北师大版数学八年级上册第二章份-4_公园有多宽55
公园有多宽教案北师大版

- 比例尺
- 地图
3. 测量实践与问题解决
- 测量实践
- 问题解决
典型例题讲解
例题1:计算公园的周长
公园的宽度是500米,长度是800米,计算公园的周长。
解答:
周长 = 2 × (宽度 + 长度)
周长 = 2 × (500米 + 800米)
周长 = 2 × 1300米
周长 = 2600米
教学难点与重点
1. 教学重点
- 理解并掌握长度单位米和千米的换算关系。
- 学会使用测量工具进行实际距离的测量,并能准确记录数据。
- 能够运用比例尺从地图上读取并计算实际距离。
- 通过实际案例,计算公园的宽度,并理解其与周长、面积的关系。
举例解释:
- 长度单位换算:重点在于让学生理解1千米等于1000米的概念,并在实际情境中应用。
3. 实物教具:提供真实的测量工具,如卷尺、测距仪等,让学生在实际操作中掌握测量技能,提高教学效果。
教学流程
(一)课前准备(预计用时:5分钟)
学生预习:
发放预习材料,引导学生提前了解公园宽度测量的学习内容,标记出有疑问或不懂的地方。设计预习问题,如“你知道如何使用卷尺吗?”和“比例尺在地图上是如何表示的?”,激发学生思考,为课堂学习做好准备工作。
实际距离 = 5厘米 × 100000
实际距离 = 500000厘米
实际距离 = 5000米
例题4:测量误差的处理
测量一段距离,第一次测得300米,第二次测得298米,第三次测得299米,计算平均距离。
解答:
平均距离 = (第一次距离 + 第二次距离 + 第三次距离) ÷ 3
2.4 课件 公园有多宽 (北师大版八年级上册)7

3
3
a 10 b,那么a、 2. 10 在两个连续整数a和b之间, b的值分别是 .
3.估算 37 (误差小于0.1)的大小是( ) A. 6 B. 6.3 C. 6.8 D.6.0~6.1 4. 下列各式估算正确的是( ) 90 30 B.600 250 C. 18 5.2 D. 17 4.1
果用一圆柱形的容器(底面直径等于高)来装这些液体, 这个容器大约有多高(误差小于1米)? 解:设圆柱的高为x,那么它的底面半径为0.5x,则:
1 x 2
2
x 40 , x x
3
160
, ,
3
160
∴X ≈ 4 .
这节课你有哪些收获?
用自己的语言表达学习这节内容的感想.
2
2
x 32 ,
即
5 x 6 ,
25 x 36 ;
2
A
5.6 x 5.7 , 31.36 x 32.49 ;
2
x 5 .6 .
x
6
1 6 3
B
C
学以致用
甲、乙两船同时从A港出发,甲朝 北偏东60°方向行驶,乙朝南偏东30° 方向行驶。已知甲、乙两船的速度分别 是45千米每小时和50 千米每小时,经 过2小时航行后,试估算两船相距多少千 米?(精确到0.1千米)
(1)通过这节课的学习,你掌握了哪些知识? (2)通过学习这些知识,对你有怎样的启发? (3)对于这节课的学习,你还有哪些疑问?
估算一个无理数的大小
探求无理数估算结果的合理性
学会估算一个无理数的大致范围 用估算来解决实际问题和数学问题
作业:习题2.6 1,2,3,6.
北师大版数学八年级上册课后习题参考精品解析含答案

八年级上册数学课后练习题答案(北师大版)第一章勾股定理课后练习题答案说明:因录入格式限制,“√”代表“根号”,根号下内用放在“()”里面;“⊙”,表示“森哥马”,§,¤,♀,∮,≒,均表示本章节内的类似符号。
§1.l探索勾股定理随堂练习1.A所代表的正方形的面积是625;B所代表的正方形的面积是144。
2.我们通常所说的29英寸或74cm的电视机,是指其荧屏对角线的长度,而不是其长或宽,同时,因为荧屏被边框遮盖了一部分,所以实际测量存在误差.1.1知识技能1.(1)x=l0;(2)x=12.2.面积为60cm:,(由勾股定理可知另一条直角边长为8cm).问题解决12cm2。
1.2知识技能1.8m(已知直角三角形斜边长为10m,一条直角边为6m,求另一边长).数学理解2.提示:三个三角形的面积和等于一个梯形的面积:联系拓广3.可以将四个全等的直角三角形拼成一个正方形.随堂练习12cm、16cm.习题1.3问题解决1.能通过。
.2.要能理解多边形ABCDEF’与多边形A’B’C’D’E’F’的面积是相等的.然后剪下△OBC和△OFE,并将它们分别放在图③中的△A’B’F’和△D’F’C’的位置上.学生通过量或其他方法说明B’E’F’C’是正方形,且它的面积等于图①中正方形ABOF和正方形CDEO的面积和。
即(B’C’)2=AB2+CD2:也就是BC2=a2+b2。
,这样就验证了勾股定理§l.2 能得到直角三角形吗随堂练习l.(1) (2)可以作为直角三角形的三边长.2.有4个直角三角影.(根据勾股定理判断)数学理解2.(1)仍然是直角三角形;(2)略;(3)略问题解决4.能.§1.3 蚂蚁怎样走最近13km提示:结合勾股定理,用代数办法设未知数列方程是解本题的技巧所在习题1.5知识技能1.5lcm.问题解决2.能.3.最短行程是20cm。
4.如图1~1,设水深为x尺,则芦苇长为(x+1)尺,由勾股定理解得x=12,则水池的深度为12尺,芦苇长为13尺。
初二(八年级)上册数学书练习题答案(北师大版)

初二(八年级)上册数学书练习题答案(北师大版)初二(八年级)下册数学书练习题答案很重要,初二(八年级)下册数学书练习题答案是什么呢?下面是初二(八年级)下册数学书练习题答案,跟初二(八年级)下册数学书练习题答案对事先您做的对吗?八年级上册数学课后练习题答案(北师大版)第一章勾股定理课后练习题答案说明:因录入格式限制,〝√〞代表〝根号〞,根号下内用放在〝()〞外面;〝⊙〞,表示〝森哥马〞,§,¤,♀,∮,≒,均表示本章节内的相似符号。
§1.l探求勾股定理随堂练习1.A所代表的正方形的面积是625;B所代表的正方形的面积是144。
2.我们通常所说的29英寸或74cm的电视机,是指其荧屏对角线的长度,而不是其长或宽,同时,由于荧屏被边框遮盖了一局部,所以实践测量存在误差.1.1知识技艺1.(1)x=l0;(2)x=12.2.面积为60cm:,(由勾股定理可知另一条直角边长为8cm).效果处置12cm2。
1.2知识技艺1.8m(直角三角形斜边长为10m,一条直角边为6m,求另一边长).数学了解2.提示:三个三角形的面积和等于一个梯形的面积:联络拓广3.可以将四个全等的直角三角形拼成一个正方形.随堂练习12cm、16cm.习题1.3效果处置1.能经过。
.2.要能了解多边形ABCDEF’与多边形A’B’C’D’E’F’的面积是相等的.然后剪下△OBC和△OFE,并将它们区分放在图③中的△A’B’ F’和△D’F’C’的位置上.先生经过量或其他方法说明B’ E’F’C’是正方形,且它的面积等于图①中正方形ABOF和正方形CDEO的面积和。
即(B’C’) 2=AB2+CD2:也就是BC2=a2+b2。
,这样就验证了勾股定理§l.2 能失掉直角三角形吗随堂练习l.(1) (2)可以作为直角三角形的三边长.2.有4个直角三角影.(依据勾股定理判别)数学了解2.(1)依然是直角三角形;(2)略;(3)略效果处置4.能.§1.3 蚂蚁怎样走最近13km提示:结合勾股定理,用代数方法设未知数列方程是解此题的技巧所在习题 1.5知识技艺1.5lcm.效果处置2.能.3.最短行程是20cm。
北师大版数学八年级上册教材目录

第一章勾股定理
1.探索勾股定理
2.能得到直角三角形吗
3.蚂蚁怎样走最近
回顾与思考
复习题1.数怎么又不够用了
2.平方根
3.立方根
4.公园有多宽
5.用计算器开方
6.实数
回顾与思考
复习题
第三章图形的平移与旋转
1.生活中的平移
2.简单的平移作图
3.生活中的旋转
4.简单的旋转作图
回顾与思考
复习题
总复习
第六章一次函数
1.函数
2.一次函数
3.一次函数的图象
4.确定一次函数表达式
5.一次函数图象的应用
回顾与思考
复习题
第七章二元一次方程组
1.谁的包裹多
2.解二元一次方程组
3.鸡兔同笼
4.增收节支
5.里程碑上的数
6.二元一次方程与一次函数
回顾与思考
复习题
第八章数据的代表
1.平均数
2.中位数与众数
3.利用计算器求平均数
5.它们是怎样变过来的
6.简单的图案设计
回顾与思考
复习题
第四章四边形性质探索
1.平行四边形的性质
2.平行四边形的判别
3.菱形
4.矩形、正方形
5.梯形
6.探索多边形的内角和与外角和
7.平面图形的密铺
8.中心对称图形
回顾与思考
复习题
第五章位置的确定
1.确定位置
2.平面直角坐标系
3.变化的鱼
回顾与思考
复习题
北师大版八年级数学教案-实数-公园有多宽-计算器开方
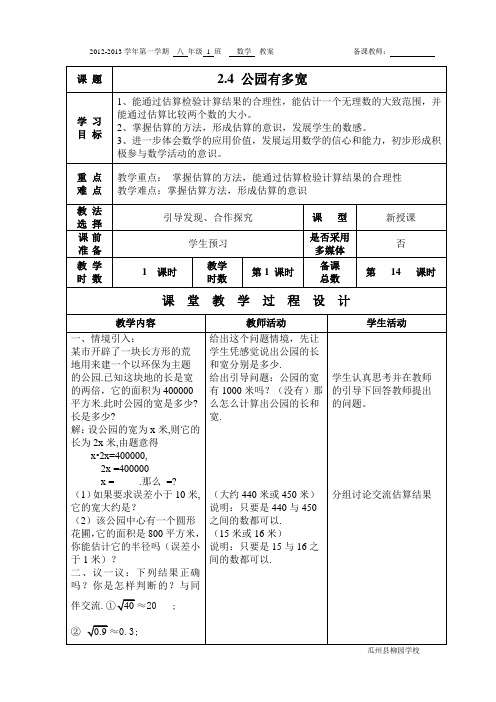
课题 2.4 公园有多宽学习目标1、能通过估算检验计算结果的合理性,能估计一个无理数的大致范围,并能通过估算比较两个数的大小。
2、掌握估算的方法,形成估算的意识,发展学生的数感。
3、进一步体会数学的应用价值,发展运用数学的信心和能力,初步形成积极参与数学活动的意识。
重点难点教学重点:掌握估算的方法,能通过估算检验计算结果的合理性教学难点:掌握估算方法,形成估算的意识教法选择引导发现、合作探究课型新授课课前准备学生预习是否采用多媒体否教学时数1 课时教学时数第1 课时备课总数第14 课时课堂教学过程设计教学内容教师活动学生活动一、情境引入:某市开辟了一块长方形的荒地用来建一个以环保为主题的公园.已知这块地的长是宽的两倍,它的面积为400000平方米.此时公园的宽是多少?长是多少?解:设公园的宽为x米,则它的长为2x米,由题意得x•2x=400000,2x =400000x = .那么=? (1)如果要求误差小于10米,它的宽大约是?(2)该公园中心有一个圆形花圃,它的面积是800平方米,你能估计它的半径吗(误差小于1米)?二、议一议:下列结果正确吗?你是怎样判断的?与同伴交流.①40≈20 ;②0.9≈0.3; 给出这个问题情境,先让学生凭感觉说出公园的长和宽分别是多少.给出引导问题:公园的宽有1000米吗?(没有)那么怎么计算出公园的长和宽.(大约440米或450米)说明:只要是440与450之间的数都可以.(15米或16米)说明:只要是15与16之间的数都可以.学生认真思考并在教师的引导下回答教师提出的问题。
分组讨论交流估算结果③100000≈500;④3900≈96.三、例1:生活表明,靠墙摆放梯子时,若梯子底端离墙距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6米的梯子,当梯子稳定摆放时,他的顶端最多能到达多高(保留到0.1)设梯子稳定摆放时的高度为x 米,此时梯子底端离墙的距离恰为梯子长度的,根据勾股定理有四、你能比较512-与12的大小吗?你是怎样想的?五、随堂练习1.估算下列数的大小:(1)6.13(误差小于0.1)(2)3800(误差小于1)2.估算比较6与2.5的大小.六、小结:你的收获?你得到怎样的启发?教师讲解并板书:x2+(31×6)2=62即x2=32,x=32因为5.62=31.36<32所以32>5.6因此,梯子稳定摆放时,它的顶端能够达到5.6米高的墙教师组织学生讨论交流如何比较大小出示练习,组织学生练习,在运算、交流形成共识后,教师要学生完成。
北师大版数学八年级上册4《公园有多宽》教学设计5

北师大版数学八年级上册4《公园有多宽》教学设计5一. 教材分析《公园有多宽》这一节是北师大版数学八年级上册第四单元的教学内容。
本节课的主要内容是让学生掌握公园宽度的计算方法,学会使用平行四边形面积公式解决实际问题。
通过本节课的学习,学生能够将所学的数学知识与生活实际相结合,提高解决实际问题的能力。
二. 学情分析学生在学习本节课之前,已经掌握了平行四边形的性质,以及面积公式的推导过程。
但是,将面积公式应用于解决实际问题,对学生来说还较为陌生。
因此,在教学过程中,教师需要引导学生将所学的数学知识与生活实际相结合,提高解决实际问题的能力。
三. 教学目标1.知识与技能:掌握公园宽度的计算方法,学会使用平行四边形面积公式解决实际问题。
2.过程与方法:通过观察、操作、思考、交流等活动,提高学生解决实际问题的能力。
3.情感态度与价值观:培养学生热爱生活,关注身边的数学,增强对数学学科的兴趣。
四. 教学重难点1.重点:掌握公园宽度的计算方法,学会使用平行四边形面积公式解决实际问题。
2.难点:将所学的数学知识与生活实际相结合,提高解决实际问题的能力。
五. 教学方法1.情境教学法:通过设置公园场景,引导学生观察、分析、解决实际问题。
2.启发式教学法:教师引导学生思考,激发学生的学习兴趣,培养学生独立解决问题的能力。
3.合作学习法:学生分组讨论,共同解决问题,提高学生的团队协作能力。
六. 教学准备1.教具:多媒体课件、公园场景图、练习题、黑板、粉笔。
2.学具:学生手册、练习本、文具。
七. 教学过程导入(5分钟)教师出示一张公园场景图,引导学生观察公园的形状,并提出问题:“请大家想一想,如何计算这个公园的宽度?”学生根据已知的平行四边形性质,尝试回答问题。
呈现(10分钟)教师讲解公园宽度的计算方法,引导学生理解并掌握平行四边形面积公式。
通过讲解,让学生明白公园宽度与平行四边形面积之间的关系。
操练(10分钟)教师出示一组练习题,让学生运用平行四边形面积公式计算公园宽度。
北师大版数学八年级上册4《公园有多宽》教学设计4

北师大版数学八年级上册4《公园有多宽》教学设计4一. 教材分析《公园有多宽》这一节内容是北师大版数学八年级上册第四单元的一节实践性较强的课程。
通过这一节课的学习,让学生能够运用测量的方法,结合图形和数据,估算出公园的宽度。
教材以实际情境为背景,引导学生通过实践操作,培养学生的动手操作能力、观察能力以及解决问题的能力。
二. 学情分析学生在学习这一节内容时,已经掌握了测量的基本方法,对图形和数据有一定的认识。
但部分学生在实际操作中,可能对测量方法的运用还不够熟练,对数据的处理和估算能力有待提高。
此外,学生对实际情境与数学知识的联系还需加强。
三. 教学目标1.知识与技能:让学生掌握测量的基本方法,能够运用图形和数据进行简单的估算。
2.过程与方法:培养学生动手操作、观察、思考和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生积极参与数学活动的意识,提高学生运用数学知识解决实际问题的能力。
四. 教学重难点1.重点:测量方法的正确运用,数据的处理和估算。
2.难点:如何将实际情境与数学知识相结合,提高解决问题的能力。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究。
2.运用实践活动,培养学生的动手操作能力。
3.以小组合作的形式,让学生在讨论中解决问题,提高学生的团队协作能力。
4.采用启发式教学,引导学生独立思考,提高学生的问题解决能力。
六. 教学准备1.教师准备公园的图片、测量工具(如尺子、卷尺等)、数据处理软件(如Excel等)。
2.学生准备测量工具(如尺子、卷尺等)、笔记本、草稿纸。
七. 教学过程1.导入(5分钟)教师出示公园的图片,引导学生观察公园的宽度。
提问:“你们认为公园的宽度大约是多少?”让学生发表自己的看法,从而引出本节课的主题。
2.呈现(10分钟)教师简要介绍测量的基本方法,如尺子、卷尺等工具的使用。
然后让学生分组,每组选择一种测量工具,对公园的宽度进行实际测量。
北师大版数学八年级上册4《公园有多宽》教学设计2

北师大版数学八年级上册4《公园有多宽》教学设计2一. 教材分析《公园有多宽》这一节内容是北师大版数学八年级上册第四单元中的一节。
本节课的主要内容是让学生掌握公园宽度的计算方法,并运用这个方法解决实际问题。
教材通过引入公园宽度的计算,让学生体会数学在生活中的应用,提高学生学习数学的兴趣。
在这一节课中,学生需要了解公园宽度的计算方法,能够运用这个方法计算不同形状公园的宽度,并解决实际问题。
二. 学情分析在八年级的学生中,大部分学生已经掌握了相似多边形的性质和计算方法。
但是,学生在解决实际问题时,往往会因为对问题的理解不深入而无法正确运用所学的知识。
因此,在教学过程中,教师需要帮助学生理解公园宽度的计算方法,并引导学生将所学的知识运用到实际问题中。
三. 教学目标1.知识与技能目标:学生能够理解公园宽度的计算方法,并能够运用这个方法计算不同形状公园的宽度。
2.过程与方法目标:通过解决实际问题,学生能够提高自己的数学思维能力。
3.情感态度与价值观目标:学生能够体会数学在生活中的应用,增强学习数学的兴趣。
四. 教学重难点1.重点:公园宽度的计算方法。
2.难点:将所学的知识运用到实际问题中。
五. 教学方法在教学过程中,我将采用问题驱动法和案例教学法。
问题驱动法能够激发学生的思考,让学生主动参与到学习过程中;案例教学法能够帮助学生将所学的知识运用到实际问题中,提高学生的解决问题的能力。
六. 教学准备1.教具准备:多媒体课件、公园图片、实际问题案例。
2.教材准备:北师大版数学八年级上册教材。
七. 教学过程1.导入(5分钟)通过向学生展示一些公园的图片,让学生观察并思考:如何计算公园的宽度?这样能够激发学生的兴趣,让学生主动参与到学习过程中。
2.呈现(10分钟)在这个环节中,教师向学生介绍公园宽度的计算方法。
通过讲解和示例,让学生理解公园宽度的计算方法,并能够运用这个方法计算不同形状公园的宽度。
3.操练(10分钟)教师给出一些实际问题,让学生独立解决。
北师大版八年级上册数学课本课后练习题答案

第一章勾股定理课后练习题答案§1.l探索勾股定理随堂练习1.A所代表的正方形的面积是625;B所代表的正方形的面积是144。
2.我们通常所说的29英寸或74cm的电视机,是指其荧屏对角线的长度,而不是其长或宽,同时,因为荧屏被边框遮盖了一部分,所以实际测量存在误差.1.1知识技能1.(1)x=l0;(2)x=12.2.面积为60cm:,(由勾股定理可知另一条直角边长为8cm).问题解决12cm2。
1.2知识技能1.8m(已知直角三角形斜边长为10m,一条直角边为6m,求另一边长).数学理解2.提示:三个三角形的面积和等于一个梯形的面积:联系拓广3.可以将四个全等的直角三角形拼成一个正方形.随堂练习12cm、16cm.习题1.3问题解决1.能通过。
.2.要能理解多边形ABCDEF’与多边形A’B’C’D’E’F’的面积是相等的.然后剪下△OBC和△OFE,并将它们分别放在图③中的△A’B’F’和△D’F’C’的位置上.学生通过量或其他方法说明B’E’F’C’是正方形,且它的面积等于图①中正方形ABOF和正方形CDEO的面积和。
即(B’C’)2=AB2+CD2:也就是BC2=a2+b2。
,这样就验证了勾股定理§l.2 能得到直角三角形吗随堂练习l.(1) (2)可以作为直角三角形的三边长.2.有4个直角三角影.(根据勾股定理判断)数学理解2.(1)仍然是直角三角形;(2)略;(3)略问题解决4.能.§1.3 蚂蚁怎样走最近13km习题1.5知识技能1.5lcm.问题解决2.能.3.最短行程是20cm。
4.如图1~1,设水深为x尺,则芦苇长为(x+1)尺,由勾股定理解得x=12,则水池的深度为12尺,芦苇长为13尺。
复习题知识技能1.蚂蚁爬行路程为28cm. 2.(1)能;(2)不能;(3)不能;(4)能 3.200km.4.169cm。
5.200m。
数学理解6.两直角边上的半圆面积之和等于斜边上半圆的面积. 7.提示:拼成的正方形面积相等:8.能. 9.(1)18;(2)能.问题解决11.(1)24m;(2)不是,梯子底部在水平方向上滑动8m. 12.≈30.6。
公园有多宽ppt 北师大版

估算一个无理数的大小
探求无理数估算结果的合理性
学会估算一个无理数的大致范围 用估算来解决实际问题和数学问题
作业巩固:习题2.6 1,2,3,6.
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
用估算来解决实际问题 公园宽
200000 ?
(1)如果要求误差小于10米,它的宽大约是?
(大约440米或450米,其实440米与450米之间的值都可以)
(2)该公园中心有一个圆形花圃,它的面积 是800平方米,你能估计它的半径吗(误差小 于1米)? (15米与16米之间的值均可)
用估算来解决实际问题 画能挂上去吗? 生活表明,靠墙摆放梯子时,若梯子底端离墙距 离为梯子长度的三分之一,则梯子比较稳定。现 有一长度为6米的梯子,当梯子稳定摆放时, (1)他的顶端最多能到达多高(保留到0.1)? (2)现在如果请一个同学利用这个梯子在墙高5.9 米的地方张贴一副宣传画,他能办到吗?
1、聪明的人有长的耳朵和短的舌头。 ——弗莱格 2、重复是学习之母。 ——狄慈根 3、当你还不能对自己说今天学到了什么东西时,你就不要去睡觉。 ——利希顿堡 4、人天天都学到一点东西,而往往所学到的是发现昨日学到的是错的。 ——B.V 5、学到很多东西的诀窍,就是一下子不要学很多。 ——洛 克 6、学问是异常珍贵的东西,从任何源泉吸收都不可耻。 ——阿卜· 日· 法拉兹 7、学习是劳动,是充满思想的劳动。 ——乌申斯基 8、聪明出于勤奋,天才在于积累 --华罗庚 9、好学而不勤问非真好学者。 10、书山有路勤为径,学海无涯苦作舟。 11、人的大脑和肢体一样,多用则灵,不用则废 -茅以升 12、你想成为幸福的人吗?但愿你首先学会吃得起苦 --屠格涅夫 13、成功=艰苦劳动+正确方法+少说空话 --爱因斯坦 14、不经历风雨,怎能见彩虹 -《真心英雄》 15、只有登上山顶,才能看到那边的风光。 16只会幻想而不行动的人,永远也体会不到收获果实时的喜悦。 17、勤奋是你生命的密码,能译出你一部壮丽的史诗。 1 8.成功,往往住在失败的隔壁! 1 9 生命不是要超越别人,而是要超越自己. 2 0.命运是那些懦弱和认命的人发明的! 21.人生最大的喜悦是每个人都说你做不到,你却完成它了! 22.世界上大部分的事情,都是觉得不太舒服的人做出来的. 23.昨天是失效的支票,明天是未兑现的支票,今天才是现金. 24.一直割舍不下一件事,永远成不了! 25.扫地,要连心地一起扫! 26.不为模糊不清的未来担忧,只为清清楚楚的现在努力. 27.当你停止尝试时,就是失败的时候. 28.心灵激情不在,就可能被打败. 29.凡事不要说"我不会"或"不可能",因为你根本还没有去做! 30.成功不是靠梦想和希望,而是靠努力和实践. 31.只有在天空最暗的时候,才可以看到天上的星星. 32.上帝说:你要什么便取什么,但是要付出相当的代价. 33.现在站在什么地方不重要,重要的是你往什么方向移动。 34.宁可辛苦一阵子,不要苦一辈子. 35.为成功找方法,不为失败找借口. 36.不断反思自己的弱点,是让自己获得更好成功的优良习惯。 37.垃圾桶哲学:别人不要做的事,我拣来做! 38.不一定要做最大的,但要做最好的. 39.死的方式由上帝决定,活的方式由自己决定! 40.成功是动词,不是名词! 20、不要只会吃奶,要学会吃干粮,尤其是粗茶淡饭。
北师大版数学八年级上册4《公园有多宽》教学设计2

北师大版数学八年级上册4《公园有多宽》教学设计2一. 教材分析《公园有多宽》这一节是北师大版数学八年级上册第4课的内容。
本节课的主要内容是让学生掌握平行四边形的性质,并能运用这些性质解决实际问题。
通过这一节课的学习,学生能够进一步理解平行四边形的概念,提高解决问题的能力。
二. 学情分析学生在学习这一节课之前,已经学习了平行四边形的概念和一些基本性质,但他们对这些性质的理解可能还不够深入,无法灵活运用到实际问题中。
此外,学生的空间想象能力和逻辑思维能力有待提高。
三. 教学目标1.知识与技能目标:让学生掌握平行四边形的性质,并能运用这些性质解决实际问题。
2.过程与方法目标:通过观察、操作、思考、交流等活动,培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养他们勇于探究、合作交流的良好学习习惯。
四. 教学重难点1.重点:平行四边形的性质及运用。
2.难点:如何引导学生发现并证明平行四边形的性质。
五. 教学方法1.情境教学法:通过设置实际问题,激发学生的学习兴趣,引导学生主动参与。
2.合作学习法:引导学生分组讨论,培养学生的团队协作能力和沟通能力。
3.启发式教学法:引导学生观察、思考、发现,培养学生的创新能力。
4.反馈评价法:及时了解学生的学习情况,调整教学策略。
六. 教学准备1.教学课件:制作精美、清晰的课件,帮助学生直观地理解平行四边形的性质。
2.教学素材:准备一些实际问题,供学生练习运用平行四边形的性质解决。
3.学生活动用品:如直尺、三角板等,方便学生在课堂上进行操作。
七. 教学过程1.导入(5分钟)利用课件展示公园的图片,引导学生观察公园的形状,提出问题:“公园是一个平行四边形,你知道它的宽是多少吗?”从而引出本节课的主题。
2.呈现(10分钟)展示平行四边形的性质,引导学生观察、思考,发现平行四边形的对边相等、对角相等等性质。
3.操练(10分钟)分组讨论:让学生以小组为单位,运用平行四边形的性质解决实际问题。
北师大版-数学-八年级上册-第二章第四节公园有多宽课堂作业 .

初中-数学-打印版
初中-数学-打印版 《八年级上第二章第四节公园有多宽》课堂作业
第1课时
1、 X 是整数, x 介于3 的两个平方根之间,则x 的取值的个数( )
A 、1
B 、 2
C 、3
D 、 4
答案:C
2
在两个连续整数之间,这两个整数是
答案:3,4
3、估算面积是20平方米的正方形,它的边长是___(误差小于0.1米)
答案:4.5
4、通过运算,比较6与2.5的大小 答案:6<2.5
5、一个人每天平均饮用大约0.0015米3的各种液体,按70岁计算,他所饮用的液体总量大约为40米3,如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高?(误差小于1米 答案:5.5米。
北师大版八年级上册数学课本课后练习题答案

八年级上册数学课后练习题答案(北师大版)第一章勾股定理课后练习题答案说明:因录入格式限制,“√”代表“根号”,根号下内用放在“()”里面;“⊙”,表示“森哥马”,§,¤,♀,∮,≒,均表示本章节内的类似符号。
§1.l探索勾股定理随堂练习1.A所代表的正方形的面积是625;B所代表的正方形的面积是144。
2.我们通常所说的29英寸或74cm的电视机,是指其荧屏对角线的长度,而不是其长或宽,同时,因为荧屏被边框遮盖了一部分,所以实际测量存在误差.1.1知识技能1.(1)x=l0;(2)x=12.2.面积为60cm:,(由勾股定理可知另一条直角边长为8cm).问题解决12cm。
21.2知识技能1.8m(已知直角三角形斜边长为10m,一条直角边为6m,求另一边长).数学理解2.提示:三个三角形的面积和等于一个梯形的面积:联系拓广3.可以将四个全等的直角三角形拼成一个正方形.随堂练习12cm、16cm.习题1.3问题解决1.能通过。
.2.要能理解多边形ABCDEF’与多边形A’B’C’D’E’F’的面积是相等的.然后剪下△OBC和△OFE,并将它们分别放在图③中的△A’B’F’和△D’F’C’的位置上.学生通过量或其他方法说明B’E’F’C’是正方形,且它的面积等于图①中正方形ABOF和正方形CDEO的面积和。
即(B’C’)=AB+CD:也就是BC=a+b。
,222222这样就验证了勾股定理§l.2 能得到直角三角形吗随堂练习l.(1) (2)可以作为直角三角形的三边长.2.有4个直角三角影.(根据勾股定理判断)数学理解2.(1)仍然是直角三角形;(2)略;(3)略问题解决4.能.§1.3 蚂蚁怎样走最近13km提示:结合勾股定理,用代数办法设未知数列方程是解本题的技巧所在习题1.5知识技能1.5lcm.问题解决2.能.3.最短行程是20cm。
4.如图1~1,设水深为x尺,则芦苇长为(x+1)尺,由勾股定理解得x=12,则水池的深度为12尺,芦苇长为13尺。
2.4 课件 公园有多宽 (北师大版八年级上册)4

A
议一议
(1)通过估算,你能比较 5 1 与 1 的大小吗?
2
2
你是怎样想的?与同伴交流
5 1 (2)小明是这样想的: 2 1
与
它们的分子就可以了。因为
5 >2,所以 5 -1 >1,因此 1 5 1 > 2 2
2
的分母相同,只要比较
———通过估算,比较下面各组数的大小:
( 1) ( 2)
C O
B
A
1 估算无理数的方法是(1)通过平方运算,采 用“接近法”,确定真值所在范围;(2)根据 问题中误差允许的范围,在真值的范围内取出近 似值。
2 “精确到”与“误差小于”意义不同。如精确 到1m是四舍五入到个位,答案惟一;误差小于 1m,答案在真值左右1m都符合题意,答案不惟 一。在本章中误差小于1m就是估算到个位,误差 小于10m就是估算到十位。
1、估算: A、2和3之间
17 1 的值在(
) D、5和6之间
B、3和4之间 C、4和5之间
2、估算下列各数的大小: (1) 15.9 (误差小于0.1)
5 1 2
(2)
3
1111
(误差小于1)
3、求出所有大于 17 且小于 11 的整数。 4、通过估算,比较
5 与 8
的大小。
课本第49页第1、2、3、5题
2 “精确到”与“误差小于”意义不同。如精确 到1m是四舍五入到个位,答案惟一;误差小于 1m,答案在真值左右1m都符合题意,答案不惟 一。在本章中误差小于1m就是估算到个位,误差 小于10m就是估算到十位。
例1 生活经验表明, 靠墙摆放梯子时,若 C 梯子底端离墙的距离 约为梯子长度的1/3, 则梯子比较稳定。现 有一长度为6米的梯子, 当梯子稳定摆放时, B 它的顶端能达到5.6米 高的墙头吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
** 公园有多宽
班级:___________________________姓名:___________________________
一、选择题
**的算术平方根在( )
**与0.06之间
B.0.02与0.03之间 **与0.003之间 D.0.2与0.3之间
2.在无理数5,6,7,8中,其中在
218+与2126+之间的有( ) **个
B.2个
C.3个
D.4个 3.化简2)521(-的结果为( ) A.21-5
B.5-21
C.-21-5
D.不能确定 4.设a 1=61,b 1=2
21,下列关系中正确的是( ) **>b
B.a ≥b
C.a<b
D.a ≤b 5.一个正方体的体积为28360立方厘米,正方体的棱长估计为( ) **厘米
B.27厘米
C.30.5厘米
D.40厘米
二、填空题 6.|2-1|=______,|3-2|=______. 7.将75,7
5,75三数按从小到大的顺序用“<”号连接起来________. 8.不等式(2-5)x >0的解集为__________.
9.大于-317且小于310的整数有______.
**是的整数部分,b 是的整数部分,则a2+b2=______.
三、解答题
11.估算下列数的大小(误差小于1)
(1)91 (2)5.23 (3)542 (4)-1002
12.通过估计,比较大小.
(1)5117 与109; (2)24与5.1; (3)10与3
10
13.用一根长为6米的绳子,能否做一个直角△ABC ,使得∠C =90°,AC =1米,BC =2米,请说明你的理由.
14.一片矩形小树林,长是宽的3倍,而对角线的长为44000米,每棵树占地1米2,这片树林共有多少棵树?小树林的长大约是多少米?(结果精确到1米)
15.如图,公路MN 和公路PG 在点P 处交汇,点A 处有一所中学,且A 点到MN 的距离是8704米.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN 上沿PN 方向行驶时,学校是否会受到噪声影响?说明理由;如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
答案:
一、1.B 2.D 3.B 4.C 5.C
二、6.2-1 2-3 7.75 <75<7
5 8.x <0 9.-2,-1,0,1,2 10.13 三、11.(1)9.5 (2)4.8 (3)23.3 (4)-32
12.(1)> (2)< (3)< 13.能 14.13194 199
15.有影响,理由略 学校受影响的时间为4秒。
