流体力学第四章(20160223)
合集下载
流体力学4

第四章
流体动力学基础
u f ( x, y, z, t ), x, y, z f (t )
u x u x u x 1 p dux 1 u x ※则: X dt dx dy dz x dt dt t x y z u y u x u x u z ux uy uz t x y z
— 推导惯性和非惯性参考 1 p a b p dy 2 y 系(相对一个惯性系如 dz dy 物体转动或匀加速运动 z o 参照系)中伯努力方程。
z
c
dx
p
1 p dy 2 y
设:六面体中心 a 点压 力为 p( xyz) ,平均密度 ( xyz),加速度 a( xyz) 。
u z dz u z ) ( p 2 ) z 下面 ( p 2 z 2 z
zx dz zx z 2
zy dz zy z 2
第四章
流体动力学基础
二、粘性流体运动方程 根据:
F
x
max ,
F
y
may ,
F
z
maz
u x ( p 2 ) u x dx x 则: Xdxdydz [( p 2 ) ]d ydz x x 2 u x ( p 2 ) u x dx x [( p 2 ) ) d ydz x x 2 zx dz zx dz [( zx )dxdy ( zx ) dxdy ] z 2 x 2 yx dy yx dy dux [( yx ) ( yx ) dxdy ] m y 2 y 2 dt
u z 2 x ( y u x 2 y ( z
2
流体力学第四章

由连续方程 V2
2
A1 V1 A2
,代入上式,有
A V A h j (1 1 ) 2 1 ,即1 (1 1 ) 2 A2 2 g A2
如以
V1
A2 则有 V2代入,则有 A1
2 A2 2 V2 h j ( 1) , 即 2 ( A2 1) 2 A1 2g A1
4.3.2 混合长度理论
4.3.3 湍流的速度分布 1、粘性底层(层流底层)
dv (1) 很大; dy
(2)粘性底层的厚度δ很小。 2、湍流核心
dv (1) dy
很小;
(2)区域大。 3、 过渡层—有时可将它算在湍流核心的 范围。
速度分布:在粘性底层中速度分布是直 线规律;湍流核心中为对数关系。 粗糙度 Δ 管壁凹凸不平的平均尺寸。 水利光滑管 δ>Δ 粗糙度对湍流核心几乎没有影响。 水利粗糙管 δ<Δ 粗糙度的大小对湍流特性产生直接影响。
《流体力学》
教学课件
第4章 流体在圆管中的流动
1 流体在固体内部的管中流动和缝隙中流动; 2 流体在固体外部的绕流; 3 流体在固体一侧的明渠流动; 4 流体与固体不相接触的孔口出流和射流。
4.1 雷诺实验
雷诺实验
雷诺实验发现 1.用不同的流体在相同直径的管道中进行实验,
所测得的临界速度 vk 是各不相同的;
T
有
W W W ,代入上式,得
T
1 1 W W W dt W W dt T0 T0 T 1 所以 T W dt 0 0
T
即脉动量的时均值
W 0
运用时均统计法就将湍流分为两个组成部分:一部分是用时均值表示 的时均流动;另一部分是用脉动值表示的脉动运动。时均流动代表运动 的主流,脉动反映湍流的本质。
流体力学(经典课件)第4章

第4章 量纲分析与 相似理论
第4章 量纲分析与相似理论
第4章 量纲分析与相似理论
第4章 量纲分析与相似理论
第4章 量纲分析与相似理论
★本章重点掌握:
量纲分析方法(瑞利法、 定理)
相似理论及其应用(相似准则、模型实验设 计)
§4.1 量纲分析的基本概念
一、单位与量纲
单位:表征各物理量的大小。 如长度单位m、cm、mm; 时间单位小时、分、秒等。 量纲:表征各物理量单位的种类。 如m、cm、mm等同属于长度类,用L表示; 小时、分、秒等同属于时间类,用T表示; 公斤、克等同属于质量类,用M表示。
F (q1, q2 ,..., qn ) 0
而这些变量中含有m个基本物理量,则可组合这些变量成为(n – m)个无量纲π数的函数关系,即
(1, 2 ,..., nm ) 0
例题2
§4.3 流动相似的基本概念
§4.3 流动相似的基本概念
一、几何相似
原型和模型对应的线性长度均成一固定比尺。
§4.4 流动相似的准则
故得雷诺准则方程:
v l vl vl 1 or ( ) p ( ) m
即要保证原型流动和模型流动的粘性力相似,则要求两 者对应的雷诺数 Re vl / 必须相等.
§4.4 流动相似的准则
三、欧拉准则:压力相似
要保证原型流动和模型流动的压力相似,则根据 动力相似要求有:
F F
p
I
式中,压力比尺:
F
p
( pA) p ( pA) m
p l
2
§4.4 流动相似的准则
故得欧拉准则方程:
p v
2
p p 1 or ( 2 ) p ( 2 ) m pv pv
第4章 量纲分析与相似理论
第4章 量纲分析与相似理论
第4章 量纲分析与相似理论
第4章 量纲分析与相似理论
★本章重点掌握:
量纲分析方法(瑞利法、 定理)
相似理论及其应用(相似准则、模型实验设 计)
§4.1 量纲分析的基本概念
一、单位与量纲
单位:表征各物理量的大小。 如长度单位m、cm、mm; 时间单位小时、分、秒等。 量纲:表征各物理量单位的种类。 如m、cm、mm等同属于长度类,用L表示; 小时、分、秒等同属于时间类,用T表示; 公斤、克等同属于质量类,用M表示。
F (q1, q2 ,..., qn ) 0
而这些变量中含有m个基本物理量,则可组合这些变量成为(n – m)个无量纲π数的函数关系,即
(1, 2 ,..., nm ) 0
例题2
§4.3 流动相似的基本概念
§4.3 流动相似的基本概念
一、几何相似
原型和模型对应的线性长度均成一固定比尺。
§4.4 流动相似的准则
故得雷诺准则方程:
v l vl vl 1 or ( ) p ( ) m
即要保证原型流动和模型流动的粘性力相似,则要求两 者对应的雷诺数 Re vl / 必须相等.
§4.4 流动相似的准则
三、欧拉准则:压力相似
要保证原型流动和模型流动的压力相似,则根据 动力相似要求有:
F F
p
I
式中,压力比尺:
F
p
( pA) p ( pA) m
p l
2
§4.4 流动相似的准则
故得欧拉准则方程:
p v
2
p p 1 or ( 2 ) p ( 2 ) m pv pv
流体力学第四章

时均速度 u
脉动速度u’ u' u u
1 t0 T udt t 0 T
4-3 圆管内紊流流动规律
一、紊流的基本特征及时均分析法
时均分析法 时均压强与脉动压强 1 t0 T p' p p p pdt t 0 T 准定常流——紊流流场中,任意定点处的时均参数 (u ,p) 不随时
4-4 沿程阻力损失的分析和计算
二、沿程损失计算
l c2 hf d 2g 64 层流流动,沿程阻力系数 Re f (Re) 紊流流动,沿程阻力系数不仅与雷诺数有关,还与相对粗糙度 d
f (Re, )
d
有关
尼古拉兹实验与实验曲线 人工粗糙管:在圆管内壁上涂胶,然后贴上具有相同半径的球形沙子, 造成不同粗糙度的圆管
4-4 沿程阻力损失的分析和计算
二、沿程损失计算
莫迪图——确定工业实际管道“λ”的曲线图 莫迪根据尼古拉兹实验结果,结合经验公式及工业管道实验总结绘 出的“λ”随“Re”、“ε/d”而变化的关系曲线图 ' ”为当量绝对粗糙度 图中“
4-4 沿程阻力损失的分析和计算
二、沿程损失计算
4-4 沿程阻力损失的分析和计算
二、沿程损失计算
4-4 沿程阻力损失的分析和计算
二、沿程损失计算
尼古拉兹实验与实验曲线 Re 2000 ),层 Ⅰ区(ab线, 流区λ=f(Re) 2000 Re 4000 ), Ⅱ区(bc线, 过渡区λ=f(Re) 8 7 4000 Re 27 ( d / ) Ⅲ区(cd线, ), 紊流光滑区λ=f(Re) 8 .85 27(d / ) 7 Re 4160(d / 2 ) 0) Ⅳ区(cd、ef之间曲线族, , 紊流过渡区λ=f(Re,ε/d) Re 4160(d / 2 ) 0.85 ),紊流粗糙区λ=f(ε/d) Ⅴ区(ef右侧水平的直线族 尼古拉兹实验曲线意义和不足 意义——揭示了管道流动中“λ”随 “Re”、“ε/d”的变化关系,为 计算“hf”奠定了基础。 不足——人工粗糙管与工业实际管道的粗糙情况不同,上面的结果不 便直接应用
流体力学学习课件第四章流体动力学

x y z
dt
dt
dt
1、公式推导前提条件:恒定流(条件之一)即
p 0, u 0 ux uy uz 0
t
t
t t t
因为恒定流动时,流线与迹线重合,则此时的dx,dy,dz与时间 dt 的比为速度
分量,即有:
ux
dx dt
uy
dy dt
uz
dz dt
则:①
dux dt
dx
duy dt
y dt
单位质量流体的惯 性力在X、Y、Z坐 标轴上分量
Z 1 p duz
z dt
(1)物理意义:作用在单位质量流体上的质量力与表面力之代数和等于其加
速度。 (2)适用条件:a.无粘性流体。
b.可压缩流体及不可压缩流体 c.恒定流及非恒定流
二、粘性流体运动微分方程
1、以应力表示的实际流体运动微分方程 (1)方程推导依据:
g 2g
g
h pA pB u2
g g 2g
理论流速: u 2 pA pB 2gh
实际流速: u 2gh
μ:修正系数,数值接近于1,由实验确定,μ =0.97 ; h:为两管水头差。
四、实际液体元流能量方程
实际液体具有粘滞性,由于内摩擦阻力的影响,液体流动
时,其能量将沿程不断消耗,总水头线因此沿程下降,固
dy
duz dt
dz uxdux
uyduy
uz duz
1 d (u 2 ) 2
因此,方程是沿流线才适用的。——条件之二
②
p dx p dy p dz dp
x y z
(3)
则(1)式
( Xdx Ydy Zdz) 1 (p dx p dy p dz)
流体力学 第4章 第3节

应分别满足柯西—黎曼条件
2 2 2 2 , ; 2 0, 2 0 2 2 x y y x x y x y
由上述条件可以证明 , 在 平面内也满足拉氏方程,
2 2 0 2 2
R 1 1 R2 2
2
2
2c
2c
z c2
1 2 2v1 v2
平面上的两条线的夹角在 z 平面上变换为原夹角的2倍。
4.13
茹柯夫斯基变换
平面通过 c 点的光滑曲线在 z 平面变换为尖角
1 2
(参阅《Fundamental Mechanics of Fluids》, pp.92-97)
4.12 保角变换
保角变换 f z 把
z 平面中的拉氏方程转换为 平面中 的拉氏方程,即如果 x, y 在 z 平面内是调和函数, ,
在 平面内也必然是调和函数。
4.12 保角变换
4.11
镜像法
镜像法
a2 z0
z0
当流体外部流场中存在奇点(如点源、点涡 等)时,常用镜像法求得满足边界条件的复 位势,其作法是在物体内部适当位置也布置 奇点,称为外部奇点的镜像,使得由奇点及 其镜像产生的复速度势满足物体边界总是一 条流线
a
如欲求圆柱外一位于 z0 点,强度为 的点涡的复位势,可在圆柱内 z0 点 添加一强度为 的点涡,在原点添加一强度为 的点涡,三个奇点在圆柱 外共同产生的复位势即所求的复位势,且保证圆柱面本身是一条流线。 请注意圆内 a 点即对于圆外一点 z0 的所谓镜像点,它们的模的乘积等于 a2 z0 z0 a 2 ; 它们的圆心处于同一条直线上,即 z 0 和 圆半径的平方, 2 a z0 有相同的幅角。 z
流体力学第四章
流体力学
动量方程16-运动控制体
已知V = 30m/s,U = 10m/s,忽略重力和摩擦力, 已知V = 30m/s,U = 10m/s,忽略重力和摩擦力, 出口截面A11= 0.003m22,求Rxx和 Ryy 出口截面A = 0.003m ,求R 和 R
解:(1) 坐标系 (2) 控制体
r r r Vr = V − U
流体力学
动量方程15-运动控制体
∂ ∂t
∫
CV
r r r r r ρVr dτ + ∫ ρVrVr ⋅ ndS = ΣF
CS
流体仅在控制面的有限个区域流入流出且 ρ,V 在进出口截面均布,定常流动
r r & ∑ F = ∑ mriVri
(
)
out
−∑
(
r & mriVri
)
in
r r r 其中 Vr = V − VCV
φ
流体力学
雷诺输运方程1
欧拉方法描述系统物理量对时间的变化率
CSIII CSI I
t
r V
II
III
dS3
dS1 r n
r n
r V
t +δ t
DN sys Dt
流体力学
= lim
N sys (t + δt ) − N sys (t )
δt → 0
δt
雷诺输运方程2
DN sys Dt
DN sys Dt
流体力学
质点导数与系统导数
质点导数
r Dφ ∂φ = + (V ⋅ ∇ )φ Dt ∂t
流体质点某物理量随时间的变化率同空 间点上物理量之间的关系 系统导数
DN ∂ = Dt ∂t r r φV ⋅ ndS
动量方程16-运动控制体
已知V = 30m/s,U = 10m/s,忽略重力和摩擦力, 已知V = 30m/s,U = 10m/s,忽略重力和摩擦力, 出口截面A11= 0.003m22,求Rxx和 Ryy 出口截面A = 0.003m ,求R 和 R
解:(1) 坐标系 (2) 控制体
r r r Vr = V − U
流体力学
动量方程15-运动控制体
∂ ∂t
∫
CV
r r r r r ρVr dτ + ∫ ρVrVr ⋅ ndS = ΣF
CS
流体仅在控制面的有限个区域流入流出且 ρ,V 在进出口截面均布,定常流动
r r & ∑ F = ∑ mriVri
(
)
out
−∑
(
r & mriVri
)
in
r r r 其中 Vr = V − VCV
φ
流体力学
雷诺输运方程1
欧拉方法描述系统物理量对时间的变化率
CSIII CSI I
t
r V
II
III
dS3
dS1 r n
r n
r V
t +δ t
DN sys Dt
流体力学
= lim
N sys (t + δt ) − N sys (t )
δt → 0
δt
雷诺输运方程2
DN sys Dt
DN sys Dt
流体力学
质点导数与系统导数
质点导数
r Dφ ∂φ = + (V ⋅ ∇ )φ Dt ∂t
流体质点某物理量随时间的变化率同空 间点上物理量之间的关系 系统导数
DN ∂ = Dt ∂t r r φV ⋅ ndS
流体力学第四章 流体动力学基本定理及其应用.ppt

f x dx
1
p dx u x
u dx v u dx w u dx
x
y
z
f y dy
1
p dy u y
v dy v v dy w v dy
x
y
z
(4-4)
1 p
w
w
w
f z dz
dz u z
dz v
x
y
dz w z
dz
由流线微分方程, 有
udy=vdx ydz=wdy wdx=udz
先分析x方向的运动,在垂直于x轴的左右两个平面中
心点上的压强各等于 p p dx
x 2
p p dx x 2
图 4-1 推导欧拉运动微分方程用图
由于是微元面积,所以这些压强可以作为各表面上的
平均压强。设在六面体形心上的单位质量的质量力分量为
fx、fy和fz ,则作用在微元平行六面体的流体微团上的质量
x y z
udu vdv wdw 1 d(u 2 v 2 w2 ) 1 dV 2
2
2
假设质量力只有重力,fx=0,fy=0,fz=-g,即z轴垂直
向上,oxy为水平面。则式(4-7)可写成
gdz 1 dp 1 dV 2 0
2
又假设为不可压缩均质流体,即ρ=常数,积分后得
gz p V 2 常数
z1
p1
g
V12 2g
z2
p2
g
V22 2g
(4-9)
在特殊情况下,绝对静止流体V=0,由式(4-8)可以得 到静力学基本方程
z p 常数
g
二、方程的物理意义和几何意义 为了进一步理解理想流体微元流束的伯努利方程,
流体力学 第4章 第1节

r r u, p •后者求解过程中, u, p 耦合在一起需联立求解,对于势流 不再 r 耦合在一起,可分开求解:先求出Φ, u = ∇Φ ,即可求得速度场,再求
解伯努利方程得到压强场。
拉氏方程解的可叠加性
∇ 2Φ = 0
如 Φ1 ,Φ2 是解,则
Φ = c1Φ1 +c2Φ2
也是解,其中 c1 ,c2 是不全为零的常数。 在后续章节会经常用到线性方程的这一性质。
Qu = ∂Φ ∂Ψ ∂Φ ∂Ψ = , v= =∂x ∂y ∂y ∂x
∂Φ ∂Ψ ∂x = ∂y ∴ ∂Φ = - ∂Ψ ∂y ∂x
上式称柯西-黎曼条件。 流函数和速度势函数中有一个已知,另一个即可以由上式求出。
复位势
4.2 复位势和复速度
构造复函数, F(z)=Φ+ iψ z= x + i y
r
r ∇× u = 0 。 或
速度势函数
r r ∇ × u = 0 ⇔ u = ∇Φ
Φ称速度势函数。
不可压缩流体
r ∇ ⋅ u = 0 → ∇ ⋅∇Φ = 0
在不可压缩流体条件下Φ满足拉普拉斯方程
势流基本方程组
∇ 2Φ = 0 ∂Φ p 1 + + ∇Φ ⋅∇Φ + gz = f(t) ∂t ρ 2
平面无旋运动和解析函数之间存在一一对应的关系。 复变函数是强有力的数学工具。复变函数的方法不能推广到三维 流动中去。
4.3 均匀流
从本节开始将给出一些基本流动的复位势。 F(z)= c z (c为实数) W(z) = c = u – i v
u = c v = 0
如沿x轴方向速度为U, 则 F(z) = U z
4.4 点源(汇)和点涡 点源(
解伯努利方程得到压强场。
拉氏方程解的可叠加性
∇ 2Φ = 0
如 Φ1 ,Φ2 是解,则
Φ = c1Φ1 +c2Φ2
也是解,其中 c1 ,c2 是不全为零的常数。 在后续章节会经常用到线性方程的这一性质。
Qu = ∂Φ ∂Ψ ∂Φ ∂Ψ = , v= =∂x ∂y ∂y ∂x
∂Φ ∂Ψ ∂x = ∂y ∴ ∂Φ = - ∂Ψ ∂y ∂x
上式称柯西-黎曼条件。 流函数和速度势函数中有一个已知,另一个即可以由上式求出。
复位势
4.2 复位势和复速度
构造复函数, F(z)=Φ+ iψ z= x + i y
r
r ∇× u = 0 。 或
速度势函数
r r ∇ × u = 0 ⇔ u = ∇Φ
Φ称速度势函数。
不可压缩流体
r ∇ ⋅ u = 0 → ∇ ⋅∇Φ = 0
在不可压缩流体条件下Φ满足拉普拉斯方程
势流基本方程组
∇ 2Φ = 0 ∂Φ p 1 + + ∇Φ ⋅∇Φ + gz = f(t) ∂t ρ 2
平面无旋运动和解析函数之间存在一一对应的关系。 复变函数是强有力的数学工具。复变函数的方法不能推广到三维 流动中去。
4.3 均匀流
从本节开始将给出一些基本流动的复位势。 F(z)= c z (c为实数) W(z) = c = u – i v
u = c v = 0
如沿x轴方向速度为U, 则 F(z) = U z
4.4 点源(汇)和点涡 点源(
流体力学ppt课件-流体动力学

g
g
2g
水头
,
z
p
g
v2
2g
总水头, hw 水头损失
第二节 热力学第一定律——能量方程
水头线的绘制
总水头线
hw
对于理想流体,总水
1
v12 2g
2
v22 2g
头线是沿程不变的,
测压管水头线
p2
为一水平直线,对于
g
实际流体,总水头沿 程降低,但测压管水
p1 g
头线沿程有可能降低、
z2
不变或者升高。
z1
v2 A2 e2
u22 2
gz2
p2
v1A1 e1
u12 2
gz1
p1
微元流管即为流线,如果不 可压缩理想流体与外界无热 交换,热力学能为常数,则
u2 gz p 常数
2
这个方程是伯努利于1738年首先提出来的,命名为伯努利 方程。伯努利方程的物理意义是沿流线机械能守恒。
第二节 热力学第一定律——能量方程
皮托在1773年用一根弯成直角的玻璃管,测量了法国塞纳河 的流速。原理如图所示,在液体管道某截面装一个测压管和 一个两端开口弯成直角的玻璃管(皮托管),皮托管一端正 对来流,一端垂直向上,此时皮托管内液柱比测压管内液柱 高h,这是因为流体流到皮托管入口A点受到阻滞,速度降为 零,流体的动能变化为压强势能,形成驻点A,A处的压强称 为总压,与A位于同一流线且在A上游的B点未受测压管的影 响,其压强与A点测压管测得的压强相等,称为静压。
第四章 流体动力学
基本内容
• 雷诺输运公式 • 能量方程 • 动量方程 • 流体力学方程应用
第一节 雷诺输运方程
• 前面解决了流体运动的表示方法,但要在流 体上应用物理定律还有困难.
流体力学第四章ppt课件

对于定常无旋运动,式(4-3)括弧内的函数
不随空间坐标x,y,z和时间t变化,因此
它在整个流场为常数。精选课件
10
U p V2 C
2
(通用常数)
对于理想、不可压缩流体、在重力作用下的 定常无、旋运动,因U=-gz,上式可写成
p V2
z
C
(通用常数)
2g
上式为上述条件下的拉格朗日积分式,C在
整个流场都适用的通用常数,因此它在整个流场
建立了速度和压力之间精的选课件关系。
11
若能求出了流场的速度分布(理论或实验的 方法),就能用拉格朗日积分式求流场的压力分 布,再将压力分布沿固体表面积分,就可求出流 体与固体之间的相互作用力。
应用拉格朗日积分式,可解释许多重要的物
理现象:如机翼产生升力的原因;两艘并排行
U 2
2
g
近似代替 20
适用于有限大流束的伯努利方成为:
z p U2 const
2g
或
z1p1U 21g2 z2p2
U22 2g
方程适用条件:
(13) (14)
(1)理想流体,定常流动;
(2)只有重力的作用;
(3)流体是不可压缩的;
(4)1.2截面处流动须是渐变流。但1.2两断
面间不必要求为渐变流精动选课件。
驶而又靠得很近的船舶为什么会产生互相吸引
的“船吸现象”;以及在浅水航道行驶的船舶为
什么会产生“吸底现象”等等。
精选课件
12
讨论: 1. 如果理想、不可压缩流体作定常、无旋流
动且只有重力作用时,同一水平面上的两 点,其速度和压力的关系如何? 2. 两艘并排行驶而又靠得很近的船舶为什么会产 生互相吸引的“船吸现象”。
流体力学第四章

雷诺数物理意义:雷诺数反映了惯性力和粘性力的对比关系。 因此可用来判别流态。
当Re较小时粘性力作用大,对质点运动起约束作用,流体 质点表现为有秩序互补掺混的层流状态。
当Re>Recr时,惯性力起主导作用,粘性力控制减弱,不足以 控制和约束外界扰动,惯性力将微小扰动不断扩大,形成紊流。
§层流、紊流和雷诺数
紊流
Байду номын сангаас
§层流、紊流和雷诺数
二、沿程损失与流动状态
实验装置
§层流、紊流和雷诺数
实验结果 层流: h v1.0 f 紊流: h f v1.75~2.0 结论: 沿程损失与流动状态有关,故 计算各种流体通道的沿程损失,必 须首先判别流体的流动状态。
§层流、紊流和雷诺数
三、流态的判别准则—临界雷诺数
第四章 流动阻力和能量损失
§4.1 沿程损失和局部损失
§4.2 §4.3 §4.4 §4.5
§4.6 §4.7 §4.8 §4.9
层流与紊流、雷诺数 圆管中的层流运动 紊流运动的特征和紊流阻力 尼古拉兹实验
工业管道紊流阻力系数的计算公式 非圆管的沿程损失 管道流动的局部损失 减小阻力的措施
z1
§层流、紊流和雷诺数
[惯性力]=[m][a] [ ][L]3 [ L] /[T ]2 [ ][ L]2 [v]2 [粘性力]
du [ ][ A] [ ][L]2 [v] /[L] [ ][L][v] dn
[惯性力] [ ][ L]2 [v]2 [ ][ L][v] [Re] [粘性力] [ ][ L][v] [ ]
16.6 106 vc Rec 2000 0.166 m/s d 0.2
流体力学第四章

g
2v22
2g
hw
Fx Q(2vx2 1vx1) Fy Q(2vy2 1vy1) Fz Q(2vz2 1vz1)
质量、能量和动量方程旳应用实例
1. 水流对弯管旳作用力 2.水流对分叉管道旳作用力 3.水流射流对管壁旳作用力
【例4-2】 水平放置在混凝土支座上旳变直径弯管,弯管两端与
uz
u y z
Z
1
p z
ux
uz x
uy
uz y
uz
uz z
两边同乘以 dx
dy
dz
沿流线旳微小位移ds在三个坐标轴上旳投影为dx、dy和dz
Xdx
1
p x
dx
ux
ux x
dx
uy
ux y
dx
uz
ux z
dx
Ydy
1
p y
dy
ux
u y x
dy
uy
u y y
dy
uz
u y z
dy
Zdz
x Dt
同理
Y 1 p Duy
y Dt
Z 1 p Duz
z Dt
展开成欧拉法旳体现 式(3-9)
无黏性流体运动微分方程 (欧拉运动微分方程)
X
1
p x
ux t
ux
u x x
uy
ux y
uz
ux z
Y
1
p y
u y t
ux
u y x
uy
u y y
uz
u y z
Z
1
p z
uz t
所以1,2断面间的水头损失为0.83米。
应用恒定总流能量方程式时应注意几点
2v22
2g
hw
Fx Q(2vx2 1vx1) Fy Q(2vy2 1vy1) Fz Q(2vz2 1vz1)
质量、能量和动量方程旳应用实例
1. 水流对弯管旳作用力 2.水流对分叉管道旳作用力 3.水流射流对管壁旳作用力
【例4-2】 水平放置在混凝土支座上旳变直径弯管,弯管两端与
uz
u y z
Z
1
p z
ux
uz x
uy
uz y
uz
uz z
两边同乘以 dx
dy
dz
沿流线旳微小位移ds在三个坐标轴上旳投影为dx、dy和dz
Xdx
1
p x
dx
ux
ux x
dx
uy
ux y
dx
uz
ux z
dx
Ydy
1
p y
dy
ux
u y x
dy
uy
u y y
dy
uz
u y z
dy
Zdz
x Dt
同理
Y 1 p Duy
y Dt
Z 1 p Duz
z Dt
展开成欧拉法旳体现 式(3-9)
无黏性流体运动微分方程 (欧拉运动微分方程)
X
1
p x
ux t
ux
u x x
uy
ux y
uz
ux z
Y
1
p y
u y t
ux
u y x
uy
u y y
uz
u y z
Z
1
p z
uz t
所以1,2断面间的水头损失为0.83米。
应用恒定总流能量方程式时应注意几点
流体力学 第四章

水塔截面积很大,水位恒定。已
知管道直径d=200mm,水头 H=4.5m,引水流量Q=100 L/s。 试求水流的总水头损失。
解:选取水塔自由面为断面1-1, 引水管出口为断面2-2,基准面 通过2-2的中心。
分析:断面1-1:
断面2-2:
由恒定总流的能量方程:
Z1 H,P1 0,V1 0 Z2 0,P2 0,V2 V
V2 2
,
求通过管道的流量。
2g
文丘里流量计是一种量测管道中流量的 设备。在管道中安装一段逐渐收缩后又 逐渐扩散的管段,并在收缩段的前后断 面各安装一根测压管。收缩段前后的管 径为d1和d2。只需测出两测压管中的水 面高差,即可求得通过管道的流量。试 导出流量计的流量公式。
例题1 水塔引水管如图示,
量Q=0.03m3/s, 断面1和断面2形心处
的压强分别为p1=49.0KN/m2和 p2=39.2KN/m2, 断面1和2的法线 方向与ox轴的夹角分别为θ1=0˚和 θ2= 60˚。试计算支座所受的作用 力。
一水管将水流射至一三角形 楔体上,并于楔体顶点处沿 水平面分为两股,两股水流 的方向分别与x轴成30 ˚。已 知管道出口直径d=8cm,总 流量 Q=0.05m3/s, 每股流量 均为Q/2。设水流通过楔体 前后的流速大小不变,求水 流对楔体的水平作用力。
测压管水头线
水力坡度
d (z p V 2 )
J
g 2g dhw
ds
ds
测压管坡度
d(z p )
Jp
g
ds
总流能量方程的应用
z1
p1
g
1V12
2g
流体力学第四章

1.渐变流及其特性
渐变流过水断面近似为平面,即渐变流是流线接近于
平行直线的流动。均匀流是渐变流的极限。
动压强特性:在渐变流同一过水断面上,各点动压强
按静压强的规律式分布,即
注:上述结论只适用于渐变流或均匀流的同一过水断面上 的 各点,对不同过水断面,其单位势能往往不同。
选取:控制断面一般取在渐变流过水断面或其极限情况均匀 流断面上。
即J=JP。 5.总水头线和测压管水头线之间的距离为相应段
的流速水头。
6.如果测压管水头线在总流中心线以上,压强就 是正职;如相反,则压强为负值,则有真空。
4.总流能量方程在推导过程中的限制条件
(1)不可压缩流体;
(2)恒定流;
(3)质量力只有重力,所研究的流体边界是静止 的(或处于平衡状态);
取管轴0-0为基准面,测压管所在断面
1,2为计算断面(符合渐变流),断面的形
心点为计算点,对断面1,2写能量方程(4-
15),由于断面1,2间的水头损失很小,
可视
,取α1=α2=1,得
由此得:
故可解得:
式中,K对给定管径是常量,称为文丘里流 量计常数。
实际流量 : μ——文丘里流量计系数,随流动情况和管
流体力学
第四章 流体动力学基础
本章是工程流体力学课程中最重要的一 章。本章建立了控制流体运动的微分方程, 即理想流体运动微分方程和实际流体的运 动微分方程;并介绍了求解理想流体运动 微分方程的伯努利积分形式;构建了工程 流体力学中应用最广的恒定总流运动的三 大基本方程:连续性方程、伯努利方程 (即能量方程)和动量方程。通过本章的 学习要培养综合运用三大基本方程分析、 计算实际总流运动问题的能力。
道收缩的几何形状而不同。
流体力学第四章

消公共因子 : 2 4 R' ' r R' r 4 ( R ) P' (1) 2 2 1 ' ' ' 2 ( R ) P (2),' 表示对R微商 r r r R' 2 ( R ) 0 (3) r
流体力学第四章
总32页
10
代边界条件 : R ( ) U , c3 U , c4 0 ( ) U , c3 U , c4 0 c1 c2 R(a ) 3 U 0 a a c1 c2 ( a ) 3 U 0 2a 2a 3 c1 2 aU 1 3 c2 a U 2
P [( prr ) r a cos ( pr ) r a sin )]d
[( prr ) r a cos ( pr ) r a sin )]2a sin ad
0
4 ga 3 6Ua 浮力 阻力,其中阻力p 6Ua 3
1 vr r 2 sin 2、存在流函数 (r , ), 1 v r sin r 3 a 1 a3 求积可得 : a (r , ) Ur 3 sin 2 ( ) 3 4r 4r
流体力学第四章 总32页 13
§3、流体对小球的Stokes阻力
总32页 3
p 2 v 0
流体力学第四章
性质:
1 不可压、小数 Re 流动, 压力p为调和函数, 即 2 p 0 、 对方程 : 1
p 2 v p 2 v两边取散度
p 2 p 2 v 2 ( v ) 0 2、 若流动为二维, 则流函数满足双调和方程 2 ( 2 ) 0 引ς v, (ς 涡度矢) ( v ) ( v ) 2 v 2 v 即 2 v ς p ς
流体力学第四章
总32页
10
代边界条件 : R ( ) U , c3 U , c4 0 ( ) U , c3 U , c4 0 c1 c2 R(a ) 3 U 0 a a c1 c2 ( a ) 3 U 0 2a 2a 3 c1 2 aU 1 3 c2 a U 2
P [( prr ) r a cos ( pr ) r a sin )]d
[( prr ) r a cos ( pr ) r a sin )]2a sin ad
0
4 ga 3 6Ua 浮力 阻力,其中阻力p 6Ua 3
1 vr r 2 sin 2、存在流函数 (r , ), 1 v r sin r 3 a 1 a3 求积可得 : a (r , ) Ur 3 sin 2 ( ) 3 4r 4r
流体力学第四章 总32页 13
§3、流体对小球的Stokes阻力
总32页 3
p 2 v 0
流体力学第四章
性质:
1 不可压、小数 Re 流动, 压力p为调和函数, 即 2 p 0 、 对方程 : 1
p 2 v p 2 v两边取散度
p 2 p 2 v 2 ( v ) 0 2、 若流动为二维, 则流函数满足双调和方程 2 ( 2 ) 0 引ς v, (ς 涡度矢) ( v ) ( v ) 2 v 2 v 即 2 v ς p ς
流体力学第四章
2
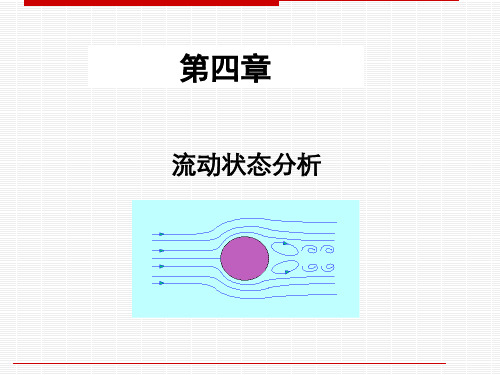
k 0 .4
2
u
*2
du 2 ( k y) ( ) dy
u* du dy ky
积分有
u* u ln y C k
y
速度分布的 指数形式
u u max
y n ( ) a
1
a (a-y) d x
0
Re 410 2.3
4
104
1.1 105
1.1 106
2.0 106
8Lu 32 Lu h f P 2 R d2
范宁摩擦因子 f (Fanning friction factor)
摩擦因子的定义:流体在壁面处的剪应力与管内单位体积流 体的平均动能之比
1 d P f 2 u / 2 4 L u2/ 2
s
L u2 L u2 P 4 f λ d 2 d 2
普朗特混合 长度假说
y
du u c1l dy v c2 u c1c2 l du dy
u
l
y
b A a 0
u l y
u
v u
x 涡体
l
b a
l 称为混合长度
2 ( c1l
2 l 2 c1 c2l 2
du du du 2 2 ) 2 )( )( c1c2l (c1 c2l ) dy dy dy 2 du 2 2 l ( ) dy
伯金汉(Buckingham)定理
一个物理方程可以变换为无因次准数方程,独立准数的个数 N 等于原方程变量数 n 减去基本因次数 m。
N nm
根据实验结果,直管层流摩擦阻力损失与管长成正比,指数 b=1
du d P 2 K d L u
k 0 .4
2
u
*2
du 2 ( k y) ( ) dy
u* du dy ky
积分有
u* u ln y C k
y
速度分布的 指数形式
u u max
y n ( ) a
1
a (a-y) d x
0
Re 410 2.3
4
104
1.1 105
1.1 106
2.0 106
8Lu 32 Lu h f P 2 R d2
范宁摩擦因子 f (Fanning friction factor)
摩擦因子的定义:流体在壁面处的剪应力与管内单位体积流 体的平均动能之比
1 d P f 2 u / 2 4 L u2/ 2
s
L u2 L u2 P 4 f λ d 2 d 2
普朗特混合 长度假说
y
du u c1l dy v c2 u c1c2 l du dy
u
l
y
b A a 0
u l y
u
v u
x 涡体
l
b a
l 称为混合长度
2 ( c1l
2 l 2 c1 c2l 2
du du du 2 2 ) 2 )( )( c1c2l (c1 c2l ) dy dy dy 2 du 2 2 l ( ) dy
伯金汉(Buckingham)定理
一个物理方程可以变换为无因次准数方程,独立准数的个数 N 等于原方程变量数 n 减去基本因次数 m。
N nm
根据实验结果,直管层流摩擦阻力损失与管长成正比,指数 b=1
du d P 2 K d L u
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 p u 2 u x fx ( ) 2(u z y u y z ) x x 2 t 1 p u 2 u y fy ( ) 2(u x z u z x ) y y 2 t 1 p u 2 u z fx ( ) 2(u y x u x y ) z z 2 t
得:
u12 p2 u 2 2 z1 z2 2g 2g p1
4.2 理想流体元流的伯努利方程
4.2.2理想流体元流伯努利方程的物理意义
1、理想流体元流伯努利方程的物理意义 z是元流过流断面上单位重量流体从某一 基准面算起所具有的位能,称单位位能。 p/ρg是元流过流断面上单位重量流体从 某一基准面算起所具有的压能,称单位 压能。 z+p/ρg 是元流过流断面上单位重量流 体从某一基准面算起所具有势能,称单 位势能。 u 2/ 2g是元流过流断面上单位重量流体 所具有的动能(kinetic energy),称 单位动能。 物理意义:元流各过流断面上单位重量流体 所具有的总机械能沿流程保持不变;同时, 亦表示了元流在不同过流断面上单位重量流 体所具有的位能、压能、动能之间可以相互 转化的关系。 2、理想流体元流伯努利方程的几何意 义 z是位臵水头 p/ρg 是压强水头。 z+p/ρg是测压管水头 u 2/ 2g是速度 水头
u y u x 0 t t
不可压缩流体,即 =Const u 运动方程 1 p x
X x
ux x
uy
u x y
u y u y Y 1 p u x uy y x y
连续性方程 u x
u y 0 x y
4.3 理想流体元流的伯努利方程
4.3.1速度势的性质
恒定势流中必然存在速度势函数φ (x、 2、速度势值相等的点所连成的空 y、z),满足: 间曲面称等势面,与流线相正交, ux ,uy 即为过流断面。d u dl 0 x y 1、速度势对任意方向 m 的偏导数,等 3、速度势值沿流线 s 方向增大。 d uds 于速度 u 在该方向的速度分量 um 4、速度势满足拉普拉斯方程,是 x y z 调和函数。 2 2 m x m y m z m
t x y z 1 p u z u u u fz ux z u y z uz z z t x y z 当恒定流时 ux u y uz 0 t t t
y
当静止时
ux u y uz 0
边界条件:一般包括固体边界和自由表 面等处的运动要素情况。 固体边界: u ( x, y, z, t ) n 0 自由表面: p( x, y, z , t ) pa ( x, y, z , t )
p ( x, y , z , t )
t 0
p0 ( x, y, z )
4.1 理想流体的运动微分方程—欧拉运动方程
4.1.2葛罗米柯(又称兰姆)运动微分方程
欧拉运动微分方程变化为区分有势流、有涡流的运动微分方程。 u y 将 u y 和 uz uz 加到欧拉微分方程第一式等号的右边,整理。 x x 同理对第二、三式作类似处理得:
将流体运动分为有势流和有涡流。严格 讲,实际流体的运动都不是有势流,只 有理想流体的运动才有可能是有势流。 因为:理想流体没有粘性,不存在切应 力,不能传递旋转(转动)运动;它既不 能使不旋转的流体微元产生旋转,也不 能使已旋转的流体微元停止旋转。 解决实际流体运动,将流场划分为两个 区间: 一个是紧靠固体边界的粘性起作用的 区间,用粘性流体边界层理论; 一个是不受固体边界阻力影响的、粘性 不起作用的区间用无粘性(理想)流体势 流理论。 恒定平面势流基本方程组(不可 压缩恒定二元势流 ): 平面无旋,即 z 0 恒定流,即
4.1 理想流体的运动微分方程—欧拉运动方程
4.1.1理想流体的运动微分方程—欧拉运动方程
1 、用微元分析法推导流体的运动微分 方程 :设点M的坐标为x、y、z,压 强为p。 x 轴方向受力分析: 利用 泰勒级数, ABCD 和 EFGH 中心点处的 dx p 压强分别为: p dx p p 2 x 2 x 表面力为:
4.1.1理想流体的运动微分方程—欧拉运动方程
2、区分恒定流和非恒定流的欧拉运动 3、欧拉运动微分方程和求解条件 微分方程 :加速度表示式展开,欧 方程式中有ρ、 fx、fy、fz、 ux、uy、 拉运动微分方程写为 uz、p八个物理量 。 u u u 1 p u x fx u x x u y x u z x 初始条件:在起始时刻 t=0 时,各处的 x t x y z 流速、压力值;对于恒定流,则不 u u u 1 p u y 存在条件。 u ( x, y, z, t ) t 0 u0 ( x, y, z ) fy ux y u y y uz y
cos( m, x) cos( m, y ) cos( m, z) x y z 意义:平面势流的问题就归结为在 u x cos(m, x) u y cos(m, y ) uz cos(m, z)
2 0 2 2 x y
一维几何理解 d dx d
(p
质量力为:
1 p 1 p dx)dydz ( p dx)dydz 2 x 2 x
du 惯性力为: dxdydz x dt 根据牛顿第二定律
(p
f x dxdydz
化简移项后得: f x 1 p dux
x
dt
同理 :
fy
1 p du y y dt
fz
1 p du z y dt
du 1 p 1 p dx)dydz ( p dx)dyd f x dxdydz dxdydz x 2 x 2 x dt
上面三式为理想流体的运动微分方程, 又称欧拉运动微分方程。
4.1 理想流体的运动微分方程—欧拉运动方程
4.3.2流函数及其性质
流体平面运动(不一定是势流)的流 1、函数Ψ对任意方向 m 的偏导数, 等于速度u在该方向顺时针旋转 90°后 线方程为: dx dy 的 m’方向的速度分量um ’ ux u y 2、流函数值相等的点连成的曲线称 u x dy u y dx 0 所以 等流函数线,即为流线;或者说,同 不可压缩均质流体平面运动的连续 一流线上的流函数相等。 性方程为: u x u y 3、流函数值沿流线s方向逆时针旋转 0 x y 90°后n的方向增大。 存在函数Ψ(x,y)的全微分: 4、任意两条流线的流函数值之差 (Ψ2-Ψ1),等于该两条流线间所通过 d u x dy u y dx 的单宽流量q 函数Ψ(x,y)称流函数 5、平面势流的流函数满足拉普拉斯 适用范围:无旋流、有旋流、实际 方程,是调和函数 流体、理想流体的不可压缩 流体 意义:求出流函数,即可求得任一 的平面流动 点的两个速度分量,这样就简化了分 析的过程。
第四章
理想流体力学和平面势流
王浩 1251934
本章概论
4.1理想流体的运动微分方程 ——欧拉微分方程
4.2 理想流体元流的伯努利方程
4.3 恒定平面势流
流体动力学
1、流体动力学(hydrodynamics//fluid dynamics):是研究流体运动而涉及力的规律及 其在工程中的应用。 2、理想流体的动压强与流体静压强一样亦具 有两个特性。 一是:动压强的方向总是沿着作用面的内法 线方向; 二是:理想流体中任一点的动压强大小与其 作用面的方位无关
称葛罗米柯运动微分方程,又称兰姆(Lamb)运动微分方程。
4.1 理想流体的运动微分方程—欧拉运动方程
4.1.3理想流体运动微分方程的积分、伯努利方程
1、 伯努利方程(能量方程)的推导: 2、伯努利方程的物理内涵: 满足下列条件下: 伯努利方程是说明能量守恒概念的, 因此又称能量方程。它说明:在流场中 (1)流体是不可压缩均质的理想流体, 任一点单位质量流体的位势能 W、压势 密度为常数; 能 p/ρ和动能u2/2 的总和保持一常数 (2)质量力是有势的; 值,而这三种机械能可以相互转化。 (3)恒定流理想流体运动微分方程简化 3、伯努利方程的应用条件: 为: dx dy dz 静止流体 p u2 d (W ) 2 x y z 2 整个有势流 即流场中所有各点的总机 ux u y uz 械能保持不变,不限于在同一条流线上。 (4)行列式为零 dx dy dz 有涡流 但限于同一条流线上各点的总 x y z 0 机械能保持不变;不同流线上各点的总 ux u y uz 机械能则是不同的。这和有势流的情况 2 p u 化简得 W 2 const 不同。 ux u y uz 上式为伯努利方程(Bernoulli equation)。 整个螺旋流 为螺旋流
u cos(u, m) um
d cos( m, x ) d m d x dm dx u x cos( m, x ) um
特定的边界条件下解拉普拉斯方程, 把解两个未知函数 ux 、uy (或 ur 、 uθ ) 的问题变为 解一个未 知函数 φ 的问题。
4.3 理想流体元流的伯努利方程
pS u A2 p A 2g
整理得
式中:pA、uA分别为A点处在皮托管 放入前的压强和速度。
1 pS p A u A 2 2
pA 为静压
1 2 u A 为动压 2
uA
2( pS p A )
ps 为全压或总压
4.3 理想流体元流的伯努利方程
有势流近似处理条件
gdA1ds1dtz1 gdA2 ds2 dtz 2 dQdt ( z1 z 2 )
p1dA1u1dt p2 dA2u2 dt d定理 2 u2 u12 dQdt ( ) dQdt ( z1 z2 ) dQdt ( p1 p2 ) 2g 2g
得:
u12 p2 u 2 2 z1 z2 2g 2g p1
4.2 理想流体元流的伯努利方程
4.2.2理想流体元流伯努利方程的物理意义
1、理想流体元流伯努利方程的物理意义 z是元流过流断面上单位重量流体从某一 基准面算起所具有的位能,称单位位能。 p/ρg是元流过流断面上单位重量流体从 某一基准面算起所具有的压能,称单位 压能。 z+p/ρg 是元流过流断面上单位重量流 体从某一基准面算起所具有势能,称单 位势能。 u 2/ 2g是元流过流断面上单位重量流体 所具有的动能(kinetic energy),称 单位动能。 物理意义:元流各过流断面上单位重量流体 所具有的总机械能沿流程保持不变;同时, 亦表示了元流在不同过流断面上单位重量流 体所具有的位能、压能、动能之间可以相互 转化的关系。 2、理想流体元流伯努利方程的几何意 义 z是位臵水头 p/ρg 是压强水头。 z+p/ρg是测压管水头 u 2/ 2g是速度 水头
u y u x 0 t t
不可压缩流体,即 =Const u 运动方程 1 p x
X x
ux x
uy
u x y
u y u y Y 1 p u x uy y x y
连续性方程 u x
u y 0 x y
4.3 理想流体元流的伯努利方程
4.3.1速度势的性质
恒定势流中必然存在速度势函数φ (x、 2、速度势值相等的点所连成的空 y、z),满足: 间曲面称等势面,与流线相正交, ux ,uy 即为过流断面。d u dl 0 x y 1、速度势对任意方向 m 的偏导数,等 3、速度势值沿流线 s 方向增大。 d uds 于速度 u 在该方向的速度分量 um 4、速度势满足拉普拉斯方程,是 x y z 调和函数。 2 2 m x m y m z m
t x y z 1 p u z u u u fz ux z u y z uz z z t x y z 当恒定流时 ux u y uz 0 t t t
y
当静止时
ux u y uz 0
边界条件:一般包括固体边界和自由表 面等处的运动要素情况。 固体边界: u ( x, y, z, t ) n 0 自由表面: p( x, y, z , t ) pa ( x, y, z , t )
p ( x, y , z , t )
t 0
p0 ( x, y, z )
4.1 理想流体的运动微分方程—欧拉运动方程
4.1.2葛罗米柯(又称兰姆)运动微分方程
欧拉运动微分方程变化为区分有势流、有涡流的运动微分方程。 u y 将 u y 和 uz uz 加到欧拉微分方程第一式等号的右边,整理。 x x 同理对第二、三式作类似处理得:
将流体运动分为有势流和有涡流。严格 讲,实际流体的运动都不是有势流,只 有理想流体的运动才有可能是有势流。 因为:理想流体没有粘性,不存在切应 力,不能传递旋转(转动)运动;它既不 能使不旋转的流体微元产生旋转,也不 能使已旋转的流体微元停止旋转。 解决实际流体运动,将流场划分为两个 区间: 一个是紧靠固体边界的粘性起作用的 区间,用粘性流体边界层理论; 一个是不受固体边界阻力影响的、粘性 不起作用的区间用无粘性(理想)流体势 流理论。 恒定平面势流基本方程组(不可 压缩恒定二元势流 ): 平面无旋,即 z 0 恒定流,即
4.1 理想流体的运动微分方程—欧拉运动方程
4.1.1理想流体的运动微分方程—欧拉运动方程
1 、用微元分析法推导流体的运动微分 方程 :设点M的坐标为x、y、z,压 强为p。 x 轴方向受力分析: 利用 泰勒级数, ABCD 和 EFGH 中心点处的 dx p 压强分别为: p dx p p 2 x 2 x 表面力为:
4.1.1理想流体的运动微分方程—欧拉运动方程
2、区分恒定流和非恒定流的欧拉运动 3、欧拉运动微分方程和求解条件 微分方程 :加速度表示式展开,欧 方程式中有ρ、 fx、fy、fz、 ux、uy、 拉运动微分方程写为 uz、p八个物理量 。 u u u 1 p u x fx u x x u y x u z x 初始条件:在起始时刻 t=0 时,各处的 x t x y z 流速、压力值;对于恒定流,则不 u u u 1 p u y 存在条件。 u ( x, y, z, t ) t 0 u0 ( x, y, z ) fy ux y u y y uz y
cos( m, x) cos( m, y ) cos( m, z) x y z 意义:平面势流的问题就归结为在 u x cos(m, x) u y cos(m, y ) uz cos(m, z)
2 0 2 2 x y
一维几何理解 d dx d
(p
质量力为:
1 p 1 p dx)dydz ( p dx)dydz 2 x 2 x
du 惯性力为: dxdydz x dt 根据牛顿第二定律
(p
f x dxdydz
化简移项后得: f x 1 p dux
x
dt
同理 :
fy
1 p du y y dt
fz
1 p du z y dt
du 1 p 1 p dx)dydz ( p dx)dyd f x dxdydz dxdydz x 2 x 2 x dt
上面三式为理想流体的运动微分方程, 又称欧拉运动微分方程。
4.1 理想流体的运动微分方程—欧拉运动方程
4.3.2流函数及其性质
流体平面运动(不一定是势流)的流 1、函数Ψ对任意方向 m 的偏导数, 等于速度u在该方向顺时针旋转 90°后 线方程为: dx dy 的 m’方向的速度分量um ’ ux u y 2、流函数值相等的点连成的曲线称 u x dy u y dx 0 所以 等流函数线,即为流线;或者说,同 不可压缩均质流体平面运动的连续 一流线上的流函数相等。 性方程为: u x u y 3、流函数值沿流线s方向逆时针旋转 0 x y 90°后n的方向增大。 存在函数Ψ(x,y)的全微分: 4、任意两条流线的流函数值之差 (Ψ2-Ψ1),等于该两条流线间所通过 d u x dy u y dx 的单宽流量q 函数Ψ(x,y)称流函数 5、平面势流的流函数满足拉普拉斯 适用范围:无旋流、有旋流、实际 方程,是调和函数 流体、理想流体的不可压缩 流体 意义:求出流函数,即可求得任一 的平面流动 点的两个速度分量,这样就简化了分 析的过程。
第四章
理想流体力学和平面势流
王浩 1251934
本章概论
4.1理想流体的运动微分方程 ——欧拉微分方程
4.2 理想流体元流的伯努利方程
4.3 恒定平面势流
流体动力学
1、流体动力学(hydrodynamics//fluid dynamics):是研究流体运动而涉及力的规律及 其在工程中的应用。 2、理想流体的动压强与流体静压强一样亦具 有两个特性。 一是:动压强的方向总是沿着作用面的内法 线方向; 二是:理想流体中任一点的动压强大小与其 作用面的方位无关
称葛罗米柯运动微分方程,又称兰姆(Lamb)运动微分方程。
4.1 理想流体的运动微分方程—欧拉运动方程
4.1.3理想流体运动微分方程的积分、伯努利方程
1、 伯努利方程(能量方程)的推导: 2、伯努利方程的物理内涵: 满足下列条件下: 伯努利方程是说明能量守恒概念的, 因此又称能量方程。它说明:在流场中 (1)流体是不可压缩均质的理想流体, 任一点单位质量流体的位势能 W、压势 密度为常数; 能 p/ρ和动能u2/2 的总和保持一常数 (2)质量力是有势的; 值,而这三种机械能可以相互转化。 (3)恒定流理想流体运动微分方程简化 3、伯努利方程的应用条件: 为: dx dy dz 静止流体 p u2 d (W ) 2 x y z 2 整个有势流 即流场中所有各点的总机 ux u y uz 械能保持不变,不限于在同一条流线上。 (4)行列式为零 dx dy dz 有涡流 但限于同一条流线上各点的总 x y z 0 机械能保持不变;不同流线上各点的总 ux u y uz 机械能则是不同的。这和有势流的情况 2 p u 化简得 W 2 const 不同。 ux u y uz 上式为伯努利方程(Bernoulli equation)。 整个螺旋流 为螺旋流
u cos(u, m) um
d cos( m, x ) d m d x dm dx u x cos( m, x ) um
特定的边界条件下解拉普拉斯方程, 把解两个未知函数 ux 、uy (或 ur 、 uθ ) 的问题变为 解一个未 知函数 φ 的问题。
4.3 理想流体元流的伯努利方程
pS u A2 p A 2g
整理得
式中:pA、uA分别为A点处在皮托管 放入前的压强和速度。
1 pS p A u A 2 2
pA 为静压
1 2 u A 为动压 2
uA
2( pS p A )
ps 为全压或总压
4.3 理想流体元流的伯努利方程
有势流近似处理条件
gdA1ds1dtz1 gdA2 ds2 dtz 2 dQdt ( z1 z 2 )
p1dA1u1dt p2 dA2u2 dt d定理 2 u2 u12 dQdt ( ) dQdt ( z1 z2 ) dQdt ( p1 p2 ) 2g 2g
