(完整版)数学模型第四版课后答案姜启源版
姜启源编《数学模型》第四版_第七章_稳定性模型

设x(t)是方程的解,若从x0 某邻域的任一初值出发,
都有
lim
t
x(t)
x0
,
称x0是方程(1)的稳定平衡点.
不求x(t), 判断x0稳定性的方法——直接法
F (x0 ) 0 x0 稳定 F (x0 ) 0 x0 不稳定
第六页,共61页。
产量模型 x(t) F (x) rx(1 x ) Ex N
c2 )
p2N 2
第九页,共61页。
捕捞 过度
• 封闭式捕捞追求利润R(E)最大
• 开放式捕捞只求利润R(E) > 0
ER
r (1 2
c) pN
R(E) T (E) S(E)
pNE (1
E ) cE
令
=0
r
c Es r(1 pN )
R(E)=0时的捕捞强度Es=2ER
~ 临界强度
临界强度下的渔场鱼量
x1 (t )
r1x1 (1
x1 N1
)
x2 (t)
r2 x2 (1
x 2
N
)
2
• 两种群在一起生存时,乙对甲增长的阻滞作用
与乙的数量成正比; 甲对乙有同样的作用.
模型
x1 (t )
r1 x1 1
x1 N1
1
x2 N2
x2 (t)
r2 x2 1
2
x1 N1
x2 N2
对于消耗甲的资源而言,
乙(相对于N2)是甲(相对于 N1) 的 1 倍.
建模
h(x)=Ex, E~捕捞强度
记 F(x) f (x) h(x)
有捕捞情况下渔场 鱼量满足
x(t) F (x) rx(1 x ) Ex
姜启源版《数学模型》第四章习题第题

姜启源版《数学模型》第四章习题第7题一、问题重述某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割后出售。
从钢管厂进货时得到的原料钢管的长度都是1850mm现有一客户需要15根290mm 28根315mm 21根350mn和30根455mn的钢管。
为了简化生产过程,规定所使用的切割模式的种类不能超过4种,使用频率最高的一种切割模式按照一根原料钢管价值的1/10增加费用,使用频率次之的切割模式按照一根原料钢管价值的2/10增加费用,依次类推,且每种切割模式下的切割次数不能太多(一根钢管最多生产5根产品)。
此外,为了减少余料浪费,每种切割模式下的余料不能超过100mm 为了使总费用最小,应如何下料?二、基本假设1、假设所研究的每根钢管的长度均为1850mm勺钢管。
2、假设每次切割都准确无误。
3、假设切割费用短时间内不会波动为固定值。
5、假设钢管余料价值为0。
6假设一切运作基本正常不会产生意外事件。
四、模型建立根据题目要求,不妨假设叫左勺王%,于是得到目标函数:4min M X i 1 0.1ii 1需求量的约束:每一种切法不能超过限制1850,余料不超过100(即产品加起来不小于1750)极限情况下,根数的范围:D j le n jj 11850 一根原料钢管最多生产5根产品:4r j5,i 1,2,3,4j 1钢管根数和切割方法都为非负整数:r ijZ ,x iZ五、模型求解model :!数学模型132页题7; sets :!定义4种切割模式,每种模式用 x(i)根管材;qiegemoshi/m1..m4/:x; !定义四种长度,每种有需求;cha ngdu/cd1..cd4/:le n,dema nd;!定义切法矩阵,行为模式,列为需要的长度类型 ;lin ks(qiegemoshi,cha ngdu):r; en dsets!目标函数,每种切割模式按切割频率增加 10%的费用;min = @sum(qiegemoshi(i):x(i)*(1+i*0.1)); !假设4种切法,一种比一种切得少;@for (qiegemoshi(i)|i#lt#4:x(i)>=x(i+1)); !需求量的约束; @for (changdu(j):约束条件如下:x-i x 2 x 3x 4(4.1 )D j ,j 1,2,3, 4(4.2 )41750r ij le n j j 11850,i 123,4(4.3)D j1850 len j(4.4)@sum(qiegemoshi(i):r(i,j)*x(i))>=demand(j));! 整数约束;@for (qiegemoshi(i): @gin (x(i)));@for (links(i,j): @gin (r(i,j)));! 每一种切法不能超过限制1850 ,余料不超过100( 即产品加起来不小于@for1750 ) (qiegemoshi(i):@sum(changdu(j):r(i,j)*len(j))>=1750);@for (qiegemoshi(i): @sum(changdu(j):r(i,j)*len(j))<=1850);! 极限情况下,最多22 根,最少19 根; @sum(qiegemoshi:x)>=19;@sum(qiegemoshi:x)<=22;! 一根原料钢管小于5 根产品; @for (qiegemoshi(i):@sum(changdu(j):r(i,j))<=5);data : demand=15 28 21 30; len=290 315 350 455;enddataend在lingo11 中运行,得到如下结果:Local optimal solution found.Objective value: 21.50000Objective bound: 21.50000Infeasibilities: 0.000000Extended solver steps: 155Total solver iterations: 20017Variable Value Reduced CostX( M1) 14.00000 -0.1000000X( M2) 4.000000 0.000000X( M3) 1.000000 0.1000000X( M4) 0.000000 0.2000000LEN( CD1) 290.0000 0.000000LEN( CD2) 315.0000 0.000000LEN( CD3) 350.0000 0.000000LEN( CD4) 455.0000 0.000000DEMAND( CD1) 15.00000 0.000000DEMAND( CD2) 28.00000 0.000000DEMAND( CD3) 21.00000 0.000000DEMAND( CD4) 30.00000 0.000000QIEFA( M1, CD1) 1.000000 0.000000QIEFA( M1, CD2) 2.000000 0.000000 QIEFA( M1, CD3) 0.000000 0.000000 QIEFA( M1, CD4) 2.000000 0.000000 QIEFA( M2, CD1) 0.000000 0.000000 QIEFA( M2, CD2) 0.000000 0.000000 QIEFA( M2, CD3) 5.000000 0.000000 QIEFA( M2, CD4) 0.000000 0.000000 QIEFA( M3, CD1) 2.000000 0.000000 QIEFA( M3, CD2) 0.000000 0.000000 QIEFA( M3, CD3) 1.000000 0.000000 QIEFA( M3, CD4) 2.000000 0.000000 QIEFA( M4, CD1) 1.000000 0.000000 QIEFA( M4, CD2) 0.000000 0.000000 QIEFA( M4, CD3) 3.000000 0.000000 QIEFA( M4, CD4) 1.000000 0.000000。
姜启源编数学模型第四版

一般模型 x(t) ~甲方兵力,y(t) ~乙方兵力
模型 假设
• 每方战斗减员率取决于双方的兵力和战斗力. • 每方非战斗减员率与本方兵力成正比. • 甲乙双方的增援率为u(t), v(t).
x(t) f (x, y) x u(t), 0
tm~传染病高潮到来时刻
tm
1
ln
1 i0
1
t i 1 ?
(日接触率) tm
病人可以治愈!
第6页/共76页
模型3
传染病无免疫性——病人治愈成 为健康人,健康人可再次被感染. SIS 模型
增加假设 3)病人每天治愈的比例为 ~日治愈率
建模 N[i(t t) i(t)] Ns(t)i(t)t Ni(t)t
di
dt
i(1 i)
i
i[i (1 1 )]
i(0) i0
/
~ 日接触率 1/ ~感染期
~ 一个感染期内每个病人的
有效接触人数,称为接触数.
第7页/共76页
模型3
di/dt
di i[i (1 1 )]
dt
接触数 (感染期内每个
病人的有效接触人数)
i
i
>1
i0
>1
1
1-1/
接触率
N[i(t t) i(t)] [s(t)]Ni(t)t
di si
dt
s(t) i(t) 1
di
i(1 i)
dt
i(0) i0
第5页/共76页
模型2
i
di
i(1 i)
dt
i(0) i0
Logistic 模型
1
i(t)
姜启源第四版数学模型-第7章

F(x)0
x N(1E),x0
平衡点
0
r1
稳定性判断 F (x 0 ) E r , F (x 1 ) r E
E r F (x 0 ) 0 ,F (x 1 ) 0 x0稳定,x1不稳定
E r F (x 0 ) 0 ,F (x 1 ) 0 x0不稳,定 x1稳定
x2 1 2 2 2
A
fx1 gx1
fx2 P0
g x2
2 p q 0
p
(
f x1
g) x2
P0
q
det
A
p>0且q>0
p<0或q<0
平衡点 P0稳定(对(2),(1)) 平衡点 P0不稳定(对(2),( Nx22
x1(t)f(x1,x2) x2(t)g(x1,x2) (1)
x (t)f(x0,x0)x ( x0)f(x0,x0)x ( x0)
1
x 1 1 2 1 1
x2 1 2 2 2
x (t)g(x0,x0)x ( x0) g(x0,x0)x ( x0) (2 )
2
x 1 1 2 1 1
过度 支出 S(E)cE r
=0 临界强度Es
pN/2cpN(c/Np2c/N) Es Es1E*经济学捕捞过度
pNE S(E)
pNE/2 S(E)
cpN/2 (p2c/N)
T(E)
Es Es2 E*生态学捕捞过度 0
Es1 E*
Es2 r
E
捕鱼业的 在自然增长和捕捞情况的合理假设下建模. 持续收获 用平衡点稳定性分析确定渔场鱼量稳定条件,
f (x , x ) 0
姜启源等编《数学模型》第四版课件第1章

河
小船(至多2人) 3名商人
3名随从
决策~ 每一步(此岸到彼岸或彼岸到此岸)船上的人员. 要求~在安全的前提下(两岸的随从数不比商人多),经 有限步使全体人员过河.
模型构成
xk~第k次渡河前此岸的商人数
yk~第k次渡河前此岸的随从数 sk=(xk , yk) ~过程的状态 xk, yk=0,1,2,3;
( x y ) 30 750 ( x y ) 50 750
求解
x=20 y =5
答:船速为20km/h.
航行问题建立数学模型的基本步骤
• 作出简化假设(船速、水速为常数)
• 用符号表示有关量(x, y分别表示船速和水速) • 用物理定律(匀速运动的距离等于速度乘以 时间)列出数学式子(二元一次方程)
dz x z , t 2, dt x 1100e t , z (2) 236.5
λ=0.1386 (不变),μ =0.1155×2=0.2310
z(t ) 1650e0.1386t 1609.5e0.2310t , t 2
施救方案
1200 1000 x(t) 800
k=1,2,…
S ~ 允许状态集合 S={(x , y) x=0, y=0,1,2,3; x=3, y=0,1,2,3; x=y=1,2}
uk~第k次渡船上的商人数
vk~第k次渡船上的随从数
uk, vk=0, 1, 2;
k=1,2,…
dk=(uk , vk) ~过程的决策 D ~允许决策集合 D={(u , v) u+v=1, 2, u, v=0, 1, 2} 状态因决策而改变
14电气照明是建筑电气技术的基本内容是保证建筑物发挥基本功能的必要条件合理的照明对提高工作效率保证安全生产和保护视力都具有重要的意义数学建模的一般步骤模型准备模型假设模型构成模型求解模型分析模型检验模型应用了解实际背景明确建模目的搜集有关信息掌握对象特征形成一个比较清晰的问题电气照明是建筑电气技术的基本内容是保证建筑物发挥基本功能的必要条件合理的照明对提高工作效率保证安全生产和保护视力都具有重要的意义针对问题特点和建模目的作出合理的简化的假设在合理与简化之间作出折中用数学的语言符号描述问题发挥想像力使用类比法尽量采用简单的数学工具数学建模的一般步骤电气照明是建筑电气技术的基本内容是保证建筑物发挥基本功能的必要条件合理的照明对提高工作效率保证安全生产和保护视力都具有重要的意义模型求解各种数学方法软件和计算机技术
数学建模_姜启源第四章__数学规划模型

DO RANGE(SENSITIVITY) ANALYSIS?
(约束条件不变) x1系数范围(64,96)
64.000000 8.000000 16.000000 x2系数范围(48,72) RIGHTHAND SIDE RANGES CURRENT ALLOWABLE ALLOWABLE RHS INCREASE DECREASE
模型求解
OBJECTIVE FUNCTION VALUE 1) 3460.800 VARIABLE VALUE REDUCED COST X1 0.000000 1.680000 X2 168.000000 0.000000 X3 19.200001 0.000000 X4 0.000000 0.000000 X5 24.000000 0.000000 X6 0.000000 1.520000 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 3.160000 3) 0.000000 3.260000 4) 76.000000 0.000000 5) 0.000000 44.000000 6) 0.000000 32.000000 NO. ITERATIONS= 2
结果解释
每天销售168 千克A2 和19.2 千克B1, 利润3460.8(元) 8桶牛奶加工成A1,42桶 牛奶加工成A2, 将得到的24千克A1全部 加工成B1 除加工能力外均 为紧约束
30元可增加1桶牛奶,3元可增加1小时时间, 应否投资?现投资150元,可赚回多少?
Max z 72x1 64x2
z=c (常数) ~等值线
0
l5
Z=0
x1 D Z=2400
在B(20,30)点得到最优解 最优解一定在凸多边 形的某个顶点取得。
姜启源课后习题

第一部分 练习与思考题第1章 建立数学模型1.1 在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何?(稳定的椅子问题见姜启源《数学模型》第6页)1.2 在商人们安全过河问题中,若商人和随从各四人,怎样才能安全过河呢?一般地,有n 名商人带n 名随从过河,船每次能渡k 人过河,试讨论商人们能安全过河时,n 与k 应满足什么关系。
(商人们安全过河问题见姜启源《数学模型》第7页)1.3 人、狗、鸡、米均要过河,船需要人划,另外至多还能载一物,而当人不在时,狗要吃鸡,鸡要吃米。
问人、狗、鸡、米怎样过河?1.4 有3对夫妻过河,船至多载两人,条件是任一女子不能在其丈夫不在的情况下与其他的男子在一起。
问怎样过河?1.5 如果银行存款年利率为5.5%,问如果要求到2010年本利积累为100000元,那么在1990年应在银行存入多少元?而到2000年的本利积累为多少元?1.6 某城市的Logistic 模型为2610251251N N dt dN ⨯-=,如果不考虑该市的流动人口的影响以及非正常死亡。
设该市1990年人口总数为8000000人,试求该市在未来的人口总数。
当∞→t 时发生什么情况。
1.7 假设人口增长服从这样规律:时刻t 的人口为)(t x ,最大允许人口为m x ,t 到t t ∆+时间内人口数量与)(t x x m -成正比。
试建立模型并求解,作出解的图形并与指数增长模型和阻滞增长模型的结果进行比较。
1.8 一昼夜有多少时刻互换长短针后仍表示一个时间?如何求出这些时间?1.9 你在十层楼上欲乘电梯下楼,如果你想知道需要等待的时间,请问你需要有哪些信息?如果你不愿久等,则需要爬上或爬下几个楼层?1.10 居民的用水来自一个由远处水库供水的水塔,水库的水来自降雨和流入的河流。
水库的水可以通过河床的渗透和水面的蒸发流失。
如果要你建立一个数学模型来预测任何时刻水塔的水位,你需要哪些信息?第2章 初等模型2.1 学校共1000名学生,235人住在A 宿舍,333人住在B 宿舍,432人住在C 宿舍。
数学模型第四版(姜启源)作业对于6.4节蛛网模型讨论下列问题:【范本模板】

对于6。
4节蛛网模型讨论下列问题:(1)因为一个时段上市的商品不能立即售完,其数量也会影响到下一时段的价格,所以第k+1时段的价格1+k y 由第k+1和第k 时段的数量1+k x 和k x 决定。
如果设1+k x 仍只取决于k y ,给出稳定平衡的条件,并与6.4的结果进行比较。
(2)若除了1+k y 由1+k x 和k x 决定之外,1+k x 也由前两个时段的价格k y 和1-k y 决定,试分析稳定平衡的条件是否还会放宽。
解:(1)设1+k y 由1+k x 和k x 的平均值决定,即价格函数表示为:)2(11k k k x x f y +=++ 则 0),2(0101>-+-=-++ααx x x y y k k k 0),(001>-=-+ββy y x x k k消去y, 得到 012)1(22x x x x k k k +=++++αβαβαβ ,k=1,2,….该方程的特征方程为022=++αβαβλλ与6.4节中 )2(11-++=k k k y y g x 时的特征方程一样, 所以0〈αβ〈2, 即为0p 点的稳定条件。
(2)设 )2(11k k k x x f y +=++ )2(11-++=k k k y y g x , 则有 0),2(0101>-+-=-++ααx x x y y k k k 0),2(0101>-+=--+ββy y y x x k k k 消去y ,得到0123)1(424x x x x x k k k k +=++++++αβαβαβαβ 该方程的特征方程为02423=+++αβαβλαβλλ令λ=x ,αβ=a , 即求解三次方程0a 2ax ax 4x 23=+++ 的根 在matlab 中输入以下代码求解方程的根x :syms x asolve(4*x^3+a*x^2+2*a*x+a==0,x)解得 1x = (36*a^2 — 216*a — a^3 + 24*3^(1/2)*(-a^2*(a — 27))^(1/2))^(1/3)/12 — a/12 + (a*(a — 24))/(12*(36*a^2 — 216*a — a^3 + 24*3^(1/2)*(-a^2*(a — 27))^(1/2))^(1/3));2x = -(2*a*(36*a^2 - 216*a — a^3 + 24*3^(1/2)*(—a^2*(a - 27))^(1/2))^(1/3) — 3^(1/2)*a*24*i — 3^(1/2)*(36*a^2 — 216*a — a^3 + 24*3^(1/2)*(—a^2*(a — 27))^(1/2))^(2/3)*i - 24*a + 3^(1/2)*a^2*i+ (36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a — 27))^(1/2))^(2/3) + a^2)/(24*(36*a^2 — 216*a - a^3 + 24*3^(1/2)*(-a^2*(a — 27))^(1/2))^(1/3));3x =—(2*a*(36*a^2 - 216*a — a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3) + 3^(1/2)*a *24*i + 3^(1/2)*(36*a^2 - 216*a — a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3)*i — 24*a - 3^(1/2)*a^2*i + (36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3) + a^2)/(24*(36*a^2 — 216*a — a^3 + 24*3^(1/2)*(—a^2*(a -27))^(1/2))^(1/3));其中1x 为实根,2x 与3x 为一对共轭虚根。
数学模型课后答案姜启源

数学模型课后答案姜启源【篇一:姜启源《数模》习题选解】方案模型构成:以阈值0,1分别标记“不在”和“在”,记第k次渡河前此岸的人阈值为xk,猫阈值为yk,鸡阈值为zk,米阈值为wk,将四维向量sk=(xk,yk,zk,wk)定义为状态,xk,yk,zk,wk=0,1。
安全渡河条件下的状态集合为允许状态集合,记作s。
以穷举法得到s:s={(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),(0,0,1,0),( 0,1,0,0),(0,0,0,1),(0,0,0,0)} 记第k次渡船上四个对象(人、猫、鸡、米)的阈值分别为ak,bk,ck,dk,并将四维向量ek=(ak,bk,ck,dk)定义为决策。
允许决策集合记作e={(a,b,c,d)|0≤b+c+d≤1,a=1,b,c,d=0,1}因为k为奇数时,船从此岸驶向彼岸,k为偶数时船由彼岸驶向此岸,所以,状态sk随决策ek变化的规律是sk+1=sk+(-1)kek该式称状态转移律,该问题就转换成多步决策模型:求决策∈?? ??=1,2,?,?? ,使状态∈??按照转移律,由初始状态s1=(1,1,1,1)经有限步n到达状态sn+1=(0,0,0,0)。
模型求解:本解答试尝用图解法,由于无法利用平面来表达四维坐标系,所以采取其投影即三维空间的方法来构建模型。
把人的阈值xk抽离出来,分别标记0系坐标系(即当xk=0时,(yk,zk,wk)的空间坐标),和1系坐标系,可允许状态点如下标示(红色点):由于a=1是恒成立的,所以,决策是0系坐标系和1系坐标系的点集间的连接,而非任意坐标系内部的连接。
如图1所示,两正方体中心重合,且对应顶点的连线通过中心,称为二合正方体(四维空间不具有包性,即a/b两正方体并没有包含的关系)。
二合正方体的一个顶点为(a,b),称为共顶点,即二合正方体共有8个共顶点。
(完整版)数学模型(第四版)课后详细答案
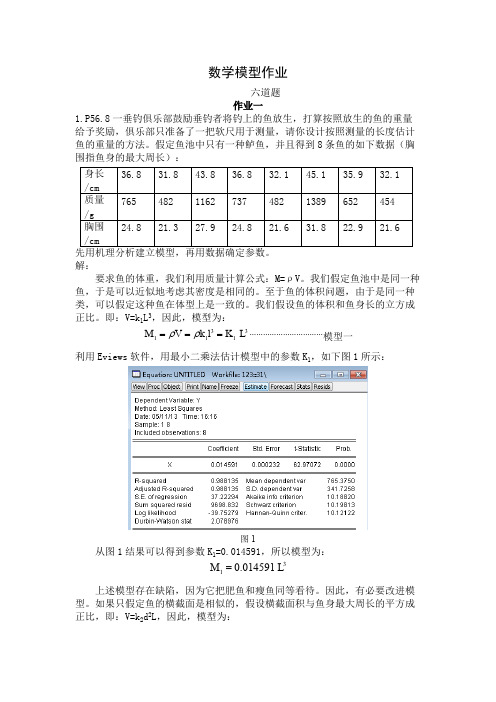
数学模型作业六道题作业一1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数。
解:要求鱼的体重,我们利用质量计算公式:M=ρV。
我们假定鱼池中是同一种鱼,于是可以近似地考虑其密度是相同的。
至于鱼的体积问题,由于是同一种类,可以假定这种鱼在体型上是一致的。
我们假设鱼的体积和鱼身长的立方成正比。
即:V=k 1L 3,因此,模型为:……………………………模型一33111M V k l K L ρρ===利用Eviews 软件,用最小二乘法估计模型中的参数K 1,如下图1所示:图1从图1结果可以得到参数K 1=0.014591,所以模型为:31M 0.014591 L =上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。
因此,有必要改进模型。
如果只假定鱼的横截面是相似的,假设横截面积与鱼身最大周长的平方成正比,即:V=k 2d 2L ,因此,模型为:身长/cm 36.831.843.836.832.145.135.932.1质量/g 76548211627374821389652454胸围/cm24.821.327.924.821.631.822.921.6t h i ng sin………………………………模型二22222M V k d K d L L ρρ===利用Eviews 软件,用最小二乘法估计模型中的参数K 2,如下图2所示:图2从图2可以得到参数K 2=0. 032248,所以模型为:22M 0.032248d L=将实际数据与模型结果比较如表1所示:表1实际数据M 76548211627374821389652454模型一M 1727.165469.2141226.061727.165482.6291338.502675.108482.619模型二M 2729.877465.2481099.465729.877482.9601470.719607.106483.9602.P131.2 一家出版社准备在某市建立两个销售代理点,向7个区的大学生售书,每个区的大学生数量(单位:千人)已经表示在图上。
数学模型第四版课后规范标准答案姜启源版

.
再由初始条件,得
又由
其解为
(1)
即乙方取胜时的剩余兵力数为
又令
注意到 .
(2) 若甲方在战斗开始后有后备部队以不变的速率 增援.则
相轨线为
此相轨线比书图11中的轨线上移了 乙方取胜的条件为
《数学模型》作业解答
第六章(2008年11月20日)
1.在6.1节捕鱼模型中,如果渔场鱼量的自然增长仍服从Logistic规律,而单位时间捕捞量为常数h.
S取最大值.
由 解得
此时 =20 =350(元)
2.某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量以及可获利润如下表:
货物
体积
(立方米/箱)
重量
(百斤/箱)
利润
(百元/箱)
甲
5
2
20
乙
4
5
10
已知这两种货物托运所受限制是体积不超过24立方米,重量不超过13百斤.试问这两种货物各托运多少箱,使得所获利润最大,并求出最大利润.
A
B
C
3 2 2
3 3 3
4 5 5
4 4 3
5 5 5
6 6 7
总计
10 10 10
15 15 15
2.试用微积分方法,建立录像带记数器读数n与转过时间的数学模型.
解:设录像带记数器读数为n时,录像带转过时间为t.其模型的假设见课本.
考虑 到 时间内录像带缠绕在右轮盘上的长度,可得 两边积分,得
《数学模型》作业解答
故应改变订货策略.改变后的订货策略(周期)为T = ,能节约费用约53.33元.
《数学模型》作业解答
第四章(2008年10月28日)
笔记-数学模型(第四版) 姜启源等编

dx kx 当 t 0 得微分方程: dt x(0) x0
解微分方程
dx kdt x 1 x dx kdt ln( x) kt c1 x ce kt , c x0 x x0 e kt
dm dm 由死亡率的定义可得: dr ( r , t ), (r , t )dr m m
解得
( r ,t ) dr m( ) ln(m) | (r , t )dr , e m( )
t 时刻年龄为 的人的存活时间之和为: h( ) 所以时刻 t 年龄为 的人的期望寿命为:
P174 习题 4 1.设 x(t ), y (t ) 分别为 t 时刻甲乙双方的兵力,满足下列微分方程
x ay , (1) y bx, (2) x ( 0) x 0 , y ( 0) y 0 a 4, x 0 y 0 则当乙方取胜时,乙方的剩余兵力是多少?战斗时间 b 是多少? (2) 若甲方在战斗开始后,有后备兵力以不变的速率 r 增援,试重新建立模 型, 讨论如何判断双方的胜负
0
( r , t ) dr
0
d
解:
设 t 时刻年龄为 的人的数目随时间变化的规律为: m m( r ), r 0
dm dm 由死亡率的定义可得: dr ( r , t ), (r , t )dr m m
解得
( r ,t ) dr m( ) ln(m) | (r , t )dr , e 0 0 m(0)
2.试推导 logistic 人口增长模型.即设时刻 t 的人口为 x(t ) ,单位时间内人口的 增量与 x(1
姜启源等编《数学模型》第四版-课件-第九章--概率模型

问题分析
• 进入稳态后为保证生产系统的周期性运转,应假 定工人们的生产周期相同,即每人作完一件产品 后,要么恰有空钩经过他的工作台,使他可将产 品挂上运走,要么没有空钩经过,迫使他放下这 件产品并立即投入下件产品的生产.
• 可以用一个周期内传送带运走的产品数占产品 总数的比例,作为衡量传送带效率的数量指标.
J(u)在u+x=S处达到最小
I(x)
J(u)与I(x)相似
I(S)+c0
I(x)在x=S处达到最小值I(S) I(S)
I(x)图形 I(S)
0s
I(x)c0I(S)的最小正根 s
S
x
9.4 轧钢中的浪费
背 轧制钢材 • 粗轧(热轧) ~ 形成钢材的雏形 景 两道工序 • 精轧(冷轧) ~ 得到钢材规定的长度
如 设每只挂钩为空的概率为q,则 p=1-q 何 求 设每只挂钩不被一工人触到的概率为r,则 q=rn
概 设每只挂钩被一工人触到的概率为u,则 r=1-u 率
一周期内有m个挂钩通过每一工作台的上方
u=1/m
p=1-(1-1/m)n
D=m[1-(1-1/m)n]/n
模型解释
传送带效率(一周期内运走 产品数与生产总数之比)
随机性模型
对象
X(t) ~ 时刻 t 的人口, 随机变量. Pn(t) ~概率P(X(t)=n), n=0,1,2,…
PP (xl) P P (x l)
切掉多余部 分的概率
整根报废 的概率
p(概率密度)
m P,P
P
m P ,P
存在最佳的m使总的浪费最小 0
PP´´ l
P mm
x
建模 选择合适的目标函数
姜启源编《数学建模》第四版 第十二章:马氏链模型

需求不超过存量,需求被售
需求超过存量,存量被售
[ j P ( D j S i ) iP ( D i S i ) ] P ( S i ) n n n n n
i 1 j 1
0 . 632 0 . 285 0 . 896 0 . 263 0 . 977 0 . 452 0.857
状态与状态转移
1 , 第 n 年健康 状态概率 a ( n ) P ( X i ), i n 状态 X n 2 , 第 n 年疾病 i 1 , 2 ,n 0 , 1 ,
转移概率 p P ( X j X i ), i , j 1 , 2 , n 0 , 1 , ij n 1 n
a (n) 1
i 1 i
k j 1
k
转移概率 p P ( X j X i ), p 0 , p 1 ,i 1 , 2 , , k ij n 1 n ij ij
基本方程
a ( n 1 ) a ( n ) p ,i 1 , 2 , , k i j ji
1. 正则链 ~ 从任一状态出发经有限次转移 能以正概率到达另外任一状态 (如例1) .
N 正则链 N , P 0
正则链 w , a ( n ) w ( n )w ~ 稳态概率
w 满足 wP w
0 .8 0 .2 例 1 . P 0 . 7 0 . 3
背景与问题
钢琴销售量很小,商店的库存量不大以免积压资金.
一家商店根据经验估计,平均每周的钢琴需求为1架. 存贮策略:每周末检查库存量,仅当库存量为零时, 才订购3架供下周销售;否则,不订购. • 估计在这种策略下失去销售机会的可能性有多大? 以及每周的平均销售量是多少?
数学模型第四版姜启源

盟军(英)
盟军(美一) 强化
盟军 缺口 (预备队)
原地 待命
德军 撤退 进攻
东进 盟 军 (美三 )
双方应该如何决策 ?
模型假设
? 博弈参与者为两方(盟军和德军)
? 盟军有3种使用其预备队的行动:强化缺口,原地 待命,东进;德军有 2种行动:向西进攻或向东撤退 .
? 博弈双方完全理性 ,目的都是使战斗中己方获得
(p*, q*): 混合(策略)纳什均衡(Mixed NE) 最优值均为 2/5
模型评述
?? 0 M ??1
0 ?? 0?
?占优(dominate) :盟军的行动 2占优于1
??? 1 1?? (前面的非常数和博弈 M' 类似)
?混合策略似乎不太可行 ! 但概率可作为参考. ----现实:盟军让预备队原地待命(行动 2),而德军
O
x
vb=vs 1 vs
单一价格战略效率为
1x
? ? ? ? x 0 (vb ? vs )dvsdvb ? 3x(1 ? x) ? 3 / 4
? ?1 0
vb 0
(vb
?
vs )dvs dvb
x=0.5
效率最大 (3/4)
线性价格战略
卖方报价 ps(vs) = as+csvs; 买方报价 pb(vb) =ab+cbvb.
多个决策主体
博弈模型 合作博弈
决策主体的决策 行为发生直接相 互作用 (相互影响 )
博弈模型 (Game Theory)
非合作博弈
静态、动态 信息完全、不完全
军事、政治、经济、企业管理和社会科学中应用广泛
11.1 进攻与撤退的抉择
背 ? 1944年6月初,盟军在诺曼底登陆成功 . 景 ? 到8月初的形势:
姜启源 第四版《数学模型》PPT 第1章

1.3.3 如何施救药物中毒 场景
两位家长带着孩子急匆匆来到医院急诊室. 诉说两小时前孩子一次误吞下11片治疗哮喘病、剂量 100mg/片的氨茶碱片,已出现呕吐、头晕等不良症状. 按照药品使用说明书,氨茶碱的每次用量成人是 100~200mg ,儿童是3~5 mg/kg.
过量服用可使血药浓度(单位血液容积中的药量)过高, 100μg/ml浓度会出现严重中毒, 200μg/ml浓度可致命.
数学模型第四版
第一章
建立数学模型
1.1 从现实对象到数学模型
1.2 数学建模的重要意义
1.3 数学建模示例 1.4 数学建模的基本方法和步骤 1.5 数学模型的特点和分类 1.6 数学建模能力的培养
1.1
从现实对象到数学模型
我们常见的模型
玩具、照片、飞机、火箭模型… ~ 实物模型
水箱中的舰艇、风洞中的飞机… ~ 物理模型 地图、电路图、分子结构图… ~ 符号模型
dy x y y 1100et dt y (0) 0
药物排除的半衰期为6 h
dy y dt
只考虑血液对药物的排除
y(t ) ae
( t )
y( ) a, y( 6) a / 2
(ln 2) / 6 0.1155(1/ h)
用数学语言把椅子位置和四只脚着地的关系表示出来 . 椅子位置 利用正方形(椅脚连线)的对称性. • 用(对角线与x轴的夹角)表示椅子位置 . • 四只脚着地 椅脚与地面距离为零 距离是的函数. 四个距离( 四只脚)
C
B´ B A´
O
A
x
D
D´
正方形 对称性
两个距离
C´
A,C 两脚与地面距离之和 ~ f()
数学模型(第四版)课后详细答案

数学模型作业六道题 作业一1. P56.8 —垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量 给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计 鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数 解:要求鱼的体重,我们利用质量计算公式: M=p V 。
我们假定鱼池中是同一种 鱼,于是可以近似地考虑其密度是相同的。
至于鱼的体积问题,由于是同一种 类,可以假定这种鱼在体型上是一致的。
我们假设鱼的体积和鱼身长的立方成 正比。
即:V=k i L 3,因此,模型为:利用Eviews 软件,用最小二乘法估计模型中的参数 K i ,如下图1所示:□ Equition: UNKTLED Workfile; 123::31\*1 諭][Pror][口bject] [Print][Mame|[Frea«]旦tinatdForecast]甌:Dependent Variable: Y Method: I east SquaresDate-05/11/13 Trne;16;16Samplv; 1 8Included ob5e[v<itcins;8Coefficient Std Errort-StatisticProb.X0.014591 0.0C0232 62.9T 072 O.QOOOR-squanedAd listed R-squared S-E. of rearession Sum squared residLog IlkfilihODd DurtJin-Wats^n stat0.988135 0.988135 37r 22294 9698.B32 -39.75279 2.076976Mean dependert var S.D. dependentvar Akaike info criteionSchwarz criterion Hannan-Quinn triter765.3750 341.7258 10.18820 101S313 10.12122图1从图1结果可以得到参数K=0.014591,所以模型为:上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。
2021-11第4版姜启源数学模型复习总结(1)

2021-11第4版姜启源数学模型复习总结(1) 第四版姜启源数学模型复习总结第1章:了解模型的概念与分类,熟练掌握数学模型的定义,数学模型的重要应用,建模的重要例子-指数模型,Logist模型。
建模的一般方法及其在建模中的应用。
建模的一般步骤(每步的主要内容与问题)。
建模的全过程(框图)4个环节的含义。
模型的特点(技艺性)。
模型分类(表现特征),建模中的能力培养。
数学建模实例的建模思想及其步骤§1 数学模型的概念:模型:模型是为了一定目的,对客观事物的一部分信息进行简缩、抽象、提炼出来的原型的替代物。
模型的分类:具体模型(或物质模型,实的),包括直观模型,物理模型。
抽象模型(或理想模型,虚的),包括思维模型,符号模型,数学模型。
数学模型:对于一个现实对象,为了一个特定目的,根据其内在规律,作出必要的简化假设,运用适当的数学工具,得到的一个数学结构。
1-1-1 模型是为了特定的目的,将原型的()而得到的原型替代物。
1-1-2数学模型可以描述为:对于一个现实对象,()。
1-1-3 关于数学模型的如下论述中正确的是() A。
数学模型是以现实世界的特定问题为研究对象。
B。
数学模型只是对实际问题的近似表示,其中包含一些简化假设。
C。
数学模型表示是某一特定问题的内在规律的数学表示,是以方程和函数关系表示的数学结构。
D。
数学模型是现实问题的真实的描述,不能做任何假设和简化。
1-1-4 关于数学建模的如下论述中正确的是() A。
数学模型和数学建模是完全相同的概念。
B。
数学建模是一个全过程,包括表述、求解、解释和验证四个环节。
C。
数学建模全过程涉及两个世界是现实世界和虚拟世界,涉及的“双向翻译”是同声翻译和文献翻译。
D.数学建模过程是一个从理论-实践-再理论-再实践不断改进的过程。
§2 建模的重要意义(1)数学以空前的广度和深度向一切领域渗透在一般工程技术领域数学建模仍然大有用武之地;在高新技术领域数学建模几乎是必不可少的工具了; 数学进入一些新领域,为数学建模开辟了许多处女地. 数学建模的具体应用:分析与设计,预测与决策,优化与控制,规划与管理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2 3 4 5
A
B
C
235117.578.3 58.75 …
333166.511183.25 …
43221614410886.4
将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A、B、C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位.你能解释这种方法的道理吗?
但 及 均有 ,即 不稳定;
③当 时,得到两个平衡点:
,
易知 , ,
平衡点 不稳定,平衡点 稳定.
2 .最大持续产量的数学模型为:
即 ,易得 此时 ,但 这个平衡点不稳定.
要获得最大持续产量,应使渔场鱼量 ,且尽量接近 ,但不能等于 .
《数学模型》第七章作业
(2008年12月4日)
1.对于7.1节蛛网模型讨论下列问题:
S取最大值.
由 解得
此时 =20 =350(元)
2.某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量以及可获利润如下表:
货物
体积
(立方米/箱)
重量
(百斤/箱)
利润
(百元/箱)
甲
5
2
20
乙
4
5
10
已知这两种货物托运所受限制是体积不超过24立方米,重量不超过13百斤.试问这两种货物各托运多少箱,使得所获利润最大,并求出最大利润.
第三章1(2008年10月14日)
1.在3.1节存贮模型的总费用中增加购买货物本身的费用,重新确定最优订货周期和订货批量.证明在不允许缺货模型中结果与原来的一样,而在允许缺货模型中最优订货周期和订货批量都比原来结果减少.
解:设购买单位重量货物的费用为 ,其它假设及符号约定同课本.
对于不允许缺货模型,每天平均费用为:
解:设安排生产甲型微波炉 件,乙型微波炉 件,相应的利润为S.
则此问题的数学模型为:
max S=3x +2y
s.t.
这是一个整线性规划问题
用图解法进行求解
可行域为:由直线 :2x+3y=100, :4x+2y=120
及x=6,y=12组成的凸四边形区域.
直线 :3x+2y=c在此凸四边形区域内平行移动.易知:当 过 与 的交点时, S取最大值.
(2)恒速静脉滴注(持续时间为 ): 设滴注速率为 解得
(3) 口服或肌肉注射:
3种情况下的血药浓度曲线如下:
第五章3(2008年11月18日)
8.在5.5节香烟过滤嘴模型中,
(1) 设
求
(2) 若有一支不带过滤嘴的香烟,参数同上,比较全部吸完和只吸到 处的情况下,进入人体毒物量的区别.
解
,
(2) 对于一支不带过滤嘴的香烟,全部吸完的毒物量为
(2) 若甲方在战斗开始后有后备部队以不变的速率 增援,重新建立模型,讨论如何判断双方的胜负规战争模型可近似表示为:
现求(1)的解: (1)的系数矩阵为
.
再由初始条件,得
又由
其解为
(1)
即乙方取胜时的剩余兵力数为
又令
注意到 .
(2) 若甲方在战斗开始后有后备部队以不变的速率 增援.则
解:由题意可得贮存量 的图形如下:
贮存费为
又
, 贮存费变为
于是不允许缺货的情况下,生产销售的总费用(单位时间内)为
.
, 得
易得函数 取得最小值,即最优周期为:
. 相当于不考虑生产的情况.
. 此时产量与销量相抵消,无法形成贮存量.
第三章2(2008年10月16日)
3.在3.3节森林救火模型中,如果考虑消防队员的灭火速度 与开始救火时的火势 有关,试假设一个合理的函数关系,重新求解模型.
令 , 解得
由 , 得
与不考虑购货费的结果比较,T、Q的最优结果没有变.
对于允许缺货模型,每天平均费用为:
令 , 得到驻点:
与不考虑购货费的结果比较,T、Q的最优结果减少.
2.建立不允许缺货的生产销售存贮模型.设生产速率为常数 ,销售速率为常数 , .在每个生产周期T内,开始的一段时间 一边生产一边销售,后来的一段时间 只销售不生产,画出贮存量 的图形.设每次生产准备费为 ,单位时间每件产品贮存费为 ,以总费用最小为目标确定最优生产周期,讨论 和 的情况.
解:按分段价格,单位时间内的销售量为
又 .于是总利润为
=
=
, 得到最优价格为:
在销售期T内的总销量为
于是得到如下极值问题:
利用拉格朗日乘数法,解得:
即为 的最优值.
第三章3(2008年10月21日)
6.某厂每天需要角钢100吨,不允许缺货.目前每30天定购一次,每次定购的费用为2500元.每天每吨角钢的贮存费为0.18元.假设当贮存量降到零时订货立即到达.问是否应改变订货策略?改变后能节约多少费用?
只吸到 处就扔掉的情况下的毒物量为
4.在5.3节正规战争模型(3)中,设乙方与甲方战斗有效系数之比为
初始兵力 相同.
(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定.
(2) 若甲方在战斗开始后有后备部队以不变的速率 增援,重新建立模型,讨论如何判断双方的胜负.
解:用 表示甲、乙交战双方时刻t的士兵人数,则正规战争模型可近似表示为:
解:已知:每天角钢的需要量r=100(吨);每次订货费 =2500(元);
每天每吨角钢的贮存费 =0.18(元).又现在的订货周期T =30(天)
根据不允许缺货的贮存模型:
得:
令 ,解得:
由实际意义知:当 (即订货周期为 )时,总费用将最小.
又 =300+100k
=353.33+100k
- =(353.33+100k)-(300+100k) =53.33.
此方法的分配结果为:
此方法的道理是:记 和 为各宿舍的人数和席位(i=1,2,3代表A、B、C宿舍). 是每席位代表的人数,取 从而得到的 中选较大者,可使对所有的 尽量接近.
再考虑 的分配方案,类似地可得名额分配结果.现将3种方法两次分配的结果列表如下:
宿舍
(1) (2) (3)
(1) (2) (3)
(1)分别就 , , 这3种情况讨论渔场鱼量方程的平衡点及其稳定状况.
(2)如何获得最大持续产量,其结果与6.1节的产量模型有何不同.
解:设时刻t的渔场中鱼的数量为 ,则由题设条件知: 变化规律的数学模型为
记
(1).讨论渔场鱼量的平衡点及其稳定性:
由 ,得 .
即
,
(1)的解为:
①当 , ,(1)无实根,此时无平衡点;
解:设甲货物、乙货物的托运箱数分别为 , ,所获利润为 则问题的数学模型可表示为
这是一个整线性规划问题.
用图解法求解.
可行域为:由直线
及 组成 直线 在此凸四边形区域内平行移动.
易知:当 过 与 的交点时, 取最大值
由 解得
.
3.某微波炉生产企业计划在下季度生产甲、乙两种型号的微波炉.已知每台甲型、乙型微波炉的销售利润分别为3和2个单位.而生产一台甲型、乙型微波炉所耗原料分别为2和3个单位,所需工时分别为4和2个单位.若允许使用原料为100个单位,工时为120个单位,且甲型、乙型微波炉产量分别不低于6台和12台.试建立一个数学模型,确定生产甲型、乙型微波炉的台数,使获利润最大.并求出最大利润.
记
① 令 ,得 , .
平衡点为 . 又 , .
平衡点 是稳定的,而平衡点 不稳定.
②最大持续产量的数学模型为:
由前面的结果可得
,令
得最大产量的捕捞强度 .从而得到最大持续产量 ,此时渔场鱼量水平 .
3.设某渔场鱼量 (时刻 渔场中鱼的数量)的自然增长规律为:
其中 为固有增长率, 为环境容许的最大鱼量.而单位时间捕捞量为常数 .
②当 , ,(1)有两个相等的实根,平衡点为 .
, 不能断定其稳定性.
但 及 均有 ,即 . 不稳定;
③当 , 时,得到两个平衡点:
,
易知: , , ,
平衡点 不稳定,平衡点 稳定
(2)最大持续产量的数学模型为
即 ,
易得 此时 ,
但 这个平衡点不稳定.这是与6.1节的产量模型不同之处.
要获得最大持续产量,应使渔场鱼量 ,且尽量接近 ,但不能等于 .
(1)因为一个时段上市的商品不能立即售完,其数量也会影响到下一时段的价格,所以第 时段的价格 由第 和第 时段的数量 和 决定,如果仍设 仍只取决于 ,给出稳定平衡的条件,并与7.1节的结果进行比较.
2.与Logistic模型不同的另一种描述种群增长规律的是Gompertz模型: .其中r和N的意义与Logistic模型相同.
设渔场鱼量的自然增长服从这个模型,且单位时间捕捞量为 .讨论渔场鱼量的平衡点及其稳定性,求最大持续产量 及获得最大产量的捕捞强度 和渔场鱼量水平 .
解: 变化规律的数学模型为
故应改变订货策略.改变后的订货策略(周期)为T = ,能节约费用约53.33元.
《数学模型》作业解答
第四章(2008年10月28日)
1.某厂生产甲、乙两种产品,一件甲产品用 原料1千克, 原料5千克;一件乙产品用 原料2千克, 原料4千克.现有 原料20千克, 原料70千克.甲、乙产品每件售价分别为20元和30元.问如何安排生产使收入最大?
《数学模型》作业答案
第二章(1)(2012年12月21日)
1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍.学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:
(1). 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者;
