九年级中考复习-圆专题
2023年九年级数学中考复习 圆综合压轴题 解答题专题训练(含解析)

2022-2023学年九年级数学中考复习《圆综合压轴题》解答题专题训练(附答案)1.如图.在Rt△ABC中,∠ACB=90°,D为AB边的中点,连接CD.以CD为直径作⊙O,分别与AC,BC相交于点M,N.过点N作⊙O的切线交AB于点E.(1)求证:∠BEN=90°.(2)若AB=10,请填空:①迮接OE,ON,当NE=时,四边形OEBN是平行四边形;②连接DM,DN,当AC=时,四边形CMDN为正方形.2.如图,以AB为直径的半圆中,点O为圆心,点C在圆上,过点C作CD∥AB,且CD =OB.连接AD,分别交OC,BC于点E,F,与⊙O交于点G,若∠ABC=45°.(1)求证:①△ABF∽△DCF;②CD是⊙O的切线.(2)求的值.3.如图,△ABC内接于⊙O,AB为直径,点D为半径OA上一点,过点D作AB的垂线交AC于点E,交BC的延长线于点P,点F在线段PE上,且PF=CF.(1)求证:CF是⊙O的切线;(2)连接AP与⊙O相交于点G,若∠ABC=2∠P AC,求证:AB=BP;(3)在(2)的条件下,若AC=4,BC=3,求CF的长.4.如图,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.(1)判断直线AF与⊙O的位置关系并说明理由;(2)若⊙O的半径为6,AF=2,求AC的长;(3)在(2)的条件下,求阴影部分的面积.5.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F,连接AD.(1)求证:EF是⊙O的切线.(2)求证:△FBD∽△FDA.(3)若DF=4,BF=2,求⊙O的半径长.6.如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG.(1)判断CG与⊙O的位置关系,并说明理由;(2)求证:2OB2=BC•BF;(3)如图2,当∠DCE=2∠F,DG=2.5时,求DE的长.7.已知:△ABC内接于⊙O,连接AO并延长交BC于点D,且AD⊥BC于点D.(1)如图1,求证:∠B=∠C;(2)如图2,点E在上,连接AE,CE,∠ACE=∠ACB,求证:∠CAE=2∠ACE;(3)如图3,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.8.在Rt△ABC中,∠ACB=90°,AC=6,∠B=30°,点M是AB上的动点,以M为圆心,MB为半径作圆交BC于点D,(1)若圆M与AC相切,如图1,求圆的半径;(2)若AM=2MB,连接AD,如图2.①求证:AD与圆M相切;②求阴影部分的面积.9.如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于D,DE交BC于F,且EF=EC.(1)求证:EC是⊙O的切线;(2)求证:△OAC∽△ECF;(3)若BD=4,BC=8,圆的半径OB=5,求EC的长.10.如图,已知以BC为斜边的Rt△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,过点D作DE∥BC交AB的延长线于点E,连接DB,DC.(1)求证:ED为⊙O的切线;(2)求证:BC2=2ED•FC;(3)若tan∠ABC=2,AD=,求BC的长.11.已知△ABC内接于⊙O,D是弧AC上一点,连接BD、AD,BD交AC于点M,∠BMC =∠BAD.(1)如图1,求证:BD平分∠ABC;(2)如图2,过点D作⊙O的切线,交BA的延长线于点F,求证:DF∥AC;(3)如图3,在(2)的条件下,BC是⊙O的直径,连接DC,AM=1,DC=,求四边形BFDC的面积.12.如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,P为弧AD上一点.(1)如图1,连接AC、PC、P A,求证:∠APC=∠ACD;(2)如图2,连接PB,PB交CD于E,过点P作⊙O的切线交CD的延长线于点F,求证:FE=PF;(3)如图3,在(2)的条件下,连接AE,且∠P AE=∠F,过点A作AG⊥PF,垂足为G,若PG=6,,求BH的长.13.如图,⊙O的半径为1,点A是⊙O的直径BD延长线上的一点,C为⊙O上的一点,AD=CD,∠A=30°.(1)求证:直线AC是⊙O的切线;(2)求△ABC的面积;(3)点E在上运动(不与B、D重合),过点C作CE的垂线,与EB的延长线交于点F.①当点E运动到与点C关于直径BD对称时,求CF的长;②当点E运动到什么位置时,CF取到最大值,并求出此时CF的长.14.如图所示,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,作AF ⊥PC于点F,连接CB.(1)求证:AC平分∠F AB.(2)求证:BC2=CE•CP.(3)当AB=4时,求劣弧BC长度(结果保留π).15.已知:如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,连接CE,BD是⊙O的切线与OE的延长线相交于点D.(1)求证:∠D=∠AEC;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,,求FH的长.16.如图,在平面直角坐标系xOy中,已知点A(0,8),点B是x轴正半轴上一点,连接AB,过点A作AC⊥AB,交x轴于点C,点D是点C关于点A的对称点,连接BD,以AD为直径作⊙Q交BD于点E,连接并延长AE交x轴于点F,连接DF.(1)求线段AE的长;(2)若∠ABE=∠FDE,求EF的值.(3)若AB﹣BO=4,求tan∠AFC的值.17.如图,在Rt△ABC中,∠B=90°,AE平分∠BAC,交BC于点E,点D在AC上,以AD为直径的⊙O经过点E,点F在⊙O上,且EF平分∠AED,交AC于点G,连接DF.(1)求证:△DEF∽GDF;(2)求证:BC是⊙O的切线;(3)若cos∠CAE=,DF=10,求线段GF的长.18.如图,⊙O是△ABC的外接圆,AC是⊙O的直径,过圆心O的直线PF⊥AB于D,交⊙O于E,F,PB是⊙O的切线,B为切点,连接AP,AF.(1)求证:直线P A为⊙O的切线;(2)求证:AC2=4OD•OP;(3)若BC=6,,求AC的长.19.如图,AB是半圆O的直径,AB=10.C是弧AB上一点,连接AC,BC,∠ACB的平分线交AB于点P,过点P分别作PE⊥AC,PF⊥BC,垂足分别为E、F.(1)求证:四边形CEPF是正方形;(2)当sin A=时,求CP的长;(3)设AP的长为x,图中阴影部分的面积为y,求y与x之间的函数关系式,并写出y 的最大值.20.问题提出(1)如图①,△ABC为等边三角形,若AB=2,则△ABC的面积为.问题探究(2)如图②,在Rt△ABC中,∠ABC=90°,AC=3,BD是△ABC的角平分线,过点D作DE⊥BD交BC边于点E.若AD=1,求图中阴影部分的面积.问题解决(3)如图③,是某公园的一个圆形施工区示意图,其中⊙O的半径是4米,公园开发部门计划在该施工区内设计一个四边形绿化区域ABCD,连接AC、BD,现准备在△ADC 区域种植花卉供游人欣赏.按设计要求,A、B、C、D四个点都在圆上,∠ADB=∠BDC =60°.设BD的长为x米,△ADC的面积为y平方米.①求y与x之间的函数关系式;②按照设计要求,为让游人有更好的观赏体验,△ADC花卉区域的面积越大越好,那么请求出花卉区域△ADC面积的最大值.参考答案1.(1)证明:如图,连接ON,DN,∵CD是⊙O的直径,∴∠CND=∠DNB=90°,∵NE是⊙O的切线,∴∠ONE=90°,∴∠BNE=∠OND,∵ON=OD,∴∠ODN=∠OND,∴∠ODN=∠BNE,∵D是斜边AB的中点,∴CD=AD=BD,∴∠B=∠BCD,∵∠BCD+∠ODN=90°,∴∠B+∠BNE=90°,∴∠NEB=90°;(2)解:①∵四边形OEBN是平行四边形,∴BE=ON=,∵E为BD的中点,∴N为BC的中点,∴NE为△BCD的中位线,∴NE∥CD,且NE=CD=.故答案为:;②∵四边形CMDN为正方形,∴∠MCD=∠MDC=45°,∠CMD=90°,∴MC=MD=CD,∵AD=DC,∴M是AC的中点,AC=2MC=CD,∴CD=AB=5,∴AC=5.故答案为:5.2.(1)证明:①∵CD∥AB,∴∠F AB=∠D,∵∠AFB=∠DFC,∴△ABF∽△DCF;②∵∠ABC=45°,∴∠AOC=2∠ABC=90°,∵CD∥AB,∴∠DCO=∠AOC=90°,∵OC是半圆的半径,∴CD是⊙O的切线;(2)解:过点F作FH∥AB交OC于H,设圆的半径为2a,∵CD=OB=OA,CD∥AB,∴CE=OE=a,AE=DE,由勾股定理得:AE==a,∴AD=2a,∵△ABF∽△DCF,∴==,∵FH∥AB,∴==,∵FH∥AB,∴==,∴EF=,∵CD是⊙O的切线,∴DC2=DG•DA,即(2a)2=DG•2a,解得:DG=,∴FG=a﹣﹣=,∴==.3.(1)证明:连接OC,∵PF=FC,OC=OB,∴∠PCF=∠CPF,∠OCB=∠OBC,∵PD⊥AB,∴∠PDB=90°,∴∠CPF+∠OBC=90°,∴∠PCF+∠OCB=90°,∴∠FCO=90°,∴OC⊥CF,∴CF是⊙O的切线.(2)证明:连接BG,∵,∴∠P AC=∠PBG,∵∠PBA=2∠P AC,∴∠PBA=2∠PBG,∵AB为⊙O的直径,∴∠AGB=∠PGB=90°,∴∠APB=∠P AB,∴AB=BP;(3)解:∵AB为⊙O的直径,∴∠ACB=90°,∵AC=4,BC=3,∴AB===5,∴AB=BP=5,∴PC=2,∵∠PDA=∠PCA=90°,P A=P A,∠APB=∠P AB,∴△APC≌△APD(AAS),∴AD=PC=2,PD=AC=4,∠P AC=∠APD,∴AE=PE,设DE=x,AE=PE=4﹣x,在Rt△AED中,AD2+DE2=AE2,即22+x2=(4﹣x)2,解得x=,∴EP=4﹣x=,∵∠PEC=90°﹣∠EPC,∠FCE=90°﹣∠PCF,即∠PEC=∠FCE,∴EF=CF=PF,∴CF=.4.解:(1)直线AF与⊙O相切.理由如下:连接OC,∵PC为圆O切线,∴CP⊥OC,∴∠OCP=90°,∵OF∥BC,∴∠AOF=∠B,∠COF=∠OCB,∵OC=OB,∴∠OCB=∠B,∴∠AOF=∠COF,∵在△AOF和△COF中,,∴△AOF≌△COF(SAS),∴∠OAF=∠OCF=90°,∴AF⊥OA,又∵OA为圆O的半径,∴AF为圆O的切线;(2)∵∠AOF=∠COF,OA=OC,∴E为AC中点,即AE=CE=AC,OE⊥AC,∵∠OAF=90°,OA=6,AF=2,∴tan∠AOF=,∴∠AOF=30°,∴AE=OA=3,∴AC=2AE=6;(3)∵AC=OA=6,OC=OA,∴△AOC是等边三角形,∴∠AOC=60°,OC=6,∵∠OCP=90°,∴CP=OC=6,∴S△OCP=OC•CP==18,S扇形AOC==6π,∴阴影部分的面积为S△OCP﹣S扇形AOC=18﹣6π.5.(1)证明:连接OD,如图所示:∵AB为⊙O的直径,∴∠ADB=90°.∴AD⊥BC.∵AB=AC,∴CD=BD=BC.∵OA=OB,∴OD是△ABC的中位线,∴OD∥AC.∵EF⊥AC,∴EF⊥OD.∵OD是半径,∴EF与⊙O相切.(2)证明:∵AB为直径,∴∠ADB=90°,∴∠BAD+∠ABD=90°,∵OD⊥DE,∴∠FDB+∠ODB=90°,∵OB=OD,∴∠OBD=∠ODB,∴∠BAD=∠FDB,∵∠F=∠F,∴△FBD∽△FDA;(3)解:设⊙O的半径为r,则AB=2r,∵△FBD∽△FDA,∴,∵DF=4,BF=2,∴,∴r=3.6.解:(1)CG与⊙O相切,理由如下:如图1,连接CO,∵AB是⊙O的直径,∴∠ACB=∠ACF=90°,∵点G是EF的中点,∴GF=GE=GC,∴∠AEO=∠GEC=∠GCE,∵OA=OC,∴∠OCA=∠OAC,∵OF⊥AB,∴∠OAC+∠AEO=90°,∴∠OCA+∠GCE=90°,即OC⊥GC,∵OC是圆的半径,∴CG与⊙O相切;(2)证明:∵∠AOE=∠FCE=90°,∠AEO=∠FEC,∴∠OAE=∠F,又∵∠B=∠B,∴△ABC∽△FBO,∴,即BO•AB=BC•BF,∵AB=2BO,∴2OB2=BC•BF;(3)由(1)知GC=GE=GF,∴∠F=∠GCF,∴∠EGC=2∠F,又∵∠DCE=2∠F,∴∠EGC=∠DCE,∵∠DCE=∠AOD=45°,∴∠EGC=45°,又∵∠OCG=90°,∴△OCG为等腰直角三角形,∴GC=OC,OG=OC,∴OD+DG=OC,即OC+2.5=OC,解得OC=,∵GF=GE=GC=OC,∴DE=GE﹣DG=OC﹣DG=.7.(1)证明:∵AD⊥BC,AD过圆心O,∴BD=CD,且AD⊥BC,∴AB=AC,∴∠B=∠C;(2)证明:连接BE,设∠ACE=α,则∠ACB=3α,∴∠ABC=∠ACB=3α,∵∠ABE=∠ACE=α,∴∠CBE=∠ABC﹣∠ABE=3α﹣α=2α,∴∠CAE=∠CBE=2α=2∠ACE;(3)解:过点E作EG⊥AC于点G,在CG上截取GH=AG,连接EH,∴EH=AE=5,∴∠AHE=∠EAH=2α,∴∠CEH=∠AHE﹣∠ECH=2α﹣α=α=∠ECH,∴CH=EH=5,∵AC=AB=13,∴AH=AC﹣CH=13﹣5=8,∴AG=GH=4,∴CG=4+5=9,在Rt△AEG中,EG===3,在Rt△CEG中,CE===3,∵,∴,∴.8.解:(1)过点M作MN⊥AC于点N,∵圆M与AC相切,∴MN=MB,∵∠ACB=90°,AC=6,∠B=30°,∴AB=12,设MN=MB=R.∴AM=12﹣R,∵∠ACB=90°,MN⊥AC,∴MN∥BC,∴∠B=∠AMB=30°,∴,∴,解得R=24﹣36.(2)①连接DM,由题意可知MB=MD,∴∠B=∠MDB=30°,∴∠AMD=60°,∵AM=2MB,∴AM=2MD,∵∠ACB=90°,∠B=30°,∴AB=2AC,∠BAC=60°,∴△AMD∽△ABC,∴∠ADM=∠ACB=90°,∴AD与圆M相切;②∵AB=12,AM=2MB,∴BM=4,AM=8,∵∠ADM=90°,∴AD==4,∴S阴影部分=4.9.(1)证明:∵OC=OB,∴∠OBC=∠OCB,∵DE⊥AB,∴∠OBC+∠DFB=90°,∵EF=EC,∴∠ECF=∠EFC=∠DFB,∴∠OCB+∠ECF=90°,∴OC⊥CE,∴EC是⊙O的切线;(2)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠ABC+∠A=90°,∠ABC+∠BFD=90°,∴∠BFD=∠A,∴∠A=∠BFD=∠ECF=∠EFC,∵OA=OC,∴∠OCA=∠A=∠BFD=∠ECF=∠EFC,∴△OAC∽△ECF;(3)解:∵AB是⊙O的直径,∴∠ACB=90°,∵OB=5,∴AB=10,∴AC===6,∵cos∠ABC=,∴,∴BF=5,∴CF=BC﹣BF=3,∵△OAC∽△ECF,∴,∴EC==.10.(1)证明:如图1,连接OD.∵BC为⊙O的直径,∴∠BAC=90°.∵AD平分∠BAC,∴.∴OD⊥BC,∵DE∥BC,∴OD⊥ED,又∵OD为半径,∴ED为⊙O的切线;(2)证明:由(1)可得△BCD为等腰直角三角形.∵DE∥BC,∴∠E=∠ABC=∠ADC,∠BDE=∠DBC=∠DCB=45°.∴△BED∽△FDC,∴,即BD2=DE•FC,又,∴BC2=2ED•FC;(3)解:如图2,过点D作DG⊥AD,交AC的延长线于点G.∴∠CDG+∠ADC=90°,∠DGC=∠DAG=45°.又∵∠ADB+∠ADC=90°,∴∠ADB=∠GDC,∵DB=DC,∠BAD=∠DGC=45°,∴△ABD≌△GCD(AAS),∴AB=CG.∵∠DAG=45°,∠ADG=90°,∴△ADG为等腰直角三角形,∴AB+AC=AG=AD==3,∵tan∠ABC=2,∴设AB=x,则AC=2x.∴3x=3,∴x=1.即AB=1,AC=2.∴BC===.11.(1)证明:∵∠BMC=∠BAD,又∵∠BMC=∠BAC+∠ABD,∠BAD=∠BAC+∠DAM,∴∠ABD=∠DAC,又∵弧DC=弧DC,∴∠DAC=∠DBC,∴∠ABD=∠CBD,∴BD平分∠ABC;(2)证明:连接OA、OB、OD,OD交AC于点N,∵FD是⊙O的切线,D为切点,OD是⊙O的半径,∴OD⊥FD,∴∠FDO=90°,又∵∠AOD=2∠ABD,∠DOC=2∠DBC,∠ABD=∠CBD,∴∠AOD=∠COD,又∵AO=CO,∴ON⊥AC,∴∠ANO=90°,∴∠ANO=∠FDO,∴AC∥FD;(3)解:连接OD,交AC于N,∵BC是⊙O的直径,∴∠BAC=∠BDC=90°,∴∠F AC=180°﹣∠BAC=90°,又∵∠ANO=∠FDN=90°,∴四边形ANDF是矩形,∴AF=DN,∠F=90°,又∵ON⊥AC,∴AN=CN,∴设MN=a,则AN=CN=MN+AM=a+1,∴CM=MN+CN=2a+1,在Rt△MDC中,cos∠ACD=,在Rt△NDC中,cos∠ACD=,∴,解得a1=﹣(舍去),a2=1,∴MN=1,CN=a+1=2,∴DN=AF==,又∵MN=AM=1,∠AMB=∠NMD,∠BAM=∠MND=90°,∴△BAM≌△DNM(AAS),∴BA=ND=,∴BF=AB+AF=2,∴AN=FD=a+1=2,∴BD==2,∴S△BFD=,S△DBC=BD•CD==3,∴S四边形BFDC=S△BFD+S△BDC=2.12.(1)证明:连接AD,∵AB是⊙O的直径,弦CD⊥AB,∴,∴∠ACD=∠DC,∵,∴∠APC=∠ADC,∴∠APC=∠ACD;(2)证明:连接OP,∵PF是⊙O的切线,∴OP⊥PF,即∠EPF+∠OPE=90°,∵OP=OB,∴∠OPB=∠OBP,∵CD⊥AB,∴∠HEB+∠HBE=90°,∵∠PEF=∠HEB,∴∠PEF=∠FPE,∴FE=PF;(3)解:过E作EM⊥PF,垂足为M,∵AG⊥PF,∴∠GAP+∠GP A=90°,∵∠APE=90°,∴∠GP A+∠EPM=90°,∵∠AGP=∠EMP=90°,∴△GP A∽△MEP,∴,∵∠P AE=∠F,∴tan∠P AE=tan∠F,则,∵,∴,∴MF=PG=6,设PM=x,∵PE2﹣PM2=EF2﹣FM2,∴,解得:x1=﹣10,x2=4,即PM=4,∴EM==8,∵,即,∴P A=3,∵CD⊥AB,AB是直径,∴∠BHE=∠APB=90°,∴∠HEB=∠BAP,∵∠MPE=∠HEB,∴tan∠P AB=,即,∴PB=6,∴BE=PB﹣PE=2,∵sin∠HEB=,即,∴BH=4.13.(1)证明:连接OC,如图1,∵AD=CD,∠A=30°,∴∠ACD=30°,∴∠CDB=60°,∵OD=OC,∴∠OCD=60°,∴∠ACO=∠ACD+∠OCD=90°,∵OC是半径,∴直线AC是⊙O的切线;(2)解:∵∠OCD=60°,OC=OD,∴△DCO是等边三角形,∴CD=AD=OD=1,作CH⊥BD于点H,则DH=,如图2,∴CH===,∵AB=AD+BD=3,∴S△ABC==.(3)①当点E运动到与点C关于直径AB对称时,CE⊥AB于点K,如图3,∵BD为⊙O的直径,CK=,∴CE=2CK=,∵CF⊥CE,∴∠ECF=90°,∵∠CDB=∠CEB=60°,∴CF=CE•tan60°==3,②∵点E在上运动过程中,∠CDB=∠CEB=60°,在Rt△ECF中,tan60°=,∴CF=CE,∴当CE最大时,CF取得最大值,∴当CE为直径,即CE=2时,CF最大,最大值为2.14.(1)证明:连接AC,BC,∵OC=OA,∴∠OCA=∠OAC,∵PF是⊙O的切线,CE⊥AB,∴∠OCP=∠F=90°,∴AF∥OC,∴∠F AC=∠OCA,∴∠F AC=∠OAC,∴CA平分∠F AB.(2)证明:∵CD是直径,∴∠CBD=90°,∴∠CBP=90°,∵CE⊥OB,∴∠CEB=∠CBP=90°,∵PC切⊙O于点C,∴∠PCB=∠CAB,∵AB是直径,∴∠ACB=90°,∴∠ABC+∠CAB=90°,∠BCE+∠ABC=90°,∵∠CAB=∠BCE,∴∠PCB=∠BCE,∴△BCE∽△PCB,∴,∴BC2=CE•CP;(3)解:,设CF=3a,CP=4a,∵BC2=CE•CP=3a•4a=12a2,∴BC=2a,在Rt△BCE中,sin∠CBE=,∴∠CBE=60°,∴∠BCE=30°,∴△COB是等边三角形,∵AB=4,∴OB=BC=2,∴劣弧BC的长==π.15.(1)证明:∵BD是⊙O的切线,∴∠OBD=90°,∠ABC+∠DBC=90°,∵BC⊥OD,∴∠D+∠DBC=90°,∴∠ABC=∠D,∵∠AEC=∠ABC,∴∠D=∠AEC;(2)证明:连接AC,如图所示:∵OF⊥BC,∴,∴∠CAE=∠ECB,∵∠CEA=∠HEC,∴△CEH∽△AEC,∴,∴CE2=EH•EA;(3)解:连接BE,过O作OG⊥BE于G,如图所示:∵AB是⊙O的直径,∴∠AEB=90°,∵⊙O的半径为5,∴AB=10,∵cos∠BCE=,∴cos∠BAE==,∴AE=8,∴BE===6,∵,∴BE=CE=6,∵CE2=EH•EA,∴EH=,在Rt△BEH中,BH=.∵OG⊥BE,OB=OE,∴BG=3,∴OG===4,∴BF•OE,∴BF=,∴HF=BH﹣BF=.16.解:(1)∵点A(0,8),∴AO=8,∵AD是⊙Q的直径,∴∠AEB=∠AED=90°,∴∠AEB=∠AOB=90°,∵BA垂直平分CD,∴BC=BD,∴∠ABO=∠ABE在△ABE和△ABO中,,∴△ABE≌△ABO(AAS),∴AE=AO=8;(2)∵∠ABE=∠FDE,∴AB∥DF,∴△CAB∽△CDF,∴,又∵∠ABE=∠FDE,∠AEB=∠FED∴△DEF∽△BEA,∴,∴EF=2AE=16;(3)设BO=x,则AB=x+4,在Rt△ABO中,由AO2+OB2=AB2得:82+x2=(x+4)2,解得:x=6,∴OB=BE=6,AB=10,∵∠EAB+∠ABE=90°,∠ACB+∠ABC=90°,∴∠EAB=∠ACB,∵∠BF A=∠AFC,∴△BF A∽△AFC,∴;设EF=m,则AF=8+m,BF=(8+m),∵在Rt△BEF中,BE2+EF2=BF2,∴62+m2=[(8+m)]2,解得:m=,即EF=,∴tan∠AFC=.17.(1)证明:如图1,∵EF平分∠AED,∴∠AEF=∠FED,∵∠AEF=∠ADF,∴∠FED=∠ADF,∵∠GFD=∠DFE,∴△GFD∽△DFE;(2)证明:如图2,∵AE平分∠BAC,∴∠BAE=∠EAO,∵OA=OE,∴∠EAO=∠OEA,∴∠BAE=∠OEA,∴AB∥OE,∴∠OEC=∠B,∵∠B=90°,∴∠OEC=90°,∵OE为半径,∴BC是⊙O的切线;(3)解:如图3,连接OF、AF,∵AD为直径,∴∠AFD=∠AED=90°,∵EF平分∠AED,∴∠AEF=∠FED=45°,∴∠AFD=∠AEF=45°,∴△AFD为等腰直角三角形,∵DF=10,OA=OD∴AD=DF=×10=20,OF⊥AD,OA=OD=OF=10,∵cos∠CAE=,∴AE=AD•cos∠CAE=20×=10,∵∠AEF=∠ADF,∠AGE=∠FGD,∴△AGE∽△FGD,∴,∴AG=GF,∵AG=AO+OG=10+OG,∴10+OG=GF,∴OG=GF﹣10,在Rt△FOG中,GF2=OF2+OG2,∴GF2=102+(GF﹣10)2,解得:GF=或(不符合题意,舍去),∴线段GF的长为.18.(1)证明:连接OB,∵PB是⊙O的切线,∴∠PBO=90°,∵OA=OB,BA⊥PO于D,∴AD=BD,∠POA=∠POB,又∵PO=PO,∴△P AO≌△PBO(SAS),∴∠P AO=∠PBO=90°,∵OA为圆的半径,∴直线P A为⊙O的切线;(2)证明:∵∠P AO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OP A+∠AOP=90°,∴∠OAD=∠OP A,∴△OAD∽△OP A,∴,∴OA2=OD•OP,又∵AC=2OA,∴AC2=4OD•OP;(3)解:∵OA=OC,AD=BD,BC=6,∴OD=BC=3,设AD=x,∵tan∠F=,∴FD=2x,OA=OF=2x﹣3,在Rt△AOD中,由勾股定理,得,(2x﹣3)2=x2+32,解之得,x1=4,x2=0(不合题意,舍去),∴AD=4,OA=2x﹣3=5,∵AC是⊙O的直径,∴AC=2OA=10.∴AC的长为10.19.(1)证明:∵∠ACB=90°,PE⊥AC,PF⊥BC,∴四边形PECF是矩形,∵CP平分∠ACB,PE⊥AC,PF⊥BC,∴PE=PF,∴四边形CEPF是正方形;(2)解:∵sin A=,AB=10,∴,∴BC=8,∴AC===6,∴tan A=,设PE=CE=m,则AE=6﹣m,∴tan A=,∴m=,∴PC=PE=;(3)解:∵四边形CEPF是正方形,∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,∴将△APE绕点P顺时针旋转90°,得到△A′PF,P A′=P A,如图所示:则A′、F、B三点共线,∠APE=∠A′PF,∴∠A′PF+∠BPF=90°,即∠A′PB=90°,∴S△P AE+S△PBF=S△P A′B=P A′•PB=x(10﹣x),∴y与x之间的函数关系式为y=﹣+5x,∵y=﹣+5x=﹣,∴x=5时,y有最大值为.20.解:(1)如图①,AD⊥BC,∵△ABC为等边三角形,AB=2,∴∠B=60°,BC=AB=2,∵AD⊥BC,∴∠ADB=90°,在Rt△ABD中,=sin B=sin60°,∴=,∴AD=,∴△ABC的面积=AB•AD=×2×=,故答案为:;(2)如图②,过点D作DH⊥BC于点H,∵∠ABC=90°,BD是△ABC的角平分线,∴∠DBC=∠ABD=45°,∵DE⊥BD,∴∠BDE=90°,∴∠DEB+∠DBE=90°,∴∠DEB=90°﹣∠DBE=90°﹣45°=45°,∴BD=ED,∵DH⊥BC,∴BH=EH,∴DH=BE=BH=EH,设DH=BH=EH=a,∵∠ABC=90°,∴AB⊥BC,∵DH⊥BC,∴AB∥DH,∴△CDH∽△CAB,∴==,∵AD=1,AC=3,∴CD=3﹣1=2,∴==,∴AB=a,CE=a,∴BC=CE+BE=a+2a=3a,∵AB2+BC2=AC2,∴a2+9a2=9,∴a2=1,∴S阴影=S△ABC﹣S△BDE=AB•BC﹣BE•DH=×a•3a﹣×2a•a=a2﹣a2=a2=1;(3)①设AC与BD相交于点E,连接OB,OA,OC,过点O作OH⊥AB于点H,∵∠ADB=∠BDC=60°,∴AB=BC,∠BAC=∠BDC=60°,∴△ABC是等边三角形,∴∠ACB=60°,AB=AC=BC,在△ABO和△ACO中,,∴△ABO≌△ACO(SSS),同理△ABO≌△CBO(SSS),∴S△ABO=S△ACO=S△CBO,∴S△ABC=3S△ABO,∵∠AOB=2∠ACB,∴∠AOB=120°,在Rt△OAH和Rt△OBH中,,∴Rt△OAH≌Rt△OBH(HL),∴∠AOH=∠BOH,AH=BH,在Rt△OAH中,OA=4,∠AOH=∠AOB=60°,∴cos∠AOH=cos60°==,sin∠AOH=sin60°==,∴OH=OA=2,AH=OA=2,∴AB=2AH=4,∴S△ABC=3S△ABO=3××4×2=12,∵∠ABE=∠DBA,∠BAE=∠BDA=60°,∴△ABE∽△DBA,∴===,即S△DBA=S△ABE,∵∠CBE=∠DBC,∠BCE=∠BDC=60°,∴△CBE∽△DBC,∴===,即S△DBC=S△CBE,∴S四边形ABCD=S△DBA+S△DBC=S△ABE+S△CBE,=(S△ABE+S△CBE)=S△ABC=×12=x2,∴S△ADC=S四边形ABCD﹣S△ABC=x2﹣12,即y=x2﹣12;∵BD的长度大于AB,小于等于直径,∴4<x≤8,∴y与x之间的函数关系式为y=x2﹣12(4<x≤8);②由①知,y与x之间的函数关系式为y=x2﹣12,则对称轴为y轴,∵>0,∴x>0时,y随x的增大而增大,∵4<x<8,∴当x=8时,y有最大值,即当BD为⊙O的直径时,y取最大值,即y=×82﹣12=4,∴花卉区域△ADC面积的最大值是4.。
中考复习--圆专题(所有知识点和题型(大全),全)

《圆》题型分类资料一.圆的有关概念:1.下列说法:①直径是弦②弦是直径③半圆是弧,但弧不一定是半圆④长度相等的两条弧是等弧,正确的命题有( )A。
1个B.2个C。
3个D。
4个2.下列命题是假命题的是( )A.直径是圆最长的弦B.长度相等的弧是等弧C.在同圆或等圆中,相等的圆心角所对的弧也相等D.如果三角形一边的中线等于这条边的一半,那么这个三角形是直角三角形.3。
下列命题正确的是( )A.三点确定一个圆B.长度相等的两条弧是等弧C.一个三角形有且只有一个外接圆D。
一个圆只有一个外接三角形4.下列说法正确的是()A.相等的圆周角所对的弧相等B.圆周角等于圆心角的一半C.长度相等的弧所对的圆周角相等D.直径所对的圆周角等于90°5。
下面四个图中的角,为圆心角的是( )A.B.C.D.二.和圆有关的角:1. 如图1,点O是△ABC的内心,∠A=50 ,则∠BOC=_________图1 图22。
如图2,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数为( )A.116°B.64°C。
58°D。
32°3. 如图3,点O为优弧AB所在圆的圆心,∠AOC=108°,点D在AB的延长线上,BD=BC,则∠D的度数为A图3 图44。
如图4,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧BC上的一点,已知∠BAC=80°,那么∠BDC=_________度.5。
如图5,在⊙O中,BC是直径,弦BA,CD的延长线相交于点P,若∠P=50°,则∠AOD=.A图5 图66. 如图6,A,B,C,是⊙O上的三个点,若∠AOC=110°,则∠ABC=°.7.圆的内接四边形ABCD中,∠A:∠B:∠C=2:3:7,则∠D的度数为。
8。
若⊙O的弦AB所对的劣弧是优弧的13,则∠AOB=。
9。
中考数学复习《圆》专题训练-附带有答案

中考数学复习《圆》专题训练-附带有答案一、选择题1.下列有关圆的一些结论:①平分弧的直径垂直于弧所对的弦;②平分弦的直径垂直于弦;③在同圆或等圆中,相等的弦所对的圆周角相等;④同弧或等弧所对的弦相等,其中正确的有()A.①④B.②③C.①③D.②④2.在同一平面内,已知⊙O的半径为3cm,OP=4cm,则点P与⊙O的位置关系是()A.点P在⊙O圆外B.点P在⊙O上C.点P在⊙O内D.无法确定3.如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°()A.66°B.33°C.24°D.30°4.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠CDA=118°,则∠C的度数为()A.32°B.33°C.34°D.44°5.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=26°,则∠D等于()A.26°B.48°C.38°D.52°6.如图,四边形ABCD内接于⊙O,∠C=100°,那么∠A是()A.60°B.50°C.80°D.100°7.如图,AB为⊙O的直径,C是⊙O上的一点,若∠BCO=35°,AO=2,则AC⌢的长度为()A.29πB.59πC.πD.79π8.如图,点A、B、C、D、E都是⊙O上的点AC⌢=AE⌢,∠D=130°则∠B的度数为()A.130°B.128°C.115°D.116°二、填空题9.半径为6的圆上,一段圆弧的长度为3π,则该弧的度数为°.10.如图,在△ABC中,∠ACB= 130°,∠BAC=20°,BC=2.以C为圆心,CB为半径的圆交AB于点D,则BD的长为.11.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= √2,则BD的长为.12.如图,四边形ABCD为⊙O的内接四边形,若∠ADC=85°,则∠B=.13.如图,在△ABC中∠ACB=90°,O为BC边上一点CO=2.以O为圆心,OC为半径作半圆与AB边交π,则阴影部分的面积为.于E,且OE⊥AB.若弧CE的长为43三、解答题14.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,OD∥BC(1)求证:AD=CD;(2)若AC=8,DE=2,求BC的长.15.如图,AB是⊙O的直径,F为⊙O上一点,AC平分∠FAB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.(1)求证:CD是⊙O的切线.(2)若DC=3,AD=9,求⊙O半径.⌢上一点,AG与DC的延长线交于点F.16.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是AC(1)如CD=8,BE=2,求⊙O的半径长;(2)求证:∠FGC=∠AGD.17.如图,在△ABC中AB=AC,以底边BC为直径的⊙O交两腰于点D,E .(1)求证:BD=CE;⌢的长.(2)当△ABC是等边三角形,且BC=4时,求DE18.如图,在△ABC中,经过A,B两点的⊙O与边BC交于点E,圆心O在BC上,过点O作OD⊥BC交⊙O 于点D,连接AD交BC于点F,且AC=FC.(1)试判断AC与⊙O的位置关系,并说明理由;(2)若FC=√3,CE=1.求图中阴影部分的面积(结果保留π).参考答案1.A2.A3.B4.C5.C6.C7.D8.C9.9010.2√311.2√212.95°π13.4√3−4314.(1)证明:∵AB是⊙O的直径∴∠ACB=90°∵OD∥BC∴∠AEO=∠ACB=90°⌢=CD⌢∴AD∴AD=CD;(2)解:∵OD⊥AC,AC=8AC=4∴AE=12设⊙O的半径为r∵DE=2∴OE=OD﹣DE=r﹣2在Rt△AEO中,AE2+OE2=AO2∴16+(r﹣2)2=r2解得:r=5∴AB=2r=10在Rt△ACB中,BC=√AB2−AC2=√102−82=6∴BC的长为6.15.(1)证明:连接OC∵AC平分∠FAB∴∠FAC=∠CAO∵AO=CO∴∠ACO=∠CAO∴∠FAC=∠ACO∴AD∥OC∵CD⊥AF∴CD⊥OC∵OC为半径∴CD是⊙O的切线;(2)解:过点O作OE⊥AF于EAF,∠OED=∠EDC=∠OCD=90°∴AE=EF=12∴四边形OEDC为矩形∴CD=OE=3,DE=OC设⊙O的半径为r,则OA=OC=DE=r∴AE=9﹣r∵OA2﹣AE2=OE2∴r2﹣(9﹣r)2=32解得r=5.∴⊙O半径为5.16.(1)解:连接OC.设⊙O的半径为R.∵CD⊥AB∴DE=EC=4在Rt △OEC中,∵OC2=OE2+EC2∴R2=(R−2)2+42解得R=5.(2)解:连接AD∵弦CD⊥AB̂ = AĈ∴AD∴∠ADC=∠AGD∵四边形ADCG是圆内接四边形∴∠ADC=∠FGC∴∠FGC=∠AGD.17.(1)证明:∵AB=AC∴∠B=∠C⌢=BE⌢∴CD⌢=CE⌢∴BD∴BD=CE;(2)解:连接OD、OE∵△ABC 是等边三角形∴∠B =∠C =60°∴∠COD =120°∴∠COD +∠BOE =∠COE +∠DOE +∠BOD +∠DOE =240° ∴∠DOE =240°−180°=60°∵BC =4∴⊙O 的半径为 2∴DE ⌢ 的长 =60π×2180=2π3 .18.(1)解:AC 与⊙O 的相切,理由如下∵AO =DO∴∠D =∠OAD∵CF =CA∴∠CAF =∠CFA又∵∠CFA =∠OFD∴∠CAF =∠OFD∵OD ⊥BC∴∠OFD +∠ODF =90°∴∠CAF +∠OAF =90°∴OA ⊥AC∵OA 是半径∴AC 是⊙O 的切线∴ AC 与⊙O 的相切;(2)解:过A 作AM ⊥BC 于M ,如图设OA=OE=r∵FC=√3,CE=1在Rt△CAO中AO=r,AC=FC=√3,OC=OE+EC=r+1AO2+AC2=OC2∴r2+(√3)2=(r+1)2解得r=1∴OC=OE+EC=2∴AO=12 OC∴∠C=30°∴∠AOC=60°∴∠AOB=180−∠AOC=120°在Rt△CAM中AM=12AC=12FC=√32∴S△AOB=12⋅OB⋅AM=12×1×√32=√34∴S扇形AOB=120360π×1=π3∴S阴影部分=S△AOB−S扇形AOB=π3−√34.。
九年级中考数学《圆证明题》专题复习试卷及解析

九年级中考数学《圆证明题》专题复习试卷及分析九年级中考数学《圆证明题》专题复习试卷及分析1、如图,点 A,B 在⊙ O上,直线 AC是⊙ O的切线, OC⊥OB,连结 AB交 OC于点 D.求证: AC=CD.2、如图, AD是⊙ O的切线,切点为 A,AB是⊙ O的弦.过点 B 作 BC∥AD,交⊙ O于点 C,连结AC,过点 C作 CD∥AB,交 AD于点 D.连结 AO并延伸交 BC于点 M,交过点 C的直线于点P,且∠BCP=∠ ACD.(1)判断直线 PC与⊙ O的地点关系,并说明原因;(2)若 AB=9,BC=6.求 PC的长.3、如图,在△ ABC中,∠ ACB=90°,点 D 是 AB上一点,以 BD为直径的⊙ O和 AB相切于点 P.(1)求证: BP均分∠ ABC;(2)若 PC=1,AP=3,求 BC的长.14、已知:如图, AC是⊙ O的直径, BC是⊙ O的弦,点 P 是⊙ O外一点,∠ PBA=∠ C.(1)求证: PB是⊙ O的切线.(2)若 OP∥BC,且 OP=8,∠ C=60°,求⊙ O的半径.5、如图,在△ ABC中, AB=AC,以 AB为直径的⊙ O交 BC于点 M,MN⊥AC于点 N.求证: MN是⊙ O的切线.6、如图, AB是⊙ O的直径,点 C 在 AB的延伸线上, CD与⊙ O相切于点 D,CE⊥AD,交 AD的延伸线于点 E.(1)求证:∠ BDC=∠A;(2)若 CE=4,DE=2,求⊙ O的直径.7、已知: AB是⊙ O的直径, BD是⊙ O的弦,延伸 BD到点 C,使 AB=AC,连结 AC,过点 D 作DE⊥AC,垂足为 E.( 1)求证: DC=BD( 2)求证: DE为⊙ O的切线.8、如图, AB是⊙ O的直径, C为⊙ O上一点,经过点 C 的直线与 AB的延伸线交于点 D,连结AC,BC,∠BCD=∠CAB.E 是⊙ O上一点,弧 CB=弧 CE,连结 AE并延伸与 DC的延伸线交于点 F.( 1)求证: DC是⊙ O的切线;( 2)若⊙ O的半径为 3,sin D=,求线段AF的长.9、如图,已知 MN是⊙ O的直径,直线 PQ与⊙ O相切于 P 点, NP均分∠MNQ.( 1)求证: NQ⊥PQ;( 2)若⊙ O的半径 R=2,NP=,求NQ的长.10、已知: AB是⊙ O的直径, BD是⊙ O的弦,延伸 BD到点 C,使 AB=AC;连结 AC,过点 D作DE⊥AC,垂足为 E.(1)求证: DC=BD(2)求证: DE为⊙ O的切线11、如图,以 Rt△ABC的 AC边为直径作⊙ O交斜边 AB于点 E,连结 EO并延伸交 BC的延伸线于点 D,点 F 为 BC的中点,连结 EF和 AD.(1)求证: EF是⊙ O的切线;(2)若⊙ O的半径为 2,∠ EAC=60°,求 AD的长.12、如图, AB是⊙ O的直径,点 E 是上的一点,∠ DBC=∠ BED.⑴求证: BC是⊙ O的切线;⑵已知 AD=3, CD=2,求 BC的长.13、如图,已知 AB是⊙ O的直径,点 C、D在⊙ O上,点 E 在⊙ O外,∠ EAC=∠D=60°.(1)求∠ ABC的度数;(2)求证: AE是⊙ O的切线;(3)当 BC=4时,求劣弧 AC的长.14、已知△ ABC,以 AB为直径的⊙ O分别交 AC于 D, BC于 E,连结 ED,若 ED=EC.(1)求证: AB=AC;(2)若 AB=4,BC=2 ,求 CD的长.15、如图,以△ ABC的边 AB上一点 O为圆心的圆经过 B、C两点,且与边 AB订交于点 E,D是弧 BE的中点, CD交 AB于 F,AC=AF.( 1)求证: AC是⊙ O的切线;( 2)若 EF=5,DF= ,求⊙ O的半径.参照答案1、∵直线 AC与⊙ O相切,∴ OA⊥ AC,∴∠ OAC=90°,即∠ OAB+∠CAB=90°,∵OC⊥OB,∴∠BOC=90°,∴∠B+∠ODB=90°,而∠ODB=∠ADC,∴∠ADC+∠B=90°,∴OA=OB,∴∠ OAB=∠B,∴∠ ADC=∠CAB,∴ AC=CD.2、( 1)解: PC与圆 O相切,原因为:过C点作直径CE,连结EB,如图,∵CE为直径,∴∠ EBC=90°,即∠ E+∠BCE=90°,∵ AB∥DC,∴∠ ACD=∠BAC,∵∠ BAC=∠E,∠ BCP=∠ACD.∴∠ E=∠ BCP,∴∠ BCP+∠BCE=90°,即∠ PCE=90°,∴ CE⊥ PC,∴ PC与圆 O相切;( 2)解:∵ AD是⊙ O的切线,切点为 A,∴ OA⊥AD,∵BC∥AD,∴ AM⊥BC,∴ BM=CM= BC=3,∴ AC=AB=9,在 Rt△ AMC中,AM= =6,设⊙ O的半径为 r ,则 OC=r,OM=AM﹣r=6 ﹣r ,2 2 2 2 2 2在 Rt△ OCM中, OM+CM=OC,即 3 +(6 ﹣ r ) =r,解得 r= ,∴ CE=2r= ,OM=6 ﹣= ,∴ BE=2OM= ,∵∠ E=∠ MCP,∴ Rt △PCM∽Rt△ CEB,∴=,即=,∴ PC= 3、( 1)证明:连结 OP,∵OP=OB,∴∠ OPB=∠OBP,∴∠ PBC=∠ OBP,∴ BP均分∠ ABC(2)作 PH⊥AB于 H.∵ PB均分∠ ABC,PC⊥BC, PH⊥AB,∴ PC=PH=1,在 Rt△ APH中, AH==2,∵∠ A=∠A,∠ AHP=∠ C=90°,∴△ APH∽△ ABC,∴=,∴=,∴ AB=3,∴ BH=AB﹣AH=,在 Rt△ PBC和 Rt△PBH中,,∴ Rt△PBC≌Rt△PBH,∴ BC=BH=.4、( 1)证明:连结 OB,∵ AC是⊙ O直径,∴∠ ABC=90°,∵OC=OB,∴∠ OBC=∠C,∵∠ PBA=∠C,∴∠ PBA=∠OBC,即∠ PBA+∠ OBA=∠ OBC+∠ ABO=∠ABC=90°,∴ OB⊥PB,∵ OB为半径,∴ PB是⊙ O的切线;(2)解:∵ OC=OB,∠ C=60°,∴△ OBC为等边三角形,∴ BC=OB,∵ OP∥BC,∴∠ CBO=∠ POB,∴∠ C=∠POB,在△ ABC和△ PBO中∵,∴△ ABC≌△ PBO(ASA),∴ AC=OP=8,即⊙ O的半径为4.5、证明:连结 OM,∵ AB=AC,∴∠ B=∠ C,∵ OB=OM,∴∠ B=∠OMB,∴∠ OMB=∠C,∴OM∥AC,∵ MN⊥AC,∴ OM⊥MN.∵点 M在⊙ O上,∴ MN是⊙ O的切线.6、( 1)证明:连结 OD,∵CD是⊙ O切线,∴∠ ODC=90°,即∠ ODB+∠ BDC=90°,∵AB为⊙ O的直径,∴∠ ADB=90°,即∠ ODB+∠ADO=90°,∴∠ BDC=∠ADO,∵OA=OD,∴∠ ADO=∠A,∴∠ BDC=∠A;(2)∵ CE⊥ AE,∴∠ E=∠ADB=90°,∴DB∥EC,∴∠ DCE=∠ BDC,∴∠ DCE=∠A,∵ CE=4, DE=2∴在 Rt △ACE中,可得 AE=8∴ AD=6在在 Rt △ADB中可得BD=3∴依据勾股定理可得7、证明:( 1)连结 AD,∵ AB是⊙ O的直径,∴∠ ADB=90°,又∵ AB=AC,∴ DC=BD;(2)连结半径 OD,∵ OA=OB, CD=BD,∴ OD∥AC,∴∠ ODE=∠CED,又∵ DE⊥ AC,∴∠ CED=90°,∴∠ ODE=90°,即 OD⊥DE.∴ DE是⊙ O的切线.8、( 1)证明:连结 OC,BC,∵ AB是⊙ O的直径,∴∠ ACB=90°,即∠ 1+∠3=90°.∵OA=OC,∴∠ 1=∠ 2.∵∠ DCB=∠BAC=∠1.∴∠ DCB+∠ 3=90°.∴ OC⊥ DF.∴ DF 是⊙ O的切线;( 2)解:在 Rt△ OCD中, OC=3,sin D=.∴ OD=5,AD=8.∵=,∴∠ 2=∠4.∴∠ 1=∠4.∴ OC∥AF.∴△ DOC∽△ DAF.∴.∴ AF=.9、( 1)证明:连结 OP,如图,∴直线PQ与⊙ O相切,∴ OP⊥PQ,∵OP=ON,∴∠ ONP=∠ OPN,∵ NP均分∠ MNQ,∴∠ ONP=∠ QNP,∴∠ OPN=∠QNP,∴OP∥ NQ,∴ NQ⊥PQ;( 2)解:连结 PM,如图,∵ MN是⊙ O的直径,∴∠ MPN=90°,∵NQ⊥PQ,∴∠ PQN=90°,而∠ MNP=∠ QNP,∴ Rt △NMP∽Rt△ NPQ,∴=,即=,∴ NQ=3.10、( 1)证明:( 1)连结 AD;∵ AB是⊙ O的直径,∴∠ ADB=90°.又∵ AB=AC∴ DC=BD(2)连结半径 OD;∵ OA=OB, CD=BD,∴ OD∥AC.∴∠ 0DE=∠CED.又∵ DE⊥ AC,∴∠ CED=90°.∴∠ ODE=90°,即 OD⊥DE.∴ DE是⊙ O的切线.11、( 1)证明:连结 CE,如下图:∵AC为⊙ O的直径,∴∠ AEC=90°.∴∠ BEC=90°.∵点F 为 BC的中点,∴ EF=BF=CF.∴∠ FEC=∠FCE.∵OE=OC,∴∠ OEC=∠OCE.∵∠ FCE+∠ OCE=∠ ACB=90°,∴∠ FEC+∠OEC=∠OEF=90°.∴ EF是⊙ O的切线.( 2)解:∵ OA=OE,∠EAC=60°,∴△ AOE是等边三角形.∴∠ AOE=60°.∴∠COD=∠AOE=60°.∵⊙ O的半径为 2,∴ OA=OC=2在 Rt △OCD中,∵∠ OCD=90°,∠ COD=60°,∴∠ ODC=30°.∴ OD=2OC=4,∴ CD=.在Rt△ ACD中,∵∠ ACD=90°,AC=4,CD=.∴AD==.12、1)AB是⊙ O的直径,得∠ ADB=90°,进而得出∠ BAD=∠DBC,即∠ ABC=90°,即可证明BC是⊙ O的切线;( 2)可证明△ ABC∽△ BDC,则=,即可得出BC=;13、解:( 1)∵∠ ABC与∠ D 都是弧 AC所对的圆周角,∴∠ ABC=∠D=60°;( 2)∵ AB是⊙ O的直径,∴∠ ACB=90°.∴∠ BAC=30°,∴∠ BAE=∠BAC+∠EAC=30°+60°=90°,即 BA⊥AE,∴ AE是⊙ O的切线;( 3)如图,连结 OC,∵∠ ABC=60°,∴∠ AOC=120°,∴劣弧 AC的长为.14、( 1)证明:∵ ED=EC,∴∠ EDC=∠ C,∵∠ EDC=∠B,∴∠ B=∠C,∴ AB=AC;(2)解:连结 AE,∵ AB为直径,∴ AE⊥BC,由( 1)知 AB=AC,∴ BE=CE= BC=,九年级中考数学《圆证明题》专题复习试卷及分析九年级中考数学《圆证明题》专题复习试卷及分析∵△ CDE∽△ CBA,∴,∴ CE?CB=CD?CA,AC=AB=4,∴?2 =4CD,∴ CD= .15、( 1)证明:连结 OD、 OC,如图,∵ D 是弧 BE的中点,∴ OD⊥BE,∴∠ D+∠3=90°,∵∠ 3=∠ 2,∴∠ D+∠2=90°,∵ AF=AC,OD=OC,∴∠ 1=∠2,∠ D=∠ 4,∴∠ 1+∠ 4=90°,∴ OC⊥AC,∴ AC是⊙ O的切线;( 2)解:设⊙ O的半径为 r ,则 OF=OE﹣ EF=r﹣5,22222 2在 Rt△ ODF中,∵ OD+OF=DF,∴ r +( r ﹣ 5) =(),整理得 r 2﹣5r ﹣ 6=0,解得 r 1 =6,r 2=﹣1,∴,⊙ O的半径为 6.10。
2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)
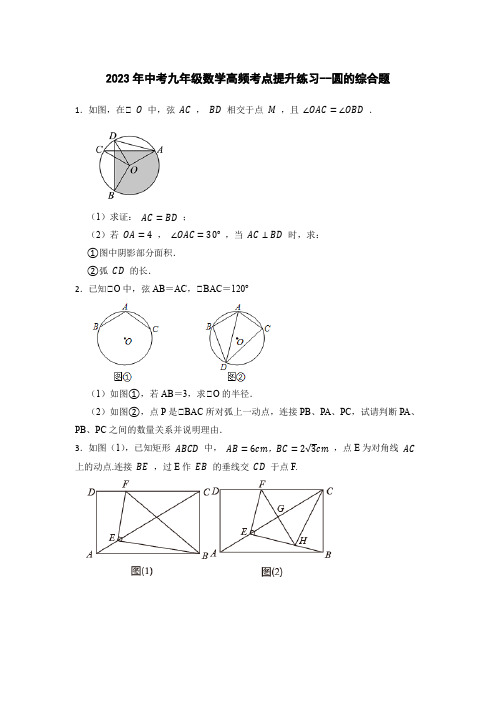
2023年中考九年级数学高频考点提升练习--圆的综合题1.如图,在⊙ O中,弦AC,BD相交于点M,且∠OAC=∠OBD.(1)求证:AC=BD;(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:①图中阴影部分面积.②弧CD的长.2.已知⊙O中,弦AB=AC,⊙BAC=120°(1)如图①,若AB=3,求⊙O的半径.(2)如图②,点P是⊙BAC所对弧上一动点,连接PB、PA、PC,试请判断PA、PB、PC之间的数量关系并说明理由.3.如图(1),已知矩形ABCD中,AB=6cm,BC=2√3cm,点E为对角线AC 上的动点.连接BE,过E作EB的垂线交CD于点F.(1)探索BE与EF的数量关系,并说明理由.(2)如图(2),过F作AC垂线交AC于点G,交EB于点H,连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动,设E的运动时间为ts.①是否存在t,使得H与B重合?若存在,求出t的值;若不存在,说明理由;②t为何值时,△CFH是等腰三角形;③当CG=GH时,求△CGH的面积.4.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD是⊙O的切线;(2)求证:⊙C=2⊙DBE.(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)5.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,⊙ABC中,点D 是BC边上一点,连结AD,若AD2=BD⋅CD,则称点D是⊙ABC中BC边上的“好点”.(1)如图2,⊙ABC的顶点是4×3网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)⊙ABC中,BC=9,tanB=43,tanC=23,点D是BC边上的“好点”,求线段BD的长.(3)如图3,⊙ABC是⊙O的内接三角形,OH⊙AB于点H,连结CH并延长交⊙O于点D.①求证:点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9,⊙ABD=90°,OH=6,请直接写出CHDH的值.6.如图,⊙O为等边⊙ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B 重合),连接DA,DB,DC.(1)求证:DC是⊙ADB的平分线;(2)设四边形ADBC的面积为S,线段DC的长为x,试用含x的代数式表示S;(3)若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D 运动到每一个确定的位置,⊙DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.7.在⊙ABC中,D,E分别是⊙ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在⊙ABC的内部或边上,则称弧DE为⊙ABC的中内弧.例如,图1中弧DE是⊙ABC其中的某一条中内弧.(1)如图2,在边长为4 √3的等边⊙ABC中,D,E分别是AB,AC的中点.画出⊙ABC的最长的中内弧DE,并直接写出此时弧DE的长;(2)在平面直角坐标系中,已知点A(2 √3,6),B(0,0),C(t,0),在⊙ABC中,D,E分别是AB,AC的中点.①若t=2 √3,求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;②请写出一个t的值,使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.8.如图,⊙O是⊙ABC的外接圆,AC是直径,过点O作OD⊙AB于点D,延长DO 交⊙O于点P,过点P作PE⊙AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)若⊙POC=60°,AC=12,求劣弧PC的长;(结果保留π)(2)求证:OD=OE;(3)求证:PF是⊙O的切线.9.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=32CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ=,DF=.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)当点P在点A右侧时,作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长.10.如图,⊙ABC中,⊙ACB=90°,D是边AB上一点,且⊙A=2⊙DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.(1)求证:AB是⊙O的切线;(2)若CD的弦心距为1,BE=EO,求BD的长.11.已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM 在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持⊙ABP=90°不变,BP边与直线l相交于点P.(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;(2)请利用如图1所示的情形,求证:ABPB=OMBM;(3)若AO=2 √6,且当MO=2PO时,请直接写出AB和PB的长.12.(问题情境)如图①,小区A、B位于一条笔直的道路l的同侧,为了方便A,B两个小区居民投放垃圾,现在l上建一个垃圾分类站C,使得C与A,B的距离之比为2:1.(1)(初步研究)在线段AB上作出点C,使CACB=2.如图,做法如下:第一步:过点A作射线AM,以A为圆心,任意长为半径画弧,交AM于点P1;以P1为圆心,AP1长为半径画弧,交AM于点P2;以P2为圆心,AP1长为半径画弧,交AM于点P3.第二步:连接BP3,作∠AP2C=∠AP3B,交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.(2)(深入思考)如图,点C在线段AB上,点D在直线AB外,且DADB=CACB=2.求证:DC是∠ADB的平分线.(3)(问题解决)如图,已知点A,B和直线l,点C在线段AB上,且CACB=2.用直尺和圆规完成下列作图.(保留作图痕迹,不写作法)(⊙)在直线AB上作出点E(异于点C),使EAEB=2;(⊙)在直线l上作出点F,使FAFB=2.13.在矩形ABCD中,BC=2AB,点E是对角线AC上任意一点,过点E作AD的垂线分别交AD,BC于点F,G,作FH平行AC交CD于点H.(1)证明:EF=CH.(2)连结GH交AC于点K,若AE:CK=3,求AE:EK的值.(3)作⊙FGH的外接圆⊙O,且AB=1.①若⊙O与矩形的边相切时,求CH的长.②作点E关于GH的对称点E',当E'落在⊙O上时,直接写出⊙FGH的面积。
2023年春九年级数学中考高分复习圆综合压轴解答题专题训练原卷版

2023年春九年级数学中考高分复习圆综合压轴解答题专题训练原卷版1.如图,⊙O为正△ABC的外接圆.(1)尺规作图:作∠ABC的角平分线⊙O于点D.(2)过点D作⊙O的切线DE,交AB的延长线于点M.①求证:AC∥DE.②连接OM,若AM=2,求⊙O的半径.2.如图,△ABC内接于⊙O,AB是⊙O的直径,CD平分∠ACB交⊙O于点D,交AB于点F,弦AE⊥CD于点H,连接CE、OH.(1)延长AB到圆外一点P,连接PC,若PC2=PB•P A,求证:PC是⊙O的切线;(2)求证:CF•AE=AC•BC;(3)若=,⊙O的半径是,求tan∠AEC和OH的长.3.已知四边形ABCD内接于⊙O,AB=AD.(1)如图1,求证:点A到∠C两边的距离相等;(2)如图2,已知BD与AC相交于点E,BD为⊙O的直径.①求证:tan∠CAD=;②若∠CBD=30°,AD=,求AE的长.4.如图,在▱ABCD中,AB=5,AD=3,∠ADB=90°,P为线段BD上一点,以PD为直径作圆分别交线段CD,AP于点E,F,延长AP交直线BC于点G,连接DF,EF,EP.(1)当∠DEF=45°时,求证:=.(2)当BG=2时,求tan∠FEP的值.(3)①当△DEF是以DE为腰的等腰三角形时,求DP的长.②记线段EF交BD于点Q,若=,则BG的长为.5.如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.(1)求证:PG与⊙O相切:(2)若,求的值;(3)在(2)的条件下,若⊙O的半径为4,PD=OD,求EC的长.6.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上(不与点B、D重合),以O为圆心,以OB为半径作圆O交BD于点E.(1)sin∠ABD=;(2)若圆O经过点A,求圆O的面积;(3)若圆O与△ACD的边所在直线相切,求OB的长.7.如图1,AB为⊙O的直径,C为弧BE的中点,AD和过点C的直线相交于D,交⊙O于点E.连接OC,BE,相交于点F,DE=CF.(1)求证:CD是⊙O的切线;(2)连接AC,交BE于点P,若EP=2,CD=3,求直径AB的长;(3)猜想AE、AB和AD之间的数量关系,并证明.8.如图1,在⊙O中,点H是直径AB上的一点,过H点作弦CD⊥AB,点E 是的中点,过点E作BD的平行线交DC延长线于点F,连接BE,交CD 于点G.(1)求证:EF是⊙O的切线;(2)求证:BD+EF=DF;(3)如图2,连接DE,若=k,则当k为何值时,线段DE=EF?9.如图1,点C在以AB为直径的⊙O上,P是AB延长线上一点,∠PCB=∠P AC,过点C作CE⊥AB,垂足为D,交⊙O于点E.(1)求证:PC是⊙O的切线;(2)若点D是P A的中点,求∠P的度数;(3)如图2,过点B作BM∥PC交⊙O于点M,交CD于点N,连接AM.若tan∠P=,CN=5,求AM的长.10.如图,在矩形ABCD中,AB=6,BC=8,点A在直线l上,AD与直线l相交所成的锐角为60°,点P在直线上l,AP=8,过点作EF⊥l,垂足为点E,且与点P重合,EF=6,以EF为直径,在EF的左侧作半圆O,点M是半圆O上任意一点.(1)连接AM,求线段AM的最大值;(2)矩形ABCD保持不动,半圆O沿直线l向左平移,当点F落在边AD上时,求半圆O与矩形ABCD重合部分的面积S;(3)在平移过程中,当半圆O与矩形ABCD的边相切时,求平移的距离.(参考数据:tan75°≈2+,结果保留根号)11.如图,AB是⊙O的直径,C、D是⊙O上两点.AE与过点C的切线垂直,垂足为E,直线EC与直径AB的延长线相交于点P,弦CD交AB于点F,连接AC、AD、BC、BD.(1)若∠ABC=∠ABD=60°,判断△ACD的形状,并证明你的结论;(2)若CD平分∠ACB,求证:PC=PF;(3)在(2)的条件下,若AD=5,PF=5,求由线段PC、和线段BP所围成的图形(阴影部分)的面积.12.李老师在上课时的屏幕上有如下内容:如图,AB是⊙O的直径,点C为弧BD的中点,连结AC交BD于点E,CE =1,,老师要求同学们在矩形方框中添加一个条件和结论后,编制成一道完整的题目,并解答.(1)李老师在方框中添加的内容是“BE=3,求AB的长”,请你解答;(2)以下是小童和小诗的对话:小童:我加的内容是“BE=3,连结CD,求CD的长”.小诗:我加的内容是“sin∠CBE=,连结OC,求tan∠ABD的值”.请你帮小诗完成解答:(3)参考第(1)题中李老师添加的内容及第(2)题中的对话,写出你想添加的内容(可以添线添字母,但所添内容不能与(1)、(2)中的内容相同),编制成一道完整的题目,并解答.13.已知,如图1,在△ABC中,AB=AC,点D是BC边上动点,E是△ABD 外接圆⊙O上的点,且,连结DE,BE.(1)求证:CD=BE;(2)如图2,当AE∥BC时.①求证:AC是⊙O的切线;②若AC=15,BC=18,求⊙O的半径.14.如图,四边形ABCD内接于⊙O,对角线AC是⊙O的直径,BD平分∠ABC,BD交AC于点E,过点D作DF⊥DB,DF交BA延长线于点F.(1)求证:AF=BC;(2)如果AB=3AF,求的值;(3)过点F作FG∥BD交CA延长线于点G,求证:AG=CE.15.如图1,已知AB是⊙O的直径,CD为⊙O的弦,连接AD,BC,相交于点E,连接OE并双向延长,交CD于点F,交⊙O于点P,点Q.(1)如图2,当AB∥CD时,且OE=3,EF=2时,求⊙O的半径;(2)如图3,当AB与CD不平行(假设∠ABC<∠DAB),过点F作AB的平行线,交BC的延长线于点M,交AD于点N.①求证:△MCF∽△DNF;②若OE=4,EF=3,求⊙O的半径;(3)在(2)②的条件下,连接AC,BD.若∠DEB=45°,求四边形ACDB的面积.16.若四边形的一组对角α,β,满足∠α+∠β=180°,我们把这个四边形称为可衍生四边形,∠β为二倍角.(1)如图1,在四边形ABCD中,AD⊥CD,∠A=130°,当四边形ABCD 为可衍生四边形,且∠C为二倍角时,求∠B的度数;(2)如图2,四边形ABCD内接于⊙O,点E是圆上一点,连结并延长CE,AD交于点F,延长CD,BA交于点G,CD•DG=AD•DF,求证:四边形ABCF 是可衍生四边形;(3)如图3,在(2)的条件下,连结AE,EG,若CD是⊙O的直径,AF⊥EG,AG=5AB,求sin∠F AG的值.17.【问题提出】小明在学习了“圆心角”和“圆周角”的知识后,发现了顶点在圆内(顶点不在圆心)的角,命名为圆内角.比如图1中,∠APC、∠BPD 是圆内角,所对的弧分别是、,圆内角的大小与所对弧的度数之间有什么关系呢?【问题解决】小明想到了将∠APC转化为学过的两种角,即圆周角、圆心角.解:连接BC,OA,OC,OB,OD.如图2,在△PBC中,∠APC=∠PBC+∠PCB∵∠PBC=∠AOC,∠PCB=∠BOD∴∠APC=∠AOC+∠BOD=(∠AOC+∠BOD)即:∠APC的度数=(的度数+的度数)(1)如图1,在⊙O中,弦AB、CD相交于点P,若的度数是60°,的度数是80°,则∠APD的度数是.【问题探究】顶点在圆外且两边与圆相交的角,命名为圆外角,圆外角的大小呢?(2)如图3,点P是⊙O外一点,点A、点C在圆上,连接P A、PC,分别与⊙O相交于点B、点D,试探索∠APC的度数与、度数之间的关系,并说明理由.【解释应用】直接利用前面发现的结论,解决问题.(3)如图4,平面直角坐标系内,点A(﹣,1)在⊙O上,点B、点C 是线段OM上的两个动点,且AB=AC,延长AB、AC分别与⊙O相交于点D、E,延长DE交y轴于点F,试探究∠F的度数是否变化,如果不变,请求出它的度数.18.定义:过三角形的一个顶点作该三角形的高线和角平分线,这两条线段所夹的角称为该三角形的珍珠角.(1)如图1,∠DAE是△ABC的珍珠角,∠B=α,∠C=β,α>β,请用α和β表示∠DAE.(2)如图2,△ABC中,∠BAC>∠B>∠C,以AC为直径作⊙O交BC于点D,点F在上,AF交DC于点E,∠FDC=∠BAE.求证:∠DAE是△ABC的珍珠角.(3)在(2)的条件下,如图3,连接OD,交AE于点G,OG=AB.若GF=m,BD=n,求BC的长(用含m,n的式子表示).19.如图,在平面直角坐标系xOy中,A,B两点的坐标分别为(26,0),(0,26).以AB为直径作⊙P,点C在直径AB上,且AC=a,点Q为⊙P上一动点.(1)若a=6,如图1,①求点C的坐标.②若CQ∥y轴,求点Q的坐标.(2)若a=5,如图2,点D在弦OA上,△QCD是以CQ为斜边的等腰直角三角形,求点Q的坐标.20.问题提出:(1)如图①,正方形ABCD内有一以BC为直径的半圆O,请通过画图在半圆O上找一点E,使得E到AD的距离最小.问题探究:(2)如图②,在Rt△ABC中,∠ACB=90°,AC=BC=4,点E为AB边上一点,BE=3AE,且∠CEF=45°,求CF的长.问题解决:(3)如图③,十四届全运会场馆外有一不规则区域.其中,AD∥BC,弧CD 所对的圆心角为60°,AE是区域内一条笔直的小路,即AE⊥BC于点E.组委会计划将本区域设计成为一个休闲娱乐区,规划在AB边上确定一点M作为一个入口,在AE、弧CD上分别确定点N、P,将△PNE修建成花园.为保持美观且节约成本,要求∠EMN=90°,且△PNE面积最小.已知AB=130m,BE=50m,AD=CE=150m,求△PNE面积的最小值.。
中考数学复习《圆》经典题型及测试题(含答案)
中考数学复习《圆》经典题型及测试题(含答案)【专题分析】圆在中考中的常见考点有圆的性质及定理,圆周角定理及其推论,圆心角、圆周角、弧、弦之间的“等推”关系;切线的判定,切线的性质,切线长定理,弧长及扇形面积的计算,求阴影部分的面积等.对圆的考查在中考中以客观题为主,考查题型多样,关于圆的基本性质一般以选择题或填空题的形式进行考查,切线的判定等综合性强的问题一般以解答题的形式进行考查;圆在中考中的比重约为10%~15%.【解题方法】解决圆的有关问题常用的数学思想就是转化思想,方程思想和数形结合思想;常用的数学方法有分类讨论法,设参数法等.【知识结构】【典例精选】如图,⊙O的半径是3,点P是弦AB延长线上的一点,连结OP,若OP =4,∠APO=30°,则弦AB的长为( )A.2 5 B. 5C.213 D. 13【思路点拨】先过点O作OC⊥AP,连结OB,根据OP=4,∠APO=30°,求出OC的值,在Rt△BCO中,根据勾股定理求出BC的值,进而得出AB的值.【解析】如图,过点O作OC⊥AP于点C,连结OB,∵OP=4,∠APO=30°,∴OC=4×sin 30°=2.∵OB=3,∴BC=OB2-OC2=32-22=5,∴AB=2 5.故选A.答案:A规律方法:利用垂径定理进行证明或计算,通常是在半径、圆心距和弦的一半所组成的直角三角形中,利用勾股定理构建方程求出未知线段的长.如图,从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )A.4 2 m B.5 m C. 30 m D.215 m【思路点拨】首先连结AO,求出AB,然后求出扇形的弧长BC,进而求出扇形围成的圆锥的底面半径,最后应用勾股定理求出圆锥的高即可.【解析】如图,连结AO,∵AB=AC,点O是BC的中点,∴AO⊥BC.又∵∠BAC=90°,∴∠ABO=∠ACO=45°,∴AB=2OB=2×(8÷2)=42(m).∴l BC=90π×42180=22π(m).∴将剪下的扇形围成的圆锥形的半径是22π÷2π=2(m).∴圆锥的高是422-22=30(m).故选C.答案:C规律方法:解决圆锥的相关问题,可以利用圆的周长等于扇形的弧长建立方程,利用方程解决问题.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心、ED 为半径作半圆,交A,B所在的直线于M,N两点,分别以MD,ND为直径作半圆,则阴影部分的面积为( )A.9 5 B.18 5 C.36 5 D.72 5【思路点拨】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN 的面积-大半圆的面积,MN为半圆的直径,从而可知∠MDN=90°,在Rt△MDN 中,由勾股定理可知MN2=MD2+DN2,从而可得到两个小半圆的面积=大半圆的面积,故此阴影部分的面积=△DMN的面积,在Rt△AED中,ED=AD2+AE2=62+32=35,所以MN=65,然后利用三角形的面积公式求解即可.【解析】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积.∵MN为大半圆的直径,∴∠MDN=90°.在Rt△MDN中,MN2=MD2+DN2,∴两个小半圆的面积和=大半圆的面积.∴阴影部分的面积=△DMN 的面积.在Rt△AED中,ED=AD2+AE2=62+32=35,∴阴影部分的面积=△DMN的面积=12MN·AD=12×65×6=18 5.故选B.答案:B规律方法:求阴影部分的面积,一般是将所求阴影部分进行分割组合,转化为规则图形的和或差.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连结CD.(1)求证:∠A=∠BCD.(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.【思路点拨】(1)根据圆周角定理可得∠ADC=90°,根据直角三角形的性质可得∠A+∠ACD=90°,再由∠DCB+∠ACD=90°,可得∠A=∠BCD;(2)当点M是BC的中点时,直线DM与⊙O相切.连结DO,证明∠ODM =90°,进而证得直线DM与⊙O相切.【自主解答】(1)证明:∵AC为直径,∴∠ADC=90°,∴∠A+∠ACD=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°,∴∠A=∠BCD.(2)解:当点M是BC的中点时,直线DM与⊙O相切.理由如下:如图,连结DO,∵DO=CO,∴∠1=∠2.∵∠BDC=90°,点M是BC的中点,∴DM=CM,∴∠4=∠3.∵∠2+∠4=90°,∴∠1+∠3=90°,∴直线DM与⊙O相切.规律方法:在判定一条直线是圆的切线时,如果这条直线和圆有公共点,常作出经过公共点的半径,证明这条直线与经过公共点的半径垂直,概括为“连半径,证垂直,得切线”.【能力评估检测】一、选择题1.如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连结BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( B )A.40° B.50° C.60° D.20°2.如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( C )A. 3 B.3 C.2 3 D.43.如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( A )A.25° B.50° C.60° D.30°4.如图,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP 的度数为( B )A.15° B.30° C.60° D.90°5.如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心、AB长为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( D )A.6 B.7 C.8 D.96.如图,已知AB为⊙O的直径,AD切⊙O于点A,EC=CB.则下列结论中不一定正确的是( D )A.BA⊥DA B.OC∥AEC.∠COE=2∠CAE D.OD⊥AC7.如图,菱形ABCD的对角线BD,AC分别为2,23,以B为圆心的弧与AD,DC相切,则阴影部分的面积是( D )A.23-33π B.43-33πC.43-π D.23-π8.如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( B )A .13π cmB .14π cmC .15π cmD .16π cm9.如图,在矩形ABCD 中,AB =4,AD =5,AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A. 133B. 92C. 4313 D .2 5 解:如图,连接OE ,OF ,ON ,OG .∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO =∠AFO =∠OFB =∠BGO =90°.∴四边形AFOE ,FBGO 都是正方形.∴AF =BF =AE =BG =2.∴DE =3.∵DM 是⊙O 的切线,∴DN =DE =3,MN =MG . ∴CM =5-2-MN =3-MN .在Rt △DMC 中,DM 2=CD 2+CM 2,∴(3+MN )2=(3-MN )2+42.∴NM =43.∴DM =3+43=133.故选A. 答案:A二、填空题10.在平面直角坐标系中,O 为坐标原点,则直线y =x +2与以O 点为圆心,1为半径的圆的位置关系为 相切.11.如图,圆内接四边形ABCD 两组对边的延长线分别相交于点E ,F ,且∠A =55°,∠E =30°,则∠F =40° .12.如图,正三角形ABC 的边长为2,点A ,B 在半径为2的圆上,点C 在圆内,将正三角形ABC 绕点A 逆时针旋转,当点C 第一次落在圆上时,点C 运动的路线长为 .【解析】设点C 落在圆上的点为C ′,连结OA ,OB ,OC ′,则OA =OB = 2.又∵AB =2,∴OA 2+OB 2=AB 2,∴∠AOB =90°,∴∠OAB =45°,同理∠OAC ′=45°,∴∠BAC ′=90°.∵△ABC 为等边三角形,∴∠CAB =60°,∴∠CAC ′=30°,∴点C 运动的路线长为30π×2180=π3.故答案为π3. 答案:π3 13.如图,在△ABC 中,∠BAC =90°,AB =5 cm ,AC =2 cm ,将△ABC 绕顶点C按顺时针方向旋转45°至△A 1B 1C 的位置,则线段AB 扫过区域(图中的阴影部分)的面积为 cm 2.【解析】在Rt△ABC 中,BC =AC 2+AB 2=29(cm),S 扇形BCB 1=45π×292360=29π8(cm 2),S △CB 1A 1=12×5×2=5(cm 2),S 扇形CAA 1=45π×22360=π2(cm 2),故S 阴影部分=S 扇形BCB 1+S △CB 1A 1-S △ABC -S 扇形CAA 1=29π8+5-5-π2=25π8(cm 2). 答案:25π8三、解答题14.如图,AB 是⊙O 的直径,BC 切⊙O于点B ,OC 平行于弦AD ,过点D 作DE ⊥AB 于点E ,连结AC ,与DE 交于点P .求证:(1)PE =PD ;(2)AC ·PD =AP ·BC .证明:(1)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴EP BC =AE AB .又∵AD ∥OC ,∴∠DAE =∠COB ,∴△AED ∽△OBC ,∴ED BC =AE OB =AE 12AB =2AE AB .∴ED =2EP ,∴PE =PD . (2)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴AP AC =PE BC .∵PE =PD ,∴AP AC =PD BC,∴AC ·PD =AP ·BC . 15.如图,在△OAB 中,OA =OB =10,∠AOB =80°,以点O 为圆心,6为半径的优弧MN 分别交OA ,OB 于点M ,N .(1)点P 在右半弧上(∠BOP 是锐角),将OP 绕点O 逆时针旋转80°得OP ′,求证:AP =BP ′;(2)点T 在左半弧上,若AT 与弧相切,求点T 到OA 的距离;(3)设点Q 在优弧MN 上,当△AOQ 的面积最大时,直接写出∠BOQ 的度数.(1)证明:如图,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,∠BOP′=∠POP′+∠BOP=80°+∠BOP,∴∠AOP=∠BOP′.又∵OA=OB,OP=OP′,∴△AOP≌△BOP′.∴AP=BP′.(2)解:如图,连结OT,过点T作TH⊥OA于点H.∵AT与MN相切,∴∠ATO=90°.∴AT=OA2-OT2=102-62=8.∵12OA·TH=12AT·OT,即12×10×TH=12×8×6,∴TH=245,即点T到OA的距离为245.(3)10°,170°.16.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;(2)若AC=3,∠B=30°.①求⊙O的半径;②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).解:(1)直线BC与⊙O相切.理由如下:如图,连结OD,∵OA=OD,∴∠OAD=∠ODA,∵∠BAC的角平分线AD交BC边于点D,∴∠CAD=∠OAD,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.∴直线BC与⊙O相切.(2)①设OA=OD=r,∵在Rt△BDO中,∠B=30°,∴OB=2r,∴在Rt△ACB中,∠B=30°,∴AB=2AC=6,∴3r=6,解得r=2.②∵在Rt△ODB中,∠B=30°,∴∠BOD=60°,∴S扇形ODE=60π×22360=23π,∴阴影部分面积为S△BOD-S扇形ODE=23-23π.11。
2025年九年级中考数学复习专题六 圆
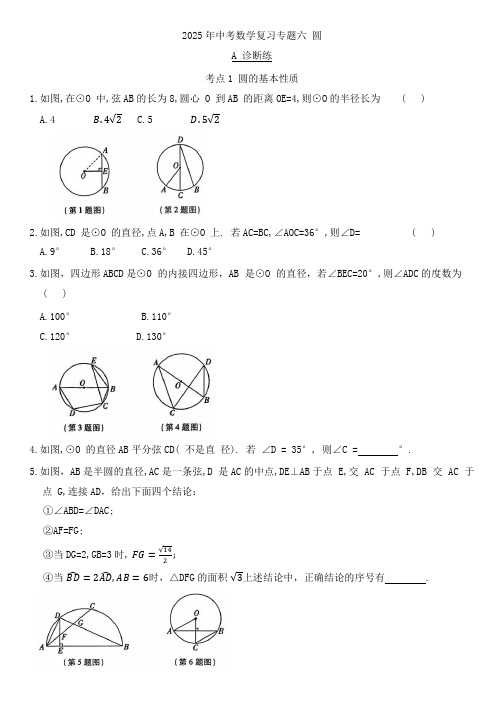
2025年中考数学复习专题六圆A 诊断练考点1 圆的基本性质1.如图,在⊙O 中,弦AB的长为8,圆心 O 到AB 的距离OE=4,则⊙O的半径长为 ( )A.4B.4√2C.5D.5√22.如图,CD 是⊙O 的直径,点A,B 在⊙O 上. 若AC=BC,∠AOC=36°,则∠D= ( )A.9°B.18°C.36°D.45°3.如图,四边形ABCD是⊙O 的内接四边形,AB 是⊙O 的直径,若∠BEC=20°,则∠ADC的度数为( )A.100°B.110°C.120°D.130°4.如图,⊙O 的直径AB平分弦CD( 不是直径). 若∠D = 35°, 则∠C =°.5.如图,AB是半圆的直径,AC是一条弦,D 是AC的中点,DE⊥AB于点 E,交 AC 于点 F,DB 交 AC 于点 G,连接AD,给出下面四个结论:①∠ABD=∠DAC;②AF=FG;;③当DG=2,GB=3时,FG=√142̂=2AD̂,AB=6时,△DFG的面积√3上述结论中,正确结论的序号有 .④当BD考点2 与圆有关的位置关系6.如图,⊙O 中,弦AB 的长为√3,点 C在⊙O 上,OC⊥AB,∠ABC30°.⊙O所在的平面内有一点 P,若OP=5,则点 P与⊙O 的位置关系是 ( )A.点 P在⊙O上B.点 P在⊙O内C.点P在⊙O外D.无法确定7.如图,以AB 为直径的⊙O与AC相切于点 A,以AC 为边作平行四边形ACDE,点 D,E 均在⊙O 上,DE 与AB交于点F,连接CE,与⊙O交于点 G,连接 DG. 若 AB = 10,DE = 8,则 AF = ,DG=.8.如图,⊙O 是△ABC的外接圆,D 是直径AB 上一点,∠ACD 的平分线交AB 于点E,交⊙O于另一点F,FA=FE.(1)求证:CD⊥AB;(2)设FM⊥AB,垂足为M.若OM=OE=1,求AC的长.9.如图,△ABC 内接于⊙O,AB=AC=10,过点A作AE∥BC,交⊙O 的直径 BD的延长线于点 E,连接CD.(1)求证:AE 是⊙O 的切线;,求 CD 和DE 的长.(2)若tan∠ABE=12考点3 与圆有关的计算10.两个半径相等的半圆按如图方式放置,半圆O'的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是 ( )A.43π−√3B.43πC.23π−√3D.43π−√3411.已知圆锥的底面圆半径为 4,母线长为 5,则圆锥的侧面积为 .12.铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,AB所在圆的圆心C恰好是△ABO 的内心,若.AB=2√3,则花窗的周长 ( 图中实线部分的长度 ) = .(结果保留π)B 考点突破练考点4 圆的基本性质基础考向1 弧、弦、圆心角的关系1.如图,AB是⊙O 的直径,BC=CD,∠COD=52°,,则∠AOD 的大小为 .2.如图,在⊙O中,AB̂=CD,有下列结论:①AB = CD;②AC = BD;③∠AOC=∠BOD;④AĈ=BD̂,其中正确的是 (填序号).考向2 垂径定理及其推论3.如图,OA,OB,OC都是⊙O的半径,AC,OB 交于点 D.若AD=CD=8,OD=6,则BD的长为 ( )A.5B.4C.3D.24.如图,⊙O 是一个盛有水的容器的横截面,⊙O的半径为10 cm,水的最深处到水面AB 的距离为4 cm,则水面AB的宽度为 cm.考向3 圆周角定理及其推论5.如图,在⊙O 中,弦AB,CD 相交于点 P,若∠A= 48°,∠APD=80°,则∠B的度数为( )A.32°B.42°C.48°D.52°6.如图,四边形 ABCD 内接于⊙O,AC,BD 为对角线,BD 经过圆心 O. 若∠BAC=40°,则∠DBC的度数为( )A.40°B.50°C.60°D.70°7.如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接AB,则∠BAD的度数为 .8.如图,AB 为⊙O 的直径,CD 为⊙O 的一条弦,∠BCD 的平分线交⊙O 于点E,AD,BE 的延长线交于点 F.(1)若∠BAD=70°,求∠ABE 的度数. (2)求证:AB=AF.考向4 圆内接四边形9.如图,圆内接四边形ABCD 中,∠BCD = 105°,连接 OB,OC,OD,BD,∠BOC=2∠COD.则∠CBD 的度数是( )A.25°B.30°C.35°D.40°10.如图,四边形ABCD 内接于⊙O,BC∥AD,AC⊥BD. 若∠AOD =120°,AD √3 则∠CAO 的度数与 BC 的长分别为 ( )A.10°,1B.10°, √2C.15°,1D.15°, √211.如图,四边形ABCD 内接于 ⊙O,点 E 在 CD 的延长线上. 若∠ADE=70°,则∠AOC= °.12.如图,四边形AB-CD 内接于 ⊙O,连接 AC,BD, ∠ABD =∠ADC,过点D 作DP∥AB,交⊙O 于点M,交BC 的延长线于点 P. (1)求证:BP=BD;诊断区检测区突破区,AB=10,求 CP 的长.(2)若cos∠ABD=2513.下列说法中正确的个数是 ( )①同圆或等圆中,同弧所对的圆周角相等;②在同圆或等圆中,同一条弦所对的圆周角相等;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦,并且平分弦所对的弧.A.1B.2C.3D.4提升1.如图,已知点A,B,C,D都在⊙O上,OB⊥AC,BC=CD,下列说法错误的是 ( )̂=BĈ B.∠AOD=3∠BOCA.ABC. AC=2CDD. OC⊥BD2.如图,在⊙O中,OA⊥BC,∠ADB=30°,BC=√3,则OC( )A.1B.2C.√3D.43.在半径为2的⊙O中,弦AB的长度为2,点C 为⊙O上异于A,B两点的一个动点,则∠BCA=°.,E,F 分别为AC,BC的中点,弦EF 分别4.如图,AB 为半圆O的直径,C为半圆上一点且sin∠CAB=35交AC,CB 于点 M,N. 若MN=3√2,则 AB =5.如图,OA,OB,OC都是⊙O 的半径,∠ACB=2∠BAC.(1)求证:∠AOB=2∠BOC;(2)若AB=4,BC=√5,求⊙O的半径.6.如图,以△ABC的边AC为直径作⊙O,交 BC 边于点 D,过点 C 作CE ∥AB 交⊙O 于点 E, 连接AD, DE,∠B=∠ADE.(1)求证:AC=BC;(2)若 tan B=2,CD=3,求AB 和DE 的长.7.如图,在扇形 AOB 中,OA=8,点 C 在半径 OA 上,将△BOC沿BC翻折,点 O 的对应点 D 恰好落在弧 AB 上,再将弧 AD 沿着 CD 翻折至弧A₁D(点A₁是点A的对应点),那么 OA₁的长为 .考点5 与圆有关的位置关系基础考向1 点、直线和圆的位置关系1.在同一平面内,已知⊙O的半径为2,圆心O到直线l的距离为3,点P为圆上的一个动点,则点P 到直线l的最大距离是 ( )A.2B.5C.6D.82.已知平面内有⊙O 和点A,B,若⊙O 的半径为3 cm,线段OA=4cm,OB=3cm,则直线AB与⊙O的位置关系为 ( )A.相离B.相交C.相切D.相交或相切3.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD 是AB 边上的高,AB=4,若圆C是以点 C 为圆心,2为半径的圆,那么下列说法正确的是 ( )A.点 D 在圆 C 上,点 A,B 均在圆C外B.点 D 在圆 C 内,点 A,B 均在圆C外C.点A,B,D 均在圆C外D.点A在圆C外,点D在圆C内,点B在圆C上考向2 切线的性质及判定4.如图,AC 是⊙O 的切线,B 为切点,连接OA,OC.若∠A=30°,AB=√3,BC=3则OC的长度是( )A,3 B.√3C√13 D.65.如图,AB 切⊙O 于点B,连接OA交⊙O 于点C,BD∥OA交⊙O 于点D.连接CD,若∠OCD=25°,则∠A的度数为( )A.25°B.35°C.40°D.45°̂上. 已知∠A = 50°, 6.如图,点 A 是⊙O 外一点,AB,AC分别与⊙O 相切于点 B,C,点 D 在BDC则∠D 的度数是 .7.如图,已知△ABC 内接于⊙O,CO 的延长线交AB 于点 D,交⊙O 于点E,交⊙O 的切线AF于点F,且AF∥BC.(1)求证:AO∥BE;(2)求证:AO 平分∠BAC.∠A,点O在BC上,以点O为圆心的8.如图,在△ABC 中,∠ACB=90°,点 D 是 AB 上一点,且∠BCD=12圆经过C,D两点.(1)试判断直线 AB 与⊙O 的位置关系,并说明理由;,⊙O的半径为3,求AC的长.(2)若sinB=35考向3 三角形的外接圆与内切圆9.如图,点O 是△ABC外接圆的圆心,点I 是△ABC 的内心,连接OB,IA.若∠CAI=35°,则∠OBC的度数为( )A.15°B.17.5°C.20°D.25°10.如图的方格纸中,每个方格的边长为1,A,O两点皆在格线的交点上.今在此方格纸格线的交点上另外找两点 B,C,使得△ABC 的外心为 O,求 BC 的长度()A.4B.5C.√10D.√2011.如图,⊙O是锐角三角形 ABC 的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为 D,E,F,连接 DE,EF,FD.若DE+DF=6.5,△ABC 的周长为21,则EF 的长为 ( )A.8B.4C.3.5D.312.如图,△ABC的内切圆⊙I与BC,CA,AB 分别相切于点 D,E,F,若⊙I的半径为r,∠A=α,则(BF+CE-BC)的值和∠FDE 的大小分别为 ( )A.2r,90°-αB.0,90°-αC.2r,90∘−α2D.0,90∘−α213.如图所示的网格由边长为1个单位长度的小正方形组成,点A,B,C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC 内心的坐标为 .14.在同一平面内,点P不在⊙O上,若点P到⊙O上的点的最大距离是11,最小距离是5,则⊙O的半径是 .提升1.已知点A在半径为3的圆O 上,如果点 A 到直线a 的距离是6,那么圆O与直线a的位置关系是( )A.相交B.相离C.相切D.以上答案都不对2.已知一个三角形的内心与外心重合,若它的内切圆的半径为2,则它的外接圆的面积为 ( )A.4πB.8πC.12πD.16π3.如图,在四边形AB-CD中,AB∥CD,AD⊥AB,以 D 为圆心,AD 为半径的弧恰好与 BC 相切,切点为E.若ABCD =13,则 sin C的值 ( )A 23 c 344.如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD 是矩形.当餐盘正立且紧靠支架于点A ,D 时,恰好与 BC 边相切,则此餐盘的半径等于 cm.5.如图,在平面直角坐标系中,已知点A(1,0),P(-1,0),⊙P 过原点O ,且与x 轴交于另一点D ,AB 为⊙P 的切线,B 为切点,BC 是⊙P 的直径,则∠BCD 的度数为 °.6.如图,在△ABC 中,AB=BC,以BC 为直径作⊙O 与AC 交于点D,过点 D 作DE⊥AB,交CB 延长线于点 F,垂足为点 E.(1)求证:DF 为⊙O 的切线;(2)若 BE =3,cosC =45,求 BF 的长.B.√53D.√747.如图,分别过矩形ABCD的四个顶点作其内部的⊙O 的切线,切点分别为E,F,G,H,若AE = a,BF = b, DH = c, 则 CG 的长为 .(用含a,b,c的代数式表示)考点6 与圆有关的计算基础考向1 圆内接正多边形的计算1.如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠BAE-∠COD= ( )A.60°B.54°C.48°D.36°2.如图,点 P₁~P₈是⊙O 的八等分点.若△P₁P₃P₇,四边形 P₃P₄P₆P₇的周长分别为a,b,则下列正确的是( )A. a<bB. a=bC. a>bD. a,b大小无法比较考向2 弧长与扇形面积的计算3.圆心角为90°,半径为3的扇形弧长为 ( )A.2πB.3π C32D.12π4.“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC 的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于 ( )A.πB.3πC.2πD.2π−√35.马面裙(图(1)),又名“马面褶裙”,是我国古代女子穿着的主要裙式之一.将图(1)中的马面裙抽象成数学图形,如图(2)中的阴影部分所示,AD 和BC所在圆的圆心均为点O,且点A在 OB 上,点 D 在 OC 上,若OA=AB=6 dm,OA⊥OD,则该马面裙裙面(图(2)中阴影部分)的面积为 ( )A.36πdm²B.27πdm²C.18πdm²D.12πdm²6.如图,在矩形ABCD中,AB=3,BC=6,E为BC的中点,连接AE,DE.以E为圆心,EB 长为半径画弧,分别与AE,DE交于点M,N,则图中阴影部分的面积和是 (结果保留π).考向3 圆锥的有关计算7.如图,用圆心角为120°半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是.8.如图,小珍同学用半径为8cm ,圆心角为 100°的扇形纸片,制作一个底面半径为2cm 的圆锥侧面,则圆锥上粘贴部分的面积是 cm².9.如图,圆锥形烟囱帽的底面半径为30cm ,母线长为50cm ,则烟囱帽的侧面积为 cm².(结果保留π)10.如图,在△ABC 中,AC=3,AB=4,BC 边上的高AD=2,将△ABC 绕着BC 所在的直线旋转一周得到的几何体的表面积为 .考向4 与圆有关的阴影部分面积11.如图,在△ABC 中,∠ABC=90°,∠ACB=30°,AB=4,点O 为BC 的中点,以O 为圆心,OB 长为半径作半圆,交AC 于点 D ,则图中阴影部分的面积是( )A.5√3−√33π B.5√3−4πC.5√3−2πD.10√3−2π12.如图,矩形ABCD 内接于⊙O,分别以AB,BC,CD,AD 为直径向外作半圆.若AB=4,BC=5,则阴影部分的面积是 ( )检测区突破区A.414π−20B.412π−20C.20πD.2013.如图,Rt△BCO中,∠BCO=90°,∠CBO=30°,BO=4cm,将△BCO绕点 O逆时针旋转至△B'C'O,点 C'恰好落在 BO 延长线上,则边 BC 扫过区域(图中阴影部分)的面积为 ( )A.πcm²B.(π+√3)cm2C.4πcm²D.(4π+√3)cm214.如图,点B在半圆O 上,直径AC=12,∠BAC=40°,则图中阴影部分的面积为(结果保留π).15.如图,△ABC的周长为20,⊙O 的半径为1,⊙O从与AB 相切的切点D的位置出发,在△ABC外部,按顺时针方向沿三角形的边无滑动滚动,当滚动一周又回到点 D 的位置时,⊙O的圆心O运动的长度 (填“>”“=”或“<”)三角形的周长,运动长度为 .提升1.如图,正六边形AB-CDEF内接于⊙O,点P在AB上,点Q是DÊ的中点,则∠CPQ的度数为 ( ) A.30° B.45° C.36° D.60°2.如图,正六边形AB-CDEF的外接圆⊙O 的半径为2,过圆心 O 的两条直线l₁,l₂的夹角为60°,则图中的阴影部分的面积为 ( )A.43π−√3B.43π−√32C.23π−√3D.23π−√323.如图,已知点 C 为圆锥母线 SB 的中点,AB 为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从A 点爬到C 点,则蚂蚁爬行的最短路程为 ( )A.5B.√3C.3√2D.2√34.如图,在▱ABCD中,AB=√3+1,BC=2,AH⊥CD,垂足为H,AH=√3.以点 A 为圆心,AH 长为半径画弧,AB,AC,AD 分别交于点E,F,G.若用扇形AEF围成一个圆锥的侧面,记这个圆锥底面圆的半径为r₁;用扇形AHG 围成另一个圆锥的侧面,记这个圆锥底面圆的半径为r₂,则r₁−r₂=.(结果保留根号) 5.如图,在△ABC 中,AB=4,∠C=64°,以AB 为直径的⊙O 与AC 相交于点 D,E 为ABD̂上一点,且∠ADE=40°.(1)求BÊ的长;(2)若∠EAD=76°, 求证:CB为⊙O 的切线.6.将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图(1),正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图(2),其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图(2)中(1)∠α= 度;(2)中间正六边形的中心到直线l的距离为 (结果保留根号).C 检测验收练一、选择题(每小题5分,共20分)1.如图,AB是⊙O 的直径,∠E=35°,则∠BOD= ( )A.80°B.100°C.120°D.110°2.数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是在工件圆弧上任取两点A,B,连接AB,作AB 的垂直平分线 CD 交AB于点D,交AB 于点 C,测出AB=40 cm, CD=10cm,则圆形工件的半径为 ( )A.50cmB.35 cmC.25 cmD.20cm3.刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式. 如图,Rt△ABC 中,∠C =90°, AB,BC,CA 的长分别为c,a,b.则可以用含c,a,b的式子表示出△ABC 的内切圆直径d,下列表达式错误的是 ( )A. d=a+b-cB.d=2aba+b+cC.d=√2(c−a)(c−b)̅̅̅̅̅̅̅̅̅ D. d=|(a-b)(c-b)|4.如图,两个半径长均为 1 的直角扇形的圆心分别在对方的圆弧上,扇形 CFD 的圆心 C 是弧 AB的中点,且扇形 CFD 绕着点 C 旋转,半径 AE,CF交于点G,半径BE,CD交于点 H,则图中阴影部分的面积等于 ( )A.π2−1B.π2−12C.π-1D.π-2二、填空题(每小题5分,共30分)5.如图,AB 是圆的直径,∠1,∠2,∠3,∠4的顶点均在 AB上方的圆弧上,∠1,∠4的一边分别经过点A,B,则∠1+∠2+∠3+∠4=°.6.如图,四边形ABCD是⊙O 的内接四边形,点O 在四边形ABCD内部,过点C作⊙O 的切线交AB的延长线于点P,连接 OA,OB. 若∠AOB = 140°,∠BCP =35°,则∠ADC 的度数为 .7.[2024 浙江杭州校级二模]如图,正六边形AB-CDEF与正方形AGDH都内接于⊙O,则劣弧BG 所对圆周角的度数为 .8.如图,△ABC 内接于⊙O,点 O 在AB上,AD 平分∠BAC 交⊙O 于D,连接BD.若AB=10,BD=√5,则BC的长为 .9.如图,在边长为6的正六边形 ABCDEF中,以点 F为圆心,以 FB 的长为半径作BD,剪下图中阴影部分做一个圆锥的侧面,则这.个圆锥的底面半径为 .̂的圆心10.如图,四边形ABCD 是正方形,曲线DA₁B₁C₁D₁A₂B₂…叫做“正方形的渐开线”,其中DA1为点A,半径为AD;A₁B₁的圆心为点B,半径为BA₁;B₁C₁的圆心为点C,半径为(CB₁;C₁D₁的圆心为点 D,半径为DC₁;……,DA₁,A₁B₁,B₁C₁,C₁D₁,…I的圆心依次按A,B,C,D 的顺序循环,当AB=1时,的长是 .三、解答题(11 题 10 分,12 题 12 分, 13 题13分,14题15分,共50分)11.日晷仪也称日晷,是观测日影计时的仪器,主要根据日影的位置,以指定当时的时辰或刻数,是我国古代较为普遍使用的计时仪器,如图(1)所示. 小东为了探究日晷的奥秘,在不同时刻对日晷进行了观察探究.(1)探究1:如图(2),日晷的平面是以点O为圆心的圆,直线l是日晷的底座,OA⊥l于点A,与⊙O交于点B,点P在⊙O 上,OP 为某一时刻晷针的影长,PB的延长线与直线l交于点 C.连接A P,当AP=AC时,求证:AP与⊙O相切.(2)探究2:当小东观察到影长OP 落在图(3)所示位置时,连接AP,交⊙O 于点D,若∠POD=90∘,OA=√10,AD=√2,求⊙O的半径.12.已知△AOB 中,∠ABO =30°,AB为⊙O 的弦,直线MN与⊙O 相切于点 C.(1)如图(1),若AB∥MN,直径 CE 与 AB 相交于点 D,求∠AOB 和∠BCE的大小;(2)如图(2),若OB∥MN,CG⊥AB,垂足为G,CG与OB 相交于点 F,OA=3,求线段 OF的长.13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点 D,交AC于点 E,过点 D 作DF⊥AC 于点 F,FD 的延长线交AB 的延长线于点 G.(1)若AB=10,BC=12,求△DFC的面积;(2)若 tan C=2,AE=6,求 BG的长.14.如图(1),O 是正方形ABCD对角线上一点,以O为圆心,OC长为半径的⊙O 与AD 相切于点E,与AC 相交于点 F.(1)求证:AB 与⊙O 相切;(2)若正方形ABCD 的边长为√2+1,求⊙O的半径;̂于点 N.(3)如图(2),在(2)的条件下,若点 M是半径OC 上的一个动点,过点 M 作MN⊥OC 交CE当CM:FM=1:4时,求CN的长.。
中考数学复习《圆》专题训练-带有参考答案

中考数学复习《圆》专题训练-带有参考答案一、选择题1.已知⊙O 的半径是3cm ,则⊙O 中最长的弦长是( )A .3cmB .6cmC .1.5cmD .√3cm2.如图,AB 是⊙O 的直径,C 、D 在⊙O 上∠CAB =20°,则∠ADC 等于( )A .70°B .110°C .140°D .160°3.如图,AB 是⊙O 的直径,过点A 作⊙O 的切线AC ,连接BC ,与⊙O 交于点D ,E 是⊙O 上一点,连接AE ,DE .若∠C =48°,则∠AED 的度数为( )A .42°B .48°C .32°D .38°4.如图,线段AB 经过⊙O 的圆心,AC ,BD 分别与⊙O 相切于点C ,D .若AC =BD =2√3,∠A =30°,则CD⌢的长度为( )A .πB .23πC .√23πD .2π5.如图,⊙O 的半径为9,PA 、PB 分别切⊙O 于点A ,B 若P =60∘,则AB⌢的长为( )A .133πB .136πC .6πD .52π⌢的中点,点E是BC⌢上的一点,若∠ADC=110°,则∠DEC 6.如图,四边形ABCD是⊙O的内接四边形,点D是AC的度数是()A.35°B.45°C.50°D.55°7.如图,正六边形ABCDEF内接于00,若0 O的周长等于6π,则正六边形的边长为()A.√3B.3 C.2√3D.√68.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为()A.2πB.2√2C.2π−4D.2π−2√2二、填空题9.如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD= °.10.如图,等边三角形ABC内接于⊙O,BD为内接正十二边形的一边,CD=5√2cm,则⊙O的半径R为11.如图,秋千拉绳长3m,静止时踩板离地面(CD)0.5m.一名小朋友荡秋千时,秋千在最高处时踩板离地面(BE)2m(左右对称),则该秋千从B荡到A经过的圆弧长为m.12.如图,已知⊙O上三点A,B,C,切线PA交OC延长线于点P,若OP=2OC,则∠ABC=.13.如图,一个扇形纸片的圆心角为90°,半径为6,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,则阴影部分的面积为.三、解答题14.如图.为的直径,连接,点E在上,AB=BE.求证:(1)平分;(2).15.如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,点C在⊙O上,连接OA,OC,AC.(1)求证:∠AOC=2∠PAC;(2)连接OB,若AC//OB,⊙O的半径为5,AC=6,求AP的长.16.如图,AB是⊙O的直径,BC是⊙O的弦,AE⊥OC于点D,交BC于F,与过点B的直线交于点E,且BE=EF.(1)求证:BE是⊙O的切线;(2)若⊙O的半径为10,OD=6求BE的长.17.如图,⊙O是△ABC的外接圆,直径BD与AC交于点E,过点D作⊙O的切线,与BC的延长线交于点F.(1)求证:∠F=∠BAC;(2)若DF∥AC,若AB=8,CF=2求AC的长.18.如图,在中,AB=AC以为直径的分别与、相交于点D、E,连接过点作,垂足为点(1)求证:是的切线;(2)若的半径为4,求图中阴影部分的面积.参考答案1.B2.B3.A4.B5.C6.A7.B8.C9.4010.511.2π12.30°13.9√3−3π14.(1)证明:∵∴∴∴平分(2)证明:∵∠BAD=∠DAC∴∴由(1)知∴∴∠ABC=∠ECB∴AB∥CE.15.(1)证明:过O作OH⊥AC于H∴∠OHA=90°∴∠AOH+∠OAC=90°∵PA是⊙O的切线∴∠OAP=90°∴∠OAC+∠PAC=90°∴∠AOH=PAC∵OA=OC∴∠AOC=2∠AOH∴∠AOC=2∠PAC;(2)解:连接OB,延长AC交PB于E∵PA,PB是⊙O的切线∴OB⊥PB,PA=PB∵AC//OB∴AC⊥PB∴四边形OBEH是矩形∴OH=BE,HE=OB=5∵OH⊥AC,OA=OC∴AH=CH=12AC=3∴OH=√OC2−CH2=4∴BE=OH=4,AE=AH+HE=8∵PA2=AE2+PE2∴PA2=82+(PA−4)2∴PA=10.16.(1)证明:∵BE=EF∴∠EBF=∠EFB∵∠CFD=∠EFB∴∠EBF=∠CFD∵OC=OB∴∠OCB=∠OBC∵AE⊥OC∴∠OCB+∠CFD=90°∴∠OBC+∠EBF=90°=∠ABE∴AB⊥BE∵AB是⊙O的直径∴BE是⊙O的切线;(2)解:∵⊙O的半径为10∴OA=OB=OC=10∴AB=20∵AE⊥OC∴∠ADO=90°∴在Rt△ADO中AD=√AO2−DO2∵OD=6∴AD=√AO2−DO2=√102−62=8∵结合(1),可知∠ABE=∠ADO=90°,∠BAE=∠DAO ∴△ADO∽△ABE∴BEAB =DOAD,即BE=DOAD×AB∵AD=8,AB=20,DO=6∴BE=DOAD ×AB=68×20=15即所求的值为15.17.(1)证明:∵DF是⊙O的切线∴OD⊥DF∴∠ODF=90°∴∠F+∠DBC=90°∵BD是⊙O的直径∴∠BAD=90°∴∠BAC+∠DAC=90°∵∠DBC=∠DAC∴∠F=∠BAC;(2)解:连接CD∵DF∥AC,∠ODF=90°∴∠BEC=∠ODF=90°∴直径BD⊥AC于E∴AE=CE=12AC∴AB=BC=8∵BD是⊙O的直径∴∠BCD=90°∴∠DBC+∠BDC=90°∵∠DBC+∠F=90°∴∠BDC=∠F∵∠BCD=∠FCD=90°∴△BCD∽△DCF∴BCDC =DCCF,即8DC=DC2∴DC=4∴BD=√BC2+CD2=√82+42=4√5∵在△BCD中SΔBCD=12BC⋅CD=12BD⋅CE∴12×8×4=12×4√5⋅CE∴CE=85√5∴AC=2CE=165√5.18.(1)证明:连接.是的直径.又AB=AC∴D是BC的中点.连接;由中位线定理,知又.是的切线;(2)解:连接的半径为。
九年级中考数学考点分类复习——圆

中考数学考点分类复习——圆一、选择题1.下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等.其中是真命题的是()A.①②B.②③C.①③D.①②③2.已知⊙O的半径为5,圆心O到点P的距离为4,则点P与⊙O的位置关系是( )A.点P在⊙O内B.点P的⊙O上C.点P在⊙O外D.点P在⊙O上或⊙O外3.如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )A.18° B.36° C.54° D.72°4.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )A. 2B.22-2C.2- 2D.2-15.如图,PA,PB为⊙O的切线,A,B分别为切点,∠APB=60∘,点P到圆心O的距离OP=2,则⊙O的半径为( )A.12B.1 C.32D.26.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C.若∠ABO=20°,则∠C 的度数是( )A.70°B.50°C.45°D.20°7.如图,有一半径是1米的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形,用此扇形铁皮围成一个圆锥,该圆锥的底面圆的半径长为( )A.2米B.22米 C.24米 D.28米8. 如图,△ABC是☉O的内接三角形,下列选项中,能使过点A的直线EF与☉O相切于点A的条件是()A.∠EAB=∠CB.∠B=90∘C.EF⊥ACD.AC是☉O的直径9.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )A.10B.8 2C.413D.24110.如图,P 是⊙O 外一点,PA 、PB 分别和⊙O 切于A 、B 两点,C 是AB ︵上任意一点,过C作⊙O 的切线分别交PA 、PB 于D 、E .若△PDE 的周长为12,则PA 的长为( )A .12B .6C .8D .411.如图,AB 与⊙O 相切于点C ,OA =OB ,⊙O 的直径为6 cm ,AB =6 3 cm ,则阴影部分的面积为( )A.()93-π cm 2B.()93-2π cm 2C.()93-3π cm 2D.()93-4π cm 212. 一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )A.①B.③C.②D.④13.如图,已知⊙O 的半径是2,点A ,B ,C 在⊙O 上,若四边形OABC 为菱形,则图中阴影部分面积为( )A.23π-2 3B.23π- 3C.43π-2 3D.43π- 3 14. 如图,直线l 1 // l 2,⊙O 与l 1和l 2分别相切于点A 和点B .点M 和点N 分别是l 1和l 2上的动点,MN 沿l 1和l 2平移.⊙O 的半径为1,∠1=60∘.下列结论错误的是( )A.MN =4√33B.l 1和l 2的距离为2C.若∠MON =90∘,则MN 与⊙O 相切D.若MN 与⊙O 相切,则AM =√315.如图,⊙O 的半径为3,四边形ABCD 内接于⊙O ,连接OB ,OD.若∠BOD =∠BCD ,则BD ︵的长为( )A.πB.32π C.2π D.3π 二.填空题16.在Rt △ABC 中,∠C =90°,CA =8,CB =6,则△ABC 内切圆的周长为______.17. △ABC 中,∠C =90∘,AB =4cm ,BC =2cm ,以点A 为圆心,以3.4cm 的长为半径画圆,则点C 在⊙O ________,点B 在⊙O ________.18.扇形的半径是9 cm ,弧长是3π cm ,则此扇形的圆心角为 度.19.如图,已知⊙O 的半径为2,△ABC 内接于⊙O ,∠ACB =135°,则AB =______.20.如图,正六边形ABCDEF 内接于⊙O ,则∠ADF 的度数为 .21.如图,在圆O 中,AB 为直径,AD 为弦,过点B 的切线与AD 的延长线交于点C ,AD =DC ,则∠C =______度.22.如图,PA ,PB 分别与⊙O 相切于点A ,B ,⊙O 的切线EF 分别交PA ,PB 于点E ,F ,切点C 在AB ︵上.若PA 的长为2,则△PEF 的周长是 .23.如图,点A ,B ,C 均在6×6的正方形网格格点上,过A ,B ,C 三点的外接圆除经过A ,B ,C 三点外还能经过的格点数为 .24.如图,AB 是⊙O 的直径,点C 在⊙O 上,过点C 的切线与BA 的延长线交于点D ,点E 在弧BC 上(不与点B 、C 重合),连结BE 、CE .若∠D =40°,则∠BEC =_______度.25.如图,在平面直角坐标系中有一正方形AOBC ,反比例函数y =k x经过正方形AOBC 对角线的交点,半径为6-32的圆内切于△ABC ,则k 的值为 .26. 如图,与相切,切点为,交于点,点是优弧上一点,若,则的度数为________.27. 如图,在⊙O 中,弦AB 、CD 相交于点E ,∠BDC =45∘,∠BED =95∘,则∠C 的度数为________度.28.如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F .已知∠A =110°,∠C =30°,则∠DFE 的度数是______.29. 如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为√2,则BF的长为________.30. 如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧DE交AB于E点,若AB=8cm,则图中阴影部分的面积为________cm2.(取准确值)三、解答题31.如图所示,CD是△ABC的中线,AB=2CD,∠B=60∘.求证:△ABC的外接圆的半径为CB.32. 如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36∘,求∠COD的度数.33.如图,在△ABC中,以AC为直径的⊙O分别交AB,BC于点D,E,连接DE,AD=BD,∠ADE=120°.(1)试判断△ABC的形状,并说明理由;(2)若AC=2,求图中阴影部分的面积.34.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.(1)求证:CB∥PD;(2)若BC=3,sin∠BPD=35,求⊙O的直径.35.如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,DE⊥AC,垂足为E.(1)判断DE与⊙O的位置关系,并证明你的结论;(2)如果⊙O的直径为9,cos B=13,求DE的长36.如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A 点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于点G.(1)求证:EF是⊙O的切线;(2)求AE的长.37.如图, Rt △ABC 中,∠ABC=90°,以AB 为直径的⊙O 交AC 于点D ,过点D 的切线交BC 于E .(1)求证:12DE BC =;(2)若tanC=25,DE=2,求AD 的长.38.已知,在四边形ABCD 中,E 是对角线AC 上一点,ED =EC ,以AE 为直径的⊙O 与边CD 相切于D , 点B 在⊙O 上,连结OB .(1)求证:DE =OE ;(2)若AB ∥CD ,求证:四边形ABCD 是菱形.39.如图,在ABC ∆中,AB AC =,以AB 为直径作O 交BC 于点D ,过点D 作O 的切线DE 交AC 于点E ,交AB 延长线于点F .(1)求证:DE AC ⊥;(2)若10,8AB AE ==,求BF 的长.40. 如图,正六边形ABCDEF 内接于⊙O ,BE 是⊙O 的直径,连接BF ,延长BA ,过F 作FG ⊥BA ,垂足为G .(1)求证:FG 是⊙O 的切线;(2)已知FG =2√3,求图中阴影部分的面积.41.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,点P 在⊙O 上,PB 与CD 交于点F ,∠PBC=∠C .(1)求证:CB ∥PD ;(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.42.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△PBD∽△DCA;(3)当AB=6,AC=8时,求线段PB的长.AH ,以点O为圆心,OA的长为半径作⊙O,过43.如图,点O是线段AH上一点,3点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作ABCD.(1)求证:AD 是⊙O 的切线;(2)若13OH AH =,求四边形AHCD 与⊙O 重叠部分的面积; (3)若13NH AH =,54BN =,连接MN ,求OH 和MN 的长.44.已知ABC 内接于O ,BAC ∠的平分线交O 于点D ,连接DB ,DC .(1)如图①,当120BAC ∠=时,请直接写出线段AB ,AC ,AD 之间满足的等量关系式: ;(2)如图②,当90BAC ∠=时,试探究线段AB ,AC ,AD 之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求AD AB AC+ 的值.。
2023年春九年级数学中考复习《圆综合压轴解答题》专题提升训练(附答案)

2023年春九年级数学中考复习《圆综合压轴解答题》专题提升训练(附答案)1.如图,已知四边形ACBD内接于⊙O,AB是⊙O的直径,AB=10,点D是半圆的中点,连接CD,点I是CD上一点,且DI=DB.(1)求证:点I是△ABC的内心;(2)若BC=6,求△BIC的面积;(3)随着点C的变化,点I的位置也发生改变,请探求CI长度的取值范围.2.如图,在△ABC中,AB=4,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作⊙O的切线DH交AC于点H,且DH⊥AC,连接DE与AB交于点G.(1)求证:AB=AC;(2)填空:①当BD=时,四边形EODA为菱形;②若∠EGA=∠EAG,则GO 的长为.3.如图,AB是⊙O的直径,点D在⊙O上,连接AD并延长至点C,连接BC交⊙O于点E,AB=BC=10,AC=12,过点D作DF⊥BC于点F.(1)求证:直线DF是⊙O的切线;(2)连接DE,设△CDE的面积为S1,四边形ADEB的面积为S2,求的值;(3)点P在上,且的长为,点Q为线段BD上一动点,连接PQ,求的最小值.4.(1)如图①,在△ABC中,∠BAC=90°,AB=4,AC=3,若AD平分∠BAC交CB于点D,那么点D到AC的距离为;(2)如图②,四边形ABCD内接于⊙O,AC为直径,点B是半圆AC的三等分点(弧AB<弧BC),连接BD,若BD平分∠ABC,且BD=8,求四边形ABCD的面积.(3)如图③,有一块半径为1的⊙O,若⊙O的内接四边形ABCD满足∠ABC=60°,AB=AD,且AD+DC=2,求AB的长.5.如图1,△ABC内接于⊙O,弦AE交BC于点D,连接BO,且∠ABO=∠DAC.(1)求证:AE⊥BC;(2)如图2,点F在弧AC上,连接CF、BF,BF交AE于点M,若∠ACF=∠OBC,求证:MD=ED;(3)如图3,在(2)的条件下,∠BFC=3∠EAC,若BM=,AM=3时,求弦CF 的长.6.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,连接BO并延长交边AC于点D.(1)如图1,求证:∠BAC=2∠ABD;(2)如图2,过点B作BH⊥AC于点H,延长BH交⊙O于点G,连接OC,CG,OC 交BG于点F,求证:BF=2HG;(3)如图3,在(2)的条件下,若AD=2,CD=3,求线段BF的长.7.如图,等边△ABC内接于⊙O,点D是弧AC上一点,连接BD交AC于E.(1)如图1,求证∠ADB=∠CDB;(2)如图2,点F为线段BD上一点,连接CF,若∠BCF=2∠ABD时,求证:BF=DE+AD;(3)在(2)的条件下,作∠BCF的平分线交⊙O于M,在CM上取点R,连接AR交CF于点T,若TR=1,MR=5,∠CAT=3∠ACD,求AT的长.8.如图,在△ABC中,∠C=90°,AC=BC=2.(1)若点D、E、F分别在AB,AC,BC边上(如图1),连接DE,DF,EF,且∠EDF =90°,DE=DF.①四边形DECF的四个顶点是否在同一个圆上,并说明你的理由;②EF最小值为;四边形CEDF的面积是;(请直接写出答案)③点C到线段EF的最大距离为;(请直接写出答案)(2)若点D、E、F分别在AC,BC,AB边上(如图2),连接DE,DF,EF,且∠EDF =90°,DE=DF,求EF的最小值.9.已知,△ABC内接于⊙O,AD⊥BC于点G,连接AO.(1)如图1,求证:∠BAO=∠CAD;(2)如图2,过点O作ON⊥BC于N,过点B作BH⊥AC于H,交AD于点E,交⊙O 于点F,求证:AE=2ON;(3)如图3,在(2)的条件下,直线OE交AB于点P,交AC于点Q,若HC:EF=:2,BP=11,CQ=2,求线段AD的长.10.(1)如图1,P是半径为5的⊙O上一点,直线l与⊙O交于A、B两点,AB=8,则点P到直线l的距离的最大值为.问题探究:(2)如图2,在等腰△ABC中,BA=BC,∠ABC=45°,F是高AD和高BE的交点,求S△ABF:S△BFD的值.问题解决:(3)如图3,四边形ABCD是某区的一处景观示意图,AD∥BC,∠ABC=60°,∠BCD =90°,AB=60m,BC=80m,M是AB上一点,且AM=20m.按设计师要求,需在四边形区域内确定一个点N,修建花坛△AMN和草坪△BCN,且需DN=25m.已知花坛的造价是每平米400元,草坪的造价是每平米200元,请帮设计师算算修好花坛和草坪预算最少需要多少元?11.如图,AB是⊙O的直径,P为AB上一点,弦CD与弦EF交于点P,PB平分∠DPF,连DF交AB于点G.(1)求证:CD=EF;(2)若∠DPF=60°,PE:PF=1:3,AB=2,求OG的长.12.已知⊙O是△ABC的外接圆,BC为⊙O的直径,弧AB上一点D满足DB=DA,连结CD交AB于点E.(1)求∠AED+∠ABC的值.(2)求证:AC•BC=CE•CD;(3)连接OE,若∠BOE=∠BEO,求△BEO与△BED的面积比.13.【基础巩固】(1)如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE∼△BCF;【尝试应用】(2)如图2,AB是半圆⊙O的直径,弦长AC=BC=4,E,F分别是AC,AB上的一点,∠CFE=45°,若设AE=y,BF=x,求出y与x的函数关系及y的最大值.【拓展提高】(3)已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上.如图3,如果AD:BD=1:2,求CE:CF的值.14.如图1,▱ABCD为⊙O的内接四边形,已知,以A为顶点作∠P AZ=45°,交BC于P,交CD于Z.(1)求证:四边形ABCD为正方形;(2)若BC=4BP,求DZ:CZ的值;(3)如图2,过P作PQ⊥AD于Q,过Z作ZX⊥AB于X,交PQ于Y.若,求四边形ZYPC的面积.15.如图1,在Rt△ABC中,∠C=90°,AC=16cm,AB=20cm,动点D由点C向点A 以每秒1cm速度在边AC上运动,动点E由点C向点B以每秒cm速度在边BC上运动,若点D、点E从点C同时出发,运动t秒(t>0),联结DE.(1)求证:△DCE∽△BCA;(2)如图2,设经过点D、C、E三点的圆为⊙P;①当⊙P与边AB相切时,求t的值;②在点D、点E运动过程中,若⊙P与边AB交于点F、G(点F在点G左侧,如图3),联结CP并延长交边AB于点M,连接PF,当△PFM与△CDE相似时,求CE的长.16.问题解决:(1)如图①,半圆O的直径AB=6,点P是半圆O上的一个动点,则△P AB的面积最大值是.(2)如图②,在扇形OAB中,∠AOB=90°,OA=6,点C、D分别在OA和OB上,且AC=2,D是OB的中点,点E在弧AB上.连接CE、DE,四边形CODE的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.(3)如图③,四边形ABCD中,AB=AD=6,∠BAD=60°,∠BCD=120°,四边形ABCD的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.17.给出定义:有两个内角分别是它们对角的两倍的四边形叫做倍对角四边形.(1)如图1,在倍对角四边形ABCD中,∠D=2∠B,∠A=2∠C,求∠B与∠C的度数之和;(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO,∠OBA 的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.求证:四边形DBCF是倍对角四边形;(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当4DH=3BG时,求△BGH与△ABC的面积之比.18.【概念提出】圆心到弦的距离叫作该弦的弦心距.【数学理解】如图①,在⊙O中,AB是弦,OP⊥AB,垂足为P,则OP的长是弦AB的弦心距.(1)若⊙O的半径为5,OP的长为3,则AB的长为.(2)若⊙O的半径确定,下列关于AB的长随着OP的长的变化而变化的结论:①AB的长随着OP的长的增大而增大;②AB的长随着OP的长的增大而减小;③AB的长随着OP的长的确定而确定;④AB的长与OP的长无关.其中所有正确结论的序号是.【问题解决】如图②,已知线段EF,MN,点Q是⊙O内一定点.(3)用直尺和圆规过点Q作弦AB,满足AB=EF;(保留作图痕迹,不写作法)(4)若弦AB,CD都过点Q,AB+CD=MN,且AB⊥CD.设⊙O的半径为r,OQ的长为d,MN的长为l.①求AB,CD的长(用含r,d,l的代数式表示);②写出作AB,CD的思路.19.阅读,然后解答问题:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.(1)根据“奇异三角形”的定义,请你证明:“三边分别为3,,5的三角形是奇异三角形;(2)在Rt△ABC中,AB=c,AC=b,BC=1,且c>b>1,若Rt△ABC是奇异三角形,求b和c;(3)如图,AB是⊙的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.①求证:△ACE是奇异三角形;②当△ACE是直角三角形时,求∠AOC的度数.20.问题情境:如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则P A是点P 到⊙O上的点的最短距离.(1)探究证明:如图2,在⊙O上任取一点C(不与点A,B重合),连接PC,OC.求证:P A<PC.(2)直接应用:如图3,在Rt△ABC中,∠ACB=90°,AC=BC=3,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是.(3)构造运用:如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A1MN,连接A1B,则A1B 长度的最小值为.(4)综合应用:如图5,平面直角坐标系中,分别以点A(﹣2,3),B(4,5)为圆心,以1,2为半径作⊙A,⊙B,M,N分别是⊙A,⊙B上的动点,P为x轴上的动点,直接写出PM+PN的最小值为.参考答案1.(1)如图1,证明:∵点D是半圆的中点,∴∠ACD=∠ABD=∠BCD=∠DAB,∵DI=DB.∴∠DIB=∠DBI,∴∠DCB+∠CBI=∠ABD+∠ABI,∴∠CBI=∠ABI,∴点I是△ABC的内心;(2)如图2,作AE⊥CD于E,∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,∴∠ACD=∠ABD=∠BCD=∠DAB=45°,在Rt△ABC中,BC=6,AB=10,∴AC=8,在Rt△ACE中,AE=CE=AC=4,在Rt△ADE中,AE=4,BD=AD==5,∴DE=3,∴CD=CE+DE=7,∵DI=BI=5,∴CI=2,作IJ⊥BC于J,∴IJ=CI=2,∴S△BIC===6;(3)如图3,∵DI=BD=5,∴I在以D为圆心,5为半径的圆上一段弧上运动,作⊙O的直径DC′与⊙D交于点I′,当C与C′重合,I与I′重合时,IC最大,C′I′=10﹣5,∴0<CI≤10﹣52.(1)证明:连接OD,∵DH为⊙O的切线,D为切点,∴OD⊥DH,∵DH⊥AC,∴∠ODH=∠DHC=90°,∴OD∥AC,∴∠ODB=∠C,∵OB=OD,∴∠OBD=∠ODB,∴∠OBD=∠C,∴AB=AC;(2)解:①如图,连接AD、OD、EO,∵四边形EODA为菱形,∴AD=OD=AB=2,∵AB为⊙O的直径,∴∠ADB=90°,∴BD=,故答案为:2;②∵∠EGA=∠EAG,∴∠EAG=∠OGD,∵AE∥OD,∴∠CED=∠ODE,∠EAG=∠AOD,∴∠OGD=∠GOD,∴OD=DG,∵∠B=∠AED,∴∠ODE=∠B,又∵∠OGD=∠DGB,∴△OGD∽△DGB,设OG=x,∴,∴,∵x>0,∴x=﹣1,∴OG=﹣1,故答案为:﹣1.3.(1)证明:连接OD,∵AO=OD,∴∠OAD=∠ODA,∵AB=BC,∴∠OAD=∠C.∴OD∥BC,∵DF⊥BC,∴DF⊥OD,∵OD是⊙O的半径,∴直线DF是⊙O的切线;(2)解:∵AB是⊙O的直径,∴∠ADB=90°,∵AB=BC,∴AD=DC=6,∵四边形ADEB是⊙O的内接四边形,∴∠ADE+∠ABE=180°,∵∠ADE+∠CDE=180°,∴∠CDE=∠ABC,∵∠C=∠C,∴△CDE∽△CBA,∴=,∴;(3)如图,过点Q作QG⊥AB于点G,∵sin∠ABD=,∴QG=BQ,∴PQ+BQ=PQ+QG,∴当P,Q,G三点共线时,PQ+BQ有最小值为PG,∵的弧长为π,∴,∴∠POB=60°,∴PG=OP•sin60°=,∴PQ+BQ的最小值为.4.解:(1)如图1,作DE⊥AC于E,作DF⊥AB于F,∵AD平分∠BAC,∴DE=DF,由S△ABC=S△ABD+S△ACD得,AB•AC=,∴4×3=4•DE+3DE,∴DE=,故答案是;(2)如图2,作CE⊥BD于E,作AF⊥BD于F,∵AC是直径,∴∠ABC=90°,∵BD平分∠ABC,∴∠DBC=∠ABD=,∴=,∠ECB=90°﹣∠DBC=45°=∠DBC,∴AD=CD,BE=CE,∵点B是半圆AC的三等分点(弧AB<弧BC),∴的度数是60°,的度数是120°,∴∠ADB=30°,∠BDC=60°,∴∠ADB=∠DCE=30°,∴△ADF≌△DCE(AAS),∴AF=DE,∴AF+CE=DE+BE=8,∴S四边形ABCD=S△ABD=====32;(3)如图3连接AC,延长CD至E,使DE=AD,连接AE,∵AB=AD,∴=,∴∠ACB=∠ACE,∵四边形ABCD内接于⊙O,∴∠ADE=∠ABC=60°,∴△ADE是等边三角形,∴∠E=60°,∴∠B=∠E,又∵AC=AC,∴△ABC≌△AEC(AAS),∴BC=CE,∵CE=DE+CD=AD+CD=2,∴BC=2.∵⊙O的半径是1,∴BC是⊙O的直径,∴∠BAC=90°,∴AB=BC•cos60°=1.5.(1)证明:延长BO交⊙O于G,连接AG,如图:∵=,∴∠G=∠C,∵∠ABO=∠DAC,∴∠G+∠ABO=∠C+∠DAC,∵BG为⊙O直径,∴∠BAG=90°,∴∠G+∠ABO=∠C+∠DAC=90°,∴∠ADC=90°,∴AE⊥BC;(2)证明:设BF交AC于N,延长BO交⊙O于G,连接CG,BE,如图:∵BG为⊙O直径,∴∠BCG=90°,∴∠G+∠OBC=90°,∵∠G=∠BFC,∠OBC=∠ACF,∴∠BFC+∠ACF=90°,∴∠CNF=90°,∴∠NBC+∠NCB=90°,由(1)知:AE⊥BC有∠DAC+∠NCB=90°,∴∠NBC=∠DAC,∵=,∴∠DAC=∠DBE,∴∠NBC=∠DBE,又∠BDM=∠BDE=90°,BD=BD,∴△BDM≌△BDE(ASA),∴MD=ED;(3)解:连接AF、BE,如图:∵=,∴∠BFC=∠BAC,∵∠BFC=3∠EAC,∴∠BAC=3∠EAC,∴∠BAE=2∠EAC,由(2)知∠EAC=∠DBE=∠DBM,BE=BM=,∴∠EBM=2∠EAC,∴∠EBM=∠BAE,又∠BEM=∠AEB,∴△BEM∽△AEB,∴==,∵AM=3,∴==,解得:EM=2,AB=5,在Rt△AMN中,MN2+AN2=AM2=9(Ⅰ),在Rt△ABN中,(+MN)2+AN2=AB2=25(Ⅱ),由(Ⅰ)、(Ⅱ)可得:MN=,AN=,∵∠AMF=∠BME,∠AFM=∠BEM,∴△BEM∽△AFM,∴=,即=,∴MF=,∴NF=MF﹣MN=,∵cos∠BAC=cos∠BFC,∴=,即=,∴CF=.6.(1)如图1,证明:连接OA,OC,∴OB=OC,又AB=AC,OA=OA,∴△AOB≌△AOC(SSS),∴∠OAC=∠OAB,∴∠BAC=2∠OAB,∵OA=OB,∴∠ABD=∠OAB,∴∠BAC=2∠ABD;(2)如图2,证明:连接AG,OG,延长AO交BG于M,交BC于P,交⊙O于N,由(1)知,∠BAO=∠CAO,∴=,∵AB=AC,∴AP⊥BC,∵BH⊥AC,∠AMH=∠BMP,∴∠CBG=∠CAO,∵=,∴∠CAG=∠CBG,∴∠CAG=∠CAO,∴AM=AG,=,∴GM=2GH,∠BON=∠COG,∵OB=OG,∴∠OBG=∠OGB,∴△BOM≌△GOF(ASA),∴BM=GF,∴BM+MF=GF+MF,即BF=MG=2GH;(3)如图3,解:设∠ABD=α,由(1)(2)知,∠BAC=2∠ABD=2α,∠CAG=,连接AG,作DT⊥AB于T,截取TK=AT,∴AD=DK=2,∴∠DKA=∠DAK=2α,∵∠BDK=∠AKD﹣∠ABD=2α﹣α=α,∴BK=DK=2,∴AK=AB﹣BK=3,∴AT=KT==,∴DT===,∴cos2α===,tanα==,在Rt△ABH中,AH=AB•cos2α=5×=,在Rt△AHG中,GH=AH•tanα==,∴BF=2GH=.7.解:(1)证明:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∴=,∴∠ADB=∠CDB;(2)证明:如图,作∠BCF的角平分线,交BD于点G,设∠ACD=α,∵=,∴∠ABD=∠ACD=α,∵∠BCF=2∠ABD,∴∠FCG=∠BCG=∠ACD=α,∵△ABC是等边三角形,∴BC=AC,∵=,∴∠DAC=∠DBC,在△ADC与△BGC中,,∴△ADC≌△BGC(SAS),∴BG=AD,DC=GC,∵=,∴∠BDC=∠BAC=60°,∴△DGC是等边三角形,∴∠FGC=∠EDC=60°,在△CED与△CFG中,,∴△CED≌△CFG(ASA),∴ED=FG,∴BF=BG+GF=AD+DE,即BF=DE+AD;(3)解:设∠ACD=α,则∠CAT=3∠ACD=3α,如图,延长CF交⊙O点P,交AM于N点,连接P A,过M点作MQ∥AP,交AR于Q 点,连接PM,∵CM是∠BCF的平分线,由(2)得∠FCG=∠BCG=∠ACD=α,∴∠ACP=∠ACB﹣∠BCF=60°﹣2α,∠BAT=∠BAC﹣∠CAT=60°﹣3α,∵=,=,∴∠MAB=∠BCG=α,∠MAP=∠FCG=α,∴∠MAC=∠BAC+∠BAM=60°+α,∴∠MAT=∠MAC﹣∠CAT=60°+α﹣3α=60°﹣2α,∠P AT=∠MAT+∠MAP=60°﹣2α+α=60°﹣α,∵=,∴∠AMP=∠ACP=60°﹣2α,∴∠AMP=∠MAT=60°﹣2α,∴MP∥AR,∴∠AMQ=∠MAP=α,∠MQT=∠P AR=60°﹣α,∵=,∴∠AMC=∠ABC=60°,∴∠QMR=∠AMC﹣∠AMQ=60°﹣α,∴∠QMR=∠MQR=60°﹣α,∴QR=MR=5,∵设MP=AQ=m,则QT=QR﹣TR=5﹣1=4,∴AT=QT+AQ=4+m,∵=,∴∠MPC=∠MAC=60°+α,又∵∠MNP=∠ANT=∠APC+∠P AM=60°+α,∠ATN=∠ACP+∠CAT=60°﹣2α+3α=60°+α,∴∠MNP=∠MPC=∠ANT=∠ATN=60°+α,∴MP=MN,AN=AT,∴AM=MN+AN=MP+AT=m+4+m=4+2m,在△AMR中,∠AMR=60°,AM=4+2m,MR=5,AR=5+m,如图,过R点作AM边的高HR,∴∠MRH=30°,∴MH=MR=,HR==MR=,∴AH=AM﹣MH=+2m,在Rt△AHR中,HR2+AH2=AR2,∴()2+(+2m)2=(5+m)2,解得:m=2或﹣(舍去),∴AT=4+m=6.8.解:(1)①取EF中点P,连接CP,DP,∵点P为EF中点,∴PE=PF=EF.∵∠ACB=∠EDF=90°,∴CP=DP=AC,∴PE=PF=PC=PD,∴点E、D、F、C在以P为圆心,EF为半径的同一个圆上;②当DE⊥AC时,DE的长度最小,此时EF最短,∵∠A=45°,AD=,∴DE=1,∵DE=DF,∴EF==;∵D是AB的中点,∴AD=BD=CD=,CD⊥AB,∠BCD=45°,∵DE⊥DF,∴∠EDF=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF(ASA),∴S△ADE=S△CDF,∴S四边形DECF=S△DEC+S△DCF=S△DEC+S△ADE=S△ADC=××=1;故答案为;1.③由②可知当EF取最小值时,点C到线段EF的最大距离为EF=.故答案为.(2)过点F分别作FG⊥CA于点G,设DC=a,CE=b,∵∠CDE+∠GDF=∠GDF+∠DFG=90°,∴∠CDE=∠DFG,∵∠C=∠DGF,DE=DF,∴△DCE≌△FGD(AAS),∴FG=DC=a,GD=CE=b,则2a+b=2,a2+b2=DF2,∴DF2=a2+(2﹣2a)2,=5a2_8a+4=5,当a=时,DF2最小,此时EF2最小,∴EF的最小值为.9.(1)证:如图1,作直径AE,连接BE,∴∠ABE=90°,∴∠BAO=90°﹣∠E,∵=,∴∠E=∠C,∴∠BAO=90°﹣∠C,∵AD⊥BC,∴∠AGC=90°,∴∠CAD=90°﹣∠C,∴∠BAO=∠CAD;(2)证:如图2,∵ON⊥BC,∴BC=2CN,作直径CM,连接BM,AM,∴MB⊥BC,∵ON⊥BC,∴ON∥BM,∴△CON∽△CMB,∴==2,∴BM=2ON,∵=,∴∠BAM=∠BCM,∴∠BAM=∠BCM=90°﹣∠BMC,∵=,∴∠BMC=∠BAC,∴∠BAM=90°﹣∠BAC,∵∠AHB=90°,∴∠ABH=90°﹣∠BAC,∴∠BAM=∠ABH,∴BE∥AM,∴四边形AMBE是平行四边形,∴AE=BM,∴AE=2ON;(3)解:如图3,连接AF,CF,连接CE并延长交AB于I,连接OB、OC和BD,作OJ⊥AB于J,∵AG⊥BC,BH⊥AC,∴CI⊥AB,又∵∠AEH=∠BEG,∴∠GBE=∠EAH,∵=,∴∠F AC=∠GBE,∴∠F AC=∠EAH,∵∠AHF=∠AHE=90°,AH=AH,∴△AHE≌△AHF(ASA),∴EH=FH,∴FH=,同理可得:EG=DG=,∴tan∠BFC===,∴∠BFC=60°,∵=,∴∠BAC=∠BFC=60°,∴∠BOC=2∠BAC=120°,∵OB=OC,ON⊥BC,∴∠BON==60°,∴OA=OB=2ON,∵AE=2ON,∴AO=AE,∴∠AOE=∠AEO,∴∠AOP=∠AEQ,∵∠BAO=∠CAD,∵△AOP≌△AEQ(ASA),∴AP=AQ,∴△APQ是等边三角形,∴∠APQ=60°,∵∠AEH=90°﹣∠BAC=30°,∴∠AEH=∠ABH=30°,∴PE=PB=11,设AP=AQ=PQ=x∴OP=EQ=PQ﹣PE=x﹣11,AC=AQ+CQ=x+2,在Rt△AIC中,∠BAC=60°,AC=x+2,∴AI=AC=(x+2),CI=(x+2),∴BI=AB﹣AI=(x+11)﹣(x+2)=+10,在Rt△BIC中,BC2=BI2+CI2,=()2+[(x+2)]2,在Rt△POJ中,∠APH=60°,OP=x﹣11,∴PJ=(x﹣11),OJ=(x﹣11),∴AJ=AP﹣PJ=x﹣(x﹣11)=,在Rt△AOJ中,OA2=OJ2+AJ2=[(x﹣11)]2+()2,∴OB2=[(x﹣11)]2+()2,∵BN=OB,∴BC=2BN=OB,∴BC2=3OB2=3•[(x﹣11)]2+()2,∴3•[(x﹣11)]2+()2=()2+[(x+2)]2,化简,得,x2﹣23x+130=0,∴x1=13,x2=10(舍去),∴AB=x+11=24,AC=x+2=15,∴BH=AB=12,AH=12,∴CH=AC﹣AH=3,∴BC==21,∵∠CAD=∠CBH,∠AGC=∠BHC=90°,∴△ACG∽△BCH,△BGE∽△AGC,∴==,=∴===,∴AG=,CG=,∴BG=BC﹣CG,=21﹣=,∴=,∴DG=EG=,∴AD=AG+DG=+=.10.解:(1)点P到直线l距离的最大值,即过圆心O向直线l作垂线交圆O于点P,连接OA,∵AB=8,OC⊥AB,∴AC=4,由勾股定理得:OC=3,∴PC=8,故答案为:8;(2)过点F作FG⊥AB,∵∠ABC=45°,AD⊥BC,∴△ABD为等腰直角三角形,∴AB=BD,又∵△ABC为等腰三角形,且AB=BC,BE⊥AC,∴BE平分∠ABC,又∵FD⊥BC,FG⊥AB,∴FG=FD,∴S△ABF=×AB×FG,S△BDF=×BD×DF,∴;(3)连接MC,过点A作AP⊥BC于点P,∵∠ABC=60°,AB=60,∴BP=30,AP=30,∴CD=30,设总费用为W元,∴W=400S△AMN+200S△BNC,∴W=200(2S△AMN+S△BNC),∴当2S△AMN+S△BNC最小时,总费用最小,又∵AM=20米,BM=40米,∴2S△AMN=S△BMN,∴当S△BMN+S△BNC最小时,费用最小,即S四边形BMNC最小时,费用最小,又∵S四边形BMNC=S△BMC+S△CMN,过点M作MH⊥BC,垂足为H,∵∠ABC=60°,BM=40米,∴BH=20米,MH=20米,MC=40米,∴∠BCM=30°,∴∠DCM=60°,∴S△BMC==800(平方米),∴当S△CMN最小时,费用最小,∴S△CMN=×NQ=20NQ,∴当NQ最小时,费用最小,∵ND=25米,∴N点在以D为圆心,25为半径的圆上运动,过圆心D向MC作垂线交⊙D于N点,交MC于Q,即此时NQ最小,∵CQ=15米,DQ=45米,∴NQ=45﹣25=20(米),∴S△MNC最小值=×20=400(平方米),∴S四边形BMNC最小值=1200(平方米)∴W最小值=200×1200=240000(元),11.(1)证明:如图,过点O作OM⊥EF于点M,ON⊥CD于点N,连接OF、OD,则∠OMF=∠OND=90°,∵PB平分∠DPF,OM⊥EF,ON⊥CD,∴OM=ON,在Rt△OFM和Rt△ODN中,,∴Rt△OFM≌Rt△ODN(HL),∴FM=DN,∵OM⊥EF,ON⊥CD,∴EF=2FM,CD=2DN,∴CD=EF;(2)∵PE:PF=1:3,∴设PE=x,PF=3x,则EF=PE+PF=4x,∵OM⊥EF,∴EM=FM=EF=2x,∴PM=EM﹣PE=2x﹣x=x,∵PB平分∠DPF,∠DPF=60°,∴∠FPB=DPB=DPF=30°,∴OM=x,OP=x,在Rt△OPM和Rt△OPN中,,∴Rt△OPM≌Rt△OPN(HL),∴PM=PN,由(1)知:FM=DN,∴PM+FM=PN+DN,∴PF=PD,∵∠DPF=60°,∴△PDF是等边三角形,∵PB平分∠DPF,∴PB⊥DF,垂足为G,∴DF=PF=3x,FG=DF=,∴PG===,∴OG=PG﹣OP=﹣x=,∵AB=2,∴OF=AB=,在Rt△OFG中,根据勾股定理,得OG2+FG2=OF2,∴()2+()2=()2,整理,得x2=3,解得x=±(负值舍去),∴x=,∴OG===.12.(1)解:∵BC是直径,∴∠CAB=90°,∴∠ACB+∠ABC=90°,∴∠ACB+∠ABC=45°,∵BD=AD,∴=,∴∠ACD=∠BCD,∵∠AED=∠ACD+∠CAE,∴∠AED+∠ABC=90°+∠ACB+∠ABC=135°;(2)证明:∵=,∴∠ACD=∠BCE,∵∠CBE=∠ADC,∴△CBE∽△CDA,∴=,∴AC•BC=CE•CD;(3)解:如图,过点B作BT⊥OE交CD于点T,连接OT.∵BO=BE,∴BO垂直平分线段OE,TB平分∠ABC,∴TO=TE,∴TB平分∠OTE,∵CE平分∠ACB,∴∠BTD=∠TCB+∠TBC=(∠ACB+∠ABC)=45°,∴∠OTE=90°,∴OT⊥CD,∴CT=TD,∵BC是直径,∴∠BDT=90°,∴∠BTD=∠DBT=45°,∴BD=DT=CT,∵CO=OB,CT=TD,∴BD=2OT,∴DT=CT=2ET,∴CE=3DE,∴S△BEC=3S△ADE,∵BO=OC,∴S△BEC=2S△BEO,∴2S△BEO=3S△DEB,∴=.13.(1)证明:∵∠A=∠EFC,∴∠E+∠EF A=∠EF A+∠CFB,∴∠E=∠CFB,∵∠A=∠B,∴△AFE∽△BCF;(2)解:∵AB是⊙O的直径,∴∠ACB=90°,∴AB==8,∵AC=BC,∴∠A=∠B=45°,∴∠A=∠B=∠CFE=45°,由(1)可得△AFE∽△BCF,∴,即,∴y=﹣x2+x(0≤x≤8),∴当x=4时,y最大=2;(3)解:连接DE,DF,∵△EFC与△EFD关于EF对称,∴∠EDF=∠ECF=60°,EC=ED,FC=FD,∵∠BDF+∠EDF=∠BDE=∠A+∠DEA,∵∠EDF=∠A=60°,∴∠BDF=∠DEA,∴△ADE∽△BFD,设AD=x,CE=DE=a,CF=DF=b,∵AD:BD=1:2,∴DB=2x,∴AB=3x=AC=BC,∴AE=3x﹣a,BF=3x﹣b,∵△ADE∽△BFD,∴,∴,由前两项得,2ax=b(3x﹣a),由后两项得,(3x﹣a)(3x﹣b)=2x2,即:3x(3x﹣a)﹣b(3x﹣a)=2x2,∴3x(3x﹣a)﹣2ax=2x2,∴a=x,∴,∴CE:CF=4:5.14.(1)∵四边形ABCD为平行四边形,∴∠B=∠D.又∵∠B+∠D=180°,∴∠B=∠D=90°.∴四边形ABCD为矩形,∵,∴AB=AD.∴四边形ABCD为正方形.(2)延长CD至点Q,使得DQ=BP,连接AQ,如图,∵四边形ABCD为正方形,∴∠ABP=∠ADQ=90°.在△ABP和△ADQ中,,∴△ABP≌△ADQ(SAS),∴AP=AQ,∠BAP=∠DAQ.∵∠BAD=90°,∴∠DAP+∠BAD=90°.∴∠DAP+∠QAD=90°.∴∠QAP=90°.∵∠P AZ=45°,∴∠P AZ=∠QAZ=45°.在△APZ和△AQZ中,,∴△APZ≌△AQZ(SAS).∴PZ=QZ.设AB=4a,DZ=t,则BP=a,ZC=4a﹣t,ZP=t+a,在Rt△CPZ中,∵ZC2+CP2=ZP2,∴(4a﹣t)2+(3a)2=(t+a)2.解得:t=.∴DZ=a,CZ=a,∴DZ:CZ=3:2.(3)∵四边形ABCD为正方形,PQ⊥AD,ZX⊥AB,∴四边形AXYQ,AXZD,XBPY,XBCZ均为矩形.设AB=a,AX=m,AQ=n,则mn=.由(2)可知,PZ=DZ+BP=m+n,CZ=XB=a﹣m,CP=DQ=a﹣n.在Rt△CPZ中,∵ZC2+PC2=PZ2,∴(a﹣m)2+(a﹣n)2=(m+n)2.化简得:a2﹣(m+n)a=mn.∴S四边形ZYPC=(a﹣m)(a﹣n)=a2﹣(m+n)a+mn=2mn=2×=5.15.(1)证明:∵∠C=90°,AC=16,AB=20,∴BC==12,∴=,∵==,∴=,∵∠C=∠C,∴△DCE∽△BCA;(2)解:①如图1,作PG⊥AC于G,PF⊥BC于F,作PH⊥AB于H,设CD=3a,CE=4a,DE=5a,由题意得,PH=PC=DE=,PF=CG=CD=a,FG=2a,∵S△ABC=S△APB+S△PBC+S△P AC,∴BC•AC=AB•PH++,∴12×16=20×a+12×a+16×2a,∴a=,∴t=3a=;②如图2,设CD=3a,CE=4a,DE=5a,∴PF=DE=a,由(1)知,△DCE∽△BCA,当△PMF∽△DCE时,∴△PMF∽△BCA,==,∴PM=a,FM=2a,由S△ABC=得20•CM=12×16,∴CM=,∵CP+PM=CM,∴a+a=,∴4a=,即CE=,当△PMF∽△ECD时,类比上可得,a+2a=,∴4a=,∴CE=,综上所述:CE=或.16.解:(1)点P运动至半圆O的中点时,如图1:此时底边AB上的高最大,即P'O=r=3,△P AB的面积最大值,∴S△P'AB=×3×6=9,故答案为:9;(2)四边形CODE的面积存在最大值,作OG⊥CD,垂足为G,延长OG交弧AB于点E′,则此时△CDE'的面积最大,如图2:∵OA=OB=6,AC=2,点D为OB的中点,∴OC=4,OD=3,在Rt△COD中,CD=5,OG=2.4,∴GE′=6﹣2.4=3.6,∴四边形CODE'面积为S△CDO+S△CDE′=×3×4+×5×3.6=15,∴四边形CODE的面积的最大值为15;(3)四边形ABCD的面积存在最大值,连接BD,作△ABD的外接圆O,过A作AE⊥BD于E,如图3:∵∠DAB=60°,∠DCB=120°,∴∠DAB+∠DCB=180°,∴A、B、C、D四点共圆,即C在⊙O上,∵AD=AB,∠DAB=60°,∴△ADB是等边三角形,有BD=AB=AD=6,在Rt△ABE中,BE=AB=3,AE=BE=3,∴S△ABD=BD•AE=×6×3=9,当C为中点,即A、E、C共线时,△BDC的面积最大,此时∠ACB=∠ADB=60°,AC为⊙O直径,∴∠CAB=30°,∴AC==4,∴CE=AC﹣AE=,∴S△BDC=BD•CE=×6×=3,∴S四边形ABCD=S△ABD+S△BDC=12,即四边形ABCD的面积的最大值是12.17.(1)解:在倍对角四边形ABCD中,∠D=2∠B,∠A=2∠C,∵∠A+∠B+∠C+∠D=360°,∴3∠B+∠3∠C=360°,∴∠B+∠C=120°,∴∠B与∠C的度数之和为120°;(2)证明:在△BED与△BEO中,,∴△BED≌△BEO(SAS),∴∠BDE=∠BEO,∵∠BOE=2∠BCF,∴∠BDE=2∠BCF连接OC,设∠EAF=α,则∠AFE=2α,∴∠EFC=180°﹣∠AFE=180°﹣2α,∵OA=OC,∴∠OAC=∠OCA=α,∴∠AOC=180°﹣∠OAC﹣∠OCA=180°﹣2α,∴∠EFC=∠AOC=2∠ABC,∴四边形DBCF是倍对角四边形;(3)解:过点O作OM⊥BC于M,∵四边形DBCF是倍对角四边形,∴∠ABC+∠ACB=120°,∴∠BAC=60°,∴∠BOC=2∠BAC=120°,∵OB=OC,∴∠OBC=∠OCB=30°,∴BC=2BM=BO=BD,∵DG⊥OB,∴∠HGB=∠BAC=60°,∵∠DBG=∠CBA,∴△DBG∽△CBA,∴==,∵4DH=3BG,BG=2HG,∴DG=,∴==,∴=.18.解:(1)连接OA,∵OP⊥AB,∴AP=,∵OA=5,OP=3,∴AP==4,∴AB=2AP=8,故答案为:8;(2)设半径为r不变,∴AB=2AP=2,当r不变,OP的长增大时,AB减小;OP长确定时,AB也确定,故选:②③;(3)如图,利用△MPF和△OP'B全等,首先作EF的垂直平分线,再取FM=r,然后以点O为圆心,MP为半径画圆,再以OQ为直径画圆,两圆交点为P',从而画出线段AB,如图,线段AB即为所求;(4)①解:设AB=2m,CD=2n,如图,可得:,解得:,∴AB=,CD=,②作图思路:先作斜边为4r,一条直角边为2,另一条直角边为的直角三角形;再作斜边为,一条直角边为l,另一条直角边为的直角三角形;再在⊙O中作出长为的弦,再如(3)中作法,过点Q作弦AB;最后过点Q作AB的垂直弦CD.19.(1)证明:在△ABC中,三边长分别是3,和5,∵32+52=2()2,。
中考专题复习——圆的相关证明(附答案)
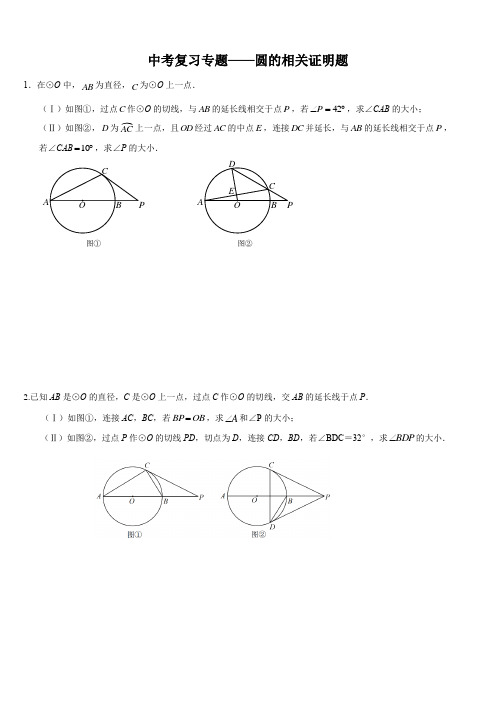
中考复习专题——圆的相关证明题1.在⊙O 中,AB 为直径,C 为⊙O 上一点.(Ⅰ)如图①,过点C 作⊙O 的切线,与AB 的延长线相交于点P ,若P ∠︒=42,求∠CAB 的大小; (Ⅱ)如图②,D 为上一点,且OD 经过AC 的中点E ,连接DC 并延长,与AB 的延长线相交于点P , 若∠CAB ︒=10,求∠P 的大小.2.已知AB 是⊙O 的直径,C 是⊙O 上一点,过点C 作⊙O 的切线,交AB 的延长线于点P .(Ⅰ)如图①,连接AC ,BC ,若OB BP =,求A ∠和∠P 的大小;(Ⅱ)如图②,过点P 作⊙O 的切线PD ,切点为D ,连接CD ,BD ,若∠BDC =32°,求BDP ∠的大小.图①图②O B COB D CPE AC3.已知点A ,B ,C 是⊙O 上的三个点,︒=∠120AOB . (Ⅰ)如图①,若AC =BC ,求C ∠和CAO ∠的大小;(Ⅱ)如图②,过点C 作⊙O 的切线,交BA 的延长线于点D ,若AC =AD ,求CAO ∠的大小.4.已知AB 为⊙O 的直径,C 为⊙O 上一点,AD 和过点C 的切线互相垂直,垂足为D ,AD 交⊙O 于点E .(Ⅰ)如图①,求证:AC 平分DAB ∠;(Ⅱ)如图②,过B 作BF AD ∥交⊙O 于点F ,连接CF ,若45AC =4DC =,求CF 和⊙O 半径的长. ABCDEO图①ABCDEO图②F5.已知,△DBC内接于⊙O,DB=DC.(Ⅰ)如图①,过点B作射线BE交⊙O于点A,若∠EAD=75°,求∠BDC的度数.(Ⅱ)如图②,分别过点B、点D作⊙O的切线相交于点E,若∠E=30°,求∠BDC的度数.①②6.已知P A,PB分别与⊙O相切于点A,B,PO交⊙O于点F,且其延长线交⊙O于点C,∠BCP=28°,E为CF上一点,延长BE交⊙O于点D.(Ⅰ)如图1,求∠CDB与∠APB的大小;(Ⅱ)如图2,当BC=CE时,求∠PBE的大小.7.在ABC △中90B ∠=︒D 为AC 上一点,以CD 为直径的⊙O 与AB 相切于点E ,与BC 相交于点F ,连接CE .(Ⅰ)如图①,若27ACE ∠=︒,求A ∠和ECB ∠的大小; (Ⅱ)如图②,连接EF ,若//EF AC ,求A ∠的大小.8. 已知:在⊙O 中OA BC ⊥垂足为E ,点D 在⊙O 上.(Ⅰ)如图①若50AOB ∠=︒,求ADC ∠和∠CAO 的大小;(Ⅱ)如图②CD ∥AO ,过点D 作⊙O 的切线,与BC 的延长线相交于点P ,若26∠=︒ABC 求∠P 的大小.图①图②ABCF OED ABCOED F 图①O EDCBA图②POE DCBA9.如图,在⊙O 中,直径AB 与弦CD 相交于点E ,58ABC ∠=︒. (Ⅰ)如图①若85AEC ∠=︒,求BAD ∠和CDB ∠的大小;(Ⅱ)如图②若CD AB ⊥过点D 作⊙O 的切线DF ,与AB 的延长线相交于点F ,求F ∠的大小.10. 已知AB 是⊙O 的直径,CD 、CB 是⊙O 的弦,且AB CD ∥.(Ⅰ)如图①若25ABC ∠=︒,求BAC ∠和ODC ∠的大小;(Ⅱ)如图②过点C 作⊙O 的切线,与BA 的延长线交于点F 若OD CF ∥求ABC ∠的大小.图①图②EABO DCFE ABO DC图②图①11. 如图,⊙O 是△ABC 的外接圆,AE 切⊙O 于点A ,AE 与直径BD 的延长线相交于点E .(Ⅰ)如图①,若∠C =71°,求∠E 的大小;(Ⅱ)如图②,当AE =AB ,DE =2时,求∠E 的大小和⊙O 的半径.12. 已知DA 、DC 分别与⊙O 相切于点A 点C ,延长DC 交直径AE 的延长线于点P . (Ⅰ)如图①若DC =PC ,求∠P 的度数;(Ⅱ)如图②在⊙O 上取一点B ,连接AB 、BC 、BE ,当四边形ABCD 是平行四边形时,求∠P 及∠AEB 的大小. OEEDCBAD O C BA图①图②DECAPOB图① 图②ECAPOD13.如图①,AB 是⊙O 的弦,OE ⊥AB ,垂足为P ,交AB 于点E ,且OP =3PE ,AB =74.(Ⅰ)求⊙O 的半径;(Ⅱ)如图②过点E 作⊙O 的切线CD ,连接OB 并延长与该切线交于点D ,延长OA 交CD 于C ,求OC 的长. 图②图①EP A BCODP EOBA参考答案1.解:(Ⅰ)如图,连接OC∵ ⊙O 与PC 相切于点C ∴ OC PC ⊥,即90OCP ∠=︒ ∵ 42P ∠=︒∴ 9048COB P ∠=︒-∠=︒ 在Rt OPC △中,48CAB ACO COP ∠+∠=∠=︒ ∵OA =OC ∴∠CAB =∠ACO ∴ 24CAB ∠=︒(Ⅱ)∵ E 为AC 的中点∴ OD AC ⊥,即90AEO ∠=︒在Rt AOE △中,由10EAO ∠=︒得9080AOE EAO ∠=︒-∠=︒ ∴ 1402ACD AOD ∠=∠=︒∵ ACD ∠是ACP △的一个外角∴ 30P ACD CAP ∠=∠-∠=︒2. 解:(Ⅰ)如图①连接OC ∵PC 是⊙O 的切线∴︒=∠90OCP ∵OB BP =∴OB BC =∵OC OB =∴BOC ∆为等边三角形, ∴∠BOC=60° ∴︒=∠=∠3021BOC A ∠P=90°-∠COB =30°(Ⅱ)如图② 连接OC 、OD 设CD 交OP 于点E∵PC ,PD 是⊙O 的切线∴PD PC = ︒=∠=∠90ODP OCP ∵OD OC =∴OP 为CD 的垂直平分线 ∴︒=∠=∠90DEP CEP∵∠BDC =32°∴∠OBD =90°-∠BDC =58° ∵OB OD =∴∠ODB =∠OBD =58° ∴∠BDP =90°-58°=32°3.解: (Ⅰ)∵︒=∠120AOB ∴∠ACB= 12 ∠AOB=60°如图① 连接OC∵AC =BC ∴∠AOC=∠BOC∵∠AOC+∠BOC +∠AOB=360° ∴∠AOC =12 (360°-120°)=120° ∵OA OC ∴∠CAO=∠ACO=12(180°-120°)=30°O AB PCOAB D CPE(Ⅱ)如图② 连接OC设∠ACD= x ∵ACAD ∴∠ACD =∠ADC= x∴∠CAB=2x ∵∠AOB=120°OAOB ∴∠OAB =∠OBA= 12(180°-120°)=30°∵CD 是⊙O 的切线∴∠OCD=90° ∵OAOC ∴∠OCA =∠OAC∴90°-x=2x -30° 解得x=40° ∴∠CAB=80°∴∠CAO=∠CAB -∠OAB =50°4.(Ⅰ)证明:连接OC ∵CD 为⊙的切线∴OC CD ⊥即90OCM OCD ∠=∠=︒ ∵AD CD ⊥垂足为D ∴90ADC ∠=︒ ∵90ADC OCM ∠=∠=︒∴OC AD ∥ ∴DAC ACO ∠=∠∵OC OA =∴CAO ACO ∠=∠∴DAC CAO ∠=∠∴AC 平分DAB ∠ (Ⅱ)解:连接AF 延长CO 交AF 于G ∵AB 为⊙的直径 ∴=90AFB ∠︒ ∵OC AD BF AD ∥,∥ ∴CO BF ∥∴90AFB AGC ∠=∠=︒ ∴OC AF ⊥由垂径定理可得AC=CF∴45AC CF == ∵90ADC ∠=︒22O O ABC DEOF GABCDEOM∴90ADC DCO AGC ∠=∠=∠=︒ ∴四边形ADCG 是矩形∴8AD CG == 4CD AG == 在Rt AGO 中,得222AG OG AO += 设OC x =则,8OA x OG x ==- 可得方程()22248x x +-=解得5x =. ∴⊙半径的长为545CF =.5.(Ⅰ)解:∵四边形ABCD 是⊙O 的内接四边形∴∠DAB +∠C =180° ∵∠EAD +∠DAB =180° ∴∠C =∠EAD ∵∠EAD =75° ∴∠C =75° ∵DB =DC∴∠DBC =∠C =75°∴∠BDC =180°﹣∠C ﹣∠DBC =30°(Ⅱ)解:连结OB OD∵EB ED 与⊙O 相切于点B 点D∴ED OD ⊥⊥,EB OB ∴ ︒=∠︒=∠90ODE 90,OBE∵︒=∠+∠+∠+∠360BOD ODE E OBE ︒=∠30E ∴︒=∠150BOD∴︒=∠=∠7521BOD C ∵DB =DC ,∴∠DBC =∠C =75°,∴∠BDC =180°﹣∠C ﹣∠DBC =30° O6. (I )解:连接OB∵P A 、PB 与圆O 相切于点A 点,B∴PO 平分∠APB 且∠PBO =90° ∵∠BCP =28°∴∠BOP =2∠BCP =28°×2=56° ∴∠BPO =90°-∠BOP =90°-56°=34° ∴∠APB =2∠BPO =2×34°=68°又∠BDC =BOC ∠21=)180(21BOP ∠- ∴∠BDC = 62)56180(21=-∴∠APB =68°∠BDC= 62 (II )连接OB∵BC =CE ∴∠CBE =∠CEB∵∠BCP =28° ∴∠CBE =76228180=-∵OB =OC ∴∠OBC =∠OCB =28° ∴∠EBO =∠CBE -∠OBC =76°-28°=48° ∵P A 与圆O 相切于点A∴OB ⊥PB ∴∠PBO =90°∴∠PBE =90°- ∠EBO =90°-48°=42°7.解:(Ⅰ)如图连接OE .∵ AB 与⊙O 相切∴ OE AB ⊥,即90AEO ∠=︒ ∵ 27ACE ∠=︒∴ 254AOE ACE ∠=∠=︒ ∴ 9036A AOE ∠=︒-∠=︒ ∵ OE OC =∴ OEC OCE ∠=∠∵ 90B ∠=︒∴ //OE BC ∴ ECB OEC ∠=∠ ∴ 27ECB ∠=︒ (Ⅱ)如图,连接OE OF∵ //OE BC //EF AC ∴ 四边形OEFC 为平行四边形 ∴ OE CF = ∴ OC OF CF == ∴ 60ACB ∠=︒∴ 9030A ACB ∠=︒-∠=︒ABCOED F ABCF OED8. 解:(Ⅰ)∵OA BC ⊥ ∴AB AC = 90∠=︒AEC∴∠=∠ACB ADC ∵1252∠=∠=︒ACB AOB∴25∠=∠=︒ADC ACB9065∠=︒-∠=︒CAO ACB(Ⅱ)连接BD . 由OA BC ⊥知,90∠=∠=︒AEB BEO∴ 9064∠=︒-∠=︒OAB ABC ∵AO ∥CD ∴90∠=∠=︒BCD BEO ∴BD 是⊙O 的直径又PD 与⊙O 相切∴⊥BD PD . 即90∠=︒BDP∵=OA OB ∴64∠=∠=︒OBA OAB∴642636∠=∠-∠=︒-︒=︒CBD ABO ABC ∴9052∠=︒-∠=︒P CBD9. (Ⅰ)∵∠AEC 是ΔBEC 的一个外角 58ABC ∠=︒85AEC ∠=︒27C AEC ABC ∴∠=∠-∠=︒∵在⊙O 中BAD C ∠=∠27BAD ∴∠=︒ AB 为⊙O 的直径90ADB ∴∠=︒ ∵在⊙O 中58ADC ABC ∠=∠=︒ 又CDB ADB ADC ∠=∠-∠32CDB ∴∠=︒(Ⅱ)连接OD∵CD ⊥AB 90CEB ∴∠=︒.9032E E CB BC =-∴∠=∠︒︒∴264DOB DCB ∠=∠=︒ ∵DF 是⊙O 的切线∴90ODF ∠=︒90906426F DOB ∴∠=︒-∠=︒-︒=︒图②POE DCBA图①O E DCBA10. 解:(Ⅰ)如图连接OC ∵ AB 是⊙O 的直径 ∴ 90ACB ∠=︒∴ 90BAC ABC ∠+∠=︒由25ABC ∠=︒得65BAC ∠=︒又AB CD ∥得25ABC BCD ∠=∠=︒ ∵ OB OC = ∴ 25OCB ABC ∠==∠=︒ 则50OCD OCB BCD ∠=∠+∠=︒ 由OC OD =得50ODC OCD ∠=∠=︒(Ⅱ)如图,连接OC∵CF 切⊙O 于点C ∴OC FC ⊥则90OCF ∠=︒∵ OD CF ∥ ∴ 90DOC OCF ∠=∠=︒ 又OC OD =则45ODC OCD ∠==∠=︒ 由AB CD ∥得45BOD ODC ∠=∠=︒∴135BOC DOC BOD ∠=∠+∠=︒ ∵ OC OB = ∴22.5ABC OCB ∠=∠=︒11. 解:(Ⅰ)连接OA .∵AE 切⊙O 于点A ∴OA ⊥AE ,∴∠OAE =90° ∵∠C =71° ∴∠AOB =2∠C =2×71°=142° 又∵∠AOB +∠AOE =180° ∴∠AOE =38° ∵∠AOE +∠E =90° ∴∠E =90°﹣38°=52° (Ⅱ)连接OA 设∠E = x .∵AB =AE ∴∠ABE =∠E = x ∵OA =OB ∴∠OAB =∠ABO = x ∴∠AOE =∠ABO +∠BAO =2x∵AE 是⊙O 的切线∴OA ⊥AE ,即∠OAE =90°在△OAE 中∠AOE +∠E =90°即2x +x =90°解得30x =︒∴∠E =30° 在Rt △OAE 中OA =21OE∵OA =OD ∴OA =OD =DE∵DE =2∴OA =2即⊙O 的半径为212.解:(Ⅰ)∵DA 、DC 是⊙O 的切线 ∴DA =DC OA ⊥DA ∴∠DAO =90°∵DC =PC ∴DA =DC =PC ∵∠DAP =90° ∴sin P=DP AD =21∴∠P=30° (Ⅱ)连接OC 、AC∵DA ,DC 是⊙O 的切线 ∴DA =DC∵四边形ABCD 是平行四边形∴□ABCD 是菱形 ∴DA =DC =CB =AB ∠ABC =∠ADC ∵∠AOC =2∠ABC ∴∠AOC =2∠ADC∵DA 、DC 是⊙O 的切线∴OA ⊥AD OC ⊥DC ∴∠DAO =∠DCO =90°∵∠ADC +∠DCO+∠AOC +∠DAO =360° ∴∠ADC +∠AOC =180°∴3∠ADC =180°∴∠ADC =60°∴∠P =90°-∠ADC =30°,∠ABC =60°又AB =BC ∴△ABC 是等边三角形 ∴∠ACB =60° ∴∠AEB =∠ACB=60°13. 解:(Ⅰ)∵OE ⊥AB∴1272APAB 设PE =x 则OP =3x OA =OE =4x在Rt OAP △中222OA OP AP =+即2216928x x =+ 解得x =2(负舍)∴4x =8 ∴半径OA 为8 (Ⅱ)∵ CD 为⊙O 的切线 ∴OE ⊥CD又∵OE ⊥AB ∴AB //CD ∴34OA OP OCOE∴323OCECAPODB。
(完整版)中考初三圆知识点专题复习

、圆中重要的知识点 1、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:( 1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 简称2推3定理:此定理中共 5个结论中,只要知道其中 2个即可推出其它3个结论,即:3、如图,已知在O O 中,弦AB CD ,且AB CD ,垂足为H , 0E(1) 求证:四边形OEHF 是正方形.(2) 若CH 3 , DH 9,求圆心0到弦AB 和CD 的距离.以上共4个定理,①AB 是直径 ②AB CD ③ CEDE ④弧BC 弧BD ⑤弧AC 弧AD中任意2个条件推出其他3个结论。
推论2:圆的两条平行弦所夹的弧相等。
即:在O O 中,••• AB // CD•••弧 AC 弧 BD例题1、基本概念1. F 面四个命题中正确的一个是( A. 平分一条直径的弦必垂直于这条直径 •平分一条弧的直线垂直于这条弧所对的弦C. 弦的垂线必过这条弦所在圆的圆心 .在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心2. F 列命题中,正确的是().A.过弦的中点的直线平分弦所对的弧B.过弦的中点的直线必过圆心C.弦所对的两条弧的中点连线垂直平分弦,且过圆心D.弦的垂线平分弦所对的弧例题2、垂径定理1、在直径为 52cm 的圆柱形油槽内装入一些油后,为 16cm, 那么油面宽度AB 是cm.2、在直径为52cm 的圆柱形油槽内装入一些油后,,如果油面宽度是 48cm,那么油的最大深度为 _______ cm.AB 于 E , OF CD 于 F .截面如图所示,如果油的最大深度4、已知:△ ABC内接于O O, AB=AC半径OB=5cm圆心O到BC的距离为3cm,求AB的长.5、如图,F是以O为圆心,BC为直径的半圆上任意一点,A是〒的中点,AD丄BC于D,求证:AD=1 BF.2F例题3、度数问题1、已知:在O O中,弦AB 12cm , 0点到AB的距离等于AB的一半,求:AOB的度数和圆的半径2、已知:O O的半径0A 1,弦AB AC的长分别是J2、J3.求BAC的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级圆专题复习第21题圆这道题对于升学考高中的学生来说是一道必得分题,随着中考复习的逐步深入,学生从知识上对于这道题已经很熟练了,都知道这道题的第(2)问主要考查圆与相似、三角函数、勾股定理等等。
如果不进行归类,学生的脑海中还是显得比较杂,比较乱。
在复习的过程中,教师如何引导学生进行归类,如何提升学生的转化能力,这些则是教学最需要突破的地方。
如果教师能够引导学生对第21题考查的题型结构进行有效的归类,那么学生在面对这道题的时候,首先将这道题归纳为几个重要的熟悉的题型,然后利用自己对这几个题型的熟练理解,则可以大大提高解决问题的速度和准确性。
一、历年题型对比分析及2017年中考题型预测1. (2013•武汉四月调考)在圆O 中,AB 为直径,PC 为弦,且PA=PC. (1)如图1,求证:OP//BC ;(2)如图2,DE 切圆O 于点C ,若DE//AB ,求tan ∠A 的值。
2. (2013•武汉中考)如图,已知△ABC 是⊙O 的内接三角形,AB =AC ,点P 是弧AB 的中点,连接PA 、PB 、PC(1)如图①,若∠BPC =60°,求证:AP AC 3 ;(2)如图②,若sin ∠BPC=2524,求tan ∠PAB 的值。
3. (2014•武汉四月调考)已知:P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B 两点,点C 为⊙O 上一点.(1)如图1,若AC 为直径,求证:OP ∥BC ; (2)如图2,若sin ∠P=,求tan ∠C 的值.4.(2014•武汉中考)如图,AB 是⊙O 的直径,C 、P 是弧AB 上两点,AB =13,AC =5 (1) 如图(1),若点P 是弧AB 的中点,求PA 的长 (2) 如图(2),若点P 是弧BC 的中点,求PA 得长5.(2015•武汉四月调考)已知:⊙O 为Rt △ABC 的外接圆,点D 在边AC 上,AD =AO . (1)如图1,若弦BE ∥OD ,求证:OD=BE ;(2)如图2,点F 在边BC 上,BF =BO ,若OD =22,OF =3,求⊙O 的直径.6.(2015•武汉中考)如图,AB 是⊙O 的直径,∠ABT=45°,A T=AB . (1)求证:AT 是⊙O 的切线;(2)连接OT 交⊙O 于点C ,连接AC ,求tan ∠TAC .7.(2016•武汉四月调考) 已知⊙O 为△ABC 的外接圆,点E 是△ABC 的内心,AE 的延长线交BC 于点F ,交⊙O 于点D .(1)如图1,求证:BD= ED ;(2)如图2,AO 为⊙O 的直径,若BC= 6,sin ∠BAC=53,求OE 的长.E D OA B CFDOA BC8.(2016•武汉中考)如图,点C 在以AB 为直径的⊙O 上,AD 与过点C 的切线垂直,垂足为点D ,AD 交⊙O 于点E .(1) 求证:AC 平分∠DAB ;(2) 连接BE 交AC 于点F ,若cos ∠CAD =54,求FCAF 的值.9.(2017•武汉四月调考)如图,□ABCD 的边AD 与经过A 、B 、C 三点的⊙O 相切(1) 求证:弧AB =弧AC(2) 如图2,延长DC 交⊙O 于点E ,连接BE ,sin ∠E =1312,求tan ∠D 的值归纳:1.从知识上归纳:(1)已知三角函数求三角函数的有:(2017•武汉四月调考)、(2013•武汉中考)、(2014•武汉四月调考)(2)已知三角函数求比值的:(2016•武汉中考)(2015•武汉中考) (3)已知三角函数求长度:(2016•武汉四月调考)(5)求三角函数:(2013•武汉四月调考)、(2015•武汉中考) (6)已知勾股定理求长度:(2014•武汉中考)(2015•武汉四月调考) 2.从题型上归纳:(1)考查圆周角转到圆心角一半的位置及圆中等腰三角型有:(2014•武汉四月调考)、(2016•武汉四月调考)、(2013•武汉中考)、(2017•武汉四月调考)(2)考查1,2,5三角型的有:(2015•武汉中考) (3)考查垂径定理和勾股定理的有:(2014•武汉中考) (4)考查旋转型相似与圆中构矩形的有:(2016•武汉中考)预测:近几年的四调和中考,对圆中三角函数的考查的年份占到很大的比例,单独考勾股定理的年份较少,仅仅只有2014年中考和2015年四调,其他年份都涉及三角函数,而且今年的四调更是已知三角函数求三角函数。
纵观2016年全国各地中考题对圆的考查,逐步在降低难度,主要集中在圆的第2问。
而第2问主要考查学生转化、计算的能力和方程思想。
那么三角函数不管作为条件,还是结论,不管是计算还是证明,学生都知道要有直角,原处作垂直还是转化?怎么转?往哪个方向转?转了之后有什么意义?怎么打通条件和结论的连接点。
这恰恰时学生的难点,也是我们教师需要传递给学生的地方。
如果教师能够引导学生将第21题第(2)问考查的题型结构归纳为几个重要的熟悉的题型,那么学生就非常自信,相信按照老师的指导方法一定能够做出这道题来,让考生百分百在道题上能得分,是我们老师需要研究的。
二、几种重要的题型和结构(一)圆中等腰三角形的结构及其类似结构知识储备:等腰三角形的顶角与底角之间的三角函数是可以任意切换的。
只需要作底上的高和腰上的高即可。
(1)已知顶角三角函数求底角三角函数,顶角半角的三角函数 例1.1.如图,已知在等腰ABC 中,AB AC =, 3sinA 5=,求tan B ,cos 2A(2)已知底角三角函数求顶角三角函数,顶角半角的三角函数。
例 1.2.如图,已知在等腰ABC 中,AB AC =, tanC 2=,求cos A ,sin2A(3)已知顶角半角的三角函数,求顶角的三角函数和底角的三角函数例1.3.如图,如图,已知在等腰ABC 中,AB AC =,310cos 210A =, 求sin A ,tan B转化一:圆中没有等腰三角形可以观察是否可以转化到一个等腰三角形中,变成熟悉的题型例1.4.(2014•武汉四月调考)已知:P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B 两点,点C 为⊙O 上一点.(1)如图1,若AC 为直径,求证:OP ∥BC ; (2)如图2,若sin ∠P=,求tan ∠C 的值.转化二:圆中有等腰三角形根据需要作底上的高(注意证明共线)和腰上的高 例 1.5.如图,AC 为O 的直径,ABD 为O 的内接三角形,AB BD =,BD 交AC 于F 点,BE AD 交AC 的延长线于E 点。
(1)求证:BE 为O 的切线;(2)若4AF CF =,求tan BAE ∠的值。
例 1.6..如图,AB 是O 的直径,点C 是O 上一动点,点D 是优弧AC 的中点,连接DO ,若点C 为AB 上任意一点(不与A 、B 重合),连接AC ,当tan 2BAC ∠=时,求DAB ∠的值。
转化三:圆中等腰三角形顶角的三角函数通常可以转化到圆心角的一半处例1.7.(2016•武汉四月调考) 已知⊙O 为△ABC 的外接圆,点E 是△ABC 的内心,AE 的延长线交BC 于点F ,交⊙O 于点D .(1)如图1,求证:BD= ED ;(2)如图2,AO 为⊙O 的直径,若BC= 6,sin ∠OFCBAODCBABAC=53,求OE的长.例1.8.如图,在ABCD中,过A、B、C三点的O交AD于E,且与CD相切。
(1)求证:CD CE=(2)若4AB=,6BE=,求cos EBC∠转化四:圆中非等腰三角形的结构中,圆周角的三角函数都可以放在圆心角的一半处例1.9.(2017•武汉四月调考)如图,□ABCD的边AD与经过A、B、C三点的⊙O相切(1) 求证:弧AB=弧AC(2) 如图2,延长DC交⊙O于点E,连接BE,sin∠E=1312,求tan∠D的值例 1.10.如图,在O中,AB AC=,D为AB上任意一点,若3cos4BDC∠=,求tan ADC∠的值(二)切线长定理与射影图结构图形结构:方法归纳:OECBAABOCDA切线长定理产生对称射影图,对称射影图中,任意知道两条线段,其他线段均可求。
转化手段有,相似、三角函数,面积,勾股定理例2如图,AC 为O 的直径,且PA AC ⊥,点B 在O 上,PB 交AC 的延长线于点D ,C 为AD 的中点,2DB BP =。
(1)求证:PB 为O 的切线。
(2)点E 为O 上一点,求cos BEA ∠的值。
(三)圆与1,2,5的三角形等腰直角三角形的一直角边作为直径作圆都可以归为1,2,5型例3.1(2015•武汉中考)如图,AB 是⊙O 的直径,∠ABT=45°,AT=AB . (1)求证:AT 是⊙O 的切线;(2)连接OT 交⊙O 于点C ,连接AC ,求tan ∠TAC .变式一:延长TO 交O 于M ,连接AM ,求tan M ∠的值。
变式二:延长TO 交O 于M ,连接EM ,求tan BEM ∠的值OEC BA变式三:连TO 交O 于F ,连接BF ,求tan TBF ∠,sin ABF∠的值。
变式四:如图,AB 是O 的直径,045ABT ∠=,AT AB =。
(1)求证:AT 是O 的切线;(2)若C 是TB 上一点,12BC CT =,连接OC ,AC ,求tan ACO ∠的值。
(四)母子型结构知识结构:BAD BCA结论:①BAD C ∠=∠ ②2BA BD BC =⋅; ③字母比=tan tan BD BA ADC BAC BA BC AC===∠=∠例 4.1.如图ABC ,O 为BC 上一点,O 过A 、C 两点交BC 于D ,BA 为O 的切线,若3sin 5B ∠=,求tan BAD ∠(五)弧(非半圆)的中点与赵州桥问题结构TOCBA条件的给法:①点F 为BE 的中点;②AF 平分BAE ∠。
连接OF 交BE 于K ,如果给拱高FK 和跨度BE 的长,可以在BOK 中用勾股定理,如果给拱高FK 和BF 的长,则可以在BOK 和BFK 中用双勾股列方程。
例5.1.如图,AC DC =,AC 平分DAB ∠。
(1)求证:AB 是O 的切线;(2)若5AC AD =,求sin BAD ∠的值。
例5.2.四边形ABCD 内接于O ,AB 为O 的直径,BC DC =(1)求证:OC AD ;(2)OF AD ⊥于E ,交CD 的延长线于F ,若27BC AD =,求cos F ∠的值(六)旋转型相似与矩形结构条件的给法:CD AD ⊥,AC 平分BAD ∠(或者)点C 为BE 的中点 转化手段:①DAC CAB ;②连接BE 、CO 交于K 点,则得矩形EDCK ;③连接OC ,过点O 作OQ 垂直AE 于点Q ,则得矩形OCDQ ; ④连接OD 交AC 于点F ,则可用X 型转化比例; ⑤连接BE 交AC 于点H ,则可用X 型转化比例; ⑥过点B 向直线DC 作垂线则形成母子型相似。
