卷积和
向量a,b卷积和互相关的公式

向量a、b的卷积和互相关是信号处理和数字图像处理中常用的运算,具有广泛的应用。
在本文中,我们将介绍向量a、b的卷积和互相关的数学公式和计算方法。
一、向量a、b的卷积公式如果a和b是长度为n的向量,那么它们的卷积可以表示为以下形式:c[i] = Σ (a[j] * b[i-j]),其中j的取值范围为0到n-1,c[i]表示卷积结果的第i个元素。
从上述公式可以看出,向量a和b的卷积结果c的长度为n,计算过程是将向量a和b按照一定的规则进行相乘,并将相乘的结果累加得到卷积结果。
二、向量a、b的互相关公式与卷积类似,向量a和b的互相关可以表示为以下形式:c[i] = Σ (a[j] * b[j+i]),其中j的取值范围为0到n-1,c[i]表示互相关结果的第i个元素。
与卷积不同的是,互相关在计算过程中,向量b的元素是按照顺序平移后与向量a的对应元素相乘并累加得到互相关结果。
三、卷积和互相关的区别卷积和互相关在数学上有一定的区别。
在卷积中,向量b的元素是按照逆序进行相乘并累加;而在互相关中,向量b的元素是按照顺序进行相乘并累加。
这意味着它们在计算过程中,对向量b的处理方式不同。
四、卷积和互相关的计算方法1. 基本计算方法对于长度为n的向量a和b,可以使用双重循环的方法来计算卷积和互相关。
具体步骤是先将向量a和b进行填充,然后进行相乘并累加得到结果。
2. 快速计算方法为了提高计算效率,可以使用快速傅里叶变换(FFT)来进行卷积和互相关的计算。
FFT是一种高效的计算方法,可以在O(nlogn)的时间复杂度内完成卷积和互相关的计算。
五、卷积和互相关的应用1. 信号处理领域卷积和互相关在信号处理领域有着广泛的应用,用于滤波、频域变换等方面。
2. 数字图像处理领域在数字图像处理中,卷积和互相关被广泛应用于图像匹配、特征提取等方面。
3. 人工智能领域在人工智能领域,卷积神经网络(CNN)中的卷积层就是利用了卷积的原理进行特征提取。
课件:6.7卷积和

序列
存在区间
序列样值数 nA个 nB个 nA +nB-1个
三、卷积和的性质
1.交换律 2.分配律
三、卷积和的性质
3.结合律
三、卷积和的性质
4.卷积的移不变性
若
则
5.序列与 δ(n)的卷积
6.序列与u(n)的卷积
信号与系统
§6.7 卷积和
一、卷积和的定义
一般序列 x(n)与单位样值序列 δ(n)的关系
对于LTI离散系统, x(n)激励系统产生的零状态响应为Fra bibliotek 一、卷积和的定义
上式称为序列x(n) 和h(n)的卷积和,或者称为离散卷积, 简称卷积,通常用符号 或*表示卷积和运算:
对式(6.7.2)进行变量置换得到卷积和的另一种表示式
二、卷积和的计算
1.解析法 解析法就是定义法,依据卷积和的定义,通过解析式进 行计算。
2.图形法 使用图解法计算 x(n)和h(n)卷积的过程: (1) 以m为自变量作出做出x(m)的波形; (2) 以m为自变量作出做出h(m)的波形,将 h(m)反褶得 到 h(-m) ,然后将 h(-m)平移 n得到h(n-m) 的波形; (3) 将x(m)和h(n-m)相乘,得到 x(m) h(n-m) ; (4) 计算和
这说明,两个序列进行卷积的次序无关紧要,可以互换。
二、卷积和的计算
• 由卷积和的定义可知,其计算过程与卷积积分过程类 似,包括四个步骤:反褶、时移、相乘、求和。
• 由于系统的因果性或激励信号存在时间的局限性,卷 积和的求和上下限会有所变化,因此卷积和的计算中 求和限的确定是非常关键的。
• 在计算序列卷积和时,常用的方法有三种,请注意 这些方法的特点和不足之处,适用条件及相互关系。
§7.6 离散卷积(卷积和)

三.卷积计算 y(n) = x(n)* h(n) = ∑x(m)h(n − m)
m=−∞
∞
m的范围由x(n)、h(n)的范围共同决定。 范围由x 范围共同决定。
1.y(n)的序列元素个数? 1.y 序列元素个数 元素个数?
若x(n)的序列长度为n1、 h(n)的序列长度为n2, 的序列长度为n 的序列长度为n 则y(n)的序列长度为n1 + n2 -1 的序列长度为n 若:
返回
例7-6-1 已知x(n) =αnu(n) (0 <α <1) , h(n) = u(n),求卷积
y(n) = x(n)∗h(n)。
y(n) = x(n) ∗h(n) =
m=−∞
∑α
∞
m
要点: 要点: u(m)u(n − m) 定上下限
量 宗 : m ≥ 0, m ≤ n 即: m ≤ n, n ≥ 0 0≤
1 2 m=−∞ 1 3
∞
∞
m=−∞
= x1(n)*x2(n)+ x1(n)* x3(n) )*x 4.其它一些性质 x(n)* δ(n)= x(n) .
x(n)* u(n)=∑ x (n )
i = −∞
n
y(n-n1-n2)=x1(n-n1)* x2(n-n2) y(n)= x1(n)* x2(n)= x1(n)* x2(n)
• •
n +6
• o
•
1 2 3 4 5
m o
2
6
m
o
n +2
m
再将x 再将x2(n-m)平移,并分区间求出卷积结果。 平移,并分区间求出卷积结果。
x1(m)
4
• o
•
卷积和的性质

n
1 y[n] y[n 1] x[n] 2 x[n 1] 3 x[n 2] 5 1 1
9 1 n h( n) 1 66( 5 ) 5 n 2 n 0
稳定系统
第3章 离散时间系统的时域分析
3.8 反卷积及其应用(自学)
h1[n]
h[n]
h[n] k [n]
可逆性:由y[n]可确定x[n].
条件
x[n]
h[n] h1[n] [n]
y[n]
h1[n]
x[n]
第3章 离散时间系统的时域分析
•LTI离散系统的互联
对于级联系统:
x[n] h1[n] h2 [n] y[n]
h[n] h1[n] h2 [n]
1 x1[k ] n[n 1]u[n] 2 k
n
x2 (n) [u(n 6) u(n 1)] (n 6) (n 1)
y( n) x1[n] x2 [n]
k
x [k ] x [n]
1 2
n
1 n( n 1)u[n] { [n 6] [n 1]} 2
三.卷积和的性质
2.分配律:
第3章 离散时间系统的时域分析
1.交换律: x1[n]* x2 [n] x2 [n]* x1[n]
x1[n] x2[n]* x[n] x1[n] x[n] x2[n]* x[n]
3.结合 律: { x1[n] * x2 [n]}* x3 [n] x1[n] * { x2 [n] * x3 [n]}
第3章 离散时间系统的时域分析
例:试用系统模拟图来表示下列方程所描述的LTI系统
信号与系统卷积和及几类常见题目

⏹卷积☐卷积的定义☐卷积的物理意义☐卷积的性质☐卷积的计算⏹信号的分解☐信号分解为基本信号之和☐…δ(t )是卷积的单位元δ(t-t 0)是卷积的延迟器u (t )是卷积的积分器δ’(t )是卷积的微分器温故知新,上讲回顾第二章信号的时域分析§2.1常用信号及其基本特性§2.2信号的时域运算Array§2.3信号的时域分解§2.4卷积积分§2.5卷积和信号分类;基本信号特性;信号分解与运算;卷积/卷积和周期/非周期判断;奇异函数运算;信号展缩平移;卷积/卷积和1. 掌握卷积和的定义/性质并进行计算(解析法、图解法、竖式法、性质求解)2. 习题课(信号时域分析几类常见题目)§2.5卷积和一、卷积和的定义及物理意义二、卷积和的性质三、卷积和的计算设x 1(n ) 和x 2(n )是两个序列,则1212()()()()k k k x n x n x x n ∞=−∞∗=−∑如果x 1(n ) 和x 2(n )都是因果序列,则11202()()()()nk x n x n x k x n k =∗=−∑1212()()()()d f t f t f f t τττ∞−∞∗=−⎰卷积和:卷积积分:1. 定义任意序列x (n ) 可以表示为单位样值信号δ(n ) 的移位加权和。
{}()=+(1)(1)+(0)()+(1)(1)+(2)(2)+()()()()k x n x n x n x n x n x k n k x k n k δδδδδδ∞=−∞−+−−+−+=− LTI 系统δ(n )h (n )x (n )?2. 物理意义输入δ(n-k )h (n-k )输出时不变x (k )δ(n-k )x (k )h (n-k )齐次性()=()()k x n x k n k δ∞=−∞−∑zs =()()()*(())k y n x k h n k h x n n ∞=−∞−∑ 可加性系统特性LTI 系统δ(n )h (n )卷积和卷积和的物理意义:揭示了LTI离散系统零状态响应与输入信号和系统单位样值响应之间的关系。
卷积和的概念

卷积和的概念卷积和的概念卷积和是一种在信号处理、图像处理、数值分析和控制理论等领域广泛应用的数学运算。
其主要用于处理具有周期性特征的数据,如正弦波、余弦波等。
一、卷积和的定义卷积和通常用符号"*" 表示,对于两个函数f(t) 和g(t),其卷积和定义为:(f * g)(t) = ∫(-∞to ∞) f(τ) g(t - τ) dτ这表示将函数f(t) 向右平移,与函数g(t) 在每个位置上进行相乘,然后将所得的积分求和。
这个过程也被称为卷积积分。
二、卷积和的性质1. 交换律:f * g = g * f2. 结合律:f * (g * h) = (f * g) * h3. 单位元:e * f = f4. 反元素:f * (f^-1) = e三、卷积和的应用1. 在信号处理中,卷积和是描述信号的线性滤波和卷积的关键工具。
它能够揭示信号中的特定频率分量,对于提取信号中的关键信息具有不可替代的作用。
在数字信号处理中,通过将一个信号与一个滤波器函数进行卷积和,可以精确地调整信号的频率成分,从而提取出特定的频率分量。
这一过程不仅在通信、语音识别等领域有着广泛的应用,同时也是其他领域如图像处理、数值分析等的重要基础。
2. 在图像处理中,卷积和被用于实现图像的滤波和锐化,是图像处理的关键工具之一。
通过将图像与特定的滤波器函数进行卷积和,可以增强图像的特定特征,如边缘、纹理等。
这一技术在计算机视觉、图像分析等领域发挥着重要的作用,为机器视觉、人脸识别等复杂任务提供了可能。
3. 在数值分析中,卷积和是数值积分和微分方程求解的重要手段之一。
在科学研究和工程实践中,许多复杂的问题需要用数学模型进行描述和解决,而卷积和在这其中扮演着关键的角色。
例如,通过将一个函数与一个基函数(例如正弦函数或余弦函数)进行卷积和,可以获得该函数的离散化数值表示,为解决复杂的数学问题提供了有效的途径。
4. 在控制理论中,卷积和是描述系统的稳定性和响应特性的重要工具。
卷积和矩阵的关系

卷积和矩阵的关系
卷积和矩阵之间的关系可以从多个角度来理解,其中最常见的是在卷积神经网络中的应用。
在卷积神经网络中,卷积层是由多个卷积核(也称为滤波器或权重矩阵)组成的,这些卷积核对输入数据进行卷积运算,生成新的特征图。
每个卷积核都可以看作是一个矩阵,而卷积运算的过程就是将这个矩阵与输入数据进行矩阵乘法运算。
因此,可以说卷积运算在卷积神经网络中是通过矩阵乘法实现的。
从数学角度来看,卷积可以被看作是一种特殊的矩阵乘法。
假设我们有一个输入矩阵X和一个卷积核K,卷积运算可以表示为:Y=X* K,其中“*”表示卷积运算。
这种运算方式实际上是将卷积核K看作一个可学习的权重矩阵,然后将其与输入矩阵X进行矩阵乘法运算,从而得到一个新的特征图Y。
此外,在信号处理中,卷积也是一种常用的信号处理方法,它可以用来提取信号中的某些特征或进行滤波操作。
在这种情况下,卷积也可以被看作是一种特殊的矩阵乘法。
具体来说,如果我们将信号表示为一个矩阵,那么卷积运算就可以看作是这个矩阵与另一个矩阵(即滤波器)进行乘法运算的过程。
这个过程可以通过一些数学技巧来加速,例如通过离散傅里叶变换(DFT)来将时域信号转换为频域信号,然后在频域中进行矩阵乘法运算。
总的来说,卷积和矩阵之间的关系在于它们都可以用来进行信号处理和特征提取。
在卷积神经网络中,卷积运算通过矩阵乘法实现,而卷积核则可以被看作是一个可学习的权重矩阵。
卷积和求法
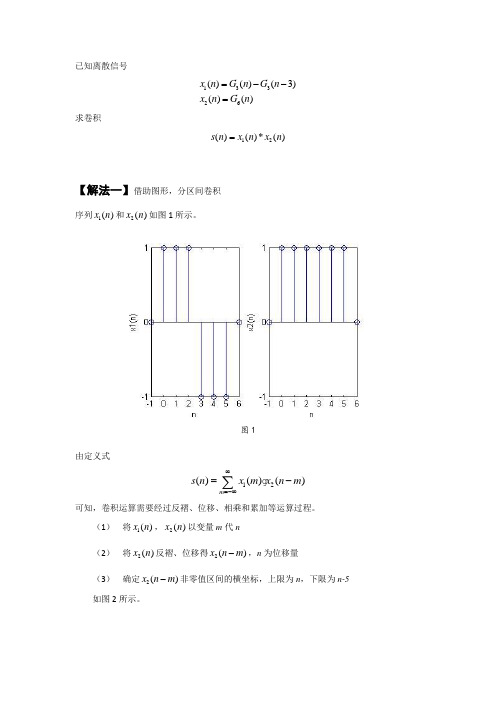
已知离散信号13326()()(3)()()x n G n G n x n G n =--=求卷积12()()*()s n x n x n =【解法一】借助图形,分区间卷积序列1()x n 和2()x n 如图1所示。
图1由定义式12()()()m s n x m x n m ∞=-∞=-∑ 可知,卷积运算需要经过反褶、位移、相乘和累加等运算过程。
(1) 将1()x n ,2()x n 以变量m 代n(2) 将2()x n 反褶、位移得2()x n m -,n 为位移量(3) 确定2()x n m -非零值区间的横坐标,上限为n ,下限为n-5 如图2所示。
图2从图2可知,当位移量0n <时,2()x n m -与1()x m 非零值没有重叠部分,故12()()*()0s n x n x n == 0n <当02n ≤≤时120111()()()nm nm n s n x m x n m ===+=-=∑∑当35n ≤≤时3212011113(2)5()()()nm m nm n ns n x m x n m ===-=--=-=-=∑∑∑当052n ≤-≤,即57n ≤≤时51252553()()11115()m n m n m x m x n m n s n =-=-=-=-=-=∑∑∑当355n ≤-≤,即810n ≤≤时55115125(1)1()()()m n n m n s n x m x n m =-=-=--=-=∑∑当56n -≥,即11n ≥时,2()x n m -与1()x m 非零值没有重叠部分,因此12()()*()0s n x n x n ==将各区间结果汇总,得0,01,025,3711,8100,11()n n n nn n n n s n <⎧⎪+≤≤⎪⎪-≤≤⎨⎪-≤≤⎪≥⎪⎩=结果如图3所示。
图3 s(n)【解法二】利用单位样值序列求卷积。
卷积和相关

1 2 * R12 ( ) T f1 (t ) f 2 (t )dt ,其中星号表示复共轭。 T 2
卷积和相关
如果 f 1 ( t ) 和 f 2 ( t ) 是两个不同的函数,则称为 互相关函数, 表示为
R12 ( ) ,如果 f 1 ( t ) 和 f 2 ( t ) 是同一个函数,则称为自相关函数, 表示为 R( ), Rxx ( ) 等。
f ( t ) f1 ( ) f 2 ( t )d f1 ( t ) f 2 ( t )
卷积和相关
任何函数与冲激函数卷积得出函数f(t)本身
f (t ) * (t ) f ( ) (t )d f (t )
f (t ) * (t T ) f (t T )
R ( ) R ( ) f ( t ) f ( t ) 12 21 注意: 1 , 2 次序一般不可交换。可证
当
f 1 ( t ) , f 2 ( t ) 为实函数时,有 R12 ( ) R21( )
R( ) R* ( )
R( ) R ( )
相关定理:
R( ) lim
FT ( )
S ( )
卷积和相关
自相关函数的性质: * R ( ) R ( ) ,实部为 的偶函 1、复对称性: 数,虚部为 的奇函数 2 R ( 0 ) f ( t ) dt E 能量 2、对于能量信号: T 1 2 2 对于功率信号: R(0) T f (t ) dt 平均功率 T 2 3、 R(0) R( ) 4、周期信号自相关也是同周期的周期函数
卷积和相关

都是两个函数通过某种运算得到另一函数。 一个函数是输入函数(待观测量、输入信号), 一个函数描述观测方式或观测仪器的特征(或作用 特点) 另外一个函数就是输出函数(信号),即观测得到 的结果。 “某种运算”:就是观测方式或观测仪器对输入 函数作用的数学描述。
平移量等于两者的平移量之和。
8、函数 f ( x, y) 与
d
函数的卷积
根据 1. d-函数是偶函数, 2. d-函数的筛选性质, 有:
f ( x) d ( x) f ( )d ( x )d f ( x)
即任意函数与d(x) 卷积后不变 利用卷积的位移不变性可得:
g(x)称为函数f(x)与h(x)的卷积. 二维函数的卷积:
g ( x, y ) f ( x, y ) h ( x, y )
f ( , )h( x , y )d d
三、卷积的物理意义和几何意义
物理意义:像强度分布是物强度分布与单位强度点 光源对应的像强度分布的卷积.
若右边园孔上加p 位相板, 则 t (x, y)
=
x2 y2 circ l/2
*
d (x+d/2 - d (x-d/2)]
练习 1-12
若f(x) * h(x) = g(x), 证明 (1) f(x- x0) * h(x) = g(x - x0) (2) h(x) * f(x) = g(x)
卷积运算:可用来表示一个观测系统或一个 观测仪器对输入信号的作用过程,等等。
卷积和

图解法求卷积和例1
例1:f1(k)、 f2(k)如图所示,已 知f(k) = f1(k)* f2(k),求f(2) =?
f1( ik ) 1.5 1 -1 0 1 -1 0 1 1 f2( ik ) 1.5
2
-2
2
3
k i
解: f (2) f1 (i ) f 2 (2 i ) i (1)换元 (2) f2(i)反转得f2(– i) (3) f2(–i)右移2得f2(2–i) (4) f1(i)乘f2(2–i) (5)求和,得f(2) = 4.5
举例:P102
■ 第 5页
注意2:因果序列的卷积和求和上下限
用定义求卷积和例
例:f (k) = a kε(k), h(k) = b kε(k) ,求yzs(k)。
解: yzs(k) = f (k) * h(k)
i
f (i )h(k i )
i
i k i a ( i ) b (k i )
■ 第 16 页
四、卷积和的性质
1. 满足乘法的三律:(1) 交换律, (2) 分配律,(3) 结合律. 2. f(k)*δ(k) = f(k) , f(k)*δ(k– k0) = f(k – k0) 3. f(k)*ε(k) =
i
f (i)
k
4. f1(k – k1)* f2(k – k2) = f1(k – k1 – k2)* f2(k)
f2(–i )
-2
f2(2–i)
2 3
ik
f1( i )f2( k- i )
2 1.5 1 -1 0 1 2
■
3
i
§3.3 卷积和

∑ =
⎪⎪ ⎨i=−∞
f1
(i)
f
2
(0
−
i)
=
3,
⎪∞
∑ ⎪
⎪i=−∞
f1
(i)
f
2
(1
−
i)
=
3,
⎪⎪1
⎪⎩0
k ≤ −2 k = −1
k =0
k =1 k =2 k ≥3
13
三、不进位乘法求卷积
∞
∑ f (k) = f1 (i) f2 (k − i) i = −∞ = L + f1(−1) f2 (k +1) + f1(0) f2 (k) + f1(1) f2 (k −1) + f1(2) f2 (k − 2) +L + f1(i) f2 (k − i) +L
17
2. 复合系统的单1 (k )
+ y(k)
h1 (k )
h2 (k)
+ h2 (k)
f (k) h2 (k)
y(k) h1 (k )
h(k) = h1(k) + h2 (k)
h(k) = h1(k) * h2 (k) = h2 (k) * h1(k)
3. f(k)*δ(k) = δ(k) *f(k)=f(k),f(k)*δ(k– k0) = f(k – k0) k
k < −1 k = −1 k =0 k =1 k=2 k =3 k >3
22
解法III: (图解法)
f1(i)
2
∞
∑ f1(k) ∗ f2 (k) = f1(i) ∗ f2 (k − i) i = −∞
1
1
卷积和计算方法

卷积和计算方法
卷积是当今被广泛应用于信息处理机制中的一种重要方法,它是一种基于信号和图像处理技术来处理和组织数据的近似方法。
它可以用来处理和提取图像和信号中的有用信息,以及计算图像的特征。
它的应用远不止这些,它也可以用来实现各种机器学习的任务,例如图像分类、特征检测和物体识别。
卷积的基本原理是在一个输入信号的基础上,不断地滑动一个称为“卷积核”的窗口,并且将每次窗口覆盖的子信号乘以核中的参数,然后求和。
这种计算过程称为卷积,因其功能而得名。
经过卷积操作之后,采用激活函数来提取信号特征,从而得到有意义的结果。
卷积运算技术是一种用于处理和组织数据的重要技术,它可以被广泛用于处理图像,信号以及目标识别中的信息处理任务。
除了传统卷积操作外,现在也有一种叫做“卷积神经网络”的深度学习技术,它可以用来训练模型来识别特征,而不是像传统卷积操作那样仅仅提取特征。
卷积神经网络的主要优点是它的强大的特征提取能力,以及其灵活的模型结构,可以用于解决复杂的问题。
此外,卷积神经网络还可以用于解决复杂的任务,例如文本分析,自然语言处理,图像分割和检索等。
卷积神经网络可以提取每个输入信号的局部特征,并将它们组合成更高级的特征,从而实现有意义的结果。
卷积和计算方法可以为计算机视觉、自动驾驶、机器人技术以及其他各种人工智能应用提供有效而准确的基础。
随着技术的发展,卷
积与计算方法将会更加普及,为信号处理,图像处理,人工智能及其他领域提供更多令人期待的解决方案。
第8讲 卷积和

4. x n n x n
x n n n1 x n n1 x n n2 n n1 x n n1 n2
4
三.卷积计算
x n hn
m
x m hn m
2.6 卷积和
1. 卷积和定义 2. 离散卷积的性质 3. 卷积计算及图解说明
1
1 卷积和
一.卷积和定义
任意序列x n 表示为 n 的加权移位之线性组合:
x n x 1 n 1 x 0 n x 1 n 1 x m n m
x m n m
x n hn
x m hn m
处由 x m 加权。 卷积和的公式表明:
系统对 x n 的响应 每一样值产生的响应之和,在各
hn将输入输出联系起来, 即零状态响应 x n hn。
3
二.离散卷积的性质
利用分配律
x ( n) h( n) ( n) 2 ( n 1) 3 ( n 2)
( n 1) 2 ( n 2) 3 ( n 3) ( n 2) 2 ( n 3) 3 ( n 4) ( n) 3 ( n 1) 6 ( n 2) 5 ( n 3) 3( n 4)
0 m n m 0 宗量 : m n n 0 从图中可见求和上限n,下限0
n m y( n) u(u(n m )
要点: 定上下限
1 n1 un 1
1.交换律
x ( n) h( n) h( n) x ( n)
2.结合律 x( n) h1 ( n) h2 ( n) x( n) [h1 ( n) h2 ( n)] 3.分配律
§7.6 离散卷积(卷积和)ppt课件

o 123
m
n0
o 123
m
n 1
y(n) u(n) n αm 1 αn1 un 1 yn
m0
1α
11
当n 时,yn 1
1α
o 1234
n
X
第
例7-6-2
8 页
已知x1(n)
4
,
n0
3,
2,
1,x2(n)
3
,
n0
2,
1, ,
求:yn x1(n) x2(n)
使用对位相乘求和法求卷积 步骤: 两序列右对齐→ 逐个样值对应相乘但不进位→ 同列乘积值相加(注意n=0的点)
信号与系统
7.5 7.7
§7.6 卷积(卷积和)
•卷积和定义 •离散卷积的性质 •卷积计算烟台大学光Βιβλιοθήκη 学院1一.卷积和定义
第 2
页
任意序列xn表示为 n的加权移位之线性组合:
xn x 1 n 1 x0 n x1 n 1 xm n m
xm n m
m
x(n)
y(n)
(n)
h(n)
X
第 9
页
x1n : x2 n :
4 321
n0
3
21
n0
4321
86 4 2
12 9 6 3
yn : 12 17 16 10 4 1 n0
所以yn 12 , 17, 16, 10, 4,1
n0
X
例7-6-3
已知x(n)
R3 n,
h(n)
1
,2,3,求x(n)
n0
h(n)。
第 10
页
x(n) 1 1 1
123
离散卷积(卷积和)

y(n)= x1(n)* x2(n)= x1(n)* x2(n)
n
x1(n)*i x2
i =
x1(n)*
x2(n)
n
i
si
=
n i
x1
i
*x2(n)=
x1(n)*
n i
x2
i
返回
三.卷积计算 yn
xn* hn
xmhn m
m
m的范围由x(n)、h(n)的范围共同决定。
6
*
n
6
n
1
1 n 6n 7un 6 un 15un un 5
2
1 n 1n 2un 1 un 5
2
这与前面所得结果是相同的,但运算过程比较简单。
返回
例7-6-7已知离散信号 x1(n)=n[u(n)-u(n-6)]
利用单x2位(n样)=值u(信n+号6)d-(un()n求+1卷) 积 y(n)= x1(n)*x2(n)
mumun m 6 mum 6un m 6
m
m
mumun m 1 mum 6un m 1
m
m
n6
mun
6
n6
mun
n1
mun
1
n1
mun
5
m0
m6
m0
m6
n6
mun
6
n6
m
5
mun
n1
mun
1
n1
m
5
mun 5
i
i
i0 i6
1 2
nn
1un
1 2
nn
1un
15un
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f (k 1) [2 2(k1) ] (k 1) 2(1 2k ) (k 1)
任意序列作用下的零状态响应
f (k) 根据h(k)的定义:
δ(k)
LTI系统 零状态
yf(k) h(k)
由时不变性: δ(k -i)
h(k -i)
由齐次性: f (i)δ(k-i)
f (i) h(k-i)
= (k+1)ε(k) – (k+1 – 5)ε(k – 5)
= (k+1)ε(k) – (k– 4)ε(k – 5)
h1(k) y(k)
例 如图复合系统由两个子系统
级联组成,其中
h1(k) = 2cos(kπ),
f(k ) h1(k)
h2(k) = akε(k),
激励f(k)= δ(k)–aδ(k-1),求复合
常用序列的卷积和公式 表 常用序列的卷积和公式
h2(k) y(k)
系统的零状态响应响应yf (k) 。
解 yf (k) = f(k)* h1(k) * h2(k) = 2cos(kπ)*[akε(k)]*[δ(k)–aδ(k-1)]
= 2cos(kπ)*[akε(k) - akε(k -1)]
= 2cos(kπ)* δ(k)
= 2cos(kπ)
由叠加性: f (i) (k i)
f (i)h(k i)
‖ i
‖ i
f (k)
yf(k)
y f (k) f (i)h(k i) 卷积和
i
零状态响应与卷积和
➢ 单位抽样响应:由单位序列δ(k)所引起的零状态 响应称为单位序列响应或单位样值响应或单位取 样响应,或简称单位响应,记为h(k)。
<0,即i>k时,f2(k-i)=0, 因而和式的上限可改写为k,也就是
k
f1(k ) f2 (k ) f1(i) f2 (k i) (1-3)
i
如果f1(k)和f2(k)均为因果序列, 则有
k
f1(k ) f2 (k ) f1(i) f2 (k i) (1-4)
i
k i0
2i
1
2k 21 1 21
2 2k
上式中k≥0, 故有
f (k) 2k (k) (k) (2 2k ) (k)
再应用卷积和性质 3,求得
f1(k) f2(k) 2(k1) (k 1) (k 2) f (k 1 2)
ε(k – 5),求复合系统的
∑
f(k)
单位序列响应h (k) 。
h2(k)
解 根据h(k)的定义,有
h(k)= [δ(k)* h1(k) –δ(k)* h2(k) ]* h1(k) = [h1(k) – h2(k) ]* h1(k) = h1(k) * h1(k) –h2(k) * h1(k) = ε(k)* ε(k) – ε(k – 5) *ε(k)
性质 2 任一序列f(k)与单位脉冲序列δ(k)的卷 积和等于 序列f(k)本身, 即
f (k) (k) (k) f (k) f (k)
性质 3 若f1(k)*f2(k)=f(k),则
f1(k) f2(k k1) f1(k k1) f2(k) f (k k1)
(n 2) 2 (n 3) 3 (n 4)
(n) 3 (n 1) 6 (n 2) 5 (n 3) 3(n 4)
卷积的图解法
f (k) f1 (i) f2 (k i) i
卷积过程可分解为四步: (1)换元: k换为 i→得 f1(i), f2(i) (2)反转平移:由f2(i)反转→ f2(–i)右移k → f2(k – i) (3)乘积: f1(i) f2(k – i) (4)求和: i 从 –∞到∞对乘积项求和。 注意:k 为参变量。 举例略。
卷积和
卷积和的定义
已知定义在区间( – ∞,∞)上的两个函数f1(k)和f2(k), 则定义和
f (k) f1(i) f2 (k i) (1-1) i
为f1(k)与f2(k)的卷积和,简称卷积;记为 f(k)= f1(k)*f2(k)
注意:求和是在虚设的变量 i 下进行的, i 为求和变 量,k 为参变量。结果仍为k 的函数。
n N 1
y(n)
N 1
anm
m0
an
1 aN 1 a1
h(n) anu(n)
x(n)
N 1
a
n
1
a (n1) 1 a1
an
1 aN 1 a1
N 1
例 如图复合系统由三个
子系统组成,其中
h1(k) = ε(k), h2(k) =
h1(k)
序列与一个移位的单位取样序列δ(n-n0)的线性卷
积等于序列本身移位n0
卷积和的计算
xn hn xmhn m m
m范围由x(n), h(n)范围共同决定。 离散卷积过程:序列倒置移位相乘取和
1.解析式法 2.图解法 3.对位相乘求和法求卷积 4.利用性质
x(n) (n) (n 1) (n 2)
h(n) (n) 2 (n 1) 3 (n 2)
利用分配律 x(n) h(n) (n) 2 (n 1) 3 (n 2)
(n 1) 2 (n 2) 3 (n 3)
求解过程中对k没有限制,故上式可写为 x(k)*y(k)=y(k)*x(k)=1.5 -∞<k<∞
可见,x(k)*y(k)运算满足交换律。
例 已知序列f1(k)=2-(k+1) ε(k+1)和f2(k)=ε(k-2),试计算
卷积和f1(k)*f2(k)
解:应用卷积和性质 3, 先计算:
f (k) (2)k (k) (k) (2)i (i) (k i)
f1(k k1) f2(k k2 ) f1(k k2 ) f2(k k1) f (k k1 k2 )
式中k1 , k2均为整数。
例 已知序列x(k)=(3)-kε(k) ,y(k)=1, -∞<k<∞, 试验证x(k) 和y(k)的卷积和运算满足交换律,即
x(k) y(k) y(k) x(k)
例 设f1(k)=e-kε( k),f2(k)=ε(k), 求f1(k)*f2(k)。
解 由卷积和定义式(1-1)得
f1(k ) f2 (k ) ei1(i) (k i)
i
考虑到f1(k)、f2(k)均为因果序列,根据式(1-4),可将上式表示为
f1(k) f2(k) ei (k i) ei
解 先计算x(k)*y(k),考虑到x(k)是因果序列,根据式(1-2),有
x(k) y(k) x(i) y(k i)
i
(3)i (i) 1 (3)i
i
i0
1 1 1
3 2
1.5
3
再计算y(k)*x(k),同样考虑到x(k)是因果序列,可得
12 9 6 3
yn : 12 17 16 10 4 1 n0
yn 12 17 16 10 4 1
n0
y(n)的元素个数?
若: 例如:
x(n)
nA
h(n)
nB
y(n)
nC nA nB 1
x(n)序列
n1 n n2,
h(n)序列
n3 n n4
➢ 零状态响应:已知输入f( n )和h( n )时,则系统的 零状态响应为
n
y(n) f (n) * h(n) f (k)h(n k) k 0
25-3
例如:已知 h(n) anu(n) 0 a 1,
x(n) G(n) u(n) u(n N)
求零状态响应 y(n) ?
y(k ) x(k) y(i)x(k i) 1 (3)(ki) (k i)
i
i
k
k
(3)(ki) (3)k 3i
i
i
(3)k (3)k 3 1.5 1 3
所以
x(k) y(k) y(k) x(k) 1.5
例:f (k) = a kε(k), h(k) = b kε(k) ,求yf(k)。
解: yf(k) = f (k) * h(k)
f (i)h(k i) ai (i)bki (k i)
i
i
当i < 0,ε(i) = 0;当i > k时,ε(k - i) = 0
解 y(n) x(n)*h(n)
n 0 h(n) 0
0 n N 1 y(n) x(n m)h(m) anmu(n m)[u(m) u(m N)]
m0
m0
n
anm
m0
an
n
am
m0
an
1 a(n1) 1 a1
3
,
n0
2,
1, ,
求:yn x1(n) x2(n)
使用对位相乘求和法求卷积 步骤: 两序列右对齐→ 逐个样值对应相乘但不进位→ 同列乘积值相加(注意n=0的点)
x1 n : x2 n :
4 321
