模糊控制实例1

合集下载

模糊控制案例001

10) 11) 12) 13) 14) 15) 16) 17) 18) 19)
If E=Z and EC=PB or PS then U=PS If E=Z and EC=Z then U=Z If E=NS and EC=NB or NS then U=Z If E=NS and EC=Z or PS then U=PS If E=NS and EC=PB then U=PM If E=NM and EC=NB then U=PS If E=NM and EC=Z or NS then U=PM If E=NB and EC=NS or NB then U=PM If E=NM and EC=PB or PS then U=PB If E=NB and EC=Z or PS or PB then U=PB
以不是，甚至可以不是一个整数，经变
换后，是基本论域上的元素。
• 模糊控制的特点所谓的模糊控制，既不是指被控制的对象是模糊的，也不是模糊控制器是不确定的，模糊控制有着自己的一套精确的理论和算法。所谓的模糊是指在表示知识，概念上的模糊性。虽然模糊控制器的算法是通过模糊语言描述的，但它所完成的是一项完全确定性的工作。
表4 模糊控制规则表格
E Ai
U Ck EC Bj
A1 PB
NM C6 R2 NB C7
A2 PM
NS C5 R4 NM C6 R5 NB C7 R3
A3 PS
Z C4 R6 NS C5 R7 NM C6 R6
A4 Z
PS C3 R10 Z C4 R11 NS C5 R9
A5 NS
PM C2 R14 PS C3 R13 Z C4 R12
A6 NM
PB C1 R18 PM C2 R16 PS C3 R15

模糊控制应用实例

模糊控制应用实例模糊控制是一种基于模糊逻辑的控制方法，它能够处理模糊的输入和输出，使得控制系统具有更好的鲁棒性和适应性。

下面将介绍一个模糊控制的应用实例。

某工厂的生产线上有一台机器人，它需要根据生产线上的物品进行分类和分拣。

由于生产线上的物品形状、颜色、大小等特征存在一定的模糊性，传统的控制方法很难实现准确的分类和分拣。

因此，工厂决定采用模糊控制方法来解决这个问题。

首先，需要对机器人的控制系统进行建模。

假设机器人的控制系统包括三个输入变量和一个输出变量。

其中，三个输入变量分别为物品的大小、颜色和形状，输出变量为机器人的动作，包括分类和分拣两种动作。

接下来，需要确定输入变量和输出变量的模糊集合和模糊规则。

假设物品的大小、颜色和形状分别属于三个模糊集合：小、中、大；红、绿、蓝；圆、方、三角。

输出变量也分别属于两个模糊集合：分类、分拣。

根据这些模糊集合，可以确定一些模糊规则，例如：如果物品大小为小且颜色为红且形状为圆，则机器人动作为分类；如果物品大小为中且颜色为绿且形状为方，则机器人动作为分拣；如果物品大小为大且颜色为蓝且形状为三角，则机器人动作为分类。

最后，需要进行模糊推理和模糊控制。

当机器人接收到一个物品时，它会根据物品的大小、颜色和形状，将它们映射到对应的模糊集合中。

然后，根据模糊规则进行模糊推理，得到机器人的动作。

最后，根据机器人的动作，控制机器人进行分类或分拣。

通过模糊控制方法，机器人可以更准确地分类和分拣物品，提高生产效率和质量。

同时，模糊控制方法还具有较好的鲁棒性和适应性，能够应对物品特征的变化和噪声的干扰。

总之，模糊控制是一种有效的控制方法，它能够处理模糊的输入和输出，使得控制系统具有更好的鲁棒性和适应性。

在工业生产、交通运输、医疗健康等领域都有广泛的应用。

模糊控制实例

x2 2 x5 A1 ( x ) 3 , 8 x 5 x 8 3
y 5 B1 ( y ) 3 11 y 3 z 1 C1 ( z ) 3 7 z 3 5 y 8 , 8 y 11
计算机控制算法
属函数 C ( z ) 为：
(1)以连续型重心法作为解模糊化机构：首先找出
因此
z 1 1 z 3 3 2 3 z 5 3 7 z C ( z ) 5 z 6 3 1 6 z 8 3 9 z 8 z9 3 3 z 1 52 67 z 81 99 z zdz zdz zdz zdz zdz 1 3 5 6 8 3 3 3 3 3 z 3 z 1 52 67 z 81 99 z dz dz dz dz 1 3 3 3 5 3 6 3 8 3 dz 28 16 49 28 25 18 3 18 6 18 2 4 1 2 1 3 3 2 3 6 4.7
{负大，负中，负小，负零，正零，正小，正中，正大}
{NB，NM，NS，NO，PO，PS，PM，PB}
第3章
计算机控制算法
2.变量的模糊化
基本论域：某个变量变化的实际范围误差的基本论域为 [ xe ， xe ] 误差变化的基本论域为[ xc ， xc ] 输出变量的基本论域为[ yu ， yu ]
变量的模糊子集论域 {n, n 1,
,0,
, n 1, n}
基本论域到模糊子集论域的转换公式
2n a b y x ba 2
模糊化就是将清晰的某个输入变量按隶属度转换到与之相对应的模糊量的过程。
第3章
计算机控制算法

模糊控制在matlab中的实例

模糊控制在matlab中的实例
MATLAB 是一种广泛使用的数学软件，可以用于模糊控制的研究和应用。

以下是一些在 MATLAB 中的模糊控制实例:
1. 模糊控制器的设计：可以通过建立模糊控制器的数学模型，使用 MATLAB 进行建模和优化，以实现精确的控制效果。

2. 模糊控制应用于电动机控制：可以使用 MATLAB 对电动机进行模糊控制，以实现精确的速度和位置控制。

3. 模糊控制在工业过程控制中的应用：在工业过程中，可以使用模糊控制来优化生产过程，例如温度控制、流量控制等。

4. 模糊控制在交通运输中的应用：在交通运输中，可以使用模糊控制来优化车辆的行驶轨迹和速度，以提高交通运输的安全性和效率。

5. 模糊控制在机器人控制中的应用：可以使用模糊控制来优化机器人的运动和操作，以实现更准确和高效的操作。

这些实例只是模糊控制应用的一部分，MATLAB 作为一种强大的数学软件，可以用于各种模糊控制的研究和应用。

模糊控制实例1

Page 12
摘要
模糊控制器設計步驟
實際例子分析
Matlab Fuzzy Toolbox實現
Page 13
實際例子分析
2 定義輸入及輸出變數輸入變數:物體位置與目標位置之誤差 (追蹤誤差=目標位置-物體位置) 輸出變數:力量
Page 15
實際例子分析
1 問題描述(搬運一質量m之物體至1公尺遠處)
0.7
0.5 0.3
1234567 y
∑ yMOM =
m j=1
wj m
= 4 +5 = 4.5 2
∑∑ yCOA =
n j=1
µC
(
y
j
)
⋅
y
j
n j =1
µC
(
y
j
)
= 2×0.5+ 3×0.5+ 4×0.7 +5×0.7 + 6×0.3 0.5+ 0.5+ 0.7 + 0.7 + 0.3
= 3.9
0.6
0.4
0.2
0
0
1
2
3
4
5
6
7
8
9 10
time(sec)
25
20
15
10
5
con_u 0 (Nt) -5
-10
-15
-20
-25
time(sec) m=1 0
1
2
3
4
5
6
7
8
9 10
2
1.8
1.6
1.4
p(oms_)x
1.2 1
0.8
0.6
0.4

模糊控制应用示例讲解

0.4
0.2
0
-3
-2
NS
ZR
PS
-1
0
1
PB
2
u3
e de NB NS ZR PS PB
模糊推理规则
NB NS ZR PS PB
PB PB PS PS ZR PB PS PS ZR ZR PS PS ZR ZR NS PS ZR ZR NS NS ZR ZR NS NS NB
模糊控制系统设计
% Example 3.8 % 典型二阶系统的模糊控制 % %被控系统建模 num=20; den=[1.6,4.4,1]; [a1,b,c,d]=tf2ss(num,den); x=[0;0];
第5次课
例1：工业工程控制
例2：典型二阶环节的模糊控制
例1：工业过程
例1: 某一工业过程要根据测量的温度（t）和压力（p）来确定阀门开启的角
度: f (t, P) 这种关系很难用数
学模型精确描述。实际中由有经验的操作员完成，因此通常可设计模糊控制器取而代之。
输入输出变量的论域
0
0
0.5
1
1.5
2
2.5 压力 3
阀门开启角度的模糊隶属度函数
“负” “零” “正”
1 0.8 0.6 0.4 0.2
0 -10 -8 -6 -4 -2 0 2 4 6 8 10
角度增量
隶属度函数
模糊推理规则库
模糊推理规则有3条：
If 温度“冷” and 压力“高”，则阀门角度增量为“正”
If 温度“热” and 压力“高”，则阀门角度增量为“负”
If 压力“正常”，则阀门角度增量为“零 ”

模糊控制算法实例解析(含代码)

模糊控制算法实例解析（含代码）
首先来看一个实例，控制进水阀S1和出水阀S2，使水箱水位保持在目标水位O处。

按照日常操作经验，有以下规则：
1、若当前水位高于目标水位，则向外排水，差值越大，排水越快；
2、若当前水位低于目标水位，则向内注水，差值越大，注水越快；
3、若当前水位和目标水位相差很小，则保持排水速度和注水速度相等。

下面来设计一个模糊控制器
1、选择观测量和控制量
一般选择偏差e，即目标水位和当前水位的差值作为观察量，选取阀门开度u为控制量。

2、输入量和输出量的模糊化
将偏差e划分为5个模糊集，负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB)，e为负表示当前水位低于目标水位，e 为正表示当前水位高于目标水位。

设定e的取值范围为[-3，3]，隶属度函数如下。

偏差e对应的模糊表如下：隶属度
变化等级-3 -2
-1
1
2
3模糊集
PB 0 0 0 0 0 0.5
1PS 0
0 0.5 1 0.5 0ZO
0 0.5 1 0.5 0
0NS
0 0.5 1 0.5 0
0NB
0.5 0 0 0 0 0。

模糊控制器设计实例

模糊控制器在智能家居中的应用
总结词
提升家居舒适度
详细描述
智能家居系统中的温度、湿度、光照等环境因素的控制可以通过模糊控制器实现。通过将传感器采集的环境参数进行模糊化处理，根据模糊逻辑规则进行推理，实现对家居环境的智能调节，提升家居的舒适度。
模糊控制器在智能家居中的应用
总结词：节能环保
详细描述：在智能家居中，模糊控制器能够根据家庭成员的生活习惯和环境参数，智能调节家电的运行状态，实现节能环保。例如，根据室内外温度和光照强度，模糊控制器可以智能调节空调和照明设备的运行状态，减少能源的浪费。
进方向。
模糊控制器性能优化
算法优化
改进模糊控制器的核心算法，提高响应速度和控制精度。
参数调整
根据实际应用需求，调整模糊控制器的参数，以优化控制效果。
抗干扰设计
增强模糊控制器的抗干扰能力，提高系统的稳定性和鲁棒性。
人机交互优化
改进用户界面和操作方式，提高模糊控制器的易用性。
05
模糊控制器发展趋势与展望
高医疗设备的安全性和可靠性。
模糊控制器在医疗设备中的应用
总结词
辅助医生诊断
VS
详细描述
在医疗影像诊断中，模糊控制器可以对医学影像数据进行处理和分析，辅助医生进行疾病诊断。通过对医学影像数据进行模糊化处理，提取病变特征，并根据模糊逻辑规则进行推理，帮助医生快速准确地判断病情。
04
模糊控制器性能评估
02
模糊控制器设计实例
模糊控制器实例选择
实例选择
选择一个适合的模糊控制器实例，例如温度控制器、速度控制器等，需要考虑控制对象的特性和控制要求。
实例分析
对所选实例进行详细分析，了解其输入输出变量、控制规则等，为后续设计提供基础。

模糊控制应用实例

模糊控制应用实例1. 引言模糊控制是一种基于模糊逻辑的控制方法，它能够处理不确定性和模糊性问题。

本文将介绍模糊控制的应用实例，包括模糊控制在机器人导航、温度控制和交通信号灯控制等方面的应用。

2. 模糊控制在机器人导航中的应用2.1 模糊控制器设计在机器人导航中，模糊控制可以用于控制机器人的运动路径。

首先，需要设计一个模糊控制器，该控制器包括输入和输出变量以及一组模糊规则。

输入变量可以是机器人与障碍物的距离、机器人当前的角度等。

输出变量通常是机器人的速度和转向角度。

2.2 模糊控制器实现在机器人导航中，可以使用传感器来获取机器人与障碍物的距离和机器人当前的角度。

这些信息可以作为输入变量输入到模糊控制器中。

模糊控制器根据一组模糊规则来计算机器人的速度和转向角度，然后将其作为输出变量输出给机器人的控制系统。

2.3 模糊控制器优势相比于传统的控制方法，模糊控制在机器人导航中具有一定的优势。

首先，模糊控制能够处理不确定性和模糊性问题，使得机器人能够更好地适应复杂的环境。

其次，模糊控制可以通过调整模糊规则和输入变量的权重来优化机器人的导航性能。

最后，模糊控制可以很容易地与其他控制方法结合使用，以实现更高级的导航功能。

3. 模糊控制在温度控制中的应用3.1 温度控制系统在温度控制中，模糊控制可以用于调节加热器或制冷器的功率，以维持目标温度。

温度控制系统通常包括一个温度传感器、一个控制器和一个执行器。

温度传感器用于测量当前的温度，控制器根据温度的变化来调整执行器的功率。

3.2 模糊控制器设计在温度控制中，需要设计一个模糊控制器来根据当前的温度误差和误差变化率来调整执行器的功率。

模糊控制器的输入变量可以是温度误差和误差变化率，输出变量可以是执行器的功率。

通过选择适当的模糊规则和调整输入变量的权重，可以实现温度的稳定控制。

3.3 模糊控制器实现在温度控制中，可以使用一个模糊控制器来计算执行器的功率。

模糊控制器根据一组模糊规则来决定执行器的功率大小，然后将其输出给执行器。

模糊控制程序实例

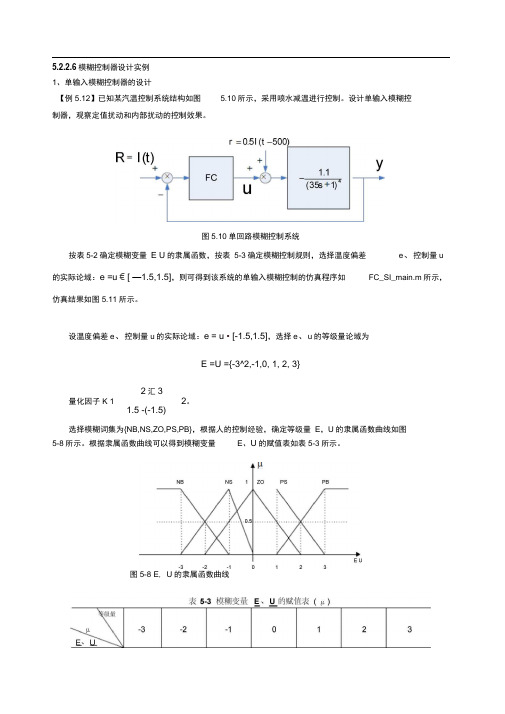
5.2.2.6模糊控制器设计实例1、单输入模糊控制器的设计【例5.12】已知某汽温控制系统结构如图 5.10所示，采用喷水减温进行控制。

设计单输入模糊控制器，观察定值扰动和内部扰动的控制效果。

图5.10单回路模糊控制系统按表5-2确定模糊变量E U的隶属函数，按表5-3确定模糊控制规则，选择温度偏差e、控制量u 的实际论域：e =u € [ —1.5,1.5]，则可得到该系统的单输入模糊控制的仿真程序如FC_SI_main.m所示，仿真结果如图5.11所示。

设温度偏差e、控制量u的实际论域：e = u • [-1.5,1.5]，选择e、u的等级量论域为E =U ={-3^2,-1,0, 1, 2, 3}2汇3量化因子K 1 2。

1.5 -(-1.5)选择模糊词集为{NB,NS,ZO,PS,PB}，根据人的控制经验，确定等级量E，U的隶属函数曲线如图5-8所示。

根据隶属函数曲线可以得到模糊变量E、U的赋值表如表5-3所示。

图5-8 E, U的隶属函数曲线依据人手动控制的一般经验，可以总结出一些控制规则，例如: 若误差E为0,说明温度接近希望值，喷水阀保持不动；若误差明温度低于希望值，应该减少喷水；若误差明温度高于希望值，应该增加喷水。

若采用数学符号描述，可总结如下模糊控制规则：若E负大，则U正大；若E负小，贝U U正小；若E为零，则U为零；若E正小，则U负小；若E正大，则U负大。

写成模糊推理句：if E=NB then U=PBif E=NS then U=PSif E=Z0 then U=Z0if E=PS then U=NSif E=PB then U=NB由上述的控制规则可得到模糊控制规则表，如表5-4所示。

模糊控制规则实际上是一组多重条件语句，它可以表示从误差论域旦到控制量论域U的模糊关系R。

按着上述控制规则，可以得到该温度偏差与喷水阀门开度之间的模糊关系R:R=E U=(NB E PB U)U(NS E PS U)U(Z0E Z0U)U(PS E NS U)U(PB E NB U) 计算模糊关系矩阵R的子程序如F_Relation_1.m 所示。

模糊pid控制实例

模糊pid控制实例以下是一个模糊PID控制的简单实例：假设我们要控制一台电机的转速，目标是使电机转速尽可能稳定在设定值附近。

根据模糊PID控制器的工作原理，我们可以进行以下步骤：1. 设定目标值和初始设定值：设定电机转速的目标值，例如1000转/分钟。

同时设置初始的PID参数。

- 设定值（SP，Set Point）= 1000 RPM- 比例增益 (Kp) = 1- 积分时间(Ti) = 1- 微分时间(Td) = 0.12. 测量电机转速：使用传感器或编码器来测量电机当前的转速，得到当前的反馈值。

3. 模糊控制规则建立：基于当前误差（设定值减去反馈值）和误差的变化率，建立一组模糊逻辑规则，例如： - 如果误差为"NB"并且误差变化率为"PB"，则输出为"NB"。

- 如果误差为"NB"并且误差变化率为"NM"，则输出为"NM"。

- ...4. 模糊推理和模糊输出：根据模糊逻辑规则，进行模糊推理，即将当前的误差和误差变化率映射到模糊输出的隶属度值上。

5. 解模糊：将模糊输出映射回具体的控制量，例如根据模糊输出计算PID控制器的输出量。

6. 更新PID参数：根据误差的变化和模糊输出的结果来更新PID控制器的参数，例如根据误差的大小和变化率来调整PID参数，以使控制更加精确。

7. 反馈控制：将PID控制器的输出量应用于电机，调整电机的转速。

8. 循环控制：循环执行上述步骤，不断更新PID参数和反馈控制，使得电机转速尽可能稳定在设定值附近。

需要注意的是，以上是一个简单的示例，实际的模糊PID控制根据具体的应用情况和系统特点会有所差异。

参数的选择和模糊规则的建立都需要根据具体的控制对象进行优化和调整。

此外，在实际应用中，还需要考虑到系统的鲁棒性、性能指标等因素。

模糊控制详细讲解实例

一、速度控制算法：首先定义速度偏差-50 km/h ≤e （k ）≤50km/h ，-20≤ec （i ）= e （k ）- e （k-1）≤20，阀值e swith =10km/h设计思想：油门控制采用增量式PID 控制算法,刹车控制采用模糊控制算法，最后通过选择规则进行选择控制量输入。

选择规则：e （k ）<0 ① e （k ）>- e swith and throttlr_1≠0 选择油门控制② 否则：先将油门控制量置0，再选择刹车控制 0<e （k ）先选择刹车控制，再选择油门控制 e （k ）=0 直接跳出选择刹车控制：刹车采用模糊控制算法1.确定模糊语言变量 e 基本论域取[-50,50]，ec 基本论域取[-20,20]，刹车控制量输出u 基本论域取[-30,30]，这里我将这三个变量按照下面的公式进行离散化：)]2(2[ba x ab n y +--= 其中，],[b a x ∈，n 为离散度。

E 、ec 和u 均取离散度n=3，离散化后得到三个量的语言值论域分别为：E=EC=U={-3,-2,-1,0,1,2,3}其对应语言值为{ NB,NM,NS,ZO, PS,PM,PB } 2.确定隶属度函数E/EC 和U 取相同的隶属度函数即：E EC U(,5,1)(,3,2,0)(,3,1,1)u (,2,0,2)(,1,1,3)(,0,2,3)(,1,5)g x trig x trig x trig x trig x trig x g x ∧∧--⎧⎪--⎪⎪--⎪=-⎨⎪-⎪⎪⎪⎩说明：边界选择钟形隶属度函数，中间选用三角形隶属度函数，图像略实际EC 和E 输入值若超出论域范围，则取相应的端点值。

3.模糊控制规则由隶属度函数可以得到语言值隶属度（通过图像直接可以看出）如下表：表1：E/EC 和U3.模糊推理由模糊规则表3可以知道输入E 与EC 和输出U 的模糊关系，这里我取两个例子做模糊推理如下：if (E is NB) and (EC is NM) then (U is PB) 那么他的模糊关系子矩阵为：1211U EC E R R R R ⨯⨯=其中，711)0,,0,5.0,1(0⨯== P R E ,即表1中NB 对应行向量，同理可以得到，712)0,,0,5.0,1,0(1⨯== P R EC , 711)0,,0,5.0,1(0⨯== P R U77210000000000005.05.00005.010)0,,0,5.0,1,0()0,,0,5.0,1(⨯⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⨯=⨯TEC E R R 49121)0,,0,5.0,5.0,0,0,0,0,0,5.0,1,0(⨯= EC E R7491211000000005.05.00005.0100000)0,,0,5.0,1()0,,5.0,1,0(⨯⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⨯=⨯= TU EC E R R Rif (E is NVB or NB) and (EC is NVB) then (U is PVB)1112U EC E R R R R ⨯⨯= 结果略按此法可得到27个关系子矩阵，对所有子矩阵取并集得到模糊关系矩阵如下：)27,,2,1(21 ==i R R R R i 由R 可以得到模拟量输出为：()U E EC R =⨯4.去模糊化由上面得到的模拟量输出为1×7的模糊向量，每一行的行元素（u （z ij ））对应相应的离散变量z j ，则可通过加权平均法公式解模糊：)21,,2,1()()(210210 ===∑∑==j i zu z zu u i iji jij从而得到实际刹车控制量的精确值u 。

模糊控制在matlab中的实例

模糊控制在matlab中的实例以下是一个简单的模糊控制器在 MATLAB 中的实例：假设你有一个被控对象，它的输出值 y 取决于输入值 u。

你想要设计一个模糊控制器来控制该对象。

首先，你需要定义模糊控制器的输入和输出变量以及它们的隶属度函数。

示例中，我们定义了两个输入变量 x1 和 x2 以及一个输出变量y，每个变量都由三个隶属度函数组成。

```matlab% 定义输入和输出变量及其隶属度函数x1 = fuzzyvar("input", [-5 5], "bellmf", [1 2 3]);x2 = fuzzyvar("input", [-5 5], "trimf", [-4 0 4]);y = fuzzyvar("output", [-10 10], "trimf", [-8 0 8]);```接下来，我们需要定义规则库。

规则库是一系列模糊规则的集合，每条规则由前提和结论组成。

在这个示例中，我们定义了九条规则，将输入变量 x1 和 x2 映射到输出变量 y。

```matlab% 定义规则库ruleList = ["If (x1 is 1) and (x2 is 1) then (y is -7)";"If (x1 is 1) and (x2 is 2) then (y is -9)";"If (x1 is 1) and (x2 is 3) then (y is -9)";"If (x1 is 2) and (x2 is 1) then (y is -5)";"If (x1 is 2) and (x2 is 2) then (y is -7)";"If (x1 is 2) and (x2 is 3) then (y is -8)";"If (x1 is 3) and (x2 is 1) then (y is -3)";"If (x1 is 3) and (x2 is 2) then (y is -5)";"If (x1 is 3) and (x2 is 3) then (y is -6)";];```现在我们可以创建模糊控制器，并将输入变量和输出变量与规则库相结合。

自动化控制系统中的模糊控制技术应用案例分析

自动化控制系统中的模糊控制技术应用案例分析摘要：自动化控制系统在各个领域中起着至关重要的作用，而模糊控制技术作为一种重要的控制方法，具有适应性强、可靠性高等特点，广泛应用于各种实际问题中。

本文通过分析两个实际案例，探讨了模糊控制技术在自动化控制系统中的应用。

1. 引言自动化控制系统是指利用计算机和现代控制技术对工业过程、机械设备等进行监测、控制和优化的系统。

模糊控制技术作为一种基于模糊逻辑的控制方法，具有适应性强、抗干扰能力好等优点，被广泛应用于自动化控制系统中。

2. 模糊控制技术基本原理模糊控制技术的基本原理是将模糊集合理论引入到控制系统中，通过设计模糊规则集合和模糊推理机制，实现对系统的控制。

模糊控制系统主要由模糊化、模糊推理和解模糊三个部分组成。

3. 应用案例一：自动驾驶汽车的模糊控制自动驾驶汽车的模糊控制是近年来自动化领域的热点研究之一。

在自动驾驶汽车中，模糊控制技术可以用于实现车辆的路径规划和操控。

通过使用激光雷达等传感器获取周围环境信息，将信息输入到模糊控制系统中进行处理，计算出车辆应该采取的行驶方向和速度。

在路径规划方面，模糊控制系统可以根据当前位置和目标位置之间的距离进行判断，并结合交通规则、路况等因素，确定车辆的行驶路径。

在操控方面，模糊控制系统可以根据车辆与前方障碍物的距离、速度等信息，计算出合适的减速或转向指令，实现安全和平稳的行驶。

4. 应用案例二：温度控制系统中的模糊控制温度控制是很多工业生产过程中的常见问题，而模糊控制技术可以在这方面发挥重要的作用。

在温度控制系统中，通过模糊控制技术可以实现对温度的精确控制，提高生产过程的稳定性和效率。

以热处理工业过程为例，对于不同的热处理设备和工件，模糊控制系统可以根据设备和工件的特性，设定合适的温度范围和控制要求。

然后，通过温度传感器获取实时温度信息，将其输入到模糊控制系统中进行处理。

模糊控制系统会根据温度与设定值之间的差异，计算出合适的加热或冷却指令，控制加热或冷却装置的工作状态，使温度保持在设定范围内。

3.5模糊控制应用实例

VL(z) (z 40) / 20
0 z 10 0 z 10
10 z 25 10 z 25
25 z 40 25 z 40
40 z 60 40 z 60
图3.5.3 洗涤时间隶属函数
6
4. 建立模糊控制规则
IF 污泥多 AND 油脂多，THEN 洗涤时间长
洗涤时间
泥污度
3) 规则前件隶属度的聚集
Rule1: min(4 5,3 5) 3 5 Rule2 : min(4 5,2 5) 2 5 Rule3 : min(1 5,3 5) 1 5 Rule4 : min(1 5,2 5) 1 5
9
4）每条规则的推理输出
Rule1 : min(3 5, M (z)) Rule2 : min(2 5, L(z)) Rule3 : min(1 5, L(z)) Rule4 : min(1 5 , VL(z))
LG(y)(y50)/50
0y50 0y50
50y100 50y100
图3.5.2 油性肮脏度隶属函数
5
VS(z) (10 z) / 10
S
(z)
z /10 (25 z)
/
15
洗
涤
时
＝间 M
(
z)
(z 10) / 15 (40 z) / 15
L
(z)
(z 25) / 15
(60
z)
/
20
3.5 模糊控制应用实例——洗衣机的模糊控制
一、重点解决三个问题：
1.
物理量的测定
2.
控制量的确定
3.
控制知识库
1.
二、关键技术：
1.
布质、布量传感器

模糊控制应用实例

图7.14 输入变量旳隶属函数 (a)负载量；(b)水；(c)质料
• 2）输出变量
图7.15 输出变量旳隶属函数
• （4）解模糊判决成果 • 据此又细提成如下旳洗涤控制： • ①水流9种； • ②洗涤时间16种； • ③清洗时间6种； • ④脱水时间6种。
• 7.2 智能手机充电器
• 7.2.1 智能充电原理
• 根据这些控制规律，就可制定出如下满足模糊控制要求旳控制规则：
• 规则1：假如NC=+3时R=VG且C=G且 A=VG，那么NC=3；
• 规则2：假如NC=+2时R=VG且C=G且 A=VG，那么NC=2；
• 规则3：假如NC=+1时R=VG且C=G且 A=VG，那么NC=1；
• 规则4：假如NC=0时 R=VG且A=G，那么
度
• C：（Comfort of riding）乘坐舒适性 • E：（Energy saving）节省能源 • R：（Running time ）行驶时间 • S：（Safety）安全性 • T：（Traceability of speed）速度跟踪
性
• 用5个符号表达模糊概念旳等级： • VG：（Very Good）非常好 • G：（Good）好 • M ：（Medium）中档 • B：（Bad）差 • VB：（Very Bad）非常差 • （1）停车精确度 • （2）乘坐舒适度 • （3）节省能源
• 规则1：假如N =0时，S=G且C=G且E=G，那么N=0；
• 规则2：假如N =P7时，S=G且C=G且 T=B，那么N=P7；
• 规则3：假如N=B7时，S=B，那么N=（N （t）+Bmax）/2；
• 规则4：假如NC=4时，S=G且C=G且 T=VG，那么NC=4；

模糊控制应用实例

模糊控制应用实例模糊控制在自动驾驶中的应用实例自动驾驶技术是近年来备受关注的热门话题，它的出现旨在解决驾驶过程中的安全问题，并提高驾驶的便利性和舒适度。

而模糊控制作为自动驾驶技术中的重要一环，有着广泛的应用。

本文将以自动驾驶中的模糊控制为例，探讨其应用实例。

在自动驾驶的过程中，模糊控制被用来处理传感器数据，并作出相应的决策。

以自动驾驶汽车的转向控制为例，模糊控制可以根据车辆的位置、速度、前方障碍物等数据，决定车辆的转向角度，以保证车辆在道路上行驶的安全性和稳定性。

模糊控制通过模糊化处理将传感器数据转化为模糊集合。

例如，车辆的位置可以被模糊化为"靠左"、"靠右"、"居中"等模糊集合，车辆的速度可以被模糊化为"缓慢"、"中等"、"快速"等模糊集合。

然后，利用一系列的模糊规则来推导出车辆转向角度的模糊集合。

例如，如果车辆靠左，并且速度较快，那么转向角度可能是"向右转"；如果车辆居中，并且速度较慢，那么转向角度可能是"保持直行"。

最后，通过去模糊化处理将模糊集合转化为具体的转向角度。

在自动驾驶中，模糊控制的应用不仅限于转向控制，还包括加速控制、制动控制等。

例如，在车辆的加速控制中，模糊控制可以根据车辆的加速度和前方障碍物的距离，决定车辆的加速度大小，以保证车辆在道路上的安全跟随。

同样，在车辆的制动控制中，模糊控制可以根据车辆的速度和前方障碍物的距离，决定车辆的制动力大小，以保证车辆在紧急情况下的安全停车。

除了在自动驾驶中的应用，模糊控制还广泛应用于其他领域。

例如，在温控系统中，模糊控制可以根据室内温度和设定温度，决定空调的制冷或制热强度，以保持室内的舒适温度。

在机器人的路径规划中，模糊控制可以根据环境的复杂性和机器人的速度，决定机器人的行走路径，以避免障碍物的碰撞。

模糊控制的应用实例与分析

模糊控制的应用实例与分析模糊控制是一种针对模糊系统进行控制的方法，它通过运用模糊逻辑和模糊规则来进行控制决策。

模糊控制广泛应用于各个领域，以下是几个不同领域的模糊控制应用实例和相关分析。

1.模糊控制在温度控制系统中的应用：温度控制系统是模糊控制的一个常见应用领域。

传统的温度控制系统通常使用PID控制器，但是由于环境和外部因素的干扰，PID控制器往往不能很好地应对这些复杂情况。

而模糊控制可以通过建立模糊规则来实现对温度的精准控制。

例如，如果设定的温度为25度，模糊控制系统可以根据当前的温度和温度变化率等信息，通过判断当前温度是偏低、偏高还是处于目标温度范围内，然后根据这些模糊规则来决定是否增加或减少加热器的功率，从而实现温度的稳定控制。

2.模糊控制在交通信号灯控制中的应用：交通信号灯控制是一个动态复杂的系统，传统的定时控制往往不能适应不同时间段、不同拥堵程度下的交通流需求。

而模糊控制可以通过模糊规则来根据交通流的情况进行动态调整。

例如，交通信号灯的绿灯时间可以根据路口的车辆数量和流动情况进行自适应调整。

当车辆较多时，绿灯时间可以延长，以减少拥堵；当车辆较少时，绿灯时间可以缩短，以提高交通效率。

模糊控制可以将车辆数量和流动情况等模糊化，然后利用模糊规则来决策绿灯时间，从而实现交通信号灯的优化控制。

3.模糊控制在飞行器自动驾驶中的应用：飞行器自动驾驶是一个高度复杂的系统，传统的控制方法往往不能满足复杂的空中飞行任务。

模糊控制可以通过模糊规则来根据飞行器的状态和目标任务要求进行决策。

例如，飞行器的高度控制可以利用模糊控制来应对不同高度要求的任务。

通过将目标高度和当前高度模糊化处理，然后利用模糊规则来决策飞行器的升降舵和发动机功率等参数，从而实现对飞行器高度的精准控制。

综上所述，模糊控制作为一种针对模糊系统进行控制的方法，具有很大的应用潜力。

它可以通过建立模糊规则来解决传统控制方法难以解决的复杂问题。

虽然模糊控制存在一些问题，如规则的设计和调试等工作比较困难，但是随着计算机技术的发展和模糊控制理论的不断完善，模糊控制在各个领域中的应用将会越来越广泛。

模糊控制应用实例

模糊控制应用实例模糊控制是一种部分基于逻辑的控制方法，它通过将模糊集合理论应用于控制系统中的输入和输出来模拟人类决策的过程。

与传统的精确控制方法相比，模糊控制更适合于处理模糊的、不确定的和复杂的系统。

在现实世界中，模糊控制广泛应用于各个领域，例如工业自动化、交通控制、飞行器导航等。

在本文中，我将介绍几个模糊控制的应用实例，以帮助读者更好地了解其实际应用价值。

1. 交通信号灯控制系统交通信号灯控制是一个典型的实时决策问题，涉及到多个信号灯的切换以及车辆和行人的流量控制。

传统的定时控制方法往往无法适应实际交通状况的变化，而模糊控制可以根据不同时间段和交通流量的变化，动态地调整信号灯的切换时间和优先级，以实现交通拥堵的缓解和行车效率的提高。

2. 温度控制系统在许多工业生产过程中，温度的精确控制对产品质量和产量的影响非常重要。

模糊控制可以根据温度传感器采集到的实时数据，结合事先建立的模糊规则库，调整加热或制冷设备的输出，以实现温度的稳定和精确控制。

与传统的PID控制方法相比，模糊控制对于非线性和时变的系统具有更好的适应性和鲁棒性。

3. 汽车制动系统汽车制动系统是保证驾驶安全的重要组成部分，而制动力的控制是其关键。

模糊控制可以根据制动踏板的压力以及车辆的速度和加速度等信息，动态地调整制动力的输出，以实现舒适而有效的制动。

模糊控制还可以考虑路面的湿滑情况和车辆的负荷情况等因素，自适应地调整制动力的分配，提高制动系统的性能和安全性。

4. 智能家居系统智能家居系统通过感应器、执行器和控制器等组件，实现对家庭设备和环境的智能控制。

模糊控制可以根据家庭成员的习惯和偏好，结合各种传感器采集到的数据，自动地调节室内温度、湿度、光线等参数，提高居住舒适度并节约能源。

在夏天的炎热天气中，模糊控制可以根据室内外温度、湿度和人体感觉来控制空调的开关和风速，实现智能舒适的环境控制。

总结回顾：模糊控制在各个领域都有着广泛的应用。

它通过基于模糊集合理论的推理和决策方法，实现对复杂系统的智能控制。