2.2三角形面积的计算练习题及答案
三角形四边形看图形周长面积专项练习30题(有答案)ok
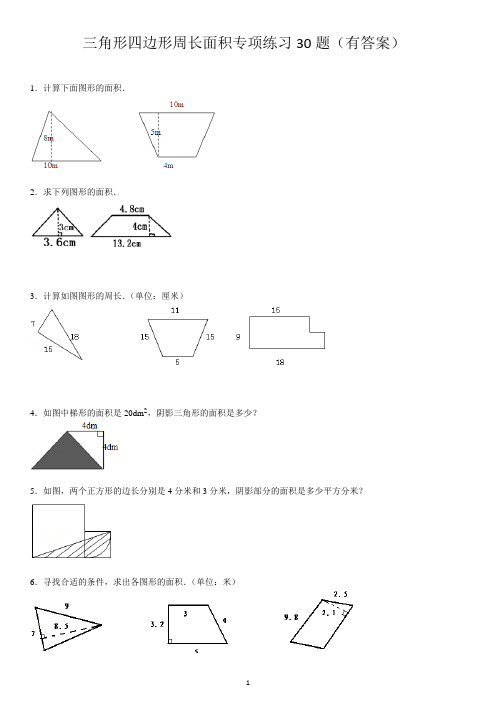
三角形四边形周长面积专项练习30题(有答案)1.计算下面图形的面积.2.求下列图形的面积.3.计算如图图形的周长.(单位:厘米)4.如图中梯形的面积是20dm2,阴影三角形的面积是多少?5.如图,两个正方形的边长分别是4分米和3分米,阴影部分的面积是多少平方分米?6.寻找合适的条件,求出各图形的面积.(单位:米)7.算出下面图形的面积.8.求阴影部分面积.单位:厘米.9.图形王国展风采.(求下面图形的周长,单位:厘米.)10.找准所需条件,计算下列图形的面积.(单位:米)11.求下面图形的面积.12.如图:三角形ABC的面积是6cm2,AB长4cm,求AB边上的高CD的长.13.如图所示,BC长为5,求画阴影线的两个三角形的面积之和.14.找准所需条件,计算下列图形的面积.(单位:米)15.如图,直角三角形的三条边分别长3cm、4cm、5cm,求最长边上的高为多少厘米.16.17.选择合适的数据计算下面图形的面积.18.求下面图形的面积.(单位:厘米)请同学们先写出每个图形的面积计算字母公式,然后再进行计算.19.计算下面图形或阴影部分的面积.(单位:cm)20.找出如图所需数据再求出面积.(单位:cm)21.一个三角形的底长是5m,如果底边延长1m,那么面积就增加1.5m2,请你求出原来三角形的面积是多少平方米?22.三角形ABC是一个正三角形,求这个图形的周长.23.求下面图形中阴影部分的面积.24.求下面各图形中涂色部分的面积25.如图,长方形的长是12cm,宽是5cm,三角形①的面积是24cm2,阴影部分面积是多少?26.求下面图形的面积.(单位:厘米)27.28.下面平行四边形中,涂色部分的面积是10平方分米求空白部分的面积.(单位:分米)29.30.如图数字分别表示两个长方形和一个直角三角形的面积,另一个三角形面积是_________.参考答案:1.三角形的面积:10×8÷2=80÷2,=40(m2);梯形的面积:(4+10)×5÷2=14×5÷2,=35(m2);答:三角形的面积为40(m2);梯形的面积为35(m2).2.(1)3.6×3÷2=5.4(平方厘米);(2)(4.8+13.2)×4÷2,=18×4÷2,=36(平方厘米);答:三角形的面积是5.4平方厘米,梯形的面积是36平方厘米3.①7+15+18=40(厘米);②5+11+15×2,=16+30,=46(厘米);③(18+9)×2=27×2,=54(厘米).答:三角形的周长是40厘米,等腰梯形的周长是46厘米,六边形的周长是54厘米.4.20﹣4×4÷2,=20﹣8,=12(平方分米),答:阴影三角形的面积是12平方分米.5.(4+3)×3÷2﹣(3×3﹣×3.14×32),=7×3÷2(9﹣7.065),=10.5﹣1.935,=8.565(平方分米);答:阴影部分的面积是8.565平方分米6.(1)三角形的面积:7×8.5÷2,=59.5÷2,=29.75(平方米);(2)梯形的面积:(3+5)×3.2÷2,=8×3.2÷2,=25.6÷2,=12.8(平方米);(3)平行四边形的面积:9.8×2.1=20.58(平方米);答:三角形的面积是29.75平方米,梯形的面积是12.8平方米,平行四边形的面积是20.58平方米7.(1)3.6×2.5÷2=4.5(平方厘米);(2)(1.4+4.6)×3.2÷2=6×3.2÷2=9.6(平方分米);(3)6.2×3.5=21.7(平方米);答:三角形的面积是4.5平方厘米;梯形的面积是9.6平方分米;平行四边形的面积是21.7平方米.8.12×12×=36(平方厘米);答:阴影部分的面积为36平方厘米.9.①6+7+9=22(厘米);②(13+24)×2=37×2,=74(厘米);③7+8+6+5+3+4=33(厘米);④32×4=128(厘米);答:三角形的周长是22厘米,长方形的周长是74厘米,六边形的周长是33厘米,正方形的周长是128厘米.10.(1)6×8÷2=24(平方米);(2)(14+24)×10÷2,=38×10÷2,=190(平方米);答:三角形的面积是24平方米;梯形的面积是190平方米11.(1)2.4×0.9÷2=1.08(平方厘米);(2)2.2×1.2+2.2×0.8÷2,=2.64+0.88,=3.52(平方分米);答:甲图形的面积是1.08平方厘米,乙图形的面积是3.52平方分米.12.6×2÷4,=12÷4,=3(cm);答:AB边上的高CD的长为3厘米.13.(5×5÷2﹣5×2÷2)×2,=(12.5﹣5)×2,=7.5×2,=15,答:阴影线的两个三角形的面积之和是15.14.三角形的面积:3×4÷2,=12÷2,=6(平方米);梯形的面积:(8+12)×10÷2,=20×10÷2,=200÷2,=100(平方米);组合图形的面积:6.3×4×2,=25.2×2,=50.4(平方米);答:三角形的面积是6平方米,梯形的面积是100平方米,组合图形的面积是50.4平方米15.3×4÷2×2÷5,=12÷5,=2.4(厘米),答:这个三角形最长边上的高2.4厘米,16.(27×2÷9)×5÷2,=(54÷9)×5÷2,=6×5÷2,=30÷2,=15(平方米);答:阴影部分的面积是15平方米.17.(1)30×40÷2,=1200÷2,=600(平方厘米),答:三角形的面积是600平方厘米;(2)15×8=120(平方分米),答:平行四边形的面积是120平方分米;(3)(8+15)×10÷2,=23×10÷2,=230÷2,=115(平方厘米),答:梯形的面积是115平方厘米.18.S△=ah÷2,=8×6÷2,=48÷2,=24(平方厘米);S▱=ah,=12×15,=180(平方厘米);S梯形=(a+b)h÷2,=(10+18)×12÷2,=28×12÷2,=336÷2,=168(平方厘米);答:三角形、平行四边形和梯形的面积分别是24平方厘米、180平方厘米和168平方厘米19.(1)12×4.5÷2,=4.5×6,=27(平方厘米),(2)8×8=64(平方厘米),(3)42×2÷15=5.6(厘米),(4.5+15)×5.6÷2,=19.5×5.6÷2,=54.6(平方厘米).20.(1)20×22÷2=220(平方厘米);答:三角形的面积是220平方厘米.(2)(18+12)×10÷2,=30×10÷2,=150(平方厘米);答:图形的面积是150平方厘米.(3)10×8=80(平方厘米);答:平行四边形的面积是80平方厘米21.原三角形的高:1.5×2÷1=3(米),原三角形的面积:5×3÷2=7.5(平方米);答:原来三角形的面积是7.5平方米.22.6×2+3.14×6×,=12+9.42,=21.42(厘米),答:这个图形的周长是21.42厘米.23.14×12÷2=84(平方厘米);答:阴影部分的面积是84平方厘米.24.(60+80)×30÷2﹣60×20÷2,=2100﹣600,=1500(平方厘米);答:图形中涂色部分的面积1500平方厘米25.阴影部分的面积:12×5﹣24=36(平方厘米);答:阴影部分的面积是36平方厘米.26.(1)8×6÷2,=48÷2,=24(平方厘米);(2)12×15=180(平方厘米);(3)(10+18)×12÷2,=28×12×,=28×6,=168(平方厘米),答:三角形的面积是24平方厘米,平行四边形的面积是180平方厘米,梯形的面积是168平方厘米.27.8×5÷2,=40÷2,=20,答:阴影部分是面积是20.28.因为空白部分的高=阴影部分的高,所以空白部分梯形的高为:10×2÷5=4(分米);空白部分的面积:(3+3+5)×4÷2,=11×4÷2,=44÷2,=22(平方分米);答:空白部分的面积是22平方分米.29.7×4﹣7×4÷2,=28﹣14,=14(平方厘米).答:阴影部分的面积是14平方厘米.30.因为AO×OD=15,OC×OE=12,所以AO×OD×OC×OE=15×12,而OD×OE=5×2=10,所以OA×OC=15×12÷10=18,所以另一个三角形面积是:18÷2=9,答:另一个三角形面积是9,故答案为:9。
面积计算(学生)

面积计算1.1已知图18-1中,三角形ABC 的面积为8平方厘米,AE =ED ,BD=23 BC ,求阴影部分的面积。
练习1.11、 如图18-2所示,AE =ED ,BC=3BD ,S △ABC =30平方厘米。
求阴影部分的面积。
2、 如图18-3所示,AE=ED ,DC =13 BD ,S △ABC =21平方厘米。
求阴影部分的面积。
3、 如图18-4所示,DE =12 AE ,BD =2DC ,S △EBD =5平方厘米。
求三角形ABC 的面积。
1.2两条对角线把梯形ABCD 分割成四个三角形,如图18-5所示,已知两个三角形的DB C18-1BD 18-2CDCD 18-4面积,求另两个三角形的面积各是多少?练习1.21、 两条对角线把梯形ABCD 分割成四个三角形,(如图18-6所示),已知两个三角形的面积,求另两个三角形的面积是多少? 2、 已知AO =13 OC ,求梯形ABCD 的面积(如图18-7所示)。
3、 已知三角形AOB 的面积为15平方厘米,线段OB 的长度为OD 的3倍。
求梯形ABCD的面积。
(如图18-8所示)。
1.3四边形ABCD 的对角线BD 被E 、F 两点三等分,且四边形AECF 的面积为15平方厘BC18-5 B C 18-6 B C 18-7D米。
求四边形ABCD 的面积(如图18-9所示)。
练习1.31、 四边形ABCD 的对角线BD 被E 、F 、G 三点四等分,且四边形AECG 的面积为15平方厘米。
求四边形ABCD 的面积(如图18-10)。
2、 已知四边形ABCD 的对角线被E 、F 、G 三点四等分,且阴影部分面积为15平方厘米。
求四边形ABCD 的面积(如图18-11所示)。
3、 如图18-12所示,求阴影部分的面积(ABCD 为正方形)。
1.4如图18-13所示,BO =2DO ,阴影部分的面积是4平方厘米。
那么,梯形ABCD18-9BCBC 18-10C18-11 E 18-12的面积是多少平方厘米?练习1.41、 如图18-14所示,阴影部分面积是4平方厘米,OC =2AO 。
数学五年级上册《三角形的面积》一课一练(含答案)

【同步专练B】6.2 三角形的面积(巩固提升篇)一、单选题(共10题)1.等底等高的两个三角形()A. 形状相同B. 周长相等C. 面积相等D.完全不同2.一个三角形的底是2a cm,高是底的一半,它的面积是( )cm2.A. a2B. 2aC. 2a2D. 4a3.一个三角形的底和髙相等,如果将底减少1分米,高増加1分米,那么这个三角形的面积会().A. 增加B. 减少C. 不变D. 无法确定4.一个三角形与一个平行四边形的面积相等,高也相等.平行四边形的底是5cm,三角形的底是().A. 2.5cmB. 5cmC. 10cmD.20cm5.两个三角形的周长相等,面积()A. 一定相等B. 不可能相等C. 可能相等D.不等6.平行四边形的面积是32平方厘米,与它等底等高的三角形的面积是()A. 32平方厘米B. 64平方厘米C. 16平方厘米7.一个三角形的底扩大到原来的5倍,高不变,面积会().A. 扩大到原来的5倍B. 扩大到原来的25倍C. 不变D. 缩小到原来的8.一个三角形和一个平行四边形面积相等,底也相等,若平行四边形的高是6厘米,则三角形的高是()厘米.A. 3B. 6C. 129.一个直角三角形的三条边分别是3厘米,4厘米,5厘米,这个三角形的面积是().A. 12B. 6C. 1510.一个三角形与平行四边形等底,平行四边形的高是三角形的高的4倍,则平行四边形的面积是三角形面积的()倍.A. 4B. 8C. 16D. 2二、填空题(共10题)11.一个直角三角形的面积是50平方厘米.它的一条直角边长10厘米,另一条直角边长是________厘米12.一个三角形的底和高都是10分米,它的面积是________平方分米.13.一个平行四边形的底12厘米,高8厘米,它的面积是________平方厘米;与它等底等高的三角形的面积是________平方厘米.14.一个三角形和一个平行四边形等底等高.已知三角形的面积是26cm2,平行四边形的面积是________平方厘米.15.等腰直角三角形的一条直角边是0.8厘米,它的面积________16.一个三角形和一个平行四边形等底等高,如果三角形的面积是15平方厘米,那么平行四边形的面积是________平方厘米;如果平行四边形的面积是15平方厘米,那么三角形的面积是________平方厘米.17.在一个长30厘米,宽20厘米的长方形纸板上剪下一个最大的三角形,这个三角形的面积是________平方厘米.18.一个三角形和一个平行四边形的底和面积都相同,三角形的高是8cm,平行四边形的高是________cm.19.一个三角形的面积是32dm²,高是40cm,底边是________dm.20.一个三角形的面积是60cm2,底是12cm,高是________ cm.三、判断题(共10题)21.每个三角形都有三条高,三条高都在三角形内.()22.三角形面积等于和它同底等高的平行四边形面积的一半.()23.一个三角形的面积是176m2,底是22m,高是8m.()24.平行四边形的面积是三角形面积的2倍.()25.三角形和平行四边形面积和底都相等,三角形的高是平行四边形高的2倍. ()26.两个周长相等的三角形,面积也相等.()27.用两个完全一样的正三角形可以拼成一个平行四边形. ()28.两个三角形的面积相等,则这两个三角形一定等底等高.()29.等底等高的两个三角形,形状不一定相同,但面积一定相等.()30.一个三角形的面积是35平方厘米,底长7厘米,则它的高是5厘米.()四、计算题(共3题)31.求阴影部分的面积(单位:cm).32.计算下面图形的面积.(单位:cm)(1)(2)33.计算下面图形的面积五、解决问题(共5题)34. (1)(2)(3)35.(单位:厘米)36.有一个三角形,它的三个顶点所在的位置分别是A(0,2)、B(8,0)、C(4,4),请在图中画出这个三角形;如果每个小方格的面积是1格,那么,它的面积是多少格.37.下面是张大爷种的一块长方形菜地,涂色的部分种上了白菜,其余的地方种萝卜.请你算一下种白菜的面积.每平方米需施肥0.25kg,这块地共需施肥多少kg?38.希望小学图书馆落成了,学校老师为图书馆制作了一个指示牌(如图).制作这样一个指示牌至少需要多大面积的铁皮?参考答案一、单选题1. C2. A3. B4. C5. C6. C7. A8. C9. B10. B二、填空题11. 1012. 5013. 96;4814. 5215. 0.32平方厘米16. 30;7.517. 30018. 419. 1620. 10三、判断题21. ×22. √23. ×24. ×25. √26. ×27. √28. ×29. √30. ×四、计算题31.解:(2+3+2)×2÷2﹣(3+2)×2÷2 =7×2÷2﹣5×2÷2=7﹣5=2(平方厘米)答:阴影部分的面积是2平方厘米32.(1)解:3×6÷2=9平方厘米(2)解:40×10÷2=200平方厘米33.解:7.2×9.6÷2=34.56(cm2)五、解决问题34.(1)解:4.2×5.4÷2=11.34(平方厘米) (2)解:5.9×8÷2=23.6(平方分米)(3)解:2.5×12÷2=15(平方米)35.解: 12×16÷2=12×8=96(平方厘米)所以三角形的面积是96平方厘米.36.解:画图如下:8×4-8×2÷2-4×3÷2-5×2÷2=32-8-6-5=13(格)答:它的面积是13格.37.解:长方形面积:4×2.2=8.8(平方米)种白菜面积:8.8÷2=4.4(平方米)8.8×0.25=2.2(kg)答:种白菜的面积是4.4平方米,这块地共需施肥2.2kg.38. 解:6×8=48dm2(2+6+2)×5÷2=25dm225+48=73dm2。
2022年五年级上册数学同步练习 三角形的面积 (含答案)

五年级上册数学一课一练三角形的面积一、单选题1.三角形的面积是()A. 161B. 116C. 232D. 3222.下面图形(单位:厘米)的面积是()A. 99.15平方厘米B. 432平方厘米C. 112平方厘米D. 15.99平方厘米3.把三角形的底和高都扩大到原来的2倍,面积扩大到原面积的( )倍。
A. 2B. 4C. 6D. 8二、判断题4.判断对错三角形的底等于三角形的面积除以高5.底乘以另一条底上的高也可以求出三角形的面积。
6.如果两个三角形的面积相等,那么它们一定是等底等高。
三、填空题7.出下面图形的面积________.(单位:分米)8.有一个三角形,底是分米,高是底的一半,这个三角形的面积是________平方分米9.一个三角形的面积是60cm2,底是12cm,高是________ cm。
10.直角三角形三条边的长度分别为6厘米、8厘米、10厘米,它的面积是________平方厘米.11.下面图形(单位:厘米)的面积是________四、解答题12.如图,四边形的面积是多少平方厘米?五、综合题13.先测量下面各图形的底和高,再分别算出它们的面积。
(精确到毫米。
)(1)底________高________面积________(2)底________高________面积________六、应用题14.先画出如图底边上的高,再量出所需的数据(取整厘米数),求出它的面积.15.图中直线l与直线平行,点A、B在直线上,点C、D、E、F在直线l上.△ABC、△ABD、△AEB、△AFB 的面积一样吗?说一说理由.参考答案一、单选题1.【答案】B【解析】【解答】2982=116平方厘米。
【分析】根据三角形面积的计算公式直接计算即可。
2.【答案】D【解析】【解答】7.8×4.1÷2=31.98÷2(平方厘米)【分析】这道题考查的是求三角形的面积的知识,解答此题要运用三角形面积=底×高÷2的公式,然后代入数据计算即可。
苏教版五年级上册数学分层作业设计2.2三角形的面积(附答案)

2.2 三角形的面积(练习)一、学习重难点1、学习重点:掌握三角形的面积公式,并能运用公式解决实际问题。
2、学习难点:理解三角形的面积公式的推导过程。
二、知识梳理1、三角形的面积计算公式的推导。
三角形的面积公式及用字母表示公式。
三角形的面积=底×高÷2如果用S表示三角形的面积,a表示三角形的底,h表示三角形的高,那么三角形的面积计算公式可以写成s=a×h÷22、三角形面积计算公式的应用。
运用三角形的面积计算公式解决简单的实际问题时,要做到“一找”“二算”。
一找:分析题意,找出已知什么,求什么。
二算:列式计算真题基础过关练一、选择题1.(2023秋·湖北荆门·五年级统考期末)一个三角形与一个平行四边形的面积相等,高也相等,三角形的底是6厘米,平行四边形的底是()厘米。
A.6B.3C.122.(2021秋·广东茂名·五年级统考期末)如图,三角形ABC的面积是32cm2,阴影部分的面积是()cm2。
A.48B.16C.643.(2022秋·甘肃酒泉·五年级统考期末)一个三角形的底不变,如果高扩大4倍,那么它的面积()。
A.扩大4倍B.扩大2倍C.无法确定4.(2020秋·辽宁沈阳·五年级统考期末)一个三角形和一个平行四边形的高相等,面积也相等。
如果平行四边形的底边是3cm,那么三角形的底是()厘米。
A.1.5B.3C.65.(2023秋·辽宁鞍山·五年级统考期末)下图中三角形()的面积可以用“4×3÷2”进行计算。
A.B.C.二、填空题6.(2023秋·山东枣庄·五年级统考期末)把一个长方形框架用力一拉,拉成一个平行四边形,与原来框架比,周长( ),面积( );如果拉成的平行四边形的面积是32cm2,与它等底等高的三角形的面积是( )cm2。
数学三角形试题答案及解析

数学三角形试题答案及解析1.一张正方形纸,从一边的中点到邻边的中点连一条线段,沿这条线段剪去一个角,剪去的面积是8平方厘米,剩下的面积是多少平方厘米?(先画出图示,再进行解答)【答案】56平方厘米【解析】根据正方形的特征,从一组邻边的中点剪的是一个等腰直角三角形,又知剪去就分面积是8平方厘米,即可求出剪去这个等腰直角三角形的直角边,从而求出原正方形的边长,由正方形的边长可求出正方形的面积,用正方形的面积减去剪去部分的面积就是剩下的面积.解:如图,8×2=16(平方厘米),16=4×4,即剪去等腰直角三角形的直角边是4厘米;4×2=8(厘米),8×8﹣8,=64﹣8,=56(平方厘米),答:剩下的面积是56平方厘米;故答案为:56平方厘米点评:本题是考查图形的拼切、三角形的面积和正方形的面积的计算.解答此题的关键是求出正方形的边长,要求正方形的边长关键是求出剪去部分的直角边长.2.在下面(3×5)点子图上,能连多少个面积是3平方厘米的三角形.(两点之间最小距离为1厘米).【答案】28个【解析】在(3×5)点子图上面积是3平方厘米的三角形,一种它的底是3厘米高是2厘米;另一种它的底是2厘米高是3厘米;还有斜连线的三角形共三种,找出每种三角形的个数然后相加即可.解:底3厘米,高2厘米的三角形12个;底2厘米,高3厘米的三角形12个,类同如图所示的三角形4个.12+12+4=28(个),总共能连28个面积是3平方厘米的三角形.答:能连28个面积是3平方厘米的三角形.点评:按类找出三角形的个数,然后相加.3.如图中平行四边形ABCD的面积比直角三角形BCF的面积大80平方厘米.已知BC=20厘米,CF=16厘米,求CE的长.【答案】12厘米【解析】根据三角形的面积公式S=ab÷2,求出直角三角形BCF的面积,再求出平行四边形ABCD的面积,由平行四边形的面积公式S=ah,知道h=S÷a,求出平行四边形的高EC的长度.解:(20×16÷2+80)÷20,=240÷20,=12(厘米),答:CE的长是12厘米.点评:本题主要是灵活利用三角形的面积公式S=ab÷2与平行四边形的面积公式S=ah解决问题.4.如图.正方形ABGD与正方形EFGC并放在一起.已知小正方形EFGC的边长是6,求三角形AEC(阴影部分)的面积.【答案】18【解析】设大正方形ABCD的边长=a,因为CH∥AD,所以△GHC∽△GAD,所以HC:AD=CG:DG,所以HC:a=6:(6+a),所以HC=6a÷(6+a),EH=EC﹣HC=6﹣6a÷(6+a);三角形AEC(阴影部分)的面积=三角形AEH的面积+三角形GEH的面积=EH×AB÷2+EH×GC÷2=EH×(AB+CG)÷2=[6﹣6a÷(6+a)]×(a+6)÷2=[6×6+6a﹣6a]÷2=6×6÷2=18解:设大正方形ABCD的边长=a,因为CH∥AD,所以△GHC∽△GAD,所以HC:AD=CG:DG,所以HC:a=6:(6+a),所以HC=6a÷(6+a),EH=EC﹣HC=6﹣6a÷(6+a);三角形AEC(阴影部分)的面积=三角形AEH的面积+三角形GEH的面积,=EH×AB÷2+EH×GC÷2=EH×(AB+CG)÷2,=[6﹣6a÷(6+a)]×(a+6)÷2,=[6×6+6a﹣6a]÷2,=6×6÷2,=18;答:三角形AEC(阴影部分)的面积是18.点评:关键是设出大正方形的边长,再用设出的数表示出EH,最后根据三角形的面积公式解决问题.5.一根铁丝,可以围成一个直径为4.5分米的圆,如果把这根铁丝折成一个等边三角形,这个三角形的边长是多少分米?【答案】4.71分米【解析】先求出圆的周长,就是等边三角形的周长,再根据等边三角形的特点(三条边相等),即可求出三角形的边长.解:3.14×4.5÷3,=3.14×4.5×,=3.14×1.5,=4.71(分米),答:这个三角形的边长是4.71分米.点评:解答此题的关键是,根据铁丝的长度不变,即圆的周长就是等边三角形的周长,再根据等边三角形的特点,即可求出要求的答案.6.有一块三角形的广告牌,底是16分米,高是底的一半,做10块这祥的广告牌需三合板多少平方米?【答案】6.4平方米【解析】先求出三角形广告牌的高,再利用三角形的面积=底×高÷2,求出一个三角形广告牌的面积,将面积单位化成平方米后,再乘10,问题即可得解.解:16×(16÷2)÷2,=16×8÷2,=64(平方分米),64平方分米=0.64平方米,0.64×10=6.4(平方米).答:做10块这祥的广告牌需三合板6.4平方米.点评:此题主要考查三角形的面积的计算方法的灵活应用,解答时要注意单位的换算.7.永太经济开发区准备拍卖一块三角形土地,底是90米,高是70米.底价为180元/m2.一位开发商想参加竞拍,他准备了60万元,够起拍价吗?请说明理由.【答案】够【解析】根据“三角形的面积=底×高÷2”计算出这块三角形土地的面积,然后用“总价=单价×数量”进行解答即可.解:90×70÷2×180,=3150×180,=567000(元),因为60万元>567000元,所以够起拍价.点评:解答此题的关键是根据三角形的面积计算公式先计算出三角形土地的面积,进而根据单价、数量和总价之间的关系进行解答.8.请你替老板想一想,应该接手这块广告牌吗?为什么?【答案】应该,因为成本远远低于对方的出价【解析】先依据三角形的面积公式求出广告牌的面积,再乘96,然后将结果与6000元相比较即可得解.解:16×5÷2×96,=40×96,=3840(元);3840<6000,答:应该接手这块广告牌,因为成本远远低于对方的出价.点评:此题主要考查三角形的面积的计算方法在实际生活中的应用.9.计算下面每个三角形的面积.【答案】24dm2,16dm2【解析】根据三角形的面积公式:面积=底×高÷2,代入数据列式解答即可.解:(1)12×4÷2=24(dm2).答:面积是24dm2.(2)8×4÷2=16(dm2).答:面积是16dm2.点评:本题主要是灵活利用三角形的面积公式:三角形面积=底×高÷2解决问题.10.如果三角形的两条边分别是10厘米和4厘米,第三条的边长度可能是多少厘米?(取整厘米数)【答案】7、8、9、10、11、12、13厘米【解析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可.解:10﹣4<第三边<10+4,6<第三边<14,那么第三边的长度可能是7、8、9、10、11、12、13厘米;答:三边的长度可能是7、8、9、10、11、12、13厘米.点评:解答此题的关键是根据三角形的特性进行分析、解答即可.11.求下面三角形的面积.(1)底是1.8分米,高是4.6分米.(2)直角三角形的两条直角边分别为3.2厘米,4.5厘米.【答案】4.14平方分米,7.2平方厘米【解析】三角形的面积S=ah,据此代入数据即可求解.解:(1)1.8×4.6÷2=4.14(平方分米);答:三角形的面积是4.14平方分米.(2)3.2×4.5÷2=7.2(平方厘米);答:直角三角形的面积是7.2平方厘米.点评:此题主要考查三角形的面积的计算方法.12.计算下面三角形的面积.【答案】6平方厘米;3平方米;30平方米;6平方分米【解析】三角形的面积S=ah,据此代入数据即可求解.解:(1)=6(平方厘米);(2)=3(平方米);(3)=30(平方米);(4)=6(平方分米).点评:此题主要考查三角形的面积的计算方法.13.计算下面各个三角形的面积.面积面积面积.【答案】2.66平方米;3.6平方分米;3.96平方厘米【解析】根据三角形的面积公式:面积=底×高÷2,代入数据依次列式解答即可.解:①2.8×1.9÷2=2.66(平方米);②4.8×1.5÷2=3.6(平方分米);③3.6×2.2÷2=3.96(平方厘米).故答案为:2.66平方米;3.6平方分米;3.96平方厘米.点评:本题主要是灵活利用三角形的面积公式:三角形面积=底×高÷2解决问题,找出三角形的底和高,是解答此题的关键.14.一块总面积为48平方米的苗圃的平面图如图所示.(1)种冬青树苗的面积是多少平方米?(2)种松树苗的面积是多少平方米?(3)种杉树苗的面积是多少平方米?【答案】18平方米,12平方米,18平方米【解析】分别利用长方形、三角形和平行四边形的面积公式即可求解.解:(1)3×6=18(平方米);答:种冬青树苗的面积是18平方米.(2)4×6÷2=12(平方米);答:种松树苗的面积是12平方米.(3)3×6=18(平方米);答:种杉树苗的面积是18平方米.点评:此题主要考查长方形、三角形和平行四边形的面积的计算方法在实际生活中的应用.15.如图的直角三角形中有一个长方形,根据已知条件你能求出长方形的面积吗?(单位:厘米)【答案】35平方厘米【解析】设长方形的长为a厘米,宽为b厘米,则两个三角形的面积分别为×5a平方厘米,×7b平方厘米,长方形的面积是ab平方厘米,大三角形的面积是(a+7)×(b+5),再根据两个三角形的面积加长方形的面积等于大三角形的面积,即可求出ab的积,即长方形的面积.解:设长方形的长为a厘米,宽为b厘米,则两个三角形的面积分别为×5a平方厘米,×7b平方厘米,长方形的面积是ab平方厘米,大三角形的面积是(a+7)×(b+5),×5a+×7b+ab=(a+7)×(b+5),a+b+ab=++b+,=,ab=35,答:长方形的面积是35平方厘米.点评:关键是设出未知数,找出各个图形的面积,再根据数量关系等式列方程解答即可.16.求下列三角形的周长.(1)三角形的三条边分别是a厘米、b厘米和c厘米.(2)一个等腰三角形,底边长a分米,腰长b分米.【答案】a+b+c厘米;a+2b分米【解析】(1)三角形的周长是三条边的长度之和,据此把三条边的长度相加即可;(2)因为等腰三角形的两条腰相等,所以等腰三角形的周长=腰长×2+底边长;据此解答即可.解:(1)周长为:a+b+c(厘米).答:三角形的周长是a+b+c厘米.(2)周长为:a+b×2=a+2b(分米).答:三角形的周长为a+2b分米.点评:此题主要考查三角形的周长计算.17.有一个直角三角形,两条直角边是两个质数,和为12cm,这个直角三角形的面积是多少平方厘米?【答案】17.5平方厘米【解析】根据一个直角三角形,两条直角边是两个质数,和为12cm,可以求出两条直角边的长,再根据直角三角形的面积公式求出直角三角形的面积.解:因为一个直角三角形,两条直角边是两个质数,和为12cm,所以两条直角边分别是5cm,7cm,所以这个直角三角形的面积是:×5×7=17.5(平方厘米).答:这个直角三角形的面积是17.5平方厘米.点评:本题考查了质数的定义和直角三角形面积的求法,理解直角三角形的面积等于其两直角边长乘积的一半是解题的关键.18.一个直角三角形的两条直角边分别是60cm和80cm,它的面积是多少平方厘米?这个三角形的斜边长100cm,这条斜边上的高是多少厘米?【答案】2400平方厘米;48厘米【解析】由于两条直角边的长度,依据三角形的面积公式求出这个三角形的面积,再依据同一个三角形的面积不变求出斜边上的高.解:三角形的面积:60×80÷2,=4800÷2,=2400(平方厘米);斜边上的高:2400×2÷100,=4800÷100,=48(厘米).答:这个三角形的面积是2400平方厘米;斜边上的高是48厘米.点评:解答此题的关键是:先确定出计算三角形的面积需要的线段的长度,再据同一个三角形的面积不变,求出斜边上的高.19.明明准备把一根17厘米长的铁丝围成一个三角形(每条边长都是整厘米),3条铁丝的边长分别是多少厘米?第一条边【答案】【解析】题目要求,根据构成三角形的条件,周长为17厘米,可逐步分析,将每个符合题意的三角形写出即可.解:由题意,符合题意的三角形各边分别为:点评:本题考查了在定周长的条件下构成三角形的问题,要求学生掌握此类问题并能运用,注意要不重不漏.20.一个等腰三角形的底是32厘米,腰是23厘米.则它的周长是多少厘米?【答案】78厘米【解析】三角形的周长就是三角形三条边的和,据此即可解答.解:23×2+32,=46+32,=78(厘米);答:它的周长是78厘米.点评:此题主要考查三角形的周长的计算方法.注意等腰三角形的两腰相等.21.计算面积.【答案】8.1平方厘米【解析】根据三角形的面积公式S=ah÷2,把三角形的底4.5厘米,高3.6厘米代入公式即可求出面积.解:4.5×3.6÷2,=16.2÷2,=8.1(平方厘米),答:三角形的面积是8.1平方厘米.点评:此题主要利用了三角形的面积公式S=ah÷2解决问题.22.一块白菜地的形状是三角形.它的底是21米,高是18米.如果每平方米可栽白菜10棵,这块地一共可栽白菜多少棵?【答案】1890棵【解析】根据三角形的面积公式S=ah÷2,求出三角形菜地的面积,再根据单产量×数量=总产量,求出这块地一共可栽白菜的棵数.解:21×18÷2×10,=189×10,=1890(棵),答:这块地一共可栽白菜1890棵.点评:本题主要是利用三角形的面积公式S=ah÷2与数量关系单产量×数量=总产量解决问题.23.一块三角形菜地,底长80m,高60m,画在比例尺是1:500的地图上,面积是多少平方厘米?【答案】192 cm2【解析】要求三角形菜地的图上面积是多少厘米,先根据“实际距离×比例尺=图上距离”求出三角形菜地的图上的底和高,进而根据“三角形的面积=底×高÷2”进行解答即可.解:80m=8000cm,60m=6000cm,(8000×)×(6000×),=16×12,=192(cm2);答:这块菜地的图上面积是192 cm2.点评:解答此题应根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论;用到的知识点:三角形面积计算方法.24.计算下列各图形的周长.【答案】10厘米,8厘米,7厘米【解析】长方形的周长=(长+宽)×2,正方形的周长=边长×4,三角形的周长计算它的三条边的长度和.由此解答即可.解:(3+2)×2,=5×2,=10(厘米);2×4=8(厘米);2+2+3=7(厘米);答:长方形的周长是10厘米,正方形的周长是8厘米,三角形的周长是7厘米.点评:此题主要考查长方形、正方形、三角形周长公式的灵活运用.25.右图中涂色的两个三角形面积相等..【答案】正确【解析】依据等底等高的三角形面积相等,即可做出判断.解:如图所示,因为阴影三角形ABF和DEF的面积分别加上公共部分三角形BEF的面积,就形成了两个等底等高的三角形,则三角形ABE和三角形DEB的面积相等,减去公共部分三角形BEF的面积,也就是阴影部分,面积仍然相等.故答案为:正确.点评:此题主要考查等底等高的三角形面积相等.26.一块三角形的铁板底长6米,是高的,这块铁板的面积是多少?【答案】54平方米【解析】由题意可知:三角形的高是(6÷)米,于是利用三角形的面积=底×高÷2,即可求出这块铁板的面积.解:6×(6÷)÷2,=6×18÷2,=108÷2,=54(平方米);答:这块铁板的面积是54平方米.点评:此题主要考查三角形的面积的计算方法,关键是先求出三角形的高.27.一面三角形的红旗,底是0.8米,高是1.5m,制作一面这样的红旗需要用布多少平方米?【答案】0.6平方米【解析】三角形的面积=底×高÷2,将数据代入公式即可求解.解:0.8×1.5÷2=0.6(平方米);答:制作一面这样的红旗需要用布0.6平方米.点评:此题主要考查三角形的面积的计算方法的灵活应用.28.我能算出下面图形的周长.(单位:cm)【答案】22厘米,15厘米,22厘米,20厘米【解析】(1)根据长方形的周长公式C=(a+b)×2,把长7厘米,宽4厘米,代入公式解答即可;(2)把三角形的三条边分别加起来即可;(4)把四边形的四条边加起来即可;(5)根据正方形的周长公式C=4a,把边长5厘米代入公式解答即可.解:(1)(7+4)×2,=11×2,=22(厘米),答:长方形的周长是22厘米,(2)4+6+5=15(厘米),答:三角形的周长是15厘米,(3)5+5+3+9=22(厘米),答:四边形的周长是22厘米,(4)4×5=20(厘米),答:正方形的周长的20厘米.点评:本题主要是根据长方形的和正方形的周长公式及周长的意义解决问题.29.人民医院制作底和高都是8分米的救护包扎用的三角巾,用长6.4米,宽1.6米的白布可以做多少块这样的三角巾?【答案】32块【解析】两个底与高都是8分米的三角巾都可以拼成一个边长8分米的正方形,据此先计算出用长6.4米,宽1.6米的白布可以做多少块这样的正方形,再乘2即可解答.解:6.4米=64分米,1.6米=16分米,(64÷8)×(16÷8),=8×2,=16(个),16×2=32(个),答:可以做32块这样的三角巾.点评:解答此题的关键是明确两个这样的三角巾可以拼成边长是8分米的正方形,据此先求出剪出的正方形的个数,再乘2.30.见图ABCD平行四边形,E是BC的中点,平行四边形ABCD的面积比三角形ABE的面积多多少倍?【答案】3倍【解析】三角形ABC的面积是平行四边形ABCD的面积的一半,而三角形ABE的面积又是三角形ABC的面积的一半,则平行四边形ABCD的面积是三角形ABE的面积的四倍,从而问题得以解决.解:平行四边形ABCD的面积是三角形ABC的面积的2倍,三角形ABC的面积又是三角形ABE的面积的2倍,所以平行四边形ABCD的面积是三角形ABE的面积的4倍.则平行四边形ABCD的面积比三角形ABE的面积多3倍.答:平行四边形ABCD的面积比三角形ABE的面积多3倍.点评:此题主要考查等底等高的图形之间的倍比关系,结合图形推算即可.31.某医院计划用长为30米,宽为1.8米的白布,做成两直角边都是0.6米的救护用的三角巾,可以做成多少块?【答案】300块【解析】根据题意是求长方形布的面积里面包含多少个直角三角形巾的面积,根据长方形和三角形的面积公式解答即可.解:30×1.8÷(0.6×0.6÷2)=54÷0.18=300(块);答:可以做成300块.点评:此题主要考查长方形和三角形的面积计算,直接根据公式解答即可.32.求下面各图形中涂色部分的面积【答案】1500平方厘米【解析】由图可以看出:阴影部分的面积=梯形的面积﹣三角形的面积,将数据代入公式即可求得结果.解:(60+80)×30÷2﹣60×20÷2,=2100﹣600,=1500(平方厘米);答:图形中涂色部分的面积1500平方厘米.点评:此题主要考查三角形及梯形的面积公式,将数据代入公式即可求得结果.33.(2011•北海模拟)如图平行四边形的面积是36平方米,求阴影部分的面积.(单位:米)【答案】6平方米【解析】此题可以先求平行四边形的底,再用底减4即为阴影的底,然后用三角形的面积公式就可以求其面积.解:36÷6=6(米);6﹣4=2(米);2×6÷2=6(平方米).答:阴影部分的面积是6平方米.点评:此题主要考查平行四边形公式:S=ah;三角形的面积公式:S=ah;将数据代入公式即可求得结果.34.(2012•石阡县模拟)图中圆的周长是25.12厘米,求阴影部分的面积.【答案】8平方厘米【解析】由图意可知:阴影部分是一个等腰直角三角形,直角边就是圆的半径,圆的周长已知,可以先求出圆的半径,从而利用三角形的面积公式即可求出阴影部分的面积.解:圆的半径:25.12÷(2×3.14),=25.12÷6.28,=4(厘米);阴影部分的面积:4×4÷2,=16÷2,=8(平方厘米);答:阴影部分的面积是8平方厘米.点评:解答此题的关键是明白:阴影部分是一个什么样的三角形,它的边与圆的半径有什么关系,弄清楚后即可求解.35.【答案】20【解析】阴影部分的面积是以8为底,5为高的三角形的面积,由此根据三角形的面积公式S=ah÷2,列式解答即可.解:8×5÷2,=40÷2,=20,答:阴影部分是面积是20.点评:关键是根据三角形的面积公式S=ah÷2解决问题.36.用60厘米长的铁丝围成一个直角三角形,三角形三条边的比是3:4:5.求该三角形的面积?【答案】150平方厘米【解析】三角形的周长和三条边的比已知,又因在直角三角形中,斜边最长,因此利用按比例分配的方法,即可分别求出两条较短边(直角边)的长度,进而利用三角形的面积公式即可求解.解:60×=15(厘米),60×=20(厘米),15×20×=150(平方厘米);答:这个三角形的面积是150平方厘米.点评:此题主要考查三角形的面积的计算方法的灵活应用,只求出两条直角边的长度即可.37.(2008•江都市模拟)(1)A点用数对表示.(2)画出将梯形向右平移5格后的图形.(3)画出将梯形绕A点顺时针方向旋转90°后的图形.(4)按2:1的比画出三角形放大后的图形.(5)放大后的三角形与原三角形的面积的比是.【答案】(3,7);;4:1【解析】(1)数对表示位置的方法是:第一个数字表示列,第二个数字表示行;(2)根据平移的性质,抓住梯形的四个顶点进行平移,然后顺次连接即可;(3)根据图形旋转的性质,抓住与A相连的两条边进行旋转,即可确定旋转后的梯形的位置;(4)根据放大与缩小的性质,抓住两条直角边放大2倍,即可确定这个放大后的三角形的大小;(5)设每个小方格的长度为1,分别计算出这两个三角形的面积即可解决问题.(1)根据数对表示位置的方法可得:A点用数对表示为:(3,7);(2)根据平移的性质,把梯形的四个顶点向右平移5格,然后顺次连接即可得到梯形1;(3)根据图形旋转的性质,先把与A相连的两条边顺时针旋转90°,即可确定旋转后的梯形2;(4)根据放大与缩小的性质,把三角形的两条直角边放大2倍,即可得出放大后的三角形3,(5)设每个小方格的长度为1,则原来三角形的面积为:3×1÷2=;放大后的三角形面积为:2×6÷2=6;所以它们的面积之比是:6:=4:1.故答案为:(1)(3,7);(5)4:1.点评:此题考查了数对表示位置的方法;图形的平移、旋转、放大与缩小等性质的灵活应用.38.如图,长方形ABCD中,E是AD中点,F是CE中点,长方形ABCD的面积是48cm2,求△BDF的面积.【答案】6cm2【解析】根据矩形的性质可得三角形BCD的面积,根据中点的定义可求三角形BCF的面积,三角形CDF的面积,再由△BDF的面积=三角形BCD的面积﹣三角形BCF的面积﹣三角形CDF的面积即可求解.解:48÷2﹣48÷2÷2﹣48÷2÷2÷2,=24﹣12﹣6,=6(cm2).答:△BDF的面积是6cm2.点评:考查了矩形的性质,三角形的中线,三角形的面积,本题关键是得到三角形BCD的面积,三角形BCF的面积,三角形CDF的面积.39.操作题(1)如图是一个面积为4平方厘米的正方形纸片.请你把它折成一个面积是2平方厘米的正方形(在图中画出折痕).(2)有一块长12米,宽8米的长方形花圃,喷水嘴安装在长方形对角线交点P处.现计划从点P引三条射线把花圃分成面积相等的三部分,分别种植三种不同的花(不考虑各部分的空隙).请你通过计算,提出一个方案,并根据方案画出三条射线以及它们与长方形有关边的交点位置.【答案】;【解析】(1)分别找到两组对边的中点,再如图所示,沿相邻两个中点的连线折叠,所得到的正方形的面积就是原正方形的面积的一半,即为2平方厘米.(2)将长方形的长和宽分别三等分,再将每个等分点与点P相连,则长方形被分成了12个面积相等的三角形,所以可以找到M、N点与B点共同将长方形均分成3份,如下图所示.解:(1)如图所示,即为所要求作的图形:;(2);点评:解答此题的主要依据是:等底等高的三角形的面积相等.40.量出计算阴影部分面积所需要的数据(量得结果取整厘米数并写在图上),再计算出阴影部分的面积.【答案】6平方厘米【解析】阴影部分是一个三角形,根据三角形面积=底×高÷2,可知:计算面积需要测量出三角形的底和对应的高,测量再计算即可.解:如图所示:,经过测量,三角形的底是4厘米,高是3厘米,面积为:4×3÷2,=12÷2,=6(平方厘米).答:阴影部分的面积为6平方厘米.点评:解决本题的关键是先分析阴影部分是一个什么图形,测量出所需数据,再根据面积公式计算.41.如图直角等腰三角形的面积是平方厘米.【答案】144【解析】如图:做出三角形的高,因为三角形ABC是直角三角形,所以CD=AB=×24=12(厘米),再根据三角形的面积公式S=ab÷2可以求出三角形ABC的面积.解:24×(24×)÷2,=24×12÷2,=144(平方厘米),答:直角等腰三角形的面积是144平方厘米.故答案为:144.点评:本题主要是用等腰直角三角形的性质求出斜边上的高,再利用三角形的面积公式解决问题.42.一个三角形底缩小3倍,高扩大3倍,则面积的变化是.【答案】不变【解析】根据三角形的面积公式S=ah,知道三角形底缩小3倍,高扩大3倍,面积的变化是×3=1;据此解答.解:因为三角形的面积S=ah,所以S′=×a×3h=ah=S,故答案为:不变.点评:考查了三角形的面积,解答此题的关键是根据三角形的面积公式S=ah与积的变化规律解决问题.43.如图,在边长为12厘米的正方形ABCD中,以AB为底边作腰长为10厘米的等腰三角形PAB.则三角形PAC的面积等于平方厘米.【答案】12【解析】如图所示,先依据三角形的面积公式求出三角形PAB的高PG的长度,进而得出PH的长度,也就能求出CF、DE的长度,进而即可求出PE的长度于是得出三角形DPC和三角形DPA的面积,最后依据“阴影部分的面积=三角形DAC的面积﹣三角形DPC和三角形DPA的面积”即可得解.解:因为102﹣(12÷2)2=64,则PG的长度为8厘米,则PH=CF=DE=12﹣8=4厘米,又因102﹣82=36,则PE的长度为6厘米,所以三角形DPC的面积为:12×4÷2=24(平方厘米),三角形DPA的面积为:12×6÷2=36(平方厘米),阴影部分的面积为:12×12÷2﹣(24+36),=72﹣60,=12(平方厘米);答:三角形PAC的面积等于12平方厘米.故答案为:12.点评:解答此题的主要依据是:三角形的面积的计算方法的灵活应用.44.如图,平行四边形底边的中点是A,它的面积是48m2.阴影部分的面积是m2.【答案】12【解析】如下图,先作辅助线,把这个平行四边形分成4个与阴影部分等底等高的4个三角形,由此可以得此阴影部分的面积是这个平行四边形面积的,根据求一个数的几分之几是多少,用乘法解答.解:如图:因为平行四边形底边的中点是A,4个三角形等底等高;所以阴影部分的面积是这个平行四边形面积的,48×=12(平方厘米);答:阴影部分的面积是12平方厘米.故答案为:12.点评:此题主要考查平行四边形和三角形的面积计算,根据等底等高的三角形的面积相等,再根据求一个数的几分之几是多少,用乘法解答即可.45.一个三角形的底是15cm,高是8cm,它的面积是cm2.与它等底等高的平行四边形的面积是cm2.【答案】60,120【解析】(1)根据三角形的面积=底×高÷2计算即可;(2)因为平行四边形的面积是和它等底等高的三角形的面积的2倍,所以用(1)三角形的面积乘2即可解答.解:(1)三角形的面积为:15×8÷2=60(平方厘米).答:三角形的面积是60平方厘米.(2)平行四边形的面积为:60×2=120(平方厘米).答:与它等底等高的平行四边形的面积是120平方厘米.故答案为:60,120.点评:此题主要考查三角形面积的计算及等底等高的三角形和平行四边形的面积之间的关系.46.一个直角三角形的两条直角边分别是8厘米和6.5厘米,这个直角三角形的面积是平方厘米.【答案】26。
高中试卷-2.2 基本不等式 练习(1)(含答案)

第二章 一元二次函数、方程和不等式2.2等式性质与不等式性质(共2课时)(第1课时)一、选择题1.(2019·内蒙古集宁一中高一期末)下列不等式一定成立的是( )A .a b2B .a b 2≤C .x +1x ≥2D .x 2+1x 2≥2【答案】D【解析】当a ,b ,x 都为负数时,A,C 选项不正确.当a ,b 为正数时,B 选项不正确.根据基本不等式,有x 2+1x 2≥=2,故选D.2.(2019山东师范大学附中高一期中)已知x >0,函数9y x x=+的最小值是( )A .2B .4C .6D .8【答案】C【解析】∵x >0,∴函数96y x x =+³=,当且仅当x=3时取等号,∴y 的最小值是6.故选:C .3.(2019广东高一期末)若正实数a ,b 满足a +b =1,则下列说法正确的是( )A .ab 有最小值14BC .1a +1b 有最小值4D .a 2+b 2【答案】C【解析】∵a >0,b >0,且a +b =1;∴1=a +b ≥∴ab ≤14;∴ab 有最大值14,∴选项A 错误;=a +b =1+1+=2,∴B 项错误.1a+1b ==1ab ≥4,∴1a +1b 有最小值4,∴C 正确;a 2+b 2=(a +b )2―2ab =1―2ab ≥1―2×14=12,∴a 2+b 2的最小值是12,不是∴D 错误.4.(2019·柳州市第二中学高一期末)若x >―5,则x +4x 5的最小值为( )A .-1B .3C .-3D .1【解析】x +4x5=x +5+4x 5―5≥2×2―5=―1,当且仅当x =―3时等号成立,故选A.5.(2019吉林高一月考)若()12f x x x =+- (2)x >在x n =处取得最小值,则n =( )A .52B .3C .72D .4【答案】B 【解析】:当且仅当时,等号成立;所以,故选B.6.(2019·广西桂林中学高一期中)已知5x 2³,则f(x)= 24524x x x -+-有A .最大值B .最小值C .最大值1D .最小值1【答案】D【解析】()()()2211112122222x f x x x x -+éù==-+³=ê--ëû当122x x -=-即3x =或1(舍去)时, ()f x 取得最小值1二、填空题7.(2019·宁夏银川一中高一期末)当1x £-时,1()1f x x x =++的最大值为__________.【答案】-3.【解析】当1x £-时,()11[(1)111f x x x x x =+=--+--++又1(1)21x x -+-³+,()11[(1)1311f x x x x x =+=--+--£-++,故答案为:-38.(2019·上海市北虹高级中学高一期末)若0m >,0n >,1m n +=,且41m n+的最小值是___.【答案】9【解析】∵0m >,0n >,1m n +=,4()5414519n m m n m n m n m n æö\+=++=+++=ç÷èø…,当且仅当12,33n m == 时“=”成立,故答案为9.9.(2019·浙江高一期末)已知0a >,0b >,若不等式212ma b a b+³+恒成立,则m 的最大值为【答案】9.【解析】由212m a b a b +³+得()212m a b a b æö£++ç÷èø恒成立,而()212225a b a b a b b a æö++=++ç÷èø5549³+=+=,故9m £,所以m 的最大值为9.10.(2019·浙江高一月考)设函数24()(2)(0)f x x x x x=-++>.若()4f x =,则x =________.【答案】2【解析】因为2(2)0y x =-³,当2x =时,取最小值;又0x >时,44y x x=+³=,当且仅当06(,),即2x =时,取最小值;所以当且仅当2x =时,24()(2)f x x x x=-++取最小值(2)4f =.即()4f x =时,2x =.故答案为2三、解答题11.(2016·江苏高一期中)已知a >0,b >0,且4a +b =1,求ab 的最大值;(2)若正数x ,y 满足x +3y =5xy ,求3x +4y 的最小值;(3)已知x <54,求f (x )=4x -2+145x -的最大值;【答案】(1)的最大值;(2)的最小值为5;(3)函数的最大值为【解析】(1),当且仅当,时取等号,故的最大值为(2),当且仅当即时取等号(3)当且仅当,即时,上式成立,故当时,函数的最大值为.12.(2019·福建高一期中)设0,0,1a b a b >>+= 求证:1118a b ab++³ 【答案】可以运用多种方法。
【北师大版】四年级下册数学一课一练-2.2三角形分类(含答案)

四年级下册数学一课一练-2.2三角形分类一、单选题1.一个三角形中有两个角相等,那么这个三角形一定是()。
A. 锐角三角形B. 直角三角形C. 等腰三角形2.有一个直角三角形,两个锐角分别是()A. 48°和52。
B. 38°和42°C. 48°和42°D. 60°和35°3.一个三角形的两个内角分别是65°和35°,这个三角形是()。
A. 锐角三角形B. 直角三角形C. 钝角三角形4.一个三角形的最小内角是48°,按角分,这是一个()三角形。
A. 钝角B. 锐角C. 直角D. 无法确定5.下面这个三角形被遮住了一部分,请判断,这个三角形是什么三角形?()。
A. 直角三角形B. 锐角三角形C. 钝角三角形D. 以上都有可能二、判断题6.等边三角形的每一个内角都是锐角。
7.一个三角形中,至少有两个角是锐角.8.三条线段组成的图形一定是三角形.9.一个顶角是80度的等腰三角形,一定是一个钝角三角形。
10.一个三角形的两个内角都是锐角,这个三角形一定是锐角三角形。
三、填空题11.纸飞机的翅膀可以看做________。
12.一个等腰三角形的底角是36°,它的顶角是________°,它按角分类是________三角形。
13.有一个三角形,它的三个内角的度数的比是7∶3∶10,最小的角是________,这是一个________三角形。
14.一个三角形,三个内角的度数比是2:3:4,最大的内角是________度,这个三角形按角分类是________三角形。
15.在一个三角形的3个角中,一个是35°,一个是110°,这个三角形既是________三角形,又是________三角形。
四、解答题16.观察下面的三角形,你能按边给它们分类吗?17.下面是三块三角形玻璃打碎后留下的碎片,你能判断出它们原来各是什么三角形吗?五、应用题18.一个等腰三角形的底边是3厘米,周长为37厘米.它的一条腰是多少?参考答案一、单选题1.【答案】C【解析】【解答】解:一个三角形中有两个角相等,那么这个三角形一定是等腰三角形。
数学五年级上册《三角形的面积》同步练习题(含答案)

62 三角形的面积1.(2020秋•射阳县期中)我国古代数学名著《九章算术》中记载了三角形面积的计算方法是“半广以乘正从”.就是指三角形的面积为()A .底乘高的一半B .底的一半乘高C .底的一半乘高的一半D .底乘高2.(2020秋•高台县期中)一个三角形,高不变,底扩大3倍,面积()A .扩大3倍B .扩大6倍C .扩大9倍D .不变3.(2020秋•赣榆区期中)一个三角形桃园,底54米,高40米.如果平均每棵桃树占地9平方米,这个桃园一共种树棵.4.(2020秋•偃师市期中)如图,这个平行四边形的面积是40平方米,小直角三角形的面积是平方米.5.(2020•云梦县)一个等腰三角形的两条边是5cm、10cm,那么它的周长可能是20cm或25cm.(判断对错)6.(2019•福建模拟)一个三角形的面积是2.4平方米,高是1.2米,它的底是4米.(判断对错)7.计算如图各图形的周长.8.求图中三角形的面积.9.(2019春•普陀区期中)乙三角形的面积比甲三角形的面积大多少平方厘米?10.(2018秋•福州期末)工人叔叔给一块底是10米,高是4米的三角形广告牌刷油漆,每平方米大约要用油漆0.34千克,工人叔叔带来了7千克油漆,要刷完这块广告牌,这些油漆够吗?11.一块三角形的棉田,底长为240m,是高的1.6倍,共产皮棉1170kg.平均每公顷棉田可产皮棉多少千克?12.(2019•保定模拟)爷爷家有一块三角形的小麦地,底32米、高15米,今年一共收小麦134.4千克.平均每平方米收小麦多少千克?13.(2018秋•水城县校级期中)一面用纸做成的直角三角形小旗,底是12厘米,高是20厘米.做10面这样的小旗,至少需要这种纸多少平方厘米?14.(2019•防城港模拟)一块三角形地,底是48米,是高的2.4倍,在这块地里栽树苗,每棵树苗占地1.2平方米,这块地一共可以栽树苗多少棵?1.一个直角三角形的面积是220cm,一条直角边是5cm,另一条直角边是()A .8cmB .4 cmC .2 cm2.如图中,甲、乙两个平行四边形形状完全一样,则阴影部分面积相比()A .甲大于乙B .甲小于乙C .甲等于乙3.(2020•石阡县)现有5厘米、8厘米的小棒各一根,请你再选1根长度是整厘米的小棒围成的三角形,这个三角形的周长最大是厘米,最小是厘米.4.(2018秋•江城区期末)一个三角形周长是26cm,两条边长是8厘米和5.5cm,另一条边长厘米.5.(2015春•尚志市期末)如果一个等腰三角形的周长是84厘米,底边长是24厘米,它的一条腰长是厘米.6.(2019•株洲模拟)两个周长相等的三角形,面积也一定相等.(判断对错).7.(2018•海安县)一个等腰三角形有两条边的长度分别是5厘米和12厘米,这个等腰三角形的周长可能是22厘米. (判断对错)8.计算下列图形的面积:(单位:厘米)9.计算如图图形阴影部分的面积(单位:厘米)10.一块三角形的稻田,底是90米,相当于高的1.5倍,每平方米稻田需要施肥0.2千克.这块稻田一共需要施肥多少千克?11.(2017秋•海安县校级期末)有一块三角形麦地底45米,高86.2米,如果每公顷可收小麦4600千克,这块地共收小麦多少千克?12.(2020秋•赣榆区期中)有一块三角形的花圃,底是25米,高是20米.平均每平方米产鲜花50枝,这块花圃一共可以产鲜花多少枝?13.(2016秋•遵义期末)块三角形的玻璃,底是12.5分米,高是7.6分米,每平方分米玻璃的价钱是68元,买这块玻璃要用多少元?参考答案1.【分析】“半广以乘正从”.“广是指三角形的底边,正从是指底边上的高.整句话的意思是:三角形的面积等于高与底边边长乘积的一半,据此解答.【解答】解:我国古代数学名著《九章算术》中记载了三角形面积的计算方法是“半广以乘正从”.就是指三角形的面积为底的一半乘高.故选:B.2.【分析】根据三角形的面积计算公式“2=÷”及在乘法算式中,一个因数不变,另一个加数扩大或缩小S ah多少倍,积也随之扩大或缩小相同的倍数,一个三角形,高不变,底扩大3倍,面积扩大3倍.【解答】解:一个三角形,高不变,底扩大3倍,面积扩大3倍.故选:A.3.【分析】根据三角形的面积公式:2=÷,把数据代入公式求出这个桃园的面积,然后根据“包含”除法S ah的意义,用桃园的面积除以每棵桃树的占地面积即可.【解答】解:544029⨯÷÷10809=÷=(棵)120答:这个桃园一共种树120棵.故答案为:120.4.【分析】根据平行四边形的面积公式:S ah÷=(米),然后求三角形的底:=,求平行四边形的底:40410=÷,计算其面积即可.S ah1064-=(米),利用三角形面积公式:2【解答】解:(4046)42÷-⨯÷(106)42=-⨯÷=⨯÷4428=(平方米)答:小直角三角形的面积是8平方米.故答案为:8.5.【分析】根据三角形3条边之间的关系,在三角形中任意两边之和大于第三边,任意两边之差小于第三边,由此可知,三角形的腰长是10厘米,底边是5厘米,根据三角形的周长公式解答即可.【解答】解:1025⨯+=+20525=(厘米)答:这个三角形的周长是25厘米.因此,一个等腰三角形的两条边是5cm、10cm,那么它的周长可能是20cm或25cm.这种说法是错误的.故答案为:⨯.6.【分析】根据三角形的面积公式2=÷,代入数据即可求出底.a S hS ah=÷,知道2【解答】解:2.42 1.2⨯÷=÷4.8 1.2=(米)4答:它的底是4米.故题干的说法是正确的.故答案为:√.7.【分析】根据多边形周长的计算方法,把围成多边形的各边的长度合并起来即可.【解答】解:(1)34512++=(厘米)答:三角形的周长是28厘米.(2)30408060210+++=(毫米)答:梯形的周长是210毫米.(3)12918122172++++=(米)答:五边形的周长是72米.8.【分析】图中的三角形的底是1165=÷进行解答.S ah-=厘米,高是8厘米,由此利用三角形的面积公式2【解答】解:(116)82-⨯÷=⨯÷582=÷402=(平方厘米)20答:图中三角形的面积是20平方厘米.9.【分析】由图意可知:乙三角形的面积比甲三角形面积大的面积也就是乙加上空白部分与甲加上空白部分的差,根据三角形的面积公式求出甲加上空白部分的面积和乙加上空白部分的面积,从而可以求出甲与乙的面积差.【解答】解:(862)(482)⨯÷-⨯÷=-2416=(平方厘米)8答:乙三角形的面积比甲三角形的面积大8平方厘米.10.【分析】要想知道7千克油漆够还是不够,首先根据三角形的面积公式:2=÷,求出这个广告牌的面S ah积,然后用广告牌的面积乘每平方米用油漆的质量求出共用油漆多少千克,如果用油漆的质量等于或小于7千克,说明够,否则就不够.【解答】解:10420.34⨯÷⨯=⨯200.34=(千克)6.86.8千克7<千克答:这些油漆够.11.【分析】已知三角形的底是240米,是高的1.6倍,根据已知一个数的几倍是多少,求这个数,用除法求出高,再根据三角形的面积公式:2=÷,把数据代入公式求出棉田的面积是多少公顷,然后根据单产量=总产量S ah÷数量,据此列式解答.【解答】解:240 1.6150÷=(米)⨯÷=(平方米)24015021800018000平方米 1.8=公顷÷=(千克)1170 1.8650答:平均每公顷棉田可产皮棉650千克.12.【分析】先利用三角形面积公式求出这块地的面积,总产量除以这块地的面积,就是每平方米的小麦产量.【解答】解:134.4(32152)÷⨯÷,=÷134.4240=(千克);0.56答:平均每平方米收小麦0.56千克.13.【分析】先依据三角形的面积=底⨯高2÷,计算出一面旗子的面积,再乘10,即可得解.【解答】解:1220210⨯÷⨯12010=⨯=(平方厘米)1200答:至少需要1200平方厘米纸.14.【分析】已知底是48米,是高的2.4倍,因此用48米除以2.4即可求出三角形底边上的高,再根据三角形的面积公式2=÷,求出三角形土地的面积,再除以1.2平方米就是要求的答案.S ah【解答】解:48(48 2.4)2 1.2⨯÷÷÷=⨯÷÷48202 1.2=÷÷9602 1.2400=(棵);答:这块地一共可以栽树苗400棵.强化提优练答案解析1.【分析】根据三角形的面积公式:2=÷,把数据代入公式解答.S ahh S a=÷,那么2【解答】解:2025⨯÷405=÷=(厘米)8答:另一条直角边是8厘米.故选:A.2.【分析】这两个平行四边形中,阴影部分面积都是平行四边形面积的一半,由此即可判断它们面积的大小.【解答】解:两图中,阴影部分均为平行四边形面积的一半,而两个平行四边形的面积相等,由此可得:阴影部分的面积都相等.故选:C.3.【分析】三角形的两边之和大于第三边,两边之差小于第三边.用5和8的和与差求出第三边的长度,进而求出周长.【解答】解:(1)5813+=(厘米)第三条边要比13厘米小,比13小的最大整厘米数是12厘米,第三边长12厘米,此时周长是:581225++=(厘米)(2)853-=(厘米)第三边要比3厘米大,比3大的最小整厘米数是4厘米,第三边长4厘米,此时周长是:45817++=(厘米)答:这个三角形的周长最大是25厘米,最小是17厘米.故答案为:25,17.4.【分析】因为三角形的周长是指三角形三条边的和,已知三角形的两条边,求斜边,用周长分别减去两条边的长度即可.【解答】解:268 5.512.5--=(厘米);答:另一条边长12.5厘米;故答案为:12.5.5.【分析】等腰三角形的两条腰相等,用三角形的周长减去底边的长度再除以2,就等于三角形的腰长.【解答】解:(8424)2-÷602=÷=(厘米)30答:它的一条腰长是30厘米.故答案为:30.6【分析】根据周长和面积的定义作答,周长是指围成图形的长度;而面积是组成此图形的面的大小.【解答】解:因为三角形的周长是指围成三角形的三条边的和,计算方法为:C a b c=++,而三角形的面积是指三角形的面的大小,计算公式为:2=÷,S ah如果两个三角形的周长相等,但两个三角形的底与高的乘积不相等,那么面积就不相等,所以两个周长相等的三角形,面积也一定相等,此说法是错误的.故答案为:⨯.7.【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;判断出该三角形的腰为12厘米,进而根据三角形的周长计算方法解答即可.【解答】解:12125++=+245=(厘米)29答:这个等腰三角形的周长是29厘米.故答案为:⨯.8.【分析】根据三角形的面积公式2=÷进行解答即可.S ah【解答】解:2.4 1.82⨯÷4.322=÷=(平方厘米)2.16答:图形的面积是2.16平方厘米.9.【分析】先依据长方形的面积公式S ab=计算出长方形的长,由图意可知:阴影部分是一个等腰直角三角形,它的底和高都等于长方形的长减去长方形的宽,从而利用三角形的面积公式2=÷即可求解.S ah【解答】解:4058÷=(厘米)(85)(85)2-⨯-÷=⨯÷332=÷92=(平方厘米)4.5答:阴影部分的面积是4.5平方厘米.10.【分析】已知三角形的底是高的1.5倍,先求出高,根据三角形的面积公式:2=÷,把数据代入公式求S ah出这块稻田的面积是多少平方米,然后每平方米的施肥量乘稻田的面积就是总施肥量.【解答】解:90 1.560÷=(米)⨯÷⨯906020.2=⨯27000.2=(千克)540答:这块稻田一共需要施肥540千克.11.【分析】根据“三角形的面积=底⨯高2÷”计算出这块三角形土地的面积,然后用“每公顷收小麦的重量⨯小麦地的面积”进行解答即可.【解答】解:4586.221939.5⨯÷=(平方米)1939.5平方米0.19395=公顷⨯=(千克)46000.19395892.17答:这块地共收小麦892.17千克.12.【分析】已知块三角形花圃,底是25米,高是20米,根据三角形的面积公式:2=÷可求出花圃的面积,S ah 再乘50即可.【解答】解:2520250⨯÷⨯25050=⨯=(枝)12500答:这块花圃一共可以产鲜花12500枝.13.【分析】先根据三角形的面积公式:2=÷,计算出这块三角形玻璃的面积,然后再用玻璃的面积乘每S ah平方分米的价格,列式解答即可.【解答】解:12.57.6268⨯÷⨯=⨯47.568=(元)3230答:买这块玻璃要用3230元.11。
小学数学九册三角形、平行四边形、梯形的面积综合练习题

梯形的面积练习题:一、求下面梯形的面积:1.上底2米下底3米高5米2.上底4分米下底5分米高2分米3.上底48米,下底56米,高35米。
4.上底124米,下底76米,高82米。
5.上底80米,下底50米,高60米。
6.上底14米,下底26米,高12米。
7. 上底15分米,下底9分米,高比下底长1分米。
8.下底24厘米,上底是下底的一半,高1分米。
9.上底5厘米,下底8厘米,高是上底和下底的差。
10.上底分米,下底分米,高是上下底的和。
二、填空:1、两个完全一样的梯形可以拼成一个()形,这个拼成的图形的底等于梯形的()与()的和,高等于梯形的(),每个梯形的面积等于拼成的平行四边形面积的()。
2、梯形的上底是a,下底是b,高是c,则它的面积=()3、一个梯形上底与下底的和是15米,高是4米,面积是()平方米。
4、一个梯形的面积是8平方厘米,如果它的上底、下底和高各扩大2倍,它的面积是()平方厘米。
5、用两个完全一样的梯形拼成一个平行四边形,已知每个梯形的面积是24平方分米,拼成的平行四边形的面积是()平方分米?三、判断:1、梯形的面积等于平行四边形的面积的一半。
()2、两个完全相同的直角梯形,可以拼成一个长方形。
()3、一个上底是5厘米,下底是8厘米,高是3厘米的梯形,它的面积是39平方厘米。
()4、一个梯形的上底是3分米,下底是5分米,高是4分米,面积就是16平方分米。
()四、应用题1、一座小型拦河坝,横截面的上底5米,下底131米,高21米。
这座拦河坝的横截面积是多少?2、一块梯形稻田,上底长8米,下底比上底长1.2米,高是上底的2倍。
这块稻田的面积是多少平方米?3、一块梯形草坪的面积是90平方米,上底是6米,下底是12米,高是多少米?4、一块梯形的果园,它的上底是160米,下底是120米,高30米。
如果每棵果树占地10平方米,这个果园共有树多少棵?5、用65米长的篱笆沿墙边围一个直角梯形的鸡舍,梯形的直角边是15米,你能计算出围成的鸡舍的面积吗?6、一块三角形地,底长38米,高是27米,如果每平方米收小麦0.7千克,这块地可以收小麦多少千克?1、有一块梯形地,上底长64米,比下底短16米,高50米。
三角形、平行四边形、梯形的面积综合练习题 (2)

梯形的面积练习题:一、求下面梯形的面积:上底2米下底3米高5米上底4分米下底5分米高2分米上底48米,下底56米,高35米。
上底124米,下底76米,高82米。
上底80米,下底50米,高60米。
上底15分米,下底9分米,高比下底长1分米。
下底24厘米,上底是下底的一半,高1分米。
上底5厘米,下底8厘米,高6厘米上底2.4分米,下底7.6分米,高8分米二、填空:1、两个完全一样的梯形可以拼成一个()形,这个拼成的图形的底等于梯形的()与()的和,高等于梯形的(),每个梯形的面积等于拼成的平行四边形面积的()。
2、梯形的上底是a,下底是b,高是c,则它的面积=()3、一个梯形上底与下底的和是15米,高是4米,面积是()平方米。
4、一个梯形的面积是8平方厘米,如果它的上底、下底和高各扩大2倍,它的面积是()平方厘米。
5、用两个完全一样的梯形拼成一个平行四边形,已知每个梯形的面积是24平方分米,拼成的平行四边形的面积是多少平方分米?三、判断:1、梯形的面积等于平行四边形的面积的一半。
()2、两个完全相同的直角梯形,可以拼成一个长方形。
()3、一个上底是5厘米,下底是8厘米,高是3厘米的梯形,它的面积是12平方厘米。
()4、一个梯形的上底是3分米,下底是5分米,高是4分米,面积就是32平方分米。
()四、应用题1、一座小型拦河坝,横截面的上底5米,下底131米,高21米。
这座拦河坝的横截面积是多少?2、一块梯形稻田,上底长8米,下底比上底长1.2米,高是上底的2倍。
这块稻田的面积是多少平方米?3、一块梯形草坪的面积是90平方米,上底是6米,下底是12米,高是多少米?4、一块梯形的果园,它的上底是160米,下底是120米,高30米。
如果每棵果树占地10平方米,这个果园共有树多少棵?5、用65米长的篱笆沿墙边围一个直角梯形的鸡舍,梯形的直角边是15米,你能计算出围成的鸡舍的面积吗?6、一块三角形地,底长38米,高是27米,如果每平方米收小麦0.7千克,这块地可以收小麦多少千克?1、有一块梯形地,上底长64米,比下底短16米,高50米。
苏教版数学五年级上册2.2《三角形面积的计算》教案

苏教版数学五年级上册2.2《三角形面积的计算》教案一. 教材分析苏教版数学五年级上册2.2《三角形面积的计算》是小学数学的重要内容,主要让学生掌握三角形面积的计算方法。
本节课的内容在学生已经掌握了平行四边形和梯形面积计算的基础上进行,为后续学习其他多边形的面积计算打下基础。
教材通过生动的图形和实际问题,引导学生探究三角形面积的计算方法,培养学生的空间观念和解决问题的能力。
二. 学情分析五年级的学生已经具备了一定的几何图形知识,对平行四边形和梯形的面积计算有一定的了解。
但学生在计算三角形面积时,容易混淆公式,对三角形的底和高概念理解不清晰。
因此,在教学过程中,需要帮助学生巩固三角形的基本概念,明确三角形面积计算的方法。
三. 教学目标1.知识与技能:让学生掌握三角形面积的计算方法,能熟练运用公式计算三角形的面积。
2.过程与方法:通过观察、操作、探究等环节,培养学生的空间观念和解决问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生合作、交流的良好学习习惯。
四. 教学重难点1.重点:三角形面积的计算方法。
2.难点:三角形底和高概念的理解,以及在不同情境下灵活运用面积公式。
五. 教学方法1.情境教学法:通过生活实例和图形,引导学生观察、操作,激发学生的学习兴趣。
2.启发式教学法:引导学生主动探究,发现问题,解决问题。
3.合作学习法:学生分组讨论,培养学生的团队协作能力。
六. 教学准备1.教学课件:制作课件,展示三角形面积的计算过程和实例。
2.学具:准备三角形模型、剪刀、直尺等学具,方便学生操作。
3.练习题:挑选合适的练习题,巩固学生对三角形面积计算的掌握。
七. 教学过程导入(5分钟)1.复习旧知识:回顾平行四边形和梯形的面积计算方法。
2.提问:同学们,你们知道三角形面积怎么计算吗?三角形面积与哪些因素有关?呈现(10分钟)1.展示三角形模型,引导学生观察三角形的特征。
2.提问:请大家思考,如何将三角形转化为已学过的图形,以便计算面积?操练(10分钟)1.分组讨论:让学生动手剪三角形,尝试将三角形转化为平行四边形或梯形。
五年级数学三角形面积的计算计算题练习题

三角形面积的计算(200道)班级:姓名:学号:∙三角形的底边是38cm,高是13cm,面积是∙三角形的底边是59cm,高是28cm,面积是∙三角形的底边是20cm,高是37cm,面积是∙三角形的底边是69cm,高是10cm,面积是∙三角形的底边是50cm,高是20cm,面积是∙三角形的底边是96cm,高是42cm,面积是∙三角形的底边是74cm,高是38cm,面积是∙三角形的底边是96cm,高是12cm,面积是∙三角形的底边是27cm,高是15cm,面积是∙三角形的底边是36cm,高是15cm,面积是∙三角形的底边是98cm,高是40cm,面积是∙三角形的底边是98cm,高是49cm,面积是∙三角形的底边是37cm,高是45cm,面积是∙三角形的底边是70cm,高是30cm,面积是∙三角形的底边是92cm,高是17cm,面积是∙三角形的底边是15cm,高是18cm,面积是∙三角形的底边是93cm,高是34cm,面积是∙三角形的底边是21cm,高是21cm,面积是∙三角形的底边是59cm,高是36cm,面积是∙三角形的底边是78cm,高是37cm,面积是∙三角形的底边是21cm,高是31cm,面积是∙三角形的底边是61cm,高是28cm,面积是∙三角形的底边是89cm,高是18cm,面积是∙三角形的底边是65cm,高是44cm,面积是∙三角形的底边是55cm,高是41cm,面积是∙三角形的底边是42cm,高是47cm,面积是∙三角形的底边是74cm,高是41cm,面积是∙三角形的底边是96cm,高是45cm,面积是∙三角形的底边是54cm,高是16cm,面积是∙三角形的底边是40cm,高是44cm,面积是∙三角形的底边是80cm,高是22cm,面积是∙三角形的底边是26cm,高是22cm,面积是∙三角形的底边是88cm,高是11cm,面积是∙三角形的底边是66cm,高是36cm,面积是∙三角形的底边是13cm,高是49cm,面积是∙三角形的底边是89cm,高是49cm,面积是∙三角形的底边是40cm,高是10cm,面积是∙三角形的底边是97cm,高是31cm,面积是∙三角形的底边是10cm,高是35cm,面积是∙三角形的底边是12cm,高是46cm,面积是∙三角形的底边是49cm,高是13cm,面积是∙三角形的底边是64cm,高是33cm,面积是∙三角形的底边是99cm,高是15cm,面积是∙三角形的底边是48cm,高是38cm,面积是∙三角形的底边是17cm,高是22cm,面积是∙三角形的底边是25cm,高是42cm,面积是∙三角形的底边是36cm,高是36cm,面积是∙三角形的底边是21cm,高是23cm,面积是∙三角形的底边是77cm,高是14cm,面积是∙三角形的底边是80cm,高是23cm,面积是∙三角形的底边是54cm,高是17cm,面积是∙三角形的底边是68cm,高是30cm,面积是∙三角形的底边是68cm,高是40cm,面积是∙三角形的底边是78cm,高是39cm,面积是∙三角形的底边是13cm,高是30cm,面积是∙三角形的底边是49cm,高是46cm,面积是∙三角形的底边是46cm,高是49cm,面积是∙三角形的底边是43cm,高是41cm,面积是∙三角形的底边是39cm,高是29cm,面积是∙三角形的底边是39cm,高是46cm,面积是∙三角形的底边是23cm,高是40cm,面积是∙三角形的底边是32cm,高是34cm,面积是∙三角形的底边是36cm,高是41cm,面积是∙三角形的底边是85cm,高是39cm,面积是∙三角形的底边是32cm,高是25cm,面积是∙三角形的底边是10cm,高是12cm,面积是∙三角形的底边是20cm,高是11cm,面积是∙三角形的底边是85cm,高是31cm,面积是∙三角形的底边是73cm,高是40cm,面积是∙三角形的底边是66cm,高是17cm,面积是∙三角形的底边是19cm,高是14cm,面积是∙三角形的底边是67cm,高是41cm,面积是∙三角形的底边是38cm,高是23cm,面积是∙三角形的底边是86cm,高是43cm,面积是∙三角形的底边是13cm,高是17cm,面积是∙三角形的底边是74cm,高是26cm,面积是∙三角形的底边是26cm,高是28cm,面积是∙三角形的底边是72cm,高是34cm,面积是∙三角形的底边是58cm,高是48cm,面积是∙三角形的底边是71cm,高是39cm,面积是∙三角形的底边是12cm,高是10cm,面积是∙三角形的底边是81cm,高是20cm,面积是∙三角形的底边是83cm,高是10cm,面积是∙三角形的底边是71cm,高是25cm,面积是∙三角形的底边是95cm,高是29cm,面积是∙三角形的底边是99cm,高是30cm,面积是∙三角形的底边是32cm,高是24cm,面积是∙三角形的底边是49cm,高是43cm,面积是∙三角形的底边是43cm,高是14cm,面积是∙三角形的底边是64cm,高是18cm,面积是∙三角形的底边是93cm,高是33cm,面积是∙三角形的底边是33cm,高是21cm,面积是∙三角形的底边是35cm,高是33cm,面积是∙三角形的底边是63cm,高是13cm,面积是∙三角形的底边是31cm,高是26cm,面积是∙三角形的底边是14cm,高是47cm,面积是∙三角形的底边是34cm,高是32cm,面积是∙三角形的底边是52cm,高是11cm,面积是∙三角形的底边是85cm,高是13cm,面积是∙三角形的底边是37cm,高是27cm,面积是∙三角形的底边是10cm,高是47cm,面积是∙三角形的底边是91cm,高是43cm,面积是∙三角形的底边是26cm,高是16cm,面积是∙三角形的底边是30cm,高是33cm,面积是∙三角形的底边是98cm,高是33cm,面积是∙三角形的底边是77cm,高是29cm,面积是∙三角形的底边是48cm,高是21cm,面积是∙三角形的底边是70cm,高是25cm,面积是∙三角形的底边是17cm,高是49cm,面积是∙三角形的底边是91cm,高是47cm,面积是∙三角形的底边是95cm,高是30cm,面积是∙三角形的底边是77cm,高是44cm,面积是∙三角形的底边是62cm,高是33cm,面积是∙三角形的底边是63cm,高是40cm,面积是∙三角形的底边是67cm,高是14cm,面积是∙三角形的底边是11cm,高是33cm,面积是∙三角形的底边是46cm,高是20cm,面积是∙三角形的底边是85cm,高是32cm,面积是∙三角形的底边是35cm,高是38cm,面积是∙三角形的底边是94cm,高是32cm,面积是∙三角形的底边是51cm,高是24cm,面积是∙三角形的底边是89cm,高是29cm,面积是∙三角形的底边是66cm,高是35cm,面积是∙三角形的底边是45cm,高是35cm,面积是∙三角形的底边是93cm,高是13cm,面积是∙三角形的底边是37cm,高是47cm,面积是∙三角形的底边是89cm,高是43cm,面积是∙三角形的底边是10cm,高是32cm,面积是∙三角形的底边是25cm,高是28cm,面积是∙三角形的底边是79cm,高是33cm,面积是∙三角形的底边是59cm,高是13cm,面积是∙三角形的底边是82cm,高是14cm,面积是∙三角形的底边是52cm,高是26cm,面积是∙三角形的底边是31cm,高是28cm,面积是∙三角形的底边是60cm,高是25cm,面积是∙三角形的底边是42cm,高是37cm,面积是∙三角形的底边是17cm,高是35cm,面积是∙三角形的底边是31cm,高是18cm,面积是∙三角形的底边是25cm,高是34cm,面积是∙三角形的底边是70cm,高是41cm,面积是∙三角形的底边是31cm,高是44cm,面积是∙三角形的底边是76cm,高是12cm,面积是∙三角形的底边是50cm,高是18cm,面积是∙三角形的底边是47cm,高是48cm,面积是∙三角形的底边是90cm,高是33cm,面积是∙三角形的底边是17cm,高是16cm,面积是∙三角形的底边是17cm,高是19cm,面积是∙三角形的底边是55cm,高是39cm,面积是∙三角形的底边是97cm,高是44cm,面积是∙三角形的底边是31cm,高是31cm,面积是∙三角形的底边是90cm,高是12cm,面积是∙三角形的底边是26cm,高是14cm,面积是∙三角形的底边是50cm,高是20cm,面积是∙三角形的底边是54cm,高是40cm,面积是∙三角形的底边是89cm,高是13cm,面积是∙三角形的底边是46cm,高是42cm,面积是∙三角形的底边是35cm,高是34cm,面积是∙三角形的底边是71cm,高是42cm,面积是∙三角形的底边是64cm,高是31cm,面积是∙三角形的底边是21cm,高是26cm,面积是∙三角形的底边是18cm,高是34cm,面积是∙三角形的底边是37cm,高是25cm,面积是∙三角形的底边是96cm,高是49cm,面积是∙三角形的底边是79cm,高是28cm,面积是∙三角形的底边是65cm,高是14cm,面积是∙三角形的底边是54cm,高是25cm,面积是∙三角形的底边是99cm,高是23cm,面积是∙三角形的底边是97cm,高是43cm,面积是∙三角形的底边是80cm,高是17cm,面积是∙三角形的底边是61cm,高是37cm,面积是∙三角形的底边是99cm,高是39cm,面积是∙三角形的底边是92cm,高是16cm,面积是∙三角形的底边是55cm,高是36cm,面积是∙三角形的底边是89cm,高是42cm,面积是∙三角形的底边是44cm,高是35cm,面积是∙三角形的底边是77cm,高是35cm,面积是∙三角形的底边是17cm,高是13cm,面积是∙三角形的底边是41cm,高是29cm,面积是∙三角形的底边是10cm,高是49cm,面积是∙三角形的底边是15cm,高是47cm,面积是∙三角形的底边是87cm,高是20cm,面积是∙三角形的底边是70cm,高是27cm,面积是∙三角形的底边是99cm,高是49cm,面积是∙三角形的底边是96cm,高是10cm,面积是∙三角形的底边是46cm,高是31cm,面积是∙三角形的底边是63cm,高是43cm,面积是∙三角形的底边是46cm,高是21cm,面积是∙三角形的底边是30cm,高是13cm,面积是∙三角形的底边是50cm,高是23cm,面积是∙三角形的底边是13cm,高是22cm,面积是∙三角形的底边是50cm,高是42cm,面积是∙三角形的底边是17cm,高是34cm,面积是。
三角形的周长和面积计算

三角形的周长和面积计算一、三角形的周长计算1.1 概念:三角形周长是指三角形三条边的总长度。
1.2 计算方法:已知三角形的三边长a、b、c,周长P=a+b+c。
1.3 单位:周长的单位通常为米、厘米、千米等长度单位。
二、三角形的面积计算2.1 概念:三角形面积是指三角形所占平面区域的面积大小。
2.2 计算方法:(1)已知三角形的三边长a、b、c,高h,面积S=(a×h)/2 或 S=(b×h)/2。
(2)已知三角形的两边长a、b和它们夹角C,面积S=(a×b×sinC)/2。
2.3 单位:面积的单位通常为平方米、平方厘米、平方千米等面积单位。
三、三角形分类3.1 按边长分类:(1)不等边三角形:三边长都不相等。
(2)等腰三角形:有两条边相等,底边不等于腰。
(3)等边三角形:三条边都相等。
3.2 按角度分类:(1)锐角三角形:三个内角都小于90°。
(2)直角三角形:有一个内角为90°。
(3)钝角三角形:有一个内角大于90°。
四、三角形性质4.1 内角和:三角形的三个内角和等于180°。
4.2 外角和:三角形的三个外角和等于360°。
4.3 对边相等:三角形中,相对的两边相等。
4.4 对角相等:三角形中,相对的两个角相等。
4.5 中线定理:三角形的中线等于对应边的一半。
五、实际应用5.1 计算三角形周长和面积,解决生活中的实际问题,如测量土地、计算物体表面积等。
5.2 利用三角形的性质和计算方法,解决几何问题,如证明三角形全等、相似等。
5.3 了解三角形分类,便于对三角形进行更深入的研究和应用。
六、学习建议6.1 掌握三角形周长和面积的计算方法,熟练运用公式。
6.2 理解三角形分类,掌握各类三角形的特点。
6.3 熟练运用三角形性质,解决几何问题。
6.4 结合实际应用,提高解决实际问题的能力。
6.5 注重练习,提高计算速度和准确性。
数学五年级上册《三角形的面积》同步训练(含答案)

第六单元《多边形的面积》第2课时三角形的面积一.选择题1.(2015•如皋市模拟)在一个上底是4厘米,下底是6厘米,高是5厘米的梯形中剪下一个最大的三角形,这个三角形的面积是()平方厘米.A .10B .12C .152.(2013秋•唐河县期末)图中两个阴影部分的面积相比(a)b.A .大于B .小于C .等于3.(2014秋•怀柔区期中)如果两个三角形的面积相等,那么,这两个三角形是()A .同底等高B .不同底不等高C .等底不等高4.如图中A是梯形上底的中点,甲三角形和乙三角形的面积比较,是()A .甲=乙B .甲>乙C .甲<乙二.填空题5.(2020秋•偃师市期中)一个三角形和一个平行四边形的面积相等,底也相等,平行四边形的高是10厘米,三角形的高是.6.(2018秋•满洲里市期末)一个平行四边形的面积是28平方厘米,与它等底等高的三角形的面积是平方厘米.7.(2018秋•江城区期末)一个三角形周长是26cm,两条边长是8厘米和5.5cm,另一条边长厘米.8.(2013•福田区校级模拟)一个等边三角形与一个正六边形的周长相等,如果三角形的面积是36平方厘米,那么六边形的面积是平方厘米.9.一个三角形周长28厘米,三角形内一点到三条边的距离都是6厘米,这个三角形面积是平方厘米.三.判断题10.(2018秋•北票市期末)三角形面积是平行四边形的一半.(判断对错)11.(2016秋•东台市月考)直角三角形的三条边分别长5米、4米和3米,面积是6平方米(判断对错)12.(2016春•红河县校级期末)底和高都分别相等的两个三角形,它们的形状一定相同..(判断对错)13.一个平行四边形的面积是10平方分米,那么三角形的面积一定是5平方分米..(判断对错)四.计算题14.张大伯家有一块240m的三角形菜地,公路拓宽后菜地被割去一个角(如图),如果每平方米菜地国家赔偿225元,张大伯可以得到多少赔偿金?15.计算阴影部分的面积.16.求下面图形中阴影部分的面积.(单位:米)五.应用题17.(2018秋•江都区期末)一块三角形菜地,底是50米,高是20米.如果每棵白菜占地10平方分米,这块菜地一共可以种多少棵白菜?18.(2019春•市南区校级期末)一根铁丝可以围成一个边长为12厘米的等边三角形,如果改围一个正方形,那么这个正方形的边长是多少厘米?19.有一个三角形的花园,底长6米,如果底延长1米,那么,它的面积就增加2平方米,原来三角形花园的面积是多少平方米?20.一块三角形的稻田,底是90米,相当于高的1.5倍,每平方米稻田需要施肥0.2千克.这块稻田一共需要施肥多少千克?21.如图,梯形的面积是22.5平方分米,求阴影三角形的面积.22.一个油菜地的形状是三角形,底边长120米,是高的1.5倍,如果每平方米油菜地可以收油菜籽0.8千克,这块油菜地一共可以收油菜籽多少千克?六.解答题23.(2019秋•武川县期末)一个三角形草坪的底边长18.4米,高是2.5米,如果每平方米草坪价格是18元,这个草坪共需多少元钱?24.(2018秋•水城县校级期中)一面用纸做成的直角三角形小旗,底是12厘米,高是20厘米.做10面这样的小旗,至少需要这种纸多少平方厘米?25.(2016秋•平顶山期末)一块三角形菜地,底是280米,高是50米.这块菜地的面积是多少公顷?26.(2015秋•合川区期末)算出图形的周长.27.(2018秋•北票市期末)一块三角形玉米地,底是240米,高是150米,共收玉米9360千克,求每公顷可以收玉米多少千克?28.(2016秋•怒江州期末)有一块三角形菜地的面积是24平方米,底是120分米,高是多少米?29.(2016秋•北京期末)一个三角形的布料面积是45平方米,一条边长为5米,求这条边上的高为多少米?30.(2017秋•抚宁区期末)下面是张大爷种的一块长方形菜地,涂色的部分种上了白菜,其余的地方种萝卜.请你算一下种白菜的面积.每平方米需施肥0.25kg,这块地共需施肥多少kg?31.(2016秋•遵义期末)块三角形的玻璃,底是12.5分米,高是7.6分米,每平方分米玻璃的价钱是68元,买这块玻璃要用多少元?参考答案第六单元《多边形的面积》第2课时三角形的面积一.选择题1.(2015•如皋市模拟)在一个上底是4厘米,下底是6厘米,高是5厘米的梯形中剪下一个最大的三角形,这个三角形的面积是()平方厘米.A .10B .12C .15【解答】解:652⨯÷=÷302=(平方厘米).15答:这个三角形的面积是15平方厘米.故选:C.2.(2013秋•唐河县期末)图中两个阴影部分的面积相比(a)b.A .大于B .小于C .等于【解答】解:两个三角形的面积等底等高,所以它们的面积相等.故选:C.3.(2014秋•怀柔区期中)如果两个三角形的面积相等,那么,这两个三角形是()A .同底等高B .不同底不等高C .等底不等高【解答】解:根据三角形的面积公式:2=÷,可知:同底等高的两个三角形的面积相等;S ah面积相等时,它们不一定是等底等高,如底和高分别是6和2的三角形与底和高分别是4和3的三角形面积也相等.故选:AB.4.如图中A是梯形上底的中点,甲三角形和乙三角形的面积比较,是()A .甲=乙B .甲>乙C .甲<乙【解答】解:由分析可知:三角形甲和三角形乙的底和高分别相等,所以甲的面积=乙的面积.故选:A.二.填空题5.(2020秋•偃师市期中)一个三角形和一个平行四边形的面积相等,底也相等,平行四边形的高是10厘米,三角形的高是20厘米.【解答】解:因为一个三角形和一个平行四边形的面积相等,底也相等,所以三角形的高:10220⨯=(厘米).答:三角形的高是20厘米.故答案为:20厘米.6.(2018秋•满洲里市期末)一个平行四边形的面积是28平方厘米,与它等底等高的三角形的面积是14平方厘米.【解答】解:28214÷=(平方厘米)答:与它等底等高的三角形的面积是14平方厘米.故答案为:14.7.(2018秋•江城区期末)一个三角形周长是26cm,两条边长是8厘米和5.5cm,另一条边长12.5厘米.【解答】解:268 5.512.5--=(厘米);答:另一条边长12.5厘米;故答案为:12.5.8.(2013•福田区校级模拟)一个等边三角形与一个正六边形的周长相等,如果三角形的面积是36平方厘米,那么六边形的面积是54平方厘米.【解答】解:设正六边形的边长为a,大正三角形的边长为b,根据题意可得:63a b=,则:3:61:2a b==;又由于大正三角形里面的每一个小正三角形的边长等于大正三角形边长(B )的12,所以大正三角形里面的每一个小正三角形的面积等于正六边形里面的每一个小正三角形的面积;因此每一个小正三角形的面积是:3649÷=(平方厘米),正六边形的面积是:9654⨯=(平方厘米).答:正六边形的面积是54平方厘米.故答案为:54.9.一个三角形周长28厘米,三角形内一点到三条边的距离都是6厘米,这个三角形面积是 84 平方厘米.【解答】解:如图,111222S ABC S PAC S PAB S PBC AC PF AB PD BC PE ∆=∆+∆+∆=⨯+⨯+⨯ 因为6PF PD PE ===厘米,代入上式,得:16()2S ABC AC AB BC ∆=⨯⨯++ 328=⨯84=(平方厘米);答:这个三角形的面积是84平方厘米;故答案为:84.三.判断题 10.(2018秋•北票市期末)三角形面积是平行四边形的一半. ⨯ (判断对错)【解答】解:等底等高的三角形的面积等于平行四边形的一半,原题中没说是等底等高,所以说法错误.故答案为:⨯.11.(2016秋•东台市月考)直角三角形的三条边分别长5米、4米和3米,面积是6平方米 √ (判断对错)【解答】解:因为直角三角形的斜边最长,所以两条直角边是4米和3米;432⨯÷122=÷6=(平方米).答:这个三角形的面积是6平方米.所以“直角三角形的三条边分别长5米,4米和3米,面积是6平方米”的说法是正确的.故答案为:√.12.(2016春•红河县校级期末)底和高都分别相等的两个三角形,它们的形状一定相同.⨯.(判断对错)【解答】解:如图所示,下面两个三角形等底等高,但是它们的形状不一样:面积相等的三角形,形状不一定相同.说成形状一定相同是错误的.故答案为:⨯.13.一个平行四边形的面积是10平方分米,那么三角形的面积一定是5平方分米.⨯.(判断对错)【解答】解:一个平行四边形的面积是10平方分米,那么和这个平行四边形等底等高的三角形的面积是5平方分米.而这个三角形不一定和这个平行四边形等底等高.故答案为:⨯.四.计算题14.张大伯家有一块240m的三角形菜地,公路拓宽后菜地被割去一个角(如图),如果每平方米菜地国家赔偿225元,张大伯可以得到多少赔偿金?【解答】解:402108⨯÷=(米)⨯÷=(平方米)2.58210102252250⨯=(元)答:张大伯可以得到2250元的赔偿金.15.计算阴影部分的面积.【解答】解:7.2(2126)⨯⨯÷=⨯7.27=(平方厘米)50.4答:阴影部分的面积是50.4平方厘米.16.求下面图形中阴影部分的面积.(单位:米)【解答】解:742⨯÷=÷282=(平方米)14答:阴影部分的面积是14平方米.五.应用题17.(2018秋•江都区期末)一块三角形菜地,底是50米,高是20米.如果每棵白菜占地10平方分米,这块菜地一共可以种多少棵白菜?【解答】解:10平方分米0.1=平方米⨯÷÷502020.15000.1=÷=(棵)5000答:这块菜地一共可以种5000棵白菜.18.(2019春•市南区校级期末)一根铁丝可以围成一个边长为12厘米的等边三角形,如果改围一个正方形,那么这个正方形的边长是多少厘米?【解答】解:1234⨯÷=÷3649=(厘米),答:这根正方形的边长是9厘米.19.有一个三角形的花园,底长6米,如果底延长1米,那么,它的面积就增加2平方米,原来三角形花园的面积是多少平方米?【解答】解:设三角形的高是x米,+⨯÷-÷=x x(61)2622-=x x3.532x=0.52x÷=÷0.50.520.5x=4原来三角形花园的面积为:⨯÷642=÷2422m=12()答:原来三角形花园的面积是12平方米.20.一块三角形的稻田,底是90米,相当于高的1.5倍,每平方米稻田需要施肥0.2千克.这块稻田一共需要施肥多少千克?【解答】解:90 1.560÷=(米)⨯÷⨯906020.2=⨯27000.2=(千克)540答:这块稻田一共需要施肥540千克.21.如图,梯形的面积是22.5平方分米,求阴影三角形的面积.【解答】解:(73)[22.52(37)]2-⨯⨯÷+÷=⨯÷÷4[4510]2=⨯÷4 4.52182=÷=(平方分米)9答:阴影三角形的面积是9平方分米.22.一个油菜地的形状是三角形,底边长120米,是高的1.5倍,如果每平方米油菜地可以收油菜籽0.8千克,这块油菜地一共可以收油菜籽多少千克?【解答】解:120(120 1.5)20.8⨯÷÷⨯1208020.8=⨯÷⨯=⨯48000.8=(千克)3840答:这块油菜地一共可以收油菜籽3840千克.六.解答题23.(2019秋•武川县期末)一个三角形草坪的底边长18.4米,高是2.5米,如果每平方米草坪价格是18元,这个草坪共需多少元钱?【解答】解:18.4 2.5218⨯÷⨯,=÷⨯,46218=⨯,2318414=(元),答:这个草坪共需414元.24.(2018秋•水城县校级期中)一面用纸做成的直角三角形小旗,底是12厘米,高是20厘米.做10面这样的小旗,至少需要这种纸多少平方厘米?【解答】解:1220210⨯÷⨯=⨯12010=(平方厘米)1200答:至少需要1200平方厘米纸.25.(2016秋•平顶山期末)一块三角形菜地,底是280米,高是50米.这块菜地的面积是多少公顷?【解答】解:280502⨯÷=⨯28025=(平方米)70007000平方米0.7=公顷答:这块菜地的面积是0.7公倾.26.(2015秋•合川区期末)算出图形的周长.【解答】解:(1)623185++=+9385=(厘米)178(2)(124)2+⨯=⨯16232=(厘米)答:三角形的周长是178厘米,长方形的周长是32厘米.27.(2018秋•北票市期末)一块三角形玉米地,底是240米,高是150米,共收玉米9360千克,求每公顷可以收玉米多少千克?【解答】解:2401502⨯÷=÷36000218000=(平方米)18000平方米 1.8=公顷9360 1.85200÷=(千克)答:每公顷收玉米5200千克.28.(2016秋•怒江州期末)有一块三角形菜地的面积是24平方米,底是120分米,高是多少米?【解答】解:120分米12=米⨯÷24212=÷4812=(米)4答:高是4米.29.(2016秋•北京期末)一个三角形的布料面积是45平方米,一条边长为5米,求这条边上的高为多少米?【解答】解:4525⨯÷=÷905=(米)18答:这条边上的高是18米.30.(2017秋•抚宁区期末)下面是张大爷种的一块长方形菜地,涂色的部分种上了白菜,其余的地方种萝卜.请你算一下种白菜的面积.每平方米需施肥0.25kg,这块地共需施肥多少kg?【解答】解:4 2.28.8⨯=(平方米)÷=(平方米)8.82 4.48.80.25⨯=⨯⨯2.2(40.25)2.21=⨯=(千克)2.2答:种白菜的面积是4.4平方米,共需施肥2.2千克.31.(2016秋•遵义期末)块三角形的玻璃,底是12.5分米,高是7.6分米,每平方分米玻璃的价钱是68元,买这块玻璃要用多少元?【解答】解:12.57.6268⨯÷⨯=⨯47.568=(元)3230答:买这块玻璃要用3230元.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时三角形面积的计算(1)
开心预习新课,轻松搞定基础。
1. (1)两个完全一样的三角形可以拼成一个( )。
(2)三角形的面积等于与它等底等高的( )面积的( )。
因为平行四边形的面积=( ),所以三角形的面积=( ),用字母表示为( )。
重难疑点,一网打尽。
2. 计算下面每个三角形的面积。
(1)(2)(3)
3. 一个三角形树林的底是180米,高是300米,这个树林的面积是多少平方米?
4. 一种用纸做成的三角形小旗,底长是12厘米,高是18厘米,做20面这样的小旗,至少需要这样的纸多少平方厘米?
源于教材、宽于教材、拓展探究显身手。
5. 一个三角形和一个平行四边形的底和高分别相等,如果平行四边形的面积是96平方米,那么三角形的面积是( )平方米;如果三角形的面积是96平方米,那么平行四边形的面积是( )平方米。
6. 学校授予最清洁班级的卫生流动红旗如右图所示,这面流动红旗的面积是多少?
7. 一张三角形的彩纸,面积是84平方分米,底是12分米,高是多少分米?
第2课时
1. (1)平行四边形
(2)平行四边形一半底×高底×高÷2S=ah÷2
2. (1)42平方厘米(2)36平方厘米(3)56平方厘米
3. 27000平方米
4. 2160平方厘米
5. 48 192
6. 630平方厘米
7. 14分米。
