零阶保持器研究
零阶保持器

T / 2
e
自动控制原理
第七章 采样数据控制系统分析
因为
T
2π
s
,所以
j π
2 π sin ( π / s ) G h ( j ) e s π / s
|G h ( j ) |
s
零阶保持器的 频率特性:
T
O -
s
2s
3s
G h ( j )
≥ 2
s
m ax
时,则由采样得到的离散信号能无失真地恢 复到原来的连续信号,这就是采样定理,也 称为香农(Shannon)定理。
自动控制原理
第七章 采样数据控制系统分析
物理意义:如果选择这样一个采样角频率 ≥ 2 ,使得对连续信号中所含的最高 s m ax 频率信号来说,能做到在其一个周期内采 样两次以上,则在经采样所获得的离散信 号中将包含连续信号的全部信息。反之, 如果采样次数太少,就做不到无失真地再 现原连续信号。
自动控制原理
第七章 采样数据控制系统分析
第七章 采样数据控制系统分析
7.1 概 述 一、采样控制系统 采样控制系统,又称断续控制系统、离散 控制系统,它是建立在采样信号基础上的。 如果控制系统中有一处或几处信号是断续 的脉冲或数码,则这样的系统称为离散系统。 通常,把系统中的离散信号是脉冲序列形 式的离散系统,称为采样控制系统; 而把数字序列形式的离散系统,称为数字 控制系统或计算机控制系统。
自动控制原理
第七章 采样数据控制系统分析
7.2 信号的采样与保持 一、采样过程 把连续信号转换成离散信号的过程,叫作 采样过程。 实现采样的装置叫作采样开关或采样器。
e(t) e(t) T e * (t) e * (t)
对具有纯滞后的一阶惯性环节的设计

中央民族大学信息工程学院计算机控制技术综合设计实验报告学生姓名:学号:指导教师:实验地点:实验名称:加热炉系统温度控制器设计目录一、设计题目及要求 (4)二、设计方案与结构图 (4)1、计算机控制系统结构图 (4)2、硬件结构图 (5)三、电路硬件设计 (6)1、电桥电路 (6)2、放大环节 (7)3、滤波电路 (7)4、A/D转换器 (8)5、D/A 转换电路 (9)四、参数计算及仿真 (10)1、0θ=时数字调节器D (z )的实现 (10)a 、无控制作用下系统伯德图 ....................................................................................... 10 b 、最少拍下调节器函数 ............................................................................................... 12 C 、最少拍下系统伯德图 ............................................................................................... 14 d 、单位阶跃响应下系统输出 ....................................................................................... 15 e 、施加阶跃干扰信号 ................................................................................................... 17 f 、施加随机信号影响.................................................................................................... 19 2、/20.374T θ==时数字调节器D (z )的实现 . (20)a 、无控制作用下系统伯德图 ....................................................................................... 20 b 、达林算法下调节器函数 ........................................................................................... 23 C 、达林算法下系统伯德图(未加增益) ................................................................... 25 d 、达林算法下系统伯德图(加增益) ....................................................................... 26 e 、单位阶跃响应下系统输出 ....................................................................................... 28 f 、施加阶跃干扰信号.................................................................................................... 29 g 、施加随机信号影响 (30)五、心得与体会 (32)一、设计题目及要求1、 针对一个具有纯滞后的一阶惯性环节()1sKe G s Ts τ-=+的温度控制系统和给定的系统性能指标:✧ 工程要求相角裕度为30°~60°,幅值裕度>6dB✧ 要求测量范围-50℃~200℃,测量精度0.5%,分辨率0.2℃2、 书面设计一个计算机控制系统的硬件布线连接图,并转化为系统结构图;3、 选择一种控制算法并借助软件工程知识编写程序流程图;4、 用MATLAB 和SIMULINK 进行仿真分析和验证;对象确定:K=10*log(C*C -sqrt(C)),rand(‘state ’,C),T=rang(1), 考虑θ=0或T/2两种情况。
零阶保持器

零阶保持器的作用是使采样信号e*(t) 每一采样瞬时的值e(kT)一直保持到 下一个采样瞬时e[(k+1)T],从而使采样信号变成阶梯信号eh(t)。
由于处在每个采样区间内的信号值为常数,其导数为零,故称为零阶保持
器。
(kT+)
O kT
t
-1
1(t kT ) 1(t kT ) g (t kT )
(t
kT
)
0
, ,
t kT t kT
e*(t) e(kT )g g (t kT )
k0
将持续时间 移至和式外
e*(t) e(kT )g (t kT )
k0 取采样过程的数学描述为
e*(t) e(kT )g (t kT )
z z e jT
1 z(ejT e jT )
2j
z
2
z(ejT
e jT
)
1
z2
z sinT 2z cosT
1
7. 设 E( s) ,求1e*(t) 的 Z 变换。 s(s 1)
将 E(s) 进行部分分式展开
E(s) 1 1 1 s(s 1) s s 1
再求其拉氏反变换
e(t)
证明: (1)
Z [e(t nT )] e(kT nT )zk k0
zne[(k n)T ]zk zz k0
zne[(k n)T ]z(kn) k0
zn e(jT )zj ( j k n) jn
由于 j<0 时,e(jT)=0,所以和式下标取值从 j = 0 开始,有
k0 进行拉氏变换
E*(s) L [e*(t )] e(kT )ekTs
吉林大学《控制工程基础》期末考试备考资料(七)

吉大《控制工程基础》(七)第七章 采样系统的分析零阶保持器的模型及其对控制系统的影响摘要 在计算机控制系统中,由于连续信号的离散化后,需要引入保持器对离散信号进行重构,由于零阶保持器的引入,控制系统的性能将会受到响应的影响,尤其是稳定性,本文对零阶保持器的的数学模型进行了简单的分析,它对控制系统稳定性的影响进行了数学分析和仿真说明。
关键词:零阶保持器,计算机控制系统,稳定性1 零阶保持器的数学模型零阶保持器即使采样系统中的D/A 运算的一种,其输入输出关系如图1所示,它的作用是在信号传递过程中,把第nT 时刻的采样信号值一直保持到第(n+1)T 时刻的前一瞬时,把第(n+1)T 时刻的采样值一直保持到(n+2)T 时刻,依次类推,从而把一个脉冲序列e *(t)变成一个连续的阶梯信号e h (t)。
因为在每一个采样区间内e h (t)的值均为常值,亦即其一阶导数为零,故称为零阶保持器,可用“ZOH ”来表示。
如果把阶梯信号e h (t)的中点连起来,则可以得到与e(t)形状一致而时间上迟后半个采样周期(T/2)的响应曲线e(t-T/2)。
图1 零阶保持器的输入输出关系由零阶保持器的单位脉冲响应,我们可以得到她的传递函数而零阶保持器的频率特性为22)2sin(1)(T T T T j e j G T j h ωωωωωω-∠=-=-2 零阶保持器对系统性能的影响根据零阶保持器的频率特性可以得知,其频率幅频特性和相频特性如图2所示图2 零阶保持器的相频特性可见零阶保持器的频率特性不很理想。
信号经过零阶保持器以后,其高频分量不能完全滤掉。
此外零阶保持器具有ωT/2的相角滞后。
因此,零阶保持器的引入将会使系统的稳定性变差。
不过,这个影响与零阶保持器周期T 的选择有着很大的关系。
零阶保持器对系统稳定性的影响对于工业上很多实际的对象,可用二阶惯性加纯滞后的模型来描述其动态特性,采用这种模型来近似这些高阶对象的精度通常很高,足以满足在生产过程的要求 ,本文主要考虑零阶保持器对系统性能的影响。
零阶保持器
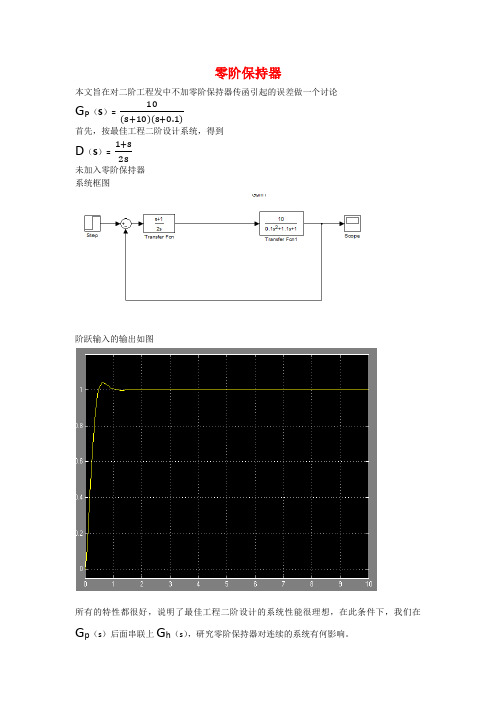
零阶保持器本文旨在对二阶工程发中不加零阶保持器传函引起的误差做一个讨论G P(s)= 10(s+10)(s+0.1)首先,按最佳工程二阶设计系统,得到D(s)= 1+s2s未加入零阶保持器系统框图阶跃输入的输出如图所有的特性都很好,说明了最佳工程二阶设计的系统性能很理想,在此条件下,我们在G p(s)后面串联上G h(s),研究零阶保持器对连续的系统有何影响。
首先,我们利用系统所给的零阶保持器,来看看系统性能有何变化系统的框图如下首先使零阶保持器的T为0.1s,阶跃输入的输出如下发现系统的超调有了增加,但稳定时间略有改进,原来的课上分析说,这是零阶保持器引入了零点的结果现在我们再将采样周期T改为0.5s,看看结果如何仿真出来的结果如下图我们可以发现,当采样周期改变后,超调变得我们无法接受了那么,将采样周期改小会如何呢?将T改为0.01s结果如下所示我们惊讶的发现,性能比最佳工程二阶更好了由于不清楚matlab中的零阶保持器具体实现过程,我自己构造了零阶保持器的环节,具体框图如下取T=0.01s,0.5s和0.1s结果如下这里的延时环节相当明显这和系统的零阶保持器做出来的结果大相径庭为了了解零阶保持器对连续系统性能实际的影响,我们对1−e −Tss进行深入分析首先,e −Ts 作泰勒级数展开,得到如下结果>>symsTs f=exp(-Ts) T= taylor(f,8) f =exp(-Ts) T =1-Ts+1/2*Ts^2-1/6*Ts^3+1/24*Ts^4-1/120*Ts^5+1/720*Ts^6-1/5040*Ts^7>> m=1-T m =Ts-1/2*Ts^2+1/6*Ts^3-1/24*Ts^4+1/120*Ts^5-1/720*Ts^6+1/5040*Ts^7可以看到,上面是一系列的零点,抱着探究性的态度,我们以二阶的近似式,也就是T – 0.5Ts +0.167Ts 2来近似,先取T=0.1s 的情况系统框图结果出现了错误,如下图,可能和MATLAB众对微分的定义有关,但是研究似乎不能进行下去了后来,在南杰胤同学的提示下,我改用pade 近似来模拟延时环节 二阶的pade 近似结果如下[a,b]=pade(0.1,2) a =1 -60 1200 b =1 60 1200即e −Ts =s 2−60s+1200s 2+60s+1200 由此得到1−e −Tss=120s s +60s +120s =120s +60+120上面的T=0.1s ,可以发现,对极点分析,结果如下>> p = [1 60 120] roots(p) p =1 60 120ans =-57.9285 -2.0715也就是说,在一定的近似情况下,零阶保持器引入了两个极点,其中的一个还是相当靠近虚轴的用此式来进行模拟,框图如下仿真结果如下超调比较大。
(完整版)自动控制原理简答题

47、传递函数:传递函数是指在零初始条件下,系统输出量的拉式变换与系统输入量的拉式变换之比。
48、系统校正:为了使系统达到我们的要求,给系统加入特定的环节,使系统达到我们的要求,这个过程叫系统校正。
49、主导极点:如果系统闭环极点中有一个极点或者一对复数极点据虚轴最近且附近没有其他闭环零点,则它在响应中起主导作用称为主导极点。
51、状态转移矩阵:()At t e φ=,描述系统从某一初始时刻向任一时刻的转移。
52、峰值时间:系统输出超过稳态值达到第一个峰值所需的时间为峰值时间。
53、动态结构图:把系统中所有环节或者元件的传递函数填在系统原理方块图的方块中,并把相应的输入输出信号分别以拉氏变换来表示从而得到的传递函数方块图就称为动态结构图。
54、根轨迹的渐近线:当开环极点数 n 大于开环零点数 m 时,系统有n-m 条根轨迹终止于 S 平面的无穷远处,且它们交于实轴上的一点,这 n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近线。
55、脉冲传递函数:零初始条件下,输出离散时间信号的z 变换()C z 与输入离散信号的变换()R z 之比,即()()()C z G z R z=。
56、Nyquist 判据(或者奈氏判据):当ω由-∞变化到+∞时, Nyquist 曲线(极坐标图)逆时针包围(-1,j0)点的圈数N ,等于系统G(s)H(s)位于s 右半平面的极点数P ,即N=P ,则闭环系统稳定;否则(N ≠P )闭环系统不稳定,且闭环系统位于s 右半平面的极点数Z 为:Z=∣P-N ∣57、程序控制系统: 输入信号是一个已知的函数,系统的控制过程按预定的程序进行,要求被控量能迅速准确地复现输入,这样的自动控制系统称为程序控制系统。
58、稳态误差:对单位负反馈系统,当时间t 趋于无穷大时,系统对输入信号响应的实际值与期望值(即输入量)之差的极限值,称为稳态误差,它反映系统复现输入信号的(稳态)精度。
零阶保持器频率特性的仿真研究

0 引言
由于零阶保持器具有最小相位滞后、 结构简单 和易于实现等特点, 常用于闭环离散系统 J 。如 图 l 所示 , 零阶保持器把采样 时刻 . j } 的采样值保持到 ( 十 1 时刻。即在时间 t . ,k 1 ] k ) j ( 十 ) 区间 E[ } 内, 它的输出量一直保持为 ( 这个值。依次类 后) 推, 从而把离散信号恢复成了一个 阶梯形的连续信
中圈分类号 : P 3 T 1 文献标识码 : A 文章编号 :0 80 8 2 1 1 0 00 10 -66(0 2 - 4 -3 J 0 O
S m u a i n Re e r h o h e u n y Ch r c e it fZe o Or e l e i l t s a c n t e Fr q e c a a t rsi o r d r Ho d r o c
W ANG u - i Ch n x a
( et fEetcl n i en S a ni nvrt Tcnl y H nhn 2 03,C ia D p.o l ra gn r go h ax i syo e oo , a zog7 30 ci E e i f U ei f h g hn )
第3 4卷 第 1期 21 0 2年 2月
实验一 控制系统典型环节的模拟实验
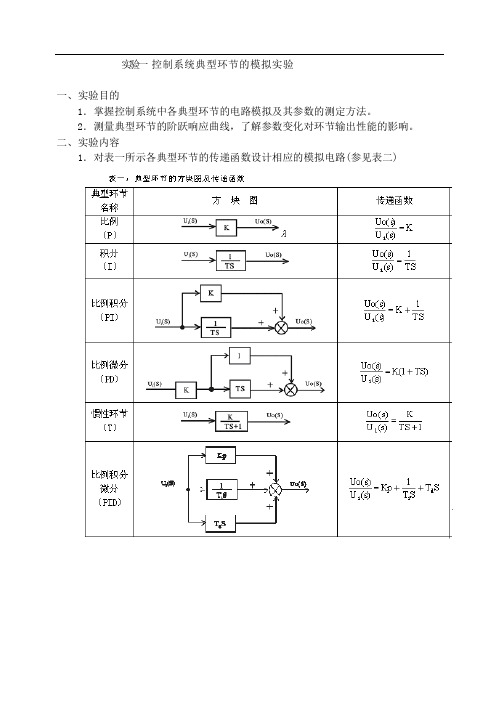
实验一控制系统典型环节的模拟实验一、实验目的1.掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2.测量典型环节的阶跃响应曲线,了解参数变化对环节输出性能的影响。
二、实验内容1.对表一所示各典型环节的传递函数设计相应的模拟电路(参见表二)2.测试各典型环节在单位阶跃信号作用下的输出响应。
3.改变各典型环节的相关参数,观测对输出响应的影响。
三、实验内容及步骤1.观测比例、积分、比例积分、比例微分和惯性环节的阶跃响应曲线。
①准备:使运放处于工作状态。
将信号发生器单元U1的ST端与+5V端用“短路块”短接,使模拟电路中的场效应管(K30A)夹断,这时运放处于工作状态。
②阶跃信号的产生:电路可采用图1-1所示电路,它由“阶跃信号单元”(U3)及“给定单元”(U4)组成。
具体线路形成:在U3单元中,将H1与+5V端用1号实验导线连接,H2端用1号实验导线接至U4单元的X端;在U4单元中,将Z端和GND端用1号实验导线连接,最后由插座的Y端输出信号。
以后实验若再用阶跃信号时,方法同上,不再赘述。
实验步骤:①按表二中的各典型环节的模拟电路图将线接好(先接比例)。
(PID先不接)②将模拟电路输入端(U i)与阶跃信号的输出端Y相连接;模拟电路的输出端(Uo)接至示波器。
③按下按钮(或松开按钮)SP时,用示波器观测输出端的实际响应曲线Uo(t),且将结果记下。
改变比例参数,重新观测结果。
④同理得积分、比例积分、比例微分和惯性环节的实际响应曲线,它们的理想曲线和实际响应曲线参见表三。
2.观察PID环节的响应曲线。
实验步骤:①将U1单元的周期性方波信号(U1 单元的ST端改为与S端用短路块短接,S11波段开关置于“方波”档,“OUT”端的输出电压即为方波信号电压,信号周期由波段开关S11和电位器W11调节,信号幅值由电位器W12调节。
以信号幅值小、信号周期较长比较适宜)。
②参照表二中的PID模拟电路图,按相关参数要求将PID电路连接好。
基于平行控制的离散非线性系统的事件触发近似最优控制-214

2021年12月Chinese Journal of Intelligent Science and Technology December 2021 第3卷第4期智能科学与技术学报V ol.3No.4 基于平行控制的离散非线性系统的事件触发近似最优控制廖泽华1,2,梁子钰1,3,周天民1,卢经纬1,2,魏庆来1,2(1. 中国科学院自动化研究所复杂系统管理与控制国家重点实验室,北京 100190;2. 中国科学院大学人工智能学院,北京 100049;3. 天津大学智能电网教育部重点实验室,天津300072)摘 要:针对离散非线性系统提出了一种基于平行控制的事件触发近似最优控制方法。
首先,基于时间触发的最优值函数和最优控制律,提出了一种新型的触发条件,并基于李雅普诺夫方法证明了闭环系统的渐近稳定性。
其次,为了实施设计的触发条件,提出了一种采用神经网络和自适应动态规划技术的平行控制方法,以预测系统的下一步状态,并获得最优值函数和最优控制律。
最后,通过仿真实验验证了所提方法的有效性。
关键词:事件触发控制;非线性最优控制;平行控制;自适应动态规划中图分类号:TP273文献标识码:Adoi: 10.11959/j.issn.2096−6652.202142Parallel control-based event-driven approximate optimalcontrol of discrete-time nonlinear systemsLIAO Zehua1,2, LIANG Ziyu1,3, ZHOU Tianmin1, LU Jingwei1,2, WEI Qinglai1,21. The State Key Laboratory for Management and Control of Complex Systems, Institute of Automation, Chinese Academy of Sciences, Beijing 100086, China2. School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing 100049, China3. Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin 300072, ChinaAbstract: A parallel control-based event-driven approximate optimal control method was proposed for discrete-time non-linear systems. Firstly, based on the time-triggered optimal value function and optimal control law, a novel triggering condition was developed and the asymptotic stability of the closed-loop system was proved based on the Lyapunov me-thod. Secondly, a parallel control method using neural networks and adaptive dynamic programming techniques was proposed to predict the next state of the system and to obtain the optimal value function and control law. Finally, the ef-fectiveness of the developed method was validated by numerical examples.Key words: event-driven control, nonlinear optimal control, parallel control, adaptive dynamic programming1 引言在过去的数十年中,随着计算能力的提升,智能控制方法得到了长足的进步[1-6]。
零阶保持器
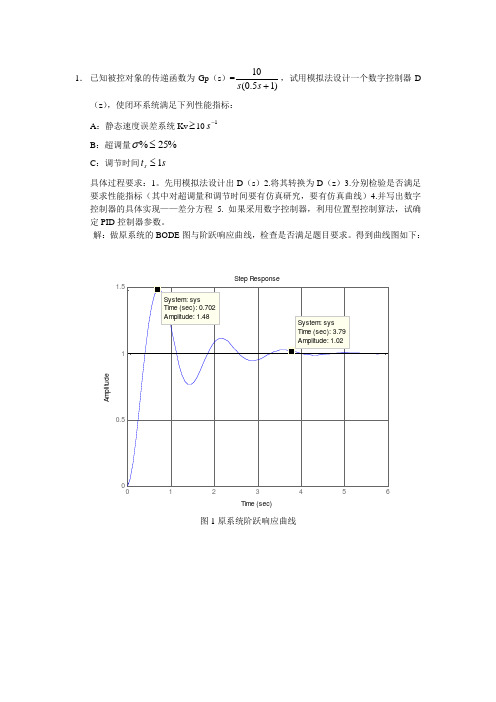
1. 已知被控对象的传递函数为Gp (s )=)15.0(10+s s ,试用模拟法设计一个数字控制器D(z ),使闭环系统满足下列性能指标: A :静态速度误差系统Kv ≥101-s B :超调量%25%≤σ C :调节时间s t s 1≤具体过程要求:1。
先用模拟法设计出D (s )2.将其转换为D (z )3.分别检验是否满足要求性能指标(其中对超调量和调节时间要有仿真研究,要有仿真曲线)4.并写出数字控制器的具体实现——差分方程 5. 如果采用数字控制器,利用位置型控制算法,试确定PID 控制器参数。
解:做原系统的BODE 图与阶跃响应曲线,检查是否满足题目要求。
得到曲线图如下:12345600.511.5Step ResponseTime (sec)A m p l i t u d e图1原系统阶跃响应曲线-60-40-200204060M a g n i t u d e (d B )10-110101102-180-135-90P h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/sec) , P m = 25.2 deg (at 4.25 rad/sec)Frequency (rad/sec)图2原系统bode 图由图可知原系统的性能指标(程序见附录1):①调节时间为ts=3.79s >1s ,超调量%48%=σ>%25,不满足要求;1010)(lim 0≥==→s sGp Kv s 满足要求。
②幅值稳定裕度:Lh=20lg(Gm)=∞dB ,-π穿越频率:∞=g ωrad/s ,相位稳定裕度:=γ 18.25 ,剪切频率:=c ω 4.25rad/s 。
分析可知,需要对原系统采取如下措施:加快反应速度,降低超调量,适当增大相位稳定裕度,这样我们可以设计超前校正器D(s),再将其离散化为D(z),其过程如下所示: ⑴设计超前校正器传递函数 设超前校正器传递函数为11)(D ++=Ts Ts s α,设定校正后的相位稳定裕度为=0γ18.45则,又41.0)sin(1)sin(1=+-=m m φφα;超前校正器传递函数计算(程序见附录1)可得:11)(D ++=Ts Ts s α=105.013774.0++s s⑵校验校正后系统性能指标00255=+-=γγφmGp’(s)=D(s) Gp (s)=)15.0(10+s s *105.013774.0++s sStep ResponseTime (sec)A m p l i t u d e00.20.40.60.81 1.20.20.40.60.811.21.4图3校正后连续系统阶跃响应曲线-100-5050M a g n i t u d e (d B )10-110101102103P h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/sec) , P m = 65.4 deg (at 7.28 rad/sec)Frequency (rad/sec)图4校正后连续系统bode 图由图可知原系统的性能指标(程序见附录1):①调节时间为ts=0.721s <1s ,超调量%6%=σ<%25, 1010)(lim '≥==→s sGp Kv s 满足要求。
零阶保持器
从频域看是把由于采样离散化而产生的高频分量 滤去,而将采样函数的离散频谱恢复成连续函数的主 频谱分量。
连续系统离散化过程
信号重构器不是理想的滤波器会给信号带来幅 值的衰减和相位的延迟,故:
用Z变换方法求脉冲传递函数
Gz
Y U
z z
Z
Gh
s
Gs
若G(s)=k
s a
,采用零阶保持器,则Gh
s
1
eTs s
Gz
Z
1
esT s
s
k
a
z
1 z
Z
k
ss
a
z
1 z
Z
k a
1 s
s
1
a
k a
z
1 z
z
z 1
z
z eaT
Байду номын сангаас
k 1 eaT a z eaT
利用Z逆变换求得其差分方程模型:
t
X t tx0 t BU d
其中
0
t eAt L1 sI A 1
求通解的方法2:
通过展开 d eAtxt 求 xt 的通解: dt
d eAt xt AeAt xt eAt xt eAt Axt xt eAt But
dt
上式两边从 t0到 t 积分可得
t
eAt xt eAt0 xt0 eA Bu d
1 s2
eTs
由Z变换的线性性质和位移定理可得
Gz
Tz
z 12
1 z
计算机控制实验报告-离散化方法研究解析

东南大学自动化学院实验报告课程名称:计算机控制技术第 2 次实验实验名称:实验三离散化方法研究院(系):自动化学院专业:自动化姓名:学号:实验室:416 实验组别:同组人员:实验时间:2014年4月10日评定成绩:审阅教师:一、实验目的1.学习并掌握数字控制器的设计方法(按模拟系统设计方法与按离散设计方法);2.熟悉将模拟控制器D(S)离散为数字控制器的原理与方法(按模拟系统设计方法);3.通过数模混合实验,对D(S)的多种离散化方法作比较研究,并对D(S)离散化前后闭环系统的性能进行比较,以加深对计算机控制系统的理解。
二、实验设备1.THBDC-1型控制理论·计算机控制技术实验平台2.PCI-1711数据采集卡一块3.PC机1台(安装软件“VC++”及“THJK_Server”)三、实验原理由于计算机的发展,计算机及其相应的信号变换装置(A/D和D/A)取代了常规的模拟控制。
在对原有的连续控制系统进行改造时,最方便的办法是将原来的模拟控制器离散化。
在介绍设计方法之前,首先应该分析计算机控制系统的特点。
图3-1为计算机控制系统的原理框图。
图3-1 计算机控制系统原理框图由图3-1可见,从虚线I向左看,数字计算机的作用是一个数字控制器,其输入量和输出量都是离散的数字量,所以,这一系统具有离散系统的特性,分析的工具是z变换。
由虚线II向右看,被控对象的输入和输出都是模拟量,所以该系统是连续变化的模拟系统,可以用拉氏变换进行分析。
通过上面的分析可知,计算机控制系统实际上是一个混合系统,既可以在一定条件下近似地把它看成模拟系统,用连续变化的模拟系统的分析工具进行动态分析和设计,再将设计结果转变成数字计算机的控制算法。
也可以把计算机控制系统经过适当变换,变成纯粹的离散系统,用z变化等工具进行分析设计,直接设计出控制算法。
按模拟系统设计方法进行设计的基本思想是,当采样系统的采样频率足够高时,采样系统的特性接近于连续变化的模拟系统,此时忽略采样开关和保持器,将整个系统看成是连续变化的模拟系统,用s域的方法设计校正装置D(s),再用s域到z域的离散化方法求得离散传递函数D(z)。
自动控制原理实验指导书

目录第一部分使用说明书 (1)第一章系统概述 (1)第二章硬件的组成及使用 (2)第二部分实验指导书 (5)第一章控制理论实验 (5)实验一典型环节的电路模拟 (5)实验二二阶系统的瞬态响应 (11)实验三高阶系统的瞬态响应和稳定性分析 (14)实验五典型环节和系统频率特性的测量 (16)实验七典型非线性环节的静态特性 (21)实验十三采样控制系统的分析 (26)附录上位机软件使用流程 (29)第一部分使用说明书第一章系统概述“THKKL-6”型控制理论及计算机控制技术实验箱是我公司结合教学和实践的需要而进行精心设计的实验系统。
适用于高校的控制原理、计算机控制技术等课程的实验教学。
该实验箱具有实验功能全、资源丰富、使用灵活、接线可靠、操作快捷、维护简单等优点。
实验箱的硬件部分主要由直流稳压电源、低频信号发生器、阶跃信号发生器、交/直流数字电压表、电阻测量单元、示波器接口、CPU(51单片机)模块、单片机接口、步进电机单元、直流电机单元、温度控制单元、通用单元电路、电位器组等单元组成。
数据采集部分采用USB2.0接口,它可直接插在IBM-PC/AT 或与之兼容的计算机USB通讯口上,有4路单端A/D模拟量输入,转换精度为12位;2路D/A模拟量输出,转换精度为12位;上位机软件则集中了虚拟示波器、信号发生器、Bode图等多种功能于一体。
在实验设计上,控制理论既有模拟部分的实验,又有离散部分实验;既有经典控制理论实验,又有现代控制理论实验;计算机控制系统除了常规的实验外,还增加了当前工业上应用广泛、效果卓著的模糊控制、神经元控制、二次型最优控制等实验;第二章硬件的组成及使用一、直流稳压电源直流稳压电源主要用于给实验箱提供电源。
有+5V/0.5A、±15V/0.5A及+24V/2.0A四路,每路均有短路保护自恢复功能。
它们的开关分别由相关的钮子开关控制,并由相应发光二极管指示。
其中+24V主要用于温度控制单元。
零阶保持器状态空间方程

零阶保持器状态空间方程1. 引言1.1 什么是零阶保持器状态空间方程零阶保持器状态空间方程是控制系统理论中的重要概念之一,它是描述系统动态行为的数学模型。
通常情况下,一个动态系统可以通过状态方程和输出方程来描述其行为。
而零阶保持器状态空间方程是指在状态空间中,系统的输出和状态变量之间存在一定的关系,通过这个关系,可以描述系统在任意时间点上的状态。
\dot{x}(t) = Ax(t) + Bu(t)y(t) = Cx(t) + Du(t)x(t)表示系统的状态向量,u(t)表示系统的输入向量,y(t)表示系统的输出向量,A、B、C和D分别是状态方程和输出方程的系数矩阵。
通过这个数学模型,我们可以更好地理解系统的动态特性,从而设计控制器以实现系统的稳定性和性能要求。
零阶保持器状态空间方程在控制领域具有广泛的应用,可以用于分析系统的稳定性、设计控制器以及优化系统性能。
通过研究和理解零阶保持器状态空间方程,我们可以更好地掌握控制系统的工作原理,提高系统的控制效果和性能。
1.2 研究零阶保持器状态空间方程的意义研究零阶保持器状态空间方程的意义在于提高系统控制的稳定性和性能。
零阶保持器是一种特殊的控制器,其传递函数为1,即控制信号等于输入信号,该控制器可用于提高系统的响应速度和抑制系统的误差。
在实际控制系统中,往往需要根据系统的特性和要求设计合适的控制器来实现所期望的性能。
零阶保持器状态空间方程是描述系统动态行为的重要数学模型,通过分析系统的状态空间方程可以更好地理解系统的稳定性和动态特性。
研究零阶保持器状态空间方程的意义在于提高系统控制的效果、提升系统的鲁棒性和稳定性,为实现系统的自动化控制和智能化管理奠定了重要基础。
2. 正文2.1 零阶保持器状态空间方程的推导零阶保持器状态空间方程的推导是控制理论中的关键内容之一。
在推导过程中,我们首先需要了解什么是状态空间方程以及什么是零阶保持器。
状态空间方程是描述系统动态行为的数学模型,它由一组一阶微分方程组成,通过状态向量来表示系统的状态。
零阶保持器

保持器
信号的复现:把采样信号恢复为原来的连续信号 称为信号的复现。 零阶保持器(恒值外推)
保持器
一阶保持器(线性外推)
零阶保持器的输入输出信号 主要特点: 1、输出信号是阶梯波,含有高次谐波。 2、相位滞后。
gh (t ) 1(t ) 1(t T )
1 e jT Gh ( j ) Gh ( j ) Gh ( j ) j T sin(T / 2) Gh ( j ) Gh ( j ) T 2 T / 2
2
2 sin ( s ) j ( s ) Gh ( j ) e s ( s )
零阶保持器对系统的影响
1 e Ts Gh ( s ) s
e
Ts 2
小结
离散系统:系统中有一处或几处信号是脉冲串或数码 系统类型 :
采样系统 — 时间离散,数值连续 数字系统 — 时间离散,数值离散
A/D 字长足够 : D/A: 用 ZOH 实现 Shannon定理
t << T
等效为理想采样开关
e* (t ) e(t ) T (t )
2 s 2 h T规律 外推的保持器。
e(nT ) e[( n 1)T ] eh (t ) e(nT ) (t T ) T
nT t (n 1)T
一阶保持器的数学模型
1 2 1 g h (t ) 1(t ) t (t ) 2(t T ) t (t T ) 1(t 2T ) t (t 2T ) T T T 1 1 2 Ts 2 Ts 1 2Ts 1 2Ts Gh ( s) 2 e 2 e e 2 e s Ts s Ts s Ts
传递函数零阶保持离散化

传递函数零阶保持离散化1.引言1.1 概述在控制系统中,传递函数是描述系统动态特性的重要数学模型。
传递函数可以用于描述连续系统的输入与输出之间的关系,通过它我们可以预测系统的响应和行为。
然而,在实际应用中,我们常常需要将连续系统进行离散化处理,以适应数字控制系统的要求。
离散化是将连续系统转化为离散系统的过程,它的目的是将连续信号转换为离散信号,并用离散数学方法对其进行处理和分析。
对于传递函数的离散化来说,就是将连续传递函数转换为离散传递函数的过程。
在离散控制算法中,离散传递函数扮演着重要的角色,它可以描述离散系统的输入和输出之间的关系。
本文将探讨传递函数零阶保持离散化的问题。
零阶保持器是一种常用的离散化方法,它的基本原理是将连续信号在某个特定时间间隔内进行采样,然后在每个采样点上保持采样值不变,以离散的形式表示连续信号。
通过对零阶保持器的定义和原理的介绍,我们将了解它在传递函数中的作用,并探讨离散化对传递函数的影响和应用。
同时,我们还将展望传递函数零阶保持离散化的意义和应用,并总结本文的内容。
在接下来的章节中,我们将深入探讨零阶保持器和离散化方法,并分析它们对传递函数的影响。
通过这些内容的学习,读者将能够更加全面地了解传递函数零阶保持离散化的原理和应用。
随着数字控制技术的发展,离散化方法在工程领域的应用将会越来越广泛,因此对于传递函数零阶保持离散化的研究具有重要的现实意义和应用价值。
1.2文章结构1.2 文章结构本文主要围绕传递函数的零阶保持离散化展开讨论。
文章分为引言、正文和结论三个主要部分,具体结构如下:引言部分首先概述了本文的研究内容和目的,对传递函数的零阶保持离散化进行了简要介绍。
接着介绍了本文的结构安排,明确了每个小节的主要内容和意义。
最后,明确了本文的目的,即探讨传递函数的零阶保持离散化在工程应用中的意义和潜在影响。
正文部分主要分为两个小节,分别是零阶保持器和离散化方法。
在2.1小节中,将详细讨论零阶保持器的定义和原理,包括其在控制系统中的作用和优势。
ad采样0点偏移处理方法_解释说明以及概述

ad采样0点偏移处理方法解释说明以及概述1. 引言1.1 概述本文旨在介绍ad采样0点偏移处理方法的概念、原理和应用。
随着科技的发展和电子设备的普及,AD转换器(Analog-to-Digital Converter,简称ADC)在各种数码设备中得到了广泛应用。
然而,由于制造工艺以及环境等因素的影响,ADC存在着一些误差,其中之一就是0点偏移误差。
因此,针对这个问题提出并实施有效的处理方法对于保证AD转换器性能至关重要。
1.2 文章结构本文内容共分为五个部分:引言、ad采样0点偏移处理方法、去除直流分量法、零阶保持器法以及结论与展望。
在引言中将概述文章背景和目标;接下来,在ad采样0点偏移处理方法部分将详细介绍什么是ad采样0点偏移以及为什么需要处理它;然后,在两个独立的部分中将对去除直流分量法和零阶保持器法进行具体说明;最后,在结论与展望部分总结整篇文章并对未来研究提出建议。
1.3 目的本文的目的主要有两个方面。
首先,通过介绍ad采样0点偏移处理方法的原理和步骤,希望读者能够全面理解这个问题以及其处理的必要性。
其次,对现有的去除直流分量法和零阶保持器法进行实验验证和效果评估,以便读者能够掌握这些方法的应用场景、局限性以及改进方向。
最终,通过本文的阐述,希望为未来关于ad采样0点偏移处理方法的研究提供思路和展望。
以上为“1. 引言”部分的详细内容描述。
2. ad采样0点偏移处理方法:2.1 什么是ad采样0点偏移:在模拟信号转换为数字信号的过程中,AD(模数)转换器采样引脚会收集到一个称为0点偏移或者直流分量的信号。
这个信号并不代表输入的真实变化,而是由于AD转换器存在一些非理想特性所导致的。
0点偏移可能存在于AD转换器输出的时间序列中,并影响信号的准确度和质量。
2.2 为什么需要处理ad采样0点偏移:AD采样0点偏移会导致数字信号的动态范围有所降低,并且可能引入误差,影响后续数据处理和分析。
因此,对于需要高精度和准确性的应用,特别是在要求低噪声和高动态范围时,就需要处理ad采样0点偏移。
零阶保持器传递函数推导

零阶保持器传递函数推导零阶保持器是指可以将一个信号不加改变地保持下去的电路。
在实际应用中,零阶保持器被广泛使用,比如在数据采集中,输入信号需要经过采样保持电路进行采样后进行数字化处理。
本文将详细介绍零阶保持器传递函数的推导方法。
一、零阶保持器的概念零阶保持器是指可以将一个信号不加改变地保持下去的电路。
其输出与输入信号相同,因此也被称为样保持器。
二、零阶保持器的基本原理零阶保持器的基本原理是通过一个开关电路,在采样时刻的瞬间将输入信号的值存储起来,然后在下一个采样时刻输出这个存储的值。
这样,零阶保持器的输出就能够保持与输入信号相同的数值,形成样保持的作用。
三、零阶保持器的传递函数零阶保持器的传递函数可以通过对其基本原理进行数学推导得到。
假设采样周期为T,零阶保持器的输入信号为x(t),输出信号为y(t),则有:y(nT) = x(nT)从上式可以看出,在采样时刻nT,零阶保持器的输出等于输入,在其余时间内输出为零。
利用这个特性,可以将信号用冲激串的形式表示:x(nT) = x(t)|t=nT = ∑(k=-∞)∞ δ(t - kT)将其带入上式中,得到:y(nT) = ∑(k=-∞)∞ x(kT) δ(n - k)上式中的n表示采样时刻,k表示历史时刻。
因为零阶保持器的输出信号只在采样时刻存在,所以可以将上式转换为z域传递函数的形式:Y(z) = X(z)·H(z)其中,X(z)和Y(z)表示输入和输出信号的z变换,H(z)为零阶保持器的传递函数。
根据上式,零阶保持器的传递函数可推导为:H(z) = 1 / (1 - z^-1)四、结论综上所述,零阶保持器的传递函数为H(z) = 1 / (1 - z^-1)。
在实际应用中,零阶保持器是样值采集的最基本电路,具有广泛的应用价值。
零阶保持函数

零阶保持函数零阶保持函数是指输出与输入之间没有任何时间延迟,因此输出与输入信号是完全一致的。
在信号处理领域中,零阶保持函数扮演着非常重要的角色,因为它能够帮助处理信号,并使其保持其原始形态。
在本文中,我们将深入探讨零阶保持函数的作用、特点及其应用。
一、零阶保持函数的定义零阶保持函数(或“零阶保持器”)是一种信号处理器件,其输出信号与输入信号之间的关系非常简单。
它接收来自信号源的输入信号,并立即将该信号以与输入信号等效的方式输出。
这意味着输出信号的幅度和形态与输入信号相同,而且没有任何时间延迟。
二、零阶保持函数的特点1. 零阶保持函数不引入延迟:单纯的零阶保持函数并不引入任何时间延迟,因此它可以帮助输入信号保持其原始形态。
2. 稳态误差为零:由于零阶保持函数保留输入信号的所有特征,因此它不会引入任何稳态误差。
3. 无需外部电源:作为一个被动的器件,零阶保持函数不需要外部电源来工作,它的全部能量都来自输入信号。
4. 线性特性:零阶保持函数具有线性传输特性,这意味着其输出信号与输入信号之间的关系是线性的。
三、零阶保持函数的应用零阶保持函数广泛应用于各种数字信号处理应用中,具有如下应用:1. 时间量化:零阶保持函数可以将连续时间信号转换为离散时间信号,这在数字信号处理中非常有用。
2. 数字滤波器:零阶保持器可以用作数字滤波器,帮助去除输入信号中的高频或低频噪声。
3. 采样保持器:零阶保持器也可以用作样本保持器,它可以在输入信号上“冻结”一段时间,从而允许输入信号在此时间段内保持不变。
4. 增益均衡器:零阶保持器可以用作增益均衡器,这有助于提高输入信号的幅度,并使其更适合进一步处理。
总之,零阶保持函数是信号处理中非常重要的一个组成部分,它可以用来处理各种类型的信号,并保持信号的原始形态。
零阶保持函数具有很多特点及其应用于各种应用,包括时间量化、数字滤波器、采样保持器和增益均衡器。
在实际应用过程中,我们需要结合具体的问题和信号特征来选择合适的零阶保持函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本文旨在对二阶工程发中不加零阶保持器传函引起的误差做一个讨论G P(s)= 10
(s+10)(s+0.1)
首先,按最佳工程二阶设计系统,得到
D(s)= 1+s
2s
未加入零阶保持器
系统框图
阶跃输入的输出如图
所有的特性都很好,说明了最佳工程二阶设计的系统性能很理想,在此条件下,我们在G p(s)后面串联上G h(s),研究零阶保持器对连续的系统有何影响。
首先,我们利用系统所给的零阶保持器,来看看系统性能有何变化
系统的框图如下
首先使零阶保持器的T为0.1s,阶跃输入的输出如下
发现系统的超调有了增加,但稳定时间略有改进,原来的课上分析说,这是零阶保持器引入了零点的结果
现在我们再将采样周期T改为0.5s,看看结果如何
仿真出来的结果如下图
我们可以发现,当采样周期改变后,超调变得我们无法接受了那么,将采样周期改小会如何呢?将T改为0.01s
结果如下所示
我们惊讶的发现,性能比最佳工程二阶更好了
由于不清楚matlab中的零阶保持器具体实现过程,我自己构造了零阶保持器的环节,具体框图如下
取T=0.01s,0.5s和0.1s结果如下
这里的延时环节相当明显
这和系统的零阶保持器做出来的结果大相径庭
为了了解零阶保持器对连续系统性能实际的影响,我们对
1−e −Ts
s
进行深入分析
首先,
e −Ts 作泰勒级数展开,得到如下结果
>> syms Ts f=exp(-Ts) T= taylor(f,8) f =
exp(-Ts) T =
1-Ts+1/2*Ts^2-1/6*Ts^3+1/24*Ts^4-1/120*Ts^5+1/720*Ts^6-1/5040*Ts^7
>> m=1-T m =
Ts-1/2*Ts^2+1/6*Ts^3-1/24*Ts^4+1/120*Ts^5-1/720*Ts^6+1/5040*Ts^7
可以看到,上面是一系列的零点,抱着探究性的态度,我们以二阶的近似式,也就是
T – 0.5Ts +0.167Ts 2来近似,先取T=0.1s 的情况
系统框图
结果出现了错误,如下图,可能和MATLAB众对微分的定义有关,但是研究似乎不能进行下去了
后来,在南杰胤同学的提示下,我改用pade 近似来模拟延时环节 二阶的pade 近似结果如下
[a,b]=pade(0.1,2) a =
1 -60 1200 b =
1 60 1200
即e −Ts =s 2
−60s+1200s 2+60s+1200
由此得到
1−e −Ts
s
=120s
s +60s +120s =120
s +60+120
上面的T=0.1s ,可以发现,对极点分析,结果如下
>> p = [1 60 120] roots(p) p =
1 60 120
ans =
-57.9285 -2.0715
也就是说,在一定的近似情况下,零阶保持器引入了两个极点,其中的一个还是相当靠近虚轴的
用此式来进行模拟,框图如下
仿真结果如下
超调比较大。
由上面三种分析结果看来,三种方式模拟得到的结果各不相同,但是除了系统所给的零阶保持器外,其它的模拟传函都使系统性能得到了较大的变化。
