巧用补形法解平面几何题
两道几何题的补形解法

两道几何题的补形解法泰州市朱庄中学 曹开清“司公限有品”,看到这个词组,真有些不知所云.这不,下面出场的老者也被这个词组难住了.老者姓万名能,尤其精通古汉语.一日,一青年向万老先生请教“司公限有品”是什么意义,万老先生思索良久,不能作答.为顾及脸面,只得胡乱敷衍:司公,乃古代的一种官职,类似于司马;限,限制;有品,有品德.青年对万老先生的解释不甚满意,万老先生便要求青年拿出原题,以带回去继续研究.这时青年拿出原题,只见上面写着:“司公限有品食××××××”(从右向左读).这个故事固然有些夸张,但它给我们的启示是:解几何题时,不应该孤立地而应该全面地看一个问题,以“识”问题的“庐山真面貌”.今举二例说明之.例 1 已知△ABC 中,AB =29,BC =37,AC =24,求△ABC 的面积.分析:常规方法是作高,用勾股定理来求,但是由于涉及到多个二次根式运算,计算相当繁复.从全局考虑,将△ABC 置于网格中,可得解题真谛.解:如图,考虑格点△ABC ,根据勾股定理,得AB =2252+=29,BC =2216+=37,AC =2244+=24.∴S△ABC 44211621522156⨯⨯-⨯⨯-⨯⨯-⨯==14.例2 如图,AD 是△ABC 的高,∠BAC =45°,BD =3,DC =2,求△ABC 的面积.分析:本题的关键是求出△ABC 的高AD .由于AD 将45°的角分成两部分,已知条件不能充分运用,直接求解是“山重水复已无路”.若联想到曾经做过的这样一个题目:“如右上图,B 、C 分别为正方形AEGF 的边EG 、FG 上的点,且∠BAC =45°,AD ⊥BC 于D ,求证:AD =AE .”这时可就“柳暗花明又一村”了.解:将△ABD 翻折到△ABE 的位置,将△ACD 翻折到△ACF 的位置,分别延长EB 、FC 交于点G ,由已知条件,易知四边形AEGF 是正方形.设AD =x ,则正方形AEGF 的边长也为x .在Rt △BGC 中,BG =EG ―BE =x ―3,CG =FG ―CF =x ―2,BC =3+2=5,根据勾股定理,得(x ―3) 2+( x ―2) 2=52,解得x =6(―1不合题意,舍去),即AD =6.∴S△ABC 6521⨯⨯==15.。
7 例析利用割补法解题题型 高中常用数学方法的介绍 例析 体验 练习

【学生版】例析利用割补法解题题型所谓割补法:就是将复杂的或不熟悉的几何图形转化为简单的熟悉的几何图形(如:三角形、正方形、长方形、平行四边形或梯形等)或几何体(如:柱体、锥体和球体);也就是把一个复杂长度、面积或体积的计算分割成若干个简单图形的有关计算或将一个不易求出长度、面积或体积的几何图形补足为较易计算的几何图形;例如,把曲边形割补成规则图形、把斜棱柱割补成直棱柱、把三棱柱补成平行六面体、把三棱锥补成三棱柱或平行六面体、把多面体切割成锥体(特别是三棱锥)、把不规则的几何体割补成规则的几何体,从而把未知的转化为已知的、把陌生的转化为熟悉的、把复杂的转化为简单的、把不够直观的转化为直观易懂的。
一、“分割”非规则图形为规则图形几何图形或几何体的“分割”,即将已知的几何图形或几何体按照结论的要求,分割成若干个易求长度、面积或体积的几何图形或几何体。
例1、为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( ) A .3+64 km 2B .3-64km 2C .6+34 km 2D .6-34km 2【提示】 【解析】 【评注】例2、如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=2,∠A 1B 1C 1=90°,AA 1=4,BB 1=3,CC 1=2,求: (1)该几何体的体积; (2)截面ABC 的面积。
【提示】 【解析】二、将非规则图形“补形”规则图形几何图形或几何体的“补形”,即将已知的几何图形或几何体按照结论的要求,补全成若干个易求长度、面积或体积的几何图形或几何体。
例3、已知三棱锥A —BCD 的所有棱长都为2,则该三棱锥的外接球的表面积为________例4、如图,在直三棱柱A 1B 1C 1-ABC 中,∠BCA =90°,点E ,F 分别为AB ,AC 的中点, 若BC =CA =CC 1,则B 1E 与A 1F 所成的角的余弦值为________.三、几何体的“割补”几何体的割补,即将已知的几何体按照结论的要求,既要分割又要补全成若干个易求体积的几何体。
巧用补形法研究四面体问题
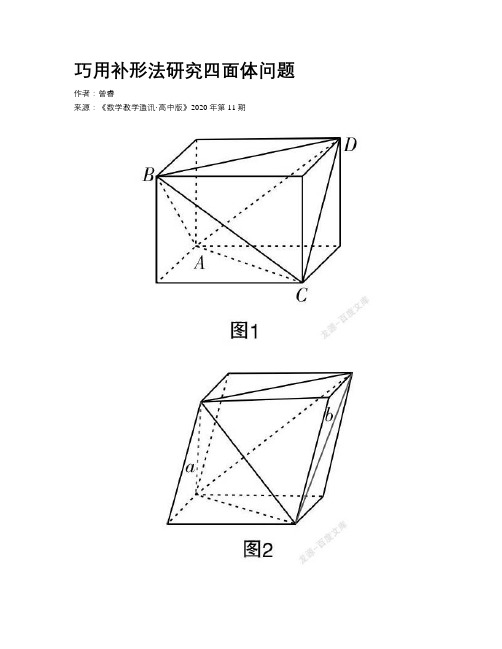
巧用补形法研究四面体问题作者:***来源:《数学教学通讯·高中版》2020年第11期[摘要] 立体几何问题中,有一类问题可以通过补形法,得到一个常见的几何体,使复杂的线面关系变得清晰明了. 文章从一道例题出发分析解决这类问题的方法,并在此基础上总结规律,归纳常见的一些四面体的补形方法.[关键词] 立体几何;四面体;补形教学中,遇到这样一个问题:已知在半径为2的球面上有A,B,C,D 四点,若AB=CD=2,则四面体ABCD的体积最大值为多少?这是某年数学全国卷的第12题,主要考查几何体的体积的计算、球的性质、异面直线间的距离,通过球这个载体考查学生的空间想象能力和推理计算能力.解答是这样的:过CD作平面PCD,使AB垂直于平面PCD,交AB于P. 设点P到CD的距离为h,则有V■=■×■×2×h×2=■h,当直径通过AB与CD中点时,h■=2■=2■,故V■=■.本小题这个解答当中,学生比较疑惑的有两点:(1)为什么可以过CD作平面PCD,使AB垂直于平面PCD,能这样作的前提是AB和CD要垂直,那为什么认定体积最大时AB和CD要垂直?(2)为什么直径通过AB与CD中点时,距离h最大?要解释清楚这两个疑点,首先需要补充说明一个公式.四面体体积公式:如果一个四面体的两条相对棱的长分别是a,b,它们的距离为d,所成的角为θ,那么它的体积为V■=■abdsinθ(证明见后).根据这个公式,我们首先得到结论:AB和CD必须垂直,即sinθ=90°时才能得到最大的体积.其次,由于AB=CD=R(球的半径),所以连结球心O和四个顶点,则容易知道△OAB 和△OCD都是正三角形.设AB的中点为E,CD的中点为F,则OE⊥AB,OF⊥CD.设AB与CD间的距离为d,有d≤EF≤OE+OF. (异面直线间公垂线段最短)因此,OEF共线时,四面体的体积可以达到最大值,因为OE=OF=■,故V■=■.?摇?摇这样解决一个选择题比较花费时间,而且在高中数学教学中,不涉及四面体的体积公式,异面直线的距离即公垂线段的长度在教学中也仅仅要求了解.下面我们用补形的思路来解决这个问题.因为题目当中两条线段长度一样,所以考虑把这个四面体补形成一个长方体:如图1:则四面体的外接球即是长方体的外接球,四面体的体积是长方体的体积减去四个全等的小三棱锥的体积.设长方体的边长为a,b,c,体对角线即为外接球的直径,得到:a2+b2+c2=42,b2+c2=22,所以a=2■,则V■=V■-4V■=abc-4×■×■abc=■abc=■.又b2+c2=22 ,所以V■=■≤■(b2+c2)=■,当且仅当b=c=■时,等号成立.从等号成立的条件可以比较容易地看出是在AB和CD垂直时,四面体的体积取到了最大值.我们会发现,使用补形,一下子把陌生的几何体变得熟悉了,原本错综复杂的线面关系也变得清晰起来. 利用这一方法解决某些几何问题,思路清晰明朗,较其他方法简洁明了.比如刚才提到的四面体的体积公式也可以用补形法得到.一个四面体的两条相对棱的长分别是a,b,它们的距离为d,所成的角为θ,将四面体补形成平行六面体(因为相对棱的长度不确定,相等的时候才能补成长方体).如图2:那么该平行六面体的底面积为S=■absinθ,平行六面体的体积为V■=■abdsinθ. 同样,该平行六面体由原四面体和四个全等的三棱锥构成. 三棱锥与平行六面体的高相等,底面积为平行六面体的一半,V■=■×■×■absinθ=■absinθ.所以V■=V■-4×V■=■absinθ.一起来看一下常见的几种四面体补形方式:一、把四面体的四个面各补上一个三棱锥,最后形成一个平行六面体. 其中正四面体是最特殊的形式,可以补成正方体. 而对棱相等的四面体则可以补形成一个长方体.例1:正四面体棱长为a,求外接球的半径R.正四面体补形为一个正方体,正四面体的外接球即为正方体的外接球.如图3:正方体的面对角线是正四面体的棱长,体对角线为外接球的直径.设正方体边长为b,则a=■b,2R=■b,所以R=■a.例2:在三棱锥A-BCD中,AB=CD=3,AD=BC=4,AC=BD=5,求三棱锥A-BCD外接球的半径.因为有三组对棱相等,把四面体补成一个长方形,如图4:长方体的三个面的面对角线是三棱锥的棱长,体对角线是外接球的直径.设长方体的棱长为a,b,c,外接球的半径为R,则a2+b2=32,b2+c2=42,a2+c2=52,(2R)2=a2+b2+c2,所以R=■.二、把四面体的一个角作为平行六面体的一个角补形成平行六面体.例3:四面体ABCD,侧棱AB,AC,AD两两垂直,AB=2,AC=3,AD=4,求四面体的外接球的半径R.因为四面体的侧棱两两垂直,所以可以把这个角看作长方体的一个角,把四面体补形成一个长方体,则四面体的外接球就是长方体的外接球四面体的三条侧棱就是长方体的长、宽、高,外接球的直径就是长方体的体对角线,则(2R)2=AB2+AC2+AD2=29,所以R=■.例4:若三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2■,AB=1,AC=2,∠BAC=60°,求球O的半径R.根据已知条件可以得到△ABC是直角三角形,把四面体补成一个长方体,则四面体的外接球就是长方体的外接球,外接球的直径就是长方体的体对角线.则(2R)2=SA2+AC2=16,所以R=2.例5:已知四面体PABC的侧面PAC与平面ABC垂直,∠ABC=90°,BC=2■,AB=2,且PA⊥PC,PA=PC,求异面直线PC与AB所成角的余弦值.解答:把四面体补成如图所示平行六面体,异面直线PC与AB所成角即為PC与CD所成角的补角的余弦值.取AC中点M,PA=PC,则PM⊥AC,又因为平面PAC与平面ABC垂直,所以PM⊥平面ABC.△ABC中,∠ABC=90°,AB=2,BC=2■,所以∠ACB=30°,AC=4.△PAC中,PA⊥PC,PA=PC,AC=4,所以PM=2,PC=2■.底面四边形ABDC中,DM2=DC2+CM2-2DC·CM·cos120°,得到DM=2■.Rt△PMD中,PD=4.△PCD中,cos∠PCD=■= -■.所以异面直线PC与AB所成角的余弦值为■.此题也可以用空间向量法解答,用补形能更好地体现线面关系.三、把四面体补形成三棱柱例6:已知某几何体底面ABC是棱长为1的等边三角形,PA⊥平面ABC,PA=3,求该几何体的外接球的半径.解答:将该四面体补形成一个三棱柱四面体的外接球就是三棱柱的外接球.先求三棱柱底面三角形外接圆半径r=■·■=■.又因为PA⊥平面ABC,PA=3,所以三棱柱的外接球半径为R=■=■.四面体的问题可以通过补形变成正方体、长方体乃至平行六面体的问题.尤其在正方体和长方体中,点线面的关系是我们所熟悉的. 一些几何题的证明和求解,由原几何图形分析探究会比较烦琐,通过补形填补成一个新的几何图形,能使原问题的本质得到充分的体现,解决起来比较容易. 本文着重讨论四面体的补形问题,希望窥一斑而知全豹,探究立体几何中补形法这一重要的转化策略.。
巧借“补形”思维,妙解立体几何问题

ʏ孙海鹰利用 补形 思维这一桥梁,可以使数学的思维方法更加活跃㊁简捷,应用起来更加灵活㊁多样,能有效培养同学们思维的灵活性㊁独创性㊂利用 补形 思维可以把空间立体几何中的一些不规则形体㊁不熟悉形体㊁残缺形体补成相应的规则形体㊁熟悉形体㊁完整形体等,对解决问题起到化繁为简㊁一目了然的作用,使得数学思维更加灵活,数学知识结构更加完整㊁充实,数学思想方法更加完美㊂一㊁还原补形法例1为了给数学家帕西奥利的‘神圣的比例“画插图,列奥纳多㊃达㊃芬奇绘制了一些多面体,图1所示的多面体就是其中之一㊂它是由一个正方体沿着各棱的中点截去八个三棱锥后剩下的部分,这个多面体的各棱长均为2,则该多面体外接球的体积为()㊂图1A.16πB.8πC.16π3D.32π3分析:对于此类空间立体几何中的不规则形体 多面体,直接处理起来有较大的难度,可借助空间几何体的还原补形法,把该多面体进行还原补形为正方体,结合补形前后对应图形中相关元素的位置关系与变化情况,进行合理分析与运算㊂解:结合图1,把该多面体进行还原补形为正方体,如图2所示㊂图2由所给多面体的棱长为2,可得正方体的棱长为22,那么正方体的中心即为多面体的外接球的球心,所以球心到多面体顶点的距离为(2)2+(2)2=2,即多面体外接球的半径R=2㊂故该多面体外接球的体积V=43πR3=32π3㊂应选D㊂还原是回归问题本质的一种逻辑推理方式㊂在解决一些空间几何体问题中,合理回归,完整地进行还原与补形是解题的关键㊂在处理空间几何体的还原补形时,要注意回归的简单几何体与 补 上去的小几何体之间要素的联系与图形之间的变化,正确构建相互之间的关系,不要出现添加或遗漏㊂二㊁联系补形法例2已知正三棱锥P-A B C,点P,A, B,C都在半径为3的球面上,若P A,P B, P C两两相互垂直,则球心到截面A B C的距离为㊂分析:此类不同空间几何体间(正三棱锥与球)的联系问题,需要进行合理补形,将正三棱锥与球这两种不同的空间几何体联系在一起,使得问题的处理直观易懂,从而便于分析与计算㊂解:由于正三棱锥的侧棱P A,P B,P C5知识结构与拓展高一数学2023年4月Copyright©博看网. All Rights Reserved.两两互相垂直,故以P A ,P B ,P C 为棱补成正方体,如图3所示㊂图3球心O 为正方体的体对角线P D 的中点,且P O =3,则正方体的棱长为2㊂设点P 到平面A B C 的距离为h ㊂根据正三棱锥的体积,借助等体积法得13ˑ34ˑ(22)2㊃h =13ˑ12ˑ2ˑ2ˑ2,解得h =233,所以所求球心到截面AB C 的距离为3-233=33㊂寻找联系是构建不同数学元素之间的桥梁㊂在空间立体几何问题中,抓住不同空间几何体之间的联系,合理补形(如三条侧棱两两互相垂直,可补形为正方体或长方体),使得问题更加直观易求㊂三㊁对称补形法 图4例3 如图4所示,在斜截圆柱中,已知圆柱的底面直径为40c m ,母线最短与最长的分别为50c m ,80c m ,则该斜截圆柱的体积V =㊂分析:此类空间几何体中的残缺形体,属于不太规则的空间几何体,直接求解无从下手,可借助空间几何体的几何特征进行合理的对称补形,将题设条件中的斜截圆柱按斜截面吻合对接,补全为一个完整的圆柱,再利用圆柱的体积公式求解㊂解:将题设条件中的斜截圆柱按斜截面吻合对接,补全为一个完整的圆柱(即斜截圆柱进行翻转对接)㊂由题意知所求体积V =12ˑ(πˑ202)ˑ(50+80)=26000π(c m 3)㊂对称是数学中的一种重要关系,也是充分展示数学美的一种表现形式㊂在解决空间几何体问题时,对于一些特殊的残缺形体,要善于发现图形中的对称关系与几何特征,借助相同图形之间的对称补形法进行化归与转化,对空间想象能力的提升很有帮助㊂编者的话: 补形 思维解决立体几何问题,是整体思想的一种具体体现,可将不规则的㊁陌生的㊁复杂的几何体补成规则的㊁熟悉的㊁简单的几何体(如常见的长方体㊁正方体㊁平行六面体㊁圆柱等),在所补成的空间几何体中研究原几何体的有关元素的位置关系㊁空间角或空间距离的计算等,从而实现问题的顺利解决㊂这类问题,能全面考查数学基础知识㊁基本技能㊁基本思想㊁基本活动经验这 四基 的落实情况,以及发现问题㊁提出问题㊁分析问题和解决问题能力的培养与提升㊂若三棱锥P -A B C 中最长的棱P A =2,且各面均为直角三角形,则此三棱锥外接球的体积是㊂图5提示:根据题意,可把该三棱锥补成长方体,如图5所示,则该三棱锥的外接球即为该长方体的外接球㊂易得外接球的半径R =12P A =1,所以该三棱锥外接球的体积V =43ˑπˑ13=43π㊂作者单位:江苏省江阴中等专业学校高新区校区(责任编辑 郭正华)6知识结构与拓展 高一数学 2023年4月Copyright ©博看网. All Rights Reserved.。
中考数学复习指导:补形法在几何题中的应用

补形法在几何题中的应用一些几何题的证明或求解,由原图形分析探究,有时显得十分繁难,若通过适当的“补形”来进行,即添置适当的辅助线,将原图形填补成一个完整的、特殊的、简单的新图形,则能使原问题的本质得到充分的显示,通过对新图形的分析,使原问题顺利获解。
这种方法,我们称之为补形法,它能培养思维能力和解题技巧。
我们学过的三角形、特殊四边形、圆等都可以作为“补形”的对象。
现就常见的添补的图形举例如下,以供参考。
一、补成三角形1.补成三角形例1.如图1,已知E为梯形ABCD的腰CD的中点;证明:△ABE的面积等于梯形ABCD面积的一半。
分析:过一顶点和一腰中点作直线,交底的延长线于一点,构造等面积的三角形。
这也是梯形中常用的辅助线添法之一。
略证:2.补成等腰三角形例2 如图2.已知∠A=90°,AB=AC,∠1=∠2,CE⊥BD,求证:BD=2CE分析:因为角是轴对称图形,角平分线是对称轴,故根据对称性作出辅助线,不难发现CF=2CE,再证BD=CF即可。
略证:3.补成直角三角形例3.如图3,在梯形ABCD中,AD∥BC,∠B+∠C=90°,F、G分别是AD、BC的中点,若BC=18,AD=8,求FG的长。
分析:从∠B、∠C互余,考虑将它们变为直角三角形的角,故延长BA、CD,要求FG,需求PF、PG。
略解:图34.补成等边三角形例4.图4,△ABC 是等边三角形,延长BC 至D ,延长BA 至E ,使AE =BD ,连结CE 、ED 。
证明:EC =ED分析:要证明EC =ED ,通常要证∠ECD =∠EDC ,但难以实现。
这样可采用补形法即延长BD 到F ,使BF =BE ,连结EF 。
略证:二、补成特殊的四边形 1.补成平行四边形例5.如图5,四边形ABCD 中,E 、F 、G 、H 分别是AB 、CD 、AC 、BD 的中点,并且E 、F 、G 、H 不在同一条直线上,求证:EF 和GH 互相平分。
空间几何体中几种常见的补形法

s△^船 ·AA =丁1×24×8=96 .
【小结 】比较 上述 两种 方 法 ,补 形
图3
法显 然 比分割法要简 洁得 多 ,计算 量也很 小 ,但 要抓 住 图形
的对 称性 ,巧妙的补成熟悉的几何 体 ,并找到 原几何 体 与补
形后 的几何体 的关 系 ,实现化繁为 简的奇效.
了一种构造思 想 ,同时也反 映了对 立统一的辩证思想 .
利用补形 法解决立体几何 问题 的基本 步骤是 :
第一步 :把不熟悉 的或 复杂 的几 何体 延 伸或 补加 成 熟
悉的或简单 的几何 体 ,把不完整 的图形 补成完整 的图形 ;
第二 步 :运用常见几何体 的知识 等计算结果 ;
第三 步 :得 出结论.
以外接球直径 2R= ,所 以 R= ,所 以外接 球 的表 面积
s球=挚.
方 法 二 联 系补 形 例 2 已知 三棱 锥 P—ABC,PA=BC=5,朋 :AC= 4,PC:AB= l,求三棱 锥的体积. 【思路 】如按常规求法 ,需求三棱锥 的底 面积和 高 ,而高 很 难求 出.由已知三组相对棱相 等这一 特点 ,联想长 方体对 面不平行 的对 角线恰 好组 成对 棱相 等 的三棱 锥 ,因此 可把 三棱锥 P—ABC补成长方体 ,再将长方体 分割成三棱锥 P— ABC和 四个相 同体积 的三棱锥.
在高考 中 ,补形法既可 以在选 择填空 题 中体 现 ,也 可以
在解答题 中体 现 ,常见的补形法 有对称 补形 、联系补 形 和还
原补形 ,还原补形主要涉及 台体 中“还台为锥 ”.下 面结合 实
例进行剖析 :
方法一 对称补形
善用“补形”,巧解图形问题

— —
分 析探究 . 有 时显 得 十分 繁难 . 若 通 过 适 当 的“ 补形 ” 来 进行 . 即添 置 适 当的 辅 助 线 .
将原 图形填补 成一个完 整的 、特殊 的 、 简 BC=
单 的 新 图形 . 则 能 使 原 问题 的 本 质 得 到 充
【 分析 】 本 题 利用 所 给直 角 , 延 长 AD、
l = 2. C E上B D.试 说 明 : BD= 2 C E.
四 、补 成 平 行 四 边 形
侈 0 4 攻 图4 , 四边 形AB C D中 , E、 F、 G、 G、 不在 同一 条 直 线上 ,试 说 明 : 剧1 和G 日
互相平分.
C D、 AC、 B D的 中点 , 并 且 E、 F、 【 分析 】 因为角是轴 对称 图形 , 角 平 分 日分 别是 B、
例 5 如 图 5, 凸五 边 形
1 2
D
AB C DE 中, LA = AB = 1 2 0  ̄ , E A= E
AB = B C = 2 , C D= D E = 4 , 则 其 面
二 、补 成 等 边 三角 形
例2 如图2 , △AB C 是 等 边 三 角形 ,
线 是 对 称 轴 .故 根 据 对 称 性 作 出 辅 助 线 .
不难发现C F = 2 C E. 再 证 BD=C Fl l l 可.
【 分析 】 因 为平 行 四边 形 的 对 角 线 互 相
平分 . 故要证 结论 . 需 考 虑 四边 形 G E HF 是
平 行 四边 形.
五 、补 成 菱 形
延 长 BC至 D . 延 长 BA至 E, 使 E= B D, 连 接
巧用补形法妙解几何题

分析
由于 六 边 形 的
弧B C 的度 数 为 6 0 。 , LB A C= 3 O ’ , 容易 想 到圆 周角 定理 , 于 。
是 可把 原 图 形 补 成 圆.
每个 内 角都 是 1 2 0 。 , 所 以 它 的每个外角均为 印 。 , 因
此 在其 外部可补 出两个等
丽
— 一 : 1— — 4 8 — 2 5 4 — 8 — 2 5
即A : C= 2 0 1 3 : 4 8 2 5
- - ‘ 0◆
-◆
-◆
-◆
‘
八、 利用特殊角 。 补成 等 腰 梯 形
九、 利用圆的有关性质 , 补成 圆
例 8 一个六边形 的六个 内角都是 1 2 0 。 , 连续 四边 的长依次是 1 、 3 、 3 2 , 那么这个六边形的周长为 (
六、 利用邻边相等 , 补成菱形
例6 如图6 , 凸五边形 A B C D E 中, A:/ _ B=
2 ( 1 + 一 争 ) 一 了 1 = 2 了 1 .
, 7
四、 利 用 一 组对 边 平行 , 补成 平行 四边 形 椤 9 4 如图 4 , A B 4 , D B上A B, E A上A B, D B:3 , E A
边 三角形 , 如 图 8所 示 , 这
解
将 工 件 补 成 o0, 连 结
B C , 连 结 ’ , 从 而 原 四边 形
易证 四边形 A B C D为正方形
。
CBE :9 0o. BM L CE
.
‘
.
1=/2, 又A 曰=C B, B A F= C8 E=9 0 。 .
B A F C BE. . A F :B E
巧用补形法解平面几何题

巧用补形法解平面几何题王立文 王兴林补形法就是根据题设的条件和图形,经过观察、分析和联想,运用添加辅助线的方法,将其拓展为范围更广的、其特征更明显、更为熟悉的几何图形,从而沟通条件和结论之间的联系.下面就补形法,谈谈它在解平面几何题中的应用.一、补成直角三角形例1 如图1,四边形ABCD 中,∠A=60°,∠B=∠D=90°,CD=1,AB=2,求BC 、AD 的长。
解:延长BC 交AD 的延长线于E 。
∵∠A=60°,∠B=90°,∴∠E=30°在△CED 中,∵∠CDE=∠ADC=90°,CD=1,∴CE=2CD=2,DE=3CD 3=。
在△AEB 中,同理有:AE=2AB=4,32AB 3BE ==。
∴BC=BE -EC=23-2,AD=AE -DE=4-3。
二、补成等腰三角形例2 已知:如图2,△ABC 中,BC 31AB =,∠ABC 的平分线交AC 于E ,CD ⊥BE 于D ,求证:BE=ED 。
证明:延长BA交CD的延长线于F。
易证△BCF是等腰三角形(ASA)。
∴CF21CD,BFBC==。
∵BC31AB=,∴AF21AB,BF31AB==。
作DG∥CA交BF于点G。
∴ABAG,AF21AG==,∴BE=ED。
三、补成等边三角形例3如图3,凸五边形ABCDE,有∠A=∠B=120°,EA=AB=BC=2,CD=DE=4,求这个五边形的面积。
简解延长DE、BA相交于K,延长DC、AB相交于M。
易知△DKM为等边三角形。
S五边形ABCDE=S等边三角形DKM-2S等边三角形AKE=222432643⨯⨯-⨯37=四、补成平行四边形例4如图4,已知六边形ABCDEF中,若∠A=∠B=∠C=∠D=∠E=∠F=120°,且AB+BC=11,AF-CD=3,求BC+DE的长。
解:延长FA 、CB 交于点P ,延长CD 、FE 交于点Q 。
专项训练2 巧用坐标求图形的面积的四种方法

专项训练2巧用坐标求图形的面积的四种方法方法总结:1.规则图形的面积可用几何图形的面积公式求解,对于不规则图形的面积,通常可采用补形法或分割法将不规则图形的面积转化为规则图形的面积和或差求解.2.求几何图形的面积时,底和高往往通过计算某些点的横坐标之差的绝对值或纵坐标之差的绝对值去实现.直接求图形的面积1.如图,已知A(-2,0),B(4,0),C(-4,4),求△ABC的面积.(第1题)利用补形法求图形的面积2.已知在四边形ABCD中,A(-3,0),B(3,0),C(3,2),D(1,3),画出图形,求四边形ABCD的面积.3.如图,已知点A(-3,1),B(1,-3),C(3,4),求三角形ABC的面积.(第3题)利用分割法求图形的面积4.在如图所示的平面直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(-4,10),B(-12,8),C(-14,0),求四边形OABC的面积.(第4题)已知三角形的面积求点的坐标5.已知点O(0,0),点A(-3,2),点B在y轴的正半轴上,若△AOB的面积为12,则点B 的坐标为()A.(0,8) B.(0,4) C.(8,0) D.(0,-8)6.已知点A(-4,0),B(6,0),C(3,m),如果三角形ABC的面积是12,求m的值.7.已知A(-3,0),B(5,0),C(x,y).(1)若点C在第二象限内,且|x|=3,|y|=3,求点C的坐标,并求△ABC的面积;(2)若点C在第四象限内,且△ABC的面积为8,|x|=4,求点C的坐标.参考答案1.解:因为C 点的坐标为(-4,4),所以△ABC 的AB 边上的高为4.因为点A ,B 的坐标分别为(-2,0),(4,0),所以AB =6.所以S △ABC =12×6×4=12. 2.解:如图.过D 点作DE 垂直于BC ,交BC 的延长线于点E ,则四边形DABE 为直角梯形. 又由题意知DE =2,AB =6,BE =3,EC =1,所以S 四边形ABCD =S 梯形DABE -S △CDE=12×(2+6)×3-12×1×2 =11.(第2题)3.解:如图,作长方形CDEF ,则S 三角形ABC =S 长方形CDEF -S 三角形ACD -S 三角形ABE -S 三角形BCF =CD·DE -12AD·CD -12AE·BE -12BF·CF =6×7-12×3×6-12×4×4-12×2×7=18. (第3题)(第4题)4.解:如图,过A 点作AD ⊥x 轴,垂足为点D ,过B 点作BE ⊥AD ,垂足为点E.易知OD =4,AD =10,DE =8,BE =-4-(-12)=8,AE =10-8=2,CD =-4-(-14)=10,所以S四边形OABC =S 三角形AOD +S 三角形ABE +S 梯形DEBC =12OD·AD +12AE·BE +12(BE +CD)·DE =12×4×10+12×2×8+12×(8+10)×8=100.方法指导:本题的解题技巧在于把不规则的四边形OABC 分割为几个规则图形,实际上分割的方法不是唯一的,并且不仅可以用分割法,还可以用补形法.5.A6.解:AB =6-(-4)=10.根据三角形的面积公式,得12AB ·|m|=12, 即12×10·|m|=12,解得|m|=2.4. 因为点C(3,m),所以点C 在第一象限或第四象限.当点C 在第一象限时,m >0,则m =2.4;当点C 在第四象限时,m <0,则m =-2.4.综上所述,m 的值为-2.4或2.4.7.解:(1)因为点C 在第二象限内,且|x|=3,|y|=3,所以点C 的坐标为(-3,3),S △ABC =12×[5-(-3)]×3=12. (2)由题意可知AB =8.因为点C 在第四象限内,|x|=4,所以x =4.因为△ABC 的面积为8,所以S △ABC =12×8×|y|=8. 所以|y|=2.又因为点C 在第四象限内,所以y =-2.所以点C 的坐标为(4,-2).。
巧用补形法,妙解立体几何题

则G ()m =e m -ma ()m -1<e 2-e 2=0,而G ()m G ()2<0,所以存在零点x 0∈()1,2使G ()x =0,即F ()x 有唯一极值点且为极小值x 0∈()1,2,因为F ()x 0=ae x 0x 0-ln x0,G ()x 0=e x 0-x 0a ()x 0-1=0,e x=x 0a ()x 0-1,所以F ()x 0=1x 0-1-ln x 0,因为F '()x 0=-1()x 0-12-1x 0<0,所以F ()x 0=1x 0-1-ln x 0在()1,2上单调递减,故F ()x 0>F ()2=1-ln 2>0,所以F ()x >0,综上可知,当a >2e 2时,总有f ()x >0.该不等式中含有多项式,于是通过移项、作差,将不等式变形,以便构造出新函数F ()x =ae xx-ln x ,再利用导数法证明函数F ()x 的极小值大于0,从而达到证明不等式的目的.对于含有指数、对数式的不等式恒成立问题,在构造出新函数后,通常需借助导数法,对函数求导,研究导函数与函数单调性之间的关系,根据函数单调性求得函数的最值.由此可见,解答不等式恒成立问题,关键在于将不等式与函数关联起来,利用函数、导函数的性质来解题.这就需将不等式进行合适的变形,如分离参数、构造出函数,以将问题转化为函数最值问题来求解.(作者单位:江苏省南京市第一中学)有些立体几何问题较为复杂,或几何图形不规则,我们采用常规方法很难求得问题的答案.此时,可巧用补形法,根据已知条件和图形,添加合适的辅助线,将不规则的、陌生的、不易计算边角的几何图形割补为规则的、熟悉的、易计算边角的图形,取得化难为易的效果.而运用补形法求解立体几何问题,关键在于如何巧妙地割补图形,主要有以下几种思路.一、将棱锥补成棱柱棱锥是常见的几何体,如三棱锥、四棱锥、五棱锥等.有些棱锥的高很难找到或求得,此时我们可以将棱锥补成棱柱,如将正三棱锥补为正方体,将对棱的长相等的三棱锥补为长方体,再根据正方体、长方体的性质,便能快速求得三棱锥的边、角的大小,从而使问题顺利获解.例1.如图1所示,三棱锥S-ABCD 的所有棱长都为2,四个顶点在同一球面上,则球的表面积为().图1A.3πB.4πC.33πD.6π解:如图2,将正三棱锥补为正方体,并使正方体的棱长为1,图2解题宝典42则正方体的对角线长为1+1+1=3,故球的半径为r =,所以球的表面积为4π×èø2=3π,因此正确选项为A .我们仅根据三棱锥的特征,很难确定其外接球的球心,为了便于计算,需采用补形法,将正三棱锥补形为正方体,那么正方体的中心即为三棱锥外接球的球心,即正方体的对角线就是球的直径,据此建立关系式,即可快速求得球的半径和表面积.二、将斜三棱柱补成四棱柱对于正三棱锥,一般很容易确定其高,但对于斜三棱柱,我们却很难确定其高.此时可采用补形法,将斜三棱柱补形为四棱柱,这样根据四棱柱的特点,可快速确定其高,求得顶点与底面之间、点与点之间的距离.例2.已知斜三棱柱的侧面A 1ACC 1与平面ABC 垂直,∠ABC =90°,BC =2,AC =23,且AA 1⊥A 1C ,AA 1=A 1C ,求点C 到侧面A 1ABB 1的距离.图3解:如图3所示,将斜三棱柱ABC -A 1B 1C 1补为四棱柱,设点C 到侧面A 1ABB 1的距离为d ,由四棱柱的上下底面平行的性质可知,d 也是平面ABB 1A 1与平面CMM 1C 1的距离,作A 1D ⊥AC 于点D ,作A 1E ⊥AB 于点E ,∵AA 1=A 1C ,AC =23,AA 1⊥A 1C ,∴A 1D =3,∵∠ABC =90°,BC =2,∴AB =22,∵侧面A 1ACC 1与平面ABC 垂直,A 1D ⊥AC 于点D ,∴A 1D ⊥AB ,A 1E ⊥AB ,∴AB ⊥面A 1ED ,∴AB ⊥ED ,即∠ABC =90°,∴DE ∥BC ,D 为AC 中点,且DE =12BC =1,∴A 1E =A 1D 2+DE 2=2,而V 四棱柱=S ABMC ∙A 1D =S A 1ABB 1∙d ,∴d =S ABMC ∙A 1D S A 1ABB 1==3.为了便于计算,将斜三棱柱补为四棱柱,从而将线面距离转化为面面距离,再利用等体积变换法使问题得解.三、将棱台补为棱锥棱台较为特殊,它的上下底面平行,且成比例,但侧棱相交于一点.为了便于计算,我们可采用补形法,将棱台补形为棱锥,这样便可构造出几组相似的三角形、多边形,借助相似图形的性质建立关系式,便可顺利求得棱台的边、高的长度.例3.如图4所示,平面EB 1C 1F 将三棱柱ABC -A 1B 1C 1分成体积为V 1,V 2两部分,其中AB ,AC 的中点分别是E ,F ,则V 1:V 2为______.图4解:延长A 1A 到A 2,B 1B 到B 2,C 1C 到C 2,使得A 1A =AA 2,B 1B =BB 2,C 1C =CC 2,并延长B 1E ,C 1F ,可知V ABC -A 2B 2C 2=V ABC -A 1B 1C 1,∵A 2A :A 2A 1=1:2,∴V A 2-AEF=18V A 2-A 1B 1C 1,∵V A2-AEF=14V A2-ABC=14×13V ABC -A 2B 2C 2=112×V ABC -A 1B 1C 1,∴V AEF -A 1B 1C 1=7V A 2-AEF =712V ABC -A 1B 1C 1,∴V 1:V 2=7:5.将棱台补成棱锥,利用棱锥A 2-AEF 的性质以及相似三角形的性质求得各条棱的长和各个三棱锥的体积,再借助棱台ABC -A 1B 1C 1与棱柱ABC -A 2B 2C 2之间的位置关系进行转换,即可顺利解题.由上述分析可以看出,对于一些较为复杂的立体图形、立体几何问题,采用补形法求解,能使问题快速获解.因此,在解答立体几何问题时,同学们要学会联想,根据几何体的结构特征合理添加辅助线,将棱锥补成棱柱,将斜三棱柱补成四棱柱,将棱台补为棱锥,以便根据棱柱、四棱柱、棱锥的性质来解题.(作者单位:江苏省如皋市第二中学)解题宝典43。
(甘志国)补形法,正四面体的最佳解法

补形法,正四面体的最佳解法甘志国(该文已发表 数学金刊(高考),2011(3):39)在求解正四面体的问题时,若把它放在正方体中,常常便于求解.下面以普通高中课程标准实验教科书《数学·选修2-1·A 版》(人民教育出版社,2007年第2版) (下简称《选修2-1》)中的三道题来介绍这一技巧.例1 (《选修2-1》第111页练习第1题)如图1,空间四边形ABCD 的每条边和BD AC ,的长都等于a ,点N M ,分别是CD AB ,的中点,求证:CD MN AB MN ⊥⊥,.证明 易得正四面体ABCD ,把它放在正方体中(如图2),则欲证结论显然成立(因为MN 垂直于图2中正方体的上下表面).图1 图2例2 (《选修2-1》第112页习题第5(1)题)如图3,空间四边形OABC 的各边以及BO AC ,的长都是1,点E D ,分别是边BC OA ,的中点,连结DE .(1)计算DE 的长;(2)求点O 到平面ABC 的距离.图3 图4解 易得正四面体OABC ,把它放在正方体中(如图4).(1)DE 的长即图4中正方体的棱长22. (2)我们在图4中求正四面体OABC 的体积V :122222221314224423=⋅⎪⎪⎭⎫ ⎝⎛⋅⋅-⎪⎪⎭⎫ ⎝⎛=-=-=--OAGB OAB G V V V V V 正方体正方体设点O 到平面ABC 的距离为h ,得︒⋅⋅⋅⋅===∆60sin 11213131122h S V ABC 36=h例3 (《选修2-1》第107-108页例3)如图5,一块均匀的正三角形面的钢板的质量为500kg ,在它的顶点处分别受力F 1, F 2, F 3,每个力与同它相邻的三角形的两边之间的角都是︒60,且|F 1|=|F 2|=|F 3|=200 kg.这块钢板在这些力的作用下将会怎样运动?这三个力最小都为多少时,才能提起这块钢板?图5 图6 图 7《选修2-1》是按图6建立空间直角坐标系来求解的,确实运算量很大,思维量也不小,而下面的解法却很简洁.解 易知图5中的三个力F 1, F 2, F 3必交于一点(设为点F ),且有正四面体FABC ,可不妨设该正四面体的棱长为)0(2>a a .我们把正四面体FABC 放在图 7中的棱长为a 的正方体中,并按图7建立空间直角坐标系,得),0,0(),,,(),0,,0(),0,0,(a C a a a B a A a F),0,(),,,0(),0,,(a a a a a a -=--=-=a 2===及图5中的F 1, F 2, F 3满足|F 1|=|F 2|=|F 3|=200,得F 1),0(2200a a a -=,, F 2),0(2200a a a --=,, F 3),0(2200a a a -=, F 1+ F 2+F 3)1,1,1(2200)2a ,22(2200--=--=a a a ,|F 1+ F 2+F 3|6200= 因为5006200<,所以这块钢板在这些力的作用下将会静止不动.设|F 1|=|F 2|=|F 3|=x ,则可得F 1+ F 2+F 3)1,1,1(2)2,22(2--=--=x a a a a x,|F 1+ F 2+F 3|6x = 当且仅当5006>x 即63250>x 时,才能提起这块钢板.(请注意:原问题“这三个力最小都为多少时,才能提起这块钢板”是无法回答的,建议把此问改为“这三个大小相等的力满足怎样的条件才能提起这块钢板”.)例4 (2013年高考课标全国卷II 卷理科第7题也即文科第9题)一个四面体的顶点在空间直角坐标系xyz O -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为( )解 A.由图8可求解(先把这个正四面体放置在正方体中):图8本文介绍的技巧“把正四面体放在正方体中”实际上就是一种补形法,在立体几何中还有很多用补形法简洁解题的例子,比如把直角四面体(该四面体从一点出发的三条棱两两垂直)补成长方体,请读者留意.。
巧用“补形法”妙解几何题

。
囱6
半 圆 补 成 整 圆 , 延 长P 、 D, 再 C P 把 P 化 为 圆 周 角 , 时 运 用 转 同 圆 的 对称 性 求 出这 个 圆周 角 所 对 弧 的 度 数 , 题 迎 刃 而解 。 本 解 把半 圆补 成 整 圆 , 别 延 长 P 、 D交 圆 于E F 分 CP 、。
由J 边 Ac= 矩 Bn一 △ D— △D , . 边形 BD 2。 S 形 BD S 形 c :S AE S cF得 s 四 四 Ac=1 五 、 成 正 方 形 补
例 5 已 知 △ B C中 , A= 5 , 上BC于 D, D= DC= 4 。AD B 3, 析 , 求 问题 的答 案 , 种 方 法 称 为 “ 形 法 ” 探 这 补 。补 形 法 不 仅 能 2. 三 角 形ABC的 面积 求 t i 大 大 地 缩 短 从 已 知 到 未 知 的 探 求 过 程 ,使 解 题 方 法 简 洁 、 明 分 析 : 图5, 如 以AB为 轴 快 . 且 还 能 逐 步 培 养 学 生 丰 富 的想 象 力 , 进 学 生 创 造 性 思 而 促 补 画一 个 与 三 角 形A曰D对 称 维的发展。 的 直 角 三 角形 A E,再 以 C B 补 成 等 腰 三 角 形 为 轴 补 画一 个 与 三 角 形AC D 例 1 △A C , D是 A的 平 分 线 , B 中 A 且AD A = B。C M垂 直 对 称 的 直 角 三 角 形 AC 延 F. , , A D的 延 长 线 于 , 证 : B AC 2 M。 求 A + =A 长 E F 交 于 点 G, 由 B、 C 分 析 : 图 l 由 1 如 , =/2, AM j C, _ C AB= 5 4  ̄. 易 知 四 边 形 e 自然 地 想 到 等腰 三 角 形 的 三 线 合 一 定 理 AEGF. 正 方 形 且 边 长 等 于 为 延 长A曰与C M交 于 .于 是 将 原 图 形 补 成 G
补形法巧解平面几何问题

船 一 明 一 删
AF 、 2
1
’ .
’
C F :A E. C A = AB. HM = MG
. ‘ .日F = ME
【 而 J
8
雎 一 髓 一
‘ . .
FM = HM —HF = MG —ME : EG .G H :2 E F
s ,= 1则有 S 2= 7
苎 一
.
.
2 ( y+z )一 2
二 :2 2z
‘ . .
Hale Waihona Puke E F = ME = 2 A F = PM —P A —M F : 4
’ . .
AB + C +C D +DE +E F +F A = 1+3 +3 +2+2 +
2 +4 = 1 5
: y: z = 5: 3: 2
P A =P B =1 Q c:Q D =3 ME =MF = Q M —Q E :P Q —Q E =7 —5 = 2
。
图5
解析 : 如图 5 , 以 为对称 中心 , 把 AA B C补成一个平行 四边 形 A B C D, 设B G= , =Y , H M = 则 C O / / A E, P C / / A F
,
又 G 日≥B C, B C=2 . ‘ .2 E F≥ 2 即E F≥ l
八
, 、
例5 . 如 图5 , 已知 AA B C中 , E、 F为 B C的三等分点 , 肘为 A C的 中点 , B M于 A E、 A F分别相交于 G 、 H, 求B G : G H: H M
q
图 6
圈 7
在直角三角形 D C E中, C D =÷ C E, D E=3 则c D=
第14讲 立体几何知多少(含解析)-【高中数学】一题多解拔尖训练

一题多解第14讲立体几何知多少,位置关系空间角典型例题【例1】如图141 ,在矩形ABCD 中,E 为边AB 的中点,将ADE 沿直线DE 翻转成1A DE ,若M 为线段1A C 的中点,则在ADE 的翻转过程中,正确的命题是________.(1)BM 是定值;(2)点M 在球面上运动;(3)一定存在某个位置,使1DE A C ;(4)一定存在某个位置,使MB ∥平面1A DE .【例2】如图145 ,在Rt ABC中,4,3,,2AB AC A ,AP mPB AQ nQC (,0)m n ,且满足111,2M m n 是BC 的中点,对任意的,QP QM R 的最小值记为 f m ,则对任意的0,m f m 的最大值为________.【例3】如图147 ,在四棱锥P ABCD 中,E 为AD 上一点,PE 平面,,,2,ABCD AD BC AD CD BC ED AE F ∥为PC 上一点,且2CF FP (I)求证:PA ∥平面;BEF (证明略)(II)若PE ,求二面角F BE C 的平面角的大小.【例4】已知,a b 是异面直线,,,,,,A B a C D b AC b BD b ,且2,1AB CD ,则异面直线,a b 所成的角等于________.【例5】已知三棱锥P ABC 满足60APB BPC CPA ,三个侧面,,APB BPC CPA 的面积分别为,2,12,则这个三棱锥的体积是________.【例6】已知在四棱柱1111ABCD A B C D 中,侧棱1AA 底面1,2ABCD AA ,底面ABCD 的边长均大于2,且45DAB,点P 在底面ABCD 内运动且在,AB AD 上的射影分别为,M N ,若2PA ,则三棱锥1P D MN 体积的最大值为________.强化训练1.在四棱锥S ABCD 中,底面ABCD 是平行四边形,,M N 分别是,SA BD 上的点.有下列命题:(1)若SM DN MA NB,则MN ∥平面SCD ;(2)若SM DN MA NB ,则MN ∥平面SCB ;(3)若平面SDA 平面ABCD ,且平面SDB 平面ABCD ,则SD 平面ABCD .其中正确命题的序号为________.2.如图1426 ,在四棱锥P ABCD 中,E 为AD 上一点,PE 平面,ABCD //,AD BC AD ,CD 22,BC ED AE 3,EB F 为PC 上一点,且2CF FP .(I)求证://PA 平面BEF ;(II)若二面角F BE C 的平面角的大小为60,求直线PB 与平面ABCD 所成角的大小.3.如图1427 ,在三棱锥A BCD 中,3,2,AB AC BD CD AD BC M 是AD的中点,则异面直线,CM AB 所成角的大小为________.4.已知三棱锥P ABC 的体积为16,点,D E 分别在侧棱,PB PC 上,且2,PD DB 3PE EC ,则三棱锥P ADE 的体积为________.5.过凸四边形ABCD 的对角线交点O 作该四边形所在平面的垂线段SO ,使SO 3 ,若22,S AOD S BOC V a V b ,当S ABCD V 最小时,ABCD 的形状为________.一题多解第14讲立体几何知多少,位置关系空间角典型例题【例1】如图141 ,在矩形ABCD 中,E 为边AB 的中点,将ADE 沿直线DE 翻转成1A DE ,若M 为线段1A C 的中点,则在ADE 的翻转过程中,正确的命题是________.(1)BM 是定值;(2)点M 在球面上运动;(3)一定存在某个位置,使1DE A C ;(4)一定存在某个位置,使MB ∥平面1A DE .【解析】【解法1】设CD 中点为S ,则111=2MS A D MS A D ,∥,且MS 为定值,又因为,,DS BE DS BE ∥,所以四边形DSBE 是平行四边形,所以BS DE ∥且BS 为定值.由余弦定理可得2222212cos 2cos MB MS SB MS SB MSB MS SB MS SB A DE ,所以MB 是定值,(1)正确.因为B 是定点,所以点M 是在以B 为圆心,MB 为半径的球面上,所以(2)正确.若当DE EC 时,如图14-2:1110DE A C DE A E EC DE A E DE EC ,(3)错误因为1,SB DE MS A D ∥∥,又因为1,SB SM S DE A D D ∩∩,所以平面MSB ∥平面1A ED ,所以MB ∥平面1A ED ,(4)正确.【点拨】利用向量数量积判定线线的垂直关系.【解法2】如图 143,1 正确,由余弦定理可知MB 为定值,同【解法1】;(2)正确,同【解法1】;(3)错误,若2AB AD ,则DE EC .若1DE A C ,又因为1A C 在平面ABCD 的射影在AC 上,所以.DE AC 由题意知AC 与DE 不垂直,所以(3)不正确.(4)正确,取DC 中点F ,则11,,,FB DE MF A D FB MF F A D DE D ∩∩∥∥,所以平面//MFB 平面1A ED ,所以MB ∥平面1A ED .【点拨】先利用假设反证法证明不垂直再利用面面平行证明线段平行.【解法3】如图144 ,(1)正确,延长DE 交CB 的延长线于点N ,连结,AN DAN 绕着DN旋转,因为1A N 为定值,所以MB 为定值;(2)正确,点M 在以B 为圆心,MB 为半径的球面上运动;(3)错误,同【解法2】;(4)正确,取EC 中点P ,可以类似【解法2】证明平面MPB ∥平面1A ND ,所以MB ∥平面1.A ED 【点拨】从不同角度构造辅助线.【赏析】本题涉及立体几何的考点比较多,如线面平行、面面平行、线面垂直、面面垂直.熟练掌握线面、面面平行及垂直的判定和性质定理、线面角、二面角的定义及求法是解立体几何题的关键.【例2】如图145 ,在Rt ABC中,4,3,,2AB AC A ,AP mPB AQ nQC (,0)m n ,且满足111,2M m n 是BC 的中点,对任意的,QP QM R 的最小值记为 f m ,则对任意的0,m f m 的最大值为________.【解析】【解法1】设 ,0,0,P a Q b ,以A 为坐标原点,,AB AC 所在直线分别为x 轴,y 轴建立如图146 所示的平面直角坐标系.则 4,,3,a m a AP mPB b n b AQ nQC因为1112m n ,所以4312a b a b ,所以86551a b,所以直线PQ 过点86,55N ,结合向量模长的几何意义可知QP QM 可等价视为点0430,22M ,即32,2M与直线PQ 上点连线的距离,所以最大值 f m 就是点M 到直线PQ 的距离的最大值,当MN PQ 时,M 到直线PQ 距离最大.所以max 1()2f m MN.【点拨】依据题意建立平面直角坐标系,使向量坐标化,从而实现数量化运算.【解法2】由,AP mPB AQ nQC 可知1111AP AB m AQ AC n,取点N 使得45AN AM ,所以2121211555AP AQ AB AC AN m n ,因为21212111215552m n,所以,,P Q N 三点共线,下同【解法1】,可知max 11()52f m MN AM .【点拨】利用向量运算,添加必要的辅助线实现向量的转化.【赏析】本题考查向量坐标形式的运算及点到直线距离公式,【解法1】利用向量坐标运算,【解法2】添加必要的辅助线实现向量的转化,【解法1】是常用的基本方法,易上手好操作.【解法2】巧妙构造,要求对重要结论熟练掌握并能灵活运用.【例3】如图147 ,在四棱锥P ABCD 中,E 为AD 上一点,PE 平面,,,2,ABCD AD BC AD CD BC ED AE F ∥为PC 上一点,且2CF FP (I)求证:PA ∥平面;BEF (证明略)(II)若PE ,求二面角F BE C 的平面角的大小.【解析】【解法1】连结CE ,在平面PCE 内,过点F 作FH CE 于点H .因为FH PE ∥,所以FH 平面ABCD .过点H 作HM BE 于点M ,连结FM .由三垂线定理得FM BE ,所以FMH 为二面角F BE C 的平面角.因为FH 平面ABCD ,PE 平面ABCD ,所以FH PE ∥,所以23FH CF PE CP ,所以22333FH PE AE ,同理1233MH BC AE ,所以在Rt FHM 中,tan 3FH FMH HM所以3FMH ,即二面角F BE C 的平面角为3.【点拨】在平面内的一条直线如果和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直,当点F 在一个半平面上时,通常用三垂线定理法求二面角的大小.【解法2】排除多余信息,若我们只考虑二面角F BE C ,我们很快发现,直四棱锥P EBCD 可以补成长方体,如图149所示.连结EC ,在平面PEC 内,过点F 作FO EC 于点O ,过点O 作OM BE 于点M ,连结FM ,如图1410 .因为PE 平面EBCD ,PE 平面PEC ,所以平面PEC 平面EBCD ,且平面PEC 平面EBCD EC .因为FO 平面,PEC FO ED ,所以FO 平面EBCD ,所以FMO 是二面角F BE C 的平面角,设AE a,则2,(0)ED a PE a,因为PE 平面ACD ,FO 平面ACD ,所以PE FO ∥,所以23FO CO CF PE CE CP ,所以233FO a ,又因为OM BC ∥,所以13OM EO BC CE ,得23OM a ,所以3tan 23FO FMO OM a 所以3FMH ,所以二面角F BE C 的平面角为3.【点拨】利用图形的特征,采用补形方法解决问题.【解法3】如图1411 ,连结CE ,在平面PCE 内过点F 作FH CE 于点H .因为PE 平面ABCD ,CE 平面ABCD ,所以FH PE ∥,所以FH 平面ABCD .过点H 作HM BE 于点M ,连结FM .由三垂线定理得FMBE ,所以FMH 为二面角F BE C 的平面角.设(0)AE a a ,则2,BC ED a PE ,所以24,.33MH a FM a (同【解法2】)由射影面积法得Δ112cos ,1232HEB FEBBE MH S FMH FMH S BE FM 所以二面角F BE C 的平面角为3.【点拨】利用射影面积法求解.【解法4】延展平面BEF 为平面BEMF ,如图1412 所示,则平面BEF ∩平面PAD EM ,在平面PAD 中,作MO 平面ABCD 于点O ,如图1413.因为PE 平面ABCD ,所以MO PE ∥,所以MO 与PE 共面,因为M 平面PAD ,所以.O AD 则OE BE ,由三垂线定理知MEBE ,所以MEO 是所求二面角的平面角.由(I )可知//ME PA ,所以2DM DE MP EA,又因为MO PE ∥,所以23MO DO DM PE ED PD ,不妨设(0)AE a a ,则2,ED a PE,因此得2,,tan 3a MO MO OE MEO OE 3MEO ,所以二面角F BE C 的平面角为3.【点拨】延展平面BEF 为平面BEMF ,将过点F 作平面EBCD 垂线的间题转化为过点M 作平面EBCD 垂线的问题.如图1414 ,延长CB 至点M ,使得2MB BC ,所以,,MB BC AE MB AE MB AE ED∥,所以AEMB 是平行四边形.因为,AM EB AM ∥平面EFB ,EB 平面EFB ,所以AM ∥平面EFB .由 I 得PA ∥平面,EFB AM PA A ,所以平面PAM ∥平面FEB ,则二面角P AM C 的平面角即为二面角F EB C 的平面角,因为PE 平面,EBCD EA AM ,所以PAE 是二面角P AM C 的平面角.不妨设(0)AE a a ,由三垂线定理得PA AM ,则,tan PE PE PAE AE.所以二面角P AM C 的平面角是3,即二面角F EB C 的平面角是3.【点拨】寻找二面角的平面角较困难,根据平面平移不改变与另一个平面构成的角的大小的原理,如果能把二面角中的一个平面平移,找出辅助平面与另一个平面的交线,就可以作出二面角的平面角.【解法6】以E 为坐标原点,分别以,,EA EB EP 所在直线为x 轴、y 轴、z 轴,建立如图14-15所示的空间直角坐标系.不妨设(0),EA a a EB b ,则22,BC ED AE a PE易知0,0,0,,0,,0E P B b ,设平面ABCD 的法向量 1111,,n x y z ,因为2CF FP所以 223223,,,,,,0,,0,333333b b F a a EF a a EB b因为2200EF EB n n,即222220,3330,b ax y az by 令21z,则2x ,可得平面EBF的一个法向量2 n .设二面角F BE C 的平面角为 ,所以12121211cos cos ,22 n n n n n n ,所以3.所以二面角F BE C 的平面角为3.【点拨】设12,n n 分别是二面角l 的面, 的法向量,则向量12,n n 的夹角,即为l 的平面角或其补角(需要根据具体情况判断相等或互补).【赏析】本题主要考查与二面角有关的立体几何综合知识.推荐【解法5】为最佳解答.求二面角的平面角的常用方法有定义法、三垂线定理法、射影面积法、平移平面法、补形法、空间向量的坐标法等,以下对各个解法进行分析.【解法1】应用三垂线定理法解题.联系到PE 平面ABCD ,有的同学大胆猜想(像一个魔术师,下子从帽子里变出一只兔子),得出了正确的结论;相应地,还有很大一部分同学被复杂的空间图形吓退,找不到二面角的确切位置,无从下手.【解法2】应用构造补形法解题,联系到长方体,比【解法1】更易得出.FO EBCD 平面【解法3】应用射影面积法解题,联系到点F 在底面EBCD 的射影,依据射影公式求二面角.【解法4】应用垂线平移法解题,联系【解法3】,过F 点作垂线,那么垂足落在哪里?有很多同学是含糊不清、模棱两可的,那么我们为什么不换一个点呢?将过点F 作平面EBCD 垂线的问题转化为过点M 作平面EBCD 垂线的问题.【解法5】应用平面平移法解题,将求二面角F BE C 的平面角的问题转化为求二面角P AM C 的平面角的问题.【解法6】应用空间向量求解法,是一种十分简捷且传统的解法.当题目条件中垂直关系明显时,利用空间坐标系不失为一种更有效的方法.【例4】已知,a b 是异面直线,,,,,,A B a C D b AC b BD b ,且2,1AB CD ,则异面直线,a b 所成的角等于________.【解析】【解法1】如图1416 ,在长方体中,因为//BE CD ,所以ABE 就是异面直线,a b 所成的角,又因为,,,,A B a C D b BD b ,所以,,CE b AC b AC CE C ,所以b 平面ACE ,所以b AE ,所以BE AE ,所以ABE 是直角三角形.又因为2,1AB CD ,所以1BE ,所以1cos 2BE ABE AB ,所以60.ABE 【点拨】构造长方体求解.【解法2】如图1417 所示,过点A 作AE CD ∥,=AE CD ,连结BE ,则EAB 是异面直线,a b 所成的角,由题意知ACDE 是矩形,所以,AE DE AE BD ,因为DE BD D ,所以AE平面BED ,所以AE BE .所以ABE 是直角三角形,又因为2,1AB CD ,所以1cos 2EAB ,所以60EAB.【点拨】利用平移法把异面直线平移为相交直线.【解法3】以A 为坐标原点,分别以,,AC AE CD 方向为x 轴,y 轴,z 轴正方向,建立如图1418 所示的空间直角坐标系,所以 0,0,0,,0,0,0A C a a ,则,0,1,D a B ,所以,0,0,1AB CD ,所以1cos 2AB CD AB CD 又因为 0,90,所以异面直线,a b 所成的角为60.【点拨】在构造长方体的基础上建立空间直角坐标系解决问题.【赏析】本题是一道典型的异面直线成角间题,与常见问题不同的是,本题中的异面直线不是直接出现在立体几何图形中.【解法1】和【解法3】都是将两条异面直线放置在长方体中求解.【解法1】将直线CD 平移到BE 处,从而易解.【解法3】则借助空间向量的方法求解.【解法2】利用异面直线所成角的概念,将CD 平移至AE 处后,在Rt BAE 中求解.在求两条异面直线所成角的大小时,要注意异面直线所成角的范围是0,2.利用中位线或平行四边形来添加辅助线的方法,有时也可对空间图形使用.【例5】已知三棱锥P ABC 满足60APB BPC CPA ,三个侧面,,APB BPC CPA 的面积分别为3,2,12,则这个三棱锥的体积是________.【解析】【解法1】由各侧面的面积可得13sin6022APB S PA PB ,所以2PA PB ,同理8343,33PB PC PA PC ,所以833PA PB PC ,构造三棱锥P A B C ,使得60A PB A PC B PC ,2,PA PB PC 所以13P A B C V ,因为P ABC P A B C V PA PB PC V PA PB PC,所以269P ABC P A B C PA PB PC V V PA PB PC【点拨】由三角形面积公式求得三棱锥的侧棱长,构造一个特殊的三棱锥,利用体积关系解决问题.【解法2】由题意得1sin60242APB S PA PB PA PB (1),1sin60224BPC S PC PB PB PC (2)13sin60124CAP S PA PC PA PC (3)由(1)(2)(3)联立解得431,2,3PA PB PC.如图1420 ,过点B 作BD 平面APC 于点D ,作DE PA 于点E ,连结BE ,易证AP 平面BDE ,所以AP BE ,在Rt BPE 中,2,60PB BPA,所以1PE .因为60APB APC BPC,所以点D 在APC 的平分线上,即30APD CPD,所以在Rt PDE 中,易得233PD ,同理,3BD ,所以111114332626sin601332323239P ABC APC V S BD PA PC BD .【点拨】求出三条棱长,过某一顶点作高,直接法求解体积.【解法3】设,,PA PB PC 的长度分别为,,a b c ,同【解法2】,则易得431,2,3a b c .如图1421 ,设点A 在平面BPC 上的射影为点O ,因为60APB APC BPC,所以30BPO CPO,所以3cos 3 ,所以26sin 1cos 3,所以点A 到平面PBC 的距离6sin 3AO PA,所以11161626sin602.3323339P ABC PBC V S AO PB PB 【点拨】作出点A 在平面PBC 上的投影,利用三余弦定理解题.注:三余弦定理证明:如图14-22,在三棱锥A BCD 中,AO 平面BCD ,过点O 作OE BC 交BC 于点E ,连结AE ,易得BC 平面AOE ,所以BEAE .在Rt AOB 中,cos OB ABO AB ,在Rt ABE 中,cos BE ABE AB,在Rt BOE 中,cos BE OBE BO,所以cos cos cos BE OB BE OBE ABO ABE BO AB AB,所以cos cos cos .ABE OBE ABO 【赏析】【解法1】巧妙地补形成一个特殊的三棱锥,利用一个平面 截三棱锥P ABC ,分别交三棱锥的棱,,PA PB PC 于点,,D E F ,则.P ABC P DEF V PA PB PC V PD PE PF解法23、实质相同,都是求底面和高,【解法3】利用三余弦定理求出三棱锥的高.【例6】已知在四棱柱1111ABCD A B C D 中,侧棱1AA 底面1,2ABCD AA ,底面ABCD 的边长均大于2,且45DAB,点P 在底面ABCD 内运动且在,AB AD 上的射影分别为,M N ,若2PA ,则三棱锥1P D MN 体积的最大值为________.【解析】【解法1】如图1423 ,设AP ,0,45N ,所以sin 2sin ,sin 452sin 45PN PA PM PA ,所以1sin135sin 45,2PMN S PM PN111212sin 45sin 245333P D MN D PMN V V ,所以当22.5 时,1P D MN V 取得最大值1.3【点拨】引入角度为变量﹐建立体积的三角函数式,利用三角函数法求最值.【解法2】因为2PA ,知点P 在以点A 为圆心,半径为2的圆弧上,因为45,90,90,DAB PMA PNA所以,,,A M P N 四点在以AP 为直径的圆F 上,如图14-24,所以1190,2122MFN FM FN AP ,所以MN在PMN 中,2222||||2cos135MN PM PN PM PN 因为22||2PM PN PM PN ,当且仅当222PM PN 时取等号,所以22PN PM PN所以2PM PN 所以1112121223323D PMN PMN V S .所以1D PMN V 的最大值为213.【点拨】利用平面几何法求得MN 的值,进而可利用均值不等式法求得PMN 面积的最大值,最后求得体积的最大值.【解法3】1112233P D MN D PMN PMN PMN V V S S 如图1425 所示,设,BAP DAP ,122sin 2sin sin135cos cos 22PMN Scos 12222,当且仅当22.5 时取等号,所以1P D MN V 的最大值为13.【点拨】引入两个角度,建立体积的代数表达式,结合积化和差公式可由两角和与差的余弦公式解决问题.【赏析】本题依托立体几何背景﹐涉及线面垂直﹑线线垂直和棱锥体积的求法.如何求解PMN 的面积的最大值是本题的关键.【解法1】从角度出发,将各边长转为为三角函数形式,利用三角函数值的有界性解答.【解法2】从平面几何的角度出发,利用基本不等式取得最值.这两种方法都是处理解三角形问题的基本方法.【解法3】从两角的关系出发,使用积化和差公式,实质是利用角的变换,和【解法1】有异曲同工之妙.强化训练1.在四棱锥S ABCD 中,底面ABCD 是平行四边形,,M N 分别是,SA BD 上的点.有下列命题:(1)若SM DN MA NB,则MN ∥平面SCD ;(2)若SM DN MA NB ,则MN ∥平面SCB ;(3)若平面SDA 平面ABCD ,且平面SDB 平面ABCD ,则SD 平面ABCD .其中正确命题的序号为________.【解析】答案:①③2.如图1426 ,在四棱锥P ABCD 中,E 为AD 上一点,PE 平面,ABCD //,AD BC AD ,CD 22,BC ED AE 3,EB F 为PC 上一点,且2CF FP .(I)求证://PA 平面BEF ;(II)若二面角F BE C 的平面角的大小为60,求直线PB 与平面ABCD 所成角的大小.【解析】(Ⅰ)证明:连结AC 交BE 于点M ,连结FM .因为//EM CD ,所以12AM AE PF MC ED FC,所以//FM AP ,又因为FM 平面,BEF PA 平面BEF ,所以//PA 平面BEF(Ⅱ)解:以E 为坐标原点,EB ,EA ,EP 所在直线分別为x 轴,y 轴,z 轴建立空间直角坐标系,如答图141 所示.设点(0,0,)P t ,因为PE 平面ABCD ,则向量(0,0,PE ,t )即为平面BEC 的法向量.因为//,,22,3AD BC AD CD BC ED AE EB ,所以四边形BCDE 为矩形,(3,0,0),(3,2,0)B C ,因为F 为PC 上一点,且2CF FP ,则有22221,,,1,,,(3,0,0)3333F t EF t EB设平面BEF 的法向量(,,)n x y z ,则n EF ,即有n .0EF ,即22033x y zt ,又0EB n ,即30x ,所以10,1,n t.因为二面角F BE C 的平面角大小为60,则PE 与n 的夹角为120 ,所以21cos1202||||11n PE n PE t t ,解得t 33),933P PB .因为PE 平面ABCD ,所以PBE 即为直线PB 与平面ABCD 所成的角.在Rt PBE 中,3cos 223BE PBE PBE PB 6,所以直线PB 与平面ABCD 所成角为6.3.如图1427 ,在三棱锥A BCD 中,3,2,AB AC BD CD AD BC M 是AD的中点,则异面直线,CM AB所成角的大小为________.【解析】取BD 中点N ,连结MN ,CN ,如答图14-2因为3,2,AB AC BD CD AD BC M 是AD 的中点,所以//MN AB ,且1322MN AB ,所以(CMN 或其补角)是异面直线CM ,AB 所成的角.因为CM 2227cos 29BD CD BC BDC BD CD 所以222172cos 4CN DN CD DN CD BDC .所以2222cos 22MN CM CN CMN MN CM .所以4CMN .所以异面直线CM ,AB 所成角的大小为4.4.已知三棱锥P ABC 的体积为16,点,D E 分别在侧棱,PB PC 上,且2,PD DB 3PE EC ,则三棱锥P ADE 的体积为________.【解析】由答图143 可知:P ABC P ADE V PA PB V PA PD .34223PC PE ,所以8P ADE V .5.过凸四边形ABCD 的对角线交点O 作该四边形所在平面的垂线段SO ,使SO 3 ,若22,S AOD S BOC V a V b ,当S ABCD V 最小时,ABCD 的形状为________.【解析】由已知,易得22,AOD DOC S a S b .设,AOB COD S x S y ,则22.S ABCD V a b x y 因为22AOD COD AOB DOC S S a DO y x S OB S b,所以22xy a b .而2(x y xy ab 设0,0a b ),于是222()a b x y a b ,当且仅当x y ab 时取等号,这时2.AOD DOC S AO a a OC S y b 同理,DO a OB b ,所以AO OC DO OB,所以//AD BC .另一方面:当x y ab 时,2,AOD DOC S AO a a BO OC S y b OD 2DOC DOC S b b S y a(1)当a b b a ,即22,AOD COD a b S S 时,AO BO OC OD,所以//AB CD .此时,四边形ABCD 是平行四边形.(2)当a bb a,即22,AOD Da b S S时,AO BOOC OD,所以AB与CD不平行.此时,四边形ABCD是梯形.。
巧用正四面体的_补形正方体_解题_曹开清

妙用“补形法”巧解几何题

( i 2 sn _ + C s O
砂 J “ 彩 浩" } 补 》
陈培东
铒 几何 题
( 江苏省南菁高级 中学 24 0 ) 140
“ 补形法 ” 是几何 中较常用 的基 本方 法之 一, 根据几何 问题 的条件和 图形特 征 , 巧妙添 加有关 的点 和线 , 原题 将
B +C D E= ∞ E 显然有 ∞ E> D, 而 +C . +C E,
=
( ) 告 .
所以当 志= m+ 1时猜想上述等式 成立的条件均为0 =季 ,
又上 述等式成立的条件均为 0 { , : 故最小值为
()()一专 =厨 号=专H () 2
法 同解 法 1 .
最值 大求
故 小 为 () 丢 H=()。 最 值 号 =( ) 丢 号 = _
20 年第 6 09 期
中学数学月刊
・4 5・
吾 y ,、 ,=-V 丧 , 1 V , V V = 2 即1 2 = 一 故
:V2— 7:5 .
C
,
3 将 四面体补成 四棱柱
例 3 —个 给定 的四面体 A C B D中 , B= 四 , C= A A
+ 妒
所 以 ( ≥ 2Os ≥ … ≥ , ( s 2 。 ()i 0 n 2 i  ̄ 0= n-
所 ≥专一i≥丢一・ ) (0c s s s z =譬 以 州( ()s () ( s +s i =n ≥i 詈 () n z 譬 i o n i n n 2z 2 2 H H 。
, , 1 、 n
2 专) 最 值 法 解 . √( . 大 求 同 法1
本饵法利用 了递推与放缩的思想 , 而这种思想也 正是 我们处理此类 问题 的 自然想法. 题者的 出发点是 想通过 命
五年级数学思维 割补法巧算面积 利用差不变求面积 练习题

利用差不变求面积1.如图是两个相同的直角三角形组合而成。
请问:阴影部分的面积是多少平方厘米?2.下面是将两个完全相同的直角三角形ABC 与DEF 叠放在一起形成的图形,AB 长2 厘米,BE 长1 厘米,OE 长1.5 厘米。
求阴影部分的面积。
3.下面是两个完全相同的直角三角形叠放在一起形成的图形。
求阴影部分的面积。
4.下图是两个相同的直角梯形重叠在一起形成的组合图形,其中AB=8cm、CD=10cm、D=20cm。
请问:阴影部分的面积是多少平方厘米?5.下面是两个相同的直角梯形ABCD 和EFGH 叠放在一起形成的图形,FG 长10 厘米,OG 长5 厘米,OC 长2 厘米。
求阴影部分的面积。
6.下面是边长分别是4 厘米、3 厘米的两个正方形,它们重叠部分的面积是2 平方厘米。
求这两个正方形中阴影部分的面积差。
7.下图中,正方形ABCD 与长方形EFHG 交于I、J 两点,正方形ABCD 的边长是9 厘米,EG 长7 厘米,EF 长5 厘米。
求两个阴影部分的面积差。
8.下图中,两个正方形的边长分别是8 厘米和6 厘米,图中阴影部分是重叠部分。
两个正方形的空白部分的面积差是多少平方厘米?9.下面是将两个完全相同的直角三角形叠放在一起形成的图形,AB 长5 厘米,BF 长3.4 厘米,AC 长3 厘米。
求阴影部分的面积。
10.求下图中甲、乙两个阴影三角形的面积差。
11.下面是长方形ABCD与平行四边形CDEF叠放在一起形成的图形,且AB、EF在同一条直线上,AD长7厘米,CD长4厘米,BH长3厘米。
求阴影部分的面积。
12.下图中,平行四边形ABCD 的底边BC 是6 厘米,直角三角形BCE 的直角边CE 是5 厘米,两阴影部分的面积和比三角形FEG 的面积大12 平方厘米。
求平行四边形ABCD 的面积。
13.下图中,平行四边形ABCD 的底边BC 是12 厘米,直角三角形BCE 的直角边CE 是10 厘米,两阴影部分的面积和比三角形FEG 的面积大24 平方厘米。
大招1外接球秒杀之补形法

大招1外接球秒杀之补形法大招总结结论:长方体各顶点可在一个球面上,故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,a b c ,其体对角线为l .当球为长方体的外接球时,截面图为长方体的对角面和其外接圆,故球的半径22222l a b c R ++==. 补形法:把几何体放到规则图形里面规则的锥体,如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,把多面体放到规则几何体里面类型1:有一条棱垂直于底面类型2:对棱相等利用长方体相对面的对角线长度相等,把四面体放人其中如图所示,,,AB CD AD CB AC D B ==='''''',三棱锥D ACB '-'可以放在长方体中,外接球直径2R 为长方体体对角线.典型例题例1.已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( )A.16πB.20πC.24πD.32π解:用公式22222462R ++==,则2424S R ππ==,故选C. 例2.长、宽、高分别为432、、的长方体的外接球的体积为( )A. C.92π D.9π解:由题意长方体的对角线就是球的直径.长方体的对角线长为=,外接球的体积343V π=⨯=⎝⎭,故选B.例3. 已知直三棱柱 ABC −A 1B 1C 1 的 6 个顶点都在球 O 的球面上, 若 AB ⊥AC,AA 1=12,AB =3,AC = 4 , 则球 O 的半径为 ( )A. 3√172B. 2√10C. 132D. 3√10解 因为三棱柱 ABC −A 1B 1C 1 的 6 个顶点都在球 O 的球面上, 若 AB =3,AC =4,AB ⊥AC,AA 1= 12 , 所以三棱柱的底面是直角三角形, 侧棱与底面垂直, 侧面 B 1BCC 1, 经过球的球心, 球的直径 是其对角线的长, 因为 AB =3,AC =4,BC =5,BC 1=13, 所以球的半径为 132. 故选 C .例4. 在三棱锥 A −BCD 中, AB =CD =√13,AD =BC =3,AC =BD =4, 则三棱锥 A −BCD 外接球的表面 积为解 将三棱锥补形为长方体, 三个长度为三对面的对角线长, 设长方体的长、 宽、高分别为 a,b,c ,则 a 2+b 2=9,b 2+c 2=13,c 2+a 2=16,∴2(a 2+b 2+ c 2)=9+13+16=38,a 2+b 2+c 2=19,∴4R 2=19,∴S =19π.例5. (2019 - 新课标 I ) 已知三棱锥 P −ABC 的四个顶点在球 O 的球面上, PA =PB =PC,△ABC 是边 长为 2 的正三角形, E,F 分别是 PA,AB 的中点, ∠CEF =90∘, 则球 O 的体积为 ( )A. 8√6πB. 4√6πC. 2√6πD. √6π解如图, 由PA=PB=PC,△ABC是边长为 2 的正三角形, 可知三棱锥P−ABC为正三棱锥, 则顶点P在底面的射影O为底面三角形的中心, 连接BO 并延长, 交AC于G, 则AC⊥BG, 又PO⊥AC,PO∩BG=O, 可得AC⊥平面PBG, 则PB⊥AC,∵E,F分别是PA,AB的中点, ∴EF//PB, 又∠CEF=90∘, 即EF⊥CE,∴PB⊥CE, 得PB⊥平面PAC,∴正三棱锥P−ABC的三条侧棱两两互相垂直, 把三棱锥补形为正方体, 则正方体外接球即为三棱锥的外接球, 其直径为D=√PA2+PB2+PC2=√6, 故半径为√62, 则球O的体积为4 3π×(√62)3=√6π. 故选D.例6.在四面体ABCD中, △BCD是边长为 2 的等边三角形, △ABD是以BD为斜边的等腰直角三的等腰直角三角形,平面ABD⊥平面ABC, 则四面体ABCD的外接球的表面积为( )A. 8πB. √6πC. 6πD. 2√2π解;在四面体ABCD中, △BCD是边长为 2 的等边三角形,△ABD是以BD为斜边的等腰直角三角形, AB=AD=√2, 平面ABD⊥平面ABC,如图, 可知AD⊥平面ABC, 可得AD⊥AC, 所以△BAC是等腰直角三角形, 所以三棱锥A−BCD是正方体的一个角,如图:外接球的直径就是长方体的体对角线的长度, 所以2r=√6,r=√62, 四面体ABCD的外接球的表面积为:4πr2=6π. 故选C自我检测1. 若三棱锥的三条侧棱两两垂直, 且侧棱长均为 √3, 则其外接球的表面积是 依题可以构造一个正方体, 其体对角线就是外接球的直径. 2r =√3+3+3=3,r =32;S 表面稆 =4πr 2=9π. 故答案为 9π.2. 在正三棱锥 S −ABC 中, M,N 分别是棱 SC 、BC 的中点, 且 MN ⊥AM , 若侧棱 SA =√3, 则正三棱锥 S −ABC 外接球的表面积是解;第 2 题图 2. ∵M,N 分别是棱 SC 、BC 的中点, ∴MN//SB,MN ⊥AM , 可得 SB ⊥AM , 由正三棱锥的性质可得 SB ⊥ AC,∴SB ⊥ 平面 SAC ⇒SB ⊥SA 且 SB ⊥AC,∵ 三棱锥 SABC 是正三棱锥, ∴SA 、SB 、SC 三条侧棱两 两互相垂直. ∵ 侧棱 SA =√3,∴ 正三棱锥 S −ABC 的外接球的直径为 :2R =3, 外接球的半径为 R =32, ∴ 正三棱锥 S −ABC 的外接球的表面积是 S =4πR 2=9π. 故答案为 9π.3.三棱锥 P −ABC 的侧棱 PA,PB,PC 两两互相垂直, 且 PA =PB =PC =2, 则三棱锥 P −ABC 的外接 球的体积是( )C. 16√33π B. 4√3πD. 8√3πA. 2√3π解;以 PA 、PB 、PC 为过同一顶点的三条棱, 作长方体如图,则长方体的外接球同时也是三棱锥P−ABC外接球. ∵长方体的对角线长为2√3,∴外接球的直径为2R=2√3, 半径R=√3, 因此,三棱锥P−ABC外接球的体积是43πR3=43π×(√3)3=4√3π, 故选B.4.(2021 秋- 湖南月考)在四面体ABCD中, AB=CD=√10,AC=BD=√5,AD=BC=√13, 则四面体的外接球的表面积为()A.6√3πB.8√3πC.16√33πD. 16π解;由题意可采用割补法,考虑到四面体ABCD的四个面为全等的三角形,所以可在其每个面补上一个以√10,√5,√13为三边的三角形作为底面,且以分别x,y,z 长、两两垂直的侧棱的三棱锥,从而可得到一个长、宽、高分别为x,y,z的长方体,并且x2+y2=10,x2+z2=5,y2+z2=13, 则有(2R)2=x2+y2+z2=14 ( R为球的半径), 得R2=72, 所以球的表面积为S=4πR2=14π, 故选C.5.(2021 - 柳州三模)在三棱锥V−ABC中, 底面△ABC是等边三角形,顶点V在底面ABC的投影是底面的中心, 侧面VAB⊥侧面VAC, 则此三棱锥的体积与其外接球的体积之比为( )A. √272πB. √636πC. √39πD. √69π解;将该三棱锥放置在正方体当中, 如图所示, 设正方体的棱长为 1 . 此三棱锥的体积V1=13×(12×1×1)×1=16, 外接球的半径R=√32, 外接球的体积V2=43πR3=43π×(√32)3=√32π,∴此三棱锥的体积与其外接球的体积之比为:V1 V2=16√32π=√39π. 故选C.6.(2021 - 榆林模拟)阳马,中国古代算数中的一种几何体, 它是底面为长方形,两个三角面与底面垂直的四棱锥. 已知在阳马P−ABCD中, PD⊥平面ABCD,PD= 3, 且阳马P−ABCD的体积为9 , 则阳马P−ABCD外接球表面积的最小值是()A. 9√3π2B. 9√3πC. 27πD. 27√3π解;由题意可知阳马的体积为: 13AB⋅BC⋅PD=AB⋅BC=9, 设阳马的外接球的半径为R, 则4R2=AB2+BC2+PD2=AB2+BC2+9⩾2AB⋅BC+9=27, 当且仅当AB=BC时等号成立,所以阳马的外接球的表面积4πR2⩾27π. 故选C.7.(2021 - 甘肃模拟)《九章算术商功》有如下叙述: “斜解立方, 得两堵斜解堑堵, 其一为阳马,一为鳖臑. 阳马居二, 鳖臑居一, 不易之率也.” (阳马和鳖臑是我国古代对一些特殊锥体的称谓). 取一个长方体, 按如图所示将其一分为二, 得两个一模一样的三棱柱,均称为堑堵, 再沿堑堵的一顶点与相对的棱剖开, 得四棱锥和三棱锥各一个. 其中以矩形为底, 有一棱与底面垂直的四棱锥, 称为阳马. 余下的三棱锥是由四个直角三角形组成的四面体,称为憋臑. 那么如图所示, a=3,b=4,c=5的阳马外接球的表面积是( )堑堵阳马牧臑A. 20√2πB. 25√2πC. 50πD. 200π解;因为长方体、堑堵、阳马、鳖臑,各个几何体的顶点都在同一个外接球的表面积上,所以它们的外接球是相同的,外接球的直径就是长方体的体对角线的长度,所以外接球的半径为: R=12√32+42+52=√502, 阳马外接球的表面积是4πR2=50π. 故选C.8.(2021 - 新乡二模)在四面体ABCP中, PB⊥平面ABC, 且AB⊥AC,AB=AC.若四面体ABCP外接球的半径为√192PB. 则PA与平面ABC所成角的正切值为()A. 12B. 13C. 2D. 3解;因为PB⊥平面ABC, 且AB⊥AC, 所以四面体ABCP可以补形为一个长方体, 故其外接球的半径R=√AB2+AC2+PB22=√2AB2+PB22=√192PB, 则AB=3PB.因为PA与平面ABC所成角为∠PAB, 所以tan∠PAB=PBAB =13. 故选B.。
2024高考数学专项立体几何系统班7、外接球与内切球

第7讲外接球与内切球知识与方法1.外接球与内切球是全国高考常考题型,模型杂、方法多,但归纳起来不外乎两大类处理方法.(1)补形:将几何体补全成长方体、正方体、直棱柱等常见几何体,计算外接球半径.(2)构建平面截球模型:寻找截面圆心以及球心到截面的距离,通过222R r d =+计算外接球半径.2.设球的半径为R ,有5个常用计算公式.(1)正方体外接球半径:R =,其中a 为正方体棱长,如图1.(2)长方体外接球半径:R =a ,b ,c 分别为长方体的长、宽、高,如图2.(3)正四面体外接球半径,4R a =,其中a 为正四面体棱长,如图3.(4)直三棱柱外接球半径:R =,其中r 为底面外接圆半径,h 为直三棱柱的高,如图4.(5)圆柱外接球半径:R =,其中r 为底面圆半径,h 为圆柱的母线长,如图5.提醒:①上面列出了一些简单模型的外接球半径计算公式,需结合图形将其记住,还有一些其他模型可以通过补形的方法转化为上述模型处理;②一些不能通过简单补形求解的模型,如球内接正棱锥,球内接圆锥等,可以通过分析几何关系,转化为平面截球模型计算外接球的半径.题组一1.(★★)已知一个正方体的所有顶点在一个球面上.若这个正方体的表面积为18,则这个球的体积为_______.【解析】设正方体的棱长为a ,则2618a =,故a =3322R a ==,其体积34932V R ππ==.【答案】92π2024高考数学专项立体几何系统班7、外接球与内切球【提炼】正方体棱长a 与其外接球半径R 之间的关系为32R =.2.(★★★)如图,在等腰梯形ABCD 中,22AB DC ==,60DAB ∠=︒,E 为AB 中点,将ADE 与BEC 分别沿ED ,EC 向上折起,使点A ,B 重合于点P ,则三棱锥P DCE -的外接球的体积为()【解析】由题意,可将平面图形等腰梯形ABCD 补全为正三角形FAB ,如图,那么在完成题干所描述的翻折后,还可将CDF △沿着CD 翻折,使得点F 也与点P 重合,显然此时得到的是一个棱长为1的正四面体,即三棱锥P DCE -是棱长为1的正四面体,其外接球半径R =343V R π==.【答案】C【提炼】正四面体的棱长为a ,则其外接球半径为64a ,内切球半径为612a ,证明方法可参考附赠的小册子《高考数学常用二级结论》.3.(★★)长方体的长,宽,高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为______.【解析】长方体的外接球半径R =,其中a ,b ,c 分别为长、宽、高,故R =O 的表面积2414S R ππ==.【答案】14π【提炼】设长方体的长、宽、高分别为a ,b ,c ,则其外接球半径2R =4.(★★)已知底面边长为1的正四棱柱的各顶点均在同一个球面上,则该球的体积为()A.323π B.4π C.2π D.43π【解析】首先得知道什么是正四棱柱,它指的是底面为正方形、侧棱与底面垂直的四棱柱,也是一种特殊的长方体,高考这种名词都是直接给,必须清楚其结构特征.外接球半径1R ==,故该球的体积34433V R ππ==.【答案】D5.(★★)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π【解析】设正四棱柱底面边长为a ,则2416a =,即2a =,其外接球的半径2242R ==,故所求球的表面积2424S R ππ==.【答案】C 6.(★★★)一个正四棱柱的各个顶点在一个直径为2的球面上,如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为______cm 2.【解析】设正四棱柱的高为h cm ,则1112=,故h =,即该棱柱的表面积(2S =+cm 2.【答案】2+题组二7.(★★★)已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若3AB =,4AC =,AB AC ⊥,112AA =,则球O 的半径为()B. C.132D.【解析】这道题可能不少同学会有这么一个困惑,就是题干没给出三棱柱111ABC A B C -为直三棱柱,是不是题干有问题呢?当然不是,事实上,斜棱柱是没有外接球的,所以题干的说法本身就隐含了三棱柱111ABC A B C -为直三棱柱这一条件.本题的直三棱柱可通过补形为长方体来计算外接球半径,如图,三棱柱111ABC A B C -与长方体有相同的外接球,该球的半径为34121322R ==.【答案】C 8.(★★★)3______.【解析】本模型一般称为墙角三棱锥,可补形为正方体(或长方体)来处理.如图,将三棱锥B ACD -补全为正方体,并放到了球体之中,可以看到二者有相同的外接球,正方体棱332R =,故外接球表面积249S R ππ==.【答案】9π【提炼】三条侧棱两两垂直的三棱锥(墙角三棱锥)可补形为长方体或正方体来计算外接球半径.题组三9.(★★★)设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为()A.2a π B.273a π C.2113a π D.25a π【解析】如图,设G 为ABC △的中心,ABC △外接圆半径233323r AG ==⨯=,1122a OG AA ==,球的半径22712R r OG a =+,故球的表面积22743S R a ππ==.【答案】B【提炼】①设直三棱柱底面外接圆半径为r ,高为h ,则其外接球半径222h R r ⎛⎫=+ ⎪⎝⎭;②关键是计算底面三角形外接圆半径,对于直角三角形,外接圆半径等于斜边长的一半,若是倍,等于高的23倍;若是普通的三角形,则可利用正弦定理计算外接圆半径.10.(★★★)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA -==,120BAC ∠=︒,则此球的表面积等于______.【解析】如图,在ABC △中,由余弦定理得222122222122BC ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭,解得BC =.由正弦定理得42sin BC r BAC ==∠,解得2r =,故1112OG AA ==,所以球的半径R ==,故球的表面积2420S R ππ==.【答案】20π题组四11.(★★★)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC -体积的最大值为()A. B. C. D.【解析】如图,先计算ABC △外接圆的半径r ,设ABC △边长为a .则2122a ⋅⋅=,解得6a =,所以62sin 60r =︒,解得r =,所以2OG ==,当D 点位于GO 延长线上时,三棱锥D ABC -的高最大,底面积不变,此时体积最大,最大值为()1243V =⨯+=【答案】B【提炼】本题三棱锥D ABC -的体积最大时,D ABC -是正三棱锥,正三棱锥外接球的计算问题,解题的关键是构建AOG △,在这个三角形中,满足222OA AG OG =+,即222R r d =+,其实这就是前一小节的平面截球模型,只要是正棱锥,都可以采用这个办法处理.12.(★★★)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A.814πB.16πC.9πD.274π【解析】如图,由题意,得14PO =,1AO =设外接球的半径为R ,则OA OP R ==,故14OO R =-.在1OO A △中,22211AO OO AO +=,即()2224R R +-=,解得94R =,故该球的表面积28144S R ππ==.【答案】A【提炼】正四棱锥外接球的有关计算,关键是构建1AOO ,在这个三角形中,利用22211OA AO OO =+建立等量关系,其实就是平面截球模型的处理方法.13.(★★★)正四棱锥S ABCD -点S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为_____.【解析】解法1:如图1,设正方形ABCD 的中心为1O ,由题意,11AO =,11SO =.设正四棱锥外接球球心为O ,半径为R ,则OA R =,11OO R =-,在1AOO 中,22211OO AO AO +=,故()2211R R -+=,解得1R =,即外接球体积为34433V R ππ==.解法2:设正方形ABCD 的中心为1O ,由题意,11AO =,11SO ==,因为11SO AO =,所以1O 即为球心,球的半径为1,体积34433V R ππ==,本题实际的图形是图2.【答案】43π14.(2021·全国甲卷·理·11·★★★)已知A ,B ,C 是半径为1的球O 的球面上的三个点,且AC BC ⊥,1AC BC ==,则三棱锥O ABC -的体积为()A.212B.312C.24D.34【解析】如图,由题意,2AB =,设D 为ABC △的外心,则1222AD AB ==,2222OD OA AD =-=,所以1112211332212O ABC ABC V S OD -=⋅=⨯⨯⨯⨯ .【答案】A题组五15.(★★)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.34πC.2π D.4π【解析】如图,由题意得1OA =,112OO =,故132O A =,圆柱体积233124V ππ⎛⎫=⋅= ⎪ ⎪⎝⎭.【答案】B【提炼】圆柱外接球半径222h R r ⎛⎫=+ ⎪⎝⎭,其中r 为底面圆半径,h 为圆柱的高.16.(★★★★)如图,半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是______.【解析】设圆柱的底面半径为r ,高为h ,则2224h r R rh +=≥,当且仅当2h r =时等号成立,故圆柱的侧面积2S rh π=的最大值为22R π,此时球的表面积与圆柱的侧面积之差为222422R R R πππ-=.【答案】22R π题组六17.(★★)正方体的内切球与其外接球的体积之比为()A. B.1:3C.1:D.1:9【解析】设正方体的棱长为a ,则其内切球、外接球的半径分别为12aR =,2R =,故正方体的内切球与其外接球的体积之比3113224343R V V R ππ==.【答案】C【提炼】设正方体的棱长为a ,则其内切球的半径2a R =.18.(★★)如图,圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是______.【解析】如图,设球的半径为R ,则213223423V R R V R ππ⋅==.【答案】3219.(2020·新课标Ⅲ卷·理·15·★★★)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_______.【解析】如图,该圆锥内半径最大的球即圆锥的内切球,设其半径为R ,则OB OG R ==,1AB AG ==.由题意得PG =OP R =-,2PB PA AB =-=.在POB 中,222OB PB OP =+,故()224R R +=,解得22R =,即球的体积3433V R π==.【答案】2320.(★★★★)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球.若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是()A.4π B.92π C.6π D.323π【解析】要解决这道题,得先搞清楚一件事,那就是最大的球到底是和棱柱的侧面相切,还是与底面相切?如图,可求得底面直角三角形的斜边10AC =,将底面Rt ABC △单独拿出来分析其内切圆半径r ,图中BP NQ r ==,故8PC r =-,即8CM PC r ==-,PN BQ r ==,故6AQ r =-,即6AM AQ r ==-,所以8614210AC CM AM r r r =+=-+-=-=,解得2r =,由123r AA >=知最大球的半径为32,体积3439322V ππ⎛⎫=⨯=⎪⎝⎭.【答案】B题组七21.(★★★)已知A,B是球O的球面上两点,90AOB∠=︒,C为该球面上的动点.若三棱锥O ABC-体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π【解析】设球O的半径为R,当点C位于如图所示位置(OC⊥平面AOB)时,三棱锥O ABC-的体积最大,最大值为321136326RR R⨯⨯==,即6R=,故球O的表面积24144S Rππ==.【答案】C22.(★★★)已知三棱锥S ABC-的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA AC=,SB BC=,三棱锥S ABC-的体积为9,则球O的表面积为________.【解析】如图,由题意知,SAC△,SBC△都是以SC为斜边的等腰直角三角形,设球O的半径为R,故31129323S ABCRV R R R-=⋅⋅⋅⋅==,即3R=,故球O的表面积2436S Rππ==.【答案】36π第8讲经典模型之对棱相等知识与方法四面体ABCD 中,AB CD m ==,AC BD n ==,AD BC t ==,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类四面体的外接球问题.如图,设长方体的长宽高分别为a 、b 、c ,则222222222a b t b c n a c m ⎧+=⎪+=⎨⎪+=⎩,三式相加可得2222222m n t a b c ++++=,而显然四面体和长方体有相同的外接球,设外接球半径为R ,则22224a b c R ++=,所以R =.典型例题【例题】四面体ABCD中,AB CD ==AC BD ==,5AD BC ==,则该四面体外接球的体积为_______.【解析】由题意,四面体ABCD是对棱相等模型3464233R V R π⇒===.【答案】3变式1三棱锥A BCD -中,6AB CD ==,5AC BD AD BC ====,则该三棱锥外接球表面积为()C.432π D.43π【解析】由题意,四面体ABCD是对棱相等模型24432R S R ππ⇒====.【答案】D 变式2A 、B 、C 、D四点在半径为2的球面上,且5AC BD ==,AD BC ==,AB CD =,则四面体ABCD 的体积为______.【解析】由题意,四面体ABCD 是对棱相等模型,设AB CD x ==,则R x ==ABCD补全为如图所示的长方体,设长方体的长、宽、高分别为a 、b 、c ,则222222413425a b b c a c ⎧+=⎪+=⎨⎪+=⎩,解得:453a b c =⎧⎪=⎨⎪=⎩,所以四面体ABCD 的体积1134543452032V =⨯⨯-⨯⨯⨯⨯⨯=.【答案】20强化训练1.(★★★)四面体ABCD中,AB CD ==AC BD ==,AD BC ==,则四面体ABCD 外接球的表面积为()A.25πB.45πC.50πD.100π【解析】由题意,四面体ABCD是对棱相等模型,2524502R S R ππ====.【答案】C2.(★★★)半径为1的球面上有不共面的A 、B 、C 、D 四点,且AB CD x ==,BC AD y ==,AC BD z ==,则222x y z ++=()A.16B.8C.4D.2【解析】由题意,四面体ABCD是对棱相等模型,22218R x y z =⇒++=【答案】B3.(★★★)四面体ABCD 中,5AB CD ==,AC BD ==,AD BC ==接球的半径为()A.2B. C.132 D.13【解析】由题意,四面体ABCD是对棱相等模型,132R =【答案】C4.(★★★)在四面体ABCD 中,2AB CD ==,AC BD AD BC ====接球的表面积为_______.【解析】由题意,四面体ABCD是对棱相等模型,2144R S R ππ==⇒==【答案】4π5.(★★★★)在三棱锥P ABC -中,2PA BC ==,PB AC =,PC AB =,且4PB PC ⋅=,则三棱锥P ABC -的外接球的表面积的最小值为________.【解析】设PB AC x ==,PC AB y ==,则4xy =,所以三棱锥P ABC -的外接球半径62R =≥,当且仅当2x y ==时取等号,所以三棱锥P ABC -的外接球的表面积的最小值为246ππ⨯=⎝⎭.【答案】6π6.(★★★★)四面体ABCD 的顶点都在球O 的表面上,4AB BC CD DA ====,AC BD ==,E 为AC 中点,过点E 作球O 的截面,则截面面积的最大值与最小值之比为()A.5:42D.5:2【解析】四面体ABCD是对棱相等模型,所以R =,将四面体ABCD 放入长方体如图,截面面积的最大值为215S R ππ==,当截面面积最小时,截面与OE 垂直,其中O 为球心,设FA a =,FB b =,FC c =,则222222216182216a a b a c b OE b r c b c =⎧⎧+=⎪⎪+=⇒=⇒=⇒=⎨⎨⎪⎪=+=⎩⎩,即截面面积的最小值为222S r ππ==,故12:5:2S S =.【答案】D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧用补形法解平面几何题
王立文王兴林
补形法就是根据题设的条件和图形,经过观察、分析和联想,运用添加辅助线的方法,将其拓展为范围更广的、其特征更明显、更为熟悉的几何图形,从而沟通条件和结论之间的联系.下面就补形法,谈谈它在解平面几何题中的应用.
一、补成直角三角形
例1如图1,四边形ABCD中,∠A=60°,∠B=∠D=90°,CD=1,AB=2,求BC、AD的长。
解:延长BC交AD的延长线于E。
∵∠A=60°,∠B=90°,
∴∠E=30°
在△CED中,
∵∠CDE=∠ADC=90°,CD=1,
∴CE=2CD=2,DE=。
在△AEB中,同理有:AE=2AB=4,。
∴BC=BE-EC=2-2,
AD=AE-DE=4-。
二、补成等腰三角形
例2已知:如图2,△ABC中,,∠ABC的平分线交AC于E,CD⊥BE 于D,求证:BE=ED。
证明:延长BA交CD的延长线于F。
易证△BCF是等腰三角形(ASA)。
∴。
∵,
∴。
作DG∥CA交BF于点G。
∴,
∴BE=ED。
三、补成等边三角形
例3如图3,凸五边形ABCDE,有∠A=∠B=120°,EA=AB=BC=2,CD=DE=4,求这个五边形的面积。
简解延长DE、BA相交于K,延长DC、AB相交于M。
易知△DKM为等边三角形。
S
五边形ABCDE =S
等边三角形DKM
-2S
等边三角形AKE
=
四、补成平行四边形
例4如图4,已知六边形ABCDEF中,若∠A=∠B=∠C=∠D=∠E=∠F=120°,且AB+BC=11,AF-CD=3,求BC+DE的长。
解:延长FA、CB交于点P,延长CD、FE交于点Q。
∵∠A=∠B=120°,
∴∠PAB=∠PBA=60°,
∴∠P=60°,
∴△ABP是等边三角形。
同理可得:△DEQ是等边三角形。
∴∠P=∠Q=60°。
∵∠C=∠F=120°,
∴四边形PCQF为平行四边形。
∴PF=CQ。
于是PA+AF=CD+DQ,
∴AF-CD=DQ-PA=DE-AB。
∵AF-CD=3,∴DE-AB=3。
∵AB+BC=11,
∴BC+DE=14。
五、补成矩形
例5如图5,在四边形ABCD中,∠BCD=∠CDA=120°,BC=5,CD=4,DA=6,求AB的长。
解:过D作BC延长线的垂线,垂足为M,过点A作MD延长线的垂线,垂足为N,过B作NA延长线的垂线,垂足为P,则四边形PBMN为矩形。
由已知及含30°角的直角三角形的性质。
又∵CM=2,DM=,AN=3,。
∴AP=5+2-3=4。
BP=DM=DN=。
∴。
六、补成正方形
例6在△ABC中,AD⊥BC,∠BAC=45°,BD=2cm,CD=3cm,求△ABC的面积。
解:如图6,作△ABD,△ACD关于AB、AC对称的△ABE、△ACH,延长FB、HC 交于F,则四边形AHFE是正方形。
设AD=x,知正方形的边长等于x,CF=HF-CH=x-3,BF=EF-BE=x-2。
在Rt△BCF中,
,
∴,
解得x=6。
=·AD
∴S
△ABC
七、补成圆形
例7已知:如图7,在四边形ABCD中,AB∥DC,AB=AC=AD=3,BC=2,求对角线BD的长。
解:以A为圆心,AB长为半径作⊙A。
∵AB=AC=AD=3,
∴C、D两点也在⊙A上。
延长BA交⊙A于E,
则BE=2AB=6。
∵AB∥DC,
∴。
∴DE=BC=2。
又∵BE为⊙A的直径,
∴∠BDE=90°。
∴BD=。
年级初中学科数学版本期数
内容标题巧用补形法解平面几何题
分类索引
号
G.622.46 分类索引描述辅导与自学
主题词巧用补形法解平面几何题栏目名
称
学法指导
供稿老师审稿老
师。
