机器人关节的变换1点的旋转变换

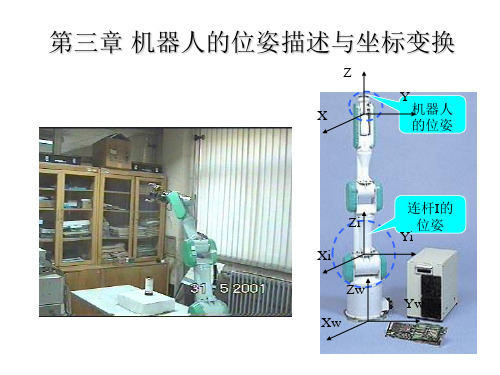
机器人的位姿描述与坐标变换

0
1
0
⎥ ⎥
⎢⎣− sinθ 0 cosθ ⎥⎦
Zi Zj
θ
θ Xi
Xj
Yi Y j
⎡cosθ − sinθ 0⎤
j i
R(Zi
,θ
)
=
⎢⎢sinθ
cosθ
0⎥⎥
⎢⎣ 0
0 1⎥⎦
Zi Zj
θ
Xi Xj
Yj
θ
Yi
⎡1 0
0⎤
j i
R(
X
i
,θ
)
=
⎢⎢0
cosθ
−
sinθ
⎥ ⎥
⎢⎣0 sinθ cosθ ⎥⎦
￥￥假设机器人的连杆和关节都是刚体￥￥
位置矢量
⎡x0 ⎤
P o '
o
=
⎢ ⎢
y0
⎥ ⎥
⎢⎣ z0 ⎥⎦
Z b Z'
O' Y' t n X' O
X Y
姿态矢量
O' O
R
=
[
O' O
X
OO'Y
⎡cos(∠X ' X )
O' O
Z
]3×3
=
⎢ ⎢
cos(∠X
'Y
)
⎢⎣cos(∠X ' Z )
单位主矢量
cos(∠Y ' X ) cos(∠Y 'Y ) cos(∠Z ' Z )
cos(∠Z ' X )⎤
cos(∠Z
'Y
)
⎥ ⎥
cos(∠Z ' Z ) ⎥⎦
姿态矩阵R的特点：

第四章(机器人学动力学)

机器人动力学

第四章机器人静力学和动力学
静力学和动力学分析，是机器人操作机设计和动态性能分析的基础。特别是动力学分析，它还是机器人控制器设计、动态仿真的基础。机器人静力学研究机器人静止或缓慢运动式，作用在机器人上的力和力矩问题。特别是当手端与环境接触时，各关节力（矩）与接触力的关系。机器人动力学研究机器人运动与关节驱动力（矩）间的动态关系。描述这种动态关系的微分方程称为动力学模型。由于机器人结构的复杂性，其动力学模型也常常很复杂，因此很难实现基于机器人动力学模型的实时控制。然而高质量的控制应当基于被控对象的动态特性，因此，如何合理简化机器人动力学模型，使其适合于实时控制的要求，一直是机器人动力学研究者追求的目标。 2
3
按静力学方法，把这些力、力矩简化到 Li 的固联坐标系 oi xi yi zi ，可得： Fi Fi 1 G i M i M i 1 r i F i 1 r Ci G i i 1 或 i i i 0
4.1 机器人静力学
一、杆件之间的静力传递在操作机中，任取两连杆 Li， i 1 。设在杆 Li 1上的 Oi 1 点 L 作用有力矩 M i 1和力 F i 1；在杆 Li 上作用有自重力 G i 〔过质 r 心 Ci ）；i 和 rCi 分别为由 Oi 到 Oi 1 和 Ci 的向径。 M i 1 F i 1
18
4.4.4 牛顿——欧拉法基本运动方程
刚体的运动可分解为随质心的移动和绕质心的转动。借助于杆件运动学知识，我们把达朗贝尔原理用于每个杆件，描述机器人各杆件的运动。达朗贝尔原理可应用于任意瞬时，它实质上是牛顿第二运动定律的一种变型，可表示为： d mi vi ( Fi ) Fi mi vi 牛顿定理 : dt d I ii Ni I ii i ( I ii ) 欧拉方程 : ( Ni ) dt 式中：mi — 杆i 质量； Fi — 杆i上所有外力合力； N i — 杆i上所有外力对质心的合力矩；

(优选)机器人位姿描述详解.

R
B
p
A B
R
B
p
A p C p A pCo
Ap
A B
R
B
p
A pBo
24
旋转部分平移部分
三、齐次坐标和齐次变化
齐次坐标
a P b
c
直角坐标
x
P
y z
齐次坐标
非零的比例因子
a x
b y
c z
25
1）点的齐次坐标：
P x y z T
0
P 2 3 4 1T , P 4 6 8 2T
5
2、方位的描述
为了规定空间某刚体B的方位，设一坐标系{B}与此刚体固连。用坐标系{B}的三个单位主矢量 , xB, y相B 对zB 于{A}的方向余弦组成的3x3矩阵来表示刚体B相对于坐标系{A}的方位。
BAR AxB A yB AzB
r11 r12 r13
A B
R
r21
r22
r23
A p BAR B p cos( yA, xB )
cos( yA, yB )
cos(
yA
,
zB
)
pBy
18
cos(zA, xB ) cos(zA, yB ) cos(zA, zB ) pBz
绕一个坐标轴旋转的转动矩阵
ZA ZB
q q
XA
X
B
1）RX
YB YA
ZA ZB
ZA ZB
q
已知点P在B坐标系的坐标：
B P [x B y B zB ]T
求点P在A坐标系的坐标：
AP [x A y A zA ]T
15
ZB
ZA

任务1 工业机器人手动操作基础知识

5加载工业机器人工件
选择“导入模型库”，“设备”“training object”中的curving thing，见图，添加后工件，如图所示。
工件离机器人较远，显示工业机器人的工作区域操作方法为：鼠标右键单击布局中的“IRB120_3_58_01”，选择“显示机器人工作区域”，其白色空间内为机器人可达区域，如图所示。
工件不在工业机器人的工作区域，需设置curving thing的位置，其操作方法为：鼠标右键单击curving thing，选择设定位置，如图411所示。在弹出的对话框中设置其合适位置，设定完毕后，点击应用，再点击关闭。
注意：设定位置时，以大地坐标为参考坐标，坐标原点在机身底座的中心，xyz方向以图箭头所指示。至此一个最小的工业机器人仿真系统建立完成，如图所示。
转化为手动模式后，点击左上角主菜单，如图所示
在弹出的如图所示的对话框中，点击“控制面板”。
在弹出的如图所示的对话框中，点击“语言”菜单，从如图所示的界面中选择想要更改的语言
点击“确定”后，在弹出的“重启 FlexPendant”对话框中点击“是”，重启后生效。
1单轴运动
点击左上角主菜单，点击手动操纵，点击“Enable”，如图 4-35所示使使能器工作，变为绿色后机器人将处于电机开启状态。
6.创建控制系统
在“基本”功能选项卡，单击“机器人系统”的“ 从布局”，如图所示。
设定好系统名称和位置，注意路径建议不要出现中文，选择RobotWare（如果安装有多个，选择对应的RobotWare版本），单击“下一个”，如图所示。
单击“选项”，如图所示。
在弹出如图所示的对话框中，作以下修改：
“840-2 PROFIBUS Anybus Device”。

第3章机器人位姿的数学描述与坐标变换

x=a(1-cos) , y=a(1-sinθ)
第3章机器人位姿的数学描述与坐标变换
3.1 机器人位姿的数学描述
#假设机器人的连杆和关节都是刚体（1）首先，建立一个参考坐标系；（2）然后，在刚体上任意建立一个刚体坐标系。
Z Z'
O' Y'
O
X'
X Y
第3章机器人位姿的数学描述与坐标变换
刚体位置：
,
)
=
？
j i
R(,q
,
)
=
R(Z
,
)
R(Y
,q
)R(Z
,
)
绕动坐标轴依次转动时，每个旋转矩阵要从左往右乘。
Z2
Zj
Zi (Z1)
q
q
Yj
（Y2 )
q Y1
Yi
Xi
X1 X2 X j
第3章机器人位姿的数学描述与坐标变换
cos − sin 0 cosq 0 sinq cos − sin 0
R(Z
i
,q
)
=
s
inq
cosq
0
0
0 1
Zi Zj
q Xi
Xj
Yj q
Yi
第3章机器人位姿的数学描述与坐标变换
1 0
0
j i
R(
X
i
,q
)
=
0
cosq
−
s in q
0 sinq cosq
cosq 0 sinq
j i
R(Yi
,q
)
=
0
1
0
− sinq 0 cosq

3机器人的位姿描述与坐标变换

利用旋转矩阵的正交性质:
假设：
整理得：
旋转变换通式
讨论：
（1）
（2）
（3）
例：坐标系B原来与A重合，将坐标系B绕过原点O的轴线
转动
，求旋转矩阵
解答：
1）
2）
3）带入旋转通式得：
2、等效转轴与等效转角
转轴和转角
旋转矩阵
1
2？
1）将方程两边矩阵的主对角线元素分别相加，则
2）将方程两边矩阵的非对角线元素成对相减得：
►绕多个坐标轴旋转的转动矩阵
1）、绕固定坐标系旋转
2）、绕运动坐标系旋转
ZYZ欧拉角
注意：多个旋转矩阵连乘时，次序不同则含义不同。1）绕新的动坐标轴依次转动时，每个旋转矩阵要从左往右乘，即旋转矩阵的相乘顺序与转动次序相同；2）绕旧的固定坐标轴依次转动时，每个旋转矩阵要从右往左乘，即旋转矩阵的相乘顺序与转动次序相反。
解：
1）
2）
Z
i
X
i
Y
i
P
坐标系j由坐标系i旋转而成
求点P在i坐标系的坐标：
已知点P在j坐标系的坐标：
P
☺
►姿态矢量矩阵
坐标系j相对于i的方位
旋转矩阵的性质：
旋转矩阵
►绕一个坐标轴旋转的转动矩阵
1）RX
2）RY
3）RZ
转动矩阵的特点：(1) 主对角线上有一个元素为1，其余均为转角的余弦/正弦；(2) 绕轴转动的次序与元素1所在的行、列号对应；(3) 元素1所在的行、列，其它元素均为0；(4) 从元素1所在行起，自上而下，先出现的正弦为负，后出现的为正，反之依然。
2、变换矩阵T的相乘 ★矩阵相乘的顺序一般不可换，特殊可换的情况为变换都是同参考系下的平移或绕同一坐标轴的旋转。

第03章机器人的运动学和动力学

教案首页课程名称农业机器人任课教师李玉柱第3章机器人运动学和动力学计划学时 3教学目的和要求：1.概述，齐次坐标与动系位姿矩阵，了解平移和旋转的齐次变换；2.机器人的运动学方程的建立与求解*；3.机器人的动力学*重点：1.机器人操作机运动学方程的建立及求解；2.工业机器人运动学方程3.机器人动力学难点：1. 机器人动力学方程及雅可比矩阵基本原理思考题：1.简述齐次坐标与动系位姿矩阵基本原理。

2.连杆参数及连杆坐标系如何建立？3.机器人动力学方程及雅可比矩阵基本原理是什么？第3章机器人运动学和动力学教学主要内容：3.2 齐次坐标与动系位姿矩阵3.3 齐次变换3.4 机器操作机运动学方程的建立与求解3.5 机器人运动学方程3.6 机器人动力学本章将主要讨论机器人运动学和动力学基本问题。

先后引入了齐次坐标与动系位姿矩阵、齐次变换，通过对机器人的位姿分析，介绍了机器人运动学方程；在此基础上有对机器人运动学方程进行了较为深入的探讨。

3.1 概述机器人，尤其是关节型机器人最有代表性。

关节型机器人实质上是由一系列关节连接而成的空间连杆开式链机构，要研究关节型机器人，必须对运动学和动力学知识有一个基本的了解。

分析机器人连杆的位置和姿态与关节角之间的关系，理论称为运动学，而研究机器人运动和受力之间的关系的理论则是动力学。

3.2 齐次坐标与动系位姿矩阵3.2.1 点的位置描述在关节型机器人的位姿控制中，首先要精确描述各连杆的位置。

为此，先定义一个固定的坐标系，其原点为机器人处于初始状态的正下方地面上的那个点，如图3-1（a）所示。

记该坐标系为世界坐标系。

在选定的直角坐标系{A}中，空间任一点P的位置可以用3×1的位置向量A P表示，其左上标表示选定的坐标系{A}，此时有A P=XYZ P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦式中：P X、P Y、P Z—点P在坐标系{A}中的三个位置坐标分量，如图3-1（b）。

3.2.2 齐次坐标将一个n维空间的点用n+1维坐标表示，则该n+1维坐标即为n维坐标的齐次坐标．．．．。

机器人学--坐标转换

1
p px py pz T ,n nx ny nz T ,o ox oy oz T ,a ax ay az T
Robotics 数学基础
2.4 物体的变换及逆变换
3.变换方程初步 {B}:基坐标系 {T}:工具坐标系 {S}:工作台坐标系 {G}:目标坐标系
或工件坐标系满足方程
A P
1
A B
R
0
A
PB 1
0
B P
1
P点在{A}和{B}中的位置矢量分别增广为:
(2-14)
AP Ax A y Az 1T ,BP Bx B y Bz 1T
而齐次变换公式和变换矩阵变为:
A P ABTB P,
ABT
A B
R
0
A
PB0 1
(2-15,16)
Robotics 数学基础
ny
oy
ay
0
fx
f
yvers
f z s
fy fyvers c
fz fyvers fxs 0
nz 0
oz 0
az 0
0 1
fx
f z v ers 0
f y s
fy fzvers fxs 0
fz fzvers c 0
0 1
将上式对角线元素相加,并简化得
nx
oy
az
(
f
2 x
f
2 y
f
2023最新整理收集 do
something
机器人技术数学基础
Mathematic Preparation for Robotics
2.1 位置和姿态的表示 2.2 坐标变换 2.3 齐次坐标变换 2.4 物体的变换及逆变换 2.5 通用旋转变换

极坐标系中的旋转变换

极坐标系中的旋转变换在数学中，极坐标系是一种用来描述平面上点的坐标系，它由极径和极角两个参数组成。

而旋转变换则是指将一个图形或点绕着某个中心旋转一定角度的变换。

本文将以极坐标系中的旋转变换为主题，探讨其原理、应用以及相关的数学概念。

一、极坐标系的基本概念极坐标系中，一个点的坐标由极径（r）和极角（θ）两个参数确定。

极径表示点到原点的距离，极角表示该点与极坐标系的极轴之间的夹角。

极径可以是正数、零或负数，极角的取值范围通常是[0, 2π)或[-π, π)。

二、极坐标系中的旋转变换旋转变换是指将一个图形或点绕着某个中心旋转一定角度的变换。

在极坐标系中，我们可以通过旋转变换来改变一个点的极角，从而改变其位置。

对于一个点P(r, θ)，我们可以将其绕着原点O旋转α角度得到一个新的点P'(r, θ + α)。

这里，α是旋转的角度，可以是正数也可以是负数。

当α为正数时，点P'相对于点P是顺时针旋转的；当α为负数时，点P'相对于点P是逆时针旋转的。

三、极坐标系中的旋转公式在极坐标系中，我们可以通过旋转公式来计算旋转后的坐标。

假设点P(r, θ)绕着原点O旋转α角度后得到点P'(r', θ')，那么我们有以下公式：r' = rθ' = θ + α其中，r表示点P到原点O的距离，θ表示点P与极坐标系的极轴之间的夹角，r'表示点P'到原点O的距离，θ'表示点P'与极坐标系的极轴之间的夹角。

四、极坐标系中旋转变换的应用极坐标系中的旋转变换在许多领域都有广泛的应用。

以下是其中几个常见的应用：1. 图形变换：将一个图形绕着某个中心旋转一定角度，可以改变图形的位置和方向。

例如，在计算机图形学中，可以通过旋转变换来实现图像的旋转效果。

2. 机器人运动：在机器人技术中，旋转变换可以用来控制机器人的运动。

通过旋转机器人的关节，可以使机器人朝着特定的方向移动。

发那科机器人操作说明书

）以进行动作指令的示教。 ? F5“点修正”（位置修改），用于对已经示教的位置数据进行再示
教。
动作类型指定向指定位置的移动轨迹。动作类型有：不进行轨迹控制、姿态控制的直线动作、以及圆弧动作。 ? 关节动作（ J） ? 直线动作（包含旋转移动）（ L） ? 圆弧动作（ C）
--- 10 -精选3.程序创建记录程序设定程序详细信息修改标准指令语句示教动作指令示教控制指令
记录程序
记录程序录时，创建一个新的空程序。
设定程序详细信息时，设定程序的属性。
修改标准指令语句时，重新设定动作指令的示教时要使用的标准指令。
示教动作指令时，对动作指令和动作附加指令进行示教。示教控制指令时，对对码垛指令和控制指令进行示教。
程序的创建或修改，通过示教操作盘进行操作。要通过示教盘进行程序创建或修改，通常情况下示教器应设定在有效状态。
输入程序名设定程序详细信息
记录程序时，输入程序名，记录程序。程序名由 8 个字符以下的英文数字、机构等构成，必须与其他程序分开来。
输入程序名的方法有 3 种。 Words（字）一最多可 5 个预约可以作为程序名的下的字（ PRG.MAIN.SUB和. TEST） .--
-5-
与执行相关的键而在机器人或空间上进行定义的位置坐标系统。坐标系有关节坐标系、
关节坐标系是设定在机器人的关节中的坐标系。关节坐标系中的机器人的位置和状态，以各关节的底座侧的关节坐标系为基准而确定。
? ? ? ?
横摆指令是使机器人执行横摆的指令。横摆指令有以下种类的指令。 Weave（模式） [i] （摆动（模式））指令 Weave（模式） [Hz， mm ， sec，sec]指令 Weave End（摆动结束）指令 Weave End[i](摆动结束 ) 指令使用横摆指令时，必须指定横摆模式。 SIN 型横摆

机器人技术基础[课后习题答案解析]

0.1简述工业机器人的定义，说明机器人的主要特征。

答：机器人是一种用于移动各种材料、零件、工具、或专用装置，通过可编程动作来执行种种任务并具有编程能力的多功能机械手。

1.机器人的动作构造具有类似于人或其他生物体某些器官〔肢体、感官等〕的功能。

2.机器人具有通用性，工作种类多样，动作程序灵活易变。

3.机器人具有不同程度的智能性，如记忆、感知、推理、决策、学习等。

4.机器人具有独立性，完整的机器人系统在工作中可以不依赖于人的干预。

0.2工业机器人与数控机床有什么区别？答：1.机器人的运动为开式运动链而数控机床为闭式运动链；2.工业机器人一般具有多关节，数控机床一般无关节且均为直角坐标系统；3.工业机器人是用于工业中各种作业的自动化机器而数控机床应用于冷加工。

4.机器人灵活性好，数控机床灵活性差。

0.5简述下面几个术语的含义：自有度、重复定位精度、工作X围、工作速度、承载能力。

答：自由度是机器人所具有的独立坐标运动的数目，不包括手爪〔末端执行器〕的开合自由度。

重复定位精度是关于精度的统计数据，指机器人重复到达某一确定位置准确的概率，是重复同一位置的X围，可以用各次不同位置平均值的偏差来表示。

工作X围是指机器人手臂末端或手腕中心所能到达的所有点的集合，也叫工作区域。

工作速度一般指最大工作速度，可以是指自由度上最大的稳定速度，也可以定义为手臂末端最大的合成速度〔通常在技术参数中加以说明〕。

承载能力是指机器人在工作X围内的任何位姿上所能承受的最大质量。

0.6什么叫冗余自由度机器人？答：从运动学的观点看，完成某一特定作业时具有多余自由度的机器人称为冗余自由度机器人。

0.7题0.7图所示为二自由度平面关节型机器人机械手，图中L1=2L2，关节的转角X围是0゜≤θ1≤180゜,-90゜≤θ2≤180゜,画出该机械手的工作X围〔画图时可以设L2=3cm〕。

1.1点矢量v为[10.0020.0030.00] T，相对参考系作如下齐次坐标变换：0.8660.5000.00011.0A= 0.5000.0000.8660.0000.0001.0003.09.0 0001写出变换后点矢量v的表达式，并说明是什么性质的变换，写出旋转算子Rot及平移算子Trans。

旋转的认识与旋转变换

旋转的认识与旋转变换旋转是我们生活中常见的一种运动形式，它可以描述物体在空间中围绕某个中心点旋转的情况。

在几何学和数学中，旋转不仅有着重要的理论意义，还被广泛应用于各个领域，如计算机图形学、物理学和工程学等。

本文将探讨旋转的认识以及旋转变换的相关内容。

一、旋转的认识1. 旋转的定义和特点在几何学中，旋转是指物体绕其自身或者其他某个中心点旋转的运动。

根据旋转轴的不同，我们可以将旋转分为二维旋转和三维旋转。

二维旋转通常是围绕平面上的某个点旋转，而三维旋转则涉及到绕一条指定轴旋转。

旋转的特点有以下几个方面：- 旋转是一种刚体运动，旋转后物体的内部结构保持不变；- 旋转是一种连续运动，物体在旋转过程中每一时刻都处于不同的位置和姿态；- 旋转可以是顺时针或逆时针方向的，根据旋转角度的正负确定。

2. 旋转的数学描述为了描述旋转，我们需要使用一些数学工具和概念。

在二维情况下，我们常用的是极坐标系。

极坐标系由中心点和极径组成，我们可以使用极坐标系中的角度来描述旋转的方向和角度。

在三维情况下，我们通常使用旋转矩阵或四元数来描述旋转。

旋转矩阵是一个3×3的矩阵，通过乘以旋转向量来实现旋转变换。

而四元数则是一种复数的扩展，可以用来表示旋转角度和旋转轴。

二、旋转变换1. 旋转变换的定义和应用旋转变换是指在空间中对物体进行旋转的变换操作。

它可以将一个初始位置的物体通过旋转操作转变为目标位置。

在计算机图形学中，旋转变换被广泛应用于三维模型的变换和动画效果的实现。

旋转变换的实现通常需要指定旋转角度和旋转轴。

通过将旋转矩阵或四元数应用于初始位置的顶点集合，我们可以得到旋转后的目标位置。

旋转变换可以用来实现物体的旋转、镜像效果的生成和动画的呈现等。

2. 旋转变换的数学表示旋转变换可以使用矩阵或四元数来表示。

以二维旋转变换为例，假设我们希望绕原点逆时针旋转一个角度θ，我们可以使用下面的旋转矩阵表示：[cos(θ) -sin(θ)][sin(θ) cos(θ)]对于三维情况，旋转矩阵为一个3×3的矩阵，具体表示方法较为复杂。

坐标变换

齐次变换具有较直观的几何意义，非常适合描述坐标系之间的变换关系。

另外，齐次变换可以将旋转变换与平移变换用一个矩阵来表达，关系明确，表达简洁。

所以常用于解决工业机器人运动学问题。

下面我们先介绍有关齐次坐标和齐次变换的内容。

2.2.1 点的位置描述如图2-1所示，在选定的三维空间直角坐标系{A}中，空间任一点P 的坐标可以用一个(3×1)列阵（或称三维列向量）Ap 表示，即：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=z y x p A(2-1)式中：X ，y ，z 是点P 在坐标系{A}中的三个坐标分量；Ap 的左上标A 代表选定的参考坐标系。

2.2.2 齐次坐标如果用四个数组成的(4×1)列阵（或称四维列向量）表示三维空间直角坐标系{A}中的点P ，即：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1z y x p(2-2)则定义列阵[x y z 1]T 为三维空间点P 的齐次坐标。

必须注意，齐次坐标的表示不是唯一的。

如果将列阵p 中的元素同乘一非零系数w 后，仍然代表同一点P ，即：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=w c b a z y x 1p(2-3)式中：x ＝a/w ，y ＝b/w ，z ＝c/w 。

2.2.3 坐标轴的描述如图2-2所示，i 、j 、k 分别是直角坐标系中X 、Y 、Z 坐标轴的单位矢量，若用齐次坐标来描述X 、Y 、Z 轴，则定义下面三个(4×1)列阵分别为单位矢量i 、j 、k （即X 、Y 、Z 坐标轴）的方向列阵。

i ＝[1 0 0 0]T ；j ＝[0 1 0 0]T ；k ＝[0 0 1 0]T 图2-2中所示矢量v 的单位矢量h 的方向列阵为：h ＝[a b c 0]T ＝[cos α cos β cos γ 0]T (2-4)式中，α、β、γ分别是矢量v 与坐标轴X 、Y 、Z 的夹角，0︒≤α≤180︒，0︒≤β ≤180︒，0︒≤γ ≤180︒。

机器人参考答案1

1.1 点矢量v 为]00.3000.2000.10[T ，相对参考系作如下齐次坐标变换：A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10000.9000.1000.0000.00.3000.0866.0500.00.11000.0500.0866.0 写出变换后点矢量v 的表达式，并说明是什么性质的变换，写出旋转算子Rot 及平移算子Trans 。

解：v ，=Av=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10000.9000.1000.0000.00.3000.0866.0500.00.11000.0500.0866.0⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡100.3000.2000.10=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡13932.1966.9 属于复合变换：旋转算子Rot （Z ，30̊）=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1000010000866.05.0005.0866.0 平移算子Trans （11.0，-3.0，9.0）=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10000.91000.30100.110011.2 有一旋转变换，先绕固定坐标系Z 0 轴转45̊，再绕其X 0轴转30̊，最后绕其Y 0轴转60̊，试求该齐次坐标变换矩阵。

解：齐次坐标变换矩阵R=Rot(Y ，60̊）Rot （X ，30̊）Rot(Z ，45̊）=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1000010000707.0707.000707.0707.010000866.05.0005.0866.000001100005.00866.000100866.005.0=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----10000433.0436.0436.005.0612.0612.00750.0047.0660.0 1.3 坐标系{B}起初与固定坐标系{O}相重合，现坐标系{B}绕Z B 旋转30̊，然后绕旋转后的动坐标系的X B 轴旋转45̊，试写出该坐标系{B}的起始矩阵表达式和最后矩阵表达式。

《机器人运动学》试题及答案

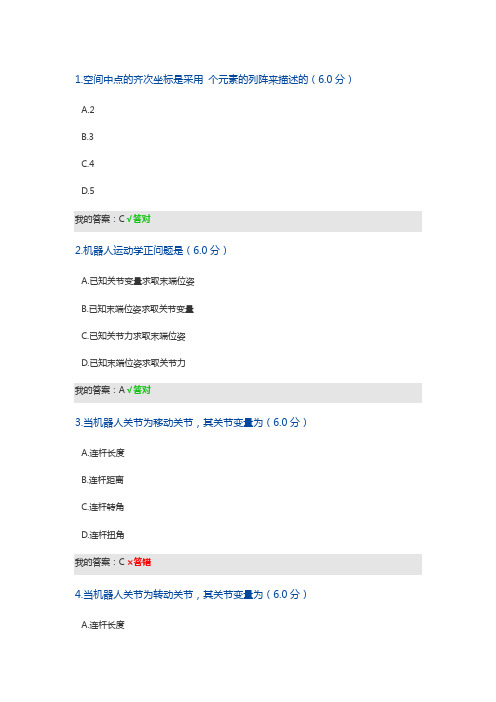
1.空间中点的齐次坐标是采用个元素的列阵来描述的（6.0分）A.2B.3C.4D.5我的答案：C√答对2.机器人运动学正问题是（6.0分）A.已知关节变量求取末端位姿B.已知末端位姿求取关节变量C.已知关节力求取末端位姿D.已知末端位姿求取关节力我的答案：A√答对3.当机器人关节为移动关节，其关节变量为（6.0分）A.连杆长度B.连杆距离C.连杆转角D.连杆扭角我的答案：C×答错4.当机器人关节为转动关节，其关节变量为（6.0分）A.连杆长度C.连杆转角D.连杆扭角我的答案：B×答错5.采用齐次法描述空间中任意矢量的方向，其最后一个元素为（6.0分）A.0B.1C.2D.3我的答案：A√答对1.机器人运动学正问题可用以（8.0分））A.求取机器人末端位姿B.求取机器人关节变量C.求取机器人工作空间D.用以实现机器人控制我的答案：BD×答错2.机器人连杆参数包括（8.0分））A.连杆长度B.连杆距离C.连杆转角我的答案：ABCD√答对3.机器人运动学逆问题可用以（8.0分））A.求取机器人末端位姿B.求取机器人关节变量C.求取机器人工作空间D.用以实现机器人控制我的答案：BD√答对4.齐次矩阵可用以描述（8.0分））A.一个坐标系相对于另一个坐标系的位姿B.刚体在空间中的位姿C.刚体的一系列运动D.关节与末端位姿的变换关系我的答案：AD×答错5.机器人关节变量一般为（8.0分））A.连杆长度B.连杆距离C.连杆转角D.连杆扭角我的答案：BC√答对1.机器人运动学用以建立末端位姿与关节变量之间的关系（6.0分）我的答案：正确√答对2.描述刚体位姿的齐次矩阵是一4*4的矩阵（6.0分）我的答案：正确√答对3.运动学正问题是已知机器人末端位姿求各关节运动变量（6.0分）我的答案：错误√答对4.在齐次变换中，如果相对于固定坐标系运动，需右乘变换算子（6.0分）我的答案：错误√答对5.连杆坐标系是建立在连杆上，与连杆固定连接的坐标系（6.0分）我的答案：正确√答对。

工业机器人考试题库附答案

工业机器人考试题库附答案一、判断题1．机械手亦可称之为机器人。

（Y）2．完成某一特定作业时具有多余自由度的机器人称为冗余自由度机器人。

（Y）3、关节空间是由全部关节参数构成的。

（Y）4、任何复杂的运动都可以分解为由多个平移和绕轴转动的简单运动的合成。

（Y）5、关节i的坐标系放在i-1关节的末端。

（N）6．手臂解有解的必要条件是串联关节链中的自由度数等于或小于6。

（N）7．对于具有外力作用的非保守机械系统，其拉格朗日动力函数L可定义为系统总动能与系统总势能之和。

（N）8．由电阻应变片组成电桥可以构成测量重量的传感器。

（Y）9．激光测距仪可以进行散装物料重量的检测。

（Y）10．运动控制的电子齿轮模式是一种主动轴与从动轴保持一种灵活传动比的随动系统。

（Y）11．谐波减速机的名称来源是因为刚轮齿圈上任一点的径向位移呈近似于余弦波形的变化。

（N）12．轨迹插补运算是伴随着轨迹控制过程一步步完成的，而不是在得到示教点之后，一次完成，再提交给再现过程的。

（Y）13．格林（格雷）码被大量用在相对光轴编码器中。

（N）14．图像二值化处理便是将图像中感兴趣的部分置1，背景部分置2。

（N）15．图像增强是调整图像的色度、亮度、饱和度、对比度和分辨率，使得图像效果清晰和颜色分明。

（Y）二、填空题1.机器人是指代替原来由人直接或间接作业的自动化机械。

2.在机器人的正面作业与机器人保持300mm以上的距离。

3.手动速度分为:微动、低速、中速、高速。

4.机器人的三种动作模式分为:示教模式、再现模式、远程模式。

5.机器人的坐标系的种类为:关节坐标系、直角坐标系、圆柱坐标系、工具坐标系、用户坐标系。

6.设定关节坐标系时，机器人的S、L、U、R、B、T各轴分别运动。

7.设定为直角坐标系时，机器人控制点沿X、Y、Z轴平行移动。

8.用关节插补示教机器人轴时，移动命令为MOVJ。

9.机器人的位置精度PL是指机器人经过示教的位置时的接近程度，可以分为9个等级，分别是PL=0，PL=1，PL=2，PL=3，PL=4，PL=5，PL=6，PL=7，PL=8。

坐标旋转变换公式

坐标旋转变换公式在计算机图形学和几何学中，坐标旋转变换公式是一种重要的数学工具，用于描述物体在平面上或空间中的旋转运动。

通过坐标旋转变换公式，我们可以将一个点或一组点绕某个轴进行旋转，从而实现模拟物体的旋转效果。

在本文中，我们将介绍二维和三维空间中的坐标旋转变换公式，以及如何利用这些公式进行旋转操作。

二维坐标旋转变换公式在二维空间中，我们常用的坐标旋转变换公式如下：对于一个点(x,y)，绕原点逆时针旋转$\\theta$角度后的新坐标(x′,y′)计算公式如下：$$ x' = x \\cdot \\cos(\\theta) - y \\cdot \\sin(\\theta) $$$$ y' = x \\cdot \\sin(\\theta) + y \\cdot \\cos(\\theta) $$其中，$\\theta$为旋转角度，在数学上通常以弧度为单位。

三维坐标旋转变换公式在三维空间中，坐标旋转变换稍显复杂，我们可以通过矩阵乘法的形式来描述旋转操作。

对于一个三维点(x,y,z)，围绕单位向量(a,b,c)与旋转角度$\\theta$进行旋转后的新坐标(x′,y′,z′)计算公式如下：$$ \\begin{bmatrix} x' \\\\ y' \\\\ z' \\end{bmatrix} = \\begin{bmatrix}\\cos(\\theta) + a^2(1-\\cos(\\theta)) & ab(1-\\cos(\\theta)) - c\\sin(\\theta) & ac(1-\\cos(\\theta)) + b\\sin(\\theta) \\\\ ab(1-\\cos(\\theta)) + c\\sin(\\theta) & \\cos(\\theta) + b^2(1-\\cos(\\theta)) & bc(1-\\cos(\\theta)) - a\\sin(\\theta)\\\\ ac(1-\\cos(\\theta)) - b\\sin(\\theta) & bc(1-\\cos(\\theta)) + a\\sin(\\theta) & \\cos(\\theta) + c^2(1-\\cos(\\theta)) \\end{bmatrix} \\cdot \\begin{bmatrix}x \\\\ y \\\\ z \\end{bmatrix} $$其中，(a,b,c)为单位向量，$\\theta$为旋转角度。

机器人现场编程-运动命令

动；如果指定的距离为负值，机器人向前移动或向工具坐标系Z轴的正方
向运动。
一、运动命令- JDEPART / LDEPART
示例:
JDEPART 80 LDEPART 2∗offset 机器人工具以关节插补动作、向工具坐标系-Z 方向上的80mm 处后退移动。机器人工具以直线插补动作，向工具坐标系-Z 方向上的2∗offset(200 mm，如果offset = 100)处后退移动。
起始点
JMOVE LMOVE
#a1 #a2
一、运动命令-C1MOVE / C2MOVE
#a1
# a2
起始点 # a3
LMOVE #a1 C1MOVE #a2 C2MOVE #a3
C1MOVE将机器人移动到圆弧轨迹的中间任意一点（不一定是中点）， C2MOVE将机器人移动至该圆弧轨迹的结束点。 C1MOVE 命令后必须跟有C1MOVE 或 C2MOVE 命令。C1MOVE 命令必须先于C2MOVE 命令。
指令格式：
DRAW
X 平移量, Y 平移量, Z 平移量, X 旋转量, Y 旋转量, Z 旋转量, 速度
TDRAW X 平移量, Y 平移量, Z 平移量, X 旋转量, Y 旋转量, Z 旋转量, 速度
功
能:机器人从当前位姿，以直线插补动作，以指定的速度，向X，Y，Z
轴方向上指定的距离处移动，并且绕各轴旋转指定的旋转量。 DRAW 命令按基础坐标系移动机器人
运动命令一运动命令基本运动命令jmove以关节各轴插补动作移动机器人lmove以直线插补动作移动机器人c1move以圆弧插补动作移动c2move以圆弧插补动作移动home移动到原点位姿delay停止机器人运动指定长度的时间一运动命令其他运动命令stable各轴不设置一致时轴一致停止机器人运动指定长度的时间