高中数学立体几何外接球7大模型
高中数学 立体几何 2.(第二次修订版)八个有趣模型——搞定空间几何体的外接球与内切球(教师版)

八个有趣模型——搞定空间几何体的外接球与内切球当讲到付雨楼老师于2018年1月14日总第539期微文章,我如获至宝.为有了教学的实施,我以付老师的文章主基石、框架,增加了我个人的理解及例题,形成此文,仍用文原名,与各位同行分享.不当之处,敬请大家批评指正.一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).初图1初图22.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法). 四、与台体相关的,此略. 五、八大模型第一讲 柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)图1-1图1-2图1-3图1-4方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32 解: 162==h a V ,2=a ,24164442222=++=++=h a a R ,π24=S ,选C ;(2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 π9 解:933342=++=R ,ππ942==R S ;(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .π36 解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1, 取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH , 则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,ΘBC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD , ∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, ΘMN AM ⊥,MN SB //,∴SB AM ⊥,ΘSB AC ⊥,∴⊥SB 平面SAC , ∴SA SB ⊥,SC SB ⊥,ΘSA SB ⊥,SA BC ⊥, ∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,(3)题-1(引理)AC(3)题-2(解答图)AC∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36. (4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( D )π11.A π7.B π310.C π340.D 解:在ABC ∆中,7120cos 2222=⋅⋅-+=οBC AB AB AC BC ,7=BC ,ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ,∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是 解:由已知得三条侧棱两两垂直,设三条侧棱长分别为c b a ,,(+∈R c b a ,,),则⎪⎩⎪⎨⎧===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S , (6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为解:3)2(2222=++=c b a R ,432=R ,23=Rπππ2383334343=⋅==R V 球,类型二、对棱相等模型(补形为长方体) 题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =) 第一步:画出一个长方体,标出三组互为异面直线的对棱; 第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=, (6)题图(6)题直观图P图2-1补充:图2-1中,abc abc abc V BCD A 31461=⨯-=-. 第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .思考:如何求棱长为a 的正四面体体积,如何求其外接球体积?例2(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解:对棱相等,补形为长方体,如图2-1,设长宽高分别为c b a ,,,110493625)(2222=++=++c b a ,55222=++c b a ,5542=R ,π55=S(1)题图B(2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为 .π229 解:如图2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S (3)正四面体的各条棱长都为2,则该正面体外接球的体积为 (3)解答题解:正四面体对棱相等的模式,放入正方体中,32=R ,23=R ,ππ2383334=⋅=V (4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解:如解答图,将正四面体放入正方体中,截面为1PCO ∆,面积是2.类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1图3-2 图3-3题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ; 第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高); 第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=,解出R例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为 解:设正六边形边长为a ,正六棱柱的高为h ,底面外接圆的半径为r ,则21=a ,正六棱柱的底面积为833)21(4362=⋅⋅=S ,89833===h Sh V 柱,∴3=h ,4)3(14222=+=R 也可1)21()23(222=+=R ),1=R ,球的体积为34π=球V ; (2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 . 解:32=BC ,4120sin 322==οr ,2=r ,5=R ,π20=S ; (3)已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为 .π16 解:折叠型,法一:EAB ∆的外接圆半径为31=r ,11=OO ,231=+=R ;法二:231=M O ,21322==D O r ,4413432=+=R ,2=R ,π16=表S ; 法三:补形为直三棱柱,可改变直三棱柱的放置方式为立式,算法可同上,略.换一种方式,通过算圆柱的轴截面的对角线长来求球的直径:162)32()2(222=+=R ,π16=表S ;(4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为 .π3160解:法一:282164236162=⋅⋅⋅-+=BC ,72=BC ,37423722==r ,372=r , 3404328)2(2122=+=+=AA r R ,π3160=表S ;法二:求圆柱的轴截面的对角线长得球直径,此略.第二讲 锥体背景的模型类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)图4-1图4-2图4-3图4-41.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点. 解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);(3)题第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ;事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则 利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径) 21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=; 第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R . 例4 (1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为 . 解:法一:由正弦定理(用大圆求外接球直径);法二:找球心联合勾股定理,72=R ,ππ4942==R S ;(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为 解:方法一:找球心的位置,易知1=r ,1=h ,r h =,故球心在正方形的中心ABCD 处,1=R ,34π=V 方法二:大圆是轴截面所的外接圆,即大圆是SAC ∆的外接圆,此处特殊,SAC Rt ∆的斜边是球半径,22=R ,1=R ,34π=V . (3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( ) A .433 B .33 C .43 D .123解:高1==R h ,底面外接圆的半径为1=R ,直径为22=R ,设底面边长为a ,则260sin 2==οaR ,3=a ,433432==a S ,三棱锥的体积为4331==Sh V ; (4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为ο60,则该三棱锥外接球的体积为( ) A .π B.3π C. 4π D.43π 解:选D ,由线面角的知识,得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上,在圆锥中求解,1=R ; (5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )AA.6 BC.3 D.2解:36)33(12221=-=-=r R OO ,362=h ,62362433131=⋅⋅==Sh V 球 类型五、垂面模型(一条直线垂直于一个平面)1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ; 第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的 三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的 顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示,则该几何体外接球的表面积为( )C A .π3 B .π2 C .316πD .以上都不对解:选C , 法一:(勾股定理)利用球心的位置求球半径,球心在圆锥的高线上,221)3(R R =+-,32=R ,ππ31642==R S ;法二:(大圆法求外接球直径)如图,球心在圆锥的高线上,故圆锥的轴截面三角形PMN 的外接圆是大圆,于是3460sin 22==οR ,下略;第三讲 二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)俯视图侧视图正视图解答图图6第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ; 第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,; 第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+ 注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 . 解:如图,3460sin 22221===οr r ,3221==r r ,312=H O , 35343121222=+=+=r H O R ,315=R ; 法二:312=H O ,311=H O ,1=AH , 352121222=++==O O H O AH AO R ,315=R ; (2)在直角梯形ABCD 中,CD AB //,ο90=∠A ,ο45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为 π4(2)题-2(2)题-1→A(3)题解:如图,易知球心在BC 的中点处,π4=表S ;(1)题(3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为 π6 解:如图,法一:33)2cos(cos 211-=+∠=∠πO OO B SO , 33sin 21=∠O OO ,36cos 21=∠O OO , 22cos 21211=∠=O OO O O OO ,232112=+=R ,ππ642==R S ; 法二:延长1BO 到D 使111r BO DO ==,由余弦定理得6=SB ,2=SD ,大圆直径为62==SB R ;(4)在边长为32的菱形ABCD 中,ο60=∠BAD ,沿对角线BD 折成二面角C BD A --为ο120的四面体ABCD ,则此四面体的外接球表面积为 π28解:如图,取BD 的中点M ,ABD ∆和CBD ∆的外接圆半径为221==r r ,ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离(弦心距)为121==d d , 法一:四边形21MO OO 的外接圆直径2=OM ,7=R ,π28=S ;法二:31=OO ,7=R ;法三:作出CBD ∆的外接圆直径CE ,则3==CM AM , 4=CE ,1=ME ,7=AE ,33=AC ,72147227167cos -=⋅⋅-+=∠AEC ,7233sin =∠AEC ,72723333sin 2==∠=AEC AC R ,7=R ;(5)在四棱锥ABCD 中,ο120=∠BDA ,ο150=∠BDC ,2==BD AD ,3=CD ,二面角CBD A --(4)题图的平面角的大小为ο120,则此四面体的外接球的体积为解:如图,过两小圆圆心作相应小圆所在平面的垂线确定球心,→抽象化(5)题解答图-2(5)题解答图-11B32=AB ,22=r ,弦心距32=M O ,13=BC ,131=r ,弦心距321=M O , ∴2121=O O ,72120sin 21==οO O OM , 法一:∴292222=+==OM MD OD R ,29=R ,∴329116π=球V ; 法二:2522222=-=M O OM OO ,∴29222222=+==OO r OD R ,29=R ,∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设:如图7,ο90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为( )A .π12125 B .π9125 C .π6125 D .π3125解:(1)52==AC R ,25=R ,6125812534343πππ=⋅==R V ,选C(2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCDA -的外接球的表面积为 .解:BD 的中点是球心O ,132==BD R ,ππ1342==R S .第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径. 第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高; 第三步:由POE ∆相似于PDH ∆,建立等式:PDPODH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高;第三步:由POG ∆相似于PFH ∆,建立等式:PFPOHF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 (1)棱长为a 的正四面体的内切球表面积是 62a π,解:设正四面体内切球的半径为r ,将正四面体放入棱长为2a的正方体中(即补形为正方体),如图,则 2622313133aa V V ABC P =⋅==-正方体,又Θr a r a Sr V ABC P 223343314314=⋅⋅⋅=⋅=-, ∴263332a r a =,62a r =,∴内切球的表面积为(1)题D图8-1A图8-26422a r S ππ==表(注:还有别的方法,此略)(2)正四棱锥ABCD S -的底面边长为2,侧棱长为37解:如图,正四棱锥ABCD S -的高7=h ,正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ,正四棱锥ABCD S -的表面积为284+=表S ,正四棱锥ABCD S -的体积为r r S V ABCDS ⋅+==-328431表, ∴3743284=⋅+r , 771427)122(7221728474-=-=+=+=r (3)三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则32解:如图,3=∆ABC S ,2==∆∆ACP ABP S S ,7=∆BCP S ,743++=表S ,三棱锥ABC P -的体积为332=-ABCP V , 另一表达体积的方式是r r S V ABC P ⋅++==-347331表, ∴3323473=⋅++r ,∴47332++=r习题: 1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ) A.3 B.6 C.36 D.9 解:【A 】616164)2(2=++=R ,3=R【三棱锥有一侧棱垂直于底面,且底面是直角三角形】【共两种】2. 三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA,则该三(2)题(3)题B棱锥的外接球体积等于 . 332π解:260sin 32==οr ,16124)2(2=+=R ,42=R ,2=R ,外接球体积332834ππ=⋅ 【外心法(加中垂线)找球心;正弦定理求球小圆半径】3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 .解:ABC ∆外接圆的半径为 ,三棱锥ABC S -的直径为3460sin 22==οR ,外接球半径32=R , 或1)3(22+-=R R ,32=R ,外接球体积2733233834343πππ=⋅==R V , 4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:PAC ∆的外接圆是大圆,3460sin 22==οR ,32=R , 5. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ,81216)97(1sin 22⋅=-=∠P ,924sin =∠P ,42922992422===R ,829=R 6. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABCP -外接球的半径为 .解:AC 是公共的斜边,AC 的中点是球心O ,球半径为1=R。
2022高考数学立体几何外接球专题(含解析)
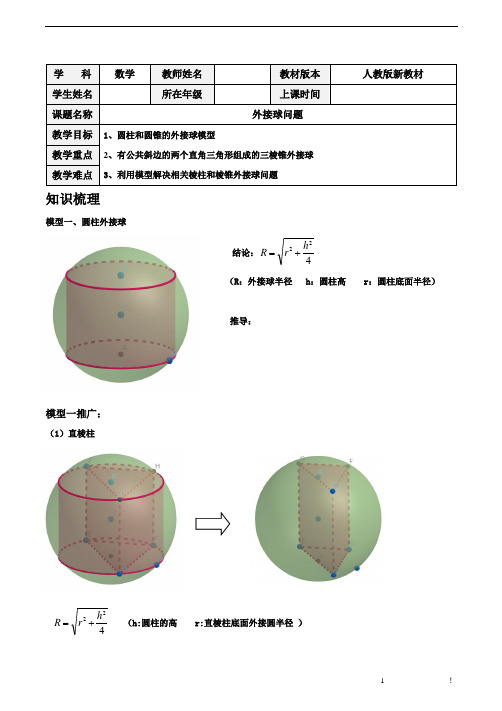
知识梳理模型一、圆柱外接球结论:422h r R +=(R:外接球半径 h:圆柱高 r:圆柱底面半径)推导:模型一推广:(1)直棱柱422h r R += (h:圆柱的高 r:直棱柱底面外接圆半径 )学 科 数学 教师姓名 教材版本 人教版新教材学生姓名所在年级上课时间课题名称外接球问题教学目标 1、圆柱和圆锥的外接球模型2、有公共斜边的两个直角三角形组成的三棱锥外接球3、利用模型解决相关棱柱和棱锥外接球问题教学重点 教学难点(2)侧面为三角形,底面为矩形,侧面和底面垂直的四棱锥(3)侧棱垂直于底面的棱锥【2017深二模】已知三棱锥S-ABC,△ABC是直角三角形,其斜边AB=8,SC⊥平面ABC,SC=6,则三棱锥的外接球的表面积为( )(A)64π(B)68π(C)72π(D)100π模型二、圆锥外接球结论:hh r R 222+=(R:外接球半径 h:圆锥高 r:圆锥底面半径)推导:模型二推广:(1)棱锥(上顶点在底面外心正上方)外接球hh r R 222+= (h:棱锥的高 r:棱锥底面外接圆半径 )【2018深一模】如图,网格纸上小正方形的边长为1,某几何体的三视图如图所示,则该几何体的外接球表面积为()A.B.C.16πD.25π【2017全国一卷文 16】已知三棱锥S−ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S−ABC的体积为9,则球O的表面积为______________.【2019 全国一卷理 12】已知三棱锥P−ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为A.B.C.D模型一、二总结题型:求几何体的外接球模型一: 422h r R += (圆柱模型) 模型二: h h r R 222+=(圆锥模型)适用于: 适用于:1、所有的圆柱、直棱柱 上顶点在底面外心正上方的棱锥2、侧棱垂直于底面的棱锥3、侧面为任意三角形,底面为矩形, 且侧面垂直于底面的四棱锥模型三、有公共斜边的两个直角三角形组成的三棱锥 ,球心在公共斜边的中点处如下图,∠ABC=∠ADC=90°,则O 为外接球球心1、在矩形ABCD 中,AB =4,BC =3,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为A. π12125B.π9125C.π6125D.π31252.三棱锥S ABC -的所有顶点都在球O的球面上,且SA AC SB BC ====4SC =,则该球的体积为A 2563πB 323π C 16π D 64π专题练习类型一 构造法(补形法)【例1】已知是球上的点, , , ,则球的表面积等于________________.【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术•商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )A .B .C .3πD .4π,,,S A B C O SA ABC ⊥平面AB BC ⊥1SA AB ==BC =O【举一反三】1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为A.B.C.D.2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥S−ABC中,,则三棱锥S−ABC外接球的表面积为()A.25ΠB.C.50ΠD.3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为()A.7πB.8πC.9πD.10π类型二 正棱锥与球的外接【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( ) A . B . C . D .【举一反三】1、球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大值为( )A .33 B . 3 C .2 3 D .42. 【四川省德阳市2018届高三二诊】正四面体ABCD 的体积为,则正四面体ABCD 的外接球的体积为______.814π16π9π274π3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥P −ABC 中,√2PA =AB =4√2,点E 在棱PA 上,且PE =3EA .正三棱锥P −ABC 的外接球为球O ,过E 点作球O 的截面α,α截球O 所得截面面积的最小值为__________.类型三 直棱柱的外接球【例4】直三棱柱的各顶点都在同一球面上,若,, 则此球的表面积等于 .【举一反三】1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球O 的球面上,AB =AC =2,BC =2√2,若球O 的表面积为72Π,则这个直三棱柱的体积是( ) A .16 B .15C .D .2、已知三棱柱的6个顶点都在球的球面上,,,,则球的半径为()A B . C.D .3、 正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最111ABC A B C -12AB AC AA ===120BAC ∠=︒111ABC A B C -O 34AB AC ==,AB AC ⊥112AA =O 1321111ABCD A B C D -R值,为 .答案与解析类型一 构造法(补形法)【例1】已知是球上的点, , , ,则球的表面积等于________________. 【答案】 【解析】由已知S,A,B,C 是球O 表面上的点,所以 ,又,,所以四面体的外接球半径等于以长宽高分别以SA,AB,BC 三边长为长方体的外接球的半径,因为, ,所以,所以球的表面积.【指点迷津】当一三棱锥的三侧棱两两垂直时,可将三棱锥补成一个长方体,将问题转化为长方体(正方体)来解.长方体的外接球即为该三棱锥的外接球.【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术•商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )A .B .C .3πD .4π,,,S A B C O SA ABC ⊥平面AB BC ⊥1SA AB ==BC =O 4πOA OB OC OS ===SA ABC ⊥平面AB BC ⊥S ABC -1SA AB ==BC =22,1R R ==O 244S R ππ==【答案】B【解析】由题意可知阳马为四棱锥,且四棱锥的底面为长方体的一个底面,四棱锥的高为长方体的一棱长,且阳马的外接球也是长方体的外接球,由三视图可知四棱锥的底面是边长为1的正方形,四棱锥的高为1,∴长方体的一个顶点处的三条棱长分别为1,1,1,∴长方体的对角线为,∴外接球的半径为,∴外接球的体积为.故选:B.【指点迷津】当一四面体或三棱锥的棱长相等时,可以构造正方体,在正方体中构造三棱锥或四面体,利用三棱锥或四面体与正方体的外接球相同来解即可.【举一反三】1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为A.B.C.D.【答案】C【解析】如图所示,将直三棱柱补充为长方体,则该长方体的体对角线为,设长方体的外接球的半径为R,则2R=4,R=2,所以该长方体的外接球的体积,故选C.2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥S−ABC中,,则三棱锥S−ABC外接球的表面积为()A.25蟺B.C.50蟺D.【答案】C【解析】解:如图,把三棱锥S−ABC补形为长方体,设长方体的长、宽、高分别为,则,∴三棱锥外接球的半径∴三棱锥S−ABC外接球的表面积为.故选:C.3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为()A .7πB .8πC .9πD .10π 【答案】C 【解析】由三视图可得,该几何体为一个三棱锥,放在长、宽、高分别为2,1,2的长方体中,此三棱锥和长方体的外接球是同一个,长方体的外接球的球心在体对角线的中点处,易得其外接球的直径为,从而外接球的表面积为9π.故答案为:C.类型二 正棱锥与球的外接【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( )A .B .C .D .【答案】A .814π16π9π274π【指点迷津】求正棱锥外接球的表面积或体积,应先求其半径,在棱锥的高上取一点作为外接球的球心,构造直角三角形,利用勾股定理求半径. 【举一反三】1、球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大值为( )A .33 B . 3 C .2 3 D .4 【答案】A【解析】 (1)由于平面SAB ⊥平面ABC ,所以点S 在平面ABC 上的射影H 落在AB 上,根据球的对称性可知,当S 在“最高点”,即H 为AB 的中点时,SH 最大,此时棱锥S -ABC 的体积最大.学科*网因为△ABC 是边长为2的正三角形,所以球的半径r =OC =23CH =23×32×2=233.在Rt △SHO 中,OH =12OC =33,所以SH =⎝ ⎛⎭⎪⎫2332-⎝ ⎛⎭⎪⎫332=1, 故所求体积的最大值为13×34×22×1=33.2. 【四川省德阳市2018届高三二诊】正四面体ABCD 的体积为,则正四面体ABCD 的外接球的体积为______. 【答案】【解析】 解:如图,设正四面体ABCD 的棱长为x ,过A 作AD ⊥BC , 设等边三角形ABC 的中心为O ,则AO =23AD =√33x ,,,即x=√2a.再设正四面体ABCD的外接球球心为G,连接GA,则,即.∴正四面体ABCD的外接球的体积为.故答案为:.3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥P−ABC中,√2PA=AB=4√2,点E在棱PA上,且PE=3EA.正三棱锥P−ABC的外接球为球O,过E点作球O的截面α,α截球O所得截面面积的最小值为__________.【答案】3π【解析】因为PA=PC=PB=4,AB=AC=BC=4√2,所以PA2+PC2=AC2,所以∠CPA=π2,同理∠CPB=∠BPA=π2,故可把正三棱锥补成正方体(如图所示),其外接球即为球O,直径为正方体的体对角线,故2R=4√3,设PA的中点为F,连接OF,则OF=2√2且OF⊥PA,所以OE=√8+1=3,当OE⊥平面α时,平面α截球O的截面面积最小,此时截面为圆面,其半径为√(2√3)2−32=√3,故截面的面积为3π.填3π.类型三 直棱柱的外接球 【例4】直三棱柱的各顶点都在同一球面上,若,, 则此球的表面积等于 . 【答案】【解析】在中,,可得,由正弦定理,可得外接圆半径r=2,设此圆圆心为,球心为,在中,易得球半径,故此球的表面积为.【指点迷津】直棱柱的外接球的球心在上、下底面的外接圆的圆心的连线上,确定球心,用球心、一底面的外接圆的圆心,一顶点构成一个直角三角形,用勾股定理得关于外接球半径的关系式,可球的半径. 【举一反三】1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球O 的球面上,AB =AC =2,BC =2√2,若球O 的表面积为72蟺,则这个直三棱柱的体积是( ) A .16 B .15 C .D .【答案】A 【解析】 由题,,因为AB =AC =2,BC =2√2,易知三角形ABC 为等腰直角三角形, 故三棱柱的高故体积V =12脳2脳2脳8=16 故选A111ABC A B C -12AB AC AA ===120BAC ∠=︒ABC ∆2AB AC ==120BAC ∠=︒BC =ABC ∆O 'O RT OBO '∆R =2420R ππ=2、已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为 ( )A .B .C .D .【答案】C【解析】由球心作面ABC 的垂线,则垂足为BC 中点M.计算AM=,由垂径定理,OM=6,所以半径,选C.3、 正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最值,为 . 【答案】大111ABC A B C -O 34AB AC ==,AB AC ⊥112AA =O 213252132=1111ABCD A B C D -R。
立体几何高考专题--外接球的几种常见求法

立体几何高考专题--外接球的几种常见求法高三微专题:外接球在立体几何中,外接球问题是一个重点和难点。
其实质是确定球心O的位置和使用勾股定理求解外接球半径(其中底面外接圆半径r可根据正弦定理求得)。
一、由球的定义确定球心在空间中,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心。
简单多面体外接球问题是立体几何中的重点和难点。
二、球体公式球的表面积公式为S=4R²,球体积公式为V=4/3R³。
三、球体几个结论:1)长方体、正方体外接球直径等于体对角线长。
2)侧棱相等,顶点在底面投影为底面外接圆圆心。
3)直径所对的球周角为90°(大圆的圆周角)。
4)正三棱锥对棱互相垂直。
四、外接球几个常见模型1.长方体(正方体)模型例1:长方体的长、宽、高分别为3、2、1,其顶点都在球O的球面上,则球O的表面积为14。
练1:体积为8的正方体的顶点都在同一球面上,则该球的表面积为12。
2.正棱锥(圆锥)模型对于侧棱相等,底面为正多边形的正棱锥,其外接球的球心位置位于顶点与底面外心连线线段(或延长线)上。
半径公式为R²=(h-R)²+r²(其中R为外接球半径,r为底面外接圆半径,h为棱锥的高,r可根据正弦定理a=2rsinA求得)。
例2:已知各顶点都在同一个球面上的正四棱锥高为h,体积为V,则这个球的表面积为____。
正四棱锥的高为h,体积为V,易知底面面积为,底面边长为。
正四棱锥的外接球的球心在它的高上,记为,得,在中。
由勾股定理,所以球的表面积为。
练2:正三棱锥S-ABC中,底面ABC是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于。
解析:ABC外接圆的半径为,三棱锥S-ABC的直径为2R=,外接球半径R=,外接球体积V=4/3R³=。
对于侧棱与底面垂直的直棱柱和圆柱,其外接球的球心位置在上下底面外心连线中点处。
立体几何专题:外接球问题中常见的8种模型(学生版)

立体几何专题:外接球问题中常见的8种模型1.知识梳理一、墙角模型适用范围:3组或3条棱两两垂直;可在长方体中画出该图且各顶点与长方体的顶点重合直接用公式(2R )2=a 2+b 2+c 2,即2R =a 2+b 2+c 2,求出R【补充】图1为阳马,图2和图4为鳖臑二、麻花模型适用范围:对棱相等相等的三棱锥对棱相等指四面体的三组对棱分别对应相等,且这三组对棱构成长方体的三组对面的对角线。
推导过程:三棱锥(即四面体)中,已知三组对棱分别相等,(AB =CD ,AD =BC ,AC =BD )第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为a ,b ,c ,AD =BC =x ,AB =CD =y ,AC =BD =z ,列方程组,a 2+b 2=x 2b 2+c 2=y 2c 2+a 2=z 2⇒(2R )2=a 2+b 2+c 2=x 2+y 2+z 22,补充:V A −BCD =abc −16abc ×4=13abc 第三步:根据墙角模型,2R =a 2+b 2+c 2=x 2+y 2+z 22,R 2=x 2+y 2+z 28,R =x 2+y 2+z 28,求出R .三、垂面模型适用范围:有一条棱垂直于底面的棱锥。
推导过程:第一步:将ABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步:O 1为ABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r(三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=csin C =2r ,OO 1=12PA .第三步:利用勾股定理求三棱锥的外接球半径:(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式:R 2=r 2+h 24四、切瓜模型适用范围:有两个平面互相垂直的棱锥推导过程:分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线,两条垂线的交点即为球心0,取B C 的中点为E ,连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式:R 2=r 21+r 22-l 24五、斗笠模型适用于:顶点的投影在底面的外心上的棱锥推导过程:取底面的外心01,连接顶点与外心,该线为空间几何体的高h ,在h 上取一点作为球心0,根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式:R =r 2+h 22h六、矩形模型适用范围:两个直角三角形的斜边为同一边,则该边为球的直径推导过程:图中两个直角三角形ΔPAB 和ΔQAB ,其中∠APB =∠AQB =90°,求外接圆半径取斜边AB 的中点O ,连接OP ,OQ ,则OP =12AB =OA =OB =OQ 所以O 点即为球心,然后在ΔPOQ 中解出半径R 公式:R 2=l22(l 为斜边长度)七、折叠模型适用范围:两个全等三角形或等腰三角形拼在一起,或菱形折叠.推导过程:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角∠A EC =α,CE =A E =h .如图,作左图的二面角剖面图如右图:H 1和H 2分别为△BCD ,△A BD 外心,分别过这两个外心做这两个平面的垂线且垂线相交于球心O CH 1=r =BD 2sin ∠BCD,EH 1=h -r ,OH 1=(h -r )tanα2由勾股定理可得:R 2=OC 2=OH 21+CH 21=r 2+(h -r )2tan 2α2.公式:R 2=r 2+(h -r )2tan 2α2八、鳄鱼模型适用范围:所有二面角构成的棱锥,普通三棱锥方法:找两面外接圆圆心到交线的距离m ,n ,找二面角α,找面面交线长度l 推导过程:取二面角两平面的外心分别为O 1,O 2并过两外心作这两个面的垂线,两垂线相交于球心O ,取二面角两平面的交线中点为E ,则O ,O 1,E ,O 2四点共圆,由正弦定理得:OE =2r =O 1O 2sin α①在ΔO 1O 2E 中,由余弦定理得:O 1O 2 2=O 1E 2+O 2E 2-2O 1E O 2E cos α②由勾股定理得:OD 2=O 1O 2+O 1D 2③由①②③整理得:OD2=O 1O 2+O 1D 2=OE 2-O 1E 2+O 1D 2=O 1O 2sin α2-O 1E 2+O 1D 2=O 1E2+O 2E 2-2O 1E O 2E cos αsin 2α-O 1E 2+O 1D 2=O1E2+O2E2-2O1EO2Ecosαsin2α-O1E2+O1B2记O1E=m,O2E=n,AB=l,则R2=m2+n2-2mn cosαsin2α+l22公式:R2=m2+n2-2mn cosαsin2α+l222.常考题型3.题型精析题型一:墙角模型1(2023·高一单元测试)三棱锥A-BCD中,AD⊥平面BCD,DC⊥BD,2AD=BD=DC=2,则该三棱锥的外接球表面积为()A.3π2B.9π2C.9πD.36π1.(2022秋·陕西西安·高一统考期末)在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑A-BCD中,满足AB⊥平面BCD,且AB=BD=5,BC=3,CD=4,则此鳖臑外接球的表面积为()A.25πB.50πC.100πD.200π2.(2023·高一课时练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图P-ABCD是阳马,PA⊥平面ABCD,PA=5,AB=3,BC=4.则该阳马的外接球的表面积为()A.1252π3B.50πC.100πD.500π33.(2023·广西南宁·统考二模)在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑A -BCD 中,AB ⊥平面BCD ,CD ⊥AD ,AB =BD =2,已知动点E 从C 点出发,沿外表面经过棱AD 上一点到点B 的最短距离为10,则该棱锥的外接球的体积为.4.(2023春·辽宁朝阳·高二北票市高级中学校考阶段练习)已知四棱锥P -ABCD 的外接球O 的表面积为64π,PA ⊥平面ABCD ,且底面ABCD 为矩形,PA =4,设点M 在球O 的表面上运动,则四棱锥M -ABCD 体积的最大值为.题型二:麻花模型1(2023春·广东梅州·高二统考期中)已知三棱锥S -ABC 的四个顶点都在球O 的球面上,且SA =BC =2,SB =AC =7,SC =AB =5,则球O 的体积是()A.83π B.3223π C.423π D.823π1.(2022春·江西景德镇·高一景德镇一中校考期中)在△ABC 中,AB =AC =2,cos A =34,将△ABC 绕BC 旋转至△BCD 的位置,使得AD =2,如图所示,则三棱锥D -ABC 外接球的体积为.2.(2023秋·吉林·高一吉林一中校考阶段练习)如图,在△ABC 中,AB =25,BC =210,AC =213,D ,E ,F 分别为三边中点,将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起,使A ,B ,C 重合为点P ,则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π3.(2023·江西·统考模拟预测)在三棱锥P -ABC 中,已知PA =BC =213,AC =BP =41,CP =AB =61,则三棱锥P -ABC 外接球的表面积为()A.77πB.64πC.108πD.72π4.(2022·全国·高三专题练习)已知四面体ABCD 的棱长满足AB =AC =BD =CD =2,BC =AD =1,现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中,使得四面体ABCD 可以在圆锥中任意转动,则圆锥侧面积的最小值为.题型三:垂面模型1(2023·高一单元测试)在三棱锥P -ABC 中,PA ⊥平面ABC ,PA =6,BC =3,∠CAB =π6,则三棱锥P -ABC 的外接球半径为()A.3B.23C.32D.61.(2023·全国·高一专题练习)已知A ,B ,C ,D 在球O 的表面上,△ABC 为等边三角形且边长为3,AD ⊥平面ABC ,AD =2,则球O 的表面积为()A.4πB.8πC.16πD.32π2.(2020春·天津宁河·高一校考期末)在三棱锥P -ABC 中,AP =2,AB =3,PA ⊥面ABC ,且在△ABC 中,C =60°,则该三棱锥外接球的表面积为()A.20π3B.8πC.10πD.12π3.(2023·全国·高一专题练习)已知A ,B ,C ,D 在球O 的表面上,△ABC 为等边三角形且其面积为334,AD ⊥平面ABC ,AD =2,则球O 的表面积为()A.πB.2πC.4πD.8π4.(2022春·山东聊城·高一山东聊城一中校考阶段练习)在四棱锥P -ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为矩形,BC =2,PC 与平面PAB 所成的角为30o ,则该四棱锥外接球的体积为()A.433π B.43πC.823πD.833π题型四:切瓜模型1(2023·贵州贵阳·校联考模拟预测)在三棱锥A -BCD 中,已知AC ⊥BC ,AC =BC =2,AD =BD =6,且平面ABD ⊥平面ABC ,则三棱锥A -BCD 的外接球表面积为()A.8πB.9πC.10πD.12π1.(2023·四川达州·统考二模)三棱锥A -BCD 的所有顶点都在球O 的表面上,平面ABD ⊥平面BCD ,AB =AD =6,AB ⊥AD ,∠BDC =2∠DBC =60°,则球O 的体积为()A.43πB.32π3C.49π3D.323π2.(2023春·陕西西安·高一长安一中校考期中)在直三棱柱ABC -A 1B 1C 1中,AB ⊥BC ,AB =BC =AA 1=4,点P 为B 1C 1的中点,则四面体PABC 的外接球的体积为()A..41416π B.41413π C.41412π D.4141π3.(2022·高一单元测试)四棱锥P -ABCD 的顶点都在球O 的表面上,△PAD 是等边三角形,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,若AB =2,BC =3,则球O 的表面积为()A.12πB.16πC.20πD.32π4.(2021·高一课时练习)在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,且ABCD 为矩形,∠DPA =π2,AD =23,AB =2,PA =PD ,则四棱锥P -ABCD 的外接球的体积为()A.163π B.323π C.643π D.16π5.(2023春·全国·高一专题练习)在四棱锥P-ABCD中,ABCD是边长为2的正方形,AP=PD=10,平面PAD⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为()A.4πB.8πC.136π9D.68π3题型五:斗笠模型1(2023·全国·高一专题练习)正四面体S-ABC内接于一个半径为R的球,则该正四面体的棱长与这个球的半径的比值为()A.64B.33C.263D.31.(2022·高一专题练习)已知正四棱锥P-ABCD(底面四边形ABCD是正方形,顶点P在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为10,若该正四棱锥的体积为50 3,则此球的体积为()A.18πB.86πC.36πD.323π2.(2022·全国·高一专题练习)某四棱锥的底面为正方形,顶点在底面的射影为正方形中心,该四棱锥内有一个半径为1的球,则该四棱锥的表面积最小值是()A.16B.8C.32D.243.(2022春·安徽·高三校联考阶段练习)在三棱锥P-ABC中,侧棱PA=PB=PC=10,∠BAC=π4,BC=22,则此三棱锥外接球的表面积为.题型六:矩形模型1(2022春·全国·高一期末)已知三棱锥A-BCD中,CD=22,BC=AC=BD=AD=2,则此几何体外接球的表面积为()A.2π3B.2π C.82π3D.8π1.(2022春·广东惠州·高一校考期中)在矩形ABCD中,AB=6,BC=8,现将△ABC沿对角线AC翻折,得到四面体DABC,则该四面体外接球的体积为()A.1963π B.10003π C.4003π D.5003π2.(2022春·河北沧州·高一校考阶段练习)矩形ABCD中,AB=4,BC=3,沿AC将三角形ABC折起,得到的四面体A-BCD的体积的最大时,则此四面体外接球的表面积值为()A.25πB.30πC.36πD.100π3.(2022春·四川成都·高一统考期末)在矩形ABCD 中,AB =6,AD =8,将△ABC 沿对角线AC 折起,则三棱锥B -ACD 的外接球的表面积为()A.36πB.64πC.100πD.与二面角B -AC -D 的大小有关题型七:折叠模型1(2022春·陕西西安·高一长安一中校考期末)已知菱形ABCD 的边长为3,∠ABC =60°,沿对角线AC 折成一个四面体,使平面ACD 垂直平面ABC ,则经过这个四面体所有顶点的球的体积为().A.5152π B.6πC.515πD.12π1.已知等边△ABC 的边长为2,将其沿边AB 旋转到如图所示的位置,且二面角C -AB -C 为60°,则三棱锥C -ABC 外接球的半径为2.(2023·广西南宁·统考二模)蹴鞠,又名“蹴球”“蹴圈”等,“蹴”有用脚蹴、踢的含义,鞠最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的足球,现已知某“鞠”的表面上有四个点A ,B ,C ,D 满足AB =BC =CD =DA =DB =433cm ,AC =23cm ,则该“鞠”的表面积为cm 2.3.(2022秋·福建泉州·高三校考开学考试)在三棱锥S -ABC 中,SA =SB =AC =BC =2,SC =1,二面角S -AB -C 的大小为60°,则三棱锥S -ABC 的外接球的表面积为.4.(2022秋·山东德州·高二统考期中)已知在三棱锥中,S -ABC 中,BA ⊥BC ,BA =BC =2,SA =SC =22,二面角B -AC -S 的大小为5π6,则三棱锥S -ABC 的外接球的表面积为()A.56π3B.58π3C.105π4D.124π9题型八:鳄鱼模型1(2022春·四川成都·高一树德中学校考期末)已知在三棱锥S-ABC中,AB⊥BC,AB=BC=2,SA =SC=22,二面角B-AC-S的大小为2π3,则三棱锥S-ABC的外接球的表面积为()A.124π9B.105π4C.105π9D.104π91.(2023春·全国·高一专题练习)如图,在三棱锥P-ABC,△PAC是以AC为斜边的等腰直角三角形,且CB=22,AB=AC=6,二面角P-AC-B的大小为120°,则三棱锥P-ABC的外接球表面积为()A.5103π B.10π C.9π D.4+23π2.(2023·陕西榆林·统考三模)在三棱锥A-BCD中,AB⊥BC,BC⊥CD,CD=2AB=2BC= 4,二面角A-BC-D为60°,则三棱锥A-BCD外接球的表面积为()A.16πB.24πC.18πD.20π3.(2023春·安徽阜阳·高三阜阳市第二中学校考阶段练习)如图1,四边形ABCD中,AB=AD =2,CB=CD=2,AB⊥AD,将△ABD沿BD翻折至△PBD,使二面角P-BD-C的正切值等于2,如图2,四面体PBCD的四个顶点都在同一个球面上,则该球的表面积为()A.4πB.6πC.8πD.9π4.(2023·江西南昌·校联考模拟预测)在平面四边形ABCD中,AD=CD=3,∠ADC=∠ACB =90°,∠ABC=60°,现将△ADC沿着AC折起,得到三棱锥D-ABC,若二面角D-AC-B的平面角为135°,则三棱锥D-ABC的外接球表面积为.5.(2023春·广东广州·高三统考阶段练习)在三棱锥P-ABC中,△ABC为等腰直角三角形,AB=AC=2,△PAC为正三角形,且二面角P-AC-B的平面角为π6,则三棱锥P-ABC的外接球表面积为.。
高考数学空间几何体的外接球与内切球常见题型

高考数学空间几何体的外接球与内切球常见题型本文介绍了空间几何体的外接球与内切球的经典类型,其中第一种类型为墙角模型,即三条棱两两垂直,不需要找球心的位置即可求出球半径。
具体方法是找到三条两两垂直的线段,然后使用公式2R=a+b+c或2R=a^2+b^2+c^2来求出R。
例如,在已知各顶点都在同一球面上的正四棱柱的高为4,体积为16的情况下,可以求出该球的表面积为32π。
第二种类型为对棱相等模型,补形为长方体。
在这种情况下,需要找到对棱相等的空间几何体,并补成长方体。
例如,如果三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积为36π。
除此之外,文章还给出了一些具体的例子,如正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA=23,则正三棱锥S-ABC外接球的表面积为36π。
同时,文章还提到了一些需要注意的引理,如正三棱锥的对棱互相垂直等。
需要注意的是,文章中存在一些格式错误和明显有问题的段落,需要进行删除或修改。
题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD,AD=BC,AC=BD)首先,我们可以画出一个长方体,标出三组互为异面直线的对棱,如图2-1所示。
设出长方体的长宽高分别为a,b,c,AD=BC=x,AB=CD=y,AC=BD=z,列方程组:a^2+b^2=x^2b+c=yc^2+a^2=z^2根据墙角模型,我们可以得到2R=a+b+c=2(x^2+y^2+z^2)/(x^2+y^2+z^2),化简得到R=sqrt(2)/2*(x^2+y^2+z^2)/(x^2+y^2+z^2),求出R即可。
例2(1)如下图所示三棱锥A-BCD,其中AB=CD=5,AC=BD=6,AD=BC=7,则该三棱锥外接球的表面积为。
2)在三棱锥A-BCD中,AB=CD=2,AD=BC=3,AC=BD=4,则三棱锥A-BCD外接球的表面积为。
3)正四面体的各条棱长都为2,则该正面体外接球的体积为。
外接球与内切八大模型—老师专用
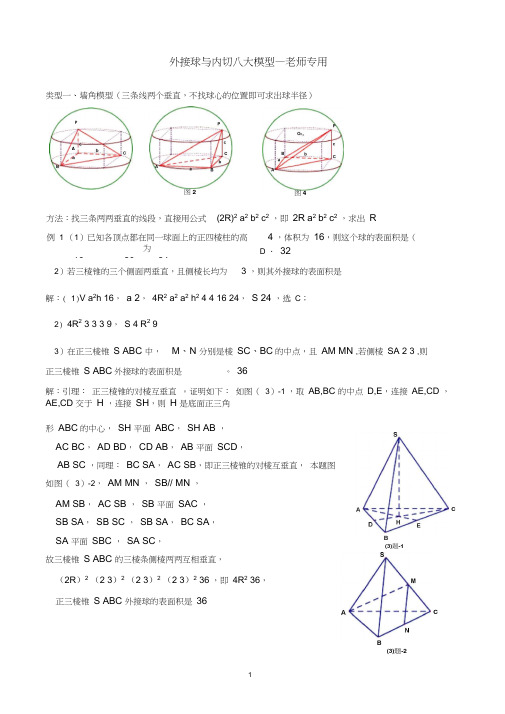
外接球与内切八大模型—老师专用类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径)正三棱锥 S ABC 外接球的表面积是。
36解:引理: 正三棱锥的对棱互垂直 。
证明如下: 如图( 3)-1 ,取 AB,BC 的中点 D,E ,连接 AE,CD ,AE,CD 交于 H ,连接 SH ,则 H 是底面正三角 形 ABC 的中心, SH 平面 ABC , SH AB ,AC BC , AD BD , CD AB , AB 平面 SCD ,AB SC ,同理: BC SA , AC SB ,即正三棱锥的对棱互垂直, 本题图如图( 3)-2, AM MN , SB// MN ,AM SB , AC SB , SB 平面 SAC , SB SA , SB SC , SB SA , BC SA , SA 平面 SBC , SA SC ,故三棱锥 S ABC 的三棱条侧棱两两互相垂直,(2R )2 (2 3)2 (2 3)2 (2 3)2 36 ,即 4R 2 36,正三棱锥 S ABC 外接球的表面积是 36方法:找三条两两垂直的线段,直接用公式 (2R)2 a 2 b 2 c 2 ,即 2R a 2 b 2 c 2 ,求出 R 例 1 (1)已知各顶点都在同一球面上的正四棱柱的高为A . 16B . 20C . 244 ,体积为 16,则这个球的表面积是( D . 322)若三棱锥的三个侧面两垂直,且侧棱长均为3 ,则其外接球的表面积是解:( 1)V a 2h 16, a 2, 4R 2 a 2 a 2 h 2 4 4 16 24, S 24 ,选 C ;2) 4R 2 3 3 3 9, S 4 R 2 9 3)在正三棱锥 S ABC 中,M 、N 分别是棱 SC 、 B C 的中点,且 AM MN ,若侧棱 SA 2 3 ,则PAB图2图4C(3)题-1C(3)题-24)在四面体 S ABC 中, SA 平面ABC , BAC 120 ,SA AC 2,AB 1,则该四面体的外接6)已知某几何体的三视图如图所示,三视图是腰长为何体外接球的体积为1的等腰直角三角形和边长为 1的正方形,则该几ab 122 2 2 2 2bc 8 , abc 24, a 3,b 4,c 2,(2R)2a 2b 2c 2 29, S 4 R 2 29 ,ac 6② R 2 r 2 OO 12 R r 2 OO 12球的表面积为( D ) A.11 B.75) 如果三棱锥的三个侧面两两垂直,它们的面积分别为C.106、4、 40 D.33,那么它的外接球的表面积是解析: (4)在 ABC 中, BC 2 AC 2 AB 2 2AB BC cos120 7 ,BC 7 , ABC 的外接球直径为 2r BCsin BAC 7 2 7, 332 2 2(2R)2 (2r)2SA 2440,S 4033,选 D 5)三条侧棱两两生直,设三条侧棱长分别为a,b,c ( a,b,c R ),则6)(2R)2 a 2 b 2 c 2 3,R 2 43 ,R3V4 R3 4 3 3 3 ,3 3 8 2类型二、垂面模型(一条直线垂直于一个平面)1.题设:如图 5, PA 平面 ABC 解题步骤:第一步:将 ABC 画在小圆面上, A 为小圆直径的一个端点,作小圆的直径 AD ,连接 PD ,则 PD 必过球心 O ;第二步: O 1为 ABC 的外心,所以 OO 1 平面 ABC ,算出小圆 O 1的半径 O 1D r (三角形的外接圆直径算法:利用正弦定理,得sin A sin Bsin c C2r ), OO 1 21PA ;第三步:利用勾股定理求三棱锥的外接球半径:①2 2 2(2R)2PA 2 (2r)22R PA 2 (2r)2 ;2.题设:如图6,7,8,P 的射影是ABC的外心三棱锥P ABC的三条侧棱相等解题步骤:第一步:确定球心O 的位置,取ABC的外心O1,则P , O, O1三点共线;第二步:先算出小圆O1 的半径AO1 r ,再算出棱锥的高PO1 h (也是圆锥的高);第三步:勾股定理:OA2 O1A2 O1O2R2 (h R)2 r 2,解出R方法二:小圆直径参与构造大圆。
高中数学立体几何外接球7大模型

02
03
04
例题1
已知长方体的长为3,宽为4 ,高为5,求其外接球的半径
。
解法
根据长方体外接球半径计算方 法,可得出外接球的半径为 1/2*sqrt(3^2+4^2+5^2)=
3/2*sqrt(10)。
例题2
已知长方体的长为6,宽为8 ,高为10,求其外接球的半
径。
解法
根据长方体外接球半径计算方 法,可得出外接球的半径为 1/2*sqrt(6^2+8^2+10^2) =1/2*sqrt(100+64+100)=1 /2*sqrt(264)=sqrt(66)。
长方体的每个面都是 矩形或正方形,相对 的两个面完全相同。
长方体外接球半径计算方法
01
设长方体的长、宽、高分别为a、 b、c,则长方体的体对角线长度 为sqrt(a^2+b^2+c^2)。
02
外接球的半径为体对角线长度的 一半,即 R=1/2*sqrt(a^2+b^2+c^2)。
典型例题解析
01
外接球半径$R = frac{sqrt{3}a}{3}$
典型例题解析
题目
在正四面体$P-ABC$中,点$P,A,B,C$都在同一球面上,若$angle PAB = angle PBA = angle BPC = angle ACP = 90^{circ}$,则该球的表面积为____.
解析
首先根据正四面体的性质,我们可以计算出外接球的半径$R = frac{sqrt{3}a}{3}$。然后 根据球的表面积公式$S = 4pi R^{2}$,我们可以计算出球的表面积为$S = 4pi (frac{sqrt{3}a}{3})^{2} = frac{4pi a^{2}}{3}$。
高考数学多面体的外接球专题模型总结终极版(七大模型)

多面体的外接球专题模型总结终极版题型一、长方体的外接球1.长方体外接球半径R=√a2+b2+c22a2.正方体外接球半径R=√323.长方体外接球的切割体(从长方体八个顶点中任取四个顶点)(1)三条侧棱两两垂直的三棱锥简称墙角型(2)一条侧棱垂直于底面,底面是直角三角形的三棱锥(双垂直)(3)各棱相等的三棱锥(正四面体)(4)对棱相等的三棱锥专题练习例1.在三棱锥BCD A −中,侧棱AB 、AC 、AD 两两垂直,ABC ∆、ACD ∆、ADB ∆的面积分别为22、32、62,则三棱锥BCD A −的外接球的体积为( )A .6πB .26πC .36πD .46π例2. 如图所示,已知球O 的面上有四点A 、B 、C 、D ,2===⊥⊥BC AB DA BC AB ABC DA ,,面,则球O 的体积等于 .例 3.已知三棱锥BCD A −的所有棱长都为2,则该三棱锥外接球的体积为_________例4.四面体BCD A −中,5==CD AB ,34==BD AC ,41==BC AD ,则四面体BCD A −外接球的表面积为( )A .π50B .π100C .π150D .π200变式练习1.在三棱锥ABC P −中,4==BC PA ,5==AC PB ,11==AB PC ,则三棱锥ABC P −的外接球的表面积为( )A .π8B .π12C .π26D .π242.已知三棱锥ABC P −的顶点都在球O 的表面上,若PA ,PB ,PC 两两互相垂直,且2===PC PB PA ,则球O 的体积为( ) A .π312 B .π28 C .π34 D .π43.《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥ABC P −为鳖臑,⊥PA 平面ABC ,2==AB PA ,4=AC ,三棱锥ABC P −的四个顶点都在球O 的球面上,则球O 的表面积为( ) A .π8 B .π12 C .π20 D .π244.已知三棱锥ABC S −的各顶点都在一个半径为r 的球面上,且1===SC SB SA ,2===AC BC AB ,则球的表面积为( )A .π12B .π8C .π4D .π35.已知三棱锥ABC P −的各顶点都在同一球面上,且⊥PA 平面ABC ,若该棱锥的体积为332,2=AB ,1=AC ,︒=∠60BAC ,则此球的表面积等于( ) A .π5 B .π8 C .π16 D .π206.三棱锥ABC P −的四个顶点都在球O 的球面上,已知PA ,PB ,PC 两两垂直,1=PA ,4=+PC PB ,当三棱锥的体积最大时,球O 的体积为( ) A .π36 B .π9C .29π D .49π7.如图所示,平面四边形ABCD 中,2===CD AD AB ,22=BD ,CD BD ⊥,将其沿对角线BD 折成四面体ABCD ,使平面ABD ⊥平面BCD ,若四面体ABCD 的顶点在同一个球面上,则该球的体积为( )A .π328B .π24C .π34题型二、上下对称几何体外接球(直棱柱)直棱柱外接球半径R=√r 2+h 24,其中r 是底面外接圆半径,h 是直棱柱的高 r =a 2sinA(正弦定理)例1.设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( )A.πa 2B.73.πa 2 C. 113πa 2 D. 5πa 2例2.如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为 .例3.如图,三棱锥的所有顶点都在一个球面上,在ABC ∆中,3=AB ,︒=∠60ACB ,︒=∠90BCD ,CD AB ⊥,22=CD ,则该球的体积为 .例4. 如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( ) A .320πB .π8C .π9D .319π例5. 如图,某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形,若该三棱锥的顶点都在同一球面上,则该球的表面积为( ) A .π27 B .π48 C .π64D .π81变式练习1.已知A ,B ,C ,D 是同一球面上的四个点,其中ABC ∆是正三角形,⊥AD 平面ABC ,62==AB AD ,则该球的体积为( ) A .π332 B .π48 C .π24 D .π162.四面体ABCD 的四个顶点都在球O 的表面上,⊥AB 平面BCD ,三角形BCD 是边长为3的等边三角形,若4=AB ,则球O 的表面积为( ) A .π36B .π28C .π16D .π43.已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为32π的等腰三角形,则该三棱锥外接球的表面积为( ) A .π20B .π17C .π16D .π8题型三、正N 棱锥外接球正N 棱锥外接球半径R=l 22ℎ,其中l 是侧棱长度,h 是正棱锥的高例1. 正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81π4B. 16πC. 9πD.27π4题型四、等腰三角形底边与一直角三角形斜边构成二面角的四面体如上图中,ABC △为等腰三角形,且AC AB =,DBC △是以BC 为斜边的△Rt ,D BC A −−二面角为α,令ABC △的外接圆半径为2r ,BC 边上的高为21h AO =,12r BC =,F 为ABC △的外心,则根据剖面图可知,外接球半径R 满足以下恒等式()21222221212sin r r h R E O OO OE +⎪⎭⎫ ⎝⎛−==+=α.例1在四面体ABC S −中,BC AB ⊥,2==BC AB ,SAC △为等边三角形,二面角B AC S −−的余弦值为33−,则四面体ABC S −的外接球表面积为 .CB图3图4图5作二面角剖面⇒例2.在四面体ABCD 中,AB=AD=2,∠BAD =60。
高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型墙角模型是指三条线段两两垂直的几何体,通过公式(2R) = a + b + c,即2R = a^2 + b^2 + c^2,可以求出其外接球半径R。
例1:1)已知顶点都在同一球面上的正四棱柱的高为4,体积为16,求该球的表面积。
解:由V = ah = 16,得a = 2,4R = a + a + h = 4 + 4 + 16 = 24,S = 24π,答案为C。
2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,求其外接球的表面积。
解:由2R = a + b + c = 3 + 3 + 3 = 9,得R = 9/4,S =4πR^2 = 9π。
3)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA = 23,求正三棱锥S-ABC外接球的表面积。
解:由墙角模型的特点可知,正三棱锥的对棱互垂直。
连接AB、BC的中点D、E,连接AE、CD,交于H,则H是底面正三角形ABC的中心。
由AM⊥MN,SB//MN,可得AM⊥SB,AC⊥SB,故SB⊥平面SAC,SB⊥SA,SB⊥SC,即SB⊥SA,BC⊥SA,故SA⊥平面SBC,SA⊥SC。
因此,三棱锥S-ABC的三棱条侧棱两两互相垂直,由2R^2 = 23^2 + 23^2 + 23^2 = 36,得R^2 = 9,S = 36π。
类型二、棱台模型棱台模型是指上底面和下底面都是正多边形,且两底面中心连线与侧棱垂直的几何体。
通过勾股定理和相似三角形,可以求出其外接球半径R和内切球半径r。
例2:1)已知棱台的上底面和下底面都是正三角形,上底边长为3,下底边长为6,侧棱长为5,求其外接球半径R和内切球半径r。
解:由勾股定理可得棱台的高为4√3.设外接球半径为R,内切球半径为r,则有R/r = (a + b + c)/(a + b - c) = (3 + 6 +5)/(3 + 6 - 5) = 7,解得R = 7r。
高中数学 立体几何 3.(第二次修订版)八个有趣模型——搞定空间几何体的外接球与内切球(学生版)

八个有趣模型——搞定空间几何体的外接球与内切球当讲到付雨楼老师于2018年1月14日总第539期微文章,我如获至宝.为有了教学的实施,我以付老师的文章主基石、框架,增加了我个人的理解及例题,形成此文,仍用文原名,与各位同行分享.不当之处,敬请大家批评指正.一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).初图1初图22.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法). 四、与台体相关的,此略. 五、八大模型第一讲 柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)图1-1图1-2图1-3图1-4方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( ) A .π16 B .π20 C .π24 D .π32 (2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 (3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1, 取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH , 则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,ΘBC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD , ∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, ΘMN AM ⊥,MN SB //,∴SB AM ⊥,ΘSB AC ⊥,∴⊥SB 平面SAC , ∴SA SB ⊥,SC SB ⊥,ΘSA SB ⊥,SA BC ⊥, ∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理)AC(3)题-2(解答图)AC(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( )π11.A π7.B π310.C π340.D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是 (6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为类型二、对棱相等模型(补形为长方体) 题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =) 第一步:画出一个长方体,标出三组互为异面直线的对棱; 第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=, 补充:图2-1中,abc abc abc V BCD A 31461=⨯-=-. 第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .例2(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .(6)题图图2-1(1)题图B(2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为 . (3)正四面体的各条棱长都为2,则该正面体外接球的体积为(4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是 .(4)题类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1图3-2图3-3题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ; 第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高); 第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=,解出R .例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为(2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 .(3)已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为 . (4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为 .第二讲 锥体背景的模型类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)图4-1图4-2图4-31.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点. 解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ;事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则 利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=; 第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R . 例4 (1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为 .(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为 (3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( )A .433 B .33 C .43 D .123(4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为ο60,则该三棱锥外接球的体积为( )A .π B.3π C. 4π D.43π (5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )A.6 B.6 C.3 D.2类型五、垂面模型(一条直线垂直于一个平面)1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直图5径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的 三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的 顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示,则该几何体外接球的表面积为( ) A .π3 B .π2 C .316πD.以上都不对侧视图正视图第三讲 二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)图6第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ; 第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,; 第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+ 注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 . (2)在直角梯形ABCD 中,CD AB //,ο90=∠A ,ο45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为(3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为(4)在边长为32的菱形ABCD 中,ο60=∠BAD ,沿对角线BD 折成二面角C BD A --为ο120的四面体ABCD ,则此四面体的外接球表面积为(5)在四棱锥ABCD 中,ο120=∠BDA ,ο150=∠BDC ,2==BD AD ,3=CD ,二面角C BD A --的平面角的大小为ο120,则此四面体的外接球的体积为类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设:如图7,ο90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为( )A .π12125 B .π9125 C .π6125 D .π3125(2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为 .第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径. 第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高; 第三步:由POE ∆相似于PDH ∆,建立等式:PDPODH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;图8-1A第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高; 第三步:由POG ∆相似于PFH ∆,建立等式:PFPOHF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 (1)棱长为a 的正四面体的内切球表面积是(2)正四棱锥ABCD S -的底面边长为2,侧棱长为3,则其内切球的半径为(3)三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则该三棱锥的内切球半径为习题: 1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ) A.3 B.6 C.36 D.9 2. 三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于 . 3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 .4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .5. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 . 6. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .。
十种求外接球与内切球模型(解析版)

十种求外接球与内切球模型【必备知识点】模型一:墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长.使用范围:3组或3条棱两两垂直;或可在长方体中画出该图且各顶点与长方体的顶点重合推导过程:长方体的体对角线就是外接球的直径公式:找三条两两垂直的线段,直接用公式(2R)2=a2+b2+c2,即2R=a2+b2+c2,求出R.例1.四面体ABCD的每个顶点都在球O的球面上,AB,AC,AD两两垂直,且AB=3,AC=2,AD= 3,则球O的表面积为( )A.64πB.16πC.4πD.π【答案】B【详解】四面体ABCD的外接球O即为以AB,AC,AD为长、宽、高的长方体的外接球,∴球O的外接球半径R=12AB2+AC2+AD2=2,∴球O的表面积S=4πR2=16π.故选:B.例2.在边长为2的正方形ABCD中,E,F分别为线段AB,BC的中点,连接DE,DF,EF,将△ADE,△CDF,△BEF分别沿DE,DF,EF折起,使A,B,C三点重合,得到三棱锥O-DEF,则该三棱锥外接球的表面积为( )A.3πB.6πC.6πD.24π【答案】C【详解】解:在正方形ABCD中,AD⊥AE,CD⊥CF,BE⊥BF,折起后OD,OE,OF两两垂直,故该三棱锥外接球即以OD,OE,OF为棱的长方体外接球.因为OD=2,OE=1,OF=1,所以2R=OD2+OE2+OF2=6,所以R=62,所以该三棱锥外接球的表面积为S表=4πR2=6π,故选:C.例3.已知P,A,B,C为球O的球面上的四个点,若PA⊥平面ABC,AC⊥BC,PA=1,AC=BC= 2,则球O的表面积为( )A.2πB.3πC.4πD.5π【答案】D【详解】解:在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,故可将三棱锥P-ABC补形成如图所示的长方体.若P,A,B,C为球O的球面上的四个点,则该长方体的各顶点亦在球O的球面上.设球O的半经为R,则该长方体的体对角线长为2R,即2R=PA2+AC2+BC2=5,从而有S球O=4πR2=π(2R)2=5π,故选:D.例4.如图,在矩形ABCD中,AB=2,BC=2,E为BC中点,把△ABE和△CDE分别沿AE,DE折起,使点B与点C重合于点P,若三棱锥P-ADE的四个顶点都在球O的球面上,则球O的表面积为( )A.3πB.4πC.5πD.9π【答案】C【详解】依题意,PE⊥PA,PE⊥PD,PA∩PD=P,PA,PD⊂平面PAD,则PE⊥平面PAD,又PA=PD=2,AD=2,即有PA2+PD2=AD2,则PA⊥PD,因此可将三棱锥P-ADE补形成以PE,PA,PD为相邻三条棱的长方体,若三棱锥P-ADE的四个顶点都在球O的球面上,则该长方体的各顶点亦在球O的球面上,设球O的半径为R,则该长方体的体对角线长为2R,即2R=PE2+PA2+PD2=5,所以球O的表面积为S=4πR2=π(2R)2=5π.故选:C例5.在正三棱锥S -ABC 中, 点M 是SC 的中点,且AM ⊥SB ,底面边长AB =22,则正三棱锥S -ABC 的外接球的表面积为()A.6πB.12πC.32πD.36π【答案】B【详解】因为三棱锥S -ABC 为正三棱锥, 所以SB ⊥AC ,又AM ⊥SB ,AC ∩AM =A ,AC ,AM ⊂平面SAC , 所以SB ⊥平面SAC,所以SB ⊥SA ,SB ⊥SC ,同理SA ⊥SC ,即SA ,SB ,SC 三线两两垂直,且AB =22,所以SA =SB =SC =2,所以(2R )2=3×22=12,所以球的表面积S =4πR 2=12π,故选 B .例6.将一个边长为4的正三角形ABC 沿其中线BD 折成一个直二面角,则所得三棱锥A -BCD 的外接球的体积为_________.【答案】2053π【详解】由题意得:AB =BC =4,AD =CD =2,BD ⊥AD ,CD ⊥BD ,即BD ⊥平面ADC ;∵二面角A -BD -C 为直二面角,∴AD ⊥CD ,则三棱锥A -BCD 的外接球即为以BD ,CD ,AD 为长宽高的长方体的外接球,又BD =16-4=23,∴三棱锥A -BCD 的外接球半径R =12AD 2+CD 2+BD 2=124+4+12=5,∴三棱锥A -BCD 的外接球体积V =43πR 3=2053π.故答案为:2053π.例7.在正三棱锥S -ABC 中,M ,N 分别是棱SC ,BC 的中点,且AM ⊥MN , 若侧棱SA =23,则正三棱锥S -ABC 外接球的表面积是_________.【答案】36π【详解】∵AM ⊥MN ,SB ⎳MN ,∴AM ⊥SB ,∵AC ⊥SB ,∴SB ⊥平面SAC,∴SB ⊥SA ,SB ⊥SC ,∵SB ⊥SA ,BC ⊥SA ,∴SA ⊥平面SBC ,∴SA ⊥SC ,故三棱锥S -ABC 的三棱条侧棱两两互相垂直,∴(2R )2=(23)2+(23)2+(23)2=36,即4R 2=36,∴正三棱锥S -ABC 外接球的表面积是36π.例8.在长方体ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为32的正方形,AA 1=3,E 是线段A 1B 1上一点, 若二面角A -BD -E 的正切值为3,则三棱锥A -A 1D 1E 外接球的表面积为_________.【答案】35π【详解】过点E 作EF ⎳AA 1交AB 于F ,过F 作FG ⊥BD 于G ,连接EG ,则∠EGF 为二面角A -BD -E 的平面角,∵tan ∠EGF =3,∴EF FG=3,∵EF =AA 1=3,∴FG =1,则BF =2=B 1E , ∴A 1E =22,则三棱锥A -A 1D 1E 外接球的直径为8+9+18=35,因此三棱锥A -A 1D 1E 外接球的表面积S =35π.模型二:对棱相等模型使用范围:对棱相等的三棱锥推导过程:通过对棱相等,可以将其补全为长方体,补全的长方体体对角线为外接球直径,设长方体的长宽高为别为a ,b ,cAD =BC AB =CD AC =BD ⇒a 2+b 2=BC 2=λ2b 2+c 2=AC 2=μ2c 2+a 2=AB 2=k 2⇒a 2+b 2+c 2=λ2+μ2+k 22⇒R =λ2+μ2+k 28V A -BCD =abc -16abc ×4=13abc 例1.如图,在△ABC 中,AB =25,BC =210,AC=213,D ,E ,F 分别为三边中点,将△BDE,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起,使A ,B ,C 重合为点P ,则三棱锥P -DEF 的外接球表面积为( )A.72πB.7143πC.14πD.56π【答案】C【详解】由题意可知,PE =DF =10,PF =DE =13,PD =EF =5,即三棱锥P-DEF 的对棱相等,先将该三棱锥补充成长方体,如图所示:设FH =x ,HD =y ,HP =z ,则x 2+y 2=10,y 2+z 2=5,x 2+z 2=13,所以x 2+y 2+z 2=14,于是三棱锥P -DEF 的外接球直径为14,半径为142,所以该三棱锥外接球的表面积为:4π⋅1422=14π.故选:C .例2.在△ABC 中,AB =AC =2,cos A =34,将△ABC 绕BC 旋转至△BCD 的位置,使得AD =2,如图所示,则三棱锥D -ABC 外接球的体积为_____________.【答案】556π【详解】在△ABC 中,由余弦定理得BC 2=22+22-2×2×2×34=2,所以BC =2.在三棱锥D -ABC 中,AB =AC =DB =DC =2,AD =BC =2.将三棱锥D -ABC 放入长方体,设长方体的长、宽、高分别为a ,b ,c ,棱锥D -ABC 外接球的半径为R ,则a 2+b 2=4,b 2+c 2=4,a 2+c 2=2,所以a 2+b 2+c 2=5,所以R =12a 2+b 2+c 2=52,从而三棱锥D -ABC 外接球的体积V =43πR 3=556π.故答案为:556π例3.已知三棱锥P -ABC 的每条侧棱与它所对的底面边长相等,且PA =32,PB =PC =5,则该三棱锥的外接球的表面积为______.【答案】34π【详解】解:根据题意,三棱锥P -ABC 可以嵌入一个长方体内,且三棱锥的每条棱均是长方体的面对角线,设长方体交于一个顶点的三条棱长为a ,b ,c ,如图所示,则a 2+b 2=PA 2=18,a 2+c 2=PB 2=25,b 2+c 2=PC 2=25,解得a =3,b =3,c =4.所以该三棱锥的外接球的半径为R =a 2+b 2+c 22=32+32+422=342,所以该三棱锥的外接球的表面积为S =4πR 2=4π×342 2=34π.故答案为:34π例4.已知四面体ABCD 的棱长满足AB =AC =BD =CD =2,BC =AD =1,现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中,使得四面体ABCD 可以在圆锥中任意转动,则圆锥侧面积的最小值为________.【答案】274π【详解】根据题意,只需四面体ABCD 在圆锥的内切球内,下面求四面体ABCD 的外接球半径.如图所示,将四面体放入长方体中,设长方体的长宽高分别为a ,b ,c ,则a 2+b 2=4,a 2+c 2=4,b 2+c 2=1,故4R 2=a 2+b 2+c 2=92,可得四面体ABCD 的外接球半径为324.当圆锥的侧面积最小时,该圆锥的内切球即四面体ABCD 的外接球,则此时圆锥的内切球的半径为R =324,底面圆的半径为r =324×3=364,母线长为324×2=322,所以侧面积为S =π×364×362=27π4.故答案为:27π4.例5.在三棱锥P -ABC 中,PA =BC =25,PB =AC =13,AB =PC =5,则三棱锥P -ABC 的外接球的表面积是______.【答案】29π【详解】由题意,PA =BC =25,PB =AC =13,PC =AB =5,将三棱锥P -ABC 放到长方体中,可得长方体的三条面对角线分别为25,13,5,设长方体的长宽高分别为a,b ,c ,即a 2+b 2=25,c 2+b 2=13,a 2+c 2=5,解得:a =4,b =2,c =3.长方体的体对角线即为三棱锥和长方体公共外接球的直径2R ,∴(2R )2=a 2+b 2+c 2⇒4R 2=29⇒S 球=4πR 2=29π﹒故答案为:29π.例6.已知三棱锥A -BCD ,三组对棱两两相等,且AB =CD =1,AD =BC =3,若三棱雉A -BCD的外接球表面积为9π2.则AC =______.【答案】5【详解】将四面体A-BCD放置于长方体中, ∵四面体A-BCD的顶点为长方体八个顶点中的四个,∴长方体的外接球就是四面体A-BCD的外接球,∵AB=CD=1,AD=BC=3,且三组对棱两两相等,∴设AC=BD=x,得长方体的对角线长为1212+(3)2+x2=124+x2,可得外接球的直径2R=124+x2,所以 R=24+x24,∵三棱锥A-BCD的外接球表面积为9π2,∴4πR2=9π2,解得 R=32 4, 即24+x24=324,解之得x=5, 因即AC=BD=5.模型三:汉堡模型适用范围:有一条侧棱垂直于底面的柱体推导过程:如图,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形).第一步:确定球心O的位置,O1是ABC的外心,则OO1⊥平面ABC.第二步:算出小圆O1的半径AO1=r,OO1=12AA1=12h AA1=h也是圆柱的高).第三步:勾股定理:OA2=O1A2+O1O2⇒R2=h22+r2⇒R=r2+h2 2,求出R.公式:R=r2+h 22例1.已知某圆柱的高为42,体积为42π,则该圆柱外接球的表面积为( )A.32πB.36πC.40πD.44π【答案】B【详解】设圆柱底面圆的半径为r,则πr2×42=42π,解得r=1.设该圆柱的两底面中心分别为O1、O2,则该圆柱外接球的球心O为线段O1O2的中点,球O 的半径为R =12+422 2=3,故球O 的表面积S =4πR 2=36π.故选:B .例2.已知三棱柱的各个侧面均垂直于底面,底面为正三角形,侧棱长与底面边长之比为3:2,顶点都在一个球面上,若三棱柱的侧面积为162,则该球的表面积为( )A.120πB.129πC.129πD.180π【答案】C【详解】由题意,设球的半径为r ,底面三角形边长为2x ,因为侧棱长与底面边长之比为3:2,所以侧棱长为3x ,因为三棱柱的侧面积为162,即满足3⋅3x ⋅2x =18x 2=162,解得x =3,可知侧棱长为9,底面边长为6,如图所示,设N ,M 分别是上、下底面的中心,MN 的中点O 是三棱柱ABC -A 1B 1C 1外接球的球心,则AM =33×6=23,OM =12MN =12AA 1=92,r =OA =OM 2+AM 2=92 2+23 2=1292,所以S =4πr 2=4π×12922=129π.故选:C .例3.已知三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上,AB =AC =AA 1=2,∠BAC =120∘,则球O 的表面积是( )A.4πB.163πC.16πD.20π【答案】D【详解】由余弦定理得BC 2=AB 2+AC 2-2AB ⋅AC ⋅cos ∠BAC =22+22-2×2×2×-12 =12,∴BC =23,设△ABC 外接圆的圆心为O 1,半径为CO 1,由正弦定理得BC sin ∠BAC =2CO 1 ,即2332=2CO 1,解得CO 1=2,设外接球的半径为R =CO ,∵O 1O =12AA 1=1,∴R =CO =CO 1 2+OO 1 2=22+12=5,球O 的表面积为S =4πR 2=20π,故选:D .例4.直三棱柱ABC -A 1B 1C 1所有顶点都在球O 的表面上,且∠BAC =π6,AA 1=22,AC =3AB =3,则球O 的表面积为________.【答案】20π【详解】解:直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上,且∠BAC =π6,AA 1=22,,AC =3AB =3,∴BC =AB 2+AC 2-2AB ⋅AC cos π6=3+9-2×3×3×32=3,设ΔABC 为外接圆的圆心为E ,2r =3sin π6=23,所以r =3,设外接球的球心为O ,设球的半径为R ,所以R =r 2+12AA 1 2=5,故S 球=4π⋅(5)2=20π.故答案为:20π.例5.在四面体ABCD 中,AB =CD =1,BC =2,且AB ⊥BC ,CD ⊥BC ,异面直线AB ,CD 所成角为π3,则该四面体外接球的表面积为______.【答案】16π3或8π【详解】由题意可以将四面体ABCD 补成一个如图所示的直三棱柱,因为异面直线AB ,CD 所成角为π3,所以∠ABE =π3或2π3,设△ABE 的外接圆半径为r ,当∠ABE =π3时,1sin60∘=2r ,r =33 ,当∠ABE =2π3时,AE =3 ,则3sin120∘=2r ,r =1,设四面体的外接球半径为R ,则R =r 2+BC 2 2=r 2+1 ,所以该四面体外接球的半径R =233或2,则外接球的表面积为.4πR 2=16π3或8π,故答案为:16π3或8π模型四:垂面模型适用范围:有一条棱垂直于底面的椎体推导过程:第一步:将ABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步:O 1为ABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=c sin C =2r ,OO 1=12PA .第三步:利用勾股定理求三棱锥的外接球半径:(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式:R 2=r 2+h 24例1.已知三棱锥P -ABC ,其中PA ⊥平面ABC ,∠BAC =120°,PA =AB =AC =2,则该三棱锥外接球的表面积为( )A.12πB.16πC.20πD.24π【答案】C【详解】根据题意设底面△ABC 的外心为G ,O 为球心,所以OG ⊥平面ABC ,因为PA ⊥平面ABC ,所以OG ⎳PA ,设D 是PA 中点,因为OP =OA ,所以DO ⊥PA ,因为PA ⊥平面ABC ,AG ⊂平面ABC ,所以AG ⊥PA ,因此OD ⎳AG ,因此四边形ODAG 是平行四边形,故OG =AD =12PA =1,由余弦定理,得BC =AB 2+AC 2-2AB ⋅AC ⋅cos120°=4+4-2×2×2×-12=23,由正弦定理,得2AG =2332⇒AG =2,所以该外接球的半径R 满足R 2=OG 2+AG 2=5⇒S =4πR 2=20π,故选:C .例2.已知四面体ABCD 的每个顶点都在球O 的球面上,CD ⊥平面ABC ,AC =23,△ABC 是正三角形,△ACD 是等腰三角形,则球O 的体积为( )A.2053πB.86πC.2873πD.36π【答案】C【详解】∵CD ⊥平面ABC ,AC ⊂平面ABC ,∴CD ⊥AC ,又△ACD 是等腰三角形,∴CD =AC .∵△ABC 是正三角形,∴AB =BC =AC =CD =23.设E 为△ABC 外接圆的圆心,则CE =23×32×23=2,OE =12CD =3,∴OC =OE 2+CE 2=7,∴球O 的体积V =43π×7 3=2873π.故选:C .例3.在三棱锥S -ABC 中, 侧棱SA ⊥底面ABC ,AB =5,BC =8,∠ABC =60°,SA =25, 则该三棱锥的外接球的表面积为()A.643π B.2563π C.4363π D.2048327π【答案】B【详解】 由题意知,AB =5,BC =8,∠ABC =60°,则在△ABC 中, 由余弦定理得 AC 2=AB 2+BC 2-2×AB ×BC ×cos ∠ABC ,解得AC =7,设△ABC 的外接圆半径为 r ,则△ABC 的外接圆直径2r =AC sin ∠ABC =772,∴r =73, 又∵侧棱SA ⊥底面ABC ,∴三棱锥的外接球的球心到平面ABC 的距离 h =12SA =5,则外接球的半径R =732+(5)2=643,则该三棱锥的外接球的表面积为S =4πR 2=2563π.例4.已知四棱锥P -ABCD 的五个顶点在球O 的球面上,PA ⊥底面ABCD ,PA =4,AB =AD ,BC=CD ,∠BAD =120°,且四边形ABCD 的面积为934,则球O 的表面积为___________.【答案】25π【详解】如图所示,在四边形中ABCD ,连结BD ,AC ,由AB =AD ,BC =CD ,所以△ABC ≌△ADC ,所以∠ABC =∠ADC ,∠BAC =∠DAC ,因为A ,B ,C ,D 在同一圆上,所以∠ABC =∠ADC =90°,又因为∠BAD =120°,所以∠BCD =60°,则∠BAC =∠DAC =60°,在Rt △ABC 中,可得BC =3AB ,因为底面ABCD 的面积为934,所以2×12AB ⋅3AB =934,解得AB =32,则BC =332,AC =3322+322=3,所以Rt △ABC 外接圆的半径r =32,将四棱锥P -ABCD 补成直四棱柱PEFG -ABCD ,该直棱柱的所有顶点都在球O 的球面上,设底面四边形ABCD 所在圆的圆心为O 1,连接OO 1,则OO 1⊥平面ABCD ,过OM ⊥PA ,垂足为M ,由球的对称性可知,球心O 到底面ABCD 的距离为d =OO 1=AM =12PA =2,所以球O 的半径R 满足R 2=d 2+r 2=254,所以球O 的表面积S 球O =4πR 2=25π.故答案为:25π.例5.在三棱锥P -ABC 中,PA ⊥平面ABC ,∠BAC =120°,AC =2,AB =1,设D 为BC 中点, 且直线PD 与平面ABC 所成角的余弦值为55, 则该三棱雉外接球的表面积为___________.【答案】 373π【详解】在△ABC 中,∠BAC =120°,AC =2,AB =1,由余弦定理得:BC 2=AC 2+AB 2-2AC ⋅BC ⋅cos ∠BAC ,即BC 2=22+12-2×2×1×cos120°=7,解得:BC =7. 设△ABC 的外接圆半径为r ,由正弦定理得2r =BC sin ∠BAC =7sin120°=273解得:r =73=213;且cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC =12+(7)2-222×1×7=277,又D 为BC 中点, 在△ABD 中,BD =12BC =72,AB =1,cos ∠ABD =277. 由余弦定理得:AD 2=AB 2+BD 2-2AB ⋅BD cos ∠ABD ,即:AD 2=12+722-2×1×72×277=34,解得AD =32.又因为PA ⊥平面ABC , 所以 ∠PDA 为直线PD 与平面ABC 所成角, 由cos ∠PDA =55,得 sin ∠PDA =255,tan ∠PDA =2所以在Rt △PAD 中, PA =AD ⋅tan ∠PDA =32⋅2=3. 设三棱锥P -ABC 的外接球半径为R , 所以R =PA 22+r 2=322+2132=3712,三棱锥P -ABC 外接球表面积为S =4πR 2=373π.模型五:斗笠模型使用范围:正棱雉或顶点的投影在底面的外心上推导过程:取底面的外心01, 连接顶点与外心,该线为空间几何体的高h ,在h 上取一点作为球心0,根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式:R =r 2+h 22h例1.已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1, 则球O 的表面积为()A.64πB.48πC.36πD.32π【答案】A 【详解】设⊙O 1的半径为r ,球的半径为R ,依题意,得πr 2=4π,∴r =2.由正弦定理可得ABsin60°=2r ,∴AB =2r sin60°=2 3.∴OO 1=AB =2 3.根据球的截面性质,得OO 1⊥平面ABC ,∴OO 1⊥O 1A ,R =OA =OO 21+O 1A 2=OO 21+r 2=4,∴球O 的表面积S =4πR 2=64π.故选A .例2.正四棱锥的顶点都在同一球面上, 若该棱锥的高为4 , 底面边长为2 , 则该球的表面积为()A.81π4B.16πC.9πD.27π4【答案】A 【详解】如图所示,设球半径为R ,底面中心为O 且球心为O ,∵正四棱锥P -ABCD 中 AB =2,∴AO =2,∵PO =4,∴在Rt △AOO 中, AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×942=81π4.例3.已知一个圆锥的母线长为26,侧面展开图是圆心角为23π3的扇形,则该圆锥的外接球的体积为( )A.36πB.48πC.36D.242【答案】A 【详解】设圆锥的底面半径为r ,由侧面展开图是圆心角为23π3的扇形得:2πr =23π3×26,解得:r =22.作出圆锥的轴截面如图所示:设圆锥的高为h ,则h =26 2-22 2=4.设该圆锥的外接球的球心为O ,半径为R ,则有R =h -R2+r 2,即R =4-R2+22 2,解得:R =3,所以该圆锥的外接球的体积为4πR 33=4π333=36π.故选:A .例4.在三棱锥P -ABC 中,侧棱PA =PB =PC =10,∠BAC =π4,BC =22,则此三棱锥外接球的表面积为_______.【答案】50π3【详解】因为PA =PB =PC =10,所以点P 在底面ABC 的射影为△ABC 的外心O 1,所以球心O 在直线PO 1上,设三棱锥外接球的半径为R ,因为2AO 1=22sin π4,所以AO 1=2,PO 1=6,由AO 2=OO 21+AO 21可得,R 2=6-R 2+4,解得R =56,故此三棱锥外接球的表面积为4πR 2=4π×256=503π.故答案为:50π3.例5.已知正四面体的棱长为4,则此四面体的外接球的表面积是为________.【答案】24π【详解】如图正四面体ABCD 棱长为4,AH ⊥平面BCD 于H ,则H 是△BCD 中心,BH =33×4=433,AH ⊥平面BCD ,BH ⊂平面BCD ,则AH ⊥BH ,AH =42-4332=463,设外接球球心为O ,则O 在AH ,则OA =OB =R 为外接半径,由BH 2+OH 2=BO 2得4332+463-R2=R 2,解得R =6,∴S =4πR 2=24π.故答案为:24π.例6.在三棱雉P -ABC 中,PA =PB =PC =26,AC =AB =4,且AC ⊥AB ,则该三棱锥外接球的表面积为________.【答案】36π【详解】设顶点P 在底面中的射影为O 1,由于PA =PB =PC ,所以O 1A =O 1B =O 1C ,即点O 1 是底面△ABC 的外心,又AC ⊥AB ,所以O 1为BC 的中点,因为PA =PB =PC =26,AC =AB =4,所以BC =42,AO 1=22,PO 1=4,设外接球的球心为O ,半径为R ,则O 必在PO 1上, O 1O =4-R ,在Rt △O 1OA 中, (4-R )2+(22)2=R 2, 解得R =3,所以S 2=4πR 2=36π.例7..一个圆锥恰有三条母线两两夹角为60°, 若该圆雉的侧面积为33π,则该圆雉外接球的表面积为________.【答案】27π2【详解】设∠ASB =∠BSC =∠CSA =60°,则SA =SB =SC =AB =AC =BC .设AB =x ,则底面圆的直径为2r =x sin60°=2x 3,该圆锥的侧面积为12π⋅2x3⋅x =33π,解得x =3,高OS =32-(3)2= 6.∴r =33= 3.设圆锥外接球的半径为R ,所以(6-R )2+r 2=R 2,解得R =364, 则外接球的表面积为4πR 2=27π2.类型六:切瓜模型使用范围:有两个平面互相垂直的棱雉推导过程:分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线, 两条垂线的交点即为球心0,取B C 的中点为E , 连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式:R 2=r 21+r 22-l 24例1.已知四棱锥P -ABCD 中,底面ABCD 为边长为4的正方形,侧面PAB ⊥底面ABCD ,且△PAB为等边三角形,则该四棱锥P -ABCD 外接球的表面积为( )A.112π3B.64π3C.64πD.16π【答案】A【详解】如图所示,在四棱锥P -ABCD 中,取侧面△PAB 和底面正方形ABCD 的外接圆的圆心分别为O 1,O 2,分别过O 1,O 2作两个平面的垂线交于点O ,则由外接球的性质知,点O 即为该球的球心,取线段AB 的中点E ,连O 1E ,O 2E ,O 2D ,OD ,则四边形O 1EO 2O 为矩形,在等边△PAB 中,可得PE =23,则O 1E =233,即OO 2=233,在正方形ABCD 中,因为AB =4,可得O 2D =22,在直角△OO 2D 中,可得OD 2=OO 22+O 2D 2,即R 2=OO 22+O 2D 2=283,所以四棱锥P -ABCD 外接球的表面积为S =4πR 2=112π3.故选:A .例2.已知三棱锥A -BCD 中, △ABD 与△BCD 是边长为2的等边三角形且二面角A -BD -C 为直二面角, 则三棱雉A -BCD 的外接球的表面积为()A.10π3B.5πC.6πD.20π3【答案】D 【详解】取BD 的中点M ,连接AM ,CM ,∠AMC =90°,AF :FM =2:1,CE :EM =2:1,OF ⊥AM ,OE ⊥MC ,OE ∩OF =O 连接OC ,点 O 是三棱锥A -BCD 的外接球的球心,因为棱长都是2 ,所以OE =FM =33,EC =233,所以在△OEC 中,R =OC =OE 2+EC 2=153,那么外接球的表面积是S =4πR 2=203π ,故选D .例3.已知四棱锥P -ABCD 的体积是363,底面ABCD 是正方形,△PAB 是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P -ABCD 的外接球的体积为________.【答案】2821π【详解】设正方形ABCD 的边长为2x ,在等边三角形PAB 中,过P 点作PE ⊥AB 于E ,由于平面PAB ⊥平面ABCD ,∴PE ⊥平面ABCD .由于△PAB 是等边三角形,则PE =3x ,∴V P -ABCD =13⋅S ABCD ⋅PE =13×2x 2×3x =363,解得x =3.设四棱锥外接球的半径为R ,O 1为正方形ABCD 中心,O 2为等边三角形PAB 中心,O 为四棱锥P -ABCD 外接球球心,则易知OO 2EO 1为矩形,则OO 2=EO 1=12AD =x =3,PO 2=23PE =23⋅33=23,R =OP =OO 22+PO 22=9+12=21,∴外接球体积V =43π×(21)3=2821π.故答案为:2821π.例4.已知四面体ABCD 中,△ABD 和△BDC 是等边三角形,二面角A -BD -C 为直二面角.若AB =43,则四面体ABCD 外接球的表面积为__________________.【答案】80π【详解】如图所示:设O 1为△BCD 的中心,O 为四面体ABCD 的外接球的球心,则OO 1⊥平面BDC .设M 为线段BD 的中点,外接球的半径为R ,连接AM ,CM ,OA ,过O 作OG ⊥AM 于点G ,易知G 为△ABD 的中心,则OO 1=OG =MO 1=MG ,因为MA =32×43=6,故MG =OG =13×6=2,GA =4,在Rt △AGO 中,GA 2+GO 2=OA 2,故22+42=R 2,则R =25.所以外接球的表面积为S =4πR 2=80π,故答案为:80π.例5.已知在三棱锥A -BCD 中,平面ABD ⊥平面BCD ,△BCD 和△ABD 均是边长为23的正三角形,则该三棱锥的外接球体积为___________.【答案】2053π【详解】依题意,平面ABD ⊥平面BCD ,△BCD 和△ABD 均是边长为23的正三角形,设G 是BD 的中点,则AG ⊥BD ,CG ⊥BD ,由于平面ABD ⊥平面BCD 且交线为BD ,所以AG ⊥平面BCD ,CG ⊥平面ABD .设E ,F 分别是等边三角形ABD 和等边三角形BCD 的中心,则AE =CF =2GE =2GF =23CG =23×3=2,设O 是三棱锥A -BCD 外接球的球心,则OE ⊥平面ABD ,OF ⊥平面BCD .所以外接球的半径R =OF 2+CF 2=12+22=5,所以外接球的体积为4π3×5 3=2053π.故选:2053π模型七:折叠模型使用范围:两个全等三角形或等腰三角形拼在一起,或菱形折叠.推导过程:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角∠A EC =α,CE =A E =h .如图,作左图的二面角剖面图如右图:H 1和H 2分别为△BCD ,△A BD 外心,CH 1=r =BD2sin∠BCD,EH1=h-r,OH1=(h-r)tan α2故R2=OC2=OH21+CH21=r2+(h-r)2tan2α2.公式:R2=r2+(h-r)2tan2α2例1.已知菱形ABCD中,∠DAB=60°,AB=3,对角线AC与BD的交点为O,把菱形ABCD沿对角线BD折起, 使得∠AOC=90°,则折得的几何体的外接球的表面积为()A.15πB.15π2C.7π2D.7π【答案】A【解析】菱形ABCD中,∠DAB=60°,AB=3,三角形ABD的外接圆的半径为r=32sin60°=3,高h=332,对角线AC与BD的交点为O,使得α=∠AOC=90°,则折得的几何体的外接球的半径为:R=(3)2+332-32tan245°=152,外接球的表面积为S=4π152 2=15π, 故选 A.例2.在三棱雉P-ABC中,PA=PB=AC=BC=2,AB=23,PC=1,则三棱雉P-ABC的外接球的表面积为()A.4π3B.4πC.12πD.52π3【答案】D【解析】取AB中点D,因为PA=PB=AC=BC=2,所以PD=CD=1,又 PD⊥AB,CD⊥AB,则面PDC⊥面ABC,设△ABC的外心为O1,外接圆半径为r,三棱锥P-ABC的外接球的球心为O,则OO1⊥面ABC,∠ACB=120°,由r=AB2sin120°=2,h=1,设∠PDC=α=60°(二面角平面角),外接球的半径为 R,R=r2+(h-r)2tan2α2=(2)2+(1-2)2tan230°=133,所以三棱雉P-ABC的外接球的表面积为4πR2=52π3,故选 D.例3.在边长为23的菱形ABCD中,∠BAD=60°,沿对角线AC折成二面角B-AC-D为120°的四面体ABCD,则此四面体的外接球表面积为________.【答案】84π【解析】如图所示, 典型的全等等腰三角形共底边:ED=h=3,O2D=r=23,∠BED=α=120°,可根据几何性质知道 ∠O 2EO =60°,OO 2=EO 2tan60°=3,R =OO 22+DO 22=(3)2+(23)2=21,或者可以通过公式R =r 2+(h -r )2tan 2α2=(23)2+(3-23)2tan 260°=21,S =4πR 2=84π.模型八:已知球心或球半径模型例1.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.【答案】36π【解析】如图, 连接AO ,OB ,∵SC 为球O 的直径,∴点O 为SC 的中点, ∵SA =AC ,SB =BC ,∴AO ⊥SC ,BO ⊥SC ,∵平面SCA ⊥平面SCB , 平面SCA ∩平面SCB =SC ,∴AO ⊥平面SCB , 设球O 的半径为R ,则OA =OB =R ,SC =2R .∴V S ⋅ABC =V A -SBC =13×S △SBC ×AO =13×12×SC ×OB ×AO , 即9=13×12×2R ×R ×R , 解得R =3,∴球O 的表面积为S =4πR 2=4π×32=36π.例2.已知三棱锥A -BCD 的所有顶点都在球O 的球面上,AB 为球O 的直径,若该三棱雉的体积为3,BC =3,BD =3,∠CBD =90°, 则球O 的体积为________.【答案】32π3【解析】设A 到平面BCD 的距离为h∵三棱锥的体积为3,BC =3,BD =3,∠CBD =90°∴13×12×3×3×h =3,∴h =2,∴球心O 到平面BCD 的距离为1.设CD 的中点为E ,连接OE ,则由球的截面性质可得OE ⊥平面CBD ,∵△BCD 外接圆的直径CD =23,∴球O 的半径OD =2,∴球O 的体积为32π3.例3.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形, SC 为球O的直径, 且SC =2,则此棱锥的体积为()A.26B.36C.23D.22【答案】A【解析】由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点, 因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,S △ABC =34×AB 2=34, 高OD =12-332=63,∴V S -ABC =2V O -ABC =2×13×34×63=26. 故选 A .例4.三棱锥S -ABC 的底面各棱长均为3 , 其外接球半径为2 , 则三棱锥S -ABC 的体积最大时,点S 到平面ABC 的距离为()A.2+3B.2-3C.3D.2【答案】C【解析】如图, 设三棱锥S -ABC 底面三角形ABC 的外心为G , 三棱锥外接球的球心为O , 要使三棱锥 S -ABC 的体积最大, 则O 在SG 上,由底面三角形的边长为3,可得AG =32sin60°=3.连接OA ,在 Rt △OGA 中,由勾股定理求得OG =OA 2-GA 2=22-(3)2=1.∴点S 到平面ABC 的距离为 OS +OG =2+1=3. 故选 C .模型九:最值模型最值问题的解法有两种方法:一种是几何法,即在运动变化过䅣中得到最值,从而转化为定值问题求解.另一种是代数方法,即建立目标函数,从而求目标函数的最值.例1.在边长为6的菱形ABCD 中,∠A =π3,现将△ABD 沿BD 折起,当三棱锥A -BCD 的体积最大时,三棱锥A -BCD 的外接球的表面积为( )A.60πB.30πC.70πD.50π【答案】A 【分析】当三棱锥A -BCD 的体积最大值时,平面ABD ⊥平面BCD ,即可求出外接圆的半径,从而求出面积.【详解】当三棱锥A -BCD 的体积最大值时,平面ABD ⊥平面BCD ,如图,取BD 的中点为H ,连接AH ,CH ,则AH ⊥BD .设O 1,O 2分别为△ABD ,△BCD 外接圆的圆心,O 为三棱锥A -BCD 的外接球的球心,则O 1在AH 上,O 2在CH 上,且AO 1=2O 1H =23AH =23,且O 2H ⊥BD ,OO 1⊥平面ABD ,OO 2⊥平面BCD .∵平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,AH ⊂平面ABDAH ⊥平面ABD ,AH ⎳O 2O ,同理CH ⎳O 1O ∴四边形O 1OO 2H 为平行四边形∵AH ⊥平面BCD ,O 2H ⊂平面BCD ∴AH ⊥O 2H ,即四边形O 1OO 2H 为矩形.∴OO 2=O 1H =3CO 2=23×32×6=23∴外接球半径R =OO 22+CO 22=3+12=15∴外接球的表面积为4πR 2=60π故选:A .例2.在四棱锥S -ABCD 中,侧面SAD ⊥底面ABCD ,且SA =SD ,∠ASD =90°,底面ABCD 是边长为2的正方形,设P 为该四棱锥外接球表面上的动点,则三棱锥P -SAD 的最大体积为( )A.1+2B.2+223C.2+23D.1+23【答案】D 【详解】连接AC ,BD 交于点O ,取AD 中点为M ,连接SM ,OS ,作图如下:因为AS =DS ,∠ASD =90°,又M 为AD 的中点,故M 为Rt △SAD 的外心,又平面SAD ⊥平面ABCD ,且面SAD ∩面ABCD =AD ,又OM ⊥AD ,OM ⊂面ABCD ,故可得OM ⊥面SAD ,故OA =OS =OD ;又四边形ABCD 为正方形,且O 为对角线交点,故可得OA =OB =OC =OD ,综上所述,OA =OB =OC =OD =OS ,故O 为四棱锥S -ABCD 的外接球的球心.则其外接球半径R =OD =12BD =2.又P 为该四棱锥外接球表面上的动点,若使得三棱锥P -SAD 的体积最大,则此时点P 到平面SAD 的距离h =OM +R =1+2,故其体积的最大值V =13S △SAD ×h =13×12×AD ×SM ×1+2 =13×12×2×1×1+2 =1+23.故选:D .例3.已知P ,A ,B ,C ,D 都在同一个球面上,平面PAB ⊥平面ABCD ,ABCD 是边长为2的正方形,∠APB =60°,当四棱锥P -ABCD 的体积最大时,该球的半径为______.【答案】213【分析】先求出四棱锥P -ABCD 的体积最大时,△PAB 为等边三角形,再找出外接球的球心,通过勾股定理即可求得半径.【详解】如图,过点P 作PQ ⊥AB 于Q ,平面PAB ⊥平面ABCD ,平面PAB ∩平面ABCD =AB ,∴PQ ⊥平面ABCD ,V P -ABCD =13⋅PQ ⋅S ABCD ,故四棱锥P -ABCD 的体积最大,即PQ 最大,∵AB =2,PQ 最大,即△PAB 面积最大,由∠APB =60°,S △PAB =12⋅PA ⋅PB ⋅sin ∠APB =34⋅PA ⋅PB ,得cos ∠APB =AP 2+BP 2-42AP ⋅BP=12,AP 2+BP 2=AP ⋅BP +4≥2AP ⋅BP ,得AP ⋅BP ≤4,当且仅当AP =BP =2时取等号,此时△PAB 面积最大,△PAB 为等边三角形.取△PAB 的外心为O 1,正方形ABCD 的外心为O 2,过O 1,O 2分别作所在平面的垂线,交点为O ,O 即为四棱锥P -ABCD 外接球的球心,四边形OO 2QO 1为矩形,OO 1=O 2Q =1 ,PO 1=23PQ =233,设外接球半径为R ,则R =12+2332=213.故答案为:213.例4.A ,B ,C ,D 四点均在同一球面上,∠BAC =120∘,△BCD 是边长为2的等边三角形,则△ABC 面积的最大值为__________,四面体ABCD 体积最大时球的表面积为___________.【答案】 33 20π3【分析】①由于S △ABC =12AB ⋅AC sin ∠BAC =34AB ⋅AC ,求△ABC 面积的最大值即是求AB ⋅AC 的最大值,利用余弦定理结合重要不等式即可求解②当面ABC⊥面BCD时四面体的体积最大,确定出球心后计算出球的半径即可求解【详解】①因为∠BAC=120∘所以S△ABC=12AB⋅AC sin∠BAC=34AB⋅AC又BC2=AB2+AC2-2AB⋅AC⋅cos120∘即4=AB2+AC2+AB⋅AC≥2AB⋅AC+AB⋅AC=3AB⋅AC所以AB⋅AC≤4 3所以S△ABC=34AB⋅AC≤34×43=33即△ABC面积的最大值为3 3②过A作AH⊥BC,垂足为H, S△ABC=12AH⋅BC=AH则△ABC面积的最大时,AH最大,AH的最大值为3 3,此时△ABC为等腰三角形,H为BC中点S△BCD=12×2×2×32=3,V A-BCD=13S△BCD⋅h=33h则当AH⊥平面BCD时, h最大,此时面ABC⊥面BCD如图,设O为四面体ABCD 外接球的球心, O1,O2分别为△ABC,△BCD的外接圆的圆心. OO1⊥平面ABC,OO2⊥平面BCD,在△ABC中BCsin∠BAC=433=2O2A⇒O2A=33DO1=23DH=23×32×2=233OO1=O2H=O2A-AH=33∴四面体ABCD外接球的半径R=OO21+O1D2=53外接球的表面积为4πR2=20π3模型十:内切球模型以三棱雉P-ABC为例, 求其内切球OE的半径推导过程:等体积法,三棱雉P-ABC体积等于内切球球心与四个面构成的四个三棱雉的体积之和.第一步:先求出四个表面的面积和整个雉体体积;第二步:设内切球的半径为r ,球心为O ,建立等式:V P -ABC =V O -ABC +V O -PAB +V O -PAC +V O -PBC ⇒V P -ABC =13S △ABC ⋅r +13S △PAB ⋅r +13S △PAC ⋅r +13S △PBC ⋅r =13S△ABC+S △PAB +S △PAC +S △PBC ⋅r 第三步:解出r =3V P -ABC S O -ABC +S O -PAB +S O -PAC +S O -PBC =3VS 表.公式:r =3VS 表例1.已知点O 到直三棱柱ABC -A 1B 1C 1各面的距离都相等,球O 是直三棱柱ABC -A 1B 1C 1的内切球,若球O 的表面积为16π,ABC 的周长为4,则三棱锥A 1-ABC 的体积为( )A.43B.163C.833D.1633【答案】B 【详解】解:设直三棱柱ABC -A 1B 1C 1的高为h ,AB =c ,BC =a ,AC =b ,内切球O 的半径为r ,则h =2r ,由题意可知球O 的表面积为16π=4πr 2,解得r =2,∴h =4,又△ABC 的周长为4,即a +b +c =4,∴连接OA ,OB ,OC ,OA 1,OB 1,OC 1可将直三棱柱ABC -A 1B 1C 1分成5个棱锥,即三个以原来三棱柱侧面为底面,内切球球心为顶点的四棱锥,两个以原来三棱柱底面为底面,内切球球心为顶点的的三棱锥,∴由体积相等可得直三棱柱ABC -A 1B 1C 1的体积为S △ABC h =13ahr +13bhr +13chr +2×13S △ABC r ,即4S △ABC =13(a +b +c )hr +43S △ABC ,∴S △ABC =4,∴三棱锥A 1-ABC 的体积为13S △ABC h =13×4×4=163.故选:B .例2.在《九章算术·商功》中,将四个面都为直角三角形的四面体称为鳖臑,如图在鳖臑ABCD 中,AB ⊥平面BCD ,AB =BC =CD =1,BC ⊥CD ,则鳖臑ABCD 内切球的表面积为( )。
高中数学丨外接球与内切球解题方法,8大模型

高中数学I夕卜接球与内切球解题方法,8大模型空间几何体的外接球与内切球-、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球。
2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).初图1初图22.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正弦定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直。
外接球与内切球九大模型(解析版)

空间几何体的外接球与内切球九大模型模型一墙角模型【方法总结】墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=a2+b2+c2.),秒杀公式:R2=a2+b2+c24.可求出球的半径从而解决问题.有以下四种类型:【例题选讲】[例](1)已知三棱锥A-BCD的四个顶点A,B,C,D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=3,BC=2,CD=5,则球O的表面积为()A.12πB.7πC.9πD.8π答案A解析由AC⊥平面BCD,BC⊥CD知三棱锥A-BCD可构造以AC,BC,CD为三条棱的长方体,设球O的半径为R,则有(2R)2=AC2+BC2+CD2=3+4+5=12,所以S球=4πR2=12π,故选A.(2)若三棱锥ABCS-的三条侧棱两两垂直,且2=SA,4==SCSB,则该三棱锥的外接球半径为().A.3B.6C.36D.9答案A解析616164)2(2=++=R,3=R,故选A.(3)已知S,A,B,C,是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=2,则球O的表面积等于().A.4πB.3πC.2πD.π答案解析由已知,222211(2)2R=++=,244S Rπ∴==球π.(4)在正三棱锥S-ABC中,M,N分别是棱SC,BC的中点,且AM MN⊥,若侧棱SA=S-ABC外接球的表面积是________.答案π36解析 MNAM⊥,MNSB//,∴SBAM⊥, SBAC⊥,∴⊥SB平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,222(2)(2R ∴=+2+36=,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(5)(2019全国Ⅰ)已知三棱锥P -ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为().A .68πB .64πC .6πD .6π答案D 解析解法一:, PA PB PC ABC == △为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥ 平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分,2R =,即344π2338R V R π=∴==⨯=,故选D .解法二:设2PA PB PC x ===,, E F 分别为, PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,CF ∴=,又90CEF ∠=︒,1 2CE AE PA x ∴===,AEC △中,由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯作PD AC ⊥于D ,PA PC = ,D ∴为AC 的中点,cos E ∠12AD AC PA x==,2243142x x x x +-+∴=,221212 2x x x ∴+=∴==,,PA PB PC ∴===,又2AB BC AC ===,, , PA PB PC ∴两两垂直,2R ∴==,R ∴=,34433V R ππ∴==⨯8=,故选D .(6)已知二面角α-l -β的大小为π3,点P ∈α,点P 在β内的正投影为点A ,过点A 作AB ⊥l ,垂足为点B ,点C ∈l ,BC =22,PA =23,点D ∈β,且四边形ABCD 满足∠BCD +∠DAB =π.若四面体PACD 的四个顶点都在同一球面上,则该球的体积为________.答案86π解析∵∠BCD +∠DAB =π,∴A ,B ,C ,D 四点共圆,直径为AC ,∵PA ⊥平面β,AB ⊥l ,∴易得PB ⊥l ,即∠PBA 为二面角α-l -β的平面角,即∠PBA =π3,∵PA =23,∴BA =2,∵BC =22,∴AC=23.设球的半径为R ,则23-R 2-(3)2=R 2-(3)2,∴R =6,V =4π3(6)3=86π.模型二对棱相等模型【方法总结】对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长,即2R =(长方体的长、宽、高分别为a 、b 、c ).秒杀公式:R 2=x 2+y 2+z 28(三棱锥的三组对棱长分别为x 、y 、z ).可求出球的半径从而解决问题.【例题选讲】[例](1)正四面体的各条棱长都为,则该正面体外接球的体积为________.答案解析这是特殊情况,但也是对棱相等的模式,放入长方体中,32=R ,23=R ,ππ2383334=⋅=V .(2)在三棱锥A -BCD 中,AB =CD =2,AD =BC =3,AC =BD =4,则三棱锥BCD A -外接球的表面积为__.答案292π解析构造长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S .(3)在三棱锥A -BCD 中,AB =CD =6,AC =BD =AD =BC =5,则该三棱锥的外接球的体积为____.答案6解析依题意得,该三棱锥的三组对棱分别相等,因此可将该三棱锥补形成一个长方体,设该长方体的长、宽、高分别为a 、b 、c ,且其外接球的半径为R ,2+b 2=62,2+c 2=52,2+a 2=52,得a 2+b 2+c 2=43,即(2R )2=a 2+b 2+c 2=43,易知2R =,即为该三棱锥的外接球的半径,所以该三棱锥的外接球的表面积为3436R π=.(4)在正四面体A BCD -中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +,则该正四面体的外接球的体积是()A B .6πC D .32π答案A解析将侧面ABC ∆和ACD ∆展成平面图形,如图所示:设正四面体的棱长为a ,则BP PE +的最小值为2BE ==,2a ∴=.在正四面体A BCD -的边长为2,外接球的半径42R ==,外接球的体积343V R π==.(5)已知三棱锥A BCD -,三组对棱两两相等,且1AB CD ==,AD BC ==,若三棱锥A BCD -的外接球表面积为92π.则AC =________.答案解析将四面体A BCD -放置于长方体中, 四面体A BCD -的顶点为长方体八个顶点中的四个,∴长方体的外接球就是四面体A BCD -的外接球,1AB CD == ,AD BC ==,且三组对棱两两相等,∴设AC BD x ==,得长方体的对角线长为=,可得外接球的直径2R =以R =, 三棱锥A BCD -的外接球表面积为92π,2942R ππ∴=,解得4R =,324=,解之得x =AC BD ==模型三汉堡模型【方法总结】汉堡模型是直棱柱的外接球、圆柱的外接球模型,用找球心法(多面体的外接球的球心是过多面体的两个面的外心且分别垂直这两个面的直线的交点.一般情况下只作出一个面的垂线,然后设出球心用算术方法或代数方法即可解决问题.有时也作出两条垂线,交点即为球心.)解决.以直三棱柱为例,模型如下图,由对称性可知球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=2h ,2224h R r ∴=+.【例题选讲】[例](1)(2013辽宁)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上.若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为().A .3172B .210C .132D .310答案C 解析如图所示,由球心作平面ABC 的垂线,则垂足为BC 的中点M .又AM =12BC =52,OM =12AA 1=6,所以球O 的半径R =OA =522+62=132.另解过C 点作AB 的平行线,过B 点作AC 的平行线,交点为D ,同理过C 1作A 1B 1的平行线,过B 1作A 1C 1的平行线,交点为D 1,连接DD 1,则ABCD -A 1B 1C 1D 1恰好成为球的一个内接长方体,故球的半径r 132=.故选C .(2)设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为().A .2a πB .273a πC .2113a πD .237a π答案B 解析222222274312a a R OB OE BE a ==+=+=,22743S a a ππ∴==.故选B .(3)(2009全国Ⅰ)直三棱柱ABC -A 1B 1C 1的各顶点都在同一球面上,若AB =AC =AA 1=2,∠BAC =120°,则此球的表面积等于().A .10πB .20πC .30πD .40π答案B解析如图,先由余弦定理求出BC =23,再由正弦定理求出r =AO 1=2,外接球的直径R =12+22=5,所以该球的表面积为4πR 2=20π.故选B .(4)已知圆柱的高为2,底面半径为3,若该圆柱的两个底面的圆周都在同一个球面上,则这个球的表面积等于()A .4πB .16π3C .32π3D .16π答案D解析由题意知圆柱的中心O 为这个球的球心,于是,球的半径r =OB =OA 2+AB 2=12+(3)2=2.故这个球的表面积S =4πr 2=16π.故选D .(5)若一个圆柱的表面积为12π,则该圆柱的外接球的表面积的最小值为()A .12)π-B .C .3)πD .16π答案A解析设圆柱的底面半径为r ,高为h ,则22212r rh πππ+=,则6h r r=-.设该圆柱的外接球的半径为R ,则22222221659()()333244h R r r r r r r =+=+-=+--=- ,当且仅当22594r r =,即4365r =时,等号成立.故该圆柱的外接球的表面积的最小值为43)12)ππ-=.模型四垂面模型【方法总结】垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球,由对称性可知球心O 的位置是△CBD的外心O 1与△AB 2D 2的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=2h ,2224h R r ∴=+.【例题选讲】[例](1)已知在三棱锥S -ABC 中,SA ⊥平面ABC ,且∠ACB =30°,AC =2AB =23,SA =1.则该三棱锥的外接球的体积为()A .13813πB .13πC .136πD .13136π答案D解析∵∠ACB =30°,AC =2AB =23,∴△ABC 是以AC 为斜边的直角三角形,其外接圆半径r =AC2=3,则三棱锥外接球即为以△ABC 为底面,以SA 为高的三棱柱的外接球,∴三棱锥外接球的半径R 满足R =132,故三棱锥外接球的体积V =43πR 3=13136π.故选D .第(1)小题图第(2)小题图1第(2)小题图2(2)三棱锥P -ABC 中,平面PAC ⊥平面ABC ,AB ⊥AC ,PA =PC =AC =2,AB =4,则三棱锥P -ABC 的外接球的表面积为()A .23πB .234πC .64πD .643π答案D解析如图1,设O 为三棱锥外接球的球心,O 1为正△PAC 的中心,则OO 1=12AB =2.2AO 1=2sinπ3=433,AO 1=233,R 2=OA 2=O 1A 2+O 1O 2=43+4=163,故几何体外接球的表面积S =4πR 2=643.另解:如图2,设O ′为正△PAC 的中心,D 为Rt △ABC 斜边的中点,H 为AC 中点.由平面PAC ⊥平面ABC ,则O ′H ⊥平面ABC .作O ′O ∥HD ,OD ∥O ′H ,则交点O 为三棱锥外接球的球心,连接OP ,又O ′P =23=23×32×2=233,OO ′=DH =12AB =2.∴R 2=OP 2=O ′P 2+O ′O 2=43+4=163.故几何体外接球的表面积S =4πR 2=643π.(3)在三棱锥S -ABC 中,侧棱SA ⊥底面ABC ,AB =5,BC =8,∠ABC =60°,SA =25,则该三棱锥的外接球的表面积为()A .643πB .256πC .4363πD .2048327π答案B解析由题意知,AB =5,BC =8,∠ABC =60°,则在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2×AB ×BC ×cos ∠ABC ,解得AC =7,设△ABC 的外接圆半径为r ,则△ABC 的外接圆直径2r =ACsin ∠ABC =732,∴r =73,又∵侧棱SA ⊥底面ABC ,∴三棱锥的外接球的球心到平面ABC 的距离h =12SA =5,则外接球的半径R =732+(5)2=643,则该三棱锥的外接球的表面积为S =4πR 2=2563π.(4)在三棱锥P -ABC 中,已知PA ⊥底面ABC ,∠BAC =120˚,PA =AB =AC =2,若该三棱锥的顶点都在同一个球面上,则该球的表面积为()A .103πB .18πC .20πD .93π答案C解析如图1,先由余弦定理求出BC =23,再由正弦定理求出r =AO 1=2,外接球的直径R =12+22=5,所以该球的表面积为4πR 2=20π.第(3)小题图第(4)小题图1第(4)小题图2另解如图2,该三棱锥为图中正六棱柱内的三棱锥P -ABC ,PA =AB =AC =2,所以该三棱锥的外接球即该六棱柱的外接球,所以外接球的直径2R =42+22=25⇒R =5,所以该球的表面积为4πR 2=20π.(5)在三棱锥P ABC -中,PA ⊥平面ABC ,120BAC ∠=︒,2AC =,1AB =,设D 为BC 中点,且直线PD与平面ABC 所成角的余弦值为5,则该三棱锥外接球的表面积为________.答案373π解析在ABC ∆中,120BAC ∠=︒,2AC =,1AB =,由余弦定理得:22BC AC =+22cos AB AC BC BAC -⋅⋅∠,即22221221cos1207BC =+-⨯⨯⨯︒=,解得:BC =.设ABC ∆的外接圆半径为r ,由正弦定理得2sin BC r BAC ===∠解得:r ==;且222cos 2AB BC AC ABC AB BC +-∠==,又D 为BC 中点,在ABD ∆中,122BD BC ==,1AB =,cos 7ABD ∠=.由余弦定理得:2222cos AD AB BD AB BD ABD =+-∠ ,即:22231()212274AD =+-⨯⨯=,解得2AD =.又因为PA ⊥平面ABC ,所以PDA ∠为直线PD 与平面ABC 所成角,由cos 5PDA ∠=,得sin 5PDA ∠=,tan 2PDA ∠=,所以在Rt PAD ∆中,tan 22PA AD PDA =∠== .设三棱锥P ABC -的外接球半径为R ,所以R =,三棱锥P ABC -外接球表面积为23743S R ππ==.模型五切瓜模型【方法总结】切瓜模型是有一侧面垂直底面的棱锥型,常见的是两个互相垂直的面都是特殊三角形且平面ABC ⊥平面BCD ,如类型Ⅰ,△ABC 与△BCD 都是直角三角形,类型Ⅱ,△ABC 是等边三角形,△BCD 是直角三角形,类型Ⅲ,△ABC 与△BCD 都是等边三角形,解决方法是分别过△ABC 与△BCD 的外心作该三角形所在平面的垂线,交点O 即为球心.类型Ⅳ,△ABC 与△BCD 都一般三角形,解决方法是过△BCD 的外心O 1作该三角形所在平面的垂线,用代数方法即可解决问题.设三棱锥A -BCD 的高为h ,外接球的半径为R ,球心为O .△BCD 的外心为O 1,O 1到BD 的距离为d ,O 与O 1的距离为m 2=r 2+m 2,2=d 2+(h -m )2,解得R .可用秒杀公式:R 2=r 12+r 22-l 24(其中r 1、r 2为两个面的外接圆的半径,l 为两个面的交线的长)【例题选讲】[例](1)已知在三棱锥P -ABC 中,V P ABC =433,∠APC =π4,∠BPC =π3,PA ⊥AC ,PB ⊥BC ,且平面PAC ⊥平面PBC ,那么三棱锥P -ABC 外接球的体积为________.答案32π3解析如图,取PC 的中点O ,连接AO ,BO ,设PC =2R ,则OA =OB=OC =OP =R ,∴O 是三棱锥P -ABC 外接球的球心,易知,PB =R ,BC =3R ,∵∠APC =π4,PA ⊥AC ,O 为PC 的中点,∴AO ⊥PC ,又平面PAC ⊥平面PBC ,且平面PAC ∩平面PBC =PC ,∴AO ⊥平面PBC ,∴V P ABC =V A PBC =13×12×PB ×BC ×AO =13×12×R ×3R ×R=433,解得R =2,∴三棱锥P -ABC 外接球的体积V =43πR 3=32π3.(2)如图,已知平面四边形ABCD 满足AB =AD =2,∠A =60˚,∠C =90˚,将△ABD 沿对角线BD 翻折,使平面ABD ⊥平面CBD ,则四面体ABCD 外接球的体积为__.答案323π27解析在四面体ABCD 中,∵AB =AD =2,∠BAD =60˚,∴△ABD为正三角形,设BD 的中点为M ,连接AM ,则AM ⊥BD ,又平面ABD ⊥平面CBD ,平面ABD ∩平面CBD =BD ,∴AM ⊥平面CBD .∵△CBD 为直角三角形,∴其外接圆的圆心是斜边BD 的中点M ,由球的性质知,四面体ABCD 外接球的球心必在线段AM 上,又△ABD 为正三角形,∴球心是△ABD 的中心,则外接球的半径为23×2×32=233,∴四面体ABCD 外接球的体积为43×π×(233)3=323π27.(3)已知三棱锥A -BCD 中,△ABD 与△BCD 是边长为2的等边三角形且二面角A -BD -C 为直二面角,则三棱锥A -BCD 的外接球的表面积为()A .10π3B .5πC .6πD .20π3答案D解析如图,取BD 中点M ,连接AM ,CM ,取△ABD ,△CBD 的中心即AM ,CM 的三等分点P ,Q ,过P 作平面ABD 的垂线,过Q 作平面CBD 的垂线,两垂线相交于点O ,则点O 为外接球的球心,如图,其中OQ =33,CQ =233,连接OC ,则外接球的半径R =OC =153,表面积为4πR 2=20π3,故选D .(4)已知ABC ∆是以BC 为斜边的直角三角形,P 为平面ABC 外一点,且平面PBC ⊥平面ABC ,3BC =,PB =PC =,则三棱锥P ABC -外接球的表面积为________.答案10π解析由题意知BC 的中点O 为ABC ∆外接圆的圆心,且平面PBC ⊥平面ABC ,过O 作面ABC 的垂线l ,则垂线l 一定在面ABC 内.根据球的性质,球心一定在垂线l 上, 球心1O 一定在平面PBC 内,且球心1O 也是PBC ∆外接圆的圆心.在PBC ∆中,由余弦定理得222cos 22PB BC PC PBC PB BC +-∠==,sin 2PBC ∴∠=,由正弦定理得:2sin PCR PBC=∠,解得2R =,∴三棱锥的外接球的表面积2410R ππ==.(5)已知等腰直角三角形ABC 中,AB =AC =2,D ,E 分别为AB ,AC 的中点,沿DE 将△ABC 折成直二面角(如图),则四棱锥A -DECB 的外接球的表面积为________.答案10π解析取DE 的中点M ,BC 的中点N ,连接MN (图略),由题意知,MN ⊥平面ADE ,因为△ADE是等腰直角三角形,所以△ADE 的外接圆的圆心是点M ,四棱锥A -DECB 的外接球的球心在直线MN 上,又等腰梯形DECB 的外接圆的圆心在MN 上,所以四棱锥A -DECB 的外接球的球心就是等腰梯形DECB 的外接圆的圆心.连接BE ,易知△BEC 是钝角三角形,所以等腰梯形DECB 的外接圆的圆心在等腰梯形DECB 的外部.设四棱锥A -DECB 的外接球的半径为R ,球心到BC 的距离为d 2=d 2+(2)2,2=(d +222+(22)2,解得R 2=52,故四棱锥A -DECB 的外接球的表面积S =4πR 2=10π.模型六斗笠模型【方法总结】圆锥、顶点在底面的射影是底面外心的棱锥.秒杀公式:R =h 2+r 22h(其中h 为几何体的高,r 为几何体的底面半径或底面外接圆的圆心)【例题选讲】[例](1)一个圆锥恰有三条母线两两夹角为60︒,若该圆锥的侧面积为,则该圆锥外接球的表面积为________.答案272π解析设60ASB BSC CSA ∠=∠=∠=︒,则SA SB SC AB AC BC =====.设AB x =,则底面圆的直径为2sin 60x r ==︒,该圆锥的侧面积为12x π=,解得3x =,高OS =.r ∴=.设圆锥外接球的半径为R ,所以222)R r R -+=,解得R =,则外接球的表面积为22742R ππ=.(2)(2020·全国Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为()A .64πB .48πC .36πD .32π答案A解析设⊙O 1的半径为r ,球的半径为R ,依题意,得πr 2=4π,∴r =2.由正弦定理可得ABsin 60°=2r ,∴AB =2r sin 60°=23.∴OO 1=AB =23.根据球的截面性质,得OO 1⊥平面ABC ,∴OO 1⊥O 1A ,R =OA =OO 21+O 1A 2=OO 21+r2=4,∴球O 的表面积S =4πR 2=64π.故选A .(3)在三棱锥P ABC -中,PA PB =26, 4PC AC AB ====,且AC AB ⊥,则该三棱锥外接球的表面积为________.答案36π解析设顶点P 在底面中的射影为1O ,由于PA PB PC ==,所以111O A O B O C ==,即点1O 是底面ABC ∆的外心,又AC AB ⊥,所以1O 为BC 的中点,因为PA PB = 4PC AC AB ====,所以11 4BC AO PO ===,设外接球的球心为O ,半径为R ,则O 必在1PO 上,=-14O O R ,在∆1Rt O OA中,()(2224R R -+=,解得3R =,所以22436S R ππ==.(4)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A .81π4B .16πC .9πD .27π4答案A解析如图所示,设球半径为R ,底面中心为O ′且球心为O ,∵正四棱锥P ABCD 中AB =2,∴AO ′=2,∵PO ′=4,∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×942=81π4.(5)如图所示,在正四棱锥P -ABCD 中,底面ABCD 是边长为4的正方形,E ,F 分别是AB ,CD 的中点,cos ∠PEF =22,若A ,B ,C ,D ,P 在同一球面上,则此球的体积为________.答案36π解析由题意,得底面ABCD 是边长为4的正方形,cos ∠PEF =22,故高PO 1为2.易知正四棱锥P -ABCD 的外接球的球心在它的高PO 1上,记球心为O ,则AO 1=22,PO =AO =R ,PO 1=2,OO 1=2-R 或OO 1=R -2(此时O 在PO 1的延长线上),在直角△AO 1O 中,R 2=AO 21+OO 21=(22)2+(2-R )2,解得R =3,所以球的体积为V =43πR 3=4π3×33=36π.(6)在三棱锥P ABC -中,2PA PB PC ===,1AB AC ==,3BC =棱锥外接球的体积为()A .43πB .823πC .3πD .323π答案A解析由PA PB PC ===P 作PG ⊥平面ABC ,垂足为G ,则G 为三角形ABC 的外心,在ABC ∆中,由1AB AC ==,BC =,可得120BAC ∠=︒,则由正弦定理可得:2AG =,即1AG =.1PG ∴==.取PA 中点H ,作HO PA ⊥交PG 于O ,则O 为该三棱锥外接球的球心.由PHO PGA ∆∆∽,可得PH PG PO PA =,则211PH PA PO PG === .可知O 与G 重合,即该棱锥外接球半径为1.∴该三棱锥外接球的体积为43π.模型七已知球心或球半径模型【例题选讲】[例](1)(2017·全国Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.答案36π解析如图,连接AO ,OB ,∵SC 为球O 的直径,∴点O 为SC 的中点,∵SA =AC ,SB =BC ,∴AO ⊥SC ,BO ⊥SC ,∵平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,∴AO ⊥平面SCB ,设球O 的半径为R ,则OA =OB =R ,SC =2R .∴V S ABC =V A SBC =13×S △SBC ×AO =13×SC ×AO ,即9=13×R ×R ,解得R =3,∴球O 的表面积为S =4πR 2=4π×32=36π.(2)已知三棱锥A -BCD 的所有顶点都在球O 的球面上,AB 为球O 的直径,若该三棱锥的体积为3,BC =3,BD =3,∠CBD =90˚,则球O 的体积为________.答案32π3解析设A 到平面BCD 的距离为h ,∵三棱锥的体积为3,BC =3,BD =3,∠CBD =90˚,∴13×12×3×3×h =3,∴h =2,∴球心O 到平面BCD 的距离为1.设CD 的中点为E ,连接OE ,则由球的截面性质可得OE ⊥平面CBD ,∵△BCD 外接圆的直径CD =23,∴球O 的半径OD =2,∴球O 的体积为32π3.(3)(2012全国Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为()A .26B .36C .23D .22答案A解析由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,如图所示,S △ABC =34×AB 2=34,高OD =12-332=63,∴V S -ABC =2V O -ABC =2×13×34×63=26.故选A .(4)(2020·新高考全国Ⅰ)已知直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为________.答案2π2解析如图,设B 1C1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q ,连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形,∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形,则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心,设截面圆的半径为r ,则r =R 2球-D 1E 2=5-3=2.又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ .又D 1P =5,∴B 1P =D 1P 2-D 1B 21=1,同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点,∴∠PEQ =π2,知 PQ的长为π2×2=2π2,即交线长为2π2.(5)三棱锥S -ABC 的底面各棱长均为3,其外接球半径为2,则三棱锥S -ABC 的体积最大时,点S 到平面ABC 的距离为()A .2+3B .2-3C .3D .2答案C 解析如图,设三棱锥S -ABC 底面三角形ABC 的外心为G ,三棱锥外接球的球心为O ,要使三棱锥S -ABC 的体积最大,则O 在SG 上,由底面三角形的边长为3,可得AG =32sin60°=3.连接OA ,在Rt △OGA 中,由勾股定理求得OG =OA 2-GA 2=22-(3)2=1.∴点S 到平面ABC 的距离为OS +OG =2+1=3.故选C .模型八最值模型【方法总结】最值问题的解法有两种方法:一种是几何法,即在运动变化过程中得到最值,从而转化为定值问题求解.另一种是代数方法,即建立目标函数,从而求目标函数的最值.【例题选讲】[例](1)已知三棱锥P -ABC 的顶点P ,A ,B ,C 在球O 的球面上,△ABC 是边长为3的等边三角形,如果球O 的表面积为36π,那么P 到平面ABC 距离的最大值为________.答案3+22解析依题意,边长是3的等边△ABC 的外接圆半径r =12·3sin 60°=1.∵球O 的表面积为36π=4πR 2,∴球O 的半径R =3,∴球心O 到平面ABC 的距离d =R 2-r 2=22,∴球面上的点P 到平面ABC 距离的最大值为R +d =3+22.(2)在四面体ABCD 中,AB =1,BC =CD =3,AC =2,当四面体ABCD 的体积最大时,其外接球的表面积为()A .2πB .3πC .6πD .8π答案C 解析∵AB =1,BC =3,AC =2,由勾股定理可得AB 2+AC 2=BC 2,所以△ABC 是以BC 为斜边的直角三角形,且该三角形的外接圆直径为BC =3,当CD ⊥平面ABC 时,四面体ABCD 的体积取最大值,此时,其外接球的直径为2R =BC 2+CD 2=6,因此,四面体ABCD 的外接球的表面积为4πR 2=π×(2R )2=6π.故选C .(3)已知四棱锥S -ABCD 的所有顶点在同一球面上,底面ABCD 是正方形且球心O 在此平面内,当四棱锥的体积取得最大值时,其表面积等于16+163,则球O 的体积等于()A .42π3B .162π3C .322π3D .642π3答案D解析由题意得,当四棱锥的体积取得最大值时,该四棱锥为正四棱锥.因为该四棱锥的表面积等于16+163,设球O 的半径为R ,则AC =2R ,SO =R ,如图,所以该四棱锥的底面边长AB =2R ,则有(2R )2+4×12×2R ×16+163,解得R =22,所以球O 的体积是43πR 3=6423π.故选D .(4)三棱锥A -BCD 内接于半径为5的球O 中,AB =CD =4,则三棱锥A -BCD 的体积的最大值为()A .43B .83C .163D .323答案C解析如图,过CD 作平面ECD ,使AB ⊥平面ECD ,交AB 于点E ,设点E 到CD 的距离为EF ,当球心在EF 上时,EF 最大,此时E ,F 分别为AB ,CD 的中点,且球心O 为EF 的中点,所以EF =2,所以V max =13×12×4×2×4=163,故选C .(5)已知正四棱柱的顶点在同一个球面上,且球的表面积为12π,当正四棱柱的体积最大时,正四棱柱的高为_.答案8解析设正四棱柱的底面边长为a ,高为h ,球的半径为r ,由题意知4πr 2=12π,所以r 2=3,又2a 2+h 2=(2r )2=12,所以a 2=6-h 22,所以正四棱柱的体积V =a 2h ,则V ′=6-32h 2,由V ′>0,得0<h <2,由V ′<0,得h >2,所以当h =2时,正四棱柱的体积最大,V max =8.模型九内切球模型【方法总结】以三棱锥P -ABC 为例,求其内切球的半径.方法:等体积法,三棱锥P -ABC 体积等于内切球球心与四个面构成的四个三棱锥的体积之和;第一步:先求出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,球心为O ,建立等式:V P -ABC =V O -ABC +V O -P AB +V O -P AC +V O -PBC ⇒V P -ABC =13S △ABC ·r +13S △P AB ·r +13S △P AC ·r +13S △r =13S △ABC +S △P AB +S △P AC +S △PBC )·r ;第三步:解出r =3V P -ABC S O -ABC +S O -P AB +S O -P AC +S O -PBC =3VS 表.秒杀公式(万能公式):r =3VS 表【例题选讲】[例](1)已知一个三棱锥的所有棱长均为2,则该三棱锥的内切球的体积为________.答案354π解析由题意可知,该三棱锥为正四面体,如图所示.AE =AB ·sin 60°=62,AO =23AE =63,DO =AD 2-AO 2=233,三棱锥的体积V D ABC =13S △ABC ·DO =13,设内切球的半径为r ,则V D ABC =13r (S △ABC +S △ABD +S △BCD +S △ACD )=13,r =36,V 内切球=43πr 3=354π.(2)(2020·全国Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.答案23π解析圆锥内半径最大的球即为圆锥的内切球,设其半径为r .作出圆锥的轴截面PAB ,如图所示,则△PAB 的内切圆为圆锥的内切球的大圆.在△PAB 中,PA =PB =3,D 为AB 的中点,AB =2,E 为切点,则PD =22,△PEO ∽△PDB ,故PO PB =OEDB ,即22-r 3=r 1,解得r =22,故内切球的体积为43π223=23π.(3)阿基米德(公元前287年~公元前212年)是古希腊伟大的哲学家、数学家和物理学家,他和高斯、牛顿并列被称为世界三大数学家.据说,他自己觉得最为满意的一个数学发现就是“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”.他特别喜欢这个结论.要求后人在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边.若表面积为54π的圆柱的底面直径与高都等于球的直径,则该球的体积为()A .4πB .16πC .36πD .64π3答案C解析设该圆柱的底面半径为R ,则圆柱的高为2R ,则圆柱的表面积S =S 底+S 侧=2×πR 2+2·π·R ·2R =54π,解得R 2=9,即R =3.∴圆柱的体积为V =πR 2×2R =54π,∴该圆柱的内切球的体积为23×54π=36π.故选C .(4)已知三棱锥P -ABC 的三条侧棱PA ,PB ,PC 两两互相垂直,且PA =PB =PC =2,则三棱锥P -ABC 的外接球与内切球的半径比为________.答案33+32解析以PA ,PB ,PC 为过同一顶点的三条棱,作长方体,由PA =PB =PC =2,可知此长方体即为正方体.设外接球的半径为R ,则R =4+4+42=3,设内切球的半径为r ,则内切球的球心到四个面的距离均为r ,由13(S △ACP +S △APB+S △PCB +S △ABC )·r =13·S △PCB ·AP ,解得r =23+3,所以Rr =323+3=33+32.(5)正四面体的外接球和内切球上各有一个动点P 、Q ,若线段PQ ,则这个四面体的棱长为________.答案4解析设这个四面体的棱长为a ,则它的外接球与内切球的球心重合,且半径R =外,r =内,依题意得4123a a +=,4a ∴=.。
外接球与内切八大模型—老师专用

外接球与内切八大模型—老师专用外接球与内切八大模型—老师专用墙角模型墙角模型是一种求解球半径的方法。
只需找到三条两两垂直的线段,就可以使用公式(2R) = a + b + c 或 2R = a^2 + b^2 + c^2 来求出球半径R。
例如,已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是多少?解:V = ah = 16,a = 2,4R = a + a + h = 4 + 4 + 16 = 24,S = 24π。
在另一个例子中,若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是9π。
解:4R = 3 + 3 + 3 = 9,S = 4πR = 9π。
正三棱锥的对棱互垂直。
证明如下:如图(3)-1,取AB,BC的中点D,E,连接AE,CD,AE,CD交于H,连接SH,则H是底面正三角形ABC的中心,因此SH垂直于平面ABC,又SH垂直于AB,因此SH垂直于平面SCD,即AB垂直于SC,同理可证BC垂直于SA,AC垂直于SB,即正三棱锥的对棱互垂直。
在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM垂直于MN,若侧棱SA=23,则正三棱锥S-ABC外接球的表面积是36π。
解:由前面的证明可知,正三棱锥S-ABC 的三棱条侧棱两两互相垂直,因此可以使用公式4R^2 = a^2 +b^2 + c^2 来求解。
由于SA=23,因此可以得到4R^2 = 36,即R^2 = 9,因此R = 3,外接球的表面积为36π。
如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是多少?球的表面积为(D)11π。
这个问题有误,因为三个侧面两两垂直的三棱锥不存在,因此无法回答这个问题。
已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为多少?这个问题可以使用解析几何的方法来求解。
根据三视图可以得到该几何体的顶点坐标为(0,0,0),(0,0,1),(1,0,0),(0,1,0)和(1,1,1)。
高中数学立体几何之外接球与内切球问题常见模型归纳(完整版)
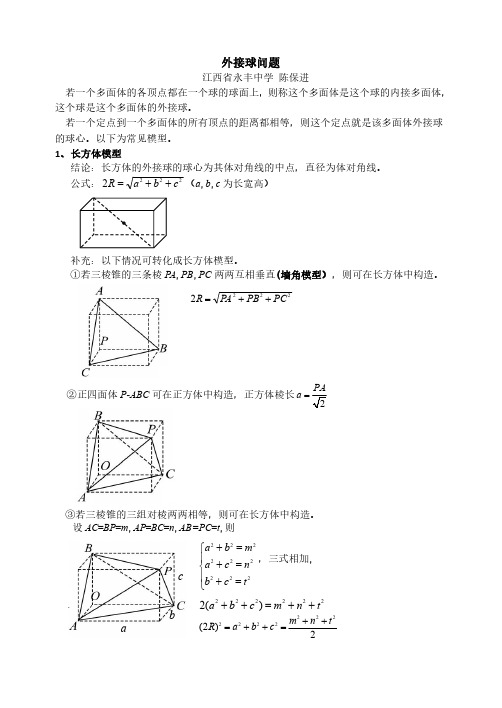
外接球问题江西省永丰中学陈保进若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
若一个定点到一个多面体的所有顶点的距离都相等,则这个定点就是该多面体外接球的球心。
以下为常见模型。
1、长方体模型结论:长方体的外接球的球心为其体对角线的中点,直径为体对角线。
公式:2222c b a R ++=(a ,b ,c 为长宽高)补充:以下情况可转化成长方体模型。
①若三棱锥的三条棱PA ,PB ,PC 两两互相垂直(墙角模型),则可在长方体中构造。
2222PC PB P A R ++=②正四面体P -ABC 可在正方体中构造,正方体棱长2=PA a ③若三棱锥的三组对棱两两相等,则可在长方体中构造。
设AC =BP =m ,AP =BC =n ,AB=PC =t ,则⎪⎩⎪⎨⎧=+=+=+222222222t c b n c a m b a ,三式相加,222222)(2t n m c b a ++=++2)2(2222222t n m c b a R ++=++=abc2、直三棱柱模型结论:直三棱柱外接球的球心是上、下底面外心连线的中点,222()2hR r =+r 为底面三角形外接圆的半径,可用正弦定理求,h 为直三棱柱的高。
补充:有一条侧棱垂直底面的三棱锥可补成直三棱柱,如图P -ABC 中,PA ⊥平面ABC ,则可补成直三棱柱PB 1C 1-ABC ,外接球半径公式同上。
提醒:底面具有外接圆的直棱柱才有外接球,比如正棱柱,且球心在上、下底面外心连线的中点,底面无外接圆的直棱柱,以及所有斜棱柱均无外接球。
3、共斜边模型四面体D-ABC 中,DC AD ⊥,BC AB ⊥,AC 为公共的斜边,O 为AC 的中点,则O 为四面体D-ABC 外接球的球心。
4、正棱锥模型外接球的球心在正棱锥的高所在直线上,如图正三棱锥A-BCD 中,作AO 1⊥平面BCD ,则易得BO 1=CO 1=DO 1,所以O 1为△BCD 的外心,设O 为其外接球球心,半径为R ,则BO =AO =R ,设AO 1=h ,BO 1=r ,则由BO 2=BO 12+OO 12,得R 2=r 2+(h-R )2。
高考数学专题:外接球与内切球九大模型(解析版)

空间几何体的外接球与内切球九大模型模型一墙角模型【方法总结】墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2.),秒杀公式:R 2=a 2+b 2+c 24.可求出球的半径从而解决问题.有以下四种类型:【例题选讲】[例](1)已知三棱锥A -BCD 的四个顶点A ,B ,C ,D 都在球O 的表面上,AC ⊥平面BCD ,BC ⊥CD ,且AC =3,BC =2,CD =5,则球O 的表面积为()A .12πB .7πC .9πD .8π答案A解析由AC ⊥平面BCD ,BC ⊥CD 知三棱锥A -BCD 可构造以AC ,BC ,CD 为三条棱的长方体,设球O 的半径为R ,则有(2R )2=AC 2+BC 2+CD 2=3+4+5=12,所以S 球=4πR 2=12π,故选A .(2)若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为().A .3B .6C .36D .9答案A解析616164)2(2=++=R ,3=R ,故选A .(3)已知S ,A ,B ,C ,是球O 表面上的点,SA ⊥平面ABC ,AB ⊥BC ,SA =AB =1,BC =2,则球O 的表面积等于().A .4πB .3πC .2πD .π答案解析由已知,222211(2)2R =++=,244S R π∴==球π.(4)在正三棱锥S -ABC 中,M ,N 分别是棱SC ,BC 的中点,且AM MN ⊥,若侧棱23SA =,则正三棱锥S -ABC 外接球的表面积是________.答案π36解析 MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,222(2)(23)(23)R ∴=+2(23)+36=,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(5)(2019全国Ⅰ)已知三棱锥P -ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为().A .68πB .64πC .62πD .6π答案D 解析解法一:, PA PB PC ABC == △为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥ 平面PAC ,∴PB ⊥平面PAC ,2APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体的一部分,2222R =++,6=,即364466,π62338R V R ππ=∴==⨯=,故选D .解法二:设2PA PB PC x ===,, E F 分别为, PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,3CF ∴=,又90CEF ∠=︒,213, 2CE x AE PA x ∴=-==,AEC △中,由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯作PD AC ⊥于D ,PA PC = ,D ∴为AC 的中点,cos E ∠12AD AC PA x==,2243142x x x x +-+∴=,2212212 22x x x ∴+=∴==,,,2PA PB PC ∴===,又2AB BC AC ===,, , PA PB PC ∴两两垂直,22226R ∴=++=,62R ∴=,34433V R ππ∴==⨯668=6π=,故选D .(6)已知二面角α-l -β的大小为π3,点P ∈α,点P 在β内的正投影为点A ,过点A 作AB ⊥l ,垂足为点B ,点C ∈l ,BC =22,PA =23,点D ∈β,且四边形ABCD 满足∠BCD +∠DAB =π.若四面体PACD 的四个顶点都在同一球面上,则该球的体积为________.答案86π解析∵∠BCD +∠DAB =π,∴A ,B ,C ,D 四点共圆,直径为AC ,∵PA ⊥平面β,AB ⊥l ,∴易得PB ⊥l ,即∠PBA 为二面角α-l -β的平面角,即∠PBA =π3,∵PA =23,∴BA =2,∵BC =22,∴AC=23.设球的半径为R ,则23-R 2-(3)2=R 2-(3)2,∴R =6,V =4π3(6)3=86π.模型二对棱相等模型【方法总结】对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长,即2222R a b c =++(长方体的长、宽、高分别为a 、b 、c ).秒杀公式:R 2=x 2+y 2+z 28(三棱锥的三组对棱长分别为x 、y 、z ).可求出球的半径从而解决问题.【例题选讲】[例](1)正四面体的各条棱长都为2,则该正面体外接球的体积为________.答案32π解析这是特殊情况,但也是对棱相等的模式,放入长方体中,32=R ,23=R ,ππ2383334=⋅=V .(2)在三棱锥A -BCD 中,AB =CD =2,AD =BC =3,AC =BD =4,则三棱锥BCD A -外接球的表面积为__.答案292π解析构造长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S .(3)在三棱锥A -BCD 中,AB =CD =6,AC =BD =AD =BC =5,则该三棱锥的外接球的体积为____.答案43436π解析依题意得,该三棱锥的三组对棱分别相等,因此可将该三棱锥补形成一个长方体,设该长方体的长、宽、高分别为a 、b 、c ,且其外接球的半径为R ,则a 2+b 2=62,b 2+c 2=52,c 2+a 2=52,得a 2+b 2+c 2=43,即(2R )2=a 2+b 2+c 2=43,易知432R =,即为该三棱锥的外接球的半径,所以该三棱锥的外接球的表面积为34434336R ππ=.(4)在正四面体A BCD -中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +的最小值为7,则该正四面体的外接球的体积是()A .6πB .6πC .3632πD .32π答案A解析将侧面ABC ∆和ACD ∆展成平面图形,如图所示:设正四面体的棱长为a ,则BP PE +的最小值为22172cos1207422a BE a a a a =+-︒== ,2a ∴=.在正四面体A BCD -的边长为2,外接球的半径6642R a ==,外接球的体积3463V R ππ==.(5)已知三棱锥A BCD -,三组对棱两两相等,且1AB CD ==,3AD BC ==,若三棱锥A BCD -的外接球表面积为92π.则AC =________.答案5解析将四面体A BCD -放置于长方体中, 四面体A BCD -的顶点为长方体八个顶点中的四个,∴长方体的外接球就是四面体A BCD -的外接球,1AB CD == ,3AD BC ==,且三组对棱两两相等,∴设AC BD x ==,得长方体的对角线长为222211[1(3)](4)22x x ++=+,可得外接球的直径212(4)2R x =+,所以22(4)4x R +=, 三棱锥A BCD -的外接球表面积为92π,2942R ππ∴=,解得324R =,即22(4)3244x +=,解之得5x =,因即5AC BD ==.模型三汉堡模型【方法总结】汉堡模型是直棱柱的外接球、圆柱的外接球模型,用找球心法(多面体的外接球的球心是过多面体的两个面的外心且分别垂直这两个面的直线的交点.一般情况下只作出一个面的垂线,然后设出球心用算术方法或代数方法即可解决问题.有时也作出两条垂线,交点即为球心.)解决.以直三棱柱为例,模型如下图,由对称性可知球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=2h ,2224h R r ∴=+.【例题选讲】[例](1)(2013辽宁)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上.若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为().A .3172B .210C .132D .310答案C 解析如图所示,由球心作平面ABC 的垂线,则垂足为BC 的中点M .又AM =12BC =52,OM =12AA 1=6,所以球O 的半径R =OA =522+62=132.另解过C 点作AB 的平行线,过B 点作AC 的平行线,交点为D ,同理过C 1作A 1B 1的平行线,过B 1作A 1C 1的平行线,交点为D 1,连接DD 1,则ABCD -A 1B 1C 1D 1恰好成为球的一个内接长方体,故球的半径r =22234121322++=.故选C .(2)设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为().A .2a πB .273a πC .2113a πD .237a π答案B 解析222222274312a a R OB OE BE a ==+=+=,22743S a a ππ∴==.故选B .(3)(2009全国Ⅰ)直三棱柱ABC -A 1B 1C 1的各顶点都在同一球面上,若AB =AC =AA 1=2,∠BAC =120°,则此球的表面积等于().A .10πB .20πC .30πD .40π答案B解析如图,先由余弦定理求出BC =23,再由正弦定理求出r =AO 1=2,外接球的直径R =12+22=5,所以该球的表面积为4πR 2=20π.故选B .(4)已知圆柱的高为2,底面半径为3,若该圆柱的两个底面的圆周都在同一个球面上,则这个球的表面积等于()A .4πB .16π3C .32π3D .16π答案D解析由题意知圆柱的中心O 为这个球的球心,于是,球的半径r =OB =OA 2+AB 2=12+(3)2=2.故这个球的表面积S =4πr 2=16π.故选D .(5)若一个圆柱的表面积为12π,则该圆柱的外接球的表面积的最小值为()A .(12512)π-B .123πC .(1233)π+D .16π答案A解析设圆柱的底面半径为r ,高为h ,则22212r rh πππ+=,则6h r r=-.设该圆柱的外接球的半径为R ,则222222222165959()()3233532444h R r r r r r r r r =+=+-=+--=- ,当且仅当22594r r =,即4365r =时,等号成立.故该圆柱的外接球的表面积的最小值为4(353)(12512)ππ-=-.模型四垂面模型【方法总结】垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球,由对称性可知球心O 的位置是△CBD的外心O 1与△AB 2D 2的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=2h ,2224h R r ∴=+.【例题选讲】[例](1)已知在三棱锥S -ABC 中,SA ⊥平面ABC ,且∠ACB =30°,AC =2AB =23,SA =1.则该三棱锥的外接球的体积为()A .13813πB .13πC .136πD .13136π答案D解析∵∠ACB =30°,AC =2AB =23,∴△ABC 是以AC 为斜边的直角三角形,其外接圆半径r =AC2=3,则三棱锥外接球即为以△ABC 为底面,以SA 为高的三棱柱的外接球,∴三棱锥外接球的半径R 满足R =r 2+SA 22=132,故三棱锥外接球的体积V =43πR 3=13136π.故选D .第(1)小题图第(2)小题图1第(2)小题图2(2)三棱锥P -ABC 中,平面PAC ⊥平面ABC ,AB ⊥AC ,PA =PC =AC =2,AB =4,则三棱锥P -ABC 的外接球的表面积为()A .23πB .234πC .64πD .643π答案D解析如图1,设O 为三棱锥外接球的球心,O 1为正△PAC 的中心,则OO 1=12AB =2.2AO 1=2sinπ3=433,AO 1=233,R 2=OA 2=O 1A 2+O 1O 2=43+4=163,故几何体外接球的表面积S =4πR 2=643π.另解:如图2,设O ′为正△PAC 的中心,D 为Rt △ABC 斜边的中点,H 为AC 中点.由平面PAC ⊥平面ABC ,则O ′H ⊥平面ABC .作O ′O ∥HD ,OD ∥O ′H ,则交点O 为三棱锥外接球的球心,连接OP ,又O ′P =23PH =23×32×2=233,OO ′=DH =12AB =2.∴R 2=OP 2=O ′P 2+O ′O 2=43+4=163.故几何体外接球的表面积S =4πR 2=643π.(3)在三棱锥S -ABC 中,侧棱SA ⊥底面ABC ,AB =5,BC =8,∠ABC =60°,SA =25,则该三棱锥的外接球的表面积为()A .643πB .2563πC .4363πD .2048327π答案B解析由题意知,AB =5,BC =8,∠ABC =60°,则在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2×AB ×BC ×cos ∠ABC ,解得AC =7,设△ABC 的外接圆半径为r ,则△ABC 的外接圆直径2r =ACsin ∠ABC =732,∴r =73,又∵侧棱SA ⊥底面ABC ,∴三棱锥的外接球的球心到平面ABC 的距离h =12SA =5,则外接球的半径R =732+(5)2=643,则该三棱锥的外接球的表面积为S =4πR 2=2563π.(4)在三棱锥P -ABC 中,已知PA ⊥底面ABC ,∠BAC =120˚,PA =AB =AC =2,若该三棱锥的顶点都在同一个球面上,则该球的表面积为()A .103πB .18πC .20πD .93π答案C解析如图1,先由余弦定理求出BC =23,再由正弦定理求出r =AO 1=2,外接球的直径R =12+22=5,所以该球的表面积为4πR 2=20π.第(3)小题图第(4)小题图1第(4)小题图2另解如图2,该三棱锥为图中正六棱柱内的三棱锥P -ABC ,PA =AB =AC =2,所以该三棱锥的外接球即该六棱柱的外接球,所以外接球的直径2R =42+22=25⇒R =5,所以该球的表面积为4πR 2=20π.(5)在三棱锥P ABC -中,PA ⊥平面ABC ,120BAC ∠=︒,2AC =,1AB =,设D 为BC 中点,且直线PD 与平面ABC 所成角的余弦值为55,则该三棱锥外接球的表面积为________.答案373π解析在ABC ∆中,120BAC ∠=︒,2AC =,1AB =,由余弦定理得:22BC AC =+22cos AB AC BC BAC -⋅⋅∠,即22221221cos1207BC =+-⨯⨯⨯︒=,解得:7BC =.设ABC ∆的外接圆半径为r ,由正弦定理得7272sin sin1203BC r BAC ===∠︒解得:72133r ==;且222cos 2AB BC AC ABC AB BC +-∠=2221(7)2277217+-==⨯⨯,又D 为BC 中点,在ABD ∆中,1722BD BC ==,1AB =,27cos 7ABD ∠=.由余弦定理得:2222cos AD AB BD AB BD ABD =+-∠ ,即:222772731()212274AD =+-⨯⨯⨯=,解得32AD =.又因为PA ⊥平面ABC ,所以PDA ∠为直线PD 与平面ABC 所成角,由5cos 5PDA ∠=,得25sin 5PDA ∠=,tan 2PDA ∠=,所以在Rt PAD ∆中,3tan 232PA AD PDA =∠== .设三棱锥P ABC -的外接球半径为R ,所以222232137()()()22312PA R r =+=+=,三棱锥P ABC -外接球表面积为23743S R ππ==.模型五切瓜模型【方法总结】切瓜模型是有一侧面垂直底面的棱锥型,常见的是两个互相垂直的面都是特殊三角形且平面ABC ⊥平面BCD ,如类型Ⅰ,△ABC 与△BCD 都是直角三角形,类型Ⅱ,△ABC 是等边三角形,△BCD 是直角三角形,类型Ⅲ,△ABC 与△BCD 都是等边三角形,解决方法是分别过△ABC 与△BCD 的外心作该三角形所在平面的垂线,交点O 即为球心.类型Ⅳ,△ABC 与△BCD 都一般三角形,解决方法是过△BCD 的外心O 1作该三角形所在平面的垂线,用代数方法即可解决问题.设三棱锥A -BCD 的高为h ,外接球的半径为R ,球心为O .△BCD 的外心为O 1,O 1到BD 的距离为d ,O 与O 1的距离为m ,则R 2=r 2+m 2,R 2=d 2+(h -m )2,解得R .可用秒杀公式:R 2=r 12+r 22-l 24(其中r 1、r 2为两个面的外接圆的半径,l 为两个面的交线的长)【例题选讲】[例](1)已知在三棱锥P -ABC 中,V P ABC =433,∠APC =π4,∠BPC =π3,PA ⊥AC ,PB ⊥BC ,且平面PAC ⊥平面PBC ,那么三棱锥P -ABC 外接球的体积为________.答案32π3解析如图,取PC 的中点O ,连接AO ,BO ,设PC =2R ,则OA =OB=OC =OP =R ,∴O 是三棱锥P -ABC 外接球的球心,易知,PB =R ,BC =3R ,∵∠APC =π4,PA ⊥AC ,O 为PC 的中点,∴AO ⊥PC ,又平面PAC ⊥平面PBC ,且平面PAC ∩平面PBC =PC ,∴AO ⊥平面PBC ,∴V P ABC =V A PBC =13×12×PB ×BC ×AO =13×12×R ×3R ×R=433,解得R =2,∴三棱锥P -ABC 外接球的体积V =43πR 3=32π3.(2)如图,已知平面四边形ABCD 满足AB =AD =2,∠A =60˚,∠C =90˚,将△ABD 沿对角线BD 翻折,使平面ABD ⊥平面CBD ,则四面体ABCD 外接球的体积为__.答案323π27解析在四面体ABCD 中,∵AB =AD =2,∠BAD =60˚,∴△ABD为正三角形,设BD 的中点为M ,连接AM ,则AM ⊥BD ,又平面ABD ⊥平面CBD ,平面ABD ∩平面CBD =BD ,∴AM ⊥平面CBD .∵△CBD 为直角三角形,∴其外接圆的圆心是斜边BD 的中点M ,由球的性质知,四面体ABCD 外接球的球心必在线段AM 上,又△ABD 为正三角形,∴球心是△ABD 的中心,则外接球的半径为23×2×32=233,∴四面体ABCD 外接球的体积为43×π×(233)3=323π27.(3)已知三棱锥A -BCD 中,△ABD 与△BCD 是边长为2的等边三角形且二面角A -BD -C 为直二面角,则三棱锥A -BCD 的外接球的表面积为()A .10π3B .5πC .6πD .20π3答案D解析如图,取BD 中点M ,连接AM ,CM ,取△ABD ,△CBD 的中心即AM ,CM 的三等分点P ,Q ,过P 作平面ABD 的垂线,过Q 作平面CBD 的垂线,两垂线相交于点O ,则点O 为外接球的球心,如图,其中OQ =33,CQ =233,连接OC ,则外接球的半径R =OC =153,表面积为4πR 2=20π3,故选D .(4)已知ABC ∆是以BC 为斜边的直角三角形,P 为平面ABC 外一点,且平面PBC ⊥平面ABC ,3BC =,22PB =,5PC =,则三棱锥P ABC -外接球的表面积为________.答案10π解析由题意知BC 的中点O 为ABC ∆外接圆的圆心,且平面PBC ⊥平面ABC ,过O 作面ABC 的垂线l ,则垂线l 一定在面ABC 内.根据球的性质,球心一定在垂线l 上, 球心1O 一定在平面PBC 内,且球心1O 也是PBC ∆外接圆的圆心.在PBC ∆中,由余弦定理得2222cos 22PB BC PC PBC PB BC +-∠==,2sin 2PBC ∴∠=,由正弦定理得:2sin PCR PBC=∠,解得102R =,∴三棱锥的外接球的表面积2410R ππ==.(5)已知等腰直角三角形ABC 中,AB =AC =2,D ,E 分别为AB ,AC 的中点,沿DE 将△ABC 折成直二面角(如图),则四棱锥A -DECB 的外接球的表面积为________.答案10π解析取DE 的中点M ,BC 的中点N ,连接MN (图略),由题意知,MN ⊥平面ADE ,因为△ADE是等腰直角三角形,所以△ADE 的外接圆的圆心是点M ,四棱锥A -DECB 的外接球的球心在直线MN 上,又等腰梯形DECB 的外接圆的圆心在MN 上,所以四棱锥A -DECB 的外接球的球心就是等腰梯形DECB 的外接圆的圆心.连接BE ,易知△BEC 是钝角三角形,所以等腰梯形DECB 的外接圆的圆心在等腰梯形DECB 的外部.设四棱锥A -DECB 的外接球的半径为R ,球心到BC 的距离为d ,则R 2=d 2+(2)2,R 2=(d +22)2+(22)2,解得R 2=52,故四棱锥A -DECB 的外接球的表面积S =4πR 2=10π.模型六斗笠模型【方法总结】圆锥、顶点在底面的射影是底面外心的棱锥.秒杀公式:R =h 2+r 22h(其中h 为几何体的高,r 为几何体的底面半径或底面外接圆的圆心)【例题选讲】[例](1)一个圆锥恰有三条母线两两夹角为60︒,若该圆锥的侧面积为33π,则该圆锥外接球的表面积为________.答案272π解析设60ASB BSC CSA ∠=∠=∠=︒,则SA SB SC AB AC BC =====.设AB x =,则底面圆的直径为22sin 603x x r ==︒,该圆锥的侧面积为123323xx ππ= ,解得3x =,高223(3)6OS =-.333r ∴=.设圆锥外接球的半径为R ,所以222(6)R r R -+=,解得36R =,则外接球的表面积为22742R ππ=.(2)(2020·全国Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为()A .64πB .48πC .36πD .32π答案A解析设⊙O 1的半径为r ,球的半径为R ,依题意,得πr 2=4π,∴r =2.由正弦定理可得ABsin 60°=2r ,∴AB =2r sin 60°=23.∴OO 1=AB =23.根据球的截面性质,得OO 1⊥平面ABC ,∴OO 1⊥O 1A ,R =OA =OO 21+O 1A 2=OO 21+r2=4,∴球O 的表面积S =4πR 2=64π.故选A .(3)在三棱锥P ABC -中,PA PB =26, 4PC AC AB ====,且AC AB ⊥,则该三棱锥外接球的表面积为________.答案36π解析设顶点P 在底面中的射影为1O ,由于PA PB PC ==,所以111O A O B O C ==,即点1O 是底面ABC ∆的外心,又AC AB ⊥,所以1O 为BC 的中点,因为PA PB =26, 4PC AC AB ====,所以1142, 22, 4BC AO PO ===,设外接球的球心为O ,半径为R ,则O 必在1PO 上,=-14O O R ,在∆1Rt O OA中,()()222422R R -+=,解得3R =,所以22436S R ππ==.(4)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A .81π4B .16πC .9πD .27π4答案A解析如图所示,设球半径为R ,底面中心为O ′且球心为O ,∵正四棱锥P ABCD 中AB =2,∴AO ′=2,∵PO ′=4,∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×942=81π4.(5)如图所示,在正四棱锥P -ABCD 中,底面ABCD 是边长为4的正方形,E ,F 分别是AB ,CD 的中点,cos ∠PEF =22,若A ,B ,C ,D ,P 在同一球面上,则此球的体积为________.答案36π解析由题意,得底面ABCD 是边长为4的正方形,cos ∠PEF =22,故高PO 1为2.易知正四棱锥P -ABCD 的外接球的球心在它的高PO 1上,记球心为O ,则AO 1=22,PO =AO =R ,PO 1=2,OO 1=2-R 或OO 1=R -2(此时O 在PO 1的延长线上),在直角△AO 1O 中,R 2=AO 21+OO 21=(22)2+(2-R )2,解得R =3,所以球的体积为V =43πR 3=4π3×33=36π.(6)在三棱锥P ABC -中,2PA PB PC ===,1AB AC ==,3BC =,则该三棱锥外接球的体积为()A .43πB .823πC .43πD .323π答案A解析由2PA PB PC ===,过P 作PG ⊥平面ABC ,垂足为G ,则G 为三角形ABC 的外心,在ABC ∆中,由1AB AC ==,3BC =,可得120BAC ∠=︒,则由正弦定理可得:32sin120AG =︒,即1AG =.221PG PA AG ∴=-=.取PA 中点H ,作HO PA ⊥交PG 于O ,则O 为该三棱锥外接球的球心.由PHO PGA ∆∆∽,可得PH PG PO PA =,则22211PH PA PO PG ⨯=== .可知O 与G 重合,即该棱锥外接球半径为1.∴该三棱锥外接球的体积为43π.模型七已知球心或球半径模型【例题选讲】[例](1)(2017·全国Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.答案36π解析如图,连接AO ,OB ,∵SC 为球O 的直径,∴点O 为SC 的中点,∵SA =AC ,SB =BC ,∴AO ⊥SC ,BO ⊥SC ,∵平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,∴AO ⊥平面SCB ,设球O 的半径为R ,则OA =OB =R ,SC =2R .∴V S ABC =V A SBC =13×S △SBC ×AO =13×12×SC ×OB ×AO ,即9=13×12×2R ×R ×R ,解得R =3,∴球O 的表面积为S =4πR 2=4π×32=36π.(2)已知三棱锥A -BCD 的所有顶点都在球O 的球面上,AB 为球O 的直径,若该三棱锥的体积为3,BC =3,BD =3,∠CBD =90˚,则球O 的体积为________.答案32π3解析设A 到平面BCD 的距离为h ,∵三棱锥的体积为3,BC =3,BD =3,∠CBD =90˚,∴13×12×3×3×h =3,∴h =2,∴球心O 到平面BCD 的距离为1.设CD 的中点为E ,连接OE ,则由球的截面性质可得OE ⊥平面CBD ,∵△BCD 外接圆的直径CD =23,∴球O 的半径OD =2,∴球O 的体积为32π3.(3)(2012全国Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为()A .26B .36C .23D .22答案A解析由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,如图所示,S △ABC =34×AB 2=34,高OD =12-332=63,∴V S -ABC =2V O -ABC =2×13×34×63=26.故选A .(4)(2020·新高考全国Ⅰ)已知直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为________.答案2π2解析如图,设B 1C 1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q ,连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形,∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形,则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心,设截面圆的半径为r ,则r =R 2球-D 1E 2=5-3=2.又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ .又D 1P =5,∴B 1P =D 1P 2-D 1B 21=1,同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点,∴∠PEQ =π2,知 PQ的长为π2×2=2π2,即交线长为2π2.(5)三棱锥S -ABC 的底面各棱长均为3,其外接球半径为2,则三棱锥S -ABC 的体积最大时,点S 到平面ABC 的距离为()A .2+3B .2-3C .3D .2答案C 解析如图,设三棱锥S -ABC 底面三角形ABC 的外心为G ,三棱锥外接球的球心为O ,要使三棱锥S -ABC 的体积最大,则O 在SG 上,由底面三角形的边长为3,可得AG =32sin60°=3.连接OA ,在Rt △OGA 中,由勾股定理求得OG =OA 2-GA 2=22-(3)2=1.∴点S 到平面ABC 的距离为OS +OG =2+1=3.故选C .模型八最值模型【方法总结】最值问题的解法有两种方法:一种是几何法,即在运动变化过程中得到最值,从而转化为定值问题求解.另一种是代数方法,即建立目标函数,从而求目标函数的最值.【例题选讲】[例](1)已知三棱锥P -ABC 的顶点P ,A ,B ,C 在球O 的球面上,△ABC 是边长为3的等边三角形,如果球O 的表面积为36π,那么P 到平面ABC 距离的最大值为________.答案3+22解析依题意,边长是3的等边△ABC 的外接圆半径r =12·3sin 60°=1.∵球O 的表面积为36π=4πR 2,∴球O 的半径R =3,∴球心O 到平面ABC 的距离d =R 2-r 2=22,∴球面上的点P 到平面ABC 距离的最大值为R +d =3+22.(2)在四面体ABCD 中,AB =1,BC =CD =3,AC =2,当四面体ABCD 的体积最大时,其外接球的表面积为()A .2πB .3πC .6πD .8π答案C 解析∵AB =1,BC =3,AC =2,由勾股定理可得AB 2+AC 2=BC 2,所以△ABC 是以BC 为斜边的直角三角形,且该三角形的外接圆直径为BC =3,当CD ⊥平面ABC 时,四面体ABCD 的体积取最大值,此时,其外接球的直径为2R =BC 2+CD 2=6,因此,四面体ABCD 的外接球的表面积为4πR 2=π×(2R )2=6π.故选C .(3)已知四棱锥S -ABCD 的所有顶点在同一球面上,底面ABCD 是正方形且球心O 在此平面内,当四棱锥的体积取得最大值时,其表面积等于16+163,则球O 的体积等于()A .42π3B .162π3C .322π3D .642π3答案D解析由题意得,当四棱锥的体积取得最大值时,该四棱锥为正四棱锥.因为该四棱锥的表面积等于16+163,设球O 的半径为R ,则AC =2R ,SO =R ,如图,所以该四棱锥的底面边长AB =2R ,则有(2R )2+4×12×2R ×16+163,解得R =22,所以球O 的体积是43πR 3=6423π.故选D .(4)三棱锥A -BCD 内接于半径为5的球O 中,AB =CD =4,则三棱锥A -BCD 的体积的最大值为()A .43B .83C .163D .323答案C解析如图,过CD 作平面ECD ,使AB ⊥平面ECD ,交AB 于点E ,设点E 到CD 的距离为EF ,当球心在EF 上时,EF 最大,此时E ,F 分别为AB ,CD 的中点,且球心O 为EF 的中点,所以EF =2,所以V max =13×12×4×2×4=163,故选C .(5)已知正四棱柱的顶点在同一个球面上,且球的表面积为12π,当正四棱柱的体积最大时,正四棱柱的高为_.答案8解析设正四棱柱的底面边长为a ,高为h ,球的半径为r ,由题意知4πr 2=12π,所以r 2=3,又2a 2+h 2=(2r )2=12,所以a 2=6-h 22,所以正四棱柱的体积V =a 2h =6-h 22h ,则V ′=6-32h 2,由V ′>0,得0<h <2,由V ′<0,得h >2,所以当h =2时,正四棱柱的体积最大,V max =8.模型九内切球模型【方法总结】以三棱锥P -ABC 为例,求其内切球的半径.方法:等体积法,三棱锥P -ABC 体积等于内切球球心与四个面构成的四个三棱锥的体积之和;第一步:先求出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,球心为O ,建立等式:V P -ABC =V O -ABC +V O -P AB +V O -P AC +V O -PBC ⇒V P -ABC =13S △ABC ·r +13S △P AB ·r +13S △P AC ·r +13S △PBC ·r =13(S △ABC +S △P AB +S △P AC +S △PBC )·r ;第三步:解出r =3V P -ABC S O -ABC +S O -P AB +S O -P AC +S O -PBC =3VS 表.秒杀公式(万能公式):r =3VS 表【例题选讲】[例](1)已知一个三棱锥的所有棱长均为2,则该三棱锥的内切球的体积为________.答案354π解析由题意可知,该三棱锥为正四面体,如图所示.AE =AB ·sin 60°=62,AO =23AE =63,DO =AD 2-AO 2=233,三棱锥的体积V D ABC =13S △ABC ·DO =13,设内切球的半径为r ,则V D ABC =13r (S △ABC +S △ABD +S △BCD +S △ACD )=13,r =36,V 内切球=43πr 3=354π.(2)(2020·全国Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.答案23π解析圆锥内半径最大的球即为圆锥的内切球,设其半径为r .作出圆锥的轴截面PAB ,如图所示,则△PAB 的内切圆为圆锥的内切球的大圆.在△PAB 中,PA =PB =3,D 为AB 的中点,AB =2,E 为切点,则PD =22,△PEO ∽△PDB ,故PO PB =OEDB ,即22-r 3=r 1,解得r =22,故内切球的体积为43π223=23π.(3)阿基米德(公元前287年~公元前212年)是古希腊伟大的哲学家、数学家和物理学家,他和高斯、牛顿并列被称为世界三大数学家.据说,他自己觉得最为满意的一个数学发现就是“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”.他特别喜欢这个结论.要求后人在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边.若表面积为54π的圆柱的底面直径与高都等于球的直径,则该球的体积为()A .4πB .16πC .36πD .64π3答案C解析设该圆柱的底面半径为R ,则圆柱的高为2R ,则圆柱的表面积S =S 底+S 侧=2×πR 2+2·π·R ·2R =54π,解得R 2=9,即R =3.∴圆柱的体积为V =πR 2×2R =54π,∴该圆柱的内切球的体积为23×54π=36π.故选C .(4)已知三棱锥P -ABC 的三条侧棱PA ,PB ,PC 两两互相垂直,且PA =PB =PC =2,则三棱锥P -ABC 的外接球与内切球的半径比为________.答案33+32解析以PA ,PB ,PC 为过同一顶点的三条棱,作长方体,由PA =PB =PC =2,可知此长方体即为正方体.设外接球的半径为R ,则R =4+4+42=3,设内切球的半径为r ,则内切球的球心到四个面的距离均为r ,由13(S △ACP +S △APB+S △PCB +S △ABC )·r =13·S △PCB ·AP ,解得r =23+3,所以Rr =323+3=33+32.(5)正四面体的外接球和内切球上各有一个动点P 、Q ,若线段PQ 长度的最大值为463,则这个四面体的棱长为________.答案4解析设这个四面体的棱长为a ,则它的外接球与内切球的球心重合,且半径64R a =外,612r =内,依题意得6664123a a +=,4a ∴=.。
五个无敌模型——全搞定空间几何的外接球

专题:五个无敌模型——全搞定空间几何的外接球一、知识要点如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点. 考查学生的空间想象能力以及化归能力.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.二、典型例题模型一:直接公式法(用于长方体、正方体中)【例1】已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( ).A. 16πB. 20πC. 24πD. 32π【例2】一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为______________.解析:要求球的体积,还是先得求出球的半径,而球的直径正好是正方体的体对角线,因此,由正方体表面积可求出棱长,从而求出正方体的体对角线是233故该球的体积为43π.模型二:构造补形法(用于墙角、正四面体、对棱相等的四面体中)【例3】若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是 思路提示:此题属于墙角模型(三条线两个垂直,不找球心的位置即可求出球半径)c abCP A Babc 图2PCBAabc 图3CBPAa bc 图4PCO 2BA方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R解答:933342=++=R ,ππ942==R S【例4】 2 )A. 3πB. 4πC. 33πD. 6π【例5】在等腰梯形ABCD 中,AB=2DC=2,0DAB=60∠,E 为AB 的中点,将ADE ∆与BEC∆分布沿ED 、EC 向上折起,使A B 、重合于点P ,则三棱锥P-DCE 的外接球的体积为( ).A. 327B. 62C. 68D. 624解析:因为AE=EB=DC=1,0DAB=CBE=DEA=60∠∠∠,所以AE=EB=BC=DC=DE=CE=1AD =,即三棱锥P-DCE 为正四面体,至此,这与例6就完全相同了,故选C.【例6】在三棱锥BCD A -中,,4,3,2======BD AC BC AD CD AB 则三棱锥BCD A -外接球的表面积为 。
