角的大小比较PPT优选课件
合集下载
角大小的比较和直角的认识优秀课件PPT

学习永远不晚。 JinTai College
思考二:怎样比较两个角的大小? 小结:顶点对齐,一组边重合,看角的另一边,在外面的边对应的角大。
直பைடு நூலகம்的初步认识
我们把这样的角叫做直角
找一找生活中的直角
怎样判断直角?
判断方法:
(1)动手操作:怎样制作直角?
(2)画直角
感谢您的阅读! 为 了 便于学习和使用, 本文档下载后内容可 随意修改调整及打印。
角大小的比较和直角的认识
2013.10.18
一、知识回顾:
1、角的特征是什么? 有一个顶点和两条边
(顶点)(边) ( 边 )
2、画角应注意什么?步骤是怎么样的?
二、角的大小比较 思考一:角的大小和什么有关?
小结:角的大小只与角张开的大小有关。
1、如果把这个角的两边延长这个角就变大了。( × )
2、用放大镜看一个角,这个角就变大了。 ( × )
角的大小比较PPT教学课件
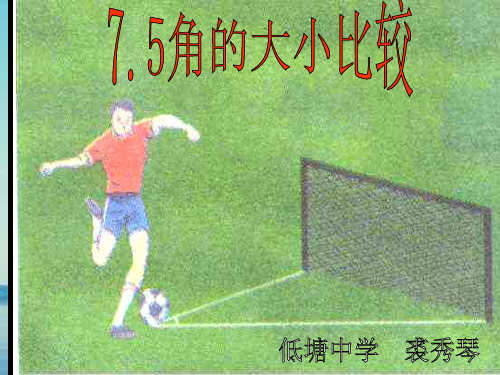
C( F )
ABC = DEF
B ( E)
A ( D)
C B
角
2
1
的
O
A
和
( AOC为 1 和 2 的和
记作 AOC = 1 + 2 )
与
B
差
21
C
O
A
( AOC为 1 和 2 的差
记作 AOC = 1 – 2 )
01 23 4 5
利用一副三角板,你能画 出哪些度数的角?
15º,30º,45º,60º,75º,90º, 105º,120º,135º,150º,165º等
一﹑角的大小比较
图1
图2
思考:你认为图中时针和分针所成的角哪个角大?
度量法
角的大小是指它们的度数的大小,所以比较两个 角的大小,可以量出它们的度数来进行。
C
F
。 60
。 30
B
A
E
D
ABC > DEF
C F
ABC> DEF
B (E)
A( D )
F
叠
C
合
AB C< DEF
法
B ( E)
A ( D)
B
右图),把这张透明纸折叠,使角的两边OB和OC
A
重合,然后把这张纸展开、铺平,画出折痕OA。
∠ AOB与∠ AOC之间有怎样的大小关系?
∠ AOB=∠ AOC
O
C
从一个角的顶点引出的一条射线,把这个角分 成两个相等的角,这条射线叫做这个角的平分线。
如上面“做一做”的图中,由 ∠ AOB=∠ AOC知,射线OA是∠ BOC 的平分线。
猎人合唱是德国作曲家韦伯的著名歌剧 《自由射手》第三幕里的一段选曲。这部 歌剧创作于1820年。故事取材于德国和捷 克斯洛伐克广为流传的、一个名叫《黑猎 人》的民间传说。它描写年轻的猎人马克 斯与守林人的女儿阿格泰相爱,并战胜重 重困难,最后结为夫妻的故事。
《角的大小》PPT课件

根据右图解下列问题
(2)比较∠AOB、∠AOC ∠AOD、∠AOE的大小
(1)找出图中的直角、锐角和钝角
解:(2)由右图可以看出: ∠ AOB < ∠ AOC < ∠ AOD < ∠ AOE
解:(1)图中的直角有∠AOC,∠BOD ,∠ COE;
锐角有∠ AOB, ∠ BOC ,∠ COD, ∠ DOE;
D
E
因为
方法一:度量法 用量角器测量一个角,角的大小也可以按其度数比较,度数大的角则大,度数小的则小
注意:使用量角器应注意的问题.即三点:对中;重合;读数.
方法二:叠合法 把两个角的顶点和一条边重合,并使两个角的另一条边在重合边的同侧,再通过观察两个角的另一边的位置进行判断.
钝角有∠ AOD, ∠ BOE。
小试牛刀
(1) 画射线AC ;
A C
(2) 在射线AC上截取AB=a.
B
所以 AB=a.
画 法:
解:已知线段a,求解;线段AB,使AB=a.
复习:
画一条线段等于已知线段
利用尺规,作一个角等于已知角.已知:∠AOB(如图).求作:∠AˊOˊBˊ,使∠ AˊOˊBˊ=∠AOB.
交流提纲:⑴你是怎样思考的;⑵讨论:按怎么样的顺序画比较方便; ⑶画角时特别应注意什么?
作法与示范
作法
示范
(1)作射线O′A′:
(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;
1、请同学们拿出已经做好的三角形,并与同桌比较一下三角形各个角的大小。
做一做,比一比
2、下列说法正确的是( )A,角的边越长,则角越大。B,角的大小与边的长短无关。C,角的大小与顶点的位置有关。D,角的大小决定于始边旋转的方向。
(2)比较∠AOB、∠AOC ∠AOD、∠AOE的大小
(1)找出图中的直角、锐角和钝角
解:(2)由右图可以看出: ∠ AOB < ∠ AOC < ∠ AOD < ∠ AOE
解:(1)图中的直角有∠AOC,∠BOD ,∠ COE;
锐角有∠ AOB, ∠ BOC ,∠ COD, ∠ DOE;
D
E
因为
方法一:度量法 用量角器测量一个角,角的大小也可以按其度数比较,度数大的角则大,度数小的则小
注意:使用量角器应注意的问题.即三点:对中;重合;读数.
方法二:叠合法 把两个角的顶点和一条边重合,并使两个角的另一条边在重合边的同侧,再通过观察两个角的另一边的位置进行判断.
钝角有∠ AOD, ∠ BOE。
小试牛刀
(1) 画射线AC ;
A C
(2) 在射线AC上截取AB=a.
B
所以 AB=a.
画 法:
解:已知线段a,求解;线段AB,使AB=a.
复习:
画一条线段等于已知线段
利用尺规,作一个角等于已知角.已知:∠AOB(如图).求作:∠AˊOˊBˊ,使∠ AˊOˊBˊ=∠AOB.
交流提纲:⑴你是怎样思考的;⑵讨论:按怎么样的顺序画比较方便; ⑶画角时特别应注意什么?
作法与示范
作法
示范
(1)作射线O′A′:
(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′ A′于点C′;
1、请同学们拿出已经做好的三角形,并与同桌比较一下三角形各个角的大小。
做一做,比一比
2、下列说法正确的是( )A,角的边越长,则角越大。B,角的大小与边的长短无关。C,角的大小与顶点的位置有关。D,角的大小决定于始边旋转的方向。
《角的大小比较》优质公开课PPT

α β
思考:你能找出一个角的补角或余角吗?
补角的性质:
同角或等角的补角相等.
余角的性质:
同角或等角的余角相等.
练习1:如图,已知:点O为直线AB上一点, OC是∠AOB的平分线,OD在∠COB内,看图 填空(填“<”“>”“﹦”)
C (1 )∠AOD < ∠AOB ∠AOD > ∠DOB = ∠BOC ∠AOC O A ∠BOD (2) ∠AOD的补角是 . ∠BOD ∠COD的余角是 . ∠AOD ∠BOD的补角是 . ∠BOC ∠AOC的补角是 .
活动一: 任意画一个角∠AOB,和同桌画 的角 比一比,两个角的大小如何?
◆
请你观察并估计下列哪个角较大?
1
2
角有大小,角的大小与角两边张开的程度有关, 与角两边画出的长短没有关系.
E
E
C
D A
C
D
A
B ∠ECD>∠AOB
O
O
B
或 ∠AOB <∠ECD
∠ECD =∠AOB
∠ABC > ∠DEF 或∠DEF <∠ABC
通过本节的学习,我们应做到以下几点: 1.会比较角的大小; 2.理解角平分线的概念; 3. 理解补(余)角的概念,并灵活运用 补( 余)角的性质; 4.会用角的和与差的形式来表示某个角.
作业:习题4.5第3、4、5题
谢谢!
D
B
C
E
F
例1 : 如图,求解下列问题
A B C
O
D
(1)比较∠AOC与∠BOC;∠BOD与∠COD的大小; (2)将∠AOC写成两个角的和与两个角的差的形式; 解:(1)由图可知: ∠AOC>∠BOC;(OB在∠AOC内) ∠BOD>∠ COD.(OC在∠ BOD内) (2)∠AOC= ∠AOB+∠BOC, ∠AOC= ∠AOD-∠ COD
思考:你能找出一个角的补角或余角吗?
补角的性质:
同角或等角的补角相等.
余角的性质:
同角或等角的余角相等.
练习1:如图,已知:点O为直线AB上一点, OC是∠AOB的平分线,OD在∠COB内,看图 填空(填“<”“>”“﹦”)
C (1 )∠AOD < ∠AOB ∠AOD > ∠DOB = ∠BOC ∠AOC O A ∠BOD (2) ∠AOD的补角是 . ∠BOD ∠COD的余角是 . ∠AOD ∠BOD的补角是 . ∠BOC ∠AOC的补角是 .
活动一: 任意画一个角∠AOB,和同桌画 的角 比一比,两个角的大小如何?
◆
请你观察并估计下列哪个角较大?
1
2
角有大小,角的大小与角两边张开的程度有关, 与角两边画出的长短没有关系.
E
E
C
D A
C
D
A
B ∠ECD>∠AOB
O
O
B
或 ∠AOB <∠ECD
∠ECD =∠AOB
∠ABC > ∠DEF 或∠DEF <∠ABC
通过本节的学习,我们应做到以下几点: 1.会比较角的大小; 2.理解角平分线的概念; 3. 理解补(余)角的概念,并灵活运用 补( 余)角的性质; 4.会用角的和与差的形式来表示某个角.
作业:习题4.5第3、4、5题
谢谢!
D
B
C
E
F
例1 : 如图,求解下列问题
A B C
O
D
(1)比较∠AOC与∠BOC;∠BOD与∠COD的大小; (2)将∠AOC写成两个角的和与两个角的差的形式; 解:(1)由图可知: ∠AOC>∠BOC;(OB在∠AOC内) ∠BOD>∠ COD.(OC在∠ BOD内) (2)∠AOC= ∠AOB+∠BOC, ∠AOC= ∠AOD-∠ COD
角的大小比较PPT课件

2020年10月2日
3
6
例1 根据图形解下列问题: (1)比较∠AOB, ∠ AOC, ∠ AOD,
∠ AOE的大小; (2)找出图中的直角、锐角和钝角。
AB
2020年10月2日
O
Cቤተ መጻሕፍቲ ባይዱ
D
E
7
从一个角的顶点引出的一条射线,把 这个角分成两个相等的角,这条射线叫做 这个角的平分线.
∵OC是∠AOB的平分线 A
C ∴ ∠AOC=∠BOC
∠AOC=∠BOC= 12∠AOB
O
B ∠AOB=2 ∠AOC=2∠BOC
2020年10月2日
8
怎样用量角器画一个角的 平分线?
先用量角器量出这个角的大小,再 以这个角的顶点为顶点, 一边为始边,
在角的内部画一条线,使它与始边所 成的角的大小是原角的一半,这条射 线就是这个角的平分线。
汇报人:XXX 汇报日期:20XX年10月10日
13
1.度量法:即用量角器量出角的度数,
通过比较角的度数来比较角的大小. 度数大的角大,度数小的角小;
2.叠合法:即把两个角叠合在一起
(使角的顶点各它的一边重合在一 起)进行比较。
2020年10月2日
4
用叠合法比较的三种情况:
F A
1.AB在∠ FED的内部,
B E
C D
∠ABC<∠ FED;
AF
2.AB在∠ FED的外部,
角的大小比较
2020年10月2日
1
如何比较两条线段的长短?
A
BC
D
1、测量法 —— 分别量出两线段的长 度,然后再比较大小
2、叠合法 —— 把两条线段叠合在一 起比较大小。
角的大小课件

一个角是另一个角的倍数,其度数等于一个角的度数乘以倍数的值。例如,如果一个角是30度,3倍 的角是90度。
角的半数
一个角是另一个角的半数,其度数等于一个角的度数除以2。例如,如果一个角是60度,半的角是30 度。
角的补角和余角
补角
两个角的和为90度,这两个角互为补 角。例如,如果一个角是30度,另一 个角是60度,它们互为补角。
在日常生活中,角度的应用还涉及到安全问题,如车辆的 转向角度、电梯的倾斜角度等,都需要控制在安全范围内 ,以保障人们的生命安全。
角度在科学中的应用
角度在科学中有着广泛的应用,如物理学中的力矩、化学中的键角、生物学中的 关节角度等。这些角度的大小和方向对科学现象的解释和预测具有重要意义。
在科学实验中,角度的测量和控制也是非常重要的,如光谱分析中的入射角和折 射角、望远镜的指向角等,都需要精确测量和控制,以保证实验结果的准确性和 可靠性。
角度在机械设计中的应用
01
02பைடு நூலகம்
03
机械零件的配合
在机械设计中,许多零件 需要精确的角度配合,如 齿轮、轴承等,以确保机 器的正常运转。
机械运动的控制
通过调整机械运动中的角 度,可以精确控制机器的 运动轨迹和方向。
机械强度与刚度
合理的角度设计可以提高 机械零件的强度和刚度, 从而提高机器的整体性能 和使用寿命。
角度在运动学中的应用
运动轨迹的控制
在运动学中,角度是一个重要的 参数,通过调整角度可以精确控
制物体的运动轨迹和方向。
运动员技术的提高
在体育比赛中,许多技术动作需 要精确的角度控制,如投掷、跳 高等,通过训练可以提高运动员
的角度控制能力。
运动伤害的预防
角的半数
一个角是另一个角的半数,其度数等于一个角的度数除以2。例如,如果一个角是60度,半的角是30 度。
角的补角和余角
补角
两个角的和为90度,这两个角互为补 角。例如,如果一个角是30度,另一 个角是60度,它们互为补角。
在日常生活中,角度的应用还涉及到安全问题,如车辆的 转向角度、电梯的倾斜角度等,都需要控制在安全范围内 ,以保障人们的生命安全。
角度在科学中的应用
角度在科学中有着广泛的应用,如物理学中的力矩、化学中的键角、生物学中的 关节角度等。这些角度的大小和方向对科学现象的解释和预测具有重要意义。
在科学实验中,角度的测量和控制也是非常重要的,如光谱分析中的入射角和折 射角、望远镜的指向角等,都需要精确测量和控制,以保证实验结果的准确性和 可靠性。
角度在机械设计中的应用
01
02பைடு நூலகம்
03
机械零件的配合
在机械设计中,许多零件 需要精确的角度配合,如 齿轮、轴承等,以确保机 器的正常运转。
机械运动的控制
通过调整机械运动中的角 度,可以精确控制机器的 运动轨迹和方向。
机械强度与刚度
合理的角度设计可以提高 机械零件的强度和刚度, 从而提高机器的整体性能 和使用寿命。
角度在运动学中的应用
运动轨迹的控制
在运动学中,角度是一个重要的 参数,通过调整角度可以精确控
制物体的运动轨迹和方向。
运动员技术的提高
在体育比赛中,许多技术动作需 要精确的角度控制,如投掷、跳 高等,通过训练可以提高运动员
的角度控制能力。
运动伤害的预防
角的大小比较ppt课件
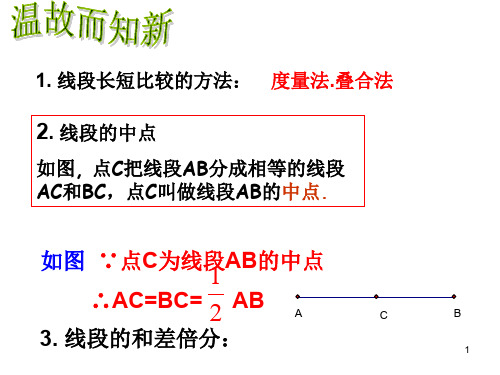
1. 线段长短比较的方法: 度量法.叠合法
2. 线段的中点
如图, 点C把线段AB分成相等的线段 AC和BC,点C叫做线段AB的中点.
如图 ∵点C为线段1 AB的中点
∴AC=BC= 2 AB A
C
B
3. 线段的和差倍分: 1
4.角是由两条有公共端点的射线组成的
图形
----静止的
角也可以看成是由一条射线绕着它的端 点旋转而成的图形----运动的
B
已知则∠∠ABOOBC==1-4--5-1°--7-0和---°∠---或A---O1--2C-0-°=-25°
C A
A C
分类 思想
O
B
O
B
12
请你说一说:
你的收获!你的困惑!
你的新想法和新发现.
13
1、课本作业题1-6 2、作业本6.6节
14
5. 角的三种表示方法:
2
3
你知道∠A、∠B、 ∠C 、∠P、 ∠Q、 ∠O的度数吗?
你会比较它们的大小吗?
30°
45°
45°
60°
4
先观察下列各组角,并估计其中哪一个角较大, 然后用量角器量一量,看看你的估计是否正确。
(1)
1
2
(2)
а
β
∠1> ∠2
A
∠ α< ∠β
思考 :∠α = 12.30°,∠β = 12°30′这两个角 一样大吗?为什么?
(2)找出图中的直角、锐角和钝角.
解(1)由图可以看出:
∠AOB﹤∠AOC﹤∠AOD﹤∠AOE
A
B
(2)图中的直角有∠AOC,∠BOD,∠COE
锐角有∠AOB,∠BOC,
O
2. 线段的中点
如图, 点C把线段AB分成相等的线段 AC和BC,点C叫做线段AB的中点.
如图 ∵点C为线段1 AB的中点
∴AC=BC= 2 AB A
C
B
3. 线段的和差倍分: 1
4.角是由两条有公共端点的射线组成的
图形
----静止的
角也可以看成是由一条射线绕着它的端 点旋转而成的图形----运动的
B
已知则∠∠ABOOBC==1-4--5-1°--7-0和---°∠---或A---O1--2C-0-°=-25°
C A
A C
分类 思想
O
B
O
B
12
请你说一说:
你的收获!你的困惑!
你的新想法和新发现.
13
1、课本作业题1-6 2、作业本6.6节
14
5. 角的三种表示方法:
2
3
你知道∠A、∠B、 ∠C 、∠P、 ∠Q、 ∠O的度数吗?
你会比较它们的大小吗?
30°
45°
45°
60°
4
先观察下列各组角,并估计其中哪一个角较大, 然后用量角器量一量,看看你的估计是否正确。
(1)
1
2
(2)
а
β
∠1> ∠2
A
∠ α< ∠β
思考 :∠α = 12.30°,∠β = 12°30′这两个角 一样大吗?为什么?
(2)找出图中的直角、锐角和钝角.
解(1)由图可以看出:
∠AOB﹤∠AOC﹤∠AOD﹤∠AOE
A
B
(2)图中的直角有∠AOC,∠BOD,∠COE
锐角有∠AOB,∠BOC,
O
2023年北京版数学三年级上册5认识直角、锐角、钝角及角的大小优选课件

►Suffering is the most powerful teacher of life. 苦难是人生最伟大的老师。 ►For man is man and master of his fate. 人就是人,是自己命运的主人。 ►A man can't ride your back unless it is bent. 你的腰不弯,别人就不能骑在你的背上。
北京课改版 数学 三年级 上册
5 角的初步认识
认识直角、锐角、钝角 及角的大小
课前导入
探究新知
课堂练习
课堂小结
课后作业
课前导入
小朋友,你们认识它吗? 它叫什么名字?
一个角有( 1 )个顶点,( 2 )些是角?
╳
√
√
╳
像这样的角, 是什么角?
探究新知
像这样的角, 叫直角。
课堂小结
这节课你们都学会了哪些知识?
像这样的角 是锐角。
课堂小结
这节课你们都学会了哪些知识?
像这样的角 是钝角。
课后作业
1.从教材课后习题中选取; 2.从课时练中选取。
►为你理想的人,否则,爱的只是你在他身上找到的你的影子。 ►有时候,我们愿意原谅一个人,并不是我们真的愿意原谅他,而是我们 不愿意失去他。不想失去他,惟有假装原谅他。不管你爱过多少人,不管 你爱得多么痛苦或快乐。最后,你不是学会了怎样恋爱,而是学会了,怎 样去爱自己。
►1Our destiny offers not the cup of despair, but the chalice of opportunity. ►So let us seize it, not in fear, but in gladness. · 命运给予我们的不是失望之酒,而是机会之杯。 因此,让我们毫无畏惧,满心愉悦地把握命运
角的比较PPT市公开课一等奖省优质课获奖课件

第5页
B
D
O
A O′
C
②若边OB与边OD重合
则∠A0B = ∠CO ′D
第6页
B
D
O
A O′
C
②若边OB 在∠CO ′ D外部
则∠A0B > ∠CO ′D
第7页
角大小与角两边画出长短相关吗? 如图所表示,角大小与角两边画出长短没 相关系.角两边叉开得越小,角度就越小.
第8页
如图,求解以下问题(1)比较∠AOB,∠AOC,∠AOD, ∠AOE大小,并指出其中锐角、直角、钝角、平角;
AB
O
C
ED
锐角∠AOB,∠BOC,∠EOD, ∠DOC 直角∠AOC,∠EOC 钝角∠DOB,∠BOE,∠AOD
(2)试比较∠BOC和∠DOE大小.
第9页
在纸上画一个角并剪下,将它对折使其两边重合,
折痕与角两边所成两个角大小关系怎样?
B 如图所表示,因为∠BOD=∠AOD
O
D 所以射线OD平分∠AOB,
则∠COD= 45° ,
DB
∠BOC= 30° ,
C
∠AOB= 60° .
O
A
解析:由题意可知,图中等量关系为 ∠COD=3∠BOD,∠BOC=2∠BOD, ∠AOB=2∠BOC
第16页
3.如图所表示,已知直线AB,CD相交于点O,OE平
分∠COB,若∠EOB=55°,则∠BOD度数是 ( C )
∴∠AOC=60°,而∠BOC=70°
∴∠AOC≠∠BOC 故OC不是∠AOB平分线
∵∠DOC=30°,∠AOD=30° ∴∠DOC=∠AOD
∴OD是∠AOC平分线
第11页
如图所表示,(1)预计∠AOB,∠DEF度数; (2)量一量,验证你预计.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C ∴ ∠AOC=∠BOC
∠AOC=∠BOC= 12∠AOB
O
B ∠AOB=2 ∠AOC=2∠BOC
2020/10/18
8
怎样用量角器画一个角的 平分线?
先用量角器量出这个角的大小,再 以这个角的顶点为顶点, 一边为始边, 在角的内部画一条线,使它与始边所 成的角的大小是原角的一半,这条射 线就是这个角的平分线。
感谢阅读!为了方便学习和使用,本文档的内容可以在下载后随意修改,调整和打印。欢迎下载!
汇报人:XXX 日期:20XX年XX月XX日
∠AOB是多少度?
ED C B
2020/10/18
O
A11
利用一幅三角尺,你能 画出哪些度数的角?
利用一幅三角尺,可以画出的角有: 15°,30°,45°,60°, 90°,105°,120°, 135°,150°,165°等。
2020/10/18
12
谢谢您的聆听与观看
THANK YOU FOR YOUR GUIDANCE.
2020/10/18
9
例2: 如右图,∠ ABC=90° , ∠ CDB=30° ,BP平分 ∠ ABD。 求∠ ABP的度数。
DCP
2020/10/18
B
A
10
练习:已知 OB是∠AOC的平分线,OD是 ∠COE平 分线。
(1)如果∠AOB=40度,∠DOE=30度,那么
∠BOD是多少度?
(2)如果∠AOE=140度,∠COD=30度,那么
2020/10/18
3
6
例1 根据图形解下列问题: (1)比较∠AOB, ∠ AOC, ∠ AOD,
∠ AOE的大小; (2)找出图中的直角、锐角和钝角。
AB
2020/10/18
O
C
D
E
7
从一个角的顶点引出的一条射线,把 这个角分成两个相等的角,这条射线叫做 这个角的平分线.
∵OC是∠AOB的平分线 A
角的大小比较
2020/10/18
1
如何比较两条线段的长短?
A
BC
D
1、测量法 —— 分别量出两线段的长 度,然后再比较大小
2、叠合法 —— 把两条线段叠合在一 起比较大小。
2020/10/18
2
如下图,如何比较两角∠BAC与∠EDF 的大小呢?
A D
C
2020/10/18
BF
E
3
角的大小比较的两种方法:
1.度量法:即用量角器量出角的度数,
通过比较角的度数来比较角的大小. 度数大的角大,度数小的角小;
2.叠合法:即把两个角叠合在一起
(使角的顶点各它的一边重合在一 起)进行比较。Leabharlann 2020/10/184
用叠合法比较的三种情况:
F A
1.AB在∠ FED的内部,
B E
C D
∠ABC<∠ FED;
AF
2.AB在∠ FED的外部,
B
C ∠ABC>∠ FED;
E
D
FA
3.AB与EF重合,
B E
C D
∠ABC=∠ FED.
2020/10/18
5
按角的大小来分,还记得我们可以把 角分成哪几类吗?
锐角:小于直角的角. 1
直角:等于90°的角
∟
2
角
(直角可以用Rt∠表示,画图时常在
直角的顶点处加上“┐ ”来表示
这个角是直角.)
钝角:大于直角而小于平角的角.
