2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 9
2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 1

2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 11.Physics _____ much easier for me since Mrs. Yang began to teach us. A. have beenB. has beenC. wasD. were2.The girl students are discussing the walls in the classroom.A. what to paintcolorB. to paint what colorC. which color to paintD. to paint which color3.—I wonder if I can learn English well.—______________________. All things are difficult before they are easy. A.I am afraid so B. You’re slow C. It takes timeD. It’s a piece of cake4.—The doctor told me not to eat too much, but I find it difficult. —The doctor is right.______ you eat, ______ you will be. A.The less; the healthier B.The less; the more healthier C.The more; the healthierD.The more; the more healthier5.— What’s the___________ of the car at present? — It’s about 70 kilometers an hour.A. placeB. speedC. priceD. mark6.My deskmate is really . She likes to attend different activities after school.A.activeB.quietzyD.honest7.--Shall we go for a picnic tomorrow?―Well, it all ______ the weather.A.belongs toB.happens toC.depends onD.concentrates on8. you can have a good future yourhard work today.A. Whether or not; depend onB. If or not; depend onC. Whether or not; depends onD. If or not; depends on9.—Would you mind taking some photos for us?—Certainly not. It’s a piece of cake.(选出可以替代 _线部分的最佳选项)A. a kind of foodB. a difficult thingC. an easy thingD. a photo10.﹣In Shenzhen the city center will be connected to all the districts by metro in several years.﹣Great, I'm proud of living in Shenzhen. A. closed to B. joined to C. added to11.Keeping an English diary can help us improve our writing__________(能力). 12.She practices the p____ of English words every day to improve her spoken English. 13.I think having(交谈)with foreigners can improve my English.14.Taiyuan and Zhengzhou have a lot in c . For example, they are both big cities with a long history.15.The s of light is about 300 million meters per second. 16.Jenny has learnt Chinese in China for many years. She has more k of Chinese culturethan I.17.write down, increase, wise, partner, be born with1. I think the number of cars in China is now.2.the telephone numberbefore you forget it.3. In order to finish this task, he needs two .4. The young manmade a decision to give up the plan.5. Heagood memory. How lucky he is!18.我不知道如何提高我的阅读速度。
2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 8

2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 81.—You don’t look well. ____ with you? 一I have a fever and can’t stop coughing.A.What's happeningB.What is itC.What’s onD.What’s the matter2.He made up his mind to devote his life_______ pollution_______ happily. A.to prevent; from liveB.to prevent; from livingC.to preventing; from livingD.to preventing; to live3.— Look! _______is dancing under the tree. —Oh, that’s my cousin, Anna. A. EverybodyB. AnybodyC. NobodyD. Somebody4.His family are worried about him because they haven’t _____ letters from him for a long time. A.accepted B.received C.writtenD.collected5.The new basketball Dave. He bought it yesterday. A. isB. is belongC. belongsD. belongs to6.―Why are you looking in class all day?―Because I can’t finish my homework until eleven every night . A. awake B. asleep C. sleeping D. sleepy7.一Would you like to eat? —Yes, please. A. anything delicious B. delicious anything C. something delicious 8.一 father took part in the charity activity in the neighbourhood yesterday?— Peter’s.A. WhoseB. WhatC. WhichD. Who9.—Who do you think will be the winner of the 21st World Cup in Russia?—I guess the gold medal will Germany. A. belong to B . take up C. make up D. stick to10.—Look! Tina is still working. It’s too late. —Wow, she is so ! I could never do like that.A. simpleB. creativeC. popularD. energetic 11.Mr. Liu wants to ____(表达) his thanks to his teachers. 12.Don’t make any n____ when you are in a library.13.Now the man doesn’t get help from a____ else because he never helps others. 14.Children are looking forward to ____(receive) gifts on Christmas Day. 15.Wearing masks can help ____(prevent) people from catching a cold. 16.Some think Stonehenge was built to celebrate a ____(胜利). 17.The old can get ____(医疗的)care from the government.18.它能预防疾病,使人们保持健康。
2020-2021学年人教版九年级上册数学期末复习试卷(有答案)
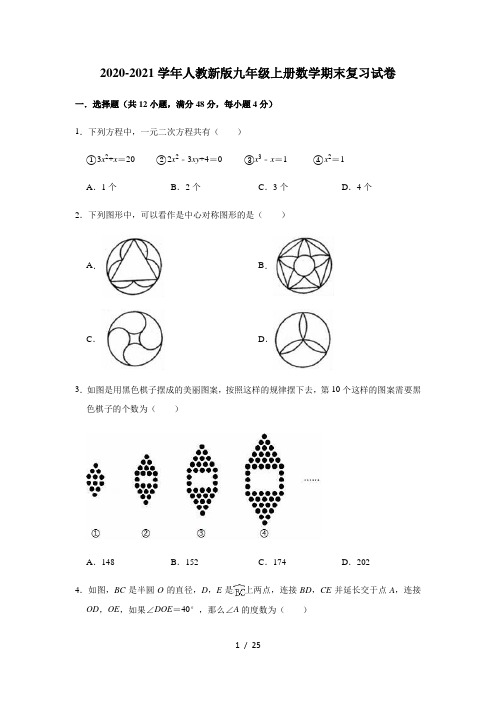
2020-2021学年人教新版九年级上册数学期末复习试卷一.选择题(共12小题,满分48分,每小题4分)1.下列方程中,一元二次方程共有()①3x2+x=20 ②2x2﹣3xy+4=0 ③x3﹣x=1 ④x2=1A.1个B.2个C.3个D.4个2.下列图形中,可以看作是中心对称图形的是()A.B.C.D.3.如图是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为()A.148B.152C.174D.2024.如图,BC是半圆O的直径,D,E是上两点,连接BD,CE并延长交于点A,连接OD,OE,如果∠DOE=40°,那么∠A的度数为()A.35°B.40°C.60°D.70°5.从,0,π,,,0.3010010001……(两个1之间依次多一个0)这六个数中随机抽取一个数,抽到无理数的概率是()A.B.C.D.6.下列语句不是命题的是()A.连结AB B.对顶角相等C.相等的角是对顶角D.同角的余角相等7.新冠病毒主要是经呼吸道飞沫传播的,在无防护下传播速度很快,已知有1个人患了新冠,经过两轮传染后共有625个人患了新冠,每轮传染中平均一个人传染m人,则m的值为()A.24B.25C.26D.278.如图,二次函数y=a(x+1)2+k的图象与x轴交于A(﹣3,0),B两点,下列说法错误的是()A.a<0B.图象的对称轴为直线x=﹣1C.点B的坐标为(1,0)D.当x<0时,y随x的增大而增大9.如图,在平面直角坐标系中,将点P(﹣4,2)绕原点O顺时针旋转90°,则其对应点Q的坐标为()A.(2,4)B.(2,﹣4)C.(﹣2,4)D.(﹣2,﹣4)10.不透明的袋子中装有红球1个、绿球1个、白球2个,除颜色外无其他差别.随机摸出一个小球后不放回,再摸出一个球,则两次都摸到白球的概率是()A.B.C.D.11.如图,将边长为3的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为()A.3B.6C.9D.3π12.如果数m使关于x的方程(m+1)x2﹣(2m﹣1)x+m=0有实数根,且使关于x的分式方程有正分数解,那么所有满足条件的整数m的值的和为()A.﹣6B.﹣5C.﹣4D.﹣3二.填空题(共6小题,满分24分,每小题4分)13.已知抛物线y=2(x﹣1)2+1,当0<x<3时,y的取值范围是.14.已知关于x的一元二次方程(m﹣1)2x2+3mx+3=0有一实数根为﹣1,则该方程的另一个实数根为.15.张老师上班途中要经过1个十字路口,十字路口红灯亮30秒、黄灯亮5秒、绿灯亮25秒,张老师希望上班经过路口是绿灯,但实际上这样的机会是.16.如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为.17.A,B两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发小时后与乙相遇.18.为响应“双十二购物狂欢节”活动,某零食店推出了甲、乙、丙三类饼干礼包,已知甲、乙、丙三类礼包均由A、B、C三种饼干搭配而成,每袋礼包的成本均为A、B、C三种饼干成本之和.每袋甲类礼包有5包A种饼干、2包B种饼干、8包C种饼干;每袋丙类礼包有7包A种饼干、1包B种饼干、4包C种饼干.已知甲每袋成本是该袋中A种饼干成本的3倍,利润率为30%,每袋乙的成本是其售价的,利润是每袋甲利润的;每袋丙礼包利润率为25%.若该网店12月12日当天销售甲、乙、丙三种礼包袋数之比为4:6:5,则当天该网店销售总利润率为.三.解答题(共2小题,满分16分,每小题8分)19.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C、直线BC的表达式为y=﹣x+3.(1)求抛物线的表达式;(2)求△DBC的面积;(3)在直线BC上有一点P,若使PO+PA的值最小,则点P的坐标为.20.在乐山市关工委组织的“五好小公民”主题教育活动中,我市蓝天学校组织全校学生参加了“红旗队飘,引我成长”知识竞赛,赛后机抽取了部分参赛学生的成绩,按从高分到低分将成绩分成A,B,C,D,E五类,绘制成下面两个不完整的统计图:根据上面提供的信息解答下列问题:(1)本次抽取了名参赛学生的成绩,D类所对应的圆心角是度;(2)样本中成绩的中位数落在类中;(3)若A类含有2名男生和2名女生,从中随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好选到1名男生和1名女生的概率.四.解答题(共5小题,满分50分,每小题10分)21.(1)计算:①a(a﹣2b)﹣(2a﹣b)2;②(x+3+)÷.(2)解方程:①x2﹣2x=1;②(x+2)(2x﹣1)=1.22.如图,Rt△ABC中,∠C=90°,BE是它的角平分线,D在AB边上,以DB为直径的半圆O经过点E.(1)试说明:AC是圆O的切线;(2)若∠A=30°,圆O的半径为4,求图中阴影部分的面积.23.抗击“新冠肺炎”疫情期间,口罩是重要的防护物资,今年2月,某社区根据实际需要,采购了5000个口罩,一部分用于社区家庭,其余部分用于社区工作人员.(1)为了保证社区抗疫工作顺利开展,用于社区工作人员的口罩个数应不少于用于社区家庭口罩个数的1.5倍,问用于该社区家庭的口罩最多有多少个?(2)据统计,2月份,该社区有200户家庭有口罩需求,平均每户需要10个,其余口罩刚好满足社区工作人员的抗疫需要,随着疫情的发展,3月份,该社区对口罩的总需求量比2月份增加了20%,需要口罩的家庭户数比2月份增加了a%,社区工作人员需要口罩的个数比2月份增如了1.5a%,同时,由于该社区加大了管控力度,平均每户家庭的口罩需求量减少了a%,求a的值.24.如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF.试说明这是中心对称图形.25.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A.B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C,D,连接AC,BD.(1)求出点C,D的坐标;(2)设y轴上一点P(0,m),m为整数,使关于x,y的二元一次方程组有正整数解,求点P的坐标;的值(3)在(2)的条件下,若Q点在线段CD上,横坐标为n,△PBQ的面积S△PBQ 不小于0.6且不大于4,求n的取值范围.五.解答题(共1小题,满分12分,每小题12分)26.四边形的一条对角线将这个四边形分成两个三角形,如果这两个三角形相似(不全等),那么我们将这条对角线叫做这个四边形的相似对角线.(1)如图1,四边形ABCD中,∠DAB=100°,∠DCB=130°,对角线AC平分∠DAB,求证:AC是四边形ABCD的相似对角线;(2)如图2,直线y=﹣x+分别与x,y轴相交于A,B两点,P为反比例函数y =(k<0)上的点,若AO是四边形ABOP的相似对角线,求反比例函数的解析式;(3)如图3,AC是四边形ABCD的相似对角线,点C的坐标为(3,1),AC∥x轴,∠BCA=∠DCA=30°,连接BD,△BCD的面积为.过A,C两点的抛物线y=ax2+bx+c (a<0)与x轴交于E,F两点,记|m|=AC+1,若直线y=mx与抛物线恰好有3个交点,求实数a的值.参考答案与试题解析一.选择题(共12小题,满分48分,每小题4分)1.解:一元二次方程有:3x2+x=20,x2=1,共2个,故选:B.2.解:A、不是中心对称图形,故本选项不合题意;B、不是中心对称图形,故本选项不合题意;C、是中心对称图形,故本选项符合题意;D、不是中心对称图形,故本选项不合题意;故选:C.3.解:根据图形,第1个图案有12枚棋子,第2个图案有22枚棋子,第3个图案有34枚棋子,…第n﹣1个图案有2(1+2+…+n+1)+2(n﹣2)=n2+5n﹣2枚棋子,第n个图案有2(1+2+…+n+2)+2(n﹣1)=n2+7n+4枚棋子,故第10个这样的图案需要黑色棋子的个数为102+7×10+4=100+70+4=174(枚).故选:C.4.解:连接CD,∵BC为⊙O的直径,∴∠BDC=90°,∴∠ADC=90°,∵∠DOE=40°,∴∠ACD=∠DOE=20°,∴∠A=180°﹣∠ADC﹣∠ACD=70°,故选:D.5.解:在所列的6个数中,无理数有,π,0.3010010001…这3个,∴这六个数中随机抽取一个数,抽到无理数的概率是,故选:A.6.解:A、连结AB,不是命题,符合题意;B、对顶角相等,是命题,不符合题意;C、相等的角是对顶角,是命题,不符合题意;D、同角的余角相等,是命题,不符合题意;故选:A.7.解:依题意,得:1+m+m(m+1)=625,解得:m1=24,m2=﹣26(不合题意,舍去).8.解:观察图象可知a<0,由抛物线的解析式可知对称轴x=﹣1,∵A(﹣3,0),A,B关于x=﹣1对称,∴B(1,0),故A,B,C正确,∵当﹣1<x<0时,y随x的增大而减小,∴选项D错误.故选:D.9.解:作图如下,∵∠MPO+∠POM=90°,∠QON+∠POM=90°,∴∠MPO=∠QON,在△PMO和△ONQ中,∵,∴△PMO≌△ONQ,∴PM=ON,OM=QN,∵P点坐标为(﹣4,2),∴Q点坐标为(2,4),10.解:画树状图为:共有12种等可能的结果数,其中两次摸出的球都是的白色的结果共有2 种,所以两次都摸到白球的概率是=,故选:B.11.解:∵正方形ABCD的边长为3,∴AB=BC=CD=AD=3,即的长是3+3=6,∴扇形DAB的面积是6×3=9,故选:C.12.解:当m+1=0时,∴m=﹣1,∴3x﹣1=0,∴x=,符合题意,当m+1≠0时,此时△≥0,∴﹣8m+1≥0,∴m≤,∵使关于x的分式方程有正分数解,∴=﹣1,∴x=>0,∴m>﹣4,∴﹣4<m≤,∴m=﹣3或﹣2或﹣1或0,∵是正分数,∴m=﹣3或﹣1,∴﹣3+(﹣1)=﹣4,故选:C.二.填空题(共6小题,满分24分,每小题4分)13.解:∵抛物线y=2(x﹣1)2+1,∴当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,∴x=0和x=2的函数值相等,当x=3时,y=9,当x=1时,y=1,∴当0<x<3时,y的取值范围是1≤y<9,故答案为:1≤y<9.14.解:∵方程(m﹣1)2x2+3mx+3=0是关于x的一元二次方程,∴(m﹣1)2≠0即m≠1.把x=﹣1代入原方程得,(m﹣1)2﹣3m+3=0,即:m2﹣5m+4=0,解得,m=4,m=1(不合题意舍去),当m=4时,原方程变为:9x2+12x+3=0,即,3x2+4x+1=0,由根与系数的关系得:x1•x2=,又x1=﹣1,∴x2=﹣故答案为:﹣.15.解:张老师上班经过路口是绿灯的机会是:==,故答案为:.16.解:如图,连接BD,∵将△ABC绕点A逆时针旋转60°,得到△ADE,∴AB=AD,∠BAD=60°,∴△ABD为等边三角形,∴∠ABD=60°,AB=BD,又∵AE=DE,BE=BE,∴△ABE≌△DBE(SSS)∴∠ABE=∠DBE=30°∴∠ABE=∠DBE=30°,又∵∠BDE=∠ADB﹣∠ADE=15°,∴∠BED=135°.故答案为:135°.17.解:甲减速后的速度为:(20﹣8)÷(4﹣1)=4(km/h),一道速度为:20÷5=4(km/h),设甲出发x小时后与乙相遇,根据题意得8+4(x﹣1)+4x=20,解得x=2.即甲出发2小时后与乙相遇.故答案为:2.18.解:设每包A、B、C三种饼干的成本分别为x、y、z,依题意得:5x+2y+8z=15x,∴5x=y+4z,由甲礼包的利润率为30%,则可求甲礼包的售价为19.5x,成本15x;∵每袋乙的成本是其售价的,利润是每袋甲利润,可知每袋乙礼包的利润是4.5x×=2x,则乙礼包的售价为12x,成本为10x;由丙礼包的组成可知,丙礼包的成本为7x+y+4z=12x,∵每袋丙礼包利润率为25%,∴丙礼包的售价为15x,成本为12x;∵甲、乙、丙三种礼包袋数之比为4:6:5,∴×100%=25%,∴总利润率是25%,故答案为25%.三.解答题(共2小题,满分16分,每小题8分)19.解:(1)把x=0代入y=﹣x+3,得:y=3,∴C(0,3),把y=0代入y=﹣x+3,得:x=3,∴B(3,0),将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:,解得:,∴抛物线的解析式为y=﹣x2+2x+3;(2)由y=﹣x2+2x+3=﹣(x﹣1)2+4,∴D(1,4),又∵C(0,3)、B(3,0)、D(1,4),∴CD==,BC==3,DB==2∴CD2+BC2=BD2,∴∠BCD=90°.即△BCD是直角三角形;S=BC×CD=3×=3;△BCD(3)如图所示:作点O关于BC的对称点O′,则O′(3,3).∵O′与O关于BC对称,∴PO=PO′.∴OP+AP=O′P+AP≥AO′.∴当A、P、O′在一条直线上时,OP+AP有最小值.设AP的解析式为y=kx+b,则,解得:.∴AP的解析式为y=x+.将y=x+与y=﹣x+3联立,解得:y=,x=,故点P的坐标为:(,),故答案为:(,).20.解:(1)30÷30%=100 (人),100×40%=40(人),100﹣4﹣40﹣30﹣6=20(人),360°×=72°,故答案为:100,72;(2)A类有4人,B类有40人,C类有30人,将100个数据从小到大排列后处在第50、51位的两个数都在C类,因此中位数在C类,故答案为:C.(3)用列表法表示所有可能出现的结果如下:由上表可知,从4名学生中任意选取2名学生共有12种等可能结果,其中恰好选到1名男生和1名女生的结果有8种∴恰好选到1名男生和1名女生的概率为.四.解答题(共5小题,满分50分,每小题10分)21.解:(1)①a(a﹣2b)﹣(2a﹣b)2=a2﹣2ab﹣4a2+4ab﹣b2=﹣3a2﹣6ab﹣b2;②原式=•=•=•=x﹣1;(2)①x2﹣2x=1,配方,得x2﹣2x+1=1+1,(x﹣1)2=2,开方,得x﹣1=,解得:x1=1+,x2=1﹣;②(x+2)(2x﹣1)=1,整理得:2x2+3x﹣3=0,b2﹣4ac=32﹣4×2×(﹣3)=33,x==,解得:x1=,x2=.22.解:(1)∵OB=OE,∴∠BEO=∠EBO,∵BE平分∠CBO,∴∠EBO=∠CBE,∴∠BEO=∠CBE,∴EO∥BC,∵∠C=90°,∴∠AEO=∠C=90°,则AC是圆O的切线;(2)在Rt△AEO中,∠A=30°,OE=4,∴OA=2OE=8,∠AOE=60°,根据勾股定理得:AE==4,则S阴影=S△AOE﹣S扇形EOD=×4×4﹣=8﹣.23.解:(1)设用于该社区家庭的口罩有x个,则用于社区工作人员的口罩有(5000﹣x)个,依题意,得:5000﹣x≥1.5x,解得:x≤2000.答:用于该社区家庭的口罩最多有2000个.(2)依题意,得:200(1+a%)×10(1﹣a%)+(5000﹣200×10)(1+1.5a%)=5000×(1+20%),整理,得:a2﹣225a+5000=0,解得:a1=25,a2=200(不合题意,舍去).答:a的值为25.24.解:连接CD,交AB于O.∵在△ACO与△BDO,,∴△ACO≌△BDO(AAS),∴OA=OB,OC=OD.∵DE∥CF,∴∠DEO=∠CFO,在△ODE和△OCF中,∴△ODE≌△OCF(AAS),∴OE=OF,∵OA=OB,OE=OF,OC=OD,∴是中心对称图形.25.解:(1)∵点A,B的坐标分别为(﹣1,0),(3,0),将点A.B分别向上平移2个单位,再向右平移1个单位得到对应点C,D,∴C(0,2),D(4,2);(2),∴①+②得:x=.∵x为正整数,∴m<﹣3.∴m=﹣4时,方程组的正整数解是,∴P(0,﹣4);(3)过点P作x轴的平行线,过点B作y轴的平行线交CD于点F,两平行直线交于点E,=3×6=18.∵S四边形PEFCS=+×3×4+×2×(3﹣n).四边形PEFC+6+3﹣n=18.∴3n+S△PBQ=9﹣2n.∴S△PBQ∵S的值不小于0.6且不大于4,△PBQ∴0.6≤9﹣2n≤4.解得2.5≤n≤4.2.又∵Q点在线段CD上,∴0≤n≤4,∴n的取值范围是2.5≤n≤4.五.解答题(共1小题,满分12分,每小题12分)26.解:(1)如图1,设∠ACD=α,则∠ACB=130°﹣α,∴∠B=180°﹣∠BAC﹣∠ACB=180°﹣50°﹣(130°﹣α)=α,在△ABC和△ACD中,∠B=∠ACD,∠BAC=∠CAD,∴△ABC∽△ACD,∴AC是四边形ABCD的相似对角线;(2)①当∠APO为直角时,当∠OAP=30°时,过点P作PH⊥x轴于点H,设OH=x,则HP=x,HA=3x,则x+3x=4,解得:x=1,故点P(1,﹣),故k=﹣;当∠AOP=30°时,同理可得:k=﹣3;②当∠OAP为直角时,当∠OPA=30°时,点P(4,﹣4),k=﹣16;当∠AOP=30°时,同理可得:k=﹣(舍去);综上,反比例函数的表达式为:y=﹣或y=﹣或y=﹣;(3)如图3,过点B作BH⊥CD于点H,则∠CBH=90°﹣∠BCD=30°,故CH=BC,则BH=BC,△BCD的面积=CD•BH=CD×CB=,故CD•BC=4而△BAC∽△ACD,故CA2=BC•CD=4,故CA=2,则点A(1,1),而点C(3,1),将点A、C的坐标代入抛物线表达式并解得:抛物线的表达式为:y=ax2﹣4ax+3a+1,AC=2,则m=±3,故直线的表达式为:y=±3x,直线y=﹣3x与抛物线有两个交点,而直线y=mx与抛物线恰好有3个交点,则直线y=3x与抛物线有一个交点,联立直线y=3x与抛物线的表达式并整理得:ax2﹣(4a+3)x+3a+1=0,△=(4a+3)2﹣4a(3a+1)=0,解得:a=﹣或﹣;此外,当抛物线过原点时,直线和抛物线也有三个交点,即3a+1=0,解得:a=﹣;综上,a=﹣或﹣或﹣.。
人教版2021年九年级数学上册期末考试卷及答案【精编】

人教版2021年九年级数学上册期末考试卷及答案【精编】 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.﹣3的相反数是( )A .13-B .13C .3-D .32.下列分解因式正确的是( )A .24(4)x x x x -+=-+B .2()x xy x x x y ++=+C .2()()()x x y y y x x y -+-=-D .244(2)(2)x x x x -+=+-3.□ABCD 中,E 、F 是对角线BD 上不同的两点,下列条件中,不能得出四边形AECF 一定为平行四边形的是( )A .BE=DFB .AE=CFC .AF//CED .∠BAE=∠DCF4.在平面直角坐标中,点M(-2,3)在( )A .第一象限B .第二象限C .第三象限D .第四象限5.已知正多边形的一个外角为36°,则该正多边形的边数为( ).A .12B .10C .8D .6 6.对于二次函数,下列说法正确的是( )A .当x>0,y 随x 的增大而增大B .当x=2时,y 有最大值-3C .图像的顶点坐标为(-2,-7)D .图像与x 轴有两个交点7.如图,将一张含有30角的三角形纸片的两个顶点叠放在矩形的两条对边上,若244∠=,则1∠的大小为( )A.14B.16C.90α-D.44α-8.二次函数y=ax2+bx+c的图象如图所示,对称轴是x=-1.有以下结论:①abc>0,②4ac<b2,③2a+b=0,④a-b+c>2,其中正确的结论的个数是()A.1 B.2 C.3 D.49.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是()A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B +∠BDC=180°10.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是()A. B.C.D.二、填空题(本大题共6小题,每小题3分,共18分)1.计算:2131|32|2218-⎛⎫--+=⎪⎝⎭____________.2.分解因式:a2b+4ab+4b=_______.3.已知x=2是关于x 的一元二次方程kx 2+(k 2﹣2)x+2k+4=0的一个根,则k 的值为__________.4.如图,△ABC 中,∠BAC =90°,∠B =30°,BC 边上有一点P (不与点B ,C 重合),I 为△APC 的内心,若∠AIC 的取值范围为m °<∠AIC <n °,则m +n =__________.5.如图,点A ,B 是反比例函数y=k x(x >0)图象上的两点,过点A ,B 分别作AC ⊥x 轴于点C ,BD ⊥x 轴于点D ,连接OA ,BC ,已知点C (2,0),BD=2,S △BCD =3,则S △AOC =__________.6.在平面直角坐标系中,点A 的坐标为(a ,3),点B 的坐标是(4,b ),若点A 与点B 关于原点O 对称,则ab=__________.三、解答题(本大题共6小题,共72分)1.解方程:2142242x x x x +-+--=12.已知关于x 的一元二次方程()22x 2k 1x k k 0-+++= (1)求证:方程有两个不相等的实数根;(2)若△ABC 的两边AB 、AC 的长是方程的两个实数根,第三边BC 的长为5.当△ABC 是等腰三角形时,求k 的值3.如图,抛物线212y x bx c =-++过点(3,2)A ,且与直线72y x =-+交于B 、C两点,点B 的坐标为(4,)m .(1)求抛物线的解析式;(2)点D 为抛物线上位于直线BC 上方的一点,过点D 作DE x ⊥轴交直线BC 于点E ,点P 为对称轴上一动点,当线段DE 的长度最大时,求PD PA +的最小值;(3)设点M 为抛物线的顶点,在y 轴上是否存在点Q ,使45AQM ︒∠=?若存在,求点Q 的坐标;若不存在,请说明理由.4.如图,四边形ABCD 内接于⊙O ,∠BAD=90°,点E 在BC 的延长线上,且∠DEC=∠BAC .(1)求证:DE 是⊙O 的切线;(2)若AC ∥DE ,当AB=8,CE=2时,求AC 的长.5.在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m ),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:(1)图1中a的值为;(2)求统计的这组初赛成绩数据的平均数、众数和中位数;(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.6.某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.(1)降价前商场每月销售该商品的利润是多少元?(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、D2、C3、B4、B5、B6、B7、A8、C9、A10、B二、填空题(本大题共6小题,每小题3分,共18分)1、2+2、b (a+2)23、﹣34、255.5、5.6、12三、解答题(本大题共6小题,共72分)1、x=12、(1)详见解析(2)k 4=或k 5=3、(1)抛物线的解析式21722y x x =-++;(2)PD PA +;(3)点Q 的坐标:1(0,2Q 、2(0,2Q .4、(1)略;(2)AC 的长为5. 5、(1) 25 ; (2) 这组初赛成绩数据的平均数是 1.61.;众数是 1.65;中位数是1.60;(3)初赛成绩为1.65 m 的运动员能进入复赛.6、(1) 4800元;(2) 降价60元.。
2021年人教版新目标2021年九年级上册英语期末考试试卷及答案

C九年级上册英语期末考试试卷(总分120分时间100分钟)注意:所有答案写在答题卡上,只交答题卡听力部分(本大题分为A 、B 、C 三部分,每小题1分,共20分)A.听句子。
选择符合题意的图画回答问题,每小题听一遍。
( )1. How does Jim study to improve English?A. B C.( )2. What is Carla afraid of now?( )3. What is not allowed here?A. B C.( )4. Which animal is the speaker talking about?A. B C.( )5. Which thing belongs to John?A. B C.B . 听对话,根据你所听对话内容选择正确答案(每段对话听两遍)听第一段对话,回答第6小题( )6. When does Mike get up on weekends? A.6:30B. 7:00C.7:30 听第二段对话,回答第7小题。
( )7. Who is good at Chinese?A. LilyB. LindaC. Lucy A. B听第三段对话,回答第8小题。
( )8. What are the coats made of? A. Wool B. Cotton C. Paper听第四段对话,回答第9小题。
( )9. How many students are there in his school this year?A. 750B. 735C. 765听第五段对话,回答第10小题。
( )10. Why does Lily want to change her job?A. Because she feels boring.B. Because her father asks her to do so.C. Because it’s too hard for her to do it.听第六段对话,回答11-12小题。
2020-2021学年人教 版九年级上册数学期末复习试卷(有答案)
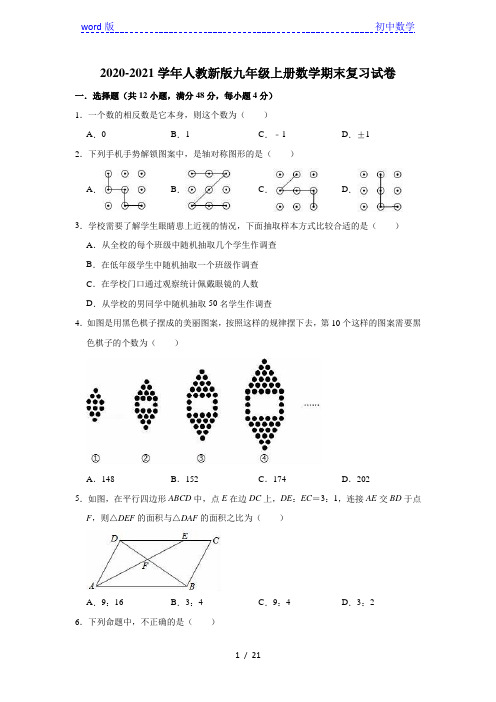
2020-2021学年人教新版九年级上册数学期末复习试卷一.选择题(共12小题,满分48分,每小题4分)1.一个数的相反数是它本身,则这个数为()A.0B.1C.﹣1D.±12.下列手机手势解锁图案中,是轴对称图形的是()A.B.C.D.3.学校需要了解学生眼睛患上近视的情况,下面抽取样本方式比较合适的是()A.从全校的每个班级中随机抽取几个学生作调查B.在低年级学生中随机抽取一个班级作调查C.在学校门口通过观察统计佩戴眼镜的人数D.从学校的男同学中随机抽取50名学生作调查4.如图是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为()A.148B.152C.174D.2025.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△DAF的面积之比为()A.9:16B.3:4C.9:4D.3:26.下列命题中,不正确的是()A.对角线相等的矩形是正方形B.对角线垂直平分的四边形是菱形C.矩形的对角线平分且相等D.顺次连结菱形各边中点所得的四边形是矩形7.估计的值应在()A.5和6之间B.6和7之间C.7和8之间D.8和9之间8.当x分别取﹣5和5时,多项式﹣x2+7x4+x6﹣2019的值的关系是()A.相等B.互为相反数C.互为倒数D.异号9.如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.若大圆半径为2,小圆半径为1,则AB的长为()A.2B.2C.D.210.如图,某大楼DE的顶部竖有一块广告牌CD,小林在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:2.4,AB=26米,AE=30米.则广告牌CD的高度约为()(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)A.35B.30C.24D.2011.如图,点A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为8,则k的值为()A.8B.﹣8C.4D.﹣412.若a使得关于x的分式方程有正整数解,且关于x的不等式组的解集为x<﹣5,则满足条件所有整数a的和为()A.﹣6B.﹣7C.﹣8D.﹣9二.填空题(共6小题,满分24分,每小题4分)13.计算:﹣1+2﹣1=.14.如图,△ABC内接于⊙O,AB=AC,∠ABC的平分线交⊙O于点D,=7:8,连接CD,AD,⊙O的半径是4cm,则扇形OBCD的面积为cm2.15.为配合我市创建省级文明城市,某校对九年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下条形统计图,则九年级各班文明行为劝导志愿者人数中位数是.16.如图,AB是⊙O的直径,AB=2,∠ABC=60°,P是⊙O上一动点,D是AP的中点,连接CD,则CD的最小值为.17.某人预计步行从家去火车站,从家步行走到6分钟时,以同样的速度回家取忘带的物品,然后从家乘出租赶往火车站,结果到火车站的时间比预计步行的时间提前了3分钟,该人离家的路程s(米)与时间t(分钟)之间的函数图象如图所示,那么从家到火车站的路程是.18.某工程队由甲乙两队组成,承包我市河东东街改造工程,规定若干天完成,已知甲队单独完成这项工程所需时间比规定时间多32天,乙队单独完成这项工程所需时间比规定时间多12天,如果甲乙两队先合作20天,剩下的甲队单独做,则延误两天完成,那么规定时间是天.三.解答题(共8小题,满分78分)19.化简求值:,其中x=.20.如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.21.如图,直线l1:y=x+6与直线l2:y=kx+b相交于点A,直线l1与y轴相交于点B,直线l2与y轴负半轴相交于点C,OB=2OC,点A的纵坐标为3.(1)求直线l2的解析式;(2)将直线l2沿x轴正方向平移,记平移后的直线为l3,若直线l3与直线l1相交于点D,且点D的横坐标为1,求△ACD的面积.22.某新建的商场有3000m2的地面花岗岩需要铺设,现有甲、乙两个工程队希望承包铺设地面的过程:甲工程队平均每天比乙工程队多铺50m2,甲工程队单独完成该工程的工期是乙工程队单独完成该工程所需工期的.(1)求甲、乙两个工程队完成该工程各需几天?(2)由于该工程的施工时间不能超过14天,商场考虑先让乙工程队做m天,剩下的工程由甲、乙两队共同完成,求m的最大值.23.某市教育局为了了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图.请你根据图中提供的信息,回答下列问题:(1)扇形统计图中a的值为;(2)补全频数分布直方图;(3)在这次抽样调查中,众数是天,中位数是天;(4)请你估计该市初二学生每学期参加综合实践活动的平均天数约是多少?(结果保留整数)24.如图,平行四边形ABCD中,点P为CB延长线上点,连接DP交AC于点M、交AB于点N,已知DA=DC,∠ACD=45°.(1)求证:四边形ABCD为正方形;(2)连接BM,若N为AB的中点,求tan∠BMP的值;(3)若MN=2,PN=6,求DM的长.25.如图,以矩形ABCD的边CD为直径作⊙O,点E是AB的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.(1)若连接AO,试判断四边形AECO的形状,并说明理由;(2)求证:AH是⊙O的切线;(3)若AB=6,CH=2,则AH的长为.26.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y 轴交于点N,其顶点为D.(1)求抛物线及直线AC的函数关系式;(2)若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t;①当S△ACP=S△ACN时,求点P的坐标;②是否存在点P,使得△ACP是以AC为斜边的直角三角形?若存在,求点P的坐标;若不存在,请说明理由;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.参考答案与试题解析一.选择题(共12小题,满分48分,每小题4分)1.解:一个数的相反数是它本身,则这个数为0.故选:A.2.解:A、是轴对称图形,故此选项正确;B、不是轴对称图形,故此选项错误;C、不是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项错误.故选:A.3.解:A、从全校的每个班级中随机抽取几个学生作调查适合抽样调查,故A符合题意;故选:A.4.解:根据图形,第1个图案有12枚棋子,第2个图案有22枚棋子,第3个图案有34枚棋子,…第n﹣1个图案有2(1+2+…+n+1)+2(n﹣2)=n2+5n﹣2枚棋子,第n个图案有2(1+2+…+n+2)+2(n﹣1)=n2+7n+4枚棋子,故第10个这样的图案需要黑色棋子的个数为102+7×10+4=100+70+4=174(枚).故选:C.5.解:∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∵DE:EC=3:1,∴DE:AB=DE:DC=3:4,∵DE∥AB,∴△DEF∽△BAF,∴==,∴△DEF的面积与△DAF的面积之比=EF:AF=3:4.故选:B.6.解:A、对角线垂直的矩形是正方形,所以A选项为假命题;B、对角线垂直平分的四边形是菱形,所以B选项为真命题;C、矩形的对角线平分且相等,所以C选项为真命题;D、顺次连结菱形各边中点所得的四边形是矩形,所以D选项为真命题.故选:A.7.解:∵<<,∴6<<7,∴的值应在6和7之间.故选:B.8.解:当x=﹣5时,原式=﹣(﹣5)2+7×(﹣5)4+(﹣5)6﹣2019=﹣52+7×54+56﹣2019,当x=5时,原式=﹣52+7×54+56﹣2019,则当x分别等于5和﹣5时,多项式﹣x2+7x4+x6﹣2019的值相等,故选:A.9.解:如图:连接OP,AO∵AB是⊙O切线∴OP⊥AB,∴AP=PB=AB在Rt△APO中,AP==∴AB=2故选:A.10.解:过B作BG⊥DE于G,BH⊥AE于H,如图:则BG=AH+AE,GE=BH,在Rt△ABF中,i=tan∠BAH=1:2.4=,∴AH=2.4BH,∴AB ==2.6BH =26,∴BH =10,AH =24,∴BG =AH +AE =24+30=54,在Rt △BGC 中,∠CBG =45°,∴CG =BG =54.在Rt △ADE 中,∠DAE =53°,∴∠ADE =90°=53°=37°,∵tan ∠ADE ==tan37°≈0.75,∴DE =AE =40.∴CD =CG +GE ﹣DE =54+10﹣40=24(米);即广告牌CD 的高度约为24米;故选:C .11.解:作AE ⊥BC 于E ,如图,∵四边形ABCD 为平行四边形,∴AD ∥x 轴,∴四边形ADOE 为矩形,∴S 平行四边形ABCD =S 矩形ADOE ,而S 矩形ADOE =|﹣k |,∴|﹣k |=8,而k <0,即k <0,∴k =﹣8.故选:B .12.解:,去分母得﹣ax=4﹣x+2,解得x=且x≠2,当整数a为0,﹣1,﹣5时,分式方程的解为正整数解,解不等式组为,而不等式组的解集为x<﹣5,所以a≥﹣5,∴满足条件的整数a的值为0,﹣1,﹣5,和为0﹣1﹣5=﹣6.故选:A.二.填空题(共6小题,满分24分,每小题4分)13.解:﹣1+2﹣1=﹣1+=﹣.故答案为:﹣.14.解:∵=7:8,∴∠ABD:∠BAC=7:8设∠ABD=7x,∠BAC=8x,∵BD平分∠ABC∴∠ABD=∠DBC=7x,∴∠ABC=14x,∵AB=AC∴∠ABC=∠ACB=14x∵∠BAC+∠ABC+∠ACB=180°∴8x+14x+14x=180°∴x=5°∴∠ABD=∠DBC=7x=35°,∠BAC=40°∴∠BAD=∠BAC+∠CAD=∠BAC+∠DBC=75°∵∠BOD=2∠BAD∴∠BOD=2×75°=150°==∴S扇形OBCD故答案为:15.解:因为参与统计的班级总数为4+5+4+3+2+2=20个,所以中位数为第10、11个数据的平均数为=4(名),故答案为:4名.16.解:如图,取OA是中点T,连接CT,DT,OP,OC,过点C作CH⊥AB于H.∵OB=OC,∠OBC=60°,∴△OBC是等边三角形,∵CH⊥OB,∴OH=HB=,CH=OH=,∵AT=TO=,AD=DP,∴DT=OP=,在Rt△CTH中,∵TH=OT+OH=1,CH=,∴CT===,∴CD≥CT﹣DT,∴CD≥﹣,∴CD的最小值为﹣.17.解:步行的速度为:480÷6=80米/分钟,∵t=16时,s=80×16=1280,∴相遇时的点的坐标为(16,1280),设s=kt+b,则,解得,所以s=320t﹣3840;设步行到达的时间为t,则实际到达是时间为t﹣3,由题意得,80t=320(t﹣3)﹣3840,解得t=20.所以家到火车站的距离为80×20=1600m.故答案为:1600m.18.解:设规定的时间是x天,则甲队单独完成需要(x+32)天,乙队单独完成需要(x+12天),由题意,得20×+=1,解得:x=28.经检验,x=28是元方程的解.答:规定的时间是28天.故答案是:28.三.解答题(共8小题,满分78分)19.解:原式=•==﹣x(x+1)=﹣x2﹣x当x=时,原式=﹣2﹣.20.证明:在AC上取AF=AE,连接OF,∵AD平分∠BAC、∴∠EAO=∠FAO,在△AEO与△AFO中,∴△AEO≌△AFO(SAS),∴∠AOE=∠AOF;∵AD、CE分别平分∠BAC、∠ACB,∴∠ECA+∠DAC=∠ACB+∠BAC=(∠ACB+∠BAC)=(180°﹣∠B)=60°则∠AOC=180°﹣∠ECA﹣∠DAC=120°;∴∠AOC=∠DOE=120°,∠AOE=∠COD=∠AOF=60°,则∠COF=60°,∴∠COD=∠COF,∴在△FOC与△DOC中,,∴△FOC≌△DOC(ASA),∴DC=FC,∵AC=AF+FC,∴AC=AE+CD.21.解:(1)∵当x=0时,y=0+6=6,∴B(0,6),∵OB=2OC,∴C(0,﹣3),∵点A的纵坐标为3,∴﹣3=x+6,解得x=﹣3,∴A(﹣3,3),则,解得.故直线l2的解析式为y=﹣2x﹣3;(2)∵点D的横坐标为1,∴y=1+6=7,∴D(1,7),∴△ACD的面积=10×4﹣×3×6﹣×4×4﹣×1×10=18.22.解:(1)设乙工程队平均每天铺xm2,则甲平均每天铺(x+50)m2,由题意得,,解得:x=150,经检验,x=150是原方程的解.答:甲完成该工程需15天,乙完成该工程需20天.(2)150m+(150+200)(14﹣m)≥3000,解得:m≤9.5.∵m为正整数,∴m的最大值为9.答:m的最大值为9.23.解:(1)a%=100%﹣(15%+20%+30%+10%+5%)=20%,故答案为:20%;(2)∵被调查的总人数为30÷15%=200人,∴3天的人数为200×20%=40人、5天的人数为200×20%=40人、7天的人数为200×5%=10人,补全图形如下:(3)众数是4天、中位数为=4天,故答案为:4、4;(4)估计该市初二学生每学期参加综合实践活动的平均天数约是2×15%+3×20%+4×30%+5×20%+6×10%+7×5%=4.05≈4(天).24.(1)证明:∵四边形ABCD是平行四边形,DA=DC,∴四边形ABCD是菱形,∵DA=DC,∴∠ACD=∠CAD=45°,∴∠ADC=90°,∴四边形ABCD为正方形;(2)解:作BE⊥PD,如图所示:则∠PEB=∠MEB=90°,设正方形ABCD的边长为a,∵四边形ABCD是正方形,∴AD∥BC,AB∥CD,AB=AD=a,∠PBN=∠DAB=∠BCD=90°,∵N为AB的中点,∴AN=BN=AB=a,在△BPN和△ADN中,,∴△BPN≌△ADN(ASA),∴BP=AD=a,PN=DN===a,PC=BP+BC=2a,∴PD=2DN=a,∵AD∥BC,∴△ADM∽△CPM,∴==,∴PM=PD=a,∵∠PEB=∠PCD=90°,∠P=∠P,∴△PBE∽△PDC,∴==,即==,解得:BE=a,PE=a,∴EM=PM﹣PE=a,∴tan∠BMP==;(3)解:MN=2,PN=6,∴MP=8,∵AB∥CD,∴AM:MC=MN:MD,∵AD∥BC,∴AM:MC=DM:MP,∴MN:MD=DM:MP,∴MD2=MN•MP=2×8=16,∴MD=4.25.(1)解:连接AO,四边形AECO是平行四边形.∵四边形ABCD是矩形,∴AB∥CD,AB=CD.∵E是AB的中点,∴AE=AB.∵CD是⊙O的直径,∴OC=CD.∴AE∥OC,AE=OC.∴四边形AECO为平行四边形.(2)证明:由(1)得,四边形AECO为平行四边形,∴AO∥EC∴∠AOD=∠OCF,∠AOF=∠OFC.∵OF=OC∴∠OCF=∠OFC.∴∠AOD=∠AOF.∵在△AOD和△AOF中,AO=AO,∠AOD=∠AOF,OD=OF ∴△AOD≌△AOF(SAS).∴∠ADO=∠AFO.∵四边形ABCD是矩形,∴∠ADO=90°.∴∠AFO=90°,即AH⊥OF.∵点F在⊙O上,∴AH是⊙O的切线.(3)∵CD为⊙O的直径,∠ADC=∠BCD=90°,∴AD,BC为⊙O的切线,又∵AH是⊙O的切线,∴CH=FH,AD=AF,设BH=x,∵CH=2,∴BC=2+x,∴BC=AD=AF=2+x,∴AH=AF+FH=4+x,在Rt△ABH中,∵AB2+BH2=AH2,∴62+x2=(4+x)2,解得x=.∴.故答案为:.26.解:(1)将A(﹣1,0),C(2,3)代入y=﹣x2+bx+c中,得,解得∴抛物线解析式为y=﹣x2+2x+3,设直线AC解析式为y=mx+n,则,解得,∴直线AC解析式为y=x+1;(2)①在y=﹣x2+2x+3中,令x=0,得y=3,∴N(0,3),∵点P的横坐标为t;∴P(t,﹣t2+2t+3),过点P作PH⊥y轴于H,连接PN,设直线AC交y轴于G,则G(0,1),∠PHN=90°∴OA=OG=1,PH=t,HN=OH﹣ON=﹣t2+2t,∴∠AGO=∠CGN=45°∵S△ACP =S△ACN∴PN∥AC∴∠PNH=∠CGN=45°∴PH=HN∴t=﹣t2+2t,解得:t1=0(舍去),t2=1,∴P(1,4);②如图2,过P作PS⊥x轴于S,过C作CK⊥PS于K,则∠CKP=∠PSA=90°∵P(t,﹣t2+2t+3),A(﹣1,0),C(2,3),∴CK=2﹣t,PK=﹣t2+2t,PS=﹣t2+2t+3,AS=t﹣(﹣1)=t+1,∵△ACP是以AC为斜边的直角三角形∴∠APS+∠CPK=∠APC=90°∵∠PCK+∠CPK=90°∴∠APS=∠PCK∴△APS∽△PCK∴=,即=解得:t=∵P是抛物线上位于直线AC上方的一个动点,∴﹣1<t<2,但>2∴t=∴P(,).(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4∴顶点D(1,4)∴B(1,2),BD=2,以B,D,E,F为顶点的四边形能为平行四边形.设点E(m,m+1),则F(m,﹣m2+2m+3),EF=,∵EF∥BD∴EF=BDword 版初中数学 21 / 21 ∴=2,解得:m 1=0,m 2=1(舍去),m 3=,m 4=; ∴点E 的坐标为:(0,1)或(,)或(,).。
2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 3

2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 31.There are_________ floors in the building and my home is on the_________ floor. A.twenty; fifteenth B.twenty; fifteen C.twentieth; fifteen D.twentieth; fifteenth2.— The Internet has made communication much more_________.— I agree. For example, I can communicate with my friends on WeChat any time. A.popular B.necessary C.important D.convenient 3.—What fruit would you like?—Some________, please. They are my favorite. A.dessert B.juice C.grapes D.biscuits 4.— Does my question sound ______enough?— I don’t think so. You can ask more______ by using “could” instead of “can”.A.politely; politelyB.politely; politeC.polite; politelyD.polite; polite5.—Which of the two T -shirts will you take?—I’ll take_______ . One is for my brother and the other is for myself.A.eitherB.bothC.allD.neither6.—Dad, can you tell me ________? I miss her very much. —Next month, dear.A.when my mum will come backB.when will my mum come backC.how my mum goes to workD.where will my mum go7.一 Ms Petty, can you tell me ________? 一Africa.A. what the baby giraffe likes eatingB. why the baby giraffe looks unhappyC. when the baby giraffe was bornD. where the baby giraffe came from8.—Excuse me, could you please tell me where the bookstore is? — ? I didn’t hear clearly, A. Pardon B. How are youC. Yes, pleaseD. Excuse9.一I don’t care . In this camp, there’s only one hairstyle—short! Understand?—Yes, madam!A. what you are used to likingB. what you used to be likeC. what are you used to likingD. what did you use to be like10.If you are free when you , I hope you can come to see me.A. pass byB. pass awayC. pass onD. pass out11.He answered all questions (correct), so he got a high grade in the final exam. 12.It’s i to talk with your mouth full during a meal.13.Scientists often (suggestion) that farmers use natural ways to grow fruits. 14.Our manager greeted the guests (polite) with a smile at the entrance. 15.He is driving fast along the road in the (direct) of Nanjing. 16.We all know that Chinese has the most (speak) in the world.17.Shopping online is cbecause people needn’t go out.18.阅读在英语学习中是很重要的。
2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 7

2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 71.一Gould I smoke here?—Sorry. Look at the sign! Smoking here. A. isn’t allowed B. is allowed C. doesn’t allow D. isn’t allowing2.The people who are more confident have more to make themselves successful. A. educationB. chancesC. prideD. excuses3.He doesn’t do his homework , though he has . A. carefully enough ; enough time B. careful enough ; time enough C. careful enough ; enough time D. enough carefully; time enough4.---Why doesn’t the surgeon stop ____________ lunch?---Because he is too busy __________ a dying patient in the operation room. A.to have; to save B. having; to save C.to have; saving D. having; saving5.To make our city more beautiful, rubbish into the river. A. needn’t be thrown B. mustn’t be thrown C. can’t throw D.may not throw6.My father has made a that he will buy a camera for me. A. suggestionB. secretC. problem D . decision7.You don't know I want to see you again. It's a year since I last saw you. A. how soon B. how long C. how oftenD. how much8.My computer doesn’t work any more. I have to get it______. A. repairB. repairingC. repairedD. repairs9.—Excuse me, you are_______ of my passing through. I’m sorry. Here you go. A. on the wayB. out the wayC. in the wayD. off the way10. Every week, Xiao Ying plans to use 180 minutes to practice her listening. According to the table, it takes her_________ hour(s) to do it on weekdays.A. 1B. 2C. 311.—I am sorry. I broke your camera by accident. (awful)—Never mind. I'm sure you didn't do it on purpose and it can’t be helped. 12.They should take care of__________(them).13.She is very excited about__________( get ) a part -time job. She really likes working in the__________(shop) center.14. Her mother doesn’t allow her__________(practice)__________(swim) every day. 15. We have nothing against__________(run), but we think that our son needs to be realistic. 16. Parents should encourage their children__________(do) social work. 17.我们应该远离污染,保持健康。
2020-2021学年人教版九年级上册数学期末复习试卷(有答案)
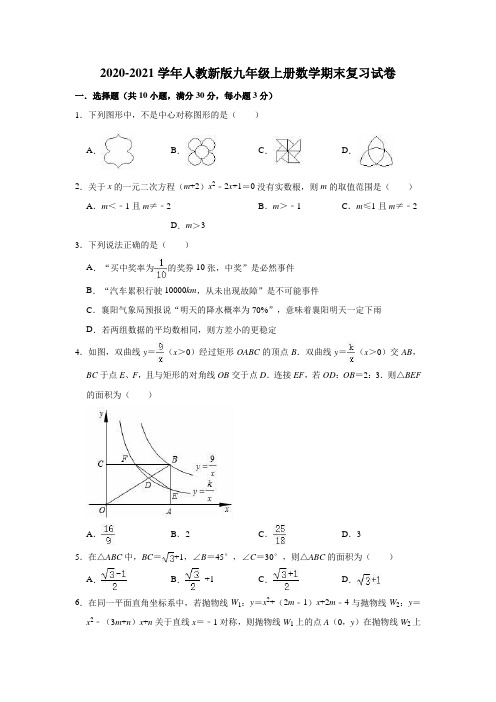
2020-2021学年人教新版九年级上册数学期末复习试卷一.选择题(共10小题,满分30分,每小题3分)1.下列图形中,不是中心对称图形的是()A.B.C.D.2.关于x的一元二次方程(m+2)x2﹣2x+1=0没有实数根,则m的取值范围是()A.m<﹣1且m≠﹣2B.m>﹣1C.m≤1且m≠﹣2D.m>33.下列说法正确的是()A.“买中奖率为的奖券10张,中奖”是必然事件B.“汽车累积行驶10000km,从未出现故障”是不可能事件C.襄阳气象局预报说“明天的降水概率为70%”,意味着襄阳明天一定下雨D.若两组数据的平均数相同,则方差小的更稳定4.如图,双曲线y=(x>0)经过矩形OABC的顶点B.双曲线y=(x>0)交AB,BC于点E、F,且与矩形的对角线OB交于点D.连接EF,若OD:OB=2:3.则△BEF 的面积为()A.B.2C.D.35.在△ABC中,BC=+1,∠B=45°,∠C=30°,则△ABC的面积为()A.B.+1C.D.6.在同一平面直角坐标系中,若抛物线W1:y=x2+(2m﹣1)x+2m﹣4与抛物线W2:y=x2﹣(3m+n)x+n关于直线x=﹣1对称,则抛物线W1上的点A(0,y)在抛物线W2上的对应点A′坐标是()A.(﹣2,8)B.(﹣2,10)C.(﹣2,12)D.(﹣2,14)7.一个圆锥的底面半径是4cm,其侧面展开图的圆心角是120°,则圆锥的母线长是()A.8cm B.12cm C.16cm D.24cm8.如图,△ABC的中线BE与CD交于点G,连接DE,下列结论不正确的是()A.点G是△ABC的重心B.DE∥BCC.△ABC的面积=2△ADE的面积D.BG=2GE9.在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为()A.(4,﹣3)B.(﹣4,3)C.(﹣3,4)D.(﹣3,﹣4)10.如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连接CD、OD,给出以下四个结论:①AC∥OD;②CD=DE;③△ODE∽△ADO;④2CD2=CE•AB.其中正确结论的个数是()A.1个B.2个C.3个D.4个二.填空题(共5小题,满分15分,每小题3分)11.抛物线y=﹣x2+bx+c的部分图象如图所示,则关于x的一元二次方程﹣x2+bx+c=0的解为.12.有一个人患了新冠肺炎,经过两轮传染后共有169人患了新冠肺炎,每轮传染中平均一个人传染了个人.13.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=4cm,∠BCD=22°30′,则⊙O的半径为cm.14.如图所示,在平面直角坐标系xOy中,四边形OABC为矩形,点A、C分别在x轴、y 轴上,点B在函数y1=(x>0,k为常数且k>2)的图象上,边AB与函数y2=(x >0)的图象交于点D,则阴影部分ODBC的面积为.(结果用含k的式子表示)15.已知对任意锐角α、β均有:cos(α+β)=cosα•cosβ﹣sinα•sinβ,则cos75°=.三.解答题(共7小题,满分55分)16.解方程(1)2y2+6y+5=0;(2)x(2x﹣5)=4x﹣10.17.如图,A、B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次,转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止,请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和大于4的概率.18.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A、B两点,点A的坐标是(﹣2,1),点B的坐标是(1,n);(1)分别求一次函数与反比例函数的解析式;(2)求△AOB的面积;(3)直接写出不等式kx+b≥的解集.19.如图,某地修建高速公路,要从A地向B地修一座隧道(A、B在同一水平面上),为了测量A、B两地之间的距离,某工程师乘坐热气球从B地出发,垂直上升120米到达C 处,在C处观察A地的俯角为42°,求A、B两地之间的距离.(结果精确到1米)[参考数据:sin42°=0.67,co42°=0.74,tan42°=0.90]20.用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)(1)在图①中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?(2)在图②中,如果不诱钢材料总长度为12米,当x为多少时,矩形架ABCD的面积S最大?最大面积是多少?(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?21.如图,在正方形ABCD中,AB=4,动点P从点A出发,以每秒2个单位的速度,沿线段AB方向匀速运动,到达点B停止.连接DP交AC于点E,以DP为直径作⊙O交AC于点F,连接DF、PF.(1)求证:△DPF为等腰直角三角形;(2)若点P的运动时间t秒.①当t为何值时,点E恰好为AC的一个三等分点;②将△E FP沿PF翻折,得到△QFP,当点Q恰好落在BC上时,求t的值.22.如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).(1)求抛物线的函数解析式;(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.参考答案与试题解析一.选择题(共10小题,满分30分,每小题3分)1.解:A.既是轴对称图形,又是中心对称图形,故本选项不合题意;B.既是轴对称图形,又是中心对称图形,故本选项不合题意;C.属于中心对称图形,故本选项不合题意;D.是轴对称图形,不是中心对称图形,故本选项符合题意;故选:D.2.解:由题意可知:△=4﹣4(m+2)<0且m+2≠0,∴m>﹣1故选:B.3.解:A、“买中奖率为的奖券10张,中奖”是随机事件,故本选项错误;B、汽车累积行驶10000km,从未出现故障”是随机事件,故本选项错误;C、襄阳气象局预报说“明天的降水概率为70%”,意味着明天可能下雨,故本选项错误;D、若两组数据的平均数相同,则方差小的更稳定,故本选项正确;故选:D.4.解:设D(2m,2n),∵OD:OB=2:3,∴A(3m,0),C(0,3n),∴B(3m,3n),∵双曲线y=(x>0)经过矩形OABC的顶点B,∴9=3m•3n,∴mn=1,∵双曲线y=(x>0)经过点D,∴k=4mn,∴双曲线y=(x>0),∴E(3m,n),F(m,3n),∴BE=3n﹣n=n,BF=3m﹣m=m,∴S=BE•BF=mn=,△BEF故选:C.5.解:过A点作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°=∠B,∴AD=BD,设BD=x,则AD=x,∵∠C=30°,∴tan C=,∴,∵BC=+1,∴x+x=+1,∴x=1,即AD=1,∴.故选:C.6.解:∵抛物线W1:y=x2+(2m﹣1)x+2m﹣4与抛物线W2:y=x2﹣(3m+n)x+n关于直线x=﹣1对称,∴(﹣+)=﹣1,∴m+n=﹣5,∴抛物线W1上的点A(0,y)在抛物线W2上的对应点A′坐标是(﹣2,y),∴2m﹣4=4+2(3m+n)+n,∴4m+3n=﹣8,解得m=7,∴y=2m﹣4=10,∴在抛物线W2上的对应点A′坐标是(﹣2,10),故选:B.7.解:圆锥的底面周长为2π×4=8πcm,即为展开图扇形的弧长,由弧长公式得=8π,解得,R=12,即圆锥的母线长为12cm.故选:B.8.解:∵△ABC的中线BE与CD交于点G,∴点G是△ABC的重心,∴DE∥BC且DE=BC,所以选项A、B正确;∵点G是△ABC的重心,根据重心性质或利用三角形相似可得BG=2GE,∴选项D正确;由△ADE∽△ABC,可知△ABC的面积=4△ADE的面积,所以选项C错误.故选:C.9.解:如图所示,建立平面直角坐标系,点B的坐标为(﹣4,3).故选:B.10.解:①∵AB是半圆直径,∴AO=OD,∴∠OAD=∠ADO,∵AD平分∠CAB交弧BC于点D,∴∠CAD=∠DAO=∠CAB,∴∠CAD=∠ADO,∴AC∥OD,∴①正确.②作ON⊥C D,∵AD平分∠CAB交弧BC于点D,∴∠CAD=×45°=22.5°,∴∠COD=45°,∵AB是半圆直径,∴OC=OD,∴∠OCD=∠ODC=67.5°,∠AEO=90°﹣22.5°=67.5°,∴∠DCE=∠CED=67.5°,∴CD=DE,∴②正确.③∵在△ODE和△ADO中,只有∠ADO=∠EDO,∵∠COD=2∠CAD=2∠OAD,∴∠DEO≠∠DAO,∴不能证明△ODE和△ADO相似,∴③错误;④∵AD平分∠CAB交弧BC于点D,∴∠CAD=×45°=22.5°,∴∠COD=45°,∵AB是半圆直径,∴OC=OD,∴∠OCD=∠ODC=67.5°∵∠CAD=∠ADO=22.5°(已证),∴∠CDE=∠ODC﹣∠ADO=67.5°﹣22.5°=45°,∴△CED∽△COD,∴=,∴CD2=OD•CE=AB•CE,∴2CD2=CE•AB.∴④正确.综上所述,只有①②④正确.故选:C.二.填空题(共5小题,满分15分,每小题3分)11.解:观察图象可知,抛物线y=﹣x2+bx+c与x轴的一个交点为(1,0),对称轴为x =﹣1,∴抛物线与x轴的另一交点坐标为(﹣3,0),∴一元二次方程2x2﹣4x+m=0的解为x1=1,x2=﹣3.故本题答案为:x1=1,x2=﹣3.12.解:设每轮传染中平均一个人传染了x个人,根据题意,得x+1+(x+1)x=169x=12或x=﹣14(舍去).答:每轮传染中平均一个人传染了12个人.故答案为:12.13.解:连接OB,∵∠BCD=22°30′,∴∠BOD=2∠BCD=45°,∵CD是直径,弦AB⊥CD,∴BE=AE=AB=2cm,在Rt△BOE中,由勾股定理可求得OB=4cm,即⊙O的半径为4cm,故答案为:4.14.解:∵D是反比例函数图象上一点∴根据反比例函数k的几何意义可知:△AOD的面积为=1.∵点B在函数(x>0,k为常数且k>2)的图象上,四边形OABC为矩形,∴根据反比例函数k的几何意义可知:矩形ABCO的面积为k.∴阴影部分ODBC的面积=矩形ABCO的面积﹣△AOD的面积=k﹣1.故答案为:k﹣1.15.解:∵cos(α+β)=cosα•cosβ﹣sinα•sinβ,∴cos75°=cos(30°+45°)=cos30°•cos45°﹣sin30°•sin45°=×﹣×=.故答案为:.三.解答题(共7小题,满分55分)16.解:(1)∵a=2,b=6,c=5,∴△=62﹣4×2×5=﹣4<0,∴此方程无实数根;(2)∵x(2x﹣5)﹣2(2x﹣5)=0,∴(2x﹣5)(x﹣2)=0,则2x﹣5=0或x﹣2=0,解得x1=2.5,x2=2.17.解:画树状图为:共有12种等可能的结果数,其中指针所指区域内的数字之和大于4的结果数为9, 所以指针所指区域内的数字之和大于4的概率==.18.解:(1)把点A 的坐标(﹣2,1)代入一反比例函数y =,可得:m =﹣2×1=﹣2, ∴反比例函数为y =﹣,∵反比例函数y =的图象经过B 点,∴n =﹣=﹣2,∴B (1,﹣2),把A (﹣2,1),B (1,﹣2)代入y =kx +b 得解得k =﹣1,b =﹣1∴一次函数为y =﹣x ﹣1;(2)在直线y =﹣x ﹣1中,令x =0,则y =﹣1,∴C (0,﹣1),即OC =1,∴S △AOB =S △AOC +S △BOC =OC ×2+OC ×1=×1×(2+1)=;(3)不等式kx+b ≥的解集是x ≤﹣2或0<x ≤1.19.解:在Rt △ABC 中,∵∠ABC =90°,∠A =42°,∴tan42°=,∴AB=≈133(米)答:A、B两地之间的距离约为133米.20.解:(1)AD=(12﹣3x)÷3=4﹣x,列方程:x(4﹣x)=3,x2﹣4x+3=0,∴x1=1,x2=3,答:当x=1或3米时,矩形框架ABCD的面积为3平方米;(2)AD=(12﹣4x)÷3=4﹣x,S=x(4﹣x),=﹣x2+4x,当x=﹣=时,S==3,最大答:当x=时,矩形架ABCD的面积S最大,最大面积是3平方米;(3)AD=(a﹣nx)÷3=﹣x,S=x(﹣x),=﹣x2+x,当x=﹣=时S==.最大答:当x=时,矩形ABCD的面积S最大,最大面积是平方米.21.证明:(1)∵四边形ABCD是正方形,AC是对角线,∴∠DAC=45°,∵在⊙O中,所对的圆周角是∠DAF和∠DPF,∴∠DAF=∠DPF,∴∠DPF=45°,又∵DP是⊙O的直径,∴∠DFP=90°,∴∠FDP=∠DPF=45°,∴△DFP是等腰直角三角形;(2)①当AE:EC=1:2时,∵AB∥CD,∴∠DCE=∠PAE,∠CDE=∠APE,∴△DCE∽△PAE,∴,∴,解得,t=1;当AE:EC=2:1时,∵AB∥CD,∴∠DCE=∠PAE,∠CDE=∠APE,∴△DCE∽△PAE,∴,∴,解得,t=4,∵点P从点A到B,t的最大值是4÷2=2,∴当t=4时不合题意,舍去;由上可得,当t为1时,点E恰好为AC的一个三等分点;②如右图所示,∵∠DFP=90°,∴∠DPF=∠FDP=45°,∵∠DPF=∠FPQ,∴∠OPF=90°,∴∠DPA+∠QPB=90°,∵∠DPA+∠PDA=90°,∴∠PDA=∠QPB,∵点Q落在BC上,∴∠DAP=∠B=90°,∴△DAP∽△PBQ,∴,∵DA=AB=4,AP=2t,∠DAP=90°,∴DP==2,PB=4﹣2t,设PQ=a,则PE=a,DE=DP﹣a=2﹣a,∵△AEP∽△CED,∴,即,解得,a=,∴PQ=,∴,解得,t1=﹣﹣1(舍去),t2=﹣1,即t的值是﹣1.22.解:(1)∵抛物线y=x2+bx+c经过A(﹣1,0)、B(0,﹣3),∴,解得,故抛物线的函数解析式为y=x2﹣2x﹣3;(2)令x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则点C的坐标为(3,0),∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴点E坐标为(1,﹣4),设点D的坐标为(0,m),作EF⊥y轴于点F,∵DC2=OD2+OC2=m2+32,DE2=DF2+EF2=(m+4)2+12,∵DC=DE,∴m2+9=m2+8m+16+1,解得m=﹣1,∴点D的坐标为(0,﹣1);(3)∵点C(3,0),D(0,﹣1),E(1,﹣4),∴CO=DF=3,DO=EF=1,根据勾股定理,CD===,在△COD和△DFE中,∵,∴△COD≌△DFE(SAS),∴∠EDF=∠DCO,又∵∠DCO+∠CDO=90°,∴∠EDF+∠CDO=90°,∴∠CDE=180°﹣90°=90°,∴CD⊥DE,①分O C与CD是对应边时,∵△DOC∽△PDC,∴=,即=,解得DP=,过点P作PG⊥y轴于点G,则==,即==,解得DG=1,PG=,当点P在点D的左边时,OG=DG﹣DO=1﹣1=0,所以点P(﹣,0),当点P在点D的右边时,OG=DO+DG=1+1=2,所以,点P(,﹣2);②OC与DP是对应边时,∵△DOC∽△CDP,∴=,即=,解得DP=3,过点P作PG⊥y轴于点G,则==,即==,解得DG=9,PG=3,当点P在点D的左边时,OG=DG﹣OD=9﹣1=8,所以,点P的坐标是(﹣3,8),当点P在点D的右边时,OG=OD+DG=1+9=10,所以,点P的坐标是(3,﹣10),综上所述,满足条件的点P共有4个,其坐标分别为(﹣,0)、(,﹣2)、(﹣3,8)、(3,﹣10).。
2020-2021学年人教版九年级上册数学期末复习试题

.
2
14.点 A(﹣3,y1),B( 2, y2 ),C(3,y 3)在抛物线 y=2x ﹣4x+c 上,则 y 1, y2 ,y3 的大小关系是
.
15.如图,在同一平面内, 将△ ABC绕点 A逆时针旋转 40°到△ AED的位置,恰好使得 EC∥AB,则∠ CAB的大小为
.
16.若点 P(﹣ m,1﹣2m)关于原点对称的点在第一象限,那么 m的取值范围是
.
20.如图, AB为⊙O 的直径,弦 CD⊥AB于点 E,已知 CD=6,EB=1,则⊙ O的半径为
.
三.解答题(共 60 分, 1 题 12 分, 2 题 6 分, 3-8 题各 7 分)
1. 解方程:(3*4=12 分)
(1).2
x
2
-
4x-
5=
0(
公式法解
)
(2).
x
2
-
4x
+
1=
0(
配方法解
5.如图 , 所示的三张卡片上分别写有一个整式,把它们背面朝上洗匀,小明闭上眼睛,从中随机抽取一张卡片,再从 剩下的卡片中随机抽取另一张,第一次抽取的卡片上的整式作为分子,第二次抽取的卡片上的整式作为分母,用列表 法或画树状图法求能组成分式的概率是多少?
6.如图,已知三角形 ABC的边 AB是⊙ 0 的切线,切点为 B.AC经过圆心 0 并与圆相交于点 D、 C,过 C 作直线 CE丄 AB,交 AB的延长线于点 E. ( 1)求证: CB平分∠ ACE; (2)若 BE=3,CE=4,求⊙ O的半径.
2
570m,问道路应多宽?
3.为了改善小区环境,某小区决定要在一块一边靠墙(墙长
25m)的空地上修建一个矩形绿化带 ABCD,绿化带一边
2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 11

2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 111.—I believe we will achieve our China Dream earlier if all of us _____. —I agree. Let's do what we can from now on. A.pull together B.have a point C.pay attentionD.keep our cool2.Mr. Li asks us to remember that careful we are, mistakes we will make. A.the more; the fewer B.the fewer; the more C.the more; the more D.the less; the fewer3.Nancy doesn’t like doing chores. But she was made ________ the dishes yesterday. A. washB. to washC. washingD. to washing4.—This dress was last year’s style.—I think it still looks perfect it has gone out this year. A.so that B.as if C.even though D.ever since5.—What should I do to learn English as a beginner? —_________, you should memorize some words. A. In the endB. In this wayC. To start withD. To my surprise 6.---Why don’t you get used to the life in Beijing?---_______ the crowded traffic _________ the high living cost. The only reason is the badlypolluted air.A. Not only; but alsoB. Either; orC. Both; andD. Neither; nor7. you practice, you will be at math. A.The more; the better B.The more; the best C.The most; the better D.The most; the best8.Many children ask their parents to give money to charity_________ buy them snacks. A. later on B. even though C. rather thanD. in order to9.Neither Jim nor Tom _______Australia before, but they know the country very well. A. has gone to B. has been to C. have gone to D. have been to10.—Excuse me, is the supermarket far from here? —No, it’s about . A. 5 minutes walk B. 5 minute walk C. 5 minutes’ walk D. 5 minute’s walk11. We should learn how to (communicate) with our parents.12. I think you should stop (talk) to him in English. He can’t understand you at all. 13. I think health is a kind of (wealth).14. I have an (comfortable) feeling that we will be late. 15. Have you heard from Lily (late)? 16. Mary has a p face. She must be ill. 17. Many ads are__________(aim) at teenagers. 18. 如果你们齐心协力,你们一定会成功。
人教新版2020-2021学年九年级上册数学期末复习试题(有答案)

人教新版2020-2021学年九年级上册数学期末复习试题一.选择题(共6小题,满分18分,每小题3分)1.下列方程一定是一元二次方程的是()A.x2+2x=x2﹣x+1B.(x﹣1)2=2x﹣3C.D.ax2+bx=c=02.下列图案中既是中心对称图形,又是轴对称图形的是()A.B.C.D.3.已知点A(﹣2,a),B(2,b),C(4,c)是抛物线y=x2﹣4x上的三点,则a,b,c 的大小关系为()A.b>c>a B.b>a>c C.c>a>b D.a>c>b4.下列事件中,属于必然事件的是()A.三角形的外心到三边的距离相等B.某射击运动员射击一次,命中靶心C.任意画一个三角形,其内角和是180°D.抛一枚硬币,落地后正面朝上5.如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为()A.12 B.4C.8D.66.如图,△ABC是一张周长为18cm的三角形纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为()A.13cm B.8cmC.6.5cm D.随直线MN的变化而变化二.填空题(共8小题,满分32分,每小题4分)7.一个扇形的面积为12πcm2,圆心角为120°,则该扇形的半径是.8.若a是方程x2﹣3x+1=0的根,计算:a2﹣3a+=.9.如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=50°,则∠ADC的度数是°.10.当﹣3≤x≤2时,函数y=ax2﹣4ax+2(a≠0)的最大值是8,则a=.11.如图,在矩形ABCD中,AB=4,AD=3,以D为圆心的圆,与线段AB有公共点,则圆的半径r的取值范围是.12.已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是.13.如图,弦AB⊥直径CD于E,若AB=10,CE=1,则CD=.14.观察一列数:,,,,,…根据规律,请你写出第10个数是.三.解答题(共4小题,满分20分,每小题5分)15.(用配方法解一元二次方程):2x2+x﹣1=0.16.如图,在边长为1的小正方形组成的网格中,△OAB的顶点都在格点上.(1)请作出△OAB关于直线CD对称的△O1A1B1;(2)请将△OAB绕点B顺时针旋转90°,画出旋转后的△BO2A2.17.如图①,用一块长100cm,宽80cm的薄钢片,在四个角上截去四个相同的小正方形,可以做成如图②所示的底面积为4800cm2的没有盖的长方体盒子,求截去的小正方形的边长.18.已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.(1)求证:DC是⊙O的切线;(2)若AB=2,求DC的长.四.解答题(共2小题,满分14分,每小题7分)19.如图是由转盘和箭头组成的两个转盘A、B,这两个转盘除了表面颜色不同外,其它构造完全相同,游戏者同时转动两个转盘,如果一个转盘转出红色,另一个转盘转出蓝色,那么红色和蓝色在一起能配成紫色.请你用列表法或树状图法,求游戏者不能配成紫色的概率.20.已知二次函数y=﹣x2+bx+c,函数值y与自变量x之间的部分对应值如表:(1)写出二次函数图象的对称轴.(2)求二次函数的表达式.(3)当﹣4<x<﹣1时,写出函数值y的取值范围.五.解答题(共2小题,满分16分,每小题8分)21.如图,AB是⊙O的直径,CD是⊙O的一条弦,且C D⊥AB于点E.(1)求证:∠BCO=∠D;(2)若CD=,AE=2,求⊙O的半径.22.如图,半圆的直径AB=20,C、D、E是半圆的四等分点.(1)求∠CAE的度数;(2)求阴影部分面积.六.解答题(共2小题,满分20分,每小题10分)23.某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)设每月的销售利润为W,请直接写出W与x的函数关系式;(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?24.如图①,二次函数y=﹣x2+bx+4的图象与直线l交于A(﹣1,2)、B(3,n)两点.点P是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图象于点N,设点P的横坐标为m.(1)b=,n=;(2)若点N在点M的上方,且MN=3,求m的值;(3)将直线AB向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).①记△NBC的面积为S1,△NAC的面积为S2,是否存在m,使得点N在直线AC的上方,且满足S1﹣S2=6?若存在,求出m及相应的S1,S2的值;若不存在,请说明理由.②当m>﹣1时,将线段MA绕点M顺时针旋转90°得到线段MF,连接FB、FC、OA.若∠FBA+∠AOD﹣∠BFC=45°,直接写出直线OF与该二次函数图象交点的横坐标.参考答案与试题解析一.选择题(共6小题,满分18分,每小题3分)1.解:A:两边的项消去后,不含二次项,所以不是一元二次方程;B:符合一元二次方程的定义,是一元二次方程;C:是分式方程,不是整式方程,当然不是一元二次方程;D:要强调a≠0,否则不是一元二次方程.故选:B.2.解:A、是轴对称图形,不是中心对称图形,故错误;B、是轴对称图形,不是中心对称图形,故错误;C、是轴对称图形,又是中心对称图形,故正确;D、是轴对称图形,不是中心对称图形,故错误.故选:C.3.解:∵抛物线y=x2﹣4x=(x﹣2)2﹣4,∴该抛物线的对称轴是直线x=2,当x>2时,y随x的增大而增大,当x<2时,y随x 的增大而减小,∵点A(﹣2,a),B(2,b),C(4,c)是抛物线y=x2﹣4x的三点,∵2﹣(﹣2)=4,2﹣2=0,4﹣2=2,∴a>c>b,故选:D.4.解:A、三角形的外心到三角形的三个顶点的距离相等,三角形的内心到三边的距离相等,只有三角形是等边三角形时才符合,故本选项不符合题意;B、某射击运动员射击一次,命中靶心是随机事件,故本选项不符合题意;C、三角形的内角和是180°,是必然事件,故本选项符合题意;D、抛一枚硬币,落地后正面朝上,是随机事件,故本选项不符合题意;故选:C.5.解:∵旋转后AC的中点恰好与D点重合,即AD=AC′=AC,∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,∴∠DAD′=60°,∴∠DAE=30°,∴∠EAC=∠ACD=30°,∴AE=CE,在Rt△ADE中,设AE=EC=x,则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=×6=2,根据勾股定理得:x2=(6﹣x)2+(2)2,解得:x=4,∴EC=4,则S=EC•AD=4.△AEC故选:B.6.解:由切线长定理得,BD=BG,CP=CG,MH=MD,NH=NP,∴BD+CP=BG+CG=5,∴AD+AP=18﹣10=8,∴△AMN的周长=AM+MN+AN=AM+MD+AN+NP=AD+AP=8,故选:B.二.填空题(共8小题,满分32分,每小题4分)7.解:设该扇形的半径是rcm,则12π=,解得r=6.故答案为:68.解:∵a是方程x2﹣3x+1=0的根,∴a2﹣3a+1=0,则a2﹣3a=﹣1,a2+1=3a,所以原式=﹣1+1=0,故答案为:0.9.解:由题意得到OA=OB=OC=OD,作出圆O,如图所示,∴四边形ABCD为圆O的内接四边形,∴∠ABC+∠ADC=180°,∵∠ABC=50°,∴∠ADC=130°,故答案为:130.10.解:∵函数y=ax2﹣4ax+2(a≠0)的对称轴为直线x=﹣=2,∴当a>0时,则x=﹣3时,函数y=ax2﹣4ax+2(a≠0)的最大值是8,∴把x=﹣3代入得,9a+12a+2=8,解得a=;∴当a<0时,则x=2时,函数y=ax2﹣4ax+2(a≠0)的最大值是8,∴把x=2代入得,4a﹣8a+2=8,解得a=﹣,故答案为或﹣.11.解:在直角△ABD中,CD=AB=4,AD=3,则BD==5.由图可知3≤r≤5.故答案为:3≤r≤512.解:由图象可得,该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),故抛物线与x轴的另一个交点为(3,0),故当y<0时,x的取值范围是﹣1<x<3.13.解:连接OA,∵弦AB⊥直径CD于E,∴AE=EB=5,设圆的半径为r,则OE=r﹣1,由勾股定理得,r2=52+(r﹣1)2,解得,r=13,则CD=2r=26,故答案为:26.14.解:,,,,,…根据规律可得第n个数是,∴第10个数是,故答案为;.三.解答题(共4小题,满分20分,每小题5分)15.解:∵2x2+x﹣1=0,∴x2+x+=,∴(x+)2=,∴x=﹣1或;16.解:(1)如图所示,△O1A1B1即为所求;(2)如图所示,△BO2A2即为所求.17.解:设截去的小正方形的边长为xcm,则长方形盒子的底面为长(100﹣2x)cm,宽为(80﹣2x)cm的长方形,依题意,得:(100﹣2x)(80﹣2x)=4800,化简,得:x2﹣90x+800=0,解得:x1=10,x2=80(不合题意,舍去).答:截去的小正方形的边长为10cm.18.(1)证明:连接OC.∵OB=OC,∠B=30°,∴∠OCB=∠B=30°.∴∠COD=∠B+∠OCB=60°.(1分)∵∠BDC=30°,∴∠BDC+∠COD=90°,DC⊥OC.(2分)∵BC是弦,∴点C在⊙O上,∴DC是⊙O的切线,点C是⊙O的切点.(2)解:∵AB=2,∴OC=OB==1.∵在Rt△COD中,∠OCD=90°,∠D=30°,∴DC=OC=.四.解答题(共2小题,满分14分,每小题7分)19.解:A转盘红色区域是蓝色区域的2倍,B转盘蓝色区域是红色区域的2倍,画树状图如图:共有9个等可能的结果,游戏者不能配成紫色的结果有4个,∴游戏者不能配成紫色的概率=.20.解:(1)∵x=﹣4、x=0时的函数值相等,都是﹣2,∴此函数图象的对称轴为直线x==﹣2;(2)将(﹣1,1)、(0,﹣2)代入y=﹣x2+bx+c,得:,解得:,∴二次函数的表达式为:y=﹣x2﹣4x﹣2;(3)∵y=﹣x2﹣4x﹣2=﹣(x+2)2+2,∴当x=﹣2时,y取得最大值2,由表可知当x=﹣4时y=﹣2,当x=﹣1时y=1,∴当﹣4<x<﹣1时,﹣2<y≤2.五.解答题(共2小题,满分16分,每小题8分)21.(1)证明:如图.∵OC=OB,∴∠BCO=∠B.∵∠B=∠D,∴∠BCO=∠D;(2)∵AB是⊙O的直径,且CD⊥AB于点E,∴CE=CD=×4=2,在Rt△OCE中,OC2=CE2+OE2,设⊙O的半径为r,则OC=r,O E=OA﹣AE=r﹣2,∴r2=(2)2+(r﹣2)2,解得:r=3,∴⊙O的半径为3.22.解:(1)∵C、D、E是半圆的四等分点,∴∠CAE=××180°=45°;(2)连接OC、OE、CE,∵△ACE和△COE等底等高,∴S△ACE =S△COE,∵C、D、E是半圆的四等分点,AB=20,∴∠COE=180°÷2=90°,OA=10,∴阴影部分的面积=S扇形COE==25π.六.解答题(共2小题,满分20分,每小题10分)23.解:(1)当50≤x≤80时,y=210﹣(x﹣50),即y=260﹣x,当80<x<140时,y=210﹣(80﹣50)﹣3(x﹣80),即y=420﹣3x.则,(2)由利润=(售价﹣成本)×销售量可以列出函数关系式w=﹣x2+300x﹣10400(50≤x≤80)w=﹣3x2+540x﹣16800(80<x<140),(3)当50≤x≤80时,w=﹣x2+300x﹣10400,当x=80有最大值,最大值为7200,当80<x<140时,w=﹣3x2+540x﹣16800,当x=90时,有最大值,最大值为7500,故售价定为90元.利润最大为7500元.24.解:(1)将点A(﹣1,2)代入二次函数y=﹣x2+bx+4中,得﹣1﹣b+4=2,∴b=1,∴二次函数的解析式为y=﹣x2+x+4,将点B(3,n)代入二次函数y=﹣x2+x+4中,得n=﹣9+3+4=﹣2,故答案为:1,﹣2;(2)设直线AB的解析式为y=kx+a,由(1)知,点B(3,﹣2),∵A(﹣1,2),∴,∴,∴直线AB的解析式为y=﹣x+1,由(1)知,二次函数的解析式为y=﹣x2+x+4,∵点P(m,0),∴M(m,﹣m+1),N(m,﹣m2+m+4),∵点N在点M的上方,且MN=3,∴﹣m2+m+4﹣(﹣m+1)=3,∴m=0或m=2;(3)①如图1,由(2)知,直线AB的解析式为y=﹣x+1,∴直线CD的解析式为y=﹣x+1+4=﹣x+5,令y=0,则﹣x+5=0,∴x=5,∴C(5,0),∵A(﹣1,2),B(3,﹣2),∴直线AC的解析式为y=﹣x+,直线BC的解析式为y=x﹣5,过点N作y轴的平行线交AC于K,交BC于H,∵点P(m,0),∴N(m,﹣m2+m+4),K(m,﹣m+),H(m,m﹣5),∴NK=﹣m2+m+4+m﹣=﹣m2+m+,NH=﹣m2+9,=NK×(x C﹣x A)=(﹣m2+m+)×6=﹣3m2+4m+7,∴S2=S△NACS1=S=NH×(x C﹣x B)=﹣m2+9,△NBC∵S1﹣S2=6,∴﹣m2+9﹣(﹣3m2+4m+7)=6,∴m=1+(由于点N在直线AC上方,所以,舍去)或m=1﹣;∴S2=﹣3m2+4m+7=﹣3(1﹣)2+4(1﹣)+7=2﹣1,S1=﹣m2+9=﹣(1﹣)2+9=2+5;②如图2,记直线AB与x轴,y轴的交点为I,L,由(2)知,直线AB的解析式为y=﹣x+1,∴I(1,0),L(0,1),∴OL=OI,∴∠ALD=∠OLI=45°,∴∠AOD+∠OAB=45°,过点B作BG∥OA,∴∠ABG=∠OAB,∴∠AOD+∠ABG=45°,∵∠FBA=∠ABG+∠FBG,∠FBA+∠AOD﹣∠BFC=45°,∴∠ABG+∠FBG+∠AOD﹣∠BFC=45°,∴∠FBG=∠BFC,∴BG∥CF,∴OA∥CF,∵A(﹣1,2),∴直线OA的解析式为y=﹣2x,∵C(5,0),∴直线CF的解析式为y=﹣2x+10,过点A,F分别作过点M平行于x轴的直线的垂线,交于点Q,S,由旋转知,AM=MF,∠AMF=90°,∴△AMF是等腰直角三角形,∴∠FAM=45°,∵∠AIO=45°,∴∠FAM=∠AIO,∴AF∥x轴,∴点F的纵坐标为2,∴F(4,2),∴直线OF的解析式为y=x①,∵二次函数的解析式为y=﹣x2+x+4②,联立①②解得,或,∴直线OF与该二次函数图象交点的横坐标为或.。
2021年最新人教版九年级数学上册期末复习试题(有答案)

人教版九年级数学上册期末复习试题(满分120分;时间:120分钟)一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 下列方程中,是一元二次方程的是( )A.x2+2x+y=1B.x2+1−1=0xC.x2=0D. (x+1)(x+3)=x2−12. 二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是()A.a<0,b<0,c>0,b2−4ac>0B.a>0,b<0,c>0,b2−4ac<0C.a<0,b>0,c<0,b2−4ac>0D.a<0,b>0,c>0,b2−4ac>03. 若关于x的一元二次方程2x2−3x−k=0的一个根为1,则另一个根为()A.2B.−1C.12D.724. 抛物线y=ax2+bx+c的对称轴为直线x=−1,与x轴相交于A,B两点,已知点B 坐标为(2,0),则点A坐标为()A.(−4,0)B.(−3,0)C.(0,−3)D.(0,−4)5. 平面直角坐标系内一点P(3,−1)关于原点对称的点的坐标是()A.(3,−1)B.(−3,1)C.(−3,−1)D.(3,1)6. 若c(c≠0)为关于x的一元二次方程x2+bx+c=0的根,则c+b的值为()A.1B.−1C.2D.−27. 芳芳在平面直角坐标系画了一个二次函数的图象,并将该图象的特点写在如图所示的卡片上,则该二次函数的解析式为()①开口向下;②顶点是原点;③过点(6, −6).A.y=−16x2 B.y=16x2 C.y=−6x2 D.y=6x28. 关于x的一元二次方程mx2−3x−1=0有两个不相等的实数根,则m的取值范围是()A.m≥−94B.m<94且m≠0 C.m>−94且m≠0D.m<949. 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系为p=at2+bt+c(a、b、c是常数),如图记录了三次实验的数据.根据上述函数实验数据,可得到最佳加工时间为()A.4.25分钟B.4.00分钟C.3.75分钟D.3.50分钟10. 如图,为等边三形内的一点,,将线段以点为旋转中心逆时针旋转60∘得到线段,下列结论:①点与点的距离为5;②;③可以由绕点进时针旋转60∘得到;④点到的距离为3;⑤,其中正确的有()A.2个B.3个C.4个D.5个二、填空题(本题共计8 小题,每题3 分,共计24分,)11. 若m<3,则关于x的一元二次方程(m−2)2x2+(2m+1)x+1=0根的情况是4________.12. 已知3是关于x的方程x2−5x+c=0的一个根,则这个方程的另一个根是________.13. 已知α,β是一元二次方程x2−4x−5=0的两实数根,则代数式(α−1)(β−1)=________14. 如图,在平面直角坐标系中,抛物线y=a(x−1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD // x轴,与抛物线交于点D.若点A的坐标为(−1, 0),则线段OB与线段CD的长度和为________.15. 把一个小球在离地面2m处向上抛起,上升的高度s(m)与时间t(s)的关系为s=10t−5t2,则小球运动到最高处时距离地面________m.16. 二次函数y=x2+4x−3的最小值是________.17. 当a−1≤x≤a时,函数y=x2−2x+1的最小值为1,则a的值为________.18. 如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为________.三、解答题(本题共计7 小题,共计66分,)19. 如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:(1)旋转△ADF可得到哪个三角形?(2)旋转中心是哪一点?旋转了多少度?(3)BE与DF的数量关系、位置关系如何?为什么?20. 如图,△ABC三个顶点的坐标分别为A(−1,3),B(−4,1),C(−2,1).(1)画出△ABC绕原点O顺时针旋转90∘后得到的△A1B1C1;(2)画出△ABC关于原点对称的△A2B2C2;(3)在(1)的条件下,求出点B旋转到点B1所经过的路径长(结果保留根号和π).21. 下面的图形是由边长为1的正方形按照某种规律排列而组成的.(1)推测第4个图形中,正方形的个数为________,周长为________;(2)推测第n个图形中,正方形的个数为________,周长为________;(都用含n的代数式表示)(3)这些图形中,任意一个图形的周长记为a,它所含正方形个数记为b,则a,b之间满足的数量关系为________.(用含a,b的等式表示)22. 已知抛物线y=−12x2+bx+c经过点(1, 0),(0, 32).(1)求该抛物线的函数表达式;(2)将抛物线y=−12x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.23. 在平面直角坐标系中,将坐标是(0, 4),(1, 0),(2, 4),(3, 0),(4, 4)的点用线段依次连接起来形成一个图案.(1)在坐标系中画出这个图案;(2)图形中哪些点在坐标轴上,它们的坐标有什么特点?(3)图中有与坐标轴平行的线段吗?线段上的点的纵坐标有什么特点?24. 将图中的A型(正方形)、B型(菱形)、C型(等腰直角三角形)纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.(1)搅匀后从中摸出1个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是________;(2)搅匀后先从中摸出1个盒子(不放回),再从余下的2个盒子中摸出1个盒子,把摸出的2个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)25. 随着新冠病毒在全世界蔓延,口罩成为紧缺物资,甲、乙两家工厂积极响应政府号召,准备跨界投资生产口罩.根据市场调查,甲、乙两家工厂计划每天各生产6万片口罩,但由于转型条件不同,其生产的成本不一样,甲工厂计划每生产1万片口罩的成本为0.6万元,乙工厂计划每生产1万片口罩的成本为0.8万元.(1)按照计划,甲、乙两家工厂共生产2000万片口罩,且甲工厂生产口罩的总成本不高于乙工厂生产口罩的总成本的,求甲工厂最多可生产多少万片的口罩?(2)实际生产时,甲工厂完全按计划执行,但乙工厂的生产情况发生了一些变化.乙工厂实际每天比计划少生产0.5m万片口罩,每生产1万片口罩的成本比计划多0.2m万元,最终乙工厂实际每天生产口罩的成本比计划多1.6万元,求m的值.参考答案一、选择题(本题共计10 小题,每题3 分,共计30分)1.【答案】C【解答】解:A,x2+2x+y=1,含有两个未知数,不符合一元二次方程的定义,故错误;−1=0,分母含有未知数,不符合一元二次方程的定义,故错误;B,x2+1xC,x2=0,符合一元二次方程的定义;D,(x+1)(x+3)=x2−1,可化简为4x+4=0,不符合一元二次方程的定义,故错误. 故选C.2.【答案】D【解答】解:∵抛物线的开口向下,∴a<0,∵对称轴在y轴右边,∴a,b异号即b>0,∵抛物线与y轴的交点在正半轴,∴c>0,∵抛物线与x轴有2个交点,∴b2−4ac>0.故选D.3.【答案】C【解答】解:根据题意得:2×1−3×1−k=0∴k=−1∴方程为:2x2−3x+1=0.解得:x1=1,x2=12故选C.4.【答案】A【解答】解:设点A坐标为(x,0),则2+x=−1,解得x=−4,2∴点A坐标为(−4,0).故选A.5.【答案】B【解答】解:根据中心对称的性质,得点P(3,−1)关于原点对称的点的坐标是(−3,1). 故选B.6.【答案】B【解答】解:把x=c代入方程x2+bx+c=0,可得c2+bc+c=0,即c(b+c+1)=0,又∵c≠0,∴b+c+1=0,∴c+b=−1.故选B.7.【答案】A【解答】解:设抛物线解析式为y=ax2,把(6, −6)代入得36a=−6,解得a=−1,6所以抛物线解析式为y=−1x2.6故选A.8.【答案】C【解答】解:∵关于x的一元二次方程mx2−3x−1=0有两个不相等的实数根,∴m≠0,且△=b2−4ac=9+4m>0,∴m>−9且m≠0.4故选C.9.【答案】C【解答】解:把(3,0.7),(4,0.8),(5,0.5)代入解析式,得到:{9a +3b +c =0.716a +4b +c =0.825a +5b +c =0.5解得:{a =−0.2b =1.5c =−2即:p =−0.2t 2+1.5t −2则对称轴是直线x =− 1.52×(−0.2)=3.75则最佳加工时间为3.75分钟故选:C10.【答案】B【解答】解:连结DD ′,如图,线段AD以点A为旋转中心逆时针旋转60∘得到线段AD′AD=AD′ ∠DAD′=60∘△ADD为等边三角形,DD′=5,所以②正确;△ABC为等边三角形,AB=AC ∠EAC=60∘.把△ABD逆时针旋转60∘后,AB与AC重合,AD与AD‘重合,△ACD’可以由△ABD绕点A逆时针旋转60∘得到,所以③正确;D:′=DB==DC=3在ΔDD′C中,32+42=52∴DC2+D′C2=DD2△DDC为直角三角形,∠DCD′=90∘△ADD/为等边三角形,∠AOD′=60∘∴ ADC≠150∘,所以②错误;∠DCD′=90∘DC⊥CD′…点D到CD的距离为3,所以④正确;四边形{A DCD= 5\Delta {\triangle ADD}+ S_{\triangle DDC}= \dfrac{\sqrt{3}}{4}\times 5^{2}+ \dfrac{1}{2}\times 3\times 4= 6+ \dfrac{25\sqrt{3}}{4}},所以③错误.故选:{B}$.二、填空题(本题共计8 小题,每题3 分,共计24分)11.【答案】无实数根【解答】解:∵△=(2m+1)2−4×(m−2)2×1=20m−15,,又∵m<34∴20m−15<0,即△<0,∴关于x的一元二次方程(m−2)2x2+(2m+1)x+1=0无实数根;故答案为:无实数根.12.【答案】x=2【解答】∵3是关于x的方程x2−5x+c=0的一个根,∴32−5×3+c=0,即−6+c=0,解得,c=6;∴由原方程,得x2−5x+6=0,即(x−2)(x−3)=0,∴x−2=0或x−3=0,解得,x=2或x=3,∴方程的另一个根是x=2;13.【答案】−8【解答】∵α、β是一元二次方程x2−4x−5=0的两实数根,∴α+β=4,αβ=−5,∴(α−1)(β−1)=αβ−(α+β)+1=−5−4+1=−8.14.【答案】5【解答】∵抛物线y=a(x−1)2+k(a、k为常数),∴对称轴为直线x=1,∵点A和点B关于直线x=1对称,且点A(−1, 0),∴点B(3, 0),∴OB=3,∵C点和D点关于x=1对称,且点C(0, a+k),∴点D(2, a+k),∴CD=2,∴线段OB与线段CD的长度和为5,15.【答案】7【解答】解:由题意可知:小球与地面的高度ℎ(m)与时间t(s)的关系为:ℎ=s+2=−5t2+10t+ 2=−5(t−1)2+7≤7,∴抛物线顶点坐标(1, 7)图象开口向下,当t=1时有最大值为7,∴小球运动到最高处时距离地面7m.故答案为:716.【答案】−7【解答】解:∵y=x2+4x−3=(x+2)2−7,∵a=1>0,∴x=−2时,y有最小值−7.故答案为:−7.17.【答案】0或3【解答】解:y=x2−2x+1=(x−1)2,∵最小值是1,∴(x−1)2=1,解得:x=0或x=2.∵抛物线y=(x−1)2对称轴是x=1,开口方向向上,∴ x<1时,y随x的增大而减小.∵a−1≤x≤a,∴x=a时y的值最小,即a=0;∴x>1时,y随x的增大而增大,∴ x=a−1时,y的值最小,即a−1=2,故a=3.故答案为:0或3.18.【答案】(8+2x)(5+2x)=70【解答】解:∵风景画的长为0+2x,宽为5+2x,∴可列方程为(8+2x)(5+2x)=70.故答案为(8+2x)(5+2x)=70.三、解答题(本题共计7 小题,每题10 分,共计70分)19.【答案】解:(1)旋转△ADF可得△ABE,理由如下:∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠DAF=90∘,在△ADF和△ABE中,{AF=AE∠FAD=∠BAEAD=AB,∴△ADF≅△ABE,∴旋转△ADF可得△ABE;(2)由旋转的定义可知:旋转中心为A,因为AD=AB,所以AD和AB之间的夹角为旋转角即90∘;(3)BE=DF且BE⊥BE.理由如下:延长BE交F于H点,如图,∵四边形ABCD为正方形,∴AD=AB,∠DAB=90∘,∵△ABE按逆时针方向旋转90∘△ADF,∴BE=DF,∠1=∠2,∵∠3=∠4,∴∠DHB=∠BAE=90∘,∴BE⊥DF.【解答】解:(1)旋转△ADF可得△ABE,理由如下:∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠DAF=90∘,在△ADF和△ABE中,{AF=AE∠FAD=∠BAEAD=AB,∴△ADF≅△ABE,∴旋转△ADF可得△ABE;(2)由旋转的定义可知:旋转中心为A,因为AD=AB,所以AD和AB之间的夹角为旋转角即90∘;(3)BE=DF且BE⊥BE.理由如下:延长BE交F于H点,如图,∵四边形ABCD为正方形,∴AD=AB,∠DAB=90∘,∵△ABE按逆时针方向旋转90∘△ADF,∴BE=DF,∠1=∠2,∵∠3=∠4,∴∠DHB=∠BAE=90∘,∴BE⊥DF.20.【答案】解:(1)由题意,△ABC绕原点O顺时针旋转90∘后,得到△A1B1C1,如图.(2)△A2B2C2即为所求三角形,如图.(3)连接BO,B1O,如图,由题意得,r=√42+12=√17,所以,l弧=nπr180∘=90∘π×√17180∘=√172π.【解答】解:(1)由题意,△ABC绕原点O顺时针旋转90∘后,得到△A1B1C1,如图.(2)△A2B2C2即为所求三角形,如图.(3)连接BO,B1O,如图,由题意得,r=√42+12=√17,所以,l弧=nπr180∘=90∘π×√17180∘=√172π.21.【答案】23,485n+3,10n+8a=2b+2【解答】解:(1)第①个图形中,正方形的个数为8,周长为18;第②个图形中,正方形的个数为8+5=13,周长为18+10=28;第③个图形中,正方形的个数为8+5×2=18,周长为18+10×2=38;则第④个图形中,正方形的个数为8+5×3=23,周长为18+10×3=48.故答案为:23;48.(2)由(1)中的规律可得,第n 个图形中,正方形的个数为8+5(n −1)=5n +3,周长为18+10(n −1)=10n +8. 故答案为:5n +3;10n +8.(3)由(2)可知,第n 个图形中,正方形的个数为5n +3,周长为10n +8,则2×(5n +3)+2=10n +8,即任意一个图形的周长=所含正方形个数×2+2,∵ 任意一个图形的周长记为a ,它所含正方形个数记为b ,∴ a =2b +2.故答案为:a =2b +2.22.【答案】把(1, 0),(0, 32)代入抛物线解析式得:{−12+b +c =0c =32, 解得:{b =−1c =32,则抛物线解析式为y =−12x 2−x +32;抛物线解析式为y =−12x 2−x +32=−12(x +1)2+2,将抛物线向右平移一个单位,向下平移2个单位,解析式变为y =−12x 2.【解答】把(1, 0),(0, 32)代入抛物线解析式得:{−12+b +c =0c =32,解得:{b =−1c =32,则抛物线解析式为y =−12x 2−x +32;抛物线解析式为y =−12x 2−x +32=−12(x +1)2+2,将抛物线向右平移一个单位,向下平移2个单位,解析式变为y =−12x 2.23.【答案】解:(1)如图所示:(2)点(0, 4)在y 轴上,点(1, 0),(3, 0)在x 轴上,y轴上点的横坐标都是0,x轴上个点纵坐标是0.(3)有,线段上各点的纵坐标都相等.【解答】解:(1)如图所示:(2)点(0, 4)在y轴上,点(1, 0),(3, 0)在x轴上,y轴上点的横坐标都是0,x轴上个点纵坐标是0.(3)有,线段上各点的纵坐标都相等.24.【答案】23 (2)画树状图为:共有6种等可能的情况,其中拼成的图形是轴对称图形的情况有2种:A和C,C和A,∴拼成的图形是轴对称图形的概率为26=13.【解答】解:(1)搅匀后从中摸出1个盒子,可能为A型(正方形)、B型(菱形)或C型(等腰直角三角形)这3种情况,其中既是轴对称图形又是中心对称图形的有2种,∴盒中的纸片既是轴对称图形又是中心对称图形的概率是23.故答案为:23.(2)画树状图为:共有6种等可能的情况,其中拼成的图形是轴对称图形的情况有2种:A和C,C和A,∴拼成的图形是轴对称图形的概率为26=13.25.【答案】(1)甲工厂最多可生=100万片的口罩;(2)m 的值为4.【解答】(1)设甲工厂生产x 万片口罩,则乙工厂生n ¯=(2000−x )万片口罩,由题意得:0.6x ≤0.8(2000−x )×34解得:x ≤1000答:甲工厂最多可生万片的口罩.(2)由题意得:(6−0.5m )(0.8+0.2m )=6×0.8+1.6整理得:m 2−8m +16=0解得:m 1=m 2=4答:m 的值为4.。
2020-2021学年人教新版九年级上册数学期末复习试卷(含下册部分内容)(有答案)

2020-2021学年人教新版九年级上册数学期末复习试卷一.选择题(共10小题,满分20分,每小题2分)1.下列各组线段,能成比例线段的是()A.3cm,6cm,7cm,9cm B.2cm,5cm,0.6dm,8cmC.3cm,9cm,1.8dm,6cm D.1cm,2cm,3cm,4cm2.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是()A.B.C.D.3.某班从甲、乙、丙、丁四位选手中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是()A.B.C.D.4.若菱形的两条对角线长分别为8和6,则这个菱形的面积是()A.96B.48C.24D.125.方程(x+1)2=0的根是()A.x1=x2=1B.x1=x2=﹣1C.x1=﹣1,x2=1D.无实根6.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE (不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有()A.4个B.5个C.6个D.7个7.受非洲猪瘟及其他因素影响,2019年9月份猪肉价格两次大幅度上涨,瘦肉价格由原来23元/千克,连续两次上涨x%后,售价上升到60元/千克,则下列方程中正确的是()A.23(1﹣x%)2=60B.23(1+x%)2=60C.23(1+x2%)=60D.23(1+2x%)=608.如图所示,在平面直角坐标系中,等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴于点A,点C在函数y=(x>0)的图象上,若OA=1,则k的值为()A.4B.2C.2D.9.用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,下列说法正确的是()A.种植10棵幼树,结果一定是“有9棵幼树成活”B.种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活”C.种植10n棵幼树,恰好有“n棵幼树不成活”D.种植n棵幼树,当n越来越大时,种植成活幼树的频率会越来越稳定于0.910.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和B,与y轴的正半轴交于点C,下列结论:①abc>0;②4a﹣2b+c>0;③2a﹣b>0,其中正确的个数为()A.0个B.1个C.2个D.3个二.填空题(共6小题,满分18分,每小题3分)11.已知二次函数y=﹣2x2+4x+6,用配方法化为y=a(x﹣m)2+k的形式为,这个二次函数图象的顶点坐标为.12.四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若AB:A'B'=2:3,则OB:OB'=.13.如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y=的图象上,把△OAB向右平移a个单位长度,对应得到△O′A′B′当这个函数图象经过△O′A′B′一边的中点时,则a的值是.14.已知三角形的两边长分别是4和7,第三边长是方程x2﹣20x+99=0的根,则第三边的边长是.15.如图,四边形ABCD∽四边形A'B'C'D',则α=.16.如图,在矩形ABCD中,AD=3AB=3,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=.三.解答题(共3小题,满分22分)17.已知非零实数a、b、c、x、y、z满足==,求的值.18.解方程:2x2+3x﹣1=0.19.在△ABC中,AB=AC,∠BAC=120°,过点C作CD∥AB,且CD=2AB,连接BD,BD=2.求△ABC的面积.四.解答题(共2小题,满分16分,每小题8分)20.有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字﹣1,0,1,2;B布袋中有二个除标号外完全相同的小球,小球上分别标有数字0,1.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.(1)若用(m,n)表示小明取球时m与n的对应值,请用树状图或列表法表示(m,n)的所有取值;(2)求关于x的一元二次方程x2﹣mx+n=0有实数根的概率.21.已知A(a,﹣2a)、B(﹣2,a)两点是反比例函数y=与一次函数y=kx+b图象的两个交点.(1)求一次函数和反比例函数的解析式;(2)求△ABO的面积;(3)观察图象,直接写出不等式kx+b﹣>0的解集.五.解答题(共1小题,满分10分,每小题10分)22.如图,在四边形ABCD中,∠BAD=110°,∠CBA=50°,∠DCB=70°,M,N分别为线段AB,CD的中点,P为线段MN上的一点,满足,且PA=PC,求∠CPA 的度数.六.解答题(共1小题,满分10分,每小题10分)23.某服装厂生产A品种服装,每件成本为71元,零售商到此服装厂一次性批发A品牌服装x件时,批发单价为y元,y与x之间满足如图所示的函数关系,其中批发件数x为10的正整数倍.(1)当100≤x≤300时,y与x的函数关系式为.(2)某零售商到此服装厂一次性批发A品牌服装200件,需要支付多少元?(3)零售商到此服装厂一次性批发A品牌服装x(100≤x≤400)件,服装厂的利润为w 元,问:x为何值时,w最大?最大值是多少?七.解答题(共1小题,满分12分,每小题12分)24.四边形ABCD中,∠ABC+∠ADC=180°,对角线BD平分∠ABC.(1)如图1,延长BC,AD交于点M.求证:①△MCD∽△MAB;②AD=CD;(2)如图2,连接AC交BD于点F,将△ABC沿着AC翻折得到△AEC,连接DE,若CE∥BD,BC=6,CD=4,求CF的长.八.解答题(共1小题,满分12分,每小题12分)25.如图,已知二次函数y=x2+bx+c的图象与x轴交于点A(1,0)、B(3,0),与y轴交于点C.(1)求二次函数的解析式;(2)若点P为抛物线上的一点,点F为对称轴上的一点,且以点A、B、P、F为顶点的四边形为平行四边形,求点P的坐标;(3)点E是二次函数第四象限图象上一点,过点E作x轴的垂线,交直线BC于点D,求四边形AEBD面积的最大值及此时点E的坐标.参考答案与试题解析一.选择题(共10小题,满分20分,每小题2分)1.解:A、3×9≠6×7,故错误;B、0.6dm=6cm,2×8≠5×6,故错误;C、1.8dm=18cm,3×18=6×9,故正确;D、1×4≠2×3,故错误.故选:C.2.解:从左面看易得第一层有2个正方形,第二层最左边有一个正方形.故选:B.3.解:根据题意画图如下:共有12种等可能数,其中恰好选中甲、乙两位选手的有2种,则恰好选中甲、乙两位选手的概率是=;故选:C.4.解:∵四边形ABCD是菱形,∴S=×6×8=24.故选:C.5.解:由于(x+1)2=0,∴x+1=0,∴x1=x2=﹣1故选:B.6.解:如图,所以使得△ADE∽△ABC的格点三角形一共有6个.故选:C.7.解:当猪肉第一次提价x%时,其售价为23+23x%=23(1+x%);当猪肉第二次提价x%后,其售价为23(1+x%)+23(1+x%)x%=23(1+x%)2.∴23(1+x%)2=60.故选:B.8.解:作BD⊥AC于D,如图,∵△ABC为等腰直角三角形,∴BD是AC的中线,∴AC=2BD,∵CA⊥x轴于点A,∵AC⊥x轴,BD⊥AC,∠AOB=90°,∴四边形OADB是矩形,∴BD=OA=1,∴AC=2,∴C(1,2),把C(1,2)代入y=得k=1×2=2.故选:C.9.解:用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,是在大量重复实验中得到的概率的近似值,故A、B、C错误,D正确,故选:D.10.解:①∵由抛物线的开口向下知a<0,∵对称轴位于y轴的左侧,∴a、b同号,即ab>0.∵抛物线与y轴交于正半轴,∴c>0,∴abc>0;故①符合题意;②如图,当x=﹣2时,y>0,4a﹣2b+c>0,故②符合题意;③对称轴为x=﹣>﹣1,得2a<b,即2a﹣b<0,故③不符合题意;故选:C.二.填空题(共6小题,满分18分,每小题3分)11.解:y=﹣2x2+4x+6=﹣2(x2﹣2x)+6=﹣2(x﹣1)2+8,∴顶点(1,8).故答案为:y=﹣2(x﹣1)2+8,(1,8).12.解:∵四边形ABCD与四边形A′B′C′D′位似,∴AB∥A′B′,∴△OAB∽△OA′B′,∴OB:OB′=AB:A′B′=2:3,故答案为:2:3.13.解:如图,过点A作AC⊥OB,垂足为C,设OA的中点为M,AB的中点为N,∵点B(4,0),等边三角形OAB,∴OC=BC=2,OA=OB=AB=4,∴AC==2,∴A(2,2),∴k=2×2=4,∴反比例函数关系式为y=,∵O(0,0),A(2,2),B(4,0),∴M(1,),N(3,),当y=时,x==4,∴a=4﹣1=3或a=4﹣3=1,故答案为:3或1.14.解:x2﹣20x+99=0,(x﹣11)(x﹣9)=0,x﹣9=0,x﹣11=0,解得:x1=9;x2=11,∵4+7=11=11,由于三角形两边之和大于第三边,只能取x=9,故答案为:9.15.解:∵四边形ABCD∽四边形A′B′C′D′,∴∠A=∠A'=62°,∠B=∠B'=75°,∴α=360°﹣140°﹣62°﹣75°=83°,故答案为:83°.16.解:分两种情况:①MN为等腰△PMN的底边时,作PF⊥MN于F,如图1所示:则∠PFM=∠PFN=90°,∵四边形ABCD是矩形,∴AB=CD,BC=AD=3AB=3,∠A=∠C=90°,∴AB=CD=1,BD===,∵点P是AD的中点,∴PD=AD=,∵∠PDF=∠BDA,∴△PDF∽△BDA,∴=,即=,解得:PF=,∵CE=2BE,∴BC=AD=3BE,∴BE=CD,∴CE=2CD,∵△PMN是等腰三角形且底角与∠DEC相等,PF⊥MN,∴MF=NF,∠PNF=∠DEC,∵∠PFN=∠C=90°,∴△PNF∽△DEC,∴==2,∴MF=NF=2PF=,∴MN=2NF=;②MN为等腰△PMN的腰时,作PF⊥BD于F,如图2所示:由①得:PF=,MF=,设MN=PN=x,则FN=﹣x,在Rt△PNF中,()2+(﹣x)2=x2,解得:x=,即MN=;综上所述,MN的长为或,故答案为:或.三.解答题(共3小题,满分22分)17.解:∵==,∴=,=,=,∴=,=,=,∴=•••••=•••••=1.18.解:这里a=2,b=3,c=﹣1,∵△=9+8=17,∴x=.19.解:过点B作BE∥AC交CD于E,过B作BF⊥CD于F,∵CD∥AB,AB=AC,∴四边形ABEC是菱形,∴BE=CE=AB,∵∠BAC=120°,∴∠ABE=60°,∴∠BED=∠ABE=60°,∵CD=2AB,BD=2,∴CE=DE=BD=2,∴△BDE是等边三角形,∴△BDE的高BF==,∴S△ABC =S菱形ABEC=×2×=,故△ABC的面积为.四.解答题(共2小题,满分16分,每小题8分)20.解:(1)画树状图如下:由图表知,(m,n)有8种可能;(2)由方程得△=m 2﹣2n ,当(m ,n )的对应值是(﹣1,0),(0,0),(1,0),(2,0),(2,1)时,△≥0,原方程有实数根,则关于x 的一元二次方程x 2﹣mx +n =0有实数根的概率是.21.解:(1)∵A (a ,﹣2a )、B (﹣2,a )两点在反比例函数y =的图象上, ∴m =﹣2a •a =﹣2a ,解得a =1,m =﹣2,∴A (1,﹣2),B (﹣2,1),反比例函数的解析式为y =﹣.将点A (1,﹣2)、点B (﹣2,1)代入到y =kx +b 中, 得:,解得:,∴一次函数的解析式为y =﹣x ﹣1.(2)在直线y =﹣x ﹣1中,令y =0,则﹣x ﹣1=0,解得x =﹣1,∴C (﹣1,0),∴S △AOB =S △AOC +S △BOC =×1×2+×1=;(3)观察函数图象,发现:当x <﹣2或0<x <1时,反比例函数图象在一次函数图象的上方,∴不等式kx +b ﹣>0的解集为x <﹣2或0<x <1. 五.解答题(共1小题,满分10分,每小题10分)22.解:延长AD ,BC ,连接ME ,NE ,∴∠DCE=180°﹣∠BCD=110°=∠BAD,∴△DCE∽△BAE,∴===,∴△NCE∽△MAE,∴∠NEC=∠MEN,==,∴∠MEC=∠NEA,∴∠MEP=∠NEP,∴∠PEB=∠PEA,作PF⊥BC于F,PG⊥AD于G,∴PF=PG,∵PA=PC,∴Rt△PCF≌Rt△PAG(HL),∴∠FPC=∠GPA,∴∠APC=∠GPA+∠CPG=∠FPC+∠CPG=∠FPG,∵∠B+∠BAD+∠AEB=180°,∠FPG+∠AEB=180°,∴∠FPG=∠B+∠BAD=110°+50°=160°,∴∠APC=160°.23.解:(1)当100≤x≤300时,设y与x的函数关系式为:y=kx+b,根据题意得出:,解得:,∴y与x的函数关系式为:y=﹣x+110,故答案为:y=﹣x+110;(2)当x=200时,y=﹣20+110=90,∴90×200=18000(元),答:某零售商一次性批发A品牌服装200件,需要支付18000元;(3)分两种情况:①当100≤x≤300时,w=(﹣x+110﹣71)x=﹣+39x=﹣(x﹣195)2+3802.5,∵批发件数x为10的正整数倍,∴当x=190或200时,w有最大值是:﹣(200﹣195)2+3802.5=3800;②当300<x≤400时,w=(80﹣71)x=9x,当x=400时,w有最大值是:9×400=3600,∴一次性批发A品牌服装x(100≤x≤400)件时,x为190元或200元时,w最大,最大值是3800元.24.(1)证明:①∵∠ABC+∠ADC=180°,∠MDC+∠ADC=180°,∴∠MDC=∠ABC,又∵∠M=∠M,∴△MCD∽△MAB;②连接AC,如图1所示:∵①△MCD∽△MAB,∴=,∴=,又∵∠M=∠M,∴△MBD∽△MAC,∴∠MBD=∠MAC,∵∠ABC+∠ADC=180°,BD平分∠ABC,∴2∠MBD+∠ADC=180°,∵∠ADC+∠MAC+∠DCA=180°,∴∠DCA=∠MBD,∴∠DCA=∠MAC,∴AD=CD;(2)解:连接BE交AC于点N,如图2所示:∵将△ABC沿着AC翻折得到△AEC,∴点B与点E关于AC对称,EC=BC=6,∴BN=EN,∵CE∥BD,∴∠CEN=∠FBN,在△CEN和△FBN中,,∴△CEN≌△FBN(ASA),∴EC=BF=6,∵∠ABC+∠ADC=180°,∴A、B、C、D四点共圆,∴∠DAC=∠DBC,∵AD=CD,∴∠DAC=∠DCA,∴∠DBC=∠DCA,又∵∠BDC=∠BDC,∴△DBC∽△DCF,∴==,∴DB•DF=DC2,∴DB•(DB﹣BF)=DC2,∴DB2﹣6DB=16,解得:DB=8,或DB=﹣2(舍去),∵=,即=,解得:CF=3.八.解答题(共1小题,满分12分,每小题12分)25.解:(1)用交点式函数表达式得:y=(x﹣1)(x﹣3)=x2﹣4x+3;故二次函数表达式为:y=x2﹣4x+3;(2)①当AB为平行四边形一条边时,如图1,则AB=PF=2,则点P坐标为(4,3),当点P在对称轴左侧时,即点C的位置,点A、B、P、F为顶点的四边形为平行四边形,故:点P(4,3)或(0,3);②当AB是四边形的对角线时,如图2,AB中点坐标为(2,0)设点P的横坐标为m,点F的横坐标为2,其中点坐标为:,即:=2,解得:m=2,故点P(2,﹣1);故:点P(4,3)或(0,3)或(2,﹣1);(3)直线BC的表达式为:y=﹣x+3,设点E坐标为(x,x2﹣4x+3),则点D(x,﹣x+3),S=AB(y D﹣y E)=﹣x+3﹣x2+4x﹣3=﹣x2+3x,四边形AEBD∵﹣1<0,故四边形AEBD面积有最大值,当x=,其最大值为,此时点E(,﹣).。
2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 10

2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 101. I find ________ difficult to remember everything, though I’m still young. A.that B.this C.it D.what2.—Does Ted tell you if he _______ next Sunday? —No, he doesn’t. But if he ____, I’ll give you a ring. A.will come; will come B.will come; comes es; will come es; come3.Li Lei’s words made her ____________.A.happilyB.angrilyC.cryingD.angry4.Our classes are over ________ noon and then we go to have a rest ________ 1:00 in the afternoon.A. at; atB. in; inC. in; atD. at; in5.Amazing China (《厉害了, 我的国》) wins high praise from the public. I think the documentary is well worth__________.A.watchB.to watchC.watchingD.watched6.After the final exam , we will feel and we’ll have a summer holiday.A. relaxing; relaxingB. relaxing; relaxedC. relaxed; relaxedD. relaxed; relaxing7.一I seldom keepon my computer for more than an hour.一Is that so? But you seem to be comfortable games on your iPad for hours. A. working; playing B. working; play C. to work; playingD. to work; play8.It’s necessary for you to make plans your friends in Switzerland.A. seeB. seeingC. to seeD. to seeing9.—I haven’t worked the problem out yet. What am I supposed to do? 一Try again! It’s only difficult. A. a lot B. a bit C. too much D. too many10.You were to close the windows. Why were you so careless? A. allowed B. supposed C. caused D. forgotten11.Some classical pieces at the concert are traditional and have a lasting(价值).12.We should master the b skills of reading, writing and communicating. 13.They b differently when you were not around. 14. The old man is Gina’s grandfather, so Gina is his g .15.There are four s in a year. They are spring, summer, autumn and winter.16.The ccity of the US is not New York, but Washington D. C.17.In Switzerland, if you are 15 minutes late for dinner, your friend may get (很生气).18.在日本和美国人们在餐桌上的举止很不同。
2020-2021学年人教版新目标九年级上册期末考试试题及答案

人教版新目标九年级上册期末考试试题(满分120 分,考试时间100 分钟)第一部分:基础知识运用(共两节;满分40分)第一节单项选择(共20小题;每小题1分,满分20分)从每小题所给的四个选项中选出最佳选项,并在答题卡上将该项涂黑。
()1.She usually has egg and some porridge for breakfast.A. an,theB. an,\C. a,theD. a,\()2. -I have two soccer balls,what about you?-Oh,I don't have .A.someB. noC. anyD. much( )3. The film reminded him _____ what he had seen in American.A. toB. inC. ofD. for( )4. What animal do you like ______, a dog, a cat or a pig?A. wellB. betterC. bestD. very( )5. He traveled all over the world _____ he had a man-made leg.A. ifB. asC. becauseD. though( )6. Not only I but also Tom and Jack _____ interested in English because it _____ useful.A. is, isB. is, areC. are, isD. are, are( )7. I can’t go _____ because I have to go home at once.A. else anywhereB. anywhere elseC. else nowhereD. somewhere else( )8. Why does this woman decided _____ these places?A. not goB. doesn’t goC. not goingD. not to go( )9. Would you please help me _____ the picture on the wall?A. put upB. put onC. put intoD. put off( )10. Excuse me, could you _____ me your new dictionary?A. borrowB. keepC. lendD. take( )11. He is a _____ boy, so he can’t go to the park by himself.A. six-year-oldB. six year oldC. six-years-oldD. six years old ( )12. We have never seen _____ good a car _____ this.A. as, asB. so, asC. such, thatD. so, that( )13. _____ of them is a farm worker.A. BothB. AllC. NeitherD. Some( )14. It _____ us five hours to work out the problem.A. costB. spentC. paidD. took( )15. Let’s write them _____ before we forget them.A. downB. onC. toD. With( )16.-----Why don’t you take your lovely dog with you?-----It ______ for a long time. I feel lonely without him.A . has been dead B. died C. is dying D. was died( )17..Almost all the boys in our class are ________playing football. They play it a lot after school.A. interested atB. interesting inC. interesting atD. interested in( )18. The computer is still quite warm . It ________be used by somebody just now.A. mustB. mustn’tC. needD. can’t( )19. This story happened _____ the night of January twenty-first.A. atB.onC. inD. of( )20. Tom told me he had some problems _______ Chinese. He wanted me to help him.A. speakingB. talkingC. tellingD. saying第二节完形填空(共10 小题;每小题2 分,满分20分)先通读下面短文,掌握其大意,然后从短文后面各题所给的选项中选出最佳选项,并在答题卡上将该项涂黑。
2021届九年级上学期人教新目标 期末复习单元知识点精品测试卷 Unit 4

2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 41.—WeChat (微信) really influences people’s life. —____. It is easier for us to keep in touch with others. A. Mainly B. Exactly C. Simply D. Mostly2.— Lily won first prize in yesterday’s dancing competition. — Really? Then her mother must be her. A.mad at B.worried about C.interested in D.proud of3.—Simon failed the exam again.—That’s not surprising. Computer games___________ too much of his time. A.take inB.take onC.take offD.take up4.一I think it’s necessary to learn how to work in groups. —I quite agree. Sometimes it's even than grades.A. less importantB. more importantC. the least importantD. the most important5.______ Frank left school at 16, he still became a successful writer. A. Ever sinceB. In factC. After allD. Even though6.John live in the city, but he living in the countryside now.A. was used to; used toB. is used to; is used toC. used to; is used toD. used to; was used to 7.一 Did Gina use to be outgoing? 一. She used to be quiet.A. Yes, she didB. No, she didn’tC. Yes, she doesD. No, she doesn’t 8.—, Kang Li!一Yes, I used to be shy but now I’m pretty outgoing.A. You look beautifulB. You’re so shyC. You’ve changed a lotD. You stay the same9.Tom is a boy and his little sister Jean is only . A. fifteen -year -old; five -year -old B. fifteen years old; five -year -old C. fifteen -year -old; five years old D. fifteen years old; five years old10.—I’ve tried hard at my schoolwork but still . —Don’t be upset. Sometimes losing is only a sign that you really tried A. failedB. worriedC. improvedD. succeeded11.Quite a lot of teenagers have no idea how to (处理)with stress. 12.After that, his parents had much more (communicate) with him than theyused to.13.There are a lot of (activity) after class in our school. 14.The(普遍的)opinion is that the meeting was a success.15.I trust his ability to pass the (考试)easily, because he spent much time gettingready for it.16.Tom’s parents died when he was a child. His (happy) was understandable. 17.(Britain) people often begin their conversation by talking about weather.18.我们为莫言感到骄傲,因为他是第一个获得诺贝尔 文学奖的中国人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021届九年级上学期人教新目标期末复习单元知识点精品测试卷 Unit 91.Do you know the girl ______ father owns a company? A.who B.which C.that D.whose2.The young man ________ is a friend of mine. A.who I had a talk B.whom I had a talk with C.which I had a talk with D.whom I had a talk3.Many tourists prefer five -star hotels because they think expensive hotels always ________ guests with better service.A. prevent B. protect C . presentD. provide4.--The government is trying to protect the environment now. --Yeah. It is reported that some factories will be______ soon.A.set upB.shut downC.given upD.turned off 5.一CCTV has produced a TV show—Chinese Poetry Competition. Have you seen it? —Sure. Wu Yishu, 16, _____ studies at High School Affiliated to Fudan, is the winner. A.whichB.whereC.whoD.whom6.There are twelve boys and thirteen girls in Class Four, which means there are 25 students _____. A. in total B. in person C. in silence D. in fact7.I prefer_____ some shopping to _____ camping since the weather isn't lovely.A. do; going B . doing; go C. do; goD. doing; going8.—You should eat _____ fruit and vegetables. —Fruit is OK. But I don’t feel like _____ vegetables.A. a little; eatB. a lots of; to eatC. plenty of; eatingD. plenty of; to eat 9.My best friend was hurt in a traffic accident. I’d like to . A. dress him up B. pick him up C. cheer him upD. give him up10.He tried his best his dream and it. A. to achieve; stick onB. achieving; stick toC. to achieve; stick toD. achieve; stick on11.I prefer shoes that__________ cool. (be)12.In my spare time ,I often have funny d__________ with my foreign friends.13.Guo Feng is one of my favorite__________(sing), because he can write his own songs. 14.Many famous (director) wives appeared at the film festival with theirhusbands.15.Mary (shut) the door and windows before she went to bed. 16.Many people say dolphins are (intelligent)than dogs. 17.这是我听过的最令人感动的故事之一。
This is stories that I have ever heard.18.昨晚,我的一个中国朋友带我去听了一场中国民 乐的演奏会。
Last night, one of my Chinese friendsa concert of Chinese folk music.19. 这是我听过的最令人感动的乐曲。
This is music that I’ve ever heard.20. 他看起来很难过,所以我们尽力使他振作起来。
He looked sad, so we tried to .此卷只装订不密封 班级 姓名 准考证号 考场号 座位号答案以及解析1.答案:D解析:试题分析:本句中先行词the girl和下文句子主语father是所有关系,故引导词用whose,谁的,选D。
点评:定语从句引导词的用法比较复杂,其关键就是根据先行词的不同选择不同的引导词.并注意作介词宾语的引导词只能使用宾格形式.that不能用于非限制性定语从句中。
2.答案:B解析:试题分析:本句中先行词young man为下文从句的逻辑宾语,talk 不能直接接宾语。
Talk with和……谈话。
英语中指人的引导词作介词宾语时,需要用宾格形式whom,故选B。
3.答案:D解析:考查动词辨析。
句意:许多游客更愿意选五星级旅馆,因为他们认为昂贵的旅馆总是为客人提供更好的服务。
表示"为某人提供某物”,应用provide sb. with sth.或provide sth. for sb.。
故选D.4.答案:B解析:考查固定短语。
set up "建立";shut down"关闭";give up "放弃";turn off"截断(电流、水等)"。
结合句意"——政府现在正在努力保护环境。
——是的,据报道有些工厂很快就会被_____。
"可知,空处填shut down合适。
故选B。
5.答案:C解析:考查定语从句。
句意:——中央电视台制作了一档电视节目(中国诗词大会)。
你看过吗?——当然。
在复旦大学附中学习的16岁的武亦姝是获胜者。
定语从句的关系词:which用来指物;where用来指地点; who和whom用来指人,前者在定语从句中一般作主语,后者作宾语。
这里指代武亦姝,在从句中作主语。
故选C。
6.答案:A解析:考查固定短语。
in total “总共”;in person“亲自”;in silence“静静地”;in fact“事实上”。
结合句意“四班有12名男孩,13名女孩,即_____25名学生”可知空处用in total最合适。
故选A。
7.答案:D解析:考查固定搭配。
句意:既然天气不好,比起野营我更喜欢购物。
prefer... to...后跟动词时,需用动词-ing 形式。
故选D。
8.答案:C解析:考查固定搭配。
第一个空后为可数名词复数,a little后跟不可数名词,a lots of本身不对,故排除A、B 选项。
plenty of后跟不可数名词或可数名词复数。
feel like doing sth.是固定搭配,意为“想要做某事”,故选C。
9.答案:C解析:句意:我最好的朋友在交通事故中受伤了。
我想使他振奋起来。
dress up"装扮";pick up"(开车)接;cheer up ”(使)振奋起来";give up"放弃"。
根据句意可知选C。
10.答案:C解析:句意:他尽他最大的努力去实现他的梦想并且坚持它。
try one’s best to do sth."尽某人最大的努力做某事";stick to "坚持"。
11.答案:are解析:关系词that作从句主语时,从句的谓语动词要与先行词shoes保持一致,故用复数形式are。
12.答案:dialogues解析:have dialogues with sb. “和某人对话” 是短语搭配。
13.答案:singers解析:考查one of +名词复数, 故适当形式为singers。
14.答案:directors’解析:由空前的形容间Many可知,应用名词复数。
由空后的wives可知,应用名词所有格形式,作定语,故填directors’。
15.答案:shut解析:句意:玛丽上床睡觉前关好了门窗由后面的went可知,此处时态为一般过去时。
16.答案:more intelligent解析:句意:许多人说海称比狗更聪明:由空后的than可知,这里应用intelligent的比较级。
17.答案:one of the most moving18.答案:took me to19.答案:the; most; moving; piece; of20.答案:cheer; him; up。
