方差分析的基本思想
方差分析

二期矽肺 100.67 93.47 74.97 88.06 113.52 101.14 95.10 118.98
三期矽肺 97.58 83.58 103.81 107.10 108.42 82.58 89.01 77.11
方差分析的基本思想
总变异:从例中看出,32个观察值大小参差不 齐,这种个体值与总均数之间的差异称为总变 异。
多个样本均数间的多重比较
多个样本均数间的多重比较:也称为两两 比较,主要用于探索与证实多组均数中, 哪两个总体均数间有差别,哪两个均数间 没有差别。 如果多组均数的比较采用两样本均数比较 的t检验,会加大I型错误。
多个样本均数间的多重比较
LSD-t检验:最小显著差法
容易获得P<0.05,但是假阳性率较高;
完全随机设计资料的方差分析
方差分析结果表 变异来源 总 组间 组内 SS 86.740 45.091 41.649 ν 39 3 36 MS F P <0.05
15.030 12.990 1.157
3.确定P值和作出推断结论:以ν组间=3,ν组内=36, 查F界值表得P<0.05, 按α=0.05水准拒绝H0 ,接受 H1,故可以认为给予不同剂量的三菱莪术液,小鼠瘤 重间差别有统计学意义。
方差分析
主要内容
方差分析的基本思想 完全随机设计、随机区组设计、拉丁方设 计、交叉设计和析因设计资料方差分析的 基本过程
多个样本均数的比较
两个样本均数的比较:
1次t-test,α=0.05;
三个样本均数的比较:
3次t-test,α=1-(1-0.05)3=0.14;
四个样本均数的比较:
6次t-test,α=1-(1-0.05)6=0.26;
方差分析的基本思想
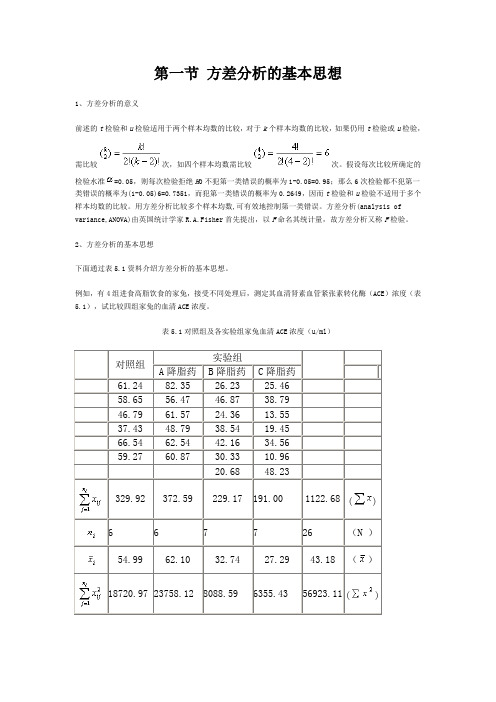
第一节方差分析的基本思想1、方差分析的意义前述的t检验和u检验适用于两个样本均数的比较,对于k个样本均数的比较,如果仍用t检验或u检验,需比较次,如四个样本均数需比较次。
假设每次比较所确定的检验水准=0.05,则每次检验拒绝H0不犯第一类错误的概率为1-0.05=0.95;那么6次检验都不犯第一类错误的概率为(1-0.05)6=0.7351,而犯第一类错误的概率为0.2649,因而t检验和u检验不适用于多个样本均数的比较。
用方差分析比较多个样本均数,可有效地控制第一类错误。
方差分析(analysis of variance,ANOVA)由英国统计学家R.A.Fisher首先提出,以F命名其统计量,故方差分析又称F检验。
2、方差分析的基本思想下面通过表5.1资料介绍方差分析的基本思想。
例如,有4组进食高脂饮食的家兔,接受不同处理后,测定其血清肾素血管紧张素转化酶(ACE)浓度(表5.1),试比较四组家兔的血清ACE浓度。
表5.1对照组及各实验组家兔血清ACE浓度(u/ml)对照组实验组A降脂药B降脂药C降脂药61.24 82.35 26.23 25.4658.65 56.47 46.87 38.7946.79 61.57 24.36 13.5537.43 48.79 38.54 19.4566.54 62.54 42.16 34.5659.27 60.87 30.33 10.9620.68 48.23329.92 372.59 229.17 191.00 1122.68 () 6 6 7 7 26 (N )54.99 62.10 32.74 27.29 43.18 ()18720.97 23758.12 8088.59 6355.43 56923.11 ()由表5.1可见,26只家兔的血清ACE浓度各不相同,称为总变异;四组家兔的血清ACE浓度均数也各不相同,称为组间变异;即使同一组内部的家兔血清ACE 浓度相互间也不相同,称为组内变异。
第九章 方差分析

第九章方差分析前面介绍了两个样本均数比较的t检验,那么多个样本均数的比较应该采用什么方法?方差分析(analysis of variance, ANOV A)是20世纪20年代发展起来的一种统计方法,由英国著名统计学家R.A.Fisher提出,又称F检验,是通过对数据变异的分析来推断两个或多个样本均数所代表总体均数是否有差别的一种统计学方法。
本章首先介绍方差分析的基本思想和应用条件,然后结合研究设计类型分别介绍各类方差分析方法。
第一节方差分析的基本思想和应用条件一、方差分析的基本思想方差分析的基本思想是把全部观察值间的变异按设计类型的不同,分解成两个或多个组成部分,然后将各部分的变异与随机误差进行比较,以判断各部分的变异是否具有统计学意义。
例9.1 为研究大豆对缺铁性贫血的恢复作用,某研究者进行了如下实验:选取已做成贫血模型的大鼠36只,随机等分为3组,每组12只,分别用三种不同的饲料喂养:不含大豆的普通饲料、含10%大豆饲料和含15%大豆饲料。
喂养一周后,测定大鼠红细胞数(×1012/L),试分析喂养三种不同饲料的大鼠贫血恢复情况是否不同?表9.1 喂养三种不同饲料的大鼠红细胞数(×1012/L)普通饲料10%大豆饲料15%大豆饲料合计X 4.78 4.65 6.80 4.65 6.92 5.913.984.447.284.04 6.167.51 3.445.997.51 3.776.677.743.65 5.298.194.91 4.707.154.795.058.185.316.01 5.534.055.677.795.16 4.688.03in12 12 12 36 (n)i X ∑ 52.53 66.23 87.62 206.38(X ∑)i X4.385.52 7.30 5.73 (X ) 2i X ∑ 234.2783373.2851647.73121255.2946(2X ∑)表9.1按完全随机设计获得的36个数据(X )中包含以下三种变异: 1. 总变异 36只大鼠喂养一周后测定红细胞数X 各不相同,即X 与总均数X 不同,这种变异称为总变异(total variation)。
方差分析SPSS

F界值为单尾
4、根据统计推断结果,结合相应的专业知识,给出一个专 业的结论。
随机区组设计的两因素方差分析
配伍设计有两个研究因素,区组因素和处理因素。 事先将全部受试对象按某种或某些特征分为若干个 区组,使每个区组内研究对象的特征尽可能相近。 每个区组内的观察对象与研究因素的水平数k相等, 分别使每个区组内的观察对象随机地接受研究因素 某一水平的处理。
k ni
SS总=
( Xij X )2 ,总 N 1
i1 j 1
组间变异:各处理组的样本均数也大小不等。大小可用各组
均数 X i 与总均数 X 的离均差平方和表示。
k
SS组间= ni ( X i X )2 , 组间 k 1, MS组间=SS组间 组间 i 1
组内变异:各处理组内部观察值也大小不等,可用各处理组
内部每个观察值 X ij与组均数 X i 的离均差平方和表示。
k ni
SS组内=
( Xij Xi )2,组内 N k,MS组内=SS组内 组内
i1 j1
三种变异的关系
SS总 SS组间 SS组内
并且该等式和上面的等式存在如下的对应关系 总变异=随机变异+处理因素导致的变异
总变异=组内变异 + 组间变异
=0.05
2、选定检验方法,计算检验统计量
F MS处理 MS误差;F MS区组 MS误差 3、确定P值,作出推断结论
F F ,P (处理,误差 ) F F ,P (处理,误差 )
F界值为单尾
4、根据统计推断结果,结合相应的专业知识,给出一个专 业的结论。
多重比较
LSD-t 检验:适用于检验k组中某一对或某几对在 专业上有特殊意义的均数是否相等。
F检验1

3.3
4.4
3.6
3.6
4.4
4.4
4.3
3.4
5.1
4.1
4.2
5.0
4.2
4.7
5.5
3.3
4.2
4.7
每次不犯第一类错误的概率为 (1-0.05)=0.95,
当这些检验独立进行时,则每次比较均 不犯错误的概率为0.953=0.8574,相应犯第 一类错误的概率为1-0.8574=0.1426,远大 于设定的0.05,并且随着比较次数的增大, 犯第一类错误的总概率将不断增大并趋向于 1。
均方差,均方(mean square,MS)
变异程度除与离均差平方和的大小有关外, 还与其自由度有关,由于各部分自由度不相等, 因此各部分离均差平方和不能直接比较,须将 各部分离均差平方和除以相应自由度,其比值 称为均方差,简称均方(mean square,MS)。组 间均方和组内均方的计算公式为:
363.51
322.98
355.99
309.60
288.76
219.72
338.83
386.67
143.17
表3 大鼠肾组织液中NO水平(ca/μmol·L-1)
正常对照组 肾缺血60min组 肾缺血60min再灌流组 合计
437.98
322.75
284.04
…..
…..
……
338.83
386.67
1.4 f( F)
1.2
F 分布曲线
1.0
0.8
0.6
0.4
0.2
0.0
0
1
2F
3
4
1.4 f( F)
1.2
1.0
5第六章方差分析

练习
• 以小鼠研究正常肝核糖核酸(RNA)对癌细 胞的生物学作用,试验分为对照组(生理 盐水)、水层 RNA组和酚层RNA组,分别用 此三种不同处理诱导肝细胞的FDP酶活力, 得数据如下。该三组资料均服从正态分布, 试比较三组均数有无差别?
ex_36.sas
表 6.1 对照组
2.79 2.69 3.11 3.47 1.77 2.44 2.83 2.52
复相关系数(确定系数),变异系数,均方根,总均数
对自变量的检验
R-Square:等于模型的平方和除以总 平方和,用于度量在因变量的变差 里能够由模型决定的比例有多少, 越接近1,效果越好。
检验的显著水平、自由度、 误差均方
具有相同字母的组间 均值差异没有统计学意义。
第2组具有A和B两个字母,所以 第二组和第三组,第一组均没有差异。
单因素方差分析
假设某单因素试验有k个处理,每个处理有n次重 复,共有nk个观测值。这类试验资料的数据模式
如下表所示。
(一)总平方和的分解 在上表中,反映全部观测值总变异的总平方和
是各观测值xij与总平均数的离均差平方和,记 为SST。即
kn
SST
( xij x.. ) 2
i1 j 1
nj 组内样本容量j 1,2,,n ki 组数,即水平数i 1,2,,k x.. 总平均数 xij i水平下第 j个样样本
变 差
组间 变差
总 变 差 组内 变差
组数(水平数)
(二)总自由度的剖分
在计算总平方和时,资料中的各个观测值要
kn
受 (xij x这..) 一0 条件的约束,故总自由度等于 i1 j1
资料中观测值的总个数减1,即kn-1。
dfT kn 1 df t k 1 df e dfT df t
方差分析

第三节 随机区组设计资料的方差分析
一、随机区组设计
1。随机区组设计
随机区组设计又称配伍组设计,是配对设计的扩展。 首先从总体中随机抽样,然后将样本中的所有受试对 象,按条件相同或相近配成若干组(随机区组或配伍 组),再将每组中的几个受试对象随机分配到不同的 处理组中去,这种设计的方法称随机区组设计。
变异程度。计算公式如下:
SS总
2
Xij X
X
2 ij
C
其中:
C X 2 N
用离均差平方和表示总变异大小受样本容量
的影响,样本容量越大,SS越大,所以必须扣 除n的影响,严格的讲是扣除ν的影响。
总变异的自由度:ν 总=N-1
SS总总 称为总变异的均方,用MS总表示。
2。完全随机设计资料的分析方法
完全随机设计资料在进行统计分析时,需根 据数据的分布特征选择方法,对于正态分布且方 差齐的资料,常采用完全随机设计的单因素方差
分析(one-way ANOVA)或两样本t检验(g=2);
对于非正态或方差不齐的资料,可进行数据变换 或采用秩和检验。
二、完全随机设计方差分析
SS区组 区组
MS区组 MS误差
误差 SS总 SS处理 SS区组 (g 1)(n 1) SS误差 误差
其中:C ( X )2 N
例4-4 某研究者采用随机区组设计进行实验,比较三 种抗癌药物对小白鼠肉瘤抑瘤效果,先将15只染有肉瘤 小白鼠按体重大小配成5个区组,每个区组内3只小白鼠 随机接受三种抗癌药物(具体分配结果见例4-3),以 肉瘤的重量为指标,试验结果见表4-9。问三种不同的 药物的抑瘤效果有无差别?
方差分析的基本思想

H1: i (i=1,…,c)不全相等
作统计推断。
显然,组间离均差平方和的大小与自 由度有关。能够客观反映组间变异的 是组间均方
,
MSTR SSTR / TR (10.5)
数学上可以证明
SST SSTR SSe (10.6)
,
,,
T
TR
e (10.7)
F MS TR MS e
(10.8)
式(10.8)反映了组间变异与组内变 异的比值,可以应用式对检验假设
MSe SSe / e (10.3)
不同处理组样本均数之间的差异称 为组间变异。产生组间变异的原因 一方面是个体变异,另一方面是各 组总体均数之间可能存在的实质性 差异差别。用组间离均差平方和反 映组间变异。
c
SSTR ni (xi x)2 (10.4) i 1
相应的自由度为 TR c 1
c ni
SST
( X ij x)2
i1 j1
(10.1)
相应的自由度为νT=N-1。
处理组内每个观察值之间的差异来源 于同一总体内的个体变异,称为组内
变异,可用组内离均差平方和表示:
c ni
SSe
( X ij xi ) 2 (10.2)
i1 j1
相应的自由度νe=N-c。
由于的大小与自由度有关,能够客观 反映组内变异的是组内均方:
第一节 方差分析的基本思想
方差分析的基本思想是,首先将总 变异分解为几个部分,每部分与特 定的因素相联系。之后构造检验统 计量F,实现对总体均数的推断。 方差分析的应用条件是各组资料取 自正态分布,各总体方差齐同。
现以随机设计为例来说明方差分析基 本思想。
方差分析的基本思路

方差分析的基本思想是:通过分析研究不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
方差分析的基本思想可以归纳为根据研究设计的类型,将全部测量值总的离均差平方和及其自由度分解为两个或多个部分,每个部分的变异都由某个因素的作用(或某几个因素的交互作用)引起。
通过比较不同变异来源的均方,借助F分布做出统计推断,从而推论各种处理因素对研究结果有无影响。
对样本均数进行比较的方差分析方法与研究设计类型有关。
方差分析中分析的数据是按照特定研究设计进行试验所得的数据,不同的研究设计其总变异的分解有所不同。
因此在应用方差分析时,要结合具体的研究设计方法来选择相应的方差分析方法。
常用的设计有:随机单位组设计/拉丁方设计/交叉设计/析因设计/正交设计/嵌套设计/裂区设计/重复测量数据/协方差分析等。
进行方差分析时同样要求资料满足正态分布且方差相等两个基本假设(与独立样本t检验的条件一样一样滴)。
即:各样本组内观察值相互独立,且服从正态分布。
各样本组内观察值总体方差相等,即方差齐性(homogeneity of variance)。
本节只涉及最基本的一种设计形式—完全随机设计。
完全随机设计(Completely Random Design)是指将受试单位随机地分配到各处理组中进行实验研究,或分别从互相独立的不同总体里随机抽取样本进行比较的一种设计方法。
例:某高原研究组将籍贯相同、年龄相同、身高体重接近的30名新战士随机分为3组,对照组按常规训练;锻炼组每天除常规训练外,还接受中速长跑与健身操锻炼;药物组除常规训练外,服用抗疲劳药物,1个月后测量第1秒用力肺活量(L),结果见表1所示。
试比较3组第1秒用力肺活量有无差别。
方差分析

ni
x x
i i
xi
ij
2 ij
6 23.48 140.87 3317.85
6 17.18 103.09 1780.96
6 14.68 87.79 1289.92
6 24 13.92 1 7.30 83.50 425.25 1167.03 7555.78
区组间的变异是指每一区组的样本均数各不 相同,与总体数也不相同。既反映了区组不同的 影响,同时也包括了随机误差(含个体差异和随 机测量误差)。 由于区组内的个体特征比较一致,减少了个体 间差异对研究结果的影响,因此可提高研究的效 率。
SSe 组内 X ij X i
i 1 j i
k
ni
2
即观察值Xij与组均数 X 的离均差平方和 i
SS总 SS组间 SS组内
总 N 1
组间 k 1
组内 N k
总 组间 组内
单因素方差分析的计算公式
变异来源 总 组间 离均差平 自由度v 方和SS 2 N-1
三.随机区组设计资料方差分析中变异的分解
处理间变异 MS组间 MS A 总变异 处理因素+随机 误差的作用 。 区组因素+随机 误差的作用 随机 误差的作用
MS总
区组间变异 MS区组 MS B。
误差 MS误差 MS E
F1 MS A MSe F2 MS B MS e
随机区组设计方差分析的计算公式
方差分析表
变异来原 υ SS MS 组间 2 6226.07 3113.035 组内 33 4306.53 130.50 总变异 35 10532.60 F 23.85 P <0.01
方差分析

• 区组间
∑
j
b-1
υ区组
SS误差
SS误差
• =SS总—SS处理 --SS 区组
(K −1)(b−1)
N = ∑ni
υ误差
k为处理组数
(∑ X )2 C=
N
例9-20
在抗癌药物筛选试验中,拟用 只小白鼠按体重相近者为一 在抗癌药物筛选试验中,拟用20只小白鼠按体重相近者为一 个区组,一共五个区组,每个区组各有四只小白鼠。 个区组,一共五个区组,每个区组各有四只小白鼠。分别观察四种药 物对小白鼠移植性肉瘤( 的抑瘤效果,结果见表9-17。问四种 物对小白鼠移植性肉瘤(S180)的抑瘤效果,结果见表 。 药物的抑瘤效果有无差别? 药物的抑瘤效果有无差别?
M 区组 = S
•
SS区组
υ区组
0.11233 = = 0.02808 4
方差分析
钟崇洲 zcz5460@
方差分析也是统计 检验的一种。由英 国著名统计学家: R.A.FISHER推导出 来的,也叫F检验。
• 一、方差分析的基本思想
组内变异 反映随机误差(E)大小。 反映随机误差(E)大小。 (E)大小 MS组内或MSe
总变异
全部观察值之间的变异 MS总或MST
• 二.应用 的条件是: 的条件是:
),即要求各观察值之 (1)独立性(independence),即要求各观察值之 )独立性( ), 间相互独立; 间相互独立; ),即要求样 (2)正态性(normality),即要求样 本来 )正态性( ), 自正态分布的总体; 自正态分布的总体; (3)方差齐性( homogeneity), 即要 )方差齐性( ), 体方差相等。 求两样本所对应的总 体方差相等。 • •
方差分析的基本思想

方差分析的基本思想
方差分析是检验多个总体均值是否相等的统计方法。
它是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。
方差分析的基本思想是根据研究目的和设计类型,将总变异中的离均差平方和SS及其自由度分别分解成相应的若干部分,然后求各相应部分的变异;再用各部分的变异与组内(或误差)变异进行比较,得出统计量F值;最后根据F值的大小确定P值,作出统计推断。
方差分析的检验假设H0为各样本来自均数相等的总体,H1为各总体均数不等或不全相等。
若不拒绝H0时,可认为各样本均数间的差异是由于抽样误差所致,而不是由于处理因素的作用所致。
理论上,此时的组间变异与组内变异应相等,两者的比值即统计量F为1;由于存在抽样误差,两者往往不恰好相等,但相差不会太大,统计量F应接近于1。
若拒绝H0,接受H1时,可认为各样本均数间的差异,不仅是由抽样误差所致,还有处理因素的作用。
此时的组间变异远大于组内变异,两者的比值即统计量F明显大于1。
在实际应用中,当统计量F值远大于1且大于某界值时,拒绝H0,接受H1,即意味着各样本均数间的差异,不仅是由抽样误差所致,还有处理因素的作用。
方差分析的基本思想

185
A2 A3
184 206
198 191
179 218
190 224
表中A1是强调运输方便性的广告,A2是强调节省燃料的经济 性的广告,A3是强调噪音低的优良性的广告. 试判断:新闻广 告的类型对该种机械的销售量是否有显著影响? 若影响显著, 哪一种广告内容为好?
解 新闻广告是所要检验的因素,三种不同的内容可看作三 个水平,因而这是一个单因素三水平的试验.
第7.1节
方差分析的基本思想
实例 某食品集团的产品销售覆盖全国, 主要分布于25个省 份,是一个颇受消费者青睐的品牌.集团营业部根据其销售情 况, 将这25个省份划分为东北、华北、东南、西北和中部5个 销售区域,每个区域由一名销售经理负责.年末将近,各部门 经理都在准备年度报告.营业部总经理准备分析一下过去一年 里各区域的销售业绩.他从营业部专员手中得到了各省份销售 情况.总经理由此发现,东北地区今年对集团的收入贡献不大规模比其他地区小,消费习惯存在差异等.当然,这种差异也 可能是由于偶然因素.但如果各区域间具有显著差异,则应当 引起销售部门的注意,从而进一步研究不同区域的不同特征, 进一步进行市场细分,采取适当的营销策略. 在形成报告之前,总经理决定对各地区的销售量进行分析, 首先检验各区域间的差异是否由于偶然原因所致,确认各区域 销售量之间是否存在着明显的差异.
研究对象的特征值,即所考察的试验(其涵义包括调查, 收集等)结果(如产品质量、数量、销量、成本等)称为试 验指标,简称指标,常用x 表示.
在试验中对所关心的“指标”有影响的、 要加以考察
而改变状态的原因称为因素,用A、B、C等大写英文字母表 示. 因素在试验中所取的各种不同状态称为因素的水平. 因 素A的r个水平常用A1,A2,…,Ar 表示,其中r称为因素A的 水平数. 若在试验中考虑了因素的全部水平,则该因素称为固定 因素;若在试验中仅随机选择了因素的部分水平,则该因素称 为随机因素.
方差分析(ANOVA)

方差分析(ANOVA)一、方差分析的基本思想1. 方差分析的概念方差分析(ANOVA)又称变异数分析或F检验,其目的是推断两组或多组资料的总体均数是否相同,检验两个或多个样本均数的差异是否有统计学意义。
我们要学习的主要内容包括单因素方差分析即完全随机设计或成组设计的方差分析和两因素方差分析即配伍组设计的方差分析。
2. 方差分析的基本思想下面我们用一个简单的例子来说明方差分析的基本思想:如某克山病区测得11例克山病患者和13名健康人的血磷值(mmol/L)如下,患者:0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11健康人:0.54 0.64 0.64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 1.56 1.87问该地克山病患者与健康人的血磷值是否不同?从以上资料可以看出,24个患者与健康人的血磷值各不相同,如果用离均差平方和(SS)描述其围绕总均数的变异情况,则总变异有以下两个来源:(1)组内变异,即由于随机误差的原因使得各组内部的血磷值各不相等;(2)组间变异,即由于克山病的影响使得患者与健康人组的血磷值均数大小不等。
而且:SS总=SS组间+SS组内v总=v组间+v组内如果用均方(即自由度v去除离均差平方和的商)代替离均差平方和以消除各组样本数不同的影响,则方差分析就是用组内均方去除组间均方的商(即F值)与1相比较,若F值接近1,则说明各组均数间的差异没有统计学意义,若F值远大于1,则说明各组均数间的差异有统计学意义。
实际应用中检验假设成立条件下F值大于特定值的概率可通过查阅F界值表(方差分析用)获得。
3. 方差分析的应用条件应用方差分析对资料进行统计推断之前应注意其使用条件,包括:(1)可比性,若资料中各组均数本身不具可比性则不适用方差分析。
(2)正态性,即偏态分布资料不适用方差分析。
对偏态分布的资料应考虑用对数变换、平方根变换、倒数变换、平方根反正弦变换等变量变换方法变为正态或接近正态后再进行方差分析。
方 差 分 析

16
任务
方差分析
三、双因素方差分析
(二)无重复作用的双因素方差分析的基本步骤
1.提出假设
(1)假设一
响。
H01 : 1 2 r
H11 : 1 ,2 , ,r
,因素A(自变量A)对因变量没有显著影响。 不全相等,因素A(自变量A)对因变量有显著影
其中, i 为行因素A第i水平的均值。
17
任务
即 B1 ,B2 , ,Bs 。将因素A,B水平的每对组合 (Ai ,Bj ) ,(i 1,2, ,r ;j 1,2, ,s)
都看作一个总体,则有rs个总体。对每个总体 都做一次试验或抽取容量为1的
随机样本,其试验结果或观察值记为 xij (i 1,2 , ,r ;j 1,2 , ,s) 。
表7-6略。
18
任务
方差分析
三、双因素方差分析
(二)无重复作用的双因素方差分析的基本步骤
2.计算有关均值
① 令xi 表示行因素A第i个水平下各观察值的均值,则
s
xij
xi
j 1
s
(i 1,2 , ,r)
(7-17)
② 令 x j 表示列因素B第j个水平下各观察值的均值,则
(三)计算误差平方和
任务
10
方差分析
二、单因素方差分析
② 水平项误差平方和SSA是各组平均值 xi (i 1,2, ,k) 总平均值 x 的误差平方和,反映了各水平总体的样本均 值之间的差异程度,因此又称为组间平方和,用公式表示 为
k ni
k
SSA
(xi x )2 ni (xi x )2
。三个平方和所对应的自由度如下所示。
01 SST的自由度为 ,其中n为全部观察值的个数。 02 SSA的自由度为 ,其中k为因素水平(总体)的个数。 03 SSE的自由度为 。
方差分析的基本思想

复习思考题
1. 方差分析的基本思想 2. 方差分析的步骤 3. 组内离差平方和,组间离差平方 和与总离差平方和各反映了什么? 4. 方差分析的适用条件是什么?
则有
SS 总= SS 间+ SS 内
上 述称 为 平方 和 分 解公 式 (经 简 单推 导就 可 得 ) 注意: MS
总
=
MS
间
+
MS
内
?
六、方差分析的实质
按指定来源分解变异, 按指定来源分解变异, 方差分析是分解变异 的一种技巧。 的一种技巧。
七、关于方差分析适用条件的说明 1.各总体均服从正态分布 2.各样本相互独立 3.各总体方差相等 其实以上并非方差分析的适用条 件,而是实际问题的条件。
xk 2
┆
x1n1 x1
1 x= ∑ ni
k n ij
┆
x2n 2 x2
┆
xknk xk
∑∑ x
i =1 i =1
欲推断: 有无显著异 欲推断: u1 , u2 …uk 有无显著异
SS间 MS间 = n间
k n
SS内 MS内= n内
先考虑总离差平方和 SS 总
SS总 = ∑
i =1
∑
i =1
( xi内离差构成
1. 若各组内个体大小一致 则 SS 总即为 SS 间 , 将各组内个体 x ij 取成 xi , 此时
SS 间=SS 总=
∑∑
i j
( xi x ) 2 = ∑ n k ( xi x ) 2
i =1
k
2.若各组平均水平一致, 则 SS 总即为 SS 内, 故用 xij xi 代替 x ij
x1 , x2 , x3 之间有差异。 现在的任务是通过样本推断 1 , 2 , 3 之
方差分析(ANOVA)

n4
n3 n2 n1
Y4
Y3 Y2
Y1
例子:某研究者在某单位工作人员中进行了体重指 数(BMI)抽样调查,随机抽取不同年龄组男性受试 者各16名,测量了被调查者的身高和体重值,由此按 照BMI=体重/身高2公式计算了体重指数,请问,不 同年龄组的体重指数有无差异。
项目
样本量 平均值 标准差
关于因素与水平
因素也称为处理因素(factor) 每一处理因素至少有两个水平(level)(也称“处理组”
)。
完全随机设计:
将实验对象随机分配到不同处理组的单因素 设计方法。针对一个处理因素,通过比较该 因素不同水平组均值,推断该处理因素不同 水平组的均值是否存在统计学差异。
例 在评价某药物耐受性及安全性的I期临床试验 中,对符合纳入标准的30名健康自愿者随机分为 3组每组10名,各组注射剂量分别为0.5U、1U、 2U,观察48小时部分凝血活酶时间(s)试问不 同剂量的部分凝血活酶时间有无不同?
当各组样本含量不同,选择Scheffe法,得结果:
Dependent Variable: no Scheffe
Multiple Comparisons
M ea n
Di ffe re nce
(I) group (J) group
(I-J)
Std. Error
Si g.
1
2
13.61250 26.51068
方差分析步骤 :
(1)提出检验假设,确定检验水准
H0:μ1=μ2=μ3 H1:μ1,μ2,μ3不全相同 a=0.05
(2)计算检验统计量F 值
(3)确定P值,做出推断结论
F0.05(2,26) =2.52,F>F0.05(2,26) ,P<0.05,拒绝 H0。 三种不同剂量48小时部分凝血活酶时间 不全相同。
方差分析

区组
k(x
j
b
j
x)
2
或
( xij ) 2 k
C*
b–1 N–k–b+1 或 (k–1) (b–1) N–1
误差
SS总 SS处理 SS区组
( x ) 2 x N
2
总
或
x
2
C
*
SS 总 N 1
*C
( xij ) 2
i j
k
b
N
( x ) 2
N
三、随机区组设计的方差分析
变异来源 SS v MS F P
组间 组内
总
2384.03 5497.84
7811.87
2 1192.01 27
29
203.62
5.8540
<0.01 (0.0077)
(3)确定P值和作出统计推断:
P<0.01,拒绝原假设,接受备择假设,可认 为三种人群的载脂蛋白不同。
三、随机区组设计的方差分析
例2. 对小白鼠喂以A、B、C三种不同的营养 素,目的是了解不同营养素增重的效 果。采用随机区组设计方法,以窝别 作为划分区组的特征,以消除遗传因 素对体重增长的影响。现将同品系、 同体重的 24只小白鼠分为8个区组,每 个区组3只小白鼠。三周后体重增加结 果(克)列于表3。问小白鼠经三种不 同营养素喂养后所增体重有无差别?
随机区组设计方差分析的计算公式 变异来源 离均差平方和(SS) 自由度(df) 均方(MS)
k i
F
处理组
n (x
i i
k
i
x)
2
或
b j
( xij ) 2
j
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
推断 1 , 2 和 3 之间有无显著差异。 由 x1 , x2 , x3 不相等, 不能直接得出 1 , 2 , 3 不尽相等的 结论,原因是:造成 x1 , x2 , x3 不相等可能有两个方面因素: 一是 1 , 2 , 3 不等,二是 1 2 3 ,但由于抽样误差, 造成 x1 , x2 , x3 之间有差异。现在的任务是通过样本推断
┆
x
i 1 j 1
k
ni
ij
, 2 k 1 欲推断: 有无显著异
SS间 MS间 n间
k ni
SS内 MS内= n内
先考虑总离差平方和 SS 总
SS 总
i 1
j 1
( x ij x ) 2
SS 总由组间离差和组内离差构成
1. 若各组内个体大小一致 则 SS 总即为 SS 间 ,
二、方差分析的直观思想
2.如果 1 , 2 , 3 有差异,则组间差异不仅 有个体差异的影响还要受到总体差异的影 响,这时组间方差 MS 比组内方差MS 大得
间
内
多,据此,可以按假设检验的方法来处理 组间方差 H : 。如果 不是太大,则接受 组内方差
0 1 2 3
原假设;若比值很大则否定原假设。具体 定量检验ቤተ መጻሕፍቲ ባይዱ要了解比值的分布并且要给出
MS间 MS内
F~F (k 1, N k )
,n内 ) (n间
查表得 F 结论
的值
五、平方和分解公式
由前面知
SS 总 =(X
ij
2 X)
SS 间= ni ( x i x ) 2
2 SS内=(x ij x i)
SS = SS + SS 总 间 内 则有
上述称为平方和分解公式(经简单推导就可得) 注意:下式是否成立 MS 总 = MS 间 + MS 内 ?
方差分析的基本思想
一、 二、 三、 四、 五、 六、 七、 八、 问题的提出 方差分析的直观思想 MS 间 和MS 的数量表示 F检验 平方和分解公式 方差分析的实质 关于方差分析适用条件的说明 复习思考题
内
一、问题的提出
例 8.1 为了探索简便易行的发展大学生心血 管系统机能水平的方法,在某年级各项身 体发育水平基本相同,同年龄女生中抽取 36人随机分为三组,用三种不同的方法进 行训练,三个月后,测得哈佛台阶指数如 表8.1 ,试分析三种不同的训练方法对女大 学生心血管系统的影响有无显著性差异。
1 , 2 , 3 之间有无显著性差异。
二、方差分析的直观思想
1.如果 1 , 2 , 3 之间没有差异,则三 个样本之间的差异(以组间方差衡量)由 抽样误差带来, 实质上由各组内个体之间 的差异造成,组内个体之间的差异的大 小,以组内方差来衡量。这时,组间方差
MS MS 内 相近 间 与组内方差
k 1, n内 (ni 1) ni k n间
故
SS间 ni ( xi x )2 MS间 n k 1 间
ni 1 n总
MS 内=
SS 间 n内
(x x n k
ij i
i
)2
四、F检验
H0 :
F
1 2 k
x 将各组内个体 ij
取成 xi ,
( xi x ) ni ( xi x ) 2
2 i 1 k
此时
SS 间=SS 总= i j
2.若各组平均水平一致, 则 SS 总即为 SS 内, 故用 xij xi 代替 x ij
2 SS SS ( x x ) ij i 内 此时 总
六、方差分析的实质
按指定来源分解变异, 方差分析是分解变异 的一种技巧。
七、关于方差分析适用条件的说明 1.各总体均服从正态分布 2.各样本相互独立 3.各总体方差相等 其实以上并非方差分析的适用条 件,而是实际问题的条件。
复习思考题
1. 方差分析的基本思想与实质 2. 组内离差平方和,组间离差平方和
表 8.1
2 , N( 1 )
2 ( , N 2 )
N ( 3 , 2 )
A3
编号 1 2 ┆ 12 x
A1
A2
76.53 60.05 ┆ 56.24 60.15
43.12 42.54 ┆ 42.40 56.19
61.31 60.00 ┆ 67.26 69.05
分析
根据研究目的,这里有三个正态总体N ( 1 , 2 ) ,N ( 2 , 2 ) ,
MS间 和 MS内 的计算表达式
三、 MS间 和MS内 的数量表示 考虑一般情况
N ( 1 , 2 ) N ( 2 , 2 )
x21 x22
┄ ┄ ┄ ┄ ┄ ┄ ┄
N ( k , 2 )
xk1 xk 2 xknk xk
1 x11 x12 ┆ x1n1 x1
1 x ni
2
K
┆ x2 n 2 x2
与总离差平方和各反映了什么? 3. 总方差与组间方差和组内方差的关 系
