扭转习题1(精选)
圆轴扭转练习带答案

六章圆轴的扭转一、填空题1、圆轴扭转时的受力特点是:一对外力偶的作用面均____________________ 于轴的轴线,其转向 _________ 。
2、圆轴扭转变形的特点是:轴的横截面积绕其轴线发生_____________________ 。
3、在受扭转圆轴的横截面上,其扭矩的大小等于该截面一侧(左侧或右侧)轴段上所有外力偶矩的_________ 。
4、圆轴扭转时,横截面上任意点的切应力与该点到圆心的距离成___________________________ 。
5、试观察圆轴的扭转变形,位于同一截面上不同点的变形大小与到圆轴轴线的距离有关,显然截面边缘上各点的变形为最 ________________________________ , 而圆心的变形为________________ 。
6、圆轴扭转时,在横截面上距圆心等距离的各点其切应力必然_______________________ 。
7、从观察受扭转圆轴横截面的大小、形状及相互之间的轴向间距不改变这一现象,可以看出轴的横截面上无___________________ 力。
8、圆轴扭转时,横截面上切应力的大小沿半径呈 ________________ 规律分布。
10、圆轴扭转时,横截面上内力系合成的结果是力偶,力偶作用于面垂直于轴线,相应的横截面上各点的切应力应垂直于________________ 。
11、受扭圆轴横截面内同一圆周上各点的切应力大小是___________________ 的。
12、产生扭转变形的一实心轴和空心轴的材料相同,当二者的扭转强度一样时,它们的___________ 截面系数应相等。
13、横截面面积相等的实心轴和空心轴相比,虽材料相同,但________________________ 轴的抗扭承载能力要强些。
16 、直径和长度均相等的两根轴,其横截面扭矩也相等,而材料不同,因此它们的最大剪应力是 ___________ 同的,扭转角是 __________ 同的。
扭转习题1
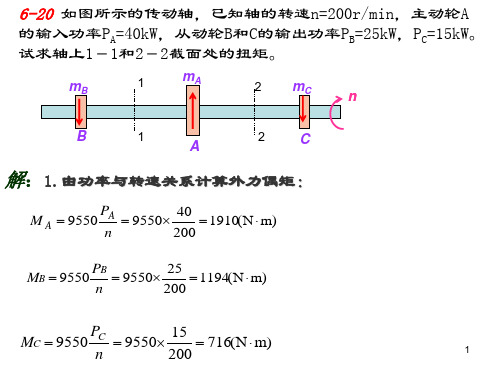
mB
mA
mC
n
(b)
B
A
C
3
解:1.由功率与转速关系计算外力偶矩:
MA
9550 PA n
9550 36 200
1719(N m)
MB 9550 PB 9550 22 1050(N m)
n
200
MC 9550 PC 9550 14 669(N m)
(2)1-1截面的最大剪应力
(3)轴AB的最大剪应力
1 mC=0.2kNm
mB=0.1kNm
φ50 φ40
A
1D
mA=0.3kNm
解:画扭矩图
T
0.3kNm
+
C
B
0.1kNm
+
x
8
(1)在AD段上,D1=50mm,T1=300N.m
Ip1=0.1D14=0.1 ×504 =6.25×105
当ρ=20mm 时 ,
=
T1 I1
300 6.25105
20=0.9610-2(Mpa)
(2)在AD段上,R1=25mm
m ax1
T1 Ip1
R1
300 6.25105
25 1.2102 (Mpa)
(3)在DC段上, T1=300N.m, D2=40mm ,R2=20mm
Ip2=0.1D24=0.1 ×404 =2.56×105
14
6--28实心圆轴如图所示,已知输出扭矩MB=MC=1.64kN.m; MD=2.18kN.m,材料G=80Mpa,【τ】=40Mpa,【θ】=1。/m。 (1)求输入扭矩MA;
(2)试设计轴的直径;
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
材料力学-扭转1
max
T Wt
1930 29 106
66.7106 Pa
66.7MPa [ ] 70MPa 满足强度要求
例 如把上例中的传动轴改为实心 轴,要求它与原来的空心轴强度相 同,试确定其直径。并比较实心轴 和空心轴的重量。
解:当实心轴和空心轴的最大应力同 为[]时,两轴的许可扭矩分别为
解:1)作扭矩图
Tmax 4.5KN m
2)设计轴的直径
由强度条件:
max
Tm a x WP
≤
由刚度条件:
max
Tmax GI p
180
[ ]
取 d = 102 mm
d 3 16Tmax 66mm
[ ]
d 4
32Tmax 180
G 2[ ]
102mm
3)计算全轴的相对扭转角D-A
(2)求所需键数n。
P
§5-6 扭转静不定问题
扭转静不定问题
已知:AB 阶梯轴两端固定,C 处作用 A 外力偶矩Me, AC抗扭刚度为G1Ip1, CB抗扭刚度为G2Ip2 。求:轴的扭矩。
Me
CB Me
解:1)静力学关系
mx 0, Me M A M B 0
2)变形几何关系
BA CA BC 0
G → G
G
d
dx
方向垂直于半径。
三)静力关系:
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dx
G
d
dx
T Ip
二、圆轴中τmax的确定
横截面上 —
扭转习题

第三章 扭转习题一、单项选择题1、横截面都为圆的两个杆,直径分别为d 和D ,并且d=。
两杆横截面上扭矩相等两杆横截面上的最大切应力之比maxDmaxdττ为A 、2倍,B 、4倍,C 、8倍,D 、16倍。
二、1、扭转变形时,公式pTlGI τ=中的 表示单位长度的扭转角,公式中的T 表示横截面上的 ;G 表示杆材料的 弹性模量;I P 表示杆横截面对形心的 ;GI P 表示杆的抗扭 。
2、截面为圆的杆扭转变形时,所受外力偶的作用面与杆的轴线 .3、实心圆轴扭转时,横截面上的切应力分布是否均匀,横截面上离圆心愈远的点处切应力 ,圆心处的切应力为 ,圆周上切应力4、两根实心圆轴的直径d 和长度L 都相同,而材料不同,在相同扭矩作用下,它们横截面上的最大切应力是否相同 ,单位长度的扭转角是否相同 。
5、剪切虎克定律的表达式 G τγ=,式中的G 表示材料的 模量,式中的γ称为 。
6、根据切应力互等定理,单元体两互相垂直截面上在其相交处的切应力成对存在, 且 相等,而 现反。
三、 1、如图所示圆轴,一端固定。
圆轴横截面的直径D=100mm ,所受的外力偶矩M 1=6kN•m,M 2=4kN•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:圆轴横截面上的最大扭矩为 kN•m;圆轴横截面上的最大切应力为 Mpa 。
2、如图所示阶梯形圆轴,一端固定。
圆轴横截面的直径分别为外力偶矩M C =1200 N•m,M B =1800 N•m。
试求BC 段横截面上的扭矩和该阶梯轴的最 大切应力。
答:BC 段横截面上的扭矩为 N•m;该阶梯轴的最大切应力为 Mpa 。
3、如图所示圆轴,一端固定。
圆轴横截面的直径d=100mm ,所受的外力偶矩M 1=7000 N•mM 2=5000 N•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:最大扭矩为 N •m 。
最大切应力为 Mpa 。
4、某传动轴为实心圆轴,轴内的最大扭矩=1.5kN m T g,许用切应力[]=50MPa τ,试确定该轴的横截面直径。
【精品】材料力学复习题第三章 扭 转.docx

第三章扭转一、判断题1.圆杆受扭时,杆内各点均处于纯剪切状态。
()2.非圆截面杆不能应用圆杆扭转切应力公式,是因为非圆截面杆扭转时“平面假设”不能成立。
()3.当剪应力超过材料的剪切比例极限时,剪应力互等定律亦成立。
()4.一点处两个相交面上的剪应力大小相等,方向指向(或背离)该两个而的交线。
()5.有径和长度柑同,材料不同的两根轴,受相同的扭转力偶矩作用,它们的最大剪应力和最大扭转角都相同。
6.杆件受扭时,横截面上最大切应力发生在距截面形心最远处。
7.薄星圆管和空心圆管的扭转切应力公式完全一样。
()&圆杆扭转变形实质上是剪切变形。
()9.横截面的角点处的切应力必为零。
()1.V2. V3. V4. X5. X6. X (非圆截面)7. X8. V9. X二、讥项选择题1.图示圆轴曲面C左、右两侧的扭矩血和的()。
—A.大小相等,止负号相同;B.大小不等,止负号相同;Q ({))cC.大小不等,正负号不同;D.大小相等,止负号不同。
》2.点径为D的实心圆轴,两端受扭转力矩作用。
轴内最大剪应力工,若轴的直径改为D/2,则轴内的绘大剪应力变为()o A. 2 T ;B. T; C. 8 T; D. 16 T O3.阶梯圆轴的最大切应力发生在()。
A.抓矩最大的截面:B.直径最小的截面;C.单位长度扭转角最大的截面;D.不能确定。
4.空心圆轴的外径为D,内径为d, a=d/Do其抗扭截面系数为()。
3 3 3宀)A.昭=晋(1 —a);B。
叫=晋(1 —c?);c。
必=^L(l-a3)D. W p5.扭转的切应力公式T=^p适用于()杆件。
° XA.任意截面;B.任意实心截面;C.任意材料的圆截面;D.线弹•性材料的圆面。
6.单位长度扭转角0与()无关。
A.杆的长度;B.扭矩;C.材料性质;D.截而的儿何性质。
7.切应力互等定理与剪切胡克定律的止确适用范围是()。
A.都只在比例极限范围内成立;B.超过比例极限时都成立;C. 切应力互等定理在比例极限范围内成立,剪切胡克定律不受比例极限限制;D. 剪切胡克立律在比例极限范围内成立,切应力互等定理不受比例极限限制。
9-1扭转习题

0 lBC GIP GIP
2lAB
取mx Tmax 110N m ,
IP
32
24
108
1.57 108 m4
AC
110 0.2 80109 1.57 108
(1
100 ) 2 200
0.0219rad
1.25
4.图(a)所示传动轴的转速n为200r/min,从主动轮上输 入功率kW,由从动轮1、3、4及5输出的功率分别为10kW、
32
mxb d
d 4 / 32
a
d
mxax
A
B
2d
A
mxb
x
B
答案: 1/8
l
(a)
l (b)
4.多边形截面棱柱受扭转力偶作用,根据( )定理可
以证明其横截面角点上的剪应力为( )。
答案: 剪应力互等,零。
二、选择
1.空心圆轴外径为D,内径为d,在计算最大剪应力时需要确定抗扭
截面系数WWtp,, 以下正确的是( )。
max
Tmax
G d4
180
32
d
4
32 2149180
81109 2 0.5
7.5102 m=75mm
综上述所以取d 75mm
5. 如图(a)所示,实心轴和空心轴通过牙式离合器 连接在一起。已知轴的转速n=100r/min,传递的
功率P= 7.5kW,材料的许用切应力 40MPa。试
答案:
3.应用公式 =T/IP计算扭转剪应力的基本条件是等截面
直圆杆,最大剪应力不超过材料的剪切比例极限。 ( )
扭转习题1

扭 转 习 题
1、图示圆截面轴,直径50=d mm ,扭矩=T 的A 点处的扭转切应力A τ答案:MPa 6.32=A τ,MPa 7.40max =τ
2、 图示空心圆截面轴,外径D =m kN 1⋅=T ,试计算mm A 15=ρ的A 上的最大、最小扭转切应力。
答案:MPa 7.63=A τ,MPa 9.84max =τ
3、如图所示,圆轴AB 与套管CD 直径mm 56=d ,许用切应力80][1=τmm 80=D ,壁厚mm 6=δ,许用切应力][2τ偶矩M 的许用值。
答案:m kN 922.1][⋅=M 4、某传动轴,转速r/min 300=n ,轮1为主动轮,输入功率kW 501=P ,轮2、轮3与轮4为从动轮,输出功率分别为kW 102=P ,kW 2043==P P 。
(1)试画轴的扭矩图,并求轴的最大扭矩;
(2)设许用切应力MPa .80][=τ,试确定轴径d ;
(3)若将轮1与轮3的位置对调,轴的最大扭矩变为何值,对轴的强度是否有利。
答案:(a ) m kN 273.1max ⋅=T ;(b )mm 3.43=d ;(c) m kN 955.0'max ⋅=T 。
5、一圆截面钢轴,转速min /250r n =,所传递功率kW 60=P ,许用切应力MPa 40][=τ,单位长度的许用扭转角m /)(8.0][0
=θ,切变模量GPa 80=G ,试确定轴径。
mm 68≥d 。
材料力学专项习题练习扭转

扭 转1. 一直径为1D 的实心轴,另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案:(A) 21α-; (B)(C); (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案:(A) τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:7. 图示圆轴料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D重量比21W W 9. 想弹塑性材料, 等直圆轴的极限扭矩是刚开始出现塑性变形时扭矩的 倍。
10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ,扭转加载到整个截面全部屈服,将扭矩卸掉所产生的残余应力如图所示,试证明图示残余应力所构成的扭矩为零。
证:截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。
12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示,式中C ,m 为由实验测定的已知常数,试证明该轴的扭转切应力计算公式为:1/e (31)/2π()23m 1mm mM m d ρρτ+=+s /3证:几何方面 d d xρϕγρ= 物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰1//221/0d 2πd d m d mC x ϕρρ+⎛⎫= ⎪⎝⎭⎰(31)/1/()d 22π(31)d m mmd C m x mϕ+⎛⎫= ⎪+⎝⎭1/e (31)/(31)d d 2π()2mm m M m d x Cm ϕ++⋅⎛⎫=⎪⎝⎭⋅ 所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。
材料力学第3章扭转习题及答案

材料力学第3章扭转习题及答案第三章扭转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(× ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(× )3.圆杆扭转变形实质上是剪切变形。
(√ )4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(× ) 6.切应力互等定理,仅适用于纯剪切情况。
(× ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√ ) 9.受扭圆轴的最大切应力只出现在横截面上。
(× ) 10.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
(√ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径(小)。
2.当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3.直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4.一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5.直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是(相)同的,扭转角φ是(不)同的。
6.等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
三、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ ,这时横截面上内边缘的切应力为( B )。
[课件]扭转练习题答案.docPPT
![[课件]扭转练习题答案.docPPT](https://img.taocdn.com/s3/m/71d013f6360cba1aa811dac0.png)
P 1 4 1 M 9 5 4 9 ( 9 5 4 9 ) N m 6 6 8 N m e 1 n 2 0 0
P 3 0 1 4 1 M 9 5 4 9 ( 9 5 4 9 ) N m 7 6 4 N m e 2 n 2 0 0
M 6 6 8 N m e 1
T 9 5 4 9 ( 9 5 4 9 ) N m A B n 1 2 0 3 5 1 2 k N m
T 5 1 2 1 6 A B3 3 P a 1 7 . 9 M P a [ ] 2 0 M P a A B m a x W 0 . 1 t
各轴均满足强度要求
3.5 阶梯形圆轴的直径分别为d1=40mm, d2=70mm,轴上装有三个带轮,如图所示。已知 由轮3输入的功率为P3=30kW,轮1输出的功率为 P1=14kW。轴作匀速转动,转速n=200r/min。材 料的剪切许用应力[τ]=60MPa,G=80GPa,许用 扭转角[φ’]=2(0)/m 。试校核轴的强度和刚度。 解:
水轮机主轴的强度 1 5 0 0 0 T 9 5 4 9 N m 5 7 3 k N m 2 5 0 横截面上最大切应力为 T T m ax W p D3 (1 4 ) 16 5 7 3 0 0 0 P a 1 9 . 2 M P a 3 0 . 5 5 d4 [ 1 ( )] 1 6 D 主轴满足强度要求。
T 2 . 1 5 1 00 . 0 2 3 2 7 0 ( M P a ) I 0 . 0 5
4 P
3 T 2 . 1 51 0 1 6 8 7 . 6 ( M P a ) 3 W 0 . 0 5 t
材料力学 扭转习题

IP2
T1 G1IP1 T2 G2IP2
2
1
扭转练习题
圆轴由两种材料组成,其剪切模量分别为G1和G2。设受扭时二者 之间无相对滑动,G1 2G2,则其横截面上的剪应力分布为( )。
T oG1 G2 d
G1 o G2
( A)
G1 o G2
(B)
D
答案: D
G1 o G2
(C )
处于线弹性、小变形状态,则(c)加载情况下的应力
与变形等于(a)和(b)两种情况的叠加。 ( )
m1
d l
m2
d l/2 l/2
m2 m1
d l/2 l/2
(a)
(b)
(c)
答案:
一内径为d、外径为D=2d的空心圆管与一直径为d的实
心圆杆结合成一组合圆轴,共同承受转矩Me。圆管与圆 杆的材料不同,其切变模量分别为G1和G2,且G1=G2/2, 假设两杆扭转变形时无相对转动,且均处于线弹性范围。
扭转练习题
一、填空
1.空心圆轴外径为D,内径为d=D/2,两端受扭转力偶 mx 作 用,则其横截面上剪应力呈( )分布, max ( ), min ( )。
答案:
线性,12556mDx3
,1
/
2
。
max
2.圆截面杆扭转时,其变形特点是变形过程中横截面始 终保持( ),即符合( )。非圆截面杆扭转时,其 变形特点是变形过程中横截面发生( ),即不符合 ( )。
试问两杆横截面上的最大切应力之比τ1/τ2为多大?并画 出沿半径方向的切应力变化规律。
因两杆扭转变形时无相对转动
Me 1 2
1 2
T1
D 2
材料力学扭转习题
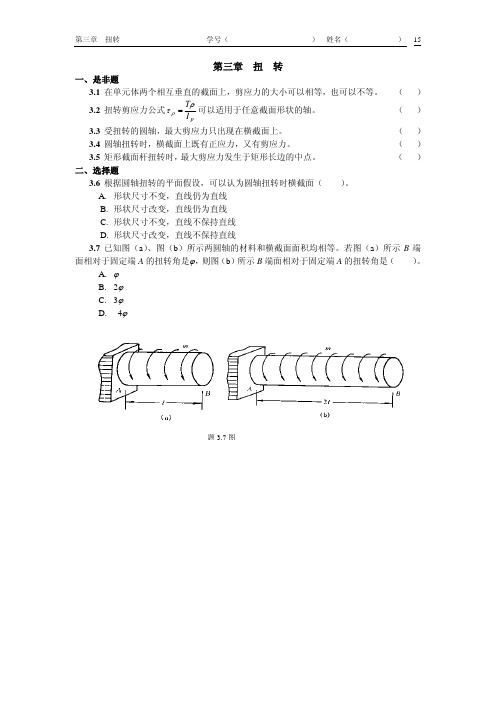
第三章 扭 转一、是非题3.1 在单元体两个相互垂直的截面上,剪应力的大小可以相等,也可以不等。
( )3.2 扭转剪应力公式pI T ρτρ=可以适用于任意截面形状的轴。
( ) 3.3 受扭转的圆轴,最大剪应力只出现在横截面上。
( )3.4 圆轴扭转时,横截面上既有正应力,又有剪应力。
( )3.5 矩形截面杆扭转时,最大剪应力发生于矩形长边的中点。
( )二、选择题3.6 根据圆轴扭转的平面假设,可以认为圆轴扭转时横截面( )。
A. 形状尺寸不变,直线仍为直线B. 形状尺寸改变,直线仍为直线C. 形状尺寸不变,直线不保持直线D. 形状尺寸改变,直线不保持直线3.7 已知图(a )、图(b )所示两圆轴的材料和横截面面积均相等。
若图(a )所示B 端面相对于固定端A 的扭转角是ϕ,则图(b )所示B 端面相对于固定端A 的扭转角是( )。
A.ϕ B.2ϕ C.3ϕ D. 4ϕ题3.7图三、计算题3.8作图示各杆的扭转图(图c中各量单位kN •m)。
101530m m m 3m20(a) (b) (c)题3.8图3.9T为圆杆横截面上的扭矩,试画出截面上与T对应的剪应力分布图。
(a) (b)(c)题3.9图3.10 发电量为15000kW 的水轮机主轴如图所示。
D = 550 mm ,d = 300 mm ,正常转速n = 250 r/min 。
材料的许用剪应力 [τ] = 50MPa 。
试校核水轮机主轴的强度。
3.11 阶梯形圆轴直径分别为d 1=40 mm ,d 2=70 mm ,轴上装有三个皮带轮,如图所示。
已知由轮3输入的功率为N 3=30 kW ,轮1输出的功率为N 1=13kW ,轴作匀速转动,转速n =200r/min ,材料的剪切许用应力[]τ=60 MPa ,G =80 GPa ,许用扭转角[]ϕ=2°/m 。
试校核轴的强度和刚度。
题3.10图 题3.11图3.12 实心轴和空心轴通过牙嵌式离合器连接在一起。
圆轴的扭转习题+答案

13、一空心圆轴在产生扭转变形时,其危险截面外缘处具有全轴的最大剪应力,而危险截面内缘处的剪应力为零。 ( )
14、粗细和长短相同的二圆轴,一为钢轴,另一为铝轴,当受到相同的外力偶作用产生弹性扭转变形时,其横截面上最大剪应力是相同的。 ( )
5、圆轴扭转时,横截面上任意点的剪应变与该点到圆心的距离成___________。
6、试观察圆轴的扭转变形,位于同一截面上不同点的变形大小与到圆轴轴线的距离有关,显然截面边缘上各点的变形为最_______,而圆心的变形为__________。
7、圆轴扭转时,在横截面上距圆心等距离的各点其剪应变必然_________。
13、横截面面积相等的实心轴和空心轴相比,虽材料相同,但_________轴的抗扭承载能力要强些。
16、直径和长度均相等的两根轴,其横截面扭矩也相等,而材料不同,因此它们的最大剪应力是________同的,扭转角是_______同的。
17、产生扭转变形的实心圆轴,若使直径增大一倍,而其他条件不改变,则扭转角将变为原来的_________。
17、内外径比值d/D=的空心圆轴受扭转,若将内外径都减小到原尺寸的一半,同时将轴的长度增加一倍,则圆轴的抗扭刚度会变成原来的( )。
A、1/2 B、1/4 C、1/8 D、1/16
18、等截面圆轴扭转时的单位长度扭转角为θ,若圆轴的直径增大一倍,则单位长度扭转角将变为( )。
A、θ/16 B、θ/8 C、θ/4 D、θ/2
5、扭矩就是受扭杆件某一横截面在、右两部分在该横截面上相互作用的分布内力系合力偶矩。 ( )
7、扭矩的正负号可按如下方法来规定:运用右手螺旋法则,四指表示扭矩的转向,当拇指指向与截面外法线方向相同时规定扭矩为正;反之,规定扭矩为负。 ( )
6第六章 圆轴的扭转习题+答案

一、填空题1、圆轴扭转时的受力特点是:一对外力偶的作用面均_______于轴的轴线,其转向______。
2、圆轴扭转变形的特点是:轴的横截面积绕其轴线发生________。
3、在受扭转圆轴的横截面上,其扭矩的大小等于该截面一侧(左侧或右侧)轴段上所有外力偶矩的_______。
4、在扭转杆上作用集中外力偶的地方,所对应的扭矩图要发生________,_________值的大小和杆件上集中外力偶之矩相同。
5、圆轴扭转时,横截面上任意点的剪应变与该点到圆心的距离成___________。
6、试观察圆轴的扭转变形,位于同一截面上不同点的变形大小与到圆轴轴线的距离有关,显然截面边缘上各点的变形为最_______,而圆心的变形为__________。
7、圆轴扭转时,在横截面上距圆心等距离的各点其剪应变必然_________。
8、从观察受扭转圆轴横截面的大小、形状及相互之间的轴向间距不改变这一现象,可以看出轴的横截面上无____________力。
9、圆轴扭转时,横截面上剪应力的大小沿半径呈______规律分布。
11、受扭圆轴横截面内同一圆周上各点的剪应力大小是_______的。
12、产生扭转变形的一实心轴和空心轴的材料相同,当二者的扭转强度一样时,它们的_________截面系数应相等。
13、横截面面积相等的实心轴和空心轴相比,虽材料相同,但_________轴的抗扭承载能力要强些。
16、直径和长度均相等的两根轴,其横截面扭矩也相等,而材料不同,因此它们的最大剪应力是________同的,扭转角是_______同的。
17、产生扭转变形的实心圆轴,若使直径增大一倍,而其他条件不改变,则扭转角将变为原来的_________。
18、两材料、重量及长度均相同的实心轴和空心轴,从利于提高抗扭刚度的角度考虑,以采用_________轴更为合理些。
二、判断题1、只要在杆件的两端作用两个大小相等、方向相反的外力偶,杆件就会发生扭转变形。
材料力学习题扭转知识分享

材料力学习题扭转扭转基本概念题一、选择题(如果题目有5个备选答案,选出2~5个正确答案,有4个备选答案选出一个正确答案。
)1.图示传动轴,主动轮A的输入功率为P A = 50 kW,从动轮B,C,D,E 的输出功率分别为P B = 20 kW,P C = 5 kW,P D = 10 kW,P E = 15 kW。
则轴上T出现在( )。
最大扭矩maxA.BA段B.AC段C.CD段D.DE段题1图2.图示单元体的应力状态中属正确的纯剪切状态的是()。
题2图3.上题图示单元体的应力状态中属正确的是()。
4.下列关于剪应力互等定理的论述中正确的是()。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C . 剪应力互等定理适用于各种受力杆件D .剪应力互等定理仅适用于弹性范围E .剪应力互等定理与材料的性能无关 5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是( )。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D 时,设轴内的最大剪应力为τ,若轴的直径改为2D ,其它条件不变,则轴内的最大剪应力变为( )。
A .τ8B .τC .τ16D .16τ7. 受扭空心圆轴(D d =α),在横截面积相等的条件下,下列承载能力最大的轴是( )。
A .0=α(实心轴)B .5.0=αC .6.0=αD .8.0=α8. 扭转应力公式ρτρpI T =的适用范围是( )。
A .各种等截面直杆 B .实心或空心圆截面直杆C .矩形截面直杆D .弹性变形E .弹性非弹性范围9. 直径为D 的实心圆轴,最大的容许扭矩为T ,若将轴的横截面积增加一倍,则其最大容许扭矩为( )。
A .T 2B .T 2C .T 22D .T 410. 材料相同的两根圆轴,一根为实心,直径为1D ;另一根为空心,内径为2d ,外径为2D ,α=22D d 。
若两轴横截面上的扭矩T ,和最大剪应力m ax τ均相同,则两轴外径之比21D D 为( )。
测试题-扭转-答案
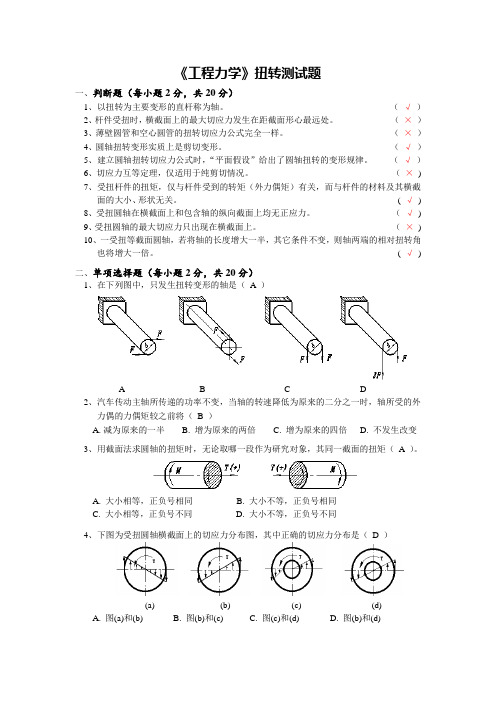
《工程力学》扭转测试题一、判断题(每小题2分,共20分)1、以扭转为主要变形的直杆称为轴。
(√)2、杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3、薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)4、圆轴扭转变形实质上是剪切变形。
(√)5、建立圆轴扭转切应力公式时,“平面假设”给出了圆轴扭转的变形规律。
(√)6、切应力互等定理,仅适用于纯剪切情况。
(×)7、受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √)8、受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)9、受扭圆轴的最大切应力只出现在横截面上。
(×)10、一受扭等截面圆轴,若将轴的长度增大一半,其它条件不变,则轴两端的相对扭转角也将增大一倍。
( √)二、单项选择题(每小题2分,共20分)1、在下列图中,只发生扭转变形的轴是(A )A B C D2、汽车传动主轴所传递的功率不变,当轴的转速降低为原来的二分之一时,轴所受的外力偶的力偶矩较之前将(B )A.减为原来的一半B. 增为原来的两倍C. 增为原来的四倍D. 不发生改变3、用截面法求圆轴的扭矩时,无论取哪一段作为研究对象,其同一截面的扭矩(A )。
A. 大小相等,正负号相同B. 大小不等,正负号相同C. 大小相等,正负号不同D. 大小不等,正负号不同4、下图为受扭圆轴横截面上的切应力分布图,其中正确的切应力分布是(D )(a) (b) (c) (d)A. 图(a)和(b)B. 图(b)和(c)C. 图(c)和(d)D. 图(b)和(d)5、一内径为d ,外径为D 的空心圆轴,其扭转截面系数为( C )A. 16π16π33p d D W −=B. 32π32π33p d D W −= C. Dd D W 16)(π44p −= D. 32π32π44p d D W −=6、建立圆轴的扭转切应力公式p I T ρτρ=时,以下哪个关系式没有用到?( C ) A. 变形的几何协调关系 B. 剪切胡克定律C. 切应力互等定理D. 切应力ρτ与扭矩的关系A T A d ρτρ⎰=7、图示等截面圆轴上装有四个皮带轮,如何合理安排?( B ) A. 将轮B 与轮D 对调 B. 将轮C 与轮D 对调 C. 将轮B 与轮C 对调D. 将轮B 与轮D 对调,然后再将轮B 与轮C 对调8、一圆轴用碳钢制作,校核其扭转角时,发现单位长度扭转角超过了许用值。
扭转——精选推荐

第三章 扭转一、填空题1、圆环形截面的扭转截面系数W p = 。
答案:()43116απ-D二、选择题问题3-1、图中所示传动轴的转速min 300r n =,主动轴A 的输入功率为kW 500,从动轮B 、C 的输出功率分别为kW 150,D 的输出功率为kW 200。
下列结论中正确的是 ?A :各轮的转向与轮作用于轴的扭转力偶矩方向一致;B :轴向最大扭矩m kN T ⋅=8.47max; C :轴向最大扭矩m kN T ⋅=37.6max; D :轴向最大扭矩m kN T⋅=55.9max。
正确答案D 。
提示:1、主动轮转动的方向与扭转方向一致;从动轮转动的方向与扭转方向相反。
2、外力偶矩的计算式:n N T 9549=;最大扭矩出现在CA 段;C B T T T+=max问题3-2、圆轴AB 的两端受扭转力偶矩e M 作用,如图所示。
假想将轴在截面C 处截开,对于左右两个分离体,截面C 上的扭矩分别用T 和'T 表示,则下列结论中 是正确的。
A :T 为正,'T 为负; B :T 为负,'T 为正; C :T 和'T 均为负; D :T 和'T 均为正。
提示:扭矩T 的符号规定:按右手螺旋法则把T 表示为矢量,当矢量方向与截面的外法线的方向一致时,T 为正;反之为负。
问题3-3、阶梯形圆杆承受外力偶矩如图所示,试作扭矩图。
(单位:m kN ⋅)A :0;)(-B :0;)(+B :50;)(-C :50;)(+C :30;D :30。
问题3-4、图示等直圆轴,试作扭矩图。
(单位:m kN ⋅)A :-15;)(-B :-15;)(+B :-50;)(-C :-50。
问题3-5、图示等直圆轴,试作扭矩图。
(单位:m kN ⋅)A :4;)(-B :4;)(+B :3;)(-C :3;)(+C :-3;)(-D :-3;)(+D :-5;E :-5。
材料力学专项习题练习扭转

扭 转1. 一直径为1D 的实心轴,另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案:(A) 21α-; (B)(C); (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案:(A) τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D 重量比21W W 9. 10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ,扭转加载到整个截面全部屈服,将扭矩卸掉所产生的残余应力如图所示,试证明图示残余应力所构成的扭矩为零。
证:截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。
12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示,式中C ,m 式为:证:几何方面 d d xρϕγρ=物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。
