chapter7水力学
水力学流体静力学PPT课件

在水利工程中,液体相对平衡 的原理被广泛应用于水坝、水 库等水工建筑物的设计和施工 中。
在医学领域,液体相对平衡的 原理也被应用于血液动力学和 药物输送等方面的研究。
04
液体内部压强与浮力
Chapter
液体内部压强的计算
压强定义
单位面积上所受的压力,用p表示 ,单位为Pa。
计算公式
p = F/A,其中F为压力,A为受力 面积。
了解液体运动的描述方法和基本方程 ;
能够运用所学知识分析和解决工程实 际问题。
教学方法与手段
01
02
03
教学方法
采用讲授、讨论、案例分 析等多种教学方法相结合 的方式。
教学手段
使用PPT课件、动画演示 、实验演示等教学手段辅 助教学。
考核方式
采用平时成绩、期末考试 成绩和实验成绩相结合的 考核方式。
的气体量来调节浮力大小。
05
流体静力学在水利工程中的应 用
Chapter
水库水位与坝体稳定性分析
水库水位确定
根据水库地形、库容曲线 及入库流量等资料,确定 水库在不同运行条件下的 水位。
坝体稳定性分析
运用土力学、岩石力学等 原理,分析坝体在静水压 力、扬压力等作用下的稳 定性,确保大坝安全。
渗流控制
液体相对平衡是流体静力学研究的基础。
等压面的形成与性质
等压面是指在液体内部,压强相等的各点所组成的面。
在重力场中,等压面是一个水平面,因为在同一水平面上,各点受到的重力作用相 同,所以压强也相等。
等压面具有传递压强的性质,即等压面上的压强可以传递到液体内部的任意一点。
液体相对平衡的应用
液体相对平衡的原理可以应用 于测量液体的密度和深度。
水力学第2-7章答案(吕宏兴__裴国霞等)
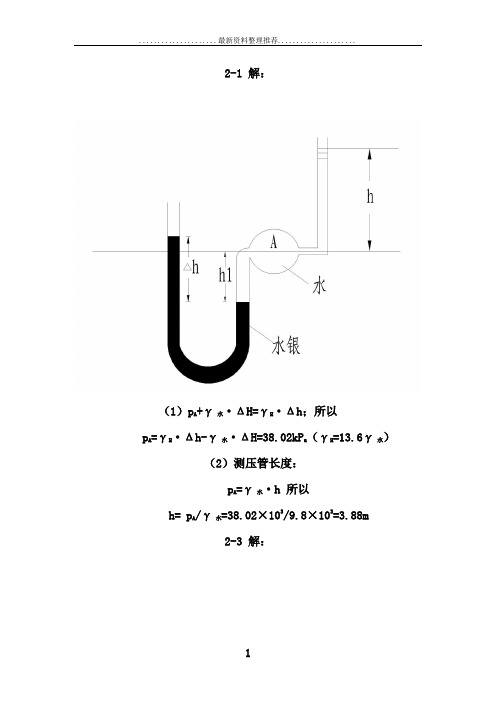
2-1 解:(1)p A+γ水·ΔH=γH·Δh;所以p A=γH·Δh-γ水·ΔH=38.02kP a(γH=13.6γ水)(2)测压管长度:p A=γ水·h 所以h= p A/γ水=38.02×103/9.8×103=3.88m2-3 解:P A-γh=p B-γ(h1+h2+h)+γH h1 所以,p A-p B=γH h1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2)=53.68kPa2-6解:p A=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kp a2-7 解:(1)左支:绝对:p c'=p0'+γh0=86.5+9.8×2=106.1kPa(2)右支:p c'=p a+γ水h; h=(p c'-p a)/γ水=(106.1-9.8)/9.8=0.827m 2-8 解:p A=0.6p a=0.6×98=58.8kp a(1)左支:p A=γh1 h1=p A/γ=58.8/9.8=6m(2)右支:p A+γh=γH h2 h2=(p A+γh)/γH=0.456m2-10解:设管嘴内的绝对压强为p',则p'+γh= p aP v=p a- p'=γh=9.8×0.6=5.886kp a2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)p=9.8×2(4.9/9.8-1)=-9.8kN/㎡(2)相对压强为0 p=γh(1-a/g)=0 由式可知 a/g-1=0 a=g=9.8m/s2时,p=02-142-16解:下游无水时,h1=1.2m,h2=1.85m,b=3m(1)求静水总压力P方法10:P=Ωb=1/2[γh1+γ(h1+h2)]×AB×b=1/2×9.8×(2×1.2+1.85)×2.14×3=133.7kN方法20:P=γh c A=γ(h1+h2/2)×AB×b=133.7kN(2)计算P的作用点D的位置:e=l/3·(2h1+h2ˊ)/(h1+h2ˊ)=0.915m(其中hˊ=h1+h2)(3)计算T:因为ΣM a=0 则:P·AC+G·AO·cos600 其中:AC=AB-e=2.14-0.915=AO=AB/2133.7×(2.14-0.915)+9.8×2.14/2×1/2=T×2.14×1/2所以 T=158kN下游有水时,AB=2.14,b=3m,p A=γh1=9.8×1.2=11.76kPa,p A=p B (1)静水总压力P左=γ·h c1A1=9.8×(h1+h2/2)×AB×b=P1=133.7kN (其中h c1=h1+h2/2 A1=AB×b) e1=0.915mP右=γ·h c2A2=9.8×h2/2×AB×b=P2=58.2kN(其中h c2=h2/2)e2=l/3=2.14/3=0.71m(2)因为ΣM a=0P1×(AB-e1)+G×AO×cos600=T×AB×cos600+P2×(AB-e2)T=80.2kN2.18已知:H=3m,b=5m,R=4.3m,θ=450 求P及作用点2=3mH=Rsin450=4.3×2(1)水平分力:P x =γh e A x =9.8×1.5×3×5=220.5(KN) (2)铅垂分力:P z =γv=γΩ×b=9.8×1.143×5=56.01(KN) 其中:Ω=S 梯OABC —S 扇OAC =8.4-7.257=1.143㎡ S 梯OABC =0.5×[4.3+(4.3-3)]×3=8.4㎡ S 扇OAC =360450πR 2=360450×3.14×4.32=7.257㎡(3)P=P Pz x22+=01.565.22022+=227.5(KN )(4)P 与水平面的夹角α: α=arctan PP xz =arctan5.22001.56=14.250=14015` 2-192-20 解:已知b=10m,k=8m(1)夹角计算:Sinβ1=(173-170)/8=3/8=0.375(cosβ1=550.5/8)β1=22.020 Sinβ2=(170-165)/8=5/8=0.625(cosβ2=0.781)β2=38.680(2)水平方向水压力P x:(闸门宽b=10m)公式:P x=γh c A x=9.8×4×8×10=3136kN(另法:P x=1/2×9.8×8×8×10=31363136kN)(3)垂直方向水压力P z=γV关键计算压力体体积V=[三角形ofc(11.12㎡)+扇形ocd(33.88㎡)-梯形ofed(34.36)]×b所以 V=(11.12+33.86-34.36)×10=10.636×10=106.36m³P z=γV=9.8×106.36=1042.33kN(4)总压力P:P=(P x2+P z2)=3304.7kN作用方向α=arctan1042.3/3304.7=17.510P与水平面夹角17.510,且过o点。
水力学教学课件ppt作者裴国霞唐朝春7,8,9章第九章明渠恒定非均..
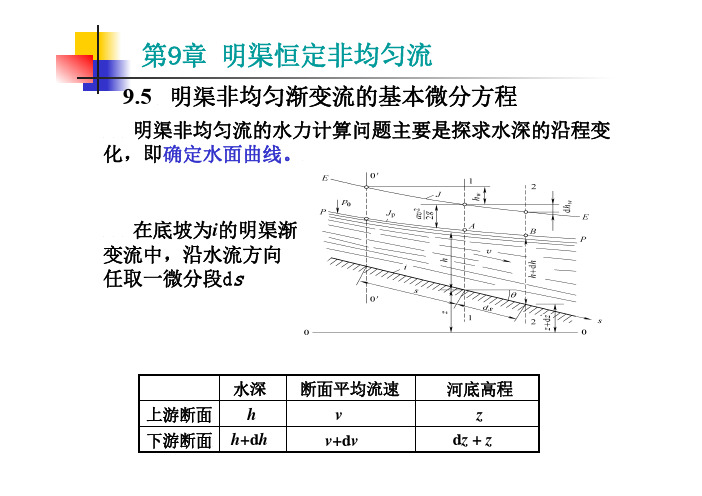
9.5 的明渠渐 d z + zv+d vzv河底高程断面平均流速对微小流段建立能量方程idsdz -=1)θsin =i dsdzds z z -=-=219.6 明渠非均匀渐变流水面曲线分析区号1:h cr 2:h cr 3:h cr各区编号M 1M 2M 3N CNcrh 0h cri i < 陡坡上均匀流K K NNcrh 0h 1s 2s 3s CC N N cri i >i = i crN N ,C C,N crh h 03c 1c 平坡渠道i = 0crh 3h逆坡渠道i < 0Ccrh 2A 3A 2A 水面曲线形式9.6.1⒈S 3S 1S 2NC C cri i > ⒉ 陡坡渠道( )cr i i >表 陡坡水面线类型及特性h h →h h →控制水深壅水急流降水 水平线壅水 缓流急流 下游趋向上游趋向 水面形态 流态 水跃 控制水深、水跌i=2H3i = 0表 平坡水面线类型及特性A 2i < 0CC A 30<i 表 逆坡水面线类型及特性当h→ 时,与C-C线有成垂直的趋势;cr h 9.6.4 水面曲线的共性与绘制步骤 ⒈ 水面曲线的共性1、3区为壅水曲线;2区为降水曲线当h→h 0时,以N-N线为渐近线;当h→∞时,以水平线为渐近线每一区域内只有相应的一条水面曲线● 渠道水面线总结⏹ 1 区水面线均为壅水曲线⏹ 2 区水面线均为降水曲线⏹ 3 区水面线均为壅水曲线⏹ 水面线通过 C-C线产生水跃或水跌⏹ 水面线:起始:N-N线,或水库水面⏹ 回落:N-N线,或水库水面,或临界水深⏹ 中间:符合12种水面曲线的变化规律⏹画水面线必须表明水面的类型号例9.7 明渠非均匀渐变流水面曲线的计算Wh 渐变流水头损失仅考虑沿程水头损失fW h h ∆≈∆明渠均匀流l∆Ji g e l -∆=∆/这就是分段计算水面曲线的有限差式,称为分段求和法公式。
分段求和法计算水面曲线的步骤:9.7.23)由控制断面向下游(或上游)取给定的 ,便可定出断。
水力学PPT课件

§1-4 液体的主要物理性质
§1-5 作用在流体上的力
第一章 绪
论
§1-1绪 论
一、水力学的定义:
用这
水力学是研究液体的运动规律,以及如何运 些规律来解决工程实际问题的科学。
水力学包括:
⑴水力学基础:
主要是研究液体在各种情况下的平衡运动规律 ,为研究的方便起见,该内容又分为流体静力学和流体 动力学。
3、内摩擦力的大小:
⑴、与相邻运动液体层的接触面积成正比
⑵、与速度梯度成正比
⑶、视液体的性质而定
⑷、与压力的大小无关
第一章 绪
4论、牛顿内摩擦定律:
F A du dy
F A du
dy
单位面积上的力,称为切应力τ。
F du
A dy
μ——液体性质的一个系数,称为粘性系数或动力 粘性系数 (单位:N·S/m2)
三、水力学在给排水工程中的应用
1、供水工程方面:管网和渠道中的水力计算;
2、水处理厂:各构筑物间的衔接和水流情况;
3、环境的分析和预测:污水排入河中混合情况。
第一章 绪 论
四、课程的性质和学习方法
性质:为应用科学,专业基础课,即有理论也 有实验。
方法:除理论推导外,实验也不可忽视。
五、教学参考书:
第一章 绪 论
§1-3 量纲、单位
一、量纲:表示物理量的特征。
如:长度、时间、质量等。在科学文献中,一般 用〔〕符号来表示量纲。例如〔长度〕或〔L〕。
二、量纲的分类:基本量纲和导出量纲。
1、基本量纲:必须具有独立性,即一个量纲不能从 其它基本量纲推导出来,也就是不依赖于其它基本 量纲。
如〔L〕、〔T〕和〔M〕是相互独立的,不能从〔
水力学第七章课后习题答案

8.12梯形断面土渠,底宽b =3m ,边坡系数m =2,水深h =1.2m ,底坡i =0.0002,渠道受到中等养护,试求通过流量。
解: ()()1.23 1.22 6.48A h b hm =+=⨯+⨯=(m 2)232 1.28.367b b χ=+=+=+⨯=(m )0.7745AR χ==(m ),取0.0225n =(见教材153页表6-4)∴231 6.480.7745 3.4350.0225Q n⨯===(m 3/s )答:通过流量 3.435Q =m 3/s 。
修建混凝土砌面(较粗糙)的矩形渠道,要求通过流量Q =9.7s m /3,底坡i =0.001,试按水力最优断面设计断面尺寸。
解: 对矩形断面,水力最优断面满足2b h =。
∴22A bh h ==,24b h h χ=+=,∴2242h hR h ==∵1Q An=0.001i =,0.017n =∴23222h h ⎛⎫⋅= ⎪⎝⎭,83110.0179.7 4.14nQ h ⨯=== 1.70h =(m ), 3.40b =(m ) 答:断面尺寸为 1.70h =m , 3.40b =m 。
.14修建梯形断面渠道,要求通过流量Q =1s m /3,边坡系数m =1.0,底坡i =0.0022,粗糙系数n =0.03,试按不冲允许流速[]max v =0.8s m /,设计断面尺寸。
解: ∵ max 0.8v v ≤=,∴0.8QA≤,max 1 1.250.8Q A v ≥==(m 2) 又∵[]max 1v v n =≤,即[]2max 3120.502n v R i ≤== 0.366R =∴有 21.25hb mh +≥20.366≤即有2 1.253.42hb h b ⎫+≥⎪⎬+≥⎪⎭解得:2 1.870.6840h h -+=0.51.37h ⎧=⎨⎩, 2.012.455b ⎧=⎨-⎩∴ 2.00b =(m ),0.5h =(m )答:断面尺寸为 2.00b =m ,0.5h =m 。
水力学第七章

渐近线 1: h 0, A 0, Es 横坐标为渐近线
渐近线 2: h , A , Es 坐标轴成 45°直线
Es m in
d Es dh
d dh
h
aQ2 2gA2
1
aQ2 d A gA3 d h
B
d A B(水面宽) dh
d
d Es 1 aQ2B 1 av2 1 Fr2
6
dh d Q2 dh dh Q2dA dh Q2dA dh v2B ds dh 2gA2 ds ds (1 A3gdh ) = ds (1 A3gdh ) ds (1 gA ) dEs dh (1 Fr2 ) ds ds
第三节 临界底坡、缓坡和陡坡
给定 Q、n、渠道断面形状尺 b /m 4.0
Fr
F G
1
2
L2 v 2 gL3
1
2
v
gL
<1 =1 >1
Fr 是流态判别的准数
二、缓流和急流的能量分析
(一) 断面单位能量(断面比能) 1. 断面比能定义
右图为一明渠非均匀流,以渠 底为基准面,过水断面单位液重的 总能量为
Es
h cos
av2 2g
h cos
aQ2 2gA2
顺水波: vw ' v vw v gh (微波传播方向和水流方向一致) 式中, vw ' 顺水波传
播波速。
逆水波: vw ' v vw v gh (微波传播方向和水流方向相反) 式中,vw ' 逆水波传播
波速.
(二)明渠水流流态判别的标准——佛劳德数
佛劳德数:流速与波速之比,以 Fr 表示 Fr v v vw gh
第七章明渠恒定非均匀流
水力学ppt课件

设计原则
泄水建筑物设计应遵循安全、经济、适用等原则,同时考虑地形、 地质、水文等因素。
实例分析
以某水库溢洪道设计为例,介绍泄水建筑物设计的步骤和方法,包 括选址、确定设计标准、选择泄流方式、计算泄流量等。
经验总结
结合实例分析,总结泄水建筑物设计的经验和教训,提出改进和优化 建议。
2024/1/25
32
5
静压力与动压力概念
静压力
静止液体作用在与其接触的某个平面上法向的总压力。
动压力
运动液体作用在与其接触的某个平面上法向的总压力。
2024/1/25
6
连续性方程与伯努利方程
连续性方程
单位时间内流入、流出控制体的质量流量之差,等于控制体 内质量的变化率。
2024/1/25
伯努利方程
理想液体在重力场作稳态流动时,具有压力能、位能和动能 三种形式,它们之间可以相互转化,且总和保持不变。
气球通过改变自身体积来实现浮沉。当气球受到的空气浮力 大于自身重力时,气球上升;当空气浮力小于自身重力时, 气球下降。因此,通过改变气球的体积,可以调节气球所受 的空气浮力,从而控制气球的浮沉。
2024/1/25
12
03 流体动力学基础知识
2024/1/25
13
流动类型及判别方法
层流与湍流
根据流体微团的运动轨迹是否规则,将流动分为层流和湍流。层流中流体微团运 动轨迹规则,而湍流中流体微团运动轨迹不规则。
A
沿程损失产生原因
流体在管道内流动时,由于摩擦阻力的作用, 使得流体能量逐渐减小。
沿程损失计算方法
采用达西公式或海曾-威廉公式进行计算, 根据管道长度、管径、流速等参数确定沿 程损失。
水力学第2-7章参考答案(吕宏兴__裴国霞等)

2-1 解:(1)p A+γ水·ΔH=γH·Δh;所以p A=γH·Δh-γ水·ΔH=38.02kP a(γH=13.6γ水)(2)测压管长度:p A=γ水·h 所以h= p A/γ水=38.02×103/9.8×103=3.88m2-3 解:P A-γh=p B-γ(h1+h2+h)+γH h1所以,p A-p B=γH h1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解:p A=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kp a 2-7 解:(1)左支:绝对:p c'=p0'+γh0=86.5+9.8×2=106.1kPa(2)右支:p c'=p a+γ水h;h=(p c'-p a)/γ水=(106.1-9.8)/9.8=0.827m 2-8 解:p A=0.6p a=0.6×98=58.8kp a(1)左支:p A=γh1 h1=p A/γ=58.8/9.8=6m(2)右支:p A+γh=γH h2 h2=(p A+γh)/γH=0.456m2-10解:设管嘴内的绝对压强为p',则p'+γh= p aP v=p a- p'=γh=9.8×0.6=5.886kp a2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)p=9.8×2(4.9/9.8-1)=-9.8kN/㎡(2)相对压强为0 p=γh(1-a/g)=0 由式可知a/g-1=0a=g=9.8m/s2时,p=02-142-16解:下游无水时,h1=1.2m,h2=1.85m,b=3m(1)求静水总压力P方法10:P=Ωb=1/2[γh1+γ(h1+h2)]×AB×b=1/2×9.8×(2×1.2+1.85)×2.14×3=133.7kN方法20:P=γh c A=γ(h1+h2/2)×AB×b=133.7kN(2)计算P的作用点D的位置:e=l/3·(2h1+h2ˊ)/(h1+h2ˊ)=0.915m(其中hˊ=h1+h2)(3)计算T:因为ΣM a=0 则:P·AC+G·AO·cos600 其中:AC=AB-e=2.14-0.915=AO=AB/2133.7×(2.14-0.915)+9.8×2.14/2×1/2=T×2.14×1/2所以T=158kN下游有水时,AB=2.14,b=3m,p A=γh1=9.8×1.2=11.76kPa,p A=p B (1)静水总压力P左=γ·h c1A1=9.8×(h1+h2/2)×AB×b=P1=133.7kN (其中h c1=h1+h2/2 A1=AB×b)e1=0.915mP右=γ·h c2A2=9.8×h2/2×AB×b=P2=58.2kN(其中h c2=h2/2)e2=l/3=2.14/3=0.71m(2)因为ΣM a=0P1×(AB-e1)+G×AO×cos600=T×AB×cos600+P2×(AB-e2)T=80.2kN2.18已知:H=3m,b=5m,R=4.3m,θ=450 求P 及作用点 H=Rsin450=4.3×22=3m (1)水平分力:P x =γh e A x =9.8×1.5×3×5=220.5(KN) (2)铅垂分力:P z =γv=γΩ×b=9.8×1.143×5=56.01(KN) 其中:Ω=S 梯OABC —S 扇OAC =8.4-7.257=1.143㎡ S 梯OABC =0.5×[4.3+(4.3-3)]×3=8.4㎡ S 扇OAC =360450πR 2=360450×3.14×4.32=7.257㎡ (3)P=PPzx22+=01.565.22022+=227.5(KN )(4)P 与水平面的夹角α: α=arctanPPxz =arctan5.22001.56=14.250=14015` 2-192-20 解:已知b=10m ,k=8m(1)夹角计算:Sin β1=(173-170)/8=3/8=0.375(cos β1=550.5/8)β1=22.020Sin β2=(170-165)/8=5/8=0.625(cos β2=0.781) β2=38.680(2)水平方向水压力P x :(闸门宽b=10m)公式:P x =γh c A x =9.8×4×8×10=3136kN(另法:P x =1/2×9.8×8×8×10=31363136kN )(3)垂直方向水压力P z =γV关键计算压力体体积V=[三角形ofc (11.12㎡)+扇形ocd (33.88㎡)-梯形ofed (34.36)]×b所以 V=(11.12+33.86-34.36)×10=10.636×10=106.36m ³P z =γV=9.8×106.36=1042.33kN(4)总压力P:P=(P x 2+P z 2)=3304.7kN作用方向α=arctan1042.3/3304.7=17.51P 与水平面夹角17.510,且过o 点。
水力学 第七章课后题答案

为什么低堰的流量系数小而泄流量大
(1)因不考虑淹没情况和侧向收缩情况,泄流量可采用公式
= 23Τ2
因为 = 0.4988 1 Τ 2
可计算出1 = 10时, = 0.4939 = 1270.42 3 Τ
3 = −0.282 = −4.84
17.18
1.85
3
2 2
= 0
根据不同 Τ 可查的不同的
267 = 6309 3 Τ 269 = 7556 3 Τ
(3) = 0.502
可利用流量公式试算出H=15.64m
上游水位高程为266.31m
7.5某灌溉进水闸为三孔,每孔宽为10m;闸墩头部为半圆形,闸墩厚d为3m;边墩头部为
思考题
7.1何谓堰流,堰流的类型有哪些?它们有哪些特点?如何判断
堰流:在水利工程中,为了引水或泄水,常修建水闸或溢流坝等建筑物,以控制河流或渠道的水位及流
量。当这类建筑物顶部闸门完全开启,闸门下缘脱离水面,闸门对水流不起控制作用时,水流从建筑物
顶部自由下泄,这种水流状态称为堰流。
类型及判断:
根据过流堰顶的水流形态随堰坎厚度与堰顶水头之比 而变
(1)设计堰的剖面形状,及堰顶高程 311页
(2)当上游水位高程分别是267m和269m时,所设计的堰剖面通过的流量各为多少(下游水位低于
堰顶。
(3)通过流量为6000时,所需要的上游水位高程
(1)闸墩和边墩均为圆形,测收缩系数可求
= 1 − 0.0058
H为堰顶作用水头,WES坝的流量系数为0.502
流量系数可以由经验公式求出
水力学(1)第七章

三. 紊流的基本方程 紊流的基本方程指的是时均流场所满足的方程,紊流流动的 瞬时量仍满足连续方程和 N-S 方程。 通过对瞬时量所满足的连续方程和 N-S 方程两边取平均的方 法可以得到紊流时均流动的连续方程和运动方程。 因为连续方程的各项都是线性项,取平均值后脉动量不出 现。 瞬时量满足 ∂ (u x + u ′ ) ∂ (u y + u ′y ) ∂ (u z + u ′ ) x z + + =0 的连续方程 ∂x ∂y ∂z
lghf
n=1.75-2.0
n=1
过 渡 层流 区
紊流
lgv
§7—2 层流流动
层流流动可直接从 N-S 方程出发求解,但一般来说是很困难 层流流动可直接从 N-S 方程出发求解,但一般来说是很困难 的,只有在极少数情况下才有解析解。下面给出两个例子。 的,只有在极少数情况下才有解析解。下面给出两个例子。 一. 两平行平板间不可压流 体的层流流动(Couette流) N-S 方 程 最 简 单 的 一 个 N-S 方 程 最 简 单 的 一 个 解。它是 x-y 平面上的平面 解。它是 x-y 平面上的平面 流动,uy=0,ux =ux(y) .. 流动 流动,u =0,u =u (y) 流动 的起因是:质量力(重 的起因是:质量力(重 力)、压差和上下板之间的 力)、压差和上下板之间的 相对运动。 相对运动。
扰动因素
对比 抗衡
v ν
粘性稳定
d
Re =
vd
ν
利于稳定
圆管中恒定流动的流态转化仅取决于雷诺数,这是客观规律用 圆管中恒定流动的流态转化仅取决于雷诺数,这是客观规律用 无量纲量表达的又一例证,也是粘性相似准则的实际应用。 无量纲量表达的又一例证,也是粘性相似准则的实际应用。
水力学

x = x(a,b,c,t) ⎫
y
=
y(a, b, c, t)
⎪ ⎬
z = z (a, b, c, t ) ⎪⎭
式中,a, b, c, t 为拉格朗
日变数。
液体质点的速度、加速度
ux
=
∂x ∂t
=
∂x(a,b, c,t) ∂t
⎫ ⎪ ⎪
uy
=
∂y ∂t
=
∂y(a,b, c,t) ∂t
⎪ ⎬ ⎪
uz
= ∂z ∂t
fx fy
= =
Fx Fy
/M /M
⎫ ⎪ ⎬
fz
=
Fz
/M
⎪ ⎭
f = Xi+Y j+Zk
第二章 水静力学
第一节 概述
¾静水压强特性及其分布规律 ¾作用与平面和曲面的静水总压力
第二节 静水压强及其特性
p = lim ΔP = dP ΔA→0 ΔA dA
¾静水压强的方向总是垂直指向于作用面 ¾静止液体中任一点处各方向的静水压强大
倾斜式空气压差计
p1 − p2 = ρg(Δh' sinθ − a)
例题
静水压强分布图
pA = ρmg(∇1 −∇2)−ρg(∇3 −∇2)+ρmg(∇3 −∇4)−ρg(∇5 −∇4)
5
静水压强分布图
静水压强分布图
第六节 作用于平面上的静水总压力
¾解析法 ¾图解法
解析法
解析法适用 于置于水中任意 方位和任意形状 的平面。
第一章 绪论
第一节 水力学的定义、任务和发展简史
水力学是研究液体平衡和机械运动规律 及其应用的一门学科。 ¾ 水静力学 ¾ 水动力学
水力学第七章

2
2 gh'' gh'
h'2h'' h'h''2 2q2 0 g
h
h 2
1
ቤተ መጻሕፍቲ ባይዱ
8q 2 gh3
1
h h'' 2
1 8Fr22 1
h
h 2
1
8q 2 gh3
1
h h 2
1 8Fr12 1
矩形断面渠道共轭水深与临界水深的关系
h2h hh2 2q2 0 g
h2h hh2 2hc3r 0
水跃的动量方程
′"
c
c
取1-1,2-2断面间水体为控制体 1)底坡水平; 2)忽略渠床对水体的摩擦力作用; 3)两个断面上的动量校正系数α01=α02=1; 4)1-1和2-2断面是渐变流断面。
水平方向的动量方程为
yc1 A1
yc2 A2
Q
g
v2
v1
′"
c
c
v1 Q / A1
v2 Q / A2
yc1 A1
Q2 gA1
yc2 A2
Q2 gA2
平底坡棱柱形渠道的水 跃基本方程
根据平底坡棱柱形渠道的水跃方程
yc1 A1
Q2 gA1
yc2 A2
Q2 gA2
由于y和A均是水深h的函数,定义水跃函数
yc
A
Q2 gA
J
h
J h' J h''
共扼水深h`和h``是使水跃函数值相等的两个水 深。
水跃函数曲线
• 共扼水深就是同一条铅垂线与水跃函数曲线相 交的两点所对应的水深。跃前水深愈小对应的跃 后水深愈大。
2024版水力学全套课件

水力学全套课件contents •引言•水静力学•水动力学基础•水流阻力与水头损失•有压管道中的恒定流•明渠恒定流•堰流与闸孔出流目录引言水力学概述水力学的定义研究液体(主要是水)的平衡和机械运动规律及其应用的科学。
水力学的重要性在水利、能源、交通、环保等领域有广泛应用,对于国民经济和社会发展具有重要意义。
水力学与其他学科的关系与流体力学、水文学、水利工程学等学科密切相关,相互促进、共同发展。
水力学的研究对象和任务研究对象01研究任务02实际应用03发展历史现状发展趋势030201水力学的发展历史与现状课程内容及学习方法课程内容学习方法水静力学静水压强及其特性静水压强的特性静水压强的定义静水压强具有方向性,垂直于受压面并指向该面;在同一点上,静水压强的大小与受压面的方位无关。
压强的表示方法1 2 3液体平衡微分方程的概念液体平衡微分方程的建立液体平衡微分方程的应用液体平衡微分方程重力作用下液体平衡重力作用下液体平衡的概念等压面的概念重力作用下液体平衡的应用液体的相对平衡液体的相对平衡的概念液体相对平衡的原理液体相对平衡的应用液体作用在平面上的总压力的概念总压力的计算方法总压力的应用液体作用在曲面上的总压力的概念01总压力的计算方法02总压力的应用03水动力学基础描述液体运动的方法宏观描述微观描述欧拉法与拉格朗日法欧拉法拉格朗日法以流体质点为研究对象,追踪流体质点的运动轨迹,考察其在运动过程中各物理量的变化规律。
流场流线迹线流管液体运动的基本概念连续性方程实质质量守恒定律在流体力学中的具体表述。
意义反映了流体运动在空间上的连续性,即流体不可能在某一区域内突然消失或出现。
应用用于求解流体的密度、速度等物理量在空间和时间上的变化规律。
伯努利方程及其应用实质意义应用动量方程及其应用实质意义应用水流阻力与水头损失由于水流与固体边界之间的摩擦而产生的阻力,其大小与水流速度、边界粗糙度等因素有关。
摩擦阻力形状阻力兴波阻力涡流阻力由于物体形状对水流的阻碍而产生的阻力,与物体的形状、尺寸和在水流中的位置有关。
水力学第七章(3)

dh / ds
在上游
i J
( ) 0
f
0
E s 0
产生水跌
Es 0
在下游
h h0
dh / ds
i J
0 ( )
f
0
0
与N-N线渐近相切
2
2
2
>
陡坡(i>icr)上c区的水面曲线
缓坡
平底坡
陡坡 >
h cr h 0 h
() (0)
1
水面线产生水跃
1
1
陡坡(i>icr)上a区的水面曲线
缓坡
平底坡
陡坡 >
h h cr h 0
反底
h h0
h h cr
J
f
Q /=K
2
2
iK 0 / K
2
2
i
i J
f
0
E s 0
临界坡 =
dh / ds
i J E s
f
( ) ( )
i J
0 ( )
f
0
Es 0
0
与N-N线渐近相切
2
2
2
>
临界底坡(i=icr)上的水面曲线
N-N线与K-K线重合,即没有b区,只有a区和c区, 也即只有a3型和c3型水面曲线。 a3型曲线的变化规律介于a1和a2之间,c3型曲线 的变化规律介于c1和c2之间,即a3和c3曲线只能 是两条水平线。
K N
1
a b h 01 i1> icr c
M N N M
水力学基本概念

目录绪论: (1)第一章:水静力学 (1)第二章:液体运动的流束理论 (3)第三章:液流形态及水头损失 (3)第四章:有压管中的恒定流 (5)第五章:明渠恒定均匀流 (5)第六章:明渠恒定非均匀流 (6)第七章:水跃 (7)第八章:堰流及闸空出流 (8)第九章:泄水建筑物下游的水流衔接与消能 (9)第十一章:明渠非恒定流 (10)第十二章:液体运动的流场理论 (10)第十三章:边界层理论 (11)第十四章:恒定平面势流 (11)第十五章:渗流 (12)第十六章:河渠挟沙水流理论基础 (12)第十七章:高速水流 (12)绪论:1 水力学定义:水力学是研究液体处于平衡状态和机械运动状态下的力学规律,并探讨利用这些规律解决工程实际问题的一门学科。
2 理想液体:易流动的,绝对不可压缩,不能膨胀,没有粘滞性,也没有表面张力特性的连续介质。
3 粘滞性:当液体处在运动状态时,若液体质点之间存在着相对运动,则质点见要产生内摩擦力抵抗其相对运动,这种性质称为液体的粘滞性。
可视为液体抗剪切变形的特性。
(没有考虑粘滞性是理想液体和实际液体的最主要差别)4 动力粘度:简称粘度,面积为1m2并相距1m的两层流体,以1m/s做相对运动所产生的内摩擦力。
5 连续介质:假设液体是一种连续充满其所占空间毫无空隙的连续体。
6 研究水力学的三种基本方法:理论分析,科学实验,数值计算。
第一章:水静力学要点:(1)静水压强、压强的量测及表示方法;(2)等压面的应用;(3)压力体及曲面上静水总压力的计算方法。
7 静水压强的两个特性:1)静水压强的方向与受压面垂直并指向受压面2)任一点静水压强的大小和受压面方向无关,或者说作用于同一点上各方向的静水压强大小相等。
8 等压面:1)在平衡液体中等压面即是等势面2)等压面与质量力正交3)等压面不能相交4)绝对静止等压面是水平面5)两种互不相混的静止液体的分界面必为等压面6)不同液体的交界面也是等压面9 静水压强的计算公式:p=p0+10 绕中心轴作等角速度旋转的液体:11 绝对压强:以设想没有大气存在的绝对真空状态作为零点计量的压强,称为绝对压强。
水力学(吴持恭)高等教育出版社
P242-260
6.5、6.6、6.8、6.11、6.13
了解临界水深实际发生的场所,掌握明渠恒定非均匀渐变流的微分方程式,掌握恒定非均匀渐变流的水面曲线分析,掌握水面曲线的计算方法。
十七周
第七章
7.1棱柱体水平明渠的水跃方程
7.2棱柱体水平明渠水跃共轭水深的计算
十五周
第六章
6.1明渠均匀流的三种流态
6.2断面比能与临界水深
6.3临界底坡、缓坡与陡坡
P228-241
6.1、6.2、6.3、6.4
熟悉明渠水流的三种流态及其判别方法,掌握临界水深的计算方法。
十六周
6.4临界水深的一些实例
6.5明渠恒定非均匀渐变流的微分方程式
6.6棱柱体明渠中恒定非均匀渐变流水面曲线分析
第七周第三章31水头损失的物理概念及其分类32液体边界几何条件对水头损失的影响33均匀流沿程水头损失与切应力关系p11812631理解水头损失的物理概念及其分类理解均匀流沿程水头损失与切应力关系第八周34液体运动的两种形态35圆管中层流运动及其沿程水头损失的计算36紊流的特征p1261473233343536了解液体运动的两种形态了解层流运动时沿程水头损失的计算方法了解紊流的特征
第二周
第一章
1.1静水压强及其特性
1.2液体平衡微分方程式及其积分
1.3等压面
1.4重力作用下静水压强的基本公式
P13-23
1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8
掌握静水压强及其特性,熟悉液体平衡的微分方程式及其积分,了解等压面。
第三周
1.6绝对压强与相对压强
1.7压强的测量
5.3明渠均匀流的计算公式
武大水力学教材第7章
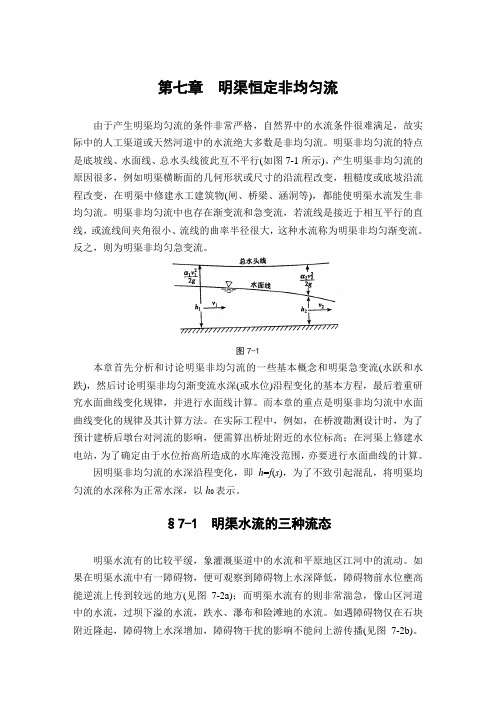
第七章明渠恒定非均匀流由于产生明渠均匀流的条件非常严格,自然界中的水流条件很难满足,故实际中的人工渠道或天然河道中的水流绝大多数是非均匀流。
明渠非均匀流的特点是底坡线、水面线、总水头线彼此互不平行(如图7-1所示)。
产生明渠非均匀流的原因很多,例如明渠横断面的几何形状或尺寸的沿流程改变,粗糙度或底坡沿流程改变,在明渠中修建水工建筑物(闸、桥梁、涵洞等),都能使明渠水流发生非均匀流。
明渠非均匀流中也存在渐变流和急变流,若流线是接近于相互平行的直线,或流线间夹角很小、流线的曲率半径很大,这种水流称为明渠非均匀渐变流。
反之,则为明渠非均匀急变流。
图7-1本章首先分析和讨论明渠非均匀流的一些基本概念和明渠急变流(水跃和水跌),然后讨论明渠非均匀渐变流水深(或水位)沿程变化的基本方程,最后着重研究水面曲线变化规律,并进行水面线计算。
而本章的重点是明渠非均匀流中水面曲线变化的规律及其计算方法。
在实际工程中,例如,在桥渡勘测设计时,为了预计建桥后墩台对河流的影响,便需算出桥址附近的水位标高;在河渠上修建水电站,为了确定由于水位抬高所造成的水库淹没范围,亦要进行水面曲线的计算。
因明渠非均匀流的水深沿程变化,即h=f(s),为了不致引起混乱,将明渠均匀流的水深称为正常水深,以h0表示。
§7-1 明渠水流的三种流态明渠水流有的比较平缓,象灌溉渠道中的水流和平原地区江河中的流动。
如果在明渠水流中有一障碍物,便可观察到障碍物上水深降低,障碍物前水位壅高能逆流上传到较远的地方(见图7-2a);而明渠水流有的则非常湍急,像山区河道中的水流,过坝下溢的水流,跌水、瀑布和险滩地的水流。
如遇障碍物仅在石块附近隆起,障碍物上水深增加,障碍物干扰的影响不能问上游传播(见图7-2b)。
上述两种情况表明,明渠水流存在两种不同的流态。
它们对于所产生的干扰波(Disturbance Wave)的传播,有着不同的影响。
障碍物的存在可视为对水流发生的干扰,下面分析干扰波在明渠中传播的特点。
水力学第七章(1)

nQ 2 1 m 1 23 12 Q AR i h0 0.625 n i 0.1875 m
0.375
2
0.25
1.303(m)
(2)用附图I求解
b h0 0.606
h0 b 1.65
m 1.5
b 2.67 nK 0.2 b 0.79 m, h0 1.31m
均匀流的解法
1.直接解法 (1)当其他量已知,求流量或底坡或粗糙系数 时,可直接由均匀流渠道中的流量表达式求解。
1 Q AC Ri A R 2 / 3 i 1 / 2 n
(2)宽矩形断面渠道求正常水深h0。
R h0
A bh0
Q
1 1 2/3 AR 2 / 3i1/ 2 bh0 h0 i1/ 2 n n
i1 2 b mh0 h0 n b 2h 1 m 2 0
23
b h0
Q
i
12
n 2 1 m2
m
5/ 3
h08 3
23
h0
nQ 2 1 m 58 i 3 16 m
38
2
14
2.试算法或图解法 (1)当已知Q、i、n、m、b(或h0)求h0(或b) 时,由于此时需要求解关于h0和b的非线性方程, 不能直接求解,只能采用试算法,或者应用附图 Ⅰ的图解曲线求解。
当渠床的粗糙系数n、底坡i及过水断面积A一定 时,湿周χ愈小流量Q愈大。
梯形断面的水力最佳断面
水力最佳断面的条件:过水断面面积A为常数和湿 周χ最小。
A (b mh)h
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水跃函数曲线具有如下的特性:
水跃函数有极小值 J(h)min,其对应水深是临界水深 hK ; 当 h > hK 时(相当于曲线的 上半支);J(h) 随着 h 即跃 后水深的减小而减小;
当 h < hK 时(相当于曲线的 下半支);J(h) 随着 h 即跃 前水深的减小而增加。
EXIT 27
7.3.2 水跃段水头损失的计算
根据能量方程,有: Ej (h1
1v12
2g
) (h2
2 2v2
2g
)
h1 v1 对矩形明渠: v2 v1 h2
2 1 v 2 1 Fr1 gh1 2
整理得棱柱体矩形水平明渠水跃段的水头损失为:
水跃段水头损失在总水头损失中所占的比例为:
Ej
1 1 2 1 3 E 1
EXIT 30
Ej E
是跃前断面弗劳德数 Fr1 的函数,随 Fr1 的增加而增大。
当 Fr1 <2.3 时,
当 Fr1 =4.5 时,
Ej E Ej E
<50%,水跃的消能效果不佳。
已达到90%。
整理水跃函数对水深的微分, 有:
Q2 dA d AhC Q2 2 2 B A0 gA dh dh gA Q 2 A3 g B
上式即为临界水深 hK 满足的方程。因此, J(h)min 对应的水 深即是临界水深。
例 7.2 分析水跃段中的低槛对跃后水深的影响。
FR Q2 Q2 1 hC 2 A1hC A2 gA1 gA2 g FR ) J (h1) J (h2 g
无槛时的水跃方程为: J (h1 ) J (h2 ) 由于有、无槛时跃前水深相同,故有:
J (h1) J (h1 ) J (h2 )
FR FR ) J (h1) ) J (h2 ) J (h2 J (h2 ) J (h2 g g
由于水跃函数随跃后水深的减小而减 小,故有为:
EXIT 24
水跃的共轭水深计算是以水跃方 程为依据的。在推导该理论方程 的时候,曾经作过一些假定。
对棱柱体矩形水平明渠中的水跃 进行了大量的实验研究,积累了 丰富的实验资料,并验证了上述 假定的合理性。 其它断面形状的水平明渠中的水 跃实验也证实了水跃方程的准确 性。
EXIT 25
7.3 棱柱体水平明渠中水跃的能量损失
均匀流
hj 0,hw hf l v2 hf 4R 2 g
Re 500
急流 临界流 缓流
J i v C Ri 1 1 C R6 n
可能,但无 工程意义
Q( 2 v2 1v1 ) F
湍流
Re 500
恒定流
急流
层流
明渠流动
临界流
缓流
渐变流
Re 500
EXIT
6
EXIT
7
表面旋滚起点过水断面 1-1 称为跃前断面,该断面处水深 h1 称为跃前水深。表面旋滚末端的过水断面2-2称为跃后断面, 该断面处的水深 h2 称为跃后水深。跃前、后水深之差称为跃 高,之间的距离称为跃长。
EXIT
8
水跃是否产生水面旋滚以及 旋滚的剧烈程度取决于跃前 断面的弗劳德数Fr。
7.1 7.2 7.3 7.4 7.5
棱柱体水平明渠的水跃方程 棱柱体水平明渠中水跃共轭水深的计算 棱柱体水平明渠中水跃的能量损失 棱柱体水平明渠中水跃跃长的确定 非棱柱体明渠中的水跃
EXIT 11
7.1 棱柱体水平明渠的水跃方程
对下图所示的产生于棱柱体水平明渠中的水跃进行研究。
采用恒定总流的动量方程 来推导水跃方程。对跃前、 跃后断面写出动量方程。 (为何不用能量方程?)
棱柱体水平明渠中的水跃方程也可应用于底坡较小的明渠。
EXIT 14
7.2 棱柱体水平明渠中水跃共轭水深的计算
当棱柱体明渠断面的几何要素和渠中流量已知时,由已知的 一个水深计算另一个水深称为共轭水深的计算。
7.2.1 共轭水深计算的一般方法
水跃方程中的 A 和 hC 都是水深的复杂函数,因此共轭水深 不易直接由水跃方程解出。 试算法
h2 h2
有槛时跃后水深较无槛时小。工程上 常通过反冲力来降低跃后水深。
7.2.2 梯形明渠共轭水深的计算
梯形明渠共轭水深可以运用迭代公式计算:
2 J1hi Q2 2 h2,i 1 2 g [b 0.5(m1 m2 )hi ] b 0.5(m1 m2 )hi
式中 AhC 是过水断面对水面线 0-0 的面积静矩。 给水深 h 以增量 dh,其相应的静矩增量 d( AhC ) 为:
dh dh d AhC [ A(hC dh) Bdh ] AhC Adh dA 2 2
EXIT 18
略去二阶微量,得:
d AhC Adh
Q bq ,
h A bh , hC 2
将以上关系式代入水跃方程,则得到棱柱体矩形水平明渠的 水跃方程如下:
2 q 2 h12 q 2 h2 gh1 2 gh2 2
整理,可得:
2q hh h h 0 g
2 1 2 2 1 2
2
EXIT 23
解方程,可得:
h1 q2 h2 1 8 3 1 2 gh 1
本章习题
7.2、7.3、7.5
第六章内容的简要回顾
明渠水流的三种流态;
断面比能公式及掌握临界水深的计算公式; 临界底坡、缓坡与陡坡; 明渠恒定非均匀渐变流的微分方程; 棱柱体明渠中恒定非均匀渐变流水面曲线分析; 明渠恒定非均匀渐变流水面曲线的计算。
∑F=0,F 包括 G 等质量力,FP、Ff 等表面力,G=mg,
E jj (h2
2g
) (h3
2g
)
近似地令 h3=h2,v3=v2 及 α3=1, 上式可简化为:
2 v2 Ejj ( 2 1) 2g
h1 E jj 2 1 1 4
EXIT 29
7.3.4 水跃总水头损失和水跃段水头损失的近似计算
v32 v12 E Ej Ejj 根据能量方程,有: E (h1 ) (h3 ) 2g 2g h1 h1 3 E 2 1 1 Ej 1 2 1 1 jj 4 4 h1 3 E 1 故有 4
图解法
EXIT 15
试算法
在应用试算法解共轭水深时,可先假设一个欲求的共轭水深 代入水跃方程,如假设的水深能满足水跃方程,则该水深即 为所求的共轭水深。否则,必须重新假设直至水跃方程得到 满足为止。试算法可得较高的精确度,但计算比较麻烦。
图解法:利用水跃函数曲线来直接求解共轭水深 当流量和明渠断面的形状尺寸给定时,可假设不同水深,计 算出相应水跃函数 J(h) ,以 h 为纵轴、J(h) 为横轴,可绘 出水跃函数曲线。水跃函数曲线具有如下的特性:
24 Re
急流 临界流 缓流
棱柱体明渠
湍流
管道流动
非恒定流
急变流
Q2 v2 hf 2 l,hj K 2g
dh iJ ds 1 Fr 2
12种水面线
第七章 水跃
本章学习基本要求:
掌握水跃的概念; 掌握棱柱体水平明渠的水跃方程、共轭水深的计算; 了解水跃消能机理、效率、能量损失计算及跃长计算的经 验公式。
h1 3 Ej 1 2 1 1 2 0.85Fr12/3 0.25 4 α2 为 2-2 断面的动能修正系数,其值随 Fr1 的增加而增大。
EXIT 28
7.3.3 跃后段水头损失的计算
根据能量方程,有:
2 2v2 2 3v3
1.0<Fr<1.7,波状水跃 1.7<Fr<2.5,弱水跃 2.5<Fr<4.5,不稳定水跃 4.5<Fr<9.0,稳定水跃 9.0<Fr, 强水跃
EXIT
9
当1<Fr1<1.7时,水跃 为波状水跃,不产生表 面旋滚,消能效果差。 有表面旋滚的水跃称为 完全水跃。
EXIT 10
EXIT
EXIT
5
水流由急流过渡到缓流,会产生一种水面突然跃起的特殊的 局部水力现象,称为水跃。
水跃段内,水流运动要素急剧变化,水流湍动、混掺强烈, 旋滚与主流间不断发生质量和动量交换,致使水跃段内产生 较大的能量损失。常利用水跃来消除泄水建筑物下游高速水 流中的巨大动能。 消能:部分势能转化为动能;部分通过摩擦、旋滚、扩散、 撞击、变成热能耗散。
ρQ( β2v2 β1v1 ) F
EXIT 12
ρQ( β2v2 β1v1 ) FP1 FP2 Ff
假定: 水跃跃前、跃后断面的水流为渐变流(动水压强近似服从 静水压强分布); 摩阻力Ff=0; 动量修正系数β1=β2=1。 应用恒定总流的动量方程和连续性方程,经整理可得: Q2 Q2 A1hC1 A2 hC 2 gA1 gA2
当明渠流量及断面形态确定时,跃前水深越小则跃后水深越 大;反之,跃前水深越大,跃后水深则越小。
EXIT 17
例 7.1 证明与 J(h)min 相应的水深即临界水深。
证:若水跃函数取极小值,则满足:
Q2 d AhC 2 d J h gA Q dA d AhC 0 2 dh dh gA dh dh
EXIT 13
当明渠断面的形状、尺寸以及渠中的流量一定时,水跃方程 的左右两边都仅是水深的函数。
Q2 Q2 A1hC1 A2 hC 2 gA1 gA2
