编译原理第七章 中间代码生成(1)
07-第7章-中间代码生成-编译原理PDF精讲课件-中国科技大学(共13讲)

中国科学技术大学 计算机科学与技术学院 陈意云
第七章 中间代码生成
记号 分析 流 器 本章内容
–介绍几种常用的中间表示:后缀表示、图形表示 和三地址代码 –用语法制导定义和翻译方案来说明源语言的各种 构造怎样被翻译成中间形式
静态 检查 器
中间 代码 中间 代码 生成 代码 生成 器 器
7.1 中 间 语 言
7.1.2 图形表示 • 语法树是一种图形化的中间表示 • 有向无环图也是一种中间表示
assign a + + a assign +
+ c uminus d uminus c c d d b b (b) DAG (a) 语法树 a = (b + cd) + cd的图形表示
7.1 中 间 语 言
7.1.4 静态单赋值形式 • 一种便于某些代码优化的中间表示 • 和三地址代码的主要区别
– 所有赋值指令都是对不同名字的变量的赋值 – 一个变量在不同路径上都定值的解决办法 if (flag) x = 1; else x = 1; y = x a; 改成 if (flag) x1 = 1; else x2 = 1; x3 = (x1, x2); //由flag的值决定用x1还是x2
E E1 E2 E.nptr = mkNode( ‘’, E1.nptr, E2.nptr) E.nptr = mkUNode( ‘uminus’, E1.nptr) E E1 E (E1) F id E.nptr = E1.nptr E.nptr = mkLeaf (id, id.entry)
符号表实例
7.2 声 明 语 句
• 符号表的特点
–各过程有各自的符号表 –符号表之间有双向链 –构造符号表时需要符号表栈 –构造符号表需要活动记录栈 sort var a:…; x:…; readarray var i:…; exchange quicksort var k, v:…; partition var i, j:…;
编译原理课件-第7章中间代码生成

● example
例2 suppose the function f has been defined in C as in the previous example. Then, the call
f ( 2+3, 4) 请写出the call三地址码。
解: translates to the three-address code begin_args t1 = 2 + 3 arg t1 arg 4 call f
2023/6/1
● If Statements if ( E ) S1 else S2
Three-Address Code :
If语句前的代码 If测试的代码
<code to evaluate E to t1>
条件
if_false t1 goto L1
<code for S1> goto L2
True情况下的代码
(sub, x, 1, t3 ) (asn, t3, x, _ ) (eq, x, 0, t4 ) (if_f, t4, L2, _) (wri, fact, _, _ ) (lab, L1, _ , _ ) halt, _, _, _ )
2023/6/1
例2 请写出TINY program三地址码的三元式表示。
7.4 Code Generation of Procedure and Function Calls 过程 和函数调用的代码生成
2023/6/1
7.1 Intermediate Code and Data Structures for Code Generation 中间代码和用于代码生成的数据结构
{ AddrKind kind; Union
编译原理 第七章——语义分析和中间代码生成

中间语言
常见的中间语言的形式: 后缀式(逆波兰式) 三地址代码 - 三元式 - 四元式 - 间接三元式 DAG图
后缀式
又称逆波兰表示法,把运算量(操作数)写在前面,把算 符写在后面(后缀)。 如:a+b 写成 ab+ a+b*c 写成 abc*+ 定义: 1.如果表达式E是一个变量或常量,则E的后缀式是E自身; 2.如果E是E1 op E2形式的表达式 (op为二元操作符) ,则E的 后缀式为E1’E2’op。E1’ 、E2’分别为E1、E2的后缀式; 3.如果E式(E1)形式的表达式,则E1的后缀式就是E的后缀式。 •这种表达式不需要括号 这种表达式不需要括号
(0) (=[ ],x,i) (1) (:=,(0),y)
([ ]=,y,-,x[i]) //变址存数四元式
(0) ( [ ]=,y,i) (1) (:=,x,(0))
(=[ ],y[i] ,-,x) //变址取数四元式
如a:=b*-c+b*-c
四元式
op (0) (1) (2) (3) (4) (5) arg1 arg2 resul t T1 uminus C
如a*(b+c) 写成 abc+* (a+b)*(c+d) 写成 ab+cd+*
* a b + c a + b c *
+
d
将表达式翻译为后缀式的语义规则
产生式
E→E1 op E2 E→(E) E→id
语义规则
E.code:=E1.code||E2.code|| op E.code:=E1.code E.code:=id
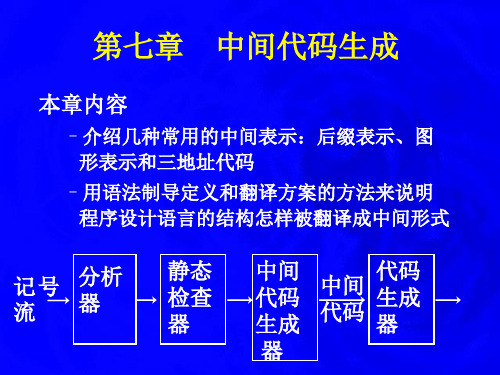
a:=b*-c+b*-c的三地址代码为:
T1 := -c T2 :=b*T1 T3 := -c T4 :=b*T3 T5 :=T2 +T4 a := T5
编译原理第七章中间代码生成汇编
*
b
*
b
uminus
c
a= b*-c + b*-c
c abc uminus * bc numinus *+ assign
抽象语法树
• 构造赋值语句语法树的语法制导定义: 产生式
S→id = E E→E1 + E2 E→E1 * E2 E→- E1 E→(E1)
• param x1 • param x2 • …… • param x2 • call p, n n表示实参个数。return y中y为过程返回的一个值
– 形如x = y[i]及x[i] = y的索引赋值。
– 形如x = &y, x = *y和*x = y的地址和指针赋值。象形式。 • 这些语句可以以带有操作符和操作数域的记录 来实现。四元式、三元式及间接三元式是三种 这样的表示。
x = y op z
其中,x、y和z是名字,常量或编译器生成的临时变量 op代表任何操作符(定点运算符、浮点运算符、逻辑运算 符等)
• 像x+y*z这样的表达式要翻译为:
T1 = y * z
T2 = x + T1 其中T1 ,T2为编译时产生的临时变量。
三地址语句的类型
• 三地址语句类似于汇编语言代码。语句可以有 符号标号,而且存在各种控制流语句。
– 临时变量也要填入符号表中。
三元式
• 为了避免把临时变量填入符号表,可以通过计 算临时值语句的位置来引用该临时变量。 • 这样三地址代码的记录只需要三个域op, arg1 和arg。
• 对于单目运算符op, arg1和arg2只需用其一。
编译原理第7章-中间代码生成

-16-
表达式代码生成的例子
College of Computer Science & Technology
class[5].age + *ptr.age
typedef struct { char name[30]; int age; float height; }person;
int x[10]; person class[10]; person *ptr;
(cSlaUsBs[I5,]5, 0,t4t5) (MULTI, t5, 33, t6) cla(sAsA[5D].aDg,eclasst,1t6, t4) (AADD , t4, 30, t1) *p(t*Arp.astsgrieg,ptt7tr2, _, t7) (AADD , t7, 30, t2)
-7-
四元式
• 表达式运算符 College of Computer Science & Technology
– ADDI, ADDF, SUBI, SUBF, MULTI, MULTF,
– DIVI, DIVF, MOD,
– AND, OR, EQ, NE, GT, GE, LT, LE
• I/O 操作
Compiler Construction Principles & Implementation Techniques
-12-
7.2 表达式的四元式代码
College of Computer Science & Technology
• 表达式的运算分量可以很复杂:
– 多维数组下标变量:A[i][j][k] – 结构体域名变量:st.address.city – 函数调用:f(x,y) – 指针引用:*(p+1) – ……
编译原理中间代码生成7

7.1 中 间 语 言
7.1.4 静态单赋值形式 • 一种便于某些代码优化的中间表示 • 和三地址代码的主要区别
– 所有赋值指令都是对不同名字的变量的赋值 – 一个变量在不同路径上都定值的解决办法
if (flag) x = 1; else x = 1; y = x a; 的条件语句改成 if (flag) x1 = 1; else x2 = 1;
assign
assign
a
+
a
+
+
+
uminus c
d
uminus
c
d
c
d
b (a) 语法树
b (b) dag
a = (b + cd) + cd的图形表示
7.1 中 间 语 言
构造赋值语句语法树的语法制导定义
产生式
语义规则
S id =E S.nptr = mkNode(‘assign’, mkLeaf (id, id.entry), E.nptr)
a = (b + cd ) + cd 语法树的代码
t1 = b t2 = c d t3 = t1 + t2 t4 = c d t5 = t3 + t4 a = t5
uminus
7.1 中 间 语 言
三地址代码是语法树或dag的一种线性表示
a = (b + cd ) + cd
语法树的代码 dag的代码
7.2 声 明 语 句
P M D; S {addWidth (top (tblptr), top (offset) ); pop(tblptr); pop (offset) }
编译原理中的中间代码生成

编译原理中的中间代码生成编译原理是计算机科学中非常重要的一门课程,它研究的是将高级语言程序转化为低级语言程序,实现计算机能够理解和运行的目的。
但是高级语言相较于机器语言更为抽象和复杂,所以需要经过多个步骤的处理,其中中间代码生成就是其中的一个重要环节。
中间代码是指一种介于高级语言和机器语言之间的表示方式,它的作用是将高级语言程序转化为更容易被计算机处理的形式,同时它也提供了一种通用的平台,可以将同一份高级语言程序转化为多种低级语言程序,如汇编语言、机器语言等。
如今,多数编译器都采用中间代码进行转化和优化,它不仅可以提高代码执行效率,还可以提高程序的可移植性和可维护性。
那么,中间代码的生成是如何进行的呢?和编译器的其它部分一样,中间代码生成也是经过多个步骤的处理,其中最主要的步骤包括词法分析、语法分析、语义分析和中间代码生成。
词法分析的作用是将源程序的字符序列转换为单词序列。
它依靠的是正则表达式的特性,对源程序进行识别和划分,得到一系列单词。
这些单词包括关键字、标识符、常数、字符等,在很大程度上决定了接下来的语法分析和语义分析。
语法分析是将单词序列转化为抽象语法树的过程,它将程序以树的形式进行表示,更为直观和容易理解。
通过对抽象语法树的遍历,可以得到程序的各种信息,如变量名、函数名、常量、运算符和控制语句等。
对于每个节点,编译器会根据其语义和上下文信息,进行类型检查、错误检测和决策生成等操作,最终得到一个可运行的程序。
语义分析是识别程序中不符合语言规范或逻辑错误的部分,它是整个编译过程中最为复杂的一个环节。
在这个过程中,编译器需要根据程序的上下文信息,判断其意义和合理性,并进行正确的处理。
例如,当编译器遇到一个未定义的变量或函数时,它将会报错并停止编译。
语义分析可以避免很多程序运行时的错误,同时也是编译器优化的重要基础。
当编译器通过词法分析、语法分析和语义分析,得到一个完整、正确的程序后,就可以进行中间代码生成了。
编译原理课件-中间代码生成

(3) E→not E1 { E.true:= E 1.false; E.Codebegin:= E 1.codebegin; E.false:= E 1.true
(翻譯不是最優)
語句 if a<b or c<d and e<f then S1 else S2 的四元式
(1) if a<b goto (7) //轉移至(E.true )
(2) goto (3)
(3) if c<d goto (5)
(4) goto (p+1)
//轉移至(E.false)
(5) if e<f goto (7) (6) goto (p+1) (7)( S1的四元式
不同層次的中間代碼
源語言
中間代碼
(高級語言) (高級)
中間代碼 (中級)
中間代碼 (低級)
float a[10][20]; a[i][j+2];
t1 = a[i, j+2]
t1 = j + 2 t2 = i * 20 t3 = t1 + t2 t4 = 4 * t3 t5 = addr a t6 = t5 + t4 t7 = *t6
語義描述使用的變數和過程:
E.true : “真”鏈, E.false : “假”鏈
E.codebegin : E 的第一個四元式
Nextstat: 下一四元式地址
编译原理实验 中间代码生成

实验四中间代码生成一.实验目的:掌握中间代码的四种形式(逆波兰式、语法树、三元式、四元式)。
二.实验内容:1、逆波兰式定义:将运算对象写在前面,而把运算符号写在后面。
用这种表示法表示的表达式也称做后缀式。
2、抽象(语法)树:运算对象作为叶子结点,运算符作为内部结点。
3、三元式:形式序号:(op,arg1,arg2)4、四元式:形式(op,arg1,arg2,result)三、以逆波兰式为例的实验设计思想及算法(1)首先构造一个运算符栈,此运算符在栈内遵循越往栈顶优先级越高的原则。
(2)读入一个用中缀表示的简单算术表达式,为方便起见,设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”。
(3)从左至右扫描该算术表达式,从第一个字符开始判断,如果该字符是数字,则分析到该数字串的结束并将该数字串直接输出。
(4)如果不是数字,该字符则是运算符,此时需比较优先关系。
做法如下:将该字符与运算符栈顶的运算符的优先关系相比较。
如果,该字符优先关系高于此运算符栈顶的运算符,则将该运算符入栈。
倘若不是的话,则将此运算符栈顶的运算符从栈中弹出,将该字符入栈。
(5)重复上述操作(1)-(2)直至扫描完整个简单算术表达式,确定所有字符都得到正确处理,我们便可以将中缀式表示的简单算术表达式转化为逆波兰表示的简单算术表达式。
四、程序代码://这是一个由中缀式生成后缀式的程序#include<iostream.h>#include<string.h>#include<math.h>#include<ctype.h>#define maxbuffer 64void main(){char display_out(char out_ch[maxbuffer], char ch[32]);//int caculate_array(char out_ch[32]);static int i=0;static int j=0;char ch[maxbuffer],s[maxbuffer],out[maxbuffer];cout<<"请输入中缀表达式: ";cin>>ch;for(i=0;i<maxbuffer;i++){out[i]=ch[i];}cout<<"请确认您输入的表达式:"; while(out[j]!='#'){cout<<out[j];j++;}cout<<'#'<<endl;display_out(s,out);//caculate_array;}char display_out(char out_ch[32],char ch[]) {int top=-1;int i=0,data[maxbuffer],n;int j=0;char sta[20];while(ch[i]!='#'){if(isalnum(ch[i])){while(isalnum(ch[i])){out_ch[j]=ch[i];j++;i++;}out_ch[j]=' ';j++;}else{switch(ch[i]){case '+':case '-': if(sta[top]=='('||top==-1){top++;sta[top]=ch[i];i++;}else{//j--;out_ch[j]=sta[top];j++;top--;//i++;}break;//break;case '*':case '/':if(sta[top]=='*'&&sta[top]=='/'){out_ch[j]=sta[top];j++;//i++;top--;}else{top++;sta[top]=ch[i];i++;}break ;//break;case '(':top++;sta[top]=ch[i];i++;break;case ')':if(sta[top]=='('){top--;i++;}if(top==-1){//cout<<"错误: 第"<<j<<"个位置的")"没有找到与之匹配的"(""; ch[i]='#';j=0;}else{//while(sta[top]!=‘(‘){out_ch[j]=sta[top];top--;j++;//}break;}break;/*case ‘#‘: out_ch[j]=‘#‘;j++;break;*/default:cout<<" your input is error"<<endl; ch[i]='#';j=0;break;}}}while(top!=-1){out_ch[j]=sta[top];j++;top--;}out_ch[j]='#';n=0;cout<<"逆波兰表达式为: ";while(out_ch[n]!='#'){cout<<out_ch[n];n++;}cout<<endl;j=0;return out_ch[maxbuffer];}五、实验结果:要求:自己给出3个测试用例,观察结果。
编译原理第七章中间代码生成

3
循环语句的中间代码生成
循环结构的代码生成方式有多种,并根据循环类型和常量优化代码。
中间代码生成的优化技术
常量合并
把具有相同值的常量合并 为一个。
• 可以节省空间。 • 会改变代码原有结
构,需要小心。
表达式优化
采用数学方法对表达式求 解结果,优化表达式产生 的中间代码。
• 用于优化表达式的 运算过程,提高效
高效的编写代码方法
既要运用科学原理,又要具 备实践经验。而编译原理的 学习可以为我们提供更好的 编写代码方法。
追求突破与创新的开发 者
不断优化自己的编码方式可 以让您编写出更高质量的程 序,使你更好的成为一个有 追求的开发者!
编译原理第七章中间代码 生成
学习了编译原理基础后,我们来进一步了解关于中间代码生成的章节。
课程背景
1 编译器
2 中间代码
将高级语言代码转换成低级语言代码的 程序。
与源代码和目标代码位于中间的代码, 更容易优化和转换。
中间代码生成的定义和作用
定义
中间代码是一种抽象的机器语言,用于编 译过程中的代码转换。化
按照代码的实际运转过程, 进行代码生成顺序的优化。
• 可避免一些冗余工 作,加快程序的执
• 行需要速一度些。优化算法, 不易实现。
总结 and 结论
精通编译原理,写出高 效代码!
各种方法都是在实际生产环 境中总结出来的经验,并根 据实际需要进行选择和判断。
作用
可以用于优化和改变代码结构,同时还可 以提高生成目标代码的速度。
中间代码生成的方法
语法制导的方法
通过语法规则来约束产生 的中间代码,便于生成和 优化代码。
• 可用于处理语法规 则固定的语句。
编译原理chapter7 语义分析及中间代码生成

编译原理
chapter7
语义分三元式 三元式顾名思义就是带有三个域的记录结构。 三元式顾名思义就是带有三个域的记录结构。 一般形式为: (i)( ,arg1,arg2) 一般形式为: )(op, )( , ) 其中,( )为三元式的编号, 其中,(i)为三元式的编号,也代表了该式的运算 ,( 结果, , 的含义与四元式类似, 结果,op,arg1,arg2的含义与四元式类似,区别在 , 的含义与四元式类似 于arg可以是某三元式的序号,表示用该三元式的结果 可以是某三元式的序号, 可以是某三元式的序号 作为运算对象。 作为运算对象。
编译原理
chapter7
语义分析和中间代码生成
对于文法G[E]: E →E+T | T 例:对于文法 T→ digit 产生式 ) E→ E(1)+T E→ T T→ digit 语 法 分 析 栈 T + E … # 语义子程序 ) {E.Val=E(1).Val+T.Val} {E.Val=T.Val} {T.Val=digit} T.Val 语 义 ‘+’ ) E(1).Val 分 析 … 栈 #
编译原理
chapter7
语义分析和中间代码生成
三地址代码可以看成是抽象语法树一种线性表示。 三地址代码可以看成是抽象语法树一种线性表示。 线性表示 例: a=b*-c+b*-c = a + T1=-c T2=b*T1 T3=-c
*
b
* - b
c
c
T4=b*T3 T5=T2+T4 a=T5
编译原理
语义分析和中间代码生成
图表示法—抽象语法树 图表示法 抽象语法树 在语法树中去掉一些对翻译不必要的信息后 在语法树中去掉一些对翻译不必要的信息后,获得 去掉一些对翻译不必要的信息 的更有效的源程序的中间表示, 的更有效的源程序的中间表示,这种经过变换后的语法 树称为抽象语法树。 树称为抽象语法树。 内部结点代表操作符,它的孩子代表对应的操作数。 内部结点代表操作符,它的孩子代表对应的操作数。 例:a+a*(b-c)+(b-c)*d ( ) ( ) + + a a b
编译原理第七章中间代码生成
7.2 声 明 语 句
7.2.2 作用域信息的保存
• 所讨论语言的文法
PDS D D ; D | id : T | proc id ; Dktable(previous) enter(table, name, type, offset) addwidth(table, width) enterproc(table, name, newtable)
四元式
• 一个四元式是带有四个域的记录结构,这四个 域分别称为op, arg1, arg2及result。
– 域op包含一个代表运算符的内部码
– 三地址语句x=y op z通过将y放入arg1,z放入arg2 ,并且将x放入result,=为算符。
– 像x=y或x=-y这样的一元操作符语句不使用arg2 – 像param这样的运算符仅使用arg1域。 – 条件和无条件语句将目标标号存入result域。
7.2 声 明 语 句
7.2.1 过程中的声明
计算被声明名字的类型和相对地址 P {offset = 0} D S DD;D D id : T {enter ( , T.type, offset); offset = offset + T.width } T integer {T.type = integer; T.width = 4 } T real {T.type = real; T.width = 8 } T array [ num ] of T1 {T.type = array (num.val, T1.type); T.width = num.val T1.width} T T1 {T.type = pointer (T1.type); T.width = 4 }
uminus
编译原理第七章 中间代码生成(1)

带括号表达式的后缀式例子
中缀式: (a + (d + b) * c ) + e #
后缀式: a d b + c * +e +
Operator stack 运算符栈 S1
Operand stack
运算分量栈 S2
7.1 常见的中间表示
抽象语法树-AST 无环有向图-DAG(共享的AST)
+ +
ad*bc*+e+
先根遍历生成前缀式:
c
++*ad*bce
抽象语法树
由Token序列生成后缀式(1)
(1)初始化: S1和S2为空; (2) 读token: tk=ReadOne(); (3) Switch tk of (i) #: if (S1为空) exit; else while (S1不为空) /*产生剩余操作符的后缀表示*/ {op = pop(S1); (str1, str2)=pop(2); push(S2, str2 + str1+ “op”);} (ii)运算分量: push(tk, S2); goto (2); (iii)运算符: if (S1为空 || tk优先级大于Top(S1)) { push (tk, S1); goto(2);} else { while(tk小于等于Top(S1) && S1不为空)) { op = pop(S1); (str1, str2)=pop(2); push(S2, str2+str1 + “op”); } push(tk, S1); goto (2); }
---
把id1的值赋值给id2(长度为n)
第七章 中间代码生成

7.2.1 过程中的说明语句
一个过程中的所有说明语句作为一个类集来 处理。用一个全程变量Offset来记录下一个数椐 在活动记录中的位置。 相对地址:相对静态数据区基址或活动记录中局 部数据区基址的一个偏移值。
7.2.2 作用域信息的保存
1 .问题的提出 一般的语言中,标识符的作用在程序正文 中有一个确定的范围。因此,同一个标识符在不同 的程序正文中可能标识不同的对象,具有不同的性 质,要求分配不同的存储空间。于是提出下面的问 题:如何组织符号表,使得同一个标识符在不同的 作用域中得到正确的引用而不产生混乱。
7.1.3 三地址代码
三地址代码是由下面一般形式的语句构成的序列: X:=y op z 其中,x、y、z为名字、常数或编译时产生的临时 变量;op代表运算符号如定点运算符、浮点运算符、 逻辑运算符等。每个语句的右边只能有一个运算符。 表达式x + y z翻译成的三地址语句序列是 t1 := y z t2 := x + t1 三地址代码通常有两种表示方法:四元式、三元式
构造赋值语句语法树的语法制导定义
产 生 式 语 义 规 则 S id :=E S.nptr := mknode(‘assign’, mkleaf (id, id.entry), E.nptr) E E1 +E2 E.nptr := mknode( ‘+’, E1.nptr, E2.nptr)
第七章 中间代码生成
本章内容: 介绍几种常用的中间表示:后缀表示、图形 表示和三地址代码 用语法制导定义和翻译方案的方法来说明程 序设计语言的结构怎样被翻译成中间形式
编译原理课件07语义分析和中间代码产生

语义分析阶段中的关键问题和 挑战
语义分析阶段面临着许多关键问题和挑战,例如识别复杂的语义错误、处理 不完整的代码等。
在处理大型程序时,编译器需确保语义分析的效率和准确性,并能处理各种 语法结构。
中间代码的定义和作用
中间代码是一种介于高级语言和底层机器代码之间的形式,它是一种可读性 较强且易于生成和优化的表示。
语义分析的基本任务和目标
语义分析的主要任务是识别和验证程序中的语义错误,例如类型不匹配、变量未定义等。 它的目标是确保程序的语义是一致的,以便于理解和执行。语义语义分析使用了各种技术和方法,包括符号表、类型检查、控制流分析等。 符号表用于记录变量和函数的信息,类型检查用于比较表达式和操作数的类 型是否一致。 控制流分析用于检测条件语句、循环语句和函数调用等代码块的流程。
编译原理课件07语义分析 和中间代码产生
在这一节中,我们将学习关于语义分析和中间代码产生的定义、概述以及它 们在编译过程中的作用。我们将探讨语义分析的任务、方法和挑战,以及中 间代码产生的基本原理和实际应用。
语义分析和中间代码产生的定义和概述
语义分析是编译过程中的重要阶段,用于分析程序的意义和语法结构,并生成中间代码。中间代码产生是将高 级语言代码转换为更低级的可执行形式的过程。 在这一阶段,编译器将检查语法的正确性和静态语义的正确性,以确保程序在执行时没有语法错误。 语义分析和中间代码产生是编译器的核心部分,它们直接影响了程序的性能和可读性。
中间代码作为编译器和解释器的输入,是程序在执行前的一个中间阶段,并 可用于代码优化和跨平台编译。
中间代码产生的基本原理和方法
中间代码产生的基本原理是将程序的语义结构转换为一系列指令序列,这些指令不依赖于具体的计算机体系结 构。 中间代码生成的方法包括源代码到抽象语法树的转换、语法树到中间代码的转换等。
编译原理第七章 中间代码生成

(1) (2) (3) (4)
(1) (2) (3) (4)
语法制导方法
语法制导方法 基于文法结构,在每个产生
式的右部增加语义动作,在语法分析过程中, 如遇语义动作,就完成对应的语义处理。
类型检查和类型转换
各种条件表达式的类型是否是布尔类型? 各种条件表达式的类型是否是布尔类型? 运算符的运算分量是否相容? 运算符的运算分量是否相容? 赋值语句的左、右部类型是否相容? 赋值语句的左、右部类型是否相容? 实参与形参的类型是否相容? 实参与形参的类型是否相容? 下标表达式的类型是否为所允许的类型? 下标表达式的类型是否为所允许的类型? 函数说明中的函数类型与返回值的类型是否 一致? 一致?
(Entryf,Labelf,Sizef,Lf) (ADDF, k, k, t0) (ASSIG, t0,f) (ENDFUNC,……) (ENDFUNC, ) 50, (VALACT, 50,β1,1) ,true,t1 (CALL, Labelf,true,t1) (ASSIG, t1, u) (MULTF, u,x, t2) (ASSIG, t2, y) (ENDPROC, ……) )
While语句的中间代码 While语句的中间代码
while语句的文法 语句的文法: 语句的文法
S→ while E do S
while语句的中间代码形式 语句的中间代码形式
(WHILE, _, _, _) E的中间代码 的中间代码 (DO, E.FORM, _, _) S的中间代码 的中间代码 (ENDWHILE, _, _, _)
三地址中间代码
三元式:i:(ω 三元式:i:(ω,op1,op2) 四元式: ,op1,op2, 四元式:( ω,op1,op2,result) b×c+b× 如:a:= b×c+b×d
编译原理语法制导翻译和中间代码生成

第七章 语法制导翻译和中间代码生成编译程序的任务是把源程序翻译成目标程序,这个目标程序必须和源程序的语义等同,也就是说,尽管它们的语法结构完全不同,但它们所表达的结果应完全相同。
通常,在词法分析程序和语法分析程序对源程序的语法结构进行分析之后,要么由语法分析程序直接调用相应的语义子程序进行语义处理,要么首先生成语法树或该结构的某种表示,再进行语义处理。
编译中的语义处理是指两个功能:第一,审查每个语法结构的静态语义,即验证语法结构合法的程序是否真正有意义。
第二,如果静态语义正确,语义处理则要执行真正的翻译,即,要么生成程序的一种中间表示形式(中间代码),要么生成实际的目标代码。
为什么有的编译程序直接生成目标代码,有的编译程序采用中间代码,所谓中间代码,也称中间语言,是复杂性介于源程序语言和机器语言的一种表示形式。
一般,快速编译程序直接生成目标代码,没有将中间代码翻译成目标代码的额外开销。
但是为了使编译程序结构在逻辑上更为简单明确,常采用中间代码,这样可以将与机器相关的某些实现细节置于代码生成阶段仔细处理,并且可以在中间代码一级进行优化工作使得代码优化比较容易实现。
本章重点:属性文法、语法制导翻译方法的基本思想、几种典型的中间代码形式、一些语法成分的翻译工作。
第一节 属性文法现在很多编译程序采用语法制导翻译方法。
这仍不是一种形式系统,但它是比较接近形式化的。
这种方法使用属性文法为工具来说明程序设计语言的语义。
一个属性文法包含一个上下文无关文法和一系列语义规则,这些语义规则附在文法的每个产生式上,在语法分析过程中,完成附加在所使用的产生式上的语义规则描述的动作,从而实现语义处理。
首先简单介绍属性文法。
属性,常用以描述事物或人的特征、性质、品质等等。
比如,谈到一个物体,可以用“颜色”描述它,谈起某人,可以使用“有幽默感”来形容他。
对编译程序使用的语法树的结点,可以用“类型”、“值”或“存储位置”来描述它。
编译原理语义分析和中间代码产生ppt课件
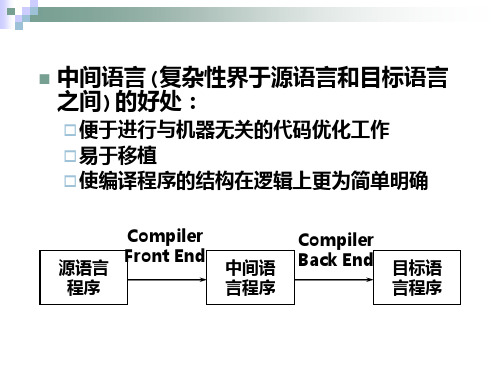
a:=b*(-c)+b*(-c)的图表示法
assign
assign
a
+
a
*
*
b uminus b uminus
+
*
b
umi语句抽象语法树的属性文法
产生式
语义规则
S→id:=E S.nptr:=mknode(‘assign’,
mkleaf(id,id.place),E.nptr)
三元式 四元式 间接三元式 DAG图表示
7.1.1 后缀式
后缀式表示法:Lukasiewicz发明的一种表 示表达式的方法,又称逆波兰表示法。
一个表达式E的后缀形式可以如下定义:
1. 如果E是一个变量或常量,则E的后缀式是E 自身。
2. 如果E是E1 op E2形式的表达式,其中op是 任何二元操作符,则E的后缀式为E1 E2 op, 其中E1 和E2 分别为E1 和E2的后缀式。
7.1.2 图表示法
图表示法
DAG 抽象语法树
7.1.2 图表示法
无循环有向图(Directed Acyclic Graph,简称DAG)
对表达式中的每个子表达式,DAG中都有一个结 点
一个内部结点代表一个操作符,它的孩子代表 操作数
在一个DAG中代表公共子表达式的结点具有多个 父结点
7.2 声 明 语 句
sort 空 表头
a x readarray exchange quicksort
指向readarray 指向exchange
readarrary 表头 i
语法树的代码 dag的代码
t1 := b t2 := c d t3 := t1 + t2 t4 := c d t5 := t3 + t4 a := t5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c
++*ad*bce
抽象语法树
由Token序列生成后缀式(1)
(1)初始化: S1和S2为空; (2) 读token: tk=ReadOne(); (3) Switch tk of (i) #: if (S1为空) exit; else while (S1不为空) /*产生剩余操作符的后缀表示*/ {op = pop(S1); (str1, str2)=pop(2); push(S2, str2 + str1+ “op”);} (ii)运算分量: push(tk, S2); goto (2); (iii)运算符: if (S1为空 || tk优先级大于Top(S1)) { push (tk, S1); goto(2);} else { while(tk小于等于Top(S1) && S1不为空)) { op = pop(S1); (str1, str2)=pop(2); push(S2, str2+str1 + “op”); } push(tk, S1); goto (2); }
+ +
a*c + a*c + e
e
+ +
e
* a
c a AST
* c a
* c
* a
DAG c
7.1 常见的中间表示
三地址中间代码
三地址:两个操作分量和一个结果的抽象地址; 为方便起见, 通常用变量名代替抽象地址; 三元式 No. (op, operand1, operand2) 编号 (操作符, 操作分量1, 操作分量2) 其中操作分量可以是变量名(抽象地址)或者编号 四元式 (op, operand1, operand2, result) (操作符, 操作分量1, 操作分量2, 结果) 其中操作分量可以是变量名(抽象地址)或者临时变量 (抽象地址)
通常用于表达式的中间表示
中缀 (运算符在操作数的中间) a*b 前缀式(运算符在操作数的前面) *ab 后缀式(运算符在操作数的后面) ab*
由抽象语法树生成后缀式
中缀式: a*d + b*c + e
+ + * a d b * e 后根遍历生成后缀式:
ad*bc*+e+
先根遍历生成前缀式:
操作分量
常量: 整数或者实数 标号: 标号名 变量: 需要更多信息用于形成其目标地址 函数/过程:需要更多信息用于得到其代码的目标地址
操作分量的ARG结构 --- 抽象地址结构
常量: (valKind, C) 标号: (labelKind, label) 变量: (varKind, level, offset, mode) 函数/过程:
由Token序列生成后缀式(2)
带括号表达式的后缀式例子
中缀式: (a + ( + b) * c ) + e #
后缀式: a d b + c * +e +
Operator stack 运算符栈 S1
Operand stack
运算分量栈 S2
7.1 常见的中间表示
抽象语法树-AST 无环有向图-DAG(共享的AST)
中间代码生成
M1
源程序
词 法 Token 分 析 序列 器
语 法 语法 分 分析 析 树 器
语 义 分 析 器
中 间 代 中间代码 码 生 成 器
…
Mn
7.1 常见的中间表示
后缀式,逆波兰式 抽象语法树 无环有向图 三元式
四元式
三地址中间代码
7.1 常见的中间表示
后缀式(逆波兰式)
生成后缀式的例子
中缀式: a * d + b * c + e #
运算符栈 S1
运算分量栈 S2
注意: 任何运算符的优先级都大于 ‘(’; (1)初始化: S1和S2为空; (2) 读token: tk=ReadOne(); (3) Switch tk of (i) #: if (S1为空) exit; else while (S1不为空) /*产生剩余操作符的后缀表示*/ {op = pop(S1); (str1, str2)=pop(2); push(S2, str2 + str1 + “op” );} (ii)operand: push(tk, S2); goto (2); ‘(’ : push(‘(‘, S1); goto (2); (iii)operator: if (S1为空 || tk优先级大于Top(S1)) { push (tk, S1);goto(2); } else { while(tk小于等于Top(S1) && Top(S1) ≠ ‘(’ && S1不为空))) { op = pop(S1); (str1, str2)=pop(2); push(S2, str2+str1 + “op”); } push(tk, S1); goto (2);} } (iv) ‘)’: while (Top(S1) ≠ ‘(’ ) {op = pop(S1); (str1, str2)=pop(2); push(S2, str2+str1 + “op”);} pop(S1); goto (2);
三地址代码的例子
a*d + b*c + e
三元式
四元式
(1) (*, a, d) (2) (*, b, c) (3) (+, (1), (2)) (4) (+, (3), e)
(*, a, d, t1) (*, b, c, t2) (+, t1, t2, t3) (+, t3, e, t4)
操作分量的抽象地址
中间代码生成在编译器中的作用
词法分析 目标代码生成
语法分析
中间代码优化
语义分析
中间代码生成
分析
合成
中间代码生成
中间代码生成是将源程序翻译成中间表示的 过程 目的:增强语言的可移植性、进行优化; 中间代码生成方法:
语法制导的翻译方法:属性文法和动作文法 基于Token序列
基于抽象语法树
实在函数/过程: (funKind, actual, label) 形参函数/过程: (funKind, formal, level, offset)
