中考数学平行四边形-经典压轴题含答案解析
中考数学—平行四边形的综合压轴题专题复习附答案解析

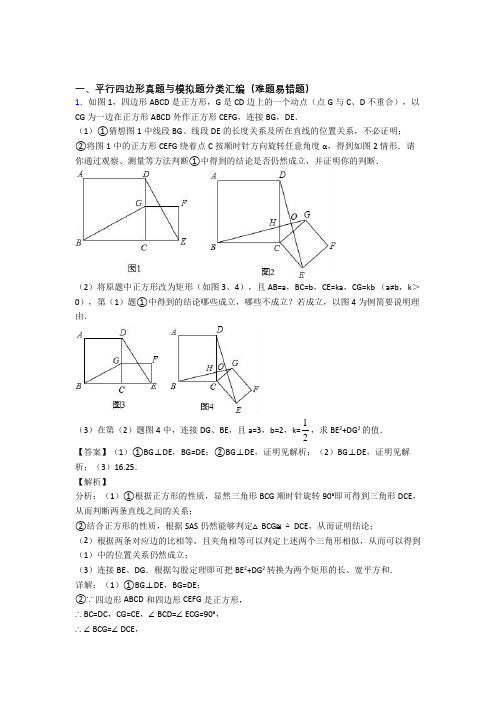
一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;(2)当点P在边AD上移动时,求证:△PDH的周长是定值;(3)当BE+CF的长取最小值时,求AP的长.【答案】(1)证明见解析.(2)证明见解析.(3)2.【解析】试题分析:(1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8;(3)过F作FM⊥AB,垂足为M,则FM=BC=AB,证明△EFM≌△BPA,设AP=x,利用折叠的性质和勾股定理的知识用x表示出BE和CF,结合二次函数的性质求出最值.试题解析:(1)解:如图1,∵PE=BE,∴∠EBP=∠EPB.又∵∠EPH=∠EBC=90°,∴∠EPH-∠EPB=∠EBC-∠EBP.即∠PBC=∠BPH.又∵AD∥BC,∴∠APB=∠PBC.∴∠APB=∠BPH.(2)证明:如图2,过B 作BQ ⊥PH ,垂足为Q .由(1)知∠APB=∠BPH ,又∵∠A=∠BQP=90°,BP=BP ,在△ABP 和△QBP 中,{90APB BPHA BQP BP BP∠=∠∠=∠=︒=,∴△ABP ≌△QBP (AAS ),∴AP=QP ,AB=BQ ,又∵AB=BC ,∴BC=BQ .又∠C=∠BQH=90°,BH=BH ,在△BCH 和△BQH 中,{90BC BQC BQH BH BH=∠=∠=︒=,∴△BCH ≌△BQH (SAS ),∴CH=QH .∴△PHD 的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8.∴△PDH 的周长是定值.(3)解:如图3,过F 作FM ⊥AB ,垂足为M ,则FM=BC=AB .又∵EF 为折痕,∴EF ⊥BP .∴∠EFM+∠MEF=∠ABP+∠BEF=90°,∴∠EFM=∠ABP .又∵∠A=∠EMF=90°,在△EFM 和△BPA 中,{EFM ABPEMF A FM AB∠=∠∠=∠=,∴△EFM ≌△BPA (AAS ).∴EM=AP .设AP=x在Rt △APE 中,(4-BE )2+x 2=BE 2.解得BE=2+28x ,∴CF=BE-EM=2+28x -x , ∴BE+CF=24x -x+4=14(x-2)2+3. 当x=2时,BE+CF 取最小值,∴AP=2.考点:几何变换综合题.2.如图,在正方形ABCD 中,E 是边BC 上的一动点(不与点B 、C 重合),连接DE 、点C 关于直线DE 的对称点为C ′,连接AC ′并延长交直线DE 于点P ,F 是AC ′的中点,连接DF . (1)求∠FDP 的度数;(2)连接BP ,请用等式表示AP 、BP 、DP 三条线段之间的数量关系,并证明; (3)连接AC ,若正方形的边长为2,请直接写出△ACC ′的面积最大值.【答案】(1)45°;(2)BP +DP 2AP ,证明详见解析;(32﹣1.【解析】【分析】(1)证明∠CDE =∠C 'DE 和∠ADF =∠C 'DF ,可得∠FDP '=12∠ADC =45°; (2)作辅助线,构建全等三角形,证明△BAP ≌△DAP '(SAS ),得BP =DP ',从而得△PAP '是等腰直角三角形,可得结论;(3)先作高线C 'G ,确定△ACC ′的面积中底边AC 为定值2,根据高的大小确定面积的大小,当C'在BD上时,C'G最大,其△ACC′的面积最大,并求此时的面积.【详解】(1)由对称得:CD=C'D,∠CDE=∠C'DE,在正方形ABCD中,AD=CD,∠ADC=90°,∴AD=C'D,∵F是AC'的中点,∴DF⊥AC',∠ADF=∠C'DF,∴∠FDP=∠FDC'+∠EDC'=12∠ADC=45°;(2)结论:BP+DP=2AP,理由是:如图,作AP'⊥AP交PD的延长线于P',∴∠PAP'=90°,在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP,由(1)可知:∠FDP=45°∵∠DFP=90°∴∠APD=45°,∴∠P'=45°,∴AP=AP',在△BAP和△DAP'中,∵BA DABAP DAP AP AP'=⎧⎪∠=∠⎨='⎪⎩,∴△BAP≌△DAP'(SAS),∴BP=DP',∴DP+BP=PP'2AP;(3)如图,过C'作C'G⊥AC于G,则S△AC'C=12AC•C'G,Rt △ABC 中,AB =BC =2, ∴AC =22(2)(2)2+=,即AC 为定值,当C 'G 最大值,△AC 'C 的面积最大,连接BD ,交AC 于O ,当C '在BD 上时,C 'G 最大,此时G 与O 重合,∵CD =C 'D =2,OD =12AC =1, ∴C 'G =2﹣1,∴S △AC 'C =112(21)2122AC C G '•=⨯-=-. 【点睛】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.3.如图,在Rt △ABC 中,∠B=90°,AC=60cm ,∠A=60°,点D 从点C 出发沿CA 方向以4cm/秒的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以2cm/秒的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是t 秒(0<t≤15).过点D 作DF ⊥BC 于点F ,连接DE ,EF .(1)求证:AE=DF ;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值,如果不能,说明理由; (3)当t 为何值时,△DEF 为直角三角形?请说明理由.【答案】(1)见解析;(2)能,t=10;(3)t=152或12. 【解析】【分析】(1)利用t 表示出CD 以及AE 的长,然后在直角△CDF 中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)△DEF为直角三角形,分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解:(1)证明:∵在Rt△ABC中,∠C=90°﹣∠A=30°,∴AB=12AC=12×60=30cm,∵CD=4t,AE=2t,又∵在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴DF=AE;(2)能,∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,∴当t=10时,AEFD是菱形;(3)若△DEF为直角三角形,有两种情况:①如图1,∠EDF=90°,DE∥BC,则AD=2AE,即60﹣4t=2×2t,解得:t=152,②如图2,∠DEF=90°,DE⊥AC,则AE=2AD,即2t2(604t)=-,解得:t=12,综上所述,当t=152或12时,△DEF为直角三角形.4.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=1MC,∴EG=CG.2(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.5.如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.(1)试猜想AE与GC有怎样的关系(直接写出结论即可);(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.(3)在(2)中,若E是BC的中点,且BC=2,则C,F两点间的距离为.【答案】(1) AE=CG,AE⊥GC;(2)成立,证明见解析; (3)2.【解析】【分析】(1)观察图形,AE、CG的位置关系可能是垂直,下面着手证明.由于四边形ABCD、DEFG都是正方形,易证得△ADE≌△CDG,则∠1=∠2,由于∠2、∠3互余,所以∠1、∠3互余,由此可得AE⊥GC.(2)题(1)的结论仍然成立,参照(1)题的解题方法,可证△ADE≌△CDG,得∠5=∠4,由于∠4、∠7互余,而∠5、∠6互余,那么∠6=∠7;由图知∠AEB=∠CEH=90°﹣∠6,即∠7+∠CEH=90°,由此得证.(3)如图3中,作CM⊥DG于G,GN⊥CD于N,CH⊥FG于H,则四边形CMGH是矩形,可得CM=GH,CH=GM.想办法求出CH,HF,再利用勾股定理即可解决问题.【详解】(1)AE=CG,AE⊥GC;证明:延长GC交AE于点H,在正方形ABCD与正方形DEFG中,AD=DC,∠ADE=∠CDG=90°,DE=DG,∴△ADE≌△CDG(SAS),∴AE,CG,∠1=∠2∵∠2+∠3=90°,∴∠1+∠3=90°,∴∠AHG=180°﹣(∠1+∠3)=180°﹣90°=90°,∴AE⊥GC.(2)答:成立;证明:延长AE和GC相交于点H,在正方形ABCD和正方形DEFG中,AD=DC,DE=DG,∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,∴∠1=∠2=90°﹣∠3;∴△ADE ≌△CDG(SAS),∴AE =CG ,∠5=∠4;又∵∠5+∠6=90°,∠4+∠7=180°﹣∠DCE =180°﹣90°=90°,∴∠6=∠7,又∵∠6+∠AEB =90°,∠AEB =∠CEH ,∴∠CEH+∠7=90°,∴∠EHC =90°,∴AE ⊥GC .(3)如图3中,作CM ⊥DG 于G ,GN ⊥CD 于N ,CH ⊥FG 于H ,则四边形CMGH 是矩形,可得CM =GH ,CH =GM .∵BE =CE =1,AB =CD =2,∴AE =DE =CG ═DG =FG 5∵DE =DG ,∠DCE =∠GND ,∠EDC =∠DGN ,∴△DCE ≌△GND(AAS),∴GCD =2,∵S △DCG =12•CD•NG =12•DG•CM , ∴2×25, ∴CM =GH 45, ∴MG =CH 22CG CM -35, ∴FH =FG ﹣FG 5, ∴CF 22FH CH +22535()()55+2. 2.【点睛】 本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.6.如图1,在△ABC中,AB=AC,AD⊥BC于D,分别延长AC至E,BC至F,且CE=EF,延长FE交AD的延长线于G.(1)求证:AE=EG;(2)如图2,分别连接BG,BE,若BG=BF,求证:BE=EG;(3)如图3,取GF的中点M,若AB=5,求EM的长.【答案】(1)证明见解析(2)证明见解析(3)5 2【解析】【分析】(1)根据平行线的性质和等腰三角形的三线合一的性质得:∠CAD=∠G,可得AE=EG;(2)作辅助线,证明△BEF≌△GEC(SAS),可得结论;(3)如图3,作辅助线,构建平行线,证明四边形DMEN是平行四边形,得EM=DN=12AC,计算可得结论.【详解】证明:(1)如图1,过E作EH⊥CF于H,∵AD⊥BC,∴EH∥AD,∴∠CEH=∠CAD,∠HEF=∠G,∵CE=EF,∴∠CEH=∠HEF,∴∠CAD=∠G,∴AE =EG ;(2)如图2,连接GC ,∵AC =BC ,AD ⊥BC ,∴BD =CD ,∴AG 是BC 的垂直平分线,∴GC =GB ,∴∠GBF =∠BCG ,∵BG =BF ,∴GC =BE ,∵CE =EF ,∴∠CEF =180°﹣2∠F ,∵BG =BF ,∴∠GBF =180°﹣2∠F ,∴∠GBF =∠CEF ,∴∠CEF =∠BCG ,∵∠BCE =∠CEF+∠F ,∠BCE =∠BCG+∠GCE ,∴∠GCE =∠F ,在△BEF 和△GCE 中,CE GCE F CG BF EF =⎧⎪∠=∠⎨⎪=⎩,∴△BEF ≌△GEC (SAS ),∴BE =EG ;(3)如图3,连接DM ,取AC 的中点N ,连接DN ,由(1)得AE =EG ,∴∠GAE =∠AGE ,在Rt △ACD 中,N 为AC 的中点,∴DN =12AC =AN ,∠DAN =∠ADN , ∴∠ADN =∠AGE ,∴DN ∥GF ,在Rt △GDF 中,M 是FG 的中点, ∴DM =12FG =GM ,∠GDM =∠AGE , ∴∠GDM =∠DAN ,∴DM ∥AE ,∴四边形DMEN 是平行四边形, ∴EM =DN =12AC , ∵AC =AB =5, ∴EM =52. 【点睛】 本题是三角形的综合题,主要考查了全等三角形的判定与性质,直角三角形斜边中线的性质,等腰三角形的性质和判定,平行四边形的性质和判定等知识,解题的关键是作辅助线,并熟练掌握全等三角形的判定方法,特别是第三问,辅助线的作法是关键.7.已知90AOB ∠=︒,点C 是AOB ∠的角平分线OP 上的任意一点,现有一个直角MCN ∠绕点C 旋转,两直角边CM ,CN 分别与直线OA ,OB 相交于点D ,点E .(1)如图1,若CD OA ⊥,猜想线段OD ,OE ,OC 之间的数量关系,并说明理由. (2)如图2,若点D 在射线OA 上,且CD 与OA 不垂直,则(1)中的数量关系是否仍成立?如成立,请说明理由;如不成立,请写出线段OD ,OE ,OC 之间的数量关系,并加以证明.(3)如图3,若点D 在射线OA 的反向延长线上,且2OD =,8OE =,请直接写出线段CE 的长度.【答案】(1)详见解析;(2)详见解析;(334【解析】【分析】(1)先证四边形ODCE 为矩形,再证矩形ODCE 为正方形,由正方形性质可得;(2)过点C 作CG OA ⊥于点G ,CH OB ⊥于点H ,证四边形OGCH 为正方形,再证()CGD CHE ASA ∆≅∆,可得;(3)根据()CGD CHE ASA ∆≅∆,可得2OE OD OH OG OC -=+=.【详解】解:(1)∵90AOB ∠=︒,90MCN ∠=︒,CD OA ⊥,∴四边形ODCE 为矩形.∵OP 是AOB ∠的角平分线,∴45DOC EOC ∠=∠=︒,∴OD CD =,∴矩形ODCE 为正方形, ∴2OC OD =,2OC OE =.∴2OD OE OC +=.(2)如图,过点C 作CG OA ⊥于点G ,CH OB ⊥于点H ,∵OP 平分AOB ∠,90AOB ∠=︒,∴四边形OGCH 为正方形,由(1)得:2OG OH OC +=,在CGD ∆和CHE ∆中, 90CGD CHE CG CHDCG ECH ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩, ∴()CGD CHE ASA ∆≅∆,∴GD HE =,∴2OD OE OC +=.(3)2OG OH OC +=, ()CGD CHE ASA ∆≅∆,∴GD HE =. ∵OD GD OG =-,OE OH EH =+,∴2OE OD OH OG OC -=+=, ∴32OC =,∴34CE =,CE 的长度为34.【点睛】考核知识点:矩形,正方形的判定和性质.熟练运用特殊四边形的性质和判定是关键.8.在平面直角坐标系中,O 为原点,点A (﹣6,0)、点C (0,6),若正方形OABC 绕点O 顺时针旋转,得正方形OA′B′C′,记旋转角为α:(1)如图①,当α=45°时,求BC 与A′B′的交点D 的坐标;(2)如图②,当α=60°时,求点B′的坐标;(3)若P 为线段BC′的中点,求AP 长的取值范围(直接写出结果即可).【答案】(1)(662,6)-;(2)(333,333)-+;(3)323323AP -+.【解析】【分析】(1)当α=45°时,延长OA′经过点B ,在Rt △BA′D 中,∠OBC =45°,A′B =626-,可求得BD 的长,进而求得CD 的长,即可得出点D 的坐标;(2)过点C′作x 轴垂线MN ,交x 轴于点M ,过点B′作MN 的垂线,垂足为N ,证明△OMC′≌△C′NB′,可得C′N =OM =33,B′N =C′M =3,即可得出点B′的坐标;(3)连接OB ,AC 相交于点K ,则K 是OB 的中点,因为P 为线段BC′的中点,所以PK =12OC′=3,即点P 在以K 为圆心,3为半径的圆上运动,即可得出AP 长的取值范围. 【详解】解:(1)∵A (﹣6,0)、C (0,6),O (0,0),∴四边形OABC 是边长为6的正方形,当α=45°时,如图①,延长OA′经过点B ,∵OB =62,OA′=OA =6,∠OBC =45°,∴A′B =626-,∴BD =(626-)×21262=-,∴CD =6﹣(1262-)=626-,∴BC 与A′B′的交点D 的坐标为(662-,6);(2)如图②,过点C′作x 轴垂线MN ,交x 轴于点M ,过点B′作MN 的垂线,垂足为N ,∵∠OC′B′=90°,∴∠OC′M =90°﹣∠B′C′N =∠C′B′N ,∵OC′=B′C′,∠OMC′=∠C′NB′=90°,∴△OMC′≌△C′NB′(AAS ),当α=60°时,∵∠A′OC′=90°,OC′=6,∴∠C′OM =30°,∴C′N =OM =33,B′N =C′M =3,∴点B′的坐标为()333,333-+;(3)如图③,连接OB ,AC 相交于点K ,则K 是OB 的中点,∵P 为线段BC′的中点,∴PK =12OC′=3,∴P 在以K 为圆心,3为半径的圆上运动,∵AK =32,∴AP 最大值为323+,AP 的最小值为323-,∴AP 长的取值范围为323323AP -+.【点睛】本题考查正方形性质,全等三角形判定与性质,三角形中位线定理.(3)问解题的关键是利用中位线定理得出点P 的轨迹.9.如图1,在长方形纸片ABCD 中,AB=mAD ,其中m ⩾1,将它沿EF 折叠(点E. F 分别在边AB 、CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 相交于点P ,连接EP .设AM n AD=,其中0<n ⩽1.(1)如图2,当n=1(即M 点与D 点重合),求证:四边形BEDF 为菱形;(2)如图3,当12n =(M 为AD 的中点),m 的值发生变化时,求证:EP=AE+DP ; (3)如图1,当m=2(即AB=2AD),n 的值发生变化时,BE CF AM -的值是否发生变化?说明理由.【答案】(1)证明见解析;(2)证明见解析;(3)值不变,理由见解析.【解析】试题分析:(1)由条件可知,当n=1(即M 点与D 点重合),m=2时,AB=2AD ,设AD=a ,则AB=2a ,由矩形的性质可以得出△ADE ≌△NDF ,就可以得出AE=NF ,DE=DF ,在Rt △AED 中,由勾股定理就可以表示出AE 的值,再求出BE 的值就可以得出结论.(2)延长PM 交EA 延长线于G ,由条件可以得出△PDM ≌△GAM ,△EMP ≌△EMG 由全等三角形的性质就可以得出结论.(3)如图1,连接BM 交EF 于点Q ,过点F 作FK ⊥AB 于点K ,交BM 于点O ,通过证明△ABM ∽△KFE ,就可以得出EK KF AM AB =,即BE BK BC AM AB -=,由AB=2AD=2BC ,BK=CF 就可以得出BE CF AM -的值是12为定值. (1)∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠A=∠B=∠C=∠D=90°.∵AB=mAD ,且n=2,∴AB=2AD .∵∠ADE+∠EDF=90°,∠EDF+∠NDF=90°,∴∠ADE=∠NDF .在△ADE 和△NDF 中,∠A =∠N ,AD =ND ,∠ADE =∠NDF ,∴△ADE ≌△NDF (ASA ).∴AE=NF ,DE=DF .∵FN=FC ,∴AE=FC .∵AB=CD ,∴AB-AE="CD-CF." ∴BE="DF." ∴BE=DE .Rt △AED 中,由勾股定理,得222AE DE AD =-,即2222AE AD AE AD ()=--,∴AE=34AD.∴BE=2AD-34AD=54.∴554334ADBEAE AD==.(2)如图3,延长PM交EA延长线于G,∴∠GAM=90°.∵M为AD的中点,∴AM=DM.∵四边形ABCD是矩形,∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,AB∥CD.∴∠GAM=∠PDM.在△GAM和△PDM中,∠GAM=∠PDM,AM=DM,∠AMG=∠DMP,∴△GAM≌△PDM(ASA).∴MG=MP.在△EMP和△EMG中,PM=GM,∠PME=∠GME,ME=ME,∴△EMP≌△EMG(SAS).∴EG=EP.∴AG+AE=EP.∴PD+AE=EP,即EP=AE+DP.(3)12BE CFAM-=,值不变,理由如下:如图1,连接BM交EF于点Q,过点F作FK⊥AB于点K,交BM于点O,∵EM=EB,∠MEF=∠BEF,∴EF⊥MB,即∠FQO=90°.∵四边形FKBC是矩形,∴KF=BC,FC=KB.∵∠FKB=90°,∴∠KBO+∠KOB=90°.∵∠QOF+∠QFO=90°,∠QOF=∠KOB,∴∠KBO=∠OFQ.∵∠A=∠EKF=90°,∴△ABM∽△KFE.∴EK KFAM AB=即BE BK BCAM AB-=.∵AB=2AD=2BC,BK=CF,∴12BE CFAM-=.∴BE CFAM-的值不变.考点:1.折叠问题;2.矩形的性质;3.全等三角形的判定和性质;4.勾股定理;5.相似三角形的判定和性质.10.(本题满分10分)如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.(1)求矩形ABCD的边AD的长.(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式【答案】(1)AD=3;(2)y=-其中,0<x<3;(3)x=;(4)S=.【解析】试题分析:(1)根据折叠图形的性质和勾股定理求出AD的长度;(2)根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式;(3)过点N作NQ⊥CD,根据Rt△NPQ 的勾股定理进行求解;(4)根据Rt△ADM的勾股定理求出MP与x的函数关系式,然后得出函数关系式.试题解析:(1)根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得:AD=3.(2)由折叠可知AM=MP,在Rt△MPD中,∴∴y=-其中,0<x<3.(3)当点N在AB上,x≥3,∴PC≤3,而PN≥3,NC≥3.∴△PCN为等腰三角形,只可能NC=NP.过N点作NQ⊥CD,垂足为Q,在Rt△NPQ中,∴解得x=.(4)当点M在CD上时,N在AB上,可得四边形ANPM为菱形.设MP=y,在Rt△ADM中,,即∴ y=.∴ S=考点:函数的性质、勾股定理.。
中考数学与平行四边形有关的压轴题含答案解析
本题考查四边形综合题、等腰直角三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.
7.(1)问题发现:
如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;
6.问题情境
在四边形ABCD中,BA=BC,DC⊥AC,过点D作DE∥AB交BC的延长线于点E,M是边AD的中点,连接MB,ME.
特例探究
(1)如图1,当∠ABC=90°时,写出线段MB与ME的数量关系,位置关系;
(2)如图2,当∠ABC=120°时,试探究线段MB与ME的数量关系,并证明你的结论;
∴∠DEC=90°,
∴∠DCE=∠CDE=45°,
∴EC=ED,∵MC=MD,
∴EM垂直平分线段CD,EM平分∠DEC,
∴∠MEC=45°,
∴△BME是等腰直角三角形,
∴BM=ME,BM⊥EM.
故答案为BM=ME,BM⊥EM.
(2)ME= MB.
证明如下:连接CM,如解图所示.
∵DC⊥AC,M是边AD的中点,
∴ AB•CF= AC•PE﹣ AB•PD.
∵AB=AC,
∴CF=PD﹣PE;
结论运用:过点E作EQ⊥BC,垂足为Q,如图④,
∵四边形ABCD是长方形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=16,CF=6,
∴BF=BC﹣CF=AD﹣CF=5,
由折叠可得:DF=BF,∠BEF=∠DEF.
∴DF=5.
∴PG+PH的值为8;
迁移拓展:如图,
由题意得:A(0,8),B(6,0),C(﹣4,0)
(必考题)初中八年级数学下册第十八章《平行四边形》经典练习卷(含答案解析)

一、选择题1.如图,三个正方形围成一个直角三角形,64、400分别为所在正方形的面积,则图中字母M 所代表的正方形面积可表示为( )A .40064-B .2240064-C .2240064-D .40064+A解析:A【分析】 要求图中字母所代表的正方形的面积,根据面积=边长×边长=边长的平方,设M 的边长为a ,直角三角形斜边的长为c ,另一直角边为b ,则2400c =,264b =,已知斜边和一直角边的平方,由勾股定理即可求出2a ,即可得到答案.【详解】设M 的边长为a ,直角三角形斜边的长为c ,另一直角边为b ,则2400c =,264b =,如图所示,在该直角三角形中,由勾股定理得:22240064a c b =-=-,故选:A .【点睛】本题主要考查勾股定理的应用和正方形的面积公式,解题的关键在于熟练运用勾股定理求出正方形的边长的平方.2.如图,将长方形纸片沿对角线折叠,重叠部分为BDE ,则图中全等三角形共有( )A .0对B .1对C .2对D .3对C解析:C【分析】因为图形对折,所以首先△CDB ≌△ABD ,由于四边形是长方形,进而可得△ABE ≌△CDE ,如此答案可得.【详解】解:∵△BDC 是将长方形纸片ABCD 沿BD 折叠得到的,∴CD=AB ,AD=BC ,∵BD=BD ,∴△CDB ≌△ABD (SSS ),∴∠CBD=∠ADB∴EB=ED∴CE=AE又AB=CD∴△ABE ≌△CDE ,∴图中全等三角形共有2对故选:C【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、SSA 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要由易到难,循序渐进. 3.如图,在平行四边形ABCD 中,90B ∠<︒,BC AB >.作AE BC ⊥于点E ,AF CD ⊥于点F ,记EAF ∠的度数为α,AE a =,AF b =.则以下选项错误的是( )A .::a b CD BC =B .D ∠的度数为αC .若60α=︒,则四边形AECF 的面积为平行四边形ABCD 面积的一半D .若60α=︒,则平行四边形ABCD )433a b +C 解析:C【分析】由平行四边形的性质得出//AD BC ,AD BC =,AB CD =,B D ∠=∠,得出180D C ∠+∠=︒,求出180EAF C ∠+∠=︒,得出B D EAF α∠=∠=∠=;由平行四边形ABCD 的面积得出::a b CD BC =;若60α=︒,则60B D ∠=∠=︒,求出30BAE DAF ∠=∠=︒,由直角三角形的性质得出33BE AE ==,33DF ,得出232AB BE =,232AD DF ==,求出平行四边形ABCD 的周长2())AB AD a b =+=+;求出ABE ∆的面积212BE AE =⨯=,ADF ∆的面积2=,平行四边形ABCD 的面积BC AE a =⨯=⨯=,得出四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半;即可得出结论. 【详解】 解:四边形ABCD 是平行四边形,//AD BC ∴,AD BC =,AB CD =,B D ∠=∠,180D C ∴∠+∠=︒,AE BC ⊥于点E ,AF CD ⊥于点F ,360290180EAF C ∴∠+∠=︒-⨯︒=︒,B D EAF α∴∠=∠=∠=;平行四边形ABCD 的面积BC AE CD AF =⨯=⨯,AE a =,AF b =,BC a CD b ∴⨯=⨯,::a b CD BC ∴=;若60α=︒,则60B D ∠=∠=︒,30BAE DAF ∴∠=∠=︒,BE AE ∴==,DF =,2AB BE ∴==,2AD DF ==,∴平行四边形ABCD 的周长2())AB AD a b =+=+;ABE ∆的面积21122BE AE a =⨯=⨯=,ADF ∆的面积21122DF AF b =⨯=⨯,平行四边形ABCD 的面积BC AE a =⨯=⨯=, ∴四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半; 综上所述,选项A 、B 、D 不符合题意,选项C 符合题意;故选:C .【点睛】本题考查了平行四边形的性质、直角三角形的性质、三角形面积等知识;熟练掌握平行四边形的性质和直角三角形的性质是解题的关键.4.下列命题中,错误的是 ( )A .有一个角是直角的平行四边形是正方形;B .对角线相等的菱形是正方形;C .对角线互相垂直的矩形是正方形;D .一组邻边相等的矩形是正方形.A 解析:A【分析】根据正方形的判定逐项作出判断即可求解.【详解】解:A. 有一个角是直角的平行四边形是正方形,判断错误,应该是矩形,符合题意;B. 对角线相等的菱形是正方形,判断正确,不合题意;C. 对角线互相垂直的矩形是正方形,判断正确,不合题意;D. 一组邻边相等的矩形是正方形,判断正确,不合题意.故选:A【点睛】本题考查了正方形的判定,熟练掌握正方形的判定方法是解题关键.5.如果平行四边形ABCD 的对角线相交于点O ,那么在下列条件中,能判断平行四边形ABCD 为菱形的是( )A .OAB OBA ∠=∠;B .OAB OBC ∠=∠; C .OAB OCD ∠=∠;D .OAB OAD ∠=∠.D解析:D【分析】根据菱形的判定方法判断即可.【详解】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠OAB=∠ACD ,∵∠OAB=∠OAD ,∴∠DAC=∠DCA ,∴AD=CD , ∴四边形ABCD 是菱形(邻边相等的平行四边形是菱形)故选:D .【点睛】本题考查菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.6.如图,在123A A A △中,160A ∠=︒,230A ∠=︒,131A A =,3+n A 是1(1,2,3)n n A A n +=⋅⋅⋅的中点,则202120222023A A A △中最短边的长为( )A .100912 B .101012 C .101112 D .102112B解析:B【分析】根据已知条件和图形的变化可得前几个图形的最短边的长度,进而可得结论.【详解】解:在△A 1A 2A 3中,∠A 1A 3A 2=90°,∠A 2=30°,A 1A 3=1,A n+3是A n A n+1(n=1、2、3…)的中点,可知:A 4A 5//A 1A 3,A 3A 4=A 2A 4,∴∠A 3A 5A 4=90°,∠A 4A 3A 2=∠A 2=30°,∴△A 1A 2A 3是含30°角的直角三角形,同理可证△A n A n+1A n+2是含30°角的直角三角形.△A 1A 2A 3中最短边的长度为A 1A 3=1=012, △A 3A 4A 5中最短边的长度为A 4A 5=12=112, △A 5A 6A 7中最短边的长度为A 5A 7=21142=, …, 所以△A n A n+1A n+2中最短边的长度为1212n -,则△A 2019A 2020A 2021中最短边的长度为120211221122n --==101012. 故选:B .【点睛】 本题考查了规律型:图形的变化类,解决本题的关键是观察图形的变化寻找规律.也考查了直角三角形斜边的中线,三角形的中位线,平行线的性质,含30°角的直角三角形的性质,以及等腰三角形的性质等知识.7.顺次连接矩形ABCD 各边的中点,所得四边形是( )A .平行四边形B .正方形C .矩形D .菱形D解析:D【分析】利用三角形中位线定理,矩形对角线的性质,菱形的判定判断即可.【详解】如图,设矩形ABCD各边的中点依次为E,F,G,H,∴EF,FG,GH,HE分别是△ABC,△BCD,△CDA,△DAB的中位线,∴EF=12AC,FG=12BD,GH=12AC,EH=12BD,∵四边形ABCD是矩形,∴AC=BD,∴EF=FG=GH=HE,∴四边形EFGH是菱形,故选D.【点睛】本题在矩形背景考查了三角形中位线定理,菱形的判定,矩形的性质,熟练运用三角形中位线定理,矩形的性质,菱形的判定是解题的关键.8.下列命题中,正确的命题是()A.菱形的对角线互相平分且相等B.顺次联结菱形各边的中点所得的四边形是矩形C.矩形的对角线互相垂直平分D.顺次连结矩形各边的中点所得的四边形是正方形B解析:B【分析】根据菱形的性质、矩形的性质、中点四边形的定义逐一判断即可.【详解】解:A. 菱形的对角线互相平分,但不相等,该命题错误;B. 顺次联结菱形各边的中点所得的四边形是矩形,该命题正确;C. 矩形的对角线互相平分,但是不垂直,该命题错误;D. 顺次连结矩形各边的中点所得的四边形是菱形,该命题错误;故选:B.【点睛】本题考查特殊四边形的判定和性质,掌握菱形的性质、矩形的性质、中点四边形的定义是解题的关键.9.如图,在平行四边形ABCD 中,点F 是AB 的中点,连接DF 并延长,交CB 的延长线于点E ,连接AE .添加一个条件,使四边形AEBD 是菱形,这个条件是( )A .BAD BDA ∠=∠B .AB DE =C .DF EF =D .DE 平分ADB ∠D解析:D【分析】 先证明△ADF ≌△BEF ,得到AD=BE ,推出四边形AEBD 是平行四边形,再逐项依次分析即可.【详解】解:在平行四边形ABCD 中,AD ∥BC ,∴∠DAB=∠EBA ,∵点F 是AB 的中点,∴AF=BF ,∵∠AFD=∠BFE ,∴△ADF ≌△BEF ,∴AD=BE ,∵AD ∥BE ,∴四边形AEBD 是平行四边形,A 、当BAD BDA ∠=∠时,得到AB=BD ,无法判定四边形AEBD 是菱形,故该选项不符合题意;B 、AB=BE 时,无法判定四边形AEBD 是菱形,故该选项不符合题意;C 、DF=EF 时,无法判定四边形AEBD 是菱形,故该选项不符合题意;D 、当DE 平分ADB ∠时,四边形AEBD 是菱形,故该选项符合题意;故选:D .【点睛】此题考查平行四边形的性质,全等三角形的判定及性质,菱形的判定,熟记平行四边形的性质是解题的关键.10.如图,菱形ABCD 中,4AB =,60A ∠=︒,点E 是线段AB 上一点(不与A ,B 重合),作EDF ∠交BC 于点F ,且60EDF ∠=︒,则BEF 周长的最小值是( )A .6B .43C .43+D .423+D解析:D【分析】 只要证明DBE DCF ∆≅∆得出DEF ∆是等边三角形,因为BEF ∆的周长4BE BF EF BF CF EF BC EF EF =++=++=+=+,所以等边三角形DEF ∆的边长最小时,BEF ∆的周长最小,只要求出DEF ∆的边长最小值即可.【详解】解:连接BD ,菱形ABCD 中,60A ∠=︒,ADB ∴∆与CDB ∆是等边三角形,60DBE C ∴∠=∠=∠︒,BD DC =,60EDF ∠=︒,BDE CDF ∴∠=∠,在BDE ∆和CDF ∆中,DBE C BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,DBE DCF ∴∆≅∆,DE DF ∴=,BDE CDF ∠=∠,BE CF =,60EDF BDC ∴∠=∠=︒,DEF ∴∆是等边三角形,BEF ∆的周长4BE BF EF BF CF EF BC EF EF =++=++=+=+,∴等边三角形DEF ∆的边长最小时,BEF ∆的周长最小,当DE AB ⊥时,DE 最小23=,BEF ∴∆的周长最小值为423+,故选:D .【点睛】本题考查菱形的性质、全等三角形的判定和性质、等边三角形的判定和性质、最小值问题等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,学会转化的思想解决问题,所以中考常考题型.二、填空题11.如图,直线a 过正方形ABCD 的顶点A ,点B 、D 到直线a 的距离分别为1、3,则正方形的边长为_______.【分析】先由正方形的性质可知再证明Rt △AFD ≌Rt △BEA 再由全等三角形的性质可得;最后在在Rt △BEA 中由勾股定理得:即得本题答案【详解】解:在正方形中;∵∴;∵∴;在Rt △AFD 和Rt △BEA 10【分析】先由正方形的性质可知DA AB =,再证明Rt △AFD ≌Rt △BEA ,再由全等三角形的性质可得3DF AE ==,1AF BE ==;最后在在Rt △BEA 中,由勾股定理得:2210AB AE BE =+=【详解】解:在正方形ABCD 中,AD AB =;∵DF AF ⊥,BE AE ⊥,∴90AFD AEB ∠=∠=︒,90ADF DAF ∠+∠=︒;∵90DAF BAE ∠+∠=︒,∴ADF BAE =∠∠;在Rt △AFD 和Rt △BEA 中,AFD AEB ADF BAE AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴Rt △AFD ≌Rt △BEA (AAS ),∴3DF AE ==,1AF BE ==;在Rt △BEA 中,由勾股定理得:22223110AB AE BE =+=+= 10.【点睛】本题主要考查正方形的性质,三角形全等的性质与判定以及勾股定理的知识. 12.如图,Rt ABC △中,90,5∠=︒=B AB ,D 为AC 的中点, 6.5=BD ,则BC 的长为__________.12【分析】根据直角三角形斜边上的中线等于斜边的一半可求出再根据勾股定理求解即可【详解】解:∵D 为的中点∴∴故答案是:12【点睛】考查了勾股定理和直角三角形斜边上的中线熟悉相关性质是解题的关键解析:12.【分析】根据直角三角形斜边上的中线等于斜边的一半,可求出AC ,再根据勾股定理求解即可.【详解】解:∵90B ∠=︒,D 为AC 的中点, 6.5=BD∴22 6.513AC BD ==⨯=, ∴222212135BC AC AB =--,故答案是:12.【点睛】考查了勾股定理和直角三角形斜边上的中线,熟悉相关性质是解题的关键.13.菱形ABCD 有一个内角是60°,它的边长是2,则此菱形的对角线AC 长为_________.或2【分析】根据菱形有一个内角为60°可以得到等边三角形分两种情况画出图形结合勾股定理求出AC 的长【详解】解:∵四边形ABCD 是菱形∴AC ⊥BDOA=OCOB=ODAD=AB=2若∠BAD=60°∴ 解析:232【分析】根据菱形有一个内角为60°可以得到等边三角形,分两种情况,画出图形,结合勾股定理求出AC 的长.【详解】解:∵四边形ABCD 是菱形,∴AC ⊥BD ,OA=OC ,OB=OD ,AD=AB=2,若∠BAD=60°,∴△ABD 是等边三角形,∴BD=2,∴OD=1,∴22213-=, ∴AC=3若∠ABC=60°,∴△ABC 是等边三角形,∴AC=2;故答案为:23或2.【点睛】此题考查了菱形的性质和勾股定理,等边三角形的判定和性质,要记住菱形的对角线互相平分且垂直,菱形的四条边都相等.14.如图,在ABC ∆中,点,D E 分别在边,AB AC 上,且BD CE =,连接,CD DE ,点,,M N P 分别是,,DE BC CD 的中点,34PMN ∠=,则MPN ∠的度数是_______.【分析】根据点MNP 分别是DEBCCD 的中点可以证明MP 是ΔDEC 的中位线NP 是ΔDBC 的中位线根据中位线定理可得到MP=NP 再根据等腰三角形的性质得到∠PMN=∠PNM 最后根据三角形的内角和定理可解析:112【分析】根据点 M ,N ,P 分别是 DE ,BC ,CD 的中点,可以证明MP 是ΔDEC 的中位线,NP 是ΔDBC 的中位线,根据中位线定理可得到MP=NP ,再根据等腰三角形的性质得到∠PMN=∠PNM ,最后根据三角形的内角和定理可以得到∠MPN .【详解】解:如图∵点 M,N,P 分别是 DE,BC,CD 的中点∴MP是ΔDEC的中位线,∴MP=1EC,2NP是ΔDBC的中位线∴NP=1BD,2又∵BD=CE∴MP=NP∴∠PMN=∠PNM=34∘∴∠MPN=180∘-∠PMN-∠PNM=180∘-34∘-34∘=112∘故答案位:112°【点睛】本题考查了三角形的中位线定理,等腰三角形的性质和判定,以及三角形的内角和定理,解题的关键是灵活运用三角形的中位线定理求线段的长度.15.如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P 不与写B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连结EF,则EF的最小值等于__________.48【分析】连接由菱形的性质解得再根据勾股定理解得继而证明四边形为矩形得到根据垂线段最短解得当时有最小值最后根据三角形面积公式解题即可【详解】连接四边形是菱形四边形为矩形当时有最小值此时的最小值为故解析:4.8【分析】连接OP ,由菱形的性质解得118,622BO BD OC AC ====,再根据勾股定理解得10BC =,继而证明四边形OEPF 为矩形,得到FE OP =,根据垂线段最短解得当OP BC ⊥时,OP 有最小值,最后根据三角形面积公式解题即可.【详解】 连接OP ,四边形ABCD 是菱形,12,16AC BD ==,AC BD ∴⊥118,622BO BD OC AC ==== 22643610BC OB OC ∴=+=+=,,PE AC PF BD AC BD ⊥⊥⊥∴四边形OEPF 为矩形,FE OP ∴=当OP BC ⊥时,OP 有最小值,此时1122OBC S OB OC BC OP =⋅=⋅ 68 4.810OP ⨯∴== EF ∴的最小值为4.8,故答案为:4.8.【点睛】本题考查菱形的性质、矩形的判定与性质、勾股定理、垂线段最短等知识,是重要考点,难度较易,掌握相关知识是解题关键.16.如图,在Rt ABC ∆中,90,6,10ACB AC AB ∠===,过点A 作//,AM CB CE 平分ACB ∠交AM 于点,E Q 是线段CE 上的点,连接BQ ,过点B 作BP BQ ⊥交AM 于点P ,当PBQ ∆为等腰三角形时,AP =________________________.【分析】过点P作PG⊥CB交CB的延长线于点G过点Q作QF⊥CB运用AAS定理证明△QBF≌△BPG根据平行线的性质和角平分线的定义求得△AEC为等腰直角三角形利用勾股定理求得线段BC的长然后结合全解析:10【分析】过点P作PG⊥CB,交CB的延长线于点G,过点Q作QF⊥CB,运用AAS定理证明△QBF≌△BPG,根据平行线的性质和角平分线的定义求得△AEC为等腰直角三角形,利用勾股定理求得线段BC的长,然后结合全等三角形和矩形的性质求解.【详解】解:过点P作PG⊥CB,交CB的延长线于点G,过点Q作QF⊥CB∵BP BQ⊥,PG⊥CB∴∠1+∠2=90°,∠2+∠3=90°∴∠1=∠3∵QF⊥CB,BP BQ⊥∴∠QFB=∠PGB=90°又∵PBQ∆为等腰三角形∴QB=PB在△QBF和△BPG中1=3QFB PGB QB PB∠∠⎧⎪∠=∠⎨⎪=⎩∴△QBF≌△BPG∴PG=BF,BG=QF∵∠ACB=90°,CE平分ACB∠∴∠ACE=∠ECB=45°又∵AM∥CB,∴∠AEC=∠ECB=45°∴∠AEC=∠ACE=45°∴△AEC为等腰直角三角形∵AM∥BC,∠ACB=90°∴∠CAM+∠ACB=180°,即∠CAM=90°∴∠CAM=∠ACB=∠PGB=90°∴四边形ACGP为矩形,∴PG=AC=6,AP=CG在Rt △ABC 中,BC=228AB AC -=∴CF=BC-BF=BC-PG=8-6=2∵QF ⊥BC ,∠ECB=45°∴△CQF 是等腰直角三角形,即CF=QF=2∴AP=CG=BC+BG=BC+QF=8+2=10【点睛】本题考查矩形的判定和性质、全等三角形的判定和性质以及勾股定理,掌握相关性质定理正确推理论证是解题关键17.如图,平面直角坐标系中,已知点()9,9A ,点B 、C 分别在y 轴、x 轴上,AB AC ⊥且AB AC =,若B 点坐标为()0,a ,则OC =______(用含a 的代数式表示).18-【分析】过A 作AE ⊥y 轴于EAD ⊥x 轴于D 构造正方形AEOD 再证△AEB ≌△ADC (SAS )得BE=CD 由EB=EO-BO=9-可求CD=9-求出OC=OD+CD=9+9-=18-即可【详解】解析:18-a .【分析】过A 作AE ⊥y 轴于E ,AD ⊥x 轴于D ,构造正方形AEOD ,再证△AEB ≌△ADC (SAS ),得BE=CD ,由EB=EO-BO=9-a ,可求CD=9-a ,求出OC=OD+CD=9+9-a =18-a 即可.【详解】过A 作AE ⊥y 轴于E ,AD ⊥x 轴于D ,∵点()9,9A ,AE=AD=OE=OD=9,∠ADO=90º,四边形AEOD 为正方形,∵AB AC ⊥,∠EAD=90°,∴∠EAB+∠BAD=90°,∠BAD+∠DAC=90°,∴∠BAE=∠CAD ,∵AB AC =,AE=AD ,∴△AEB ≌△ADC (SAS ),∴BE=CD ,∵EB=EO-BO=9-a ,∴CD=9-a ,OC=OD+CD=9+9-a =18-a ,故答案为:18-a .【点睛】本题考查正方形的判定与性质,三角形全等判定与性质,掌握正方形的判定方法与性质,三角形全等判定的方法与性质是解题关键.18.如图,将长方形纸片ABCD 沿着对角线BD 翻折,点C 落在点C '处,BC '与AD 交于点E .若20AD cm =,5AB cm =,则DE =_______cm .【分析】根据题意得到BE =DE 然后根据勾股定理得到关于线段ABAEBE 的方程解方程即可【详解】解:设ED =x 则AE =20﹣x ∵四边形ABCD 为矩形∴AD ∥BC ∴∠EDB =∠DBC ;由题意得:∠EBD 解析:858【分析】根据题意得到BE =DE ,然后根据勾股定理得到关于线段AB 、AE 、BE 的方程,解方程即可.【详解】解:设ED =x ,则AE =20﹣x ,∵四边形ABCD 为矩形,∴AD ∥BC ,∴∠EDB =∠DBC ;由题意得:∠EBD =∠DBC ,∴∠EDB =∠EBD ,∴EB =ED =x ;由勾股定理得:BE 2=AB 2+AE 2,即x 2=52+(20﹣x )2,解得:x =858, ∴ED =858. 【点睛】本题主要考查了几何变换中的翻折变换及其应用问题;解题的关键是根据翻折变换的性质,结合全等三角形的判定及其性质、勾股定理等几何知识,灵活进行判断、分析、推理或解答.19.在ABCD 中,BE AD ⊥于E ,BF CD ⊥于F ,若60EBF ︒∠=,且3AE =,2DF =,则EC =_______.【分析】由▱ABCD 中BE ⊥ADBF ⊥CD 可得∠D=120°继而求得∠A 与∠BCD 的度数然后由勾股定理求得ABBEBC 的长继而求得答案【详解】解:∵BE ⊥ADBF ⊥CD ∴∠BFD=∠BED=∠BFC91【分析】由▱ABCD 中,BE ⊥AD ,BF ⊥CD ,可得∠D=120°,继而求得∠A 与∠BCD 的度数,然后由勾股定理求得AB ,BE ,BC 的长,继而求得答案.【详解】解:∵BE ⊥AD ,BF ⊥CD ,∴∠BFD=∠BED=∠BFC=∠BEA=90°,∵∠EBF=60°,∴∠D=120°,∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠BCD=∠A=60°,∵在△ABE中,∠ABE=30°,∴AB=2AE=2×3=6,∴CD=AB=6,BE=2233AB AE-=,∴CF=CD-DF=6-2=4,∵在△BFC中,∠CBF=30°,∴BC=2CF=2×4=8,∴CE=2291BE BC+=,故答案为:91.【点睛】此题考查了平行四边形的性质、勾股定理以及含30°角的直角三角形的性质.此题难度适合,注意掌握数形结合思想的应用.20.在长方形ABCD中,52AB=,4BC=,CE CF=,CF平分ECD∠,则BE=_________.【分析】延长CF交EA的延长线于点G连接EF过点F作FH⊥CE于点H过点E作EM⊥CF于点M由题意易得FH=FDFH=EMEC=EG进而可得△CDF≌△CME然后可得CM=CD=由勾股定理可得BG=解析:7 6【分析】延长CF,交EA的延长线于点G,连接EF,过点F作FH⊥CE于点H,过点E作EM⊥CF于点M,由题意易得FH=FD,FH=EM,EC=EG,进而可得△CDF≌△CME,然后可得CM=CD=52,由勾股定理可得BG=3,设BE=x,则有EC=EG=3+x,最后利用勾股定理可求解.【详解】解:延长CF,交EA的延长线于点G,连接EF,过点F作FH⊥CE于点H,过点E作EM⊥CF于点M,如图所示:∵四边形ABCD 是矩形,4BC =,52AB =∴BC=AD ,52AB DC ==,AB ∥DC ,∠D=∠ABC=∠CBE=90° ∴∠DCF=∠G ,∵CF 平分∠ECD ,∴∠DCF=∠ECF ,DF=FH ,∴∠G=∠ECF ,∴EC=EG ,∴△ECG 是等腰三角形,∴CM=MG ,∵CE=CF ,∴△ECF 是等腰三角形, ∵EM 、FH 分别是等腰三角形ECF 腰上的高线,∴FH=EM=DF ,∴Rt △CDF ≌Rt △CME (HL ), ∴52CM DC ==, ∴CG=5,∴在Rt △CBG 中,223BG CG CB -=,设BE=x ,则有EC=EG=3+x ,在Rt △CBE 中,222BC BE CE +=,∴()22243x x +=+, 解得:76x =, ∴76BE =; 故答案为76. 【点睛】本题主要考查等腰三角形的性质与判定、矩形的性质及勾股定理,熟练掌握等腰三角形的性质与判定、矩形的性质及勾股定理是解题的关键.三、解答题21.如图,四边形ABCD是矩形,对角线AC与BD相交于点O,∠AOD=60°,AD=2,求AC的长度.解析:4【分析】根据矩形的性质和等边三角形的性质,可以得到OA的长,从而可以求得AC的长.【详解】解:∵四边形ABCD是矩形,∴OA=OC=OB=OD,∵∠AOD=60°,AD=2,∴△AOD是等边三角形,∴OA=OD=2,∴AC=2OA=4,即AC的长度为4.【点睛】本题考查了矩形的性质,等边三角形的判定与性质,熟记性质并判断出△AOB是等边三角形是解题的关键.22.如图,已知,四边形ABCD是平行四边形,AE∥BD,交CD的延长线于点E, 交BC延长线于点F,求证:四边形ABFD是等腰梯形.EF BC解析:见解析.【分析】首先证明四边形ABDE是平行四边形,即可得AB=DE,等量代换可得CD=DE,根据直角三角形斜边中线的性质定理可得DF=CD=DE,进而可得AB=DF,再说明线段AB和DF不平行即可求证结论.【详解】∵四边形ABCD是平行四边形,=.∴AD∥BC,AB∥CD,AB CD∴AB∥DE;又∵AE∥BD,∴四边形ABDE是平行四边形.=.∴AB DE∴CD DE=.⊥,∵EF BC∴DF=CD=DE.=.∴AB DF∵CD、FD交于点D,∴线段AB与线段FD不平行.∴四边形ABFD是等腰梯形.【点睛】本题考查平行四边形的判定及其性质、梯形的判定,直角三角形的斜边中线的性质定理,解题的关键是掌握两腰相等的梯形是等腰梯形.23.综合与实践:问题情境:数学活动课上,老师和同学们一起以“矩形的旋转”开展数学活动.具体操作如下:第一步:如图1,将长与宽都相等的两个矩形纸片ABCD和EFGH叠放在一起,这时对角线AC和EG互相重合.第二步:固定矩形ABCD,将矩形EFGH绕AC的中点O逆时针方向旋转,直到点E与点B重合时停止.问题解决:(1)奋进小组发现:在旋转过程中,当边AB与EF交于点M,边CD与GH交于点N,如图2、图3所示,请写出线段AM与CN始终存在的数量关系,并利用图2说明理由.(2)奋进小组继续探究发现:在旋转开始后,当两个矩形纸片重叠部分为四边形MRNQ 时,如图3所示,请你猜测四边形MRNQ 的形状,并试着证明你的猜想.探索发现:(3)奋进小组还发现在问题(2)中的四边形MRNQ 中MQN ∠与旋转角AOE ∠存在着特定的数量关系,请你写出这一关系,无需说明理由.解析:(1)AM CN =,理由见解析;(2)四边形MRNQ 为菱形,证明见解析;(3)MQN ∠=AOE ∠【分析】(1)结论:AM=CN .先证明(AAS)AOS COT ≌△△,推出AS CT =,OS OT =,34∠=∠,再证明(ASA)ESM GTN ≌△△即可解决问题.(2)过点Q 作QK ⊥EF ,QL ⊥CD ,垂足分别为点K ,L .首先证明四边形QMRN 是平行四边形,再证明QM=QN 即可.(3)结论:∠MQN=∠AOE .理由三角形的外角的性质以及平行线的性质即可解决问题.【详解】(1)关系:AM CN =理由:如图:设EG 分别与AB 、CD 相交于点S 、T ;∵四边形ABCD 与EFGH 都是矩形,且点O 为对角线的中点;∴//AB CD ,//EF GH ,OA OC =,OE OG =;∴12∠=∠;又AOS COT ∠=∠∴(AAS)AOS COT ≌△△∴AS CT =,OS OT =;∴ES GT =;又//EF GH ,∴56∠=∠;又12∠=∠;∴34∠=∠∴(ASA)ESM GTN ≌△△ ∴SM TN =,则AS SM CT TN +=+即AM CN =(2)四边形MRNQ 为菱形.证明:过点Q 作QK ⊥EF ,QL ⊥CD ,垂足分别为点K ,L .由题可知:矩形ABCD ≌矩形EFGH∴AD=EH ,AB ∥CD ,EF ∥HG∴四边形QMRN 为平行四边形,∵QK ⊥EF ,QL ⊥CD ,∴QK=EH ,QL=AD ,∠QKM=∠QLN=90°∴QK=QL ,又∵AB ∥CD ,EF ∥HG ,∴∠KMQ=∠MQN ,∠MQN=∠LNQ ,∴∠KMQ=∠LNQ ,∴△QKM ≌△QLN (AAS )∴MQ=NQ∴四边形MRNQ 为菱形.(3)结论:∠MQN=∠AOE .理由:如图中,∵∠QND=∠1+∠2,∠AOE=∠1+∠3,又由题意可知旋转前∠2与∠3重合,∴∠2=∠3,∴∠QND═∠AOE,∵AB∥CD,∴∠MQN=∠QND,∴∠MQN=∠AOE.【点睛】本题属于四边形综合题,考查了矩形的性质,菱形的判定和性质,全等三角形的判定和性质等知识,解题的关键是正确寻找确定的三角形解决问题,属于中考压轴题.24.如图,将长方形ABCD边AD沿折痕AE折叠,使点D落在BC上的点F处,已知AB=6,△ABF的面积是24,求DE的长.解析:10 3【分析】先根据三角形的面积公式求得BF的长,然后根据勾股定理可求得AF=10,由翻折的性质和矩形的性质可知BC=10,故此FC=2,最后在△EFC中,由勾股定理列方程求解即可.【详解】解:∵S△ABF=24,∴12AB•BF=24,即12×6×BF=24.解得:BF=8.在Rt△ABF中由勾股定理得:22AB BF=10.由翻折的性质可知:BC=AD=AF=10,ED=FE.∴FC=10-8=2.设DE=x ,则EC=6-x .在Rt △EFC 中,由勾股定理得:EF 2=FC 2+EC 2,x 2=4+(6-x )2.解得:x=103, ∴DE=103. 【点睛】本题主要考查的是矩形与折叠、三角形的面积公式、勾股定理的应用,根据勾股定理列出关于x 的方程是解题的关键.25.如图,在ABC 中,AB AC =,10BC =.(1)尺规作图:(要求:保留作图痕迹,不写作法)①作BAC ∠的平分线交BC 于点D ;②作边AC 的中点E ,连接DE ;(2)在(1)所作的图中,若12AD =,则DE 的长为__________.解析:(1)①见解析;②见解析;(2)6.5【分析】(1)①以A 为圆心,小于AB 的长度为半径画圆,交AB 、AC 于两个点,再分别以这两个点为圆心,一样的半径画弧,交于一点,连接这个点与点A ,即可得到BAC ∠的平分线,再画出它与BC 的交点D ;②作线段AC 的垂直平分线,即可找到线段AC 的中点E ,连接DE ;(2)由等腰三角形“三线合一”的性质得152BD BC ==,AD BC ⊥,用勾股定理求出AB 的长,再根据中位线的性质得到DE 的长.【详解】解:(1)①如图所示:②如图所示:(2)∵AB AC =,AD 平分BAC ∠, ∴152BD BC ==,AD BC ⊥, 在Rt ABD △中,2213AB AD BD =+=, ∵E 、D 分别是AC 和BC 的中点,∴1 6.52DE AB ==, 故答案是:6.5.【点睛】 本题考查等腰三角形的性质,中位线的定理,以及角平分线和垂直平分线的作法,解题的关键是熟练掌握这些几何的性质定理以及作图方法.26.已知:如图,在ABCD 中,4,6,AC BD CA AB ==⊥,求ABCD 的周长和面积. 解析:521+,5【分析】依据平行四边形的对角线互相平分,即可得到2AO =,3BO =,再根据勾股定理即可得出AB 与BC 的长,进而得到ABCD 的周长和面积. 【详解】解:如图所示,4AC =,6BD =,2AO ∴=,3BO =,又CA AB ⊥, Rt AOB ∴∆中,2222325AB BO AO =-=-Rt ABC 中,2222(5)421BC AB AC =+=+=ABCD ∴的周长2(521)25221==,ABCD 的面积5445AB AC =⨯=⨯=.【点睛】本题主要考查了平行四边形的性质以及勾股定理的运用,解题时注意:平行四边形的对角线互相平分.27.已知:如图,ABCD 中,AE 、CF 分别是BAD ∠和BCD ∠的角平分线,分别交边DC 、AB 于点E 、F ,求证:AE CF =.解析:见解析【分析】根据平行四边形的性质及角平分线的定义,证明ADE CBF ∆≅∆即可判断AE CF =.【详解】解:四边形ABCD 是平行四边形,DAB DCB ∴∠=∠,D B ∠=∠,AD BC =.AE ∵、CF 分别是BAD ∠和BCD ∠的角平分线,DAE BCF ∴∠=∠.()ADE CBF ASA ∴∆≅∆.AE CF ∴=.【点睛】本题主要考查了平行四边形的性质、全等三角形的判定和性质.证明线段相等的技巧一般是找到两个线段的相关三角形,通过全等求解.28.如图,AD 为ABC ∆的中线,BE 为ABD ∆的中线.(1)15ABE ∠=︒,40BAD ∠=︒,求 BED ∠的度数;(2)若ABC ∆的面积为40,5BD =,则E 到BC 边的距离为多少.解析:(1)55︒;(2)4.【分析】(1)根据三角形内角与外角的性质解答即可;(2)过E 作BC 边的垂线即可得:E 到BC 边的距离为EF 的长,然后过A 作BC 边的垂线AG ,再根据三角形中位线定理求解即可.【详解】解:(1)BED ∠是ABE ∆的外角, 154055BED ABE BAD ;(2)过E 作BC 边的垂线,F 为垂足,则EF 为所求的E 到BC 边的距离,过A 作BC 边的垂线AG ,AD ∴为ABC ∆的中线,5BD =,22510BC BD ∴==⨯=,ABC ∆的面积为40, ∴1402BC AG ,即110402AG ,解得8AG =,∵AD 为ABC ∆的中线, ∴11402022ABD ABC S S , 又∵BE 为ABD ∆的中线, ∴11201022EBD ABD S S , 则有:1151022BD EFEF 4EF ∴=.即E 到BC 边的距离为4.【点睛】本题考查了三角形外角的性质、三角形中位线的性质及三角形的面积公式,添加适当的辅助线是解题的关键.。
中考数学平行四边形综合经典题含答案解析

一、平行四边形真题与模拟题分类汇编(难题易错题)1.已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;(2)如图2,当b>2a时,点M在运动的过程中,是否存在∠BMC=90°,若存在,请给与证明;若不存在,请说明理由;(3)如图3,当b<2a时,(2)中的结论是否仍然成立?请说明理由.【答案】(1)见解析;(2)存在,理由见解析;(3)不成立.理由如下见解析.【解析】试题分析:(1)由b=2a,点M是AD的中点,可得AB=AM=MD=DC=a,又由四边形ABCD 是矩形,即可求得∠AMB=∠DMC=45°,则可求得∠BMC=90°;(2)由∠BMC=90°,易证得△ABM∽△DMC,设AM=x,根据相似三角形的对应边成比例,即可得方程:x2﹣bx+a2=0,由b>2a,a>0,b>0,即可判定△>0,即可确定方程有两个不相等的实数根,且两根均大于零,符合题意;(3)由(2),当b<2a,a>0,b>0,判定方程x2﹣bx+a2=0的根的情况,即可求得答案.试题解析:(1)∵b=2a,点M是AD的中点,∴AB=AM=MD=DC=a,又∵在矩形ABCD中,∠A=∠D=90°,∴∠AMB=∠DMC=45°,∴∠BMC=90°.(2)存在,理由:若∠BMC=90°,则∠AMB+∠DMC=90°,又∵∠AMB+∠ABM=90°,∴∠ABM=∠DMC,又∵∠A=∠D=90°,∴△ABM∽△DMC,∴AM ABCD DM=,设AM=x,则x aa b x =-,整理得:x2﹣bx+a2=0,∵b>2a,a>0,b>0,∴△=b2﹣4a2>0,∴方程有两个不相等的实数根,且两根均大于零,符合题意,∴当b>2a时,存在∠BMC=90°,(3)不成立.理由:若∠BMC=90°,由(2)可知x2﹣bx+a2=0,∵b<2a,a>0,b>0,∴△=b2﹣4a2<0,∴方程没有实数根,∴当b<2a时,不存在∠BMC=90°,即(2)中的结论不成立.考点:1、相似三角形的判定与性质;2、根的判别式;3、矩形的性质2.如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.(1)用尺规将图1中的△ABC分割成两个互补三角形;(2)证明图2中的△ABC分割成两个互补三角形;(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为、、的三角形,并计算图3中六边形DEFGHI的面积.②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.【答案】(1)作图见解析(2)证明见解析(3)①62;②6【解析】试题分析:(1)作BC边上的中线AD即可.(2)根据互补三角形的定义证明即可.(3)①画出图形后,利用割补法求面积即可.②平移△CHG到AMF,连接EM,IM,则AM=CH=BI,只要证明S△EFM=3S△ABC即可.试题解析:(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.(2)如图2中,延长FA到点H,使得AH=AF,连接EH.∵四边形ABDE,四边形ACGF是正方形,∴AB=AE,AF=AC,∠BAE=∠CAF=90°,∴∠EAF+∠BAC=180°,∴△AEF和△ABC是两个互补三角形.∵∠EAH+∠HAB=∠BAC+∠HAB=90°,∴∠EAH=∠BAC,∵AF=AC,∴AH=AB,在△AEH和△ABC中,∴△AEH≌△ABC,∴S△AEF=S△AEH=S△ABC.(3)①边长为、、的三角形如图4所示.∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,∴S六边形=17+13+10+4×5.5=62.②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,∵AM∥CH,CH⊥BC,∴AM⊥BC,∴∠EAM=90°+90°﹣x=180°﹣x,∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,∴∠EAM=∠DBI,∵AE=BD,∴△AEM≌△DBI,∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,∴△DBI和△ABC是互补三角形,∴S△AEM=S△AEF=S△AFM=2,∴S△EFM=3S△ABC=6.考点:1、作图﹣应用与设计,2、三角形面积3.如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).(1)当点N落在边BC上时,求t的值.(2)当点N到点A、B的距离相等时,求t的值.(3)当点Q沿D→B运动时,求S与t之间的函数表达式.(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF 与四边形PQMN的面积比为2:3时t的值.【答案】(1)(2)2(3)S=S菱形PQMN=2S△PNQ=t2;(4)t=1或【解析】试题分析:(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;(3)当0≤t≤时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当≤t≤时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.(4)MN、MQ与边BC的有交点时,此时<t<,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.试题解析:(1)∵△PQN与△ABC都是等边三角形,∴当点N落在边BC上时,点Q与点B重合.∴DQ=3∴2t=3.∴t=;(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,∴PD=DQ,当0<t<时,此时,PD=t,DQ=2t∴t=2t∴t=0(不合题意,舍去),当≤t<3时,此时,PD=t,DQ=6﹣2t∴t=6﹣2t,解得t=2;综上所述,当点N到点A、B的距离相等时,t=2;(3)由题意知:此时,PD=t,DQ=2t当点M在BC边上时,∴MN=BQ∵PQ=MN=3t,BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①,当0≤t≤时,S△PNQ=PQ2=t2;∴S=S菱形PQMN=2S△PNQ=t2,如图②,当≤t≤时,设MN、MQ与边BC的交点分别是E、F,∵MN=PQ=3t,NE=BQ=3﹣2t,∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,∵△EMF是等边三角形,∴S△EMF=ME2=(5t﹣3)2.;(4)MN、MQ与边BC的交点分别是E、F,此时<t<,t=1或.考点:几何变换综合题4.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.5.已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且,.现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P ==OB OD86为点D的对应点,再将纸片还原。
第十八章全国通用版中考数学:《平行四边形》与坐标系结合压轴题(二)—解析版

第十八章专题:《平行四边形》与坐标系结合压轴题(二)1.如图,在平面直角坐标系中,AB //OC, A (0, 12), B (a, c) , C (b, 0),并且a, b满足b= 府市 /口' + 16. 一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点 B 运动;动点Q 从点。
出发在线段OC上以每秒1个单位长度的速度向点C运动,点P、Q分别从点A、O同时出发,当点P 运动到点B时,点Q随之停止运动.设运动时间为t (秒)(1)求B、C两点的坐标;(2)当t为何值时,四边形PQCB是平行四边形?并求出此时P、Q两点的坐标;(3)当t为何值时,APQC是以PQ为腰的等腰三角形?并求出P、Q两点的坐标.(1) •, b= ^a-21 J^T^+16,••.a=21, b=16,故B (21, 12) C (16, 0); (2)由题意得:AP=2t, QO=t,贝U: PB=21-2t , QC=16-t,•••当PB=QC时,四边形PQCB是平行四边形,.•.21-2t=16-t,解得:t=5,,P (10, 12) Q (5, 0);(3)当PQ=CQ 时,过Q 作QN^AB,由题意得:122+t2=(16-t) 2, 解得:t=3.5,故P (7, 12), Q (3.5, 0),当PQ=PC时,过P作PM ±x轴,由题意得:QM=t , CM=16-2t ,则t=16-2t,解得:t=16, 2t=32, 3 3故P( 32,12), Q(16,3 30).2.如图1,在平面直角坐标系中, AB ,y 轴于点A, BC ,x 轴于点B,点D 为线段BC 的中点,若AB=a , CD=b ,且J 2 a 8 v 5 +/4我 a +2屈=b .连接AD ,在线段OC 上取一点E,使/ EAD= / DAB .(1)贝U a=, b=(2)求证:AE=OE+CD ;【解答】(1) a =4 v15 , b =2 后,(2)由(1)可知 AB=4 75, CD=BD=2 V 5 , • . AB=CB ,,.AB ±y 轴于点 A, BC±x 轴于点 B,,乙 BAO= / B= / AOC=90° ,••・四边形ABCO 是矩形,••・AB=CB , ••・四边形ABCO 是正方形,延长 CO 至u M ,使得 OM=BD ,贝u ^ABD AOM , ,/4=/M, Z1 = Z2=Z3,. OA//BC, . ・/4=/2+/5=/5+/3=/EAM , . . / M= / EAM , • . AE=EM=OE+OM=OE+BD ••• BD=CD , .1. AE=OE+CD .(3)如图 2 中,设 AE=EM=x .在 RtAAOE 中,AO 2+OE 2=AE 2, - x 2= (4<5 ) 2+ (x-2 J 5 ) 2, . . x=5石, OE=3 而,•.D (4V 5, 2 45), E (3V5 , 0), •. F (0, -6V5 )风0)3.如图,在平面直角坐标系中,有一矩形ABCD,其中A(0, 0), B (m, 0) , D (0, n), m是最接近质的整数,n是16的算术平方根,若将4ABC沿矩形又•角线AC所在直线翻折,点B落在点E处,AE与边CD相交于点M .(1)求AC的长;(2)求4AMC的面积;(3)求点E的坐标.【解答】(1)•' m是最接近#5的整数,• ' m=8,.「n 是16 的算术平方根,,n=4,,B (8, 0), D (0, 4),.••点C 矩形ABCD 的一个顶点,..C (8, 4),,AB=8, BC=4 ,AC=4 J5 ,(2)由折叠有,CE=AD=BC=4 , AE=AB=8 ,设DM=x 则CM=8-x ,・. /ADM= / CEM , /AMD=/CME, /.A ADM ^ACEM , • .AM=CM=8-x , ME=MD , 在RtAADM 中,AD=4 , DM=x , AM=8-x ,根据勾股定理有:AD2+DM 2=AM 2,即:16+x2= (8-x) 2, •1- x=3 , DM=3 , CM=5 , S AAMC = —Ch/|X AD=)>^M=10,2 2(3)过点E作EFXCD,如图,由(2)有,CM=5 , CE=4, ME=DM=3在Rt^CEM 中,由射影定理得,CE2=CFXCM , 16=CFX5,,CF=3.2,••・Ma CE=CMK EF (直角三角形的面积的两种计算) ,,EF=2.4,• . DF=CD -CF=4.8 , BC+EF=6.4 , . . E (4.8, 6.4)4 .已知正方形OABC 在平面直角坐标系中,点 A, C 分别在x 轴,y 轴的正半轴上,等腰直角三角形OEF 的直角顶点O 在原点,E, F 分别在OA, OC 上,且OA=4 , OE=2 .将AOEF 绕点O 逆 时针旋转,得△OE I F I ,点E, F 旋转后的对应点为Ei, Fi.(I )①如图①,求EiFi 的长;②如图②,连接CFi, AEi,求证△OAEi^^OCFi;「(II)将AOEF 绕点O 逆时针旋转一周,当 OEi//CFi 时,求点Ei 的坐标(直接写出结果即可)姝 姝CB C 石【解答】(I )①解:二.等腰直角三角形 OEF 的直角顶点O 在原点,OE=2, / EOF=90 , OF=OE=2 ,「. EF=2 血,・ ••将AOEF 绕点 O 逆时针旋转,得△OE i F i, ••.E i F i =EF=2 J 2 ; ②证明:四边形OABC 为正方形,OC=OA .・ •・将AOEF 绕点 O 逆时针旋转,得 △OE i F i,AOE i =/COF i, • △OEF 是等腰直角三角形,・•.△OEiFi 是等腰直角三角形, ••OE i =OF i.在 AOAE i 和 ^OCF i 中,OA=OC, /AOEi=/COF i, OEi=OFi% E・•.△OAE 卢^OCF i (SAS);(n)解:••• OEXOF,卜过点F与OE平行的直线有且只有一条,并与OF垂直,当三角板OEF绕。
2020年中考数学压轴题-专题08 动点产生的平行四边形(解析版)

专题08 动点产生的平行四边形教学重难点1.理解平行四边形的性质和判定;2.能应用平行四边形的性质和判定进行相关计算和证明;3.培养学生能在点的运动过程中寻找平行四边形,继而解决相关问题;4.培养学生分类讨论的能力,能应用分类讨论思想解决相关问题;5.体验运动过程,培养学生动态数学思维能力。
【备注】:1.根据后面两个图让学生回顾平行四边形的性质和判定,为后面的例题讲解做好准备;2.部分地方引导学生填空,让学生自己回顾。
时间大概5分钟。
平行四边形的性质:平行四边形的判定:【备注】:1.以下每题教法建议,请老师根据学生实际情况参考;2.在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;3.可以根据各题的“教法指导”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;4.例题讲解,可以根据“参考教法”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;5.引导的技巧:直接提醒,问题式引导,类比引导等等;6.部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;7.每个题目的讲解时间根据实际情况处理,建议每题7分钟,选讲例题在时间足够的情况下讲解。
1.(2019·辽宁中考真题)如图1,在平面直角坐标系中,一次函数y =﹣34x +3的图象与x 轴交于点A ,与y 轴交于B 点,抛物线y =﹣x 2+bx +c 经过A ,B 两点,在第一象限的抛物线上取一点D ,过点D 作DC ⊥x 轴于点C ,交直线AB 于点E .(1)求抛物线的函数表达式(2)是否存在点D ,使得⊥BDE 和⊥ACE 相似?若存在,请求出点D 的坐标,若不存在,请说明理由; (3)如图2,F 是第一象限内抛物线上的动点(不与点D 重合),点G 是线段AB 上的动点.连接DF ,FG ,当四边形DEGF 是平行四边形且周长最大时,请直接写出点G 的坐标. 【整体分析】(1)根据334y x =-+,求出A ,B 的坐标,再代入抛物线解析式中即可求得抛物线解析式;(2)⊥BDE 和⊥ACE 相似,要分两种情况进行讨论: ⊥⊥BDE⊥⊥ACE ,求得13(4D ,3);⊥⊥DBE⊥⊥ACE ,求得23(12D ,50)9; (3)由DEGF 是平行四边形,可得DE⊥FG ,DE=FG ,设213(,3)4D m m m -++,3(,3)4E m m -+,213(,3)4F n n n -++,3(,3)4G n n -+,根据平行四边形周长公式可得:DEGF 周长=23892()48m --+,由此可求得点G 的坐标. 【满分解答】(1)在334y x =-+中,令0x =,得3y =,令0y =,得4x =,(4,0)A ∴,(0,3)B ,将(4,0)A ,(0,3)B 分别代入抛物线2y x bx c =-++中,得:24403b c c ⎧-++=⎨=⎩,解得:1343b c ⎧=⎪⎨⎪=⎩,∴抛物线的函数表达式为:21334y x x =-++. (2)存在.如图1,过点B 作BH CD ⊥于H ,设(,0)C t ,则213(,3)4D t t t -++,3(,3)4E t t -+,(,3)H t ;334EC t ∴=-+,4AC t =-,BH t =,2134DH t t =-+,24DE t t =-+BDE ∆∵和ACE ∆相似,BED AEC ∠=∠BDE ACE ∴∆∆∽或DBE ACE ∆∆∽⊥当BDE ACE ∆∆∽时,90BDE ACE ∠=∠=︒,∴BD AC DE CE=,即:BD CE AC DE =g g 23(3)(4)(4)4t t t t t ∴-+=-⨯-+,解得:10t =(舍去),24t =(舍去),3134t =,13(4D ∴,3)⊥当DBE ACE ∆∆∽时,BDE CAE ∠=∠ BH CD ⊥Q90BHD ∴∠=︒,∴tan tan BH CEBDE CAE DH AC=∠=∠=,即:BH AC CE DH =g g 2313(4)(3)()44t t t t t ∴-=-+-+,解得:10t =(舍),24t =(舍),32312t =,23(12D ∴,50)9; 综上所述,点D 的坐标为13(4,3)或23(12,50)9;(3)如图3,Q 四边形DEGF 是平行四边形 //DE FG ∴,DE FG =设213(,3)4D m m m -++,3(,3)4E m m -+,213(,3)4F n n n -++,3(,3)4G n n -+,则:24DE m m =-+,24FG n n =-+,2244m m n n ∴-+=-+,即:()(4)0m n m n -+-=,0m n -≠Q 40m n ∴+-=,即:4m n +=过点G 作GK CD ⊥于K ,则//GK AC EGK BAO ∴∠=∠∴cos cos GK AOEGK BAO EG AB=∠=∠=,即:GK AB AO EG =g g 5()4n m EG ∴-=,即:5()4EG n m =-DEGF ∴周长2253892()2[(4)()]2()448DE EG m m n m m =+=-++-=--+20-<Q ,∴当34m =时,DEGF ∴Y 周长最大值898=, 13(4G ∴,9)16【点睛】此题考查二次函数综合题,综合难度较大,解答关键在于结合函数图形进行计算,再利用待定系数法求解析式,配合辅助线利用相似三角形的性质进行解答.2.如图,在平面直角坐标系中,直线b kx y +=分别与x 轴负半轴交于点A ,与y 轴的正半轴交于点B ,⊙P 经过点A 、点B (圆心P 在x 轴负半轴上),已知AB=10,425=AP 。
中考平行四边形压轴题+答案

平行四边形1-20一.解答题(共19小题)1.(1)如图1,已知矩形ABCD中,点E是BC上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H,试证明CH=EF+EG;(2)若点E在BC的延长线上,如图2,过点E作EF⊥BD于点F,EG⊥AC的延长线于点G,CH⊥BD于点H,则EF、EG、CH三者之间具有怎样的数量关系,直接写出你的猜想;(3)如图3,BD是正方形ABCD的对角线,L在BD上,且BL=BC,连接CL,点E是CL上任一点,EF⊥BD于点F,EG⊥BC于点G,猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想;(4)观察图1、图2、图3的特性,请你根据这一特性构造一个图形,使它仍然具有EF、EG、CH这样的线段的关系,并满足(1)或(2)的结论,写出相关题设的条件和结论.2.(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E 是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.第1页(共33页)3.如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.(1)若AE=2,求EC的长;(2)若点G在DC上,且∠AGC=120°,求证:AG=EG+FG.4.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD (不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为时,求正方形的边长.第2页(共33页)5.(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,▱ABCD 中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?根据习题背景,写出面积相等的一对平行四边形的名称为和;(2)如图2,点P为▱ABCD内一点,过点P分别作AD、AB的平行线分别交▱ABCD的四边于点E、F、G、H.已知S▱BHPE=3,S▱PFDG=5,则S△PAC=;(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,则菱形EFGH的周长为.6.如图,E是正方形ABCD的边AD上的动点,F是边BC延长线上的一点,且BF=EF,AB=12,设AE=x,BF=y.(1)当△BEF是等边三角形时,求BF的长;(2)求y与x的函数解析式,并写出它的定义域;(3)把△ABE沿着直线BE翻折,点A落在点A′处,试探索:△A′BF能否为等腰三角形?如果能,请求出AE的长;如果不能,请说明理由.7.已知矩形ABCD和点P,当点P在BC上任一位置(如图(1)所示)第3页(共33页)时,易证得结论:PA2+PC2=PB2+PD2,请你探究:当点P分别在图(2)、图(3)中的位置时,PA2、PB2、PC2和PD2又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论.答:对图(2)的探究结论为;对图(3)的探究结论为;证明:如图(2)8.已知:如图所示,O为等腰直角△BCD斜边BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.(1)求证:△BCE≌△DCF;(2)OG与BF有什么数量关系?证明你的结论;(3)若GE•GB=4﹣2,求△DBG的面积.9.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点第4页(共33页)E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF 于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC 上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.10.如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.(1)猜想四边形EFGH的形状,直接回答,不必说明理由;(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.第5页(共33页)11.如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.探究:线段MD、MF的关系,并加以证明.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.第6页(共33页)12.正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F.如图1,当点P与点O重合时,显然有DF=CF.(1)如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE 交CD于点E.①求证:DF=EF;②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;(2)若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD 于点E.请完成图3并判断(1)中的结论①、②是否分别成立?若不成立,写出相应的结论.(所写结论均不必证明)13.如图,正方形ABCD,BE⊥ED,连接BD,CE.(1)求证:∠EBD=∠ECD;(2)设EB,EC交AD于F,G两点,若AF=2FG,探究线段CG与DG之间的数量关系并证明.第7页(共33页)14.如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.(1)求证:EF+AC=AB;(2)点C1从点C出发,沿着线段CB向点B运动(不与点B重合),同时点A1从点A出发,沿着BA的延长线运动,点C1与A1的运动速度相同,当动点C1停止运动时,另一动点A1也随之停止运动.如图2,A1F1平分∠BA1C1,交BD于点F1,过点F1作F1E1⊥A1C1,垂足为E1,请猜想E1F1,A1C1与AB三者之间的数量关系,并证明你的猜想;(3)在(2)的条件下,当A1E1=3,C1E1=2时,求BD的长.15.如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.(1)若BF=BD=,求BE的长;(2)若∠ADE=2∠BFE,求证:FH=HE+HD.第8页(共33页)16.如图,小明将一张直角梯形纸片沿虚线剪开,得到矩形ABCD和三角形EGF两张纸片,测得AB=5,AD=4,EF=.在进行如下操作时遇到了下面的几个问题,请你帮助解决.(1)请你求出FG的长度.(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为.y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x 的值.(3)在(2)的操作中,小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).17.如图,将一三角板放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于Q.探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系,并写出函数自变量x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置.并求出相应的x值,如果不可能,试说明理由.第9页(共33页)18.如图,△ABC中,点P是边AC上的一个动点,过P作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:PE=PF;(2)当点P在边AC上运动时,四边形AECF可能是矩形吗?说明理由;(3)若在AC边上存在点P,使四边形AECF是正方形,且.求此时∠BAC的大小.19.如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b (a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.第10页(共33页)平行四边形1-20参考答案与试题解析一.解答题(共19小题)1.(1)如图1,已知矩形ABCD中,点E是BC上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H,试证明CH=EF+EG;(2)若点E在BC的延长线上,如图2,过点E作EF⊥BD于点F,EG⊥AC的延长线于点G,CH⊥BD于点H,则EF、EG、CH三者之间具有怎样的数量关系,直接写出你的猜想;(3)如图3,BD是正方形ABCD的对角线,L在BD上,且BL=BC,连接CL,点E是CL上任一点,EF⊥BD于点F,EG⊥BC于点G,猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想;(4)观察图1、图2、图3的特性,请你根据这一特性构造一个图形,使它仍然具有EF、EG、CH这样的线段的关系,并满足(1)或(2)的结论,写出相关题设的条件和结论.【解答】(1)证明:过E点作EN⊥CH于N.∵EF⊥BD,CH⊥BD,∴四边形EFHN是矩形.∴EF=NH,FH∥EN.∴∠DBC=∠NEC.∵四边形ABCD是矩形,∴AC=BD,且互相平分∴∠DBC=∠ACB∴∠NEC=∠ACB∵EG⊥AC,EN⊥CH,∴∠EGC=∠CNE=90°,又∵EC=CE,∴△EGC≌△CNE.∴EG=CN∴CH=CN+NH=EG+EF;(2)解:猜想CH=EF﹣EG;(3)解:EF+EG=BD;(4)解:点P是等腰三角形底边所在直线上的任意一点,点P到两腰的距离的和(或差)等于这个等腰三角形腰上的高.如图①,有CG=PF﹣PN.第11页(共33页)2.(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E 是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.【解答】(1)证明:∵四边形ABCD是正方形,∴BC=CD,∠B=∠CDF=90°,∵∠ADC=90°,∴∠FDC=90°.∴∠B=∠FDC,∵BE=DF,∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明:如图2,延长AD至F,使DF=BE,连接CF.由(1)知△CBE≌△CDF,∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,∴∠GCF=∠GCE=45°.∵CE=CF,GC=GC,∴△ECG≌△FCG.∴GE=GF,∴GE=GF=DF+GD=BE+GD.(3)解:如图3,过C作CG⊥AD,交AD延长线于G.在直角梯形ABCD中,∵AD∥BC,∴∠A=∠B=90°,又∵∠CGA=90°,AB=BC,∴四边形ABCG为正方形.∴AG=BC.…(7分)∵∠DCE=45°,根据(1)(2)可知,ED=BE+DG.…(8分)∴10=4+DG,即DG=6.设AB=x,则AE=x﹣4,AD=x﹣6,在Rt△AED中,∵DE2=AD2+AE2,即102=(x﹣6)2+(x﹣4)2.解这个方程,得:x=12或x=﹣2(舍去).…(9分)第12页(共33页)∴AB=12.∴S梯形ABCD=(AD+BC)•AB=×(6+12)×12=108.即梯形ABCD的面积为108.…(10分)3.如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.(1)若AE=2,求EC的长;(2)若点G在DC上,且∠AGC=120°,求证:AG=EG+FG.【解答】(1)解:如图,连接EF,在正方形ABCD中,AB=AD,∠B=∠D,在△ABE和△ADF中,,∴△ABE≌△ADF(SAS),∴AE=AF,∵∠EAF=60°,∴△AEF是等边三角形,∴EF=AE=2,∵BE=DF,BC=CD,∴BC﹣BE=CD﹣DF,即CE=CF,∴△CEF是等腰直角三角形,∴EC=EF=×2=;(2)方法一:证明:∵∠AGC=120°,∴∠AGF=180°﹣∠AGC=180°﹣120°=60°,又∵△AEF是等边三角形,(已证)∴∠AEF=60°,∴点A、E、G、F四点共圆,∴∠AGE=∠AFE=60°,∴∠CGE=∠AGC﹣∠AGE=120°﹣60°=60°,如图(2)①延长GE交AB的延长线于H,∵AB∥CD,∴∠H=∠CGE=60°,∴∠H=∠AGF,又∵∠GAF+∠EAG=∠EAF=60°,∠HAE+∠EAG=∠GAB=60°,∴∠GAF=∠HAE,第13页(共33页)在△AFG和△AEH中,,∴△AFG≌△AEH(AAS),∴AG=AH,FG=EH,∵∠AGE=60°,∴△AGH是等边三角形,∵AH=GH=EG+EH=EG+FG,即AG=EG+FG.方法二:如图(2)②在AG上截取GH=FG,∵∠AGC=120°,∴∠AGF=60°,∴△FGH是等边三角形,∴FH=FG,∠FHG=60°,∵△AEF是等边三角形,∴∠AFE=60°,∴∠AFE=∠GFH=60°,∴∠AFE﹣∠EFH=∠GFH﹣∠EFH,即∠AFH=∠EFG,在△AFH和△BFG中,,∴△AFH≌△EFG(SAS),∴AH=GE,∴AG=AH+GH=EG+FG,即AG=EG+FG.4.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为时,求正方形的边长.第14页(共33页)【解答】(1)证明:∵△ABE是等边三角形,∴BA=BE,∠ABE=60°.∵∠MBN=60°,∴∠MBN﹣∠ABN=∠ABE﹣∠ABN.即∠MBA=∠NBE.又∵MB=NB,∴△AMB≌△ENB(SAS).(2)解:①当M点落在BD的中点时,A、M、C三点共线,AM+CM的值最小.②如图,连接CE,当M点位于BD与CE的交点处时,AM+BM+CM的值最小.理由如下:连接MN,由(1)知,△AMB≌△ENB,∴AM=EN,∵∠MBN=60°,MB=NB,∴△BMN是等边三角形.∴BM=MN.∴AM+BM+CM=EN+MN+CM.根据“两点之间线段最短”可知,若E、N、M、C在同一条直线上时,EN+MN+CM取得最小值,最小值为EC.在△ABM和△CBM中,,∴△ABM≌△CBM,∴∠BAM=∠BCM,∴∠BCM=∠BEN,∵EB=CB,∴若连接EC,则∠BEC=∠BCE,∵∠BCM=∠BCE,∠BEN=∠BEC,∴M、N可以同时在直线EC上.∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC 的长.(3)解:过E点作EF⊥BC交CB的延长线于F,∴∠EBF=∠ABF﹣∠ABE=90°﹣60°=30°.设正方形的边长为x,则BF=x,EF=.在Rt△EFC中,∵EF2+FC2=EC2,∴()2+(x+x)2=.解得x1=,x2=﹣(舍去负值).∴正方形的边长为.第15页(共33页)第16页(共33页)5.(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,▱ABCD 中,过对角线BD 上一点P 作EF ∥BC ,HG ∥AB ,图中哪两个平行四边形的面积相等?为什么?根据习题背景,写出面积相等的一对平行四边形的名称为 ▱AEPH 和 ▱PGCF ;(2)如图2,点P 为▱ABCD 内一点,过点P 分别作AD 、AB 的平行线分别交▱ABCD 的四边于点E 、F 、G 、H .已知S ▱BHPE =3,S ▱PFDG =5,则S △PAC = 1 ;(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD 的面积为11,则菱形EFGH 的周长为 24 .【解答】解:(1)∵▱ABCD 中,EF ∥BC ,HG ∥AB , ∴S △ABD =S △BCD ,S △PBE =S △PBG ,S △PDH =S △PDF , ∴S ▱AEPH =S ▱PGCF ,S ▱ABGH =S ▱EBCF ,S ▱AEFD =S ▱HGCD ,故答案为:▱AEPH 和▱PGCF 或▱ABGH 和▱EBCF 或▱AEFD 和▱HGCD ;(2)根据(1)可得:S △ABC =S △ADC ,S △PAE =S △PAG ,S △PCH =S △PCF , ∵S ▱BHPE =3,S ▱PFDG =5,∴S △PAC =S △PAG +S △PCF +S ▱PFDG ﹣S △ACD =S △PAG +S △PCF +S ▱PFDG ﹣S ▱ABCD =S △PAG +S △PCF +S ▱PFDG ﹣(2S △PAG +2S △PCF +S ▱BHPE +S ▱PFDG )=S ▱PFDG ﹣(S ▱BHPE +S ▱PFDG )=1;故答案为:1;(3)∵①②③④四个平行四边形面积的和为14, ∴S 1+S 2+S 3+S 4=14,∵四边形ABCD 的面积为11, ∴S 5=11﹣14×=4,∴S 菱形EFGH =S 1+S 2+S 3+S 4+S 5=18, ∵菱形EFGH 的一个内角为30°, ∴设边长为x , 则x•xsin30°=18, 解得:x=6,∴菱形EFGH 的周长为24. 故答案为:24.6.如图,E 是正方形ABCD 的边AD 上的动点,F 是边BC 延长线上的一点,且BF=EF ,AB=12,设AE=x ,BF=y .(1)当△BEF 是等边三角形时,求BF 的长; (2)求y 与x 的函数解析式,并写出它的定义域;(3)把△ABE 沿着直线BE 翻折,点A 落在点A′处,试探索:△A′BF 能否为等腰三角形?如果能,请求出AE 的长;如果不能,请说明理由.【解答】解:(1)当△BEF是等边三角形时,∠ABE=30°.∵AB=12,∴AE=,∴BF=BE=.(2)作EG⊥BF,垂足为点G,根据题意,得EG=AB=12,FG=y﹣x,EF=y,∴y2=(y﹣x)2+122,∴所求的函数解析式为(0<x<12).(3)∵∠AEB=∠FBE=∠FEB,∴点A'落在EF上,∴A'E=AE,∠BA'F=∠BA'E=∠A=90,∴要使△A'BF成为等腰三角形,必须使A'B=A'F.而A'B=AB=12,A'F=EF﹣A'E=BF﹣A'E,∴y﹣x=12.∴﹣x=12.整理得x2+24x﹣144=0,解得,经检验:都原方程的根,但不符合题意,舍去,当AE=时,△A'BF为等腰三角形.7.已知矩形ABCD和点P,当点P在BC上任一位置(如图(1)所示)时,易证得结论:PA2+PC2=PB2+PD2,请你探究:当点P分别在图(2)、图(3)中的位置时,PA2、PB2、PC2和PD2又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论.答:对图(2)的探究结论为PA2+PC2=PB2+PD2;对图(3)的探究结论为PA2+PC2=PB2+PD2;第17页(共33页)证明:如图(2)【解答】解:结论均是PA2+PC2=PB2+PD2.(1)如图2,过点P作MN∥AB,交AD于点M,交BC于点N,∴四边形ABNM和四边形NCDM均为矩形,根据(1)中的结论可得,在矩形ABNM中有PA2+PN2=PB2+PM2,在矩形NCDM中有PC2+PM2=PD2+PN2,两式相加得PA2+PN2+PC2+PM2=PB2+PM2+PD2+PN2,∴PA2+PC2=PB2+PD2.(2)如图3,过点P作MN∥AB,交AB的延长线于点M,交CD的延长线于点N,∴四边形BCNM和四边形ADNM均为矩形,同样根据(1)中的结论可得,在矩形BCNM中有PC2+PM2=PB2+PN2,在矩形ADNM中有PA2+PN2=PD2+PM2,两式相加得PA2+PN2+PC2+PM2=PD2+PM2+PB2+PN2,∴PA2+PC2=PB2+PD2.8.已知:如图所示,O为等腰直角△BCD斜边BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.(1)求证:△BCE≌△DCF;(2)OG与BF有什么数量关系?证明你的结论;(3)若GE•GB=4﹣2,求△DBG的面积.【解答】(1)证明:在△BCE与△DCF中,,∴△BCE≌△DCF.(2)解:OG=BF.理由如下:∵△BCE≌△DCF,∴∠CEB=∠F,∵∠CEB=∠DEG,∴∠F=∠DEG,∵∠F+∠GDE=90°,第18页(共33页)第19页(共33页)∴∠DEG +∠GDE=90°, ∴BG ⊥DF ,∴∠BGD=∠BGF ,又∵BG=BG ,∠DBG=∠FBG , ∴△BGD ≌△BGF , ∴DG=GF ,∵O 为正方形ABCD 的中心, ∴DO=OB ,∴OG 是△DBF 的中位线, ∴OG=BF .(3)解:设BC=x ,则DC=x ,BD=,由(2)知,△BGF ≌△BGD , ∴BF=BD ,∴CF=(﹣1)x ,∵∠DGB=∠EGD ,∠DBG=∠EDG , ∴△GDB ∽△GED , ∴=,∴GD 2=GE•GB=4﹣2, ∵DC 2+CF 2=(2GD )2,∴x 2+(﹣1)2x 2=4(4﹣2), (4﹣2)x 2=4(4﹣2),x 2=4,正方形ABCD 的面积是4个平方单位. ∴S △DBG =S △BDF =××x 2=个平方单位.9.数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.∠AEF=90°,且EF 交正方形外角∠DCG 的平分线CF 于点F ,求证:AE=EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM=EC ,易证△AME ≌△ECF ,所以AE=EF . 在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由. 【解答】解:(1)正确.证明:在AB 上取一点M ,使AM=EC ,连接ME . ∴BM=BE ,∴∠BME=45°,∴∠AME=135°,∵CF是外角平分线,∴∠DCF=45°,∴∠ECF=135°,∴∠AME=∠ECF,∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,∴△AME≌△ECF(ASA),∴AE=EF.(2)正确.证明:在BA的延长线上取一点N.使AN=CE,连接NE.∴BN=BE,∴∠N=∠NEC=45°,∵CF平分∠DCG,∴∠FCE=45°,∴∠N=∠ECF,∵四边形ABCD是正方形,∴AD∥BE,∴∠DAE=∠BEA,即∠DAE+90°=∠BEA+90°,∴∠NAE=∠CEF,∴△ANE≌△ECF(ASA),∴AE=EF.10.如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.(1)猜想四边形EFGH的形状,直接回答,不必说明理由;(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.【解答】解:(1)四边形EFGH是菱形.(2分)(2)成立.(3分)第20页(共33页)理由:连接AD,BC.(4分)∵∠APC=∠BPD,∴∠APC+∠CPD=∠BPD+∠CPD.即∠APD=∠CPB.又∵PA=PC,PD=PB,∴△APD≌△CPB(SAS)∴AD=CB.(6分)∵E、F、G、H分别是AC、AB、BD、CD的中点,∴EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线.∴EF=BC,FG=AD,GH=BC,EH=AD.∴EF=FG=GH=EH.∴四边形EFGH是菱形.(7分)(3)补全图形,如答图.(8分)判断四边形EFGH是正方形.(9分)理由:连接AD,BC.∵(2)中已证△APD≌△CPB.∴∠PAD=∠PCB.∵∠APC=90°,∴∠PAD+∠1=90°.又∵∠1=∠2.∴∠PCB+∠2=90°.∴∠3=90°.(11分)∵(2)中已证GH,EH分别是△BCD,△ACD的中位线,∴GH∥BC,EH∥AD.∴∠EHG=90°.又∵(2)中已证四边形EFGH是菱形,∴菱形EFGH是正方形.(12分)11.如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.探究:线段MD、MF的关系,并加以证明.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.第21页(共33页)【解答】证明:关系是:MD=MF,MD⊥MF如图,延长DM交CE于点N,连接FD、FN∵正方形ABCD,∴AD∥BE,AD=DC,∴∠1=∠2又∵AM=EM,∠3=∠4∴△ADM≌△ENM∴AD=EN,MD=MN∵AD=DC,∴DC=NE又∵正方形CGEF,∴∠FCE=∠NEF=45°,FC=FE,∠CFE=90°又∵正方形ABCD,∴∠BCD=90°.∴∠DCF=∠NEF=45°∴△FDC≌△FNE∴FD=FN,∠5=∠6∵∠CFE=90°,∴∠DFN=90°又∵DM=MN=DN,∴M为DN的中点,∴FM=DN,∴MD=MF,DM⊥MF思路一:∵四边形ABCD、CGEF是正方形,∴AB=BC=CD=AD,∠B=∠BCD=∠CDA=∠BAD=90°CF=EF=EG=CG,∠G=∠GEF=∠EFC=∠FCG=90°,∠FCE=∠FEC=45°∴∠DCF=∠FEC思路二:延长DM交CE于N,∵四边形ABCD、CGEF是正方形∴AD∥CE,∴∠DAM=∠NEM又∵∠DMA=∠NME,AM=EM,∴△ADM≌△ENM思路三:∵正方形CGEF,∴∠FCE=∠FEC=45°又∵正方形ABCD,∴∠DCB=90°.∴∠DCF=180°﹣∠DCB﹣∠FCE=45°,∠DCF=∠FEC=45°选取条件①证明:如图∵正方形ABCD,∴AD∥BE,AD=DC,∴∠1=∠2∵AD=NE,∠3=∠4,∴△ADM≌△ENM∴MD=MN又∵AD=DC,∴DC=NE又∵正方形CGEF,∴FC=FE,∠FCE=∠FEN=45°.第22页(共33页)∴∠FCD=∠FEN=45°∴△FDC≌△FNE∴FD=FN,∠5=∠6,∴∠DFN=∠CFE=90°∴MD=MF,MD⊥MF选取条件②证明:如图,延长DM交FE于N∵正方形ABCD、CGEF∴CF=EF,AD=DC,∠CFE=90°,AD∥FE.∴∠1=∠2又∵MA=ME,∠3=∠4,∴△AMD≌△EMN∴MD=MN,AD=EN.∵AD=DC,∴DC=NE又∵FC=FE,∴FD=FN又∵∠DFN=90°,∴FM⊥MD,MF=MD.选取条件③证明:如图,延长DM交FE于N.∵正方形ABCD、CGEF∴CF=EF,AD=DC,∠CFE=90°,AD∥FE∴∠1=∠2又∵MA=ME,∠3=∠4,∴△AMD≌△EMN∴AD=EN,MD=MN.∵CF=2AD,EF=2EN∴FD=FN.又∵∠DFN=90°,∴MD=MF,MD⊥MF附加题:证明:如图过点E作AD的平行线分别交DM、DC的延长线于N、H,连接DF、FN 则∠ADC=∠H,∠3=∠4.∵AM=ME,∠1=∠2,∴△ADM≌△ENM∴DM=NM,AD=EN.∵正方形ABCD、CGEF∴AD=DC,FC=FE,∠ADC=∠FCG=∠CFE=90°,CG∥FE∴∠H=90°,∠5=∠NEF,DC=NE∴∠DCF+∠7=∠5+∠7=90°∴∠DCF=∠5=∠NEF∵FC=FE,∴△DCF≌△NEF∴FD=FN,∠DFC=∠NFE.∵∠CFE=90°∴∠DFN=90°.∴DM=FM,DM⊥FM.第23页(共33页)12.正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F.如图1,当点P与点O重合时,显然有DF=CF.(1)如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE 交CD于点E.①求证:DF=EF;②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;(2)若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD 于点E.请完成图3并判断(1)中的结论①、②是否分别成立?若不成立,写出相应的结论.(所写结论均不必证明)【解答】解:(1)如图2,延长FP交AB于点Q,①∵AC是正方形ABCD对角线,∴∠QAP=∠APQ=45°,∴AQ=PQ,∵AB=QF,∴BQ=PF,∵PE⊥PB,∴∠QPB+∠FPE=90°,∵∠QBP+∠QPB=90°,∴∠QBP=∠FPE,∵∠BQP=∠PFE=90°,∴△BQP≌△PFE,∴QP=EF,∵AQ=DF,∴DF=EF;②如图2,过点P作PG⊥AD.∵PF⊥CD,∠PCF=∠PAG=45°,∴△PCF和△PAG均为等腰直角三角形,∵四边形DFPG为矩形,∴PA=PG,PC=CF,∵PG=DF,DF=EF,∴PA=EF,∴PC=CF=(CE+EF)=CE+EF=CE+PA,即PC、PA、CE满足关系为:PC=CE+PA;(2)结论①仍成立;结论②不成立,此时②中三条线段的数量关系是PA﹣PC=CE.如图3:①∵PB⊥PE,BC⊥CE,∴B、P、C、E四点共圆,∴∠PEC=∠PBC,在△PBC和△PDC中有:BC=DC(已知),∠PCB=∠PCD=45°(已证),PC 边公共边,∴△PBC≌△PDC(SAS),第24页(共33页)∴∠PBC=∠PDC,∴∠PEC=∠PDC,∵PF⊥DE,∴DF=EF;②同理:PA=PG=DF=EF,PC=CF,∴PA=EF=(CE+CF)=CE+CF=CE+PC即PC、PA、CE满足关系为:PA﹣PC=CE.13.如图,正方形ABCD,BE⊥ED,连接BD,CE.(1)求证:∠EBD=∠ECD;(2)设EB,EC交AD于F,G两点,若AF=2FG,探究线段CG与DG之间的数量关系并证明.【解答】(1)证明:如图,过点C作CM⊥BE于M,作CN⊥DE交ED的延长线于N,∵BE⊥ED,∴四边形CNEM是矩形,∴∠DCN+∠DCM=∠MCN=90°,又∵∠BCM+∠DCM=∠BCD=90°,∴∠BCM=∠DCN,正方形ABCD中,BC=CD,在△BCM和△DCN中,,∴△BCM≌△DCN(AAS),∴CM=CN,∴矩形CNEM是正方形,∴∠CEM=45°,又∵四边形ABCD是正方形,∴∠BDC=45°,设BD、CE交于点O,在△BEO中,∠EBO+∠EOB+∠BEO=180°,在△CDO中,∠COD+∠ODC+∠OCD=180°,∵∠BOE=∠COD,∴∠EBO=∠OCD,即:∠EBD=∠ECD;第25页(共33页)(2)解:CG=DG.理由如下:如图,过点B作BP⊥CE于P,BP的延长线交CD于点Q,连接FQ,∵∠BEP=45°,∴∠EBP=90°﹣45°=45°,延长DC到点Q,使CR=AF,在正方形ABCD中,AB=BC,在△ABF和△CBR中,,∴△ABF≌△CBR(SAS),∴BF=BR,∠ABF=∠CBR,∴∠QBR=∠QBC+∠CBR=∠QBC+∠ABF=90°﹣∠EBP=45°,∴∠QBR=∠QBF=45°,在△FBQ和△RBQ中,,∴△FBQ≌△RBQ(SAS),∴FQ=QR,∵BP⊥CE,∴∠CBQ+∠BCP=90°,又∵∠BCP+∠DCG=∠BCD=90°,∴∠CBQ=∠DCG,在△BCQ和△CDG中,,∴△BCQ≌△CDG(ASA),∴DG=CQ,设FG=x,DG=CQ=a,则AF=CR=2FG=2x,AD=AF+FG+DG=2x+x+a=3x+a,FQ=QR=CQ+CR=DG+AF=a+2x,FD=FG+DG=x+a,DQ=CD﹣CQ=AD﹣DG=3x+a﹣a=3x,在Rt△DQF中,FQ2=FD2+DQ2,即(a+2x)2=(x+a)2+(3x)2,解得a=3x,∴CD=AD=3x+a=2a,在Rt△CDG中,CG===a,∴CG=DG.第26页(共33页)14.如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.(1)求证:EF+AC=AB;(2)点C1从点C出发,沿着线段CB向点B运动(不与点B重合),同时点A1从点A出发,沿着BA的延长线运动,点C1与A1的运动速度相同,当动点C1停止运动时,另一动点A1也随之停止运动.如图2,A1F1平分∠BA1C1,交BD于点F1,过点F1作F1E1⊥A1C1,垂足为E1,请猜想E1F1,A1C1与AB三者之间的数量关系,并证明你的猜想;(3)在(2)的条件下,当A1E1=3,C1E1=2时,求BD的长.【解答】(1)证明:如图1,过点F作FM⊥AB于点M,在正方形ABCD 中,AC⊥BD于点E.∴AE=AC,∠ABD=∠CBD=45°,∵AF平分∠BAC,∴EF=MF,又∵AF=AF,∴Rt△AMF≌Rt△AEF,∴AE=AM,∵∠MFB=∠ABF=45°,∴MF=MB,MB=EF,∴EF+AC=MB+AE=MB+AM=AB.(2)E1F1,A1C1与AB三者之间的数量关系:E1F1+A1C1=AB证明:如图2,连接F1C1,过点F1作F1P⊥A1B于点P,F1Q⊥BC于点Q,∵A1F1平分∠BA1C1,∴E1F1=PF1;同理QF1=PF1,∴E1F1=PF1=QF1,又∵A1F1=A1F1,∴Rt△A1E1F1≌Rt△A1PF1,∴A1E1=A1P,同理Rt△QF1C1≌Rt△E1F1C1,∴C1Q=C1E1,由题意:A1A=C1C,∴A1B+BC1=AB+A1A+BC﹣C1C=AB+BC=2AB,∵PB=PF1=QF1=QB,∴A1B+BC1=A1P+PB+QB+C1Q=A1P+C1Q+2E1F1,即2AB=A1E1+C1E1+2E1F1=A1C1+2E1F1,∴E1F1+A1C1=AB.(3)解:设PB=x,则QB=x,∵A1E1=3,QC1=C1E1=2,Rt△A1BC1中,A1B2+BC12=A1C12,即(3+x)2+(2+x)2=52,∴x1=1,x2=﹣6(舍去),∴PB=1,∴E1F1=1,又∵A1C1=5,由(2)的结论:E1F1+A1C1=AB,第27页(共33页)∴AB=,∴BD=.15.如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.(1)若BF=BD=,求BE的长;(2)若∠ADE=2∠BFE,求证:FH=HE+HD.【解答】(1)解:∵四边形ABCD正方形,∴∠BCD=90°,BC=CD,∴Rt△BCD中,BC2+CD2=BD2,即BC2=()2﹣(BC)2,∴BC=AB=1,∵DF⊥DE,∴∠ADE+∠EDC=90°=∠EDC+∠CDF,∴∠ADE=∠CDF,在△ADE和△CDF中,∵,∴△ADE≌△CDF(ASA),∴AE=CF=BF﹣BC=﹣1,∴BE=AB﹣AE=1﹣(﹣1)=2﹣;(2)证明:在FE上截取一段FI,使得FI=EH,∵△ADE≌△CDF,∴DE=DF,∴△DEF为等腰直角三角形,∴∠DEF=∠DFE=45°=∠DBC,∵∠DHE=∠BHF,∴∠EDH=∠BFH(三角形的内角和定理),在△DEH和△DFI中,∵,∴△DEH≌△DFI(SAS),∴DH=DI,又∵∠HDE=∠BFE,∠ADE=2∠BFE,∴∠HDE=∠BFE=∠ADE,∵∠HDE+∠ADE=45°,∴∠HDE=15°,∴∠DHI=∠DEH+∠HDE=60°,即△DHI为等边三角形,∴DH=HI,第28页(共33页)∴FH=FI+HI=HE+HD.16.如图,小明将一张直角梯形纸片沿虚线剪开,得到矩形ABCD和三角形EGF两张纸片,测得AB=5,AD=4,EF=.在进行如下操作时遇到了下面的几个问题,请你帮助解决.(1)请你求出FG的长度.(2)在(1)的条件下,小明先将三角形的边EG和矩形边AB重合,然后将△EFG沿直线BC向右平移,至F点与B重合时停止.在平移过程中,设G点平移的距离为x,两纸片重叠部分面积为.y,求在平移的整个过程中,y与x的函数关系式,并求当重叠部分面积为10时,平移距离x 的值.(3)在(2)的操作中,小明发现在平移过程中,虽然有时平移的距离不等,但两纸片重叠的面积却是相等的;而有时候平移的距离不等,两纸片重叠部分的面积也不可能相等.请探索这两种情况下重叠部分面积y的范围(直接写出结果).【解答】(1)解:∵EG=AB=5,EF=5,∠EGF=90°,在△EFG中,由勾股定理得:FG===10,答:FG的长度是10.(2)解:有两种情况:①如图1:∵矩形ABCD,∠EGF=90°,EG=AB,∴AB∥CD∥EG,∴=,即=,∴BM=5﹣x,∴y=(BM+EG)×BG=•(5﹣x+5)•x,∴y=﹣x2+5x(0≤x≤4);第29页(共33页)②如图2:与求BM的方法类似,得出=,∴CN=7﹣x,∴y=×(BM+CN)×BC=•(5﹣x+7﹣x)•4,y=﹣2x+24(4<x≤10);综合上述:y与x的关系式是y=,把y=10代入y=﹣x2+5x得:﹣x2+5x=10,解得:x1=10+2>4(舍去),x2=10﹣2;把y=10代入y=﹣2x+24得:﹣2x+24=10,解得:x=7.(3)解:当4≤y<16时,平移的距离不等,两纸片重叠的面积可能相等,0≤y<4或y=16时,平移的距离不等,两纸片重叠部分的面积也不可能相等.17.如图,将一三角板放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于Q.探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系,并写出函数自变量x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置.并求出相应的x值,如果不可能,试说明理由.【解答】解:(1)PQ=PB,(1分)过P点作MN∥BC分别交AB、DC于点M、N,在正方形ABCD中,AC为对角线,∴AM=PM,又∵AB=MN,∴MB=PN,∵∠BPQ=90°,∴∠BPM+∠NPQ=90°;又∵∠MBP+∠BPM=90°,∴∠MBP=∠NPQ,在Rt△MBP≌Rt△NPQ中,第30页(共33页)。
中考数学与平行四边形有关的压轴题附答案解析
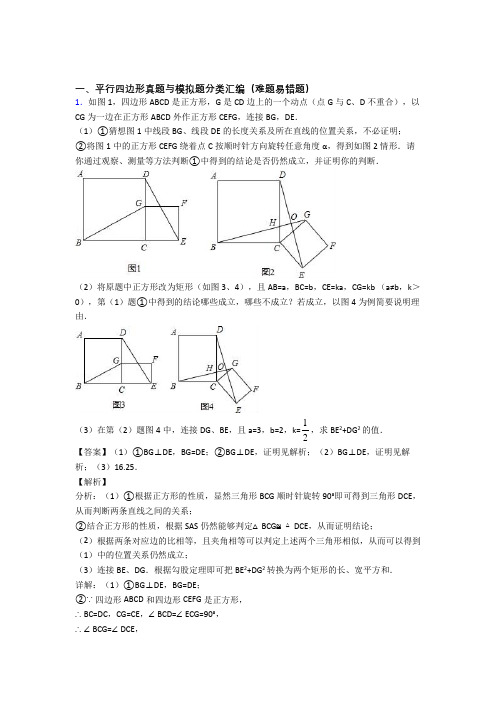
一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.(1)①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并证明你的判断.(2)将原题中正方形改为矩形(如图3、4),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图4为例简要说明理由.(3)在第(2)题图4中,连接DG、BE,且a=3,b=2,k=12,求BE2+DG2的值.【答案】(1)①BG⊥DE,BG=DE;②BG⊥DE,证明见解析;(2)BG⊥DE,证明见解析;(3)16.25.【解析】分析:(1)①根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;②结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论;(2)根据两条对应边的比相等,且夹角相等可以判定上述两个三角形相似,从而可以得到(1)中的位置关系仍然成立;(3)连接BE、DG.根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和.详解:(1)①BG⊥DE,BG=DE;②∵四边形ABCD和四边形CEFG是正方形,∴BC=DC,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,∴△BCG≌△DCE,∴BG=DE,∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(2)∵AB=a,BC=b,CE=ka,CG=kb,∴BC CG b==,DC CE a又∵∠BCG=∠DCE,∴△BCG∽△DCE,∴∠CBG=∠CDE,又∵∠CBG+∠BHC=90°,∴∠CDE+∠DHG=90°,∴BG⊥DE.(3)连接BE、DG.根据题意,得AB=3,BC=2,CE=1.5,CG=1,∵BG⊥DE,∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25.点睛:此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理.2.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.413【答案】(1)证明见解析;(2【解析】分析:(1)根据平行四边形ABCD 的性质,判定△BOE ≌△DOF (ASA ),得出四边形BEDF 的对角线互相平分,进而得出结论;(2)在Rt △ADE 中,由勾股定理得出方程,解方程求出BE ,由勾股定理求出BD ,得出OB ,再由勾股定理求出EO ,即可得出EF 的长.详解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴∠A=90°,AD=BC=4,AB ∥DC ,OB=OD ,∴∠OBE=∠ODF ,在△BOE 和△DOF 中,OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF (ASA ),∴EO=FO ,∴四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,BD ⊥EF ,设BE=x ,则 DE=x ,AE=6-x ,在Rt △ADE 中,DE 2=AD 2+AE 2,∴x 2=42+(6-x )2,解得:x=133, ∵∴OB=12∵BD ⊥EF ,∴∴EF=2EO=3. 点睛:本题主要考查了矩形的性质,菱形的性质、勾股定理、全等三角形的判定与性质,熟练掌握矩形的性质和勾股定理,证明三角形全等是解决问的关键3.在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,且∠EAF=∠CEF=45°.(1)将△ADF 绕着点A 顺时针旋转90°,得到△ABG(如图①),求证:△AEG ≌△AEF ;(2)若直线EF 与AB ,AD 的延长线分别交于点M ,N(如图②),求证:EF 2=ME 2+NF 2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF ,BE ,DF 之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF ,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题4.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.(1)证明:BE=CF.(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.【答案】(1)见解析;(2)43;(3)见解析【解析】试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.试题解析:(1)证明:连接AC,∵∠1+∠2=60°,∠3+∠2=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=∠ADC=60°∵四边形ABCD是菱形,∴AB=BC=CD=AD,∴△ABC、△ACD为等边三角形∴∠4=60°,AC=AB,∴在△ABE和△ACF中,,∴△ABE≌△ACF.(ASA)∴BE=CF.(2)解:由(1)得△ABE≌△ACF,则S△ABE=S△ACF.故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值.作AH⊥BC于H点,则BH=2,S四边形AECF=S△ABC===; (3)解:由“垂线段最短”可知,当正三角形AEF 的边AE 与BC 垂直时,边AE 最短.故△AEF 的面积会随着AE 的变化而变化,且当AE 最短时,正三角形AEF 的面积会最小,又S △CEF =S 四边形AECF ﹣S △AEF ,则△CEF 的面积就会最大.由(2)得,S △CEF =S 四边形AECF ﹣S △AEF =﹣=.点睛:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE ≌△ACF 是解题的关键.5.问题情境在四边形ABCD 中,BA =BC ,DC ⊥AC ,过点D 作DE ∥AB 交BC 的延长线于点E ,M 是边AD 的中点,连接MB ,ME.特例探究(1)如图1,当∠ABC =90°时,写出线段MB 与ME 的数量关系,位置关系;(2)如图2,当∠ABC =120°时,试探究线段MB 与ME 的数量关系,并证明你的结论; 拓展延伸(3)如图3,当∠ABC =α时,请直接用含α的式子表示线段MB 与ME 之间的数量关系.【答案】(1)MB =ME ,MB ⊥ME ;(2)ME 3.证明见解析;(3)ME =MB·tan 2 .【解析】【分析】(1)如图1中,连接CM .只要证明△MBE 是等腰直角三角形即可;(2)结论:EM=3MB .只要证明△EBM 是直角三角形,且∠MEB=30°即可; (3)结论:EM=BM•tan2 .证明方法类似;【详解】(1) 如图1中,连接CM .∵∠ACD=90°,AM=MD ,∴MC=MA=MD ,∵BA=BC ,∴BM 垂直平分AC ,∵∠ABC=90°,BA=BC ,∴∠MBE=12∠ABC=45°,∠ACB=∠DCE=45°, ∵AB ∥DE ,∴∠ABE+∠DEC=180°,∴∠DEC=90°,∴∠DCE=∠CDE=45°,∴EC=ED ,∵MC=MD ,∴EM 垂直平分线段CD ,EM 平分∠DEC ,∴∠MEC=45°,∴△BME 是等腰直角三角形,∴BM=ME ,BM ⊥EM .故答案为BM=ME ,BM ⊥EM . (2)ME =3MB .证明如下:连接CM ,如解图所示.∵DC ⊥AC ,M 是边AD 的中点,∴MC =MA =MD .∵BA =BC ,∴BM 垂直平分AC .∵∠ABC =120°,BA =BC ,∴∠MBE =12∠ABC =60°,∠BAC =∠BCA =30°,∠DCE =60°. ∵AB ∥DE ,∴∠ABE +∠DEC =180°,∴∠DEC =60°,∴∠DCE =∠DEC =60°,∴△CDE 是等边三角形,∴EC =ED .∵MC =MD ,∴EM 垂直平分CD ,EM 平分∠DEC , ∴∠MEC =12∠DEC =30°, ∴∠MBE +∠MEB =90°,即∠BME =90°.在Rt △BME 中,∵∠MEB =30°,∴ME =3MB .(3) 如图3中,结论:EM=BM•tan 2α.理由:同法可证:BM ⊥EM ,BM 平分∠ABC ,所以EM=BM•tan2α. 【点睛】本题考查四边形综合题、等腰直角三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.6.如图,抛物线y=mx 2+2mx+n 经过A (﹣3,0),C (0,﹣32)两点,与x 轴交于另一点B .(1)求经过A ,B ,C 三点的抛物线的解析式;(2)过点C 作CE ∥x 轴交抛物线于点E ,写出点E 的坐标,并求AC 、BE 的交点F 的坐标 (3)若抛物线的顶点为D ,连结DC 、DE ,四边形CDEF 是否为菱形?若是,请证明;若不是,请说明理由.【答案】(1)y=12x2+x﹣32;(2)F点坐标为(﹣1,﹣1);(3)四边形CDEF是菱形.证明见解析【解析】【分析】将A、C点的坐标代入抛物线的解析式中,通过联立方程组求得该抛物线的解析式;根据(1)题所得的抛物线的解析式,可确定抛物线的对称轴方程以及B、C点的坐标,由CE∥x轴,可知C、E关于对称轴对称。
中考数学《压轴题》专题训练含答案解析

压轴题1、已知,在平行四边形OABC 中,OA=5,AB=4,∠OCA=90°,动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动,同时动点Q 从A 点出发沿射线AB 方向以每秒1个单位的速度移动.设移动的时间为t 秒. (1)求直线AC 的解析式;(2)试求出当t 为何值时,△OAC 与△PAQ 相似; (3)若⊙P 的半径为58,⊙Q 的半径为23;当⊙P 与对角线AC 相切时,判断⊙Q 与直线AC 、BC 的位置关系,并求出Q 点坐标。
解:(1)42033y x =-+ (2)①当0≤t≤2.5时,P 在OA 上,若∠OAQ=90°时, 故此时△OAC 与△PAQ 不可能相似.当t>2.5时,①若∠APQ=90°,则△APQ ∽△OCA ,∵t>2.5,∴符合条件.②若∠AQP=90°,则△APQ ∽△∠OAC ,∵t>2.5,∴符合条件.综上可知,当时,△OAC 与△APQ 相似.(3)⊙Q 与直线AC 、BC 均相切,Q 点坐标为(109,531)。
2、如图,以矩形OABC 的顶点O 为原点,OA 所在的直线为x 轴,OC 所在的直线为y 轴,建立平面直角坐标系.已知OA =3,OC =2,点E 是AB 的中点,在OA 上取一点D ,将△BDA 沿BD 翻折,使点A 落在BC 边上的点F 处. (1)直接写出点E 、F 的坐标;(2)设顶点为F 的抛物线交y 轴正半轴...于点P ,且以点E 、F 、P 为顶点的三角形是等腰三角形,求该抛物线的解析式;(3)在x 轴、y 轴上是否分别存在点M 、N ,使得四边形MNFE 的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.解:(1)(31)E ,;(12)F ,.(2)在Rt EBF △中,90B ∠=, 2222125EF EB BF ∴=+=+=.设点P 的坐标为(0)n ,,其中0n >,顶点(12)F ,, ∴设抛物线解析式为2(1)2(0)y a x a =-+≠.①如图①,当EF PF =时,22EF PF =,221(2)5n ∴+-=.解得10n =(舍去);24n =.(04)P ∴,.24(01)2a ∴=-+.解得2a =. ∴抛物线的解析式为22(1)2y x =-+(第2题)②如图②,当EP FP =时,22EP FP =,22(2)1(1)9n n ∴-+=-+. 解得52n =-(舍去).③当EF EP =时,53EP =<,这种情况不存在. 综上所述,符合条件的抛物线解析式是22(1)2y x =-+. (3)存在点M N ,,使得四边形MNFE 的周长最小. 如图③,作点E 关于x 轴的对称点E ',作点F 关于y 轴的对称点F ',连接E F '',分别与x 轴、y 轴交于点M N ,,则点M N ,就是所求点.(31)E '∴-,,(12)F NF NF ME ME '''-==,,,.43BF BE ''∴==,.FN NM ME F N NM ME F E ''''∴++=++=22345+=.又5EF =,∴55FN NM ME EF +++=+,此时四边形MNFE 的周长最小值是553、如图,在边长为2的等边△ABC 中,A D ⊥BC,点P 为边AB 上一个动点,过P 点作PF//AC 交线段BD 于点F,作PG ⊥AB 交AD 于点E,交线段CD 于点G,设BP=x . (1)①试判断BG 与2BP 的大小关系,并说明理由;②用x 的代数式表示线段DG 的长,并写出自变量x 的取值范围;(2)记△DEF 的面积为S,求S 与x 之间的函数关系式,并求出S 的最大值;(3)以P 、E 、F 为顶点的三角形与△EDG 是否可能相似?如果能相似,请求出BP 的长,如果不能,请说明理由。
2024年中考数学压轴题型(广东专用)专题04特殊平行四边形中全等相似与最值问题(学生版)

专题04特殊平行四边形中全等相似与最值问题通用的解题思路:一、四边形与全等相似1.三角形与全等之六大全等模型:(1)一线三等角模型锐角一线三等角(2)手拉手模型(3)半角模型(4)倍长中线模型模型(6)雨伞等模型(5)平行线中等模型2.三角形与相似之四大相似模型:(1)A字模型(3)手拉手模型(2)8字模型(4)一线三等角模型B 二、四边形线段最值问题囹 1 C B D 02B (1)将军饮马模型两定一动模型一定两动模型两线段相减的最大值模型(三点共线)• B(2)费马点模型:将边以A 为顶点逆时针旋转60。
,得到AQE,连接P0则^APQ 为等边三角形,PA=PQ O1. (2023-r 东深圳•中考真题)(1)如图,在矩形ABCD 中,E 为AD 边上一点,连接BE,①若= 过C 作CFLBE 交BE 于点、F ,求证:AABE^AFCB ;②若S 矩形倔8 = 2。
时,则BECF=(2)如图,在菱形ABCD 中,cosA = |,过。
作CE1AB 交A8的延长线于点E,过E 作EF _LAD 交AD 于点、F ,若S 菱形*d =24时,求EF BC 的值.(3)如图,在平行四边形ABCD 中,匕4 = 60。
,AB = 6, AD=5,点E 在CD 上,且CE = 2,点F 为BC 上一点,连接时,过E 作EGLEF 交平行四边形ABCD 的边于点G,若EF ・EG = 70时,请直接写出AG 的长.D,E E a C C A B AB备用图2.(2022广东广州•中考真题)如图,在菱形ABCQ中,0BAD=120°,AB=6,连接8Q.⑴求BQ的长;⑵点E为线段BQ上一动点(不与点B,。
重合),点E在边AQ上,且BE二也DF,①当CE±AB时,求四边形的面积;②当四边形的面积取得最小值时,CE+右CT的值是否也最小?如果是,求CE+也CF的最小值;如果不是,请说明理由.题型一特殊平行四边形中全等相似计算1.(2024-P东汕头•一模)(1)如图1,在矩形ABCD中,E为AD边上一点,连接8E,①若BE=BC,过。
2024年中考数学二次函数压轴题专题10平行四边形的存在性问题(学生版)

专题10平行四边形的存在性问题_、知识导航考虑到求证平行四边形存在,必先了解平行四边形性质:(1) 对应边平行且相等;(2) 对角线互相平分.这是图形的性质,我们现在需要的是将其性质运用在在坐标系中:(1)对边平行且相等可转化为:x A -x B =x D - x cy A -y B = yD-y c可以理解为点B 移动到点A,点。
移动到点O,移动路径完全相同.(2)对角线互相平分转化为:\ z 乙,、2 一 2可以理解为AC 的中点也是BQ 的中点.D【小结】虽然由两个性质推得的式子并不一样,但其实可以化为统一:X A~X B =X D~ X C -y B = yD-y c + x c = + X by A + % = % + 为x A +x c ^x B +x D2 _ 2 \X A +X C=X B +X D总 + % 二 % + 北 U a + %=% + %、2 — 2当AC 和BQ 为对角线时,结果可简记为:A+C = B + D (各个点对应的横纵坐标相加)以上是对于平行四边形性质的分析,而我们要求证的是平行四边形存在性问题,此处当有一问:若坐标系 中的4个点A 、B 、。
、D 满足"A+O8+ZT,则四边形ABCQ 是否一定为平行四边形?反例如下:之所以存在反例是因为“四边形ABCQ 是平行四边形”与“AC 、BD 中点是同一个点”并不是完全等价的转化, 故存在反例.虽有反例,但并不影响运用此结论解题,另外,还需注意对对角线的讨论:(1) 四边形A8CQ 是平行四边形:AC. BQ 一定是对角线.(2) 以A 、B 、。
、。
四个点为顶点是四边形是平行四边形:对角线不确定需要分类讨论.平行四边形存在性问题通常可分为“三定一动”和“两定两动”两大类问题.1.三定一动已知A (1, 2) B (5, 3) C (3, 5),在坐标系内确定点。
使得以A 、B 、。
、。
四个点为顶点的四边形是 平行四边形.思路1:利用对角线互相平分,分类讨论:设。
中考数学与平行四边形有关的压轴题附详细答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.(1)、动手操作:如图①:将矩形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=20°,那么的度数为 .(2)、观察发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.(3)、实践与运用:将矩形纸片ABCD按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC 边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F 重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.【答案】(1)125°;(2)同意;(3)60°【解析】试题分析:(1)根据直角三角形的两个锐角互余求得∠AEB=70°,根据折叠重合的角相等,得∠BEF=∠DEF=55°,根据平行线的性质得到∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°;(2)根据第一次折叠,得∠BAD=∠CAD;根据第二次折叠,得EF垂直平分AD,根据等角的余角相等,得∠AEG=∠AFG,则△AEF是等腰三角形;(3)由题意得出:∠NMF=∠AMN=∠MNF,MF=NF,由对称性可知,MF=PF,进而得出△MNF≌△MPF,得出3∠MNF=180°求出即可.试题解析:(1)、∵在直角三角形ABE中,∠ABE=20°,∴∠AEB=70°,∴∠BED=110°,根据折叠重合的角相等,得∠BEF=∠DEF=55°.∵AD∥BC,∴∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°.;(2)、同意,如图,设AD与EF交于点G由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.由折叠知,∠AGE=∠DGE=90°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE.所以AE=AF,即△AEF为等腰三角形.(3)、由题意得出:∠NMF=∠AMN=∠MNF,∴MF=NF,由折叠可知,MF=PF,∴NF=PF,而由题意得出:MP=MN,又∵MF=MF,∴△MNF≌△MPF,∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,即3∠MNF=180°,∴∠MNF=60°.考点:1.折叠的性质;2.等边三角形的性质;3.全等三角形的判定和性质;4.等腰三角形的判定2.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由(3)若|CF﹣AE|=2,3△POF为等腰三角形时,请直接写出线段OP的长.【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP的长为62或233.【解析】【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再根据直角三角形斜边中线等于斜边一半即可得OF=OE;(2)如图2中,延长EO交CF于K,由已知证明△ABE≌△BCF,△AOE≌△COK,继而可证得△EFK是等腰直角三角形,由等腰直角三角形的性质即可得OF⊥EK,OF=OE;(3)分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】(1)如图1中,延长EO交CF于K,∵AE⊥BE,CF⊥BE,∴AE∥CK,∴∠EAO=∠KCO,∵OA=OC,∠AOE=∠COK,∴△AOE≌△COK,∴OE=OK,∵△EFK是直角三角形,∴OF=12EK=OE;(2)如图2中,延长EO交CF于K,∵∠ABC=∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,∴∠BAE=∠CBF,∵AB=BC,∴△ABE≌△BCF,∴BE=CF,AE=BF,∵△AOE≌△COK,∴AE=CK,OE=OK,∴FK=EF,∴△EFK是等腰直角三角形,∴OF⊥EK,OF=OE;(3)如图3中,点P在线段AO上,延长EO交CF于K,作PH⊥OF于H,∵|CF﹣AE|=2,EF=23,AE=CK,∴FK=2,在Rt△EFK中,tan∠FEK=3,∴∠FEK=30°,∠EKF=60°,∴EK=2FK=4,OF=12EK=2,∵△OPF是等腰三角形,观察图形可知,只有OF=FP=2,在Rt△PHF中,PH=12PF=1,HF=3,OH=2﹣3,∴OP=()2212362+-=-.如图4中,点P在线段OC上,当PO=PF时,∠POF=∠PFO=30°,∴∠BOP=90°,∴323综上所述:OP6223.【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等,综合性较强,正确添加辅助线是解题的关键.3.如图,在正方形ABCD 中,E 是边AB 上的一动点,点F 在边BC 的延长线上,且CF AE =,连接DE ,DF ,EF . FH 平分EFB ∠交BD 于点H .(1)求证:DE DF ⊥;(2)求证:DH DF =:(3)过点H 作HM EF ⊥于点M ,用等式表示线段AB ,HM 与EF 之间的数量关系,并证明.【答案】(1)详见解析;(2)详见解析;(3)22EF AB HM =-,证明详见解析.【解析】【分析】(1)根据正方形性质, CF AE =得到DE DF ⊥.(2)由AED CFD △△≌,得DE DF =.由90ABC ∠=︒,BD 平分ABC ∠, 得45DBF ∠=︒.因为FH 平分EFB ∠,所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.(3)过点H 作HN BC ⊥于点N ,由正方形ABCD 性质,得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥,,得HM HN =.因为4590HBN HNB ∠=︒∠=︒,,所以22sin 45HN BH HN HM ===︒. 由22cos 45DF EF DF DH ===︒,得22EF AB HM =-. 【详解】(1)证明:∵四边形ABCD 是正方形,∴AD CD =,90EAD BCD ADC ∠=∠=∠=︒.∴90EAD FCD ∠=∠=︒.∵CF AE =。
中考数学四边形压轴题+解析

九年级上册四边形压轴题2一.解答题(共30小题)1.(2009•临沂)数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.2.(2009•宁德)如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.3.(2009•黄石)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA 的平分线于点E,交∠BCA的外角平分线于点F.(1)探究:线段OE与OF的数量关系并加以证明;(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?4.(2009•无锡校级二模)如图,在平面直角坐标系中,点A、点C同时从点O出发,分别以每秒2个单位、1个单位的速度向x轴、y轴的正半轴方向运动,以OA、OC为边作矩形OABC.以M(4,0),N(9,0)为斜边端点作直角△PMN,点P在第一象限,且,当点A出发时,△PMN同时以每秒0.5个单位的速度沿x轴向右平移.设点A运动的时间为t秒,矩形OABC与△PMN重叠部分的面积为S.(1)求运动前点P的坐标;(2)求S与t的函数关系式,并写出自变量t的取值范围;(3)若在运动过程中,要使对角线AC上始终存在点Q,满足∠OQM=90°,请直接写出符合条件的t的值或t的取值范围.5.(2008•北京)请阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,探究PG与PC的位置关系及的值.小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题:(1)写出上面问题中线段PG与PC的位置关系及的值;(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明;(3)若图1中∠ABC=∠BEF=2α(0°<α<90°),将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出的值(用含α的式子表示).6.(2008•厦门)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE.(1)求证:四边形AFCE是菱形;(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;(3)在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.7.(2008•嘉兴)小丽参加数学兴趣小组活动,提供了下面3个有联系的问题,请你帮助解决:(1)如图1,正方形ABCD中,作AE交BC于E,DF⊥AE交AB于F,求证:AE=DF;(2)如图2,正方形ABCD中,点E,F分别在AD,BC上,点G,H分别在AB,CD上,且EF⊥GH,求的值;(3)如图3,矩形ABCD中,AB=a,BC=b,点E,F分别在AD,BC上,且EF⊥GH,求的值.8.(2008•宁夏)如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的;(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.9.(2008•昌平区二模)如图,已知△ABC的顶点B、C为定点,A为动点(不在直线BC上),B′是点B 关于直线AC的对称点,C′是点C关于直线AB的对称点,连接BC′、CB′、BB′、CC′.(1)猜想线段BC′与CB′的数量关系,并证明你的结论;(2)当点A运动到怎样的位置时,四边形BCB′C′为菱形?这样的位置有几个?请用语言对这样的位置进行描述(不用证明);(3)当点A在线段BC的垂直平分线(BC的中点及到BC的距离为的点除外上运动时,判断以点B、C、B′、C′为顶点的四边形的形状,画出相应的示意图.(不用证明)10.(2007•常德)如图1,已知四边形ABCD是菱形,G是线段CD上的任意一点时,连接BG交AC于F,过F作FH∥CD交BC于H,可以证明结论成立.(考生不必证明)(1)探究:如图2,上述条件中,若G在CD的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(2)计算:若菱形ABCD中AB=6,∠ADC=60°,G在直线CD上,且CG=16,连接BG交AC所在的直线于F,过F作FH∥CD交BC所在的直线于H,求BG与FG的长.(3)发现:通过上述过程,你发现G在直线CD上时,结论还成立吗?11.(2007•宜昌)如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.(1)判断四边形ABCE是怎样的四边形,说明理由;(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.①四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED 的面积;②当线段BP的长为何值时,△PQR与△BOC相似.12.(2007•潍坊)已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外),过P点作EF∥AB,分别交AC,BC于E,F点,作PM∥AC,交AB于M点,连接ME.(1)求证:四边形AEPM为菱形;(2)当P点在何处时,菱形AEPM的面积为四边形EFBM面积的一半?13.(2007•永州)在梯形ABCD中,AB∥CD,∠ABC=90°,AB=5,BC=10,tan∠ADC=2.(1)求DC的长;(2)E为梯形内一点,F为梯形外一点,若BF=DE,∠FBC=∠CDE,试判断△ECF的形状,并说明理由.(3)在(2)的条件下,若BE⊥EC,BE:EC=4:3,求DE的长.14.(2007•常州)已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.(1)当DG=2时,求△FCG的面积;(2)设DG=x,用含x的代数式表示△FCG的面积;(3)判断△FCG的面积能否等于1,并说明理由.15.(2007•海南)如图,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.(1)求证:△ADE≌△CDE;(2)过点C作CH⊥CE,交FG于点H,求证:FH=GH;(3)设AD=1,DF=x,试问是否存在x的值,使△ECG为等腰三角形?若存在,请求出x的值;若不存在,请说明理由.16.(2007•哈尔滨)如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD 于点F.(1)求证:EF+AC=AB;(2)点C1从点C出发,沿着线段CB向点B运动(不与点B重合),同时点A1从点A出发,沿着BA 的延长线运动,点C1与A1的运动速度相同,当动点C1停止运动时,另一动点A1也随之停止运动.如图2,A1F1平分∠BA1C1,交BD于点F1,过点F1作F1E1⊥A1C1,垂足为E1,请猜想E1F1,A1C1与AB三者之间的数量关系,并证明你的猜想;(3)在(2)的条件下,当A1E1=3,C1E1=2时,求BD的长.17.(2006•河南)如图△ABC中,∠ACB=90度,AC=2,BC=3.D是BC边上一点,直线DE⊥BC于D,交AB于点E,CF∥AB交直线DE于F.设CD=x.(1)当x取何值时,四边形EACF是菱形?请说明理由;(2)当x取何值时,四边形EACD的面积等于2?18.(2006•温州)如图,在▱ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB交BC于M,PN∥AD交DC于N.连接AM.设AP=x(1)四边形PMCN的形状有可能是菱形吗?请说明理由;(2)当x为何值时,四边形PMCN的面积与△ABM的面积相等?19.(2006•沈阳)如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.20.(2006•成都)已知:如图,在正方形ABCD中,AD=12,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平分线FP分别交AD,AE,BC于点F,H,G,交AB的延长线于点P.(1)设DE=m(0<m<12),试用含m的代数式表示的值;(2)在(1)的条件下,当时,求BP的长.21.(2006•汾阳市)如图,点E在正方形ABCD的边CD上运动,AC与BE交于点F.(1)如图1,当点E运动到DC的中点时,求△ABF与四边形ADEF的面积之比;(2)如图2,当点E运动到CE:ED=2:1时,求△ABF与四边形ADEF的面积之比;(3)当点E运动到CE:ED=3:1时,写出△ABF与四边形ADEF的面积之比;当点E运动到CE:ED=n:1(n是正整数)时,猜想△ABF与四边形ADEF的面积之比(只写结果,不要求写出计算过程);(4)请你利用上述图形,提出一个类似的问题22.(2005•资阳)阅读以下短文,然后解决下列问题:如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”,如图①所示,矩形ABEF即为△ABC的“友好矩形”,显然,当△ABC是钝角三角形时,其“友好矩形”只有一个.(1)仿照以上叙述,说明什么是一个三角形的“友好平行四边形”;(2)如图②,若△ABC为直角三角形,且∠C=90°,在图②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;(3)若△ABC是锐角三角形,且BC>AC>AB,在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.23.(2005•重庆)已知四边形ABCD中,P是对角线BD上的一点,过P作MN∥AD,EF∥CD,分别交AB、CD、AD、BC于点M、N、E、F,设a=PM•PE,b=PN•PF,解答下列问题:(1)当四边形ABCD是矩形时,见图1,请判断a与b的大小关系,并说明理由;(2)当四边形ABCD是平行四边形,且∠A为锐角时,见图2,(1)中的结论是否成立?并说明理由;(3)在(2)的条件下,设,是否存在这样的实数k,使得?若存在,请求出满足条件的所有k的值;若不存在,请说明理由.24.(2005•大连)如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG >BC),取线段AE的中点M.探究:线段MD、MF的关系,并加以证明.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.25.(2005•湖州)如图,四边形ABCD和BEFG均为正方形,则=.(结果不取近似值)26.(2005•郴州)附加题:E是四边形ABCD中AB上一点(E不与A、B重合).(1)如图,当四边形ABCD是正方形时,△ADE、△BCE和△CDE的面积之间有着怎样的关系?证明你的结论.(2)若四边形ABCD是矩形时,(1)中的结论是否仍然成立?为什么?ABCD是平行四边形呢?(3)当四边形ABCD是梯形时,(1)中的结论还成立吗?请说明理由.27.(2005•深圳校级自主招生)如图,将一三角板放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于Q.探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系,并写出函数自变量x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q的位置.并求出相应的x值,如果不可能,试说明理由.28.(2004•贵阳)如图,四边形ABCD中,AC=6,BD=8且AC⊥BD.顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2…如此进行下去得到四边形A n B n C n D n.(1)证明:四边形A1B1C1D1是矩形;(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积;(3)写出四边形A n B n C n D n的面积;(4)求四边形A5B5C5D5的周长.29.(2004•无为县)(1)如图(1),在正方形ABCD中,对角线AC、BD相交于点O,易知AC⊥BD,=;(2)如图(2),若点E是正方形ABCD的边CD的中点,即,过D作DG⊥AE,分别交AC、BC 于点F、G.求证:;(3)如图(3),若点P是正方形ABCD的边CD上的点,且(n为正整数),过点D作DN⊥AP,分别交AC、BC于点M、N,请你先猜想CM与AC的比值是多少,然后再证明你猜想的结论.30.(2004•佛山)如果正方形的一边落在三角形的一边上,其余两个顶点分别在三角形的另外两条边上,则这样的正方形叫做三角形的内接正方形.(1)如图①,在△ABC中,BC=a,BC边上的高AD=h a,EFGH是△ABC的内接正方形.设正方形EFGH 的边长是x,求证:;(2)在Rt△ABC中,AB=4,AC=3,∠BAC=90度.请在图②,图③中分别画出可能的内接正方形,并根据计算回答哪个内接正方形的面积最大;(3)在锐角△ABC中,BC=a,AC=b,AB=c,且a<b<c.请问这个三角形的内接正方形中哪个面积最大?并说明理由.九年级上册四边形压轴题2参考答案与试题解析一.解答题(共30小题)1.(2009•临沂)数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.考点:正方形的性质;全等三角形的判定与性质;角平分线的性质.专题:几何综合题;压轴题.分析:(1)在AB上取一点M,使AM=EC,连接ME,根据已知条件利用ASA判定△AME≌△ECF,因为全等三角形的对应边相等,所以AE=EF.(2)在BA的延长线上取一点N,使AN=CE,连接NE,根据已知利用ASA判定△ANE≌△ECF,因为全等三角形的对应边相等,所以AE=EF.解答:解:(1)正确.证明:在AB上取一点M,使AM=EC,连接ME.∴BM=BE,∴∠BME=45°,∴∠AME=135°,∵CF是外角平分线,∴∠DCF=45°,∴∠ECF=135°,∴∠AME=∠ECF,∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,∴△AME≌△ECF(ASA),∴AE=EF.(2)正确.证明:在BA的延长线上取一点N.使AN=CE,连接NE.∴BN=BE,∴∠N=∠NEC=45°,∵CF平分∠DCG,∴∠FCE=45°,∴∠N=∠ECF,∵四边形ABCD是正方形,∴AD∥BE,∴∠DAE=∠BEA,即∠DAE+90°=∠BEA+90°,∴∠NAE=∠CEF,∴△ANE≌△ECF(ASA),∴AE=EF.点评:此题主要考查学生对正方形的性质,角平分线的性质及全等三角形的判定方法的掌握情况.2.(2009•宁德)如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.考点:正方形的性质;全等三角形的判定与性质;矩形的性质.专题:压轴题;动点型.分析:(1)根据三角形判定方法进行证明即可.(2)作FH⊥MN于H.先证△ABE≌△EHF,得到对应边相等,从而推出△CHF是等腰直角三角形,∠FCH的度数就可以求得了.(3)本题也是通过构建直角三角形来求度数,作FH⊥MN于H,∠FCH的正切值就是FH:CH.解答:(1)证明:∵四边形ABCD和四边形AEFG是正方形,∴AB=AD,AE=AG,∠BAD=∠EAG=90°,∴∠BAE+∠EAD=∠DAG+∠EAD,∴∠BAE=∠DAG,∴△BAE≌△DAG.(2)解:∠FCN=45°,理由是:作FH⊥MN于H,∵∠AEF=∠ABE=90°,∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,∴∠FEH=∠BAE,又∵AE=EF,∠EHF=∠EBA=90°,∴△EFH≌△ABE,∴FH=BE,EH=AB=BC,∴CH=BE=FH,∵∠FHC=90°,∴∠FCN=45°.(3)解:当点E由B向C运动时,∠FCN的大小总保持不变,理由是:作FH⊥MN于H,由已知可得∠EAG=∠BAD=∠AEF=90°,结合(1)(2)得∠FEH=∠BAE=∠DAG,又∵G在射线CD上,∠GDA=∠EHF=∠EBA=90°,∴△EFH≌△GAD,△EFH∽△ABE,∴EH=AD=BC=b,∴CH=BE,∴==;在Rt△FEH中,tan∠FCN===,∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=.点评:本题考查了正方形,矩形的判定及全等三角形的判定方法等知识点的综合运用,其重点是通过证三角形全等或相似来得出线段的相等或成比例.3.(2009•黄石)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA 的平分线于点E,交∠BCA的外角平分线于点F.(1)探究:线段OE与OF的数量关系并加以证明;(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?考点:正方形的判定;平行线的性质;角平分线的性质;等腰三角形的性质;菱形的判定.专题:几何综合题;压轴题.分析:(1)利用平行线的性质由角相等得出边相等;(2)假设四边形BCFE,再证明与在同一平面内过同一点有且只有一条直线与已知直线垂直相矛盾;(3)利用平行四边形及等腰直角三角形的性质证明四边形AECF是正方形.解答:解:(1)OE=OF.证明如下:∵CE是∠ACB的平分线,∴∠1=∠2.∵MN∥BC,∴∠1=∠3.∴∠2=∠3.∴OE=OC.同理可证OC=OF.∴OE=OF.(3分)(2)四边形BCFE不可能是菱形,若四边形BCFE为菱形,则BF⊥EC,而由(1)可知FC⊥EC,在平面内过同一点F不可能有两条直线同垂直于一条直线.(3分)(3)当点O运动到AC中点时,且△ABC是直角三角形(∠ACB=90°)时,四边形AECF是正方形.理由如下:∵O为AC中点,∴OA=OC,∵由(1)知OE=OF,∴四边形AECF为平行四边形;∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,∴∠2+∠5=90°,即∠ECF=90°,∴▱AECF为矩形,又∵AC⊥EF.∴▱AECF是正方形.∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.(3分)点评:本题考查的是平行线、角平分线、正方形、平行四边形的性质与判定,涉及面较广,在解答此类题目时要注意角的运用,一般通过角判定一些三角形,多边形的形状,需同学们熟练掌握.4.(2009•无锡校级二模)如图,在平面直角坐标系中,点A、点C同时从点O出发,分别以每秒2个单位、1个单位的速度向x轴、y轴的正半轴方向运动,以OA、OC为边作矩形OABC.以M(4,0),N(9,0)为斜边端点作直角△PMN,点P在第一象限,且,当点A出发时,△PMN同时以每秒0.5个单位的速度沿x轴向右平移.设点A运动的时间为t秒,矩形OABC与△PMN重叠部分的面积为S.(1)求运动前点P的坐标;(2)求S与t的函数关系式,并写出自变量t的取值范围;(3)若在运动过程中,要使对角线AC上始终存在点Q,满足∠OQM=90°,请直接写出符合条件的t的值或t的取值范围.考点:矩形的性质;圆周角定理;切线的性质.专题:压轴题;动点型.分析:(1)过点P作PH⊥x轴于H,可求出MH的长即点P的横坐标,再根据tan∠PMN=,及勾股定理便可求出点P的坐标.(2)因为点A;点C同时从点O出发,点M(4,0),△PMN同时以每秒0.5个单位的速度沿x 轴向右平移,运动t秒后,OA=2t,OM=4+0.5t,①当0<OA≤OM,即0<2t≤时,两图形无交点;②当OM<OA≤OH,即4+0.5t<2t≤8+0.5t时,即<t≤时,矩形OABC与△PMN重叠部分的面积为S等于重叠的三角形的面积.③当OH<OA≤ON,即8+0.5t<2t≤9+0.5t,即<t≤6时,矩形OABC与△PMN重叠矩部分的面积为S等于△MNP的面积减去不重叠的三角形的面积.④当OA>ON,即2t>9+0.5t,t>6时,矩形OABC与△PMN重叠矩部分的面积为S等于△MNP的面积.(3)根据圆周角定理可知,当以OM为直径的圆与AC有公共点时,公共点即是符合条件的点Q,即可求出t的取值范围.解答:解:(1)如图,过点P作PH⊥x轴于H.∵MN=9﹣4=5,tan∠PMN=,∴PM=,PN=,∴PH=2,MH=4,NH=1.∴P(8,2).(2)运动t秒后,OA=2t,OC=t,OM=4﹣0.5t.当0<t≤时,S=0;当<t≤时,S=t2﹣3t+4;当<t≤6时,S=﹣t2+27t﹣76;当t>6时,S=5.(3)当以OM为直径的圆与AC有公共点时,公共点即是符合条件的点Q.当以OM为直径的圆与AC相切时,t=,∴t的取值范围是:0<t≤.点评:此题是典型的动点问题,比较复杂,考查了同学们对圆及三角形,矩形,等相关知识的掌握情况,有一定的难度.5.(2008•北京)请阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,探究PG与PC的位置关系及的值.小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题:(1)写出上面问题中线段PG与PC的位置关系及的值;(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明;(3)若图1中∠ABC=∠BEF=2α(0°<α<90°),将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出的值(用含α的式子表示).考点:菱形的性质;全等三角形的判定与性质;锐角三角函数的定义.专题:压轴题.分析:(1)根据题意可知小聪的思路为,通过判定三角形DHP和PGF为全等三角形来得出证明三角形HCG为等腰三角形且P为底边中点的条件;(2)思路同上,延长GP交AD于点H,连接CH,CG,本题中除了如(1)中证明△GFP≌△HDP (得到P是HG中点)外还需证明△HDC≌△GBC(得出三角形CHG是等腰三角形).(3)∠ABC=∠BEF=2α(0°<α<90°),那么∠PCG=90°﹣α,由(1)可知:PG:PC=tan(90°﹣α).解答:解:(1)∵CD∥GF,∠PDH=∠PFG,∠DHP=∠PGF,DP=PF,∴△DPH≌△FGP,∴PH=PG,DH=GF,∵CD=BC,GF=GB=DH,∴CH=CG,∴CP⊥HG,∠ABC=60°,∴∠DCG=120°,∴∠PCG=60°,∴PG:PC=tan60°=,∴线段PG与PC的位置关系是PG⊥PC,=;(2)猜想:(1)中的结论没有发生变化.证明:如图2,延长GP交AD于点H,连接CH,∵P是线段DF的中点,∴FP=DP,∵AD∥GF,∴∠HDP=∠GFP,∵∠GPF=∠HPD,∴△GFP≌△HDP(ASA),∴GP=HP,GF=HD,∵四边形ABCD是菱形,∴CD=CB,∠HDC=∠ABC=60°,∵∠ABC=∠BEF=60°,菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,∴∠GBF=60°,∴∠HDC=∠GBF,∵四边形BEFG是菱形,∴GF=GB,∴HD=GB,∴△HDC≌△GBC,∴CH=CG,∠HCD=∠GCB∴PG⊥PC(到线段两端点距离相等的点在线段的垂直平分线上)∵∠ABC=60°∴∠DCB=∠HCD+∠HCB=120°∵∠HCG=∠HCB+∠GCB∴∠HCG=120°∴∠GCP=60°∴=tan∠GCP=tan60°=;(3)∵∠ABC=∠BEF=2α(0°<α<90°),∴∠PCG=90°﹣α,由(1)可知:PG:PC=tan(90°﹣α),∴=tan(90°﹣α).点评:本题是一道探究性的几何综合题,主要考查菱形的性质,全等三角形的判定及三角函数的综合运用.6.(2008•厦门)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE.(1)求证:四边形AFCE是菱形;(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;(3)在线段AC上是否存在一点P,使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.考点:菱形的判定;勾股定理;矩形的性质;相似三角形的判定与性质.专题:压轴题;开放型;存在型.分析:(1)因为是对折所以AO=CO,利用三角形全等证明EO=FO,四边形便是菱形;(2)因为面积是24,也就是AB、BF的积可以求出,所以求周长只要求出AB、BF的和就可以,而结合勾股定理它们和的平方减去乘积二倍就是AF的平方;(3)因为AC=AO所以可以从与△AOE相似的角度考虑,即过E作EP⊥AD.解答:(1)证明:连接EF交AC于O,当顶点A与C重合时,折痕EF垂直平分AC,∴OA=OC,∠AOE=∠COF=90°(1分)∵在矩形ABCD中,AD∥BC,∴∠EAO=∠FCO,∴△AOE≌△COF(ASA).∴OE=OF(2分)∴四边形AFCE是菱形.(3分)(2)解:四边形AFCE是菱形,∴AF=AE=10.设AB=x,BF=y,∵∠B=90,∴(x+y)2﹣2xy=100①又∵S△ABF=24,∴xy=24,则xy=48.②(5分)由①、②得:(x+y)2=196(6分)∴x+y=14,x+y=﹣14(不合题意舍去)∴△ABF的周长为x+y+AF=14+10=24.(7分)(3)解:过E作EP⊥AD交AC于P,则P就是所求的点.(9分)证明:由作法,∠AEP=90°,由(1)得:∠AOE=90°,又∠EAO=∠EAP,∴△AOE∽△AEP,∴=,则AE2=AO•AP(10分)∵四边形AFCE是菱形,∴AO=AC,AE2=AC•AP(11分)∴2AE2=AC•AP(12分)即P的位置是:过E作EP⊥AD交AC于P.点评:本题主要考查(1)菱形的判定方法“对角线互相垂直且平分的四边形”,(2)相似三角形的判定和性质.7.(2008•嘉兴)小丽参加数学兴趣小组活动,提供了下面3个有联系的问题,请你帮助解决:(1)如图1,正方形ABCD中,作AE交BC于E,DF⊥AE交AB于F,求证:AE=DF;(2)如图2,正方形ABCD中,点E,F分别在AD,BC上,点G,H分别在AB,CD上,且EF⊥GH,求的值;(3)如图3,矩形ABCD中,AB=a,BC=b,点E,F分别在AD,BC上,且EF⊥GH,求的值.考点:矩形的性质;全等三角形的判定与性质;正方形的性质;相似三角形的判定与性质.专题:几何综合题;压轴题.分析:(1)证明AE=DF,只要证明三角形ABE和DAF全等即可.它们同有一个直角,且AB=AD,又因为∠AEB=90°﹣∠BAE=∠AFD,这样就构成了全等三角形判定中的AAS,两三角形就全等了;(2)可通过构建与已知条件相关的三角形来求解.作AM∥EF交BC于M,作DN∥GH交AB 于N,那么AM=EF,DN=GH,(1)中我们已证得△ABM、△DAN全等,那么AM=DN,即EF=GH,它们的比例也就求出来了;(3)做法同(2)也是通过构建三角形来求解.作AM∥EF交BC于M,作DN∥GH交AB于N,只不过证明三角形全等改为了证明其相似.解题思路和步骤是一样的.解答:(1)证明:∵DF⊥AE∴∠AEB=90°﹣∠BAE=∠AFD又∵AB=AD,∠ABE=∠DAF=90°∴△ABE≌△DAF,∴AE=DF;(2)解:作AM∥EF交BC于M作DN∥GH交AB于N则AM=EF,DN=GH由(1)知,AM=DN∴EF=GH,即(3)解:作AM∥EF交BC于M作DN∥GH交AB于N则AM=EF,DN=GH∵EF⊥GH∴AM⊥DN∴∠AMB=90°﹣∠BAM=∠AND又∵∠ABM=∠DAN=90°∴△ABM∽△DAN∴∴.点评:本题中(1)(2)和(3)虽然所求不一样,但是解题思路和步骤是一样的,都是通过构建与已知和所求的条件相关的三角形,然后证明其全等或相似来得出线段间的相等或比例关系.8.(2008•宁夏)如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC 于点Q.(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;。
中考数学平行四边形-经典压轴题附详细答案

(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
【答案】见解析
【解析】
试题分析:探究:由四边形ABCD、四边形CEFG均为菱形,利用SAS易证得△BCE≌△DCG,则可得BE=DG;
应用:由AD∥BC,BE=DG,可得S△ABE+S△CDE=S△BEC=S△CDG=8,又由AE=3ED,可求得△CDE的面积,继而求得答案.
试题解析:
探究:∵四边形ABCD、四边形CEFG均为菱形,
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
【答案】(1)见解析;(2) ;(3)见解析
【解析】
试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;
∵∠CBN+∠ABN=90°,
∴∠ABN+∠BAM=90°,
∴∠APB=90°,
∴AM⊥BN.
(2)如图②中,以AB为斜边向外作等腰直角三角形△AEB,∠AEB=90°,作EF⊥PA于E,作EG⊥PB于G,连接EP.
∵∠EFP=∠FPG=∠G=90°,
∴四边形EFPG是矩形,
∴∠FEG=∠AEB=90°,
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
中考数学压轴题之平行四边形(中考题型整理,突破提升)含答案解析

考点:1.正方形的性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.旋转的性 质.
3.如图,△ ABC 中,AD 是边 BC 上的中线,过点 A 作 AE∥ BC,过点 D 作 DE∥ AB,DE 与 AC、AE 分别交于点 O、点 E,连接 EC. (1)求证:AD=EC;
(2)当∠ BAC=Rt∠ 时,求证:四边形 ADCE 是菱形.
【答案】(1)见解析; (2)见解析. 【解析】 【分析】 (1)先证四边形 ABDE 是平行四边形,再证四边形 ADCE 是平行四边形即可; (2)由∠ BAC=90°,AD 是边 BC 上的中线,得 AD=BD=CD,即可证明. 【详解】 (1)证明:∵ AE∥ BC,DE∥ AB , ∴ 四边形 ABDE 是平行四边形, ∴ AE=BD, ∵ AD 是边 BC 上的中线, ∴ BD=DC, ∴ AE=DC, 又∵ AE∥ BC, ∴ 四边形 ADCE 是平行四边形. (2) 证明:∵ ∠ BAC=90°,AD 是边 BC 上的中线. ∴ AD=CD ∵ 四边形 ADCE 是平行四边形, ∴ 四边形 ADCE 是菱形. 【点睛】 本题考查了平行四边形的判定、菱形的判定、直角三角形斜边中线定理.根据图形与已知条 件灵活应用平行四边形的判定方法是证明的关键.
初二平行四边形所有知识点总结和常考题提高难题压轴题练习(含答案解析)

A C BD 初二平行四边形所有知识点总结和常考题知识点:1、平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
2、平行四边形的性质:⑴平行四边形的对边相等;⑵平行四边形的对角相等:⑶平行四边形的对角线互相平分。
3平行四边形的判定:⑴.两组对边分别相等的四边形是平行四边形; ⑵对角线互相平分的四边形是平行四边形;⑶两组对角分别相等的四边形是平行四边形; ⑷一组对边平行且相等的四边形是平行四边形。
4、矩形的定义:有一个角是直角的平行四边形。
5、矩形的性质:⑴矩形的四个角都是直角;⑵矩形的对角线相等。
6、矩形判定定理:⑴ 有三个角是直角的四边形是矩形;⑵对角线相等的平行四边形是矩形。
7、中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
直角三角形斜边上的中线等于斜边的一半。
(连接三角形两边中点的线段叫做三角形的中位线。
)8、菱形的定义 :有一组邻边相等的平行四边形。
9、菱形的性质:⑴菱形的四条边都相等;⑵菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
S 菱形=1/2×ab (a 、b 为两条对角线长)10、菱形的判定定理:⑴四条边相等的四边形是菱形。
⑵对角线互相垂直的平行四边形是菱形。
11、正方形定义:一个角是直角的菱形或邻边相等的矩形。
12正方形判定定理:⑴ 邻边相等的矩形是正方形。
⑵有一个角是直角的菱形是正方形。
(矩形+菱形=正方形)常考题:一.选择题(共14小题)1.矩形具有而菱形不具有的性质是( )A .两组对边分别平行B .对角线相等C .对角线互相平分D .两组对角分别相等2.平行四边形ABCD 中,AC 、BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( )A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD3.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形4.顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形5.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)6.如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.117.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.168.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°9.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.1010.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.1711.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.812.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.1913.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF ⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣414.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°二.填空题(共13小题)15.已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为cm2.16.如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于.17.如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO 的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米.18.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD 和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为.19.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是.20.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于度.21.如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是.22.如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF⊥CD于F,∠B=60°,则菱形的面积为.23.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是.24.如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C (0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为.25.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标.26.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.27.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.三.解答题(共13小题)28.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.29.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.30.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.31.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:BE=CF.32.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.33.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.34.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?35.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.36.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:(1)△AEH≌△CGF;(2)四边形EFGH是菱形.37.如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.(1)求证:△ABD≌△EBD;(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.38.如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:△BCP≌△DCP;(2)求证:∠DPE=∠ABC;(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE=度.39.在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.40.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.初二平行四边形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共14小题)1.(2013•宜宾)矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分 D.两组对角分别相等【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.2.(2014•河池)平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD【分析】根据对角线相等的平行四边形是矩形判断.【解答】解:A、是邻边相等,可得到平行四边形ABCD是菱形,故不正确;B、是对角线相等,可推出平行四边形ABCD是矩形,故正确;C、是对角线互相垂直,可得到平行四边形ABCD是菱形,故不正确;D、无法判断.故选B.【点评】本题主要考查的是矩形的判定定理.但需要注意的是本题的知识点是关于各个图形的性质以及判定.3.(2008•扬州)如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;C、有一个角是直角的平行四边形是矩形,故C选项正确;D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;综上所述,符合题意是D选项;故选:D.【点评】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.4.(2011•张家界)顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形【分析】顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形.【解答】解:连接BD,已知任意四边形ABCD,E、F、G、H分别是各边中点.∵在△ABD中,E、H是AB、AD中点,∴EH∥BD,EH=BD.∵在△BCD中,G、F是DC、BC中点,∴GF∥BD,GF=BD,∴EH=GF,EH∥GF,∴四边形EFGH为平行四边形.故选:A.【点评】本题三角形的中位线的性质考查了平行四边形的判定:三角形的中位线平行于第三边,且等于第三边的一半.5.(2006•南京)在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)【分析】因为D点坐标为(2,3),由平行四边形的性质,可知C点的纵坐标一定是3,又由D点相对于A点横坐标移动了2,故可得C点横坐标为2+5=7,即顶点C的坐标(7,3).【解答】解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),∵AB在x轴上,∴点C与点D的纵坐标相等,都为3,又∵D点相对于A点横坐标移动了2﹣0=2,∴C点横坐标为2+5=7,∴即顶点C的坐标(7,3).故选:C.【点评】本题主要是对平行四边形的性质与点的坐标的表示及平行线的性质和互为余(补)角的等知识的直接考查.同时考查了数形结合思想,题目的条件既有数又有形,解决问题的方法也要既依托数也依托形,体现了数形的紧密结合,但本题对学生能力的要求并不高.6.(2014•河南)如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.11【分析】利用平行四边形的性质和勾股定理易求BO的长,进而可求出BD的长.【解答】解:∵▱ABCD的对角线AC与BD相交于点O,∴BO=DO,AO=CO,∵AB⊥AC,AB=4,AC=6,∴BO==5,∴BD=2BO=10,故选:C.【点评】本题考查了平行四边形的性质以及勾股定理的运用,是中考常见题型,比较简单.7.(2013•南充)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.16【分析】在矩形ABCD中根据AD∥BC得出∠DEF=∠EFB=60°,由于把矩形ABCD 沿EF翻折点B恰好落在AD边的B′处,所以∠EFB=∠DEF=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中可知∠DEF=∠EFB=∠EB′F=60°故△EFB′是等边三角形,由此可得出∠A′B′E=90°﹣60°=30°,根据直角三角形的性质得出A′B′=AB=2,然后根据矩形的面积公式列式计算即可得解.【解答】解:在矩形ABCD中,∵AD∥BC,∴∠DEF=∠EFB=60°,∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,∴∠DEF=∠EFB=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中,∵∠DEF=∠EFB=∠EB′F=60°∴△EFB′是等边三角形,Rt△A′EB′中,∵∠A′B′E=90°﹣60°=30°,∴B′E=2A′E,而A′E=2,∴B′E=4,∴A′B′=2,即AB=2,∵AE=2,DE=6,∴AD=AE+DE=2+6=8,∴矩形ABCD的面积=AB•AD=2×8=16.故选D.【点评】本题考查了矩形的性质,翻折变换的性质,两直线平行,同旁内角互补,两直线平行,内错角相等的性质,解直角三角形,作辅助线构造直角三角形并熟记性质是解题的关键.8.(2013•扬州)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°【分析】连接BF,根据菱形的对角线平分一组对角求出∠BAC,∠BCF=∠DCF,四条边都相等可得BC=DC,再根据菱形的邻角互补求出∠ABC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,根据等边对等角求出∠ABF=∠BAC,从而求出∠CBF,再利用“边角边”证明△BCF和△DCF全等,根据全等三角形对应角相等可得∠CDF=∠CBF.【解答】解:如图,连接BF,在菱形ABCD中,∠BAC=∠BAD=×80°=40°,∠BCF=∠DCF,BC=DC,∠ABC=180°﹣∠BAD=180°﹣80°=100°,∵EF是线段AB的垂直平分线,∴AF=BF,∠ABF=∠BAC=40°,∴∠CBF=∠ABC﹣∠ABF=100°﹣40°=60°,∵在△BCF和△DCF中,,∴△BCF≌△DCF(SAS),∴∠CDF=∠CBF=60°.故选:B.【点评】本题考查了菱形的性质,全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,综合性强,但难度不大,熟记各性质是解题的关键.9.(2015•河南)如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC 于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.10【分析】由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.【解答】解:连结EF,AE与BF交于点O,如图,∵AB=AF,AO平分∠BAD,∴AO⊥BF,BO=FO=BF=3,∵四边形ABCD为平行四边形,∴AF∥BE,∴∠1=∠3,∴∠2=∠3,∴AB=EB,而BO⊥AE,∴AO=OE,在Rt△AOB中,AO===4,∴AE=2AO=8.故选C.【点评】本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.10.(2013•凉山州)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.17【分析】根据菱形得出AB=BC,得出等边三角形ABC,求出AC,长,根据正方形的性质得出AF=EF=EC=AC=4,求出即可.【解答】解:∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=4,∴正方形ACEF的周长是AC+CE+EF+AF=4×4=16,故选C.【点评】本题考查了菱形性质,正方形性质,等边三角形的性质和判定的应用,关键是求出AC的长.11.(2013•泰安)如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC 的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.8【分析】由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF 为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD 与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF 与三角形ECF全等,得出AF=EF,即可求出AE的长.【解答】解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,∵平行四边形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4.故选:B【点评】此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.12.(2013•菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.19【分析】由图可得,S1的边长为3,由AC=BC,BC=CE=CD,可得AC=2CD,CD=2,EC=;然后,分别算出S1、S2的面积,即可解答.【解答】解:如图,设正方形S2的边长为x,根据等腰直角三角形的性质知,AC=x,x=CD,∴AC=2CD,CD==2,∴EC2=22+22,即EC=;∴S2的面积为EC2==8;∵S1的边长为3,S1的面积为3×3=9,∴S1+S2=8+9=17.故选:B.【点评】本题考查了正方形的性质和等腰直角三角形的性质,考查了学生的读图能力.13.(2013•连云港)如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣4【分析】根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE 的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的倍计算即可得解.【解答】解:在正方形ABCD中,∠ABD=∠ADB=45°,∵∠BAE=22.5°,∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,∴∠DAE=∠AED,∴AD=DE=4,∵正方形的边长为4,∴BD=4,∴BE=BD﹣DE=4﹣4,∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF=BE=×(4﹣4)=4﹣2.故选:C.【点评】本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等角对等边的性质,正方形的对角线与边长的关系,等腰直角三角形的判定与性质,根据角的度数的相等求出相等的角,再求出DE=AD是解题的关键,也是本题的难点.14.(2014•福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE 相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.【解答】解:∵四边形ABCD是正方形,∴AB=AD,又∵△ADE是等边三角形,∴AE=AD=DE,∠DAE=60°,∴AB=AE,∴∠ABE=∠AEB,∠BAE=90°+60°=150°,∴∠ABE=(180°﹣150°)÷2=15°,又∵∠BAC=45°,∴∠BFC=45°+15°=60°.故选:C.【点评】本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°.二.填空题(共13小题)15.(2008•恩施州)已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为24cm2.【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.【解答】解:由已知得,菱形的面积等于两对角线乘积的一半即:6×8÷2=24cm2.故答案为:24.【点评】此题主要考查菱形的面积等于两条对角线的积的一半.16.(2015•梅州)如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD 的周长等于20.【分析】根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得结果.【解答】解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AB=CD,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE,∴AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴▱ABCD的周长=4+4+6+6=20,故答案为:20.【点评】本题考查了平行四边形的性质,解答本题的关键是根据平行线的性质和角平分线的性质得出∠ABE=∠AEB.17.(2013•厦门)如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=3厘米.【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF 是△OAB的中位线即可得出EF的长度.【解答】解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AC+BD=24厘米,∴OA+OB=12cm,∵△OAB的周长是18厘米,∴AB=6cm,∵点E,F分别是线段AO,BO的中点,∴EF是△OAB的中位线,∴EF=AB=3cm.故答案为:3.【点评】本题考查了三角形的中位线定理,解答本题需要用到:平行四边形的对角线互相平分,三角形中位线的判定定理及性质.18.(2007•临夏州)如图,矩形ABCD的对角线AC和BD相交于点O,过点O 的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为3.【分析】根据矩形是中心对称图形寻找思路:△AOE≌△COF,图中阴影部分的面积就是△BCD的面积.【解答】解:∵四边形ABCD是矩形,∴OA=OC,∠AEO=∠CFO;又∵∠AOE=∠COF,在△AOE和△COF中,,∴△AOE≌△COF,∴S△AOE =S△COF,∴图中阴影部分的面积就是△BCD的面积.S△BCD=BC×CD=×2×3=3.故答案为:3.【点评】此题主要考查了矩形的性质以及全等三角形的判定和性质,能够根据三角形全等,从而将阴影部分的面积转化为矩形面积的一半,是解决问题的关键.19.(2014•宿迁)如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B 的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是(5,4).【分析】利用菱形的性质以及勾股定理得出DO的长,进而求出C点坐标.【解答】解:∵菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D 在y轴上,∴AB=5,∴DO=4,∴点C的坐标是:(5,4).故答案为:(5,4).【点评】此题主要考查了菱形的性质以及坐标与图形的性质,得出DO的长是解题关键.20.(2015•黄冈)如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.【分析】根据正方形的性质得出∠BAE=∠DAE,再利用SAS证明△ABE与△ADE 全等,再利用三角形的内角和解答即可.【解答】解:∵正方形ABCD,∴AB=AD,∠BAE=∠DAE,在△ABE与△ADE中,,∴△ABE≌△ADE(SAS),∴∠AEB=∠AED,∠ABE=∠ADE,∵∠CBF=20°,∴∠ABE=70°,∴∠AED=∠AEB=180°﹣45°﹣70°=65°,故答案为:65【点评】此题考查正方形的性质,关键是根据正方形的性质得出∠BAE=∠DAE,再利用全等三角形的判定和性质解答.21.(2013•十堰)如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是1.【分析】根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,根据直角三角形性质求出CE长,即可求出AB的长.【解答】解:∵四边形ABCD是平行四边形,∴AB∥DC,AB=CD,∵AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE=CD,即D为CE中点,∵EF⊥BC,∴∠EFC=90°,∵AB∥CD,∴∠DCF=∠ABC=60°,∴∠CEF=30°,∵EF=,∴CE==2,∴AB=1,故答案为:1.【点评】本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.22.(2013•黔西南州)如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF ⊥CD于F,∠B=60°,则菱形的面积为.【分析】根据已知条件解直角三角形ABE可求出AE的长,再由菱形的面积等于底×高计算即可.【解答】解:∵菱形ABCD的边长为4,∴AB=BC=4,∵AE⊥BC于E,∠B=60°,∴sinB==,∴AE=2,∴菱形的面积=4×2=8,故答案为8.【点评】本题考查了菱形的性质:四边相等以及特殊角的三角函数值和菱形面积公式的运用.23.(2013•鞍山)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是11.【分析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解.【解答】解:∵BD⊥CD,BD=4,CD=3,∴BC===5,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=AD,EF=GH=BC,∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,又∵AD=6,∴四边形EFGH的周长=6+5=11.故答案为:11.【点评】本题考查了三角形的中位线定理,勾股定理的应用,熟记三角形的中位线平行于第三边并且等于第三边的一半是解题的关键.24.(2015•攀枝花)如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).【分析】由矩形的性质得出∠OCB=90°,OC=4,BC=OA=10,求出OD=AD=5,分情况讨论:①当PO=PD时;②当OP=OD时;③当DP=DO时;根据线段垂直平分线的性质或勾股定理即可求出点P的坐标.【解答】解:∵四边形OABC是矩形,∴∠OCB=90°,OC=4,BC=OA=10,∵D为OA的中点,∴OD=AD=5,①当PO=PD时,点P在OD得垂直平分线上,∴点P的坐标为:(2.5,4);②当OP=OD时,如图1所示:则OP=OD=5,PC==3,∴点P的坐标为:(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,DE==3;分两种情况:当E在D的左侧时,如图2所示:OE=5﹣3=2,∴点P的坐标为:(2,4);当E在D的右侧时,如图3所示:OE=5+3=8,∴点P的坐标为:(8,4);综上所述:点P的坐标为:(2.5,4),或(3,4),或(2,4),或(8,4);故答案为:(2.5,4),或(3,4),或(2,4),或(8,4).【点评】本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;本题有一定难度,需要进行分类讨论才能得出结果.25.(2013•阜新)如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D 的坐标(3,2),(﹣5,2),(1,﹣2).【分析】首先根据题意画出图形,分别以BC,AB,AC为对角线作平行四边形,即可求得答案.【解答】解:如图:以A,B,C为顶点的平行四边形的第四个顶点D的坐标分别为:(3,2),(﹣5,2),(1,﹣2).故答案为:(3,2),(﹣5,2),(1,﹣2).【点评】此题考查了平行四边形的性质.注意坐标与图形的关系.26.(2014•丹东)如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.【分析】延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF 是等边三角形,再利用菱形的边长为4求出时间t的值.。
中考数学复习---特殊平行四边形综合压轴题练习(含作案解析)

中考数学复习---特殊平行四边形综合压轴题练习(含作案解析)一.平行四边形的性质1.(2022•日照)如图,在平面直角坐标系中,平行四边形OABC的顶点O在坐标原点,点E是对角线AC上一动点(不包含端点),过点E作EF∥BC,交AB于F,点P在线段EF上.若OA=4,OC=2,∠AOC=45°,EP=3PF,P点的横坐标为m,则m的取值范围是()A.4<m<3+B.3﹣<m<4C.2﹣<m<3D.4<m<4+【答案】A【解答】解:可得C(,),A(4,0),B(4+,),∴直线AB的解析式为:y=x﹣4,∴x=y+4,直线AC的解析式为:y=﹣,∴x=4+y﹣2y,∴点F的横坐标为:y+4,点E的横坐标为:4+y﹣2y,∴EF=(y+4)﹣(4+y﹣2y)=2,∵EP=3PF,∴PF=EF=y,∴点P的横坐标为:y+4﹣y,∵0<y<,∴4<y+4﹣y<3+,故答案为:A.2.(2022•无锡)如图,在▱ABCD中,AD=BD,∠ADC=105°,点E在AD 上,∠EBA=60°,则的值是()A.B.C.D.【答案】D【解答】解:如图,过点B作BH⊥AD于H,设∠ADB=x,∵四边形ABCD是平行四边形,∴BC∥AD,∠ADC=∠ABC=105°,∴∠CBD=∠ADB=x,∵AD=BD,∴∠DBA=∠DAB=,∴x+=105°,∴x=30°,∴∠ADB=30°,∠DAB=75°,∵BH⊥AD,∴BD=2BH,DH=BH,∵∠EBA=60°,∠DAB=75°,∴∠AEB=45°,∴∠AEB=∠EBH=45°,∴EH=BH,∴DE=BH﹣BH=(﹣1)BH,∵AB===(﹣)BH=CD,∴=,故选:D.二.矩形的性质3.(2022•泰安)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为()A.B.C.﹣D.﹣2【答案】D【解答】解:如图,取AD的中点O,连接OB,OM.∵四边形ABCD是矩形,∴∠BAD=90°,AD=BC=4,∴∠BAP+∠DAM=90°,∵∠ADM=∠BAP,∴∠ADM+∠DAM=90°,∴∠AMD=90°,∵AO=OD=2,∴OM=AD=2,∴点M在以O为圆心,2为半径的⊙O上,∵OB===,∴BM≥OB﹣OM=﹣2,∴BM的最小值为﹣2.故选:D.4.(2022•丽水)如图,标号为①,②,③,④的矩形不重叠地围成矩形PQMN.已知①和②能够重合,③和④能够重合,这四个矩形的面积都是5.AE=a,DE=b,且a>b.(1)若a,b是整数,则PQ的长是;(2)若代数式a2﹣2ab﹣b2的值为零,则的值是.【答案】a﹣b;3+2.【解答】解:(1)由图可知:PQ=a﹣b,故答案为:a﹣b;(2)∵a2﹣2ab﹣b2=0,∴a2﹣b2=2ab,(a﹣b)2=2b2,∴a=b+b(负值舍),∵四个矩形的面积都是5.AE=a,DE=b,∴EP=,EN=,则======3+2.故答案为:3+2.5.(2022•宿迁)如图,在矩形ABCD中,AB=6,BC=8,点M、N分别是边AD、BC的中点,某一时刻,动点E从点M出发,沿MA方向以每秒2个单位长度的速度向点A匀速运动;同时,动点F从点N出发,沿NC方向以每秒1个单位长度的速度向点C匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接EF,过点B作EF的垂线,垂足为H.在这一运动过程中,点H所经过的路径长是.【答案】π【解答】解:如图1中,连接MN交EF于点P,连接BP.∵四边形ABCD是矩形,AM=MD,BN=CN,∴四边形ABNM是矩形,∴MN=AB=6,∵EM∥NF,∴△EPM∽△FPN,∴===2,∴PN=2,PM=4,∵BN=4,∴BP===2,∵BH⊥EF,∴∠BHP=90°,∴点H在BP为直径的⊙O上运动,当点E与A重合时,如图2中,连接OH,ON.点H的运动轨迹是.此时AM=4,NF=2,∴BF=AB=6,∵∠ABF=90°,BH⊥AF,∴BH平分∠ABF,∴∠HBN=45°,∴∠HON=2∠HBN=90°,∴点H的运动轨迹的长==π.故答案为:π.6.(2022•西宁)矩形ABCD中,AB=8,AD=7,点E在AB边上,AE=5.若点P是矩形ABCD边上一点,且与点A,E构成以AE为腰的等腰三角形,则等腰三角形AEP的底边长是.【答案】5或4【解答】解:如图所示,①当AP=AE=5时,∵∠BAD=90°,∴△AEP是等腰直角三角形,∴底边PE=AE=5;②当P1E=AE=5时,∵BE=AB﹣AE=8﹣5=3,∠B=90°,∴P1B=,∴底边AP1=;综上所述:等腰三角形AEP1的底边长为5或4;故答案为:5或4.三.正方形的性质和判定7.(2022•泸州)如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为()A.B.C.D.1【答案】B【解答】解:作FH⊥BG交于点H,作FK⊥BC于点K,∵BF平分∠CBG,∠KBH=90°,∴四边形BHFK是正方形,∵DE⊥EF,∠EHF=90°,∴∠DEA+∠FEH=90°,∠EFH+∠FEH=90°,∴∠DEA=∠EFH,∵∠A=∠EHF=90°,∴△DAE∽△EHF,∴,∵正方形ABCD的边长为3,BE=2AE,∴AE=1,BE=2,设FH=a,则BH=a,∴,解得a=1;∵FK⊥CB,DC⊥CB,∴△DCN∽△FKN,∴,∵BC=3,BK=1,∴CK=2,设CN=b,则NK=2﹣b,∴,解得b=,即CN=,∵∠A=∠EBM,∠AED=∠BME,∴△ADE∽△BEM,∴,∴,解得BM=,∴MN=BC﹣CN﹣BM=3﹣﹣=,故选:B.8.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为()A.B.2C.2D.4【答案】C【解答】解:如图,连接AE,∵四边形DEFG是正方形,∴∠EDG=90°,EF=DE=DG,∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴AE=CG,∴d1+d2+d3=EF+CF+AE,∴点A,E,F,C在同一条线上时,EF+CF+AE最小,即d1+d2+d3最小,连接AC,∴d1+d2+d3最小值为AC,在Rt△ABC中,AC=AB=2,∴d1+d2+d3最小=AC=2,故选:C.9.(2022•广西)如图,在正方形ABCD中,AB=4,对角线AC,BD相交于点O.点E是对角线AC上一点,连接BE,过点E作EF⊥BE,分别交CD,BD于点F,G,连接BF,交AC于点H,将△EFH沿EF翻折,点H的对应点H′恰好落在BD上,得到△EFH′.若点F为CD的中点,则△EGH′的周长是.【答案】5+【解答】解:如图,过点E作EM⊥BC于M,作EN⊥CD于N,过点F作FP⊥AC于P,连接GH,∵将△EFH沿EF翻折得到△EFH′,∴△EGH'≌△EGH,∵四边形ABCD是正方形,∴AB=CD=BC=4,∠BCD=90°,∠ACD=∠ACB=45°,∴BD=BC=8,△CPF是等腰直角三角形,∵F是CD的中点,∴CF=CD=2,∴CP=PF=2,OB=BD=4,∵∠ACD=∠ACB,EM⊥BC,EN⊥CD,∴EM=EN,∠EMC=∠ENC=∠BCD=90°,∴∠MEN=90°,∵EF⊥BE,∴∠BEF=90°,∴∠BEM=∠FEN,∵∠BME=∠FNE,∴△BME≌△FNE(ASA),∴EB=EF,∵∠BEO+∠PEF=∠PEF+∠EFP=90°,∴∠BEO=∠EFP,∵∠BOE=∠EPF=90°,∴△BEO≌△EFP(AAS),∴OE=PF=2,OB=EP=4,∵tan∠OEG==,即=,∴OG=1,∴EG==,∵OB∥FP,∴∠OBH=∠PFH,∴tan∠OBH=tan∠PFH,∴=,∴==2,∴OH=2PH,∵OP=OC﹣PC=4﹣2=2,∴OH=×2=,在Rt△OGH中,由勾股定理得:GH==,∴△EGH′的周长=△EGH的周长=EH+EG+GH=2+++=5+.故答案为:5+.10.(2022•安徽)如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F 作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:(1)∠FDG=°;(2)若DE=1,DF=2,则MN=.【答案】45°【解答】解:由题知,△BEF是以E为直角顶点的等腰直角三角形,∴∠AEB+∠GEF=90°,∵∠AEB+∠ABE=90°,∴∠GEF=∠ABE,在△ABE和△GEF中,,∴△ABE≌△GEF(AAS),∴EG=AB=AD,GF=AE,即DG+DE=AE+DE,∴DG=AE,∴DG=GF,即△DGF是等腰直角三角形,∴∠FDG=45°,故答案为:45°;(2)∵DE=1,DF=2,由(1)知,△DGF是等腰直角三角形,∴DG=GF=2,AB=AD=CD=ED+DG=2+1=3,延长GF交BC延长线于点H,∴CD∥GH,∴△EDM∽△EGF,∴,即,∴MD=,同理△BNC∽△BFH,∴,即,∴,∴NC=,∴MN=CD﹣MD﹣NC=3﹣﹣=,故答案为:.11.(2022•达州)如图,在边长为2的正方形ABCD中,点E,F分别为AD,CD边上的动点(不与端点重合),连接BE,BF,分别交对角线AC于点P,Q.点E,F在运动过程中,始终保持∠EBF=45°,连接EF,PF,PD.下列结论:①PB=PD;②∠EFD=2∠FBC;③PQ=PA+CQ;④△BPF为等腰直角三角形;⑤若过点B作BH⊥EF,垂足为H,连接DH,则DH的最小值为2﹣2,其中所有正确结论的序号是.【答案】①②④⑤【解答】解:如图,∵四边形ABCD是正方形,∴CB=CD,∠BCP=∠DCP=45°,在△BCP和△DCP中,,∴△BCP≌△DCP(SAS),∴PB=PD,故①正确,∵∠PBQ=∠QCF=45°,∠PQB=∠FQC,∴△PQB∽△FQC,∴=,∠BPQ=∠CFQ,∴=,∵∠PQF=∠BQC,∴△PQF∽△BQC,∴∠QPF=∠QBC,∵∠QBC+∠CFQ=90°,∴∠BPF=∠BPQ+∠QPF=90°,∴∠PBF=∠PFB=45°,∴PB=PF,∴△BPF是等腰直角三角形,故④正确,∵∠EPF=∠EDF=90°,∴E,D,F,P四点共圆,∴∠PEF=∠PDF,∵PB=PD=PF,∴∠PDF=∠PFD,∵∠AEB+∠DEP=180°,∠DEP+∠DFP=180°,∴∠AEB=∠DFP,∴∠AEB=∠BEH,∵BH⊥EF,∴∠BAE=∠BHE=90°,∵BE=BE,∴△BEA≌△BEH(AAS),∴AB=BH=BC,∵∠BHF=∠BCF=90°,BF=BF,∴Rt△BFH≌Rt△BFC(HL),∴∠BFC=∠BFH,∵∠CBF+∠BFC=90°,∴2∠CBF+2∠CFB=180°,∵∠EFD+∠CFH=∠EFD+2∠CFB=180°,∴∠EFD=2∠CBF,故②正确,将△ABP绕点B顺时针旋转90°得到△BCT,连接QT,∴∠ABP=∠CBT,∴∠PBT=∠ABC=90°,∴∠PBQ=∠TBQ=45°,∵BQ=BQ,BP=BT,∴△BQP≌△BQT(SAS),∴PQ=QT,∵QT<CQ+CT=CQ+AP,∴PQ<AP+CQ,故③错误,连接BD,DH,∵BD=2,BH=AB=2,∴DH≥BD﹣BH=2﹣2,∴DH的最小值为2﹣2,故⑤正确,故答案为:①②④⑤.12.(2022•南通)如图,点O是正方形ABCD的中心,AB=3.Rt△BEF中,∠BEF=90°,EF过点D,BE,BF分别交AD,CD于点G,M,连接OE,OM,EM.若BG=DF,tan∠ABG=,则△OEM的周长为.【答案】3+3【解答】解:如图,连接BD,过点F作FH⊥CD于点H.∵四边形ABCD是正方形,∴AB=AD=3,∠A=∠ADC=90°,∵tan∠ABG==,∴AG=,DG=2,∴BG===2,∵∠BAG=∠DEG=90°,∠AGB=∠DGE,∴△BAG∽△DEG,∴==,∠ABG=∠EDG,∴==,∴DE=,EG=,∴BE=BG+EG=2+=,∵∠ADH=∠FHD=90°,∴AD∥FH,∴∠EDG=∠DFH,∴∠ABG=∠DFH,∵BG=DF=2,∠A=∠FHD=90°,∴△BAG≌△FHD(AAS),∴AB=FH,∵AB=BC,∴FH=BC,∵∠C=∠FHM=90°,∴FH∥CB,∴==1,∴FM=BM,∵EF=DE+DF=+2=,∴BF==4,∵∠BEF=90°,BM=MF,∴EM=BF=2,∵BO=OD,BM=MF,∴OM=DF=,∵OE=BD=×6=3,∴△OEM的周长=3++2=3+3,解法二:辅助线相同.证明△BAG≌△FHD,推出AB=HF=3,再证明△FHM≌△BCM,推出CM=HM=,求出BD,DF,BF,利用直角三角形斜边中线的性质,三角形中位线定理,可得结论.故答案为:3+3.13.(2022•攀枝花)如图,以△ABC的三边为边在BC上方分别作等边△ACD、△ABE、△BCF.且点A在△BCF内部.给出以下结论:①四边形ADFE是平行四边形;②当∠BAC=150°时,四边形ADFE是矩形;③当AB=AC时,四边形ADFE是菱形;④当AB=AC,且∠BAC=150°时,四边形ADFE是正方形.其中正确结论有(填上所有正确结论的序号).【答案】①②③④【解答】解:①∵△ABE、△CBF是等边三角形,∴BE=AB,BF=CB,∠EBA=∠FBC=60°;∴∠EBF=∠ABC=60°﹣∠ABF;∴△EFB≌△ACB(SAS);∴EF=AC=AD;同理由△CDF≌△CAB,得DF=AB=AE;由AE=DF,AD=EF即可得出四边形ADFE是平行四边形,故结论①正确;②当∠BAC=150°时,∠EAD=360°﹣∠BAE﹣∠BAC﹣∠CAD=360°﹣60°﹣150°﹣60°=90°,由①知四边形AEFD是平行四边形,∴平行四边形ADFE是矩形,故结论②正确;③由①知AB=AE,AC=AD,四边形AEFD是平行四边形,∴当AB=AC时,AE=AD,∴平行四边形AEFD是菱形,故结论③正确;④综合②③的结论知:当AB=AC,且∠BAC=150°时,四边形AEFD既是菱形,又是矩形,∴四边形AEFD是正方形,故结论④正确.故答案为:①②③④.四.菱形的性质14.(2022•丽水)如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG∥AD交AE于点G.若cos B=,则FG的长是()A.3B.C.D.【答案】B【解答】解:方法一,如图,过点A作AH⊥BE于点H,过点F作FQ⊥AD 于点Q,∵菱形ABCD的边长为4,∴AB=AD=BC=4,∵cos B==,∴BH=1,∴AH===,∵E是BC的中点,∴BE=CE=2,∴EH=BE﹣BH=1,∴AH是BE的垂直平分线,∴AE=AB=4,∵AF平分∠EAD,∴∠DAF=∠FAG,∵FG∥AD,∴∠DAF=∠AFG,∴∠FAG=∠AFG,∴GA=GF,设GA=GF=x,∵AE=CD=4,FG∥AD,∴DF=AG=x,cos D=cos B==,∴DQ=x,∴FQ===x,∵S梯形CEAD=S梯形CEGF+S梯形GFDA,∴×(2+4)×=(2+x)×(﹣x)+(x+4)×x,解得x=,则FG的长是.或者:∵AE=CD=4,FG∥AD,∴四边形AGFD的等腰梯形,∴GA=FD=GF,则x+x+x=4,解得x=,则FG的长是.方法二:如图,作AH垂直BC于H,延长AE和DC交于点M,∵菱形ABCD的边长为4,∴AB=AD=BC=4,∵cos B==,∴BH=1,∵E是BC的中点,∴BE=CE=2,∴EH=BE﹣BH=1,∴AH是BE的垂直平分线,∴AE=AB=4,所以AE=AB=EM=CM=4,设GF=x,则AG=x,GE=4﹣x,由GF∥BC,∴△MGF∽△MEC,∴=,解得x=.故选:B.15.(2022•甘肃)如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为()A.B.2C.3D.4【答案】B【解答】解:在菱形ABCD中,∠A=60°,∴△ABD为等边三角形,设AB=a,由图2可知,△ABD的面积为3,∴△ABD的面积=a2=3,解得:a1=2,a2=﹣2(舍去),故选:B.27。
中考数学平行四边形-经典压轴题

1.已知,在矩形 ABCD 中,AB=a,BC=b,动点 M 从点 A 出发沿边 AD 向点 D 运动.
(1)如图 1,当 b=2a,点 M 运动到边 AD 的中点时,请证明∠ BMC=90°; (2)如图 2,当 b>2a 时,点 M 在运动的过程中,是否存在∠ BMC=90°,若存在,请给与 证明;若不存在,请说明理由; (3)如图 3,当 b<2a 时,(2)中的结论是否仍然成立?请说明理由. 【答案】(1)见解析; (2)存在,理由见解析; (3)不成立.理由如下见解析. 【解析】 试题分析:(1)由 b=2a,点 M 是 AD 的中点,可得 AB=AM=MD=DC=a,又由四边形 ABCD 是矩形,即可求得∠ AMB=∠ DMC=45°,则可求得∠ BMC=90°; (2)由∠ BMC=90°,易证得△ ABM∽ △ DMC,设 AM=x,根据相似三角形的对应边成比 例,即可得方程:x2﹣bx+a2=0,由 b>2a,a>0,b>0,即可判定△ >0,即可确定方程有 两个不相等的实数根,且两根均大于零,符合题意; (3)由(2),当 b<2a,a>0,b>0,判定方程 x2﹣bx+a2=0 的根的情况,即可求得答 案. 试题解析:(1)∵ b=2a,点 M 是 AD 的中点, ∴ AB=AM=MD=DC=a, 又∵ 在矩形 ABCD 中,∠ A=∠ D=90°, ∴ ∠ AMB=∠ DMC=45°, ∴ ∠ BMC=90°. (2)存在, 理由:若∠ BMC=90°, 则∠ AMB+∠ DMC=90°, 又∵ ∠ AMB+∠ ABM=90°, ∴ ∠ ABM=∠ DMC, 又∵ ∠ A=∠ D=90°, ∴ △ ABM∽ △ DMC, ∴ AM AB ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在四边形 ABCD 中,∠ D+∠ B=180°,∠ B=90°, ∴ ∠ D=90°, ∵ ∠ DAB=120°,AC 平分∠ DAB, ∴ ∠ DAC=∠ BAC=60°, ∵ ∠ B=90°,
∴ AB= 1 AC,同理 AD= 1 AC.
2
2
∴ AC=AD+AB.
(2)(1)中的结论成立,理由如下:以 C 为顶点,AC 为一边作∠ ACE=60°,∠ ACE 的另
【答案】(1)①45°;②BC 的中点,45°;(2)不会发生变化,证明参见解析;(3)不 会发生变化,作图参见解析. 【解析】 试题分析:(1)当点 P 在线段 BC 上时,①由折叠得到一对角相等,再利用正方形性质求 出∠ DAE 度数,在三角形 AFD 中,利用内角和定理求出所求角度数即可;②由 E 为 DF 中 点,得到 P 为 BC 中点,如图 1,连接 BE 交 AF 于点 O,作 EG∥ AD,得 EG∥ BC,得到 AF 垂直平分 BE,进而得到三角形 BOP 与三角形 EOG 全等,利用全等三角形对应边相等得到 BP=EG=1,得到 P 为 BC 中点,进而求出所求角度数即可;(2)若点 P 是线段 BC 上任意一 点时(不与 B,C 重合),∠ AFD 的度数不会发生变化,作 AG⊥DF 于点 G,如图 1(a)所 示,利用折叠的性质及三线合一性质,根据等式的性质求出∠ 1+∠ 2 的度数,即为∠ FAG 度数,即可求出∠ F 度数;(3)作出相应图形,如图 2 所示,若点 P 在 BC 边的延长线上 时,∠ AFD 的度数不会发生变化,理由为:作 AG⊥DE 于 G,得∠ DAG=∠ EAG,设 ∠ DAG=∠ EAG=α,根据∠ FAE 为∠ BAE 一半求出所求角度数即可. 试题解析:(1)①当点 P 在线段 BC 上时,∵ ∠ EAP=∠ BAP=30°,∴ ∠ DAE=90°﹣ 30°×2=30°,在△ ADE 中,AD=AE,∠ DAE=30°,∴ ∠ ADE=∠ AED=(180°﹣30°)÷2=75°,在 △ AFD 中,∠ FAD=30°+30°=60°,∠ ADF=75°,∴ ∠ AFE=180°﹣60°﹣75°=45°;②点 E 为 DF 的中点时,P 也为 BC 的中点,理由如下:
∴ △ CDA≌ △ CBE, ∴ AD=BE, ∴ AD+AB=AE. 在 Rt△ ACE 中,∠ CAB=45°,
∴ AE= AC = 2AC cos45
∴ AD AB= 2AC .
2.已知,在矩形 ABCD 中,AB=a,BC=b,动点 M 从点 A 出发沿边 AD 向点 D 运动.
(1)如图 1,当 b=2a,点 M 运动到边 AD 的中点时,请证明∠ BMC=90°; (2)如图 2,当 b>2a 时,点 M 在运动的过程中,是否存在∠ BMC=90°,若存在,请给与 证明;若不存在,请说明理由; (3)如图 3,当 b<2a 时,(2)中的结论是否仍然成立?请说明理由. 【答案】(1)见解析; (2)存在,理由见解析; (3)不成立.理由如下见解析. 【解析】 试题分析:(1)由 b=2a,点 M 是 AD 的中点,可得 AB=AM=MD=DC=a,又由四边形 ABCD 是矩形,即可求得∠ AMB=∠ DMC=45°,则可求得∠ BMC=90°; (2)由∠ BMC=90°,易证得△ ABM∽ △ DMC,设 AM=x,根据相似三角形的对应边成比 例,即可得方程:x2﹣bx+a2=0,由 b>2a,a>0,b>0,即可判定△ >0,即可确定方程有 两个不相等的实数根,且两根均大于零,符合题意; (3)由(2),当 b<2a,a>0,b>0,判定方程 x2﹣bx+a2=0 的根的情况,即可求得答 案. 试题解析:(1)∵ b=2a,点 M 是 AD 的中点, ∴ AB=AM=MD=DC=a, 又∵ 在矩形 ABCD 中,∠ A=∠ D=90°, ∴ ∠ AMB=∠ DMC=45°, ∴ ∠ BMC=90°. (2)存在, 理由:若∠ BMC=90°, 则∠ AMB+∠ DMC=90°, 又∵ ∠ AMB+∠ ABM=90°, ∴ ∠ ABM=∠ DMC,
一边交 AB 延长线于点 E,
∵ ∠ BAC=60°, ∴ △ AEC 为等边三角形, ∴ AC=AE=CE, ∵ ∠ D+∠ ABC=180°,∠ DAB=120°, ∴ ∠ DCB=60°, ∴ ∠ DCA=∠ BCE, ∵ ∠ D+∠ ABC=180°,∠ ABC+∠ EBC=180°, ∴ ∠ D=∠ CBE,∵ CA=CE, ∴ △ DAC≌ △ BEC, ∴ AD=BE, ∴ AC=AD+AB.
在△ ADE 中,AD=AE,AG⊥DE,∵ AG 平分∠ DAE,即∠ 2=∠ DAG,且 ∠ 1=∠ BAP,∴ ∠ 1+∠ 2= ×90°=45°,即∠ FAG=45°,则∠ AFD=90°﹣45°=45°;(3)如图 2 所示,∠ AFE 的大小不会发生变化,∠ AFE=45°,
作 AG⊥DE 于 G,得∠ DAG=∠ EAG,设∠ DAG=∠ EAG=α, ∴ ∠ BAE=90°+2α,∴ ∠ FAE= ∠ BAE=45°+α,∴ ∠ FAG=∠ FAE﹣∠ EAG=45°,在 Rt△ AFG 中, ∠ AFE=90°﹣45°=45°. 考点:1.正方形的性质;2.折叠性质;3.全等三角形的判定与性质. 5.如图,在正方形 ABCD 中,E 是边 BC 上的一动点(不与点 B、C 重合),连接 DE、点 C 关于直线 DE 的对称点为 C′,连接 AC′并延长交直线 DE 于点 P,F 是 AC′的中点,连接 DF. (1)求∠ FDP 的度数; (2)连接 BP,请用等式表示 AP、BP、DP 三条线段之间的数量关系,并证明;
【解析】
【分析】
(1)由折叠的性质知,
,
,
,则由
得到
;
(2)由
,可得
,又由
,即可求得 的长,然后在
中,利用勾股定理即可求得 的长,再过点 作
于 ,由角平分线的性
质,可得
,易证得四边形
是矩形,继而可求得答案.
【详解】
(1) 四边形
为矩形,
,
,
又
,
;
(2)
,
,
,
,
在
中,
,
过点 作
于,
,
,
,
,
,
,
、 、 共线,
如图 1,连接 BE 交 AF 于点 O,作 EG∥ AD,得 EG∥ BC,∵ EG∥ AD,
DE=EF,∴ EG= AD=1,∵ AB=AE,∴ 点 A 在线段 BE 的垂直平分线上,同理可得点 P 在线段 BE 的垂直平分线上,∴ AF 垂直平分线段 BE,∴ OB=OE,∵ GE∥ BP,∴ ∠ OBP=∠ OEG, ∠ OPB=∠ OGE,∴ △ BOP≌ △ EOG,∴ BP=EG=1,即 P 为 BC 的中点,∴ ∠ DAF=90°﹣ ∠ BAF,∠ ADF=45°+∠ BAF,∴ ∠ AFD=180°﹣∠ DAF﹣∠ ADF=45°;(2)∠ AFD 的度数不会 发生变化,作 AG⊥DF 于点 G,如图 1(a)所示,
,
四边形
是矩形,
,
. 【点睛】 此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾 股定理等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意掌握辅助线的作 法,注意数形结合思想的应用.
4.操作:如图,边长为 2 的正方形 ABCD,点 P 在射线 BC 上,将△ ABP 沿 AP 向右翻折, 得到△ AEP,DE 所在直线与 AP 所在直线交于点 F. 探究:(1)如图 1,当点 P 在线段 BC 上时,①若∠ BAP=30°,求∠ AFE 的度数;②若点 E 恰为线段 DF 的中点时,请通过运算说明点 P 会在线段 BC 的什么位置?并求出此时∠ AFD 的度数. 归纳:(2)若点 P 是线段 BC 上任意一点时(不与 B,C 重合),∠ AFD 的度数是否会发 生变化?试证明你的结论; 猜想:(3)如图 2,若点 P 在 BC 边的延长线上时,∠ AFD 的度数是否会发生变化?试在 图中画出图形,并直接写出结论.
又∵ ∠ A=∠ D=90°, ∴ △ ABM∽ △ DMC, ∴ AM AB ,
CD DM
设 AM=x,则 x a , a bx
整理得:x2﹣bx+a2=0, ∵ b>2a,a>0,b>0, ∴ △ =b2﹣4a2>0, ∴ 方程有两个不相等的实数根,且两根均大于零,符合题意, ∴ 当 b>2a 时,存在∠ BMC=90°, (3)不成立. 理由:若∠ BMC=90°, 由(2)可知 x2﹣bx+a2=0, ∵ b<2a,a>0,b>0, ∴ △ =b2﹣4a2<0, ∴ 方程没有实数根, ∴ 当 b<2a 时,不存在∠ BMC=90°,即(2)中的结论不成立. 考点:1、相似三角形的判定与性质;2、根的判别式;3、矩形的性质
△ PAP'是等腰直角三角形,可得结论; (3)先作高线 C'G,确定△ ACC′的面积中底边 AC 为定值 2,根据高的大小确定面积的大 小,当 C'在 BD 上时,C'G 最大,其△ ACC′的面积最大,并求此时的面积. 【详解】 (1)由对称得:CD=C'D,∠ CDE=∠ C'DE, 在正方形 ABCD 中,AD=CD,∠ ADC=90°, ∴ AD=C'D, ∵ F 是 AC'的中点, ∴ DF⊥AC',∠ ADF=∠ C'DF,
由.
(3)如图 3,若 DAB 90 ,探究边 AD 、 AB 与对角线 AC 的数量关系并说明理由.
【答案】(1) AC AD AB .证明见解析;(2)成立;(3) AD AB
