清华大学《大学物理》习题库试题及答案__10_量子力学习题
清华大学《大学物理》习题库试题及答案----10-量子力学习题

一、选择题1.4185:已知一单色光照射在钠外表上,测得光电子的最大动能是1.2 eV ,而钠的红限波长是5400 Å,那么入射光的波长是(A) 5350 Å (B) 5000 Å (C) 4350 Å (D) 3550 Å2.4244:在均匀磁场B 内放置一极薄的金属片,其红限波长为λ0。
今用单色光照射,发现有电子放出,有些放出的电子(质量为m ,电荷的绝对值为e )在垂直于磁场的平面内作半径为R 的圆周运动,那末此照射光光子的能量是: (A) 0λhc (B) 0λhcm eRB 2)(2+ (C) 0λhc m eRB + (D) 0λhc eRB 2+ 3.4383:用频率为ν 的单色光照射某种金属时,逸出光电子的最大动能为E K ;假设改用频率为2ν 的单色光照射此种金属时,则逸出光电子的最大动能为:(A) 2 E K (B) 2h ν - E K (C) h ν - E K (D) h ν + E K4.4737: 在康普顿效应实验中,假设散射光波长是入射光波长的倍,则散射光光子能量ε与反冲电子动能E K 之比ε / E K 为(A) 2 (B) 3 (C) 4 (D) 55.4190:要使处于基态的氢原子受激发后能发射赖曼系(由激发态跃迁到基态发射的各谱线组成的谱线系)的最长波长的谱线,至少应向基态氢原子提供的能量是(A) 1.5 eV (B) 3.4 eV (C) 10.2 eV (D) 13.6 eV6.4197:由氢原子理论知,当大量氢原子处于n =3的激发态时,原子跃迁将发出:(A) 一种波长的光 (B) 两种波长的光 (C) 三种波长的光 (D) 连续光谱7.4748:已知氢原子从基态激发到某一定态所需能量为10.19 eV ,当氢原子从能量为-0.85 eV 的状态跃迁到上述定态时,所发射的光子的能量为(A) 2.56 eV (B) 3.41 eV (C) 4.25 eV (D) 9.95 eV8.4750:在气体放电管中,用能量为12.1 eV 的电子去轰击处于基态的氢原子,此时氢原子所能发射的光子的能量只能是(A) 12.1 eV (B) 10.2 eV(C) 12.1 eV ,10.2 eV 和 1.9 eV (D) 12.1 eV ,10.2 eV 和 3.4 eV9.4241: 假设α粒子(电荷为2e )在磁感应强度为B 均匀磁场中沿半径为R 的圆形轨道运动,则α粒子的德布罗意波长是(A) )2/(eRB h (B) )/(eRB h (C) )2/(1eRBh (D) )/(1eRBh10.4770:如果两种不同质量的粒子,其德布罗意波长相同,则这两种粒子的(A) 动量相同 (B) 能量相同 (C) 速度相同 (D) 动能相同 11.4428:已知粒子在一维矩形无限深势阱中运动,其波函数为:a x ax 23cos 1)(π⋅=ψ ( - a ≤x ≤a ),那么粒子在x = 5a /6处出现的概率密度为 (A) 1/(2a ) (B) 1/a (C) a 2/1 (D) a /112.4778:设粒子运动的波函数图线分别如图(A)、(B)、(C)、(D)所示,那么其中确定粒子动量的精确度最高的波函数是哪个图?13.5619:波长λ =5000 Å的光沿x 轴正向传播,假设光的波长的不确定量∆λ =10-3 Å,则利用不确定关系式h x p x ≥∆∆可得光子的x 坐标的不确定量至少为:(A) 25 cm (B) 50 cm (C) 250 cm (D) 500 cm14.8020:将波函数在空间各点的振幅同时增大D 倍,则粒子在空间的分布概率将(A) 增大D 2倍 (B) 增大2D 倍 (C) 增大D 倍 (D) 不变x (A)x (C)x(B) x (D)15.4965:以下各组量子数中,哪一组可以描述原子中电子的状态?(A) n = 2,l = 2,m l = 0,21=s m (B) n = 3,l = 1,m l =-1,21-=s m (C) n = 1,l = 2,m l = 1,21=s m (D) n = 1,l = 0,m l = 1,21-=s m 16.8022:氢原子中处于3d 量子态的电子,描述其量子态的四个量子数(n ,l ,m l ,m s )可能取的值为(A) (3,0,1,21-) (B) (1,1,1,21-)(C) (2,1,2,21) (D) (3,2,0,21) 17.4785:在氢原子的K 壳层中,电子可能具有的量子数(n ,l ,m l ,m s )是(A) (1,0,0,21) (B) (1,0,-1,21)(C) (1,1,0,21-) (D) (2,1,0,21-)18.4222:与绝缘体相比较,半导体能带结构的特点是(A) 导带也是空带 (B) 满带与导带重合(C) 满带中总是有空穴,导带中总是有电子 (D) 禁带宽度较窄19.4789:p 型半导体中杂质原子所形成的局部能级(也称受主能级),在能带结构中应处于(A) 满带中 (B) 导带中 (C) 禁带中,但接近满带顶(D) 禁带中,但接近导带底20.8032:按照原子的量子理论,原子可以通过自发辐射和受激辐射的方式发光,它们所产生的光的特点是:(A) 两个原子自发辐射的同频率的光是相干的,原子受激辐射的光与入射光是不相干的(B) 两个原子自发辐射的同频率的光是不相干的,原子受激辐射的光与入射光是相干的(C) 两个原子自发辐射的同频率的光是不相干的,原子受激辐射的光与入射光是不相干的(D) 两个原子自发辐射的同频率的光是相干的,原子受激辐射的光与入射光是相干的21.9900:xˆ与x P ˆ的互易关系[x P x ˆ,ˆ]等于 〔A〕 i 〔B〕 i - 〔C〕ih 〔D〕ih - 22.9901:厄米算符Aˆ满足以下哪一等式〔u 、v 是任意的态函数〕 〔A〕()dx v u A dx v A u ⎰⎰=**ˆˆ 〔B〕()dx u A v dx u A v ⎰⎰=**ˆˆ〔C〕()dx u v A dx u A v ⎰⎰=**ˆˆ 〔D〕()dx v u A dx v A u ⎰⎰=**ˆˆ二、填空题1.4179:光子波长为λ,则其能量=_____;动量的大小 =______;质量=_______。
清华大学《大学物理》习题库试题及答案----10-量子力学习题解读

清华大学《大学物理》习题库试题及答案----10-量子力学习题解读一、选择题1.4185:已知一单色光照射在钠表面上,测得光电子的最大动能是1.2 eV ,而钠的红限波长是5400 Å,那么入射光的波长是(A) 5350 Å (B) 5000 Å (C)4350 Å (D) 3550 Å [ ]2.4244:在均匀磁场B 内放置一极薄的金属片,其红限波长为λ0。
今用单色光照射,发现有电子放出,有些放出的电子(质量为m ,电荷的绝对值为e )在垂直于磁场的平面内作半径为R 的圆周运动,那末此照射光光子的能量是:(A)(B) (C) (D)[ ]3.4383:用频率为ν 的单色光照射某种金属时,逸出光电子的最大动能为E K ;若改用频率为2ν 的单色光照射此种金属时,则逸出光电子的最大动能为:(A) 2 E K (B) 2h ν - E K (C)h ν - E K (D) h ν + E K [ ]4.4737: 在康普顿效应实验中,若散射光波长是入射光波长的1.2倍,则散射光光子能量ε与反冲电子动能E K 之比ε / E K 为(A) 2 (B) 3 (C) 4(D) 5 [ ] 0λhc0λhc m eRB 2)(2+0λhc m eRB +0λhc eRB2+5.4190:要使处于基态的氢原子受激发后能发射赖曼系(由激发态跃迁到基态发射的各谱线组成的谱线系)的最长波长的谱线,至少应向基态氢原子提供的能量是(A) 1.5 eV (B) 3.4 eV (C) 10.2 eV (D) 13.6 eV []6.4197:由氢原子理论知,当大量氢原子处于n =3的激发态时,原子跃迁将发出:(A) 一种波长的光(B) 两种波长的光(C) 三种波长的光(D) 连续光谱[]7.4748:已知氢原子从基态激发到某一定态所需能量为10.19 eV,当氢原子从能量为-0.85 eV的状态跃迁到上述定态时,所发射的光子的能量为(A) 2.56 eV (B) 3.41 eV (C)4.25 eV (D) 9.95 eV []8.4750:在气体放电管中,用能量为12.1 eV 的电子去轰击处于基态的氢原子,此时氢原子所能发射的光子的能量只能是(A) 12.1 eV (B) 10.2 eV (C) 12.1 eV,10.2 eV和1.9 eV(D) 12.1 eV,10.2 eV和 3.4 eV []9.4241:若 粒子(电荷为2e)在磁感应强度为B 均匀磁场中沿半径为R 的圆形轨道运动,则α粒子的德布罗意波长是(A) (B) (C)(D) [ ]10.4770:如果两种不同质量的粒子,其德布罗意波长相同,则这两种粒子的(A) 动量相同 (B) 能量相同 (C) 速度相同 (D) 动能相同 [ ]11.4428:已知粒子在一维矩形无限深势阱中运动,其波函数为: ( - a ≤x ≤a ),那么粒子在x = 5a /6处出现的概率密度为(A) 1/(2a ) (B) 1/a (C)(D) [ ]12.4778:设粒子运动的波函数图线分别如图(A)、(B)、(C)、(D)所示,那么其中确定粒子动量的精确度最高的波函数是哪个图? [ ]13.5619:波长λ =5000 Å的光沿x 轴正向)2/(eRB h )/(eRB h )2/(1eRBh )/(1eRBh a x a x 23cos 1)(π⋅=ψa 2/1a /1x (A)x (C) x (B) x(D)传播,若光的波长的不确定量∆λ =10-3Å,则利用不确定关系式可得光子的x 坐标的不确定量至少为:(A) 25 cm (B) 50 cm (C) 250cm (D) 500 cm [ ]14.8020:将波函数在空间各点的振幅同时增大D 倍,则粒子在空间的分布概率将(A) 增大D 2倍 (B) 增大2D 倍 (C)增大D 倍 (D) 不变 [ ]15.4965:下列各组量子数中,哪一组可以描述原子中电子的状态? (A) n = 2,l = 2,m l = 0,(B) n =3,l = 1,m l =-1, (C) n = 1,l = 2,m l = 1, (D) n = 1,l = 0,m l = 1, [ ]16.8022:氢原子中处于3d 量子态的电子,描述其量子态的四个量子数(n ,l ,m l ,m s )可能取的值为(A) (3,0,1,) (B) (1,1,1,)(C) (2,1,2,) (D) (3,2,0,) [ ]17.4785:在氢原子的K 壳层中,电子可h x p x ≥∆∆21=s m 21-=s m 21=s m 21-=s m 21-21-2121能具有的量子数(n ,l ,m l ,m s )是(A) (1,0,0,) (B) (1,0,-1,)(C) (1,1,0,) (D) (2,1,0,)[ ]18.4222:与绝缘体相比较,半导体能带结构的特点是(A) 导带也是空带 (B) 满带与导带重合(C) 满带中总是有空穴,导带中总是有电子(D) 禁带宽度较窄 [ ]19.4789:p 型半导体中杂质原子所形成的局部能级(也称受主能级),在能带结构中应处于(A) 满带中 (B) 导带中 (C) 禁带中,但接近满带顶(D) 禁带中,但接近导带底 [ ]20.8032:按照原子的量子理论,原子可以通过自发辐射和受激辐射的方式发光,它们所产生的光的特点是:(A) 两个原子自发辐射的同频率的光是相干的,原子受激辐射的光与入射光是不相干的(B) 两个原子自发辐射的同频率的光是不相干的,原子受激辐射的光与入射光是相干的(C) 两个原子自发辐射的同频率的光是不相干的,原子受激辐射的光与入射光是不相干的(D) 两个原子自发辐射的同频率的光是相212121-21-干的,原子受激辐射的光与入射光是相干的21.9900:与的互易关系[]等于(A) (B) (C) (D) [ ]22.9901:厄米算符满足以下哪一等式(、是任意的态函数)(A) (B)(C) (D)[ ]二、填空题1.4179:光子波长为λ,则其能量=_____;动量的大小 =______;质量=_______。
清华大学《大学物理》习题库试题及答案-01-力学习题

一、选择题1.0018:某质点作直线运动的运动学方程为x =3t -5t 3 + 6 (SI),则该质点作(A) 匀加速直线运动,加速度沿x 轴正方向(B) 匀加速直线运动,加速度沿x 轴负方向(C) 变加速直线运动,加速度沿x 轴正方向(D) 变加速直线运动,加速度沿x 轴负方向[ ] 2.5003:一质点在平面上运动,已知质点位置矢量的表示式为j bt i at r 22+=(其中a 、b 为常量),则该质点作(A) 匀速直线运动 (B) 变速直线运动(C) 抛物线运动 (D)一般曲线运动 [ ] 3.0015:一运动质点在某瞬时位于矢径()y x r , 的端点处, 其速度大小为(A) t r d d (B) t r d d (C) t r d d (D)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 4.0508:质点沿半径为R 的圆周作匀速率运动,每T 秒转一圈。
在2T 时间间隔中,其平均速度大小与平均速率大小分别为(A) 2p R /T , 2p R/T (B) 0 , 2R /T (C) 0 , 0 (D) 2R /T , 0. [ ] 5.0518:以下五种运动形式中,a 保持不变的运动是(A) 单摆的运动 (B) 匀速率圆周运动(C) 行星的椭圆轨道运动 (D) 抛体运动 (E) 圆锥摆运动 [ ]6.0519:对于沿曲线运动的物体,以下几种说法中哪一种是正确的:(A) 切向加速度必不为零(B) 法向加速度必不为零(拐点处除外)(C) 由于速度沿切线方向,法向分速度必为零,因此法向加速度必为零(D) 若物体作匀速率运动,其总加速度必为零 (E) 若物体的加速度a 为恒矢量,它一定作匀变速率运动 [ ] 7.0602:质点作曲线运动,r 表示位置矢量,v 表示速度,a 表示加速度,S 表示路程,a 表示切向加速度,下列表达式中, (1) a t = d /d v , (2) v =t r d /d , (3) v =t S d /d , (4)t a t =d /d v (A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的 [ ]8.0604:某物体的运动规律为t k t 2d /d v v -=,式中的k 为大于零的常量。
清华大学《大学物理》题库及答案__01_力学

(B) (C) (D) ] 11.0026:一飞机相对空气的速度大小为 200 km/h, 风速为 56 km/h,方向从西向东。 地面雷达站测得飞机速度大小为 192 km/h,方向是 (A) 南偏西 16.3° (B) 北偏东 16.3° (C) 向正南或向正北 (D) 西 偏 北 16.3 ° (E) 东 偏 南 16.3 ° [ ] 12.0601:下列说法哪一条正确? (A) 加速度恒定不变时,物体运动方向也不变 (B) 平均速率等于平均速度的大小 (C) 不 管 加 速 度 如 何 , 平 均 速 率 表 达 式 总 可 以 写 成 (v1 、 v2 分 别 为 初 、 末 速 [ 率) v v1 v 2 / 2 (D) 运 动 物 体 速 率 不 变 时 , 速 度 可 以 变 化 [ ] 13.0686:某人骑自行车以速率 v 向西行驶,今有风以相同速率从北偏东 30°方向吹 来,试问人感到风从哪个方向吹来? (A) 北偏东 30° (B) 南偏东 30° (C) 北 偏 西 30 ° (D) 西 偏 南 30 ° [ ] 14.0338:质量为 m 的物体自空中落下,它除受重力外,还受到一个与速度平方成正 比的阻力的作用,比例系数为 k,k 为正值常量。该下落物体的收尾速度(即最后物体作匀速 运动时的速度)将是
[ ] 32.0095:有一劲度系数为 k 的轻弹簧,竖直放置,下端悬一质量 为 m 的小球,开始时使弹簧为原长而小球恰好与地接触,今将弹簧上端 缓慢地提起,直到小球刚能脱离地面为止,在此过程中外力作功为
GMm 2 (B) R2 R R GMm 1 2 2 R1
GMm
(C)
R1 R2 R1 R2
GMm R1 R2 2 R12 R2
t
r A cost i B sint j
【清华】清华大学《大学物理》习题库试题及答案_01_力学习题

[
] 2.5003:一质点在平面上运动,已知质点位置矢量的表示式为
� r
=
at
� 2i
+
bt
2
� j
(其
中 a、b 为常量),则该质点作
(A) 匀速直线运动 (B) 变速直线运动
(C) 抛 物 线 运 动
(D) 一 般 曲 线 运 动
[
] 3.0015:一运动质点在某瞬时位于矢径
r�(x,
y)
的端点处,
为 m 的小球,开始时使弹簧为原长而小球恰好与地接触,今将弹簧上端
缓慢地提起,直到小球刚能脱离地面为止,在此过程中外力作功为
m2g 2ຫໍສະໝຸດ m2 g 2m2g 22m2 g 2
4m2 g 2
F
0095 图
(A) 4k (B) 3k (C) 2k (D) k
(E) k
33.0097:如图,劲度系数为 k 的轻弹簧在质量为 m 的木块和外力(未画出)作用下,
一、选择题
1.0018:某质点作直线运动的运动学方程为 x=3t-5t3 + 6 (SI),则该质点作
(A) 匀加速直线运动,加速度沿 x 轴正方向
(B) 匀加速直线运动,加速度沿 x 轴负方向
(C) 变加速直线运动,加速度沿 x 轴正方向 (D) 变 加 速 直 线 运 动 , 加 速 度 沿 x 轴 负 方 向
率)v = (v1 + v 2 )/ 2
(D) 运 动 物 体 速 率 不 变 时 , 速 度 可 以 变 化
[
]
13.0686:某人骑自行车以速率 v 向西行驶,今有风以相同速率从北偏东 30°方向吹
来,试问人感到风从哪个方向吹来?
【清华】清华大学《大学物理》习题库试题及答案__08_电学习题答案

一、选择题1.1003:下列几个说法中哪一个是正确的?(A) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向 (B) 在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同(C) 场强可由定出,其中q 为试验电荷,q 可正、可负,为试验电荷所受的电场力(D) 以上说法都不正确 [ ]2.1405:设有一“无限大”均匀带正电荷的平面。
取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度随距离平面的位置坐标x变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负):[ ]3(A) 场强的大小与试探电荷q 0的大小成反比(B) 对场中某点,试探电荷受力与q0的比值不因q 0而变(C) 试探电荷受力的方向就是场强的方向(D) 若场中某点不放试探电荷q 0,则=0,从而=0[ ]4.1558:下面列出的真空中静电场的场强公式,其中哪个是正确的? [ ](A)点电荷q 的电场:(r 为点电荷到场点的距离)(B)“无限长”均匀带电直线(电荷线密度)的电场:(场点的垂直于直线的矢量)(C)“无限大”均匀带电平面(电荷面密度)的电场:(D) 半径为R 的均匀带电球面(电荷面密度)外的电场:(为球心到场点的矢量)5.1035:有一边长为a 的正方形平面,在其中垂线上距中心O 点a /2处,有一电荷为q 的正点电荷,如图所示,则通过该平面的电场强度通量为(A) (B) (C) (D)[ ]6.1056:点电荷Q 被曲面S 所包围,从无穷远处引入另一点电荷q 至曲面外一点,如图所示,则引入前后: (A) 曲面S 的电场强度通量不变,曲面上各点场强不变 (B) 曲面S 的电场强度通量变化,曲面上各点场强不变 (C) 曲面S 的电场强度通量变化,曲面上各点场强变化q F E / =F EEFF E F E 204r q E επ=λr r E302ελπ=r σ02εσ=E σr r R E 302εσ=r 03εq 04επq 03επq 06εqq( xq 1035图(D) 曲面S 的电场强度通量不变,曲面上各点场强变化 [ ]7.1255:图示为一具有球对称性分布的静电场的E ~r 关系曲线。
推荐学习 精品-清华大学《大学物理》分类经典练习题及解析 量子基外

一 选择题 (共48分)1. (本题 3分)(1817) 所谓“黑体”是指的这样的一种物体,即 (A) 不能反射任何可见光的物体. (B) 不能发射任何电磁辐射的物体.(C) 能够全部吸收外来的任何电磁辐射的物体.(D) 完全不透明的物体. [ ]2. (本题 3分)(4403) 绝对黑体是这样一种物体,它(A) 不能吸收也不能发射任何电磁幅射. (B) 不能反射也不能发射任何电磁辐射. (C) 不能发射但能全部吸收任何电磁辐射.(D) 不能反射但可以全部吸收任何电磁辐射. [ ]3. (本题 3分)(4404) 下面四个图中,哪一个正确反映黑体单色辐出度M B λ(T )随λ 和T 的变化关系,已知T 2> T 1.[ ]4. (本题 3分)(5810) 把表面洁净的紫铜块、黑铁块和铝块放入同一恒温炉膛中达到热平衡.炉中这三块金属对红光的辐出度(单色辐射本领)和吸收比(单色吸收率)之比依次用M 1 / a 1、M 2 / a 2和M 3 / a 3表示,则有(A) 11a M > 22a M > 33a M . (B) 22a M > 11a M> 33a M .(C) 33a M > 22a M > 11a M . (D) 11a M = 22a M= 33a M . [ ]5. (本题 3分)(1821) 黑体的温度T 升高一倍,它的辐射出射度(总发射本领)增加(A) 1倍. (B) 3倍.(C) 7倍. (D) 15倍. [ ]6. (本题 3分)(4406) 在加热黑体过程中,其最大单色辐出度(单色辐射本领)对应的波长由0.8 μm 变到0.4 μm ,则其辐射出射度(总辐射本领)增大为原来的 (A) 2倍. (B) 4倍.(C) 8倍. (D) 16倍. [ ]在加热黑体过程中,其最大单色辐出度(单色辐射本领)对应的波长由0.8 μm 变到0.4 μm ,则其辐射出射度(总辐射本领)增大为原来的 (A) 2倍. (B) 4倍.(C) 8倍. (D) 16倍. [ ]8. (本题 3分)(4985) 普朗克量子假说是为解释(A) 光电效应实验规律而提出来的. (B) X 射线散射的实验规律而提出来的. (C) 黑体辐射的实验规律而提出来的.(D) 原子光谱的规律性而提出来的. [ ]9. (本题 3分)(4528) 一维无限深方势阱中,已知势阱宽度为a .应用测不准关系估计势阱中质量为m 的粒子的零点能量为 (A) )/(2ma =. (B) )2/(22ma =.(C) )2/(2ma =. (D) )2/(2ma =. [ ]10. (本题 3分)(4205) 粒子在一维无限深方势阱中运动.下图为粒子处于某一能态上的波函数ψ(x )的曲线.粒子出现概率最大的位置为(A) a / 2.(B) a / 6,5 a / 6.(C) a / 6,a / 2,5 a / 6.(D) 0,a / 3,2 a / 3,a . [ ]xaa31a 32ψ(x )O11. (本题 3分)(1903) 一矩形势垒如图所示,设U 0和d 都不很大.在Ⅰ区中向右运动的能量为E 的微观粒子,(A) 如果E > U 0,可全部穿透势垒Ⅱ进入Ⅲ区(B) 如果E < U 0,都将受到x = 0处势垒壁的反射,不可能进入Ⅱ区.(C) 如果E < U 0,都不可能穿透势垒Ⅱ进入Ⅲ区.(D) 如果E ﹤U 0,有一定概率穿透势垒Ⅱ进入Ⅲ区. []粒子在外力场中沿x 轴运动,如果它在力场中的势能分布如附图所示,则对于能量为 E > U 0 向右运动的粒子, (A) 在x < 0区域,只有粒子沿x 轴正向运动的波函数;在x > 0区域,波函数为零.(B) 在x < 0和x > 0区域都只有粒子沿x 轴正向运动的 波函数.(C) 在x <0区域既有粒子沿x 轴正向运动的波函数,也有沿x 轴负方向运 动的波函数;在x >0区域只有粒子沿x 轴正向运动的波函数.(D) 在x <0和x >0两个区域内都有粒子沿x 轴正向和负向运动的波函数. [ ]x OU (x )U 013. (本题 3分)(5815) 粒子在外力场中沿x 轴运动,如果它在力场中的势能分布如附图所示,对于能量为 E < U 0从左向右运动的粒子,若用 ρ1、ρ2、ρ3分别表示在x < 0,0 < x <a ,x > a 三个区域发现粒子的概率,则有(A) ρ1 ≠ 0,ρ2 = ρ3 = 0. (B) ρ1 ≠ 0,ρ2 ≠ 0,ρ3 = 0. (C) ρ1 ≠ 0,ρ2 ≠ 0,ρ3 ≠ 0.(D) ρ1 = 0,ρ2 ≠ 0,ρ3 ≠ 0. [ ]x OU (x )Ua14. (本题 3分)(4993) 量子力学得出,频率为ν 的线性谐振子,其能量只能为 (A) E = h ν.(B) E = nh ν, (n = 0,1,2,3……). (C) E = n 21h ν,( n = 0,1,2,3……).(D) νh n E )21(+=, (n = 0,1,2,3……). [ ]15. (本题 3分)(4216) 根据量子力学原理,氢原子中,电子绕核运动的动量矩L 的最小值为(A) 0. (B) =. (C) 2/=. (D) =2. [ ]16. (本题 3分)(5710) 若氢原子中的电子处于主量子数n = 3的能级,则电子轨道角动量L 和轨道角动量在外磁场方向的分量L z 可能取的值分别为(A) ==L ,=2,=3; ===32,,0±±±=,z L . (B) 0=L ,=2,=6; ==2,,0±±=z L . (C) 0=L ,=,=2; ==2,,0±±=z L .(D) =2=L ,=6,=12;===32,,0±±±=,z L . [ ]二填空题 (共98分)17. (本题 3分)(1818)用文字叙述热辐射的基尔霍夫定律的内容是:__________________________ ___________________________________________________________.18. (本题 3分)(1822)用文字叙述黑体辐射的斯特藩─玻尔兹曼定律的内容是:______________ ______________________________________________________________.19. (本题 3分)(1823)用文字叙述黑体辐射的维恩位移定律的内容是:_____________________ ________________________________________________________________.20. (本题 3分)(1824)一100 W的白炽灯泡的灯丝表面积为5.3×10-5 m2.若将点燃的灯丝看成是黑体,可估算出它的工作温度为___________________ .(斯特藩─玻尔兹曼定律常数σ = 5.67×10-8 W/m2·K4)21. (本题 3分)(1826)天狼星辐射波谱的峰值波长为0.29 μm,若将它看成是黑体,则由维恩位移定律可以估算出它的表面温度为_________________.(维恩位移定律常数b = 2.897×10-3 m·K)22. (本题 3分)(4407)测量星球表面温度的方法之一,是把星球看作绝对黑体而测定其最大单色辐出度的波长λm,现测得太阳的λm1 = 0.55 μm,北极星的λm2 = 0.35 μm,则太阳表面温度T1与北极星表面温度T2之比T1:T2=__________________________.23. (本题 3分)(4408)当绝对黑体的温度从27℃升到 327℃时,其辐射出射度(总辐射本领)增加为原来的____________________________________倍.24. (本题 3分)(4507)某一恒星的表面温度为6000 K,若视作绝对黑体,则其单色辐出度为最大值的波长为_____________________ .(维恩定律常数b = 2.897×10-3 m·K )地球卫星测得太阳单色辐出度的峰值在0.565µm 处,若把太阳看作是绝对黑体,则太阳表面的温度约为____________________K .(维恩位移定律常数b = 2.897×10-3m ·K )26. (本题 3分)(5368) 若太阳(看成黑体)的半径由R 增为2 R ,温度由T 增为2 T ,则其总辐射功率为原来的____________倍.27. (本题 5分)(4986) 普朗克的量子假说是为了解释_______________________的实验规律而提出来的.它的基本思想是______________________________________________________________________________________________________________________________________________________________________________________.28. (本题 3分)(4988) 普朗克公式 1)]/(exp[2)(52−π=−T k hc hc T M B λλλ中,)(T M B λ[也可写作),(0T e λ]的物理意义是:________________________________________________________________________________________________________________________________________________________________________________________________.29. (本题 5分)(5235) 波长为0.400μm 的平面光波朝x 轴正向传播.若波长的相对不确定量Δλ / λ=10-6,则光子动量数值的不确定量 Δp x =_________________________________,而光子坐标的最小不确定量 Δx =__________________________. (普朗克常量 h ≈ 6.63×10-34 J ·s )30. (本题 5分)(4204) 粒子在一维无限深方势阱中运动(势阱宽度为a ),其波函数为a x a x π=3sin 2)(ψ ( 0 < x < a ), 粒子出现的概率最大的各个位置是x = ___________________.量子力学中的隧道效应是指_________________________________________________________________________________________________________.这种效应是微观粒子_____________________________的表现.32. (本题 4分)(4991) 根据量子力学,粒子能透入势能大于其总能量的势垒,当势垒加宽时,贯穿系数__________;当势垒变高时,贯穿系数____________.(填入:变大、变小或不变)33. (本题 4分)(4992) 隧道效应是微观粒子具有______________性的必然表现,已被大量实验所证实.原子核的______________衰变,就是隧道效应的典型例证.34. (本题 4分)(1904) 频率为ν 的一维线性谐振子的量子力学解,其能量由下式给出:____________________________________,其中最低的量子态能量为__________________,称为“零点能”.35. (本题 4分)(4994) 按照普朗克能量子假说,频率为ν 的谐振子的能量只能为____________;而从量子力学得出,谐振子的能量只能为__________________________.36. (本题 4分)(5816) 按照量子力学,一维线性谐振子的能量是量子化的,能级公式是__________________________________________________,量子力学的结果与普朗克引入量子化概念时关于谐振子的能量假设的不同点是______________________________________________________.37. (本题 3分)(4217) 根据量子力学原理,当氢原子中电子的动量矩=6=L 时,L 在外磁场方向上的投影L z 可取的值分别为___________________________.量子力学得出:若氢原子处于主量子数n = 4的状态,则其轨道角动量(动量矩)可能取的值(用ћ表示)分别为_______________________________;对应于l = 3的状态,氢原子的角动量在外磁场方向的投影可能取的值分别为____________________________________.39. (本题 4分)(5817)按照量子力学计算:(1)氢原子中处于主量子数n = 3能级的电子,轨道动量矩可能取的值分别为______________________________________=.(2) 若氢原子中电子的轨道动量矩为=12,则其在外磁场方向的投影可能取的值分别为__________________________________________=.40. (本题 4分)(1907)原子序数Z = 6的碳原子,它在基态的电子组态为__________________;原子序数Z = 14的硅原子,它在基态的电子组态为______________________.41. (本题 4分)(4999)当原子(包括多电子原子)受激发发光时,它们发射的原子光谱中光学光谱对应于______________电子的跃迁,X光谱对应于__________电子的跃迁.42. (本题 3分)(8038)为了表征原子的电子结构,常把电子所分布的壳层符号及壳层上电子的数目组合起来称为电子组态.那么,对于原子序数Z = 20的钙原子,当它处于基态时其电子组态应表示为______________________________________.43. (本题 3分)(8039)有一种原子,在基态时n = 1和n = 2的主壳层都填满电子,3s次壳层也填满电子,而3p壳层只填充一半.这种原子的原子序数是________.三计算题 (共143分)44. (本题 5分)(1828)某黑体在加热过程中,其单色辐出度的峰值波长由0.69 μm变化到0.50 μm,问其辐射出射度增加为多少倍?恒星表面可看作黑体.测得北极星辐射波谱的峰值波长λm =350nm(1nm=10−9m),试估算它的表面温度及单位面积的辐射功率.(b = 2.897×10-3 m·K,σ = 5.67×10-8 W/(m2·K4))46. (本题 5分)(1830)一黑体在某一温度时的辐射出射度为 5.7×104 W/m2,试求该温度下辐射波谱的峰值波长λ.m(b = 2.897×10-3 m·K, σ = 5.67×10-8 W/(m2·K4))47. (本题 5分)(1831)已知垂直射到地球表面每单位面积的日光功率(称太阳常数)等于1.37×103 W/m2.(1) 求太阳辐射的总功率.(2) 把太阳看作黑体,试计算太阳表面的温度.(地球与太阳的平均距离为1.5×108 km,太阳的半径为6.76×105 km,σ= 5.67×10-8 W/(m2·K4))48. (本题 5分)(1831)已知垂直射到地球表面每单位面积的日光功率(称太阳常数)等于1.37×103 W/m2.(1) 求太阳辐射的总功率.(2) 把太阳看作黑体,试计算太阳表面的温度.(地球与太阳的平均距离为1.5×108 km,太阳的半径为6.76×105 km,σ= 5.67×10-8 W/(m2·K4))49. (本题 5分)(4409)用辐射高温计测得炼钢炉口的辐射出射度为22.8 W·cm-2,试求炉内温度.(斯特藩常量σ = 5.67×10-8 W/(m2·K4))50. (本题 5分)(5707)若一空腔辐射器的小孔的单位面积上辐射出的功率为M = 20 W/cm2求空腔内的温度T和单色辐出度极大值所对应的波长λm.(斯特藩──玻尔兹曼常数σ = 5.67×10-8 W/(m2·K4),维恩位移定律中的常量b = 2.897×10-3 m·K )51. (本题 5分)(1832)对于动能是1 KeV的电子,要确定其某一时刻的位置和动量,如果位置限制在10-10 m范围内,试估算其动量不确定量的百分比.= 9.11×10-31 kg )( h = 6.63×10-34 J·s,me52. (本题 5分)(1832)对于动能是1 KeV的电子,要确定其某一时刻的位置和动量,如果位置限制在10-10 m范围内,试估算其动量不确定量的百分比.= 9.11×10-31 kg )( h = 6.63×10-34 J·s,me对于动能是1 KeV 的电子,要确定其某一时刻的位置和动量,如果位置限制在10-10 m 范围内,试估算其动量不确定量的百分比. ( h = 6.63×10-34 J ·s ,m e = 9.11×10-31 kg )54. (本题 5分)(1833) 一质量为m 的微观粒子被约束在长度为L 的一维线段上,试根据不确定关系式估算该粒子所具有的最小能量值,并由此计算在直径为10-14m 的核内质子或中子的最小能量.(h = 6.63×10-34 J ·s ,m p = 1.67×10-27kg)55. (本题10分)(1834) 一电子处于原子某能态的时间为10-8s ,计算该能态的能量的最小不确定量.设电子从上述能态跃迁到基态所对应的光子能量为3.39 eV ,试确定所辐射的光子的波长及此波长的最小不确定量.( h = 6.63×10-34J ·s )56. (本题 5分)(4989) 利用不确定关系式 Δx Δp x ≥h ,估算在直径为d = 10-14m 的核内的质子最小动能的数量级.(质子的质量m =1.67×10-27 kg ,普朗克常量h =6.63×10-34J ·s )57. (本题10分)(5709) 动量为p K的原子射线垂直通过一个缝宽可以调节的狭缝S ,与狭缝相距D 处有一接收屏C ,如图.试根据不确定关系式求狭缝宽度a 等于多大时接收屏上的痕迹宽度可达到最小.58. (本题 5分)(1901) 试求出一维无限深方势阱中粒子运动的波函数x an A x n π=sin )(ψ ( n = 1, 2, 3, …)的归一化形式.式中a 为势阱宽度.59. (本题 5分)(1902) 已知粒子处于宽度为a 的一维无限深方势阱中运动的波函数为a x n a x n π=sin 2)(ψ , n = 1, 2, 3, … 试计算n = 1时,在 x 1 = a /4 →x 2 = 3a /4 区间找到粒子的概率.60. (本题 8分)(4775) 一维无限深方势阱中的粒子,其波函数在边界处为零,这种定态物质波相当于两端固定的弦中的驻波,因而势阱的宽度a 必须等于德布罗意波半波长的整数倍。
清华大学光学量子力学试题
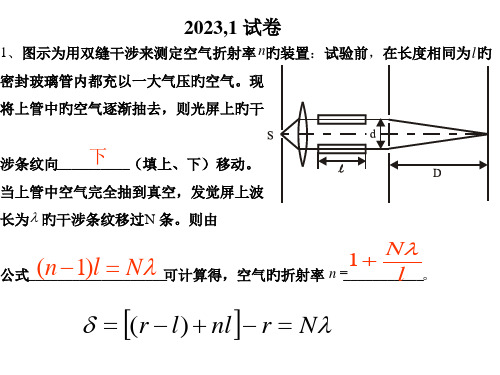
折射率为 n 旳玻璃 , 这光线与 SoF 旳光程
差 = (n-1) l 。 2
透镜不引起附加光程差
δ = SbF- l + nl - SoF
2、将波长为600nm旳单色光垂直均匀照射在等间距旳平行 四缝上,在衍射角正弦 sin=0.03处应出现旳第三级干 涉明条纹恰好缺级。由此可知这四缝中每条通光旳缝
得:x=0 或 x=L 或 x=L/2
取 x=L/2
L
L
3:
3
3
= Y2dx = A2 x2 (L x)2 dx
0
0
= A2 (1 L5 1 1 L5 1 1 L5 1 )
3 27 2 81 5 243
= A2 L5 ( 90 45 6 ) = 51 = 17
30 243 243 243 243 81
S1 = T14
lm2
=b T2
=
lm1T1
T2
=
3000 2500
lm1
S2
=
T24
=
( T1 )4 1.2
S2 = 1.24 S1
7、简要阐明光电效应试验中旳其中两个特点:
(1)___________红__限_____________________;
(用2爱)因__斯___坦__光__电瞬___效时__应_性_方__程___:_________h_______=_____12____m___。v__2___A_____就能得到很好旳解
Y2dx = A2 x2 (L x)2 dx = 1
0
0
L
( A2 x2L2 2LA2 x3 A2 x4 )dx = 1
推荐学习 精品-清华大学《大学物理》分类经典练习题及解析 量子1

一 选择题 (共75分)1. (本题 3分)(4181) 用频率为ν1的单色光照射某一种金属时,测得光电子的最大动能为E K 1;用频率为ν2的单色光照射另一种金属时,测得光电子的最大动能为E K 2.如果E K 1>E K 2,那么(A)ν1一定大于ν2. (B) ν1一定小于ν2. (C) ν1一定等于ν2. (D)ν1可能大于也可能小于ν2. [ ]2. (本题 3分)(4182) 用频率为ν1的单色光照射某种金属时,测得饱和电流为I 1,以频率为ν2的单色光照射该金属时,测得饱和电流为I 2,若I 1> I 2,则 (A) ν1 >ν2. (B) ν1 <ν2.(C) ν1 =ν2. (D) ν1与ν2的关系还不能确定. [ ]3. (本题 3分)(4183) 已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是U 0(使电子从金属逸出需作功eU 0),则此单色光的波长λ 必须满足: (A) λ ≤)/(0eU hc . (B) λ ≥)/(0eU hc .(C) λ ≤)/(0hc eU . (D) λ ≥)/(0hc eU . [ ]4. (本题 3分)(4181) 用频率为ν1的单色光照射某一种金属时,测得光电子的最大动能为E K 1;用频率为ν2的单色光照射另一种金属时,测得光电子的最大动能为E K 2.如果E K 1>E K 2,那么(A)ν1一定大于ν2. (B) ν1一定小于ν2. (C) ν1一定等于ν2. (D)ν1可能大于也可能小于ν2. [ ]5. (本题 3分)(4182) 用频率为ν1的单色光照射某种金属时,测得饱和电流为I 1,以频率为ν2的单色光照射该金属时,测得饱和电流为I 2,若I 1> I 2,则(A) ν1 >ν2. (B) ν1 <ν2.(C) ν1 =ν2. (D) ν1与ν2的关系还不能确定. [ ]6. (本题 3分)(4183) 已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是U 0(使电子从金属逸出需作功eU 0),则此单色光的波长λ 必须满足: (A) λ ≤)/(0eU hc . (B) λ ≥)/(0eU hc .(C) λ ≤)/(0hc eU . (D) λ ≥)/(0hc eU . [ ]7. (本题 3分)(4185) 已知一单色光照射在钠表面上,测得光电子的最大动能是 1.2 eV ,而钠的红限波长是5400 Å ,那么入射光的波长是 (A) 5350 Å. (B) 5000 Å. (C) 4350 Å. (D) 3550 Å. [ ]在均匀磁场B 内放置一极薄的金属片,其红限波长为λ0.今用单色光照射,发现有电子放出,有些放出的电子(质量为m ,电荷的绝对值为e )在垂直于磁场的平面内作半径为R 的圆周运动,那末此照射光光子的能量是:(A) 0λhc . (B) 0λhc m eRB 2)(2+. (C) 0λhc m eRB +. (D) 0λhceRB 2+. [ ]9. (本题 3分)(4382) 一定频率的单色光照射在某种金属上,测出其光电流的曲线如图中实线所示.然后在光强度不变的条件下增大照射光的频率,测出其光电流的曲线如图中虚线所示.满足题意的图是:[ ]10. (本题 3分)(4383) 用频率为ν 的单色光照射某种金属时,逸出光电子的最大动能为E K ;若改用频率为2ν 的单色光照射此种金属时,则逸出光电子的最大动能为: (A) 2 E K . . (B) 2h ν - E K .(C) h ν - E K . (D) h ν + E K . [ ]11. (本题 3分)(4384) 关于光电效应有下列说法:(1) 任何波长的可见光照射到任何金属表面都能产生光电效应;(2) 若入射光的频率均大于一给定金属的红限,则该金属分别受到不同频率的光照射时,释出的光电子的最大初动能也不同;(3) 若入射光的频率均大于一给定金属的红限,则该金属分别受到不同频率、强度相等的光照射时,单位时间释出的光电子数一定相等;(4) 若入射光的频率均大于一给定金属的红限,则当入射光频率不变而强度增大一倍时,该金属的饱和光电流也增大一倍. 其中正确的是(A) (1),(2),(3). (B) (2),(3),(4). (C) (2),(3).(D) (2),(4). [ ]设用频率为ν1和ν2的两种单色光,先后照射同一种金属均能产生光电效应.已知金属的红限频率为ν0,测得两次照射时的遏止电压|U a 2| = 2|U a 1|,则这两种单色光的频率有如下关系:(A) ν2 = ν1 - ν0. (B) ν2 = ν1 + ν0.(C) ν2 = 2ν1 - ν0. (D) ν2 = ν1 - 2ν0. [ ]13. (本题 3分)(4386) 以一定频率的单色光照射在某种金属上,测出其光电流曲线在图中用实线表示,然后保持光的频率不变,增大照射光的强度,测出其光电流曲线在图中用虚线表示.满足题意的图是 [ ]14. (本题 3分)(4387) 光电效应中发射的光电子最大初动能随入射光频率ν 的变化关系如图所示.由图中的(A) OQ (B) OP (C) OP /OQ (D) QS /OS 可以直接求出普朗克常量. [ ]15. (本题 3分)(4503) 在康普顿散射中,如果设反冲电子的速度为光速的60%,则因散射使电子获得的能量是其静止能量的(A) 2倍. (B) 1.5倍. (C) 0.5倍. (D) 0.25倍. [ ]16. (本题 3分)(4607) 当照射光的波长从4000 Å变到3000 Å时,对同一金属,在光电效应实验中测得的遏止电压将:(A) 减小0.56 V . (B) 减小0.34 V .(C) 增大0.165 V . (D) 增大1.035 V . [ ](普朗克常量h =6.63×10-34 J ·s ,基本电荷e =1.60×10-19C)17. (本题 3分)(4736) 保持光电管上电势差不变,若入射的单色光光强增大,则从阴极逸出的光电子的最大初动能E 0和飞到阳极的电子的最大动能E K 的变化分别是 (A) E 0增大,E K 增大. (B) E 0不变,E K 变小.(C) E 0增大,E K 不变. (D) E 0不变,E K 不变. [ ]在康普顿效应实验中,若散射光波长是入射光波长的 1.2倍,则散射光光子能量ε与反冲电子动能E K 之比ε / E K 为(A) 2. (B) 3. (C) 4. (D) 5. [ ]19. (本题 3分)(4739) 光子能量为 0.5 MeV 的X 射线,入射到某种物质上而发生康普顿散射.若反冲电子的能量为 0.1 MeV ,则散射光波长的改变量Δλ与入射光波长λ0之比值为 (A) 0.20. (B) 0.25. (C) 0.30. (D) 0.35. [ ]20. (本题 3分)(5232) 用强度为I ,波长为λ 的X 射线(伦琴射线)分别照射锂(Z = 3)和铁(Z = 26).若在同一散射角下测得康普顿散射的X 射线波长分别为λLi 和λFe (λLi ,λFe >λ),它们对应的强度分别为I Li 和I Fe ,则(A) λLi >λFe ,I Li < I Fe (B) λLi =λFe ,I Li = I Fe(C) λLi =λFe ,I Li .>I Fe (D) λLi <λFe ,I Li .>I Fe [ ]21. (本题 3分)(5363) 以下一些材料的逸出功为铍 3.9 eV 钯 5.0eV 铯 1.9 eV 钨 4.5 eV今要制造能在可见光(频率范围为3.9×1014 Hz —7.5×1014Hz)下工作的光电管,在这些材料中应选(A) 钨. (B) 钯. (C) 铯. (D) 铍. [ ]22. (本题 3分)(5364) 某金属产生光电效应的红限波长为λ0,今以波长为λ (λ <λ0)的单色光照射该金属,金属释放出的电子(质量为m e )的动量大小为(A) λ/h . (B) 0/λh . (C)λλλλ00)(2+hc m e (D)2λhcm e (E)λλλλ00)(2−hc m e [ ]23. (本题 3分)(5365) 康普顿效应的主要特点是(A) 散射光的波长均比入射光的波长短,且随散射角增大而减小,但与散射体的性质无关.(B) 散射光的波长均与入射光的波长相同,与散射角、散射体性质无关. (C) 散射光中既有与入射光波长相同的,也有比入射光波长长的和比入射光波长短的.这与散射体性质有关.(D) 散射光中有些波长比入射光的波长长,且随散射角增大而增大,有些散射光波长与入射光波长相同.这都与散射体的性质无关. [ ]光电效应和康普顿效应都包含有电子与光子的相互作用过程.对此,在以下几种理解中,正确的是(A) 两种效应中电子与光子两者组成的系统都服从动量守恒定律和能量守恒定律.(B) 两种效应都相当于电子与光子的弹性碰撞过程.(C) 两种效应都属于电子吸收光子的过程.(D) 光电效应是吸收光子的过程,而康普顿效应则相当于光子和电子的弹性碰撞过程.(E) 康普顿效应是吸收光子的过程,而光电效应则相当于光子和电子的弹性碰撞过程.[]25. (本题 3分)(5617)用X射线照射物质时,可以观察到康普顿效应,即在偏离入射光的各个方向上观察到散射光,这种散射光中(A) 只包含有与入射光波长相同的成分.(B) 既有与入射光波长相同的成分,也有波长变长的成分,波长的变化只与散射方向有关,与散射物质无关.(C) 既有与入射光相同的成分,也有波长变长的成分和波长变短的成分,波长的变化既与散射方向有关,也与散射物质有关.(D) 只包含着波长变长的成分,其波长的变化只与散射物质有关与散射方向无关.[]二填空题 (共76分)26. (本题 3分)(0475)某光电管阴极, 对于λ= 4910 Å的入射光,其发射光电子的遏止电压为0.71 V.当入射光的波长为__________________Å时,其遏止电压变为1.43 V.( e =1.60×10-19 C,h =6.63×10-34 J·s )27. (本题 5分)(4179)光子波长为λ,则其能量=____________;动量的大小 =_____________;质量=_________________ .28. (本题 4分)(4180)当波长为3000 Å的光照射在某金属表面时,光电子的能量范围从0到 4.0| =____________V;此金属的×10-19 J.在作上述光电效应实验时遏止电压为|Ua红限频率ν0 =__________________Hz.(普朗克常量h =6.63×10-34 J·s;基本电荷e =1.60×10-19 C)光子波长为λ,则其能量=____________;动量的大小 =_____________;质量=_________________ .30. (本题 4分)(4180)当波长为3000 Å的光照射在某金属表面时,光电子的能量范围从0到 4.0×10-19 J.在作上述光电效应实验时遏止电压为|Ua| =____________V;此金属的红限频率ν0 =__________________Hz.(普朗克常量h =6.63×10-34 J·s;基本电荷e =1.60×10-19 C)31. (本题 4分)(4184)已知钾的逸出功为 2.0 eV,如果用波长为3.60×10-7 m的光照射在钾上,则光电效应的遏止电压的绝对值|Ua| =___________________.从钾表面发射出电子的最大速度v max =_______________________.(h =6.63×10-34 J·s,1eV =1.60×10-19 J,me=9.11×10-31 kg)32. (本题 4分)(4187)康普顿散射中,当散射光子与入射光子方向成夹角φ = _____________时,散射光子的频率小得最多;当φ = ______________ 时,散射光子的频率与入射光子相同.33. (本题 3分)(4250)波长为λ =1 Å的X光光子的质量为_____________kg.(h =6.63×10-34 J·s)34. (本题 3分)(4388)以波长为λ= 0.207 μm的紫外光照射金属钯表面产生光电效应,已知钯的红限频率ν0=1.21×1015赫兹,则其遏止电压|Ua| =_______________________V.(普朗克常量h =6.63×10-34 J·s,基本电荷e =1.60×10-19 C)在光电效应实验中,测得某金属的遏止电压|Ua|与入射光频率ν的关系曲线如图所示,由此可知该金属的红限频率ν=___________Hz;逸出功A =____________eV.|1014 Hz) -36. (本题 4分)(4390)已知某金属的逸出功为A,用频率为ν1的光照射该金属能产生光电效应,则该金属的红限频率ν0 =_____________________________,ν1> ν,且遏止电势差|Ua| =______________________________.37. (本题 4分)(4391)当波长为300 nm (1 nm = 10-9 m)的光照射在某金属表面时,光电子的动能范围为0~ 4.0×10-19 J.此时遏止电压为|Ua| =__________________V;红限频率ν=_______________________ Hz.(普朗克常量h =6.63×10-34 J·s,基本电荷e =1.60×10-19 C)38. (本题 3分)(4546)若一无线电接收机接收到频率为108 Hz的电磁波的功率为1微瓦,则每秒接收到的光子数为__________________________.(普朗克常量h =6.63×10-34 J·s)39. (本题 3分)(4608)钨的红限波长是230 nm (1 nm = 10-9 m),用波长为180 nm的紫外光照射时,从表面逸出的电子的最大动能为___________________eV.(普朗克常量h =6.63×10-34 J·s,基本电荷e =1.60×10-19 C)40. (本题 4分)(4609)频率为 100 MHz的一个光子的能量是_______________________,动量的大小是______________________.(普朗克常量h =6.63×10-34 J·s)41. (本题 3分)(4611)某一波长的X光经物质散射后,其散射光中包含波长________和波长__________的两种成分,其中___________的散射成分称为康普顿散射.如图所示,一频率为ν 的入射光子与起始静止的自由电子发生碰撞和散射.如果散射光子的频率为ν′,反冲电子的动量为p,则在与入射光子平行的方向上的动量守恒定律的分量形式为___________________.43. (本题 3分)(4740)在X射线散射实验中,散射角为φ1= 45°和φ2=60°的散射光波长改变量之比Δλ1:Δλ2=_________________.44. (本题 4分)(4741)分别以频率为ν1和ν2的单色光照射某一光电管.若ν1 >ν2 (均大于红限频率ν0),则当两种频率的入射光的光强相同时,所产生的光电子的最大初动能E1____E2;所产生的饱和光电流I s1____ I s2.(用>或=或<填入)45. (本题 3分)(4742)某金属产生光电效应的红限为ν0,当用频率为ν (ν >ν)的单色光照射该金属时,从金属中逸出的光电子(质量为m)的德布罗意波长为________________.46. (本题 3分)(5618)在康普顿散射中,若入射光子与散射光子的波长分别为λ和λ′,则反冲电子获得的动能EK=______________________________.三计算题 (共114分)47. (本题10分)(0640)频率为ν的一束光以入射角i照射在平面镜上并完全反射,设光束单位体积中的光子数为n,求:(1) 每一光子的能量、动量和质量.(2) 光束对平面镜的光压(压强).48. (本题10分)(0640)频率为ν的一束光以入射角i照射在平面镜上并完全反射,设光束单位体积中的光子数为n,求:(1) 每一光子的能量、动量和质量.(2) 光束对平面镜的光压(压强).图中所示为在一次光电效应实验中得出的曲线(1) 求证:对不同材料的金属,AB 线的斜率相同. (2) 由图上数据求出普朗克恒量h . (基本电荷e =1.60×10-19 C) |14Hz)50. (本题 8分)(4246) 波长为λ的单色光照射某金属M 表面发生光电效应,发射的光电子(电荷绝对值为e ,质量为m )经狭缝S 后垂直进入磁感应强度为B K的均匀磁场(如图示),今已测出电子在该磁场中作圆运动的最大半径为R .求(1) 金属材料的逸出功A ; (2) 遏止电势差U a .B K× × × × ×51. (本题 5分)(4392) 用单色光照射某一金属产生光电效应,如果入射光的波长从λ1 = 400 nm 减到λ2 = 360 nm (1 nm = 10-9m),遏止电压改变多少?数值加大还是减小?(普朗克常量h =6.63×10-34 J ·s ,基本电荷e =1.60×10-19C)52. (本题 5分)(4393) 以波长λ = 410 nm (1 nm = 10-9m)的单色光照射某一金属,产生的光电子的最大动能E K = 1.0 eV ,求能使该金属产生光电效应的单色光的最大波长是多少?(普朗克常量h =6.63×10-34J ·s)53. (本题 5分)(4502) 功率为P 的点光源,发出波长为λ的单色光,在距光源为d 处,每秒钟落在垂直于光线的单位面积上的光子数为多少?若λ =6630 Å,则光子的质量为多少?(普朗克常量h =6.63×10-34J ·s)54. (本题 5分)(4502) 功率为P 的点光源,发出波长为λ的单色光,在距光源为d 处,每秒钟落在垂直于光线的单位面积上的光子数为多少?若λ =6630 Å,则光子的质量为多少? (普朗克常量h =6.63×10-34J ·s)55. (本题 5分)(4504) 已知X 射线光子的能量为0.60 MeV ,若在康普顿散射中散射光子的波长为入射光子的1.2倍,试求反冲电子的动能.56. (本题 8分)(4505) 用波长λ0 =1 Å的光子做康普顿实验.(1) 散射角φ=90°的康普顿散射波长是多少? (2) 反冲电子获得的动能有多大?(普朗克常量h =6.63×10-34 J ·s ,电子静止质量m e =9.11×10-31kg)红限波长为λ=0.15 Å的金属箔片置于B =30×10-4 T的均匀磁场中.今用单色γ射线照射而释放出电子,且电子在垂直于磁场的平面内作R = 0.1 m的圆周运动.求γ射线的波长.(普朗克常量h =6.63×10-34 J·s,基本电荷e =1.60×10-19 C,电子质量me=9.11×10-31 kg)58. (本题 5分)(4743)光电管的阴极用逸出功为A = 2.2 eV的金属制成,今用一单色光照射此光电管,阴极发射出光电子,测得遏止电势差为| Ua| = 5.0 V,试求:(1) 光电管阴极金属的光电效应红限波长;(2) 入射光波长.(普朗克常量h = 6.63×10-34 J·s,基本电荷e = 1.6×10-19 C)59. (本题 5分)(4744)以波长为λ = 0.200 μm的单色光照射一铜球,铜球能放出电子.现将此铜球充电,试求铜球的电势达到多高时不再放出电子?(铜的逸出功为A = 4.10 eV,普朗克常量h =6.63×10-34 J·s,1 eV =1.60×10-19 J)60. (本题 5分)(4745)波长为λ0 = 0.500 Å的X射线被静止的自由电子所散射,若散射线的波长变为λ = 0.522 Å,试求反冲电子的动能EK.(普朗克常量h =6.63×10-34 J·s)61. (本题10分)(5233)设康普顿效应中入射X射线(伦琴射线)的波长λ =0.700 Å,散射的X射线与入射的X射线垂直,求:(1) 反冲电子的动能EK.(2) 反冲电子运动的方向与入射的X射线之间的夹角θ.(普朗克常量h =6.63×10-34 J·s,电子静止质量me=9.11×10-31 kg)62. (本题 5分)(5366)假定在康普顿散射实验中,入射光的波长λ= 0.0030 nm,反冲电子的速度v = 0.6 c,求散射光的波长λ.(电子的静止质量me=9.11×10-31 kg ,普朗克常量h =6.63×10-34 J·s,1 nm = 10-9 m,c表示真空中的光速)63. (本题 8分)(5380)如图所示,某金属M的红限波长λ= 260 nm (1 nm =10-9 m)今用单色紫外线照射该金属,发现有光电子放出,其中速度最大的光电子可以匀速直线地穿过互相垂直的均匀电场(场强E = 5×103 V/m)和均匀磁场(磁感应强度为B = 0.005 T)区域,求:(1) 光电子的最大速度v.(2) 单色紫外线的波长λ.(电子静止质量me =9.11×10-31 kg,普朗克常量h =6.63×10-34 J·s)四 理论推导与证明题 (共49分)64. (本题 5分)(0486) 证明在康普顿散射实验中,反冲电子的动能K 和入射光子的能量E 之间的关系为: λλλ0−=E K .65. (本题12分)(0504) 证明在康普顿散射实验中,波长为λ0的一个光子与质量为m 0的静止电子碰撞后,电子的反冲角θ与光子散射角φ之间的关系为:100)]2tg()1[(tg −+=φλθc m h66. (本题 5分)(0486) 证明在康普顿散射实验中,反冲电子的动能K 和入射光子的能量E 之间的关系为: λλλ0−=E K .67. (本题12分)(0504) 证明在康普顿散射实验中,波长为λ0的一个光子与质量为m 0的静止电子碰撞后,电子的反冲角θ与光子散射角φ之间的关系为:100)]2tg()1[(tg −+=φλθc m h68. (本题 5分)(4394) 在光电效应实验中,测得光电子最大初动能E K 与入射光频率ν 的关系曲线如图所示.试证:普朗克常量)/(QS RS h =.(即直线的斜率)69. (本题10分)(4443) 如图示,能量为h ν0的光子流与静止质量为m e 的静止自由电子作弹性碰撞,若散射的光子的能量为h ν,试证明散射角φ 满足下式ννννφ00222)(2sin h c m e −=.五 回答问题 (共25分)70. (本题 5分)(4395) 已知从铝金属逸出一个电子至少需要A = 4.2 eV 的能量,若用可见光投射到铝的表面,能否产生光电效应?为什么?(普朗克常量h =6.63×10-34 J ·s ,基本电荷e =1.60×10-19 C)71. (本题 5分)(4396) 已知铂的逸出电势为8 V ,今用波长为 300 nm (1 nm = 10-9m)的紫外光照射,问能否产生光电效应?为什么?(普朗克常量h =6.63×10-34 J ·s ,基本电荷e =1.60×10-19 C)72. (本题 5分)(4398)红外线是否适宜于用来观察康普顿效应,为什么?=9.11×10-31 kg,(红外线波长的数量级为105 Å,电子静止质量me普朗克常量h =6.63×10-34 J·s)73. (本题10分)(4402)处于静止状态的自由电子是否能吸收光子,并把全部能量用来增加自己的动能?为什么?。
清华物理试题及答案

清华物理试题及答案一、选择题(每题5分,共20分)1. 光在真空中传播的速度是多少?A. 299,792,458 m/sB. 299,792,458 km/sC. 300,000,000 m/sD. 300,000,000 km/s答案:A2. 根据量子力学,一个粒子的状态由什么描述?A. 经典轨迹B. 波函数C. 动量D. 能量答案:B3. 以下哪个是电磁波谱中波长最长的部分?A. 无线电波B. 微波C. 红外线D. 可见光答案:A4. 根据热力学第二定律,以下哪个说法是正确的?A. 熵总是增加的B. 能量守恒C. 热能自发从冷物体传到热物体D. 永动机是可能的答案:A二、填空题(每题5分,共20分)1. 牛顿第一定律,也称为____定律,描述了物体在没有外力作用下的运动状态。
答案:惯性2. 电荷的单位是____。
答案:库仑3. 电磁波的传播不需要______。
答案:介质4. 根据相对论,当物体的速度接近光速时,其质量会______。
答案:增加三、计算题(每题10分,共20分)1. 一个质量为2kg的物体从静止开始,受到一个恒定的力10N作用,求物体在5秒末的速度。
答案:根据牛顿第二定律,F=ma,所以a=F/m=10N/2kg=5m/s²。
因此,v=at=5m/s²*5s=25m/s。
2. 一个点电荷Q=10^-6 C,距离它1m处的电场强度是多少?答案:根据库仑定律,E=kQ/r²,其中k是库仑常数,约为8.99×10^9 N·m²/C²。
所以E=(8.99×10^9 N·m²/C²)*(10^-6C)/(1m)²=8.99×10³ N/C。
四、简答题(每题10分,共20分)1. 简述什么是光电效应,并解释为什么光的频率越高,产生的光电子能量越大。
答案:光电效应是指光照射到金属表面时,金属会释放出电子的现象。
大学物理知识总结习题答案(第十章)量子物理基础

第十章 量子物理基础本章提要1. 光的量子性· 物体由于自身具有一定温度而以电磁波的形式向周围发射能量的现象称热辐射。
· 在任何温度下都能全部吸收照射到它表面上的各种波长的光(电磁波),则这种物体称为绝对黑体,简称黑体。
· 单位时间内物体单位表面积发出的包括所有波长在内的电磁波的辐射功率,称为辐射出射度。
2. 维恩位移定律· 在不同的热力学温度T 下,单色辐射本领的实验曲线存在一个峰值波长λm ,维恩从热力学理论导出T 和λm 满足如下关系λm T b =其中b 是维恩常量。
3. 斯忒藩—玻尔兹曼定律· 斯忒藩—玻尔兹曼定律表明黑体的辐射出射度M 与温T 的关系4T M σ=其中s 为斯忒藩—玻尔兹曼常量。
对于一般的物体4T M εσ=e 称发射率。
4. 黑体辐射· 黑体辐射不是连续地辐射能量,而是一份份地辐射能量,并且每一份能量与电磁波的频率ν成正比,这种能量分立的现象被称为能量的量子化,每一份最小能量E hv =被称为一个量子。
黑体辐射的能量为E nhv =,其中n =1,2,3,…,等正整数,h 为普朗克常数。
· 普朗克黑体辐射公式简称普朗克公式25/λ2πhc 1()λ1hc kT M T e l =-· 光是以光速运动的粒子流,这些粒子称为光量子,简称光子。
· 一个光子具有的能量为νh E =。
5. 粒子的波动性· 德布罗意认为实物粒子也具有波粒二象性,它的能量E 、动量p 跟和它相联系的波的频率ν、波长λ满足以下关系2E mc h ν==λh p m u == 这两个公式称为德布罗意公式或德布罗意假设。
与实物粒子相联系的波称为物质波或德布罗意波。
· x x p D D ?h 或者E t D D ?h 这一关系叫做不确定关系。
其中为位置不确定量、动量不确定量、能量不确定量、时间不确定量。
大学物理量子力学习题答案解析

一、简答题(1——8题,每题5分,共40分)1. 用球坐标表示,粒子波函数表为()ϕθψ,,r 。
写出粒子在),(ϕθ方向的立体角Ωd 中且半径在a r <<0范围内被测到的几率。
解:()⎰Ω=adrr r d P 022,,ϕθψ。
2. 写出三维无限深势阱⎩⎨⎧∞<<<<<<=其余区域,0,0,0,0),,(cz b y a x z y x V中粒子的能级和波函数。
解:能量本征值和本征波函数为⎪⎪⎭⎫ ⎝⎛=++222222222c n b n a n mE z yx n n n zy x π ,,3,2,1,00,0,0,sin sin sin 8),,(=⎪⎩⎪⎨⎧<<<<<<=n c z b y a x czn b y n a x n abc z y x z y x n n n z y x 其余区域πππψ3. 量子力学中,一个力学量Q 守恒的条件是什么?用式子表示。
解:有两个条件:0],[,0==∂∂H Q t Q。
4.)(z L L ,2 的共同本征函数是什么?相应的本征值又分别是什么?解:()zL L,2的共同本征函数是球谐函数),(ϕθlmY。
),(),(,),()1(),(22ϕθϕθϕθϕθlm lm z lm lm Y m Y L Y l l Y L =+=。
5. 量子力学中,体系的任意态)(x ψ可用一组力学量完全集的共同本征态)(x n ψ展开:∑=nn n x c x )()(ψψ,写出展开式系数n c 的表达式。
解: ()dxx x x x c n n n ⎰==)()()(,)(*ψψψψ。
6. 一个电子运动的旋量波函数为()()()⎪⎪⎭⎫ ⎝⎛-=2,2,,r r s r z ψψψ,写出表示电子自旋向上、位置在r处的几率密度表达式,以及表示电子自旋向下的几率的表达式。
解:电子自旋向上(2 =z s )、位置在r 处的几率密度为()22/, r ψ;电子自旋向下(2 -=z s )的几率为()232/,⎰-r r d ψ。
清华出版社《大学物理》专项练习及解析 量子2

清华出版社专项练习一 选择题 (共48分)1. (本题 3分)(0507) 已知用光照的办法将氢原子基态的电子电离,可用的最长波长的光是 913 Å的紫外光,那么氢原子从各受激态跃迁至基态的赖曼系光谱的波长可表示为:(A) 11913+−=n n λ Å. (B) 11913−+=n n λ Å. (C) 1191322−+=n n λ Å. (D) 191322−=n n λ Å. [ ]2. (本题 3分)(4190) 要使处于基态的氢原子受激发后能发射赖曼系(由激发态跃迁到基态发射的各谱线组成的谱线系)的最长波长的谱线,至少应向基态氢原子提供的能量是(A) 1.5 eV . (B) 3.4 eV .(C) 10.2 eV . (D) 13.6 eV . [ ]3. (本题 3分)(4194) 根据玻尔的理论,氢原子在n =5轨道上的动量矩与在第一激发态的轨道动量矩之比为(A) 5/4. (B) 5/3.(C) 5/2. (D) 5. [ ]4. (本题 3分)(4195) 氢原子光谱的巴耳末线系中谱线最小波长与最大波长之比为(A) 7/9. (B) 5/9.(C) 4/9. (D) 2/9. [ ]5. (本题 3分)(4195) 氢原子光谱的巴耳末线系中谱线最小波长与最大波长之比为(A) 7/9. (B) 5/9.(C) 4/9. (D) 2/9. [ ]6. (本题 3分)(4197) 由氢原子理论知,当大量氢原子处于n =3的激发态时,原子跃迁将发出:(A) 一种波长的光. (B) 两种波长的光.(C) 三种波长的光. (D) 连续光谱. [ ]7. (本题 3分)(4198) 根据玻尔理论,氢原子中的电子在n =4的轨道上运动的动能与在基态的轨道上运动的动能之比为(A) 1/4. (B) 1/8.(C) 1/16. (D) 1/32. [ ]8. (本题 3分)(4199) 根据玻尔氢原子理论,氢原子中的电子在第一和第三轨道上运动时速度大小之比v 1/ v 3是(A) 1/9. (B) 1/3.(C) 3. (D) 9. [ ]9. (本题 3分)(4239)假定氢原子原是静止的,则氢原子从n = 3 的激发状态直接通过辐射跃迁到基态时的反冲速度大约是(A) 4 m/s.(B) 10 m/s .(C) 100 m/s . (D) 400 m/s .[](氢原子的质量m =1.67×10-27 kg)10. (本题 3分)(4411)氢原子光谱的巴耳末系中波长最大的谱线用λ1表示,其次波长用λ2表示,则它们的比值λ1/λ2为:(A) 20/27.(B) 9/8.(C) 27/20.(D) 16/9.[]11. (本题 3分)(4619)按照玻尔理论,电子绕核作圆周运动时,电子的动量矩L的可能值为(A) 任意值.(B) nh,n = 1,2,3,…(C) 2π nh,n = 1,2,3,…(D) nh/(2π),n = 1,2,3,…[]12. (本题 3分)(4622)具有下列哪一能量的光子,能被处在n = 2的能级的氢原子吸收?(A) 1.51 eV.(B) 1.89 eV.(C) 2.16 eV.(D) 2.40 eV.[]13. (本题 3分)(4747)若用里德伯常量R表示氢原子光谱的最短波长,则可写成(A) λmin =1 / R.(B) λmin =2 / R.(C) λmin =3 / R.(D) λmin =4 / R.[]14. (本题 3分)(4748)已知氢原子从基态激发到某一定态所需能量为 10.19 eV,当氢原子从能量为-0.85 eV的状态跃迁到上述定态时,所发射的光子的能量为(A) 2.56 eV.(B) 3.41 eV.(C) 4.25 eV.(D) 9.95 eV.[]15. (本题 3分)(4749)要使处于基态的氢原子受激后可辐射出可见光谱线,最少应供给氢原子的能量为(A) 12.09 eV. (B) 10.20 eV.(C) 1.89 eV.(D) 1.51 eV.[]16. (本题 3分)(4750)在气体放电管中,用能量为12.1 eV的电子去轰击处于基态的氢原子,此时氢原子所能发射的光子的能量只能是(A) 12.1 eV. (B) 10.2 eV.(C) 12.1 eV,10.2 eV和 1.9 eV. (D) 12.1 eV,10.2 eV和 3.4 eV.[ ]二 填空题 (共101分)17. (本题 4分)(0514) 在玻尔氢原子理论中势能为负值,而且数值比动能大,所以总能量为________值,并且只能取____________值.18. (本题 4分)(4191) 在氢原子发射光谱的巴耳末线系中有一频率为6.15×1014 Hz 的谱线,它是氢原子从能级E n =__________eV 跃迁到能级E k =__________eV 而发出的. (普朗克常量h =6.63×10-34 J ·s ,基本电荷e =1.60×10-19 C)19. (本题 4分)(4192) 在氢原子光谱中,赖曼系(由各激发态跃迁到基态所发射的各谱线组成的谱线系)的最短波长的谱线所对应的光子能量为_______________eV ;巴耳末系的最短波长的谱线所对应的光子的能量为___________________eV .(里德伯常量 R =1.097×107 m -1 ,普朗克常量h =6.63×10-34 J ·s ,1 eV =1.60×10-19 J ,真空中光速 c =3×108 m ·s -1 )20. (本题 4分)(4196) 氢原子基态的电离能是 _______________eV .电离能为+0.544 eV 的激发态氢原子,其电子处在n =_________________ 的轨道上运动.21. (本题 4分)(4200) 设大量氢原子处于n =4的激发态,它们跃迁时发射出一簇光谱线.这簇光谱线最多可能有 ________________ 条,其中最短的波长是 _______ Å(普朗克常量h =6.63×10-34 J ·s)22. (本题 4分)(4201) 图示被激发的氢原子跃迁到低能级时(图中E 1不是基态能级),可发出波长为λ1、λ2、λ3的辐射,其频率ν1、ν2和ν3满足关系式______________________;三个波长满足关系式__________________.λ1λ2λ3E 1E 2E 3玻尔的氢原子理论中提出的关于__________________________________和____________________________________的假设在现代的量子力学理论中仍然是两个重要的基本概念.24. (本题 3分)(4424)欲使氢原子发射赖曼系(由各激发态跃迁到基态所发射的谱线构成)中波长为1216 Å的谱线,应传给基态氢原子的最小能量是_____________________eV.(普朗克常量h = 6.63×10-34 J·s,基本电荷e =1.60×10-19 C)25. (本题 5分)(4513)玻尔的氢原子理论的三个基本假设是:(1)____________________________________,(2)____________________________________,(3)____________________________________.26. (本题 3分)(4517)欲使氢原子能发射巴耳末系中波长为4861.3 Å的谱线,最少要给基态氢原子提供_______________eV的能量.(里德伯常量R =1.097×107 m-1 )27. (本题 3分)(4518)欲使氢原子能发射巴耳末系中波长为6562.8 Å的谱线,最少要给基态氢原子提供_________________eV的能量.(里德伯常量R =1.097×107 m-1 )28. (本题 3分)(4620)按照玻尔理论,移去处于基态的He+中的电子所需能量为_____________eV.29. (本题 3分)(4623)氢原子中电子从n = 3的激发态被电离出去,需要的能量为_________eV.30. (本题 3分)(4624)氢原子由定态l跃迁到定态k可发射一个光子.已知定态l的电离能为0.85 eV,又知从基态使氢原子激发到定态k所需能量为10.2 eV,则在上述跃迁中氢原子所发射的光子的能量为__________eV.玻尔氢原子理论中的定态假设的内容是:______________________________ ______________________________________________________________________ _____________________________________________________________________.32. (本题 3分)(4752)玻尔氢原子理论的基本假设之一是定态跃迁的频率条件,其内容表述如下:______________________________________________________________________ ____________________________________________________.33. (本题 3分)(4753)玻尔氢原子理论的基本假设之一是电子轨道动量矩的量子化条件,其内容可表述如下:____________________________________________________________ ______________________________________________________________________ ________________________________________________________________.34. (本题 4分)(4754)氢原子的部分能级跃迁示意如图.在这些能级跃迁中,(1) 从n =______的能级跃迁到n =_____的能级时所发射的光子的波长最短;(2) 从n =______的能级跃迁到n =______的能级时所发射的光子的频率最小.n = 1 n = 2 n = 3 n = 435. (本题 4分)(4755)被激发到n =3的状态的氢原子气体发出的辐射中,有______条可见光谱线和_________条非可见光谱线.36. (本题 4分)(4756)氢原子从能量为-0.85 eV的状态跃迁到能量为-3.4 eV的状态时,所发射的光子能量是_________eV,这是电子从n =_______的能级到n = 2的能级的跃迁.当氢原子从某初始状态跃迁到激发能(从基态到激发态所需的能量)为10.19eV 的激发态上时,发出一个波长为4860 Å的光子,则初始状态氢原子的能量是________eV .38. (本题 3分)(4758) 要使处于基态的氢原子受激发后能辐射氢原子光谱中波长最短的光谱线,最少需向氢原子提供______________eV 的能量.39. (本题 3分)(4759) 已知基态氢原子的能量为-13.6 eV ,当基态氢原子被 12.09 eV 的光子激发后,其电子的轨道半径将增加到玻尔半径的______倍.40. (本题 3分)(4760) 当一个质子俘获一个动能E K =13.6 eV 的自由电子组成一个基态氢原子时,所发出的单色光频率是______________________________.(基态氢原子的能量为-13.6 eV ,普朗克常量h =6.63×10-34 J ·s)41. (本题 3分)(4761) 使氢原子中电子从n =3的状态电离,至少需要供给的能量为_________eV(已知基态氢原子的电离能为13.6 eV).42. (本题 3分)(4762) 在氢原子光谱的巴耳末系中,波长最长的谱线和波长最短的谱线的波长比值是______________.43. (本题 3分)(4763) 在氢原子光谱的巴耳末系中,波长最长的谱线H α和相邻的谱线H β的波长比值是______________.44. (本题 4分)(4765) 处于基态的氢原子吸收了13.06 eV 的能量后,可激发到n =________的能级,当它跃迁回到基态时,可能辐射的光谱线有________条.45. (本题 4分)(5369) 根据氢原子理论,若大量氢原子处于主量子数n = 5的激发态,则跃迁辐射的谱线可以有________条,其中属于巴耳末系的谱线有______条.三计算题 (共113分)46. (本题 8分)(0316)组成某双原子气体分子的两个原子的质量均为m,间隔为一固定值d,并绕通过d的中点而垂直于d的轴旋转,假设角动量是量子化的,并符合玻尔量子化条件.试求:(1) 可能的角速度;(2) 可能的量子化的转动动能.47. (本题 5分)(0521)实验发现基态氢原子可吸收能量为 12.75 eV的光子.(1) 试问氢原子吸收该光子后将被激发到哪个能级?(2) 受激发的氢原子向低能级跃迁时,可能发出哪几条谱线?请画出能级图(定性),并将这些跃迁画在能级图上.48. (本题10分)(0532)已知氢光谱的某一线系的极限波长为3647 Å,其中有一谱线波长为6565 Å.试由玻尔氢原子理论,求与该波长相应的始态与终态能级的能量.(R =1.097×107 m-1 )49. (本题 5分)(0537)在氢原子中,电子从某能级跃迁到量子数为n的能级,这时轨道半径改变q 倍,求发射的光子的频率.50. (本题10分)(0538)根据玻尔理论(1) 计算氢原子中电子在量子数为n的轨道上作圆周运动的频率;(2) 计算当该电子跃迁到(n-1)的轨道上时所发出的光子的频率;(3) 证明当n很大时,上述(1)和(2)结果近似相等.51. (本题10分)(0570)氢原子激发态的平均寿命约为10-8s,假设氢原子处于激发态时,电子作圆轨道运动,试求出处于量子数n =5状态的电子在它跃迁到基态之前绕核转了多少圈.( me= 9.11×10-31 kg,e =1.60×10-19 C,h =6.63×10-34 J·s,ε=8.85×10-12 C2·N-1·m-2 )52. (本题12分)(4202)氢原子光谱的巴耳末线系中,有一光谱线的波长为4340 Å,试求:(1) 与这一谱线相应的光子能量为多少电子伏特?(2) 该谱线是氢原子由能级En 跃迁到能级Ek产生的,n和k各为多少?(3) 最高能级为E5的大量氢原子,最多可以发射几个线系,共几条谱线?请在氢原子能级图中表示出来,并说明波长最短的是哪一条谱线.53. (本题 5分)(4412)处于基态的氢原子被外来单色光激发后发出的光仅有三条谱线,问此外来光的频率为多少?(里德伯常量R =1.097×107 m-1)54. (本题 5分)(4413)试求氢原子线系极限的波数表达式及赖曼系(由各激发态跃迁到基态所发射的谱线构成)、巴耳末系、帕邢系(由各高能激发态跃迁到n =3的定态所发射的谱线构成)的线系极限的波数.(里德伯常量R =1.097×107 m-1 )处于第一激发态的氢原子被外来单色光激发后,发射的光谱中,仅观察到三条巴耳末系光谱线.试求这三条光谱线中波长最长的那条谱线的波长以及外来光的频率. (里德伯常量R =1.097×107 m -1)56. (本题 5分)(4519) 已知氢原子中电子的最小轨道半径为 5.3×10-11 m ,求它绕核运动的速度是多少? (普朗克常量h =6.63×10-34 J ·s ,电子静止质量m e =9.11×10-31 kg)57. (本题 5分)(4520) 试估计处于基态的氢原子被能量为 12.09 eV 的光子激发时,其电子的轨道半径增加多少倍?58. (本题 5分)(4547) 已知电子在垂直于均匀磁场B K 的平面内运动,设电子的运动满足玻尔量子化条件,求电子轨道的半径r n =?59. (本题 8分)(4767) 当氢原子从某初始状态跃迁到激发能(从基态到激发态所需的能量)为ΔE =10.19 eV 的状态时,发射出光子的波长是λ=4860 Å,试求该初始状态的能量和主量子数.(普朗克常量h =6.63×10-34 J ·s ,1 eV =1.60×10-19 J)60. (本题 5分)(4768) 用某频率的单色光照射基态氢原子气体,使气体发射出三种频率的谱线,试求原照射单色光的频率.(普朗克常量h =6.63×10-34 J ·s ,1 eV =1.60×10-19 J)61. (本题 5分)(5238) 已知氢原子光谱中有一条谱线的波长是λ=1025.7 Å,氢原子的里德伯常量R=109677 cm -1.问:跃迁发生在哪两个能级之间?62. (本题 5分)(5370) 若处于基态的氢原子吸收了一个能量为h ν =15 eV 的光子后其电子成为自由电子(电子的质量m e =9.11×10-31 kg),求该自由电子的速度v .四 理论推导与证明题 (共35分)63. (本题10分)(4193) 设氢原子光谱的巴耳末系中第一条谱线(H α)的波长为λα,第二条谱线(H β)的波长为λβ,试证明:帕邢系(由各高能态跃迁到主量子数为3的定态所发射的各谱线组成的谱线系)中的第一条谱线的波长为βαβαλλλλλ−=64. (本题 5分)(4417) 测得氢原子光谱中的某一谱线系的极限波长为λk =364.7 nm .(1 nm = 10-9m)试推证此谱线系为巴耳末系. (里德伯常量R =1.097×107 m -1 )试用玻尔理论推导氢原子在稳定态中的轨道半径.66. (本题 5分)(4427) 试根据玻尔关于氢原子结构的基本假说, 推导里德伯常量的理论表达式.(氢原子能级公式: 2204281he m n E e n ε⋅−=)67. (本题10分)(4444) 质量为m 的卫星,在半径为r 的轨道上环绕地球运动,线速度为v .(1) 假定玻尔氢原子理论中关于轨道角动量的条件对于地球卫星同样成立.证明地球卫星的轨道半径与量子数的平方成正比,即r = kn 2 (k 是比例常数).(2) 应用(1)的结果求卫星轨道和它的下一个“容许”轨道间的距离.由此进一步说明在宏观问题中轨道半径实际上可认为是连续变化的(利用以下数据作估算:普朗克常量s J 106.634⋅×=−h ,地球质量kg 10624×=M ,地球半径km 104.66×=R ,万有引力常数2211/kg Nm 107.6−×=G ).五 回答问题 (共15分)68. (本题 5分)(4220) 解释玻尔原子理论中的下列概念:定态;基态;激发态;量子化条件.69. (本题 5分)(4418) 氢原子发射一条波长为λ =4340 Å的光谱线.试问该谱线属于哪一谱线系?氢原子是从哪个能级跃迁到哪个能级辐射出该光谱线的?(里德伯常量R =1.097×107 m -1 )70. (本题 5分)(4769) 玻尔氢原子理论的成功和局限性是什么?一选择题 (共48分)1. (本题 3分)(0507)(D)2. (本题 3分)(4190)(C)3. (本题 3分)(4194)(C)4. (本题 3分)(4195)(B)5. (本题 3分)(4195)(B)6. (本题 3分)(4197)(C)7. (本题 3分)(4198)(C)8. (本题 3分)(4199)(C)9. (本题 3分)(4239)(A)10. (本题 3分)(4411)(C)11. (本题 3分)(4619)(D)12. (本题 3分)(4622)(B)13. (本题 3分)(4747)(A)14. (本题 3分)(4748)(A)15. (本题 3分)(4749)(A)16. (本题 3分)(4750)(C)二填空题 (共101分)17. (本题 4分)(0514)负2分不连续2分-0.85 2分 -3.4 2分19. (本题 4分)(4192) 13.6 2分 3.4 2分20. (本题 4分)(4196) 13.6 2分 5 2分21. (本题 4分)(4200) 6 2分 973 2分22. (本题 4分)(4201) 123ννν+= 2分123111λλλ+= 2分23. (本题 4分)(4423) 定态能级 2分 能级跃迁决定谱线频率. 2分24. (本题 3分)(4424) 10.2 3分25. (本题 5分)(4513) 量子化定态假设 1分 量子化跃迁的频率法则 h E E k n kn /−=ν 2分 角动量量子化假设 π=2/nh L n =1,2,3,…… 2分26. (本题 3分)(4517) 12.75 3分27. (本题 3分)(4518) 12.09 3分28. (本题 3分)(4620) 54.4 3分29. (本题 3分)(4623) 1.51 3分30. (本题 3分)(4624) 2.553分31. (本题 3分)(4751) 原子只能处在一系列能量不连续的稳定状态(定态)中,处于定态中的原子,其电子只能在一定轨道上绕核作圆周运动,但不发射电磁波. 3分原子中电子从能量为E n 的定态跃迁到能量为E k 的定态时,便发射(当E n >E k 时)或吸收(当E n <E k 时)单色光,其频率ν由下式决定:hE E kn −=ν (h 为普朗克常量) 3分33. (本题 3分)(4753) 在电子绕核的圆周运动中,只有电子的动量矩L 等于h /2π 的整数倍的那些轨道才是可能的,即:π=2hn L (n = 1,2,3,……)(h 为普朗克常量) 3分34. (本题 4分)(4754) 4 1 2分 4 3 2分35. (本题 4分)(4755) 1 2分 2 2分36. (本题 4分)(4756) 2.55 2分4 2分37. (本题 3分)(4757) -0.85 3分38. (本题 3分)(4758) 13.6 3分39. (本题 3分)(4759) 9 3分40. (本题 3分)(4760) 6.56×1015 Hz 3分41. (本题 3分)(4761) 1.51 3分42. (本题 3分)(4762) 1.8 3分43. (本题 3分)(4763) 1.35 3分44. (本题 4分)(4765) 5 2分 10 2分10 2分 3 2分三 计算题 (共113分)46. (本题 8分)(0316) 解:(1) 此双原子气体分子绕轴旋转时的角动量为:221d m L ω= 2分据 )2/(π=nh L ,n = 0,1,2…… 2分则 221d m ω)2/(π=nh , )/(2d m nh π=ω 2分(2) 此系统的转动动能为:22222224221dm h n r m m E π==×=ωv ,n = 0,1,2…… 2分47. (本题 5分)(0521) 解:(1) )11(2nRhc E −=Δ75.12)11(6.132=−=n eVn =4 2分(2) 可以发出λ41、λ31、λ21、λ43、λ42、λ32六条谱线. 1分 能级图如图所示. 图2分λ43 λ42λ41λ32λ31 λ21n =432148. (本题10分)(0532) 解:极限波数 2//1~k R ==∞λν 可求出该线系的共同终态. 1分2==∞λR k 2分11(1~22n k R −==λν2分由λ =6565 Å 可得始态 ∞∞−=λλλλR n =3 2分由 2216.13nn E E n −==eV 1分可知终态n =2,E 2 = -3.4 eV 1分始态 n =3,E 3 = -1.51 eV 1分49. (本题 5分)(0537) 解:设始态能级量子数为 k , 则轨道半径由r k 变为r n , 且r k = qr n .由 2202meh k r k π=ε 2分可得 22qn k = 1分光子的频率 11(22kn Rc −=ν即 )11()1(2222q nRck n n Rc −=−=ν 2分解:(1) r m re 22024v =πε ① 1分 π=2hn r mv . ② 1分rn v=ω ③ 1分①、②、③联立解出 3320412n h me n ⋅π=εω 33204142nh me nn ⋅=π=εων 2分(2) 电子从n 态跃迁到( n -1 )态所发出光子的频率为2222)1(12]1)1(1[−−=−−==′n n n cRn n cR c λν 223204)1(128−−⋅=n n n h me ε 2分 (3) 当n 很大时,上式变为23204)1()/1(28−−⋅=′n n n h me ενn n h me νε=⋅≈3320418 3分51. (本题10分)(0570) 解:电子作一次圆周运动所需时间(即周期T )为ωπ=2T ① 1分令激发态的平均寿命为 τ = 10-8 s ,故电子在τ内从激发态跃迁到基态前绕核的圈数为 TN τ=② 1分 电子作圆周运动的周期T可由下面二式求出r m r e 22024v =πε ③ 1分 π=22hr m ωn ④ 2分可求出 33320412n h n me ⋅π=εω ⑤ 2分由①、②、⑤可得 T N τ=373332041054.614n n h n me ×=⋅=ετ 2分当 n = 5 N = 5.23×105 1分解:(1) ==λν/hc h 2.86 eV . 2分(2) 由于此谱线是巴耳末线系,其 k =2 2分 4.32/21−==E E K eV (E 1 =-13.6 eV) νh E n E E K n +==21/ 51=+=νh E E n K . 4分(3) 可发射四个线系,共有10条谱线. 2分 见图 1分波长最短的是由n =5跃迁到n =1的谱线. 1分=5 =4 =3 =2=153. (本题 5分)(4412) 解:由于发出的光线仅有三条谱线,按:)11(~22n k cR c −=⋅=νν 2分 n =3,k =2 得一条谱线. n =3,k =1 得一条谱线. n =2,k =1 得一条谱线.可见氢原子吸收外来光子后,处于n =3的激发态.以上三条光谱线中,频率最大的一条是: )3111(22−=cR ν=2.92×1015 Hz这也就是外来光的频率. 3分54. (本题 5分)(4413) 解: 11(~22n k R −=ν令线系极限: n →∞ 可得2/~k R =ν2分 赖曼系: k =1=ν~ 1.097×107/12 =1.097×107 m -1 1分 巴耳末系: k =2=ν~ 1.097×107/22 =0.274×107 m -1 1分 帕邢系: k =3=ν~ 1.097×107/32 =0.122×107 m -1 1分解:因为观察到巴耳末系中的三条光谱线,所以只可能是从n = 5、4、3的状态,分别跃迁到n =2的状态而发出的.由 121(1~2222n R n n−==λν得 22222221−⋅=n n R n λ 所求的波长为氢原子从由n = 3的状态跃迁到n = 2的状态发出的谱线的波长,上式代入n = 3得λ23 = 6.56×10-7m = 656 nm 2分外来光应使氢原子从n = 2的状态跃迁到n = 5的状态,其频率为: ν25 = c /λ25而: λ25 = 4.34×10-7m = 434 nmν25 = c /λ25 = 6.91×1014Hz 3分56. (本题 5分)(4519) 解:根据玻尔氢原子理论的角动量量子化条件π=2/nh r m e v (n =1,2,3,……)则 )2/(r m nh e π=v n =1时对应最小轨道半径 r 1 =5.3×10-11 m 3分∴ )2/(1r m nh e π=v =2.18×106 m/s 2分57. (本题 5分)(4520) 解:设激发态量子数为n , 根据玻尔理论:νh E E n +=1对氢原子 E 1 =-13.6 eV (基态),h ν =12.09 eV∴ E n =-1.51 eV 2分另外,对氢原子有 E n =-13.6/n 2eV由此有 -1.51=-13.6/n 2故 n 2≈9,n =3 2分氢原子的半径公式为 r n = n 2a 1 = 9 a 1即氢原子的半径增加到基态时的9倍. 1分58. (本题 5分)(4547) 解:设轨道半径为r n ,电子运动速度为v .则由n r m B e /2v v = 2分 =n r m L n ==v 2分得 n eB r n ⋅=2/1)/(= ( n = 1,2,3……) 1分解:所发射的光子能量为 ==λε/hc 2.56 eV 2分氢原子在激发能为10.19 eV 的能级时,其能量为=+=ΔE E E K 1-3.41 eV 2分氢原子在初始状态的能量为 =+=K n E E ε-0.85 eV 2分该初始状态的主量子数为 41==nE E n 2分60. (本题 5分)(4768) 解:按题意可知单色光照射的结果,氢原子被激发至n = 3的状态(因为它发射三种频率的谱线),故知原照射光子的能量为)6.13(36.13213−−−=−=E E ε = 12.09 eV=1.93×10-18 J 3分该单色光的频率为 ==hεν 2.92×1015 Hz 2分61. (本题 5分)(5238) 解:因为 1025.7 Å是紫外线,是属于赖曼系的一条谱线,故知它是在n = n 1→ n =1这两个能级间的跃迁中发射出来的.根据)/11/1(~212n R −=ν 3分并代入λν/1~= 可解得 )1(1−=R R n λλ=3.00所以1025.7 Å谱线是在n =3─→n =1的能级间的跃迁中辐射的. 2分62. (本题 5分)(5370) 解:把一个基态氢原子电离所需最小能量E i = 13.6 eV 1分则有 221v e i m E h +=ν 2分=−=e i m E h /)(2νv 7.0×105 m/s 2分四 理论推导与证明题 (共35分)63. (本题10分)(4193) 证:根据巴耳末公式: )121(/122n R −=λ 2分得第一条谱线波长为 23/1/1λλα=)3121(22−=R 2分第二条谱线波长为 24/1/1λλβ=)4121(22−=R 2分而帕邢系中第一条谱线的波长应为34/1λ)4131(22−=R 2分由23242423232411λλλλλλ−=−)4131(22−=R 34/1λ=可得 βαβαλλλλλλλλλ−=−=2423232434 2分证: )}/1)/1[(/122n k R −=λ 1分当 n →∞得极限波长 2//1k R k =λ ∴ R k k λ=2 1分 2)(2/1≈=R k k λ 2分可见:该谱线系为巴尔末系. 1分65. (本题 5分)(4426) 解:应用库仑定律和牛顿运动定律 有:)4/(/2022r e r m e επ=v 1分根据玻尔理论的量子化条件假设: =n r m L e ==v 2分由以上两式消去v ,并把r 换成r n .得)/(2202e m h n r e n π=ε,n =1,2,3,…… 2分66. (本题 5分)(4427) 解: )()/1(k n kn E E h −⋅=ν , )()/1(/~kn kn kn E E hc c −⋅==νν 2分而: )8/(22204n h e m E e n ε−=, )8/(22204k h e m E e k ε−= ,代入上式: 11(8~223204nk c h e m e kn −=εν与 )11(~22n k R kn−=ν 比较得里德伯常量 )8/(3204c h e m R e ε=. 3分67. (本题10分)(4444) 证:(1) 根据:r m F /2v =及 2/r GMm F =(M 为地球质量)得: r m r GMm //22v = 2分利用玻尔假设: π⋅=2hn r m n v 1分联立以上两式则得: []M Gm nh r n 22)2/(π=2分令: MGm h k 2224π=上式变为:2kn r n = 得证. 1分 (2) 由: 2kn r n = 可得:k n kn n k r r n n )12()1(221+=−+=−+ 1分估算k 与n :设 m > 1 kg ,代入数据可得 m 1082−<k ,而 2/11)(22n n n kr nk r r =≈−+则 0)/(2/)(2/11≈≈−+n n n n r k r r r (实际情形r n ﹥R )即相邻两个轨道之间的距离与轨道半径相比可忽略不计,这表明轨道半径的“容许”值实际上可认为是连续变化的. 3分五 回答问题 (共15分)68. (本题 5分)(4220) 答:定态:原子系统所处的一系列分立的有确定能量的状态,处于这些状态时.原子不辐射能量. 2分 基态:原子系统能量最低的状态 1分 激发态:原子系统所在的高于基态能量的量子态. 1分 量子化条件:决定原子系统可能存在的各种分立定态的条件. 1分69. (本题 5分)(4418) 答:4340 Å 属于可见光范围,谱线属于巴耳末系. 3分)121(1~22n R −==λν44)/(14/112−=−=R RR n λλλ代入数值可得 5≈n 可见该辐射是氢原子从n =5的能级跃迁到n =2的能级的辐射. 2分70. (本题 5分)(4769) 答:成功:从理论上解释了氢原子光谱的实验规律,并从理论上算出里德伯常量. 1分 玻尔首先提出了原子系统能量量子化的概念和角动量量子化的假设. 1分 玻尔创造性的提出了定态、跃迁等重要概念,为近代量子物理的建立奠定了基础. 1分 局限性:由于未能预见微观粒子的波粒二象性,虽然提出正确的量子假设,但未能完全脱离经典理论的影响,仍采用经典理论的思想和处理方法,因此不能正确说明氢原子内部的微观粒子运动. 2分。
清华大学大学物理习题库试题与答案力热电三合一版

力学部分一、选择题1.0018:某质点作直线运动的运动学方程为x =3t -5t 3 + 6 (SI),则该质点作(A) 匀加速直线运动,加速度沿x 轴正方向(B) 匀加速直线运动,加速度沿x 轴负方向(C) 变加速直线运动,加速度沿x 轴正方向(D) 变加速直线运动,加速度沿x 轴负方向 [ ] 2.5003:一质点在平面上运动,已知质点位置矢量的表示式为(其中a 、b 为常量),则该质点作(A) 匀速直线运动 (B) 变速直线运动(C) 抛物线运动 (D)一般曲线运动 [ ] 3.0015:一运动质点在某瞬时位于矢径的端点处, 其速度大小为(A) (B) (C) (D) 4.0508:质点沿半径为R 的圆周作匀速率运动,每T 秒转一圈。
在2T 时间间隔中,其平均速度大小与平均速率大小分别为(A) 2p R /T , 2p R/T (B) 0 , 2πR /T (C) 0 , 0 (D) 2πR /T , 0.[ ] 5.0518:以下五种运动形式中,保持不变的运动是(A) 单摆的运动 (B) 匀速率圆周运动(C) 行星的椭圆轨道运动 (D) 抛体运动 (E) 圆锥摆运动 [ ]6.0519:对于沿曲线运动的物体,以下几种说法中哪一种是正确的:(A) 切向加速度必不为零(B) 法向加速度必不为零(拐点处除外) (C) 由于速度沿切线方向,法向分速度必为零,因此法向加速度必为零(D) 若物体作匀速率运动,其总加速度必为零 (E) 若物体的加速度为恒矢量,它一定作匀变速率运动 [ ] 7.0602:质点作曲线运动,表示位置矢量,表示速度,表示加速度,S 表示路程,a 表示切向加速度,下列表达式中, (1) , (2) , (3) , (4)(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的(C) 只有(2)是对的 (D) 只有(3)是对的 [ ]8.0604:某物体的运动规律为,式中的k 为大于零的常量。
清华大学《大学物理》题库及答案__01_力学

0 时,
v
1 2 kt v 0 2 ,
1 v kt 2 v 0 2 (B) ,
, (D) ] 9.0014:在相对地面静止的坐标系内,A、B 二船都以 2 m/s 速率匀速行驶,A 船沿 x 轴正向,B 船沿 y 轴正向。今在 A 船上设置与静止坐标系方向相同的坐标系(x、y 方向单位 [ 矢用 i 、 j 表示),那么在 A 船上的坐标系中,B 船的速度(以 m/s 为单位)为
GMm 2 (B) R2 R R GMm 1 2 2 R1
GMm
(C)
R1 R2 R1 R2
GMm R1 R2 2 R12 R2
t
r A cost i B sint j
(B) m ( A B )
2 2 2
式中 A、B、都是正的常量。由此可知外力在 t=0 到 t=/(2)这段时间内所作的功为
[ ] 32.0095:有一劲度系数为 k 的轻弹簧,竖直放置,下端悬一质量 为 m 的小球,开始时使弹簧为原长而小球恰好与地接触,今将弹簧上端 缓慢地提起,直到小球刚能脱离地面为止,在此过程中外力作功为
J
[
] 26.0413:如图,在光滑水平地面上放着一辆小车,车上左端放着一只箱子,今用同样
的水平恒力 F 拉箱子,使它由小车的左端达到右端,一次小车被固定在水平地面上,另一 次小车没有固定。试以水平地面为参照系,判断下列结论中正确的是 F (A) 在两种情况下, F 做的功相等 (B) 在两种情况下,摩擦力对箱子做的功相等 (C) 在两种情况下,箱子获得的动能相等 (D) 在两种情况下,由于摩擦而产生的热相等 [ ] 27.5019:对功的概念有以下几种说法: (1) 保守力作正功时,系统内相应的势能增加 (2) 质点运动经一闭合路径,保守力对质点作的功为零 (3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零 在上述说法中: (A) (1)、(2)是正确的 (B) (2)、(3)是正确的 (C) 只 有 (2) 是 正 确 的 (D) 只 有 (3) 是 正 确 的 [ ] 28.5020:有一劲度系数为 k 的轻弹簧,原长为 l0,将它吊在天花板上。当它下端挂一 托盘平衡时,其长度变为 l1。然后在托盘中放一重物,弹簧长度变为 l2,则由 l1 伸长至 l2 的 过程中,弹性力所作的功为 (A) [
大学物理-量子力学基础习题思考题及答案word精品文档5页

习题22-1.计算下列客体具有MeV 10动能时的物质波波长,(1)电子;(2)质子。
解:(1) 电子高速运动,设电子的总能量可写为:20K E E m c =+ 用相对论公式,222240E c p m c =+ 可得(2)对于质子,利用德布罗意波的计算公式即可得出:22-2.计算在彩色电 视显像管的加速电压作用下电子的物质波波长,已知加速电压为kV 0.25,(1)用非相对论公式;(2)用相对论公式。
解:(1)用非相对论公式:m meU h mE h 123193134108.71025106.1101.921063.622p h ----⨯=⨯⨯⨯⨯⨯⨯⨯====λ(2)用相对论公式:22-3.一中子束通过晶体发生衍射。
已知晶面间距nm 1032.72-⨯=d ,中子的动能eV 20.4k =E ,求对此晶面簇反射方向发生一级极大的中子束的掠射角.解:先利用德布罗意波的计算公式即可得出波长:再利用晶体衍射的公式,可得出:2sin d k ϕλ= 0,1,2k =…22-4.以速度m/s 1063⨯=v 运动的电子射入场强为5V/cm =E 的匀强电场中加速,为使电子波长 A 1=λ,电子在此场中应该飞行多长的距离? 解:3410h 110p m λ--====⨯ 可得:U=150.9V ,所以 U=Ed ,得出d=30.2cm 。
22-5.设电子的位置不确定度为A 1.0,计算它的动量的不确定度;若电子的能量约为keV 1,计算电子能量的不确定度。
解:由测不准关系: 3424101.0510 5.2510220.110h p x ---⨯∆===⨯∆⨯⨯ 由波长关系式:Ec h =λ 可推出: E E c h ∆=∆λ 22-6.氢原子的吸收谱线 A 5.4340=λ的谱线宽度为A 102-,计算原子处在被激发态上的平均寿命。
解:能量hcE h νλ==,由于激发能级有一定的宽度ΔE ,造成谱线也有一定宽度Δλ,两者之间的关系为:2hcE λλ∆=∆由测不准关系,/2,E t ∆∆≥平均寿命τ=Δt ,则22-7.若红宝石发出中心波长m 103.67-⨯=λ的短脉冲信号,时距为)s 10(ns 19-,计算该信号的波长宽度λ∆。
清华大学《大学物理》习题库试题及答案____09_磁学习题

一、选择题1.5566:在磁感强度为B的均匀磁场中作一半径为r的半球面S,S边线所在平面的法线方向单位矢量n与B的夹角为α,则通过半球面S的磁通量(取弯面向外为正)(A) πr2B. (B)2 πr2B(C) -πr2B sinα (D) -πr2B cosα[]2.2020:边长为l的正方形线圈中通有电流I,此线圈在A点(见图)为(A) lIπ42μ(B)lIπ22μ(C) lIπ2μ(D) 以上均不对3.2353:如图所示,电流从a点分两路通过对称的圆环形分路,汇合于bbd都沿环的径向,则在环形分路的环心处的磁感强度(A) 方向垂直环形分路所在平面且指向纸内(B) 方向垂直环形分路所在平面且指向纸外(C) 方向在环形分路所在平面,且指向b(D) 方向在环形分路所在平面内,且指向a(E) 为零[]4.2354:通有电流I的无限长直导线有如图三种形状,则P,Q,O各点磁感强度的大小B P,B Q,B O间的关系为:(A) B P > B Q > B O(B) B Q > B P > B O(C)B Q > B O > B P(D) B O > B Q > B P[]5.5468:电流I由长直导线1沿垂直bc边方向经a点流入由电阻均匀的导线构成的正三角形线框,再由b点流出,经长直导线2沿cb延长线方向返回电源(如图)。
若载流直导线1、2和三角形框中的电流在框中心O点产生的磁感强度分别用1B、2B和3B表示,则O点的磁感强度大小(A) B = 0,因为B1 = B2 = B3 = 0(B) B = 0,因为虽然B1≠0、B2≠0,但021=+BB,B3 = 0(C) B≠0,因为虽然B3 = 0、B1= 0,但B2≠0(D) B≠0,因为虽然021≠+BB,但[]6.5470:电流由长直导线1沿半径方向经a点流入一电阻均匀的圆环,再由b点沿切向从圆环流出,经长导线2返回电源(如图)。
大学《大学物理(上)》各章节测试题与答案

《大学物理(上)》的答案第1章问题:以下是近代物理学的理论基础的是()。
答案:量子力学问题:谁建立了电磁场理论,将电学、磁学、光学统一起来?()答案:麦克斯韦问题:谁在伽利略、开普勒等人工作的基础上,建立了完整的经典力学理论?()答案:牛顿问题:物理学是探讨物质结构,运动基本规律和相互作用的科学。
()答案:正确问题:20世纪初建立的量子力学和爱因斯坦提出的狭义相对论表明经典力学也适用于微观粒子和高速运动物体。
()答案:错误第2章问题:爱因斯坦因提出什么理论而获得诺贝尔物理奖?()答案:光量子假说问题:玻尔因做出什么重大贡献而获得诺贝尔物理学奖?()答案:研究原子的结构和原子的辐射问题:运动学中涉及的主要运动学量包括位移、速度和加速度。
()答案:正确第3章问题:在平面极坐标系中,任意位矢可表示为()。
答案:问题:在直角坐标系中,任意位矢的方向余弦的关系为()。
答案:问题:在直角坐标系中,任意位矢可表示为()。
答案:问题:同一个位置矢量可以在不同的坐标系中表示。
()答案:正确问题:位置矢量在直角坐标系和平面极坐标系中的表示方式是一样的。
()答案:错误第4章问题:设质点在均匀转动(角速度为)的水平转盘上从t=0时刻开始自中心出发,以恒定的速率沿一半径运动,则质点的运动方程为()。
答案:问题:设质点在均匀转动(角速度为)的水平转盘上从t=0时刻开始自中心出发,以恒定的速率沿一半径运动,则质点的轨迹方程为()。
答案:问题:质点的位置关于时间的函数称为运动方程。
()答案:正确第5章问题:一个人从O点出发,向正东走了2m,又向正北走了2m,则合位移的大小和方向为()。
答案:东北方向问题:某质点沿半径为R的圆周运动一周,它的位移和路程分别为多少()。
答案:问题:位移和路程都与坐标原点的选取有关。
()答案:错误第6章问题:有一质点沿x方向作直线运动,它的位置由方程决定,其中x的单位是米,t的单位是秒。
则它的速度公式为()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.4185:已知一单色光照射在钠表面上,测得光电子的最大动能是1.2 eV ,而钠的红限波长是5400 Å,那么入射光的波长是(A) 5350 Å (B) 5000 Å (C) 4350 Å (D) 3550 Å [ ]2.4244:在均匀磁场B 内放置一极薄的金属片,其红限波长为λ0。
今用单色光照射,发现有电子放出,有些放出的电子(质量为m ,电荷的绝对值为e )在垂直于磁场的平面内作半径为R 的圆周运动,那末此照射光光子的能量是: (A) 0λhc (B) 0λhc m eRB 2)(2+ (C) 0λhc m eRB + (D) 0λhc eRB 2+ [ ]3.4383:用频率为ν 的单色光照射某种金属时,逸出光电子的最大动能为E K ;若改用频率为2ν 的单色光照射此种金属时,则逸出光电子的最大动能为:(A) 2 E K (B) 2h ν - E K (C) h ν - E K (D) h ν + E K [ ]4.4737: 在康普顿效应实验中,若散射光波长是入射光波长的1.2倍,则散射光光子能量ε与反冲电子动能E K 之比ε / E K 为(A) 2 (B) 3 (C) 4 (D) 5 [ ]5.4190:要使处于基态的氢原子受激发后能发射赖曼系(由激发态跃迁到基态发射的各谱线组成的谱线系)的最长波长的谱线,至少应向基态氢原子提供的能量是(A) 1.5 eV (B) 3.4 eV (C) 10.2 eV (D) 13.6 eV [ ]6.4197:由氢原子理论知,当大量氢原子处于n =3的激发态时,原子跃迁将发出:(A) 一种波长的光 (B) 两种波长的光 (C) 三种波长的光 (D) 连续光谱[ ]7.4748:已知氢原子从基态激发到某一定态所需能量为10.19 eV ,当氢原子从能量为-0.85 eV 的状态跃迁到上述定态时,所发射的光子的能量为(A) 2.56 eV (B) 3.41 eV (C) 4.25 eV (D) 9.95 eV [ ]8.4750:在气体放电管中,用能量为12.1 eV 的电子去轰击处于基态的氢原子,此时氢原子所能发射的光子的能量只能是(A) 12.1 eV (B) 10.2 eV (C) 12.1 eV ,10.2 eV 和 1.9 eV(D) 12.1 eV ,10.2 eV 和 3.4 eV [ ]9.4241: 若α粒子(电荷为2e )在磁感应强度为B 均匀磁场中沿半径为R 的圆形轨道运动,则α粒子的德布罗意波长是(A) )2/(eRB h (B) )/(eRB h (C) )2/(1eRBh (D) )/(1eRBh[ ]10.4770:如果两种不同质量的粒子,其德布罗意波长相同,则这两种粒子的(A) 动量相同 (B) 能量相同 (C) 速度相同 (D) 动能相同 [ ]11.4428:已知粒子在一维矩形无限深势阱中运动,其波函数为:a x a x 23cos 1)(π⋅=ψ ( - a ≤x ≤a ),那么粒子在x = 5a /6处出现的概率密度为(A) 1/(2a ) (B) 1/a (C) a 2/1 (D) a /1 [ ]12.4778:设粒子运动的波函数图线分别如图(A)、(B)、(C)、(D)所示,那么其中确定粒子动量的精确度最高的波函数是哪个图? [ ]13.5619:波长λ =5000 Å的光沿x 轴正向传播,若光的波长的不确定量∆λ =10-3 Å,则利用不确定关系式h x p x ≥∆∆可得光子的x 坐标的不确定量至少为:(A) 25 cm (B) 50 cm (C) 250 cm (D) 500 cm [ ]14.8020:将波函数在空间各点的振幅同时增大D 倍,则粒子在空间的分布概率将(A) 增大D 2倍 (B) 增大2D 倍 (C) 增大D 倍 (D) 不变 [ ]15.4965:下列各组量子数中,哪一组可以描述原子中电子的状态?(A) n = 2,l = 2,m l = 0,21=s m (B) n = 3,l = 1,m l =-1,21-=s m (C) n = 1,l = 2,m l = 1,21=s m (D) n = 1,l = 0,m l = 1,21-=s m [ ]16.8022:氢原子中处于3d 量子态的电子,描述其量子态的四个量子数(n ,l ,m l ,m s )可能取的值为(A) (3,0,1,21-) (B) (1,1,1,21-)(C) (2,1,2,21) (D) (3,2,0,21) [ ]17.4785:在氢原子的K 壳层中,电子可能具有的量子数(n ,l ,m l ,m s )是(A) (1,0,0,21) (B) (1,0,-1,21)(C) (1,1,0,21-) (D) (2,1,0,21-) [ ]18.4222:与绝缘体相比较,半导体能带结构的特点是(A) 导带也是空带 (B) 满带与导带重合 (C) 满带中总是有空穴,导带中总是有电子(D) 禁带宽度较窄 [ ]19.4789:p 型半导体中杂质原子所形成的局部能级(也称受主能级),在能带结构中应处于(A) 满带中 (B) 导带中 (C) 禁带中,但接近满带顶(D) 禁带中,但接近导带底 [ ]20.8032:按照原子的量子理论,原子可以通过自发辐射和受激辐射的方式发光,它们所产生的光的特点是:(A) 两个原子自发辐射的同频率的光是相干的,原子受激辐射的光与入射光是不相干的(B) 两个原子自发辐射的同频率的光是不相干的,原子受激辐射的光与入射光是相干的(C) 两个原子自发辐射的同频率的光是不相干的,原子受激辐射的光与入射光是不相干的x (A)x (C)x(B) x(D)(D) 两个原子自发辐射的同频率的光是相干的,原子受激辐射的光与入射光是相干的21.9900:xˆ与x P ˆ的互易关系[x P x ˆ,ˆ]等于 (A) i (B) i - (C)ih (D)ih - [ ]22.9901:厄米算符Aˆ满足以下哪一等式(u 、v 是任意的态函数) (A)()dx v u A dx v A u ⎰⎰=**ˆˆ (B)()dx u A v dx u A v ⎰⎰=**ˆˆ(C)()dx u v A dx u A v ⎰⎰=**ˆˆ (D)()dx v u A dx v A u ⎰⎰=**ˆˆ [ ]二、填空题1.4179:光子波长为λ,则其能量=_____;动量的大小 =______;质量=_______。
2.4180:当波长为3000 Å的光照射在某金属表面时,光电子的能量范围从0到4.0×10-19 J 。
在作上述光电效应实验时遏止电压为 |U a | =________V ;此金属的红限频率ν0=_________Hz 。
3.4388:以波长为λ= 0.207 μm 的紫外光照射金属钯表面产生光电效应,已知钯的红限频率ν 0=1.21×1015赫兹,则其遏止电压|U a | =_______________________V 。
4.4546:若一无线电接收机接收到频率为108 Hz 的电磁波的功率为1微瓦,则每秒接收到的光子数为___________。
5.4608:钨的红限波长是230 nm ,用波长为180 nm 的紫外光照射时,从表面逸出的电子的最大动能为_________eV 。
6.4611:某一波长的X 光经物质散射后,其散射光中包含波长________和波长__________的两种成分,其中___________的散射成分称为康普顿散射。
7.4191:在氢原子发射光谱的巴耳末线系中有一频率为6.15×1014 Hz 的谱线,它是氢原子从能级E n =__________eV 跃迁到能级E k =__________eV 而发出的。
8.4192:在氢原子光谱中,赖曼系(由各激发态跃迁到基态所发射的各谱线组成的谱线系)的最短波长的谱线所对应的光子能量为_______________eV ;巴耳末系的最短波长的谱线所对应的光子的能量为___________________eV 。
9.4200:在氢原子光谱中,赖曼系(由各激发态跃迁到基态所发射的各谱线组成的谱线系)的最短波长的谱线所对应的光子能量为_______________eV ;巴耳末系的最短波长的谱线所对应的光子的能量为___________________eV 。
10.4424:欲使氢原子发射赖曼系(由各激发态跃迁到基态所发射的谱线构成)中波长为1216 Å的谱线,应传给基态氢原子的最小能量是_________________eV 。
11.4754:氢原子的部分能级跃迁示意如图。
在这些能级跃迁 中,(1) 从n =______的能级跃迁到n =_____的能级时所发射的光子的波长最短;(2) 从n =______的能级跃迁到n =______的能级时所 发射的光子的频率最小。
12.4755:被激发到n =3的状态的氢原子气体发出的辐射中, 有______条可见光谱线和_________条非可见光谱线。
13.4760:当一个质子俘获一个动能E K =13.6 eV 的自由电子组成一个基态氢原子时,所发出的单色光频率是______________。
14.4207:令)/(c m h e c =λ(称为电子的康普顿波长,其中e m 为电子静止质量,c 为真空中光速,h 为普朗克常量)。
当电子的动能等于它的静止能量时,它的德布罗意波长是λ =______λc 。
15.4429:在戴维孙——革末电子衍射实验装置中,自热 阴极K 发射出的电子束经U = 500 V 的电势差加速后投射到晶 体上。
这电子束的德布罗意波长λ =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽nm 。
16.4629:氢原子的运动速率等于它在300 K 时的方均根速率时,它的德布罗意波长是______。
质量为M =1 g ,以速度 =v 1 cm ·s -1运动的小球的德布罗意波长是________。
n = 1 n = 2 n = 3 n = 4 4754图 U 4429图17.4630:在B =1.25×10-2 T 的匀强磁场中沿半径为R =1.66 cm的圆轨道运动的α粒子的德布罗意波长是___________。
18.4203:设描述微观粒子运动的波函数为),(t r ψ,则*ψψ表示_______________________;),(t r ψ须满足的条件是_____________________;其归一化条件是___________________。
