生成树的计数及其应用
离散数学中的图的树与生成树的计数

在离散数学中,图是一个由点和边组成的抽象数学模型。
其中,树是一种特殊的图,它是一个无环连通图。
在图论中,树扮演了重要的角色,它具有许多有趣的性质和应用。
而生成树则是树的一个特殊子集,它由给定图中的所有顶点和部分边构成。
本文将介绍图的树的基本概念,并探讨生成树的计数方法。
首先,让我们来看看图的树。
树是一种无环连通图,其中任意两个顶点之间存在唯一一条路径。
它具有以下性质:1.n个顶点的树有n-1条边。
这可以通过归纳法证明:当n=1时,结论成立;假设n=k时成立,那么n=k+1时,只需要添加一个顶点和一条边,即可构成n=k+1个顶点的树。
因此,结论成立。
2.连接树上任意两个顶点的边都是桥。
即如果一条边被删除,那么树就会变成两个或更多个不相连的子树。
3.树是一个高度平衡的结构。
对于一个n个顶点的树,任意两个叶子结点之间的路径长度至多相差1。
4.树的任意两个顶点之间有唯一一条路径,路径长度为顶点之间的边数。
接下来,让我们来讨论生成树的计数方法。
生成树是树的一个特殊子集,它是由给定图中的所有顶点和部分边构成。
生成树的计数在图论中具有重要的意义和应用。
对于一个具有n个顶点的连通图来说,其生成树的个数可以通过Cayley公式计算得到。
Cayley公式是由亚瑟·凯利于1889年提出的,它给出了完全图的生成树数目。
据此,我们可以得到生成树的计数公式为:T = n^(n-2),其中T表示生成树的个数。
此外,还有一种常见的计数方法是基于度数矩阵和邻接矩阵的矩阵树定理。
矩阵树定理由高斯于1847年提出,它提供了一种计算图的生成树个数的方法。
根据矩阵树定理,一个无向图G的生成树数目等于该图度数矩阵的任意一个(n-1)阶主子式的行列式的值。
其中,度数矩阵是一个对角矩阵,它的对角线上的元素为各个顶点的度数。
邻接矩阵则是一个关于顶点间连接关系的矩阵,其中1表示相邻顶点之间存在边,0表示不存在边。
除了数学方法,还存在一种基于图的遍历的计数方法,称为Kirchhoff矩阵树定理。
图论中的生成树计数算法

图论中的生成树计数算法生成树是图论中重要的概念之一,它是指由给定图的节点组成的树形结构,其中包含了原图中的所有节点,但是边的数量最少。
生成树的计数问题是指在一个给定的图中,有多少种不同的生成树。
生成树计数算法是解决这个问题的关键步骤,本文将介绍一些常见的生成树计数算法及其应用。
1. Kirchhoff矩阵树定理Kirchhoff矩阵树定理是图论中经典的生成树计数方法之一。
该定理是由Kirchhoff在19世纪提出的,它建立了图的Laplacian矩阵与其生成树个数的关系。
Laplacian矩阵是一个$n\times n$的矩阵,其中$n$是图中的节点数。
对于一个连通图而言,Laplacian矩阵的任意一个$n-1$阶主子式,其绝对值等于该图中生成树的个数。
应用示例:假设我们有一个无向连通图,其中每个节点之间的边权均为1。
我们可以通过计算图的Laplacian矩阵的任意一个$n-1$阶主子式的绝对值来得到该图中的生成树个数。
2. Prufer编码Prufer编码是一种编码方法,可用于求解生成树计数问题。
它是基于树的叶子节点的度数的编码方式。
Prufer编码将一个树转换为一个长度为$n-2$的序列,其中$n$是树中的节点数。
通过给定的Prufer序列,可以构造出对应的生成树。
应用示例:假设我们有一个具有$n$个节点的有标号的无根树。
我们可以通过构造一个长度为$n-2$的Prufer序列,然后根据Prufer编码的规则构造出对应的生成树。
3. 生成函数方法生成函数方法是一种利用形式幂级数求解生成树计数问题的方法。
通过将图的生成树计数问题转化为生成函数的乘法运算,可以得到生成函数的一个闭形式表达式,从而求解生成树的个数。
应用示例:假设我们有一个具有$n$个节点的有根树,其中根节点的度数为$d$。
我们可以通过生成函数方法求解出该有根树中的生成树个数。
4. Matrix-Tree定理Matrix-Tree定理是对Kirchhoff矩阵树定理的一种扩展,适用于带权图中生成树计数的问题。
离散数学中的生成树与生成树计数

离散数学是计算机科学中的重要学科,其中生成树是一个重要的概念。
在图论中,生成树是一棵树,它包含了图中的所有顶点,并且是由图边组成的无环连通子图。
生成树在图论中有着重要的应用,特别是在计算机网络、运筹学和电路设计等领域。
生成树的概念与基础就是组成它的边是有限的,并且连接图中的所有顶点,但没有形成圈回到起点。
生成树通常是用来描述一个系统的最小连接方式。
生成树可以应用于计算机网络的设计中,用于构建最小生成树算法,以便在网络中选择最小的数据传输路径。
此外,在运筹学中,生成树被用于求解最小生成树问题,即为一个加权图找到一棵包含所有顶点的生成树,使得树中边的权重之和最小。
在离散数学中,生成树计数是一个重要的研究分支。
生成树计数是指对给定图,计算其生成树的数目。
生成树计数的问题可以通过使用基于图论和组合数学的算法来解决。
通常,生成树计数的问题与相应图的特性和性质密切相关。
对于一个简单图来说,如果图中任意两点之间至少有一条边,那么该图一定存在生成树。
对于有 n 个顶点的连通图来说,它的生成树数量可以通过Cayley公式计算得到。
Cayley公式表明,一个有 n 个标号的顶点的完全图的生成树数量等于 n^(n-2)。
而对于非完全图,生成树的计数问题则较为困难。
在处理非完全图的生成树计数问题时,可以使用基于递归和动态规划的算法来解决。
一个常见的方法是使用Kirchhoff矩阵树定理,它将生成树计数的问题转化为计算矩阵的行列式的问题。
Kirchhoff矩阵树定理提供了一种计算给定图的生成树数目的有效算法,通过计算图的基尔霍夫矢量的一个特征值,可以得到图的生成树的数目。
另一个常见的方法是使用Prufer编码,它是一个用于描述无环连通图的序列。
通过Prufer编码,我们可以将计算生成树的问题转化为计数树的问题。
通过对无向图进行Prufer编码,我们可以计算出生成树的数目,并且可以根据生成树的数目来确定该无向图的种类和特征。
离散数学 求生成树的个数

在离散数学中,生成树(Spanning Tree)是一个图(Graph)的子图,它包含图中的所有顶点,并且是一个树(Tree)。
生成树的一个重要性质是它不包含任何环(Cycle)。
求一个给定图的生成树个数是一个经典问题,通常使用矩阵树定理(Matrix Tree Theorem)来解决。
矩阵树定理给出了一个图的生成树个数的计算公式,它基于图的拉普拉斯矩阵(Laplacian Matrix)的行列式。
拉普拉斯矩阵是一个方阵,其大小为图的顶点数,矩阵的元素定义如下:•如果i和j是不同的顶点,则矩阵的第i行第j列的元素是顶点i和j之间的边的权重(如果存在边的话),否则是0。
•对于每个顶点i,矩阵的第i行第i列的元素是顶点i的度(即与顶点i相邻的边的数量)的负值。
矩阵树定理指出,图的生成树个数等于其拉普拉斯矩阵的任何一个n-1阶主子式的行列式值的绝对值。
n是图的顶点数,n-1阶主子式意味着去掉矩阵中的一行和一列后得到的矩阵。
下面是一个简单的例子,说明如何使用矩阵树定理计算生成树的个数:假设有一个包含4个顶点的简单图,其边和权重如下:A -- 2 -- B| |1 3 1| |C -- 4 -- D1 -3 1 00 1 -3 40 0 1 -4主子式的行列式值。
去掉第一行和第一列后,我们得到:1 01 -3 40 1 -4x3矩阵的行列式,我们得到:1 * 1) - (0 * 0) = 12 - 1 = 11过程可能涉及复杂的行列式计算,特别是对于大型图来说。
在实际应用中,通常会使用专门的数学软件或库(如Python中的NumPy或SciPy)来进行这些计算。
此外,还有一些算法(如Kruskal算法和Prim算法)可以用来构造生成树,但它们并不直接计算生成树的总数。
这些算法通常用于找到图的一个生成树,而不是计算所有可能的生成树的数量。
NOI国家集训队论文分类(至2008)(摘抄自C博客)

摘抄自C博客组合数学计数与统计2001 - 符文杰:《Pólya原理及其应用》2003 - 许智磊:《浅谈补集转化思想在统计问题中的应用》2007 - 周冬:《生成树的计数及其应用》2008 - 陈瑜希《Pólya计数法的应用》数位问题2009 - 高逸涵《数位计数问题解法研究》2009 - 刘聪《浅谈数位类统计问题》动态统计2004 - 薛矛:《解决动态统计问题的两把利刃》2007 - 余江伟:《如何解决动态统计问题》博弈2002 - 张一飞:《由感性认识到理性认识——透析一类搏弈游戏的解答过程》2007 - 王晓珂:《解析一类组合游戏》2009 - 曹钦翔《从“k倍动态减法游戏”出发探究一类组合游戏问题》2009 - 方展鹏《浅谈如何解决不平等博弈问题》2009 - 贾志豪《组合游戏略述——浅谈SG游戏的若干拓展及变形》母函数2009 - 毛杰明《母函数的性质及应用》拟阵2007 - 刘雨辰:《对拟阵的初步研究》线性规划2007 - 李宇骞:《浅谈信息学竞赛中的线性规划——简洁高效的单纯形法实现与应用》置换群2005 - 潘震皓:《置换群快速幂运算研究与探讨》问答交互2003 - 高正宇:《答案只有一个——浅谈问答式交互问题》猜数问题2003 - 张宁:《猜数问题的研究:<聪明的学生>一题的推广》2006 - 龙凡:《一类猜数问题的研究》数据结构数据结构2005 - 何林:《数据关系的简化》2006 - 朱晨光:《基本数据结构在信息学竞赛中的应用》2007 - 何森:《浅谈数据的合理组织》2008 - 曹钦翔《数据结构的提炼与压缩》结构联合2001 - 高寒蕊:《从圆桌问题谈数据结构的综合运用》2005 - 黄刚:《数据结构的联合》块状链表2005 - 蒋炎岩:《数据结构的联合——块状链表》2008 - 苏煜《对块状链表的一点研究》动态树2006 - 陈首元:《维护森林连通性——动态树》2007 - 袁昕颢:《动态树及其应用》左偏树2005 - 黄源河:《左偏树的特点及其应用》跳表2005 - 魏冉:《让算法的效率“跳起来”!——浅谈“跳跃表”的相关操作及其应用》2009 - 李骥扬《线段跳表——跳表的一个拓展》SBT2007 - 陈启峰:《Size Balance Tree》线段树2004 - 林涛:《线段树的应用》单调队列2006 - 汤泽:《浅析队列在一类单调性问题中的应用》哈希表2005 - 李羽修:《Hash函数的设计优化》2007 - 杨弋:《Hash在信息学竞赛中的一类应用》Splay2004 - 杨思雨:《伸展树的基本操作与应用》图论图论2005 - 任恺:《图论的基本思想及方法》模型建立2004 - 黄源河:《浅谈图论模型的建立与应用》2004 - 肖天:《“分层图思想”及其在信息学竞赛中的应用》网络流2001 - 江鹏:《从一道题目的解法试谈网络流的构造与算法》2002 - 金恺:《浅谈网络流算法的应用》2007 - 胡伯涛:《最小割模型在信息学竞赛中的应用》2007 - 王欣上:《浅谈基于分层思想的网络流算法》2008 - 周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》最短路2006 - 余远铭:《最短路算法及其应用》2008 - 吕子鉷《浅谈最短径路问题中的分层思想》2009 - 姜碧野《SPFA算法的优化及应用》欧拉路2007 - 仇荣琦:《欧拉回路性质与应用探究》差分约束系统2006 - 冯威:《数与图的完美结合——浅析差分约束系统》平面图2003 - 刘才良:《平面图在信息学中的应用》2007 - 古楠:《平面嵌入》2-SAT2003 - 伍昱:《由对称性解2-SAT问题》最小生成树2004 - 吴景岳:《最小生成树算法及其应用》2004 - 汪汀:《最小生成树问题的拓展》二分图2005 - 王俊:《浅析二分图匹配在信息学竞赛中的应用》Voronoi图2006 - 王栋:《浅析平面Voronoi图的构造及应用》偶图2002 - 孙方成:《偶图的算法及应用》树树2002 - 周文超:《树结构在程序设计中的运用》2005 - 栗师:《树的乐园——一些与树有关的题目》路径问题2009 - 漆子超《分治算法在树的路径问题中的应用》最近公共祖先2007 - 郭华阳:《RMQ与LCA问题》划分问题2004 - 贝小辉:《浅析树的划分问题》数论欧几里得算法2009 - 金斌《欧几里得算法的应用》同余方程2003 - 姜尚仆:《模线性方程的应用——用数论方法解决整数问题》搜索搜索2001 - 骆骥:《由“汽车问题”浅谈深度搜索的一个方面——搜索对象与策略的重要性》2002 - 王知昆:《搜索顺序的选择》2005 - 汪汀:《参数搜索的应用》启发式2009 - 周而进《浅谈估价函数在信息学竞赛中的应用》优化2003 - 金恺:《探寻深度优先搜索中的优化技巧——从正方形剖分问题谈起》2003 - 刘一鸣:《一类搜索的优化思想——数据有序化》2006 - 黄晓愉:《深度优先搜索问题的优化技巧》背包问题2009 - 徐持衡《浅谈几类背包题》匹配2004 - 楼天城:《匹配算法在搜索问题中的巧用》概率概率2009 - 梅诗珂《信息学竞赛中概率问题求解初探》数学期望2009 - 汤可因《浅析竞赛中一类数学期望问题的解决方法》字符串字符串2003 - 周源:《浅析“最小表示法”思想在字符串循环同构问题中的应用》多串匹配2004 - 朱泽园:《多串匹配算法及其启示》2006 - 王赟:《Trie图的构建、活用与改进》2009 - 董华星《浅析字母树在信息学竞赛中的应用》后缀数组2004 - 许智磊:《后缀数组》2009 - 罗穗骞《后缀数组——处理字符串的有力工具》字符串匹配2003 - 饶向荣:《病毒的DNA———剖析一道字符匹配问题解析过程》2003 - 林希德:《求最大重复子串》动态规划动态规划2001 - 俞玮:《基本动态规划问题的扩展》2006 - 黄劲松:《贪婪的动态规划》2009 - 徐源盛《对一类动态规划问题的研究》状态压缩2008 - 陈丹琦《基于连通性状态压缩的动态规划问题》状态设计2008 - 刘弈《浅谈信息学中状态的合理设计与应用》树形DP2007 - 陈瑜希:《多角度思考创造性思维——运用树型动态规划解题的思路和方法探析》优化2001 - 毛子青:《动态规划算法的优化技巧》2003 - 项荣璟:《充分利用问题性质——例析动态规划的“个性化”优化》2004 - 朱晨光:《优化,再优化!——从《鹰蛋》一题浅析对动态规划算法的优化》2007 - 杨哲:《凸完全单调性的加强与应用》计算几何立体几何2003 - 陆可昱:《长方体体积并》2008 - 高亦陶《从立体几何问题看降低编程复杂度》计算几何思想2004 - 金恺:《极限法——解决几何最优化问题的捷径》2008 - 程芃祺《计算几何中的二分思想》2008 - 顾研《浅谈随机化思想在几何问题中的应用》圆2007 - 高逸涵:《与圆有关的离散化》半平面交2002 - 李澎煦:《半平面交的算法及其应用》2006 - 朱泽园:《半平面交的新算法及其实用价值》矩阵矩阵2008 - 俞华程《矩阵乘法在信息学中的应用》高斯消元2002 - 何江舟:《用高斯消元法解线性方程组》数学方法数学思想2002 - 何林:《猜想及其应用》2003 - 邵烜程:《数学思想助你一臂之力》数学归纳法2009 - 张昆玮《数学归纳法与解题之道》多项式2002 - 张家琳:《多项式乘法》数形结合2004 - 周源:《浅谈数形结合思想在信息学竞赛中的应用》黄金分割2005 - 杨思雨:《美,无处不在——浅谈“黄金分割”和信息学的联系》其他算法遗传算法2002 - 张宁:《遗传算法的特点及其应用》2005 - 钱自强:《关于遗传算法应用的分析与研究》信息论2003 - 侯启明:《信息论在信息学竞赛中的简单应用》染色与构造2002 - 杨旻旻:《构造法——解题的最短路径》2003 - 方奇:《染色法和构造法在棋盘上的应用》一类问题区间2008 - 周小博《浅谈信息学竞赛中的区间问题》序2005 - 龙凡:《序的应用》系2006 - 汪晔:《信息学中的参考系与坐标系》物理问题2008 - 方戈《浅析信息学竞赛中一类与物理有关的问题》编码与译码2008 - 周梦宇《码之道—浅谈信息学竞赛中的编码与译码问题》对策问题2002 - 骆骥:《浅析解“对策问题”的两种思路》优化算法优化2002 - 孙林春:《让我们做得更好——从解法谈程序优化》2004 - 胡伟栋:《减少冗余与算法优化》2005 - 杨弋:《从<小H的小屋>的解法谈算法的优化》2006 - 贾由:《由图论算法浅析算法优化》程序优化2006 - 周以苏:《论反汇编在时间常数优化中的应用》2009 - 骆可强《论程序底层优化的一些方法与技巧》语言C++2004 - 韩文弢:《论C++语言在信息学竞赛中的应用》策略策略2004 - 李锐喆:《细节——不可忽视的要素》2005 - 朱泽园:《回到起点——一种突破性思维》2006 - 陈启峰:《“约制、放宽”方法在解题中的应用》2006 - 李天翼:《从特殊情况考虑》2007 - 陈雪:《问题中的变与不变》2008 - 肖汉骏《例谈信息学竞赛分析中的“深”与“广”》倍增2005 - 朱晨光:《浅析倍增思想在信息学竞赛中的应用》二分2002 - 李睿:《二分法与统计问题》2002 - 许智磊:《二分,再二分!——从Mobiles(IOI2001)一题看多重二分》2005 - 杨俊:《二分策略在信息学竞赛中的应用》调整2006 - 唐文斌:《“调整”思想在信息学中的应用》随机化2007 - 刘家骅:《浅谈随机化在信息学竞赛中的应用》非完美算法2005 - 胡伟栋:《浅析非完美算法在信息学竞赛中的应用》2008 - 任一恒《非完美算法初探》提交答案题2003 - 雷环中:《结果提交类问题》守恒思想2004 - 何林:《信息学中守恒法的应用》极限法2003 - 王知昆:《浅谈用极大化思想解决最大子矩形问题》贪心2008 - 高逸涵《部分贪心思想在信息学竞赛中的应用》压缩法2005 - 周源:《压去冗余缩得精华——浅谈信息学竞赛中的“压缩法”》逆向思维2005 - 唐文斌:《正难则反——浅谈逆向思维在解题中的应用》穷举2004 - 鬲融:《浅谈特殊穷举思想的应用》目标转换2002 - 戴德承:《退一步海阔天空——“目标转化思想”的若干应用》2004 - 栗师:《转化目标在解题中的应用》类比2006 - 周戈林:《浅谈类比思想》分割与合并2006 - 俞鑫:《棋盘中的棋盘——浅谈棋盘的分割思想》2007 - 杨沐:《浅析信息学中的“分”与“合”》平衡思想2008 - 郑暾《平衡规划——浅析一类平衡思想的应用》。
扇图的生成树的计数

扇图的生成树的计数
刘珊
【期刊名称】《喀什师范学院学报》
【年(卷),期】2013(034)006
【摘要】应用计算生成树个数的有向图方法、分块矩阵的行列式计算法以及常系数线性递归方程的解法,得到扇图的生成树个数的计算公式.
【总页数】2页(P11-12)
【作者】刘珊
【作者单位】肇庆学院数学与信息科学学院,广东肇庆526061
【正文语种】中文
【中图分类】O157.5
【相关文献】
1.无圈竞赛图的内(外)生成树与路的计数 [J], 郭廷花;杨爱民
2.基于最小生成树扇度的蚁群算法 [J], 丁怡心;廖勇毅
3.基于最小生成树扇度的蚁群算法 [J], 丁怡心;廖勇毅
4.二部图生成树的新的计数公式(英文) [J], 谭尚旺;张德龙
5.基于路的多重完全图相关图生成树计数 [J], 谭秋月
因版权原因,仅展示原文概要,查看原文内容请购买。
生成树的名词解释

生成树的名词解释生成树(Spanning Tree)是图论中的一个重要概念,用来描述在一个无向连通图中连接所有顶点的极小连通子图。
在一个无向连通图中,如果能够找到一颗包含所有顶点且边数最少的子图,那么这个子图就是该图的生成树。
生成树的概念最早由Otto Schönflies于1885年提出,并且在图论研究和实际应用中得到了广泛的运用。
生成树在电网规划、通信网络设计、计算机网络以及城市交通规划等领域都有着重要的应用价值。
生成树的定义可以用简洁的方式表述:在一个无向连通图中,生成树是保留了原图的所有顶点,但只保留了足够的边来使得这个子图连通,并且不包含任何环的一种连通子图。
换句话说,生成树是一个无向连通图中的极小连通子图,它连接了所有的顶点,并且不存在回路。
生成树具有很多重要的性质和应用。
首先,生成树的边数比原图的顶点数少一个。
这是因为生成树是一个连通子图,而且不包含任何环。
因此,生成树中的边数等于原图的顶点数减去1。
这个性质经常用于生成树的构造和推导。
其次,生成树可以用于表示图中的最小连接网络。
在一个无向连通图中,如果存在多个连通子图,那么通过连接这些子图的最少的边,就可以得到一个生成树。
这个生成树可以看作是一个最小的连通网络,其中所有顶点都能够通过最短路径相互到达。
此外,生成树还可以用于网络设计和优化问题。
在电网规划、通信网络设计和计算机网络中,生成树常常被用于实现信息的传输和路由的优化。
通过构造合适的生成树,可以使得信息的传输路径更加简洁和高效。
生成树有多种构造算法,其中最常用的是Prim算法和Kruskal算法。
Prim算法是一种贪心算法,它从一个任意选定的顶点开始,逐步构建生成树。
具体地,Prim算法每次选择与已有的生成树连接边权值最小的顶点,并将其加入生成树。
重复这个过程,直到生成树包含了所有的顶点。
Kruskal算法是一种基于边的方法,它首先将图中的边按照权值从小到大排序,然后依次将边加入生成树,直到生成树包含了所有的顶点为止。
tg数学公式

tg数学公式TG数学公式,即生成树计数公式,是图论中的一个重要定理。
它可以用于计算一个给定图的生成树的数量。
在这篇文章中,我们将介绍TG数学公式的定义、推导过程和应用。
一、TG数学公式的定义TG数学公式是由英国数学家Tutte在20世纪50年代提出的。
它用于计算一个连通图的生成树的数量。
生成树是指一个连通图中包含所有顶点且没有回路的子图。
生成树的数量对于图的结构和性质有着重要的影响,因此TG数学公式具有很高的研究和应用价值。
二、TG数学公式的推导过程TG数学公式的推导过程相对复杂,需要借助一些图论的基本概念和定理。
这里我们简要介绍一下推导的思路。
我们需要引入一个重要的定理,即基尔霍夫矩阵-树定理。
该定理指出,一个连通图的生成树的数量等于该图的任意一个割集的割集矩阵的行列式的绝对值。
接下来,我们需要定义割集和割集矩阵。
割集是指将一个连通图分割成两个非空子图的边的集合。
割集矩阵是一个n×n的矩阵,其中n是图的顶点数,矩阵的元素a[i][j]表示边(i,j)是否属于割集。
然后,我们可以利用割集矩阵来计算生成树的数量。
具体步骤如下:1. 构造图的割集矩阵。
2. 选择任意一行或一列,将其除去。
3. 计算剩余矩阵的行列式的绝对值。
4. 将步骤3中得到的结果乘以(-1)的行号加列号的幂次方。
5. 对所有行列式的结果求和,即为生成树的数量。
三、TG数学公式的应用TG数学公式在图论和网络分析中有着广泛的应用。
以下是一些典型的应用场景:1. 最小生成树:在一个带权图中,如果我们希望找到一棵生成树,使得树中所有边的权重之和最小,可以利用TG数学公式来计算生成树的数量,并通过枚举所有生成树,选择权重和最小的生成树。
2. 网络设计:在网络设计中,我们常常需要考虑如何将节点连接起来,以满足一定的性能要求。
TG数学公式可以帮助我们计算不同网络拓扑下生成树的数量,从而为网络设计提供参考。
3. 社交网络分析:在社交网络分析中,我们希望了解网络中各个节点之间的关系和连接方式。
最小生成树算法及应用

最小生成树算法及应用
二、求图的最小生成树算法小结 Prim算法和Kruskal算法 三、应用举例
例2、最优布线问题(wire.???) 学校有n台计算机,为了方便数据传输,现要将它们用数据线连接起来。两台计算机被连接是指它们时 间有数据线连接。由于计算机所处的位置不同,因此不同的两台计算机的连接费用往往是不同的。
算法分析
2、套用最小生成树的经典算法求解
以机器蛇为顶点,以不受屏蔽的通信线路为边构建图,就可以直 接套用最小生成树的经典算法求解。由于几乎每两条机器蛇间都 会有一条边,因此应选用Prim算法。
设
const maxn=200 ; oo=2000000000;{ 机器蛇数的上限和无穷大} type TPoint=record {坐标} x,y:longint; end; var s,w1,w2:array[1..maxn] of TPoint; { 机器蛇的坐标和屏蔽线的坐标 } n,m,i,j,k:integer; ba:array[1..maxn] of boolean; { 机器蛇的访问标志} d:array[1..maxn] of longint; {d[i]以机器蛇i为头的最短边长} min:longint; ans:double;
题目中要求信息可以在任意两条机器蛇间传递、通讯网 络的总长度要尽可能的短,显然这是一个求图的最小生 成树问题。这道题在构造图的过程中还涉及到一点计算 几何的知识。 1、判断线段相交 两条线段AB、CD,相交的充要条件是:A、B在直线CD 的异侧且C、D在直线AB的异侧。也就是说从AC到AD的 方向与从BC到BD的方向不同,从CA到CB的方向也与从 DA到DB的方向不同。
机器蛇
Matlab实现生成树计数

Matlab 实现生成树计数摘要在信息学竞赛中,有关生成树的最优化问题如最小生成树等是我们经常遇到的,而对生成树的计数及其相关问题则少有涉及。
事实上,生成树的计数是十分有意义的,在许多方面都有着广泛的应用。
本文首先介绍了行列式的基本概念、性质,并在此基础上引入Matrix Tree -定理。
关键字:生成树的计数、Matrix Tree -定理Matrix Tree -定理(Kirchhoff 矩阵-树定理)。
Matrix Tree -定理是解决生成树计数问题最有力的武器之一。
它首先于1847年被Kirchhoff 证明。
在介绍定理之前,我们首先明确几个概念:1、G 的度数矩阵[]D G 是一个n 阶矩阵,并且满足:0;().ij G i i j d d v i j =⎧=⎨≠⎩ ,()G i d v 为顶点i v 的度数(度数即与顶点i v 关联的边的个数)。
2、G 的邻接矩阵[]A G 也是一个n 阶矩阵, 并且满足:01i j ij i j v v a v v ⎧=⎨⎩;;没直接连接直接连接 我们定义G 的Kirchhoff 矩阵(也称为拉普拉斯算子)[]C G 为[][][]C G D G A G =-,则Matrix Tree -定理可以描述为:G 的所有不同的生成树的个数等于其Kirchhoff 矩阵[]C G 任何一个1n -阶主子式的行列式的绝对值。
所谓1n -阶主子式,就是对于()1r r n ≤≤,将[]C G 的第r 行、第r 列同时去掉后得到的新矩阵,用[]Cr G 表示。
Matlab 程序:function n=STREEC( D,A )C=D-A;,n=size(C);C(:,n)=[]; %删除矩阵C 的第n 列C(n,:)=[]; %删除矩阵C 的第n 行,形成了Cr ,为了节约空间,这里没有定义新的变量Cr,用C 代替Crn=abs(det(C)); %这里C 表示Cr.end。
步数可变循环图中生成树的计数

可 靠性尸 ∑ A 一 ) k 为网 结点的 一 ( 户m 其中 P1 n i 络中 个数, m为边 A 为 个 数, 具有 结点五 的 条边 连通子
^ 一 1
图的 个数 . 于 个 结点 的 网络 要连 通 , 对 至少 要 有 一1条边 . 以 尸一 一P ( - p 一 , 所 一 1 ) A 一 为生 成树
( c o l f C m u e ce c a d C mmu i t n 。 a z o nv ri f S in e n eh oo y, a z o 3 0 0 C ia S h o o o p t S i e n o r n nc i s L n h u U ies y o c c d T c n lg L n h u 7 0 5 , h n ) ao t e a
Ab ta t sr c : Th u b ro p n ig te si r p n t r en m e fs a n n r e n ag a h( e wo k)i a mp ra t s ni o t n ,welsu idq a tt .No l—t de u n iy
Ke r s y wo d : s a n n r e;n n f e t p cr u a t g a h;Ch b s e o y o a p n i g te o —i d s e ic l n r p x e y h v p l n mi l
对 于一 个通 信 网络 , 2个结点 间有 可能 断 开 , 设 断开 的可 能性 为 1 每 假 一户, 么 可以估 计 此 网络连 通 的 那
Fo m ul s f r t e N u b r o p nn n e s i n— i e t p r a o h m e f S a i g Tr e n No f x d S e
最小生成树应用场合

最小生成树算法
1.网络布局问题:在一个连通加权无向图中,最小生成树算法可以帮助找到一个包含所有顶点的最小权重树,从而在地图上实现有效的布局。
2.地图着色问题:在地图着色问题中,最小生成树算法可以用于优化颜色分配,使得相邻区域的颜色不同,同时最小化所需的颜色数量。
3.车辆路径优化问题:在物流和运输行业中,最小生成树算法可以用于优化车辆的行驶路径,使得车辆能够更高效地完成配送任务,降低运输成本。
4.通信网络设计:在通信网络设计中,最小生成树算法可以用于构建高效的数据传输网络,使得数据能够在不同的节点之间快速传输。
5.电力系统设计:在电力系统的设计中,最小生成树算法可以用于构建高效的输电网络,使得电能能够从发电厂传输到各个用户。
请注意,这些应用场景中都需要用到最小生成树算法来寻找最优解。
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)
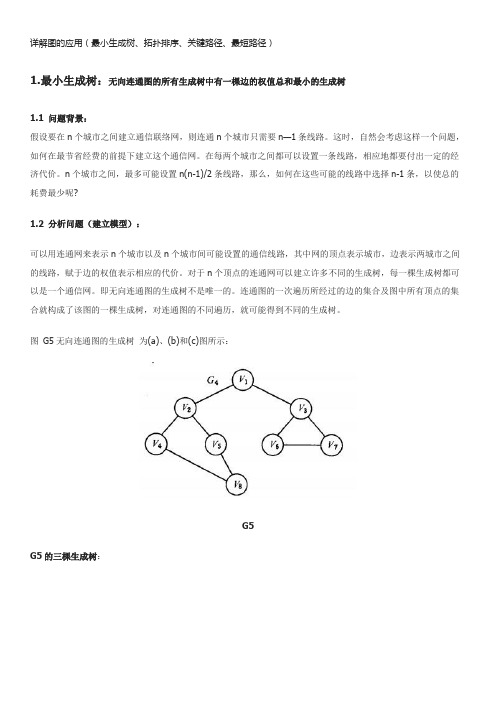
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)1.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?1.2 分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1 条边。
1.3最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{ E}) 是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
1.4 解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。
图论中的生成树计数算法

图论中的生成树计数算法在图论中,生成树是指一个无向连通图的一个子图,它包含图中的所有顶点,并且是一个树。
生成树计数算法是指计算一个无向连通图中生成树的数量的方法。
本文将介绍图论中的一些常见生成树计数算法。
1. Cayley公式Cayley公式是最简单的生成树计数算法之一,它适用于完全图。
完全图是指图中的任意两个不同顶点之间都有一条边相连。
假设完全图有n个顶点,那么生成树的数量为n^(n-2)个。
Cayley公式的证明可以利用普鲁夫树(Prüfer Tree)的概念,这里不再详述。
2. Kirchhoff矩阵树定理Kirchhoff矩阵树定理是另一种生成树计数算法,它适用于任意连通图。
矩阵树定理的原理是利用图的拉普拉斯矩阵(Laplacian Matrix)的性质。
图的拉普拉斯矩阵定义为:对于一个n个顶点的图,其拉普拉斯矩阵L的定义为:L=D-A,其中D是一个对角矩阵,对角线上的元素是该顶点的度数,A是图的邻接矩阵。
根据Kirchhoff矩阵树定理,一个图的所有生成树的数量等于该图的任意一个n-1阶主子式的行列式的绝对值。
主子式是指原矩阵去掉若干行和列后形成的子矩阵。
基于这个定理,我们可以通过计算图的拉普拉斯矩阵的主子式来得到生成树的数量。
3. Prufer编码Prufer编码是一种用序列表示带标号图中生成树的方法。
给定一个有n个顶点的生成树T,Prufer编码可以将T转化为一个长度为n-2的序列,该序列的元素由图中的顶点标号组成。
具体的编码方法如下:- 第一步:选择标号最小的叶子节点,并将与之相邻的节点记录下来。
- 第二步:删除该叶子节点,并将该叶子节点的标号记录下来。
- 重复以上两步,直到所有顶点都被删除为止。
通过Prufer编码,我们可以将生成树的计数问题转化为序列的计数问题。
在给定n个顶点的情况下,长度为n-2的Prufer序列的数量为n^(n-2)。
除了上述介绍的几种生成树计数算法外,还有其他更复杂的算法,如Chow定理、Matrix-Tree定理等。
离散数学中的图的树与生成树计数算法

离散数学是数学的一个重要分支,它研究的是离散的对象和离散的结构。
图论作为离散数学的分支之一,研究的是图的性质和结构。
在离散数学中,图的树是一种重要的概念,而生成树则是树的一种特殊类型。
本文将介绍图的树以及生成树的计数算法。
在图论中,图是由节点和边组成的集合。
树是一种特殊的图,它是一个无环图,并且其中的任意两个节点都是通过唯一的路径连接在一起的。
树的一个重要性质是它具有n个节点的话,就有n-1条边。
这个性质可以通过归纳法进行证明。
生成树是图的一个特殊类型,它是包含所有节点并且没有环的子图。
图中可能存在多个生成树,而生成树的计数是一个重要的问题。
一个图有多少种不同的生成树取决于图的结构和节点之间的连接关系。
在计算生成树数量时,有一些经典的算法可以使用。
其中,几个著名的算法包括Matrix Tree 定理、Kirchhoff定理和Prufer编码。
Matrix Tree 定理是一个重要的生成树计数定理。
该定理指出,一个图的生成树数量等于其拉普拉斯矩阵中任意一个不连通的块的行列式。
拉普拉斯矩阵是一个图的特殊矩阵,其中的元素是节点之间的连接关系。
通过计算拉普拉斯矩阵的行列式,我们可以得到图的生成树数量。
Kirchhoff定理是图论中的另一个重要定理。
它指出,一个图的所有生成树组成的集合,可以通过这个图的基尔霍夫矩阵的任意一个不连通部分的代数余子式求和得到。
基尔霍夫矩阵是一个与图的边相关的矩阵,通过对基尔霍夫矩阵的计算,我们可以得到图的生成树数量。
Prufer编码是一个用于计算生成树数量的编码技术。
在Prufer编码中,我们将图的生成树转化为一个特殊的序列。
通过对这个序列的计算和转化,我们可以得到图的生成树数量。
Prufer编码是一个相对简单的方法,但它可以应用于不同类型的图,因此是一个实用且灵活的生成树计数方法。
总之,在离散数学中,图的树和生成树是重要的概念。
图的树是一种无环图,而生成树是包含所有节点且没有环的子图。
算法合集之《最小生成树算法及其应用》

第 5 页 共 29 页
IOI2004 国家集训队论文 吴景岳
图 3 Kruskal 算法的执行流程 Kruskal 算法在图 G=(V,E)上的运行时间取决于如何实现集合的合并。我们可 以采用路径压缩的优化方法,这是目前所知的最有效的。初始化需占用时间 O(V),第 4 行中对边进行排序需要的运行时间为 O(ElgE);对分离集的森林要进 行 O(E)次操作,总共需要时间为 O(Eα(E,V)),其中α函数为 Ackermann 函数的 反函数。因为α(E,V)=O(lgE)。所以 Kruskal 算法的全部运行时间为 O(ElgE)。 Prim 算法: 正如 Kruskal 算法一样。Prim 算法也是最小生成树一般算法的特例。它的执 行非常类似于寻找图的最短通路的 Dijkstra 算法。Prim 算法的特点是集合 A 中 的边总是只形成单棵树。如图 4 所示,阴影覆盖的边属于正在生成的树,树中的 结点为黑色。在算法的每一步,树中与树外的结点确定了图的一个割,并且通过 该割的轻边被加进树中。树从任意根结点 r 开始形成并逐渐生长直至该树跨越了 V 中的所有结点。在每一步,连接 A 中某结点到 V-A 中某结点的轻边被加入到 树中。由推论 1,该规则总是加入对 A 安全的边,因此当算法终止时,A 中的边 就成为一棵最小生成树。因为每次添加到树中的边都是使树的权尽可能小的边, 因此上述策略是“贪心”的。 有效实现 Prim 算法的关键是设法较容易地选择一条新的边添加到由 A 的边 所形成的树中,在下面的伪代码中,算法的输入是连通图 G 和将生成的最小生 成树的根 r。在算法执行过程中,不在树中的所有结点都驻留于优先级基于 key 域的队列 Q 中,对每个结点 v,key[v]是连结 v 到树中结点的边所具有的最小权 值;按常规,若不存在这样的边则 key[v]=∞。域π[v]表示点 v 的“父亲结点”。 在算法执行中,GENERIC-MST 的集合 A 隐含地满足: A={(v,π[v]):v∈V-{r}-Q} 当算法终止时,优先队列 Q 为空,因此 G 的最小生成树 A 满足: A={(v,π[v]): v∈V-{r}}
生成树计数算法

⽣成树计数算法⽣成树计数问题:给出⼀个⽆向图,求它的⽣成树的个数。
预备知识(1)⼀个n个顶点的⽆向图G,定义它的度数矩阵D,D是⼀个n*n的矩阵。
对于顶点u,设度数为deg[u],如果i=j,那么D[i][j]=deg[i],否则D[i] [j]=0.(2)⼀个n个顶点的⽆向图G,定义它的邻接矩阵A,A是⼀个n*n的矩阵。
如果i和j之间有边,那么A[i][j]=1,否则等于0。
(3)⼀个n个顶点m条边的⽆向图G,定义它的关联矩阵B,B是⼀个n*m的矩阵。
对于第i条边e[i]=(u,v),那么B[u][i]和B[v][i]中⼀个是1,⼀个是-1,第i列其他值为0。
那么我们有所以对于如果i=j,它是顶点i的度数,否则,如果i和j之间有边,那么它等于-1,否则它等于0.(4)对于⼀个n个顶点m条边的⽆向图G,定义它的Kirchhoff矩阵C,C是⼀个n*n的矩阵,很显然,C=D-AMatrix-Tree定理对于⼀个⽆向图G,它的⽣成树个数等于其Kirchhoff矩阵任何⼀个n-1阶主⼦式的⾏列式的绝对值。
所谓n-1阶主⼦式,就是对于任意⼀个r,将C的第r⾏和第r列同表⽰时删去后的新矩阵,⽤下⾯的字母表⽰C_{r}接下来,我们⾸先证明下⾯四个性质:性质1:对于任何⼀个图的Kirchhoff矩阵C,它的⾏列式为0。
性质2:对于不连通的图,它的Kirchhoff矩阵C的任⼀个n-1阶主⼦式的⾏列式均为0。
性质3:如果G是⼀棵树,它的Kirchhoff矩阵C的任⼀个n-1阶主⼦式的⾏列式均为1。
性质4:柯西-⽐内公式。
设A和B分别是n*m和m*n的矩阵,那么其中S是⼀个⼦集,⼤⼩为n,也就是S取遍所有的n⼦集,相应的As和Bs为从A和B中取出S元素下标的所有列和所有⾏。
性质1证明:由C的性质可得,它的每⼀⾏每⼀列和均为0,那么我们把第2到第n⾏都加到第⼀⾏,那么第⼀⾏就全部是0了。
有⼀⾏全部是0,那么它的⾏列式就是0了。
第4讲-生成树

图G
· u·
·v ···w
· x··
图G的生成树T
· u·
·v ···w
· x··
T的余树
2021/4/4
9
割集
• 割集的定义:连通图G的一个边集 BE(G),如果它是使得G-B不 连通的极小边集,则称B为G的割 集。
• 例:图的割集
2021/4/4
10
2.2 割 集
定义:连通图G的一个边集BE(G),如果它是使G-B不连通的
11
定理2.6 设B为连通图G的割集,则ω(G-B)=2 证:用反证法。 设 B为连通图G的割集,且ω(G-B)≥3,将B中任一边e添回到GB中,一条边只能使两分支连接,故G-B+e仍是不连通的,而 B-e是B的真子集,这与B为极小边集矛盾,故ω(G-B)=2。
*割边为只含一条边的割集。
记号:对V 的子集V1 和V2,用[V1,V2]表示一个端点在V1 中另 一个端点在V2 中的所有边的集。 定义:若S ⊂V,记 S V/S,则边集 [ S ,S ] 称为G 中的割。
• 等价说法:图G中的割点v为满足于 ω(G-v)> ω(G)的顶点v。
• G-v是什么? ω(G)是什么?
2021/4/4
6
关于割点的结论
• 定理: v为图G的割点的充要条件是G 中存在与v不同的两个顶点u和w,使 得图G所有的uw路都通过v。
• 证明?
• 定理:树G中的每个d(v) > 1的顶点
2021/4/4
22
破圈法求解结果
v2
1
3
v1
3
3 v7
v6
v3 7
2 v4
v5
2021/4/4
生成树的计数

生成树的计数郑艺容;周雪【摘要】In this paper, we explored the possibility of counting spanning tree in a combinatorial approach. We got three combinatorial identifies applying the inclusion-exclusion principle. Based on these identifies and mathematics induction, we gave an easy proof for the Cayley’s formula using a combinatorial argument. The approach combines the problem of graphical enumeration with classical problems in combinatorial mathematics and reveals the essence of the problem of counting spanning trees with better effect.%从组合数学的角度研究生成树的计数。
先利用容斥原理,得到3个组合恒等式,再从组合数学的角度出发,并利用数学归纳法给出了Cayley’s 公式的又一简便证明。
该计数方法将图的计数问题与组合数学中的经典问题联系起来,更好地揭示了生成树计数的本质。
【期刊名称】《厦门理工学院学报》【年(卷),期】2015(000)001【总页数】3页(P95-97)【关键词】Cayley’s 公式;生成树;容斥原理;数学归纳法【作者】郑艺容;周雪【作者单位】厦门理工学院应用数学学院,福建厦门361024; 福州大学离散数学中心,福建福州350003;福州大学离散数学中心,福建福州350003【正文语种】中文【中图分类】O157计算图的不同生成树的个数是图的计数问题中的一个重要研究课题.1857年,Cayley [1] 在研究给定碳原子数n的饱和碳氢化合物(CnH2n+2)的同分异构体的数目时,提出“树”的概念,即不含圈的连通图.如果连通图G的一个子图T是一棵树,且包含G的所有顶点,则该子图T称为G的生成树(Spanning Tree).设G 是一个图,t(G)表示G中不同生成树的个数.Cayley于1889年给出计算n阶完全图的不同生成树个数的公式,即著名的Cayley’s 公式.定理1 [2] (Cayley’s 公式) n阶完全图的不同生成树的个数Cayley’s 公式有很多不同的证明方法,参见文献[2-5].本文又给出Cayley’s 公式的又一简单证明.首先介绍一些基本概念和结论.容斥原理是组合数学中一个非常重要的定理,其内容如下:定理2[6 ] (容斥原理) 设A是有限集,Ai⊆A(i=1,2,…,n,n≥2),则设N={1,2,…,n},M={1,2,…,m},A表示N上所有p维数组构成的集合,其中p<m≤n.因为p<m,那么对A中的任意一个p维数组s,存在M中的元素i∉s.令Ai(i=1,2,…,m)表示A中不含有i的p维数组构成的集合,易知A=A1∪A2∪…∪Am.引理m.定理3 设n,m,p∈N+,p<m≤n,则以下组合恒等式成立证明A,Ai(i=1,2,…,m)定义如上.首先,由乘法原理可知.又A=A1∪A2∪…∪Am,根据容斥原理、对称性及引理1可得:特别地,当p=n-2时可得以下推论:推论(n≥3).以下给出Cayley’s 公式的另一简单证明.设T表示所有n阶生成树构成的集合,tn表示所有n阶生成树的个数,即.Ti(i=1,2,…,n)表示顶点i为树叶的所有n阶生成树构成的集合.引理2 集合T1∩T2∩…∩Tk满足:.证明由上述定义可知:T1∩T2∩…∩Tk那么表示顶点1,2,…,k(1≤k≤n)均为树叶的n阶生成树构成的集合,这样的任意一棵树可经过下述两个步骤得到.(i)由顶点k+1,k+2,…,n导出的子图T是一棵树,易知恰好有tn-k个这样的T;(ii)把顶点1,2,…,k添加到T中得到树T,使得顶点i(1,2,…,k)为T的树叶,即顶点i 恰好与顶点k+1,k+2,…,n中的某一个顶点相邻,这样的方式共有(n-k)k种,根据乘法计数原理可得:=(n-k)ktn-k .引理3 n阶不同生成树的个数tn满足:tn=1(n=1,2);(n≥3).证明T表示所有n阶生成树构成的集合,Ti(i=1,2,…n)表示所有n阶生成树中顶点i为树叶的生成树构成的集合,由于每棵非平凡树至少有两片树叶,故T=T1∪T2∪…∪Tn,由容斥原理、对称性及引理2可知:以下给出Cayley’s 公式的另一证明.定理4 所有不同n阶生成树的个数tn=nn-2 ( Cayley’s 公式)证明用数学归纳法(i)易知t1=t2=1,t3=3 结论显然成立.(ⅱ)假设定理对小于n的正整数都成立.(ⅲ)以下证明对n结论成立.根据引理3Cayley’s 公式是图计数中的经典公式,已有很多不同的证明方法,本文利用由容斥原理得到的组合恒等式并借助数学归纳法给出Cayley’s 公式的又一简单证明.接下来可进一步研究Cayley’s 公式的不同证明方法,特别是能将图的其它经典问题与图的计数问题联系起来证明Cayley’s 公式,更好地揭示图论中的一些本质联系.2【相关文献】[1]CAYLEY A.On the theory of the analytical forms called trees[J].Philophical Magazine,1857,13(4):172-176.[2]CAYLEY A.A theorem on trees[J].Quart J Math,1989,23:376-378.[3]SHOR P W.A new proof of Cayley’s formula for counting l abeled trees[J].J Combin Theory:Series A,1995,71:154-158.[4]ARIANNEJAD M,EMAMI M.A new proof of Cayley’s formula for counting labeled spanning trees[J].Electronic Notes in Discr Math,2014,45:99-102.[5]GODSIL C,ROYLE G.Algebraic graph theory[M].New York:Springer-Verlag,2001.[6]曹汝成.组合数学[M].广州:华南理工大学出版社,2000.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生成树的计数及其应用目录生成树的计数及其应用 (1)目录 (1)摘要 (2)关键字 (2)问题的提出 (2)[例一]高速公路(SPOJ p104 Highways) (2)[分析] (2)预备知识 (2)排列 (3)行列式 (4)新的方法 (7)介绍 (7)证明 (9)理解 (12)具体应用 (12)[例二]员工组织(UVA p10766 Organising the Organisation) (13)[分析] (13)[例三]国王的烦恼(原创) (13)[分析] (14)总结 (14)参考文献 (14)摘要有关生成树的最优化问题如最小生成树等是我们经常遇到的,而对生成树的计数及其相关问题则少有涉及。
事实上,生成树的计数是十分有意义的,在许多方面都有着广泛的应用。
首先介绍了一种指数级的动态规划算法,然后介绍了行列式的基本概念、性质,并在此基础上引入Matrix-Tree定理,同时通过与一道数学问题的对比,揭示了该定理所包含的数学思想。
最后通过几道例题介绍了生成树的计数的应用,并进行总结。
关键字生成树的计数Matrix-Tree定理问题的提出[例一]高速公路(SPOJ p104 Highways)一个有n座城市的组成国家,城市1至n编号,其中一些城市之间可以修建高速公路。
现在,需要有选择的修建一些高速公路,从而组成一个交通网络。
你的任务是计算有多少种方案,使得任意两座城市之间恰好只有一条路径?数据规模:1≤n≤12。
[分析]我们可以将问题转化到成图论模型。
因为任意两点之间恰好只有一条路径,所以我们知道最后得到的是原图的一颗生成树。
因此,我们的问题就变成了,给定一个无向图G,求它生成树的个数t(G)。
这应该怎么做呢?经过分析,我们可以得到一个时间复杂度为O(3n*n2)的动态规划算法,因为原题的规模较小,可以满足要求。
但是,当n再大一些就不行了,有没有更优秀的算法呢?答案是肯定的。
在介绍算法之前,首先让我们来学习一些基本的预备知识。
预备知识下面,我们介绍一种重要的代数工具——行列式。
为了定义行列式,我们首先来看一下排列的概念。
排列定义1 由1,2,…,n 组成的一个有序数组i 1i 2…i n 称为1,2,…,n 的一个排列。
由排列的定义可知,i 1,i 2,…,i n 表示了n 个不同的自然数,同时i 1,i 2,…,i n 中的每个自然数都是集合S n ={1,2,…,n }中的一个元素,换句话说,n i n i i →→→,,, 2121定义了集合S n 到自身上的一个一一对应。
这个一一对应可以用符号⎪⎪⎭⎫⎝⎛n i i i n 2121记之,称为置换,而上述一一对应可以改写为n j n j j i j i j i j →→→,,, 212其中j 1j 2…j n 是1,2,…,n 的一个排列。
所以这个一一对应也可以用符号⎪⎪⎭⎫ ⎝⎛n j j j n i i i j j j 2121记之,因此对1,2,…,n 的任一排列j 1j 2…j n ,可定义⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛n j j j n n i i i j j j i i i n 21212121任取一个排列i 1i 2…i n ,将其中两个相邻的自然数i j -1,i j 对换一下,便造出一个新的排列i 1i 2…i j -2i j i j -1 i j +1…i n ,称为原来排列的对换排列,这样一种步骤成为对换。
显然,对于任何一个排列经过若干次对换后都可以变成标准排列12…n 。
不过,不管经过什么途径作对换,在给定排列i 1i 2…i n 后,关于对换的次数有下列重要定理。
定理1 将任意一个排列i 1i 2…i n 通过对换变成标准排列12…n ,所需的对换次数的奇偶性与对换方式无关。
利用这个定理,我们引入定义2 一个排列i 1i 2…i n 称为偶(奇)排列,如果有一种方式,经过偶(奇)数次对换后,可以将排列i 1i 2…i n 变为标准排列12…n 。
设排列i 1i 2…i n 经过t 次对换后变为标准排列12…n ,则数值(-1)t 和对换方式无关。
将它改写成ni i i n2112δ,即()⎩⎨⎧-=-=的奇排列时。
,,,是,当的偶排列时;,,,是,当n i i i n i i i i i i n n n tn 211211112212121δn 个确定自然数1,2,…,n 的排列,可以看作是集合S n ={1,2,…,n }到自身上的一个一一对应。
将这个概念推广,任取n 个元素的集合S ={a 1,a 2,…,a n }。
对于集合S 到自身上的一一对应n i n i i a a a a a a →→→,,, 2121n i i i a a a 21称为n a a a ,,, 21的一个排列。
容易看出,n i i i a a a 21是n a a a ,,, 21的排列的充要条件是i 1i 2…i n 是1,2,…,n 的排列。
同样,排列n i i i a a a 21变为标准排列n a a a 21的对换总次数的奇偶性和对换方式无关,因此引入符号()⎩⎨⎧-=-=的奇排列时。
是,当的偶排列时;是,当n i i i n i i i ti i i n a a a a a a a a a a a a a a a a a a n n n,,,1,,,11212121212121 δ其中t 是某一种将n i i i a a a 21变为n a a a 21的对换方式的对换总次数。
下面我们介绍行列式。
行列式一阶行列式是一个变量a 11的函数det(a 11)= a 11,也可以改写成为()∑⎪⎪⎭⎫ ⎝⎛==1111111111det a a a δ二阶行列式是四个变量a 11,a 12,a 21,a 22的函数1212221122211211det a a a a a aa a -=⎪⎪⎭⎫⎝⎛,也可以改写成∑⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛21211221212221121112det i i i i a a i i a a a a δ 三阶行列式是九个变量a ij (i ,j =1,2,3)的函数322311332112312213322113312312332211333231232221131211det a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++=⎪⎪⎪⎭⎫ ⎝⎛,同样可以改写成为321321321123321333231232221131211123det i i i i i i a a a i i i a a a a a a a a a ∑⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛δ通过观察一、二、三阶行列式的定义,我们得出了n 阶行列式的一般定义。
定义3 n 阶矩阵A 的行列式是一实数,记作det A ,它定义为n n ni i i i i i n n a a a i i i nA 212121122112det ∑⎪⎪⎭⎫ ⎝⎛=δ行列式有下列几种常用的符号:A a a a a a a a a A nnn n nn n n ==⎪⎪⎪⎭⎫ ⎝⎛= 11111111det det由行列式的定义可知,利用定义直接计算行列式是很困难的,只有在阶数低时才可以直接用定义计算。
为了能够进行计算,需要先导出行列式的若干基本性质,在通过这些性质,将复杂的行列式计算化为简单的行列式计算,也可以将高阶行列式的计算化为低阶行列式的计算。
性质1 设A 是n 阶矩阵,则det A T =det A 。
这个定理的重要意义在于,它告诉我们行列式的行和列的地位是平等的。
确切地说,每个关于行的性质,对列必然成立;反之亦然。
性质2 行列式的任两行(或两列)互换,行列式变号。
推论 行列式的某两行(或两列)相同时,行列式的值为0。
性质3 用实数λ乘以一行(或列)后,所得到的行列式等于原来的行列式乘以λ。
推论 行列式有两行(或两列)成比例,则该行列式的值为零。
特别的,当行列式有一行(或列)全为零时,行列式的值为零。
性质4nnn n j j jn j nj j n nnn n j j jn j nj j n nnn n j j jn jn j j n j j n a a a a b b a a a a a a a a a a a a a a a a a a b a b a a a a a1,11,11,11,11111,11,11,11,11111,11,111,11,1111++--++--++--+=++ 对列也有同样性质。
推论 将行列式的任意行(或一列)乘以实数λ,再相应地加到另一行(或另一列)上去,则行列式的值不变。
例如,当j ≠1时nnn n n nnn n jnn j a a a a a a a a a a a a a a122111112211111λλ=++下面我们介绍一种计算行列式的方法。
首先,不难证明nnn nnnn nnnnn n n a a a a a a a a a a a a a a a a a a a12221122221121121222211100== 今取行列式nnn nb b b b B 1111det =我们可以将B 化为上三角形式,记为'B ,同时记录行交换次数S 。
根据定理11,易知:()nnnnSb b b b b b B B '0''0''''det 1det 22211211=-=再利用刚才的结论,得()∏=-=ni iiSb B 1'1det 。
对于矩阵A ,任取2p 个自然数1≤i 1<i 2<…<i p <=n ,1≤j 1<j 2<…<j p <=n在矩阵A 中取出第i 1,i 2,…,i p 行第j 1,j 2,…,j p 列的交叉元素,按原来的次序排成p 阶矩阵。
这个矩阵的行列式称为矩阵A 的p 阶子式,记作pp p pj i i j i i p p a a a a j j j i i i A 11212111=⎪⎪⎭⎫⎝⎛根据这个定义,下面我们再介绍中一个非常重要的公式——Binet -Cauchy 公式。
定理8(Binet -Cauchy 公式) 设A 和B 各为p *q 及q *p 矩阵,则有⎪⎪⎪⎩⎪⎪⎪⎨⎧<⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=>=∑<=<<<=时。
当时;当时;当q p p j j j B j j j p A q p BA q p AB q j j p p p1121212121det det ,0det特别的,det AA T =(det A )2。
