描述性统计量及检验
实验一常用计算方法及描述统计量分析

实验一常用计算方法及描述统计量分析1.引言描述统计量是统计学中常用的数据分析方法。
通过统计样本数据的各种特征指标,可以对总体数据的一些性质进行分析和描述。
本实验主要介绍几种常用的计算方法及描述统计量分析。
2.均值均值是描述数据集中趋势的一个重要统计量。
一组数据的均值可以通过将所有观察值相加,然后除以观察值的总数来计算。
均值可以用来描述一个数据集的集中趋势,通常用符号μ来表示。
3.中位数中位数是将一组有序数据划分为较小和较大两部分的值,位于中间位置的值。
对于一个有序的数据集,中位数就是位于中间位置的数值。
如果数据集的观察值个数是奇数,则中位数是排在中间的值;如果数据集的观察值个数是偶数,中位数是排在中间两个值的平均值。
4.众数众数是数据集中出现频率最高的数值。
一个数据集可以有一个或多个众数。
众数可以用来描述数据集中出现频率最高的数值,通常用符号Mo 表示。
5.极差极差是描述数据集分散程度的一个统计量。
它是数据集中最大值与最小值的差别。
极差可以用来描述数据集的波动性,如果极差较大,说明数据分散程度较大。
6.方差方差是描述数据集分散程度的一个统计量。
方差是数据与其均值之间差异的平均平方值。
方差可以用来描述数据集的波动性,如果方差较大,说明数据分散程度较大。
7.标准差标准差是描述数据集分散程度的一个统计量。
标准差是方差的平方根,用符号σ来表示。
标准差可以用来描述数据集的波动性,如果标准差较大,说明数据分散程度较大。
8.相关系数相关系数是描述两个变量之间关系强度的一个统计量。
相关系数的取值范围在-1到1之间,当相关系数为正时,表示两个变量正相关,当相关系数为负时,表示两个变量负相关。
相关系数可以用来描述两个变量之间的关联程度。
9.回归分析回归分析是一种描述和预测变量之间关系的方法。
回归分析可以用来研究因变量与自变量之间的关系,并通过建立回归方程对因变量进行预测和解释。
10.结论通过实验一的学习,我们了解了常用的计算方法及描述统计量分析。
第三章描述性统计分析

描述性统计分析指标
统计量可分为两类
一类表示数据的中心位置,例如均值、中位数、众 数等 一类表示数据的离散程度,例如方差、标准差、极 差等用来衡量个体偏离中心的程度。
描述单变量分布的三种方式
用数字呈现一个变量的分布 用表格呈现一个变量的分布 用图形呈现一个变量的分布
Frequencies
在交叉列联表中,除了频数外还引进了各种百分 比。例如表中第一行中的33.3%, 33.3%, 33.3 %分别是高级工程师3人中各学历人数所占的比例 ,称为行百分比(Row percentage),一行的百 分比总和为100%;表中第一列的25.0%,25.0% ,50.0%分别是本科学历4人中各职称人数所占的 比例,称为列百分比(Column percentage), 一列的列百分比总和为100%,表中的6.3%,6.3 %,12.5%等分别是总人数16人中各交叉组中人 数所占的百分比,称为总百分比(Total percentage),所有格子中的总百分比之和也为 100%。
例子
假设我们有以下的三组观测值:
观测A:11,12,13,16,16,17,18,21 观测B:14,15,15,15,16,16,16,17 观测C:11,11,11,12,19,20,20,20
这三组观测值的均值都是15.5,那么这三组数 据是否相似呢?
离散趋势
离散趋势的描述
本科 职称 高 级工 程师 Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total 1 33.3% 25.0% 6.3% 1 25.0% 25.0% 6.3% 2 33.3% 50.0% 12.5% 0 .0% .0% .0% 4 25.0% 100.0% 25.0%
实验五描述性统计分析

第二篇 数据分析基础实验五 描述性统计分析实验目的:了解相关系数和偏相关系数的计算方法。
实验工具:SPSS 描述性统计分析菜单项。
知识准备:一、统计整理统计整理是根据统计研究的目的,对统计调查所获得的大量原始资料(初级资料),进行科学的分类和汇总,使之条理化、系统化,得出能够反映现象总体特征的综合资料的工作过程。
统计整理的结果为统计表与统计图。
统计表主要表现为频数表,而统计图的表现形式多样,前面已经介绍了各种统计图的制作方法,此处不在专门进行介绍。
二、集中趋势的测量集中趋势是指一组数据向某一中心值靠拢的倾向,测度集中趋势也就是寻找数据一般水平的代表值或中心值。
集中趋势主要依赖各种平均指标进行反映。
1、算术平均数算术平均数又称为均值,其定义为:设1X ,2X ,…,n X 是取自某总体的一个样本,它的算术平均数∑==ni i X n X 11算术平均数有四个重要性质:①各变量值与平均数离差之和等于零;②各个变量值与平均数离差平方和为最小值;③常数的算术平均数是其本身;④对于任何两个变量x 和y ,它们的代数和的算术平均数就等于两个变量的算术平均数的代数和。
2、调和平均数调和平均数是根据标志值的倒数计算的,它是标志值倒数的算术平均数的倒数。
调和平均数的计算公式为:使用调和平均数要注意三个问题:①变量X 的取值不能为零,因为零不能作为分母,此时调和平均数无法计算;②调和平均数与算术平均数一样,易受极端值的影响③调和平均数只适用于特殊的数据情况,所以要注意区分它的适用条件。
在SPSS 中,调和平均数可以在Report 子菜单的4个报表过程中计算输出。
3、几何平均数几何平均数是n 个变量值乘积的n 次方根。
凡是现象的连乘积等于现象的总比率或总速度都可用几何平均数来计算它们的平均比率和平均速度。
其计算公式为:n n n x x x x x G ∏=⋅⋅⋅⋅= (321)式中:标志值个数。
连乘符号;各个标志值;数;几何平均------------∏n x G在SPSS 中,几何平均数可以在Report 子菜单的4个报表过程中计算输出。
stata描述性统计分析报告

stata描述性统计分析报告describedescribe命令可以描述数据文件的整体,包括观测总数,变量总数,生成日期,每个变量的存储类型(storagetype),标签(label)等。
list[varlist][if exp][in range]summarize[varlist][weight][if exp][in range][,detail]summarize可以提供varlist指定变量(可以不止一个)的如下统计量:Percentiles(分位数),四大最大的数和四个最小的数,Variance(方差),Std.Dev.(标准差),Skewness(偏度),Kurtosis(斜度)tabstattabstat varlist[weight][if exp][in range][,stats(statname[...])]tabstat提供[,stats(statname[...])]指定的统计量,可供选择的有mean(均值),count(非缺失观测值个数),sum(总和),max(最大值),min(最小值),range(最大值-最小值),sd (标准差),var(方差),cv(变易系数=标准差/均值),skewness(偏度),kurtosis(斜度),median(中位数),p1(1%分位数,类似地有p5, p10,p25,p50,p75,p95,p99),iqr(interquantile range=p75–p25)。
比如,想知道变量pop在整个样本的均值和方差,可以使用如下命令:tabstat pop,stats(mean var)anova命令anova y x1 x2anova做方差分析(analysis of variance),研究y的平均值在分类变量x1和x2不同取值之间的差异。
signrank命令signrank y1=y2signrank做Wilcoxon秩检验。
报告中常用的统计指标和描述性统计方法

报告中常用的统计指标和描述性统计方法统计学作为一门研究数量关系的科学,广泛应用于各个领域。
在进行统计分析时,我们常常需要使用各种统计指标和描述性统计方法,来帮助我们更好地理解和呈现数据的特征。
本文将针对报告中常用的统计指标和描述性统计方法展开详细论述,包括以下六个主题:一、平均数的计算与应用平均数是最常见的统计指标之一,它能够反映数据的集中趋势。
我们常用的平均数有算术平均数、加权平均数和几何平均数等。
在报告中,我们可以通过计算平均数,来描述一组数据的整体水平。
同时,平均数还可以用于比较不同组的数据,并进行定量分析。
二、离散程度的度量与解释离散程度是描述数据分散情况的统计指标,常用的离散程度指标有方差和标准差等。
方差反映了数据相对平均值的分散程度,而标准差是方差的平方根。
这些指标能够帮助我们了解数据的波动情况,并进行风险管理和预测。
三、分布形态的描述与判断数据的分布形态是指数据的分布特征,常见的分布形态有对称分布、偏态分布和峰态分布等。
在报告中,我们可以使用偏度和峰度等统计指标,来定量描述数据的分布形态,并判断数据是否符合正态分布。
这能够提供有关数据的进一步洞察,为后续分析提供参考。
四、相关性的分析与解释相关性分析可以帮助我们揭示数据之间的关联程度。
常见的相关性指标有皮尔逊相关系数、斯皮尔曼相关系数和判定系数等。
这些指标可以帮助我们判断变量之间的线性相关性,并进行因果关系的推断。
在报告中,相关性分析有助于我们发现变量之间的相互作用,进而指导决策和行动。
五、显著性检验的原理与应用显著性检验是统计推断的重要工具,用于判断样本数据与总体之间是否存在显著差异。
在报告中,我们可以借助显著性检验的方法,来分析样本的统计显著性,并进行结论的推断。
常用的显著性检验方法有 t 检验、方差分析和卡方检验等,它们可以帮助我们进行统计推论和决策。
六、回归分析的原理与应用回归分析是用于建立变量之间关系的统计方法。
常见的回归分析方法有线性回归、多项式回归和逻辑回归等。
Eviews数据统计与分析教程4章 图形和统计量分析(课堂讲课)

专业课件
12
EViews统计分析基础教程
二、描述性统计量
2.序列组窗口下的描述性统计量
在序列组(Group)对象窗口下选择工具栏中的“View”| “Descriptive Statistics”(描述性统计量)选项,将弹出3 个选项。
专业课件
13
EViews统计分析基础教程
二、描述性统计量
2.序列组窗口下的描述性统计量
第二个选项是“Stats Table”(统计表),它将描述性统计 量值通过电子表格的形式显示在对象窗口中。
第三个选项是“Stats by Classification”(分类统计量), 它将样本分为若干组后再对各组观测值分别进行描述统计。
第四个选项是“Boxplots by Classification”(分类箱线图/ 箱尾图),将序列分布按照箱线图/箱尾图进行分类。箱线 图(Boxplot)也称为箱尾图,是利用数据统计量来描述数 据的一种方法。
打开序列组对象窗口,选择工具栏中的“View”|“Granger Causality”选项,在弹出的对话框中输入滞后期,然后单击 “OK”按钮,就会得到下图所示的分析结果。一般情况下 Granger因果检验的滞后期要根据AIC和SC准则来确定。
专业课件
1
EViews统计分析基础教程
一、图形对象
1.图形对象的建立
选择对象窗口工具栏中的“View”| “Graph”选项。“Graph” 的菜单中有6种图形可供选择。
“Line”表示生成的是折线图 “Area”表示生成面积图 “Bar”表示为条形图 “Spike”表示尖峰图 “Seasonal Stacked Line”表示生成的是季节性堆叠图 “Seasonal Split Line”表示生成的是季节性分割线
实验三、描述性统计分析实验报告

实验三、描述性统计分析实验报告上海对外贸易学院实验报告⼀、实验⽬的和要求1.熟练掌握描述性统计分析的基本原理2.熟练掌握频数分析原理、SPSS操作及案例分析3.熟练掌握基本描述统计量原理、SPSS操作及案例分析4.熟练掌握探索性分析原理、SPSS操作及案例分析5.熟练掌握原理交叉列联表原理、SPSS操作及案例分析6.熟练掌握多选项分析的SPSS操作及案例分析⼆、实验内容及结果分析1.频数分析(数据⽂件:3-studentscore.sav)(1)完成各门成绩的统计结果(抓图后复制到下⾯)图1分析解释:(2)完成语⽂成绩区间频度分布表(抓图后复制到下⾯)图2分析解释:(3)计算全部学⽣各门成绩的平均值、标准差、极差和四分位数(抓图后复制到下⾯)图3分析解释:2.基本描述统计量(数据⽂件:3-studentscore.sav)计算全部学⽣各部门成绩的平均值、标准差、最⼤值和最⼩值(抓图后复制到下⾯)图4分析解释:3.探索性分析(数据⽂件:3-studentscore.sav)(1)完成语⽂成绩茎叶图和箱图(抓图后复制到下⾯)图5分析解释:图6分析解释:(2)语⽂成绩正态分布检验的Q-Q概率图(抓图后复制到下⾯)(数据⽂件:4-Explore.sav)图7分析解释:(3)完成考察学⽣“英语”、“数学”、“语⽂”三门课程成绩的分布、极端值以及正态分布性和⽅差的齐性。
(抓图后复制到下⾯)图8分析解释:4.交叉列联表分析(数据⽂件:4-crosstabulation.sav)(1)⼆维交叉列联表(P64,抓图后复制到下⾯)图9分析解释:(2)X2检验结果(P671,抓图后复制到下⾯)图10分析解释:三、思考题(P79-P80)完成思考题3、4,并将关健图抓下来粘贴到相应题下⾯,并进⾏简单的解释。
四、学完“描述性统计分析”章节后的收获。
【STATA精品教程】第五章 描述性统计分析

使用tabstat命令计算描述性统计量
. tabstat varlist [if] [in] [weight] [, options]
选项 含义
mean 平均数
count / n 观测值数目
s
range 极差
sd 标准差
var
方差
cv 变异系数 (sd/mean)
meanonly
仅计算和显示平均数,本选项在编程中比较有用。
format
使用变量的显示格式。
separator(#) 每#个变量画一条分界线,默认为separator(5), separator(0) 禁止使用分界线。
【例5-1】现在我们利用小时工资数据集举例说明summarize的使用。 要求使用summarize命令对wage.dta执行如下操作: (1)对wage、educ、exper、tenure、nonwhite、female、married 做基本的统计分析, (2)Summarize命令加上detail选项容许我们对某些重要的变量做 更加详尽的分析, (3)在summarize后使用in或者if来限制条件,可以获得对某个子 样本的描述性统计。 (4)使用outreg2命令导出描述性统计量。
sfrancia varlist [if] [in]
④D’ Agostino检验
sktestdc varlist [=exp] [if exp] [in range] [, noadjust]
【例5-4】下面我们依次举例说明这四个命令的使用,这里用到的 数据仍然是小时工资数据集wage1.dta。 首先我们对wage变量进行偏度—峰度检验, (2)接下来我们对wage变量分别进行W检验Swilk(Shapiro-Wilk W test for normality)和 W' 检验Sfrancia(Shapiro-Francia W' test for normality), (3)最后演示D’ Agostino检验,使用的命令是sktestdc,这里我 们使用未经调整过的卡方检验,即添加noadjust选项:
调查数据分析--描述性统计结果
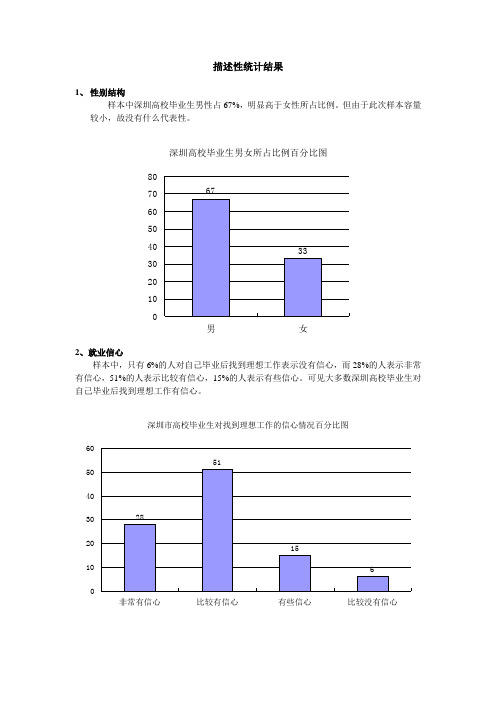
描述性统计结果1、 性别结构样本中深圳高校毕业生男性占67%,明显高于女性所占比例。
但由于此次样本容量较小,故没有什么代表性。
深圳高校毕业生男女所占比例百分比图01020304050607080男女2、就业信心样本中,只有6%的人对自己毕业后找到理想工作表示没有信心,而28%的人表示非常有信心,51%的人表示比较有信心,15%的人表示有些信心。
可见大多数深圳高校毕业生对自己毕业后找到理想工作有信心。
深圳市高校毕业生对找到理想工作的信心情况百分比图102030405060非常有信心比较有信心有些信心比较没有信心3、接受学校或政府提供的就业辅导或培训的情况样本中,66%的人表示没有接受过学校或政府提供的就业辅导或培训,人数比例明显高于有接受过此类培训的。
深圳市高校毕业生接受就业辅导或培训的情况百分比图010203040506070接受过没有接受过4、薪酬要求样本中,一半人找工作对月薪的要求不高于3000元,深圳市高校毕业生对工作月薪要求的平均水平为3653元。
对月薪的要求主要集中在3000-5000元,最低要求为2000元,最高要求为10000元。
深圳市高校毕业生对工作月薪要求的情况表变量关系检验的描述5、不同性别的人对找到理想工作的信心情况对比 (注,因为样本容量不够,所以“非常有信心”“比较有信心”合并为“有信心”;将“有些信心”“比较没有信心”“合并为“比较没有信心”;“非常没有信心”没有人选故省去该选项。
)男女对找到工作的信心指数被分为“有信心”“比较没有信心”两项,采用两个独立样本卡方检验的统计方法,对比就业信心情况在不同性别上的凸显度。
F 检验结果为0.629,在0.05水平上不显著,说明男女在这个问题上总体的方差没有显著性差异。
可以推断,不同性别的人在就业信心情况上没有显著差异。
(由图表也可分析出同一结果)不同性别的人对照到理想工作的信心情况比较0.00%10.00%20.00%30.00%40.00%50.00%60.00%70.00%80.00%90.00%有信心比较没有信心6、不同性别的人接受学校或政府提供的就业辅导或培训的情况对比根据有没有接受过学校或政府提供的就业辅导或培训的情况分为两个选项,采用两个独立样本卡方检验的统计方法,对比接受就业辅导或培训的情况在不同性别上的凸显度。
临床研究资料常用统计分析方法

临床研究资料常用统计分析方法统计分析是临床研究中不可或缺的部分,它通过收集和整理研究数据,对数据进行加工处理和解释,以达到对研究问题进行评估和推断的目的。
本文将介绍一些常用的临床研究资料统计分析方法,包括描述性统计分析、推断统计分析和相关性分析。
一、描述性统计分析描述性统计分析是对研究数据进行整理、描述和总结的方法,通过计算和展示数据的中心趋势、离散程度、分布和关联性,以对数据进行初步的解释和理解。
1. 中心趋势的描述中心趋势是描述一组数据集中值的指标,常用的计算方法有平均值、中位数和众数。
平均值是数据的算术平均数,通常用来衡量数据的集中程度。
中位数是将数据按照大小排序后,处于中间位置的数值,它对异常值不敏感,常用来描述有偏态分布的数据。
众数是数据中出现频率最高的数值,可以用来描述数据的集中情况。
2. 离散程度的描述离散程度描述了数据集的分散程度,常用的计算方法有标准差、方差和范围。
标准差是数据偏离平均值的平均距离,它可以衡量数据的波动性。
方差是标准差的平方,它表示数据的离散程度。
范围是最大值减去最小值,它描述了数据的变异范围。
3. 分布的描述分布描述了数据在某一区间内出现的频率或概率分布情况。
常用的方法有频数分布表、频率分布直方图、正态分布曲线等。
频数分布表用来列出每个数值所对应的频数或频率,直方图展示了数据的频数分布情况,正态分布曲线则是用来描述数据服从正态分布的情况。
二、推断统计分析推断统计分析是通过对样本数据进行统计推断,来对总体数据进行估计、推断和判断的方法。
1. 参数估计参数估计是通过样本数据来估计总体参数的方法,常用的方法有点估计和区间估计。
点估计是根据样本数据计算出的参数值作为总体参数的估计值,区间估计是根据样本数据计算出的参数范围作为总体参数的估计范围。
2. 假设检验假设检验是通过对样本数据进行假设检验,来对总体参数进行推断和判断的方法。
它包括设定原假设和备择假设,计算检验统计量和P 值,从而判断原假设是否成立。
SPSS统计分析—描述性统计分析

• 各地区城乡居民消费水平比较
已知有2005年各省城乡居民消费水平, 试按地区对各省城乡消费 水平之比进行分析, 并比较不同地区之间城乡消费水平是否有较 大差异。
• 执行【Analyze】/【Descriptive Statistics】/【Ratio】命令, 弹出如 下图所示对话框
• 结果解读
SPSS统计分析—描述性统计 分析
描述性统计量
集中趋势
分布情况
均值
Mean
标准差 Std.deviatiom 偏度
Skewness
中位数 Median
Variance
峰度
Kurtosis
众数
Mode
极小值
Minimum
和
Sum
极大值
Maximum
Range
均值的标准 误差
S.E.mean
• 【Descriptive Statistics】子菜单
• ⑤ Ratio: 计算两个变量相对比的统计量特征。
• ⑥ P-P Plots: 绘制P-P图,检验数据服从的分布情况。
• ⑦ Q-Q Plots: 绘制Q-encies
• 频数分析简介 • 频数分析表是描述性统计中最常用的方法之一,它主要包括以下几
• 结果解读
• 1、列联表 • 2.卡方检验结果
3.条图
相对比描述——Ratio
• 在实际问题中,研究者有时除了希望了解变量自身的统计特征,还希望 得到两个变量相对比之间的统计描述。
• 法一: 通过对两个变量作除法形成一个新变量,然后分析新变量的统计 特征来得到。
• 法二: 直接通过【Ratio】过程来分析两个变量之间的相对比关系,并 且可以得到多于第一种方法的信息。
小胖说统计之临床试验中的描述性统计分析

小胖说统计之临床试验中的描述性统计分析The purpose of the field of statistics is to characterize a population based on the information contained in a sample taken from that population。
上述论述中,包含的三个要素是population、samples和characterization。
那么具体怎么characterization呢?无非有两种,一种就是我们所谓的descriptive statistics(描述性统计分析),一种是inferential statistics(推断性统计分析)。
具体到我们的临床试验中,描述性统计分析占到了我们最后统计分析报告的绝大部分,这是因为除了你事先有检验假设的一些终点的分析会用到推断性统计分析外,你几乎所有的人口学和基线变量的总结、疗效数据的总结、安全性数据的总结都要用到描述性统计分析。
而具体的描述性统计分析,又根据不同的数据类型有不同的描述方式,对于连续性变量来说,我们最常用到的是均数、标准差、中位数、最小值和最大值;对于分类型变量来说,主要用到的是频数表的方式即频数及百分比;对于time to event数据来说,我们则最主要基于Kaplan-Meier来进行统计描述。
此外,除了用表格的形式对临床试验数据进行描述性总结之外,我们还会用到一些figures来进行统计描述,最常见的如Line Plot,Bar Chart,Box Plot,K-M curve等。
我们在统计分析计划或研究方案中的统计分析部分,特别是在统计分析的一般原则中一般会对描述性统计分析常有以下类似的描述:对于连续型变量,将列出未缺失的受试者个数、均数、标准差、中位数、最小值和最大值。
对于分类变量,将以频数表的形式(频数和百分数)列出。
而有些比较详细的统计分析计划会对各描述性统计分析统计量的小数位数加以规定,从而使table更加标准化,当然小数位数的规定也不是绝对统一的标准,以下的例子的描述供大家参考:对于连续型变量,将列出未缺失的受试者个数、均数、标准差、中位数、最小值和最大值。
品质评价实验报告——描述性检验法

食品品质评价—描述检验法一、实验目的通过实验了解定量描述检验法的定义、特点及其应用;初步学会定量描述检验的方法。
本实验是利用定量描述检验法评价两种品牌的西红柿薯条和薯片的总体品质,分析其感官差异。
二、实验方法原理制定具体实验方案、对实验的样品进行准备,组织同学进行品尝并参加样品的品尝,根据人的感觉包括味觉、嗅觉、视觉、听觉和触觉等,用语言、文字、符号或数据进行记录,再运用概率统计原理进行统计分析,画出风味剖面图并对剖面图进行分析从而得出结论,对食品的色、香、味、形、质地、口感等各项指标做出评价。
三、样品及器具1.样品:两种番茄味薯片(可比克,上好佳)2.器具:被子,托盘,纸条,笔,纸巾四、方法步骤1.召开信息会,熟悉产品,确定产品特性特征及强度等级,采用GB12313-90标度 A(数字);2.确定评价方法:独立方法;3.评价组长按定量描述检验法程序做好样品的‘描述检验问卷’;4 两种薯条 /片样品以随机三位数编号,放在托盘内,呈递给评价员;5.评价员在熟悉薯条 /片产品的各项特性特征,独立品评,并填写问卷表;5.数据处理分组:按编号分成两大组进行数据统计分析,其中:1-22 号为第一大组(薯条),23-44 号为第二大组(薯片),结果报告形式:用QDA图报告总体评价结果;用方差分析报告样品间和评价员差异。
五、心得体会本次实验我对描述检验方法有了更进一步的认识,初步学会了定量描述检验的方法。
作为实验员,从样品特性特征的鉴定、感觉顺序的确定、采用数字法进行强度评价、余味和滞留度的测定、综合印象的评估,到实验的前期准备工作以及本次实验的内容——利用定量描述检验法评价两种品牌的番茄薯片的总体品质,整个过程我都参与了。
虽然多花了许多时间,但也有很多收获。
我对定量描述检验法的整个流程有了深层理解和深刻印象,同时也交到了很多朋友。
只有亲自动手实践,理论联系实际,才能更好地掌握理论知识,将所学内容应用于实践当中。
SPSS描述性分析统计操作步骤

SPSS的描述性分析操作步骤第一步:打开并输入数据
SPSS的打开方式有以上几种选择“打开现有的数据库”点击确定。
结果如下图显示。
第二步:在菜单栏里选择分析—描述统计—描述如下:选择左侧栏里需要统计的变量双击到右侧变量栏里。
如下
在右上角的选项里选择你需要的统计量:如下点击继续—确定—就可以得到数据量如下图所示
单样本的T检验在选项里分析—比较均值—单样本T检验如下图所示在右上角的选项里可以选择置信区间如下
点击继续—确定就可以得到我们想要的单样本t检验
心理1203班周昱衡
20120223189
2014年6月10号。
样本描述性统计与假设检验

数据分析-何帆
Statistics对话框
分位数
集中趋势统计 量
离散趋势统计 量
偏度和峰度
数据分析-何帆
Chart按钮
选择图形
定义是按照频数 还是按百分比作 图
数据分析-何帆
应用实例
练习2
在有小麦丛矮病的麦田里,调查了13株病株 和11株健株的植株高度,分析健株高度是否 高于病株?其调查数据如下: 健株 26.0 32.4 37.3 37.3 43.2 47.3 51.8 55.8 57.8 64.0 65.3 病株 16.7 19.8 19.8 23.3 23.4 25.0 36.0 37.3 41.4 41.7 45.7 48.2 57.8 该数据保存在“丛矮病的麦田.SAV”文件中
结果分析
自由度 t统计量 值 P值 置信区间 的上下限
数据分析-何帆
练习1
有一种新型农药防治柑桔红蜘蛛,进行了9 个小组的实验,其防治效果为: 95%,92%,88%,92%,93%,95%, 89%,98%,92% 与原用农药的防治效果90%比较,分析其 效果是否高于原用农药。
数据分析-何帆
数据分析-何帆
假设检验一般理论
对H0 进行检验: (1)寻找检验统计量 (2)对给定小概率,寻找拒绝域0 P{(x1,x2,…,xn) 0 | H0 为真时}= 接受域1 : 1∪0= (样本空间)
当样本观测值: (x1,x2,…,xn) 0 时,拒绝H0 (x1,x2,…,xn) 1 时,接受H1
数据分析-何帆
基本数学模型-离散趋势统计量
SAS中的描述性统计过程

SAS中的描述性统计过程(2012-08—01 18:07:01)转载▼分类:数据分析挖掘标签:杂谈SAS中的描述性统计过程描述性统计指标的计算可以用四个不同的过程来实现,它们分别是means过程、summary过程、univariate过程以及tabulate过程。
它们在功能范围和具体的操作方法上存在一定的差别,下面我们大概了解一下它们的异同点。
相同点:他们均可计算出均数、标准差、方差、标准误、总和、加权值的总和、最大值、最小值、全距、校正的和未校正的离差平方和、变异系数、样本分布位置的t检验统计量、遗漏数据和有效数据个数等,均可应用by语句将样本分割为若干个更小的样本,以便分别进行分析。
不同点:(1)means过程、summary过程、univariate过程可以计算样本的偏度(skewness)和峰度(kurtosis),而tabulate过程不计算这些统计量;(2)univariate过程可以计算出样本的众数(mode),其它三个过程不计算众数;(3)summary过程执行后不会自动给出分析的结果,须引用output语句和print过程来显示分析结果,而其它三个过程则会自动显示分析的结果;(4)univariate过程具有统计制图的功能,其它三个过程则没有;(5)tabulate过程不产生输出资料文件(存储各种输出数据的文件),其它三个均产生输出资料文件.统计制图的过程均可以实现对样本分布特征的图形表示,一般情况下可以使用的有chart过程、plot过程、gchart过程和gplot过程。
大家有没有发现前两个和后两个只有一个字母‘g’(代表graph)的差别,其实它们之间(只差一个字母g的过程之间)的统计描述功能是相同的,区别仅在于绘制出的图形的复杂和美观程度.chart过程和plot过程绘制的图形类似于我们用文本字符堆积起来的图形,只能概括地反映出资料分布的大体形状,实际上这两个过程绘制的图形并不能称之为图形,因为他根本就没有涉及一般意义上图形的任何一种元素(如颜色、分辨率等)。
统计学实验报告1统计计量描述

分析报告(一)实验项目:统计量描述实验日期:2012-3-16 实验地点:8教80680实验目的:熟悉描述性统计量的类型划分及作用;准确理解各种描述性统计量的构造原理;熟练掌握计算描述性统计量的SPSS操作;培养运用描述统计方法解决身边实际问题的能力。
实验内容:(1):分析被调查者的户口和收入的基本情况(2):分析储户存款金额的分布情况(3):计算存款金额的基本描述统计量,并对城镇和农村户口进行比较分析(4):分析储户存款数量是否存在不均衡现象实验步骤:analysze—Descriptive statistics-- Frequencies实验结果:【注释】:其中2.00表示收入基本不变【注释】:这是对城镇户口,农村户口的收入情况的描述性分析,frequency代表频率,percent 代表所占总体的百分比标准差是6881.827,标准误是0.141【注释】:本表描述的是城镇户口和农村户口的最小值,最大值,均值,标准差,标准误。
实验分析:(一)、总体看来,城镇户口和农村户口的收入情况:基本不变占据很大比例,说明经济发展较稳定(二)、城镇户口的收入增加所占的比例为34.3%,远超过农村户口的18.9%,说明农村的发展相较于城镇,还有很大的发展空间。
(三)、存款金额最大值(80502)和最小值(1)之间差距过大,说明贫富差距过大,从长远角度来看,不利于经济的发展,我们国家也有出台一些减小贫富差距的政策,加快城镇化建设之类的。
实验小结:备注:分析报告(二)姓名:李懿帆班级:统计2班学号:2010101213实验项目:单样本t检验实验日期:2012-3-23 实验地点:8教80680实验目的:准确掌握单样本t检验的方法原理;熟练掌握单样本t检验的SPSS操作;学会利用单样本t检验方法解决身边的实际问题实验内容:(1):某银行居民的平均存款与2500在95%的置信度下是否具有显著性差异(2):求某银行居民的平均存款在95%的置信度下的置信区间实验步骤:analysze—Compare Means—One-Sample T Test实验结果:【注释】:这是该银行居民存款的描述性分析,包括有平均值=2454.27(千元),标准差=6881.827,均值的标准误差=397.322【注释】:单样本的检验结果是t检验统计量:-.115,自由度df=299,双侧概率p值大于显著性水平0.05,不应该拒绝原假设,即居民的平均存款与2500在95%的置信度下不存在显著性差异居民的平均存款在95%的置信度下的置信区间:为[2500-827.63,2500+736.17]实验分析:在95%的保证水平下,该银行居民的平均存款在2500元左右。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对任意概率P:Pi <P< Pi+1,有P=Pi +a( Pi+1-Pi),
那么
Q(P)=(1-a)Q(Pi) +aQ(Pi+1)
第二节 描述性统计量及检验
第二节 描述性统计量及检验
偏度和峰度都是用来测定收益率分布的形状,且 都以正态分布为基准的。
正态分布:偏度=0,峰度=3。
第二节 描述性统计量及检验
偏度的符号反映了分布偏斜的方向: 当偏度S 值=0时,序列分布是对称的。 当偏度S >0时,称为正偏,意味着序列分布有长的
右拖尾。 当偏度S <0时,称为负偏,意味着序列分布有长的
6
4
其中n是样本个数,S是偏度,K是峰度
由于正态分布的偏度S=0,峰度K=3,所以 JB 统计量 是用来衡量偏度和峰度偏离0和3的程度。
JB 统计量是用来检验时间序列是否服从正态分布的。
第二节 描述性统计量及检验
检验步骤: 原假设:时间序列服从正态分布。
计算S、K,并计算JB统计量。 在原假设下,JB 统计量服从自由度为2的X^2分布,
80
Skewness 0.783449
Kurtosis
2.267514
40
0 1000
2000
3000
4000
5000
6000
Jarque-Bera 124.6544 Probability 0.000000
上证综合指数收益率曲线
.100 .075 .050 .025 .000 -.025 -.050 -.075 -.100
0.000550 0.000353 0.088875 -0.092562 0.018805 -0.460843 6.365833
Jarque-Bera 506.9232 Probability 0.000000
第二节 描述性统计量及检验
Quantile—Quantile图 Q-Q图是借助分位数来比较两个分布的一种简单而
重要的工具(比JB统计量的用途更加广泛)。
分位数(Quantile):对于介于0,1之间的数 q,满 足如下条件的数 x(q) 称为 q 的分位数: P( x< x(q) ) < q
第二节 描述性统计量及检验
分位数的计算:
对于一组观察值,取概率:Pi=(i-0.5)/n ,i=1,…,n。
与Pi对应的分位数是把数据从小到大排列后的第i个 数,记为Q(Pi)。
主菜单:File/New/Filework 工作窗口: Unstructured/Deservation/OK 主菜单窗口: Data/空格/变量名/回车 工作窗口: 导入数据/view/Descriptive Ststistics(描述统计量)
/Histogram and Stats(直方图和统计量)
500
750
1000
上证综合指数收盘价曲线统计量
240
Series: SH
Sample 1 1000
200
Observations 1000
160
Mean
2501.364
Median
1743.640
Maximum 6092.060
120
imum
1011.500
Std. Dev.
1460.333
第二节 描述性统计量及检验
例2.1 右表是我国1992-2003 年的实际GDP增长率(可比价 格),对其进行描述性统计分 析。
1992 14.2 1993 13.5 1994 12.6 1995 10.5
1996 9.6 1997 8.8 1998 7.8 1999 7.1 2000 8.0 2001 7.5 2002 8.0 2003 9.1
比正态分布更大的概率。 用公式表示为:P{ <c}>p{X<c},c是一个比较小的
数。 服从尖峰分布随机变量,X服从正态分布。
第二节 描述性统计量及检验
在实际中,意味着来自于尖峰分布的随机样本会有 更多的极端值。
如果小概率事件发生的可能性大于正态分布所描述 的情形,那该变量的分布应当用尖峰分布来描述。
即 JB ~ X^2(2)。以检验水平5%为例,对应的临界值 =5.99,即P(X>5.99)=0.05。
若计算的JB >5.99,则拒绝原假设,分布不是正态
分布。否则接受原假设。
上证综合指数收盘价曲线
7,000 6,000 5,000 4,000 3,000 2,000 1,000
0
SH
250
分布,即相对于正态分布更平坦。
正态分布的峰度K=3。
第二节 描述性统计量及检验
K=3
K>3
K<3
正态分布的峰度=3
第二节 描述性统计量及检验
峰度也反映了分布尾部的厚薄。
正态分布的峰度K=3。K-3称为超出峰度。
具有正的超出峰度的分布称为尖峰分布。 尖峰分布具有厚尾性,即该分布在其支撑的尾部有
例2.1中GDP增长率的统计量:
第二节 描述性统计量及检验
例2.1中GDP增长率的偏度是0.78,峰度K为2.14 ,
说明GDP增长率的分布是不对称的,相对于正态分 布也是平坦的。
第二节 描述性统计量及检验
2.2. 统计量的检验
Jarque-Bera检验
统计量
JB n [S 2 (K 3)2 ]
SHR
250
500
750
1000
上证综合指数收益率统计量
240
200
160
120
80
40
0
-0.05
0.00
0.05
Series: SHR Sample 1 1000 Observations 999
Mean Median Maximum Minimum Std. Dev. Skewness Kurtosis
这在金融市场风险研究中有着重要的意义。
第二节 描述性统计量及检验
样本均值
E(r)
1 T
T
rt
t 1
样本方差
var(r)
2
1 T 1
T t 1
(rt
)2
样本偏度
s
1 T 1
T t 1
(rt
)3
3
样本峰度
k
T
1 1
T t 1
(rt
)4
4
第二节 描述性统计量及检验
Eviews操作:
左拖尾。
偏度的大小反映了分布偏斜的程度。
第二节 描述性统计量及检验
S=0 均值=中位数
S>0 均值>中位数
S<0 均值<中位数
第二节 描述性统计量及检验
峰度反应分布隆起的程度: 当峰度K>3时,序列分布曲线的凸起程度大于正态
分布,即相对于正态分布更隆起; 当峰度K<3时,序列分布曲线的凸起程度小于正态
