热力学统计物理第二章课件
合集下载
2010-09级热力学统计物理第二章

1 Oct.18, 2010
重庆大学光电工程学院
重庆大学光电工程学院
2
热力学统计物理 第二章
热力学统计物理 第二章
一、特性函数
1.特性函数的定义 对于简单的 p-V 的均匀热力学系统 可逆过程的热力学基本方程为:
TdS dU pdV (2.1.2) 式中有五个变量,选取两个为独立变量,还有 三个未知函数,按理说,要确定它们需要除了 (2.1.2)时外,还要补充两个方程,才能确定这 些函数。实际上,只要再增加一个能量方程 U U S ,V (2.1.3) 就行了。这里内能 U(S,V) 是以 S,V 为变量的 特性函数,它的全微分为: (2.1.4) dU TdS pdV
F F dF dT dV T V V T
G G dG dT p dp T p T
U(S,V) H(S,p) F(T,V) G(T,p)
dU TdS pdV
•
选T,p为独立变量,特性函数为G(T,p), 其全微 分为:
H V p
S
dU TdS pdV
U T S V
,
G S T p
, F S T V ,
F p V T
G V p T
Oct.18, 2010
3.吉布斯函数的物理意义: dG=-SdT+Vdp
考虑一个装在密封圆筒容器中的气体及带有活塞的膨涨系 统,它的能量为E=U+pV(内能+势能), dE=dU+d(pV)=TdS-pdV+pdV+Vdp=TdS+Vdp Vdp的含义,绝热过程中膨涨系统作的功等于 能量的减少。即膨涨系统作的功应为 dWe=-(dE)S=-Vdp 在等温过程中, -(dG)T=- Vdp 显然,在等温过程中吉布斯函数的减少等于 在绝热过程中膨胀系统做的功。
重庆大学光电工程学院
重庆大学光电工程学院
2
热力学统计物理 第二章
热力学统计物理 第二章
一、特性函数
1.特性函数的定义 对于简单的 p-V 的均匀热力学系统 可逆过程的热力学基本方程为:
TdS dU pdV (2.1.2) 式中有五个变量,选取两个为独立变量,还有 三个未知函数,按理说,要确定它们需要除了 (2.1.2)时外,还要补充两个方程,才能确定这 些函数。实际上,只要再增加一个能量方程 U U S ,V (2.1.3) 就行了。这里内能 U(S,V) 是以 S,V 为变量的 特性函数,它的全微分为: (2.1.4) dU TdS pdV
F F dF dT dV T V V T
G G dG dT p dp T p T
U(S,V) H(S,p) F(T,V) G(T,p)
dU TdS pdV
•
选T,p为独立变量,特性函数为G(T,p), 其全微 分为:
H V p
S
dU TdS pdV
U T S V
,
G S T p
, F S T V ,
F p V T
G V p T
Oct.18, 2010
3.吉布斯函数的物理意义: dG=-SdT+Vdp
考虑一个装在密封圆筒容器中的气体及带有活塞的膨涨系 统,它的能量为E=U+pV(内能+势能), dE=dU+d(pV)=TdS-pdV+pdV+Vdp=TdS+Vdp Vdp的含义,绝热过程中膨涨系统作的功等于 能量的减少。即膨涨系统作的功应为 dWe=-(dE)S=-Vdp 在等温过程中, -(dG)T=- Vdp 显然,在等温过程中吉布斯函数的减少等于 在绝热过程中膨胀系统做的功。
大学物理热学第二章_(热平衡态的统计分布律)

即: p 2
思考: f()
3kBT
m O p
f()
m m'
2
O 1 2 O
31
第二章 热平衡态的统计分布律
说明 一般三种速率用途各不相同
• 讨论速率分布一般用 v p
• 讨论分子的碰撞次数用v
• 讨论分子的平均平动动能用 v 2
dN 仅是 的函数.
Nd
f(v)
•曲线下面的总面积,等于分
布在整个速率范围内所有各个
速率间隔中的分子数与总分子 O
数的比率的总和
f (v )dv 1
(归一化条件)
0
26
第二章 热平衡态的统计分布律
(2) 不同气体, 不同温度下的速率分布曲线的关系
由于曲线下的面积不变,由此可见 ① m 一定,T 越大, v p 越大, 这时曲线向右移动 ② T 一定, m 越大, v p 越小, 这时曲线向左移动
f(v) T1
f(v) m2(> m1)
T2(> T1)
m1
O v p1 v p2
v O v p2 v p1
v
27
第二章 热平衡态的统计分布律
三. Maxwell速率分布律的实验验证
➢与实验曲线相符密勒-库士实验:
1. 实验装置 2. 测量原理 (1) 能通过细槽到达检测器 D
的分子所满足的条件
v L
又
dN (vx ,vy ) N
f (vx )dvx f (v y )dvy f (vx ,v y )dvxdvy
dN (vx ,v y ) N
所以 f (vx ,vy ) f (vx ) f (vy )
同理可得,在三维空间 f (vx ,vy ,vz ) f (vx ) f (vy ) f (vz2)2
思考: f()
3kBT
m O p
f()
m m'
2
O 1 2 O
31
第二章 热平衡态的统计分布律
说明 一般三种速率用途各不相同
• 讨论速率分布一般用 v p
• 讨论分子的碰撞次数用v
• 讨论分子的平均平动动能用 v 2
dN 仅是 的函数.
Nd
f(v)
•曲线下面的总面积,等于分
布在整个速率范围内所有各个
速率间隔中的分子数与总分子 O
数的比率的总和
f (v )dv 1
(归一化条件)
0
26
第二章 热平衡态的统计分布律
(2) 不同气体, 不同温度下的速率分布曲线的关系
由于曲线下的面积不变,由此可见 ① m 一定,T 越大, v p 越大, 这时曲线向右移动 ② T 一定, m 越大, v p 越小, 这时曲线向左移动
f(v) T1
f(v) m2(> m1)
T2(> T1)
m1
O v p1 v p2
v O v p2 v p1
v
27
第二章 热平衡态的统计分布律
三. Maxwell速率分布律的实验验证
➢与实验曲线相符密勒-库士实验:
1. 实验装置 2. 测量原理 (1) 能通过细槽到达检测器 D
的分子所满足的条件
v L
又
dN (vx ,vy ) N
f (vx )dvx f (v y )dvy f (vx ,v y )dvxdvy
dN (vx ,v y ) N
所以 f (vx ,vy ) f (vx ) f (vy )
同理可得,在三维空间 f (vx ,vy ,vz ) f (vx ) f (vy ) f (vz2)2
热力学与统计物理—第二章

§2.2 麦氏关系的简单应用
一、以T, V为状态参量
U p T p V T T V U S CV T T V T V
能态方程
CV p dS dT dV T T V
dS dU pdV T
4 d(VT 3 ) 3 4 S VT 3 S 0 3
3.物态方程 :
1 1 p u (T ) T 4 3 3
1 c J u cu T 4 T 4 4 4
Ju T 4
斯特藩—玻耳兹曼定律
三 . 红外技术及应用
红外探测
dG
V m ( )T , p 0 ( )T ,H H p
磁致伸缩 压磁效应
G G G dT dp dH T p H
G G V , 0 m p T ,H H T , p
§2.4 热辐射的热力学理论
第二章 均匀物质的热力学性质
1. 麦克斯韦关系及应用
2. 热辐射的热力学理论
3. 磁介质热力学
§2.1 麦克斯韦关系
热力学基本微分方程:
dU T dS Yi dyi
i
四个全微分(简单系统):
dU TdS pdV
H U pV
dH TdS Vdp dF SdT pdV
p dU CV dT T p dV T V
二
、以T, p为状态 dp T T p Tpp T
V dH C p dT V T dp T p
3. 辐射能量密度u:
U= u (T)V
4. 辐射通量密度:
热力学与统计物理

∂S = ∂S ∂T ∂V p ∂T p ∂V p
κ T
κ S
=
∂S ( ∂T
)p
/
∂S ( ∂T
)V
= Cp CV
=γ
平衡稳定性要求: 以上四量皆为正。
一个有效方法: 运用雅可比行列式进行导数变换
设: u = u(x, y), v = v(x, y)
有:
∂u
∂(u, v) ∂(x, y)
=
( ∂x ) y ∂v
自变量为 x,y,z,……的函数L(x,y,z,…)的全微分 dL = Rdx + Qdy + Wdz +
其中
R=
∂L ∂x
,
Q
=
∂L ∂y
,W
=
∂L ∂z
,
均为x, y, z,…的函数
若以R代替x,即选R, y, z,…为自变量,则通过勒让德变换:
L = L − Rx
两边求微分: dL = dL − Rdx − xdR
= −T
∂ 2V ∂T 2
T
p
∂S ∂p
= − ∂V ∂T
T
p
Cp (T ,
p)
=
Cp (T ,
p 0
)
−
⌠p ⌡p
T
∂ 2V ∂T 2
dp
p
Cp
p
0
C
0 p
=
C p (T ,
p 0
),
V
= V (T ,
p)
由实验测定
p 0
dH = CpdT +
V −T
∂V ∂T
dp
p
dS = Cp dT − T
热力学统计物理第二章课件
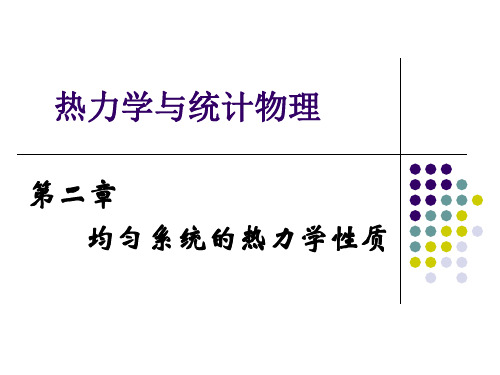
V p T p T V
C p TVp
Ch2.1热力学势的全微分和麦韦关系
例4:证明
CV CP
s T
例5:证明
CV C P
TV 2
T
Ch2.2热力学基本函数的计算
一、目的
通过三个热力学基本函数来确定系 统的主要热力学性质。
dV ( V ) p dT ( V )T dp T p VdT VV T
的确定
由热力学基本方程:dU = TdS - pdV 得到:
U V T
T
S V T
p T
p T V
p
对理想气体: 对范氏气体:
p
RT V
p T V
p R V T
U V T
0
a V2
p VRTb Va2
d ) dT
作 业:
2.2 2.4 2.8
2、非简单系统的推广 例如: 表面系的热力学基本方程为 dU = TdS +σ dA
与简单系统的基本方程比较 dU = TdS - p dV 容易看出对应关系 p - σ , V A
地位和意义:
将不能直接观测到的物理量用麦氏关系 转化为可以直接观测到的物理量表示。
S A
-σ
T
Ch2.1热力学势的全微分和麦韦关系
热力学与统计物理
第二章 均匀系统的热力学性质
Ch2.1热力学势的全微分和麦韦关系
全微分dz、偏微分∂z和变分δz
全微分:如果函数 z f x, y 在点(x,y)的全增量
z f x x, y y f x, y
热力学与统计物理学.pptx

具体来说有:全微分法、系数比较法、循环关系法、 复合函数微分、混合二阶偏导法
系数比较法(适用对象:求U、H、F、G的偏导数) 复合函数的偏导数法(适用对象:求两个函数偏导数之差)
f f f y (x)z (x)y(y)x(x)z
循环关系法(适用对象:求脚标为U、H、F、G的偏导数) x y z
例、求能态方程和焓态方程及Cp 、 Cv
熵变的计算
S是状态函数。在给定的初态和终态之间,系统 无论通过何种方式变化(经可逆过程或不可逆过程), 熵的改变量一定相同。
当系统由初态A通过一可逆过程R到达终态B时求熵
变的方法:直接用
SB SA
B dQ
(
A
T
)R
来计算。
当系统由初态A通过一不可逆过程到达终态B时求熵变
的方法:
(1)把熵作为状态参量的函数表达式推导出来,再将
T V
V T
UFTSFTF
CV
U T V
H=U+pV
TV ,G=F+pV
(2)吉布斯函数G=G(T、p)
由G=G(T、p)和dG=—SdT+Vdp
例:求表面系统的热力学函数
表面系统指液体与其它相的交界面。
表面系统的状态参量: 、A、T 表面系统的实验关系: =(T) 分析:对于流体有f(p,V,T)=0, 对应于表面系统:p,AV
PA
p p(T)
B
固 A
液 C
气
在T—p图中,描述复相系统平衡热力学性Βιβλιοθήκη OLALC T
B P
固
液
PC
C
PA
A
气
O
LA
LC T
A---三相点 C---临界点
系数比较法(适用对象:求U、H、F、G的偏导数) 复合函数的偏导数法(适用对象:求两个函数偏导数之差)
f f f y (x)z (x)y(y)x(x)z
循环关系法(适用对象:求脚标为U、H、F、G的偏导数) x y z
例、求能态方程和焓态方程及Cp 、 Cv
熵变的计算
S是状态函数。在给定的初态和终态之间,系统 无论通过何种方式变化(经可逆过程或不可逆过程), 熵的改变量一定相同。
当系统由初态A通过一可逆过程R到达终态B时求熵
变的方法:直接用
SB SA
B dQ
(
A
T
)R
来计算。
当系统由初态A通过一不可逆过程到达终态B时求熵变
的方法:
(1)把熵作为状态参量的函数表达式推导出来,再将
T V
V T
UFTSFTF
CV
U T V
H=U+pV
TV ,G=F+pV
(2)吉布斯函数G=G(T、p)
由G=G(T、p)和dG=—SdT+Vdp
例:求表面系统的热力学函数
表面系统指液体与其它相的交界面。
表面系统的状态参量: 、A、T 表面系统的实验关系: =(T) 分析:对于流体有f(p,V,T)=0, 对应于表面系统:p,AV
PA
p p(T)
B
固 A
液 C
气
在T—p图中,描述复相系统平衡热力学性Βιβλιοθήκη OLALC T
B P
固
液
PC
C
PA
A
气
O
LA
LC T
A---三相点 C---临界点
热力学与统计物理学第二章 热力学函数及关系

• 目的在于: (1)对某可逆等值过程,用态函数差计算 过程量A或Q;(2)对不可逆过程,用某态函数差判 别过程进行方向。
•两个重要的概念:热力学势,特性函数。
• 问题关键:可逆过程态的热一律和热二律(Q=TdS) 相结合的微分形式,找出二变量态函数全微分中的 偏导数之间的对应关系。
2
• 焓的性质:
• 焓的应用:用它定义定压热容量
在可逆等压过程中,统系吸热等于它的焓增,加即
dHp Qp CpdT
dH
H T
p
dT
H p
T
dp
比较以上两时,:有Cp
H T
p
5
二、自由能
定义为:F=U-TS,在常温环境中,利用它计算功 是非常方便的。
可逆过程dU:TdSA,那么 dUd(TS) dFTdSAd(TS) SdTA
(3)S p ; VT TV
(4) S pT
V . Tp
记住麦氏关系的小窍门:
(1) 等式两边对角线上的量的乘积、分子与脚标的乘积应具 有能量量纲;
(2) 若分子分母性质(广延量或强度量)相同,则等号两边 取正号,性质不同,取负号;
(3) 若分式的分母乘以脚标具有能量量纲,需倒置到分母, 则可用麦氏关系。
第二章 热力学函数及关系
动机和目的 一、焓、自由能和吉布斯函数 二、特性函数与麦克斯韦关系 三、热均匀物质热力学 四、热辐射的热力学
小结和习题课
1
• 动机:前一章用到了内能U和熵S,但还不够用来 分析一些等值过程,本章引入另外三个态函数:焓 H、自由能F、吉布斯函数G。它们分别于等压、等 温、等压等温过程。
S V
V S
比较以上两个等式,有
T U , p U
•两个重要的概念:热力学势,特性函数。
• 问题关键:可逆过程态的热一律和热二律(Q=TdS) 相结合的微分形式,找出二变量态函数全微分中的 偏导数之间的对应关系。
2
• 焓的性质:
• 焓的应用:用它定义定压热容量
在可逆等压过程中,统系吸热等于它的焓增,加即
dHp Qp CpdT
dH
H T
p
dT
H p
T
dp
比较以上两时,:有Cp
H T
p
5
二、自由能
定义为:F=U-TS,在常温环境中,利用它计算功 是非常方便的。
可逆过程dU:TdSA,那么 dUd(TS) dFTdSAd(TS) SdTA
(3)S p ; VT TV
(4) S pT
V . Tp
记住麦氏关系的小窍门:
(1) 等式两边对角线上的量的乘积、分子与脚标的乘积应具 有能量量纲;
(2) 若分子分母性质(广延量或强度量)相同,则等号两边 取正号,性质不同,取负号;
(3) 若分式的分母乘以脚标具有能量量纲,需倒置到分母, 则可用麦氏关系。
第二章 热力学函数及关系
动机和目的 一、焓、自由能和吉布斯函数 二、特性函数与麦克斯韦关系 三、热均匀物质热力学 四、热辐射的热力学
小结和习题课
1
• 动机:前一章用到了内能U和熵S,但还不够用来 分析一些等值过程,本章引入另外三个态函数:焓 H、自由能F、吉布斯函数G。它们分别于等压、等 温、等压等温过程。
S V
V S
比较以上两个等式,有
T U , p U
热力学与统计物理学-第二章
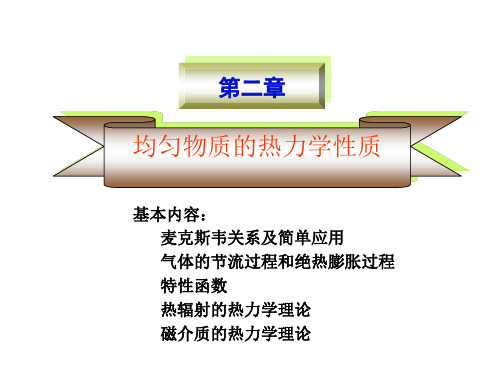
dG=-SdT+VdP
S V
P T
T P
Good Physicists Have Studied Under Very Fine Teachers
太阳照在小树上
(
S V
)T
(
p T
)V
(河流)由山峰流向山谷
照向和流向方向一致取正号,否则取负号。看对 方的分母,取自己的脚标。
T
p
T
V
( V
)S
( S
)V
;
( p )S ( S ) p
( S V
)T
(
p T
)V
;
( V T
)p
(
S p
)T
——麦克斯韦关系
Sun
太阳 peak
山峰
Tree
小树 Valley
山谷
§2-2 麦克斯韦关系的简单应用
麦克斯韦关系的应用有:
⑴用实验可测量的量(如状态方程,热容量
Summary
dU=TdS-PdV dH=TdS+VdP
P T S V V S
T V
P S
S P
G
T
P
F
H
V
S
U
dF=-SdT -PdV
S P
V T
T V
一.能态方程和定容热容量
U T p p V T T V
CV
T S T
V
第一式给出了温度不变时, 系统内能随体积的变化率与物态方程的关系,称 为能态方程;第二式是定容热容量。
热力学与统计物理第2章

x
⎜⎛ ⎝
∂U ∂x
⎟⎞ ⎠y
∂(S,P) ⎜⎛∂S⎟⎞ ⎜⎛∂P⎟⎞ −⎜⎛∂S⎟⎞ ⎜⎛∂P⎟⎞
⎜⎛∂P⎟⎞2
CP
=T⎜⎛∂S⎟⎞ ⎝∂T⎠P
=T∂(S,P) ∂(T,P)
=T
∂(T,V) ∂(T,P) ∂(T,V)
=T⎝∂T⎠V⎝∂V⎠T ⎝∂V⎠T⎝∂T⎠V ⎜⎛∂P⎟⎞ ⎝∂V⎠T
=CV
−T⎝∂T⎠V ⎜⎛∂P⎟⎞ ⎝∂V⎠T
7、可测量的量和不可测量的量 可以直接测量的量:状态变量 (P,V,T……..) 各种热容
不可以直接测量的量:U,H,F,G…….. 和它们的某些偏微商
(二) 气体节流过程和焦耳-汤姆孙效应
ΔQ = 0 W = P1V1 − P2V2
U 2 + P2V2 = U1 + P1V1
这是一个不可逆过程
− ⎜⎛ ∂P ⎟⎞ = ∂2U ⎝ ∂S ⎠V ∂V∂S
⎜⎛ ∂T ⎟⎞ = −⎜⎛ ∂P ⎟⎞ ⎝ ∂V ⎠ S ⎝ ∂S ⎠V
H (S, P)
dH = ⎜⎛ ∂H ⎟⎞ dS + ⎜⎛ ∂H ⎟⎞ dP
⎝ ∂S ⎠ P
⎝ ∂P ⎠ S
dH = TdS + VdP
⎜⎛ ∂H ⎟⎞ = T ⎝ ∂S ⎠ P
⎟⎞ ⎠P
= T ⎜⎛ ∂S ⎝ ∂T
⎟⎞ ⎠P
⎜⎛ ∂H ⎟⎞ = T ⎜⎛ ∂S ⎟⎞ +V ⎝ ∂P ⎠T ⎝ ∂P ⎠T
(定义热容量的表达 式)
从麦氏 ⎜⎛ ∂S ⎟⎞ = −⎜⎛ ∂V ⎟⎞ 代入上式得:
⎝ ∂P ⎠T ⎝ ∂T ⎠ P
⎜⎛ ∂H ⎟⎞ = V − T ⎜⎛ ∂V ⎟⎞
热力学与统计物理第二章均匀物质的热力学性质

(1)(3)两式比较,即有
H V ( )T T ( ) p V p T
H S CP T T P T P
定压膨胀系数: 1 ( V ) P
V T
焓态方程:
H ( )T TV V p
dH CP dT [T 1]Vdp (可测)
dG SdT VdP
dF SdT pdV
(1)由热力学的基本微分方程: dU=TdS-pdV 内能:U=U(S,V),全微分为
U U dU dS dV S V V S
U U 对比可得: S T , V P V S
五、求证:
CP CV T
P T V
2
P V T
证明:
( S , P) S CP T T T (T , P) P
( S , P) T (T , V )
(T , P) (T , V )
(3)麦氏关系记忆 • 规律:相邻3个变量为一组,按顺序(顺、逆时针都可 以)开始第一变量放在分子,中间变量作分母,末尾 量放在括号外作下标,构成一偏导数.则此偏导数等 于第4个变量按相反方向与相邻的另两个量构成的 偏导数(符号:广延量对广延量正号,否则负号).
§2.2 麦氏关系的简单应用
上节导出了麦氏关系:
u (u , y ) 性质: ( 1 ) ( ) y= x ( x, y ) (u, y ) u y u y u 证明: ( ) y ( )x ( )x ( ) y ( ) y ( x, y ) x y y x x (u, v) (v, u ) (u , v) (u , v) ( x, s ) (2) (3) ( x, y ) ( x, y ) ( x, y ) ( x, s ) ( x, y ) (u, v) 1 (4) ( x, y ) ( x, y ) (u , v)
热力学统计物理 第二章 课件

T V
S
p S
V
S
p
T
V T
p
S V
T
p T
V
➢ 麦氏关系应用
选取T、V为状态参量,内能U的全微分为
而由
dU
U T
V
dT
U V
T
dV
dU = TdS - pdV
及以T、V为自变量时熵的全微分表达式
dS
S T
V
dT
S V
T
dV
可得
dU
T
S T
V
dT
第二章 均匀物质的热力学性质
§2.1 内能、焓、自由能和吉布斯函数的全微分
➢ 内能
热力学基本方程
dU = TdS - pdV
给出了相邻两个平衡态的内能、熵和体积之间的关系。
上式可以看作是内能U作为S、V的函数的全微分的表 达式。
内能U作为S、V的函数,其全微分为
dU
U S
V
dS
U V
S
dV
H
C p dT
V
T
V T
dp
p
H0
此式为焓的积分表达式。由U=H-pV即可求得内能。
关于熵函数,其全微分为
dS
Cp T
dT
V T
p
dp
求线积分,得
S
C
p
T
dT
V T
p
dp
S0
此式即熵的积分表达式。
为什么物态方程、内能 和熵函数是最基本的?
§2.5 特性函数
p T
V
dV
求线积分,得
S
CV T
dT
p T
2、 均物热学性质

表示熵的物态方程为: f(S,T,p)=0.偏导数存在关系,
T p
S
p S
S T T
p
1
T p
S
p
1
S
S p
T
S
S T T p T p
T p
S
S p
T
S
T p
麦氏
S p
T
V T
p
Cp
T
S T
p
V T p
Cp T
T Cp
V T
一、节流过程
1.节流过程 2.焦耳-汤姆逊效应:节流 p1 前后气体的温度发生变化.
节流阀
p1 p2
p2
3.理论分析:假设在节流过程中有一定量(M)的气体, 从左向右通过节流阀,其压强,体积,内能分别在截流前
后为:(p1,V1,U1) (p2,V2,U2).
节流过程中外界对这部分气体(M)做功(p1V1-p2V2), 而节流过程是绝热过程,则,系统从外界所吸收的热量,
S F , p F S p
T V
V T V T T V
对于吉布斯函数G=G(T,p),有
S
G ,V T p
G p
T
S p
T
V T
p
利用上述各关系式,通过数学推演得出简单系统平衡
性质的关系,并导出简单系统热力学函数一般表达式.
4
总结以上各式,即得麦克斯韦(Maxwell)关系式
T
S T
p
V p
T
S p
((TT④,,Vp分)) 母:雅可比性质1
V p
T
T
V T
p
T S T
p
T
T p
S
p S
S T T
p
1
T p
S
p
1
S
S p
T
S
S T T p T p
T p
S
S p
T
S
T p
麦氏
S p
T
V T
p
Cp
T
S T
p
V T p
Cp T
T Cp
V T
一、节流过程
1.节流过程 2.焦耳-汤姆逊效应:节流 p1 前后气体的温度发生变化.
节流阀
p1 p2
p2
3.理论分析:假设在节流过程中有一定量(M)的气体, 从左向右通过节流阀,其压强,体积,内能分别在截流前
后为:(p1,V1,U1) (p2,V2,U2).
节流过程中外界对这部分气体(M)做功(p1V1-p2V2), 而节流过程是绝热过程,则,系统从外界所吸收的热量,
S F , p F S p
T V
V T V T T V
对于吉布斯函数G=G(T,p),有
S
G ,V T p
G p
T
S p
T
V T
p
利用上述各关系式,通过数学推演得出简单系统平衡
性质的关系,并导出简单系统热力学函数一般表达式.
4
总结以上各式,即得麦克斯韦(Maxwell)关系式
T
S T
p
V p
T
S p
((TT④,,Vp分)) 母:雅可比性质1
V p
T
T
V T
p
T S T
p
T
热力学与统计物理学第二讲

——在准静态绝热过程中,气体的温度随体积的变化率
讨论: 因为V不变,T 又因为CV是正的 所以,等号右边总是负的 ——表明体积膨胀时,温度总是要降低。 (在液化气体的过程中,可利用这个 特性作为降温手段) P
H )P T,( )S V S P
再利用求偏导数的次序可以交换的性质,同理可求得: (3)F(T,V) 由
T V ( )S ( )P P S
dF SdT PdV
同理可求得:
F F S P ( )V S , ( )T P; ( )T ( )V T V V T
V )P ] dP 得: T T 1 V ( )H [T( )P V ]..........( 1 ) P CP T
为描述节流过程前后气体温度随压强的变化率,引进Joule—Thomson系数
(
T )H P
代入(1)式得: 1 [ T ( V )P V ] V ( T 1 )......( 2 )
S V ) ( ) T P V T
根据麦氏关系:(
1 V 1 P 又 ( ), ( ), K T P P V V T P T
——两容量之差与物 态方程的关系
得:C P CV TV
2
KT
四、气体的节流过程和绝热膨胀
1、节流过程 实验装置: Joule—Thomson (焦耳—汤姆孙)效应: 气体经节流(膨胀)过程 而发生温度变化的现象 初态 P1(高) T1 T2 P2(底)
第二讲
第二章 均匀物质的热力学性质
一、热力学函数全微分表达式 其偏导数可以给出系统状态的热力学参量。它的微分为全微分, 并能单值地确定系统状态的函数。 例如:内能、焓、熵、自由能等 1、内能的全微分表达式 热力学函数:
讨论: 因为V不变,T 又因为CV是正的 所以,等号右边总是负的 ——表明体积膨胀时,温度总是要降低。 (在液化气体的过程中,可利用这个 特性作为降温手段) P
H )P T,( )S V S P
再利用求偏导数的次序可以交换的性质,同理可求得: (3)F(T,V) 由
T V ( )S ( )P P S
dF SdT PdV
同理可求得:
F F S P ( )V S , ( )T P; ( )T ( )V T V V T
V )P ] dP 得: T T 1 V ( )H [T( )P V ]..........( 1 ) P CP T
为描述节流过程前后气体温度随压强的变化率,引进Joule—Thomson系数
(
T )H P
代入(1)式得: 1 [ T ( V )P V ] V ( T 1 )......( 2 )
S V ) ( ) T P V T
根据麦氏关系:(
1 V 1 P 又 ( ), ( ), K T P P V V T P T
——两容量之差与物 态方程的关系
得:C P CV TV
2
KT
四、气体的节流过程和绝热膨胀
1、节流过程 实验装置: Joule—Thomson (焦耳—汤姆孙)效应: 气体经节流(膨胀)过程 而发生温度变化的现象 初态 P1(高) T1 T2 P2(底)
第二讲
第二章 均匀物质的热力学性质
一、热力学函数全微分表达式 其偏导数可以给出系统状态的热力学参量。它的微分为全微分, 并能单值地确定系统状态的函数。 例如:内能、焓、熵、自由能等 1、内能的全微分表达式 热力学函数:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
?T
?
?
1 V
? ?V
? ?
?p
? ? ?T
? ? ?T? p
Cp
?
CV
?
VT? ?T
2
?
0
.
15
水的密度在4oC,有极大值,表明此时体积有 极小值,即
?
?
1 ? ?V V ?? ?T
? ??p
?
0?
?
?
p(,S
V)
.
4
6.麦克斯韦关系式
由:
(?U ?S
)V
?
T (,S
V);(?U ?V) NhomakorabeaS
?
?
p(,S
V)
? ?U (?V )S ( ?S
)V
?
?T ( ?V )S ;(
? ?U ?S )V ( ?V )S
?
?
(
?p ?S
)V
注意:交换求导顺序时,脚标要 跟着交换。
?T (?V )S
??
?p (?S )V
第二章 均匀物质的热力学性质
§2.0 引言
如何描述物理过程及规律? 古代希腊人假定:定律是关于某个全过程或某个物 体完整形状的描述。 伽利略和牛顿提出了现代物理中新的描述方法:
不是试图一步直接建立一个过程所有状态之间的关 系式,而是把过程的一个状态和下一个状态联系起来。
用某个状态在无穷小的时间和空间的变化率即导数 及增量描述对邻近状态的影响 。这种自然定律就是一个 状态和邻近状态之间关系的表达式。
V
p
?S (?T )p
?
?S ( ?T )V
?
?S ( ?V )T(
?V ?T ) p
CCp T? V ?
? ?S ?? ?V
? ??T
? ?V ?? ?T
? ??p
?
T
? ?p ?? ?T
? ??V
? ?V ?? ?T
? ??p
.
普适式
14
?
?
1 V
? ??
?V ?T
? ??p
?
?
1 ? ?p ? p ?? ?T ??V
全微分 dU ? ???U ?? dT ? ?? ?U ?? dV
? ?T ?V
? ?V ?T
由基本方程 dU ? TdS ? pdV,并令S=S(T,V)得
dU
?
T[???
?S ?T
? ??V
dT
?
? ?S ?? ?V
? ??T
dV] ?
pdV
?
T
? ??
?S ?T
? ??V
dT
?
? ??T
? ??
)V
;
(?V ?T
)p
??
?S ( ?p )T
——麦克斯韦关系
Sun
太阳 peak
山峰
Tree
小树 Valley
山谷
.
6
太阳照在小树上
?S (?V )T
?
?p ( ?T )V
(河流)由山峰流向山谷
照向和流向方向一致取正号,否则取负号。看对
方的分母,取自己的脚标。
.
7
Summary
dU=TdS-PdV
通常CV也不容易测定
.
9
⑵用实验可以测量的量表示某些物理效应 及物理量的变化率(§2.3的内容)
⑶求基本热力学函数和特性函数,进而求 出所有热力学函数(§2.3、§2.4的内容)
⑷讨论某些物质的热力学性质(§2.6、 §2.7的内容)
.
10
二、能态方程和焓态方程及Cp 、 CV
⒈能态方程与CV
令 U ? U ?T,V?
再通过这种微小增量的积累,获得全过程整体关系。
§2.1 内能、焓、自由能和吉布斯函数的全微分 一、热力学重要函数和方程 ⒈基本热力学函数
物态方程 P=P(T,V);内能:U ;熵 S 。
2.自由能和其它热力学势
自由能:F =U-TS
内能: U
焓: H =U+pV
吉布斯函数: G=U-TS+pV=F+pV
?
T
?? ?
?S ?T
?? ?p
给出Cp的又一个计算公式
????
?H ?p
????T
?
V
? T ?? ?V ?? ? ?T ?p
叫焓态方程。
.
13
三、热容差 C p ? CV
应与物态方程联系
S T Cp
?
CV
?
T
? ??
?S ?T
? ??p
?
T
? ??
?S ?T
? ??V
S(T, p) ??S ?T,V ?T, p???
?
?? ?
?P ?S
?? ?V
?
?? ?
?T ?V
?? ?S
dH=TdS+VdP
?? ?
?T ?P
?? ?S
?
?? ?
?V ?S
?? ?P
G
T
P
F
H
VS U
dF=-SdT -PdV
?? ?
?S ?V
?? ?T
?
?? ?
?P ?T
?? ?V
dG=-SdT+VdP
? ?? ?S ?? ? ?? ?V ??
?S ?V
? ??T
?
? pd??
V
.
11
两式比较,并用麦氏关系
? ?S ?? ?V
? ??T
?
? ?p ?? ?T
? ??V
? ?U ?? ?V
? ??T
?
T
? ??
?p ?T
? ??V
?
p
称为能态方程
得到
CV
?
? ?U ?? ?T
? ??V
?
T
? ??
?S ?T
? ??V
给出CV的又一个计算公式
.
2
3.基本方程 由热力学第一定律和第二定律可得:
dUT? dS ? pdV
U ? US(V, )
4.方程的其它形式
dH ? dU ??pdV Vdp ? TdS ? Vdp
dH ? TdS ? Vdp
同理可得
H ? HS( , p)
dF ? ? SdT ? pdV
F ? FT( V, )
dG ? ? SdTV? dp . G ? GT( , p) 3
同理,由H, F 的全微分表达式和函数关系,得
?T ( ?p )S
?
?V ( ?S ) p ;(
?S ?V )T
?
?p ( ?T )V;(
?S ?p )T
?
?
(
?V ?T
)
p
.
5
( ?T ?V
)S
??
?p ( ? S )V ;
?T ( ?p )S
?
?V ( ?S )p
?S
( ?V
)T
?
?p
( ?T
5.热力学势函数特性
热力学势 U,H,F ,G,从状态参量T,p,V和熵S中选 择特定两个参量作为自己的自变量,由热力学
理论就可推知系统的性质。
U ? US(V, )
dU
?
(?U ?S
)V
dS
?
(
?U ?V
)S
dV
比较
dUT? dS ? pdV
(
?U ?S
)V
?
T (,S
V);
?U ( ?V )S
因为物态方程 p ? pV( T, )
在实验上是可测的,因此常把其它偏导数利用 麦氏关系改写为与物态方程联系的形式。
.
12
⒉焓态方程与Cp
令H=H(T,p),微分并与dH=TdS+Vdp比较,
再由麦氏关系
????
?S ?p
????T
?
??? ?V ?? ? ?T ?p
得到
Cp
?
?? ?
?H ?T
?? ?p
? ?P ?T
? ?T ?P
Good Physicists Have Studied Under Very Fine Teachers
.
8
§2.2 麦克斯韦关系的简单应用
一、麦克斯韦关系的应用有:
? ⑴用实验可测量的量(如状态方程,热容
量Cp 、 CV、膨胀系数 ? 、压缩系数 ? T
等)来表示不能直接测量的量(如U、H 、F、G等)
