高中数学 1.2极坐标系 新人教A版选修4-4
合集下载
高中数学 1.2极坐标系课件 新人教A版选修4-4
栏
(2)把点 P 的直角坐标(0，－2)化成极坐标是________．
目 链
接
．(1)(－ 2， 2)
(2)2，3π2
ppt精选
13
例 3 在极坐标系中，已知 A2，π6 ，B2，－π6 ，求 A，B 两 点间的距离．
解析：解法一 如图所示，
栏
目
链
接
π ∵∠AOB＝ 3 ，又 OA＝OB＝2，
∴△ABO 为等边三角形．∴AB 的长度为 2.
两点间的距离公式求解．
ppt精选
15
►变式训练
3．已知两点的极坐标 A3，π2 ，B3，π6 ，求： (1)A、B 两点间的距离；
(2)△AOB 的面积；
栏
目
(3)直线 AB 与极轴正方向所成的角．
链 接
解析：如下图所示：
ppt精选
16
πππ ∵OA＝OB＝3，∠AOB＝ 2 － 6 ＝ 3 ，
目
π＜θ≤π)．
链 接
解析：如下图所示：
ppt精选
7
关于极轴的对称点为
π
B2，－
3
.
栏
关于直线 l 的对称点为 C2，23π.
目 链 接
关于极点 O 的对称点为 D2，－23π.
ppt精选
8
点评：点与点的位置关系中，(ρ，θ)关于极点的 对称点为(ρ，θ＋π)，关于直线α＝的对称点为(ρ， π－θ)，关于极轴的对称点为(ρ，－θ)．
点评：(1)写极坐标要注意顺序，极径ρ在前，极角θ在后，不能把 顺序写错了．
(2)点的极坐标是不唯一的，但若限制ρ>0，0≤θ<2π，则除极点外， 点的极坐标唯一确定．
1.2.2《极坐标和直角坐标的互化》 课件(人教A版选修4-4)(2)
2 12
所以线段AB中题8分，共24分）
7.极坐标系中，点（6，7 ）的直角坐标为_______.
3
【解析】∵x=ρcosθ=6cos 7 =3,
3
y=ρsinθ=6sin 7 = 3 3 ,
∴点的极坐标（6，7 ）化为直角坐标为（3， 3）. 3
【解析】∵tanθ= - ,
5 5 4 3 ＜θ＜π, 2
∴cosθ= - 3 ，sinθ= 4 , ∴x=5cosθ=-3,y=5sinθ=4, ∴点M的直角坐标为(-3,4). 答案：(-3,4)
三、解答题（共40分）
x=2x 10.（12分）已知点P的直角坐标按伸缩变换 变换为点 y= 3y
2.直角坐标系中，点（1， 3）的极坐标可以是( -
)
【解析】
3.把点的直角坐标(3,-4)化为极坐标(ρ ,θ )(ρ ≥0,0≤θ ＜
2π )，则( ) （B）ρ =5,θ =4
（A）ρ =3,θ =4
（C）ρ =5,tanθ = 4
3
（D）ρ =5,tanθ =-
4 3 x 3
【解析】选D.由公式得ρ= x 2 +y2 = 32 +(-4)2 =5, tanθ = y =- 4 ,
θ∈［0,2π).
4.在极坐标系中，点A(2,
(A)1 (B)2
)与B(2,- )之间的距离为( 6 6
)
(C)3
6
(D)4
)的直角坐标分别 6
【解析】选B.方法一：点A(2, )与B(2,为( 3,1)与( 3,-1), 于是|AB|= ( 3- 3)2 +(1+1)2 =2.
方法二：由点A(2, )与B(2,- )知|OA|=|OB|=2,∠AOB= ,
所以线段AB中题8分，共24分）
7.极坐标系中，点（6，7 ）的直角坐标为_______.
3
【解析】∵x=ρcosθ=6cos 7 =3,
3
y=ρsinθ=6sin 7 = 3 3 ,
∴点的极坐标（6，7 ）化为直角坐标为（3， 3）. 3
【解析】∵tanθ= - ,
5 5 4 3 ＜θ＜π, 2
∴cosθ= - 3 ，sinθ= 4 , ∴x=5cosθ=-3,y=5sinθ=4, ∴点M的直角坐标为(-3,4). 答案：(-3,4)
三、解答题（共40分）
x=2x 10.（12分）已知点P的直角坐标按伸缩变换 变换为点 y= 3y
2.直角坐标系中，点（1， 3）的极坐标可以是( -
)
【解析】
3.把点的直角坐标(3,-4)化为极坐标(ρ ,θ )(ρ ≥0,0≤θ ＜
2π )，则( ) （B）ρ =5,θ =4
（A）ρ =3,θ =4
（C）ρ =5,tanθ = 4
3
（D）ρ =5,tanθ =-
4 3 x 3
【解析】选D.由公式得ρ= x 2 +y2 = 32 +(-4)2 =5, tanθ = y =- 4 ,
θ∈［0,2π).
4.在极坐标系中，点A(2,
(A)1 (B)2
)与B(2,- )之间的距离为( 6 6
)
(C)3
6
(D)4
)的直角坐标分别 6
【解析】选B.方法一：点A(2, )与B(2,为( 3,1)与( 3,-1), 于是|AB|= ( 3- 3)2 +(1+1)2 =2.
方法二：由点A(2, )与B(2,- )知|OA|=|OB|=2,∠AOB= ,
人教A版高中数学选修4-4课件：1.2.2极坐标与直角坐标的互化 (共17张PPT)
(2) 将点M的直角坐标( 3， 1)化成极坐标.
练习：互化下列直角坐标与极坐标
直角坐标 ( 2 3 ,2) 极坐标
(4, ) 6
(0,1)
(3,0)
( 3, )
(1, ) 2
直角坐标 (3, 3 )
极坐标
5 (2 3 , ) 6
( 3 ,1) ( 5,0)
7 ( 2, ) 6
y x y , tan ( x 0) O x
x
M y N x
三、极坐标与直角坐标的互化 公式
y 直化极： x y , tan ( x 0) x
2 2 2
极化直： x cos , y sin
2 例 (1) 将点M 的极坐标(5, )化成直角坐标. 3
P
O X
线上取一点M，使OM= ;
如图示：
M
新课讲解
2、负极径的实例 在极坐标系中画出点:M（－3，/4）的位置 [1]作射线OP，使XOP= /4 [2]在OP的反向延长线上取一 点M，使OM= 3; 如图示： M（－3，/4）
●
P
= /4
O X
M
新课讲解
3、关于负极径的思考 “负极径”真是“负”的吗？
极坐标与直角坐标的互化 把直角坐标系的原点作为极点，x轴 的正半轴作为极轴，并在两种坐标系中 取相同的长度单位. 设M是平面内任意一 点，它的直角坐标是(x,y),极坐标是(,). 从下图可以得出它们之间的关系：
x cos , y sin .
2 2 2
①y 由①又可得到下面的关系式：
于极点对称的点 的一个坐标是 (A)
A.(8, ) 6
人教版高中数学选修4-4 第一讲 坐标系 二 极坐标系 (共34张PPT)教育课件
A. y 1
sin t
1
x t2
C.
1
yt 2
x cos t
B. y 1
cos t
x tan t
D. y 1
tan t
7.极坐标方程
2
arcsin化(为 直0)角坐标方程的形
式是 （ ）
A. x2 y2 x 0
B．y x(1 x)
C. 2x 1 4y2 1 D.．y (x 1)
2.极坐标（,）与(ρ，2kπ+θ)( k )表z 示 同一个点.即一点的极坐标的统一的表达式 为(ρ，2kπ+θ)
3.如果规定ρ＞0,0≤θ＜2π，那么除 极 点外,平面内的点和极坐标就可以一一对 应了。
我们学了直角坐标,也学了极坐 标，那么这两种坐标有什么关系呢? 已知点的直角坐标为,如何用极坐标 表示这个点呢?
M (, )
0
x
2
4
5
6
C
1.如图，在极坐标系中，写出点 AF(,6B, ,4C3 ,)D的, G极(坐5, 标53，所) 并在标的出位E置( 72 , ) ,
E D BA
O
X
4 F
3
G 5
3
解：如图可得A,B,C,D的坐标分别为
(4,0)
(2, )
(3, )
(1, 5 )
4
2
6
点E,F,G的位置如图所示
1
4.极坐标方程ρ=cosθ与ρcosθ= 的2 图形是（ ） B
A
B
C
D
解x=：12把，ρc故os排θ=除A，、12 化D；为又直圆角ρ坐=c程os，θ显得然: 过点 (0,1)，又排除C，故选B。
5、若A、B的两点极坐标为A(4,
1.2 极坐标系 课件-高中数学人教A版选修4-4 (共17张PPT)
问题3：已知角 终边上有一点 P(1, 3) 如何 求角 的大小及点P到原点距离？
1.互化条件
(1)极点就是坐标原点; (2)极轴为x的正半轴；
(3)具有相同的单位长度.
M(x,y)
2.互化公式
M(,)
. x
y
cos (为极径，为极角) sin
极坐标
直角坐标 O x
x2 y2
y
X
tan y (x 0)
极点；极轴；长度单位； 角度单位和它的正方向。
[2] 点的直角坐标与极坐标互化？
x y
cos (为极径，为极角) sin
极坐标
直角坐标
x2 y2 tan y (x 0)
x
谢谢各位老师的 聆听！
O
X
这样就建立了一个极坐标系
问题1:类比直角坐标系确定点只需知 道横纵坐标， 那么在极坐标中如何确定一点的位置？
引入距离和方位角
x
二、极坐标的表示方法
(1)极径：对于极坐标平面上任意点M到极点O
的距离|OM|叫点M的极径，用表示，=|OM|
（；2）以极轴为始边旋转到射线OM的角 MOX叫点M的极角，记为MOX，= ;
a(1 sin )
极坐标系
如何确定以下两船 的位置关系呢？
（1）距离： 12海里 （2）方向：
发生故障!!!
拯救船
20º
O
x
云南大学北门
银杏大道
从这往南走100米！
一、极坐标系的建立
(1)在平面内取一个定点O，叫做极点。
(2)从极点O引一条射线OX，叫做极轴。
(3)选定一个长度单位和角度单位及 它的正方向（以逆时针方向旋转为 正角）
(3)有序数对（，）就叫做M的极坐标
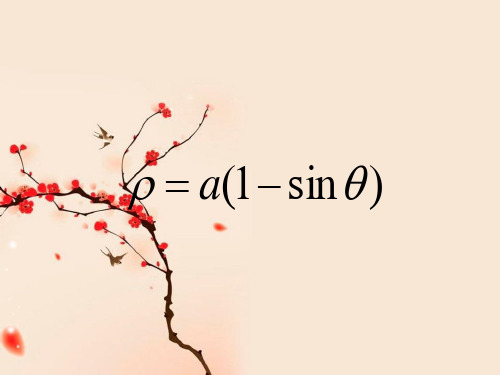
1.互化条件
(1)极点就是坐标原点; (2)极轴为x的正半轴；
(3)具有相同的单位长度.
M(x,y)
2.互化公式
M(,)
. x
y
cos (为极径，为极角) sin
极坐标
直角坐标 O x
x2 y2
y
X
tan y (x 0)
极点；极轴；长度单位； 角度单位和它的正方向。
[2] 点的直角坐标与极坐标互化？
x y
cos (为极径，为极角) sin
极坐标
直角坐标
x2 y2 tan y (x 0)
x
谢谢各位老师的 聆听！
O
X
这样就建立了一个极坐标系
问题1:类比直角坐标系确定点只需知 道横纵坐标， 那么在极坐标中如何确定一点的位置？
引入距离和方位角
x
二、极坐标的表示方法
(1)极径：对于极坐标平面上任意点M到极点O
的距离|OM|叫点M的极径，用表示，=|OM|
（；2）以极轴为始边旋转到射线OM的角 MOX叫点M的极角，记为MOX，= ;
a(1 sin )
极坐标系
如何确定以下两船 的位置关系呢？
（1）距离： 12海里 （2）方向：
发生故障!!!
拯救船
20º
O
x
云南大学北门
银杏大道
从这往南走100米！
一、极坐标系的建立
(1)在平面内取一个定点O，叫做极点。
(2)从极点O引一条射线OX，叫做极轴。
(3)选定一个长度单位和角度单位及 它的正方向（以逆时针方向旋转为 正角）
(3)有序数对（，）就叫做M的极坐标
人教A版高中数学选修4-4课件1.1.2极坐标系
如果规定 0, 0 2 ，那么除极点外，平面内 的点可用唯一的极坐标 ， 表示. 同时，极坐标 ， 表示的点也是唯一确定的.
默认： 0， R. 第9页
负极径
默认： 0， R. 第9页
对称点
思考：设P , 是平面内一点，则点P关于 极轴、极垂线 过极点且垂直于极轴的直线 、 极点对称的点的坐标是什么？
2 B 5， 6
例5 把下列点的直角坐标化成极坐标：
0, 0 2
4 1 A 1, 1； 2 B 4， 3 ;
3 3 3 , 2 2
x cos y sin
x y
2 2
2
y tan x 0 x
例4 把下列点的极坐标化成直角坐标： 14 1 A 4， ； 3
2 B 5， 6
例4 把下列点的极坐标化成直角坐标： 14 1 A 4， ； 3
60m
A教学楼 B体育馆
思考：在极坐标中 4， ， 4 ， 2 ， 4 ， 4 ， 6 6 6 2 表示的点有什么关系？ 4， 6
一般地，极坐标 ， 与 ， 2k k Z 表示 同一个点.平面内一个点的极坐标有无数种表示.
（ ， ） M
x
注意：（1）一般地，不作特殊说明时，我们认为ρ≥0， 可取任意实数。 （2）当M在极点时，它的极坐标为（0，θ），可取任 意值。
例1 如图，在极坐标系中，写出点A, B , C的极坐标.
A 1， 0
B 4， 2
人教版高中数学选修4-4课件1.2-极坐标系 (共38张PPT)
阶段小结
1、建立一个极坐标系需要哪些要素? 极点；极轴；长度单位；计算角度的正方向.
2、极坐标系内一点的极坐标有多少种表达式？ 无数，极角有无数个.
3、一点的极坐标有否统一的表达式？
有。（ρ ，2kπ +θ ）
4、结论：
极坐标(, ) 与(, ＋2k)(k∈Z)表示同一个点. 和直角坐标不同，平
（3）在空间直角坐标系上，空间上所有点的集合与全体三元有序实数对（x , y , z）的集合建立一 一对应；
复习回顾
1. 直角坐标系
数
平面直角坐标
轴
系
R
（x , y)
空间直角坐标 系
（x , y , z)
复习回顾
建立坐标系是为了确定点的位置。由此，在所创建的坐标系中，应满 足： 任意一点都存在一个坐标与之对应；反之，依据一个点的坐标就能确 定这个点的位置； 而确定点的位置即为求出此点在设定的坐标系中的坐标。
区别吗？
思考: ①平面上一点的极坐标是否唯一？
若不唯一，那有多少种表示方法？ ②不同的极坐标是否可以写出统一表达式？
1、点的极坐标的表达式的研究
如图：OM的长度为4，
4
请说出点M的极坐标的表达式？
思考：这些极坐标之间有何异同？
M
O
4，π 4
+2kπ
X
极径相同，不同的是极角.
A
2
11 7
6
6
C
3
5
4
3
3
2
2
3
B
6
D
A
2
11
6
3
高中数学人教A版选修(4-4)1.2 同步练习 极坐标和直角坐标的互化(人教A版).doc
《极坐标系和直角坐标的互化》
同步练习
赵县实验中学赵连霞
1．点P的直角坐标为(－，)，那么它的极坐标可表示为()．
A.B.C.D.
2．已知A，B的极坐标分别是和，则A和B之间的距离等于
()．
A.B.
C.D.
3.已知点M的极坐标是，它关于直线θ＝的对称点坐标是()．
A.B.
C.D.
4.已知点M的直角坐标为(－3，－3)，若ρ>0，0≤θ<2π，则点M的极坐标是________．
答案 B
4.答案
5.x＝－5cos＝－，y＝－5sin＝－.
∴点M的直角坐标是.
6..ρ＝＝2，tanθ＝＝.
又∵点N在第三象限，ρ>0.∴最小正角θ＝π.
故点N的极坐标是.
7.
8.解 求两点间的距离可用如下公式：
|AB|＝＝＝2.
S△AOB＝|ρ1ρ2sin(θ1－θ2)|＝＝×2×4＝4.
5.把点M的极坐标化成直角坐标；
6.把点N的直角坐标(－，－1)化成极坐标．
7.把点N的直角坐标(1，－1)化成极坐标
8.已知A、B两点的极坐标分别是，，求A、B两点间的距离和△AOB的面积．
答案和解析
1.解析 直接利用极坐标与直角坐标的互化公式．
答案 B
2.解析 极坐标系中两点A(ρ1，θ1)，B(ρ2，θ2)的距离|AB|＝
.
答案 C
3.解析 当ρ<0时，我们找它的极角应按反向延长
线上去找．描点时，先找到角－的
终边．又因为ρ＝－2<0，所以再沿反向延长线上
找到离极点2个单位的点即是点.
直线θ＝，就是由极角为的那些点的集合．
故M关于直线θ＝的对称点为M′，但是选择支没有这
同步练习
赵县实验中学赵连霞
1．点P的直角坐标为(－，)，那么它的极坐标可表示为()．
A.B.C.D.
2．已知A，B的极坐标分别是和，则A和B之间的距离等于
()．
A.B.
C.D.
3.已知点M的极坐标是，它关于直线θ＝的对称点坐标是()．
A.B.
C.D.
4.已知点M的直角坐标为(－3，－3)，若ρ>0，0≤θ<2π，则点M的极坐标是________．
答案 B
4.答案
5.x＝－5cos＝－，y＝－5sin＝－.
∴点M的直角坐标是.
6..ρ＝＝2，tanθ＝＝.
又∵点N在第三象限，ρ>0.∴最小正角θ＝π.
故点N的极坐标是.
7.
8.解 求两点间的距离可用如下公式：
|AB|＝＝＝2.
S△AOB＝|ρ1ρ2sin(θ1－θ2)|＝＝×2×4＝4.
5.把点M的极坐标化成直角坐标；
6.把点N的直角坐标(－，－1)化成极坐标．
7.把点N的直角坐标(1，－1)化成极坐标
8.已知A、B两点的极坐标分别是，，求A、B两点间的距离和△AOB的面积．
答案和解析
1.解析 直接利用极坐标与直角坐标的互化公式．
答案 B
2.解析 极坐标系中两点A(ρ1，θ1)，B(ρ2，θ2)的距离|AB|＝
.
答案 C
3.解析 当ρ<0时，我们找它的极角应按反向延长
线上去找．描点时，先找到角－的
终边．又因为ρ＝－2<0，所以再沿反向延长线上
找到离极点2个单位的点即是点.
直线θ＝，就是由极角为的那些点的集合．
故M关于直线θ＝的对称点为M′，但是选择支没有这
选修4-4 1.2 极坐标系
y x y , tan ( x 0) x
2 2 2
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件：
1. 极点与直角坐标系的原点重合; 2. 极轴与直角坐标系的x轴的正半
轴重合; 3. 两种坐标系的单位长度相同.
例1. 将点M的极坐标
2 (5, ) 3
5 5 3 ) 所以, 点M的直角坐标为( , 2 2
题组一：说出下图中各点的极坐标
2
5 6
C E D O B A X
4
4 3
F
G
5 3
特别规定： 当M在极点时，它的 极坐标=0，可以取任意值。
想一想？
①平面上一点的极坐标是否唯一？ ②若不唯一，那有多少种表示方法？ ③坐标不唯一是由谁引起的？
④不同的极坐标是否可以写出统一表达式？
三、点的极坐标的表达式的研究
如图：OM的长度为4， 4 请说出点M的极坐标的其 他表达式。 O X 思：这些极坐标之间有何异同？ 极径相同，不同的是极角 思考：这些极角有何关系？ 这些极角的始边相同，终边也相同。也 就是说它们是终边相同的角。
π 2kπ+ 4 本题点M的极坐标统一表达式：4，
C (5,0) E ( 3,3)
D (0,2)
π），（3， ） π 例3 已知两点（2，
求两点间的距离.
用余弦定理求 AB的长即可.
3
π 解：∠AOB =
6
B
A
2
推广： 在极坐标下，任意两点P ( 1 ,1 ), P2 ( 2 , 2 ) 1
o
x
之间的距离可总结如下：
2 PP2 12 2 2 1 2 cos(1 2 ) 1
高中新课程数学(新课标人教A版)选修4-4《1.2.1极坐标系的的概念》导学案
1.2.1极坐标系的的概念学习目标1．能在极坐标系中用极坐标刻画点的位置.2.体会在极坐标系和平面直角坐标系中刻画点的位置的区别.学习过程一、学前准备情境1：军舰巡逻在海面上，发现前方有一群水雷，如何确定它们的位置以便将它们引爆？情境2：如图为某校园的平面示意图，假设某同学在教学楼处。
（1）他向东偏60°方向走120M 后到达什么位置？该位置唯一确定吗？（2）如果有人打听体育馆和办公楼的位置，他应如何描述？问题1：为了简便地表示上述问题中点的位置，应创建怎样的坐标系呢？ 问题2：如何刻画这些点的位置？ 二、新课导学◆探究新知（预习教材P 8～P 10，找出疑惑之处）1、如右图，在平面内取一个 O ，叫做 ； 自极点O 引一条射线Ox ，叫做 ；再选定一个 ，一个 （通常取 ）及其 （通常取 方向），这样就建立了一个 。
2、设M 是平面内一点，极点O 与M 的距离||OM 叫做点M 的 ，记为 ；以极轴Ox 为始边，射线OM 为终边的角xOM 叫做点M 的 ，记为 。
有序数对 叫做点M 的 ，记作 。
3、思考：直角坐标系与极坐标系有何异同？ ___________________________________________. ◆应用示例例题1：(1)写出图中A ，B ，C ，D ，E ，F ，G 各点的极坐标)20,0(πθρ<≤>.（2）：思考下列问题，给出解答。
①平面上一点的极坐标是否唯一？②若不唯一，那有多少种表示方法？③坐标不唯一是由谁引起的？④不同的极坐标是否可以写出统一表达式？ ⑤本题点G 的极坐标统一表达式。
答：◆反馈练习小结：在平面直角坐标系中，一个点对应 个坐标表示，一个直角坐标对应 个点。
极坐标系里的点的极坐标有 种表示，但每个极坐标只能对应 个点。
三、总结提升1．已知5,3M π⎛⎫⎪⎝⎭，下列所给出的能表示该点的坐标的是A ．⎪⎭⎫⎝⎛-3,5π B ．⎪⎭⎫ ⎝⎛34,5π C ．⎪⎭⎫ ⎝⎛-32,5π D ．55,3π⎛⎫- ⎪⎝⎭ 2、在极坐标系中,与(ρ,θ)关于极轴对称的点是( )A 、),(θρB 、),(θρ-C 、),(πθρ+D 、),(θπρ-(3,0)(6,2)(3,)245(5,)(3,)(4,)365(6,)3A B C D E F G ππππππ。
数学：1.2.2《极坐标和直角坐标的互化》课件(新人教选修4-4)
重合;
3. 两种坐标系的单位长度相同.
3 3 1 3） 2 tan （ 1
2 2
极坐标与直角坐标的互化关系式: 设点M的直角坐标是 (x, y) 极坐标是 (ρ,θ)
x=ρcosθ, y=ρsinθ
y x y , tan ( x 0) x
2 2 2
互化公式的三个前提件：
1. 极点与直角坐标系的原点重合; 2. 极轴与直角坐标系的x轴的正半轴
问题: 极坐标系是怎样定义的?
极坐标系与直角坐标系有何异同? 平面内的一个点的直角坐标是(1, 3 ) 3
这个点如何用极坐标表示?
在直角坐标系中, 以原点作为极点, x轴的正半轴作为极轴, 并且两种坐标系中取相 同的长度单位 (1, 3) 点M的直角坐标为 (1, 3)
y
M (1, 3)
θ
O
x
设点M的极坐标为(ρ,θ)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x＝8cos23π＝－4， y＝8sin23π＝4 3.
即点 M 的直角坐标为(－4，4 3)．
ppt课件
ρ2＝x2＋y2，
(2)由坐标变换公式 tan
θ＝xy（x≠0），
得 ρ＝ （－ 3）2＋（－1）2＝2 2，
tan
θ＝－ 62＝－3
3 .
栏
∵点 M 在第四象限，ρ＞0，
目 链
接
∴最小正角 θ＝116π.
(1)A，B 两点间的距离为 3.
栏 目
链
接
(2)△AOB 的面积 S＝12×3×3sin 60°＝943.
(3)直线 AB 与极轴正方向所成的角为π－π6 ＝56π.
ppt课件
析疑难
提
能
力栏 目 链
接
ppt课件
1．2 极 坐 标 系
ppt课件
栏 目 链 接
ppt课件
1．了解极坐标的基本概念． 2．能在极坐标系中用极坐标刻画点的位置，体 会在极坐标系和平面直角坐标系中刻画点的位置 的区别． 3．能进行极坐标与平面直角坐标的互化．
ppt课件
栏 目 链 接
ppt课件
题型一 坐标的概念 例1 写出下图中各点的极坐标(ρ>0，0≤θ<2π， 且各线之间间距相等)．
ppt课件
解法二 将点 A 化为直角坐标为( 3，1)，点 B 化为直角坐标为
( 3，－1)．
∴A、B 两点间的距离
d＝ ( 3－ 3)2＋[1－（－1）]2＝2.
栏 目 链
接
答案：2
点评：在极坐标系中我们没有定义两点间的距离，我们只要画出
图形便可以得到结果或把两点极坐标转化为直角坐标，用直角坐标的
因此，点 M 的极坐标是2
2，116π.
答案：(1)(－4，4 3)
(2)2
2，116π
ppt课件
点评：直角坐标化极坐标时，先求出tan θ的值，再 栏
由直角坐标确定θ所在的象限，然后求出符合条件的 目
极角，一般只要取θ∈[0，2π)就可以了
链 接
ppt课件
►变式训练
2．(1)把点 M 的极坐标2，3π4 化成直角坐标是________．
两点间的距离公式求解．
ppt课件
►变式训练
3．已知两点的极坐标 A3，π2 ，B3，π6 ，求： (1)A、B 两点间的距离；
(2)△AOB 的面积；
栏
目
(3)直线 AB 与极轴正方向所成的角．
链 接
解析：如下图所示：
ppt课件
πππ ∵OA＝OB＝3，∠AOB＝ 2 － 6 ＝ 3 ，
∴△AOB 为正三角形．
栏 目 链 接
ppt课件
题型二 极坐标与直角坐标的互化
例 2 (1)把点 M 的极坐标8，23π化为直角坐标形式是________；
(2)把点 M 的直角坐标( 6，－ 2)化成极坐标(ρ≥0，0≤θ＜2 栏
目
π)是________．
链
接
解析：(1)由坐标变换公式
x＝ρcos y＝ρsin
θ， θ得
栏
(2)把点 P 的直角坐标(0，－2)化成极坐标是________．
目 链
接
．(1)(－ 2， 2)
(2)2，3π2
ppt课件
例 3 在极坐标系中，已知 A2，π6 ，B2，－π6 ，求 A，B 两 点间的距离．
解析：解法一 如 ∵∠AOB＝ 3 ，又 OA＝OB＝2，
∴△ABO 为等边三角形．∴AB 的长度为 2.
点评：(1)写极坐标要注意顺序，极径ρ在前，极角θ在后，不能把 顺序写错了．
(2)点的极坐标是不唯一的，但若限制ρ>0，0≤θ<2π，则除极点外， 点的极坐标唯一确定．
ppt课件
►变式训练
1．设点 A2，π3 ，直线 l 为过极点且垂直于极轴的直线，分别
求出点 A 关于极轴、直线 l、极点的对称点的极坐标(限定 ρ＞0，－ 栏
目
π＜θ≤π)．
链 接
解析：如下图所示：
ppt课件
关于极轴的对称点为
π
B2，－
3
.
栏
关于直线 l 的对称点为 C2，23π.
目 链 接
关于极点 O 的对称点为 D2，－23π.
ppt课件
点评：点与点的位置关系中，(ρ，θ)关于极点的 对称点为(ρ，θ＋π)，关于直线α＝的对称点为(ρ， π－θ)，关于极轴的对称点为(ρ，－θ)．
栏 目 链 接
ppt课件
分析：根据极坐标定义，若 M 是平面上任一点，ρ表示 OM 的
长度，θ表示以射线 Ox 为始边，射线 OM 为终边所成的角，则 M
的极坐标为(ρ，θ)．
解析：A(5，0)，B2，π6 ，C4，π2 ，D5，3π4 ，E(2，π)，
栏 目 链
接
F5，4π3 ，G3.5，5π3 .