简单的三元一次方程组的解法
三元一次方程组的解法

三元一次方程组的解法
三元一次方程组是一种重要的数学工具,常用于解决实际问题。
它的解法备受人们的关注,被广泛运用于数学分析、工程设计等领域。
三元一次方程组是由三个未知数和三个方程所组成,它们存在三
个相互抵消的关系,其中最重要两个是线性方程和非线性方程。
它们
经过改写得出一个普通的式子,写出三元一次方程组的一般形式:ax + by + cz = d
ex + fy + gz = h
ix + jy + kz = l
其中a、b、c、d、e、f、g、h、i、j、k和l都是实数,而x、y 和z是未知数,此式称为三元一次方程组的一般形式。
三元一次方程的解法主要由以下步骤组成:首先,确定每个方程
的变量,即确定未知数x、y和z;其次,将每个方程两边部分展开,
形成部分格式;接着,可以将每组关系整理在同一行,也可以将关系
分别整理到各自的行中;最后,利用消元法、逆矩阵法以及其他求解
方法,求出未知数的值,这样就可以得到方程的解了。
在三元一次方程的解法中,需要用到复杂的矩阵计算,通过矩阵
的乘法和消元法实现求解,大大减少了我们的计算复杂度,又可以有
效地提升求解效率,并且对实际问题的解决也有极大地帮助。
因此可以看出,三元一次方程组具有重要的应用价值,不仅可以
用它来解决线性方程和非线性方程,而且还可以应用于例如工程设计、概率论和统计学等各门学科,因此,学习如何解决三元一次方程组,
对我们也是非常有必要的。
三元一次方程组的解法公式

三元一次方程组的解法公式
三元一次方程组是数学中比较重要的一类方程组,在很多领域,如科学、工程、经济学等都有着重要的应用。
它是由三个未知数和三个等号组成的等式组,用来求解三个未知数的值。
三元一次方程组的解法公式是:
若a、b、c均不为0,则方程组的解为:
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a},y=\frac{a\cdot x+c}{b}$$
若a=0,则方程组的解为:
$$x=\frac{c}{b},y=\frac{c}{a}$$
若b=0,则方程组的解为:
$$x=\frac{-c}{a}, y=\frac{a\cdot x+c}{b}$$
若c=0,则方程组的解为:
$$x=0,y=\frac{-b}{a}$$
若a=b=0,则方程组的解为:
$$x=y=\frac{-c}{a}$$
若a=b=c=0,则方程组无解。
三元一次方程组的解法公式很容易理解,但实际的求解过程中,还是可能出现一些麻烦。
比如,当a=b=c=0时,方程组就没有解,就不能使用上面的公式进行求解。
此外,有时候,三元一次方程组的解法公式求出来的解可能不太容易理解,比如当a、b、c都不为0时,求出来的解可能会比较复杂,需要大量的计算,而且解的形式也可能是不确定的。
因此,在求解三元一次方程组的时候,除了要正确使用上面的解法公式,还要注意检查方程组的系数是否满足要求,以及求出来的解是否符合预期,这样才能得到正确的结果。
如何解三元一次方程组

如何解三元一次方程组解三元一次方程组的一种常见方法是使用消元法。
下面是一个示例:假设我们有以下三元一次方程组:1. 2x + 3y + 4z = 102. 3x + 2y + z = 53. x + y + 2z = 7首先,我们可以使用第一条方程来消去x的系数。
将第一条方程乘以3,将第二条方程乘以2,然后将它们相减,得到一个新的方程:6x + 9y + 12z = 30-6x - 4y - 2z = -10---------------------5y + 10z = 20 (新方程1)接下来,我们可以使用第一条方程来消去y的系数。
将第一条方程乘以2,将第三条方程乘以3,然后将它们相减,得到另一个新的方程:4x + 6y + 8z = 20-3x - 3y - 6z = -21---------------------x + 2z = -1 (新方程2)现在,我们有两个新方程:5y + 10z = 20 (新方程1)x + 2z = -1 (新方程2)我们可以使用这两个方程来解决y和z的值。
首先,将新方程2中的x用新方程1中的y和z表示。
将新方程2中的x替换为-2z-1,得到:-2z - 1 + 2z = -10 = 0我们可以看到,这个方程恒成立,说明y和z的值可以是任意数。
因此,我们无法得到唯一的解。
总结起来,这个三元一次方程组有无穷多个解。
可以用参数化的方式表示解,如:x = -2z - 1y = t (其中t为任意实数)z = s (其中s为任意实数)这只是解三元一次方程组的一种方法,还有其他方法,如代入法、矩阵法等。
具体使用哪种方法取决于具体的方程组和个人偏好。
三元一次方程组的一般形式和加减消元法求解过程

三元一次方程组的一般形式和加减消元法求解过程方程组中含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,这就构成了一个三元一次方程组.三元一次方程组的一般形式为:a1x+b1y+c1z=d1①a2x+b2y+c2z=d2②a3x+b3y+c3z=d3 ③可以采用类似二元一次方程组的加减消元的方法求解.将①式乘以c2,②式乘以c1,可得:a1c2x+b1c2y+c1c2z =d1c2④a2c1x+b2c1y+c1c2z =d2c1 ⑤④式减⑤式得:(a1c2- a2c1)x+(b1c2- b2c1)y =d1c2- d2c1⑥将②式乘以c3,③式乘以c2,可得:a2c3x+b2c3y+c2c3z =d2c3⑦a3c2x+b3c2y+c2c3z =d3c2⑧⑦式减⑧式得:(a2c3- a3c2)x+(b2c3- b3c2)y =d2c3- d3c2⑨由⑥⑨两式可得二元一次方程组:(a1c2- a2c1)x+(b1c2- b2c1)y =d1c2- d2c1(a2c3- a3c2)x+(b2c3- b3c2)y =d2c3- d3c2这样就将一个三元一次方程组转化成了一个二元一次方程组.解这个二元一次方程组可得:x=d1b2c3− d1b3c2− d2b1c3+ d2b3c1+ d3b1c2− d3b2c1 a1b2c3− a1b3c2− a2b1c3+ a2b3c1+ a3b1c2− a3b2c1y=a1d2c3− a1d3c2− a2d1c3+ a2d3c1+ a3d1c2− a3d2c1 a1b2c3− a1b3c2− a2b1c3+ a2b3c1+ a3b1c2− a3b2c1再将以上x、y的解代入①或②或③式中可解得:z=a1b2d3− a1b3d2− a2b1d3+ a2b3d1+ a3b1d2− a3b2d1 a1b2c3− a1b3c2− a2b1c3+ a2b3c1+ a3b1c2− a3b2c1即方程组的解为:x=d1b2c3− d1b3c2− d2b1c3+ d2b3c1+ d3b1c2− d3b2c1 a1b2c3− a1b3c2− a2b1c3+ a2b3c1+ a3b1c2− a3b2c1y=a1d2c3− a1d3c2− a2d1c3+ a2d3c1+ a3d1c2− a3d2c1 a1b2c3− a1b3c2− a2b1c3+ a2b3c1+ a3b1c2− a3b2c1.z=a1b2d3− a1b3d2− a2b1d3+ a2b3d1+ a3b1d2− a3b2d1 a1b2c3− a1b3c2− a2b1c3+ a2b3c1+ a3b1c2− a3b2c1可以看出,三元一次方程组和二元一次方程组一样,当知道了每个方程中未知数的系数和等号右边的常数项时,方程解可以由这些数直接计算得到.因此我们可以用分离系数的方法求解三元一次方程组.。
三元一次方程组解法举例

6. 写出方程组的解,并检验解的正确性。
代入法应用举例
例如,对于三元一次方程组
$\left\{ \begin{array}{l} x + y + z = 6 \ x - y + 2z = 3 \ 3x + 2y - z = 8 \end{array} \right.$可以使用代入法求解
解法选择策略与注意事项
选择策略
在面对三元一次方程组时,首先观察方程组 的系数特点,如果系数简单且易于代入,可 以选择代入法;如果存在明显可消元的变量 ,可以尝试消元法;对于复杂方程组,建议 采用矩阵法进行求解。
注意事项
在使用代入法和消元法时,要注意选择合适 的变量进行代入或消元,避免计算过于复杂 ;在使用矩阵法时,需要确保理解矩阵运算 的基本原理,正确构建系数矩阵和常数矩阵 ,以保证求解的准确性。
三元一次方程组解法 举例
汇报人: 日期:
目录
• 三元一次方程组概述 • 三元一次方程组解法——代入法 • 三元一次方程组解法——消元法 • 三元一次方程组解法——矩阵法 • 三种解法的比较与总结
01
三元一次方程组概述
三元一次方程组的定义
定义
三元一次方程组是指包含三个未知数的一次方程所组成的方程组。
杂的方程组,可以通过计算机进行高效求解。
• 缺点:需要一定的线性代数基础知识,对于初学者可能难以
03
理解。
适用范围的讨论
代入法
适用于变量系数较为简单 ,易于进行代入计算的情 况。
消元法
适用于方程组中存在较为 明显的可消元变量的情况 。
矩阵法
三元一次方程组的解

三元一次方程组的解三元一次方程组是指含有三个未知数的一次方程组,我们可以通过一定的方法来求解这些方程的解。
下面就让我来为大家详细介绍一下三元一次方程组的解法。
一、初等变换法初等变换法是指通过对方程组进行加法、减法、乘法等基本运算,来得到方程组的解。
这种方法相对简单,适用于一些比较简单的方程组。
下面是一个使用初等变换法解三元一次方程组的例子:$x + y + z = 10$$2x - y + 3z = 5$$3x + 4y - 2z = 7$先将第2个式子加到第3个式子上,得到:$x + y + z = 10$$2x - y + 3z = 5$$5x + 3y + z = 12$再将第1个式子乘以2,得到:$2x + 2y + 2z = 20$$2x - y + 3z = 5$$5x + 3y + z = 12$将第1个式子减去第2个式子,得到:$x + 3y - z = 15$$2x - y + 3z = 5$$5x + 3y + z = 12$将第2个式子乘以3,得到:$x + 3y - z = 15$$6x - 3y + 9z = 15$$5x + 3y + z = 12$将第2个式子乘以2,得到:$x + 3y - z = 15$$12x - 6y + 18z = 30$$5x + 3y + z = 12$将第2个式子减去第1个式子的3倍,得到:$x + 3y - z = 15$$3x - 15z = 3$$5x + 3y + z = 12$再将第3个式子减去第1个式子的5倍,得到:$x + 3y - z = 15$$3x - 15z = 3$$4y - 4z = -63$由第2个式子得:$x = 5z + 1$将上面的式子带入第1个和第3个式子中,得到:$20z + 16y = 79$$25z + 14y = 47$解得 $y=-\dfrac{1}{2}$,$z=\dfrac{9}{5}$,最终得到:$x=3$,$y=-\dfrac{1}{2}$,$z=\dfrac{9}{5}$二、高斯消元法高斯消元法是求解三元一次方程组的一种比较常用的方法,它的主要思想是通过消元的方式,将方程组化成为一个上三角矩阵,然后就可以通过回带的方法来解方程组。
3三元一次方程组解法举例

三元一次方程组解法举例一、学习内容熟练掌握简单的三元一次方程的解法。
二、例题分析第一阶梯[例1]解方程组提示:解一次方程的思想是什么?可以采取什么方法来实现?参考答案:解:把①代入②得5x+3(2x-7)+2z=2整现得11x+2z=23 ④④×2+③得25x=50,x=2把x=2代入①和③得y=-3,z=∴是原方程的解说明:解三元一次方程,可以先消去一个未知数化为二元一次方程来解,即三元转化二元转化一元,因此代入消元、加减消元法均可运用。
[例2]提示:此方程组是一个三元一次方程组,我们知道,解二元一次方程组的基本方法是代入法和加减法,事实上,在求解过程中,不管是代入或是加减,其目的是消元,把二元转化为一元,从而求解,类似,三元一次方程组的解法也可以设法将三元二元一元,观察方程组,①中含有两个未知数,可以变形为y=2x-7 ④,把④分别代入②,③,便于消去y,得到一个关于x,z的二元一次方程组,通过求解x,z便可求出y的值,从而达到解三元一次方程组的目的。
参考答案:解:由①得y=2x-7④将④分别代入②③得⑤-⑥得12x=48∴x=4把x=4代入⑤得4+z=3∴z=-1把x=4,z=-1代入②得4+2y+5(-1)=12y=2∴y=1说明:此题也可以用代入法求解x,z,一般来说,当方程组中某个未知数为1时,用“代入法”来求解比较简,当某个未知数的系数绝对值相等或成整数倍时用"加减法"消元比较容易,特别对多元一次方程组,两者可以结合起来。
第二阶梯[例1]提示:考虑用加减法,三个方程中,z的系数比较简单,设法先消去z,① + ③可以消去z,得到一个只含x,y的方程,进一步② + ③×2,也可以消去z得到一个只含x,y的方程,这样,就得到了一个关于x,y的二元一次方程组。
参考答案:① + ③得 5x + 5y = 25 ④② + ③×2得 5x + 7y = 31 ⑤解这个方程组⑤ - ④得∴把x = 2,y = 3代入①得3×2 + 2×3 + z = 13 ∴z = 1说明:此题是根据观察三个未知数的系数,先要考虑好消去哪个未知数,这是根据谁的系数简单,就消去谁,此题还可以利用① - ②×3,③ - ②×2消去x或① - ②×2,③ - ②×3消去y,都可以利用消元法求解方程组,可见消元法是解多元一次方程组基本方法。
三元一次方程组的公式解
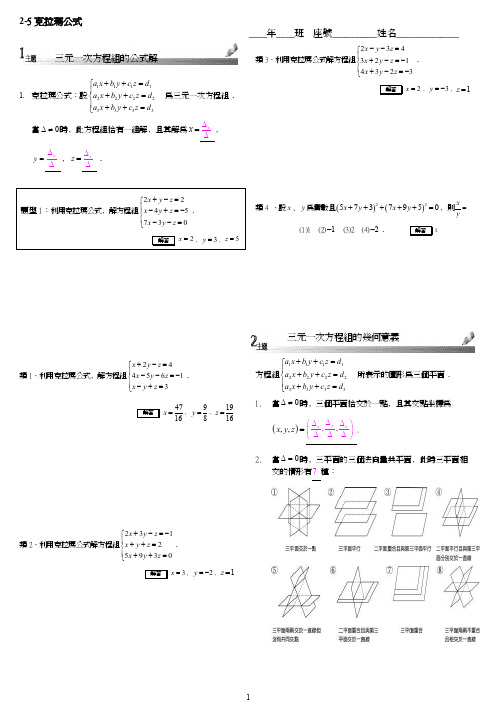
____年____班 座號__________姓名______________三元一次方程組的公式解1. 克拉瑪公式:設111122223333a x b y c z d a x b y c z d a x b y c z d++=⎧⎪++=⎨⎪++=⎩ 為三元一次方程組﹒當0∆≠時﹐此方程組恰有一組解﹐且其解為x =x∆∆﹐y =y ∆∆﹐z =z∆∆﹒類1、利用克拉瑪公式﹐解方程組2445613x y z x y z x y z +-=⎧⎪--=-⎨⎪-+=⎩﹒4716x =﹐98y =﹐1916z =類2、利用克拉瑪公式解方程組23125930x y z x y z x y z +-=-⎧⎪++=⎨⎪++=⎩﹒3x =﹐2y =-﹐1z =類3、利用克拉瑪公式解方程組2343214323x y z x y z x y z --=⎧⎪+-=-⎨⎪+-=-⎩﹒2x =﹐3y =-﹐1z =類4 、設x ﹑y 為實數且()()225737950x y x y +++++=﹐則x y= (1)1 (2)1- (3)2 (4)2-﹒4三元一次方程組的幾何意義方程組111122223333a x b y c z d a x b y c z d a x b y c z d++=⎧⎪++=⎨⎪++=⎩ 所表示的圖形為三個平面﹒1. 當0∆≠時﹐三個平面恰交於一點﹐且其交點坐標為(),,x y z =,,y x z ∆⎛⎫∆∆ ⎪∆∆∆⎝⎭.2.當0∆=時﹐三平面的三個法向量共平面﹐此時三平面相交的情形有7種:類1、解方程組3234351x y zx y zx y z++=⎧⎪++=⎨⎪++=⎩﹐並說明三平面的相交情形﹒無解﹐三平面兩兩相交於一直線﹐沒有共同交點類2、設三平面1:379E x y z--=-﹑2:3E x y z++=﹑3:320E x y z-+=﹐則三平面的相交情形為何﹖(1)三平面互相平行(2)三平面交於一直線(3)三平面兩兩交於一線﹐而這三直線互相平行(4) 2類3、說明下列各方程組所表示的平面相交的情形﹕(1)2306380250x y zx y zx y z+-=⎧⎪+-=⎨⎪-+=⎩﹒(2)22134341x y zx y zx y z-+=⎧⎪--=⎨⎪++=⎩﹒(1)交於一點;(2)交於一點類1、三平面為212121ax y zx ay zx y az++=⎧⎪++=⎨⎪++=⎩﹐若此三平面相異﹐而兩兩交線互相平行﹐則a=____________﹒3-類2、試就m值﹐討論方程組()()26211m x y mx m y m⎧+-=⎪⎨-+=-⎪⎩的解﹒5m≠-且2m≠⇒恰一解﹐②5m=-⇒無解﹒③2m=⇒無限多組解﹐213x tty=⎧⎪⇒-⎨=⎪⎩﹐t為實數﹒;類3、方程組111kx y z x ky z x y kz ++=⎧⎪++=⎨⎪++=⎩無解時﹐求k =?2-類4、分別求k 值﹐使方程組()()3453258k x y kx k y ⎧++=-⎪⎨++=⎪⎩(1)恰有一組解﹒ (2)無解﹒ (3)有無限多組解﹒(1)1k≠-﹐7-;(2)7k =-;(3)1k =-類5、試就a 值討論()()231132221ax y z x a y z x y a z ⎧++=-⎪+++=⎨⎪+++=-⎩三平面相交情形﹐並求﹐ (1)當5a ⇒≠-且1a ≠時﹐表三平面交於一點﹐ (2)1a= 表兩平面重合與另一平面平行﹐無解﹒(3)5a =- ∴解為一直線x t =﹐212t y -=﹐z t =﹐t 為實數﹒類1、設方程組2315x y z x y z x ay z b --=⎧⎪++=⎨⎪+-=⎩有無限多組解﹐求a ﹐b 的值﹒1a =﹐9b =類2、設方程組3223222x y z x y z x ky z -+=⎧⎪+-=⎨⎪+-=⎩有無限多組解﹐求k 的值﹒12類3、設方程組3425157x y z x y z x y z k +-=-⎧⎪++=-⎨⎪+-=⎩有解﹐求實數k 的值18-類4、k 為一實數﹐三平面1:E x y z k -+=-﹑2:346E x ky z -+=-﹑3:34E kx y z -+=-﹐下列何者正確﹖ (1)2k ≠且5k ≠時三平面交於一點 (2)2k =時三平面交於一直線 (3)5k =時三 平面交於一直線 (4)5k =時三平面兩兩交於一直線﹐三交線 兩兩平行 (5)1k =1245類1、設方程組()111122223333:a x b y c z d L a x by c z d a x b y c z d++=⎧⎪++=⎨⎪++=⎩ 恰有一組解()4,5,6﹐且方程組()()()()111112222233333234:234234a b x b y c z d L a b x b y c z d a b x b y c z d +++=⎧⎪'+++=⎨⎪+++=⎩ 恰有一組解(),,αβγ﹐求α的值﹒故444288x x α'∆∆===⨯='∆∆﹒ 類2、111222a x b y c a x b y c +=⎧⎨+=⎩ 解為()1,2﹐則11122225302530ax by c a x b y c ++=⎧⎨++=⎩ 的解為____________﹒ 32x =-﹐65y =- 類3、設3a b d e =﹐252cb fe =﹐733a d cf =﹐求2323ax by cdx ey f +=⎧⎨+=⎩的解﹒ 52x =﹐76y =類1、設a 為實數﹐已知方程組232240x y z axax y z x x y az +-=⎧⎪++=⎨⎪++=⎩恰有一組解﹐則a的值為____________﹒ 5a ≠且23a ≠-類1、若方程組0220x ky z x ky z y x y z +-=⎧⎪+-=⎨⎪+-=⎩有0x y z ===以外的解﹐則(1)k =____________﹐(2)此方程組的解為____________﹒(1)2;(2)3x ty t z t =⎧⎪=⎨⎪=⎩﹐t 為實數類2設方程組()()010220x y az a x y z a x y z ⎧++=⎪--+=⎨⎪-++=⎩ 除()0,0,0之外尚有其他解﹐求a 值﹒23-或2類1、從上圖(1)到圖(8)中﹐選出各聯立方程組所代表之平面的關係﹕(1)4210x y z x y z x y z -+=⎧⎪+-=⎨⎪++=⎩﹒ (2)211x y x y =⎧⎪=⎨⎪+=⎩﹒ (3)⎪⎩⎪⎨⎧=-+=-+=-+33232212z y x z y x z y x ﹒ (4)1325x y z x y z x y z ++=⎧⎪++=⎨⎪++=⎩﹒ (1)1;(2)5;(3)8;(4)4。
初中数学三元一次方程组解法举例PPT课件

巩固练习:
下列方程中,不是三元一次方程组的是( D )
x y 2 (A)y z 2
z x
x -3 0 (B) x y z 20
x - y 2z 7
x y z 3 (C) x - y 2z 7
2x y z 9
x - 2 0
(D)
2 x
y
z
1
x 2y 3z 2
探究2:如何解“探究1”中列得的方程组呢?
x y z 12 ① 1.消去系数最简单
x 2y 5z 22
②
的未知数. 2.消去某个方程中
x 4y
③ 缺少的未知数.
思路:
消元的方法: 代入消元法和加减消元法
x y 8
y
z
6
z x 4
1、解三元一次方程组的基本思想:
2、解三元一次方程组前要仔细观察各方程系数特点, 选择最好的解法。 消元的关键是要选准先消元的未知数. 一般规律是: 1.消去系数最简单的未知数.
2.消去某个方程中缺少的未知数. 3.消去系数相等或互为相反数的未知数. 4.消去系数成整数倍关系的未知数.
一次方程组有何不同? 思考3:三个方程都含有三个未知数的
方程组怎样实现由“三元”转化 为“二元”? 选择代入法还是加减法?
练习:1.解三元一次方程组
x-2y -9 y-z 3 2z x 47
2x 3y - z 18 3x - 2y z 8 x 2y z 24
典例分析
例1 解三元一次方程组
3x 4z 7 2x 3y z 9 5x-9y 7z 8
了解三元一次方程组的解法及应用

了解三元一次方程组的解法及应用在数学中,方程是一个含有未知数的等式,而方程组则是由多个方程组成的一组等式。
其中,三元一次方程组指的是含有三个未知数的一组方程。
了解和掌握三元一次方程组的解法及应用,对于解决实际问题和提升数学能力都具有重要意义。
一、三元一次方程组的解法1. 代入法代入法是解三元一次方程组的一种常用方法。
首先,从其中一个方程中解出一个未知数,然后将其代入其他方程中,得到一个二元方程组。
接着,再使用二元方程组的解法求出另外两个未知数的值。
最后,将求得的两个未知数代入原方程中,求出第三个未知数的值。
2. 消元法消元法是另一种解三元一次方程组的常用方法。
通过将方程组中的某一方程乘以适当的数,使得方程组中某一未知数的系数相等,然后将这两个方程相减,从而消去该未知数。
接着,将得到的新方程与其他方程相加或相减,继续消去另一个未知数。
最后,将求得的两个未知数代入原方程中,求出第三个未知数的值。
二、三元一次方程组的应用1. 几何问题三元一次方程组在几何问题中有广泛的应用。
例如,在三维空间中,可以通过三元一次方程组来求解平面与直线的交点、直线与直线的交点等。
这些问题常常涉及到坐标系、向量和几何关系等概念,通过解方程组可以得到准确的结果。
2. 经济问题三元一次方程组在经济学中也有重要的应用。
例如,在市场经济中,供求关系是一个复杂的问题。
通过建立三元一次方程组,可以求解出市场平衡点,即供给与需求相等的点。
这对于决策者来说,可以提供重要的参考,帮助他们做出合理的经济决策。
3. 物理问题三元一次方程组在物理学中也有广泛的应用。
例如,在运动学中,可以通过三元一次方程组来求解物体的运动轨迹、速度和加速度等。
这些问题涉及到时间、距离和速度等概念,通过解方程组可以得到物理量之间的关系,进而进行科学的分析和预测。
三、三元一次方程组的挑战尽管三元一次方程组具有广泛的应用,但在实际问题中,解方程组并不总是一件容易的事情。
有时,方程组可能没有解,或者有无穷多个解。
三元一次方程组的解法及运用

__________________________________________________ 来,把这个工程交给了甲乙两个施工队,工期 50 天完成,甲乙两队合作了 30 天后,乙队因另外有任务需 要离开 10 天,于是甲队加快速度,每天多修了 0.6 千米,10 天后乙队回来,为了保证工期,甲队速度不 变,乙队每天也比原来多修 0.4 千米,结果如期完成。问:甲,乙两队原计划每天各修多少千米?
工作量=工作效率×工作时间(相对应的)
例 6.(遵义 07)某中学准备改造面积为1080m2 的旧操场,现有甲、乙两个工程队都想承建这项工程.经 协商后得知,甲工程队单独改造这操场比乙工程队多用 9 天;乙工程队每天比甲工程队多改造10m2 ;甲
船(飞机)航行问题:相对运动的合速度关系是: 顺水(风)速度=静水(无风)中速度+水(风)流速度; 逆水(风)速度=静水(无风)中速度-水(风)流速度。
车上(离)桥问题: ①车上桥指车头接触桥到车尾接触桥的一段过程,所走路程为一个车长。 ②车离桥指车头离开桥到车尾离开桥的一段路程。所走的路程为一个成长 ③车过桥指车头接触桥到车尾离开桥的一段路程,所走路成为一个车长+桥长 ④车在桥上指车尾接触桥到车头离开桥的一段路程,所行路成为桥长-车长 行程问题可以采用画示意图的辅助手段来帮助理解题意,并注意两者运动时出发的时间和地点。
例 1.有大小两种货车,2 辆大车与 3 辆小车一次可以运货 15.5 吨,5 辆大车与 6 辆小车一次可以运货 35 吨。3 辆大车与 5 辆小车一次可以运货多少吨?
•
(2)行程问题(基本关系:路程=速度×时间。) 相遇问题(相向而行),这类问题的相等关系是:各人走路之和等于总路程或同时走时两人所走的时间相 等为等量关系。甲走的路程+乙走的路程=全路程
高考数学中三元一次方程组的解法

高考数学中三元一次方程组的解法解三元一次方程组是数学高考中必考的内容之一,其解题步骤和方法也是比较固定的。
本文将从基础知识和样例分析两个方面来介绍三元一次方程组的解法。
一、基础知识1. 三元一次方程组的定义三元一次方程组是指包含三个未知数和三个方程的方程组,方程的次数都为一次,解为三个未知数满足这三个方程的共同解。
2. 解三元一次方程组的思路解三元一次方程组的基本思路是通过已知的方程式,构造新的方程式,再通过求解新的方程式,得到未知数的解。
具体来讲,可以通过以下步骤:(1)利用其中某一个方程式,通过代入减法或代入加法的方法,得到一个只包含两个未知数的二元一次方程式。
(2)重复上述方法,得到另外两个二元一次方程式。
(3)通过解决这三个二元一次方程式,求出一个通解,再将其带回原方程组中,验证是否符合题意。
3. 三元一次方程组的求解公式设三元一次方程组为:$\begin{cases}a_1x_1+b_1x_2+c_1x_3=d_1 \\a_2x_1+b_2x_2+c_2x_3=d_2 \\a_3x_1+b_3x_2+c_3x_3=d_3 \\\end{cases}$则可得到以下求解公式:$\begin{cases}x_1=\frac{d_1b_2c_3+d_2b_3c_1+d_3b_1c_2}{a_1b_2c_3+a_2b_ 3c_1+a_3b_1c_2-a_1b_3c_2-a_2b_1c_3-a_3b_2c_1} \\x_2=\frac{d_1a_3c_2+d_2a_1c_3+d_3a_2c_1}{a_1b_2c_3+a_2b_ 3c_1+a_3b_1c_2-a_1b_3c_2-a_2b_1c_3-a_3b_2c_1} \\x_3=\frac{d_1a_2b_3+d_2a_3b_1+d_3a_1b_2}{a_1b_2c_3+a_2b_ 3c_1+a_3b_1c_2-a_1b_3c_2-a_2b_1c_3-a_3b_2c_1} \\\end{cases}$二、样例分析下面就通过一个数学设计题来具体分析三元一次方程组的求解方法。
解三元一次方程组的方法

解三元一次方程组的方法三元一次方程组是指含有三个未知数的一次方程组,通常形式为:a1x + b1y + c1z = d1。
a2x + b2y + c2z = d2。
a3x + b3y + c3z = d3。
解三元一次方程组的方法主要有消元法、代入法和矩阵法。
下面将分别介绍这三种方法的具体步骤。
一、消元法。
消元法是解三元一次方程组常用的方法之一,其基本思想是通过加减消元将方程组化简为二元一次方程组,然后逐步求解。
具体步骤如下:1. 选择一个方程,通过乘以适当的系数使得其系数与另一个方程中对应未知数的系数相等,然后将两个方程相加或相减,消去该未知数的项。
2. 重复以上步骤,逐步消去另外两个未知数的项,最终得到一个二元一次方程组。
3. 解二元一次方程组,得到一个未知数的值。
4. 将求得的未知数的值代入原方程组中,求解出另外两个未知数的值。
二、代入法。
代入法是另一种解三元一次方程组的常用方法,其基本思想是通过将一个方程中的一个未知数用另外两个未知数的表达式代入另外两个方程中,从而化简为一个二元一次方程组。
具体步骤如下:1. 选择一个方程,将其中一个未知数用另外两个未知数的表达式代入另外两个方程中,得到一个包含两个未知数的方程。
2. 解得一个未知数的值。
3. 将求得的未知数的值代入原方程组中,求解出另外两个未知数的值。
三、矩阵法。
矩阵法是利用线性代数中矩阵的性质来解三元一次方程组的方法,其基本思想是将方程组写成矩阵的形式,通过矩阵运算来求解未知数的值。
具体步骤如下:1. 将方程组写成增广矩阵的形式。
2. 通过行变换将增广矩阵化简为阶梯形矩阵或行最简形矩阵。
3. 根据化简后的矩阵,逐步求解得到未知数的值。
以上就是解三元一次方程组的方法,消元法、代入法和矩阵法是三种常用的解法,可以根据具体情况选择合适的方法来求解三元一次方程组。
希望本文可以帮助到您。
解三元一次方程组

解三元一次方程组一次方程组是数学中一个重要的概念,它表达了多个未知量之间的不等式关系,通过求解一次方程组可以找到这些未知量的具体数值。
关于一次方程组,最常见的就是二元一次方程组,而这篇文章的重点将集中在解三元一次方程组上。
什么是三元一次方程组?三元一次方程组是由三个未知量所组成的等式系统,其形式如下: ax + by + cz = dex + fy + gz = hix + jy + kz = l其中,a,b,c,e,f,g,i,j,k是系数,而d、h、l是常量,x、y、z是未知量。
解三元一次方程组的基本思想解三元一次方程组的基本思想是利用矩阵的思想,通过对应的操作,将方程组转换为对应的“三元一次方程组的矩阵形式”,再利用线性代数的矩阵的求解方式求解。
三元一次方程组的矩阵形式将三元一次方程组上文中所给的形式,可以用矩阵的形式表示为: [a b ce f gi j k] * [xyz] = [dhl]其中,[a b ce f gi j k]称为系数矩阵,[x y z]称为未知量矩阵,[d h l]称为常量矩阵。
解三元一次方程组的解法在解三元一次方程组时,可以使用线性代数中的矩阵定理,即可以把一个矩阵称为A,另一个矩阵称为B,当这两个矩阵的乘积等于一个单位矩阵时,就可以求出未知量矩阵的值。
即如下形式:A *B = E其中,E是单位矩阵,为三阶单位阵,其元素均为1。
以上式子可以简写为:A * X = b,其中,X表示未知量矩阵,b 表示常量矩阵。
实际操作中,可以采取以下步骤:1.将方程组化为系数矩阵形式。
2.将系数矩阵分解为两个矩阵,其中一个矩阵是单位矩阵,另一个矩阵就是所求的未知量矩阵。
3.将上面的两个矩阵进行乘积,得到等于常数矩阵的结果,同时可求得未知量矩阵的值。
这就是解三元一次方程组的方法,下面对上述方法进行一个案例说明。
案例:设有一个三元一次方程组:2x + 3y + z = 5x + y + 2z = 03x + y 4z =2解上述方程组:1.将方程组化为系数矩阵形式:[2 3 11 1 23 1 -4] * [xyz] = [5-2]2.将系数矩阵分解为两个矩阵:[2 3 11 1 23 1 -4] * [a b cd e fg h i] * [xyz] = [5-2]3.将上面的两个矩阵进行乘积:[2 3 11 1 23 1 -4] * [a b cd e fg h i] * [xyz] = [5-2]令系数矩阵的乘积等于单位矩阵,即如下形式: [2 3 11 1 23 1 -4] * [a b cd e fg h i] = [1 0 00 1 00 0 1]可以把此方程组转化为一个9元一次方程组: 2a + 3d + g = 13a + b + h = 0a + d + i = 03b + e + h = 02b + 3e + i = 13c + f + g = 0c + e + i = 0c + 3f +h = 02c + 3f + i = 1求解此方程组,可得:a = 1b = 0c = 0d = 0e = 1f = 0g = 0h = 0i = 1代入初始方程组,可以求出未知量矩阵的值: x = 1y = 0z = 0即为方程组的解。
三一次方程组的解法步骤

三一次方程组的解法步骤
宝子,今天咱们来唠唠三元一次方程组的解法呀。
三元一次方程组呢,就是有三个未知数,并且每个方程都是一次的方程组。
那咋解呢?
咱得想办法消去一个未知数,把三元一次方程组变成二元一次方程组。
比如说,你看这三个方程,你可以先挑两个方程,然后找个合适的方法把一个未知数给消掉。
这方法就和解二元一次方程组的时候消元差不多哦。
可以用加减消元法,就看哪个未知数的系数比较好处理,要是两个方程里有一个未知数的系数相同或者互为相反数,那直接相加或者相减,这个未知数就没啦。
要是系数不一样呢,就想办法把系数变成一样的,再加减消元。
消掉一个未知数之后,就得到一个二元一次方程组啦。
这个二元一次方程组就好对付多啦。
接着再用解二元一次方程组的方法,不管是代入消元还是加减消元,再消去一个未知数,这样就能求出一个未知数的值了。
求出一个未知数的值之后呢,就可以把这个值代回到之前得到的二元一次方程组中的一个方程里,求出另一个未知数的值。
最后呀,把求出的这两个未知数的值,代入到原来三元一次方程组中的任意一个方程,就可以求出第三个未知数的值啦。
你可别觉得这很复杂哦,就像走迷宫一样,一步一步来,先把三元变二元,再把二元变一元,最后就把所有未知数都求出来啦。
多做几道题,你就会发现这其实还挺有趣的呢。
就像玩游戏闯关一样,每解出一个方程组就像闯过一关,可带劲啦。
三元一次方程组的解法举例

三元一次方程组的解法举例在数学中,三元一次方程组是由三个含有三个未知数的一次方程组成的。
解决这种方程组可以帮助我们找到未知数的值,使得所有方程都成立。
在本文中,我们将介绍三种常见的解三元一次方程组的方法。
方法一:代入消元法代入消元法是解三元一次方程组最常用的方法之一。
它的基本思想是将方程组中的一个未知数用其他未知数的表达式代入其他方程中,从而减少未知数的数量,从而简化方程组。
以下是一个具体的例子:假设我们有三元一次方程组:2x + 3y + 4z = 103x + 2y + z = 5x + 2y + 3z = 7我们可以使用代入消元法来解决这个方程组。
首先,我们可以从第一个方程中解出x的表达式:x = (10 - 3y - 4z)/2将这个表达式代入第二个方程中得到:3((10 - 3y - 4z)/2) + 2y + z = 5化简这个方程,我们可以解出y的表达式:y = (39 - 10z)/11将这个表达式代入第三个方程中得到:(10 - 3((39 - 10z)/11) - 4z)/2 + 2((39 - 10z)/11) + 3z = 7化简这个方程,我们可以解出z的表达式:z = 1将z的值代入y的表达式,然后再代入x的表达式,我们可以得到:x = 2y = 3z = 1所以方程组的解为x = 2,y = 3,z = 1。
方法二:矩阵消元法矩阵消元法是解三元一次方程组的另一种常用方法。
它的基本思想是将方程组表示为矩阵的形式,然后通过一系列行变换将矩阵化简成行最简形,从而得到方程组的解。
以下是一个具体的例子:假设我们有三元一次方程组:2x + 3y + 4z = 103x + 2y + z = 5x + 2y + 3z = 7我们可以将这个方程组表示为矩阵的形式:[2 3 4 | 10][3 2 1 | 5][1 2 3 | 7]接下来,我们通过一系列行变换将矩阵化简成行最简形。
具体的步骤如下:1.将第一个方程乘以3,第二个方程乘以2,第三个方程乘以1,并进行相减:[6 9 12 | 30][6 4 2 | 10][1 2 3 | 7]2.将第二行乘以1/2,得到:[6 9 12 | 30][3 2 1 | 5][1 2 3 | 7]3.将第一行减去两倍的第二行,得到:[0 5 10 | 20][3 2 1 | 5][1 2 3 | 7]4.将第一行乘以1/5,得到:[0 1 2 | 4][3 2 1 | 5][1 2 3 | 7]5.将第二行减去三倍的第一行,将第三行减去一倍的第一行,得到:[0 1 2 | 4][3 -1 -2 | -7][1 0 1 | 3]6.将第二行乘以-1,得到:[0 1 2 | 4][-3 1 2 | 7][1 0 1 | 3]7.将第一行加上三倍的第二行,得到:[0 0 8 | 25][-3 1 2 | 7][1 0 1 | 3]8.将第三行减去一倍的第二行,得到:[0 0 8 | 25][-3 1 2 | 7][1 0 1 | 3]9.将第一行乘以1/8,得到:[0 0 1 | 25/8][-3 1 2 | 7][1 0 1 | 3]10.将第二行加上三倍的第一行,第三行减去第一行,得到:[0 0 1 | 25/8][0 1 5 | 23/8][1 0 1 | 3]11.将第三行减去一倍的第二行,得到:[0 0 1 | 25/8][0 1 5 | 23/8][1 0 1 | 3]12.将第三行减去五倍的第二行,得到:[0 0 1 | 25/8][0 1 5 | 23/8][1 0 0 | -2/8]最后得到了行最简形的矩阵,通过回代法可以求得方程组的解:x = -1/4y = 23/8z = 25/8所以方程组的解为x = -1/4,y = 23/8,z = 25/8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x y z 26 x y 1 2 x z y 18
(1) (2) (3)
新乐市实验学校
答案
x=10 Y=9 你做对了吗?
Z=7
新乐市实验学校(1){{解:②×3+③ ,得
11x+10z=35 ④
①与④组成方程组
解下列三元一次方程组 3x+4z=7 ① 2x+3y+z=9 ② 5x-9y+7z=8 ③
解三元一次方程组.
难点:
解三元一次方程组既简单应用。
新乐市实验学校
自主学习(5分钟)
1、结合课本 21 页问题理解三元一次方 程(组)的概念; 2、结合教材 页例1理解三元一次方程组的 解题思路及一般格式。
新乐市实验学校
自学检测(1分钟)
1.下列方程组中是三元一次方程组的是( B )
x 2 y 3, x 2 y 5, A. x 2 y 4, B. 3x z 7, 2 y 3z 6 2x y 7 x y 2, x2 y z 5, C. y z 1, D. x y 6, z t 3 y xy 7 2.三元一次方程组要满足什么条件呢?
新乐市实验学校
孙小然主备
新乐市实验学校
复习巩固(2分钟)
1、二元一次方程的定义是什么?二元一次方 程组的定义是怎样的? 2、解二元一次方程组的基本思路是什么? 基本方法有哪些?
新乐市实验学校
学习目标:
1 .明确什么是三元一次方程(组); 2 .类比二元一次方程组的解法, 会解三元一次方程组。
重点:
解: 5 y z 12, ④ 把③代入①②得 6 y 5 z 22. ⑤ 解得
y 2, z 2.
x 8, ∴这个三元一次方程组的解为 y 2, z 2.
把y=2代入③,得x=8.
新乐市实验学校
随堂练习
独立完成练习(3分钟)学师学友互查
学生独立思考:
﹛
元一次方程组,也 是三元一次方程组 X=2 y=3 是三元一次方程组吗? 解的表达形式!要 注意哦! z=4
新乐市实验学校
新乐市实验学校
新乐市实验学校
学生展示3分钟
x y z 12, ① 解三元一次方程组: x 2 y 5z 22, ② x 4 y. ③
3、解三元一次方程组的一般步骤:
(1)化三一次方程组为二元一次方程组; (2)解二元一次方程组,并代入求出另一个未知数的值; (3)写出这个三元一次方程的解。
新乐市实验学校
小组思考应用三元一次方程解决 问题
新乐市实验学校
新乐市实验学校
作业:
课本
师友当堂检测:
3x+4z=7 11x+10z=35 X=5 解得: Z=-2 1 把x=5,z=-2代入②,得y=
{
因此,三元一次方程组的解为
{
3 X=5
Y=1/3 Z=-2
新乐市实验学校
小组归纳:1.解三元一次方程组的基本思路:
2.解三元一次方程组的基本思想是消元;基本方法是
加减消元法和代入消元法
(1)方程组中含有三个未知数;
(2)每个方程中含有未知数的项的次数都是1;
(3)一共有三个方程
新乐市实验学校
概念:含有三个未知数,每个方程中含未知 数的项的次数都是1,并且一共有三个方程, 像这样的方程组叫做三元一次方程组. x y z 12, 例 x 2 y 5z 22, x 4 y. 是!它是最简的三
