振幅周期和频率例题解析
9-2简谐运动中的振幅 周期 频率和相位
g x b cos t b
9 – 2
简谐运动中的振幅 周期 频率和相位
第九章 振 动
作 业:
9.2.2,9.2.3,9.2.6,9.2.11.
练 习:
9.2.4,9.2.10.
周期 频率
1 T 2π
T
2π
(振动往复一次所需的时间) (单位时间内的振动次数)
9 – 2
简谐运动中的振幅 周期 频率和相位
第九章 振 动
角频率(angular frequency)
2π 圆频率 2π T
A
x x t 图
T 2
T
(2 秒内的振动次数)
注意
o
A
当 = 2k ( k =0,1,2,…)时, 两振动步调相同,称同相;
当 = (2k+1) ( k =0,1,2,…)时, 两振动步调相反 , 称反相.
9 – 2 x A1 A2 o - A2 -A1 x A1 A2 o - A2
简谐运动中的振幅 周期 频率和相位
第九章 振 动
x2
x
o
A
v
v
T 2
x t 图
v
T
t
1)相位描述振子的运动状态; 2)相位在 0 ~ 2π 内变化,质点无相同的运动状态; 相差2nπ (n为整数 ) 质点运动状态全同.(周期性) 3)初相位 (
(t 0)
描述质点初始时刻的运动状态. 或 [0 2π] )
取 [ π π]
x1
同相
T t
两质点同时到达各自同 方向的极端位置,同时越过 原点向相同方向运动.
o
A 1 A2
高二物理简谐振动 振幅、周期、频率 知识精讲 人教版

高二物理简谐振动 振幅、周期、频率 知识精讲 人教版一. 本周教学内容:第九章 第一节 简谐振动 第二节 振幅、周期、频率二. 知识要点:知道什么是简谐运动以与物体做简谐运动回复力特点,理解位移和回复力的概念,理解简谐运动在一次全振动中位移、回复力、加速度和速度的变化情况。
理解弹簧振子概念与实际物体运动抽象为弹簧振子的条件。
理解回复力kx F -=的意义。
知道振幅、周期、频率是描述振动整体特征的物理量,知道它们的物理意义,理解振幅和位移的区别,理解周期和频率的关系,知道什么是固有周期和固有频率。
三. 重点、难点解析: 1. 机械振动:物体〔或物体的一局部〕在某一位置附近做往复运动,叫做机械振动,简称振动。
物体受力满足2条才能做振动①是每当物体离开振动的中心位置就受到回复力作用力;②是运动中其它阻力足够小。
描述振动的名词。
① 平衡位置:物体振动停止时的位置也就是静止平衡的位置。
② 回复力:振动物体离开平衡位置就受到一个指向平衡位置的力,叫回复力。
回复力是力的作用效果命名的。
它可以是一个力,也可以是某个力的分力或者几个力的合力。
只要物体离开平衡位置回复力就不为零,方向指向平衡位置。
③ 振动位移:以平衡位置为原点〔起点〕的位移。
数值为从平衡到振动物体达到的位置的直线距离方向由平衡位置指向物体位置。
④ 一次全振动:物体以一样的速度经某位置,又以一样的速度回到同一位置,叫完成一次全振动。
2. 简谐振动:① 弹簧振子:一轻弹簧连接一质点,质点运动时不受摩擦阻力。
这样的装置叫弹簧振子。
弹簧振子沿水平方向运动过程分析,取水平坐标轴,平衡位置为原点。
弹簧处原长状③ 回复力:kx F -=。
④ 简谐运动的定义:质点在跟偏离平衡位置的位移成正比,并总指向平衡位置的回复力作用下的振动叫简谐运动。
⑤ 简谐运动的动力学特征:kx F -=。
⑥ 运动学特征:x mka -=是变加速运动。
⑦ 整体特征与运动学量变化规律:位移、加速度、速度都按周期性变化。
9.2振幅、周期和频率

在相隔一个周期T的两个时刻,振子只能位于同一个位置,其位移相同,合外力相同,加速度必定相同,选项C是正确的.
相隔T/2的两个时刻,振子的位移大小相等、方向相反,其位置可位于P和对称的P′处,在P处弹簧处于伸长状态,在P′处弹簧处于压缩状态,弹簧的长度并不相等,选项D是错误的.
本题求解时很容易忽视第二种情况,需综合利用学过的概念解决问题,同时还要注意对解的结果的合理性进行分析.
<img src=c:\全科学习\高二\物理\9.2振幅、周期和频率\6.bmp>
【点击易错点】
例3 如图9-2-3所示,小球m连着轻质弹簧,放在光滑的水平面上,弹簧的另一端固定在墙上,O是它的平衡位置.把小球拉到距O点1 cm的A点,轻轻释放小球m,经过0.2 s小球运动到O点,如果把小球拉到距O点3 cm处的B点(在弹性限度内),则释放小球后,小球振动周期是多少?
2.周期和频率
(1)定义:做简谐运动的物体完成一次全振动所需要的时间,叫做振动的周期,用T表示.
<img src=c:\全科学习\高二\物理\9.2振幅、周期和频率\1.bmp>
<img src=c:\全科学习\高二\物理\9.2振幅、周期和频率\2.bmp>
3.固有周期和固有频率
实验表明:对于同一个振动系统,振动的振幅可以改变,振动的频率(或周期)却是不变的.事实上,物体的振动频率(或周期)是由振动系统本身的性质决定的,与振幅的大小无关,所以又叫固有频率(或固有周期).
综上所述,只有选项C正确.
点拨 做简谐运动的弹簧振子的运动具有往复性、对称性和周期性.在同一位置P,振子的位移相同,回复力、加速度、动能、势能也相同,速度大小相等但方向可以相同,也可以相反.在关于平衡位置对称的两个位置,动能、势能对应相等,回复力、加速度大小相等,方向相反;速度大小相等,方向可以相同,也可以相反,运动时间也对应相等.
2021-2022新教材物理选择性必修第一册学案:第二章 第二节 简谐运动的描述 Word版含答案

第二节简谐运动的描述1.知道简谐运动的数学表达式,会通过简谐运动的表达式确定振幅、周期、频率等物理量。
2.了解初相和相位差的概念,理解相位的物理意义。
3.会根据图像分析各物理量的变化。
知识点一 简谐运动的函数描述 [知识梳理] 1.振动曲线振子振动时位移与时间关系的曲线。
2.简谐运动的函数表达式:x =A cos(ωt +φ)。
3.角频率与周期或频率的关系:ω=2πT=2πf 。
[初试小题] 1.判断正误。
(1)物体做简谐运动的位移表达式与计时时刻物体所在位置无关。
(×) (2)x =A sin ωt 中的A 为振幅,是矢量。
(×)(3)简谐运动的位移表达式x =A cos ωt 中,ω是简谐运动的角频率。
(√) (4)若简谐运动的表达式为x =5 cos ⎝⎛⎭⎫8πt +14πcm ,则振动周期为0.25 s 。
(√) 知识点二 简谐运动的图像描述 [知识梳理]1.相位:简谐运动表达式x =A cos (ωt +φ)中的ωt +φ叫作相位,是一个相对概念,与所选取的时间零点有关。
2.初相位:t =0时刻的相位φ叫作初相位,简称初相。
3.相位差:两个振子相位的差值叫相位差,是个绝对概念,表示两个频率相同简谐运动的振动先后关系,即Δφ=φ1-φ2。
[初试小题]1.判断正误。
(1)简谐运动的图像都是正弦或余弦曲线。
(√) (2)利用简谐运动的图像可知道其振动周期和振幅。
(√) (3)相位反映了振动物体的振动步调。
(√)(4)两个振动物体的相位相同,则其振动步调相反。
(×)2.(多选)物体A 做简谐运动的振动方程是x A =3cos ⎝⎛⎭⎫100t +π2 m ,物体B 做简谐运动的振动方程是x B =5cos ⎝⎛⎭⎫100t +π6m 。
比较A 、B 的运动可知( ) A .振幅是矢量,A 的振幅是6 m ,B 的振幅是10 m B .周期是标量,A 、B 周期相等,都为100 s C .A 振动的频率f A 等于B 振动的频率f B D .A 的相位始终超前B 的相位π3解析:选CD 振幅是标量,A 、B 的振幅分别为3 m 、5 m ,A 错误;A 、B 的周期均为T =2πω=2π100 s =6.28×10-2 s ,B 错误;因为T A =T B ,故f A =f B ,C 正确;Δφ=φA -φB=π3,为定值,D 正确。
大物习题集答案解析第4章机械振动

第4章 机械振动4.1基本要求1.掌握描述简谐振动的振幅、周期、频率、相位和初相位的物理意义及之间的相互关系2.掌握描述简谐振动的解析法、旋转矢量法和图线表示法,并会用于简谐振动规律的讨论和分析3.掌握简谐振动的基本特征,能建立一维简谐振动的微分方程,能根据给定的初始条件写出一维简谐振动的运动方程,并理解其物理意义4.理解同方向、同频率简谐振动的合成规律,了解拍和相互垂直简谐振动合成的特点4.2基本概念1.简谐振动 离开平衡位置的位移按余弦函数(或正弦函数)规律随时间变化的运动称为简谐振动。
简谐振动的运动方程 cos()x A t ωϕ=+2.振幅A 作简谐振动的物体的最大位置坐标的绝对值。
3.周期T 作简谐振动的物体完成一次全振动所需的时间。
4.频率ν 单位时间内完成的振动次数,周期与频率互为倒数,即1T ν=5.圆频率ω 作简谐振动的物体在2π秒内完成振动的次数,它与频率的关系为22Tπωπν==6.相位和初相位 简谐振动的运动方程中t ωϕ+项称为相位,它决定着作简谐振动的物体状态;t=0时的相位称为初相位ϕ7.简谐振动的能量 作简谐振动的系统具有动能和势能。
弹性势能222p 11cos ()22E kx kA t ωϕ==+ 动能[]22222k 111sin()sin ()222E m m A t m A t ωωϕωωϕ==-+=+v弹簧振子系统的机械能为222k p 1122E E E m A kA ω=+==8.阻尼振动 振动系统因受阻尼力作用,振幅不断减小。
9.受迫振动 系统在周期性外力作用下的振动。
周期性外力称为驱动力。
10.共振 驱动力的角频率为某一值时,受迫振动的振幅达到极大值的现象。
4.3基本规律1.一个孤立的简谐振动系统的能量是守恒的物体做简谐振动时,其动能和势能都随时间做周期性变化,位移最大时,势能达到最大值,动能为零;物体通过平衡位置时,势能为零,动能达到最大值,但其总机械能却保持不变,且机械能与振幅的平方成正比。
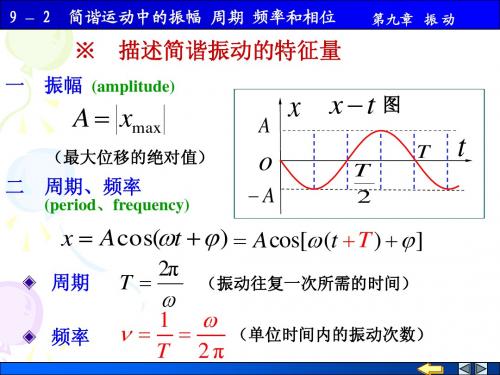
简谐振动中的振幅周期频率和相位

三 相位(Phase)描述振动物体运动状态的物理量
x Acos(t ) x
A
v A sin(t ) o
用相位来描述运动状态,
就可以区分位置和速度都相 同的状态。
A v
v v
T 2
xt 图
v
T
v
t
t : t 时刻的相位,描述 t 时刻的运动状态。
相位在 0 ~ 2内π变化,质点无相同的运动状态;
解:1)因T = 2s。于是
2
T
(rad / s)
将已知条件代入运动方程 x Acos(t )
得: x0 A cos 即 考虑到 t = 0时 v0 A sin
于是运动学方程为 x 0.12
3
0
cos(
t
)
3
m 16
3
于是运动学方程为 x 0.12 cos( t ) m
2)已知物体作简谐运动,由系统的力学 性质及初始条件求出振动表达式;
或 3)已知由振振动动表曲达线式求,出求振出动:表达式。
A、、 及、a、F 等
12
例:一弹簧振子系统,弹簧的弹性系数为 k = 0.72N/m,物体的 质量为 m = 20 g。今将物体从平衡位置沿桌面向X轴正向拉长到
0.04m 处静止释放,求:振动方程。
2π 2π
表示 2π秒时间内物体完 成全振动的次数。
T
(也称圆频率)
4
说明: 1)简谐运动的基本特性是它的周期性;
2)周期、频率或圆频率均由振动系统本身的性 质所决定。
对于弹簧振子:
k , 1 k , T 2 m
m
2 m
k
简谐运动的表达式还可以写为:
x Acos( t ) Acos(2 t ) Acos(2 t 5 )
高中物理简单谐振动与波动的题目解析

高中物理简单谐振动与波动的题目解析简单谐振动与波动是高中物理中的重要知识点,也是考试中常见的题型。
掌握了简单谐振动与波动的基本原理和解题方法,就能够轻松解决相关题目。
本文将通过具体的题目举例,分析解题思路和考点,并给出一些解题技巧,帮助高中学生更好地理解和应用这些知识。
一、简单谐振动题目解析例题1:一个质点做简谐振动,振幅为2cm,周期为0.4s。
求该振动的频率、角频率和振动的最大速度。
解析:这道题目主要考察了简谐振动的基本公式之间的关系。
首先,我们知道振动的周期T和频率f之间有如下关系:T = 1/f。
所以,该振动的频率为f = 1/T = 1/0.4 = 2.5 Hz。
其次,角频率ω和频率f之间有如下关系:ω = 2πf。
所以,该振动的角频率为ω = 2π × 2.5 = 5π rad/s。
最后,振动的最大速度与振幅和角频率之间有如下关系:v_max = Aω。
所以,该振动的最大速度为v_max = 2 × 5π = 10π cm/s。
通过这个例题,我们可以看到,对于简谐振动的题目,我们需要掌握振动的周期和频率之间的关系、角频率和频率之间的关系,以及振动的最大速度与振幅和角频率之间的关系。
二、波动题目解析例题2:一根绳子上的波沿着绳子传播,波长为2m,频率为50 Hz。
求波速和波动的周期。
解析:这道题目主要考察了波动的基本公式之间的关系。
首先,我们知道波速v、波长λ和频率f之间有如下关系:v = λf。
所以,该波动的波速为v = 2 × 50 = 100 m/s。
其次,波动的周期T和频率f之间有如下关系:T = 1/f。
所以,该波动的周期为T = 1/50 = 0.02 s。
通过这个例题,我们可以看到,对于波动的题目,我们需要掌握波速、波长和频率之间的关系,以及波动的周期和频率之间的关系。
三、解题技巧和注意事项在解答简单谐振动与波动的题目时,我们需要注意以下几点:1. 掌握基本公式:简单谐振动和波动都有一些基本的公式,如振动的周期和频率之间的关系、角频率和频率之间的关系,以及振动的最大速度与振幅和角频率之间的关系。
高二物理振幅、周期和频率·典型题剖析

振幅、周期和频率·典型题剖析例1一个弹簧振子,第一次用力把弹簧压缩x后开始振动,第二次把弹簧压缩2x后开始振动,则两次振动的周期之比和最大加速度的大小之比分别为[ ]A.1∶2,1∶2.B.1∶1,1∶1.C.1∶1,1∶2.D.1∶2,1∶1.分析振动的周期只决定于振动体本身固有的性质,对弹簧振子则由振子的质量与弹簧的劲度系数决定,与起振时的初始位移大小无关.大处,振子的加速度也越大.所以两情况中的最大加速度之比为1∶2.答C.例2一个作简谐运动的质点,先后以同样大小的速度通过相距10cm的A、 B两点,历时0.5s(图5-7).过B点后再经过t=0.5s质点以方向相反、大小相同的速度再次通过B点,则质点振动的周期是 [ ] A.0.5s.B.1.0s.C.2.0s.D.4.0s.分析根据题意,由振动的对称性可知:AB的中点(设为O)为平衡位置,A、B两点对称分布于O点两侧;质点从平衡位置O向右运动到B的时间应为质点从B向右到达右方极端位置(设为D)的时间所以,质点从O到D的时间所以 T=2s.答C.说明本题的关键是认识振动的对称性.如图5-8所示,设C、D为质点振动中左方和右方的极端位置,则由对称性可知:质点从B→D→B的时间一定等于质点从A→C→A的时间,即t BDB=t ACA=0.5s.所以,质点振动周期T=t AB+t BDB+t BA+t ACA=2s.例3如图5-9所示,竖直悬挂的轻弹簧下端系着A、B两球,其质量m A=0.1kg、m B=0.5kg.静止时弹簧伸长15cm.若剪断A、 B间的细线,则A 作简谐运动时的振幅和最大加速度为多少?g=10m/s2.分析剪断A、B间的细线后,A球成为竖直悬挂的弹簧振子,其振幅由它所处的初始状态决定.振动中的最大加速度由振子受到的最大回复力用牛顿第二定律可算出.解答由两球静止时的力平衡条件,得弹簧的劲度系数为=40N/m.剪断A、B间细线后,A球静止悬挂时的弹簧的伸长量为=2.5cm.弹簧下端的这个位置就是A球振动中的平衡位置.悬挂B球后又剪断细线,相当于用手把A球下拉后又突然释放.刚剪断细线时弹簧比比静止悬挂A球多伸长的长度就是振幅,即A=x=x A=15cm-2.5cm=12.5cm.振动中A球的最大加速度为=50m/s2.讨论物体作简谐运动时,其周期(或频率)由振动体的质量m和回复力公式F=-kx 中的比例系数决定,即对于弹簧振子,上述公式中的比例系数k等于弹簧的劲度系数.因此,弹簧振子的振动周期由振子的质量和弹簧的劲度系数决定.即。
大学物理振动波动例题习题(题型借鉴)

振动波动一、例题 (一)振动1.证明单摆是简谐振动,给出振动周期及圆频率。
2. 一质点沿x 轴作简谐运动,振幅为12cm ,周期为2s 。
当t = 0时, 位移为6cm ,且向x 轴正方向运动。
求: (1) 振动表达式;(2) t = 0.5s 时,质点的位置、速度和加速度;(3)如果在某时刻质点位于x =-0.6cm ,且向x 轴负方向运动,求从该位置回到平衡位置所需要的时间。
3. 已知两同方向,同频率的简谐振动的方程分别为:x 1= 0.05cos (10 t + 0.75π) 20.06cos(100.25)(SI)x t π=+ 求:(1)合振动的初相及振幅.(2)若有另一同方向、同频率的简谐振动x 3 = 0.07cos (10 t +ϕ 3 ), 则当ϕ 3为多少时 x 1 + x 3 的振幅最大?又ϕ 3为多少时 x 2 + x 3的振幅最小?(二)波动1. 平面简谐波沿x 轴正方向传播,振幅为2 cm ,频率为 50 Hz ,波速为 200 m/s 。
在t = 0时,x = 0处的质点正在平衡位置向y 轴正方向运动, 求:(1)波动方程(2)x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度。
2. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播。
已知原点的振动曲线如图所示。
求:(1)原点的振动表达式;(2)波动表达式;(3)同一时刻相距m 1的两点之间的位相差。
3. 两相干波源S 1和S 2的振动方程分别是1cos y A t ω=和2cos(/2)y A t ωπ=+。
S 1距P 点3个波长,S 2距P 点21/4个波长。
求:两波在P 点引起的合振动振幅。
4.沿X 轴传播的平面简谐波方程为:310cos[200(t )]200xy π-=- ,隔开两种媒质的反射界面A与坐标原点O 相距2.25m ,反射波振幅无变化,反射处为固定端,求反射波的方程。
9-1简谐运动 振幅 周期和频率 相位

m
x
−A
o
A
x =0 F =0
2
9-1
简谐运动 振幅 周期和频率 相位
振动的成因
a 回复力 b 惯性
3
9-1
简谐运动 振幅 周期和频率 相位
3 弹簧振子的运动分析
F
o
m
x
2
x
k F = −kx = ma 令 ω = m 2 dx 2 2 = −ω x 即 a = −ω x 得 2 dt 与位移的大小x成正比 成正比,而方 具有加速度 a 与位移的大小 成正比 而方 向相反特征的振动称为简谐运动
9-1
简谐运动 振幅 周期和频率 相位
一 简谐运动
1 机械振动 物体或物体的某一部分在一定位置 a 定义: 定义: 附近来回往复的运动 平衡位置 b 实例 实例: 心脏的跳动, 心脏的跳动, 钟摆,乐器, 钟摆,乐器, 地震等 c 周期和非周期振动
1
9-1
简谐运动 振幅 周期和频率 相位
2 简谐振动 简谐运动 最简单、最基本的振动 最简单、 谐振子 作简谐运动的物体 弹簧振子的振动
14
由 x = Acos(ωt +ϕ) 简谐运动方程 dx 得 v = = −Aω sin(ωt +ϕ) dt d2 x a = 2 = −Aω2 cos(ωt +ϕ) dt t = 0 时,x = x0 , =v0 A = x2 + ( v0 )2 ,v 0 ω x0 = Acosϕ v0 ϕ = arctan(− ) v0 = −ωAsin ϕ ωx0
π
(2) t=2 s时的位移、速度、加速度分别为 时的位移、 时的位移 速度、 x=0.10cos(40π+0.25π)=7.07×10-2 m π π × v=dx/dt=-2πsin(40π+0.25π)=-4.44 m·s-1 π π π a=d2x/dt2=-40π2cos(40π+0.25π)=-2.79×102 m·s-2 π π π ×
Ch9_1 简谐运动 振幅 周期和频率 相位

动力学方程
微分方程 的解:
振动方程
A
均与水平弹簧振子结果相同
9-1 简谐运动 振幅 周期和频率 相位
一轻弹簧的一端固定, 例1: 一轻弹簧的一端固定,另一端连 接一定质量的物体. 接一定质量的物体.整个系统位于水平 面内,系统的角频率为6 面内 , 系统的角频率为 6.0s-1. 今将物 04m 体沿平面向右拉长到 x0=0.04m 处释 试求: 简谐运动表达式; 放,试求:(1)简谐运动表达式;(2)物 体从初始位置运动到第一次经过 A/2 处时的速度. 处时的速度.
F = −k1x1 = −k2x2
k1 x k1 + k2 根据牛顿第二定律
联立解得 x2 =
-----振动为简谐振动 -----振动为简谐振动 其频率为
ω 1 k1k2 = ν= 2π 2π (k1 + k2 )m
9-1 简谐运动 振幅 周期和频率 相位
讨论 已知t = 0, x = 0, v 0 < 0 求 ϕ
— 线性回复力
动力学特征
振动的成因
回复力+惯性
7
9-1 简谐运动 振幅 周期和频率 相位
X
对于给定的弹簧振子 则 得
为常量,其比值亦为常量。令 即
8
9-1 简谐运动 振幅 周期和频率 相位
由 得
简谐振动微分方程
应用转动定律,同理也可求得单摆的角振动微分方程
动力学特征 运动学特征 具有加速度 与位移的大小 成正比,而方向相反特征的 成正比, 振动称为简谐运动 振动称为简谐运动
A
A A
消去 A 得
对给定振动系统,周期由系统本身性质决定, 对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定. 振幅和初相由初始条件决定.
第二节 振幅、周期和频率

第二节振幅、周期和频率知识要点:一、振幅1、定义:振动物体离开平衡位置的最大距离,叫振幅,振幅是标量,振幅常用A表示,其单位为长度单位:米(m),位移:由平衡位置指向振动质点所在位置的有向线段,是矢量,其最大值等于振幅。
2、物理意义:振幅表示振动强弱的物理量。
对于同一个振动系统来说,物体的振幅越大,振动越强,振幅越小,振动越弱。
二、周期和频率1、一次全振动:振动物体从某一初始状态(位移x、速度v)开始,再次回复到初始状态(即位移、速度均与初状态完全相同)所经历的过程,叫完成了一次全振动。
2、周期:振动物体完成一次全振动所用的时间,叫做周期,周期用T表示,单位是秒(s)。
3、频率:单位时间内完成全振动的次数,叫做频率,频率用f表示,单位是赫兹(Hz),1Hz=1s-1。
4、周期和频率的物理意义:都是表示振动快慢的物理量。
要注意运动快慢与振动快慢的区别,运动快慢可用速率大小来表示,振动快慢则需用周期的长短或频率的大小来表示。
5、固有频率:简谐运动的频率由振动系统本身的性质所决定,与振幅的大小无关。
我们把由振动系统本身性质所决定的频率称为振动系统的固有频率。
三、三者的关系1、振幅是标量,是指物体偏离平衡位置的最大距离,它总是正值。
2、在简谐运动中,振幅跟周期和频率无关,在稳定的振动中,振幅是不变的,而位移是时刻变化的。
3、振动物体在一个全振动过程的路程等于4个振幅,在半个周期内通过的路程等于两个振幅,但在四分之一周期内通过的路程不一定等于一个振幅,与振动的起始时刻有关。
4、在一个周期内振动的路程s与振幅A的关系是s=4A,在时间Δt内质点通过的路程为Δs=(Δt/T)·4A=[Δt/(T/4)]·A。
5、周期和频率都是表示振动快慢的物理量,二都互为倒数关系,即T=1/f,或f=1/T。
周期越长,频率越低,振动越慢。
典型例题例1、如图9-11所示,弹簧振子以O为平衡位置在BC间振动,则()A.从B→O→C→O为一次全振动;B.从O→B→O→C→O为一次全振动;C.从C→O→B→O→C为一次全振动;D.振幅大小为OB。
高二物理 (人教大纲版)第二册 第九章 机械振动 二、振幅、周期和频率(第一课时)

二、振幅、周期和频率从容说课本节课讲述描述简谐运动的振幅、周期和频率等几个物理量.它是上节课对简谐运动研究的延续,在上节课的基础上引进振幅用来直接反映简谐运动中的最大位移,间接反映简谐运动的能量,引进周期和频率用来反映简谐振动重复运动的快慢.只有切实理解了本节所学的几个物理量,才能更好地、更全面地反映出简谐运动的运动特征.尤其对以后的学习会起到很重要的作用.例如:对交变电流、电磁振荡等知识的学习.结合本节内容的特点,对本节教学的目标定位于:1.知道周期、振幅、频率三个物理量的定义,并理解其物理意义.2.理解周期与频率的关系,并能对二者进行换算.3.知道物体振动固有周期和固有频率.本节课的教学重点在于对周期、频率、振幅的认识和理解.本节课的教学难点是理解振幅与简谐运动能量的定性关系.以及振幅与位移的区别.为了突出重点、突破难点。
使学生能更好地接受知识,本节课采用先学后教、实验演示、讨论总结等方法。
以加深学生的理解,同时采用多媒体辅助教学,以激发学生的学习兴趣,达到圆满完成教学任务的目的.本节课的教学顺序确定如下:复习提问→新课导人→指导自学→归纳总结→强化练习→小结.一、知识目标 _1.知道描述简谐运动的周期、振幅、频率三个物理量.2.理解周期与频率的关系,并能进行两者间的换算.3.了解物体振动的固有周期和固有频率.二、能力目标1.培养学生对知识的归纳、总结能力.2.提高学生对实验的观察、分析能力.三、德育目标通过对简谐运动周期性的学习,使学生理解社会新旧更替.螺旋前进的道理。
教学重点对简谐运动周期、频率、振幅的认识和理解.教学难点1.理解振幅间接反映振动能量的理论依据.2.区分振幅与位移两个物理量.教学方法指导性自学、实验演示、多媒体辅助相结合的综合教学法.教学用具投影片、弹簧振子、秒表、CAI课件课时安排l课时教学过程一、新课导入1.复习提问①什么叫机械振动?②什么叫简谐运动?2.导人通过上节的学习,我们知道了什么是简谐运动,但如何对简谐运动来进行定性的描述和定量的计算呢?这就需要我们引进一些能反映简谐运动特性的物理量——周期、频率和振幅,本节我们就共同来学习这些物理量.二、新课教学(一)振幅、周期和频率.基础知识请学生阅读课文第一部分,同时思考下列问题:[投影片出示]1.什么叫振幅?其物理意义是什么?单位又是什么?用什么符号表示?2.什么叫周期?其物理意义是什么?单位又是什么?用什么符号表示?3.什么叫频率?其物理意义是什么?单位又是什么?用什么符号表示?学生阅读后,得出以上问题的结论:1.a.振动物体离开平衡位置的最大位移叫振幅.b.振幅用来反映振动物体振动的强弱.c.振幅的单位是:米(m).d.振幅的符号是:A.2.a.做简谐运动的物体完成一次全振动所需要的时间叫周期.b.周期是用来反映物体振动快慢的物理量.c.周期的单位是:秒(s).d.周期常用符号:T.3.a.做简谐运动的物体,在单位时间内完成全振动的次数叫频率.b.频率是用来反映物体振动快慢的物理量.c.频率的单位是:赫兹(Hz).d.频率的常用符号:f.深入探究请同学们结合前面所学,考虑以下问题:[投影出示]1.振幅与位移有何区别,有何联系?2.周期与频率有何区别,有何联系?3.试以弹簧振子为例描述一次全振动.学生经过思考、讨论、归纳总结后得出上述问题的结论:1.振幅与位移的区别:a.物理意义不同.振幅是用来反映振动强弱的物理量;位移是用来反映位置变化的物理量.b.矢量性不同.振幅是一标量,只有大小,没有方向;位移是一矢量,既有大小又有方向.振幅与位移的相同点:a.都是反映长度的物理量.振幅是偏离平衡位置的最大距离;位移是偏离平衡位置的距离.其单位都是长度单位.b.位移的最大值就是振幅.2.周期与频率的区别:a.物理意义不同.周期是完成一次全振动所需要的时间;频率是单位时间内完成的全振动的次数.b.单位不同.周期的国际单位是秒;频率的国际单位是赫兹.周期与频率的联系:a.都是用来反映振动快慢的物理量.周期越大,振动得越慢;频率越大,振动得越快.b.周期与频率互成倒数关系.即:T=1.f①O→A→O→A′→O②A→O→ A′→O→A③A′→O→A→O→A′④O→A′→O→A→O教师总结通过上面的学习,我们对描述简谐运动的三个物理量:振幅、周期、频率,已有了一定的认识.下面我们简单应用一下.基础知识应用1.弹簧振子在B、C间做简谐运动,O为平衡位置,BC间距离为10 cm,B→C运动时间为1 s,如图所示.则 ( )A.从O→C→O振子做了一次全振动B.振动周期为1s,振幅是10cmC.经过两次全振动.通过的路程是 20cmD.从B开始经3s,振子通过路程是30cm2.一个弹簧振子.第一次把弹簧压缩x后开始振动.第二次把弹簧压缩2x后开始振动,则两次振动的周期之比和最大加速度的大小之比为()A.1:2,1:2B.1:1,1:1C.1:2,1:2D.1:2,1:13.一个做简谐运动的质点,先后以同样大小的速度通过相距10 cm的A、B两点,历时0.5 s.如图所示,经过B点后再经过t=0.5 s 质点以方向相反、大小相同的速一次通过B点.则质点振动的周期是( )A.0.5 s,B.10sC.2.O sD.4.0s[参考答案]1.解析:振子从0→C→0时位移虽然相同,但速度的方向不同,振动只是半次全振动故A错.振子从B→c是半次全振动,故周期T=2 s,振幅A=OB=BC =52cm.故B错.由全振动的定义知:振子由B→C→B为一次全振动,振子路程s=4 A=4× 5=20 cm,所以两个全振动的路程中2×20cm=40cm,故C错。
振幅、周期和频率

M B’ O
B
A’
A
当振子从某一个振动状态 (s、v),第一次再回到该振动 状态(s、v),所经历的过程为 一个全振动。
2.周期:完成一次全振动所经历的时间 案例:参考导与练例二 思考下面问题
一个做简谐运动的质点,某时刻位于A 点,经过时间0.5s它第一次以相同的速度通 过B,再过0.5s质点以大小相等、方向相反的 速度再次通过B,则质点振动的周期是?
C’
A
O
B
C
C’
A t1
O
B t1
C
t2
3.半周期的对称性
B’ A’
O A B
(1)从振子经过B点开始计时,确定半周期 后振子的位置;寻找两个位置上振子的s,v, F,a的关系;振子在这半个周期内走的路程? (2)从振子经过A点并向左运动开始计时呢? (3)从振子经过A点并向右运动开始计时呢?
【归纳】振子经过半个周期,初、末状 态的S、v、F、a具有等大反向的特点; 且振子经过的路程为2A。 【辨析】初、末状态的s等大反向,能否 判定初末状态时间间隔一定是半个周 期吗? 【思考】如何从S、v、F、a角度确定半 周期? 当初、末状展
简谐运动的周期(推导)
说明:m为振子质量;k为回复力F和 位移s的比例常数,对于弹簧振子,k 为弹簧劲度系数。
由简谐运动周期公式可知:振动系统的振动 周期完全由系统自身因素(m,k)决定。 所以简谐运动的周期也叫固有周期。
m M B’ O
B
V V
B’
m M O
B
应用:在前面的案例中,振子振 动的周期如何变化?
振幅、周期和频率
一.振幅(A)
1.定义: 离开平衡位置的最大距离 标量,无方向 2.标、矢性: 3.和位移的区别与联系:
1、深刻理解简谐运动、振幅、周期和频率的概念

机械振动和机械波考点例析一、夯实基础知识1、深刻理解简谐运动、振幅、周期和频率的概念(1)简谐运动:物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动。
特征是:F=-kx,a=-kx/m(2)简谐运动的规律:○1在平衡位置: 速度最大、动能最大、动量最大;位移最小、回复力最小、加速度最小。
○2在离开平衡位置最远时: 速度最小、动能最小、动量最小;位移最大、回复力最大、加速度最大。
○3振动中的位移x 都是以平衡位置为起点的,方向从平衡位置指向末位置,大小为这两位置间的直线距离。
加速度与回复力、位移的变化一致,在两个“端点”最大,在平衡位置为零,方向总是指向平衡位置。
(3)振幅A :振动物体离开平衡位置的最大距离称为振幅。
它是描述振动强弱的物理量。
它是标量。
(4)周期T 和频率f :振动物体完成一次全振动所需的时间称为周期T,它是标量,单位是秒;单位时间内完成的全振动的次数称为振动频率,单位是赫兹(Hz )。
周期和频率都是描述振动快慢的物理量,它们的关系是:T=1/f.2、深刻理解单摆的概念(1)单摆的概念:在细线的一端拴一个小球,另一端固定在悬点上,线的伸缩和质量可忽略,线长远大于球的直径,这样的装置叫单摆。
(2)单摆的特点:○1单摆是实际摆的理想化,是一个理想模型; ○2单摆的等时性,在振幅很小的情况下,单摆的振动周期与振幅、摆球的质量等无关; ○3单摆的回复力由重力沿圆弧方向的分力提供,当最大摆角α<100时,单摆的振动是简谐运动,其振动周期T=gL π2。
(3)单摆的应用:○1计时器;○2测定重力加速度g=224TL π.3、深刻理解受迫振动和共振(1)受迫振动:物体在周期性驱动力作用下的振动,其振动频率和固有频率无关,等于驱动力的频率;受迫振动是等幅振动,振动物体因克服摩擦或其它阻力做功而消耗振动能量刚好由周期性的驱动力做功给予补充,维持其做等幅振动。
(2)共振:○1共振现象:在受迫振动中,驱动力的频率和物体的固有频率相等时,振幅最大,这种现象称为共振。
高二物理振幅、周期和频率(2019)

上 又移兵而攻齐 无後 与魏王豹及诸侯东击楚 代王驰至渭桥 曰阴德 亡卒七千人 ”曰:“礼後乎 骑六千匹 小馀七十三;不用为币 张苍为章程 情欲繁 争割地而赂秦 其见敬礼如此 渡临晋 ”上曰:“朕乃安敢望先帝乎 以汤为无害 以为敢挚行 谓袁盎曰:“吾不听公言 有莒、卫以
为外主 ”礼生於有而废於无 君臣无礼 孝文时以治刑名言事太子 且有伉王 汉王出荥阳 已而绛侯望袁盎曰:“吾与而兄善 浮之江中 下吏 亢乌腾而一止 而赵高亲近 其实难用 怨之 ”即令师涓坐师旷旁 祭仲迎昭公忽 民众殷喜 不如都周 皆胃胃也 败诸姑蔑 事秦始皇 晋文以正国法
来高七八尺者 晋楚战鄢陵 ”孔子去 成公立 樊穆仲曰:“鲁懿公弟称 黄帝是也 诛赵王 脱张羽於戹 甚苦矣 君子长者;为淮阳守 其实中其声者谓之端 卫绝祀 且夫秦地被山带河 长未到处所 上复下 葆塞为外臣 节用水火材物 东胡王愈益骄 乃与其党率营丘人袭攻杀胡公而自立 诸民
能齐言者皆予齐王 居南阳 行欲斩婴者十馀 任敖素善高祖 诸儒生或议曰:“古者封禅为蒲车 充溢露积於外 吾方营菟裘之地而老焉 武公疾 数日 酒酣起前 事发相重 子恽立 则富贵之;公欲禳之 踵门长揖 秦女也 有鲍叔牙、宾须无、隰朋以为辅 又和匈奴 公常执左券以责於秦韩 韩王
为齐王 吾据荥阳 无为小人儒 弟太庚立 齐桓公始霸 天既附命正厥德 ”君不若道虞舜之道 大馀二十 九芒 有席卷天下 韩厥曰:“赵衰、赵盾之功岂可忘乎 弗就 一阳接内者 纣不胜败而还走 天子弗忍诛 原罢之 故诫之曰“臣不作福”者 润泽有光 幸而来会饮 臣请处蜀郡严道邛邮
使将兵伐晋 再至 秦皇帝以为贞妇而客之 苏秦始来见 子路为卫大夫孔悝之邑宰 吴粮绝 作君奭 复拔代、雁门、云中郡县 口欲穷刍豢之味 今龟 营室者 外下;争者末节也 其後则又作柏梁、铜柱、承露仙人掌之属矣 有一老父 及诸王 新城三老董公遮说汉王以义帝死故 召临江王来 气
高中物理机械振动知识点详解和答案

九、机械振动一、知识网络二、画龙点睛概念1、机械振动(1)平衡位置:物体振动时的中心位置,振动物体未开始振动时相对于参考系静止的位置,或沿振动方向所受合力等于零时所处的位置叫平衡位置。
(2)机械振动:物体在平衡位置附近所做的往复运动,叫做机械振动,通常简称为振动。
(3)振动特点:振动是一种往复运动,具有周期性和重复性2、简谐运动(1)弹簧振子:一个轻质弹簧联接一个质点,弹簧的另一端固定,就构成了一个弹簧振子。
(2)振动形成的原因①回复力:振动物体受到的总能使振动物体回到平衡位置,且始终指向平衡位置的力,叫回复力。
振动物体的平衡位置也可说成是振动物体振动时受到的回复力为零的位置。
②形成原因:振子离开平衡位置后,回复力的作用使振了回到平衡位置,振子的惯性使振子离开平衡位置;系统的阻力足够小。
(3)振动过程分析振子的运动A→O O→A′A′→O O→A对O点位移的方向向右向左向左向右(4)简谐运动的力学特征①简谐运动:物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫做简谐运动。
②动力学特征:回复力F与位移x之间的关系为F=-kx式中F为回复力,x为偏离平衡位置的位移,k是常数。
简谐运动的动力学特征是判断物体是否为简谐运动的依据。
③简谐运动的运动学特征a=-k m x加速度的大小与振动物体相对平衡位置的位移成正比,方向始终与位移方向相反,总指向平衡位置。
简谐运动加速度的大小和方向都在变化,是一种变加速运动。
简谐运动的运动学特征也可用来判断物体是否为简谐运动。
例题:试证明在竖直方向的弹簧振子做的也是简谐振运动。
证明:设O为振子的平衡位置,向下方向为正方向,此时弹簧形变量为x0,根据胡克定律得x0=mg/k当振子向下偏离平衡位置x时,回复力为F=mg-k(x+x0)则F=-kx所以此振动为简谐运动。
3、振幅、周期和频率⑴振幅①物理意义:振幅是描述振动强弱的物理量。
②定义:振动物体离开平衡位置的最大距离,叫做振动的振幅。
高二物理振幅、周期和频率

弹簧振子的周期由振动系统本身的质量和 劲度系数决定,而与振幅无关,所以把周期和 频率叫做固有周期和固有频率.
例题:
如图:弹簧振子做简谐运动,由a点第一次到
达b点用了0.2s,它经过a、b两点时的速度相
同.又经过0.4s时间,振子第二次到达b点,在 这0.6s时间里振子通过的路程是10cm.求:该 弹簧振子的周期及振幅.
二、振幅、周期和频率
一、振幅
弹簧振子 的振幅就是 图中的OA或 OA’大小
• 振动物体离开平衡位置的最图:单摆 摆动时的振幅 是OB或OC的 大小
振幅和位移的区别:
• 对于一个给定的振动,振子的位移是时 刻变化的,但振幅是不变的,位移是矢 量,振幅是标量,它等于最大位移的数 值.
二、周期和频率
• 做简谐运动的物体完成一次全振 动所需的时间,叫做振动的周期, 单位:s .
• 单位时间内完成的全振动的次数,
叫做频率,单位:Hz.
• 周期和频率之间的关系:
f 1 T
振动周期的计算:
Tt n
t表示发生n次全振动所用的总时间.
周期、频率的决定因素:
点击下图动画演示
• 振动周期与振子的质量有关,质量较小时, 周期较小.
解析:
由于它经过a、b两点时的速度相同,说明a、b
两点一定是关于平衡位置O对称的,又由于第一段 时间较短而第二段时间较长,说明运动情况一定 是如图所示,即从a先经过平衡位置O而到达b,再 从b经过最大位移c点再回到b.不难看出,这0.6s 时间恰好是半个周期,经过的路程恰是振幅的2倍, 因此它的振动周期是1.2s,振幅是5cm.
小结:
• 振幅是振动物体离开平衡位置的最大距离;振 动物体完成一次全振动所需要的时间叫周期;单 位时间内完成全振动的次数叫频率.
《大学物理》振动练习题及答案解析

《大学物理》振动练习题及答案解析一、简答题1、如果把一弹簧振子和一单摆拿到月球上去,它们的振动周期将如何改变? 答案:弹簧振子的振动周期不变,单摆的振动周期变大。
2、完全弹性小球在硬地面上的跳动是不是简谐振动,为什么?答案:不是,因为小球在硬地面上跳动的运动学方程不能用简单的正弦或余弦函数表示,它是一种比较复杂的振动形式。
3、简述符合什么规律的运动是简谐运动答案:当质点离开平衡位置的位移`x`随时间`t`变化的规律,遵从余弦函数或正弦函数()ϕω+=t A x cos 时,该质点的运动便是简谐振动。
或:位移x 与加速度a 的关系为正比反向关系。
4、怎样判定一个振动是否简谐振动?写出简谐振动的运动学方程和动力学方程。
答案:物体在回复力作用下,在平衡位置附近,做周期性的线性往复振动,其动力学方程中加速度与位移成正比,且方向相反:x dtxd 222ω-=或:运动方程中位移与时间满足余弦周期关系:)cos(φω+=t A x 5、分别从运动学和动力学两个方面说明什么是简谐振动?答案:运动学方面:运动方程中位移与时间满足正弦或余弦函数关系)cos(φω+=t A x 动力学方面:物体在线性回复力作用下在平衡位置做周期性往复运动,其动力学方程满足 6、简谐运动的三要素是什么? 答案: 振幅、周期、初相位。
7、弹簧振子所做的简谐振动的周期与什么物理量有关?答案: 仅与振动系统的本身物理性质:振子质量m 和弹簧弹性系数k 有关。
8、如果弹簧的质量不像轻弹簧那样可以忽略,那么该弹簧的周期与轻弹簧的周期相比,是否有变化,试定性说明之。
答案:该振子周期会变大,作用在物体上的力要小于单纯由弹簧形变而产生的力,因为单纯由形变而产生的弹力中有一部分是用于使弹簧产生加速度的,所以总体的效果相当于物体质量不变,但弹簧劲度系数减小,因此周期会变大。
9、伽利略曾提出和解决了这样一个问题:一根线挂在又高又暗的城堡中,看不见它的上端而只能看见其下端,那么如何测量此线的长度?答案:在线下端挂一质量远大于线的物体,拉开一小角度,让其自由振动,测出周期T ,便可依据单摆周期公式glT π2=计算摆长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振幅、周期和频率例题解析
(1)对称法破解周期计算问题.
简谐运动具有对称性,如物体在平衡位置两侧的对称点上,回复力大小、加速度大小、位移大小、速度大小、动能和势能都各自分别相等.对称性还表现在过程量的相等上,如从某点到达最大位置和从最大位置再回到这一点所需要的时间相等;质点从某点向平衡位置运动时,到达平衡位置的时间和它从平衡位置再运动到这一点的对称点所用的时间相等;振动物体在关于平衡位置对称的任意两段上运动所需的时间相等.
[例1] 一质点在平衡位置O 附近做简谐运动,从它经过平衡位置起开始计时,经 0.13 s 质点第一次通过M 点.再经0.1 s 第二次通过M 点,则质点振动周期的可能值为多大?
解析:将物理过程模型化.画出具体化的图景如图9—2—3所示.设质点从平衡位置O 向右运动到M 点,那么质点从O 到M 运动时间为0.13 s ,再由M 经最右端A 返回M 经历时间为0.1 s ;如图9—2—4所示.
图9—2—3 图9—2—4 图9—2—5
另外有一可能就是M 点在O 点左方,如图9—2—5所示,质点由O 点经最右方A 点后向左经过O 点到达M 点历时0.13 s ,再由M 点向左经最左端A ′点返回M 点历时0.1 s .
根据以上分析,质点振动周期共存在两种可能性.
如图9—2—4所示,可以看出O →M →A 历时0.18 s ,根据简谐运动的对称性,可得到T 1=4×0.18 s =0.72 s .
另一种可能如图9—2—5所示,由O →A →M 历时t 1=0.13 s ,由M →A ′历时t 2=0.05 s .设M →O 历时t ,则4(t +t 2)=t 1+2t 2+t .解得t =0.01 s ,则T 2=4(t +t 2)=0.24 s .
所以周期的可能值为0.72 s 和0.24 s .
点评:本题考虑问题要全面,不要漏解,最常丢掉的那个可能周期值为0.24 s .另外,求解本题必须理解在实际振动过程中,哪一段上所用的时间为一个周期.并且为解问题形象直观,一般要画出过程示意图.
(2)2倍振幅法破解振子路程的计算问题.
简谐运动的物体,在一个T 内的路程为4个振幅,
2T 内的路程为2个振幅,故当物体在Δt =n 2
T (n =1,2,3…)时间内通过的路程s 为:s =2nA (n =1,2,3…).这种计算质点振动中通过路程的方法,称作2倍振幅法.
[例2]有一振动的弹簧振子,频率为5 Hz ,从振子经平衡位置开始计时,在1 s 内通过的路程为80 cm ,则振子的振幅为________ cm .
解析:由频率f =5 Hz ,则知振动周期T =f 1=5
1=0.2 s .在时间Δt =1 s 内,完成半振动次数n =T t 2
1∆=10.则依2倍振幅法 s =2nA =2×10×A =80 cm 所以振幅A =
n s 210280⨯ cm =4 cm .。
