上三角矩阵环中的一些斜McCoy子环
近世代数答案3

2畅 商环的应用例子 :爱森斯坦判别法的证明(整数环上多项式性质的证明)
可化归到整数环的剩余类域上 . 3畅 新域或新环的构造 :复数域(作为实数域R 上使 x2 + 1 = 0 有根的最小扩
域) ;二元域 ;集合 S 在域 F 上生成的扩域 ;商环 、剩余类环 F[ x ]/( f ( x ))(包括
§ 1 域的例子 ,复数域及二元域的构造 , 对纠一个错的码的应用
以下习题中打 倡 者为必作题 ,其余为选作题 .
倡 1畅 令
C0 =
a -b
b a
a ,b ∈ R ,
则(1)C0 对矩阵的加法和乘法成为域 .
(2) C0 中R0 =
a 0
0 a
a ∈ R 是同构于R 的子域 .
· 49 ·
(2) 若
u3
-2=
0
,把
u u
+ -
11表成
au2 +
bu + c 的形式 ,a ,b ,c ∈ Q
.
9畅 令 E = F( u) ,u 是极小多项式为奇数次的代数元 .证明 E = F( u2 ) .
促进读者巩固高等代数的知识与其它近世代数教材相比本书中域的内容包括下一章的有限域的内容放到整环的因式分解唯一性理论之前并且替代它而成为教材的核心部分内容也改变很多加入纠错码的例子和三大几何作图难题的讨论这些应用内容而舍去了可分扩张及分裂域等内容
2019年本刊分类总目录

— — — 以 天 水 市 秦 州 区 人 民 医 院 病 案 为 例 邢渊,李琴琴,王晶(3,59) 拉曼光谱在卵巢癌诊断中的应用研究 谈芳君,金 措,唐晓琳(4,60) 内蒙古优秀男子举重运动员的静息心电图分析 蒙 娜,张丽琴(4,65)
树人论坛
认知视角下藏语方位词的统计分析研究 丁海兰,于洪志(1,63)
三七与天麻复配提取液体外抗氧化作用 王 俊,康淑荷(1,69)
DNA 双链断裂损伤焦点的定量计算和分析方法研究进展 尤培蒙,黎 晨,王晨曦,何俊霞,
肖文媛,赵 晋(2,54) 香蕉皮内生细菌的分离纯化及初步鉴定 源自 王福彬,雒晓芳,郑青波,刘传丽,
— 93 —
腕部神经阻滞复合臂丛神经阻滞麻醉在老年患者手部手 术中的临床应用 米 宏,雷知雅(2,36) 子宫内膜癌早期诊断的研究进展
窦倩如,张英姿(2,39) 少肌性肥胖发病机制和诊断标准的研究进展 谢文清,陆明洁,王苗,李霞,海向军(3,44) 端粒酶在宫颈癌诊断和治疗中的研究进展 王丽丽,杨宇琴,黎晨,尤培蒙,杨田,赵晋(3,50) 乳腺癌中肿瘤相关巨噬细胞的浸润与 eIF4E 表达的关系 田世馨,尚立娜,马应全,张城(3,54) 亚临床甲状腺功能减退 患 者 TSH 与 B 型 尿 钠肽 原 水 平的 相关性研究
第七章图答案

第7章图部分答案解释如下。
2. 不一定是连通图,可能有若干连通分量 11. 对称矩阵可存储上(下)三角矩阵14.只有有向完全图的邻接矩阵是对称的 16. 邻接矩阵中元素值可以存储权值21. 只有无向连通图才有生成树 22. 最小生成树不唯一,但最小生成树上权值之和相等26. 是自由树,即根结点不确定35. 对有向无环图,拓扑排序成功;否则,图中有环,不能说算法不适合。
42. AOV网是用顶点代表活动,弧表示活动间的优先关系的有向图,叫顶点表示活动的网。
45. 能求出关键路径的AOE网一定是有向无环图46. 只有该关键活动为各关键路径所共有,且减少它尚不能改变关键路径的前提下,才可缩短工期。
48.按着定义,AOE网中关键路径是从“源点”到“汇点”路径长度最长的路径。
自然,关键路径上活动的时间延长多少,整个工程的时间也就随之延长多少。
三.填空题1.有n个顶点,n-1条边的无向连通图2.有向图的极大强连通子图3. 生成树4. 455. n(n-1)/2 6 .n i d1217. 9 8. n9. 2(n-1) 10. N-1 11. n-1 12. n 13. N-1 14. n 15. N 16. 3 17. 2(N-1) 18. 度出度 19. 第I列非零元素个数 20.n 2e21.(1)查找顶点的邻接点的过程 (2)O(n+e) (3)O(n+e) (4)访问顶点的顺序不同 (5)队列和栈22. 深度优先 23.宽度优先遍历 24.队列25.因未给出存储结构,答案不唯一。
本题按邻接表存储结构,邻接点按字典序排列。
25题(1) 25题(2)26.普里姆(prim)算法和克鲁斯卡尔(Kruskal)算法 27.克鲁斯卡尔28.边稠密边稀疏 29. O(eloge)边稀疏 30.O(n2) O(eloge)31.(1)(V i,V j)边上的权值都大的数(2)1 负值(3)为负边32.(1)n-1 (2)普里姆 (3)最小生成树 33.不存在环 34.递增负值35.16036.O(n2) 37. 50,经过中间顶点④ 38. 75 39.O(n+e)40.(1)活动(2)活动间的优先关系(3)事件(4)活动边上的权代表活动持续时间41.关键路径 42.(1)某项活动以自己为先决条件(2)荒谬(3)死循环43.(1)零(2)V k度减1,若V k入度己减到零,则V k顶点入栈(3)环44.(1)p<>nil (2)visited[v]=true (3)p=g[v].firstarc (4)p=p^.nextarc45.(1)g[0].vexdata=v (2)g[j].firstin (3)g[j].firstin (4)g[i].firstout (5)g[i].firstout(6)p^.vexj (7)g[i].firstout (8)p:=p^.nexti (9)p<>nil(10)p^.vexj=j(11)firstadj(g,v0) (12)not visited[w] (13)nextadj(g,v0,w)46.(1)0 (2)j (3)i (4)0 (5)indegree[i]==0 (6)[vex][i] (7)k==1(8)indegree[i]==047.(1)p^.link:=ch[u].head (2)ch[u].head:=p (3)top<>0 (4)j:=top(5)top:=ch[j].count(6)t:=t^.link48.(1)V1 V4 V3 V6 V2 V5(尽管图以邻接表为存储结构,但因没规定邻接点的排列,所以结果是不唯一的。
数值分析第三版课本知识题及答案解析

第一章 绪 论1. 设x >0,x 的相对误差为δ,求ln x 的误差.2. 设x 的相对误差为2%,求nx 的相对误差.3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字:*****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====⨯4. 利用公式(3.3)求下列各近似值的误差限:********12412324(),(),()/,i x x x ii x x x iii x x ++其中****1234,,,x x x x 均为第3题所给的数.5. 计算球体积要使相对误差限为1%,问度量半径R 时允许的相对误差限是多少?6. 设028,Y =按递推公式1n n Y Y -=-( n=1,2,…)计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差?7. 求方程25610x x -+=的两个根,使它至少具有四位有效数字27.982).8. 当N 充分大时,怎样求211Ndx x +∞+⎰?9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2?10. 设212S gt =假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减小.11. 序列{}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字),计算到10y 时误差有多大?这个计算过程稳定吗?12. 计算61)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好?3--13.()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式ln(ln(x x =-计算,求对数时误差有多大?14. 试用消元法解方程组{101012121010;2.x x x x +=+=假定只用三位数计算,问结果是否可靠?15. 已知三角形面积1sin ,2s ab c =其中c 为弧度,02c π<<,且测量a ,b ,c 的误差分别为,,.a b c ∆∆∆证明面积的误差s ∆满足.s a b cs a b c ∆∆∆∆≤++第二章 插值法1. 根据(2.2)定义的范德蒙行列式,令2000011211121()(,,,,)11n n n n n n n n n x x x V x V x x x x x x x xxx ----==证明()n V x 是n 次多项式,它的根是01,,n x x -,且101101()(,,,)()()n n n n V x V x x x x x x x ---=--.2. 当x = 1 , -1 , 2 时, f (x)= 0 , -3 , 4 ,求f (x )的二次插值多项式.3. 给出f (x )=ln x 的数值表用线性插值及二次插值计算ln 0.54 的近似值.4. 给出cos x ,0°≤x ≤90°的函数表,步长h =1′=(1/60)°,若函数表具有5位有效数字,研究用线性插值求cos x 近似值时的总误差界.5. 设0k x x kh =+,k =0,1,2,3,求032max ()x x x l x ≤≤.6. 设j x 为互异节点(j =0,1,…,n ),求证:i)0()(0,1,,);nk kj j j x l x xk n =≡=∑ii)()()1,2,,).nk jj j xx l x k n =-≡0(=∑7. 设[]2(),f x C a b ∈且()()0f a f b ==,求证21()()().8max max a x ba xb f x b a f x ≤≤≤≤≤-"8. 在44x -≤≤上给出()xf x e =的等距节点函数表,若用二次插值求xe 的近似值,要使截断误差不超过610-,问使用函数表的步长h 应取多少?9. 若2n n y =,求4n y ∆及4n y δ.10. 如果()f x 是m 次多项式,记()()()f x f x h f x ∆=+-,证明()f x 的k 阶差分()(0)kf x k m ∆≤≤是m k -次多项式,并且()0(m lf x l +∆=为正整数).11. 证明1()k k k k k k f g f g g f +∆=∆+∆.12. 证明110010.n n kkn n k k k k f gf g f g g f --+==∆=--∆∑∑13. 证明1200.n j n j y y y -=∆=∆-∆∑14. 若1011()n n n n f x a a x a x a x --=++++有n 个不同实根12,,,n x x x ,证明{10,02;, 1.1()n k njk n a k n j jx f x -≤≤-=-=='∑15. 证明n 阶均差有下列性质: i)若()()F x cf x =,则[][]0101,,,,,,n n F x x x cf x x x =;ii) 若()()()F x f x g x =+,则[][][]010101,,,,,,,,,n n n F x x x f x x x g x x x =+.16. 74()31f x x x x =+++,求0172,2,,2f ⎡⎤⎣⎦及0182,2,,2f ⎡⎤⎣⎦.17. 证明两点三次埃尔米特插值余项是(4)22311()()()()/4!,(,)k k k k R x f x x x x x x ++=ξ--ξ∈并由此求出分段三次埃尔米特插值的误差限.18. 求一个次数不高于4次的多项式()P x ,使它满足(0)(1)P P k =-+并由此求出分段三次埃尔米特插值的误差限.19. 试求出一个最高次数不高于4次的函数多项式()P x ,以便使它能够满足以下边界条件(0)(0)0P P ='=,(1)(1)1P P ='=,(2)1P =.20. 设[](),f x C a b ∈,把[],a b 分为n 等分,试构造一个台阶形的零次分段插值函数()n x ϕ并证明当n →∞时,()n x ϕ在[],a b 上一致收敛到()f x .21. 设2()1/(1)f x x =+,在55x -≤≤上取10n =,按等距节点求分段线性插值函数()h I x ,计算各节点间中点处的()h I x 与()f x 的值,并估计误差.22. 求2()f x x =在[],a b 上的分段线性插值函数()h I x ,并估计误差.23. 求4()f x x =在[],a b 上的分段埃尔米特插值,并估计误差.24. 给定数据表如下:试求三次样条插值并满足条件 i) (0.25) 1.0000,(0.53)0.6868;S S '='=ii)(0.25)(0.53)0.S S "="=25. 若[]2(),f x C a b ∈,()S x 是三次样条函数,证明 i)[][][][]222()()()()2()()()bbbbaaaaf x dx S x dx f x S x dx S x f x S x dx"-"="-"+""-"⎰⎰⎰⎰;ii) 若()()(0,1,,)i i f x S x i n ==,式中i x 为插值节点,且01n a x x x b =<<<=,则[][][]()()()()()()()()()baS x f x S x dx S b f b S b S a f a S a ""-"="'-'-"'-'⎰.26. 编出计算三次样条函数()S x 系数及其在插值节点中点的值的程序框图(()S x 可用(8.7)式的表达式).第三章 函数逼近与计算1. (a)利用区间变换推出区间为[],a b 的伯恩斯坦多项式.(b)对()sin f x x =在[]0,/2π上求1次和三次伯恩斯坦多项式并画出图形,并与相应的马克劳林级数部分和误差做比较. 2. 求证:(a)当()m f x M ≤≤时,(,)n m B f x M ≤≤. (b)当()f x x =时,(,)n B f x x =.3. 在次数不超过6的多项式中,求()sin 4f x x =在[]0,2π的最佳一致逼近多项式.4. 假设()f x 在[],a b 上连续,求()f x 的零次最佳一致逼近多项式.5. 选取常数a ,使301max x x ax≤≤-达到极小,又问这个解是否唯一?6. 求()sin f x x =在[]0,/2π上的最佳一次逼近多项式,并估计误差.7. 求()xf x e =在[]0,1上的最佳一次逼近多项式.8. 如何选取r ,使2()p x x r =+在[]1,1-上与零偏差最小?r 是否唯一? 9. 设43()31f x x x =+-,在[]0,1上求三次最佳逼近多项式. 10. 令[]()(21),0,1n n T x T x x =-∈,求***0123(),(),(),()T x T x T x T x .11. 试证{}*()nT x 是在[]0,1上带权ρ=的正交多项式.12. 在[]1,1-上利用插值极小化求11()f x tg x -=的三次近似最佳逼近多项式.13. 设()xf x e =在[]1,1-上的插值极小化近似最佳逼近多项式为()n L x ,若n f L ∞-有界,证明对任何1n ≥,存在常数n α、n β,使11()()()()(11).n n n n n T x f x L x T x x ++α≤-≤β-≤≤14. 设在[]1,1-上234511315165()128243843840x x x x x x ϕ=-----,试将()x ϕ降低到3次多项式并估计误差. 15. 在[]1,1-上利用幂级数项数求()sin f x x =的3次逼近多项式,使误差不超过0.005.16. ()f x 是[],a a -上的连续奇(偶)函数,证明不管n 是奇数或偶数,()f x 的最佳逼近多项式*()n nF x H ∈也是奇(偶)函数.17. 求a 、b 使[]220sin ax b x dx π+-⎰为最小.并与1题及6题的一次逼近多项式误差作比较.18. ()f x 、[]1(),g x C a b ∈,定义 ()(,)()();()(,)()()()();b baaa f g f x g x dxb f g f x g x dx f a g a =''=''+⎰⎰问它们是否构成内积?19. 用许瓦兹不等式(4.5)估计6101x dx x +⎰的上界,并用积分中值定理估计同一积分的上下界,并比较其结果.20. 选择a ,使下列积分取得最小值:1122211(),x ax dx x ax dx----⎰⎰.21. 设空间{}{}10010121,,,span x span x x 1ϕ=ϕ=,分别在1ϕ、2ϕ上求出一个元素,使得其为[]20,1x C ∈的最佳平方逼近,并比较其结果.22. ()f x x =在[]1,1-上,求在{}2411,,span x x ϕ=上的最佳平方逼近.23.sin (1)arccos ()n n x u x +=是第二类切比雪夫多项式,证明它有递推关系()()()112n n n u x xu x u x +-=-.24. 将1()sin 2f x x=在[]1,1-上按勒让德多项式及切比雪夫多项式展开,求三次最佳平方逼近多项式并画出误差图形,再计算均方误差.25. 把()arccos f x x =在[]1,1-上展成切比雪夫级数.26. 用最小二乘法求一个形如2y a bx =+的经验公式,使它与下列数据拟合,并求均方误差.27.28. 在某化学反应里,根据实验所得分解物的浓度与时间关系如下:用最小二乘拟合求.29. 编出用正交多项式做最小二乘拟合的程序框图. 30. 编出改进FFT 算法的程序框图. 31. 现给出一张记录{}{}4,3,2,1,0,1,2,3k x =,试用改进FFT 算法求出序列{}k x 的离散频谱{}k C (0,1,,7).k =第四章 数值积分与数值微分1. 确定下列求积公式中的待定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度: (1)101()()(0)()hhf x dx A f h A f A f h --≈-++⎰; (2)21012()()(0)()hh f x dx A f hA f A f h --≈-++⎰;(3)[]1121()(1)2()3()/3f x dxf f x f x -≈-++⎰;(4)[][]20()(0)()/1(0)()hf x dx h f f h ah f f h ≈++'-'⎰.2. 分别用梯形公式和辛普森公式计算下列积分:(1)120,84xdx n x =+⎰; (2)1210(1),10x e dx n x --=⎰;(3)1,4n =⎰; (4),6n =.3. 直接验证柯特斯公式(2.4)具有5次代数精度.4. 用辛普森公式求积分1x e dx-⎰并计算误差.5. 推导下列三种矩形求积公式:(1)2()()()()()2baf f x dx b a f a b a 'η=-+-⎰; (2)2()()()()()2baf f x dx b a f b b a 'η=---⎰;(3)3()()()()()224baa b f f x dx b a f b a +"η=-+-⎰.6. 证明梯形公式(2.9)和辛普森公式(2.11)当n →∞时收敛到积分()baf x dx⎰.7. 用复化梯形公式求积分()baf x dx⎰,问要将积分区间[],a b 分成多少等分,才能保证误差不超过ε(设不计舍入误差)?8. 1xedx-,要求误差不超过510-.9. 卫星轨道是一个椭圆,椭圆周长的计算公式是S a =θ,这里a 是椭圆的半长轴,c是地球中心与轨道中心(椭圆中心)的距离,记h 为近地点距离,H 为远地点距离,6371R =公里为地球半径,则(2)/2,()/2a R H h c H h =++=-.我国第一颗人造卫星近地点距离439h =公里,远地点距离2384H =公里,试求卫星轨道的周长.10. 证明等式3524sin3!5!n nn n ππππ=-+-试依据sin(/)(3,6,12)n n n π=的值,用外推算法求π的近似值.11. 用下列方法计算积分31dyy ⎰并比较结果.(1) 龙贝格方法;(2) 三点及五点高斯公式;(3) 将积分区间分为四等分,用复化两点高斯公式.12. 用三点公式和五点公式分别求21()(1)f x x =+在x =1.0,1.1和1.2处的导数值,并估计误差.()f x 的值由下表给出:第五章 常微分方程数值解法1. 就初值问题0)0(,=+='y b ax y 分别导出尤拉方法和改进的尤拉方法的近似解的表达式,并与准确解bx ax y +=221相比较。
近世代数(全)--4-1唯一分解环_2023年学习资料

4.相伴-,b∈K,若存在单位ε ∈K,使得-b=α 6,则称b与a相伴,也称b是a的相伴元-记作b~a.-5 平凡因子:-称单位和相伴元为平凡因子;-称除了平凡因子的因子(若有的话)为真因子.-例3-在Z中,-6有因 :1,-1,2,-2,3,-3,6,-6.-其中1与-1为单位,6和-6与6相伴,-2,-2,3,-3为6 真因子.-2018/11/9
例4-求Z[订中5的因子.-.a+bil5-..c+diZ[i],st.a+bic+di=5-→25=a2 b2c2+d2-→a2+b2=1,5,25-5的平凡因子:1,-1,i,-i,5,-5,5i,-5i-全部 因子为:+2士i,士1±2i-2018/11/9
6.不可约元-a∈K,a≠0,a不是单位,-若只有平凡因子,则称为不可约元;-若有真因子,称为可约元-例5 Z中全部不可约元:素数及相反数-性质:-1不可约元与单位乘积是不可约元:-2a∈K,a≠0,a有真因子-→ =bc,b,c都不是单位-2018/11/9
8.素元-p∈K,p≠0,p不是单位,若pIab,-必有pIa或者p1b,则称p为素元.-性质:素元一定是 可约元;-不可约元未必是素元-3引2+-5-2-5-32+V-5-3M2--5-例7在Z中全部素元:素数及 反数-2018/11/9
二、唯一分解环-问题:是否整环中非零、非单位的元素都能-唯一分解?-不一定-定义:如果K中任一非零非单位的 素都-能唯一分解,则称K是唯一分解环.-定理1唯一分解环的不可约元等同于素元-定理2若K有以下性质:1每一 非零、-非单位的元素α 都可以分解成不可约元的乘积;-2不可约元都是素元,则K是唯一分解环.-例8-Z为唯一 解环.-2018/11/9
山东大学材料科学基础试题库

材料科学基础》试题库 名词解释 1、铁素体、奥氏体、珠光体、马氏体、贝氏体、莱氏体 2、共晶转变、共析转变、包晶转变、包析转变3、晶面族、晶向族4 、有限固溶体、无限固溶体5 、晶胞9、相、组织 10 、不平衡共晶、伪共晶、离异共晶 12、淬透性、淬硬性13 、固溶体 置换固溶体 间隙固溶体14、均匀形核、非均匀形核 15 、成分过冷 16 、共析(共析) (包晶)反应17、临界晶核 18 、枝晶偏析 19 、钢的退火,正火,淬火,回火 20 、反应扩散 21、临界分切应力22 、调幅分解 23 、二次硬化 24 、上坡扩散 25、负温度梯度30、柏氏矢量 描述位错特征的一个重要矢量, 它集中反映了位错区域内畸变总量的大小和方向, 也是位错 扫过后晶体相对滑动的量。
31、柯氏气团 32、动态再结晶 33、交滑移 攀移 34、相 组织 35、线缺陷 36、热加工 冷加工 37、全位错 不全位错 38、位错反应 39、相律40、相图 描述各相平衡存在条件或共存关系的图解,也可称为平衡时热力学参量的几何轨迹。
41、点阵畸变 在局部范围,原子偏离其正常的点阵位置,造成点阵畸变。
42、过冷度相变过程中冷却到相变点以下某个温度后发生转变, 平衡相变温度与该实际转变温度之差称 过冷度。
43、形变织构 多晶形变过程中出现的晶体学取向择优的现象。
44、二次再结晶再结晶结束后正常长大被抑制而发生的少数晶粒异常长大的现象。
45、滑移系 晶体中一个滑移面及该面上的一个滑移方向的组合称一个滑移系。
46、孪生晶体受力后,以产生孪晶的方式进行的切变过程。
47、刃型位错和螺型位错模型将晶体上半部切开, 插入半个晶面, 再粘合起来; 这样, 在相当于刃端部为中心线的附近一 定范围,原子发生有规则的错动。
其特点是上半部受压, 下半部受拉。
这与实际晶体中的刃 型位错造成的情景相同, 称刃型6、二次渗碳体 7 回复、再结晶、二次再结晶 8 、晶体结构、空间点阵11 、临界变形度位错模型。
【国家自然科学基金】_矩阵环_基金支持热词逐年推荐_【万方软件创新助手】_20140731
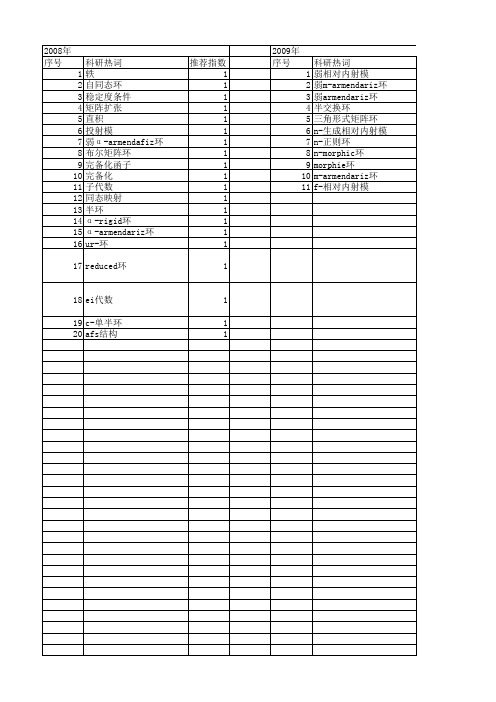
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 弱相对内射模 弱m-armendariz环 弱armendariz环 半交换环 三角形式矩阵环 n-生成相对内射模 n-正则环 n-morphic环 morphie环 m-armendariz环 f-相对内射模
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 轶 自同态环 稳定度条件 矩阵扩张 直积 投射模 弱α -armendafiz环 布尔矩阵环 完备化函子 完备化 子代数 同态映射 半环 α -rigid环 α -armendariz环 ur-环 reduced环 ei代数 c-单半环 afs结构
2014年 序号 1 2 3 4 5 6 7 8
2014年 科研热词 零因子 拟弱armendariz环 形式矩阵环 弱m-拟armendariz环 左app-环 半交换环 s-行列式 m-拟armendariz环 推荐指数 1 1 1 1 1 1 1 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10
科研热词 矩阵环 自由abel群 群环 求根问题 正交 有限矩阵群 整数分解 数字签名 代数等价 n次广义幂等矩阵
推荐指数 2 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 模范畴 唯一强clean环 唯一bleached局部环 recollement 推荐指数 2 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
一类矩阵环的斜Amenderiz性质

令 R是 环 , 口是 R 的 自同 态 , 口扩 张为 ( 上 的 自同态 : ( 一 ( , ( ) = ( 将 R) M R) R) ( 口 ): 口 : ( ). 口 )根据 文献 [] 若 尺 是 口斜 Ar n ei环 , R 的 每一个 子环 也是 Ar n ei环. 当 尺是 3, 一 medr z 则 medr z 但 r i 时对 任意 扎 , ( 不 一定 是 斜 Ar n ei 环 . i d环 g ≥2 R) me d r z 然 而 由I ] , R 是 ar i , s知 若 -i d环 则 g
g抖 1 2 , 蚪
…
…
gk 蚪 1 , 2
=
0 .
g蚪12 , 蚪1
go
…
●
。 .
O
●
:
go
因此 我们 有
fg o 。一 0 . () 1 () 2
() 3
对 任 意 p 口 1 2 … , ) , ∈{ , , 五 ,
f g , + , 1 o= 0 o, 蚪1 抖g ,
中 圈 分 类 号 : 5 . O1 3 3 文 献 标识 码 : A
16 9 5年 , pa s y在 对 AW *一 数 和 V nNe mam 正则 代数 的研究 中引人 了 B r 环 的概念. Ka ln k 代 O u r ae 在 对 B e 环 的研 究 中 , me d r E 注意 到 rd cd环 R满足 这 样 的性 质 : ar Ar n ei 妇 z eue 如果 对 于 R上 的 任 意两 个 多
GPS定位原理与应用习题集答案

第一篇《GPS定位原理与应用》习题集一、名词解释一、名词解释I、卫星星历:是描述卫星运行轨道的信息。
2、天线高:指天线的相位中心至观测点标志中心顶面的垂直距离。
3,春分点:当太阳在黄道上从天球南半球向北半球运行时,黄道与地球赤道的交点。
4、开普勒第一定律:卫星运行的轨道是一个椭圆,而该椭圆的一个焦点与地球的月心相重合。
这一定律表明,在中心引力场中,卫星绕地球运行的轨道面,是一个通过划球质心的静止平面。
5、同步环:由多台接收机同步观测的结果所构成的闭合环称为同步环。
6、多路朽效应:在GPS测量中,如果测站周围的反射物所反射的卫星信号(反射波)进入接收衫天线,这就将和直接来自卫星的信号(直接波)产生干涉,从而使观测值偏离真值产且所谓的多路径误差。
这种山于多路径的信号传播所引起的干涉时延效应称为多路径效应。
7、周跳:在接收机跟踪GPS卫星进行观测的过程中,常常山于多种原因(例如接收机天线被阻挡、外界噪声信号的千扰等),可能使载波相位观测值中的9周数不正确但其不足1整周的小数部分仍然是正确的,这种现象成为整周变跳,简称周跳。
8、绝对定位:利用GPS卫星和用户接收机间的距离观测值直接确定用户接收机天线在在WGS-84坐标系中相对地球质心的绝对位置。
9,恒星时:以春分点为参考点,由春分点的周日视运动所确定的时间,称为恒星时。
恒星时是地方时。
10、卫星的无摄运动:卫星在轨运动受到中心力和摄动力的影响。
假设地球为匀质球体,其对卫星的引力称为中心力(质量集中于球体的中心)。
中心力决定着卫星运动的4本规律和特征,此时卫星的运动称为无摄运动,山此所决定的卫星轨道可视为理想的轨道,又称卫星的无摄运动轨道。
11,精密星历:是一些国家的某些部门,根据各自建立的跟踪站所获得的精密观测资料,应用与确定预报星历相似的方法,而计算的卫星星历。
它可以向用户提供在用户观测时间的卫星星历,避免了预报星历外推的误差。
12、相对定位:用两台或多台接收机分别安置在基线的两端,并同步观测相同的GPS 卫星,以确定4线端点在协议地球坐标系中的相对位置或4线向量的定位方法。
近世代数习题解答张禾瑞三章

近世代数习题解答第三章环与域1 加群、环的定义1. 证明,本节内所给的加群的一个子集作成一个子群的条件是充分而且必要的.证 (ⅰ)若S是一个子群则S⇒∈,+a∈baSb'0是S的零元,即a+'0a=对G的零元,0+a=a0'=∴即.=-∈∴-s∈0Saa(ⅱ)若S⇒∈+,aba∈Sb今证S是子群由S,∈+⇒∈对加法是闭的,适合结合律,a,bbaSS由Saa∈=-0∈,而且得SaSa∈-⇒再证另一个充要条件:若S是子群,S∈-⇒,∈,⇒-aabSbbSa∈反之S=∈⇒-⇒∈0-=aSaaa-a∈S故S=⇒-(+,∈)-ba∈baSba2. }aR=,加法和乘法由以下两个表给定:b,,0{c,0 a b c+ 0 a bc0 0 0 0 00 0 a bca a 0 ca 0 0 0 0bb bc 0b 0 a b cac 0 a b cc c b a证明,R作成一个环证R对加法和乘法的闭的.对加法来说,由.9.2习题6,R和阶是4的非循环群同构,且为交换群.乘法适合结合律Z)((=xyx)yz事实上.当0=x 或a x =,)(A 的两端显然均为0. 当b x =或x=c,)(A 的两端显然均为yz . 这已讨论了所有的可能性,故乘法适合结合律.两个分配律都成立xz xy z y x +=+)(事实上,第一个分配律的成立和适合律的讨论完全一样, 只看0=x 或a x =以及b x =或c x =就可以了.至于第二个分配律的成立的验证,由于加法适合交换律,故可看0=y 或a y = (可省略a z z ==,0的情形)的情形,此时两端均为zx剩下的情形就只有∴R 作成一个环.2 交换律、单位元、零因子、整环1. 证明二项式定理在交换环中成立. 证 用数学归纳法证明. 当1=n 时,显然成立. 假定k n =时是成立的:看1+=k n 的情形)()(b a b a k ++(因为)()()(11kr k r k r -++=)即二项式定理在交换环中成立.2. 假定一个环R 对于加法来说作成一个循环群,证明R 是交换环.证 设a 是生成元 则R 的元可以写成na (n 整数)3. 证明,对于有单位元的环来说,加法适合交换律是环定义里其他条件的结果 (利用)11)((++b a ) 证 单位元是1,b a , 是环的任意二元, 4. 找一个我们还没有提到过的有零因子的环.证 令R 是阶为2的循环加群 规定乘法:R b a ∈,而0=ab 则R 显然为环.阶为2 ∴有R a ∈ 而 0≠a但 0=aa 即a 为零因子 或者R 为n n ⨯矩阵环.5. 证明由所有实数2b a + (b a ,整数)作成的集合对于普通加法和乘法来说是一个整环.证 令2{b a R +=b a ,(整数)}(ⅰ) R 是加群2)()()2()2(d b c a d c b a +++=+++ 适合结合律,交换律自不待言.零元 200+2b a +的负元2b a --(ⅱ)2)()2()2)(2(bc ad bd ac d c b a +++=++ 乘法适合结合律,交换律,并满足分配律.(ⅲ)单位元 201+(ⅲ) R 没有零因子,任二实数00=⇒=a ab 或0=b3 除、环、域1. =F {所有复数bi a + b a ,是有理数}证明 =F 对于普通加法和乘法来说是一个域. 证 和上节习题5同样方法可证得F 是一个整环. 并且 (ⅰ)F 有01≠+i(ⅱ) 0≠+bi a 即 b a , 中至少一个0≠022≠+∴b a 因而有,i b a b b a a 2222+-++ 使)((bi a +i b a bb a a 2222+-++1)= 故F 为域2. =F {所有实数,3b a + b a ,( 是有理数)} 证明 F 对于普通加法和乘法来说是一个域.证 只证明 03≠+b a 有逆元存在.则b a ,中至少有一个0≠ , 我们说0322≠-b a 不然的话,223b a =,0(≠b 若0=b 则 0=a 矛盾)223b a = 但 3 不是有理数既然0322≠-b a则 3b a + 的逆为3332222b a bb a a -+-4. 证明 例3的乘法适合结合律.证),)](,)(,[(332211βαβαβα又 )],)(,)[(,(332211βαβαβα-----------------+--=)()([3232132321αββαβββααα,5. 验证,四元数除环的任意元 )(),(di c bi a ++ ,这里d c b a ,,,是实数,可以写成),0)(0,()1,0)(0,()0,)(0,()0,(i d c i b a +++的形式. 证 ),(),(),(di bi c a di c bi a +=++4 无零因子环的特征1. 假定F 是一个有四个元的域,证明.(a )的特征是2;(b )F 的0≠ 或11的两个元都适合方程 证 (a ) 设F 的特征为P 则P 的(加)群F 的非零元的阶 所 4P (4是群F 的阶) 但要求P 是素数, .2=∴P (b ) 设},,1,0{b a F =由于2=P ,所以加法必然是,0=+x x ,而b a a a =+⇒≠+11 故有0 1 a b 0 0 1 a b 1 1 0 b a A a b 0 1 Bb a 1 0又 },,1{b a 构成乘群,所以乘法必然是 1,22≠≠a a a (否则b a = )b a =⇒2故有. 1 a b 1 1 a b a a b 1 b b a 1 这样, b a , 显然适合12+=x x2. 假定 ][a 是模 的一个剩余类.证明,若a 同 n 互素,那么所有][a 的书都同n 互素(这时我们说][a 同n 互素). 证 设][a x ∈ 且d n x =),( 则11,dn n dx x ==由于)(1111q n x d q dn dx nq x a nq a x -=-=-=⇒=-故有 ,a d ,且有 n d因为 1),(=n a 所以1=d3. 证明, 所有同 n 互素的模 n 的剩余类对于剩余类的乘法来说作成一个群(同 互素的剩余类的个数普通用符号)(n φ 来表示,并且把它叫做由拉φ函数)证]{[a G =而][a 同n 互素}G 显然非空,因为)1),1((]1[=∈n G(ⅰ)G b a ∈][],[则][]][[ab b a =又1),(,1),(==n b n a 有1),(=n ab(ⅱ)显然适合结合律.(ⅲ)因为n 有限,所以G 的阶有限. 若]][[]][['x a x a = 即][]['ax ax =由此可得)(''x x a ax ax n -=-',1),(x x n n a -∴= 即有][]['x x =另一个消去律同样可证成立.G 作成一个群4. 证明,若是1),(=n a , 那么)(1)(n an ≡φ(费马定理)证 ),(n a 则G a ∈][而 ][a 的阶是G 的阶 )(n φ的一个因子 因此]1[][)(=n a φ 即]1[][)(=n a φ5 子环、环的同态1. 证明,一个环的中心是一个交换子环.证 设N 是环的中心.显然N O ∈ N b a ∈,,x 是环的任意元 是子环,至于是交换环那是明显的. 2. 证明, 一个除环的中心是个域.证 设!是除环!是中心 由上题知N 是R 的交换子环,1R ∈显然N ∈1,即N 包含非零元,同时这个非零元1是的单位元.R x N a ∈∈,即xa ax =N ∴!是一个域3. 证明, 有理数域是所有复数b a bi a ,(+是有理数)作成的域)(i R 的唯一的真子域.证 有理数域R 是)(i R 的真子域.设F !是)(i R 的一个子域,则R F ⊇(因为R 是最小数域) 若,F bi a ∈+ 而0≠b则)(i F F F i =⇒∈这就是说,R 是)(i R 的唯一真子域. 4. 证明, )(i R 有且只有两自同构映射.证 有理数显然变为其自己. 假定α→i则由i i =⇒-=⇒-=αα1122或 i -=α 这就证明完毕. 当然还可以详细一些:21,φφ确是)(i R 的两个自同构映射.现在证明只有这两个. 若bi a i +=→αφ: (有理数变为其自己)则由12)(12222-=+-=+⇒-=abi b a bi a i若 102-=⇒=a b 是有理数,在就出现矛盾,所以有0=a 因而.1±=b在就是说, 只能i i → 或i i -→i5. 3J 表示模3的剩余类所作成的集合.找出加群3J 的所有自同构映射,这找出域3J !的所有自同构映射.证 1)对加群3J 的自同构映射 自同构映射必须保持!00←→ 故有i i →:1φ2)对域3J 的自同构映射.自同构映射必须保持00←→,11←→所有只有i i →:φ6. 令R 是四元数除环, R 是子集=S {一切)}0,(a 这里a 阿是实数,显然与实数域-S 同构.令-R 是把R 中S 换成-S 后所得集合;替R 规定代数运算.使-≅R R ,分别用k j i ,,表示R 的元),,0(),1,0(),0,(i i ,那么-R 的元可以写成d c b a dk cj bi a ,,,(+++是实数)的形式(参看.3.3 习题5). 验证.1222-===k j i ,.,,j ik ki i kj jk k ji ij =-==-==-=证 1)对a a →)0,(:φ来说显然-≅S S 2)=S {一切)}0,(a a 实数 =-S {一切()0,a a 实数 βα,{(=R 一切)}0,(a 复数对)(αβ是不属于S 的R 的元. =-R βα,{(一切}a规定由于S 与-S 的补足集合没有共同元,容易验证ψ是R 与-R 间的一一映射.规定-R 的两个唤的和等于它们的逆象的和的象. -R 的两个元的积等于它们的逆象的积的象.首先,这样规定法则确是-R 的两个代数运算.其次,对于这两个代数运算以及R 的两个代数运算来说在ψ之下-≅R R (3)由.3.3习题5知 这里 d c b a ,,, 实数这是因为令),0(),1,0(),0,(i k j i i ===(4)1)0,1()0,)(0,(2-=-==i i i 同样j ik ki i kj jk =-==-=,6 多项式环1. 证明, 假定R 是一个整环,那么R 上的一个多项式环][x R 也是一个整环.证 R !是交换环][x R ⇒交换环, R 有单位元11⇒是][x R 的单位元, R 没有零因子][x R ⇒没有零因子事实上,0,)(10≠++=a x a x a a x f n n 则m n m n x b a b a x g x f +++= 00)()( 因为R 没有零因子,所以0≠m n b a 因而0)()(≠x g x f 这样][x R 是整环2. 假定R 是模7的剩余类环,在][x R 里把乘积 计算出来解 原式=]2[]5[]4[]5[]5[]5[]3[]5[345345++++=-++-x x x x x x x x 3. 证明:(ⅰ) ],[],[1221ααααR R =(ⅱ) 若n x x x ,,,21 是R 上的无关未定元,那么每一个i x 都是R 上的未定元.证 (ⅰ)=],[21ααR {一切}211221i i i i a αα∑{],[12=ααR 一切}112212j j j j a αα∑由于=∑211221i i i i a αα112212j j j j a αα∑因而=],[21ααR ],[12ααR(ⅱ)设00=∑=nk k i k x a即∑=+-nk n i h i i k x x x x x a 00010101 因为n x x x ,,21是R 上的无关未定元,所以即i x 是R 上的未定元4. 证明:(ⅰ) 若是n x x x ,,21和n y y y ,,21上的两组无关未定元,那么 (ⅱ) R !上的一元多项式环][x R 能与它的一个真子环同构. 证 (ⅰ)),,(),,(:2121n n y y y f x x x f →φ根据本节定理3 ],,[~],,[2121n n y y y R x x x R容易验证),,(),,(212211n n x x x f x x x f ≠),,(),,(212211n n y y y f y y y f ≠⇒ 这样],,[],,[2121n n y y y R x x x R ≅(ⅱ)令{][=x R 一切}2210n n x a x a a +++显然][][2x R x R ⊂ 但][2x R x ∉不然的话 这与x 是R 上未定元矛盾. 所以][2x R 是][x R 上未定元显然 故有(ⅰ)}[][2x R x R ≅这就是说,][2x R 是][x R 的真子环,且此真子环与][x R 同构.7 理想1. 假定R 是偶数环,证明,所有整数r 4是ϑ的一个理想,等式!对不对? 证 R r r r r ∈∈2121,,4,4ϑ ϑ∴ 是R 的一个理想. 等式 )4(=ϑ不对这是因为R 没有单位元,具体的说)4(4∈但ϑ∉42. 假定R 是整数环,证明.1)7,3(=证 R 是整数环,显然)1(=R .1)7,3(=又 )7,3()7(13)2(1∈+-=3. 假定例3的R 是有理数域,证明,这时),2(x 是一个主理想. 证 因为2与x 互素,所以存在)(),(21x P x P 使),2()1(][x x R ==∴ 。
非交换环上的McCoy条件

摘要: 在左 ( 或右) Mc C o y环上的矩阵环和 上三角矩 阵环 中, 找到了一些左 ( 或右) Mc C o y子环
同时给 出了没有单位元的左( 或右) Mc Co y环. 说明了一个左 Mc C o y环不一定是右 Mc C o y环
一
个右 Mc C o y环不一定是左 Mc Co y环. 最后指 出 r e v e r s i b l e环满足一个 Mc Co y条件 .
第 6期 2 0 1 3年 l 1月
华 东师范 o f E a s t Ch i n a No r ma l Un i v e r s i t y( Na t u r a l S c i e n c e
N0.6
g i v e t ha t a r i g h t Mc Co y r i ng i s n o t l e t f Mc Co y a n d a l e t f Mc Co y r i n g i s n o t r i g h t Mc Co y . Co n s e q u e n t l y , r e v e r s i b l e r i n g s s a t i s f y a Mc Co y c o n d i t i o n. Ke y wo r ds : r i g h t Mc Co y r i ng ; l e f t Mc Co y r i n g ; Mc Co y r i n g ; ma t r i x r i n g ; u p pe r
Y i n i n g Xi n j i a n g 8 3 5 0 0 0 , C h i n a ;
2 . S c h o o l o f ma t h e ma t i c s a n d c o mp u t e r s c i e n c e j No r t h w e s t U n i v e r s i t y l 0 r Na t i o n a l i t i e s , L a n z h o u 7 3 0 1 2 4 C h i n a 1
一类特殊的B-M环的几个性质

一类特殊的B-M环的几个性质
陈昌南
【期刊名称】《怀化学院学报》
【年(卷),期】1987(0)6
【摘要】Szasz.F.在《RadiKale der,Ringe》一书后曾提出“讨论每一个子环都是Brown-Mc Coy根环的环”作为一个尚未解决的问题,本文试图对此问题进行探讨。
如果它不含单位元,可以证明它是一个Brown-McCoy根环。
并在此基础上,引申出几点推论。
下面将采用几个符号:“B-M环A”表示环A是Brown-McCoy根环,
也写做“A∈BM”。
“R_BM(A)”表示环A的Brown-McCoy根。
“I△A”表示
I是环A的理想。
“∑(?)I_a”表示若干个I_a的直和。
此外,还要采用一些别的常用符号。
【总页数】2页(P1-2)
【关键词】单位元;子环;根环;正则理想;半单环;B-M;既约环;表示环;遗传环;尚未解
决的问题
【作者】陈昌南
【作者单位】
【正文语种】中文
【中图分类】O1
【相关文献】
1.一类特殊的上三角矩阵环的Armendariz性质 [J], 方小利;陶颖
2.一类函数的几个特殊性质 [J], 胡小平
3.一类IBN环的商环的Grothendieck群的性质 [J], 朱晓胜
4.一类特殊分块矩阵为循环矩阵的循环分块矩阵的几个性质 [J], 毛纲源
5.一类特殊的归纳环及双向归纳环 [J], 马鑫;王世强;沈复兴
因版权原因,仅展示原文概要,查看原文内容请购买。
西工大-有限元试题(附答案)汇总
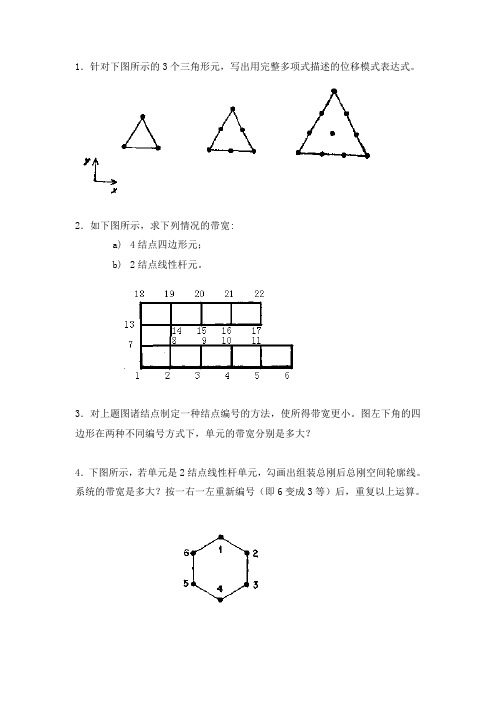
1.针对下图所示的3个三角形元,写出用完整多项式描述的位移模式表达式。
2.如下图所示,求下列情况的带宽:a)4结点四边形元;b)2结点线性杆元。
3.对上题图诸结点制定一种结点编号的方法,使所得带宽更小。
图左下角的四边形在两种不同编号方式下,单元的带宽分别是多大?4.下图所示,若单元是2结点线性杆单元,勾画出组装总刚后总刚空间轮廓线。
系统的带宽是多大?按一右一左重新编号(即6变成3等)后,重复以上运算。
5.设杆件1-2受轴向力作用,截面积为A,长度为L,弹性模量为E,试写出杆端力F1,F2与杆端位移21,uu之间的关系式,并求出杆件的单元刚度矩阵)(][ek6.设阶梯形杆件由两个等截面杆件○1与○2所组成,试写出三个结点1、2、3的结点轴向力F1,F2,F3与结点轴向位移321,,uuu之间的整体刚度矩阵[K]。
7.在上题的阶梯形杆件中,设结点3为固定端,结点1作用轴向载荷F1=P,求各结点的轴向位移和各杆的轴力。
8.下图所示为平面桁架中的任一单元,yx,为局部坐标系,x,y为总体坐标系,x轴与x轴的夹角为 。
(1)求在局部坐标系中的单元刚度矩阵)(][ek(2)求单元的坐标转换矩阵 [T];(3)求在总体坐标系中的单元刚度矩阵)(][ek9.如图所示一个直角三角形桁架,已知27/103cm N E ⨯=,两个直角边长度cm l 100=,各杆截面面积210cm A =,求整体刚度矩阵[K]。
10. 设上题中的桁架的支承情况和载荷情况如下图所示,按有限元素法求出各结点的位移与各杆的内力。
11. 进行结点编号时,如果把所有固定端处的结点编在最后,那么在引入边界条件时是否会更简便些?12. 针对下图所示的3结点三角形单元,同一网格的两种不同的编号方式,单元的带宽分别是多大?13. 下图所示一个矩形单元,边长分别为2a 与2b ,坐标原点取在单元中心。
位移模式取为xyy x v xy y x u 87654321αααααααα+++=+++=导出内部任一点位移v u ,与四个角点位移之间的关系式。
M-nil-McCoy环

M-nil-McCoy环费盼盼;吴俊;朱利民【摘要】本文引入了M-nil-McCoy环的概念,研究了M-nil-McCoy环的基本性质,给出了M-nil-McCoy环的一些刻画,讨论了M-nil-McCoy环环与其它环之间的关系.【期刊名称】《安徽师范大学学报(自然科学版)》【年(卷),期】2014(037)006【总页数】6页(P530-535)【关键词】McCoy环;Armendariz环;NI环;u.p.幺半群【作者】费盼盼;吴俊;朱利民【作者单位】安徽师范大学数学计算机科学学院,安徽芜湖241003;安徽师范大学数学计算机科学学院,安徽芜湖241003;安徽师范大学数学计算机科学学院,安徽芜湖241003【正文语种】中文【中图分类】O153.3本文中的环均指有单位元的结合环.设R为环,M是幺半群,R[x]表示R上的一元多项式环,R[M]表示R上关于M的一元多项式环,nil(R)表示R中所有幂零元之集,Un(R),Ln(R)分别表示环R上n阶上三角矩阵环和n阶下三角矩阵环.1942年,McCoy证明了[1]:若R是交换环,f(x)是R[x]的零因子,则存在0≠r∈R,使得f(x)r=0.称R是右(左)McCoy环[2],是指对任意f(x),g(x)∈R[x]\{0}时,若f(x)g(x)=0,则存在r∈R\{0},使得f(x)r=0(rg(x)=0).此后,McCoy环及其推广的研究受到众多代数工作者的关注[3-6].2010年,Hashemi引入了M-McCoy环的概念.环R称为右(左)M-McCoy环[3],是指对任意{0},如果αβ=0,则存在s∈R\{0},使得ais=0(sbj=0),任意1≤i≤m(1≤j≤n).同时文[3]还指出了,M-McCoy环是零因子可换环的推广.称R是右(左)nil-McCoy环[4],是指对任意f(x),g(x)∈R[x]\{0}时,如果f(x)g(x)∈nil(R),则存在r∈R\{0},使得f(x)r∈nil(R)(rg(x)∈nil(R)).如果R既是右nil-McCoy环,又是左nil-McCoy环,则称R是nil-McCoy环.环R是Armendariz环[7],如果对任意{0}满足f(x)g(x)=0,则对任意i,j有aibj=0.称R为M-Armendariz环[8],如果对任意满足αβ=0,则对任意i,j有aibj=0.环R称为M-nil-Armendariz环[9],如果对任意{0}满足αβ∈nil(R)[M],则对任意i,j有aibj∈nil(R).受此启发,本文引入了M-nil-McCoy环的概念,通过具体的例子说明了M-nil-McCoy环是M-McCoy环和M-nil-Armendariz环的真正推广,并对M-nil-McCoy环进行了一些研究.定义1.1 设M是幺半群,环R称为右M-nil-McCoy环,是指对任意{0},如果αβ∈nil(R)[M],则存在s∈R\{0},使得ai s∈nil(R),任意1≤i≤m.左M-nil-McCoy环的定义是类似的.易知M-nil-McCoy环是左右对称的.不难验证,若M={e},则任意环R均是M-nil-McCoy;若M是自然数加法幺半群(N,+),则R[M]≅R[x],因此,R是M-nil-McCoy环当且仅当R是nil-McCoy环.命题1.2 设R是环,M是幺半群,Un(R),Ln(R)(n≥2)均为M-nil-McCoy环.证对任意令则(R)).同样有B∈Un(R),使得BAi∈nil(Un(R)).故Un(R)是M-nil-McCoy环.同理Ln(R)是M-nil-McCoy环.推论1.3 设R,N,S是环,RNS是双模,则是M-nil-McCoy环.推论|a,b∈R}是M-nil-McCoy环.由定义可知,M-nil-Armendariz环是M-nil-McCoy环,下面的例子说明M-nil-McCoy环是M-nil-Armendariz环的真正推广.例1.5 设S=M2(Z),令易知f(x)g(x)=0∈nil(S)[x],但∉nil(S).故S不是nil-Armendariz环.由[10,proposition 2.8]知不是nil-Armendariz环,令M=(N,+),则Un(S)不是M-nil-Armendariz环,但由命题2.2知Un(S)是M-nil-McCoy环.命题1.6 设R是环,M是幺半群,若R是M-McCoy环,则R是M-nil-McCoy 环.证任意{0},假设αβ∈nil(R)[M],若αβ=0,则由M-McCoy环的定义知,存在r∈R\{0}使得air=0.故air∈nil(R),所以R是M-nil-McCoy环.若αβ≠0≠βα,则存在n,m∈N+,使得(αβ)n=(βα)m=0,其中(αβ)n-1≠0≠(βα)m-1,故有0=(αβ)n=α(βαβα…β)=αγ,0=(βα)m=β(αβαβ…α)=βω.当γ,ω有一个不为0时,不妨设γ≠0,由R是M-McCoy环知,存在r∈R\{0}使得air=0,从而air∈nil(R),且M-nil-McCoy环是左右对称的,故R是M-nil-McCoy环.当γ与ω有一个为0时,不妨取γ=β(αβ…αβ)=β(αβ)n-1=0.因为(αβ)n-1≠0,由R是M-McCoy环知,存在r∈R\{0}使得ais=0,故a is∈nil(R),且M-nil-McCoy环是左右对称的,因此R是M-nil-McCoy环.注1.7 M-nil-McCoy环不必是M-McCoy环.例如,取R=Z为整数环,则U4(R)不是左也不是右McCoy环.事实上,令则f(x)g(x)=0.若存在A=[aij]∈U4(R)\{0},使得f(x)A=0,即于是A=0,故U4(R)不是右McCoy环.同理可知U4(R)不是左McCoy环.取M=(N,+),则U4(R)[M]不是M-McCoy环,而由命题2.2知U4(R)[M]是M-nil-McCoy环.由[4,example2.2]知nil-McCoy环的子环不一定是nil-McCoy环.取M=(N,+),则M-nil-McCoy环的子环不一定是M-nil-McCoy环.设N是幺半群M的子幺半群,若R是M-nil-McCoy环,则显然R是N-nil-McCoy环.下面的例子说明N-nil-McCoy环未必是M-nil-McCoy环.例1.8 设F是域,S=M2(F)为F上的二阶方阵环,M是4阶循环群,则S不是M-nil-McCoy环.事实上,假设S是M-nil-McCoy环.取α=E11e+E12g+E21g2+E22g3,β=-E21e+E11g+E22g2-E12g3∈S[M],则αβ=0∈nil(S)[M].于是存在使得EijD∈nil(S),1≤i,j≤2.从而有(S).(S).(S).(S).故存在l,m,n,t∈N+,使得即由F是域知,aij=0,1≤i,j≤2.从而D=0.矛盾.所以S不是M-nil-McCoy环.设N是幺半群M的子幺半群,如果对任意n∈N,m∈M,有nm∈N(mn∈N),则称N是M的右(左)理想.若N既是M的右理想,又是M的左理想,则称N是M的理想[11].设M是幺半群,若对任意a,x,y∈M,ax=ay(xa=ya),有x=y,则称M是左(右)可消幺半群.若M既是左可消幺半群,又是右可消幺半群,则称M是可消幺半群. 命题1.9 设M是可消幺半群,N是M的理想,若R是N-nil-McCoy环,则R是M-nil-McCoy环.证任意{0},假设αβ∈nil(R)[M],由M是可消幺半群知,对任意k∈N,若i≠j,则kgi≠kgj且hik≠hjk.注意到N是M的理想,则[N],且(kα)(βk)∈nil(R)N,于是存在r,d∈R\{0}使得air,dbj∈nil(R).故R是M-nil-McCoy环.2 M-nil-McCoy环的性质称M是u.p.幺半群[3],若对任意非空有限子集A,B⊆M,存在g∈M,使得g有唯一的表示g=ab,a∈A,b∈B.环R称为NI环[5],若nil(R)是R的理想.定理2.1 设M是u.p.幺半群,若R是NI环,则R是M-nil-McCoy环.证任意{0},假设αβ∈nil(R)[M].因为R是NI环,所以nil(R)是R的理想,且有(R)是约化环.由[8,1,1]知,是M-Armendariz环.其中,=(ai+nil(R))gi∈(R/nil(R))[M],=(bj+nil(R))hj∈(R/nil(R))[M],易知是环同态,则有由于是M-Armendariz环,所以于是存在c,d∈R\{0},使得aic,dbj∈nil(R).故R是M-nil-McCoy环.由零因子可换环是NI环即知下面的结论是定理3.1的直接结果.推论2.2[3]’若M是u.p.幺半群,R是零因子可换环,则R是M-McCoy环.推论2.3 设M是u.p.幺半群,R是半交换环,则R是M-nil-McCoy环.证因为R是半交换环,由[5,Lemma 2.10]知nil(R)是R的理想,再由定理3.1即得.推论2.4 设M是u.p.幺半群,R是约化环(零因子可换环或对称环),则R是M-nil-McCoy环.定义2.5[3] (M,≤)是有序幺半群,若对任意g1,g2,h∈M,g1<g2,有g1h<g2h,hg1<hg2,则称(M,≤)是严格全序幺半群.易知严格全序幺半群是u.p.幺半群.推论2.6 设M是严格全序幺半群,R是NI环,则R是M-nil-McCoy环.引理2.7[5] 设R是半交换环,若C1C2…Ck=0,其中Ci∈R,则C1RC2RC3R…RCk=0.命题2.8 设R是半交换环,若a∈nil(R),b∈nil(R),则a+b∈nil(R).证由引理2.7易证.推论2.9 设M是严格全序幺半群,R是半交换环,则R是M-nil-McCoy环.且nil(R[M])=nil(R)[M].证结论的前半部分由推论2.6即得,下证nil(R[M])=nil(R)[M].任意其中g1<g2<…<gm.若α∈nil(R[M]),则存在k∈N+,使得(aigi)k=∑((a1g1)j11…(amgm)j1m)…((a1g1)jk1…(amgm)jkm)=0,其中jr1+jr2+…+jrm=1,r=1,…,k,jri=0或1.由于M是严格全序幺半群,则有((g1)j11…(gm)j1m)…((g1)jk1…(gm)jkm)<,其中j1m+…+jkm≠k.因此故即am∈nil(R).又存在β,γ∈R[M],使得由R是半交换环知,nil(R)是R的理想,于是α,amβ,γam∈nil(R)[M].由命题2.8知同理可得am-1∈nil(R),继续进行下去可有a1,…,am∈nil(R).所以nil(R[M])⊆nil(R)[M]. 反之,任意则存在ni∈N+,1≤i≤m,使得(ai)ni=0.取k=(n1+…+nm+1),有αk=(aigi)k=∑((a1g1)j11…(amgm)j1m)…((a1g1)jk1…(amgm)jkm)=0.易知αk的系数形如γ=((a1)j11…(am)j1m)…((a1)jk1…(am)jkm),于是存在at∈{a1,…,am},使得j1t+…+jkt≥nt.由于=0,R是半交换环,可得γ=0.所以αk=0.nil(R[M])⊇nil(R)[M].总之,nil(R[M])=nil(R)[M].下面给出M-nil-McCoy环的一些刻画.定理2.10 设I是环R的理想,且有I⊆nil(R),则R是M-nil-McCoy环当且仅当R/I是M-nil-McCoy环.证令⊆nil(R),易知有I.任意则αβ∈nil(R)[M]⟺[M].即存在s,t∈R\{0},使得ais,tbj∈nil(R)当且仅当存在使得).因此,R是M-nil-McCoy环当且仅当R/I是M-nil-McCoy环.x∈R称为正则元[5],若对∀r(≠0)∈R,rx≠0≠xr.定理2.11 设△为R中中心正则元构成的乘法封闭子集,则R是M-nil-McCoy环当且仅当△-1R是M-nil-McCoy环.证 (⇒)令S=△-1R,任意其中u,v∈△,αi=aiu-1,βj=bjv-1.假设γω∈nil(S)[M],则γω=αiβjgihj=aiu-1bjv-1gihj=aibj(vu)-1gihj.再令因为(vu)-1∈△,则[M],由R是M-nil-McCoy环知,存在t∈R\{0},使得ait∈nil(R).记s=tv-1,则αis=aiu-1tv-1=ait(vu)-1∈nil(S),所以S是M-nil-McCoy环.(⇐)任意假设γ1ω1∈nil(R)[M],令其中u,v∈△,则由于△-1R是M-nil-McCoy环,故存在cv-1∈△-1R\{0},使得u-1ai(cv-1)∈nil(△-1R)[M].所以aic∈nil(R).因此R是M-nil-McCoy环. [1] MCCOY N. Remarks on divisors of zero[J]. Amer Math Monhly,1942,49:286-295.[2] NIELSEN P. Semi-commutativity and the McCoy condition[J]. J Algebra, 2006,298:134-141.[3] HASHEMI E. McCoy rings relative to a monoid[J]. Comm Algebra, 2010,38(3):1075-1083.[4] ZHAO L, ZHU X, GU Q. Nilpotent elements and McCoy rings[J]. Studia Scientiarum Mathematicarum Hungarica, 2012,49(3):326-337.[5] HASHEMI E. On weak McCoy rings[J]. J Sci Tarbiat Moallem University, 2010,1:49-58.[6] YANG S, SONG X. Extensions of McCoy rings relative to a monoid[J]. J of Math Res and Exposition, 2008,28(3):659-665.[7] REGE M, CHHAWCHHARIA S. Armendariz rings[J]. Pro Japan Acad Ser A Math Sci, 1997,73:14-17.[8] LIU Z. Armendariz rings relative to a monoid[J]. Comm Algebra, 2005,33:649-661.[9] HABIBI M, MOUSSAVI A. Nilpotent elements and nil-armendariz property of monoid rings[J]. J of Algebra and Its Applications,2012,1250082:1-14.[10] RAMON A. Nilpotent elements and armendariz rings[J]. J Algebra, 2008,319:3128-3140.[11] XIE X, SONG X. Weak m-quasi-armendariz rings[J]. J of Anhui Normal University Natural Science, 2012,35(2):123-126.。
形式上三角矩阵环的导子和自同构

__________________* 湖南省教育厅资助科研项目(05C694),怀化学院青年基金项目(HHUQ2009-04).作者简介:谢乐平(1976—),男,湖南宁乡人,讲师,研究方向:矩阵代数.形式三角矩阵环的广义导子*谢乐平(怀化学院数学系,湖南,怀化418008)摘要:设B A ,是有单位元的环,M 为非零的),(B A -双模,研究形式三角矩阵环Tri ),,(B M A 的广义导子,利用代数方法得到了形式三角矩阵环Tri ),,(B M A 的广义导子可以由环B A ,的广义导子和),(B A -双模M 的广义拟线性映射表示,同时由此结论推得形式三角矩阵环Tri ),,(B M A 的导子的结构.关键词: 形式上三角矩阵环;广义导子;导子MR(2000)主题分类号:16W20;16W25;15A57 中图分类号:O151.21假定B A ,是两个有单位元的结合环,一个),(B A -双模M 是指M 是一个左A -模,也是一个右B -模,并且,A a ∈∀B b M m ∈∈,,有)()(mb a b am =.一个形式三角矩阵环定义为Tri ),,(B M A =⎭⎬⎫⎩⎨⎧∈∈∈⎪⎪⎭⎫ ⎝⎛B b M m A a b m a ,,0;, 其加法和乘法按通常矩阵的运算进行.人们对这类环进行了初步研究.例如[1]对形式三角矩阵环的各种性质做了系统的研究, [2]研究了形式三角矩阵代数的交换映射,即使0]),([=a a L 的线性映射L ,这里a 是形式三角矩阵代数的任一个元素.研究一个矩阵环或矩阵代数也是一件有意义的工作. 例如[3]证明了-C 代数A 上的上三角矩阵环的导子可以表示成一个内导子和一个A 上-C 导子诱导的导子之和. [4]证明了结合环上严格上三角矩阵代数的自同构可以表示成一个对角自同构,一个中心自同构和一个内自同构的乘积. [5-7]也研究了矩阵环和矩阵代数的导子和自同构. [8]研究了形式三角矩阵环的反自同构.本文的目的是确定形式三角矩阵环Tri ),,(B M A 的广义导子.假定B A ,是两个有单位元的结合环,M 为一个),(B A -双模。
图论第一章课后习题解答

d (v) =2m
推论 3 在任何图中,奇点个数为偶数。 推论 4 正则图的阶数和度数不同时为奇数。 定义 5 一个图 G 的各个点的度 d1, d2,…, dn 构成的非负整数组 (d1, d2,…, dn)称为 G 的 度序列。 若对一个非负整数组(d1, d2,…, dn), 则称这个数组是可图的。 定理 5 且 设有非负整数组 Π = (d1, d2,…, dn),
bi 个 (i = 1,2,…,s),则有 列。 定理 7
bi = n。故非整数组(b ,b ,…, b )是 n 的一个划分,称为 G 的频序
1 2 s
s
i 1
一个 n 阶图 G 和它的补图 G 有相同的频序列。
§1.2 子图与图的运算
且 H 中边的重数不超过 G 中对应边的 定义 1 如果 V H V G ,E H E G , 重数,则称 H 是 G 的子图,记为 H G 。有时又称 G 是 H 的母图。 当 H G ,但 H G 时,则记为 H G ,且称 H 为 G 的真子图。G 的生成子图是 指满足 V(H) = V(G)的子图 H。 假设 V 是 V 的一个非空子集。以 V 为顶点集,以两端点均在 V 中的边的全体为边集 所组成的子图,称为 G 的由 V 导出的子图,记为 G[ V ];简称为 G 的导出子图,导出子图 G[V\ V ]记为 G V ; 它是 G 中删除 V 中的顶点以及与这些顶点相关联的边所得到的子图。 若 V = {v}, 则把 G-{v}简记为 G–v。 假设 E 是 E 的非空子集。以 E 为边集,以 E 中边的端点全体为顶点集所组成的子图 称为 G 的由 E 导出的子图,记为 G E ;简称为 G 的边导出子图,边集为 E \ E 的 G 的 导出子图简记为 G E 。若 E e ,则用 G–e 来代替 G-{e}。 定理 8 简单图 G 中所有不同的生成子图(包括 G 和空图)的个数是 2m 个。 定义 2 设 G1,G2 是 G 的子图。若 G1 和 G2 无公共顶点,则称它们是不相交的;若 G1 和 G2 无公共边,则称它们是边不重的。G1 和 G2 的并图 G1∪G2 是指 G 的一个子图,其顶点 集为 V(G1)∪V(G2),其边集为 E(G1)∪E(G2);如果 G1 和 G2 是不相交的,有时就记其并图为 G1+G2。类似地可定义 G1 和 G2 的交图 G1∩G2,但此时 G1 和 G2 至少要有一个公共顶点。
与给定矩阵A的可交换子环C(A)的一些探讨

与给定矩阵A的可交换子环C(A)的一些探讨
林志兴;杨忠鹏
【期刊名称】《莆田学院学报》
【年(卷),期】2010(017)002
【摘要】收集整理现在常用的高等代数与线性代数材料中与给定矩阵A可交换的矩阵所构成的全矩阵空间pn×n的子空间C(A)的习题.指出C(A)的交换性及用A 的多项式表示问题同C(A)的维数与n有密切关系,得到n(n≥3)阶幂等矩阵A或对合矩阵A的C(A)都是不可交换的结论.
【总页数】4页(P23-26)
【作者】林志兴;杨忠鹏
【作者单位】莆田学院,数学与应用数学系,福建,莆田,351100;莆田学院,数学与应用数学系,福建,莆田,351100
【正文语种】中文
【中图分类】O151.21
【相关文献】
1.可交换矩阵空间上矩阵函数的一些性质 [J], 马翠云
2.论可交换矩阵的一些性质 [J], 布合力且木·阿不都热合木
3.可交换矩阵的一些性质 [J], 李美喜;刘军
4.上三角矩阵环中的一些斜McCoy子环 [J], 王文康
5.关于与给定矩阵可交换的矩阵的多项式表示 [J], 杨忠鹏;冯晓霞;张清新
因版权原因,仅展示原文概要,查看原文内容请购买。
1.3 环上的测度

1.3 环上的测度设X 是某个取定的集,也称为基本空间。
以X 的某些子集为元素所成的集称为X 上的集类,或简称为类。
集类用黑体英文字母表示,例如E,F,M 等。
设E 是X 上的某个集类,M 是E 的某个子集,集类{}M A MA =∈ E E .1.3.1 环、σ-环、代数、σ-代数定义1.3.1 设X 是基本空间,R 是X 上的集类,若对12,E E ∀∈R ,有1212,E E E E ∈-∈ R R , (1.3.1)则称R 是X 上的环. 若还有X ∈R ,则称R 是X 上的代数,或域。
注 由定义1.3.1可知:环是对集的“ ”和“-”运算封闭的非空集,而代数是对“余”运算也封闭的环。
※定义1.3.2 设X 是基本空间,S 是X 上的集类,若对任意一列集(1,2,)i E i ∈= S ,有121,ii EE E ∞=∈-∈ S S , (1.3.2)则称S 是X 上的σ-环,若还有X ∈S ,则称S 是X 上的σ-代数,或σ-域。
注 由定义1.3.2可知:σ-环是对集的“可列并”和“-”运算封闭的非空集; 而σ-代数是对“余”运算也封闭的σ-环。
例1.3.1 设X 是任意集,X 的有限子集(包括∅)全体所成的集类R 是X 上的一个环;当X ∈R 时,R 是X 上的一个代数。
例 1.3.2 设1R 是实数全体,0R 是由1R 中的有限个左开右闭的有限区间的并集1(,]nii i E ab ==全体所成的集类,则0R 是1R 上的一个环.注 由1R 中的有限个左闭右开的有限区间的并集1[,)niii E a b == 全体所成的集类也是1R上的一个环。
但由1R 中的有限个有限开区间(或闭区间)的并集全体所成的集类不是1R 上的环。
因为两个开区间的差集可以不再是开区间(对闭区间的情况也是如此).例1.3.3 设1R 是实数全体,1R 是由1R 中的有限个有限区间(无论是开区间、闭区间、还是半开半闭区间)的并集1,ni i i E a b ==全体所成的集类,则1R 是1R 上的一个环.例1.3.4 设X 是任意无限集,X 的有限子集(包括∅)及可列子集全体所成的集类S 是X 上的一个σ-环;当X ∈S 时,S 是X 上的一个σ-代数.例1.3.5 设X 是任意集,X 的所有子集全体所成的集类=2X S 是X 上的一个σ-代数.定理1.3.1(环的性质) 设X 是非空集,R 是X 上的环,则(1) ∅∈R ;(2) 若12,E E ∈R ,则12E E ∈ R ;(3) 若(1,2,,)i E i n ∈= R ,则1nii E=∈ R ;(4) X 上任意个环(或代数)的交集仍是X 上的环 (或代数).定理1.3.2(σ-环的性质) 设X 是非空集,S 是X 上的σ-环,则(1) ∅∈S ,且S 是X 上的环;(2) 若(1,2,)i E i ∈= S , 则1ii E∞=∈ S ;(3) 若(1,2,)i E i ∈= S , 则 lim ,lim n n n n E E →∞→∞∈∈S S ; (自习)(4) X 上任意个σ-环(或σ-代数)的交集仍是X 上的σ-环(或σ-代数).定理1.3.3 设E 是由集X 的某些子集所构成的集类,则必存在惟一的环(或代数)R ,使得(1) ⊂E R ;(2) 若 R 是包含E 的环(或代数),则⊂ R R.注1 定理1.3.3中的环(或代数)R 是包含E 的最小的环(或代数),称之为由集E 所张成的环(或代数)。
胡冠章应用近世代数第三版答案

/faculty/~ghu/html/catelog0.htm 第一章习题1.11.用2种颜色的珠子做成有5颗珠子项链,问可做出多少种不同的项链?解在学群论前我们没有一般的方法,只能用枚举法。
用笔在纸上画一下,用黑白两种珠子,分类进行计算:例如,全白只1种,四白一黑1种,三白二黑2种,…等等,可得总共8种。
2.对正四面体的顶点用2种颜色着色,有多少种本质上不同的着色方法?解类似第1题,用枚举法可得5种。
3.有4个顶点的图共有多少个?互不同构的有多少个?解由本节内容,有4个顶点的图共有64个图。
用分类计数的方法可得共有11个互不同构的图。
4.如何用圆规5等分一个圆?解用初等数学的方法求五边形的边长:作一个顶角为36°、腰长为1的等腰三角形,设底边长为a,则a就是十边形的边长,以a为半径以单位圆周上任意一点为圆心在圆周上交出两点,则这两点之间的距离就是五边形的边长。
那么a怎么求呢?只要在那个等腰三角形上作一条补助线�底角的角平分线,再利用相似三角形边长成比例的关系,可得,因而a就可作出了。
5.用根式表示3次和4次代数方程的根。
查看数学手册。
因公式较复杂,不在这里列出了。
习题1.2习题1.35. 举一个偏序集但不是全序集的例子,并画图。
解考虑到画图的方便,可举有限集的例子,例如:有限集的幂集对包含关系所构成的偏序集,有限整数集对整除关系所构成的偏序集。
详解略。
习题1.41. a=493, b=391, 求(a,b), [a,b] 和p, q。
解方法一、辗转相除法。
列以下算式:a=b+102b=3×102+85102=1×85+17由此得到 (a,b)=17, [a,b]=a×b/17=11339。
然后回代:17=102-85=102-(b-3×102)=4×102-b=4×(a-b)-b=4a-5b.所以 p=4, q=-5.方法二、大衍求一术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
()存 一 非 元S l y 满 ()=,么fx l 0 () = , () R 中 在 个 零 =I 2 J 足FxS 0 0, l 那 () = , x 2 0 x f 且f
= 0, s ≠ 0 所以 y 、2 而 , ly 和 中至少 有一 个不为 零 , R是右 斜 Mc o 故 C y环 .
0
( )
卢( 3 )
.
g ( q( 2 ) 2x) g( 1 )
如果 厂 ( =0 那么有 F( E 4=0 如果 _ ( =0 那么有 F( ) 4 lz) , x) 1 ; 厂 z) , 2 z E3
:0 下 丽设 ^( ≠ 0 . ) 且 ( ≠ 0 ) . 如果 g ( ≠ 0 那 么有 f ( g ( 1 z) , l ) 1z)= 0 因为 R是 右斜 一 C y环,所 以在 R中存在 一 个非零 , Mc o 元 r, 1满足 f ( r 1 ) l=0 从 而 F( FE = 0 如果 g ( ≠ 0 那 么有 , ( g ( , z) 1 ; 2 ) , 2 ) 2z):0 因为 R是右 ,
第 3 总第 8 2卷 2期
2 011 年 6 月
西 北 民 族 大 学 学 报( 自然科 学 版 )
Vo . 2 No 2 13 , .
Junl f otwsU i r t f aoatsNaua S i c ) ora o N r e n e i r tnli ( trl c n e h t v sy o N i i e e
口2
( R)=
口2 C2
∈
日1
右斜 一
环・
{
证 “” () ; 中 () 明 设 R[ 的F =∑二A 0 () B 0 足F ) () ] 。 ≠ , z =∑ 。 ≠ , G j 满 ( G
=
0 其 中 ,
口i Cl i a2 0 0
0 且 ( = 0 因为 F( ≠ 0那么 p( ) 0 所以 户 z) 1z ) . x) , x ≠ , ( g ( )=0 又因为 R是左斜 一 C y环, 以在 , Mco 所 R中存在一个非零元 r , 3满足 rg ( 3 1z)= 0从而 rE1 x , 3 3 )=0 O( . 从 以上可得 U3R) ( 是左斜 一Mc o 环 . Cy
“ ” [; e f ) 设Rz ]  ̄ ( =∑三a v ,( = 0 e,足 ) : , ( = p x o s g ) ∑ 6 o z () 0 z i o j v 满 g 令F )
, )3G( ( f, x): g x I, ( )3那么 F( ) x x V( )= 0因为 U ( 是左斜 一 Cy 所以在 u3R) , 3R) Mco 环, ( 中存 在一
c 0
fl 0 口i
1
fl 0 b j
1
bJ J
、 ,● ●●●●●● ,
=,中 l 口 B 【 b 令 ( = 三a = 6 0 A= 其 【 z Jj l 2 1 z ∑ 0X )∑ 。 0,= I j . ) 0 u, l ( ,
1 一
≤ 2 那 么有 ,
f1z f( )
0
PX 1 ( )
f (7J l3) 1
f lX g( )
【
0
q ) ( ]
Fz ()= I
【
() z
0 l z :I , ) G(
g( 2 )
0 1 .
g( J l )
如果 f ( 1X)= 0那 么有 F( El 0如 果 , ( , x) 3= ; 2 )=0 那 么有 F( E2 = 0 下 面设 f ( ≠ 0 , ) 2 . lX)
( 表 示环 R上的 Y × 阶矩 阵环, n R)表示 环 R上 的 × 阶上三 角矩 阵 环, 表示 矩 阵 R) t r(
环
( R)中的 单位矩 阵 .E 1 i { ≤ , ≤ 咒} M R)中的 矩 阵单 位 . R是 一个 环 , 环 R的一 是 ( 设 是
= ( C )那 么 是 M R)的一 个 同态 . (t , ) (
,v ) g( =∑ 。 ,() x 6 户 =∑ 0 ,( =∑ 。 , c q i ) 其中1 “ ≤ ,
[ 收稿 日期 】 0 1 5 0 2 1 —0 —2 [ 作者简介 ]王文康 (9 4 )女 ( 1 6 一 , 藏族 ) 甘肃天祝人, , 教授 , 主要从 事代数 学研究 .
且 ( )≠ 0 .
如果 g ( ) 0 那么有 f ( ) 1X =0 因为 .是右斜 一 C y lz ≠ , lx g ( ) , R Mc o 环, 所以在 R中存在一个非零 元 r, 1满足 l ) 1 0 从而 F( rE1 0 如 果 g ≠ 0 那 么有 , ( g ( r= , X) 1 3= ; 2x) , 2z) 2x)=0 因为 R是右 ,
从 以上 可得 【3 R) 厂( 是右 斜 一 C y环 . Mc o
“ ” [; 中 () e 设Rx ] 的, =∑三a O ≠0 () i , =∑二 ≠0 足, )() 0 - g 。 , ( g = , 满 4
F( z): f x)3 G( ( , X): g( 3那 么 F( G( X) , x) )= 0 因为 u3R)是右 斜 一Mc o ,所以在 , ( C y环
定理 12 一 个环 R是左 斜 一 C y环 当且 仅当 环 U3 R)= . Mc o (
r,,●
L
f 0 z 1
‘, ●【
c∈ R 左
斜 一 c o M C y环 .
0
证 “” 3 ) ; 中 ( =∑三A 0 () 明 设U R[ 的F ) ( z] o ≠ , z =∑ 马 G 0 ≠0 足FzG , ( ( 满 ) )
^( ) P ( z 1 ) 0 0 口( 4 ) a( 3 )
,
1≤ , l愚 ≤ 2 3≤ e h ≤ 4 ,, , , 。那 么 有 F ( ) =
,( 2 )
() P() z 2z () z
G( )= g( lx) Fra bibliotek ( ) lx
g( zz)
0
口 2i
S4 S3
,
bl d l j j b2 j
B =
0
0
tf 4
tj 3
,
A =
C21
b2 d2 j j
b 1 j
令 ( )= ∑ i )= z m口 , ( g
口 1
∑ 6 , () 。 a =∑三S z ) 。a, ( =∑i C () , () x 户 l = , z =∑ 。 z =∑ , 中 o 。 其
p ) ( =∑三C q ) o ,( =∑ , 中1 , , 么 i 0 其 ≤“ ≤2 有 那
f1X) ,( 0 P ) ( ]
f( J lz)
fi g( )
【
0
口z 1 ( )
Fz = l ()
I
,( 2 )
0 I () 1 , X = G
斜 — C y 所 以在 R中存在一个非零 元 r, Mco 环, 2满足 ,( r =0从而 F( rE =0 下面设 g =0 2 )2 , x)2 . lx) 且 g( 2 )=0 因为 G( ) 0那么 qx) 0所以 ,( q )=0又因为 R是右斜 一 Cy , 以在 . z ≠ , ( ≠ , 1 ) ( , Mco 环 所 R中存 在 一个非 零 元 r, 3满足 1x) 3= 0 从而 F( rE1 0 r , X) 3 3= .
0 如 果在 R中存在 一个 非 零元 S 使 得 ,( S=0 那 么称 环 R是 右斜 盯一 C y环 ; , , z) , Mc o 如果 在 R中存 在一
个非零 元 r 使得 r X)= 0 那 么 称环 R是左 斜 — C y环 ; , g( , Mco 如果 一个 环既是右 斜 一 C y环 又是 Mc o 左斜 — C y环 , 么称 环 R是斜 一 C y环 . Mc o 那 Mc o
一
2
一
个非零元 s :
所以 1 2 、 和 中至少有一个不为零, R是左斜 — Cy . 故 Mco 环
口1 C1
f i s: ,g。c,。 ] 。 g。 :≠ ,G , c,=g。 , 满c那 z , 而 足 么 =c且 s z
0 S4 0 S3
J n,0 1 u e2 1
上三 角矩 阵环 中的一些斜 Mc o C y子环
王 文 康
( 西北 民族 大 学 数 学与计 算机 科 学学院 , 甘肃 兰 州 7 0 2 ) 3 1 4
【 摘
要] 设 是 环 R的 一 个 同 态, 由 扩 张 的 M R) 一 个 同 态 . 本 文 中, 到 了上 三 角 矩 阵 环 中的 一 个 三 是 ( 的 在 找
个 同态 , 义 ( n 定 ( 1 主要 结果
主,} R 1 a l c E
证明 ” () ; 中 () “ 设 R[ 的F =EmAX≠0G =∑ 』 ≠0 足F )() ] = i ,() 0 0 , j I 满 ( G
马 =
r
一
令 ( z)= / ̄= io a
g() 2X
0 I .
g( J 1z)
如果 g( 1 )=0 ,那么有 E1G( 3 )= 0 如果 g ( )= 0 那 么有 E2G( ; 2z , 2 )= 0 下 面设 g ( ≠ 0 . lX) 且
g ( ≠ 0 2 X) .
如 果 f ( ≠ 0 那 么有 , ( g =0 因为 R是左 斜 一 C y环 , 以在 R中存 在一 个 非零 元 l x) , z) lx) , Mc o 所
