小学五年级奥数中等难度练习题二

合集下载

五年级奥数练习(中难度)

练习周练习（五年级）（中难度）姓名：成绩：答：第一题：牛吃草有三块草地，面积分别为5公顷、15公顷和24公顷．草地上的草一样厚，而且长得一样快．第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天．问：第三块草地可供多少头牛吃80天？第二题：阴影面积如图，在一个边长为6的正方形中，放入一个边长为2的正方形，保持与原正方形的边平行，现在分别连接大正方形的一个顶点与小正方形的两个顶点，形成了图中的阴影图形，那么阴影部分的面积为．答：答：答：第五题：排队画展9点开门，但早有人来排队入场，从第一个观众来到时起，若每分钟来的观众一样多，如果开3个入场口，9点9分就不再有人排队；如果开5个入场口，9点5分就没有人排队．求第一个观众到达的时间．答：练习周练习（五年级）答案第一题答案：解答：(法1)设1头牛1天吃草量为“1”，第一块草地可供10头牛吃30天，说明1公顷草地30天提供1030560⨯÷=份草；第二块草地可供28头牛吃45天，说明1公顷草地45天提供28451584⨯÷=份草；所以1公顷草地每天新生长的草量为()()84604530 1.6-÷-=份，1公顷原有草量为60 1.63012-⨯=．24公顷草地每天新生长的草量为1.62438.4⨯=；24公顷草地原有草量为1224288⨯=．那么24公顷草地80天可提供草量为：28838.4803360+⨯=，所以共需要牛的头数是：33608042÷=(头)牛．(法2)现在是3块面积不同的草地，要解决这个问题，也可以将3块草地的面积统一起来．由于[]5,15,24120=，那么题中条件可转化为：120公顷草地可供240头牛吃30天，也可供224头牛吃45天．设1头牛1天的吃草量为“1”，那么120公顷草地每天新生长的草量为()() 22445240304530192⨯-⨯÷-=，120 公顷草地原有草量为()240192301440-⨯=．120公顷草地可供144080192210÷+=(头)牛吃80天，那么24公顷草地可供210542÷=(头)牛吃80天．第二题答案：解答：本题中小正方形的位置不确定，所以可以通过取特殊值的方法来快速求解，也可以采用梯形蝴蝶定理来解决一般情况．解法一：取特殊值，使得两个正方形。

小学数学五年级奥数测试题及答案(K12教育文档)

(完整word)小学数学五年级奥数测试题及答案(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整word)小学数学五年级奥数测试题及答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整word)小学数学五年级奥数测试题及答案(word版可编辑修改)的全部内容。

五年级奥数一、填空（每题2分）1、某数分别与两个相邻整数相乘，所得的积相差150，这个数是（）2、每张方桌上放有12个盘子，每张圆桌上放有13个盘子。

若共有109个盘子，则圆桌有（）张，方桌有（ )张。

3、在1至1000这1000个整数中，既能被3整除有是7的倍数的整数有（）个。

4、三个连续自然数的积是120，这三个数分别是（ )、( ）、( ).5、40人参加测验，答对第一题的有30人,答对第二题的有21人,两题都答对的有15人。

两题都答错的有（）人。

6、今年八月一日是星期五，八月二十日是星期（）.7、有一排算式：1+1,2+3，3+5，4+7，1+9，2+11，3+13，4+15，1+17,2+19，3+21,…，那么（）+（）= 19948、节日之夜，广场上挂起了一排彩灯，共1999盏，排列的规律是：从头起每八盏为一组，每组的八盏灯依次为三盏红灯，二盏黄灯，三盏绿灯,那么最后一盏灯的颜色是（）。

9、在一根长100厘米的木棍上，自左至右每隔6厘米染一个红点，再自右至左每隔5厘米染一个红点,然后沿红点将木棍逐段锯开，那么长度是1厘米的木棍有（ )条。

10、A、B、C、D四个数，每次去掉一个数，将其余3个数求平均数，这样算了4次，得到以下4个数：45、60、65、70，问原来四个数的平均数是（）.11、妈妈买3千克苹果2千克梨,共付款12元；李奶奶买同样价格的苹果3千克,梨5千克，共付款21元。

小学五年级奥数题及答案-甲乙丙三人的年龄

小学五年级奥数题及答案-甲乙丙三人的年龄
编者小语：“题海无边，题型有限”。

学习数学必须要有扎实的基本功，有了扎实的基本功再进行“奥数”的学习就显得水到渠成了。

为大家准备了小学五年级奥数题，希望小编整理奥数题阴影面积问题(中等难度)，可以帮助到你们，助您快速通往高分之路!!
有甲乙丙三个人，当甲的年龄是乙的2倍时;丙是22岁，当乙的年龄是丙的2倍，甲是31岁;当甲60岁时，丙是多少岁?
解答：设丙22岁时，乙的年龄是x岁，当时甲的年龄就是2x岁.那么甲是3l岁时，乙是(31-x)岁，丙是22+ (31-2x)=53-2x岁，且有：31-x=2×(53-2x)，解得x=25，所以乙25岁时，甲50岁，丙22岁.那么甲60岁时，丙32岁.利用方程解年龄问题.设定乙的年龄之后，我们可以把各个时期甲、乙、丙的年龄都用含有x的式子表达出来，继而很方便地建立等量关系.。

小学奥数竞赛专题：五年级奥数中等难度练习题二

五年级奥数中等难度练习题二
பைடு நூலகம்
三角形面积：：（中等难度）
右图是由大、小两个正方形组成的，小正方形的边长是
4 厘米，求三角形 ABC的面积． [来源:学科网］
三角形面积答案：：
这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接
AD（见
右上图），可以看出，三角形 ABD与三角形 ACD的底都等于小正方形的边长，高都等于大正方形的边长，
年龄：：（中等难度）现在哥哥的年龄恰好是弟弟年龄的 2 倍。而 9 年前哥哥的年龄是弟弟年龄的 5 倍，则哥哥现在的年龄
是__________岁。
年龄答案：： [ 来源 :学学科科网网 ZXXK] 把弟弟 9 年前的年龄看作是 1 份，那么哥哥 9 年前的年龄是 5 份，年龄之差为 4 份。现在弟弟的年龄为 "1 份加上 9 岁" ，哥哥的年龄是弟弟年龄的 2 倍，所以年龄之差为 " 份加上 9 岁" ，所以 1 份的年龄为 9÷（ 4-1 ）＝３岁，哥哥现在的年龄为 3×5+9=24 岁。
7.3 米，分别所用的时间是 6,7,8 分
钟，所以三只蚂蚁的速度之比为： 28:24:21 ，注意题目中有一个条件，就是第一次出发的时候，他们是同
所以二等奖有 13 名。
【小结】根据题意列出方程组，解不定方程需要尝试未知数的值。
圆形跑道问题：：（中等难度）
有甲、乙、丙三人，甲每分钟行走 120 米，乙每分钟行走 100 米，丙每分钟行走 70 米。如果三人同
时同向从同地出发，沿周长是 300 米的圆形跑道行走，那么分钟之后，三个人又可以相聚。
数论问题：：（中等难度）

五年级奥数天天练(中难度)-最新推荐

学而思奥数网天天练周练习（五年级）（中难度）姓名：成绩：答：答：第一题：牛吃草有三块草地，面积分别为5公顷、15公顷和24公顷．草地上的草一样厚，而且长得一样快．第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天．问：第三块草地可供多少头牛吃80天？第二题：阴影面积如图，在一个边长为6的正方形中，放入一个边长为2的正方形，保持与原正方形的边平行，现在分别连接大正方形的一个顶点与小正方形的两个顶点，形成了图中的阴影图形，那么阴影部分的面积为．答：答：答：第三题：分数一个分数约分后是23．如果这个分数的分子减去18，分母减去22，约分后就可以得到一个新的分数35．那么，原来的分数在约分前是第四题：自然数从1，2，3，4，…，1994这些自然数中，最多可以取个数，能使这些数中任意两个数的差都不等于9．第五题：排队画展9点开门，但早有人来排队入场，从第一个观众来到时起，若每分钟来的观众一样多，如果开3个入场口，9点9分就不再有人排队；如果开5个入场口，9点5分就没有人排队．求第一个观众到达的时间．学而思奥数网天天练周练习（五年级）答案第一题答案：解答：(法1)设1头牛1天吃草量为“1”，第一块草地可供10头牛吃30天，说明1公顷草地30天提供1030560⨯÷=份草；第二块草地可供28头牛吃45天，说明1公顷草地45天提供28451584⨯÷=份草；所以1公顷草地每天新生长的草量为()()84604530 1.6-÷-=份，1公顷原有草量为60 1.63012-⨯=．24公顷草地每天新生长的草量为1.62438.4⨯=；24公顷草地原有草量为1224288⨯=．那么24公顷草地80天可提供草量为：28838.4803360+⨯=，所以共需要牛的头数是：33608042÷=(头)牛．(法2)现在是3块面积不同的草地，要解决这个问题，也可以将3块草地的面积统一起来．由于[]5,15,24120=，那么题中条件可转化为：120公顷草地可供240头牛吃30天，也可供224头牛吃45天．设1头牛1天的吃草量为“1”，那么120公顷草地每天新生长的草量为()() 22445240304530192⨯-⨯÷-=，120 公顷草地原有草量为()240192301440-⨯=．120公顷草地可供144080192210÷+=(头)牛吃80天，那么24公顷草地可供210542÷=(头)牛吃80天．第二题答案：解答：本题中小正方形的位置不确定，所以可以通过取特殊值的方法来快速求解，也可以采用梯形蝴蝶定理来解决一般情况．解法一：取特殊值，使得两个正方形的中心相重合，如右图所示，图中四个空白三角形的高均为1.5，因此空白处的总面积为6 1.5242222⨯÷⨯+⨯=，阴影部分的面积为662214⨯-=．解法二：连接两个正方形的对应顶点，可以得到四个梯形，这四个梯形的上底都为2，下底都为6，上底、下底之比为2:61:3=，根据梯形蝴蝶定理，这四个梯形每个梯形中的四个小三角形的面积之比为221:13:13:31:3:3:9⨯⨯=，所以每个梯形中的空白三角形占该梯形面积的916，阴影部分的面积占该梯形面积的716，所以阴影部分的总面积是四个梯形面积之和的716，那么阴影部分的面积为227(62)1416⨯-=．第三题答案：解答：设原来分数的分母为3x，依题意，原来分数的分子为2x；同样可知21833225xx-=-，交叉相乘得1090966x x-=-，解得24x=．于是，原来分数的分子、分母分别为222448x=⨯=．332472x=⨯=所以，原来的分数在约分前是4872．第四题答案：解答：方法一：把1994个数一次每18个分成一组，最后14个数也成一组，共分成111组．即1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18；19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36；…………………1963，1964，…，1979，1980；1981，1982， (1994)每一组中取前9个数，共取出9111999⨯=（个）数，这些数中任两个的差都不等于9．因此，最多可以取999个数．方法二：构造公差为9的9个数列（除以9的余数）{}1,10,19,28,,1990L，共计222个数{}2,11,20,29,,1991L，共计222个数{}3,12,21,30,,1992L，共计222个数{}4,13,22,31,,1993L，共计222个数{}5,14,23,32,,1994L，共计222个数{}6,15,24,33,,1986L，共计221个数{}7,16,25,34,,1987L，共计221个数{}8,17,26,35,,1988L，共计221个数{}9,18,27,36,,1989L，共计221个数每个数列相邻两项的差是9，因此，要使取出的数中，每两个的差不等于9，每个数列中不能取相邻的项．因此，前五个数列只能取出一半，后四个数列最多能取出一半多一个数，所以最多取1119999⨯=个数．第五题答案：解答：如果把入场口看作为“牛”，开门前原有的观众为“原有草量”，每分钟来的观众为“草的增长速度”，那么本题就是一个“牛吃草”问题．设每一个入场口每分钟通过“1”份人，那么4分钟来的人为39552⨯-⨯=，即1分钟来的人为240.5÷=，原有的人为：()30.5922.5-⨯=．这些人来到画展，所用时间为22.50.545÷=(分)．所以第一个观众到达的时间为8点15分．点评：从表面上看这个问题与“牛吃草”问题相离很远，但仔细体会，题目中每分钟来的观众一样多，类似于“草的生长速度”，入场口的数量类似于“牛”的数量，问题就变成“牛吃草”问题了．解决一个问题的方法往往能解决一类问题，关键在于是否掌握了问题的实质．。

五年级奥数天天练(中难度)-精选本

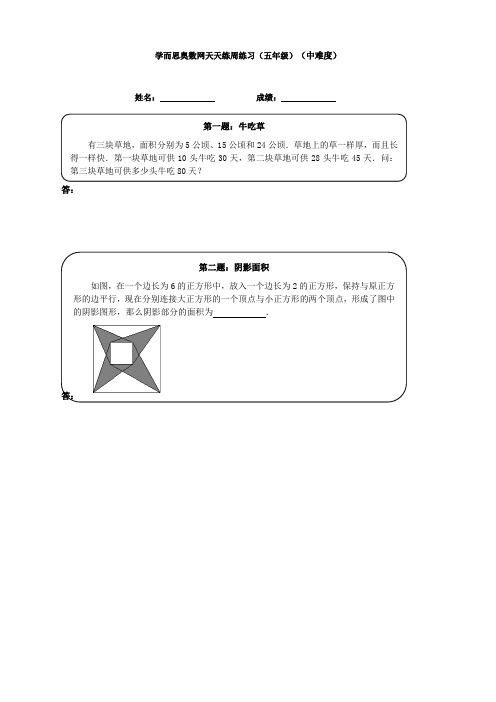
学而思奥数网天天练周练习（五年级）（中难度）姓名：成绩：答：答：第一题：牛吃草有三块草地，面积分别为5公顷、15公顷和24公顷．草地上的草一样厚，而且长得一样快．第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天．问：第三块草地可供多少头牛吃80天？第二题：阴影面积如图，在一个边长为6的正方形中，放入一个边长为2的正方形，保持与原正方形的边平行，现在分别连接大正方形的一个顶点与小正方形的两个顶点，形成了图中的阴影图形，那么阴影部分的面积为．答：答：答：第三题：分数一个分数约分后是23．如果这个分数的分子减去18，分母减去22，约分后就可以得到一个新的分数35．那么，原来的分数在约分前是第四题：自然数从1，2，3，4，…，1994这些自然数中，最多可以取个数，能使这些数中任意两个数的差都不等于9．第五题：排队画展9点开门，但早有人来排队入场，从第一个观众来到时起，若每分钟来的观众一样多，如果开3个入场口，9点9分就不再有人排队；如果开5个入场口，9点5分就没有人排队．求第一个观众到达的时间．学而思奥数网天天练周练习（五年级）答案第一题答案：解答：(法1)设1头牛1天吃草量为“1”，第一块草地可供10头牛吃30天，说明1公顷草地30天提供1030560⨯÷=份草；第二块草地可供28头牛吃45天，说明1公顷草地45天提供28451584⨯÷=份草；所以1公顷草地每天新生长的草量为()()84604530 1.6-÷-=份，1公顷原有草量为60 1.63012-⨯=．24公顷草地每天新生长的草量为1.62438.4⨯=；24公顷草地原有草量为1224288⨯=．那么24公顷草地80天可提供草量为：28838.4803360+⨯=，所以共需要牛的头数是：33608042÷=(头)牛．(法2)现在是3块面积不同的草地，要解决这个问题，也可以将3块草地的面积统一起来．由于[]5,15,24120=，那么题中条件可转化为：120公顷草地可供240头牛吃30天，也可供224头牛吃45天．设1头牛1天的吃草量为“1”，那么120公顷草地每天新生长的草量为()() 22445240304530192⨯-⨯÷-=，120公顷草地原有草量为()240192301440-⨯=．120公顷草地可供14408019221÷+=(头)牛吃80天，那么24公顷草地可供210542÷=(头)牛吃80天．第二题答案：解答：本题中小正方形的位置不确定，所以可以通过取特殊值的方法来快速求解，也可以采用梯形蝴蝶定理来解决一般情况．解法一：取特殊值，使得两个正方形的中心相重合，如右图所示，图中四个空白三角形的高均为1.5，因此空白处的总面积为6 1.5242222⨯÷⨯+⨯=，阴影部分的面积为662214⨯-=．解法二：连接两个正方形的对应顶点，可以得到四个梯形，这四个梯形的上底都为2，下底都为6，上底、下底之比为2:61:3=，根据梯形蝴蝶定理，这四个梯形每个梯形中的四个小三角形的面积之比为221:13:13:31:3:3:9⨯⨯=，所以每个梯形中的空白三角形占该梯形面积的916，阴影部分的面积占该梯形面积的716，所以阴影部分的总面积是四个梯形面积之和的716，那么阴影部分的面积为227(62)1416⨯-=．第三题答案：解答：设原来分数的分母为3x，依题意，原来分数的分子为2x；同样可知21833225xx-=-，交叉相乘得1090966x x-=-，解得24x=．于是，原来分数的分子、分母分别为222448x=⨯=．332472x=⨯=所以，原来的分数在约分前是4872．第四题答案：解答：方法一：把1994个数一次每18个分成一组，最后14个数也成一组，共分成111组．即1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18；19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36；…………………1963，1964，…，1979，1980；1981，1982， (1994)每一组中取前9个数，共取出9111999⨯=（个）数，这些数中任两个的差都不等于9．因此，最多可以取999个数．方法二：构造公差为9的9个数列（除以9的余数）{}1,10,19,28,,1990，共计222个数{}2,11,20,29,,1991，共计222个数{}3,12,21,30,,1992，共计222个数{}4,13,22,31,,1993，共计222个数{}5,14,23,32,,1994，共计222个数{}6,15,24,33,,1986，共计221个数{}7,16,25,34,,1987，共计221个数{}8,17,26,35,,1988，共计221个数{}9,18,27,36,,1989，共计221个数每个数列相邻两项的差是9，因此，要使取出的数中，每两个的差不等于9，每个数列中不能取相邻的项．因此，前五个数列只能取出一半，后四个数列最多能取出一半多一个数，所以最多取1119999⨯=个数．第五题答案：解答：如果把入场口看作为“牛”，开门前原有的观众为“原有草量”，每分钟来的观众为“草的增长速度”，那么本题就是一个“牛吃草”问题．设每一个入场口每分钟通过“1”份人，那么4分钟来的人为39552⨯-⨯=，即1分钟来的人为240.5÷=，原有的人为：()30.5922.5-⨯=．这些人来到画展，所用时间为22.50.545÷=(分)．所以第一个观众到达的时间为8点15分．点评：从表面上看这个问题与“牛吃草”问题相离很远，但仔细体会，题目中每分钟来的观众一样多，类似于“草的生长速度”，入场口的数量类似于“牛”的数量，问题就变成“牛吃草”问题了．解决一个问题的方法往往能解决一类问题，关键在于是否掌握了问题的实质．。

小学5年级中级难度奥数题答案

1概率答案：连续扔两次硬币可能出现的情况有（正，正）；（正，反）；（反，正）；（反，反）共四种情况。

约翰扔的话，两种情况记1分，两种情况记0分；汤姆扔的话三种情况记1分，一种情况记0分。

所以汤姆赢得的可能性大。

2长方体答案：设长方体的长宽高分别为a、b、c ，则有ab 、bc 、ca 的值分别为6，8，12。

可得长方体的体积的平方为，所以此长方体的体积为24。

3脚印答案：爸爸走3步和小龙走4步距离一样长，也就是说他们一共走7步，但却只会留下6个脚印，也就是说每216厘米会有6个脚印，那么有60个脚印说明总长度是厘米，也就是21.6米。

4倍数答案：（1）3个数都是3的倍数，有1种情况（2）3个数除以3都余1，有1种情况（3）3个数除以3都余2，有1种情况（4）一个除以3余1，一个除以3余2，一个是3的倍数，有：3×3×3=27种情况所以，一共有1+1+1+27=30种不同取法。

5计算答案：原式=7.816×(1.45+1.69)+3.14×2.184=7.186×3.14+3.14×2.184=31.46数字答案：在900个三位数中，三位数各不相同的有9×9×8＝648（个），三位数全相同的有9个，恰有两位数相同的有900-648-9=243（个）。

7公倍数答案：6，7，8。

提示：相邻两个自然数必互质，其最小公倍数就等于这两个数的乘积。

而相邻三个自然数，若其中只有一个偶数，则其最小公倍数等于这三个数的乘积；若其中有两个偶数，则其最小公倍数等于这三个数乘积的一半。

8行程答案：因为小红的速度不变，相遇地点不变，所以小红两次从出发到相遇的时间相同。

也就是说，小强第二次比第一次少走4分。

由（70×4）÷（90－70）＝14（分）可知，小强第二次走了14分，推知第一次走了18分，两人的家相距（52＋70）×18＝2196（米）。

【推荐】五年级奥数天天练(中难度).doc

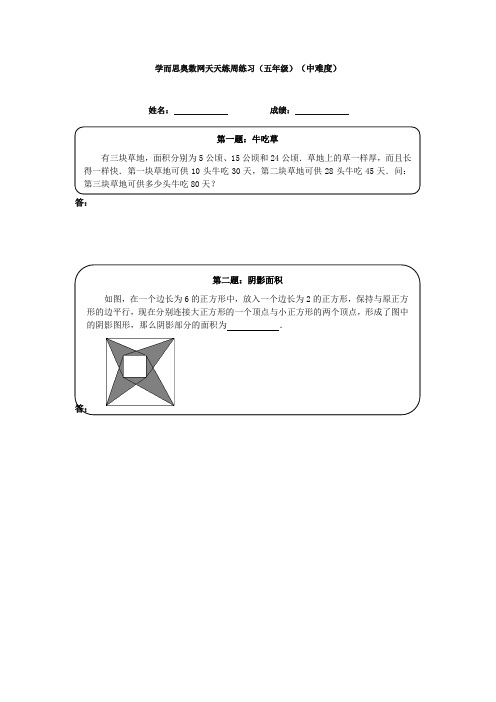
学而思奥数网天天练周练习（五年级）（中难度）姓名：成绩：答：答：第一题：牛吃草有三块草地，面积分别为5公顷、15公顷和24公顷．草地上的草一样厚，而且长得一样快．第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天．问：第三块草地可供多少头牛吃80天？第二题：阴影面积如图，在一个边长为6的正方形中，放入一个边长为2的正方形，保持与原正方形的边平行，现在分别连接大正方形的一个顶点与小正方形的两个顶点，形成了图中的阴影图形，那么阴影部分的面积为．答：答：答：第三题：分数一个分数约分后是23．如果这个分数的分子减去18，分母减去22，约分后就可以得到一个新的分数35．那么，原来的分数在约分前是第四题：自然数从1，2，3，4，…，1994这些自然数中，最多可以取个数，能使这些数中任意两个数的差都不等于9．第五题：排队画展9点开门，但早有人来排队入场，从第一个观众来到时起，若每分钟来的观众一样多，如果开3个入场口，9点9分就不再有人排队；如果开5个入场口，9点5分就没有人排队．求第一个观众到达的时间．学而思奥数网天天练周练习（五年级）答案第一题答案：解答：(法1)设1头牛1天吃草量为“1”，第一块草地可供10头牛吃30天，说明1公顷草地30天提供1030560⨯÷=份草；第二块草地可供28头牛吃45天，说明1公顷草地45天提供28451584⨯÷=份草；所以1公顷草地每天新生长的草量为()()84604530 1.6-÷-=份，1公顷原有草量为60 1.63012-⨯=．24公顷草地每天新生长的草量为1.62438.4⨯=；24公顷草地原有草量为1224288⨯=．那么24公顷草地80天可提供草量为：28838.4803360+⨯=，所以共需要牛的头数是：33608042÷=(头)牛．(法2)现在是3块面积不同的草地，要解决这个问题，也可以将3块草地的面积统一起来．由于[]5,15,24120=，那么题中条件可转化为：120公顷草地可供240头牛吃30天，也可供224头牛吃45天．设1头牛1天的吃草量为“1”，那么120公顷草地每天新生长的草量为()() 22445240304530192⨯-⨯÷-=，120 公顷草地原有草量为()240192301440-⨯=．120公顷草地可供144080192210÷+=(头)牛吃80天，那么24公顷草地可供210542÷=(头)牛吃80天．第二题答案：解答：本题中小正方形的位置不确定，所以可以通过取特殊值的方法来快速求解，也可以采用梯形蝴蝶定理来解决一般情况．解法一：取特殊值，使得两个正方形的中心相重合，如右图所示，图中四个空白三角形的高均为1.5，因此空白处的总面积为6 1.5242222⨯÷⨯+⨯=，阴影部分的面积为662214⨯-=．解法二：连接两个正方形的对应顶点，可以得到四个梯形，这四个梯形的上底都为2，下底都为6，上底、下底之比为2:61:3=，根据梯形蝴蝶定理，这四个梯形每个梯形中的四个小三角形的面积之比为221:13:13:31:3:3:9⨯⨯=，所以每个梯形中的空白三角形占该梯形面积的916，阴影部分的面积占该梯形面积的716，所以阴影部分的总面积是四个梯形面积之和的716，那么阴影部分的面积为227(62)1416⨯-=．第三题答案：解答：设原来分数的分母为3x，依题意，原来分数的分子为2x；同样可知21833225xx-=-，交叉相乘得1090966x x-=-，解得24x=．于是，原来分数的分子、分母分别为222448x=⨯=．332472x=⨯=所以，原来的分数在约分前是4872．第四题答案：解答：方法一：把1994个数一次每18个分成一组，最后14个数也成一组，共分成111组．即1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18；19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36；…………………1963，1964，…，1979，1980；1981，1982， (1994)每一组中取前9个数，共取出9111999⨯=（个）数，这些数中任两个的差都不等于9．因此，最多可以取999个数．方法二：构造公差为9的9个数列（除以9的余数）{}1,10,19,28,,1990，共计222个数{}2,11,20,29,,1991，共计222个数{}3,12,21,30,,1992，共计222个数{}4,13,22,31,,1993，共计222个数{}5,14,23,32,,1994，共计222个数{}6,15,24,33,,1986，共计221个数{}7,16,25,34,,1987，共计221个数{}8,17,26,35,,1988，共计221个数{}9,18,27,36,,1989，共计221个数每个数列相邻两项的差是9，因此，要使取出的数中，每两个的差不等于9，每个数列中不能取相邻的项．因此，前五个数列只能取出一半，后四个数列最多能取出一半多一个数，所以最多取1119999⨯=个数．第五题答案：解答：如果把入场口看作为“牛”，开门前原有的观众为“原有草量”，每分钟来的观众为“草的增长速度”，那么本题就是一个“牛吃草”问题．设每一个入场口每分钟通过“1”份人，那么4分钟来的人为39552⨯-⨯=，即1分钟来的人为240.5÷=，原有的人为：()30.5922.5-⨯=．这些人来到画展，所用时间为22.50.545÷=(分)．所以第一个观众到达的时间为8点15分．点评：从表面上看这个问题与“牛吃草”问题相离很远，但仔细体会，题目中每分钟来的观众一样多，类似于“草的生长速度”，入场口的数量类似于“牛”的数量，问题就变成“牛吃草”问题了．解决一个问题的方法往往能解决一类问题，关键在于是否掌握了问题的实质．。

5年级中等难度奥数题

约翰与汤姆掷硬币，约翰掷两次，汤姆掷两次，约翰掷两次，……，这样轮流掷下去．若约翰连续两次掷得的结果相同，则记1分，否则记0分．若汤姆连续两次掷得的结果中至少有1次硬币的正面向上，则记1分，否则记0分．谁先记满10分谁就赢（）赢的可能性较大（请填汤姆或约翰）．2长方体：（中等难度）若长方体的三个侧面的面积分别是6，8，12，则长方体的体积是（）。

3脚印：（中等难度）夜里下了一场大雪，早上，小龙和爸爸一起步测花园里一条环形小路的长度，他们从同一点同向行走，小龙每步长54厘米，爸爸每步长72厘米，两人各走完一圈后又都回到出发点，这时雪地上只留下60个脚印。

那么这条小路长（）米。

4倍数：（中等难度）从l～9这9个数码中取出3个，使它们的和是3的倍数，则不同取法有__种。

5计算：（中等难度）7.816×1.45+3.14×2.184+1.69×7.816=_____。

6数字：（中等难度）恰有两位数字相同的三位数共有多少个？7公倍数：（中等难度）三个连续自然数的最小公倍数是168，求这三个数。

8行程：（中等难度）小红和小强同时从家里出发相向而行。

小红每分走52米，小强每分走70米，二人在途中的A处相遇。

若小红提前4分出发，且速度不变，小强每分走90米，则两人仍在A处相遇。

小红和小强两人的家相距多少米？小明参加了六次测验，第三、第四次的平均分比前两次的平均分多2分，比后两次的平均分少2分。

如果后三次平均分比前三次平均分多3分，那么第四次比第三次多得几分？10行程：（中等难度）晶晶每天早上步行上学，如果每分钟走60米，则要迟到5分钟，如果每分钟走75米，则可提前2分钟到校.求晶晶到校的路程？11倒推法：（中等难度）马小虎在做一道整数减法题时，把减数个位上的1看成7，把十位上的7看成1，得出差为111，则正确答案是？12买笔：（中等难度）李老师为学校一共买了28支价格相同的钢笔，共付人民币9□.2□元.已知□处数字相同，请问每支钢笔多少元？13流水：（中等难度）甲乙两港之间相距360千米，一轮船往返共用35个小时，顺水比逆水快5个小时，现有一机帆船静水船速为每小时12千米，求它往返两港的时间是？14棋子：（中等难度）有5个小朋友，每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子请你证明，这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。

五年级奥数天天练(中难度)-优选

学而思奥数网天天练周练习（五年级）（中难度）姓名：成绩：答：答：第一题：牛吃草有三块草地，面积分别为5公顷、15公顷和24公顷．草地上的草一样厚，而且长得一样快．第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天．问：第三块草地可供多少头牛吃80天？第二题：阴影面积如图，在一个边长为6的正方形中，放入一个边长为2的正方形，保持与原正方形的边平行，现在分别连接大正方形的一个顶点与小正方形的两个顶点，形成了图中的阴影图形，那么阴影部分的面积为．答：答：答：第三题：分数一个分数约分后是23．如果这个分数的分子减去18，分母减去22，约分后就可以得到一个新的分数35．那么，原来的分数在约分前是第四题：自然数从1，2，3，4，…，1994这些自然数中，最多可以取个数，能使这些数中任意两个数的差都不等于9．第五题：排队画展9点开门，但早有人来排队入场，从第一个观众来到时起，若每分钟来的观众一样多，如果开3个入场口，9点9分就不再有人排队；如果开5个入场口，9点5分就没有人排队．求第一个观众到达的时间．学而思奥数网天天练周练习（五年级）答案第一题答案：解答：(法1)设1头牛1天吃草量为“1”，第一块草地可供10头牛吃30天，说明1公顷草地30天提供1030560⨯÷=份草；第二块草地可供28头牛吃45天，说明1公顷草地45天提供28451584⨯÷=份草；所以1公顷草地每天新生长的草量为()()84604530 1.6-÷-=份，1公顷原有草量为60 1.63012-⨯=．24公顷草地每天新生长的草量为1.62438.4⨯=；24公顷草地原有草量为1224288⨯=．那么24公顷草地80天可提供草量为：28838.4803360+⨯=，所以共需要牛的头数是：33608042÷=(头)牛．(法2)现在是3块面积不同的草地，要解决这个问题，也可以将3块草地的面积统一起来．由于[]5,15,24120=，那么题中条件可转化为：120公顷草地可供240头牛吃30天，也可供224头牛吃45天．设1头牛1天的吃草量为“1”，那么120公顷草地每天新生长的草量为()() 22445240304530192⨯-⨯÷-=，120 公顷草地原有草量为()240192301440-⨯=．120公顷草地可供144080192210÷+=(头)牛吃80天，那么24公顷草地可供210542÷=(头)牛吃80天．第二题答案：解答：本题中小正方形的位置不确定，所以可以通过取特殊值的方法来快速求解，也可以采用梯形蝴蝶定理来解决一般情况．解法一：取特殊值，使得两个正方形的中心相重合，如右图所示，图中四个空白三角形的高均为1.5，因此空白处的总面积为6 1.5242222⨯÷⨯+⨯=，阴影部分的面积为662214⨯-=．解法二：连接两个正方形的对应顶点，可以得到四个梯形，这四个梯形的上底都为2，下底都为6，上底、下底之比为2:61:3=，根据梯形蝴蝶定理，这四个梯形每个梯形中的四个小三角形的面积之比为221:13:13:31:3:3:9⨯⨯=，所以每个梯形中的空白三角形占该梯形面积的916，阴影部分的面积占该梯形面积的716，所以阴影部分的总面积是四个梯形面积之和的716，那么阴影部分的面积为227(62)1416⨯-=．第三题答案：解答：设原来分数的分母为3x，依题意，原来分数的分子为2x；同样可知21833225xx-=-，交叉相乘得1090966x x-=-，解得24x=．于是，原来分数的分子、分母分别为222448x=⨯=．332472x=⨯=所以，原来的分数在约分前是4872．第四题答案：解答：方法一：把1994个数一次每18个分成一组，最后14个数也成一组，共分成111组．即1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18；19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36；…………………1963，1964，…，1979，1980；1981，1982， (1994)每一组中取前9个数，共取出9111999⨯=（个）数，这些数中任两个的差都不等于9．因此，最多可以取999个数．方法二：构造公差为9的9个数列（除以9的余数）{}1,10,19,28,,1990，共计222个数{}2,11,20,29,,1991，共计222个数{}3,12,21,30,,1992，共计222个数{}4,13,22,31,,1993，共计222个数{}5,14,23,32,,1994，共计222个数{}6,15,24,33,,1986，共计221个数{}7,16,25,34,,1987，共计221个数{}8,17,26,35,,1988，共计221个数{}9,18,27,36,,1989，共计221个数每个数列相邻两项的差是9，因此，要使取出的数中，每两个的差不等于9，每个数列中不能取相邻的项．因此，前五个数列只能取出一半，后四个数列最多能取出一半多一个数，所以最多取1119999⨯=个数．第五题答案：解答：如果把入场口看作为“牛”，开门前原有的观众为“原有草量”，每分钟来的观众为“草的增长速度”，那么本题就是一个“牛吃草”问题．设每一个入场口每分钟通过“1”份人，那么4分钟来的人为39552⨯-⨯=，即1分钟来的人为240.5÷=，原有的人为：()30.5922.5-⨯=．这些人来到画展，所用时间为22.50.545÷=(分)．所以第一个观众到达的时间为8点15分．点评：从表面上看这个问题与“牛吃草”问题相离很远，但仔细体会，题目中每分钟来的观众一样多，类似于“草的生长速度”，入场口的数量类似于“牛”的数量，问题就变成“牛吃草”问题了．解决一个问题的方法往往能解决一类问题，关键在于是否掌握了问题的实质．。

五年级奥数天天练(中难度)【最佳】

学而思奥数网天天练周练习（五年级）（中难度）姓名：成绩：答：答：第一题：牛吃草有三块草地，面积分别为5公顷、15公顷和24公顷．草地上的草一样厚，而且长得一样快．第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天．问：第三块草地可供多少头牛吃80天？第二题：阴影面积如图，在一个边长为6的正方形中，放入一个边长为2的正方形，保持与原正方形的边平行，现在分别连接大正方形的一个顶点与小正方形的两个顶点，形成了图中的阴影图形，那么阴影部分的面积为．答：答：答：第三题：分数一个分数约分后是23．如果这个分数的分子减去18，分母减去22，约分后就可以得到一个新的分数35．那么，原来的分数在约分前是第四题：自然数从1，2，3，4，…，1994这些自然数中，最多可以取个数，能使这些数中任意两个数的差都不等于9．第五题：排队画展9点开门，但早有人来排队入场，从第一个观众来到时起，若每分钟来的观众一样多，如果开3个入场口，9点9分就不再有人排队；如果开5个入场口，9点5分就没有人排队．求第一个观众到达的时间．学而思奥数网天天练周练习（五年级）答案第一题答案：解答：(法1)设1头牛1天吃草量为“1”，第一块草地可供10头牛吃30天，说明1公顷草地30天提供1030560⨯÷=份草；第二块草地可供28头牛吃45天，说明1公顷草地45天提供28451584⨯÷=份草；所以1公顷草地每天新生长的草量为()()84604530 1.6-÷-=份，1公顷原有草量为60 1.63012-⨯=．24公顷草地每天新生长的草量为1.62438.4⨯=；24公顷草地原有草量为1224288⨯=．那么24公顷草地80天可提供草量为：28838.4803360+⨯=，所以共需要牛的头数是：33608042÷=(头)牛．(法2)现在是3块面积不同的草地，要解决这个问题，也可以将3块草地的面积统一起来．由于[]5,15,24120=，那么题中条件可转化为：120公顷草地可供240头牛吃30天，也可供224头牛吃45天．设1头牛1天的吃草量为“1”，那么120公顷草地每天新生长的草量为()() 22445240304530192⨯-⨯÷-=，120 公顷草地原有草量为()240192301440-⨯=．120公顷草地可供144080192210÷+=(头)牛吃80天，那么24公顷草地可供210542÷=(头)牛吃80天．第二题答案：解答：本题中小正方形的位置不确定，所以可以通过取特殊值的方法来快速求解，也可以采用梯形蝴蝶定理来解决一般情况．解法一：取特殊值，使得两个正方形的中心相重合，如右图所示，图中四个空白三角形的高均为1.5，因此空白处的总面积为6 1.5242222⨯÷⨯+⨯=，阴影部分的面积为662214⨯-=．解法二：连接两个正方形的对应顶点，可以得到四个梯形，这四个梯形的上底都为2，下底都为6，上底、下底之比为2:61:3=，根据梯形蝴蝶定理，这四个梯形每个梯形中的四个小三角形的面积之比为221:13:13:31:3:3:9⨯⨯=，所以每个梯形中的空白三角形占该梯形面积的916，阴影部分的面积占该梯形面积的716，所以阴影部分的总面积是四个梯形面积之和的716，那么阴影部分的面积为227(62)1416⨯-=．第三题答案：解答：设原来分数的分母为3x，依题意，原来分数的分子为2x；同样可知21833225xx-=-，交叉相乘得1090966x x-=-，解得24x=．于是，原来分数的分子、分母分别为222448x=⨯=．332472x=⨯=所以，原来的分数在约分前是4872．第四题答案：解答：方法一：把1994个数一次每18个分成一组，最后14个数也成一组，共分成111组．即1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18；19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36；…………………1963，1964，…，1979，1980；1981，1982， (1994)每一组中取前9个数，共取出9111999⨯=（个）数，这些数中任两个的差都不等于9．因此，最多可以取999个数．方法二：构造公差为9的9个数列（除以9的余数）{}1,10,19,28,,1990，共计222个数{}2,11,20,29,,1991，共计222个数{}3,12,21,30,,1992，共计222个数{}4,13,22,31,,1993，共计222个数{}5,14,23,32,,1994，共计222个数{}6,15,24,33,,1986，共计221个数{}7,16,25,34,,1987，共计221个数{}8,17,26,35,,1988，共计221个数{}9,18,27,36,,1989，共计221个数每个数列相邻两项的差是9，因此，要使取出的数中，每两个的差不等于9，每个数列中不能取相邻的项．因此，前五个数列只能取出一半，后四个数列最多能取出一半多一个数，所以最多取1119999⨯=个数．第五题答案：解答：如果把入场口看作为“牛”，开门前原有的观众为“原有草量”，每分钟来的观众为“草的增长速度”，那么本题就是一个“牛吃草”问题．设每一个入场口每分钟通过“1”份人，那么4分钟来的人为39552⨯-⨯=，即1分钟来的人为240.5÷=，原有的人为：()30.5922.5-⨯=．这些人来到画展，所用时间为22.50.545÷=(分)．所以第一个观众到达的时间为8点15分．点评：从表面上看这个问题与“牛吃草”问题相离很远，但仔细体会，题目中每分钟来的观众一样多，类似于“草的生长速度”，入场口的数量类似于“牛”的数量，问题就变成“牛吃草”问题了．解决一个问题的方法往往能解决一类问题，关键在于是否掌握了问题的实质．。

小学奥数类型题解析及专项训练(中等难度)

小学奥数类型题解析及专项训练（中等难度）一. 算术题：某学校有120个学生参加了足球比赛，他们分成4个班级参赛。

每个班级参赛人数相同。

请问每个班级有多少学生参赛？解析：假设每个班级有x个学生参赛，根据题意可以得到方程：4x = 120。

解这个方程可以得到x = 30。

所以每个班级有30个学生参赛。

算术题专项练习应用题：某商店有40个相同的玩具，要分给4个学生，要求每个学生分得的玩具个数相同。

1.请问每个学生最多能分得几个玩具？2.请问每个学生最少能分得几个玩具？3.如果要求每个学生分得的玩具个数大于等于10，最多能分几个玩具？4.如果要求每个学生分得的玩具个数小于等于5，最少能分几个玩具？5.如果要求每个学生分得的玩具个数是奇数，最多能分几个玩具？二. 概率题：一个袋子里有3个红球，2个蓝球和1个黄球，小明从袋子里随机取出一个球，问他取出红球的概率是多少？解析：总共有6个球，取出红球的可能性有3个，所以取出红球的概率是3/6，即1/2。

概率题专项练习应用题：一个骰子有六个面，上面的数字是1、2、3、4、5、6。

小明随机掷了一次骰子，请问掷出的数字是偶数的概率是多少？一个扑克牌有52张，其中红心牌有13张。

小红随机从扑克牌里抽取一张牌，请问她抽到红心牌的概率是多少？一个骰子有六个面，上面的数字是1、2、3、4、5、6。

小明随机掷了两次骰子，请问两次都出现1的概率是多少？一个扑克牌有52张，其中梅花牌有13张。

小芳随机从扑克牌里抽取两张牌，请问她抽到两张梅花牌的概率是多少？一个骰子有六个面，上面的数字是1、2、3、4、5、6。

小明随机掷了三次骰子，请问至少掷出一次6的概率是多少？三. 逻辑题：一个班级有30个学生，其中有20人是男生。

小明是这个班级的学生，问他是男生的概率是多少？解析：总共有30个学生，20人是男生，所以小明是男生的可能性有20个，所以他是男生的概率是20/30，即2/3。

逻辑题专项练习应用题：一个班级有35个学生，其中有25人是女生。

小学奥数五年级天天练(中难度)

国际数学奥林匹克竞赛国际数学奥林匹克竞赛，英文名：International Mathematical Olympiad，简称：IMO。

“数学奥林匹克”的名称源自苏联，其将体育竞赛、科学的发源地——古希腊和数学竞赛相互关联。

在20世纪上半叶，不同国家相继组织了各级各类的数学竞赛，先在学校，继之在地区，后来在全国进行，逐步形成了金字塔式的竞赛系统。

从各国的竞赛进一步发展，自然为形成最高一层的国际奥林匹克竞赛创造了必要的条件。

2023年7月12日，在第64届国际数学奥林匹克竞赛中，中国的6名选手全员获得金牌，中国队获国际数学奥赛总分五连冠。

[9]历史起源1956年罗马尼亚数学家罗曼教授提出了倡议，并于1959年7月在罗马尼亚举行了第一次国际奥林匹克数学（International Mathematical Olympiad简称IMO），当时只有保加利亚、捷克斯洛伐克、匈牙利、波兰、罗马尼亚和苏联参加。

以后每年举行（中间只在1980年断过一次），参加的国家和地区逐渐增多，参加这项赛事的代表队达80余支。

中国第一次参加国际数学奥林匹克是在1985年。

经过40多年的发展，国际数学奥林匹克的运转逐步制度化、规范化，有了一整套约定俗成的常规，并为历届东道主所遵循。

目的激发青年人的数学才能；引起青年对数学的兴趣；发现科技人才的后备军；促进各国数学教育的交流与发展。

对象参赛选手为中学生，每支代表队有学生6人，另派2名数学家为领队。

试题试题由各参赛国提供，然后由东道国精选后提交给主试委员会表决，产生6道试题。

东道国不提供试题。

试题确定之后，写成英语、法语、德语、俄语等工作语言，由领队译成本国文字。

答：答：答：第三题：分数一个分数约分后是．如果这个分数的分子减去18，分母减去22，约分后就可以23得到一个新的分数．那么，原来的分数在约分前是35第四题：自然数从1，2，3，4，…，1994这些自然数中，最多可以取个数，能使这些数中任意两个数的差都不等于9．第五题：排队画展9点开门，但早有人来排队入场，从第一个观众来到时起，若每分钟来的观众一样多，如果开3个入场口，9点9分就不再有人排队；如果开5个入场口，9点5分就没有人排队．求第一个观众到达的时间．解答：． 222448x =⨯=332472x =⨯=所以，原来的分数在约分前是． 4872第四题答案：解答：方法一：把1994个数一次每18个分成一组，最后14个数也成一组，共分成111组．即1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18；19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36； …………………1963，1964，...，1979，1980； 1981，1982， (1994)每一组中取前9个数，共取出9111999⨯=（个）数，这些数中任两个的差都不等于9．因此，最多可以取999个数．方法二：构造公差为的个数列（除以999的余数），共计个数 {}1,10,19,28,,1990 222，共计个数 {}2,11,20,29,,1991 222，共计个数 {}3,12,21,30,,1992 222，共计个数 {}4,13,22,31,,1993 222，共计个数 {}5,14,23,32,,1994 222，共计个数{}6,15,24,33,,1986 221，共计个数 {}7,16,25,34,,1987 221，共计个数 {}8,17,26,35,,1988 221，共计个数{}9,18,27,36,,1989 221每个数列相邻两项的差是9，因此，要使取出的数中，每两个的差不等于9，每个数列中不能取相邻的项．因此，前五个数列只能取出一半，后四个数列最多能取出一半多一个数，所以最多取个数． 1119999⨯=第五题答案：解答：如果把入场口看作为“牛”，开门前原有的观众为“原有草量”，每分钟来的观众为“草的增长速度”，那么本题就是一个“牛吃草”问题．设每一个入场口每分钟通过“1”份人，那么4分钟来的人为，即1分39552⨯-⨯=钟来的人为，原有的人为：240.5÷=．这些人来到画展，所()30.5922.5-⨯=用时间为(分)．所以第一个22.50.545÷=观众到达的时间为8点15分．点评：从表面上看这个问题与“牛吃草”问题相离很远，但仔细体会，题目中每分钟来的观众一样多，类似于“草的生长速度”，入场口的数量类似于“牛”的数量，问题就变成“牛吃草”问题了．解决一个问题的方法往往能解决一类问题，关键在于是否掌握了问题的实质．小学奥数的知识点汇总 1、年龄问题的三大特征年龄问题：已知两人的年龄，求若干年前或若干年后两人年龄之间倍数关系的应用题，叫做年龄问题。

中等难度试卷数学五年级

中等难度试卷数学五年级专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个数字是偶数？A. 3B. 4C. 5D. 6答案：B2. 1千米等于多少米？A. 100米B. 1000米C. 10米D. 10000米答案：B3. 下列哪个图形是四边形？A. 三角形B. 正方形C. 圆形D. 椭圆形答案：B4. 下列哪个数字是质数？A. 12B. 13C. 14D. 15答案：B5. 下列哪个数字是立方数？A. 8B. 9C. 10D. 11答案：A二、判断题（每题1分，共5分）1. 5的倍数都是奇数。

（）答案：×2. 0是最小的自然数。

（）答案：√3. 所有的偶数都是2的倍数。

（）答案：√4. 1是质数。

（）答案：×5. 1千米等于1000米。

（）答案：√三、填空题（每题1分，共5分）1. 5 + 7 = ____答案：122. 20 9 = ____答案：113. 4 × 6 = ____答案：244. 36 ÷ 6 = ____答案：65. 2的3次方等于____答案：8四、简答题（每题2分，共10分）1. 请写出2的倍数的前5个数。

答案：2、4、6、8、102. 请写出3的倍数的前5个数。

答案：3、6、9、12、153. 请写出5的倍数的前5个数。

答案：5、10、15、20、254. 请写出10以内所有的质数。

答案：2、3、5、75. 请写出10以内所有的合数。

答案：4、6、8、9五、应用题（每题2分，共10分）1. 小明有5个苹果，小红比小明多3个苹果，小红有多少个苹果？答案：8个2. 一个长方形的长是8厘米，宽是4厘米，求这个长方形的面积。

答案：32平方厘米3. 小华有20元钱，他买了一支笔花了3元，他还剩多少钱？答案：17元4. 一辆汽车每小时行驶60千米，行驶了3小时，这辆汽车行驶了多少千米？答案：180千米5. 一个班级有20名学生，其中有10名女生，求这个班级的女生比例。

【最新】五年级奥数题及答案：计算问题2(中等难度)-实用word文档 (1页)

【最新】五年级奥数题及答案：计算问题2(中等难度)-实用word文档本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！
== 本文为word格式，下载后可方便编辑和修改！ ==
五年级奥数题及答案：计算问题2(中等难度)
编者小语：“题海无边，题型有限”。

学习数学必须要有扎实的基本功，有了扎实的基本功再进行“奥数”的学习就显得水到渠成了。

数学网为大家准备了小学五年级奥数题，希望小编整理奥数题计算问题2(中等难度)，可以帮助到你们，助您快速通往高分之路!!
计算：（中等难度）
计算答案：。

奥数题及答案(合集15篇)

奥数题及答案(合集15篇)奥数题及答案1加工零件：(中等难度)甲、乙、丙3名工人准备在同样效率的3个车床上车出7个零件，加工各零件所需要的'时间分别为4，5，6，6，8，9，9分钟。

3人同时开始工作，问最少经过多少分钟可车完全部零件?加工零件答案：加工所有的零件供需：4+5+6+6+8+9+9=47分钟，平均到三台车床上加工，平均每台加工时间为分钟。

由于加工各零部件需要整数分钟，因此最快需16分钟完成，但是无论怎么分组，都做不到。

因此延长1分钟，即17分钟，有(6，9)，(6，9)，(4，5，8)，满足题意。

所以，最少经过17分钟可完成全部零件。

奥数题及答案2一大块金帝牌巧克力可以分成若干大小一样的正方形小块。

小明和小强各有一大块金帝巧克力，他们同时开始吃第一小块巧克力。

小明每隔20分钟吃1小块，14时40分吃最后1小方块;小强每隔30分钟吃1小块，18时吃最后1小方块。

那么他们开始吃第1小块的'时间是几时几分?分析：小明每隔20分钟吃1小块，小强每隔30分钟吃1小块，小强比小明多间隔10分钟，小明14时40分吃最后1小方块，小强18时吃最后1小方块，小强比小明晚3小时20分，说明在吃最后一块前面共有(3*60+20)/10=20个间隔，即已经吃了20块。

那么，20*20=400分钟=6小时40 分钟，14时40分-6小时40分=8时。

解：18时-14时40分=3小时20分=3*60+20=200分钟，已经吃的块数=200/(30-20)=20块，小明吃20块用时20*20=400分钟=6小时40分钟，开始吃第一块的时间为14时40分-6小时40分=8时。

奥数题及答案31、难度：一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？2、难度：甲乙两座城市相距530千米，货车和客车从两城同时出发，相向而行．货车每小时行50千米，客车每小时行70千米．客车在行驶中因故耽误1小时，然后继续向前行驶与货车相遇．问相遇时客车、货车各行驶多少千米？1、难度：一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？2、难度：甲乙两座城市相距530千米，货车和客车从两城同时出发，相向而行．货车每小时行50千米，客车每小时行70千米．客车在行驶中因故耽误1小时，然后继续向前行驶与货车相遇．问相遇时客车、货车各行驶多少千米？因为客车在行驶中耽误1小时，而货车没有停止继续前行，也就是说，货车比客车多走1小时．如果从总路程中把货车单独行驶小时的`路程减去，然后根据余下的就是客车和货车共同走过的．再求出货车和客车每小时所走的速度和，就可以求出相遇时间．然后根据路程＝速度×时间，可以分别求出客车和货车在相遇时各自行驶的路程．相遇时间：奥数题及答案4一、按规律填数.1）64,48,40,36,34,( ) 2）8,15,10,13,12,11,( )3)1、4、5、8、9、（）、13、（）、（）4)2、4、5、10、11、（）、（）5)5,9,13,17,21,( ),( )二、等差数列1.在等差数列3,12,21,30,39,48,…中912是第几个数?2.求1至100内所有不能被5或9整除的整数和3.把210拆成7个自然数的和,使这7个数从小到大排成一行后,相邻两个数的差都是5,那么,第1个数与第6个数分别是多少?4.把从1开始的所有奇数进行分组,其中每组的第一个数都等于此组中所有数的个数,如（1）,（3、5、7）,（9、11、13、15、17、19、21、23、25）,（27、29、……79）,（81、……）,求第5组中所有数的和三、平均数问题1.已知9个数的平均数是72,去掉一个数后,余下的数平均数为78,去掉的数是______ .2.某班有40名学生,期中数学考试,有两名同学因故缺考,这时班级平均分为89分,缺考的同学补考各得99分,这个班级中考平均分是_______ .3.今年前5个月,小明每月平均存钱4.2元,从6月起他每月储蓄6元,那么从哪个月起小明的平均储蓄超过5元?4.A、B、C、D四个数,每次去掉一个数,将其余下的三个数求平均数,这样计算了4次,得到下面4个数.23,26,30,33A、B、C、D 4个数的平均数是多少?5 A、B、C、D4个数,每次去掉一个数,将其余3个数求平均数,这样计算了4次得到下面4个数23、26、30、33,A、B、C、D4个数的和是 .四、加减乘除的简便运算1）100-98+96-94+92-90+……+8-6+4-2=（）2）1976+1977+……20xx-1975-1976-……-1999=（）3）26×99 =（）4）67×12+67×35+67×52+67=（）5)（14+28+39）×（28+39+15）-（14+28+39+15）×（28+39）五、数阵图1、△、□、〇分别代表三个不同的数,并且;△+△+△=〇+〇；〇+〇+〇+〇=□+□+□；△+〇+〇+□=60 求：△= 〇= □=2.将九个连续自然数填入3行3列的九个空格中,使每一横行及每一竖列的三个数之和都等于60.3.将从1开始的九个连续奇数填入3行3列的九个空格中,使每一横行、每一竖列及两条对角线上的三个数之和都相等.4 用1至9这9个数编制一个三阶幻方,写出所有可能的结果.所谓幻方是指在正方形的方格表的每个方格内填入不同的数,使得每行、每列和两条对角线上的各数之和相等；而阶数是指每行、每列所包含的方格的数.六、和差倍问题1.果园里一共种340棵桃树和杏树,其中桃树的棵数比杏树的3倍多20棵,两种树各种了多少棵?2.一个长方形,周长是30厘米,长是宽的.2倍,求这个长方形的面积.3.甲、乙两个数,如果甲数加上320就等于乙数了.如果乙数加上460就等于甲数的3倍,两个数各是多少?4.有两块同样长的布,第一块卖出25米,第二块卖出14米,剩下的布第二块是第一块的2倍,求每块布原有多少米?5.果园里有桃树和梨树共150棵,桃树比梨树多20棵,两种果树各有多少棵?6.甲、乙两桶油共重30千克,如果把甲桶中6千克油倒入乙桶,那么两桶油重量相等,问甲、乙两桶原有多少油?七、年龄问题1.兄弟俩今年的年龄和是30岁,当哥哥像弟弟现在这样大时,弟弟的年龄恰好是哥哥年龄的一半,哥哥今年几岁?2.母女的年龄和是64岁,女儿年龄的3倍比母亲大8岁,求母女二人的年龄各是多少岁?3.哥哥今年比小丽大12岁,8年前哥哥的年龄是小丽的4倍,今年二人各几岁?4.爷爷今年72岁,孙子今年12岁,几年后爷爷的年龄是孙子的5倍?几年前爷爷的年龄是孙子的13倍?八、假设问题1、有42个同学参加植树,男生平均每人种3棵,女生平均每人种2棵,男生比女生多种56棵.男、女生各多少人?2.某小学举行一次数学竞赛,共15道题,每做对一题得8分,每做错一题倒扣4分,小明共得了72分,他做对了多少道题?3.一张试卷有25道题,答对一题得4分,答错或不答均倒扣1分,某同学共得60分,他答对了多少道题?4.小华解答数学判断题,答对一题给4分,答错一题要倒扣4分,她答了20个判断题,结果只得了56分,她答错了多少道题?5.育才小学五年级举行数学竞赛,共10道题,每做对一道题得8分,错一题倒扣5分,张小灵最终得分为41分,她做对了多少道题?奥数题及答案5请你从01、02、03、…、98、99中选取一些数，使得对于任何由0～9当中的某些数字组成的无穷长的一串数当中，都有某两个相邻的数字，是你所选出的那些数中当中的'一个。