江苏省扬州市邗江实验学校七年级数学下册 7.1《探索直线平行的条件》(1)练习(无答案) 苏科版
苏科版初一数学下册7.1 探索直线平行的条件(考点训练)【含答案】

7.1探索直线平行的条件(考点训练)1.(2022•青海)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示()A.同旁内角、同位角、内错角B.同位角、内错角、对顶角C.对顶角、同位角、同旁内角D.同位角、内错角、同旁内角2.(2022春•嘉祥县期末)如图,∠ABD与∠BDC是()形成的内错角.A.直线AD、BC被直线BD所截B.直线AB、CD被直线BD所截C.直线AB、CD被直线AC所截D.直线AD、BC被直线AC所截3.(2022春•仪征市校级月考)如图,直线AD、BE被直线BF和AC所截,下列说法正确的是()A.∠3与∠4是同旁内角B.∠2与∠5是同位角C.∠6与∠1是内错角D.∠2与∠6是同旁内角4.(2021秋•晋江市期末)如图,直线AB,CD被AE所截,则∠A的内错角是.5.(2022春•西吉县期末)如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是.6.(2022春•嘉兴期末)如图,直线a,b被直线c所截,∠3的同旁内角是.7.(2022春•怀柔区校级期末)如图,直线a,b被c所截,下列四个结论:①∠1和∠7互为对顶角;②∠2和∠6是同位角;③∠3=∠5;④∠4和∠5是同旁内角.其中,结论一定正确的有()A.1个B.2个C.3个D.4个8.(2022春•桂林期末)如图,直线a,b被直线c所截,下列条件中不能判断a ∥b的是()A.∠2=∠6B.∠3+∠5=180°C.∠3=∠6D.∠1=∠4 9.(2022春•文山州期末)如图,下列条件中,不能判定AB∥DC的是()A.∠1=∠2B.∠D+∠BAD=180°C.∠3=∠4D.∠B=∠DCE10.(2022春•文登区期末)用两个相同的三角板如图所示摆放,直线a∥b,画图依据是:.11.(2022春•平桂区期末)如图,直线c与直线a,b相交,∠1=50°,当∠2=时,a∥b.12.(2022春•田家庵区期末)如图,直线AB,CD被直线CE所截,∠C=100°,请写出能判定AB∥CD的一个条件:.13.(2022春•望城区期末)如图,直线c与a、b相交,∠1=35°,∠2=80°,要使直线a与b平行,直线a绕点O逆时针旋转的度数至少是.14.(2021秋•杜尔伯特县期末)完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.证明:∵AB⊥AC(已知),∴∠=90°(),∵∠1=30°,∠B=60°(已知),∴∠1+∠BAC+∠B=(),即∠+∠B=180°,∴AD∥BC().15.(2022春•龙岗区期末)填空并完成以下证明:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.证明:FH⊥AB(已知)∴∠BHF=.∵∠1=∠ACB(已知)∴DE∥BC()∴∠2=.()∵∠2=∠3(已知)∴∠3=.()∴CD∥FH()∴∠BDC=∠BHF=.°()∴CD⊥AB.16.(2022春•安陆市期中)如图,已知a⊥b,a⊥c,求证:b∥c.17.(2021秋•渭城区期末)如图,已知∠EAC=∠ACD,∠ABD=∠ACD,求证:AC∥BD.18.(2022春•韩城市期末)如图,AB⊥AD,CD⊥AD,∠1=∠2,求证:DF∥EA.答案与解析1.(2022•青海)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示()A.同旁内角、同位角、内错角B.同位角、内错角、对顶角C.对顶角、同位角、同旁内角D.同位角、内错角、同旁内角【答案】D【解答】解:根据同位角、内错角、同旁内角的概念,可知第一个图是同位角,第二个图是内错角,第三个图是同旁内角.故选:D.2.(2022春•嘉祥县期末)如图,∠ABD与∠BDC是()形成的内错角.A.直线AD、BC被直线BD所截B.直线AB、CD被直线BD所截C.直线AB、CD被直线AC所截D.直线AD、BC被直线AC所截【答案】B【解答】解:∠ABD与∠BDC是直线AB、CD被直线BD所截形成的内错角.故选:B.3.(2022春•仪征市校级月考)如图,直线AD、BE被直线BF和AC所截,下列说法正确的是()A.∠3与∠4是同旁内角B.∠2与∠5是同位角C.∠6与∠1是内错角D.∠2与∠6是同旁内角【答案】D【解答】解:A、∠3与∠4是内错角,错误;B、∠2与∠5不是同位角,错误;C、∠1与∠6不是同旁内角,错误;D、∠2与∠6是同旁内角,正确;故选:D.4.(2021秋•晋江市期末)如图,直线AB,CD被AE所截,则∠A的内错角是.【答案】∠AOD【解答】解:如图,直线AB,CD被AE所截,则∠A的内错角是∠AOD.故答案为:∠AOD.5.(2022春•西吉县期末)如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是.【答案】∠2、∠4【解答】解:∠1的同位角是∠2,∠5的内错角是∠4,即∠1的同位角和∠5的内错角分别是∠2、∠4.故答案为:∠2、∠4.6.(2022春•嘉兴期末)如图,直线a,b被直线c所截,∠3的同旁内角是.【答案】∠6【解答】解:根据题意,∠3的同旁内角是∠6.故答案为:∠6.7.(2022春•怀柔区校级期末)如图,直线a,b被c所截,下列四个结论:①∠1和∠7互为对顶角;②∠2和∠6是同位角;③∠3=∠5;④∠4和∠5是同旁内角.其中,结论一定正确的有()A.1个B.2个C.3个D.4个【答案】B【解答】解:①∠1和∠7不是对顶角,原说法错误;②∠2和∠6是同位角,原说法正确;③∠3与∠5是内错角,但是不一定相等,原说法错误;④∠4和∠5是同旁内角,原说法正确.结论一定正确的有2个.故选:B.8.(2022春•桂林期末)如图,直线a,b被直线c所截,下列条件中不能判断a ∥b的是()A.∠2=∠6B.∠3+∠5=180°C.∠3=∠6D.∠1=∠4【答案】D【解答】解:A、∠2=∠6,可以判定a,b平行,故本选项不符合题意;B、∠3+∠5=180°,可以判断直线a、b平行,故本选项不符合题意;C、∠3=∠6,可以判定a,b平行,故本选项不符合题意;D、∠1=∠4,不能判定a,b平行,故本选项符合题意.故选:D.9.(2022春•文山州期末)如图,下列条件中,不能判定AB∥DC的是()A.∠1=∠2B.∠D+∠BAD=180°C.∠3=∠4D.∠B=∠DCE【答案】C【解答】解:A、当∠1=∠2时,由内错角相等,两直线平行得AB∥DC,故A 不符合题意;B、当∠D+∠BAD=180°时,由同旁内角互补,两直线平行得AB∥DC,故B不符合题意;C、当∠3=∠4时,由内错角相等,两直线平行得AD∥BC,故C符合题意;D、当∠B=∠DCE时,由同位角相等,两直线平行得AB∥DC,故D不符合题意;故选:C.10.(2022春•文登区期末)用两个相同的三角板如图所示摆放,直线a∥b,画图依据是:.【答案】内错角相等,两直线平行【解答】解:如图:由题意得:∠1=∠2,∴a∥b(内错角相等,两直线平行),故答案为:内错角相等,两直线平行.11.(2022春•平桂区期末)如图,直线c与直线a,b相交,∠1=50°,当∠2=时,a∥b.【答案】130°【解答】解:当∠2=130°时,a∥b,理由如下:∵∠1=50°,∠2=130°,∴∠1+∠2=180°,∴a∥b,故答案为:130°.12.(2022春•田家庵区期末)如图,直线AB,CD被直线CE所截,∠C=100°,请写出能判定AB∥CD的一个条件:.【答案】∠1=100°(答案不唯一)【解答】解:能判定AB∥CD的一个条件:∠1=100°(答案不唯一),理由如下:∵∠C=100°,∠1=100°,∴∠C=∠1,∴AB∥CD,故答案为:∠1=100°(答案不唯一).13.(2022春•望城区期末)如图,直线c与a、b相交,∠1=35°,∠2=80°,要使直线a与b平行,直线a绕点O逆时针旋转的度数至少是.【答案】45°【解答】解:如图,∵∠3=∠1=35°时,a∥b,∴要使直线a与b平行,直线a绕点O逆时针旋转的度数至少是80°﹣35°=45°.故答案为:45°.14.(2021秋•杜尔伯特县期末)完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.证明:∵AB⊥AC(已知),∴∠=90°(),∵∠1=30°,∠B=60°(已知),∴∠1+∠BAC+∠B=(),即∠+∠B=180°,∴AD∥BC().【解答】解:证明:∵AB⊥AC(已知),∴∠BAC=90°(垂直的定义),∵∠1=30°,∠B=60°(已知),∴∠1+∠BAC+∠B=180°(等量关系),即∠BAD+∠B=180°,∴AD∥BC(同旁内角互补,两直线平行),故答案为:BAC;垂直的定义;180°;等量关系;BAD;同旁内角互补,两直线平行.15.(2022春•龙岗区期末)填空并完成以下证明:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.证明:FH⊥AB(已知)∴∠BHF=.∵∠1=∠ACB(已知)∴DE∥BC()∴∠2=.()∵∠2=∠3(已知)∴∠3=.()∴CD∥FH()∴∠BDC=∠BHF=.°()∴CD⊥AB.【解答】证明:FH⊥AB(已知),∴∠BHF=90°.∵∠1=∠ACB(已知),∴DE∥BC(同位角相等,两直线平行),∴∠2=∠BCD.(两直线平行,内错角相等).∵∠2=∠3(已知),∴∠3=∠BCD(等量代换),∴CD∥FH(同位角相等,两直线平行),∴∠BDC=∠BHF=90°,(两直线平行,同位角相等)∴CD⊥AB.故答案为:90°;同位角相等,两直线平行;∠BCD;两直线平行,内错角相等;∠BCD;等量代换;同位角相等,两直线平行;90;两直线平行,同位角相等.16.(2022春•安陆市期中)如图,已知a⊥b,a⊥c,求证:b∥c.【解答】证明:∵a⊥b,a⊥c,∴∠1=∠2=90°,∴b∥c(同位角相等,两直线平行).17.(2021秋•渭城区期末)如图,已知∠EAC=∠ACD,∠ABD=∠ACD,求证:AC∥BD.【解答】解:∵∠EAC=∠ACD,∠ABD=∠ACD,∴∠EAC=∠ABD,∴AC∥BD.18.(2022春•韩城市期末)如图,AB⊥AD,CD⊥AD,∠1=∠2,求证:DF∥EA.【解答】证明:∵AB⊥AD,CD⊥AD,∴∠CDA=∠BAD=90°.∴∠1+∠ADF=∠2+∠DAE.∵∠1=∠2,∴∠ADF=∠DAE.∴DF∥EA。
江苏省扬州市邗江实验学校七年级数学下册 7.1《探索直
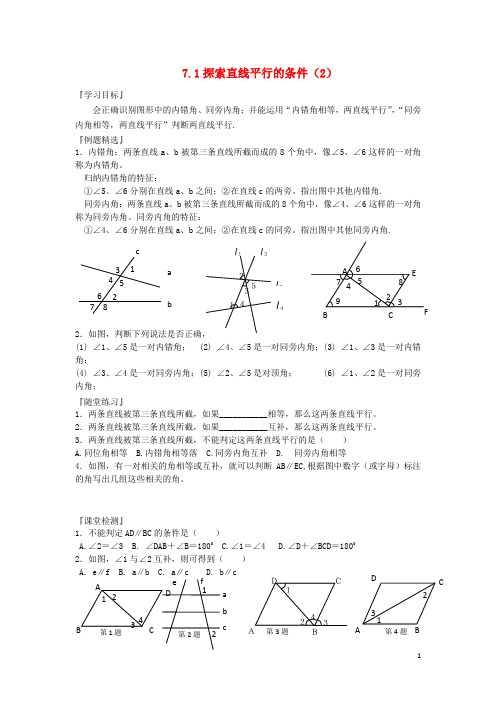
7.1探索直线平行的条件(2)『学习目标』会正确识别图形中的内错角、同旁内角;并能运用“内错角相等,两直线平行”,“同旁内角相等,两直线平行”判断两直线平行.『例题精选』1.内错角:两条直线a 、b 被第三条直线所截而成的8个角中,像∠5、∠6这样的一对角称为内错角。
归纳内错角的特征:①∠5、∠6分别在直线a 、b 之间;②在直线c 的两旁。
指出图中其他内错角.同旁内角:两条直线a 、b 被第三条直线所截而成的8个角中,像∠4、∠6这样的一对角称为同旁内角。
同旁内角的特征:①∠4、∠6分别在直线a 、b 之间;②在直线c 的同旁。
指出图中其他同旁内角.2.如图,判断下列说法是否正确,(1) ∠1、∠5是一对内错角; (2) ∠4、∠5是一对同旁内角;(3) ∠1、∠3是一对内错角;(4) ∠3、∠4是一对同旁内角;(5) ∠2、∠5是对顶角; (6) ∠1、∠2是一对同旁内角;『随堂练习』1.两条直线被第三条直线所截,如果___________相等,那么这两条直线平行。
2.两条直线被第三条直线所截,如果___________互补,那么这两条直线平行。
3.两条直线被第三条直线所截,不能判定这两条直线平行的是( ) A.同位角相等 B.内错角相等落 C.同旁内角互补 D. 同旁内角相等4.如图,有一对相关的角相等或互补,就可以判断AB ∥EC,根据图中数字(或字母)标注的角写出几组这些相关的角。
『课堂检测』1.不能判定AD ∥BC 的条件是( )A.∠2=∠3B. ∠DAB +∠B =1800C.∠1=∠4D.∠D +∠BCD =18002.如图,∠1与∠2互补,则可得到( ) A. e ∥f B. a ∥b C. a ∥c D. b ∥c1 3 2 4 5l 2 l 3l 1 l 4 BC a b c 5 6 4 8 1 2 3 7 A D BC 1 4 32第3题ab cC第4题3.如图,由下列条件可以判定哪两条直线平行,说明理由。
苏科版七年级数学下册7.1直线平行的条件和探索例题和同步练习(含练习答案)

苏科版七年级数学下册直线平行的条件和探索【直线平行的条件和性质】【学习目标】1.同位角、内错角、同旁内角的识别;2.会判定两条直线平行;3.平行线的性质.【基础知识梳理】1.如图,同位角的是;内错角的是;同旁内角的是.2.直线平行的条件:(1)基本事实:,两直线平行;(2)定理:,两直线平行;(3)定理:,两直线平行.3.平行线的性质:(1)基本事实:两直线平行,;(2)定理:两直线平行,;(3)定理:两直线平行,.【典型例题】一、三线八角模型例1:如图所示,同位角一共有对,分别是;内错角一共有对,分别是;同旁内角一共有对,分别是.【变式】已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上.例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1一同旁内角→∠9一内错角→∠3.路径2:∠1一内错角→∠12一内错角→∠6一同位角→∠10一同旁内角→∠3.试一试:(1)从起始∠1跳到终点角∠8;(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?二、平行线的判定例2:如图,点E在AC的延长线上,给出四个条件:①∠1=∠2;②∠3=∠4:③∠A=∠DCE;④∠D+∠ABD=180°.其中能判断AB∥CD的有.(填写所有满足条件的序号)三、平行线的性质例3:如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,求图2中∠AEF的度数.【变式】如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,求∠F的度数.四、综合运用例4:填空并完成以下证明:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.证明:FH⊥AB(已知)∴∠BHF=.∵∠1=∠ACB(已知)∴DE∥BC()∴∠2=.()∵∠2=∠3(已知)∴∠3=.()∴CD∥FH()∴∠BDC=∠BHF=.°()∴CD⊥AB.例5:(1)如图(1),若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由;(2)如图(2),要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.【变式】问题情境:如图1,AB∥CD,∠P AB=130°,∠PCD=120°.求∠APC度数.小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.问题迁移:(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.【拓展应用】例6:如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.【能力提升】1.如图所示,下列结论中不正确的是()A.∠1和∠2是同位角B.∠2和∠3是同旁内角C.∠1和∠4是同位角D.∠2和∠4是内错角2.在同一个平面内,不相邻的两个直角,如果它们有一条边共线,那么另一边互相()A.平行B.垂直C.共线D.平行或共线3.如图,F A⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是()A.由∠CAB=∠NCD,得AB∥CD B.由∠DCG=∠BAC,得AB∥CDC.由∠MAE=∠ACG,∠DCG=∠BAE,得AB∥CD D.由∠MAB=∠ACD,得AB∥CD4.如图,在△ABC中,以点C为顶点,在△ABC外画∠ACD=∠A,且点A与D在直线BC的同一侧,再延长BC至点E,在所作的图形中,∠A与是内错角;∠B与是同位角;∠ACB与是同旁内角.5.如图,已知∠1=(3x +24)°,∠2=(5x +20)°,要使m ∥n ,那么∠1= (度).6.如图,BE ∥CF ,则∠A +∠B +∠C +∠D = 度.7.如图,直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交,若∠1=30°,求∠2的度数.8.(1)如图①,若∠B +∠D =∠BED ,试猜想AB 与CD 的位置关系,并说明理由;(2)如图②,要想得到AB ∥CD ,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.9.如图,AD ∥BC ,∠DAC =120°,∠ACF =20°,∠EFC =140°.求证:EF ∥AD .10.【探究】如图①,∠AFH 和∠CHF 的平分线交于点O ,EG 经过点O 且平行于FH ,分别与AB 、CD 交于点E 、C .(1)若∠AFH =60°,∠CHF =50°,则∠EOF = 度,∠FOH = 度.(2)若∠AFH +∠CHF =100°,求∠FOH 的度数.【拓展】如图②,∠AFH 和∠CHI 的平分线交于点O ,EG 经过点O 且平行于FH ,分别与AB 、CD 交于点E 、G .若∠AFH +∠CHF =α,直接写出∠FOH 的度数.(用含α的代数式表示)【能力提升】答案第1题 第3题 第4题 第5题 第6题1.如图所示,下列结论中不正确的是()A.∠1和∠2是同位角B.∠2和∠3是同旁内角C.∠1和∠4是同位角D.∠2和∠4是内错角解:A、∠1和∠2是同旁内角,故本选项错误,符合题意;B、∠2和∠3是同旁内角,故本选项正确,不符合题意;C、∠1和∠4是同位角,故本选项正确,不符合题意;D、∠3和∠4是内错角,故本选项正确,不符合题意;故选:A.2.在同一个平面内,不相邻的两个直角,如果它们有一条边共线,那么另一边互相()A.平行B.垂直C.共线D.平行或共线解:如图所示:不相邻的两个直角,如果它们有一条边共线,内错角相等,或同旁内角互补,那么另一边互相平行或共线.故选:D.3.如图,F A⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是()A.由∠CAB=∠NCD,得AB∥CDB.由∠DCG=∠BAC,得AB∥CDC.由∠MAE=∠ACG,∠DCG=∠BAE,得AB∥CDD.由∠MAB=∠ACD,得AB∥CD解:A、正确,同位角∠CAB=∠NCD,故AB∥CD;B、错误,∠DCN=∠BAC不是同位角,所以B不对;C、正确,∠MAE=∠ACG,∠DCG=∠BAE,可得同位角∠BAN=∠DCN,故AB∥CD;D、正确,同位角∠MAB=∠ACD,故AB∥CD.故选:B.4.如图,在△ABC中,以点C为顶点,在△ABC外画∠ACD=∠A,且点A与D在直线BC的同一侧,再延长BC至点E,在作的图形中,∠A与是内错角;∠B与是同位角;∠ACB与是同旁内角.解:如图所示,∠A与∠ACD、∠ACE是内错角;∠B与∠DCE、∠ACE是同位角;∠ACB与∠A、∠B是同旁内角.5.如图,已知∠1=(3x+24)°,∠2=(5x+20)°,要使m∥n,那么∠1=75(度).解:如图所示:∠1+∠3=180°,∵m∥n,∴∠2=∠3,∴∠1+∠2=180°,∴3x+24+5x+20=180°,解得:x=17,则∠1=(3x+24)°=75°.6.如图,BE∥CF,则∠A+∠B+∠C+∠D=180度.解:如图所示,由图知∠A+∠B=∠BPD,∵BE∥CF,∴∠CQD=∠BPD=∠A+∠B,又∵∠CQD+∠C+∠D=180°,∴∠A+∠B+∠C+∠D=180°.7.如图,直尺的一条边经过一个含45角的直角顶点直尺的一组对边分别与直角三角尺的两边相交,若∠1=30°,求∠2的度数.解:如图,∵∠ACB=90°∴∠1+∠3=90°,∵∠1=30°,∴∠3=60°,∵a∥b,∴∠2=∠3=60°.8.(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由;(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的数量关系,试说明理由.解:(1)AB∥CD,理由:如图(1),延长BE交CD于F.∵∠BED=∠B+∠D,∠BED=∠EFD+∠D,∴∠B=∠EFD,∴AB∥CD;(2)∠1=∠2+∠3.理由如下:如图(2),延长BA交CE于F,∵AB∥CD(已知),∴∠3=∠EF A(两直线平行,同位角相等),∵∠1=∠2+∠EF A,∴∠1=∠2+∠3.9.如图,AD∥BC,∠DAC=120°,∠ACF=20°,∠EFC=140°.求证:EF∥AD.证明:∵AD∥BC,∴∠DAC+∠ACB=180°,∵∠DAC=120°,∴∠ACB=60°,又∵∠ACF=20°,∴∠BCF=∠ACB-∠ACF=40°,又∵∠EFC=140°,∴∠BCF+∠EFC=180°,∴EF∥BC,∵AD∥BC,∴EF∥AD.10. 【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.(1)若∠AFH=60°,∠CHF=50°,则∠EOF=度,∠FOH=度.(2)若∠AFH+∠CHF=100°,求∠FOH的度数.【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF =α,直接写出∠FOH的度数.(用含α的代数式表示)解:【探究】(1)∵∠AFH=60°,OF平分∠AFH,∴∠OFH=30°,又∵EG∥FH,∴∠EOF=∠OFH=30°;∵∠CHF=50°,OH平分∠CHF,∴∠FHO=25°,∴△FOH中,∠FOH=180°-∠OFH-∠OHF=125°;故答案为:30,125;(2)∵FO 平分∠AFH ,HO 平分∠CHF ,∴∠OFH =12 ∠AFH ,∠OHF =12∠CHF . ∵∠AFH +∠CHF =100°,∴∠OFH +∠OHF =12 (∠AFH +∠CHF )=12×100°=50°. ∵EG ∥FH ,∴∠EOF =∠OFH ,∠GOH =∠OHF .∴∠EOF +∠GOH =∠OFH +∠OHF =50°.∵∠EOF +∠GOH +∠FOH =180°,∴∠FOH =180°-(∠EOF +∠GOH )=180°-50°=130°.【拓展】∵∠AFH 和∠CHI 的平分线交于点O ,∴∠OFH =12 ∠AFH ,∠OHI =12∠CHI , ∴∠FOH =∠OHI -∠OFH=12(∠CHI -∠AFH ) =12(180°-∠CHF -∠AFH ) =12(180°-α) =90°-12α.。
江苏省扬州市邗江实验学校七年级数学下册 7.1《探索直线平行的条件》(2)练习(无答案) 苏科版
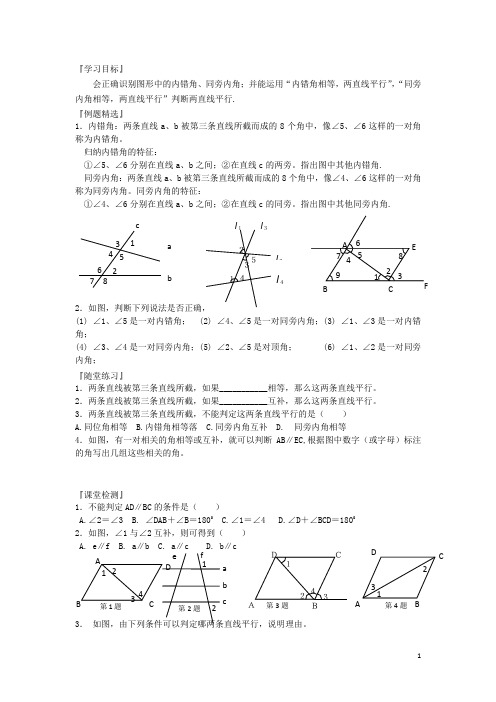
『学习目标』会正确识别图形中的内错角、同旁内角;并能运用“内错角相等,两直线平行”,“同旁内角相等,两直线平行”判断两直线平行.『例题精选』1.内错角:两条直线a 、b 被第三条直线所截而成的8个角中,像∠5、∠6这样的一对角称为内错角。
归纳内错角的特征:①∠5、∠6分别在直线a 、b 之间;②在直线c 的两旁。
指出图中其他内错角.同旁内角:两条直线a 、b 被第三条直线所截而成的8个角中,像∠4、∠6这样的一对角称为同旁内角。
同旁内角的特征:①∠4、∠6分别在直线a 、b 之间;②在直线c 的同旁。
指出图中其他同旁内角.2.如图,判断下列说法是否正确,(1) ∠1、∠5是一对内错角; (2) ∠4、∠5是一对同旁内角;(3) ∠1、∠3是一对内错角;(4) ∠3、∠4是一对同旁内角;(5) ∠2、∠5是对顶角; (6) ∠1、∠2是一对同旁内角;『随堂练习』1.两条直线被第三条直线所截,如果___________相等,那么这两条直线平行。
2.两条直线被第三条直线所截,如果___________互补,那么这两条直线平行。
3.两条直线被第三条直线所截,不能判定这两条直线平行的是( ) A.同位角相等B.内错角相等落C.同旁内角互补D. 同旁内角相等4.如图,有一对相关的角相等或互补,就可以判断AB ∥EC,根据图中数字(或字母)标注的角写出几组这些相关的角。
『课堂检测』1.不能判定AD ∥BC 的条件是( )A.∠2=∠3B. ∠DAB +∠B =1800C.∠1=∠4D.∠D +∠BCD =18002.如图,∠1与∠2互补,则可得到( ) A. e ∥f B. a ∥b C. a ∥c D. b ∥c31 3 2 4 5l 2 l 3l 1 l 4 BC a b c 5 6 4 8 1 2 3 7 A D B C 1 4 3 2 第3题 a b c A BC第4题(1) ∠1=∠2 (2) ∠A=∠3 (3) ∠C=∠3 (4) ∠A+∠2+∠4=1800 4.如图,∠1=∠2,AC平分∠DAB,你能判断哪两条直线平行,请说明理由。
2021-2022学年苏科版七年级数学下册《7-1探索直线平行的条件》同步达标测试题(附答案)

2021-2022学年苏科版七年级数学下册《7-1探索直线平行的条件》同步达标测试题(附答案)一.选择题(共8小题,满分40分)1.如图,直线a,b被直线c所截,则∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D.邻补角2.下列图形中,由∠1=∠2,能得到AB∥CD的是()A.B.C.D.3.如图,直线a,b被第三条直线c所截.由“∠1=∠2”,得到“a∥b”的依据是()A.两直线平行,同位角相等B.同位角相等,两直线平行C.两直线平行,内错角相等D.内错角相等,两直线平行4.如图,下列条件中,不能判定l1∥l2的是()A.∠1=∠3B.∠2+∠4=180°C.∠2=∠3D.∠4+∠5=180°5.如图所示,下列推理正确的是()A.∵∠1=∠4(已知)∴AB∥CD(内错角相等,两直线平行)B.∵∠2=∠3(已知)∴AE∥DF(内错角相等,两直线平行)C.∵∠1=∠3(已知)∴AB∥DF(内错角相等,两直线平行)D.∵∠2=∠3(已知)∴AE∥DC(内错角相等,两直线平行)6.如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠4=∠5;③∠8=∠1;④∠6+∠7=180°.其中,能够判断a∥b的是()A.①②③④B.①③C.②③④D.①②7.如图,在四边形ABCD中,连接BD,判定正确的是()A.若∠1=∠2,则AB∥CDB.若∠3=∠4,则AD∥BCC.若∠A+∠ABC=180°,则AD∥BCD.若∠C=∠A,则AB∥CD8.若将一副三角板按如图所示的方式放置,则下列结论不正确的是()A.∠1=∠3B.如果∠2=30°,则有AC∥DEC.如果∠2=30°,则有BC∥AD D.如果∠2=30°,必有∠4=∠C二.填空题(共6小题,满分30分)9.如图,写出一个能判定EC∥AB的条件是.10.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB∥DC的条件为.11.如图,直线a、b被c所截,∠1=130°,当∠2=°时,a∥b.12.一副三角板按如图所示叠放在一起,点C为直角顶点,边AB和边DE所在的直线交于点P.若固定三角板ABC不动,改变三角板CDE的位置(其中点C位置始终不变),则当∠APD的度数为时,DE∥AC.13.如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC =154°,则此工件.(填“合格”或“不合格”)14.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于时,AB∥CD.三.解答题(共6小题,满分50分)15.如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.16.如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H 且∠1=∠2,∠B=∠C.请问AB∥CD吗?试说明理由.17.将一副三角尺拼图,并标点描线如图所示,然后过点C作CF平分∠DCE,交DE于点F.(1)求证:CF∥AB;(2)求∠EFC的度数.18.已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°,∠DEF=∠B.求证:DE∥BC.19.如图,∠1=∠2,∠3=∠4,∠5=∠6,求证:CE∥BF.20.如图,已知∠1=∠2,∠MAE=45°,∠FEG=15°,∠NCE=75°,EG平分∠AEC,求证:AB∥EF∥CD.参考答案一.选择题(共8小题,满分40分)1.解:如图所示,∠1和∠2两个角都在被截直线b和a同侧,并且在第三条直线c(截线)的同旁,故∠1和∠2是直线b、a被c所截而成的同位角.故选:A.2.解:A、∠1、∠2是同旁内角,由∠1=∠2不能得到AB∥CD;B、∠1、∠2是内错角,由∠1=∠2能得到AB∥CD;C、∠1、∠2是同旁内角,由∠1=∠2不能得到AB∥CD;D、∠1、∠2是同旁内角,由∠1=∠2不能得到AB∥CD.故选:B.3.解:∵∠1=∠2,∴a∥b(内错角相等,两直线平行),故选:D.4.解:A、∵∠1=∠3,∴直线l1∥l2,故此选项不合题意;B、∵∠2+∠4=180°,∴直线l1∥l2,故此选项不合题意;C、∠2=∠3,不能得出直线l1∥l2,故此选项符合题意;D、∵∠2=∠5,4+∠5=180°,∴4+∠2=180°,∴直线l1∥l2,故此选项不合题意.故选:C.5.解:A、错误.∠1和∠4不是内错角,推不出AB∥CD;B、正确.内错角相等,两直线平行;C、错误.∠1和∠3不是内错角,推不出AB∥DF;D、错误.由∠2=∠3推出AE∥DF.故选:B.6.解:①∵∠1=∠2,∴a∥b,故本小题正确;②∵4=∠5,∴a∥b,故本小题正确;③∵∠8=∠1,∠8=∠2,∴∠1=∠2,∴a∥b,故本小题正确;④∵∠6+∠7=180°,∠6+∠2=180°,∴∠7=∠2,∴a∥b,故本小题正确.故选:A.7.解:A、根据∠1=∠2不能推出AB∥CD,故本选项不符合题意;B、根据∠3=∠4不能推出AD∥BC,故本选项不符合题意;C、根据∠A+∠ABC=180°能推出AD∥BC,故本选项符合题意;D、根据∠C=∠A不能推出AB∥CD,故本选项不符合题意.故选:C.8.解:A、∵∠CAB=∠EAD=90°,∴∠1=∠CAB﹣∠2,∠3=∠EAD﹣∠2,∴∠1=∠3,故本选项正确.B、∵∠2=30°,∴∠1=90°﹣30°=60°,∵∠E=60°,∴∠1=∠E,∴AC∥DE,故本选项正确.C、∵∠2=30°,∴∠3=90°﹣30°=60°,∵∠B=45°,∴BC不平行于AD,故本选项错误.D、由AC∥DE可得∠4=∠C,故本选项正确.故选:C.二.填空题(共6小题,满分30分)9.解:∵∠A=∠ACE,∴EC∥AB(内错角相等,两直线平行).故答案为:∠A=∠ACE(答案不唯一).10.解:①∵∠1=∠2,∴AB∥CD,故本选项符合题意;②∵∠3=∠4,∴BC∥AD,故本选项不符合题意;③∵∠A=∠CDE,∴AB∥CD,故本选项符合题意;④∵∠A+∠ADC=180°,∴AB∥CD,故本选项符合题意.故答案为:①③④.11.解:当∠1+∠2=180°时,a∥b,∵∠1=130°,∴∠2=180°﹣130°=50°.故答案为:50.12.解:分两种情况①如图1所示,当DE∥AC时,∠APD+∠A=180°,∵∠A=60°,∴∠APD=180°﹣∠A=180°﹣60°=120°;②如图2所示,当DE∥AC时,∠APD=∠BAC=60°,综上所述,当∠APD等于120°或60°时,CE∥AB.故答案为120°或60°.13.解:作CF∥AB,如图所示:则∠ABC+∠1=180°,∴∠1=180°﹣146°=34°,∴∠2=∠BCD﹣∠1=60°﹣34°=26°,∵∠2+∠EDC=26°+154°=180°,∴CF∥ED,∴AB∥ED;故答案为:合格.14.解:∵AB∥CD,∴∠3=∠4(两直线平行,同位角相等);又∵∠1+∠3=180°(平角的定义),∠1=140°(已知),∴∠3=∠4=40°;∵EF⊥MN,∴∠2+∠4=90°,∴∠2=50°;故答案为:50°三.解答题(共6小题,满分50分)15.证明:∵∠A=∠EDF(已知),∴AC∥DF(同位角相等,两直线平行),∴∠C=∠CGF(两直线平行,内错角相等).又∵∠C=∠F(已知),∴∠CGF=∠F(等量代换),∴BC∥EF(内错角相等,两直线平行).16.解:AB∥CD.理由如下:∵∠1=∠2(已知),∴CE∥FB(同位角相等,两直线平行),∵CE∥FB,∴∠C=∠BFD(两直线平行,同位角相等),∵∠B=∠C(已知),∴∠B=∠BFD(等量代换),∴AB∥CD(内错角相等,两直线平行).17.解:(1)∵CF平分∠DCE,且∠DCE=90°,∴∠ECF=45°,∵∠BAC=45°,∴∠BAC=∠ECF,∴CF∥AB;(2)在△FCE中,∵∠FCE+∠E+∠EFC=180°,∴∠EFC=180°﹣∠FCE﹣∠E,=180°﹣45°﹣30°=105°.18.证明:∵∠BDC+∠DHF=180°,∴BD∥FH,∴∠B=∠EFC,∵∠DEF=∠B,∴∠EFC=∠DEF,∴DE∥BC.19.证明:∵∠3=∠4,∴DF∥BC,∴∠5=∠BAF,∵∠5=∠6,∴∠6=∠BAF,∴AB∥CD,∴∠2=∠AGE,∵∠1=∠2,∴∠1=∠AGE,∴CE∥BF.20.证明:∵∠1=∠2,∴AB∥EF(同位角相等,两直线平行),∴∠MAE=∠AEF=45°,∵∠FEG=15°,∴∠AEG=60°,∴∠GEC=60°,∴∠FEC=∠FEG+∠GEC=75°,∵∠NCE=75°,∴∠FEC=∠ECN,∴EF∥CD,∴AB∥EF∥CD.。
苏科版七年级数学下册 同步练习探索直线平行的条件
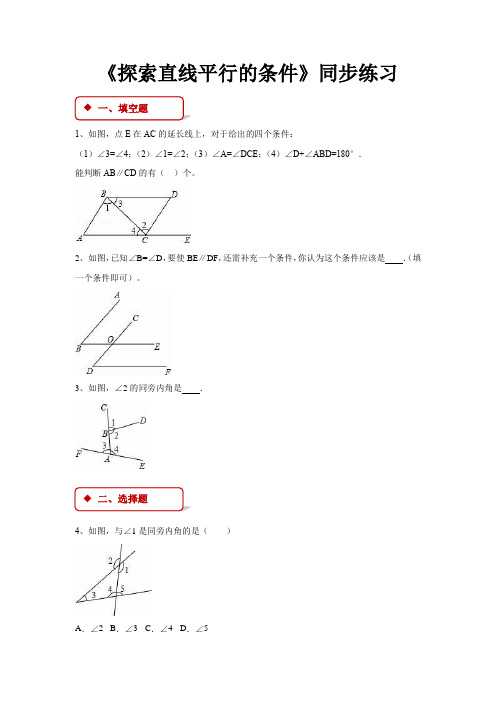
《探索直线平行的条件》同步练习1、如图,点E在AC的延长线上,对于给出的四个条件:(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.能判断AB∥CD的有()个。
2、如图,已知∠B=∠D,要使BE∥DF,还需补充一个条件,你认为这个条件应该是.(填一个条件即可)。
3、如图,∠2的同旁内角是.4、如图,与∠1是同旁内角的是()A.∠2 B.∠3 C.∠4 D.∠55、如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则()A.AB∥BC B.BC∥CD C.AB∥DC D.AB与CD相交6.如图,能判定EC∥AB的条件是()A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE7.如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是()A.两直线平行,内错角相等B.两直线平行,同位角相等C.内错角相等,两直线平行D.同位角相等,两直线平行8.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C(1)找出图中相互平行的线,说说它们之间为什么是平行的;(2)证明:∠A=∠D.答案和解析1.3解析:(1)如果∠3=∠4,那么AC∥BD,故(1)错误;(2)∠1=∠2,那么AB∥CD;内错角相等,两直线平行,故(2)正确;(3)∠A=∠DCE,那么AB∥CD;同位角相等,两直线平行,故(3)正确;(4)∠D+∠ABD=180°,那么AB∥CD;同旁内角互补,两直线平行,故(4)正确.即正确的有(2)(3)(4).故答案为:3.2.∠B=∠COE解析:添加:∠B=∠COE,∵∠B=∠D,∠B=∠COE,∴∠COE=∠D,∴BE∥DF,故答案为:∠B=∠COE.3.∠4解析:此题主要考查了同旁内角,关键是掌握同旁内角的边构成“U”形.4.D.解析:A、∠1和∠2是对顶角,不是同旁内角,故本选项错误;B、∠1和∠3是同位角,不是同旁内角,故本选项错误;C、∠1和∠4是内错角,不是同旁内角,故本选项错误;D、∠1和∠5是同旁内角,故本选项正确;5. C.解析:∵∠ABC=150°,∠BCD=30°,∴∠ABC+∠BCD=180°,∴AB∥DC.6.D.解:A、两个角不是同位角、也不是内错角,故选项错误;B、两个角不是同位角、也不是内错角,故选项错误;C、不是EC和AB形成的同位角、也不是内错角,故选项错误;D、正确.7.C.解:∵∠1与∠2是内错角,∴若∠1=∠2,则AD∥BC.故选C.8.解:(1)∵∠1=∠2,∴CE∥FB,∴∠C=∠BFD,∵∠B=∠C,∴∠B=∠BFD,∴AB∥CD;(2)证明:由(1)可得AB∥CD,∴∠A=∠D.。
探索直线平行的条件(练习)-七年级数学下册同步精品课堂(苏科版)(解析版)

第七章平面图形的认识(二)7.1探索直线平行的条件一.单选题1.如图,∠A的同位角是()A.∠BOE B.∠AOE C.∠BOD D.∠AOD【详解】解:根据同位角的定义,由图可知∠A的同位角是∠BOE.故本题选:A.2.两条直线被第三条直线所截,则()A.同位角必相等B.内错角必相等C.同旁内角互补D.同旁内角不一定互补【详解】解:∵两条被截的直线不一定平行,∴截得的同位角不一定相等,内错角不一定相等,同旁内角不一定互补.故本题选:D.3.下列条件不能使两直线平行的是()A.内错角相等B.同旁内角互补C.对顶角相等D.同位角相等【详解】解:A、内错角相等,两直线平行,不合题意;B、同旁内角互补,两直线平行,不合题意;C、对顶角相等,是两直线相交,不能够判断两直线平行,符合题意;D、同位角相等,两直线平行,不合题意.故本题选:C.4.如图,弯形管道ABCD的拐角∠ABC=120°,要保证管道AB∥CD,则∠BCD等于()A.60°B.50°C.70°D.65°【详解】解:当∠ABC+∠BCD=180°时,可得AB∥CD,∵∠ABC=120°,∴∠BCD=60°.故本题选:A.5.如图所示,直线a、b被c、d所截,下列条件中能说明a∥b的是()A.∠1=∠2B.∠2+∠4=180°C.∠3=∠4D.∠1+∠4=180°【详解】解:∵∠3=∠4,∴a∥b(同位角相等,两直线平行).故本题选:C.6.如图,能够判断DE∥BC的条件是()A.∠1=∠2B.∠4=∠C C.∠1+∠3=180°D.∠3+∠C=180°【详解】解:A、∵∠1=∠2,∴EF∥AC,故不合题意;B、∵∠4=∠C,∴EF∥AC,故不合题意;C、∵∠1+∠3=180°,∴DE∥BC,故符合题意;D、∵∠3+∠C=180°,∴EF∥AC,故不合题意.故本题选:C.7.下列图形中,∠1与∠2是同位角的是()A.B.C.D.【详解】解:A、∠1与∠2不是同位角,故A不合题意;B、∠1与∠2不是同位角,故B不合题意;C、∠1与∠2是同位角,故C符合题意;D、∠1与∠2不是同位角,故D不合题意.故本题选:C.8.如图,点E在AB的延长线上,下列条件中能够判定AB∥CD的条件有()①∠BAD+∠ABC=180°;②∠1=∠2;③∠3=∠4;④∠E+∠5=∠ADC.A.①②B.②④C.①③D.③④【详解】解:∵∠BAD+∠ABC=180°,∴BC∥AD,故①不合题意;∵∠1=∠2,∴AB∥CD,故②符合题意;∵∠3=∠4,∴BC∥AD,故③不合题意;∵∠E+∠5=∠ADC,∠EDC+∠5=∠ADC,∴∠E=∠EDC,∴AB∥CD,故④符合题意.故本题选:B.9.给出下列说法:(1)两条直线被第三条直线所截,同位角相等;(2)相等的两个角是对顶角;(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;其中正确的有()A.0个B.1个C.2个D.3个【详解】解:(1)两条平行直线被第三条直线所截,同位角相等,故原命题是假命题;(2)相等的角不一定是对顶角,故原命题是假命题;(3)同一平面内,一条直线和两条平行线中的一条相交,则它与另一条也相交,故原命题是真命题;(4)从直线外一点到这条直线的垂线段长度,叫做该点到直线的距离,故原命题是假命题;其中正确的有1个.故本题选:B.10.下列说法:(1)同位角相等;(2)平行于同一条直线的两直线平行;(3)同旁内角相等,两直线平行;(4)同旁内角的两个角的平分线互相垂直.其中说法正确的个数为()A.1B.2C.3D.4【详解】解:(1)同位角不一定相等,故说法错误;(2)平行于同一直线的两直线平行,是平行公理的推论,故说法正确;(3)同旁内角互补,两直线平行,故说法错误;(4)同旁内角的两个角的平分线不一定互相垂直,故说法错误;综上,正确的说法只有(2).故本题选:A.11.如图,下列条件中不能判定AB∥CD的是()A.∠A+∠ADC=180°B.∠A=∠ADEC.∠ABD=∠BDC D.∠ADB=∠CBD【详解】解:A、当∠A+∠ADC=180°时,可得:AB∥CD,不合题意;B、当∠A=∠ADE时,可得:AB∥CD,不合题意;C、当∠ABD=∠BDC时,可得:AB∥CD,不合题意;D、当∠ADB=∠CBD时,可得:AD∥BC,符合题意.故本题选:D.12.如图,点D,E,F分别在△ABC的边BC,AB,AC上,连接DE,DF,在下列给出的条件中,不能判定AB∥DF的是()A.∠A+∠2=180°B.∠1=∠4C.∠1=∠A D.∠A=∠3【详解】解:A.若∠A+∠2=180°,则AB∥DF(同旁内角互补,两直线平行);B.若∠1=∠4,则AB∥DF(内错角相等,两直线平行);C.若∠1=∠A,则ED∥AC(同位角相等,两直线平行);D.∠A=∠3,则AB∥DF(同位角相等,两直线平行).故本题选:C.13.如图,图中同位角的对数、内错角的对数、同旁内角的对数,分别是()A.10,8,4B.11,7,5C.12,6,6D.13,5,7【详解】解:内错角有:∠GAB与∠ABC,∠BAC与∠ABM,∠FAC与∠ACB,∠BAC与∠ACN,∠EBC与∠ACB,∠ABC与∠MCH;同位角有∠GAF与∠ABM,∠GAB与∠MBE,∠BAC与∠EBC,∠FAC与∠ABC,∠GAF 与∠ACN,∠FAC与∠NCH,∠GAB与∠ACB,∠BAC与∠BCH,∠MBE与∠MCH,∠EBC 与∠NCH,∠ABM与∠ACB,∠ABC与∠ACN;同旁内角:∠BAC与∠ACB,∠BAC与∠ABC,∠ABC与∠ACB,∠GAB与∠ABM,∠EBC 与∠BCH,∠FAC与∠AC.故本题选:C.二.填空题14.小丽将两块完全相同的直角三角尺如图所示,拼在一起,沿着三角尺的斜边画出线段AB和CD,则小丽判定AB∥CD,她的依据是.【详解】解:由题意:∠BCD=∠ABC=30°,∴AB∥CD(内错角相等,两直线平行).故本题答案为:内错角相等,两直线平行.15.如图所示,直线AB、CD被直线EF所截,交点分别为M、N,则∠AMN的内错角是.【详解】解:根据内错角的定义,观察上图可知,∠AMN的内错角是∠DNM.故本题答案为:∠DNM.16.如图,直线c与a、b相交,∠1=35°,∠2=80°,要使直线a与b平行,直线a绕点O逆时针旋转的度数至少是.【详解】解:如图,∵∠3=∠1=35°时,a∥b,∴要使直线a与b平行,直线a绕点O逆时针旋转的度数至少是80°﹣35°=45°.故本题答案为:45°.17.如图,①∠1=∠2,②∠3+∠1=180°,③∠1=∠4,④∠2=∠5,则上述条件可以推出a∥b的是(写出所有正确的序号).【详解】解:如图,①当∠1=∠2时,由内错角相等,两直线平行得c∥d,故①不合题意;②当∠3+∠1=180°时,可得∠6+∠7=180°,由同旁内角互补,两直线平行得a∥b,故②符合题意;③当∠1=∠4时,可得∠1=∠6,由同位角相等,两直线平行得a∥b,故③符合题意;④当∠2=∠5时,由同位角相等,两直线平行得a∥b,故④符合题意.故本题答案为:②③④.18.一副三角板按如图所示(共定点A)叠放在一起,若固定三角板ABC,改变三角板ADE 的位置(其中A点位置始终不变),当∠BAD=°时,DE∥AB.【详解】解:由题意得∠ADE=30°,∠ACB=∠DAE=90°,①如图,当∠BAD=∠ADE=30°时,可得AB∥DE;②如图,当∠BAD+∠D=180°时,可得AB∥DE,则∠BAD=180°﹣∠D=150°.故本题答案为:30或150.19.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是.(只填序号).【详解】解:如图,∠2与∠3是直线AB、直线BC,被直线CD所截的一对内错角,因此①符合题意;∠2与∠B是直线CD、直线BC,被直线AB所截的一对同位角,因此②符合题意;∠A与∠B是直线AC、直线BC,被直线AB所截的一对同旁内角,因此③符合题意,∠A与∠ACB是直线AB、直线BC,被直线AC所截的一对同旁内角,因此④不合题意.故本题答案为:①②③.三.解答题20.填写下列空格:已知:如图,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.证明:∵CE平分∠ACD(已知),∴().∵∠1=∠2(已知),∴∠1=().∴AB∥CD().【详解】证明:∵CE平分∠ACD(已知),∴∠2=∠3(角平分线的定义),∵∠1=∠2(已知),∴∠1=∠3(等量代换),∴AB∥CD(内错角相等,两直线平行).故本题答案为:∠2=∠3;角平分线的定义;∠3;等量代换;内错角相等,两直线平行.21.如图,直线AB与射线DE相交于点O,∠BOE=130°,∠D=50°,AB与CD平行吗?为什么?【详解】解:AB与CD平行,理由如下:∵∠BOE=130°,∴∠AOD=∠BOE=130°,∵∠D=50°,∴∠AOD+∠D=130°+50°=180°,∴AB∥CD.22.如图,已知AC、BC分别是∠BAD、∠ABE的平分线,且∠1+∠2=∠ACB.求证:AD ∥BE.如图,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有∠1=∠2,∠3=∠4,请判断光线a与光线b是否平行,并说明理由.【详解】解:平行,理由如下:如图,∵∠1=∠2,∴∠5=∠6,∵∠3=∠4,∴∠3+∠5=∠4+∠6,∴a∥b.24.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,M为边AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.试说明BD与MF的位置关系,并说明理由.【详解】解:BD∥FM,理由如下:∵∠A=90°,ME⊥BC,∴∠AFM+∠AMF=90°,∠BEM=90°,∵∠A+∠ABC+∠BEM+∠AME=360°,∴∠ABC+∠AME=180°,∵BD平分∠ABC,MF平分∠AME,∴∠AMF+∠ABD=90°,∴∠AFM=∠ABD,∴BD∥FM.25.将△ABC纸片沿DE折叠,其中∠B=∠C.(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.【详解】解:(1)AB与DF平行,理由如下:由翻折得:∠DFC=∠C,又∵∠B=∠C,∴∠B=∠DFC,∴AB∥DF;(2)如图,连接GC,由翻折得:∠DGE=∠ACB,∵∠1+∠GDC=180°=∠DGC+∠DCG+∠GDC,∴∠1+=∠DGC+∠DCG,∵∠2+∠GEC=180°=∠EGC+∠ECG+∠GEC,∴∠2=∠EGC+∠ECG,∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB,∵∠B=∠ACB,∴∠1+∠2=2∠B.提升篇26.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)符合条件的其它所有可能度数为()A.60°和135°B.45°、60°、105°、135°C.30°和45°D.以上都有可能【详解】解:当AC∥DE时,∠BAD=∠DAE=45°;当BC∥AD时,∠DAB=∠B=60°;当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.故本题选:B.27.如图,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,CD与AB 在直线EF异侧.若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,当时间t的值为时,CD与AB平行.【详解】解:分三种情况:如图①,AB与CD在EF的两侧时,∵∠BAF=110°,∠DCF=60°,∴∠ACD=180°﹣60°﹣(6t)°=120°﹣(6t)°,∠BAC=110°﹣t°,要使AB∥CD,则∠ACD=∠BAF,即120°﹣(6t)°=110°﹣t°,解得:t=2;此时(180°﹣60°)÷6=20,∴0<t<20;②CD旋转到与AB都在EF的右侧时,∵∠BAF=110°,∠DCF=60°,∴∠DCF=360°﹣(6t)°﹣60°=300°﹣(6t)°,∠BAC=110°﹣t°,要使AB∥CD,则∠DCF=∠BAC,即300°﹣(6t)°=110°﹣t°,解得:t=38,此时(360°﹣60°)÷6=50,∴20<t<50;③CD旋转到与AB都在EF的左侧时,∵∠BAF=110°,∠DCF=60°,∴∠DCF=(6t)°﹣(180°﹣60°+180°)=(6t)°﹣300°,∠BAC=t°﹣110°,要使AB∥CD,则∠DCF=∠BAC,即(6t)°﹣300°=t°﹣110°,解得:t=38,此时t>50,∵38<50,∴此情况不存在.综上,当时间t的值为2秒或38秒时,CD与AB平行.故本题答案为:2秒或38秒.28.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):(1)若∠DCE=35°,求∠ACB的度数;(2)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)请你动手操作,现将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C 顺时针方向旋转,当0°<∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.【详解】解:(1)∵∠ECB=90°,∠DCE=35°,∴∠DCB=90°﹣35°=55°,∴∠ACB=∠ACD+∠DCB=90°+55°=145°;(2)∠ACB+∠DCE=180°,理由如下:∵∠ACB=∠ACD+∠DCB=90°+∠DCB,∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°;(3)存在,当∠ACE=30°时,AD∥BC,当∠ACE=∠E=45°时,AC∥BE,当∠ACE=120°时,AD∥CE,当∠ACE=135°时,BE∥CD,当∠ACE=165°时,BE∥AD.。
七年级数学苏科版下册课时练第7单元 《7.1探索直线平行的条件》(含答案解析)(1)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!课时练7.1探索直线平行的条件1.如图,下列说法错误的是()A.∵∠1=∠2,∴l3∥l4B.∵∠2+∠5=180°,∴l3∥l4C.∵∠1=∠4,∴l1∥l2D.∵∠1=∠3,∴l1∥l22.如图,下列说法错误的是()A.∠1与∠2是对顶角B.∠1与∠3是同位角C.∠1与∠4是内错角D.∠B与∠D是同旁内角3.如图所示,点E在BA的延长线上,点F在BC的延长线上,则下列条件中能判定AB∥CD的是()A.∠1=∠2B.∠DAE=∠BC.∠D+∠BCD=180°D.∠3=∠44.如图,直线a,b被第三条直线c所截.由“∠1=∠2”,得到“a∥b”的依据是()A.两直线平行,同位角相等B.同位角相等,两直线平行C.两直线平行,内错角相等D.内错角相等,两直线平行5.下列画出的直线a与b不一定平行的是()A.B.C.D.6.如图,直线a、b被直线c所截,下列说法不正确的是()A.∠1与∠5是同位角B.∠2与∠4是对顶角C.∠3与∠6是同旁内角D.∠5与∠2是内错角7.如图,不能推出a∥b的条件是()A.∠4=∠2B.∠3+∠4=180°C.∠1=∠3D.∠2+∠3=180°8.直线AB、BC、CD、EG如图所示.若∠1=∠2,则下列结论错误的是()A.AB∥CD B.∠EFB=∠3C.∠4=∠5D.∠3=∠59.如图,直线a、b被c所截,∠1=130°,当∠2=°时,a∥b.10.如图,请添加一个条件,使得AB∥CD,添加一个符合要求的条件,可以是.11.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC =180°.其中,能推出AB∥DC的条件为.12.如图,已知∠1=∠2,则图中互相平行的线段是.13.将一副三角板如图摆放,则∥,理由是.14.如图,下列条件中,能判断AB∥CD的是.A.∠AEC=∠C B.∠C=∠BFD C.∠BEC+∠C=180°D.∠C=∠B15.如图,∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD为75°,要使OD ∥AC,直线OD绕点O按逆时针方向至少旋转度.16.如图,点A,B,C,D在同一条直线上,若满足条件,则有CE∥DF,理由是.(要求:不再添加辅助线,只需填一个答案即可)17.如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是.18.结合图(不能自己标角),用符号语言表达“同旁内角互补,两直线平行”的推理形式:∵,∴.19.如图,把三角尺的直角顶点放在直线b上.若∠1=40°,则当∠2=°时,a ∥b.20.完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.证明:∵AB⊥AC(已知),∴∠=90°(),∵∠1=30°,∠B=60°(已知),∴∠1+∠BAC+∠B=(),即∠+∠B=180°,∴AD∥BC().21.补充完成下列证明过程,并填上推理的依据.已知:如图,∠BEC=∠B+∠C.求证:AB∥CD.证明:延长BE交CD于点F,则∠BEC=∠EFC+∠C.()又∵∠BEC=∠B+∠C,∴∠B=,(等量代换)∴AB∥CD.()22.如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,请说明AE∥GF的理由.解:因为∠BAG+∠AGD=180°(),∠AGC+∠AGD=180°(),所以∠BAG=∠AGC().因为EA平分∠BAG,所以∠1=().因为FG平分∠AGC,所以∠2=,得∠1=∠2(),所以AE∥GF().参考答案1.D.2.C.3.D.4.D.5.A.6.D.7.B.8.D.9.50.10.∠BEF=∠C(答案不唯一).11.①③④.12.AB∥CD.13.BC;ED;内错角相等,两直线平行.14.A、C.15.5.16.∠6=∠D(答案不唯一),同位角相等,两直线平行(答案不唯一).17.同位角相等,两直线平行.18.∠2+∠4=180°;a∥b.19.50.20.BAC;垂直的定义;180°;等量关系;BAD;同旁内角互补,两直线平行.21.三角形的外角等于与它不相邻的两内角的和,∠EFC,内错角相等,两直线平行.22.已知;邻补角的定义;同角的补角相等;∠BAG;角平分线的定义;∠AGC;等量代换;内错角相等,两直线平行.。
2020—2021年苏教版七年级数学下册《探索直线平行的条件》同步练习题及答案(精品试题).doc

苏教版2017-2018学年七年级下册7.1探索直线平行的条件同步练习 【基础演练】 一、选择题1.在如图给出的过直线外一点作已知直线l 1的平行线l 2的方法,其依据是( )A .同位角相等,两直线平行;B .内错角相等,两直线平行;C .筒旁内角互补,两直线平行;D .两直线平行,同位角相等.2.下列命题中,正确的是( )A .两条直线被第三条直线所截,同位角相等;B .相等的角是对顶角;C .在同一平面内,平行于同一条直线的两条直线平行;D .和为180°的两个角叫做邻补角.3.如图4.1-28,下列条件中,不能判断直线ι1//ι2的是( ) A .∠1=∠3; B .∠2=∠3; C .∠4=∠5; D .∠2+∠4=180°.5l 11l 21 2 4321873465图1a bc第1题图第3题图第4题图[4.如图,直线a 、b 与直线c 相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°,其中能判断a ∥b 的是 ( )A .①③;B .①③④;C .②④;D .①②③④.5.如图两条非平行的直线AB ,CD 被第三条直线EF 所截,交点为PQ ,那么这条直线将所在平面分成( )A.5个部分;B.6个部分;C.7个部分;D.8个部分.P 第(3)题QF E DCB A第5题图第6题图二、填空题6.如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是 ,理由是 .7.在同一平面内,两条直线的位置关系是_______或_______. 8.如图,∠1与∠C 是两条直线______被第三条直线______所截构成的______角.∠2与∠B 是两条直线______被第三条直线______所截构成的______角;∠B 与∠C 是两条直线______被第三条直线______所截构成的______角.9.如图,∠1、∠2、∠3、∠4、∠5、∠6中,是同位角的有__________________;是内错角的有__________________;是同旁内角的有__________________.10.如图,直线a 、b 被直线c 所截,若要a ∥b ,需增加条件 (填一个即可). 三、解答题321EDCB A第8题图432156第9题图 第10题图11.如图,若∠1+∠3=1800,能否得出AB ∥CD ?为什么?12.如图,已知∠1=450,∠2=1350,∠D =450,问:BC 与DE 平行吗?AB与CD呢?为什么?ABCD E F123第11题图ABCDEF1 2 第12题图【能力提升】13.如图已知∠1=∠2,再添上什么条件,可使AB∥CD成立?并说明理由.14.已知:如图,AB、BE、ED、CD依次相交于B、E、D,∠E=∠B+∠D. 试说明AB∥CD.21E NMCFDB A第13题图ECDBA第14题图参考答案1.A;2.C;3.B;4.D;5.C;6.∠α=∠β,内错角相等,两直线平行;7.平行或相交;8.AE、BC、CD、同位角,AE、BC、AB、内错角;9.∠1与∠3、∠4与∠6,∠2与∠4、∠3与∠5,∠2与∠5、∠1与∠6、∠3与∠4、∠1与∠2、∠5与∠6;10.答案不唯一,如∠1=∠3;11.解:AB∥CD.因为∠2与∠3互为补角,所以∠2+∠3=1800。
苏科版七年级数学下册第七章7.1-探索直线平行的条件同步练习(内含答案)

苏科版七年级数学下册第七章7.1 探索直线平行的条件同步练习(含答案)一、选择题1.如图K-1-1,直线a,b与l相交,∠1=120°,要使a∥b,则∠2的度数是() A.60°B.80°C.100°D.120°2.如图K-1-2,∠1和∠2不是同位角的是()图K-1-2 图K-1-1 图K-1-33.如图K-1-3所示,若∠1=∠2,则下列结论正确的是()A.AD∥BC B.AB∥CD C.AD∥EF D.EF∥BC4.如图K-2-1,下列判断错误的是()A.∠1和∠2是同旁内角B.∠3和∠4是内错角C.∠5和∠6是同旁内角D.∠5和∠8是同位角图K-2-15.如图K-2-2所示,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠7=180°.其中能判定a∥b的是()A.①②③④B.①③④ C.①③D.②④K-2-2二、填空题图6.如图K-1-4,∠1与∠B是直线________和________被直线________所截构成的同位角;∠2与∠A 是直线________和________被直线________所截构成的________角.7.如图K-1-5所示,如果∠B=∠1,那么根据“____________________________”,可得DE∥BC;如果∠B=∠2,那么根据“同位角相等,两直线平行”,可得________∥__________.8.如图K-1-6,∠A=70°,O是AB上的一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD需绕点O按逆时针方向至少旋转________°图K-1-4 K-1-5 图K-1-69.如图K-2-3,已知三角形ABC,延长BC至点E,再以C为顶点,在三角形ABC外画∠ACD=∠A,且点A,D在直线BC的同一侧,在所画图形中,∠A与____________是内错角;∠B与____________是同位角;∠ACB与____________是同旁内角.10.如图K-2-4,E是AD延长线上的一点,若添加一个条件,使BC∥AD,则可添加的条件为________.(任意添加一个符合题意的条件即可)图K-2-3三、解答题11.如图K-1-7,已知∠ADE=∠ABC,∠ABC=∠EFC,请找出图中互相平行的直线,并说明理由.图K-1-712.如图K-1-8所示,直线AB,CD分别与直线EF交于点G,H,∠AGE+∠DHE=180°,GM平分∠BGE,HN平分∠DHE交直线AB于点N,则GM与HN平行吗?为什么?图K-1-813.如图K-1-9,已知∠ABC=∠ACB,BD平分∠ABC交AC于点D,CE平分∠ACB交AB于点E,∠DBF=∠F,则EC与DF有怎样的位置关系?试说明理由.图K-1-914.如图K-2-5,已知∠AED=60°,∠EDB=30°,EF平分∠AED,EF与BD有怎样的位置关系?为什么?图K-2-515.如图K-2-6所示,已知BE平分∠ABC,CE平分∠BCD,且∠1+∠2=90°,则AB和CD平行吗?为什么?图K-2-616. 一副三角尺按图K-2-7①所示的方式拼接,固定三角尺ADC,将三角尺ABC按顺时针方向旋转一个大小为α(0°<α<180°)的角得到三角形AB′C′,示意图如图②所示.(1)当α为多少度时,能使图②中的AB′∥CD?请说明理由;(2)当α分别为多少度时,能使B′C′∥AD,AC′∥CD?(不必说明理由)教师详解详析一选择题1.[解析] D根据,同位角相等,两直线平行即可求解.2.D 3.C 4.C 5.C二.填空题6.DC AB BC BC AB AC同位7.同位角相等,两直线平行DB EF8.[答案] 10[解析] 因为OD′∥AC,所以∠AOD′=180°-∠A=110°,所以∠DOD′=∠AOD′-∠AOD=110°-100°=10°.故答案为10.9.∠ACD,∠ACE∠DCE,∠ACE∠A,∠B10.[答案] ∠C=∠CDE(答案不唯一)[解析] 要使BC∥AD,通常通过同位角、内错角、同旁内角来处理.所以可以是∠CBD=∠BDA或者∠C=∠CDE或者∠C+∠CDA=180°或者∠CBA+∠A=180°.三.解答题11.解:DE∥BC,EF∥AB.理由:因为∠ADE=∠ABC,所以DE∥BC(同位角相等,两直线平行).因为∠ABC=∠EFC,所以EF∥AB(同位角相等,两直线平行).12.解:GM与HN平行.理由如下:因为∠AGE+∠DHE=180°(已知),∠AGE+∠BGE=180°(邻补角的定义),所以∠BGE=∠DHE(同角的补角相等).因为GM平分∠BGE(已知),所以∠EGM=12∠BGE(角平分线的定义).因为HN平分∠DHE(已知),所以∠EHN=12∠DHE(角平分线的定义).所以∠EGM=∠EHN(等式的性质),所以GM∥HN(同位角相等,两直线平行).13.解:EC∥DF.理由如下:因为BD平分∠ABC,CE平分∠ACB,所以∠DBC=12∠ABC,∠BCE=12∠ACB.因为∠ABC=∠ACB,所以∠DBC=∠BCE.因为∠DBF=∠F,所以∠BCE=∠F,所以EC∥DF.14..解:EF∥BD.理由如下:因为∠AED=60°,EF平分∠AED,所以∠FED=30°.又因为∠EDB=30°,所以∠EDB=∠FED,所以EF∥BD(内错角相等,两直线平行).15..解:AB∥CD.理由:因为BE平分∠ABC,CE平分∠BCD,所以∠ABC=2∠1,∠BCD=2∠2.因为∠1+∠2=90°,所以∠ABC+∠BCD=2∠1+2∠2=2(∠1+∠2)=180°,所以AB∥CD. 16.解:(1)α为15°时,能使图②中的AB′∥CD.理由如下:因为∠BAC=45°,∠ACD=30°,而三角尺ABC按顺时针方向旋转一个大小为α的角得到三角形AB′C′,所以∠B′AC′=45°.当∠B′AC=∠ACD=30°时,AB′∥CD,此时∠CAC′=45°-30°=15°,即α为15°时,能使图②中的AB′∥CD.(2)当α=45°时,B′C′∥AD;当α=150°时,AC′∥DC.。
2020-2021学年苏科版七年级数学下册《7.1 探索直线平行的条件》 试卷

苏科版七年级数学下册《7.1 探索直线平行的条件》强化提优试卷(时间:60分钟满分:100分)一.选择题(共18题;共36分)1.如图,三条直线两两相交,其中同位角共有()A.0对B.6对C.8对D.12对(第1题) (第2题) (第3题) (第4题)2.如图,其中内错角的对数是()A.5B.2C.3D.43.如图,图中共有同旁内角()A.2对B.3对C.4对D.5对4.如图,按各组角的位置,判断错误的是()A.∠1和∠2是同旁内角B.∠3和∠4是内错角C.∠5和∠6是同旁内角D.∠5和∠8是同位角5.如图,已知∠1=∠B,则下列说法正确的是( )A. AB与CD平行B. AC与DE平行C. AB与CD平行,AC与DE也平行D. 以上说法都不正确(第5题) (第6题) (第7题) (第10题)6.如图,已知∠1=30°,则下列结论正确的有(B )①若∠2=30°,则AB∥CD;②若∠5=30°,则AB∥CD;③若∠3=150°,则AB∥CD;④若∠4=150°,则AB∥CD.A. 1个B. 2个C. 3个D. 4个7.如图,∠1=120°.要使a∥b,则∠2的度数是( )A. 60°B. 80°C. 100°D. 120°8.下列说法错误的是( )A. 同一平面内的两条直线不平行就相交B. 同位角相等,两直线平行C. 过直线外一点只有一条直线与已知直线平行D. 同位角互补,两直线平行9.两条直线被第三条直线所截.下列叙述正确的是()A.同位角一定不相等B.内错角的对顶角﹣定相等C.同位角的邻补角一定相等D.两对同旁内角的和一定大于180°10.下列图形中(如图),∠1和∠2是同位角的有()A.1个B.2个C.3个D.4个.11.如图所示,以下几种说法,其中正确的个数是()①∠3和∠4是同位角;②∠6和∠7是同位角;③∠4和∠5是内错角;④∠2和∠5是同旁内角;⑤∠2和∠7是同位角;⑥∠1和∠2是同位角.A.3个B.4个C.5个D.6个(第11题) (第12题) (第13题) (第14题) (第15题)12.如图,不能判定AB∥CD的是()A. ∠B=∠DCEB. ∠A=∠ACDC. ∠B+∠BCD=180°D. ∠A=∠DCE 13.如图,下列说法正确的是()A. 如果∠1和∠2互补,那么l1∥l2B. 如果∠2=∠3,那么l1∥l2C. 如果∠1=∠2,那么l1∥l2D. 如果∠2和∠3互补,那么l1∥l214..如图,下列条件中能判定直线l1∥l2的是()A. ∠1=∠2B. ∠1=∠5C. ∠1+∠3=180°D. ∠3=∠515.如图,下列条件中,能判断AB∥CD是()A.∠1=∠5 B.∠4=∠8 C.∠1+∠2+∠3+∠4=180°D.∠2=∠616.如图,FA⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是()A.由∠CAB=∠NCD,得AB∥CDB.由∠DCG=∠BAC,得AB∥CDC.由∠MAE=∠ACG,∠DCG=∠BAE,得AB∥CDD.由∠MAB=∠ACD,得AB∥CD(第16题) (第17题) (第18题)17.如图示,直线a、b都与直线c相交,下列条件中,能说明a∥b的是()①∠1=∠2;②∠2=∠7;③∠2=∠8;④∠1+∠4=180°.A.①②B.①②③C.①②④D.①②③④18.如图,下面四种沿AB折叠的方法中,不一定能判定两条边线a,b互相平行的是( ) A. 如图①,展开后测得∠1=∠2 B. 如图②,展开后测得∠1=∠2且∠3=∠4C. 如图③,测得∠1=∠2D. 如图④,展开后测得∠1+∠2=180°二、填空题(共8题;共16分)19.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为__ __.(第19题) (第20题) (第21题) (第22题)20.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD应绕点O逆时针旋转至少____.21.如图,请你写出一个能判定l1∥l2的条件:∠1=∠2或∠3=∠5或∠3+∠4= .22.如图,∠1+∠2=240°,∠1+∠3=240°,则b与c的关系是23.如图,直线a和直线b被直线c所截,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5=∠8.其中不能判断a∥b的条件的序号是.(第23题) (第24题) (第25题) (第26题)24.如图,直线MN分别交直线AB,CD于E,F,其中,∠AEF的对顶角是∠,∠BEF的同位角是∠.25.如图,∠2的内错角是∠C,∠3与∠B是内错角角,∠B的同旁内角是.26.如图,E是AD的延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为________________________________________________________(添加一个条件即可).三、解答题(共8题;共48分)27.如图所示.(1)指出与∠5为同位角的有哪些角,分别是哪两直线被哪一条直线所截形成的;(2)指出与∠2是同旁内角的有哪些角,分别是哪两直线被哪一条直线所截形成的?28.已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)∴∠1=∠ABC,∠2=∠ADC.()∵∠ABC=∠ADC,()∴∠=∠(等量代换)∵∠1=∠3()∴∠2=∠.()∴∥.()29.如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠ECG=90°﹣∠HAE.求证:BH∥CD.30.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明BE∥AC的理由.31.如图,∠ACE=∠FEC,∠EFB=∠A,试说明FB∥AE的理由.32.如图,EC⊥DG,垂足为C,∠BAF=50°,∠ACE=140°,则AB与CD平行吗?为什么?33.如图,在四边形ABCD中,∠A=∠D,∠B=∠C,试判断AD与BC的位置关系,并说明理由.,34..(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.,教师样卷一.选择题(共18题;共36分)1.如图,三条直线两两相交,其中同位角共有(D)A.0对B.6对C.8对D.12对解:根据同位角的定义可知:图中有12对同位角.故选D.(第1题) (第2题) (第3题) (第4题)2.如图,其中内错角的对数是(D)A.5B.2C.3D.4解:如右图所示,是内错角的有:∠2与∠3;∠1与∠3;∠2与∠4;∠1与∠4.故选:D.3.如图,图中共有同旁内角(D)A.2对B.3对C.4对D.5对解:由图知:∵∠BAC和∠B在截线AB的同侧,且都在被截直线AC、BC的内侧;∴∠BAC和∠B是同旁内角.∵∠BAE和∠B在截线AB的同侧,且都在被截直线DE、BC的内侧;∴∠BAE和∠B是同旁内角.∵∠C和∠B在截线BC的同侧,且都在被截直线AB、AC的内侧;∴∠C和∠B是同旁内角.同理可得:∠C与∠BAC以及∠C与∠DAC都是同旁内角,故图中共有同旁内角共5对.故选:D.4.如图,按各组角的位置,判断错误的是(C)A.∠1和∠2是同旁内角B.∠3和∠4是内错角C.∠5和∠6是同旁内角D.∠5和∠8是同位角解:A、∠1和∠2是同旁内角,说法正确;B、∠3和∠4是内错角,说法正确;C、∠5和∠6是同旁内角,说法错误;D、∠5和∠8是同位角,说法正确,故选:C.5.如图,已知∠1=∠B,则下列说法正确的是(A )A. AB与CD平行B. AC与DE平行C. AB与CD平行,AC与DE也平行D. 以上说法都不正确(第5题) (第6题) (第7题) (第10题)6.如图,已知∠1=30°,则下列结论正确的有(B )①若∠2=30°,则AB∥CD;②若∠5=30°,则AB∥CD;③若∠3=150°,则AB∥CD;④若∠4=150°,则AB∥CD. A. 1个 B. 2个 C. 3个 D. 4个7.如图,∠1=120°.要使a∥b,则∠2的度数是(D)A. 60°B. 80°C. 100°D. 120°8.下列说法错误的是(D)A. 同一平面内的两条直线不平行就相交B. 同位角相等,两直线平行C. 过直线外一点只有一条直线与已知直线平行D. 同位角互补,两直线平行9.两条直线被第三条直线所截.下列叙述正确的是(D)A.同位角一定不相等B.内错角的对顶角﹣定相等C.同位角的邻补角一定相等D.两对同旁内角的和一定大于180°解:根据题意知,A、当两直线平行时,同位角相等,故此选项错误;B、当两直线平行时,内错角相等,其对顶角也相等,故此选项错误;C、当两直线平行时,同位角相等,等角的补角也相等,故此选项错误;D、两对同旁内角的和为360°,故此选项正确;故选:D.10.下列图形中(如图),∠1和∠2是同位角的有(D)A.1个B.2个C.3个D.4个解:下列图形中(如图),∠1和∠2是同位角的有①②③④,共4个,故选:D.11.如图所示,以下几种说法,其中正确的个数是(B)①∠3和∠4是同位角;②∠6和∠7是同位角;③∠4和∠5是内错角;④∠2和∠5是同旁内角;⑤∠2和∠7是同位角;⑥∠1和∠2是同位角.A.3个B.4个C.5个D.6个解:①由同位角的概念可知,∠3和∠4是同位角,故本选项正确;②由同位角的概念可知,∠6和∠7不是同位角,故本选项错误;③由内错角的概念可知,∠4和∠5是内错角,故本选项正确;④由同旁内角的概念可知,∠2和∠5是同旁内角,故本选项正确;⑤由同位角的概念可知,∠2和∠7不是同位角,故本选项错误;⑥由同位角的概念可知,∠1和∠2是同位角,故本选项正确;则正确的个数有4个;故选:B.(第11题) (第12题) (第13题) (第14题) (第15题)12.如图,不能判定AB∥CD的是(D )A. ∠B=∠DCEB. ∠A=∠ACDC. ∠B+∠BCD=180°D. ∠A=∠DCE 13.如图,下列说法正确的是(D )A. 如果∠1和∠2互补,那么l1∥l2B. 如果∠2=∠3,那么l1∥l2C. 如果∠1=∠2,那么l1∥l2D. 如果∠2和∠3互补,那么l1∥l214..如图,下列条件中能判定直线l1∥l2的是(C )A. ∠1=∠2B. ∠1=∠5C. ∠1+∠3=180°D. ∠3=∠515.如图,下列条件中,能判断AB∥CD是(D)A.∠1=∠5 B.∠4=∠8 C.∠1+∠2+∠3+∠4=180°D.∠2=∠6解:A、当∠1=∠5时,AD∥BC,故此选项错误;B、当∠4=∠8时,AD∥BC,故此选项错误;C、当∠1+∠2+∠3+∠4=180°时,AD∥BC,故此选项错误;D、当∠2=∠6时,AB∥CD,故此选项正确.故选:D.16.如图,FA⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是(B)A.由∠CAB=∠NCD,得AB∥CDB.由∠DCG=∠BAC,得AB∥CDC.由∠MAE=∠ACG,∠DCG=∠BAE,得AB∥CDD.由∠MAB=∠ACD,得AB∥CD解:A、正确,同位角∠CAB=∠NCD,故AB∥CD;B、错误,∠DCN=∠BAC不是同位角,所以B不对;C、正确,∠MAE=∠ACG,∠DCG=∠BAE,可得同位角∠BAN=∠DCN,故AB∥CD;D、正确,同位角∠MAB=∠ACD,故AB∥CD.故选:B.(第16题) (第17题) (第18题)17.如图示,直线a、b都与直线c相交,下列条件中,能说明a∥b的是(C)①∠1=∠2;②∠2=∠7;③∠2=∠8;④∠1+∠4=180°.A.①②B.①②③C.①②④D.①②③④解:利用同位角相等,两直线平行可知①∠1=∠2,对;利用内错角相等,两直线平行可知②∠2=∠7,对;③对顶角∠2=∠8,无法判断直线的位置关系,错;利用旁内角互补,两直线平行可知④∠1+∠4=180°,对.故选:C.18.如图,下面四种沿AB折叠的方法中,不一定能判定两条边线a,b互相平行的是(C ) A. 如图①,展开后测得∠1=∠2 B. 如图②,展开后测得∠1=∠2且∠3=∠4C. 如图③,测得∠1=∠2D. 如图④,展开后测得∠1+∠2=180°三、填空题(共8题;共16分)19.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为__平行__.(第19题) (第20题) (第21题) (第22题)20.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD应绕点O逆时针旋转至少__12°__.21.如图,请你写出一个能判定l1∥l2的条件:∠1=∠2或∠3=∠5或∠3+∠4=180°.解:若∠1=∠2,根据内错角相等,两直线平行,若∠3=∠5,根据同位角相等,两直线平行,若∠3+∠4=180°,根据同旁内角互补,两直线平行,故答案为∠1=∠2或∠3=∠5或∠3+∠4=180°22.如图,∠1+∠2=240°,∠1+∠3=240°,则b与c的关系是b∥c解:∵∠1+∠2=240°,∠1+∠3=240°,∴∠2=∠3,∴b∥c.故答案为b∥c.23.如图,直线a和直线b被直线c所截,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5=∠8.其中不能判断a∥b的条件的序号是④.解:①∠1=∠2可根据同位角相等,两直线平行得到a∥b;②∠3=∠6可根据内错角相等,两直线平行得到a∥b;③∠4+∠7=180°可得∠6+∠7=180°根据同旁内角互补,两直线平行得到a∥b;④∠5=∠8不能判定a∥b;故答案为:④.(第23题) (第24题) (第25题) (第26题)24.如图,直线MN分别交直线AB,CD于E,F,其中,∠AEF的对顶角是∠BEM,∠BEF的同位角是∠DFN.解:∠AEF的对顶角是∠BEM,∠BEF的同位角是∠DFN.25.如图,∠2的内错角是∠C,∠3与∠B是内错角角,∠B的同旁内角是∠1或∠DAB或∠C.解:∠2和∠C在截线AD和BC的内部,被截线AC的两侧,故∠2的内错角是∠C,∠3与∠B在截线AE和BC的内部,被截线AB的两侧,故∠3与∠B是内错角,∠B的同旁内角是∠1或∠DAB或∠C.26.如图,E是AD的延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE(添加一个条件即可).四、解答题(共8题;共48分)27.如图所示.(1)指出与∠5为同位角的有哪些角,分别是哪两直线被哪一条直线所截形成的;(2)指出与∠2是同旁内角的有哪些角,分别是哪两直线被哪一条直线所截形成的?解:(1)当直线AB与BC被AC所截时,∠3与∠5是同旁内角;当直线AC与BC被AB 所截时,∠4与∠5是同旁内角;(2)当直线AB与BC被AC所截时,∠2与∠5是同旁内角;当直线AB与AC被BC所截时,∠4与∠2是同旁内角;28.已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)∴∠1=∠ABC,∠2=∠ADC.()∵∠ABC=∠ADC,()∴∠=∠(等量代换)∵∠1=∠3()∴∠2=∠.()∴∥.()解:证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)∴∠1=1/2∠ABC,∠2=1/2∠ADC.(角平分线的定义)∵∠ABC=∠ADC,(已知)∴∠1=∠2,(等量代换)∵∠1=∠3,(已知)∴∠2=∠3.(等量代换)∴AB∥DC.(内错角相等,两直线平行)故答案为:角平分线的定义;已知;1,2;已知;3,等量代换;AB,DC,内错角相等,两直线平行.29.如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠ECG=90°﹣∠HAE.求证:BH∥CD.证明:过点E作EF∥BH,∴∠HAE=∠AEF,∵AE⊥CE,∴∠AEC=90°即∠AEF+∠CEF=90°,∴∠HAE+∠CEF=90°,∴∠CEF=90°﹣∠HAE,∵∠ECG=90°﹣∠HAE,∴∠CEF=∠ECG,∴EF∥CD,∵EF∥BH,∴BH∥CD.30.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明BE∥AC的理由.【解】∵BE平分∠ABD,∴∠DBE=∠ABE.∵∠ABE=∠C,∴∠DBE=∠C,∴BE∥AC(同位角相等,两直线平行)31.如图,∠ACE=∠FEC,∠EFB=∠A,试说明FB∥AE的理由.【解】∵∠FEC+∠EFB+∠FOE=180°,∴∠EFB=∠180°-∠FEC-∠FOE.∵∠ACE+∠FBD+∠BOC=180°,∴∠FBD=180°-∠ACE-∠BOC.又∵∠ACE=∠FEC,∠FOE=∠BOC,∴∠EFB=∠FBD.又∵∠EFB=∠A,∴∠FBD=∠A,∴FB∥AE(同位角相等,两直线平行).32.如图,EC⊥DG,垂足为C,∠BAF=50°,∠ACE=140°,则AB与CD平行吗?为什么?【解】AB∥CD.理由如下:∵EC⊥DG,∴∠ECG=90°.又∵∠ACE=140°,∴∠ACG=50°.又∵∠BAF=50°,∴∠BAF=∠ACG,∴AB∥CD(同位角相等,两直线平行).33.如图,在四边形ABCD中,∠A=∠D,∠B=∠C,试判断AD与BC的位置关系,并说明理由.,【解】AD∥BC.理由如下:延长BA,CD相交于点E,则∠EAD+∠EDA+∠E=180°,∠B+∠C+∠E=180°,∴∠EAD+∠EDA=∠B+∠C.∵∠BAD=∠CDA,∴∠EAD=∠EDA.又∵∠B=∠C,∴∠EAD=∠B,∴AD∥BC(同位角相等,两直线平行).34..(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.,【解】(1)AB∥CD.理由如下:∵AB⊥EF,CD⊥EF,∴AB∥CD(在同一平面内,垂直于同一条直线的两条直线互相平行).(2)如解图,延长NO′交AB于点P.,∵OM平分∠EOB,O′N平分∠CO′F,∠EOB=∠CO′F=90°,∴∠EOM=∠FO′N=45°.又∵∠FO′N=∠EO′P,∴∠EOM=∠EO′P,∴OM∥O′P,即OM∥O′N(同位角相等,两直线平行).。
2020-2021学年苏科版七年级下册数学 7.1探索直线平行的条件 同步练习 (含解析)

7.1探索直线平行的条件同步练习一.选择题1.如图,点E在射线AB上,要AD∥BC,只需()A.∠A=∠CBE B.∠A=∠C C.∠C=∠CBE D.∠A+∠D=180°2.如图所示,下列判断错误的是()A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线B.若AD∥BC,则∠1=∠2=∠3C.若∠3+∠4+∠C=180°,则AD∥BCD.若∠2=∠3,则AD∥BC3.如图,能判断直线AB∥CD的条件是()A.∠1=∠2B.∠3=∠4C.∠3+∠4=180°D.∠1+∠3=180°4.如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG =∠D,则下列判断不一定成立的是()A.AB∥CD B.AD∥BGC.∠B=∠AEF D.∠BEF+∠EFC=180°5.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为()A.0B.1C.2D.36.木工师傅用图中的角尺画平行线,他依据的数学道理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.同旁内角互补,两直线平行D.以上结论都不正确7.如图,下列不能判定DF∥AC的条件是()A.∠A=∠BDF B.∠2=∠4C.∠1=∠3D.∠A+∠ADF=180°8.如图,下列条件能得到BD∥CE的是()A.∠1=∠2B.∠A=∠F C.∠ABD=∠2D.∠C=∠D 9.如图,∠CAD=∠ADB,下列结论正确的是()A.∠BAD=∠ADC B.∠ACD=∠ABD C.AB∥CD D.AC∥BD10.如图,点D,E,F分别是三角形ABC三边上的点,依次连接DE,EF,FD.则下列条件中能推出AF∥DE的是()A.∠A=∠EDF B.∠C=∠DEF C.∠AFD=∠FDE D.∠BDE=∠DEF 二.填空题11.如图,射线CA,直线BE交于点O,已知∠C=65°,请你添加一个条件,使得BE∥CD.12.如图,是小明学习三线八角时制作的模具,经测量∠2=105°,要使木条a与b平行,则∠1的度数必须是度.13.把两块形状、大小相同的三角板按照如图所示摆放,那么ED∥BC的依据是.14.如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转.15.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n 的有.(填序号)三.解答题16.如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.17.已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF∥BC.18.如图,在△ABC中,∠EGF+∠BEC=180°,∠EDF=∠C,试判断DE与BC的位置关系并说明理由.参考答案一.选择题1.解:要AD∥BC,只需∠A=∠CBE,故选:A.2.解:A、∵AD∥BC,∴∠2=∠3,又∵∠1=∠3,∴∠1=∠2,则BD是∠ABC的平分线;B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;C、∠3+∠4+∠C=180°,即同旁内角∠ADC+∠C=180°,则AD∥BC;D、内错角∠2=∠3,则AD∥BC.故选:B.3.解:∵∠4+∠5=180°,∠3+∠4=180°,∴∠3=∠5,∴AB∥CD,故选:C.4.解:A、∵∠B=∠DCG=∠D,∴AB∥DC,AD∥BG,正确,故本选项不符合题意;B、∵∠B=∠DCG=∠D,∴AB∥DC,AD∥BG,正确,故本选项不符合题意;C、根据AB∥DC,AD∥BG不能推出EF∥BC,所以不能推出∠B=∠AEF,错误,故本选项符合题意;D、∵AB∥CD,∴∠BEF+∠EFC=180°,正确,故本选项不符合题意;故选:C.5.解:∵∠1=∠2=60°,∴a∥b,∵∠2=∠3,∴b∥c,∴a∥c,故选:D.6.解:木工师傅用图中的角尺画平行线,他依据的数学道理是同位角相等,两直线平行,故选:A.7.解:A.∠A=∠BDF,由同位角相等,两直线平行,可判断DF∥AC;B.∠2=∠4,不能判断DF∥AC;C.∠1=∠3由内错角相等,两直线平行,可判断DF∥AC;D.∠A+∠ADF=180°,由同旁内角互补,两直线平行,可判断DF∥AC;故选:B.8.解:A、如图,∵∠1=∠3,1=∠2,∴∠2=∠3,∴BD∥CE;B、∠A=∠F,不能判定BD∥CE;C、∠ABD=∠2,不能判定BD∥CE;D、∠C=∠D,不能判定BD∥CE.故选:A.9.解:如图,∵∠CAD=∠ADB,∴AC∥BD(内错角相等,两直线平行).故选:D.10.解:如图,若∠AFD=∠FDE时,AF∥DE(内错角相等,两直线平行).故选:C.二.填空题11.解:添加的条件是∠AOE=∠C,∵∠AOE=∠C,∴BE∥CD.故答案为:∠AOE=∠C(答案不唯一).12.解:如图,∵∠2=105°,∴∠3=∠2=105°,∴要使b与a平行,则∠1+∠3=180°,∴∠1=180°﹣105°=75°.故答案为:75.13.解:由题意可得:∠DEF=∠ACB,则ED∥BC(内错角相等,两直线平行).故答案为:内错角相等,两直线平行.14.解:∵OD∥AC,∴∠BOD'=∠A=70°,∴∠DOD'=78°﹣70°=8°.故答案是:8°15.解:①∵∠1=25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;③∠1+∠2=90°,不能判断直线m∥n;④∠ACB=∠1+∠2,不能判断直线m∥n;⑤∠ABC=∠2﹣∠1,判断直线m∥n;故答案为:①⑤三.解答题16.证明:∵∠A=∠EDF(已知),∴AC∥DE(同位角相等,两直线平行),∴∠C=∠CGF(两直线平行,内错角相等).又∵∠C=∠F(已知),∴∠CGF=∠F(等量代换),∴BC∥EF(内错角相等,两直线平行).17.证明:∵∠DAC=∠ACB,∴AD∥BC,∵∠D+∠DFE=180°,∴AD∥EF,∴EF∥BC.18.解:DE∥BC.理由如下:∵∠EGF+∠BEC=180°,∴DF∥AC,∴∠BFD=∠C,∵∠EDF=∠C,∴∠EDF=∠BFD,∴DE∥BC.。
江苏省扬州市邗江实验学校七下7.2探索平行线的性质练习

7.2探索平行线的性质『学习目标』能正确运用平行线的性质进行简单的说理、计算.『例题精选』1.判断题(1).在同一平面内的两条直线被第三条直线所截,那么同位角相等.()(2).如图,如果∠A+∠B=180°,那么∠C+∠D=180°.()(3).两直线平行,同旁内角相等.()(4).如果两条平行线被第三条直线所截,则一对同旁内角的平分线互相垂直.()(5).两条直线被第三条直线所截,那么这两条直线平行.()2.已知,如图,直线a∥b, c∥d , ∠1=70°, 求∠2、∠3的度数.思路点拔:运用平行线的性质,观察图中有哪些相等的角。
『随堂练习』1.如图,直线a∥b,若∠1=118°,则∠2=_________.2.如图,已知AB∥CD,BC∥DE,那么∠B +∠D =_________.3.如图,已知CE是DC的延长线,AB∥DC,AD∥BC,若∠B=60°,则∠BCE=_________,∠D=_________,∠A=_________.第1题第2题第3题第1题第2题『课堂检测』1.下列说法,其中是平行线性质的是()①两直线平行,同旁内角互补②同位角相等,两直线平行③内错角相等,两直线平行④垂直于同一条直线的两直线平行A.①B.②③C.④D.①④2.已知∠1=∠2,∠3=125°,那么∠4的度数为()A.45°B.55°C.65°D.75°3.已知AB∥D E,∠A=150°,∠D=140°,则∠C的度数是()A.60°B.75°C.70°D.50°4.∠1=∠2,能判断AB∥DF吗?为什么?若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
7.2探索平行线的性质——课外作业『基础过关』1.两条直线被第三条直线所截,如果内错角相等,则同旁内角____.2.如图,已知∠1=30°,∠B =60°,AB ⊥AC ,⑴∠DAB +∠B =_____;⑵AB 与CD 平行吗?AD 与BC 平行吗?3.如果直线AB ∥CD ,EF ∥CD ,那么AB ∥EF ,这个推理的依据是___________.4.如图,直线a 、b 被直线c 所截形成了八个角,若a ∥b ,那么这八个角中与∠1相等的角共有 个(不含∠1).5.两条直线被第三条直线所截,则( )A 同位角相等B 内错角相等C 同旁内角互补D 同旁内角不一定互补6.若两条平行线被第三条直线所截,则同一对同位角的平分线互相( )A.垂直B.平行C.重合D.相交『能力训练』7.如图,AB ∥CD ,则( )A.∠1=∠5B.∠2=∠6C.∠3=∠7D.∠5=∠88.如图,AB ∥DE ,则∠A +∠C +∠D =( ) 第7 题 第8 题A .180°B .270°C .360°D .540°9.如图,∵AB ∥CD∴∠A +_______=180°( )∵BC ∥AD ,∴∠A +_____=180°( )∴∠B =_________.10.如图,BC ∥DE ,小颖用量角器分别画出∠ABC 、∠ADE 的角平分线BG 、DH ,想一想,小颖所画的这两条射线BG 和DH 会平行吗?为什么?(请你先用量角器画出这两条角平分线)『综合应用』11.填空并完成以下推理:已知,如图,∠1=∠ACB ,∠2=∠3,FH ⊥AB 于H ,求证:CD ⊥AB .解:∵∠1=∠ACB (已知)∴DE ∥BC ( )∴∠2= ( )∵∠2=∠3(已知) ∴∠3=∴CD ∥FH ( )C A BD EF H123∴∠BDC=∠BHF()又∵FH⊥AB(已知)∴。
苏科版七年级数学下册7.1探索直线平行的条件(1)学案及练习

7.1探索直线平行的条件班级 姓名 学号 学习目标1.会正确识别图形中的同位角。
2.经历观察、操作、想象、说理、交流等数学活动,进一步发展空间观念、有条理地思考和表达的能力。
学习难点对给定的两个角,能正确指出哪两条直线被哪一条直线所截。
教学过程一、操作引入:(1)利用三角板和直尺画平行线:(2)观察:∠1与∠2相等时,所画的直线a 、b 是否平行? (3)探索:∠1与∠2不相等,所画的直线a 、b 平行吗?定义:两条直线a 、b 被第三条直线所截而成的8个角中,像∠1与∠2这样的一对角称为同位角。
(4)猜想:图中还有其它的同位角吗?(5)结论:同位角相等,两直线平行。
解:(1)AB ∥CD因为∠1与∠C 是 AB 、CD 被AC 截成的同位角, 且∠1 =∠C 所以 AB ∥CD (2)AC ∥BD.因为∠2与∠C 是BD 、AC 被CD 截成的同位角,且∠2=∠C 所以AC ∥BD例3、如图直线a.b 被c 所截∠1=35°,∠2=145°。
问直线a 与b 平行吗?二、学会应用:例1、如图,∠1和∠2是同位角的是()例2、如图所示:∠1=∠C ,∠2=∠C 请你找出图中互相平行的直线,并说明理由。
N1PMQF EDC BA3142BA CD516432ABC DEFG【课后作业】班级 姓名 学号一、填空题1、如图(1),直线AB 、CD 被直线AE 所截,∠A 和______是同位角。
2、如图(2),∠3和∠9是直线________、_______被直线_______所截而成的______角;∠6和∠9是直线_____、______被直线________所截而成的_______角。
(1) (2)3、如图(3),直线AF 和AC 被直线EB 所截,∠EBC 的同位角是_______;直线DC 、AC 被直线AF 所截,∠F AC 的同位角是________。
4、 图(4)中的角,∠5和∠4是________角,∠5和∠7是________角。
七年级数学下册7_1探索直线平行的条件练习新版苏科版

探索直线平行的条件1.(1)如图①,∠1和∠2是直线________、________被直线________所截成的________角;∠2和∠3是直线________、________被直线________所截成的________角.(2)如图②,∠1和∠2是直线________、________被直线________所截成的________角;∠4和∠3是直线_____、________被直线________所截成的________角.2.如图,∠1和∠2是同位角的是 ( )3.如图,能与∠a构成同位角的角有 ( )A.4个 B.3个 C.2个 D.1个4.如图,如果∠D=∠EFC,那么 ( )A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF5.如图,填空:(1)若∠ADE=∠ABC,则________∥________,理由:________________________;(2)若∠EFC=∠ABC,则________∥________,理由:_____________________;6.如图,直线EF和AB、CD分别相交于K、H,且EG⊥AB,∠CHF=60º,∠E=30º,试说明AB∥CD.7.如图,下列说法正确的是 ( )A.∠3和∠4不是同位角 B.∠6和∠7是同位角C.∠1和∠2是同位角 D.∠5和∠6是同位角8.如图,下列说法正确的是 ( )A.因为∠1=∠3,所以EF∥GH B.因为∠1=∠2,所以AB∥CDC.因为∠1=∠3,所以AB∥CD D.因为∠2=∠4,所以EF∥GH9.如图,小明从A处出发沿北偏东60º方向行走至B处,又沿北偏西20º方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是 ( )A.右转80º B.左转80º C.右转100ºD.左转100º10.如图,∠1、∠2互为________角,它们________(填“相等”或“不相等”),理由:________________________________.11.如图,添加一个条件________ ,则AC∥DE;添加一个条件________,则CD∥E F.12.如图,∠1=45º,∠2=135º,l 1与l2平行吗?试说明理由.13.如图,∠1=∠2=115º,∠3=65º,图中有哪些直线互相平行?试说明理由.14.如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠ADE=∠AED.试说明DE∥FB.参考答案1.(1) AB DE BC 同位 BC EF DE 同位(2) BE CF AD 同位 CF AD BE 同位2.A 3.B 4.D5.(1) DE BC同位角相等,两直线平行(2)AB EF同位角相等,两直线平行6.略7.C 8.B 9.A10.同位不相等如果∠1=∠2,那么应有a∥b,但由图形可知a与b相交,所以∠1≠∠2 11.∠ACB=∠DEB或∠A=∠EDB ∠DCB=∠FEB或∠CDB=∠EFB12.平行理由略13.因为∠3=65º,所以∠HFA=115º,所以∠HFA=∠1.所以AB∥MD.同理,∠HFA=∠2,所以HC∥GE14.略。
江苏省扬州市邗江实验学校七年级数学下册-71探索直线平行的条件2练习无答案苏科版

**探索直线平行的条件(2)『学习目标』会正确识别图形中的内错角、同旁内角;并能运用“内错角相等,两直线平行”,“同旁内角相等,两直线平行”判断两直线平行.『例题精选』1.内错角:两条直线a 、b 被第三条直线所截而成的8个角中,像∠5、∠6这样的一对角称为内错角。
归纳内错角的特征:①∠5、∠6分别在直线a 、b 之间;②在直线c 的两旁。
指出图中其他内错角.同旁内角:两条直线a 、b 被第三条直线所截而成的8个角中,像∠4、∠6这样的一对角称为同旁内角。
同旁内角的特征:①∠4、∠6分别在直线a 、b 之间;②在直线c 的同旁。
指出图中其他同旁内角.2.如图,判断下列说法是否正确,(1) ∠1、∠5是一对内错角; (2) ∠4、∠5是一对同旁内角;(3) ∠1、∠3是一对内错角;(4) ∠3、∠4是一对同旁内角;(5) ∠2、∠5是对顶角; (6) ∠1、∠2是一对同旁内角;『随堂练习』1.两条直线被第三条直线所截,如果___________相等,那么这两条直线平行。
2.两条直线被第三条直线所截,如果___________互补,那么这两条直线平行。
3.两条直线被第三条直线所截,不能判定这两条直线平行的是( ) A.同位角相等 B.内错角相等落 C.同旁内角互补 D. 同旁内角相等4.如图,有一对相关的角相等或互补,就可以判断AB ∥EC,根据图中数字(或字母)标注的角写出几组这些相关的角。
『课堂检测』1.不能判定AD ∥BC 的条件是( )A.∠2=∠3B. ∠DAB +∠B =1800C.∠1=∠4D.∠D +∠BCD =18002.如图,∠1与∠2互补,则可得到( ) A. e ∥f B. a ∥b C. a ∥c D. b ∥c1 3 2 4 5l 2 l 3l 1 l 4 A BF E C 1 5 4 3 2 9 8 7 6 a b c 5 6 4 8 1 2 3 7 A D BC 1 4 32第3题A B CD 1 2 3 4 第1题a b ce f 1 2 第2题A BCD123 第4题3.如图,由下列条件可以判定哪两条直线平行,说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
『学习目标』
会正确识别图形中的同位角,并能运用“同位角相等,两直线平行”判断两直线平行. 『例题精选』
1. 同位角:两条直线a 、b 被第三条直线所截而成的8个角中,像∠1、∠2这样的一对角
称为同位角。
同位角的特征:
①∠1、∠2分别在直线a 、b 的上方,(在被截两直线的同方向); ②都在直线c 的同旁。
指出右图中其他同位角.
2.如图, ∠1=1350,∠D=450
,试问图中的AB ∥ED 吗?请说明理由。
思路点拔:寻找图形中的同位角.
3.如图,图中∠AEF 的同位角有哪几个?根据“同位角相等,两直线平行”,图中哪两个同位角相等,可得DE ∥BC ?哪两个同位角相等,可得EF ∥BD ?
『随堂练习』
1.若∠1,∠2是同位角,则它们之间的关系是( )
A.∠1=∠2
B. ∠1>∠2
C. ∠1<∠2
D. 无法确定 2.如图,直线c 与直线a 、b 相交,与∠1是同位角的是( ) A.∠2 B.∠3 C.∠4 D.∠5
3.如图,直线c 与直线a 、b 相交,哪一个角与∠1互补可推出a ∥b ( ) A.∠2或∠3 B.∠3或∠4 C.∠2或∠5 D.∠2或∠4
4.如图,与∠AEF 是同位角的角是__________________________. 『课堂检测』
1.如图,∠A 1A 2A 3=∠A 4,可得___∥___. 2.如图,要使A 2A 5∥A 1A 6,增加条件____________________________. 3.木工师傅用角尺在工件上画出两条垂线a 、b ,这两条 垂线平行吗?为什么?由此你能得到什么结论? 4.如图,∠1、∠2、∠3、∠4、∠5、∠6、 ∠7、∠8、∠9中,哪两个角是同位角。
a b c 5 6 4 8 1 2
3 7 A B D F C E 1 B C
c
2 1 b
a 3
5 4
2、3题图
A
B C D
O E
G F
A 1
A 2
A 4
A 3
A 6
A 5
第4题图
7.1探索直线平行的条件(1)——课外作业
『基础过关』
1.如图,∠1=∠2=∠3,则( )
A. AB ∥CD
B. AB ∥EF
C. CD ∥EF
D. AB ∥CD ∥EF 2.如图,要使AB ∥CD ,则( )
A. ∠A =∠B
B. ∠A =∠DCE
C. ∠B =∠ACD
D. ∠B =∠DCE
3.如图,已知三角形ABC ,∠A =800
, ∠B =∠C, 当∠ADE 为( )时, DE ∥BC
A. 450
B. 500
C. 550
D. 600
第1题 第2题 第3题
第4题
4.如图,已知∠1=∠2,要添加下列哪些条件可使CM ∥EN 成立。
( )
①∠DMN =∠FNB ②∠AMD =∠MNF ③∠DMN +∠FNB =1800
④DM ⊥AB FN ⊥AB A. ① B. ①② C. ①②③ D. ①②③④
5. 如(第2题)图,若∠B +∠DCE =1800
,则可得∠B =_________,进而可得_____ ∥______. 6. 如图,∠D 与_______是同位角,是直线_____、______被第三条_________所截而成的。
『能力训练』
7.如图,已知∠ADE =∠B ,则____∥_____,由_____=______,得DF ∥AC. 8.如图,要使DE ∥BC ,则需要添加条件______=_______,若∠A =∠BFC ,则_____∥______。
第6题 第7题
第8题
9.如图,∠1=∠C ,∠2 =∠C,请找出图中互相平行的直线,并说明理由.
『综合应用』
10.如图,(1)∠1=1200,∠4=1200
,则可判定 ____∥_____ ,根据是______________________.
(2)∠1=1200 , 由∠3=600
,得∠4=______ 则可判定 ____∥_____ 。
(3) ∠2=600
, ∠4=______ ,可判定a ∥b ,根据 是____________________________________.
A B
C D
1
2
E
C A ED F C B 3 2 1 A C
D B E
F C F A
D E B C F G 1 3 4 2 a b
c 1 2
4
3。
