电化学阻抗谱及其数据处理与解析
合集下载
电化学阻抗谱课件
电化学阻抗谱
电 化 学 阻 抗 谱 (Electrochemical Impedance Spectroscopy，简写为 EIS)，早期的电化 学文献中称为交流阻抗(AC Impedance)。 阻抗测量原本是电学中研究线性电路网 络频率响应特性的一种方法，引用到研 究电极过程，成了电化学研究中的一种 实验方法。
电化学阻抗谱
数据处理的途径
阻抗谱的数据处理有两种不同的途径： • 依据已知等效电路模型或数学模型的数据
处理途径 • 从阻纳数据求等效电路的数据处理途径
电化学阻抗谱
阻纳数据的非线性最小二乘法拟合原理
• 一般数据的非线性拟合的最小二乘法 若且G已是知变函量数X和的m具个体参表量达C式1，：C2，…,Cm的非线性函数，
5. 若在右括号后紧接着有 一个左括号与之相邻， 则在右括号中的复合元 件的级别与后面左括号 的复合元件的级别相同。 这两个复合元件是并联 还是串联，决定于这两 个复合元件的CDC是放 在奇数级还是偶数级的 括号中。
电化学阻抗谱
计算等效电路阻纳
根据上述５条规则，可以写出等效电路的电路 描述码（CDC），就可以计算出整个电路的阻 纳。
电化学阻抗谱
拟合过程主要思想如下 ：
假设我们能够对于各参量分别初步确定一个近似 值C0k , k = 1, 2, …, m，把它们作为拟合过程的初 始值。令初始值与真值之间的差值 C0k – Ck ＝ k, k = 1, 2, …, m， 于是根据泰勒展开定理可将Gi 围绕C0k , k = 1, 2, …, m 展开,我们假定各初始值C0k与其真值非常 接近，亦即，k非常小 (k = 1, 2, …, m)， 因此可 以忽略式中 k 的高次项而将Gi近似地表达为 ：
G=G( X,C1，C2，…,Cm ） 个就C2测，是在量…控要值，制根（C变据mn量的这>X数mn的值）个数，：测值使g量为1得，X值将g12，，来这X…些估2，，参定…g量mn,的。X个n估非时参定线，量值性测C代拟到1 入合，n 非线性函数式后计算得到的曲线（拟合曲线）与实 验有测随量机数误据差符，合不得能最从好测。量由值于直测接量计值算g出i (im=个1,参2,…量,，n) 而只能得到它们的最佳估计值。
电 化 学 阻 抗 谱 (Electrochemical Impedance Spectroscopy，简写为 EIS)，早期的电化 学文献中称为交流阻抗(AC Impedance)。 阻抗测量原本是电学中研究线性电路网 络频率响应特性的一种方法，引用到研 究电极过程，成了电化学研究中的一种 实验方法。
电化学阻抗谱
数据处理的途径
阻抗谱的数据处理有两种不同的途径： • 依据已知等效电路模型或数学模型的数据
处理途径 • 从阻纳数据求等效电路的数据处理途径
电化学阻抗谱
阻纳数据的非线性最小二乘法拟合原理
• 一般数据的非线性拟合的最小二乘法 若且G已是知变函量数X和的m具个体参表量达C式1，：C2，…,Cm的非线性函数，
5. 若在右括号后紧接着有 一个左括号与之相邻， 则在右括号中的复合元 件的级别与后面左括号 的复合元件的级别相同。 这两个复合元件是并联 还是串联，决定于这两 个复合元件的CDC是放 在奇数级还是偶数级的 括号中。
电化学阻抗谱
计算等效电路阻纳
根据上述５条规则，可以写出等效电路的电路 描述码（CDC），就可以计算出整个电路的阻 纳。
电化学阻抗谱
拟合过程主要思想如下 ：
假设我们能够对于各参量分别初步确定一个近似 值C0k , k = 1, 2, …, m，把它们作为拟合过程的初 始值。令初始值与真值之间的差值 C0k – Ck ＝ k, k = 1, 2, …, m， 于是根据泰勒展开定理可将Gi 围绕C0k , k = 1, 2, …, m 展开,我们假定各初始值C0k与其真值非常 接近，亦即，k非常小 (k = 1, 2, …, m)， 因此可 以忽略式中 k 的高次项而将Gi近似地表达为 ：
G=G( X,C1，C2，…,Cm ） 个就C2测，是在量…控要值，制根（C变据mn量的这>X数mn的值）个数，：测值使g量为1得，X值将g12，，来这X…些估2，，参定…g量mn,的。X个n估非时参定线，量值性测C代拟到1 入合，n 非线性函数式后计算得到的曲线（拟合曲线）与实 验有测随量机数误据差符，合不得能最从好测。量由值于直测接量计值算g出i (im=个1,参2,…量,，n) 而只能得到它们的最佳估计值。
电化学交流阻抗谱详解
第10页，共36页。
（C）三个时间常数
CPEDL
ROX
CPEOX
RSG
CPESG
第11页，共36页。
常见的三个时间常数的电路图
第12页，共36页。
1.4. 在腐蚀与防护中的应用
（1）两个时间常数的模型
金属腐蚀机制研究
金属本 体
腐蚀产物层
第13页，共36页。
研究不同镀层的钢材的腐蚀情况
第14页，共36页。
第17页，共36页。
保护膜
钝化膜 金属本体
第18页，共36页。
金属腐蚀区
钝化膜
保护膜
第19页，
1. 保护膜电容区
2. 保护膜阻抗区 3. 钝化膜电容区 4. 钝化膜阻抗区
电容随着频率减少而增加 阻抗不随频率而变化
第20页，共36页。
保护膜层的阻抗变化
钝化膜层阻抗变化
第21页，共36页。
第35页，共36页。
优点 缺点
线性极化法
1. 快速测定金属腐蚀体系瞬间腐蚀速度
2. 对腐蚀体系的影响和干扰很少，重现性好
3. 进行连续检测和现场监控，并且可以用于筛选金属材料和缓蚀剂
以及评价金属镀层的耐腐蚀性能
1. 另行测定或者从文献中选取的塔菲尔常数不能够反映腐蚀速度随 时间的变化情况
2. 线性极化区时近似的，准确度不是很高 3. 不适用于电导率较低的体系，应用范围受到限制
Tafel区
线性极 化区
Tafel区
过渡区
a
ba
lg
ia ic
k
bk
lg
ik ic
线性极化区
a
babk
ia
2.30（3 ba +bk）ic
（C）三个时间常数
CPEDL
ROX
CPEOX
RSG
CPESG
第11页，共36页。
常见的三个时间常数的电路图
第12页，共36页。
1.4. 在腐蚀与防护中的应用
（1）两个时间常数的模型
金属腐蚀机制研究
金属本 体
腐蚀产物层
第13页，共36页。
研究不同镀层的钢材的腐蚀情况
第14页，共36页。
第17页，共36页。
保护膜
钝化膜 金属本体
第18页，共36页。
金属腐蚀区
钝化膜
保护膜
第19页，
1. 保护膜电容区
2. 保护膜阻抗区 3. 钝化膜电容区 4. 钝化膜阻抗区
电容随着频率减少而增加 阻抗不随频率而变化
第20页，共36页。
保护膜层的阻抗变化
钝化膜层阻抗变化
第21页，共36页。
第35页，共36页。
优点 缺点
线性极化法
1. 快速测定金属腐蚀体系瞬间腐蚀速度
2. 对腐蚀体系的影响和干扰很少，重现性好
3. 进行连续检测和现场监控，并且可以用于筛选金属材料和缓蚀剂
以及评价金属镀层的耐腐蚀性能
1. 另行测定或者从文献中选取的塔菲尔常数不能够反映腐蚀速度随 时间的变化情况
2. 线性极化区时近似的，准确度不是很高 3. 不适用于电导率较低的体系，应用范围受到限制
Tafel区
线性极 化区
Tafel区
过渡区
a
ba
lg
ia ic
k
bk
lg
ik ic
线性极化区
a
babk
ia
2.30（3 ba +bk）ic
电化学交流阻抗谱分析
N.B. ∆i for
summed curve = ia + |∆ic| (∆ia=x)
E
i = polarization
resistance
ic
babk 2.30（3 ba
+b
）
k
1 Rp
（IE%=1-i /i ） 1.corr 2.corr
极化曲线在腐蚀与防护中应用
铝合金在含有氯离子 的乙二醇-硼酸溶液 中的腐蚀行为研究
氨基苯唑在3.5% NaCl中铜 镍合金的防腐蚀的研究
缓蚀剂的存在改变了阳极钝化过程， 使铜镍合金更加容易钝化，增加抗 腐蚀的性能。
超疏水层状双羟基对于铝合金防腐蚀研究
F.界面电容 （C）和 常相角元件（CPE）
G.电感 （L）
通常每一个界面之间都会存 在一个电容。
A.溶液电阻 （Rs）
B. 极化阻抗 （Rp） C. 电荷转移电阻 （Rct） D. 扩散电阻 （Zw） E. 界面电容 （C）和 常相角元件（CPE）
注意事项：
1. Rp近似Rct+Zw，但不是完全的相等 2. 极化阻抗通过计划曲线也可以得到 （腐蚀
电位出切线的斜率）
1.2.2. 等效电路元件
R 阻抗 C 电容 L 电感 W 无限扩散阻抗 O 有限扩散阻抗 Q 常相角元件
导纳
阻抗
1.3 等效电路 判断电容。阻 抗等结构元件
（A）一个时间常数
Rct 或Rp
Cdl Rs
Nyquist图
相位图
大致表征几个 时间常数
Zw
Rct Cdl Rs
Nyquist图
ic
ba bk 2.30（3 ba
1 +bk）R p
电化学阻抗谱原理应用及谱图分析
电化学阻抗谱原理应用及谱图分析电化学阻抗谱原理应用及谱图分析电化学阻抗谱(Electrochemical Impedance Spectroscopy，EIS)是一种测量电化学系统的电化学行为的方法，它通过测量系统对于正弦电压或电流的响应，来研究电化学反应过程中的阻抗变化。
EIS广泛应用于材料科学、化学工程、电池研究、腐蚀研究和生物医学等领域。
EIS的原理是利用正弦电压或电流去激励待测电化学系统，并测量响应信号的振幅和相位，然后将这些数据在频率域或时间域中进行分析，从而得到电化学系统的等效电路模型，如电阻、电容、电感等等，这些参数可以反映出系统的结构、特性和电化学反应的动力学信息。
EIS的主要作用是在电化学反应的过程中研究电荷传递、离子传输、质量传递等复杂的反应机理，可以通过建立电化学反应动力学模型，分析电极表面化学反应动力学参数，优化电极材料和电解液配方，提高电化学反应效率。
以下是两个例子，说明EIS的应用及注意事项：锂离子电池的研究：EIS广泛应用于电池的研究和开发中，通过测量电池的电化学阻抗谱来评估电池的性能和寿命。
例如，在锂离子电池中，电解质的性质和电极材料的表面形貌对电池性能有很大影响。
利用EIS可以评估电池的内部电阻、扩散系数等参数，进而优化电池设计和材料配方。
注意事项是，需要确保电池在测量时处于稳态，并控制好测量温度和电压等参数。
金属腐蚀的研究：EIS也被广泛应用于金属腐蚀的研究中，通过测量金属表面的电化学阻抗谱，可以评估金属表面的保护膜的质量和稳定性，了解金属腐蚀的机制，同时也可以评估防腐涂层的性能。
注意事项是，需要确保测量条件稳定，避免干扰，同时应选择合适的电解液和电极材料。
电化学阻抗谱（EIS）的谱图是通过测量电化学系统对于正弦电压或电流的响应所得到的。
谱图提供了电化学系统的等效电路模型，这些参数可以反映出系统的结构、特性和电化学反应的动力学信息。
在谱图的分析过程中，需要注意以下几点：峰的位置和形状:电化学阻抗谱中的峰代表电化学体系中不同的特征和反应机理。
电化学阻抗谱与数据处理与解析
G 0, k 1,2,...,m Ck
可以写成一个由m个线性代数方程所组成的 方程组
从方程组可以解出 1 , 2 , .... , m 的值，将其代 入下式，即可求得Ck 的估算值：
Ck ＝ C0k + k, k = 1, 2, …, m，
计算得到的参数估计值Ck比C0k 更接近于真值。 在这种情况下可以用由上式 求出的Ck作为新的初 始值C0k，重复上面的计算，求出新的Ck 估算值 这样的拟合过程就称为是“均匀收敛”的拟合过 程。
按规则(1)将这一等效电路表示为： R CE-1 按规则(2)，CE-1可以表示为（Q CE-2）。因此 整个电路可进一步表示为： R(Q CE-2) 将复合元件CE-2表示成(Q(W CE-3))。整个等效 电路就表示成： R(Q(W CE-3)) 剩下的就是将简单的复合元件 CE-3 表示出来。 应表示为（RC）。于是电路可以用如下的 CDC 表示： R(Q(W(RC)))
电化学阻抗谱方法是一种以小振幅的 正弦波电位（或电流）为扰动信号的电化 学测量方法。由于以小振幅的电信号对体 系扰动，一方面可避免对体系产生大的影 响，另一方面也使得扰动与体系的响应之 间近似呈线性关系，这就使测量结果的数 学处理变得简单。
同时，电化学阻抗谱方法又是一种频 率域的测量方法，它以测量得到的频率范 围很宽的阻抗谱来研究电极系统，因而能 比其他常规的电化学方法得到更多的动力 学信息及电极界面结构的信息。
0 0 G G( X, C1 , C0 , C 2 m ) + 1 m
G Ck C k
S (gi - G i ) (gi - G i 1
2 0 1 1
n
n
m
G Ck ) 2 Ck
电化学阻抗谱技术与数据解析
1. lg Z − lg 图
Z = Z 2 + Z 2
Z=
RL2
+
1 2Cd2
=
1 + (RLCd )2 Cd
lg
Z
=
1 2
lg
1
+
(
RLCd
)
2
−
lg
−
lg
Cd
讨论：（1）高频区 lim →
1 2
lg
1
+
(RLCd
)2
=
lg
RLCd
则
lg Z = lg Cd
与频率无关
lg Z 是一条平行于横轴 lg 的水平线。
电解池等效电路分析
电解池等效电路的简化
1.实际测量体系中可忽略不计CAB、RA、RB
Cd
C’d
A
RfБайду номын сангаас
Rl
R‘f
B
电解池等效电路分析
2. 为突出研究电极界面阻抗，可采取措施以 略去辅助电极界面阻抗，即“辅”采用大 面积铂电极→大面积。相当于“辅”为短路
，所测得的实际等效电路阻抗只反映“研 ”界面阻抗与Rl ：
Z
Rp
= arctan RpCd
1+ (RpCd )2
溶液电阻可以忽略时电化学极化的电化学阻抗谱
Z
=
1
+
Rp2Cd ( RpCd
)2
tan
=
Z Z
=
RpCd
RpCd
=
Z Z
将此式代入 Z 中有:
Z
=
1
+
Rp (Z
)
2
=
Z = Z 2 + Z 2
Z=
RL2
+
1 2Cd2
=
1 + (RLCd )2 Cd
lg
Z
=
1 2
lg
1
+
(
RLCd
)
2
−
lg
−
lg
Cd
讨论：（1）高频区 lim →
1 2
lg
1
+
(RLCd
)2
=
lg
RLCd
则
lg Z = lg Cd
与频率无关
lg Z 是一条平行于横轴 lg 的水平线。
电解池等效电路分析
电解池等效电路的简化
1.实际测量体系中可忽略不计CAB、RA、RB
Cd
C’d
A
RfБайду номын сангаас
Rl
R‘f
B
电解池等效电路分析
2. 为突出研究电极界面阻抗，可采取措施以 略去辅助电极界面阻抗，即“辅”采用大 面积铂电极→大面积。相当于“辅”为短路
，所测得的实际等效电路阻抗只反映“研 ”界面阻抗与Rl ：
Z
Rp
= arctan RpCd
1+ (RpCd )2
溶液电阻可以忽略时电化学极化的电化学阻抗谱
Z
=
1
+
Rp2Cd ( RpCd
)2
tan
=
Z Z
=
RpCd
RpCd
=
Z Z
将此式代入 Z 中有:
Z
=
1
+
Rp (Z
)
2
=
(完整版)电化学曲线极化曲线阻抗谱分析
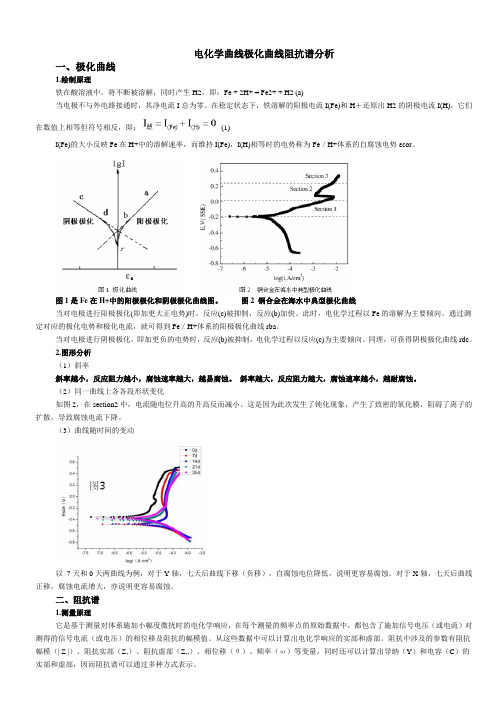
电化学曲线极化曲线阻抗谱分析一、极化曲线1.绘制原理铁在酸溶液中，将不断被溶解，同时产生H2，即：Fe + 2H+ = Fe2+ + H2 (a)当电极不与外电路接通时，其净电流I总为零。
在稳定状态下，铁溶解的阳极电流I(Fe)和H＋还原出H2的阴极电流I(H)，它们在数值上相等但符号相反，即：(1)I(Fe)的大小反映Fe在H+中的溶解速率，而维持I(Fe)，I(H)相等时的电势称为Fe／H+体系的自腐蚀电势εcor。
图1是Fe在H+中的阳极极化和阴极极化曲线图。
图2 铜合金在海水中典型极化曲线当对电极进行阳极极化(即加更大正电势)时，反应(c)被抑制，反应(b)加快。
此时，电化学过程以Fe的溶解为主要倾向。
通过测定对应的极化电势和极化电流，就可得到Fe／H+体系的阳极极化曲线rba。
当对电极进行阴极极化，即加更负的电势时，反应(b)被抑制，电化学过程以反应(c)为主要倾向。
同理，可获得阴极极化曲线rdc。
2.图形分析（1）斜率斜率越小，反应阻力越小，腐蚀速率越大，越易腐蚀。
斜率越大，反应阻力越大，腐蚀速率越小，越耐腐蚀。
（2）同一曲线上各各段形状变化如图2，在section2中，电流随电位升高的升高反而减小。
这是因为此次发生了钝化现象，产生了致密的氧化膜，阻碍了离子的扩散，导致腐蚀电流下降。
（3）曲线随时间的变动以7天和0天两曲线为例，对于Y轴，七天后曲线下移（负移），自腐蚀电位降低，说明更容易腐蚀。
对于X轴，七天后曲线正移，腐蚀电流增大，亦说明更容易腐蚀。
二、阻抗谱1.测量原理它是基于测量对体系施加小幅度微扰时的电化学响应，在每个测量的频率点的原始数据中，都包含了施加信号电压（或电流）对测得的信号电流（或电压）的相位移及阻抗的幅模值。
从这些数据中可以计算出电化学响应的实部和虚部。
阻抗中涉及的参数有阻抗幅模（| Z |）、阻抗实部（Z,）、阻抗虚部（Z,,）、相位移（θ）、频率（ω）等变量，同时还可以计算出导纳（Y）和电容（C）的实部和虚部，因而阻抗谱可以通过多种方式表示。
电化学阻抗谱及其数据处理与解析-张鉴清
• 总的说来，电化学阻抗谱的线性条件只 能被近似地满足。我们把近似地符合线 性条件时扰动信号振幅的取值范围叫做 线性范围。每个电极过程的线性范围是 不同的，它与电极过程的控制参量有关。 如：对于一个简单的只有电荷转移过程 的电极反应而言，其线性范围的大小与 电极反应的塔菲尔常数有关，塔菲尔常 数越大，其线性范围越宽。
按规则（１）将这一等效电路表示为： R CE-1 按规则（２）， CE-1 可以表示为（ Q CE-2 ）。因 此整个电路可进一步表示为： R(Q CE-2) 将复合元件CE-2表示成(Q(W CE-3))。整个等效电 路就表示成： R(Q(W CE-3)) 剩下的就是将简单的复合元件 CE-3 表示出来。应 表示为（ RC ）。于是电路可以用如下的 CDC 表示： R(Q(W(RC)))
G( ) = G’( ) + j G”( )
阻抗或导纳的复平面图
• 复合元件(RC)频响特征的阻抗复平面图
导纳平面图
Байду номын сангаас
阻抗波特（Bode）图
复合元件(RC)阻抗波特图
两个时间常数等效电路A
两个时间常数等效电路B
阻抗的复平面图
阻抗波特（Bode）图
电化学阻抗谱的基本条件
• 因果性条件:当用一个正弦波的电位信号对电极 系统进行扰动，因果性条件要求电极系统只对 该电位信号进行响应。 • 线性条件。当一个状态变量的变化足够小，才 能将电极过程速度的变化与该状态变量的关系 作线性近似处理。 • 稳定性条件。对电极系统的扰动停止后，电极 系统能回复到原先的状态，往往与电极系统的 内部结构亦即电极过程的动力学特征有关。
从阻纳数据求等效电路的数据处理方法
电路描述码 我们对电学元件、等效元件，已经用符号 RC、RL或RQ表示了R与C、L或Q串联组 成的复合元件，用符号 (RC) 、(RL) 或 (RQ)表示了R与C、L或Q并联组成的复合 元件。现在将这种表示方法推广成为描述 整个复杂等效电路的方法， 即形成电路 描述码 (Circuit Description Code, 简写为 CDC)。规则如下：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2f ω为角频率，f 用Hz表示。
精品课件
精品课件
R 电阻 C 电容 L 电感 Q (CPE) 常相位角元件 W (Warburg扩散阻抗) T 双曲正切 固体电解质 O 双曲余切 有限扩散
精品课件
Q (CPE) 常相位角元件
Constant Phase Angle Element 界面双电层 - 界面电容 弥散效应 圆心下降的半圆 0<n<1
稳定性条件：对电极系统的扰动停止后，电极 系统能恢复到原先的状态，往往与电极系统的 内部结构亦即电极过程的动力学特征有关。
精品课件
因果性条件
当用一个正弦波的电位信号对电极系统进行扰动 ，因果性条件要求电极系统只对该电位信号进行 响应。这就要求控制电极过程的电极电位以及其 它状态变量都必须随扰动信号——正弦波的电位 波动而变化。控制电极过程的状态变量则往往不 止一个，有些状态变量对环境中其他因素的变化 又比较敏感，要满足因果性条件必须在阻抗测量 中十分注意对环境因素的控制。
精品课件
总的说来，电化学阻抗谱的线性条件只能被近 似地满足。我们把近似地符合线性条件时扰动 信号振幅的取值范围叫做线性范围。每个电极 过程的线性范围是不同的，它与电极过程的控 制参量有关。如：对于一个简单的只有电荷转 移过程的电极反应而言，其线性范围的大小与 电极反应的塔菲尔常数有关，塔菲尔常数越大 ，其线性范围越宽。
精品课件
阻纳是一个频响函数，是一个当扰动与响应都是 电信号而且两者分别为电流信号和电压信号时的 频响函数。
由阻纳的定义可知，对于一个稳定的线性系统 ，当
响与扰动之间存在唯一的因果性时，GZ与GY 都决定于系 统的内部结构，都反映该系统的频响特性，故在GZ与GY 之间存在唯一的对应关系：GZ = 1/ GY
法，引用到研究电极过程，成了电化学
研究中的一种实验方法。
精品课件
电化学阻抗谱方法是一种以小振幅的 正弦波电位（或电流）为扰动信号的电化 学测量方法。由于以小振幅的电信号对体 系扰动，一方面可避免对体系产生大的影 响，另一方面也使得扰动与体系的响应之 间近似呈线性关系，这就使测量结果的数 学处理变得简单。
是 的正弦波电信号（电流或电压）Y，Y即是 响应信号。Y与X之间的关系可以用下式来表示：
Y = G(w) X
如果扰动信号X为正弦波电流信号，而Y为正弦 波电压信号，则称G为系统M的阻抗 (Impedance) 。如果扰动信号X为正弦波电压信号，而Y为正弦 波电流信号，则称G为系统M的导纳
(Admittance)。
精品课件
Z
1 Y0
jn
n = 0 , 1/Y0 单位 Ω
n = -1, H
n = 1, F
n = 1/2, S.Sec1/2
Z 相当 Z(R) , Z(L), Z(C), Z(W),
精品课件
阻抗或导纳的复平面图
复合元件(RC)频响特征的阻抗复平面图Байду номын сангаас
精品课件
导纳平面图
阻抗波特（Bode）图
复合元件RC阻抗波特图
精品课件
两个时间常数等效电路A
精品课件
两个时间常数等效电路B
精品课件
阻抗的复平面图
精品课件
阻抗波特（Bode）图
精品课件
电化学阻抗谱的基本条件
因果性条件：当用一个正弦波的电位信号对电 极系统进行扰动，因果性条件要求电极系统只 对该电位信号进行响应。
线性条件：当一个状态变量的变化足够小，才 能将电极过程速度的变化与该状态变量的关系 作线性近似处理。
电化学阻抗测量技术与 电化学阻抗谱的数据处理
理论与应用
浙江大学
张鉴清
精品课件
电化学阻抗谱
电化学阻抗谱
(Electrochemical
Impedance
Spectroscopy，简写为 EIS)，早期的电
化 学 文 献 中 称 为 交 流 阻 抗 (AC
Impedance)。阻抗测量原本是电学中研
究线性电路网络频率响应特性的一种方
精品课件
电化学阻抗谱的数据处理与解析
1. 数据处理的目的与途径 2. 阻纳数据的非线性最小二乘法拟合原理 3. 从阻纳数据求等效电路的数据处理方法
G是一个随频率变化的矢量，用变量为频率 f 或
其角
频率 的复变函数表示。故G的一般表示式可以写为：
G(w) = G’(w) + j G”(w)
精品课件
精品课件
精品课件
不同电路元件的阻抗表示不同
R
C
L
Z
R
1 ( j ) jc c
jL
，
Y
1 R
jc
1 ( j ) jL L
j 1
j 2 1 虚数单位；
在对不可逆电极过程进行测量时，要近似地满 足稳定性条件往往是很困难的。这种情况在使 用频率域的方法进行阻抗测量时尤为严重，因 为用频率域的方法测量阻抗的低频数据往往很 费时间，有时可长达几小时。这么长的时间中 ，电极系统的表面状态就可能发生较大的变化 。
精品课件
稳定结构示意图
精品课件
不稳定结构示意图
精品课件
稳定性条件
对电极系统的扰动停止后，电极系统能否恢复到 原先的状态，往往与电极系统的内部结构亦即电 极过程的动力学特征有关。一般而言，对于一个 可逆电极过程，稳定性条件比较容易满足。电极 系统在受到扰动时，其内部结构所发生的变化不 大，可以在受到小振幅的扰动之后又回到原先的 状态。
精品课件
精品课件
同时，电化学阻抗谱方法又是一种频 率域的测量方法，它以测量得到的频率范 围很宽的阻抗谱来研究电极系统，因而能 比其他常规的电化学方法得到更多的动力 学信息及电极界面结构的信息。
精品课件
阻抗与导纳
对于一个稳定的线性系统M，如以一个
角频率为 的正弦波电信号（电压或电流）X为
激励信号（在电化学术语中亦称作扰动信号）输 入该系统，则相应地从该系统输出一个角频率也
精品课件
线性条件
由于电极过程的动力学特点，电极过程速度随 状态变量的变化与状态变量之间一般都不服从 线性规律。只有当一个状态变量的变化足够小 ，才能将电极过程速度的变化与该状态变量的 关系作线性近似处理。故为了使在电极系统的 阻抗测量中线性条件得到满足，对体系的正弦 波电位或正弦波电流扰动信号的幅值必须很小 ，使得电极过程速度随每个状态变量的变化都 近似地符合线性规律，才能保证电极系统对扰 动的响应信号与扰动信号之间近似地符合线性 条件。