北京大学2016-2017学年第2学期高等数学A期末考试试卷
北京市西城区2016— 2017学年度第二学期期末考试高二理科数学试卷(word版含答案)

北京市西城区2016— 2017学年度第二学期期末试卷高二数学(理科)2017.7试卷满分:150分考试时间:120分钟一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9. 曲线1y x=在2x =处切线的斜率为______. 10. 4)12(xx -展开式中的常数项是_______.(用数字作答) 11. 离散型随机变量ξ的分布列为:且2=ξE ,则1p =_________;2p = _________.12. 某班举行的联欢会由5个节目组成,节目演出顺序要求如下: 节目甲不能排在第一个,并且节目甲必须和节目乙相邻,则该班联欢会节目演出顺序的编排方案共有_____种.13. 若函数32()f x ax ax x =-+在区间(1,0)-上恰有一个极值点,则a 的取值范围是_____.14. 已知,对于任意x ∈R ,e xax b ≥+均成立.①若e a =,则b 的最大值为__________;②在所有符合题意的b a ,中,a b -的最小值为_________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)在数列{}n a 中,11=a ,121++=+n n a nn a ,其中1,2,3,n =.(Ⅰ) 计算2a ,3a ,4a ,5a 的值;(Ⅱ) 根据计算结果,猜想{}n a 的通项公式,并用数学归纳法加以证明.16.(本小题满分13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为21与p ,且乙投球2次均未命中的概率为161. (Ⅰ)求甲投球2次,至少命中1次的概率;(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.17.(本小题满分13分)已知函数32()3f x x ax =+.(Ⅰ) 若1-=a ,求)(x f 的极值点和极值; (Ⅱ) 求)(x f 在[0,2]上的最大值.18.(本小题满分13分)一个袋中装有黑球,白球和红球共n (*n ∈N )个,这些球除颜色外完全相同. 已知从袋中任意摸出1个球,得到黑球的概率是52. 现从袋中任意摸出2个球. (Ⅰ) 用含n 的代数式表示摸出的2球都是黑球的概率,并写出概率最小时n 的值.(直接写出n 的值)(Ⅱ) 若15=n ,且摸出的2个球中至少有1个白球的概率是74,设X 表示摸出的2个球中红球的个数,求随机变量X 的分布列和数学期望. 19.(本小题满分14分)已知函数2()f x ax bx =+和x x g ln )(=.(Ⅰ) 若1==b a ,求证:()f x 的图象在()g x 图象的上方;(Ⅱ) 若()f x 和()g x 的图象有公共点P ,且在点P 处的切线相同,求a 的取值范围. 20.(本小题满分14分)已知函数()(1)e xf x x =-.(Ⅰ)求()f x 的单调区间;(Ⅱ)证明:当0>a 时,方程()f x a =在区间(1,)+∞上只有一个解;(Ⅲ)设()()ln(1)h x f x a x ax =---,其中0>a .若()0h x ≥恒成立,求a 的取值范围.北京市西城区2016 — 2017学年度第二学期期末试卷高二数学(理科)参考答案及评分标准2017.7一、选择题:本大题共8小题,每小题5分,共40分.1. A ;2.D ;3. C ;4. B ;5. C ;6. D ;7. C ;8. B . 二、填空题:本大题共6小题,每小题5分,共30分.9. 41-; 10. 24; 11. ,4211; 12. 42; 13. 1(,)5-∞-; 14. 0;1e-.注:一题两空的题目,第一空2分,第二空3分.三、解答题:本大题共6小题,共80分. 15.(本小题满分13分)解: (Ⅰ) 根据已知,24a =;99a =;416a =;525a =. …………… 4分 (Ⅱ)猜想2n a n =. …………… 6分证明:① 当1=n 时,由已知11=a ;由猜想,2111a ==,猜想成立. …………… 8分②假设当k n =(k ∈*N )时猜想成立,即2k a k =, ……………10分则1+=k n 时, 221)1(1212+=+⨯+=++=+k k kk a k k a k k . 所以,当1n k =+时,猜想也成立. ……………12分 由①和②可知,2n a n =对任意的*n ∈N 都成立. ……………13分 16.(本小题满分13分)解:(Ⅰ)设“甲投球一次命中”为事件A , 则11(),()22P A P A ==. …………… 2分 故甲投球2次至少命中1 次的概率为31()1()()4P A A P A P A -⋅=-=. …………5分(Ⅱ) 设“乙投球一次命中”为事件B .由题意得1()(1)(1)16P B B p p ⋅=--=, ……………7分解得43=p 或45(舍去), 所以31(),()44P B P B ==. ……………8分甲、乙两人各投球2次共命中3次有两种情况:甲中两次,乙中一次;甲中一次,乙中两次. ……………9分甲中两次,乙中一次的概率为1211313()()()()2224432P A P A C P B P B =⨯⨯⨯⨯=.…11分 甲中一次,乙中两次的概率为1211339()()()()2224432C P A P A P B P B =⨯⨯⨯⨯=.…12分事件“甲中两次,乙中一次”与“甲中一次,乙中两次”是互斥的,所以,所求事件概率为93332328+=. 所以甲、乙两人各投2次,共命中3次的概率为38. ……………13分 17.(本小题满分13分)解:(Ⅰ) 当1-=a 时,32()3f x x x =-,2()36f x x x '=-. ……………2分令2()360f x x x '=-=,得0x =或2x =.(f '……………4分所以,函数)(x f 的极大值点为0x =,极大值为0;极小值点为2x =,极小值为4-.……………6分(Ⅱ) 2()363(2)f x x ax x x a '=+=+. ……………7分①当0a =时,()0f x '≥(仅当0x =时,()0f x '=),函数)(x f 是增函数,)(x f 在[0,2]上的最大值为(2)8128f a =+=. ……………8分②当0a >时,在区间(0,)+∞上()0f x '>,函数)(x f 是增函数.)(x f 在[0,2]上的最大值为(2)812f a =+. ……………10分③当0a <时,()f x '与()f x 在区间(0,)+∞上的情况如下:……………11分此时,(0)0f =,(2)812f a =+. 当8120a +>,即203a -<<时,)(x f 在[0,2]上的最大值为(2)812f a =+. 12分当8120a +≤,即23a ≤-时,)(x f 在[0,2]上的最大值为(0)0f =. ………13分 综上,当23a ≤-时,)(x f 在[0,2]上的最大值为0;当23a >-时,)(x f 在[0,2]上的最大值为812a +.18.(本小题满分13分) 解:(Ⅰ) 依题意有n 52个黑球. 记“摸出的2球都是黑球”为事件A , 则225222(1)41055()(1)2525n n C n n n P A C n n n --===--. ……………4分()P A 最小时5=n . ……………5分(Ⅱ) 依题意有21565⨯=个黑球. ……………6分 设袋中白球的个数为x (个),记“从袋中任意摸出两个球至少得到一个白球”为事件B ,则2152154()17xC P B C -=-=,整理得2291200x x -+=,解得5x =或24x =(舍). ……………8分 所以袋中红球的个数为4(个).随机变量X 的取值为0,1,2. ……………9分21121511(0)21C P X C ===;1141121544(1)105C C P X C ===;242152(2)35C P X C ===. X…………12分数学期望114428012211053515EX =⨯+⨯+⨯=. ……………13分 19.(本小题满分14分)解:(Ⅰ) 当1==b a 时,2()f x x x =+.设2()ln h x x x x =+-,0x >. ……………1分则2121(21)(1)()21x x x x h x x x x x +--+'=+-==, ……………2分所以,在区间1(0,)2上()0h x '<,()h x 是减函数;在区间1(,)2+∞上()0h x '>,()h x 是增函数. ……………4分所以,()h x 的最小值为1()2h =31ln 42-,又31ln 042->,所以()0h x >恒成立. 即()f x 的图象在()g x 图象的上方. ……………5分(Ⅱ) 设00(,)P x y ,其中00x >.由已知()2f x ax b '=+,1()g x x'=. 因为在点P 处的切线相同, 所以2000000012,,ln ax b y ax bx y x x +==+=. ……………7分 消去0,b y 得200ln 10ax x +-=.根据题意,方程200ln 10ax x +-=有解. ……………8分设2()ln 1F x ax x =+-,则()F x 在(0,)+∞上有零点.2121()2ax F x ax x x+'=+=, 当0a ≥时,()0F x '>,函数()F x 在(0,)+∞上单调递增. 当1a ≥时,(1)10F a =-≥,110F =+-=≤,()F x 有零点. 当01a ≤<时,(1)10F a =-≤,22(e )e 10F a =+>,()F x 有零点. …11分 当0a <时,令()0F x '=,解得x =(F '与在区间上的情况如下:令302≥,得 312ea ≥-. 此时(1)10F a =-<.所以()F x 有零点. ……………13分 综上,所求a 的取值范围为31[,)2e -+∞. ……………14分20.(本小题满分14分)解:(Ⅰ)由已知()e (1)e e xxxf x x x '=+-=. ……………2分所以,在区间(,0)-∞上()0f x '<,函数()f x 在(,0)-∞上单调递减,在区间(0,)+∞上()0f x '>,函数()f x 在区间(0,)+∞上单调递增. ……………4分 (Ⅱ)设()()(1)e xg x f x a x a =-=--,0a >. ……………5分()e x g x x '=,由(Ⅰ)知,函数()g x 在区间(0,)+∞上单调递增.且(1)0g a =-<,11(1)e(e 1)0a a g a a a a +++=-=->.所以,()g x 在区间(1,)+∞上只有一个零点,方程()f x a =在区间(1,)+∞上只有一个解. ……………8分 (Ⅲ)设()()ln(1)h x f x a x ax =---,0>a ,()h x 定义域为}1|{>x x ,()e (e )[(1)e ]111x x x a a x h x x a x x a x x x '=--=-=-----, ……………9分 令()0h x '=,则(1)e 0xx a --=,由(Ⅱ)知,()(1)e xg x x a =--在区间(1,)+∞上只有一个零点,是增函数, 不妨设()g x 的零点为0x ,则00(1)e 0xx a --=, ……………11分 所以,()h x '与()h x 在区间(0,)+∞上的情况如下:所以,函数()h x 的最小值为0()h x ,00000()(1)e ln(1)x h x x a x ax =----,由00(1)e 0xx a --=,得001e x a x -=,所以00000()e ln ln e e x x x a ah x a ax a a a =⋅--=-. ……………13分依题意0()0h x ≥,即ln 0a a a -≥,解得0e a <≤,所以,a 的取值范围为(0,e]. ……………14分。
2016-2017学年北京市西城区高二(下)期末数学试卷(理科)(解析版)

2016-2017学年北京市西城区高二(下)期末数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.(5分)复数等于()A.﹣1+i B.﹣1﹣i C.1+i D.1﹣i2.(5分)已知函数f(x)=e﹣x,则f'(﹣1)=()A.B.C.e D.﹣e3.(5分)甲射击命中目标的概率为,乙射击命中目标的概率为.现在两人同时射击目标,则目标被击中的概率是()A.B.C.D.4.(5分)已知函数f(x)在R上可导,其部分图象如图所示,设,则下列不等式正确的是()A.a<f'(1)<f'(2)B.f'(1)<a<f'(2)C.f'(2)<f'(1)<a D.f'(1)<f'(2)<a5.(5分)直线y=x与抛物线y=x2所围成的封闭图形的面积是()A.B.C.D.6.(5分)用1,2,3,4四个数字组成无重复数字的四位数,其中比2000大的偶数共有()A.16个B.12个C.9个D.8个7.(5分)函数在区间[0,π]上的最大、最小值分别为()A.π,0B.C.D.8.(5分)5个黑球和4个白球从左到右任意排成一排,下列说法正确的是()A.总存在一个白球,它右侧的白球和黑球一样多B.总存在一个黑球,它右侧的白球和黑球一样多C.总存在一个黑球,它右侧的白球比黑球少一个D.总存在一个白球,它右侧的白球比黑球少一个二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.(5分)曲线y=在x=2处的切线的斜率为.10.(5分)展开式中的常数项是.11.(5分)离散型随机变量ξ的分布列为:且Eξ=2,则p1=;p2=.12.(5分)某班举行的联欢会由5个节目组成,节目演出顺序要求如下:节目甲不能排在第一个,并且节目甲必须和节目乙相邻,则该班联欢会节目演出顺序的编排方案共有种.13.(5分)若函数f(x)=ax3﹣ax2+x在区间(﹣1,0)上恰有一个极值点,则a的取值范围是.14.(5分)已知,对于任意x∈R,e x≥ax+b均成立.①若a=e,则b的最大值为;②在所有符合题意的a,b中,a﹣b的最小值为.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(13分)在数列{a n}中,a1=1,,其中n=1,2,3,….(Ⅰ)计算a2,a3,a4,a5的值;(Ⅱ)根据计算结果,猜想{a n}的通项公式,并用数学归纳法加以证明.16.(13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为与p,且乙投球2次均未命中的概率为.(Ⅰ)求甲投球2次,至少命中1次的概率;(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.17.(13分)已知函数f(x)=x3+3ax2.(Ⅰ)若a=﹣1,求f(x)的极值点和极值;(Ⅱ)求f(x)在[0,2]上的最大值.18.(13分)一个袋中装有黑球,白球和红球共n(n∈N*)个,这些球除颜色外完全相同.已知从袋中任意摸出1个球,得到黑球的概率是.现从袋中任意摸出2个球.(Ⅰ)用含n的代数式表示摸出的2球都是黑球的概率,并写出概率最小时n的值.(直接写出n的值)(Ⅱ)若n=15,且摸出的2个球中至少有1个白球的概率是,设X表示摸出的2个球中红球的个数,求随机变量X的分布列和数学期望.19.(14分)已知函数f(x)=ax2+bx和g(x)=lnx.(Ⅰ)若a=b=1,求证:f(x)的图象在g(x)图象的上方;(Ⅱ)若f(x)和g(x)的图象有公共点P,且在点P处的切线相同,求a的取值范围.20.(14分)已知函数f(x)=(x﹣1)e x.(Ⅰ)求f(x)的单调区间;(Ⅱ)证明:当a>0时,方程f(x)=a在区间(1,+∞)上只有一个解;(Ⅲ)设h(x)=f(x)﹣aln(x﹣1)﹣ax,其中a>0.若h(x)≥0恒成立,求a的取值范围.2016-2017学年北京市西城区高二(下)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.(5分)复数等于()A.﹣1+i B.﹣1﹣i C.1+i D.1﹣i【解答】解:复数=.故选:A.2.(5分)已知函数f(x)=e﹣x,则f'(﹣1)=()A.B.C.e D.﹣e【解答】解:根据题意,函数f(x)=e﹣x,则f′(x)=﹣e﹣x,则f′(﹣1)=﹣e﹣(﹣1)=﹣e;故选:D.3.(5分)甲射击命中目标的概率为,乙射击命中目标的概率为.现在两人同时射击目标,则目标被击中的概率是()A.B.C.D.【解答】解:设事件A表示“甲射击命中目标”,事件B表示“乙射击命中目标”,则P(A)=,P(B)=,目标被击中的对立事件是甲、乙二人都没有击中,∴目标被击中的概率:p=1﹣[1﹣P(A)][1﹣P(B)]=1﹣=.∴目标被击中的概率是.故选:C.4.(5分)已知函数f(x)在R上可导,其部分图象如图所示,设,则下列不等式正确的是()A.a<f'(1)<f'(2)B.f'(1)<a<f'(2)C.f'(2)<f'(1)<a D.f'(1)<f'(2)<a【解答】解:由图象可知,函数的增长越来越快,故函数在该点的斜率越开越大,∵,∴f′(1)<a<f′(2),故选:B.5.(5分)直线y=x与抛物线y=x2所围成的封闭图形的面积是()A.B.C.D.【解答】解:由,可得交点的坐标为(0,0),A(1,1),∴所求的封闭图形的面积为S=(x﹣x2)dx=(x2﹣x3)=﹣=,故选:C.6.(5分)用1,2,3,4四个数字组成无重复数字的四位数,其中比2000大的偶数共有()A.16个B.12个C.9个D.8个【解答】解:根据题意,要求的四位数比2000大,则其首位数字必须是2、3、4中一个,则分3种情况讨论:①、首位数字为2时,其个位数字必须为4,将1、3全排列,安排在中间两个数位,有A22=2种情况,即此时有2个比2000大的偶数,②、首位数字为3时,其个位数字必须为2或4,有2种情况,将剩下的2个数字全排列,安排在中间两个数位,有A22=2种情况,即此时有2×2=4个比2000大的偶数,③、首位数字为4时,其个位数字必须为2,将1、3全排列,安排在中间两个数位,有A22=2种情况,即此时有2个比2000大的偶数,则一共有2+4+2=8个比2000大的偶数,故选:D.7.(5分)函数在区间[0,π]上的最大、最小值分别为()A.π,0B.C.D.【解答】解:函数,∴f′(x)=1﹣cos x;令f′(x)=0,解得cos x=,又x∈[0,π],∴x=;∴x∈[0,)时,f′(x)<0,f(x)单调递减;x∈(,π]时,f′(x)>0,f(x)单调递增;且f()=﹣sin=﹣1,f(0)=0,f(π)=π;∴函数f(x)在区间[0,π]上的最大、最小值分别为π和﹣1.故选:C.8.(5分)5个黑球和4个白球从左到右任意排成一排,下列说法正确的是()A.总存在一个白球,它右侧的白球和黑球一样多B.总存在一个黑球,它右侧的白球和黑球一样多C.总存在一个黑球,它右侧的白球比黑球少一个D.总存在一个白球,它右侧的白球比黑球少一个【解答】解:5为奇数,4为偶数,故总存在一个黑球,它右侧的白球和黑球一样多,故选:B.二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.(5分)曲线y=在x=2处的切线的斜率为﹣.【解答】解:∵y=∴y′=﹣则y′=﹣∴曲线y =在x =2处的切线的斜率为﹣. 故答案为:﹣ 10.(5分)展开式中的常数项是 24 . 【解答】解:展开式的通项公式为 T r +1=•24﹣r•(﹣1)r •x 4﹣2r,令4﹣2r =0,求得r =2,可得常数项是24, 故答案为:24.11.(5分)离散型随机变量ξ的分布列为:且E ξ=2,则p 1=;p 2=.【解答】解:∵E ξ=2,∴由离散型随机变量ξ的分布列,得:,解得,P 2=.故答案为:,.12.(5分)某班举行的联欢会由5个节目组成,节目演出顺序要求如下:节目甲不能排在第一个,并且节目甲必须和节目乙相邻,则该班联欢会节目演出顺序的编排方案共有 42 种.【解答】解:根据题意,节目甲不能排在第一个,则甲必须排在第二、三、四、五的位置, 分2种情况讨论:①、若甲排在第二、三、四的位置, 甲的排法有3种,由于节目甲必须和节目乙相邻,乙可以排在甲之前或之后,有2种情况,对于剩下的3个节目,进行全排列,安排在剩余的3个空位中,有A 33=6种情况, 则此时有3×2×6=36种编排方案;②、若甲排在第五的位置,甲的排法只有1种,由于节目甲必须和节目乙相邻,乙只能排在甲之前,即第四个位置,有1种情况,对于剩下的3个节目,进行全排列,安排在前面3个空位中,有A33=6种情况,则此时有1×1×6=6种编排方案;则该班联欢会节目演出顺序的编排方案共有36+6=42种;故答案为:42.13.(5分)若函数f(x)=ax3﹣ax2+x在区间(﹣1,0)上恰有一个极值点,则a的取值范围是(﹣∞,﹣).【解答】解:由题意,f′(x)=3ax2﹣2ax+1,a=0显然不成立;a≠0时,对称轴为x=∉(﹣1,0),f′(x)在(﹣1,0)为单调函数,当f′(﹣1)f′(0)<0即5a+1<0时,函数f(x)在区间(﹣1,0)上恰有一个极值点,解得:a<﹣,a∈(﹣∞,﹣),故答案为:(﹣∞,﹣).14.(5分)已知,对于任意x∈R,e x≥ax+b均成立.①若a=e,则b的最大值为0;②在所有符合题意的a,b中,a﹣b的最小值为﹣.【解答】解:①若a=e,则对于任意x∈R,e x≥ex+b均成立,即为b≤e x﹣ex恒成立,由y=e x﹣ex的导数为y′=e x﹣e,当x>1时,y′>0,函数y递增;当x<1时,y′<0,函数y递减.可得x=1处,函数y取得最小值,且为0,则b≤0,即b的最大值为0;②对于任意x∈R,e x≥ax+b均成立,即有b≤e x﹣ax恒成立,由y=e x﹣ax的导数为y′=e x﹣a,当a≤0时,y′>0恒成立,函数y递增,无最小值;当a>0时,当x>lna时,y′>0,函数y递增;当x<lna时,y′<0,函数y递减.可得x=lna处,函数y取得最小值,且为a﹣alna,则b≤a﹣alna,即a﹣b≥alna,由f(a)=alna的导数为f′(a)=lna+1,可得a>时,f′(a)>0,f(a)递增;0<a<时,f′(a)<0,f(a)递减.可得a=时,f(a)取得最小值﹣.则a﹣b的最小值为﹣.故答案为:0,﹣.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(13分)在数列{a n}中,a1=1,,其中n=1,2,3,….(Ⅰ)计算a2,a3,a4,a5的值;(Ⅱ)根据计算结果,猜想{a n}的通项公式,并用数学归纳法加以证明.【解答】解:(Ⅰ)根据题意,数列{a n}中,a1=1,,则a2=×a1+1=4,a3=×a2+1=9,a4=×a3+1=16,a5=×a4+1=25,(Ⅱ)有(Ⅰ)可以猜测:a n=n2,用数学归纳法证明:①、当n=1时,a1=12=1,即n=1时,a n=n2成立,②、假设n=k(k≥1)时,结论成立,即a k=k2,n=k+1时,a k+1=×a k+1=(k+1)2,即n=1时,结论也成立,根据①②可得:a n=n2成立.16.(13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为与p,且乙投球2次均未命中的概率为.(Ⅰ)求甲投球2次,至少命中1次的概率;(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.【解答】解:(Ⅰ)由题意,甲投球2次,都没有命中的概率为•=,故甲至少命中1次的概率为1﹣=.(Ⅱ)∵乙投球2次均未命中的概率为(1﹣p)•(1﹣p)=,∴p=.若甲、乙两人各投球2次,求两人共命中3次,则甲只有一次没有命中、乙2次全部命中,或乙只有一次没有命中、甲2次全部命中.而甲只有一次没有命中、乙2次全部命中的概率为••(1﹣)•=,而乙只有一次没有命中、甲2次全部命中的概率为••=,故两人共命中3次的概率为+=.17.(13分)已知函数f(x)=x3+3ax2.(Ⅰ)若a=﹣1,求f(x)的极值点和极值;(Ⅱ)求f(x)在[0,2]上的最大值.【解答】解:(Ⅰ)a=﹣1时,f(x)=x3﹣3x2,f′(x)=3x2﹣6x=3x(x﹣2),令f′(x)>0,解得:x>2或x<0,令f′(x)<0,解得:0<x<2,故f(x)在(﹣∞,0)递增,在(0,2)递减,在(2,+∞)递增;故x=0是极大值点,极大值是f(0)=0,x=2是极小值点,极小值是f(2)=﹣4;(Ⅱ)f′(x)=3x2+6ax=3x(x+2a),a≥0时,f′(x)≥0,f(x)在[0,2]递增,故f(x)max=f(2)=12a+8;﹣1<a<0时,﹣2<2a<0,令f′(x)>0,解得:x>﹣2a,令f′(x)<0,解得:0<x<﹣2a,故f(x)在[0,﹣2a)递减,在(﹣2a,2]递增,若a=﹣时,f(x)max=0;若﹣1<a<﹣时,f(0)>f(2),可得f(x)max=f(0)=0;若﹣<a<0时,f(0)<f(2),可得f(x)max=f(2)=12a+8;a≤﹣1时,2a≤﹣2,f(x)在[0,2]递减,故f(x)max=f(0)=0.18.(13分)一个袋中装有黑球,白球和红球共n(n∈N*)个,这些球除颜色外完全相同.已知从袋中任意摸出1个球,得到黑球的概率是.现从袋中任意摸出2个球.(Ⅰ)用含n的代数式表示摸出的2球都是黑球的概率,并写出概率最小时n的值.(直接写出n的值)(Ⅱ)若n=15,且摸出的2个球中至少有1个白球的概率是,设X表示摸出的2个球中红球的个数,求随机变量X的分布列和数学期望.【解答】解:(Ⅰ)依题意有个黑球,记“摸出的2球都是黑球”为事件A,则P(A)===∴P(A)最小时n=5.(Ⅱ)依题意有=6个黑球,设袋中白球的个数为x个,记“从袋中任意摸出两个球到少得到一个白球”为事件B,则P(B)=1﹣=,整理,得:x2﹣29x+120=0,解得x=5或x=24(舍),∴袋中红球的个数为4个,机变量X的取值为0,1,2,P(X=0)==,P(X=1)==,P(X=2)=,∴X的分布列为:EX=.19.(14分)已知函数f(x)=ax2+bx和g(x)=lnx.(Ⅰ)若a=b=1,求证:f(x)的图象在g(x)图象的上方;(Ⅱ)若f(x)和g(x)的图象有公共点P,且在点P处的切线相同,求a的取值范围.【解答】解:(Ⅰ)证明:若a=b=1,即有f(x)=x2+x,令h(x)=f(x)﹣g(x)=x2+x﹣lnx,h′(x)=2x+1﹣==,x>0,当x>时,h′(x)>0,h(x)递增;当0<x<时,h′(x)<0,h(x)递减.可得h(x)在x=处取得极小值,且为最小值,且h()=+﹣ln>0,即有h(x)>0恒成立,则f(x)的图象在g(x)图象的上方;(Ⅱ)设P的坐标为(m,n),f(x)=ax2+bx的导数为f′(x)=2ax+b,g(x)=lnx的导数为g′(x)=,可得2am+b=,且n=am2+bm=lnm,消去b,可得am2+1﹣2am2=lnm,可得a=(m>0),令u(m)=(m>0),则u′(m)=,当m>时,u′(m)>0,u(m)递增;当0<m<时,u′(m)<0,u(m)递减.可得u(m)在m=处取得极小值,且为最小值,且u()==﹣,则a≥﹣,故a的取值范围是[﹣,+∞).20.(14分)已知函数f(x)=(x﹣1)e x.(Ⅰ)求f(x)的单调区间;(Ⅱ)证明:当a>0时,方程f(x)=a在区间(1,+∞)上只有一个解;(Ⅲ)设h(x)=f(x)﹣aln(x﹣1)﹣ax,其中a>0.若h(x)≥0恒成立,求a的取值范围.【解答】解:(Ⅰ)由已知f′(x)=e x+(x﹣1)e x=xe x,令f′(x)>0,解得:x>0,令f′(x)<0,解得:x<0,故f(x)在(﹣∞,0)递减,在(0,+∞)递增;(Ⅱ)设g(x)=f(x)﹣a=(x﹣1)e x﹣a,a>0,g′(x)=xe x,由(Ⅰ)知,函数g(x)在区间(0,+∞)递增,且g(1)=﹣a<0,g(a+1)=ae a+1﹣a=a(e a+1﹣1)>0,故g(x)在(1,+∞)上只有1个零点,方程f(x)=a在区间(1,+∞)上只有1个解;(Ⅲ)设h(x)=f(x)﹣aln(x﹣1)﹣ax,a>0,h(x)的定义域是{x|x>1},h′(x)=xe x﹣﹣a=[(x﹣1)e x﹣a],令h′(x)=0,则(x﹣1)e x﹣a=0,由(Ⅱ)得g(x)=(x﹣1)e x﹣a在区间(1,+∞)上只有1个零点,是增函数,不妨设g(x)的零点是x0,则(x0﹣1)﹣a=0,故h′(x),h(x)在区间(0,+∞)上的情况如下:∴函数h(x)的最小值是h (x0),h(x 0)=(x0﹣1)﹣aln(x0﹣1)﹣ax0,由(x0﹣1)﹣a=0,得x0﹣1=,故h(x0)=•﹣aln=a﹣alna,由题意h(x0)≥0,即a﹣alna≥0,解得:0<a≤e,故a的范围是(0,e].。
北京市昌平区2016-2017学年高二数学下学期期末考试试题 理(含解析)

北京2016~2017学年下学期高二期末考试数学试卷(理科)考试范围:导数定积分30% 统计与统计案例20% 计数原理概率随机变量及其分布20%推理证明算法复数20% 坐标系与参数方程10% 附加题解析几何13分参考公式:如果事件A,B互斥,那么P(A+B)=P(A)+P(B).如果事件A, B相互独立,那么P(A·B)=P(A)·P(B).若,,…,为样本点,为回归方程,则,,其中,. ,其中n=a+b+c+d为样本容量.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的1. 在复平面内,复数z =对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A【解析】由题意可得:,则复数z =对应的点位于第一象限 .本题选择A选项.2. 在(x+2)4的展开式中,x2的系数为A. 24B. 12C. 6D. 4【答案】A【解析】由二项式展开式的通项公式可得,展开式的通项公式为:,令可得:的系数为: .点睛:一是在T r+1=中,是该项的二项式系数,与该项的(字母)系数是两个不同的概念,前者只指,而后者是字母外的部分,前者只与n和r有关,恒为正,后者还与a,b有关,可正可负.二是二项式系数的最值与增减性与指数n的奇偶性有关,当n为偶数,中间一项的二项式系数最大;当n为奇数时,中间两项的二项式系数相等,且同时取得最大值.3. 已知函数f(x)=ln2x,则=A. B. C. D.【答案】D【解析】由复合函数求导法则可得: .本题选择D选项.点睛:求函数的导数应注意:①求导之前利用代数或三角变换先进行化简,减少运算量;②根式形式,先化为分数指数幂,再求导.③复合函数求导先确定复合关系,由外向内逐层求导,必要时可换元处理.4. 将一枚均匀硬币随机掷4次,恰好出现2次正面向上的概率为A. B. C. D.【答案】B【解析】投掷4次的所有可能结果为种,其中恰好出现2次正面向上的事件有种,据此可得,题中所求事件的概率值为: .本题选择B选项.5. 嘿哥有3个电子邮箱,他要发5封不同的电子邮件,则不同的发送方法有A. 8种B. 15种C. 种D. 种【答案】C【解析】由乘法原理可得:不同的发送方法有种.6. 设a,b,c是正整数,且a∈,当数据a,b,c的方差最小时,a+b+c的值为A. 252或253B. 253或254C. 254或255D. 267或268【答案】B【解析】设,则数据a,b,c的方差:,设a=b+m,c=b+n,则,取b=85,当m+n=0,−1,1时,s2有可能取得最小值,m=−16,n=15时,s2取得最小值.取b=84,当m+n=0,−1,1时,s2有可能取得最小值,m=−15,n=16时,s2取得最小值.∴a+b+c=79+85+90=254,或a+b+c=79+84+90=253.本题选择B选项.7. 高二第二学期期中考试,按照甲、乙两个班级学生数学考试成绩优秀和不优秀统计人数后,得到2×2列联表,则随机变量的观测值为A. 0.600B. 0.828C. 2.712D. 6.004【答案】A【解析】本题主要考查独立性检验。
北京市海淀北大附中2016_2017学年高二数学下学期期末考试试题理(含解析)

———————欢迎下载,祝您学习进步,成绩提升———————
如果您喜欢这份文档,欢迎下载!祝您成绩进步,学习愉快!
人大附中 2016-2017 学年度第二学期期末高二年级数学(理科)
一、选择题(共 8 道小题,每道小题 5 分,共 40 分,请将正确答案填涂在答题纸上.)
10.在复平面上,一个正方形的三个项点对应的复数分别是 0 、1 2i 、 2 i ,则该正方形的 第四个顶点对应的复数是__________. 【答案】 (1,3) 【解析】正方形三个顶点对应的坐标为 (0,0) , (1, 2) , (2,1) , 设第 4 个顶点为 (a,b) , 则 (a 1,b 2) (2 0,1 0) (2,1) , ∴ a 1 , b 3 ,即第 4 个顶点为 (1,3) .
(1 )若序列 A0 为1, 2 , 3 , 4 ,则序列 A2 为__________. ( 2 )若序列 A0 为1, 2 , , n ,则序列 S( A0 ) __________. 【答案】(1) 8 ,12 ( 2 ) (n 2) 2n1
【解析】(1)由题意 A1 :1 2 , 2 3 , 3 4 ,
sin
π 4
4
可化成
y
x
4
2 0,
圆
4
sin
π 4
可化成
(x
2)2 (y
2)2 4 ,
圆心 2, 2 到直线的距离 d | 2 2 4 2 | 2 r , 12 12
说明圆与直线相切.
故选 C .
D.相离
6.某光学仪器厂生产的透镜,第一次落地打破的概率为 0.3 ;第一次落地没有打破,第二次
北京大学高等数学考题未知年份高数期末考试题试题(含答案)

xk =k/n, dx=1/n
三、解答题
考察了变限积分求导
考察分步积分
考察 极限(洛必达)、变限积分求导
考察多元函数的(条件)极值
考察微分中值定理(罗尔定理,拉格朗日中值定理,柯西中值定理)、积分中值定理
二、填空题
考察二重积分概念,基本计算
a=1 b=ቤተ መጻሕፍቲ ባይዱa=-1
1. 方程e^z-xyz=0,可确定二元隐函数z=z(x,y) ,等式两边对x取
偏导(将y视为常数),则类似于之前学过的一元隐函数求导。
2.F=ez-xyz,
积分区域是圆,用极坐标表示更简便,且被积函数用极坐标 表示更简便,故使用极坐标。
文科高等数学 期末考试
一、选择题
定积分:观察积分区域是否 具有对称性,被积函数奇偶 性来简化问题计算。
多元(两元)函数的极限 ,注意:所谓二重极限,指 P(x,y)以任何方式区域P0时,f(x,y)都无限接近同一值。
换元:
掌握常见的第一类、第二类换元类型,基本积分公式 (详见课件)
x>a,f’>0 ; x<a,f’<0; x=a,f(a)=limf’(a)=0,所以A
北京市西城区2016— 2017学年度第二学期期末考试高二数学(文科)试卷答案

北京市西城区2016 — 2017学年度第二学期期末试卷高二数学(文科)参考答案及评分标准2017.7一、选择题:本大题共8小题,每小题5分,共40分.1. C ;2.D ;3. A ;4. D ;5. A ;6. D ;7. D ;8. B . 二、填空题:本大题共6小题,每小题5分,共30分.9. 对任意x ∈R ,都有e 0x ≥; 10. 14-; 11. 4; 12.13.5,[2,1]6-; 14.{4} ;{1,2,4}A =,{3,5}B =,或{1,2,5}A =,{3,4}B =,或{2,4,5}A =,{1,3}B =.注:14题第二个空只需填对一组即可;一题两空的题目,第一空2分,第二空3分.三、解答题:本大题共6小题,共80分. 15.(本小题满分13分) 解:(Ⅰ)由题意得 1146242410a d a d +=-⎧⎨+=-⎩, ……………4分解得16.(本小题满分13分)解:(Ⅰ)由32()3f x x x =-,得2()36f x x x '=-. …………… 3分令2()360f x x x '=-=,得0x =或2x =.(f '…………… 6分所以,)(x f 在区间(,0)-∞ 、(2,)+∞上单调递增;在区间(0,2)上单调递减. …8分 (Ⅱ) 由(Ⅰ)知,函数)(x f 在区间(1,0)-和(2,)+∞上单调递增;在区间(0,2)上单调递减.且(1)4f -=-;(0)0f =;(2)4f =-;(3)0f =.所以,当03m ≤≤时,)(x f 的值域为[4,0]-;当3m >时,()(3)0f m f >=,)(x f 的值域为[4,()]f m -. ……………12分所以,m 的最大值等于3. ……………13分 17.(本小题满分13分)解:(Ⅰ) 当1a =时,不等式()4f x >整理得2230x x +->,即(1)(3)0x x -+>, …………… 3分 解得3x <-或1x >,所以,不等式()4f x >的解集为{3,1}x x x <->或. …………… 6分 (Ⅱ)由已知,抛物线()y f x =的对称轴为212ax a=-=-. …………… 9分 所以函数()f x 在区间(1,2)上是单调函数.若()f x 在区间(1,2)上恰有一个零点,则(1)(2)0f f <, ……………11分 即(81)(31)0a a ++<,解得1138a -<<-. 所以,a 的取值范围为11(,)38--. ……………13分 18.(本小题满分13分)解:(Ⅰ) 当1x =时,甲用水量为5吨,需交水费4 1.81310.20⨯+⨯=元. …………2分 乙用水量为3吨,需交水费3 1.8 5.40⨯=元. ……………4分 (Ⅱ)当54x ≤,即0.8x ≤时,甲、乙两户用水量均不超过4吨.(53) 1.814.4y x x x =+⨯=; ……………6分当54x >,34x ≤,即4453x <≤时,甲用水量超过4吨,乙用水量不超过4吨.3 1.84 1.8(54)320.4 4.8y x x x =⨯+⨯+-⨯=-; ……………8分 当34x >,即43x >时,甲、乙用水量均超过4吨.(44) 1.8(5434)3249.6y x x x =+⨯+-+-⨯=-. ……………9分所以414.4,0,54420.4 4.8,,534249.6,.3x x y x x x x ⎧≤≤⎪⎪⎪=-<≤⎨⎪⎪->⎪⎩……………10分 (Ⅲ)由(Ⅱ)可知,函数()y f x =在各分段区间上都是增函数.当4[0,]5x ∈时,4()26.45y f ≤<;当44(,]53x ∈时,4()26.43y f ≤<;当4(,)3x ∈+∞时,令249.626.4x -=,解得 1.5x =.57.5x =,3 4.5x =,所以,甲用水量为7.5吨;乙用水量为4.5吨. ……………13分 19.(本小题满分14分)解:(Ⅰ) 当0k =时,()(1)e 2xf x x =-+.则()e (1)e e x x xf x x x '=+-=, ……………2分所以,在区间(,0)-∞上()0f x '<,()f x 是减函数;在区间(0,)+∞上()0f x '>,()f x 是增函数. ……………4分又(0)1f =,所以,()f x 的极小值为1;没有极大值. ……………6分 (Ⅱ) 由2()(1)e 2xf x x kx =--+,得()e 2(e 2)xxf x x kx x k '=-=-. ……………7分当0k ≤时,e 20xk ->,所以,当0x <时,()0f x '<,当0x >时,()0f x '>,()f x 在区间(,0)-∞上是减函数,在区间(0,)+∞上是增函数. ……………8分所以()f x 在区间[0,)+∞上的最小值为(0)f ,且(0)1f =,符合题意. …………9分 当0k >时,令()0f x '=,得0x =或ln 2x k =, 所以,当102k <≤时,ln 20k ≤在区间(0,)+∞上()0f x '>,()f x 是增函数, 所以()f x 在区间[0,)+∞上的最小值为(0)1f =,符合题意. ……………11分 当12k >时,ln 20k >, 当(0,ln 2)x k ∈时,()0f x '<,()f x 在区间(0,ln 2)k 上是减函数.所以(ln 2)(0)1f k f <=,不满足对于任意的[0,)x ∈+∞,()1f x ≥恒成立. …13分 综上,k 的取值范围为1(,]2-∞. ……………14分 20.(本小题满分14分)解:(Ⅰ) 当1==b a 时,2()f x x x =+.设2()ln h x x x x =+-,0x >. ……………1分则2121(21)(1)()21x x x x h x x x x x +--+'=+-==, ……………2分所以,在区间1(0,)2上()0h x '<,()h x 是减函数;在区间1(,)2+∞上()0h x '>,()h x 是增函数. ……………4分所以,()h x 的最小值为1()2h =31ln 42-,又31ln 042->,所以()0h x >恒成立. 即()f x 的图象在()g x 图象的上方. ……………6分(Ⅱ) 设00(,)P x y ,其中00x >.由已知()2f x ax b '=+,1()g x x'=. 因为在点P 处的切线相同, 所以2000000012,,ln ax b y ax bx y x x +==+=. ……………8分 消去0,b y 得200ln 10ax x +-=,依题意,方程200ln 10ax x +-=有解.……………9分设2()ln 1F x ax x =+-,则()F x 在(0,)+∞上有零点.2121()2ax F x ax x x+'=+=, 当0a ≥时,()0F x '>,函数()F x 在(0,)+∞上单调递增. 当1a ≥时,(1)10F a =-≥,0F =≤,所以()F x 有零点. 当01a ≤<时,(1)10F a =-≤,22(e )e 10F a =+>,所以()F x 有零点.……………11分当0a <时,令()0F x '=,解得x =(F '与在区间上的情况如下:令302≥,得 312ea ≥-. 此时(1)10F a =-<.所以()F x 有零点. ……………13分 综上,所求a 的取值范围为31[,)2e -+∞. ……………14分。
2002~2003 学年第二学期《高等数学》期末考试试题A卷及答案(216 学时)

0 2002~2003 学年第二学期《高等数学》期末考试试题 A 卷(216 学时) 专业班级学号 姓名一、填空题(每小题 4 分,共 12 分)(1)设 S 为: x 2+ y 2+ z 2= 4 ,则 ⎰⎰(x 2 + y 2)d S = 。
S( 2 ) 设 D= {(x , y ) | x 2 + y 2 ≤ ρ 2 } , f为 连 续 函 数 , 则lim1f (x , y )d x d y = 。
ρ →0πρ 2 ⎰⎰(3)周期为 2 的函数 f (x ) ;设它在一个周期[-1,1] 上的表达式为 f (x ) = 级数的和函数为 s (x ) ,则 s (-5) = 。
二、选择题(每小题 4 分,共 12 分)(1) 微分方程 y ' - y = ex+ 1的一个特解应有形式(式中 a , b 为常数)x ,它的傅立叶 A. ae x + bB. axe x + bxC. ae x + bxD. axe x + b♣sin 2(x 2 + y 2) ♠ x 2 + y 2 ≠ 0(2)函数 f (x , y ) = ♦ ♠♥x 2 + y 22 x 2+ y 2在点(0,0) 处= 0A.无定义B.连续C.有极限但不连续D.无极限(3) 设 L 是 y= 1 - x 2(-1 ≤ x ≤ 1) 表示的围线的正向,则⎰ L2x d x + y d y 2x 2 + y 2之值等于 A. 0B. 2π 三、(12 分)计算下列积分:C. - 2πD. 4 ln 2(1) I =⎰⎰ x d x d y ,其中 D = {(x , y ) | 0 ≤ x ≤ 1,0 ≤ y ≤ x 2}。
D(2) I =⎰⎰⎰ xy 2 z 3d x d y d z ,其中∧ 是由曲面 z = xy , y = x , x = 1及 z = 0 围成的闭区域。
∧四、(8 分)求曲面4x 2+ 4z 2-17 y 2+ 2 y -1 = 0 在点 M (2,1,0) 处的切平面方程。
北京市西城区2016-2017学年度第二学期期末考试高二数学(理科)试卷

北京市西城区2016—2017学年度第二学期期末试卷高二数学(理科)2017.7试卷满分:150分考试时间:120分钟一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9. 曲线1y x=在2x =处切线的斜率为______. 10. 4)12(xx -展开式中的常数项是_______.(用数字作答) 11. 离散型随机变量ξ的分布列为且=ξE 1_________;2 _________.12. 某班举行的联欢会由5个节目组成,节目演出顺序要求如下 节目甲不能排在第一个,并且节目甲必须和节目乙相邻,则该班联欢会节目演出顺序的编排方案共有_____种.13. 若函数32()f x ax ax x =-+在区间(1,0)-上恰有一个极值点,则a 的取值范围是_____.14. 已知,对于任意x ∈R ,e x ax b ≥+均成立.①若e a =,则b 的最大值为__________;②在所有符合题意的b a ,中,a b -的最小值为_________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)在数列{}n a 中,11=a ,121++=+n n a nn a ,其中1,2,3,n =.(Ⅰ) 计算2a ,3a ,4a ,5a 的值;(Ⅱ) 根据计算结果,猜想{}n a 的通项公式,并用数学归纳法加以证明.16.(本小题满分13分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为21与p ,且乙投球2次均未命中的概率为161. (Ⅰ)求甲投球2次,至少命中1次的概率;(Ⅱ)若甲、乙两人各投球2次,求两人共命中3次的概率.17.(本小题满分13分)已知函数32()3f x x ax =+.(Ⅰ) 若1-=a ,求)(x f 的极值点和极值; (Ⅱ) 求)(x f 在[0,2]上的最大值.18.(本小题满分13分)一个袋中装有黑球,白球和红球共n (*n ∈N )个,这些球除颜色外完全相同. 已知从袋中任意摸出1个球,得到黑球的概率是52. 现从袋中任意摸出2个球. (Ⅰ) 用含n 的代数式表示摸出的2球都是黑球的概率,并写出概率最小时n 的值.(直接写出n 的值)(Ⅱ) 若15=n ,且摸出的2个球中至少有1个白球的概率是74,设X 表示摸出的2个球中红球的个数,求随机变量X 的分布列和数学期望.19.(本小题满分14分)已知函数2()f x ax bx =+和x x g ln )(=.(Ⅰ) 若1==b a ,求证:()f x 的图象在()g x 图象的上方;(Ⅱ) 若()f x 和()g x 的图象有公共点P ,且在点P 处的切线相同,求a 的取值范围.20.(本小题满分14分)已知函数()(1)e xf x x =-.(Ⅰ)求()f x 的单调区间; (Ⅱ)证明:当0>a时,方程()f x a =在区间(1,)+∞上只有一个解;(Ⅲ)设()()ln(1)h x f x a x ax =---,其中0>a .若()0h x ≥恒成立,求a 的取值范围.北京市西城区2016 — 2017学年度第二学期期末试卷高二数学(理科)参考答案及评分标准2017.7一、选择题:本大题共8小题,每小题5分,共40分.1. A ;2.D ;3. C ;4. B ;5. C ;6. D ;7. C ;8. B . 二、填空题:本大题共6小题,每小题5分,共30分.9. 41-; 10. 24; 11. ,4211; 12. 42; 13. 1(,)5-∞-; 14. 0;1e-.注:一题两空的题目,第一空2分,第二空3分.三、解答题:本大题共6小题,共80分. 15.(本小题满分13分)解: (Ⅰ) 根据已知,24a =;99a =;416a =;525a =. …………… 4分 (Ⅱ)猜想2n a n =. (6)分证明:① 当1=n 时,由已知11=a ;由猜想,2111a ==,猜想成立. …………… 8分②假设当k n =(k ∈*N )时猜想成立,即2k a k =, (10)分则1+=k n 时, 221)1(1212+=+⨯+=++=+k k kk a k k a k k . 所以,当1n k =+时,猜想也成立. ……………12分由①和②可知,2n a n =对任意的*n ∈N 都成立. (13)分16.(本小题满分13分)解:(Ⅰ)设“甲投球一次命中”为事件A ,则11(),()22P A P A ==. …………… 2分故甲投球2次至少命中1 次的概率为31()1()()4P A A P A P A -⋅=-=. …………5分 (Ⅱ) 设“乙投球一次命中”为事件B . 由题意得1()(1)(1)16P B B p p ⋅=--=, ……………7分 解得43=p 或45(舍去), 所以31(),()44P B P B ==. ……………8分甲、乙两人各投球2次共命中3次有两种情况:甲中两次,乙中一次;甲中一次,乙中两次. ……………9分甲中两次,乙中一次的概率为1211313()()()()2224432P A P A C P B P B =⨯⨯⨯⨯=.…11分 甲中一次,乙中两次的概率为1211339()()()()2224432C P A P A P B P B =⨯⨯⨯⨯=.…12分事件“甲中两次,乙中一次”与“甲中一次,乙中两次”是互斥的,所以,所求事件概率为93332328+=.所以甲、乙两人各投2次,共命中3次的概率为38. ……………13分 17.(本小题满分13分)解:(Ⅰ) 当1-=a 时,32()3f x x x =-,2()36f x x x '=-. ……………2分令2()360f x x x '=-=,得0x =或2x =.()f x '与()f x 在R 上的情况如下: (4)分所以,函数)(x f 的极大值点为0x =,极大值为0;极小值点为2x =,极小值为4-. (6)分(Ⅱ) 2()363(2)f x x ax x x a '=+=+. ……………7分①当0a =时,()0f x '≥(仅当0x =时,()0f x '=),函数)(x f 是增函数,)(x f 在[0,2]上的最大值为(2)8128f a =+=. (8)分②当0a >时,在区间(0,)+∞上()0f x '>,函数)(x f 是增函数.)(x f 在[0,2]上的最大值为(2)812f a =+. (10)分③当0a <时,()f x '与()f x 在区间(0,)+∞上的情况如下: (11)分此时,(0)0f =,(2)812f a =+. 当8120a +>,即203a -<<时,)(x f 在[0,2]上的最大值为(2)812f a =+. 12分当8120a +≤,即23a ≤-时,)(x f 在[0,2]上的最大值为(0)0f =. ………13分综上,当23a ≤-时,)(x f 在[0,2]上的最大值为0;当23a >-时,)(x f 在[0,2]上的最大值为812a +. 18.(本小题满分13分) 解:(Ⅰ) 依题意有n 52个黑球. 记“摸出的2球都是黑球”为事件A , 则225222(1)41055()(1)2525n n C n n n P A C n n n --===--. ……………4分()P A 最小时5=n . (5)分(Ⅱ) 依题意有21565⨯=个黑球. ……………6分设袋中白球的个数为x (个),记“从袋中任意摸出两个球至少得到一个白球”为事件B ,则2152154()17xC P B C -=-=,整理得2291200x x -+=,解得5x =或24x =(舍). ……………8分所以袋中红球的个数为4(个).随机变量X 的取值为0,1,2. ……………9分21121511(0)21C P X C ===;1141121544(1)105C C P X C ===;242152(2)35C P X C ===. X 的分布列为:…………12分数学期望114428012211053515EX =⨯+⨯+⨯=. ……………13分19.(本小题满分14分)解:(Ⅰ) 当1==b a 时,2()f x x x =+.设2()ln h x x x x =+-,0x >. ……………1分则2121(21)(1)()21x x x x h x x x x x+--+'=+-==, (2)分所以,在区间1(0,)2上()0h x '<,()h x 是减函数;在区间1(,)2+∞上()0h x '>,()h x 是增函数. ……………4分所以,()h x 的最小值为1()2h =31ln 42-,又31ln 042->,所以()0h x >恒成立. 即()f x 的图象在()g x 图象的上方. ……………5分(Ⅱ) 设00(,)P x y ,其中00x >.由已知()2f x ax b '=+,1()g x x'=. 因为在点P 处的切线相同, 所以2000000012,,ln ax b y ax bx y x x +==+=. ……………7分消去0,b y 得200ln 10ax x +-=.根据题意,方程200ln 10ax x +-=有解. (8)分设2()ln 1F x ax x =+-,则()F x 在(0,)+∞上有零点. 2121()2ax F x ax x x+'=+=, 当0a ≥时,()0F x '>,函数()F x 在(0,)+∞上单调递增.当1a ≥时,(1)10F a =-≥,110F =+=≤,()F x 有零点.当01a ≤<时,(1)10F a =-≤,22(e )e 10F a =+>,()F x 有零点. …11分当0a <时,令()0F x '=,解得x =. ()F x '与()F x 在区间(0,)+∞上的情况如下:此时(1)10F a =-<.所以()F x 有零点. ……………13分综上,所求a 的取值范围为31[,)2e-+∞. ……………14分20.(本小题满分14分)解:(Ⅰ)由已知()e (1)e e x x x f x x x '=+-=. ……………2分所以,在区间(,0)-∞上()0f x '<,函数()f x 在(,0)-∞上单调递减,在区间(0,)+∞上()0f x '>,函数()f x 在区间(0,)+∞上单调递增. (4)(Ⅱ)设()()(1)e xg x f x a x a =-=--,0a >. ……………5分()e x g x x '=,由(Ⅰ)知,函数()g x 在区间(0,)+∞上单调递增.且(1)0g a =-<,11(1)e (e 1)0a a g a a a a +++=-=->.所以,()g x 在区间(1,)+∞上只有一个零点,方程()f x a =在区间(1,)+∞上只有一个解. ……………8分(Ⅲ)设()()ln(1)h x f x a x ax =---,0>a ,()h x 定义域为}1|{>x x ,()e (e )[(1)e ]111x x x a a x h x x a x x a x x x '=--=-=-----, ……………9分 令()0h x '=,则(1)e 0xx a --=,由(Ⅱ)知,()(1)e xg x x a =--在区间(1,)+∞上只有一个零点,是增函数, 不妨设()g x 的零点为0x ,则00(1)e 0xx a --=, ……………11分所以,()h x '与()h x 在区间(0,)+∞上的情况如下:0,00000()(1)e ln(1)x h x x a x ax =----,由00(1)e 0x x a --=,得001e x a x -=, 所以00000()e ln ln e ex x x a a h x a ax a a a =⋅--=-. ……………13分依题意0()0h x ≥,即ln 0a a a -≥,解得0e a <≤,所以,a 的取值范围为(0,e]. (14)。
2016-2017(下)《高等数学AⅡ》期末试卷-E卷答案 (2) (1)

下学期期末考试试卷答案课程名称:《高等数学A Ⅱ》 (试卷编号:E )一、填空题(本大题共9小题10空,每空2 分,共 20分)1.2-2. 221,,333⎛⎫- ⎪⎝⎭3.2154. (){}22,12x y xy ≤+< 5. 36. 23,137. xy xye xye +(或“()1xy xy e +”) 8.3 9. 收敛二、单项选择题(选择正确答案的字母填入括号,本大题共6小题,每小题3 分,共18 分)三、判断题(选择正确答案的字母填入括号,正确的打“√”,错误的打“×”。
本大题共5小题,每小题2分,共10分)四、计算题(本大题共5小题,每小题6分,共30分)1.解:因为22sin y zxe y x x∂=-∂,22cos y z x e y x y ∂=+∂, ――――――――2分所以(),02zx ππ∂=∂,()2,0z y ππ∂=∂, ――――――――2分 于是,所求全微分22dz dx dy ππ=+ ――――――――2分 2.解:dz z du z dv fdx u dx v dx x∂∂∂=++∂∂∂ ――――――――2分 11x v u e x=⋅+⋅+ ――――――――2分()111x x x e x=++++ ――――――――2分3.解:积分区域(){}2,1D x y xy x =≤≤≤≤所以210x Dxyd dx σ=⎰⎰⎰ ――――――――2分25122x x dx dx ⎛⎫==- ⎪⎝⎭⎰⎰ ――――――――2分1360161212x x ⎛⎫=-= ⎪⎝⎭ ――――――――2分4.解:积分区域(){}2,,01,1,11x y z z xy x Ω=≤≤≤≤-≤≤所以21111xxzdxdydz dx dy xzdz -Ω=⎰⎰⎰⎰⎰⎰ ――――――――2分2121112xxz dx dy -=⎰⎰ 21112x xdx dy -=⎰⎰ ――――――――2分 21112x xy dx -⎛⎫= ⎪⎝⎭⎰ 21122x x dx -⎛⎫=- ⎪⎝⎭⎰ 1231=46x x -⎛⎫- ⎪⎝⎭ 13=- ――――――――2分5.解:由11limlim 1n n n na n a n ρ+→∞→∞+===,得级数的收敛半径 1R =, ――――――――3分在1x =-处,幂级数成为()()111231n nn n n ∞=-=-+-++-+∑L L ,由()lim 10nn n →∞-≠知该级数发散;在1x =处,幂级数成为1n n ∞=∑,由lim 0n n →∞=∞≠知该级数发散。
北京市2016-2017学年高二下学期期末数学试卷(理科) Word版含解析

A北京市 2016-2017 学年高二下学期期末试卷(理科数学)一、选择题:本大题共 8 小题,每小题 5 分,共 40 分,在每个小题给出的四个选项中,只有一个符合题目 要求的.1.在复平面内,复数 z=对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 2.在(x+2)4 的展开式中,x 2 的系数为( ) A .24 B .12 C .6 D .43.已知函数 f (x )=ln2x ,则 f′(x )=( )A .B .C .D .4.将一枚均匀硬币随机投掷 4 次,恰好出现 2 次正面向上的概率为( )A .B .C .D .5.函数 f (x )=﹣ x 2+lnx 的极值点是()A .x=﹣1B .x=﹣C .x=1D .x=6.5 名大学生被分配到 4 个地区支教,每个地区至少分配 1 人,其中甲乙两名同学因专业相同,不能分配 在同一地区,则不同的分配方法的种数为( ) A .120 B .144 C .216 D .2407.设 a ,b ,c 是正整数,且 a ∈[70,80),b ∈[80,90),c ∈[90,100],当数据 a ,b ,c 的方差最小时, a+b+c 的值为( ) A .252 或 253 B .253 或 254 C .254 或 255 D .267 或 2688.已知函数 f (x )=e x +ax ﹣2,其中 a ∈R ,若对于任意的 x ,x ∈[1,+∞),且 x <x ,都有 x •f(x )﹣ 1 2 1 2 2 1x •f(x )<a (x ﹣x )成立,则 a 的取值范围是( ) 1 2 1 2 A .[1,+∞) B .[2,+∞) C .(﹣∞,1]D .(﹣∞,2]二、填空题:本大题共 6 个小题,每小题 5 分.、共 30 分.9.函数 f (x )=cosx ,则 f′()= .10.定积分dx 的值为 .11.设(2x+1)3=a x 3+a x 2+a x+a ,则 a +a +a +a = .3 2 1 0 0 1 2 312.由数字 1,2 组成的三位数的个数是 (用数字作答).13.在平面几何里,有勾股定理“设△ABC 的两边 AB ,AC 互相垂直,则 AB 2+AC 2=BC 2”,拓展到空间,类比 平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出正确的结论是:“设三棱锥 ﹣BCD 的三个侧面 ABC 、ACD 、ADB 两两互相垂直,则 .”14.研究函数f(x)=的性质,完成下面两个问题:①将f(2)、f(3)、f(5)按从小到大排列为;②函数g(x)=(x>0)的最大值为.三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.15.在数列{a}中,a=1,a=n•a,n=2,3,4,….n1n n﹣1(Ⅰ)计算a,a,a,a的值;2345(Ⅱ)根据计算结果,猜想{a}的通项公式,并用数学归纳法加以证明.n16.已知函数f(x)=x3+3x2﹣9x;(1)求f(x)的单调区间;(2)若函数f(x)在区间[﹣4,c]上的最小值为﹣5,求c的取值范围.17.甲参加A,B,C三个科目的学业水平考试,其考试成绩合格的概率如表,假设三个科目的考试甲是否成绩合格相互独立.科目A科目B科目C甲(Ⅰ)求甲至少有一个科目考试成绩合格的概率;(Ⅱ)设甲参加考试成绩合格的科目数量为X.求X的分布列和数学期望.18.口袋中装有2个白球和n(n≥2,n∈N*)个红球,每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.(Ⅰ)用含n的代数式表示1次摸球中奖的概率;(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;(Ⅲ)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.19.已知函数f(x)=x2e x﹣b,其中b∈R.(Ⅰ)证明:对于任意x,x∈(﹣∞,0],都有f(x)﹣f(x)≤;1212(Ⅱ)讨论函数f(x)的零点个数(结论不需要证明).20.设L为曲线C:y=e x在点(0,1)处的切线.(Ⅰ)证明:除切点(0,1)之外,曲线C在直线L的上方;(Ⅱ)设h(x)=e x﹣ax+ln(x+1),其中a∈R,若h(x)≥1对x∈[0,+∞)恒成立,求a的取值范围.北京市2016-2017学年高二下学期期末试卷(理科数学)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分,在每个小题给出的四个选项中,只有一个符合题目要求的.1.在复平面内,复数z=对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【考点】复数代数形式的乘除运算.【分析】直接由复数代数形式的乘除运算化简复数z,求出在复平面内,复数z对应的点的坐标,则答案可求.【解答】解:z==则在复平面内,复数z对应的点的坐标为:(,,),位于第一象限.故选:A.2.在(x+2)4的展开式中,x2的系数为()A.24B.12C.6D.4【考点】二项式系数的性质.【分析】直接根据二项式的展开式的通项公式即可求出.【解答】解:(x+2)4的展开式的通项公式为T=C r•24﹣r•x r,r+14令r=2,故展开式中x2的系数为C2•22=24,4故选:A.3.已知函数f(x)=ln2x,则f′(x)=()A.B.C.D.【考点】导数的运算.【分析】根据复合函数的导数公式进行求解即可.【解答】解:∵f(x)=ln2x,∴f′(x)===,故选:D4.将一枚均匀硬币随机投掷4次,恰好出现2次正面向上的概率为()A.B.C.D.【考点】列举法计算基本事件数及事件发生的概率.【分析】将一枚均匀硬币随机投掷4次,利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出恰好出现2次正面向上的概率.【解答】解:将一枚均匀硬币随机投掷4次,恰好出现2次正面向上的概率为:p==.故选:B.5.函数f(x)=﹣x2+lnx的极值点是()A.x=﹣1B.x=﹣C.x=1D.x=【考点】利用导数研究函数的极值.【分析】求出原函数的导函数,确定出函数的单调区间,由此求得函数的极值点.【解答】解:由f(x)=﹣x2+lnx,得f′(x)=(x>0),当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.∴函数f(x)在(0,1)上为增函数,在(1,+∞)上为减函数.∴函数f(x)=﹣x2+lnx的极值点为x=1.故选:C.6.5名大学生被分配到4个地区支教,每个地区至少分配1人,其中甲乙两名同学因专业相同,不能分配在同一地区,则不同的分配方法的种数为()A.120B.144C.216D.240【考点】排列、组合及简单计数问题.【分析】先求出没有限制要求的5名大学生被分配到4个地区支教,每个地区至少分配1人的种数,再排除甲乙两名同学分配在同一地区的种数,问题得以解决.【解答】解:5个人分成满足题意的4组只有1,1,1,2,即只有一个单位有2人,其余都是1人,故有C2A4=240种,54其中甲乙两名同学分配在同一地区的方法为C1A3=24种,43故甲乙两名同学因专业相同,不能分配在同一地区,则不同的分配方法的种数为240﹣24=216种,故选:C.7.设a,b,c是正整数,且a∈[70,80),b∈[80,90),c∈[90,100],当数据a,b,c的方差最小时,a+b+c的值为()A.252或253B.253或254C.254或255D.267或268【考点】极差、方差与标准差.【分析】设=,则数据a,b,c的方差s2=≥[(a﹣b)2+(b﹣c)2+(a﹣c)2],设a=b+m,c=b+n,则s2≥[m2+n2+(m+n)2],应该使得b=85,而当m+n=0,﹣1,1时,s2有可能取得最小值.【解答】解:设=,1 s s 1 s s则数据 a ,b ,c 的方差s 2=[(a ﹣b )2+(b ﹣c )2+(a ﹣c )2], 设 a=b+m ,c=b+n ,则 s 2≥[m 2+n 2+(m+n )2],= ≥取 b=85,当 m+n=0,﹣1, 时, 2 有可能取得最小值,m=﹣16,n=15 时, 2 取得最小值取 b=84,当 m+n=0,﹣1, 时, 2 有可能取得最小值,m=﹣15,n=16 时, 2 取得最小值== ..∴a+b+c=79+85+90=254,或 a+b+c=79+84+90=253. 故选:B .8.已知函数 f (x )=e x +ax ﹣2,其中 a ∈R ,若对于任意的 x ,x ∈[1,+∞),且 x <x ,都有 x •f(x )﹣ 1 2 1 2 2 1x •f(x )<a (x ﹣x )成立,则 a 的取值范围是( ) 1 2 1 2 A .[1,+∞) B .[2,+∞) C .(﹣∞,1] D .(﹣∞,2]【考点】利用导数研究函数的单调性.【分析】将不等式变形为:< 恒成立,构造函数 h (x )= ,转会为当 x <x12时,h (x )<h (x )恒成立,为了求 a 的范围,所以需要构造函数,可通过求导数,根据单调性来求它的1 2范围.【解答】解:∵对于任意的 x ,x ∈[1,+∞),且 x <x ,都有 x •f(x )﹣x •f(x )<a (x ﹣x )成立,1212211212∴不等式等价为< 成立,令 h (x )=,则不等式等价为当 x <x 时,h (x )<h (x )恒成立,1212即函数 h (x )在(0,+∞)上为增函数;h (x )=,则 h′(x )=≥0 在(0,+∞)上恒成立;∴xe x ﹣e x +2﹣a ≥0;即 a ﹣2≤xe x ﹣e x 恒成立, 令 g (x )=xe x ﹣e x ,∴g′(x )=xe x >0; ∴g (x )在(0,+∞)上为增函数; ∴g (x )>g (0)=﹣1; ∴2﹣a ≥1; ∴a ≤1.∴a 的取值范围是(﹣∞,1].A故选:C二、填空题:本大题共 6 个小题,每小题 5 分.、共 30 分.9.函数 f (x )=cosx ,则 f′()= ﹣ .【考点】导数的运算.【分析】求函数的导数,根据函数的导数公式代入直接进行计算即可. 【解答】解:∵f (x )=cosx ,∴f′(x )=﹣sinx ,f′()=﹣sin =﹣ ,故答案为:﹣10.定积分dx 的值为 .【考点】定积分.【分析】根据定积分的性质,然后运用微积分基本定理计算定积分即可.【解答】解:dx=2 x 2dx=2× x 3 = .故答案为: .11.设(2x+1)3=a x 3+a x 2+a x+a ,则 a +a +a +a = 27 . 321123【考点】二项式系数的性质.【分析】令 x=1 可得 a +a +a +a 的值.123【解答】解:令 x=1,a +a +a +a =33=27,0 1 2 3故答案为:2712.由数字 1,2 组成的三位数的个数是 8 (用数字作答). 【考点】排列、组合及简单计数问题. 【分析】直接根据分步计数原理可得.【解答】解:每一位置都有 2 种排法,故有 23=8 种, 故答案为:813.在平面几何里,有勾股定理“设△ABC 的两边 AB ,AC 互相垂直,则 AB 2+AC 2=BC 2”,拓展到空间,类比 平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出正确的结论是:“设三棱锥﹣BCD 的三个侧面 ABC 、ACD 、ADB 两两互相垂直,则 △S A BC2 △+S ACD △+S ADB 22=S△BCD2 .”【考点】类比推理.【分析】从平面图形到空间图形的类比【解答】解:建立从平面图形到空间图形的类比,于是作出猜想:△S ABC 故答案为:2+S22=S2.△S ABC△ACD△+S ADB△BCD 2+S△ACD△+SADB22=S△BCD2.14.研究函数f(x)=的性质,完成下面两个问题:①将f(2)、f(3)、f(5)按从小到大排列为f(5)<f(2)<f(3);;②函数g(x)=(x>0)的最大值为e.【考点】利用导数研究函数的单调性.【分析】①利用导数判断在(0,e)递增,(e,+∞)递减得出f(3)>f(5),运用作差判断f(2)﹣f (5),f(2)﹣f(3)即可得出大小.②构造函数ln(g(x))=lnx(x>0),令h(x)=lnx(x>0),运用导数求解极大值,得出h(x)的极大值为h(e)=lne=,结合对数求解即可.【解答】解:①∵函数f(x)=,∴f′(x)=,f′(x)==0,x=e,f′(x)=,>0,x∈(0,e)f′(x)=<0,x∈(e,+∞)∴在(0,e)递增,(e,+∞)递减∴f(3)>f(5),∵f(2)﹣f(5)===>0∴f(2)>f(5)∵f(2)﹣f(3)==<0∴f(3)>f(2)故答案:f(5)<f(2)<f(3);②∵函数g(x)=(x>0),∴ln(g(x))=lnx(x>0)(令 h (x )= lnx (x >0),h′(x )=h′(x )=h′(x )=(1﹣lnx )=0,x=e(1﹣lnx )<0,x >e(1﹣lnx )>0,0<x <e∴h (x )= lnx (x >0),在(0,e )递增,在(e ,+∞)递减,h (x )的极大值为 h (e )= lne= ,∴函数 g (x )=(x >0)的最大值为 e ,故答案为:e三、解答题:本大题共 6 小题,共 80 分,解答应写出文字说明、证明过程或演算步骤. 15.在数列{a }中,a =1,a =n•a ,n=2,3,4,….n1nn ﹣1(Ⅰ)计算 a ,a ,a ,a 的值;2 3 4 5(Ⅱ)根据计算结果,猜想{a }的通项公式,并用数学归纳法加以证明.n【考点】数学归纳法;归纳推理. 【分析】(Ⅰ)利用已知条件通过 n=2,3,4,5 直接计算 a ,a ,a ,a 的值,2345(Ⅱ)根据(Ⅰ)的计算结果,猜想的通{a }项公式,用数学归纳法的证明步骤直接证明即可.n【解答】解:(Ⅰ)a =1,a =n•a ,1 n n ﹣1可得 n=2 时,a =2;n=3 时,a =6;2 3a =24,a =120 4 5(Ⅱ)猜想 a =n!.n证明:①当 n=1 时,由已知,a =1!=1,猜想成立.1②假设当 n=k (k ∈N *)时猜想成立,即 a =k!.k则 n=k+1 时,a =(k+1)a =(k+1)k!=(k+1)!.k+1 k所以 当 n=k+1 时,猜想也成立.根据 ①和 ②,可知猜想对于任何 n ∈N *都成立16.已知函数 f (x )=x 3+3x 2﹣9x ; (1)求 f (x )的单调区间;(2)若函数 f (x )在区间[﹣4,c]上的最小值为﹣5,求 c 的取值范围. 【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性. 【分析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可; 2)通过讨论 c 的范 围,求出函数的最小值,从而求出 c 的具体范围. 【解答】解:(1)函数 f (x )的定义域是 R , f′(x )=3x 2+6x ﹣9,令 f′(x )>0,解得:x >1 或 x <﹣3,令f′(x)<0,解得:﹣3<x<1,∴f(x)在(﹣∞,﹣3)递增,在(﹣3,1)递减,在(1,+∞)递增;(2)由f(﹣4)=20结合(1)得:c≥1时,函数f(x)在[﹣4,c]上的最小值是f(1)=﹣5,﹣4<c<1时,函数f(x)在区间[﹣4,c]上的最小值大于﹣5,故c的范围是[1,+∞).17.甲参加A,B,C三个科目的学业水平考试,其考试成绩合格的概率如表,假设三个科目的考试甲是否成绩合格相互独立.科目A科目B科目C甲(Ⅰ)求甲至少有一个科目考试成绩合格的概率;(Ⅱ)设甲参加考试成绩合格的科目数量为X.求X的分布列和数学期望.【考点】离散型随机变量的期望与方差;列举法计算基本事件数及事件发生的概率;离散型随机变量及其分布列.【分析】(Ⅰ)记“甲至少有一个科目考试成绩合格”为事件M,利用对立事件概率计算公式能求出甲至少有一个科目考试成绩合格的概率.(Ⅱ)由题意得X的可能取值为0,1,2,3,分别求出相应的概率,由此能出X的分布列和EX.【解答】解:(Ⅰ)记“甲至少有一个科目考试成绩合格”为事件M,则P()=(1﹣)(1﹣)(1﹣)=,∴甲至少有一个科目考试成绩合格的概率:P(M)=1﹣P()=1﹣.(Ⅱ)由题意得X的可能取值为0,1,2,3,P(X=0)=(1﹣)(1﹣)(1﹣)=,P(X=1)=++(1﹣)×,P(X=3)=,,P(X=2)=1﹣P(X=0)﹣P(X=1)﹣P(X=3)=∴X的分布列为:123X0PEX==.18.口袋中装有2个白球和n(n≥2,n∈N*)个红球,每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.(Ⅰ)用含n的代数式表示1次摸球中奖的概率;(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;(Ⅲ)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.【考点】古典概型及其概率计算公式.【分析】(Ⅰ)设“1次摸球中奖”为事件A,利用互斥事件概率加法公式能求出用含n的代数式表示1次摸球中奖的概率.(Ⅱ)由(Ⅰ)得若n=3,则1次摸球中奖的概率为p=,由此能求出3次摸球中,恰有1次中奖的概率.(Ⅲ)设“1次摸球中奖”的概率为p,则3次摸球中,恰有1次中奖的概率为f(p)=3p3﹣6p2+3p,(0<p <1),由此利用导数性质能求出当f(p)取得最大值时,n的值.【解答】解:(Ⅰ)设“1次摸球中奖”为事件A,则P(A)==.(Ⅱ)由(Ⅰ)得若n=3,则1次摸球中奖的概率为p=,∴3次摸球中,恰有1次中奖的概率为P(1)=3(Ⅲ)设“1次摸球中奖”的概率为p,则3次摸球中,恰有1次中奖的概率为:f(p)==3p3﹣6p2+3p,(0<p<1),∵f′(p)=9p2﹣12p+3=3(p﹣1)(3p﹣1),∴当p∈(0,)时,f(p)取得最大值,令=,解得n=2或n=1(舍),∴当f(p)取得最大值时,n的值为2.19.已知函数f(x)=x2e x﹣b,其中b∈R.=3×=.(Ⅰ)证明:对于任意x,x∈(﹣∞,0],都有f(x)﹣f(x)≤1212(Ⅱ)讨论函数f(x)的零点个数(结论不需要证明).【考点】利用导数研究函数的单调性.【分析】(Ⅰ)利用导数转化为求解最大值,最小值的差证明.;(Ⅱ)根据最大值为;f(﹣2)=分类当b<0时,当b=0时,当b=﹣b,f(x)的最小值为:﹣b,时,当0<b<时,当b>时,判断即可.【解答】解:(Ⅰ)f(x)的定义域R,且f′(x)=x(x+2)e x,令f′(x)=0则x=0,或x=﹣2,12f′(x)=x(x+2)e x,x(﹣∞,﹣2)﹣2 f′(x)+0(﹣2,0)﹣f(x)增函数极大值减函数﹣b,∴f(x)在区间(﹣∞,0]上的最大值为;f(﹣2)=∵x∈(﹣∞,0],∴f(x)=x2e x﹣b≥﹣b,∴f(x)的最小值为:﹣b,∴对于任意x,x∈(﹣∞,0],都有f(x)﹣f(x)≤f(x)﹣f(x)≤;1212最大值(Ⅱ)f′(x)=x(x+2)e x,函数f(x)=x2e x﹣b,当b<0时,函数f(x)=x2e x﹣b>0恒成立,函数f(x)的零点个数为:0当b=0时,函数f(x)=x2e x,函数f(x)的零点个数为:1当b=时,函数f(x)的零点个数为;2,当0<b<时,函数f(x)的零点个数为:3,当b>时,函数f(x)的零点个数为:1,20.设L为曲线C:y=e x在点(0,1)处的切线.(Ⅰ)证明:除切点(0,1)之外,曲线C在直线L的上方;(Ⅱ)设h(x)=e x﹣ax+ln(x+1),其中a∈R,若h(x)≥1对x∈[0,+∞)恒成立,求a的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究曲线上某点切线方程.【分析】(Ⅰ)求出函数的导数,计算f′(0),从而求出切线方程即可;(Ⅱ)求出h(x)的导数,通过讨论a的范围,单调函数的单调区间,从而求出a的具体范围即可.【解答】解:(Ⅰ)设f(x)=e x,则f′(x)=e x,∴f′(0)=1,L的方程是y=x+1,令g(x)=f(x)﹣(x+1),则除切点之外,曲线C在直线L的上方等价于g(x)>0,(x∈R,x≠0),g(x)满足g(0)=0,且g′(x)=f′(x)﹣1=e x﹣1,当x<0时,g′(x)<0,故g(x)递减,当x>0时,g′(x)>0,故g(x)递增,∴g(x)>g(0)=0,∴除切点(0,1)之外,曲线C在直线L的上方;﹣a,(Ⅱ)h(x)的定义域是{x|x>﹣1},且h′(x)=e x+①a≤2时,由(Ⅰ)得:e x≥x+1,∴h′(x)=e x+﹣a≥x+1+﹣a≥2﹣a≥0,∴h(x)在[0,+∞)递增,∴h(x)≥h(0)=1恒成立,符合题意;②a>2时,由x∈[0,+∞),且h′(x)的导数h″(x)=≥0,∴h′(x)在区间[0,+∞)递增,∵h′(0)=2﹣a<0,h′(lna)=>0,于是存在x∈(0,+∞),使得h′(x)=0,00∴h(x)在区间(0,x)上递减,在区间(x,+∞)递增,00∴h(x)<h(0)=1,此时,h(x)≥1不会恒成立,不合题意,综上,a的范围是(﹣∞,2].。
20162017学年第二学期期末考试试卷

复旦大学数学科学学院2016~2017学年第二学期期末考试试卷 A 卷 课程名称:____高等数学C (下) ___ 课程代码:__ MATH120006 开课院系:____数学科学学院_______ 考试形式: 闭卷一、 (本题满分48分,每小题8分)计算下列各题: 1、 计算 2(,)(,)1lim 1,0x x y x y a a xy +→∞⎛⎫+≠ ⎪⎝⎭ 2、 设()f u 为可导函数,210()(1)x y x y z f u du f u du +-=++⎰⎰,求2z x y ∂∂∂, 22z y ∂∂.姓名:学 号:专业:(装订线内不要答题)3、 计算[4Dx y d σ⎰⎰,其中22:1,0D x y x +≤≥.4、 求幂级数11ln(1)1n n n x n ∞+=++∑的收敛半径和收敛域。
5、 已知曲线()y y x =经过原点,且在原点的切线平行于直线250x y --=,而()y x 满足369x y y y e '''-+=,求()y x .6、 某地是肝炎病高发区,有25%的人曾患甲型肝炎,有15%的人是乙型肝炎病毒携带者,有28%的人至少有一种肝炎阳性史。
普查时,从该地人群中任选一人询问,他既有甲型又有乙型阳性史的可能性有多大?二、 (10分)已知函数(,)z f x y =的全微分22dz xdx ydy =-,并且(1,1)2f =,求(,)f x y 在椭圆域 2214y x +≤上的最值。
三、(6分)计算D ydxdy⎰⎰,其中D是由直线2,0,2x y y=-==以及曲线x=四、(10分)求级数1(4)3n nnnx n∞=-+∑的和。
五、 (10分)设(,)f u v 具有连续偏导数,且满足(,)(,)u v f u v f u v uv ''+=.求2()(,)x y x e f x x -=所满足的一阶微分方程,并求其通解。
高数下期末考试试卷及答案(精选.)

⾼数下期末考试试卷及答案(精选.)2017学年春季学期《⾼等数学Ⅰ(⼆)》期末考试试卷(A )注意:1、本试卷共 3 页;2、考试时间110分钟;3、姓名、学号必须写在指定地⽅⼀、单项选择题(8个⼩题,每⼩题2分,共16分)将每题的正确答案的代号A 、B 、C 或D 填⼊下表中.1.已知a 与b都是⾮零向量,且满⾜-=+a b a b ,则必有(). (A)-=0a b (B)+=0a b (C)0?=a b (D)?=0a b 2.极限2222001lim()sinx y x y x y →→+=+( ).(A) 0(B) 1 (C) 2 (D)不存在 3.下列函数中,df f =?的是( ).(A )(,)f x y xy = (B )00(,),f x y x y c c =++为实数(C )(,)f x y =(D )(,)e x y f x y +=4.函数(,)(3)f x y xy x y =--,原点(0,0)是(,)f x y 的( ).(A )驻点与极值点(B )驻点,⾮极值点(C )极值点,⾮驻点(D )⾮驻点,⾮极值点 5.设平⾯区域2 2:(1)(1)2D x y -+-≤,若1d 4D x y I σ+=,2DI σ=,则有(). (A )123I I I << (B )123I I I >> (C )213I I I << (D )312I I I <<6.设椭圆L :13422=+y x 的周长为l ,则22(34)d L x y s +=??(). (A) l (B) l 3 (C) l 4 (D) l 127.设级数∑∞=1n na为交错级数,0()n a n →→+∞,则().(A)该级数收敛 (B)该级数发散(C)该级数可能收敛也可能发散 (D)该级数绝对收敛 8.下列四个命题中,正确的命题是(). (A )若级数1 nn a∞=∑发散,则级数21nn a∞=∑也发散(B )若级数21nn a∞=∑发散,则级数1nn a∞=∑也发散(C )若级数21nn a∞=∑收敛,则级数1nn a∞=∑也收敛1||nn a∞=∑收敛,则级数21n n a ∞=∑也收敛⼆、填空题(7个⼩题,每⼩题2分,共14分).1.直线3426030x y z x y z a -+-=??+-+=?与z 轴相交,则常数a 为 .2.设(,)ln(),y f x y x x=+则(1,0)y f '=______ _____.3.函数(,)f x y x y =+在(3,4)处沿增加最快的⽅向的⽅向导数为 .4.设22:2D x y x +≤,⼆重积分()d Dx y σ-??= .5.设()f x 是连续函数,22{(,,)|09}x y z z x y Ω=≤≤--,22()d f x y v Ω+在柱⾯坐标系下的三次积分为 .6.幂级数11(1)!nn n x n ∞-=-∑的收敛域是 . 7.将函数21,0()1,0x f x x x ππ--<≤??=?+<≤??以2π为周期延拓后,其傅⾥叶级数在点x π=处收敛于 .三峡⼤学试卷纸教学班号序号学号姓名…………………….……答题不要超过密封线………….………………………………三、综合解答题⼀(5个⼩题,每⼩题7分,共35分,解答题应写出⽂字说明、证明过程或演算步骤) 1.设(,)x u xf x y =,其,u y ??.解: 2.求曲⾯e 3z z xy ++=在点(2,1,0)处的切平⾯⽅程及法线⽅程.解:3.交换积分次序,并计算⼆次积分0sin d d xyx y yππ.解:4.设Ω是由曲⾯1,,===x x y xy z 及0=z 所围成的空间闭区域,求23d d d I xy z x y z Ω=.解:5.求幂级数11n n nx∞-=∑的和函数()S x ,并求级数12nn n ∞=∑的和.解:三峡⼤学试卷纸教学班号序号学号姓名…………………….……答题不要超过密封线………….………………………………四、综合解答题⼆(5个⼩题,每⼩题7分,共35分,解答题应写出⽂字说明、证明过程或演算步骤)1.从斜边长为1的⼀切直⾓三⾓形中,求有最⼤周长的直⾓三⾓形.解2.计算积分22()d Lx y s +?,其中L 为圆周22x y ax += (0a >).解:3.利⽤格林公式,计算曲线积分2I xy x x xy y =+++??,其中L 是由抛物线2y x =和2x y =所围成的区域D 的正向边界曲线.4.计算d x S ∑,∑为平⾯1=++z y x 在第⼀卦限部分.解:5.利⽤⾼斯公式计算对坐标的曲⾯积分d d d d d d x y y z z x S++蝌,其中∑为圆锥⾯222z x y =+介于平⾯0z =及1z =之间的部分的下侧. 解:三峡⼤学试卷纸教学班号序号学号姓名…………………….……答题不要超过密封线………….………………………………xO 2y x =2x y =y D2017学年春季学期《⾼等数学Ⅰ(⼆)》期末考试试卷(A)答案及评分标准⼀、单项选择题(8个⼩题,每⼩题2分,共16分)1.已知a 与b 都是⾮零向量,且满⾜-=+a b a b ,则必有(D ) (A)-=0a b ; (B)+=0a b ; (C)0?=a b ; (D)?=0a b .2.极限2222001lim()sin x y x y x y →→+=+ ( A ) (A) 0; (B) 1; (C) 2; (D)不存在. 3.下列函数中,d f f =?的是( B );(A ) (,)f x y xy =;(B )00(,),f x y x y c c =++为实数;(,)f x y =(D )(,)e x yf x y +=.4.函数(,)(3)f x y xy x y =--,原点(0,0)是(,)f x y 的( B ).(A )驻点与极值点;(B )驻点,⾮极值点;(C )极值点,⾮驻点;(D )⾮驻点,⾮极值点. 5.设平⾯区域D :2 2(1)(1)2x y -+-≤,若1d 4D x y I σ+=,2DI σ=,3DI σ=,则有( A )(A )123I I I <<;(B )123I I I >>;(C )213I I I <<;(D )312I I I <<.6.设椭圆L :13422=+y x 的周长为l ,则22(34)d L x y s +=??(D ) (A) l ; (B) l 3; (C) l 4; (D) l 12.7.设级数∑∞=1n na为交错级数,0()n a n →→+∞,则( C )(A)该级数收敛; (B)该级数发散;(C)该级数可能收敛也可能发散; (D) 该级数绝对收敛. 8.下列四个命题中,正确的命题是( D )(A )若级数1nn a∞=∑发散,则级数21n∞=∑也发散;(B )若级数21nn a∞=∑发散,则级数1nn a∞=∑也发散;(C )若级数21nn a∞=∑收敛,则级数1nn a∞=∑也收敛;(D )若级数1||nn a∞=∑收敛,则级数21n n a ∞=∑也收敛.⼆、填空题(7个⼩题,每⼩题2分,共14分).1.直线3426030x y z x y z a -+-=??+-+=?与z 轴相交,则常数a 为 3 。
2016-2017高数二、二期末试题答案

课程名称:高等数学(二、二)(期末试卷)答案要求:1.答案一律写在答题纸上,写在其它位置无效 2.答题纸单独收,与试卷和草稿纸分开。
一、填空题(每空3分,共15分) 1.微分方程()460yxy y ''-+=的通解中含任意常数的个数为 4 个.2. 以函数2y x Cx =+为通解的一阶微分方程为2xy x y'=+.3. 若级数1n n u ∞=∑的部分和为21n ns n =+,则级数1n n u ∞=∑的和s = 2 .4. 为使级数()11np n n∞=-∑条件收敛,则常数p 的取值范围为01p <≤.5. 设幂级数1nn n a x ∞=∑的收敛区间为()3,3-,则幂级数()111n n n na x ∞-=-∑的收敛区间为()2,4-.二、单项选择题(每小题3分,共15分) 1.设,,xxx e e-是某二阶线性非齐次微分方程的三个特解,则该微分方程的通解为( D ).(A) 12xy C x C e =+; (B) 123x x y C x C e C e -=++;(C) ()12x x y C x C e e -=+-; (D) ()()12x x y C e x C e x x -=-+-+. 2.将微分方程()21yy y '''-=降为一阶微分方程时,做变量代换y p '=,则( C ).(A) y p '''=; (B) dp y ydy ''=; (C) dp y p dy ''=; (D) dp y x dx''=. 3.微分方程23y y x '''-=的特解形式为( B ).(其中,,a b c 为常数)(A)*2y ax bx c =++; (B) ()*2y x ax bx c =++;(C) ()*y x ax b =+; (D) ()*22y x ax bx c =++. 4.若级数1nn u∞=∑收敛,则必收敛的级数为( A ).(A) ()11n n n u u ∞+=+∑ (B )()11nn n u n ∞=-∑ (C )21n n u ∞=∑ (D )()2121n n n u u ∞-=-∑5. 级数()1113n n n -∞=-∑的和s =( A ).(A)14 ; (B) 13 ; (C) 12; (D) 1 . 三、判断下列常数项级数是否收敛?若收敛,是条件收敛还是绝对收敛(每小题7分,共21分) 1.13n n n ∞=∑ ; 解:由正项级数的比值判别法11131lim lim 133n n n n n nu n u n ++→∞→∞+=⋅=<,所以该级数收敛,又因是正项级数,收敛的正项级数绝对收敛。
2017高等数学II(1)A参考答案
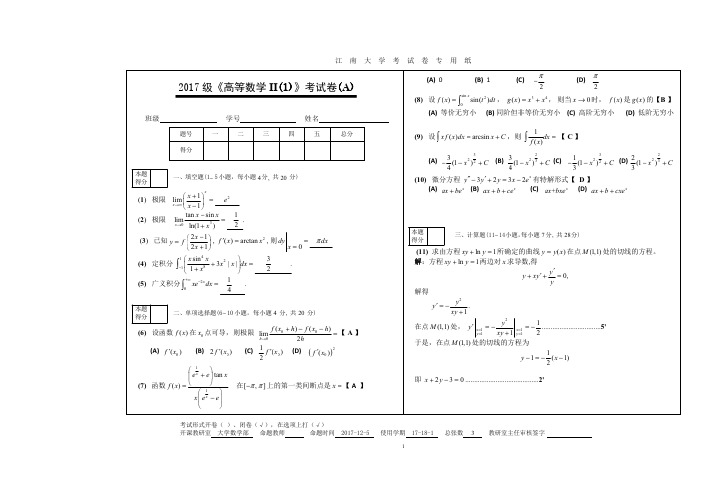
考试形式开卷( )、闭卷(√),在选项上打(√)
开课教研室 大学数学部 命题教师
命题时间 2017-12-5 使用学期 17-18-1 总张数 3 教研室主任审核签字
d
1
江南大学考试卷专用纸
(12) 求不定积分 ∫ arctan x dx .
解:令 x = t , 则 x = t2, dx = 2tdt .于是 ......................1'
本题 得分
三、计算题(11~ 14小题,每小题 7 分, 共 28分)
(11) 求由方程 xy + ln y = 1所确定的曲线 y = y(x) 在点 M (1,1) 处的切线的方程。 解:方程 xy + ln y = 1两边对 x 求导数,得
y + xy′ + y′ = 0, y
解得
y′ = − y2 . xy + 1
2
2e
所以特解为 y
==
−1 2e
1
x3e x2
+
1 x3 2
=
1 2e
1
x3 e − e x2
. ..............1'
本题 得分
四、证明题(15 ~ 16 小题,每小题 7 分,共 14 分)
(15) 证明:当 x > 0 时, ln(1 + x) > arctan x . 1+ x
江南大学考试卷专用纸
2017 级《高等数学 II(1)》考试卷(A)
班级
学号
姓名
(A) 0
(B) 1
(C) − π 2
(D) π 2
∫ (8) 设 f (x) = sin x sin(t2 )dt , g(x) = x3 + x4 , 则当 x → 0 时, f (x) 是 g(x) 的【B 】 0 (A) 等价无穷小 (B) 同阶但非等价无穷小 (C) 高阶无穷小 (D) 低阶无穷小
2016-2017(下)《高等数学AⅡ》期末试卷-E卷 (1)

第 1 页 (共 3 页)下学期期末考试试卷课程名称:《高等数学A Ⅱ》 (试卷编号:E )(本卷满分100分,考试时间120分钟)考试方式:考试考查闭卷开卷仅理论部分其他 )学院: 专业:班级: 学号: 姓名: 任课教师:考试地点: 考试时间: 月 日 时 分一、填空题(本大题共9小题10空,每空2 分,共 20分)1.已知()(),1,0,1a b ==r r2,1,-4,则a b ⋅=r r 。
2.与()2,2,1a =-r共线的单位向量e =r。
3.直线+162212x y z --==-与直线123043x y z -+-==的夹角余弦为。
4. ()22ln 2zx y=+--的定义域是 。
5.()(,)(0,3)sin limx y xy x→= 。
6.若()ln 1z xy =+,则()1,2zx ∂=∂ ,()1,2z y ∂=∂ 。
7.若xyz e =,则2zx y∂=∂∂ 。
8.若平面区域D 的面积为3,则二重积分Dd σ=⎰⎰ 。
9. 级数211n n ∞=∑的敛散性是 。
二、单项选择题(选择正确答案的字母填入括号,本大题共6小题,每小题3 分,共18 分)1. 已知,23a i j b i j k =-=+-r r r r r r r3,则a b ⨯=r r ( )。
A. 5 B. 2 C. 95i j k -+r r r 3 D. 95i j k ++r r r32.向量()1,2,a m =-r与向量()4,1,2b =r 垂直,则m =( )。
A.1- B. 0 C. 1 D.23.设23(,,)2f x y z xy y z xyz =+-,则()2,1,1yz f -=( )。
A.0 B. 4 C. 8 D. 13- 4. 函数x y x y x y x f 933),(2233-+++= 在点()1,0处( )。
A.取极大值B.取极小值C.不取极值D.无法确定 5.设()22DI xy dxdy =+⎰⎰, 其中D 是由曲线222x y a +=所围成的平面区域 ()0a >,则I =( )。
北京市西城区2016-2017学年度第二学期期末考试高二数学(文科)试卷

北京市西城区2016— 2017学年度第二学期期末试卷高二数学(文科)2017.7试卷满分:150分考试时间:120分钟题号一二三本卷总分151617181920分数一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1. 设集合2{|}A x xx ,{1,0,1,2}B ,则AB()(A ){0,2}(B ){0,1}(C ){1,2}(D ){1,2}2. 下列函数中,既是奇函数又是单调递增函数的是()(A )exy(B )ln y x(C )1yx(D )3yx3. 若等比数列{}n a 满足2420a a ,3540a a ,则公比q 等于()(A )2(B )12(C )3(D )134. 如果0a b ,那么下列不等式一定成立的是()(A )ab(B )11ab(C )11()()22ab(D )ln ln a b5. “d c b a ,,,成等差数列”是“c b d a ”的()(A )充分不必要条件(B )必要不充分条件(C )充要条件(D )既不充分也不必要条件6. 关于函数12()log f x x ,下列结论正确的是()(A )值域为(0,)(B )图象关于x 轴对称(C )定义域为R(D )在区间(,0)上单调递增7. 已知0x 是函数11()()2xf x x的一个零点,且10(,)x x ,20(,0)x x ,则()(A )1()0f x ,2()0f x (B )1()0f x ,2()0f x (C )1()0f x ,2()f x (D )1()0f x ,2()f x 8. 在股票买卖过程中,经常会用各种曲线描述某一只股票的变化趋势,其中一种曲线是即时价格曲线()y f x ,一种是平均价格曲线()y g x . 例如:(2)3f 表示开始交易后2小时的即时价格为3元,(2)4g 表示开始交易后2小时内所有成交股票的平均价格为4元. 下列给出的四个图象中,实线表示()yf x ,虚线表示()yg x . 其中可能正确的是()(A )(B )(C )(D )二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.已知命题:,e0xp xR ,则:p ______________.10. 曲线1y x在2x处切线的斜率为______.11. 当0x 时,函数24xyx的最小值为______. 12. 已知93a,ln xa ,则x______.13. 若函数1,0,1()1(),0.3x x x f x x则(1)(1)f f _______;不等式1()3f x 的解集为_______. 14. 已知非空集合,A B 同时满足以下四个条件:①{1,2,3,4,5}AB ;②A B;③()card A A ;④()card B B .注:其中()card A 、()card B 分别表示A 、B 中元素的个数.如果集合A 中只有一个元素,那么A_____;OxyOxyOxyOxy如果集合A 中有3个元素,请写出一对满足条件的集合,A B :_______________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13分)已知等差数列}{n a 的前n 项和为n S ,244S ,1051a a .(Ⅰ)求}{n a 的通项公式;(Ⅱ)设集合*{24}nA n S N,求集合A 中的所有元素.16.(本小题满分13分)已知函数32()3f x xx .(Ⅰ)求)(x f 的单调区间;(Ⅱ)若)(x f 的定义域为[1,]m 时,值域为[4,0],求m 的最大值.17.(本小题满分13分)已知函数2()21f x axax ,0a.(Ⅰ)当1a时,解不等式()4f x ;(Ⅱ)若函数()f x 在区间(1,2)上恰有一个零点,求a 的取值范围.18.(本小题满分13分)某市居民自水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨 3.00元. 某月甲、乙两户共交水费y 元,已知甲、乙两用户该月用水量分别为5,3x x 吨. (Ⅰ) 若1x ,求该月甲、乙两户的水费;(Ⅱ) 求y 关于x 的函数;(Ⅲ) 若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量.19.(本小题满分14分)已知函数2()(1)e2xf x x kx,kR .(Ⅰ)当0k时,求()f x 的极值;(Ⅱ)若对于任意的[0,)x,()1f x 恒成立,求k 的取值范围.20.(本小题满分14分)已知函数2()f x axbx 和x x g ln )(.(Ⅰ)若1b a ,求证:()f x 的图象在()g x 图象的上方;(Ⅱ)若()f x 和()g x 的图象有公共点P ,且在点P 处的切线相同,求a 的取值范围.北京市西城区2016 — 2017学年度第二学期期末试卷高二数学(文科)参考答案及评分标准2017.7一、选择题:本大题共8小题,每小题5分,共40分.1. C ;2.D ;3. A ;4. D ;5. A; 6. D; 7. D; 8. B.二、填空题:本大题共6小题,每小题5分,共30分.9. 对任意xR ,都有e0x; 10.14; 11.4; 12.e ;13. 5,[2,1]6;14.{4};{1,2,4}A ,{3,5}B ,或{1,2,5}A ,{3,4}B ,或{2,4,5}A ,{1,3}B.注:14题第二个空只需填对一组即可;一题两空的题目,第一空2分,第二空3分.三、解答题:本大题共6小题,共80分.15.(本小题满分13分)解:(Ⅰ)由题意得1146242410a d a d,……………4分解得19,2a d ,……………6分所以112)1(29)1(1n n dn a a n.……………8分(Ⅱ)n n n n ndn n na S n1022)1(92)1(21,……………10分由21024nn ,整理得210240n n,解得46n,……………12分所以集合*{24}nn S N中的所有元素为4,5,6.……………13分16.(本小题满分13分)解:(Ⅰ)由32()3f x xx ,得2()36f x xx .…………… 3分令2()360f x xx,得0x或2x.()f x 与()f x 在区间R 上的情况如下:x (,0)0(0,2)2(2,)()f x 00()f x 04…………… 6分所以,)(x f 在区间(,0)、(2,)上单调递增;在区间(0,2)上单调递减. …8分(Ⅱ)由(Ⅰ)知,函数)(x f 在区间(1,0)和(2,)上单调递增;在区间(0,2)上单调递减.且(1)4f ;(0)0f ;(2)4f ;(3)0f .所以,当03m 时,)(x f 的值域为[4,0];当3m 时,()(3)0f m f ,)(x f 的值域为[4,()]f m .……………12分所以,m 的最大值等于3.……………13分17.(本小题满分13分)解:(Ⅰ)当1a时,不等式()4f x 整理得2230xx ,即(1)(3)0x x ,…………… 3分解得3x或1x,所以,不等式()4f x 的解集为{3,1}x x x 或.…………… 6分(Ⅱ)由已知,抛物线()yf x 的对称轴为212a xa.…………… 9分所以函数()f x 在区间(1,2)上是单调函数.若()f x 在区间(1,2)上恰有一个零点,则(1)(2)0f f ,……………11分即(81)(31)0aa ,解得1138a.所以,a 的取值范围为11(,)38.……………13分18.(本小题满分13分)解:(Ⅰ)当1x时,甲用水量为5吨,需交水费4 1.81310.20元. …………2分乙用水量为3吨,需交水费3 1.8 5.40元.……………4分(Ⅱ)当54x,即0.8x 时,甲、乙两户用水量均不超过4吨.(53) 1.814.4y xx x ;……………6分当54x ,34x ,即4453x时,甲用水量超过4吨,乙用水量不超过4吨.3 1.84 1.8(54)320.4 4.8y x x x ;……………8分当34x ,即43x 时,甲、乙用水量均超过4吨.(44) 1.8(5434)3249.6y x x x .……………9分所以414.4,,54420.4 4.8,,534249.6,.3x x y x x xx……………10分(Ⅲ)由(Ⅱ)可知,函数()yf x 在各分段区间上都是增函数.当4[0,]5x时,4()26.45yf ;当44(,]53x时,4()26.43y f ;当4(,)3x时,令249.626.4x ,解得 1.5x .57.5x,3 4.5x,所以,甲用水量为7.5吨;乙用水量为 4.5吨. (13)分19.(本小题满分14分)解:(Ⅰ)当0k时,()(1)e2xf x x .则()e (1)e e xxx f x x x ,……………2分所以,在区间(,0)上()0f x ,()f x 是减函数;在区间(0,)上()0f x ,()f x 是增函数. ……………4分又(0)1f ,所以,()f x 的极小值为1;没有极大值. ……………6分(Ⅱ)由2()(1)e2xf x x kx ,得()e 2(e 2)xxf x x kx x k . ……………7分当0k时,e 20xk ,所以,当0x时,()0f x ,当0x时,()0f x ,()f x 在区间(,0)上是减函数,在区间(0,)上是增函数.……………8分所以()f x 在区间[0,)上的最小值为(0)f ,且(0)1f ,符合题意. …………9分当0k时,令()0f x ,得0x或ln 2xk ,所以,当102k时,ln 20k 在区间(0,)上()0f x ,()f x 是增函数,所以()f x 在区间[0,)上的最小值为(0)1f ,符合题意.……………11分当12k 时,ln 20k ,当(0,ln 2)xk 时,()0f x ,()f x 在区间(0,ln 2)k 上是减函数.所以(ln 2)(0)1f k f ,不满足对于任意的[0,)x,()1f x 恒成立. (13)分综上,k 的取值范围为1(,]2. (14)分20.(本小题满分14分)解:(Ⅰ)当1b a 时,2()f x xx .设2()ln h x xx x ,0x. ……………1分则2121(21)(1)()21xx x x h x x xxx,……………2分所以,在区间1(0,)2上()0h x ,()h x 是减函数;在区间1(,)2上()0h x ,()h x 是增函数. ……………4分所以,()h x 的最小值为1()2h 31ln42,又31ln042,所以()0h x 恒成立.即()f x 的图象在()g x 图象的上方.……………6分(Ⅱ) 设00(,)P x y ,其中00x .由已知()2f x ax b ,1()g x x.因为在点P 处的切线相同,所以200000012,,ln ax by axbx y x x .……………8分消去0,b y 得200ln 10axx ,依题意,方程200ln 10ax x 有解.……………9分设2()ln 1F x axx ,则()F x 在(0,)上有零点.2121()2axF x axxx,当0a时,()0F x ,函数()F x 在(0,)上单调递增. 当1a 时,(1)10F a ,11()ln0F aa,所以()F x 有零点.当01a时,(1)10F a ,22(e )e10F a ,所以()F x 有零点.……………11分当0a 时,令()0F x ,解得12xa . ()F x 与()F x 在区间(0,)上的情况如下:x1(0,)2a12a1(,)2a ()F x 0()F x 13ln22a 令13ln022a,得312e a.此时(1)10F a .所以()F x 有零点.……………13分综上,所求a 的取值范围为31[,)2e.……………14分。
厦门大学 【精品】2016-2017学年第2 学期 高等数学A期末考试试卷

厦门大学2016-2017学年第2 学期高等数学A 期末考试试卷2016~2017学年第2 学期 考试科目:高等数学A 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.二元函数2ln(21)z y x =-+的定义域为 。
2. 设向量(2,1,2)a =,(4,1,10)b =-,c b a λ=-,且a c ⊥,则λ= 。
3.经过(4,0,2)-和(5,1,7)且平行于x 轴的平面方程为 。
4.设yz u x =,则du = 。
5.级数11(1)npn n ∞=-∑,当p 满足 条件时级数条件收敛。
二、单项选择题(本大题共5小题,每小题3分,共15分)1.微分方程2()'xy x y y +=的通解是( )A .2x y Ce =B .22x y Ce =C .22y y e Cx =D .2y e Cxy = 2.求极限(,)(0,0)limx y →=( )A .14 B .12- C .14- D .123.直线:327x y zL ==-和平面:32780x y z π-+-=的位置关系是 ( )A .直线L 平行于平面πB .直线L 在平面π上C .直线L 垂直于平面πD .直线L 与平面π斜交4.D 是闭区域2222{(,)|}x y a x y b ≤+≤,则Dσ= ( )A .33()2b a π-B .332()3b a π-C .334()3b a π-D .333()2b a π-5.下列级数收敛的是 ( )A .11(1)(4)n n n ∞=++∑ B .2111n n n ∞=++∑ C .1121n n ∞=-∑ D.1n ∞=三、计算题(本大题共7小题,每小题7分,共49分) 1. 求微分方程'x y y e +=满足初始条件0x =,2y =的特解。
2. 计算二重积分22Dx y dxdy x y++⎰⎰,其中22{(,)1,1}D x y x y x y =+≤+≥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京大学高等数学 A 期末考试试卷2016~2017学年第 2 学期考试科目:高等数学 A 考试类型:(闭卷)考试考试时间: 120 分钟学号 姓名 年级专业、填空题(本大题共 5小题,每小题 3分,共15分)1.二元函数 z ln(y 22x 1) 的定义域为 。
2. 设向量 a (2,1,2) ,b (4, 1,10) , c b a ,且 a c ,则 3.经过(4,0, 2)和(5,1,7)且平行于 x 轴的平面方程为 。
4.设 u x ,则 du 。
15.级数 ( 1)n 1p ,当 p 满足条件时级数条件收敛。
n 1 n二、单项选择题 (本大题共 5小题,每小题 3分,共 15分)1.微分方程 2(xy x)y' y 的通解是( )A . y Ce 2x2 2xB . yC eC . y2e2y CxD . e2y Cxy2.求极限 lim 2 xy 4()(x,y) (0,0)xy1 1 1 1A .B .C .D .42 4 23.直线 L : x y z 和平面 :3x 2y 7z 8 0 的位置关系是 ()32 7A.直线L 平行于平面B.直线L在平面上三、计算题(本大题共 7小题,每小题 7分,共49分)1. 求微分方程 y' y e x满足初始条件 x 0, y 2的特解。
xy2. 计算二重积分 2 2 dxdy ,其中 D {( x, y) x 2 y 2 1,x y 1} D x y3.设 z z(x,y)为方程 2sin( x 2y 3z) x 4y 3z 确定的隐函数,求 xyC .直线 L 垂直于平面D .直线 L 与平面 斜交4.D 是闭区域 {( x, y)|a 2 x 2y 2 b 2} ,则 x 2 y 2dD3 32 3 3 4 3 3A . (b a )B . (b a )C . (b a ) 2 3 3 5.下列级数收敛的是1 1 n 1 A .1B . 12nC .1n 1 (n 1)(n 4) n 1 n 1 n 1 2n 1D .3(b 3a 3)2D .n11 3n(n 1)4.求曲线积分(x y)dx (x y)dy ,其中L沿x2 y2 a2(x 0, y 0) ,逆时针方L向。
5. 计算y51 x2y6dxdy ,其中D是由y 3 x,x 1及y 1所围成的区域Dn6.判断级数( 1) n 1的敛散性,并指出是条件收敛还是绝对收敛n 1 n 1 n(1 x)(2 x)展开成x的幂级数,并求其成立的区间四、解答题 (本大题共 3 小题,每小题7 分,共21 分)1.抛物面z x2 y2被平面x y z 1截成一椭圆,求原点到这椭圆的最长与最短距离。
7.将函数nn2. 求幂级数( 1) nx的和函数n 1 (n 1)!3. 设函数f(x)和g (x)有连续导数,且 f (0) 1,g(0) 0 ,L为平面上任意简单光滑闭曲线,取逆时针方向,L 围成的平面区域为 D ,已知xydx [yf(x) g(x)]dy yg(x)d ,LD求 f (x)和g(x) 。
sin cos1.5CM 参考答案一、填空题(本大题共 5小题,每小题 3分,共15分)1.{( x,y)|y 22x 1 0} 2.33.9y z 2 0 4. yzx yz 1dx zx yzln xdy yx yzln xdz 5.0 p 1二、单项选择题 (本大题共 5小题,每小题 3分,共 15分)1.C 2.C 3.C 4.B 5. A三、计算题(本大题共 7小题,每小题 7分,共49分) 1. 求微分方程 y' y e x满足初始条件 x 0, y 2的特解。
解:先求 y' y 0的通解,得 y C 1e x ⋯⋯⋯⋯⋯⋯ 2 分 采用常数变易法,设 y h(x)e x,得 y' h'(x)e xh(x)e x⋯⋯⋯3 分 代入原方程得 h'(x)e x h(x)e x h(x)e x e x⋯⋯⋯⋯⋯⋯ 4分得h(x) 1e 2x C ⋯⋯⋯⋯⋯⋯ 5 分 2故通解为 y 1e xCe x⋯⋯⋯⋯⋯⋯ 6分2将初始条件 x 0,y 2带入得C 23,故特解为 y 12e x 32e x7分2. 计算二重积分 x2 y2 dxdy ,其中 D {( x,y):x 2y 2D x y1,x y 1} 。
解:设 x r cos , y r sin 1分 所以x 2y2 D x 2 y 2dxdy 2 dsin cos2(sin cos 1)d47分r cos r sinrdr 5分6分3分3.设z z(x, y)为方程2sin( x 2y 3z) x 4y 3z 确定的隐函数,求xy 解:设 F ( x, y, z) x 4y 3z 2sin( x 2y 3z) ⋯⋯⋯⋯⋯⋯ 1 分F x 1 2cos( x 2y 3z), F y 4 4cos( x 2y 3z), F z 3 6cos( x 2y 3z) ⋯⋯⋯⋯⋯⋯4 分所以xy4. 求曲线积分(x y)dx (x y) dy,其中L沿x2 y2 a2(x 0,y 0) ,逆时针L方向。
解:圆的参数方程为:x acost , y a sint (0 t ) ⋯⋯⋯⋯⋯1分2(x y)dx (x y)dy02(a cost a sin t )da cost02(a cost a sin t)dasint ⋯⋯3 分La2 2 (cos 2t sin 2t )dt ⋯⋯⋯⋯⋯⋯ 4 分a2[sin 2t cos2t]02⋯⋯⋯⋯⋯⋯ 6 分2a2⋯⋯⋯⋯⋯⋯7 分(本题也可以利用“曲线积分与路径无关”来解)5. 计算y51 x2y6dxdy ,其中D是由y 3 x,x 1及y 1所围成的区域。
D解:D {(x,y)|3 x y 1, 1 x 1} ⋯⋯⋯⋯⋯⋯1分y 51 x2y6dxdyD 11dxy6dy 2分4分z F x 2cos(x 2y 3z) 1 x F z 3[1 2cos( x 2y 3z)] z F y 4cos(x 2y 3z) 4y F z 3[1 2cos(x 2y 3z)]6分zz 7分1 1 39 1(|x|31)dx 5分 13(x 31)dx ⋯⋯⋯⋯⋯⋯6分7分6. 判断级数n1 ( 1)nn n1的敛散性,并指出是条件收敛还是绝对收敛解:( 1)nn 1 n 1 nn 1⋯⋯⋯⋯⋯⋯ n 1 n1分1(n ) ⋯⋯⋯⋯⋯⋯ 3 分n所以级数发散。
⋯⋯⋯⋯⋯⋯ 4 分 又n 1 n ( 1) (11)1n 1 n5分( 1)n( 1)n 1n (n 1) n6分显然,交错级数 ( 1), n 1 n 收敛。
⋯⋯⋯⋯⋯⋯ 7 分n1 ( 1)n(n 1) n 都收敛,所以原级数收敛。
因此是条件7. 将函数 (1 x)(2 x) 展开成 x 的幂级数,并求其成立的区间 解:(1 x)(2 x) 1 x 2 x 2分1n 而x n, |x| 11 x n 0 3分21x 12[1 2x (x 2)2] (|x| 2)4分 所以(1 x)(2 x)1 x x212[1 2x (2x )2]5分(1 n 11) x n⋯⋯⋯⋯⋯⋯ 6分 n 0 2成立范围 |x| 1⋯⋯⋯⋯⋯⋯ 7 分 四、解答题(本大题共 3 小题,每小题 7 分,共 21 分)1. 抛物面 z x 2 y 2 被平面 x y z 1截成一椭圆,求原点到这椭圆的最长与最 短距离。
解:设椭圆上任一点 P 的坐标为 P(x,y,z), P 点满足抛物面和平面方程。
原点到这椭圆上任一点的距离的平方为 x 2 y 2 z 2 ,⋯⋯⋯⋯⋯⋯ 1 分 构造拉格朗日函数F x 2y 2z 2(x 2y 2z) (x y z 1) ⋯⋯⋯⋯⋯⋯ 2 分F x 2x 2x 0 F y 2y 2y 0F z 2z 0 ⋯⋯⋯⋯⋯⋯ 4 分 F x 2 y 2z 0F x y z 1 0解得 x 1( 1 3) ⋯⋯⋯⋯⋯⋯ 5 分2得两个驻点为 P 1 ( 1 3, 1 3,2 3), P 2 (1 3, 1 3,2 3)2 2 22 22 22⋯⋯⋯⋯⋯⋯⋯ 6 分所以最短距离为 9 5 3 ,最短距离为 9 5 3 ⋯⋯⋯⋯⋯⋯ 7 分nn2. 求幂级数( 1) nx的和函数 n 1 (n 1)!n解:因为 exx,所以 e xn 0 n! n 0nn( 1) x n!1分 S(x)n0nn ( 1) nx (n1)! n0( 1)n (n 1 1)xn (n 1)! 2分n n n n( 1)nx n( 1)nx n⋯⋯⋯⋯⋯⋯n 0 n! n 0 (n 1)!3分所以1S(x) e x (1 e x)(x 0)x 1x(1 e x) (x 0) ⋯⋯6 分 xnnxx( 1)n x ndx n 0 n!1 x 1 x x xde x 01xxxe e 1 x II3. 设函数 f(x)和g(x)有连续导数,且 f(0) 1,g(0) 0 ,L 为平面上任意简单 光滑闭曲线,取逆时针方向, L 围成的平面区域为II xx ee xxnn( 1)n x nxe n0 n! 4分( 1)n x n 1 ( 1)n x n 11 ( 1)n 1x n 1n 0 (n 1)! x n 0 (n 1)! x n 0 (n 1)!1 ( 1)n x n1 x n 0 n!1 1exe xxn 0 (n 1)!1 ( 1)n x nx n 1 n! 1 1 ( 1)n x n x x n 0 n!(x 0 )⋯ 5分故 S(x) e x 当 x 0 时, S(x) 0 。
7分 另解:当 x 0 时,( 1)n nx n 1 ( 1)n nx n 1 1 ( 1)n n 1 (n 1)! x n 1 (n 1)! x n 1 (n 1)! x ndx 01xx 0 n 1 (n 1)! dx( 1)n 1x n 1 0x( 1) xdxn 1 (n 1)!xx 0 xe 当 x 0 时,S(x) 0 。
D,已知Lxydx [yf(x) g(x)]dy yg(x)d ,求 f (x)和g(x) 。
解:由格林公式得[yf '(x) g'(x) x]dxdy yg(x)dxdy⋯⋯⋯⋯⋯⋯ 2 分DD即[yf '(x) g'(x) x yg( x)]dxdy 0 ⋯⋯⋯⋯⋯⋯ 3 分D由于区域的任意性,yf '(x) g'(x) x yg(x) 0 ⋯⋯⋯⋯⋯⋯4分又由于y的任意性,有 f '(x) g(x),g'(x) x ⋯⋯⋯⋯⋯5分2又由f(0) 1,g(0) 0得,g(x) x⋯⋯⋯⋯⋯⋯6分23所以 f (x) x 1 ⋯⋯⋯⋯⋯⋯7 分61 623 1[(1 x2 y6)2]13xdx。
