配合物晶体场理论2019
无机化学-配合物结构理论

配位化合物中M与L之间化学健的形成及 配合物的一些性质难以用经典化学健理论来 解释。
1913年Pauling 首先将分子结构中的价健 理论应用于配合物,并经不断修正补充,形 成了近代配合物价健理论。
2019年10月11 日5时28分
一、价键理论的要点
1、中心离子(M)具有空的价电子轨道,配体(L)具 有孤对电子。
2、M的空轨道在成键前必先进行杂化,然后再与 L 形成 配位健。
3、配合物的空间构型和键型取决于M 的杂化轨道。
2019年10月11 日5时28分
二、配合物的空间构型 1、配位数为2的配合物
如:[Ag(NH3) 2]+ Ag+ 4d105s05p0
2019年10月11 日5时28分
(1) 轨道杂化:
[Co(NH3)6]2+等。
2019年10月11 日5时28分
2、内轨配键、内轨型配合物
M以部分次外层的轨道(n-1)d组成杂化轨道, 与配位原子形成的配健称为内轨配键。相应的化 合物称为内轨型配合物。
如:dsp2 、dsp3 、d2sp3等。 内轨型配合物:[Cu(H2O)4]2+、[Co(NH3)6]3+、
2019年10月11 日5时28分
3、配合物的颜色 当dγ轨道(八面体场为例)上填满了电子(d10结构)
或无d电子(d0)时,配合物的电子不能在dγ~dε之 间跃迁。故配合物是无色的。
其余d1~d9情况下,dε上的电子可以吸收能量跃迁 到dγ 上。故要吸收一定谱长的光,而人们看到它们的 补色。此时配合物一般都是有色的。
2019年10月11 日5时28分
例: [Ni(NH3)4]2+ Ni 3d8
第一节晶体场理论ppt课件

释了配合物的空间构型等问题。
为了较好地解释配合物的磁性和高自旋和低自旋等问
题,1935年培特和冯弗莱克提出了晶体场理论(CFT)。
晶体场理论认为:配合物中央离子(原子)和配体之
间的相互作用,主要来源于类似于离子晶体中正负离子间
的静电作用;在此作用下,中心离子的原子轨道可能发生
分裂。
z
Hans Albrecht Bethe
——2006年高中化学竞赛试题
6-2 某钒的配合物具有 VO(N2O2)配位结构形式,所有的氮、氧原子都为配 位原子。且配合物只检测到一种 V-N键,两种 O-V键。
美国著名化学家,因阐明化学 键的本质,并以此解释了复杂分子 结构,1954年获诺贝尔化学。
看法。 他认为:所有配合物都是以共价配键结合的。并结合杂化轨道理论对
配合物的构型加以解释。
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
相对较多;
npx npy
☆pz 轨道受配体静电的排斥相对
较小,其能级升高相对较少。
E’
npz
np
四方配位场
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
⑶ d轨道
中央离子的 d 轨道有五种取向(dxy、dyz、dxz、dx2-y2、dz2),当四 个配体沿±x、±y 方向靠近中央离子时,中央离子 d 轨道受配体静电的 排斥,其能级升高,并发生能级分裂。
点平面方向。
z
z
x
y
y
x
dxz
dyz
5-2 配合物的晶体场理论

△o
设Es3+ 13 则 2Eeg +3Et2g=0 =0, (1) 3+ d CFSE=1×(- 0.4 △oo))= --0.4 △o 如 Ti Cr d CFSE=3×(- 0.4 △ = 1.2 Eeg - Et2g = △o (2) 3 联立(1)、(2)式,得 Eeg = + 5 △o = +0.6 △o 2 - 5△o = - 0.4 △o Et2g = CFSE: d 电子进入分裂轨道比处于未分裂 轨道总能量降低值。
该二轨道处于和配体迎头相碰的位置, 其电子受到静电斥力较大,能量升高。 2-y2 dz2 eg dx E Es t2g E0 自由离子 球形场中 八面体场
该三轨道插在配体的空隙中间,其电子受 到静电斥力较小,能量比前二轨道低。 2-y2 dz2 eg dx E Es dxy dxz dyz t2g E0 自由离子 球形场中 八面体场
d1 ↑ d2 ↑ ↑ d3 ↑ ↑ ↑ d4 ↑ ↑ ↑ d5 ↑ ↑ ↑ d6 ↑ ↑ ↑ d7 ↑ ↑ ↑ d8 ↑ ↑ ↑ d9 ↑ ↑ ↑ d10 ↑ ↑ ↑
↑ ↑ ↑ ↑ ↑
1 2 3 ↑ 4 高 ↑↑ 5 ↑↑ 自 4 ↑↑ 旋 3 ↑↑ 2 ↑↑ 1 ↑↑ 0
1 2 3 2 低 1 自 0 旋 1 ↑ ↑↑ 2 ↑↑ 1 ↑↑ 0
↑ ↑ ↑
↑ ↑ ↑ ↑ ↑
↑ ↑ ↑ ↑ ↑ ↑
↑ ↑ ↑ ↑ ↑ ↑ ↑
↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑
↑ ↑ ↑ ↑ ↑
d4d7构型的离子, d电子分布有高、低自 如 Cr2+ d4 旋两种方式。 [Cr(H2O)6]2+ [Cr(CN)6]4eg eg ´ △o △o t2g t2g 高自旋 低自 旋 电子成对能(P)和晶体场分裂能的相对大小 H2O是弱场 CN-是强场
配位化学配合物的晶体场理论及光谱化学序列

配位体的性质和数量可以影响 配位化学配合物的稳定性、溶 解性和反应性。
03 晶体场理论
晶体场理论的定义
01
晶体场理论是研究过渡金属配合物中金属离子的电子能级变化 的理论。
02
它将配合物置于一个晶体场中,通过金属离子与配体的相互作
用,来描述配合物的电子能级变化。
这种理论主要关注配合物在晶体场中的电子排布和能级分裂。
晶体场理论和光谱化学序列是研究配 位化学配合物的重要理论工具,有助 于深入理解配合物的结构和性质。
研究意义
深入理解配位化学配合物的结构和性 质,有助于发现新型材料和催化剂, 推动相关领域的发展。
晶体场理论和光谱化学序列的应用, 有助于揭示配合物的电子结构和光谱 性质,为实验研究和应用提供理论支 持。
对未来研究的建议
进一步研究不同晶体场对配合物性质的影响,探索更 有效的理论模型来描述配合物的电子结构和性质。
输标02入题
开展更多光谱实验,收集更全面的光谱数据,以完善 光谱化学序列的数据库,提高预测新配合物物的研究,探索其在能源、环境、 生物医学等领域的应用潜力,为解决实际问题提供科
02 配位化学配合物的基本概念
配位化学配合物的定义
配位化学配合物是由一个或多个中心原子(或离子)与一定数目的配位体通过配 位键结合形成的复杂化合物。
中心原子通常具有可用的空轨道,而配位体则提供孤对电子,形成稳定的电子对 配位键。
配位化学配合物的分类
根据中心原子的类型,配位化学 配合物可分为金属配合物和无机
学依据和技术支持。
04
加强跨学科合作,将配位化学与其他领域(如物理、 材料科学等)相结合,开拓新的研究领域和应用前景。
THANKS
光谱化学序列的分类
《晶体场理论》课件

03
通过实验测量可以获得晶体的各种物理性质数据,如通过硬度测试了解晶体的机械性能,通过电导率测试了解晶体的导电性能等。
03
CHAPTER
晶体场理论的基本概念
晶体场中电子由于受到周期性势场作用而产生的能级分裂,产生的能量差值即为晶体场稳定化能。
晶体场稳定化能
晶体场分裂能
随着晶体场强度的增加,分裂能级的间距逐渐增大。
强晶体场中分裂能级较为稳定,弱晶体场中分裂能级不稳定。
在晶体场作用下,电子云会发生变形,以适应周围势场的分布。
电子云变形
光谱线分裂
磁有序现象
化学键合作用
由于晶体场作用,光谱线会分裂成多个子线,子线的数目和位置取决于晶体场的对称性和强度。
在强晶体场中,由于电子自旋和轨道磁矩的相互作用,可导致磁有序现象的出现。
常用的数值计算方法包括有限差分法、有限元法、蒙特卡洛方法等。这些方法可以根据具体问题选择合适的数值计算方法,以获得更准确的结果。
05
CHAPTER
晶体场理论的应用
磁性材料设计
利用晶体场理论预测和解释不同材料的磁学性质,为磁性材料的设计和优化提供理论支持。
催化剂设计
通过晶体场理论模拟催化剂的电子结构和活性位点,优化催化剂的性能,提高化学反应效率。
晶体场效应
由于晶体场作用导致能级分裂的能量差值,反映了晶体场对电子的束缚强弱。
晶体场对电子的相互作用和影响,包括电子云变形和能级分裂等。
03
02
01
能级分裂类型
分裂能级数量
分裂能级间距
分裂能级的稳定性
01
02
03
04
根据晶体场强度和对称性,能级分裂可分为弱场分裂、中等强度场分裂和强场分裂。
第16讲 配合物的晶体场理论

第五章 配位化合物的化学键理论
分裂后d轨道中电子的排布—高自旋态和低自旋态 二、 分裂后d轨道中电子的排布 高自旋态和低自旋态 d轨道分裂前:在自由金属离子中,5个d轨道是简并的,电子的排 布按洪特规则分占不同轨道,且自旋平行,有唯一的一种排布方 式。 d轨道分裂后:在络合物中,金属离子的d电子排布将有两种情况: 高自旋态排布和低自旋态排布,这与分裂能 成对能 分裂能和成对能 分裂能 成对能的大小有关。
第五章 配位化合物的化学键理论
dz2, d(x2-y2)
eg
6Dq
10Dq Es
自由离子d轨道 球形场
dxz,dxy,dyz
4Dq
t2g
d轨道在Oh场中轨道能级的分裂图 可见 在八面体场中,d轨道分裂的结果是:与Es相比,eg 轨道能量上升了6Dq,而t2g轨道能量下降了4Dq.
第五章 配位化合物的化学键理论
第五章 配位化合物的化学键理论
(5)分裂能与紫外光谱 )
(a)电磁波的名称及波长范围
第五章 配位化合物的化学键理论
(b)d-d跃迁
dz2, d(x
2
-y )
2
eg
6Dq
d-d跃迁
10Dq
4Dq
Es
自由离子d轨道 球形场
dxz,dxy,dyz
t2g
d轨道在Oh场中轨道能级的分裂图
∆Ed − d = ∆分裂能 ≃ 近紫外区和可见光区的光能
3.分裂后d 3.分裂后d轨道中电子的排布 分裂后
电子在分裂后d轨道中的排布与△和P的相对大小有关。 如:对于d2组态,有两种排布方式:
△ (a) (b)
△
第五章 配位化合物的化学键理论
△ (a)
第5讲 配合物的化学键理论-晶体场理论

洛阳师范学院
2. 正四面体场
d轨道能级在Td场中的取向
dxy、dxz、dyz:指向立方体棱边的中点,用t2表示;
dz2和d x2-y2:指向立方体的面心,用e表示。
较高能级(eg)上d 电子排布不均匀时,发生大畸变。
理想八面体
0 3 6 *2 10 d , d , t e , d 2g g 3 *2 6 t e ( HS ), t 2 g ( LS ) 2g g
变形八面体
大变形
3 *1 6 *3 6 *1 t e ( HS ), t 2 g eg , t2 g eg ( LS ) 2g g 1 2 4 *2 5 *2 5 t , t , t e ( HS ), t e ( HS ), t 2g g 2g 2g 2g 2g g
洛阳师范学院
光谱化学序的一般认识 ①卤素 < 氧 < 氮 < 碳;
② I < Br < Cl < F ;
–
–
–
–
随r↓,静电场↑,△也↑。
③ NH3、H2O都是极性分子,但NH3的极化率> H2O, 所 以有较 大的诱导 偶极 , 可产生 较强的 静电场: △NH3 > △H2O; ④ 但是静电效应不能解释:
洛阳师范学院
d轨道能级在Td场中的分裂:
分裂能△t小于△o,计算表明△t=(4/9)△o 根据重心守恒原理可以求出t2及e轨道的相对能量: 3E(t2)+2E(e)=0 △t=E(t2)-E(e)=(4/9)△o
配合物的晶体场理论及配合物的光谱4h课件

对于d1,d2,d3型中心离子,按Hund规则,只有一种d电子的排布方式,即分占 三个不同的简并t2g 低能轨道;对于d4,d5,d6,d7型中心离子,分别有两种排布 方式;而对于d8,d9,d10型中心离子,也只有一种d电子的排布方式。各组态电 子排布方式:
配合物的晶体场理论及配合物的光谱4h 课件
随着新实验材料的积累,新型配合物的不断涌现,价键理论遇到了越来 越多的困难,在此基础上逐渐发展起了晶体场理论
4.1 晶体场理论(CFT)
晶体场理论是一种静电理论,它把配合物中中心原子与配体之间的相互作
用看作类似于离子晶体中阴、阳离子间的相互作用。但配体的加入,使得中
心原子五重简并的d轨道失去简并性,分裂为两组或更多的能级组,因而对
可见:八面体配合物中,只有d4,d5,d6,d7四种离子才有高、低自旋两种 可能的排布。高自旋态(P>Δ0)即是较小的弱场排列,成单电子多,不够稳 定;低自旋态(P<Δ0)即是较大的强场排列,成单电子少,较稳定
对于正四面体配合物,由于Δt=4/9Δ0,一般Δt<P,所以尚未发现低自旋配合物
正八面体配合物的稳定化能可按下式计算:
E(t2g)=-4Dq
n2 =0
CFSE=xE(eg)+yE(t2g)+(n1-n2)P=0×6Dq+5×(-4q)+(2-0)P= -20Dq+2P
由计算可知,在弱场中,体系能量相对于球形场无变化;在强场中,轨道分裂可 降低20Dq的能量,但由于有两对电子成对,又要升高2P的能量。故实际采取哪种 方式应取决于10Dq(轨道分裂能)与P(电子成对能)的相对大小。如果10Dq>P,则以 低自旋方式存在,反之则以高自旋存在
把晶体场足够强以致使得10Dq>P的配体称为强场配体,反之则称为弱场配体
金属配合物晶体场理论

第九讲:多原子分子金属配合物晶体场理论1. 金属配合物2MLn: 金属离子或原子与它周围n 个离子或分子形成的化合物价键理论(VB)例如[Fe( H2O )6]3+配合物的中央离子(或原子)和配位体之间的化学键可分为电价配键和共价配键两种。
电价配合物,带正电的中心离子和带负电或具有偶极矩的配位体之间是靠静电引力结合成键,呈高自旋状态。
共价配合物,配位体的孤对电子和中心离子空的杂化价轨道形成共价配键,呈低自旋状态。
价键理论说明了高自旋配合物和低自旋配合物产生的原因,对配合物的磁性和几何构型也都给予了一定的说明。
但作为一个定性的理论,价键理论有很大的局限性。
1). 历史3晶体场(CFT)分子轨道法(MO)1929年,H.Bethe 用量子力学结合群论初步建立了晶体场方法。
将配合物视为一个大的分子,用MO法处理。
因包含金属d 轨道,MO成分较为复杂。
在MO法中,对称性匹配原则是关键因素。
1950年代以后,人们吸收上述理论的优点,发展了配位场理论。
1932年,van Vleck 在Bethe的工作基础上,提出过渡金属配合物的化学键理论,较好地解释金属配合物的磁性和稳定性。
1. 金属配合物5.3 金属配合物晶体场理论2. 晶体场理论1)、基本思想金属配合物的成键类似于离子晶体中正负离子的作用。
(i)金属与配体的作用为静电作用,配体视为点电荷。
(i i)配体的作用是建立一个负电荷势场(晶体场),在晶体场的微扰下,金属的d轨道发生能级分裂。
(i i i)金属的电子从低到高填充分裂后的d轨道,使总能量下降,产生附加成键效应。
分裂后总能量的下降称晶体场稳定化能(CFSE)。
42. 晶体场理论8(ii)d轨道分裂模式:由晶体场的对称性决定。
中心力场O h 的不可约表示对于正八面体场,5个d轨道按O h 群的不可约表示分类(查特征标表或相关表)原来简并的d 轨道分裂为两组:e g 和t 2g 。
gz y x gzx yz xy e d d t d d d ⎪⎭⎪⎬⎫⎪⎭⎪⎬⎫-22222. 晶体场理论10两组能级的高低(直观观察)ge 2gt ∆:∆分裂能2. 晶体场理论14(i)用群论知识了解d轨道分裂为几组。
配位化合物的价键理论 配合物的晶体场理论

.配位化合物的价键理论配合物的晶体场理论一.配合物的构型与中心的杂化方式二中心杂化轨道的形成1. ns np nd 杂化1 个 4s 空轨道,3 个 4p 空轨道和2 个 4d 空轨道形成 sp3d2杂化轨道,正八面体分布。
6 个F-的 6 对孤对电子配入sp3d2空轨道中,形成正八面体构型的配合单元。
例 2 Ni(CO)4的成键情况在配体 CO 的作用下,Ni 的价层电子重排成 3d104s0形成 sp3杂化轨道,正四面体分布,4 个CO 配体与 sp3杂化轨道成配键,形成的 Ni(CO)4构型为正四面体。
例 1 和例 2 的相同点是,配体的孤对电子配入中心的外层空轨道, 即 ns np nd 杂化轨道, 形成的配合物称外轨型配合物. 所成的键称为电价配键. 电价配键不是很强.例 1 和例 2 的不同点是,CO 配体使中心的价电子发生重排,这样的配体称为强配体。
常见的强配体有 CO、 CN-、NO2-等;例1 中 F-不能使中心的价电子重排,称为弱配体。
常见的弱配体有 F-、Cl-、H2O 等。
而 NH3等则为中等强度配体。
对于不同的中心,相同的配体其强度也是不同的。
2. (n-1) d ns np 杂化例 3 讨论的成键情况形成 d2sp3杂化,使用 2 个 3d 轨道, 1 个 4s 轨道,3个4p 轨道。
用的内层 d 轨道。
形成的配离子为正八面体构型。
空出 1 个内层 d 轨道,形成 dsp2杂化轨道,呈正方形分布。
故构型为正方形。
例 3 和例 4 中,杂化轨道均用到了 ( n - 1 ) d 内层轨道,配体的孤对电子进入内层,能量低,称为内轨配合物,较外轨配合物稳定。
所成的配位键称为共价配键。
三价键理论中的能量问题内轨配合物稳定,说明其键能 E内大,大于外轨的 E外,那么怎样解释有时要形成外轨配合物呢?其能量因素如何?上面的例题中我们看到,形成内轨配合物时发生电子重排,使原来平行自旋的 d 电子进入成对状态,违反洪特规则,能量升高。
无机化学 配合物 晶体场理论超级详细 超级好
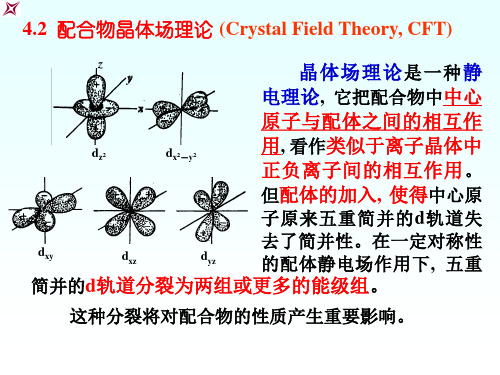
z
y
dz2
dx2-y2
晶体场理论 是一种 静 电理论, 它把配合物中中心 原子与配体之间的相互作 用, 看作类似于离子晶体中 正负离子间的相互作用 。 但配体的加入, 使得中心原
dyz
ห้องสมุดไป่ตู้dxy
dxz
子原来五重简并的 d 轨道失 去了简并性。在一定对称性 的配体静电场作用下 , 五重
该化学序代表了配体场的强度顺序。由此顺序可见, 对同一金属离子, 造成△值最大的是CN-离子, 最小的是I- 离子,通常把 CN - 、 NO 2 - 等离子称作 强场配位体 , I - 、 Br-、F-离子称为弱场配位体。
须指出的是, 上述配体场强度顺序是纯静电理论 所不能解释的。例如OH-比H2O分子场强度弱, 按静 电的观点OH-带了一个负电荷, H2O不带电荷, 因而 OH - 应该对中心金属离子的 d 轨道中的电子产生较 大的影响作用, 但实际上是OH-的场强度反而低, 显 然这就很难纯粹用静电效应进行解释。这说明了
HS
CSFE对dn的双峰曲线
既然 CFSE 引起附加成键效应,那么这种附加成 键效应及其大小必然会在配合物的热力学性质上表现 出来。
CFSE对配合物性质的影响
晶体场理论的核心是配位体的静电场与中心离子的作 用所引起的 d 轨道的分裂和 d 电子进入低能级轨道带来的稳 定化能使体系能量下降,从而产生一种附加成键作用效应。
由右图可以发现,在正八 面体弱场高自旋(HS)中, CFSE 的曲线呈现“反W”形或“双峰 ”形状, 三个极小值位于d0、d5 、d10处,两个极大值出现在d3 和d8处,而在强场低自旋(LS)中 , 曲线呈“V”形, 极小值为d0和 d10,极大值为d6。 LS
配合物晶体场理论

(2) 金属离子d轨道的主量子数
在同一副族不同过渡系的金属的对应配合物中,分裂 能值随着d轨道主量子数的增加而增大。当由第一过渡系到 第二过渡系再到第三过渡系、分裂能依次递增40~50 %和 20~25 %。这是由于4d轨道在空间的伸展较3d轨道远,5d 轨道在空间的伸展又比 4d轨道远,因而易受到配体场的强 烈作用之故。
四面体场
Td
球形场
八面体场
Oh
拉长八面体场
D4h
平面四方场
D4h
d 轨道能级在不同配体场中的分裂
二 分裂能和光谱化学序列
分裂能:中心离子的d轨道的简并能级因配体场
的影响而分裂成不同组能级之间的能量差。
分裂能的大小与下列因素有关:
1 配体场 亦即几何构型类型 如△t=(4/9)△o
2 金属离子
(1) 金属离子的电荷
sq = 17.42 Dqdx2-y2Fra bibliotek球形场
八面体场
拉长八面体场
平面四方场
sq = 17.42 Dq 总之,5条d轨道在Sq场中分裂为四组,由高到低的顺序是: ① dx2-y2, ② dxy, ③ dz2, ④ dxz和dyz。
dx2-y2
dxy dxz dyz
dxy dxz dyz
dxz dyz
一 晶体场中d轨道能级的分裂 1 正八面体场
假定有一 d 1 构型的正离子 , 当它处于一个球壳的中心,球 壳表面上均匀分布着 6 个单位的 负电荷,受负电荷的排斥, d轨 道能量升高。 另一方面,由于负电荷的 分布是球形对称的,因而不管 这个电子处在哪条 d 轨道上,它 所受到的负电荷的排斥作用都 是相同的,即 d轨道能量虽然升 高,但仍保持五重简并。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dx2-y2
球形场 八面体场 拉长八面体场 平面四方场
sq = 17.42 Dq 总之,5条d轨道在Sq场中分裂为四组,由高到低的顺序是:
① dx2-y2, ② dxy, ③ dz2, ④ dxz和dyz。
dxy dxz dyz
dx2-y2
四面体场 Td
dxy dxz dyz
●当P>△时, 因电子成对需要的能量高, 电子将尽
量以单电子排布分占不同的轨道, 取高自旋状态; ●当P<△时, 电子成对耗能较少, 此时将取低自旋
状态。
根据P和△的相对大小可以对配合物的高、低自旋 进行预言:
① 在弱场时, 由于△值较小, 配合物将取高自旋构型, 相反, 在强场时, 由于△值较大, 配合物将取低自旋构型。
-23200000
2-2080200
△hydH水mø(化水热 /合 (焓K)/Jk/Jm•o lmo)l-1
1-8206040
1-2640600
1-4202080 Sc2+ V2+ Mn2+ Co2+ Cu2+
Ca2+ Ti2+
Cr2+
第一系Z0n列2+过1 渡2金属3 离4子5(M62
+
)7F的e2+8水化9 热N1i02+n
子靠拢, 从而dx2-y2的能量升高,
这 样 eg 轨 道 发 生 分 裂 。 在 t2g 三
条轨道中, 由于xy平面上的dxy
dxz
dyz
轨道离配体要近, 能量升高, xz 和yz平面上的轨道dxz和dyz离配
拉长 八面体场
体远因而能量下降。结果, 轨道 也发生分裂。
这样,5条d轨道分成四组,能量从高到低的次序为: ① dx2-y2,② dz2, ③ dxy, ④ dxz和dyz。
[Fe(H2O)6]3+ 13700 [CrCl6]313600
[Cr(H2O)6]2+ 14000
[Fe(H2O) 6]2+ 10400
[MoCl6]319200
3 配体的本性
将一些常见配体按光谱实验测得的分裂能从小到大次
序排列起来,便得光谱化学序:
I-<Br-<OCrO32-<Cl-≈SCN-<N3-<(EtO)2PS2-<F-< SSO32-<(NH2)2CO<OCO22-<OCO2R-<ONO-≈OH-< OSO32-<ONO2-<O2CCO22-<H2O<NCS-<H2NCH2COO- ≈edta4-<py≈NH3≈PR3<en<SO32-<NH2OH<NO2-≈bipy ≈bipy≈phen<H-<CH3-≈C6H5-<C5H5-<CN-≈CO<P(OR)3
t2
4Dq
△t=(4/9)△o
6Dq
e
dz2 dx2-y2
四面体场
由于在四面体场中,这两组轨道都在一定程度下避开了
配体、没有像八面体中d轨道与配体迎头相撞的情况,可以预 料分裂能△t将小于△o,计算表明
△t=(4/9)△o 同样,根据重心守恒原理可以求出t2及e轨道的相对能量:
△t=E(t2)-E(e)=(4/9)△o 解得: E(t2)=1.78 Dq
0 0 1 2 3 4 5
LFSE
-4Dq -8Dq -12Dq -16 Dq+P -20 Dq+2P -24 Dq+2P -18 Dq+P -12Dq -6 Dq 0 Dq
CFSE对配合物性质的影响
晶体场理论的核心是配位体的静电场与中心离子的作 用所引起的d轨道的分裂和d电子进入低能级轨道带来的稳 定化能使体系能量下降,从而产生一种附加成键作用效应。
(1) 金属离子的电荷
中心金属离子电荷增加,△值增加。这是由于随着 金属离子的电荷的增加,金属离子的半径减小,因而配 体更靠近金属离子,从而对 d 轨道产生的影响增大之故, 三价离子的分裂能 比二价离子要大40~60 %(四价离子 的分裂能更大)。
(2) 金属离子d轨道的主量子数
在同一副族不同过渡系的金属的对应配合物中,分裂
两组,一组包括dxy、dxz、dyz三条轨道,用t2表示,这三条轨
道的极大值分别指向立方体棱边的中点。距配体较近,受到的
排斥作用较强,能级升高,另一组包括dz2和dx2-y2,以e表示
,这两条轨道的极大值分别指向立方体的面心,距配体较远, 受到的排斥作用较弱,能级下降。
球形场
dxy dxz dyz
dn
弱场
强场
构型 电子对数 LFSE 构型 电子对数
m1 m2
m1 m2
d1
t
1 2
g
d2
t
2 2g
0
0
-4Dq
t
1 2g
0
0
-8Dq
t
2 2g
00 00
d3
t
3 2g
0
0
-12Dq
t
3 2g
00
d4
t
3 2g
e
1 g0Biblioteka d5t3 2g
e
2 g
0
d6
t
4 2g
e
2 g
1
d7 d8 d9 d10
t
5 2g
正八面体场中心离子5个d 轨道的能级分裂
分裂能o = Eeg – Et2g = 10 Dq
自由离子的d 轨道
假想的球型场中的中 心离子的d 轨道
八面体场中的中心 离子的d 轨道
由于电子的总能量, 亦即各轨道总能量保持不变, eg能量的升高总
值必然等于t2g轨道能量下降的总值, 这就是所谓的重心守恒原理
由右图可以发现,在正八
面体弱场高自旋(HS)中, CFSE
LS
的曲线呈现“反W”形或“双峰
”形状, 三个极小值位于d0、d5
、d10处,两个极大值出现在d3
和d8处,而在强场低自旋(LS)中
, 曲线呈“V”形, 极小值为d0和
d10,极大值为d6。
HS
CSFE对dn的双峰曲线
既然CFSE引起附加成键效应,那么这种附加成 键效应及其大小必然会在配合物的热力学性质上表现 出来。
4 平面正方形场
设四个配体只在x、y平面上沿±x和±y 轴方向趋近于中心原子,因dx2-y2轨道 的极大值正好处于与配体迎头相撞的位置, 受排斥作用最强,能级升高最多。其次是 在xy平面上的dxy轨道。而dz2仅轨道的环 形部分在xy平面上,受配体排斥作用稍小, 能量稍低,简并的dxz、dyz的极大值与xy 平面成45º角,受配体排斥作用最弱,能 量最低。
该化学序代表了配体场的强度顺序。由此顺序可见, 对同一金属离子, 造成△值最大的是CN-离子, 最小的是I-
离子,通常把CN-、NO2-等离子称作强场配位体,I-、 Br-、F-离子称为弱场配位体。
须指出的是, 上述配体场强度顺序是纯静电理论 所不能解释的。例如OH-比H2O分子场强度弱, 按静 电的观点OH-带了一个负电荷, H2O不带电荷, 因而 OH-应该对中心金属离子的d轨道中的电子产生较 大的影响作用, 但实际上是OH-的场强度反而低, 显 然这就很难纯粹用静电效应进行解释。这说明了
3E(t2)+2 E(e)=0
E(e)=-2.67 Dq
3 拉长的八面体
球形场
dxy dxz dyz 八面体场
相对于正八面体而言, 在拉
长八面体中, z轴方向上的两个
配体逐渐远离中心原子, 排斥力
下 降 , 即 dz2 能 量 下 降 。 同 时 , 为了保持总静电能量不变, 在x
轴和y轴的方向上配体向中心原
Mm+(g)+∞H2O=[M(H2O)6]m+(aq) △hydHm[Mm+, (t2gNegn-N)] Mm+(dn, g) +6 H2O —△—h—ydH—m(—M—m+—, g—→) [M(H2O)6]m+(t2gNegn-N)
△hydHm{M(H2O)6]m+(dn, 球形)}
CFSE
——————————————→ [M(H2O)6]m+ (dn, 球形)
例如,以过渡金属离子的水合焓为例:
●水化热: 由气态阳离子变为水合阳离子放出的热量
Mm+(g)+∞H2O=[M(H2O)6]m+(aq) △hydHm[Mm+, (t2gNegn-N)]
显然水合焓跟中心离子的d轨道处于配体H2O静电场 有关。假定这种静电场由球形对称的静电场和正八面体 对称的静电场两部分所组成。基于此,可以写出水合焓 的玻恩-哈伯循环(下页):
能量下降的越多,即CFSE越大,络合物越稳定。
晶体场稳定化能的大小与下列因素有关: ★ 配合物的几何构型; ★ 中心原子的d电子的数目; ★ 配体场的强弱; ★ 电子成对能。
LFSE的计算
nn12::te2gg轨 轨道 道中 中的 的电 电子 子数 数
m m12: :八 球面 形体 体场 场dd中 中 轨 轨, , 道 道中 中的 的成 成对 对电 电子 子
四 晶体场稳定化能和配合物的热力学性质
1 晶体场稳定化能(CFSE) Crystal Field Stabilization Energy
d电子从未分裂的d轨道进入分裂的d轨道所产生的总
能量下降值称为晶体场稳定化能。
这种因d轨道分裂和电子填入低能级轨道给配合物 带来的额外稳定化作用将产生一种附加成键作用效应 。
(原来简并的轨道在外电场作用下如果发生分裂,则分裂后所有
轨道的能量改变值的代数和为零)。
2E(eg)+3E(t2g)=0 E(eg)-E(t2g)=△o
由此解得:
E(eg)=0.6△o = 6Dq E(t2g)=-0.4△o =-4Dq
2 正四面体场
在正四面体场中,过渡金属离子的五条d轨道同样分裂为
