小学五年级数学组合图形面积思维训练一
五年级思维拓展第一讲组合图形的面积求解

第一讲:组合图形的面积求解五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五1五五五五五五五五五五五五五五五五五五五五五五五五五五五2五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五五3五五五五五五五五五五五五五五五五五五4五五五五五五五五五五五五五五五五五五五五五五五五五五五A类题型1.求四边形ABCD的面积。
(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3.有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
4.正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
5.已知大正方形的边长是12厘米,求中间最小正方形的面积。
6.如下图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
7.求下图长方形ABCD的面积(单位:厘米)。
8.如图:长方形ABCD的面积是80平方厘米,EF分别是AB和AD的中点,求三角形EFC的面积。
9.四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?10.图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
B类题型1.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)2.下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?3.下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?4.如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
5.在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(单位:厘米)6.图中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
五年级思维训练-组合图形的面积(二)

边长是9厘米的正三角形的面积是边长为3厘米的正三角 形面积的多少倍?
1、边长是8厘米的正三角形的面积是边长为2厘米的正三 角形面积的多少倍?
2、一个梯形与一个三角形等高,梯形下底的长是上底的 2倍,梯形上底的长又是三角形底长的2倍。这个梯形的 面积是三角形面积的多少倍?。
3、有两种自然的放法将正方形内接于等腰直角三角形。 已知等腰直角三角形的面积是36平方厘米,两个正方形 的面积分别是多少?
2、把等边三角形ABC的每条边6等分,组成如下图所示的 三角形网,如果图中每个小三角形的面积都是1平方厘米, 求图中三角形DEF的面积
3、如图所示,在长方形ABCD中,AD=15厘米,AB=8厘米, 图中阴影部分的面积是68平方厘米,四边形EFGO的面积 是多少平方厘米?
在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20 平方厘米,求三角形ABC的面积。
1、把下图三角形的底边BC四等分,在下面括号里填上 “>”、“<”或“=”。
甲的面积( )乙的面积
2、如图,在三角形ABC中,D是BC的中点,E、F是AC的三 等分点。已知三角形ABC的面积是108平方厘米,求三角 形CDE的面积。
F E
D
3、下图中,BD=2厘米,DE=4厘米,EC=2厘米,F是AE的 中点,三角形ABC的BC边上的高是4厘米,阴影面积是多 少平方厘米?
1、下图中2、如下图四边形ABCD是直角梯形,AD=9厘米, CD=12厘 米,求阴影部分的面积
3、求图中阴影部分的面积
下图中,边长为10和15的两个正方体并放在一起,求三 角形ABC(阴影部分)的面积。
1、下图中,三角形ABC的面积是36平方厘米,三角形ABE 与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三 角形AFE的面积。
小学五年级组合图形面积练习题
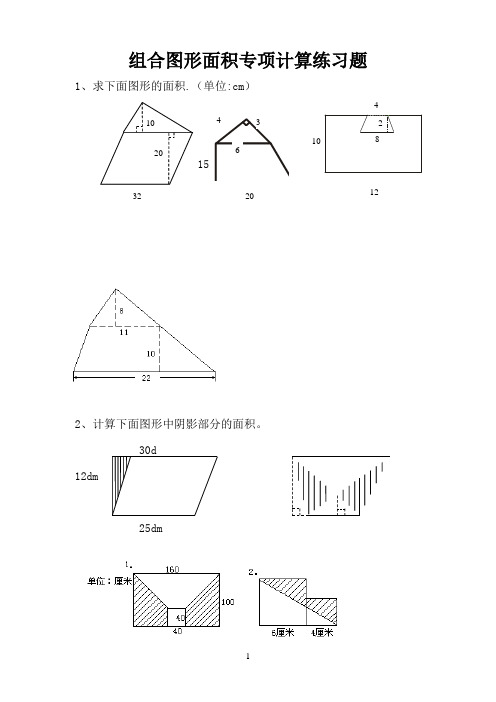
组合图形面积专项计算练习题1、求下面图形的面积.(单位:cm )152、计算下面图形中阴影部分的面积。
30d12dm25dm2010643482 1032 20123、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴.③已知:阴影部分的面积为24④求S 阴。
平方厘米,求梯形的面积。
4、求下面各图形的面积。
(单位:分米)13cm16cm12cm 7cm8dm8dm3dm5、“实践操作"显身手:6、如右图所示,平行四边形的面积是48平方厘米,求阴影部分的面积。
7、如右图所示,梯形中阴影部分的面积是150平方厘米,求梯形的面积16cm2、求下面图形的面积。
25组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合.由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3.适当采用增加辅助线等方法帮助解题;4.采用割、补、分解、代换等方法,可将复杂问题变得简单。
一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?1.求四边形ABCD的面积.(单位:厘米)2.已知正方形ABCD的边长是7厘米,求正方形EFGH的面积.3.有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米.求原来梯形的面积.正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍.求中间长方形的面积。
1.(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积.2.正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3.求下图长方形ABCD的面积(单位:厘米).四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
(尖子生培优)组合图形面积的解题技巧-2023五年级数学思维拓展含答案

(尖子生培优)组合图形面积的解题技巧2023五年级数学思维拓展我们已经学过简单的平面图形的面积的计算,这些知识是我们计算比较复杂的图形的面积的基础,将这些基础知识有意识地运用变化的观点对图形进行分割、添补、平移、旋转、添加辅助线等方法,恰当地将较复杂的图形变成我们学过的图形,达到最佳解题的目的。
一.选择题(共20小题)1.如图,每个小正方形的边长都是1cm ,涂色部分面积最大的是( )A .B .C .D .2.如图,在平行四边形中,阴影部分的面积和空白部分的面积相比较,( )A .阴影部分的面积大B.空白部分的面积大C.阴影部分和空白部分的面积一样大D.无法比较3.图中,甲、乙两部分面积的关系是()A.甲>乙B.甲=乙C.甲<乙4.如图,在半径为4m的圆形荒地中建造一个正方形的水池,并在水池的四周铺上草坪,草坪的面积是水池面积的()A.2750B.2325C.57%D.53%5.如图,在两个完全相同的平行四边形中,各剪下一个三角形,两个三角形的面积相比,()A.①<②B.①>②C.①=②D.无法比较6.如图,甲、乙是两个完全一样的平行四边形,甲、乙两图中的阴影部分的面积相比较,()A.甲阴影=乙阴影B.甲阴影>乙阴影C.甲阴影<乙阴影D.无法比较7.图中阴影甲、阴影乙是梯形中的两个三角形,它俩的面积()A.相等B.甲大C.乙大8.图是两个完全相同的平行四边形,图中阴影部分的面积相比,()A.①>②B.①<②C.①=②D.无法确定9.如图,下面三个平行四边形的面积相等。
比较图中阴影部分的面积,下面说法正确的是()A.①>②>③B.①>③>②C.①=②=③10.下面两个长方形完全相同,彩色部分的面积()A.A>B B.A=B C.A<B D.无法比较11.图中平行线所夹的三个阴影部分面积相比,()A.平行四边形面积大B.梯形面积大C.一样大12.比较如图平行四边形中阴影部分和空白部分面积的大小()A.阴影部分面积大B.空白部分面积大C.面积相等13.观察如图,可以发现小三角形、大三角形与梯形面积之间的相互关系。
(完整)五年级组合图形的面积典型例题

五年级上册组合图形面积计算题求下列图形的面积:(单位:cm )435254367886101:一个等腰直角三角形,最长的边是10厘米,这个三角形的面积是多少平方厘米?【巩固练习1】:如图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
2: 求右面平行四边形的周长。
8612【巩固练习2】:求右面三角形的AB 上的高。
典型例题3:求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)【巩固练习3】:求四边形ABCD 的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积分别是多少?【巩固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积分别是多少?典型例题5:图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
410CBA543【巩固练习5】:图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
【巩固练习6】求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?2、已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3、求下图长方形ABCD的面积(单位:厘米)。
4、如图,用48m长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?5、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=4cm,DB=6cm,两个三角形面积和是多少?DC BA 610DC BA20m墙【典型例题】【例1】已知平行四边表的面积是28平方厘米,求阴影部分的面积。
【练一练】如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)【例2】下图中甲和乙都是正方形,求阴影部分的面积。
最新苏教版五年级数学上册组合图形的面积专项练习

组合图形的面积专项练习[基础巩固]1.平行四边形的面积公式是(),用字母表示为()。
2.三角形的面积公式是(),用字母表示为()。
3.梯形的面积公式是(),用字母表示为()。
[学以致用]一、选一选。
1.两个()的三角形一定能拼成一个平行四边形。
A.底相等B.面积相等C.等底等高D.完全相同2.一个三角形的高扩大到原来的2倍,底扩大到原来的4倍,面积扩大到原来的( )倍。
A.2B.4C.6D.83.将一些练习本擦成一个长方体,再将它均匀地斜放,如图,这时从正面看到的图形是一个近似的平行四边形,比较两图从正面看到的图形,( )。
A.周长相等,面积不等B.周长不等,面积相等C.周长、面积都相等D.周长、面积都不相等4.李大爷用同样长的篱笆靠墙围了两个养鸡场,这两个养鸡场的面积相比( )。
A.①号大B.②号大C.同样大D.无法确定二、填一填。
1.在括号里填合适的单位。
(1)无锡太湖广场的面积约是67( )。
(2)地球面积约5.1亿()。
(3)港珠澳大桥沉管隧道长度约为5664( )。
(4)中央大厅的面积约3600( )。
2.39公顷=( )平方米 4800公顷=( )平方千米540000平方米=( )公顷 36平方千米=( )平方米3.一个三角形底是16厘米,面积是40平方厘米,这条底边上的高是( )厘米。
4.在一个底是8厘米,高是4厘米的平行四边形中画一个最大的三角形,这个三角形的面积是( )平方厘米。
5.一个平行四边形与一个三角形等底等高,三角形的面积是32平方厘米,平行四边形的面积是( )平方厘米。
6.一个三角形和一个平行四边形的高和面积均相等,如果平行四边形的底是8米,那么三角形的底是( )米;如果三角形的底是4米,那么平行四边形的底是( )米。
7.一个梯形和一个三角形的高相等,面积也相等。
已知梯形的上、下底分别是5分米和7分米,这个三角形的底是( )分米。
8.一个直角梯形的周长是64分米,它的两条腰分别长13分米、15分米,这个直角梯形的面积是( )平方分米。
五年级上册数学-思维训练 组合图形的面积(直线图形)汇总(含答案)人教新课标

小学数学思维训练5-5.组合图形的面积(直线图形)一、知识要点(一)常用的面积公式及其联系图(二)几种常见的解题方法对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例1:求下图阴影部分的面积(单位:厘米)。
解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:×2×4=4(平方厘米)2.相加、相减求面积:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出所求图形的面积。
例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?解答:两个正方形的面积:+=41(平方厘米)三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米)阴影部分的面积:41-33=8(平方厘米)3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
例3:平行四边形ABCD的边BC长8厘米,直角三角形ECB的直角边EC长为6厘米。
已知阴影部分的总面积比三角形EFG的面积大8平方厘米,平行四边形ABCD的面积是多少?解答:阴影部分的总面积比三角形EFG的面积大8平方厘米,分别加上梯形FBCG,得出的平行四边形ABCD比三角形EBC的面积大8平方厘米。
平行四边形ABCD的面积:8×6÷2+8=32(平方厘米4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
例4:下图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2平方厘米,CD的长是多少?解答:结合已知条件看图,很难有思路,连接DA,就可以发现:三角形ABE比三角形CDE 的面积大2平方厘米,分别加上三角形DAE得到的三角形ABD比三角形CDA的面积大2平方厘米。
小学五年级数学思维专题训练—等积变形(含答案解析)
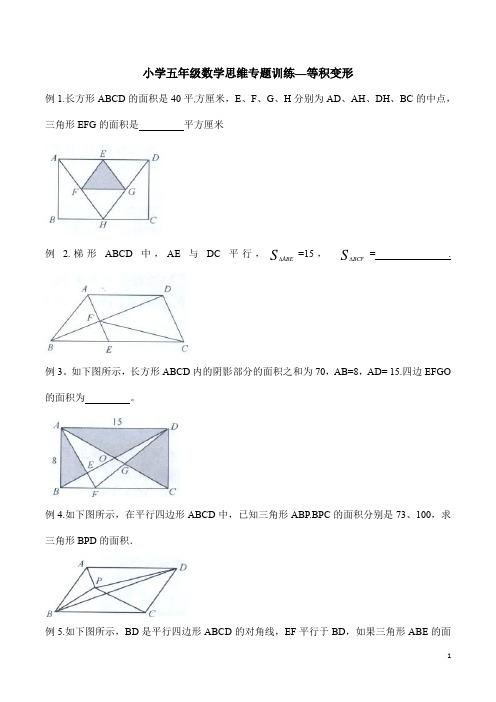
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
【精品奥数】五年级上册数学思维训练讲义-第14讲 组合图形的面积(一) 人教版(含答案)

第十四讲组合图形的面积(一)第一部分:趣味数学等腰三角形面积今有圭田广十二步,正从二十一步,问为田几何?赏析:圭田就是等腰三角形。
最早的文字记载见于《九章算术》“方田”章。
“圭田术曰:半广以乘正从。
”也就是说,三角形的面积等于高与底边边长乘积的一半。
刘徽注称:“半广者,以盈补虚为直田也。
亦可半正从以乘广。
”即如图根据“出入相补”原理、采用“以盈补虚”的方法将三角形化为与之等积的长方形,再利用“方田术”计算其面积。
解答:根据三角形的面积 =底×高÷2得出:12×21÷2=252÷2=126(步)可见我们的古人与我们现在研究平面图形面积的方法类似,都是利用转化思想,把三角形和梯形转化成我们熟悉的长方形再进行面积计算。
不同的是《九章算术》中记载的是特殊的三角形即直角三角形,特殊的梯形即直角梯形,今天我们已在此基础上把它们推广到了普通的三角形与梯形。
第二部分:奥数小练一、知识要点在组合图形中,三角形的面积出现的机会很多,解题时我们还可以记住下面三点:1.两个三角形等底、等高,其面积相等;2.两个三角形底相等,高成倍数关系,面积也成倍数关系;3.两个三角形高相等,底成倍数关系,面积也成倍数关系。
二、精讲精练【例题1】如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)【思路导航】按照一般解法,首先要求出梯形的面积,然后减去空白部分的面积即得所求面积。
其实,只要连接AC,显然三角形AEC与三角形DEC同底等高其面积相等,这样,我们把两个阴影部分合成了一个三角形ABC。
面积是:6×3÷2=9平方厘米。
练习一:1.求下图(1)中阴影部分的面积。
2.求图(2)中阴影部分的面积。
(单位:厘米)3.下图(3)的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
图(1)图(2)图(3)【例题2】下图中,边长为10和15的两个正方体并放在一起,求三角形ABC(阴影部分)的面积。
五年级-组合图形的面积
组合图形的面积知识集结知识元组合图形的面积知识讲解1.1、各图形面积公式:2、组合图形:有几个简单的图形拼出来的图形,我们把它们叫做组合图形。
3、计算组合图形的面积:(1)分割法,即将这个图形分割成几个基本的图形。
分割图形越简洁,其解题的方法也将越简单,同时又要考虑分割的图形与所给条件的关系。
(2)添补法,即通过补上一个简单的图形,使整个图形变成一个大的规则图形。
5.计算组合图形阴影部分的面积:等于组合图形的面积减去空白部分的面积。
例题精讲组合图形的面积例1.'求下图中涂色部分的面积。
(单位:cm)求阴影部分面积。
如图,小正方形ABCD的边长是5cm,大正方形CEFG的边长是10cm,求图中阴影部分面积。
'例3.'在一块梯形菜地里,有一条宽约1m的小路(如图),每平方米产菜4.5kg,这块菜地共产菜多少千克?'例4.'如图是某工艺品的展开图。
它的面积是多少?(单位:cm)'例5.'图4由3个边长是6的正方形组成,则图中阴影部分的面积是________。
计算如图阴影部分的面积.(单位:厘米)'例7.'如图,2个大正方形、2个中正方形和1个小正方形紧挨着排在一起,其中大中小正方形的边长分别为3、2、1,那么阴影部分的面积是多少?'例8.'如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD=CB,求图中阴影部分的面积和.'例9.'求图形中阴影部分的面积.(单位:dm)例10.'如图中,ADEF是一个长8CM,宽5CM的长方形,ABCD为直角梯形,BEF为直角三角形,图中阴影部分的面积是多少?'探索活动:成长的脚印知识讲解计算不规则图形的面积:估计、计算不规则图形面积的内容主要是以方格图作为背景进行估计与计算的,所以借助方格图能帮助建立估计与计算不规则图形面积的方法。
组合图形的面积--2022-2023学年五年级数学思维拓展

2022-2023学年小学五年级思维拓展专题组合图形的面积知识精讲专题简析:组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1,切实掌握有关简单图形的概念、公式,牢固建立空间观念;2,仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3,适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
典例分析【典例分析01】一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?【思路引导】由于此三角形中只知道最长的边是12厘米,所以,不能用三角形的面积公式来计算它的面积。
我们可以假设有4个这样的三角形,且拼成了下图正方形。
显然,这个正方形的面积是12×12,那么,一个三角形的面积就是12×12÷4=36平方厘米。
【典例分析02】正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
【思路引导】图中的两个小三角形平移后可拼得一个小正方形,两个大三角形平移后可拼得一个大正方形。
这两个正方形的边长分别是12÷(1+2)=4(厘米)和4×2=8(厘米)。
中间长方形的面积只要用总面积减去这两个拼起来的正方形的面积就可以得到。
即:12×12-(4×4+8×8)=64(平方厘米)【典例分析03】四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH 的面积是多少平方厘米?【思路引导】设大正方形的边长是a,小正方形的边长是b。
(1)梯形EFAD的面积是(a+b)×b÷2,三角形EFC的面积也是(a+b)×b÷2。
最新五年级组合图形面积解析及一题多解大全(重磅推出)

组合图形面积应知应会基础图形的面积:【1】平行四边形的面积=底×高,【2】三角形的面积=底×高用字母表示的三角形面积计算公式是:S=ah÷2【3】梯形的面积=(上底+下底)×高÷2s梯形=(a+b)×h÷2a=s梯形×2÷h-bb=s梯形×2÷h-ah=s梯形×2÷(a+b)二、组合图形(一)组合图形:计算时需转化成已学的基本图形,通过加、减进行计算。
(二)求组合图形的方法:1、分割法:将组合图形分成几个基本图形,通过加,求几个基本图形的和。
2、填补法:将组合图形补成一个基本图形,通过大面积减小面积,求两个基本图形的差。
组合图形的面积直接计算:根据公式计算图形的面积【1】分析:梯形的高等于三角形的高解:S阴影三角形=底×高÷2=14×12÷2=84(平方厘米)直接计算:S 阴影=S 三角形甲+S 三角形乙 【2】求阴影部分的面积。
解:S 阴影=S 三角形甲+S 三角形乙 =5×3÷2+3×3÷2 =7.5+4.5=12(平方厘米)直接计算:S 组合图形=S 平行四边形+S 三角形 【3】求组合图形的面积。
解:S 组合图形=S 平行四边形+S 三角形 =24×8+10×24÷2 =192+120 =312(平方米)直接计算:S 组合图形=S 平行四边形+S 三角形 【4】求组合图形的面积。
解:S 组合图形=S 平行四边形+S 三角形 =50×33+35×12÷2 =1650+210 =1860(平方米)直接计算:S 组合图形=S 长方形+S 三角形【5】下图为一个游泳馆的标识牌,求黄色标识牌的面积。
S 组合图形=S 长方形+S 三角形 =20×10+20×10÷ 253 甲乙单位:厘米=200+100=300(平方厘米)直接计算:S组合图形=S长方形+S三角形【6】下图为一个墙面的平面图,求这面墙面的面积。
数学五年级上册组合图形的面积解决问题复习题(含答案)

6.4组合图形的面积1.一块正方形的草地如果每边增加5米,扩大后仍为一块正方形草地,面积比原来正方形草地多425平方米,求原来的正方形草地的边长.2.下面的组合图形你一定很熟悉吧,那就请你动起手来,试一试吧如图阴影部分是梯形,左面长方形长4厘米,宽3厘米,A 为宽中点.求阴影部分的面积?3.一条长方形毛巾,长60厘米,宽25厘米,把它的4个角折向同一面(如图),所得的每个三角形的面积都是32平方厘米,求图中阴影部分面积.4.奥运会即将开幕了,全市掀起了美化城市的热潮.有位同学为一家商店设计了一副霓虹灯闪烁的原理图.图中正方形A B C D 的边长是6分米,等腰直角三角形的斜边长为20分米.正方形与三角形放在同一条直线上,C F为8分米,正方形以每秒2分米的速度沿直线向右匀速运动.问:(1)第6秒时,三角形与正方形重叠部分的面积是多少?(2)第几秒时,正方形的顶点C 恰好与FM的中点O重合,此时三角形与正方形重叠部分的面积是多少?(画出示意图,再进行计算)5.在一块梯形的地中间有一个长方形的游泳池,其余的地是草坪,草坪的面积是多少平方米?(已知梯形的上底是40m,下底是70m,高是30m,长方形的长是30m,宽是15m)6.王大爷在一块边长为20m的正方形土地上盖一个三角形养鸡场(如图),剩下的土地用来种玉米喂鸡,每平方米可收玉米1.3千克,这块地一共可收玉米多少千克?7.张大爷家有一块菜地(如图),这块菜地的面积有多少平方米?周长呢?8.幸福小学校园里有块花圃(如图所示),你能算出它的面积吗?(先在图上画出你的想法,再算出它的面积.)9.森林之家中的每一个小动物都非常爱劳动,其中小山羊种了一块白菜(如图)请计算这块菜地的面积.10.如图是一块长方形草坪,长是16米,宽是10米,中间有两条小路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大?(单位:米)11.如图是边长6米的正方形和梯形拼成的“火炬”,梯形的上底长9米,A 为上底的中点,B 为下底的中点,线段A B 恰好是梯形的高且长为3米,C D 长为2米,那么,图中阴影部分的面积是多少平方米?12.一个长方形,如果长和宽各增加8厘米,那么面积就增加384平方厘米.如果长和宽再各增加8厘米,那么面积又会增加多少平方厘米?13.一个长方形花圃,如果长增加4米,面积就增加40米;如果宽减少3米,面积就减少90米.原来这个花圃的面积是多少平方米?(画出示意图,再解答)14.有一条水渠穿过一块菜地(如图),这块菜地的面积是多少?15.有一个长25 m、宽20 m的长方形花坛,如果在这个花坛的四周修3 m宽的小路,小路的面积是多少平方米?16.给一个直角楼梯铺地毯,如下图所示(图中阴影处不铺),至少需要多少平方米的地毯?(单位:米)17.一个正方形的边长增加3厘米,面积就增加39平方厘米,原来正方形的面积是多少平方厘米?18.王爷爷家有一块地,他分别用来种植高粱、土豆和玉米(如下图)。
五年级奥数之组合图形的面积

五年级奥数之组合图形的面积组合图形的面积1,如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)2,求下图中阴影部分的面积。
3,求图中阴影部分的面积。
(单位:厘米)4,下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
5,下图中,边长为10和15的两个正方体并放在一起,求三角形ABC(阴影部分)的面积。
6,下图中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
7,图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
8,图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影部分的面积(ADFC不是正方形)。
9,两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)10,如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?11,下图的梯形ABCD中,下底是上底的2倍,E是AB 的中点。
那么梯形ABCD的面积是三角形BDE面积的多少倍?12,下图梯形ABCD中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC的面积比三角形AOD的面积大多少平方厘米?13,在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
14,把下图三角形的底边BC四等分,在下面括号里填上“>”、“<”或“=”。
甲的面积()乙的面积。
15,如图,在三角形ABC中,D是BC的中点,E、F是AC的三等分点。
已知三角形的面积是108平方厘米,求三角形CDE的面积。
16,下图中,BD=2厘米,DE=4厘米,EC=2厘米,F是AE的中点,三角形ABC的BC边上的高是4厘米,阴影面积是多少平方厘米?17,边长是9厘米的正三角形的面积是边长为3厘米的正三角形面积的多少倍?18,边长是8厘米的正三角形的面积是边长为2厘米的正三角形面积的多少倍?19,一个梯形与一个三角形等高,梯形下底的长是上底的2倍,梯形上底的长又是三角形底长的2倍。
五年级数学(上册)《组合图形的面积》试题及答案及五年级数学上册平面图形的面积归纳与练习

五年级数奥数:《组合图形的面积》1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积- 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14×2 = 42÷2= 3.5×2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10×2 = 16×8÷2= 4×2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
五年级数学 组合图形的面积 练习题(含答案)

人教版数学五年级上册6.4 组合图形的面积练习卷一、选择题1.如图,阴影部分的面积是16dm2,平行四边形的面积是()dm2.A.48B.32C.642.下图为一幅图形的密铺方案,则此影阴部分的面积与空白部分的面积比为()A.2∶1B.7∶9C.1∶1D.3∶43.如图,长方形ABCD中,AB=12厘米,BC=8厘米,平行四边形BCEF的一边BF 交CD于G,若梯形CEFG的面积为64平方厘米,则DG长为()A.3B.4C.5D.64.图中每个小方格的面积为1cm2,脚印的面积大约是()。
A.5cm2——50cm2B.10cm2——28cm2C.28cm2——50cm2 5.如下图,每个方格的面积为1平方厘米。
请你估一估,这个图案的面积约为()。
A.20平方厘米B.11平方厘米C.9平方厘米D.7平方厘米6.估计一下,下图不规则土地的面积约是()。
A.216m 36m B.224m C.2二、图形计算7.[多种思路求面积].你能计算出图中这个多边形的面积吗?8.计算下面图形的面积。
(单位:厘米)三、填空题9.如图,两个正方形的边长分别是6厘米、4厘米,阴影部分的面积是_____平方厘米。
10.如图,A是平行四边形BC边上的中点,阴影部分面积是2平方厘米,则平行四边形的面积是平方厘米.11.下图中,长方形长10厘米,宽6厘米,E为AB边上任一点,三角形EDC(即阴影部分)的面积是________平方厘米.12.如图,5个相同的小长方形拼成一个周长是88厘米的大长方形,那么大长方形的面积是_____平方厘米。
13.下图中每个小方格的面积表示21cm,估算一下,阴影部分的面积大约是( )2cm。
14.如图中三个正方形的边长分别为10,20,30,那么图中阴影部分的面积是.15.如图,大小两个正方形拼在一起,阴影部分面积为28平方厘米,小正方形边长为4厘米,则图中空白部分的面积是平方厘米.16.如图,四边形ABCD是一个梯形,由三个直角三角形拼成;它的面积是_____cm2。
(word完整版)五年级组合图形的面积典型例题

五年级上册组合图形面积计算题求下列图形的面积:(单位:cm )435254367886101:一个等腰直角三角形,最长的边是10厘米,这个三角形的面积是多少平方厘米?【巩固练习1】:如图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
2: 求右面平行四边形的周长。
8612【巩固练习2】:求右面三角形的AB 上的高。
典型例题3:求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)【巩固练习3】:求四边形ABCD 的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积分别是多少?【巩固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积分别是多少?典型例题5:图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
410CBA543【巩固练习5】:图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
【巩固练习6】求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?2、已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3、求下图长方形ABCD的面积(单位:厘米)。
4、如图,用48m长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?5、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=4cm,DB=6cm,两个三角形面积和是多少?DBA610DB A20m墙【典型例题】【例1】已知平行四边表的面积是28平方厘米,求阴影部分的面积。
【练一练】如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)【例2】下图中甲和乙都是正方形,求阴影部分的面积。
五年级组合图形的面积及解答

五年级组合图形的面积1.求下图中阴影部分的面积;分析: 使用等底、等高,其面积相等,S阴影=1025÷2=125平方厘米2.求图中阴影部分的面积;单位:厘米分析: S阴影=2820÷2+40-2820÷2=400平方厘米3.下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积;分析: S阴影=8050-801+501+11=3871平方厘米4.图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积;分析:SADC=6+1010÷2=80SDEC=1010÷2=50S阴影= S ADC - S DEC=80-50=305.图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影部分的面积ADFC不是正方形;分析:SABC =36,AC=8,则CF=9,CF与SABC的高相等S阴影=3+98÷2=486.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米分析:两个三角形高相等,底成倍数关系,面积也成倍数关系;BO=2DO,SBOC =2SDOC,SDOC=2平方厘米;两个三角形等底、等高,其面积相等,SACD =SBCD=6平方厘米;SAOD=4平方厘米;SABO=2SAOD=8平方厘米;SABCD=4+2+4+8=18平方厘米7.下图的梯形ABCD中,下底是上底的2倍,E是AB的中点;那么梯形ABCD的面积是三角形BDE 面积的多少倍分析:两个三角形高相等,底成倍数关系,面积也成倍数关系;AE=BE ;S DAE =S BED ;S BCD 与S BAD 的高相等,AD=2BC,所以S BAD = 2S BCD ,S BAD =2S DAE ;S BAD=2S DAE ;S ABCD =3S BED 8.下图梯形ABCD 中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC 的面积比三角形AOD 的面积大多少平方厘米分析:S BCD = S BOC +S DOC ;S ACD = S AOD +S DOC S BCD -S ACD = S BOC +S DOC - S AOD +S DOC = S BOC- S AODS BCD =128÷2=48平方厘米;S ACD =78÷2=28平方厘米 S BOC- S AOD =48-28=20平方厘米9.如图,在三角形ABC 中,D 是BC 的中点,E 、F 是AC 的三等分点;已知三角形的面积是108平方厘米,求三角形CDE 的面积;分析:EF=EC ;S DCE =S DEF ;BD=DC ;S BFD =S DFC ;S BCF =4S DCE ;AF=2FC ;S BCF =2S ABF S ABF =2S DCE ;S ABC =S BCF +S ABF =4S DCE +2S DCE =6S DCE ; S DCE =108÷6=18平方厘米10.下图中,BD=2厘米,DE=4厘米,EC=2厘米,F 是AE 的中点,三角形ABC 的BC边上的高是4厘米,阴影面积是多少平方厘米分析:SDAE =DEH÷2=44÷2=8平方厘米;AF=EF;SADF=SDEF;SDEF=8÷2=4平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级数学思维秋季班方法讲义:
第八讲《组合图形面积(一)》
姓名
【点燃思维】
1、一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?
2、求四边形ABCD的面积。
(单位:厘米)
3、有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
4、下图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
5、(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
6、正图长方形ABCD的面积是16平方厘米,E、F 都是所在边的中点,求三角形AEF 的面积。
7、图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
8、图中三个正方形的边长分别是1厘米、2厘米和3厘米,求图中阴影部分的面积。
9、下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)
10、边长分别为3厘米与5厘米的两个正方形拼在一起(如图)。
求阴影部分的面积。
巩固练习:
1、已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
2、求下图长方形ABCD的面积(单位:厘米)。
3、求下面图中每个小图形的阴影部分面积。
(1)
(2)
(3)。
