《数字电子技术基础》课后习题及参考标准答案
数字电子技术基础课后答案全解(供参考)

第3章 逻辑代数及逻辑门【3-1】 填空1、与模拟信号相比,数字信号的特点是它的 离散 性。
一个数字信号只有两种取值分别表示为0 和1 。
2、布尔代数中有三种最基本运算: 与 、 或 和 非 ,在此基础上又派生出五种基本运算,分别为与非、或非、异或、同或和与或非。
3、与运算的法则可概述为:有“0”出 0 ,全“1”出 1;类似地或运算的法则为 有”1”出”1”,全”0”出”0” 。
4、摩根定理表示为:A B ⋅=A B + ;A B +=A B ⋅。
5、函数表达式Y=AB C D ++,则其对偶式为Y '=()A B C D +⋅。
6、根据反演规则,若Y=AB C D C +++,则Y =()AB C D C ++⋅ 。
7、指出下列各式中哪些是四变量A B C D 的最小项和最大项。
在最小项后的( )里填入m i ,在最大项后的( )里填入M i ,其它填×(i 为最小项或最大项的序号)。
(1) A +B +D (× ); (2) ABCD (m 7 ); (3) ABC ( × ) (4)AB (C +D ) (×); (5) A B C D +++ (M 9 ) ; (6) A+B+CD (× ); 8、函数式F=AB+BC+CD 写成最小项之和的形式结果应为m ∑(3,6,7,11,12,13,14,15),写成最大项之积的形式结果应为M (∏ 0,1,2,4,5,8,9,10 )9、对逻辑运算判断下述说法是否正确,正确者在其后( )内打对号,反之打×。
(1) 若X +Y =X +Z ,则Y=Z ;( × ) (2) 若XY=XZ ,则Y=Z ;( × ) (3) 若X ⊕Y=X ⊕Z ,则Y=Z ;(√ ) 【3-2】用代数法化简下列各式(1) F 1 =1ABC AB += (2) F 2 =ABCD ABD ACD AD ++= (3)3F AC ABC ACD CD A CD=+++=+ (4) 4()()F A B C A B C A B C A BC=++⋅++⋅++=+【3-3】 用卡诺图化简下列各式(1) 1F BC AB ABC AB C =++=+ (2) 2F AB BC BC A B=++=+(3) 3F AC AC BC BC AB AC BC=+++=++ (4) 4F ABC ABD ACD CD ABC ACD A D=+++++=+或AB AC BC ++(5) 5F ABC AC ABD AB AC BD =++=++ (6) 6F AB CD ABC AD ABC A BC CD=++++=++(7) 7F AC AB BCD BD ABD ABCD A BD BD =+++++=++ (8) 8 F AC AC BD BD ABCD ABCD ABCD ABCD=+++=+++(9) 9()F A C D BCD ACD ABCD CD CD =⊕+++=+(10)F 10=10F AC AB BCD BEC DEC AB AC BD EC =++++=+++ 【3-4】 用卡诺图化简下列各式 (1) P 1(A ,B ,C )=(0,1,2,5,6,7)m AB AC BC =++∑(2) P 2(A ,B ,C ,D )=(0,1,2,3,4,6,7,8,9,10,11,14)m AC AD B CD =+++∑ (3)P 3(A ,B ,C ,D )=(0,1,,4,6,8,9,10,12,13,14,15)m AB BC AD BD =+++∑(4) P 4 (A ,B ,C ,D )=17M M A BC BC D •=+++ 【3-5】用卡诺图化简下列带有约束条件的逻辑函数(1)()1,,,(3,6,8,9,11,12)(0,1,2,13,14,15)()d P A B C D m AC BD BCD ACD =+=++∑∑或 (2) P 2(A ,B ,C ,D )=(0,2,3,4,5,6,11,12)(8,9,10,13,14,15)dm BC BC D +=++∑∑(3) P 3 =()A C D ABCD ABCD AD ACD BCD ABD ++++=++或 AB +AC =0 (4) P 4 =A B ABCD ABCD +=+(A B C D 为互相排斥的一组变量,即在任何情况下它们之中不可能两个同时为1) 【3-6】 已知: Y 1 =AB AC BD ++ Y 2 =ABCD ACD BCD BC +++ 用卡诺图分别求出Y Y 12⋅, Y Y 12+, Y Y 12⊕。
数字电子技术基础课后答案(李雪飞)

电路如下图
当M=0时,
当M=1时,
[题3.19]
[题3.20]
解:设两个5位二进制数分别为A( )和B( )。依据题意,将两个5位二进制数的高4位,即 和 分别接入比较器的数据输入端,将 和 比较的结果 , 和 分别接入级联输入的 , 和 端,其函数表达式为
[题3.21]
解:由电路写出输出Y的逻辑函数式为
因此, 的取值应满足0.57kΩ≤ ≤1.75 kΩ。
[题2.8]
0.47kΩ≤R≤4.39 kΩ
[题2.9]
这时相当于 端经过一个20 kΩ的电阻接地。假定与非门输入端多发射极三极管每个发射结的导通压降均为0.7V,则有
(1) ≈1.4V
(2) ≈0.2V
(3) ≈1.4V
(4) ≈0V
(5) ≈1.4V
[题3.5]答案见阎石数字电子技术第四版137页。
[题3.6]
真值表为
A
B
C
D
F1
F2
A
B
C
D
F1
F2
0
0
0
0
φ
φ
1
0
0
0
1
0
0
0
0
1
1
0
1
0
0
1
0
1
0
0
1
0
1
0
1
0
1
0
0
1
0
0
1
1
0ቤተ መጻሕፍቲ ባይዱ
1
1
0
1
1
1
1
0
1
0
0
1
0
1
数字电子技术基础课后答案(太原理工大学教科书)

《数字电子技术基础教程》习题与参考答案(2010.1)第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=()2=(53)8=(2B)16(3)56=()2=(70)8=(38)16(4)()2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)=177(2)=170(3)=241(4)=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=()2(2)(9C)16=()2(3)(B1)16=(1011 0001)2(4)(AF)16=()2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)22(3)5.8=(101.1100)2(4)101.71=(.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
(1);(2);(3);(4)解:(1)是正数,所以其反码、补码与原码相同,为(2)反码为,补码为(3)反码为,补码为(4)反码为,补码为【题1-8】将下列自然二进制码转换成格雷码。
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)=177(2)=170(3)=241(4)=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=()2(3)(B1)16=(1011 0001)2(4)(AF)16=()2【题1-5】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)()2=(2)()2=(3)()2=【题1-6】将下列十进制数转换为二进制数。
(1);(2);(3);(4)解:(1)=()2(2)=()2(3)=()2(4)=()2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
(1)01101100;(2);(3);(4)解:(1)01101100是正数,所以其反码、补码与原码相同,为01101100(2)反码为,补码为(3)反码为,补码为(4)反码为,补码为【题1-8】将下列自然二进制码转换成格雷码。
000;001;010;011;100;101;110;111解:格雷码:000、001、011、010、110、111、101、100【题1-9】将下列十进制数转换成BCD码。
数字电子技术基础. 第四版. 课后习题答案详解

(1)Y=A+B
(2)YABCABC
解:BCABCCABC(A+A=)
(5)Y=0
(2)(1101101)2=(6D)16=(109)10
(4)(11.001)2=(3.2)16=(3.125)10
(2)(127)10=(1111111)2=(7F)16
(4) (25.7)10(11001.1011 0011)2(19.B3)16
1.12
将下列各函数式化为最大项之积的形式
(1)Y(ABC)(ABC)(ABC)
(3)YM0⋅M3⋅M4⋅M6⋅M7
(5)YM0⋅M3⋅M5
(2)Y(ABC)(ABC)(ABC)
(4)YM0⋅M4⋅M6⋅M9⋅M12⋅M13
1.13
用卡诺图化简法将下列函数化为最简与或形式:
(3)Y(AB)(AC)ACBC
(2)Y
ACD
解:(AB)(AC)ACBC[(AB)(AC)AC]⋅BC
(ABACBCAC)(BC)BC
(5)YADACBCDC
解:Y(AD)(AC)(BCD)CAC(AD)(BCD)
ACD(BCD)ABCD
(4)YABC
(6)Y0
1.11
将函数化简为最小项之和的形式
(3)Y=1
(4)YAB CDABDAC D
解:YAD(B CBC)AD(BCC)AD
(7)Y=A+CD
(6)YAC(C DA B)BC(BADCE)
解:YBC(B⋅ADCE)BC(BAD)⋅CEABCD(CE)ABCDE
(8)YA(BC)(ABC)(ABC)
解:YA(B⋅C)(ABC)(ABC)A(AB CB C)(ABC)
数字电子技术基础(第4版)_课后习题答案

第一章1.1二进制到十六进制、十进制(1)(10010111)2=(97)16=(151)10 (2)(1101101)2=(6D)16=(109)10(3)(0.01011111)2=(0.5F)16=(0.37109375)10 (4)(11.001)2=(3.2)16=(3.125)10 1.2十进制到二进制、十六进制(1)(17)10=(10001)2=(11)16 (2)(127)10=(1111111)2=(7F)161621016210)3.19()1010 1(11001.101(25.7)(4))A D7030.6()0101 0000 0111 1101 0110 (0.0110(0.39)(3) B ====1.8用公式化简逻辑函数(1)Y=A+B (3)Y=1)=+(解:1A A 1)2(=+++=+++=+++=C B A C C B A C B Y CB AC B A Y ADC C B AD C B C B AD DC A ABD CD B A Y =++=++=++=)()(Y )4(解:(5)Y=0 (7)Y=A+CDE ABCD E C ABCD CE AD B BC CE AD B BC Y CE AD B BC B A D C AC Y =+=⋅+=+⋅=++++=)()()()()()6(解:CB AC B C B A A C B A C B A C B A C B C B A A C B A C B A C B A Y C B A C B A C B A Y +=++=+++=++++=++++⋅+=++++++=)())(())()(())()((8解:)(D A D A C B Y ++=)9(E BD E D BF E A AD AC Y ++++=)10(1.9 (a) C B C B A Y += (b) C B A ABC Y +=(c) ACD D C A D C A B A Y D AC B A Y +++=+=21,(d) C B A ABC C B A C B A Y BC AC AB Y +++=++=21, 1.10 求下列函数的反函数并化简为最简与或式(1)C B C A Y += (2)DC A Y++=CB C B AC C B AC B A BC AC C A B A BC AC C A B A Y BCAC C A B A Y +=++++=⋅+++=+++=+++=))((]))([())(())(()3(解: (4)C B A Y ++=DC ABD C B D C A D C B D A C A C D C B C A D A Y CD C B C A D A Y =++=+++=++++=+++=)())(())()(()5(解: (6)0=Y1.11 将函数化简为最小项之和的形式CB AC B A ABC BC A C B A C B A C B A ABC BC A CB A AC B B A BC A C B AC BC A Y CB AC BC A Y +++=++++=++++=++=++=)()()1(解:D C B A CD B A D C B A ABCD BCD A D C B A Y +++++=)(2)13()()()(3CD B A BCD A D BC A D C B A D C B A ABCD D ABC D C AB D C AB CD B A D C B A D C B A D C B A CD AB B A B A B A ACD D AC D C A D C A CD A D C A D C A D C A B BCD D BC D C B D C B CD B D C B D C B D C B A Y CDB A Y ++++++++++++=+++++++++++++++++++=++=解:)((4)CD B A D ABC D BC A D C AB D C AB CD B A ABCD BCD A Y +++++++= (5)MN L N M L N LM N M L N M L N M L Y +++++=1.12 将下列各函数式化为最大项之积的形式(1)))()((C B A C B A C B A Y ++++++= (2)))()((C B A C B A C B A Y ++++++= (3)76430M M M M M Y ⋅⋅⋅⋅= (4)13129640M M M M M M Y ⋅⋅⋅⋅⋅= (5)530M M M Y ⋅⋅=1.13 用卡诺图化简法将下列函数化为最简与或形式:(1)D A Y +=(3)1=Y (2)D C BC C A B A Y +++= (4)B AC B A Y ++=B A DC Y ++=AC B A Y +=(5)D C B Y ++= (6)C B AC B A Y ++=(7)C Y = (9)D C A C B D A D B Y +++=(8))14,11,10,9,8,6,4,3,2,1,0(),,,(m D C B A Y ∑= (10)),,(),,(741m m m C B A Y ∑=D A D C B Y ++=ABC C B A C B A Y ++=1.14化简下列逻辑函数(1)D C B A Y +++= (2)D C A D C Y += (3)C A D AB Y ++= (4)D B C B Y += (5)E D C A D A E BD CE E D B A Y +++++=1.20将下列函数化为最简与或式(1)AD D C B D C A Y ++= (2)AC D A B Y ++= (3)C B A Y ++= (4)D B A Y +=第二章2.1解:Vv v V V v T I mA I mA Vv T V v a o B o B BS B o B 10T 3.0~0(2.017.0230103.0207.101.57.05I V 5v 1021.5201.510V 0v )(i i ≈≈∴<=×≈=−≈∴−=×+−=截止,负值,悬空时,都行)饱和-=时,=当截止时,=当都行)=饱和,,-=悬空时,都行)饱和。
《数字电子技术基础》课后习题答案

2、2: (4)解:
(8)解:
2、3:
(2)证明:左边
《数字电子技术基础》课后习题答案
=右式 所以等式成立
(4)证明:左边=
右边= 左边=右边,所以等式成立 2、4
(1) 2、5 (3) 2、6:
(1) 2、7:
(1) 卡诺图如下:
BC A
00
01
11
10
0
1
1
1
1
1
1
所以, 2、8: (2)画卡诺图如下:
(c)
(f)
3、7、解: (a)
《数字电子技术基础》课后习题答案
3、8、解:输出高电平时,带负载的个数
N OH
I OH I IH
400 20
20
G 可带 20 个同类反相器 输出低电平时,带负载的个数
N OL
I OL I IL
8 0.45
17.78
G 反相器可带 17 个同类反相器 3、12
EN=1 时,
11
10
00
0
0
0
0
01
0
0
0
0
11
0
1
1
1
10
0
0
0
0
电路图如下:
第四章:
自测题:
一、 2、输入信号,优先级别最高的输入信号 7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C
练习题:
4、1;解:(a) (b)
(74)10 =(0111 0100)8421BCD=(1010 0111)余 3BCD (45、36)10 =(0100 0101、0011 0110)8421BCD=(0111 1000、0110 1001 )余 3BCD (136、45)10 =(0001 0011 0110、0100 0101)8421BCD=(0100 0110 1001、0111 1000 )余 3BCD (374、51)10 =(0011 0111 0100、0101 0001)8421BCD=(0110 1010 0111、1000 0100)余 3BCD 1、8、解
《数字电子技术基础》课后习题及参考答案#(精选.)

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
数字电子技术基础(数电)课后习题解答

解: ① (0011101)2 =1×24+ 1×23+ 1×22+ 1×20=(29)10
(0011101)2 =(0 011 101)2= (35)8 (0011101)2 =(0001 1101)2= (1D)16 同理:② (27.75)10,(33.6)8,(1B.C)16; ③ (439)10,(667)8,(1B7)16;
(1) Y=AB+BC+A'C'
=B+A'C'
BC
A
00 01 11 10
0
1
11
1
11
(2) Y=AB'C'+A'B'+A'D+C+BD =B’+C+D (或用圈0法)
CD 00 01 11 10
AB
00 1
1
1
1
01
1
1
1
11
1
1
1
10 1
1
1
1
(3) Y=A' (B'C+B(CD'+D))+ABC'D
1
010
1
011
1
100
1
101
1
110
1
111
0
题1.9 在举重比赛中,有甲、乙、丙三名裁判,其中甲为主裁判,乙、丙为副裁判,当主裁判 和一名以上(包括一名)副裁判认为运动员上举合格后,才可发出合格信号。列出该函数的 真值表。
(全)数字电子技术基础课后答案夏路易

《数字电子技术基础教程》习题与参考答案(2010.1)第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101 解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
《数字电子技术基础》课后习题答案

《数字电子技术基础》课后习题答案《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1) 十六进制转二进制: 4 5 C0100 0101 1100二进制转八进制:010 001 011 1002 13 4十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2) 十六进制转二进制: 6 D E . C 80110 1101 1110 . 1100 1000二进制转八进制:011 011 011 110 . 110 010 0003 3 3 6 . 6 2十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1 758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3) 十六进制转二进制:8 F E . F D1000 1111 1110. 1111 1101二进制转八进制:100 011 111 110 . 111111 0104 3 7 6 . 7 7 2十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*1 6-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(4376.772)8=(2302.98828125)10(4) 十六进制转二进制:7 9 E . F D0111 1001 1110 . 1111 1101二进制转八进制:011 110 011 110 . 111 111 0103 6 3 6 . 7 7 2十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16 -2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1 950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD (45.36)10=(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10=(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10=(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则二、2、×4、×三、1、B3、D5、C练习题:2.2:(4)解:Y=AB̅+BD+DCE+A̅D=AB̅+BD+AD+A̅D+DCE=AB̅+BD+D+DCE=AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A ̅+B ̅+C ̅)(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A ̅+B ̅+C ̅+DE ) =[(A ̅+B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A ̅+B ̅+C ̅+DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE 2.3:(2)证明:左边=A +A ̅(B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A ̅+(B +C)̅̅̅̅̅̅̅̅̅̅=A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A̅B +AB ̅)⨁C = (A̅B +AB ̅)C ̅+ (A ̅B +AB ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A ̅BC ̅+AB ̅C ̅)+A ̅B ̅̅̅̅⋅AB̅̅̅̅̅⋅C =A̅BC ̅+AB ̅C ̅+(A +B ̅)(A ̅+B )C =A̅BC ̅+AB ̅C ̅+(AB +A ̅B ̅)C =A̅BC ̅+AB ̅C ̅+ABC +A ̅B ̅C 右边= ABC +(A +B +C )AB ̅̅̅̅⋅BC ̅̅̅̅⋅CA̅̅̅̅ =ABC +(A +B +C )[(A̅+B ̅)(B ̅+C ̅)(C ̅+A ̅)] =ABC +(A +B +C )(A̅B ̅+A ̅C ̅+B ̅+B ̅C ̅)(C ̅+A ̅)=ABC +(A +B +C )(A̅B ̅C ̅+A ̅C ̅+B ̅C ̅+A ̅B ̅) =ABC +AB̅C ̅+A ̅BC ̅+A ̅B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B ̅C ̅)(A ̅+BC) 2.5(3)Y ̅=A ̅B ̅(C ̅+D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C ̅D ̅(A ̅+B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC ̅+AB ̅C +A ̅BC 2.7:(1)Y =A ̅B ̅+B ̅C ̅+AC +B ̅C 卡诺图如下: B C A 00 0111100 1 1 1111所以,Y=B̅+AC2.8:(2)画卡诺图如下:B C A 0001 11 100 1 1 0 11 1 1 1 1Y(A,B,C)=A+B̅+C̅2.9:(1)画Y(A,B,C,D)=∑m(0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:CDAB00 01 11 1000 1 1 1 101 1 111 ×××10 1 ××Y (A,B,C,D )=A̅B ̅+D ̅ 2.10:(3)解:化简最小项式: Y =AB +(A̅B +C ̅)(A ̅B ̅+C ) =AB +(A̅B A ̅B ̅+A ̅BC +A ̅B ̅C ̅+C ̅C ) =AB (C +C̅)+A ̅BC +A ̅B ̅C ̅ =ABC +ABC ̅+A ̅BC +A ̅B ̅C ̅ =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5) 2.13:(3)Y =AB̅+BC ̅+AB ̅C ̅+ABC ̅D ̅ =AB̅(1+C ̅)+BC ̅(1+AD ̅) =AB̅+BC ̅ =AB̅+BC ̅̿̿̿̿̿̿̿̿̿̿̿̿ = AB̅̅̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:B C A 00 01 11 10 0 0 0 1 0 1 0 1 1 1Y =AB +AC +BC=AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC ̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=(A ̅+B ̅)(A ̅+C ̅)(B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅+B ̅̅̅̅̅̅̅̅̅+A ̅+C ̅̅̅̅̅̅̅̅̅+B ̅+C ̅̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空;二、1、√8、√;三、1、A4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A ̅B ̅1̅̅̅̅̅̅=A +B +0=A +B(e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y1=A+B+0̅̅̅̅̅̅̅̅̅̅̅̅̅=A+B̅̅̅̅̅̅̅̅(c) Y3=A+B+1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y6=A⋅0+B⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y1=A⨁B⋅C=(A̅B+AB̅)C=A̅BC+AB̅C3.8、解:输出高电平时,带负载的个数2020400===IHOHOH I I NG 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===ILOLOL I I NG 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B ̅EN=0时,Y 1=A ̅, Y 2=B3.17根据题意,设A为具有否决权的股东,其余两位股东为B、C,画卡诺图如下,BCA00 01 11 100 0 0 0 01 0 1 1 1则表达结果Y的表达式为:Y=AB+AC=AB+AC̿̿̿̿̿̿̿̿̿̿̿̿=AB̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A、B、C、D变量的卡诺图如下:CD AB00 01 11 1000 0 0 0 001 0 0 0 011 0 1 1 110 0 0 0 0Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC ̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、3、√4、√三、5、A7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +B ̅̅̅̅̅̅̅̅̅̅̅=A ̅+B̅̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
(全)数字电子技术基础课后答案

【题
(
解:(1)A=0,B=0
(2)A=0,B=1或C=1
(3)A=1,B=0,C=1
(4)A=0,B=1或C=0
【题
(
解:(1)
A
B
C
Y
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
(2)
当A取1时,输出Y为1,其他情况Y=0。
【题
(
(
解:(1)左边 右边
【题
(1)
解:(1)25=(0010 0101)BCD
(
(
(
【题
解:4位数格雷码;
0000、0001、0011、0010、0110、0111、0101、0100、1100、1101、1111、1010、1011、1001、1000、
第
【题
图题2-1
解:
【题
图题2-2
解:
【题
图题2-3
解:
【题
图题2-4
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
数字电子技术基础课后答案(太原理工大学教科书)

《数字电子技术基础教程》习题与参考答案(2010.1)第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=()2=(53)8=(2B)16(3)56=()2=(70)8=(38)16(4)()2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)=177(2)=170(3)=241(4)=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=()2(2)(9C)16=()2(3)(B1)16=(1011 0001)2(4)(AF)16=()2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)22(3)5.8=(101.1100)2(4)101.71=(.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
(1);(2);(3);(4)解:(1)是正数,所以其反码、补码与原码相同,为(2)反码为,补码为(3)反码为,补码为(4)反码为,补码为【题1-8】将下列自然二进制码转换成格雷码。
《数字电子技术基础》习题答案
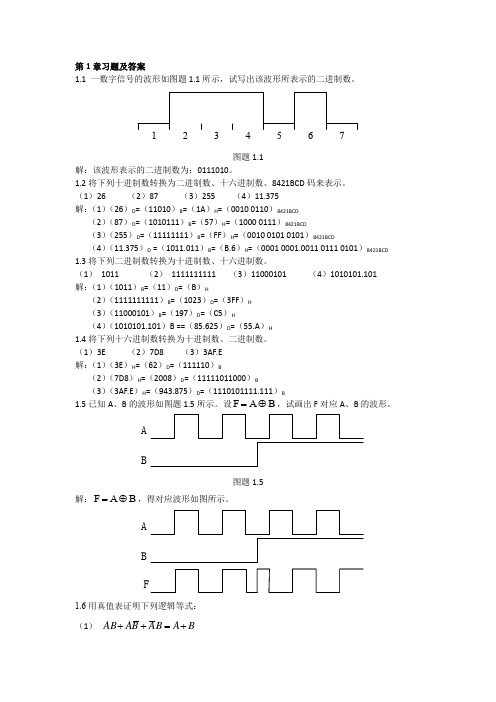
证明:(1)左边= =右边
(2)右边=
=
=
= =左边
1.8写出下列函数的对偶式 。
(1)
(2)
(3)
(4)
解:(1)
(2)
(3)
(4)
1.9写出题1.8中函数的反函数 。
解:(1)
(2)
(3)
(4)
1.10列出下列问题的真值表,并写出逻辑表达式。
(1)设三变量A、B、C当变量组合值中出现奇数个1时,输出(F1)为1,否则为0。
(1) 。
(2)
(3)
(4)
解(1)卡诺图如图解1.15(a)所示,得
图解1.15(a)
(2)卡诺图如图解1.15(b)所示,得
图解1.15(b)
(3)卡诺图如图解1.15(c)所示,得
图解1.15(c)
(4)卡诺图如图解1.15(d)和(e)所示。
按图(d)写出的化简结果为
按图(e)写出的化简结果为
(4)(1010101.101)B ==(85.625)D=(55.A)H
1.4将下列十六进制数转换为十进制数、二进制数。
(1)3E(2)7D8(3)3AF.E
解:(1)(3E)H=(62)D=(111110)B
(2)(7D8)H=(2008)D=(11111011000)B
(3)(3AF.E)H=(943.875)D=(1110101111.111)B
任一解都为最简与或式。
图解1.15(d)和(e)
1.17化简逻辑函数。
(1)
(2)
解(1)卡诺图如图解1.17(a)所示,
图解1.17(a)
(2)卡诺图如图解1.17(b)所示,
图解1.17(b)
《数字电子技术基础教程》习题与及参考答案

《数字电子技术基础教程》习题与及答案第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177 (2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101 解:(1)(1110.01)2=14.25 (2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)=177(2)=170(3)=241(4)=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=()2(3)(B1)16=(1011 0001)2(4)(AF)16=()2【题1-5】将下列二进制数转换为十进制数。
(1);(2);(3);(4)解:(1)()2=(2)()2=(3)()2=【题1-6】将下列十进制数转换为二进制数。
(1);(2);(3);(4)解:(1)=()2(2)=()2(3)=()2(4)=()2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
(1)01101100;(2);(3);(4)解:(1)01101100是正数,所以其反码、补码与原码相同,为01101100(2)反码为,补码为(3)反码为,补码为(4)反码为,补码为【题1-8】将下列自然二进制码转换成格雷码。
000;001;010;011;100;101;110;111解:格雷码:000、001、011、010、110、111、101、100【题1-9】将下列十进制数转换成BCD码。
(1)25;(2)34;(3)78;(4)152解:(1)25=(0010 0101)BCD(2)34=(0011 0100)BCD(3)78=(0111 1000)BCD(4)152=(0001 0101 0010)BCD【题1-10】试写出3位和4位二进制数的格雷码。
解:4位数格雷码;0000、0001、0011、0010、0110、0111、0101、0100、1100、1101、1111、1010、1011、1001、1000、第2章习题与参考答案【题2-1】 试画出图题2-1(a )所示电路在输入图题2-1(b )波形时的输出端B 、C 的波形。
图题2-1解:A.....B、C【题2-2】 试画出图题2-2(a )所示电路在输入图题2-2(b )波形时的输出端X 、Y 的波形。
图题2-2解:..A B..XY...【题2-3】 试画出图题2-3(a )所示电路在输入图题2-3(b )波形时的输出端X 、Y 的波形。
图题2-3解:.A B.YX....【题2-4】 试画出图题2-4(a )所示电路在输入图题2-4(b )波形时的输出端X 、Y 的波形。
图题2-4解:.A B.YX .....【题2-5】 试设计一逻辑电路,其信号A 可以控制信号B ,使输出Y 根据需要为Y =B 或Y =B 。
解:可采用异或门实现,B A B A Y +=,逻辑电路如下:=1ABY....【题2-6】 某温度与压力检测装置在压力信号A 或温度信号B 中有一个出现高电平时,输出低电平的报警信号,试用门电路实现该检测装置。
解:压力信号、温度信号与报警信号之间的关系为:B A Y +=,有如下逻辑图。
1≥AB.Y...【题2-7】 某印刷裁纸机,只有操作工人的左右手同时按下开关A 与B 时,才能进行裁纸操作,试用逻辑门实现该控制。
解:开关A 、B 与裁纸操作之间的关系为B A Y +=,逻辑图如下:&AB.Y...【题2-8】 某生产设备上有水压信号A 与重量信号B ,当两信号同时为低电平时,检测电路输出高电平信号报警,试用逻辑门实现该报警装置。
解:水压信号A 、重量信号B 与报警信号之间的关系为B A Y +=,逻辑图如下:1≥AB.Y...【题2-9】 如果如下乘积项的值为1,试写出该乘积项中每个逻辑变量的取值。
(1)AB ;(2)ABC ;(3)ABC ;(4)ABC解:(1)A=1,B=1 (2)A=1、B=1、C=0 (3)A=0,B=1,C=0 (4)A=1,B=0或C=1【题2-10】 如果如下和项的值为0,试写出该和项中每个逻辑变量的取值。
(1)A B +;(2)A B C ++;(3)A B C ++;(4)A B C ++解:(1)A=0,B=0 (2)A=0,B=1或C=1 (3)A=1,B=0,C=1 (4)A=0,B=1或C=0【题2-11】 对于如下逻辑函数式中变量的所有取值,写出对应Y 的值。
(1)Y ABC AB =+;(2)()()Y A B A B =++解:(1)Y ABC AB =+)(B C A +=(2)()()Y A B A B =++A =当A 取1时,输出Y 为1,其他情况Y=0。
【题2-12】 试证明如下逻辑函数等式。
(1)AB ABC AB +=;(2)ABC C AC AB AC ++=+(); (3)()()A BC BC AC A BC AC ++=+解:(1)左边==+=+=B A C B A C B A B A )(1右边 (2)左边==+=++AC AB AC C C AB )(右边 (3)左边=右边)()(=+=++AC BC A AC BC BC A【题2-13】 对如下逻辑函数式实行摩根定理变换。
(1)1Y A B =+;(2)2Y AB =;(3)3Y AB C D =+();(4)4Y A BC CD BC =+++()解:(1)B A B A Y =+=1 (2)B A B A Y +==2(3)D C B A D C B A D C BA Y ++=++=+=)()(3 (4)BC B A BC C B A BC D C B A C B A BC D C C B A BC CD C B A Y +=+=++=++=+++=)(()(4【题2-14】 试用代数法化简如下逻辑函数式。
(1)1()Y A A B =+;(2)2Y BC BC =+;(3)3()Y A A AB =+解:(1)1()Y A A B =+=A (2)2Y BC BC =+=C (3)3()Y A A AB =+=A【题2-15】 试用代数法将如下逻辑函数式化简成最简与或式。
(1)1 Y AB ABC ABCD ABC DE =+++;(2)2Y AB ABC A =++; (3)3Y AB A B C AB =+++() 解:(1)1 Y AB ABC ABCD ABC DE =+++B A = (2)2Y AB ABC A =++=C A +(3)3Y AB A B C AB =+++()=C AB + 【题2-16】 试用代数法将如下逻辑函数式化简成最简与或式。
(1)1()Y A BC A B C A B CD =++++;(2)2Y ABCD ABCD ABCD =++;(3)3(())Y ABC AB C BC AC =++解:(1)1()Y A BC A B C A B CD =++++=B A(2)2Y ABCD ABCD ABCD =++=CD AB + (3)3(())Y ABC AB C BC AC =++=ABC【题2-17】 将如下逻辑函数式转换成最小项之和形式。
(1)1()()Y A B C B =++;(2)2()Y A BC C =+;(3)3Y AB CD AB CD =++(); (4)4()Y AB B C BD =+解:(1)1()()Y A B C B =++=∑),,,(7651m (2)2()Y A BC C =+=∑),(75m (3)3Y AB CD AB CD =++()=∑),,,,,,(151413121173m (4)4()Y AB B C BD =+∑),(1513m【题2-18】 试用卡诺图化简如下逻辑函数式。
(1)1Y ABC ABC B =++; (2)2Y A ABC AB =++; (3)3Y AC AB AB =++; (4)4 Y AB C AC C =++解:(1)1Y ABC ABC B =++BC A 0100011110.111...111...B A Y +=1(2)2Y A ABC AB =++;BC A 0100011110111..1...A Y =2(3)3Y AC AB AB =++BC A 0100011110111..1...A Y =3(4)4 Y AB C AC C =++BC A 0100011110.111...111...C A Y +=4【题2-19】 试用卡诺图化简如下逻辑函数式。
解:(1)(,,,)(0,1,2,8,9,10,12,13,14,15)F A B C D m =∑;AB CD 0001111000011110..111111111.1....C BD B AB Y ++=1(2)(,,,)(2,4,5,6,7,11,12,14,15)F A B C D m =∑;.AB CD0001111000011110.11111111.1..ACD D C A D B B A Y +++=2(3)(,,,)(0,2,4,6,7,8,12,14,15)F A B C D m =∑AB CD 0001111000011110..11111111.1..BC D A D C Y ++=3【题2-20】 试用卡诺图化简如下具有任意项的逻辑函数式。
解:(1)(,,,)(3,5,8,9,10,12)(0,1,2,13)F A B C D m d =+∑∑;AB CD 0001111000011110..X XX11111.1X..D C C A D B B A Y +++=1(2)(,,,)(4,5,6,13,14,15)(8,9,10,12)F A B C D m d =+∑∑;AB CD 0001111000011110..111X 11X1X.X...AB D B C B Y ++=2(3)(,,,)(0,2,9,11,13)(4,8,10,15)F A B C D m d =+∑∑AB CD 0001111000011110..1111X XX1.X...D B AD Y +=3【题2-21】 将如下逻辑函数式画成真值表。
