五年级奥数数阵问题
小学五年级奥数第10讲 数阵(含答案分析)

第10讲数阵一、知识要点填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,和同学们讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二、精讲精练【例题1】把5、6、7、8、9五个数分别填入下图的五个方格里,如图a 使横行三个数的和与竖行三个数的和都是21。
练习1:1.把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2.把1—9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3.将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
【例题2】将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
练习2:1.把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2.把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
3.将1——8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
第1题第二题第三题【例题3】将1——6这六个数分别填入下图的圆中,使每条直线上三个圆内数的和相等、且最大。
练习3:1.将1——6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
2.将1——9九个数分别填入下图○内,使每边上四个○内数的和都是17。
3.将1——8八个数分别填入下图的○内,使每条安上三个数的和相等。
第1题第二题第三题【例题4】将1——7分别填入下图的7个○内,使每条线段上三个○内数的和相等。
练习4:1.将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。
五年级奥数第4讲:数阵-课件

练习五(选做)
如下图的五个连环,他们相交后分成九个区域,现在两个区域 里已分别填进数字10和6,请在另外七个区域里分别填上2、3、4、 5、6、7、9这七个数,使每个圆内数字的和都是15。
10 5
6 72
96
3
4
排除法
从两头做为突破口
两数之和等于 15-9=6
6=2+4
总结
运用数的总和与每行和的总和关系,利用数和倍数的 特点,先确定几个数,然后用排除法找出正确答案。
8
9
b2 4 8 c3
2573
小结
1. 理解幻方里总和、幻和、阶数的概念,总和=幻和×阶数, 奇数阶幻方中心数=幻和÷阶数。 2. 解决封闭数阵的时候,学会用总和的思想求顶点数,同时 利用自然数、倍数等数的特性辅助求解,并对得出的组合逐一 排除,最后得到正确答案。
2、3、5倍数的特征 什么是偶数?
还有其它填法吗?
(61,2,89)(67,2,83)(71,2,79) 两两组合共有3种
例题五(选讲)
将1~9这九个数分别填入下图的○里,使外三角形边上○内数 之和等于里面三角形边上○内数之和。
1
两个三角形2共同的点
637 45
三个数的和等于 三个数的和
618
想想符合这样的组合?
37
2
8
94
9
5
你们还能想到更多的答案吗?
所2是有质的偶数数都2不8是是质偶数数吗? 3个质数相加是偶数 奇数+偶数+奇数=不同的质数,其中的四个数都在60~90之间, 要使横行、竖行的三个数的和都是152,可以怎么填?
61 67 2 83
89
3个质数相加是偶数 奇数+偶数+奇数=152 又是偶数又是质数的是2
小学奥数 数阵图(一) 精选练习例题 含答案解析(附知识点拨及考点)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯,3年级,第6题 【解析】例题精讲知识点拨教学目标5-1-3-1.数阵图87654321【答案】87654321【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【考点】封闭型数阵图 【难度】2星 【题型】填空【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:(2)h gf ed c baa+b+c=14(1)c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行.若e=1,则c=14-(1+3)=10,不行. 若g=1,则a=8,c=4,e=7.说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点上的三个数的和是 。
小学五年级奥数数阵题doc

第十六讲数阵问题上一讲我们学习了三阶幻方数阵图的辐射数阵图,这一讲我们学习封闭型数阵图和复合型数阵图。
例1.将1~6这六个数分别填入图中的○内,使每条边上三个○内的数字之和相等。
例2.将5~14这十个自然数填入右图中的○内,使每个大圆上六个数的和是55。
例3.将1~10这十个自然数分别填入图中的十个○内,使各条线段上四个○内数的和相等,每个三角形三个顶点上○内数的和也相等。
例4.把0~9这十个整数分别填入右图圆圈中,使每个正方形顶点上四个数字之和相等。
练习与思考1.将5~10这六个自然数分别填入图中的○内,使图中每条边上三个数的和都是21。
2.将1—10这十个自然数填入图中的○内,使五边形每条边上的三个数之和相等,并使和尽可能地小。
3.将1—9这九个自然数分别填入图中九个小三角形中,使每4个小三角形组成的三角形内的4个数的和等于20。
4.将1—9这九个自然数分别填入图中九个小三角形中,要求靠近三角形每条边上五个数的和相等,并尽可能地大。
这五个数之和最大是多少?5.将1—8这八个自然数分别填入图中的○内,使每个大圆上五个○内所填数的和等于21。
6.将3—10这八个自然数填在图中立方体八个顶点上的○中,使立方体每个面四个顶点上○中数的和相等。
7.将1—9这九个自然数填入图中的○内,使对角结上五个○内数的和相等,每个正方形四个顶点上数的和也相等。
8.如图,三个正方形组成八个三角形。
现在把每个正方形的四个顶点上都分别填上2,3,4,5这四个数。
这连续的八个自然数各是多少|9.如图,三个圆相互交割成七部分,请在空白部分中分别五上2,3,5,7,使每个圆圈内四个数之和都等于15。
10.上右图是五圆连环图,相互交割成九个部分。
将1—9这九个自然数分别填入九个部分内,使每个圆圈里数的和都相等。
11.下左图中有三个正三角形,其中有三条通过四点的线段。
请你把1—9这九个自然数分别填在九个黑点的旁边,使每个正三角形顶点上三个数的和相等,每条线段上四个数的和也相等。
小学奥数:数阵图(三).专项练习及答案解析

耳tM 蚱 教学目标1 . 了解数阵图的种类2 .学会一些解决数阵图的解题方法3 .能够解决和数论相关的数阵图问题知识点拨 、数阵图定义及分类:1 .定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图 .2 .数阵是一种由幻方演变而来的数字图 .数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图 ^ 3 .二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点 (或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的 数量关系,得到关键点上所填数的范围; 第三步:运用已经得到的信息进行尝试. 这个步骤并不是对所有数阵题都适用, 很多数阵题 更需要对数学方法的综合运用.例题精讲数阵图与数论【例1】 把0—9这十个数字填到右图的圆圈内,使得五条线上的数字和构成一个等差数列,而且这个等差数列的各项之和为 55,那么这个等差数列的公差有 能的取值.【考点】数阵图与数论 【难度】3星 【题型】填空【关键词】迎春杯,三年级,初赛,第 8题【解析】设顶点分别为 A 、B G D E,有45+A +削C +D +E =55,所以A +B +C +D +E =10,所以A 、 R CH E 分别只能是0-4中的一个数字.则除之外的另外5个数(即边上的)为 45-10=35.设所形成的等差数列的首项为 a 1,公差为d .利用求和公式5(a 1 + a 1+4d ) 2=55, 得a 1+2d =11,故大于等于0+1+5=6,且为奇数,只能取 7、9或11,而对 应的公差d 分别为2、1和0.经试验都能填出来所以共有 3中情况,公差分别为2、 1、0.5-1-3-3.数阵图目地蚱_____ 种可【答案】2种可能【例2】将1~ 9填入下图的。
中,使得任意两个相邻的数之和都不是3, 5, 7的倍数.【考点】数阵图与数论【解析】根据题意可知1的两边只能是3与7; 2的两边只能是6与9; 3的两边只能是1、5 或8; 4的两边只能是7与9.可以先将3—1—7--写出来,接下来7的后面只能是4, 4的后面只能是9, 9的后面只能是2, 2的后面只能是6,可得:3—1 — 7—4 -9-2-6--,还剩下5和8两个数.由于6 8 14是7的倍数,所以接下来应该是5,这样可得:3—1—7—4 — 9—2—6 —5 —8—3.检验可知这样的填法符合题意.【答案】3 —1 — 7—4—9—2 — 6 — 5—8—3【例3】在下面8个圆圈中分别填数字1,2,3, 4, 5, 6, 7, 8(1已填出).从1开始顺时针走1步进入下一个圆圈,这个圆圈中若填n(n<8)o则从这个圆圈开始顺时针走n步进入另一个圆圈.依此下去,走7次恰好不重复地进入每个圆圈,最后进入的一个圆圈中写8 .请给出两种填法.O OO Q 0【考点】数阵图与数论【难度】4星【题型】填空【关键词】走美杯,5年级,决赛,第12题,15分【解析】按顺时针方向:1,2, 5,3, 8, 7,4, 6 或1,5,2 , 4, 8, 6, 7,3 或1,6,2,3 , 8, 5, 7, 4或1,6, 4, 2, 8, 7, 5, 3 (答对任一种给6分,总得分不超过12)由于无论如何填8都是最后一个填写,而填之前,已经走过了28步,因为28 + 8=3余4,即8永远只能在最底下的圆圈里。
五年级奥数数阵问题

课时3 数阵问题(一)一.数阵填“幻方”就是同学们比较熟悉得一种数学游戏,由幻方演变出来得数阵问题,也就是一类比较常见得填数问题。
这里,主要讨论一些数阵得填法。
解答数阵问题通常用两种方法:一就是待定数法,二就是试验法。
待定数法就就是先用字母(或符号)表示满足条件得数,通过分析、计算来确定这些字母(或符号)应具备得条件,为解答数阵问题提供方向。
试验法就就是根据题中所给条件选准突破口,确定填数得可能范围。
把分析推理与试验法结合起来,再由填数得可能情况,确定应填得数。
二.例题精析例1 把5、6、7、8、9五个数分别填入下图得五个方格里,如图a使横行三个数得与与竖行三个数得与都就是21。
先把五格方格中得数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D+E=35,A +E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一”得10个空格里,使在同一直线上得各数得与都就是12。
2、把1——9各数填入“七一”得9个空格里,使在同一直线上得各数得与都就是13。
3、将1——7七个自然数分别填入图中得圆圈里,使每条线上三个数得与相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数得与就是30。
分析设中间两个圆中得数为a、b,则两个大圆得总与就是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a与b就是1与4时,每个大圆上另外四个数分别就是(2、6,8,9)与(3、5,7,10);当a与b就是2与3时,每个大圆上另外四个数分别为(1、5,9,10)与(4,6,7,8)。
小试牛刀1、把1——8八个数分别填入下图得○内,使每个大圆上五个○内数得与相等。
2、把1——10这十个数分别填入下图得○内,使每个四边形顶点得○内四个数得与都相等,且与最大。
五年级奥数《数阵》练习题
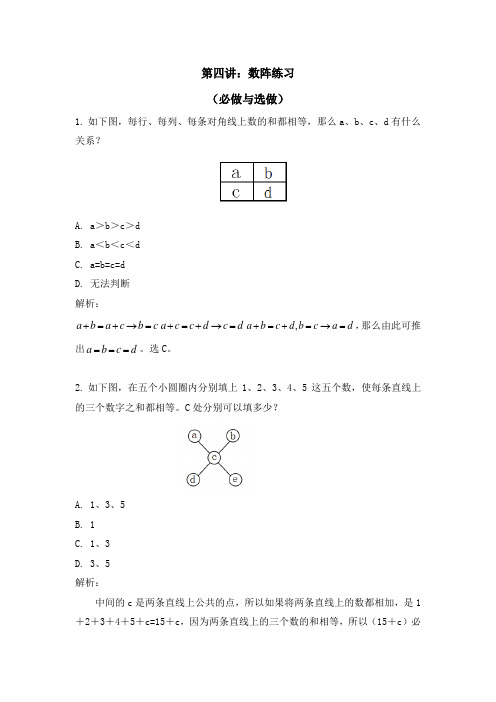
第四讲:数阵练习 (必做与选做)1. 如下图,每行、每列、每条对角线上数的和都相等,那么a 、b 、c 、d 有什么关系?A. a >b >c >dB. a <b <c <dC. a=b=c=dD. 无法判断 解析:c b c a b a =→+=+d c d c c a =→+=+d a c b d c b a =→=+=+,,那么由此可推出d c b a ===。
选C 。
2. 如下图,在五个小圆圈内分别填上1、2、3、4、5这五个数,使每条直线上的三个数字之和都相等。
C 处分别可以填多少?A. 1、3、5B. 1C. 1、3D. 3、5 解析:中间的c 是两条直线上公共的点,所以如果将两条直线上的数都相加,是1+2+3+4+5+c=15+c ,因为两条直线上的三个数的和相等,所以(15+c )必须能被2整除,即c必须为奇数,c可以是1、3、5。
选A。
3.阿派将1、2、3、4、5、6、7这七个数填入下图的七个方框里,每个数只填一次,使得三条直线上的三个数之和恰好分别是8、11、15,e可以怎么填?A. 5B. 7C. 3D. 1解析:将三条线上的数都加在一起,中间的e加了3次,其它数都加了一次,所以三条线上三个数的和=1+2+……+7+2e=28+2e,条件又说三条线上三个数的和分别是8、11、15,所以28+2e=8+11+15,e=3。
选C。
4.将1~5填入右图的○中,使得横、竖、大圆上的几个数之和都相等每个数只能用一次,e处分别可以填什么?A. 1B. 5C. 3D. 无正确答案解析:先看“十字”上的两条直线,中间的e被加了两次,如果将两条直线上的数都相加,是1+2+3+4+5+e=15+e,因为两条直线上的三个数的和相等,所以(15+e)能被2整除,即e为奇数,e可以是1、3、5。
当e=1时,其它四个数的和是2+3+4+5=14,14÷2=7,7+1=8,即每条直线上数的和是8,但是圆上的数的和是14,所以不满足;当e=3时,其它四个数的和是1+2+4+5=12,12÷2=6,6+3=9,即每条直线上数的和是9,但是圆上的数的和是12,所以不满足;当e=5时,其它四个数的和是1+2+3+4=10,10÷2=5,5+5=10,即每条直线上数的和是10,圆上的数的和也是10,满足条件。
小学奥数5-1-3-3 数阵图(三).专项练习及答案解析

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.数阵图与数论【例 1】 把0—9这十个数字填到右图的圆圈内,使得五条线上的数字和构成一个等差数列,而且这个等差数列的各项之和为55,那么这个等差数列的公差有 种可能的取值.例题精讲知识点拨教学目标5-1-3-3.数阵图【考点】数阵图与数论【难度】3星【题型】填空【关键词】迎春杯,三年级,初赛,第8题【解析】设顶点分别为A、B、C、D、E,有45+A+B+C+D+E=55,所以A+B+C+D+E=10,所以A、B、C、D、E分别只能是0-4中的一个数字.则除之外的另外5个数(即边上的)为45-10=35.设所形成的等差数列的首项为a1,公差为d.利用求和公式5(a1+a1+4d)2=55,得a1+2d=11,故大于等于0+1+5=6,且为奇数,只能取7、9或11,而对应的公差d分别为2、1和0.经试验都能填出来所以共有3中情况,公差分别为2、1、0.【答案】2种可能【例 2】将1~9填入下图的○中,使得任意两个相邻的数之和都不是3,5,7的倍数.【考点】数阵图与数论【难度】4星【题型】填空【解析】根据题意可知1的两边只能是3与7;2的两边只能是6与9;3的两边只能是1、5或8;4的两边只能是7与9.可以先将3—1—7--写出来,接下来7的后面只能是4,4的后面只能是9,9的后面只能是2,2的后面只能是6,可得:3—1—7—4—9—2—6--,还剩下5和8两个数.由于6814+=是7的倍数,所以接下来应该是5,这样可得:3—1—7—4—9—2—6—5—8—3.检验可知这样的填法符合题意.【答案】3—1—7—4—9—2—6—5—8—3【例 3】在下面8个圆圈中分别填数字l,2,3,4,5,6,7,8(1已填出).从1开始顺时针走1步进入下一个圆圈,这个圆圈中若填n(n≤8)。
小学数学五年级《数阵、数字谜综合》练习题(含答案)

《数阵、数字谜综合》练习题(含答案)解决数阵类问题可以从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格),和关键点(方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.Ⅰ、数阵问题【例1】(★★★)如图,大三角形被分成了9个小三角形.试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形3条边的每5个数相加的和相等,问这5个数的和最大可能是多少?分析:第一步:确定关键区格,计算三条边时,其中有3个角上共6个区格内的数被重复计算了2遍,而位于每条边中心位置的区格值计算了一次.第二步:由于,边上的三个数分别计算了1遍,因此(1+2+3+4+5+6+7+8+9)×2再减去三个边上的数,所得应该为3的倍数,当三条边上的三角形中分别填入1、2、3时,这个和取得最大值,各条边上的和也取得最大值28.第三步:通过试验得到可行的填法:【例2】(★★)把1,2,3,…,13这13个数分别填在下图所示的3个圆圈内,使得同一个圆圈内任意两个数相减,所得的差不在这个圆圈内.现在已经把1,4,7填在第一个圆圈内,3填在第三个圆圈内,请将其余9个数填好.31 4 7_5_4_6 _7_8_9_3 _2_12 11 125 6 8 910 1331 4 7分析:第一步:由已知可推出6只能填在中间的圆中.第二步:由已经填的数可以得到:2、5、8、11不能出现在第一个圆中,且(2、8)和(5、11)不能在第二个圆中成对出现,(2、5)(5、8)(8、11)不能在第三个圆中成对出现,判断5和8的位置的各种情况,可以得出5、8只能都填在在第二个圆中,2、11填在第三个圆中.第三步:判断其余几个数的位置关系:13只能填在第一个圆中,9只能填在第二个圆中,12只能填在第三个圆中,10只能填在第一个圆中.【例3】(★★★)请在下图的每个圆圈内填入不同的自然数,使得图中每个圆圈中所填的数都是上一行与它相邻的两个圆圈中所填数的和.分析:第一步:由于每个圆圈中所填的数都是上一行与它相邻的两个圆圈中所填数的和,所以只要填出这四个数字就能得到其他圆圈中所填的数.如果第一行填入的是x 、y 、z 、w ,则20=x+w+3(y+z ),所以y+z 不超过6(事实上不超过5,此处可以讨论一下).第二步:由于y+z 的和不超过5所以,y 和z 只可能为1和2,1和3,1和4,2和3,通过尝试可以得到不止一个答案,下面的答案是其中一个.20911638421720[前铺]把1.2,3.7,6.5,2.9,4.6分别填在下图的5个圆圈内,然后在每个方框中填上和它相连的3个圆圈中的数的平均值,再把3个方框中的数的平均值,再把3个方框中的数平均值填在三角形中.请找出一种填法,使三角形中的数尽可能小.问这个最小的数是多少?分析:设个小圆中的数依次为a1、a2、a3、a4、a5,则三个正方形中的数依次为123a +a +a 3、234a +a +a 3、345a +a +a 3,继而求出三角形中的数值为12345a +2a +3a +2a +a 9.所以,a 3中应该填入最小的数1.2,a 2、a 4中应该填入次大的2.9和3.7,a 1、a 5中填入4.6和6.5.Ⅱ、数阵问题乘法解决数字谜类问题也需要寻找关键的突破口,运用的主要知识和方法主要有: 1、 数字乘法个位数字的规律,2、 数值大小的考量,3、 加减法进位规律,4、 合数分解质因数性质,5、 奇偶数性质规律.6、 余数性质.【例4】(★★保良局亚洲区城市小学数学邀请赛)下面残缺算式中只知道三个“4”,那么补全后它的乘积是 .分析:容易看出,乘数个位为9,而被乘数个位不小于5.依次验证各种可能情况,通过奇偶性等分析乘积的十位,可知只有7可能.此时乘数十位必须是6才能使乘积十位为4.故所求为47×69=3243.[点评]本题运用到的主要知识点和数学方法有:数值大小的考量、奇偶分析等【例5】(★★★全国小学数学奥林匹克)在下面残缺的算式中,只写出了3个数字1,其余的数字都不是1,那么这个算式的乘积是 .分析:为了说明的方便,这个算式中的关键数字用英文字母表示.很明显e= 0.从c ab ⨯的个位数是1,b 可能是3,7,9三数之一,两位数ab 应是(100+f )的因数.101,103,107,109是质数,f=0或5也明显不行.102=17×6,则ab =17,C 只能取3,317c ab ⨯=⨯,不是三位数;104=13×8,则13ab =,c 可取7,c ×ab =7×13,仍不是三位数;108=27×4,则ab =27,c 是3.327c ab ⨯=⨯,还不是三位数.只有106=53×2,53ab =,c=7,753c ab ⨯=⨯是三位数.因此这个乘法算式是故这个算式的乘积是3816.[点评]本题运用到的主要知识点和数学方法有数字乘法个位数字规律.【例6】(★★★2005年全国小学数学奥林匹克)下面算式(1)是一个残缺的乘法竖式,其中□≠2,那么乘积是 .分析:如式(2),由题意a ≠2,所以b ≥6,从而d ≥6.由22□÷c ≥60和c >2知c=3,所以22□是225或228,75de =或76.因为75×399<30 000,所以76de =.再由乘积不小于30000和所有的□≠2,推出唯一的解76×396=30096.[点评]本题运用到的主要知识点和数学方法有数量大小的考量,合数的分解等.【例7】(★★★★2003年北京市迎春杯数学邀请赛)在下面的算式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字.那么,“努力力争”四个汉字所代表的四个数字的和是 .分析:观察竖式可知:乘数个位数字,“习”ד争”的个位数字是1,则“习”与“争”取值有两种情况:①“习”=3,“争”=7;②“习”=7,“争”=3.先看第①种情况:“习”=3,“争”=7时,第二个部分的积其末位与千位对齐,可知“力=0”,“数学学习”×7,积仍为四位数,则“数”只能为1,“学”只能是2.又由于“学”×7+2(进位)=“学”,不能成立.所以“习”=3,“争”=7时,不能成立,无解. 再看第②种情况:由“习”=7,“争”=3,推出“数”=2或l ,“学”=9.当“数”=2时,积千位为8,则“努”×7的末位数应为“1”,不符合条件.所以“数”=1,“学”=9,“习”=7,“争”=3,则“努”=2,“努力力争”=2003.所以“努力力争”四个汉字所代表的数字和为5.[点评]本题运用到的主要知识点和数学方法有:数字乘法个位数规律、十进制数进位规律等.【例8】(★★★香港圣公会小学数学奥林匹克)在右面的乘法算式中,每一个□中要填一个数字,不同的中文字代表不同的数字,请问:“新年”两字代表什么数字?分析:由于乘积最后一位是1,还有三个9,可知乘数是7773或3337.于是可以逐一来确定被乘数的每一位,就知7773不符合,只有3337合适,并且逐一定出被乘数是4543.4543×3337—15 159 991.所以,“新年”两字是15.[点评]本题运用到的主要数学方法和知识点有:数字乘法个位数规律、十进制数进位规律.Ⅲ、数字谜除法【例9】(★★★全国小学数学奥林匹克)下面的除法算式(1)是一个小数的除法竖式,其中所注明的两个字母要求:A<B,那么满足这个竖式的除数与商的和是.C,分析:因为能够除尽但含有两位小数,所以除数含有因子2或5.由式(2)知除数应大于60,且能整除00所以除数只能是75,C≤7.又商的整数部分是9,75×9=675,B=5,因为A<B,所以C≥5.因为5≤C C是75的倍数,所以C=6,从而被除数等于675+6=681.这个和是75+681÷75=84.08.≤7,且00[点评]本题运用到的主要知识点和数学方法主要有:整除性质、数值大小的考量等.【例10】(★★★全国小学数学奥林匹克)下面这个残缺算式中,只知道其中两个数字,请补全.那么这个除法算式的商数是.分析:容易看出,第三行首位是9.另外,第三行的个位与第四行首位数字之和不小于10.如果商的首位数字大于1,那么除数要小于50,故第四行首位数字小于5,而第三行个位数字不小于6.分别验证6,7,8,9四种情况,知均不满足条件.如果商的首位数字等于1,验证第三行个位数字各种情况,知只有2满足条件.此时除数等于92,而商等于109.[点评]本题运用到的知识点和数学方法主要有:十进制数进位规律、数值大小的考量等.【例11】(★★2004年全国小学数学奥林匹克)已知下面的除法算式中,每个□表示一个数字,那么被除数应是.分析:由竖式知,商的十位是0,并且商的千位比百位大,只能是9,所以商是9807.因为除数乘8是两位数,乘9是3位数,所以除数是12.被除数=9807×12=117 684.[点评]本题运用到的知识点和数学方法有,数值大小的考量等.【例12】(★★★2002年全国小学数学奥林匹克)在下面的算式中,只有四个4是已知的,则被除数为.分析:设除数为4m n,商为abc,根据除法竖式可知4m n×b=□□4,再由减法竖式可知4m n×b=9□4.因为4m n×c=4□□,所以m≤4.试验:m=1时,由4m n×b=9□4,推出b=7,n=2;由142×a=□□4,推出a=2;由142×c=4□□,推出c=3.所以被除数为142×273=38 766.m=2,3,4时,均无解.[点评]本题运用到的主要知识点和数学方法有:数值大小的考量、乘法个位数字规律等.练习1、(★★)有10个连续的自然数,9是其中第三大的数.现在把这10个数填到下图的10个方格中,每格内填一个数,要求图中3个2×2的正方形中的4个数之和相等.那么,这个和数的最小值是多少?分析:第一步:首先确定数阵图中的关键区格,即相邻两个正方形相交的两个区格;第二步:由于9是其中第三大的数,所以这10个连续自然数是2、3、4、5……9、10、11,计算三个正方形和的和,显然这个和能被3整除,其中有两个数被重复计算了两次,2+3+……11=65除以3余2,因此被重复计算两个数的和被3除余1,这两个数取2、5时,这个和取得最小值,第三步,由已知的两个方格中的数,得到每个正方形中的和也取得最小值24,构造各个正方形中其他几个数使每个正方形中的数和为24,如图:4697103811522、(★★武汉明心奥数挑战赛)下面是一个残缺的乘法算式,只知道其中一个数字“8”,请你补全,那么这个算式的乘积是.分析:容易看出,乘数的个位大于8,故只能是9.又被乘数的9倍是三位数,8倍是两位数,它只能是12.故所求为12×89=1068.3、(★★★★香港圣公会小学数学奥林匹克)下面算式(1)中。
图形变形解五年级数阵图奥数题的解法

图形变形解五年级数阵图奥数题的解法
图形变形解五年级数阵图奥数题的解法
导语:数阵图的题目大部分是填出一种合理的情况即可,所以对数字敏感的同学很有优势。
以下是小编为大家精心整理的图形变形解五年级数阵图奥数题的解法,欢迎大家参考!
假如能够凭借优异的数感直接通过尝试得出答案,那当然是最快捷的方法;不过对于要求填出所有可能的填法、问一共有多少种填法、或者难以通过尝试得出答案的题目,就只能通过计算来求解。
因此,解决数阵图的'方法大体分为两种:
1、猜中间数并尝试
优先尝试将最中间的待填数字填入图形的正中间,再分组配对,尝试其他位置
2、计算线和
画线尽量覆盖所有空格,根据待填数字的总和,求出可能的线和值,再尝试其是否可行;
也可以设未知数,设法直接解出未知数和线和,再尝试填出其他位置的数。
常见的图形变形,变为更顺眼的图形,可能会让解题更加顺畅。
五年级奥数-数阵图与数字谜(含解析)
数阵图与数字谜教学目标1. 熟悉数阵图与数字谜的题目特点;2. 掌握数阵图与数字谜的解题思路。
精讲讲练数阵图数阵图是把一些数按照一定规则填在某一特定图形的规定位置上而来的图形,有时简称数阵。
【例1】 (2007年“希望杯”第二试)在右图所示○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点的三个数的和是__________。
【分析】 由于每条边上的三个数的和都是12,所以把这三条边上的三个数的和都加起来,总和应为12336⨯=,在其中,A 、B 、C 各算了一次,三个顶点的三个数各算了两次,所以三个顶点的三个数的和为(3618)29-÷=。
【例2】 (2007年天津“陈省身杯”国际青少年数学邀请赛)将112:这十二个自然数分别填入右图的12个圆圈内,使得每条直线上的四个数之和都相等,这个相等的和为__________。
【分析】 由于每条直线上的四个数之和都相等,设这个相等的和为S ,把所有6条直线上的四个数之和相加,得到总和为6S ;另一方面,在这样相加中,由于每个数都恰好在两条直线上,所以每个数都被计算了两遍。
所以,6(12312)2S =++++⨯L ,得到26S =,即所求的相等的和为26。
【例3】 (2007年“走进美妙的数学花园”决赛)如右图所示,A ,B ,C ,D ,E ,F ,G ,H ,I ,J 表示110:这10个各不相同的数字。
表中的数为所在行与列的对应字母的和,例如“14G C +=”。
请将表中其它的数全部填好。
C BA【分析】 由于5A F +=,14B F +=,所以1459B A -=-=,所以A 和B 只能是0和9。
因此可以推出:0A =,9B =,6C =,3D =,2E =,5F =,8G =,1H =,4I =,7J =。
可得右下图。
【例4】 (2007年“走进美妙的数学花园”初赛)从1、2、3…20这20个数中选出9个不同的数放入33⨯的方格表中,使得每行、每列、每条对角线上的三个数的和都相等。
五年级奥数:数阵图(二)

数阵图(二)一、考点、热点回顾上一讲我们讲了仅有一个“重叠数”的辐射型数阵图的填数问题,这一讲我们讲有多个“重叠数”的封闭型数阵图。
1、一个“重叠数”的辐射型数阵图的填数问题2、有多个“重叠数”的封闭型数阵图。
一般地,在m边形中,每条边上有n个数的形如下图的图形称为封闭型m-n图。
与“辐射型m-n图只有一个重叠数,重叠次数是m-1”不同的是,封闭型m-n图有m个重叠数,重叠次数都是1次。
对于封闭型数阵图,因为重叠数只重叠一次,所以已知各数之和+重叠数之和=每边各数之和×边数。
二、典型例题例1 、将1~8这八个数分别填入右图的○中,使两个大圆上的五个数之和都等于21。
分析与解:中间两个数是重叠数,重叠次数都是1次,所以两个重叠数之和为21×2-(1+2+…+8)=6。
在已知的八个数中,两个数之和为6的只有1与5,2与4。
每个大圆上另外三个数之和为21-6=15。
如果两个重叠数为1与5,那么剩下的六个数2,3,4,6,7,8平分为两组,每组三数之和为15的只有2+6+7=15和3+4+8=15,故有左下图的填法。
如果两个重叠数为2与4,那么同理可得上页右下图的填法。
例2、将1~6这六个自然数分别填入右图的六个○内,使得三角形每条边上的三个数之和都等于11。
分析与解:本题有三个重叠数,即三角形三个顶点○内的数都是重叠数,并且各重叠一次。
所以三个重叠数之和等于11×3-(1+2+…+6)=12。
1~6中三个数之和等于12的有1,5,6;2,4,6;3,4,5。
如果三个重叠数是1,5,6,那么根据每条边上的三个数之和等于11,可得左下图的填法。
容易发现,所填数不是1~6,不合题意。
同理,三个重叠数也不能是3,4,5。
经试验,当重叠数是2,4,6时,可以得到符合题意的填法(见右上图)。
例3 、将1~6这六个自然数分别填入右图的六个○中,使得三角形每条边上的三个数之和都相等。
分析与解:与例2不同的是不知道每边的三数之和等于几。
五年级奥数数阵问题

课时3 数阵问题(一)一.数阵填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析例1 把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D +E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2、6,8,9)和(3、5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1、5,9,10)和(4,6,7,8)。
小试牛刀1、把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
五年级上册数学培优奥数讲义-第23讲数阵图

第23讲数阵图知识与方法数阵图问题千变万化,需要综合运用各种数学知识来解决问题,而往往同学们喜欢毫无顺序的“瞎试”,本讲要介绍一些通用的方法。
所以,一般是先用公式法分析出重复数,再用尝试法进行试填。
方法一:尝试法:所给的是一个等差数列,并且每条线上的数是奇数个时,中间数只能填最大数、最小数或中间数,因此可以依据这个规律进行尝试。
方法二:公式法:线和×线数=数字和+重复数×重复次数初级挑战1将1~7分别填入下图的7个○内,使每条线段上三个○内数的和相等。
思维点拨:观察发现,每条线上的三个数之和相等,而这三条线相交刚好重复了一个数,我们叫做重复数。
除去重复数,三条线上其他两数之和应相等。
1~7中,找出三组和相等的六个数即可,剩下的一个数填中间。
答案:(答案不唯一)能力探索1把1~11分别填入下图的○内,使每条线段上3个○内数的和相等。
答案:中间重复数为1或6或11。
给出一种填法:(答案不唯一)初级挑战2将数字1~8填入图中,使横行方框中的数之和与竖列方框中的数之和相等且为19。
思维点拨:本题的关键在于先确定中间重复数。
横行和竖列的和为19×2=38,而实际上所有方框中的数之和为1+2+3+4+5+6+7+8=36,38-36=2,多出来的2正好是中间重复的数。
答案:(答案不唯一)能力探索2将2~8填入下图的方框中,使横行、竖列的和相等且为20。
答案:中间重复数:20×2-(2+3+4+…+8)=5。
(答案不唯一)中级挑战1将1~10这十个自然数填入下图的○中,使每个圆上六个数的和为29。
思维点拨:两个大圆圈的和为29×2=58,而圆圈上所有的数之和为:1+2+3+…+10=55,因此中间两个圆圈数(重复数)的和为58-55=3,而3=1+2,由此可先填出中间的两个圆圈数分别为1和2,再两两配对填出其它数即可。
答案:(答案不唯一)把数字1~8分别填入下图的小圆圈内,使每个五边形上5个数的和都等于20。
经典奥数题及答案

一.数阵问题1.下面的数阵, 第14行第11个数是(180),2012位于第(45 )行第( 76)个解:n*2-1=14*2-1=27 1+3+5+...+27=196196-(27-11)=18045*45=2025 2025-2012=1345*2-1-13=762.将自然数按下列顺序排列,2012在(59)行(5)列。
解:n*(n-1)/263*64/2=2016 2016-2012+1=564-5=593.将奇数列1,3,5,7,9,11,13,15,17,19,…按下表排列.其中第11行第l0列的数为(401).解:n*n+n-1 n=行+列-111+10-1=20 20*20+(20-1)=419419-2*(20-11)=4014.下列各数,第15行最左边的数是(393)?第17行第11个数是(533),1001位于第(23)行第(17)个。
解:n*n*2-114*14*2-1+2=39316*16*2-1+11*2=53322*22*2-1=967 (1001-967)/2=175.自然数按如下方式排列,则401在第(39 )拐弯处。
第36次拐弯是(343)。
700到2012之间有( 38 )个拐角数.解:1+1+1+2+2+3+3......401-1=400=20*20 20*2-1=3936/2=18 (1+2+3+...+18)*2+1=34326*27=702 44*45=1980(44-26+1)*2=38二.计数问题1.上体育课时,我们几个同学站成一排,从1开始顺序报数,除我以外的其他同学报的数之和减去我报的数恰好等于500, 问:共有多少个同学? 我报的数是几? 解:(1+32)*32/2=528(个)(528-500)/2=1432人 142.一本书中间的某一张被撕掉了,余下的各页码数之和是1133,这本书有多少页.解:1+2+3+...+48=1176(页)48页3..把从1开始的自然数依次写出来,得到1234567…将它从左至右每四个数码分为一组成为一个四位数,1234,5678,9101,1121,3141..第120个四位数是(5126)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时3 数阵问题(一)
一.数阵
填“幻方”是同学们比较熟悉的一种数学游戏,由幻方演变出来的数阵问题,也是一类比较常见的填数问题。
这里,主要讨论一些数阵的填法。
解答数阵问题通常用两种方法:一是待定数法,二是试验法。
待定数法就是先用字母(或符号)表示满足条件的数,通过分析、计算来确定这些字母(或符号)应具备的条件,为解答数阵问题提供方向。
试验法就是根据题中所给条件选准突破口,确定填数的可能范围。
把分析推理和试验法结合起来,再由填数的可能情况,确定应填的数。
二.例题精析
例1 把5、6、7、8、9五个数分别填入下图的五个方格里,如图a使横行三个数的和与竖行三个数的和都是21。
先把五格方格中的数用字母A、B、C、D、E来表示,根据题意可知:A+B+C+D+E=35,A+E+B+C+E+D=21×2=42。
把两式相比较可知,E=42-35=7,即中间填7。
然后再根据5+9=6+8便可把五个数填进方格,如图b。
小试牛刀
把1——10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
2、把1——9各数填入“七一”的9个空格里,使在同一直线上的各数的和都是13。
3、将1——7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
例2 将1——10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
分析设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3+……+10+a+b=30×2、即55+a+b=60,a+b=5。
在1——10这十个数中1+4=5,2+3=5。
当a和b是1和4时,每个大圆上另外四个数分别是(2、6,8,9)和(3、5,7,10);当a和b是2和3时,每个大圆上另外四个数分别为(1、5,9,10)和(4,6,7,8)。
小试牛刀
1、把1——8八个数分别填入下图的○内,使每个大圆上五个○内数的和相等。
2、把1——10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
3、将1——8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
例3将1——6这六个数分别填入下图的圆中,使每条直线上三个圆内数的和相等、且最大。
分析设中间三个圆内的数是a、b、c。
因为计算三条线上的和时,a、b、c都被计算了两次,根据题意可知:1+2+3+4+5+6+(a+b+c)除以3没有余数。
1+2+3+4+5+6=21、21÷3=7没有余数,那么a+b+c的和除以3也应该没有余数。
在1——6六个数中,只有4+5+6的和最大,且除以3没有余数,因此a、b、c分别为4、5、6。
(1+2+3+4+5+6+4+5+6)÷3=12、所以有下面的填法:
小试牛刀
1、将1——6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
2、将1——9九个数分别填入下图○内,使每边上四个○内数的和都是17。
3、将1——8八个数分别填入下图的○内,使每条安上三个数的和相等。
例4将1——7分别填入下图的7个○内,使每条线段上三个○内数的和相等。
分析首先要确定中心圆内的数,设中心○内的数是a,那么,三条线段上的总和是1+2+3+4+5+6+7+2a=28+2a,由于三条线段上的和相等,所以(28+2a)除以3应该没有余数。
由于28÷3=9……1、那么2a除以3应该余2、因此,a可以为1、4或7。
当a=1时,(28+2×1)÷3-1=9,即每条线段上其他两数的和是9,因此,有这样的填法。
小试牛刀
1、将1——9填入下图的○中,使横、竖行五个数相加的和都等于25。
2、将1——11这十一个数分别填进下图的○里,使每条线上3个○内的数的和相等。
3、将1——8这八个数分别填入下图○内,使外圆四个数的和,内圆四个数的和以及横行、竖行上四个数的和都等于18。
例5如下图(a)四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数的和相等。
问这六个质数的积是多少
分析设每个小三角形三个顶点处○内数的和为X。
因为中间的小三角形顶点处的数在求和时都用了三次,所以,四个小三角形顶点处数的总和是4X=20+2X,解方程得X=10。
由此可知,每个小三角形顶点处的三个质数的和是10,这三个质数只能是2、3、5。
因此这6个质数的积是2×2×3×3×5×5=900。
如图(b)。
小试牛刀
1、将九个不同的自然数填入下面方格中,使每行、每列、每条对角线上三个数的积都相等。
2、将1——9九个自然数分别填入下图的九个小三角形中,使靠近大三角形每条边上五个数的和相等,并且尽可能大。
这五个数之和最大是多少
3、将1——9九个数分别填入下图○内,使外三角形边上○内数之和等于里面三角形边上○内数之和。
