Matlab灰色预测模型GM(1,1)代码
灰色系统G(1,1)预测步骤【模板带代码】

=3499.075e -0.1062t
3641.075
编写程序
u=alpha(2)/alpha(1) v=X0(1)-u v=3499.075 u=—3641.075
(5)进行参差检验
1)根据预测公式,计算
v=3499.075 u=—3641.075
Xˆ
1
k
1
X
0
1
for n=0:10
X2(n+1)=v*exp(-alpha(1)*n)+u
end
X2
2.0690
2)累减生成序列
Xˆ X3 =1.0e+003 * (0) 0.1420 0.4079 0.4536
0.5044
0.7713 0.8577 0.9537 1.0605
源程序:X3(1)=X2(1)
for m=1:10
kesi =
4.4388 339.0664 176.2445 203.6132
0 0.1998 1.2682 0.2130 0.8524 0.1330
0.0089
0.3767
0.2203
0.4155
{0%,19.98%,126.82%,0.89%,37.67% ,22.03% ,41.55% ,21.30%,85.24%,13.30%}
e=
179.4592 111.5134 74.1747 175.0204 159.6072 29.2461 215.2168 33.1910
3.2147 24.1540
源程序:S0=0.6745*X0std e=abs(daita0-daita0mean) 对所有的 e 都小于 S0 ,故小参差概率 P(k S0) 1 0.95
灰色预测模型及MATLAB实例

灰⾊预测模型及MATLAB实例下⾯将主要从三⽅⾯进⾏⼤致讲解,灰⾊预测概念及原理、灰⾊预测的分类及求解步骤、灰⾊预测的实例讲解。
⼀、灰⾊预测概念及原理:1.概述:关于所谓的“颜⾊”预测或者检测等,⼤致分为三⾊:⿊、⽩、灰,在此以预测为例阐述。
其中,⽩⾊预测是指系统的内部特征完全已知,系统信息完全充分;⿊⾊预测指系统的内部特征⼀⽆所知,只能通过观测其与外界的联系来进⾏研究;灰⾊预测则是介于⿊、⽩两者之间的⼀种预测,⼀部分已知,⼀部分未知,系统因素间有不确定的关系。
细致度⽐较:⽩>⿊>灰。
2.原理:灰⾊预测是通过计算各因素之间的关联度,鉴别系统各因素之间发展趋势的相异程度。
其核⼼体系是灰⾊模型(Grey Model,GM),即对原始数据做累加⽣成(或者累减、均值等⽅法)⽣成近似的指数规律在进⾏建模的⽅法。
⼆、灰⾊预测的分类及求解步骤:1.GM(1,1)与GM(2,1)、DGM、Verhulst模型的分类⽐较:预测模型适⽤场景涉及的序列GM(1,1)模型⼀阶微分⽅程,只含有1个变量的灰⾊模型。
适⽤于有较强指数规律的序列。
累加序列均值序列GM(2,1)模型适⽤于预测预测具有饱和的S形序列或者单调的摆动发展序列缺陷。
累加序列累减序列均值序列DGM模型累加序列累减序列Verhulst模型累加序列均值序列2.求解步骤思维导图:其中预测过程可能会涉及以下三种序列、⽩化微分⽅程、以及⼀系列检验,由于⼤致都相同,仅仅是某些使⽤累加和累减,⽽另外⼀些则使⽤累加、累减和均值三个序列的差别⽽已。
于是下⾯笔者将对其进⾏归纳总结再进⾏绘制思维导图,帮助读者理解。
(1)原始序列(参考数据列):(2)1次累加序列(1-AGO):(3)1次累减序列(1-IAGO ):(也就是原始序列中,后⼀项依次减去前⼀项的值,例如,[x(2)-x(1),x(3-x(2),...,x(n)-x(n-1))]。
)(4)均值⽣成序列:(这是对累加序列"(前⼀项+后⼀项)/2"得出的结果。
高级计算器灰色预测GM(1.1)模型-的计算程序

高级计算器灰色预测GM(1.1 )模型的计算程序毕 永(陕西省子长县疾病预防控制中心 子长 717399)CASIO ƒχ—3800P 计算器,置有4组最大容量135步程序存储器,体积小,价格低,功能多,是基层工作者一种理想的计算工具。
灰色预测GM(1.1 )模型公式冗长,计算过程繁琐复杂,编程运算化繁为简,变难为易,大大提高了工作效率。
在Ⅰ区程序输入x ( t ) 生成u ∧值和a∧值,在Ⅱ区程序输入t 即可得 y ∧( t ) 值。
现介绍操作方法如下:1 公式1.1 ()()1t i y t x t -=∑ 1.2 ()()()11122z t y t y t =+- 1.3 ()()()dy t ay t u d t == 1.4 ()()()1[1]1uu y t x e a t a a +=---+1.5 ()()()()()221/N N N t z t t a N x t z t z t x t D ∧===⎧⎫⎡⎤⎡⎤⎡⎤=--+⎨⎬⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎩⎭∑∑∑1.6 ()()()()()22222/N N Z N t t t t u z t x t z t Z t x t D ∧====⎧⎫⎡⎤⎡⎤⎡⎤⎡⎤=-+⎨⎬⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎩⎭∑∑∑∑1.7 ()()()22221N N t t D N z t z t ==⎡⎤⎡⎤=--⎢⎥⎢⎥⎣⎦⎣⎦∑∑ 2 写入程序2.1 准备MODE EXP (LRN 状态)SHIFT PCL (程序存储器清零)MODE ·(RUN状态)SHIFT KAC (K寄存器清零)令:2 Kin 4 Kin 3 Kin2 SHIFT Min(输入数值给需要使用的寄存器) MODE EXP (LRN状态)2.2 程序Ⅰ(进入程序Ⅰ区)Kin + 3 Kin 6 ÷ 2 + Kout 3 –Kout 6 = Kin + 5 Kin×6 χ2Kin + 2 Kout 6 Kin + 1 1 Kin + 4 Kout 4 SHIFT HLT (显示3)MR Kin-3 Kout 3 SHIFT X←→K 2 Kin×2 SHIFT X←→K 4 Kin×4 SHIFT X←→K 1 Kin×1 SHIFTX←→K 5 Kin×5 Kin×3 χ2Kin-4 Kout 5 Kin-2 Kout 1 Kin-1 Kin-3 Kout 4 Kin÷2 Kin÷3 Kout 3 Kin÷2 Kout 2 SHIFT M-(显示-0.333333333)Ⅱ(进入程序Ⅱ区)- 1 =×Kout 3 =+/- SHIFT e x ×MR + Kout 2 =SHIFT HLT -SHIFT X←→K 1 =(62步显示0.864639944)2.3 退出与运算MODE ·3 运算实例表1:1973~1980年启东县人口恶性肿瘤死亡率(/10万)[1]t 年份死亡率x ( t ) y∧( t ) x∧( t )1 1973 108.462 1974 125.87 240.143 1975 144.08 372.674 1976 127.45 506.045 1977 132.84 640.276 1978 135.55 775.367 1979 139.87 911.328 1980 134.03 1048.149 1981 136.97 1185.84 137.7110 1982 138.14 1324.43 138.5911 1983 142.42 1463.92 139.4812 1984 152.36 1604.29 140.37 3.1 使用Ⅰ区程序生成数据操作:显示:说明:MODE ·RUN状态SHIFT KAC K寄存器清零令:108.46 Kin 3 SHIFT Min 输入变量125.87Ⅰ 1144.08Ⅰ 2::::::134.03 Ⅰ 7RUN - 20427.27008 u∧ / a∧Kout 3 - 0.0063918026 a∧Kout 4 3551879.152 D3.2 使用Ⅱ区程序求出y∧( t ) 值操作:显示:说明:MODE 7 2 设定小数令:2 Ⅱ240.14 y∧(2)3Ⅱ372.67 y∧(3)4Ⅱ506.04 y∧(4)5Ⅱ640.27 y∧(5)6Ⅱ775.36 y∧(6)7Ⅱ911.32 y∧(7)8 Ⅱ1048.15 y∧(8)3.3 模型外推预测时求出y∧( t ) 、x∧( t ) 值操作:显示:说明:令:8 Ⅱ1048.15 y∧(8)RUN 1048.15 存入K1寄存器9 Ⅱ1185.85 y∧(9)RUN 137.71 x∧(9)10 Ⅱ1324.44 y∧(10)RUN 138.59 x∧(10)11 Ⅱ1463.92 y∧(11)RUN 139.48 x∧(11)12 Ⅱ1604.29 y∧(12)RUN 140.37 x∧(12)参考文献[1] 汪爱勤,鱼敏,灰色预测方法在疾病预测中的应用[J],中华流行病学杂志,1988,9(1):49 ̴52[2] 李光,疾病的灰色预测模型(GM)及其电子计算器程序[J],湖北预防医学杂志,1991,2(4):53 ̴55[3] 韩波,林华荣,孙瑞林,用计算器灰色预测环境污染[J],环境监测管理与技术,1994,6(1):44 ̴46。
建立灰色系统GM(1,1)1-AGO模型的步骤

一、建立灰色系统GM (1,1)(即:1-AGO )模型的步骤第一步:累加生成对原始数列中各同类数据依次累加,形成新的序列。
一次累加生成序列为)()}即:(1)(0)(1)(1)x x =,(1)(0)(0)(2)(1)(2)x x x =+,(1)(0)(0)(0)(3)(1)(2)(3)x x x x =++,...第二步:一次拟合参数求解如下G(1,1)模型即微分方程:(1)(1)()()dx t ax t u dt+= (1) 其中:T T T a u B B B Y 1[,]()-=,且()]解方程(1),可得响应函数为:(1)(0)ˆ(1)[(1)]ak u u xk x e a a-+=-+ 第三步:确定预测值预测函数为:(0)(1)(1)(0)ˆˆˆ(1)(1)()(1)[(1)]aa ku xk x k x k ex e a-+=+-=--第四步:精度检验精度检验的方法有三种:相对误差检验法、后验差检验法、关联度检验法1、 相对误差检验法:(仔细辨明(0)(0)ˆ(),()xk x k ) 相对误差为:(0)(0)(0)ˆ()()100%()-⨯x k xk x k 相对误差越小越好。
2、 后验差检验法:计算残差(0)(0)ˆ-X X的方差 2(0)(0)211111[()()]===-∑∑n n k k S x k x k n n2(0)(0)(0)(0)221111ˆˆ()()[()()]==⎡⎤=---⎢⎥⎣⎦∑∑n n k k S x k xk x k x k n n 计算后验差之比: 21/=C S S 计算小概率误差:(0)(0)(0)(0)2111ˆˆ()()[()()]0.6745=⎧⎫=---<⎨⎬⎩⎭∑n k p P x k xk x k x k S n,C p C 指标和是后验差检验的两个重要指标.指标越小越好121.C S S S 越小表示大而越小大表示原始数据方差大,即原始数据离散程度大. 2S C 小表示残方差小,即残差离散程度小.小就表明尽管原始数据很离散,而模型所得计算值与实际值之差并不太离散.1,,0.6745,,,.p p C p 指标越大越好越大表明残差与残差平均值之差小于给定值的点较多即拟合值(或预测值)分布比较均匀.按两个指标可综合评定预测模型的精度模型的精度由后验差和小误差概率共同刻划.一般地,将模型的精度分为四级,见下表精度检验等级参照表{},,=Max p C 模型的精度级别的级别于是的级别如果模型很差,可以考虑进行关联度检验,以便选出更好的模型。
用MATLAB实现灰色预测GM_1_1_模型_唐丽芳

社,1992.
[责任编辑:尤书才]
To Accomplish Gray Forecasting GM(1,1) Model Using the MATLAB
TANG Li-fang1,JIA Dong-qing2 ,MENG Qing-peng2
k
∑ 式中 x(1) (k) = x(0) (i) , i =1
(k=1,2,3,…,n)
% 作 1-AGO 生成序列 x (1)
for i=1:n x1(i)=sum(x0(1:i));
end
采用一阶单变量微分方程进行拟合,得到白化方程的 GM(1, 1)模型:
dx (1) + ax(1) (t) = u, 式中 a, u 是待定系数。 (3) dt
+
u
a
a
…(6)
^ (1)
% 计算 GM(1,1)模型 x (k + 1) 值
yc1(1)=x0(1); for k=1:n c=x0(1)-au(2)/au(1); yc1(k+1)=c*exp( -au(1)*k)+au(2)/au(1); end
(5)还原后的预测结果(作 IAGO)
^(0)
^(1)
end
r=r/n; % r 表示关联度
(3)方差比和小误差概率检验
方差比和小误差概率检验属后验差检验,计算公式分别
如下:
∑ 预测误差均值
−
e
=
1
n
e(i)
n i=1
∑ 原始数据均值:
−(0)
x
=
1
n
灰色模型预测GM(1,1)MATLAB程序代码

灰⾊模型预测GM(1,1)MATLAB程序代码版权所有引⽤请注明出处function gmcal=gm1(x)%% ⼆次拟合预测GM(1,1)模型%x = [5999,5903,5848,5700,7884];sizexd2 = size(x,2);%求数组长度k=0;for y1=xk=k+1;if k>1x1(k)=x1(k-1)+x(k);%累加⽣成z1(k-1)=-0.5*(x1(k)+x1(k-1));%z1维数减1,⽤于计算Byn1(k-1)=x(k);elsex1(k)=x(k);endend%x1,z1,k,yn1sizez1=size(z1,2);%size(yn1);z2 = z1';z3 = ones(1,sizez1)';YN = yn1'; %转置B=[z2 z3];au0=inv(B'*B)*B'*YN;au = au0';afor = au(1);ufor = au(2);ua = au(2)./au(1);constant1 = x(1)-ua;afor1 = -afor;x1t1 = 'x1(t+1)';estr = 'exp';tstr = 't';leftbra = '(';rightbra = ')';strcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1),tstr,rightbra,'+',leftbra,num2str(ua),rightbra) %输出时间响应⽅程k2 = 0;for y2 = x1k2 = k2 + 1;if k2 > kelseze1(k2) = exp(-(k2-1)*afor);endendsizeze1 = size(ze1,2);z4 = ones(1,sizeze1)';G=[ze1' z4];X1 = x1';au20=inv(G'*G)*G'*X1;au2 = au20';Aval = au2(1);Bval = au2(2);strcat(x1t1,'=',num2str(Aval),estr,leftbra,num2str(afor1),tstr,rightbra,'+',leftbra,num2str(Bval),rightbra) %输出时间响应⽅程nfinal = sizexd2-1 + 1; %决定预测的步骤数5 这个步骤可以通过函数传⼊%nfinal = sizexd2 - 1 + 1;%预测的步骤数 1for k3=1:nfinalx3fcast(k3) = constant1*exp(afor1*k3)+ua;end%⼀次拟合累加值for k31=nfinal:-1:0if k31>1x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1);elseif k31>0x31fcast(k31+1) = x3fcast(k31)-x(1);elsex31fcast(k31+1) = x(1);endendendx31fcast%⼀次拟合预测值for k4=1:nfinalx4fcast(k4) = Aval*exp(afor1*k4)+Bval;end%x4fcastfor k41=nfinal:-1:0if k41>1x41fcast(k41+1) = x4fcast(k41)-x4fcast(k41-1);elseif k41>0x41fcast(k41+1) = x4fcast(k41)-x(1);elsex41fcast(k41+1) = x(1);endendendx41fcast,x%⼆次拟合预测值%***精度检验p C************//////////////////////////////////k5 = 0;for y5 = xk5 = k5 + 1;if k5 > sizexd2elseerr1(k5) = x(k5) - x41fcast(k5);endend%err1%绝对误差xavg = mean(x);%xavg%x平均值err1avg = mean(err1);%err1avg%err1平均值k5 = 0;s1total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses1total = s1total + (x(k5) - xavg)^2;endends1suqare = s1total ./ sizexd2;s1sqrt = sqrt(s1suqare);%s1suqare,s1sqrt%s1suqare 残差数列x的⽅差 s1sqrt 为x⽅差的平⽅根S1k5 = 0;s2total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses2total = s2total + (err1(k5) - err1avg)^2;endends2suqare = s2total ./ sizexd2;%s2suqare 残差数列err1的⽅差S2Cval = sqrt(s2suqare ./ s1suqare);Cval%nnn = 0.6745 * s1sqrt%Cval C检验值k5 = 0;pnum = 0 ;for y5 = xk5 = k5 + 1;if abs( err1(k5) - err1avg ) < 0.6745 * s1sqrtpnum = pnum + 1;%ppp = abs( err1(k5) - err1avg )elseendendpval = pnum ./ sizexd2;pval%p检验值%arr1 = x41fcast(1:6)%预测结果为区间范围预测步长和数据长度可调整程序参数进⾏改进。
GM(1,1)模型的Matlab实现(范例2)

GM (1,1)模型的MATLAB 实现摘要 本文介绍了灰色预测()1,1GM 模型的基本原理,并在其基础上利用MATLAB 软件进行实现,给出相应的MATLAB 算法。
并通过实例检验MATLAB 算法的正确性与通用性。
关键词模型; 灰色系统; MATLAB ;1 引言1.1灰色预测理论基本介绍灰色系统是指系统论中一部分信息是已知的,但另一部分信息是未知的,系统内各因素间有不确定的关系。
而灰色预测模型是灰色系统理论的重要内容之一,其中灰色模型是邓聚龙教授在1982年提出的一种新的模型计算方法,被广泛应用于农业、工业、医学、军事、经济、交通、生态等许多科学领域,解决了许多领域中的复杂实践问题[13]-。
且对于杂乱无章表征数据,灰色预测能发现其内在必然的联系与规律,即通过鉴别系统各因素之间发展趋势的相异程度,进行关联分析,并对原始数据进行一定的处理,来寻找系统变动的规律,生成有较强规律性的数据序列,建立相应的微分方程模型,从而预见系统的未来的发展趋势及状况。
灰色预测法是用等时距观测到的反映预测对象特征的一系列数量值,构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
灰色预测有其四种常见的类型,分别为:灰色时间序列预测、畸变预测、系统预测、拓扑预测。
灰色模型(Grey Models )简称GM 模型,是灰色系统理论(Grey System Theory )的一个基本模型。
GM 模型的一般模型为,当中时,GM 模型不能做预测,只能用于分析因子之间的相互作用。
做预测用的一般为模型,其中,用的最多的则是用灰色微分拟合法建立的模型。
由于它预测要求所需样本量少(至少四组),不需要计算统计特征量、不用考虑样本变化的趋势、运算简便、在短期内精度高、预测效果好、容易检查等优点。
本文通过运用MATLAB 软件对模型进行程序实现。
增强模型通用性与实用性,方便今后对其使用。
假设我们有一段原始时间序列:为了弱化原始时间序列的随机性,在建立灰色预测模型之前,我们需要先对原始时间序列进行数据处理,经过数据处理后的时间序列称为生成列。
灰色预测模型matlab程序精确版

%x=[1019,1088,1324,1408,1601];gm1(x); 测试数据%二次拟合预测GM(1,1)模型function gmcal=gm1(x)if nargin==0x=[1019,1088,1324,1408,1601]endformat long gsizex=length(x);%求数组长度k=0;for y1=xk=k+1;if k>1x1(k)=x1(k-1)+x(k);%累加生成z1(k-1)=-0.5*(x1(k)+x1(k-1));%z1维数减1,用于计算Byn1(k-1)=x(k);elsex1(k)=x(k);endend%x1,z1,k,yn1sizez1=length(z1);%size(yn1);z2 = z1';z3 = ones(1,sizez1)';YN = yn1'; %转置%YNB=[z2 z3];au0=inv(B'*B)*B'*YN;au = au0';%B,au0,auafor = au(1);ufor = au(2);ua = au(2)./au(1);%afor,ufor,ua%输出预测的 a u 和 u/a的值constant1 = x(1)-ua;afor1 = -afor;x1t1 = 'x1(t+1)';estr = 'exp';tstr = 't';leftbra = '(';rightbra = ')';%constant1,afor1,x1t1,estr,tstr,leftbra,rightbrastrcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1),tstr,rightbra,'+ ',leftbra,num2str(ua),rightbra)%输出时间响应方程%******************************************************%二次拟合k2 = 0;for y2 = x1k2 = k2 + 1;if k2 > kelseze1(k2) = exp(-(k2-1)*afor);endend%ze1sizeze1=length(ze1);z4 = ones(1,sizeze1)';G=[ze1' z4];X1 = x1';au20=inv(G'*G)*G'*X1;au2 = au20';%z4,X1,G,au20Aval = au2(1);Bval = au2(2);%Aval,Bval%输出预测的 A,B的值strcat(x1t1,'=',num2str(Aval),estr,leftbra,num2str(afor1),tstr,rightbra,'+',lef tbra,num2str(Bval),rightbra)%输出时间响应方程nfinal = sizex-1 + 1;(其中+1可改为+5等其他数字,即可预测更多的数字)%决定预测的步骤数5 这个步骤可以通过函数传入%nfinal = sizexd2 - 1 + 1;%预测的步骤数 1for k3=1:nfinalx3fcast(k3) = constant1*exp(afor1*k3)+ua;end%x3fcast%一次拟合累加值for k31=nfinal:-1:0if k31>1x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1);elseif k31>0x31fcast(k31+1) = x3fcast(k31)-x(1);elsex31fcast(k31+1) = x(1);endendendx31fcast%一次拟合预测值for k4=1:nfinalx4fcast(k4) = Aval*exp(afor1*k4)+Bval;end%x4fcastfor k41=nfinal:-1:0if k41>1x41fcast(k41+1) = x4fcast(k41)-x4fcast(k41-1);elseif k41>0x41fcast(k41+1) = x4fcast(k41)-x(1);elsex41fcast(k41+1) = x(1);endendendx41fcast,x%二次拟合预测值%***精度检验p C************////////////////////////////////// k5 = 0;for y5 = xk5 = k5 + 1;if k5 > sizexelseerr1(k5) = x(k5) - x41fcast(k5);endend%err1%绝对误差xavg = mean(x);%xavg%x平均值err1avg = mean(err1);%err1avg%err1平均值k5 = 0;s1total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexelses1total = s1total + (x(k5) - xavg)^2;endends1suqare = s1total ./ sizex;s1sqrt = sqrt(s1suqare);%s1suqare,s1sqrt%s1suqare 残差数列x的方差 s1sqrt 为x方差的平方根S1 k5 = 0;s2total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexelses2total = s2total + (err1(k5) - err1avg)^2; endends2suqare = s2total ./ sizex;%s2suqare 残差数列err1的方差S2Cval = sqrt(s2suqare ./ s1suqare);Cval%nnn = 0.6745 * s1sqrt%Cval C检验值k5 = 0;pnum = 0 ;for y5 = xk5 = k5 + 1;if abs( err1(k5) - err1avg ) < 0.6745 * s1sqrtpnum = pnum + 1;%ppp = abs( err1(k5) - err1avg )elseendendpval = pnum ./ sizex;pval%p检验值%arr1 = x41fcast(1:6)%预测结果为区间范围预测步长和数据长度可调整程序参数进行改进运行结果x =1019 1088 1324 1408 1601ans =x1(t+1)=8908.4929exp(0.11871t)+(-7889.4929)ans =x1(t+1)=8945.2933exp(0.11871t)+(-7935.7685)x31fcast =Columns 1 through 31019 1122.89347857097 1264.43142178303 Columns 4 through 61423.80987235488 1603.27758207442 1805.36675232556 x41fcast =Columns 1 through 31019 1118.05685435129 1269.65470492098 Columns 4 through 61429.69153740195 1609.90061644041 1812.82460377782 x =1019 1088 1324 1408 1601Cval =0.139501578334155 pval =1。
用Matlab实现GM_1_1_灰色模型的供电量预测

人工智能及识别技术ARTIFICIAL INTELLIGENCE AND IDENTIFICATION TECHNIQUES1灰色预测模型GM (1,1)灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论,由我国邓聚龙教授在1982年首次提出的。
灰色系统理论具有所需样本数据少,不需要计算统计特征量等优点。
灰色预测解决了连续微分方程的建模问题。
它通过原始数据的整理来寻找数的规律。
在建模时,首先对原始数据进行累加或累减生成,形成新的序列,对新序列建立微分方程模型和解析分析,达到预测原始序列的目的。
其中GM (1,1)模型是基于灰色系统理论的常用预测模型。
因为它具有要求原始数据少、不考虑分布规律、不考虑变化趋势、运算方便、短期精度高、易于检查的优点,得到了广泛的应用。
它的基本原理是:认为原始数列是逐步增长或减少的,通过对原始数列应用累加生成这样的数据处理方法可以得到一条具有指数增长规律的上升形状数列。
由于一阶微分方程的解即是指数增长形式,因此通过建立一阶微分方程模型和累减生成还原就可以得到预测数列。
2GM (1,1)模型的建立(1)对随机序列(i=0,1,2…n )作一次累加(1…AGO)生成序列(i=0,1,2…n ),其中。
(2)按照X i (1)的指数增长规律,可知X i (1)满足下列一阶线性微分方程。
(X(1)是时间t 的函数,这是灰色方程,部分数据未知)(3)参数估计:记待定,经离散化处理,得:Y n=BA.使用最小二乘法求出A 的近似解:,将近似值代入原微分方程:(*)(原微分方程的白化方程)其中(4)Xi (1)的预测值:求解微分方程(*)得到原微分方程的近似解,其中X 1(1)=X 1(0);写成离散形式,得到X i (1)的预测值:(5)X i(0)的预测值:3应用实例用Matlab 实现GM (1,1)灰色模型的供电量预测梁智勇(广东电网公司肇庆供电局,肇庆526040)摘要:介绍灰色预测模型GM (1,1)在电力系统中的预测应用,同时在Matlab 平台上实现了灰色模型GM (1,1)函数的编制。
灰色预测MATLAB程序

灰色预测心设尹曲⑴#为原始数列,其1次累<加生成数列为炉=(孝①宀2\S,其中©=2^°:⑺卫=12…止i-1尋定文沙的灰导数为d(Jt)=玄㈣(Jt)=尤⑴的-工⑴(*-1).令尹为数列壬⑴的邻值生成数列,即尹)(町=加小(町十(1—a)x山(k-1).于是定文GM(1T1)的灰微分方程模型为d(k)+az①(上)=&_即或.严⑹+盘⑴懐)=乩⑴在式(1)中口①的称为灰导数’熬称为发展系数'弧称为白化背景值,b称为灰作用量。
将时刻表庄=23…用代入(O式有j<0)(2)-az⑴(2)=工®⑶—俺叫巧=»于是GMIL)樫型可表示为r=现在问题归结为求巧h在值。
用一元绒性回归,即最小二垂進求它们的估计值住=[]卜护跖护F奕厢上回归分析中求诂计值是用软件计算的,有标淮程博求解,如山訥甜等。
GM(1.1)的白化型对于的(1-1)的获微分方程⑴,如果将解导教矿悶的时報=%…屮观対连续叢里"则工⑴衩为时间i函敕卅®,于是-<'W耐应于导敕重级必%),白化背杲值刃(時对应于导數申⑴。
于是GM(1,1)的换微分方嗨对应于的白微分方程为写®4曲%「)=也⑵GAI(1>1)换色预刪的步叢1-數堀的椅噓弓处理为了保证©M(B1)屋複方达的可行性・需要対已却皴堀锁必要的检峻处Ho 设療皓数攥列为了-计算埶列的级比如果所有的级比都落在可容覆盖区间盂-內・则數摒列X糾可咲建立G*ICL-1)複型且可以避行页色预测。
否则,丙軌据懺适当的叢换处理,如平移銮换:取C使得敕培列严⑹二工蚀盘)+匚用二12…”的级比都落在可啓禎盖内。
(1)残差檢验:计算相对薙差Z 建立GM (L T 1)複型不妬设少弋以m 叫唠霸足上面的要求,以它芮議堀列建立GM(1>1)型蛊(仍(i)+血C1\A)=b ・用回归分祈求得目上的估计值"于是相应的白化模型为 气^十小卄工解为工叱)=0)①—勺中1-色-⑶ 应Q于是停到预测值壬⑴(上+1)=0叫1)一勺>加+仝血二12…卫一1=aa伙而相应地得到预«=x co \t +1)=x 0)(t+l)-x a)(i)3i =1,2,-?n-l ?如果对所有的^<0.1・则认为达到鞭嵩的要求:否则,若耐所有的|^)1<0^,则认対达到一般要求©(2)级比偏差値桧验:计算能)=1-呂学©如果对所有的|,则认为达列较高的要求孑吾则若对斫有的,则认为达到一般要求O灰色预测计算实例^…;=:=-■■■■昏例北方某城市1986—1992年道路交通噪声平均声级数据见表6序号年吶寺表拆市近年来交通噪声数据[眶(应)]二諾;二319S872.4第—爭:级比检验建立丢通噪屛均声级数锯时间序列如下:4198972.1j 1990?1.4 619?17201199771.6艸=(•严①卫购(2)厂卅⑺) =(711,72.4.71.4,72.1.71.4,7UQ.71.6)些(1)求级比k(k)忠防护住T)2=(几⑵山⑶.…也⑺)g=(0.982JJ.0042J.0098-0.9917J.0056)(2)级比判断由于所有的X.(10e[0.982J.009S],k=2,3.6故可以用双0)作满意的GM(1,1)建模’第二步:GM(1,1)建模(1)对原始数据X®作一次累加,即卞⑴=(71.L143.5215.9.288359.4.431.4,503)(2)构造数据矩阵B及数据向量Y-2)—H 弋3/>1⑶讦算1T心求解得F'⑴=(工倒〔1〉_-)e 弋Q f+-1*^+1)=0<l,U)--)£-t +-=-3092^--^+31000⑶求生咸数列值歸型齊看:n令“is 那血由上面的碉醯数可甲得,其中取菱由龙⑴(i}=恥壮曲5加得丁I —"炉閃=进悶-进德-尊(71儿72.4.72.2:72.1:71.9:71.7,71.6)^}=(s"a >亍⑴⑵,…,网⑺A<第三步;模型检验•>模型的各种检验指标值的计算结果见表工 •t*表7GM(1检验表<序号年俯原始值模型值残差相对误差级比偏差•>1 19S6 71.1 71.1<219S7 72.4 72.4 -0.0057 0.01%0.0023 <3 19S S 72.4 72.2 0.163S 0.23%0.0203 •>4 19S9 72.1 72.1 0.0329 0.05%-O.(K H8 •>5199071.4 71.9 -0-49S4 0.7%-0.0074 <61991 72.0 71.7 0.21599 037%0.0107<71992 71.6 71.6 0.037S0.05%-0.0032于是得到目=山的餡,立欖型7-B)'1B TY=(dt0.0023 72.6573dt+0.002ix (1>=72.657^心经验证・该模型的精度较高.可进行预测和预报计算的Matlab 程序如下:仃坝测和预报n=length(x); z=0;%取输入数据的样本量for i=1:nz=z+x(i,:)be(i,:)=z; %计算累加值,并将值赋予矩阵beend for i=2:n %对y(i-1,:)=x(i,:)%对原始数列平行移位 endfor i=1:n-1%计算数据矩阵B 的第一列数据c(i,:)=-0.5*(be(i,:)+be(i+1,:)); clCjdearxO=[71H 72.472A 72J71477m c n.lengthtxO);*'b%注意这里为列帖lamda =xD(l :n-1),A0(2:n)%计算级比range =minmaxflamda f )%计算级比的范阖 X1=cumsum(xO);%累加运算B=['0,5*(xl(l ;n ^l)+xl(2:n))t ones(n -1,1)]TY 二甸(2:町;口=B\Y%拟合参数u(l>=a .u(2)=bx=dsolve (+a 'x =b\f x(0)-xO^J ;%求徴分方程的特号解x =subs(xJ*a\,b r /xO ,Mu(l)P u(2)t xO(l)|)i%代入荷计痹擞值和初蜡值yucel =subs %求巳知数擁的扳测位y-vpa(x,6)奄其中的石表示显不白位数字yuce=[x0(l)T diff(yucel)]%羔分运算,还原数据 epsiIon=-yuce%计算战羞作用:求累加数列、求ab 的值、求预测方程、求残差clc %清屏,以使结果独立显示x=[71.172.472.472.171.472.071.6]; format long ;%设置计算精度if length(x(:,1))==1%对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x endM.I-JTVorhlllst 模型endfor j=1:n-1%计算数据矩阵B的第二列数据e(j,:)=1;endfor i=1:n-1%构造数据矩阵BB(i,1)=c(i,:);B(i,2)=e(i,:);endalpha=inv(B'*B)*B'*y;%计算参数矩阵即ab的值for i=1:n+1%计算数据估计值的累加数列,如改为n+1为n+m可预测后m-1个值ago(i,:)=(x(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha( 2,:)/alpha(1,:);%显示输出预测值的累加数列endvar(1,:)=ago(1,: )for i=1:n%显示输出预测值%如改n为n+m-1,可预测后m-1个值var(i+1,:)=ago(i+1,:)-ago(i,:);%估计值的累加数列的还原,并计算出下一预测值endfor i=1:nerror(i,:)=x(i,:)-var(i,:);%计算残差endc=std(error)/std(x);%调用统计工具箱的标准差函数计算后验差的比值cago alpha var%显示输出预测值的累加数列%显示输出参数数列%显示输出预测值error %显示输出误差c %显示后验差的比值作用:数据处理判断是否可以用灰色预测、求级比、求累加数列、求ab的值、求预测方程clc,clearx0=[71.172.472.472.171.472.071.6]';%注意这里为列向量n=length(x0);lamda=x0(1:n-1)./x0(2:n)%计算级比range=minmax(lamda')%计算级比的范围x1=cumsum(x0)%累加运算B=[-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];Y=x0(2:n);u=B\Y%拟合参数u(1)=a,u(2)=bx=dsolve('Dx+a*x=b','x(0)=x0');%求微分方程的符号解x=subs(x,{'a','b','x0'},{u(1),u(2),x0(1)})%代入估计参数值和初始值yuce1=subs(x,'t',[0:n-1]);%求已知数据的预测值y=vpa(x,6)%其中的6表示显示6位数字yuce=[x0(1),diff(yuce1)]%差分运算,还原数据。
GMn灰色模型代码

GM(,n)(灰色模型代码)%灰色预测模型GM(1,n)模型的matlab源代码,包括预测模型的建立,以及模型的精度检验指标c,p的计算%假设预测3步,N=3%如在命令窗口键入:%gm=ycgm1n([1.6,1.7,2,1.8,1.9],[2,2.4,3,3.2,3.1],[3,3.1,3.2,3.5,2.8],3)function GM=ycgm1n(data1,data2,data3,N) %data1:纵摇,data2:升沉,data3:波浪T=length(data1);PYX1=data1;PYX2=data2;PYX3=data3;%进行数据预处理,这里用初值化X0_1=PYX1./PYX1(1);X0_2=PYX2./PYX2(1);X0_3=PYX3./PYX3(1);%用AGO生成一阶累加生成模块X1_1(1)=X0_1(1);X1_2(1)=X0_2(1);X1_3(1)=X0_3(1);for i=2:TX1_1(i)=X1_1(i-1)+X0_1(i);X1_2(i)=X1_2(i-1)+X0_2(i);X1_3(i)=X1_3(i-1)+X0_3(i);end%构造累加矩阵Bfor i=1:T-1M1(i)=(0.5*(X1_1(i)+X1_1(i+1)));M2(i)=(0.5*(X1_2(i)+X1_2(i+1)));M3(i)=(0.5*(X1_3(i)+X1_3(i+1)));endB1=zeros(T-1,3);for i=1:(T-1)B1(i,1)=-M1(i); %-(X1_1(i)+X1_1(i+1)))/2;B1(i,2)=X1_2(i+1);B1(i,3)=X1_3(i+1);endB2=zeros(T-1,2);for i=1:(T-1)B2(i,1)=-M2(i); %-(X1_2(i)+X1_2(i+1)))/2;B2(i,2)=X1_3(i+1);endB3=zeros(T-1,2);for i=1:(T-1)B3(i,1)=-M3(i); %-(X1_3(i)+X1_3(i+1)))/2;B3(i,2)=1;endsave B1 B1;save B2 B2;save B3 B3;%构造常数项向量Yfor i=2:TY1(i-1)=X0_1(i);Y2(i-1)=X0_2(i);Y3(i-1)=X0_3(i);endHCS1=inv(B1'*B1)*B1'*Y1'; %用最小二乘法求灰参数HCS1H1=HCS1'; %H1=[a,b2,b3]HCS2=inv(B2'*B2)*B2'*Y2'; %用最小二乘法求灰参数HCS2H2=HCS2'; %H2=[a,b3]HCS3=inv(B3'*B3)*B3'*Y3'; %用最小二乘法求灰参数HCS3H3=HCS3'; %H3=[b,a]%计算出X3的累加序列for i=1:T+NYCX13(i)=(X0_3(1)-H3(2)/H3(1))*exp(-1*H3(1)*(i-1))+H3(2)/H3(1);endfor i=2:T+N% K(i)=XR1(i)-XR1(i-1);YCX0_3(i)=YCX13(i)-YCX13(i-1);endYCX0_3(1)=X0_3(1);%对参数作alpha,beta变换H2=H2./(1+0.5*H2(1));%还原计算出X2的预测值YCX0_2(1)=X0_2(1);for i=2:TYCX0_2(i)=H2(2).*X1_3(i)-H2(1).*X1_2(i-1);endYCX12(T)=X1_2(T);for i=T+1:T+NYCX0_2(i)=H2(2).*YCX13(i)-H2(1).*YCX12(i-1);YCX12(i)=YCX0_2(i)+YCX12(i-1);end%对参数作alpha,beta变换H1=H1./(1+0.5*H1(1));%还原计算出X1的预测值YCX0_1(1)=X0_1(1);for i=2:TYCX0_1(i)=H1(2).*X1_2(i)+H1(3).*X1_3(i)-H1(1).*X1_1(i-1);endYCX11(T)=X1_1(T);for i=T+1:T+NYCX0_1(i)=H1(2).*YCX12(i)+H1(3).*YCX13(i)-H1(1).*YCX11(i-1);YCX11(i)=YCX0_1(i)+YCX11(i-1);end%数据还原GM=YCX0_1; %.*PYX1(1);save GM GM;e0(1,T-1)=zeros;for i=1:T-1 %求X1到X5的残差值e0e0(i)=(X0_1(i+1)-YCX0_1(i+1))/X0_1(i+1); %1-YCX0_1(i+1)/X0_1(i+1); endsave e0 e0;e0_average=sum(abs(e0))/length(e0)p=1-e0_average;X_average=mean(X0_1) %求原始数据x0均值s1=std(PYX1) %求原始数据的标准差s2=std(e0)c=s2/s1 %计算方差比c,c<0.35为好end。
数学建模算法:灰色预测模型GM(1,1)及Python代码
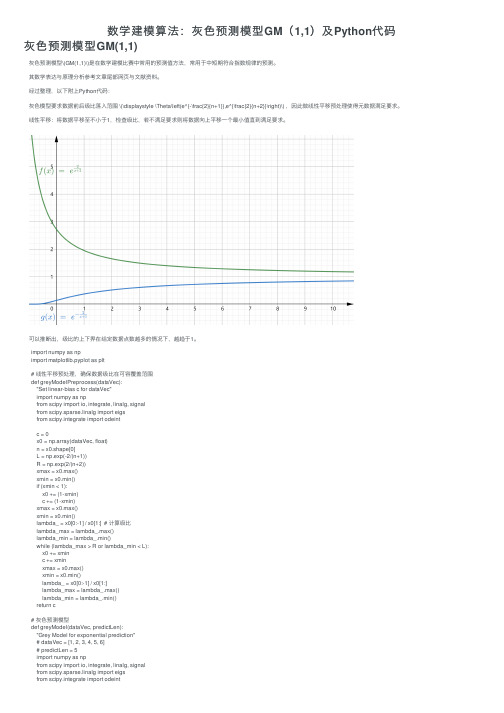
数学建模算法:灰⾊预测模型GM(1,1)及Python代码灰⾊预测模型GM(1,1)灰⾊预测模型\(GM(1,1)\)是在数学建模⽐赛中常⽤的预测值⽅法,常⽤于中短期符合指数规律的预测。
其数学表达与原理分析参考⽂章尾部⽹页与⽂献资料。
经过整理,以下附上Python代码:灰⾊模型要求数据前后级⽐落⼊范围 \(\displaystyle \Theta\left(e^{-\frac{2}{n+1}},e^{\frac{2}{n+2}}\right)\) ,因此做线性平移预处理使得元数据满⾜要求。
线性平移:将数据平移⾄不⼩于1,检查级⽐,若不满⾜要求则将数据向上平移⼀个最⼩值直到满⾜要求。
可以推断出,级⽐的上下界在给定数据点数越多的情况下,越趋于1。
import numpy as npimport matplotlib.pyplot as plt# 线性平移预处理,确保数据级⽐在可容覆盖范围def greyModelPreprocess(dataVec):"Set linear-bias c for dataVec"import numpy as npfrom scipy import io, integrate, linalg, signalfrom scipy.sparse.linalg import eigsfrom scipy.integrate import odeintc = 0x0 = np.array(dataVec, float)n = x0.shape[0]L = np.exp(-2/(n+1))R = np.exp(2/(n+2))xmax = x0.max()xmin = x0.min()if (xmin < 1):x0 += (1-xmin)c += (1-xmin)xmax = x0.max()xmin = x0.min()lambda_ = x0[0:-1] / x0[1:] # 计算级⽐lambda_max = lambda_.max()lambda_min = lambda_.min()while (lambda_max > R or lambda_min < L):x0 += xminc += xminxmax = x0.max()xmin = x0.min()lambda_ = x0[0:-1] / x0[1:]lambda_max = lambda_.max()lambda_min = lambda_.min()return c# 灰⾊预测模型def greyModel(dataVec, predictLen):"Grey Model for exponential prediction"# dataVec = [1, 2, 3, 4, 5, 6]# predictLen = 5import numpy as npfrom scipy import io, integrate, linalg, signalfrom scipy.sparse.linalg import eigsfrom scipy.integrate import odeintx0 = np.array(dataVec, float)n = x0.shape[0]x1 = np.cumsum(x0)B = np.array([-0.5 * (x1[0:-1] + x1[1:]), np.ones(n-1)]).TY = x0[1:]u = linalg.lstsq(B, Y)[0]def diffEqu(y, t, a, b):return np.array(-a * y + b)t = np.arange(n + predictLen)sol = odeint(diffEqu, x0[0], t, args=(u[0], u[1]))sol = sol.squeeze()res = np.hstack((x0[0], np.diff(sol)))return res# 输⼊数据x = np.array([-18, 0.34, 4.68, 8.49, 29.84, 50.21, 77.65, 109.36])c = greyModelPreprocess(x)x_hat = greyModel(x+c, 5)-c# 画图t1 = range(x.size)t2 = range(x_hat.size)plt.plot(t1, x, color='r', linestyle="-", marker='*', label='True')plt.plot(t2, x_hat, color='b', linestyle="--", marker='.', label="Predict")plt.legend(loc='upper right')plt.xlabel('xlabel')plt.ylabel('ylabel')plt.title('Prediction by Grey Model (GM(1,1))')plt.show()误差分析部分:可就绝对误差、相对误差、级⽐、残差做数据分析,以下⽰例为最⼩⼆乘法线性回归分析。
Matlab灰色预测模型GM(1,1)代码

Matlab灰色预测模型GM(1,1)代码function c7fun73X0=[2.874 3.278 3.307 3.39 3.679];AU=c7fun73(X0);a=AU(1);u=AU(2);m2=length(X0);for k=1:1:m2-1xx1(k+1)=(X0(1)-u/a)*exp(-a*k)+u/a;ends=0;xx0(1)=X0(1);for jj=2:1:m2;xx0(jj)=xx1(jj)-xx1(jj-1);enddisp('GM(1,1)对数列进行预测结果');xx0disp('数列1原始观测数据');X0disp('a');AU(1)disp('u');AU(2)function au=c7fun73(X0)m=length(X0);s1=0;for jj=1:1:m;X1(jj)=s1+X0(jj); s1=X1(jj); endfor ii=1:1:m-1; B(ii)=-(X1(ii)+X1(ii+1))/2; endB=[B(:),ones(m-1,1)];y=X0([2:m])';au=inv((B'*B))*B'*y;% 用MATLAB的灰色预测GM(1,1)模型%%程序中的变量定义;alpha是包含值的矩阵;ago是预测后累加值矩阵;var是预测值矩阵;error是残差矩阵;c是后验差比值function my_gm_test()clcdata=exprnd(5,1,10)%原始10个数据[ago alpha var error c]=gm1(data)plot(data)hold onplot(var','-r*')function [ago alpha var error c]=gm1(x); %定义函数gm1(x)%清屏,以使结果独立显示format long; %设置计算精度if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x';endn=length(x); %取输入数据的样本量z=0;for i=1:n %计算累加值,并将值赋予矩阵bez=z+x(i,:);be(i,:)=z;endfor i=2:n %对原始数列平行移位y(i-1,:)=x(i,:);endfor i=1:n-1 %计算数据矩阵B的第一列数据c(i,:)=-0.5*(be(i,:)+be(i+1,:));endfor j=1:n-1 %计算数据矩阵B的第二列数据e(j,:)=1;endfor i=1:n-1 %构造数据矩阵BB(i,1)=c(i,:);B(i,2)=e(i,:);endalpha=inv(B'*B)*B'*y; %计算参数矩阵for i=1:n+1 %计算数据估计值的累加数列,如改为n+1为n+m 可预测后m-1个值ago(i,:)=(x(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha(2,:)/alpha(1,:);endvar(1,:)=ago(1,:)for i=1:n %如改n为n+m-1,可预测后m-1个值var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下一预测值endfor i=1:nerror(i,:)=var(i,:)-x(i,:); %计算残差endc=std(error)/std(x); %调用统计工具箱的标准差函数计算后验差的比值cago %显示输出预测值的累加数列alpha %显示输出参数数列var %显示输出预测值error %显示输出误差c %显示后验差的比值cfunction []=greymodel(y)% 本程序主要用来计算根据灰色理论建立的模型的预测值。
数学建模灰色预测GM(1,1)

灰色预测GM (1,1)算法原理:灰色模型建立的步骤Step1:对)0(X 作1-AGO ,得序列(1)(1)(1)(1)((1),(2),,())X x x x n =Step2:对)0(X 作准光滑性检验。
由)1()()()1()0(-=k k k x xρ 当()0.5k ρ<时准光滑条件满足。
Step3:检验)1(X 是否具有准指数规律。
由)1()()()1()1()1(-=k k k x x σ 得29.1)5(,36.1)4(,54.1)3()1()1(≈≈≈σσ当k>3时,]5.1,1[)()1(∈k σ,5.0=δ,准指数规律满足,故可对)1(X 建立GM(1,1)模型。
Step4:对)1(X 作紧邻均值生成。
令)1(5.0)(5.0)()1()1()1(-+=k k k x x z得 (1)(1)(1)(1((2),(3),,())Z z z z n = 于是 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---=1)(1)3(1)2()1()1()1(n B z z z ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=)()3()2()0()0()0(n Y x x x Step5:对参数列T b a a],[ˆ=进行最小二乘估计。
得 =aˆ1)(-B B T T B Y Step6:确定模型(1)(1)d a b dt x x +=及时间响应式ab a b k e x x k a +-=--)1()0()1())1(()(ˆ Step7:求)1(X 的模拟值))5(ˆ),4(ˆ),3(ˆ),2(ˆ),1(ˆ(ˆ)1()1()1()1()1()1(x x x x x X= Step8:还原求出)0(X 的模拟值。
由(0)(1)(1)(1)(1)()()()(1)ˆˆˆˆk k k k x x x x α==--得(0)(0)(0)(0)(0)(0)ˆˆˆˆˆˆ((1),(2),(3),(4),(5))Xx x x x x = Step9:检验误差。
灰色预测系统基于GM(1-1)的matlab程序

function GM1_1(X0)%format long ;X0=input('请输入实测数据');%实测值[m,n]=size(X0);X1=cumsum(X0); %累加X2=[];for i=1:n-1X2(i,:)=X1(i)+X1(i+1);endB=-0.5.*X2 ;t=ones(n-1,1);B=[B,t] ; % 求B矩阵YN=X0(2:end) ;Pt=YN./X1(1:(length(X0)-1)) %对原始数据序列X0进行准光滑性检验, %序列X0的光滑比P(t)=X0(t)/X1(t-1)A=inv(B.'*B)*B.'*YN.' ;a=A(1)u=A(2)c=u/a ;b=X0(1)-c ;X=[num2str(b),'exp','(',num2str(-a),'k',')',num2str(c)];strcat('X(k+1)=',X)%syms k;for t=1:length(X0)k(1,t)=t-1;endkY_k_1=b*exp(-a*k)+c;for j=1:length(k)-1Y(1,j)=Y_k_1(j+1)-Y_k_1(j);endXY=[Y_k_1(1),Y] %预测值CA=abs(XY-X0) ; %残差数列Theta=CA %残差检验绝对误差序列XD_Theta= CA ./ X0 %残差检验相对误差序列AV=mean(CA); % 残差数列平均值R_k=(min(Theta)+0.5*max(Theta))./(Theta+0.5*max(Theta)) ;% P=0.5R=sum(R_k)/length(R_k) %关联度Temp0=(CA-AV).^2 ;Temp1=sum(Temp0)/length(CA);S2=sqrt(Temp1) ; %绝对误差序列的标准差%----------AV_0=mean(X0); % 原始序列平均值Temp_0=(X0-AV_0).^2 ;Temp_1=sum(Temp_0)/length(CA);S1=sqrt(Temp_1) ; %原始序列的标准差TempC=S2/S1*100; %方差比C=strcat(num2str(TempC),'%') %后验差检验 %方差比%----------SS=0.675*S1 ;Delta=abs(CA-AV) ;TempN=find(Delta<=SS);N1=length(TempN);N2=length(CA);TempP=N1/N2*100;P=strcat(num2str(TempP),'%') %后验差检验 %计算小误差概率m=input('请输入预测期数:');for g=1:(length(X0)+m)v(1,g)=g-1;endvm=b*exp(-a*v)+c;for j=1:length(v)-1l(1,j)=m(j+1)-m(j);endxyz=[m(1),l]%预测值disp(['小误差概率为:',num2str(P)]);disp(['后验方差比为:',num2str(C)]);disp(['预测值为:',num2str(xyz)]);。
灰色预测模型GM(1,1)的matlab运行代码

灰色预测模型GM(1,1)的matlab 运行代码例 由1990—2001年中国蔬菜产量,建立模型预测2002年中国蔬菜产量,并对预测结果作检验。
分析建模:给定原始时间1990—2001年资料序列X )0((k),对X )0((k)生成1-AGO(累加)序列X )1((k)及Y n 。
见下表X )1((k)=)(1i )0(i X k∑=; Y n =T X X X )]12(,),3(),2([)0()0()0( 对上述X )0((k)的GM(1,1),得到[][][][][][][][][][][]⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+-+-+-+-+-+-+-+-+-+-+-==⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----------=15236.2-1331173.5-1244348.01204848.5-1168369.5-1135943.5-1107892.5-186730.0-168581.5-148915.5-129308.0-112115.0111105.011095.01985.01875.01765.01655.01545.01435.01325.01215.01)12(1)11(1)10(1)9(1)8(1)7(1)6(1)5(1)4(1)3(1)2()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()1()()()()()()()()()()()()()()()()()()()()()()(X X X X X X X X X X X X X X X X X X X X X X z z z z z z z z z z z B 将 B 和Y n 代入辨识算式,有:10.1062105()13999.9T Tn a B B B Y b α--⎡⎤⎡⎤==•=⎢⎥⎢⎥⎣⎦⎣⎦得灰色GM(1,1)模型为(1)灰微分方程X )0((k)-0.1062105 Z )1((k)=13999.9(2)白化方程9.139991062105.0)1()1(=-X dtdX (3)白化方程的时间响应式5.1318135.151332)1()1(ˆ1062105.0)0()1(-=+⎥⎦⎤⎢⎣⎡-=+--t at e a b e a b X t X (4)还原为原始数据预测方程:)(ˆ)1(ˆ)1(ˆ)1()1()0(t X t X t X-+=+,即 t e t X1062105.0)0(15248.968)1(ˆ=+ (5)残差检验: 残差error1=e1=)()ˆ)0()0(i X i X -(,这里残差有12个。
灰色模型GM11matlab实现

单位:亿请根据1978-2012年的全国人口数据,用GM(1,1)来预测未来人口数量,能预测50年内的数据吗?100年呢?为什么?摘要:关键字:人口预测、GM(1,1)一、问题的重述二、问题的分析三、模型假设1、假设本问题所使用的数据均真实有效,具有统计分析价值2、不考虑战争、灾害、疾病对人口数目的影响;3、...4、...四、符号说明与名词解释4.1符号说明见模型假设。
4.2名词解释...五、模型的建立与求解5.1模型建立在灰色系统理论中,称抽象的逆过程为灰色模型,也称GM。
它是根据关联度、生成数灰导数,灰微分等观点和一系列数学方法建立起来的连续型的微分方程。
通常GM表示为GM(n,h)。
当n=h=1时即构成了单变量一阶灰色预测模型。
设原始时间序列为:(0)(0)(0)(0)(0)[(1),(2),(3),,()]X x x x x n=L设(1)X为(0)X的一次累加序列:即:(1)(0)(1)(1)(1)(1)(0)()(-1)(),2,, x xx k x k x k k n ⎧=⎪⎨⎪=+=⎩L得(1)(1)(1)(1)(1)[(1),(2),(3),,()] X x x x x n=L利用(1)X 计算GM(1,1)模型参数a 、u ,令ˆ[,]T aa u =, 则有1ˆ()T T N aB B B Y -= 其中(1)(1)(1)(1)(1)(1)1((1)(2))121((2)(3))121((1)())12x x x x B x n x n ⎡⎤-+⎢⎥⎢⎥⎢⎥-+⎢⎥=⎢⎥⎢⎥⎢⎥--+⎢⎥⎣⎦L L (0)(0)(0)[(2),(3),,()]T N Y x x x n =L由此获得:(1)(1)ˆ(1)((1))ak u uxk x e a a -+=-+ 于是:(0)(1)(1)ˆˆˆ(1)(1)()1xk x k x k +=+-()或(0)(0)ˆ(1)-((1))ak uxk a x e a-+=-(2)注:(1)式是根据(0)X 和(1)X 的关系的到的(2)式是利用数学求导还原得到的至于用哪个,最好看相对误差5.2模型求解:求解得:六、模型检验6.1残差检验残差大小检验,即对模型值和实际值的残差进行逐点检验。
GM11的MATLAB实现及其应用

茹(1’(t+1):I茗(o’(1)一旦Ie一∞+旦.
‘
口。
口
(7)对一次累加生成数列的预测值进行一次累减生成(1一AGO),得到原始数据的还原预测值:
;(o)(1+1)=互(1)(t+1)一互(1’(t),其中t=l,2,…,,l,并且规定;(o)=0.
针对不同的统计数据,对数据进行预测时常用很多方法,比如:定性预测法、回归预测法和时间序列预测等 方法,但是这些预测方法要求数据具有一定的规律或符合某些典型的概率分布,因此,运用这些方法进行预测 或做决策约束太多,实用性也显弱.运用灰色GM(1,1)模型[2】对数据进行灰色预测时,对样本量数据的多少和 样本有无规律都适合,而且计算量小且方便,更不会出现量化结果与定性分析结果不符的情况.因此,该方法具 有很广泛的实用价值.
和预测值之间的残差和相对误差,验证了该算法的有效性和程序的正确性,进一步预测出2007—2009年的住
宿和餐饮业收入增加值.
2.1实例应用
随着经济的不断发展,住宿餐饮业单位数量不断增加,营业额持续增长,不仅吸纳了大量的劳动力就业,也
成为繁荣经济、拉动消费需求增长的重要力量.由年鉴记录显示,我国第三产业中住宿和餐饮业收入值不断增
end
yn=ddata(2:lien)’; B(1:lien—l,1:2)=1;
for k=l:lien—l
B(k,1)=一0.5*(su础ta(k)+sumdata(k+1));
end
eoeff=inv(1t’*B)*B’*yIl%用最小二乘拟合系数
for k=aln: selre=n(nd+dlaitean(1)一eoeff(2)/eoeff(1))*exp(一酬1)*(k一1))+eoeff(2)/eoeff(1);
MATLAB实现灰色预测程序

MATLAB实现灰色预测程序function [y,p,e]=huise_1_1(X,k) %灰色模型的malab程序%Example [y,p]=gm_1_1([200 250 300 350],2)%接口描述:X的预测的初始数列,|X|>4,K是指向后进行预测的个数%命令格式:程序保存的文件名,eg:huise.m 则命令是:huise([579.8 547.5 527.0 492.3 437.0],5) if nargout>3;error('Too many output argument.');endif nargin==1,k=1;x_orig=X;elseif nargin==0|nargin>2error('Wrong number of input arguments.');endx_orig=X;predict=k; %AGO 处理,即是对初始数列进行一阶累加x=cumsum(x_orig); %计算系数(a 和u)------------------------n=length(x_orig); %生成矩阵Bfor i=1:(n-1);B(i)=-(x(i)+x(i+1))/2;endB=[B' ones(n-1,1)]; %生成矩阵Yfor i=1:(n-1);y(i)=x_orig(i+1);endY=y'; %计算系数a=au(1) u=au(2)au=(inv(B'*B))*(B'*Y); %--------------------------------------------------------%把huise模型公式转换成符号coef1=au(2)/au(1);coef2=x_orig(1)-coef1;coef3=0-au(1);costr1=num2str(coef1);costr2=num2str(abs(coef2));costr3=num2str(coef3);eq=strcat(costr1,'+',costr2,'e^',costr3,'*(t-1))'); %计算每一个值for t=1:(n+predict)mcv(t)=coef1+coef2*exp(coef3*(t-1));endx_mcv0=diff(mcv);x_mcve=[x_orig(1) x_mcv0] %输出图形中的各点x_mcv=diff(mcv(1:end-predict));x_orig_n=x_orig(2:end);x_c_error=x_orig_n-x_mcv;x_error=mean(abs(x_c_error./x_orig_n));if x_error>0.2 %相对误差的均值disp('model disqualification!');elseif x_error>0.1disp('model check out');elsedisp('model is perfect!');endplot(1:n,x_orig,'o',1:n+predict,x_mcve);p=x_mcve(end-predict+1:end); %画出预测模型和初始数列的点xlabel('年份(从第一个数据年份起)');ylabel('产水量(万吨)');title('灰度模型GM(1,1)');grid ony=eq;e=x_error;p=x_mcve(end-predict+1:end);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s=0;xx0(1)=X0(1);
for jj=2:1:m2;
xx0(jj)=xx1(jj)-xx1(jj-1);
end
disp('GM(1,1)对数列进行预测结果');xx0
disp('数列1原始观测数据');X0
disp('a');AU(1)
disp('u');AU(2)
z=z+x(i,:);
be(i,:)=z;
end
for i=2:n %对原始数列平行移位
y(i-1,:)=x(i,:);
end
for i=1:n-1 %计算数据矩阵B的第一列数据
c(i,:)=-0.5*(be(i,:)+be(i+1,:));
% 本程序主要用来计算根据灰色理论建立的模型的预测值。
% 应用的数学模型是 GM(1,1)。
% 原始数据的处理方法是一次累加法。
y=input('请输入数据 ');
n=length(y);
yy=ones(n,1);
yy(1)=y(1);
for i=2:n
yy(i)=yy(i-1)+y(i);
disp(['再下个拟合值为',num2str(ys(n+2))]);
x(0)={x(0)(1),x(0)(2),……,x(0)(N)}=
{ 724.57, 746.62, 778.27, 800.8, 827.75,871.1, 912.37, 954.28, 995.01, 1037.2}
function c7fun73
X0=[2.874 3.278 3.307 3.39 3.679];
AU=c7fun73(X0);a=AU(1);u=AU(2);m2=length(X0);
for k=1:1:m2-1
xx1(k+1)=(X0(1)-u/a)*exp(-a*k)+u/a;
for i=1:n+1 %计算数据估计值的累加数列,如改为n+1为n+m可预测后m-1个值
ago(i,:)=(x(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha(2,:)/alpha(1,:);
end
var(1,:)=ago(1,:)
end
for j=1:n-1 %计算数据矩阵B的第二列数据
e(j,:)=1;
end
for i=1:n-1 %构造数据矩阵B
B(i,1)=c(i,:);
B(i,2)=e(i,:);
end
alpha=inv(B'*B)*B'*y; %计算参数 矩阵
%清屏,以使结果独立显示
format long; %设置计算精度
if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换
x=x';
end
n=length(x); %取输入数据的样本量
z=0;
for i=1:n %计算累加值,并将值赋予矩阵be
var %显示输出预测值
error %显示输出误差
c %显示后验差的比值c
function []=greymodel(y)
a=A(1);
u=A(2);
t=u/a;
i=1:n+2;
yys(i+1)=(y(1)-t).*exp(-a.*i)+t;
yys(1)=y(1);
for j=n+2:-1:2
ys(j)=yys(j)-yys(j-1);
end
x=1:n;
xs=2:n+2;
yn=ys(2:n+2);
y=X0([2:m])';
au=inv((B'*B))*B'*y;
% 用MATLAB的灰色预测GM(1,1)模型
%
%程序中的变量定义;alpha是包含 值的矩阵;ago是预测后累加值矩阵;var是预测值矩阵;error是残差矩阵;c是后验差比值
function my_gm_test()
clc
data=exprnd(5,1,10)%原始10个数据
[ago alpha var error c]=gm1(data)
plot(data)
hold on
plot(var','-r*')
function [ago alpha var error c]=gm1(x); %定义函数gm1(x)
end
c=std(error)/std(x); %调用统计工具箱的标准差函数计算后验差的比值c
ago %显示输出预测值的累加数列 ຫໍສະໝຸດ alpha %显示输出参数 数列
function au=c7fun73(X0)
m=length(X0);
s1=0;
for jj=1:1:m;X1(jj)=s1+X0(jj); s1=X1(jj); end
for ii=1:1:m-1; B(ii)=-(X1(ii)+X1(ii+1))/2; end
B=[B(:),ones(m-1,1)];
end
B=ones(n-1,2);
for i=1:(n-1)
B(i,1)=-(yy(i)+yy(i+1))/2;
B(i,2)=1;
end
BT=B';
for j=1:n-1
YN(j)=y(j+1);
end
YN=YN';
A=inv(BT*B)*BT*YN;
plot(x,y,'^r',xs,yn,'*-b');
det=0;
for i=2:n
det=det+abs(yn(i)-y(i));
end
det=det/(n-1);
disp(['百分绝对误差为:',num2str(det),'%']);
disp(['下个拟合值为 ',num2str(ys(n+1))]);
for i=1:n %如改n为n+m-1,可预测后m-1个值
var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下一预测值
end
for i=1:n
error(i,:)=var(i,:)-x(i,:); %计算残差
