AOE关键路径知识讲解
《信息系统监理师》难点--关键路径
关键路径(CPM)AOE网(Activity On Edge network),即边表示活动的网络,与AOV网相对应的是。
它通常表示一个工程的计划或进度。
AOE网是一个有向带权图,图1中的:边:表示活动(子工程),边上的权:表示该活动的持续时间,即完成该活动所需要的时间;顶点:表示事件,每个事件是活动之间的转接点,即表示它的所有入边活动到此完成,所有出边活动从此开始。
其中有两个特殊的顶点(事件),一个称做源点,它表示整个工程的开始,亦即最早活动的起点,显然它只有出边,没有入边;另一个称做汇点,它表示整个工程的结束,亦即最后活动的终点,显然它只有入边,没有出边。
除这两个顶点外,其余顶点都既有人边,也有出边,是入边活动和出边活动的转接点。
在一个AOE网中,若包含有n个事件,通常令源点为第0个事件,汇点为第n-1个事件,其余事件的编号(即顶点序号)分别为1~n-2。
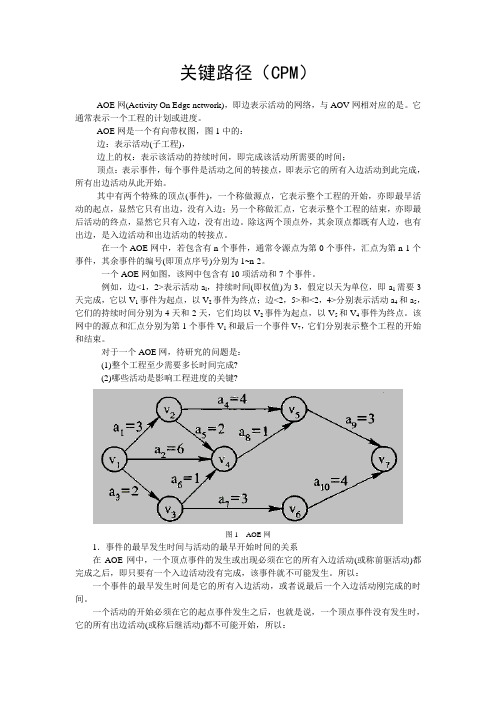
一个AOE网如图,该网中包含有10项活动和7个事件。
例如,边<1,2>表示活动a l,持续时间(即权值)为3,假定以天为单位,即a1需要3天完成,它以V1事件为起点,以V2事件为终点;边<2,5>和<2,4>分别表示活动a4和a5,它们的持续时间分别为4天和2天,它们均以V2事件为起点,以V5和V4事件为终点。
该网中的源点和汇点分别为第1个事件V1和最后一个事件V7,它们分别表示整个工程的开始和结束。
对于一个AOE网,待研究的问题是:(1)整个工程至少需要多长时间完成?(2)哪些活动是影响工程进度的关键?图1AOE网1.事件的最早发生时间与活动的最早开始时间的关系在AOE网中,一个顶点事件的发生或出现必须在它的所有入边活动(或称前驱活动)都完成之后,即只要有一个入边活动没有完成,该事件就不可能发生。
所以:一个事件的最早发生时间是它的所有入边活动,或者说最后一个入边活动刚完成的时间。
一个活动的开始必须在它的起点事件发生之后,也就是说,一个顶点事件没有发生时,它的所有出边活动(或称后继活动)都不可能开始,所以:一个活动的最早开始时间是它的起点事件的最早发生时间。
详细拼音教学aoe课件课件

汇报人: 2023-12-21
目录
• 拼音教学概述 • aoe基础知识讲解 • aoe实际应用案例分析 • aoe教学方法探讨 • aoe教学注意事项及建议
01
拼音教学概述
拼音教学的重要性
01
02
03
语言学习的基础
拼音是汉语学习的基础, 掌握拼音对于提高听说读 写能力至关重要。
拼音教学的历史与发展
古代的拼音教学
古代中国采用反切法、直音法等注音 方法,为拼音教学奠定了基础。
现代的拼音教学
拼音教学的发展趋势
随着教育改革的深入,拼音教学更加 注重实践和应用,采用多种教学方法 和手段,提高教学效果。
现代汉语拼音方案的确立,为拼音教 学提供了统一的标准。
02
aoe基础知识讲解
aoe的发音与书写规则
语言学习
对于非母语者来说,aoe的学习也是 非常有用的,能够帮助他们更好地掌 握汉语发音和拼写。
04
aoe教学方法探讨
直观教学法在aoe教学中的应用
图片、实物展示
利用图片、实物等直观教具,帮 助学生建立字母与实际事物之间
的联系,加深记忆。
动态演示
通过动态演示,展示字母的发音过 程和口型变化,帮助学生准确掌握 发音要领。
对比教学
将相似或容易混淆的字母进行对比 ,帮助学生区分和记忆。
游戏教学法在aoe教学中的应用
字母卡片游戏
利用字母卡片进行认读、拼写等 游戏,增加学习的趣味性和互动
性。
字母接龙游戏
通过字母接龙游戏,帮助学生巩 固字母顺序和发音。
字母拼图游戏
将字母视为拼图的一部分,鼓励 学生自由组合,培养创造力和想
单韵母aoe知识点总结

单韵母aoe知识点总结一、韵母aoe的发音规律韵母aoe在汉语拼音中的发音规律如下:1. a韵母的发音:a的发音是一个平舌元音,发音时舌头平放,口型呈现半圆形,声音由喉部发出。
2. o韵母的发音:o的发音是一个圆唇元音,发音时口唇要呈现圆形,声音由喉部发出。
3. e韵母的发音:e的发音是一个合口元音,发音时口型要呈现半合状态,声音由喉部发出。
二、韵母aoe在拼音中的用法韵母aoe在汉语拼音中有着多种用法:1. 作为单韵母使用:在一些汉字中,aoe会作为单韵母出现,如“烤(kǎo)”、“靠(kào)”、“老(lǎo)”等。
2. 作为复合韵母使用:aoe还可以与其他韵母合并成复合韵母使用,如“高(gāo)”、“告(gào)”、“座(zuò)”等。
三、韵母aoe在词汇运用中的示例韵母aoe在汉语词汇中有着广泛的运用,一些常用词汇示例如下:1. 高(gāo):表示高的意思,如“高山(gāo shān)”、“高楼(gāo lóu)”等。
2. 烤(kǎo):表示用热的方法烹饪食物,如“烤鸭(kǎo yā)”、“烤肉(kǎo ròu)”等。
3. 座(zuò):表示坐的意思,如“座位(zuò wèi)”、“座谈(zuò tán)”等。
四、韵母aoe的常见读音错误在汉语学习过程中,很多学习者容易在韵母aoe的发音上出现错误。
常见的错误包括:将ao读成o,将ao读成e,将o读成uo等。
因此,正确掌握韵母aoe的发音规律和用法对于避免发音错误具有重要意义。
五、韵母aoe的练习技巧为了提高对韵母aoe的发音准确度,学习者可以通过以下几种技巧进行练习:1. 反复听音频,模仿发音:可以通过听音频、视频等多媒体材料,反复模仿正确的发音来提高自己的发音准确度。
2. 多读多练,熟悉用法:可以通过朗读句子、阅读文章等方式,加深对韵母aoe的用法和运用的熟悉度,从而提高语言表达的准确性和流利度。
数据结构程序设计实验~AOE图的关键路径

数据结构课程设计报告专业网络工程班级姓名学号指导老师评分计算AOE网的关键路径AOE网即边表示活动的网络。
通常,可用AOE网来估算工程计划的完成时间。
如下所示的AOE网包括11项活动,9个事件,每个事件都有所需的完成时间。
我们现在要解决的是:(1)完成整项工程至少需要多少时间(最短时间);(2)哪些活动是影响工程进度的关键(关键活动)。
用e(i)表示活动最早开始时间,l(i)表示活动的最迟开始时间,则l(i)-e(i)为完成该活动的时间余量。
对于本例列表如下:下图就是上述AOE网的关键路径:请编程完成下列工作:1、输入:(1)顶点的信息和入度;(2)AOE网的边(始点、终点和权值)。
2、输出:(1) AOE网的邻接表(按“顶点入度:—>顶点权值”的格式输出)如a 0:-->4 5-->3 4-->2 6(2)输出关键活动每行所显示的分别为开始事件、结束事件、最早开始时间、最迟开始时间和完成活动的时间余量:当l(i)-e(i)=0时,在该行注明为关键活动。
如:a b 0 0 0 关键活动源程序#include<stdio.h>#include<stdlib.h>#include<iomanip.h>#include <process.h>//#define PROJECTNUMBER 9//10//#define PLANNUMBER 11//13typedef struct node{int adjvex;int dut;struct node *next;}edgenode;typedef struct{int projectname;int id;edgenode *link;}vexnode;//vexnode Graphicmap[PROJECTNUMBER];void CreateGraphic(vexnode* Graphicmap,int projectnumber,int activenumber){int begin,end,duttem;edgenode *p;for(int i=0;i<projectnumber;i++){Graphicmap[i].projectname=i;Graphicmap[i].id =0;Graphicmap[i].link =NULL;}printf("某项目的开始到结束在图中的节点输入<vi,vj,dut>\n");printf("如:3,4,9 回车表示第三节点到第四节点之间的活动用了9个单位时间\n"); for(int k=0;k<activenumber;k++){scanf("%d,%d,%d",&begin,&end,&duttem);p=(edgenode*)malloc(sizeof(edgenode));p->adjvex =end-1;p->dut =duttem;Graphicmap[end-1].id ++;p->next =Graphicmap[begin-1].link ;Graphicmap[begin-1].link =p;}}int SearchMapPath(vexnode* Graphicmap,int projectnumber,int activenumber,int& totaltime){int i,j,k,m=0;int front=-1,rear=-1;int* topologystack=(int*)malloc(projectnumber*sizeof(int));//用来保存拓扑排列int* vl=(int*)malloc(projectnumber*sizeof(int));//用来表示在不推迟整个工程的前提下,VJ允许最迟发生的时间int* ve=(int*)malloc(projectnumber*sizeof(int));//用来表示Vj最早发生时间int* l=(int*)malloc(activenumber*sizeof(int));//用来表示活动Ai最迟完成开始时间 int* e=(int*)malloc(activenumber*sizeof(int));//表示活动最早开始时间edgenode *p;totaltime=0;for(i=0;i<projectnumber;i++) ve[i]=0;for(i=0;i<projectnumber;i++){if(Graphicmap[i].id==0){topologystack[++rear]=i;m++;}}while(front!=rear){front++;j=topologystack[front];m++;p=Graphicmap[j].link ;while(p){k=p->adjvex ;Graphicmap[k].id --;if(ve[j]+p->dut >ve[k])ve[k]=ve[j]+p->dut ;if(Graphicmap[k].id ==0)topologystack[++rear]=k;p=p->next ;}}if(m<projectnumber){printf("\n本程序所建立的图有回路不可计算出关键路径\n");printf("将退出本程序\n");return 0;}totaltime=ve[projectnumber-1];for(i=0;i<projectnumber;i++)vl[i]=totaltime;for(i=projectnumber-2;i>=0;i--){j=topologystack[i];p=Graphicmap[j].link ;while(p){k=p->adjvex ;if((vl[k]-p->dut )<vl[j])vl[j]=vl[k]-p->dut ;p=p->next ;}}i=0;printf("| 起点 | 终点 | 最早开始时间 | 最迟完成时间 | 差值 | 备注 |\n");for(j=0;j<projectnumber;j++){p=Graphicmap[j].link;while(p){k=p->adjvex ;e[++i]=ve[j];l[i]=vl[k]-p->dut;printf("| %4d | %4d | %4d | %4d | %4d |",Graphic map[j].projectname +1,Graphicmap[k].projectname +1,e[i],l[i],l[i]-e[i]);if(l[i]==e[i])printf(" 关键活动 |");printf("\n");p=p->next ;}}return 1;}void seekkeyroot(){int projectnumber,activenumber,totaltime=0;system("cls");printf("请输入这个工程的化成图形的节点数:");scanf("%d",&projectnumber);printf("请输入这个工程的活动个数:");scanf("%d",&activenumber);vexnode* Graphicmap=(vexnode*)malloc(projectnumber*sizeof(vexnode)); CreateGraphic(Graphicmap,projectnumber,activenumber);SearchMapPath(Graphicmap,projectnumber,activenumber,totaltime);printf("整个工程所用的最短时间为:%d个单位时间\n",totaltime);system("pause");}int main(){char ch;for(;;){do{system("cls");printf("| 欢迎进入求关键路径算法程序 |");for(int i=0;i<80;i++)printf("*");printf("%s","(S)tart开始输入工程的节点数据并求出关键路径\n"); printf("%s","(E)xit退出\n");printf("%s","请输入选择:");scanf("%c",&ch);ch=toupper(ch);}while(ch!='S'&&ch!='E');switch(ch){case'S':seekkeyroot(); break; case'E':return 1; }}}。
关键路径AOE网及其如何求关键路径步骤
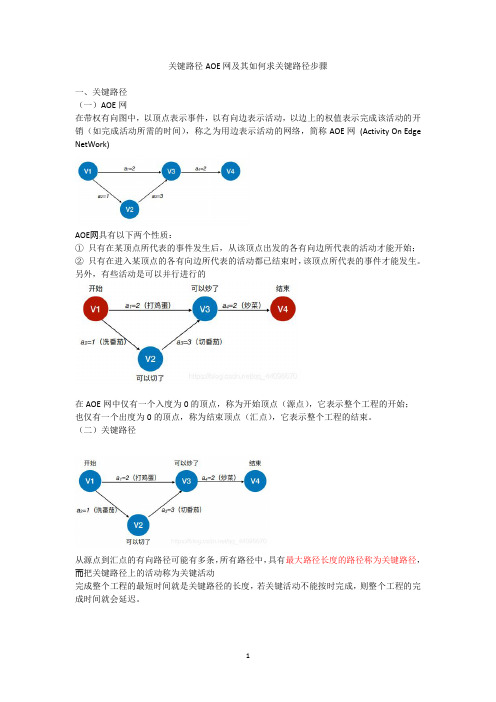
关键路径AOE网及其如何求关键路径步骤一、关键路径(一)AOE网在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称AOE网(Activity On Edge NetWork)AOE⽹具有以下两个性质:①只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始;②只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生。
另外,有些活动是可以并行进行的在AOE网中仅有一个入度为0的顶点,称为开始顶点(源点),它表示整个工程的开始;也仅有一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。
(二)关键路径从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,⽽把关键路径上的活动称为关键活动完成整个工程的最短时间就是关键路径的长度,若关键活动不能按时完成,则整个工程的完成时间就会延迟。
活动ai的时间余量d(i)=l(i)-e(i),表⽰在不增加完成整个工程所需总时间的情况下,活动ai 可以拖延的时间若一个活动的时间余量为零,则说明该活动必须要如期完成,d(i)=0即l(i)=e(i)的活动ai是关键活动由关键活动组成的路径就是关键路径(三)求关键路径的步骤(四)求所有事件的最早发生时间1.求所有事件的最早发生时间ve()(五)求所有事件的最迟发生时间1.求所有事件的最迟发生时间vl()1.求所有活动的最早发生时间e()1.求所有活动的最迟发生时间l()(八)求所有活动的时间余量(九)关键活动、关键路径的特性若关键活动耗时增加,则整个工程的工期将增长缩短关键活动的时间,可以缩短整个工程的工期当缩短到一定程度时,关键活动可能会变成非关键活动可能有多条关键路径,只提高⼀条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
关键路径AOE介绍

10 0
2018/11/5 2018/11/5
2018/10/31 2018/11/1
15 2018/11/15 1 2018/11/16
2018/11/16 2018/11/20
8 2018/11/24 4 2018/11/28
2018/10/26 A3
2018/10/31 B4
2018/11/16 C3
数据挖掘 数学建模 智能分析
项目关键路径分析
1
关键路径解决的问题 关键路径法用于在进度模型中估算项目最短工期,确定逻辑网络路径的进度灵活 性大小。这种进度网络分析技术在不考虑任何资源限制的情况下,沿进度网络路 径使用顺推与逆推法,计算出所有活动的最早开始、最早结束、最晚开始和最晚 完成日期。 项目的关键路径说明,缩短项目的非关键路径的周期无法缩短项目的周期。只有 有效的缩短关键路径周期才可以缩短项目的周期。
9
没有计划开始时间下的情况
活动名称 项目准备 需求1 需求2 需求3 开发1 开发2 开发3 开发4 测试1 测试2 测试3 版本发布1 版本发布2 现场实施
活动ID S A1 A2 A3 B1 B2 B3 B4 C1 C2 C3 D1 D2 E
2 6 4 10 16 13 12 15 10 11 8 12 14 14
2018/10/26 A3
2018/10/31 B4
2018/11/16 C3
8
项目关键路径
项目关键路径为S->A2->B3->C2->D2->E. 说明: 1、如果活动C2的计划开始时间提前1天,那么整个项目可以提前一天完成,也就是说2018/10/23开始至 2018/12/27结束,历史63天。 2、非关键路径可以在浮动范围内完成就可以。
关键路径算法

关键路径算法相关概念: (1)AOE (Activity On Edges)⽹络如果在⽆有向环的带权有向图中⽤有向边表⽰⼀个⼯程中的各项活动(Activity),⽤边上的权值表⽰活动的持续时间(Duration),⽤顶点表⽰事件(Event),则这样的有向图叫做⽤边表⽰活动的⽹络,简称AOE (Activity On Edges)⽹络。
AOE ⽹是⼀个带权的有向⽆环图。
AOE⽹络在某些⼯程估算⽅⾯⾮常有⽤。
例如,可以使⼈们了解: a、完成整个⼯程⾄少需要多少时间(假设⽹络中没有环)? b、为缩短完成⼯程所需的时间, 应当加快哪些活动? (2)关键路径(Critical Path) 在AOE⽹络中, 有些活动顺序进⾏,有些活动并⾏进⾏。
从源点到各个顶点,以⾄从源点到汇点的有向路径可能不⽌⼀条。
这些路径的长度也可能不同。
完成不同路径的活动所需的时间虽然不同,但只有各条路径上所有活动都完成了,整个⼯程才算完成。
因此,完成整个⼯程所需的时间取决于从源点到汇点的最长路径长度,即在这条路径上所有活动的持续时间之和。
这条路径长度最长的路径就叫做关键路径(Critical Path)。
(3)由于实际⼯程只有⼀个开始点和⼀个结束点,因此AOE⽹存在唯⼀的⼊度为0的开始点(⼜称源点)和唯⼀的出度为0的结束点(⼜称汇点)参数定义: (1)事件的最早发⽣时间 etv(earliest time of vertex):即顶点V k的最早发⽣时间。
(2)事件的最晚发⽣时间 ltv(latest time of vertex):即顶点V k的最晚发⽣时间,也就是每个顶点对应的事件最晚需要开始的时间,超出此事件将会延误整个⼯期。
(3)活动的最早开⼯时间 ete(earliest time of edge):即弧ak的最早发⽣时间。
(4)活动的最晚开⼯时间 lte(latest time of edge):即弧ak的最晚发⽣时间,也就是不推迟⼯期的最晚开⼯时间。
AOE网和关键路径试题实例解析

AOE网和关键路径AOE网(Activity On Edge Network)是一个带权的有向无环图。
其中用顶点表示事件,弧表示活动,权值表示两个活动持续的时间。
AOE网是以边表示活动的网。
关键路径:AOE网中从起点至终点最长的路径。
关键路径上的活动均为关键活动。
最早开始时间:在关键路径上,从开始到该任务的最早执行的时间,取最大值最晚开始时间:关键路径的总时间-反向得出该任务的时间注意:关键路径不一定只有一条松弛时间:不影响完工前提下可能被推迟完成的最大时间松弛时间=关键路径的总时间-包含该任务的关键路径花的时间松弛时间=最晚开始时间-最早开始时间计算完成项目的最少时间:计算关键路径试题:1、下图所示的AOE网表示一项包含8个活动的工程。
活动d的最早开始时间和最迟开始时间分别是()A、3和7B、12和12C、12和14D、15和15求AOE网的关键路径的步骤如下:解析:选C2、某软件项目的活动图如下图所示,其中顶点表示项目里程碑,链接顶点的边表示包含的活动,变色数字表示活动的持续时间(天)。
完成该项目的最少时间为(17)天。
由于某种原因,现在需要同一个开发人员完成BC和BD,则完成该项目的最少时间为(18)天。
(17) A.11 B.18 C.20 D.21(18) A.11 B.18 C.20 D.21【答案】B D【解析】关键路径为ABCEFJ 和ABDGFJ ,18天。
BC持续时间3天,BD持续时间2天,由一天完成,则可以把BC持续时间作为5天,BD持续时间也为5天,则关键路径为ABDGFJ,21天3、某软件项目的活动图如下图所示,其中顶点表示项目里程碑,连接顶点的边表示包含的活动,边上的数字表示活动的持续时间(天),则完成该项目的最少时间为(17)天。
活动BD 和HK 最早可以从第(18)天开始。
(活动AB、AE 和AC 最早从第1 天开始)(17) A.17 B.18 C.19 D.20(18) A.3 和10 B.4 和11 C.3 和9 D.4 和10【答案】D B【解析】因为网络图是从0开始算的,按题目要求活动AB从第1天开始的话,就是1、2、3,活动BD就是第4天开始,相应的活动HK就是第11天开始。
《aoe》教学讲解课件.

《aoe》教学讲解课件.一、教学内容本节课我们将学习《aoe》教材的第一章第三节,详细内容主要包括拼音的发音规则、声母、韵母及声调的基础知识。
通过这一部分的学习,学生将能够掌握aoe三个元音字母的正确发音,理解并运用到实际语境中。
二、教学目标1. 让学生掌握aoe三个元音字母的正确发音,并能熟练拼读。
2. 培养学生运用aoe三个元音字母进行简单词语的组合和拆分。
3. 提高学生对汉语拼音的学习兴趣,激发他们自主学习的积极性。
三、教学难点与重点教学难点:声调的正确发音和运用。
教学重点:aoe三个元音字母的正确发音及组合。
四、教具与学具准备1. 教师准备:PPT教学课件、拼音卡片、示例词语卡片。
2. 学生准备:拼音练习本、彩色笔。
五、教学过程1. 实践情景引入(5分钟)教师通过播放一段包含aoe三个元音字母的儿童歌曲,引导学生注意听辨这三个元音字母的发音。
学生跟唱歌曲,并尝试模仿发音。
2. 例题讲解(10分钟)教师展示PPT,讲解aoe三个元音字母的发音要领,并举例说明。
学生跟随教师一起练习发音,并尝试拼读示例词语。
3. 随堂练习(10分钟)教师分发拼音卡片,学生分组进行拼音接龙游戏,加强aoe 三个元音字母的拼读练习。
教师巡回指导,纠正发音错误。
4. 小组讨论与展示(15分钟)学生分组讨论如何运用aoe三个元音字母组成不同的词语。
各小组展示讨论成果,其他小组进行评价。
学生反馈学习情况,提出疑问,教师解答。
六、板书设计1. aoe三个元音字母的大写和小写,以及对应的发音。
2. 示例词语及其拼音。
3. 本节课的重点和难点。
七、作业设计1. 作业题目:请运用aoe三个元音字母,组成至少5个词语,并正确标注拼音。
答案示例:a:阿姨(ā yí)、安全(ān quán)o:哥哥(gē ge)、花朵(huā duǒ)e:饿(è)、鹅(é)2. 作业要求:字迹工整,拼音标注准确。
AOE网与关键路径简介

AOE⽹与关键路径简介前⾯我们说过的主要是为解决⼀个⼯程能否顺序进⾏的问题,但有时我们还需要解决⼯程完成需要的最短时间问题。
如果我们要对⼀个流程图获得最短时间,就必须要分析它们的拓扑关系,并且找到当中最关键的流程,这个流程的时间就是最短时间。
在前⾯讲了AOV⽹的基础上,来介绍⼀个新的概念。
在⼀个表⽰⼯程的带权有向图中,⽤顶点表⽰事件,⽤有向边表⽰活动,⽤边上的权值表⽰活动的持续时间,这种有向图的边表⽰活动的⽹,称之为AOE⽹(Activity On edge Network)。
由于⼀个⼯程,总有⼀个开始,⼀个结束,在正常情况下,AOE⽹只有⼀个源点⼀个汇点。
既然AOE⽹是表⽰⼯程流程的,所以就具有明显的⼯程属性。
只有在某顶点代表的事件发⽣后,从该顶点出发的各活动才能开始。
只有在进⼊某顶点的各活动都已经结束,该顶点代表的事件才能发⽣。
尽管AOV⽹和AOE⽹都是⽤来对⼯程建模的,但它们还是有很⼤的区别,主要体现在AOV⽹是顶点表⽰活动的⽹,它只描述活动之间的制约关系,⽽AOE⽹是⽤边表⽰活动的⽹,边上的权值表⽰活动持续的时间,如图7-9-3所⽰两图的对⽐。
因此,AOE⽹是要建⽴在活动之间制约关系没有⽭盾的基础之上,再来分析完成整个⼯程需要多少时间,或者为缩短完成⼯程所需时间,应当加快哪些活动等问题。
我们把路径上各个活动所持续的时间之后称为路径长度,从源点到汇点具有最⼤长度的路径叫关键路径,在关键路径上完成的活动叫关键活动。
显然就图7-9-3的AOE⽹⽽⾔,开始->发动机完成->部件集中到位->组装完成就是关键路径,路径长度为5.5。
如果我们需要缩短整个⼯期,去改进轮⼦的⽣产效率,哪怕改动成0.1也⽆益于整个⼯期的变化,只有缩短关键路径上的关键活动时间才才可以减少整个⼯期长度。
例如如果发动机制造缩短为2.5,整车组装缩短为1.5,那么关键路径就为4.5,整整缩短了⼀天的时间。
如果某项活动的最早开始时间和最晚开始时间⼀样,表⽰中间没有空隙,则此项活动就为关键活动。
关键路径法

关键路径算法
(1) 输入e条有向边<j,k>,建立AOE网络的存储 结构;
(2) 从源点出发,令ev[1] =0,按拓扑排序的序 列求其余各顶点的最早出现时间ev[i](2≤i≤n)。 若拓扑排序序列中的顶点个数小于网络中的顶 点数n,则说明网络中存在环路,算法中止执 行;否则执行(3);
ev[k]和Lv[k]可以采用下面的递推公式计算: (1) 向汇点递推
由源点的ev[1]=0开始,利用公式:
式向中汇p点表的示方所向有递指推向,顶可点逐的个边求的出集各合顶,点如的图ev 。 7.2意义为:从指向顶点Vk的各边的活动中 取最晚完成的一个活动的完成时间作为Vk的最 早出现时间ev[k]。
数据结构
数据结构
第七章 图
第七章 图
关键路径法
关键路径法是采用边表示活动(Activity On Edge)的网络,简称为AOE网络。
AOE网络是一个带权的有向无环路图,其中, 每个顶点代表一个事件(Event),事件说明某 些活动或某一项活动的完成,即阶段性的结 果。
离开某顶点的各条边所代表的活动,只有在 该顶点对应的事件出现后才能开始。
完成整个工程所需的时间取决于从开始点到 结束点的最长路径长度,此长度最大的路径 叫做关键路径。
分析关键路径的目的是辨别哪些是关键活动, 以便争取提高关键活动的效率,缩短整个工 期。
在描述关键路径的算法时,设活动ai由弧 <j,k>表示,要确定如下几个相关的量:
(1) 事件Vj的最早出现时间和活动的最早开始 时间:从源点V1到某顶点Vj的最长路径长度 叫作事件j的最早出现时间,表示成ev[j]。顶 点Vj的最早出现时间ev[j]决定了从Vj指出的 各条边所代表活动的最早开始时间,因为事 件j不出现,它后面的各项活动就不能开始。 我们以e[i]表示活动ai的最早开始时间。显然 e[i]= ev[j] 。
关键路径的概念和算法

关键路径的概念和算法AOE⽹:在⼀个表⽰⼯程的带权有向图中,⽤顶点表⽰事件,⽤有向边表⽰活动,边上的权值表⽰活动的持续时间,称这样的有向图叫做边表⽰活动的⽹,简称AOE⽹。
AOE⽹中没有⼊边的顶点称为始点(或源点),没有出边的顶点称为终点(或汇点)。
AOE⽹的性质:⑴只有在某顶点所代表的事件发⽣后,从该顶点出发的各活动才能开始;⑵只有在进⼊某顶点的各活动都结束,该顶点所代表的事件才能发⽣。
关键路径:在AOE⽹中,从始点到终点具有最⼤路径长度(该路径上的各个活动所持续的时间之和)的路径称为关键路径。
关键活动:关键路径上的活动称为关键活动。
关键活动:e[i]=l[i]的活动 由于AOE⽹中的某些活动能够同时进⾏,故完成整个⼯程所必须花费的时间应该为始点到终点的最⼤路径长度。
关键路径长度是整个⼯程所需的最短⼯期。
与关键活动有关的量:⑴事件的最早发⽣时间ve[k] ve[k]是指从始点开始到顶点vk的最⼤路径长度。
这个长度决定了所有从顶点vk发出的活动能够开⼯的最早时间。
⑵事件的最迟发⽣时间vl[k] vl[k]是指在不推迟整个⼯期的前提下,事件vk允许的最晚发⽣时间。
⑶活动的最早开始时间e[i] 若活动ai是由弧<vk , vj>表⽰,则活动ai的最早开始时间应等于事件vk的最早发⽣时间。
因此,有:e[i]=ve[k]⑷活动的最晚开始时间l[i] 活动ai的最晚开始时间是指,在不推迟整个⼯期的前提下,ai必须开始的最晚时间。
若ai由弧<vk,vj>表⽰,则ai的最晚开始时间要保证事件vj的最迟发⽣时间不拖后。
因此,有:l[i]=vl[j]-len<vk,vj>⽰例:所以:代码实现:123456789101112131415161718192021222324252627282930313233Status TopologicalOrder(ALGraph G, Stack &T){// 有向⽹G 采⽤邻接表存储结构,求各顶点事件的最早发⽣时间ve(全局变量)。
《数据结构与算法》AOE网及关键路径

基本概念:
AOE网:带权的有向图,其中,顶点表示事件,弧表示活 动,权表示活动持续的时间。
关键路径:AOE-网中有些活动可以并行的进行,所以完 成工程的最短时间是从开始点到完成点的最长路径的 长度(这里所说的长度是指路径上各个活动持续时间 之和,不是路径上弧的数目)。路径长度最长的路径 叫做关键路径。
a5=1 7
v9 a8=7
v8 a11=4
a3=5
4
v4 a6=2
5
a9=4 11
v6
7
从ve(0)=0开始向后推.
Ve(j)=Max{ve(i)+dut(〈i,j〉)}
(j=1,2….n-1)
1 求活动最迟发生时间 6
a1=6 v2 a4=1
16v7
a7=9
a10=2 18
v9
0 v1 a2=4
a6=12
4 a5=7 6
el a1 0 0 a2 5 5 a3 0 7 a4 0 7 a5 9 16 a6 23 23 a7 15 15 a8 15 15 a9 5 5 a10 27 27 a11 27 27 a12 35 35 a13 41 41
v5 a8=7
v3 a5=1 7
v8 a11=4
a3=5
6
v4
8 a6=2
a9=4 14
v6
10
从vl(9)=18开始向回推(倒计时)。 Ve(i)=Min{vl(j)- dut(〈i,j〉)}
(j=n-2,n-3,----,0)
例: 对下面的AOE网络,试回答下列问题: ve vl
(1)列出所有的关键路径; (2)完成整个工程至少需要多少时间?
最早发生时间:假设开始点是V1,从V1到Vi的最长的路径 的长度叫做事件Vi的最早发生时间。
详细拼音教学aoe课件课件

汉语拼音是普通话的 标准发音
课程目标与内容
掌握aoe三个单韵母的发音规则 熟悉aoe的声调与组合
学会拼读aoe与其他声母组成的音节
学习方法与建议
跟着老师反复练习发音 记忆拼音的形状和声音,建立拼音意识
多听多读,熟悉拼音的发音规则 多练习拼读,逐渐提高拼读能力
02 aoe拼音基础知识
aoe拼音的发音
呃
作为叹词,用于表达轻松、愉悦的情绪。发音时,嘴巴略微张大,声 音从喉咙发出,拖长音调。
THANKS FOR WATCHING
感谢您的观看
a
发音时,嘴巴自然张开,舌位 最低,舌尖抵住下齿龈,嘴角 向两边咧开,声带振动,发出
悠扬的声音。
o
发音时,嘴唇拢圆,舌头向后缩, 舌面后部隆起,舌位半高,声音自 肺部发出,悠扬洪亮。
e
发音时,嘴巴半开半闭,上下齿微 露,舌头平放,舌位半低,声音从 喉咙里出来,平稳洪亮。
aoe拼音的书写规则
01
02
VS
详细描述
增强拼音在实际生活中的应用能力,需在 日常生活中多使用拼音进行交流和学习。 例如,使用拼音输入法进行文字输入、使 用拼音进行阅读理解、利用拼音进行语言 沟通等。同时,教师也可通过课堂活动、 游戏等方式,让学生更好地掌握拼音知识 ,提高实际应用能力。
06 课程总结与展望
学习成果回顾与总结
学习更多字母
随着拼音知识的加深,学生可以逐步学习更多字 母的发音和书写,扩大拼音知识的储备。
3
培养自主学习的能力
通过不断练习和实践,学生可以培养自主学习的 能力,为未来的学习和生活打下坚实的基础。
07 附录:aoe拼音表
a
啊
啊,是一个感叹词,常用于表达 惊讶、惊奇、欢喜等情绪。在拼 音中,它的发音类似于“啊”音
AOV网和关键路径

数据结构重读– AOV网和关键路径与AOV网对应的,还有一个AOE网,当然它也是有DAG(向无环图)。
AOE(Activity On Edge)网:顾名思义,用边表示活动的网。
与AOV不同,活动都表示在了边上,如下图所示:如上所示,共有11项活动(11条边),9个事件(9个顶点)。
整个工程只有一个开始点和一个完成点。
即只有一个入度为零的点(源点)和只有一个出度为零的点(汇点)。
(1) 关键路径:是从开始点到完成点的最长路径的长度。
路径的长度是边上活动耗费的时间。
(2) 最早发生时间:v1到vi的最长路径叫做vi的最早发生时间,用ei表示。
例如上图中,v5的最早发生时间是max(6+1, 4+1) = 7。
(3) 最迟开始时间:在不推迟整个工程完成的前提下,活动i最迟必须开始进行的时间,用l(i)表示。
l(i) – e(i)是活动的时间余量。
(4) 关键活动:l(i)=e(i)的活动称为关键活动。
关键路径上的活动都是关键活动。
提前完成非关键活动并不能加快工程进度(类似木桶效应)。
AOE网的主要活动就是识别出哪些是关键活动,以便争取提高关键活动的工效,缩短整个工期。
当然,如果AOE网发生了改变,那么原先的关键路径也会发生变化。
因此,只有在不改变挂件路径的情况下,提供关键活动的速度,才能对整体工程进度起到帮助作用。
求关键路径的算法求关键路径,就是要求e(i) = l(i)的事件(点)。
我们首先必须分别求出所有点的e(i)和l(i)。
由于ve和vl的递推公式必须在拓扑排序下有效,因此,先要求拓扑排序0、求拓扑排序(同时顺道求ve)要增设一个栈T记录拓扑有序序列,计算求得各个顶点的ve之后,从栈顶依次弹出栈,就可以倒序遍历,求vl了。
还要使用拓扑排序的那个入度为0的栈,可以每次Pop时候顺道记录下,最后cnt如果<g->nvexs,则表示有环。
1、求最早发生时间ve[]ve(0)=0开始递推ve(j) = max{ve{i}+dut(i, j)}2、求最晚发生时间vl[]从vl(n-1)=ve(n-1)开始倒推。
2024年《aoe》完美教学讲解课件.

2024年《aoe》完美教学讲解课件.一、教学内容本节课我们将学习《aoe》教材的第二章《基础发音与字母》,详细内容包括:1. a、o、e三个元音字母的发音及书写;2. a、o、e与辅音字母组合的发音规律;3. 相关单词和简单句子的练习。
二、教学目标1. 让学生掌握a、o、e三个元音字母的发音和书写;2. 让学生理解并运用a、o、e与辅音字母组合的发音规律;3. 培养学生运用所学知识进行简单单词和句子交流的能力。
三、教学难点与重点教学难点:a、o、e与辅音字母组合的发音规律。
教学重点:a、o、e三个元音字母的发音和书写。
四、教具与学具准备1. 教具:PPT课件、教学录音机、卡片;2. 学具:练习本、铅笔、橡皮。
五、教学过程1. 实践情景引入(5分钟)利用PPT展示一个有趣的场景,如动物园,让学生观察并找出含有a、o、e发音的动物名字。
2. 新课导入(10分钟)讲解a、o、e三个元音字母的发音和书写,让学生跟随录音练习发音。
3. 例题讲解(10分钟)选取几个含有a、o、e与辅音字母组合的单词,讲解发音规律,并进行示范发音。
4. 随堂练习(10分钟)学生自主练习发音,教师进行个别指导。
5. 小组活动(10分钟)将学生分成小组,进行单词接龙游戏,要求每个单词都要含有a、o、e元音字母。
六、板书设计1. a、o、e三个元音字母的发音和书写;2. a、o、e与辅音字母组合的发音规律;3. 相关单词和简单句子。
七、作业设计1. 作业题目:(1)抄写a、o、e三个元音字母;(2)默写本节课所学的含有a、o、e的单词;(3)运用所学知识,用a、o、e拼出一个自己喜欢的动物名字。
2. 答案:(1)略;(2)略;(3)例如:我喜欢的小动物是猫,用a、o、e拼出为“mao”。
八、课后反思及拓展延伸1. 课后反思:本节课学生对a、o、e三个元音字母的掌握情况较好,但对发音规律的理解还有待提高,下节课需要加强练习。
2. 拓展延伸:让学生课后收集更多含有a、o、e的单词,并在下节课与同学分享。
《aoe》(完美)教学讲解课件pptx

2024/1/24
1
目录
2024/1/24
• 课程介绍与教学目标 • 拼音基础知识讲解 • 《aoe》课文逐句解读 • 互动环节:学生朗读与角色扮演 • 知识巩固与拓展延伸 • 课程总结与反思
2
课程介绍与教学目标
01
2024/1/24
3
《aoe》课程背景及意义
18
05 知识巩固与拓展延伸
2024/1/24
19
练习题类型及解题技巧指导
听力题
通过播放录音,让学生辨别《aoe》中的元音和辅音,提高学生的听音能力。
口语题
要求学生模仿老师的发音,练习《aoe》中的元音和辅音发音,培养学生的口语 表达能力。
2024/1/24
20
练习题类型及解题技巧指导
• 阅读题:提供包含《aoe》元音和辅音的单词、短 语或句子,让学生阅读并理解其意思,提高学生的 阅读能力。
06 课程总结与反思
2024/1/24
27
本次课程主要内容回顾
2024/1/24
拼音基础知识
01
讲解了拼音的基本概念、声母、韵母和声调等基础知识。
单韵母a、o、e的发音和书写
02
通过示范和练习,帮助学生掌握单韵母a、o、e的正确发音和书
写方法。
拼音拼读初步
03
引导学生通过拼音拼读的方式,初步接触和了解汉字的读音。
28
学生学习成果展示
2024/1/24
发音准确
学生能够准确地发出单韵母a、o、e的音,并能够区分不同的声 调。
书写规范
学生能够按照正确的笔画顺序和书写规范,书写单韵母a、o、e 。
拼读能力
汉语拼音《aoe》精ppt课件(2024)

轻声规则
在某些情况下,音节中的某个音会发轻声,不标注声调。如“guā”中的“u” 可以发轻声,读作“gu·ā”。
2024/1/28
17
拼音词组拼读示例
2024/1/28
双音节词组
如“dà mǐ”,其中“dà”和“mǐ”都是音节,分别拼读后 再连读成词组。
多音节词组
如“hóng sè de píng guǒ”,其中“hóng”、“sè”、 “de”、“píng”、“guǒ”都是音节,分别拼读后再连读 成词组。注意轻声和儿化音的读法。
汉语拼音《aoe》精ppt 课件
2024/1/28
1
目 录
2024/1/28
• 课程介绍与目标 • 基础知识讲解 • 《aoe》拼音学习 • 拼音组合与拼读练习 • 课堂互动与游戏环节 • 课程总结与回顾
2
ห้องสมุดไป่ตู้1
课程介绍与目标
2024/1/28
3
汉语拼音《aoe》背景
2024/1/28
汉语拼音的起源与发展
整体认读音节
zhi, chi, shi, ri, zi, ci, si, yi, wu, yu, ye, yue, yuan, yin, yun, ying。
9
发音规则与技巧
2024/1/28
声调的发音规则
阴平(第一声)、阳平(第二声)、上声(第三声)、去声(第 四声)。
音节的拼读方法
两拼法、三拼法。
发音
发音时,嘴半开,舌位靠后,舌 头后缩,舌根稍微抬高,声带颤
动。
书写规则
e占中格,中格正中写横线,接 笔再写多半圆。
拼音标注
在四线三格中,e要写在中间一 格,声调标在e上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 由上分析可知,辨别关键活动就是要找e(i)=l(i)的活动。为 了求得AOE-网中活动的e(i)和l(i), 首先求事件的最早发 生时间ve(j)和最迟发生时间vl(j)。如果活动ai由弧<j,k>表 示,其持续时间记为dut(<j,k>),则有如下关系:
•
e(i ) = ve(j)
(7-1)
• typedef float AdjType;
• typedef struct ArcNode
• { int adjvex;
/* 相邻顶点字段 */
• AdjType weight;
• struct ArcNode *nextarc;
/* 链字段 */
• }ArcNode;
/* 边表中的结点 */
点的入度 */ • for(i=0;i<G.vexnum;i++) • if(indegree[i]==0) / / 将入度为零的顶点入栈 • { indegree[i]=top; • top=i; •}
• while(top!=-1)
/* 栈不为空 */
• { j=top;
• top=indegree[top];
• while(p!=NULL)
• { j=p->adjvex;
• if(vl[j]-p->weight<vl[i]) vl[i]=vl[j]-p->weight;
• p=p->nextarc;
•}
•}
•}
• void counte_l(ALGraph G,AdjType *ve,AdjType *vl,AdjType *ee,AdjType *el)
• typedef struct VNode
• { VertexType data;
/* 顶点信息 */
• ArcNode *firstarc;
/* 边表头指针 */
• }VNode,AdjList[MAXVEX]; /* 顶点表中的结点 */
• typedef struct
• { AdjList vertices;
• for(k=0;k<G.vexnum;k++) /* 求事件vj可能的最早发 生时间ee(j) */
• { i=topo[k];
//k仅起控制作用
•
p=G.vertices[i].firstarc;
• while(p!=NULL)
• { j=p->adjvex;
• if(ve[i]+p->weight>ve[j]) ve[j]=ve[i]+p->weight;
•
vl(i) = Min{ vl (j) – dut(<i,j>) }
•
j
•
<i,j> ∈S , i=n-2,…,0 (7-3)
• 其中,S是所有以第i个顶点为头的弧的集 合。
• 这两个递推公式的计算必须分别在拓扑 有序和逆拓扑有序的前提下进行。也就是 说ve(j-1)必须在vj的所有前驱的最早发生时 间求得之后才能确定,而vl(j-1)则必须在vj 的所有后继的最迟发生时间求得之后才能 确定。因此,可以在拓扑排序的基础上计 算ve(j-1)和vl(j-1)。
最后一个顶点止顺序编号。
• p=p->nextarc; • }}}
• int CriticalPath(ALGraph G) /*关键路径算法*/
• { AdjType
ve[MAXVEX],vl[MAXVEX],ee[MAXEDGE],el[MAXEDGE];
• int topo[MAXVEX];
• vl[i]=ve[G.vexnum-1]; /*每个事件的最迟发生时间赋初值 为最生事件的最早发生时间(本例均为18)*/
• for(k=G.vexnum-2;k>=0;k--) /*下标从0开始,最后一个顶点 无后继,所以减2*/
• { i=topo[k];
•
p=G.vertices[i].firstarc;
• { int k;
• while(p)
/* 删除以该顶点为起点的边 */
• { k=p->adjபைடு நூலகம்ex;
• indegree[k]--;
• if(indegree[k]==0) /* 将新的入度为零的边 入栈 */
• { indegree[k]=top;
• top=k;
•}
• p=p->nextarc;
printf("V%1d ",topo[i]+1);
printf("\n");
• return TRUE;
•}
• void insert(ALGraph &G,int a,int b,float weight) • /*在表尾插入表结点*/ • { ArcNode *p,*temp; • temp=(ArcNode *)malloc(sizeof(ArcNode)); • temp->adjvex=b; • temp->nextarc=NULL; • temp->weight=weight; • p=G.vertices[a].firstarc; • if(p==NULL) • G.vertices[a].firstarc=temp; • else • { while(p->nextarc!=NULL) p=p->nextarc; /*找表尾*/ • p->nextarc=temp; •} •}
• 由此得到求关键路径的算法:
• (1)输入e条弧<j,k>,建立AOE-网的存储结构;
• (2)从源点v0出发,令ve[0]=0,按拓扑有序求 其余各顶点的最早发生时间ve[i] (1≤i≤n-1)。如果 得到的拓扑有序序列中顶点个数小于网中顶点数n, 则说明网中存在环,不能求关键路径,算法终止; 否则执行步骤(3)。
• /*计算各活动的最早发生时间和最迟发生时间,并输出关 键路径*/
• { int i=0,j,k; ArcNode *p; • printf("关键路径是: "); • for(j=0;j<G.vexnum;j++) /*求活动ai的最早开始时间ee(i)
及最晚开始时间el(i) */ • { p=G.vertices[j].firstarc; • while(p!=NULL) • { k=p->adjvex; • ee[i]=ve[j]; • el[i]=vl[k]-p->weight; • if(ee[i]==el[i]) printf("<v%1d, v%1d>, ",j+1,k+1); • i++; //i表示弧的序号。弧的序号自第一个顶点开始到
• void makeList(ALGraph &G) /*邻接表的构造*/ • { int i; • G.vexnum=9; • for(i=0;i<G.vexnum;i++) //给顶点指针域赋初值 • G.vertices[i].firstarc=NULL; • insert(G,0,1,6); insert(G,0,2,4); insert(G,0,3,5); • insert(G,1,4,1); insert(G,2,4,1); insert(G,3,5,2); • insert(G,4,6,9); insert(G,4,7,7); insert(G,5,7,4); • insert(G,6,8,2); insert(G,7,8,4); •}
• /*图的关键路径问题的算法AOE.C*/
• #include <stdio.h>
• #include <stdlib.h>
• #define MAXVEX 100
• #define TRUE 1
• #define FALSE 0
• typedef char VertexType[MAXVEX]; /*存放顶点信息的字符串*/
/* 取出当前栈顶元素 */
• topo[count++]=j;
/*ptopo数组存放拓扑序列*/
• p=G.vertices[j].firstarc;
• //取该元素边表中的第一个边结点,删除该结点,构造新的AOV网
• makeNewAOV(p,indegree,top); //对indegree数组进行修改
7.5.2 关键路径
• 与AOV-网相对应的是AOE-网(Activity On Edge) 即边表示活动的网。AOE-网是一个带权的有向无 环图,其中,顶点表示事件(Event),弧表示活动, 权表示活动持续的时间。通常,AOE-网可用来估 算工程的完成时间。
• 例如,图7.29是一个假想的有11项活动的AOE-网。 其中有9个事件v1,v2,v3,…,v9,每个事件 表示在它之前的活动已经完成,在它之后的活动 可以开始。如v1表示整个工程开始,v9表示整个 工程结束,v5表示a4和a5已经完成,a7和a8可以 开始。与每个活动相联系的数是执行该活动所需 的时间。比如,活动a1需要6天, a2需要4天等。
•}
•}
• int topoSort(ALGraph G,int *topo) /*拓扑排序算 法*/
• { ArcNode *p; • int i,j,count=0,top=-1; • int indegree[MAXVEX]; • FindInDegree(G,indegree); /* 求出图中所有顶
数组赋初值*/ • for(i=0;i<G.vexnum;i++) • { p=G.vertices[i].firstarc; • while(p) • { inDegree[p->adjvex]++; • p=p->nextarc; •} •} •}
