第8章习题答案
初二物理第八章练习题含答案

初二物理第八章练习题含答案1. 选择题(1) 以下属于力的性质是:A. 大小B. 方向C. 作用点D. 面积答案:A、B、C(2) 能够使物体发生位移的只有:A. 摩擦力B. 重力C. 弹力和悬挂力D. 正确答案全部都对答案:C(3) 法拉第一定律指出的是:A. 外力作用于物体上时,物体一定保持静止或匀速直线运动B. 外力作用于物体上时,物体的速度将发生变化C. 物体受到的合力为零时,物体一定保持静止或匀速直线运动D. 物体受到的合力为零时,物体的速度将发生变化答案:C2. 填空题(1) 一个力从右往左作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从左往右(2) 一个力从上往下作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从下往上(3) 一个物体受到A力的作用产生加速度a,如果力A的大小不变,改变作用方向,则产生的加速度为______。
答案:-a3. 解答题(1) 什么是力?力的三要素是什么?解答:力是物体之间相互作用的结果,是导致物体发生变化的原因。
力的三要素包括大小、方向和作用点。
大小表示力的强弱程度,方向表示力作用的直线方向,作用点表示力作用的具体位置。
(2) 什么是合力?如何求合力?解答:合力是同时作用在物体上的多个力的共同效果。
求合力的方法是将所有作用在物体上的力按照大小和方向合成,可以通过向量法或图示法来求解。
(3) 描述牛顿第一定律,并用实例说明其应用。
解答:牛顿第一定律也称为惯性定律,指出在没有外力作用时,物体将保持静止或匀速直线运动的状态。
例如,当我们用力推动一张光滑的桌子上的书时,如果力的大小和方向适当,书就会保持匀速直线运动,直到受到其他力的作用。
这说明物体在没有外力干扰时具有惯性,保持原来的状态不发生变化。
总结:初二物理第八章练习题主要涉及力的性质和作用、法拉第一定律等内容。
通过选择题和填空题加深对知识点的理解,同时通过解答题展开思考和拓展。
课后习题答案第8章_存储器和可编程逻辑器件

第8章半导体存储器和可编程逻辑器件8-1存储器按读写功能以及信息的可保存性分别分为哪几类?并简述各自的特点。
解答:存储器按读写功能可分为只读存储器(ROM)和随机存储器(RAM)。
随机存取存储器在工作过程中,既可从其任意单元读出信息,又可以把外部信息写入任意单元。
因此,它具有读、写方便的优点,但由于具有易失性,所以不利于数据的长期保存。
只读存储器在正常工作时其存储的数据固定不变,只能读出,不能随时写入。
ROM为非易失性器件,当器件断电时,所存储的数据不会丢失。
存储器按信息的可保存性可分为易失性存储器和非易失性存储器。
易失性存储器在系统关闭时会失去存储的信息,它需要持续的电源供应以维持数据。
非易失存储器在系统关闭或无电源供应时仍能保持数据信息。
8-2什么是SRAM?什么是DRAM?它们在工作原理、电路结构和读/写操作上有何特点?解答:SRAM(Static Random Access Memory)为静态随机存储器,其存储单元是在静态触发器的基础上附加控制电路构成的。
DRAM(Dynamic Random Access Memory)为动态随机存储器,常利用MOS管栅极电容的电荷存储效应来组成动态存储器,为了避免存储信息的丢失,必须定时地对电路进行动态刷新。
SRAM的数据由触发器记忆,只要不断电,数据就能保存,但其存储单元所用的管子数目多,因此功耗大,集成度受到限制。
DRAM一般采用MOS管的栅极电容来存储信息,由于电荷保存时间有限,为避免存储数据的丢失,必须由刷新电路定期刷新,但其存储单元所用的管子数目少,因此功耗小,集成度高。
SRAM速度非常快,但其价格较贵;DRAM的速度比SRAM慢,不过它比ROM 快。
8-3若RAM的存储矩阵为256字⨯4位,试问其地址线和数据线各为多少条?解答:存储矩阵为256字⨯4位的RAM地址线为8根,数据线为4根。
8-4某仪器的存储器有16位地址线,8位数据线,试计算其最大存储容量是多少?解答:最大存储容量为216⨯8=524288=512k bit(位)8-5用多少片256⨯4位的RAM可以组成一片2K⨯8位的RAM?试画出其逻辑图。
第8章 习题提示和答案

为 516.6m3 / min ,绝热压缩到 p2 = 1MPa 。由于磨擦作用,使出口气温度达到 350℃。求
以各级消耗的功不相等。
8-17 某高校实验室需要压力为 6.0MPa 的压缩空气。有两人分别提出下述两个方案:
A 方案采用绝热效率为 0.9 的轴流式压气机;B 方案采用活塞式气机,二级压缩。中间冷却,
两缸压缩多变指数均为 1.25。试述上述两个方案的优劣。(设 p0 = 0.1MPa、t0 = 27°C )
为 0.5MPa ,但压缩过程的指数分别为:n1 =1.4、n2 =1.25、n3 =1,试求各压气机的容积效
率(假设膨胀过程的指数和压缩过程相同)。
1
提示和答案: ηV = 1− σ (π n −1) ,ηV,1 = 0.871 、ηV,2 = 0.843 、ηV,3 = 0.76 。 8-5 某单级活塞式压气机,其增压比为 7,活塞排量为 0.009m3 ,余容比为 0.06,转 速为 750r/min,压缩过程多变指数为 1.3。求(1)容积效率;(2)生产量( kg/h );(3)理 论消耗功率(kW);(4)压缩过程中放出的热量。已知吸入空气参数为 p1 = 0.1MPa 、
应略大于
185
kW,(190.76 −185)kW 185 kW
=
3.1% ,
其误差尚在可允许范围内,所以实测基本合理。 8-14 以 R134a 为工质的制冷循环装置中,蒸发器温度为-15℃,进入压缩机工质的干
《半导体物理》习题答案第八章

第8章 半导体表面与MIS 结构2.对于电阻率为8cm Ω⋅的n 型硅,求当表面势0.24s V V =-时耗尽层的宽度。
解:当8cm ρ=Ω⋅时:由图4-15查得1435.810D N cm -=⨯∵22D d s rs qN x V εε=-,∴1022()rs s d D V x qN εε=-代入数据:11141352219145211.68.85100.24 4.9210()()7.3101.610 5.8109.2710d x cm -----⨯⨯⨯⨯⨯==⨯⨯⨯⨯⨯3.对由电阻率为5cm Ω⋅的n 型硅和厚度为100nm 的二氧化硅膜组成的MOS 电容,计算其室温(27℃)下的平带电容0/FB C C 。
解:当5cm ρ=Ω⋅时,由图4-15查得143910D N cm -=⨯;室温下0.026eV kT =,0 3.84r ε=(SiO 2的相对介电系数) 代入数据,得:1141/20002197722110.693.84(11.68.85100.026)11()11.6 1.61010010310FBr rs rs A C C kT q N d εεεε---===⨯⨯⨯+⋅+⨯⨯⨯⨯⨯此结果与图8-11中浓度为1⨯1015/cm 3的曲线在d 0=100nm 的值非常接近。
4. 导出理想MIS 结构的开启电压随温度变化的表示式。
解:按定义,开启电压U T 定义为半导体表面临界强反型时加在MOS 结构上的电压,而MOS结构上的电压由绝缘层上的压降U o 和半导体表面空间电荷区中的压降U S (表面势)两部分构成,即oST S Q U U C =-+ 式中,Q S 表示在半导体表面的单位面积空间电荷区中强反型时的电荷总数,C o 单位面积绝缘层的电容,U S 为表面在强反型时的压降。
U S 和Q S 都是温度的函数。
以p 型半导体为例,强反型时空间电荷区中的电荷虽由电离受主和反型电子两部分组成,且电子密度与受主杂质浓度N A 相当,但反型层极薄,反型电子总数远低于电离受主总数,因而在Q S 中只考虑电离受主。
《大学物理》第8章气体动理论练习题及答案

《大学物理》第8章气体动理论练习题及答案练习1一、选择题1. 在一密闭容器中,储有A、B、C三种理想气体,处于平衡状态。
A种气体的分子数密度为n1,它产生的压强为p1,B种气体的分子数密度为2n1,C种气体的分子数密度为3n1,则混合气体的压强p为( )A. 3p1;B. 4p1;C. 5p1;D. 6p1.2. 若理想气体的体积为V,压强为p,温度为T,一个分子的质量为m,k为玻尔兹曼常量,R为普适气体常量,则该理想气体的分子数为( )A. pVm⁄; B. pVkT⁄; C. pV RT⁄; D. pV mT⁄。
3. 一定量某理想气体按pV2=恒量的规律膨胀,则膨胀后理想气体的温度( )A. 将升高;B. 将降低;C. 不变;D. 升高还是降低,不能确定。
二、填空题1. 解释下列分子动理论与热力学名词:(1) 状态参量:;(2) 微观量:;(3) 宏观量:。
2. 在推导理想气体压强公式中,体现统计意义的两条假设是:(1) ;(2) 。
练习2一、选择题1. 一个容器内贮有1摩尔氢气和1摩尔氦气,若两种气体各自对器壁产生的压强分别为p 1和p 2,则两者的大小关系是 ( )A. p 1>p 2;B. p 1<p 2;C. p 1=p 2;D. 不能确定。
2. 两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数为n ,单位体积内的气体分子的总平动动能为E k V ⁄,单位体积内的气体质量为ρ,分别有如下关系 ( )A. n 不同,E k V ⁄不同,ρ不同;B. n 不同,E k V ⁄不同,ρ相同;C. n 相同,E k V ⁄相同,ρ不同;D. n 相同,E k V ⁄相同,ρ相同。
3. 有容积不同的A 、B 两个容器,A 中装有刚体单原子分子理想气体,B 中装有刚体双原子分子理想气体,若两种气体的压强相同,那么,这两种气体的单位体积的内能E A 和E B 的关系( )A. E A <E B ;B. E A >E B ;C. E A =E B ;D.不能确定。
形势与政策习题答案第8章

第八章港澳台问题一、单项选择题(每小题5分,共计25分)1.1840年,中英签订(),中国被迫割让香港岛给英国。
A.《南京条约》B.《北京条约》C.《马关条约》D.《辛丑条约》答案:A解析:1840年,英国发动鸦片战争,清政府惨败。
1842年8月29日,清政府与英国签订了中国近代历史上第一个丧权辱国的不平等条约——中英《南京条约》。
条约规定,中国将香港岛割让给英国。
随后,中英又相继签订了《五口通商章程》和《虎门条约》《北京条约》《展拓香港界址专条》等不平等条约,先后占领了九龙半岛和新界。
英国通过刺刀、洋枪与大炮的野蛮征服,实现了对中国香港地区领土的占领。
知识点:香港问题的产生难度级别:12.20世纪80年代初,为实现国家和平统一,国家领导人邓小平创造性地提出了“()”的科学构想,并首先用于解决香港问题。
A.武力统一B.一国两制C.社会主义本质D.改革开放答案:B解析:20世纪80年代初,为实现国家和平统一,国家领导人邓小平创造性地提出了“一国两制”的科学构想,并首先用于解决香港问题。
按照邓小平的论述,“一国两制”是指在一个中国的前提下,国家的主体坚持社会主义制度,香港、澳门、台湾保持原有的资本主义制度长期不变。
知识点:一国两制的提出难度级别:23.(),中国政府对香港恢复行使主权,香港特别行政区成立。
A.1998年7月1日B.1999年12月20日C.1997年7月1日D.1997年10月1日答案:C解析:1997年7月1日,中国政府对香港恢复行使主权,香港特别行政区成立,香港基本法开始实施。
香港进入了“一国两制”、“港人治港”、高度自治的历史新纪元。
作为祖国大家庭的一分子,香港同胞与内地民众共享伟大祖国的尊严与荣耀,共担中华民族伟大复兴的责任和使命。
知识点:香港回归难度级别:14.1997年,刚刚回归的香港GDP约为1774亿元,人均GDP约为2.73万美元。
2019年,香港GDP达到了()万亿元,人均GDP 约为4.88万美元。
大学物理第八章课后习题答案

大学物理第八章课后习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第八章电磁感应电磁场8 -1一根无限长平行直导线载有电流I,一矩形线圈位于导线平面内沿垂直于载流导线方向以恒定速率运动(如图所示),则()(A)线圈中无感应电流(B)线圈中感应电流为顺时针方向(C)线圈中感应电流为逆时针方向(D)线圈中感应电流方向无法确定分析与解由右手定则可以判断,在矩形线圈附近磁场垂直纸面朝里,磁场是非均匀场,距离长直载流导线越远,磁场越弱.因而当矩形线圈朝下运动时,在线圈中产生感应电流,感应电流方向由法拉第电磁感应定律可以判定.因而正确答案为(B).8 -2将形状完全相同的铜环和木环静止放置在交变磁场中,并假设通过两环面的磁通量随时间的变化率相等,不计自感时则()(A)铜环中有感应电流,木环中无感应电流(B)铜环中有感应电流,木环中有感应电流(C)铜环中感应电动势大,木环中感应电动势小(D)铜环中感应电动势小,木环中感应电动势大23分析与解 根据法拉第电磁感应定律,铜环、木环中的感应电场大小相等,但在木环中不会形成电流.因而正确答案为(A ).8 -3 有两个线圈,线圈1 对线圈2 的互感系数为M 21 ,而线圈2 对线圈1的互感系数为M 12 .若它们分别流过i 1 和i 2 的变化电流且ti t i d d d d 21<,并设由i 2变化在线圈1 中产生的互感电动势为ε12 ,由i 1 变化在线圈2 中产生的互感电动势为ε21 ,下述论断正确的是( ).(A )2112M M = ,1221εε=(B )2112M M ≠ ,1221εε≠(C )2112M M =, 1221εε<(D )2112M M = ,1221εε<分析与解 教材中已经证明M21 =M12 ,电磁感应定律t i M εd d 12121=;ti M εd d 21212=.因而正确答案为(D ). 8 -4 对位移电流,下述四种说法中哪一种说法是正确的是( )(A ) 位移电流的实质是变化的电场(B ) 位移电流和传导电流一样是定向运动的电荷(C ) 位移电流服从传导电流遵循的所有定律(D ) 位移电流的磁效应不服从安培环路定理分析与解 位移电流的实质是变化的电场.变化的电场激发磁场,在这一点位移电流等效于传导电流,但是位移电流不是走向运动的电荷,也就不服从焦耳热效应、安培力等定律.因而正确答案为(A ).48 -5 下列概念正确的是( )(A ) 感应电场是保守场(B ) 感应电场的电场线是一组闭合曲线(C ) LI Φm =,因而线圈的自感系数与回路的电流成反比(D ) LI Φm =,回路的磁通量越大,回路的自感系数也一定大 分析与解 对照感应电场的性质,感应电场的电场线是一组闭合曲线.因而正确答案为(B ).8 -6 一铁心上绕有线圈100匝,已知铁心中磁通量与时间的关系为()Wb π100sin 100.85t Φ⨯=,求在s 100.12-⨯=t 时,线圈中的感应电动势.分析 由于线圈有N 匝相同回路,线圈中的感应电动势等于各匝回路的感应电动势的代数和,在此情况下,法拉第电磁感应定律通常写成tψt ΦN ξd d d d -=-=,其中ΦN ψ=称为磁链. 解 线圈中总的感应电动势()()t tΦNξπ100cos 51.2d d =-= 当s 100.12-⨯=t 时,V 51.2=ξ. 8 -7 有两根相距为d 的无限长平行直导线,它们通以大小相等流向相反的电流,且电流均以tI d d 的变化率增长.若有一边长为d 的正方形线圈与两导线处于同一平面内,如图所示.求线圈中的感应电动势.5分析 本题仍可用法拉第电磁感应定律tΦξd d -=来求解.由于回路处在非均匀磁场中,磁通量就需用⎰⋅=SΦS B d 来计算(其中B 为两无限长直电流单独存在时产生的磁感强度B 1 与B 2 之和). 为了积分的需要,建立如图所示的坐标系.由于B 仅与x 有关,即()B B x =,故取一个平行于长直导线的宽为dx 、长为d 的面元dS ,如图中阴影部分所示,则x d S d d =,所以,总磁通量可通过线积分求得(若取面元y x S d d d =,则上述积分实际上为二重积分).本题在工程技术中又称为互感现象,也可用公式tl M E M d d -=求解. 解1 穿过面元dS 的磁通量为()x d xI μx d d x I μΦd π2d π2d d d d 0021-+=⋅+⋅=⋅=S B S B S B 因此穿过线圈的磁通量为()43ln π2d π2d π2d 02020Id μx x Id μx d x Id μΦΦd d dd =-+==⎰⎰⎰ 再由法拉第电磁感应定律,有6tI d μt ΦE d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 解2 当两长直导线有电流I 通过时,穿过线圈的磁通量为 43ln π20dI μΦ=线圈与两长直导线间的互感为 43ln π20d μI ΦM == 当电流以tl d d 变化时,线圈中的互感电动势为 tI d μt I M E d d 43ln π2d d 0⎪⎭⎫ ⎝⎛=-= 试想:如线圈又以速率v 沿水平向右运动,如何用法拉第电磁感应定律求图示位置的电动势呢此时线圈中既有动生电动势,又有感生电动势.设时刻t ,线圈左端距右侧直导线的距离为ξ,则穿过回路的磁通量()ξf ΦS,1d =⋅=⎰S B ,它表现为变量I 和ξ的二元函数,将Φ代入t ΦE d d -= 即可求解,求解时应按复合函数求导,注意,其中v =tξd d ,再令ξ=d 即可求得图示位置处回路中的总电动势.最终结果为两项,其中一项为动生电动势,另一项为感生电动势.8 -8 有一测量磁感强度的线圈,其截面积S =4.0 cm 2 、匝数N =160 匝、电阻R =50Ω.线圈与一内阻R i =30Ω的冲击电流计相连.若开始时,线圈的平面与均匀磁场的磁感强度B 相垂直,然后线圈的平面很快地转到与B 的方向平行.此时从冲击电流计中测得电荷值54.010C q -=⨯.问此均匀磁场的磁感强度B 的值为多少7分析 在电磁感应现象中,闭合回路中的感应电动势和感应电流与磁通量变化的快慢有关,而在一段时间内,通过导体截面的感应电量只与磁通量变化的大小有关,与磁通量变化的快慢无关.工程中常通过感应电量的测定来确定磁场的强弱. 解 在线圈转过90°角时,通过线圈平面磁通量的变化量为NBS NBS ΦΦΦ=-=-=0Δ12 因此,流过导体截面的电量为ii R RNBS R R Φq +=+=Δ 则 ()T 050.0=+=NSR R q B i 8 -9 如图所示,一长直导线中通有I =5.0 A 的电流,在距导线9.0 cm 处,放一面积为0.10 cm 2 ,10 匝的小圆线圈,线圈中的磁场可看作是均匀的.今在1.0 ×10-2 s 内把此线圈移至距长直导线10.0 cm 处.求:(1) 线圈中平均感应电动势;(2) 设线圈的电阻为1.0×10-2Ω,求通过线圈横截面的感应电荷.8分析 虽然线圈处于非均匀磁场中,但由于线圈的面积很小,可近似认为穿过线圈平面的磁场是均匀的,因而可近似用NBS ψ=来计算线圈在始、末两个位置的磁链.解 (1) 在始、末状态,通过线圈的磁链分别为1011π2r ISμN S NB ψ==,2022π2r IS μN S NB ψ== 则线圈中的平均感应电动势为 V 1011.111πΔ2ΔΔ8210-⨯=⎪⎪⎭⎫ ⎝⎛-==r r t IS μN t ΦE 电动势的指向为顺时针方向.(2) 通过线圈导线横截面的感应电荷为tΦE d d -= 8 -10 如图(a)所示,把一半径为R 的半圆形导线OP 置于磁感强度为B 的均匀磁场中,当导线以速率v 水平向右平动时,求导线中感应电动势E 的大小,哪一端电势较高9分析 本题及后面几题中的电动势均为动生电动势,除仍可由tΦE d d -=求解外(必须设法构造一个闭合回路),还可直接用公式()l B d ⋅⨯=⎰l E v 求解.在用后一种方法求解时,应注意导体上任一导线元dl 上的动生电动势()l B d d ⋅⨯=v E .在一般情况下,上述各量可能是dl 所在位置的函数.矢量(v ×B )的方向就是导线中电势升高的方向. 解1 如图(b)所示,假想半圆形导线O P 在宽为2R 的静止形导轨上滑动,两者之间形成一个闭合回路.设顺时针方向为回路正向,任一时刻端点O 或端点P 距 形导轨左侧距离为x ,则B R Rx Φ⎪⎭⎫ ⎝⎛+=2π212 即B R tx RB t ΦE v 2d d 2d d -=-=-= 由于静止的 形导轨上的电动势为零,则E =-2R v B .式中负号表示电动势的方向为逆时针,对OP 段来说端点P 的电势较高. 解2 建立如图(c )所示的坐标系,在导体上任意处取导体元dl ,则()θR θB l θB E o d cos d cos 90sin d d v v ==⋅⨯=l B vB R θθBR E v v 2d cos d E π/2π/2===⎰⎰- 由矢量(v ×B )的指向可知,端点P 的电势较高.10 解3 连接OP 使导线构成一个闭合回路.由于磁场是均匀的,在任意时刻,穿过回路的磁通量==BS Φ常数.由法拉第电磁感应定律tΦE d d -=可知,E =0 又因 E =E OP +E PO即 E OP =-E PO =2R v B由上述结果可知,在均匀磁场中,任意闭合导体回路平动所产生的动生电动势为零;而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势.上述求解方法是叠加思想的逆运用,即补偿的方法.8 -11 长为L 的铜棒,以距端点r 处为支点,以角速率ω绕通过支点且垂直于铜棒的轴转动.设磁感强度为B 的均匀磁场与轴平行,求棒两端的电势差.分析 应该注意棒两端的电势差与棒上的动生电动势是两个不同的概念,如同电源的端电压与电源电动势的不同.在开路时,两者大小相等,方向相反(电动势的方向是电势升高的方向,而电势差的正方向是电势降落的方向).本题可直接用积分法求解棒上的电动势,亦可以将整个棒的电动势看作是O A 棒与O B 棒上电动势的代数和,如图(b)所示.而E O A 和E O B 则可以直接利用第8 -2 节例1 给出的结果.解1 如图(a)所示,在棒上距点O 为l 处取导体元dl ,则()()r L lB ωl lB ωE L-r r AB AB 221d d --=-=⋅⨯=⎰⎰-l B v 因此棒两端的电势差为()r L lB ωE U AB AB 221--== 当L >2r 时,端点A 处的电势较高解2 将AB 棒上的电动势看作是O A 棒和O B 棒上电动势的代数和,如图(b)所示.其中221r ωB E OA =,()221r L B ωE OB -= 则()r L BL ωE E E OB OA AB 221--=-= 8 -12 如图所示,长为L 的导体棒OP ,处于均匀磁场中,并绕OO ′轴以角速度ω旋转,棒与转轴间夹角恒为θ,磁感强度B 与转轴平行.求OP 棒在图示位置处的电动势.分析 如前所述,本题既可以用法拉第电磁感应定律t ΦE d d -= 计算(此时必须构造一个包含OP 导体在内的闭合回路, 如直角三角形导体回路OPQO ),也可用()l B d ⋅⨯=⎰lE v 来计算.由于对称性,导体OP 旋转至任何位置时产生的电动势与图示位置是相同的.解1 由上分析,得()l B d ⋅⨯=⎰OP OP E v l αB l o d cos 90sin ⎰=v()()l θB θωl o d 90cos sin ⎰-=l()⎰==L θL B ωl l θB ω022sin 21d sin 由矢量B ⨯v 的方向可知端点P 的电势较高.解2 设想导体OP 为直角三角形导体回路OPQO 中的一部分,任一时刻穿过回路的磁通量Φ为零,则回路的总电动势QO PQ OP E E E t ΦE ++==-=0d d 显然,E QO =0,所以()221PQ B ωE E E QO PQ OP ==-= 由上可知,导体棒OP 旋转时,在单位时间内切割的磁感线数与导体棒QP 等效.后者是垂直切割的情况.8 -13 如图(a)所示,金属杆AB 以匀速12.0m s -=⋅v 平行于一长直导线移动,此导线通有电流I =40A .求杆中的感应电动势,杆的哪一端电势较高分析 本题可用两种方法求解.(1) 用公式()l B d ⋅⨯=⎰lE v 求解,建立图(a )所示的坐标系,所取导体元x l d d =,该处的磁感强度xI μB π20=.(2) 用法拉第电磁感应定律求解,需构造一个包含杆AB 在内的闭合回路.为此可设想杆AB 在一个静止的形导轨上滑动,如图(b)所示.设时刻t ,杆AB 距导轨下端CD 的距离为y ,先用公式⎰⋅=SΦS B d 求得穿过该回路的磁通量,再代入公式tΦE d d -=,即可求得回路的电动势,亦即本题杆中的电动势. 解1 根据分析,杆中的感应电动势为()V 1084.311ln 2πd 2πd d 50m 1.1m 1.00-⨯-=-=-==⋅⨯=⎰⎰v v v I μx x μxl E AB AB l B 式中负号表示电动势方向由B 指向A ,故点A 电势较高. 解2 设顺时针方向为回路AB CD 的正向,根据分析,在距直导线x 处,取宽为dx 、长为y 的面元dS ,则穿过面元的磁通量为x y xI μΦd 2πd d 0=⋅=S B 穿过回路的磁通量为11ln 2πd 2πd 0m1.1m 1.00⎰⎰-===S Iy μx y x I μΦΦ 回路的电动势为V 1084.32πd d 11ln 2πd d 500-⨯-=-=-=-=Iy μt y x I μt ΦE 由于静止的形导轨上电动势为零,所以 V 1084.35-⨯-==E E AB式中负号说明回路电动势方向为逆时针,对AB 导体来说,电动势方向应由B 指向A ,故点A 电势较高.8 -14 如图(a)所示,在“无限长”直载流导线的近旁,放置一个矩形导体线框,该线框在垂直于导线方向上以匀速率v 向右移动,求在图示位置处,线框中感应电动势的大小和方向.分析 本题亦可用两种方法求解.其中应注意下列两点:1.当闭合导体线框在磁场中运动时,线框中的总电动势就等于框上各段导体中的动生电动势的代数和.如图(a)所示,导体eh 段和fg 段上的电动势为零[此两段导体上处处满足()0l B =⋅⨯d v ],因而线框中的总电动势为()()()()hg ef hgef gh ef E E E -=⋅⨯-⋅⨯=⋅⨯+⋅⨯=⎰⎰⎰⎰l B l B l B l B d d d d v v v v 其等效电路如图(b)所示.2.用公式tΦE d d -=求解,式中Φ是线框运动至任意位置处时,穿过线框的磁通量.为此设时刻t 时,线框左边距导线的距离为ξ,如图(c )所示,显然ξ是时间t 的函数,且有v =tξd d .在求得线框在任意位置处的电动势E (ξ)后,再令ξ=d ,即可得线框在题目所给位置处的电动势.解1 根据分析,线框中的电动势为hg ef E E E -=()()⎰⎰⋅⨯-⋅⨯=hgef l B l B d d v v ()⎰⎰+-=2201000d 2πd 2πl l l l d I μl d I μv v ()1202πl d I I μ+=1vI 由E ef >E hg 可知,线框中的电动势方向为efgh .解2 设顺时针方向为线框回路的正向.根据分析,在任意位置处,穿过线框的磁通量为()()ξl ξξx Il μdx ξx Il μΦl 120020ln π2π21++=+=⎰ 相应电动势为()()1120π2d d l ξξl l I μt ΦξE +=-=v 令ξ=d ,得线框在图示位置处的电动势为 ()1120π2l d d l l I μE +=v 由E >0 可知,线框中电动势方向为顺时针方向.*8 -15 有一长为l ,宽为b 的矩形导线框架,其质量为m ,电阻为R .在t =0时,框架从距水平面y =0 的上方h 处由静止自由下落,如图所示.磁场的分布为:在y =0 的水平面上方没有磁场;在y =0 的水平面下方有磁感强度为B 的均匀磁场,B 的方向垂直纸面向里.已知框架在时刻t 1 和t 2 的位置如图中所示.求在下述时间内,框架的速度与时间的关系:(1) t 1 ≥t >0,即框架进入磁场前;(2) t 2 ≥t ≥t 1 ,即框架进入磁场, 但尚未全部进入磁场;(3)t >t 2 ,即框架全部进入磁场后.分析 设线框刚进入磁场(t 1 时刻)和全部进入磁场(t 2 时刻)的瞬间,其速度分别为v 10 和v 20 .在情况(1)和(3)中,线框中无感应电流,线框仅在重力作用下作落体运动,其速度与时间的关系分别为v =gt (t <t 1)和v =v 20 +g (t -t 2 )(t >t 2 ).而在t 1<t <t 2这段时间内,线框运动较为复杂,由于穿过线框回路的磁通量变化,使得回路中有感应电流存在,从而使线框除受重力外,还受到一个向上的安培力F A ,其大小与速度有关,即()A A F F =v .根据牛顿运动定律,此时线框的运动微分方程为()tv v d d m F mg A =-,解此微分方程可得t 1<t <t 2 时间内线框的速度与时间的关系式.解 (1) 根据分析,在1t t ≤时间内,线框为自由落体运动,于是()11t t gt ≤=v 其中1t t =时,gh 2101==v v(2) 线框进入磁场后,受到向上的安培力为v Rl B IlB F A 22== 根据牛顿运动定律,可得线框运动的微分方程tv m v d d 22=-R l B mg 令mRl B K 22=,整理上式并分离变量积分,有 ⎰⎰=-t t t g 110d d vv Kv v 积分后将gh 210=v 代入,可得()()[]1212t t K e gh K g g K----=v (3) 线框全部进入磁场后(t >t 2),作初速为v 20 的落体运动,故有()()()[]()222031221t t g e gh K g g Kt t g t t K -+--=-+=--v v 8 -16 有一磁感强度为B 的均匀磁场,以恒定的变化率t d d B 在变化.把一块质量为m 的铜,拉成截面半径为r 的导线,并用它做成一个半径为R 的圆形回路.圆形回路的平面与磁感强度B 垂直.试证:这回路中的感应电流为td d π4B d ρm I =式中ρ 为铜的电阻率,d 为铜的密度. 解 圆形回路导线长为πR 2,导线截面积为2πr ,其电阻R ′为22rR ρS l ρR ==' 在均匀磁场中,穿过该回路的磁通量为BS Φ=,由法拉第电磁感应定律可得回路中的感应电流为t t t d d 2πd d π1d d 122B ρRr B R R ΦR R E I ='='='= 而2ππ2r R d m =,即dm Rr π2π2=,代入上式可得 td d π4B d ρm I = 8 -17 半径为R =2.0 cm 的无限长直载流密绕螺线管,管内磁场可视为均匀磁场,管外磁场可近似看作零.若通电电流均匀变化,使得磁感强度B 随时间的变化率td d B 为常量,且为正值,试求:(1) 管内外由磁场变化激发的感生电场分布;(2) 如1s T 010.0d d -⋅=tB ,求距螺线管中心轴r =5.0 cm 处感生电场的大小和方向.分析 变化磁场可以在空间激发感生电场,感生电场的空间分布与场源———变化的磁场(包括磁场的空间分布以及磁场的变化率td d B 等)密切相关,即S B l E d d ⋅∂∂-=⎰⎰S S k t .在一般情况下,求解感生电场的分布是困难的.但对于本题这种特殊情况,则可以利用场的对称性进行求解.可以设想,无限长直螺线管内磁场具有柱对称性,其横截面的磁场分布如图所示.由其激发的感生电场也一定有相应的对称性,考虑到感生电场的电场线为闭合曲线,因而本题中感生电场的电场线一定是一系列以螺线管中心轴为圆心的同心圆.同一圆周上各点的电场强度E k 的大小相等,方向沿圆周的切线方向.图中虚线表示r <R 和r >R 两个区域的电场线.电场线绕向取决于磁场的变化情况,由楞次定律可知,当0d d <t B 时,电场线绕向与B 方向满足右螺旋关系;当0d d >t B 时,电场线绕向与前者相反.解 如图所示,分别在r <R 和r >R 的两个区域内任取一电场线为闭合回路l (半径为r 的圆),依照右手定则,不妨设顺时针方向为回路正向.(1) r <R , tB r t r E E k l k d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r E k d d 2-= r >R , t B R t r E E k lk d d πd d d π2d 2-=⋅-=⋅=⋅=⎰⎰S B l E tB r R E k d d 22-= 由于0d d >tB ,故电场线的绕向为逆时针. (2) 由于r >R ,所求点在螺线管外,因此tB r R E k d d 22-= 将r 、R 、tB d d 的数值代入,可得15m V 100.4--⋅⨯-=k E ,式中负号表示E k 的方向是逆时针的.8 -18 在半径为R 的圆柱形空间中存在着均匀磁场,B 的方向与柱的轴线平行.如图(a)所示,有一长为l 的金属棒放在磁场中,设B 随时间的变化率tB d d 为常量.试证:棒上感应电动势的大小为分析 变化磁场在其周围激发感生电场,把导体置于感生电场中,导体中的自由电子就会在电场力的作用下移动,在棒内两端形成正负电荷的积累,从而产生感生电动势.由于本题的感生电场分布与上题所述情况完全相同,故可利用上题结果,由⎰⋅=lk E l E d 计算棒上感生电动势.此外,还可连接OP 、OQ ,设想PQOP 构成一个闭合导体回路,用法拉第电磁感应定律求解,由于OP 、OQ 沿半径方向,与通过该处的感生电场强度E k 处处垂直,故0d =⋅l E k ,OP 、OQ 两段均无电动势,这样,由法拉第电磁感应定律求出的闭合回路的总电动势,就是导体棒PQ 上的电动势.证1 由法拉第电磁感应定律,有 22Δ22d d d d d d ⎪⎭⎫ ⎝⎛-==-==l R l t B t B S t ΦE E PQ 证2 由题8 -17可知,在r <R 区域,感生电场强度的大小tB r E k d d 2= 设PQ 上线元dx 处,E k 的方向如图(b )所示,则金属杆PQ 上的电动势为()()222202/2d d d 2/d d 2d cos d l R l t B x r l R t B r x θE E l k k PQ -=-==⋅=⎰⎰x E 讨论 假如金属棒PQ 有一段在圆外,则圆外一段导体上有无电动势 该如何求解8 -19 截面积为长方形的环形均匀密绕螺绕环,其尺寸如图(a)所示,共有N 匝(图中仅画出少量几匝),求该螺绕环的自感L .分析 如同电容一样,自感和互感都是与回路系统自身性质(如形状、匝数、介质等)有关的量.求自感L 的方法有两种:1.设有电流I 通过线圈,计算磁场穿过自身回路的总磁通量,再用公式IΦL =计算L .2.让回路中通以变化率已知的电流,测出回路中的感应电动势E L ,由公式t I E L L d /d =计算L .式中E L 和tI d d 都较容易通过实验测定,所以此方法一般适合于工程中.此外,还可通过计算能量的方法求解.解 用方法1 求解,设有电流I 通过线圈,线圈回路呈长方形,如图(b)所示,由安培环路定理可求得在R 1 <r <R 2 范围内的磁场分布为xNI μB π20=由于线圈由N 匝相同的回路构成,所以穿过自身回路的磁链为 12200ln π2d π2d 21R R hI N μx h x NI μN N ψS R R ==⋅=⎰⎰S B 则1220ln π2R R h N μI ψL = 若管中充满均匀同种磁介质,其相对磁导率为μr ,则自感将增大μr 倍.8 -20 如图所示,螺线管的管心是两个套在一起的同轴圆柱体,其截面积分别为S 1 和S 2 ,磁导率分别为μ1 和μ2 ,管长为l ,匝数为N ,求螺线管的自感.(设管的截面很小)分析 本题求解时应注意磁介质的存在对磁场的影响.在无介质时,通电螺线管内的磁场是均匀的,磁感强度为B 0 ,由于磁介质的存在,在不同磁介质中磁感强度分别为μ1 B 0 和μ2 B 0 .通过线圈横截面的总磁通量是截面积分别为S 1 和S 2 的两部分磁通量之和.由自感的定义可解得结果.解 设有电流I 通过螺线管,则管中两介质中磁感强度分别为I L N μnl μB 111==,I LN μnl μB 222== 通过N 匝回路的磁链为221121S NB S NB ΨΨΨ+=+=则自感2211221S μS μlN I ψL L L +==+= 8 -21 有两根半径均为a 的平行长直导线,它们中心距离为d .试求长为l的一对导线的自感(导线内部的磁通量可略去不计).分析 两平行长直导线可以看成无限长但宽为d 的矩形回路的一部分.设在矩形回路中通有逆时针方向电流I ,然后计算图中阴影部分(宽为d 、长为l )的磁通量.该区域内磁场可以看成两无限长直载流导线分别在该区域产生的磁场的叠加.解 在如图所示的坐标中,当两导线中通有图示的电流I 时,两平行导线间的磁感强度为()r d I μr I μB -+=π2π200 穿过图中阴影部分的磁通量为 aa d l μr Bl ΦS a d a -==⋅=⎰⎰-ln πd d 0S B 则长为l 的一对导线的自感为aa d l μI ΦL -==ln π0 如导线内部磁通量不能忽略,则一对导线的自感为212L L L +=.L 1 称为外自感,即本题已求出的L ,L 2 称为一根导线的内自感.长为l 的导线的内自感8π02l μL =,有兴趣的读者可自行求解. 8 -22 如图所示,在一柱形纸筒上绕有两组相同线圈AB 和A ′B ′,每个线圈的自感均为L ,求:(1) A 和A ′相接时,B 和B ′间的自感L 1 ;(2) A ′和B 相接时,A 和B ′间的自感L 2 .分析 无论线圈AB 和A ′B ′作哪种方式连接,均可看成一个大线圈回路的两个部分,故仍可从自感系数的定义出发求解.求解过程中可利用磁通量叠加的方法,如每一组载流线圈单独存在时穿过自身回路的磁通量为Φ,则穿过两线圈回路的磁通量为2Φ;而当两组线圈按(1)或(2)方式连接后,则穿过大线圈回路的总磁通量为2Φ±2Φ,“ ±”取决于电流在两组线圈中的流向是相同或是相反.解 (1) 当A 和A ′连接时,AB 和A ′B ′线圈中电流流向相反,通过回路的磁通量亦相反,故总通量为0221=-=ΦΦΦ,故L 1 =0.(2) 当A ′和B 连接时,AB 和A ′B ′线圈中电流流向相同,通过回路的磁通量亦相同,故总通量为ΦΦΦΦ4222=+=, 故L I ΦI ΦL 4422===. 本题结果在工程实际中有实用意义,如按题(1)方式连接,则可构造出一个无自感的线圈.8 -23 如图所示,一面积为4.0 cm 2 共50 匝的小圆形线圈A ,放在半径为20 cm 共100 匝的大圆形线圈B 的正中央,此两线圈同心且同平面.设线圈A 内各点的磁感强度可看作是相同的.求:(1) 两线圈的互感;(2) 当线圈B 中电流的变化率为-50 A·s-1 时,线圈A 中感应电动势的大小和方向.分析 设回路Ⅰ中通有电流I 1 ,穿过回路Ⅱ的磁通量为Φ21 ,则互感M =M 21 =Φ21I 1 ;也可设回路Ⅱ通有电流I 2 ,穿过回路Ⅰ的磁通量为Φ12 ,则21212I ΦM M == . 虽然两种途径所得结果相同,但在很多情况下,不同途径所涉及的计算难易程度会有很大的不同.以本题为例,如设线圈B 中有电流I 通过,则在线圈A 中心处的磁感强度很易求得,由于线圈A 很小,其所在处的磁场可视为均匀的,因而穿过线圈A 的磁通量Φ≈BS .反之,如设线圈A 通有电流I ,其周围的磁场分布是变化的,且难以计算,因而穿过线圈B 的磁通量也就很难求得,由此可见,计算互感一定要善于选择方便的途径.解 (1) 设线圈B 有电流I 通过,它在圆心处产生的磁感强度R I μN B B 200=穿过小线圈A 的磁链近似为 A B A A A A S RI μN N S B N ψ200== 则两线圈的互感为H 1028.6260-⨯===RS μN N I ψM A B A A (2)V 1014.3d d 4-⨯=-=tI M E A 互感电动势的方向和线圈B 中的电流方向相同.8 -24 如图所示,两同轴单匝线圈A 、C 的半径分别为R 和r ,两线圈相距为d .若r 很小,可认为线圈A 在线圈C 处所产生的磁场是均匀的.求两线圈的互感.若线圈C 的匝数为N 匝,则互感又为多少解 设线圈A 中有电流I 通过,它在线圈C 所包围的平面内各点产生的磁感强度近似为()2/322202d R IR μB +=穿过线圈C 的磁通为 ()22/32220π2r d R IR μBS ψC +==则两线圈的互感为 ()2/3222202πdR R r μI ψM +== 若线圈C 的匝数为N 匝,则互感为上述值的N 倍. 8 -25 如图所示,螺绕环A 中充满了铁磁质,管的截面积S 为2.0 cm 2 ,沿环每厘米绕有100 匝线圈,通有电流I 1 =4.0 ×10 -2 A ,在环上再绕一线圈C ,共10 匝,其电阻为0.10 Ω,今将开关S 突然开启,测得线圈C 中的感应电荷为2.0 ×10 -3C .求:当螺绕环中通有电流I 1 时,铁磁质中的B 和铁磁质的相对磁导率μr .分析 本题与题8 -8 相似,均是利用冲击电流计测量电磁感应现象中通过回路的电荷的方法来计算磁场的磁感强度.线圈C 的磁通变化是与环形螺线管中的电流变化相联系的. 解 当螺绕环中通以电流I 1 时,在环内产生的磁感强度110I n μμB r =则通过线圈C 的磁链为S I n μμN BS N ψr c 11022==设断开电源过程中,通过C 的感应电荷为q C ,则有()RS I n μμN ψR ψR qc r c c 110201Δ1=--=-= 由此得 T 10.02110===S N Rqc I n μμB r 相对磁导率1991102==I n μS N Rqc μr8 -26 一个直径为0.01 m ,长为0.10 m 的长直密绕螺线管,共1 000 匝线圈,总电阻为7.76 Ω.求:(1) 如把线圈接到电动势E =2.0 V 的电池上,电流稳定后,线圈中所储存的磁能有多少 磁能密度是多少*(2) 从接通电路时算起,要使线圈储存磁能为最大储存磁能的一半,需经过多少时间分析 单一载流回路所具有的磁能,通常可用两种方法计算:(1) 如回路自感为L (已知或很容易求得),则该回路通有电流I 时所储存的磁能221LI W m =,通常称为自感磁能.(2) 由于载流回路可在空间激发磁场,磁能实际是储存于磁场之中,因而载流回路所具有的能量又可看作磁场能量,即V w W V m m d ⎰=,式中m w 为磁场能量密度,积分遍及磁场存在的空间.由于μB w m 22=,因而采用这种方法时应首先求载流回路在空间产生的磁感强度B 的分布.上述两种方法还为我们提供了计算自感的另一种途径,即运用V w LI V m d 212⎰=求解L . 解 (1) 密绕长直螺线管在忽略端部效应时,其自感l S N L 2=,电流稳定后,线圈中电流RE I =,则线圈中所储存的磁能为J 1028.3221522202-⨯===lRSE N μLI W m 在忽略端部效应时,该电流回路所产生的磁场可近似认为仅存在于螺线管。
第8章直流稳压电源习题及答案
图8.17(a)
图8.17(b)
返回
上一题 下一页 下一题
第 பைடு நூலகம் 章 半导体器件
【解】( 1 ) 在 0≤ωt <π半个周期内,电压 a 电位最高, b点电位最低。此时二极管 D1 承受正向电压而导通,二极管 D2承受反向电压而截止,电流自 a 点经 D1 通过负载 RL 而由 O 点返回。在π≤ωt<2π半个周期内,a 点电位最低,b 点 电位最高,此时 D1 反向截止,D2 正向导通,电流自 b 点经 D2 通过负载 RL 而由 O 点返回。可见,当电源电压交变一次,两 只二极管在正,负半周各自轮流通,从而使负载得到了单向流 动的全波脉动电流和电压。
【解】 (1)负载直流电压
UO 1.2 U2 1.215 V 18 V
负载直流电流
IO
UO RL
18 A 0.06 300
A
图8.4
(2)二极管平均电流
ID
1 2
IO
1 0.06 2
A 0.03
A
一般取
IF 2ID 2 0.03A 0.06 A
返回
上一题 下一页 下一题
第 8 章 半导体器件
(2)负载直流电压平均值
1
UO 2
0
2U2 sin t dt
2
U2 0.45 U2
(3)二极管电流也就是负载电流,其平均值为
ID
IO
UO RL
0.45
U2 RL
(4)在负半周期,整流元件D所受的最大反向电压
URm U2m 2 U2
返回
上一题 上一页 下一题
第 8 章 半导体器件
8.2.7 图8.17(a)(教材图 8.06 )为一全波整流电路,试 求: (1)在交流电压的正,负半周内,电流流通的路径;
第8章 组合逻辑电路习题解答
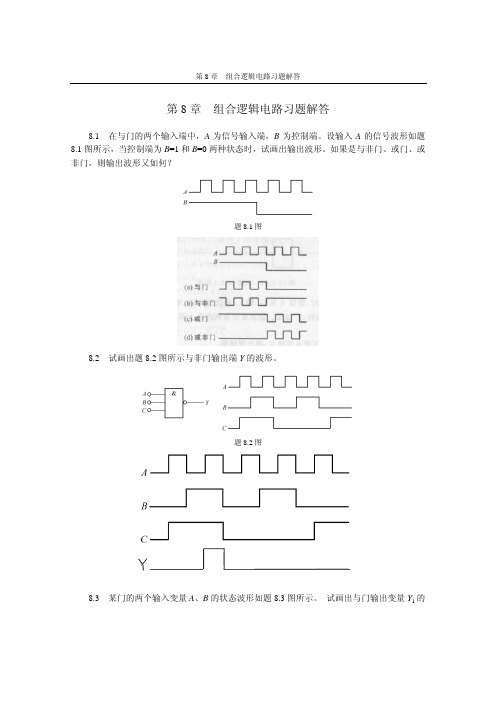
Y = BCD + ACD + ABD + ABC = BCD ⋅ ACD ⋅ ABD ⋅ ABC
全部用二输入端与非门实现:
Y = BCD + ACD + ABD + ABC
= CD ⋅ AB + BD ⋅ AC = CD ⋅ AB ⋅ BD ⋅ AC = CD ⋅ AB ⋅ BD ⋅ AC
8.5 根据下列各逻辑式,画出逻辑图。 (1)Y=(A+B)C;(2)Y=AB+BC;(3)Y=(A+B)(A+C);(4)Y=A+BC;(5)Y=A(A+B)+BC
第 8 章 组合逻辑电路
201
8.6 用与非门组成下列逻辑门: (1)与门 Y=ABC; (2)或门 Y=A+B+C; (3)非门 Y = A ; (4)与或门 Y=ABC+DEF; (5)或非门 Y = A + B + C 。
204
第 8 章 组合逻辑电路
8.11 试写出题 8.11 图各逻辑电路图的逻辑表达式。
题 8.11 图
图(a) F = A ⋅ B ⋅ C ⋅ D = A ⋅ B ⋅ C + D 图(b) A + B ⋅ ( A + B) = A + B + B + C = A + B + B ⋅ C 图(c) F = A ⋅ B ⋅ A ⋅ B = AB + BA
题 8.2 图
8.3 某门的两个输入变量 A、B 的状态波形如题 8.3 图所示。试画出与门输出变量 Y1 的
200
第 8 章 组合逻辑电路
第八章习题答案

9. 以KBrO3基准物标定Na2S2O3溶液的浓度,试问KBrO3与Na2S2O3的化学计量关系解:测定过程为:KBrO3在酸性介质中与过量的KI反应析出I2, 析出的I2用Na2S2O3溶液滴定。
相关反应方程式如下:BrO3-+I-+6H+ =3I2+3H2O+ Br-I2+ 2S2O32- =2 I-+ S4O62-综合两个反应可知:KBrO3~3I2~6Na2S2O3n KBrO3:n Na2S2O3=1:610.用同一KMnO4标准溶液分别滴定体积相等的FeSO4和H2C2O4溶液,消耗的KMnO4标准溶液体积相等,试问FeSO4和H2C2O4两种溶液浓度的比例关系为多少解:相关反应方程式如下:MnO4-+5Fe2++8H+ = Mn2++5 Fe3++4H2O2 MnO4-+5 C2O42-+16H+ = 2 Mn2++10CO2+8H2On MnO4-:n Fe2+=1:5n MnO4-:n C2O42-=2:5c(FeSO4):c(H2C2O4)=2:111.假如有一邻苯二甲酸氢钾试样,其中邻苯二甲酸氢钾含量约为90%,其余为不与酸反应的惰性杂质,现用浓度为mol·L-1的NaOH标准溶液滴定,欲使滴定时碱液消耗体枳在25mL左右,则:(1)需称取上述试样多少克(2)若以mol·L-1的NaOH标准溶液滴定,情况又如何(3)通过(1)、(2)计算结果说明为什么在滴定分析中滴定剂的浓度常采用~0. 2 mol·L-1解:(1) M邻苯二甲酸氢钾=n NaOH=×25×10-3=×10-2molm邻苯二甲酸氢钾=M邻苯二甲酸氢钾×n NaOH/90%=≈(2) n NaOH=×25×10-3=×10-4molm邻苯二甲酸氢钾=M邻苯二甲酸氢钾×n NaOH/90%≈(3) 浓度常采用~0. 2 mol·L-1之间:m邻苯二甲酸氢钾≈~之间相对误差<%。
高等数学练习册第八章习题参考答案(1)

解 令x a cos t, y a sin t,
I
2 0
1 a2
[a 2
(cos
t
sin
t
)(
sin
t
)
(cos
t
sin
t
)
cos
t
]dt
2
0 dt 2 .
p55. 2.计算 ( x2 2xy)dx ( y2 2xy)dy,其中 L
L为抛物线y x2上从点(1,1)到点(1,1)的一段弧.
C
(2)曲线弧C的重心坐标为
xG
1 x( x, y)ds
MC
,yG
1 y( x, y)ds .
MC
p51.2.设光滑曲线L关于x轴对称, L1是L在x轴上方的部分, (1)若f ( x, y)在L上连续,且关于y为奇函数,则Biblioteka f ( x, y)ds 0 ; L
(2)若f ( x, y)在L上连续,且关于y为偶函数,
(1)当p点从点A(a , 0)经位于第一象限的弧段到 B(0,b)时, F所作的功;
(2)当p点经过全椭圆时,F所作的功.
p56. 解 F | F | F 0 x2 y2 ( x , y ) x2 y2 x2 y2
( x, y),
(1) W F d s ( x)dx ( y)dy
0
22
a2
2
| cos
t
| dt
2a 2
2 cos udu 2a2 .
20
2
0
p52. 3.计算 | xy | ds,其中L :圆周x2 y2 a2. L
解法1
I 4
2
a3
sin t
第8章 习题答案-局域网技术与组网工程(第2版)-苗凤君-清华大学出版社

8.10 习题与实践1.习题(1)自顶向下网络设计方法的主要网络设计阶段有哪些?答:设计和实现网络系统遵从一定的网络系统集成模型,模型从系统开始,经历用户需求分析、逻辑网络设计、物理网络设计和测试,并贯彻网络工程监理。
既采用自顶向下的网络设计方法,从OSI参考模型上层开始,然后向下直到底层的网络设计方法。
(2)为什么了解客户的商业特点很重要?答:只有对客户的商业特点进行透彻分析,才能提出得到客户认可的网络设计方案。
(3)目前公司都有哪些商业目标?答:常见的网络设计目标包括:增加收入和利润、提高市场占有份额、拓展新的市场空间、提高在同一市场内同其他公司竞争的能力、降低费用、提高员工生产力、缩短产品开发周期、使用即时生产方法、制定解决配件短缺的计划、为新客户提供服务、支持移动性、为客户提供更好的支持、为关键要素开放网络、建立达到新水平的良好的信息网和关系网以作为网络组织化模型的基础、避免网络安全问题引发商业中断、避免自然或人为灾害引发商业中断、对过时技术进行更新改造、降低电信和网络费用并在操作上进行简化等。
(4)目前商业组织机构的典型技术目标有哪些?答:常见的网络技术目标主要包括可扩展性、可用性、网络性能、安全性、可管理性、易用性、适应性和可付性。
(5)如何区分带宽和吞吐量?答:带宽(bandwidth)用来衡量单位时间内传输比特的能力,通常用bit/s表示,分物理带宽和逻辑带宽。
吞吐量是指单位时间内无差错地传输数据的能力,通常以以bps, Bps,或分组/秒(pps)度量。
(6)如何提高网络效率?答:网络效率表明为产生所需的输出而要求的系统开销。
如为避免冲突、差错、确认而采用的控制,都会影响网络效率。
提高网络效率的通用手段是有增大帧的最大长度,因为较长的帧意味着链路具有较低的差错率,从而提高信道效率。
(7)为提高网络效率必须进行哪些折中?答:提高网络效率的通用手段是有增大帧的最大长度,一旦帧越长,比特越多,帧出错机会也会增加。
第8章 死锁习题及答案

第八章死锁习题及答案一、填空题1.进程的“同步”和“互斥”反映了进程间①和②的关系。
【答案】①直接制约、②间接制约【解析】进程的同步是指在异步环境下的并发进程因直接制约而互相发送消息,进行相互合作、相互等待,使得各进程按一定的速度执行的过程;而进程的互斥是由并发进程同时共享公有资源而造成的对并发进程执行速度的间接制约。
2.死锁产生的原因是①和②。
【答案】①系统资源不足、②进程推进路径非法【解析】死锁产生的根本原因是系统的资源不足而引发了并发进程之间的资源竞争。
由于资源总是有限的,我们不可能为所有要求资源的进程无限地提供资源。
而另一个原因是操作系统应用的动态分配系统各种资源的策略不当,造成并发进程联合推进的路径进入进程相互封锁的危险区。
所以,采用适当的资源分配算法,来达到消除死锁的目的是操作系统主要研究的课题之一。
3.产生死锁的四个必要条件是①、②、③、④。
【答案】①互斥条件、②非抢占条件、③占有且等待资源条件、④循环等待条件【解析】互斥条件:进程对它所需的资源进行排它性控制,即在一段时间内,某资源为一进程所独占。
非抢占条件:进程所获得的资源在未使用完毕之前,不能被其它进程强行夺走,即只能由获得资源的进程自己释放。
占有且等待资源条件:进程每次申请它所需的一部分资源,在等待新资源的同时,继续占有已分配到的资源,循环等待条件:存在一进程循环链,链中每一个进程已获得的资源同时被下一个进程所请求。
4.在操作系统中,信号量是表示①的物理实体,它是一个与②有关的整型变量,其值仅能由③原语来改变。
【答案】①资源,②队列,③P-V【解析】信号量的概念和P-V原语是荷兰科学家E.W.Dijkstra提出来的。
信号量是一个特殊的整型量,它与一个初始状态为空的队列相联系。
信号量代表了资源的实体,操作系统利用它的状态对并发进程共享资源进行管理。
信号量的值只能由P-V原语来改变。
5.每执行一次P原语,信号量的数值S减1。
如果S>=0,该进程①;若S<0,则②该进程,并把它插入该③对应的④队列中。
第8章习题解答

第8章思考题及习题8参考答案一、填空1. 单片机存储器的主要功能是存储和。
答:程序、数据。
2.假设外部数据存储器2000H单元的内容为80H,执行下列指令后累加器A中的内容为。
MOV P2,#20HMOV R0,#00HMOVX A,@R0答:80H。
3.在存储器扩展中,无论是线选法还是译码法最终都是为扩展芯片的端提供控制信号。
答:片选。
4.起止范围为0000H~3FFFH的数据存储器的容量是 KB。
答:16KB。
5.在AT89S52单片机中,PC和DPTR都用于提供地址,但PC是为访问存储器提供地址,而DPTR是为访问存储器提供地址。
答:程序、数据。
6.11条地址线可选个存储单元,16KB存储单元需要条地址线。
答:2K,14。
7.4KB RAM存储器的首地址若为0000H,则末地址为 H。
答:0FFF。
8.若单片机外扩32KB 数据存储器的首地址若为4000H,则末地址为 H。
答:BFFF9. 设计一个以AT89S52单片机为核心的系统,如果不外扩程序存储器,使其内部8KB闪烁程序存储器有效,则其引脚应该接。
答:EA*,+5V10.74LS138是具有3个输入的译码器芯片,其输出常作片选信号,可选中片芯片中的任一芯片,并且只有1路输出为电平,其它输出均为电平。
答:8,低,高;二、单选1.区分AT89S51单片机片外程序存储器和片外数据存储器的最可靠方法是。
A.看其位于地址范围的低端还是高端B.看其离AT89S51单片机芯片的远近C.看其芯片的型号是ROM还是RAMD.看其是与RD信号连接还是与PSEN信号连接答:D2.访问片外数据存储器的寻址方式是。
A.立即寻址B.寄存器寻址C.寄存器间接寻址D.直接寻址答:C3.若要同时扩展4片2KB的RAM和4片4KB的ROM,则最少需要根地址线。
A、12B、13C、14D、154.当EA=1时,AT89S52单片机可以扩展的外部程序存储器的最大容量为。
A. 64KB B.60KB C.58KB D.56KB答:D5. 若某数据存储器芯片地址线为12根,那么它的存储容量为。
第8章习题解答

第8章习题解答一. 选择题1. 关于类和对象,不正确的说法是()A. 类是一种数据类型,它封装了数据和函数B. 类是对某一类对象的抽象C. 可以基于类这种数据类型定义类的引用D. 一个类的对象只有一个【答案】D【解析】类是一种数据类型,可以基于“类”这种数据类型定义多个称为“对象”的变量。
2. 类定义的外部,可以被访问的类的成员有()A. public 的类成员B. public或private的类成员C. private或protected的类成员D. public或private 的类成员【答案】A【解析】类的成员数据或成员函数的访问属性分为三种情况:private、public和protected,即私有访问属性、公有访问属性和保护访问属性,类定义的外部只能访问公有访问属性的成员。
3 关于this 指针,说法错误的是()A. this指针必须显式说明B. 当创建一个对象后,this 指针就指向该对象C. 成员函数拥有this指针D. 静态成员函数拥有this指针【答案】D【解析】this指针是一种特殊的指针,它指向成员函数当前操作的数据所属的对象。
不同的对象调用相同的成员函数时,this指针将指向不同的对象,也就可以访问不同对象的成员数据。
而静态成员函数是一个类的所有对象共享的成员,而不仅仅是某一对象的成员。
因此,可以在没有任何对象存在的情况下,可以使用静态成员函数,而使用this指针必须有明确的对象所指。
4. 调用形式参数为普通对象的函数时,系统会自动调用相应类的()A. 名字不同于类名的一般成员函数B. 构造函数C. 析构函数D. 拷贝构造函数【答案】D【解析】若函数的形参为类的对象,调用函数时,实参赋值给形参,系统自动调用拷贝构造函数实现拷贝赋值。
5. 定义某类的对象后,再删除该对象,系统会自动调用()A. 名字不同于类名的一般成员函数B. 拷贝构造函数C. 构造函数D. 析构函数【答案】D【解析】当对象生存期结束时,需要调用析构函数,释放对象所占的内存空间。
现代化学基础习题第八章习题答案

第八章原子结构与元素周期律1(8-2). 讨论下列高速运动的质子与子弹的波动性。
质子的质量271.6710-⨯kg ,直径1410-cm ,速度51.3810-⨯m·s -1;子弹质量10g ,直径1cm ,速度4410⨯ m·s -1。
h h p mvλ==3422756.6310 2.8810/1.6710 1.3810m s λ----⨯==⨯⨯⨯⨯质子361.6510/m sλ-=⨯子弹质子的波长远远大于子弹的波长,质子能产生明显衍射干涉等波动性现象。
2(8-4). 量子力学中与波尔模型中的原子轨道的含义有何差异?原子轨道ϕ应由哪些量子数来规定?2ϕ的物理意义是什么?答:量子力学中原子轨道表示原子核外电子运动状态的波函数,波尔模型中的原子轨道表示电子在特定轨道上运动,轨道具有固定能量。
原子轨道ϕ由主量子数你n,角量子数m,磁量子数m 规定。
2ϕ表示空间某处单位体积内电子出现的概率,即该点概率密度3(8-10). 简述原子半径、电离能、电子亲和能、电负性的含义及其一般变化规律。
见课本概念4(8-14).某元素的原子核外有13个电子,用4个量子数表示其中能量最高的3个电子的运动状态。
13,11,2ψ(,,) 13,02ψ(,0,+)13,02ψ(,0,-)5(8-18). 写出符合下列条件的原子的元素符号:(1) 最外层电子构型为4s 2,次外层有8个电子 Ca (2) 属于零族,但无p 电子; He (3) 在3p 能级上只有一个电子 Al (4) 4s 和3d 轨道上各有2个电子 Ti6(8-22). 已知M2+的离子3d轨道中有5个电子,试推出M原子的核外电子排布和M元素在周期表中的位置。
Mn 第四周期,第ⅦB族 [Ar]3d54s27.填充下列表格原子序数原子外层电子构型未成对电子数周期数族数所属区16 3s23p4 2 3 VI A p19 4s1 1 4 I A s42 4d55s2 5 5 VI B d48 4d105s20 5 IIB ds8.Cu形成+1离子时失去的是4s电子还是3d电子?试用Slater规则的计算结果加以说明.Cu 1s22s22p63s23p63d104s1 4s 电子的σ4s=0.85×18+1×10=25.20 E4s=-13.6×(29-25.30)2/42=-11.5eVσ3d=0.35×9+1.0×18=21.15 E3d=-13.6×(29-21.15)2/32=-92.43eVE3d <E4s, 应失去4s 电子9. 如何理解屏蔽效应和钻穿效应?如何解释同一主层中的能级分裂和不同主层中的能级交错现象?答:在多电子原子中,一个电子除受原子核引力还受其它电子斥力,导致该电子有效电荷减少,即产生屏蔽效应钻穿效应是外层电子所受到的屏蔽作用小于内层电子的屏蔽作用,产生钻到内层空间的现象同一主层角量子数不同的电子受到屏蔽作用不同,则发生能级分裂;不同主层由于外层电子出现钻穿效应导致能级交错。
大学计算机第8章 习题答案

1.以下英文缩写中,表示数据库管理系统的是(B)。
A.DB B.DBMS C.DBA D.DBS2.数据库管理系统、操作系统、应用软件的层次关系从核心到外围分别是(B)。
A.数据库管理系统、操作系统、应用软件B.操作系统、数据库管理系统、应用软件C.数据库管理系统、应用软件、操作系统D.操作系统、应用软件、数据库管理系统3.数据库系统提供给用户的接口是(A)。
A.数据库语言B.过程语言C.宿主语言D.面向对象语言4.(C)是数据库系统的核心。
A.数据模型B.数据库C.数据库管理系统D.数据库管理员5.关系数据库模型通常由3部分组成,它们是(B)。
A.数据结构、数据通信、关系操作B.数据结构、关系操作、完整性约束C.数据通信、关系操作、完整性约束D.数据结构、数据通信、完整性约束6.下列说法不正确的是(A)。
A.数据库避免了一切数据重复B.数据库减少了数据冗余C.数据库数据可以为DBA认可的用户共享D.控制冗余可确保数据的一致性7.用二维表结构表示实体及实体间关系的数据模型为(C)。
A.网状模型B.层次模型C.关系模型D.面向对象模型8..一个学生可以同时借阅多本图书,一本图书只能由一个学生借阅,学生和图书之间为(B)关系。
A.一对一B.一对多C.多对多D.多对一9.一个仓库可以存放多种零件,每种零件可以存放在不同的仓库中,仓库和零件之间为(C)关系。
A.一对一B.一对多C.多对多D.多对一10.按数据的组织形式,数据库的数据模型可分为3种模型,它们是(C)。
A、小型、中型和大型B.网状、环状和链状C.层次、网状和关系D.独享、共享和实时11.数据库中有A,B两表,均有相同字段C,在两表中C字段都设为主键。
当通过C 字段建立两表关系时,则该关系为(A)。
A.一对一B.一对多C.多对多D.不能建立关系12.如果在创建表中建立“性别”字段,并要求用汉字表示,其数据类型应当是(C)。
A.是/否B.数字C.文本D.备注13.在Access数据库对象中,体现数据库设计目的的对象是(D)。
概率论与数理统计第8章假设检验习题及答案

62第8章 假设检验一、填空题1、 对正态总体的数学期望m 进行假设检验,如果在显著性水平0.05下,接受假设00:m m =H ,那么在显著性水平0.01下,必然接受0H 。
2、在对总体参数的假设检验中,若给定显著性水平为a ,则犯第一类错误的概率是a 。
3、设总体),(N ~X 2s m ,样本n 21X ,X ,X ,2s未知,则00:H m =m ,01:H m <m 的拒绝域为 )}1(/{0--<-n t nS X a m ,其中显著性水平为a 。
4、设n 21X ,X ,X 是来自正态总体),(N 2s m 的简单随机样本,其中2,sm 未知,记å==n1i i X n 1X ,则假设0:H 0=m 的t 检验使用统计量=T Qn n X )1(-.二、计算题1、某食品厂用自动装罐机装罐头食品,规定标准重量为250克,标准差不超过3克时机器工作 为正常,每天定时检验机器情况,现抽取16罐,测得平均重量252=X 克,样本标准差4=S 克,假定罐头重量服从正态分布,试问该机器工作是否正常?解:设重量),(~2s m N X05.016==a n 4252==S X(1)检验假设250:0=m H 250:1¹m H , 因为2s 未知,在0H 成立下,)15(~/250t nS X T -=拒绝域为)}15(|{|025.0tT >,查表得1315.2)5(025.0=¹t由样本值算得1315.22<=T ,故接受0H (2)检验假设9:20=s H9:201>s H因为m 未知,选统计量 222)1(s S n x -=在0H 成立条件下,2x 服从)15(2x 分布,拒绝域为)}15({205.02x x >,查表得996.24)15(205.0=x ,现算得966.24667.26916152>=´=x 拒绝0H ,综合(1)和(2)得,以为机器工作不正常2、一种电子元件,要求其使用寿命不得低于1000小时,现在从一批这种元件中随机抽取25 件,测得其寿命平均值为950小时,已知该种元件寿命服从标准差100=s 小时正态分布, 试在显著性水平0.05下确定这批产品是否合格. 解:设元件寿命),(~2s m N X ,2s 已知10002=s,05.0,950,25===a X n检验假设1000:0=m H1000:1<m H在2s 已知条件下,设统计量)1,0(~/1000N nX s m -=拒绝域为}{05.0mm<,查表得645.195.005.0-=-=m m而645.15.2205025/1001000950-<-=-=-=m拒绝假设0H 选择备择假设1H ,所以以为这批产品不合格.3. 对 显 著 水 平 a , 检 验假 设 H 0 ; m = m 0, H 1 ; m ¹ m 0, 问当 m 0, m , a 一定 时 , 增大样本量 n 必 能 使 犯 第 二 类 错 误 概 率 b减 少 对 吗 ?并 说 明 理 由 。
第八章 习题答案

第八章 习题解答8-1考虑并回答下面的问题:(a )在确定非线性元件的描述函数时,要求非线性元件不是时间的函数,并要求有斜对称性,这是为什么?(b )什么样的非线性元件是无记忆的?什么样的非线性元件是有记忆的?它们的描述函数各有什么特点?(c )线性元件的传递函数与非线性元件的描述函数,有什么是相同的?有什么是不同的?线性元件可以有描述函数吗?非线性元件可以有传递函数吗?(d )非线性系统线性部分的频率特性曲线与非线性元件的负倒描述函数曲线相交时,系统一定能产生稳定的自激振荡吗? 解:(a )描述函数法只能用来研究非线性定常系统的特性,这要求非线性元件的特性不随时间发生变化。
在用描述函数法研究非线性系统的自振特性时,要求在正弦输入下非线性特性的输出没有直流分量,这要求非线性元件的特性是斜对称的。
(b )一般情况下用代数方程描述的非线性特性是无记忆的,根据非线性环节当前的输入就可以决定非线性环节的输出。
用微分方程描述的非线性特性是有记忆的,不能简单地根据非线性环节当前的输入决定非线性环节的输出。
无记忆非线性特性的描述函数一般为实数,有记忆非线性特性的描述函数一般为复数。
(c )线性元件的传递函数与非线性元件的描述函数都是元件的外部描述。
线性元件的传递函数表述的是元件输出拉氏变换与输入拉氏变换之比,而非线性元件的描述函数表示的是元件在正弦输入下输出基波特性。
由传递函数可以得到系统的频率特性,而描述函数一般不是频率的函数,线性元件可以有描述函数,但传递函数只适用于线性系统,非线性系统没有传递函数。
(d )只有稳定的交点才对应稳定的自激振荡。
8-2设非线性元件的输入、输出特性为35135()()()()y t b x t b x t b x t =++证明该非线性元件的描述函数为2413535()48N A b b A b A =++式中A 为非线性元件输入正弦信号的幅值。
解:由于非线性特性是单值斜对称的,所以10A =,10φ=。
第8章 群论参考答案

第8章群论习题解答提示1. 仅平凡群{e}有零元,独异点(单位半群)的幂等元不一定惟一,但群的幂等元惟一。
3. (P170) 由于变换(映射)的复合运算ο是可以结合的,恒等变换I=f1,0∈G,显然I为G 单位元。
下面只证明复合运算ο在G上是封闭的,且G中每个元素有单位元。
事实上,a,b,c,d∈Q,且a,c≠0,对于x∈Q,有(fab οfcd)(x)=fab(fcd(x))=a(cx+d)+b=acx+(ad+b),又ac≠0,ac,ad+b∈Q,故=fac,ad+b∈G,所以,复合运算在G上是封闭的。
f a,b∈G,a≠0,a,b∈Q,取f1/a,-b/a∈G,有fa,b οf1/a,-b/a=fa(1/a),a(-b/a)+b=f1,0所以,fab存在逆元f。
综上,G关于变换的复合运算ο构成群。
4. 设<S;*>是单位半群,e是单位元,H是S中所有可逆元素的集合。
显然单位元e是可逆元,所以e∈H,H非空。
若a,b∈H,则存在a-1,b-1∈S,使得a-1*a=a*a-1=e,b-1*b=b*b-1=e,于是,(b-1*a-1)*(a*b)=(a*b)*(b-1*a-1)=e,因此a*b也是可逆元,故a*b∈H,<H;*>是一代数结构。
因为H是S的子集,所以运算*在H上也是可结合的,e是<H;*>的单位元。
∀a∈H,必有a-1∈S,使得a-1*a=a*a-1=e,所以a是a-1的逆元,因此a-1∈H。
由上证得,<H;*>是一个群。
6. 在等式两边同时左乘x-1,有axba=bc,再在等式两边同时左乘a-1,右乘a-1b-1,有x=a-1bca-1b-1故方程存在解。
再证惟一性。
若方程存在两解,设为x,y,即有axba=bc=ayba,由于G是群,满足消去律,有x=y。
故解是惟一的。
7. 必要性显然。
下面证明充分性。
设|G|=n,G={a1,a2,…,an}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题8
1. 简述在CPU与外部设备之间设置接口电路的原因。
2. 接口的功能有哪些?
3. I/O接口中,一般包含有三种端口,它们是:、和。
4. 端口地址的编址方式有两种,分别是:和。
5. I/O设备数据传送控制方式有哪些?各自有什么特点?
6. 什么是中断?什么是中断源?微机系统的中断源有哪些?
7. 中断识别的方法有:、和。
8. 设机器共有5级中断,中断响应的优先次序为1→2→3→4→5,各级中断的屏蔽位如表8.3所示。
其中“1”对应于屏蔽,“0”对应于开放。
表8.3 各级中断的屏蔽位
(1)求实际中断处理次序;
(2)若在运行用户程序时,同时出现2、4级中断请求,而在处理第2级中断未完成时,又同时出现1、3、5级中断请求,试画出此程序运行过程示意图。
9. 简述中断处理过程。
10. 简述DMA的三种工作方式。
11. 简述DMA的数据传输过程。
12. 简述通道的功能。
13. 根据通道的工作方式不同,通道可以分为:、和。
参考答案
习题8
1. 略
2. 略
3. 数据端口;状态端口;控制端口
4. 统一编址;独立编址
5. 略
6. 略
7. 查询法;向量法;强置程序计数器法
8. (1)实际中断处理次序为:1→4→5→2→3
(2)运行过程示意图如附图8.1所示。
附图8.1 运行过程示意图
9. 略
10. 略
11. 略
12. 略
13. 选择通道;数组多路通道;字节多路通道。
