频谱分析(完整版)
第3章-频谱分析

周期信号分解为一系列虚指数函数的离散和或连续和。 利用
信号的正弦分解思想, 系统的响应则可表示为不同频率正弦分 量产生响应的叠加。
第3章 连续时间系统的频域分析
3.1.2 傅立叶级数 1. 周期信号的三角级数表示 在电子技术、 通信工程、 自动控制等领域, 除了正弦
信号外, 非正弦周期信号也经常遇到。 把非正弦周期信号分 解为傅立叶级数是法国科学家傅立叶所做出的巨大贡献。 1807年, 傅立叶以他惊人的洞察力大胆断言: 任何周期函数都 可以用收敛的正弦级数表示。 他的关于把信号分解为正弦分 量的思想对后来的自然科学等领域产生了巨大的影响。
【例 3-4】 画出图3-4所示矩形周期信号f(t)的双边频谱图
形。
第3章 连续时间系统的频域分析
解 由
Fn
1 T
T /2 f t ejn1t dt 1 2sinn π/ 4
T / 2
4 n π/ 4
得:
F0=0.25 F±1=0.225 F±2=0.159 F±3=0.075 F±4=0 F±5=-0.045 F±6=0.053 F±7=-…
12 e jn1t dt
0
2
j4n1
e
jn 2
1
1
jn
jn
e4
e
j
n 4
jn
e 4
2
jn
e4
sin
n
n
4
故f(t)展开为指数形式的傅立叶级数为
f
t
(
2
jn
e4
sቤተ መጻሕፍቲ ባይዱn
n
) e jn1t
n
4
第3章 连续时间系统的频域分析
3.2 周期信号的频谱及特点
频谱分析

一个信号的频谱告诉我们这个信号包含哪些正弦函数。
比如,信号X(t)=2sin(3t).它的频谱只有一个点:(3,2).也就是说,这个信号它只包含了一个正弦函数,角频率为3,幅值为2。
傅立叶定理指出:任何一个周期函数都可以分解为很多正弦函数的和。
进而我们可以把一个非周期函数看作是一个周期为无限大的周期函数。
傅立叶定理有着非常广泛的应用。
加窗在进行离散傅立叶dft变换时,为了减小频谱泄漏现象要进行加窗处理比如使用海宁窗等,实际上是对序列的边界点进行了平滑处理以使得以此序列进行周期拓展时边界点是连续的.对于一已知序列在时域不加窗(或加矩形窗)和加海宁窗再进行dft,所得结果肯定不一致.在实际工程应用领域,例如电气工程中的谐波分析等不加窗后进行dft所得结果的物理意义是显而易见的.但加了窗后反而使结果没什么意义了. 从另外一种角度出发,假设序列是同步采样得到的结果,也就是边界点上没有出现跳变,自然也无需再加窗平滑处理,那此时再进行加窗处理相当于改变了输入序列的值,变换结果与原先不同也是自然的了. 是不是加窗变换后还要进行一些处理才能得到与实际意义(比如物理意义)相符的结果?通常做的ft应该都是加窗处理了的,只不过采用了一个矩形窗而你没有注意到而已。
加窗就是信号乘以窗函数,相应于频域就是离散信号的频谱与窗函数频谱的卷积。
离散的数字信号频谱是以采样率为周期的从负无穷到正无穷的周期性谱,而有限长度的时间窗对应于无限长度的频率响应,因此它与信号频谱的卷积自然也是无限长度的,也就是产生了频谱的混迭,信号带宽越宽混迭的影响就更大。
自然dtf采样到的-pi到+pi的频谱也存在了混迭,除了一些解析解信号的频谱有可能由这些频谱中推算出原始1)信号加窗与分帧是两个不同的概念.2)一首歌首先要经过分帧,下一步才是加窗.3)音频信号属于"短时平稳过程" 每一帧信号视为平稳过程,即统计特性平稳.4)因为傅立叶变换对应的是无限信号,信号经过分帧后变成有限信号,分帧的信号再进行傅立叶变换后,高频部分将有"泄露",所以要加窗.5)窗函数的拼谱都是在某高频部分截止,所以每帧信号加窗后的傅立叶变化,频谱基本"泄露"6)详细内容请参考<信号与系统>卷积中文名称:卷积英文名称:convolution定义:数学中关于两个函数的一种无穷积分运算。
频谱分析

有早期的频谱仪几乎 目前单纯的数字式频谱仪
都属于模拟滤波式或 一般用于低频段的实时分
超外差结构,并被沿 析,尚达不到宽频带高精
用至今
度频谱分析
频谱分析仪的分类(续2)
实时频谱仪和非实时频谱仪
实时分析应达到的速度与被分析信号的带宽及 所要求的频率分辨率有关。一般认为,实时分析是 指在长度为T的时段内,完成频率分辨率达到1/T的 谱分析;或者待分析信号的带宽小于仪器能够同时 分析的最大带宽。
ux 电调谐 滤波器
视频 检波器
Y放大
锯齿波 发生器
X 放大
数字滤波式频谱仪
数字滤波式频谱仪在现代频谱分析仪中占 有重要地位。数字滤波器的形状因子较小,因 而提高了频谱仪的频率分辨率;具有数字信号 处理的高精度、高稳定性、可重复性和可编程 性等普遍优点。
利用数字滤波器可以实现频分或时分复用,因此 仅用一个数字滤波器就可以实现与并行滤波式等效的 实时频谱仪。用单个数字滤波器代替多个模拟滤波器 之后,滤波器的中心频率由时基电路控制使之顺序改 变。
脉冲宽度和频带宽度(续1)
脉冲宽度与频带宽度对周期信号频谱的影响
X(t)
-2T0
-T0
-T1 T1T0/2 T0
2T0
t
连续方波信号的波形如上图所示,它在一个周
期内的时域表达式为
x(t )
1
t T1
0 T1 t T0 2
其中T0为方波的周期,脉冲宽度为2T1。
脉冲宽度和频带宽度(续2)
窄带滤波器 检波器
电
子
窄带滤波器 检波器
扫
ux 前置 放大器
窄带滤波器
检波器
描 开 关
Y放大
2 信号分析基础(频谱分析)
(2.69)
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
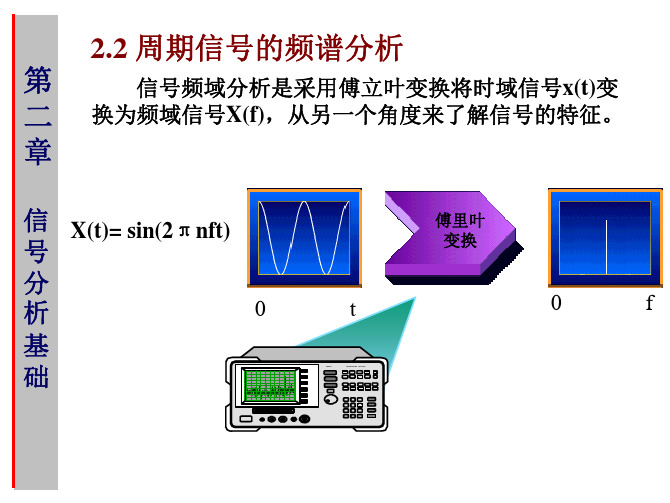
式2.68称为 x t 的傅立叶变换,称式2.69为 X 的 傅立叶逆变换,两者称为傅立叶变换对,可记为
x t X
IFT
FT
2 f 代入傅立叶积分式中,则式2.68, 2.69变为
X f x t e j 2 ft dt
Im[X ( f )] ( f ) arctgRe[ X ( f )]
x (t ) 1 X ( )e jt d 2 X ( ) x (t )e jt dt
X f 连续幅值谱
f
连续相位谱
X 频谱密度函数
2.2 周期信号的频谱分析 第 二 章
信号频域分析是采用傅立叶变换将时域信号x(t)变 换为频域信号X(f),从另一个角度来了解信号的特征。
信 X(t)= sin(2πnft) 号 分 0 析 基 础
傅里叶 变换
t
8563A
SPECTRUM ANALYZER 9 kHz - 26.5 GHz
0
f
频域分析的概念 周 期 信 号 的 频 谱 分 析
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
T0 T0 , 设有一个周期信号x(t)在区间 2 2
以傅立叶级数表示为
x t
n
ce
n
jn0t
1 式中 cn T0
T0 2 T 0 2
x t e
jn0t
dt
将其代入上式则得
n n
幅频谱 相频谱
频谱图的概念 周 期 信 号 的 频 谱 分 析
第3章 频谱分析

jn1t
n 1
F jn e
1
jn1t
式(3-9)又可写为
f t
F jn e
1
jn1t
F e
n
jn1t
(3-10)
第 3章
连续时间系统的频域分析
式(3-10)称为周期信号f(t)的指数形式傅立叶级数展开式, 其中F(jnω1)为傅立叶系数, 简写为Fn, 又称为频谱函数。 由于 Fn为复数, 所以式(3-10)又称为复系数形式傅立叶级数展开式。 傅立叶系数Fn为
(n=0, 1, 2, 3, …) 4 T /2 bn f t sin n1tdt T 0
an 0
第 3章
连续时间系统的频域分析
(3) 奇谐函数。 若周期信号f(t)波形沿时间轴平移半个周 期后与原波形相对于时间轴镜像对称, 即满足
T f t f t 2
bn 0
故
1 2 sinn π/ 4 f t a0 an cos n1t cos n1t 2 n π n 1 n 1
因此
1 a0 2
an
2 sinn π/ 4 nπ
第 3章
连续时间系统的频域分析
即 a0=0.5 a1=0.45 a2≈0.32 a3=0.15
1807年, 傅立叶以他惊人的洞察力大胆断言: 任何周期函数都
可以用收敛的正弦级数表示。 他的关于把信号分解为正弦分 量的思想对后来的自然科学等领域产生了巨大的影响。
周期信号是定义在(-∞, ∞)区间内, 每隔一定时间T按相
同规律重复变化的信号。 图3-1所示是实际的周期性非正弦信号, 它们一般表示为
频谱分析

2.1频谱分析原理时域分析只能反映信号的幅值随时间的变化情况,除单频率分量的简单波形外,很难明确提示信号的频率组成和各频率分量大小,而频谱分析能很好的解决此问题。
由于从频域能获得的主要是频率信息,所以本节主要介绍频率(周期)的估计与频谱图的生成。
2.2.1DFT与FFT对于给定的时域信号y,可以通过Fourier变换得到频域信息Y。
Y可按下式计算式中,N为样本容量,Δt = 1/Fs为采样间隔。
采样信号的频谱是一个连续的频谱,不可能计算出所有的点的值,故采用离散Fourier变换(DFT),即式中,Δf = Fs/N。
但上式的计算效率很低,因为有大量的指数(等价于三角函数)运算,故实际中多采用快速Fourier变换(FFT)。
其原理即是将重复的三角函数算计的中间结果保存起来,以减少重复三角函数计算带来的时间浪费。
由于三角函数计算的重复量相当大,故FFT能极大地提高运算效率。
2.2.2 频率、周期的估计对于Y(kΔf),如果当kΔf = 时,Y(kΔf)取最大值,则为频率的估计值,由于采样间隔的误差,也存在误差,其误差最大为Δf / 2。
周期T=1/f。
从原理上可以看出,如果在标准信号中混有噪声,用上述方法仍能够精确地估计出原标准信号的频率和周期,这个将在下一章做出验证2.2.3 频谱图为了直观地表示信号的频率特性,工程上常常将Fourier变换的结果用图形的方式表示,即频谱图。
以频率f为横坐标,|Y(f)|为纵坐标,可以得到幅值谱;以频率f为横坐标,arg Y(f)为纵坐标,可以得到相位谱;以频率f为横坐标,Re Y(f)为纵坐标,可以得到实频谱;以频率f为横坐标,Im Y(f)为纵坐标,可以得到虚频谱。
根据采样定理,只有频率不超过Fs/2的信号才能被正确采集,即Fourier 变换的结果中频率大于Fs/2的部分是不正确的部分,故不在频谱图中显示。
即横坐标f ∈[0, Fs/2]2.5.运行实例与误差分析为了分析软件的性能并比较时域分析与频域分析各自的优势,本章给出了两种分析方法的频率估计的比较,分析软件的在时域和频域的计算精度问题。
频谱分析(完整版)

Matlab 信号处理工具箱 帮助文档 谱估计专题翻译:无名网友 & Lyra频谱分析Spectral estimation (谱估计)的目标是基于一个有限的数据集合描述一个信号的功率(在频率上的)分布。
功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信号的检测。
从数学上看,一个平稳随机过程n x 的power spectrum (功率谱)和correlation sequence (相关序列)通过discrete-time Fourier transform (离散时间傅立叶变换)构成联系。
从normalized frequency (归一化角频率)角度看,有下式()()j mxx xx m S R m eωω∞-=-∞=∑注:()()2xx S X ωω=,其中()/2/21limN j n n N n N X x e Nωω→∞=-=∑πωπ-<≤。
其matlab近似为X=fft(x,N)/sqrt(N),在下文中()L X f 就是指matlab fft 函数的计算结果了使用关系2/s f f ωπ=可以写成物理频率f 的函数,其中s f 是采样频率()()2/sjfm f xx xxm S f R m eπ∞-=-∞=∑相关序列可以从功率谱用IDFT 变换求得:()()()/22//22sss f jfm f j m xx xx xx sf S e S f e R m d df f πωππωωπ--==⎰⎰序列n x 在整个Nyquist 间隔上的平均功率可以表示为()()()/2/202ss f xx xx xx sf S S f R d df f ππωωπ--==⎰⎰ 上式中的()()2xx xx S P ωωπ=以及()()xx xx sS f P f f = 被定义为平稳随机信号n x 的power spectral density (PSD)(功率谱密度) 一个信号在频带[]1212,,0ωωωωπ≤<≤上的平均功率可以通过对PSD 在频带上积分求出[]()()211212,xxxx P P d P d ωωωωωωωωωω--=+⎰⎰从上式中可以看出()xx P ω是一个信号在一个无穷小频带上的功率浓度,这也是为什么它叫做功率谱密度。
频谱分析
1. FFT的提出 DFT在18世纪就已经被提出,但是一直到20世纪,都没有被真正用 于实际的谱分析和信号处理。 直到1965年IBM的T.W.Cooley和MIT的J.W.Tuky提出了基2FFT算法 之后,使DFT算法的运算效率提高了1个数量级以上。
F (m )
N 1
f ( k )W N
6.3.1 离散傅里叶变换(DFT)
DFT的应用举例:
subplot(3,2,1);plot(wk,abs(Xk));
例:对长度为26的三角形序列x (n),编写matlab程序验证频 率采样定理。 close all;clear all;clc; M=27;N=32;n=0:M; xa=0:floor(M/2); xb= ceil(M/2)1:-1:0; xn=[xa,xb]; Xk=fft(xn,1024); X32k=fft(xn,32) x32n=ifft(X32k ); X16k=X32k(1:2:N); x16n=ifft(X16k,N/2); ) subplot(3,2,2);stem(n,xn,'.');bo x on k=0:1023;wk=2*k/1024;
(a)FT[X(n)] 200
(b) 三 角 波 序 列 ;x(n) 20 15
|X(ej )|
x(n)
100 0 0 0.5 / (c) 16点 频 域 采 样 200 1
10 5 0
0
5
10
15 n
20
25
30
(d) 16点 IDFT[X16(k)] 20
|X16(k)|
信号时域特性与频域特性的关系
频谱分析

频谱分析:将时域信号变换至频域加以分析的方法称为频谱分析。
频谱分析的目的是把复杂的时间历程波形,经过傅里叶变换分解为若干单一的谐波分量来研究,以获得信号的频率结构以及各谐波和相位信息。
(傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。
从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。
从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。
)很多情况下的振动是周期的,任何关于时间的周期函数都能展开成傅立叶级数,即无限多个测试信号的频域分析是把信号的幅值、相位或能量变换以频率坐标轴表示,进而分析其频率特性的一种分析方法,又称为频谱分析。
对信号进行频谱分析可以获得更多有用信息,如求得动态信号中的各个频率成分和频率分布范围,求出各个频率成分的幅值分布和能量分布,从而得到主要幅度和能量分布的频率值。
由时间函数求频谱函数的傅里叶变换公式就是将该时间函数乘以以频率为系数的指数函数之后,在从负无限大到正无限大的整个区间内,对时间进行积分,这样就得到了与这个时间函数对应的,以频率为自变量的频谱函数。
频谱函数是信号的频域表示方式。
根据上述傅里叶变换公式,可以求出常数(直流信号)的频谱函数为频域中位于零频率处的一个冲激函数,表示直流信号就是一个频率等于零的信号。
与此相反,冲激函数的频谱函数等于常数,表示冲激函数含有无限多个、频率无限密集的正弦成分。
同样的,单个正弦波的频谱函数就是频域中位于该正弦波频率处的一对冲激函数。
利用傅里叶变换的方法对信号进行分解,并按频率展开,使其成为频率的函数,进而在频率域中对信号进行研究和处理的一种过程,称为频谱分析。
对信号进行频谱分析,是对其进行傅里叶变换,得到其振幅谱与相位谱。
分析软件主要为Matlab。
对于信号来说,分模拟信号与数字信号。
进行频谱分析时,对于模拟信号来说,首先对其进行抽样,使其离散化,然后利用离散傅里叶变换(DFT)或者快速傅里叶变换(FFT),然后对其幅度(ABS)和相位(ANGLE)的图像进行分析,而对于数字信号来说,则可直接进行离散傅里叶变换或快速傅里叶变换。
频谱分析

频谱分析利用傅里叶变换的方法对振动的信号进行分解,并按频率顺序展开,使其成为频率的函数,进而在频率域中对信号进行研究和处理的一种过程,称为频谱分析。
怎样进行频谱分析:利用频谱分析仪进行测量,输入信号不能有失真,因此要按特定应用的要求设置频谱分析仪和优化测量步骤,以达到最好的技术指标。
下面的测量提示对这些步骤有详细的说明。
1. 选择最好的分辨率带宽 (RBW)必须认真考虑分辨率带宽 (RBW)的设置,因为他关系到频谱成分的分离,适宜的噪声基底的设置和信号的解调。
通过低电平信号的测量,可以看到使用窄RBW的优点。
在使用窄RBW时,频谱分析仪显示出较低的平均噪声级 (DANL),且动态范围增加,灵敏度有所改进。
在图3中,把RBW从100kHz改变到10kHz 将能更好地分辨-95dBm的信号。
但并非任何情况都是最窄的RBW最好。
对于调制信号,RBW一定要设置得足够宽,使它能将信号边带包括在内。
如果忽略这一点,测量将是极不精确的。
窄RBW设置的一项重要缺点是扫频速度。
更宽的RBW设置在给定频率范围内允许更快的扫频。
图4和图5比较了在200MHz频率范围内,10kHz和 3kHzRBW的扫频时间。
一定要知道RBW 选择时所必须的基本权衡因素,使得用户在明白哪些参数最为重要的时候,给以适当的优化。
但在权衡不可避免时,现代频谱分析仪可为您提供弱化,甚至消除这些因素的方法。
通过使用数字信号处理,频谱分析仪在实现更精确的测量的同时还提供更高的速度,即使是使用窄RBW。
2. 改进测量精度在进行任何测量前,必须了解有哪些可以改进幅度和频率测量精度的技术。
自校准功能可用来产生误差校正系数 (例如幅度改变—分辨率带宽),分析仪随后用它校正测量数据,得到更好的幅度测量结果,并使您能在测量过程中更灵活地改变控制。
当被测装置接到经校准的分析仪时,信号传输网络可能会使感兴趣信号减弱或变形,必须在测量中排除这一影响,见图6。
一种方法是使用分析仪的内置幅度校正功能,一个信号源以及一个功率表。
(完整word版)DFT信号频谱分析

一,实验名称: DFT 的频谱分析 二,实验目的:1. 加深对 DFT 原理的理解,熟悉DFT 的性质。
2. 掌握离散傅里叶变换的有关性质,利用Matlab 实现DFT 变换3. 深刻理解利用 DFT 分析信号频谱的原理,分析实现过程中出现的现象及解决方法三,实验原理:所谓信号的频谱分析就是计算信号的傅里叶变换。
连续信号与系统的傅里叶分析显然不便于直接用计算机进行计算,使其应用受到限制,而DFT 是一种时域和频域均离散化的变换,适合数值运算,成为分析离散信号和系统的有力工具。
工程实际中,经常遇到的连续信号Xa(t),其频谱函数Xa(jW)也是连续函数。
数字计算机难于处理,因而我们采用DFT 来对连续时间信号的傅里叶变换进行逼近,进而分析连续时间信号的频谱。
离散傅里叶变换是有限长序列的傅里叶变换,它相当于把信号的傅里叶变换进行等频率间隔采样,并且有限长序列的离散傅里叶变换和周期序列的离散傅里叶级数本质是一样的。
快速傅里叶变换(FFT )并不是一种新的变换,它是离散傅里叶变换的一种快速算法,并且主要是基于这样的思路而发展起来的:(1)把长度为N 的序列的DFT 逐次分解成长度较短的序列的DFT 来计算。
(2)利用WN(nk)的周期性和对称性,在DFT 运算中适当的分类,以提高运算速度。
(对称性nk N nk N W W N-=+2,12-=NN W ;周期性nkN nk N nrN N k rN n NW W W W ---==)(,r 为任意整数,1=nrN N W )离散傅里叶变换的推导:离散傅里叶级数定义为nk j N k p p ek x Nn x N21)(1)(π∑-==(1-1)将上式两端乘以nm j Ne π2-并对n 在0~N-1求和可得⎥⎦⎤⎢⎣⎡==∑∑∑∑∑-=---=-=-=---=-10)(110101)(1N2N2N2)()(1)(N n m k n j N N k p N n N k m k n j pN n nm j pe k X ek XNen xπππ 因为{mk 1mk 0)(N)(10)(N 2N2N2-1-1N 11=≠---=-==∑m k j m k j N n m k n jee eNπππ所以∑∑-=-=--=1010)()()(N2N k p N n nm j pm k k X en xδπ 这样∑-=-=10N2)()(N n nm j p p en x m X π用k 代替m 得∑-=-=10N2)()(N n nk j p P en x k X π (1-2)令N2πj N eW -=,则(1-2)成为DFS[]∑-===1)()()(N n nkNp p pW n x k Xn x (1-3)(1-1)成为 IDFS []∑-=-==10)(1)()(N n nkNp p p W k X N n x k X (1-4) 式(1-3)、(1-4)式构成周期序列傅里叶级数变换关系。
3-中文版-频谱分析updated

频率 采样频率
抗混滤波器 关
抗混滤波器 开
f1
2
BA 7682-11, 30
数字滤波分析仪(CPB)
传感器 前置放大器 A/D 变换 数字滤波 检波器/ 平均器 显示/ 输出
A/D
12.5 16 20kHz
RMS
6.3 8 10 kHz
输出
频率 对数坐标 20 50 31.5 63 100 200 500 1K 1K 2K 2K 5K 10K 20K 4K 8K 16K 倍频程坐标 1/3倍频程坐标
低通 频率
高通
频率 频率 带通 频率 带阻 频率
BA 7682-11, 9
滤波器响应时间
传感器 前置放大器 滤波器 检波器/ 平均器 RMS
幅值 幅值
显示/ 输出
A
A
A 8% 时间
时间
TR 1/B B TR 1
BA 7682-11, 10
带通滤波器和带宽
B 0 理想滤波器
带宽, B = f2 – f1 中心频率 = f0
Squaring 2
Averaging
1 T
Root
dt
Out
2 TA 1 TA In
线性平均
指数平均
vout = vin
2
TA
0
Time
TA = 2 = 2 RC
BA 7682-11, 17
平均时间的选择
Ripple 4 dB
1
RMS
Time Time
fm
TA = f m
BA 7682-11, 23
内容
时域与频域 信号类型
滤波器类型
音乐信号频谱分析

利用双线性变换设 计IIR滤波器( 巴特 沃斯数字低通滤波 器的设计)",首先 要设计出满足指标
要求的模拟滤波器 的传递函数Ha(s), 然后由Ha(s)通过双 线性变换可得所要 设计的IIR滤波器的
系统函数H(z)
如果给定的指标为 数字滤波器的指标, 则首先要转换成模 拟滤波器的技术指 标,这里主要是边 界频率Wp和Ws的转 换,对ap和as指标
2.语音信号的采集
但过高的采样频率并不可取,对固定长 度(T)的信号,采集到过大的数据量 (N=T/△t),给计算机增加不必要的计算 工作量和存储空间
若数据量(N)限定,则采样时间过短,会 导致一些数据信息被排斥在外
采样频率过低,采样点间隔过远,则离 散信号不足以反映原有信号波形特征, 无法使信号复原,造成信号混淆
3.低通滤波器的设计
plot(x2)
subplot(2,1,2)
title('IIR低通滤波器 滤波后的时域波形')
%画出滤波前的时域图 plot(fl) sound(fl, 44100)
title('IIR低通滤波器 滤波前的时域波形')
%画出滤波后的时域图
%播放滤波后的信号
3.低通滤波器的设计
1 散的数字语音信号
采样也称抽样,是信号在时间上的离散化,即按照一定时间间隔△t在模拟信号x(t)上逐点采取其瞬时
2值
采样时必须要注意满足奈奎斯特定理,即采样频率fs必须以高于受测信号的最高频率两倍以上的速度进
3 行取样,才能正确地重建波它是通过采样脉冲和模拟信号相乘来实现的 4 在采样的过程中应注意采样间隔的选择和信号混淆:对模拟信号采样首先要确定采样间隔 5 如何合理选择△t涉及到许多需要考虑的技术因素 6 一般而言,采样频率越高,采样点数就越密,所得离散信号就越逼近于原信号
频谱分析法

目录中文摘要 (1)Abstract (2)第一章目的及意义 (3)第二章转子系统振动监测与诊断的信息表达 (1)2.1波形分析;去 (1)2.2频谱分析法 (1)2.3轴心轨迹分析法 (2)2.4 艇跟踪分析法 (4)2.4.1奈奎斯特图分析法 (4)242波德图 (4)2.4.3瀑布图和坎贝尔图 (4)第三章转子系统的故瞳机理 (6)3.1转子不平衡 (6)3.2转子不对中 (7)3.3油膜涡动及油膜振荡 (8)3.4翳碰摩 (9)第四章转子系统的故障模拟实验研究 (10)4.1 ZT—3型转子振动实验台介绍 (10)4.2 DH动态测试分析软彳牛介绍 (13)4.3实验环境 (13)4.4实验结果分析 (14)4.4.1不平衡实验 (14)4.4.2不对中实验 (17)4.4.3碰摩实验 (19)4.4.4油膜涡动实验 (21)4.4.5升降速实验 (24)结论 (28)致谢 (29)参考文献 (30)中文摘要旋转机械(例如:航空发动机、压缩机、汽轮机等)是工业部门中应用最为广泛的一类机械设备。
这类设备常常由于出现各种故障而影响其正常运转,采用诊断技术对于保证机械设备安全可靠的运行,进而提高企业的经济效益,具有十分重要的意义。
本论文探讨了旋转机械常见故障机理及信号分析方法,分析了转子不平衡、不对中、转静碰摩、油膜涡动及升降速时振动参数的变化规律及诊断特征。
同时, 应用ZT-3型多功能转子模拟实验台进行了转子不平衡、不对中、转静碰摩、油膜涡动等故瞳的模拟,并用DH5922动态信号分析系统进行了振动数据的采集和分析,获取了振动信号的时间波形、频谱及轴心轨迹等特征,验证了转子常见故障的振动特征,本论文的硏究将为以航空发动机为代表的高速旋转机械的故障诊断奠定基础。
关键词:航空发动机;故障诊断;振动测试;转子实验台AbstractRotary machinery such as aero-engine, compressor turbine is a kind of machine employed widely in industry, and their faults often affect their normal operation. Therefore, fault diagnosis of rotary machinery is very important to ensure the safety of equipment and improve economic benefit.In this paper fault mechanism and signal analysis of rotary machine are discussed, the way of signal analysis, and the vibration characters of imbalanee, rub, oil volute movement and ascending and falling speed of rotor are researched. At the same time, using the multi-functions rotor test desk and DH5922 dynamic signal analysis system vibration data acquisition and fault characters analysis are carried out. The research of this paper will establish the base for high-speed rotary machine such as aero-engine ・Keywords: Aero-engine; Fault diagnosis; Vibration test; Rotor test desk第一章目的及意义航空发电机是一类重要的动能转子机械,旋转机械是各类型机械设备中数最多,应用最广泛的一类机械,航空发电机是一类重要的大型高速的动能转子机械,旋转机械是各类型机械设备中数量最多应用最广泛的一类, 通过对旋转机械的典型故障分析找出典型故瞳的振动特征是进行模式识别的必要条件,因而是进行精密诊断的基础。
信号的频谱分析 ppt课件

▪§1-1 信号及其分类 ▪§1-2 信号的时域及频域描述 ▪§1-3 周期信号的频谱分析 ▪§1-4 非周期信号的频谱分析 ▪§1-5 信号的相关分析 ▪§1-6 数字信号的处理与应用 ▪§1-7三维DFT谱的概念及应用
精品资料
• 你怎么称呼老师?
• 如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进?
➢ 信号:只涉及被测参量的量值特征和时变特征, 而不涉及其物理特征。
▪ 信号分析
运用数学工具对信号加以分析研究,提取有 用的信号,从中得到一些对工程有益的结论和方 法。
§ 1-1 信号及其分类 ▪ 信号的分类与描述
➢ 信号的分类主要是依据信号波形特征来划分的, 在介绍信号分类前,先建立信号波形的概念
周期信号又可分为简谐信号(单一频率)和复杂周期 信号(多个频率)。
按正弦或余弦规律变化的信号,工程称为简谐信号;复杂周期信 号波形可看成是由若干个频率比为有理数的正弦信号叠加而成。
简谐信号(简单周期信号) x(t)A 0si(n t0)
§ 1-1 信号及其分类
复杂周期信号 x ( t ) A 0 s( i 0 t n 0 ) A 1 s( i 1 t n 1 )
第三节 周期信号的频谱分析
信号的表示:★ 时间域表示,例如 x ( t ) ,简称时域信号; ★ 频率域表示,例如X ( f ),简称频域信号;
它们的关系:
x(t) FT X(f) IFT
§ 1-3 周期信号的频谱分析
信号频谱分析是采用傅立叶变换将时域信号 x(t)变换为频域信号X(f),从而帮助人们从另一个 角度来了解信号的特征。
三、指数形式的傅里叶级数。
• 三角傅里叶级数与指数傅里叶级数并不是两种不同
频谱分析

目录目录 (1)摘要 (2)一. DFT的简介 (3)1.1概述 (3)1.2.DFT的定义 (3)1.3谱分析的原理 (3)二.用DFT对连续信号进行谱分析 (4)三.用DFT进行谱分析的误差问题 (5)1.混叠现象 (5)2.栅栏效应 (5)3.截断效应 (6)四.设计实现 (6)1. 设计内容 (6)2.用Matlab软件实现 (7)五.结果分析 (11)六.结束语 (12)七致谢 (12)八参考文献 (13)摘要数字信号处理方法的一个重要用途是在离散时间域中确定一个连续时间信号的频谱,通常称为频谱分析,更具体的说它也包括能量谱或功率谱,所谓信号的谱分析就是计算信号的傅里叶变换,而DFT的实质是有限长序列傅里叶变换的有限点离散采样,从而实现了频域离散化,使数字信号处理可以在频域采样数值运算的方法进行,这样就大大提高了数字信号处理的灵活性,从而使信号的实时处理和设备的简化得以实现。
利用Matlab软件对正余弦信号进行设计程序分析并画出频谱图,所以说DFT不仅在理论上有重要意义,而且在各种信号的处理中亦起着核心的作用,数字频谱分析可以应用在很广的领域。
关键字:Matlab 频谱分析DFT一. DFT 的简介1.1概述频谱是为了是信号从时域转到频域而对信号进行分析的方法,可分为幅值谱、相位谱、实频谱、虚频谱、功率谱等,他们从不同方面描述了信号的特征,从而表示出信号的频谱信息,幅值谱和功率谱反应信号各频率的能量,相位谱可以反映信号各频率分量的初始相位,实频谱和虚频谱在工程中的应用相对比较少,而功率谱和幅值谱则比较广泛,通常在对正余弦信号进行谱分析时主要是用Matlab 对其进行分析,从而使信号的实时处理和设备的简化得以实现,而DFT 是一种时域和频域均离散化的变换,适合数值运算,成为计算机分析离散信号和系统的有力工具。
1.2.DFT 的定义设x(n)是一个长度为M 的有限长序列,则定义x(n) 的N 点离散傅里叶变换为X(k)=DFT[x (n )]=kn N N o n W n x ∑-=1)( k=0,1,…,N-1 (1)X(k)的离散离散傅里叶逆变换为x (n )=IDFT[X (k )]=N 1kn N N o n Wk X --=∑1)( n=0,1,…,N-1 (2)式中,,N 称为DFT 变换区间长度,N ≥M ,通常称(1)式和(2)式为离散傅里叶变换对。
FFT频谱分析

Matlab fftshift 详解- 信号处理基本功一. 实信号情况因为实信号以fs为采样速率的信号在fs/2 处混叠,所以实信号fft的结果中前半部分对应[0, fs/2],后半部分对应[ -fs/2, 0]1)实信号fft的结果前半部分对应[0, fs/2]是正频率的结果,后半部分对应[ -fs/2, 0]是负频率的结果。
大于fs/2的部分的频谱实际上是实信号的负频率加fs的结果。
故要得到正确的结果,只需将视在频率减去fs即可得到频谱对应的真实负频率2)如果要让实信号fft的结果与[-fs/2, fs/2]对应,则要fft后fftshift一下即可,fftshift的操作是将fft结果以fs/2为中心左右互换3)如果实信号fft的绘图频率f从[-fs/2, fs/2],并且没有fftshift,则fft正频谱对应f在[0, fs/2]的结果将混叠到(f - fs/2)的位置;fft负频谱对应f在[-fs/2, 0]的结果混叠到f + fs - fs/2 的位置,注意这里f为负值,也就是说此种情况下fft负频谱对应的视在频率减去fs/2即可得到频谱对应的真实负频率二. 复信号情况1)复信号没有负频率,以fs为采样速率的信号,fft的频谱结果是从[0, fs]的。
2)在f > fs/2 时,对复信号的fft结果进行fftshift会产生频率混叠(将下面的示例2中的频率从f=15改为f=85可以验证f=85的谱线在fftshift后跑到f = -15 = 85 - fs = 85 - 100的位置了),所以复信号也一般要求f <= fs/23)在对雷达的慢时间维(复信号)进行fft后,由于要用doppler = ((0:LFFT-1)/LFFT - 0.5)*PRF; 计算多普勒频率,所以对该慢时间信号fft后要fftshift下,以便和正确的频率单元相对应。
注意多普勒频率fd < = PRF/2 时才测的准!fftshift作用:将零频点移到频谱的中间用法:Y=fftshift(X)Y=fftshift(X,dim)描述:fftshift移动零频点到频谱中间,重新排列fft,fft2和fftn的输出结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
翻译:无名网友 & Lyra
频谱分析
Spectral estimation(谱估计)的目标是基于一个有限的数据集合描述一个信号的功 率(在频率上的)分布。功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信 号的检测。 从数学上看,一个平稳随机过程 xn 的 power spectrum(功率谱)和 correlation sequence(相关序列)通过 discrete-time Fourier transform(离散时间傅立叶变换) 构成联系。从 normalized frequency(归一化角频率)角度看,有下式
ˆ f P xx k
其中
X L fk fs L
2
, fk
kf s , k 0,1, , N 1 N
L 1
X L f k xL n e 2 jkn / N
n 0
选择 N 是大于 L 的下一个 2 的幂次是明智的, 要计算 X L f k 我们直接对 xL n 补零到 长度为 N。假如 L>N,在计算 X L f k 前,我们必须绕回 xL n 模 N。 作为一个例子,考虑下面 1001 元素信号 xn ,它包含了 2 个正弦信号和噪声 randn('state',0); fs = 1000; % Sampling frequency t = (0:fs)/fs; % One second worth of samples A = [1 2]; % Sinusoid amplitudes (row vector) f = [150;140]; % Sinusoid frequencies (column vector) xn = A*sin(2*pi*f*t) + 0.1*randn(size(t)); 注意:最后三行表明了一个方便的表示正弦之和的方法,它等价于: xn = sin(2*pi*150*t) + 2*sin(2*pi*140*t) + 0.1*randn(size(t)); 对这个 PSD 的周期图估计可以通过产生一个周期图对象(periodogram object)来计算 Hs = spectrum.periodogram('Hamming'); 估计的图形可以用 psd 函数显示。 psd(Hs,xn,'Fs',fs,'NFFT',1024,'SpectrumType','twosided')
% Sampling frequency % One-tenth of a second worth of samples % Sinusoid amplitudes % Sinusoid frequencies
0 0 Ponesided 2 Pxx 0
信号在频带 1 , 2 , 0 1 2 上的平均功率可以用单边 PSD 求出
2
P1 ,2
1
P
onesided
d
频谱估计方法
Matlab 信号处理工具箱提供了三种方法 Nonparametric methods(非参量类方法) PSD 直接从信号本身估计出来。最简单的就是 periodogram(周期图法) ,一种改进 的周期图法是 Welch's method。更现代的一种方法是 multitaper method(多椎体法) 。
M
x n Ak e jk n
k 1
其频谱是
M
X f f s Ak f f k
k 1
对一个有限长序列,就变成了
XL f
1 fs
fs / 2
M
M
fs / 2
f s Ak f k WR f d AkWR f f k
S xx f
m
R m e
xx
2 jfm / f s
相关序列可以从功率谱用 IDFT 变换求得:
Rxx m
fs / 2 S xx e jm S xx f e 2 jfm / f s d df 2 fs fs / 2
S xx
m
R m e
xx
2
j m
注: S xx X ,其中 X
lim N
1 N
N /2 n N / 2
xne jn 。其 matlab
近似为 X=fft(x,N)/sqrt(N),在下文中 X L f 就是指 matlab fft 函数的计算结果了 使用关系 2 f / f s 可以写成物理频率 f 的函数,其中 f s 是采样频率
xL n x n wR n
因为时域的乘积等效于频域的卷积,所以上式的傅立叶变换是
XL f
1 fs
fs / 2
fs / 2
X WR f d
前文中导出的表达式
ˆ f P xx
XL f fs L
2
说明卷积对周期图有影响。 正弦数据的卷积影响最容易理解。假设 x n 是 M 个复正弦的和-400Fra bibliotek-300
-200
-100 0 100 frequency/Hz
200
300
400
500
该图显示了一个主瓣和若干旁瓣,最大旁瓣大约在主瓣下方 13.5dB 处。这些旁瓣说 明了频谱泄漏效应。无限长信号的功率严格的集中在离散频率点 f k 处,而有限长信号在离 散频率点 f k 附近有连续的功率。 因为矩形窗越短,它的频率响应对 Dirac 冲击的近似性越差,所以数据越短它的频谱 泄漏越明显。考虑下面的 100 个采样的序列 randn('state',0) fs = 1000; t = (0:fs/10)/fs; A = [1 2]; f = [150;140];
Parametric methods (参量类方法) 这类方法是假设信号是一个由白噪声驱动的线性系统的输出。这类方法的例子是 Yule-Walker autoregressive (AR) method 和 Burg method。这些方法先估计假设的 产生信号的线性系统的参数。 这些方法想要对可用数据相对较少的情况产生优于传统非参数 方法的结果。 Subspace methods (子空间类) 又称为 high-resolution methods(高分辨率法)或者 super-resolution methods (超分辨率方法) 基于对自相关矩阵的特征分析或者特征值分解产生信号的频率分量。 代表 方 法 有 multiple signal classification (MUSIC) method 或 eigenvector (EV) method。这类方法对线谱(正弦信号的谱)最合适,对检测噪声下的正弦信号很有效,特 别是低信噪比的情况。 方法 周期图 Welch 多椎体 Yule-Walker AR Burg Covariance (协方差) 修正协方差 MUSIC 特征向量法 PSD 估计 重叠,加窗的信号段的平均周期图 多个正交窗(称为锥)的组合做谱估计 描述 函数 spectrum.periodogram, periodogram spectrum.welch, pwelch, cpsd, tfestimate, mscohere spectrum.mtm, pmtm
被定义为平稳随机信号 xn 的 power spectral density (PSD)(功率谱密度) 一个信号在频带 1 , 2 , 0 1 2 上的平均功率可以通过对 PSD 在频带上积分 求出
2
1 xx xx
P1 ,2
1
P d P d
时 间序列的 估计的自 相关函数 计算自回 归 spectrum.yulear, pyulear (AR)谱估计 通过最小化线性预测误差计算自回归(AR) 谱估计 spectrum.burg, pburg
通过最小化前向预测误差做时间序列的自回 spectrum.cov, pcov 归(AR)谱估计 通过最小化前向及后向预测误差做时间序列 的自回归(AR)谱估计 多重信号分类 虚谱估计 spectrum.mcov, pmcov spectrum.music, pmusic spectrum.eigenvector, peig
平均功率通过用下述求和去近似积分 求得 [Pxx,F] = psd(Hs,xn,fs,'twosided'); Pow = (fs/length(Pxx)) * sum(Pxx) Pow = 2.5059 你还可以用单边 PSD 去计算平均功率 [Pxxo,F] = psd(Hs,xn,fs,'onesided'); Pow = (fs/(2*length(Pxxo))) * sum(Pxxo) Pow = 2.5011 周期图性能 下面从四个角度讨论周期图法估计的性能:泄漏,分辨率,偏差和方差。 频谱泄漏 考虑有限长信号 xL n ,把它表示成无限长序列 x n 乘以一个有限长矩形窗 wR n 的 乘积的形式经常很有用:
ˆ f P xx
XL f fs L
2
注:这里 X L f 运用的是 matlab 里面的 fft 的定义不带归一化系数,所以要除以 L 其中
X L f xL n e2 jfn / f s
n 0
L 1
实际对 X L f 的计算可以只在有限的频率点上执行并且使用 FFT。实践上大多数周期 图法的应用都计算 N 点 PSD 估计
