完整版相交线同步练习题

合集下载

(完整版)相交线练习题及答案

相交线练习题及答案一、选择题1、如图所示,直线AB，CD相交于点O，已知∠AOD＝160°，则∠BOC的大小为( ）A．20°B．60°C．70°D．160°2、如图，下列各组角中，是对顶角的一组是（)A．∠1和∠2 B．∠2和∠3C．∠2和∠4 D．∠1和∠53、下列图形中，与互为邻补角的是（ )4、如图所示,点P到直线l的距离是( ）A．线段PA的长度 B．线段PB的长度B．C．线段PC的长度 D．线段PD的长度5、如图,将∠BAC沿DE向∠BAC内折叠，使AD与A′D重合,A′E与AE重合，若∠A=30°，则∠1+∠2=( ) A．50° B．60° C．45° D．以上都不对6、如图所示，直线AB⊥CD于点O,直线EF经过点O，若∠1=26°，则∠2的度数是( ）A．26° B．64°C．54° D．以上答案都不对7、四条直线相交于一点，总共有对顶角( ）A．8对 B．10对 C．4对 D．12对8、如图，直线l1，l2，l3相交于一点,则下列答案中，全对的一组是（）A．∠1=90°，∠2=30°，∠3=∠4=60° B．∠1=∠3=90°，∠2=∠4=30°C．∠1=∠3=90°，∠2=∠4=60° D．∠1=∠3=90°，∠2=60°，∠4=30°9、已知∠1与∠2是同位角，则A．∠1 = ∠2 B．∠1 〉∠2 C．∠1 〈∠2 D．以上都有可能10、如图,AB⊥AC，AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有（）A．2条 B．3条 C．4条 D．5条11、。

如图，与∠4是同旁内角的是（）A．∠1 B．∠ 2C．∠3 D．∠5二、填空题13、如图，直线AB，CD交于点O，OE⊥AB，若∠AOD＝50°，则∠COE的度数为________．14、如图,已知直线AB与CD相交于点O，OA平分∠COE，若∠DOE=70°，第13题图第14题图第15题图则∠BOD= ．15、如图，已知AB⊥CD，垂足为点O，直线EF经过O点，若∠1=55°，则∠COE的度数为度．16、如图直线AB，CD,EF相交于点O,图中∠AOB的对顶角是______ ，∠COF的邻补角是______ ．17、如图,直线AB，CD相交于点O,OE⊥AB，O为垂足,∠EOD=26°,则∠AOC= ，∠COB= ．第16题图第17题图第18题图18、如图所示，直线AB，CD被DE所截，则∠1和∠是同位角，∠1和∠是内错角，∠1和∠是同旁内角．19、一机器人以0.3m/s的速度在平地上按下图中的步骤行走，那么该机器人从开始到停止所需时间为s．三、简答题20、已知：线段AB和AB外一点C．求作：AB的垂线，使它经过点C（要求：尺规作图，保留作图痕迹，不写作法）．21、已知直线AB和CD相交于点O，∠AOC为锐角，过O点作直线OE、OF．若∠COE=90°,OF平分∠AOE，求∠AOF+∠COF的度数．22、如图，直线AB、CD相交于点O，OE⊥AB,O为垂足，∠DOB=2∠EOD，求∠AOC，∠COB的度数．23、陆老师布置了一道题目：过直线l外一点A做l的垂线．(用尺规作图）你认为小淇的作法正确吗？如果不正确，请画出一个反例；如果正确，请给出证明．参考答案一、选择题1、。

相交线相关试题及答案

相交线相关试题及答案一、选择题1. 下列关于相交线的说法中，正确的是（）。

A. 相交线一定有且只有一个交点B. 相交线可以是两条直线或一条直线和一条曲线C. 两条直线相交，其交点只有一个D. 两条直线相交，其交点可以有无数个答案：C2. 在同一平面内，两条直线的位置关系是（）。

A. 平行或相交B. 垂直或相交C. 垂直或平行D. 重合或相交答案：A二、填空题3. 两条直线相交所成的四个角中，有2个对角相等且都为90°时，这两条直线互相______。

答案：垂直4. 在平面直角坐标系中，若两条直线的斜率都存在，且它们的斜率互为相反数，则这两条直线的关系是______。

答案：垂直三、解答题5. 如图所示，直线l₁和l₂相交于点O，∠AOB=90°，∠BOC=45°，求∠AOC的度数。

解：由于∠AOB和∠BOC是直线l₁和l₂相交所形成的邻补角，根据题意，∠AOB=90°，∠BOC=45°。

因此，∠AOC = ∠AOB + ∠BOC = 90° + 45° = 135°。

6. 已知直线l₁：y = 2x - 1与直线l₂：y = -3x + 2相交于点P，求点P的坐标。

解：要求出点P的坐标，我们需要解这个方程组：\begin{cases}y = 2x - 1 \\y = -3x + 2\end{cases}将第二个方程的y代入第一个方程，得到：-3x + 2 = 2x - 1解得：x = 1将x的值代入任意一个方程求y，例如代入第二个方程：y = -3(1) + 2 = -1因此，点P的坐标为(1, -1)。

四、证明题7. 已知平面内两条直线l₁和l₂相交，且∠AOB和∠BOC是直线l₁和l₂相交所形成的邻补角，若∠AOB = 60°，求证：∠BOC = 120°。

证明：根据邻补角的定义，两个角的和为180°。

(完整word版)人教版初中数学七年级下册相交线练习题附参考答案

人教版初中数学七年级下册相交线练习题附参考答案1．在两条直线相交所成的四个角中，( )不能判定这两条直线垂直A．对顶角互补 B．四对邻补角 C．三个角相等 D．邻补角相等答案：B说明：两条直线相交，已有四对邻补角，因此，选项B不足以判定这两条直线垂直；而根据垂直的定义，对顶角、邻补角的性质不难判断其它选项的说法都可以判定这两条直线垂直；所以答案为B．2．如图，在三角形ABC中，AC⊥BC，CD⊥AB于D，则下列关系不成立的是( )A．AB>AC>ADB．AB>BC>CDC．AC+BC>ABD．AC>CD>BC答案：D说明：由垂线段最短的性质，可知AB>AC，AB>BC，AC>AD，BC>CD都成立，即选项A、B中的关系都是正确的；再由两点之间线段最短，可知AB<AC+BC成立，所以选项C也正确；只有选项D中CD>BC不成立，答案为D．3．图中，∠1和∠2是同位角的是( )A B C D答案：D说明：由同位角的概念可知，一条直线与两条直线相交，同位角位置相同且有一边在同一直线上，这样可以判断选项A、B、C中的∠1与∠2都不是同位角，只有选项D中的∠1与∠2是同位角，答案为D．填空题：1．如图，直线a，b，c交于O，∠1 = 30º，∠2 = 50º，则∠3 =________．答案：100º说明：如图，∠3的对顶角为∠4，所以∠3 =∠4；又∠1+∠2+∠4 = 180º，∠1 = 30º，∠2 = 50º，所以∠4 = 180º−30º−50º = 100º，即∠3 = 100º．2．如图，直线AB、CD交于O，OA平分∠EOC，且∠EOD = 120º，则∠BOD =_______．答案：30º说明：因为∠BOD =∠COA，∠EOD+∠EOC = 180º，OA平分∠EOC，所以∠EOD+2∠COA = 180º，再由∠EOD = 120º，可得∠COA = 30º，即∠BOD = 30º．3．已知如图，①∠1与∠2是_______被_______所截成的_______角；②∠2与∠3是_______被_______截成的_______角；③∠3与∠A是_______被_______截成的_______角；④AB、AC被BE截成的同位角_______，内错角_______，同旁内角_______；⑤DE、BC被AB截成的同位角是_______，内错角_______，同旁内角_______．答案：①DE、BC；BE；内错角②AC、BC；BE；同旁内角③AB、BE；AC；同位角④不存在；∠ABE与∠3；∠ABE与∠AEB⑤∠ADE与∠ABC；不存在；∠EDB与∠DBC4．在三角形ABC中，AC⊥BC，CD⊥AB于D，如图，则在图中共有______对互余的角，______对互补的角，______对邻补角，点A到CD的距离是______，到BC的距离是______，到点B的距离是______，点C 到直线AB的距离是______．答案：有4对互余的角：∠ACD与∠A；∠A与∠B；∠B与∠BCD；∠BCD与∠ACD；有3对互补的角：∠CDA与∠CDB；∠ACB与∠CDA；∠ACB与∠CDB；有1对邻补角：∠CDA与∠CDB；点A到CD的距离是AD；点A到BC的距离是AC；点A到点B的距离是AB；点C到直线AB的距离是CD．解答题：1．如图，已知直线AB、CD、EF相交于O，OG⊥AB，且∠FOG = 32º，∠COE = 38º，求∠BOD．答案：因为AB、CD、EF交于O，所以∠FOD =∠COE =38º又因为OG⊥AB，所以∠BOD = 90º−∠FOD−∠FOG = 90º−32º−38º = 20º．2．如图，已知OA⊥OB，OC⊥OD，且∠AOD：∠BOC = 4：5，求∠BOC的度数．答案：因为OA⊥OB，OC⊥OD所以∠AOB =∠DOC =90º即∠AOD+∠BOC = 180º又因为∠AOD：∠BOC = 4：5所以∠BOC = ×180º = 100º．3．如图，直线AB、CD交于O，∠AOE = 30º，∠BOC = 2∠AOC，求∠DOF．解答：∵AB、CD交于O∴∠AOC+∠BOC = 180º又∵∠BOC = 2∠AOC∴3∠AOC = 180º∴∠AOC = 60º又∵∠AOE = 30º∴∠DOF = 30º。

相交线同步练习题

5.1.1相交线同步练习题(总4页)相交线同步练习题一、选择题:(每小题3分,共15分)1.如图所示,∠1和∠2是对顶角的图形有( )12121221个个个个2.如图1所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )° ° ° °O F ED C B A(1)3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.个个个个4.如图2所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( ) ° ° ° °60︒30︒34l 3l 2l 112(2)5.如图3所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( )A.∠1=90°,∠2=30°,∠3=∠4=60°;B.∠1=∠3=90°,∠2=∠4=30C.∠1=∠3=90°,∠2=∠4=60°;D.∠1=∠3=90°,∠2=60°,∠4=30°OD C B A(3)二、填空题:(每小题2分,共16分)1. 如图4所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.34DC B A12(4)2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.3.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.O FED C B A4.如图6所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠BOD=•______.O ED C B A5.对顶角的性质是______________________.6.如图7所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.O D CB A127.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•则∠EOB=______________. O ED C B A8.如图9所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,•?且∠BOE:∠EOD=2:3,则∠EOD=________.O EDC BA三、训练平台:(每小题10分,共20分)1. 如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.O FE D C BA 122. 如图所示,L 1,L 2,L 3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.34l 3l 2l 112=。

2022-2023学年人教版数学七年级下册《相交线》同步练习

5.1相交线一、单选题1．下列图形中，1∠和2∠的位置关系不属于同位角的是（）A ．B ．C ．D ．2．下列说法正确的是（）①在同一平面内，两条直线的位置关系有相交和平行两种；①直线外一点与直线上各点连接的所有线段中，垂线段最短；①相等的两个角是对顶角；①两条直线被第三条直线所截，内错角相等；①如果一条直线和两条直线中的一条垂直，那么这条直线也和另一条垂直． A ．1个 B ．2个 C ．3个 D ．4个 3．如图，直线,AB CD 相交于点,O OE AB ⊥于点,O OF 平分12530'AOE ∠∠=︒,，则下列结论中不正确的是（）A ．13∠=∠B ．245∠=︒C ．AOD ∠与1∠互为补角 D ．3∠的余角等于6530'︒4．如图，直线AB ，CD 相交于点O ，且①AOC 比①AOD 小50°，则①AOC 和①AOD 的度数分别为( )A ．55°和125°B ．65°和115°C ．60°和120°D ．155°和105°5．如图，直线AB CD ，相交于点O ，OE CD ⊥，OF 平分BOD ∠，26AOE ∠=︒，则COF ∠的度数为（）A ．116︒B ．142︒C ．148︒D ．154︒6．如图，直线 AB 、CD 相交于点 O ，EF ①AB 于 O ，且①COE =50°，则①BOD 等于（）A ．40°B ．50°C ．45°D ．55° 7．如图，直线a ，b 相交于点O ，若1∠等于45︒，则2∠等于( )A ．45°B ．135°C ．115°D ．55°8．如图，下列说法中错误的是（）A ．,GBD HCE ∠∠是同位角B ．,ABD ACH ∠∠是同位角C ．,FBC ACE ∠∠是内错角D ．,GBC BCE ∠∠是同旁内角9．如图所示，直线a 、b 被直线c 所截，①1与①2是（）A．同位角B．内错角C．同旁内角D．邻补角10．如图，直线a，b被直线c所截，那么①1的同位角是（）A．①2B．①3C．①4D．①5二、填空题11．如图，已知直线AB、CD交于点E，EF①CD，①AEF=50°，那么①BED=____.12．平面内有四条不同的直线两两相交，若最多有m个交点，最少有n个交点，那么（-n）m= ______ ．13．如图，与①B互为内错角的角是______________14．如图，直线AB，CD相交于点O，OE①CD于O，①AOC＝36°，则①BOE的度数是_______________________度．三、解答题16．如图，已知：点A、点B及直线l．（1）请画出从点A到直线l的最短路线，并写出画图的依据．（2）请在直线l上确定一点O，使点O到点A与点O到点B的距离之和最短，并写出画图的依据．17．如图，直线m和l交于O点，已知1∠的度数．∠的补角是它的余角的4倍，求218．根据要求画图，并回答问题．已知：直线AB、CD相交于点O，且OE①AB（1）过点O画直线MN①CD；（2）若点F是（1）所画直线MN上任意一点（O点除外），且①AOC=34°，求①EOF 的度数．19．如图，OB OD ⊥，OC 平分AOD ∠，40BOC ∠=︒，求AOB ∠的大小．20．如图，直线AB 和CD 相交于点O ，90DOE ∠=︒，OD 平分BOF ∠，50BOE ∠=︒．(1)求AOC ∠的度数；(2)求EOF ∠的度数；(3)求AOF ∠的度数．21．已知OA ①OB ，①AOB ：①AOC ＝3：4，求①BOC 的度数．参考答案：1．D2．B3．D4．B5．C6．A7．B8．A9．A10．C 11．40°12．113．∠BAE或∠BAD14．54°15．4416．（1）如图所示：点E为所求，根据垂线段最短；（2）如图所示：根据两点之间线段最短．17．60︒18．（1）如图．（2）如上图：①当F在OM上时．①EO①AB，MN①CD，①①EOB=①MOD=90°，①①MOE+①EOD=90°，①EOD+①BOD=90°，①①EOF=①BOD=①AOC=34°；①当F在ON上时，如图在F′点时．①MN①CD，①①MOC=90°=①AOC+①AOM，①①AOM=90°﹣①AOC=56°，①①BON=①AOM=56°，①①EOF′=①EOB+①BON=90°+56°=146°，答：①EOF的度数是34°或146°．19．10︒20．(1)40︒(2)130︒(3)100︒21．30°或150°。

(完整版)七年级数学下册_5.1同步练习及答案

5.1.1 相交线姓名_____________一、选择题:1.如图所示,∠1和∠2是对顶角的图形有( )12121221A.1个B.2个C.3个D.4个2.如图1所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )A.150°B.180°C.210°D.120°OFE D CB A O DCBA 60︒30︒34l 3l 2l 112(1) (2) (3) 3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个4.如图2所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( )A.62°B.118°C.72°D.59°5.如图3所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( ) A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30C.∠1=∠3=90°,∠2=∠4=60°;D.∠1=∠3=90°,∠2=60°,∠4=30° 二、填空题:1. 如图4所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.34D CBA 12OFED CB A OED CBA(4) (5) (6) 2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.3.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.4.如图6所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠BOD =•______.5.对顶角的性质是______________________.6.如图7所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.ODC BA 12OE D CBA OE DCBA(7) (8) (9)7.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•则∠EOB=______________. 8.如图9所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,• 且∠BOE:∠EOD=2:3,则∠EOD=________. 三、解答题:1. 如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.OF EDCBA 122，如图所示,直线a,b,c 两两相交,∠1=2∠3,∠2=65°,求∠4的度数.cba3412答案:一、1.A 2.B 3.B 4.A 5.D 二、1.∠2和∠4 ∠3 2.155° 25° 155° 4.35° 5.对顶角相等 •6 .125° 55° 7.147.5° 8.42°三、1.∠2=60° 2.∠4=36°四、1.∠BOD=120°,∠AOE=30° 2.∠BOD=72° 3.∠4=32.5° 五、1.4条不同的直线相交于一点,图中共有12对对顶角(平角除外),n 条不同的直线相交于一点,图中共有(n 2-n)对对顶角(平角除外).2.6条直线最多可以把平面分成22个部分,n 条直线最多可以把平面分成(1)12n n +⎡⎤+⎢⎥⎣⎦个部分.六、∠AOC 与∠BOD 不一定是对顶角.如图1所示,当射线OC,OD 位于直线AB 的一侧时,不是对顶角;如图2所示,当射线OC,OD 位于直线AB 的两侧时,是对顶角.(1)O D C BA21(2)O DCBA七、140°.5.1.3同位角、内错角、同旁内角同步练习姓名_____________一、填空题1.如图1，直线a 、b 被直线c 所截，∠1和∠2是，∠3和∠4是，∠3和∠2是。

小学数学相交线练习题

小学数学相交线练习题
小学数学练习题：相交线
一、选择题
1. 下图中，两条相交线的交点是（）
A. 直角
B. 锐角
C. 退化角
D. 平角
2. 下图中，AB和CD为两条相交线，若AB为垂直于CD，那么角A和角B的关系是（）
A. 互补角
B. 对顶角
C. 钝角
D. 垂角
3. 直线l与平行线m相交，形成的两组内错角分别为40°和（）
A. 40°
B. 60°
C. 80°
D. 100°
4. 下图中，MN与PQ相交于点O，若角MON为130°，则角NOM
和角NOQ的关系是（）
A. 互补角
B. 对顶角
C. 直角
D. 无关
二、填空题
1. 直线l与平行线m相交，形成的同旁内角分别为120°和（）°。

2. 直线AB与CD相交于点O，若角AOC为60°，则角BOD为（）°。

3. 直线l与平行线m相交，形成的同旁外角分别为80°和（）°。

三、计算题
1. 下图中，直线l与m相交于点O，角BOC的度数为55°，求角AOD的度数。

（提示：角AOD与角BOC互补）
四、应用题
小明站在田地中央，看到一棵大树和一栋高楼的顶部在视线上重合。

他向前走了30米，再看到大树和高楼的顶部在视线上重合点后方6米。

已知大树的高度为12米，求高楼的高度。

（假设小明的眼睛高度为1.5米）
以上是关于小学数学相交线的练习题，希望对你有帮助！。

(完整版)相交线与平行线常考题目及答案(绝对经典)

相交线与平行线
一．选择题（共3小题）
1．在同一平面内，有8条互不重合的直线，l1，l2，l3…l8，若l1⊥l2，l2∥l3，l3⊥l4，l4∥l5…以此类推，则l1和l8的位置关系是（）
A．平行B．垂直C．平行或垂直D．无法确定
2．如图，直线AB、CD相交于O，OE⊥AB，OF⊥CD，则与∠1互为余角的有（）
26．几何推理，看图填空：
（1）∵∠3=∠4（已知）
∴∥（）
（2）∵∠DBE=∠CAB（已知）
∴∥（）
（3）∵∠ADF+=180°（已知）
∴AD∥BF（）
27．如图，直线AB、CD相交于点O，OE平分∠BOD．
（1）若∠AOC=68°，∠DOF=90°，求∠EOF的度数．
（2）若OF平分∠COE，∠BOF=30°，求∠AOC的度数．
7．将一副学生用三角板按如图所示的方式放置．若AE∥BC，则∠AFD的度数是．
评卷人
得分
三．解答题（共43小题）
8．已知：直线EF分别与直线AB，CD相交于点F，E，EM平∠FED，AB∥CD，H，P分别为直线AB和线段EF上的点．
（1）如图1，HM平分∠BHP，若HP⊥EF，求∠M的度数．
（2）如图2，EN平分∠HEF交AB于点N，NQ⊥EM于点Q，当H在直线AB上运动（不与点F重合）时，探究∠FHE与∠ENQ的关系，并证明你的结论．
（3）若点P在图（3）位置时，写出∠1、∠2、∠3之间的关系并给予证明．
15．如图，已知AB∥PN∥CD．
（1）试探索∠ABC，∠BCP和∠CPN之间的数量关系，并说明理由；
（2）若∠ABC=42°，∠CPN=155°，求∠BCP的度数．
16．如图，AD∥BC，∠EAD=∠C，∠FEC=∠BAE，∠EFC=50°

(完整版)相交线练习题

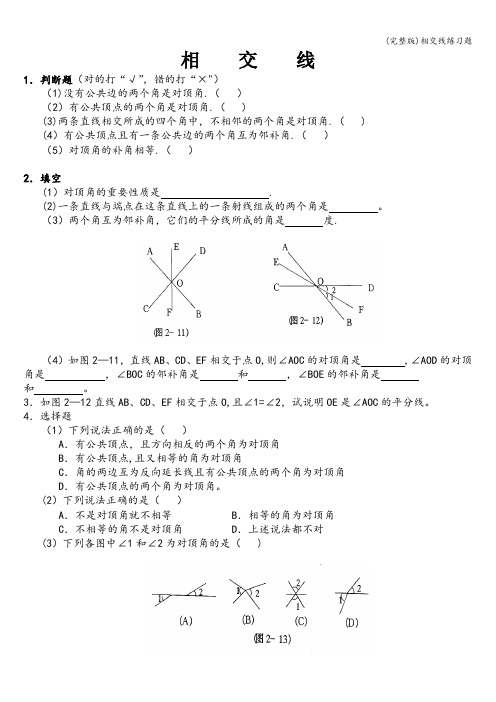
相交线1．判断题（对的打“√”，错的打“×"）（1)没有公共边的两个角是对顶角.（）（2）有公共顶点的两个角是对顶角.（ )(3)两条直线相交所成的四个角中，不相邻的两个角是对顶角.（ )(4）有公共顶点且有一条公共边的两个角互为邻补角.（）（5）对顶角的补角相等.（）2．填空(1）对顶角的重要性质是 .(2)一条直线与端点在这条直线上的一条射线组成的两个角是。

（3）两个角互为邻补角，它们的平分线所成的角是度.（4）如图2—11，直线AB、CD、EF相交于点O,则∠AOC的对顶角是 ,∠AOD的对顶角是，∠BOC的邻补角是和，∠BOE的邻补角是和。

3．如图2—12直线AB、CD、EF相交于点O,且∠1=∠2，试说明OE是∠AOC的平分线。

4．选择题（1）下列说法正确的是（）A．有公共顶点，且方向相反的两个角为对顶角B．有公共顶点,且又相等的角为对顶角C．角的两边互为反向延长线且有公共顶点的两个角为对顶角D．有公共顶点的两个角为对顶角。

(2）下列说法正确的是（）A．不是对顶角就不相等 B．相等的角为对顶角C．不相等的角不是对顶角 D．上述说法都不对(3）下列各图中∠1和∠2为对顶角的是（ )10756894321(1)（4）如果两个角的平分线相交成90°的角，那么这两个角是（ )A ．对顶角B ．互补的两个角C ．互为邻补角D ．以上答案都不对6．如图2-14，已知直线AB 、CD 、EF 相交于点O,∠1：∠2：∠3=2:3:4，求∠4的度数.7．如图2—15,已知直线AB 、CD 相交于点O ，OE 平分∠BOD,且∠BOE=10°，求∠AOC 的度数。

相交线2一、判断（每题1分，共10分）1。

顶点相同并且相等的两个角是对顶角。

( ）2。

相交直线构成的四个角中若有一个角是直角，就称这两条直线互相垂直。

( ） 3。

直线外一点到这条直线的垂线段叫做这点到这条直线的距离。

新人教版七年级下册数学(全册)同步练习随堂练习一课一练

新人教版七年级下册数学全册同步练习（课本配套，适合课堂小测、作业布置和知识强化训练）《相交线》同步练习如图，已知AB 是线1. 如图1所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.(1) (2) (3)2.如图1所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.3.如图2所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.4.如图3所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠BOD=•______.5.对顶角的性质是______________________.6.如图4所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.（4）34D CBA 12OFED CB A OED CBAODC BA 12E OE DCBA7.如图5所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°, 则∠EOB=______________. 8.如图6所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,• 且∠BOE:∠EOD=2:3,则∠EOD=________.1.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个2.如图7所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )A.150°B.180°C.210°D.120°(7) (8) (9) 3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等. A.1个 B.2个 C.3个 D.4个4.如图8所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( ) A.62° B.118° C.72° D.59°5.如图9所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( ) A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30 C.∠1=∠3=90°,∠2=∠4=60°; D.∠1=∠3=90°,∠2=60°,∠4=30°12121221OFE D CB A O DCBA 60︒30︒34l 3l 2l 1121. 如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.2. 如图所示,L 1,L 2,L 3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.3. 如图所示,AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE•的度数.4. 如图所示,直线AB 与CD 相交于点O,∠AOC:∠AOD=2:3,求∠BOD 的度数.OF EDCBA 1234l 3l 2l 112OE DCBA5. 如图所示,直线a,b,c 两两相交,∠1=2∠3,∠2=65°,求∠4的度数.答案和解析一、填一填 1、 ∠2和∠4 ∠32、155° 25° 155°3、∠BOC ∠AOD 和∠COB 50° 130°4、 35°5、对顶角相等1，46、125° 55°ODCBAcba34127、147.5° 8、42° 二、选择 1、A 2、B 3、B 4、A 5、D 三、解答题1、∠2=60°2、∠4=36°3、∠BOD=120°,∠AOE=30°4、∠BOD=72°5、∠4=32.5°《垂线》同步练习如图，已知AB 是线1.如图所示,直线AB 与直线CD 的位置关系是_______,记作_______,此时,•∠AOD=∠_____=∠______=∠______=90°.2.过一点有且只有________直线与已知直线垂直.3.画一条线段或射线的垂线,就是画它们________的垂线.O DCBA4.直线外一点到这条直线的_________,叫做点到直线的距离.1.如图1所示,下列说法不正确的是( )A.点B 到AC 的垂线段是线段AB;B.点C 到AB 的垂线段是线段ACC.线段AD 是点D 到BC 的垂线段;D.线段BD 是点B 到AD 的垂线段(1) (2)2.如图1所示,能表示点到直线(线段)的距离的线段有( ) A.2条 B.3条 C.4条 D.5条3.下列说法正确的有( )①在平面内,过直线上一点有且只有一条直线垂直于已知直线; ②在平面内,过直线外一点有且只有一条直线垂直于已知直线; ③在平面内,过一点可以任意画一条直线垂直于已知直线; ④在平面内,有且只有一条直线垂直于已知直线. A.1个 B.2个 C.3个 D.4个4.如图2所示,AD ⊥BD,BC ⊥CD,AB=acm,BC=bcm,则BD 的范围是( ) A.大于acm B.小于bcmC.大于acm 或小于bcmD.大于bcm 且小于acm 5.到直线L 的距离等于2cm 的点有( ) A.0个 B.1个 C.无数个 D.无法确定6.点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到直线m 的距离为( )A.4cmB.2cm;C.小于2cmD.不大于2cmDCBADCBA1如图所示,直线AB,CD,EF 交于点O,OG 平分∠BOF,且CD ⊥EF,∠AOE=70°, 求∠DOG 的度数.2如图所示,村庄A 要从河流L 引水入庄,需修筑一水渠,请你画出修筑水渠的路线图.3.如图6所示,O 为直线AB 上一点,∠AOC=13∠BOC,OC 是∠AOD 的平分线. (1)求∠COD 的度数;(2)判断OD 与AB 的位置关系,并说明理由.答案和解析一、填一填1、垂直 AB ⊥CD DOB BOC COA2、一条3、所在直线4、 35°5、垂线段的长度二、选择6、C7、D8、CGOFEDCBA ODC BA9、D10、C11、D三、解答题1、∠DOG=55°2、解:如图3所示.3、解:(1)∵∠AOC+∠BOC=∠AOB=180°,∴13∠BOC+∠BOC=180°,∴43∠BOC=•1 80°,∴∠BOC=135°,∠AOC=45°,又∵OC是∠AOD的平分线,∴∠COD=∠AOC=45°.(2)∵∠AOD=∠AOC+∠COD=90°,∴OD⊥AB.《同位角内错角同旁内角》同步练习如图，已知AB是线1．如图，根据图形填空．（1）∠A和_________ 是同位角；（2）∠B和_________ 是内错角；l（3）∠A和_________ 是同旁内角．2．如图所示，与∠C构成同旁内角的有个．3．如图，与图中的∠1成内错角的角是．4．如图：△ABC中，∠A的同旁内角是．5．如图，直线MN分别交直线AB，CD于E，F，其中，∠AEF的对顶角是∠，∠BEF的同位角是∠____．6．如图：图中的∠1，∠2，∠3，∠4，∠5，∠6，∠7 中同位角有对．1．如图，∠1与∠2是（）A．对顶角B．同位角C．内错角D．同旁内角2．如图，已知AB∥CD，与∠1是同位角的角是（）A．∠2 B．∠3 C．∠4 D．∠5 3．如图，与∠1是同位角的是（）A．∠2 B．∠3 C．∠4 D．∠5 4．如图，下列各语句中，错误的语句是（）A．∠ADE与∠B是同位角 B．∠BDE与∠C是同旁内角C．∠BDE与∠AED是内错角D．∠BDE与∠DEC是同旁内角5．如图，在所标识的角中，同位角是（）A．∠1和∠2 B．∠1和∠3 C．∠1和∠4 D．∠2和∠36．已知：如图，直线AB、CD被直线EF所截，则∠EMB的同位角是（）A．∠AMF B．∠BMF C．∠ENC D．∠END7．如图，若直线MN与△ABC的边AB、AC分别交于E、F，则图中的内错角有（）A．2对B．4对C．6对D．8对8．如图，下列说法中错误的是（）A．∠3和∠5是同位角B．∠4和∠5是同旁内角C．∠2和∠4是对顶角D．∠1和∠4是内错角1 如图所示，∠1与∠2，∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角？2．如图所示，BF、DE相交于点A，BG交BF于点B，交AC于点C．（1）指出ED、BC被BF所截的同位角，内错角，同旁内角；（2）指出ED、BC被AC所截的内错角，同旁内角；（3）指出FB、BC被AC所截的内错角，同旁内角．答案和解析一、填一填1、（1）∠A和∠ECD，∠BCD是同位角；（2）∠B和∠BCE是内错角；（3）∠A和∠ECA，∠BCA是同旁内角；2、33、∠BDC4、∠B和∠C5、∠BEM ∠DFN6、3二、选择12、B13、D14、C15、B16、C17、D18、C19、D三、解答题1解：左图：∠1与∠2是AB与CD被直线BD所截形成的内错角，∠3与∠4是直线AD与直线BC被直线BD所截形成的内错角；右图：∠1与∠2是AB与CD被直线BD所截形成的同旁内角，∠3与∠4是直线AD与直线BC被直线AB所截形成的同位角．2、解：（1）同位角：∠FAE和∠B；内错角：∠B和∠DAB；同旁内角：∠EAB和∠B；（2）内错角：∠EAC和∠BCA，∠DAC和∠ACG；同旁内角：∠EAC和∠ACG，∠DAC和∠BCA；（3）内错角：∠BAC和∠ACG，∠FAC和∠BCA；同旁内角：∠BAC和∠BCA，∠BAC和∠ABC，∠B和∠ACB，∠FAC和∠ACG．《平行线》同步练习如图，已知AB是线1．在同一平面内，不重合的两条直线的位置关系有_______种，分别是________．2．设a，b，c为平面内三条不同直线：（1）若a∥b，c⊥a，则b与c的位置关系是______；（2）若a∥b，b∥c，则a与c的位置关系是______．3．在同一平面内L1与L2没有公共点，则L1______L2．4．在同一平面内L1和L2有一个公共点，则L1与L2______．1．下列说法不正确的是（）A．过马路的斑马线是平行线B．100米跑道的跑道线是平行线C．若a∥b，b∥d，则a⊥dD．过直线外一点有且只有一条直线与已知直线平行2．下列说法正确的是（）A．同一平面内不相交的两线段必平行B ．同一平面内不相交的两射线必平行C ．同一平面内不相交的一条线段与一条直线必平行D ．同一平面内不相交的两条直线必平行3．如图所示，在这些四边形AB 不平行于CD 的是（）A ． ∠1和∠2B ．∠1和∠3C ．∠1和∠4D ．∠2和∠31.在同一平面内三条直线交点有多少个？甲：同一平面三直线相交交点的个数为0个，因为a ∥b ∥c ，如图（1）所示．乙：同一平面内三条直线交点个数只有1个，因为a ，b ，c 交于同一点O ，如图（2）所示．以上说法谁对谁错？为什么？2．如图所示，在5×5的网格中，AC 是网格中最长的线段，请画出两条线段与AC 平行并且过网格的格点．3.如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字“M”：（1）请从正面，上面，右侧三个不同方向上各找出一组平行线段，并用字母表示出来；（2）EF与A′B′有何位置关系？CC′与DH有何位置关系？答案和解析一、填一填1、2，相交，平行2、（1）b⊥C （2）a∥c3、∥4、相交二、选择20、C21、D22、D三、解答题1甲，乙说法都不对，各自少了三种情况．a∥b，c与a，b相交如图（1），a，b，•c两两相交如图（2），所以三条直线互不重合，交点有0个或1个或2个或3个，共四种情况．2、如图所示：EF∥AC，PQ∥AC，MN∥AC，且它们都过格点．3、（1）正面：AB∥EF，AE∥MF等等；上面：A′B′∥AB，C′D′∥CD等等；右侧： DD′∥HR，DH∥D′R（2）EF∥A′B′，CC′⊥DH《平行线的判定》同步练习1.已知三条不同的直线a,b,c在同一平面内，下列四个推理：①∵∥，∥，∴⊥；②∵∥，∥，∴∥；③∵⊥，⊥，∴⊥；④∵⊥，⊥，∴∥.其中正确的是.(填写所有正确的序号)2.在同一平面内，直线a，b相交于P，若a∥c，则b与c的位置关系是______.3.在同一平面内，若直线a，b，c满足a⊥b，a⊥c，则b与c的位置关系是______.4.如图所示，BE是AB的延长线，量得∠CBE＝∠A＝∠C.(1)由∠CBE＝∠A可以判断______∥______，根据是_________.(2)由∠CBE＝∠C可以判断______∥______，根据是_________.1.下列四幅图中都有∠1=∠2，其中能说明AB∥CD的是( ).A B C D2.如图，下列推理错误的是( ).A.∵∠1=∠2，∴∥B.∵∠1=∠4，∴∥C.∵∠2+∠3=180?，∴∥D.∵∠1=∠5，∴∥3.如图，下列条件不能判断AD∥EF的是( ).ED CBAA.∠D=∠EFCB.∠D+∠EFD=180?C.EF ∥BC ，AD ∥BCD.∠A+∠B=180?A ． ∠1和∠2B ．∠1和∠3C ．∠1和∠4D ．∠2和∠31．如图，， . 说明：AB ∥CD.2．如图，AD 是一条直线， . .说明：BE ∥CF.3. ①如图,哪两个角相等能判定直线AB ∥CD? ②如果∠1=∠2，能判定哪两条直线平行?③如果∠3=∠4，能判定哪两条直线平行?新课标第一网答案和解析一、填一填 1、②④ 2、相交 3、互相平行◆ 三、解答题 A BCD E G H123 4 54、（1）AD BC 同位角相等，两直线平行（2）CD AB 内错角相等，两直线平行二、选择23、C24、B25、D三、解答题1、∵∠1=70°∴∠3=∠1=70°∴∠1=∠2=70°∴ AB ∥CD2、∵∠2=115°∴∠BCF=65°∴∠1=∠BCF∴BE ∥CF3、①∠2=∠3 或∠4=∠5或∠1=∠2②AB ∥CD③EF∥ GD《平行线的性质》同步练习如图，已知AB是线1．如图1所示，直线a ∥b ，且a ，b 被c 所截，若∠1=40°，则∠2=______．图1 图2 图32．如图2所示，直线a ∥b ，且a ，b 被c 所截，若∠1=60°，则∠2=_______，•∠3=________．3．如图3所示，若AB ∥CD ，∠DEF=120°，则∠B=_______．4．如图4所示，砌墙师傅用重锤线检验砌的墙体是否与地面垂直，•墙体坚直线用a 表示，重锤线用b 表示，地平线用c 表示，当a ∥b 时，因为b ⊥c ，则a______c ，•这里运用了平行线的性质是_______．图4 图55．如图5所示，一块木板，AB ∥CD ，木工师傅量得∠B=80°，∠C=65°，则∠A=______，∠D=______．1．如图6所示，DE ∥BC ，DF ∥AC ，下列结论正确的个数为（） ①∠C=∠AED ②∠EDF=∠BFD ③∠A=∠BDF ④∠AED=∠DFBA．1个 B．2个 C．3个 D．4个图6 图72．如图7，在甲，乙两地之间修一条笔直公路，从甲地测得公路的走向是北偏东50°，甲，乙两地同时开工，若干天后，公路准确接通，则乙地所修公路走向是（）A．北偏45° B．南北方向 C．南偏西50° D．以上都不对3．家住湖边的小海，帮爸爸用铁丝用网箱如图8所示，若AB∥CD，AC∥BD，•若∠1=α，则：①∠3=α；②∠2=180°-α；③∠4=α，其中正确的个数有（）A．0个 B．1个 C．2个 D．3个4．如图9所示，AM平分∠BAC，AM∥EN，则与∠E•相等的角下列说法不正确的是（）A．∠BAM B．∠ABC C．∠NDC D．∠MAC图8 图91．如图，已知∠AED=60°，∠2=30°，EF平分∠AED，可以判断EF∥BD吗？为什么？2．如图所示，若∠1+∠2=180°，∠3=110°，求∠4．3．（探究题）如图所示，若AB∥CD，且∠1=∠2，试判断AM与CN位置关系，•并说明理由．答案和解析一、填一填1、40°2、60°，120°3、60°4、⊥，两直线平行，同位角相等（同旁内角互补）．5、115°，100°二、选择26、D27、C28、C29、B三、解答题1．可以，∵∠AED=60°，EF平分∠AED∴∠FED=30°又∵∠EDB=∠2=30°∴EF∥BD解题规律：证两直线平行，找内错角相等．2．设∠2对顶角为∠5，则∠2=∠5∵∠1+∠2=180°∴∠1+∠5=180°∴AB∥CD，∴∠3=∠4又∵∠3=110°∴∠4=110°解题规律：先判断AB∥CD，再运用平行线的性质定理． 3．因为AB∥CD所以∠EAB=∠ECD又因为∠1=∠2而∠EAM=∠EAB-∠1∠ACN=∠ACD-∠2即∠EAM=∠ACN所以AM∥CN（同位角相等，两直线平行）．解题技巧：判断AM∥CN，①可证∠EAM=∠ECN，②证∠MAC+∠ACN=180°，都能达到目的．《命题定理证明》同步练习如图，已知AB是线1、每个命题都由__ __和两部分组成。

《5.1相交线》练习题

(D)(C)(B)(A)22211121《5.1相交线》练习题一1、下列各图中，∠1和∠2是对顶角的是（）2、已知直线AB 、CD 相交于点O ，则与∠AOC 互补的角有（） A 、1个 B 、2个 C 、3个 D 、4个3、如图，三条直线两两相交，其中对顶角共有 ( ） A 、3对 B 、4对 C 、5对 D 、6对4、如图，直线AB 、CD 交于点O ，OE 、OF 是过O 点的两条射线，其中构成对顶角的是（）A 、∠AOF 与 ∠DOEB 、∠EOF 与∠BOEC 、∠BOC 与∠AOD D 、∠COF 与∠BOD5、下列说法错误的是（）A 、对顶角的平分线成一个平角B 、对顶角相等C 、相等的角是对顶角D 、对顶角的余角相等 6、如图，直线AB 与CD 相交于点O ，∠AOD+∠BOC=236度，则∠AOC 的度数为（）A 、72度B 、62度C 、124度D 、144度 7、如图，点A 到直线CD 的距离是指哪条线段长（）A 、ACB 、CDC 、AD D 、BD 8、在“同一平面内，过一点有且只有一条直线与已知直线垂直”中这一点的位置（）A 、在直线的上方B 、在直线的下方C 、在直线上D 、可以任意位置9、下列说法中正确的个数有（）（1）直线外一点与直线上各点连接的所有线中垂线段最短。

（2）画一条直线的垂线段可以画无数条。

（3）在同一平面内，经过一个已知点能画一条且只能画一条直线和已知直线垂直。

（4）从直线外一点到这条直线的垂线段叫做点到直线的距离。

A 、1个 B 、2个 C 、3个 D 、4个10、如图2-27，∠BAC 和∠ACD 是（）A ．同位角B ．同旁内角C ．内错角D ．以上结论都不对O F E D CBA ODCBADABC11、如图2-28，∠1与∠2不能构成同位角的图形是（）12、如图2-29，图中共有同旁内角对A ．2B ．3C ．4D ．513、如图2-30，与∠1构成同位角的共有（）A ．1个B ．2个C ．3个D ．4个 14、如图2-31，下列判断正确的是 [ ]A ．4对同位角，4对内错角，2对同旁内角B ．4对同位角、4对内错角，4对同旁内角C ．6对同位角，4对内错角，4对同旁内角D ．6对同位角，4对内错角，2对同旁内角15、如图，直线AB 、CD 相交于点O ，若∠AOC=50度，则∠BOC= ，∠AOD= ∠BOD= 。

完整版相交线和平行线测试题及答案

相交线与平行线测试题一、选择题 1. 下列正确说法的个数是 ①同位角相等 ③等角的补角相等A . 1 , B. 2. 下列说法正确的是（ A. 两点之间，直线最短； B. 过一点有一条直线平行于已知直线； C. 和已知直线垂直的直线有且只有一条； D. 在平面内过一点有且只有一条直线垂直于已知直线 3. 下列图中/ 1和/ 2是同位角的是（）A.⑴、⑵、） ②对顶角相等 ④两直线平行, C. 3, ）同旁内角相等 D. 4 II ) ⑶、⑷、⑸, ( D .4. 如果一个角的补角是 150°那么这个角的余角的度数是 A.30 ° B.60 ° C.90 ° D.1205. 下列语句中，是对顶角的语句为（ A.有公共顶点并且相等的两个角 B. 两条直线相交，有公共顶点的两个角 C. 顶点相对的两个角 D. 两条直线相交，有公共顶点没有公共边的两个角6. 下列命题正确的是（）A. 内错角相等B. 相等的角是对顶角C. 三条直线相交，必产生同位角、内错角、同旁内角D. 同位角相等，两直线平行 7. 两平行直线被第三条直线所截，同旁内角的平分线（ A.互相重合 B.互相平行 C.互相垂直 8. 在平面内，将一个图形绕一个定点沿某个方向转动一个角度, 下列图案中，不能由一个图形通过旋转而构成的是（） D.无法确定这样的图形运动称为旋转。

9. 三条直线相交于一点，构成的对顶角共有（ A 、3对 B 、4对 C 、5对 10. 如图，已知 AB // CD // EF , BC // AD ,AC与/ AGE 相等的角有（））D 、6对平分/ BAD , 那么图中BO 平分/ ABC , CO 平分/ ACB ，且 MN BC = 24 , AC = 18，^U △AMN 的周长为( B 、36 C 、42 D 、18 12.如图，若AB // CD ,则/ A 、/ E 、/ D 之间的关系是 (A. / A+ / E+ / D=180°B. / A -/ E + / D=180°C. / A+ / E -/ D=180°D. / A+ / E+ / D=270°二、填空题13. 一个角的余角是 300,则这个角的补角是 ___________ .14. 一个角与它的补角之差是 200,则这个角的大小是 __________ . 15. 时钟指向3时30分时，这时时针与分针所成的锐角是 _____________ . 16. 如图②，/ 1 = 820 , / 2 = 980 , / 3 = 80o ，则/ 4 = ______ 度. 17. 如图③，直线 AB , CD , EF 相交于点 0, AB 丄CD , OG 平分/ AOE ,则/ BOE = _________ 度,/ AOG = __________ 度.18. 如图④，AB // CD , / BAE = 1200 , / DCE = 30o ，则/一 _______O23.如图 9，如果/ 1=40° , / 2=100° ,那么/于 ________ , / 3的同旁内角等于 __________A.5个B.4个C.3个D.2个 19. 把一张长方形纸条按图⑤中， 20. 如图⑦，正方形ABCD 中, 的最小值为_________ . 21. 如图所示，当半径为 30cm 的距离为__________ c m 。

相交线练习题

相交线练习题一、选择题1. 两条直线相交，交点的个数最多有几个？A. 0个B. 1个C. 2个D. 3个2. 在同一平面内，两条直线的位置关系有几种？A. 1种B. 2种C. 3种D. 4种3. 如果两条直线相交成直角，这两条直线叫做？A. 平行线B. 垂直线C. 相交线D. 异面直线4. 下列说法正确的是：A. 两条直线一定相交B. 两条直线一定平行C. 两条直线一定重合B. 两条直线可能相交5. 如果两条直线相交，它们的位置关系是？A. 相交B. 平行C. 垂直D. 异面二、填空题6. 两条直线相交所成的角中，有一个角是直角时，这两条直线互相________。

7. 在同一平面内，不相交的两条直线叫做________。

8. 两条直线相交所成的角中，如果有一个角是锐角，则其它三个角都是________。

9. 如果两条直线相交成钝角，则这两条直线所成的角中，有________个直角。

10. 在同一平面内，两条直线的位置关系除了相交，还有________。

三、判断题11. 如果两条直线相交，它们一定相交于一点。

（）12. 两条直线相交所成的角中，最多有一个直角。

（）13. 两条直线相交，交点的个数可以是两个。

（）14. 两条平行线在任何情况下都不会相交。

（）15. 两条直线相交所成的角中，如果有一个角是锐角，那么其它三个角都是钝角。

（）四、简答题16. 请简述在同一平面内，两条直线相交时，它们的位置关系有哪些可能？17. 请解释什么是垂直线，并给出两条直线垂直相交的条件。

18. 请描述在平面几何中，两条直线相交所成的角有哪些特点？19. 当两条直线相交时，它们所成的角的大小有哪些可能？20. 请解释什么是平行线，并给出两条直线平行的条件。

五、解答题21. 在平面直角坐标系中，直线l1的方程为y=2x+3，直线l2的方程为y=-x+5。

求这两条直线的交点坐标。

22. 如果两条直线l1和l2在平面上相交，且l1的斜率为2，l2的斜率为-1/2，求l1和l2相交所成的角的度数。

人教版七年级下册第五章相交线与平行线相交线同步练习(含答案)

相交线同步练习一．选择题（共12小题）1．下列各图中，∠1=∠2一定成立的是（）A．B．C．D．2．毛泽东主席在《水调歌头游泳》中写道“一桥飞架南北，天堑变通途”．正如从黄果树风景区到关岭县城的坝陵河大桥建成后，从黄果树风景区到关岭县城经大桥通过的路程缩短20公里，用所学数学知识解释这一现象恰当的是（）A．两点确定条直线B．两点之间线段最短C．垂线段最短D．连接两点间线段的长度是两点间的距离3．下列图形中，线段AD的长表示点A到直线BC距离的是（）A．B．C．D．4．下列图形中，∠1和∠2是内错角的是（）A．B．C．D．5．如图，直线a，b相交于点O，若∠1等于30°，则∠2等于（）A．60°B．70°C．150°D．170°6．如图，下列说法正确的是（）A．∠A与∠B是同旁内角B．∠1与∠2是对顶角C．∠2与∠A是内错角D．∠2与∠3是同位角7．已知：如图，直线BO⊥AO于点O，OB平分∠COD，∠BOD=22°．则∠AOC的度数是（）A．22°B．46°C．68°D．78°8．下列结论：①平面内3条直线两两相交，共有3个交点；②在平面内，若∠AOB=40°，∠AOC=∠BOC，则∠AOC的度数为20°；⑨若线段AB=3，BC=2，则线段AC的长为1或5；④若∠α+∠β=180°，且∠α＜∠β，则∠α的余角为（∠β-∠α）．其中正确结论的个数有（）A．1个B．2个C．3个D．4个9．如图，OA⊥OB，∠BOC=30°，OD平分∠AOC，则∠BOD的大小是（）A．20°B．30°C．40°D．60°10．如图所示，直线AB与CD相交于O点，∠1=∠2．若∠AOE=140°，则∠AOC 的度数为（）A．40°B．60°C．80°D．100°11．如图，直线AB、CD相交于O，OE平分∠AOC，∠EOA：∠AOD=1：4，则∠EOB的度数为（）A．60°B．90°C．120°D．150°12．如图所示，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15°30′，则下列结论中不正确的是（）A．∠AOF=45°B．∠1=∠AOCC．∠DOE=74.3°D．∠COE=105.5°二．填空题（共6小题）13．若∠1和∠2是对顶角，∠1=35°，则∠2的补角是．14．如图，已知OA⊥OC，OB⊥OD，∠3=24°，则∠1= ．15．如图所示，∠A和∠ACD是直线AB，CD被所截形成的内错角；∠B的同位角有．16．如图，直线AB、CD相交于点O，∠1=∠2，若∠AOD=68°，则∠1的度数为．17．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=35°，则∠CON的度数为．18．如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE．（1）若∠AOC=76°，∠BOF= 度；（2）若∠BOF=36°，∠AOC= 度．三．解答题（共5小题）19．如图，直线AB，CD相交于点O，∠BOE=90°，OF平分∠AOD，∠COE=20°．（1）求∠BOD与∠DOF的度数．（2）写出∠COE的所有余角．20．如图，直线AB、CD相交于点O，OE平分∠BOC，∠COF=90°．（1）若∠BOE=64°，求∠AOF的度数；（2）若∠BOD：∠BOE=2：3，求∠AOF度数．21．直线AB，CD相交于点O，OE平分∠BOD，OF⊥CD，垂足为O，若∠EOF=54°．求∠AOF的度数．22．如图，直线AB，CD相交于点O，OE平分∠AOD，FO⊥OD于O，∠1=40°，试求∠2和∠4的度数．23．如图，直线AB与CD相交于点E，射线EG在∠AEC内（如图1）．（1）若∠BEC的补角是它的余角的3倍，则∠BEC= 度；（2）在（1）的条件下，若∠CEG比∠AEG小25度，求∠AEG的大小；（3）若射线EF平分∠AED，∠FEG=100°（如图2），则∠AEG-∠CEG= 度．参考答案1-5：CBDDC 6-10:ACABC 11-12:DC13、145°14、24°15、AC；∠ECD，∠ACE16、34°17、55°18、33；7219、（1）∵∵BOE=90°，∵∵AOE=180°-∵BOE=180°-90°=90°，∵∵COE=20°，∵∵COA=90°-∵COE=90°-20°=70°，∵∵BOD=∵COA=70°，∵∵AOD=180°-∵COA=180°-70°=110°，又∵OF平分∵AOD，∵∵DOF=0.5×110°=55°；（2）∵∵AOE=90°，∵∵AOC+∵COE=90°，∵∵BOD=∵AOC，∵∵BOD+∵COE=90°，∵∵COE的余角有：∵COA，∵BOD．20、解：（1）∵OE平分∠BOC，∴∠BOC=2∠BOE=2×64°=128°，∴∠AOC=180°-128°=52°，∵∠COF=90°，∴∠AOF=38°；（2）∵OE平分∠BOC，∴∠BOC=2∠BOE，∵∠BOD：∠BOE=2：3，∴∠BOD＝45°，∴∠AOC=∠BOD=45°，∵∠COF=90°，∴∠AOF=45°21、解：∵OF⊥CD，∠EOF=54°，∴∠DOE=90°-54°=36°，又∵OE平分∠BOD，∴∠BOD=2∠DOE=72°，∴∠AOC=72°，又∵∠COF=90°，∴∠AOF=90°+72°=162°．22、解：∵FO⊥OD于O，∠1=40°，∴∠BOD=50°，根据对顶角相等，得∠2=50°，∴∠AOD=130°，又OE平分∠AOD，∴∠4=65°．23、解：（1）设∠BEC的度数为x，则180-x=3（90-x），x=45°，∴∠BEC=45°，故答案为：45；（2）∵∠BEC=45°，∴∠AEC=135°，设∠AEG=x°，则∠CEG=x-25，由∠AEC=135°，得x+（x-25）=135，解得x=80°，∴∠AEG=80°；（3）∵射线EF平分∠AED，∴∠AEF=∠DEF，∵∠FEG=100°，∴∠AEG+∠AEF=100°，∵∠CEG=180°-100°-∠DEF=80°-∠DEF，∴∠AEG-∠CEG=100°-∠AEF-（80°-∠DEF）=20°，故答案为：20．。

人教版初中数学七年级下册第五章第一节《5.1相交线》同步练习题(含答案)

人教版初中数学七年级下册第五章第一节《 5.1相交线》同步练习题（含答案）5.1《相交线》同步练习题、选择题（每小题只有一个正确答案） 1 •如图所示，/ 1与/2不是同位角的是（）A.2 .在同一平面内，下列说法中，错误的是 A. 过两点有且只有一条直线B. 过一点有无数条直线与已知直线平行C. 过直线外一点有且只有一条直线与已知直线平行D. 过一点有且只有一条直线与已知直线垂直3 .已知：0A 丄 0C , / AOB :/ AOC , 2 : 3,则/ BOC 的度数为（），A. 30 °B.60 °C. 150 °D.30。

或 150 °4.如图，点A 到线段BC 所在直线的距离是线段（）A. / 1和/ 3是同位角B. / 1和/ 5是同位角C. / 1和/ 2是同旁内角D. / 5和/6是内错角6 .两条直线相交所构成的四个角中：①有三个角都相等；②有一对对顶角互补；③有一个角是直角；④有一对邻补角相等.其中能判定这两条直线垂直的有（） A. 1个 B. 2个 C. 3个 D. 4个7 .平面上三条直线两两相交最多能构成对顶角的对数是（ A. 7 B. 6 C. 5 D. 4二、填空题8.如图，直线a 与b 相交于点 0,直线c 丄b ,且垂足为0,若/仁35 °,则/2= ______________D.A. AC 的长度B. AD 的长度C. AE 的长度5. 如图所示，下列说法错误的是（）D. AB 的长度9 .如图，计划把河水引到水池 A 中，先作AB 丄CD ，垂足为B ，然后沿AB 开渠，能使所开的渠道最短，这样设计的依据是 _______________10 .两条直线相交所成的四个角中，有两个角分别是(2x -10)°和(110-x) °，则 x= _________11 .如图，在平面内，两条直线 l i , 12相交于点0,对于平面内任意一点 M ，若p , q 分别是点M 到直线11，12的距离，则称(p, q)为点M 的距离坐标”.根据上述规定，距离坐标”是(2，1的点共有 _____________________ 个.三、解答题13 .如图，直线 AB, CD 相交于点 0, / BOE=90°，OF 平分/ AOD / COE=20°，求/ BOD 与/ DOF 的度数.BC D(1)/ 1和/ 3是直线被直线所截得的 (2)/ 1和/ 4是直线被直线所截得的 (3)/ B 和/2是直线被直线所截得的 (4)/ B 和/4是直线被直线所截得的12 .看图填空:人教版初中数学七年级下册第五章第一节《 5.1相交线》同步练习题（含答案）14 .在同一平面内三条直线交点有多少个？甲：同一平面三直线相交交点的个数为 0个，因为a , b ,c 如图（1）所示.乙：同一平面内三条直线交点个数只有 1个，因为a , b,c 交于同一点0,如图（2）所示.以上说法谁对谁错？为什么？15 .已知，如图，直线AB 和CD 相交于点 0, / C0E 是直角，0F 平分/ AOE, / COF=34°, 求/ A0C和/ BOD 的度数.16 .探究题：(I)(1) 三条直线相交，最少有____ 个交点；最多有 _____ 个交点，画出图形，并数出图形中的对顶角和邻补角的对数；(2) 四条直线相交，最少有____ 个交点；最多有 _______ 个交点，画出图形，并数出图形中的对顶角和邻补角的对数；(3) 依次类推，n条直线相交，最少有________ 个交点；最多有_______ 个交点，对顶角有对，邻补角有__________ 对.参考答案I. B2. B3. D4. B5. B6. D7. B8. 55°9•垂线段最短10. 40 或80II. 4,12. 解析：根据同旁内角、同位角及内错角的概念可得：(1) / 1和/3是直线AB、BC被直线AC所截得的同旁内角；(2) / 1和/ 4是直线AB, BC被直线AC所截得的同位角；(3) / B和/ 2是直线AB, AC被直线BC所截得的同位角；(4) / B和/4是直线AC, BC被直线AB所截得的内错角•13. / BOD=70°, / DOF=55°解：•••/ COE=20°,Z BOE=90°,•••/ BOD=180°, 20°, 90° =70°,•••/ AOD—180°, 70° =110°,•/ OF 平分/ AOD ,1• / DOF=-/AOD=55°,•••/ BOD=70°,Z DOF=55°.14. 甲，乙说法都不对，各自少了三种情况，具体见解析解析：甲、乙说法都不对，都少了三种情况.a// b,c与a,b相交如图(1);a,b,c两两相交如图(2),所以三条直线互不重合，交点有0个或1个或2个或3个，共四种情况15. / AOC=22 , / BOD=22 .解析：，，COE=90 , , COF=34 ,,,EOF= COE , COF=56°,,OF是，AOE的平分线,,,AOE=2, EOF=112°,,,AOC=112°, 90 ° =22 ° ,,,BOD和，AOC是对顶角，,,BOD=22°,16. (1)1,3,画图见解析，对顶角有6对，邻补角有12对;(2)1,6, 画图见解析，对顶角有12对,邻补角有24对;(3)1, n n 1,n(n —1),2 n(n —1).2分析：当直线同交于一点时，只有一个交点；当直线两两相交，且不过同一点时，交点个数2最多；根据对顶角与邻补角的定义找出即可.;1三条直线相交，最少有 1个交点，最多有3个交点，如图:对顶角：6对，邻补角：12对；；2四条直线相交，最少有 1个交点，最多有6个交点，如图:对顶角：12对，邻补角：24对；n n 1(3) n 条直线相交，最少有 1个交点，最多有个交点，对顶角有 n (n - 1)对,2邻补角有2n (n - 1)对. 丄,“宀,n n 1故答案为：(1) 1, 3 ； (2) 1, 6； (3) 1, , n ( n- 1), 2n (n - 1).2。

人教版初中数学七年级下册第五章《相交线》同步练习(含答案)

《相交线与平行线》同步练习一、选择题（每小题只有一个正确答案）1．下列语句中，指的是对顶角的是（）Ａ．有公共顶点并且相等的两个角Ｂ．有公共顶点的两个角Ｃ．角的两边互为反向延长线的两个角Ｄ．两直线相交所成的两个角2．如图1，直线AB CD EF ，，相交于点O ，且AB CD ⊥，若70BOE ∠，则DOF ∠的度数为（）Ａ．10 Ｂ．20Ｃ．30 Ｄ．403．已知直线a b c ，，在同一平面内，则下列说法错误的是（）Ａ．如果a b ∥，b c ∥，那么a c ∥ Ｂ．如果a b ⊥，c d ⊥，那么a c ∥ Ｃ．如果a 与b 相交，那么a b ∥ D ．如果a b ⊥，，a c ∥，那么b c ∥4．如图，已知∠1=∠2=∠3=∠4，则图形中平行的是（）A ．AB ∥CD ∥EF;B ．CD ∥EF;C ．AB ∥EF;D ．AB ∥CD ∥EF ，BC ∥DE5．如图，已知∠1=∠2，则在结论：（1）∠3=∠4，（2）AB ∥CD ，（3）AD ∥BC 中（）A ．三个都正确B ．只有一个正确;C ．三个都不正确D ．只有一个不正确6.如图，在△ABC 中，D 、E 、F 分别在AB 、BC 、AC 上，且EF ∥AB ，要使DF ∥BC ，只需再有下列条件中的（）A ∠1=∠2B ．∠EFD=∠ADEC ．∠AFD=∠2D ．都不正确7.如果∠α与∠β的两边分别平行，∠α与∠β的3倍少36°，则∠α的度数是( )A 、18°B 、126C 、18°或126°D 、以上都不对8.P 为直线l 上的一点，Q 为l 外一点，下列说法不正确的是( )A 、过P 可画直线垂直于lB 、过Q 可画直线l 的垂线C 、连结PQ 使PQ ⊥lD 、过Q 可画直线与l 垂直9.下列关系中，互相垂直的两条直线是( )A 、互为对顶角的两角的平分线B.互为补角的两角的平分线C 、两直线相交所成的四个角中相邻两角的角平分线D 、相邻两角的角平分线10.如图，AB ⊥BC ，BC ⊥CD ，∠EBC=∠BCF ，那么∠ABE 与∠DCF 的位置和大小关系是( )A 、是同位角且相等B 、不是同位角但相等C 、是同位角但不等D 、不是同位角也不等二、填空题1．如图4，已知三条直线AB CD EF ，，两两相交于点P Q R ，，，则图中邻补角有____对，对顶角有____对（平角除外）．2.图5，90AOC = ∠，45BOC =∠，OD 平分AOB ∠，则AOD ∠的度数为____，COD ∠的度数为____．3.定点P 在直线AB 外，动点O 在直线AB 上移动，当PO 最短时，∠POA=_______，这时线段PO 所在的直线是AB 的___________，线段PO 叫做直线AB 的______________。