线段和差倍分及其应用专题

原七年级数学上册4图形的初步认识专题课堂(六)线段的和、差、倍、分计算习题课件(新版)华东师大版

第十四页，共14页。
解：∵点 M 为 AB 的中点，∴AM＝BM＝21AB＝12×12＝6 cm，∵ BC＝2MC，∴BC＋CM＝3MC＝6 cm，∴CM＝2 cm，∴AC＝AM＋MC ＝6＋2＝8 cm
第四页，共14页。
类型Ⅱ：与比例有关的计算【例 2】如图，线段 AB 上有两点 C，D，AD＝35，BC＝44，AC＝23DB，求线段 AB 的长．
第六页，共14页。
二、分类讨论的数学思想本类题型需根据点的位置不同而进行分类讨论．【例 3】已知线段 AB＝4.8 cm，C 是 AB 的中点，D 是 CB 的中点，点 E 在 AB 上，且 CE＝13AC.请你画图并计算 DE 的长．分析：易求 AC＝BD＝12AB＝2.4 cm.根据点 E 在 C 点的左侧或右侧的不同位置可得 DE＝CD－CE 或 DE＝CD＋CE，因此应分类讨论可得出 DE 的长．
点，且AB＝14，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，
设运动时间为t(t>0)秒．－6
8－5t
(1)写出数轴上点B表示的数____，点P表示的数_______；(用含t的代数式表示)
(2)动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P，Q
同时出发，问点P运动多少(duōshǎo)秒时追上点Q?
(3)设 AC＝a cm，∵点 D，E 分别是 AC 和 BC 的中点，∴DE＝CD ＋CE＝12(AC＋BC)＝12AB＝6 cm，∴不论 AC 取何值(不超过 12 cm)，DE 的长不变
第十二页，共14页。
【对应训练】
4．(2015秋·攀枝花校级期末)如图，已知数轴上点A表示的数为8，B是数轴上一
第八页，共14页。

证题技巧之三——证明线段或角的和差倍分(推荐文档)

证题技巧之三一一证明线段或角的和差倍分一、证明线段或角的倍分1、方法：①长（或大）折半 ②短（或小）加倍2、判断：两种方法有时对同一个题都能使用，但存在易繁的问题，因此，究竟是折半还是加倍要以有利于利用已知条件为准。

3、添线：①为折半或加倍而添；②为折半或加倍后创造条件或利于利用已知条件而添。

4、传递：在加倍或折半后，还不易或不能证明结论，则要找与被证二量有等量关系的量来传递，或者添加这个量来传递。

此时，添线从两方面考虑：①造等量②为证等量与被证二量相等而添。

参考例4、例5、例6。

例1 AD 是^ ABC 的中线，ABEF 和ACGH 是分别以AB 和AC 为边向形外作的正方形。

求证：FH=2AD/ BAC+ / ACN=180证明：延长AD 至N 使AD=DN则ABNC 是平行四边形CN=AB=FA AC=AH又/ FAH+ / BAC=180 •••△ FAHY NCA ••• FH=AN例 2、△ ABC 中，/ B=2 / C ,AD 是高，M 是BC 边上的中点。

$•••1求证：DM=2 AB/ 2=Z B •••/ 2=2Z 1•••/ 1 = / DNM 又 AN=DN=ND • DM=2 A B1贝J BFAC••• BF=AE•••△ AEC 心 BFD •DF 二CE 二 CD=2CE作业:1、在△ABC 中，D 为BC 的中点，E 为AD 的中点，BE 的延长 1线交AC 于F ,求证：AF=2 FC2、AB 和AC 分别切© O 于B 和C, BD 是直径。

求证/ BAC 二Z CBD3、圆内接△ ABC 的AB=AC ,过C 作切线交AB 的延长线于D , DE 垂直于AC 的延长线于E 。

求证：BD=2CE例4从平行四边形的钝角顶点 A 向BC 边作垂线，垂足为E ,证明：取AB 的中点N ，连接MN 、DN贝J MN // AC / 1 = / C••• DM=DN例 3 △ ABC 中，AB=AC , E 是AB 的中点，D 在AB 的延长线上，且 DB=AC 。

线段的和差与倍分

线段的和差与倍分学习目标：1．能用直尺和圆规作出线段的和、差。

2．理解线段中点的概念及意义，会用刻度尺画出一条线段的中点，并能用符号语言表示出来学习重难点：线段中点的应用学习过程一、知识回顾1．如何比较线段的长短？2．如图所示，A地到B地有a,b,c,d（图中从上到下）四条道路，其中最短的是，理由是。

二、预习自学活动一、作出符合要求的线段思考，木料截断的位置在什么地方？已知线段AB，画出它的中点C。

A B如图，如果点C把线段AB分成相等的两条线段AC与BC，那么点C叫做线段AB的中点。

几何语言：（1）（2）（3）三、例题分析例1、已知C是线段AB上的一点，AC=5厘米，CB=3厘米，M是线段AB的中点，画出符合要求的图形，并求出MC的长。

思考：若例1中点C是直线AB上一点，MC的长是多少呢？（四）课堂总结（1）要得到线段的中点，首先必须确保_________________________________. （2）等分点的概念：类似于中点定义，将线段等分成3份的点叫做线段的三等分点，把线段等分成4份的点叫做线段的四等分点四、达标练习1、如图，已知cm=，DC3=，D是AC的中点，且cmBC4则AB= ，AC=____.2、已知C是线段AB上的一点，6,8==,M是AB的中点。

画出符合要求的AC cm CB cm图形，并求出MC的长。

3、如图，已知线段20是线段的中点，在MB上，N为PB的中点，NB=4cm,=，M AB PAB cm求PM的长。

M P NA B五、课堂小结：本节课我们新学到哪些内容？六、课下作业1、如果点M 把线段AB 分成相等的两条线段AM 与BM ，那么点M 叫做线段AB 的中点.此时AM 、BM 和AB 有如下关系： .2、如图，已知cm AB 20=，cm CD 8=，E 、F 分别为AC 、BD 的中点，求EF 的长.3、已知线段cm AB 10=，C 是线段AB 的中点，E 、F 分别为AC 、CB 的中点,求EF 的长. 如果8AB cm =呢？12AB cm =呢？由此可以发现什么规律？4、如图：已知AB:BC:CD=2:3:4，E,F 分别是线段AB,CD 的中点，且AD=45cm ，求线段EF 的长。

方程思想在线段的和差倍分计算中的应用专题练习(解析版)

方程思想在线段的和差倍分计算中的应用专题练习一、选择题1、如图，线段AC:CB=2:3，D是CB的中点，已知AB=20 cm，求BD的长（）．A. 6 cmB. 7 cmC. 8 cmD. 9 cm答案：A解答：∵AC:CB=2:3∴设AC=2x（cm），CB=3x（cm），∵AB=20 cm∴2x+3x=20，解得x=4，∵D是CB的中点∴BD=12CB=32x=6 cm．2、如图所示，线段AB被点C、D分成2:3:4三部分，M为AC的中点，N为BD的中点，且MN=2.4，则AB的长度为（）．A. 3.4B. 3.5C. 3.6D. 3.7答案：C解答：设AC为2x，CD为3x，DB为4x，根据题中所给条件，可知MC=12AC=x，DN=12DB=2x，MN=MC+CD+DN=x+3x+2x=6x=2.4，x=0.4，∴AB=2x+3x+4x=9x=3.63、如图，已知线段AB上有C、D两点，AB=2CD，BD=23CD，AC=1，求BD的长度（）．A. 1B. 2C. 3D. 4答案：B解答：设CD=x，则AB=2x，BD=2 3 x∵AC=AB-CD-BD=13x，且AC=1∴有13x=1，解得x=3，则BD=23x=2．4、如图，点A、B在线段EF上，点M、N分别是线段EA、BF的中点，EA:AB:BF=1:2:3，若MN=8 cm，则线段EF的长是（）．A. 10 cmB. 11 cmC. 12 cmD. 13 cm答案：C解答：∵EA:AB:BF=1:2:3，设EA=x，AB=2x，BF=3x，∵M、N分别为EA、BF的中点，∴MA=12EA，NB=12BF，∴MN=MA+AB+BN=12x+2x+32x=4x，∵MN=8 cm，∴4x=8，∴x=2，∴EF=EA+AB+BF=6x=12，∴EF的长为12 cm．选C.5、如图，点B，D在线段AC上，BD=13AB=14CD，E是AB的中点，F是CD的中点，EF=5，则AB的长为（）．A. 5B. 6C. 7D. 8答案：B解答：设BD=x，则AB=3BD=3x，CD=4BD=4x，∵E、F分别为AB、CD中点，∴EB=12AB=32x，DF=12CD=2x，∴EF=EB+DF-DB=32x+2x-x=52x，∵EF=5，∴52x=5，∴x=2，∴AB=3x=3×2=6．二、填空题6、如图，已知BC=2AB，CD=4AB，且AD=7 cm，则BC的长为______ cm．答案：2解答：∵BC=2AB，CD=4AB∴设AB=x，BC=2x，CD=4x∵AD=AB+BC+CD=x+2x+4x=7∴x=1，∴BC=2x=2 cm．7、如图，D为线段AC的中点，BC=14AB，BD=9，则线段AC的长为______．答案：30解答：设BC=x，则AB=4x，AC=4x+x=5x，∵D为线段AC的中点，∴AD=CD=2.5x，∵BD=9，∴2.5x-x=9，∴x=6，∴AC=5x=30，故答案为：30．8、如图，AC=13AB，BD=14AB，AE=CD，则CE与AB之比为______．答案：1 12解答：AB=12x，AC=4x，BD=3x，CD=AB-AC-BD，∵AE=CD，AE=5x，CE=AE-AC=x，CE:AE=1:12．9、如图，已知线段AB:BC:CD=2:3:4，点E、F分别是AB、CD的中点，且EF=12 cm，则线段AD的长为______ cm．答案：18解答：设AD=9x，AB=2x，BC=3x，CD=4x，∴BE=x，CF=2x，EF=BE+BC+CF=6x=12，x=2，AD=18．三、解答题10、如图，已知AC:CD:DB=2:3:4，若E为AC的中点，F为DB的中点，若EF=5.4，求AB 的长．答案：8.1．解答：设AC=2x，∴CD=3x，DB=4x，∴AE=EC=x，DF=FB=2x，∵EF=5.4，∴EF=EC+CD+DF=6x=5.4，x=0.9，∴AB=AC+CD+DB=9x=8.1．11、如图，已知线段AB和CD的公共部分BD=13AB=14CD，线段AB、CD的中点E、F之间距离是10 cm，求AB，CD的长．答案：AB=12 cm，CD=16 cm．解答：设BD=x cm，则AB=3x cm，CD=4x cm，AC=6x cm．∵点E、点F分别为AB、CD的中点，∴AE=12AB=1.5x cm，CF=12CD=2x cm，∴EF=AC-AE-CF=6x-1.5x-2x=2.5x cm．∵EF=10 cm，∴2.5x=10，解得：x=4，∴AB=12 cm，CD=16 cm．12、已知线段AB，点C在AB的延长线上，AC=53BC，点D在AB的反向延长线上，BD=35DC.（1）在图上画出点C和点D的位置．（2）设线段AB长为x，请用含x的代数式表示BC，AD. （3）若AB=12 cm，求线段CD的长．答案：（1）画图见解析．（2）BC=32x，AD=54x．（3）CD=45．解答：（1）（2）BC=32x，AD=54x．（3）由（2）得：CD=AD+AB+BC，∴CD=54x+x+32x，∴CD=154x，∵AB=12，∴x=12，∴CD=45．13、如图，C，D是线段AB上的两点，已知AC:CD:DB=1:2:3，M、N分别是AC，BD的中点，且AB=36 cm，求线段MN的长．答案：24 cm．解答：∵AC:CD:DB=1:2:3，∴设AC=x cm，则CD=2x cm，DB=3x cm，∵AB=36 cm，∴x+2x+3x=36，解得：x=6，∵M、N分别是AC、BD的中点，∴CM=12AC=12x，DN=12BD=32x，∴MN=CM+CD+DN=12x+2x+32x=4x=4×6=24（cm）．14、如图所示，已知：BC=13AB=14CD，点E、F分别是线段AB、CD的中点，且EF=60厘米，求线段AB的长度．答案：72 cm．解答：设BC=x cm，∵BC=13AB=14CD，∴AB=3BC=3x cm，CD=4BC=4x cm，∴AD=AB+CD-BC=6x cm，∵E、F分别是线段AB、CD的中点，∴AE=12AB=32x cm，FD=12CD=2x cm，∴EF=AD-AE-FD=6x-32x-2x=52x cm∵EF=60 cm，∴52x=60，∴x=24，∴AB=3x=3×24=72 cm．。

四年级线段图解决和差倍问题

第3讲线段图解决应用题1.掌握和倍问题与差倍问题的题型特点；2.掌握线段图法解决和差倍问题的步骤。

一. 和差问题1. 题型特点已知两个数的“和”与“差”，求这两个数。

2. 基本公式大数=(和+差)÷2小数=(和-差)÷2（或者：小数=大数-差，小数=和-大数）3. 图示分析一根线绳和一根麻绳总长为48米，已知线绳比麻绳长10米，求线绳和麻绳各长多少米？1. 张明在期末考试时，语文、数学两门课的平均得分是95分，数学比语文多得8分，张明这两门功课的成绩各是多少分？2. 甲、乙两筐苹果共重75千克，从甲筐取出5千克苹果放入乙筐里，甲筐苹果还比乙筐多7千克。

甲、乙两筐原来各有苹果多少千克？二. 和倍问题1. 题型特点已知两个数的“和”与这两个数的倍数关系，求这两个数。

2. 基本公式小数=和÷(倍数+1)大数=和-小数（或者：大数=小数×倍数）3. 图示分析甲班和乙班共有图书160本。

甲班的图书本数是乙班的3倍，甲班和乙班各有图书多少本？1. 某小学有学生760人，其中男生比女生的3倍少40人，男、女生各有多少人？2. 大白兔和小灰兔共采摘了蘑菇160个，后来大白兔吃了20个，而小灰兔又采了10个，这时，大白兔的蘑菇是小灰兔的蘑菇的5倍，原来小灰兔采了多少个蘑菇？3. 三个队种数，第二队种的树是第一队的2倍，第三队种的树比第一队的2倍多4棵。

已知3个队一共种树64棵，求每个队各种树多少棵？三. 差倍问题1. 题型特点已知两个数的“差”与这两个数的倍数关系，求这两个数。

2. 基本公式：小数=差÷(倍数-1)大数=小数+差（或者：大数=小数×倍数）3. 图示分析：光明小学开展冬季体育比赛，参加跳绳比赛的人数是踢踺子人数的3倍，跳绳比赛的人数比踢踺子的多36人。

参加跳绳和踢踺子比赛的各有多少人？1. 两筐苹果重要相等，甲筐卖出去7千克后，乙筐卖出去19千克后，甲筐剩下的苹果重要是乙筐的3倍，两筐苹果原来各有多少千克？2. 小丽和小荣集邮，小丽邮票的张数是小荣的5倍，如果小丽把自己的票给小荣100张，她俩邮票的张数正好相等。

探究线段的和、差、倍、分是平面几何中常见的问题,“截

探究线段的和、差、倍、分是平面几何中常见的问题，“截长补短法”是解决这一类问题的常用方法，“截长”就是将题中的某条线段截成题中的几条线段之和；“补短”就是将题中某条线段延长（补上某线段），然后，证明它与题中某条线段相等。

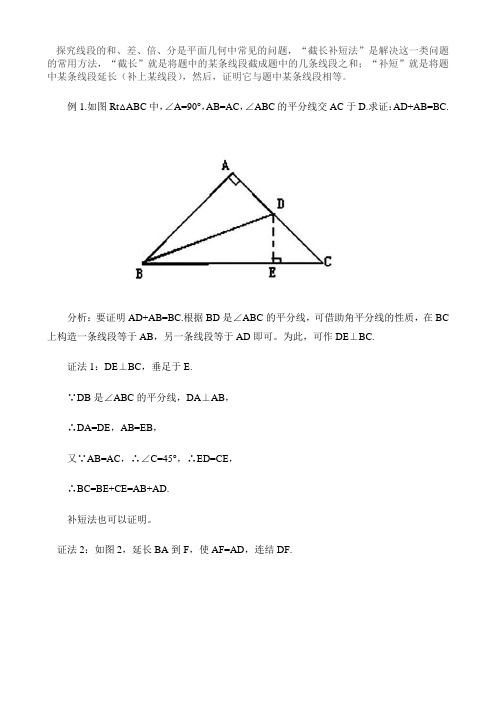
例1.如图Rt△ABC中，∠A=90°，AB=AC，∠ABC的平分线交AC于D.求证：AD+AB=BC.分析：要证明AD+AB=BC.根据BD是∠ABC的平分线，可借助角平分线的性质，在BC 上构造一条线段等于AB，另一条线段等于AD即可。

为此，可作DE⊥BC.证法1：DE⊥BC，垂足于E.∵DB是∠ABC的平分线，DA⊥AB，∴DA=DE，AB=EB，又∵AB=AC，∴∠C=45°，∴ED=CE，∴BC=BE+CE=AB+AD.补短法也可以证明。

证法2：如图2，延长BA到F，使AF=AD，连结DF.∵DA⊥AB，∴∠FAC=90°，∵AF=AD，∴∠F=45°，同理∠C=45°，∴∠F=∠C，∵∠FBD=∠CBD，BD=BD，∴△FBD≌△CBD，∴FB=BC，∵FB=BA+FA=BA+AD，∴AD+AB=BC评注：证明一条线段等于两条线段之和，一般有截长法或补短法两种变式1：△ABC中，∠A=108°，AB=AC，∠ABC的平分线交AC于D.求证：BC=AB+CD变式2: △ABC中，∠A=100°，AB=AC，∠ABC的平分线交AC于D.求证：BC=BD+AD(同学们仿照例题,中、课后思考完成)“一题多解”有利于锻炼学生思维的灵活性，活跃思路，让学生能根据题目给出的已知条件，并结合自身情况，灵活地选择解题切入点．“一题多解”有利于培养学生的创新思维，使学生不满足仅仅得出一道习题的答案，而去追求更独特、更快捷的解题方法。

“一题多解”有利于学生积累解题经验，丰富解题方法，学会如何综合运用已有的知识不断提高解题能力。

2021年中考数学热点专题复习：例析线段和差倍分问题的求解策略

2021年中考数学热点专题复习：例析线段和差倍分问题的求解策略在几何问题中，要证明一条线段是另外几条线段的和差，或是另一线段的几倍或几分之几，我们统称为线段的和差倍分问题，处理这类问题的指导思想是化归为线段的相等问题．一、利用全等形或相似形对于线段的倍分问题，通常可利用图形中特殊的分点为解题的突破口，找出图形中较短线段的倍分线段，再用全等三角形证明它与较长线段相等，或围绕特殊分点对应线段所在三角形寻找相似三角形，利用相似形对应线段的比例关系达到求证的目的．例1如图1，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD ＝45°，AD与BE交于点F，连CF．(1)求证：BF＝2AE；(2)若CD＝2，求AD的长．分析由图形的对称性，不难发现点E为AC的中点，即AC＝2AE，故问题(1)只要证明BF＝AC．(2)略．例2如图2，点A、B、C、D在⊙O上，AC⊥BD于点E，过点O作OF⊥BC于点F．(1)求证：△AEB∽△OFC；(2)AD＝2OF．二、取长补短法对于线段的和差问题，通常采用延长较短线段或截取较长线段的方式，化归为线段的相等问题（俗称取长补短法）．例3 如图3，已知点A、B、C、D顺次在⊙O上，且AB＝BD，BM⊥AC于点M，求证：AM＝CD＋CM．证明（延长法）延长DC至点N，使CN＝C M，下面只要证明AM＝DN即可．连BN，则由AB＝BD，得∠ACB＝∠ADB＝∠BAD＝∠BCN，又CN＝CM，BC为公共边，例4 如图4，在菱形ABCD中，F为BC边的中点，DF与对角线AC交于点M，过点M作ME⊥CD于点E，∠1＝∠2．(1)若CE＝1，求BC的长；(2)求证：AM＝DF＋ME．解 (1)略；(2)证法1（截取法）如图4，连BD 交AC 于点O ，分别证明AO ＝DF ，OM ＝ME 即可．证法2（延长法）如图5，延长DF 至点N ，使FN ＝ME ，只要证AM ＝DN 即可．连CN 、MB ．同证法1可得△BCD 为正三角形，M 是正△BCD 的中心．三、几何变换法用几何变换法证明线段的和差倍分问题，实质上是利用几何变换将线段移动，使较短线段在适当的位置进行“集中”，使隐含的数量关系明显化，从而达到证明的目的．例5 如图6，⊙O 外接于正方形ABCD ，P 为劣弧AD 上任意一点，求证：PA PC PB+恒为定值，并求出此定值．证明当P 与A 重合时，易知 2PA PC AC PB AB+==；一般情况下，可将△ABP绕点B顺时针旋转90°，得△CBQ，则综上，无论P为劣弧AD上哪一点，PA PCPB恒为定值2，得证．例6 如图7，在四边形ABCD中，AB∥CD，E为BC边的中点，F在DC边的延长线上，且∠BAE＝∠EAF，求证：AB＝AF＋CF．解将△ABE绕点E顺时针旋转180°，得到△GCE，则由AB∥CD、E为BC边的中点知点G在DC的延长线上．。

线段的和差倍分教案

线段的和差倍分教案篇一：三角形专题线段的和差倍分专题：三角形之线段的和差倍分1、在△ABC中，∠ACB= 900，AC=BC，直线MN经过点C，且AD ⊥MN于D，BE⊥MN于E。

（1）当直线MN绕点C旋转到图1的位置时，求证：DE=AD+BE。

（2）当直线MN绕点C旋转到图2的位置时，问DE 、AD、BE 有何关系，并说明理由。

A2、如图，在△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于点E，AD⊥CE于点D. 求证：DE?AD?BE.3、如图，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE、BE，BE⊥AE，延长AE交BC的延长线于点F.求证：（1）FC=AD；（2）AB=BC+AD4、如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．求证：?BD=CF?BD=2CE．5、?如图，在△ABC中，BD平分∠ABC，CD平分∠ACB，过D 点作EF∥BC交AB于E，交AC于F，求证：EF=BE+CF．?在△ABC中，BD平分∠ABC，CD平分∠ACG，过D点作EF∥BC 交AB于E，交AC于F，试探究BE、EF与CF的数量关系．篇二：【教案】2.4线段的和与差2.4线段的和与差教学目标1．理解线段可以相加减，掌握用直尺、圆规作线段的和、差. 2．利用线段的和与差进行简单的计算。

教学重点和难点重点：用直尺、圆规作线段的和、差。

难点：进行简单的计算。

教学时间：1课时教学类型：新授教学过程：一、复习旧知，作好铺垫1．已知线段AB，用圆规、直尺画出线段CD，使线段CD=AB. 2．两点间的距离是指（）A.连结两点的直线的长度；B.连结两点的线段的长度；C.连结两点的直线；D.连结两点的线段.二、创设情景，激趣导入1．我们知道数（如有理数）可以相加减，那么作为几何图形的线段是否可以相加减呢？12．观察：如图所示，A、B、C三点在一条直线上，1）图中有几条线段？2）这几条线段之间有怎样的等量关系？A B C学生讨论三、尝试探讨，学习新知1．显然，图中有三条线段：AB、AC、BC,它们有如下的关系AB+ BC= AC，AC- BC= AB，AC- AB= BC2．由此，你可以得到怎样的结论两条线段可以相加（或相减），它们的和（或差）也是一条线段，其长度等于这两条线段的和（或差）3．例题1：如图,已知线段a、b,1）画出一条线段, 使它等于a+b2）画出一条线段, 使它等于a-b※学生尝试画图※教师示范，（注意画图语句的叙述）解：（1）①画射线OP;②在射线OP上顺次截取OA=a,AB=b线段OB就是所要画的线段.（2）①画射线OP;②在射线OP上截取OC=a，在射线OC上截取CD=b线段OD就是所要画的线段.2 b4.在例题1中为什么CD要“倒回”截？不“倒回”截行吗？5．思考：你会作一条线段使它等于2a吗？1）学生讨论2）2a是什么意思？（a+a）3）那么na（n为正整数，且n1）具有什么意义？6．尝试：例题2 如图,已知线段a、b,画出一条线段，使它等于2a-b1）学生独立完成2）反馈，纠正这两个例题是线段的和、差、倍的具体画法，教师在画图的过程中，要边画边讲．注意讲清以下问题：(1)先画的图形是已知的线段a，b．(2)画射线的目的是确定整个图形的起点，由于在没有画完的情况下，终点不能确定，而这种只有起点而没有终点的状态，只有用射线描述最为合适．(3)什么叫“顺次截取”？就是要沿着射线的方向，从起点开始，依照计算的顺序截取．(4)线段的和、差在画图中的区别是什么？“和”是在截取时不改变方向．而“差”在截取时的方向是变化的．3通过这两个例题．使学生能够掌握线段的和、差、倍的画图．(5)两个例题讲完后可以安排一个练习：已知线段a，b，c(a＞b ＞c)，画一条线段，使它等于2a+3b-c．7．将一条线段分成两条相等线段的点叫做这条线段的中点.若已知点M是线段AB的中点，你能得到哪些等量关系.AM?MB，AM?MB，BM?ABAB?2AM，AB?2MB8．已知线段AB，你会画出它的中点C吗？除了用尺测量，你还有其他方法吗？9．介绍用尺规作线段AB 的中点C.注意语言的叙述：解：（1）以点A为圆心，以大于AB的长a为半径作弧，以点B 为圆心，以a为半径作弧，两弧分别相交于点E、点F；（2）作直线EF，交线段AB于点C.点C就是所求的线段AB的中点. 1212四、反馈小结、深化理解1．学生自己总结本节课的学习内容，应回答出线段的和、差、倍、分的画法；线段中点的定义． 4a2．线段的和、差、倍的画法中应注意的问题．如步骤、方向等．3．一些关键词的用法，如“连结”、“顺次”等．五、学习训练与学习评价建议一、判断题（每题4分，共20分）(1)连接A、B两点，那么线段AB叫做A、B两点的距离.（）(2)连接A、B两点的线段的长度，叫做A、B两点的距离.（）(3)若AB＝BC，则B是线段AC的中点.（）(4)若AB=AM+BM，则点M在线段AB上.（）(5)若点M在线段AB外，则必有ABAM+MB.（）二、填空题（每题5分，共20分）(1)点M把线段PQ分成两条相等的线段，点M叫做线段PQ的______，这时有PQ=_______=_______.(2)延长线段AB到C，使BC=AB，反向延长AC到D使AD=AC，则CD=_______AB.(3)如图1.3-4，如果A、B两点将MN三等分，C为BN的中点，BC=5cm，则MN=________.(4)如图1.3-5，在直线PQ上要找一点A，使PA=3AQ，则A点应在________.图1.3-4图1.3-5 5篇三：线段和差倍分怎样证明线段的和差倍分问题怎样证明线段的倍分问题【典型例题】常规题型1、已知：如图所示，点D、E分别是等边?ABC的边AC、BC上的点，AD=CE，BD、AE交于点P，BQ?AE于Q．求证：PQ? 12PB．B C常规题型2、已知：如图所示，在?ABC中，AB=AC，?A?120?，AB的垂直平分线MN分别交BC、AB于点M、N．求证：CM=2BM．C N A能力挑战1、如图所示，在?ABC中，AB?12BC，D是BC的中点，M是BD的中点．求证：AC=2AM． ABD能力挑战2、已知：如图所示，在?ABC中，BD是AC边上的中线，BH平分?CBD,AF?BH，分别交BD、BH、BC于E、G、F．求证：2DE=CF．AD EBQ【经典练习】1、如图所示，已知?ABC中，?1??2，AD=DB，DC?AC．求证：AC? 1AB．21 2CD 2、已知：如图所示，D是?ABC的边BC上一点，且CD=AB，?BDA??BAD，AE是?ABD的中线．求证：AC=2AE． A E?AB于3、已知：如图所示，在?ABC中，AB=AC，?BAC?120?，D 是BC的中点，DEEE．求证：EB=3EA．AED?BAC?120?，4、已知：如图所示，在?ABC中，AB=AC，P是BC 上一点，且?BAP?90?．求证：PB=2PC．B P5、已知：如图所示，锐角?ABC中，?B?2?C，BE是角平分线，AD?BE，垂足是D．求证：AC=2BD．C6、如图所示，在?ABC中，AB=AC，?BAC?90?，BE平分?ABC，交AC于D，CE?BE于E点，求证：CE?1BD．2B C怎样证明线段的和差问题【典型例题】常规题型1、如图所示，已知?ABC中，?A?60?，BD、CE分别平分?ABC和?ACB，BD、CE交于点O．求证：BE+CD=BC． AEDB C能力挑战1、如图所示，在等腰直角三角形ABC中，?BAC?90?，AD=AE，AF?BE交BC于F，过点F作FG?CD于M，交BE延长线于点G，求证：BG=AF+FG．G AEB C能力挑战2、如图所示，在?ABC中，AB=AC，?A?100?，BE平分?ABC，求证：AE+BE=BC．AC B【练习】1、如图所示，已知?ABC中，?A?2?B，CD是?ACB的平分线，求证：BC=AC+AD．BC2、如图所示，若E为正方形ABCD的边BC上一点，AF为?DAE 的平分线，AF与CD相交于F点．求证：AE=BE+DF． A DFB3、如图所示，已知?ABC和?ADE均为等边三角形，B、C、D 在一直线上，求证：CE=AC+CD．ED?C?90?，4、如图所示，已知在?ABC中，AC=BC，AD是?BAC的平分线，求证：AB=AC+CD．CDB A5、如图所示，等边?ABC和等边?BDE，点A在DE的延长线上，求证：BD+DC=AD．CA B证明线段的和差倍分问题作业1、如图所示，在等腰三角形ABC中，P是底边BC上的任意一点．（1）求证：P点(本文来自：千叶帆文摘:线段的和差倍分教案)到两腰的距离之和等于腰上的高．（2）若P点在BC的延长线上，那么点P到两腰的距离与腰上的高三者之间存在什么关系？AFE BC2、如图所示，等腰三角形ABC中，AB=AC，?A?108?，BD平分?ABC．求证：BC=AB+DC．ADC B3、如图所示，已知?ABC是等腰三角形，AB=AC，?BAC?45?，AD 和CE是高，它们相交于H，求证：AH=2BD．E H4、如图所示，在?ABC中，?ACB?90?，P是AC的中点，过A过BP的垂线交BC延长线于点D，E是垂足．若?DBE?30?，求证：BP=4PE．D。

线段的和差(53张PPT)数学

答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
CD
CB
解析由题图可知：BD＝BC＋CD，AD＝AC＋BD－CB.
(2)如果CD＝4 cm，BD＝7 cm，B是AC的中点，那么AB的长为_____cm.
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3
解析如果CD＝4 cm，BD＝7 cm，B是AC的中点，则BC＝BD－CD＝7－4＝3 cm，∴AB＝BC＝3 cm.
∴点O是线段AB的中点；∵AB＝2OB，∴点O是线段AB的中点.故选C.
答案
解析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
4.如图，C是线段AB上的一点，点D是线段BC的中点，若AB＝10，AC＝6，则AD等于( )A.4 B.6 C.7.5 D.8
D
解析 ∵BC＝AB－AC＝4，点D是线段BC的中点，∴CD＝DB＝ BC＝2，∴AD＝AC＋CD＝6＋2＝8.故选D.
中点
知识点2 与中点有关的计算
答案
自我检测2.点C是线段AB的中点，则下列结论不成立的是( )A.AC＝BC B.AC＝ ABC.AB＝2AC D.BC＝ AB
B
答案
返回

(完整版)线段和差倍分及其应用专题

线段的和差倍分及其应用专题知识点：A、线段的和、差如图：①AB= + ；②AC= －；③BC= －；B、线段的中点如图：∵点C是线段AB的中点；∴①= =21；②=2 =2 ；解题思想：求线段的长度时，通常需要依据条件将线段表示成两线段的和、差。

★☆★解题需注意题设条件中的语言表达，能准确地把文字语言转化成图形语言，并要求能准确地书写符号语言。

如：“点C在线段AB上”与“点C在直线AB上”，你能根据文字语言将其转化成图形语言吗？试一试！例题讲解：【例1】、如图,D是AB的中点, E是BC的中点,BE=51AC=2cm,线段DE的长,求线段DE的长.练习：1、如图，AB=24cm，C、D点在线段AB上，且CD=10cm，M、N分别是AC、BD的中点，求线段MN的长．A BCA BC2、如图，C为线段AB的中点，N为线段CB的中点，CN=1cm.求图中所有线段的长度的和．3、在同一条公路旁，住着五个人，他们在同一家公司上班，如图9,不妨设这五个人的家分别住在点ABDEF位置，公司在C点，若AB=4km，BC=2km，CD=3km，DE=3km，EF=1km，他们全部乘出租车上班，车费单位报销．出租车收费标准是：起步价3元（3km以内，包括3km），以后每千米1.5元（不足1km，以1km计算），每辆车能容纳3人．（1）若他们分别乘出租车去上班，公司需支付车费多少元？（2）如果你是公司经理，你对他们有没有什么建议？4、如图所示，沿江街AB段上有四处居民小区A．C．D．B，且有AC=CD=DB，为改善居民的购物环境，想在AB上建一家超市，每个小区的居民各执一词，难以定下具体的建设位置，高经理是超市负责人，从便民、获利的角度考虑，你觉得他会把超市建在哪儿？为什么？【例2】、点C 、D 顺次将线段AB 分成三部分，且AC = 2CD ，CD ：DB = 1 ：3，M 、N 分别为AC 、BD 的中点，MN = 7cm ，求线段AB 的长度。

微专题八线段及角的和差倍分计算人教版七年级数学上册完美课件

微专题八线段及角的和差倍分计算-2020秋人教版七年级数学上册课件 (共26 张PPT)
(2)∵∠CON＝30°－α＝90°－β， ∴β＝α＋60°； (3)∵OC 平分∠MON，∠MON＝90°， ∴∠CON＝∠COM＝45°，设∠AON＝5t，∠AOC＝30＋8t， ∵∠AOC－∠AON＝∠CON， ∴30＋8t－5t＝45，解得 t＝5， ∴经过 5 秒 OC 第一次平分∠MON.
微专题八线段及角的和差倍分计算
一二
一线段的和差倍分计算 (教材 P128 练习第 3 题) 如图 1，点 D 是线段 AB 的中点，C 是线段 AD 的中点，若 AB＝4 cm，求线段 CD 的长度．
图1
解：∵D 是线段 AB 的中点，AB＝4 cm， ∴AD＝BD＝2 cm. ∵C 是线段 AD 的中点， ∴CD＝AC＝1 cm.
[2019 秋·罗山期末]如图 7①，O 为直线 AB 上一点，过点 O 作射线 OC，∠AOC＝30°，将一直角三角尺(∠M＝30°)的直角顶点放在点 O 处，一边 ON 在射线 OA 上，另一边 OM 与 OC 都在直线 AB 的上方．
图7
(1)若将图①中的三角尺绕点 O 以每秒 5°的速度沿顺时针方向旋转 t 秒，当 OM 恰好平分∠BOC 时，如图②.
[2019 秋·和平区期末]点 O 为直线 AB 上一点，在直线 AB 同侧任作射线 OC，OD，使得∠COD＝90°.
图6 (1)如图 6①，过点 O 作射线 OE，当 OE 恰好为∠AOC 的平分线时，另作射线 OF，使得 OF 平分∠BOD，则∠EOF 的度数是____135 ______度；
(i)求 t 的值； (ii)试说明此时 ON 平分∠AOC. (2)将图①中的三角尺绕点 O 顺时针旋转，设∠AON＝α，∠COM＝β，当 ON 在∠AOC 内部时，试求 α 与 β 的数量关系； (3)若将图①中的三角尺绕点 O 以每秒 5°的速度沿顺时针方向旋转的同时，射线 OC 也绕点 O 以每秒 8°的速度沿顺时针方向旋转，如图③，那么经过多长时间，射线 OC 第一次平分∠MON？请说明理由．

线段图解答和倍、差倍问题

1、鸡是鸭的3倍，就把（）看成1份，（）就有这样的（）份。

（画图）2、鸡是鸭的3倍，鸡和鸭共20只，鸡（）只，鸭（）只。

3、鸡是鸭的3倍，鹅是鸭的4倍，鹅、鸡和鸭共40只，鸡（）只，鸭（），鹅（）只。

2、鸡是鸭的3倍，鹅和鸡一样多，小鸟是鸭子的2倍，鹅、小鸟、鸡和鸭共45只，鸡（）只，鸭（），鹅（）只，小鸟（）只。

3、鸡是鸭的2倍，鹅是鸡的3倍，鹅、鸡和鸭共54只，鸡（）只，鸭（），鹅（）只。

4、鸡是鸭的3倍，鹅是鸡的2倍，鹅、鸭共42只，鸡（）只，鸭（），鹅（）只。

5、鸡是鸭的3倍，鹅是鸡的2倍，鹅比鸭多40只，鸡（）只，鸭（），鹅（）只。

6、甲乙两个粮仓，甲仓存粮是乙仓的3倍，甲仓运出100吨后两仓存粮一样多。

乙仓存粮多少吨？7、甲水库有43亿立方米水，乙水库有37亿立方米水．试问：需要从甲水库调多少亿立方米水到乙水库，才能使乙水库的水是甲水库的3倍？8、有三堆煤，甲堆比乙堆的3倍多30千克，丙堆比乙堆少15千克，三堆煤共240千克，那么，甲堆有煤多少千克？9、二年级和三年级共有123人，二年级比三年级的2倍多3人.二年级和三年级各有多少人?10、二年级和三年级共有147人，二年级比三年级的2倍少3人.二年级和三年级各有多少人?11、一年级、二年级和三年级共有147人，二年级比三年级的2倍多12人，一年级比三年级多15人，一年级、二年级和三年级各有多少人?12、小玲和小军的糖加起来是9个，小玲和小方的糖加起来是8个，小军和小方的成绩加起来是7分.问他们三人各得多少分?13、甲比乙的2倍多3，丙是甲的2倍，甲、乙、丙之和是65，甲乙丙各是多少？14、甲比乙的2倍多3，丙比甲的2倍少5，甲、乙、丙之和是67，甲乙丙各是多少？15、甲数比乙数多8，乙数比丙数少5，甲比丙（）。

线段的和差倍分教案

线段的和差倍分教案篇一：三角形专题线段的和差倍分专题：三角形之线段的和差倍分1、在△ABC中，∠ACB= 900，AC=BC，直线MN经过点C，且AD ⊥MN于D，BE⊥MN于E。

（1）当直线MN绕点C旋转到图1的位置时，求证：DE=AD+BE。

（2）当直线MN绕点C旋转到图2的位置时，问DE 、AD、BE 有何关系，并说明理由。

A2、如图，在△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于点E，AD⊥CE于点D. 求证：DE?AD?BE.3、如图，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE、BE，BE⊥AE，延长AE交BC的延长线于点F.求证：（1）FC=AD；（2）AB=BC+AD4、如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．求证：?BD=CF?BD=2CE．5、?如图，在△ABC中，BD平分∠ABC，CD平分∠ACB，过D 点作EF∥BC交AB于E，交AC于F，求证：EF=BE+CF．?在△ABC中，BD平分∠ABC，CD平分∠ACG，过D点作EF∥BC 交AB于E，交AC于F，试探究BE、EF与CF的数量关系．篇二：【教案】2.4线段的和与差2.4线段的和与差教学目标1．理解线段可以相加减，掌握用直尺、圆规作线段的和、差. 2．利用线段的和与差进行简单的计算。

教学重点和难点重点：用直尺、圆规作线段的和、差。

难点：进行简单的计算。

教学时间：1课时教学类型：新授教学过程：一、复习旧知，作好铺垫1．已知线段AB，用圆规、直尺画出线段CD，使线段CD=AB. 2．两点间的距离是指（）A.连结两点的直线的长度；B.连结两点的线段的长度；C.连结两点的直线；D.连结两点的线段.二、创设情景，激趣导入1．我们知道数（如有理数）可以相加减，那么作为几何图形的线段是否可以相加减呢？12．观察：如图所示，A、B、C三点在一条直线上，1）图中有几条线段？2）这几条线段之间有怎样的等量关系？A B C学生讨论三、尝试探讨，学习新知1．显然，图中有三条线段：AB、AC、BC,它们有如下的关系AB+ BC= AC，AC- BC= AB，AC- AB= BC2．由此，你可以得到怎样的结论两条线段可以相加（或相减），它们的和（或差）也是一条线段，其长度等于这两条线段的和（或差）3．例题1：如图,已知线段a、b,1）画出一条线段, 使它等于a+b2）画出一条线段, 使它等于a-b※学生尝试画图※教师示范，（注意画图语句的叙述）解：（1）①画射线OP;②在射线OP上顺次截取OA=a,AB=b线段OB就是所要画的线段.（2）①画射线OP;②在射线OP上截取OC=a，在射线OC上截取CD=b线段OD就是所要画的线段.2 b4.在例题1中为什么CD要“倒回”截？不“倒回”截行吗？5．思考：你会作一条线段使它等于2a吗？1）学生讨论2）2a是什么意思？（a+a）3）那么na（n为正整数，且n1）具有什么意义？6．尝试：例题2 如图,已知线段a、b,画出一条线段，使它等于2a-b1）学生独立完成2）反馈，纠正这两个例题是线段的和、差、倍的具体画法，教师在画图的过程中，要边画边讲．注意讲清以下问题：(1)先画的图形是已知的线段a，b．(2)画射线的目的是确定整个图形的起点，由于在没有画完的情况下，终点不能确定，而这种只有起点而没有终点的状态，只有用射线描述最为合适．(3)什么叫“顺次截取”？就是要沿着射线的方向，从起点开始，依照计算的顺序截取．(4)线段的和、差在画图中的区别是什么？“和”是在截取时不改变方向．而“差”在截取时的方向是变化的．3通过这两个例题．使学生能够掌握线段的和、差、倍的画图．(5)两个例题讲完后可以安排一个练习：已知线段a，b，c(a＞b ＞c)，画一条线段，使它等于2a+3b-c．7．将一条线段分成两条相等线段的点叫做这条线段的中点.若已知点M是线段AB的中点，你能得到哪些等量关系.AM?MB，AM?MB，BM?ABAB?2AM，AB?2MB8．已知线段AB，你会画出它的中点C吗？除了用尺测量，你还有其他方法吗？9．介绍用尺规作线段AB 的中点C.注意语言的叙述：解：（1）以点A为圆心，以大于AB的长a为半径作弧，以点B 为圆心，以a为半径作弧，两弧分别相交于点E、点F；（2）作直线EF，交线段AB于点C.点C就是所求的线段AB的中点. 1212四、反馈小结、深化理解1．学生自己总结本节课的学习内容，应回答出线段的和、差、倍、分的画法；线段中点的定义． 4a2．线段的和、差、倍的画法中应注意的问题．如步骤、方向等．3．一些关键词的用法，如“连结”、“顺次”等．五、学习训练与学习评价建议一、判断题（每题4分，共20分）(1)连接A、B两点，那么线段AB叫做A、B两点的距离.（）(2)连接A、B两点的线段的长度，叫做A、B两点的距离.（）(3)若AB＝BC，则B是线段AC的中点.（）(4)若AB=AM+BM，则点M在线段AB上.（）(5)若点M在线段AB外，则必有ABAM+MB.（）二、填空题（每题5分，共20分）(1)点M把线段PQ分成两条相等的线段，点M叫做线段PQ的______，这时有PQ=_______=_______.(2)延长线段AB到C，使BC=AB，反向延长AC到D使AD=AC，则CD=_______AB.(3)如图1.3-4，如果A、B两点将MN三等分，C为BN的中点，BC=5cm，则MN=________.(4)如图1.3-5，在直线PQ上要找一点A，使PA=3AQ，则A点应在________.图1.3-4图1.3-5 5篇三：线段和差倍分怎样证明线段的和差倍分问题怎样证明线段的倍分问题【典型例题】常规题型1、已知：如图所示，点D、E分别是等边?ABC的边AC、BC上的点，AD=CE，BD、AE交于点P，BQ?AE于Q．求证：PQ? 12PB．B C常规题型2、已知：如图所示，在?ABC中，AB=AC，?A?120?，AB的垂直平分线MN分别交BC、AB于点M、N．求证：CM=2BM．C N A能力挑战1、如图所示，在?ABC中，AB?12BC，D是BC的中点，M是BD的中点．求证：AC=2AM． ABD能力挑战2、已知：如图所示，在?ABC中，BD是AC边上的中线，BH平分?CBD,AF?BH，分别交BD、BH、BC于E、G、F．求证：2DE=CF．AD EBQ【经典练习】1、如图所示，已知?ABC中，?1??2，AD=DB，DC?AC．求证：AC? 1AB．21 2CD 2、已知：如图所示，D是?ABC的边BC上一点，且CD=AB，?BDA??BAD，AE是?ABD的中线．求证：AC=2AE． A E?AB于3、已知：如图所示，在?ABC中，AB=AC，?BAC?120?，D 是BC的中点，DEEE．求证：EB=3EA．AED?BAC?120?，4、已知：如图所示，在?ABC中，AB=AC，P是BC 上一点，且?BAP?90?．求证：PB=2PC．B P5、已知：如图所示，锐角?ABC中，?B?2?C，BE是角平分线，AD?BE，垂足是D．求证：AC=2BD．C6、如图所示，在?ABC中，AB=AC，?BAC?90?，BE平分?ABC，交AC于D，CE?BE于E点，求证：CE?1BD．2B C怎样证明线段的和差问题【典型例题】常规题型1、如图所示，已知?ABC中，?A?60?，BD、CE分别平分?ABC和?ACB，BD、CE交于点O．求证：BE+CD=BC． AEDB C能力挑战1、如图所示，在等腰直角三角形ABC中，?BAC?90?，AD=AE，AF?BE交BC于F，过点F作FG?CD于M，交BE延长线于点G，求证：BG=AF+FG．G AEB C能力挑战2、如图所示，在?ABC中，AB=AC，?A?100?，BE平分?ABC，求证：AE+BE=BC．AC B【练习】1、如图所示，已知?ABC中，?A?2?B，CD是?ACB的平分线，求证：BC=AC+AD．BC2、如图所示，若E为正方形ABCD的边BC上一点，AF为?DAE 的平分线，AF与CD相交于F点．求证：AE=BE+DF． A DFB3、如图所示，已知?ABC和?ADE均为等边三角形，B、C、D 在一直线上，求证：CE=AC+CD．ED?C?90?，4、如图所示，已知在?ABC中，AC=BC，AD是?BAC的平分线，求证：AB=AC+CD．CDB A5、如图所示，等边?ABC和等边?BDE，点A在DE的延长线上，求证：BD+DC=AD．CA B证明线段的和差倍分问题作业1、如图所示，在等腰三角形ABC中，P是底边BC上的任意一点．（1）求证：P点(本文来自：千叶帆文摘:线段的和差倍分教案)到两腰的距离之和等于腰上的高．（2）若P点在BC的延长线上，那么点P到两腰的距离与腰上的高三者之间存在什么关系？AFE BC2、如图所示，等腰三角形ABC中，AB=AC，?A?108?，BD平分?ABC．求证：BC=AB+DC．ADC B3、如图所示，已知?ABC是等腰三角形，AB=AC，?BAC?45?，AD 和CE是高，它们相交于H，求证：AH=2BD．E H4、如图所示，在?ABC中，?ACB?90?，P是AC的中点，过A过BP的垂线交BC延长线于点D，E是垂足．若?DBE?30?，求证：BP=4PE．D。

人教七下线段的和差倍分计算专题

线段的和差倍分计算一.和差问题1.线段上有1个点。

如线段AB上有一点M和：AB=+差：AM=—BM=—2.线段上有2个点。

如点M、N是线段AB上的两个点。

和：AB=++；AN=+；MB=+差：AM=AB—;AM=AN—;MN=AB——;MN=AN—MN=MB—;NB=AB—;NB=MB—。

2．如图，若线段AC=4cm，BC=3.5cm，求线段AB的长.思路指引：（1）已知条件有哪些？求什么？（2）利用线段的和还是差来求线段AB的长？（3）在右边的框里填写推理步骤。

3．如图，若线段AC=4，AB=7，求线段CB的长.4、已知线段AB=8点C在线段AB上，且BC=3，求线段AC的长.二.线段中点的图形及符号语言：线段中点的三种表示方法：如图（1）∵C 是线段AB 中点∴=（2）∵C 是线段AB 中点∴=2或=2（3）∵C 是线段AB 中点∴=12或=12三应用新知1：已知：如图线段AB=6cm,点C 是线段AB 的中点，求线段BC 的长解：∵C 是线段AB 中点∴=12又∵AB=6∴=12=12=答：线段BC 的长是________2已知：如图，若线段CA=5cm,点C 是线段AB 的中点，求线段BC 的长3已知：如图，若线段CB=7cm,点C 是线段AB 的中点，求线段BA 的长C A练习：A 层1、已知点M 是线段AE 的中点，则AM=______,AE=____MEAM=_____AE2已知，点F 是线段AB 的中点，线段BF=6cm ，求线段AB 的长B 层1.如图：AB=4cm ，BC=3cm ，如果O 是线段AC 的中点，求线段OB 的长度．解：∵AB=4，BC=3，AC=______+______=4+3=7又∵O 为AC 的中点，∴OC=______AC=______=______∴OB=OC-BC=_____-______=__________2.已知：如图，AB=16cm ，点C 为AB 的中点，点D 为CB 的中点，求线段CD 的长3、如图，C 为线段AB 的中点，D 在线段CB 上，DA=8，DB=6，求CD 的长。

【初三】线段、角的和差倍分

初中数学竞赛专题选讲线段、角的和差倍分一、内容提要证明线段、角的和，差，倍，分，常用两种方法：一是转化为证明线段或角的相等关系；一是用代数恒等式的证明方法。

一.转化为证明相等的一般方法㈠通过作图转化1.要证明一线段（角）等于两线段（角）的和（用截长补短法）⑴分解法――把大量分成两部分，证它们分别等于两个小量⑵合成法――作出两个小量的和，证它与大量相等2.要证明一线段（角）等于另一线段（角）的2倍⑴折半法――作出大量的一半，证它与小量相等⑵加倍法――作出小量的2倍，证它与大量相等㈡应用有关定理转化1.三角形中位线等于第三边的一半，梯形中位线等于两底和的一半2.直角三角形斜边中线等于斜边的一半3.直角三角形中，含30度的角所对的直角边等于斜边的一半4.三角形的一个外角等于和它不相邻的两个内角和5.等腰三角形顶角的外角等于底角的2倍6.三角形的重心（各中线的交点）分中线为2∶17.有关比例线段定理二.用代数恒等式的证明1.由左证到右或由右证到左2.左右两边分别化简为同一个第三式3.证明左边减去右边的差为零4.由已知的等式出发，通过恒等变形，到达求证的结论二、例题例1.已知：△ABC中，∠B＝2∠C，AD是高求证：DC＝AB＋BD分析一：用分解法，把DC分成两部分，分别证与AB，BD相等。

可以高AD为轴作△ADB的对称三角形△ADE，再证EC＝AE。

∵∠AEB＝∠B＝2∠C且∠AEB＝∠C＋∠EAC，∴∠EAC＝∠C辅助线是在DC上取DE＝DB，连结AE。

分析二：用合成法，把AB，BD合成一线段，证它与DC相等。

---------------------------------------------------------------------------------------------------------------------------------仍然以高AD为轴，作出DC的对称线段DF。

线段和差倍分及其应用专题

原七年级数学上册4图形的初步认识专题课堂(六)线段的和、差、倍、分计算习题课件(新版)华东师大版

证题技巧之三——证明线段或角的和差倍分(推荐文档)

线段的和差与倍分

方程思想在线段的和差倍分计算中的应用专题练习(解析版)

四年级 线段图解决和差倍问题

探究线段的和、差、倍、分是平面几何中常见的问题,“截

2021年中考数学热点专题复习：例析线段和差倍分问题的求解策略

线段的和差倍分教案

线段的和差(53张PPT)数学

(完整版)线段和差倍分及其应用专题

微专题八线段及角的和差倍分计算人教版七年级数学上册完美课件

线段图解答和倍、差倍问题

线段的和差倍分教案

人教七下线段的和差倍分计算专题

【初三】线段、角的和差倍分

四年级线段图解决和差倍问题