直接法设计IIR滤波器
实验四 IIR数字滤波器设计
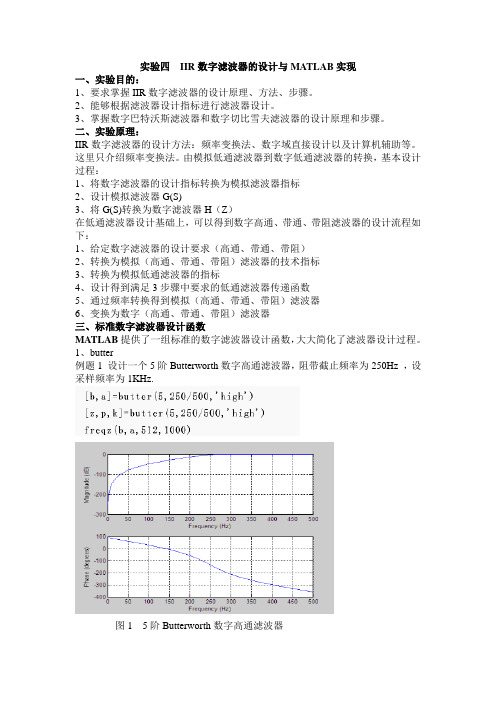
实验四IIR数字滤波器的设计与MATLAB实现一、实验目的:1、要求掌握IIR数字滤波器的设计原理、方法、步骤。
2、能够根据滤波器设计指标进行滤波器设计。
3、掌握数字巴特沃斯滤波器和数字切比雪夫滤波器的设计原理和步骤。
二、实验原理:IIR数字滤波器的设计方法:频率变换法、数字域直接设计以及计算机辅助等。
这里只介绍频率变换法。
由模拟低通滤波器到数字低通滤波器的转换,基本设计过程:1、将数字滤波器的设计指标转换为模拟滤波器指标2、设计模拟滤波器G(S)3、将G(S)转换为数字滤波器H(Z)在低通滤波器设计基础上,可以得到数字高通、带通、带阻滤波器的设计流程如下:1、给定数字滤波器的设计要求(高通、带通、带阻)2、转换为模拟(高通、带通、带阻)滤波器的技术指标3、转换为模拟低通滤波器的指标4、设计得到满足3步骤中要求的低通滤波器传递函数5、通过频率转换得到模拟(高通、带通、带阻)滤波器6、变换为数字(高通、带通、带阻)滤波器三、标准数字滤波器设计函数MATLAB提供了一组标准的数字滤波器设计函数,大大简化了滤波器设计过程。
1、butter例题1 设计一个5阶Butterworth数字高通滤波器,阻带截止频率为250Hz ,设采样频率为1KHz.图1 5阶Butterworth数字高通滤波器2、cheby1和cheby2例题2 设计一个7阶chebyshevII型数字低通滤波器,截止频率为3000Hz,Rs=30dB,采样频率为1KHz。
图2 7阶chebyshevII型数字低通滤波器四、冲激响应不变法一般来说,在要求时域冲激响应能模仿模拟滤波器的场合,一般使用该方法。
冲激响应不变法一个重要的特点是频率坐标的变换时线性的,因此如果模拟滤波器的频响带限于折叠频率的话,则通过变换后滤波器的频率响应可不失真的反映原响应与频率的关系。
例题3 设计一个中心频率为500Hz,带宽为600 Hz的数字带通滤波器,采样频率为1K Hz。
IIR数字滤波器设计实验报告

实验三IIR数字滤波器设计实验报告一、实验目的:1.通过仿真冲激响应不变法和双线性变换法2.掌握滤波器性能分析的基本方法二、实验要求:1.设计带通IIR滤波器2.按照冲激响应不变法设计滤波器系数3. 按照双线性变换法设计滤波器系数4. 分析幅频特性和相频特性5. 生成一定信噪比的带噪信号,并对其滤波,对比滤波前后波形和频谱三、基本原理:㈠IIR模拟滤波器与数字滤波器IIR数字滤波器的设计以模拟滤波器设计为基础,常用的类型分为巴特沃斯(Butterworth)、切比雪夫(Chebyshev)Ⅰ型、切比雪夫Ⅱ型、贝塞尔(Bessel)、椭圆等多种。
在MATLAB信号处理工具箱里,提供了这些类型的IIR数字滤波器设计子函数。
(二)性能指标1.假设带通滤波器要求为保留6000hz~~7000hz频段,滤除小于2000hz和大宇9000hz频段2.通带衰减设为3Db,阻带衰减设为30dB,双线性变换法中T取1s.四、实验步骤:1.初始化指标参数2.计算模拟滤波器参数并调用巴特沃斯函数产生模拟滤波器3.利用冲激响应不变法和双线性变换法求数字IIR滤波器的系统函数Hd (z)4.分别画出两种方法的幅频特性和相频特性曲线5.生成一定信噪比的带噪信号6.画出带噪信号的时域图和频谱图6.对带噪信号进行滤波,并画出滤波前后波形图和频谱图五、实验结果模拟滤波器的幅频特性和相频特性:101010101Frequency (rad/s)P h a s e (d e g r e e s )1010101011010-5100Frequency (rad/s)M a g n i t u d e在本实验中,采用的带通滤波器为6000-7000Hz ,换算成角频率为4.47-0.55,在上图中可以清晰地看出到达了题目的要求。
冲击响应不变法后的幅频特性和相频特性:0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )双线性变换法的幅频特性和相频特性:0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )00.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )通过上图比较脉冲响应不变法双线性变换法的幅频特性和相频特性,而在在幅频曲线上几乎没有差别,都能达到相同的结果。
iir数字滤波器设计原理

iir数字滤波器设计原理IIR数字滤波器设计原理IIR(Infinite Impulse Response)数字滤波器是一种常用的数字滤波器,其设计原理基于无限冲激响应。
与FIR(Finite Impulse Response)数字滤波器相比,IIR数字滤波器具有更低的计算复杂度和更窄的频率过渡带。
在信号处理和通信系统中,IIR数字滤波器被广泛应用于滤波、陷波、均衡等领域。
IIR数字滤波器的设计原理主要涉及两个方面:滤波器的结构和滤波器的参数。
一、滤波器的结构IIR数字滤波器的结构通常基于差分方程来描述。
最常见的结构是直接型I和直接型II结构。
直接型I结构是基于直接计算差分方程的形式,而直接型II结构则是通过级联和并联方式来实现。
直接型I结构的特点是简单直接,适用于一阶和二阶滤波器。
它的计算复杂度较低,但对于高阶滤波器会存在数值不稳定性的问题。
直接型II结构通过级联和并联方式来实现,可以有效地解决数值不稳定性的问题。
它的计算复杂度相对较高,但适用于高阶滤波器的设计。
二、滤波器的参数IIR数字滤波器的参数包括滤波器的阶数、截止频率、增益等。
这些参数根据实际需求来确定。
滤波器的阶数决定了滤波器的复杂度和性能。
阶数越高,滤波器的频率响应越陡峭,但计算复杂度也越高。
截止频率是指滤波器的频率响应开始衰减的频率。
截止频率可以分为低通、高通、带通和带阻滤波器。
根据实际需求,选择合适的截止频率可以实现对信号的滤波效果。
增益是指滤波器在特定频率上的增益或衰减程度。
增益可以用于滤波器的频率响应的平坦化或强调某些频率。
IIR数字滤波器的设计通常包括以下几个步骤:1. 确定滤波器的类型和结构,如直接型I或直接型II结构;2. 确定滤波器的阶数,根据要求的频率响应和计算复杂度来选择;3. 设计滤波器的差分方程,可以使用脉冲响应不变法、双线性变换法等方法;4. 根据差分方程的系数,实现滤波器的级联和并联结构;5. 进行滤波器的参数调整和优化,如截止频率、增益等;6. 对滤波器进行性能测试和验证,确保设计满足要求。
第三章 IIR滤波器设计方法.ppt

u的单位圆内部必须对应于z 的单位圆内部。 3)G(z -1) 必须是全通函数。 为使两个函数的频率响应满足一定的变换要求,z 平面的
单位圆应映射到 u 平面的单位圆上,若以 e jθ 和 e jω 分别表 示u平面和z 平面的单位圆,则由上式为
波器为
Ha
(s)
1
1
s
解 首先确定上下边界频率
T 2f
fs
1 2f1 / fs 2 105/ 1000 0.21
2 2f2 / fs 2 95/ 1000 0.19
求中心频率
coso
sin(0.21 0.19 ) sin0.21 sin0.19
解:确定数字频域的上下边带的角频率
1 2f1 / f s 0.55 2 2f 2 / f s 0.45 3 2f 3 / f s 0.6
T 2f
fs
求中心频率:
cos0
sin0.45 0.55
sin 0.45 sin 0.55
0.9695(z2 1.6188z 1) z2 1.5695z 0.9390
17
3.4 从低通数字滤波器到各种数字滤波器的 频率变换
前面讨论由模拟低通滤波器原型来设计各种数字滤波器 的方法,该设计方法同样也可直接在数字域上进行。
数字低通滤波器 原型函数Hp(z)
变换
各种数字滤 波器的H(z)
2
0.6 0.2
cos(
)
a
2
0.6 0.2
IIR滤波器直接型与级联型的设计Matlab代码

clear;clc;%%[y,fs]=wavread('music1-2');qq=16;%% 设置滤波器参数Wp=2*900;Ws=2*1500;Rp=0.1;Rs=60;Fs=32000;wp=Wp/Fs;ws=Ws/Fs;%% 选择滤波器类型%[N,Wpo]=cheb2ord(wp,ws,Rp,Rs);%求切比雪夫2型归一化模拟低通滤波器的阶数%[b,a]=cheby2(N,Rs,Wpo);%设计滤波器[N,Wpo]=cheb1ord(wp,ws,Rp,Rs);%求切比雪夫1型归一化模拟低通滤波器的阶数[b,a]=cheby1(N,Rp,Wpo);%设计滤波器%[N,Wpo]=buttord(wp,ws,Rp,Rs);%求巴特沃斯型归一化模拟低通滤波器的阶数%[b,a]=butter(N,Wpo);%设计滤波器%[N,Wpo]=ellipord(wp,ws,Rp,Rs);%求椭圆型归一化模拟低通滤波器的阶数%[b,a]=ellip(N,Rp,Rs,Wpo);%设计椭圆滤波器%% 滤波器频响[h,w]=freqz(b,a,1024);%求滤波器的幅频响应h=20*log10(abs(h)/max(abs(h)));%幅度归一figure;plot(w/2/pi*Fs,h);title('滤波器的幅频响应');grid on;bqr=intbR(b,qq);aqr=intbR(a,qq);[hr,wr]=freqz(bqr,aqr,1024);hr=20*log10(abs(hr)/max(abs(hr)));%figure;plot((0:1023)/1024,hr);figure;plot(w/2/pi*Fs,hr);title('滤波器的量化后的幅频响应');grid on;%% 级联处理[sos,g]=tf2sos(b,a);b1=sos(1,1:3);a1=sos(1,4:6);b2=sos(2,1:3);a2=sos(2,4:6);b3=sos(3,1:3);a3=sos(3,4:6);b4=sos(4,1:3);a4=sos(4,4:6);b5=sos(5,1:3);a5=sos(5,4:6);% b6=sos(6,1:3);a6=sos(6,4:6);% b7=sos(7,1:3);a7=sos(7,4:6);% b8=sos(8,1:3);a8=sos(8,4:6);% b9=sos(9,1:3);a9=sos(9,4:6);%% 级联量化bqr1=intbR(b1,qq); aqr1=intbR(a1,qq);[h1,w1]=freqz(bqr1,aqr1,1024);bqr2=intbR(b2,qq); aqr2=intbR(a2,qq);[h2,w1]=freqz(bqr2,aqr2,1024);bqr3=intbR(b3,qq); aqr3=intbR(a3,qq);[h3,w1]=freqz(bqr3,aqr3,1024);bqr4=intbR(b4,qq); aqr4=intbR(a4,qq);[h4,w1]=freqz(bqr4,aqr4,1024);bqr5=intbR(b5,qq); aqr5=intbR(a5,qq);[h5,w1]=freqz(bqr5,aqr5,1024);% bqr6=intbR(b6,qq); aqr6=intbR(a6,qq);% [h6,w1]=freqz(bqr6,aqr6,1024);% bqr7=intbR(b7,qq); aqr7=intbR(a7,qq);% [h7,w1]=freqz(bqr7,aqr7,1024);% bqr8=intbR(b3,qq); aqr8=intbR(a8,qq);% [h8,w1]=freqz(bqr8,aqr8,1024);% bqr9=intbR(b3,qq); aqr9=intbR(a9,qq);%[h9,w1]=freqz(bqr9,aqr9,1024);hh=h1.*h2.*h3;%.*h4;%.*h5.*h6.*h7;%.*h8.*h9;hh=20*log10(abs(hh)/max(abs(hh)));sos1=intbR(sos,qq);%% 信号过系统%yy=filter(bqr,aqr,y);yy=filter(b,a,y);Y=sosfilt(sos1,y);%% 画图figure;%specgram(Y);%sound(yy,fs);%plot(20*log10(abs(fft(y,1024))/max(abs(fft(y,1024)))),'g');hold on;%原信号频谱图plot(w/pi*Fs,20*log10(abs(fft(yy,1024))/max(abs(fft(yy,1024)))),'c');hold on;%直接量化后的归一化频谱图plot(w/pi*Fs,20*log10(abs(fft(Y,1024))/max(abs(fft(Y,1024)))),'r');grid on;%级联量化后的归一化频谱图%plot(hh,'g');%title('切比雪夫2幅频响应图');%legend('直接结构','级联结构','r','g');%figure(2);%zplane(b,a);%title('巴特沃斯的零极点图');。
IIR数字滤波器设计

| H ( j) |2 H ( j)H ( j) s j H (s)H (s)
版权全部 违者必究
16
模拟滤波器旳设计
由给定旳模平方函数求所需旳系统函数旳措施:
① 解析延拓:令 s j代入模平方函数得:H(s) H(s),
并求其零极点。
②取H(s)H(s) 全部左半平面旳极点作为 H (s) 旳极点。
有关极点旳讨论
在归一化频率旳情况 c=1,极点均匀分布在单位圆上
s e j(2k N 1) / 2N k
k 1,2,, N
对于物理可实现系统,它旳全部极点均应在 s旳左半平面上
版权全部 违者必究
24
模拟滤波器旳设计
Ⅱ 系统函数旳构成
滤波器旳极点求出后,可取左半平面上旳全部极点构
成系统函数。
首先设计一种合适旳模拟滤波器,然后将它 “ 变换 ” 成满足给定 指标旳数字滤波器。
这种措施适合于设计幅频特征比较规则旳滤波器,例如低通、高通 、带通、带阻等。 当把模拟滤波器旳H(s) “ 变换 ” 成数字滤波器旳H(z) 时,其实质就 是实现S平面对Z平面旳 “ 映射 ” 。这必须满足两个条件: ① 必须确保模拟频率映射为数字频率,且确保两者旳频率特征基本
频 p =100krad/s, 通带旳最大衰减为Ap= 3dB,阻带边频
版权全部 违者必究
11
数字滤波类型与指标
措施三:利用 “ 零极点累试法 ” 进行设计 若需设计滤波器旳幅频特征比较规则而且简朴时,可采用 “ 零极点累试法 ”进行设计。例如:数字陷波器
版权全部 违者必究
12
§2 模拟滤波器旳设计
因为IIR数字滤波器旳设计是基于既有旳模拟滤波器设计旳 成熟技术而完毕旳。故讨论 “ IIR数字滤波器旳设计 ”之前 ,必须简介模拟滤波器设计旳某些基本概念,并简介两种常 用旳模拟滤波器旳设计措施 :巴特沃思(Butterworth)滤波 器和切比雪夫(Chebyshev)滤波器。
iir滤波器设计方法

iir滤波器设计方法IIR滤波器设计方法数字信号处理中的滤波器是一项重要的技术,用于滤除数字信号中的噪声和干扰,并对信号进行平滑处理。
IIR滤波器作为数字滤波器的一种,被广泛应用于音频处理、图像处理等领域。
下面将介绍IIR滤波器的设计方法。
一、数字滤波器的基本原理数字滤波器是一种按照某种规律改变信号频率和幅度的系统。
数字滤波器的基本原理是,将输入信号x(n)通过一定的滤波器系统后,得到输出信号y(n)。
滤波器系统可以是连续时域滤波器,也可以是离散时域滤波器。
其中,IIR滤波器是离散时域滤波器的其中一类。
二、IIR滤波器的分类IIR滤波器可以分为两类:低通滤波器和高通滤波器。
低通滤波器用于滤除高频噪声,保留低频信息,常用于音频等信号处理。
高通滤波器则用于滤除低频噪声,保留高频信息,常用于图像边缘检测等处理。
三、IIR滤波器设计方法1. 选择滤波器类型首先需要选择合适的滤波器类型,通常是根据所要处理的信号类型选择,“低通”或“高通”滤波器。
2. 确定滤波器参数在选定滤波器类型后,需要确定滤波器参数。
通常包括切-off频率、通带增益、阻带增益等。
其中,切-off频率是指信号经过滤波器后的频率处理效果,通带增益和阻带增益是指滤波器在信号传输过程中增益的波动程度。
3. 设计滤波器传递函数设计滤波器传递函数的目的是,确定在滤波器系统中所要使用的传递函数,以实现所要求的滤波效果。
根据IIR滤波器的设计方法,通常采用应用差分方程来实现传递函数。
4. 设置初始滤波器系数通过选择合适的初始滤波器系数,可以影响整个滤波器系统的滤波效果。
在确定了滤波器的传递函数后,设计人员可以根据所要求的滤波效果来选择合适的初始滤波器系数。
5. 优化滤波器系数通过不断的调节和优化滤波器系数,可以提高整个滤波器系统的滤波效果。
优化的过程通常需要根据实际的滤波效果进行多次调整和修改。
四、总结IIR滤波器是数字信号处理中一种常用的滤波器类型,其设计方法可以通过选择合适的滤波器类型、确定滤波器参数、设计滤波器传递函数、设置初始滤波器系数和优化滤波器系数等步骤来实现。
iir数字滤波器的设计方法

iir数字滤波器的设计方法IIR数字滤波器的设计方法IIR数字滤波器是一种常用的数字信号处理工具,用于对信号进行滤波和频率域处理。
其设计方法是基于传统的模拟滤波器设计技术,通过将连续时间滤波器转换为离散时间滤波器来实现。
本文将介绍IIR数字滤波器的设计方法和一些常见的实现技巧。
一、IIR数字滤波器的基本原理IIR数字滤波器是一种递归滤波器,其基本原理是将输入信号与滤波器的系数进行加权求和。
其输出信号不仅与当前输入值有关,还与之前的输入和输出值有关,通过不断迭代计算可以得到最终的输出结果。
二、IIR数字滤波器的设计步骤1. 确定滤波器的类型:低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
2. 确定滤波器的阶数:阶数决定了滤波器的陡峭度和性能。
3. 选择滤波器的截止频率或通带范围。
4. 根据所选的滤波器类型和截止频率,设计滤波器的模拟原型。
5. 将模拟原型转换为数字滤波器。
三、IIR数字滤波器的设计方法1. 巴特沃斯滤波器设计方法:- 巴特沃斯滤波器是一种最常用的IIR数字滤波器,具有平坦的通带特性和陡峭的阻带特性。
- 设计方法为先将模拟滤波器转换为数字滤波器,然后通过对模拟滤波器进行归一化来确定截止频率。
2. 阻带衰减设计方法:- 阻带衰减设计方法是一种通过增加滤波器的阶数来提高滤波器阻带衰减特性的方法。
- 通过增加阶数,可以获得更陡峭的阻带特性,但同时也会增加计算复杂度和延迟。
3. 频率变换方法:- 频率变换方法是一种通过对滤波器的频率响应进行变换来设计滤波器的方法。
- 通过对模拟滤波器的频率响应进行变换,可以得到所需的数字滤波器。
四、IIR数字滤波器的实现技巧1. 级联结构:- 将多个一阶或二阶滤波器级联起来,可以得到更高阶的滤波器。
- 级联结构可以灵活地实现各种滤波器类型和阶数的设计。
2. 并联结构:- 将多个滤波器并联起来,可以实现更复杂的频率响应。
- 并联结构可以用于设计带通滤波器和带阻滤波器。
IIR数字滤波器的Z域直接设计法_基本节组合法

44
军 事 通 信 技 术
2000 年
表 2 2P 节增益表( dB)
r A 0. 1 0. 2 0. 3 P 12 0. 4 0. 5 0. 6 0. 7 0. 8 0. 9 0. 1 0. 2 0. 3 P 6 0. 4 0. 5 0. 6 0. 7 0. 8 0. 9 0. 1 0. 2 0. 3 P 4 0. 4 0. 5 0. 6 0. 7 0. 8 0. 9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 X 0 ( P 0. 1 P ) 12 ( P 0. 2 P ) 6 - 0. 38 - 0. 90 - 1. 38 - 2. 57 - 3. 86 - 5. 55 - 7. 69 - 10. 16 - 12. 36 ( P 0. 3 P ) 4 0. 4P 0. 5P - 1. 83 - 3. 99 - 6. 29 - 9. 39 0. 6P - 2. 33 - 4. 95 - 7. 71 0. 7P - 2. 76 - 5. 73 - 8. 84 0. 8P - 3. 09 - 6. 31 - 9. 65 0. 9P - 3. 29 - 6. 66 P - 3. 64 - 6. 78
2. 2 2P 节 2P 节如图 3, 它有两个在单位圆内的共轭极点 r e 和 r e , 极点半径 r 和幅角 A是两个可调参数以改变 其频率响应。
jA - jA
( a) 极零图 ( b ) 结构图 ( c) 幅频响应 图 3 2P 节的极零图、 结构图、 幅频响应
( a) 极 零图 ( b) 结构图 ( c) 幅频响应 图 2 1P 节的极零图、 结构图、 幅频响应
1P 节的传递函数、 频率响应和幅频增益函数如下 H 1P ( z ) = ( 1 - r ) 1 1 - r Z- 1 ( 4) ( 5) ( 6)
iir数字滤波器的设计步骤

IIR数字滤波器的设计步骤1.简介I I R(In fi ni te Im pu l se Re sp on se)数字滤波器是一种常用的数字信号处理技术,它的设计步骤可以帮助我们实现对信号的滤波和频率选择。
本文将介绍I IR数字滤波器的设计步骤。
2.设计步骤2.1确定滤波器的类型I I R数字滤波器的类型分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
根据信号的要求,我们需确定所需滤波器的类型。
2.2确定滤波器的规格根据滤波器的应用场景和信号特性,我们需确定滤波器的通带范围、阻带范围和衰减要求。
2.3选择滤波器的原型常用的I IR数字滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
根据滤波器的需求,我们需选择适合的滤波器原型。
2.4设计滤波器的传递函数根据滤波器的规格和选定的滤波器原型,我们需计算滤波器的传递函数。
传递函数表示了输入和输出之间的关系,可以帮助我们设计滤波器的频率响应。
2.5对传递函数进行分解将滤波器的传递函数进行分解,可得到II R数字滤波器的差分方程。
通过对差分方程进行相关计算,可以得到滤波器的系数。
2.6滤波器的稳定性判断根据滤波器的差分方程,判断滤波器的稳定性。
稳定性意味着滤波器的输出不会无限增长,确保了滤波器的可靠性和准确性。
2.7选择实现方式根据滤波器的设计需求和实际应用场景,我们需选择I IR数字滤波器的实现方式。
常见的实现方式有直接I I型、级联结构和并行结构等。
2.8优化滤波器性能在设计滤波器后,我们可以对滤波器的性能进行优化。
优化包括滤波器的阶数和抗混淆能力等方面。
3.总结I I R数字滤波器的设计步骤包括确定滤波器的类型和规格、选择滤波器的原型、设计滤波器的传递函数、对传递函数进行分解、判断滤波器的稳定性、选择实现方式和优化滤波器性能等。
通过这些步骤的实施,我们可以有效地设计出满足信号处理需求的II R数字滤波器。
IIR数字滤波器的设计及软件实现

IIR数字滤波器的设计及软件实现什么是IIR数字滤波器?IIR数字滤波器是一种数字信号处理滤波器,它基于递归的思想,可以对原始信号进行滤波处理。
与FIR数字滤波器相比,IIR数字滤波器具有更高的效率和更灵活的设计。
它的设计基于对滤波器的传递函数进行分析和优化,可以通过不同的传递函数来实现不同的滤波目标。
IIR数字滤波器的设计方法要设计一个IIR数字滤波器,可以采用以下步骤:步骤1:确定滤波器的类型根据滤波的目的和要求,确定滤波器的类型。
常见的滤波器类型有低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
步骤2:计算滤波器的阶数滤波器的阶数是指滤波器中的二阶段数。
阶数越高,滤波器的性能越好,但也意味着计算量和实现难度会增加。
根据滤波的要求和性能要求,计算滤波器的阶数。
步骤3:选择滤波器的截止频率滤波器的截止频率是指滤波器在截止频率附近的频率响应。
对于低通滤波器和高通滤波器,截止频率通常是一个常数。
对于带通滤波器和带阻滤波器,截止频率需要确定两个频率。
步骤4:计算滤波器的传递函数根据滤波器类型、阶数和截止频率,可以通过传递函数的计算得到滤波器的传递函数。
步骤5:采用正则化处理在计算得到传递函数后,需要进行正则化处理。
正则化处理可以消除传递函数中的不稳定性,并确保滤波器的稳定性和可变性。
步骤6:实现反馈环和前馈环根据传递函数,可以实现反馈环和前馈环。
反馈环和前馈环的选择会影响滤波器的性能。
IIR数字滤波器的软件实现要实现IIR数字滤波器,可以使用MATLAB或Python等数学软件。
这里以Python为例进行说明。
步骤1:导入必要的库import numpy as np #用于处理数组和矩阵import scipy.signal as signal #用于信号处理import matplotlib.pyplot as plt #用于绘图步骤2:指定滤波器的类型、截止频率和阶数type ='lowpass'#低通滤波器fc =2000#截止频率order =4#阶数步骤3:计算滤波器的系数b, a = signal.butter(order, fc, type)步骤4:生成信号并进行滤波t = np.linspace(0, 1, 500, endpoint=False)x = np.sin(2* np.pi *5* t) + np.sin(2* np.pi *10* t) + np.sin(2* np.pi *20* t)y = signal.filtfilt(b, a, x)步骤5:绘制原始信号和滤波后的信号plt.plot(t, x, label='original signal')plt.plot(t, y, label='filtered signal')plt.legend(loc='best')plt.show()IIR数字滤波器是数字信号处理中一种重要的滤波器。
IIR滤波器设计

IIR滤波器的DSP实现一、IIR滤波器的基本结构IIR滤波器差分方程的一般表达式为:式中x(n)为输入序列;y(n)为输出序列;和为滤波器系数.若所有系数等于0,则为FIR滤波器.IIR滤波器具有无限长的单位脉冲响应,在结构上存在反馈回路,具有递归性,即IIR滤波器的输出不仅与输入有关,而且与过去的输出有关.将上式展开得出y(n)表达式为:在零初始条件下,对上式进行z变换,得到:设N=M,则传递函数为:上式可写成:上式具有N个零点和N个极点.若有极点位于单位圆外将导致系统不稳定.由于FIR滤波器所有的系数均为0,不存在极点,不会造成系数的不稳定.对于IIR滤波器,系统稳定的条件如下: 若||<1,当n→时,h(n)→0,系统稳定;若||>1,当n→时,h(n)→,系统不稳定.IIR滤波器具有多种形式,主要有:直接型(也称直接I型)、标准型(也称直接II型)、变换型、级联型和并联型.二阶IIR滤波器,又称为二阶基本节,分为直接型、标准型和变换型.对于一个二阶IIR滤波器,其输出可以写成:1.直接型(直接I型)根据上式可以得到直接二型IIR滤波器的结构图.如图1所示.共使用了4个延迟单元().直接型二阶IIR滤波器还可以用图2的结构实现.图2 直接I型二阶IIR滤波器此时,延时变量变成了w(n).可以证明上图的结构仍满足二阶IIR滤波器输出方程.前向通道:反馈通道:将1.2式代入1.1式可得:2.标准型(直接II型)从图2可以看出,左右两组延迟单元可以重叠,从而得到标准二阶IIR滤波器的结构图,如图3所示.由于这种结构所使用的延迟单元最少(只有2个),得到了广泛地应用,因此称之为标准型IIR滤波器.图3 标准型二阶IIR滤波器二、IIR滤波器的设计IIR滤波器的设计可以利用模拟滤波器原型,借鉴成熟的模拟滤波器的设计结果进行双线性变换,将模拟滤波器变换成满足预定指标的数字滤波器,即根据模拟设计理论设计出满足要求的传递函数H(s),然后将H(s)变换成数字滤波器的传递函数H(z).设计IIR滤波器的基础是设计模拟滤波器的原型,这些原型滤波器主要有:①巴特沃兹(Butterworth)滤波器,其幅度响应在通带内具有最平特性;②切比雪夫(Chebyshev)滤波器,在通带内具有等波纹特性,且阶数小于巴特沃兹滤波器.③椭圆(Elliptic)滤波器,在通带内具有等波纹特性,且阶数最小.将模拟滤波器转换为数字滤波器常用的方法是双线性变换,其作用是完成从s平面到z平面的一个映射.其关系为:双线性变换的基本性质如下:①s平面上的轴映射到z平面的单位圆上;②s平面的左半平面映射到z平面的单位圆内;③s平面的右半平面映射到z平面的单位圆外.考虑到s平面上的虚轴映射为z平面的单位圆,令,它代表一个可变的模拟频率.其z平面上相应的数字频率为,即,将以上两式代入2.1式得:对上式求解得:模拟频率和相应的数字频率之间的映射关系如图4所示:图4 和之间的映射关系当在0~1之间变化时,在0~之间变化,为采样频率:当时,其对应的在之间.双线性变换会造成频率失真,通常采用预畸变来补偿频率失真.双线性变换设计的步骤如下:①选择一个合适的模拟传递函数H(s);②对截止频率或预定的数字频率进行畸变,并根据式2.3求得相应的模拟频率;③用对H(s)中的频率进行换算,即:④用式2.1计算H(z):三、二阶IIR滤波器的DSP实现1.标准型二阶IIR滤波器的实现在二阶IIR滤波器结构中,标准型结构是最常见的滤波器结构,其结构如图5所示:图5 标准型二阶IIR滤波器由结构图可以写出反馈通道和前向通道的差分方程:反馈通道:前向通道:由以上两式对二阶IIR滤波器进行编程,其中乘法-累加运算可采用单操作数指令或双操作数指令,数据和系数可存放在DARAM中,如图6所示:图6 双操作数数据存放和系数表2.直接型二阶IIR滤波器的实现二阶IIR滤波器可以用直接型结构来实现.在迭代运算中,先衰减后增益,系统的动态范围和鲁棒性要好些.直接型二阶IIR滤波器的结构如图7所示:图7 直接型二阶IIR滤波器直接型二阶IIR滤波器的脉冲传递函数为:差分方程为:为了实现直接型滤波,可在DARAM中开辟4个循环缓冲区,用来存放变量和系数,并采用循环缓冲区方式寻址.这4个循环缓冲区的结构如图8所示:图8 循环缓冲区结构四、总体设计方案1.利用MATLAB来确定IIR滤波器的参数;2.启动CCS,在CCS中建立一个汇编源文件、建立一个C源文件和一个命令文件,并将这三个文件添加到工程,再编译并装载程序;3.设置波形时域观察窗口,得到其滤波前后波形变化图;4.设置频域观察窗口,得到其滤波前后频谱变化图.五、主要参数f1=500Hz f2=1000Hz f s=2000六、源程序1.汇编源文件程序(.asm).global _iir,_init,_outdata_iirbset frctsub #1,t0mov t0,mmap(csr)add t0,ar0mov xar2,xdpmov ar2,cdpmov #0,ac0rpt csrmacmz *ar0-,*cdp+,ac0add t0,ar1mov xar3,xdpmov ar3,cdprpt csrmacmz *ar1-,*cdp+,ac0mar *ar1+mov hi(ac0),*ar1mov hi(ac0),t0bclr frctret_initsub #1,t0mov t0,mmap(csr)mov #0,ac0rpt csrmov ac0,*ar0+rpt csrmov ac0,*ar1+ret_outdatamov t1,ac0sub #2,ac0mov ac0,mmap(csr)add ac0,ar0rpt csrdelay *ar0-mar *ar0+mov t0,*ar0ret2.C源文件程序(.c)#includ e "math.h"#define signal_1_f 500#define signal_2_f 10000#define signal_sample_f 25000#define pi 3.1415926#define IIRNUMBER_L 2#define bufer_L 256int N_L=IIRNUMBER_L;int data_in[bufer_L];int out[bufer_L] ;int x[IIRNUMBER_L+1];int y[IIRNUMBER_L+1];int k=0;int bufer=bufer_L;int fBn[IIRNUMBER_L]={0,0x634a};int fAn[IIRNUMBER_L]={0xe5c,0xe5c};extern int iir(int *x,int *y,int *fAn,int *fBn,int N_L); extern int init(int *,int *,int);extern int outdata(int *,int,int);void inputwave();void main(){int iirout;inputwave();init(x,y,N_L);while(1){x[0]=data_in[k];iirout=iir(x,y,fAn,fBn,N_L);outdata(out,iirout,bufer);k++;if(k>=bufer_L){k=0;}}}void inputwave(){fl oat wt1;fl oat wt2;int i;for(i=0;i<=bufer_L;i++){wt1=2*pi*i*signal_1_f;wt1=wt1/signal_sample_f;wt2=2*pi*i*signal_2_f;wt2=wt2/signal_sample_f;data_in[i]=(cos(wt1)+cos(wt2))/2*32768;}}3.命令文件程序(.cmd)-stack 0x0500-sysstack 0x0500-heap 0x1000-c-u _Reset-l rts55.libMEMORY{PAGE 0:RAM(RWIX): origin=0x000100, length=0x01ff00ROM(RIX): origin=0x020100, length=0x01ff00VECS(RIX): origin=0xffff00, length=0x000200 PAGE 2:IOPORT(RWI):origin=0x000000, length=0x020000 }SECTIONS{.text >ROM PAGE 0.data >ROM PAGE 0.bss >RAM PAGE 0.const >RAM PAGE 0.sysmem >RAM PAGE 0.stack >RAM PAGE 0.cio >RAM PAGE 0.sysstack >RAM PAGE 0.switch >RAM PAGE 0.cinit >RAM PAGE 0.pinit >RAM PAGE 0.vectors >VECS PAGE 0.ioport >IOPORT PAGE 2}七、实验结果及分析1.输入波形:①时域波形:②频域波形:2.输出波形:①时域波形:②频域波形:八、心得体会课程设计是培养学生综合运用所学知识,发现,提出,分析和解决实际问题,锻炼实践能力的重要环节,是对学生实际工作能力的具体训练和考察过程.随着科学技术发展的日新日异,数字技术已经成为当今计算机应用中空前活跃的领域, 在生活中可以说得是无处不在.通过这次课设,我掌握了数字滤波器的设计过程,了解了IIR的原理和特性,学习IIR滤波器的DSP 实现原理.熟悉设计IIR数字滤波器的原理和方法,学习使用CCS的波形观察窗口观察输入输出信号波形和频谱变化情况.通过这次课程设计使我懂得了理论与实际相结合是很重要的,只有理论知识是远远不够的,只有把所学的理论知识与实践相结合起来,从理论中得出结论,才能真正为社会服务,从而提高自己的实际动手能力和独立思考的能力.DSP原理及应用课程设计报告设计课题: IIR滤波器的DSP实现专业班级: 信息07-2班姓名: 王晓萱学号: 07100637同组人: 王鑫、蔚金昌、吴杰、徐扬、李峰。
iir数字滤波器设计及c语言程序

iir数字滤波器设计及c语言程序IIR数字滤波器设计及C语言程序IIR(Infinite Impulse Response)数字滤波器是一种常用的数字信号处理技术,广泛应用于音频处理、图像处理、通信系统等领域。
本文将介绍IIR数字滤波器的设计原理,并给出相应的C语言程序实现。
一、IIR数字滤波器的设计原理IIR数字滤波器的设计基于差分方程,其输入信号和输出信号之间存在一定的差分关系。
相比于FIR(Finite Impulse Response)数字滤波器,IIR数字滤波器具有更窄的转换带宽、更高的滤波器阶数和更好的相位响应等特点。
IIR数字滤波器的设计主要包括两个关键步骤:滤波器规格确定和滤波器参数计算。
首先,根据实际需求确定滤波器的类型(低通、高通、带通或带阻)、截止频率、通带衰减和阻带衰减等规格。
然后,根据这些规格利用数字滤波器设计方法计算出滤波器的系数,从而实现对输入信号的滤波。
二、IIR数字滤波器的设计方法常见的IIR数字滤波器设计方法有脉冲响应不变法、双线性变换法和最小均方误差法等。
下面以最常用的脉冲响应不变法为例介绍设计方法。
脉冲响应不变法的基本思想是将模拟滤波器的脉冲响应与数字滤波器的单位脉冲响应进行匹配。
首先,根据模拟滤波器的传递函数H(s)确定其脉冲响应h(t)。
然后,将连续时间下的脉冲响应离散化,得到离散时间下的单位脉冲响应h[n]。
接下来,根据单位脉冲响应h[n]计算出数字滤波器的差分方程系数,从而得到滤波器的数字表示。
三、IIR数字滤波器的C语言程序实现下面给出一个简单的IIR数字滤波器的C语言程序实现示例,以低通滤波器为例:```c#include <stdio.h>#define N 100 // 输入信号长度#define M 5 // 滤波器阶数// IIR数字滤波器系数float b[M+1] = {0.1, 0.2, 0.3, 0.2, 0.1};float a[M+1] = {1.0, -0.5, 0.3, -0.2, 0.1};// IIR数字滤波器函数float IIR_filter(float *x, float *y, int n) {int i, j;float sum;for (i = 0; i < n; i++) {sum = 0;for (j = 0; j <= M; j++) { if (i - j >= 0) {sum += b[j] * x[i - j]; }}for (j = 1; j <= M; j++) { if (i - j >= 0) {sum -= a[j] * y[i - j]; }}y[i] = sum;}}int main() {float x[N]; // 输入信号float y[N]; // 输出信号int i;// 生成输入信号for (i = 0; i < N; i++) {x[i] = i;}// IIR数字滤波器滤波IIR_filter(x, y, N);// 输出滤波后的信号for (i = 0; i < N; i++) {printf("%f ", y[i]);}return 0;}```以上是一个简单的IIR数字滤波器的C语言程序实现示例。
IIR数字滤波器设计中两种主要离散化方法的比较
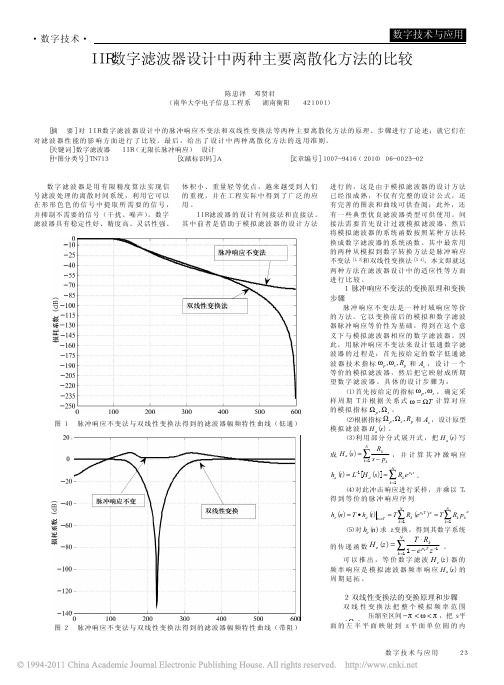
23数字技术与应用·数字技术·数字滤波器是用有限精度算法实现信号滤波处理的离散时间系统,利用它可以在形形色色的信号中提取所需要的信号,并抑制不需要的信号(干扰、噪声)。
数字滤波器具有稳定性好、精度高、灵活性强、体积小、重量轻等优点,越来越受到人们的重视,并在工程实际中得到了广泛的应用。
IIR滤波器的设计有间接法和直接法。
其中前者是借助于模拟滤波器的设计方法进行的,这是由于模拟滤波器的设计方法已经很成熟,不仅有完整的设计公式,还有完善的图表和曲线可供查阅;此外,还有一些典型优良滤波器类型可供使用。
间接法需要首先设计过渡模拟滤波器,然后将模拟滤波器的系统函数按照某种方法转换成数字滤波器的系统函数。
其中最常用的两种从模拟到数字转换方法是脉冲响应不变法[1,2]和双线性变换法[3,4],本文即就这两种方法在滤波器设计中的适应性等方面进行比较。
1 脉冲响应不变法的变换原理和变换步骤脉冲响应不变法是一种时域响应等价的方法。
它以变换前后的模拟和数字滤波器脉冲响应等价性为基础,得到在这个意义下与模拟滤波器相应的数字滤波器。
因此,用脉冲响应不变法来设计低通数字滤波器的过程是:首先按给定的数字低通滤波器技术指标p s p R ,,ωω和s A ,设计一个等价的模拟滤波器,然后把它映射成所期望数字滤波器。
具体的设计步骤为:(1)首先按给定的指标s p ωω,,确定采样周期T并根据关系式T Ω=ω计算对应的模拟指标s p ΩΩ,。
(2)根据指标p s p R ,,ΩΩ和s A ,设计原型模拟滤波器)(s H a 。
(3)利用部分分式展开式,把)(s H a 写成∑=−=Nk kkap s R s H 1)(,并计算其冲激响应∑=−==Nk t p k a a k e R s H L t h 11)]([)(。
(4)对此冲击响应进行采样,并乘以T,得到等价的脉冲响应序列∑∑=====•=Nk nk k N k n T p k nT t a e p R T e R T t h T n h k 11)()()((5)对)(n h e 求z变换,得到其数字系统的传递函数 1)(11∑=−−⋅=Nk T p ke zeR T z H k 。
IIR数字滤波器设计中两种主要数字化方法的比较

中图分类号 : T N 7 1 3
文献标识码 : A
O 引言
I I R数字滤波器 ( D i g i t  ̄f i l t e r , 以下简称 D F ) 的设计有 间 接法 和直接法 , 其 中间接法是借助 于模 拟滤 波器 ( A n M o g i f l — t e r , 以下简称 A F ) 的设 计 方 法进行 的 , 需 要 首 先设 计 过渡 A F , 然后将 A F的系统 函数按 照某种方法进行 数字化转换成
的映射关系反映的是 舟( s ) 的周期延拓与 日( ) 的关系 , 而 不 是 日( s ) 本身与 日( z ) 的关 系。因此 , 脉冲响应不变法将 H( s )
( 2 ) S 平面与 z 平面的映射关 系 按照( 1 ) 中所述 的变换原 理 , s与 =满 足 z =e 的关 系 ,
第 1 期
谢 小娟 , 等: I I R数 字 滤波 器设计 中两种 主要 数 字化方 法的 比较
2 7
射关系以及 D F的频 响分别 如 图 2的 ( a ) 、 ( b ) 和( C ) 所示。
D F的 系统 函数。其 中工程上最常用的两种方法是脉 冲响应
l J ● J
3 1 r
—
. , j l m I z ]
一
1 r , r 3 w, r
、 (
一
不变法 和双线性 变换 法[ 3 . 4 1 , 二者 皆有 条件 地遵 循数字 化 的两个基本 目标 , 即转换 前后频晌具有一致性且物理 可实
【 r = e , 即= 的 模与s 的 实部成 e 指数关系
收 稿 日期 : 2 0 1 2一l 1 — 2 3
IIR滤波器的原理与设计方法

IIR滤波器的原理与设计方法IIR(Infinite Impulse Response)滤波器是一种数字滤波器,其具有无限冲激响应的特点。
与FIR(Finite Impulse Response)滤波器相比,IIR滤波器具有更高的效率和更窄的频带特性。
本文将介绍IIR滤波器的原理和设计方法。
一、IIR滤波器的原理IIR滤波器是通过对输入信号和输出信号之间的差异进行递归运算而实现滤波的。
其核心原理是利用差分方程来描述滤波器的行为。
IIR滤波器可以被表达为如下形式:y[n] = b₀x[n] + b₁x[n-1] + ... + bₘx[n-ₘ] - a₁y[n-1] - ... - aₘy[n-ₘ]其中,x[n]表示输入信号的当前采样值,y[n]表示输出信号的当前采样值,a₁,...,aₘ和b₀,...,bₘ是滤波器的系数。
二、IIR滤波器的设计方法设计IIR滤波器需要确定滤波器的阶数、截止频率和系数等参数,以下介绍一种常用的设计方法:巴特沃斯滤波器设计方法。
1. 确定滤波器阶数滤波器的阶数决定了滤波器的复杂度和频率响应的形状。
阶数越高,频率响应越陡峭。
根据需要的滤波效果和计算复杂度,选择适当的滤波器阶数。
2. 确定截止频率截止频率是滤波器在频域上的边界,用于确定滤波器的通带和阻带。
根据信号的频谱分析以及滤波器的应用要求,确定合适的截止频率。
3. 求解滤波器系数根据巴特沃斯滤波器的设计方法,可以采用双线性变换、频率抽样和极点放置等技术求解滤波器的系数。
具体方法比较复杂,需要使用专业的滤波器设计软件或者数字信号处理工具包进行计算。
4. 评估设计结果设计完成后,需要评估滤波器的性能指标,如频率响应、相位响应、群延迟等。
可以通过频域分析和时域仿真等方法来评估滤波器的设计效果。
三、结论IIR滤波器是一种常用的数字滤波器,其具有无限冲激响应的特点。
通过对输入信号和输出信号进行递归运算,可以实现滤波效果。
设计IIR滤波器需要确定滤波器的阶数、截止频率和系数等参数,并通过专业的设计方法进行求解。
fir、iir数字滤波器的设计与实现

一、概述数字滤波器是数字信号处理中的重要部分,它可以对数字信号进行滤波、去噪、平滑等处理,广泛应用于通信、音频处理、图像处理等领域。
在数字滤波器中,fir和iir是两种常见的结构,它们各自具有不同的特点和适用场景。
本文将围绕fir和iir数字滤波器的设计与实现展开讨论,介绍它们的原理、设计方法和实际应用。
二、fir数字滤波器的设计与实现1. fir数字滤波器的原理fir数字滤波器是一种有限冲激响应滤波器,它的输出仅依赖于输入信号的有限个先前值。
fir数字滤波器的传递函数可以表示为:H(z) = b0 + b1 * z^(-1) + b2 * z^(-2) + ... + bn * z^(-n)其中,b0、b1、...、bn为滤波器的系数,n为滤波器的阶数。
fir数字滤波器的特点是稳定性好、易于设计、相位线性等。
2. fir数字滤波器的设计方法fir数字滤波器的设计通常采用频率采样法、窗函数法、最小均方误差法等。
其中,频率采样法是一种常用的设计方法,它可以通过指定频率响应的要求来确定fir数字滤波器的系数,然后利用离散傅立叶变换将频率响应转换为时域的脉冲响应。
3. fir数字滤波器的实现fir数字滤波器的实现通常采用直接型、级联型、并行型等结构。
其中,直接型fir数字滤波器是最简单的实现方式,它直接利用fir数字滤波器的时域脉冲响应进行卷积计算。
另外,还可以利用快速傅立叶变换等算法加速fir数字滤波器的实现。
三、iir数字滤波器的设计与实现1. iir数字滤波器的原理iir数字滤波器是一种无限冲激响应滤波器,它的输出不仅依赖于输入信号的有限个先前值,还依赖于输出信号的先前值。
iir数字滤波器的传递函数可以表示为:H(z) = (b0 + b1 * z^(-1) + b2 * z^(-2) + ... + bn * z^(-n)) / (1 +a1 * z^(-1) + a2 * z^(-2) + ... + am * z^(-m))其中,b0、b1、...、bn为前向系数,a1、a2、...、am为反馈系数,n为前向路径的阶数,m为反馈路径的阶数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国民航大学
电子信息工程学院 DSP技术及应用课程设计报告
题目:直接法设计IIR滤波器
专业班级:2011级通信C班
学号:
姓名:
指导教师:
二〇〇年月日
目录
一、设计目的 (1)
二、设计要求 (1)
三、设计原理及方案 (1)
四、软件流程 (3)
五、调试分析 (4)
六、设计总结 (5)
七、参考文献 (6)
一、设计目的
1、复习数字信号处理教材中讲解的滤波器的基本设计方法。
2、通过查找资料学习prony和yule-walk滤波器的知识。
3、熟练掌握matlab的常用函数,学会对信号进行处理。
4、学会使用matlab的GUI控件编辑图形用户界面。
5、学习撰写ppt和报告的技巧,培养团队合作能力。
二、设计要求
1、查阅课题相关资料,学习matlab的基本语句,以及设计滤波器的知识,制定设计计划及设计思路。
2、搭建GUI平台,使界面中可以显示原信号时域、频域波形,加噪后信号的时域、频域波形,滤波器的频率响应波形,以及去噪后声音信号的时域、频域波形,方便进行对比。
3、可以打开任意wav格式声音文件。
4、通过添加播放与音量调节按钮,可对声音信号进行播放、调节音量操作。
5、通过录音按钮,可以现场采集声音信号并保存
6、向声音信号添加不同种类噪声,并且可以改变信噪比或噪声频率等参数。
7、用prony及yule-walk方法设计不同类型的IIR滤波器,滤除噪声信号。
8、通过在窗口中输入数值,可以改变滤波器阶数,以及通带与阻带的宽度。
三、设计原理及方案
1、yule-walk法设计IIR滤波器原理:
yulewalk函数使用最小二乘拟合逼近给定的频率特性。
不像模拟滤波器原型设计,yulewalk函数设计方法不是基于低通、高通、带通、带阻的设计参数,而是基于离散区域上的特征值。
函数的用法如下:
[b,a]=yulewalk(n,f,m)
该函数返回yule-walk滤波器的系数矩阵[b,a];其中矩阵f和m是已知的
频率响应;n是滤波器的阶数。
其中频率矩阵f的元素必须处于范围[0,1]之内,而且必须是升序排列,以0开始,以1结束。
2. prony法设计IIR滤波器原理:
和yule-walk法不同,prony法是根据给定的冲激响应设计滤波器的一种方法,prony在滤波器设计、指数信号建模、系统辨识等领域都有广泛的应用。
在matlab里用prony函数实现:
[b,a]=prony(h,nb,na)
其中,nb,na指定滤波器的传递函数中分子和分母的阶数,h为给定的冲激响应,返回值中b和a的长度分别为nb+1和na+1,并且以升幂的形式给出系统的传递函数。
3
原理图说明:
(1)初始化:点击开始使用,进入主界面。
(2)添加一个声音信号或点击录制可以录制声音,点击添加后可以得到该声音信号的时域、频域波形。
(3)加入噪声:选择噪声种类、设定相关参数,点击添加后,得到加噪后的声音信号,并在界面中显示加噪后的声音信号的波形。
(4)滤波器滤波:选择适合的滤波器并设定相关参数,点击选择后获得加噪声音信号经滤波器滤波后的声音,以及它的时域、频域波形。
四、平台介绍
欢迎界面,点击“开始使用”进入主界面
在点击“录音开始后”,会在下面
的坐标中实时显示波形。
在点击“选择声音信号”,可以选
择任意声音信号。
选择声音文件后,就会看到信号的波形和频谱图。
选择噪声类型,并调整参数,点击“添加噪声信号”,即可看到加噪后信号的波形与频谱图。
选择滤波器,调整相应参
数,点击“使用滤波器”,
即可看到去噪后信号的波
形和频谱图,以及滤波器的
图。
五、调试分析
在系统编程过程中我们遇到了许多问题,以下几点主要的进行分析说明:
1、在为声音信号加入正余弦噪声时,无法直接将原始声音与噪声信号相加。
解决方法:由于噪声信号的长度与原始信号不同,必须重新设定使其长度相等,在正余弦噪声后添加“转置加”符号后,两者才可以进行相加。
2、在最开始设计滤波器时,对prony以及yule-walk方法的原理不了解,设定的各项参数不合理。
解决方法:通过上网查找资料,借阅书籍,组员之间不断探讨尝试,掌握两种方法的基本原理,设定合适的滤波器参数。
3、不知道button间的数据如何传递。
解决方法:设置全局变量,数据即可在程序中传递。
4、不知如何将下拉菜单和按钮关联。
解决方法:获取popupmenu的string属性,并设为全局变量,在按钮中直接调用即可。
5、在添加背景图后,运行时,坐标轴不能全部显示出来,只有在使用时才会显示。
解决方法:在matlab中添加背景图后,坐标轴确实没有办法完全显示,只能改为使用软件提供的背景色,对界面进行美化。
六、设计总结
通过本次应用matlab实现直接法设计IIR滤波器实验,我们巩固了数字信号处理的知识,掌握了有关滤波器的设计方法,并学习了利用prony和yulewalk 两种新的方法设计滤波器。
在使用matlab处理声音信号和设计滤波器过程中和GUI平台的搭建过程中,我们组虽然遇到很多问题,但都经过查资料和询问同学使问题得到了解决,使我们对matlab的使用有了更加深刻的理解。
这次课程设计的经历,我们都受益匪浅,在韩老师和何老师的指导下,我们不光在学术上有所收获,还在ppt设计以及答辩方便得到了很多技巧,而且这次实习还提高了我们团结合作的能力,我们相信这些宝贵的实习经历都会对我们以后的工作有所帮助。
七、参考文献
[1] 陈亚勇. MATLAB信号处理详解.北京:人民邮电出版社,
[2] 张小虹王丽娟任姝婕. 数字信号处理基础. 北京:清华大学出版社,2007
[3] 万永革.数字信号处理的MATLAB实现.北京:科学出版社,。
