必修4 平面向量总复习课件
合集下载
人教A版高中数学必修四课件:第二章 阶段复习课 平面向量 (共82张PPT)

择决定命运,环境造就人生!
1、只要有坚强的意志力,就自然而然地会有能耐、机灵和知识。2、你们应该培养对自己,对自己的力量的信心,百这种信心是靠克服障碍,培养意志和锻炼意志而获得的。 3、坚强的信念能赢得强者的心,并使他们变得更坚强。4、天行健,君子以自强不息。5、有百折不挠的信念的所支持的人的意志,比那些似乎是无敌的物质力量有更强大 的威力。6、永远没有人力可以击退一个坚决强毅的希望。7、意大利有一句谚语:对一个歌手的要求,首先是嗓子、嗓子和嗓子……我现在按照这一公式拙劣地摹仿为:对 一个要成为不负于高尔基所声称的那种“人”的要求,首先是意志、意志和意志。8、执着追求并从中得到最大快乐的人,才是成功者。9、三军可夺帅也,匹夫不可夺志也。 10、发现者,尤其是一个初出茅庐的年轻发现者,需要勇气才能无视他人的冷漠和怀疑,才能坚持自己发现的意志,并把研究继续下去。11、我的本质不是我的意志的结果, 相反,我的意志是我的本质的结果,因为我先有存在,后有意志,存在可以没有意志,但是没有存在就没有意志。12、公共的利益,人类的福利,可以使可憎的工作变为可 贵,只有开明人士才能知道克服困难所需要的热忱。13、立志用功如种树然,方其根芽,犹未有干;及其有干,尚未有枝;枝而后叶,叶而后花。14、意志的出现不是对愿 望的否定,而是把愿望合并和提升到一个更高的意识水平上。15、无论是美女的歌声,还是鬓狗的狂吠,无论是鳄鱼的眼泪,还是恶狼的嚎叫,都不会使我动摇。16、即使 遇到了不幸的灾难,已经开始了的事情决不放弃。17、最可怕的敌人,就是没有坚强的信念。18、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下 去。19、意志若是屈从,不论程度如何,它都帮助了暴力。20、有了坚定的意志,就等于给双脚添了一对翅膀。21、意志坚强,就会战胜恶运。22、只有刚强的人,才有神 圣的意志,凡是战斗的人,才能取得胜利。23、卓越的人的一大优点是:在不利和艰难的遭遇里百折不挠。24、疼痛的强度,同自然赋于人类的意志和刚度成正比。25、能 够岿然不动,坚持正见,度过难关的人是不多的。26、钢是在烈火和急剧冷却里锻炼出来的,所以才能坚硬和什么也不怕。我们的一代也是这样的在斗争中和可怕的考验中 锻炼出来的,学习了不在生活面前屈服。27、只要持续地努力,不懈地奋斗,就没有征服不了的东西。28、立志不坚,终不济事。29、功崇惟志,业广惟勤。30、一个崇高 的目标,只要不渝地追求,就会居为壮举;在它纯洁的目光里,一切美德必将胜利。31、书不记,熟读可记;义不精,细思可精;惟有志不立,直是无着力处。32、您得相 信,有志者事竟成。古人告诫说:“天国是努力进入的”。只有当勉为其难地一步步向它走去的时候,才必须勉为其难地一步步走下去,才必须勉为其难地去达到它。33、 告诉你使我达到目标的奥秘吧,我唯一的力量就是我的坚持精神。34、成大事不在于力量的大小,而在于能坚持多久。35、一个人所能做的就是做出好榜样,要有勇气在风 言风语的社会中坚定地高举伦理的信念。36、即使在把眼睛盯着大地的时候,那超群的目光仍然保持着凝视太阳的能力。37、你既然期望辉煌伟大的一生,那么就应该从今 天起,以毫不动摇的决心和坚定不移的信念,凭自己的智慧和毅力,去创造你和人类的快乐。38、一个有决心的人,将会找到他的道路。39、在希望与失望的决斗中,如果 你用勇气与坚决的双手紧握着,胜利必属于希望。40、富贵不能淫,贫贱不能移,威武不能屈。41、生活的道路一旦选定,就要勇敢地走到底,决不回头。42、生命里最重 要的事情是要有个远大的目标,并借助才能与坚持来完成它。43、事业常成于坚忍,毁于急躁。我在沙漠中曾亲眼看见,匆忙的旅人落在从容的后边;疾驰的骏马落在后头, 缓步的骆驼继续向前。44、有志者事竟成。45、穷且益坚,不坠青云之志。46、意志目标不在自然中存在,而在生命中蕴藏。47、坚持意志伟大的事业需要始终不渝的精神。 48、思想的形成,首先是意志的形成。49、谁有历经千辛万苦的意志,谁就能达到任何目的。50、不作什么决定的意志不是现实的意志;无性格的人从来不做出决定。我终 生的等待,换不来你刹那的凝眸。最美的不是下雨天,是曾与你躲过雨的屋檐。征服畏惧、建立自信的最快最确实的方法,就是去做你害怕的事,直到你获得成功的经验。 真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。生活真象这杯浓酒,不经三番五次的提炼呵,就不会这样可口!人格的完善是本,财富的确立是末能力可以慢 慢锻炼,经验可以慢慢积累,热情不可以没有。不管什么东西,总是觉得,别人的比自己的好!只有经历过地狱般的折磨,才有征服天堂的力量。只有流过血的手指才能弹 出世间的绝唱。对时间的价值没有没有深切认识的人,决不会坚韧勤勉。第一个青春是上帝给的;第二个的青春是靠自己努力的。不要因为寂寞而恋爱,孤独是为了幸福而 等待。每天清晨,当我睁开眼睛,我告诉自己:我今天快乐或是不快乐,并非由我所遭遇的事情造成的,而应该取决于我自己。我可以自己选择事情的发展方向。昨日已逝,
1、只要有坚强的意志力,就自然而然地会有能耐、机灵和知识。2、你们应该培养对自己,对自己的力量的信心,百这种信心是靠克服障碍,培养意志和锻炼意志而获得的。 3、坚强的信念能赢得强者的心,并使他们变得更坚强。4、天行健,君子以自强不息。5、有百折不挠的信念的所支持的人的意志,比那些似乎是无敌的物质力量有更强大 的威力。6、永远没有人力可以击退一个坚决强毅的希望。7、意大利有一句谚语:对一个歌手的要求,首先是嗓子、嗓子和嗓子……我现在按照这一公式拙劣地摹仿为:对 一个要成为不负于高尔基所声称的那种“人”的要求,首先是意志、意志和意志。8、执着追求并从中得到最大快乐的人,才是成功者。9、三军可夺帅也,匹夫不可夺志也。 10、发现者,尤其是一个初出茅庐的年轻发现者,需要勇气才能无视他人的冷漠和怀疑,才能坚持自己发现的意志,并把研究继续下去。11、我的本质不是我的意志的结果, 相反,我的意志是我的本质的结果,因为我先有存在,后有意志,存在可以没有意志,但是没有存在就没有意志。12、公共的利益,人类的福利,可以使可憎的工作变为可 贵,只有开明人士才能知道克服困难所需要的热忱。13、立志用功如种树然,方其根芽,犹未有干;及其有干,尚未有枝;枝而后叶,叶而后花。14、意志的出现不是对愿 望的否定,而是把愿望合并和提升到一个更高的意识水平上。15、无论是美女的歌声,还是鬓狗的狂吠,无论是鳄鱼的眼泪,还是恶狼的嚎叫,都不会使我动摇。16、即使 遇到了不幸的灾难,已经开始了的事情决不放弃。17、最可怕的敌人,就是没有坚强的信念。18、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下 去。19、意志若是屈从,不论程度如何,它都帮助了暴力。20、有了坚定的意志,就等于给双脚添了一对翅膀。21、意志坚强,就会战胜恶运。22、只有刚强的人,才有神 圣的意志,凡是战斗的人,才能取得胜利。23、卓越的人的一大优点是:在不利和艰难的遭遇里百折不挠。24、疼痛的强度,同自然赋于人类的意志和刚度成正比。25、能 够岿然不动,坚持正见,度过难关的人是不多的。26、钢是在烈火和急剧冷却里锻炼出来的,所以才能坚硬和什么也不怕。我们的一代也是这样的在斗争中和可怕的考验中 锻炼出来的,学习了不在生活面前屈服。27、只要持续地努力,不懈地奋斗,就没有征服不了的东西。28、立志不坚,终不济事。29、功崇惟志,业广惟勤。30、一个崇高 的目标,只要不渝地追求,就会居为壮举;在它纯洁的目光里,一切美德必将胜利。31、书不记,熟读可记;义不精,细思可精;惟有志不立,直是无着力处。32、您得相 信,有志者事竟成。古人告诫说:“天国是努力进入的”。只有当勉为其难地一步步向它走去的时候,才必须勉为其难地一步步走下去,才必须勉为其难地去达到它。33、 告诉你使我达到目标的奥秘吧,我唯一的力量就是我的坚持精神。34、成大事不在于力量的大小,而在于能坚持多久。35、一个人所能做的就是做出好榜样,要有勇气在风 言风语的社会中坚定地高举伦理的信念。36、即使在把眼睛盯着大地的时候,那超群的目光仍然保持着凝视太阳的能力。37、你既然期望辉煌伟大的一生,那么就应该从今 天起,以毫不动摇的决心和坚定不移的信念,凭自己的智慧和毅力,去创造你和人类的快乐。38、一个有决心的人,将会找到他的道路。39、在希望与失望的决斗中,如果 你用勇气与坚决的双手紧握着,胜利必属于希望。40、富贵不能淫,贫贱不能移,威武不能屈。41、生活的道路一旦选定,就要勇敢地走到底,决不回头。42、生命里最重 要的事情是要有个远大的目标,并借助才能与坚持来完成它。43、事业常成于坚忍,毁于急躁。我在沙漠中曾亲眼看见,匆忙的旅人落在从容的后边;疾驰的骏马落在后头, 缓步的骆驼继续向前。44、有志者事竟成。45、穷且益坚,不坠青云之志。46、意志目标不在自然中存在,而在生命中蕴藏。47、坚持意志伟大的事业需要始终不渝的精神。 48、思想的形成,首先是意志的形成。49、谁有历经千辛万苦的意志,谁就能达到任何目的。50、不作什么决定的意志不是现实的意志;无性格的人从来不做出决定。我终 生的等待,换不来你刹那的凝眸。最美的不是下雨天,是曾与你躲过雨的屋檐。征服畏惧、建立自信的最快最确实的方法,就是去做你害怕的事,直到你获得成功的经验。 真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。生活真象这杯浓酒,不经三番五次的提炼呵,就不会这样可口!人格的完善是本,财富的确立是末能力可以慢 慢锻炼,经验可以慢慢积累,热情不可以没有。不管什么东西,总是觉得,别人的比自己的好!只有经历过地狱般的折磨,才有征服天堂的力量。只有流过血的手指才能弹 出世间的绝唱。对时间的价值没有没有深切认识的人,决不会坚韧勤勉。第一个青春是上帝给的;第二个的青春是靠自己努力的。不要因为寂寞而恋爱,孤独是为了幸福而 等待。每天清晨,当我睁开眼睛,我告诉自己:我今天快乐或是不快乐,并非由我所遭遇的事情造成的,而应该取决于我自己。我可以自己选择事情的发展方向。昨日已逝,
人教A版数学必修4PPT课件平面向量4

数λ1,λ2 ,使
a 1e1 2 e2
说明:① e1 ,e2 是两个不共线的向量; ② a 是平面内的任意向量; ③ λ1,λ2为实数,且唯一确定.
人 教 A 版 数学 必修4 PPT课件 平面向 量4
人 教 A 版 数学 必修4 PPT课件 平面向 量4
我们把不共线的向量 e1 ,e2 叫做这一平面内所有向量 的一组基底.
一对实数
1, 2,使
a
1 e1
2
e
.
2
不共线的向量 e1,e2 叫做表示这一平面内 所有向量的一组基底.
言论的花,开得愈大;行为的果子,结得愈小. ——冰心
2.在等边三角形 ABC 中,A→B与B→C的夹角等于( C )
A.60°
B.90°
C.120°
D.150°
3.已知 e1 和 e2 是表示平面内所有向量的一组基底, 那么下面四组向量中不能作为一组基底的是 ( C)
A.e1 和 e1+e2 B.e1-2e2 和 e2-2e1 C.e1-2e2 和 4e2-2e1 D.e1+e2 和 e1-e2 【解析】分析四个选项知,在 C 中,4e2-2e1= -2(e1-2 e2).∴e1-2 e 2 与 4 e 2-2 e 1 共线,应选 C.
种表示是否唯一?请说明理由.
1.理解平面向量的基底的意义与作用. (重点) 2.能够在具体问题中适当地选取基底,使其他 向量都能够用基底来表达. (难点) 3.初步利用定理解决问题(如相交线交成线段 比的问题等).
人 教 A 版 数学 必修4 PPT课件 平面向 量共线的向量 e1,e2 与该
平面内的任一向量 a 之间的关系.
a
e1
e2
人 教 A 版 数学 必修4 PPT课件 平面向 量4
a 1e1 2 e2
说明:① e1 ,e2 是两个不共线的向量; ② a 是平面内的任意向量; ③ λ1,λ2为实数,且唯一确定.
人 教 A 版 数学 必修4 PPT课件 平面向 量4
人 教 A 版 数学 必修4 PPT课件 平面向 量4
我们把不共线的向量 e1 ,e2 叫做这一平面内所有向量 的一组基底.
一对实数
1, 2,使
a
1 e1
2
e
.
2
不共线的向量 e1,e2 叫做表示这一平面内 所有向量的一组基底.
言论的花,开得愈大;行为的果子,结得愈小. ——冰心
2.在等边三角形 ABC 中,A→B与B→C的夹角等于( C )
A.60°
B.90°
C.120°
D.150°
3.已知 e1 和 e2 是表示平面内所有向量的一组基底, 那么下面四组向量中不能作为一组基底的是 ( C)
A.e1 和 e1+e2 B.e1-2e2 和 e2-2e1 C.e1-2e2 和 4e2-2e1 D.e1+e2 和 e1-e2 【解析】分析四个选项知,在 C 中,4e2-2e1= -2(e1-2 e2).∴e1-2 e 2 与 4 e 2-2 e 1 共线,应选 C.
种表示是否唯一?请说明理由.
1.理解平面向量的基底的意义与作用. (重点) 2.能够在具体问题中适当地选取基底,使其他 向量都能够用基底来表达. (难点) 3.初步利用定理解决问题(如相交线交成线段 比的问题等).
人 教 A 版 数学 必修4 PPT课件 平面向 量共线的向量 e1,e2 与该
平面内的任一向量 a 之间的关系.
a
e1
e2
人 教 A 版 数学 必修4 PPT课件 平面向 量4
【课件】必修4第二章《平面向量》复习课(共81张PPT)

P123
35 35 of 22
3
第23课 第(6)题
P123
36 36 of 22
7
第23课 第(7)题
P123
37 37 of 22
B
第23课 第(7)题
P123
38 38 of 22
= 5
第23课 第(8)题
P123
39 39 of 22
23
第23课 第(8)题
P123
40 40 of 22
平面向量总复习
1 1 of 22
一张图学透
一张图学透 平面向量的
数量积
2 2 of 22
一张图学透
一张图学透 三角函数 的图像与
性质
3 3 of 22
一张图学透
一张图学透 三角函数 的图像与
性质
4 4 of 22
一张图学透
一张图学透 三角函数 的图像与
性质
5 5 of 22
四组题讲透
①②③④⑤⑥
23
第23课 第(8)题
P123
41 41 of 22
方法便笺
求向量的模或其范围的方法
第23课 方法便笺
P122
42 42 of 22
方法便笺
求向量的模或其范围的方法
提示: ①求形如 ma nb的向量的模,可通过平方,转化为数量 的运算. ②用定义法和坐标法求模的范围时,一般把它表示成某个 变量的函数,再利用函数的有关知识求解;用几何法求模 的范围时,注意数形结合的思想,长利用三角不等式进行 最值的求解.
第23课 方法便笺
P122
43 43 of 22
2 2
第23课 第(9)题
P123
44 44 of 22
35 35 of 22
3
第23课 第(6)题
P123
36 36 of 22
7
第23课 第(7)题
P123
37 37 of 22
B
第23课 第(7)题
P123
38 38 of 22
= 5
第23课 第(8)题
P123
39 39 of 22
23
第23课 第(8)题
P123
40 40 of 22
平面向量总复习
1 1 of 22
一张图学透
一张图学透 平面向量的
数量积
2 2 of 22
一张图学透
一张图学透 三角函数 的图像与
性质
3 3 of 22
一张图学透
一张图学透 三角函数 的图像与
性质
4 4 of 22
一张图学透
一张图学透 三角函数 的图像与
性质
5 5 of 22
四组题讲透
①②③④⑤⑥
23
第23课 第(8)题
P123
41 41 of 22
方法便笺
求向量的模或其范围的方法
第23课 方法便笺
P122
42 42 of 22
方法便笺
求向量的模或其范围的方法
提示: ①求形如 ma nb的向量的模,可通过平方,转化为数量 的运算. ②用定义法和坐标法求模的范围时,一般把它表示成某个 变量的函数,再利用函数的有关知识求解;用几何法求模 的范围时,注意数形结合的思想,长利用三角不等式进行 最值的求解.
第23课 方法便笺
P122
43 43 of 22
2 2
第23课 第(9)题
P123
44 44 of 22
高三数学平面向量总复习课件 必修4

10 3
3、已知|a|=18,|b|=1,a·b=-9,则a和b
的夹角θ是(A)
A.120。 B.150。 C.60。 D.30。
4、已知|a|=|b|=1,a与b的夹角为90。,
c=2a+3b,d=ka-4b,c⊥d,k=()
A. -6 B. 6 C. 3 D. -3
5、设点A(a,b),B(c,d),若径平移得
(2) 若x (1, 6 )时,不等式 f ( x) mx 16恒成立,求实数m的范围.
[解析]
(1)
a
b ,
a
b
0,
又
a
b
1,
c
2
c c
a
2
2( x2
3)a
b
(x2
3)2
b
2
x4
6x2
10
c
10, x4 6x2 10 10,
解得 6 x 6
又 而c
设a (x
R()2, 记cosfx(,x1)),ba
(cos x, b 1.
(1) 若x [0, ], 试求f ( x)的单调递
减区间; (2) 将y
2
sin
x的图
象按向量c
(m, n) ( m )平移后得 y f ( x)的图
2 象,求实数m, n的值.
[解析]
(1) a
b
2 cos 2
恒成立,即使x3 3x mx 16恒成立.
亦即:m 3 x2 16 , x
令g( x) x2 16 , 则 x
g'( x)
2x
16 x2
2( x
2)( x2 x2
2x
4)
当1 x 2时, g'( x) 0 当2 x 6时, g'( x) 0 g( x)在(1,2)上递减, 在(2, 6)上递增. x 2, g( x)达到最小值 g(2) 22 16 12
高中人教B版必修四课件:复习课(三) 平面向量

4.在平行四边形 ABCD 中,AD=1,∠BAD=60°,E 为 CD 的中点.若 AC ·BE =1,则 AB 的长为________. 解析:设| AB|=x,x>0,则 AB·AD=12x.又 AC ·BE =( AD + AB)· AD-12 AB=1-12x2+14x=1,解得 x=12,即 AB 的长为12. 答案:12
(2)解决此类问题要掌握平面向量数量积的两种求法:一是根据 数量积的定义,即 a·b=|a||b|cos θ,二是利用坐标运算,即 a·b=x1x2 +y1y2;同时还要掌握利用数量积求向量的夹角、求向量的长度和判 断两个向量垂直的方法.
[典例] (1)设 a=(1,2),b=(1,1),c=a+kb.若 b⊥c,则
[答案] (1)A (2)C
[类题通法] (1)数量积的计算通常有三种方法:数量积的定义,坐标运 算,数量积的几何意义; (2)可以利用数量积求向量的模和夹角,向量要分解成题中 已知向量的模和夹角进行计算.
[题组训练]
1.已知 a+b+c=0,|a|=2,|b|=3,|c|= 19,则向量 a 与 b
由―O→C =λ―O→A +μ―O→B ,
得(1,0)=λ(0,1)+μ 23,-12= 23μ,λ-12μ,
∴
23μ=1,
λ-12μ=0,
解得μ=2 3 3,
λ=
3 3.
∴λ+μ= 3. 答案: 3
平面向量的数量积
(1)题型既有选择题、填空题,又有解答题,主要考查数量积运 算、向量的垂直等问题,常与平面几何、三角函数、解析几何等知识 交汇命题.
3.如图,半径为 1 的扇形 AOB 的圆心角为 120°, 点 C 在 AB 上,且∠COB=30°.若―O→C =λ―O→A + μ―O→B ,则 λ+μ=________.
必修四_平面向量知识点梳理58页PPT

40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
必修四_平面向量知识点梳理
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是ห้องสมุดไป่ตู้毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
必修四_平面向量知识点梳理
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是ห้องสมุดไป่ตู้毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
人教A版高中数学必修四课件:第二章2.3.1平面向量基本定理 (共16张PPT)

x
e2
O
a 3e1 2e2
3 a x 4y 2
yn
A
a 3m 2n
当a 0时, 有且只有1 2 0时可使 0 1 e1 2 e2 , (e1 , e2不共线).
若1与2中只有一个为零 , 情况会是怎样?
若2 0, 则a 1 e1 ,即a与e1共线, 若1 0, 则a 2 e2 ,即a与e2共线,
本题在解决过程中用到了两向量共 线的等价条件这一定理,并用基向量表 示有关向量,用待定系数法列方程,通 过消元解方程组。这些知识和考虑问题 的方法都必须切实掌握好。
课堂总结 1.平面向量基本定理可以联系物理 学中的力的分解模型来理解,它说明在
同一平面内任一向量都可以表示为不共
线向量的线性组合,该定理是平面向量
D
A
N M B
C
例2.用向量的方法证明: 1 平行四边形OACB中, BD BC , OD与BA 3 1 相交于E , 求证 : BE BA. 4 D B C E
O
A
例3.证明: 向量OA, OB, OC的终点A, B, C共线 的等价条件是存在实数 、 且 1, 使得 OC OA OB.
问题 3 : 设 e1 , e2 是同一平面内两个不共 线的向量, a是这一平面内的任一向 量, 我们来通过作图研 究a与e1 , e2 之间的关系?
平面向量基本定理: 如果e1 , e2 是同一平面内两个不共 线的向量, 那 么对于平面内的任一向 量a , 有且只有一对实数
1 , 2 , 使得a 1 e1 2 e2 .
坐标表示的基础,其本质是一个向量在
其他两个向量上的分解。
2. 在实际问题中的指导意义在于
【高中数学必修4】平面向量单元复习2课件

第二章 平面向量 单元复习 第二课时
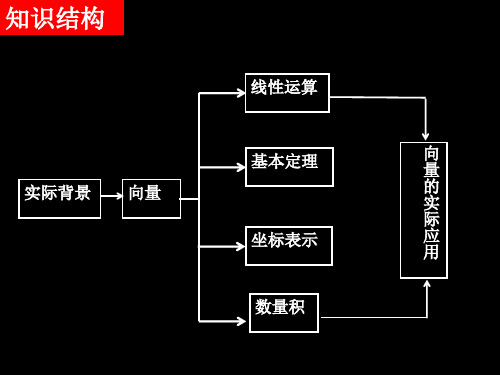
知识结构
t
p
1 2
5730
线ห้องสมุดไป่ตู้运算
基本定理
向 量
实际背景 向量
的 实
际
坐标表示
应 用
数量积
知识梳理
(1)a+b=b+a; (2)(a+b)+c=a+(b+c); (3)若a与b为相反向量,则a+b=0; (4)若b+c=a,则c=a-b; (5)|a±b|≤|a|+|b|,|a±b|≥||a|-|b||; (6)O A 1 A 1 A 2A 2 A 3 A n 1 A n O A n
(7) cos
|aa||bb |;
(8) |a|cos a|bb|.
范例分析
例1 已知向量a、b满足:|a|=4,且 a·(a-b)=12,求向量b在a方向上的投影.
1
例2 已知非零向量a、b满足: (a-b)⊥b,且(a+2b)⊥(a-2b),求向量 a与b的夹角.
60°
例3 已知向量a、b、c两两之间的夹
例6 已知向量a、b满足:|a|=4, |b|=3,(2a-3b)·(2a+b)=61,当 t∈[0,1]时,求|a+tb|的取值范围.
[2 3, 4]
作业:
P119复习参考题A组:11,13. B组:2,3.
P119复习参考题B组:1.(做书上)
角为120°,且|a|=1,|b|=2,|c|=3,
求向量a+b+c与a的夹角. 150°
例4 设向量a、b不共线,已知 AB 2a+kb,BC a+b,CD a-2b, 且A、B、D三点共线,求实数k的值.
k=-1
例5 设e为单位向量,且向量a≠e, 若对任意实数t,不等式|a-te|≥|a- e|恒成立,求证:(a-e)⊥e.
知识结构
t
p
1 2
5730
线ห้องสมุดไป่ตู้运算
基本定理
向 量
实际背景 向量
的 实
际
坐标表示
应 用
数量积
知识梳理
(1)a+b=b+a; (2)(a+b)+c=a+(b+c); (3)若a与b为相反向量,则a+b=0; (4)若b+c=a,则c=a-b; (5)|a±b|≤|a|+|b|,|a±b|≥||a|-|b||; (6)O A 1 A 1 A 2A 2 A 3 A n 1 A n O A n
(7) cos
|aa||bb |;
(8) |a|cos a|bb|.
范例分析
例1 已知向量a、b满足:|a|=4,且 a·(a-b)=12,求向量b在a方向上的投影.
1
例2 已知非零向量a、b满足: (a-b)⊥b,且(a+2b)⊥(a-2b),求向量 a与b的夹角.
60°
例3 已知向量a、b、c两两之间的夹
例6 已知向量a、b满足:|a|=4, |b|=3,(2a-3b)·(2a+b)=61,当 t∈[0,1]时,求|a+tb|的取值范围.
[2 3, 4]
作业:
P119复习参考题A组:11,13. B组:2,3.
P119复习参考题B组:1.(做书上)
角为120°,且|a|=1,|b|=2,|c|=3,
求向量a+b+c与a的夹角. 150°
例4 设向量a、b不共线,已知 AB 2a+kb,BC a+b,CD a-2b, 且A、B、D三点共线,求实数k的值.
k=-1
例5 设e为单位向量,且向量a≠e, 若对任意实数t,不等式|a-te|≥|a- e|恒成立,求证:(a-e)⊥e.
高中数学人教A版必修4 平面向量专题复习PPT全文课件

途径二:“形”“数”相守 找坐标
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
y A
B (O) C 2
x
图13
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
练习1、【2017课标3,理12】在矩形ABCD中,AB=1
AD=2,
APABAD
动点P在以点C为圆心且与BD相切的圆上.若
(五)等与不等寻定值
极化恒等式
2
2
4a b a b a b
绝对值三角不等式
因对任意实数 m,n,恒有 m n m n 成立
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
(五)等与不等寻定值
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
(五)等与不等寻定值
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
数缺形时少直观, 形少数时难入微; 数形结合百般好, 隔离分家万事休.
(2013 年浙江省数学竞赛)已知直线 AB 与抛物线 y2 4x 交于 A, B 两点, M 为 AB的
中点, C 为抛物线上一个动点,若C0 满足 C0AC0B min CACB ,则下列一定成立的是
()
A. C0M AB C. C0 A C0B
纵观近五年的高考试题,平面向量的考查主要体现在2 个方面:
人教版必修四第二单元平面向量的复习课件

变式:若等边 ABC 的边长为 2
3 ,平面内一点
M
满足 CM
1
CB
2 CA
,则
63
MA• MB ________.
题型五: 向量与三角函数的综合
例 已知向量 a (sin ,2) 与 b (1, cos ) 互相垂直,其中 (0, ) .
2 (1)求 sin 和 cos 的值;
(2)若 sin( ) 10 , 0 ,求tan( )的值.
4.注意掌握一些重要结论,灵活运用结论解题。如向量的共线定理, 平面向量基本定理,三角形四心与向量有关的常见结论等。
1. (湖南)设D、E、F分别是△ABC的三边BC、CA、AB上的点,
且 =2 , =2 , =2 ,则
()
A.反向平行
B.同向平行
C.互相垂直
A
解:
E F
D.既不平行也不垂直
B
C
D
仿照上题,用坐标运算的方法解决下列问题:
例 已知 ABC,AD 为中线,求证 AD2 1 AB2 AC2 BC 2
2
2
例 设两个向量 e1 、e2 ,满足| e1 | 2 ,| e2 | 1 ,e1 、e2 的夹角为 60°,若向量 2te1 7e2
与向量 e1 te2 的夹角为钝角,求实数 t 的取值范围.
3
3
OM ,ON, MN
B
D
M
N C
A O
题型三: 向量平行与垂直的条件
4、已知 O,N,P 在 ABC 所在平面内,且 OA OB OC , NA NB NC 0 ,
且 PA• PB PB • PC PC • PA ,则点 O,N,P 依次是 ABC 的
人教A版数学必修四第二章2.3《平面向量的坐标表示与运算》(共20张PPT)

解:设c→=x→a+→yb,即 (4,2)=x(1,1)+y(-1,1) =(x,x)+(-y,y)
X-y=4
解得
X+y=2
X=3
y=-1
=(x-y,x+y) c→=3→a-→b,故选B
随堂演练:
1、下列说法正确的有( B )个 (1)向量的坐标即此向量终点的坐标。 (2)位置不同的向量其坐标可能相同。 (3)一个向量的坐标等于它的始点坐标减去它的终点坐标。 (4)相等的向量坐标一定相同。 A2、:已1 知M→NB=(:-21,2)C:,3则-3M→ND等:于4 ( C ) A3、、已(知-3a→,=3()1B,、3)(,-6→,b=3()-C2、,(1)3,,-则6)→b-Da→、等(于-(4,C-1)) A、(-3,2)B、(3,-2)C、(-3,-2)D、(-2,-3) 4、已知A→B=(5,7),λAB→=(10,14)则实数λ=___2_
探索研究
设得问出: 向已 量知a r向b r量,a ra r b r(,x1, λa→y的1)坐,标b r 表(示x2, 吗?y2),你能
r rrr rr 解 : a b ( x 1 i r y 1 j ) r( x 2 i y 2 j )
(x1 x2)i(y1y2)j
即 a b (x 1 x 2 ,y 1 y 2 ) 同理可得
a b (x 1 x 2 ,y 1 y 2)
结论:两个向量和与差的坐标分别等 于这两个向量相应坐标的和与差.
(2)实数与向量的积的坐标表示
r
已 知 R , 向 量 a (x , y ), 那 么
a r _ _ ( _ x _ r i _ _ _ y _ u j r _ ) _ _ _ _ x _ r i _ _ _ _ y _ r _ j
人教A版数学必修四第二章平面向量单元复习课件ppt
D
A
M
MN
C N
B
1 3
MC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
例4
在Rt△ABC中,已知斜边BC=2,
线段PQ以A为中点,且PQ=4,向量 B C 与
P Q 的夹角为60°,求 BP CQ .
(5)相等向量: 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用 长度相等且方向相同的向量. (6)相反向量: 长度相等且方向相反的向量. (7)平行向量(共线向量): 方向相同或相反的非零向量. (8)向量的数量积: a·b=|a||b|cosθ.
例1设向量a=(1,-3),b=(-2,4),
c=(-1,-2),若表示向量4a,4b-2c,
2(a-c),d 的有向线段首尾相接能构 成四边形,求向量d 的坐标.
d=(-2,-6)
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
Cபைடு நூலகம்
Q
BPCQ 2 A
B
P
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
知识梳理 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
必修四平面向量复习分解课件
03 向量的向量积
向量积的定义
向量积的定义
两个向量$vec{A}$和$vec{B}$的向量积 是一个向量,记作$vec{A} times vec{B}$,它的模长为$|vec{A} times vec{B}| = |vec{A}| times |vec{B}| times sin theta$,其中$theta$是$vec{A}$和 $vec{B}$之间的夹角。
详细描述
向量数量积定义为两个向量$mathbf{A}$和$mathbf{B}$的模长之积与它们夹角 的余弦值的乘积,记作$mathbf{A} cdot mathbf{B}$。
向量数量积的几何意义
总结词
向量数量积表示两个向量在平面 上的投影长度及其夹角的余弦值 的乘积。
详细描述
向量数量积的几何意义是表示两 个向量在平面上的投影长度之积 与它们夹角的余弦值的乘积。
VS
定义的理解
向量积是一个向量,其方向垂直于作为运 算对象的两个向量,其大小等于两个向量 的模长之积与它们夹角的正弦值的乘积。
向量积的几何意义
向量积的几何意义
向量积表示一个有向面积,即以 $vec{A}$和$vec{B}$为邻边的平行四 边形的有向面积。
几何意义的应用
在物理学和工程学中,向量积常用于 描述力矩、速度和加速度等物理量。
运算律的理解
这些运算律表明,向量积满足分配律,即可 以将一个向量分配到括号内的多个向量中进 行运算。
04 向量的混合积
混合积的定义
要点一
总结词
混合积是三个向量的有序积,记作$vec{a} cdot vec{b} cdot vec{c}$。
要点二
详细描述
混合积是三个向量的有序积,表示为$vec{a} cdot vec{b} cdot vec{c}$,其中$vec{a}$、$vec{b}$和$vec{c}$是平 面向量。混合积的符号遵循右手定则,即从向量$vec{a}$ 沿向量$vec{b}$、$vec{c}$方向看去,若方向为右手方向 则结果为正,反之为负。
人教A版高中数学必修四第二章平面向量复习课件

解:设点 B 的坐标为(x,y),
则 OB (x, y), AB (x 5, y 2)
OB AB
∴ x( x-5) +y( y-2) =0
即 x2+y2 – 5x – 2y=0
①
又 OB AB
∴x2+y2=(x-5)2+(y-2)2 即 10x+4y=29 ②
2024/11/3
由①、②解得:
2
2a b
b2
3
ab
3
2024/11/3
上页 下页 返回
15、如图,E是正方形ABCD的边AB延
长线上的一点,F在BC上,且BE=BF, 用向量的坐标法证明:AF⊥CE
2024/11/3
D
C
F
A
BE
上页 下页 返回
3、已知三个力 f1、f2、f3 作用于同一质点,且 | f1 | 20, | f2 | 30, | f3 | 40 (单位:牛)若三个力在同一平面
内且两两的夹角都为1200,求协力的大小和方向
y
B
f2
oθ
f3
x
C
A f1
2024/11/3
上页 下页 返回
例2:已知向量a (cos 3 x,sin 3 x),b (cos x , sin x),
22
2
2
且x
0,2
,
求
:
(1)a
b及
a
b
;
(2)若f
(x)
a
b
2
a
b
的最小值是-
3 2
, 求的值.
x1
y1
7 2
23或xy22
3 为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、数量积的坐标运算
B
a ?b ? x1 x2 ? y1 y2
4、运算律: (1) a ?b ? b?a
Oθ
B
A
(2)(? a)?b ? ?(a ?b)? a(? ?b)1
(3)(a ? b)?c ? a ?c ? b ?c
.
5、数量积的主要性质及其坐标表示:
?1?a ? b ? a ?b ? 0 ? x1x2 ? y1 y2 ? 0
必修四 平面向量
专题 复习
.
知 识
向量的概念
零向量、单位向量、 共线向量、相等向量
解决
网
图形
络
平 面
加法、减法
向量平行的充要条件
的平 行和 比例
向 量
数乘向量
ห้องสมุดไป่ตู้
平面向量基本定理
问题 的
初
向 量
坐标表示
两向量的夹角公式
解决 步 图形 应
的垂 用
两向量数量积
向量垂直的充要条件 直和 角度,
两点. 的距离公式
坐标运算: 设 a = (x1, y1), b = (x2, y2)
则a + b = ( x1 + x2 , y1 + y2 )
.
一、平面向量概念
2.向量的减法运算
B
1)减法法则: OA-OB = BA
2)坐标运算:
O
A
若 a=( x1, y1 ), b=( x2, y2 ) 则a - b= (x1 - x2 , y1 - y2)
?5?a ?b ? a ?b
.
例1.设非零向量a , b不共线,c ? ka ? b, d ? a ? kb (k ? R), 若c // d ,试求 k.
解:∵ c // d ,
∴由向量共线的充要条件得:c ? ? d ,
即 ka ? b ? ?(a ? kb),
又∵ a ,b不共线
∴由平面向量的基本定理
1
;
2
rr (a ? 2b)
?
rr (2a ? b)时,(1+2x)(2-x)+4 ? 3=0.x=-2或x ?
7
2
.
例8. 已知 ABCD 的三个顶点 A、B、C的坐 标分别为(- 2,1)、( -1,3)、(3,4),求 顶点D的坐标.
?k ? ? ??1 ? k?
?
k ? ?1
.
r 例7.已知向量a
?
?1,
2?,
r b
?
?x,1?, 分别求出当
r r rr
a ? 2b2与 a ? b平行和垂直时实数x的值.
rr
rr
解:a ? 2b=(1+2x,4),2a ? b ?(2 ? x, 3)
rr (a ? 2b)
//
r (2a
?
r b)时,3(1+2x)-4(2-x)=0,x=
( 2 ) a ? b ? a ? b ? x1 x2 ? y1 y2 ? 0
.
(3)两个向量相等的充要条件是两个向量的
坐标即相: 等a?.?? 那么 a
(x1?, y1), ?b?
x1
? b
?
? (x2, y2)
x2且y1 ?
y2
三、平面向量的基本定理
如果 e1 , e 2 是同一平面内的两个不共线
.
一、平面向量概念
向
量 的 表
几何表示 : 有向线段
r uuur 字母表示 : a 、AB 等
示 坐标表示 : (x,y)
若 A(x1,y1), B(x2,y2) 则 AB = (x2 - x1 , y2 - y1)
.
一、平面向量概念
向量的模(长度)
1. 设 a = ( x , y ), 则 a ?
向量,那么对于这一平面内的任一向
量a ,有且只有一对实数?1 , ? 2 ,使
? ? a ? 1 e 1 ? e 2 2 .
(四) 数量积
1、平面向量数量积的定义: a ?b ? | a | ?| b | cos?
? 2、数量积的几何意义:
r
r rr
r
等于 a 的长度 | a | 与 b 在 a 方向上的投影 | b | cos. 的乘积
长度 问题
一、平面向量概念
向量定义:既有大小又有方向的量叫向量。
重要概念:
(1)零向量: 长度为0的向量,记作 0. (2)单位向量:长度为 1个单位长度的向量 . (3)平行向量:也叫共线向量,方向相同或相反
的非零向量 . (4)相等向量:长度相等且方向相同的向量 . (5)相反向量:长度相等且方向相反的向量 .
3.加法减法运算律
1)交换律: a+b=b+a 2)结合律: (a+b)+c=a+(b+c)
.
练习
填空:
uuur uuur uuur
AB ? uuur BA ? uuur
BD ? uuur BC ? uuur
__Au_Du_ru_; __uC_u_Aru__;
BC ? uuur OD ?
CA ? uuur OA ?
x2 ? y2
2. 若表示向量 a 的起点和终点的坐标分别 为A(x1,y1)、B (x2,y2) ,则
a ? AB ? ?x1 ? ? x2 2 ? ?y1 ? ? y2 2
.
一、平面向量概念
1.向量的加法运算 三角形法则
AB+BC= AC
A
C BO
平行四边形法则
B
C
OA+OB= OC
A
重要结论: AB+BC+CA= 0
则
a??
?
|
a? a?
|
.
二、平面向量之间关系
向量平行(共线)充要条件的两种形式 :
(1)a // b(b ? 0) ? a ? ?b;
(2)a // b(a ? (x1, y1),b ? (x2 , y2 ),b ? 0) ? x1 y2 ? x2 y1 ? 0
向量垂直充要条件的两种形式:
(1)a ? b ? a ? b ? 0
?2?.当a
// b时,a ?b
?
? ? ?
a
? b ,当a,b同向时
??? a ?b,当a,b反向时
2
(3)a ?a ? a , a ? a ?a ? x12 ? y12
?4?cos? ? a ?b ? x1 x2 ? y1 y2
a ?b
x12 ? y12 x22 ? y22
(a, b是两个非零向量 )
__uB_uA_u_r_;
__A_D___;
uuur uuur uuru
OA? OB ? __B_A___ .
.
一、平面向量概念 4.实数λ与向量 a 的积
定义:λa是一个 向量.
它的长度 |λa| = |λ| |a|;
它的方向 (1) 当λ≥0时,λa 的方向 与a方向相同; (2) 当λ<0时,λa 的方向 与a方向相反.
其实质就是向量的伸长或缩短! 坐标运算: 若a = (x , y), 则λa = λ (x , y)
= (λ x , λ y)
.
一、平面向量概念
定理1:两个非零向量 a?与b?平行 (方向相同或相反 )
存在唯一实数 ?,使得 a? ? ?b?.
结论: 设 a??表示与非零向量 a? 同向的单位向量 .
