有限元第二次作业
《有限元分析》课程作业

《有限元分析》课程作业任课教师:徐亚兰学生姓名:陈新杰学号:班级:1304012时间:2016-01-05一、问题描述及分析问题:如图1所示,有一矩形平板,在右侧受到P=10KN/m 的分布力,材料常数为:弹性模量Pa E 7101⨯=;泊松比3/1=μ;板的厚度为t=;试按平面应力问题利用三角形与矩形单元分别计算各个节点位移及支座反力。
图1 平面矩形结构的有限元分析分析:使用两种方案:一、基于3节点三角形单元的有限元建模,将矩形划分为两个3节点三角形单元;二、基于4节点矩形单元的有限元建模,使用一个4节点矩形单元。
利用MATLAB 软件计算出各要求量,再将两种方案的计算结果进行比较、分析、得出结论。
二、有限元建模及分析1、基于3节点三角形单元的有限元建模及分析 (1)结构的离散化与编号如图2所示,将平面矩形结构分为两个3节点三角形单P=10KN/m1m1m元。
单元①三个节点的编号为1,2,4,单元②三个节点的编号为3,4,2,各个节点的位置坐标为(),,1,2,3,4i i x y i =,各个节点的位移(分别沿x 方向和y 方向)为(),,1,2,3,4i i u v i =。
图2 方案一:使用两个3节点三角形单元(2)各单元的刚度矩阵及刚度方程 a.单元的几何和节点描述单元①有6个节点位移自由度(DOF )。
将所有节点上的位移组成一个列阵,记作(1)q ;同样,将所有节点上的各个力也组成一个列阵,记作(1)F ,则有(1)112244,,,,,)q u v u v u v =((1)112244(,,,,,)x y x y x y F F F F F F F =同理,对于单元②,有(2)334422,,,,,)q u v u v u v =(1234X y ①②(2)334422(,,,,,)x y x y x y F F F F F F F =b.单元的位移场描述对于单元①,设位移函数012012(,)(,)u x y a a x a y v x y b b x b y ⎫=++⎪⎬=++⎪⎭(1-1)由节点条件,在,i i x x y y ==处,有(,)(,)i i i i i i u x y u v x y v =⎫⎬=⎭1,2,4i = (1-2) 将式(1-1)代入节点条件式(1-2)中,可求出式(1-1)中待定系数,即011122211223444411()22u x y a u x y a u a u a u AAu x y ==++ (1-3) 11122112234441111()221u y a u y b u b u b u AAu y ==++ (1-4) 21122112234441111()221x u a x u c u c u c u AAx u ==++ (1-5) 01122341()2b a v a v a v A =++(1-6) 11122341()2b b v b v b v A =++(1-7) 21122341()2b c v c v c v A =++(1-8)在式(1-3)~式(1-8)中1122123441111()221x y A x y a a a x y ==++ (1-9)2212442442124421244(1,2,3)1111x y a x y x y x y y b y y y x c x x x ⎫==-⎪⎪⎪⎪=-=-⎬⎪⎪⎪==-+⎪⎭ (1-10) 上式中的符号(1,2,3)表示下标轮换,如12,23,31→→→同时更换。
有限元习题及答案ppt课件

病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
(完整word版)有限元分析大作业报告要点

有限元分析大作业报告试题1:一、问题描述及数学建模图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图所示。
二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模(1)设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences 为Structural(2)选择单元类型:三节点常应变单元选择的类型是Solid Quad 4 node182;六节点三角形单元选择的类型是Solid Quad 8 node183。
因研究的问题为平面应变问题,故对Element behavior(K3)设置为plane strain。
(3)定义材料参数:弹性模量E=2.1e11,泊松比σ=0.3(4)建几何模型:生成特征点;生成坝体截面(5)网格化分:划分网格时,拾取lineAB和lineBC,设定input NDIV 为15;拾取lineAC,设定input NDIV 为20,选择网格划分方式为Tri+Mapped,最后得到600个单元。
(6)模型施加约束:约束采用的是对底面BC 全约束。
大坝所受载荷形式为Pressure ,作用在AB 面上,分析时施加在L AB 上,方向水平向右,载荷大小沿L AB 由小到大均匀分布。
以B 为坐标原点,BA 方向为纵轴y ,则沿着y 方向的受力大小可表示为:}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 (1) 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图(2)六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图①最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;②结果显示三节点和六节点单元分析出来的最大应力值相差较大,原因可能是B点产生了虚假应力,造成了最大应力值的不准确性。
有限元课后习题答案

有限元课后习题答案1.1有限元法的基本思想和基本步骤是什么首先,将表示结构的连续离散为若干个子域,单元之间通过其边界上的节点连接成组合体。
其次,用每个单元内所假设的近似函数分片地表示求解域内待求的未知厂变量。
步骤:结构的离散化,单元分析,单元集成,引入约束条件,求解线性方程组,得出节点位移。
1.2有限元法有哪些优点和缺点优点:有限元法可以模拟各种几何形状复杂的结构,得出其近似解;通过计算机程序,可以广泛地应用于各种场合;可以从其他CAD软件中导入建好的模型;数学处理比较方便,对复杂形状的结构也能适用;有限元法和优化设计方法相结合,以便发挥各自的优点。
缺点:有限元计算,尤其是复杂问题的分析计算,所耗费的计算时间、内存和磁盘空间等计算资源是相当惊人的。
对无限求解域问题没有较好的处理办法。
1.3有限元法在机械工程中有哪些具体的应用静力学分析模态分析动力学分析热应力分析其他分析2.1杆件结构划分单元的原则是什么?1)杆件的交点一定要取为节点2)阶梯形杆截面变化处一定要取为节点3)支撑点和自由端要取为节点4)集中载荷作用处要取为节点5)欲求位移的点要取为节点6)单元长度不要相差太多2.2简述单元刚度矩阵的性质。
单元刚度矩阵是描述单元节点力与节点位移之间关系的矩阵。
2.3有限元法基本方程中每一项的意义是什么?{Q}---整个结构的节点载荷列阵(包括外载荷、约束力);{}---整个结构的节点位移列阵;[K]---结构的整体刚度矩阵,又称总刚度矩阵。
2.4简述整体刚度矩阵的性质和特点。
对称性奇异性稀疏性主对角上的元素恒为正2.5位移边界条件和载荷边界条件的意义是什么由于刚度矩阵的线性相关性不能得到解,从而引入边界条件。
2.6写出平面刚架问题中单元刚度矩阵的坐标变换式2.7推导平面刚架局部坐标系下的单元刚度矩阵。
2.8简述整体坐标的概念。
单元刚度矩阵的坐标变换式把平面刚架的所有单元在局部坐标系X’O’Y’下的单元刚度矩阵变换到一个统一的坐标系xOy下,这个统一的坐标系xOy称为整体坐标系。
有限元习题及答案

有限元习题及答案一判断题(×)1. 节点的位置依赖于形态,而并不依赖于载荷的位置(√)2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元(×)3. 不能把梁单元、壳单元和实体单元混合在一起作成模型(√)4. 四边形的平面单元尽可能作成接近正方形形状的单元(×)5. 平面应变单元也好,平面应力单元也好,如果以单位厚来作模型化处理的话会得到一样的答案(×)6. 用有限元法不可以对运动的物体的结构进行静力分析(√)7. 一般应力变化大的地方单元尺寸要划的小才好(×)8. 所谓全约束只要将位移自由度约束住,而不必约束转动自由度(√)9. 同一载荷作用下的结构,所给材料的弹性模量越大则变形值越小(√)10一维变带宽存储通常比二维等带宽存储更节省存储量。
二、填空1.平面应力问题与薄板弯曲问题的弹性体几何形状都是薄板,但前者受力特点是:平行于板面且沿厚度均布载荷作用,变形发生在板面内;后者受力特点是:垂直于板面的力的作用,板将变成有弯有扭的曲面。
2.平面应力问题与平面应变问题都具有三个独立的应力分量:σx ,σy ,τxy ,三个独立的应变分量:εx ,εy ,γxy ,但对应的弹性体几何形状前者为薄板,后者为长柱体。
3.位移模式需反映刚体位移,反映常变形,满足单元边界上位移连续。
4.单元刚度矩阵的特点有:对称性,奇异性,还可按节点分块。
5.轴对称问题单元形状为:三角形或四边形截面的空间环形单元,由于轴对称的特性,任意一点变形只发生在子午面上,因此可以作为二维问题处理。
6.等参数单元指的是:描述位移和描述坐标采用相同的形函数形式。
等参数单元优点是:可以采用高阶次位移模式,能够模拟复杂几何边界,方便单元刚度矩阵和等效节点载荷的积分运算。
7.有限单元法首先求出的解是节点位移,单元应力可由它求得,其计算公式为{}{}[][]e D B σδ=。
(用符号表示即可)8.一个空间块体单元的节点有 3 个节点位移: u ,v ,w9.变形体基本变量有位移应变应力基本方程平衡方程物理方程几何方程10.实现有限元分析标准化和规范化的载体就是单元三选择题1 等参变换是指单元坐标变换和函数插值采用__B___的结点和______的插值函数。
有限元作业题资料
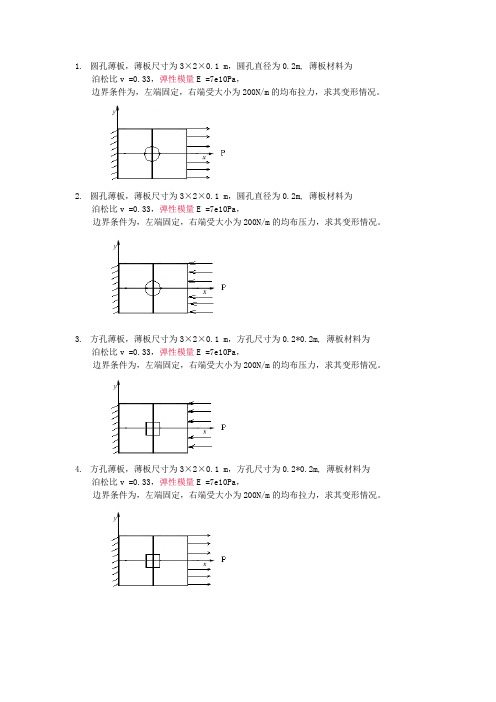
泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布拉力,求其变形情况。
2.圆孔薄板,薄板尺寸为3×2×0.1 m,圆孔直径为0.2m, 薄板材料为泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布压力,求其变形情况。
3.方孔薄板,薄板尺寸为3×2×0.1 m,方孔尺寸为0.2*0.2m, 薄板材料为泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布压力,求其变形情况。
4.方孔薄板,薄板尺寸为3×2×0.1 m,方孔尺寸为0.2*0.2m, 薄板材料为泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布拉力,求其变形情况。
泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布拉力,求其变形情况。
6.菱形孔薄板,薄板尺寸为3×2×0.1 m,菱形边长为0.2m, 薄板材料为泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布压力,求其变形情况。
7.椭圆形孔薄板,薄板尺寸为3×2×0.1 m,椭圆的短轴为0.2m,长轴为0.3m,薄板材料为泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布拉力,求其变形情况。
8.椭圆形孔薄板,薄板尺寸为3×2×0.1 m,椭圆的短轴为0.2m,长轴为0.3m,薄板材料为泊松比v =0.33,弹性模量E =7e10Pa,边界条件为,左端固定,右端受大小为200N/m的均布压力,求其变形情况。
料为泊松比v =0.33,弹性模量Ex =7e10Pa Ez=Ey=1e10Pa边界条件为,左端固定,右端受大小为200N/m的均布拉力,求其变形情况。
有限元作业试题及答案.doc

2
答:一般选用三角形或四边形单元,在满足一定精度情况,
有限元划分网格的基本原则是:
1、拓朴正确性原则。即单元间是靠单元顶点、或单元边、或单元面连接
2、几何保形原则。即网格划分后,单元的集合为原结构近似
3、特性一致原则。即材料相同,厚度相同
4、单元形状优良原则。单元边、角相差尽可能小
c j二elcm= —a
Ni = l/a2 • a x = x/a
同理可得:Nj二y/a
有限元方法及应用试题
1
答:单元离散(划分、剖分)一单元分析一整体分析
有限元分析的主要步骤主要有:
A结构的离散化
B单元分析。选择位移函数、根据几何方程建立应变与位移的关系、根据物理方程建立应力
与位移的关系、根据虚功原理建立节点力与节点位移的关系(单元刚度方程)
C等效节点载荷计算
D整体分析,建立整体刚度方程
7、图示三角形ijni为等边三角形单元,边长为1,单位面积材料密度位P,集 中力F垂直作用于nij边的中点,集度为q的均布载荷垂直作用于im边。写出三 角形单元的节点载荷向量。
q:移到m, i点F:移到m, j点重力:移到m, I, j点
要证{8}=0
只需证,Nm = 0
Nm= 1/2A (am+bmx +cmy)
(d)平面三角形单元,29个节点,38个自由度
4、什么是等参数单元?。
如果坐标变换和位移插值采用相同的节点,并且单元的形状变换函数与位移插值的形函
数一样,则称这种变换为等参变换,这样的单元称为等参单元。
5பைடு நூலகம்
v(x, y)=
答:不能取这样的位移模式,因为在平面三节点三角形单元中,位移模式应该是呈线性的。
中科大工程中的有限元作业答案(最新)

、最小势能原理法
2
1 1 12 1 2 22 1 3 32 1 1 2 2
P = 2 k d + 2 k d + 2 k d - Fq - F q
2的位移。
d1 , d 2 , d 3分别代表弹簧 (1),
( 2 ),( 3)的伸长量,q1和q2表示节点1,
= êêk21(1) k22(1) 0úú + êê0 k11(2) k12(2) úú
êë 0 0 0úû êë0 k21(2) k22(2) úû
k12(1)
0ù
ék11(1)
ê
(1)
(1)
(2)
= êk21 k22 + k11 k12(2) úú
êë 0
k21(2)
k22(2) úû
EA
é E1A1
ë
û
2
2
sinq cos
-cos q
-sinq cos
q
qù
é cos q
2
2
ê
AE sinq cosq
sin q
-sinq2cosq
-sin q úú
2
K=
ê
L ê -cos q
cos q
sinq cos
-sinq cos
q
qú
2
2
ê-sin cos
sinq cosq
cos q úû
ë q q -sin q
3
Þ RB = ql
8
3
R Bl
ql
, y BR =
= 3EI
8EI
4
3
ql
(完整版)有限元第二章课后题答案

2 弹性力学问题的有限单元法思考题2.1 有限元法离散结构时为什么要在应力变化复杂的地方采用较密网格,而在其他地方采用较稀疏网格?答:在应力变化复杂的地方每一结点与相邻结点的应力都变化较大,若网格划分较稀疏,则在应力突变处没有设置结点,而使得所求解的误差很大,若网格划分较密时,则应力变化复杂的地方可以设置更多的结点,从而使得所求解的精度更高一些。
2.2 因为应力边界条件就是边界上的平衡方程,所以引用虚功原理必然满足应力边界条件,对吗?答:对。
2.3 为什么有限元只能求解位移边值问题和混合边值问题?弹性力学中受内压和外压作用的圆环能用有限元方法求解吗?为什么?答:有限元法是一种位移解法,故只能求解位移边值问题和混合边值问题。
而应力边值问题没有确定的位移约束,不能用位移法求解,所以也不能用有限元法求解。
2.4 矩形单元旋转一个角度后还能够保持在单元边界上的位移协调吗?答:能。
矩形单元的插值函数满足单元内部和单元边界上的连续性要求,是一个协调元。
矩形的插值函数只与坐标差有关,旋转一个角度后各个结点的坐标差保持不变,所以插值函数保持不变。
因此矩形单元旋转一个角度后还能够保持在单元边界上的位移协调。
2.5 总体刚度矩阵呈带状分布,与哪些因素有关?如何计算半带宽? 答:因素:总体刚度矩阵呈带状分布与单元内最大结点号与最小结点号的差有关。
计算:设半带宽为B ,每个结点的自由度为n ,各单元中结点整体码的最大差值为D ,则B=n(D+1),在平面问题中n=2。
2.6 为什么单元尺寸不要相差太大,如果这样,会导致什么结果? 答:由于实际工程是一个二维或三维的连续体,将其分为具有简单而规则的几何单元,这样便于网格计算,还可以通过增加结点数提高单元精度。
在几何形状上等于或近似与原来形状,减小由于形状差异过大带来的误差。
若形状相差过大,使结构应力分析困难加大,误差同时也加大。
2.7 剖分网格时,在边界出现突变和有集中力作用的地方要设置结点或单元边界,试说明理由。
有限元试题及答案[1]
![有限元试题及答案[1]](https://img.taocdn.com/s3/m/124aad996bec0975f465e211.png)
一、如图所示的1D 杆结构,试用取微单元体的方法建立起全部基本方程和边界条件,并求出它的所有解答。
注意它的弹性模量为E 、横截面积A解:如图1.1所示的1D 杆结构,其基本变量为 位移 x u 应变 x ε 应力 x σ取微单元体Adx ,其应力状态如图1.2,由泰勒展开式知()⋅⋅⋅⋅⋅+∂∂+⋅∂∂+=+22221dx x dx x dx x x x x σσσσ略去2阶以上的商阶微量知()dx xdx x xx ⋅∂∂+=+σσσ 由力的平衡知0=∑i x :0=-⎪⎭⎫ ⎝⎛∂∂+A A dx x x x x σσσ即力的平衡方程为:⋅⋅⋅⋅=0dxd xσ① 位移由图1.3知(泰勒展开,略去商阶微量)()dx xu u dx x u xx ⋅∂∂+=+ dxu dxdxdx u dx x uu ABABB A xx x x x ∂=-+-∂∂+=-=∴)(''ε应变 即几何方程为:⋅⋅⋅⋅=dxdu xx ε② 根据虎克定律知⋅⋅⋅⋅⋅⋅⋅=⋅=dxdu E E xx x εσ③ 由①、②、③知该1D 杆的基本方程为⎪⎪⎪⎩⎪⎪⎪⎨⎧====dx du E E dx du dx d x x xx xxεσεσ0 在节点1时位移:00==x x u 在节点2时应力:APlx x==σ即其边界条件为00==x x u on u SAPlx x==σ on P S 由①式知⋅⋅⋅⋅⋅=0c x σ ④ ④代入③解得:dxdu Ec x=0 ⋅⋅⋅⋅⋅⋅⋅+=10c x Ec u x ⑤ 0c 、1c 为待定系数结合边界条件知⎪⎪⎩⎪⎪⎨⎧==+A P c c x Ec 010解知得APc =0,01=c ∴⎪⎪⎪⎩⎪⎪⎪⎨⎧==⋅==EA P E x EA P u A P x xx x σεσ二、设平面问题中的应力问题y a x a a x 321++=σy a x a a y 654++=σ y a x a a xy 987++=τ其中i a (1、2、………9)为常数,令所有体积力为零,对下面特殊情况说明平衡是否满足?为什么?或者i a 之间有什么关系才满足平衡。
有限元试卷(2)答案

动、静态有限元试卷(二)答案一、解:节点坐标:三角形面积: ⊿=2则:二、解:节点坐标几何矩阵02102======j m j j i i y x y x y x 400======jji i m ii m m j mm j j i y x y x a y x y x a y x y x a 211011211-======i j m mij j m i y y b y y b y y b 111211111-====-==jim im j mj i x x c x x c x x c ()()()4212/22/422/yx y c x b a N yy c x b a N y x y c x b a N m m m m j j j j i i i i --=∆++==∆++=-=∆++=[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=⎥⎦⎤⎢⎣⎡=42102420042102042000000y x y y x y x y y x N N N N N N N m j im j i 001001======j m j j i i y x y x y x 111111011==-====i j m m ij j m i y y b y y b y y b 011111111==-====ji m im j mj i x x c x x c x x c []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆=10110100101001010000000021m mjjii m j i m j ib c b c b c c c c b b b B弹性矩阵应力转换矩阵单元刚度矩阵[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10002000222100010112E E D μμμμ[][][]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----==1011010020200202002E B D S [][][]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------------=∆=1011010202001031211213010020201011014Et t S B k T e 三、解:将②、③单元采用类似单元①的局部编号,右图所示。
有限元第二次作业~付章

有限元第二次作业学院:建筑工程学院专业:结构工程姓名:付章学号:2011210038基于SAP2000的简支深梁应力分析A Simply-supported Deepbeam Stress Analysis Using SAP2000SAP2000是一款功能强大的结构通用有限元分析软件,对跨/高比小于5的深梁的应力具有很强的分析功能,本例中通过对深梁划分正方体网格,模拟六大应力分量在实体内的分布,分析其与一般梁应力分布的不同。
关键词:有限元,网格,深梁,应力分布SAP2000 is a powerful structure general finite element analysis software. Towards a deepbeam whose l/h ratio is less than 5,it has strong analytical function.In this example, through dividing the deepbeam into many cube grids, we simulate the distribution of the six stress components in the entity,and analyze the difference with general beam's.Key words:finite element analysis,grids,deepbeam,stress distribution一、概述深梁的梁高方向应力的分布不能像普通梁一样忽略,而弹性力学方法给出的解析解非常复杂,复杂的结构甚至无法得到解。
有限元方法作为一种应用广泛的近似解方法,已比较准确模拟深梁中的应力分布。
本例中 跨度l=4m ,h=1.2m ,b=0.4m ,支座简支,混凝土等级为C35,上表面均布恒载20KN/m 2,将0.4m ×0.4m ×0.4m 的正方体分割为8个网格进行分析。
中南大学有限元习题与答案(Word最新版)

中南大学有限元习题与答案通过整理的中南大学有限元习题与答案相关文档,希望对大家有所帮助,谢谢观看!中南大学有限元习题与答案习题 2.1 解释如下的概念:应力、应变,几何方程、物理方程、虚位移原理。
解应力是某截面上的应力在该处的集度。
应变是指单元体在某一个方向上有一个ΔU的伸长量,其相对变化量就是应变。
表示在x轴的方向上的正应变,其包括正应变和剪应变。
几何方程是表示弹性体内节点的应变分量与位移分量之间的关系,其完整表示如下:物理方程:表示应力和应变关系的方程某一点应力分量与应变分量之间的关系如下:虚位移原理:在弹性有一虚位移情况下,由于作用在每个质点上的力系,在相应的虚位移上虚功总和为零,即为:若弹性体在已知的面力和体力的作用下处于平衡状态,那么使弹性体产生虚位移,所有作用在弹性体上的体力在虚位移上所做的工就等于弹性体所具有的虚位能。
2.2说明弹性体力学中的几个基本假设。
连续性假设:就是假定整个物体的体积都被组成该物体的介质所填满,不存在任何间隙。
完全弹性假设:就是假定物体服从虎克定律。
各向同性假设:就是假定整个物体是由同意材料组成的。
小变形和小位移假设:就是指物体各点的位移都远远小于物体原来的尺寸,并且其应变和转角都小于1。
2.3简述线应变与剪应变的几何含义。
线应变:应变和刚体转动与位移导数的关系,剪应变表示单元体棱边之间夹角的变化。
2.4 推到平面应变平衡微分方程。
解:对于单元体而言其平衡方程:在平面中有代入上式的2.5 如题图2.1所示,被三个表面隔离出来平面应力状态中的一点,求和的值。
解:x方向上:联立二式得:2.6相对于xyz坐标系,一点的应力如下某表面的外法线方向余弦值为,,求该表面的法相和切向应力。
解:该平面的正应力全应力该平面的切应力2.7一点的应力如下MP 求主应力和每一个主应力方向的方向余弦;球该店的最大剪应力。
解:设主平面方向余弦为,由题知将代入得即,。
最大剪应力(1)当时代入式(2.21)(2)当时代入式(2.21)且2.8已知一点P的位移场为,求该点p(1,0,2)的应变分量。
中科大有限元作业答案(第一次到第五次)

有限元作业一1、对图示杆结构,已知节点 3 的位移 10mm,试用有限元法求出各节点的节点力和节点 2 的位移。
已知两段杆的长度为 l1, l2 截面积为 A 1, A 2 ,弹性模量为 E 1, E2 。
2.求解如图所示桁架节点 1 处的水平位移和垂直位移分量以及每一杆单元的应力。
已知所有 单元 A 5106m2 , E 200GPa, L 1m。
有限元作业一1、对图示杆结构,已知节点 3 的位移 10mm,试用有限元法求出各节点的节点力和节点 2 的位移。
已知两段杆的长度为 l1, l2 截面积为 A 1, A 2 ,弹性模量为 E 1, E2 。
解:将整个杆件可以划分 3 个节点,2 个单元。
如图所示:设图中力为 F,则 1 节点所受反 作用力为-F。
对单元①,单元刚度矩阵为:ke(1) 同理,单元②的单元刚度矩阵为:1 1 AE 1 1 L1 1 1 ke(2) 将单元刚度矩阵集成,有整体刚度矩阵为:A2E2 1 1 L2 1 1 k ke(1) [k]e(2)(1) (1) k11 k12 0 0 0 0 (1) (1) (2) (2) k21 k22 0 0 k11 k12 (2) (2) 0 k21 k22 0 0 0 (1) (1) k11 k12 0 (1) (1) (2) (2) k21 k22 k11 k12 (2) (2) 0 k k 21 22 E1A EA 1 1 1 0 L L1 1 E1A EA E A EA 1 1 1 2 2 2 2 L1 L2 L2 L1 EA E2 A2 2 2 0 L2 L2 F 1x F 整体节点载荷矩阵为 R F 2x 0 , F F 3x 1x 0 整体节点位移矩阵为: 2x 2x 。
有限元作业

ci y)
cm x j (i , j , m )
A 2 A jx my mx yj 得
Ni
1 2A
[
x
j
ym
xm y j
(yj
ym )
xj
3
xm
(xm
xj)
yj
3
ym
]
1 3
Nj
1 (0 2A
yj
ym ) 3
1 3
Nj
1 (0 2A
2
x2 l
2
lx
uu12
N1
N2
uu12
B N1'
N
' 2
4x l2
l
4x l l2
E
x
E
B
uu12
,即
D
E
对于矩形截面梁单元,积分: dydz A 为单元横截面面积。
BT
EAB dx
EA
l 0
2x l2
2x
2x l2
l2
2x l2
dx
4EA
3l
4EA 3l
4EA
3l
4EA 3l
(b)、 u(x) 1x 2x2 ,由边界条件确定常数1 、2 :
}
《结构分析中的有限元法》2015-有限元习题-参考答案

,
lk
(
1) 4
16x2
64 3
x
16 3
,
34 3
lk
(1)
2x2
7 6
x
1 6
根据拉格朗日插值多项式:
pn (x)
n
lk (x) f (xk )或pn (x)
k 0
nn
(
k0 j0
x xj )f xk x j
(xk ) 。
jk
将
n
2
带入:
p2
(x)
-38x2
349 6
x
35 3
2015 年 3 月 24 日作业
2、简述结构离散(或有限元建模)的内容和要求。 有限元建模的内容: 1)网格划分---即把结构按一定规则分割成有限单元 2)边界处理---即把作用于结构边界上约束和载荷处理为结点约束和结点载
荷 有限元建模的要求: 1)离散结构必须与原始结构保形---单元的几何特性 2)一个单元内的物理特性必须相同---单元的物理特性
4、说明用有限单元法解题的主要步骤。 答:研究问题的力学建模;结构离散;单元分析;整体分析与求解;结果分析及 后处理。
5、推导基于变分原理的总势能泛函极值条件。 解:有积分形式确立的标量泛函有
Π
F
u,
u x
,
dΩ
E
u,
u x
,
d
其中 u 是未知函数, F 和 E 是特定的算子, 是求解域, 是 的边界。 Π 称 为未知函数 u 的泛函,随函数 u 的变化而变化。连续介质问题的解 u 使泛函 Π 对 于微小的变化u 取驻值,即泛函的“变分”等于零 Π 0 ,此为变分法。
来待求场函数的无穷自由度问题转换为求解场函数结点值的有限自由度问题。 (3)有限元法是通过和原问题数学模型(基本方程、边界条件)等效的变分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-2 图示悬臂板, 属于平面应力问题, 其网格图及单元、 节点编号见图 2-1,E=2.1×1011 , u=0.28,演算其单刚阵到总刚阵的组集过程,并用MATLAB 软件计算总刚阵。
图 2-1答:根据图 2-1 所示列出单元节点列表:节点jk单元i1 3 5 42 2 5 33 2 6 54162(1)计算单元刚度阵0 0 0 0 0 0 1 1 1 0 0k3, 3k3,4k3 ,5111单元 1 的刚度矩阵 : k 1k 4,13k 4,14k 41,5, k 10 0 k 3 ,3 k 3, 4k 3,5 0 ;k 5,13 k 51,4k 51,5 0 0 k 41,3 k 41 ,4 k 4,510 0 k 51,3k 51, 4k 51, 40 0 00 0 00 k 22,2 k 22,3 k 22,5 0 k 22, 2 k 22, 3 0 k 22, 5 00 k 3,2 2k 3,20 k 3,2 5 0单元 2 的刚度矩阵: k2k 32, 2k 32,3 k 32,5 , k 2 3;0 0 0 0 0 0k 5,2k 52,3k 5,5220 k 52, 2 k 52, 30 k 52, 40 00 0 0 0 0 0 k 23,2 k 23,5 k 23,6 0 k 23, 2 0 0 k 23.5 k 23,60 0 0 0 0 0 单元 3 的刚度矩阵: k3k 53,2k 53,5k 53,6 , k30 0 0 ;k 63,2 k 63,5 k 63,60 k 53, 2 0 0 k 53,5 k 53,60 k 63, 20 0 k 63,5k 63,6k14,1k14,2000k14,6k14,1k14,2k14,6k24.1k24, 2000k24,6000000单元 4 的刚度矩阵:k4k24,1k24,2k24,6,k4;k64,1k64,2k64,6000000000000k64,10000k64, 64k 1k 2k 3k 4总刚度矩阵:K k ee 1k14,1k14,2000k14, 6k24,1k22,2 k23, 2 k24,2k22,30k22,5k23,5k23,6k24,60k32,2k31,3k32,3k31, 4k3,51k32,50K0k41,3k41,4k4,1500k52, 2k53,2k51,3k52,3k51,4k51,5 k52,5 k53,5k53,6k64,1k63, 2k64,200k63,5k63,6k64,6Matlab程序语言的编写:function Idexglobal gNode gElement gMaterialgNode=[0.0 0.010.5 0.011.0 0.011.0 0.00.5 0.00.0 0.0]%gNode 同样是一个矩阵,每一行表示一个结点,第点的 y 坐标1 列是结点的x 坐标,第2 列是结gElement=[3 4 52 3 52 5 6126];%gElement 是一个矩阵,每一行表示一个单元,第单元的第 2 个结点号。
1 行是单元的第 1 个结点号,第2 行是Returnfunction k=StiffnessMatrix(ie)%计算单元刚度矩阵函数global gNode gElementk=zeros(6,6);%6x6 单元刚阵E=2.1*10^11; u=0.28 ;%材料特性%材料特性t=0.01;%材料特性xi=gNode(gElement(ie,1),1); yi=gNode(gElement(ie,1),2); xj=gNode(gElement(ie,2),1); yj=gNode(gElement(ie,2),2); xm=gNode(gElement(ie,3),1);ym=gNode(gElement(ie,3),2);分量ai=xj*ym-xm*yj;aj=xm*yi-xi*ym;am=xi*yj-xj*yi;bi=yj-ym;bj=ym-yi;bm=yi-yj;ci=-(xj-xm);cj=-(xm-xi);cm=-(xi-xj);d=[1,xi,yi;1,xj,yj;1,xm,ym];area=det(d);B=[bi 0 bj 0 bm 0 ;0 ci 0 cj 0 cm;ci bi cj bj cm bm];B=B/2/area;D=[1 u 0;u 1 0;0 0 (1-u)/2];D=D*E/(1-u^2);k=transpose(B)*D*B*t*abs(area);阵Returnfunction gK=AssembleStiffnessMatrix%计算总刚阵global gElement gK iegK=zeros(12,12);for ie =1:1:4k=StiffnessMatrix(ie);for i=1:1:3for j=1:1:3for p=1:1:2for q=1:1:2m=(i-1)*2+p;%每个节点有(i-1)*2+pn=(j-1)*2+q;%每个节点有(i-1)*2+pM=(gElement(ie,i)-1)*2+p;N=(gElement(ie,j)-1)*2+q;gK(M,N)=gK(M,N)+k(m,n);end%计算节点坐标%计算单元面积%计算单元刚度矩%单元循环%节点循环%节点循环%自由度循环%自由度循环2 个自由度, i 节点的第p 个自由度为2 个自由度, i 节点的第p 个自由度为endendendendReturn则单元 1 的刚度矩阵为>>StiffnessMatrix(1)ans =1.0e+010 *2.05080-2.05080.04100-0.04100 5.69660.0319-5.6966-0.03190-2.05080.0319 2.0531-0.0729-0.00230.04100.0410-5.6966-0.0729 5.69740.0319-0.00080-0.0319-0.00230.03190.00230 -0.041000.0410-0.000800.0008单元 2 的刚度矩阵>>StiffnessMatrix(2)ans =1.0e+010 *2.0531-0.0729-2.05080.0319-0.00230.0410-0.0729 5.69740.0410-5.69660.0319-0.0008 -2.05080.0410 2.050800-0.04100.0319-5.69660 5.6966-0.03190-0.00230.03190-0.03190.002300.0410-0.0008-0.0410000.0008单元 3 的刚度矩阵为>>StiffnessMatrix(3)ans =1.0e+010 *0.00230-0.00230.03190-0.031900.00080.0410-0.0008-0.04100-0.00230.0410 2.0531-0.0729-2.05080.03190.0319-0.0008-0.0729 5.69740.0410-5.69660-0.0410-2.05080.0410 2.05080 -0.031900.0319-5.69660 5.6966单元 4 的刚度矩阵>>StiffnessMatrix(4)ans =1.0e+010 *2.0531-0.0729-2.05080.0319-0.00230.0410-0.0729 5.69740.0410-5.69660.0319-0.0008-2.05080.0410 2.050800-0.04100.0319-5.69660 5.6966-0.03190-0.00230.03190-0.03190.002300.0410-0.0008-0.0410000.0008总刚度矩阵为ans =1.0e+011 *Columns 1 through 80.2053-0.0073-0.00020.0041000 0-0.00730.56970.0032-0.0001000 0-0.00020.00320.4106-0.0073-0.00020.004100.0041-0.0001-0.0073 1.13950.0032-0.0001000-0.00020.00320.20530-0.2051 0.0041000.0041-0.000100.56970.0032 -0.56970000-0.20510.00320.2053 -0.007300000.0041-0.5697-0.0073 0.569700-0.41020.00730-0.0073-0.0002 0.0032000.0073-1.1393-0.007300.0041 -0.0001-0.20510.00410-0.0073000 00.0032-0.5697-0.00730000 0Columns 9 through 1200-0.20510.0032000.0041-0.5697-0.41020.00730-0.00730.0073-1.1393-0.007300-0.007300-0.0073000-0.00020.0041000.0032-0.0001000.4106-0.0073-0.00020.0041-0.0073 1.13950.0032-0.0001-0.00020.00320.205300.0041-0.000100.56972-3 在平面问题有限元分析中,(1)用到了哪些弹性力学中的基本方程?答:平衡微分方程、几何方程、相容方程(形变协调方程)。
(2)力的平衡条件是如何满足的?答:根据能量守恒原理,有外力所作虚功应该等于内力虚功。
也就是结构在外载荷作用下处于平衡状态则在结构上的力在任意虚功位移上所作的虚功之和等于零。
以下是用到的方程:x xy xz X 0xu, xy u vx y z x y x yx y yzY0 x y zzx zy z Z0 x y z yzv,yw,zyzzxv wz yw ux z( 3)变形协调条件是如何满足的?答:对材料进行线弹性和各向同性的假设,用弹性力学中应力-应变之间的关系得到变形协调条件。
下面是形变协调方程。
2222xyxyzxxyyz2xy 2x 2,yzxy z x y x2222yzyzxyyzzx2yz 2y 2,zxyz xy z y222yzxy2zyzx ,zx2zx 2x z x 2 z x z yx y2-4 在平面三角形单元中的位移、应变、应力具有什么特征? 位移特征: (1)必须包含单元的刚体位移;(2)必须包含单元的常应变状态; (3)必须保证不偏惠各坐标轴; (4)必须保证单元内位移连续。
