东北师范大学 【精品】2016-2017学年第2 学期 高等数学A期末考试试卷
吉林省东北师大附中2017-2018学年高一下学期期末数学试卷 Word版含解析

吉林省东北师大附中2017-2018学年高一下学期期末数学试卷一、选择题:(每小题4分,共48分)1.设a,b是非零实数,若a<b,则下列不等式成立的是()A.a2<b2B.a b2<a2b C.D.2.在等比数列{a n}中,已知a1a3a11=8,那么a2a8等于()A.4B.6C.12 D.163.直线l1:mx+(1﹣m)y=3;l2:(m﹣1)x+(2m+3)y=2互相垂直,则m的值为()A.﹣3 B.1C.0或D.1或﹣34.不等式<0的解集为()A.{x|x<﹣2或0<x<3} B.{x|﹣2<x<0或x>3} C.{x|x<﹣2或x>0} D.{x|x<0或x>3}5.点M(x0,y0)在圆x2+y2=R2外,则直线与圆的位置关系是()A.相切B.相交C.相离D.不确定6.在数列{a n}中,a1=2,a n+1=a n+ln(1+),则a n=()A.2+lnn B.2+(n﹣1)lnn C.2+nlnn D.1+n+lnn7.当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是()A.(﹣∞,﹣1]∪[1,+∞)B.[﹣1,1]C.(﹣∞,﹣1)∪(1,+∞)D.(﹣1,1)8.已知等差数列前n项和为S n.且S13<0,S12>0,则此数列中绝对值最小的项为()A.第5项B.第6项C.第7项D.第8项9.若直线y=kx+1与圆x2+y2=1相交与P,Q两点,且此圆被分成的两段弧长之比为1:2,则k的值为()A.或B.C.或D.10.下列函数中,y的最小值为4的是()A.B.C.D.y=e x+4e﹣x11.过直线x+y=0上一点P作圆(x+1)2+(y﹣5)2=2的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=﹣x对称时,∠APB=()A.30°B.45°C.60°D.90°12.若a,b,c>0且a2+2ab+2ac+4bc=12,则a+b+c的最小值是()A.B.3C.2D.二、填空题:(每小题4分,共16分)13.不等式组表示的平面区域的面积等于.14.点(x,y)在直线x+3y﹣2=0上移动时,z=2x+8y的最小值为.15.等比数列{a n}的前n项和是S n,若S30=13S10,S10+S30=140,则S20的值是.16.直线y=x+b与曲线恰有一个公共点,则b的取值范围是.三、解答题:(共56分)17.已知等差数列{a n}中a2=9,a5=21.(1)求数列{a n}的通项公式;(2)若,求数列{log2b n}的前n项和S n.18.如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?19.已知关于x的一元二次不等式(a+1)x2+ax+a>b(x2+x+1)对任意实数x都成立,试比较实数a,b的大小.20.已知平面区域恰好被面积最小的圆C:(x﹣a)2+(y﹣b)2=r2及其内部所覆盖.(1)试求圆C的方程.(2)若斜率为1的直线l与圆C交于不同两点A,B满足CA⊥CB,求直线l的方程.21.如图,直角三角形ABC的顶点坐标A(﹣2,0)、B(0,),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究是否是定值?若是,求出定值;若不是,请说明理由.四.附加题22.以数列{a n}的任意相邻两项为坐标的点P n(a n,a n+1)(n∈N*)都在一次函数y=2x+k的图象上,数列{b n}满足.(1)求证:数列{b n}是等比数列;(2)设数列{a n},{b n}的前n项和分别为S n,T n,且S6=T4,S5=﹣9,求k的值.吉林省东北师大附中2017-2018学年高一下学期期末数学试卷一、选择题:(每小题4分,共48分)1.设a,b是非零实数,若a<b,则下列不等式成立的是()A.a2<b2B.a b2<a2b C.D.考点:一元二次不等式的应用;不等关系与不等式.专题:综合题.分析:由不等式的相关性质,对四个选项逐一判断,由于a,b为非零实数,故可利用特例进行讨论得出正确选项解答:解:A选项不正确,因为a=﹣2,b=1时,不等式就不成立;B选项不正确,因为a=1,b=2时,不等式就不成立;C选项正确,因为⇔a<b,故当a<b时一定有;D选项不正确,因为a=1,b=2时,不等式就不成立;选项正确,因为y=2x是一个增函数,故当a>b时一定有2a>2b,故选C.点评:本题考查不等关系与不等式,解题的关键是熟练掌握不等式的有关性质,且能根据这些性质灵活选用方法进行判断,如本题采用特值法排除三个选项,用单调性判断正确选项.2.在等比数列{a n}中,已知a1a3a11=8,那么a2a8等于()A.4B.6C.12 D.16考点:等比数列的性质.专题:计算题.分析:根据等比数列的通项公式化简a1a3a11=8后,得到关于第5项的方程,求出方程的解即可得到第5项的值,然后根据等比数列的性质得到a2a8等于第5项的平方,把第5项的值代入即可求出所求式子的值.解答:解:a1•a3•a11=a13•q12=(a1q4)3=a53=8,∴a5=2,则a2•a8=a52=4.故选:A点评:此题考查学生灵活运用等比数列的通项公式化简求值,掌握等比数列的性质,是一道综合题.3.直线l1:mx+(1﹣m)y=3;l2:(m﹣1)x+(2m+3)y=2互相垂直,则m的值为()A.﹣3 B.1C.0或D.1或﹣3考点:直线的一般式方程与直线的垂直关系.专题:计算题;直线与圆.分析:根据两条直线垂直的条件,结合题意建立关于m的方程,解之即可得到实数m的值.解答:解:∵直线l1:mx+(1﹣m)y=3;l2:(m﹣1)x+(2m+3)y=2互相垂直,∴m(m﹣1)+(1﹣m)(2m+3)=0,解之得m=﹣3或1故选:D点评:本题给出两条直线互相垂直,求实数m的值.着重考查了直线的方程和直线的位置关系等知识,属于基础题.4.不等式<0的解集为()A.{x|x<﹣2或0<x<3} B.{x|﹣2<x<0或x>3} C.{x|x<﹣2或x>0} D.{x|x<0或x>3}考点:其他不等式的解法.专题:计算题;转化思想.分析:将“不等式<0”转化为:“x(x+2)(x+3)<0”,用穿根法求解.解答:解:依题意:原不等式转化为:x(x+2)(x+3)<0解得:x<﹣2或0<x<3故选A点评:本题主要考查分式不等式的解法,一般是转化为整式不等式,再用穿根法求解.5.点M(x0,y0)在圆x2+y2=R2外,则直线与圆的位置关系是()A.相切B.相交C.相离D.不确定考点:点与圆的位置关系.专题:直线与圆.分析:由已知得x02+y02>R2,从而圆心(0,0)到直线x0x+y0y=R2的距离d<R,由此推导出直线x0x+y0y=R2与圆相交.解答:解:∵点M(x0,y0)在圆x2+y2=R2外,∴x02+y02>R2,∴圆心(0,0)到直线x0x+y0y=R2的距离:d=<R,∴直线x0x+y0y=R2与圆相交.故选:B.点评:本题考查直线与圆的位置关系的判断,是基础题,解题时要认真审题.6.在数列{a n}中,a1=2,a n+1=a n+ln(1+),则a n=()A.2+lnn B.2+(n﹣1)lnn C.2+nlnn D.1+n+lnn考点:数列的概念及简单表示法.专题:点列、递归数列与数学归纳法.分析:把递推式整理,先整理对数的真数,通分变成,用迭代法整理出结果,约分后选出正确选项.解答:解:∵,,…∴=故选:A.点评:数列的通项a n或前n项和S n中的n通常是对任意n∈N成立,因此可将其中的n换成n+1或n﹣1等,这种办法通常称迭代或递推.解答本题需了解数列的递推公式,明确递推公式与通项公式的异同;会根据数列的递推公式写出数列的前几项.7.当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是()A.(﹣∞,﹣1]∪[1,+∞)B.[﹣1,1]C.(﹣∞,﹣1)∪(1,+∞)D.(﹣1,1)考点:简单线性规划的应用.专题:计算题.分析:先根据约束条件的可行域,再利用几何意义求最值,z=kx+y表示直线在y轴上的截距,﹣k表示直线的斜率,只需求出k的取值范围时,直线z=kx+y在y轴上的截距取得最大值的一个最优解为(1,2)即可.解答:解:由可行域可知,直线AC的斜率=,直线BC的斜率=,当直线z=kx+y的斜率介于AC与BC之间时,C(1,2)是该目标函数z=kx+y的最优解,所以k∈[﹣1,1],故选B.点评:本题主要考查了简单的线性规划,以及利用几何意义求最值的方法反求参数的范围,属于基础题.8.已知等差数列前n项和为S n.且S13<0,S12>0,则此数列中绝对值最小的项为()A.第5项B.第6项C.第7项D.第8项考点:等差数列的前n项和;数列的应用.专题:等差数列与等比数列.分析:由等差数列的性质可得a6+a7>0,a7<0,进而得出|a6|﹣|a7|=a6+a7>0,可得答案.解答:解:∵S13===13a7<0,S12===6(a6+a7)>0∴a6+a7>0,a7<0,∴|a6|﹣|a7|=a6+a7>0,∴|a6|>|a7|∴数列{a n}中绝对值最小的项是a7故选C.点评:本题考查等差数列的前n项和以及等差数列的性质,解题的关键是求出a6+a7>0,a7<0,属中档题.9.若直线y=kx+1与圆x2+y2=1相交与P,Q两点,且此圆被分成的两段弧长之比为1:2,则k的值为()A.或B.C.或D.考点:直线与圆相交的性质.专题:综合题;直线与圆.分析:根据直线y=kx+1与圆x2+y2=1相交于P、Q两点,且∠POQ=120°(其中O为原点),求出圆心到直线的距离;再根据点到直线的距离公式即可求出k的值.解答:解:因为直线y=kx+1与圆x2+y2=1相交于P、Q两点,且此圆被分成的两段弧长之比为1:2,所以∠POQ=120°(其中O为原点),如图可得∠OPE=30°;OE=OPsin30°=,即圆心O(0,0)到直线y=kx+1的距离d==,所以k=.故选:A.点评:本题考查直线和圆的位置关系,点到直线的距离公式,考查计算能力,求出圆心(0,0)到直线的距离是解题的关键.10.下列函数中,y的最小值为4的是()A.B.C.D.y=e x+4e﹣x考点:基本不等式.专题:不等式的解法及应用.分析:由基本不等式求最值的规则,逐个选项验证可得.解答:解:选项A错误,因为x可能为负数;选项B错误,化简可得y=2(+)由基本不等式可得取等号的条件为=即x2=﹣1,显然没有实数满足x2=﹣1;选项C错误,由基本不等式可得取等号的条件为sinx=2,但由三角函数的值域可知sinx≤1;选项D,由基本不等式可得当e x=2即x=ln2时,y取最小值4.故选:D.点评:本题考查基本不等式求最值,涉及基本不等式取等号的条件,属基础题.11.过直线x+y=0上一点P作圆(x+1)2+(y﹣5)2=2的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=﹣x对称时,∠APB=()A.30°B.45°C.60°D.90°考点:圆的切线方程.专题:直线与圆.分析:判断圆心与直线的关系,在直线上求出特殊点,利用切线长、半径以及该点与圆心连线构成直角三角形,求出∠APB的值.解答:解:显然圆心C(﹣1,5)不在直线y=﹣x上.由对称性可知,只有直线y=﹣x上的特殊点,这个点与圆心连线垂直于直线y=﹣x,从这点做切线才能关于直线y=﹣x对称.所以该点与圆心连线所在的直线方程为:y﹣5=x+1即y=6+x,与y=﹣x联立,可求出该点坐标为(﹣3,3),所以该点到圆心的距离为=2,由切线长、半径以及该点与圆心连线构成直角三角形,又知圆的半径为.所以两切线夹角的一半的正弦值为=,所以夹角∠APB=60°故选C.点评:本题是中档题,考查直线与圆的位置关系,直线与圆相切的关系的应用,考查计算能力,常考题型.12.若a,b,c>0且a2+2ab+2ac+4bc=12,则a+b+c的最小值是()A.B.3C.2D.考点:基本不等式在最值问题中的应用.专题:压轴题.分析:因为a+b+c的平方与已知等式有关,现将(a+b+c)2用已知等式表示,根据一个数的平方大于等于0得不等式,然后解不等式得范围.解答:解:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=(a2+2ab+2ac+4bc)+b2+c2﹣2bc=12+(b ﹣c)2≥12,当且仅当b=c时取等号,∴a+b+c≥故选项为A点评:若要求的代数式能用已知条件表示,得不等式,通过解不等式求代数式的范围.二、填空题:(每小题4分,共16分)13.不等式组表示的平面区域的面积等于25.考点:二元一次不等式(组)与平面区域.专题:计算题.分析:画出约束条件表示的可行域,求出交点坐标,然后求出三角形面积,即可求解解答:解:作出不等式组所表示的平面区域,如图所示的三角形ABC由由题意可得A(﹣2,2),B(3,7),C(3,﹣3)∴BC=10,A到直线BC的距离d=5∴S△ABC==25故答案为:25点评:本题考查二元一次不等式(组)与平面区域,考查学生作图能力,计算能力,是基础题.14.点(x,y)在直线x+3y﹣2=0上移动时,z=2x+8y的最小值为4.考点:基本不等式.专题:不等式.分析:根据基本不等式的性质进行计算即可.解答:解:∵x+3y﹣2=0,∴x+3y=2,∴z=2x+23y≥2=2=2=4,当且仅当x=3y,即x=1,y=时,“=”成立,故答案为:4.点评:本题考查了基本不等式的性质,应用性质是注意满足条件;一正二定三相等,本题是一道基础题.15.等比数列{a n}的前n项和是S n,若S30=13S10,S10+S30=140,则S20的值是40.考点:等比数列的性质.专题:计算题.分析:首先根据题意求出S10=10,S30=130,再根据S n,S2n﹣S n,S3n﹣S2n也是等比数列,得到S20=40,或者S20=﹣30,然后利用等比数列的求和公式得到答案.解答:解:因为S30=13S10,S10+S30=140,所以S10=10,S30=130.∵数列{a n}为等比数列,∴S n,S2n﹣S n,S3n﹣S2n也是等比数列,即S10,S20﹣S10,S30﹣S20也是等比数列,所以S20=40,或者S20=﹣30,因为S20=S10(1+q10),所以S20=40.故答案为40.点评:本题主要考查了等比数列的性质和数列的求和.解题的关键是利用了等比数列中S n,S2n﹣S n,S3n﹣S2n也是等比数列的性质.16.直线y=x+b与曲线恰有一个公共点,则b的取值范围是﹣3<b≤3或.考点:函数的零点.专题:计算题.分析:先整理C的方程可知曲线C的图象为半圆,要满足仅有一个公共点,有两种情况,一种是与半圆相切,根据原点到直线的距离为半径3求得b,一种是与半圆相交但只有一个交点,根据图象可分别求得b的上限和下限,最后综合可求得b的范围.解答:解:依题意可知曲线C的方程可整理成y2+x2=9(x≥0)要使直线l与曲线c仅有一个公共点,有两种情况:如下图:(1)直线与半圆相切,原点到直线的距离为3,切于A点,d==3,因为b<0,可得b=﹣3,满足题意;(2)直线过半圆的下顶点(0,﹣3)和过半圆的上顶点(3,0)之间的直线都满足,y=x+b过点(0,﹣3),可得b=﹣3,有两个交点,y=x+b过点(0,3),可得b=3,有一个交点,∴﹣3<b<3,此时直线y=x+b与曲线恰有一个公共点;综上:﹣3<b≤3或;故答案为:﹣3<b≤3或;点评:本题主要考查了直线与圆的位置关系,考查了学生对数形结合思想,分类讨论思想,转化和化归的思想的综合运用,是一道好题;三、解答题:(共56分)17.已知等差数列{a n}中a2=9,a5=21.(1)求数列{a n}的通项公式;(2)若,求数列{log2b n}的前n项和S n.考点:数列的求和;等差数列的通项公式.专题:等差数列与等比数列.分析:(1)利用a5﹣a2=3d计算可得公差,进而可得结论;(2)通过对数的性质化简可知数列是以4为首项、4为公差的等差数列,进而计算可得结论.解答:解:(1)∵a2=9,a5=21,∴a5﹣a2=3d,∴d=4,∴a n=a2+(n﹣2)•d=4n+1;(2)∵a n=4n+1,∴,∴log2==4n,∴数列是以4为首项、4为公差的等差数列,∴.点评:本题考查数列的通项及前n项和,考查运算求解能力,涉及对数的性质等基础知识,注意解题方法的积累,属于中档题.18.如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?考点:基本不等式在最值问题中的应用.专题:应用题.分析:设矩形栏目的高为acm,宽为bcm,则依题意可知ab=9000,代入广告的面积中,根据基本不等式的性质求得广告面积的最小值.根据等号成立的条件确定广告的高和宽.解答:解:设矩形栏目的高为acm,宽为bcm,则ab=9000.①广告的高为a+20,宽为2b+25,其中a>0,b>0.广告的面积S=(a+20)(2b+25)=2ab+40b+25a+500=18500+25a+40b≥18500+2=18500+2.当且仅当25a=40b时等号成立,此时b=,代入①式得a=120,从而b=75.即当a=120,b=75时,S取得最小值24500.故广告的高为140cm,宽为175cm时,可使广告的面积最小.点评:本题主要考查了基本不等式在最值问题中的应用.基本不等式在解决生活问题中常被用到,也是2015届高考应用题中热点,平时应用注意这方面的训练.19.已知关于x的一元二次不等式(a+1)x2+ax+a>b(x2+x+1)对任意实数x都成立,试比较实数a,b的大小.考点:一元二次不等式的解法.专题:不等式的解法及应用.分析:把不等式化为关于x的一元二次不等式,由不等式恒成立列出条件,求出a、b的大小关系.解答:解:不等式(a+1)x2+ax+a>b(x2+x+1)可变形为(a﹣b+1)x2+(a﹣b)x+a﹣b>0,…又不等式对任意的实数x都成立,则,…即,解得a﹣b>0;所以a>b.…点评:本题考查了一元二次不等式的恒成立问题,是基础题目.20.已知平面区域恰好被面积最小的圆C:(x﹣a)2+(y﹣b)2=r2及其内部所覆盖.(1)试求圆C的方程.(2)若斜率为1的直线l与圆C交于不同两点A,B满足CA⊥CB,求直线l的方程.考点:直线和圆的方程的应用;直线的一般式方程;圆的标准方程.专题:计算题.分析:(1)根据题意可知平面区域表示的是三角形及其内部,且△OPQ是直角三角形,进而可推断出覆盖它的且面积最小的圆是其外接圆,进而求得圆心和半径,则圆的方程可得.(2)设直线l的方程是:y=x+b.根据CA⊥CB,可知圆心C到直线l的距离,进而求得b,则直线方程可得.解答:解:(1)由题意知此平面区域表示的是以O(0,0),P(4,0),Q(0,2)构成的三角形及其内部,且△OPQ是直角三角形,所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是,所以圆C的方程是(x﹣2)2+(y﹣1)2=5.(2)设直线l的方程是:y=x+b.因为,所以圆心C到直线l的距离是,即=解得:b=﹣1.所以直线l的方程是:y=x﹣1.点评:本题主要考查了直线与圆的方程的应用.考查了数形结合的思想,转化和化归的思想.21.如图,直角三角形ABC的顶点坐标A(﹣2,0)、B(0,),顶点C在x轴上,点P为线段OA的中点,设圆M是△ABC的外接圆,若DE是圆M的任意一条直径,试探究是否是定值?若是,求出定值;若不是,请说明理由.考点:圆方程的综合应用;平面向量数量积的运算.专题:综合题;直线与圆.分析:先求出圆M的方程,再设过圆心M的任意一直线为x=my+1与圆的方程联立,利用向量的数量积公式,即可得出结论.解答:解:由题意,△AOB∽△BOC,∴=,∴|CO|=4 …∴C(4,0),AC中点为M(1,0),半径为3∴圆M的方程(△ABC的外接圆)为(x﹣1)2+y2=32…设过圆心M的任意一直线为x=my+1,…∴∴(m2+1)y2=9…设直线x=my+1与圆(x﹣1)2+y2=9的两个交点为D(x1,y1),E(x2,y2)则=(x1+1,y1),=(x2+1,y2),∴•=(x1+1)(x2+1)+y1y2=(my1+2)(my2+2)+y1y2=(m2+1)y1y2+4…由(m2+1)y2=9,得代入上式•=﹣9+4=﹣5…当ED为横轴时,D(﹣2,0),E(4,0),=(﹣1,0),=(5,0)∴•=﹣5…点评:本题考查圆的方程,考查直线与圆的位置关系,考查向量的数量积公式,考查学生分析解决问题的能力,属于中档题.四.附加题22.以数列{a n}的任意相邻两项为坐标的点P n(a n,a n+1)(n∈N*)都在一次函数y=2x+k的图象上,数列{b n}满足.(1)求证:数列{b n}是等比数列;(2)设数列{a n},{b n}的前n项和分别为S n,T n,且S6=T4,S5=﹣9,求k的值.考点:数列的求和;等比关系的确定.专题:等差数列与等比数列.分析:(1)通过将点代入y=2x+k可知a n+1=2a n+k,利用b n+1=a n+2﹣a n+1计算即得结论;(2)通过b n=(a1+k)•2n﹣1=a n+1﹣a n可知a2﹣a1=(k+a1)•20、a3﹣a2=(k+a1)•21、…、a n﹣a n﹣1=(k+a1)•2n﹣2,累加整理得b n﹣a n=k,计算即得结论.解答:(1)证明:∵点都在一次函数y=2x+k图象上,∴a n+1=2a n+k,∴b n+1=a n+2﹣a n+1=(2a n+1+k)﹣(2a n+k)=2(a n+1﹣a n)=2b n,∴=2,故{b n}是以b1=a2﹣a1=2a1+k﹣a1=k+a1为首项、2为公比的等比数列;(2)解:∵b n=(a1+k)•2n﹣1=a n+1﹣a n,∴a2﹣a1=(k+a1)•20,a3﹣a2=(k+a1)•21,…a n﹣a n﹣1=(k+a1)•2n﹣2,累加得:a n﹣a1=(k+a1)•=(k+a1)•(2n﹣1﹣1),整理得:a n=(a1+k)•2n﹣1﹣k,∴b n﹣a n=[(a1+k)•2n﹣1]﹣[(a1+k)•2n﹣1﹣k]=k,又S6=T4,即a1+a2+…+a6=b1+b2+b3+b4,∴a5+a6=4k,即,∴,∴,又S5=﹣9,∴,∴k=8.点评:本题考查等比数列的判定以及数列的求和,考查运算求解能力,注意解题方法的积累,属于中档题.。
东北师大附中2016年高二数学下学期期末试题

.精选文档 .东北师大附中2016 年高二数学放学期期末试题2015---2016学年(高二)年级上学期期末考试(理科)数学试卷一、选择题(本大题共 12 个小题,每题 5 分,在每题中,只有一项为哪一项切合题目要求的)(1)已知会合 , 则( A)(B)()( D)(2)已知复数,则实数(A)( B)()(D)(3)将点的极坐标化成直角坐标为(A)( B)()(D)(4)在同一平面的直角坐标系中,直线经过伸缩变换后,获得的直线方程为(A)(B)()( D)(5)如图,曲线和围成几何图形的面积是次抽(A)(B)()( D)(6) 10 件产品中有 3 件次品,不放回的抽取1 件,在已知第 1 次抽出的是次品的条件下,第2 件,每2 次抽到仍为次品的概率为(A)(B)()(D)(7)以下说法中,正确说法的个数是① 命题“若,则”的逆否命题为:“若,则”;② “ ” 是“ ” 的充足不用要条件;③会合,,若,则实数的全部可能取值组成的会合为(A)0 (B)1 ()2 (D)3(8)设某批产品合格率为,不合格率为,现对该产品进行测试,设第次初次测到正品,则等于(A)(B)()(D)(9)在 10 件产品中,有 3 件一等品, 7 件二等品,从这10 件产品中任取 3 件,则拿出的 3 件产品中一等品件数多于二等品件数的概率(A)( B)()(D)(10)函数存在与直线平行的切线,则实数的取值范围是(A)( B)()(D)(11)函数的大概图象为(A)( B)()(D)(12)已知曲线:上一点,曲线 : 上一点,当时,关于随意,都有恒成立,则的最小值为(A)1 (B) () (D)二、填空题(本大题共 4 个小题,每题 5 分,共20 分)13.已知随机变量听从正态散布,,则的值为.14.若函数在处取极值,则.15.如图的三角形数阵中,知足:(1)第 1 行的数为 1;(2)第 n( n≥ 2) 行首尾两数均为 n,其他的数都等于它肩上的两个数相加.则第 10 行中第 2 个数是 ________.16.在平面直角坐标系中,直线与曲线和均相切,切点分别为和 , 则的值是.三、解答题(本大题共 6 小题,共 70 分,解答应写出必需的字说明、证明过程及演算步骤)17.(本小题满分10 分)在平面直角坐标系中,圆的参数方程为,直线过点(0,2 )且倾斜角为.( Ⅰ) 求圆的一般方程及直线的参数方程;( Ⅱ) 设直线与圆交于,两点,求弦的长.18.(本小题满分12 分).精选文档.在直角坐标系中,已知直线(为参数),以坐标原点为极点,轴正半轴为极轴成立极坐标系,曲线.(Ⅰ)写出直线的一般方程和曲线的直角坐标方程;(Ⅱ)设点的直角坐标为,直线与曲线的交点为、,求的值.19.(本小题满分12 分)生产甲乙两种元件,其质量按检测指标区分为:指标大于或许等于为正品,小于为次品,现随机抽取这两种元件各件进行检测,检测结果统计以下:测试指标元件甲元件乙(Ⅰ)试分别预计元件甲,乙为正品的概率;(Ⅱ)在(Ⅰ)的前提下,记为生产 1 件甲和 1 件乙所得的正品数,求随机变量的散布列和数学希望.20.(本小题满分12 分)设函数.(Ⅰ)当时,求函数的单一区间;(Ⅱ)若对都有成立,求的取值范围.21.(本小题满分12 分)为认识家用轿车在高速公路上的车速状况,交通部门随机选用了 100 名家用轿车驾驶员进行检查,获得其在高速公路上行驶时的均匀车速状况为:在55 名男性驾驶员中,平均车速超出的有40 人,不超出的有15 人,在45 名女性驾驶员中,均匀车速超出的20 人,不超出的有25 人.(Ⅰ)依据检查数据,达成以下列联表,并判断能否有 99.5%的掌握以为“车速与性别相关” ,说明原因;(Ⅱ)以上述样本数据预计整体,且视频次为概率,若从高速公路上行驶的家用轿车中随机抽取 3 辆,记这 3 辆车均匀车速超出且为男性驾驶员的车辆数为,求随机变量的散布列和数学希望.参照公式:,此中 .参照数据:共计男性驾驶员女性驾驶员共计 10022.(此题满分12 分)已知函数.(Ⅰ)若函数在上是单一递加函数,务实数的取值范围;(Ⅱ)若,对随意,不等式恒成立,求的最小值.2015---2016学年(高二)年级上学期期末考试(理科)数学试卷答案一、选择题: DBB AB D二、填空题: 13. 0.3 14. 2 15. 46 16. 43三、解答题:17. (10分)( Ⅰ) 圆的一般方程为,直线的参数方程为,( Ⅱ) 依题意,直线的直角坐标方程为圆心到直线 l 的距离18. (12分)解:(Ⅰ),(Ⅱ)把代入中,整理得,设A,B对应的参数分别为由韦达定理由得几何意义可知,.19. (12分)解:(Ⅰ)元件甲为正品的概率约为:元件乙为正品的概率约为:(Ⅱ)随机变量的全部取值为0,1, 2,;;因此随机变量的散布列为:X012P因此:20. (12分)解:(Ⅰ)定义域为当时,,当时,;当时,;当时,,∴ 的单一增区间为,,单一减区间为.(Ⅱ)即在区间上恒成立,令,故当时,单一递减,当时,单一递加,时,,即.21. (12分)超出不超出共计男性驾驶员401555女性驾驶员202545共计 6040100解:(Ⅰ),因此有 99.5% 以上的掌握以为“车速与性别相关”.(Ⅱ)由已知得“均匀车速超出且为男性驾驶员”的概率为,而且~,因此,其散布列以下0123因此,.22.(12分)(Ⅰ)∵在上是增函数,∴ 恒成立,因此只要(Ⅱ)由于,由(Ⅰ)知,函数在上单一递加,不如设,则,可化为,设,则.因此为上的减函数,即在上恒成立,等价于在上恒成立,设,因此,因,因此,因此函数在上是增函数,因此(当且仅当时等号成立).因此.即的最小值为.。
吉林省长春2016-2017学年高一下期末数学试题(文)含答案

B
.1
C
.2
D
.3
7. 已知直线 l1 、 l2 , 平面 , l1 // l 2,l1 // ,那么 l 2 与平面 的关系是(
).
A. l1 //
B.
l2
C. l2 // 或l2
D.
l2 与 相交
8.原点和点 (1,1) 在直线 x y a 两侧,则 a 的取值范围是 ( )
A. a 0或a 2 B . 0 a 2 C . a 0或 a 2 D . 0 a 2
题目要求的。
1. 已知 | a | | b | 2 , 向量 a 与 b 的夹角为 60 ,则 a b 等于(
)
1
A.
B
.3
C
.2
D
.4
2
2
2. 有一个几何体的三视图如右图所示,这个几何体应是一个
()
A. 棱台 B. 棱锥 C. 棱柱 D. 都不对
3. 如图, ABCD- A1B1C1D1 为正方体,下面结论错AC1⊥BD
,
x≤3
(1)求此不等式组表示的平面区域的面积;
(2)求 z1 2 x 3 y 的最大值;
y3
(3)求 z2
的取值范围 .
x1
22.( 本小题满分 12 分 ) 已知直线 l 过定点 (1.4 ), 求当直线 l 在第一象限与坐标轴围成的三
角形面积最小时 , 此直线的方程 .
长春外国语学校 2016-2017 学年第二学期期末考试高一年级 数学试卷(文科)参考答案
长春 2016-2017 学年第二学期期末考试高一年级
数学试卷(文科)
出题人:马双
审题人:王先师
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共
【经典期末卷】大学高数(下)期末测试题及答案
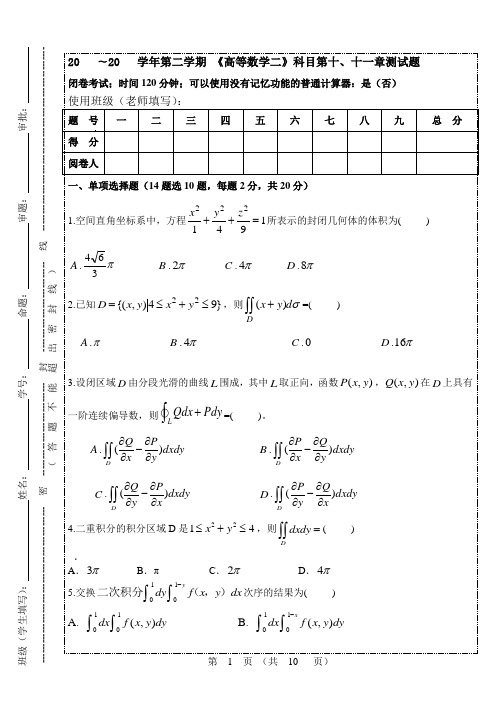
第 1 页 (共 10 页)班级(学生填写): 姓名: 学号: 命题: 审题: 审批: ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- (答题不能超出密封线)LQdx Pdy +⎰=( )dxdy )P dxdy x 二重积分的积分区域D 是221≤+x y π C .2π+⎰L Pdx Qdy在A.∂∂-=∂∂P Qy x第 2 页(共10 页)第 3 页 (共 10 页)班级(学生填写): 姓名: 学号: ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- (答题不能超出密封线)()Lx y ds +⎰= ()Lx y ds +⎰= Lydx xdy +⎰= 2sin y t =上对应22xy De dxdy --⎰⎰= 2.第 4 页 (共 10 页)三. 计算题(一)(每小题6分,共36分)1.计算:22xy De d σ+⎰⎰,其中D 是由圆周224x y +=所围成的闭区域。
2.计算三重积分xdxdydz Ω⎰⎰⎰,其中Ω为三个坐标面及平面21x y z ++=所围成的闭区域。
3.计算xyzdxdydz Ω⎰⎰⎰,其中Ω是由曲面2221x y z ++=,0,0,0x y z ≥≥≥所围成.第 5 页 (共 10 页)班级(学生填写): 姓名: 学号: ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- (答题不能超出密封线)4.求2d d Dxx y y⎰⎰,其中D 为1xy =,y x =及2x =所围成的区域。
完整word版,浙江大学2016-2017学年第2学期高等数学A期末考试试卷

复旦大学高等数学A 期末考试试卷2016~2017学年第2 学期 考试科目:高等数学A 考试类型:(闭卷)考试 考试时间: 120 分钟 学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.二元函数2ln(21)z y x =-+的定义域为 。
2. 设向量(2,1,2)a =r ,(4,1,10)b =-r,c b a λ=-r r r ,且a c ⊥r r ,则λ= 。
3.经过(4,0,2)-和(5,1,7)且平行于x 轴的平面方程为 。
4.设yz u x =,则du = 。
5.级数11(1)np n n∞=-∑,当p 满足 条件时级数条件收敛。
二、单项选择题(本大题共5小题,每小题3分,共15分)1.微分方程2()'xy x y y +=的通解是( )A .2x y Ce =B .22x y Ce =C .22y y e Cx =D .2y e Cxy = 2.求极限(,)(0,0)lim x y →= ( )A .14 B .12- C .14- D .123.直线:327x y zL ==-和平面:32780x y z π-+-=的位置关系是 ( ) A .直线L 平行于平面π B .直线L 在平面π上C .直线L 垂直于平面πD .直线L 与平面π斜交4.D 是闭区域2222{(,)|}x y a x y b ≤+≤,则Dσ= ( )A .33()2b a π- B .332()3b a π- C .334()3b a π- D .333()2b a π-5.下列级数收敛的是 ( )A .11(1)(4)n n n ∞=++∑ B .2111n n n ∞=++∑ C .1121n n ∞=-∑ D.1n ∞=三、计算题(本大题共7小题,每小题7分,共49分) 1. 求微分方程'x y y e +=满足初始条件0x =,2y =的特解。
2. 计算二重积分22Dx ydxdy x y++⎰⎰,其中22{(,)1,1}D x y x y x y =+≤+≥。
XX大学2016—2017学年度第二学期考试试卷A卷高数1-2(A)

XX 大学2016—2017学年度第二学期考试试卷A 卷高等数学1—2注意事项:1. 请考生在下列横线上填写姓名、学号和年级专业。
2 .请仔细阅读各种题目的回答要求,在规定的位置填写答案。
3. 不要在试卷上乱写乱画,不要在装订线内填写无关的内容。
4. 满分100分,考试时间120分钟专业 学号 姓名_________________一.填空题(共24分,每小题3分)1.设函数x y z =,则__________________________=dz .2.方程333z e xyz e -=确定()y x z z ,=,则__________________=∂∂x z. 3. 曲线t t x sin -=,t y cos 1-=,2sin 2tz =在π=t 处切线方程为_________________________________________. 4. 函数2u x y z =+在点(2,1,0)M 处最大的方向导数为__________________. 5. 交换二次积分222(,)y y I dy f x y dx =⎰⎰的积分次序,得__________________=I .6.设平面曲线)10(:2≤≤=x x y L ,则曲线积分__________________=⎰ds x L.7. 幂级数∑∞=12n n n x n的收敛域是 ________________________.8. 微分方程022=+'-''y y y 的通解为___________________________.二、选择题(共12分,每小题3分)1. 设曲面2232y x z +=在点)5 , 1 , 1(M 处的切平面方程为064=+-+λz y x ,则λ=( ).(A) 15- (B) 0 (C) 5- (D) 52. 函数),(y x f 在点),(y x 处可微是函数),(y x f 在该点处存在偏导数的( ). (A) 必要条件 (B) 充分条件(C) 充要条件 (D) 既非充分又非必要条件3. 设曲线L 是单位圆周122=+y x 按逆时针方向,则下列曲线积分不等于零的是( ).(A) ds y L⎰ (B) ds x L⎰ (C) dx y xdy L⎰+ (D) ⎰+-L y x ydxxdy 224. 下列级数中收敛的是( ).(A) ∑∞=122n n n (B) ∑∞=+12n n n(C) ∑∞=+1)2121(n n n (D) ∑∞=133n n n三、解答题:(共59分)1.(7分)求二元函数()3132,23---=y x xy y x f 的极值. 2. (7分)设函数2,x z f x y y ⎛⎫= ⎪⎝⎭,其中()v u f ,具有二阶连续偏导数,求yx zx z ∂∂∂∂∂2 , .3.(7分)计算二重积分dxdy xy D⎰⎰2,其中D 是由圆周422=+y x 与y 轴所围成的右半区域.4.(7分)将函数())1ln(x x f +=展成1-x 的幂级数,并写出可展区间5.(7分)计算曲面积分(2)I xy x y z dS ∑=+++⎰⎰,其中∑为平面1x y z ++=在第一卦限中的部分.6. (8分) 求微分方程x xe y y y 223=+'-''的通解.7. (8分)计算曲线积分()()y d y xy dx yx x I L⎰+-+-=2322其中L 为曲线22x x y -=从)0,2(A 到)0,0(O 的弧段. 8.(8分)利用高斯公式计算曲面积分()()d xdy x z dzdx y dydz x I ⎰⎰∑-+++=33332,其中∑为由上半球面224y x z --=与锥面22y x z +=围成的空间闭区域的整个边界曲面的外侧.四.(5分)设()f x 是在(,)-∞+∞内的可微函数, 且()()f x f x α'<, 其中01α<<. 任取实数0a , 定义1ln (),1,2,3n n a f a n -==.证明:级数11()n n n a a ∞-=-∑绝对收敛.高等数学1--2 参考答案与评分标准一、填空题(共24分,每小题3分) 1. dy xy ydx y dz x x 1ln -+= 2. 3z z yz x e xy ∂=∂- 3.2022-=-=-z y x π4.5. 2(,)xI dx f x y dy =⎰⎰6.()11127. )21, 21[- 8. )sin cos (21x c x c e y x +=二、选择题(共12分,每小题3分) 1. C 2. B 3. D 4. D 三、解答题(共64分) 1. (7分)解: 令⎪⎩⎪⎨⎧=-==-=022022y x f x y f yx 得驻点⎩⎨⎧==00y x ,⎩⎨⎧==22y x 2 分 x f xx 2-=,2=xy f ,2-=yy f 4 分 在(0,0)处, 2 , 2 , 0-===C B A04 2<-=-B AC , ∴(0,0)为非极值点. 5 分在(2,2)处 2 , 2 , 04-==<-=C B A04 2>=-B AC ∴ 1)2 , 2(=f 为函数),(y x f 的极大值. 7 分2.(7分) 解:2121f xy f yx z '+'=∂∂ 3分)21(212f xy f yy y x z '+'∂∂=∂∂∂ ])([ 22])([11222212221221112x f yx f xy f x x f y x f y f y ''+-''+'+''+-''+'-= 223122113212221f y x f y x f yx f x f y ''+''-''-'+'-= 7 分3. (7分) 解:⎰⎰⎰⎰--=224 0222y Dxdx dy y dxdy xy3分⎰--=2 2 22)4(21dy y y 5 分 1564)4(2 0 42=-=⎰dy y y 7 分4. (7分) 解:10(1)ln(1)1n n n x x n ∞+=-+=+∑ 11≤<-x 1 分)211ln(2ln )]1(2ln[)1ln(-++=⋅-+=+x x x 3分10)21(1)1(2ln +∞=∑-+-+=n n n x n∑∞=++-+-+=011)1(2)1()1(2ln n n n n x n 6分1211≤-<-x ⇒ 31≤<-x 7分5.(7分)解::1z x y ∑=--dS ∴== 2分(2DI xy ∴=+⎰⎰4分1102xDdx xydy dxdy -=⎰5分()13202xx x dx =-+6分=7分6.(8分)解 (1)先求微分方程023=+'-''y y y 的通解Y特征方程 0232=+-r r 即 0)1)(2(=--r r ,21=r ,12=rx x e c e c Y 221+= 3 分(2)求原方程的一个特解*y 2 =λ 是特征方程的根,故设 x x e bx ax e b ax x y 222)()(+=+=*5分令bx ax x Q +=2)(,则b ax x Q +='2)(,a x Q 2)(=''将)(x Q ',)(x Q ''代入方程x x Q p x Q ='++'')()2()(λ 得 x b ax a =++22则 ⎩⎨⎧=+=1212b a a , 解之得⎪⎩⎪⎨⎧==021b a , x xe y 221=*7 分 所求通解 x x x xe e c e c y 222121++= 8 分7.(8分) 解:⎰++-+-OAL dy y xy dx yx x )2()(322dxdy x y dxdy y Px Q DD)()(22⎰⎰⎰⎰+=∂∂-∂∂= 3 分 ⎰⎰⋅=θd ρd cos 2 0220 ρρθπ5 分⎰==20 443cos 4ππθθd 6 分dy y xy dx yx x I OA ⎰+-+--=)2()(43322π 7 分2434320-=-=⎰ππxdx 8 分8. (8分) 解:由高斯公式dV z y x I )333(222⎰⎰⎰Ω++= 3 分2244 03 sin d d r dr ππθφφ=⎰⎰⎰ 6 分192(152π=- 8 分9.(5分)解:对任意设2n ≥,由拉格朗日中值定理,有111212121'()ln ()ln (),()n n n n n n n n n n f a a f a f a a a a a f ξαξ----------=-=-<-2 分其中1n ξ-介于1n a -与2n a -之间. 于是有11101,2,.n n n a a a a n α---<-= 3分 又级数1101n n a a α∞-=-∑收敛, 由比较审敛法知级数11()n n n a a ∞-=-∑绝对收敛.5分。
2016级高等数学(A)(下)期末试卷含答案

2016级高等数学(A )(下)期末试卷一。
填空题(本题共10小题,每小题3分,满分30分)1.已知曲面z xy =上一点0000(,,)M x y z 处的法线垂直于平面390x y z +++=,则0x = ,0y = ,0z = ;2.交换积分次序2111d (,)d x x f x y y --=⎰⎰;3.设{},,,x y z r ==r 3divr=r; 4.设正向闭曲线C :1x y +=,则曲线积分22d d Cx y x xy y +=⎰ ;5.设幂级数nn n a x∞=∑的收敛半径为3,则幂级数11(1)n nn na x ∞+=-∑的收敛区间为 ;6.设2()e xf x =,则(2)(0)n f= ;7. 设0,0()1,0x f x x x ππ-<≤⎧=⎨+<≤⎩,其以2π为周期的Fourier 级数的和函数记为()S x ,则(3)S π= ;8.设正向圆周:1C z =,则cos d Czz z=⎰; 9.函数1()cosf z z z=的孤立奇点0z =的类型是 (如为极点,应指明是几级极点),[]Res (),0f z = ;二.(本题共2小题,每小题8分,满分16分)11.判断级数1342n n nn ∞=-∑的敛散性. 12.求幂级数1121n n n n x n ∞+=+∑的收敛域与和函数. 三.(本题共2小题,每小题9分,满分18分)14.将函数21()43f z z z =-+ 在圆环域13z <<内展开为Laurent 级数.四.(15)(本题满分9分)验证表达式 22(cos 21)d (3)d x xy x x y y +++-+ 为某一函10.使二重积分()2244d Dxy σ--⎰⎰的值达到最大的平面闭区域D 为 .13.将函数()f x x x =+ 在(1,1]-上展开为以2为周期的Fourier 级数.数的全微分,并求其原函数.五.(16)(本题满分9分)利用留数计算反常积分41d 1x x+∞+⎰. 六.(17)(本题满分10分) 已知流体的流速函数{}33333(,,),,2x y z y z z x z =--v ,求该流体流过由上半球面1z =z = 所围立体表面的外侧的流量.七.(18)(本题满分8分) 设函数([0,1])f C ∈,且0()1f x ≤<,利用二重积分证明不等式:11100()d ()d 1()1()d f x x f x x f x f x x ≥--⎰⎰⎰2016级高等数学(A )(下)期末试卷一。
东北师范大学数学与统计学院2016学年秋季学期高等代数1期末试卷

2
证明: (1)W1和W2都是Kn的子空间; (2)Kn = W1 ⊕W2. 9. 设V1和V2是线性空间V 的真子空间, 证明
V = V1 V2.
10. 设V 是 数 域K上 的 线 性 空 间, ε1, ε2, · · · , εn是V 的 一 组 基, 证 明V 上 的 线 性 变 换 f 是 单 的 当 且 仅 当 f (ε1), f (ε2), · · · , f (εn)线性无关.
1
2016学年秋季学期期末考试试题: 高等代数1
一、 简答题 1. 举出教材中至少三个等价关系的例子. 2. 设 f (x)和g(x)是 数 域K上 的 两 个 次 数 小 于2016的 多 项 式, 如 果 数 域K上 有2016个 不 同 的 数ai(i = 1, 2, · · · , 2016)使得
有无穷多组解, 计算a的值, 并在此前提下计算该线性方程组的所有解. 5. 设V = K4, V1 = L(α1, α2, α3), V2 = L(β1, β2), 其中
1 3 −1
2 −1
(α1, α2, α3)
=
2
1
0
,
(β1, β2)
=
5
2
.
−1 1 1
f (ai) = g(ai), i = 1, 2, · · · , 2016.
判断 f (x)和g(x)是否一定相等, 如果一定相等, 说明理由, 否则举出一个例子进行说明. 二、 计算题 3. 在K3中给出两组基:
ε1 = (1, 0, 1) , ε2 = (2, 1, 1) , ε3 = (1, 1, 1) ,
2016-2017(下)《高等数学AⅡ》期末试卷-E卷答案 (2) (1)

下学期期末考试试卷答案课程名称:《高等数学A Ⅱ》 (试卷编号:E )一、填空题(本大题共9小题10空,每空2 分,共 20分)1.2-2. 221,,333⎛⎫- ⎪⎝⎭3.2154. (){}22,12x y xy ≤+< 5. 36. 23,137. xy xye xye +(或“()1xy xy e +”) 8.3 9. 收敛二、单项选择题(选择正确答案的字母填入括号,本大题共6小题,每小题3 分,共18 分)三、判断题(选择正确答案的字母填入括号,正确的打“√”,错误的打“×”。
本大题共5小题,每小题2分,共10分)四、计算题(本大题共5小题,每小题6分,共30分)1.解:因为22sin y zxe y x x∂=-∂,22cos y z x e y x y ∂=+∂, ――――――――2分所以(),02zx ππ∂=∂,()2,0z y ππ∂=∂, ――――――――2分 于是,所求全微分22dz dx dy ππ=+ ――――――――2分 2.解:dz z du z dv fdx u dx v dx x∂∂∂=++∂∂∂ ――――――――2分 11x v u e x=⋅+⋅+ ――――――――2分()111x x x e x=++++ ――――――――2分3.解:积分区域(){}2,1D x y xy x =≤≤≤≤所以210x Dxyd dx σ=⎰⎰⎰ ――――――――2分25122x x dx dx ⎛⎫==- ⎪⎝⎭⎰⎰ ――――――――2分1360161212x x ⎛⎫=-= ⎪⎝⎭ ――――――――2分4.解:积分区域(){}2,,01,1,11x y z z xy x Ω=≤≤≤≤-≤≤所以21111xxzdxdydz dx dy xzdz -Ω=⎰⎰⎰⎰⎰⎰ ――――――――2分2121112xxz dx dy -=⎰⎰ 21112x xdx dy -=⎰⎰ ――――――――2分 21112x xy dx -⎛⎫= ⎪⎝⎭⎰ 21122x x dx -⎛⎫=- ⎪⎝⎭⎰ 1231=46x x -⎛⎫- ⎪⎝⎭ 13=- ――――――――2分5.解:由11limlim 1n n n na n a n ρ+→∞→∞+===,得级数的收敛半径 1R =, ――――――――3分在1x =-处,幂级数成为()()111231n nn n n ∞=-=-+-++-+∑L L ,由()lim 10nn n →∞-≠知该级数发散;在1x =处,幂级数成为1n n ∞=∑,由lim 0n n →∞=∞≠知该级数发散。
东北师范大学附属中学数学高二下期末经典测试题(含解析)
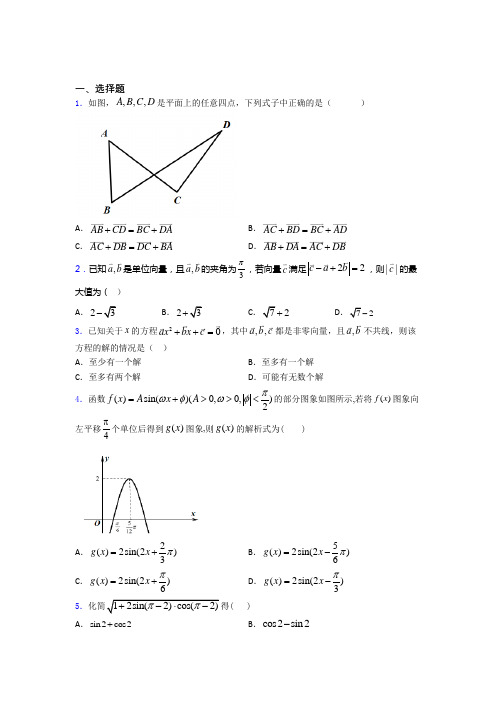
一、选择题1.如图,,,,A B C D 是平面上的任意四点,下列式子中正确的是( )A .AB CD BC DA +=+ B .AC BD BC AD +=+ C .AC DB DC BA +=+D .AB DA AC DB +=+2.已知,a b 是单位向量,且,a b 的夹角为3π,若向量c 满足22c a b -+=,则||c 的最大值为( ) A .23-B .23+C .72+D .72-3.已知关于x 的方程20ax bx c ++=,其中,,a b c 都是非零向量,且,a b 不共线,则该方程的解的情况是( ) A .至少有一个解 B .至多有一个解 C .至多有两个解D .可能有无数个解4.函数()sin()(0,0,)2f x A x A πωφωφ=+>><的部分图象如图所示,若将()f x 图象向左平移4π个单位后得到()g x 图象,则()g x 的解析式为( )A .2()2sin(2)3g x x π=+ B .5()2sin(2)6g x x π=- C .()2sin(2)6g x x π=+D .()2sin(2)3g x x π=-5.12sin(2)cos(2)ππ+-⋅-( ) A .sin2cos2+B .cos2sin2-C .sin2cos2-D .cos2sin2±-6.若函数sin()(0,||)y x ωϕωϕπ=-><的部分图象如图所示,则,ωϕ的值分别是()A .52,125πωϕ==B .5,126πωϕ==C .122,55πωϕ==D .12,56πωϕ== 7.非零向量a b ,满足:a b a -=,()0a a b ⋅-=,则a b -与b 夹角的大小为 A .135° B .120° C .60°D .45°8.若将函数1()cos 22f x x =的图像向左平移6π个单位长度,则平移后图像的一个对称中心可以为( ) A .(,0)12πB .(,0)6πC .(,0)3πD .(,0)2π9.在给出的下列命题中,是假命题的是( ) A .设O A B C 、、、是同一平面上的四个不同的点,若(1)(R)OA m OB m OC m =⋅+-⋅∈,则点、、A B C 必共线B .若向量,a b 是平面α上的两个不平行的向量,则平面α上的任一向量c 都可以表示为(R)c a b λμμλ=+∈、,且表示方法是唯一的C .已知平面向量OA OB OC 、、满足|(0)OA OB OC r r ===,且0OA OB OC ++=,则ABC ∆是等边三角形D .在平面α上的所有向量中,不存在这样的四个互不相等的非零向量a b c d 、、、,使得其中任意两个向量的和向量与余下两个向量的和向量相互垂直10.在三角形ABC 中,,CA a CB b ==,点P 在直线AB 上,且2AP PB =,则CP 可用,a b 表示为( )A .2CP a b =+B .CP a b =-C .12CP a b =- D .1233CP a b =+ 11.在ABC ∆中,已知sin 2sin()cos C B C B =+,那么ABC ∆一定是( ) A .等腰直角三角形 B .直角三角形 C .等腰三角形D .等边三角形12.已知函数()()sin 0,0,,2f x A x A x R πωϕωϕ⎛⎫=+>><∈ ⎪⎝⎭在一个周期内的图象如图所示.则()y f x =的图象,可由函数cos y x =的图象怎样变换而来(纵坐标不变)( )A .先把各点的横坐标缩短到原来的12倍,再向左平移6π个单位B .先把各点的横坐标缩短到原来的12倍,再向右平移12π个单位C .先把各点的横坐标伸长到原来的2倍,再向左平移6π个单位 D .先把各点的横坐标伸长到原来的2倍,再向右平移12π个单位13.已知函数()()sin 0,0,2f x A x A πωϕωϕ=+>>≤⎛⎫⎪⎝⎭的部分图象如图所示,则函数()y f x =的表达式是( )A .()2sin 12f x x π⎛⎫=+⎪⎝⎭ B .()2sin 23f x x π⎛⎫=+ ⎪⎝⎭ C .()22sin 23f x x π⎛⎫=-⎪⎝⎭D .()2sin 23f x x π⎛⎫=-⎪⎝⎭14.已知sin α=,则44sin cos αα-的值为 A .35B .15-C .15D .3515.已知非零向量a ⃑ =(t,0),b ⃑ =(−1,√3),若a ⃑ ⋅b ⃑ =−4,则a ⃑ +2b ⃑ 与b⃑ 的夹角( ) A .π3B .π2C .π6D .2π3二、填空题16.已知sin76m ︒=,则cos7︒=________.(用含m 的式子表示)17.求()22sin cos 2,,63f x x x x ππ⎡⎤=-+∈-⎢⎥⎣⎦的值域____. 18.空间四点,,,A B C D 满足3AB =,=7BC ,||=11CD ,||=9DA ,则·AC BD =_______.19.已知向量(12,)a k =,(1,14)b k =-,若a b ⊥,则实数k =__________.20.已知平面向量a ,b 满足|a |=1,|b |=2,|a ﹣b a 在b 方向上的投影是__________.21.已知角θ的终边上的一点P 的坐标为()3,4,则cos 21sin 2θθ=+________________.22.已知(,)P x y 是椭圆22143x y +=上的一个动点,则x y +的最大值是__________.23.已知3(,),sin 25παπα∈=,则tan()4πα-=___________ . 24.已知平面向量a 、b 满足||3a =,||2b =,a 与b 的夹角为60,若(a mb -)a ⊥,则实数m 的值是___________ .25.已知()()2,1,,3a b λ=-=,若a 与b 的夹角为钝角,则λ的取值范围是___________.(用集合表示)三、解答题26.已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+ (Ⅰ)求函数()f x 的最小正周期和图象的对称轴方程 (Ⅱ)求函数()f x 在区间[,]122ππ-上的值域 27.在已知函数()sin(),f x A x x R ωϕ=+∈(其中0,0,02A πωϕ>><<)的图象与x轴的交点中,相邻两个交点之间的距离为2π,且图象上一个最低点为2,23M π⎛⎫-⎪⎝⎭.(1)求()f x 的解析式; (2)当,122x ππ⎡⎤∈⎢⎥⎣⎦时,求()f x 的值域. 28.已知向量(1,2),(,1)a b x →→==(1)当(2)(2)a b a b +⊥-时,求x 的值;(2)若,a b <>为锐角,求x 的范围. 29.如图,在ABC ∆中, 3B π∠=, 8AB =,点D 在BC 边上,且2CD =,1cos 7ADC ∠=. (1)求sin BAD ∠; (2)求,BD AC 的长.30.已知圆C 经过1(1,0)M -,2(3,0)M ,3(0,1)M 三点. (1)求圆C 的标准方程;(2)若过点N 31)的直线l 被圆C 截得的弦AB 的长为4,求直线l 的倾斜角.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1.B 2.B 3.B 4.C5.C6.C7.A8.A9.D10.D11.C12.B13.D14.A15.A二、填空题16.【解析】【分析】通过寻找与特殊角的关系利用诱导公式及二倍角公式变形即可【详解】因为即所以所以所以又【点睛】本题主要考查诱导公式和二倍角公式的应用意在考查学生分析解决问题的能力17.【解析】【分析】由条件利用同角三角函数的基本关系化简函数解析式再利用正弦函数的定义域和值域二次函数的性质求得函数在上的值域【详解】设故在上值域等价于在上的值域即的值域为【点睛】本题考查同角三角函数的18.0【解析】【分析】由代入再由代入进一步化简整理即可【详解】因为故答案为0【点睛】本题主要考查向量的数量积运算灵活运用数量积的运算公式即可属于常考题型19.【解析】由题意则20.【解析】分析:根据向量的模求出•=1再根据投影的定义即可求出详解:∵||=1||=2|﹣|=∴||2+||2﹣2•=3解得•=1∴在方向上的投影是=故答案为点睛:本题考查了平面向量的数量积运算和投影21.【解析】分析:由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解:角的终边上的一点的坐标为那么故答案为点睛:本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求22.【解析】是椭圆=1上的一个动点设∴最大值为23.【解析】∵∴∴∴故答案为24.3【解析】∵∴∴∴∴故答案为325.【解析】∵向量与的夹角为钝角∴即;解得即的取值范围是故答案为三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.B解析:B【解析】【分析】用不同的方法表示出同一向量,然后对式子进行化简验证.【详解】=-,=-,DC AC ADDC BC BD∴AC AD BC BD-=-,∴AC BD BC AD+=+.故选:B.【点睛】本题主要考查了平面向量的加减法及其几何意义,属于容易题.2.B解析:B 【解析】不妨设(1,0)a =,13(,22b =,(,)c x y =,则2(,c a b x y -+=+,所以22(3)2c a b x -+=+=,即22(4x y +=,点(,)x y 在以(0,为圆心,2为半径的圆上,所以2c x =+2+.故选B .3.B解析:B 【解析】 【分析】根据平面向量基本定理可知(),c a b R λμλμ=+∈,从而将方程整理为()()20x a x b λμ+++=,由,a b 不共线可得200x x λμ⎧+=⎨+=⎩,从而可知方程组至多有一个解,从而得到结果. 【详解】由平面向量基本定理可得:(),c a b R λμλμ=+∈则方程20ax bx c ++=可变为:20ax bx a b λμ+++= 即:()()20xa xb λμ+++=,a b 不共线 20x x λμ⎧+=∴⎨+=⎩可知方程组可能无解,也可能有一个解∴方程20ax bx c ++=至多有一个解本题正确选项:B 【点睛】本题考查平面向量基本定理的应用,关键是能够利用定理将方程进行转化,利用向量和为零和向量不共线可得方程组,从而确定方程解的个数.4.C解析:C 【解析】 【分析】根据函数的图象求出函数()f x 的解析式,再根据图象的平移变换得到()g x 的解析式即可. 【详解】 由图象可知,A =2,541264T πππ=-=, 2T ππω∴==, 2ω∴=,又当512x π=时,52sin(2)212πφ⨯+=, 即5sin()16πφ+=, 2πφ<,3πφ∴=-,故()sin()f x x π=-223,将()f x 图象向左平移4π个单位后得到()g x , ∴ ()2sin[2()]2sin(2)436g x x x πππ=+-=+,故选:C 【点睛】本题主要考查了正弦型函数的图象与性质,图象的变换,属于中档题.5.C解析:C 【解析】 【分析】先利用诱导公式化简角,然后利用正弦的二倍角公式和完全平方式结合角在各个象限中的符号化简即可得到答案. 【详解】==,∵22ππ<<,∴sin2cos20->.∴原式sin2cos2=-. 故选C. 【点睛】本题考查诱导公式和二倍角公式以及三角函数在各个象限中的符号的应用,属于基础题.6.C解析:C 【解析】 【分析】给出三角函数图像,求相关系数,可以通过读取周期,某些特殊值来求解. 【详解】由图可以读取5=066T ππ,(,)为五点作图的第一点2512==65T ππωω⇒⇒= 1222()2565k k Z k ππϕπϕπ⨯-=∈⇒=+,||ϕπ<25πϕ⇒=选择C. 【点睛】由三角函数sin()y A x ωϕ=+图像,获取相应参数的值一般遵循先定A ,然后根据周期定ω,最后通过带值定ϕ. 7.A解析:A 【解析】 【分析】先化简()0a a b ⋅-=得2=a a b ⋅,再化简a b a -=得2b a =,最后求a b -与b 的夹角. 【详解】因为()0a a b ⋅-=,所以220=a a b a a b -⋅=∴⋅,,因为a b a -=,所以2222a a a b b =-⋅+, 整理可得22b a b =⋅, 所以有2b a =,设a b -与b 的夹角为θ,则()2cos a b b a b b a b ba bθ-⋅⋅-===-222222||a a =-, 又0180θ︒≤≤︒,所以135θ=︒, 故选A . 【点睛】本题主要考查数量积的运算和向量夹角的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.8.A解析:A 【解析】 【分析】通过平移得到1cos(2)23y x π=+,即可求得函数的对称中心的坐标,得到答案. 【详解】 向左平移6π个单位长度后得到1cos 223y x π⎛⎫=+ ⎪⎝⎭的图像,则其对称中心为(),0122k k Z ππ⎛⎫+∈ ⎪⎝⎭,或将选项进行逐个验证,选A. 【点睛】本题主要考查了三角函数的图象变换,以及三角函数的图象与性质的应用,其中解答中根据三角函数的图象变换,以及熟记三角函数的图象与性质是解答的关键,着重考查了推理与运算能力.9.D解析:D 【解析】 【分析】 【详解】由()()1OA m OB m OC OA OC m OB OC CA mCB =⋅+-⋅⇒-=⋅-⇒=⋅ 则点、、A B C 必共线,故A 正确;由平面向量基本定理可知B 正确;由 (0)OA OB OC r r ===>可知O 为ABC ∆的外心,由0OA OB OC ++=可知O 为ABC ∆的重心,故O 为ABC ∆的中心,即ABC ∆是等边三角形,故C 正确;存在四个向量(1,0),(0,1),(2,0),(0,-2)其中任意两个向量的和向量与余下两个向量的和向量相互垂直,D 错误 故选D.10.D解析:D 【解析】 【分析】利用向量三角形法则得到:1212++3333CP CA CB a b ==得到答案. 【详解】利用向量三角形法则得到:221212++()++333333CP CA AP CA AB CA CB CA CA CB a b =+==-==故选:D 【点睛】本题考查了向量的表示,也可以利用平行四边形法则得到答案.11.C【解析】 【分析】根据三角形内角和及两角和的正弦公式化简,利用三角函数性质求解. 【详解】在ABC ∆中,由()sin 2sin cos C B C B =+可得sin()2sin cos A B A B +=,化简sin cos cos sin 2sin cos A B A B A B +=,即in 0()s A B -=,由0,0A B ππ<<<<知A B ππ-<-<,所以0A B -=,故选C.【点睛】本题考查了三角形中内角和定理及两角和差的正弦公式的应用,属于中档题.解题的关键是对三角恒等式的变形.12.B解析:B 【解析】 【分析】根据图象可知1A =,根据周期为π知=2ω,过点(,1)12π求得3πϕ=,函数解析式()sin(2)3f x x π=+,比较解析式cos sin()2y x x π==+,根据图像变换规律即可求解.【详解】由()()sin 0,0,,2f x A x A x R πωϕωϕ⎛⎫=+>><∈ ⎪⎝⎭在一个周期内的图象可得1A =,11244126T πππω=⋅=+,解得=2ω,图象过点(,1)12π,代入解析式得1sin(2)12πϕ=⨯+,因为2πϕ<,所以3πϕ=,故()sin(2)3f x x π=+,因为cos sin()2y x x π==+,将函数图象上点的横坐标变为原来的12得sin 22y x π⎛⎫=+ ⎪⎝⎭,再向右平移12π个单位得sin[2()]sin(2)()1223y x x f x πππ=-+=+=的图象,故选B. 【点睛】本题主要考查了由sin()y A x ωϕ=+部分图像求解析式,图象变换规律,属于中档题.13.D解析:D 【解析】根据函数的最值求得A ,根据函数的周期求得ω,根据函数图像上一点的坐标求得ϕ,由此求得函数的解析式. 【详解】由题图可知2A =,且11522122T πππ=-=即T π=,所以222T ππωπ===, 将点5,212π⎛⎫⎪⎝⎭的坐标代入函数()()2sin 2x x f ϕ=+, 得()5262k k ππϕπ+=+∈Z ,即()23k k πϕπ=-∈Z , 因为2πϕ≤,所以3πϕ=-,所以函数()f x 的表达式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.故选D.【点睛】本小题主要考查根据三角函数图像求三角函数的解析式,属于基础题.14.A解析:A 【解析】44sin cos αα-()()2222sin cos sin cos αααα=-+22sin cos αα=-22sin 1α=-35=-,故选A.点睛:已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的,用平方差公式分解要求的算式,两个因式中一部分用同角的三角函数关系整理,另一部分把余弦变为正弦,代入题目的条件,得到结论.15.A解析:A 【解析】 【分析】根据条件容易求出t=4,从而得出a ⃑ =(4,0),从而得出a ⃑ +2b ⃑ =(2,2√3)可设a ⃑ +2b ⃑ 与b⃑ 的夹角为θ,这样根据cosθ=(a ⃑ +2b ⃑ )·b ⃑ |a⃑ +2b ⃑ ||b ⃑ | 即可求出cosθ,进而得出θ的值.【详解】因a ⃑ ⋅b⃑ =−4=−t ∴t=4;∴a ⃑ =(4,0),b ⃑ =(−1,√3),a ⃑ +2b⃑ =(2,2√3) 设a ⃑ +2b ⃑ 与b ⃑ 的夹角为θ,则:cosθ=(a ⃑ +2b ⃑ )·b ⃑|a ⃑ +2b ⃑ ||b ⃑ |=-2+64×2=12,∴θ=π3故答案为A . 【点睛】本题主要考查向量的模及平面向量数量积公式、余弦定理的应用,属于中档题.平面向量数量积公式有两种形式,一是a ⃑ ⋅b ⃑ =|a ⃑ ||b ⃑ |cosθ,二是a ⃑ ⋅b ⃑ =x 1x 2+y 1y 2,主要应用以下几个方面:(1)求向量的夹角, cosθ=a⃑ ·b ⃑ |a⃑ |·|b ⃑ | (此时a⃑ ·b ⃑ 往往用坐标形式求解);(2)求投影,a ⃑ 在b ⃑ 上的投影是a⃑ ⋅b ⃑ |b ⃑ |;(3)a ⃑ ,b ⃑ 向量垂直则a ⃑ ⋅b ⃑ =0;(4)求向量ma ⃑ +nb ⃑ 的模(平方后需求a ⃑ ⋅b⃑ ).二、填空题16.【解析】【分析】通过寻找与特殊角的关系利用诱导公式及二倍角公式变形即可【详解】因为即所以所以所以又【点睛】本题主要考查诱导公式和二倍角公式的应用意在考查学生分析解决问题的能力【解析】 【分析】通过寻找76︒,7︒与特殊角90︒的关系,利用诱导公式及二倍角公式变形即可. 【详解】因为sin76m ︒=,即()sin 9014m ︒-︒=,所以cos14m ︒=, 所以22cos 71m ︒-=,所以21cos141cos 722m+︒+︒==,又cos 7ο==【点睛】本题主要考查诱导公式和二倍角公式的应用,意在考查学生分析解决问题的能力.17.【解析】【分析】由条件利用同角三角函数的基本关系化简函数解析式再利用正弦函数的定义域和值域二次函数的性质求得函数在上的值域【详解】设故在上值域等价于在上的值域即的值域为【点睛】本题考查同角三角函数的解析:3,34⎡⎤⎢⎥⎣⎦【解析】 【分析】由条件利用同角三角函数的基本关系化简函数解析式,再利用正弦函数的定义域和值域、二次函数的性质,求得函数()f x 在2,63ππ⎡⎤-⎢⎥⎣⎦上的值域。
(整理)高数二册期末总练习题.

(整理)高数二册期末总练习题.微分复习1. 若f(x,y,z)=22y x z xy xz +-+,求f x (1,0,1). 2. 设z=ln y x -2,求yzx z ,. 3. 求函数z=22y x +在x=1,y=1处的全微分. 4. 设z=u v ,而u=2x+y ,v=3x-y ,求xz ??. 5. 设z=f(22y x xy -,),其中f 具有一阶连续偏导数,求y z x z ,. 6. 设z=z(x,y)由方程ez=xyz 所确定,求yz x z ,. 7. 球曲面z=x 2+2y 2-3在点(2,1,4)处的切平面方程.8. 求曲面?==22x z y x 上点(1,1,1)处的法平面方程,切线方程. 9. 求函数z=3(x+y)-x 3-y 3的极值.10. 从斜边之长为l 的一切直角三角形中,求有最大周长的直角三角形. 11. 设f(x,y,z)=xy 2+z 3x 2,求f zzx (2,0,1). 12. 设z=x y ,求dz|(1,2).13. 设z=x+sin(xy)-2lny ,求全微分dz|(1,1),yx z2.14. 设z=e x-2y ,而x=sint ,y=t 3,则dtdz. 15. 设z=f(yarctanx,xe y ),其中f 有一阶连续偏导数,求yz x z ,. 16. 设方程lny+z=lnz 确定z 是x ,y 的函数,求yz x z ,. 17. 求曲线x=t+cost ,y=sint ,z=e t 在对应t 0=0处的切线方程与法平面方程.18. 求函数f(x,y)=e x (x+y 2)的极值. 二重积分及其应用1. 求??--Dd y x σ224,其中D ;x 2+y 2≤4,y ≥0.2. 设平面区域D 是由y=x ,y=1与y 轴所围,求??Ddxdy 5.3. 设平面区域D 由y=x ,xy=1和x=2围成,把??Dd y x f σ),(化为二次积分.4. 由y=x+2,y=x 2围成的平面薄片,其各点处密度为21x +=ρ,求该薄片的质量.5. 交换二次积分??102),(xx dy y x f dx 的积分次序.6. 设D={(x,y)|b 2≤x 2+y 2≤a 2,b>0,a>0,x ≥0},把二重积分??+Ddxdyy x )(22表示为极坐标系下的二次积分.7. 求??--Dy xd eσ22,其中D 是由x 2+y 2=1,y=x 和x=0在第一象限所围成封闭区域. 8. 计算??Dd xσarctan,其中D 是闭区域1≤x 2+y 2≤4,0≤y ≤x. 9. 计算以xoy 面上的圆周x 2+y 2=ax 围成的闭区域为底,而以曲面z=x 2+y 2为顶的曲顶柱体体积.10. 求锥面z=22y x +被圆柱z 2=2x 所截得部分的面积. 11. 求旋转抛物面z=x 2+y 2被平面z=1所截得部分的面积.12. 计算以xoy 面上由y=x 以及y=x 2围成D 以z=x y 为顶的曲顶柱体体积.13. 求由平面x=0,y=0,y+x=1所围成z=0及抛物面x 2+y 2=6-z ,截得立体体积. 曲线积分复习题1. 设平面曲线L 下半圆周y=-21x -,求?+L ds y x )(22.2. 设一段锥面螺线L :x=e t cost ,y=e t sint ,z=e t (0≤t ≤2π)上点(x,y,z)处的线密度为μ(x,y,z)=2221zy x ++,求该构件的质量.3. 计算?L ds y 2,其中L 是抛物线y=x 2上点(0,0)与(1,1)之间的一段弧.4. 设一段折线型构件占有xoy 面上的曲线弧L ,L 为连接点A(2,0),O(0,0)与点B(0,3)的折线段,且在曲线L 上点(x,y)处的密度为μ(x,y)=x 3+y 3,求该构件质量.5. 计算?+Ly x ds e22,其中L 是由x=acost ,y=asint ,t ??∈4,0π.6. 设一质点在力→→→+=j x i y F 的作用下,沿圆周x=Rcost ,y=Rsint 上由t 1=0到t 2=2π的一段弧移动做功W.7. 计算?L ydy x 3,其中L 是抛物线y=x 2上从点(0,0)到点(1,1)的一段弧.8. 计算?-++L dy x y dx y x )()(,其中:(1)L 从(1,1)经(1,2)到(4,2)的折线(2)L 是抛物线上y 2=x 上从点(1,1,)到点(4,2)一段弧.9. 设有一平面力场→→+-=i y a x F ])[(22,将一质点沿曲线L :(x-a)2+y 2=a 2(a>0)从点(a,a)移动到点(2a,0)所做功W=1,求a.10. 设一质点在力→→→→++=k x j z i y F 的作用下,从点A(0,1,2)沿直线段移动到点B(2,3,5),求力F 做的功W.11. 计算?+++L dy y x dx y x )()(222,其中L :x 2+y 2=1,正方向.12. 就算?++-+L dy y x dx y xy x )()32(224,其中L 是曲线x 2+y 2=-2y 取正方向.13. 计算曲线积分I=?-+-L x x dy x y e dx x y e )cos (]2sin [,其中L 为曲线y=21x -上的点A(1,0)沿逆时针方向到B(-1,0)的一段弧. 14. 设L :x 2+y 2=2x 逆时针方向,求?-L xdy xdx y cos sin .15. 设有一变力在坐标上投影X=2xy-y 4+3,Y=x 2-4xy 3,这变力确定了一个立场.(1)证明质点在场内移动时,场力所做的功与路径无关(2)计算质点从(1,0)到(2,1),改变力做的功.16. 计算?+--Ldy y x dx y x )sin ()(2,其中L 为圆周y=22x x -上点(0,0)到(1,1)的一段弧.17. 设L 由x=0,x=2,y=0,y=3围成,逆时针方向、封闭,求+-Lxydy dx y 2)1(2.18. 求?-)0.2()0,0()sin (cos ydy ydx e x .19. 设L 为圆域D :x 2+y 2≤-2x 正向边界,求?-+-L dy y x dx y x )()(33.级数期末复习1. 求级数n nnn 32)1(1-∑∞=的和. 2. p nn n1)1(1-∑∞=,求p 的范围使得级数收敛或发散.3. 判断收敛性 1) nn n 11+∑∞= 15))1(1n n n -+∑∞= 2) n n 311∞=∑ 16))1ln(1 +∑∞=n nn 3) )423(1n n n +∑∞= 17))423(31nn n +∑∞= 4) 1121++∑∞=n n n 18)nn n n ++∑∞=211 5) 121-∑∞=n nn 6) )4)(1(51++∑∞=n n n 7) )11ln(31nn +∑∞= 8) nn 2sin1π∞=∑9)nn n 4sin 51π∞=∑10) !1n n n n ∞=∑ 11) !41n n n ∞=∑ 12) nn n 5!1∞=∑13) nn n 321∞=∑14) 112tan+∞=∑n n n π4.判断是否收敛,若收敛,是否绝对收敛或条件收敛1)21)1(1+-∑∞=n nn 2)1113)1(--∞=-∑n n n n3)nnn ln 1)1(1-∑∞= 4)n n n 3sin 1∞=∑5)623)1(41++-∑∞=n n nn 5.求幂级数收敛区间1)nx n n )5(1-∑∞= 2)12)1(121+-∑+∞=n x n n n 3)!0n x n n ∞=∑ 4)nn n x n !)1(11-∞=-∑ 5)1221+∑∞=n x nn n6.将函数展成幂级数1)函数f(x)=2312++x x 分别展开成x 和x+4的幂级数2)将f(x)=ln(2+x)展成x+1的幂级数 3)将函数f(x)=e -2x 展开成x 的幂级数 4)将函数f(x)=cos(x 2)展成x 的幂级数5)将函数f(x)=x1展成x+4的幂级数7.求下列级数的和函数1)11-∞=∑n n nx2)nx nn ∞=∑1。
2016-2017学年吉林省长春联考高一下期末数学理科试卷(有答案)

2016-2017学年吉林省长春联考高一(下)期末数学试卷(理科)一.选择题:(本大题共计12小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项符合题目要求.)1.(4分)△ABC中,若a=1,c=2,B=60°,则△ABC的面积为()A.B.C.1 D.2.(4分)已知,则a10=()A.﹣3 B.C.D.3.(4分)在锐角△ABC中,a=2,b=2,B=45°,则A等于()A.30°B.60°C.60°或120°D.30°或150°4.(4分)不等式组,所表示的平面区域的面积等于()A.B.C.D.5.(4分)在R上定义运算,若成立,则x的取值范围是()A.(﹣4,1)B.(﹣1,4)C.(﹣∞,﹣4)∪(1,+∞)D.(﹣∞,﹣1)∪(4,+∞)6.(4分)在△ABC中,如果sinA:sinB:sinC=2:3:4,那么cosC等于()A.B.C.D.7.(4分)一个等比数列{a n}的前n项和为48,前2n项和为60,则前3n项和为()A.63 B.108 C.75 D.838.(4分)已知x,y是正数,且,则x+y的最小值是()A.6 B.12 C.16 D.249.(4分)对于任意实数a、b、c、d,命题:①若a>b,c<0,则ac>bc;②若a>b,则ac2>bc2;③若ac2<bc2,则a<b;④;⑤若a>b>0,c>d>0,则ac>bd.其中真命题的个数是()A.1 B.2 C.3 D.410.(4分)若正数x,y满足x+3y=5xy,则3x+4y的最小值是()A.B.C.5 D.611.(4分)若不等式ax2+2ax﹣4<2x2+4x对任意实数x均成立,则实数a的取值范围是()A.(﹣2,2)B.(﹣2,2]C.(﹣∞,﹣2)∪[2,∞)D.(∞,2]12.(4分)已知方程(x2﹣mx+2)(x2﹣nx+2)=0的四个根组成一个首项为的等比数列,则|m﹣n|=()A.1 B.C.D.二.填空题(本大题共4小题,每小题4分,共16分)13.(4分)不等式>1的解集是.14.(4分)若等比数列{a n}的各项均为正数,且a7a11+a8a10=2e4,lna1+lna2+lna3+…+lna17=.15.(4分)在△ABC中,面积,则∠C等于.16.(4分)设,利用课本中推导等差数列前n项和公式的方法,可求得f(﹣5)+f(﹣4)+…+f(0)+…+f(5)+f(6)的值是.三、解答题(共56分,需要写出必要的解答和计算步骤)17.(10分)若不等式ax2+5x﹣2>0的解集是,则不等式ax2﹣5x+(a2﹣1)>0的解集是.18.(10分)已知{a n}是等差数列,S n是其前n项和.已知a1+a3=16,S4=28.(1)求数列{a n}的通项公式(2)当n取何值时S n最大,并求出这个最大值.19.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,若向量=(﹣cosB,sinC),=(﹣cosC,﹣sinB),且.(Ⅰ)求角A的大小;(Ⅱ)若b+c=4,△ABC的面积,求a的值.20.(12分)已知在△ABC中,角A,B,C的对边分别是a,b,c,且bsinA+acosB=0.(1)求角B的大小;(2)若b=2,求△ABC面积的最大值.21.(12分)数列{a n}的前n项和为S n,且S n=n(n+1)(n∈N*)(1)求数列{a n}的通项公式;(2)若数列{b n}满足:a n=+++…+,求数列{b n}的通项公式;(3)令c n=(n∈N*),求数列{c n}的前n项和T n.2016-2017学年吉林省长春联考高一(下)期末数学试卷(理科)参考答案与试题解析一.选择题:(本大题共计12小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项符合题目要求.)1.(4分)△ABC中,若a=1,c=2,B=60°,则△ABC的面积为()A.B.C.1 D.【解答】解:S===.△ABC故选B.2.(4分)已知,则a10=()A.﹣3 B.C.D.【解答】解:∵,,…写出几项发现数列是一个具有周期性的数列,且周期是3,∴,故选B.3.(4分)在锐角△ABC中,a=2,b=2,B=45°,则A等于()A.30°B.60°C.60°或120°D.30°或150°【解答】解:锐角△ABC中,由正弦定理可得=,∴sinA=.∵B=45°,a>b,再由大边对大角可得A>B,故B=60°,故选:B.4.(4分)不等式组,所表示的平面区域的面积等于()A.B.C.D.【解答】解:由约束条件作出可行域如图,=S△OBA+S△OCA∴S四边形OBAC=.故选:C.5.(4分)在R上定义运算,若成立,则x的取值范围是()A.(﹣4,1)B.(﹣1,4)C.(﹣∞,﹣4)∪(1,+∞)D.(﹣∞,﹣1)∪(4,+∞)【解答】解:因为,所以,化简得;x2+3x<4即x2+3x﹣4<0即(x﹣1)(x+4)<0,解得:﹣4<x<1,故选A.6.(4分)在△ABC中,如果sinA:sinB:sinC=2:3:4,那么cosC等于()A.B.C.D.【解答】解:由正弦定理可得;sinA:sinB:sinC=a:b:c=2:3:4可设a=2k,b=3k,c=4k(k>0)由余弦定理可得,=故选:D7.(4分)一个等比数列{a n}的前n项和为48,前2n项和为60,则前3n项和为()A.63 B.108 C.75 D.83【解答】解:由等比数列的性质可知等比数列中每k项的和也成等比数列.则等比数列的第一个n项的和为48,第二个n项的和为60﹣48=12,∴第三个n项的和为:=3,∴前3n项的和为60+3=63.故选:A.8.(4分)已知x,y是正数,且,则x+y的最小值是()A.6 B.12 C.16 D.24【解答】解:x+y=(x+y)(+)=1+9++≥10+2=10+6=16,当且仅当x=4,y=12时取等号,故x+y的最小值是16,故选:C9.(4分)对于任意实数a、b、c、d,命题:①若a>b,c<0,则ac>bc;②若a>b,则ac2>bc2;③若ac2<bc2,则a<b;④;⑤若a>b>0,c>d>0,则ac>bd.其中真命题的个数是()A.1 B.2 C.3 D.4【解答】解:①根据不等式的性质可知若a>b,c<0,则ac>bc或ac<bc,∴①错误.②当c=0时,ac2=bc2=0,∴②错误.③若ac2>bc2,则c≠0,∴a<b成立,∴③正确.④当a=1,b=﹣1时,满足a>b,但不成立,∴④错误.⑤若a>b>0,c>d>0,则ac>bd>0成立,∴⑤正确.故正确的是③⑤.故选:B.10.(4分)若正数x,y满足x+3y=5xy,则3x+4y的最小值是()A.B.C.5 D.6【解答】解:∵正数x,y满足x+3y=5xy,∴=1∴3x+4y=()(3x+4y)=+++≥+2=5当且仅当=时取等号∴3x+4y≥5即3x+4y的最小值是5故选:C11.(4分)若不等式ax2+2ax﹣4<2x2+4x对任意实数x均成立,则实数a的取值范围是()A.(﹣2,2)B.(﹣2,2]C.(﹣∞,﹣2)∪[2,∞)D.(∞,2]【解答】解:不等式ax2+2ax﹣4<2x2+4x,可化为(a﹣2)x2+2(a﹣2)x﹣4<0,当a﹣2=0,即a=2时,恒成立,合题意.当a﹣2≠0时,要使不等式恒成立,需,解得﹣2<a<2.所以a的取值范围为(﹣2,2].故选B.12.(4分)已知方程(x2﹣mx+2)(x2﹣nx+2)=0的四个根组成一个首项为的等比数列,则|m﹣n|=()A.1 B.C.D.【解答】解:设这四个根为x1,x2,x3,x4,公比为p其所有可能的值为,,,,由得x1x2x3x4=4,即,则p6=64⇒p=±2.当p=2时,四个根为,1,2,4,且,4为一组,1,2为一组,则+4=m,1+2=n,则;当p=﹣2时,不存在任两根使得x1x2=2,或x3x4=2,∴p=﹣2舍去.故选B.二.填空题(本大题共4小题,每小题4分,共16分)13.(4分)不等式>1的解集是{x|﹣2<x<﹣} .【解答】解:不等式,移项得:>0,即<0,可化为:或,解得:﹣2<x<﹣或无解,则原不等式的解集是{x|﹣2<x<﹣}.故答案为:{x|﹣2<x<﹣}14.(4分)若等比数列{a n}的各项均为正数,且a7a11+a8a10=2e4,lna1+lna2+lna3+…+lna17=34.【解答】解:∵数列{a n}为等比数列,且a7a11+a8a10=2e4,∴a7a11+a8a10=2a8a10=2e4,则a8a10=e4,∴lna1+lna2+…lna17=ln(a1a2…a17)=34,故答案为:34.15.(4分)在△ABC中,面积,则∠C等于45°.【解答】解:由三角形的面积公式得:S=absinC,而,所以absinC=,即sinC==cosC,则sinC=cosC,即tanC=1,又∠C∈(0,180°),则∠C=45°.故答案为:45°16.(4分)设,利用课本中推导等差数列前n项和公式的方法,可求得f(﹣5)+f(﹣4)+…+f(0)+…+f(5)+f(6)的值是3.【解答】解:∵,∴f(1﹣x)==∴f(x)+f(1﹣x)=∴f(﹣5)+f(﹣4)+…+f(0)+…+f(5)+f(6)=6×=3故答案为:3三、解答题(共56分,需要写出必要的解答和计算步骤)17.(10分)若不等式ax2+5x﹣2>0的解集是,则不等式ax2﹣5x+(a2﹣1)>0的解集是.【解答】解:∵ax2+5x﹣2>0的解集是,∴a<0,且,2是方程ax2+5x﹣2=0的两根韦达定理×2=,解得a=﹣2;则不等式ax2﹣5x+a2﹣1>0即为﹣2x2﹣5x+3>0,解得故不等式ax2﹣5x+a2﹣1>0的解集.故答案为:18.(10分)已知{a n}是等差数列,S n是其前n项和.已知a1+a3=16,S4=28.(1)求数列{a n}的通项公式(2)当n取何值时S n最大,并求出这个最大值.【解答】解:(1)设等差数列{a n}的公差为d,∵a1+a3=16,S4=28.∴2a1+2d=16,4a1+d=28,联立解得:a1=10,d=﹣2.∴a n=10﹣2(n﹣1)=12﹣2n.(2)令a n=12﹣2n≥0,解得n≤6.∴n=5,或6时,S n取得最大值,为S6==30.19.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,若向量=(﹣cosB,sinC),=(﹣cosC,﹣sinB),且.(Ⅰ)求角A的大小;(Ⅱ)若b+c=4,△ABC的面积,求a的值.【解答】解:(Ⅰ)∵=(﹣cosB,sinC),=(﹣cosC,﹣sinB),∴,即,∵A+B+C=π,∴B+C=π﹣A,可得cos(B+C)=,…(4分)即,结合A∈(0,π),可得.…(6分)(Ⅱ)∵△ABC的面积==,∴,可得bc=4.…(8分)又由余弦定理得:=b2+c2+bc,∴a2=(b+c)2﹣bc=16﹣4=12,解之得(舍负).…(12分)20.(12分)已知在△ABC中,角A,B,C的对边分别是a,b,c,且bsinA+acosB=0.(1)求角B的大小;(2)若b=2,求△ABC面积的最大值.【解答】解:(1)由bsinA+acosB=0及其正弦定理可得:sinBsinA+sinAcosB=0,sinA≠0,∴sinB+cosB=0,即tanB=﹣1,又0<B<π,∴B=.(2)由余弦定理,可得=≥2ac+ac,∴ac≤=2(2﹣),当且仅当a=c时取等号.∴S=sinB≤=﹣1,△ABC故△ABC面积的最大值为:﹣1.21.(12分)数列{a n}的前n项和为S n,且S n=n(n+1)(n∈N*)(1)求数列{a n}的通项公式;(2)若数列{b n}满足:a n=+++…+,求数列{b n}的通项公式;(3)令c n=(n∈N*),求数列{c n}的前n项和T n.【解答】解:(1)∵数列{a n}的前n项和为S n,且S n=n(n+1)(n∈N*),∴n≥2时,a n=S n﹣S n﹣1=n(n+1)﹣n(n﹣1)=2n.n=1时,a1=S1=2,对于上式也成立.∴a n=2n.(2)数列{b n}满足:a n=+++…+,∴n≥2时,a n﹣a n﹣1==2.∴b n=2(3n+1).n=1时,=a1=2,可得b1=8,对于上式也成立.∴b n=2(3n+1).(3)c n===n•3n+n,令数列{n•3n}的前n项和为A n,则A n=3+2×32+3×33+…+n•3n,∴3A n=32+2×33+…+(n﹣1)•3n+n•3n+1,∴﹣2A n=3+32+…+3n﹣n•3n+1=﹣n•3n+1,可得A n=.∴数列{c n}的前n项和T n=+.。
2016-2017(下)《高等数学AⅡ》期末试卷-A卷 (1)

第 1 页 (共 3 页)下学期期末考试试卷课程名称:《高等数学A Ⅱ》 (试卷编号: A )(本卷满分100分,考试时间120分钟)考试方式:考试考查闭卷开卷仅理论部分其他)学院: 专业:班级: 学号: 姓名: 任课教师:考试地点: 考试时间: 月 日 时 分一、填空题(本大题共10小题10空,每空2 分,共 20分)1.极限(,)limx y →= .2.经过两点(1,2,0)A -、(4,1,3)B -的直线方程为 .3.求两直线113:141x y z l -+==-和22:221x y zl +==--的夹角θ= . 4.球心在点(1,3,2)-且通过坐标原点的球面方程为 . 5.求直线234112x y z ---==与平面260x y z ++-=的交点坐标 . 6.设(,)f x y =,则(1,1)xy f = .7.设2sin 2z x y =,则全微分dz = . 8.计算二次积分2ln 1yx dy e dx =⎰⎰.9.若级数11p n n ∞=∑收敛,则P 的范围是 . 10.把函数2xe 展开成x 的幂级数,则2xe = .二、单项选择题(选择正确答案的字母填入括号,本大题共6小题,每小题3 分,共18 分)1.已知级数21sin n n n α∞=∑,则此级数( ). A. 发散 B. 条件收敛 C. 绝对收敛 D. 不能确定2.过点(2,0,3)-且与直线27010x y z x y z -+-=⎧⎨+-+=⎩垂直的平面方程为( ).A. 2370x y z +++=B. 2350x y z +-+=C. 2350x y z -+-=D. 2370x y z --+= 3.设函数22324z x y y =-+-,则(0,2)是( ).A. 极大值点B. 极小值点C.不是极值点D. 无法确定 4.设22(,)xy z f x y e =+,则zx∂=∂( ). A. 122xy xf xe f ''+ B. 122xy xf ye f ''+ C. 122xy yf xe f ''+ D. 122xy yf ye f ''+5.求曲线221()44z x y y ⎧=+⎪⎨⎪=⎩在点4,7)处的切线与x 轴正向之间的夹角( ). A. 30oB. 45oC. 90oD. 60o6.设25DI xy d σ=⎰⎰,其中区域{}(,)01,11D x y x y =≤≤-≤≤,则I =( ).A. 1-B. 0C. 1D. 2请考生注意:答题时不要超过“装订线”,否则后果自负。
辽宁省大连市2016-2017学年高二数学下学期期末考试试题理

12016〜2017学年度第二学期期末考试试卷高二数学(理科)第I 卷•选择题:(本大题共12小题,每小题5分,共60分•在每小题给出的四个选项中,只有一项是符合题目要求的)1 .已知i 是虚数单位,则复数i • 1=()1 -i1 31 3 A. 1 3iB.-iC.1 -3iD.i2 22 22•“任何实数的平方大于 0,因为a 是实数,所以a 2 > 0”,这个三段论推理 ( )A •大前题错误B •小前题错误C •推理形式错误D •是正确的3.某校食堂的原料费支出 x 与销售额y (单位:万元)之间有如下数据,4.用反证法证明命题“三角形的内角中至少有一个不大于60 ”时,假设正确的是 ( )A.假设三个内角都不大于 60B. 假设三个内角都大于 60C.假设三个内角至多有一个大于60 D.假设三个内角至多有两个大于 605.下面几种推理中是演绎推理的为A.由金、银、铜、铁可导电,猜想:金属都可导电;B.猜想数列1 2‘2 33 4的通项公式为a nn(n 1)(nA. 60B. 50C. 55D. 65C.由半径为r的圆的面积s -二r2,得单位圆的面积S二…;1(0,2)内取值的概率为D.由平面直角坐标系中圆的方程为 (x _a)2 • (y _b)2 =r 2,推测空间直角坐标系中球的方程为2 2 2 2(x-a) (y-b) (z-c) =r1尸2 n 1 I — c<*1 +a +a + ■■■ + a = ------------ ( a 式1,n w N ),在验证 n = 1 时,1 -a等式的左边等于 ( )A.1B. 1 aC.1 a a 2D.1 a a2 a 37.在 (2x 21 x"5)的二项展开式中,x 的系数为( )A.10B.-10C.40D.-40& 5张卡片上分别标有号码1,2, 3,4,5 ,现从中任取 3张, 则3张卡片中最大号码为 4的概率是( )1331A.BC.D.510510第II 卷6 •用数学归纳法证明39.若 |_|B( n,p),且 E()=3,D 「)=2,则 P 「T )的值为 3_ 32A.2B.C.D.11610 .将5封不同的信全部投入4个邮筒,每个邮筒至少投一封,不同的投法共有A.120 种B. 356 种C.264 种D.240 种11.袋中装有标号为1 , 2, 3的三个小球,从中任取一个,记下它的号码,放回袋中,这样连续做三次.若每次抽到各球的机会均等,事件 A 表示“三次抽到的号码之和为 6”,事件B 表示“三次抽到的号码都是2”,则P (B A )=B.12.用 0, 1,…17 D. 6279十个数字,可以组成有重复数字的三位数的个数为C.D.A.243B.252C.261D.352二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13. 已知随机变量•服从正态分布N(1f2),如图1所示.若在(0,)内取值的概率为0.4,则•在(0,2)内取值的概率为14. 掷两颗骰子,掷得的点数和大于9的概率为.5 2 3 4 515. 右(3x -1) a0a1x a2x a3x a4x a5x,贝y 印a2a3a4a5= ___ . ______2 1 4 16•若X是离散型随机变量,P(X=x J , P(X =X2),且X1:::X2.又已知E(X)二3 3 3 D(X) ,贝U x1 - x2的值为______ . ______9三•解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17. (本小题满分10分)已知复数Z1,Z2在复平面内对应的点分别为A(-2,1) , B(a,3) , ( a R ).(i)若乙一z2= J5,求a的值;(n)若复数z二乙z2对应的点在二、四象限的角平分线上,求a的值.18. (本小题满分12分)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加•现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛•(I)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自不同协会”,求事件A发生的概率;(n)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望•19. (本小题满分12分)某小组共10人,利用假期参加义工活动.已知参加义工活动次数为1, 2, 3的人数分别为3, 3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.(I)设A为事件“选出的2人参加义工活动次数之和为 4 ”,求事件A发生的概率;(n)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望•20. (本小题满分12分)某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的2):(I)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为X,求X的分布列和数学期望;(H)根据表3中数据,能否认为爱好羽毛球运动与性别有关?附:掘2 =门(口小22 -皿门21)2n i n2 n 1 n 2 21. (本小题满分12分)请考生在(21) (1), ( 21) (2)二题中任选一题作答,如果多做,则按所做的第一题记分•做答时,把所选题目的序号填在相应位置.(21) (1)选修4— 4 :坐标系与参数方程在极坐标系中,点M(1,3),曲线C的方程为‘Sin2v - cos—以极点0为原点,以极轴为x轴正半轴建立直角坐标系.(I)求点M的直角坐标及曲线C的直角坐标方程;(n)斜率为-1的直线|过点M,且与曲线C交于A,B两点,求点M到A,B两点的距离之积2 2列联表(表(21) (2)选修4— 5 :不等式选讲已知函数f (x) =2|x 1| _|x _2| , x [一3,3].(I)写出函数f(x)的分段解析表达式,并作出f (x)的图象;(n)求不等式| f(x)| .2的解集22. (本小题满分12分)请考生在(22) (1), ( 22) (2)二题中任选一题作答,如果多做,则按所做的第一题记分.做答时,把所选题目的序号填在相应位置.(22) (1)选修4— 4 :坐标系与参数方程在平面直角坐标系xOy中,曲线G : x - 2彳• y2 =4,曲线C2: x _2cos -•为参数).1' 丿2y=2 + 2s in 日(I)以坐标原点0为极点,x轴的正半轴为极轴建立极坐标系,求曲线C1, C2的极坐标方程;(n)在(I)的极坐标系中,射线'与曲线C1 , C2分别交于A , B两点,定点M(4,0),求△ MB3的面积•(22) (2)选修4— 5 :不等式选讲设对于任意实数x,不等式| x • 7 |_ m -1恒成立,且m的最大值为p.(I)求p的值;n)若a,b,c三R,且a・b・c = p,求证: 2 , 2 2 1 a b c .3352016〜2017学年第二学期期末考试试卷数学(理科)参考答案与评分标准说明:一、 本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要 考查内容比照评分标准制订相应的评分细则.二、 对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和 难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后 继部分的解答有较严重的错误,就不再给分.三、 解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、 只给整数分数,选择题和填空题不给中间分.•选择题 1.B 2.A 3.A 4.B 10.D 11.A 12.B5.C6.C7.D8.B9.C二.填空题13.0.814.1 15.3316.3617.解:(I )由复数的几何意义可知:召=_2 • i, z 2二a • 3i .因为 |乙-Z 21—5,所以 | -2 -a -2i .. (-2 -a)2(-2)2 二 5 (5)(II )复数 Z =4 z 2 =(-2 i)(a -3i) =(-2a 3) (a 6)i 由题意可知点(-2a 3, a 6)在直线y 二-x 上所以 a-(-2a 3),解得 a =9 (10)9所以事件A 发生的概率为 (4)18.解:(I )由已知,有 P(A)=CCCC 89 35(II )随机变量 X 的所有可能取值为1,2,3,4x 1 2 3 4P1 3 3 1147714随机变量X 的数学期望E(X) =1 — 2 3 3 3 4 — 5 ............................................ 14 7 7 14 219. 解:(I )由已知,有P(A)所以事件A 发生的概率为1 (4)3(II )随机变量X 的所有可能取值为0, 1, 2,c ;c 3 Vc ;15所以,随机变量X 的分布列为X 0 1 2 P4 7 4 151515,4 7 4随机变量X 的数学期望E X ;=0121 (12)分151515P(X =k)=cfc 严C; (k =1,2,3,4).12P x =o = C 3 C 3C 4C 1015’P X=2二警1533 20.解:(I )任一学生爱好羽毛球的概率为 ,故X ~ B(3,上).88(II )因为P(X =0) = C 331255、 8 512p (x =1)=c 3 x225 512,P(X =2) = C 3135P(X=3) = C 〕⑴327 _512512X 0 1 2 3P125 225 135 27 512512512 512随机变量X 的分布列为所以, 随机变量X 的数学期望E (X ) =3 -=一 (8)分8 880 (20 20 - 10 30)230汇50汉30汉5016 450. 3556 ::: 3. 841所以没有理由认为爱好羽毛球运动与性别有关 ............ 12 分21. ( 1)解:(I )点M 的直角坐标为(0,1),曲线C 的直角坐标方程为 y 2 =x (4)y =1 —tI. 2x = _—t把直线I 的参数方程2 (t 为参数)代入曲线C 的方程得LV'2y =1 t L 2t 2 3、2t 2=0,=(3、、2)2 -4 2 =10 0,设A B 对应的参数分别为t 1,t 2,则t 1 t^^ .2 ,t 1 t^2, 由t 的几何意义得| MA || MB 屮 | 化2|=出 t 2$2 (12)—x -4-3 三 x _ -1(2)解:(I ) f (x)二 3x-1 :::x :::2 x 42乞x 乞3f (x)的图象如图所示(II )直线l 的参数方程为.......................... 4 分2(II )方法一:由f(x)的表达式及图象,当f(X)=2时,可得X = 2;32 当f(x)工―2时,可得x = -2或x = -2;32 2故f (x) • 2的解集为(一,3] ;f (x) 「2的解集为(-2,——);3 32 2所以不等式| f(x)| 2的解集为(-2, - —)(—,3] ......... 12 分3 3-X -4 -3 _ x _ T方法二:由(I )可知f (x) =?3x -1 :::x :::2x 4 2 _ x _ 3所以x +4 -3 兰x £T-3x 一1 兰x vOf(x)才/3x 0 兰xv2x 4 2乞x乞3当一3乞x :::-1时,2当 < x .. 0 时,_3x 2,解得 x =:--3彳 2-1 乞 x ::32当0乞x :::2时,3x 2,解得x .32: x : 23当 2_x_3 时,x 4 2,解得 x • -22 _x _32 2 综上,f(x) >2 的解集为(_2,——)U(—,3].................................................................................. 12 分3 322. (1) (I)解:Ci : T 二4cos= , C2 二 4sin= (4)分(n) M 到射线的距离为d =4sin ,2. 33 3re兀 兀 厂| AB|= P B — P A =4sin — —4cos - =2^3—2 (2)解:(I )因为不等式|x ・7|_m-1恒成立,所以m —1乞0,即m 乞1,所以p =1 ......................... 4 (II )因为 a,b,c ・ R ,所以 a 2 ・b 2 _2abb 2c 2 _ 2bc c 2 a 2 _ 2ac即 2(a 2 b 2 c 2) _ 2(ab bc ac),2 2 2 2 2 2故 3( a b c ) - a b c 2 (ab bc ac), 于是 3(a 2 b 2 c 2) _(a b c)2,11 因为a b c =1,于是得a2 b 2 c^-.当a = b = c时取等号 (12)3333A则 S ABM —I ABl d =6-2.、3 (12)2。
2017高等数学II(1)A参考答案
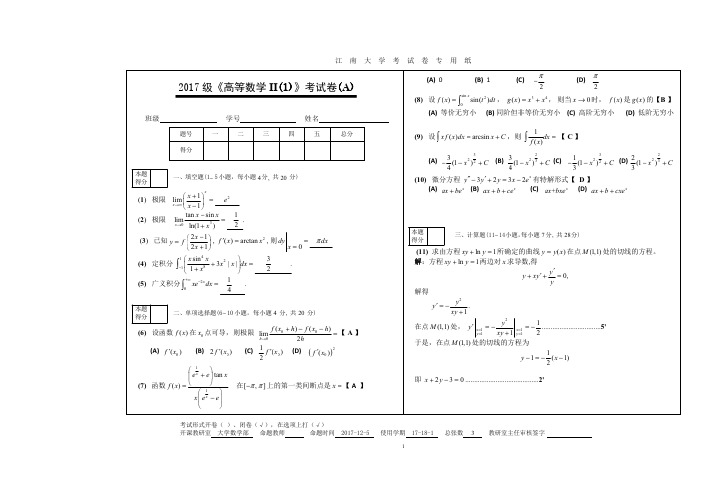
考试形式开卷( )、闭卷(√),在选项上打(√)
开课教研室 大学数学部 命题教师
命题时间 2017-12-5 使用学期 17-18-1 总张数 3 教研室主任审核签字
d
1
江南大学考试卷专用纸
(12) 求不定积分 ∫ arctan x dx .
解:令 x = t , 则 x = t2, dx = 2tdt .于是 ......................1'
本题 得分
三、计算题(11~ 14小题,每小题 7 分, 共 28分)
(11) 求由方程 xy + ln y = 1所确定的曲线 y = y(x) 在点 M (1,1) 处的切线的方程。 解:方程 xy + ln y = 1两边对 x 求导数,得
y + xy′ + y′ = 0, y
解得
y′ = − y2 . xy + 1
2
2e
所以特解为 y
==
−1 2e
1
x3e x2
+
1 x3 2
=
1 2e
1
x3 e − e x2
. ..............1'
本题 得分
四、证明题(15 ~ 16 小题,每小题 7 分,共 14 分)
(15) 证明:当 x > 0 时, ln(1 + x) > arctan x . 1+ x
江南大学考试卷专用纸
2017 级《高等数学 II(1)》考试卷(A)
班级
学号
姓名
(A) 0
(B) 1
(C) − π 2
(D) π 2
∫ (8) 设 f (x) = sin x sin(t2 )dt , g(x) = x3 + x4 , 则当 x → 0 时, f (x) 是 g(x) 的【B 】 0 (A) 等价无穷小 (B) 同阶但非等价无穷小 (C) 高阶无穷小 (D) 低阶无穷小
吉林省2016-2017学年高一数学下学期期末考试试题(含解析)

吉林省2016---2017学年度下学期高一年级数学学科期末考试试题一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设x∈R,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|=A. B. C. 2 D. 10【答案】B【解析】试题分析:两向量垂直,所以,所以,那么向量,所以考点:向量数量积的坐标表示名师点睛:对于两向量垂直的坐标表示,,.2. 已知等差数列,等比数列,则该等差数列的公差为A. 3或B. 3或C. 3D.【答案】C【解析】解:因为等差数列,等比数列,联立方程组得到等差数列的公差为3,选C3. 在10到2 000之间,形如2n(n∈N*)的各数之和为A. 1 008B. 2 040C. 2 032D. 2 016【答案】C【解析】∴∴故选C。
4. 与向量a=(-5,12)方向相反的单位向量是A. (5,-12)B. (-,)C. (,-)D. (,-)【答案】D【解析】∵向量a=(-5,12),=13,∴与向量a=(-5,12)方向相反的单位向量是()故选D.5. 用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为A. B. C. 8π D.【答案】B【解析】S圆=πr2=π⇒r=1,而截面圆圆心与球心的距离d=1,所以球的半径为R==. 所以V=πR3=,故选B.6. 已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,这个几何体的体积是A. 288+36πB. 60πC. 288+72πD. 288+18π【答案】A.....................考点:1、三视图;2、空间几何体的体积.【易错点晴】本题主要考查的是三视图和空间几何体的体积,属于容易题.解题时要看清楚是求表面积还是求体积,否则很容易出现错误.本题先根据三视图判断几何体的结构特征,再计算出几何体的体积即可.7. 若变量x,y满足约束条件且z=2x+y的最大值和最小值分别为m和n,则m-n=A. 5B. 6C. 7D. 8【答案】B【解析】试题分析:作出不等式组对应的平面区域,利用z的几何意义,进行平移即可得到结论.解:作出不等式组对应的平面区域如图:由z=2x+y,得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点A,直线y=﹣2x+z的截距最小,此时z最小,由,解得,即A(﹣1,﹣1),此时z=﹣2﹣1=﹣3,此时n=﹣3,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点B,直线y=﹣2x+z的截距最大,此时z最大,由,解得,即B(2,﹣1),此时z=2×2﹣1=3,即m=3,则m﹣n=3﹣(﹣3)=6,故选:B.考点:简单线性规划.8. 若直线l1:kx-y-3=0和l2:x+(2k+3)y-2=0互相垂直,则k等于A. -3B. -2C. -或-1D. 或1【答案】A【解析】∵直线l1:kx-y-3=0和l2:x+(2k+3)y-2=0互相垂直,∴k-(2k+3)=0,∴k=-3故选A.9. 如图所示,正四棱锥P-ABCD的底面积为3,体积为,E为侧棱PC的中点,则PA与BE所成的角为A. B. C. D.【答案】C【解析】连接AC,BD交于点O,连接OE,PO,∵正四棱锥P−ABCD的底面ABCD是正方形,∴O是AC中点,又E是PC中点,∴OE∥PA,∴PA与BE所成的角为∠BEO.∵正四棱锥P−ABD的底面积为3,体积为,∴AB=BC=,PO=,AC=,PA=,OB=,∵OE与PA在同一平面,OE是三角形PAC的中位线,则∠OEB即为PA与BE所成的角,∴OE=,∵PO⊥BD,AC⊥BD,PO∩AC=O,∴BD⊥平面APC,∴BO⊥EO,在Rt△OEB中,tan∠OEB==,∴∠OEB=.故选项为:C10. 在△ABC中,内角A,B,C对应的边分别是a,b,c,已知c=2,C=,△ABC的面积S△ABC=,则△ABC的周长为A. 6B. 5C. 4D. 4+2【答案】A【解析】在△ABC中,∵△ABC的面积S△ABC==ab⋅sin C=ab⋅∴ab=4.再由余弦定理c2=4=a2+b2−2ab⋅cos C=a2+b2−4,∴a2+b2=8,∴a+b==4,故△ABC的周长为a+b+c=4+2=6,故选A.11. 已知正项数列中,,记数列的前项和为,则的值是A. B. C. D. 11【答案】B【解析】∵所以数列为等差数列,且首项为1,公差为3,则,即,故则数列的前项和为==故=故选项为:B12. 已知正方体ABCD-A1B1C1D1棱长为1,点P在线段BD1上,当∠APC最大时,三棱锥P-ABC的体积为A. B. C. D.【答案】B【解析】连接AC交BD于O,连接PO,则∠APC=2∠APO∵tan∠APO=∴当PO最小时,∠APO最大,即PO⊥BD1时,∠APO最大,如图,作PE⊥BD于E,∵正方体ABCD-A1B1C1D1棱长为1,∴BD=,BD1=,∵OP⊥BD1,PE⊥BD,∴△BDD1∽△BPO∽△PEO,∴,∴OP=,PE=,∴三棱锥P-ABC的体积V=,,故选项为:B点睛:立体几何的核心思想:空间问题平面化.本题把问题转化到平面BDD1中,当PO最小时,即∠APO最大,借助平面几何知识易得:OP=,PE=,从而得到了三棱锥P-ABC的体积.二.填空题:本大题共4小题,每小题5分。
2016-2017(下)《高等数学AⅡ》期末试卷-E卷 (1)

第 1 页 (共 3 页)下学期期末考试试卷课程名称:《高等数学A Ⅱ》 (试卷编号:E )(本卷满分100分,考试时间120分钟)考试方式:考试考查闭卷开卷仅理论部分其他 )学院: 专业:班级: 学号: 姓名: 任课教师:考试地点: 考试时间: 月 日 时 分一、填空题(本大题共9小题10空,每空2 分,共 20分)1.已知()(),1,0,1a b ==r r2,1,-4,则a b ⋅=r r 。
2.与()2,2,1a =-r共线的单位向量e =r。
3.直线+162212x y z --==-与直线123043x y z -+-==的夹角余弦为。
4. ()22ln 2zx y=+--的定义域是 。
5.()(,)(0,3)sin limx y xy x→= 。
6.若()ln 1z xy =+,则()1,2zx ∂=∂ ,()1,2z y ∂=∂ 。
7.若xyz e =,则2zx y∂=∂∂ 。
8.若平面区域D 的面积为3,则二重积分Dd σ=⎰⎰ 。
9. 级数211n n ∞=∑的敛散性是 。
二、单项选择题(选择正确答案的字母填入括号,本大题共6小题,每小题3 分,共18 分)1. 已知,23a i j b i j k =-=+-r r r r r r r3,则a b ⨯=r r ( )。
A. 5 B. 2 C. 95i j k -+r r r 3 D. 95i j k ++r r r32.向量()1,2,a m =-r与向量()4,1,2b =r 垂直,则m =( )。
A.1- B. 0 C. 1 D.23.设23(,,)2f x y z xy y z xyz =+-,则()2,1,1yz f -=( )。
A.0 B. 4 C. 8 D. 13- 4. 函数x y x y x y x f 933),(2233-+++= 在点()1,0处( )。
A.取极大值B.取极小值C.不取极值D.无法确定 5.设()22DI xy dxdy =+⎰⎰, 其中D 是由曲线222x y a +=所围成的平面区域 ()0a >,则I =( )。
厦门大学 【精品】2016-2017学年第2 学期 高等数学A期末考试试卷

厦门大学2016-2017学年第2 学期高等数学A 期末考试试卷2016~2017学年第2 学期 考试科目:高等数学A 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.二元函数2ln(21)z y x =-+的定义域为 。
2. 设向量(2,1,2)a =,(4,1,10)b =-,c b a λ=-,且a c ⊥,则λ= 。
3.经过(4,0,2)-和(5,1,7)且平行于x 轴的平面方程为 。
4.设yz u x =,则du = 。
5.级数11(1)npn n ∞=-∑,当p 满足 条件时级数条件收敛。
二、单项选择题(本大题共5小题,每小题3分,共15分)1.微分方程2()'xy x y y +=的通解是( )A .2x y Ce =B .22x y Ce =C .22y y e Cx =D .2y e Cxy = 2.求极限(,)(0,0)limx y →=( )A .14 B .12- C .14- D .123.直线:327x y zL ==-和平面:32780x y z π-+-=的位置关系是 ( )A .直线L 平行于平面πB .直线L 在平面π上C .直线L 垂直于平面πD .直线L 与平面π斜交4.D 是闭区域2222{(,)|}x y a x y b ≤+≤,则Dσ= ( )A .33()2b a π-B .332()3b a π-C .334()3b a π-D .333()2b a π-5.下列级数收敛的是 ( )A .11(1)(4)n n n ∞=++∑ B .2111n n n ∞=++∑ C .1121n n ∞=-∑ D.1n ∞=三、计算题(本大题共7小题,每小题7分,共49分) 1. 求微分方程'x y y e +=满足初始条件0x =,2y =的特解。
2. 计算二重积分22Dx y dxdy x y++⎰⎰,其中22{(,)1,1}D x y x y x y =+≤+≥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东北师范大学2016-2017学年第2 学期高等数学A 期末考试试卷2016~2017学年第2 学期 考试科目:高等数学A 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.二元函数2ln(21)z y x =-+的定义域为 。
2. 设向量(2,1,2)a =r ,(4,1,10)b =-r,c b a λ=-r r r ,且a c ⊥r r ,则λ= 。
3.经过(4,0,2)-和(5,1,7)且平行于x 轴的平面方程为 。
4.设yz u x =,则du = 。
5.级数11(1)npn n ∞=-∑,当p 满足 条件时级数条件收敛。
二、单项选择题(本大题共5小题,每小题3分,共15分)1.微分方程2()'xy x y y +=的通解是( )A .2x y Ce =B .22x y Ce =C .22y y e Cx =D .2y e Cxy = 2.求极限(,)(0,0)limx y →=( )A .14 B .12- C .14- D .123.直线:327x y zL ==-和平面:32780x y z π-+-=的位置关系是 ( )A .直线L 平行于平面πB .直线L 在平面π上C .直线L 垂直于平面πD .直线L 与平面π斜交4.D 是闭区域2222{(,)|}x y a x y b ≤+≤,则Dσ= ( )A .33()2b a π-B .332()3b a π-C .334()3b a π-D .333()2b a π-5.下列级数收敛的是 ( )A .11(1)(4)n n n ∞=++∑ B .2111n n n ∞=++∑ C .1121n n ∞=-∑ D.1n ∞=三、计算题(本大题共7小题,每小题7分,共49分) 1. 求微分方程'x y y e +=满足初始条件0x =,2y =的特解。
2. 计算二重积分22Dx y dxdy x y++⎰⎰,其中22{(,)1,1}D x y x y x y =+≤+≥。
3.设(,)z z x y =为方程2sin(23)43x y z x y z +-=-+确定的隐函数,求z z x y∂∂+∂∂。
4.求曲线积分()()Lx y dx x y dy ++-⎰,其中L 沿222(0,0)x y a x y +=≥≥,逆时针方向。
5.计算Dy ⎰⎰,其中D是由y =1x =-及1y =所围成的区域。
6.判断级数1(1)1n n n n ∞=-+∑的敛散性,并指出是条件收敛还是绝对收敛。
7.将函数1(1)(2)x x --展开成x 的幂级数,并求其成立的区间。
四、解答题(本大题共 3 小题,每小题 7 分,共 21 分)1.抛物面22z x y =+被平面1x y z ++=截成一椭圆,求原点到这椭圆的最长与最短距离。
2. 求幂级数1(1)(1)!n nn nx n ∞=-+∑的和函数。
3. 设函数()f x 和()g x 有连续导数,且(0)1f =,(0)0g =,L 为平面上任意简单光滑闭曲线,取逆时针方向,L 围成的平面区域为D ,已知[()()]()LDxydx yf x g x dy yg x d σ++=⎰⎰⎰Ñ,求()f x 和()g x 。
参考答案一、填空题(本大题共5小题,每小题3分,共15分) 1.2{(,)|210}x y y x -+> 2.33.920y z --= 4.1ln ln yz yz yz yzx dx zx xdy yx xdz -++ 5.01p <≤ 二、单项选择题(本大题共5小题,每小题3分,共15分)1.C 2.C 3.C 4.B 5.A三、计算题(本大题共7小题,每小题7分,共49分)1. 求微分方程'x y y e +=满足初始条件0x =,2y =的特解。
解:先求'0y y +=的通解,得1x y C e -=………………2分采用常数变易法,设()x y h x e -=,得''()()x x y h x e h x e --=-………3分 代入原方程得'()()()x x x x h x e h x e h x e e ----+=………………4分得21()2x h x e C =+………………5分故通解为12x x y e Ce -=+………………6分将初始条件0x =,2y =带入得32C =,故特解为1322x x y e e -=+…………7分2. 计算二重积分22Dx y dxdy x y++⎰⎰,其中22{(,):1,1}D x y x y x y =+≤+≥。
解:设cos ,sin x r y r θθ==………………1分则10,12sin cos r πθθθ≤≤≤≤+………………3分所以1212220sin cos cos sin Dx y r r dxdy d rdr x y r πθθθθθ+++=+⎰⎰⎰⎰………………5分 20(sin cos 1)d πθθθ=+-⎰………………6分42π-=………………7分3. 设(,)z z x y =为方程2sin(23)43x y z x y z +-=-+确定的隐函数,求z zx y∂∂+∂∂。
解:设(,,)432sin(23)F x y z x y z x y z =-+-+-………………1分12cos(23),44cos(23),36cos(23)x y z F x y z F x y z F x y z =-+-=--+-=++-………………4分2cos(23)14cos(23)4,3[12cos(23)]3[12cos(23)]y x z z F F z x y z z x y z x F x y z y F x y z ∂+--∂+-+=-==-=∂++-∂++-……6分 所以1z z x y∂∂+=∂∂………………7分4. 求曲线积分()()Lx y dx x y dy ++-⎰,其中L 沿222(0,0)x y a x y +=≥≥,逆时针方向。
解:圆的参数方程为:cos ,sin (0)2x a t y a t t π==≤≤……………1分220()()(cos sin (cos sin )cos )sin Lx y dx x y dy a t a t da a t a t da t t ππ++-=+-+⎰⎰⎰……3分220(cos 2sin 2)at t dt π=-⎰………………4分220[sin 2cos 2]2a t t π=+………………6分 2a =-………………7分(本题也可以利用“曲线积分与路径无关”来解)5.计算Dy ⎰⎰,其中D是由y =1x =-及1y =所围成的区域。
解:{(,)|1,11}D x y y x =≤≤-≤≤………………1分111Dydx y -=⎰⎰⎰………………2分31262112[(1)63x y -=-⨯+-⎰………………4分1311(||1)9x dx -=--⎰………………5分 1302(1)9x dx =--⎰………………6分16=………………7分 6.判断级数1(1)1n n n n ∞=-+∑的敛散性,并指出是条件收敛还是绝对收敛。
解:(1)11n n n n n -=++1分)n →∞:………………3分 所以级数发散。
………………4分 又(1)1(1)(111n n n n n -=--++5分1n n +=………………6分显然,交错级数1n n ∞=1nn ∞=都收敛,所以原级数收敛。
因此是条件收敛。
………………7分7. 将函数1(1)(2)x x --展开成x 的幂级数,并求其成立的区间。
解:111(1)(2)12x x x x=-----………………2分而1,||11n n x x x ∞==<-∑………………3分 211[1()](||2)2222x xx x =+++<-L ………………4分所以22111[1()](1)(2)222x xx x x x =+++-+++--L L ………………5分101(1)2n n n x ∞+==-∑………………6分 成立范围||1x <………………7分四、 解答题(本大题共 3 小题,每小题 7 分,共 21 分)1. 抛物面22z x y =+被平面1x y z ++=截成一椭圆,求原点到这椭圆的最长与最短距离。
解:设椭圆上任一点P 的坐标为(,,)P x y z ,P 点满足抛物面和平面方程。
原点到这椭圆上任一点的距离的平方为222x y z ++,………………1分 构造拉格朗日函数22222()(1)F x y z x y z x y z λμ=++++-+++-………………2分2222022020010x yzF x x F y y F z F x y z F x y z λμλμλμλμ=++=⎧⎪=++=⎪⎪=-+=⎨⎪=+-=⎪=++-=⎪⎩………………4分解得1(12x =-………………5分得两个驻点为121111(2(22222P P =---=---- …………………6分………………7分2. 求幂级数1(1)(1)!n nn nx n ∞=-+∑的和函数。
解:因为0!n xn x e n ∞==∑,所以0(1)!n n xn x e n ∞-=-=∑,………………1分00(1)(1)(11)()(1)!(1)!n n n nn n nx n x S x n n ∞∞==--+-==++∑∑………………2分00(1)(1)!(1)!n n n nn n x x n n ∞∞==--=-+∑∑………………3分(1)!n nx n x e n ∞-=-=∑………………4分 110010010(1)(1)!11(1)1(11(1)1)(1)!(1)!1(1)1(1)1!1!!n n n n n n n n n n n n n n n n n x n x x x n x n x x x x n x e x x n x xn x n ∞+++∞∞==∞∞=∞-===--=-++⎡⎤--=-=--⎢⎥⎣⎦=-=+--=-∑∑∑∑∑∑ (0)x ≠…………5分所以1()(1)(0)x x S x e e x x --=--≠故1()(1)(0)x x S x e e x x--=--≠……6分当0x =时,()0S x =。
………7分另解:当0x ≠时,11110(1)1(1)1(1)(1)!(1)!(1)!n n n n x n n n n n n x x n x n x n x n d x +∞∞∞===⎡⎤---==⎢⎥++-⎣⎦⎰∑∑∑ 1111001(1)1(1)(1)!(1)!n n n x n n n x x n x n x x dx x dx -∞∞==-⎧⎫⎡⎤⎡⎤--⎪⎪==-⎨⎬⎢⎥⎢⎥--⎪⎪⎣⎦⎣⎦⎩⎭⎰⎰∑∑ 001(1)!n x n n x n x x dx ∞=-=-∑⎰11xxx x x dx e x d e x x --=-=⎰⎰()11x x e e x x--=+- 11x x e e x x --=+-当0x =时,()0S x =。
