利用多项式拟合获得汽车发动机外特性曲线的几种方法
基于MATLAB的发动机万有特性曲线绘制方法

坐标的万有特性曲线运用最广 , 绘制该万有特性 曲线需要画出等燃油消耗率曲线 、 等功率曲线和边 界线 ,具体绘制方法如表 1 所示 。
表1 发动机万有特性曲线绘制方法 线型 等燃 油 消 耗 率 曲线 边界线 等功率曲线 绘制方法 先建立燃油消耗率与转速和扭 矩的 关 系 模 型 , 绘 出 三 维 曲 面 图 ,再生成二维的等值线图 。 根据发动机外特性曲线的数据 绘制边界线 。 公式 Pe = Ttq nΠ 9550 绘制 ,绘出三 维曲面图 ,再生成二维等值线图 采用 ( 建立) 的模型
492. 2 471. 2
由式 ( 1 ) , 根据最小二 乘 法 原 理 , J = ∑e i =
i =0
E ・ E值为最小 , 此时
T
9J | 9A
A=A
= 0 。进而得到 B =
G ×A ,从理论上讲系数矩阵 G 的阶数 l 越大越能更
好地实现等燃油消耗率曲线的拟合 ,然而 l 变大时 ,
( kW・ be ( gΠ h) ) 的三维曲面图 , 再利用 MAT LAB 语言
Ttq 、 n 数据绘制在平面上 ,形成 Ttq - n 关系曲线 ,构
成发动机万有特性曲线的边界线 , 此时油量调节机 构固定在标定循环供油量位置 , 万有特性曲线上的 转速和扭矩不可能超出边界线的范围。 根据公式 Pe = Ttq nΠ 9550 ,选择不同的 Ttq 、 n ,利 用 interp1 进行拟合 , 得到函数 Pe = f ( Ttq , n ) , 绘制 得到三维曲线 ,利用 contour 命令得到的双曲线即是 等功率曲线 。
1 2 1 3 1 4
引 言
为了能全面反映发动机的性能 , 把发动机的多 个参数画在一张图上而形成的多参数的特性曲线叫 做发动机的万有特性曲线 , 传统用作图法制取万 有特性曲线是将不同转速下的负荷特性曲线绘制在 同一张坐标图上 ,形成曲线簇 ,然后从曲线簇上把等 油耗点逐一投影到万有特性图上 , 并圆滑地连接成 等油耗曲线 ,再做出等功率曲线 , 画出外特性曲线 , 进而得到发动机的万有特性曲线 , 这种万有特性曲 线的手工绘制方法费时费力 , 难以保证数据和图形 [2 ] 的精度 ,而 MAT LAB 软件具有强大的矩阵计算和 [3 ] 数据可视化能力 , 为万有特性曲线的绘制提供了 一种新的方法 。国内开展了利用 MAT LAB 进行万有 特性曲线绘制的研究 , 由于外特性曲线拟合较为简
发动机外特性曲线:效率与转速特性曲线
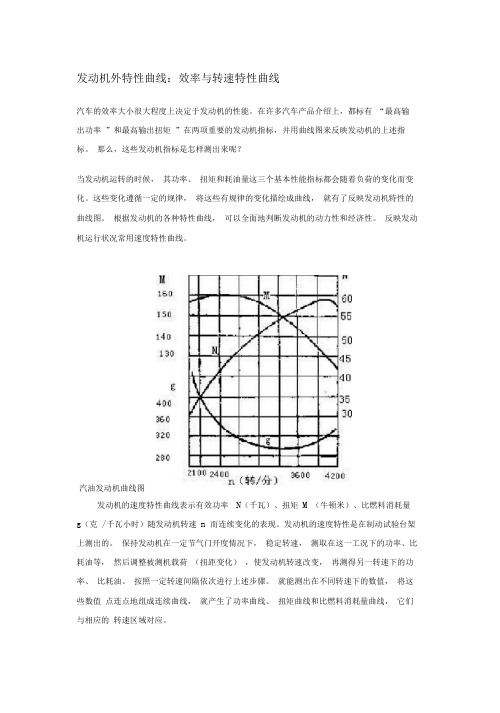
发动机外特性曲线:效率与转速特性曲线汽车的效率大小很大程度上决定于发动机的性能。
在许多汽车产品介绍上,都标有“最高输出功率”和最高输出扭矩”在两项重要的发动机指标,并用曲线图来反映发动机的上述指标。
那么,这些发动机指标是怎样测出来呢?当发动机运转的时候,其功率、扭矩和耗油量这三个基本性能指标都会随着负荷的变化而变化。
这些变化遵循一定的规律,将这些有规律的变化描绘成曲线,就有了反映发动机特性的曲线图。
根据发动机的各种特性曲线,可以全面地判断发动机的动力性和经济性。
反映发动机运行状况常用速度特性曲线。
汽油发动机曲线图发动机的速度特性曲线表示有效功率N(千瓦)、扭矩M (牛顿米)、比燃料消耗量g(克/千瓦小时)随发动机转速n 而连续变化的表现。
发动机的速度特性是在制动试验台架上测出的。
保持发动机在一定节气门开度情况下,稳定转速,测取在这一工况下的功率、比耗油等,然后调整被测机载荷(扭距变化),使发动机转速改变,再测得另一转速下的功率、比耗油。
按照一定转速间隔依次进行上述步骤。
就能测出在不同转速下的数值,将这些数值点连点地组成连续曲线,就产生了功率曲线、扭矩曲线和比燃料消耗量曲线,它们与相应的转速区域对应。
当汽油机节气门完全开启(或者柴油机喷油泵在最大供油量时)的速度特性,称为发动机的外特性,它表示发动机所能得到的最大动力性能。
从外特性曲线上可以看到发动机所能输出的最大功率、最大扭矩以及它们相应的转速和燃料消耗量,汽车产品介绍书上大都采用发动机外特性曲线图,但一般只标出功率和扭矩曲线。
发动机外特性曲线是在发动机最好的工作状态下能使发动机发出最大功率的情况下测出来的。
它表现的曲线特征是∶功率曲线和扭矩曲线都呈现凸形曲线,但两者表现是不一样的。
在汽油发动机外特性曲线中∶功率曲线在较低转速下数值很小,但随转速增加而迅速增长,但转速增加到一定区间后,功率增长速度变缓,直至最大值后就会下降,尽管此时转速仍会继续增长。
读懂汽车发动机特性曲线图
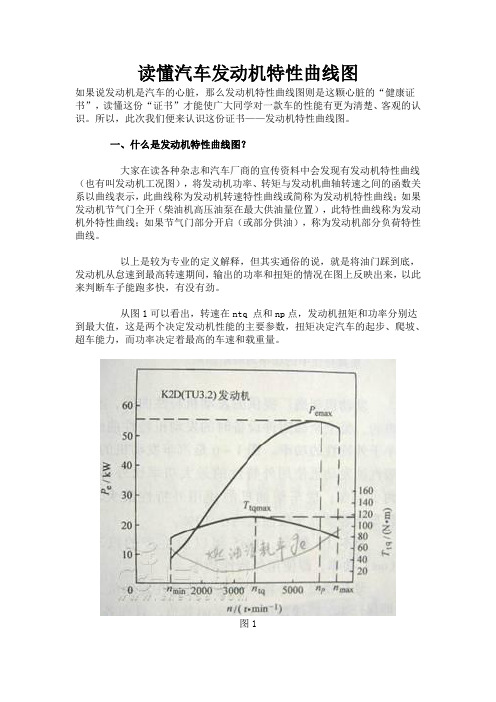
读懂汽车发动机特性曲线图如果说发动机是汽车的心脏,那么发动机特性曲线图则是这颗心脏的“健康证书”,读懂这份“证书”才能使广大同学对一款车的性能有更为清楚、客观的认识。
所以,此次我们便来认识这份证书——发动机特性曲线图。
一、什么是发动机特性曲线图?大家在读各种杂志和汽车厂商的宣传资料中会发现有发动机特性曲线(也有叫发动机工况图),将发动机功率、转矩与发动机曲轴转速之间的函数关系以曲线表示,此曲线称为发动机转速特性曲线或简称为发动机特性曲线;如果发动机节气门全开(柴油机高压油泵在最大供油量位置),此特性曲线称为发动机外特性曲线;如果节气门部分开启(或部分供油),称为发动机部分负荷特性曲线。
以上是较为专业的定义解释,但其实通俗的说,就是将油门踩到底,发动机从怠速到最高转速期间,输出的功率和扭矩的情况在图上反映出来,以此来判断车子能跑多快,有没有劲。
从图1可以看出,转速在ntq 点和np点,发动机扭矩和功率分别达到最大值,这是两个决定发动机性能的主要参数,扭矩决定汽车的起步、爬坡、超车能力,而功率决定着最高的车速和载重量。
图1二、如何由曲线图判断发动机性能那么怎样的发动机曲线才能代表发动机性能是较好的呢?让我们看图说话,从汽车的起步、超车和极速这3个方面分析。
起步加速能力图2拿到一张发动机曲线图,如图2,我们可以看到,扭矩在2000转的时候达到100Nm,升至3500转的过程中有一个快速的提升过程,而如果此区间内的斜线倾斜度越大,越光滑,则代表发动机可以用较短的时间达到扭矩的峰值,并且加速平稳线性,与此同时,功率也随转速的增加而增加。
在实际的驾车当中,随着我们踩第一脚油,汽车克服地面摩擦力,开始起步,随着发动机转速提高,汽车的扭矩会快速提升,一般的发动机在3000转左右来到扭矩峰值,而人们经常提及的“3000转换挡”的惯性操作,实际目的就是为了能够保持这个最大的牵引力,通过换挡,使发动机保持在最高扭矩转速附近,这样我们就可以用更短的时间提高车速。
汽车驱动力及发动机转矩曲线在python中拟合

汽车驱动力及发动机转矩曲线在python 中拟合确定汽车的动力性就必须掌握沿汽车行驶方向的作用于汽车的各种外力,即驱动力和行驶阻力,今天我们一起学习一下汽车的驱动力。
汽车的驱动力是由汽车发动机产生的转矩,经由传动系传至驱动轮上产生的。
汽车行驶时,作用于驱动轮上的转矩t T 产生一个对地面的圆周力0F ,地面对驱动轮的反作用力t F 即是驱动汽车的外力,称为汽车的驱动力,如下图所示。
rT t t =F公式中,t T 为作用于驱动轮的转矩,r 为车轮半径。
作用于驱动轮上的转矩t T 是由发动机产生的转矩经传动系传至驱动轮的,所以可以得到r i i T T 0g tq t η=F公式中tq T 表示发动机转矩,g i 表示变速器的传动比,0i 表示主减速器的传动比,T η表示传动系的机械功率。
在加速过程的不稳定工况下,发动机所能提供的功率比稳定工况时稍有下降,电喷汽油机比化油器汽油机要下降得更多些。
在进行动力性评估师,一般沿用稳态工况时发动里台架试验所得到的使用外特性中的功率和转矩曲线。
为了便于计算,常采用多项式来描述由试验台测得的,接近于抛物线的发动机转矩曲线。
主要是由最小二乘法来对数据进行拟合,拟合阶数K 随特性曲线而异,一般取值在2至5之间。
下面举一个例子,使用python 进行数据处理。
一款车,试验测得的转矩特性如下: 转速n1000 1500 2000 2500 3000 3500 3800 4000 转矩tq T 135 147 153 157 147 138 133 126 在python 中输入以下代码:import numpy as npimport matplotlib.pyplot as pltnum1= [1000,1500,2000,2500,3000,3500,3800,4000]x = np.array(num1)print('x is :\n',x)num2 = [135,147,153,157,147,138,134,126]y = np.array(num2)print('y is :\n',y)f1 = np.polyfit(x, y, 5)print('f1 is :\n',f1)p1=np.poly1d(f1)print("p1 is :\n",p1)xnew=np.arange(1000,4000,1)ynew=p1(xnew)plot1=plt.plot(x,y,'r*',label='original values')plot2=plt.plot(xnew,ynew,'b',label='polyfit values') plt.xlabel('n')plt.ylabel('Ttq')plt.title('engeneer')plt.legend()plt.show()按F5运行后即可得到以下输出:输出结果就包括了发动机转矩曲线拟合图像及拟合多项式的系数值。
Matlab程序模拟汽车理论中的数据特性图1
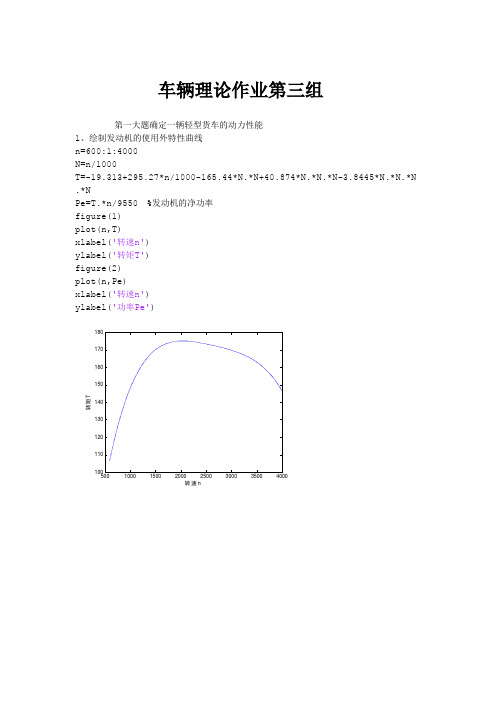
车辆理论作业第三组第一大题确定一辆轻型货车的动力性能 1、绘制发动机的使用外特性曲线 n=600:1:4000 N=n/1000T=-19.313+295.27*n/1000-165.44*N.*N+40.874*N.*N.*N-3.8445*N.*N.*N .*NPe=T.*n/9550 %发动机的净功率 figure(1) plot(n,T) xlabel('转速n') ylabel('转矩T') figure(2) plot(n,Pe) xlabel('转速n') ylabel('功率Pe')5001000150020002500300035004000100110120130140150160170180转速n转矩T5001000150020002500300035004000010203040506070转速n功率P e2、绘制驱动力---行驶阻力平衡图 i0=6.17; %减速器的传动比 ig(1)=6.09 % 一档的传动比 ig(2)=3.09 ig(3)=1.71 ig(4)=1.00 nT=0.85 r=0.367 f=0.013 m1=3880 m2=9590 CdA=2.77 Ff1=m1*9.8*f Ff2=m2*9.8*fft1=T*ig(1)*i0*nT/r %一档所产生的驱动力 ft2=T*ig(2)*i0*nT/r ft3=T*ig(3)*i0*nT/r ft4=T*ig(4)*i0*nT/r Ft=[ft1;ft2;ft3;ft4]';ua1=0.377*r*n/(ig(1)*i0) %一档的速度 ua2=0.377*r*n/(ig(2)*i0) ua3=0.377*r*n/(ig(3)*i0) ua4=0.377*r*n/(ig(4)*i0) ua=[ua1;ua2;ua3;ua4]';fw1=CdA*ua1.^2/21.15+Ff1 %一档的行驶阻力 fw2=CdA*ua2.^2/21.15+Ff1 fw3=CdA*ua3.^2/21.15+Ff1 fw4=CdA*ua4.^2/21.15+Ff1Fz1=[fw1;fw2;fw3;fw4]'; figure(3)plot(ua,Ft) %绘制各档的驱动力曲线hold onplot(ua,Fz1) %绘制行驶阻力曲线 hold onplot(ua4,Ff2) %绘制滚动阻力曲线 xlabel('ua/(km.h)')ylabel('F/N')title('汽车驱动力-行驶阻力平衡图')text(20,12000,'Ft1'); text(30,6000,'Ft2'); text(40,4000,'Ft3'); text(80,3000,'Ft4');text(90,2200,'(空载)Ff+fw'); text(105,1450,'满载Ff')102030405060708090200040006000800010000120001400016000ua/(km.h)F /N汽车驱动力-行驶阻力平衡图Ft1Ft2Ft3Ft4(空载)Ff+Fw满载Ff一档的驱动力很大,可用于爬坡且坡度较大;二档用于直接原地起步加速 3、绘制动力特性图D=(Ft-Fw)/(m1*9.8) %求动力因数f1=0.0076+0.000056*ua %一定车速条件下的滚动阻力 figure(4) plot(ua,D) hold onplot(ua,f1) text(20,0.3,'I') text(20,0.154,'II') text(40,0.1,'III') text(80,0.05,'IV') text(110,0.025,'f') title('汽车动力特性图') xlabel('ua/(km.h)') ylabel('D')1020304050607080900.050.10.150.20.250.30.350.40.45IIIIIIIVf汽车动力特性图ua/(km.h)DIf=0.218Iw1=1.798 Iw2=3.598die1=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(1).^2)/(m1*r^2);%一档的旋转质量换算系数die2=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(2).^2)/(m1*r^2); die3=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(3).^2)/(m1*r^2); die4=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(4).^2)/(m1*r^2); die=[die1;die2;die3;die4]';a1=9.8*D(:,1)/die1-9.8*f/die1; %求一档的加速度 a2=9.8*D(:,2)/die2-9.8*f/die2; a3=9.8*D(:,3)/die3-9.8*f/die3; a4=9.8*D(:,4)/die4-9.8*f/die4; aI=1./a1 %求一档的加速度倒数 aII=1./a2 aIII=1./a3 aIV=1./a4aa=[aI,aII,aIII,aIV]';figure(5) %绘制各档的加速度倒数曲线 plot(ua1,aI) hold on plot(ua2,aII) hold onplot(ua3,aIII) hold onplot(ua4,aIV)axis([5 99 0.01 10])10203040506070809012345678910aI aII aIIIaIV加速度倒数曲线ua/(km.h)1/a由图可知,加速度倒数没有交点,则可以在每档达到最大车速时换挡 nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=6.17;If=0.218; Iw1=1.798;Iw2=3.598;L=3.950;a=2.000;hg=0.9;m=3880;g=9.8; G=m*g; ig=[6.09 3.09 1.71 1.00 ]; nmin=600;nmax=4000; u1=0.377*r*nmin./ig/i0; u2=0.377*r*nmax./ig/i0;deta=0*ig; for i=1:4deta(i)=1+(Iw1+Iw2)/(m*r^2)+(If*(ig(i))^2*i0^2*nT)/(m*r^2); endua=[0:0.01:99];N=length(ua);n=0;Tq=0;Ft=0;inv_a=0*ua;delta=0*ua; Ff=G*f;Fw=CDA*ua.^2/21.15; for i=1:N k=i;if ua(i)<=u2(2)n=ua(i)*(ig(2)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000)^.4;Ft=Tq*ig(2)*i0*nT/r;inv_a(i)=(deta(2)*m)/(Ft-Ff-Fw(i)); delta(i)=0.01*inv_a(i)/3.6; elseif ua(i)<=u2(3)n=ua(i)*(ig(3)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4;Ft=Tq*ig(3)*i0*nT/r;inv_a(i)=(deta(3)*m)/(Ft-Ff-Fw(i)); delta(i)=0.01*inv_a(i)/3.6;else ua(i)<=u2(4)n=ua(i)*(ig(4)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft=Tq*ig(4)*i0*nT/r;inv_a(i)=(deta(4)*m)/(Ft-Ff-Fw(i)); delta(i)=0.01*inv_a(i)/3.6; enda=delta(1:k); t(i)=sum(a); endplot(t,ua,'b','LineWidth',2);axis([0 100 0 100]);title('四档汽车二档原地起步换挡加速时间曲线'); xlabel('时间t (s )');ylabel('速度ua (km/h )');1020304050607080901000102030405060708090100四档汽车二档原地起步换挡加速时间曲线时间t (s )速度u a (k m /h )第二大题n=600:1:4000 N=n/1000T=-19.313+295.27*n/1000-165.44*N.*N+40.874*N.*N.*N-3.8445*N.*N.*N .*NPe=T.*n/9550 figure(1) plot(n,T)text(1000,120,'转矩T') hold on plot(n,Pe)text(2000,20,'发动机净功率Pe')5001000150020002500300035004000020406080100120140160180转矩T发动机净功率Pei0=6.17; ig(1)=6.09 ig(2)=3.09 ig(3)=1.71 ig(4)=1.00 nT=0.85 r=0.367 f=0.013 m1=3880 m2=9590 CdA=2.77ua1=0.377*r*n/(ig(1)*i0) ua2=0.377*r*n/(ig(2)*i0) ua3=0.377*r*n/(ig(3)*i0) ua4=0.377*r*n/(ig(4)*i0); ua=10:1:100Pf=m1*9.8*f.*ua/(3600) Pw=CdA*ua.^3/(76140) figure(2) plot(ua1,Pe) hold on plot(ua2,Pe) hold on plot(ua3,Pe) hold onplot(ua4,Pe) hold onplot(ua,(Pf+Pw)/nT)010203040506070809010010203040506070评价:一二三档的后备功率都比较大,可在一定坡度的道路上直接启动加速; 在最高档达到最高车速时,n0=[815 1207 1614 2012 2603 3006 3403 3884]B00=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7] B10=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291] B20=[72.379 36.657 14.524 7.0035 4.4763 2.8593 2.9788 0.71113]B30=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215]B40=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230 -0.000038568] B0=spline(n0,B00,n) B1=spline(n0,B10,n) B2=spline(n0,B20,n) B3=spline(n0,B30,n) B4=spline(n0,B40,n)Pf3=m1*9.8*f.*ua3/(3600) Pw3=CdA*ua3.^3/(76140) Pf4=m1*9.8*f.*ua4/(3600) Pw4=CdA*ua4.^3/(76140) Ff1=m1*9.8*ffz3=CdA*ua3.^2/21.15+Ff1 fz4=CdA*ua4.^2/21.15+Ff1 %Pe3=fz3.*ua3./(3600*nT); %Pe4=fz4.*ua4./(3600*nT); Pe3=(Pf3+Pw3)/nTPe4=(Pf4+Pw4)/nTb3=B0+B1.*Pe3+B2.*Pe3.^2+B3.*Pe3.^3+B4.*Pe3.^4 b4=B0+B1.*Pe4+B2.*Pe4.^2+B3.*Pe4.^3+B4.*Pe4.^4Qs4=Pe4.*b4./(1.02*ua4*7.10*9.8) Qs3=Pe3.*b3./(1.02*ua3*7.10*9.8) figure(3)plot(ua4,Qs4) hold on plot(ua3,Qs3)01020304050607080901.41.61.822.22.42.62.8n=600:1:4000 N=n/1000T=-19.313+295.27*n/1000-165.44*N.*N+40.874*N.*N.*N-3.8445*N.*N.*N .*NPe=T.*n/9550 i0=6.17; ig(1)=6.09 ig(2)=3.09 ig(3)=1.71 ig(4)=1.00 nT=0.85 r=0.367 f=0.013 m1=3880 m2=9590 CdA=2.77ua1=0.377*r*n/(ig(1)*i0) ua2=0.377*r*n/(ig(2)*i0) ua3=0.377*r*n/(ig(3)*i0) ua4=0.377*r*n/(ig(4)*i0);n0=[815 1207 1614 2012 2603 3006 3403 3884]B00=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7] B10=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291]B20=[72.379 36.657 14.524 7.0035 4.4763 2.8593 2.9788 0.71113]B30=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215]B40=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230 -0.000038568]B0=spline(n0,B00,n)B1=spline(n0,B10,n)B2=spline(n0,B20,n)B3=spline(n0,B30,n)B4=spline(n0,B40,n)Pf3=m1*9.8*f.*ua3/(3600) %三档的滚动阻力功率Pw3=CdA*ua3.^3/(76140) %三档的的空气阻力功率Pf4=m1*9.8*f.*ua4/(3600)Pw4=CdA*ua4.^3/(76140)Ff1=m1*9.8*fPe3=(Pf3+Pw3)/nT %三档的发动机净功率Pe4=(Pf4+Pw4)/nT %四档的发动机净功率b3=B0+B1.*Pe3+B2.*Pe3.^2+B3.*Pe3.^3+B4.*Pe3.^4b4=B0+B1.*Pe4+B2.*Pe4.^2+B3.*Pe4.^3+B4.*Pe4.^4Qs4=Pe4.*b4./(1.02*ua4*7.10) %四档的百公里油耗Qs3=Pe3.*b3./(1.02*ua3*7.10) %三档的百公里油耗ua=[25 40 50]ss=[50 250 250]fz=CdA*ua.^2/21.15+Ff1 %匀速条件下的阻力Pee=fz.*ua/(3600*nT);b=spline(b4,Pe4,Pee) %匀速条件下的燃油消耗率Qsy=Pee.*b./(1.02*ua*7.10)a=[0.2 0.2 -0.36]dt1=1/(3.6*0.2)dt2=1/(3.6*0.2)dt3=1/(3.6*(0.36))ua11=25:1:40ua22=40:1:50ua33=50:-1:25b11=spline(ua4,b4,ua11) %在加速条件下的各个速度节点的燃油消耗率b22=spline(ua4,b4,ua22)b33=spline(ua4,b4,ua33)If=0.218Iw1=1.798Iw2=3.598die4=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(4).^2)/(m1*r^2);Pej1=(m1*9.8*f.*ua11/(3600)+CdA.*ua11.^3/(76140)+(die4*m1.*ua11/3600)*0.2)/nT %在三个加速条件下的各个速度节点Pej2=(m1*9.8*f.*ua22/(3600)+CdA.*ua22.^3/(76140)+(die4*m1.*ua22/3 600)*0.2)/nT %的发动机净功率Pej3=(m1*9.8*f.*ua33/(3600)+CdA.*ua33.^3/(76140)+(die4*m1.*ua33/3 600)*0.2)/nT %Qstj1=Pej1.*b11/(367.1*7.10) %在三中加速条件下的,各自的单位时间的燃油消耗量Qstj2=Pej2.*b22/(367.1*7.10)Qstj3=Pej3.*b33/(367.1*7.10)i11=size(Qstj1)i22=size(Qstj2)i33=size(Qstj3)i1=i11(2)i2=i22(2)i3=i33(2)Qt1=Qstj1(2:i1-1)Qt2=Qstj2(2:i2-1)Qt3=Qstj3(2:i3-1)q1=((Qstj1(1)+Qstj1(i1))*dt1./2+sum(Qt1)*dt1)/10q2=((Qstj2(1)+Qstj2(i2))*dt2./2+sum(Qt2)*dt2)/10q3=((Qstj3(1)+Qstj3(i3))*dt3./2+sum(Qt3)*dt3)/10Qall=(q1+q2+q3+Qsy(:,1)+Qsy(:,2)+Qsy(:,3))*100/1075q1 =5.8526q2 =4.9810 q3 =6.0186 Qall =2.7916第三大题(1)m0=4880; %空载质量m/kghg0=0.845; %空载质心高L0=3.95; %空载轴距a0=2.100; %空载质心至前轴距离m=9290; %满载质量m/kghg=1.170; %满载质心高L=3.95; %满载轴距a=2.950; %满载质心至前轴距离BB=0.38; %B为制动力分配系数g=9.8;G=m*g;b=L-a;G0=m0*g;b0=L0-a0;Fu1 =0:1000:100000;Fu2=1/2*(G/hg*(b^2+4*hg*L/G*Fu1).^0.5-(G*b/hg+2*Fu1));Fu02=1/2*(G0/hg0*(b0^2+4*hg0*L0/G0*Fu1).^0.5-(G0*b0/hg0+2*Fu1));F2=(1-B)*Fu1/B;plot(Fu1,Fu2) %绘制满载时的I曲线hold onplot(Fu1,Fu02) %绘制空载时的I曲线hold onplot(Fu1,F2); %%绘制beta曲线title('beta线和I曲线')text(30000,50000,'beta曲线')text(25000,10000,'空载时I曲线')text(25000,30000,'满载时I曲线')xlabel('Fu1')ylabel('Fu2')figure(2)fe=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9];for i=1:10Fxb1fk=0:100:120000;Fxb1rk=0:100:120000;Fxb2fk=(L0-fe(i)*hg0)/(fe(i)*hg0).*Fxb1fk-G0*b0/hg0;Fxb2rk=(-1*fe(i)*hg0)/(L0+fe(i)*hg0).*Fxb1rk+fe(i)*G0*a0/(L0+fe(i )*hg0);plot(Fxb1fk,Fxb2fk)hold onplot(Fxb1rk,Fxb2rk,'r')hold onendxlabel('Fxb1')ylabel('Fxb2')axis([0 120000 0 40000])title('空载时的f、r线组图')figure(3)for i=1:10Fxb1fk=0:100:220000;Fxb1rk=0:100:220000;Fxb2fk=(L-fe(i)*hg)/(fe(i)*hg).*Fxb1fk-G*b/hg;Fxb2rk=(-1*fe(i)*hg)/(L+fe(i)*hg).*Fxb1rk+fe(i)*G*a/(L+fe(i)*hg); plot(Fxb1fk,Fxb2fk)hold onplot(Fxb1rk,Fxb2rk,'r')hold onendxlabel('Fxb1')ylabel('Fxb2')axis([0 220000 0 80000])title('满载时的f、r线组图')012345678910x 104-2024681012141618x 104beta 线和I 曲线beta 曲线空载时I 曲线满载时I 曲线Fu1F u 2024681012x 10400.511.522.533.54x 104Fxb1F x b 2空载时的f 、r 线组图00.20.40.60.81 1.21.4 1.6 1.822.2x 105012345678x 104Fxb1F x b 2满载时的f 、r 线组图(2)-(3)m0=4880; %空载质量m/kghg0=0.845; %空载质心高L0=3.95; %空载轴距a0=2.100; %空载质心至前轴距离m=9290; %满载质量m/kghg=1.170; %满载质心高L=3.95; %满载轴距a=2.950; %满载质心至前轴距离BB=0.38; %B 为制动力分配系数g=9.8;G=m*g;b=L-a;G0=m0*g;b0=L0-a0;z=0:0.1:1; %制动强度fef=B*z*L./(b+z*hg);fef0=B*z*L0./(b0+z*hg0);fer=(1-B)*z*L./(a-z*hg);fer0=(1-B)*z*L0./(a0-z*hg0);figure(1)plot(z,fef,z,fef0,z,fer,z,fer0,z,z)text(0.8,1.5,'空车后轮')text(0.8,1.2,'满载后轮')text(0.7,0.6,'满载前轮')text(0.8,0.4,'空车前轮')figure(2)Ef=z./fef*100Ef0=z./fef0*100Er=z./fer*100Er0=z./fer0*100plot(fef,Ef,fer,Er)hold onplot(fef0,Ef0,fer0,Er0)axis([0 1 0 100])text(0.3,90,'Ef')text(0.8,90,'Er 满载')text(0.3,70,'Er 空载')00.10.20.30.40.50.60.70.80.9100.20.40.60.811.21.41.61.82空车后轮满载后轮满载前轮空车前轮00.10.20.30.40.50.60.70.80.910102030405060708090100Ef Er 满载Er 空载m0=4880;hg=0.845;l=3.950;a=2.100;b=1.850;beita=0.38;g=9.8;G0=m0*g ;m=9290;Hg=1.170;L=3.950;A=2.950;B=1.050;beita=0.38;g=9.8;G=m*g;t1=0.02;t2=0.02;ua0=30;fai=0.80;z=0:0.01:1.0;faifk=beita*z*l./(b+z*hg);faifm=beita*z*L./(B+z*Hg);fairk=(1-beita)*z*l./(a-z*hg);fairm=(1-beita)*z*L./(A-z*Hg);Efk=z./faifk*100;Efm=z./faifm*100;Erk=z./fairk*100;Erm=z./fairm*100;ak1=Erk(81)*g*fai/100;am1=Erm(81)*g*fai/100;Sk1=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*ak1);Sm1=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*am1);disp('空载时,汽车制动距离Sk1=');disp(Sk1);disp('满载时,汽车制动距离Sm1=');disp(Sm1);ak2=fai*g*a/(l+fai*hg);am2=fai*g*A/(L+fai*Hg);ak3=fai*g*b/(l-fai*hg);am3=fai*g*B/(L-fai*Hg);Sk2=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*ak2);Sm2=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*am2);Sk3=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*ak3);Sm3=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*am3);disp('空载时,前制动器损坏,汽车制动距离Sk2=');disp(Sk2);disp('满载时,前制动器损坏,汽车制动距离Sm2=');disp(Sm2);disp('空载时,后制动器损坏,汽车制动距离Sk3=');disp(Sk3);disp('满载时,后制动器损坏,汽车制动距离Sm3=');disp(Sm3);空载时,汽车制动距离Sk1=7.8668满载时,汽车制动距离Sm1=5.6354空载时,前制动器损坏,汽车制动距离Sk2=10.0061满载时,前制动器损坏,汽车制动距离Sm2=7.5854空载时,后制动器损坏,汽车制动距离Sk3=8.0879满载时,后制动器损坏,汽车制动距离Sm3=12.9629。
多项式函数拟合曲线

多项式函数拟合曲线
多项式函数拟合曲线是一种数学方法,用于通过已知数据点来拟合一个多项式函数,以便更好地描述数据点之间的关系。
多项式函数拟合曲线通常使用最小二乘法或其他优化算法来找到最佳拟合多项式。
在多项式函数拟合曲线中,首先需要选择一个多项式次数,然后使用最小二乘法或其他优化算法来找到最佳拟合多项式。
最小二乘法是一种数学优化技术,通过最小化误差的平方和来找到最佳拟合多项式。
多项式函数拟合曲线的应用非常广泛,例如在回归分析、数据预测、信号处理、控制系统等领域中都有应用。
通过拟合曲线,可以更好地理解数据点之间的关系,并预测未来的趋势和行为。
总之,多项式函数拟合曲线是一种重要的数学方法,可以帮助我们更好地描述数据点之间的关系,并预测未来的趋势和行为。
发动机速度特性曲线测试与分析(指导书)_工学_高等教育_教育专区

发动机速度特性曲线测试与分析(指导书)一、实验目的1、了解发动机测试台架及其装置的构造和工作原理,并掌握其使用方法2、了解发动机速度特性曲线的意义3、掌握发动机速度特性的测定方法4、掌握试验数据处理与速度特性曲线拟合的方法二、实验原理及方法1、发动机速度特性曲线的概念内燃机的速度特性,是指内燃机在油量调节机构(油量调节齿条、拉杆或节气门)保持不变的情况下,主要性能指标(转矩、油耗、功率、排气温度、烟度等)随内燃机转速的变化关系。
当油量调节机构固定在标定位置时,测得的特性为全负荷速度特性(简称外特性);油量低于标定位置时,测得的特性称为部分特性。
由于外特性反映了内燃机所能达到的最高动力性能,确定了最大功率、最大转矩以及对应的转速,因此在速度特性中最为重要。
内燃机在出厂时必须提供此特性。
2、发动机测试台架的工作原理和系统框图发动机测试台架是发动机性能试验的一种主要设备。
发动机测试台架需要完成动力性、经济性相关特性的测试;也需要为被测发动机提供一个标准的测试条件。
台架由各种传感器和测试仪器组成。
测功机控制电路基本原理是将测功机的转速实际值与可调的设定值进行比较,比较后的差值经过PID放大器放大,用于调节涡流制动器的励磁电流,从而改变发动机的转速,使其等于设定值。
3、发动机速度特性测试方法在发动机试验台架上,运行发动机,使发动机油温、水温和油压等参数达正常值。
保持节气门或油门开度固定不变,调整测功机负荷, 使转速达到预定值, 测量计算G T 、g e 、Ne 和Me,在特性曲线图上标出该点。
再调节测功机负荷,使转速达到第二个预定值, 再测量计算G T 、g e 、Ne 和Me,并在特性曲线图上标出该点… 将所有点用一条光滑曲线连接。
4、数据处理方法运用最小二乘法对实验数据进行拟合(取5~8个点),按拟合结果绘制光滑的特性曲线。
三、实验仪器和设备1、电涡流测功机电涡流测功机的主机是一台电涡流制动器,主要由转子部分,摆动部分和固定部分组成, 如图。
基于MATLAB语言的发动机万有特性曲线的绘制

基于MATLAB语言的发动机万有特性曲线的绘制
黄美美;赵志伟;靳华磊;贾延涛;孙海鹏
【期刊名称】《现代制造技术与装备》
【年(卷),期】2011(000)005
【摘要】利用MATLAB语言的强大的数据处理和绘图功能,在建立发动机万有特性曲线曲面拟合数学模型的基础上,运用其矩阵运算、三维绘图等功能,进行曲线、曲面拟合,绘制了万有特性曲线.该方法具有数据处理精度高、明显直观和实用性强等优点.
【总页数】2页(P19,24)
【作者】黄美美;赵志伟;靳华磊;贾延涛;孙海鹏
【作者单位】山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100
【正文语种】中文
【相关文献】
1.基于MATLAB语言的发动机万有特性研究 [J], 关志伟;杨玲;施继红;吴明
2.基于Matlab语言的液压特性曲线的绘制 [J], 陈立胜;李业庆
3.汽车发动机万有特性曲线簇计算机绘制算法 [J], 彭炜;李志中;段明磊
4.基于MATLAB的发动机万有特性曲线绘制方法 [J], 周广猛;郝志刚;刘瑞林;陈东;管金发;张春海
5.多项式插值法绘制发动机万有特性曲线 [J], 李小华;罗福强;汤东
因版权原因,仅展示原文概要,查看原文内容请购买。
汽车发动机万有特性曲线簇计算机绘制算法

因而, 三次 B样条 曲线矢量方 程可表示
为I
CI . . ( u ) =N1 . . ( u ) P i l + N2 . ‘ ( u ) Pi + N3 , 4 ( u ) P i 十 1 +N‘ , ‘ ) P { + 2
( 4 )
至此, 所有的 Mj 均已求得。
2 . 2 . 2 最优逼近 曲线
对象 , 采用本文后面的传统 B样条曲线拟和
方式. 拟和 的 曲线在节 点容 易 出现奇 异性 , 从 图 形 上看就 是 曲线 两 次 经过 同一 节点 处 , 即
其中, X 一 i  ̄X<X j , h j =】 【 j -Xj 一 1 , j =1 ,
2, … … , N。
“ 打折 , 这样的情况必须避免 。 本 文 处理 方法 是 以 节 点作 为 特 征 , 多边 形控翩点构造二阶导数连续的 B样条曲线 。 若从空间 n + 1个顶 点 P i O;0 , 1 , …n ) 中选取 相 邻 的 四个 硬点 , 可 构造 出一段 三 次 B样条 曲线 , 其相 应 的基 函数 是 :
油耗 ) 。
x轴代表转速 , Y轴代表扭矩 , z代表油
移动 式试车 线在 我 国单缸 柴 油机试 车 中 的 真正 使用 , 仅 有一 年 多的 时问 , 其突 出的优 越 性 已赢 得 生产 厂 家 的 信赖 , 并 在 行 业 中 引 起 很大 反 响 。随着 它在 生 产实践 和使 用过 程 中 的 不 断改进 和提 高 , 必 将 显 示 出强 大 的 生 命力。 在 多缸 汽 油机 和柴 油机的 出厂试 验 中 , 这 种移 动式 试车 线 也必将 会占有 一席 之地
・21 ・
若i , j 的高 度值 不 等 , 则当f <O时 , 等 值 线 必 与 棱 边 有 唯 一 交 点 ; 当f >o , 两 者 无 交点 I 而当 f 一0时 , 等值 线过 节点 i 或j , 见 图 2 。值得 注意 的是 , f =O的情 形 极易 引起后 面
基于Matlab的发动机与液力变矩器匹配特性计算

基于Matlab的发动机与液力变矩器匹配特性计算王向东;李智;吴金才【摘要】发动机与液力变矩器匹配是否合理对动力系统工作性能有着重要影响.论文采用Matlab软件对发动机与液力变矩器匹配计算过程进行了详细说明,并绘制了二者共同工作的输出特性图.【期刊名称】《机电产品开发与创新》【年(卷),期】2017(030)002【总页数】4页(P43-46)【关键词】Matlab;发动机;液力变矩器;匹配特性【作者】王向东;李智;吴金才【作者单位】中国人民解放军96658部队,北京100094;中国人民解放军96658部队,北京100094;中国人民解放军96658部队,北京100094【正文语种】中文【中图分类】TP391.7由于液力变矩器具有良好的适应性,在重型载重汽车、各种工程机械、船舶等方面有着广泛的应用。
液力变矩器作为发动机动力输出路径中关键环节,其与发动机性能匹配的好坏,直接影响车辆的动力性、经济性等。
发动机与液力变矩器匹配后,可以看作是一种新的动力装置,好的匹配方案能够充分发挥二者各自的优点,从而达到良好的整机性能。
本文采用Matlab软件,并利用实例对发动机与液力变矩器的匹配过程进行计算,绘制匹配后的整机输出特性图。
根据汽车理论相关知识,发动机外特性是指节气门全开时发动机功率、扭矩、以及燃油消耗率与发动机转速之间的关系。
发动机外特性通常在试验台架上测得,即每隔一定转速测测量发动机的输出扭矩、油耗等,并将测得的数据进行拟合,从而得到发动机外特性曲线。
本文中以发动机外特性中的转矩特性为例介绍匹配计算过程,其他特性的计算过程可参照此方法进行。
发动机外特性中的转矩特性拟合通常采用多项式描述,即:式中,系数a0、a1、a2……ak可由最小二乘法确定;拟合的阶数k随发动机外特性曲线而异,一般在2,3,4,5中选取。
(1)液力变矩器外特性。
液力变矩器的外特性是指在泵轮转速nB不变、工作油一定和油温一定的条件下,泵轮转矩MB、涡轮输出转矩-MT以及效率η等与涡轮转速nT之间的关系。
用origin软件绘制发动机万有特性曲线

用origin软件绘制发动机万有特性曲线方法一、万有特性数据输入在excel中整理好发动机万有特性数据,主要包括发动机转速、扭矩、燃油消耗率及功率数据。
打开origin,将excel中整理好的数据直接复制粘贴到Book1中即可,可以在左下方的信息栏对Book1进行重命名。
origin中表格操纵与excel中类似。
可以编辑数据的名称、单位、备注等信息,也可空着以后再绘制好的图表上修改。
同时选中燃油消耗率和功率数据两列,点右键选择Set as Z,也可以在Column菜单下点选Set as Z,如下图所示。
二、绘制万有特性曲线选中表格中所有数据列表,在绘图命令菜单Plot下绘制等高线命令Contour的颜色填充Color Fill选项,将出现图表窗口,如下图所示。
三、万有特性曲线图调整上一步完成的万有特性曲线只是一个雏形,与常见的还很不一样,需要进行调整细化。
在已绘制好的万有特性曲线图中,由于点选的是颜色填充的绘制方法,数据源有两组Z轴分量,相当于在一张图上绘制了两层,而等燃油消耗率曲线在等功率曲线的下方,被覆盖住无法看到。
因此,需要取消等功率曲线图层的颜色填充效果。
如图所示,在图片窗口左上角的1上右击,选择图层属性Layer Properties命令,在弹出的对话框中打开图层Layer1的下一级,选中转速、扭矩、功率曲线,并去掉Color Fill Control下Enabled之前的勾选,即可取消等功率曲线图层的颜色填充效果。
等燃油消耗率曲线还需要进行进一步的调整,才能变成最常见的样子。
需要调整曲线的层次间隔,让等值曲线分布的疏密合理,还要加上等值线的数据标注,以便于观看查阅。
同样是在图层属性对话框里,选中转速、扭矩、燃油消耗率曲线,在列标题或单元格编辑表格中,单击列标题或单元格可以完成曲线的层次、填充颜色、层次线型及添加数据标注的修改。
如图所示,单击Level栏表头,弹出Set Level设置层次对话框,先点击find min/max命令,找到燃油消耗率的最小值与最大值,并自动设置为等值曲线变化范围,选择线性变化,并选中增量increment选项,设置增量值为1,既让等燃油消耗率曲线从184.5g/kw.h开始,每隔1g/kw.h就绘制一条,直至367g/kw.h结束,一共183条。
基于Matlab的发动机特性研究

a
=
arcsin(
Fi ma g
)
,从
图
1
可
知,
YC6J190-33 发动机时汽车最大车速是 87km/h,I 档最大爬
坡度 ilmax=57.9%,最大爬坡角 almax=30.08。;由图 2 可知,康
明斯 ISBE4+225 发动机时汽车最大车速是 90km/h,I 档最大
Polyval、Polytool、Polyconf 等函数均可对上述曲线拟合。 转 矩(332.156N•m)初 选 玉 柴 YC6J190-33 发 动 机、康 明 斯
ISBE4+225 发动机与德国曼 D0836LFL 发动机,通过其模拟曲
51
理论与算法
2019.08
线图,分别对发动机的转矩特性以及比油特性进行计算,借 助 Matlab 对多项式进行拟合,得出三种发动机的转矩和比油 特性拟合曲线。 2.1 动力性能计算
Research on Engine Characteristics Based on Matlab
Yuan Jian (BYD automobile industry co., LTD.,Shenzhen Guangdong,518118)
Abstract: In this paper, the engine’s external characteristic curve is drawn by using matlab, and the engine’s different torque characteristics and specific fuel consumption characteristics are obtained, and the quadratic polynomial fitting is carried out. The results show that the selected engine has better matching performance. Key words:matlab;engine;characteristics;comparative analysis
发动机速度特性曲线测试与分析(指导书)
发动机速度特性曲线测试与分析(指导书)一、实验目的1、了解发动机测试台架及其装置的构造和工作原理,并掌握其使用方法2、了解发动机速度特性曲线的意义3、掌握发动机速度特性的测定方法4、掌握试验数据处理与速度特性曲线拟合的方法二、实验原理及方法1、发动机速度特性曲线的概念内燃机的速度特性,是指内燃机在油量调节机构(油量调节齿条、拉杆或节气门)保持不变的情况下,主要性能指标(转矩、油耗、功率、排气温度、烟度等)随内燃机转速的变化关系。
当油量调节机构固定在标定位置时,测得的特性为全负荷速度特性(简称外特性);油量低于标定位置时,测得的特性称为部分特性。
由于外特性反映了内燃机所能达到的最高动力性能,确定了最大功率、最大转矩以及对应的转速,因此在速度特性中最为重要。
内燃机在出厂时必须提供此特性。
2、发动机测试台架的工作原理和系统框图发动机测试台架是发动机性能试验的一种主要设备。
发动机测试台架需要完成动力性、经济性相关特性的测试;也需要为被测发动机提供一个标准的测试条件。
台架由各种传感器和测试仪器组成。
测功机控制电路基本原理是将测功机的转速实际值与可调的设定值进行比较,比较后的差值经过PID放大器放大,用于调节涡流制动器的励磁电流,从而改变发动机的转速,使其等于设定值。
3、发动机速度特性测试方法在发动机试验台架上,运行发动机,使发动机油温、水温和油压等参数达正常值。
保持节气门或油门开度固定不变,调整测功机负荷, 使转速达到预定值, 测量计算G T 、g e 、Ne 和Me,在特性曲线图上标出该点。
再调节测功机负荷,使转速达到第二个预定值, 再测量计算G T 、g e 、Ne 和Me,并在特性曲线图上标出该点… 将所有点用一条光滑曲线连接。
4、数据处理方法运用最小二乘法对实验数据进行拟合(取5~8个点),按拟合结果绘制光滑的特性曲线。
三、实验仪器和设备1、电涡流测功机电涡流测功机的主机是一台电涡流制动器,主要由转子部分,摆动部分和固定部分组成, 如图。
[汇总]利用多项式拟合获得汽车发动机外特性曲线的几种方法
![[汇总]利用多项式拟合获得汽车发动机外特性曲线的几种方法](https://img.taocdn.com/s3/m/dc96a1342e60ddccda38376baf1ffc4ffe47e28e.png)
利用多项式拟合获得汽车发动机外特性曲线的几种方法发动机外特性是汽车动力性计算的主要依据,基本车型的发动机外特性应由制造厂提供。
发动机外特性为非线形曲线,通过多项式拟合的方法可以获得描述发动机外特性的数学方程。
已有研究结果证明标明再工程应用上采用二次方程来描述汽车发动机外特性已具足够精度,即2e e e T an +bn c =+ (1-1)式中:e T ——发动机输出扭矩,N m ;e n ——发动机输出转速,r min 。
式(1-1)中系数a ,b ,c 可以由外特性确定,获得途径有多少种: 1.多点拟合法如果已知发动机外特性确定曲线N 个点(ei ei n ,T ),i=1,2,3,……,N,则利用最小二乘法可以获得系数a,b,c 的估计值,令:()()22NN2ei ei ei ei i 1i 1eE T T an+bn c T ===-=+-∑∑由()()()N22ei ei ei ei i 1N 2ei ei ei ei i 1N 2ei ei ei i 1E2an +bn c T n 0aE 2an +bn c T n 0a E 2an +bn c T 0a ===⎫∂=+-=⎪∂⎪⎪∂=+-=⎬∂⎪⎪∂=+-=⎪∂⎭∑∑∑ (1-2)得 N N N N4322ei ei ei ei ei i 1i 1i 1i 1N N N N32ei ei ei ei ei i 1i 1i 1i 1N N N2ei ei ei i 1i 1i 1n a n b n c T n n a n b n c T n n a n b N c T ===========⎫⎛⎫⎛⎫⎛⎫++=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪⎪⎛⎫⎛⎫⎛⎫⎪++=⎬ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪⎪⎛⎫⎛⎫⎪++= ⎪ ⎪⎪⎝⎭⎝⎭⎭∑∑∑∑∑∑∑∑∑∑∑(1-3)解此线性方程组,即可以求出系数a,b 和c 。
2.三点插值法如果已知发动机外特性曲线上的三个点(ei ei n ,T ),i=1,2,3,则利用拉格朗日插值法可以求出系数a,b 和c 。
MATLAB曲线拟合在发动机特性拟合中的应用

MATLAB曲线拟合工具箱在发动机特性拟合中的应用摘要:详细介绍了MA TLAB的曲线拟合工具箱(Curve Fitting Toolbox)的GUI交互式图形界面和函数调用两种方式的使用方法,并以某柴油发动机稳态工况下的试验数据绘制万有特性图为例,介绍了利用曲线拟合工具箱进行曲面拟合的步骤和方法,并给出了关键代码。
对拟合结果的数理统计校验表明,拟合结果完全符合要求。
结果表明,MA TLAB的曲线拟合工具箱为发动机特性的曲面拟合提供了极大的便利。
主题词:发动机特性,曲面拟合,多元回归,曲线拟合工具箱中图分类号: TK421 文献标识码:AApplication of MATLAB Curve Fitting Toolbox on Engine Characteristic Maps FittingAbstract:The usage of MATLAB Curve Fitting Toolbox GUI mode and function mode is detailed introduced. The procedures and method of surface fitting employ Curve Fitting Toolbox are demonstrated with the universal characteristic map plotting of a diesel engine steady state test data. Key codes are provided also. The statistics results show that the fitting accuracy is very high. The results prove that MATLAB Curve Fitting Toolbox can provide much convenience to the surface fitting of engine characteristics.Key Words:Engine Characteristic Map, Surface Fitting, Multiple Regression, Curve Fitting Toolbox引言根据发动机稳态工况下的性能试验数据绘制转速特性、负荷特性和万有特性曲线的过程较为繁琐,工作量较大,目前一般应用计算机编制程序对大量的试验数据进行处理,从而得到万有特性曲线[1] ;尤其是MA TLAB 软件,因其强大的数值计算和绘图功能,越来越广泛的被应用于发动机万有特性的研究[2,3,4]。
发动机数学模型

第七章发动机性能数学模型 (100)7.1 数学模型的内容、分类和建模方法 (100)7.2 发动机稳态性能数学模型 (101)7.2.1用总体法建立的I级性能模型 (101)7.2.2用部件法建立的II级性能模型 (101)7.2.2.1气体热力性质 (102)7.2.2.2部件特性及其出口气流参数计算 (103)7.2.2.3确定共同工作点 (106)7.2.2.4确定发动机推力、耗油率和燃油流量 (108)7.3 发动机过渡态性能数学模型 (108)第七章 发动机性能数学模型7.1 数学模型的内容、分类和建模方法数学模型是根据设计任务和优化课题建立起来的产品设计参数与性能参数之间的数学关系。
不同的设计对象和设计任务,具有不同的设计参数和性能参数,它们的数学模型也将完全不同。
例如,优化压气机流路形状时,设计参数是流路尺寸,性能参数是压气机特性和压气机质量,它的数学模型是由已知流路的尺寸和设计要求而能求得压气机特性和质量的计算方法组成。
又例如,优化涡轮盘型面时,要求在满足给定应力限制的条件下使涡轮盘的质量最轻,这时设计参数为涡轮盘型面尺寸,目标参数为涡轮盘质量,应力限制为约束,数学模型是涡轮盘型面尺寸和涡轮盘质量、应力之间的数学关系。
在发动机设计中,发动机的主要设计参数是发动机类型、发动机循环参数、空气流量、控制方案、进气道和喷管类型、进气道和喷管的主要几何参数和控制方案。
主要性能参数是推力、装耗油率、最大直径、最大长度、发动机重量、噪声级水平和成本等。
因此发动机数学模型应由这样一些计算方法组成,它们可以根据进气道、发动机、喷管的设计参数求得发动机性能参数。
本章将系统介绍在工程上广泛应用的发动机稳态和过渡态性能数学模型。
由于发动机的复杂性,它的数学模型也很复杂,相应的计算机程序将占有相当大的内存,运行机时较长,因此要求发动机数学模型和程序既能正确反映发动机性能、重量、尺寸和设计参数之间的关系,又能计算迅速和占用内存少。
基于LabVIEW的发动机万有特性曲线建立

基于LabVIEW的发动机万有特性曲线建立施水娟;李文文【摘要】发动机万有特性图通常包括等油耗曲线和等功率曲线.采用LabVIEW 2011编程,先通过ActiveX控件读取Excel文件中的试验数据.然后构造曲面网格,利用Biharmonic Spline二维离散点插值方法拟合三维曲面.最后,采用Contour Line.vi绘制等高线水平可定义的等油耗曲线和等功率曲线(二维等高线图),并由三次样条插值得到的外特性曲线和坐标轴构成的多边形边界删除等油耗曲线和等功率曲线的界外点,成功建立万有特性曲线.【期刊名称】《微型机与应用》【年(卷),期】2016(035)015【总页数】4页(P14-17)【关键词】Excel读取;二维离散点插值;等高线图绘制;万有特性曲线【作者】施水娟;李文文【作者单位】南通职业大学汽车与交通工程学院,江苏南通226007;中国一汽无锡油泵油嘴研究所,江苏无锡214063【正文语种】中文【中图分类】U467.2发动机试验需要离线处理的数据包括负荷特性数据(功率、比油耗、气体排放、烟度等)、外特性数据(转速、扭矩、比油耗、烟度、排温、进气量、充气效率、空燃比等)、万有特性数据和其他相关试验数据。
万有特性曲线反映的是在不同发动机转速和负荷下的油耗率,主要包括等油耗曲线和等功率曲线,根据需要还可以画出等过量空气系数等曲线[1] 。
周广猛等人利用MATLAB及其拟合方法绘制了万有特性曲线[2]。
鉴于虚拟仪器技术在发动机测试领域的广泛应用,本文利用NI LabVIEW软件实现了发动机万有特性曲线的建立。
主要涉及了基于LabVIEW的试验数据读取、二维离散点的网格生成和曲面插值、外特性曲线的建立等内容,可作为发动机数据采集系统离线数据处理的子模块。
目前,大多数发动机台架保存的试验数据为Excel格式数据文件。
本文采用Excel 2007提供的Microsoft Excel 12.0 Object Library Version 1.6 ActiveX控件和LabVIEW编写的有限状态机来读取文件中的试验数据。
发动机性能试验数据处理方法的研究

-40.5198+0.11423 N e=
1233.26-0.73411
n -3.82766 n;
× 10-5 n2, n ≤ 1530 n >1530
695.69-0.6243 ge =
-8952.6+5.6529
n +2.3627 n,
× 10-4 n2, n ≤ 1610 n >1610
机型在正常情况下性能指标的变化情况。 由拟合所 得方程可以求解整机特征值。
图 1 调速特性曲线
Fig.1 The governing characteristics curve
5 结 论
参数变化规律的依据; 2) 利用坐标平移对原观测数据进行适当变换能
用计算机对发动机性能试验数据进行处理、拟 减小计算机运算的舍入误差;
续, 相邻两段的多项式在分界点上的函数值必须相
等, 且要求 qj 阶导数也相等 (qj < p j )。
最小二乘法的关键是确定多项式系数 bji, 使根 据拟合的多项式算出的 yδ 值与相应的各试验点的 y
值之间差值的平方和 (残差平方和)w 为最小, 即
n
∑ m in w =
yδi - y i 2。
我国国标 (GB1105-74 ) 规定标准大气状况, 对 陆用内燃机为环境温度 20 ℃, 大气压力为 101.325 kPa (760 mmHg ) , 相对湿度为 60% 。 [6]
如果试验时大气状况与标准状况不符合, 对于 柴油机其功率和燃油消耗率应按下列规定进行换
算。
N e0 = N e C ,
据有效位数超过机内能表示的最多位数时, 由于计 压 (kPa ) ; T 为环境温度 (K) ; Υ为相对湿度 (% ) ; pw
python多条曲线拟合方法

python多条曲线拟合方法在数据分析和科学研究中,经常需要使用曲线拟合的方法来描述两个变量之间的关系。
Python作为一种强大的编程语言,提供了多种曲线拟合的方法,使得这一过程变得简单而有效。
本文将介绍几种在Python中进行多条曲线拟合的方法。
一、曲线拟合的基本概念曲线拟合是通过选择合适的数学模型来描述两个变量之间的关系。
通过拟合一系列数据点,我们可以得到最佳的模型参数,从而更好地理解数据的特点和趋势。
Python提供了许多用于曲线拟合的库,如scipy和numpy等。
这些库提供了丰富的函数和方法,可以方便地进行曲线拟合。
三、多项式拟合多项式拟合是最基本的一种曲线拟合方法,通过选择不同的多项式阶数(如1次、2次、3次等)来描述数据。
在Python中,可以使用SciPy库中的polyfit函数进行多项式拟合。
示例代码:```pythonimport numpy as npfrom scipy.optimize import curve_fitimport matplotlib.pyplot as plt# 生成示例数据x = np.linspace(0, 10, 50)y = 3 * x**2 + 2 * x + 1 + np.random.randn(x.shape[0]) * 0.5 # 生成带有噪声的数据# 进行多项式拟合popt, pcov = curve_fit(np.poly1d, x, y)# 输出拟合结果print("拟合多项式为:", popt[0](x))```四、非线性拟合非线性拟合是更为复杂的一种曲线拟合方法,需要选择合适的非线性函数模型来进行拟合。
在Python中,可以使用SciPy库中的curve_fit_online函数进行非线性拟合。
示例代码:```pythonimport numpy as npfrom scipy.optimize import curve_fit_onlineimport matplotlib.pyplot as plt# 生成示例数据x = np.linspace(0, 10, 50)y = np.exp(-x / 5) * (1 + np.sin(2 * np.pi * x / 10)) # 带有非线性项的数据# 进行非线性拟合popt, pcov, r, t, p = curve_fit_online(f=exp_sin_func, x=x, y=y)# 输出拟合结果print("拟合结果:", popt)```其中,exp_sin_func是自定义的非线性函数模型,可以根据具体需求进行编写。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用多项式拟合获得汽车发动机外特性曲线的几种方法
发动机外特性是汽车动力性计算的主要依据,基本车型的发动机外特性应由制造厂提供。
发动机外特性为非线形曲线,通过多项式拟合的方法可以获得描述发动机外特性的数学方程。
已有研究结果证明标明再工程应用上采用二次方程来描述汽车发动机外特性已具足够精度,即
2
e e e T an +bn c =+ (1-1)
式中:e T
——发动机输出扭矩,N m ;
e n ——发动机输出转速,r min 。
式(1-1)中系数a ,b ,c 可以由外特性确定,获得途径有多少种: 1.多点拟合法
如果已知发动机外特性确定曲线N 个点(ei ei n ,T ),i=1,2,3,……,N,则利用最小二乘法可以获得系数a,b,c 的估计值,令:
()()
2
2
N
N
2
ei ei ei ei i 1
i 1
e
E T T an
+bn c T ===
-=
+-∑∑
由
()()(
)
N
22
ei ei ei ei i 1
N 2
ei ei ei ei i 1N 2
ei ei ei i 1E
2an +bn c T n 0a
E 2an +bn c T n 0a E 2an +bn c T 0a ===⎫∂=+-=⎪∂⎪
⎪∂=+-=⎬∂⎪
⎪∂=+-=⎪∂⎭∑∑∑ (1-2) 得
N N N N
4322
ei ei ei ei ei i 1i 1i 1i 1N N N N
32ei ei ei ei ei i 1i 1i 1i 1N N N
2ei ei ei
i 1i 1i 1n a n b n c T n n a n b n c T n n a n b N c T ===========⎫⎛⎫⎛⎫⎛⎫
++=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭
⎪
⎪⎛⎫⎛⎫⎛⎫⎪
++=⎬
⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪
⎪⎛⎫⎛⎫
⎪++= ⎪ ⎪⎪⎝⎭⎝⎭⎭∑∑∑∑∑∑∑∑∑∑∑ (1-3) 解此线性方程组,即可以求出系数a,b 和c 。
2.三点插值法
如果已知发动机外特性曲线上的三个点(ei ei n ,T ),i=1,2,3,则利用拉格朗日插值法可以求出系数a,b 和c 。
拉格朗日插值三项式可以写成
()()
()()
()()
()()
()()
()()
e
e2e e3e
e1e e3e
e1e e2e1
e2e1e3e2
e1e2e3e3
e1e3e2e e1
e2
e3
n n n n n n n n n n n n T T T T n
n n n n
n n n n
n n n ------=++------ (1-4)
由式(1-1)和(1-4)可以得
()()()()()()()()()()()()()()()()()()()()e1e2e1e3e2e1e2e3e3e1e3e2e2e3e1e3e1e2e1e2e1e3e2e1e2e3e3e1e3e2e2e3e1e3e1e2e1e2e1e3e2e1e2e3e3e1e e1
e2
e3
e1e2e3e1e2e3
T T T a n n n n n n n n n n n n n n T n n T n n T b n n n n n n n n n n n n n n T n n T n n T c n n n n n n n n n n n =
+
+
------+++=---------=+-
-----()3e2n ⎫
⎪⎪
⎪⎪
⎬
⎪
⎪
⎪⎪-⎭
(1-5)
3.经验公式
如果仅仅知道发动机的最大输出功率,最大输出转矩及其相应的转速,常用下列经验公式描述发动机的外特性:
()
()2
T e 2
T
P em p
e em T T T T n n n
n -=-
-- (1-6)
式中:em T —发动机最大输出转矩N m ;
T n ——发动机最大输出转矩时的曲轴转速,r min ; P
n ——发动机最大输出功率时的曲轴转速,r min ; p
T ——发动机最大输出功率时的输出转矩,N m ;
em P
p p T 9549
n =,
em
P 为发动机最大输出功率,kW 。
由式(1-1)和式(1-6)可得:
()()()
()2
T P T 2
T P 2T 2
T P em p
em p em p em T T a n n 2n T T b n n T T c T n n n ⎫
-+=⎪⎪-⎪⎪-⎪
=⎬-⎪⎪
-⎪
=-⎪-⎪⎭
(1-7) 在以上介绍的三种确定系数a,b,c 的方法中,三点插值法既有较高是精度,其计算也比较简单。
应该指出的是技术文件中给出的发动机外特性曲线是台架试验测量出来的,
台架试验室时发动机处于相对稳定工况,且为带来风扇,水泵分、等附件,因此对台架试验数据用修正系数μ加以修正,才能得到发动机使用外特性。
各国的台架试验所执行的标准不同,故修正系数μ的取值也不同。
按SAE标准试验(美法意)μ=0.81~0.84
按BS标准试验(英)μ=0.83~0.85
按GB标准试验(中)μ=0.85~0.91
按JIS标准试验(日)μ=0.88~0.91
按DIN标准试验(德)μ=0.90~0.92。
