高一数学填空题
高一数学试题及答案免费

高一数学试题及答案免费一、选择题(每题3分,共30分)1. 下列哪个选项不是实数?A. πB. -2C. √2D. i2. 函数f(x) = x^2 + 2x + 1的最小值出现在x等于:A. -1B. 0C. 1D. 23. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∪B的结果:A. {1, 2, 3}B. {1, 2, 3, 4}C. {2, 3}D. {1, 4}4. 以下哪个不等式是正确的?A. |-3| > |3|B. |-3| < |3|C. |-3| = |3|D. |-3| ≠ |3|5. 若a > b > 0,c < d < 0,下列哪个选项是正确的?A. ac > bdB. ac < bdC. ad > bcD. ac = bd6. 已知等差数列的首项a1 = 3,公差d = 2,求第5项a5的值:A. 9B. 11C. 13D. 157. 圆的半径为5,圆心到直线的距离为3,求圆与直线的位置关系:A. 相离B. 相切C. 相交D. 直线过圆心8. 函数y = sin(x) + cos(x)的最大值出现在x等于:A. 0B. π/4C. π/2D. π9. 已知三角形ABC,若∠A = 60°,∠B = 45°,求∠C的度数:A. 75°B. 120°C. 45°D. 30°10. 下列哪个是二次方程的判别式?A. b^2 - 4acB. b^2 + 4acC. a^2 - b^2D. a^2 + b^2二、填空题(每题2分,共20分)11. 若a + b = 10,且a - b = 2,则a = ______,b = ______。
12. 一个正六边形的内角和为________。
13. 一个圆的周长为44cm,其半径为________。
高一上《1-4章》数学基础知识填空题

数学基础知识训练题1(集合部分)1.集合{0,1,2}的子集有,真子集有 .2.已知A={不大于3的自然数},U={0,1,2,3,4,5},则C U A= .3.已知A={a,b,c,d,e,f },B={b,d,e,g },则A∩B= ,A∪B = .4.集合M∩N=M是M N的条件,M∪N=是M=N=的条件5.满足关系{1,2}ÍMÍ{1,2,3,4,5}的集合M的个数是 .6.已知集合A={x|x≤2}, B={x|x<a},满足A ÊB,则a的取值范围是 .7.命题:“一个实数x,使得2x+3<0”的非命题是 .8.若p真q假,则p∧q为命题;p∨q为命题; (p∨q)为命题;p→q为命题;p→q为命题.9.A={( x , y )| x+y=1},B={( x , y )| x-y=-1}则A∩B.10.设U=Z,A={2m-1| m∈Z} 则C U A=11.空集表示的集合,记为,它是任意非空集合的.12. x2=4是x=-2或x=2的________________条件;13. ab=0是a=0或b=0的__________________条件;14. 已知M={ x│x≤19},a=32,则a与M的关系是 .15.已知A={ x│-5≤x<1},B={ x│-3<x<4},则A∩B= .16.设全集U=N,A={ n│n∈N且n≥3},则C U A=.数学基础知识训练题 2(不等式)1. 方程x 2-2x -1=0的解集为 .2. 不等式-3x ≤6的解集为 .3. 不等式5+x£3≥312-4x £«18的解集为 . 4. 不等式组x 2£x 3£¾£ 1 ¡¢Ù2(x £3)£3(x £2)£¼0¡¡ ¢Ú的解集为 .5. 不等式x 2-2x -3>0的解集为 .6. 不等式-x2-3x +4≥0的解集为 .7. 不等式|2x +3|≤7的解集为 .8. 不等式|x -3|>2的解集为 .11. 不等式x 2+2x +1≥0的解集为 .12. 不等式x2+2x +3>0的解集为 .13.不等式x 2-3x +5<0的解集为 .14.不等式3x £«1x £3>0的解集为 .15.求不等式3£2x x £4≥1的解集为 .16.二次不等式ax 2+bx +1>0的解集是(-1,13)则a = ,b = . (均值定理) 1.若x >0, 则4x -2+ 的最小值是 .2.函数f (x )=1+4x 2+21x 的最小值是 .3.y =2-3x -4x(x >0)的最大值是 . 4.y =x +1x £3-2(x >3)最小值是 .数学基础知识训练题3(函数的定义域、值域)1. 函数y=£x2£«2x£«3的定义域是 ,值域是 .2. f(x)=1的定义域是,值域是 .3. 函数y=(x£2)0lgx的定义域是 .4. 函数y=log0. 5(1£x)的定义域是 .5. 函数y=-3sin(2x+φ)-5的值域是 .6. 函数y=3cos2x-4sin2x的值域是 .7. 函数y=sin x-sin2x+cos x的值域是 .8. 函数y=cos2x-2sin x cos x-sin2x的值域是 .9. 函数y=x2-3x-5的值域是 .10.函数y=3-x-1x(x>0)的值域是 .数学基础知识训练题 4 (函数的奇偶性、单调性)1. 函数y=x3的奇偶性是;在R上的单调性是 .2. 函数y=-ax-3+bx5(其中a、b不同时为0)的奇偶性是 .3. 函数y=2x2的奇偶性是;若x∈(-1,1],则该函数的奇偶性是 .4. 函数y=-x4+1的奇偶性是 .5. 函数y=0的奇偶性是 .6. 函数y=cos x的奇偶性是;y=cos x+1的奇偶性是 .7. 函数y=sin x的奇偶性是;y=sin x+cos x的奇偶性是 .8. 函数y=x cos x的奇偶性是;y=x sin x的奇偶性是 .9. 函数y=sin x cos x的奇偶性是;y=(sin x-2)2的奇偶性是10.函数y=cos(3x+11p2)的奇偶性是;函数y=sin(2x-2001p2)的奇偶性是 .11.若函数y=mx2+(1+m)x-3是偶函数,则该函数在[0, +∞)上的单调性是 .12.若函数y=f(x)是R上的奇函数,且在[0, +∞)上是增函数,则此函数在(-∞,0]上的单调性是;f(-1),f(2),f(π)的大小关系是;f(0)= .13. 若函数y=f(x)是R上的偶函数,且在[0, +∞)上是增函数,则此函数在(-∞,0]上的单调性是;f(-1),f(2),f(π)的大小关系是 .14.已知y=f(x)是R上的奇函数,f(3)=5,则f(-3)= .15.已知y=f(x)是R上的奇函数,f(-3)=5,则f(3)= .16.已知y=f(x)是R上的偶函数,f(3)=5,则f(-3)= .17.已知y=f(x)是R上的偶函数,f(-7)=-2,则f(7)= .数学基础知识训练题5(函数的对称性)1.奇函数的图像关于对称;2.偶函数的图像关于对称;3.互为反函数的两个函数的图像关于对称。
高一数学试题及答案

高一数学试题及答案一、选择题(每题4分,共40分)1. 下列哪个选项是函数y=|x|在x=0处的极限值?A. 1B. 0C. 2D. 不存在2. 已知函数f(x) = 3x^2 - 2x + 1,求f(2)的值。
A. 10B. 11C. 12D. 133. 若a、b为等差数列的连续项,且a+b=10,而a与b的倒数之和为\(\frac{2}{5}\),则a的值为:A. 1B. 2C. 3D. 44. 一个圆的半径为5cm,求该圆的面积(圆周率取3.14)。
A. 78.5平方厘米B. 85平方厘米C. 90平方厘米D. 95平方厘米5. 已知一个等比数列的前三项分别为2, 6, 18,求该数列的公比。
A. 2B. 3C. 4D. 66. 若x满足方程x^2 - 5x + 6 = 0,求x的值。
A. 2, 3B. 1, 4C. 1, 6D. 3, 47. 直线y = 2x + 3与x轴的交点坐标为:A. (-1.5, 0)B. (1.5, 0)C. (-3, 0)D. (3, 0)8. 已知一个三角形的三边长分别为3cm, 4cm, 5cm,该三角形的面积是多少?A. 6平方厘米B. 7.5平方厘米C. 9平方厘米D. 12平方厘米9. 函数y = |2x - 3|与x轴所围成的图形面积为:A. 2B. 3C. 4D. 610. 若a, b, c是等差数列,且a + c = 2b,若b = 5,则a + c的值为:A. 5B. 10C. 15D. 20二、填空题(每题4分,共20分)11. 若f(x) = x^3 - 6x^2 + 11x - 6,求f(2) = ______。
12. 一个圆的直径为10cm,求该圆的周长(圆周率取3.14)为______。
13. 已知等比数列的前两项为3和9,求该数列的第四项为______。
14. 若x和y满足方程组\(\begin{cases} 2x + y = 8 \\ x - y = 2 \end{cases}\),求x的值为______。
高一数学考试题库及答案

高一数学考试题库及答案一、选择题(每题4分,共40分)1. 下列函数中,哪一个是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x答案:B2. 已知集合A={1, 2, 3},集合B={2, 3, 4},则A∩B等于:A. {1, 2, 3}B. {2, 3}C. {1, 4}D. {1, 2, 3, 4}答案:B3. 函数y=2x+3的图像是:A. 一条直线B. 一条曲线C. 一个圆D. 一个椭圆答案:A4. 已知等差数列{an}的首项a1=2,公差d=3,则a5的值为:A. 14B. 17C. 20D. 23答案:A5. 下列哪个选项是正确的不等式?B. 3x < 6C. 5x ≤ 10D. 7x ≥ 14答案:D6. 已知函数f(x)=x^2-4x+3,求f(2)的值:A. -1B. 1C. 3D. 5答案:A7. 函数y=x^2-6x+8的顶点坐标是:A. (3, -1)B. (-3, 1)D. (-3, -1)答案:C8. 已知向量a=(1, 2),向量b=(3, 4),则向量a+b的坐标为:A. (4, 6)B. (-2, -2)C. (2, 6)D. (4, 2)答案:A9. 已知圆的方程为(x-2)^2+(y-3)^2=9,该圆的半径为:A. 3B. 6C. 9D. 12答案:A10. 函数y=sin(x)的值域是:A. (-1, 1)B. (-∞, +∞)C. [0, +∞)D. (-∞, 0]答案:A二、填空题(每题4分,共20分)11. 已知函数f(x)=x^2-6x+8,求该函数的对称轴方程为:__________。
答案:x=312. 已知等比数列{bn}的首项b1=2,公比q=2,则b3的值为:__________。
答案:813. 函数y=cos(x)的周期为:__________。
答案:2π14. 已知向量a=(2, -1),向量b=(-1, 3),则向量a·b的值为:__________。
高一数学考试试题及答案

高一数学考试试题及答案一、选择题(每题3分,共30分)1. 若函数f(x)=2x+1,则f(-1)的值为:A. -1B. 1C. 3D. -3答案:A2. 已知集合A={1,2,3},B={2,3,4},则A∩B的元素个数为:A. 1B. 2C. 3D. 4答案:B3. 函数y=x^2-4x+3的顶点坐标为:A. (2,-1)B. (2,1)C. (-2,1)D. (-2,-1)答案:A4. 圆的方程为(x-2)^2+(y-3)^2=25,则圆心坐标为:A. (2,3)B. (-2,-3)C. (-2,3)D. (2,-3)答案:A5. 直线y=2x+3与x轴的交点坐标为:A. (-3/2, 0)B. (3/2, 0)C. (0, -3/2)D. (0, 3/2)答案:B6. 函数y=|x|的图像是:A. 一条直线B. 两条直线C. 一条曲线D. 两条曲线答案:B7. 已知等差数列{an}的前三项分别为2, 5, 8,则该数列的公差为:A. 1B. 2C. 3D. 4答案:B8. 函数y=sin(x)的周期为:B. 2πC. π/2D. 4π答案:B9. 已知向量a=(3, -4),b=(2, 5),则a·b的值为:A. -1B. 11C. -11D. 1答案:C10. 圆的方程为x^2+y^2-6x+8y-24=0,则该圆的半径为:A. 2B. 4C. 6D. 8答案:C二、填空题(每题4分,共20分)11. 函数y=3x-2的反函数为______。
答案:y=(1/3)x+2/312. 已知等比数列{bn}的前三项分别为3, 6, 12,则该数列的公比为______。
13. 若a, b, c是三角形的三边长,且满足a^2+b^2=c^2,则该三角形为______三角形。
答案:直角14. 函数y=1/x的图像在第二象限内是______的。
答案:递减15. 已知向量a=(4, 1),b=(2, -3),则|a+b|的值为______。
高一数学必修测试题及答案
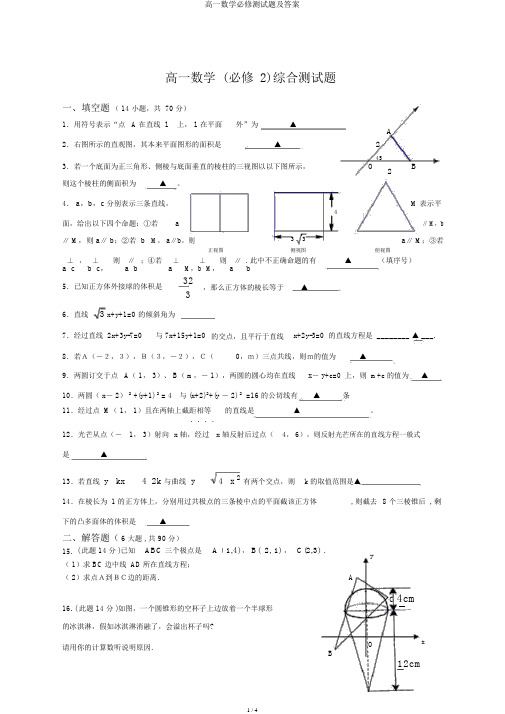
高一数学 (必修 2)综合测试题一、填空题( 14 小题,共 70 分)1.用符号表示“点 A 在直线l上, l在平面外”为▲A 2.右图所示的直观图,其本来平面图形的面积是▲23.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图以以下图所示,O 45B2则这个棱柱的侧面积为▲。
4.a,b,c分别表示三条直线,4M表示平面,给出以下四个命题:①若a∥ M,b ∥ M,则 a∥ b;②若 b M, a∥b,则33a∥ M;③若正视图侧视图俯视图⊥,⊥则∥;④若⊥⊥M,则a∥ . 此中不正确命题的有▲(填序号)a cb c, a b a M,b b5.已知正方体外接球的体积是32,那么正方体的棱长等于▲36.直线 3 x+y+1=0的倾斜角为7.经过直线 2x+3y-7=0与 7x+15y+1=0的交点,且平行于直线x+2y-3=0 的直线方程是 ________ ▲ ___. 8.若A(-2,3),B(3,-2),C(0,m)三点共线,则m的值为▲9.两圆订交于点 A( 1, 3)、 B( m,- 1),两圆的圆心均在直线x- y+c=0上,则 m+c的值为▲10.两圆( x― 2)2 +(y+1) 2 = 4与 (x+2)2+(y ― 2) 2 =16 的公切线有▲条11.经过点 M( 1, 1)且在两轴上截距相等的直线是▲。
....12.光芒从点(―1, 3)射向x 轴,经过x 轴反射后过点(4, 6),则反射光芒所在的直线方程一般式是▲13.若直线y kx 4 2k 与曲线y4x 2有两个交点,则k 的取值范围是▲14.在棱长为 1 的正方体上,分别用过共极点的三条棱中点的平面截该正方体, 则截去8 个三棱锥后 , 剩下的凸多面体的体积是▲二、解答题( 6 大题 , 共 90 分)15.( 此题 14 分 )已知ABC 三个极点是 A (1,4), B( 2, 1) ,C(2,3).y( 1)求 BC边中线 AD所在直线方程;( 2)求点A到BC边的距离.AC 4cm16.( 此题 14 分 )如图,一个圆锥形的空杯子上边放着一个半球形的冰淇淋,假如冰淇淋消融了,会溢出杯子吗?请用你的计算数听说明原因.O xB12cm17. (本 15 分 )如, ABCD是正方形, O是正方形的中心,PO 底面 ABCD, E 是 PC的中点.P求:( 1)PA∥平面 BDE;(2)平面 PAC 平面 BDE.18. (本15 分 )已知直 l 点P(1,1),并与直 l 1:x E- y+3=0 和l2:2x+y - 6=0 分交于点A、B,若段 AB 被点 P 平分,求:(Ⅰ)直l 的方程;D C (Ⅱ)以 O心且被l 截得的弦8 5的的方程.O5A B19.( 本16 分) 已知数a足 0<a<2,直l1:ax- 2y- 2a+4=0 和l2:2x+a2y- 2a2- 4=0 与两坐成一个四形。
高一数学含金试题及答案

高一数学含金试题及答案一、选择题(每题4分,共40分)1. 下列函数中,为奇函数的是()A. y = x^2B. y = |x|C. y = x^3D. y = x^2 + 1答案:C2. 已知集合A={1, 2, 3},B={2, 3, 4},则A∩B为()A. {1, 2, 3}B. {2, 3}C. {1, 4}D. {3, 4}答案:B3. 若f(x) = 2x + 3,g(x) = x - 1,则f[g(x)]等于()A. 2x - 2 + 3B. 2x + 2C. 3x + 1D. 3x - 2答案:A4. 函数y = x^2 - 4x + 4的最小值是()A. 0B. 1C. 4D. -4答案:A5. 已知向量a = (3, -1),b = (1, 2),则向量a·b等于()A. 5B. -1C. 4D. -5答案:B6. 函数y = sin(x)的值域是()A. (-∞, +∞)B. [0, +∞)C. [-1, 1]D. (-1, 1)答案:C7. 已知直线l的方程为y = 2x + 3,点P(1, 2)在直线l上,则点P关于直线l的对称点Q的坐标为()A. (0, 1)B. (-1, 0)C. (1, 0)D. (2, 3)答案:A8. 已知等差数列{an}的首项a1 = 2,公差d = 3,则a5等于()A. 14B. 17C. 20D. 23答案:A9. 已知抛物线C:y^2 = 4x,焦点F(1, 0),点P在抛物线上,且|PF| = 2,则点P的坐标为()A. (1, 2)B. (1, -2)C. (0, 2)D. (0, -2)10. 已知函数f(x) = x^2 - 2x + 1,则f(-1)等于()A. 4B. 3C. 2D. 1答案:A二、填空题(每题4分,共20分)11. 已知函数f(x) = x^3 - 3x,求f'(x) = _________。
数学题高一试题及答案

数学题高一试题及答案一、选择题1. 若函数f(x) = 2x^2 - 4x + 3,求f(2)的值。
A. 1B. 3C. 5D. 7答案:B2. 已知等差数列{an}的前三项分别为a1 = 1,d = 2,求a3的值。
A. 5B. 6C. 7D. 8答案:A3. 函数y = x^3 - 3x^2 + 2x + 1的极值点个数是:A. 0B. 1C. 2D. 3答案:C二、填空题4. 计算复数(1 + 2i)(3 - 4i)的结果为______。
答案:11 - 10i5. 已知圆的方程为x^2 + y^2 - 6x + 8y - 24 = 0,求该圆的半径。
答案:5三、解答题6. 已知函数f(x) = x^3 - 3x^2 + 2,求证f(x)在x = 2处取得极小值。
证明:首先求导数f'(x) = 3x^2 - 6x。
令f'(x) = 0,解得x = 0 或x = 2。
验证f''(x) = 6x - 6,代入x = 2,得到f''(2) = 6 > 0,因此f(x)在x = 2处取得极小值。
7. 解不等式:x^2 - 4x + 4 > 0。
解:将不等式转化为(x - 2)^2 > 0,由于平方项总是非负的,所以不等式成立当x ≠ 2。
因此,解集为{x|x ≠ 2}。
四、计算题8. 计算定积分∫(0到1) (2x + 3) dx。
解:首先求被积函数(2x + 3)的原函数F(x) = x^2 + 3x。
计算定积分,得到F(1) - F(0) = (1^2 + 3*1) - (0^2 + 3*0) = 4。
答案:49. 已知函数f(x) = √x,求f(x)在区间[1, 4]上的平均变化率。
解:平均变化率定义为(f(b) - f(a)) / (b - a),代入f(x) = √x,得到平均变化率= (√4 - √1) / (4 - 1) = (2 - 1) / 3 = 1/3。
高一数学必刷试题及答案

高一数学必刷试题及答案一、选择题(每题4分,共40分)1. 若函数f(x)=x^2-2x+2,以下哪个选项是f(x)的最小值?A. 1B. 2C. 3D. 42. 已知等差数列{an}的前三项分别为1,4,7,求该数列的通项公式an。
A. an = 3n - 2B. an = n + 2C. an = 3n - 1D. an = 2n + 13. 圆的方程为x^2 + y^2 - 6x - 8y + 25 = 0,圆心坐标为?A. (3, 4)B. (-3, -4)C. (3, -4)D. (-3, 4)4. 函数y = sin(x)的图像在x=π/2处的切线斜率是?A. 1B. -1C. 0D. 不存在5. 集合A={1, 2, 3},集合B={2, 3, 4},求A∪B。
B. {2, 3, 4}C. {1, 2, 3, 4}D. {1, 2, 3, 4, 5}6. 已知向量a=(2, 3),向量b=(-1, 2),求向量a与向量b的点积。
A. 4B. -1C. 1D. 07. 函数f(x)=x^3-3x^2+4x-1,求f'(x)。
A. 3x^2 - 6x + 4B. x^2 - 6x + 4C. 3x^2 - 9x + 4D. x^2 - 3x + 48. 已知三角形ABC中,角A=60°,边a=3,边b=4,求边c的长度。
A. 5B. √7C. 2√3D. √139. 抛物线y^2=4x的准线方程是?A. x=-1B. x=1C. y=-1D. y=110. 函数f(x)=x^3-6x^2+11x-6,求f'(x)=0的解。
A. 1, 2, 3C. 1, 3, 5D. 2, 4, 6二、填空题(每题4分,共20分)1. 已知函数f(x)=x^3-3x^2+2,求f'(x)=0的解。
答案:1, 22. 圆x^2 + y^2 - 4x + 6y - 12 = 0的半径是:答案:√103. 已知等比数列{an}的前三项分别为2,4,8,求该数列的公比。
高一数学期末试题及答案

高一数学期末试题及答案一、选择题(每题4分,共40分)1. 若函数f(x)=2x+1,则f(-1)的值为()A. -3B. -1C. 1D. 32. 已知集合A={1, 2, 3},B={2, 3, 4},则A∩B为()A. {1, 2, 3}B. {2, 3}C. {1, 4}D. {1, 2, 3, 4}3. 以下哪个函数是奇函数()A. f(x) = x^2B. f(x) = x^3C. f(x) = x + 1D. f(x) = -x4. 已知等差数列{an}的首项a1=1,公差d=2,则a5的值为()A. 9B. 10C. 11D. 125. 以下哪个不等式是正确的()A. 2x > x + 1B. 3x ≤ 2x + 1C. 4x < 3x + 2D. 5x ≥ 4x + 16. 已知函数f(x)=x^2-4x+3,求f(2)的值()A. -1B. 1C. 3D. 57. 若cosθ=-1/2,则θ的值为()A. π/3B. 2π/3C. 4π/3D. 5π/38. 已知向量a=(3, -1),b=(2, 4),则a·b的值为()A. 10B. 8C. 6D. 49. 以下哪个是二项式定理的展开式()A. (x+y)^n = C(n, 0)x^n + C(n, 1)x^(n-1)y + ... + C(n, n)y^nB. (x-y)^n = C(n, 0)x^n - C(n, 1)x^(n-1)y + ... - C(n, n)y^nC. (x+y)^n = C(n, 0)x^n + C(n, 1)x^(n-1)y + ... + C(n, n)y^nD. (x-y)^n = C(n, 0)x^n + C(n, 1)x^(n-1)y + ... + C(n, n)y^n10. 已知方程x^2-5x+6=0的根为x1和x2,则x1+x2的值为()A. 2B. 3C. 5D. 6二、填空题(每题4分,共20分)11. 已知函数f(x)=x^2-6x+8,求f(1)的值。
高一数学集合练习题及答案(5篇)

高一数学集合练习题及答案(5篇)高一数学练习题及答案篇1一、填空题.(每题有且只有一个正确答案,5分×10=50分)1、已知全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 ,6 },那么集合 { 2 ,7 ,8}是 ( )2 . 假如集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是 ( )A.0B.0 或1C.1D.不能确定3. 设集合A={x|1A.{a|a ≥2}B.{a|a≤1}C.{a|a≥1}.D.{a|a≤2}.5. 满意{1,2,3} M {1,2,3,4,5,6}的集合M的个数是 ( )A.8B.7C.6D.56. 集合A={a2,a+1,1},B={2a1,| a2 |, 3a2+4},A∩B={1},则a的值是( )A.1B.0 或1C.2D.07. 已知全集I=N,集合A={x|x=2n,n∈N},B={x|x=4n,n∈N},则 ( )A.I=A∪BB.I=( )∪BC.I=A∪( )D.I=( )∪( )8. 设集合M= ,则 ( )A.M =NB. M NC.M ND. N9 . 集合A={x|x=2n+1,n∈Z},B={y|y=4k±1,k∈Z},则A 与B的关系为 ( )A.A BB.A BC.A=BD.A≠B10.设U={1,2,3,4,5},若A∩B={2},( UA)∩B={4},( UA)∩( UB)={1,5},则以下结论正确的选项是( )A.3 A且3 BB.3 B且3∈AC.3 A且3∈BD.3∈A且3∈B二.填空题(5分×5=25分)11 .某班有同学55人,其中音乐爱好者34人,体育爱好者43人,还有4人既不爱好体育也不爱好音乐,则班级中即爱好体育又爱好音乐的有人.12. 设集合U={(x,y)|y=3x1},A={(x,y)| =3},则 A= .13. 集合M={y∣y= x2 +1,x∈ R},N={y∣ y=5 x2,x∈ R},则M∪N=_ __.14. 集合M={a| ∈N,且a∈Z},用列举法表示集合M=_15、已知集合A={1,1},B={x|mx=1},且A∪B=A,则m的值为三.解答题.10+10+10=3016. 设集合A={x, x2,y21},B={0,|x|,,y}且A=B,求x, y的值17.设集合A={x|x2+4x=0},B={x|x2+2(a+1)x+a21=0} ,A∩B=B,求实数a的值.18. 集合A={x|x2ax+a219=0},B={x|x25x+6=0},C={x|x2+2x8=0}.?(1)若A∩B=A∪B,求a的值;(2)若A∩B,A∩C= ,求a的值.19.(本小题总分10分)已知集合A={x|x23x+2=0},B={x|x2ax+3a5=0}.若A∩B=B,求实数a的取值范围.20、已知A={x|x2+3x+2 ≥0}, B={x|mx24x+m10 ,m∈R}, 若A∩B=φ, 且A∪B=A, 求m的取值范围.21、已知集合,B={x|2参考答案C B AD C D C D C B26 {(1,2)} R {4,3,2,1} 1或1或016、x=1 y=117、解:A={0,4} 又(1)若B= ,则,(2)若B={0},把x=0代入方程得a= 当a=1时,B=(3)若B={4}时,把x=4代入得a=1或a=7.当a=1时,B={0,4}≠{4},∴a≠1.当a=7时,B={4,12}≠{4},∴a≠7.(4)若B={0,4},则a=1 ,当a=1时,B={0,4},∴a=1综上所述:a18、.解:由已知,得B={2,3},C={2,4}.(1)∵A∩B=A∪B,∴A=B于是2,3是一元二次方程x2ax+a219=0的两个根,由韦达定理知:解之得a=5.(2)由A∩B ∩ ,又A∩C= ,得3∈A,2 A,4 A,由3∈A,得323a+a219=0,解得a=5或a=2?当a=5时,A={x|x25x+6=0}={2,3},与2 A冲突;当a=2时,A={x|x2+2x15=0}={3,5},符合题意.∴a=2.19、解:A={x|x23x+2=0}={1,2},由x2ax+3a5=0,知Δ=a24(3a5)=a212a+20=(a2)(a10).(1)当2(2)当a≤2或a≥10时,Δ≥0,则B≠ .若x=1,则1a+3a5=0,得a=2,此时B={x|x22x+1=0}={1} A;若x=2,则42a+3a5=0,得a=1,此时B={2,1} A.综上所述,当2≤a10时,均有A∩B=B.20、解:由已知A={x|x2+3x+2 }得得.(1)∵A非空,∴B= ;(2)∵A={x|x }∴ 另一方面,,于是上面(2)不成立,否则,与题设冲突.由上面分析知,B= .由已知B= 结合B= ,得对一切x 恒成立,于是,有的取值范围是21、∵A={x|(x1)(x+2)≤0}={x|2≤x≤1},B={x|1∵ ,(A∪B)∪C=R,∴全集U=R。
高一数学试题及答案(8页)

高一数学试题及答案第一部分:选择题1. 设函数f(x) = x^2 4x + 3,求f(2)的值。
A. 1B. 0C. 1D. 22. 已知等差数列{an}的公差为2,且a1 = 3,求a5的值。
A. 7B. 9C. 11D. 133. 设集合A = {x | x > 0},B = {x | x < 5},求A∩B的值。
A. {x | x > 0, x < 5}B. {x | x > 5}C. {x | x < 0}D. {x | x < 5, x > 0}4. 若直线y = kx + 2与圆x^2 + (y 1)^2 = 4相切,求k的值。
A. 1B. 1C. 2D. 25. 设函数g(x) = |x 1| + |x + 1|,求g(x)的最小值。
A. 0B. 1C. 2D. 36. 若等比数列{bn}的首项为2,公比为3,求bn的第5项。
A. 162B. 243C. 4D. 7297. 已知函数h(x) = x^3 3x^2 + 2x,求h(x)的导数。
A. 3x^2 6x + 2B. 3x^2 6x 2C. 3x^2 + 6x + 2D. 3x^2 + 6x 28. 若直线y = mx + 1与直线y = 2x + 4平行,求m的值。
A. 2B. 2C. 1D. 19. 设集合C = {x | x^2 5x + 6 = 0},求C的值。
A. {2, 3}B. {1, 4}C. {2, 4}D. {1, 3}10. 若函数f(x) = ax^2 + bx + c(a ≠ 0)的顶点坐标为(2,3),求b的值。
A. 12B. 12C. 6D. 6答案:1. A2. C3. A4. B5. B6. D7. A8. D9. C10. B第一部分:选择题答案解析1. 解析:将x = 2代入f(x) = x^2 4x + 3中,得到f(2) =2^2 42 + 3 = 1。
高一数学考试题库及答案

高一数学考试题库及答案一、选择题(每题3分,共30分)1. 下列哪个选项是实数集合的符号表示?A. ZB. NC. QD. R答案:D2. 函数f(x) = 2x + 3的值域是:A. (-∞, +∞)B. [3, +∞)C. (-∞, 3]D. [0, +∞)答案:A3. 已知集合A = {1, 2, 3},集合B = {2, 3, 4},则A∩B等于:A. {1}B. {2, 3}C. {4}D. {1, 2, 3}答案:B4. 计算下列三角函数值:sin(π/6)的值是:A. 1/2B. √3/2C. 1/√2D. √2/2答案:A5. 已知等差数列{an}的首项a1=2,公差d=3,则a5的值是:A. 14B. 17C. 20D. 23答案:A6. 函数y = x^2 - 6x + 5的顶点坐标是:A. (3, -4)B. (3, 4)C. (-3, 4)D. (-3, -4)答案:B7. 已知复数z = 2 + 3i,求z的共轭复数:A. 2 - 3iB. -2 + 3iC. -2 - 3iD. 2 + 3i答案:A8. 已知向量a = (3, 4),向量b = (-1, 2),则向量a与向量b的点积为:A. 10B. -2C. 2D. -10答案:B9. 计算下列极限:lim(x→0) [sin(x)/x]的值是:A. 1B. 0C. ∞D. -1答案:A10. 已知圆的方程为x^2 + y^2 = 9,圆心坐标为:A. (0, 0)B. (3, 0)C. (0, 3)D. (-3, 0)答案:A二、填空题(每题4分,共20分)11. 函数f(x) = x^3 - 3x在x=1处的导数是______。
答案:212. 集合{1, 2, 3}的补集在全集U={1, 2, 3, 4, 5}中是______。
答案:{4, 5}13. 已知等比数列{bn}的首项b1=4,公比q=2,则b3的值是______。
高一数学填空题练习试题集

高一数学填空题练习试题答案及解析1.若方程表示圆心在第四象限的圆,则实数的范围为 .【答案】【解析】由方程可得,因为圆心在第四象限,则有,解得.故答案为.【考点】圆的方程.2.若实数满足则的最小值是 .【答案】1【解析】为增函数,故只需求的最小值,设,则,根据约束条件画出可行域,可知在原点处取得最小值,则的最小值是。
【考点】利用线性规划求非线性目标函数的最值3.已知满足,,则.【答案】【解析】,故.【考点】向量的数量积运算.4.已知向量=(x,2),=(1,y),其中x>0,y>0.若•=4,则+的最小值为.【答案】【解析】因为所以当且仅当时取等号.【考点】基本不等式求最值5.已知,且是第二象限角,则;【答案】【解析】,又因为是第二象限角,所以【考点】同角基本关系式6.已知是上增函数,若,则a的取值范围是【答案】【解析】利用增函数的定义,可知.【考点】增函数的定义.7.已知且,,当时均有,则实数的取值范围是 .【答案】【解析】解:,当时,变开为:,构造函数,,其中,且,由图像可知,当时,的图像在的图像下方.当时,有,即,得,即当时,有,即,得,即,由(1)(2)可知,实数的取值范围是【考点】本题考查二次函数的图像与性质,指数函数的图像与性质,考查函数的恒成立问题.8.已知集合=,,则= .【答案】【解析】.【考点】本题考查交集及其运算,定义域值域的求法.9.设奇函数f(x)的定义域为[-5,5],在上是减函数,又f(-3)=0,则不等式xf(x)<0的解集是 .【答案】【解析】先根据奇函数图象关于原点对称得到其在上的图象,在把所求不等式转化结合图象即可得到结论.由题意可画之内的示意图,因为所以自变量和函数值符号相反,由图可知【考点】函数奇偶性的性质;函数的图象;其他不等式的解法.10.直线的倾斜角为_____________________【答案】【解析】根据题意,由于直线的斜率为y=x-1,即可知斜率为1,借助于特殊角的正切值为1可知,其倾斜角为,故答案为【考点】直线的斜率与倾斜角点评:本题考查直线的斜率与倾斜角的关系,是基础题.11.已知是同一平面内两个不共线的向量,且=2+k,=+3,=2-,如果A,B,D三点共线,则实数k的值为;【答案】;【解析】因为=+3,=2-,所以=+=-(+3)+(2-)=-4;又因为A,B,D三点共线,所以存在实数,使=,即2+k=(-4),故=2,k=-8.【考点】本题主要考查平面向量的线性运算,共线向量定理,相反向量。
高一数学练习题及答案

高一数学练习题及答案一、选择题(每题5分,共30分)1. 已知函数\( f(x) = 3x^2 - 2x + 1 \),求\( f(-1) \)的值。
A. 6B. 4C. 2D. -22. 若\( a \)和\( b \)是方程\( x^2 - 5x + 6 = 0 \)的两个根,则\( a + b \)的值为:A. 3B. 5C. 6D. 83. 已知\( \sin 45^\circ = \frac{\sqrt{2}}{2} \),求\( \cos 45^\circ \)的值。
A. \( \frac{\sqrt{2}}{2} \)B. \( \frac{1}{2} \)C. \( \frac{\sqrt{3}}{2} \)D. \( \frac{\sqrt{6}}{3} \)4. 圆的半径为5,圆心到直线的距离为3,求圆与直线的位置关系。
A. 相离B. 相切C. 相交D. 包含5. 已知等差数列的首项是2,公差是3,求第5项的值。
A. 17B. 14C. 11D. 86. 函数\( y = \log_2 x \)的定义域是:A. \( x > 1 \)B. \( x < 1 \)C. \( x \geq 1 \)D. \( x \geq 0 \)二、填空题(每题4分,共20分)1. 若\( a \),\( b \),\( c \)是三角形的三边,且\( a^2 + b^2= c^2 \),则此三角形是________。
2. 已知\( \tan \theta = 3 \),求\( \sin \theta \)的值。
3. 函数\( y = x^3 - 3x^2 + 2 \)的导数是________。
4. 已知\( \cos \alpha = \frac{4}{5} \),\( \alpha \)在第一象限,求\( \sin \alpha \)的值。
5. 等比数列\( 2, 4, 8, \ldots \)的第6项是________。
2023-2024学年上海市松江区高一上册期末数学试题(含解析)

2023-2024学年上海市松江区高一上册期末数学试题一、填空题1.已知集合{1,0,1,2}A =-,{|03}B x x =<<,则A B = ___________【正确答案】{1,2}【分析】利用交集的定义进行求解.【详解】因为{1,0,1,2}A =-,{|03}B x x =<<,所以{1,2}A B = .故答案为.{1,2}2.函数()()lg 1f x x =-的定义域为______.【正确答案】()1,+∞根据对数型复合函数定义域可得:010x x ≥⎧⎨->⎩,解不等式即可求解.【详解】由()()lg 1f x x =-,则010x x ≥⎧⎨->⎩,解得1x >,所以函数的定义域为()1,+∞.故()1,+∞3.若41log 2x =,则x =__________.【正确答案】2【分析】将对数式化为指数式,由此求得x .【详解】由于41log 2x =,所以1242x ===.故24.已知1x 、2x 是方程2330x x +-=的两个根,则1211x x +=______.【正确答案】1【分析】利用根与系数关系求得正确答案.【详解】由题意得12123,3x x x x +=-=-,所以121212111x x x x x x ++==.故15.设a 、b 为实数,比较两式的值的大小:22a b +_______222a b --(用符号,,,>≥<≤或=填入划线部分).【正确答案】≥【分析】利用作差比较法求得正确答案.【详解】因为2222(222)(1)(1)0a b a b a b +---=-++≥,1,1a b ==-时等号成立,所以22222a b a b +≥--.故≥6.已知()y f x =是奇函数,当0x >时,()2f x x =-,则1()2f -的值为________.【正确答案】32##1.5【分析】根据奇函数的定义求值.【详解】由题意1113(()(2)2222f f -=-=--=.故32.7.函数2()lg(4)f x x x =-的严格减区间是_________.【正确答案】[)2,4先由函数解析式,求出定义域,再由对数型复合函数单调性的判定方法,即可求出减区间.【详解】由2()lg(4)f x x x =-可得240x x ->,解得04x <<,即2()lg(4)f x x x =-的定义域为()0,4,令24t x x =-,则24t x x =-是开口向下,对称轴为2x =的二次函数,所以24t x x =-在(]0,2上单调递增,在[)2,4上单调递减,又lg y t =是增函数,所以函数2()lg(4)f x x x =-的严格减区间是[)2,4.故[)2,48.已知函数()1||x f x x =+,则不等式(3)(2)0f x f x -+>的解集为____【正确答案】(1,+∞)【分析】由已知条件得出函数()f x 为奇函数,并且在在R 时单调递增,由此可得出关于x 不等式,解之可得不等式的解集.【详解】因为()()1||1||x x f x f x x x --==-=-+-+,所以函数()f x 为奇函数,又01()1,01x x x x f x x x x x ⎧≥⎪⎪+==⎨+⎪<⎪-⎩,,当0x ≥时,1+11()111+1+x x f x x x x -===-+,所以函数()f x 在[)0+∞,时单调递增;当0x <时,111()1+111x x f x x x x--==-=----,所以函数()f x 在()0-∞,时单调递增,所以函数()f x 在R 时单调递增.所以不等式(3)(2)0f x f x -+>化为(3)(2)(2)f x f x f x ->-=-,所以3>-2x x -,解得>1x ,所以不等式(3)(2)0f x f x -+>的解集为()1+∞,,故答案为.()1+∞,本题考查根据函数的奇偶性和单调性求解不等式,属于中档题.9.若存在实数x 使13x a x -+-≤成立,则实数a 的取值范围是___________.【正确答案】2 4.a -≤≤【考点定位】本题主要考察绝对值不等式的性质及其运用【详解】试题分析:本题的几何意义是:存在在数轴上到的距离与到的距离之和小于的点.有13a -≤,24a ∴-<<.含绝对值的不等式的解法.【易错点晴】本题主要考查了含绝对值不等式的解法.含有多个绝对值符号的不等式,一般可用零点分段法求解,对于形如或,利用实数绝对值的几何意义求解较简便.选择或填空题可采用绝对值几何意义的方法,解答题要采用零点分段求解的方法.本题难度不大,属于中档题.10.对任意的正实数x 、y≤m 的取值范围是________.【正确答案】)+∞【分析】分离参数为m ≥的最大值即得.【详解】由题意得m因为22()2x y x y +=≤=+,当且仅当x y =时取等号,所以m ≥m的取值范围是)+∞.故)+∞.11.设平行于y 轴的直线l 分别与函数2log y x =和2log 1y x =-的图像相交于点A 、B ,若在函数2log y x =的图像上存在点C ,使得ABC 是以AB 为斜边的等腰直角三角形,则点C 的横坐标为_______.【正确答案】12【分析】设22(,log ),(,log 1)A t t B t t -,求得C 点坐标并代入2log y x =,求得t ,进而求得C 的横坐标.【详解】设22(,log ),(,log 1)A t t B t t -,线段AB 的中点坐标为22log 1,2t t -⎛⎫ ⎪⎝⎭,122AB =,因为ABC 是以AB 为斜边的等腰直角三角形,所以22log 11(,)22t C t --,因为点C 在函数2log y x =的图像上,所以222log 11log (22t t -=-,22221111log log (log (2222t t t t -=---=,所以21log 122t t =-,所以12212t t =-,解得22t +=,所以点C 的横坐标为11222t -=.故1212.已知()32,,x x a f x x x a⎧≤=⎨>⎩,若存在实数b ,使函数()()g x f x b =-有两个零点,则a 的取值范围是________.【正确答案】()(),01,-∞⋃+∞【分析】由()()g x f x b =-有两个零点可得()f x b =有两个零点,即()y f x =与y b =的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a 的范围【详解】()()g x f x b =- 有两个零点,()f x b ∴=有两个零点,即()y f x =与y b =的图象有两个交点,由32x x =可得,0x =或1x =①当1a >时,函数()f x 的图象如图所示,此时存在b ,满足题意,故1a >满足题意②当1a =时,由于函数()f x 在定义域R 上单调递增,故不符合题意③当01a <<时,函数()f x 单调递增,故不符合题意④0a =时,()f x 单调递增,故不符合题意⑤当a<0时,函数()y f x =的图象如图所示,此时存在b 使得,()y f x =与y b =有两个交点综上可得,a<0或1a >故()(),01,-∞⋃+∞本题考查了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.二、单选题13.下列四组函数中,同组的两个函数是相同函数的是()A .2()y x =与y x=B .y x =与ln e x y =C .22x y =与4x y =D .y x =与11y x -⎛⎫= ⎪⎝⎭【正确答案】C【分析】根据相同函数的知识对选项进行分析,从而确定正确答案.【详解】A 选项,2y =的定义域是[)0,∞+,y x =的定义域是R ,不是相同函数.B 选项,y x =的定义域是R ,ln e x y =的定义域是()0,∞+,不是相同函数.C 选项,224x x y ==,定义域、值域、和对应关系完全相同,是相同函数,C 选项正确.D 选项,y x =的定义域是R ,11y x -⎛⎫= ⎪⎝⎭的定义域是{}|0x x ≠,不是相同函数.故选:C14.已知函数()y f x =可表示为x 02x <<24x ≤<46x ≤<68x ≤≤y 1234则下列结论正确的是()A .()()43f f =B .()f x 的值域是{}1,2,3,4C .()f x 的值域是[]1,4D .()f x 在区间[]4,8上单调递增【正确答案】B ()()42f f =,所以选项A 错误;由表得()f x 的值域是{}1,2,3,4,所以选项B 正确C 不正确;()f x 在区间[]4,8上不是单调递增,所以选项D 错误.【详解】A.()()(4)3,4(3)2f f f f ===,所以该选项错误;B.由表得()f x 的值域是{}1,2,3,4,所以该选项正确;C.由表得()f x 的值域是{}1,2,3,4,不是[]1,4,所以该选项错误;D.()f x 在区间[]4,8上不是单调递增,如:54>,但是(5)=(4)=3f f ,所以该选项错误.故选:B方法点睛:判断函数的性质命题的真假,一般要认真理解函数的定义域、值域、单调性等的定义,再根据定义分析判断.15.设x 、y 是实数,则“0x >”是“x y >且11x y >”的()A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件【正确答案】B【分析】根据充分必要条件的定义判断.【详解】0x >时不能推出x y >且11x y >,例如3x =,2y =满足0x >,此时x y >但11x y <,当x y >且11x y>同时成立时,110--=>y x x y xy ,而0y x -<,因此有0xy <,而x y >,所以0x y >>,即0x >成立,因此题中应不必要非充分条件.故选:B .16.已知函数13,0()3,0x x x f x x +⎧-≥=⎨<⎩,若123x x x <<,且123()()()f x f x f x ==,则2123()x f x x x ⋅+的取值范围是()A .10,8⎛⎫ ⎪⎝⎭B .10,2⎛⎫ ⎪⎝⎭C .3(0,2D .30,8⎛⎤ ⎥⎝⎦【正确答案】D【分析】结合对称性以及二次函数的性质求得正确答案.【详解】由解析式易得()f x 的图象如下图所示,当0x <时,1()33x f x +=<,令|3|3x -=,得0x =或6x =,因为123x x x <<,且123()()()f x f x f x ==,所以2326,03x x x +=<<,所以2212222223()()11333(3)()0,666288x f x x f x x x x x x ⋅⋅⎛⎤==-=--+∈ ⎥+⎝⎦,故选:D三、解答题17.已知全集U =R ,集合{}2230A x x x =--<,{}1216x B x =<<.(1)求A B ⋃;(2)设集合{3,}D x a x a a =<<+∈R ,若D A ⊆,求实数a 的取值范围.【正确答案】(1)()1,4A B =- (2)(,4][3,)∞∞--⋃+.【分析】(1)解不等式求得集合,A B ,由此求得A B ⋃.(2)根据D A ⊆列不等式,由此求得a 的取值范围.【详解】(1)因为{}2230A x x x =--<,{}1216x B x =<<,()()223310x x x x --=-+<,解得13x -<<.412162x <<=,解得04x <<.所以{13}A x x =-<<,{04}B x x =<<.所以()1,4A B =- .(2)因为{|1A x x =≤-或}3x ≥,由题意得31a +≤-或3a ≥,解得4a ≤-或3a ≥,所以实数a 的取值范围是(,4][3,)∞∞--⋃+.18.已知函数2||1()1x f x x +=-.(1)证明:函数()y f x =为偶函数;(2)证明:函数()y f x =在区间(1,)+∞上是严格减函数.【正确答案】(1)证明见解析(2)证明见解析【分析】(1)根据奇偶性定义证明;(2)根据单调性的定义证明.【详解】(1)因为2||1()1x f x x +=-,所以()f x 的定义域为{|D x x R =∈,且1}x ≠±.对于任意x D ∈,因为2211()()()11x x f x f x x x -++-===---,所以()f x 为偶函数.(2)当(1,)x ∈+∞时,211()11x f x x x +==--.任取12,(1,)x x ∈+∞,且12x x <,那么2112121211()()11(1)(1)x x f x f x x x x x --=-=----因为121x x <<,所以210x x ->,12()1(1)0x x ->-,所以12())0(f x f x ->,即12()()f x f x >.所以()f x 是(1,)+∞上的严格减函数.19.环保生活,低碳出行,新能源电动汽车正成为人们购车的热门选择.某型号国产电动汽车,在一段平坦的国道进行测试,国道限速80km/h (不含80km/h ).经多次测试得到,该汽车每小时耗电量M (单位:Wh )与速度v (单位:km/h )的下列数据:v0204060M 0300056009000为了描述国道上该汽车每小时耗电量与速度的关系,现有以下三种函数模型供选择:321()40M v v bv cv =++,2()800()3v M v a =+,()500log (1)a M v v b =++.(1)当080v ≤<时,请选出符合表格所列实际数据的函数模型,并求出相应的函数解析式;(2)现有一辆同型号汽车在200km 的国道上行驶,如何行使才能使得总耗电量最少,最少为多少?【正确答案】(1)321()40M v v bv cv =++符合,且321()218040M v v v v =-+(2)此汽车以40km/h 的速度行驶时,总耗电量最少,最少为28000Wh【分析】(1)利用特殊值以及函数的单调性求得正确答案.(2)结合二次函数的性质求得正确答案.【详解】(1)选321()40M v v bv cv =++,理由如下:若()500log (1)a M v v b =++,由(0)0M =得0b =,由(20)3000M =得1621a =;由(40)5600M =得55641a =,矛盾,舍若2()800()3v M v a =+,此时函数是减函数,(40)(60)M M <,不符合题意;若321()40M v v bv cv =++,由323212020203000401404040560040b c b c ⎧⨯+⨯+⨯=⎪⎪⎨⎪⨯+⨯+⨯=⎪⎩,解得2180b c =-⎧⎨=⎩,321()218040M v v v v =-+,将()60,9000代入,也符合.(2)汽车在200km 的国道上行驶所用时间为200v ,总耗电量为()2322002001()(2180)5402800040S M v v v v v v v =⋅=⋅-+=-+,由于080v ≤<,所以当40v =时,min =28000WhS 所以,此汽车以40km/h 的速度行驶时,总耗电量最少,最少为28000Wh .20.已知函数2()1x f x x -=+.(1)求不等式(4)1(2)f x f x -+<+的解集;(2)若关于x 的方程()0f x m -=在[1,)x ∈+∞上有解,求实数m 的最大值;(3)证明:函数()y f x =关于点(1,1)--中心对称.【正确答案】(1)()3,3-(2)最大值为12(3)证明见解析【分析】(1)解分式不等式来求得不等式(4)1(2)f x f x -+<+的解集.(2)通过求()f x 在[)1,+∞上的值域来求得m 的取值范围,进而求得m 的最大值.(3)通过证明(,)P a b 、(2,2)Q a b ----都在()y f x =的图象上来证得函数()y f x =关于点(1,1)--中心对称.【详解】(1)()f x 的定义域为{}|1x x ≠-,因为(4)1(2)f x f x -+<+,所以2422133x x x x -+--+<-+,即3033x x x +<-+,所以290(3)(3)x x x +<-+,因为290x +>,所以(3)(3)0x x -+<,解得33x -<<,由4121x x -≠-⎧⎨+≠-⎩,解得3x ≠±,所以不等式(4)1(2)f x f x -+<+的解集为()3,3-.(2)由题意得关于x 的方程()0f x m -=在[1,)x ∈+∞上有解,则m 的取值范围即()f x 在[)1,+∞上的值域.因为23()111x f x x x -==-+++,所以3312,012x x +≥<≤+,所以11()2f x -<≤,即112m -<≤,所以实数m 的最大值为12.(3)在函数()y f x =的图象上任意取一点(,)P a b ,关于点()1,1--的对称点(2,2)Q a b ----,由()f a b =得21a b a -=+,即2(1)1b a b b -=≠-+,把2x a =--代入得224(2)211a a f a a a +++--==--+--24+3611221311bb b b b b b b -+++==⋅=---+---+,所以对称点(2,2)Q a b ----在函数()y f x =的图象上.即函数()y f x =的图象关于()1,1--中心对称.21.函数()y f x =的定义域为D ,若存在正实数k ,对任意的x D ∈,总有|()()|f x f x k --≤,则称函数()f x 具有性质()P k .(1)分别判断函数()2021f x =与()g x x =是否具有性质(1)P ,并说明理由;(2)已知()y f x =为二次函数,若存在正实数k ,使得函数()y f x =具有性质()P k .求证:()y f x =是偶函数;(3)已知0a k >,为给定的正实数,若函数()2()log 4x f x a x =+-具有性质()P k ,求a 的取值范围.【正确答案】(1)()f x 具有性质(1)P ,()g x 不具有性质(1)P ,理由见解析(2)证明见解析(3)[2,2]k k -【分析】(1)根据性质()P k 的定义对函数()2021f x =与函数()g x x =进行判断,从而确定正确答案.(2)性质()P k 的定义列不等式,求得b ,进而判断出()f x 是偶函数.(3)性质()P k 的定义列不等式,结合对数函数、指数函数的知识求得a 的取值范围.【详解】(1)对任意x ∈R ,得|()()||20212021|01f x f x --=-=<,所以()f x 具有性质(1)P ;对任意x ∈R ,得|()()||()||2|g x g x x x x --=--=.易得只需取1x =,则|(1)(1)|21g g --=>,所以()g x 不具有性质(1)P .(2)设二次函数2()(0)f x ax bx c a =++≠满足性质()P k .则对任意x ∈R ,满足22|()()||()||2|f x f x ax bx c ax bx c bx k --=++--+=≤.若0b ≠,取00||k x b =>,000|()()||2|2f x f x bx k k --==>,矛盾.所以0b =,此时2()(0)f x ax c a =+≠,满足()()f x f x -=,即()y f x =为偶函数(3)由于0a >,函数2()log (4)x f x a x =+-的定义域为R .易得22()log (4)log (22)x x x f x a x a -=+-=+⋅.若函数()f x 具有性质()P k ,则对于任意实数x ,有22|()()||log (22)log (22)|x x x x f x f x a a ----=+⋅-+⋅222|log |22x xx xa k a --+⋅=≤+⋅,即222log 22x x x x a k k a --+⋅-≤≤+⋅.即24log 14x x a k k a +-≤≤+⋅.由于函数2log y x =在(0,)+∞上严格递增,得42214x kk x a a -+≤≤+⋅.即112214k k x a a a a --≤+≤+⋅.当1a =时,得212k k -≤≤,对任意实数x 恒成立.当1a >时,易得10a a ->,由141x a +⋅>,得10114x a <<+⋅,得11014x a a a a a -<<-+⋅,得11114xa a a a a a -<+<+⋅.由题意得112214k k x a a a a --≤+≤+⋅对任意实数x 恒成立,所以122k k a a -⎧≥⎪⎨⎪≤⎩,即12.k a <≤当1a <时,易得10a a -<,由141x a +⋅>,得10114x a <<+⋅,得11014x a a a a a ->>-+⋅,得11114xa a a a a a ->+>+⋅.由题意得112214k k x a a a a --≤+≤+⋅对任意实数x 恒成立,所以212kk a a-⎧≥⎪⎨≤⎪⎩,即12.k a ->≥综上所述,a 的取值范围为[2,2]k k -.求解新定义函数类型的题目,关键点是理解和运用新定义,将新定义的知识,转化为学过的知识来进行求解.求解含参数的不等式问题,需要对参数进行分类讨论,分类讨论要做到不重不漏.。
上海市高一上学期期末数学试题(解析版)

一、填空题1.若扇形的弧长为,半径为2,则该扇形的面积是__________ 2π【答案】2π【分析】根据扇形面积公式求得正确答案. 【详解】依题意,扇形的面积为.12π22π2⨯⨯=故答案为:2π2.已知一元二次方程的两个实根为,则____ 20(0)x ax a a --=>12x x 、1211x x +=【答案】1-【分析】先利用韦达定理得到,再由代入即可求解.1212,x x x x +12121211x xx x x x ++=【详解】因为一元二次方程的两个实根为, 20(0)x ax a a --=>12x x 、所以. 1212,x x a x x a +==-故121212111x x a x x x x a++===--故答案为: 1-3.函数的定义域是__________. 22log 1x y x +=-【答案】(,2)(1,)-∞-+∞ 【分析】先利用对数式中真数为正得到,再将分式不等式化为一元二次不等式进行求解. 201x x +>-【详解】要使有意义,须, 22log 1x y x +=-201x x +>-即,解得或, (2)(1)0x x +->1x ><2x -即函数的定义域是. 22log 1x y x +=-(,2)(1,)-∞-+∞ 故答案为:.(,2)(1,)-∞-+∞4.已知,则__________cos160m = tan20= 【答案】【分析】根据诱导公式及同角三角函数的基本关系求得的值,进而求得的值. sin20 cos20 【详解】因为,所以, cos160m = cos20cos160m=-=-所以,sin 20=== 所以sin 20tan 20cos 20===故答案为:5.定义且,若,则______{A B xx A -=∈∣}x B ∉{}{}1,3,5,7,9,2,3,5A B ==()()A B B A -⋃-=【答案】{}1,2,7,9【分析】根据题目定义,分别求得和,再利用并集运算即可得出结果.{}1,7,9A B -={}2B A -=【详解】根据集合且的定义可知, {A B xx A -=∈∣}x B ∉当时,可得,; {}{}1,3,5,7,9,2,3,5A B =={}1,7,9A B -={}2B A -=所以 ()(){}1,2,7,9A B B A -⋃-=故答案为:{}1,2,7,96.将函数的图象向左平移__________个单位可得到函数的图象. 2x y =32x y =⋅【答案】2log 3【分析】根据指数对数的运算知,即可求解. 22log 3log 322232x x x y +=⋅==⋅【详解】因为,22log 3log 322232x x x y +=⋅==⋅所以将函数的图象向左平移个单位可得函数的图象. 2x y =2log 332x y =⋅故答案为:2log 37.当,时,则的最小值是__________. lg lg a b =()a b ≠13a b+【答案】【分析】由且,得出,用均值不等式即可得出答案. lg lg a b =a b ¹1ab =【详解】,且,而函数在上单调递增,lg lg a b = a b ¹lg y x =()0,+∞,即,且,,lg lg lg 0ab a b ∴=+=1ab =0a >0b >, 13a b ∴+≥=当且仅当,即13a b =b =a =故答案为:8.已知关于的方程有四个不相等的实数根,则的取值范围___________.x 265x x a -+=a 【答案】.(0,4)【分析】由题知转化为函数与有个不同的交点,画出函数的图265y x x =-+y a =4265y x x =-+像即可求出的取值范围.a 【详解】方程有四个不相等的实数根,265x x a -+=等价于函数与有个不同的交点.265y x x =-+y a =4由函数的图像知:265y x x =-+的取值范围为:.a 04a <<故答案为:(0,4)【点睛】本题主要考查方程的根的问题,转化为函数的交点问题为解题的关键,属于中档题.9.德国数学家狄利克雷在数学领域成就显著,以其命名函数,该函数被1,()0,x y D x x ⎧==⎨⎩为有理数为无理数称为狄利克雷函数.若存在三个点、、,使得为等边三角11(,())A x D x 22(,())B x D x 33(,())C x D x ABC A 形,则________. 123()()()D x D x D x ++=【答案】1【分析】由狄利克雷函数分析得出的位置有两种情况,逐一分析即可得出答案.ABC A 【详解】,1,()0,x y D x x ⎧==⎨⎩为有理数为无理数或1,∴()0D x =存在三个点、、,使得为等边三角形,11(,())A x D x 22(,())B x D x 33(,())C x D x ABC A 不同时为0或1,∴123(),(),()D x D x D x 不妨设,123x x x <<分析得的位置有两种情况,ABC A第一种情况:当为有理数时,即,如图,1x 1()1D x =过点作,垂足为,得,,B BD AC ⊥D 1BD =AD =AB AC BC ===可知,为无理数, 211x x AD x =+=31x x =即,,与图形不一致,舍去; 2()0D x =3()0D x =第二种情况:当为无理数时,即,如图,1x 1()0D x =过点作,垂足为,得,,B BD AC ⊥D 1BD =AD =AB AC BC ===可知,, 211x x AD x =+=31x x =存在,且 1x =210Q x x ==∈31x x ==即,与图形一致,符合题意, 2()1D x =3()0D x =此时,,123()()()0101D x D x D x ++=++=故答案为:1. 10.已知函数在是严格增函数,在上为严格减函数,若对任意()1ln xf x x+=(]0,1[)1,+∞,都有,则k 的取值范围是_________()0,x ∞∈+e x x k ≤【答案】1,e ∞⎡⎫+⎪⎢⎣⎭【分析】根据函数的单调性求出函数最大值可求出的最大值,对两边取自然对数,ln x x -e x x k ≤分离,利用不等式恒成立求解即可. ln k 【详解】因为在是严格增函数,在上为严格减函数, ()1ln xf x x+=(]0,1[)1,+∞所以. 1ln ()(1)1xf x f x+=≤=由,可得,0x >ln 1x x -≤- 又时,由可得, ()0,x ∞∈+e x x k ≤ln ln(e )ln x x k k x ≤=+即恒成立, ln ln x x k -≤所以,即.ln 1k ≥-1ek ≥故答案为:1,e ∞⎡⎫+⎪⎢⎣⎭二、单选题11.若为第三象限角,则( ) αA . B . C . D .cos 20α>cos20α<sin 20α>sin 20α<【答案】C【解析】利用为第三象限角,求所在象限,再判断每个选项的正误. α2α【详解】因为为第三象限角,所以, α3222k k πππαπ+<<+()k Z ∈可得 , 24234k k ππαππ+<<+()k Z ∈所以是第第一,二象限角, 2α所以,不确定, sin 20α>cos 2α故选:C【点睛】本题主要考查了求角所在的象限以及三角函数在各个象限的符号,属于基础题.12.已知定义域为的函数满足:①对任意,恒成立;②若R ()y f x =,R x y ∈()()()f x y f x f y +=⋅则.以下选项表述不正确的是( )x y ≠()()f x f y ≠A .在上是严格增函数 B .若,则()y f x =R (3)10f =(6)100f =C .若,则 D .函数的最小值为2(6)100f =1(3)10f -=()()()F x f x f x =+-【答案】A【分析】根据给定条件,探讨函数的性质,再举例判断A ;取值计算判断B ,C ;借助均值不()f x 等式求解判断D 作答.【详解】任意,恒成立,,R x y ∈()()()f x y f x f y +=⋅且,假设,则有,R a ∈0a ≠()0f a =(2)()()()0()f a f a a f a f a f a =+=⋅==显然,与“若则”矛盾,假设是错的,因此当且时,,2a a ≠x y ≠()()f x f y ≠R a ∈0a ≠()0f a ≠取,有,则,于是得,,0,0x a y =≠=()()(0)f a f a f =⋅(0)1f =R x ∀∈()0f x ≠,,,R x ∀∈2()([()]0222x x x f x f f =+=>()()(0)1f x f x f ⋅-==对于A ,函数,,,1()()2xf x =,x y ∀∈R 111()()()()()()222x y x y f x y f x f y ++==⋅=⋅并且当时,,即函数满足给定条件,而此函数在上是严格减函数,x y ≠()()f x f y ≠1()()2xf x =R A 不正确;对于B ,,则,B 正确;(3)10f =(6)(3)(3)100f f f =⋅=对于C ,,则,而,有,又,因此(6)100f =(3)(3)100f f ⋅=(3)0f >(3)10f =(3)(3)1f f ×-=,C 正确; 1(3)10f -=对于D ,,,则有,()()1f x f x ⋅-=()0f x >()()()1F x f x f x =+-³=当且仅当,即时取等号,所以函数的最小值为2,D 正确. ()()1f x f x =-=0x =()()()F x f x f x =+-故选:A【点睛】关键点睛:涉及由抽象的函数关系求函数值,根据给定的函数关系,在对应的区间上赋值即可.13.Logistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠病毒感染累计人数(的单位:天)的Logistic 模型:其中为最大病毒感()I t t ()()0.23531e t K I t --=+K 染数.当时,标志着该地区居民工作生活进入稳定窗口期.在某地区若以2022年12月()0.95I t K ≥15日为天,以Logistic 模型为判断依据,以下表述符合预期的选项是( ) 1t =A .该地区预计2023年元旦期间进入稳定窗口期; B .该地区预计2023年1月底进入稳定窗口期; C .该地区预计2023年2月中下旬进入稳定窗口期; D .该地区预计2023年某时刻不起再有新冠病毒感染者. 【答案】C【分析】根据条件列不等式,解指数型不等式即可. 【详解】由题意知,,0.23(53)0.951et K K --≥+即:, 0.23(53)201e19t --+≤所以, ln19353535313660.230.23t ≥+≈+≈+=因为以2022年12月15日为天,所以天,即预计2023年2月18日后该地区进入稳定窗1t =66t ≥口期,即该地区预计2023年2月中下旬进入稳定窗口期.故选:C.14.已知函数,定义域为,值域为.则以下选项正确的是( )()()23log 2f x mx x m =-+A B A .存在实数使得 m R A B ==B .存在实数使得 m R A B =⊆C .对任意实数 10,m A B -<<⋂≠∅D .对任意实数 0,m A B >⋂≠∅【答案】D【分析】设,考虑,,,,,几种情22y mx x m =-+1m >1m =01m <<0m =10m -<<1m ≤-况,分别计算集合和,再对比选项得到答案..A B 【详解】设,当,即时, 22y mx x m =-+2440m ∆=->11m -<<设对应方程的两根为,,不妨取,1x 2x 12x x <当时,,,且; 1m >2440m ∆=-<R A =R B ≠B ≠∅当时,,;1m =()(),11,A =-∞+∞ R B =当时,,,; 01m <<2440m ∆=->()()12,,A x x =-∞+∞ R B =当时,,;0m =(),0A =-∞R B =当时,,,,故;10m -<<2440m ∆=->()12,A x x =max 1y m m =-31,log B m m ⎛⎤⎛⎫=-∞- ⎪ ⎥⎝⎭⎝⎦当时,函数无意义.1m ≤-对选项A :根据以上情况知不存在的情况,错误; R A B ==对选项B :根据以上情况知不存在的情况,错误; R A B =⊆对选项C :假设任意实数,, 10m -<<A B ⋂≠∅取,解得,则, 119m m -=m =(],2B =-∞-对于,有220mx x m -+=1x =此时应满足,解得, 12x =<-405m -<<易得,错误; m =A B ⋂=∅对选项D :根据以上情况知对任意实数,正确; 0,m A B >⋂≠∅故选:D【点睛】关键点睛:本题考查了对数型复合函数的定义域和值域,意在考查学生的计算能力,转化能力和综合应用能力,其中,根据二次函数的开口方向和的正负讨论的范围,进而计算集合∆a A 和是解题的关键,分类讨论的方法是常考方法,需要熟练掌握.B三、解答题15.如图所示:角为锐角,设角的始边与轴的非负半轴重合,终边与单位圆交于点ααx ,将射线绕坐标原点按逆时针方向旋转后与单位圆交于点. 2,cos 3P α=OP O π2()11,Q x y(1)求的值; tan α(2)求的值. 1y【答案】 (2) 23【分析】(1)确定,计算得到答案.sin 0α>sin α=sin tan cos ααα=(2)设终边对应的角度为,则,,计算得到答案. OQ βπ2βα=+1cos y α=【详解】(1)角为锐角,,,则, αsin 0α>2cos 3α=sin α===sin tan cos ααα==(2)设终边对应的角度为,,OQ βπ,π2β⎛⎫∈ ⎪⎝⎭则,π2βα=+1π2sin sin cos 23y βαα⎛⎫==+== ⎪⎝⎭16.集合{为严格增函数}.S =()()(),0,f x f x x y x∈+∞=∣()()2121(0),(0)f x x x f x x x =+>=>(1)直接写出是否属于集合 ()()12,f x f x ;S (2)若.解不等式:()m x S ∈()()223223ee e e xxxx m m -+⋅<⋅(3)证明:“”的充要条件是“” ()()()()120H x af x bf x ab =+≠()H x S ∈0,0b a ><【答案】(1)不属于集合,属于集合 ()1f x S ()2f x S (2) ()3,1-(3)证明见解析【分析】(1)根据定义直接判断即可; (2)由,可得函数为增函数,不等式,即为不等式()m x S ∈()m x y x=()()223223e ee e x x xx m m -+⋅<⋅,再根据函数的单调性解不等式即可;()()222332e e e e x xxxm m ++<(3),即函数在定义域内为增函数,根据函数的单调性结合充分条件和必要条()H x S ∈()H x y x=件的定义证明即可. 【详解】(1)因为在定义域内为减函数, ()()1110f x y x x x==+>所以不属于集合, ()1f x S 因为在定义域内为增函数, ()()20f x y x x x==>所以属于集合; ()2f x S (2)不等式,()()223223ee ee xxxx m m -+⋅<⋅即为不等式,()()222332e e e e x xxxm m ++<因为, ()m x S ∈所以函数为增函数, ()m x y x=所以,223e e xx+<所以,解得, 223x x +<31x -<<所以不等式的解集为;()()223223ee ee xxxx m m -+⋅<⋅()3,1-(3),()()()()2120H x af x bf x bx ax a ab =+=++≠则, ()()0H x abx a x x x=++>令, ()()0ag x bx a x x=++>当,则在上递增, ()H x S ∈()()0ag x bx a x x=++>()0,∞+令,120x x <<则对任意的恒成立,()()210g x g x -≥12,x x ()()2121212112a x x a abx a bx a b x x x x x x -⎛⎫++-++=-- ⎪⎝⎭恒成立,()()211212x x bx x a x x --=≥即恒成立, 120bx x a -≥因为,所以, 0ab ≠0,0a b ≠≠当时,恒成立, 0b >12ax x b ≥因为,所以, 120x x >0ab≤又,所以, 0,0b a >≠a<0当时,恒成立, 0b <12ax x b≤因为没有最大值,所以不恒成立,与题意矛盾, 120x x >12ax x b≤综上所述,当在上递增时,, ()()0ag x bx a x x=++>()0,∞+0,0b a ><当时, 0,0b a ><则函数在上都是增函数, ,ay bx y a x==+()0,∞+所以函数在上是增函数, ()()0ag x bx a x x=++>()0,∞+综上所述,“”的充要条件是“”.()H x S ∈0,0b a ><【点睛】关键点点睛:解决本题的关键在于把握新定义的含义,以及函数单调性的判定及利用函数的单调性解不等式.。
高一数学必考试题及答案

高一数学必考试题及答案一、选择题(每题3分,共30分)1. 下列函数中,为奇函数的是:A. y = x^2B. y = |x|C. y = x^3D. y = sin(x)答案:C2. 若函数f(x) = 2x + 1在区间[-1, 2]上是增函数,则下列说法正确的是:A. f(x)在[-1, 2]上单调递减B. f(x)在[-1, 2]上单调递增C. f(x)在[-1, 2]上先增后减D. f(x)在[-1, 2]上先减后增答案:B3. 已知集合A={1, 2, 3},集合B={2, 3, 4},则A∩B的元素个数为:A. 0B. 1C. 2D. 3答案:C4. 函数y = 3x - 2的图像不经过第几象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:B5. 已知等差数列{an}的前三项分别为1, 4, 7,则其第10项为:A. 26B. 27C. 28D. 29答案:A6. 圆的方程为x^2 + y^2 - 6x + 8y - 24 = 0,其圆心坐标为:A. (3, -4)B. (-3, 4)C. (3, 4)D. (-3, -4)答案:A7. 函数f(x) = x^2 - 6x + 8的最小值是:A. -1B. 0C. 1D. 2答案:B8. 直线y = 2x + 3与x轴的交点坐标为:A. (-3/2, 0)B. (3/2, 0)C. (0, 3)D. (0, -3)答案:B9. 已知三角形ABC中,∠A = 60°,∠B = 45°,则∠C的大小为:A. 45°B. 60°C. 75°D. 30°答案:D10. 函数f(x) = |x - 2| + |x + 3|的最小值是:A. 5B. 1C. 0D. 2答案:A二、填空题(每题4分,共20分)1. 已知函数f(x) = x^2 - 4x + 3,其顶点坐标为______。
高一数学集合10道填空题练习题及详细答案解析A4

高一数学集合10道填空题练习题及详细答案解析1.若集合C={x∈R|cx²+cx+9=0}只有一个元素,则c= .2.已知集合C={x|x²≥9,x∈R},D={-3,-2,0,3, 8},则(CᵣC)∩D= .3.已知集合G={x|(x-213)²>0},H={x||x|≤213,x∈Z},则G∩H= .4.已知集合G={x|x-19x+1≤0},H={x∈N|x²+24x-25≤0},则G∩H= .5.若集合W={225, 15p},集合V={p²,225},且W=V,则p= .6.已知集合C={214,c},D={2c-22,214},且C=D,则实数c的取值为.7.已知集合G={x|-84≤x≤-78},集合H=|x|x=2n-1,n∈Z},则G∩H= .8.集合W={x∈Z|x²≤16},结合V={x∈N|x<14},则W∩V的子集个数= .9.集合S={x|x≥-289},集合T={x|x≤-241},则S∩(CᵣT)= .10.已知集合S={-117,9,63,121,172},T={x|(x+118)(x-122)≤0},则S∩T= .高一数学集合10道填空题解答详细解析1.若集合C={x ∈R|cx ²+cx+9=0}只有一个元素,则c= .解:当c=0,代入可有9=0,矛盾;当c ≠0时,元素满足的方程是一元二次方程,根据题意只有一个元素,则方程只有一个解,故方程的判别式为0,即:c ²-4*c*9=0,进一步知c =4*9=36,即为本题答案。
2.已知集合C={x|x ²≥9,x ∈R},D={-3,-2,0,3, 8},则(CᵣC)∩D= .解:对于集合C :x ²≥9,则对于该集合的补集CᵣC 有:x ²<9,解出:-3<x <3,可知端点的值取不到,再与集合D 取交集的元素只有-2和0,故答案为{-2,0}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学填空题专项训练
1.不等式01
2
≤+-x x 的解集为 .
2.已知等比数列{}n a 中,各项都是正数,且2312,2
1
,a a a 成等差数列,则87109a a a a ++= .
3.一组数据8,9,x ,11,12的平均数是10,则这组数据的标准差是_________.
4. 阅读下列程序:
Read S ←1
For I from 1 to 5 step 2 S ←S+I Print S End for End
输出的结果是 .
5.某校为了解高三男生的身体状况,检测了全部480名高三男生的体重(单位㎏)。
所得数据都在区间[50,75]中,其频率分布直方图如图所示。
若图中从左到右的前3个小组的频率之比为1:2:3,则体重小于60㎏的高三男生人数为_______。
(第4题)
6.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为4cm 的圆面,中间有边长为1cm 的正方形孔,若随机向铜钱上滴一滴油(油滴不出边界),则油滴整体(油滴是直径为0.2cm 的球)正好落入孔中的概率是 .(不作近似计算)
7. 在ABC ∆中,角A,B,C 的对边分别为,,,c b a 若
8. 已知实数x ,y 满足22,052y x y x +=++那么的最小值为 .
9. 对一切实数x ,不等式01||2
≥++x a x 恒成立,则实数a 的取值范围是 .
10. 已知数列{}n a 满足1a =1,13211
1
3121--++++
=n n a n a a a a (N n n ∈≥,2)
,若 n a =2006,求数列{}n a 的通项公式 .
11. 某人从2002年1月1日起, 每年这一天到银行存一年定期a 元, 若年利率r 保持不变,且每年到期的存款将本和利都再存入新一年的定期, 到2009年1月1日, 将所有的存款和利息全部取回, 他可取回的钱为________元.
12. 在斜三角形ABC 中,角C B A ,,所对的边分别为c b a ,,,若
1tan tan tan tan =+B
C
A C ,则 =+2
2
2c b a .
13.在等差数列{}n a 中,n S 表示其前n 项,若m n S n =,)(n m n
m S m ≠=,则m n S +的取值范围是 .
14.(1)过)1,2(P 且横截距等于纵截距两倍的直线方程为042=-+y x .
(2)α
αsin 4
sin +
(),0(πα∈)的最小值为4. (3)已知两点),(),,(2211y x P y x P ,
则方程)())((1211y y y y x x ----)(21x x -=0能表示所有的直线。
(4)已知数列{}n a 通项公式n n a n λ+=2
为增数列,则λ的取值范围是2-≥λ
请写出正确命题的序号 .。
