有限元C++编程实践
有限元算例二维传热c++程序源代码4

//please turn to page 158 for more detailsprintf("计算基函数系数值...\n");for(id=0;id<nx*ny*2;id++){for(i=0;i<3;i++){if(i==0) j=1,k=2;else if(i==1) j=2,k=0;else if(i==2) j=0,k=1;pE[id].A=( (pE[id].nd[j].x-pE[id].nd[i].x)*(pE[id].nd[k].y-pE[id].nd[i].y)-(pE[id].nd[j].y-pE[id].nd[i].y)*(pE[id].nd[k].x-pE[id].nd[i].x) )/2.0;D=2.0*pE[id].A;pE[id].a[i]=( pE[id].nd[j].x*pE[id].nd[k].y- pE[id].nd[k].x*pE[id].nd[j].y )/D;pE[id].b[i]=( pE[id].nd[j].y-pE[id].nd[k].y )/D;pE[id].c[i]=( pE[id].nd[k].x-pE[id].nd[j].x )/D;}}printf("OK!\n");printf("计算单元有限元特征式系数矩阵...\n");int l,m;for(i=0;i<nx;i++) //计算单元有限元特征式系数矩阵for(j=0;j<ny;j++){for(l=0;l<3;l++) //for the first triangle in the rectanglefor(m=0;m<3;m++){pE[i*2+j*ny*2].Aij[l][m]=( pE[i*2+j*ny*2].b[l]*pE[i*2+j*ny*2].b[m] +pE[i*2+j*ny*2].c[l]*pE[i*2+j*ny*2].c[m] ) * pE[i*2+j*ny*2].A;}for(l=0;l<3;l++) //for the second triangle in the rectangle for(m=0;m<3;m++){pE[i*2+j*ny*2+1].Aij[l][m]=( pE[i*2+j*ny*2+1].b[l]*pE[i*2+j*ny*2+1].b[m] + pE[i*2+j*ny*2+1].c[l]*pE[i*2+j*ny*2+1].c[m] ) * pE[i*2+j*ny*2+1].A;}}printf("OK!\n");printf("计算积分值,填充到f函数向量数组...\n");static int js[2]={4,4}; //每一层积分区间均分为4个子区间int idx=0;for(i=0;i<nx;i++) //计算积分值,填充到f函数向量数组for(j=0;j<ny;j++){for(idx=0;idx<3;idx++) //for the first triangle in the rectangle。
三结点三角形有限单元程序设计C 语言

fclose(fp) ;
int NN2=NN*2; int NBW=NN2;
//半带宽 NBW
float GK[50][50];
float DU[50];
int *count=new int [NN];
float (*strain)[3]=new float [NN][3];
float (*stress)[3]=new float [NN][3];
int ngn[3]; for(i=0;i<3;i++)ngn[i]=NGN[NOE-1][i];
float cn[3][2]; for(i=0;i<3;i++) for(j=0;j<2;j++) cn[i][j]=CN[ngn[i]-1][j];
float a[3]={0,0,0}; float b[3]={0,0,0}; float c[3]={0,0,0};
void elestrain_stress(
intNOE,intNGN[][3],floatCN[][2],
floatDU[50],floatE0,floatU0,floatt,
intNE,intNN,floatelestrain[3],floatelestress[3]);
#endif
Ⅴ.节点应力-应变头文件 NodeStrainStress.h
fscanf(fp,"%s",&newlin); for(i=0;i<NN;i++)
for(j=0;j<2;j++) fscanf(fp, "%f", &CN[s",&newlin); int NRE=0; fscanf(fp, "%d", &NRE) ; int *restrict=new int [NRE]; for(i=0;i<NRE;i++)
有限单元法 cad cam实验报告

CAD/CAM 技术实验报告有限单元法一、实验目的1、通过上机练习,学习3D实体建模的基本知识。
2、了解有限元法作为一种数值计算方法解决工程实际问题的全过程。
3、知道如何进行有限元离散、单元分析和整体分析,并得出相应的分析结果。
二、实验原理I-DEAS软件是当今国内、外应用最为广泛的几种大型CAD/CAM/CAE一体化软件之一,具有较强的有限元分析功能。
在航空航天、核工业、铁路运输业、石油化工、机械制造、能源、汽车、电子、造船和水利等领域得到广泛的应用,为各领域内的产品设计和科学研究做出了很大贡献。
用I-DEAS软件进行结构偶有限元分析的步骤:(1)前处理程序:前处理程序的功能是根据一个实际问题的物理模型,用尽可能接近自然语言的方式,向计算机输入尽可能少的定义有限元模型和控制分析过程的数据,自动生成有限元分析主体程序所需要的全部输入文件。
几何造型:几何造型是指在选定的坐标(常用的是直角坐标系、圆柱坐标系和球坐标系)内通过几何元素(点、线、面、体)的生成和对他们的编辑,生成有限元分析对象的几何构造和图形。
网格生成:1、转换生成法:这是直接将几何元素的点、线、面和体直接转化成有限元的结点、线单元、面单元和体单元。
2、自动生成法:这是在商业软件中常被采用的方法。
他在任意形状的平面或空间裁剪曲面上可生成三角形或四边形单元;对单元几何实体或由曲面围成的封闭空间,可生成四面体或六面体实体单元。
(2)后处理程序:后处理程序的功能是对用户在前处理程序中指明需要输出的计算结果进一步处理和图形显示。
主要计算结果中通常需要处理的物理量是位移(矢量或各个分量)、应力(等效应力或各个分量)和温度等。
为了清晰地观察变形图和未变形图对比的显示结果,变形图可以由用户给出放大倍数。
三、使用仪器、材料计算机、I-DEAS软件四、实验步骤(一)初步熟悉I-DEAS软件1、了解软件界面的不同分区,包含图形区、执行命令输出信息区、提示区和功能按钮区。
有限元分析中《结构力学》矩阵位移法C语言程序(附例题)

程序:#include "stdafx.h"#include "stdio.h"#include "math.h"#include "stdlib.h"void main(){int loc[3][2]={0},ifix[6]={0};float area[3]={0.0},fint[3]={0.0},cx[4]={0.0},cy[4]={0.0},f[12]={0.0},fr[12]= {0.0},fe[3][6]={0.0};int nn,ne,nd,nfix;float ea;int i,j,k;FILE *shuru,*shuchu;shuru=fopen("shuru.dat","r");shuchu=fopen("shuchu.dat","w");fscanf(shuru,"%d%d%d%d%f",&nn,&ne,&nd,&nfix,&ea);fprintf(shuchu,"nn ne nd nfix e\n%d %d %d %d %f\n",nn,ne,nd,nfix,ea);i=0;while(i<=ne-1){fscanf(shuru,"%d%d%f%f",&loc[i][0],&loc[i][1],&area[i],&fint[i]);i++;}fprintf(shuchu,"element node1 node2 area fint\n");i=0;while(i<=ne-1){fprintf(shuchu,"%d %d %d %f %f\n",i+1,loc[i][0],loc[i][1],area[i],fint[i]);i++;}j=0;while(j<=nn-1){fscanf(shuru,"%f%f",&cx[j],&cy[j]);j++;}fprintf(shuchu,"node x-coord y-coord\n");j=0;while(j<=nn-1){fprintf(shuchu,"%d %f %f\n",j+1,cx[j],cy[j]);j++;}k=0;while(k<=nfix-1){fscanf(shuru,"%d",&ifix[k]);k++;}fprintf(shuchu,"ifix=");k=0;while(k<=nfix-1){fprintf(shuchu,"%d ",ifix[k]);k++;}fprintf(shuchu,"\n");void cst(int (*loc)[2],int *ifix,float *area,float *fint,float *cx,float *cy,float*f,float *fr,float (*fe)[6],FILE *shuru,FILE *shuchu,float ea);cst(loc,ifix,area,fint,cx,cy,f,fr,fe,shuru,shuchu,ea);fprintf(shuchu,"node x-disp y-disp thita\n");i=0;while(i<=3){fprintf(shuchu,"%d %f %f %f\n",i+1,f[3*i],f[3*i+1],f[3*i+2]);i++;}fprintf(shuchu,"reaction nodal forces from the equations\n");fprintf(shuchu,"node x-load y-load moment\n");i=0;while(i<=3){fprintf(shuchu,"%d %f %f %f\n",i+1,fr[3*i],fr[3*i+1],fr[3*i+2]);i++;}fprintf(shuchu,"element axi-f shear-q moment-m\n");i=0;while(i<=ne-1){fprintf(shuchu,"%d %f %f %f %f %f %f\n",i+1,fe[i][0],fe[i][1],fe[i][2],fe[i][3],fe [i][4],fe[i][5]);i++;}fclose(shuru);fclose(shuchu);}void cst(int (*loc)[2],int *ifix,float *area,float *fint,float *cx,float *cy,float*f,float *fr,float (*fe)[6],FILE *shuru,FILE *shuchu,float ea){int np,nvd;float p1[3][6]={0.0},p2[3][6]={0.0},gk[12][12]={0.0},gk1[12][12]={0.0},al[3]= {0.0},tt[3][6][6]={0.0},bkl[3][6][6]={0.0};float t[6][6]={0.0},css[3]={0.0},snn[3]={0.0},ek[6][6]={0.0},ekl[6][6]={0.0},ekk[3] [6][6]={0.0},xx[6]={0.0},ba[6][6]={0.0};int nn=4,ne=3,nd=12,nfix=6;int ii,jj,i,j,k,l,inode,nodei,idofn,nrows,nrowe,jnode,nodej,jdofn,ncols,ncole;int i1,i2,ie,ix;float x12,y12,q,eal,eil1,eil2,eil3;i=0;{for(;i<=ne-1;i++){i1=loc[i][0];i2=loc[i][1];x12=cx[i2-1]-cx[i1-1];y12=cy[i2-1]-cy[i1-1];al[i]=sqrt(pow(x12,2)+pow(y12,2));css[i]=x12/al[i];snn[i]=y12/al[i];}}fscanf(shuru,"%d%d",&np,&nvd);if(np!=0)i=0;for(;i<=np-1;i++){fscanf(shuru,"%d%f%f%f",&i,&f[3*i],&f[3*i+1],&f[3*i+2]); }if(nvd!=0)i=0;for(;i<=nvd-1;i++){fscanf(shuru,"%d%f",&ie,&q);i1=loc[ie-1][0];i2=loc[ie-1][1];p1[ie-1][1]=q*al[ie-1]/2;p1[ie-1][2]=q*al[ie-1]*al[ie-1]/12;p1[ie-1][4]=q*al[ie-1]/2;p1[ie-1][5]=-q*al[ie-1]*al[ie-1]/12;}i=0;for(;i<=nd-1;i++){j=0;for(;j<=nd-1;j++){gk[i][j]=0.0;}}for(i=0;i<=ne-1;i++){j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){ekl[j][k]=0.0;ek[j][k]=0.0;t[j][k]=0.0;}}eal=ea*area[i]/al[i];eil1=ea*fint[i]/al[i];eil2=ea*fint[i]/(al[i]*al[i]);eil3=ea*fint[i]/(al[i]*al[i]*al[i]);ekl[0][0]=eal;ekl[1][1]=12.0*eil3;ekl[2][2]=4.0*eil1;ekl[3][3]=eal;ekl[4][4]=12.0*eil3;ekl[5][5]=4.0*eil1;ekl[2][1]=6.0*eil2;ekl[3][0]=-eal;ekl[4][1]=-12.0*eil3;ekl[4][2]=-6.0*eil2;ekl[5][1]=6.0*eil2;ekl[5][2]=2.0*eil1;ekl[5][4]=-6.0*eil2;ii=0;for(;ii<=4;ii++){jj=ii+1;for(;jj<=5;jj++){ekl[ii][jj]=ekl[jj][ii];}}k=0;for(;k<=5;k++){l=0;for(;l<=5;l++){{ekk[i][k][l]=ekl[k][l];fprintf(shuchu,"%d %d %d %f %f\n",i+1,k+1,l+1,ekl[k][l],ekk[i][k][l]);} }}t[0][0]=css[i];t[0][1]=-snn[i];t[1][0]=snn[i];t[1][1]=css[i];t[2][2]=1.0;t[3][3]=css[i];t[3][4]=-snn[i];t[4][3]=snn[i];t[4][4]=css[i];t[5][5]=1.0;j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){tt[i][j][k]=t[j][k];p2[i][j]=p2[i][j]+t[j][k]*p1[i][k];}}ii=0;for(;ii<=5;ii++){j=0;for(;j<=5;j++){ba[ii][j]=0.0;k=0;for(;k<=5;k++){ba[ii][j]=ba[ii][j]+tt[i][ii][k]*ekl[k][j];}}}ek[ii][j]=0.0;ii=0;for(;ii<=5;ii++){j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){ek[ii][j]=ek[ii][j]+ba[ii][k]*tt[i][j][k];}}}j=0;for(;j<=5;j++){ii=0;for(;ii<=5;ii++){fprintf(shuchu,"i,ii,j,ek,tt=%d %d %d %f %f\n",i+1,ii+1,j+1,ek[ii][j],tt[i][ii][j]); }}inode=0;while(inode<=1){nodei=loc[i][inode];idofn=0;while(idofn<=2){nrows=(nodei-1)*3+idofn;nrowe=inode*3+idofn;f[nrows]=f[nrows]+p2[i][nrowe];jnode=0;while(jnode<=1){nodej=loc[i][jnode];jdofn=0;while(jdofn<=2){ncols=(nodej-1)*3+jdofn;ncole=jnode*3+jdofn;gk[nrows][ncols]=gk[nrows][ncols]+ek[nrowe][ncole];jdofn++;}jnode++;}idofn++;}inode++;}}i=0;for(;i<=nd-1;i++){j=0;for(;j<=nd-1;j++){gk1[i][j]=gk[i][j];}}fprintf(shuchu,"nodal forces from applied loads\node x-load y-load moment\n"); i=0;for(;i<=nn-1;i++){fprintf(shuchu,"%d %f %f %f\n",i+1,f[3*i],f[3*i+1],f[3*i+2]);}i=0;for(;i<=nd-1;i++){j=0;for(;j<=nd-1;j++){fprintf(shuchu,"i,j,gk1 %d %d %f\n",i+1,j+1,gk[i][j]);}}i=0;for(;i<=nfix-1;i++){ix=ifix[i];gk[ix-1][ix-1]=gk[ix-1][ix-1]*1.0e20;}void gauss(float (*a)[12],float *b,int n);gauss(gk,f,nd);i=0;for(;i<=nd-1;i++){fr[i]=0.0;j=0;for(;j<=nd-1;j++){fr[i]=fr[i]+gk1[i][j]*f[j];fr[i]=fr[i]-f[i];}}for(i=0;i<=ne-1;i++){i1=loc[i][0];i2=loc[i][1];xx[0]=f[3*i1-3];xx[1]=f[3*i1-2];xx[2]=f[3*i1-1];xx[3]=f[3*i2-3];xx[4]=f[3*i2-2];xx[5]=f[3*i2-1];j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){bkl[i][j][k]=0.0;l=0;for(;l<=5;l++){bkl[i][j][k]=bkl[i][j][k]+ekk[i][j][l]*tt[i][k][l];}}}j=0;for(;j<=5;j++){fe[i][j]=0.0;k=0;for(;k<=5;k++){fe[i][j]=fe[i][j]+bkl[i][j][k]*xx[k];}}j=0;for(;j<=5;j++){fe[i][j]=fe[i][j]-p1[i][j];}}}void gauss(float (*a)[12],float *b,int n){int i,i1,j,m;i=0;for(;i<=n-1;i++){i1=i+1;for(j=i1;j<=n-1;j++)a[i][j]=a[i][j]/a[i][i];b[i]=b[i]/a[i][i];a[i][i]=1.0;for(j=i1;j<=n-1;j++){for(m=i1;m<=n-1;m++)a[j][m]=a[j][m]-a[j][i]*a[i][m];b[j]=b[j]-a[j][i]*b[i];}}i=n-2;for(;i>=0;i--){j=i+1;for(;j<=n-1;j++){b[i]=b[i]-a[i][j]*b[j];}}}一、如图所示平面刚架的内力,各杆面积A=76.3cm2,惯性矩I=15760cm4,弹性模量E=2×105MPa程序:#include "stdafx.h"#include "stdio.h"#include "math.h"#include "stdlib.h"void main(){int loc[3][2]={0},ifix[6]={0};float area[3]={0.0},fint[3]={0.0},cx[4]={0.0},cy[4]={0.0},f[12]={0.0},fr[12]={0.0},fe[3][6]={0.0};int nn,ne,nd,nfix;float ea;int i,j,k;FILE *shuru,*shuchu;shuru=fopen("shuru.dat","r");shuchu=fopen("shuchu.dat","w");fscanf(shuru,"%d%d%d%d%f",&nn,&ne,&nd,&nfix,&ea);fprintf(shuchu,"nn ne nd nfix e\n%d %d %d %d %f\n",nn,ne,nd,nfix,ea);i=0;while(i<=ne-1){fscanf(shuru,"%d%d%f%f",&loc[i][0],&loc[i][1],&area[i],&fint[i]);fprintf(shuchu,"element node1 node2 area fint\n");i=0;while(i<=ne-1){fprintf(shuchu,"%d %d %d %f %f\n",i+1,loc[i][0],loc[i][1],area[i],fint[i]);i++;}j=0;while(j<=nn-1){fscanf(shuru,"%f%f",&cx[j],&cy[j]);j++;}fprintf(shuchu,"node x-coord y-coord\n");j=0;while(j<=nn-1){fprintf(shuchu,"%d %f %f\n",j+1,cx[j],cy[j]);j++;}k=0;while(k<=nfix-1){fscanf(shuru,"%d",&ifix[k]);k++;}fprintf(shuchu,"ifix=");k=0;while(k<=nfix-1){fprintf(shuchu,"%d ",ifix[k]);k++;}fprintf(shuchu,"\n");void cst(int (*loc)[2],int *ifix,float *area,float *fint,float *cx,float *cy,float*f,float *fr,float (*fe)[6],FILE *shuru,FILE *shuchu,float ea);cst(loc,ifix,area,fint,cx,cy,f,fr,fe,shuru,shuchu,ea);fprintf(shuchu,"node x-disp y-disp thita\n");i=0;while(i<=3){fprintf(shuchu,"%d %f %f %f\n",i+1,f[3*i],f[3*i+1],f[3*i+2]);i++;}fprintf(shuchu,"reaction nodal forces from the equations\n");fprintf(shuchu,"node x-load y-load moment\n");i=0;while(i<=3){fprintf(shuchu,"%d %f %f %f\n",i+1,fr[3*i],fr[3*i+1],fr[3*i+2]);i++;}fprintf(shuchu,"element axi-f shear-q moment-m\n");i=0;while(i<=ne-1){fprintf(shuchu,"%d %f %f %f %f %f %f\n",i+1,fe[i][0],fe[i][1],fe[i][2],fe[i][3],fe [i][4],fe[i][5]);fclose(shuru);fclose(shuchu);}void cst(int (*loc)[2],int *ifix,float *area,float *fint,float *cx,float *cy,float*f,float *fr,float (*fe)[6],FILE *shuru,FILE *shuchu,float ea){int np,nvd;float p1[3][6]={0.0},p2[3][6]={0.0},gk[12][12]={0.0},gk1[12][12]={0.0},al[3]= {0.0},tt[3][6][6]={0.0},bkl[3][6][6]={0.0};float t[6][6]={0.0},css[3]={0.0},snn[3]={0.0},ek[6][6]={0.0},ekl[6][6]={0.0},ekk[3] [6][6]={0.0},xx[6]={0.0},ba[6][6]={0.0};int nn=4,ne=3,nd=12,nfix=6;int ii,jj,i,j,k,l,inode,nodei,idofn,nrows,nrowe,jnode,nodej,jdofn,ncols,ncole;int i1,i2,ie,ix;float x12,y12,q,eal,eil1,eil2,eil3;i=0;{for(;i<=ne-1;i++){i1=loc[i][0];i2=loc[i][1];x12=cx[i2-1]-cx[i1-1];y12=cy[i2-1]-cy[i1-1];al[i]=sqrt(pow(x12,2)+pow(y12,2));css[i]=x12/al[i];snn[i]=y12/al[i];}}fscanf(shuru,"%d%d",&np,&nvd);if(np!=0)i=0;for(;i<=np-1;i++){fscanf(shuru,"%d%f%f%f",&i,&f[3*i],&f[3*i+1],&f[3*i+2]);}if(nvd!=0)i=0;for(;i<=nvd-1;i++){fscanf(shuru,"%d%f",&ie,&q);i1=loc[ie-1][0];i2=loc[ie-1][1];p1[ie-1][1]=q*al[ie-1]/2;p1[ie-1][2]=q*al[ie-1]*al[ie-1]/12;p1[ie-1][4]=q*al[ie-1]/2;p1[ie-1][5]=-q*al[ie-1]*al[ie-1]/12;}i=0;for(;i<=nd-1;i++){j=0;for(;j<=nd-1;j++){gk[i][j]=0.0;}}for(i=0;i<=ne-1;i++){j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){ekl[j][k]=0.0;ek[j][k]=0.0;t[j][k]=0.0;}}eal=ea*area[i]/al[i];eil1=ea*fint[i]/al[i];eil2=ea*fint[i]/(al[i]*al[i]);eil3=ea*fint[i]/(al[i]*al[i]*al[i]); ekl[0][0]=eal;ekl[1][1]=12.0*eil3;ekl[2][2]=4.0*eil1;ekl[3][3]=eal;ekl[4][4]=12.0*eil3;ekl[5][5]=4.0*eil1;ekl[2][1]=6.0*eil2;ekl[3][0]=-eal;ekl[4][1]=-12.0*eil3;ekl[4][2]=-6.0*eil2;ekl[5][1]=6.0*eil2;ekl[5][2]=2.0*eil1;ekl[5][4]=-6.0*eil2;ii=0;for(;ii<=4;ii++){jj=ii+1;for(;jj<=5;jj++){ekl[ii][jj]=ekl[jj][ii];}}k=0;for(;k<=5;k++){l=0;for(;l<=5;l++){{ekk[i][k][l]=ekl[k][l];fprintf(shuchu,"%d %d %d %f %f\n",i+1,k+1,l+1,ekl[k][l],ekk[i][k][l]);} }}t[0][0]=css[i];t[0][1]=-snn[i];t[1][0]=snn[i];t[1][1]=css[i];t[2][2]=1.0;t[3][3]=css[i];t[3][4]=-snn[i];t[4][3]=snn[i];t[4][4]=css[i];t[5][5]=1.0;j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){tt[i][j][k]=t[j][k];p2[i][j]=p2[i][j]+t[j][k]*p1[i][k];}}ii=0;for(;ii<=5;ii++){j=0;for(;j<=5;j++){ba[ii][j]=0.0;k=0;for(;k<=5;k++){ba[ii][j]=ba[ii][j]+tt[i][ii][k]*ekl[k][j];}}}ek[ii][j]=0.0;ii=0;for(;ii<=5;ii++){j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){ek[ii][j]=ek[ii][j]+ba[ii][k]*tt[i][j][k];}}}j=0;for(;j<=5;j++){ii=0;for(;ii<=5;ii++){fprintf(shuchu,"i,ii,j,ek,tt=%d %d %d %f %f\n",i+1,ii+1,j+1,ek[ii][j],tt[i][ii][j]); }}inode=0;while(inode<=1){nodei=loc[i][inode];idofn=0;while(idofn<=2){nrows=(nodei-1)*3+idofn;nrowe=inode*3+idofn;f[nrows]=f[nrows]+p2[i][nrowe];jnode=0;while(jnode<=1){nodej=loc[i][jnode];jdofn=0;while(jdofn<=2){ncols=(nodej-1)*3+jdofn;ncole=jnode*3+jdofn;gk[nrows][ncols]=gk[nrows][ncols]+ek[nrowe][ncole];jdofn++;}jnode++;}idofn++;}inode++;}}i=0;for(;i<=nd-1;i++){j=0;for(;j<=nd-1;j++){gk1[i][j]=gk[i][j];}}fprintf(shuchu,"nodal forces from applied loads\node x-load y-load moment\n"); i=0;for(;i<=nn-1;i++){fprintf(shuchu,"%d %f %f %f\n",i+1,f[3*i],f[3*i+1],f[3*i+2]);}i=0;for(;i<=nd-1;i++){j=0;for(;j<=nd-1;j++){fprintf(shuchu,"i,j,gk1 %d %d %f\n",i+1,j+1,gk[i][j]); }}i=0;for(;i<=nfix-1;i++){ix=ifix[i];gk[ix-1][ix-1]=gk[ix-1][ix-1]*1.0e20;}void gauss(float (*a)[12],float *b,int n);gauss(gk,f,nd);i=0;for(;i<=nd-1;i++){fr[i]=0.0;j=0;for(;j<=nd-1;j++){fr[i]=fr[i]+gk1[i][j]*f[j];fr[i]=fr[i]-f[i];}}for(i=0;i<=ne-1;i++){i1=loc[i][0];i2=loc[i][1];xx[0]=f[3*i1-3];xx[1]=f[3*i1-2];xx[2]=f[3*i1-1];xx[3]=f[3*i2-3];xx[4]=f[3*i2-2];xx[5]=f[3*i2-1];j=0;for(;j<=5;j++){k=0;for(;k<=5;k++){bkl[i][j][k]=0.0;l=0;for(;l<=5;l++){bkl[i][j][k]=bkl[i][j][k]+ekk[i][j][l]*tt[i][k][l];}}}j=0;for(;j<=5;j++){fe[i][j]=0.0;k=0;for(;k<=5;k++){fe[i][j]=fe[i][j]+bkl[i][j][k]*xx[k]; }}j=0;for(;j<=5;j++){fe[i][j]=fe[i][j]-p1[i][j];}}}void gauss(float (*a)[12],float *b,int n) {int i,i1,j,m;i=0;for(;i<=n-1;i++){i1=i+1;for(j=i1;j<=n-1;j++)a[i][j]=a[i][j]/a[i][i];b[i]=b[i]/a[i][i];a[i][i]=1.0;for(j=i1;j<=n-1;j++){for(m=i1;m<=n-1;m++)a[j][m]=a[j][m]-a[j][i]*a[i][m];b[j]=b[j]-a[j][i]*b[i];}}i=n-2;for(;i>=0;i--){j=i+1;for(;j<=n-1;j++){b[i]=b[i]-a[i][j]*b[j];}}}程序输出:nn ne nd nfix e4 3 12 6 200000000.000000element node1 node2 area fint1 12 0.007630 0.0001582 3 1 0.007630 0.0001583 24 0.007630 0.000158node x-coord y-coord1 0.000000 5.0000002 6.400000 5.0000003 0.000000 0.0000004 9.600000 0.000000ifix=7 8 9 10 11 121 1 1 238437.500000 238437.5000001 12 0.000000 0.0000001 1 3 0.000000 0.0000001 1 4 -238437.500000 -238437.5000001 1 5 0.000000 0.0000001 1 6 0.000000 0.0000001 2 1 0.000000 0.0000001 2 2 1442.871094 1442.8710941 2 3 4617.187500 4617.1875001 2 4 0.000000 0.0000001 2 5 -1442.871094 -1442.8710941 2 6 4617.187500 4617.1875001 3 1 0.000000 0.0000001 32 4617.187500 4617.1875001 3 3 19700.000000 19700.0000001 3 4 0.000000 0.0000001 3 5 -4617.187500 -4617.1875001 3 6 9850.000000 9850.0000001 4 1 -238437.500000 -238437.5000001 42 0.000000 0.0000001 4 3 0.000000 0.0000001 4 4 238437.500000 238437.5000001 4 5 0.000000 0.0000001 4 6 0.000000 0.0000001 5 1 0.000000 0.0000001 52 -1442.871094 -1442.8710941 5 3 -4617.187500 -4617.1875001 5 4 0.000000 0.0000001 5 5 1442.871094 1442.8710941 5 6 -4617.187500 -4617.1875001 6 1 0.000000 0.0000001 62 4617.187500 4617.1875001 6 3 9850.000000 9850.0000001 6 4 0.000000 0.0000001 6 5 -4617.187500 -4617.1875001 6 6 19700.000000 19700.000000i,ii,j,ek,tt=1 1 1 238437.500000 1.000000 i,ii,j,ek,tt=1 2 1 0.000000 0.000000i,ii,j,ek,tt=1 3 1 0.000000 0.000000i,ii,j,ek,tt=1 4 1 -238437.500000 0.000000 i,ii,j,ek,tt=1 5 1 0.000000 0.000000i,ii,j,ek,tt=1 6 1 0.000000 0.000000i,ii,j,ek,tt=1 1 2 0.000000 0.000000i,ii,j,ek,tt=1 2 2 1442.871094 1.000000i,ii,j,ek,tt=1 3 2 4617.187500 0.000000 i,ii,j,ek,tt=1 4 2 0.000000 0.000000i,ii,j,ek,tt=1 5 2 -1442.871094 0.000000 i,ii,j,ek,tt=1 6 2 4617.187500 0.000000 i,ii,j,ek,tt=1 1 3 0.000000 0.000000i,ii,j,ek,tt=1 2 3 4617.187500 0.000000 i,ii,j,ek,tt=1 3 3 19700.000000 1.000000 i,ii,j,ek,tt=1 4 3 0.000000 0.000000i,ii,j,ek,tt=1 5 3 -4617.187500 0.000000 i,ii,j,ek,tt=1 6 3 9850.000000 0.000000 i,ii,j,ek,tt=1 1 4 -238437.500000 0.000000 i,ii,j,ek,tt=1 2 4 0.000000 0.000000i,ii,j,ek,tt=1 3 4 0.000000 0.000000i,ii,j,ek,tt=1 4 4 238437.500000 1.000000 i,ii,j,ek,tt=1 5 4 0.000000 0.000000i,ii,j,ek,tt=1 6 4 0.000000 0.000000i,ii,j,ek,tt=1 1 5 0.000000 0.000000i,ii,j,ek,tt=1 2 5 -1442.871094 0.000000 i,ii,j,ek,tt=1 3 5 -4617.187500 0.000000 i,ii,j,ek,tt=1 4 5 0.000000 0.000000i,ii,j,ek,tt=1 5 5 1442.871094 1.000000 i,ii,j,ek,tt=1 6 5 -4617.187500 0.000000 i,ii,j,ek,tt=1 1 6 0.000000 0.000000i,ii,j,ek,tt=1 2 6 4617.187500 0.000000 i,ii,j,ek,tt=1 3 6 9850.000000 0.000000 i,ii,j,ek,tt=1 4 6 0.000000 0.000000i,ii,j,ek,tt=1 5 6 -4617.187500 0.000000 i,ii,j,ek,tt=1 6 6 19700.000000 1.000000 2 1 1 305200.000000 305200.0000002 1 2 0.000000 0.0000002 13 0.000000 0.0000002 1 4 -305200.000000 -305200.0000002 1 5 0.000000 0.0000002 1 6 0.000000 0.0000002 2 1 0.000000 0.0000002 2 2 3025.919922 3025.9199222 23 7564.800293 7564.8002932 2 4 0.000000 0.0000002 2 5 -3025.919922 -3025.9199222 2 6 7564.800293 7564.8002932 3 1 0.000000 0.0000002 3 2 7564.800293 7564.8002932 3 3 25216.001953 25216.0019532 3 4 0.000000 0.0000002 3 5 -7564.800293 -7564.8002932 3 6 12608.000977 12608.0009772 4 1 -305200.000000 -305200.0000002 4 2 0.000000 0.0000002 43 0.000000 0.0000002 4 4 305200.000000 305200.0000002 4 5 0.000000 0.0000002 4 6 0.000000 0.0000002 5 1 0.000000 0.0000002 5 2 -3025.919922 -3025.9199222 53 -7564.800293 -7564.8002932 5 4 0.000000 0.0000002 5 5 3025.919922 3025.9199222 5 6 -7564.800293 -7564.8002932 6 1 0.000000 0.0000002 6 2 7564.800293 7564.8002932 63 12608.000977 12608.0009772 6 4 0.000000 0.0000002 6 5 -7564.800293 -7564.8002932 6 6 25216.001953 25216.001953i,ii,j,ek,tt=2 1 1 3025.919922 0.000000 i,ii,j,ek,tt=2 2 1 0.000000 1.000000i,ii,j,ek,tt=2 3 1 -7564.800293 0.000000 i,ii,j,ek,tt=2 4 1 -3025.919922 0.000000 i,ii,j,ek,tt=2 5 1 0.000000 0.000000i,ii,j,ek,tt=2 6 1 -7564.800293 0.000000 i,ii,j,ek,tt=2 1 2 0.000000 -1.000000i,ii,j,ek,tt=2 2 2 305200.000000 0.000000 i,ii,j,ek,tt=2 3 2 0.000000 0.000000i,ii,j,ek,tt=2 4 2 0.000000 0.000000i,ii,j,ek,tt=2 5 2 -305200.000000 0.000000 i,ii,j,ek,tt=2 6 2 0.000000 0.000000i,ii,j,ek,tt=2 1 3 -7564.800293 0.000000 i,ii,j,ek,tt=2 2 3 0.000000 0.000000i,ii,j,ek,tt=2 3 3 25216.001953 1.000000 i,ii,j,ek,tt=2 4 3 7564.800293 0.000000 i,ii,j,ek,tt=2 5 3 0.000000 0.000000i,ii,j,ek,tt=2 6 3 12608.000977 0.000000 i,ii,j,ek,tt=2 1 4 -3025.919922 0.000000 i,ii,j,ek,tt=2 2 4 0.000000 0.000000i,ii,j,ek,tt=2 3 4 7564.800293 0.000000 i,ii,j,ek,tt=2 4 4 3025.919922 0.000000 i,ii,j,ek,tt=2 5 4 0.000000 1.000000i,ii,j,ek,tt=2 6 4 7564.800293 0.000000i,ii,j,ek,tt=2 1 5 0.000000 0.000000i,ii,j,ek,tt=2 2 5 -305200.000000 0.000000 i,ii,j,ek,tt=2 3 5 0.000000 0.000000i,ii,j,ek,tt=2 4 5 0.000000 -1.000000i,ii,j,ek,tt=2 5 5 305200.000000 0.000000 i,ii,j,ek,tt=2 6 5 0.000000 0.000000i,ii,j,ek,tt=2 1 6 -7564.800293 0.000000 i,ii,j,ek,tt=2 2 6 0.000000 0.000000i,ii,j,ek,tt=2 3 6 12608.000977 0.000000 i,ii,j,ek,tt=2 4 6 7564.800293 0.000000 i,ii,j,ek,tt=2 5 6 0.000000 0.000000i,ii,j,ek,tt=2 6 6 25216.001953 1.000000 3 1 1 257061.218750 257061.2187503 1 2 0.000000 0.0000003 1 3 0.000000 0.0000003 14 -257061.218750 -257061.2187503 1 5 0.000000 0.0000003 1 6 0.000000 0.0000003 2 1 0.000000 0.0000003 2 2 1808.063232 1808.0632323 2 3 5366.628906 5366.6289063 24 0.000000 0.0000003 2 5 -1808.063232 -1808.0632323 2 6 5366.628906 5366.6289063 3 1 0.000000 0.0000003 3 2 5366.628906 5366.6289063 3 3 21238.716797 21238.7167973 34 0.000000 0.0000003 3 5 -5366.628906 -5366.6289063 3 6 10619.358398 10619.3583983 4 1 -257061.218750 -257061.2187503 4 2 0.000000 0.0000003 4 3 0.000000 0.0000003 4 4 257061.218750 257061.2187503 4 5 0.000000 0.0000003 4 6 0.000000 0.0000003 5 1 0.000000 0.0000003 5 2 -1808.063232 -1808.0632323 5 3 -5366.628906 -5366.6289063 54 0.000000 0.0000003 5 5 1808.063232 1808.0632323 5 6 -5366.628906 -5366.6289063 6 1 0.000000 0.0000003 6 2 5366.628906 5366.6289063 6 3 10619.358398 10619.3583983 64 0.000000 0.0000003 6 5 -5366.628906 -5366.6289063 6 6 21238.716797 21238.716797i,ii,j,ek,tt=3 1 1 75979.257813 0.539054 i,ii,j,ek,tt=3 2 1 -115892.476563 -0.842271 i,ii,j,ek,tt=3 3 1 4520.158203 0.000000i,ii,j,ek,tt=3 4 1 -75979.257813 0.000000 i,ii,j,ek,tt=3 5 1 115892.476563 0.000000 i,ii,j,ek,tt=3 6 1 4520.158203 0.000000i,ii,j,ek,tt=3 1 2 -115892.476563 0.842271 i,ii,j,ek,tt=3 2 2 182890.046875 0.539054 i,ii,j,ek,tt=3 3 2 2892.901367 0.000000i,ii,j,ek,tt=3 4 2 115892.476563 0.000000 i,ii,j,ek,tt=3 5 2 -182890.046875 0.000000 i,ii,j,ek,tt=3 6 2 2892.901367 0.000000i,ii,j,ek,tt=3 1 3 4520.158203 0.000000i,ii,j,ek,tt=3 2 3 2892.901367 0.000000i,ii,j,ek,tt=3 3 3 21238.716797 1.000000 i,ii,j,ek,tt=3 4 3 -4520.158203 0.000000 i,ii,j,ek,tt=3 5 3 -2892.901367 0.000000 i,ii,j,ek,tt=3 6 3 10619.358398 0.000000 i,ii,j,ek,tt=3 1 4 -75979.257813 0.000000 i,ii,j,ek,tt=3 2 4 115892.476563 0.000000 i,ii,j,ek,tt=3 3 4 -4520.158203 0.000000 i,ii,j,ek,tt=3 4 4 75979.257813 0.539054 i,ii,j,ek,tt=3 5 4 -115892.476563 -0.842271 i,ii,j,ek,tt=3 6 4 -4520.158203 0.000000 i,ii,j,ek,tt=3 1 5 115892.476563 0.000000 i,ii,j,ek,tt=3 2 5 -182890.046875 0.000000 i,ii,j,ek,tt=3 3 5 -2892.901367 0.000000 i,ii,j,ek,tt=3 4 5 -115892.476563 0.842271 i,ii,j,ek,tt=3 5 5 182890.046875 0.539054 i,ii,j,ek,tt=3 6 5 -2892.901367 0.000000 i,ii,j,ek,tt=3 1 6 4520.158203 0.000000i,ii,j,ek,tt=3 2 6 2892.901367 0.000000i,ii,j,ek,tt=3 3 6 10619.358398 0.000000 i,ii,j,ek,tt=3 4 6 -4520.158203 0.000000 i,ii,j,ek,tt=3 5 6 -2892.901367 0.000000 i,ii,j,ek,tt=3 6 6 21238.716797 1.000000 nodal forces from applied loadsode x-load y-load moment1 0.000000 -192.000000 -204.8000032 0.000000 -192.000000 204.8000033 0.000000 0.000000 0.0000004 0.000000 0.000000 0.000000 i,j,gk1 1 1 241463.421875i,j,gk1 1 2 0.000000i,j,gk1 1 3 7564.800293i,j,gk1 1 4 -238437.500000i,j,gk1 1 5 0.000000i,j,gk1 1 6 0.000000i,j,gk1 1 7 -3025.919922i,j,gk1 1 8 0.000000i,j,gk1 1 9 7564.800293i,j,gk1 1 10 0.000000i,j,gk1 1 11 0.000000i,j,gk1 1 12 0.000000i,j,gk1 2 1 0.000000i,j,gk1 2 2 306642.875000i,j,gk1 2 3 4617.187500i,j,gk1 2 4 0.000000i,j,gk1 2 5 -1442.871094i,j,gk1 2 6 4617.187500i,j,gk1 2 7 0.000000i,j,gk1 2 8 -305200.000000i,j,gk1 2 9 0.000000i,j,gk1 2 10 0.000000i,j,gk1 2 11 0.000000i,j,gk1 2 12 0.000000i,j,gk1 3 1 7564.800293i,j,gk1 3 2 4617.187500i,j,gk1 3 3 44916.000000i,j,gk1 3 4 0.000000i,j,gk1 3 5 -4617.187500i,j,gk1 3 6 9850.000000i,j,gk1 3 7 -7564.800293i,j,gk1 3 8 0.000000i,j,gk1 3 9 12608.000977i,j,gk1 3 10 0.000000i,j,gk1 3 11 0.000000i,j,gk1 3 12 0.000000i,j,gk1 4 1 -238437.500000i,j,gk1 4 2 0.000000i,j,gk1 4 3 0.000000i,j,gk1 4 4 314416.750000i,j,gk1 4 5 -115892.476563i,j,gk1 4 6 4520.158203i,j,gk1 4 8 0.000000i,j,gk1 4 9 0.000000i,j,gk1 4 10 -75979.257813 i,j,gk1 4 11 115892.476563 i,j,gk1 4 12 4520.158203 i,j,gk1 5 1 0.000000i,j,gk1 5 2 -1442.871094 i,j,gk1 5 3 -4617.187500 i,j,gk1 5 4 -115892.476563 i,j,gk1 5 5 184332.921875 i,j,gk1 5 6 -1724.286133 i,j,gk1 5 7 0.000000i,j,gk1 5 8 0.000000i,j,gk1 5 9 0.000000i,j,gk1 5 10 115892.476563 i,j,gk1 5 11 -182890.046875 i,j,gk1 5 12 2892.901367 i,j,gk1 6 1 0.000000i,j,gk1 6 2 4617.187500i,j,gk1 6 3 9850.000000i,j,gk1 6 4 4520.158203i,j,gk1 6 5 -1724.286133 i,j,gk1 6 6 40938.718750 i,j,gk1 6 7 0.000000i,j,gk1 6 8 0.000000i,j,gk1 6 9 0.000000i,j,gk1 6 10 -4520.158203 i,j,gk1 6 11 -2892.901367 i,j,gk1 6 12 10619.358398 i,j,gk1 7 1 -3025.919922 i,j,gk1 7 2 0.000000i,j,gk1 7 3 -7564.800293 i,j,gk1 7 4 0.000000i,j,gk1 7 5 0.000000i,j,gk1 7 6 0.000000i,j,gk1 7 7 3025.919922i,j,gk1 7 8 0.000000i,j,gk1 7 9 -7564.800293 i,j,gk1 7 10 0.000000i,j,gk1 7 11 0.000000i,j,gk1 7 12 0.000000i,j,gk1 8 1 0.000000i,j,gk1 8 2 -305200.000000i,j,gk1 8 4 0.000000i,j,gk1 8 5 0.000000i,j,gk1 8 6 0.000000i,j,gk1 8 7 0.000000i,j,gk1 8 8 305200.000000 i,j,gk1 8 9 0.000000i,j,gk1 8 10 0.000000i,j,gk1 8 11 0.000000i,j,gk1 8 12 0.000000i,j,gk1 9 1 7564.800293i,j,gk1 9 2 0.000000i,j,gk1 9 3 12608.000977i,j,gk1 9 4 0.000000i,j,gk1 9 5 0.000000i,j,gk1 9 6 0.000000i,j,gk1 9 7 -7564.800293i,j,gk1 9 8 0.000000i,j,gk1 9 9 25216.001953i,j,gk1 9 10 0.000000i,j,gk1 9 11 0.000000i,j,gk1 9 12 0.000000i,j,gk1 10 1 0.000000i,j,gk1 10 2 0.000000i,j,gk1 10 3 0.000000i,j,gk1 10 4 -75979.257813 i,j,gk1 10 5 115892.476563 i,j,gk1 10 6 -4520.158203 i,j,gk1 10 7 0.000000i,j,gk1 10 8 0.000000i,j,gk1 10 9 0.000000i,j,gk1 10 10 75979.257813 i,j,gk1 10 11 -115892.476563 i,j,gk1 10 12 -4520.158203 i,j,gk1 11 1 0.000000i,j,gk1 11 2 0.000000i,j,gk1 11 3 0.000000i,j,gk1 11 4 115892.476563 i,j,gk1 11 5 -182890.046875 i,j,gk1 11 6 -2892.901367 i,j,gk1 11 7 0.000000i,j,gk1 11 8 0.000000i,j,gk1 11 9 0.000000i,j,gk1 11 10 -115892.476563i,j,gk1 11 11 182890.046875i,j,gk1 11 12 -2892.901367i,j,gk1 12 1 0.000000i,j,gk1 12 2 0.000000i,j,gk1 12 3 0.000000i,j,gk1 12 4 4520.158203i,j,gk1 12 5 2892.901367i,j,gk1 12 6 10619.358398i,j,gk1 12 7 0.000000i,j,gk1 12 8 0.000000i,j,gk1 12 9 0.000000i,j,gk1 12 10 -4520.158203i,j,gk1 12 11 -2892.901367i,j,gk1 12 12 21238.716797node x-disp y-disp thita1 -0.020768 -0.000749 -0.0041792 -0.021164 -0.014385 0.0078233 -0.000000 -0.000000 0.0000004 0.000000 -0.000000 0.000000reaction nodal forces from the equationsnode x-load y-load moment1 0.249791 -191.991058 -204.7498172 0.253289 -191.827469 204.7061163 94.456879 228.500870 -209.7956244 -94.456657 155.499146 -54.196941element axi-f shear-q moment-m1 94.456924 228.500854 262.488831 -94.456924 155.499146 -28.8833622 228.500870 -94.456879 -209.795624 -228.500870 94.456879 -262.4888313 181.889847 -4.264181 28.883371 -181.889847 4.264181 -54.196941。
有限元方法编程范文

有限元方法编程范文有限元方法(Finite Element Method,简称FEM)是一种数值分析方法,用于求解连续介质的强度、振动、流体、热传导等问题。
它是一种将物理问题转化为代数方程组的方法,通过将解域(问题的空间范围)离散化为许多小单元,再对这些小单元进行处理,最终得到整个解域的近似解。
1.离散化:首先将解域进行离散化,将其分割为许多小单元,称为有限元单元。
这些单元可以是一维线段、二维三角形或四边形、三维四面体等形状。
通过适当的划分精度和方法,确定离散化的步长,使得在每个单元上的近似解足够接近精确解。
2.定义变量:根据问题的性质和假设,定义相应的物理量和变量。
例如,对于强度分析问题,可以定义位移、应力、应变等变量。
将这些变量表示为一个向量,并对其进行数值处理。
3.得到局部方程:根据物理方程和边界条件,利用数学方法得到每个单元上的局部方程。
这些局部方程可以表示为刚度矩阵和载荷向量的形式。
刚度矩阵描述了每个单元上的物理性质和相互作用关系。
4.组装全局方程:将所有单元上的局部方程组装成全局方程。
这需要将单元之间的连续性纳入考虑,以确保解域的连续性。
这样可以得到一个大规模的代数方程组,以求解未知变量。
5.施加边界条件:根据问题的边界条件,将其施加到全局方程中。
常见的边界条件有位移边界条件、力边界条件和自然边界条件等。
6.求解代数方程组:使用适当的数值求解方法,例如高斯消元法、迭代法或者直接法,对代数方程组进行求解。
由于求解的规模很大,可能需要采用优化算法和并行计算技术来提高效率。
7.后处理结果:将求解得到的数值结果转化为工程可分析的形式,例如绘制等值线、曲线或进行一些定量的计算。
这些结果可以用来评估结构的强度、振动特性等。
有限元方法的编程实现可以使用不同的编程语言和软件工具。
常用的编程语言包括C、C++、Fortran和Python等。
一些流行的软件包,如ANSYS和ABAQUS,提供了用户友好的界面和功能强大的求解器,可以方便地进行有限元分析。
c++面向对象的有限元程序设计

《C++面向对象的有限元程序设计》一、引言在计算机科学和工程中,有限元方法是一种数值分析技术,广泛应用于工程设计和科学研究领域。
C++作为一种流行的编程语言,在有限元程序设计中也扮演了重要角色。
本文将从深度和广度两个方面对C++面向对象的有限元程序设计进行全面评估,并撰写一篇有价值的文章,以帮助读者更全面、深刻地理解这一主题。
二、C++面向对象的有限元程序设计的基本概念1. 有限元方法的基本原理有限元方法是一种数值计算方法,用于求解偏微分方程和积分方程。
通过将求解区域分割为有限个单元,建立单元之间的联系,将连续的问题转化为离散的代数问题,从而得到数值解。
在有限元程序设计中,需要考虑如何有效地表示和处理单元、节点、边界条件等信息。
2. 面向对象的程序设计思想面向对象的程序设计思想强调将现实世界中的问题抽象成对象,通过封装、继承和多态等机制构建模块化、可复用的代码结构。
在C++中,类和对象是面向对象程序设计的核心概念,有限元程序设计可以通过抽象出单元、节点、网格等对象来实现。
三、深入探讨C++面向对象的有限元程序设计1. C++语言特性在有限元程序设计中的应用在C++语言中,有丰富的特性可以用于实现面向对象的有限元程序设计。
类的封装可以用于表示单元和节点对象的属性和行为,继承可以用于构建具体单元类型的层次结构,多态可以实现对不同单元类型的统一处理。
2. 优化设计思路下的C++面向对象有限元程序设计针对大规模的有限元计算,优化的设计思路是必不可少的。
C++中提供了丰富的性能优化手段,如模板元编程、内联函数、移动语义等,可以在面向对象的有限元程序设计中发挥重要作用。
四、总结和回顾在本文中,我们对C++面向对象的有限元程序设计进行了全面评估,并撰写了一篇有价值的文章。
通过深入探讨原理、语言特性和优化设计思路,帮助读者更全面地理解了这一主题。
从我的个人观点看,C++面向对象的有限元程序设计是一个值得深入研究的领域,它不仅涉及到程序设计技术,还涉及到数值计算和工程应用等多个领域的知识。
《有限元与程序设计》课程的实践和思考

中国科教创新导刊I 中国科教创新导刊2008N O .35C hi na Educa t i on I nnov at i on H er al d 科教研究自70年代有限元法诞生起,由于能够解决许多手工无法分析的复杂工程问题而得到了极大发展,限元法成功应用于机械、航天、建筑、水利工程等许多科学领域当中。
《有限元与程序设计》是三峡大学为水利水电工程专业的本科生开设的一门重要的选修课程。
课程性质为公共选修课,学时32。
虽然是选修课,但开设这门课的意义重大。
这主要表现在以下几个方面。
(1)实现水利工程领域的计算技术的现代化是时代发展的必然趋势,不学习有限元法,不掌握先进的结构程序设计方法,今后很难胜任工作。
利用专门的有限元分析软件,可使设计工作中的大量的繁重的计算由电脑完成,实现设计工作自动化。
(2)有利于巩固和深化算法语言课程,有利于提高学生的计算机应用和程序编程能力。
(3)毕业设计阶段有的课题要用到有限元法,如果在之前选修了就会带来很大的方便。
有限元法还是攻读硕士后进一步深化的主干课程,做数值计算方向的研究生,几乎都要采用有限元方法。
因此,本科阶段对有限元进行初步学习并掌握有限元的基本概念,培养初步的编程能力就显得极为必要和十分迫切。
1使用教材和软件结合本科生的特点,并且照顾一些领悟能力以及动手能力略差的学生,因此,决定了课程目的是培养学生有限元的基本知识及思路,并初步掌握一门大型有限元软件的操作。
课程内容包括:学习有限元的基本原理、公式、上机学习本专业大型有限元软件。
考核方式为平时考勤及作业占30%,期末采取闭卷或上机大作业的形式,占70%。
有限元原理部分的教材采用《工程中的有限元方法》第三版,是翻译的美国的经典教程材。
该书将复杂的原理和公式写得通俗易懂,适应本科生阅读,因此可以满足教学要求。
有限元上机用软件采用ANSYS 教育版,这是ANSY S 公司对各个高校有限元法教学推出的教学软件,清华大学的有限元课程就采用了该软件。
有限元编程的c++实现算例

有限元编程的c++实现算例1. #include<>2. #include<>3.4.5. #define ne 3 #define nj 4 #define nz6 #define npj 0 #define npf1 #define nj3 12 #define dd6 #define e0 #definea0 #define i0 #define pi16.17.18. int jm[ne+1][3]={{0,0,0},{0,1,2},{0,2,3},{0,4,3}}; /*gghjghg*/19. double gc[ne+1]={,,,};20. double gj[ne+1]={,,,};21. double mj[ne+1]={,a0,a0,a0};22. double gx[ne+1]={,i0,i0,i0};23. int zc[nz+1]={0,1,2,3,10,11,12};24. double pj[npj+1][3]={{,,}};25. double pf[npf+1][5]={{0,0,0,0,0},{0,-20,,,}};26. double kz[nj3+1][dd+1],p[nj3+1];27. double pe[7],f[7],f0[7],t[7][7];28. double ke[7][7],kd[7][7];29.30.31.36. void jdugd(int);38. void zb(int);39. void gdnl(int);40. void dugd(int);41.42.43. void main()46. int i,j,k,e,dh,h,ii,jj,hz,al,bl,m,l,dl,zl,z,j0;47. double cl,wy[7];48. int im,in,jn;49.50.54. if(npj>0)55. {56. for(i=1;i<=npj;i++)57. { j=pj[i][2];59. p[j]=pj[i][1];60. }61. }62. if(npf>0)63. {64. for(i=1;i<=npf;i++)65. { hz=i;67. gdnl(hz);68. e=(int)pf[hz][3];69. zb(e); for(j=1;j<=6;j++) {72. pe[j]=;73. for(k=1;k<=6;k++) {75. pe[j]=pe[j]-t[k][j]*f0[k];76. }77. }78. al=jm[e][1];79. bl=jm[e][2];80. p[3*al-2]=p[3*al-2]+pe[1]; p[3*al-1]=p[3*al-1]+pe[2];82. p[3*al]=p[3*al]+pe[3];83. p[3*bl-2]=p[3*bl-2]+pe[4];84. p[3*bl-1]=p[3*bl-1]+pe[5];85. p[3*bl]=p[3*bl]+pe[6];86. }87. }89.90. for(e=1;e<=ne;e++) {94. dugd(e); for(i=1;i<=2;i++) {97. for(ii=1;ii<=3;ii++)98. {99. h=3*(i-1)+ii; dh=3*(jm[e][i]-1)+ii; for(j=1;j<=2 ;j++)102. {103. for(jj=1;jj<=3;jj++) {105. l=3*(j-1)+jj; zl=3*(jm[e][j]-1)+jj; dl=zl-dh+ 1; if(dl>0)109. kz[dh][dl]=kz[dh][dl]+ke[h][l]; }111. }112. }113. }114. }115.116. for(i=1;i<=nz;i++) {119. z=zc[i]; kz[z][l]=; for(j=2;j<=dd;j++)122. {123. kz[z][j]=; }125. if((z!=1))126. {127. if(z>dd)128. j0=dd;129. else if(z<=dd)130. j0=z; for(j=2;j<=j0;j++)132. kz[z-j+1][j]=;133. }134. p[z]=; }136.137.138.140. for(k=1;k<=nj3-1;k++)141. {142. if(nj3>k+dd-1) im=k+dd-1;144. else if(nj3<=k+dd-1)145. im=nj3;146. in=k+1;147. for(i=in;i<=im;i++)148. {149. l=i-k+1;150. cl=kz[k][l]/kz[k][1]; jn=dd-l+1;152. for(j=1;j<=jn;j++)153. {154. m=j+i-k;155. kz[i][j]=kz[i][j]-cl*kz[k][m];156. }157. p[i]=p[i]-cl*p[k]; }159. }160.161.162.163.164. p[nj3]=p[nj3]/kz[nj3][1]; for(i=nj3-1;i>=1;i--)166. {167. if(dd>nj3-i+1)168. j0=nj3-i+1;169. else j0=dd; for(j=2;j<=j0;j++)171. {172. h=j+i-1;173. p[i]=p[i]-kz[i][j]*p[h];174. }175. p[i]=p[i]/kz[i][1]; }177. printf("\n");178. printf("_____________________________________________________________\n");179. printf("NJ U V CETA \n"); for(i=1;i<=nj;i++)181. {182. printf(" %-5d % % %\n",i,p[3*i-2],p[3*i-1],p[3*i]);183. }184. printf("_____________________________________________________________\n");185. printf("E N Q M \n");187. for(e=1;e<=ne;e++) {190. jdugd(e); zb(e); for(i=1;i<=2;i++) 193. {194. for(ii=1;ii<=3;ii++)195. {196. h=3*(i-1)+ii;197. dh=3*(jm[e][i]-1)+ii; wy[h]=p[dh];199. }200. }201. for(i=1;i<=6;i++)202. {203. f[i]=;204. for(j=1;j<=6;j++)205. {206. for(k=1;k<=6;k++) {208. f[i]=f[i]+kd[i][j]*t[j][k]*wy[k];209. }210. }211. }212. if(npf>0)213. {214. for(i=1;i<=npf;i++) if(pf[i][3]==e) {217. hz=i;218. gdnl(hz); for(j=1;j<=6;j++) {221. f[j]=f[j]+f0[j];222. }223. }224. }225. printf("%-3d(A) % % %\n",e,f[1],f[2],f[3]); printf(" (B) % % %\n",f[4],f[5],f[6]); }228. return;229. }230.232.236. void gdnl(int hz)237. {238. int ind,e;239. double g,c,l0,d;240.241.242. g=pf[hz][1]; c=pf[hz][2]; e=(int)pf[hz][3];ind=(int)pf[hz][4]; l0=gc[e]; d=l0-c;248. if(ind==1)249. {250. f0[1]=;251. f0[2]=-(g*c*(2-2*c*c/(l0*l0)+(c*c*c)/(l0*l0*l0)))/2; f0[3]=-(g*c*c)*(6-8*c/l0+3*c*c/(l0 *l0))/12;253. f0[4]=;254. f0[5]=-g*c-f0[2];255. f0[6]=(g*c*c*c)*(4-3*c/l0)/(12*l0);256. }257. else258. {259. if(ind==2) {261. f0[1]=;262. f0[2]=(-(g*d*d)*(l0+2*c))/(l0*l0*l0);263. f0[3]=-(g*c*d*d)/(l0*l0);264. f0[4]=;265. f0[5]=(-g*c*c*(l0+2*d))/(l0*l0*l0);266. f0[6]=(g*c*c*d)/(l0*l0);267. }268. else270. f0[1]=-(g*d/l0); f0[2]=;272. f0[3]=;273. f0[4]=-g*c/l0;274. f0[5]=;275. f0[6]=;276. }277. }278. }279.280. void zb(int e)284. {285. double ceta,co,si;286. int i,j;287. ceta=(gj[e]*pi)/180; co=cos(ceta); 289. si=sin(ceta);290. t[1][1]=co; t[1][2]=si;292. t[2][1]=-si;293. t[2][2]=co;294. t[3][3]=;295. for(i=1;i<=3;i++)296. {297. for(j=1;j<=3;j++) {299. t[i+3][j+3]=t[i][j];300. }301. }302. }303.304.305.306. void jdugd(int e)310. {311. double A0,l0,j0;312. int i;314.315.316. A0=mj[e]; l0=gc[e]; j0=gx[e];320.321. for(i=0;i<=6;i++)322. for(j=0;j<=6;j++) kd[i][j]=;324.325. kd[1][1]=e0*A0/l0;326. kd[2][2]=12*e0*j0/pow(l0,3);327. kd[3][2]=6*e0*j0/pow(l0,2);328. kd[3][3]=4*e0*j0/l0;329. kd[4][1]=-kd[1][1];330. kd[4][4]=kd[1][1];331. kd[5][2]=-kd[2][2]; kd[5][3]=-kd[3][2];333. kd[5][5]=kd[2][2];334. kd[6][2]=kd[3][2];335. kd[6][3]=2*e0*j0/l0;336. kd[6][5]=-kd[3][2];337. kd[6][6]=kd[3][3];338.339. for(i=1;i<=6;i++)340. for(j=1;j<=i;j++) kd[j][i]=kd[i][j];342. }343.344.345. void dugd(int e)349. {350. int i,k,j,m;351. jdugd(e); zb(e); for(i=1;i<=6;i++)354. {355. for(j=1;j<=6;j++)356. {357. ke[i][j]=;358. for(k=1;k<=6;k++)359. {360. for(m=1;m<=6;m++)361. {362. ke[i][j]=ke[i][j]+t[k][i]*kd[k][m]*t[m][j]; } 364. }365. }366. }367. }368.369.370.372.373.374. </></>。
平面桁架有限元C#编程

1题目结构如图所示: 杆的弹性模量E 为200000Mpa ,横截面面积A 为3250mm 2。
图 1 桁架示意图2实验材料PC 机一台,Microsoft Visual Studio 软件,Ansys 软件。
3实验原理(1)桁架结构特点桁架结构中的桁架指的是桁架梁,是格一种梁式结构。
桁架结构常用于大跨度的厂房、展览馆、体育馆和桥梁等公共建筑中。
由于大多用于建筑的屋盖结构,桁架通常也被称作屋架。
结构上由光滑铰链连接,载荷只作用于节点处,只约束线位移,各杆只有轴向拉伸和压缩。
(2)平面桁架有限元分析1、单元分析局部坐标系中的干单元如图所示:图 2 局部坐标系中的杆单元以下公式描述了整体位移和局部位移之间的关系:U=Tu 其中U=[ U ix U iy U jx U jy ],T=[cos θ−sin θ00sin θcos θ0000cos θ−sin θ00sin θcos θ],u=[u ix u iy u jx u jy ]U 和u 分别代表整体坐标系和局部坐标系XY 系和局部坐标系xy 下节点i 和节点j 的位移。
T 是变形从局部坐标转换到整体坐标系下的变换阵,类似的局部力和整体力也有以下关系:F=Tf其中F=[ F ixF iy F jx F jy ] ,是整体坐标系下施加在节点i 和j 上的力的分量而且f=[ f ix f iy f jx f jy ],代表局部坐标系下施加在节点i和j上的分量。
在假设的二力杆条件下,杆只能沿着局部坐标系的x方向变形,内力也总是沿着局部坐标系x的方向,因此将y方向的位移设置为0,局部坐标系下内力和位移通过刚度矩阵有如下关系:[f ixf iyf jxf jy]=|k0−k00000−k0k00000|=[U ixU iyU jxU jy]这里k=k eq=AE/L,写成矩阵形式有:f=Ku将f和u替换成F和U有:T-1F=KT-1U将方程两边乘以T得到:F=TKT-1U其中T-1是变换矩阵T的逆矩阵,替换方程中的TKT-1和U矩阵的值,相乘后得到:[F ixF iy F jx F jy]= k[cos2θsinθcosθ−cos2θ−sinθcosθsinθcosθsin2θ−sinθcosθ−sin2θ−cos2θ−sinθcosθcos2θsinθcosθ−sinθcosθ−sin2θsinθcosθsin2θ][U ixU iyU jxU jy]上述方程代表了施加外力、单元刚度矩阵和任意单元节点的整体位移之间的关系。
有限元C++编程实践

基于有限元算法的编程实践学号:2011043010031姓名:廖校毅电子科技大学物理电子学院【摘要】本文就有限元算法在电磁场分析中的应用展开研究与实践,从电磁场的Maxwell方程出发,根据电磁场的边值问题及变分公式建立了有限元方程组。
具体在实践中,将这些知识运用到C++语言和Matlab中,并将这两种语言有机结合,编程并实现二维FEM。
程序最后通过计算含两种介质的电位槽电位分布来验证其正确性。
关键词: 有限元变分法C++ MatlabThe Programming Practice Based on The Finite Element Algorithm Student ID:2011043010031Name:Liao Xiaoyi University of Electronic Science and technology &School of PhysicalElectronicsAbstract In this paper, we take the application of finite element method in electromagnetic field analysis into research and practice. Starting from Maxwell equations of electromagnetic field, the electromagnetic field boundary value problems and variational formula established the finite element equations. In specific practice, this knowledge will be applied to the C++ language and Matlab, and the organic combination of two languages, programming and implementation of two-dimensional FEM. Finally, through the program to verify the validity of the calculation of potential distribution in channel potential containing two kinds of medium.Key words The finite element method The variational method C++ Matlab一、前言在数学中,有限元法(FEM,Finite Element Method)是一种为求得偏微分方程边值问题近似解的数值技术。
有限元上机实习任务

《结构分析中的有限元法》上机实习任务本课程共有12个上机学时,每次实习课2个学时,共6次,下面是各次实习课任务。
♦实习一实习目的:掌握Visual C++ 6.0集成开发环境的基本操作方法主要内容:1.参见教材“附录A VC++ 6.0集成开发环境使用方法简介”,熟悉Visual C++ 6.0集成开发环境的使用方法。
2.熟悉Visual C++ 6.0的界面,练习集成开发环境中的新建工程、打开已有源文件并插入工程、编译连接和运行调试等功能。
实习作业:学生上交的实习报告内容为:Visual C++ 6.0集成开发环境的基本操作步骤。
♦实习二实习目的:掌握pff程序的基本使用方法主要内容:1.根据教材1.8节介绍的内容,利用例1.4练习pff程序在平面刚架结构中的基本使用方法。
包括原始数据文件的准备,结构数据文件的阅读等。
2.用程序pff计算实习作业。
包括:准备原始数据文件、输出实习结果、绘制内力图等。
实习作业:1-13(a)、(b)、(e)、(f)。
学生上交的实习报告内容为:原始数据文件,以及相应的内力图。
(将输入和输出文件打出来,并将内力图画在下面)♦实习三实习目的:掌握pff程序的进阶使用方法主要内容:1.平面刚架结构中包含:二力杆、刚性杆、全桁铰结点等时,pff程序的使用方法。
2.平面刚架结构中包含:弹簧支座、支座位移和温度变化、斜支座等时,pff 程序的使用方法。
实习作业:1.必做作业:1-13(c)、(d),1-14。
学生上交的实习报告内容为:原始数据文件,以及相应的内力图。
2.选做作业:1-15,1-16。
学生上交的实习报告内容为:修改后的pff.cpp和pff.exe电子文档,原始数据文件以及相应的内力图。
(说明:选做作业不影响学生的上机成绩,但对学生的总成绩有正面影响。
下同。
)♦实习四实习目的:掌握用pff_all程序计算连续梁和平面桁架的使用方法主要内容:1.根据教材中2.6节所述的内容,练习用pff_all程序计算各类平面结构的方法。
有限元编程大作业报告

本科生实验报告书四节点等参单元有限元分析的程序目录1.问题概述 (1)2.四节点四边形等参单元介绍 (1)3.单元应力磨平方法介绍 (4)4.程序流程设计 (6)4.1 程序设计概述4.2 流程图5.程序结构及程序说明 (8)6.程序应用及算例分析 (9)6.1 算例概述6.2 算例求解6.3 算例程序数值解6.4 算例分析7. 总结 (15)7. 附录……………………………………………………()1.问题概述等参单元是有限元方法中使用最广泛的单元类型。
等参单元的位移模式和坐标变换均采用相同的形函数,这种坐标变换叫做等参变换。
通过等参变换可以将自然(局部)坐标中几何形状规则的单元转换成总体(笛卡尔)坐标中形状扭曲的单元,因而使得单元有较好的适应性。
本问题首先对平面四节点四边形等参单元的形函数、应力矩阵和等效节点力矩阵、应力磨平公式等的推导和计算求解。
并通过设计求解程序进行编程求解,最后给出算例(受集中荷载的悬臂梁)并进行求解,将解及的解进行比较。
在这个过程中,采用了高斯三点积分和高斯两点积分,这种积分方法的求解效率较高而且精度也较好。
在问题的最后,尝试去分析引起数值解误差的原因,并分析四节点等参单元的若干特性。
2.四节点四边形等参单元介绍边长为2的正方形单元(如下图所示),在其形心处安置一个局部坐标οξη。
单元角结点i的坐标(ξi,ηi)分别为±1,因此单元四条边界的方程可用简单公式ξ±1=0和η±1=0逐一给出。
图2-1 母单元图2-2 四边形单元形函数N i的表达式:N i =(1+ξi ξ)(1+ηi η)/4位移函数:∑==41i N u i i u ∑==41i N v i i v坐标变换式:∑==41i x N x i i ,∑==41i y N y i i单元应变矩阵{}[]{}[]{}ee B B B B B x v y u y v x u δδε4321==⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂= 式中{}[]TT T T T 4321e δδδδδ=——单元节点的位移列阵;[]{}),,,(432100,,,,=⎭⎬⎫⎩⎨⎧=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=i v u N N N N B i i i x i y i y i x i i δ 这里记号x N i x ∂∂=/N ,i ,y /N y ,i ∂∂=i N 。
有限元方法编程

有限元方法编程【原创版3篇】篇1 目录1.有限元方法概述2.有限元方法的编程步骤3.有限元方法的应用实例4.有限元方法的优缺点篇1正文一、有限元方法概述有限元方法是一种数值分析方法,它通过将待求解的连续体划分为有限个小的、简单的子区域(即有限元),从而将连续体问题转化为有限元上的离散问题。
这种方法可以大大简化问题的求解过程,并可以在计算机上进行高效的数值计算。
有限元方法被广泛应用于固体力学、流体力学、热传导、电磁场等领域。
二、有限元方法的编程步骤1.几何建模:首先需要对问题进行几何建模,即将问题的实际物理区域抽象为计算机可以处理的几何形状。
2.网格划分:将几何模型划分为有限个小的、简单的子区域,即有限元。
这一步需要考虑网格的密度和网格的类型,以保证求解的精度和效率。
3.选择合适的有限元公式:根据问题的性质和求解的目标,选择合适的有限元公式来描述问题的物理过程。
4.编写或选用求解器:根据所选公式,编写或选用相应的求解器,进行数值计算。
5.后处理:对计算结果进行处理,包括结果的可视化和结果的解析等。
三、有限元方法的应用实例有限元方法被广泛应用于各种工程问题中,例如飞机翼的强度分析、汽车底盘的振动分析、建筑物的抗震分析等。
四、有限元方法的优缺点优点:1.可以大大简化问题的求解过程,提高求解效率。
2.可以在计算机上进行高效的数值计算,便于进行结果的可视化和解析。
3.可以适用于各种复杂的几何形状和物理过程。
缺点:1.需要进行几何建模和网格划分,这需要耗费一定的时间和精力。
2.网格的选取对求解结果的精度和效率有重要影响,需要进行适当的选择。
篇2 目录1.有限元方法概述2.有限元方法编程的基本步骤3.有限元方法编程的实际应用4.有限元方法编程的挑战与未来发展篇2正文一、有限元方法概述有限元方法是一种数值分析方法,广泛应用于固体力学、流体力学、热传导等领域。
它的基本思想是将待求解的连续体划分为有限个小的、简单的子区域,即单元,然后用有限个简单的基本函数来近似描述每个单元的物理特性。
面向对象有限元分析程序设计及其VC++实现说明书

文章编号:1000_0887(2002)12_1283_06面向对象有限元分析程序设计及其V C++实现X马永其 冯 伟(上海大学,上海市应用数学和力学研究所,上海200072)(张禄坤推荐)摘要: 采用面向对象的方法确定了有限元分析过程的对象、对象间的关系及类库,并使用VC++语言,利用其MFC 类库实现了有限元分析类库及相应窗口图形化界面的程序体序# 程序系统具有良好的可靠性,可再用性和可扩充性# 为进一步开发大型、通用、功能性强的面向对象的有限元分析软件提供参考#关 键 词: 面向对象; 有限元; 程序; 设计; VC++中图分类号: TP311;O241 文献标识码: A引 言有限元分析程序涉及力学、应用数学和计算机科学3个不同学科的理论和方法,因而其编制工作十分复杂,且程序庞大易错# 因此,有限元软件的开发一直寻求从方法上得以改善# 面向对象程序设计方法的出现,给有限元软件的开发提供了新的途径# 国外学者于1990年开始应用面向对象方法进行有限元分析程序的设计[1,2]# 经过10余年的发展,目前已编制出能够进行非线性及流体问题有限元分析,并与CAD 或数据库等其它软件集成的有限元分析程序[3,4,5],但使用VC++语言的少见报道# 国内在此领域的研究目前正在起步,仅有个别文献涉足[6,7]# 本文将通过研究设计及编程实践,讨论应用面向对象的程序设计方法进行有限元程序设计的基本思想,及采用面向对象的VC++语言进行有限元分析程序编制的基本方法# 希望引起更多国内学者的兴趣和参与,进而开发出大型、通用、功能性强的面向对象的有限元工具软件#1 面向对象方法及VC++语言面向对象程序设计方法是计算机程序开发方法的一种变革# 其主要特征是:信息隐藏性;便于在概念上体现并行和分布式结构;便于软件的演化和扩充;增加程序设计的灵活性和可理解性[8]# 面向对象程序设计过程在形式上为认定类和组织类之间关系的过程,而实质为数据抽象和代码重用# 通常归结为3个步骤:识别对象;识别对象间的关系;识别类#1283应用数学和力学,第23卷第12期(2002年12月) Applied Mathematics and Mechanics应用数学和力学编委会编重庆出版社出版 X 收稿日期: 2001_10_12;修订日期: 2002_05_21作者简介: 马永其(1966)),男,宁夏人,博士(E _mail:mayongqi@)#1284马永其冯伟Microsoft Visual C++是建立在Windows95和WindowsNT32位应用程序上的强有力的复杂开发工具,是一个Windows集成开发环境(IDE:integrated development environment)[9]#其最大的优点是节约时间,不必编译、链接便可看到应用程序的式样,可用键盘或鼠标来完成可视化设计及应用程序的许多编程工作#因此它允许在较短的时间内开发很复杂的Windows程序#面向对象的编程基础是类,Visual C++中的MFC(Mic rosoft Foundation Class)类库提供了强大的面向对象编程接口,简化了可在屏幕上创建和操纵窗口、处理绘图、使程序连接到帮助文件、便利线程、管理内存等的复杂的API(Application Programming Interface)函数调用,使应用程序的编制可以用众多的可视化控件来实现#本文的程序是在Visual C++ 5.0环境中开发编制的#2程序的设计在有限元分析过程中,主要应用了结构、载荷、节点、单元、自由度、矩阵、材料、高斯积分点、边界条件、求解和辅助计算等物理概念#因此,根据面向对象程序设计方法可确定有限元分析过程的对象为:结构对象、载荷对象、节点对象、单元对象、自由度对象、矩阵对象、材料对象、高斯积分点对象、边界条件对象、求解对象和辅助计算对象等#单元是有限元分析过程中最为重要的物理概念,它是整个有限元分析过程的核心,贯穿于整个过程的始终#因此,在标识对象间关联的过程中,单元对象确定为最关键和重要的对象#其余对象,根据其与单元对象的关系可基本分为两类对象,一类是服务于单元对象的对象,另一类是被单元对象服务的对象#在两类对象的每一类中,根据所起作用的不同又可分为包容和利用两种#其中载荷对象、节点对象、材料对象、矩阵对象、高斯积分点对象是服务于单元对象的对象,而载荷对象、节点对象和材料对象是被单元对象包容的对象,矩阵对象、高斯积分点对象是被单元对象利用的对象#结构对象、求解对象和辅助计算对象是被单元对象服务的对象,结构对象包容单元对象,求解对象和辅助计算对象利用单元对象#边界条件对象、自由度对象间接作用于单元对象,边界条件对象被结构对象包容并被单元对象间接利用#自由度对象被节点对象包容并被单元对象间接包容#根据确定的有限元分析过程的对象和所标识的对象间的关联,便形成了一个由单元类、节点类、自由度类、载荷类、材料类、边界条件类、结构类、求解类以及矩阵类和高斯节点类等组成的有限元分析类库#具体设计以单元类为例,单元类要实现的任务是:1)单元材料系数矩阵的计算、位移_应变矩阵的计算、单元刚度矩阵的计算和单元载荷列阵的计算;2)单元内节点的管理#其成员数据主要有载荷、材料物性、高斯积分点、单元应变矩阵对象数组、单元刚度矩阵、单元载荷列阵和节点对象数组等#在对具体结构进行有限元分析时,将采用具体单元类型,如一维单元、二维单元、三维单元等#因此,视单元类为虚基类,采用protec ted关键字以便其子类能够存取有关数据,采用virtual关键字以实现多态性#这样就构筑了类之间的层次和体系结构,形成了继承关系#单元一旦确定后,利用单元的自然坐标可直接建立不同类型单元的插值函数,并可计算出相应的Jac obi矩阵与其行列式#因此,具体单元类除了继承单元类的所有数据成员和数据函数外,还要增加两个成员数据即插值函数矩阵和Jacobi矩阵与其行列式,成员函数也需增加操作这两个成员数据的相关函数,以便计算具体单元的刚度矩阵#设计程序的系统控制如图1所示#结构类接受用户界面输入的材料、载荷、边界条件和节点位置等信息后,发送消息并构造具体单元类、节点类、自由度类#然后由结构类、具体单元类、节点类和自由度类向求解类通讯并发送消息# 最后由结构类、具体单元类、节点类和求解类向辅助计算类通讯并发送消息# 从而完成一个结构的有限元分析过程#图1 类之间的关系及程序控制3 系统的实现根据以上有限元分析过程的面向对象程序设计,用VC++语言具体描述类库,以单元类为例,它是Visual C++的MFC 类库中的C Object 类的继承类,具体表示如下:class CElement:public CObject{protected:int noelement; //element numberint numnodes;//number of element nodes CMaterial *elmaterial;//pointer to element material CLoad *elload;//pointer to element load CGausspoint *gausspoint;//pointer to gausspoint class CMatrix *Dmat;//pointer to element constitutive matrix CObArray BmatArray;//a rray of e lement strain_displacement matrix CMatrix *kemat;//pointer to element stiffness matrix CMatrix *fevec;//pointer to element load ma trix int *lma rray;//pointer to equation numbe r of dof of element .s node CObArray nodearray;//a rray of e lement nodespublic:CElement();//construc tor CElement(int);//construc tor virtual ~CElement();//destructor 1285面向对象有限元分析程序设计及其VC++实现1286马永其冯伟virtual void setDma t()=0;//sets the element constitutive ma trixvirtual void setBmatArra y()=0;virtual void setkemat()=0;virtual void setfevec()=0;virtual void setnodearray()=0;virtual CMatrix*getDma t()=0;//returns the element constitutive matrixvirtual CObArray*getBmatArray()=0;virtual CMatrix*getkemat()=0;virtual CMatrix*getfe vec()=0;Virtual CObArray*getnodearray()=0;//,(other member data and functions)};利用Visual C++的App Wizard工具生成多文档界面(MDI)有限元分析系统的WINDWS应用程序框架,共生成6个类:About对话框的对话框类(C AboutDlg)、整个应用程序的CWinApp 类(C MyApp)、文档类(CMyDos)、视图类(CMyVie w)、框架类(CMainFra me)和子框架类(CChild-Frame)#加入有限元分析过程类库,并将有限元分析过程归纳、抽象、定义为一个问题类,由有限元分析的结构类、求解类和应力类组合而成,其成员数据为结构类对象、求解类对象和应力类对象#将问题类作为WI NDOWS应用程序框架中文档类的公共类型属性变量,加入其中,具体问题类和文档类属性变量描述如下:class CProblem:public CObject{private:CString name;//string of problem nameCStructure*structure;//pointer to structureCLinea rsolver*solver;//pointer to solverCStress*stress;//pointer to stresspublic:CProblem();//constructorCProblem(CString);//constructorvirtual~CProblem()://destructorvoid setT(CString);//sets the problem nameCString getT();//returns the problem namevoid setstructure(CStructure*);//sets the struc tureCStructure*getstruc ture();//returns the structurevoid setsolver(CLinearsolver*);//sets the solverCLinea rsolver*getsolver();//returns the solvervoid setstress(CStress*);//set the stressCStress*getstress();//returns the stress//,(other member func tions)};class CMyDoc:public CDocum ent{protected://c reate from serializa tion onlyCMyDoc();DECLARE -DYNCREATE(CMyDoc )//Attributespublic:CProblem m -problem;//attribute of CMyDoc problem //,(other member date and functions)};利用WI NDOWS 操作系统的消息循环机制,建立起相应的系统通讯体系,其作用方式通过图2所示#由MFC 类库中提供的丰富的for WI NDOW S 的窗口、菜单、对话框、属性表等类库,通过继承、修改和扩充编制所需的人机对话界面,如数据和分析等菜单项,结构对话框类(CStructure -Dialog)等窗口图形化界面#当用户要完成对一个结构进行有限元应力分析的计算过程时,只要将鼠标点到菜单(界面层)上,即发出消息将/菜单对话0激活,菜单对象产生反应# 通过完成对话框界面的人机交互后,发出消息至WI NDOW S 操作系统的消息队列中参加消息循环# /问题对象0(有限元分析层)获此消息后,产生相应的计算动作,完成有限元分析的计算过程#图2 系统消息流图4 小 结通过对有限元分析过程进行面向对象的程序设计,确立了相应的对象及对象间的关系,并建立了相应的类库,说明面向对象方法是一种易于用来进行科学和工程计算程序设计的强有力的程序设计方法# 采用VC++语言描述了有限元分析类库,通过继承、修改和扩充,利用MFC 类库方便地建立了面向对象的有限元分析及相应窗口图形化界面的程序体系,即保证了有限元分析类库的灵活使用,又保证了系统操作的清晰简便,从而提高了程序的可靠性,可再用性和可扩充性#本文的开发实践将为进一步开发大型、通用、功能性强的面向对象的有限元分析软件提供有价值参考#1287面向对象有限元分析程序设计及其VC++实现1288马永其冯伟[参考文献][1]Forde B W R,Foschi R O,Stiemer S F.Objec t_oriented finite elem ent analysis[J].Computer s andStr uctur es,1990,34(3):355)374.[2]Fenves G F.Object_oriented programming for engineering software development[J].Engin eer in gWith Com puter s,1990,6(1):1)15.[3]Archer G C,Fenves G,Thewalt C.A new objec t_oriented finite element analysis[J].Com puter s andStru ctur es,1999,70(1):63)75.[4]Robe rt Ian Mackie.An object_oriented approach to ca lculation control in finite element prog rams[J].Com puter s a nd Stru ctur es,2000,77(5):461)474.[5]YU Li_chao,Kuma r Ashok V.An object_oriented modular framework for implementing the finite ele-ment method[J].Computer s and Str uctur es,2001,79(9):919)928.[6]孔祥安.C++语言与面向对象有限元程序设计[M].成都:西南交通大学出版社,1995.[7]马永其,陈罕,李斯特.采用面向对象方法的有限元程序[J].北京化工大学学报,2000,27(3):51)55.[8]宛延凯.C++语言和面向对象程序设计[M].(第二版).北京:清华大学出版社,1998.[9]Kate Gregory.Visual C++5开发使用手册[M].康博创作室译,文珍审校.北京:机械工业出版社,1998.Object_Oriented Finite Eleme nt Analysisand Programming in VC++MA Yong_qi FENG W ei(Sha ngha i In stitut e of Applied Mathem atics and Mecha nics,Shan gha i Univer sity Shanghai200072,P R China)Abs tract:The design of finite element analysis program using objec t_oriented programm ing(OOP) techniques is presented.The objects,classes and the subclasses used in the programm ing are ex-plained.The system of classes library of finite element ana lysis program and Windows_type Graphica l User Interfaces by VC++and its MFC are developed.The reliability,reusability and extensibility of program are enhanced.It is a reference to develop the large_scale,versatile and powerful systems of object_oriented finite elem ent software.Key wo rds:object_oriented program ming;finite elem ent method;program;design;VC++。
在VC++编程平台上实现面向对象有限元程序

在VC++编程平台上实现面向对象有限元程序
曹骥; 阮红河; 等
【期刊名称】《《工程设计CAD与智能建筑》》
【年(卷),期】2002(000)001
【摘要】如何在面向对象有限元理论基础上实现一个实用的有限元软件系统是本文的研究重点。
本文首先在对编程语言、类库以及编程平台的选择作了一番讨论后,确定用VC++编程平台实现面向对象有限元程序。
然后探讨了有限元程序的面向对象编程、MFC类库的使用以及VC++编辑器的使用等具体问题。
文末给出了一个面向对象有限元程序实例(OOFEA)。
【总页数】4页(P14-17)
【作者】曹骥; 阮红河; 等
【作者单位】同济大学建筑工程系
【正文语种】中文
【中图分类】TP311.1
【相关文献】
1.VC++面向对象编程初探 [J], 康芊
2.面向对象通用优化程序在VC++平台上的实现 [J], 鲍弋海;曹骥;袁勇
3.地下工程有限元程序面向对象的设计与实现 [J], 李晓军;朱合华
4.面向对象有限元程序设计及其VC++与Matlab混合编程实现 [J], 史贵才;葛修润
5.利用VC++实现有限元程序设计 [J], 王居林;周彦;高立名
因版权原因,仅展示原文概要,查看原文内容请购买。
平板有限元C#编程
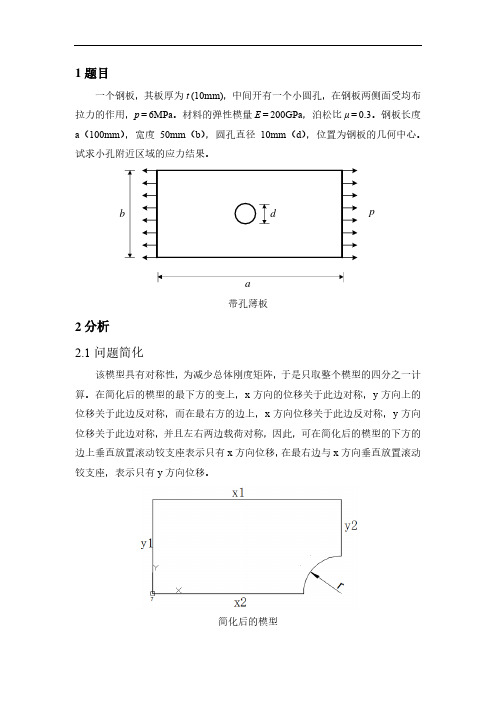
1题目一个钢板,其板厚为t (10mm),中间开有一个小圆孔,在钢板两侧面受均布拉力的作用,p = 6MPa 。
材料的弹性模量E = 200GPa ,泊松比μ = 0.3。
钢板长度a (100mm ),宽度50mm (b ),圆孔直径10mm (d ),位置为钢板的几何中心。
试求小孔附近区域的应力结果。
p带孔薄板2分析 2.1问题简化该模型具有对称性,为减少总体刚度矩阵,于是只取整个模型的四分之一计算。
在简化后的模型的最下方的变上,x 方向的位移关于此边对称,y 方向上的位移关于此边反对称,而在最右方的边上,x 方向位移关于此边反对称,y 方向位移关于此边对称,并且左右两边载荷对称,因此,可在简化后的模型的下方的边上垂直放置滚动铰支座表示只有x 方向位移,在最右边与x 方向垂直放置滚动铰支座,表示只有y 方向位移。
简化后的模型2.2网格划分方法本题使用线性三角形单元分析,网格划分为均匀的三角形网格。
网格划分的方法为,将x1边m 等分,y1以及y2边n 分,再将圆弧m0等分,最后将x2边(m-m0)等分,并找到各个等分点的坐标。
再将x1边的等分点按照顺序分别与x2边和圆弧边的等分点进行连接,找出各条线段的n 等分点的坐标,然后依次连接各个等分点形成4边形网格,最后连接四边形网格的一条对角线形成三角形网格。
节点和单元编号的方法为从上到下从左至右,每一列编号完成后,立即跳至下一列的顶端,向下编号,直到编号完成。
2.3单元分析本问题为平面应力问题,在z 面上没有内力,其应力状态为:Txyxy=[]对于平面应力问题,胡克定律的通用形式为:x xx y yy 2xyxy10E 1011002或者写为:,其中E 是弹性模量,是泊松比。
对于线性三角形单元,用形函数和节点位移表示的位移变量为:i ix j jx k kx u S U S U S U i iyj jyk ky vS U S U S U将上式写为矩阵形式:ix iy i j k jxij k jykx kyU U S 0S 0S 0U u 0S 0S 0S U v U U然后将应变也用位移表示,并写成矩阵形式:ix iy x ijkjxy i j kjy xyiijjkkkx kyU U 0U 100U 2AU U 其中ij kY Y jk iY Y ki jY Y ik j X X ji kX X kj i X X ,进一步将上述方程写成:BU 。
元编程的c实现算例修订稿

元编程的c实现算例公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]有限元编程的c++实现算例1. #include<>2. #include<>3.4.5. #define ne 3 #define nj 4#define nz 6#define npj 0#define npf 1#define nj3 12#define dd 6#define e0 #define a0 #define i0 #define pi16.17.18. int jm[ne+1][3]={{0,0,0},{0,1,2},{0,2,3},{0,4,3}}; /*gghjghg*/19. double gc[ne+1]={,,,};20. double gj[ne+1]={,,,};21. double mj[ne+1]={,a0,a0,a0};22. double gx[ne+1]={,i0,i0,i0};23. int zc[nz+1]={0,1,2,3,10,11,12};24. double pj[npj+1][3]={{,,}};25. double pf[npf+1][5]={{0,0,0,0,0},{0,-20,,,}};26. double kz[nj3+1][dd+1],p[nj3+1];27. double pe[7],f[7],f0[7],t[7][7];28. double ke[7][7],kd[7][7];29.30.31.36. void jdugd(int);38. void zb(int);39. void gdnl(int);40. void dugd(int);41.42.43. void main()45. {46. int i,j,k,e,dh,h,ii,jj,hz,al,bl,m,l,dl,zl,z,j0;47. double cl,wy[7];48. int im,in,jn;49.50.54. if(npj>0)55. {56. for(i=1;i<=npj;i++)57. { j=pj[i][2];59. p[j]=pj[i][1];60. }61. }62. if(npf>0)63. {64. for(i=1;i<=npf;i++)65. { hz=i;67. gdnl(hz);68. e=(int)pf[hz][3];69. zb(e); for(j=1;j<=6;j++) {72. pe[j]=;73. for(k=1;k<=6;k++) {75. pe[j]=pe[j]-t[k][j]*f0[k];76. }77. }78. al=jm[e][1];79. bl=jm[e][2];80. p[3*al-2]=p[3*al-2]+pe[1]; p[3*al-1]=p[3*al-1]+pe[2];82. p[3*al]=p[3*al]+pe[3];83. p[3*bl-2]=p[3*bl-2]+pe[4];84. p[3*bl-1]=p[3*bl-1]+pe[5];85. p[3*bl]=p[3*bl]+pe[6];86. }87. }88.89.90. for(e=1;e<=ne;e++){94. dugd(e); for(i=1;i<=2;i++) {97. for(ii=1;ii<=3;ii++)98. {99. h=3*(i-1)+ii; dh=3*(jm[e][i]-1)+ii; for(j=1;j<=2;j++) 102. {103. for(jj=1;jj<=3;jj++) {105. l=3*(j-1)+jj; zl=3*(jm[e][j]-1)+jj; dl=zl-dh+1; if(dl>0) 109. kz[dh][dl]=kz[dh][dl]+ke[h][l]; }111. }112. }113. }114. }115.116. for(i=1;i<=nz;i++) {119. z=zc[i]; kz[z][l]=;for(j=2;j<=dd;j++)122. {123. kz[z][j]=;}125. if((z!=1))126. {127. if(z>dd)128. j0=dd;129. else if(z<=dd)130. j0=z; for(j=2;j<=j0;j++)132. kz[z-j+1][j]=;133. }134. p[z]=;}136.137.138.139.140. for(k=1;k<=nj3-1;k++)141. {142. if(nj3>k+dd-1) im=k+dd-1;144. else if(nj3<=k+dd-1)145. im=nj3;146. in=k+1;147. for(i=in;i<=im;i++)148. {149. l=i-k+1;150. cl=kz[k][l]/kz[k][1]; jn=dd-l+1; 152. for(j=1;j<=jn;j++)153. {154. m=j+i-k;155. kz[i][j]=kz[i][j]-cl*kz[k][m]; 156. }157. p[i]=p[i]-cl*p[k]; }159. }160.161.162.163.164. p[nj3]=p[nj3]/kz[nj3][1]; for(i=nj3-1;i>=1;i--)166. {167. if(dd>nj3-i+1)168. j0=nj3-i+1;169. else j0=dd; for(j=2;j<=j0;j++)171. {172. h=j+i-1;173. p[i]=p[i]-kz[i][j]*p[h];174. }175. p[i]=p[i]/kz[i][1]; }177. printf("\n");178. printf("_____________________________________________________________\n"); 179. printf("NJ U V CETA \n"); for(i=1;i<=nj;i++)181. {182. printf(" %-5d % % %\n",i,p[3*i-2],p[3*i-1],p[3*i]);183. }184. printf("_____________________________________________________________\n"); 185. printf("E N Q M \n");187. for(e=1;e<=ne;e++) {190. jdugd(e); zb(e); for(i=1;i<=2;i++)193. {194. for(ii=1;ii<=3;ii++)195. {196. h=3*(i-1)+ii;197. dh=3*(jm[e][i]-1)+ii; wy[h]=p[dh];199. }200. }201. for(i=1;i<=6;i++)202. {203. f[i]=;204. for(j=1;j<=6;j++)205. {206. for(k=1;k<=6;k++) {208. f[i]=f[i]+kd[i][j]*t[j][k]*wy[k];209. }210. }211. }212. if(npf>0)213. {214. for(i=1;i<=npf;i++) if(pf[i][3]==e) {217. hz=i;218. gdnl(hz); for(j=1;j<=6;j++) {221. f[j]=f[j]+f0[j];222. }223. }224. }225. printf("%-3d(A) % % %\n",e,f[1],f[2],f[3]);printf(" (B) % % %\n",f[4],f[5],f[6]);}228. return;229. }230.232.236. void gdnl(int hz)237. {238. int ind,e;239. double g,c,l0,d;240.241.242. g=pf[hz][1]; c=pf[hz][2]; e=(int)pf[hz][3]; ind=(int)pf[hz][4]; l0=gc[e]; d=l0-c;248. if(ind==1)249. {250. f0[1]=;251. f0[2]=-(g*c*(2-2*c*c/(l0*l0)+(c*c*c)/(l0*l0*l0)))/2; f0[3]=-(g*c*c)*(6-8*c/l0+3*c*c/(l0*l0))/12;253. f0[4]=;254. f0[5]=-g*c-f0[2];255. f0[6]=(g*c*c*c)*(4-3*c/l0)/(12*l0);256. }257. else258. {259. if(ind==2) {261. f0[1]=;262. f0[2]=(-(g*d*d)*(l0+2*c))/(l0*l0*l0);263. f0[3]=-(g*c*d*d)/(l0*l0);264. f0[4]=;265. f0[5]=(-g*c*c*(l0+2*d))/(l0*l0*l0);266. f0[6]=(g*c*c*d)/(l0*l0);267. }268. else269. {270. f0[1]=-(g*d/l0); f0[2]=;272. f0[3]=;273. f0[4]=-g*c/l0;274. f0[5]=;275. f0[6]=;276. }277. }278. }279.280. void zb(int e)284. {285. double ceta,co,si;286. int i,j;287. ceta=(gj[e]*pi)/180; co=cos(ceta); 289. si=sin(ceta);290. t[1][1]=co; t[1][2]=si;292. t[2][1]=-si;293. t[2][2]=co;294. t[3][3]=;295. for(i=1;i<=3;i++)296. {297. for(j=1;j<=3;j++) {299. t[i+3][j+3]=t[i][j];300. }301. }302. }303.304.305.306. void jdugd(int e)310. {311. double A0,l0,j0;312. int i;313. int j;314.315.316. A0=mj[e]; l0=gc[e]; j0=gx[e]; 320.321. for(i=0;i<=6;i++)322. for(j=0;j<=6;j++) kd[i][j]=;324.325. kd[1][1]=e0*A0/l0;326. kd[2][2]=12*e0*j0/pow(l0,3);327. kd[3][2]=6*e0*j0/pow(l0,2);328. kd[3][3]=4*e0*j0/l0;329. kd[4][1]=-kd[1][1];330. kd[4][4]=kd[1][1];331. kd[5][2]=-kd[2][2]; kd[5][3]=-kd[3][2];333. kd[5][5]=kd[2][2];334. kd[6][2]=kd[3][2];335. kd[6][3]=2*e0*j0/l0;336. kd[6][5]=-kd[3][2];337. kd[6][6]=kd[3][3];338.339. for(i=1;i<=6;i++)340. for(j=1;j<=i;j++) kd[j][i]=kd[i][j];342. }343.344.345. void dugd(int e)349. {350. int i,k,j,m;351. jdugd(e); zb(e); for(i=1;i<=6;i++)354. {355. for(j=1;j<=6;j++)356. {357. ke[i][j]=;358. for(k=1;k<=6;k++)359. {360. for(m=1;m<=6;m++)361. {362. ke[i][j]=ke[i][j]+t[k][i]*kd[k][m]*t[m][j]; } 364. }365. }366. }367. }368.369.370.372.373.374. </></>。
C语言编写有限元语言

元计算有限元语言及其编译器是元计算公司开发的 将“有限元语言”翻译为“C++语言”直至可执行 程序的软件,其主要工作流程:有限元语言(FEL source code)→ 有限元语言及其编译器(FELAC) → C++语言代码(C++ source code)→ C++ 编译器(C++ compiler)→ 目标代码(object code)→ 可执行程序(executables)。
谢谢
ቤተ መጻሕፍቲ ባይዱ
元计算科技发展有限公司成立于2009年11月,落 户在中新天津生态城,在北京、武汉设有子公司。 元计算有限元语言是全球首次发明并且优于当前高 级编程语言的智能化模型语言,处于独一无二的位 置,它可以在数天甚至数小时内完成通常采用高级 语言需要数年才能完成的编程工作。 元计算公司以中国科学院数学与系统科学研究院有 限元自动生成核心技术,通过自身不懈的努力与完 善,对产品重新架构并设计形成一系列具有高度前 瞻性和创造性的产品。
利用C语言开发高效率的有限元程序

利用C语言开发高效率的有限元程序
叶又;戚燕
【期刊名称】《计算机工程与应用》
【年(卷),期】1997(033)011
【摘要】本文通过与FORTRAN语言的比较,说明利用C语言开发有限元程序的可行性。
结果表明,C语言不仅可以提供更强大实用的编程环境,同时由于提供指针变量、动态内存分配函数和结构变量,使其编写的软件在维护性、可读性和内存利用效率方面具有明显的优势,是有限元软件的发展方向。
【总页数】4页(P43-46)
【作者】叶又;戚燕
【作者单位】上海交大国家模具CAD工程中心;上海交大国家模具CAD工程中心【正文语种】中文
【中图分类】TP311.52
【相关文献】
1.利用Visual Basic语言开发工程项目施工质量管理软件 [J], 杨炯
2.利用FEPG进行Navier-Stokes方程的有限元程序的生成 [J], 万水;M.P.尼尔森
3.利用Maple编制平面问题有限元程序 [J], 凡大林;方诗圣
4.利用Visual Basic语言开发应用程序的探讨 [J], 吴海昕
5.DDE技术在利用C语言开发AutoCAD中的应用 [J], 刘广华;张日华
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于有限元算法的编程实践学号:2011043010031姓名:廖校毅电子科技大学物理电子学院【摘要】本文就有限元算法在电磁场分析中的应用展开研究与实践,从电磁场的Maxwell方程出发,根据电磁场的边值问题及变分公式建立了有限元方程组。
具体在实践中,将这些知识运用到C++语言和Matlab中,并将这两种语言有机结合,编程并实现二维FEM。
程序最后通过计算含两种介质的电位槽电位分布来验证其正确性。
关键词: 有限元变分法C++ MatlabThe Programming Practice Based on The Finite Element Algorithm Student ID:2011043010031Name:Liao Xiaoyi University of Electronic Science and technology &School of PhysicalElectronicsAbstract In this paper, we take the application of finite element method in electromagnetic field analysis into research and practice. Starting from Maxwell equations of electromagnetic field, the electromagnetic field boundary value problems and variational formula established the finite element equations. In specific practice, this knowledge will be applied to the C++ language and Matlab, and the organic combination of two languages, programming and implementation of two-dimensional FEM. Finally, through the program to verify the validity of the calculation of potential distribution in channel potential containing two kinds of medium.Key words The finite element method The variational method C++ Matlab一、前言在数学中,有限元法(FEM,Finite Element Method)是一种为求得偏微分方程边值问题近似解的数值技术。
它通过变分方法[1],使得误差函数达到最小值并产生稳定解。
类比于连接多段微小直线逼近圆的思想,有限元法包含了一切可能的方法,这些方法将许多被称为有限元的小区域上的简单方程联系起来,并用其去估计更大区域上的复杂方程。
它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。
这个解不是准确解,而是近似解,因为实际问题被较简单的问题所代替。
由于大多数实际问题难以得到准确解,而有限元不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。
因其理论依据的普遍性,作为一种声誉很高的数值分析方法,,已被普遍推广并成功地用来解决各种结构工程、热传导、渗流、流体力学、空气动力学、土壤力学、机械零件强度分析、电磁工程问题等,并且大量可靠的基于有限元算法的软件如ANSYS 被开发和使用。
有限元法有以下特点:一,离散化过程保持了明显的物理意义。
因为变分原理描述了支配物理现象的物理学中的最小作用原理(如力学中的最小势能原理、静电学中的汤姆逊定理等),基于问题固有的物理特性而予以离散化处理,列出计算公式,是保证方法的正确性、数值解的存在与稳定性等前提要素。
二,优异的解题能力。
与其他数值方法相比较,有限元法在适应场域边界几何形状及媒质物理性质变异情况的复杂问题求解上,有突出优点:不受几何形状和媒质分布的复杂程度限制;不同媒质分界面上的边界条件是自动满足的;不必单独处理第二、三类边界条件;离散点配置比较随意,通过控制有限单元剖分密度和单元插值函数的选取,可以充分保证所需的数值计算精度。
二、 算法原理2.1 变分基本原理: 对于一般的问题,可以给出下列对应于一个自变量x 的简单形式的泛函21[](,,')x x J y F x y y dx =⎰函数y 稍有变化时:21[](,,'')x x J y y F x y y y y dx δδδ+=++⎰21[][][(,,)(,,)]d x x J J y y J y F x y y y y F x y y xδδδ∆=+-'''=++-⎰上式用多元函数的泰勒公式加以展开:2222222231{[][()2d 2()]}FF F F y y y y y yJ xFy y y y y y J J J Jδδδδδδδδδδ∂∂∂'++'∂∂∂∆=∂∂''+++''∂∂∂=+++≈⎰称为泛函的一阶变分。
泛函同一般函数的极值特性相似,泛函的取极值的条件是泛函的一阶变分为零,泛函值为拐点的条件是二阶变分为零。
所以,根据一阶变分为零,有下式成立:2211-0'[](,,')0'x x x x F d F y dx y J y F x y y dx F e h y ⎧⎛⎫∂∂=⎪ ⎪∂∂⎝⎭⎪=⇔⎨⎡⎤∂⎪=⎢⎥⎪∂⎣⎦⎩⎰2.2 有限元算法基本原理[2]:2.2.1 有限元网格划分的基本原则鉴于实际应用中三角形的网格剖分方式比较常见,下面以三角形网格剖分为例,介绍有限元网格划分基本原则:1.不同媒质的分界线,不容许跨越分界线的三角元2.三角元的边逼近边界3.三角形要求不要太尖或太钝4.顶点编号相差不能太悬殊,对多区域的编号,按区域连续编号,5.三角形节点编号按逆时针顺序编号图 2 网格划分示意图J δ2.2.1 有限元分片差值取任意一个网格如图,在有限单元(三角形)上进行分片线性插值,基函数为:123(,)e x y x y ϕααα=++123123123i i ij j j m m mx y x y x y ϕαααϕαααϕααα⎧=++⎪=++⎨⎪=++⎩由线性代数知识从而有:()()()123/2/2/2i i j j m m i i j j m m i i j j m m a a a b b b c c c αϕϕϕαϕϕϕαϕϕϕ⎧=++∆⎪⎪=++∆⎨⎪=++∆⎪⎩ 其中()12i j m m ji j m i m ji j j i a x y x y b y y c x x b c b c =-=-=-∆=- 把 代入三角元上的线性插值函数,[],,1(,)()2()() =(,)e i i i i j j j j m m m m e s s i j mx y a b x c y a b x c y a b x c y N x y ϕϕϕϕϕ=++∆++++++∑1(,)() 2 (,,)e s s s s N x y a b x c y s i j m =++∆=其中: {}{}(,), , i e e e e i j m j e e m x y N N N N ϕϕϕϕϕ⎡⎤⎢⎥⎡⎤==⎢⎥⎣⎦⎢⎥⎣⎦下面进行单元的泛函分析[][]222ee e e e D J J dxdy x y εϕϕϕϕ⎡⎤⎛⎫⎛⎫∂∂≈=+⎢⎥ ⎪ ⎪∂∂⎢⎥⎝⎭⎝⎭⎣⎦⎰⎰()2/2ei i j j m m b b b xϕαϕϕϕ∂==++∆∂()224ee i i j j m m D dxdy b b b x ϕεεϕϕϕ⎛⎫∂=++ ⎪∂∆⎝⎭⎰⎰{}{}{}{}1 ,, 4 i i i j i m i T i j m j i j j j m j e e e m i m j m m m bb bb bb b b b b b b K b b b b b b ϕεϕϕϕϕϕϕϕ⎧⎫⎧⎫⎪⎪⎪⎪=⎨⎬⎨⎬∆⎪⎪⎪⎪⎩⎭⎩⎭= {}1 4 i i i j i m j i j j j m e m i m j m m b b b b b b where K b b b b b b b b b b b b ε⎧⎫⎪⎪=⎨⎬∆⎪⎪⎩⎭ 同理:{}{}{}22e e Te e e D dxdy K y ϕεϕϕ⎛⎫∂= ⎪∂⎝⎭⎰⎰ {}2 4 i i i j i m j i j j j m em i m j m m c c c c c c where K c c c c c c c c c c c c ε⎧⎫⎪⎪=⎨⎬∆⎪⎪⎩⎭单元上总的泛函:[]222ee e eD J dxdyx y εϕϕϕ⎡⎤⎛⎫⎛⎫∂∂=+⎢⎥ ⎪⎪∂∂⎢⎥⎝⎭⎝⎭⎣⎦⎰⎰{}{}{}{}{}{}{}{}{}12112212T Te e e e e e Te e eK K K ϕϕϕϕϕϕ=+=图 2 插值示意图 123,,ααα{}{}{}12 e e ee e e ii ij im e e eji jj jm e e e mi mj mm K K K K K K K K K K K K =+⎧⎫⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎩⎭其中() 4e e rs sr r s r s where K K b b c c ε==+∆总体合成:改写扩充单位阵 到所有单位,即把扩充部分添零,为方便总体矩阵的处理。
[][]{}{}{}{}{}{}111212NNT e e e e TJ J K K ϕϕϕϕϕϕ==⎛⎫≈= ⎪⎝⎭=∑∑()1,1,2,Neij ij e where K K i j N ===∑变分问题被离散化的多元二次函数的极值问题:[](){}{}{}12,11,,,21min 2TN Nij i j i j J J K K ϕϕϕϕϕϕϕϕ=≈===∑ 根据函数极值理论:0 (1,2,,)iJi N ϕ∂==∂ 所以有下式成立:,10 (1,2,,)Nijji j K j N ϕ===∑{}{}{}0K ϕ=三、 仿真实现[4][5]3.1 仿真实例采用有限元法仿真并求解如图的含有介质体的静场电位分布。
