11月月考成绩(指标)

合集下载

九年级月考成绩总结(3篇)

九年级月考成绩总结（3篇）九年级月考成绩总结（精选3篇）九年级月考成绩总结篇1着时间的流逝，不知不觉间，距离中考只有30天的时间了。

和一模、二模相比较，在刚刚过去的三模考试中，很多同学凭借自己的努力，取得了可喜的成绩。

回忆当初，一模考试在总分800分的前提下，全年级700分以上人数只有58人，600分以上只有836人;二模考试总分760分(未考体育)，660分以上只有125人，560分以上1088人;三模考试总分790分(除理化试验)，700分以上就有180人，690分以上竟有281人，600分以上1091人，590分以上1158人。

虽然这个成绩与学校董事会给我们提出的20__年中考目标还有一些差距，但我们可以清楚的看到，在老师的精诚合作与同学们的奋力拼搏下，我们取得了明显的进步。

我们还有时间，我们相信，在剩下的一个月内，在全体老师和同学们的共同努力下，我们一定能够完成学校给我们定的目标，创造辉煌!同学们有没有信心?古人说过，“行百里者半于九十”。

王校长前不久也在毕业班领导组会议上指出：“后期30天是黄金时间，应该当黄金来用。

”可见，后期的复习安排尤为重要!根据前几届的后期复习来看，最后一个月的冲刺，总分普遍可增加20分以上，希望同学们在后期备考阶段，每位同学都要有精细的规划，合理安排好时间复习应考。

下面就如何合理安排后期的复习，给同学们提出建议。

一、要清醒的认识到自己的优势和不足，这段时间在跟上老师复习节奏的同时，可从本人的实际情况出发，主动征求老师意见，制定恰当的复习计划。

为了保证同学们后期复习的有效性，各备课组老师都给同学们提出合理的复习建议。

语文读懂文章再动笔阅读在语文试卷中所占分值较多，又相对难以把握。

复习现代文阅读时，同学们要把握议论、记叙、说明三种不同文体的阅读规律，将老师平时讲的这三种文体的阅读技巧运用起来。

要有意识地按不同文体阅读文章，不要完全凭语感。

同学们在阅读中出现的问题就是没有读懂文章，就草草答题，这是不可取的，要完全读懂文章后再开始答题。

【名校】重庆八中2025届学年高三语文11月试卷+答案

重庆市第八中学2024年11月高三月考语文一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1～5题。

①在公共生活中的说理是一种理性交流、表达看法、解释主张并对别人可能有说服作用的话语形式。

说服就是运用语言来对具体的他人作劝说、解释、说明，以期对他们有所影响。

《伊索寓言》中有一则《太阳与风》的故事：太阳与风进行比赛，看谁能使穿着外套的行人脱掉外套。

风刮了又刮，但刮得越凶，那个行人就把外套裹得越紧。

然后太阳出来了，照在行人的身上，行人感到身体出汗了，就把外套脱了下来。

这个故事可以用作“说服强于强制”的寓言。

希腊哲学家芝诺对说服有相似的说法，他称说服是一只摊开的手掌，而不是一个攥紧的拳头。

说服是欢迎他人加入对话，不是企图限制他们有自己的看法，更不是威胁他们不准有自己的看法。

②说理通过说明和协商，而不是暴力或战争来解决人间可能出现的矛盾和冲突，并形成一种可以称之为“讲理”的文明秩序。

所有的战争和混乱都是在没有协商、无理可讲的情况下发生的。

说理使得人类能够用“摊开的手掌”，而不是“攥紧的拳头”来相互交往，人类才得以进入文明社会。

然而，当下互联网中的说理常常被当作是攥紧拳头，而非摊开手掌的话语行为。

这样的“说理”便成为“占领话语阵地”“口诛笔伐”“论战”和向对方报以“投枪”和“匕首”。

这种“说理”观念令无数人深受其害而浑然不知。

例如，药家鑫驾车撞人后又将伤者刺了八刀致其死亡，他被判死刑之后，人们对死刑存废问题提出不同的看法。

在一篇主张废除死刑的文章下，一位网友留言道：“像你这样的作家，我只能称你为垃圾，你已经在违背你的道德，真不知道你学的是什么，假如有人杀了你妻子，你还会维护下去吗？”另一位网友反驳这则留言道：“某位（读者）看来智力与情感有双重问题，根本不懂得如何辩论，只会情感宣泄式的喊口号，动不动就是‘如果他们杀了你的孩子后，你会怎么样之类’的无理假设，这种网络愤青只能显示自己的无知。

月考反思教研活动记录(3篇)

第1篇一、活动背景为了进一步提高我校教师的教育教学水平，促进教师之间的交流与合作，及时发现和解决教学中存在的问题，我校于XX年XX月XX日开展了月考反思教研活动。

本次活动旨在通过对月考成绩的分析，查找教学中的不足，为今后的教学工作提供改进方向。

二、活动目的1. 通过对月考成绩的分析，找出学生在各学科、各知识点上的薄弱环节，为教师调整教学策略提供依据。

2. 促进教师之间的交流与合作，共同探讨教学中的问题，提高教学效果。

3. 引导教师进行教学反思，总结经验，改进教学方法，提高自身素质。

三、活动内容1. 月考成绩分析首先，各学科教师分别对月考成绩进行了详细的分析，包括各学科的平均分、及格率、优秀率等数据。

然后，针对各学科、各知识点的得分情况，教师们展开了热烈的讨论。

2. 教学问题探讨在分析月考成绩的基础上，教师们针对教学过程中存在的问题进行了深入探讨。

主要包括以下几个方面：（1）教学目标是否明确，是否符合学生的实际需求？（2）教学方法是否合理，能否激发学生的学习兴趣？（3）教学评价是否科学，能否及时反馈学生的学习情况？（4）教学资源是否充足，能否满足教学需求？3. 教学改进措施针对上述问题，教师们提出了以下改进措施：（1）明确教学目标，关注学生的实际需求。

教师应根据学生的实际情况，制定合理的教学目标，确保教学活动具有针对性和实效性。

（2）改进教学方法，提高教学效果。

教师应灵活运用多种教学方法，激发学生的学习兴趣，提高学生的参与度。

（3）科学进行教学评价，及时反馈学生学习情况。

教师应采用多元化的评价方式，关注学生的学习过程，及时发现并解决学习中存在的问题。

（4）充分利用教学资源，提高教学质量。

教师应积极挖掘和利用各类教学资源，丰富教学内容，提高教学质量。

四、活动总结本次月考反思教研活动取得了圆满成功。

通过本次活动，教师们对月考成绩有了更深入的了解，对教学中的问题有了更清晰的认识，为今后的教学工作奠定了基础。

11月月考分析和反思

13单招语文月考考试分析与反思单招班11月份的月考已经结束，表面看好像成绩不错，因为这次考场的安排是按照上次考试的年纪排名进行的，第一、二考场几乎都能够及格，甚至还有几个高分，但是当整体的数字呈现在我们面前时，才发现情况比上次还糟。

于是我们语文教研组集体在经过教研之后，针对各班情况，都进行了总结和反思。

现汇报如下：一、试卷分析(一)试卷整体层面：这次期中考试语文试题考试时间为120分钟，试卷满分为100分。

由基础知识及运用、课内外阅读积累、阅读分析（含现代文阅读和文言文阅读）、作文四个部分组成。

不过考察内容和教学进度要求不太一致，按进度应该考前三单元，不包括文言文。

但我们对教材进行了整合处理，所以还有文言文。

本次命题以教材为本，比较全面地考察了学生对教材中基础知识、基本技能的掌握情况。

对语言的积累、语感能力的形成都有不同程度的考察。

整张试卷难易适度，覆盖面广、形式比较单一，有广度却无深度；想考查学生平时的学习结果，关注平时的训练与应用，学习过程中一次与一次的变化和发展。

基本上准确把握了教材中需要掌握的知识点。

词语积累、课文识记、唯一这次涉及了一点课外阅读部分、作文这次相比于以往多了一点灵活性、开放性，可以发散学生的思维。

（二）分值分析:试卷中共有七道大题，可以分为四类。

其中第一大类：积累运用占38分，第二大类：阅读理解占23分，第三大类：应用文写作7分，第四大类：作文占30分整体看，本次试卷命题难度适中，其中较难题10％，中等难度题30％，简单题60％，面向了大多数学生，符合命题要求。

二、成绩统计：最高分：84分；最低分：40分；平均分63.7优秀： 1人三、与九月份考试对比注：高一年级题型和高二基本一致，基础部分几乎都能拿到该拿的分，但是两个现代文阅读学生十分比较严重。

有些学生20分一分都得不到，导致成绩总体比较低。

从这我们发现学生对短文的理解还浮于文字表面，对短文只是粗粗的读过缺少思考与品味，因此有些题的回答不完整。

北京市五年级上学期数学月考试卷(11月)

北京市五年级上学期数学月考试卷（11月）姓名:________ 班级:________ 成绩:________亲爱的小朋友们，这一段时间的学习，你们收获怎么样呢？今天就让我们来检验一下吧！一、填空．（21分） (共11题；共21分)1. （3分） 6平方米=________平方分米6立方米=________立方分米1.6平方米=________平方分米1.6立方米=________立方分米2. （3分） (2017六上·黄埔期末) 在横线上填上“＜”“＞”或“=”（1）÷ ________ ×（2）1÷ ________1×（3）÷4________ × ．3. （2分）(2019·中山) 2018年国庆黄金周，广东全省共接待游客50496000人次，横线上的数读作________人次，改写成用“万”作单位的数是________万人次。

4. （3分）用竖式计算（1）9.5÷0.05=（2）1.7÷2.5=（3）7÷1.4=（4）26.26÷26=5. （2分） (2018五上·寻乌期中) 口袋里只有8枚黑棋，任意摸出一枚，________是黑棋．（填“可能”“不可能”或“一定”）6. （1分）表中的“大”用数对（5，1）表示。

像这样，找一找“数”“学”的位置，并用数对表示。

数（________，________），学（________，________）7. （1分） 0.907缩小到原数的是________；扩大到原数的100倍是________．8. （2分）在自然数中，最小的偶数是________，最小的质数是________。

9. （2分）0.305÷0.13的商保留两位小数，近似值是________；保留三位小数，近似值是________．10. （1分）计算并凑整到百分位．(用四舍五入法)（1）3.25×0.42≈________（2）7.83×1.39≈________11. （1分）填空0.2×0.15=________5-1.42=________二、判断． (共5题；共5分)12. （1分）判断对错．1.2里面有12个十分之一．13. （1分）在计算3.6×4×2.5＝3.6×(4×2.5)利用的是乘法分配律。

辽宁省沈阳市2023-2024学年八年级上学期11月月考语文试题(含答案)

2023—2024学年度上学期八年级阶段练习（二）语文（范围：第1、2、3、4、5单元+第6单元课外古诗词诵读；语法：词性、短语、句子主干；名著：《红星照耀中国》《昆虫记》）满分120分，时间120分钟。

注意事项：1．同学们须用0.5mm黑色字迹的签字笔在本练习题规定位置填写自己的班级、姓名及练习号；2．须在答题卡上作答；3．本练习题包括4道大题，23道小题，共8页。

一、积累与运用（17分）1．下列词语中加点字的字音、字形完全正确的一项是（（2分）A．凌空（líng）抵赖（dǐ）匿名（mì）春寒料峭（qiào）B．沉溺（nì）滞留（zhì）国殇（shāng）殚精竭虑（dān）C．僵绳（jiāng）吹嘘（xǔ）踱步（duó）精疲力尽（jīng）D．狼藉（jí）上朔（sù）主宰（zhǎi）触目伤怀（chù）2．依次填入下面句子横线处的词语最恰当的一项是（）（2分）黄河是中原大地上最为雄浑_________的奇观。

_________早在《诗经》中就有对黄河的描写，但只有到了李白的笔下，才真正写出了黄河的气魄，写出了黄河的灵魂。

在这里，黄河_________，一泻千里，奔腾咆哮，气势恢宏。

最著名的如“黄河之水天上来，奔流到海不复回”，这句子千百年来，传诵不衰。

难怪林庚先生要击节赞叹：“每一个读到这样诗句的人，就都会感染到他要冲破一切_________的力量。

”A．壮美虽然势不可挡束缚B．壮美虽然锐不可当禁锢C．美好也许锐不可当约束D．美好也许势不可挡限制3．下列各项中分析不正确的一项是（）（2分）“元旦京港澳天宫对话”，将远隔千里的三地青年学子和身处中国空间站的航天员们“聚”在一起。

他们谈梦想、说奋斗、聊青春、话未来，堪称一堂别开生面的新年第一课。

我印象最深的是“太空画展”、中航天员们展示的《太空旅行》《美丽的太空家园》等画作。

月考后，总结反思很重要！务必做好试卷分析（内附成绩分析表模板）

月考后，总结反思很重要！务必做好试卷分析（内附成绩分析表模板）试卷分析有策略所谓考后试卷分析，是指考试后订正试卷中出现的错误，分析考试的收获以及考试暴露出的问题，然后归类，逐一进行对照并制订出自我提高的措施与方法。

一般试卷分析要讲究以下四个策略：1.从逐题分析到整体分析从每一道错题入手，分析错误的知识原因、能力原因、解题习惯原因等。

分析思路是：①这道题考查的知识点是什么？②知识点的内容是什么？③这道题是怎样运用这一知识点解决问题的？④这道题的解题过程是什么？⑤这道题还有其他的解法吗？在此基础上，学生就可以进行整体分析，拿出一个总体结论。

通常情况下，学生考试丢分的原因大体有三种，即知识不清、问题情景不清和表述不清。

“知识不清”，就是在考试之前没有把知识学清楚，丢分发生在考试之前，与考试发挥没有关系。

“问题情景不清”，就是审题不清，没有把问题看明白，或是不能把问题看明白。

这是一个审题能力、审题习惯问题。

“表述不清”，指的是虽然知识具备、审题清楚，问题能够解决，但表述凌乱、词不达意。

上述问题逐步由低级发展到高级。

研究这三者所造成的丢分比例，用数字说话，也就能够得到整体结论，找到整体方向了。

2.从数字分析到性质分析要点有三：①统计各科因各种原因的丢分数值。

如计算失误失分、审题不清失分、考虑不周失分、公式记错失分、概念不清失分等。

②找出最不该丢的5～10分。

这些分数是最有希望获得的，找出来很有必要。

在后续学习中，努力找回这些分数可望可即。

如果真正做到这些，那么不同学科累计在一起，总分提高也就很可观了。

③任何一处失分，有可能是偶然性失分，也有可能是必然性失分，学生要学会透过现象看本质，找到失分的真正原因。

3.从口头分析到书面分析从潜意识的存在到口头表达是一次进步，从口头表达到书面表达又是一次进步。

书面表达是考后试卷分析的最高级形式。

建议学生在考试后写出书面的试卷分析。

这个分析是反观自己的一面镜子，是以后进步的重要阶梯。

二年级上册 11月数学月考试卷

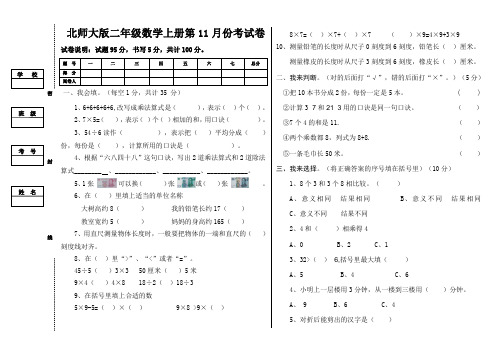
学校班级姓名密封线考号北师大版二年级数学上册第11月份考试卷试卷说明：试题95分，书写5分，共计100分。

题号一二三四五六七总分得分阅卷人一、我会填。

（每空1分，共计35 分）1、6+6+6+6+6,改写成乘法算式是（），表示（）个（）。

2、7×5=（），表示（）个（）相加的和，用口诀（）。

3、54÷6读作（），表示把（）平均分成（）份，每份是（），计算所用的口诀是（）。

4、根据“六八四十八”这句口诀，写出2道乘法算式和2道除法算式________ 、____________、___________、____________。

5、1张可以换（）张或（）张。

6、在（）里填上适当的单位名称大树高约8（）我的铅笔长约17（）教室宽约5（）妈妈的身高约165（）7、用直尺测量物体长度时，一般要把物体的一端和直尺的（）刻度线对齐。

8、在（）里“>”、“<”或者“=”。

45÷5（）3×3 50厘米（）5米9×4（）4×8 18÷2（）18÷39、在括号里填上合适的数5×9-5=（）×（） 9×8 >9×（）8×7=（）×7+（）×7 （）×9=4×9+3×910、测量铅笔的长度时从尺子0刻度到6刻度，铅笔长（）厘米。

测量橡皮的长度时从尺子3刻度到6刻度，橡皮长（）厘米。

二、我来判断。

（对的后面打“√”，错的后面打“×”。

）（5分）①把10本书分成2份，每份一定是5本。

( )②计算3×7和21÷3用的口诀是同一句口诀。

（）③7个4的和是11. （）④两个乘数都8，列式为8+8. （）⑤一条毛巾长50米。

（）三、我来选择。

（将正确答案的序号填在括号里）（10分）1、8个3和3个8相比较。

2024年11月班级工作总结范文5篇

2024年11月班级工作总结范文5篇篇1一、引言本月，班级工作围绕着提高学生学习积极性、促进班级文化建设、增强团队凝聚力等方面展开。

经过全班的共同努力，我们取得了一系列成果，也积累了一定的经验。

现将本月班级工作进行总结，以期更好地为未来工作提供指导。

二、班级工作总体情况（一）教育教学方面1. 学习积极性显著提高。

本月，班级内学习气氛浓厚，同学们自觉性增强，课后积极复习与预习，参与课堂讨论的积极性明显提高。

2. 教学方法创新。

教师团队积极探索新的教学方法，运用多媒体和网络资源，丰富课堂教学内容，提高教学效果。

3. 考试成绩稳步提升。

本月月考成绩稳中有升，各科目平均分和及格率均有所增长。

（二）班级建设方面1. 班级文化建设成效显著。

班级墙报定期更新，展示学生作品和班级活动照片，增强了班级荣誉感和凝聚力。

2. 班会活动丰富多彩。

本月组织了多次班会活动，包括学习经验交流、心理辅导讲座等，有效促进了学生的交流与成长。

3. 班级纪律进一步规范。

通过班规的制定和执行，班级纪律明显好转，迟到、旷课现象明显减少。

（三）课外活动方面1. 文体活动活跃。

组织了篮球比赛、运动会等文体活动，增强了学生体质，提高了团队凝聚力。

2. 社会实践活动丰富。

开展了志愿者活动、社会实践等，让学生接触社会、了解社会，增强了社会责任感。

3. 学科竞赛成绩突出。

在各类学科竞赛中，班级学生表现优异，获得了多项奖项，为学校争得了荣誉。

三、重点工作推进情况（一）学业指导与帮扶工作本月，班级开展了学业指导与帮扶工作，针对学习困难的学生进行个别辅导，提高了学习效果。

同时，开展了学习经验交流会，让优秀学生分享学习经验，促进了全班学生的学习进步。

（二）心理健康教育心理健康教育是本月班级工作的重点之一。

通过心理辅导讲座、个别咨询等方式，帮助学生解决心理问题，缓解学习压力，提高了学生的心理健康水平。

（三）家校合作与沟通本月，班级加强了与家长的联系与沟通，通过家长会、电话、微信等方式，及时与家长反馈学生学习情况和生活表现，形成了家校共同关注孩子成长的良好氛围。

重庆市第一中学校2024-2025学年高三上学期11月月考数学试题

D．1- 2i
2．已知平面向量
ar
=
(1,
2
)
,
r b
=
(
m,
-1)
，则“
m
<
2
”是“
ar
与
r b
的夹角为钝角”的（
）
A．充分不必要条件 C．充要条件
B．必要不充分条件 D．既不充分也不必要条件
{ } 3． Sn 为等比数列 an 的前 n 项和，若 a1 = 2 ，且 a2022 + a2023 = 0 ，则 S2025 等于（）
.
13．点 O 为平面直角坐标系的原点， A(-3,0) ，点 P 满足
PA PO
= 2 ，点 Q 为圆
C : (x - 3)2 + ( y - 4)2 = 1 上一动点，则 PQ + PC 的最小值为
.
14．若数列{an} 满足对任意 n Î N*
都有 an+1
£
an
+ an+2 2
，则称数列{an} 为 N* 上的“凹数
B．若关于 x 的方程 g ( x) = a 有两个不相等的实根 x1, x2 ，且 x1 < x2 ，则 x1 + 2x2 > 3
C．若 a
> 0,"x
>
0 ，不等式
f
æ ç è
a × ex x
ö ÷
³
ø
f
a
( x - lnx +1) 恒成立，则的取值范围为
é êë
2 e
,
+¥
ö ø÷
试卷第31 页，共33 页
（参考数据：若 X ~ N (u,s 2 ) ，则 P (u -s £ X £ u + s ) = 0.6827 ，

2025届巴蜀中学高三11月适应性月考(三)物理试题

物理试卷注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。

2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

在试题卷上作答无效。

3．考试结束后，请将本试卷和答题卡一并交回。

满分100分，考试用时75分钟。

一、单项选择题：本大题共7小题，每小题4分，共28分。

在每小题给出的四个选项中，只有一项符合题目要求。

1. 如图，一轻绳跨过光滑定滑轮，绳一端系物块P ，P 置于水平桌面上，与桌面间存在摩擦；绳的另一端悬挂一轻盘（质量可忽略），盘中放置砝码。

改变盘中砝码总质量m ，并测量P 的加速度大小a ，得到a m −图像。

重力加速度大小为g 。

在下列a m −图像中，可能正确的是（）A. B. C. D. 2. 某电动小车在平直路面上以恒定功率P 启动，经过时间t 达到最大速度v ，该过程电动小车前进距离为x 。

若电动小车的质量为m ，所受阻力的大小恒为f ，下列说法错误的是（）A. 小车做加速度不变的加速运动B. 小车速度为v 时，所受牵引力大小等于阻力大小C. 该过程，电动机对小车所做的功为212fx mv +D. 该过程，电动机对小车所做的功为Pt3. 下图甲为用手机和轻弹簧制作的一个振动装置。

手机加速度传感器记录了手机在竖直方向的振动情况，以向上为正方向，得到手机振动过程中加速度a 随时间t 变化的曲线为正弦曲线，如图乙所示，下列说法正确的是（）的的A. 0t =时，弹簧的弹性势能为0B. 0.2s t =时，手机位于平衡位置上方C. 从0t =至0.2s t =，手机的机械能不变D. a 随t 变化的关系式为24sin 2.()5πm/s a t =4. 2024年4月25日，神舟十八号飞船与天宫空间站顺利对接，运载火箭先将飞船送入圆轨道Ⅰ上，通过变轨进入预定圆轨道。

如图所示，飞船与空间站在对接前在各自预定的圆轨道I 、Ⅲ上运动，Ⅱ为对接转移轨道，不考虑飞船质量的变化，下列说法正确的是（）A. 飞船从椭圆轨道Ⅱ进入预定圆轨道Ⅲ需要减速B. 飞船在Ⅰ轨道上的运行速度小于在Ⅲ轨道上的运行速度C. 飞船在Ⅱ轨道上的机械能大于在Ⅰ轨道上的机械能D. 飞船在三个轨道上运行时与地球连线在单位时间内扫过的面积相等5. 如图所示电路，电源内阻不计，P 点是电容器两极板间的一个定点，C 为电容器的电容，E 为电源的电动势．滑动变阻器滑片最初处于a 端且电路处于稳定状态，现滑片从a 端缓慢滑到b 端，则该过程中（）A. 电容器两极板间的电压先增大后减小B. c 点电势比d 点电势略高C. 流过3R 横截面的电荷量等于CED. P 点的电势升高6. 如图所示，在竖直y 轴上固定两个点电荷，电荷量为+Q 的点电荷在02y 处、电荷量m 为4Q −的点电荷在03y 处。

七年级第一次月考成绩分析

七年级第一次月考成绩分析七年级第一次月考分析上周，我校举行了六—九年级第一次月考，从此次月考成绩来看，成绩极不理想，与预期目标差距较大。

通过这次月考充分暴露出存在我们同学身上的一些问题。

下面我就从几个方面对本次月考做以分析：一、月考成绩相关数据七年级一二班参考总人数：106人。

语文试卷总分：120 分。

其中优秀人数：0人，合格人数：65 人；最高分99分，最低分44分。

评定分56.06. 数学试卷总分：120 分。

其中优秀人数：0人，合格人数：15人；最高分93分，最低分21分。

评定分33.48.英语试卷总分：120 分。

其中优秀人数：0人，合格人数：3人；最高分78分，最低分16分。

评定分19.9.总体来看：尖子生不尖，差生过差。

举例：杨永华、肖雨、张文凯虽为年级第一，但三位同学三科均未达到优秀。

后两名杨星、王强三门总分90几分，均分才30多分。

二、试卷难度分析此次语文月考试卷总分共120 分，其中基础知识占到26分，阅读理解占到44分，作文占到50分。

题目难易结合。

数学试卷总分120分，其中选择、填空题占48分，填空计算问答占到72分，基础、新知难易结合；英语试卷总分120分，其中选择题占70分，阅读写作占到50分。

基础性知识考的多。

三、学生作答情况分析通过仔细检查学大家的卷子，发现达到优秀率的学生对于基础知识掌握很牢固，丢分现象极少。

丢分多出现在计算、阅读、写作，这些操作理解题上，主要原因是因为平时对综合题的练习不够，思路无法展开，导致做不出或者是思路出现错误。

此次月考成绩低于60分的学生过多，语文达到41人，占两个班的39%；数学未及格人数91人，占两个班的86%；英语未及格人数103人，占两个班的97.2%。

通过对这些同学的试卷分析，发现问题主要出在基础知识上，语文科基本的课文内容掌握不是很好。

大部分不合格的学生对于阅读理解题也存在着重大的问题；数学科基础能力、计算能力过差，例如：第18题找正整数、负整数、正数、正分数，一部分同学都能做错。

月考后教研活动记录数学(3篇)

第1篇一、活动时间2023年11月15日（星期三）下午2:00-4:30二、活动地点学校会议室三、参与人员数学组全体教师四、活动主题1. 分析月考成绩，查找教学中的不足。

2. 探讨提高学生数学成绩的有效策略。

3. 分享优秀教学经验和教学方法。

4. 安排下一阶段的教学工作。

五、活动内容（一）月考成绩分析1. 整体情况分析：- 全体数学老师首先对本次月考的整体成绩进行了汇报，包括及格率、优秀率、平均分等关键指标。

- 通过数据对比，分析了不同年级、不同班级的成绩差异，以及学生在不同题型上的得分情况。

2. 具体问题分析：- 针对薄弱环节，如选择题、填空题和解答题的得分情况进行了深入分析。

- 探讨了学生在应用题、几何题等复杂题型上的失分原因。

3. 学生个体分析：- 对部分成绩优秀和成绩落后的学生进行了个别分析，找出其成功或失败的原因。

（二）教学策略探讨1. 针对薄弱环节，加强基础知识教学：- 针对学生在基础知识掌握上的不足，老师们提出了加强基础知识教学的重要性。

- 建议通过课堂讲解、课后辅导、小组合作等多种方式，帮助学生巩固基础知识。

2. 提高课堂效率，激发学生学习兴趣：- 通过创设有趣的教学情境、运用多媒体教学手段等方法，提高课堂效率。

- 鼓励学生参与课堂讨论，激发学生的学习兴趣。

3. 关注个体差异，实施分层教学：- 针对不同层次的学生，制定不同的教学目标和教学方法。

- 关注学困生的学习进步，给予他们更多的关爱和帮助。

（三）优秀教学经验分享1. 教学案例分享：- 由经验丰富的老师分享了他们在教学中的成功案例，如如何设计课堂活动、如何处理课堂突发事件等。

2. 教学方法交流：- 老师们就如何运用多种教学方法提高教学质量进行了深入交流，如翻转课堂、项目式学习等。

（四）下一阶段教学工作安排1. 加强备课，提高教学质量：- 要求老师们认真备课，针对学生的薄弱环节进行针对性教学。

2. 加强课堂管理，营造良好学习氛围：- 加强课堂纪律，关注学生的学习状态，营造良好的学习氛围。

四川省成都市2024-2025学年高三上学期11月期中考试数学试题含答案

成都市高2022级高三11月月考数学试题（答案在最后）总分150分时间120分钟一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若命题p ：20430x x x ∃>-+>，，则命题p ⌝为（）A.20430，∃>-+≥x x xB.20430，∃≤-+≤x x xC.20430，∀>-+≤x x xD.20430，∀≤-+≤x x x 【答案】C 【解析】【分析】根据存在量词命题的否定为全称量词命题，写出结论即可.【详解】命题p 是一个存在性命题，说明存在使2430x x -+>的正数x ，则它的否定是：不存在使2430x x -+>的正数x ，即对任意的正数2430x x -+>都不能成立，由以上的分析，可得p ⌝为：20430，∀>-+≤x x x ，故选：C.2.在ABC V 中，“π6A >”是“1sin 2A >”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】结合正弦函数的性质由1sin 2A >，可得π5π66A <<，再根据充分条件和必要条件的定义判断即可.【详解】在ABC V 中，()0,πA ∈，由1sin 2A >，可得π5π66A <<，所以“π6A >”是“1sin 2A >”的必要不充分条件.故选：B .3.已知向量,a b的夹角为2π3，且5,4a b == ，则a 在b 方向上的投影向量为（）A.38b -B.58b -C.58bD.78b- 【答案】B 【解析】【分析】根据投影向量的计算公式，结合已知条件，直接求解即可.【详解】由题可知：12π54cos 523448a b a b b b b b bb bb⎛⎫⨯⨯- ⎪⋅⎝⎭⋅=⨯=⨯=-，故a在b 方向上的投影向量为58b - .故选：B.4.已知等差数列{}n a 和{}n b 的前n 项和分别为n S 、n T ，若342n n S n T n +=+，则62102a b b +（）A.11113B.3713C.11126D.3726【答案】B 【解析】【分析】计算出11113713S T =，由等差数列的性质得611116a S T b =，6621062a a b b b =+，从而得到答案.【详解】因为等差数列{}n a 和{}n b 的前n 项和分别为n S 、n T ，满足342n n S n T n +=+，所以111131143711213S T ⨯+==+，又11161116111111()211()2a a a Sb b T b +==+，故666210662322371a a a b b b b ===+，故选：B5.遗忘曲线由德国心理学家艾宾浩斯研究发现，描述了人类大脑对新事物遗忘的规律，某同学利用信息技术拟合了“艾宾浩斯遗忘曲线”，得到记忆率y 与初次记忆经过的时间x （小时）的大致关系：0.0610.6y x =-，则记忆率为20%时经过的时间约为（）（参考数据：lg 20.30≈，lg 30.48≈）A.80小时B.90小时C.100小时D.120小时【答案】C 【解析】【分析】根据题设得到0.0643x =，两边取对数求解，即可得出结果.【详解】根据题意得0.06110.65x =-，整理得到0.0643x =，两边取以10为底的对数，得到4lg 0.06lg 3x =，即2lg 2lg 30.06lg x -=，又lg 20.30,lg 30.48≈≈，所以0.60.48lg 2lg1000.06x -≈==，得到100x ≈，故选：C.6.已知圆锥的侧面展开图是一个半径为43，面积为4π3的扇形，则该圆锥的外接球的表面积为（）A.256π63B.4πC.9π2D.9π【答案】A 【解析】【分析】求出圆锥的底面圆半径和高，再求出外接球的半径，由此求得圆锥的外接球的面积.【详解】设圆锥的底面圆半径为r ，则该圆锥的侧面展开图扇形弧长为2πr ，于是144π2π233r ⋅⋅=，解得1r =，该圆锥的高为73h ==，设该圆锥的外接球的半径为R ，则球心到圆锥底面圆距离||d h R =-，由球的性质知，2227)13R R -+=，解得R =所以该圆锥的外接球的面积为22564ππ63S R ==.故选：A 7.若()*n n ∈N次多项式()()1212100nn nnn n P t a ta t a t a t a a --=++⋅⋅⋅+++≠满足()cos cos n P x nx =，则称这些多项式()n P t 为切比雪夫多项式．如，由2cos 22cos 1θθ=-可得切比雪夫多项式()2221P x x =-，同理可得()3343P x x x =-．利用上述信息计算sin 54︒=（）A.14+ B.14C.48 D.48【答案】A 【解析】【分析】根据切比雪夫多项式得()33cos 4cos 3cos cos3P θθθθ=-=，即可取18θ= ，结合二倍角公式以及同角关系求解.【详解】由于()33cos 4cos 3cos cos3P θθθθ=-=,cos54sin 36︒=︒，即3cos544cos 183cos182sin18cos18︒=︒-︒=︒︒，变形可得24cos 1832sin18︒-=︒，即214sin 182sin18-=︒，解可得：51sin184︒=或514-（舍)，则有21cos3612sin 184+︒=-=︒，即1sin 544+︒=，故选：A8.函数()2e 12e 21x x xh x -=++，不等式()()2222h ax h ax -+≤对x ∀∈R 恒成立，则实数a 的取值范围是（）A.()2,-+∞ B.(),2-∞ C.()0,2 D.[]2,0-【答案】D 【解析】【分析】令()()1f x h x =-，根据奇偶性定义判断()f x 为奇函数，再应用导数研究()f x 的单调性，进而将目标式转化为2220ax ax +-≤在R 上恒成立，求参数范围.【详解】因为()2e 122e e e 2121x x xx x xh x --=+=-+++，所以()()22222e e e e 221212121x x x x xx x x x h x h x ---⋅+-=+-++-=+=++++，令()()1f x h x =-，则()()0f x f x +-=，得()f x 为奇函数，又()()()222ln41ln4e e e e e 121e 21222x x x x x xx x x x xf x --'⎛⎫=+-=+-=+- ⎪+⎝⎭+++''，1e 2e x x +≥，当且仅当1e e xx =，即0x =时等号成立；ln4ln4ln2142222x x ≤=++，当且仅当122xx=，即0x =时等号成立；所以()0f x '>，得()f x 在R 上为增函数，因为()()()()()()22222222022h ax h ax f ax f ax f ax f ax -+≤⇔-+≤⇔-≤-，所以2220ax ax +-≤在R 上恒成立，显然0a =时满足；当0a ≠，需满足20Δ480a a a <⎧⎨=+≤⎩，解得20a -≤<，综上，[]2,0a ∈-.故选：D【点睛】关键点点睛：注意构造()()1f x h x =-，判断其奇偶性、单调性，最后将问题化为2220ax ax +-≤在R 上恒成立为关键.二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.设1z ，2z 为复数，且120z z ≠，则下列结论正确的是（）A.1212z z z z = B.1212z z z z +=+C.若12=z z ，则2212z z = D.1212z z z z ⋅=⋅【答案】ABD 【解析】【分析】根据题意，由复数的运算，代入计算，逐一判断，即可得到结果.【详解】设1i z a b =+，2i z c d =+(,,,)a b c d ∈R ，对于选项A ，因为12(i)(i)()()i z z a b c d ac bd ad bc =++=-++，所以12z z =且12z z 1212z z z z =，故A 正确；对于选项B ，因为12()()i z z a c b d +=+++，1i z a b =-，2i z c d =-，则12()()z z a c b d i +=+-+，12()()i z z a c b d +=+-+，所以1212z z z z +=+，故B 正确；对于选项C ，若12=z z ，例如11i z =+，21i z =-，满足12z z ==，但221(1i)2i z =+=，222(1i)2i z =-=-，即2212z z ≠，故C 错误；对于选项D ，因为21(i)(i)()()i z a b c d ac bd c z ad b ⋅=++=-++，所以21()()i z ac bd a b z d c ⋅=--+，12(i)(i)()()i z z a b c d ac bd ad bc ⋅=--=--+，所以1212z z z z ⋅=⋅，故D 正确.故选：ABD.10.下列关于概率统计的知识，其中说法正确的是（）A.数据1-，0，2，4，5，6，8，9的第25百分位数是1B.已知随机变量(),X B n p ，若()40E X =，()30D X =，则160n =C.若事件M ，N 的概率满足()()0,1P M ∈，()()0,1P N ∈且()()1P N M P N +=，则M 与N 相互独立D.若一组样本数据(),i i x y （1i =，2，…，n ）的对应样本点都在直线132y x =-+上，则这组样本数据的相关系数为12-【答案】ABC 【解析】【分析】根据百分位数的定义计算判断A ，由二项分布的数学期望与方差公式计算可判断B ，根据相互独立事件及条件概率的概率公式计算可判断C ，根据相关系数的定义可判断D.【详解】对于选项A ，8个数据从小到大排列，由于825%2⨯=，所以第25百分位数应该是第二个与第三个的平均数0+2=12，故A 正确；对于选项B ，因为(),X B n p ~，()40E X =，()30D X =，所以40(1)30np np p =⎧⎨-=⎩，解得1,1604p n ==，故B 正确；对于选项C ，由()()1P N M P N +=，可得()()1P N M P N =-，即()()()P NM P N P M =，即()()()P NM P N P M =，所以M 与N 相互独立，故C 正确；对于选项D ，因为样本点都在直线132y x =-+上，说明是负相关且线性相关性很强，所以相关系数为1-，故D 错误.故选：ABC.11.“曼哈顿距离”是十九世纪的赫尔曼•闵可夫斯省所创词汇，用以标明两个点在标准坐标系上的绝对轴距总和，其定义如下：在直角坐标平面上任意两点()()1122,,,A x y B x y 的曼哈顿距离()1212,d A B x x y y =-+-，则下列结论正确的是（）A.若点()()1,3,2,4P Q ，则(),2d P Q =B.若对于三点,,A B C ，则“()()(),,,d A B d A C d B C +=”当且仅当“点A 在线段BC 上”C.若点M 在圆224x y +=上，点P 在直线280x y -+=上，则(),d P M 的最小值是25-D.若点M 在圆224x y +=上，点P 在直线280x y -+=上，则(),d P M 的最小值是4【答案】AD 【解析】【分析】由定义即可判断A 选项，由数形结合即可判断出B 选项，C,D 选项是求点与点的“曼哈顿距离”距离，由基本不等式转化成点到点的平面距离，借助数形结合即可得出判断．【详解】对于A 选项：由定义可知(),21432d P Q =-+-=，故A 选项正确；对于B 选项：设点()()()112233,,,,,A x y B x y C x y 则()()()121213132323,,,,d A B d A C x x y y x x y y d B C x x y y +=-+-+-+-=-+-显然，当点A 在线段BC 上时，121323121323,x x x x x x y y y y y y -+-=--+-=-，()()(),,,d A B d A C d B C ∴+=成立，如图：过点B 作BE y ⊥轴，过点C 作EE x ⊥轴，且相交于点E ，过点A 作AD BE ⊥与D ，过点A 作AF CE ⊥与F ，由图可知121213132323x x y y x x y y BD AD AF CF BE CE x x y y -+-+-+-=+++=+=-+-，显然此时点A 不在线段BC 上，故B 选项不正确；对于C ，D 选项：当0,0a b >>a b ≥+≥∴想要(),d P M 最小，点M 到直线距离最小时取得，∴过原点O 作OM ⊥直线280x y -+=交圆于M ，如图：设(),M a b ，则25452,55OMbk M a ⎛⎫==-∴- ⎪ ⎪⎝⎭设点0,0，则()00,d P M x y =+-，又当0,ab a b =+≥①当005x +=时，由()00544,25x y d P M =+=-+004x y =++-=-②当04505y -=时，由002885x y =-=-()00,8d P M x y =+-=-又48-<- ；(),d P M ∴的最小值为：4.故C 选项错误，D 选项正确.故选：AD【点睛】思路点睛：本题考查了新概念问题，解决新概念问题首先要确定新概念的定义或公式，将其当做一种规则和要求严格按照新概念的定义要求研究，再结合所学相关知识处理即可.三､填空题：本题共3小题，每小题5分，共15分.12.6(12)(13)x x -+的展开式中，含2x 的项的系数为________．（用数字作答）【答案】99【解析】【分析】先求二项式6(13)x +的展开式的通项，再由乘法法则求出6(12)(13)x x -+的展开式中含2x 的项即可得解.【详解】由题意得6(13)x +的展开式的通项为()166C 33C rr r r rr T x x +==，所以6(12)(13)x x -+的展开式中，含2x 的项为2221112663C 23C 99x x x x -⋅=，所以展开式中含2x 的项的系数为99.故答案为：99.13.已知椭圆2222:1(0)x y C a b a b+=>>的右焦点和上顶点分别为F 和A ，连接AF 并延长交椭圆C 于B ，若32AOB AOF S S = ，则椭圆C 的离心率为_______．【答案】3【解析】【分析】先根据面积比例关系得出点B 的横坐标，点在直线AF 上得出B 的坐标，最后应用点B 在椭圆上得出2213c a =得出离心率.【详解】因为32AOB AOF S S = ，所以132122BAOB AOF OA x S S OA c ⨯==⨯ ，所以32B x c =，设()()0,,,0A b F c ，设直线():bAF y x c c =--，点B 在直线AF 上，所以2B by =-，点B 在椭圆上，可得22229441b ca b +=，所以2213c a =，即得3c a =.故答案为:3.14.设数列{}n a 的前n 项和为21212,1,1,23n nn n a a S a a a +++===．对任意()()*22221N ,21log log n n n n S a a λ+∈++>恒成立，则λ的取值范围为______.【答案】3,2∞⎛⎫-+ ⎪⎝⎭【解析】【分析】根据递推关系可得{}1n n a a +-为等比数列，即可结合累加法求解12n n a -=，由等比求和公式得21nn S =-，即可代入不等式化简得()22212n n n λ+>-⋅，构造()2212n nn b n =-⋅，作差得数列单调性，即可求解.【详解】由21213n nn a a a +++=，得()2112n n n n a a a a +++-=-，又211a a -=，所以数列{}1n n a a +-是以2为公比，1为首项的等比数列，所以112n n n a a -+-=，则()()()1231111221112222211212n n n n n n n n n a a a a a a a a --------=-+-++-+=+++++=+=- ，进而数列{}n a 是以2为公比，1为首项的等比数列，可得122112nn n S -==--，不等式()()2222121log log n n n S a a λ+++>恒成立，即()()()2222122212nnn n n n λλ-+>⇒+>-⋅．设()2212n n n b n =-⋅，则()()()()()223211112121221221212n n n n n n n n n b b n n n n ++++-+--=-=+⋅-⋅-⋅+⋅，当1n ≥时，10n n b b +-<，为递减数列，所以()1max 12n b b ==，所以122λ+>，解得32λ>-．故答案为：3,2∞⎛⎫-+ ⎪⎝⎭.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.锐角ABC V 的内角,,A B C 所对的边分别为,,a b c ，若2cos 2b a B c +=，且a =，3b =.（1）求边c 的值；（2）求内角A 的角平分线AD 的长．【答案】（1）2c =（2）5AD =【解析】【分析】（1）根据正弦定理结合三角恒等变换运算求解可得1cos 2A =，即可利用余弦定理求解1c =或2c =，利用锐角三角形即可得2c =；（2）利用等面积法，结合三角形的面积公式即可求解．【小问1详解】因为2cos 2b a B c +=，由正弦定理可得：()sin 2sin cos 2sin 2sin 2sin cos 2cos sin B A B C A B A B A B +==+=+，即sin 2cos sin B A B =，又因为π02B <<，则sin 0B ≠，可得1cos 2A =，又因为π02A <<，所以π3A =．由余弦定理可得2222cos a b c bc A =+-，即227323cos60c c =+-⨯⨯⨯︒，则2320c c -+=，解得：1c =，或2c =，由于三角形为锐角三角形，故2220a c b +->，故220c ->，进而只取2c =，故2c =.【小问2详解】根据面积关系可得ABC ABD ACD S S S =+ ，即11123sin 602sin 303sin 30222AD AD ⨯⨯⨯︒=⨯⨯⨯︒+⨯⨯⨯︒，解得：5AD =．16.如图，在四棱锥P ABCD -中，2PD =，1AD =，PD DA ⊥，PD DC ⊥，底面ABCD 为正方形，M ，N 分别为AD ，PD 的中点.（1）求点B 到平面MNC 的距离；（2）求直线MB 与平面BNC 所成角的余弦值.【答案】（1）63（2）5【解析】【分析】（1）建立空间直角坐标系，运用向量点到平面的距离公式计算即可；（2）先求出直线与平面所成的角，可通过向量法，求出平面的法向量，再根据向量的夹角公式求出直线与平面所成角的正弦值，最后根据三角函数关系求出余弦值.【小问1详解】因为2PD =，1AD =，PD DA ⊥，PD DC ⊥，底面ABCD 为正方形，以D 为原点，DA 为x 轴，DC 为y 轴，DP 为z 轴建立空间直角坐标系，则(0,0,0)D ，(1,0,0)A ，(1,1,0)B ，(0,1,0)C ，(0,0,2)P ，因为M ，N 分别为DA ，DP 中点，所以1(,0,0)2M ，(0,0,1)N ，则1(,0,1)2MN =- ，1(,1,0)2MC =- ，1(,1,0)2MB = ，设平面MNC 的法向量为(,,)n x y z =，由00n MN n MC ⎧⋅=⎪⎨⋅=⎪⎩ ，即102102x z x y ⎧-+=⎪⎪⎨⎪-+=⎪⎩，令2x =，则1y =，1z =，所以(2,1,1)n = ，则12111022MB n ⋅=⨯+⨯+⨯=，||n == 根据点B 到平面MNC的距离公式|63|||MB n d n ==⋅=.【小问2详解】首先设平面BNC 的法向量(,,)m a b c =，(1,1,1)BN =-- ，(1,0,0)BC =- ，由00m BN m BC ⎧⋅=⎪⎨⋅=⎪⎩，即00a b c a --+=⎧⎨-=⎩，令1c =，则0a =，1b =，所以(0,1,1)m = ，设直线MB 与平面BNC 所成角为θ，则10111012MB m ⋅=⨯+⨯+⨯=，5||2MB ==，||m == ，所以||10sin 5||||MB m MB m θ⋅== ，因为22sin cos 1θθ+=，所以cos 5θ==，则直线MB 与平面BNC 所成角的余弦值155.17.某工厂生产某款电池，在满电状态下能够持续放电时间不低于10小时的为合格品，工程师选择某台生产电池的机器进行参数调试，在调试前后，分别在其产品中随机抽取样本数据进行统计，制作了如下的22⨯列联表：产品合格不合格合计调试前451560调试后35540合计8020100（1）根据表中数据，依据0.01α=的独立性检验，能否认为参数调试与产品质量有关联；（2）现从调试前的样本中按合格和不合格，用分层随机抽样法抽取8件产品重新做参数调试，再从这8件产品中随机抽取3件做对比分析，记抽取的3件中合格的件数为X ，求X 的分布列和数学期望；（3）用样本分布的频率估计总体分布的概率，若现在随机抽取调试后的产品1000件，记其中合格的件数为Y ，求使事件“Yk =”的概率最大时k 的取值.参考公式及数据：()()()()22()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.α0.0250.010.0050.001x α5.0246.6357.87910.828【答案】（1）依据0.01α=的独立性检验，可认为参数调试与产品质量无关联（2）分布列见解析，数学期望为94（3）875【解析】【分析】（1）计算2χ的值，将其与0.01α=对应的小概率值比较即得；（2）先算出抽取的8件产品中的合格品与不合格品的数目，再从中抽取3件，根据合格品件数X 的可能值运用超几何分布概率计算出概率，列出分布列计算数学期望即得；（3）分析得出7(1000,8Y B ，利用二项分布概率公式得出1000100071()C ()(),0,1,,1000,88kk k P Y k k -=== 再利用作商法分析得875k =时，事件“Y k =”的概率最大.【小问1详解】零假设为0H ：假设依据0.01α=的独立性检验，认为参数调试与产品质量无关联；则220.01100(4553515) 2.344 6.63580204060x χ⨯-⨯=≈<=⨯⨯⨯，故依据0.01α=的独立性检验，没有充分证据说明零假设0H 不成立，因此可认为0H 成立，即认为参数调试与产品质量无关联；【小问2详解】依题意，用分层随机抽样法抽取的8件产品中，合格产品有458660⨯=件，不合格产品有2件，而从这8件产品中随机抽取3件，其中的合格品件数X 的可能值有1,2,3.则126238C C 3(1),C 28P X ===216238C C 15(2),C 28P X ===363802C C 10(3)C 28P X ===.故X 的分布列为：X123P32815281028则15109()12328284328E X =⨯+⨯+⨯=；【小问3详解】依题意，因随机抽取调试后的产品的合格率为357408=，故7(1000,8Y B ，则1000100071()C ()(),0,1,,1000,88kkkP Y k k -=== 由1199910001000100071C (()(1)10007000788771()11C ()()88k k k kk k P Y k k k P Y k k k ++--=+--====++，故由7000711k k ->+可解得78748k <，因Z k ∈，故当0874k <≤时，()P Y k =单调递增；由7000700011k k -≤+可解得78748k ≥，即当875k ≥时，()P Y k =单调递减.故当事件“Y k =”的概率最大时，875k =.【点睛】方法点睛：（1）计算卡方值，并与小概率值比较得出结论；（2）求随机变量的分布列关键在于判断X 满足的概率模型；（3）对于二项分布中概率最大值问题，一般考虑作商后分析判断商与1的大小即得.18.已知双曲线()2222:10,0x y C a b a b-=>>的实轴长为4，渐近线方程为12y x =±.（1）求双曲线C 的标准方程；（2）双曲线的左､右顶点分别为12A A ､，过点()3,0B 作与x 轴不重合的直线l 与C 交于P Q ､两点，直线1A P 与2A Q 交于点S ，直线1AQ 与2A P 交于点T .（i ）设直线1A P 的斜率为1k ，直线2A Q 的斜率为2k ，若12k k λ=，求λ的值；（ii ）求2A ST 的面积的取值范围.【答案】（1）2214x y -=（2）（i ）15-；（ii ）2522,,933∞⎡⎫⎛⎫⋃+⎪⎢ ⎪⎪⎝⎭⎣⎭【解析】【分析】（1）根据双曲线性质计算即可；（2）设直线l 方程及P Q 、坐标，联立双曲线方程，根据韦达定理得出纵坐标和积关系，（i ）利用两点斜率公式消元计算即可；（ii ）联立直线方程求出S T 、坐标，并求出ST ，利用三角形面积公式及2t 范围计算即可.【小问1详解】由题意知：124,2b a a ==，解得2,1a b ==，双曲线方程为2214xy -=.【小问2详解】因为直线l 斜率不为0，设直线l 方程为3x ty =+，易知()()122,0,2,0A A -，设()()1122,,,P x y Q x y ，联立2214x y -=，得()224650t y ty -++=，则212212240Δ06454t t y y t y y t ⎧-≠⎪>⎪⎪⎨+=--⎪⎪=⎪-⎩，且()121256y y y y t =-+，（i ）()()21121121212121223222325ty k y x y ty y y k x y ty y ty y y λ+--+==⋅=⋅=++++()()121121212255165525556y y y y y y y y y y -++-===--+-++；（ii ）由题可得：()()2211:2,:2A Q y k x A P y k x =-=+.联立可得：()2112124410,333s k k x S k k k +⎛⎫==⇒ ⎪-⎝⎭，即()11104,332y S x ⎛⎫ ⎪ ⎪+⎝⎭，同理()22104,332y T x ⎛⎫ ⎪ ⎪+⎝⎭.()()()121212121212125101010532235535256y y y y y y ST x x ty ty t y y t y y -∴=-=-=++++-++++==，故2212A ST A S S ST x x =-= ，20t ≥且24t ≠，222,,933A STS ∞⎡⎫⎛⎫∴=∈⋃+⎪⎢ ⎪⎪⎝⎭⎣⎭ .【点睛】关键点点睛：反设直线线并设点，联立双曲线方程后得出P Q 、纵坐标的和积关系，为后面消元转化减轻计算量.19.已知定义：函数()f x 的导函数为()f x '，我们称函数()f x '的导函数()f x ''为函数()f x 的二阶导函数，如果一个连续函数()f x 在区间I 上的二阶导函数()0f x ''≥，则称()f x 为I 上的凹函数;二阶导函数()0f x ''≤，则称()f x 为I 上的凸函数.若()f x 是区间I 上的凹函数，则对任意的12,,x x n x I ∈，有不等式()()()1212n n f x f x f x x x x f n n ++++++⎛⎫≤⎪⎝⎭恒成立（当且仅当12n x x x === 时等号成立）.若()f x 是区间I 上的凸函数，则对任意的12,,n x x x I ∈ ，有不等式()()()1212n n f x f x f x x x x f n n ++++++⎛⎫≥⎪⎝⎭恒成立（当且仅当12n x x x === 时等号成立）.已知函数()1f x x x =+，π0,2x ⎛⎤∈ ⎥⎝⎦.（1）试判断()f x 在π0,2⎛⎤ ⎥⎝⎦为凹函数还是凸函数?（2）设12,x x ，L ，0n x >，2n ≥，且121n x x x +++= ，求1212111n nx x xW x x x =++++++ 的最大值;（3）已知*N a ∈，且当π0,2x ⎛⎤∈ ⎥⎝⎦，都有()()()sin sin 31cos 0x ax x f x x +-+>恒成立，求实数a 的所有可能取值.【答案】（1）凸函数（2）1n f n ⎛⎫⋅⎪⎝⎭（3）{}2【解析】【分析】（1）根据凹凸函数的定义判断即可；（2）由（1）知()f x 在π0,2⎛⎤⎥⎝⎦为凸函数，根据凸函数的性质结合题意即可求解；（3）令()sin sin 3cos h x x ax x x =+-，π0,2x ⎛⎤∈ ⎥⎝⎦，则问题转化为ℎ>0在π0,2⎛⎤ ⎥⎝⎦上恒成立，对a 分类讨论，结合导数的运算研究函数的单调性即可求解.【小问1详解】()1x f x x =+，π0,2x ⎛⎤∈ ⎥⎝⎦，所以()()211f x x ='+，″()321x =-+，因为π0,2x ⎛⎤∈ ⎥⎝⎦，所以″0<，所以()f x 在π0,2⎛⎤ ⎥⎝⎦为凸函数.【小问2详解】由（1）知()1x f x x =+在π0,2⎛⎤⎥⎝⎦内为凸函数，又1212111n nx x xW x x x =++++++ ，且121n x x x +++= （12,x x ，L ，0n x >，2n ≥），所以()()()12121.nn x x x W f x f x f x n f n f n n +++⎛⎫⎛⎫=+++≤⋅=⋅ ⎪⎪⎝⎭⎝⎭所以max 1.W n f n ⎛⎫=⋅ ⎪⎝⎭【小问3详解】令()sin sin 3cos h x x ax x x =+-，π0,2x ⎛⎤∈ ⎥⎝⎦，则ℎ>0在π0,2⎛⎤ ⎥⎝⎦上恒成立，则()cos 2cos 3sin h x a ax x x x =+'-，且()02h a '=-，当1a =，πππ3ππ3πsin sin cos 204444424h ⎛⎫⎫=+-=-<⎪ ⎪⎝⎭⎝⎭，不合题意舍去;当2a =，则()sin sin23cos h x x x x x =+-，故()2cos22cos 3sin h x x x x x =-+'，令()()k x h x ='，则()4sin25sin 3cos 8sin cos 5sin 3cos k x x x x x x x x x x=-++=-++'5sin 5sin cos 3cos 3sin cos x x x x x x x =-+-()()5sin 1cos 3cos sin x x x x x =-+-，令()sin g x x x =-，π0,2x ⎛⎤∈ ⎥⎝⎦，则()1cos 0g x x ='->，所以()g x 在π0,2x ⎛⎤∈ ⎥⎝⎦上递增，所以sin x x >，所以()'0k x >，即()()'k x h x =在π0,2x ⎛⎤∈ ⎥⎝⎦上递增，又()020h a -'==，则ℎ′>0，所以ℎ在π0,2x ⎛⎤∈ ⎥⎝⎦上递增，又()00h =，即ℎ>0，π0,2x ⎛⎤∈ ⎥⎝⎦，符合题意;当3a ≥，令0ππ0,12x a ⎛⎤=∈ ⎥-⎝⎦，则()0001πax x x a -=-=，()00sin sin πax x =+，所以()()00000000000sin sin 3cos sin sin 3cos 3cos 0h x x ax x x x x x x x x π=+-=++-=-≤，不合题意舍去，综上，正整数a 的取值集合为{}2.【点睛】方法点睛：求解“新定义”题目，主要分如下几步：（1）对定义进行信息提取，明确新定义的名称和符号；（2）对新定义所提取的信息进行加工，探求解决方法和相近的知识点，明确它们的相同点和相似点；（3）对定义中提取的知识进行提取和转换，如果题目是新定义的运算、法则，直接按照法则计算即可；如果新定义是性质，一般要判断性质的适用性，能否利用定义的外延，可用特值排除.。

高三历次月考成绩临界生分析表(含公式)

647 369 242 597 686 381 543 126 925 453 603 756 349 124 316 294 631 350 188 391 345 360 272 236 570 141 489 572 616 182 500 858 500 672 855 395 229 761 850 756 320 306 741 393 584 699 658 522 530 116 133 775 627 784 340 768 781 420 793 493 903 769 917 781
姓名
9月月 10月月 11月月 12月月 1月月 2月月 3月月 4月月 5月月 9月月考 10月月考 11月月考 12月月考 1月月考 2月月考 3月月考 4月月考考级考级排考级排考级排考级排考级排考级考级考级临界生临界生临界生临界生临界生临界生临界生临界生排名名名名名名排名排名排名
二本一本一本二本二本临界一本临界二本一本专科一本临界二本二本临界一本一本一本一本二本一本一本一本临界一本一本一本一本二本一本二本二本二本一本二本三本二本二本三本一本临界一本二本临界三本二本临界一本一本二本临界一本临界二本二本临界二本二本二本一本一本三本二本三本一本二本临界三本一本临界三本二本专科二本临界专科三本
一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本一本

2024-2025学年高二上学期11月月考语文试卷

（选自周怀宗《童道明：错过契诃夫，是这个时代阅读的遗憾》）
6．下列对文本一相关内容和艺术特色的分析鉴赏，不正确的一项是（3分）
A．第④段生动描述胖子和瘦子相遇后的场景，心中满是遇到老友的惊喜，这符合朋友重逢的真实生活逻辑。
B．第⑫段画线句子通过行李“蜷缩”这一拟人化的描写，侧面表现出瘦子的卑躬屈膝，具有强烈的讽刺意味。
契诃夫生前的名声并不是很大，但是他去世100多年之后，他的声誉比当初高了不知多少倍，原因就在于他的作品是现代性的，他在现代性之初，就发现了现代性中隐藏的种种隐忧，直到今天，他的作品所反映出来的东西，依旧在我们的身边，他永远不落伍。
大约在20世纪50年代，契诃夫的作品首先得到了西方的重视，那个时代正是西方现代派戏剧崛起的时代，以荒诞派为代表。主要的特点是表现人们源于精神世界的痛苦，源于社会压迫所产生的痛苦，这样的戏剧中没有正面人物，也没有反面人物。后来人们追溯它的源头，发现原来契诃夫早就开始这样创作了。相比较19世纪的其他俄国作家来说，契诃夫是很温和的。他并不非常激烈，他更善于挖掘人性本身的问题，而不仅仅是一个革命作家。
B．以影视、游戏等为代表的当代“中国经验”不断走向国际，受到外界的认可，未来也将会有更多优质的文化产品走出去。
C．受日韩将自身传统文化内核隐藏在文化产品中的启发，中国游戏从业者首次在《黑神话：悟空》中加入中国传统元素。
D．近年来，国内游戏玩家对高性能个人电脑的需求逐渐降低，而《黑神话：悟空》的出现将有可能再次繁荣高性能个人电脑市场。
绝密★启用前
2024-2025学年高二上学期11月月考试卷
语文
考试时间：150分钟试卷分数：150分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息。
2．请将答案正确填写在答题卡上。

2025届高考语文一元思辨类(单概念类)作文11月精选(真题呈现+审题指导+立意参考+高分范文)

2025届高考作文分类【一元思辨类（单概念类）]作文各省市及名校模拟考试11月精选（真题呈现+审题指导+立意参考+高分范文）（湖北省襄阳市第五中学2025届高三11月月考）“松弛感”四、作文（60分）23、阅读下面材料，根据要求写作。

“松弛感”源于一位微博写手的一段经历。

她乘坐飞机时，遇到一家人出门旅游，因妈妈没有登机，所有行李都被退回了。

博主预计这家人会在电话里吵一架。

结果，飞机上的一家人完全没有生气，气氛全程都非常松弛。

博主对于“原来世界上真有这么松弛的家庭关系”的感慨，引发了很多网友的跟帖。

奥运赛事虽已结束，中国“00后奥运小将，展现真正的松弛感”的话题却仍在被热议。

他们努力拼搏，实力超群，从容淡定；全红婵挂满迪士尼玩偶挂件的“痛包”和丑鱼拖鞋充满了生活趣味；夺冠后陈艺文给昌雅妮的公主抱……他们用松弛感为严肃紧张的竞技赛场添加了活力，展现了年轻一代运动员的独特风范。

上述材料引发了你怎样的感悟和思考？请你以“松弛感”为话题，写一篇文章。

要求：选准角度，确定立意，明确文体，自拟标题；不要套作，不得抄袭；不得泄露个人信息；不少于800字。

【解析】【详解】本题考查学生的写作能力。

【审题】这是一道话题作文题。

本题以“松弛感”一词的来源和“00后奥运小将展现松弛感”为引子，要求考生围绕“松弛感”这一话题进行文章创作。

审题时，可以从以下几个维度进行深入分析：首先，理解“松弛感”的内涵。

在本应焦虑或愤怒的场合以及紧张的奥运赛场上，“松弛感”不仅仅是指外在的轻松自在、不拘小节，更是一种内在的心理状态——即在高度竞争、压力巨大的环境下，依然能够保持冷静、自信，甚至带有些许幽默与趣味的生活态度。

它体现了人们对生活的充分而正确的认知；运动员们对比赛的深刻理解、对自我能力的充分信任，以及面对挑战时的从容不迫。

所以，题目中所谓的“松弛感”，更多指向一种心态，即在不确定的当下，于过程中努力，而对结果保持开放的心态。

“松”在快速发展的当代社会，是对“从前慢”的复古怀旧，也是高效率中的“变奏变频”。