乘法器电路的设计
4位乘法器
一、概述利用四位二进制寄存器、全加器以及D触发器等元器件,实现四位二进制乘法器的控制部分和乘法的实现部分。
成法是加法的简便运算乘法运算只能通过加法运算以及移位运算来实现。
在控制端用四个触发器产生四个控制信号来控制实现的加法移位功能,实现端在控制端信号作用下依次执行置零、加法、移位和循环操作。
二、方案说明设计一个4位二进制乘法器,可以存储其乘积。
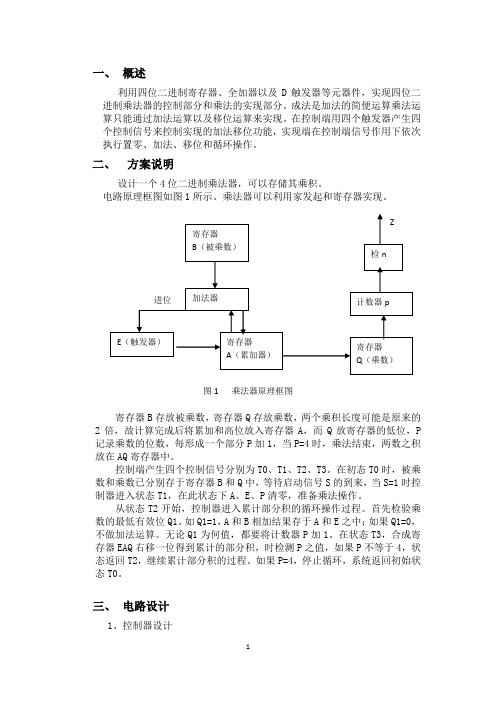
电路原理框图如图1所示。
乘法器可以利用家发起和寄存器实现。
图1 乘法器原理框图寄存器B存放被乘数,寄存器Q存放乘数,两个乘积长度可能是原来的2倍,故计算完成后将累加和高位放入寄存器A,而Q放寄存器的低位,P 记录乘数的位数,每形成一个部分P加1,当P=4时,乘法结束,两数之积放在AQ寄存器中。
控制端产生四个控制信号分别为T0、T1、T2、T3。
在初态T0时,被乘数和乘数已分别存于寄存器B和Q中,等待启动信号S的到来,当S=1时控制器进入状态T1,在此状态下A、E、P清零,准备乘法操作。
从状态T2开始,控制器进入累计部分积的循环操作过程。
首先检验乘数的最低有效位Q1。
如Q1=1,A和B相加结果存于A和E之中;如果Q1=0,不做加法运算。
无论Q1为何值,都要将计数器P加1。
在状态T3,合成寄存器EAQ右移一位得到累计的部分积,时检测P之值,如果P不等于4,状态返回T2,继续累计部分积的过程。
如果P=4,停止循环,系统返回初始状态T0。
三、电路设计1、控制器设计根据图2所示的ASM图表,可以设计二进制乘法器的控制器。
图2 二进制乘法器ASM图表四个D触发器的驱动方程为:D0=T0S’+T3Z=((T0S’)’·(T3Z)’)’D1=T0S=((T0S)’)’D2=T1+T3Z’=(T1’·(T3Z’)’)’D3=T2控制器仿真电路如图2所示。
控制器中S为启动信号,高电平有效,系统开始工作时应使T0=1,T1=T2=T3=0,故图中设置了Reset信号(负脉冲)图2 二进制乘法器的控制逻辑图2. 二进制乘法器数据处理器(1) A寄存器A寄存器具有并入、移位、同步清0和保持功能。
4位乘法器的设计

4位乘法器的设计乘法器是计算机中非常重要的组成部分,用于实现数字乘法运算。
在设计4位乘法器时,需要考虑到多个方面,如计算的准确性、速度和功耗等。
本文将详细探讨4位乘法器的设计原理、逻辑电路实现以及性能分析。
1.乘法器的基本原理乘法操作是通过将被乘数与乘数一位一位地相乘,再将各位的结果相加得到最终的乘积。
因此,4位乘法器的设计需要考虑到每一位乘法的计算和结果的累加。
2.乘法器的逻辑电路实现2.14位乘法器的简单实现最简单的方法是采用两个4位二进制数相乘的定义,即将每一位的乘积相加得到最终的结果。
这可以通过4个并行的与门和一些全加器来实现。
具体的逻辑电路图如下所示:A0───────┐┌─────A1───────┤├─────A2───────┤├─────A3───────┤├─────AND0 OR0 CoutB0───────┐│B1───────┤XOR0B2───────┤B3───────┘从上图可以看出,A0到A3和B0到B3分别作为输入,经过与门得到各位的乘积,然后通过一系列的全加器将乘积相加得到最终结果。
在这种设计中,每个位的计算之间是并行的,因此可以快速得到乘法运算的结果。
2.2优化的4位乘法器上述简单实现的4位乘法器虽然能够实现乘法运算,但其性能方面存在一些不足。
为了提高性能,可以采用更复杂的逻辑电路设计。
一种常见的优化方法是使用布斯加算器(Booth's Algorithm)来实现乘法运算。
这种方法通过将乘法运算转化为位移和加减运算来减少乘法的次数,从而提高性能。
具体的实现方法如下:1)将被乘数和乘数拓展到5位,比特位B4作为符号位,初始值为0。
2)将被乘数拓展为4位乘子,乘数拓展为5位乘数。
3)初始化中间结果为0。
4)迭代循环4次进行乘法运算,每次进行下面的步骤:-如果乘数的最低位和符号位相同,什么都不做。
-如果乘数的最低位为0且前一位为1,将乘数和被乘数相加。
-如果乘数的最低位为1且前一位为0,将乘数和被乘数相减。
数字电路课程设计之乘法器精选全文完整版

基于Verilog 的乘法器设计一、设计目标使用Verilog 语言实现4bit*4bit 乘法器设计,并使用Quartes 编写程序,使用modelsin 进行仿真验证设计二、基本原理2.1半加器半加器是为两输入两输出的加法电路,输入无进位,真值表如下图所示,输入X,Y,输出C,SX Y C S 0 0 0 0 0 1 0 1 1 0 0 1 111最简积之和式为 S=X`Y+XY`=X ○+Y;C=XY. 电路图为:2.2全加器全加器是为三输入两输出,输入存在进位,真值表如下图所示,输入X,Y,Z,输出C,SX Y Z C S 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 11111化简最简积之和式为:S=X`Y`Z+X`YZ`+XY`Z`+XYZ; C=XY+XZ+YZ; 通过使用半加器组成全加器进行化简为:S=Z(X`Y`+XY)+Z`(X`Y+XY`)=Z(X ○+Y)`+Z`(X ○+Y)=X ○+Y ○+Z123YX C123123Y X`X Y`123S123C123X YSguan tian liangC 的卡诺图如下图X YZ 00 01 11 10 0 0 0 1 0 1111按两两结合 C=XY+YZ+XZ 换一种结合方式 C= XY+XY`Z+X`YZ=Z(XY`+X`Y)+XY=Z(X ○+Y)+XY 电路图如下所示(使用两个半加器与一个或门)123123X Y123123SZ123C多位二进制加法实现 2.2.1 行波进位加法器B2A3B3C3C4C2C1C0S0S1S2S3FA FALL_ADD A1B2Cout 3Cin4S5FA FALL_ADD A1B2Cout 3Cin4S5FAFALL_ADDA1B2Cout 3Cin4S5FAFALL_ADD A1B 2Cout 3Cin4S5A0B0A1B1A2行波进位加法器优点在于结构逻辑简单,缺点速度很慢,在最坏情况下,进位必须从最低有效位传到最高有效加法器,假设同时给出所有加数位,则总的最长延迟为:CinSCinCout ABCout ADD t t n t t +⨯−+=)2(ABCoutt 为最低有效级上从A 或B 到Cout 的延迟,CinCoutt 为中间级上Cin 与Cout 的延迟,CinSt 为最高有效位上从Cin 到S 的延迟。
乘法器幅度调制电路

《高频电子线路》设计报告基于MC1596乘法器的调幅电路制作人:李超08111100谢攀08111040汪新皓08111041乘法器幅度调制电路一、 设计目的1.复习和巩固以前所学内容,了解乘法器1596的工作原理。
2.熟练multisium 等仿真软件的使用,提高实际动手能力。
二、 设计原理方案1. 调幅信号的分析(1) 普通调幅波(AM )调制信号为单一频率的余弦波:t U u m Ω=ΩΩcos ,载波信号为t U u c cm c ωcos =,普通调幅波(AM )的表达式为: t t m U t t U u c a cm c AM AM ωωcos )cos 1(cos )(Ω-==式中,m a 称为调幅系数和调幅度,由于调幅系数m a 与调制电压的振幅成正比,即m U Ω越大,m a 越大,调幅波幅度变化越大,m a 应小于或等于1。
如果m a >1,调幅波产生失真,这种情况称为过调幅。
调幅波波形(2)普通调幅波的频谱普通调幅波的表达式展开得:它由三个高频分量组成。
将这三个高频用图画出,便可得到如下图所示的频谱图。
在这个图上调幅波的每一个正弦分量用一个线段表示,线段的长度代表其幅度,线段早横轴上的位置代表其频率。
普通调幅波的频谱图调幅的过程就是在频谱上将低频调制信号搬移到高频载波分量两侧的过程。
再单调频调制时,其调幅波的频带宽度为调制信号频谱的两倍,即B=2F 。
(3)普通调幅波的功率 载波分量功率:Lcm c R U P 221= R L 为负载电阻值,上边频分量功率:c a L cm a L cm a P m R U m R U m P 2222141811)2(21=== 边频分量功率:c a L cm a L cm a P m R U m R U m P 2222241811)2(21=== 因此,调幅波在调制信号的一个周期内的平均功率为:c a c P m P P P P )21(221+=++= 可见,边频功率随m a 的增大而增加,当m a =1时,边频功率最大,即c P P 32=这时上、下边功率之和只有载波功率的一半,这也就是说,用这种调制方式,发送端发送的功率被不携带信息的载波占去了很大的比例,显然,功率利用率不高。
十六位硬件乘法器电路设计报告

课程名称电子设计自动化题目十六位硬件乘法器电路院系班级信息学院11电子信息工程A班姓名学号指导老师凌朝东2013 年 12 月 5 日题目名称:十六位硬件乘法器电路摘要:设计一个16位硬件乘法器电路.要求2位十进制乘法,能用LED数码管同时显示乘数,被乘数和积的值.本设计利用Quartus II软件为设计平台,通过移位相加的乘法原理:即从被乘数的最低位开始,若为1,则乘数左移后与上一次的和相加;若为0,左移后以全零相加,直至被乘数的最高位。
经软件仿真和硬件测试验证后,以达到实验要求。
目录1.题目名称 (2)2.摘要 (2)3.目录 (3)4.正文 (4)4.1. 系统设计 (4)4.1 设计要求 (4)4.2 系统设计方案 (4)4.2 单元电路设计 (4)4.2.1十进制计算模块 (5)4.2.2 BCD码转二进制模块 (5)4.2.3 8位右移寄存器模块 (6)4.2.4 8位加法器模块 (7)4.2.5 1乘法器multi_1模块 (7)4.2.6 16位移位寄存器reg_16模块 (8)4.2.7 16位二进制转BCD码B_BCD模块 (9)4.2.8 8位乘法器multi_8x8顶层设计 (10)4.3 软件设计 (12)4.3.1设计平台和开发工具 (12)4.3.2程序流程方框图 (13)4.4 系统测试 (14)4.1仿真分析 (14)4.2硬件验证 (15)5. 结论 (15)6. 参考文献 (15)7. 附录 (15)4.正文4.1系统设计1.1设计要求题目要求设计一个16位硬件乘法器电路.要求2位十进制乘法;能用LED数码管同时显示乘数,被乘数和积的信息.设置一个乘法使能端,控制乘法器的计算和输出.1.2系统设计方案此设计问题可分为乘数和被乘数输入控制模块,乘法模块和输出乘积显示模块基本分.乘数和被乘数的输入模块使输入的十进制数转化为二进制数输入乘法模块,乘法模块利用移位相加的方法将输入的两组二进制数进行相乘,并将16位乘积输出到乘积输出显示模块.显示模块将输入的二进制数按千,百,十,个位分别转化为十进制数输出.乘数和被乘数的输入可用数据开关K1~K10分别代表数字1,2,…,9,0,用编码器对数据开关K1~K10的电平信号进行编码后输入乘法器进行计算.但此方案所用硬件资源较多,输入繁琐,故不采取.方案二是利用硬件箱自带16进制码发生器,由对应的键控制输出4位2进制构成的1位16进制码,数的范围是0000~1111,即0H~FH.每按键一次,输出递增1,输出进入目标芯片的4位2进制数将显示在该键对应的数码管.乘数和被乘数的输入模块将16进制码的A~F码设计成输出为null.使得减少了无用码的输入.两数相乘的方法很多,可以用移位相加的方法,也可以将乘法器看成计数器,乘积的初始值为零,每一个时钟周期将乘数的值加到积上,同时乘数减一,这样反复执行,直到乘数为零.本设计利用移位相加的方法使得程序大大简化.系统总体电路组成原理图如下图所示:4.2单元电路设计下面分解8位乘法器的层次结构,分为以下7个模块:1. 十进制计算模块:使用4个十进制计数模块,输入乘数的十位个位,被乘数的十位个位。
乘法器电路的设计与实现

乘法器电路的设计与实现乘法器电路是一种用于实现数字信号的乘法运算的电路。
在数字电子系统中,乘法运算是十分常见的操作之一。
乘法器电路的设计与实现对于数字电子系统的性能和效率具有重要影响。
乘法器电路的设计是基于数字逻辑门电路的原理。
在数字电子系统中,逻辑门电路是基本的构建模块。
常用的逻辑门包括与门、或门、非门等。
乘法器电路的设计可以通过组合逻辑电路和时序逻辑电路来实现。
组合逻辑电路是指输出只与当前的输入有关,不依赖于之前的输入。
而时序逻辑电路是指输出不仅与当前的输入有关,还与之前的输入有关。
乘法器电路的设计过程可以分为几个关键步骤。
首先是确定乘法器的位数。
乘法器电路的位数决定了它可以处理的数字的范围。
位数越多,乘法器可以处理的数字范围越大。
然后是确定乘法器的输入和输出的编码方式。
在数字电子系统中,常用的编码方式包括二进制和十进制。
接下来是确定乘法器的运算规则。
乘法器可以实现有符号数和无符号数的乘法运算。
最后是选择适当的逻辑门电路来实现乘法器。
乘法器电路的实现需要考虑一些关键因素。
首先是电路的布局和连接。
乘法器电路中的逻辑门电路需要正确地布局和连接,以确保信号能够正确地传输和处理。
其次是电源和地的连接。
电源和地的连接是电路正常工作的基础,必须保证良好的接触和稳定的电源供应。
此外,还需要考虑电路的稳定性和抗干扰能力。
乘法器电路需要能够稳定地工作,并且能够抵抗来自外部的干扰。
乘法器电路的设计和实现也可以通过计算机辅助设计软件来完成。
计算机辅助设计软件可以提供方便快捷的设计工具和仿真环境,大大提高了设计的效率和准确性。
通过计算机辅助设计软件,设计人员可以轻松地进行逻辑门电路的布局和连接,并进行电路的仿真和验证。
乘法器电路的设计与实现是数字电子系统设计的重要组成部分。
乘法器电路的性能和效率对于数字电子系统的整体性能具有重要影响。
设计人员需要仔细考虑乘法器电路的位数、编码方式、运算规则等因素,并选择适当的逻辑门电路来实现乘法器。
定点原码一位乘法器的设计

定点原码一位乘法器的设计定点原码乘法器是一种基本的数字运算电路,用于实现两个定点原码数的乘法运算。
在设计定点原码乘法器时,需要考虑两个关键方面:乘法运算的算法和乘法运算电路的实现。
一、乘法运算的算法设计:1.符号位的处理:定点原码乘法器需要考虑乘法运算的符号位。
根据乘法运算的规则,当两个数的符号位不同时,乘积的符号位为负;当两个数的符号位相同时,乘积的符号位为正。
因此,在乘法运算时,首先需要对两个乘数的符号位进行判断和处理。
2.乘法运算的主体部分:乘法运算的主体部分是通过将两个乘数的每一位进行相乘,并将结果相加得到乘积的每一位。
一般来说,乘法运算可以采用移位和加法的方式来实现。
a.移位操作:在乘法运算中,需要将乘数的每一位与被乘数的每一位相乘,并将结果相加。
因此,首先需要将乘数的每一位与被乘数的每一位相乘,移位操作可以实现该过程。
b.加法操作:乘法运算中,需要将乘数的每一位与被乘数的每一位相乘,得到中间的结果,然后将中间结果相加,得到最终的乘积。
这一步骤可以通过加法器电路来实现。
二、乘法运算电路的实现设计:在设计定点原码乘法器的电路时,需要考虑各个功能模块的实现:1.符号位处理电路:由于定点原码乘法器需要考虑两个乘数的符号位,因此需要设计一个符号位处理电路。
该电路可以根据两个乘数的符号位来判断乘积的符号位,并给出相应的控制信号。
2.移位操作电路:移位操作电路用于实现乘数的每一位与被乘数的每一位相乘。
可以采用多路选择器和移位寄存器来实现。
多路选择器用于选择当前操作的两个数位,移位寄存器用于保存被乘数的每一位。
3.加法器电路:加法器电路用于将乘数的每一位与移位操作电路中移位后的结果相加。
可以采用并行加法器来实现,通过级联多个全加器,实现两个二进制数的加法运算。
4.乘积结果输出电路:乘积结果输出电路用于将最终的乘积输出。
可以通过选择器来选择最后一位的结果,并将结果输出到寄存器中,供后续电路使用。
设计定点原码乘法器的步骤如下:1.分析乘法运算的算法,确定各个功能模块的需求和输入输出信号。
乘法运算电路设计

乘法运算电路设计通常涉及到模拟或数字电路设计。
这里提供一种基于数字电路设计的简单示例,说明如何设计一个二进制乘法器。
一、二进制乘法器设计
1. 设计原理:
假设有两个两位的二进制数A1 A0和B1 B0,它们相乘的结果是Y3 Y2 Y1 Y0。
这个设计基于基本的二进制乘法原理。
2. 逻辑电路图:
根据乘法的定义,可以归纳出输出4位二进制数与输入的两位二进制数之间的逻辑关系,并据此设计逻辑电路图。
3. 仿真波形图:
通过仿真测试,验证设计的正确性。
二、硬件乘法器电路设计
1. 设计思路:
利用硬件箱自带的16进制码发生器,通过对应的键控制输出4位2进制构成的1位16进制码,数的范围是0000~1111,即
0H~FH。
每按键一次,输出递增1,输出进入目标芯片的4位2进制数将显示在该键对应的数码管。
2. 乘数和被乘数的输入模块:
将16进制码的A~F码设计成输出为null,减少无用码的输入。
3. 程序设计:
利用移位相加的方法简化程序。
以上是一个简单的乘法运算电路设计的概述,具体的电路设计还需要根据实际需求和条件进行优化和调整。
乘法器电路设计

乘法器电路设计1.引言在现代电子系统中,乘法器作为一种基本算术运算单元,广泛应用于信号处理、控制系统、通信等领域。
乘法器电路的设计直接关系到系统的性能、功耗和成本。
因此,对乘法器电路设计进行深入研究和优化具有重要意义。
本文将对乘法器的工作原理、电路实现以及性能优化进行详细阐述。
2.乘法器的工作原理乘法器的基本功能是将两个二进制数相乘,输出它们的积。
在二进制数中,每一位都表示一个权值,从低位到高位分别为2的0次方、2的1次方、2的2次方等。
因此,将两个二进制数相乘的过程可以看作是将其中一个数的每一位与另一个数相乘,然后相加得到最终结果。
为了实现这一功能,乘法器电路可以分为两部分:数据选择器和加法器。
数据选择器负责选择两个输入数中的每一位,并根据该位的权值将其相乘得到部分积。
加法器则将这些部分积相加得到最终结果。
具体来说,当乘数的一位为1时,与其对应的被乘数将被加到加法器的输入端;当乘数的一位为0时,加法器的输入端保持不变。
3.乘法器电路的实现根据上述工作原理,乘法器电路的实现可以采用多种方法。
其中,基于查找表(LUT)的方法是一种常用的实现方式。
LUT是一种存储固定输入和对应输出的存储器,通过查找表中的地址来获取相应的输出值。
在乘法器电路中,LUT 可以存储预先计算好的部分积,根据输入的乘数和被乘数的每一位,直接输出相应的部分积,从而避免了重复计算。
这样能够大大减小乘法器的硬件开销和计算时间,提高运算效率。
除了基于LUT的方法外,还可以采用其他实现方式,如组合逻辑电路、流水线乘法器和阵列乘法器等。
这些实现方式各有优缺点,需要根据具体应用场景和性能要求进行选择。
4.乘法器电路的性能优化为了提高乘法器的性能,可以从多个方面进行优化。
首先,可以采用高性能的触发器和数据总线来提高信号传输速度和降低功耗。
其次,可以优化查找表的地址编码方式,以减少存储空间和提高查询速度。
此外,可以通过采用并行处理技术来加快运算速度,例如将多个输入同时送入LUT中进行查找。
数字设计原理与实践_课程设计_乘法器

数字设计原理与实践课程设计题目名称:学生姓名:学号:指导老师:1.设计题目乘法器电路设计:设计一个乘法器,能够完成两个4位二进制无符号数的乘法运算。
2.设计目标设计一个乘法器,使之能完成两个4位的二进制数的乘法运算。
3.设计思路4位二进制数的乘法,按照十进制的乘法规则,可进行相应的运算。
比如a1a2a3a4和b1b2b3b4运算过程见右图。
如图所示,乘开之后,就产生了许多的两个二进制数相乘,即两个二进制数相与的过程。
如果利用合适的加法器把这些二进制数相与的结果进行合适的累加,最后即可得到4位二进制数相乘的结果。
也就是说4位二进制数的乘法可以分解成许多相与项相加(积之和)的形式,最后实现题目的要求。
4.设计电路推导由题可知,两个4位二进制数相乘结果位为8位。
其中a1b1可直接输出作为积的(第八位)最低位。
然后是a2b1与a1b2的和作为积的第七位,并且向前进位。
接着a3b1、a2b2、a1b3相加,此时可以用加法器级联,以此类推,所有的相与项都能加起来。
在加法器方面,选择4位二进制加法器74ls283。
74LS283的引脚图和逻辑原理图见上,可知,74LS283是4位二进制全加器。
两个加数输入端分别为A0~A3,和B0~B3,和为C0~C3,S1为进位输入端,S3为进位输出端。
了解了各引脚之后,我们计划使用三个74LS283,其中a1b1直接输出,不需要接入加法器。
然后a1b2、a1b3、a1b4分别接入第一个加法器的A0~A2端,a2b1、a2b2、a2b3、a2b4分别接第一个加法器的B0~B3接口。
这样第一个接口的输出端:和的最低位C0 就是a1b2+a2b1,所以直接输出就是最后乘积的第七位(次低位)。
现在讨论下两片74LS283的级联。
SUM的最低位是作为积的一位直接输出,然后后几位依次与下一个74238的输入A1~A4相连,就完成了两个74283的级联。
这样做的原理已在前面的讨论中给出,这里不做赘述。
乘法器verilog设计的设计方法

乘法器verilog设计的设计方法【1.乘法器的Verilog设计概述】乘法器是数字电路设计中常见的组件,其作用是将两个二进制数相乘得到结果。
Verilog是一种通用的硬件描述语言,可以用于描述和实现数字电路。
乘法器的Verilog设计就是利用Verilog语言实现乘法器的功能。
【2.乘法器Verilog设计的基本原理】乘法器Verilog设计的基本原理是通过移位和相加操作实现两个二进制数的乘积。
典型的乘法器架构包括全加器、半加器和数据选择器等。
在全加器中,乘数和被乘数分别经过多次移位操作后与乘法器输出相加,从而得到最终结果。
【3.乘法器Verilog设计的实现步骤】乘法器Verilog设计的实现步骤如下:1) 确定乘法器的输入和输出:根据需求确定乘法器的输入信号,如乘数和被乘数,以及输出信号,如乘积。
2) 编写Verilog代码:利用Verilog语言编写乘法器的逻辑功能,包括移位、相加和数据选择等操作。
3) 仿真和验证:对编写好的Verilog代码进行仿真和验证,确保其功能正确。
4) 优化和调试:根据仿真结果对代码进行优化和调试,以提高性能和减少资源占用。
5) 下载和测试:将设计好的乘法器下载到目标硬件,进行实际测试。
【4.乘法器Verilog设计的优化策略】1) 优化代码结构:合理划分模块,减少模块间的耦合度,提高代码的可读性和可维护性。
2) 采用高效的算法:如布斯算法、Wallace树等,提高乘法器的运算速度。
3) 减少资源占用:通过合理分配信号位数、使用紧凑型数据结构等方法,降低硬件成本。
4) 电源和时序优化:针对功耗和时序要求,采用适当的电路设计和优化技术。
【5.乘法器Verilog设计的应用领域】乘法器Verilog设计广泛应用于各类电子设备和系统中,如数字信号处理、图像处理、通信系统等。
在这些领域,乘法器作为基本组件,为实现高速、高效、低功耗的数字信号处理提供了有力支持。
【6.总结与展望】乘法器Verilog设计是数字电路设计的重要内容。
乘法器常规调幅电路设计

辽宁工业大学高频电子线路课程设计(论文)题目:乘法器常规调幅电路设计院(系):工程学院专业班级:学号:学生姓名:指导教师:教师职称:起止时间:课程设计(论文)任务及评语院(系):电子与信息工程学院教研室:通信工程教研室学号学生姓名专业班级课程设计题目乘法器常规调幅电路设计课程设计(论文)任务设计内容:1.采用乘法器常规调幅,并对已调波进行放大10倍2.用EWB仿真,能够观察输入输出波形。
设计参数:输入信号频率15000HZ,电压500mV左右,调幅系数为0.5,输入信号载波频率10000HZ,载波电压为100mV,放大倍数10左右。
设计要求:1.分析设计要求,明确性能指标。
必须仔细分析课题要求、性能、指标及应用环境等,广开思路,构思出各种总体方案,绘制结构框图。
2 .确定合理的总体方案。
以电路的先进性、结构的繁简、成本的高低及制作的难易等方面作综合比较,并考虑器件的来源,敲定可行方案。
3 .设计各单元电路。
总体方案化整为零,分解成若干子系统或单元电路,逐个设计。
4.组成系统。
在一定幅面的图纸上合理布局,通常是按信号的流向,采用左进右出的规律摆放各电路,并标出必要的说明。
指导教师评语及成绩平时成绩(20%):答辩成绩(30%):论文成绩(50%):总成绩:指导教师签字:年月日摘要随着电子技术的发展,集成模拟乘法器应用也越来越广泛,它不仅应用于模拟量的运算,还广泛应用于通信、测量仪表、自动控制等科学技术领域。
集成模拟乘法器是实现两个模拟信号相乘的器件,它广泛用于乘法、除法、乘方和开方等模拟运算,同时也广泛用于信息传输系统作为调幅、解调、混频、鉴相和自动增益控制电路,是一种通用性很强的非线性电子器件,目前已有多种形式、多品种的单片集成电路,同时它也是现代一些专用模拟集成系统中的重要单元。
关键词:集成模拟乘法器;二极管;三极管;滑动变阻器目录第1章绪论 (1)1.1乘法器常规调幅电路的概况 (1)1.2设计的要求及技术指标 (1)第2章乘法器常规调幅电路设计 (2)2.1设计方案论证 (2)2.2总体设计方案框图及分析 (2)2.3乘法器常规调幅电路设计 (3)第3章乘法器常规调幅电路整体电路设计 (5)3.1乘法器常规调幅整体仿真电路图 (5)3.2乘法器常规调幅电路参数计算 (6)3.3电路仿真波形 (7)3.4电路仿真结果分析 (8)3.5电路性能分析 (9)第4章课程设计总结 (10)参考文献 (11)附录:元器件清单 (12)第1章绪论1.1乘法器常规调幅电路的概况用集成模拟乘法器可以构成性能优良的调幅和解调电路,,其电路元件参数通常采用器件典型应用参数值。
ai处理器单元中的矩阵乘法器电路设计

本人处理器单元中的矩阵乘法器电路设计本人处理器在近年来得到了快速发展,其中的矩阵乘法器电路设计是其中的重要组成部分。
矩阵乘法是深度学习中的核心运算,因此其电路设计对于本人处理器的性能和效率至关重要。
1. 矩阵乘法的重要性矩阵乘法在深度学习中起着至关重要的作用。
在神经网络的训练过程中,大量的矩阵运算需要进行,尤其是在卷积神经网络中。
矩阵乘法的高效运算可以大大加速神经网络的训练和推理过程,因此其电路设计的优化对于本人处理器的性能至关重要。
2. 传统的矩阵乘法器电路设计传统的矩阵乘法器电路设计通常采用乘法-累加器(MAC)单元来实现。
MAC单元通过并行计算多个乘法和加法操作来实现矩阵乘法,但是在面对大规模矩阵计算时,传统的MAC单元往往会面临运算速度慢、能耗高等问题。
3. 新型矩阵乘法器电路设计随着技术的不断发展,新型的矩阵乘法器电路设计不断涌现。
其中,基于硬件加速的矩阵乘法器设计成为了一种重要的趋势。
FPGA和ASIC等专用芯片逐渐成为了优化矩阵乘法运算的选择,通过定制化的硬件设计和指令集,可以大大提高矩阵乘法的运算速度和能效比。
4. 个人观点和理解在我看来,矩阵乘法器电路设计的优化是本人处理器发展中的关键一环。
随着深度学习应用的不断扩展,对于矩阵乘法运算的需求也越来越大,因此如何设计高效的矩阵乘法器电路至关重要。
我认为,未来的发展方向可能会越来越向着定制化、专用化的方向发展,通过硬件加速来实现对矩阵乘法运算的优化。
总结回顾在本人处理器单元中,矩阵乘法器电路设计是其中的核心组成部分。
传统的MAC单元在面对大规模矩阵计算时往往效率低下,因此新型的基于硬件加速的矩阵乘法器设计成为了重要的发展方向。
个人认为,未来的发展方向可能会越来越向着定制化、专用化的方向发展,以实现对矩阵乘法运算的高效优化。
在这篇文章中,我对本人处理器单元中矩阵乘法器电路设计进行了深入的探讨,并共享了自己的观点和理解。
希望这篇文章能够帮助你更深入地理解这一重要的主题。
电路中的乘法器设计

电路中的乘法器设计乘法器作为数字电路中重要的基本组件之一,被广泛应用于各种数字信号处理系统中。
乘法器的设计与优化对于提高性能、节省资源以及降低功耗都有着重要的价值。
一、乘法器的原理和分类乘法器是一种将两个输入信号相乘并输出结果的电路。
在数字电路中,乘法器有多种不同的实现方式,常见的有布斯乘法器、波尔久杰斯基乘法器以及Wallace树乘法器等。
布斯乘法器是一种基于二进制补码运算的乘法器。
它通过将两个输入信号逐位相乘,并将结果相加得到最终的乘积。
此种乘法器的优点是结构简单,实现方便,但缺点是速度相对较慢。
波尔久杰斯基乘法器是一种通过分解乘法运算来提高速度的乘法器。
它将两个输入信号分别展开成若干个中间变量,并通过特定的组合电路将这些变量相乘,并最终将结果相加得到最终的乘积。
该乘法器相比布斯乘法器具有更快的运算速度,但需要更多的硬件资源。
Wallace树乘法器则是一种通过并行计算实现高速乘法的乘法器。
它将输入信号分组,并通过特定的组合电路实现了并行计算的功能,从而大大提高了运算速度。
然而,该乘法器在实现过程中,需要大量的硬件资源,且相对复杂。
二、乘法器的设计优化在实际乘法器的设计过程中,往往需要考虑多个因素,如运算速度、资源利用率、功耗以及抗干扰能力等。
为了达到更好的设计效果,我们可以采取一些优化策略。
第一,使用合适的乘法算法。
不同的乘法算法在运算速度、资源利用率以及功耗等方面会有所不同,根据具体的应用需求选择合适的乘法算法是非常重要的。
第二,考虑并行计算。
众所周知,乘法操作是一个非常耗时的运算,可以通过并行计算的方式来提高运算速度。
比如,可以采用布斯树和Wallace树等并行计算的方法来实现高速乘法。
第三,精确控制电路延迟。
在进行乘法运算时,电路延迟是一个重要的因素,可以通过合理设计电路结构、选用合适的器件以及优化布线等方式来减少电路延迟,提高乘法器的运算速度。
第四,采用节能技术。
如今,节能已经成为电路设计不可忽视的因素之一。
乘法和除法电路
–VEE
I0 2
RX ux
I0 2
RX
I0 2
RY
uY
I0 2
RY
负反馈电阻,用以 扩大 uX、uY 范围
uO
4 RC Rx RY I0
uX uY
KuXuY
K 4RC Rx RY I0
ux
KXY X
uy Y
uo
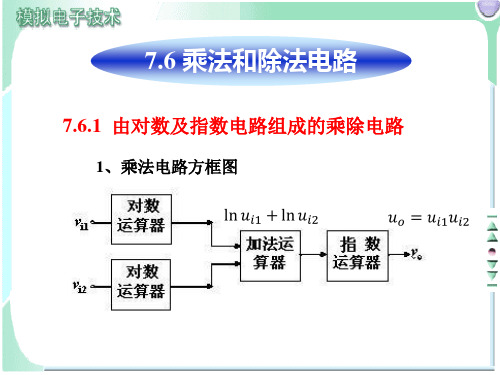
7.6 乘法和除法电路
7.6.1 由对数及指数电路组成的乘除电路
1、乘法电路方框图
2、除法电路方框图
7.6.2 模拟乘法器 一、模拟乘法器的基本特性
符号
uO = Kuxuy K — 比例系数
类型
单象限乘法器 ux、uy 皆
为固定极性 二象限乘法器 一个为固定极 性,另一个为可正可负
四象限乘法器 ux、uy 皆为
可正可负
二、可变跨导乘法器的工作原理
uO rbe
β
RC rbe
uX
rbb (1 β)
UT I E1
(1 β) 2UT IC3
uO
β RC IC3 2(1 β)UT
uX
RC IC3 2U T
uX
当 uY > uBE3 时,IC3≈uY/RE
uO
RC 2 REU T
uXuY
KuXuY
KXY
u'O
X Y
R
8
uI R
uO KuO2 uI
uO
uI K
uO
(uI < 0)
4、压控增益
KXY
uY
X
Y
uo
uX
uO = KuXuY 设 uX = UXQ 则 uO = (KUXQ)uY 调节直流电压 UXQ , 则调节电路增益
四位二进制乘法器电路的设计

四位二进制乘法器电路的设计一、前言在数字电路设计中,四位二进制乘法器是一个常见的电路设计,它可以将两个四位的二进制数相乘,并输出八位的结果。
本文将详细介绍四位二进制乘法器电路的设计原理和实现方法。
二、四位二进制乘法器电路的原理1. 乘法运算原理在十进制数中,两个数相乘的运算过程是将其中一个数每一位与另一个数相乘,并将每次得到的结果相加。
例如,计算12×13时,先用12分别与3和1相乘,得到36和12,然后将这两个结果相加即可得到156。
在二进制数中也是同样的道理。
例如,计算1010(10)×1101(13)时,先用1010分别与1、0、1、1相乘,得到1010、0000、1010、1010四个结果;然后将这四个结果左移0、4、8、12位(即对应不同位置上的十进制值),再相加即可得到11100110(230)。
2. 四位二进制乘法器电路原理根据以上运算原理,在数字电路中可以设计出四位二进制乘法器电路。
该电路由以下几部分组成:① 两个四位二进制数输入端:分别为被乘数和乘数,每个输入端有四个二进制位。
② 乘法器:该电路的核心部分,用于实现两个四位二进制数的相乘。
具体实现方式为将被乘数的每一位与乘数相乘,并将结果存储在一个8×4的矩阵中。
其中,矩阵的第i行第j列表示被乘数第i位和乘数第j位相乘的结果(i和j均从0开始计数)。
例如,当被乘数为1010、乘数为1101时,该矩阵如下所示:1 0 1 0---------1 | 1 0 1 01 | 0 0 00 | 1 01 | 1其中,第一列表示被乘数的最低位与乘数相乘的结果,第二列表示被乘数次低位与乘数相乘的结果,以此类推。
③ 加法器:用于将矩阵中每一行的结果相加,并输出一个八位二进制结果。
具体实现方式为将矩阵中同一行的四个二进制数字依次左移不同位置后相加,并将得到的八位结果输出。
例如,在上述示例中,对于第一行来说,需要将1010左移0、4、8、12位,分别得到10100000、00000000、00000000和00000000,然后将这四个数相加,得到10100110(166),即为最终结果。
ad834乘法器电路

ad834乘法器电路AD834是一款高性能乘法器电路芯片,广泛应用于射频(RF)和微波领域。
它使用先进的集成电路技术,能够实现高精度的模拟乘法功能。
下面我将从不同角度来介绍AD834乘法器电路。
1. 基本原理:AD834乘法器电路的基本原理是利用四象限乘法器实现信号的乘法运算。
它接受两个输入信号,分别称为X和Y,经过乘法运算后输出结果为Z。
乘法器的原理是将输入信号X和Y进行乘法运算,得到的结果与输入信号的幅度和相位相关。
2. 工作频率范围:AD834乘法器电路适用于宽频带的应用,其工作频率范围通常在几百MHz到几GHz之间。
这使得它在射频和微波系统中能够处理高频信号,并实现频率转换、调制解调、幅度调制等功能。
3. 电路结构:AD834乘法器电路采用集成电路技术,通常由多个功能模块组成。
其中包括输入缓冲放大器、四象限乘法器、输出缓冲放大器等。
这些模块相互配合,实现了高性能的乘法运算。
4. 特点和性能:AD834乘法器电路具有以下特点和性能:高线性度,能够实现高精度的乘法运算,输出结果与输入信号的幅度和相位关系准确。
宽动态范围,能够处理大幅度的输入信号,适用于各种信号强度情况。
低功耗,采用低功耗设计,适合用于电池供电或功耗敏感的应用。
高速响应,能够快速响应输入信号的变化,适用于高速数据处理和调制解调等应用。
5. 应用领域:AD834乘法器电路广泛应用于射频和微波系统中,包括无线通信、卫星通信、雷达、无线电广播、电视、航空航天等领域。
它在这些领域中扮演着重要的角色,实现了信号处理、频率转换、调制解调等功能。
总结:AD834乘法器电路是一款高性能的乘法器芯片,具有高线性度、宽动态范围、低功耗和高速响应等特点。
它在射频和微波系统中应用广泛,能够实现信号的乘法运算,并在无线通信、雷达、电视等领域中发挥重要作用。
组成原理——定点原码一位乘法器设计与实现

组成原理——定点原码一位乘法器设计与实现定点原码一位乘法器是一种用于进行定点数乘法运算的电路。
它是计算机系统中常用的基本算术电路,用于实现乘法操作。
在本文中,我们将讨论定点原码一位乘法器的设计原理以及其实现方法。
定点数表示法是一种用整数表示的数值表示法,其中小数点的位置是固定的。
在定点数乘法运算中,我们需要将两个输入数值进行相乘,并将结果输出。
定点原码一位乘法器的设计目标是实现高精度的乘法运算,同时保持低功耗和低延迟。
定点原码一位乘法器的设计原理基于布尔代数和逻辑电路。
其主要包括以下几个步骤:1.输入信号:定点原码一位乘法器通常有两个输入信号,分别代表两个乘数。
这些信号通常由时钟信号触发,以确保同步操作。
2.加法器和移位器:定点原码一位乘法器使用加法器和移位器来实现乘法操作。
移位器用于将乘数(或加数)进行位移操作,以便选择正确的乘积位。
加法器用于将部分乘积相加,并输出最终的乘积结果。
3.乘积位选择:乘积位选择决定了哪些部分乘积需要相加以得到最终乘积结果。
这通常通过导线连接来实现,其中每根导线对应于一个部分乘积位。
4.符号位处理:定点原码一位乘法器还需要处理符号位。
这涉及到对符号位进行逻辑与门操作,以确保最终结果的符号正确。
定点原码一位乘法器的实现通常使用逻辑门、移位寄存器、加法器等电路元件。
它的实现过程可以分为以下几个步骤:1.设计逻辑电路:根据定点原码一位乘法器的设计原理,设计逻辑电路图,其中包括逻辑门、移位寄存器和加法器等。
2.实现逻辑电路:根据设计的逻辑电路图,使用逻辑门、移位寄存器和加法器等电路元件,来实现电路的物理连接。
3.进行仿真:使用仿真工具,对设计的电路进行仿真测试,以验证电路的正确性和性能。
4.调整和优化:根据仿真结果,对电路进行调整和优化,以提高电路的性能和功耗。
5.布局和布线:根据最终设计的电路图,对电路进行布局和布线,以保证电路的可靠性和稳定性。
6.制造和测试:将电路进行制造和测试,以确保制造的电路符合设计要求,并具有良好的性能和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
parameter size = 8;
input[size:1] a, b;
// 源操作数
output[2*size:1] outcome; // 乘积
assign outcome = a*b; endmodule
// 相乘
8位并行乘法器RTL图
9.2.2 移位相加乘法器
结构 移位寄存器 加法器
reg[3:0] address; // 存储器地址
always @( posedge clk ) begin
address = { a, b }; case( address )
4'h0: out = 4'b0000; 4'h1: out = 4'b0000; 4'h2: out = 4'b0000; 4'h3: out = 4'b0000; 4'h4: out = 4'b0000; 4'h5: out = 4'b0001; 4'h6: out = 4'b0010; 4'h7: out = 4'b009;
reg[3:0] firsta, firstb; // 操作数高4位 reg[3:0] seconda, secondb; // 操作数低4位 wire[7:0] outa, outb, outc, outd; // 乘积每8位1组
always @( posedge clk ) begin
firsta = a[7:4]; seconda = a[3:0]; firstb = b[7:4]; secondb = b[3:0]; end
always @( a or b ) begin
outcome = 4’h0; for( i = 1; i <= size; i = i+1 )
if( b[i] ) outcome = outcome + ( a << (i-1) ); end endmodule
乘法器的功能仿真波形图
9.2.3 查找表乘法器
优点 耗用资源少
【例9.16】8位二进制数的乘法 module mult_for( outcome, a, b ); parameter size = 8; input[size:1] a, b; output[2*size:1] outcome; reg[2*size:1] outcome; integer i;
lookup m1( outa, firsta, firstb, clk ), // 元件调用 m2( outb, firsta, secondb, clk ), m3( outc, seconda, firstb, clk ), m4( outd, seconda, secondb, clk );
always @( posedge clk ) begin
out = ( outa << 4 ) + ( outb << 2 ) // 乘积 + ( outc << 2 ) + outd;
end endmodule
4位查找表乘法器仿真波形图
/*************** 8×8查找表乘法器 ****************/ module mult8x8( out, a, b, clk ); output[15:0] out; // 乘积 input[7:0] a, b; // 操作数 input clk; reg[15:0] out;
/*************** 4×4查找表乘法器 ****************/ module mult4x4( out, a, b, clk ); output[7:0] out; // 乘积 input[3:0] a, b; // 操作数 input clk; reg[7:0] out;
8位查找表乘法器 Y = A×B A = A1×24+A2 B = B1×24+B2 则 Y = ( A1×24+A2 )×( B1×24+B2 ) = A1×B1×28 + A1×B2×24 + A2×B1×24 + A2×B2
【例9.5】 8×8查找表乘法器 /********** 2×2查找表乘法器 *********/ module lookup( out, a, b, clk ); output[3:0] out; // 乘积 input[1:0] a, b; // 操作数 input clk; reg[3:0] out;
reg[1:0] firsta, firstb; // 操作数高2位 reg[1:0] secondቤተ መጻሕፍቲ ባይዱ, secondb; // 操作数低2位 wire[3:0] outa, outb, outc, outd; // 乘积每2位1组
always @( posedge clk ) begin
firsta = a[3:2]; seconda = a[1:0]; firstb = b[3:2]; secondb = b[1:0]; end
结构 操作数:地址 乘积:存储器
优点 运算速度快
缺点 耗用存储资源多
设计思路
4位查找表乘法器 Y = A×B A = A1×22+A2 B = B1×22+B2 则 Y = ( A1×22+A2 )×( B1×22+B2 ) = A1×B1×24 + A1×B2×22 + A2×B1×22 + A2×B2
9.2 乘法器设计
应用 数字信号处理和数字通信 地位 影响系统的运行速度 实现
并行乘法器 移位相加乘法器 查找表乘法器 加法树乘法器
9.2.1 并行乘法器
结构 用乘法运算符描述 由EDA软件综合
优点 运算速度快
缺点 耗用资源多
【例9.4】8位并行乘法器
module mult( outcome, a, b);
4'h8: out = 4'b0000; 4'h9: out = 4'b0010; 4'ha: out = 4'b0100; 4'hb: out = 4'b090; 4'hc: out = 4'b0000; 4'hd: out = 4'b009; 4'he: out = 4'b090; 4'hf: out = 4'b1001; default: out = 4'bx; endcase end endmodule
