初三数学下期中第一次模拟试题及答案
【人教版】九年级数学下期中第一次模拟试题(附答案)

一、选择题1.如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为()A.5米B.6米C.8米D.10米2.下列每个选项的两个图形,不是相似图形的是()A. B.C.D.3.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为()A.21cm B.14cm C.6cm D.24cmEG BC,分别交AB,AD,AC于4.如图,已知在ABC中,D为BC上一点,//点E,F,G,则下列比例式正确的是()A .AE EF BE BD =B .EF AF DC AD = C .AC FG CG DC = D .AE FG AB DC= 5.大自然巧夺天工,一片小心树叶也蕴含着“黄金分割”.如图,P 为AB 的黄金分割点(AP >PB ),如果AP 的长度为8cm ,那么AB 的长度是( )A .45-4B .12-45C .12+45D .45+4 6.如图,在△ABC 中,DE ∥BC ,12AD BD =,则AE EC=( )A .13B .12C .23D .327.已知函数()0k y k x=≠中,在每个象限内,y 的值随x 的值增大而增大,那么它和函数()0y kx k =-≠在同一直角坐标平面内的大致图像是( ).A .B .C .D .8.已知()()()112233,,,,,A x y B x y C x y 是反比例函数2y x =上的三点,若123x x x <<,213y y y <<,则下列关系式不正确的是 ( ) A .120x x < B .130x x < C .230x x <D .120x x +< 9.已知反比例函数2y -x=,点A (a-b ,2),B (a-c ,3)在这个函数图象上,下列对于a ,b ,c 的大小判断正确的是( )A .a <b <cB .a <c <bC .c <b <aD .b <c <a 10.已知0k >,函数y kx k =+和函数k y x=在同一坐标系内的图象大致是( ) A . B .C .D .11.反比例函数y=kb x的图象如图所示,则一次函数y=kx+b (k≠0)的图象的图象大致是( )A .B .C .D .12.如图,△ABC 的三个顶点分别为A (1,2),B (2,5),C (6,1).若函数在第一象限内的图像与△ABC 有交点,则的取值范围是A .2≤≤B .6≤≤10C .2≤≤6D .2≤≤二、填空题13.如图,在四边形ABCD 中,AC 平分∠BAD ,AD=AC ,以A 为圆心,AB 长为半径画弧,交AC 于点E ,连接DE 、BE ,并延长BE 交CD 于点F ,下列结论:①△BAC ≌ △EAD ,②BC+CF=DE+EF ,③∠ABE+∠ADE=∠BCD ,其中正确的有____(填序号)14.如图1,课本中有一道例题:有一块三角形余料ABC ,它的边120BC mm =,高80AD mm =.要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB ,AC 上.设PN xmm =,用x 的代数式表示AE =________mm ,由//PN BC ,可得APN ABC ∽△△,再利用相似三角形对应高的比等于相似比,可求得PN =________mm .拓展:原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图2,此时,PN =________mm .15.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P 为AB 的黄金分割点()AP PB >,如果AB 的长度为8cm ,那么AP 的长度是_____________.16.如图是用卡钳测量容器内径的示意图,现量得卡钳上A ,D 两个端点之间的距离为10cm ,23AO DO BO CO ==,则容器的内径是______.17.已知点(,7)M a 在反比例函数21y x=的图象上,则a=______. 18.如图,在方格纸中(小正方形的边长为1),反比例函数k y x=的图象与直线AB 的交点A 、B 在图中的格点上,点C 是反比例函数图象上的一点,且与点A 、B 组成以AB 为底的等腰△,则点C 的坐标为________.19.如图,直线y=12x﹣2与x轴、y轴分别交于点A和点B,点C在直线AB上,且点C的纵坐标为﹣1,点D在反比例函数y=kx的图象上,CD平行于y轴,S△OCD=52,则k的值为________.20.如图,点P,Q在反比例函数y=kx(k>0)的图像上,过点P作PA⊥x轴于点A,过点Q作QB⊥y轴于点B.若△POA与△QOB的面积之和为4,则k的值为_________.三、解答题21.在如图所示的12个小正方形组成的网格中,ABC的三个顶点都在小正方形的顶点上.仅用无刻度的直尺按要求完成下列作图.(1)在图1网格中找格点D,作直线BD,使直线BD与AC的交点P是AC的中点.(2)在图2网格中找格点E,作直线BE交AC于点Q,使得CQ CB.22.作图题:如图所示,图中的小方格都是边长为1的正方形,△ABC 与△A 'B 'C '是以点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O ;(2)△A 'B 'C '与△ABC的位似比是 ;(3)以位似中心O 为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A 'B 'C '关于点O 中心对称的△A "B "C ",并直接写出△A "B "C "各顶点的坐标. 23.如图,建筑物BC 上有一个旗杆AB ,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度,他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED ,小明沿CD 后退,发现地面上的点F 、树顶E 、旗杆顶端A 恰好在一条直线上,继续后退,发现地面上的点G 、树顶E 、建筑物顶端B 恰好在一条直线上,已知旗杆3AB =米,4DE =米,5DF =米,1.5FG =米,点、、A B C 在一条直线上,点C D F G 、、、在一条直线上,AC ED 、均垂直于CG ,根据以上信息,请求出这座建筑物的高BC .24.已知y 是x 的反比例函数,且当x =4时,1y =-.(1)求y 与x 之间的函数解析式;(2)求当132x -≤≤-时,y 的取值范围. 25.如图,一块含30°,60°,90°的直角三角板,直角顶点O 位于坐标原点,斜边AB 垂直于x 轴,顶点A 在函数y 1=1k x (x >0)的图象上,顶点B 在函数y 2=2k x (x >0)的图象上,∠ABO=30°,求12k k 的值.26.某校园艺社计划利用已有的一堵长为10m 的墙,用篱笆围一个面积为212m 的矩形园子.(1)如图,设矩形园子的相邻两边长分别为()x m 、()y m .①求y 关于x 的函数表达式;②当4y 时,求x 的取值范围;(2)小凯说篱笆的长可以为9.5m ,洋洋说篱笆的长可以为10.5m.你认为他们俩的说法对吗?为什么?【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据同一时刻,物体的实际高度和影长成正比例列出比例式即可解答.【详解】解:如图,假设没有墙,电线杆AB 的影子落在E 处,∵同一时刻,物体的实际高度和影长成正比例,∴CD:DE=1:0.5=2:1,∴AB:BE=2:1,∵CD=2,BE=BD+DE,∴BE=3+1=4,∴AB:4=2:1,∴AB=8,即电线杆AB的高为8米,故选:C.【点睛】本题考查了相似三角形的应用、比例的性质,解答的关键是理解题意,将实际问题转化为相似三角形中,利用同一时刻,物体的实际高度和影长成正比例列出方程求解.2.D解析:D【分析】根据相似图形的定义,对选项进行一一分析,排除错误答案.【详解】解:A、形状相同,但大小不同,符合相似形的定义,故不符合题意;B、形状相同,但大小不同,符合相似形的定义,故不符合题意;C、形状相同,但大小不同,符合相似形的定义,故不符合题意;D、形状不相同,不符合相似形的定义,故符合题意;故选:D.【点睛】本题考查的是相似形的定义,是基础题.3.A解析:A【分析】根据题意可画出图形,再根据相似三角形的性质对应边成比例解答即可.【详解】解:如图所示,∵DE∥BC,∴△AED∽△ABC,∴AE DEAC BC=,设屏幕上的图形高是x cm,则307 90x=,解得:x=21.答:屏幕上图形的高度为21cm,故选:A.【点睛】本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.4.D解析:D【分析】根据相似三角形的判定推出△AEF∽△ABD,△AFG∽△ADC,△AEG∽△ABC,再根据相似三角形的性质得出比例式即可.【详解】A、∵EG∥BC,即EF∥BD,∴△AEF∽△ABD,∴AE EF=,AB BD≠,故本选项不符合题意;∵AB BEB、∵EF∥BD,∴△AEF∽△ABD,∴EF AF=,BD AD∵BD≠DC,故本选项不符合题意;C、∵EG∥BC,即FG∥DC,∴△AFG∽△ADC,∴AG FG=,AC DC∵AG AC≠,故本选项不符合题意;AC CGD、∵EG∥BC,∴△AEG∽△ABC,∴AE AG=,AB AC∵FG∥DC,∴△AFG∽△ADC,∴AG FG=,AC DC∴AE FG=,故本选项符合题意;AB DC故选:D【点睛】本题考查了相似三角形的性质和判定,能正确的识别图形、灵活运用定理进行推理是解此题的关键.5.D解析:D【分析】根据黄金分割的定义得到AB ,然后把AP=8代入后可求出AB 的长. 【详解】∵P 为AB 的黄金分割点(AP >PB ),∴AB ,∴)8414==(cm ), 故选:D .【点睛】本题考查了黄金分割以及分母有理化.把线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC=AC :BC ),叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点.其中AC=12AB .并且线段AB 的黄金分割点有两个. 6.B解析:B【分析】直接利用平行线分线段成比例定理得出答案即可.【详解】解:∵DE ∥BC , ∴AE EC =12AD BD =. 故选:B .【点睛】 本题考查了平行线分线段成比例定理,了解定理的内容是解答此题的关键.7.A解析:A【分析】首先根据反比例函数图象的性质判断出k 的范围,再确定其所在象限,进而确定正比例函数图象所在象限,即可得到答案.【详解】解:∵函数k y x=中,在每个象限内,y 随x 的增大而增大,∴k<0,∴双曲线在第二、四象限,∴函数y=-kx的图象经过第一、三象限,故选:A.【点睛】此题主要考查了反比例函数图象的性质与正比例函数图象的性质,图象所在象限受k的影响.8.A解析:A【分析】根据反比例函数2yx=和x1<x2<x3,y2<y1<y3,可得点A,B在第三象限,点C在第一象限,得出x1<x2<0<x3,再选择即可.【详解】解:∵反比例函数2yx=中,2>0,∴在每一象限内,y随x的增大而减小,∵x1<x2<x3,y2<y1<y3,∴点A,B在第三象限,点C在第一象限,∴x1<x2<0<x3,∴x1•x2>0,x1•x3<0,x2•x3<0,x1+x2<0,故选:A.【点睛】本题考查了反比例函数图象上点的坐标特征,解答此题的关键是熟知反比例函数的增减性,本题是逆用,难度有点大.9.B解析:B【分析】利用反比例函数图象上点的坐标特征得到2(a-b)=-2,3(a-c)=-2,则a-b=-1<0,a-c=-2 3<0,再消去a得到-b+c=-13<0,然后比较a、b、c的大小关系.【详解】∵点A(a-b,2),B(a-c,3)在函数2y-x=的图象上,∴2(a-b)=-2,3(a-c)=-2,∴a-b=-1<0,a-c=-23<0,∴a<b,a<c,∵-b+c=-13<0,∴c<b,∴a<c<b.故选B.【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数y=kx(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.10.D解析:D【解析】根据题意,在函数y=kx+k和函数kyx=中,有k>0,则函数y=kx+k过一二三象限.且函数kyx=在一、三象限,则D选项中的函数图象符合题意;故选D.11.D解析:D【分析】先由反比例函数的图象得到k,b同号,然后分析各选项一次函数的图象即可.【详解】∵y=kbx的图象经过第一、三象限,∴kb>0,∴k,b同号,选项A图象过二、四象限,则k<0,图象经过y轴正半轴,则b>0,此时,k,b异号,故此选项不合题意;选项B图象过二、四象限,则k<0,图象经过原点,则b=0,此时,k,b不同号,故此选项不合题意;选项C图象过一、三象限,则k>0,图象经过y轴负半轴,则b<0,此时,k,b异号,故此选项不合题意;选项D图象过一、三象限,则k>0,图象经过y轴正半轴,则b>0,此时,k,b同号,故此选项符合题意;故选D.考点:反比例函数的图象;一次函数的图象.12.A解析:A【分析】把A点的坐标代入即可求出k的最小值;当反比例函数和直线BC相交时,求出b2﹣4ac的值,得出k的最大值.【详解】把点A(1,2)代入kyx=得:k=2;C的坐标是(6,1),B的坐标是(2,5),设直线BC的解析式是y=kx+b,则25 61 k bk b+=⎧⎨+=⎩,解得:17kb=-⎧⎨=⎩,则函数的解析式是: y=﹣x+7,根据题意,得:kx=﹣x+7,即x2﹣7x+k=0,△=49﹣4k≥0,解得:k≤494.则k的范围是:2≤k≤494.故选A.考点:反比例函数综合题.二、填空题13.①②③【分析】先由已知条件利用SAS证明△BAC≌△EAD得到①;由全等得到BC=DE然后再通过证明△ABE∽△ACD得到∠ABE=∠ACD=∠AEB进而再得到CF=EF得到BC+CF=DE+EF即解析:①②③【分析】先由已知条件利用SAS证明△BAC ≌△EAD,得到①;由全等得到BC=DE,然后再通过证明△ABE∽△ACD,得到∠ABE=∠ACD=∠AEB,进而再得到CF=EF,得到BC+CF=DE+EF,即②正确;由∠ABE=∠ACD,∠BCA=∠EDA,可得到∠ABE+∠ADE=∠BCD,即③正确.【详解】解:由题意可知,∠BAC=∠CAD,AB=AE,在△BAC和△EAD中,AB AE BAC CAD AC AD =⎧⎪=⎨⎪=⎩∠∠∴△BAC ≌ △EAD ,故①正确;∵△BAC ≌ △EAD ,∴BC=ED ,∠BCA=∠EDA ,由于AB=AE ,AC=AD ,∠BAC=∠CAD , ∴AB AE AC AD=, ∴△ABE ∽△ACD ,且△ABE 和△ACD 都为等腰三角形,∴∠ABE=∠ACD=∠AEB ,∵∠AEB=∠CEF ,∴∠ECF=∠CEF ,∴CF=EF ,∴BC+CF=DE+EF ,故②正确;由以上过程知道∠ABE=∠ACD ,∠BCA=∠EDA ,∴∠ABE+∠ADE=∠ACD+∠BCA=∠BCD ,故③正确.故答案为:①②③.【点睛】本题考查了全等三角形的判定和性质,相似三角形的判定和性质,正确找到全等三角形是解题的关键.14.48【分析】根据相似三角形的性质可得对应高的比等于相似比进行计算然后根据矩形的性质可设则进行求解即可;【详解】设则∵PN ∥BC ∴∴即解得∴拓展:设则∵PN ∥BC ∴∴∴解得∴;故答案是:;48;【点睛解析:80x -484807 【分析】根据相似三角形的性质可得对应高的比等于相似比进行计算,然后根据矩形的性质可设BQ x =,则2PN x =,80AE x =-,进行求解即可;【详解】设PN xmm =,则PN PQ ED xmm ===,()80AE AD ED x mm =-=-,∵PN ∥BC ,∴APN ABC , ∴PN AE BC AD =, 即8012080x x -=,解得48x =,∴48PN mm =,拓展:设PQ xmm =,则2PN xmm =,()80AE AD ED x mm =-=-,∵PN ∥BC ,∴APN ABC , ∴PN AE BC AD =, ∴28012080x x -=,解得2407x =, ∴48027PN x ==; 故答案是:80x -;48;4807. 【点睛】 本题主要考查了相似三角形的应用,准确分析计算是解题的关键.15.()cm 【分析】利用黄金分割的定义计算出AP 【详解】为的黄金分割点故答案为:()cm 【点睛】此题考查黄金分割的定义黄金分割物体的较大部分等于与整体的解析:(4)cm【分析】利用黄金分割的定义计算出AP .【详解】 P 为AB 的黄金分割点()AP PB >,()118422AP AB cm ∴==⨯=故答案为:(4)cm.【点睛】. 16.【分析】连接ADBC 后可知△AOD ∽△BOC 再由相似三角形的性质和已知条件可以得到问题解答【详解】解:如图连接ADBC 则在△AOD 和△BOC 中∴△AOD ∽△BOC (cm )故答案为15cm 【点睛】本题解析:15cm【分析】连接AD 、BC 后可知△AOD ∽△BOC ,再由相似三角形的性质和已知条件可以得到问题解答.【详解】解:如图,连接AD 、BC ,则在△AOD 和△BOC 中,AO DO BO CO DOA BOC⎧=⎪⎨⎪∠=∠⎩,∴△AOD ∽△BOC ,233,1015322AD AO BC AD BC BO ====⨯=(cm ), 故答案为15cm .【点睛】本题考查相似三角形的应用,熟练掌握相似三角形的判定及性质并灵活运用是解题关键. 17.3【分析】把点代入反比例函数解析式求解即可【详解】解:∵点在反比例函数的图象上∴解得故答案为:3【点睛】本题考查反比例函数上点的坐标特征掌握反比例函数上点的坐标特征是解题的关键解析:3【分析】把点(,7)M a 代入反比例函数解析式,求解即可.【详解】解:∵点(,7)M a 在反比例函数21y x=的图象上, ∴217a=,解得3a =, 故答案为:3.【点睛】 本题考查反比例函数上点的坐标特征,掌握反比例函数上点的坐标特征是解题的关键. 18.(22)或(-2-2)【分析】先求得反比例函数的解析式为设C 点的坐标为()根据AC=BC 得出方程求出即可【详解】由图象可知:点A 的坐标为(-1-4)代入得:所以这个反比例函数的解析式是设C 点的坐标为解析:(2,2)或(-2,-2)【分析】先求得反比例函数的解析式为4y x =,设C 点的坐标为(x ,4x),根据AC=BC 得出方程,求出x 即可.【详解】 由图象可知:点A 的坐标为(-1,-4), 代入k y x=得:4k xy ==, 所以这个反比例函数的解析式是4y x =, 设C 点的坐标为(x ,4x), ∵A (-1,-4),B (-4,-1),AC=BC , 即()()2222441441x x x x ⎛⎫⎛⎫--+--=--+-- ⎪ ⎪⎝⎭⎝⎭, 解得:2x =±,当2x =时,422y ==, 当2x =-时,422y ==--, 所以点C 的坐标为(2,2)或(-2,-2).故答案为:(2,2)或(-2,-2).【点睛】本题考查了等腰三角形的性质、用待定系数法求反比例函数的解析式、反比例函数图象上点的坐标特征等知识点,能求出反比例函数的解析式是解此题的关键.19.3【详解】试题分析:把x=2代入y=x ﹣2求出C 的纵坐标得出OM=2CM=1根据CD ∥y 轴得出D 的横坐标是2根据三角形的面积求出CD 的值求出MD 得出D 的纵坐标把D 的坐标代入反比例函数的解析式求出k 即解析:3【详解】试题分析:把x=2代入y=12x ﹣2求出C 的纵坐标,得出OM=2,CM=1,根据CD ∥y 轴得出D 的横坐标是2,根据三角形的面积求出CD 的值,求出MD ,得出D 的纵坐标,把D 的坐标代入反比例函数的解析式求出k 即可.解:∵点C 在直线AB 上,即在直线y=12x ﹣2上,C 的横坐标是2,∴代入得:y=12×2﹣2=﹣1,即C(2,﹣1),∴OM=2,∵CD∥y轴,S△OCD=52,∴12CD×OM=52,∴CD=52,∴MD=52﹣1=32,即D的坐标是(2,32),∵D在双曲线y=kx上,∴代入得:k=2×32=3.故答案为3.考点:反比例函数与一次函数的交点问题.点评:本题考查了反比例函数与一次函数的交点问题、一次函数、反比例函数的图象上点的坐标特征、三角形的面积等知识点,通过做此题培养了学生的计算能力和理解能力,题目具有一定的代表性,是一道比较好的题目.20.4【分析】根据反比例函数的性质确定△POA与△QOB的面积均为2然后根据反比例函数的比例系数的几何意义确定其值即可【详解】根据题意得:点P和点Q关于原点对称所以△POA与△QOB的面积相等∵△POA解析:4【分析】根据反比例函数的性质确定△POA与△QOB的面积均为2,然后根据反比例函数的比例系数的几何意义确定其值即可.【详解】根据题意得:点P和点Q关于原点对称,所以△POA与△QOB的面积相等,∵△POA 与△QOB 的面积之和为4,∴△POA 与△QOB 的面积均为2, ∴2k=2,∴|k|=4,∵反比例函数的图象位于一、三象限,∴k=4,故答案为4.【点睛】此题考查了反比例函数的比例系数的几何意义及反比例函数的图象上点的坐标特征的知识,解题的关键是求得△POA 与△QOB 的面积,难度不大.三、解答题21.(1)画图见解析;(2)画图见解析.【分析】(1)根据题意画图即可;(2)由平行线性质得到MAQ NCQ ∠=∠,继而可证明AMQ CNQ ∽△△,再根据相似三角形的性质解得35CQ AC =,最后根据勾股定理解题即可. 【详解】(1)如图1所示,取格点D ,连接AD ,CD ,则四边形ABCD 为矩形,连接BD 交AC 于点P ,由于矩形对垂线互相平分,则点P 为AC 中点,故图1中直线BD ,格点D 即为所求.(2)如图2所示,找格点M ,N ,使得2AM =,3CN =,连接MN 与AC 交于点Q ,连接BQ 并延长交格点于点E ,则格点E 即为所求.∵//AM CN ,MAQ NCQ ∴∠=∠,又AQM CQN ∠=∠(对顶角相等)AMQ CNQ ∴∽△△,23AM AQ CN CQ ∴==, 即35CQ AC =, 由勾股定理得:222AC AB BC =+,又4AB =,3BC =,22435AC ∴=+=335355CQ AC CB ∴==⨯==, 故CQ CB =,∴格点E 即为所求.【点睛】本题考查网格作图,涉及相似三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.22.(1)画图见解析;(2)1:2;(3)画图见解析;A "(6,0),B "(3,-2),C "(4,-4)【分析】(1)连接CC′并延长,连接BB′并延长,两延长线交于点O ;(2)由OB=2OB′,即可得出△A′B′C′与△ABC 的位似比为1:2;(3),连接B′O 并延长,使OB ″=OB′,延长A′O 并延长,使OA″=OA′,C′O 并延长,使OC″=OC′,连接A″B″,A″C″,B″C″,则△A″B″C″为所求,从网格中即可得出△A″B″C″各顶点的坐标.【详解】解:(1)图中点O 为所求;(2)△A′B′C′与△ABC 的位似比等于1:2;故答案为:1:2;(3)△A″B″C″为所求;A″(6,0);B″(3,-2); C″(4,-4).【点睛】此题考查了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.23.这座建筑物的高BC 为 14米【分析】根据两组相似三角形ACF EDF ∆∆∽和BCG EDG ∆∆∽,利用对应边成比例,列出CD 和BC 的关系式,然后解方程求出BC 的长.【详解】解:由题意可得90ACF EDF AFC EFD ︒∠∠∠∠==,=,ACF EDF ∴∆∆∽,AC CF ED DF∴=, 即3545BC CD ++=, 554BC CD -∴=, 由题意可得,90BCG EDG BGC EGD ︒∠∠∠∠==,=,BCG EDG ∴∆∆∽,BC CG ED DG ∴=, 即5 1.545 1.5BC CD ++=+,6.54( 6.5)BC CD ∴+=,556.54264BC BC -∴=⨯+, 14BC ∴=,∴这座建筑物的高BC 为 14米.【点睛】本题考查相似三角形的应用,解题的关键是利用相似三角形对应边成比例的性质列式求边长.24.(1)4y x =-;(2)4y 83≤≤. 【分析】(1)利用待定系数法确定反比例函数的解析式即可;(2)根据自变量的取值范围确定函数值的取值范围即可.【详解】解:(1)设反比例函数的解析式为k y x =, ∵当x=4,y=-1,∴k=-1×4=-4,∴反比例函数的解析式为4y x =-; (2)当x=-3时,43y =,当x=-12时,y=8, ∴当-3≤x≤-12时,y 的取值范围是43≤y≤8. 【点睛】本题考查了反比例函数的性质,求得反比例函数的解析式是解答本题的关键.25.13【分析】设AC=a ,则OA=2a ,,根据直角三角形30°角的性质和勾股定理分别计算点A 和B 的坐标,写出A 和B 两点的坐标,代入解析式求出k 1和k 2的值,即可求12k k 的值. 【详解】设AB 与x 轴交点为点CRt △AOB 中,∠B=30°,∠AOB=90°,∴∠OAC=60°,∵AB ⊥OC ,∴∠ACO=90°,∴∠AOC=30°,设AC=a ,则OA=2a ,22OA AC -3, ∴3,a),∵A 在函数y 1=1k x(x >0)的图象上, ∴k 1332,Rt △BOC 中,3,∴22OB OC -,∴B 3a ,-3a ),∵B 在函数y 2=2k x(x >0)的图象上, ∴k 2332, ∴12k k 223a 33a -=-13, 故答案为:-13. 【点睛】本题考查了反比例函数图象上点的坐标特征.直角三角形30°的性质,熟练掌握直角三角形30°角所对的直角边是斜边的一半,正确写出A .B 两点的坐标是本题的关键. 26.(1)①1265y x x ⎛⎫=⎪⎝⎭,②635x ;(2)小凯的说法错误,洋洋的说法正确. 【分析】(1)①根据矩形的面积公式计算即可,注意自变量的取值范围;②构建不等式即可解决问题;(2)构建方程求解即可解决问题;【详解】(1)①由题意xy =12,1265y x x ⎛⎫∴= ⎪⎝⎭②y ⩾4时,124x ≥,解得3x ≤ 所以635x . (2)当1229.5x x +=时,整理得:2419240,0x x -+=∆<,方程无解. 当12210.5x x+=时,整理得2421240,570x x -+=∆=>,符合题意; ∴小凯的说法错误,洋洋的说法正确.【点睛】本题考查反比例函数的应用.(1)①中需注意,因为墙的宽度为10m ,所以y≤10,据此可求得自变量x 的取值范围;②中求得x 的取值要与①中取公共解集;(2)能根据根的判别式判断一元二次方程解的情况是解决此问的关键.。
【人教版】初三数学下期中第一次模拟试题及答案

一、选择题1.如图,D是△ABC的边BC上一点,AC=4,AD=2,∠DAB=∠C.如果△ACD的面积为15,那么△ABD的面积为()A.15 B.10 C.152D.52.如图,在四边形ABCD中,对角线BD平分∠ABC,∠DBC=30°,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F,若CD=2,则BF的长为()A.235B.233C.635D.4353.有下列四种说法:其中说法正确的有()①两个菱形相似;②两个矩形相似;③两个平行四边形相似;④两个正方形相似.A.4个B.3个C.2个D.1个4.如图,在△ABC中,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为()A.6 B.8 C.10 D.125.如图,直线l1//l2//l3,分别交直线m、n于点A、B、C、D、E、F.若AB∶BC=5∶3,DE=15,则EF的长为()A .6B .9C .10D .256.如图,△ABC 中,DE ∥BC ,25AD AB =,DE =3,则BC 的长为( )A .7.5B .4.5C .8D .67.如图,正方形ABCD 的顶点A 的坐标为()1,0-,点D 在反比例函数m y x =的图象上,B 点在反比例函数3y x=的图像上,AB 的中点E 在y 轴上,则m 的值为( )A .-2B .-3C .-6D .-88.如图,A 、B 是函数1y x=的图像上关于原点对称的任意两点,BC //x 轴,AC //y 轴,ABC 的面积记为S ,则( )A .1S =B .2S =C .24S <<D .4S =9.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,∠ABC=90°,CA ⊥x 轴,点C 在函数y=k x(x >0)的图象上,若AB=2,则k 的值为( )A .4B .22C .2D .210.如图,函数y =kx (k >0)与函数2y x=的图象相交于A ,C 两点,过A 作AB ⊥y 轴于B ,连结BC ,则三角形ABC 的面积为( )A .1B .2C .k 2D .2k 211.如图,点A 是反比例函数2(0)y x x =>的图象上任意一点,AB x 轴交反比例函数3y x=-的图象于点B ,以AB 为边作ABCD ,其中C 、D 在x 轴上,则ABCD S 为( )A .2.5B .3.5C .4D .512.如图, O 为坐标原点,点B 在x 轴的正半轴上,四边形OBCA 是平行四边形, 45sin AOB ∠=,反比例函数()0m y m x=>在第一象限内的图像经过点A ,与BC 交于点F ,若点F 为BC 的中点,且AOF 的面积为12,则m 的值为( )A .16B .24C .36D .48二、填空题13.如图,在矩形纸片ABCD 中,AB=6,BC=10,点E 在CD 上,将△BCE 沿BE 折 叠,点C恰落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,点A 恰落在线段BF 上的点H 处,有下列结论:①∠EBG=45°;②△DEF ∽△ABG ;③S △ABG = 1.5 S △FGH ;④AG+DF=FG ;其中正确的是______________.(填写正确结论的序号)14.如图,⊙O 的直径为5,在⊙O 上位于直径AB 的异侧有定点C 和动点P ,已知BC :CA =4:3,点P 在半圆弧AB 上运动(不与A ,B 重合),过C 作CP 的垂线CD 交PB 的延长线于D 点.则△PCD 的面积最大为______________.15.如果23a c b d ==,其中20b d +≠,那么22a c b d +=+________. 16.如图,90A B ∠=∠=︒,AB a ,AD BC <,在边AB 上取点P ,使得PAD △,PBC 与PDC △两两相似,则AP 长为___________.(结果用含a 的代数式表示)17.反比例函数()0k y x x=<的图象如图所示,下列关于该函数图象的四个结论:①0k >;②当0x <时,y 随x 的增大而增大;③该函数图象关于直线y x =-对称;④若点()2,3-在该反比例函数图象上,则点()1,6-也在该函数的图象上.其中正确结论的有_________(填番号).18.函数25(1)n y n x -=+是反比例函数,且图象位于第二、四象限内,则n =____. 19.如图,在平面直角坐标系中,反比例函数y=k x(k≠0),经过▱ABCD 的顶点B .D ,点A 的坐标为(0,-1),AB ∥x 轴,CD 经过点(0,2),▱ABCD 的面积是18,则点C 的坐标是______.20.如图,已知反比例函数y =k x(x >0)与正比例函数y =x (x ≥0)的图象,点A (1,4),点A '(4,b )与点B '均在反比例函数的图象上,点B 在直线y =x 上,四边形AA 'B 'B 是平行四边形,则B 点的坐标为______.三、解答题21.如图,已知ABC 和点A '.(1)以点A '为顶点求作A B C ''',使A B C ABC '''∽,4A B C ABC SS '''=;(尺规作图,保留作图痕迹,不写作法) (2)设D 、E 、F 分别是ABC 三边AB 、BC 、AC 的中点,D '、E '、F '分别是你所作的A B C '''三边A B ''、B C ''、A C ''的中点,求证:DEF D E F '''∽.22.如图,在1010⨯的正方形网格中,每个小正方形的边长为1,建立如图所示的坐标系,ABC 的三个顶点均在格点上.(1)若将ABC 沿x 轴对折得到111A B C △,则1C 的坐标为________.(2)以点B 为位似中心,将ABC 各边放大为原来的2倍,得到22A BC ,请在这个网格中画出22A BC .(3)在(2)的条件下,求22A BC 的面积是多少?23.如图,在等边ABC 中,点D ,E 分别在AB ,AC 上,连接DE ,DC (E ,C 两点不重合),当AED DCB ∠=∠时,我们把AE EC称为AD DB 的“类似比”,(1)若12AD DB =,则“类似比”AE EC =___________; (2)若(1)AD k k DB =<时,求“类似比”AE EC 的值(用含k 的代数式表示); (3)直接写出AED ∠和“类似比”AE EC 的取值范围. 24.如图,已知一次函数12y x b =+的图象与反比例函数()0k y x x=<的图象交于点A(-1,2)和点B .(1)求b 和k 的值; (2)请求出点B 的坐标,并观察图象,直接写出关于x 的不等式12k x b x+>的解集; (3)若点P 在y 轴上一点,当PA PB +最小时,求点P 的坐标.25.如图,在平面直角坐标系中,一次函数1(0)y kx b k =+≠的图象与反比例函数()2m y m 0x=≠的图象相交于第一、三象限内的A (3,5),B (a ,﹣3)两点,与x 轴交于点C .(1)求该反比例函数和一次函数的解析式; (2)直接写出当1y >2y 时,x 的取值范围;(3)在y 轴上找一点P 使PB ﹣PC 最大,求PB ﹣PC 的最大值及点P 的坐标.26.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min 时,材料温度降为600℃.如图,煅烧时温度y (℃)与时间x min ()成一次函数关系:锻造时,温度y (℃)与时间x min ()成反比例函数关系。
初三数学下期中一模试卷(附答案)
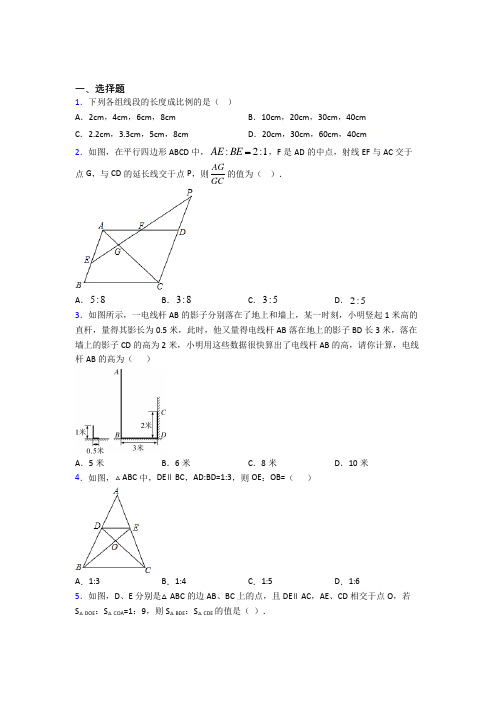
一、选择题1.下列各组线段的长度成比例的是()A.2cm,4cm,6cm,8cm B.10cm,20cm,30cm,40cmC.2.2cm,3.3cm,5cm,8cm D.20cm,30cm,60cm,40cm2.如图,在平行四边形ABCD中,:2:1AE BE ,F是AD的中点,射线EF与AC交于点G,与CD的延长线交于点P,则AGGC的值为().A.5:8B.3:8C.3:5D.2:53.如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为()A.5米B.6米C.8米D.10米4.如图,ABC中,DE∥BC,AD:BD=1:3,则OE:OB=()A.1:3 B.1:4 C.1:5 D.1:65.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:9,则S△BDE:S△CDE的值是().A .1:2B .1:3C .1:4D .2:56.如图,在ABCD 中,7AB =,3BC =,ABC ∠的平分线交CD 于点F ,交的延长线于点E ,若2BF =,则线段EF 的长为( )A .4B .3C .83D .747.一次函数y kx b =+和反比例函数xb y k =的部分图象在同一坐标系中可能为( ) A . B . C . D . 8.如图,在平面直角坐标系中,直线y x =-与双曲线k y x=交于A 、B 两点,P 是以点(2,2)C 为圆心,半径长1的圆上一动点,连结AP ,Q 为AP 的中点.若线段OQ 长度的最大值为2,则k 的值为( )A .12-B .32-C .2-D .14- 9.如图,函数k y x=-与1y kx =+(0k ≠)在同一平面直角坐标系中的图像大致( )A .B .C .D .10.已知反比例函数y=21k x+的图上象有三个点(2,1y ), (3, 2y ),(1-, 3y ),则1y ,2y ,3y 的大小关系是( )A .1y >2y >3yB .2y >1y >3yC .3y >1y >2yD .3y >2y >1y 11.在函数()0k y k x=<的图象上有()11,A y ,()21,B y -,()32,B y -三个点,则下列各式中正确的是( )A .123y y y <<B .132y y y <<C .321y y y <<D .231y y y <<12.已知1(3A -,1)y 、1(2B -,2)y 、3(1,)C y 是一次函数3y x b =-+的图象上三点,则1y ,2y ,3y 的大小关系是( )A .123y y y <<B .213y y y <<C .312y y y <<D .321y y y <<二、填空题13.如图,△ABC 中,∠C =90°,BC =8cm ,AC =6cm ,点P 沿BC 边以2cm/s 的速度从点B 向点C 移动,同时点Q 沿CA 边以1cm/s 的速度从点C 向点A 移动.若以点C 、P 、Q 构成的三角形与△ABC 相似,则运动时间为____________秒.14.如图,在正方形ABCD 中,4AB =,P 是BC 边上一动点(不与B ,C 重合),DE AP ⊥于E .若PA x =,DE y =,则y 关于x 的函数解析式为_____.15.如图,矩形ABCD 中,2AB =,E 为CD 的中点,连接AE 、BD 交于点P ,过点P 作PQ BC ⊥于点Q ,则PQ =________.16.如图,在矩形ABCD 中,M N 、分别是边AD BC 、的中点,点P Q 、在DC 边上,且14PQ DC =.若8,10AB BC ==,则图中阴影部分的面积是_____________17.有5张正面分别有数字-1,14-,0,1,3的卡片,它们除数字不同外全部相同,将它们背面朝上,洗匀后从中随机的抽取一张.记卡片上的数字为a ,则使以x 为自变量的反比例函数37a y x-=经过二、四象限,且关于x 的一元二次方程2230ax x -+=有实数解的概率是__________. 18.如图,矩形ABCD 的边AB 与x 轴平行,顶点A 的坐标为(2,1),点B ,D 都在反比例函数6y x=的图像上,则矩形ABCD 的面积为_____.19.如图,△DEF 的三个顶点分别在反比例函数=xy n 与()0,0xy m x m n =>>>的图象上,若DB ⊥x 轴于B 点,FE ⊥x 轴于C 点,若B 为OC 的中点,△DEF 的面积为6,则m 与n 的关系式是____.20.如图,在平面直角坐标系中,菱形ABCD 的顶点A 、B 在反比例函数y k x=(k >0,x >0)的图象上,横坐标分别为1,4,对角线BD ∥x 轴,若菱形ABCD 的面积为9.则k 的值为____.三、解答题21.如图是一块三角形钢材ABC ,其中边60cm BC =,高40cm AD =,把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB ,AC 上,这个正方形零件的边长是多少?22.如图,Rt △ABO 的顶点A 是双曲线y =k x 与直线y =﹣x +(k +1)在第四象限的交点,AB ⊥x 轴于点B ,且S △ABO =32.(1)求这两个函数的表达式;(2)求直线与双曲线的交点A和C的坐标及△AOC的面积.(3)写出反比例函数y=kx的值大于一次函数y=﹣x+(k+1)时的x的取值范围.23.如图,一次函数y=ax+b的图象与反比例函数y=kx的图象交于M(-3,1),N(1,n)两点.(1)求这两个函数的表达式;(2)过动点C(m,0)且垂直于x轴的直线与一次函数及反比例函数的图象分别交于D、E两点,当点E位于点D上方时,直接写出m的取值范围.24.如图,已知在平面直角坐标系中,O是坐标原点,点A(2,5)在反比例函数1kyx的图象上.一次函数y2=x+b的图象过点A,且与反比例函数图象的另一交点为B.(1)求反比例函数和一次函数的解析式;(2)连结OA和OB,求△OAB的面积;(3)根据图象直接写出y1>y2时,x的取值范围.25.如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.(1)当矩形DEFG是正方形时,求正方形的边长.(2)设EF=x,矩形DEFG的面积为S,求S关于x的函数关系式,当x为何值时S有最大值,并求出最大值.26.如图,在ABC ∆中,点D 、E 、F 分别在AB 、AC 、BC 上,DE //BC ,EF //AB .(1)求证:ADE ∆∽EFC ∆;(2)如果6AB =,4=AD,求ADE EFCS S ∆∆的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段,对每一项进行分析即可.【详解】解:A 、2×8≠4×6,故本选项错误;B 、10×40≠20×30,故选项错误;C 、2.2×8≠3.3×5,故选项错误;D 、20×60=30×40,故本选项正确.故选:D .【点睛】此题考查了比例线段,用到的知识点是成比例线段的概念,注意在相乘的时候,最小的和最大的相乘,另外两个相乘,看它们的积是否相等.2.D解析:D【分析】证明AFE △≌△()DFP AAS ,推出=AE DP ,由:2:1AE BE =,设BE k =,2AE k =,推出3AB CD k ==,5PC k =,由//AE BC ,可得AG AE GC CP =的值. 【详解】∵四边形ABCD 是平行四边形,∴//AB PC ,AB CD =,∴AEF P ∠=∠,∵AFE DFP ∠=∠,AF DF =,∴AFE △≌△()DFP AAS ,∴=AE DP ,∵:2:1AE BE =,设BE k =,2AE k =,∴3AB CD k ==,5PC k =,∵//AE BC , ∴2255AG AE k GC CP k ===, 故选:D .【点睛】 本题考查了平行四边形的性质,全等三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是学会利用已知条件证明三角形全等、利用参数解决问题,属于中考常考题型.3.C解析:C【分析】根据同一时刻,物体的实际高度和影长成正比例列出比例式即可解答.【详解】解:如图,假设没有墙,电线杆AB 的影子落在E 处,∵同一时刻,物体的实际高度和影长成正比例,∴CD :DE=1:0.5=2:1,∴AB :BE=2:1,∵CD=2,BE=BD+DE ,∴BE=3+1=4,∴AB :4=2:1,∴AB=8,即电线杆AB 的高为8米,故选:C .【点睛】本题考查了相似三角形的应用、比例的性质,解答的关键是理解题意,将实际问题转化为相似三角形中,利用同一时刻,物体的实际高度和影长成正比例列出方程求解. 4.B解析:B【分析】先根据DE ∥BC ,得出ADE ∽ABC ,进而得出1=4AD DE AB BC = ,再根据DE ∥BC ,得到ODE ∽OCB ,进而得到1=1:44OE DE OB CB ==. 【详解】解:∵DE ∥BC , ∴ADE ∽ABC , ∴=AD DE AB BC, 又∵1=3AD BD , ∴1=4AD DE AB BC =, ∵DE ∥BC , ∴ODE ∽OCB , ∴1=1:44OE DE OB CB ==. 故选:B .【点睛】 本题主要考查了相似三角形的判定与性质,平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.5.A解析:A【分析】根据DE ∥AC 可得到△DOE ∽△COA 和△DBE ∽△ABC ,再根据相似三角形的性质即可得出12BE EC =,再根据同高三角形的面积比等于底之比即可求出. 【详解】∵DE ∥AC∴△DOE ∽△COA ,△DBE ∽△ABC∵S △DOE :S △COA =1:9 ∴13DE AC = ∴13DE BE AC BC == ∴12BE EC = ∴S △BDE :S △CDE =1:2故答案选A .【点睛】本题主要考察了相似三角形的性质,准确记住面积比等于相似比平方是解题关键. 6.C解析:C【分析】平行四边形的对边相等且平行,利用平行四边形的性质以及平行线的基本性质求解.【详解】解:∵平行四边形ABCD∴AD ∥CB ,AD=BC=4.∴∠CBE=∠AEB∵∠ABC 的平分线交AD 于点E∴∠ABE=∠CBE∴∠ABE=∠AEB∴AE=AB=7∴DE=AE-AD=7-3=4.∵AD ∥CB ,∴△DEF ∽△CBF ∴EF DE BF BC= ∴423EF = 即83EF = 故选:C .【点睛】 本题主要考查了平行四边形的性质和相似三角形的性质和判定,掌握相关知识是解题的关键.7.C解析:C【分析】运用一次函数和反比例函数的图象性质逐项分析即可.先观察反比函数看k 、b 是同号还是异号,再由一次函数图象判断k 、b 是同号还是异号,如果两者相一致就是正确选项,否则是错误选项.【详解】【点睛】 此题考查反比例函数和一次函数的图象特点.其关键是要弄清图象特点与关系式中k 、b 同号还是异号.8.A解析:A【分析】连接BP ,证得OQ 是△ABP 的中位线,当P 、C 、B 三点共线时PB 长度最大,PB=2OQ=4,设 B 点的坐标为(x ,-x ),根据点(2,2)C ,可利用勾股定理求出B 点坐标,代入反比例函数关系式即可求出k 的值.【详解】解:连接BP ,∵直线y x =-与双曲线k y x=的图形均关于直线y=x 对称, ∴OA=OB ,∵点Q 是AP 的中点,点O 是AB 的中点∴OQ 是△ABP 的中位线,当OQ 的长度最大时,即PB 的长度最大,∵PB≤PC+BC ,当三点共线时PB 长度最大,∴当P 、C 、B 三点共线时PB=2OQ=4,∵PC=1,∴BC=3,设B 点的坐标为(x ,-x ),则()()22BC=2-23x x ++=, 解得1222,22x x ==-(舍去) 故B 点坐标为22,⎛⎫- ⎪ ⎪⎝⎭, 代入k y x=中可得:12k =-, 故答案为:A .【点睛】本题考查三角形中位线的应用和正比例函数、反比例函数的性质,结合题意作出辅助线是解题的关键.9.B解析:B【分析】分k >0和k <0两种情况分类讨论即可确定正确的选项.【详解】解:当k >0时,函数1y kx =+的图象经过一、二、三象限,反比例函数k y x =-的图象分布在二、四象限,没有选项符合题意;当0k <时,函数1y kx =+的图象经过一、二、四象限,反比例函数k y x =-的图象分布在一、三象限,B 选项正确,故选:B.【点睛】考查了反比例函数和一次函数的性质,解题的关键是能够分类讨论,难度不大. 10.A解析:A【分析】先判断出k 2+1是正数,再根据反比例函数图象的性质,比例系数k >0时,函数图象位于第一三象限,在每一个象限内y 随x 的增大而减小判断出y 1、y 2、y 3的大小关系,然后即可选取答案.【详解】解:∵k 2≥0,∴k 2+1≥1,是正数,∴反比例函数y =21k x+的图象位于第一三象限,且在每一个象限内y 随x 的增大而减小,∵(2,y 1),(3,y 2),(﹣1,y 3)都在反比例函数图象上,∴0<y 2<y 1,y 3<0,∴y 1>y 2>y 3.故选:A .【点睛】本题考查了反比例函数图象的性质,对于反比例函数y =k x(k ≠0),(1)k >0,反比例函数图象在一、三象限;(2)k <0,反比例函数图象在第二、四象限内,本题先判断出比例系数k 2+1是正数是解题的关键.11.B解析:B【分析】根据反比例函数图象上点的坐标特征得到11y k ⨯=,21y k -⨯=,32y k -⨯=,然后计算出1y 、2y 、3y 的值再比较大小即可.【详解】 解:(0)k y k x=<的图象上有1(1,)A y 、2(1,)B y -、3(2,)C y -三个点, 11y k ∴⨯=,21y k -⨯=,32y k -⨯=,1y k ∴=,2y k =-,312y k =-, 而k 0<,132y y y ∴<<.故选:B .【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数k y x=(k 为常数,且0k ≠)的图象是双曲线,图象上的点(),x y 的横纵坐标的积是定值k ,即xy k =.12.C解析:C【分析】 分别计算自变量为13-,12-和1时的函数值,然后比较函数值的大小即可. 【详解】 1(3A -,1)y 、1(2B -,2)y 、3(1,)C y 是一次函数3y x b =-+的图象上三点, 11y b ∴=+,232y b =+,33y b =-+. 3312b b b -+<+<+, 312y y y ∴<<.故选:C .【点睛】本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足其解析式.也考查了一次函数的性质.二、填空题13.或【分析】首先设点P 移动t 秒时△CPQ 与△ABC 相似然后分别从当即时△CPQ ∽△CBA 与当即时△CPQ ∽△CAB 去分析求解即可求得答案【详解】设点P 移动t 秒时△CPQ 与△ABC 相似∵点P 从点B 以2c 解析:125或3211【分析】 首先设点P 移动t 秒时△CPQ 与△ABC 相似,然后分别从当CP CQ CB CA =,即8286t t -=时,△CPQ ∽△CBA ,与当CQ CP CB CA =,即8286t t -=时,△CPQ ∽△CAB ,去分析求解即可求得答案.【详解】设点P 移动t 秒时△CPQ 与△ABC 相似,∵点P 从点B 以2cm/s 的速度向点C 移动,点Q 以1cm/s 的速度从点C 向点A 移动, ∴BP =2tcm ,CQ =tcm ,则CP =CB−BP =8−2t (cm ),∵∠C 是公共角,∴当CP CQ CB CA=,即8286t t -=时,△CPQ ∽△CBA , 解得:t =125; 当CQ CP CB CA=,即8286t t -=时,△CPQ ∽△CAB ,解得:t =3211, ∴点P 移动125s 或3211s 时△CPQ 与△ABC 相似. 故答案为:125或3211【点睛】 此题考查了相似三角形的判定.此题难度适中,注意掌握数形结合思想、分类讨论思想以及方程思想的应用.14.【分析】根据正方形的性质以及DE ⊥AP 即可判定△ADE ∽△PAB 根据相似三角形的性质即可列出y 与x 之间的关系式需要注意的是x 的范围【详解】解:∵四边形ABCD 为正方形∴∠BAD =∠ABC =90°∴∠解析:(164y x x =<< 【分析】根据正方形的性质以及DE ⊥AP 即可判定△ADE ∽△PAB ,根据相似三角形的性质即可列出y 与x 之间的关系式,需要注意的是x 的范围.【详解】解:∵四边形ABCD 为正方形,∴∠BAD =∠ABC =90°,∴∠EAD +∠BAP =90°,∠BAP +∠APB =90°,∴∠EAD =∠APB ,又∵DE ⊥AP ,∠AED =∠B =90°,∴△ADE ∽△PAB . ∴=AD DE AP AB ,即4=4y x∴(164y x x=<<.故答案为:(164y x x =<< 【点睛】 本题考查相似三角形,解题关键是熟练运用相似三角形的判定与性质,本题属于中等题型.15.【分析】根据矩形的性质得到AB ∥CDAB=CDAD=BC ∠BAD=90°根据线段中点的定义得到DE=CD=AB 根据相似三角形的性质即可得到结论【详解】解:∵四边形ABCD 是矩形∴AB ∥CDAB=CD 解析:43 【分析】 根据矩形的性质得到AB ∥CD ,AB=CD ,AD=BC ,∠BAD=90°,根据线段中点的定义得到DE=12CD=12AB ,根据相似三角形的性质即可得到结论. 【详解】解:∵四边形ABCD 是矩形,∴AB ∥CD ,AB=CD ,AD=BC ,∠BAD=90°,∵E 为CD 的中点,∴DE=12CD=12AB , ∴△ABP ∽△EDP ,∴AB PB DE PD =, ∴21PB PD = , ∴23PB BD = , ∵PQ ⊥BC ,∴PQ ∥CD ,∴△BPQ ∽△DBC ,∴23PQ BP CD BD ==, ∵CD=2, ∴PQ=43, 故答案为:43.【点睛】本题考查了相似三角形的判定和性质,矩形的性质,正确的识别图形是解题的关键. 16.【分析】连接MN 过点O 作于点E 交CD 于点F 先证明得到相似比是然后求出和的面积用矩形MNCD 的面积减去这两个三角形的面积得到阴影部分面积【详解】解:如图连接MN 过点O 作于点E 交CD 于点F ∵四边形ABC 解析:23【分析】连接MN ,过点O 作OE MN ⊥于点E ,交CD 于点F ,先证明OMN PQO ,得到相似比是4:1,然后求出OMN 和PQO 的面积,用矩形MNCD 的面积减去这两个三角形的面积得到阴影部分面积.【详解】解:如图,连接MN ,过点O 作OE MN ⊥于点E ,交CD 于点F ,∵四边形ABCD 是矩形,∴//AD BC ,AD BC =,∵M 、N 分别是边AD 、BC 的中点,∴DM CN =,∴四边形MNCD 是平行四边形,∴//MN CD ,∴OMN PQO ,相似比是:4:1MN PQ =,∴:4:1OE OF =, ∵152EF BC ==, ∴4OE =,1OF =, ∴184162MNO S =⨯⨯=,12112PQOS =⨯⨯=,8540MNCD S =⨯=, ∴4016123S =--=阴影.【点睛】本题考查相似三角形的性质和判定,解题的关键是掌握相似三角形的性质和判定. 17.【分析】根据反比例函数图象经过第二四象限关于x 的一元二次方程ax2-2x+3=0有实数解列出不等式求出a 的取值范围从而确定出a 的值再根据概率公式计算即可【详解】解:∵反比例函数图象经过第二四象限∴3解析:25【分析】根据反比例函数图象经过第二、四象限,关于x 的一元二次方程ax 2-2x+3=0有实数解,列出不等式求出a 的取值范围,从而确定出a 的值,再根据概率公式计算即可.【详解】解:∵反比例函数图象经过第二、四象限,∴3a-7<0,解得73a < 关于x 的一元二次方程ax 2-2x+3=0有实数解,则△=4-12a≥0,且a≠0,解得:,a≤13,且(a≠0),综上,a≤13,且(a≠0), ∴ a 可取-1,-14, ∴使以x 为自变量的反比例函数37a y x -=经过二、四象限,且关于x 的一元二次方程ax 2-2x+3=0有实数解的概率是25. 故答案为:25. 【点睛】 本题考查了概率公式,用到的知识点是反比例函数图象的性质、根的判别式、概率公式,熟记性质以及判别式求出a 的值是解题的关键.18.8【分析】根据A 点坐标及反比例解析式求出B 和D 点坐标进而得到矩形的长和宽即可求出面积【详解】解:∵A 点坐标为(21)∴D 点横坐标为2又D 点在反比例函数上∴D(23)B 点纵坐标为1又B 点在反比例函数上解析:8【分析】根据A 点坐标及反比例解析式求出B 和D 点坐标,进而得到矩形的长和宽,即可求出面积.【详解】解:∵A 点坐标为(2,1)∴D 点横坐标为2,又D 点在反比例函数6y x =上,∴D(2,3) B 点纵坐标为1,又B 点在反比例函数6y x=上,∴B(6,1) ∴AB=6-2=4,AD=3-1=2∴矩形ABCD 的面积=AB×AD=4×2=8.故答案为8.本题考查了反比例函数上点的坐标的求法及矩形的面积公式,熟练掌握反比例函数的图形性质是解决此类题的关键.19.【分析】设点D 点坐标根据B 是OC 的中点求出E 点坐标进而得到F 点坐标在根据梯形DFCB 的面积减去梯形DECB 的面积即可列出等量关系求解【详解】解:∵∴DE 所在的反比例函数是设由B 是OC 的中点可知E 点坐 解析:24-=m n【分析】设点D 点坐标,根据B 是OC 的中点,求出E 点坐标,进而得到F 点坐标,在根据梯形DFCB 的面积减去梯形DECB 的面积即可列出等量关系求解.【详解】解:∵n m <∴D 、E 所在的反比例函数是=xy n 设(,)n D a a ,由B 是OC 的中点可知E 点坐标为:(2,)2n a a,又F 点和E 点横坐标相同,且F 在=xy m 上, 故F 点坐标为:(2,)2m a a又11==()()22梯形梯形DECB ∆-+-+DEF DFCB S S S DB FC BC DB EC BC 111()()=()22224=+-+-n m n n a a m n a a a a 又∵△DEF 的面积为6 ∴1()64-=m n ∴24-=m n .故答案为:24-=m n【点睛】 本题考查了反比例函数上点的坐标运算,当两点在反比例函数上时,设其中一个点的坐标,则另一个点的坐标根据题中给定的等量关系用设好的坐标的代数式表示.20.2【分析】根据题意利用面积法求出AE 设出点B 坐标表示点A 的坐标应用反比例函数上点的横纵坐标乘积为k 构造方程求k 【详解】连接AC 分别交BDx 轴于点EF 由已知AB 横坐标分别为14∴BE=3∵四边形ABC解析:2.【分析】根据题意,利用面积法求出AE ,设出点B 坐标,表示点A 的坐标.应用反比例函数上点的横纵坐标乘积为k 构造方程求k .连接AC 分别交BD 、x 轴于点E 、F .由已知,A 、B 横坐标分别为1,4,∴BE =3.∵四边形ABCD 为菱形,AC 、BD 为对角线,∴S 菱形ABCD =412⨯AE •BE =9, ∴AE 32=,设点B 的坐标为(4,y ),则A 点坐标为(1,y 32+) ∵点A 、B 同在y k x =图象上, ∴4y =1•(y 32+), ∴y 12=, ∴B 点坐标为(4,12), ∴k =2故答案为:2.【点睛】 此题考查菱形的性质,反比例函数图象上点的坐标与k 之间的关系,解题关键在于掌握其性质定义.三、解答题21.24cm【分析】设正方形零件的边长为cm x .则 c m EG EF x ==,由题意易得KD EG x ==,进而可得AEF ABC ∽,然后根据相似三角形的性质可求解.【详解】解:设正方形零件的边长为cm x .则 c m EG EF x ==,由题可知,四边形KEGD 是矩形,∴KD EG x ==,∵AD AK KD =+,40AD =,∴40AK x =-,∵AD BC ⊥,∴90ADB ∠=︒,∵四边形EGHF 为正方形,∴//BC EF ,∴90AKE ∠=︒,∴AK EF ⊥,∵//BC EF ,∴AEF ABC ∽, ∴EF AK BC AD=, ∴406040x x -=, 解得24x =.即()24cm EG =,答:正方形零件的边长为24cm .【点睛】本题主要考查相似三角形的应用,熟练掌握相似三角形的性质与判定是解题的关键. 22.(1)y=3x -和y=-x-2;(2)交点A 为(1,-3),C 为(-3,1);4;(3)-3<x <0或x >1.【分析】(1)设出A 坐标(x ,y ),表示出OB 与AB ,进而表示出三角形ABO 面积,由已知面积确定出反比例函数k 的值,进而确定出一次函数;(2)联立反比例函数与一次函数解析式,求出A 与C 坐标即可;由一次函数解析式求出交点的坐标,然后三角形AOC 面积=两个三角形面积的和,求出即可;(3)根据图象即可求得.【详解】解:(1)设A 点坐标为(x ,y ),且x >0,y <0, 则113||||(),222ABO S OB AB x y ∆=⋅⋅=⋅⋅-= ∴xy=-3,∴k=xy=-3,代入y =﹣x +(k +1),得y=-x-2;∴所求的两个函数的解析式分别为y=3x-和y=-x-2; (2)解:求两个函数图象交点,得32y x y x ⎧=-⎪⎨⎪=--⎩ 13,?31x x y y ==-⎧⎧⎨⎨=-=⎩⎩∴交点A 为(1,-3),C 为(-3,1);由y=-x-2,令x=0,得y=-2.∴直线y=-x+2与y 轴的交点的坐标为(0,-2), 则112123422AOC S ∆=⨯⨯+⨯⨯= (3)∵交点A 为(1,-3),C 为(-3,1),∴由图象可知:反比例函数y=k x的值大于一次函数y=-x+(k+1)时, x 的取值范围为-3<x <0或x >1.【点睛】 此题考查了一次函数与反比例函数的交点问题,以及三角形面积,解题关键是熟练掌握待定系数法.23.(1)y=3x -;2y x =--;(2)m >1或-3<m <0 【分析】(1)把M 代入反比例函数的解析式即可求得k 的值,然后求得n 的值,利用待定系数法即可求得一次函数的解析式;(2)先画出两函数的图象,再根据两函数图象的上下位置关系结合交点的横坐标即可得出m 的取值范围.【详解】(1)∵点M (-3,1)和N (1,n )在反比例函数k y x =的图象上, ∴3k =-,3n =-.∴反比例函数表达式为3x=-, 点N 的坐标为N (1,3-),∵点M (-3,1)和N (1,3-)在一次函数y ax b =+的图象上,∴313a b a b -+=⎧⎨+=-⎩, 解得12a b =-⎧⎨=-⎩, ∴一次函数表达式为2y x =--;(2)一次函数2y x =--的图象与反比例函数3y x=-的图象相交于点M (-3,1)和N (1,3-),观察函数图象可知:若过动点C (m ,0)且垂直于x 轴的直线分别与反比例函数图象和一次函数图象交于E 、D 两点,当点E 位于点D 上方时,则m 的取值范围是:m >1或-3<m <0.【点睛】本题是反比例函数与一次函数的综合题,考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及待定系数法求函数解析式,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.24.(1)反比例函数110y x =,一次函数23y x =+(2)212(3)5x <-或02x << 【分析】(1)本题根据待定系数法,将点A 坐标代入函数解析式求解即可.(2)本题首先求得点B 的坐标,继而求解直线与坐标轴的交点坐标,最后利用割补法求解本题.(3)本题根据图像即可直接作答.【详解】(1)∵点(2,5)A 是直线2y x b =+与反比例函数1k y x =的图象的一个交点, ∴将A 点分别代入得:52b =+;52k =, ∴3b =,10k =.故反比例函数和一次函数的解析式分别为110y x =和23y x =+. (2)如下图所示:联立方程12103y x y x ⎧=⎪⎨⎪=+⎩,得25x y =⎧⎨=⎩或52x y =-⎧⎨=-⎩, ∴点(5,2)B --.∵点C 与点D 分别是直线23y x =+与y 轴的交点和与x 轴的交点,∴点(0,3)C ,点(3,0)D -,即3OD OC ==, ∴11213532222AOB AOD BOD S S S =+=⨯⨯+⨯⨯=. 故△OAB 的面积为212. (3)观察函数图象可知,12y y > 时,x 的取值范围为:5x <-或02x <<.【点睛】本题考查反比例函数与一次函数的综合,待定系数法求解解析式需要熟练掌握,其次求解不规则图形的面积通常利用割补法,比较函数大小时,利用图像法更为高效. 25.(1)409;(2)()254204S x =--+,当x =4时,S 有最大值20 【分析】(1)GF ∥BC 得△AGF ∽△ABC ,利用相似三角形对应边上高的比等于相似比,列方程求解;(2)根据相似三角形的性质求出GF =10−54x ,求出矩形的面积,运用二次函数性质解决问题.【详解】(1)设HK =y ,则AK =AH ﹣KH =AH ﹣EF =8﹣y ,∵四边形DEFG 为矩形,∴GF ∥BC ,∴△AGF ∽△ABC ,∴AK :AH =GF :BC ,∵当矩形DEFG 是正方形时,GF =KH =y ,∴(8﹣y):8=y :10,解得:y =409;(2)设EF =x ,则KH =x .∴AK =AH ﹣EF =8﹣x ,由(1)可知:8108GF x -=, 解得:GF =10﹣54x , ∴s =GF•EF =(10﹣54x )x =﹣54(x ﹣4)2+20, ∴当x =4时S 有最大值,并求出最大值20.【点睛】 本题考查了相似三角形的性质,二次函数的最值,矩形的性质的应用,注意:矩形的对边相等且平行,相似三角形的对应高的比等于相似比,题目是一道中等题,难度适中. 26.(1)证明见解析;(2)4.【分析】(1)根据平行线的性质可得∠A =∠CEF ,∠AED =∠C ,即可得结论;(2)根据线段的和差关系可得BD 的长,由DE //BC ,EF //AB 可得四边形DBFE 是平行四边形,根据平行四边形的性质可得EF 的长,根据相似三角形的面积比等于相似比的平方即可得答案.【详解】(1)∵DE//BC ,EF//AB ,∴∠A =∠CEF ,∠AED =∠C ,∴△ADE ∽△EFC .(2)∵AB =6,AD =4,∴DB =6-4=2,∵DE//BC ,EF//AB ,∴四边形DBFE 是平行四边形,∴EF =DB=2,∵△ADE ∽△EFC ,224()()42∆∆===ADE EFC S AD S EF . 【点睛】本题考查平行线的性质、平行四边形的判定与性质及相似三角形的判定与性质,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;相似三角形的面积比等于相似比的平方;熟练掌握相关判断定理及性质是解题关键.。
【人教版】初三数学下期中第一次模拟试卷带答案

一、选择题1.如图,在平行四边形ABCD 中,以对角线AC 为直径的圆O 分别交BC ,CD 于点M ,N ,若13AB =,14BC =,9CM =,则线段MN 的长为( )A .18013B .10C .12613D .1 2.如图,直线////a b c ,直线m 分别交直线a ,b ,c 于点A ,B ,C ,直线n 分别交直线a ,b ,c 于点D ,E ,F ,若23=AB BC ,则DE DF 的值为( )A .13B .23C .25D .353.如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图一定相似的有( )A .1个B .2个C .3D .4个 4.已知如图,DE 是△ABC 的中位线,AF 是BC 边上的中线,DE 、AF 交于点O .现有以下结论: ①DE ∥BC ;②OD =14BC ;③AO =FO ;④AOD S =14ABC S .其中正确结论的个数为( )A .1B .2C .3D .45.下列判断中,不正确的有( )A .三边对应成比例的两个三角形相似B .两边对应成比例,且有一个角相等的两个三角形相似C .有一个锐角相等的两个直角三角形相似D .有一个角是100°的两个等腰三角形相似6.如图,要使ABC ACD ∆∆,需补充的条件不能是( )A .ADC ACB ∠=∠B .ABC ACD ∠=∠ C .AD AC AC AB = D .AD BC AC DC ⋅=⋅ 7.下列函数中,y 总随x 的增大而减小的是( )A .4y x =-B .4y x =-C .4y x =D .4y x =- 8.下列式子中表示y 是x 的反比例函数的是( )A .24y x =-B .y=5x 2C .y=21xD .y=13x9.关于反比例函数3y x =,下列说法错误的是( ) A .图象关于原点对称 B .y 随x 的增大而减小C .图象分别位于第一、三象限D .若点(,)M a b 在其图象上,则3ab = 10.如图,在平面直角坐标系中,菱形OBCD 的边OB 在x 轴上,反比例函数()0k y x x=>的图象经过菱形对角线的交点,A 且与边BC 交于点F ,点C 的坐标为()8,4,则OBF ∆的面积为( )A .104B .83C .103D .11411.如图,菱形ABCD 的边AD 与x 轴平行,A 、B 两点的横坐标分别为1和3,反比例函数y=3x的图象经过A 、B 两点,则菱形ABCD 的面积是( )A .42B .4C .22D .2 12.如图,矩形ABCD 的顶点A ,B 在x 轴的正半轴上,反比例函数k y x =在第一象限内的图象经过点D ,交BC 于点E .若4AB =,2CE BE =,34AD OA =,则线段BC 的长度为( )A .1B .32C .2D .23二、填空题13.如图,已知Rt ABC 中,AC=b ,BC=a ,D 1是斜边AB 的中点,过D 1作D 1E 1⊥AC 于E 1,连结BE 1交CD 1于D 2;过D 2作D 2E 2⊥AC 于E 2,连结BE 2交CD 1于D 3;过D 3作D 3E 3⊥AC 于E 3,…,如此继续,可以依次得到点D 4,D 5,…,D n ,分别记BD 1E 1,BD 2E 2,BD 3E 3,…,BD n E n 的面积为S 1,S 2,S 3,…S n .则(1)1E C =__________,(2)S n =__________.14.如图,ABC 中,1BC =.若113AD AB =,且11//D E BC ,照这样继续下去,12113D D D B =,且22//D E BC ;23213D D D B =,且33//DE BC ;…;1113n n n D D D B --=,且//n n D E BC 则101101=D E _________.15.下列五组图形中,①两个等腰三角形;②两个等边三形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有_______(填序号)16.如图,ABC 是等边三角形,被一平行于BC 的矩形所截,AB 被截成三等分,则图中阴影部分的面积是ABC 的面积的______.17.如图,一次函数1y k x b =+的图象过点()0,4A ,且与反比例函数()20k y x x=>的图象相交于B 、C 两点,若2BC AB =,则12k k ⋅的值为______.18.反比例函数16y x =与2k y x=()0k <的图像如图所示,点P 是x 正半轴上一点,过点P 作x 轴的垂线,分别交反比例函数16y x =与2k y x =()0k <的图像于点A ,B ,若4AB PB =,则k 的值为_______.19.如图,已知双曲线(0)k y x x=>经过矩形OABC 边AB 的中点F ,交BC 于点E ,且四边形OEBF 的面积为2,则k =_______.20.若A 、B 两点关于y 轴对称,且点A 在双曲线y =12x上,点B 在直线y =x +6上,设点A 的坐标为(a ,b ),则a b b a +=_____. 三、解答题21.作图题:如图所示,图中的小方格都是边长为1的正方形,△ABC 与△A 'B 'C '是以点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O ;(2)△A 'B 'C '与△ABC 的位似比是 ;(3)以位似中心O 为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A 'B 'C '关于点O 中心对称的△A "B "C ",并直接写出△A "B "C "各顶点的坐标. 22.△ABC 在边长为1的正方形网格中如图所示.(1)以点C 为位似中心,作出△ABC 的位似图形△A 1B 1C 1,使其位似比为1:2.且△A 1B 1C 1位于点C 的异侧,并表示出A 1的坐标.(2)作出△ABC 绕点C 顺时针旋转90°后的图形△A 2B 2C 2.23.已知y 是x 的反比例函数,且当x =4时,1y =-.(1)求y 与x 之间的函数解析式;(2)求当132x -≤≤-时,y 的取值范围. 24.如图,直线y =12x 与双曲线y =k x (k >0)交于A 、B 两点,且点A 的横坐标为4. (1)求k 的值;(2)若双曲线y =k x(k >0)上一点C 的纵坐标为8,求△AOC 的面积.25.如图所示,一次函数y kx b =+的图象与反比例函数m y x=的图象交于A(-2,1),B(1,n)两点.(1)求反比例函数和一次函数的表达式;(2)求ABO ∆的面积; (3)根据图像直接写出当一次函数的值大于反比例函数的值时x 的取值范围.26.如图1,在矩形ABCD 中,AD =2,点E 是AD 的中点,连接BE ,且BE ⊥AC 交AC 于点F.(1)求证:△EAB∽△ABC;(2)求AB,EF的长;(3)如图2,连接DF,BD,求DFBD的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】连结AM,AN,根据圆周角定理可知△ABM是直角三角形,利用勾股定理即可求出AC的长;易证△AMN∽△ACD,根据相似三角形的性质即可求出MN的长.【详解】解:连结AM,AN,∵AC是⊙O的直径,∴∠AMC=90°,∠ANC=90°,∵AB=13,BM=5,∴22AB BM,∵CM=9,∴AC=15,∵∠MCA=∠MNA,∠MCA=∠CAD,∴∠MNA=∠CAD,∵∠AMN=∠ACN,∴∠AMN=∠ACN,∵△NMA∽△ACD,∴AM :MN=CD :AC ,∴12:MN=13:15,∴MN=18013. 故选:A .【点睛】本题考查了圆周角定理运用、勾股定理的运用、相似三角形的判定和性质,题目的综合性较强,难度中等,解题的关键是添加辅助线构造相似三角形.2.C解析:C【分析】 先由23AB BC =得出25AB AC =,再根据平行线分线段成比例定理即可得到结论. 【详解】 ∵23AB BC =, ∴25AB AC =, ∵a ∥b ∥c , ∴25DE AB DF AC ==, 故选:C .【点睛】 本题考查了平行线分线段成比例定理,掌握三条平行线截两条直线,所得的对应线段成比例是解题的关键.3.C解析:C【分析】根据相似多边形的判定定理对各个选项进行分析,从而确定最后答案.【详解】矩形的原图与外框不相似,因为其对应角的度数一定相同,但对应边的比值不一定相等,不符合相似的条件;锐角三角形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件;正五边形相似,因为它们的边长都对应成比例、对应角都相等,符合相似的条件;菱形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件. 综上,外框与原图一定相似的有3个,故选:C .【点睛】本题主要考查了相似图形的概念,注意边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形.4.C解析:C【分析】①根据三角形中位线定理进行判断;②根据三角形中位线定理进行判断;③根据三角形中位线定理进行判断;④由相似三角形△ADO ∽△ABF 的面积之比等于相似比的平方进行判断.【详解】∵DE 是△ABC 的中位线,∴DE ∥BC ,故①正确;∴DE=12BC , ∴OD=12BF , ∵AF 是BC 边上的中线,∴BF=12BC , ∴OD=12BF=14BC ,故②正确; ∵DE 是△ABC 的中位线,∴AD=DB ,DE ∥BC ,∴AO =FO ,故③正确;④∵DE ∥BC ,即DO ∥BF ,∴△ADO ∽△ABF , ∴22ADO ABF 1124S AD S AB ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, 又∵AF 是BC 边上的中线,∴ABF ABC 12SS =, ∴ADO ABC18S S =,故④错误. 综上所述,正确的结论是①②③,共3个.故选:C .【点睛】本题考查了三角形中位线定理、相似三角形的判定与性质.本题利用了“相似三角形的面积之比等于相似比的平方”的性质.正确的识别图形是解题的关键.5.B解析:B【分析】由相似三角形的判定依次判断可求解.【详解】解:A、三边对应成比例的两个三角形相似,故A选项不合题意;B、两边对应成比例,且夹角相等的两个三角形相似,故B选项符合题意;C、有一个锐角相等的两个直角三角形相似,故C选项不合题意;D、有一个角是100°的两个等腰三角形,则它们的底角都是40°,所以有一个角是100°的两个等腰三角形相似,故D选项不合题意;故选:B.【点睛】本题考查了相似三角形的判定,熟练运用相似三角形的判定是本题的关键.6.D解析:D【分析】要使两三角形相似,已知有一组公共角,则可以再添加一组角相等或添加该角的两边对应成比例.【详解】∵∠DAC=∠CAB∴当∠ACD=∠ABC或∠ADC=∠ACB或AD:AC=AC:AB时,△ABC∽△ACD.故选:D【点睛】本题考查相似三角形的判定方法的开放性的题,相似三角形的判定方法:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.7.A解析:A【分析】根据正比例函数的性质,可判断A;根据一次函数的性质,可判断B;根据反比例函数的性质,可判断C、D.【详解】A选项:y随x的增大而减小,符合题意,故A正确;B选项:y随x的增大而增大,不符合题意,故B错误;C选项:在每个象限内y随x的增大而减小,不符合题意,故C错误;D选项:在每个象限内y随x的增大而增大,不符合题意,故D错误.故选:A.【点睛】本题主要考查了反比例函数的增减性,关键是要注意反比例函数在叙述增减性时必须强调在每个象限内.8.D解析:D【分析】根据反比例函数的定义逐项分析即可.【详解】A. 24y x =-,y 是x 的一次函数,故不符合题意;B. y=5x 2,y 是x 的正比例函数,故不符合题意; C. 21y x=,y 是x²的反比例函数,故不符合题意; D. y=13x,y 是x 的反比例函数,符合题意; 故选:D .【点睛】 本题考查了反比例函数的定义,一般地,形如k y x=(k 为常数,k ≠0)的函数叫做反比例函数. 9.B解析:B【分析】根据题目中的函数解析式和反比例函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.【详解】解:∵反比例函数3y x=, ∴该函数图象关于原点轴对称,故选项A 正确;在每个象限内,y 随x 的增大而减小,故选项B 错误;该函数图象为别位于第一、三象限,故选项C 正确;若点M (a ,b )在其图象上,则ab=3,故选项D 正确;故选:B .【点睛】本题考查反比例函数的性质,解答本题的关键是明确题意,利用反比例函数的性质解答. 10.C解析:C【分析】根据菱形的性质可求出点A 坐标,将点A 的坐标代入到反比例函数解析式可求得k 值,即可确定函数的解析式,过点A 作AM ⊥x 轴于点M ,过点C 作CN ⊥x 轴于点N ,如图,首先在Rt △CNB 中,根据勾股定理建立方程求出OB 的长,进而可求得点B 的坐标,然后利用待定系数法可求得直线BC 的解析式,再联立直线和双曲线的解析式求出交点F 坐标,然后根据三角形的面积公式求解可.【详解】解:∵四边形OBCD 是菱形,∴OA =AC ,∵C (8,4),∴A (4,2),把点A (4,2)代入反比例函数()0k y x x =>,得到k =8,∴反比例函数的解析式为y =8x; 过点A 作AM ⊥x 轴于点M ,过点C 作CN ⊥x 轴于点N ,如图,设OB =x ,则BC =x ,BN =8﹣x ,在Rt △CNB 中,x 2﹣(8﹣x )2=42,解得:x =5,∴点B 的坐标为(5,0),设直线BC 的函数表达式为y =ax +b ,把点B (5,0),C (8,4)代入得:∴5084a b a b +=⎧⎨+=⎩,解得:43203a b ⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线BC 的解析式为42033y x =-, 解方程组420338y x y x⎧=-⎪⎪⎨⎪=⎪⎩,得:18x y =-⎧⎨=-⎩或643x y =⎧⎪⎨=⎪⎩, ∴点F 的坐标为F (6,43), 作FH ⊥x 轴于H ,连接OF ,∴S △OBF =12OB •FH =14105233⨯⨯=, 故选:C .【点睛】本题考查了菱形的性质、利用待定系数法求函数的解析式、两个函数的交点问题以及勾股定理等知识,属于常考题型,熟练掌握上述知识是解题的关键.11.A解析:A【分析】作AH ⊥BC 交CB 的延长线于H ,根据反比例函数解析式求出A 的坐标、点B 的坐标,求出AH 、BH ,根据勾股定理求出AB ,根据菱形的面积公式计算即可.【详解】如图,作AH ⊥BC 交CB 的延长线于H ,∵反比例函数y=3x 的图象经过A 、B 两点,A 、B 两点的横坐标分别为1和3, ∴A 、B 两点的纵坐标分别为3和1,即点A 的坐标为(1,3),点B 的坐标为(3,1), ∴AH=3﹣1=2,BH=3﹣1=2,由勾股定理得,AB=222222+=,∵四边形ABCD 是菱形,∴BC=AB=22,∴菱形ABCD 的面积=BC×AH=42,故选A .【点睛】本题考查的是反比例函数的系数k 的几何意义、菱形的性质,根据反比例函数解析式求出A 的坐标、点B 的坐标是解题的关键.12.B解析:B【分析】设OA 为4a ,则根据题干中的比例关系,可得AD=3a ,CE=2a ,BE=a ,从而得出点D 和点E 的坐标(用a 表示),代入反比例函数可求得a 的值,进而得出BC 长.【详解】设OA=4a根据2CE BE =,34AD OA =得:AD=3a ,CE=2a ,BE=a ∴D(4a ,3a),E(4a+4,a)将这两点代入解析得;444a k a a ⎪⎪⎨⎪=⎪+⎩解得:a=12∴BC=AD=32 故选:B【点睛】本题考查反比例函数和矩形的性质,解题关键是用含有字母的式子表示出点D 、E 的坐标,然后代入解析式求解.二、填空题13.b 【分析】根据直角三角形的性质以及相似三角形的性质利用在△ACB 中D2为其重心可得D2E1=BE1然后从中找出规律即可解答【详解】解:∵D1E1⊥ACBC ⊥AC ∴D1E1∥BC ∴∵D1是斜边AB 的中 解析:12b 22(1)ab n + 【分析】根据直角三角形的性质以及相似三角形的性质,利用在△ACB 中,D 2为其重心可得D 2E 1=13BE 1,然后从中找出规律即可解答. 【详解】解:∵D 1E 1⊥AC ,BC ⊥AC ,∴D 1E 1∥BC , ∴1111AE AD CE BD =, ∵D 1是斜边AB 的中点,∴AD 1=BD 1, ∴11111AE AD CE BD ==, ∵AC =b , ∴AE 1=E 1C =12b , ∵D 1E 1∥BC , ∴BD 1E 1与CD 1E 1同底同高,面积相等,以此类推;根据直角三角形的性质以及相似三角形的性质可知:D 1E 1=12BC ,CE 1=12AC ,S 1=22∴在ACB 中,D 2为其重心, ∴D 2E 1=13BE 1, ∴D 2E 2=13BC ,CE 2=13AC ,S 2=213S △ABC , ∵D 2E 2:D 1E 1=2:3,D 1E 1:BC =1:2,∴BC :D 2E 2=2D 1E 1:23D 1E 1=3, ∴CD 3:CD 2=D 3E 3:D 2E 2=CE 3:CE 2=3:4,∴D 3E 3=14D 2E 2=14×13BC =14BC ,CE 3=34CE 2=14×13AC =14AC ,S 3=214S △ABC …; ∴S n =21(1)n +S △ABC =21(1)n +×12ab =22(1)ab n +. 故答案为:12b ,22(1)ab n +.【点睛】此题主要考查相似三角形的判定与性质和三角形的重心等知识,解决本题的关键是根据直角三角形的性质以及相似三角形的性质得到第一个三角形的面积与原三角形的面积的规律.也考查了重心的性质即三角形三边中线的交点到顶点的距离等于它到对边中点距离的两倍.14.【分析】由D1E1∥BC 可得△AD1E1∽△ABC 然后由相似三角形的对应边成比例证得继而求得D1E1的长又由D1D2=可得AD2=继而求得D2E2的长同理可求得D3E3的长于是可得出规律则可求得答案解析:10121()3- 【分析】由D 1E 1∥BC ,可得△AD 1E 1∽△ABC ,然后由相似三角形的对应边成比例,证得111D E AD BC AB =,继而求得D 1E 1的长,又由D 1D 2= 113D B ,可得AD 2= 59AB ,继而求得D 2E 2的长,同理可求得D 3E 3的长,于是可得出规律,则可求得答案.【详解】解:∵D 1E 1∥BC ,∴△AD 1E 1∽△ABC , ∴111D E AD BC AB=, ∵BC=1,AD 113AB =, ∴D 1E 113=, ∵D 1D 2=113D B , ∴AD 2= 59AB , 同理可得:22254211()993D E ==-=-, 3331921()273D E ==-, ∴21().3n n n D E =-∴101101D E =10121()3-. 故答案为:10121()3-.【点睛】 此题考查了相似三角形的判定与性质.得到规律21().3nn n D E =-是关键. 15.②⑤【分析】根据相似图形的性质对各个选项逐个分析即可得到答案【详解】两个等腰三角形的顶角不一定相等故不一定相似;两个等边三角形一定相似;两个菱形的内角不一定相等故不一定相似;两个矩形的相邻边长比例不解析:②⑤【分析】根据相似图形的性质对各个选项逐个分析,即可得到答案.【详解】两个等腰三角形的顶角不一定相等,故不一定相似;两个等边三角形一定相似;两个菱形的内角不一定相等,故不一定相似;两个矩形的相邻边长比例不一定相等,故不一定相似;两个正方形一定相似;故答案为:②⑤.【点睛】本题考查了图形相似的知识;解题的关键是熟练掌握相似图形的性质,从而完成求解. 16.【分析】根据题意易证△AEH ∽△AFG ∽△ABC 利用相似三角形的性质解决问题即可【详解】解:∵AB 被截成三等分∴△AEH ∽△AFG ∽△ABC ∴∴S △AFG :S △ABC=4:9S △AEH :S △ABC= 解析:13【分析】根据题意,易证△AEH ∽△AFG ∽△ABC ,利用相似三角形的性质解决问题即可.【详解】解:∵AB 被截成三等分,∴△AEH ∽△AFG ∽△ABC , ∴11,,23AE AE AF AB ==, ∴S △AFG :S △ABC =4:9,S △AEH :S △ABC =1:9, ∴S 阴影部分的面积=49S △ABC -19S △ABC =13S △ABC , ∴图中阴影部分的面积是ABC 的面积的13. 故答案为:13. 【点睛】 本题主要考查了利用三等分点求得各相似三角形的相似比,从而求出面积比计算阴影部分的面积,难度适中.17.﹣3【分析】由题意可设一次函数的解析式为y =k1x+4然后联立两个函数的解析式可得等式k1x2+4x ﹣k2=0进而可根据根与系数的关系得出x1+x2=﹣x1x2=﹣再由可得点C 的横坐标是点B 横坐标的解析:﹣3【分析】由题意可设一次函数的解析式为y =k 1x +4,然后联立两个函数的解析式可得等式k 1x 2+4x ﹣k 2=0,进而可根据根与系数的关系得出x 1+x 2=﹣14k ,x 1x 2=﹣21k k ,再由2BC AB =可得点C 的横坐标是点B 横坐标的3倍,不妨设x 2=3x 1,然后对上述的两个式子整理变形即得结果.【详解】解:∵一次函数y =k 1x +b 的图象过点A (0,4),∴一次函数的解析式为y =k 1x +4,由k 1x +4=2k x,得k 1x 2+4x ﹣k 2=0, 设上述方程的两个实数根为x 1、x 2,则x 1+x 2=﹣14k , x 1x 2=﹣21k k , ∵BC =2AB ,∴点C 的横坐标是点B 横坐标的3倍,不妨设x 2=3x 1,∴x 1+x 2=4x 1=﹣14k ,x 1x 2=3x 12=﹣21k k , ∴221113k k k ⎛⎫⨯-=- ⎪⎝⎭,整理得:k 1k 2=﹣3. 故答案为﹣3.【点睛】本题考查了一次函数与反比例函数的交点、一元二次方程的根与系数的关系等知识,熟练掌握上述知识、掌握求解的方法是关键.18.-2【分析】设点A 横坐标为m 分别表示出ABPB 根据得到关于k 的方程解方程即可【详解】解:设点A 横坐标为m 则点A 纵坐标为∵AB ⊥x 轴∴点B 纵坐标为∴AB=PB=∵∴∴∴故答案为:-2【点睛】本题考查了解析:-2【分析】设点A 横坐标为m ,分别表示出AB 、PB ,根据4AB PB =,得到关于k 的方程,解方程即可.【详解】解:设点A 横坐标为m ,则点A 纵坐标为6m , ∵ AB ⊥x 轴,∴点B 纵坐标为k m , ∴AB =66k k m m m--= ,PB =k k m m =-, ∵4AB PB =, ∴64k k m m-=- , ∴64k k -=- ,∴2k =-.故答案为:-2【点睛】本题考查了反比例函数图象上点的表示,解题的关键是根据4AB PB =列出方程,注意表示PB 时,注意式子符号问题.19.2【分析】如果设F (xy )表示点B 坐标再根据四边形OEBF 的面积为2列出方程从而求出k 的值【详解】解:∵双曲线经过矩形边的中点设F (xy )E (ab )那么B (x2y )∵点E 在反比例函数解析式上∴S △C解析:2【分析】如果设F (x ,y ),表示点B 坐标,再根据四边形OEBF 的面积为2,列出方程,从而求出k 的值.【详解】解:∵双曲线(0)k y x x =>经过矩形OABC 边AB 的中点F 设F (x ,y ),E (a ,b ),那么B (x ,2y ),∵点E 在反比例函数解析式上,∴S △COE =12ab=12k , ∵点F 在反比例函数解析式上,∴S △AOF =12xy=12k ,即xy=k ∵S 四边形OEBF =S 矩形ABCO -S △COE -S △AOF ,且S 四边形OEBF =2,∴2xy-12k-12xy=2, ∴2k-12k-12k=2, ∴k=2.故答案为:2.【点睛】本题的难点是根据点F 的坐标得到其他点的坐标.在反比例函数上的点的横纵坐标的积等于反比例函数的比例系数.20.70【分析】根据点关于y 轴对称的特点写出B 点坐标再把两点坐标分别代入所求关系式即可解答【详解】解:根据点A 在双曲线y =上得到2ab =1即ab =根据AB 两点关于y 轴对称得到点B (﹣ab )根据点B 在直线解析:70【分析】根据点关于y 轴对称的特点写出B 点坐标,再把两点坐标分别代入所求关系式即可解答.【详解】解:根据点A 在双曲线y =12x 上,得到2ab =1,即ab =12, 根据A 、B 两点关于y 轴对称,得到点B (﹣a ,b ).根据点B 在直线y =x +6上,得到a +b =6, ∴22a b a b b a ab++= =2()2a b ab ab+- =2162212-⨯=36112-=70.故答案为:70.【点睛】 此题考查了反比例函数、一次函数图象上点的坐标特征,能够根据解析式求得点的坐标之间的关系式;熟悉两个点关于y 轴对称的点的坐标关系:纵坐标不变,横坐标互为相反数;能够把要求的代数式变成和或积的形式.三、解答题21.(1)画图见解析;(2)1:2;(3)画图见解析;A "(6,0),B "(3,-2),C "(4,-4)【分析】(1)连接CC′并延长,连接BB′并延长,两延长线交于点O ;(2)由OB=2OB′,即可得出△A′B′C′与△ABC 的位似比为1:2;(3),连接B′O 并延长,使OB″=OB′,延长A′O 并延长,使OA″=OA′,C′O 并延长,使OC″=OC′,连接A″B″,A″C″,B″C″,则△A″B″C″为所求,从网格中即可得出△A″B″C″各顶点的坐标.【详解】解:(1)图中点O 为所求;(2)△A′B′C′与△ABC的位似比等于1:2;故答案为:1:2;(3)△A″B″C″为所求;A″(6,0);B″(3,-2);C″(4,-4).【点睛】此题考查了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.22.(1)图见解析;(3,﹣3);(2)图见解析.【分析】(1)首先找到A、B、C点对应点A1、B1、C1,然后连接即可;(2)利用网格特点和旋转的性质画出A、B的对应点A2、B2即可【详解】解:(1)如图,△A1B1C1所作,点A1的坐标为(3,﹣3);(2)如图,△A2B2C2为所作.【点睛】本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了旋转变换.23.(1)4yx=-;(2)4y83≤≤.【分析】(1)利用待定系数法确定反比例函数的解析式即可;(2)根据自变量的取值范围确定函数值的取值范围即可.【详解】解:(1)设反比例函数的解析式为kyx =,∵当x=4,y=-1,∴k=-1×4=-4,∴反比例函数的解析式为4yx=-;(2)当x=-3时,43y=,当x=-12时,y=8,∴当-3≤x≤-12时,y的取值范围是43≤y≤8.【点睛】本题考查了反比例函数的性质,求得反比例函数的解析式是解答本题的关键.24.(1)8;(2)15.【详解】解:(1)∵点A的横坐标为4,点A在直线y=12x上,∴点A的纵坐标为y=12×4=2,即A(4,2).又∵点A(4,2)在双曲线y=kx上,∴k=2×4=8;(2)∵点C在双曲线y=8x上,且点C纵坐标为8,∴C(1,8).如图,过点C作CM⊥x轴于M,过点A作AN⊥x轴于N.∵S△COM=S△AON=82=4,∴S△AOC=S四边形CMNA=12×(|y A|+|y C|)×(|x A|-|x c|)=15.【点睛】主要考查了待定系数法求反比例函数的解析式和反比例函数y=kx中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.25.(1)反比例函数的解析式是y=-2x,一次函数的解析式是y=-x-1;(2)1.5;(3)x<-2或0<x<1.【分析】(1)把A的坐标代入反比例函数的解析式即可求出反比例函数的解析式,把B的坐标代入求出B的坐标,把A、B的坐标代入一次函数y=kx+b即可求出函数的解析式;(2)求出C的坐标,求出△AOC和△BOC的面积,即可求出答案;(3)根据函数的图象和A、B的坐标即可得出答案.【详解】(1)∵把A(-2,1)代入y=mx得:m=-2,∴反比例函数的解析式是y=-2x∵B(1,n)代入反比例函数y=-2x得:n=-2,∴B的坐标是(1,-2),把A、B的坐标代入一次函数y=kx+b得:122k bk b-+⎧⎨-+⎩==,解得:k=-1,b=-1,∴一次函数的解析式是y=-x-1;(2)∵把y=0代入一次函数的解析式y=-x-1得:0=-x-1,x=-1∴C(-1,0),△AOB的面积S=S AOC+S△BOC=12×|-1|×1+12×|-1|×|-2|=1.5;(3)从图象可知:当一次函数的值大于反比例函数的值时x的取值范围x<-2或0<x<1.【点睛】本题是反比例函数与一次函数的综合题,考查了用待定系数法求一次函数的解析式,根据函数图像判断不等式解集等知识点的综合运用,以及学生的计算能力和观察图形的能力,运用了数形结合思想.26.(1)见解析;(2)AB =EF ;(3)3【分析】 (1)根据矩形的性质得出90EAB ABC ∠=∠=︒和∠AEB =∠BAC ,即可证明结论;(2)由(1)的结论,得AB EA BC AB=,即可求出AB 的长,再由勾股定理求出BE 的长,再由△AEF ∽△CBF ,即可求出EF 的长;(3)由△AFE ∽△CFB 得12EF AE BF CB ==,证明3ED EF BE ED ==,则△DEF ∽△BED ,即可求出结果.【详解】解:(1)∵四边形ABCD 为矩形,∴90BAE CBA ∠=∠=︒ ,AD ∥BC ,AD =BC ,AB ∥CD ,AB =CD ,∴90BAC CAE ∠+∠=︒,∵BE ⊥AC ,∴90CAE AEB ∠+∠=︒,∴∠AEB =∠BAC ,∴△EAB ∽△ABC ;(2)由(1)知△EAB ∽△ABC , ∴AB EA BC AB=, ∵AD =2,点E 是AD 的中点,∴AE =1,BC =2,∴22AB AE BC =⋅=, ∴AB =在Rt △ABE 中,BE =, ∵AD ∥BC ,∴△AEF ∽△CBF , ∴12EF AE BF CB ==,∴13EF BE ==; (3)∵AD ∥BC ,∴△AFE ∽△CFB , ∴12EF AE BF CB ==, ∴3BE EF ==∴3ED EF BE ED ==, ∵∠DEB =∠FED , ∴△DEF ∽△BED , ∴DF EF BD ED =,∴3DF BD =. 【点睛】本题考查相似三角形的性质和判定,解题的关键是掌握相似三角形的性质和判定.。
初三数学下期中第一次模拟试卷带答案

一、选择题1.如图,抛物线y =ax 2+bx +c 的顶点坐标为(1,﹣4a ),点A (4,y 1)是该抛物线上一点,若点B (x 2,y 2)是该抛物线上任意一点,有下列结论:①4a ﹣2b +c >0;②抛物线y =ax 2+bx +c 与x 轴交于点(﹣1,0),(3,0);③若y 2>y 1,则x 2>4;④若0≤x 2≤4,则﹣3a ≤y 2≤5a .其中,正确结论的个数是( )A .0B .1C .2D .32.在二次函数2y ax bx c =++中,函数值y 与自变量x 的部分对应值如下表 则m 的值为( ). x -2 -1 0 1 2 3 4 y72-1-2m27A .1B .-1C .2D .-23.抛物线222=++y x x 与y 轴的交点坐标为( ) A .(1,0)B .(0,1)C .(0,0)D .(0,2)4.如图,抛物线y =ax 2+bx +c 的对称轴是x =1,下列结论:①abc >0;②b 2﹣4ac >0; ③8a +c <0; ④5a +b +2c >0,正确的是( )A .①②③B .②③④C .①②④D .②③5.已知抛物线2y ax bx c =++(a ,b ,c 是常数0a ≠,1c >)经过点(2,0),其对称轴是直线12x =.有下列结论:①0abc >;②关于x 的方程20ax bx c ++=有两个不等的实数根;③12a <-.其中正确结论的个数是( ) A .0B .1C .2D .36.在同一直角坐标系中,一次函数y ax c =+和二次函数2y ax c =--的图象可能为( )A .B .C .D .7.如图,某河堤迎水坡AB 的坡比tan 1:3CAB i =∠=,堤高5BC m =,则坡面AB 的长是( )A .5mB .10mC .53mD .8m8.如图,Rt ABC △中,90ACB ∠=︒,CD AB ⊥,4tan 3B =,若10BC =,则AD 的长为( )A .6B .323C .7.5D .10 9.在ABC 中,90,13,12C AB BC ∠=︒==,则sin B 的值为( )A .1213B .512C .513D .13510.如图,在33⨯正方形网格中,ABC 的顶点都在格点上,则sin CAB ∠=( )A 3B .22C .12D 311.如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC =α,∠ADC =β,则竹竿AD 与AB 的长度之比为( )A .tan tan a βB .tan tan aβC .sin sin a βD .cos cos aβ12.如图,直线y =-33x +2与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 顺时针旋转60°后得到△AO'B',则点B'的坐标是( ) A .(4,23)B .(23,4)C .(3,3)D .(23+2,2)二、填空题13.已知将抛物线2y ax c =+向右平移2个单位,再向上平移3个单位后得到的抛物线经过点(0,5),则1234a c +-的值为______.14.当x >m 时,二次函数y =﹣x 2+3x 的函数值y 随x 的增大而减小,则实数m 的取值范围是_____.15.抛物线()20y ax bx c a =++≠的部分图象如图所示,其与x 轴的一个交点坐标为()4,0-,对称轴为1x =-,则0y >时,x 的取值范围________.16.将抛物线()214y x =+-向上平移a 个单位后得到的抛物线恰好与x 轴只有一个交点,则a 的值为_________;17.如图是我国古代数学家赵爽在注解《周牌算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形与二个正方形拼成的.如果大正方形的面积是125,小正方形面积是25,则cos θ的值为______.18.如图,在Rt ABC 中,C 90∠=︒,25AC =,2cos 3B =,则AB =______.19.如图,在边长为1的小正方形网格中,点A ,B ,C ,D 都在这些小正方形的顶点上,AB ,CD 相交于点O ,则cos ∠BOD =_____.20.在ABC 中,若213sin cos 02A B ⎛-+= ⎝⎭,则C ∠的度数是_____________.三、解答题21.如图,在矩形ABCD 中,AB =6cm ,BC =12cm ,点P 从点A 出发沿着AB 以每秒1cm 的速度向点B 移动;同时点Q 从点B 出发沿着BC 以每秒2cm 的速度向点C 运动.设△DPQ 的面积为S ,运动时间为t 秒.(1)用含t 的代数式表示出BP 的长为 cm ,CQ 的长为 cm ; (2)写出S 与t 之问的函数关系式;(3)当△DPQ 的面积最小时,请判断线段PQ 与对角线AC 的关系,并说明理由.22.如图,在平面直角坐标系中,已知抛物线252y ax bx =++与x 轴交于()5,0A ,()1,0B -两点,与y 轴交于点C .(1)求抛物线的解析式;(2)若点M 是抛物线的顶点,连接AM ,CM ,求AMC 的面积;(3)若点Р是抛物线上的一个动点,过点Р作PE 垂直y 轴于点E ,交直线AC 于点D ,过点D 作x 轴的垂线,垂足为点F ,连接EF ,当线段EF 的长度最短时,求出点P 的坐标.23.已知二次函数223(0)y mx mx m m =-->的图像与x 轴交于A ,B 两点(点A 在点B 左侧),顶点为C .(1)求A ,B 两点的坐标;(2)连接,BC AC ,若ABC 为等边三角形,求m 的值.24.如图,海中有一个小岛A ,它的周围25海里内有暗礁,今有货船由西向东航行,开始在A 岛南偏西60°的B 处,往东航行20海里后到达该岛南偏西45°的C 处后,货船继续向东航行,你认为货船在航行途中有没有触礁的危险.25.如图,已知△OAB ,点A 的坐标为(2,2),点B 的坐标为(3,0). (1)求sin ∠AOB 的值;(2)若点P 在y 轴上,且△POA 与△AOB 相似,求点P 的坐标.26.(1)计算:03tan 30|32|(2021)π︒++-(2)已知::9:11:15a b c =,且70a b c ++=.求a 的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】利用对称轴公式和顶点坐标得出﹣4a =a +b +c ,b =﹣2a ,c =﹣3a ,则可对①进行判断;抛物线解析式为y =ax 2﹣2ax ﹣3a ,配成交点式得y =a (x ﹣3)(x +1),可对②进行判断;根据二次函数对称性和二次函数的性质可对③进行判断;计算x =4时,y =5a ,则根据二次函数的性质可对④进行判断.解:①∵二次函数y =ax 2+bx +c (a ≠0)的顶点坐标为(1,﹣4a ),∴x =﹣2ba=1,且﹣4a =a +b +c , ∴b =﹣2a ,c =﹣3a ,∵抛物线开口向上,则a >0,∴4a ﹣2b +c =4a +4a ﹣3a =5a >0,故结论①正确; ②∵b =﹣2a ,c =﹣3a ,∴y =ax 2﹣2ax ﹣3a =a (x ﹣3)(x +1),∴抛物线y =ax 2+bx +c 与x 轴交于点(﹣1,0),(3,0),故结论②正确; ③∵点A (4,y 1)关于直线x =1的对称点为(﹣2,y 1), ∴当y 2>y 1,则x 2>4或x 2<﹣2,故结论③错误; ④当x =4时,y 1=16a +4b +c =16a ﹣8a ﹣3c =5a , ∴当0≤x 2≤4,则﹣4a ≤y 2≤5a ,故结论④错误. 故选:C . 【点睛】本题考查了二次函数的图象与性质,掌握二次函数图象与性质的相关知识并能灵活运用所学知识求解是解题的关键.2.B解析:B 【分析】根据二次函数的性质,结合题意,将0x =、1y =-代入到2y ax bx c =++,得c 的值;将1x =-、2y =和1x =、2y =-代入到21y ax bx =+-,通过求解二元一次方程,即可得到a 、b 的值,从而得到二次函数解析式,经计算即可得到答案. 【详解】根据题意,将0x =、1y =-代入到2y ax bx c =++,得1c =- ∴21y ax bx =+-将1x =-、2y =和1x =、2y =-代入到21y ax bx =+-,得1212a b a b --=⎧⎨+-=-⎩∴1a =,2b =- ∴221y x x =--当2x =时,222211m =-⨯-=- 故选:B . 【点睛】本题考查了二次函数、二元一次方程组的知识;解题的关键是熟练掌握二次函数、二元一次方程组的性质,从而完成求解.3.D【分析】令x=0,则y=2,抛物线与y 轴的交点为 (0,2) 【详解】 令x=0,则y=2,∴抛物线与y 轴的交点为(0,2), 故选:D . 【点睛】本题考查二次函数的图象及性质;熟练掌握二次函数的图象及性质,会求函数图象与坐标轴的交点是解题的关键;4.B解析:B 【分析】由函数图像与对称轴的方程结合可判断①,由抛物线与x 轴有两个交点,可判断②,由抛物线的对称轴为:1,2bx a=-= 可得2,b a =-结合图像可得当2x =-时,42y a b c =-+<0, 可判断③,由图像可得当2x =时,4+2y a b c =+>0,当1x =-时,y a b c =-+>0,两式相加可得:52a b c ++>0,可判断④,从而可得答案. 【详解】 解:图像开口向下, a ∴<0,12bx a==->0, b ∴>0,函数图像与y 轴交于正半轴,c ∴>0,abc ∴<0,故①不符合题意; 抛物线与x 轴有两个交点,24b ac ∴->0, 故②符合题意;抛物线的对称轴为:1,2bx a=-= 2,b a ∴=-当2x =-时,42y a b c =-+<0,()422a a c ∴-⨯-+<0,8a c ∴+<0,故③符合题意;当2x =时,4+2y a b c =+>0,当1x =-时,y a b c =-+>0,两式相加可得:52a b c ++>0,故④符合题意; 故选:.B 【点睛】本题考查的是抛物线的图像与系数之间的关系,二次函数的性质,掌握以上知识是解题的关键.5.C解析:C 【分析】由二次函数的对称性及题意可得该抛物线与x 轴的另一个交点坐标为()1,0-,进而可得抛物线的开口方向向下,则有a 0,b 0,c 0<>>,然后根据二次函数的性质可进行排除选项. 【详解】解:∵抛物线2y ax bx c =++(a ,b ,c 是常数0a ≠,1c >)经过点(2,0),其对称轴是直线12x =, ∴抛物线与x 轴的另一个交点的横坐标为12212⨯-=-, ∴该点坐标为()1,0-,∴抛物线的开口方向向下,即0a <, 根据“左同右异”可得0b >, ∴0abc <,故①错误;∴令y=0,则关于x 的方程20ax bx c ++=的解为:122,1x x ==-,故②正确; 根据根与系数的关系可得122cx x a==-, ∴21c a =->,解得12a <-,故③正确; ∴正确的个数有2个; 故选C . 【点睛】本题主要考查二次函数的图像与性质,熟练掌握二次函数的图像与性质是解题的关键.6.D解析:D 【分析】根据二次函数的开口方向,与y 轴的交点;一次函数经过的象限,与y 轴的交点可得相关图象. 【详解】解:∵一次函数经过y 轴上的(0,c ),二次函数经过y 轴上的(0,-c ),∴两个函数图象交于y 轴上的不同点,故A ,C 选项错误;当a <0,c <0时,二次函数开口向上,一次函数经过二、三、四象限,故B 选项错误; 当a <0,c >0时,二次函数开口向上,一次函数经过一、二、四象限,故D 选项正确; 故选:D . 【点睛】本题考查二次函数及一次函数的图象的性质;用到的知识点为:二次函数和一次函数的常数项是图象与y 轴交点的纵坐标;一次函数的一次项系数大于0,图象经过一、三象限;小于0,经过二、四象限;二次函数的二次项系数大于0,图象开口向上;二次项系数小于0,图象开口向下.7.B解析:B 【分析】根据坡比求出AC 的长度,再利用勾股定理求出AB 即可. 【详解】解:∵tanCAB BC i AC ==∠=,5BC m =, ∴AC =,∴10AB m ===,故选:B .【点睛】此题考查解直角三角形的实际应用,勾股定理,熟记坡比的计算公式是解题的关键.8.B解析:B 【分析】设DC=4x ,BD=3x ,根据勾股定理求CD ,再根据∠ACD=∠B ,用三角函数求AD . 【详解】解:∵CD AB ⊥,4tan 3DBB DC==,设DC=4x ,BD=3x , (3x )2+(4x )2=102, ∵x>0,解得x=2, ∴BD=6,CD=8∵∠ACD+∠BCD=90°,∠B+∠BCD=90°, ∴∠ACD=∠B , ∴4tan 3ACD ∠=, ∴43AD CD =,CD=8,∴323AD =, 故选:B .【点睛】 本题考查了三角函数,勾股定理等知识,解题关键是根据已知的正切值求出线段长. 9.C解析:C【分析】先根据勾股定理求得AC ,再根据正弦的定义求解即可;【详解】∵在ABC 中,90C ∠=︒,13AB =,12BC =,∴2213125AC =-=,∴5sin 13AC B AB ==; 故答案选C .【点睛】本题主要考查了勾股定理与解直角三角形,准确理解计算是解题的关键.10.B解析:B【分析】利用勾股定理可得AC 10,BC 5AB 5∠ABC =90°,在Rt △ABC 中求解sin ∠CAB 的值即可.【详解】由勾股定理,得:AC 221310+=BC 22125+=AB 22125+= ∵AB 2+BC 2=AC 2,∴∠ACB =90°,在Rt △ABC 中,sin ∠BAC =BC AC 510=22. 故选:B .【点睛】此题考查了特殊角的三角函数值,属于基础题,解答本题的关键是求出AB 、AC 、BC 的长度,判断出△ABC 是直角三角形.11.C解析:C【分析】先在Rt △ABC 和Rt △ADC 中,求出AB =sin AC a 、AD =sin AC β,再求长度之比即可. 【详解】解:在Rt △ABC 中,∵sin ∠ABC =AC AB ,即sinα=AC AB , ∴AB =sin AC a, 在Rt △ADC 中,∵sin ∠ADC =AC AD ,即sinβ=AC AD , ∴AD =sin AC β, ∴AD AB =sin sin ACAC βα=sin sin a β, 故选:C .【点睛】本题考查锐角的三角函数、解直角三角形的应用,借助中间参数AC ,利用正弦函数的定义求解是解答的关键.12.B解析:B【分析】根据直线解析式求出点A 、B 的坐标,从而得到OA 、OB 的长度,再求出∠OAB =30°,利用勾股定理列式求出AB ,然后根据旋转角是60°判断出AB′⊥x 轴,再写出点B′的坐标即可.【详解】令y =0,则−x +2=0, 解得x =,令x =0,则y =2,所以,点A (0),B (0,2),所以,OA =OB =2,∵tan ∠OAB =OB OA ==, ∴∠OAB =30°,由勾股定理得,AB 4==,∵旋转角是60°,∴∠OAB′=30°+60°=90°,∴AB′⊥x 轴,∴点B′(4).故选:B .【点睛】本题考查了坐标与图形性质−旋转,一次函数图象上点的坐标特征,勾股定理的应用,三角函数的应用,求出AB′⊥x 轴是解题的关键. 二、填空题13.【分析】首先求出平移后的抛物线的解析式把点(05)代入解析式得变形为再把变形为代入求值即可【详解】解:抛物线向右平移2个单位解析式为再向上平移3个单位后得到的抛物线解析式为∵抛物线经过点∴∴∴=故答 解析:【分析】首先求出平移后的抛物线的解析式2(2)3y a x c =-++,把点(0,5)代入解析式得435a c ++=,变形为42a c +=,再把1234a c +-变形为3(4)4a c +-代入求值即可.【详解】解:抛物线2y ax c =+向右平移2个单位,解析式为2(2)y a x c =-+,再向上平移3个单位后得到的抛物线解析式为2(2)3y a x c =-++∵抛物线经过点(0,5),∴435a c ++=∴42a c +=∴1234a c +-=3(4)4a c +- 324=⨯-64=-2=故答案为:2.【点睛】本题考查了二次函数的图象与几何变换,掌握旋转及平移的规律是解题的关键. 14.m≥【分析】根据题目中的函数解析式和二次函数的性质可以得到当x 为何值时y 随x 的增大而减小从而可以得到m 的取值范围【详解】解:∵二次函数y =﹣x2+3x =﹣(x ﹣)2+∴当x≥时y 随x 的增大而减小∵当解析:m ≥32 【分析】根据题目中的函数解析式和二次函数的性质,可以得到当x 为何值时,y 随x 的增大而减小,从而可以得到m 的取值范围.【详解】解:∵二次函数y =﹣x 2+3x =﹣(x ﹣32)2+94, ∴当x≥32时,y 随x 的增大而减小, ∵当x >m 时,二次函数y =﹣x 2+3x 的函数值y 随x 的增大而减小,∴m≥32, 故答案为:m≥32. 【点睛】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答. 15.或【分析】根据抛物线与x 轴的一个交点坐标和对称轴由抛物线的对称性可求抛物线与x 轴的另一个交点再根据抛物线的增减性可求当y <0时x 的取值范围【详解】解:∵抛物线y=ax2+bx+c (a≠0)与x 轴的一解析:4x <-或2x >【分析】根据抛物线与x 轴的一个交点坐标和对称轴,由抛物线的对称性可求抛物线与x 轴的另一个交点,再根据抛物线的增减性可求当y <0时,x 的取值范围.【详解】解:∵抛物线y=ax 2+bx+c (a≠0)与x 轴的一个交点坐标为(-4,0),对称轴为x=-1, ∴抛物线与x 轴的另一个交点为(2,0),由图象可知,当y >0时,x 的取值范围是x <-4或x >2.故答案为:x <-4或x >2.【点睛】本题考查了抛物线与x 轴的交点,二次函数的性质,关键是得到抛物线与x 轴的另一个交点.16.4【分析】根据上加下减左加右减的规律写出平移后抛物线的解析式由新抛物线恰好与x 轴有一个交点得到△由此求得的值【详解】抛物线y =(x+1)2﹣4向上平移a 个单位后得到的抛物线的解析式为y =(x+1)2解析:4【分析】根据“上加下减,左加右减”的规律写出平移后抛物线的解析式,由新抛物线恰好与x 轴有一个交点得到△0=,由此求得a 的值.【详解】抛物线y =(x +1)2﹣4向上平移a 个单位后得到的抛物线的解析式为y =(x +1)2﹣4+a ,即223y x x a =+-+∵新抛物线恰好与x 轴有一个交点,∴△()244430b ac a =-=--+= 解得4a =故答案为:4.【点睛】此题考查了抛物线与x 轴的交点坐标,二次函数图象与几何变换.由于抛物线平移后的形状不变,故a 不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.17.【分析】根据正方形的面积公式可得大正方形的边长为小正方形的边长为5再根据直角三角形的边角关系列式即可求解;【详解】∵大正方形的面积是125小正方形的面积为25∴大正方形的边长为小正方形的边长为5设直【分析】根据正方形的面积公式可得大正方形的边长为 ,小正方形的边长为5 ,再根据直角三角形的边角关系列式即可求解;【详解】∵ 大正方形的面积是125,小正方形的面积为25,∴ 大正方形的边长为,小正方形的边长为5 ,设直角三角形中θ所对的直角边为x ,则()(2225x x ++= , 解得:x 1=5,x 2=-10(舍去),∴ sin θ5,∴ cos θ ,. 【点睛】本题考查了解直角三角形的应用,勾股定理的证明,正方形的面积,难度适中. 18.6【分析】设BC=2x 根据余弦的定义用x 表示出AB 根据勾股定理列式计算得到答案【详解】解:设BC=2x 在Rt △ABC 中∠C=90°∴∴AB=3x 由勾股定理得AC2+BC2=AB2即(2)2+(2x )解析:6【分析】设BC=2x ,根据余弦的定义用x 表示出AB ,根据勾股定理列式计算,得到答案.【详解】解:设BC=2x ,在Rt △ABC 中,∠C=90°,2cos 3B =, ∴23BC AB =, ∴AB=3x ,由勾股定理得,AC 2+BC 2=AB 2,即(2+(2x )2=(3x )2,解得,x=2,∴AB=3x=6,故答案为:6.【点睛】本题考查的是锐角三角函数的定义,掌握锐角A 的邻边b 与斜边c 的比叫做∠A 的余弦是解题的关键.19.【分析】设左下角顶点为点F 取BF 的中点E 连接CEDE 由点C 为AF 的中点点E 为BF 的中点可得出进而可得出∠BOD =∠DCE 在△DCE 中由DC2=CE2+DE2可得出∠DEC =90°再利用余弦的定义即可解析:5【分析】设左下角顶点为点F ,取BF 的中点E ,连接CE ,DE ,由点C 为AF 的中点、点E 为BF 的中点可得出//CE AB ,进而可得出∠BOD =∠DCE ,在△DCE 中,由DC 2=CE 2+DE 2可得出∠DEC =90°,再利用余弦的定义即可求出cos ∠BOD 的值,此题得解.【详解】解:设左下角顶点为点F ,取BF 的中点E ,连接CE ,DE ,如图所示.∵点C为AF的中点,点E为BF的中点,∴//CE AB,∴∠BOD=∠DCE,在△DCE中,DC10,DE=2,CE2,∵DC2=CE2+DE2,∴∠DEC=90°,∴cos∠DCE=CECD25510=∴cos∠BOD55【点睛】本题考查了解直角三角形、勾股定理逆定理、余弦的定义、中位线以及平行线的性质,构造出含有一个锐角等于∠AOD的直角三角形是解题的关键.20.120°【分析】直接利用非负数的性质以及特殊角的三角函数值计算得出答案【详解】解:∵∴sinA-=0cosB-=0∴sinA=cosB=∴∠A=30°∠B=30°∴∠C的度数是:180°-30°-3解析:120°【分析】直接利用非负数的性质以及特殊角的三角函数值计算得出答案.【详解】解:∵213sin cos02A B⎛-+=⎝⎭,∴sinA-12=0,3,∴sinA=12,3∴∠A=30°,∠B=30°,∴∠C的度数是:180°-30°-30°=120°.故答案为:120°.【点睛】此题主要考查了非负数的性质以及特殊角的三角函数值,正确记忆相关数据是解题关键.三、解答题21.(1)(6-t),(12-2t);(2)S=t2-6t+36;(3)PQ∥AC,理由见解析【分析】(1)由题意可得出答案;(2)根据△PQD的面积=矩形ABCD的面积-△APD的面积-△PBQ的面积-△CDQ的面积可得出答案;(3)由二次函数的性质及中位线定理可得出答案.【详解】解:(1)根据题意得:AP=t(cm),BQ=2t(cm),则BP=(6-t)cm,CQ=(12-2t)cm,故答案为:(6-t),(12-2t);(2)∵BP=6-t(cm),CQ=12-2t(cm),∴△PQD的面积=矩形ABCD的面积-△APD的面积-△PBQ的面积-△CDQ的面积=12×6-12×12t-12×2t×(6-t)-12×6(12-2t)=t2-6t+36,∴S=t2-6t+36;(3)∵S=t2-6t+36=(t-3)2+27,且1>0,∴当t=3时,S最小;即经过3s时,△PQD的面积最小,此时,PQ∥AC.理由:∵t=3,∴AP=PB=3(cm),CQ=BQ=6(cm),∴PQ∥AC..【点睛】本题考查了矩形的性质,二次函数的最值,中位线定理,熟练掌握二次函数的性质是解题的关键.22.(1)y=−12x2+2x+52;(2)152;(3)(25,2)或(25-2)【分析】(1)利用二次函数的交点式,结合待定系数法即可求解;(2)△AMC的面积=S△MHC+S△MHA=12×MH×OA,即可求解;(3)点D在直线AC上,设点D(m,−12m+52),由题意得,四边形OEDF为矩形,故EF=OD,即当线段EF的长度最短时,只需要OD最短即可,进而求解.【详解】解:(1)令x=0,则y=52,即C(0,52),设抛物线的表达式为y=a(x−5)(x+1),将点C的坐标代入上式得:52=a(0−5)(0+1),解得a=−12,∴抛物线的表达式为:y=−12(x−5)(x+1)=−12x2+2x+52;(2)由抛物线的表达式得:顶点M(2,92),过点M作MH∥y轴交AC于点H,设直线AC的表达式为y=kx+t,则5205tk t⎧⎪⎨⎪⎩==+,解得:1252kt⎧-⎪⎪⎨⎪⎪⎩==,∴直线AC的表达式为:y=−12x+52,当x=2时,y=32,则MH=92−32=3,则△AMC的面积=S△MHC+S△MHA=12×MH×OA=12×3×5=152;(3)点D 在直线AC 上,设点D (m ,−12m +52), 由题意得,四边形OEDF 为矩形,故EF =OD ,即当线段EF 的长度最短时,只需要OD 最短即可,∴EF 2=OD 2=m 2+(−12m +52)2=54m 2−52m +254, ∵54>0,故EF 2存在最小值(即EF 最小),此时m =1, ∴点D (1,2),∵点P 、D 的纵坐标相同,∴2=−12x 2+2x +52,解得x =25± 故点P 的坐标为(25+2)或(25-,2).【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,是解题的关键.23.(1)(1,0)A -,(3,0)B ;(2)3m =【分析】(1)把y=0代入,解方程即可;(2)求出顶点坐标,过C 作CD AB ⊥于D ,求出CD 即可.【详解】解:(1)2230mx mx m --=,∵0m >,方程两边同时除以m 得, 2230x x --=解得,13x =,21x =-∴A ,B 两点的坐标分别为:(1,0)A -,(3,0)B .(2)抛物线223(0)y mx mx m m =-->的顶点横坐标为:212m x m -=-=, 把x=1代入223y mx mx m =--得,y=-4m ,抛物线的顶点C 的坐标为:(1,4)C m -由(1)得,AB=4,过C 作CD AB ⊥于D ,∵ABC 为等边三角形,∴AD=2,AC=4, ∴22224223CD AC AD =-=-=∵点C 在第四象限,∴423m =∴3m =. 【点睛】 本题考查求二次函数与x 轴交点,等边三角形的性质,解题关键是熟练的解一元二次方程,根据已知条件,找到坐标与线段的关系.24.货船在航行途中无触礁的危险【分析】过点A 作AD ⊥BC ,垂足为D ,解直角三角形即可得到结论.【详解】解:过点A 作AD BC ⊥,垂足为DABC 30∠=︒,ACD 45∠=︒CD AD x ∴==,3tan 30x BD x ==︒320BC BD CD x x ∴=-=-=解得10310x =+ 即:AD=10310+∵10310+>25所以货船在航行途中无触礁的危险. 【点睛】本题考查了解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.25.(1)22;(2)点P 的坐标为(0,3)或(0,83). 【分析】(1)证明∠AOB=45°,可得结论.(2)分两种情形,利用相似三角形的性质分别求解即可.【详解】解:(1)如图,过点A 作AH ⊥OB 于H .∵A (2,2),∴AH =OH =2,∴∠AOB =45°,∴sin ∠AOB =22. (2)由(1)可知,∠AOP =∠AOB =45°,OA =2,当△AOP′∽△AOB 时,OA OA =OP OB',可得OP ′=OB =3,∴P ′(0,3),当△AOP ∽△BOA 时,OA OB =OP OA,∴3, ∴OP =83, ∴P (0,83), 综上所述,满足条件的点P 的坐标为(0,3)或(0,83). 【点睛】本题考查相似三角形的性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.26.(1)3;(2)18【分析】(1)分别利用特殊角的三角函数值、绝对值的性质、零指数幂计算各部分即可求解; (2)设9a k =,11b k =,15c k =,利用70a b c ++=求出k 的值,即可求解.【详解】解:(1)原式3213=+=; (2)::9:11:15a b c =,91115a b c ∴== 设91115a b c k ===,则9a k =,11b k =,15c k = 70a b c ++=9111570k k k ∴++=2k ∴=18a ∴=.【点睛】本题考查实数的运算、比例的性质,掌握特殊角的三角函数值、绝对值的性质、零指数幂以及见比设参的方法是解题的关键.。
初三数学下期中第一次模拟试题附答案

初三数学下期中第一次模拟试题附答案一、选择题1.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于()A.B.C.D.2.已知反比例函数y=﹣6x,下列结论中不正确的是()A.函数图象经过点(﹣3,2)B.函数图象分别位于第二、四象限C.若x<﹣2,则0<y<3D.y随x的增大而增大3.在反比例函数y=1kx的每一条曲线上,y都随着x的增大而减小,则k的值可以是()A.-1B.1C.2D.34.如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段AC 的长为()A.43B.42C.6D.45.如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为()A.4B.3C.2D.16.观察下列每组图形,相似图形是()A .B .C .D .7.如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是()A.32OBCD=B .32αβ=C .1232SS=D.1232CC=8.如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞()A.8米B.9米C.10米D.11米9.如图,在平行四边形中,点在边上, 与相交于点,且,则与的周长之比为()A.1 : 2B.1 : 3C.2 : 3D.4 : 910.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为()A.12m B.13.5m C.15m D.16.5m11.在小孔成像问题中,如图所示,若为O到AB的距离是18 cm,O到CD的距离是6 cm,则像CD的长是物体AB长的()A.13B.12C.2倍D.3倍12.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是()A.360元B.720元C.1080元D.2160元二、填空题13.计算:cos245°-tan30°sin60°=______.14.如图,菱形ABCD的边AD与x轴平行,A、B两点的横坐标分别为1和3,反比例函数y=3x的图象经过A、B两点,则菱形ABCD的面积是_____;15.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是______步.16.已知反比例函数y=2mx,当x>0时,y随x增大而减小,则m的取值范围是_____.17.已知线段a=2厘米,c=8厘米,则线段a和c的比例中项b是______厘米.18.如图,将矩形ABCD折叠,折痕为EF,BC的对应边B'C′与CD交于点M,若∠B′MD=50°,则∠BEF的度数为_____.19.近视眼镜的度数(y 度)与镜片焦距(x 米)呈反比例,其函数关系式为120.y x =如果近似眼镜镜片的焦距0.3x =米,那么近视眼镜的度数y 为______.20.如图,l 1∥l 2∥l 3,AB=25AC ,DF=10,那么DE=_________________.三、解答题21.某学校数学兴趣小组想利用数学知识测量某座山的海拔高度,如图,他们在山腰A 处测得山顶B 的仰角为45°,他们从A 处沿着坡度为i=1 : 3的斜坡前进1000 m 到达D 处,在D 处测得山顶B 的仰角为58°,若点A 处的海拔为12米,求该座山顶点B 处的海拔高度,(结果保留整数,参考数据:tan 58°≈1.60,sin 58°≈0. 85,cos 58°≈0.53,3≈1. 732)22.如图,在ABC V 中,AB AC =,点E 在边BC 上移动(点E 不与点B ,C 重合),满足DEF B ∠=∠,且点D 、F 分别在边AB 、AC 上.(1)求证:BDE CEF △∽△.(2)当点E 移动到BC 的中点时,求证:FE 平分DFC ∠.23.如图,在平面直角坐标系中,正方形OABC 的顶点O 与坐标原点重合,其边长为2,点A ,点C 分别在轴,轴的正半轴上.函数2y x =的图象与CB 交于点D ,函数k y x=(k 为常数,0k ≠)的图象经过点D ,与AB 交于点E ,与函数2y x =的图象在第三象限内交于点F ,连接AF 、EF .(1)求函数k y x=的表达式,并直接写出E 、F 两点的坐标. (2)求△AEF 的面积. 24.如图,已知O 是原点,,B C 两点的坐标分别为()3,1-,()2,1.(1)以点O 为位似中心,在y 轴的左侧将OBC V 扩大为原来的两倍(即新图与原图的相似比为2),画出图形,并写出点,B C 的对应点的坐标;(2)如果OBC V 内部一点M 的坐标为(),x y ,写出点M 的对应点M '的坐标.25.如图,在四边形ABCD 中,AC 平分∠DAB ,AC 2=AB•AD ,∠ADC=90°,点E 为AB 的中点.(1)求证:△ADC ∽△ACB .(2)若AD=2,AB=3,求的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据作图可以证明△AOB是等边三角形,则∠AOB=60°,据此即可求解.【详解】连接AB,由图可知:OA=0B,AO=AB∴OA=AB=OB,即三角形OAB为等边三角形,∴∠AOB=60°,∴cos∠AOB=cos60°=.故选B.【点睛】本题主要考查了特殊角的三角函数值,正确理解△ABC是等边三角形是解题的关键.2.D解析:D【解析】【分析】根据反比例函数的性质及图象上点的坐标特点对各选项进行逐一分析即可.【详解】A、∵当x=﹣3时,y=2,∴此函数图象过点(﹣3,2),故本选项正确;B、∵k=﹣6<0,∴此函数图象的两个分支位于第二、四象限,故本选项正确;C、∵当x=﹣2时,y=3,∴当x<﹣2时,0<y<3,故本选项正确;D、∵k=﹣6<0,∴在每个象限内,y随着x的增大而增大,故本选项错误;故选:D.【点睛】本题考查的是反比例函数的性质,熟知反比例函数的增减性是解答此题的关键.3.A解析:A【解析】【分析】利用反比例函数的增减性,y 随x 的增大而减小,则求解不等式1-k>0即可.【详解】∵反比例函数y=1−kx 图象的每一条曲线上,y 随x 的增大而减小,∴1−k>0,解得k<1.故选A.【点睛】此题考查反比例函数的性质,解题关键在于根据其性质求出k 的值.4.B解析:B【解析】【分析】由已知条件可得ABC DAC ~V V ,可得出AC BC DC AC =,可求出AC 的长. 【详解】解:由题意得:∠B =∠DAC ,∠ACB =∠ACD,所以ABC DAC ~V V ,根据“相似三角形对应边成比例”,得AC BC DC AC=,又AD 是中线,BC =8,得DC=4,代入可得AC= 故选B.【点睛】本题主要考查相似三角形的判定与性质.灵活运用相似的性质可得出解答. 5.A解析:A【解析】【分析】根据互余角性质得∠PAM =∠PBC ,进而得△PAM ∽△PBC ,可以判断①;由相似三角形得∠APM =∠BPC ,进而得∠CPM =∠APB ,从而判断②;根据对角互补,进而判断③;由△APB ∽△NAB 得AP AN BP AB=,再结合△PAM ∽△PBC 便可判断④. 【详解】解:∵AP ⊥BN ,∴∠PAM+∠PBA =90°,∵∠PBA+∠PBC =90°,∴∠PAM =∠PBC ,∵∠PMA =∠PCB ,∴△PAM ∽△PBC ,故①正确;∵△PAM ∽△PBC ,∴∠APM=∠BPC,∴∠CPM=∠APB=90°,即PM⊥PC,故②正确;∵∠MPC+∠MBC=90°+90°=180°,∴B、C、P、M四点共圆,∴∠MPB=∠MCB,故③正确;∵AP⊥BN,∴∠APN=∠APB=90°,∴∠PAN+∠ANB=90°,∵∠ANB+∠ABN=90°,∴∠PAN=∠ABN,∵∠APN=∠BPA=90°,∴△PAN∽△PBA,∴AN PA BA PB=,∵△PAM∽△PBC,∴Al AP BC BP=,∴AN AM AB BC=,∵AB=BC,∴AM=AN,故④正确;故选:A.【点睛】本题考查了相似三角形的判定和性质,正方形的性质、四点共圆,同角的余角相等,判断出PM⊥PC是解题的关键.6.D解析:D【解析】【分析】根据相似图形的定义,形状相同,可得出答案.【详解】解:A、两图形形状不同,故不是相似图形;B、两图形形状不同,故不是相似图形;C、两图形形状不同,故不是相似图形;D、两图形形状相同,故是相似图形;故选:D.【点睛】本题主要考查相似图形的定义,掌握相似图形形状相同是解题的关键.7.D解析:D【解析】A选项,在△OAB∽△OCD中,OB和CD不是对应边,因此它们的比值不一定等于相似比,所以A选项不一定成立;=,所以B选项不成立;B选项,在△OAB∽△OCD中,∠A和∠C是对应角,因此αβC选项,因为相似三角形的面积比等于相似比的平方,所以C选项不成立;D选项,因为相似三角形的周长比等于相似比,所以D选项一定成立.故选D.8.C解析:C【解析】如图所示,AB,CD为树,且AB=13,CD=8,BD为两树距离12米,过C作CE⊥AB于E,则CE=BD=8,AE=AB-CD=6,在直角三角形AEC中,AC=10米,答:小鸟至少要飞10米.故选C.9.C解析:C【解析】【分析】根据已知可得到相似三角形,从而可得到其相似比,再根据相似三角形的周长比等于相似比就可得到答案.【详解】∵四边形ABCD是平行四边形,∴DC∥AB,CD=AB.∴△DFE∽△BFA,∵DE:EC=1:2,∴EC:DC=CE:AB=2:3,∴C△CEF:C△ABF=2:3.故选C.10.D解析:D【解析】【分析】利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明同学的身高即可求得树高AB.【详解】∵∠DEF=∠BCD=90°,∠D=∠D,∴△DEF∽△DCB,∴BC DC EF DE=,∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,∴由勾股定理求得DE=40cm,∴20 0.30.4 BC=,∴BC=15米,∴AB=AC+BC=1.5+15=16.5(米).故答案为16.5m.【点睛】本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型.11.A解析:A【解析】【分析】作OE⊥AB于E,OF⊥CD于F,根据题意得到△AOB∽△COD,根据相似三角形的对应高的比等于相似比计算即可.【详解】作OE⊥AB于E,OF⊥CD于F,由题意得,AB∥CD,∴△AOB∽△COD,∴CDAB=OFOE=13,∴像CD的长是物体AB长的1 3 .故答案选:A.【点睛】本题考查了相似三角形的应用,解题的关键是熟练的掌握相似三角形的应用.12.C解析:C【解析】【分析】根据题意求出长方形广告牌每平方米的成本,根据相似多边形的性质求出扩大后长方形广告牌的面积,计算即可.【详解】3m×2m=6m2,∴长方形广告牌的成本是120÷6=20元/m2,将此广告牌的四边都扩大为原来的3倍,则面积扩大为原来的9倍,∴扩大后长方形广告牌的面积=9×6=54m2,∴扩大后长方形广告牌的成本是54×20=1080元,故选C.【点睛】本题考查的是相似多边形的性质,掌握相似多边形的面积比等于相似比的平方是解题的关键.二、填空题13.0【解析】【分析】直接利用特殊角的三角函数值代入进而得出答案【详解】=故答案为0【点睛】此题主要考查了特殊角的三角函数值正确记忆相关数据是解题关键解析:0【解析】【分析】直接利用特殊角的三角函数值代入进而得出答案.【详解】2cos 45tan30sin60︒-︒︒=223311()023222-⨯=-= . 故答案为0.【点睛】 此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.14.【解析】【分析】作AH⊥BC 交CB 的延长线于H 根据反比例函数解析式求出A 的坐标点B 的坐标求出AHBH 根据勾股定理求出AB 根据菱形的面积公式计算即可【详解】作AH⊥BC 交CB 的延长线于H∵反比例函数y解析:42【解析】【分析】作AH ⊥BC 交CB 的延长线于H ,根据反比例函数解析式求出A 的坐标、点B 的坐标,求出AH 、BH ,根据勾股定理求出AB ,根据菱形的面积公式计算即可.【详解】作AH ⊥BC 交CB 的延长线于H ,∵反比例函数y =3x的图象经过A 、B 两点,A 、B 两点的横坐标分别为1和3, ∴A 、B 两点的纵坐标分别为3和1,即点A 的坐标为(1,3),点B 的坐标为(3,1),∴AH =3﹣1=2,BH =3﹣1=2,由勾股定理得,AB 2222+=2,∵四边形ABCD 是菱形,∴BC =AB =2,∴菱形ABCD 的面积=BC×AH =2, 故答案为2【点睛】本题考查的是反比例函数的系数k 的几何意义、菱形的性质,根据反比例函数解析式求出A 的坐标、点B 的坐标是解题的关键.15.【解析】【分析】如图根据正方形的性质得:DE∥BC 则△ADE∽△ACB 列比例式可得结论【详解】如图∵四边形CDEF 是正方形∴CD=EDDE∥CF 设ED=x 则CD=xAD=12-x∵DE∥CF∴∠AD解析:60 17.【解析】【分析】如图,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论.【详解】如图,∵四边形CDEF是正方形,∴CD=ED,DE∥CF,设ED=x,则CD=x,AD=12-x,∵DE∥CF,∴∠ADE=∠C,∠AED=∠B,∴△ADE∽△ACB,∴DEBC=ADAC,∴x5=12-x12,∴x=60 17,故答案为60 17.【点睛】本题考查了相似三角形的判定和性质、正方形的性质,设未知数,构建方程是解题的关键.16.m>2【解析】分析:根据反比例函数y=当x>0时y随x增大而减小可得出m﹣2>0解之即可得出m的取值范围详解:∵反比例函数y=当x>0时y随x 增大而减小∴m﹣2>0解得:m>2故答案为m>2点睛:本解析:m>2.【解析】分析:根据反比例函数y=2mx,当x>0时,y随x增大而减小,可得出m﹣2>0,解之即可得出m的取值范围.详解:∵反比例函数y =2m x-,当x >0时,y 随x 增大而减小,∴m ﹣2>0,解得:m >2.故答案为m >2. 点睛:本题考查了反比例函数的性质,根据反比例函数的性质找出m ﹣2>0是解题的关键.17.4【解析】∵线段b 是ac 的比例中项∴解得b =±4又∵线段是正数∴b=4点睛:本题考查了比例中项的概念利用比例的基本性质求两条线段的比例中项的时候负数应舍去解析:4【解析】∵线段b 是a 、c 的比例中项,∴216b ac ==,解得b =±4,又∵线段是正数,∴b =4. 点睛:本题考查了比例中项的概念,利用比例的基本性质求两条线段的比例中项的时候,负数应舍去.18.70°【解析】【分析】设∠BEF=α则∠EFC=180°﹣α∠DFE=∠BEF=α∠CFE=40°+α依据∠EFC=∠EFC 即可得到180°﹣α=40°+α进而得出∠BEF 的度数【详解】∵∠C=∠C解析:70°【解析】【分析】设∠BEF=α,则∠EFC=180°﹣α,∠DFE=∠BEF=α,∠C'FE=40°+α,依据∠EFC=∠EFC',即可得到180°﹣α=40°+α,进而得出∠BEF 的度数.【详解】∵∠C'=∠C=90°,∠DMB'=∠C'MF=50°,∴∠C'FM=40°,设∠BEF=α,则∠EFC=180°﹣α,∠DFE=∠BEF=α,∠C'FE=40°+α,由折叠可得,∠EFC=∠EFC',∴180°﹣α=40°+α,∴α=70°,∴∠BEF=70°,故答案为:70°.【点睛】本题考查了矩形的性质、折叠的性质,熟练掌握相关的性质是解题的关键.19.400【解析】分析:把代入即可算出y 的值详解:把代入故答案为400点睛:此题主要考查了反比例函数的定义本题实际上是已知自变量的值求函数值的问题比较简单解析:400【解析】分析:把0.3x =代入120y x=,即可算出y 的值.详解:把0.3x =代入120x, 400y =,故答案为400.点睛:此题主要考查了反比例函数的定义,本题实际上是已知自变量的值求函数值的问题,比较简单.20.【解析】试题解析::∵l1∥l2∥l3∴∵AB=AC ∴∴∵DF=10∴∴DE=4 解析:【解析】试题解析::∵l 1∥l 2∥l 3, ∴AB DE AC DF=. ∵AB=25AC , ∴25AB AC =, ∴25DE DF =. ∵DF=10, ∴2105DE =, ∴DE=4. 三、解答题21.1488米.【解析】【分析】过D 作DE ⊥BC 于点E ,作DF ⊥AC 于点F ,易知四边形DECF 为矩形,在Rt △ADF 中,利用三角函数可求出DF 和AF ,设BE=x 米,在Rt △BDE 中,利用三角函数可表示出DE 的长度,再根据AC=BC 建立方程求出x 的值,最后用BC 加上A 点的海拔高度即为B 处的海拔高度.【详解】解:如图,过D 作DE ⊥BC 于点E ,作DF ⊥AC 于点F ,∵DE ⊥BC ,DF ⊥AC ,∠C=90°∴四边形DECF 为矩形,∴DE=FC ,DF=EC∵山坡AD 的坡度为3∴∠DAF=30°, ∴1DF=AD sin 30=1000=5002⋅⨯o 米, 3AF=AD cos30=1000=5003⋅o 设BE=x 米,在Rt △BDE 中,∠BDE=58°, ∴BE DE=tan 58 1.6≈o x 米, 在Rt △ABC 中,∠BAC=45°,∴AC=BC∴AF+FC=BE+EC ,即50035001.6=+x x 解得400034000976-=≈x ∴BC=BE+EC=976+500=1476米∵A 处的海拔高度为12米,∴B 处的海拔高度为1476+12=1488米答:该座山顶点B 处的海拔高度为1488米.【点睛】本题考查解直角三角形的应用,作辅助线构造直角三角形,再根据三角函数建立方程是解题的关键.22.见解析【解析】试题分析:(1)由三角形内角和定理可得:∠BDE=180°-∠B-∠DEB ,∠CEF=180°-∠DEF-∠DEB ,结合∠B=∠DEF ,可得∠BDE=∠CEF ;由AB=AC 可得∠B=∠C ,由此即可证得:△BDE∽△CEF ;(2)由(1)中结论:△BDE ∽△CEF 可得:BE DE CF EF=,结合BE=EC 可得:CE DE CF EF=,再结合∠C=∠B=∠DEF ,证得:△DEF ∽△ECF ,由此可得∠DFE=∠EFC ,从而得到结论EF 平分∠DFC.试题解析:(1)∵AB AC =,∴B C ∠=∠,∵180BDE B DAB ∠=︒-∠-∠,180CEF DEF DEB ∠=︒-∠-∠,∵DEF B ∠=∠,∴BDE CEF ∠=∠,BDE CEF V V ∽.(2)∵BDE CEF V V ∽,∴BE DE CF EF=, ∵E 是BC 中点,BE CE =,∴CE DE CF EF=, ∵DEF B C ∠=∠=∠,∴DEF ECF V V ∽,∴DFE CFE ∠=∠,∴EF 平分DFC ∠.23.(1)2y x =,E (2,1),F (-1,-2);(2)32. 【解析】【分析】(1)先得到点D 的坐标,再求出k 的值即可确定反比例函数解析式;(2)过点F 作FG ⊥AB ,与BA 的延长线交于点G .由E 、F 两点的坐标,得到AE=1,FG=2-(-1)=3,从而得到△AEF 的面积.【详解】解:(1)∵正方形OABC 的边长为2,∴点D 的纵坐标为2,即y=2,将y=2代入y=2x ,得到x=1,∴点D 的坐标为(1,2). ∵函数k y x =的图象经过点D ,∴21k =,∴k=2, ∴函数k y x =的表达式为2y x =. (2)过点F 作FG ⊥AB ,与BA 的延长线交于点G .根据反比例函数图象的对称性可知:点D 与点F 关于原点O 对称∴点F 的坐标分别为(-1,-2),把x=2代入2y x=得,y=1; ∴点E 的坐标(2,1);∴AE=1,FG=2-(-1)=3,∴△AEF 的面积为:12AE•FG=131322⨯⨯= .24.(1)如图,OB C ''△即为所求,见解析;点B 的对应点的坐标为()6,2-,点C 的对应点的坐标为()4,2--;(2)点(),M x y 的对应点M '的坐标为()2,2x y --.【解析】【分析】(1)延长BO ,CO 到B′、C′,使OB′、OC′的长度是OB 、OC 的2倍.顺次连接三点即可;(2)从这两个相似三角形坐标位置关系来看,对应点的坐标正好是原坐标乘以-2的坐标,所以M 的坐标为(x ,y ),写出M 的对应点M′的坐标为(-2x ,-2y ).【详解】(1)如图,OB C ''△即为所求,点B 的对应点的坐标为()6,2-,点C 的对应点的坐标为()4,2--.(2)从这两个相似三角形坐标位置关系来看,对应点的坐标正好是原坐标乘以-2的坐标,所以M的坐标为(x,y),写出M的对应点M′的坐标为(-2x,-2y).【点睛】考查了直角坐标系和相似三角形的有关知识,注意做这类题时,性质是关键,看图也是关键.很多信息是需要从图上看出来的.25.(1)证明见解析;(2).【解析】【分析】(1)根据角平分线的定义得到∠DAC=∠CAB,根据相似三角形的判定定理证明;(2)根据相似三角形的性质得到∠ACB=∠ADC=90°,根据直角三角形的性质得到 CE=AE,根据等腰三角形的性质、平行线的判定定理证明=,由相似三角形的性质列出比例式,计算即可.【详解】(1)证明:∵AC 平分∠DAB,∴∠DAC=∠CAB,∵AC2=AB•A D,∴=,∴△ADC∽△ACB;(2)∵△ADC∽△ACB,∴∠ACB=∠ADC=90°,∵点 E 为 AB 的中点,∴CE=AE= AB= ,∴∠EAC=∠ECA,∴∠DAC=∠EAC,∴∠DAC=∠ECA,∴CE∥AD;∴==,∴=.【点睛】本题考查的是直角三角形的性质、平行线的判定、相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.。
【人教版】初三数学下期中第一次模拟试卷含答案
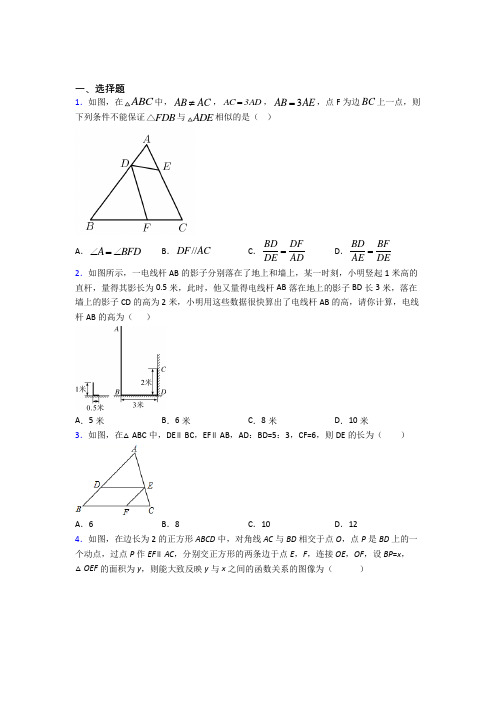
一、选择题1.如图,在ABC 中,AB AC ≠,AC 3AD =,3AB AE =,点F 为边BC 上一点,则下列条件不能保证FDB △与ADE 相似的是( )A .A BFD ∠=∠B .//DF AC C .BD DF DE AD = D .BD BF AE DE = 2.如图所示,一电线杆AB 的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB 落在地上的影子BD 长3米,落在墙上的影子CD 的高为2米,小明用这些数据很快算出了电线杆AB 的高,请你计算,电线杆AB 的高为( )A .5米B .6米C .8米D .10米 3.如图,在△ABC 中,DE ∥BC ,EF ∥AB ,AD :BD=5:3,CF=6,则DE 的长为( )A .6B .8C .10D .124.如图,在边长为2的正方形ABCD 中,对角线AC 与BD 相交于点O ,点P 是BD 上的一个动点,过点P 作EF ∥AC ,分别交正方形的两条边于点E ,F ,连接OE ,OF ,设BP =x ,△OEF 的面积为y ,则能大致反映y 与x 之间的函数关系的图像为( )A.B.C.D.5.下列条件中,不能判断△ABC与△DEF相似的是()A.∠A=∠D,∠B=∠F B.BC ACEF DF=且∠B=∠DC.AB BC ACDE EF DF==D.AB ACDE DF=且∠A=∠D6.如图所示,一般书本的纸张是原纸张多次对开得到,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,那么ADAB等于()A2B.22C.512D.27.如图,ABO中,∠ABO=45°,顶点A在反比例函数y=3x(x>0)的图象上,则OB2﹣OA2的值为()A .3B .4C .5D .6 8.与点()2,3-在同一反比例函数图象上的点是( ) A .()1.5,4- B .()1,6-- C .()6,1 D .()2,3-- 9.如图,在平面直角坐标系中,正方形ABCD 的顶点A 的坐标为(﹣1,1),点B 在x 轴正半轴上,点D 在第三象限的双曲线y =8x 上,过点C 作CE ∥x 轴交双曲线于点E ,则CE 的长为( )A .85B .235C .3.5D .510.如图,矩形ABCD 的顶点A ,B 在x 轴的正半轴上,反比例函数k y x =在第一象限内的图象经过点D ,交BC 于点E .若4AB =,2CE BE =,34AD OA =,则线段BC 的长度为( )A .1B .32C .2D .2311.如图,已知点A ,B 分别在反比例函数12y x =-和2k y x=的图象上,若点A 是线段OB 的中点,则k 的值为( ).A .8-B .8C .2-D .4-12.已知1(3A -,1)y 、1(2B -,2)y 、3(1,)C y 是一次函数3y x b =-+的图象上三点,则1y ,2y ,3y 的大小关系是( )A .123y y y <<B .213y y y <<C .312y y y <<D .321y y y <<二、填空题13.如图圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则:ABM AFM S S =△△___________.14.如图,////AB GH CD ,点H 在BC 上,AC 与BD 交于点G ,2AB =,3CD =,则GH 的长为 .15.下列五组图形中,①两个等腰三角形;②两个等边三形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有_______(填序号)16.如图,在Rt ABC ∆中,90ACB ∠=︒,//CD AB ,ABC ∠的平分线BD 交AC 于点E ,若10AB =,6BC =,则AE =_______.17.双曲线y=kx经过点A(a,﹣2a),B(﹣2,m),C(﹣3,n),则m_____n(>,=,<).18.如图,点M是反比例函数kyx=(0k>)的图像上一点,MP x⊥轴,垂足为点P,如果MOP△的面积为7,那么k的值是___________.19.如图,四边形OABC和ADEF均为正方形,反比例函数8yx=的图象分别经过AB的中点M及DE的中点N,则正方形ADEF的边长为___20.点A(a,b)是一次函数y=2x-3与反比例函数9yx=的交点,则2a2b-ab2=_____.三、解答题21.如图,在1010⨯的正方形网格中,每个小正方形的边长为1,建立如图所示的坐标系,ABC的三个顶点均在格点上.(1)若将ABC 沿x 轴对折得到111A B C △,则1C 的坐标为________.(2)以点B 为位似中心,将ABC 各边放大为原来的2倍,得到22A BC ,请在这个网格中画出22A BC .(3)在(2)的条件下,求22A BC 的面积是多少?22.如图,Rt ABC ∆中,90ACB ∠=︒,顶点A 、B 都在反比例函数()0k y x x=>的图象上,直线AC x ⊥轴,垂足为D ,连结OA ,使OA AB ⊥于A ,连结OC ,并延长交AB 于点E ,当2AB OA =时,点E 恰为AB 的中点,若()1,A n .(1)求反比例函数的解析式;(2)求EOD ∠的度数.23.如图,在平面直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象与反比例函数y =m x(x <0)的图象交于第二象限内的A 、B 两点,过点A 作AC ⊥x 轴于点C ,OA =5,OC =4,点B 的纵坐标为6.(1)求反比例函数和一次函数的解析式;(2)求△AOB 的面积;(3)写出kx +b ﹣m x<0的解集.24.如图,已知反比例函数y=kx的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.(1)求k和m的值;(2)若点C(x,y)也在反比例函数y=kx的图象上,当-3≤x≤-1时,求函数值y的取值范围.25.小芳从家骑自行车去学校,所需时间y(min)与骑车速度x(/m min)之间的反比例函数关系如图.(1)小芳家与学校之间的距离是多少?(2)写出y与x的函数表达式;(3)若小芳7点20分从家出发,预计到校时间不超过7点28分,请你用函数的性质说明小芳的骑车速度至少为多少?26.如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.(1)当矩形DEFG是正方形时,求正方形的边长.(2)设EF=x,矩形DEFG的面积为S,求S关于x的函数关系式,当x为何值时S有最大值,并求出最大值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】先根据已知条件可证得ADE ACB ∽,由此可得AED B ∠=∠,再利用相似三角形的判定对选项逐个判断即可.【详解】解:∵AC 3AD =,3AB AE =, ∴AD AE 1AC AB 3==, 又∵A A ∠=∠, ∴ADE ACB ∽,∴AED B ∠=∠, A 选项:∵A BFD ∠=∠,B B ∠=∠,∴BFD BAC ∽,故选项A 正确;B 选项:∵//DF AC ,∴C BFD ∠=∠,∠=∠A BDF ,∴BFD BCA △∽△,故选项B 正确; C 选项:BD DF DE AD=无法证明FDB △与ADE 相似; D 选项:∵BD BF AE DE=, AED B ∠=∠, ∴BFD EDA △∽△,故选项D 正确;故选:C .【点睛】 本题考查了相似三角形的判定及性质,熟练掌握相似三角形的判定是解决本题的关键. 2.C解析:C【分析】根据同一时刻,物体的实际高度和影长成正比例列出比例式即可解答.【详解】解:如图,假设没有墙,电线杆AB 的影子落在E 处,∵同一时刻,物体的实际高度和影长成正比例,∴CD :DE=1:0.5=2:1,∴AB :BE=2:1,∵CD=2,BE=BD+DE ,∴BE=3+1=4,∴AB :4=2:1,∴AB=8,即电线杆AB 的高为8米,故选:C .【点睛】本题考查了相似三角形的应用、比例的性质,解答的关键是理解题意,将实际问题转化为相似三角形中,利用同一时刻,物体的实际高度和影长成正比例列出方程求解. 3.C解析:C【分析】根据DE ∥BC ,EF ∥AB ,判断出DE BF =,在根据DE ∥BC ,EF ∥AB ,便可以找到分的线段成比例。
初三数学下期中第一次模拟试题含答案

一、选择题1.如图,在Rt ABC 中,90C ∠=︒,7AC =,24BC =,将它绕着BC 中点D 顺时针旋转一定角度后到A B C ''',恰好使//B C AB '',A C ''与边AB 交于点E ,则A E '的长为( )A .72B .4924C .8425 D .91252.如图,在菱形ABCD 中,660AB DAB =∠=︒,,A ,E 分别交BC 、BD 于点E 、F ,2CE =,连接CF ,以下结论:①ABF CBF ≌;②点E 到AB 的距离是23;③ADF 与EBF △的面积比为3∶2:④ABF 的面积为为1835,其中正确的是( )A .①④B .①③④C .①②④D .①②③④3.如图,在直角坐标系中,矩形OABC 的顶点O 在原点,边OA 在x 轴上,OC 在y 轴上,如果OA B ''△与OAB 关于点O 位似,且OA B ''△的面积等于OAB 面积的14,则点B '的坐标为( )A .3,12⎛⎫⎪⎝⎭B .3,12⎛⎫⎪⎝⎭或3,12⎛⎫-- ⎪⎝⎭C .()3,2D .()3,2或()3,2--4.下列条件中,不能判断△ABC 与△DEF 相似的是( )A .∠A =∠D ,∠B =∠F B .BC ACEF DF=且∠B =∠D C .AB BC ACDE EF DF== D .AB ACDE DF=且∠A =∠D 5.如图,地面上点A 处有一只兔子,距它10米的B 处有一根高1.6米的木桩,大树、木桩和兔子刚好在一条直线上.一只老鹰在9.6米高的树顶上刚好看见兔子,则大树C 离木桩B( )米.A .60B .50C .40D .456.下列相似图形不是位似图形的是( )A .B .C .D .7.如图,过反比例函数()0ky x x=>的图象上一点A 作AB x ⊥轴于点B ,连接AO ,若2AOB S =△,则k 的值为( )A .2B .3C .4D .58.函数y a x a =+与(0)ay a x=≠在同一直角坐标系中的图像可能是( ) A . B . C .D .9.在反比例函数13my x-=图象上有两点()11,A x y ,()22,B x y ,120x x <<,12y y <,则m 的取值范围是( )A .13m >B .13m <C .13m ≥D .13m ≤10.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,∠ABC=90°,CA ⊥x 轴,点C 在函数y=kx(x >0)的图象上,若AB=2,则k 的值为( )A .4B .2C .2D 211.反比例函数ky x=经过点(2,1),则下列说法错误..的是( ) A .2k =B .函数图象分布在第一、三象限C .当0x >时,y 随x 的增大而增大D .当0x >时,y 随x 的增大而减小12.对于反比例函数5y x=-,下列说法中不正确的是( ) A .图象经过点(1,5)-B .当0x >时,y 的值随x 的值的增大而增大C .图像分布在第二、四象限D .若点11()A x y ,,22()B x y ,都在图像上,且12x x <,则12y y <.二、填空题13.如图圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则:ABM AFM S S =△△___________.14.如图,已知菱形ABCD 的边长为4,点E 、F 分别是AB 、AD 上的点,若BE =AF =1,∠BAD =120°,GFEG=_____.15.如图,在ABC 中,//DE BC ,若9AB =,8AC =,3AD =,则EC 的长是______.16.如图,在平行四边形ABCD 中,点E 在边BC 上,EC =2BE ,连接AE 交BD 于点F ,若△BFE 的面积为2,则△AFD 的面积为_____.17.如图,边长为1的正方形OABC 中顶点B 在一双曲线上,请在图中画出一条过点B 的直线,使之与双曲线的另一支交于点D ,且满足线段BD 最短,则BD =________.18.如图,一次函数1y k x b =+的图象过点()0,4A ,且与反比例函数()20k y x x=>的图象相交于B 、C 两点,若2BC AB =,则12k k ⋅的值为______.19.如图,点M 是反比例函数ky x=(0k >)的图像上一点,MP x ⊥轴,垂足为点P ,如果MOP △的面积为7,那么k 的值是___________.20.设A (x 1,y 1),B (x 2,y 2)为函数21k y x-=图象上的两点,且x 1<0<x 2,y 1>y 2,则实数k 的取值范围是__.三、解答题21.作图题:如图所示,图中的小方格都是边长为1的正方形,△ABC 与△A 'B 'C '是以点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O ;(2)△A 'B 'C '与△ABC 的位似比是 ;(3)以位似中心O 为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A 'B 'C '关于点O 中心对称的△A "B "C ",并直接写出△A "B "C "各顶点的坐标. 22.下图是由边长为1的小正方形组成的5×4网格,A 、B 、C 、D 、E 、F 、P 、Q 均为网格格点,请用无刻度直尺作图,保留作图痕迹,不写画法. (1)在线段AB 上找到一点M ,使△AQM ≌△BPM. (2)在线段CD 上找点N ,使△ECN ∽△FDN.23.定义:有一组对角互补的四边形叫做互补四边形.(1)在互补四边形ABCD 中,A ∠与C ∠是一组对角,若::2:3:4,B C D ∠∠∠=则A ∠= °(2)如图,在ABC 中,点,D E 分别在边,AB BC 上,且,BE BC AB BD ⋅=⋅求证:四边形ADEC 是互补四边形.24.如图,已知点A (1,-2)在反比例函数y =kx的图象上,直线y =-x +1与反比例函数y =kx的图象的交点为点B 、D .(1)求反比例函数和直线AB 的表达式; (2)求S △AOB ;(3)动点P (x ,0)在x 轴上运动,若△OAP 是等腰三角形时,直接写出点P 的坐标. 25.实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y (毫克/百毫升)与时间A (时)成正比例;1.5小时后(包括1.5小时)B 与C 成反比例.根据图中提供的信息,解答下列问题:(1)求一般成人喝半斤低度白酒后,D 与x 之间的两个函数关系式及相应的自变量x 取值范围;(2)依据人的生理数据显示,当y ≥80时,肝部正被严重损伤,请问喝半斤低度白酒后,肝部被严重损伤持续多少小时?26.如图,一次函数1y x =+的图象与反比例函数ky x=的图象相交,其中一个交点的横坐标是2.(1)求反比例函数的表达式;(2)将一次函数1y x =+的图象向下平移2个单位,求平移后的图象与反比例函数k y x=图象的交点坐标;(3)直接写出一个一次函数,使其过点(0,5),且与反比例函数ky x=的图象没有公共点.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】过点D 作DF ⊥AB 于F ,易证四边形EFDC´是矩形,可得C´E=DF ,由勾股定理求得AB 的长,根据已知和相似三角形的判定可证明△ACB ∽△DFB ,可得AC ABDF BD=,J 进而求得DF 值,由A´E=A´C´﹣C´即可求解. 【详解】解:过点D 作DF ⊥AB 于F ,则∠DFB=90°,∵△ABC 绕着BC 中点D 顺时针旋转一定角度后到A B C ''',恰好使//B C AB '',∴∠C=∠C´=∠A´EB=90°,AC=A´C´=7,CD=BD=12, ∴四边形EFDC´为矩形, ∴C´E=DF ,∵在Rt △ACB 中,∠C=90°,AC=7,BC=24, ∴222272425AC BC +=+=,∵∠C=∠DFE ,∠B=∠B , ∴△ACB ∽△DFB , ∴AC AB DF BD =即72512DF =,∴DF=8425=C´E ,∴A´E=A´C´﹣C´E=7﹣8425=9125, 故选:D . 【点睛】本题考查了旋转的性质、矩形的判定与性质、相似三角形的判定与性质、勾股定理等知识,熟练掌握这些知识的灵活运用,添加恰当的辅助线是解答的关键.2.C解析:C 【分析】根据菱形的性质得出△ABF 和△CBF 全等的条件,从而可判断①成立;过点E 作EG ⊥AB ,过点F 作MH ⊥AB ,求得EG 的长度,则可判断②是否成立;由AD ∥BE ,可判定△ADF ∽△EBF ,由相似三角形的性质可得△ADF 与△EBF 的面积比,从而可判断③是否成立;利用相似三角形的性质和等边三角形的性质,可求得△ABF 在AB 边上的高,进而求得△ABF 的面积,则可判断④是否成立. 【详解】解:∵四边形ABCD 是菱形,AB=6, ∴BC=AB=6, ∵∠DAB=60°,∴AB=AD=DB=6,∠ABD=∠DBC=60°, 在△ABF 与△CBF 中,AB BC ABF FBC BF BF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABF ≌△CBF (SAS ),故①成立;如图,过点E 作EG ⊥AB 延长线于点G ;过点F 作MH ⊥AB 交AB ,CD 于点H ,M , 则由菱形的对边平行可得MH ⊥CD ,∵CE=2,BC=6,∠ABC=120°, ∴BE=6-2=4,∠EBG=60° ∵EG ⊥AB , ∴33= 故②成立; ∵AD ∥BE ,∴△ADF ∽△EBF ,∴2269()(),44ADF EBF S AD S BE ∆∆=== 故③不成立; ∵△ADF ∽△EBF ,32DF AD FB EB ∴== ∵DB=6, ∴BF= 125∴FH=125, ∴S △ABF =12AB•FH=162⨯=, 故④成立.综上所述,一定成立的有①②④. 故选:C . 【点睛】本题考查了菱形的性质、全等三角形的判定、相似三角形的判定与性质及三角形的面积计算,熟练掌握相关性质及定理是解题的关键.3.D解析:D 【分析】由OA B ''△与OAB 关于点O 位似,且OA B ''△的面积等于OAB 面积的14,利用相似三角形的面积比等于相似比的平方,即可求得OA B ''△与OAB 的位似比为1:2,又由点B 的坐标为(6,4),即可求得答案. 【详解】解:∵OA B ''△与OAB 关于点O 位似, ∴OA B ''△∽OAB ,∵OA B ''△的面积等于OAB 面积的14, ∴位似比为1:2, ∵点B 的坐标为(6,4),∴点B′的坐标是:(3,2)或(-3,-2). 故选D . 【点睛】此题考查了位似图形的性质.此题难度不大,注意位似图形是特殊的相似图形,注意掌握相似三角形的面积比等于相似比的平方定理的应用,注意数形结合思想的应用. 4.B解析:B【分析】直接根据三角形相似的判定方法分别判断得出答案.【详解】解:A 、A D ∠=∠,B F ∠=∠,根据有两组角对应相等的两个三角形相似,可以得出ABC DFE ∽△△,故此选项不合题意;B 、BC AC EF DF =,且BD ∠=∠,不是两边成比例且夹角相等,故此选项符合题意; C 、AB BC AC DE EF DF==,根据三组对应边的比相等的两个三角形相似,可以得出ABC DEF ∽△△,故此选项不合题意;D 、AB AC DE DF=且A D ∠=∠,根据两组对应边的比相等且夹角对应相等的两个三角形相似,可以得出ABC DEF ∽△△,故此选项不合题意;故选:B .【点睛】此题主要考查了相似三角形的判定,关键是掌握三角形相似的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似. 5.B解析:B【分析】如图,证明△ABE ∽△ACD ,根据相似三角形的性质列式求解即可.【详解】解:如图,根据题意得,△ABE ∽△ACD ,∴AB BE AC CD= ∵AB=10m ,BE=1.6m ,CD=9.6m∴10 1.6=9.6AC ∴AC=60m ∴BC=AC-AB=60-10=50m故选:B .【点睛】此题主要考查了相似三角形的应用,善于观察题目的信息是解题以及学好数学的关键. 6.D解析:D【分析】根据位似变换的概念判断即可.【详解】解:D 中两个图形,对应边不互相平行,不是位似图形,A 、B 、C 中的图形符合位似变换的定义,是位似图形,故选:D .【点睛】本题考查的是位似变换,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.7.C解析:C【分析】根据点A 在反比例函数图象上结合反比例函数系数k 的几何意义,即可得出关于k 的含绝对值符号的一元一次方程,解方程求出k 值,再结合反比例函数在第一象限内有图象即可确定k 值.【详解】解:∵点A 在反比例函数k y x=的图象上,且AB x ⊥轴于点B , ∴设点A 坐标为(,)x y ,即||k xy =,∵点A 在第一象限,x y ∴、都是正数,1122AOB S OB AB xy ∴=⋅=, 2AOB S =,4k xy ∴==.故选:C .【点睛】本题考查了反比例函数的性质以及反比例函数系数k 的几何意义,解题的关键是找出关于k 的含绝对值符号的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k 的几何意义找出关于k 的含绝对值符号的一元一次方程是关键.8.B解析:B【分析】分a >0与a <0两种情况,根据一次函数和反比例函数的图象与性质解答即可.【详解】解:当a >0时,y =|a |x +a =ax +a 的图象在第一、二、三象限,a y x =的图象在第一、三象限,此时选项B 正确;当a <0时,y =|a |x +a =﹣ax +a 的图象在第一、三、四象限,a y x=的图象在第二、四象限,此时没有正确选项;故选:B .【点睛】本题考查了一次函数与反比例函数的图象与性质,属于常考题型,熟练掌握上述知识是解题关键. 9.A解析:A【分析】根据反比例函数的图象与性质,可得该反比例函数图象的两个分支分别位于第二、四象限,从而可确定1-3m 的取值,进而求出m 的取值范围.【详解】解:∵120x x <<时,12y y <,∴反比例函数图象位于第二、四象限,∴1-3m <0, 解得:13m >, 故选:A .【点睛】此题主要考查了反比例函数的图象与性质,熟练掌握相关性质是解答此题的关键. 10.A解析:A【解析】【分析】作BD ⊥AC 于D ,如图,先利用等腰直角三角形的性质得到,,再利用AC ⊥x 轴得到C ,),然后根据反比例函数图象上点的坐标特征计算k 的值.【详解】作BD ⊥AC 于D ,如图,∵△ABC 为等腰直角三角形,∴,∴BD=AD=CD=2,∵AC⊥x轴,∴C(2,22),把C(2,22)代入y=kx得k=2×22=4,故选A.【点睛】本题考查了等腰直角三角形的性质以及反比例函数图象上点的坐标特征,熟知反比例函数y=kx(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k是解题的关键. 11.C解析:C【分析】将点(2,1)代入kyx=中求出k值,再根据反比例函数的性质对四个选项逐一分析即可.【详解】将点(2,1)代入kyx=中,解得:k=2,A.k=2,此说法正确,不符合题意;B.k=2﹥0,反比例函数图象分布在第一、三象限,此书说法正确,不符合题意;C.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,此说法错误,符合题意;D.k=2﹥0且x﹥0,函数图象位于第一象限,且y随x的增大而减小,此说法正确,不符合题意;故选:C.【点睛】本题考查了反比例函数的性质,熟练掌握反比例函数的性质,理解函数图象上的点与解析式的关系是解答的关键.12.D解析:D【分析】根据反比例函数的性质判断即可.【详解】解:A. 把(1,5)-代入反比例函数得,55-=-,本选项正确;B. 50-<,图象分别位于第二、四象限,函数在x<0上为增函数、在x>0上同为增函数,本选项正确;C. 50-<,因此图像分布在第二、四象限,本选项正确;D. 函数在x<0上为增函数、在x>0上同为增函数,若点11()A x y ,,22()B x y ,都在图像上,当120x x <<或120x x <<时,12y y <,本选项错误.故选:D .【点睛】本题考查的知识点是反比例函数的性质,牢记反比例函数图象的性质是解此题的关键.二、填空题13.【分析】根据正六边形的性质判断出△AMB ∽△BAF 再根据相似三角形的性质求解即可【详解】由题意可知∠AFB=∠ABF=∠CAB=30°则△AMB ∽△BAF 且在△BAF 中∠BAF=120°∴△BAF 是 解析:12【分析】根据正六边形的性质,判断出△AMB ∽△BAF ,再根据相似三角形的性质求解即可.【详解】由题意,可知∠AFB=∠ABF=∠CAB=30°,则△AMB ∽△BAF ,且在△BAF 中,∠BAF=120°,∴△BAF 是顶角为120°的等腰三角形,作AP ⊥BF ,∵∠ABF=30°,∴AB=2AP,,AP , ∴AB BF =, ∴△AMB ∽△BAF∴:1:3ABM AFB S S =△△ ∴1:1:22ABM AFM S S ==, 故答案为:12.【点睛】本题考查正多边形的性质及相似三角形的判定与性质,准确推断出相似三角形,且注意相似三角形的面积比等于相似比的平方是解题关键.14.【分析】过点E 作EM ∥BC 交AC 下点M 点根据菱形的性质可得△AEM 是等边三角形则EM=AE=3由AF ∥EM 对应线段成比例即可得结论【详解】解:过点E 作EM ∥BC 交AC 于点M ∵四边形ABCD 是菱形∴A 解析:13【分析】过点E 作EM ∥BC 交AC 下点M 点,根据菱形的性质可得△AEM 是等边三角形,则EM=AE=3,由AF ∥EM ,对应线段成比例即可得结论.【详解】解:过点E 作EM ∥BC 交AC 于点M ,∵四边形ABCD 是菱形,∴AB =4,AD ∥BC ,∴∠AEM =∠B =60°,∠AME =∠ACB =60°,∴△AEM 是等边三角形,则EM =AE =3,∵AF ∥EM ,∴13GF AF GE EM ==, 故答案为:13. 【点睛】 本题考查了平行线分线段成比例,菱形的性质,熟练运用菱形的性质、等边三角形性质是解题的关键.15.【分析】先根据相似三角形的判定与性质可得从而可得AE 的长再根据线段的和差即可得【详解】解得则故答案为:【点睛】本题考查了相似三角形的判定与性质熟练掌握相似三角形的判定与性质是解题关键解析:163【分析】 先根据相似三角形的判定与性质可得AD AE AB AC=,从而可得AE 的长,再根据线段的和差即可得.【详解】 //DE BC ,ADE ABC ∴,AD AE AB AC∴=, 9AB =,8AC =,3AD =,398AE ∴=, 解得83AE =, 则816833EC AC AE =-=-=, 故答案为:163. 【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键. 16.18【分析】根据平行四边形的性质可得BC ∥AD 进而可判定△ADF ∽△EBF 然后用相似三角形面积的比等于相似比的平方即可求出△AFD 的面积【详解】解:∵ABCD 是平行四边形∴AD ∥BCAD =BC ∴△A解析:18【分析】根据平行四边形的性质可得BC ∥AD ,进而可判定△ADF ∽△EBF ,然后用相似三角形面积的比等于相似比的平方即可求出△AFD 的面积.【详解】解:∵ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴△ADF ∽△EBF ,∵EC =2BE ,∴BC =3BE ,即AD =3BE ,∴S △AFD =9S △EFB =18.故答案为:18.【点睛】本题考查了平行四边形的性质和相似三角形的判定和性质,属于常考题型,熟练掌握上述知识是解题的关键.17.2【分析】作直线OB交双曲线另一支于点D根据双曲线对称性得到BD最短根据勾股定理和双曲线对称性即可求解【详解】解:如图作直线OB交双曲线另一支于点D∵双曲线关于直线y=x及直线y=−x对称∵四边形O解析:22【分析】作直线OB,交双曲线另一支于点D,根据双曲线对称性得到BD最短,根据勾股定理和双曲线对称性即可求解.【详解】解:如图,作直线OB,交双曲线另一支于点D,∵双曲线关于直线y=x及直线y=−x对称,∵四边形OABC是正方形,∴线段BD在直线y=x上,∴易得∠BDD'>90∘∴BD最短.在Rt△OBC中,OB=222OC BC+=,∴BD=22.故答案为:22【点睛】本题主要考查了反比例函数图象的中心对称性,勾股定理等知识,熟知反比例函数图形的对称性是解题关键.18.﹣3【分析】由题意可设一次函数的解析式为y=k1x+4然后联立两个函数的解析式可得等式k1x2+4x﹣k2=0进而可根据根与系数的关系得出x1+x2=﹣x1x2=﹣再由可得点C的横坐标是点B横坐标的解析:﹣3【分析】由题意可设一次函数的解析式为y=k1x+4,然后联立两个函数的解析式可得等式k1x2+4x﹣k2=0,进而可根据根与系数的关系得出x1+x2=﹣14k,x1x2=﹣21kk,再由2BC AB=可得点C 的横坐标是点B 横坐标的3倍,不妨设x 2=3x 1,然后对上述的两个式子整理变形即得结果.【详解】解:∵一次函数y =k 1x +b 的图象过点A (0,4),∴一次函数的解析式为y =k 1x +4,由k 1x +4=2k x,得k 1x 2+4x ﹣k 2=0, 设上述方程的两个实数根为x 1、x 2,则x 1+x 2=﹣14k , x 1x 2=﹣21k k , ∵BC =2AB ,∴点C 的横坐标是点B 横坐标的3倍,不妨设x 2=3x 1,∴x 1+x 2=4x 1=﹣14k ,x 1x 2=3x 12=﹣21k k , ∴221113k k k ⎛⎫⨯-=- ⎪⎝⎭,整理得:k 1k 2=﹣3. 故答案为﹣3.【点睛】本题考查了一次函数与反比例函数的交点、一元二次方程的根与系数的关系等知识,熟练掌握上述知识、掌握求解的方法是关键. 19.14【分析】根据点是反比例函数()的图像上一点可得到M 点的坐标;轴垂足为点可知P 点横坐标等于M 点横坐标;再通过的面积建立等式即可计算得到答案【详解】∵是反比例函数()的图像上一点设横坐标∴∵轴垂足为 解析:14【分析】根据点M 是反比例函数k y x=(0k >)的图像上一点,可得到M 点的坐标;MP x ⊥轴,垂足为点P ,可知P 点横坐标等于M 点横坐标;再通过MOP △的面积建立等式,即可计算得到答案.【详解】 ∵M 是反比例函数k y x=(0k >)的图像上一点 设M 横坐标x a = ∴,k M a a ⎛⎫ ⎪⎝⎭∵MP x ⊥轴,垂足为点P∴P 点横坐标等于M 点横坐标∴(),0P a∴=a OP ,k MP a= 又∵MP x ⊥轴,垂足为点P∴=90MPO ∠∴MOP △为直角三角形 ∴11222k k S OP MP a a =⨯=⨯=△MOP ∵7S =△MOP ∴=72k ∴14k = 故答案为:14.【点睛】本题考察了反比例函数、直角坐标系、直角三角形的知识;求解的关键的熟练掌握反比例函数、直角三角形性质,结合直角坐标系,从而计算得到答案.20.﹣1<k <1【分析】根据函数值的大小关系判别函数的图象位置根据位置判定比例系数的大小再解不等式【详解】因为A (x1y1)B (x2y2)为函数图象上的两点且x1<0<x2y1>y2所以函数图象分支在二解析:﹣1<k <1【分析】根据函数值的大小关系,判别函数的图象位置,根据位置判定比例系数的大小,再解不等式.【详解】因为A (x 1,y 1),B (x 2,y 2)为函数21k y x-=图象上的两点,且x 1<0<x 2,y 1>y 2, 所以函数图象分支在二、四象限所以k 2-1<0解得﹣1<k <1故答案为:﹣1<k <1【点睛】考核知识点:反比例函数的图象.数形结合,熟记反比例函数的性质是关键.三、解答题21.(1)画图见解析;(2)1:2;(3)画图见解析;A "(6,0),B "(3,-2),C "(4,-4)【分析】(1)连接CC′并延长,连接BB′并延长,两延长线交于点O ;(2)由OB=2OB′,即可得出△A′B′C′与△ABC 的位似比为1:2;(3),连接B′O并延长,使OB″=OB′,延长A′O并延长,使OA″=OA′,C′O并延长,使OC″=OC′,连接A″B″,A″C″,B″C″,则△A″B″C″为所求,从网格中即可得出△A″B″C″各顶点的坐标.【详解】解:(1)图中点O为所求;(2)△A′B′C′与△ABC的位似比等于1:2;故答案为:1:2;(3)△A″B″C″为所求;A″(6,0);B″(3,-2);C″(4,-4).【点睛】此题考查了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.22.(1)见解析(2)见解析【分析】(1)连接PQ,AB交点即为所求;(2)找到F点关于CD的对称点F’,连接CD,EF’,交点即为所求.【详解】(1)如图,M点为所求;(2)如图,N点为所求.【点睛】此题主要考查网格中作图,解题的关键是熟知熟知网格的特点、对称性、全等三角形与相似三角形的判定方法.23.(1)90;(2)见解析 【分析】(1)根据互补四边形的定义得到180A C ∠+∠=︒,由四边形内角和得180B D ∠+∠=︒,根据三个角的比例,列式求出各个角的度数; (2)根据两组对应边成比例且夹角相等,证明BDE BCA ,得到BED A ∠=∠,可以证明180A CED ∠+∠=︒,就可以证明四边形ADEC 是互补四边形. 【详解】(1)∵四边形ABCD 是互补四边形,且A ∠与C ∠是一组对角, ∴180A C ∠+∠=︒, ∵四边形内角和是360︒, ∴180B D ∠+∠=︒,∵::2:3:4B C D ∠∠∠=,∴设2B x ∠=,3C x ∠=,4D x ∠=, 24180x x +=︒,解得30x =︒,∴390C x ∠==︒,则1809090A ∠=-=︒︒︒, 故答案是:90;(2)∵BE BC AB BD ⋅=⋅,∴BE BDAB BC=, ∵B B ∠=∠,∴BDE BCA , ∴BED A ∠=∠,∴180A CED BED CED ∠+∠=∠+∠=︒, ∴四边形ADEC 是互补四边形. 【点睛】本题考查相似三角形的性质和判定,解题的关键是掌握相似三角形的性质和判定.24.(1)y= 2x-, y=x-3;(2)S △AOB =32;(3))10P ,()20P ,()320P ,,4502P ,⎛⎫⎪⎝⎭. 【分析】(1)运用待定系数法先求出反比例函数解析式,再求出B 的坐标,从而求出直线AB 的解析式;(2)利用反比例函数k 的几何意义进行面积转化求解即可; (3)列出各边长的表达式,根据不同情况进行分类讨论即可. 【详解】(1)将()1,2A -代入k y x=,得2k =-,故反比例函数解析式为2y k =-,联立21y x y x ⎧=-=-+⎪⎨⎪⎩,解得21x y =⎧⎨=-⎩或12x y =-⎧⎨=⎩,即:()2,1B -,()1,2D - 设直线AB 的解析式为:y mx n =+,将()1,2A -,()2,1B -代入得:221m n m n +=-+=-⎧⎨⎩,解得:13m n ==-⎧⎨⎩ , 则直线AB 的解析式为:3y x =-∴反比例函数解析式为2y k=-,直线AB 的解析式为:3y x =-; (2)作AM x ⊥轴,BN x ⊥轴,AH y ⊥轴,则AOB OAH OBN OHAM MABN S S S S S ++=+△△△矩形梯形, 根据反比例函数k 的几何意义可知:122OAH OBN OHAM k S S S ===△△矩形, ()()()1132121222AOB MABN S S MN AM BN ∴==+=⨯-⨯+=△梯形, 32AOB S ∴=△;(3)由题:5OA OP x =,()214AP x =-+①若OA OP =5x =,解得5x =,故:)150P ,()250P -;②若OA AP =()2514x =-+2x =或0(舍去),故:()320P ,;③若OP AP =,则()214x x =-+52x =,故:4502P ,⎛⎫⎪⎝⎭; 综上,所有P 的坐标为:)150P ,()250P -,()320P ,,4502P ,⎛⎫⎪⎝⎭. 【点睛】本题考查了反比例函数与一次函数综合问题,以及等腰三角形的判定与性质,熟练掌握反比例函数k的几何意义,以及分类讨论的思想是解题的关键.25.(1)100(0 1.5)225( 1.5)x x y x x≤≤⎧⎪=⎨≥⎪⎩ ;(2)2.0125(或16180)(小时)【解析】分析: (1)首先根据题意,1.5小时内其血液中酒精含量y (毫克/百毫升)与时间A (时)成正比例;1.5小时后(包括1.5小时)B 与C 成反比例,y 与t 的函数关系式为ay x=(a 为常数),将数据代入用待定系数法可得反比例函数的关系式; (2)把y =80代入两个函数求得x 值相减即可求得肝部被严重损伤持续时间. 详解:(1)由题意,得 ①当0 1.5x ≤≤时, 设函数关系式为:y kx =, 则150 1.5k =,解得100k =, 故100y x =, ②当 1.5x ≥时, 设函数关系式为:a y x=, 则150 1.5225a =⨯=,解得 225a =, 故 225y x=综上所述:()()1000 1.52251.5x x y x x ⎧≤≤⎪=⎨≥⎪⎩(2)当80y =时,80100x = 解得0.8x =(或45x =) 当80y =时,22580x =解得 2.8125x =(或4516x = ) 由图象可知,肝部被严重损伤持续时间 2.81250.8 2.0125=-=(或45416116580=-=)(小时) 点睛: 本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式. 26.(1)6y x=;(2)(2,3),(3,2)--;(3)25y x =-+(答案不唯一) 【分析】(1)将x=2代入一次函数,求出其中一个交点是(2,3),再代入反比例函数ky x=即可解答;(2)先求出平移后的一次函数表达式,联立两个函数解析式得到一元二次方程260x x --=即可解答;(3)设一次函数为y=ax+b (a≠0),根据题意得到b=5,联立一次函数与反比例函数解析式,得到2560ax x +-=,若无公共点,则方程无解,利用根的判别式得到25240a ∆=+<,求出a 的取值范围,再在范围内任取一个a 的值即可. 【详解】解:(1)∵一次函数1y x =+的图象与反比例函数ky x=的图象的一个交点的横坐标是2,∴当2x =时,3y =, ∴其中一个交点是(2,3).∴236k =⨯=.∴反比例函数的表达式是6y x=. (2)∵一次函数1y x =+的图象向下平移2个单位, ∴平移后的表达式是1y x =-. 联立6y x=及1y x =-,可得一元二次方程260x x --=, 解得12x =-,23x =.∴平移后的图象与反比例函数图象的交点坐标为(2,3),(3,2)-- (3)设一次函数为y=ax+b (a≠0), ∵经过点(0,5),则b=5, ∴y=ax+5,联立y=ax+5以及6y x=可得:2560ax x +-=, 若一次函数图象与反比例函数图象无交点,则25240a ∆=+<,解得:2524a <-, ∴25y x =-+(答案不唯一). 【点睛】本题考查了一次函数与反比例函数图象交点问题以及函数图象平移问题,解题的关键是熟悉函数图象上点的特征,第(3)问需要先确定a 的取值范围.。
最新九年级数学下期中第一次模拟试题及答案

一、选择题1.对于二次函数2y x bx c =++(b ,c 是常数)中自变量x 与函数y 的部分对应值如下表:x1- 0 1 2 34 y10 52 125A .函数图像开口向上B .当5x =时,10y =C .当2x >时,y 随x 的增大而增大.D .方程20x bx c ++=有两个不相等的实数根2.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,在下列六个结论中:①20a b -<;②0abc <;③0a b c ++<;④0a b c -+>;⑤420a b c ++>;⑥240b ac -<.其中正确的个数有( )A .1个B .2个C .3个D .4个3.小凯在画一个开口向上的二次函数图象时,列出如下表格: x … -1 0 1 2 … y…1211…A .(-1,1)B .(0,2)C .(1,1)D .(2,1)4.已知二次函数24y x x m =-+的图象与x 轴有两个交点,若其中一个交点的横坐标为1,则另一个交点的横坐标为( ) A .1- B .2-C .2D .35.飞机着陆后滑行的距离s (单位:m )与滑行的时间t (单位:s )的函数解析式是260 1.5s t t =-,那么飞机着陆后滑行多长时间才能停下来.( )A .10sB .20sC .30sD .40s6.已知二次函数2y ax bx c =++的图象如图所示,则下列结论正确的个数有( ) ①0c >;②240b ac -<;③0a b c -+>;④当1x >时,y 随x 的增大而减小A .4个B .3个C .2个D .1个7.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A 滑行至B ,已知AB=500米,则这名滑雪运动员的高度下降了__米.(sin34°≈0.56,cos34°≈0.83,tan34°≈0.67) ( )A .415B .280C .335D .2508.如图,四边形ABCD 中,∠B =∠C =90°,CD =2米,BC =5米,5sin 13A =,则AB =( )A .8米B .10米C .12米D .14米9.如图,某建筑物AB 在一个坡度为1:0.75i =的山坡CE 上,建筑物底部点B 到山脚点C 的距离20BC =米,在距山脚点C 右侧水平距离为60米的点D 处测得建筑物顶部点A的仰角是24°,建筑物AB 和山坡CE 的剖面的同一平面内,则建筑物AB 的高度约为( )(参考数据:sin 240.41︒≈,cos240.91︒≈,tan 240.45︒≈)A .32.4米B .20.4米C .16.4米D .15.4米10.如图,是一个正六棱柱的主视图和左视图,则图中x 的值为( )A .2B .3C .3D .33211.如图,要测量小河的宽度,在小河边取PA 的垂线PB 上的一点C ,测得50PC m =,35PCA ∠=︒,则小河的宽度PA 等于( )A .50tan35m ︒B .50sin55m ︒C .50sin35m ︒D .50tan55m ︒12.在正方形网格中,∠AOB 如图所示放置,则sin ∠AOB 的值为( )A .12B 5C 25D .8510二、填空题13.已知()11y ,,()23y ,是函数226y x x c =-++图像上的点,则1y ,2y 的大小关系是______.14.设()()y x a x b =++的图象与x 轴有m 个交点,函数(1)(1)y ax bx =++的图象与x 轴有n 个交点,则所有可能的数对(,)m n 是__________.15.若A (m-2,n ),B (m+2,n )为抛物线2()2020y x h =--+上两点,则n=_______.16.如图,矩形OABC 中,3OA =,5AB =,抛物线2y x bx c =++的顶点为P ,且经过点(),M m n 和()4,N m n +,其中点M ,N 位于矩形OABC 的内部(不含边界),则MNP ∆的面积是___________,b c +的取值范围是___________.17.如图,有一个三角形的钢架ABC ,∠A=30°,∠C=45°,AC=2(3+1)m .工人师傅搬运此钢架_______(填“能”或“不能”)通过一个直径为2.1m 的圆形门?18.如图,测角仪CD 竖直放在距建筑物AB 底部8m 的位置,在D 处测得建筑物顶端A 的仰角为50°.若测角仪CD 的高度是1.5m ,则建筑物AB 的高度约为_____m .(结果精确到个位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)19.如图,在平面直角坐标系中,点B 在第一象限,BA x ⊥轴于点A ,反比例函数()0ky x x=>的图象与线段AB 相交于点C ,且C 是线段AB 的中点,点C 关于直线y x =的对称点'C 的坐标为()()1,1n n ≠,若OAB 的面积为4.则下列结论:①2n =;②4k =;③不等式kx x<的解集是2x >;④tan 2ABO ,其中正确结论的序号是________.20.如图,在菱形ABCD 中,AC 、BD 相交于点O ,60BAD ∠=︒,BD 长为4,则菱形ABCD 的面积是__________.三、解答题21.某旅馆有客房120间,经市场调查发现,客房每天的出租数量y (间)与每间房的日租金x (元)的关系如图所示,为保证旅馆的收益,每天出租的房间数不少于90间. (1)结合图象,求出客房每天的出租的房间数y (间)与每间房的日租金x (元)之间的函数关系式和自变量的取值范围;(2)设客房的日租金总收入为W (元),不考虑其它因素,旅馆将每间客房的日租金定为多少元时,客房的日租金总收入最高?最高总收入为多少?22.如图,抛物线223y x x =--与x 轴交于A 、B 两点.(1)抛物线与x 轴的交点坐标为______; (2)求抛物线与坐标轴围成的ABC 的面积;(3)设(1)中的抛物线上有一个动点P ,当点P 在该抛物线上滑动到什么位置时,满足6PAB S =△,并求出此时P 点的坐标.23.如图,在平面直角坐标系中,点A 的坐标是()0,2.试寻找一些点,使他们满足“到点A 与到x 轴的距离相等”.小明在探究过程中首先想到了OA 的中点M 满足条件,点M 到点A 和x 轴的距离都是1.接着,小明过x 轴上一点()4,0B 作x 轴的垂线l .他认为在l 上应该有一个点N 到点A 与到x 轴的距离相等.(1)请你用尺规作图找出点N(不写画法,保留作图痕迹)并求出点N的坐标;(2)小明用同样的方法又找出了一些符合条件的点,并把这些点用平滑的曲线连接起来他发现这些点在一条对称轴为y轴的抛物线上.请你根据以上探究和发现,求出这条抛物线的解析式;(3)请直接写出平面内到点A和直线2y=-距离相等的点所在抛物线的解析式.24.如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高(结果保留根号).25.如图1,直线y=34x和直线y=﹣12x+5相交于点A,直线y=﹣12x+5与x轴交于点C,点P在线段AC上,PD⊥x轴于点D,交直线y=34x于点Q.(1)点A的坐标为;(2)当QP=OA时,求Q点的坐标及△APQ的面积;(3)如图2,在(2)的条件下,∠OQP平分线交x轴于点M.①直接写出点M 的坐标 ; ②点N 在直线y =34x 的上方,当OQN 和OQM 全等时直接写出N 点坐标 .26.如图,ABC 中,90,,ACB CD CE ∠=︒分别是ABC 的高和中线,过点C 作CE 的垂线交AB 的延长线于点F . (1)求证:CBFACF △△(2)若14,tan 2AF BCD =∠=,求BF 的长.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据表格中的数据和二次函数图象具有对称性即可判断各个选项中的说法是否正确,从而可以解答本题. 【详解】解:由表格可得,当x <2时,y 随x 的值增大而减小;当x >2时,y 随x 的值增大而增大,该函数开口向上,故选项A 、C 不符合题意; ∴点(−1,10)的对称点是(5,10),∴点(5,10)在该函数的图象上,故选项B 不符合题意;由表格可得,该抛物线开口向上,且最小值是1,则该抛物线与x 轴没有交点, ∴方程20x bx c ++=无实数根,故选项D 符合题意. 故选:D . 【点睛】本题考查二次函数的性质、二次函数的最值、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.2.D解析:D 【分析】由抛物线的开口方向判断a 与0的关系,由抛物线与y 轴的交点判断c 与0的关系,利用图象判断1,-1,2所对应的y 的值,进而对所得结论进行判断. 【详解】解:①∵由函数图象开口向下可知,a <0,由函数的对称轴12b a ->-,故12b a<, ∵a <0, ∴b >2a ,∴2a -b <0,①正确;②∵a <0,对称轴在y 轴左侧,a ,b 同号,图象与y 轴交于负半轴,则c <0,故abc <0;②正确;③当x=1时,y=a+b+c <0,③正确; ④当x=-1时,y=a -b+c <0,④错误; ⑤当x=2时,y=4a+2b+c <0,⑤错误; ⑥∵图象与x 轴无交点, ∴b 2-4ac <0,⑥正确;故正确的有①②③⑥,共4个. 故选:D . 【点睛】此题主要考查了二次函数图象与系数的关系,熟练利用数形结合得出是解题关键.3.A解析:A 【分析】观察图表数据,根据二次函数的对称性即可判断出计算错误的一组数据,然后再利用二次函数的增减性得出结论. 【详解】解:观察y 值发现y =1时x 有三个不同的值,因此这三个值中必有一对计算错误. 由二次函数的对称性:如果(-1,1),(1,1)是图象的两个对称点,那么根据描点得到这个函数图象的开口应该是向下的.同理若(-1,1),(2,1)是两个对称点,那么该函数图象的开口也是向下的,所以(1,1),(2,1)是图象的两个对称点,因此该图像的对称轴为直线032x =,根据二次函数的增减性,当开口向上时,在对称轴的左边,y 随x 的增大而减小,所以1x =-时,y 一定是大于1的, 故选A . 【点睛】本题考查了二次函数的图象,找出图表数据特点,根据函数的对称性解答即可,熟练掌握二次函数的图象和性质,是解答的关键.4.D解析:D 【分析】函数的对称轴为:x=-22ba=,一个交点的坐标为(1,0),则另一个交点的坐标为(3,0),即可求解. 【详解】解:∵二次函数y=x 2-4x+m 中a=1,b=-4, ∴函数的对称轴为:x=-22ba=, ∵一个交点的坐标为(1,0)与另一个交点的坐标关于对称轴对称, ∴另一个交点的坐标为(3,0),即另一个交点的横坐标为3. 故选:D . 【点睛】本题考查的是抛物线与x 轴的交点,主要考查函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.5.B解析:B 【分析】当s 取最大值时,飞机停下来,求函数最大值时的自变量即可. 【详解】∵当s 取最大值时,飞机停下来, ∴t= 6022( 1.5)b a -=-⨯-=20, 故选:B . 【点睛】本题考查了二次函数应用-飞机着陆问题,熟练把问题转化为二次函数的最值问题是解题的关键.6.B解析:B 【分析】根据二次函数的图象与y 轴的交点判断c 的正负;根据二次函数的图象与x 轴交点个数,判断②的正确性;根据1x =-时,y 取值的正负,判断③的正确性;根据图象中函数的增减性判断④的正确性. 【详解】解:∵二次函数的图象与y 轴的交点在正半轴, ∴0c >,故①正确;∵二次函数的图象与x 轴有两个交点, ∴方程20ax bx c ++=有两个不相同的实数根, ∴240b ac ->,故②错误;当1x =-时,0y >,即0a b c -+>,故③正确; 根据图象,当1x >时,y 随x 的增大而减小,故④正确. 故选:B . 【点睛】本题考查二次函数,解题的关键是根据二次函数的图象分析解析式中系数的关系.7.B解析:B 【分析】根据正弦的定义求解即可; 【详解】由题可知sin 340.56500280AC AB =︒=⨯=(米); 故选B . 【点睛】本题主要考查了解直角三角形的应用,准确计算是解题的关键.8.D解析:D 【分析】过点D 作DE ⊥AB 于E ,得到四边形DEBC 是矩形,得到BE=DC=2米,DE=BC=5米,根据5sin 13A =,求得AD=13米,根据勾股定理求出AE=12米,即可得到答案. 【详解】过点D 作DE ⊥AB 于E , ∴∠DEB=∠B =∠C =90°, ∴四边形DEBC 是矩形, ∴BE=DC=2米,DE=BC=5米, ∵5sin 13A =, ∴513DE AD =, ∴AD=13米,∴AE=222213512AD DE -=-=米,∴AB=AE+BE=12+2=14米,故选:D ..【点睛】此题考查矩形的判定及性质,勾股定理,锐角三角函数,正确引出辅助线构建直角三角形解决问题是解题的关键.9.C解析:C【分析】延长AB 交CD 反向延长线于F .根据题意可知43BF FC =,则设BF=4x ,FC=3x .由正切可求出AF 的长.再在Rt BFC △中,由勾股定理可求出x 的值.最后即可利用=AB AF BF -求出AB 长.【详解】 如图延长AB 交CD 反向延长线于F ,由题意可知BF DF ⊥.∵建筑物AB 在一个坡度为i =1:0.75的山坡CE 上,∴10.75BF FC =,即43BF FC =. 设BF=4x 米,则FC=3x 米,DF=(60+3x )米,∵24D ∠=︒,∴tan tan 240.45AF D DF∠=︒==, ∴0.45(603)(27 1.35)AF x x =+=+米. 在Rt BFC △中,222BF FC BC +=,即222(4)(3)20x x +=,∴1244x x ==-,(舍).∴4416BF =⨯=米,27 1.354=32.4AF =+⨯米.∴=32.4-16=16.4AB AF BF -=米.故选:C.【点睛】本题考查解直角三角形的实际应用和勾股定理.作出常用的辅助线是解答本题的关键.10.D解析:D【分析】先画出俯视图,利用主视图与左视图,求出边长AB,构造三角形ABC与三角形ABE,利用三角函数解直角三角形即可【详解】由正六棱柱的主视图和左视图,得俯视图如图,标注字母如图,由主视图可得到正六棱柱的最长的对角线长BD是6,BF=1BD2=3,则边长AB为3,连AC交BD于E,则AC⊥BD,由左视图得AE=CE=x,在△ABC中,AB=BC=3,∠ABC=120°,∴在Rt△ABE中,∠BAE=30°,AB=3,∴BE=32,33,即33故选择:D.【点睛】本题考查了正六棱柱的三视图,掌握三视图中俯视图的画法,利用主视图与左视图画出准确的俯视图,注意题目中的隐含条件及左视图的特点,可将其转化到直角三角形中解答.培养了学生的空间想象能力.11.A解析:A【分析】根据正切函数可求小河宽PA 的长度.【详解】解:∵PA ⊥PB ,PC=50米,∠PCA=35°,∴小河宽PA=PCtan ∠PCA=50tan35°(米).故选:A .【点睛】考查考查了解直角三角形的应用,解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.12.C解析:C【分析】根据图形找出角的两边经过的格点以及点O 组成的直角三角形,利用勾股定理求出OA ,再根据锐角的正弦值等于对边比斜边求解.【详解】如图:AE ⊥OB ,在Rt △AOE 中,AE=4,OE=2, ∴2225OA AE OE =+=,∴sin ∠AOB=25525AE OA ==, 故选:C .【点睛】此题考查求网格中角的三角函数值,熟记角的三角函数值的计算公式,并正确确定角所在的直角三角形是解题的关键.二、填空题13.【分析】经过配方后确定抛物线的对称轴进而确定抛物线的增减性根据自变量的大小关系可确定函数值的大小关系【详解】解:∵∴抛物线的对称轴为∵a=-2<0∴抛物线开口向下∵1比3更接近对称轴∴故答案为:【点 解析:12y y >【分析】经过配方后确定抛物线的对称轴,进而确定抛物线的增减性,根据自变量的大小关系可确定函数值的大小关系.【详解】解:∵()2223926=23222y x x c x x c x c ⎛⎫=-++--+=--++ ⎪⎝⎭ ∴抛物线的对称轴为32x =∵a=-2<0∴抛物线开口向下 ∵1比3更接近对称轴,∴12y y >故答案为:12y y >.【点睛】本题考查了二次函数值的大小比较,根据二次函数的解析式确定对称轴的位置是解题的关键.14.(11)(10)(21)(22)【分析】分别对ab 的值分类讨论根据直线和二次函数的交点式:y =a (x ﹣x1)(x ﹣x2)(abc 是常数a≠0)得出抛物线与x 轴的交点坐标情况即可求解【详解】因为是二次解析:(1,1),(1,0),(2,1),(2,2)【分析】分别对a 、b 的值分类讨论,根据直线和二次函数的交点式:y =a (x ﹣x 1)(x ﹣x 2)(a ,b ,c 是常数,a≠0),得出抛物线与x 轴的交点坐标情况,即可求解.【详解】因为()()y x a x b =++ 是二次函数,令()()y x a x b =++=0,有0x a +=或0x b +=,解得:x a =-或x b =-;对m 来说,①当a b =时,图像与x 轴有一个交点,即1m =;② 当a b 时,图像与x 轴有两个交点,即2m =;函数(1)(1)y ax bx =++:令(1)(1)0y ax bx =++=,有10ax +=或10bx +=, 对n 来说,①当0a b =≠时,关于x 的方程有一个解,图象与x 轴有1个交点,即1n =; ②当0a b 时,关于x 的方程无解,图像与x 轴没有交点,即0n =;③当a b 且0ab =时,关于x 的方程有一个解,图象与x 轴有1个交点,即1n =; ④ 当a b 且0ab ≠时,关于x 的方程有两个不相等的解,图像与x 轴有两个交点,即2n =; 综上所述,当a b =时,1n =或0n =;当a b 时,1n =或2n =. ∴所有可能的数对(,)m n 是(1,1),(1,0),(2,1),(2,2)故答案为:(1,0)或(2,1)或(1,1)或(2,2).【点睛】本题考查了二次函数与x 轴的交点问题,解决本题的关键是正确理解二次函数的交点式. 15.2016【分析】根据二次函数的图象与性质可得抛物线的对称轴为再利用m-2+m+2=2h 解得m=h 则可得A (h−2n )B (h +2n )将B (h +2n )代入函数关系式即可求出结果【详解】解:∵A (m-2n解析:2016【分析】根据二次函数的图象与性质可得抛物线2()2020y x h =--+的对称轴为x h =,再利用m-2+m+2=2h ,解得m=h ,则可得A (h−2,n ),B (h +2,n ),将B (h +2,n )代入函数关系式即可求出结果.【详解】解:∵A (m-2,n ),B (m+2,n )是抛物线2()2020y x h =--+上两点, ∴抛物线2()2020y x h =--+的对称轴为x h =,∴m-2+m+2=2h ,解得m=h ,∴A (h−2,n ),B (h +2,n ),当x =h +2时,n =−(h +2−h )2+2020=2016,故答案为:2016.【点睛】本题考查了二次函数的图象与性质,解题的关键是掌握二次函数图象上的点的坐标特征并灵活运用所学知识解决问题.16.【分析】根据题意先把抛物线的一次项系数和常数项用含的式子表示出来从而表示出点P 的坐标再利用两点间的距离求出MN 的长和点P 到MN 的距离即可求出三角形的面积;再根据点MN 在矩形内部求出的范围进而可求的范 解析:42b c -<+<【分析】根据题意,先把抛物线的一次项系数和常数项用含,m n 的式子表示出来,从而表示出点P 的坐标,再利用两点间的距离求出MN 的长,和点P 到MN 的距离,即可求出三角形的面积;再根据点M ,N 在矩形内部求出,m n 的范围,进而可求b c +的范围【详解】点M 和点N 的纵坐标均为n 可知,M 与N 关于对称轴对称,点M (m 、n )点N (4m +、n )∴MN 的距离为:44m m +-=∴点P 的横坐标为:2m +抛物线2y x bx c =++的对称轴为:2b x =- 22b m ∴-=+ 24b m ∴=--将点 M (m 、n )代入2y x bx c =++得:2m bm c n ++=,则24c m m n =++①,点P 为抛物线的顶点,则点P 的纵坐标为:22244416164444ac b c m m c m m a ----==---,将①式代入得P 点的坐标为(2m +、4n -)∴点P 到MN 的距离为:()44n n --=14482PMN S ∴=⨯⨯=△ 2224424b c m m m n m m n +=--+++=++-②点M 在矩形的内部,045m m >⎧∴⎨+<⎩01m ∴<<点N 在矩形的内部03n ∴<<代入②式有:42b c -<+<故答案为:①8;②42b c -<+<【点睛】本题考查了二次函数的性质以及二次函数图像上点的特征,解题关键是用含,m n 式子表示出点P 的坐标,结合题意求出,m n 的范围17.能【分析】过B 作BD ⊥AC 于D 解直角三角形求出AD=xmCD=BD=xm 得出方程求出方程的解即可【详解】解:工人师傅搬运此钢架能通过一个直径为21m 的圆形门理由是:过B 作BD ⊥AC 于D ∵AB >BDB解析:能【分析】过B 作BD ⊥AC 于D ,解直角三角形求出xm ,CD=BD=xm ,得出方程,求出方程的解即可.【详解】解:工人师傅搬运此钢架能通过一个直径为2.1m 的圆形门,理由是:过B 作BD ⊥AC 于D ,∵AB>BD,BC>BD,AC>AB,∴求出DB长和2.1m比较即可,设BD=xm,∵∠A=30°,∠C=45°,∴DC=BD=xm,AD=3BD=3xm,∵AC=2(3+1)m,∴x+3x=2(3+1),∴x=2,即BD=2m<2.1m,∴工人师傅搬运此钢架能通过一个直径为2.1m的圆形门.【点睛】本题考查了解直角三角形的应用,解一元一次方程等知识点,能正确求出BD的长是解此题的关键.18.11【分析】根据题意作辅助线DE⊥AB然后根据锐角三角函数可以得到AE 的长从而可以求得AB的长本题得以解决【详解】解:作DE⊥AB于点E由题意可得DE=CD=8m∵∠ADE=50°∴AE=DE•ta解析:11【分析】根据题意,作辅助线DE⊥AB,然后根据锐角三角函数可以得到AE的长,从而可以求得AB 的长,本题得以解决.【详解】解:作DE⊥AB于点E,由题意可得,DE=CD=8m,∵∠ADE=50°,∴AE=DE•tan50°≈8×1.19=9.52(m),∵BE=CD=1.5m,∴AB=AE+BE=9.52+1.52=11.2≈11(m),故答案为:11.本题考查了解直角三角形的应用-仰角俯角问题,解答本题的关键是明确题意,利用数形结合的思想解答.19.②④【分析】根据对称性求出C 点坐标进而得OA 与AB 的长度再根据已知三角形的面积列出n 的方程求得n 进而用待定系数法求得k 再利用相关性质即可判断【详解】解:∵点C 关于直线y=x 的对称点C 的坐标为(1n ) 解析:②④【分析】根据对称性求出C 点坐标,进而得OA 与AB 的长度,再根据已知三角形的面积列出n 的方程求得n ,进而用待定系数法求得k ,再利用相关性质即可判断.【详解】解:∵点C 关于直线y=x 的对称点C'的坐标为(1,n )(n≠1),∴C (n ,1),∴OA=n ,AC=1,∴AB=2AC=2,∵△OAB 的面积为4, ∴12n×2=4, 解得,n=4,故①不正确;∴C (4,1),B (4,1),∴k=4×1=4,故②正确;解方程组4y x y x =⎧⎪⎨=⎪⎩,得:22x y =⎧⎨=⎩(负值已舍), ∴直线y=x 反比例函数(0)k y x x=>的图象的交点为(2,2),观察图象,不等式k x x<的解集是02x <<,故③不正确; ∵B (4,1),∴OA=4,AB=2, ∴tan ABO 2OA AB∠==,故④正确; 故答案为:②④.本题是反比例函数图象与一次函数图象的交点问题,主要考查了一次函数与反比例函数的性质,对称性质,正切函数等,关键是根据对称求得C点坐标及由三角形的面积列出方程.20.【分析】根据菱形的性质可知∠BAO=30°△ABD是等边三角形得到AB=BD=4再利用三角函数求得OA则AC可求再用菱形面积公式即可【详解】∵四边形ABCD是菱形∠BAD=60°∴AB=BD∠BAO解析:【分析】根据菱形的性质可知∠BAO=30°,△ABD是等边三角形,得到AB=BD=4,再利用三角函数求得OA,则AC可求,再用菱形面积公式即可.【详解】∵四边形ABCD是菱形,∠BAD=60°,∴ AB=BD,∠BAO=30°,BD⊥AC,AC=2OA,∴△ABD是等边三角形,AB=BD=4,在Rt△ABO中,OA=AB•cos30°=4×2=,∴ AC=2OA=∴S菱形ABCD=11AC BD=22⋅⨯故填:【点睛】本题考查菱形的性质、等边三角形的判定、菱形的面积公式、勾股定理,求得对角线的长度是关键.三、解答题21.(1)32165y x=-+,160210x≤≤;(2)每间客房的日租金定为180元时,客房日租金的总收入最高为19440元【分析】(1)首先假设出一次函数解析式,再利用待定系数法求一次函数解析式即可;(2)根据客房日租金的总收入为W=每间客房的日租金×每天客房出租数,再利用配方法求出二次函数的最值即可.【详解】解:(1)设客房每天的出租数量y(间)与每间房的日租金x(元)之间的函数关系式(0)y kx b k=+≠.把(160,120),(170,114)代入得160120170114k b k b +=⎧⎨+=⎩, 解得35216k b ⎧=-⎪⎨⎪=⎩,∴ 32165y x =-+, 由题意得:321690532161205x ⎧-+≥⎪⎪⎨⎪-+≤⎪⎩ ∴160210x ≤≤∴自变量x 的取值范围是160210x ≤≤(2)由题意得:()2332161801944055W y x x x x ⎛⎫=⋅=-+⋅=--+ ⎪⎝⎭∵305-<,160210x ≤≤ ∴当180x =时,19440w =最大.答:每间客房的日租金定为180元时,客房日租金的总收入最高为19440元.【点睛】此题主要考查了二次函数的应用以及待定系数法求一次函数解析式以及二次函数最值问题,得出客房日租金的总收入为W=每间客房的日租金×每天客房出租数是解题关键. 22.(1)()1,0-或()3,0;(2)6;(3)点P的坐标为()1、()1、()0,3-、()2,3-.【分析】(1)令y=0,转化为一元二次方程,方程的根就是与x 轴交点的横坐标;(2)求出AB 的长度,OC 的长度,按公式计算即可;(3)利用面积公式,抛物线的解析式转化成一元二次方程求解即可.【详解】解:(1)当0y =时,2230x x --=,解得 11x =-,23x =,∴抛物线与x 轴的交点坐标为()1,0-或()3,0,故答案为:()1,0-或()3,0.(2)由(1)点()1,0A -,()3,0B ,()0,3C-, ∴()314AB =--=,3OC =, ∴14362ABC S =⨯⨯=△. (3)∵点()1,0A -,点()3,0B ,()222314y x x x =--=--,∴此抛物线有最小值,此时4y =-,()314AB =--=,∵6PAB S =△,抛物线上有一个动点P ,∴点P 的纵坐标的绝对值为6234⨯=, ∴2233x x --=或2233x x --=-, 解得,117x =,217x =,30x =,42x =,∴点P 的坐标为()17,3、()17,3-、()0,3-、()2,3-.【点睛】本题考查了二次函数与坐标轴的交点,抛物线上的内接三角形的面积,动点问题,熟练掌握性质,并能灵活运用是解题的关键.23.(1)见解析;N ()4,5;(2)2114y x =+;(3)218y x = 【分析】(1)利用尺规作图,作出线段AB 的垂直平分线即可;(2)设出抛物线的解析式,结合题意分析出点M 为抛物线的顶点,点N 在抛物线上,利用待定系数法直接求解即可;(3)设出抛物线解析式,结合题意分析出抛物线经过原点,且经过点(4、2)点(-4、2)利用待定系数法求解即可.【详解】解:(1)如图,连接AB ,作线段AB 的垂直平分线,与直线l 相交于点N ,点N 即为所求.连接AN ,过点A 作AH BN ⊥于点H ,设点N 的坐标为()4,y由作图可知AN y =,在Rt ANH ∆中,4AH =,2NH y =-,22(2)16y y ∴=-+,解得5y =∴点N 的坐标为()4,5;(2)此抛物线关于y 轴对称,∴点()0,1M 是抛物线的顶点,设抛物线的解析式为21y ax =+,将点()4,5N 代入得,14a =, ∴抛物线的解析式为2114y x =+. (3)设抛物线的解析式为:2y ax bx c =++,结合题意可知抛物线经过原点,和点(4、2)点(-4、2)则有164216420a b b c +=⎧⎪-=⎨⎪=⎩解得1800a b c ⎧=⎪⎪=⎨⎪=⎪⎩∴抛物线的解析式为:218y x =. 【点睛】本题考查了线段垂直平分线的尺规作图,待定系数法求函数解析式,解题关键是结合题意确定满足条件的点.24.古塔BD的高为()10m【分析】在Rt △ABD 和Rt △BCD 中,分别解直角三角形,用BD 表示AB 和BC ,然后根据BC-AB=20m ,可求得塔BD 的高度.【详解】解:根据题意得45BAD ∠=︒,30BCD ∠=︒,20AC m =,在Rt △ABD 中,∵45BAD BDA ∠=∠=︒,∴AB BD =,在Rt BDC 中, ∵tan BD BCD BC ∠=,∴BD BC =,则BC =,又∵BC AB AC -=,∴20BD -=,解得()10BD m ==. 答:古塔BD的高为()10m +.【点睛】本题考查了解直角三角形的应用,解答本题的关键是利用仰角建立直角三角形,利用解直角三角形的知识分别用BD 表示出AB 、BC 的长度.25.(1)()4,3;(2)()8,6Q ;10;(3)()3,6,()1.4,4.8【分析】(1)把两个函数解析式联立方程组计算即可;(2)设P 的横坐标n ,根据勾股定理求出P ,Q 的坐标,计算即可;(3)①作MH OQ ⊥,根据勾股定理和三角函数值求出M 的坐标计算即可;②当四边形NOMQ 为平行四边形和当△NOQ 与△MOQ 关于OQ 对称时分别计算即可得到结果;【详解】(1)由题意可得: 34152y x y x ⎧=⎪⎪⎨⎪=-+⎪⎩, 化简得:31542x x =-+, 解得:4x =, 把4x =代入y =34x 中,得3y =, ∴()4,3A ;故答案是()4,3;(2)如图,把0y =代入152y x =-+中,得到10x =, ∴()10,0C ,设P 的横坐标n ,把xn =代入152y x =-+得()154102y n n =-+≤≤, ∴1,52P n n ⎛⎫-+ ⎪⎝⎭, 把xn =代入34y x =得34y n =, ∴3,4Q n n ⎛⎫ ⎪⎝⎭,∵()4,3A ,∴5OA ==,31555424PQ n n n ⎛⎫=--+=- ⎪⎝⎭, ∵QP OA =, ∴5554n -=,∴8n =,∴()8,6Q ,作AG x ⊥轴,则()△115841022APQ S PQ GD ==⨯⨯-=; (3)①作MH OQ ⊥,∵MQ 平分OQP ∠,∴HM DM =,设(),0M m (m >0),则OM m =,8DM m =-, ∴8HM m =-,∵sin HM QOD OM∠=,sin QD QOD OQ ∠=, ∴HM DQ OM OQ=, ∵()8,6Q ,∴10OQ =,6DQ =, ∴8610m m-=, ∴5m =,∴()5,0M ;②如图,当四边形NOMQ 为平行四边形时,△△NQO MOQ ≅,则NQ 由OM 平移得到,()5,0M 平移到点()8,6Q ,则853-=,则横坐标加上3,606-=,则纵坐标加上6,∵()0,0O ,∴()13,6N ;当△NOQ 与△MOQ 关于OQ 对称时,△△NOQ MOQ ≅,设()2,N a b , ∵6sin 0.610QD QOD QO ∠===, ∴0.6HM OM =, ∴0.65HM =, ∴3HM =,∴226N M HM ==,作2N F x ⊥轴,则2FN M QOD ∠=∠, ∴228cos 6 4.810FN MN QOD =∠=⨯=, 26sin 6 3.610PM N M QOD =∠=⨯=, 5 3.6 1.4OF MO FM =-=-=, ∴()2 1.4,4.8N ;综上所述,符合条件的N 点的坐标为()3,6,()1.4,4.8.【点睛】本题主要考查了一次函数综合应用,结合三角函数定义、勾股定理、三角形全等计算是解题的关键.26.(1)见解析;(2)1【分析】(1)由90ACB FCE ∠=∠=︒可证ACE BCF ∠=∠,由CE 是ABC ∆中线得AE=CE ,所以ACE CAE ∠=∠,从而可得BCF CAE ∠=∠,结合BFC CFA ∠=∠可证CBF ACF △△;(2)证明A BCD ∠=∠,根据1tan 2BCD ∠=利用相似三角形的性质求得11,2,4222CF BF CF ===,从而可求出BF 的值. 【详解】解:(1)证明:90ACB ∠=︒,90BCE ACE ∴∠+∠=︒,又CE CF ⊥,90BCE BCF ∴∠+∠=︒, ACE BCF ∴∠=∠又CE 是ABC ∆中线,AE CE ∴=,ACE CAE ∴∠=∠ BCF CAE ∴∠=∠又BFC CFA ∠=∠CBF ACF ∴∆∆(2)解:由(1)知CBFACF ∆∆ BF CF CB CF AF AC ∴== 又CD 是Rt ABC ∆的高,90ACB ∠=︒,90CDB ∴∠=︒90,90BCD CBD A CBD ∴∠+∠=︒∠+∠=︒,A BCD ∴∠=∠ 又1tan 2BCD ∠=, 1tan tan 2A BCD ∴∠=∠= 12CB BD AC CD ∴==, 12BF CF CB CF AF AC ∴=== 又4AF =,11,2,4222CF BF CF ∴=== 1BF ∴=.【点睛】此题主要考查了相似三角形的判定与性质以及解直角三角形,熟练掌握相关性质是解答此题的关键.。
最新九年级数学下期中第一次模拟试题附答案

一、选择题1.如图,抛物线2y ax bx c =++的顶点坐标为(1,4)a -,点()14,A y 是该抛物线上一点,若点()22,B x y 是该抛物线上任意一点.有下列结论:①420a b c -+>;②抛物线2y ax bx c =++与x 轴交于点(1,0)-,(3,0); ③若21y y >,则24x >;④若204x ≤≤,则235a y a -≤≤. 其中,正确结论的个数是( ) A .0B .1C .2D .3 2.抛物线y =x 2﹣2x ﹣1的对称轴是( )A .直线x =﹣2B .直线x =﹣1C .直线x =1D .直线x =23.将进货价为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨1元,其销售量就减少5个,设这种商品的售价为x 元时,获得的利润为y 元,则下列关系式正确的是( ) A .()()352005y x x =-- B .()()354005y x x =-- C .()()402005y x x =--D .()()403755y x x =--4.二次函数()20y ax bx c a =++≠的图象如图所示,给出下列四个结论:①240b ac -<;②0a b c ++<;③2a b >;④0abc >,其中正确的结论是( ). A .①② B .②④C .③④D .②③④5.函数k y x=与()20y kx k k =-≠在同一直角坐标系中的图象大致是下图中的( )A .B .C .D .6.将抛物线()2214y x =--+向右平移3个单位,再向下平移2个单位,得到抛物线的解析式为( ) A .()2241y x =-++ B .()2221y x =--+ C .()2246y x =--+D .()2242y x =--+7.如图,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AEF 是等边三角形,连接AC 交EF 于点G ,有下列结论:①15BAE DAF ∠=∠=︒;②AC EF ⊥;③BE DF EF +=;④3AG GC =.其中正确的个数为( )A .1B .2C .3D .48.在RtΔABC 中,若∠C=90°,cosA=35,则sinA 的值为( ) A .35B .45 C .34D .549.如图,边长为23的等边三角形AOB 的顶点B 在x 轴的正半轴上,点C 为AOB 的中心,将AOB 绕点O 以每秒60︒的速度逆时针旋转,则第2021秒,AOB 的中心C 的对应点2021C 的坐标为( )A .()0,2-B .)3,1-C .(3D .(3-10.如图,四边形ABCD 中,∠B =∠C =90°,CD =2米,BC =5米,5sin 13A =,则AB =( )A .8米B .10米C .12米D .14米11.如图,四边形ABCD 是边长为1的正方形,BPC △是等边三角形,连接DP 并延长交CB 的延长线于点H ,连接BD 交PC 于点Q ,下列结论:①135BPD ︒∠=;②BDP HDB △∽△;③:1:2DQ BQ =;④314BDPS-=.其中正确的有( )A .①②③B .②③④C .①②③④D .①②④12.tan60︒的值为( ) A .33B .23C .3D .2二、填空题13.函数y =ax 2+bx +c (a ≠0)图像如图所示,过点(﹣1,0),对称轴为x =2,下列结论正确的是_____. ①4a +b =0; ②24a +2b +3c <0;③若A (﹣3,y 1),B (﹣0.5,y 2),C (3.5,y 3)三点都在抛物线上,y 1<y 2<y 3; ④当y 1>﹣1时,y 随x 增大而增大.14.如图所示,二次函数2(0)y ax bx c a =++≠的图像与x 轴交于点()3,0,对称轴为直线1x =.则方程20cx bx a ++=的两个根为_____.15.如果抛物线y=x 2-6x+c-2的顶点到x 轴的距离是4,则c 的值等于_________. 16.二次函数224y x x =-++的最大值是______.17.如图,在平面直角坐标系中,Rt ABC 的顶点A C 、的坐标分别是()0,3、3,0.90ACB ∠=︒,2AC BC =,反比例函数()0ky x x=>的图象经过点B ,则k 的值为________.18.如图,在菱形纸片ABCD 中,3AB =,60A ∠=︒,将菱形纸片翻折,使点A 落在CD 的中点E 处,折痕为FG ,点F ,G 分别在边AB ,AD 上,则tan EFG ∠的值为________.19.计算:()201232cos 4520212π-⎛⎫---- ⎪⎝⎭=__________20.在ABC 中,若213sin tan 02A B ⎫-+-=⎪⎪⎝⎭,则C ∠的度数为__________. 三、解答题21.如图,已知矩形ABCD 的周长为36cm ,矩形绕它的一条边CD 旋转形成一个圆柱.设矩形的一边AB 的长为cm(0)x x >,旋转形成的圆柱的侧面积为2cm S .(1)用含x 的式子表示:矩形的另一边BC 的长为______cm ;旋转形成的圆柱的底面圆的周长为______cm . (2)求S 关于x 的函数解析式及自变量x 的取值范围; (3)求当x 取何值时,矩形旋转形成的圆柱的侧面积最大;(4)若矩形旋转形成的圆柱的侧面积等于218cm π,则矩形的长是______cm ,宽是______cm .22.天气寒冷,某百货商场准备销售一种围巾,围巾的进货价格为每条50元,并且每条的售价不低于进货价,经过市场调查,每月的销售量y (条)与每条的售价x (元)之间满足人体所示的函数关系.(1)求每月销售y (条)与售价x (元)的函数关系式;(2)物价部门规定,该围巾的每条利润不允许高于进货价的30%,设这种围巾每月的总利润为w (元),那么售价定为多少元可获得最大利润?最大利润是多少?23.如图,抛物线y =﹣x 2+bx +c 与x 轴相交于A (﹣3,0),D (1,0)两点,其中顶点为B .(1)求该抛物线的解析式;(2)若该抛物线与y 轴的交点为C ,求△ABC 的面积.24.如图,在矩形ABCD 中,BE 交AD 于点E 且平分∠ABC ,对角线BD 平分∠EBC .(1)求DEAE的值. (2)求tan ABD ∠.25.如图,海中有一个小岛A ,它的周围25海里内有暗礁,今有货船由西向东航行,开始在A 岛南偏西60°的B 处,往东航行20海里后到达该岛南偏西45°的C 处后,货船继续向东航行,你认为货船在航行途中有没有触礁的危险.26.如图,ABC 中,90,,ACB CD CE ∠=︒分别是ABC 的高和中线,过点C 作CE 的垂线交AB 的延长线于点F . (1)求证:CBFACF △△(2)若14,tan 2AF BCD =∠=,求BF 的长.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】利用对称轴公式和顶点坐标得出4a a b c -=++,2b a =-,3c a =-,则可对①进行判断;抛物线解析式为223y ax ax a =--,配成交点式得()()31y a x x =-+,可对②进行判断;根据二次函数对称性和二次函数的性质可对③进行判断;计算4x =时5y a =,根据二次函数的性质可对④进行判断 【详解】①根据抛物线()20y ax bx c a =++≠的图像可知抛物线的对称轴12bx a=-= 2b a ∴=-顶点坐标为(1、4a -)4a a b c ∴-=++3c a ∴=-424435a b c a a a a ∴-+=+-= 抛物线开口向上,则0a >420a b c ∴-+>故结论①正确 ②2b a =-,3c a =-()()22331y ax ax a a x x ∴=--=-+∴抛物线()20y ax bx c a =++≠与x 轴交于(1-、0),(3、0)故结论②正确 ③A (4、1y )关于直线1x =的对称点为(2-、1y )∴当21y y >时,则24x >或22x <-故结论③错误④当4x =时,116416835y a b c a a a a =++=--=∴当204x ≤≤时,245a y a -≤≤故结论④错误 故选:C . 【点睛】本题考查了抛物线与x 轴的交点,也考查了二次函数的性质,解题关键是把求二次函数与x 轴交点问题转化为解关于x 一元二次方程,并熟练掌握二次函数的性质.2.C解析:C 【分析】先将抛物线化为顶点式,即可解决问题. 【详解】解:因为抛物线y =x 2﹣2x ﹣1=x 2﹣2x +1﹣2=(x ﹣1)2﹣2, 所以对称轴是直线x =1. 故选:C . 【点睛】本题考查了二次函数的性质,解题的关键是能将抛物线化为顶点式.3.B解析:B 【分析】根据售价减去进价表示出实际的利润. 【详解】解:设这种商品的售价为x 元时,获得的利润为y 元,根据题意可得:[](35)2005(40)y x x =--- 即y=(x-35)(400-5x ),故选:B . 【点睛】本题考查了二次函数的应用,解题的关键是理解“商品每上涨1元,其销售量就减少5个”.4.B解析:B 【分析】根据抛物线与x 轴交点可判断①;根据x=1时,y <0,可判断②;对称轴x=-1可判断③;根据抛物线开口方向、对称轴、与y 轴交点可判断④. 【详解】解:①由抛物线图象与x 轴有两个交点可知240b ac ->,故①错误; ②由图象知,当x=1时,y=a+b+c <0,故②正确; ③抛物线对称轴x=-1,即-2ba=-1<0,即b=2a <0,即③错误; ④由抛物线图象得:开口向下,即a <0;c >0,b <0,∴abc >0,故④正确; 所以正确的有:②④, 故选:B . 【点睛】主要考查图象与二次函数系数之间的关系,掌握二次函数y=ax 2+bx+c 系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点、抛物线与x 轴交点的个数确定是解题的关键.5.B解析:B 【分析】根据k>0,k<0,结合反比例函数及二次函数图象及其性质分类讨论. 【详解】解:分两种情况讨论:①当k>0时,反比例函数k y x=在一、三象限,而二次函数()20y kx k k =-≠开口向上,与y 轴交点在原点下方,故C 选项错误,B 选项正确;②当k<0时,反比例函数k y x=在二、四象限,而二次函数()20y kx k k =-≠开口向下,与y 轴交点在原点上方,故A 选项与D 选项错误. 故选B . 【点睛】本题考查了反比例函数图象性质和二次函数图象性质.关键是根据k>0,k<0,结合反比例函数及二次函数图象及其性质分类讨论.6.D解析:D 【分析】根据“左加右减、上加下减”的原则进行解答即可. 【详解】解:将抛物线y=-2(x-1)2+4向右平移3个单位,再向下平移2个单位长度后得到抛物线的解析式为:y=-2(x-1-3)2+4-2,即y=-2(x-4)2+2; 故选:D . 【点睛】此题主要考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.7.C解析:C 【分析】通过HL 证明ABE ADF ≌,从而得到,BAE DAF BE DF ∠=∠=由正方形的性质可以得出EC FC =,从而得出AC 垂直平分EF 可得结论①②正确,设EC x =,根据勾股定理,表示出等边三角形边长EF =,分别计算出AG ,CG ,再计算BE 、EF 的长,可比较BE DF +的长与EF 的长,即可判断结论③错误,结论④正确.【详解】四边形ABCD 是正方形,,90AB AD B D ∴=∠=∠=︒AEF 是等边三角形 ,60AE AF EAF ∴=∠=︒ 30BAE DAF ∴∠+∠=︒在Rt ABE △和Rt ADF 中AE AFAB AD =⎧⎨=⎩∴Rt ABE △≌Rt ADFBE DF ∴= BC CD =BC BE CD DF -=-∴,即CE CF = ∴AC 是EF 的垂直平分线AC EF ∴⊥∴AC 平分EAF ∠160302EAC FAC ∴∠=∠=⨯︒=︒45BAC DAC ∠=∠=︒ 15BAE DAF ∠∠∴==︒ 故结论①②正确;sin 60sin 602sin 6022AG AE EF CG =︒⋅=︒⋅=⨯⋅︒=⨯AG ∴=故结论④正确; 设EC x =,则FC x =由勾股定理得EF =12CG EF x ==,则2x AC CG AG CG =+=+=(12AB x+∴==()1122x x BE AB CE x +∴=-=-=))1212x BE DF x ∴+=⨯=≠故结论③错误综上所述结论①②④正确,结论③错误故选:C .【点睛】本题考查了正方形的性质,全等三角形的判定以性质,勾股定理,等边三角形的性质,解题关键是熟练运用这些性质,利用勾股定理计算边的长度.8.B解析:B【分析】根据正弦和余弦的平方和等于1求解.【详解】解:∵()()22sin cos 1A A +=,∴4sin 5A ===, 故选B .【点睛】本题考查锐角三角函数的性质,熟练掌握正弦函数与余弦函数的平方和等于1的性质是解题关键. 9.B解析:B 【分析】通过计算画出第2021秒,AOB 的位置,过C′作C′D ⊥x 轴于点D ,连接OC′,BC′,求出DC′的长,即可求解.【详解】∵360°÷60°=6,∴AOB 的位置6秒一循环,而2021=6×336+5,∴第2021秒,AOB 的位置如图所示, 设点C 的对应点C′,过C′作C′D ⊥x 轴于点D ,连接OC′,BC′,则∠DOC′=30°,,∴DC′=OD∙tan ∠3=1,∴C′)1-. 故选B .【点睛】本题主要考查图形于=与坐标,等边三角形的性质,锐角三角函数,找到图形的变化规律,画出图形,是解题的关键.10.D解析:D【分析】过点D 作DE ⊥AB 于E ,得到四边形DEBC 是矩形,得到BE=DC=2米,DE=BC=5米,根据5sin 13A =,求得AD=13米,根据勾股定理求出AE=12米,即可得到答案. 【详解】过点D 作DE ⊥AB 于E ,∴∠DEB=∠B =∠C =90°,∴四边形DEBC 是矩形,∴BE=DC=2米,DE=BC=5米, ∵5sin 13A =, ∴513DE AD =, ∴AD=13米,∴AE=222213512AD DE -=-=米,∴AB=AE+BE=12+2=14米,故选:D ..【点睛】此题考查矩形的判定及性质,勾股定理,锐角三角函数,正确引出辅助线构建直角三角形解决问题是解题的关键.11.D解析:D【分析】由等边三角形及正方形的性质求出∠CPD=∠CDP=75°、∠PCB=∠CPB=60°,从而判断①;证∠DBH=∠DPB=135°可判断②;作QE⊥CD,设QE=DE=x,则QD=2x,CQ=2QE=2x,CE=3x,由CE+DE=CD求出x,从而求得DQ、BQ的长,据此可判断③,证DP=DQ=6-22,根据BDPS=12BD•PDsin∠BDP求解可判断④.【详解】解:∵△PBC是等边三角形,四边形ABCD是正方形,∴∠PCB=∠CPB=60°,∠PCD=30°,BC=PC=CD,∴∠CPD=∠CDP=75°,则∠BPD=∠BPC+∠CPD=135°,故①正确;∵∠CBD=∠CDB=45°,∴∠DBH=∠DPB=135°,又∵∠PDB=∠BDH,∴△BDP∽△HDB,故②正确;如图,过点Q作QE⊥CD于E,设QE=DE=x,则QD2x,CQ=2QE=2x,∴CE3,由CE+DE=CD知x3x=1,解得x=3-12,∴QD2=6-22,∵BD2∴BQ=BD−DQ26-232-6,则DQ∶6-2∶32-6∶2,故③错误;∵∠CDP=75°,∠CDQ=45°,∴∠PDQ=30°,又∵∠CPD =75°,∴∠DPQ =∠DQP =75°,∴DP =DQ =2,∴BDP S =12BD•PDsin ∠BDP =12×2×12=14 ,故④正确; 故选:D .【点睛】本题主要考查相似三角形的判定与性质,解题的关键是熟练掌握等边三角形和正方形的性质、等腰三角形的判定与性质及相似三角形的判定等知识点.12.C解析:C【分析】根据特殊角的三角函数值解答即可.【详解】tan60°,故选C.【点睛】本题考查了特殊角三角函数值,熟记特殊角的三角函数值是解题关键.二、填空题13.①②③【分析】由抛物线的对称轴可判断①;由①可得出过点(﹣10)代入可得出c =﹣5a 代入化简即可判断②;根据二次函数的增减性知抛物线上点离对称轴水平距离越小函数值越大据此可判断③;由抛物线的图像的增 解析:①②③【分析】由抛物线的对称轴可判断①;由①可得出=4b a -,过点(﹣1,0),代入可得出c =﹣5a ,代入化简即可判断②;根据二次函数的增减性知抛物线上点离对称轴水平距离越小,函数值越大,据此可判断③;由抛物线的图像的增减性直接判断④.【详解】函数y =ax 2+bx +c (a ≠0)的对称轴2b x a =-, ∵ 对称轴2x =, ∴=22b a-, ∴=4b a -,∴ 4+=0a b ,故①正确;有图可知,a <0,∴=4b a -,∴ 2=8b a -,过点(﹣1,0),∴ a-b+c =0,∴ b=a+c ,即a+c=﹣4a ,∴ c =﹣5a ,∴24a +2b +3c =24a -8a -15a =a <0,故②正确;当x =0时,y =c ,∵A (﹣3,y 1),B (﹣0.5,y 2),C (3.5,y 3)三点都在抛物线上,点A 与2x =的水平距离为5,点B 与2x =的水平距离为2.5,点C 与2x =的水平距离为1.5,∵5>2.5>1.5,∴ 123y y y <<,故③正确;有图可知,当11y >-,y 随x 增大先增大后减小,故④不正确;综上,正确的有:①②③.故答案为:①②③.【点睛】本题考查的是二次函数图象与系数的关系,要求学生熟悉函数的基本性质,能熟练求解函数与坐标轴的交点及顶点的坐标等.14.【分析】根据题意和二次函数的性质可以得到二次函数的图像与轴的另一个交点然后得到的解然后再变形即可得到方程的两个根;【详解】∵二次函数的图象与x 轴交于点对称轴为直线∴该函数与x 轴的另一个交点为∴当时可 解析:11x =-,213x =【分析】根据题意和二次函数的性质,可以得到二次函数2(0)y ax bx c a =++≠的图像与x 轴的另一个交点,然后得到20ax bx c ++=的解,然后再变形,即可得到方程的两个根;【详解】∵二次函数2(0)y ax bx c a =++≠的图象与x 轴交于点()3,0,对称轴为直线1x =, ∴该函数与x 轴的另一个交点为()1,0-,∴当0y =时,20ax bx c =++,可得:11x =-,23x =,当20ax bx c ++=,0x ≠时,可得2110a b c x x ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭, 设1t x=,可得20ct bt a ++=, ∴11t =-,213t =, 由上可得,方程20cx bx c ++=的两个根为11x =-,213x =;故答案为:11x =-,213x =. 【点睛】本题主要考查了二次函数与一元二次方程的应用,准确分析计算是解题的关键. 15.7或15【分析】根据题意可知抛物线顶点纵坐标是±4化成顶点式求解即可【详解】解:∵抛物线y=x2-6x+c-2的顶点到x 轴的距离是4∴抛物线顶点纵坐标是±4抛物线y=x2-6x+c-2化成顶点式为:解析:7或15.【分析】根据题意可知,抛物线顶点纵坐标是±4,化成顶点式求解即可.【详解】解:∵抛物线y=x 2-6x+c-2的顶点到x 轴的距离是4,∴抛物线顶点纵坐标是±4,抛物线y=x 2-6x+c-2化成顶点式为:y=(x-3)2+c-11,c-11=4,c=15,c-11=-4,c=7,故答案为:7或15.【点睛】本题考查了抛物线的顶点坐标,解题关键是理解到x 轴的距离是纵坐标的绝对值,注意:分类讨论.16.【分析】利用二次函数的配方法确定最值即可【详解】∵∵a=-1<0∴二次函数有最大值且最大值为5;故答案为:5【点睛】本题考查了二次函数的最值问题熟练运用配方法确定二次函数的最值是解题的关键解析:【分析】利用二次函数的配方法确定最值即可.【详解】∵224y x x =-++2(24)x x =---2[(1)14]x =----2(1)5x =--+,∵a= -1<0,∴二次函数224y x x =-++有最大值,且最大值为5;故答案为:5.【点睛】本题考查了二次函数的最值问题,熟练运用配方法确定二次函数的最值是解题的关键. 17.【分析】过作于求解再求解证明由可得再求解从而可得答案【详解】解:过作于由故答案为:【点睛】本题考查的是勾股定理的应用等腰直角三角形的判定与性质锐角三角函数的应用利用待定系数法求解反比例函数的解析式掌 解析:27.4 【分析】 过B 作BH OC ⊥于,H 求解2232,AC OA OC =+= 再求解32,2BC =证明,CH BH = 由cos ,CH BCH BC ∠= 可得2,232= 再求解3,2CH = 339,3,222BH OH ==+= 从而可得答案. 【详解】解:过B 作BH OC ⊥于,H90,BHC AOC ∴∠=︒=∠()()0,3,3,0,A B3,OA OC ∴==2232,AC OA OC ∴=+=2,AC BC =2BC ∴= 90,45,ACB ACO ∴∠=︒∠=︒45,BCH CBH ∠=︒=∠,CH BH ∴= 由cos ,CH BCH BC∠=2=3,2CH ∴= 339,3,222BH OH ∴==+= 93,,22B ⎛⎫∴ ⎪⎝⎭3927.224k xy ∴==⨯= 故答案为:27.4【点睛】本题考查的是勾股定理的应用,等腰直角三角形的判定与性质,锐角三角函数的应用,利用待定系数法求解反比例函数的解析式,掌握以上知识是解题的关键. 18.【分析】连接AE 交GF 于O 连接BEBD 则△BCD 为等边三角形设AF=x=EF 则BF=3-x 依据勾股定理可得Rt △BEF 中BF2+BE2=EF2解方程(3-x )2+()2=x2即可得到EF=再根据Rt解析:3【分析】连接AE 交GF 于O ,连接BE ,BD ,则△BCD 为等边三角形,设AF=x=EF ,则BF=3-x ,依据勾股定理可得Rt △BEF 中,BF 2+BE 2=EF 2,解方程(3-x )2+2=x 2,即可得到EF=218,再根据Rt △EOF 中,=tan ∠EFG=EO FO =. 【详解】解:如图,连接AE 交GF 于O ,连接BE ,BD ,则△BCD 为等边三角形,∵E 是CD 的中点,∴BE ⊥CD ,∴∠EBF=∠BEC=90°,Rt △BCE 中,CE=cos60°×3=1.5,BE=sin60°332 ∴Rt △ABE 中,372由折叠可得,AE ⊥GF ,EO=12374设AF=x=EF ,则BF=3-x , ∵Rt △BEF 中,BF 2+BE 2=EF 2,∴(3-x )2+3322=x 2, 解得x=218,即EF=218, ∴Rt △EOF 中,223218AF AO -= ∴tan ∠EFG=233EO FO = 233【点睛】 本题考查了菱形的性质、解直角三角形以及折叠的性质:折叠是一种对称变换,对应边和对应角相等.解题时,常设要求的线段长为x ,然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案. 19.0【分析】直接利用负整数指数幂绝对值的性质特殊角的三角函数值及零指数幂分别化简得出答案【详解】解:原式=4-(3-)--1=4-3+--1=0故答案为0【点睛】本题主要考查了实数运算正确化简各数是解解析:0【分析】直接利用负整数指数幂、绝对值的性质、特殊角的三角函数值及零指数幂,分别化简得出答案.【详解】解:原式2222-1=0,故答案为0.【点睛】本题主要考查了实数运算,正确化简各数是解题的关键.20.120º【分析】根据绝对值和平方的非负数性质可得sinA=tanB=根据特殊角的三角函数值可得出∠A ∠B 的度数根据三角形内角和定理即可得答案【详解】∵∴sinA-=0-tanB=0∴sinA=tan解析:120º【分析】根据绝对值和平方的非负数性质可得sinA=12,tanB=3,根据特殊角的三角函数值可得出∠A 、∠B 的度数,根据三角形内角和定理即可得答案.【详解】∵21sin tan 02A B ⎫-+=⎪⎪⎝⎭,∴sinA-12=0,3-tanB=0,∴sinA=12,tanB=3, ∴∠A=30°,∠B=30°,∠C=180°-30°-30°=120°,故答案为:120°【点睛】本题考查了特殊角的三角函数值、非负数的性质及三角形内角和定理,根据非负数性质得出sinA=12, 三、解答题21.(1)(18)x -,2(18)x π-;(2)2=236(018)S x x x ππ-+<<;(3)9x =;(4)(9+,(9-【分析】(1)根据矩形的性质,圆的周长公式求解即可.(2)根据圆柱的侧面积公式求解即可.(3)利用二次函数的性质求解即可.(4)构建方程求解即可.【详解】解:(1)BC=12(36-2x )=(18-x )cm ,旋转形成的圆柱的底面圆的周长为2π(18-x )cm .故答案为:(18)x -,2(18)x π-;(2)22(18)236(018)S x x x x x πππ=-⋅=-+<<(3)222362(9)162S x x x ππππ=-+=--+∵-2π<0,∴当9x =时,矩形旋转形成的圆柱的侧面积最大:(4)由题意:-2πx 2+36πx=18π,∴x 2-18x+9=0,解得或(舍弃),∴矩形的长是()cm ,宽是()cm .故答案为:(9+,(9-.【点睛】本题考查圆柱的计算,二次函数的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.22.(1)y 101200x =-+(x≥50);(2)售价定为65元可获得最大利润,最大利润8250元.【分析】(1)设一次函数解析式y kx b =+ (x≥50),利用待定系数法将(60,600),(80,400)代入即得解得解析式;(2)根据题意列出函数关系式,再利用二次函数的性质求最大利润即可,注意考虑自变量的范围,围巾的每条利润不允许高于进货价的30%.【详解】解:(1)设一次函数解析式y kx b =+ (x≥50).由函数图像可知(60,600),(80,400)在函数图像上,代入即得: 6006040080k b k b =+⎧⎨=+⎩解得:101200k b =-⎧⎨=⎩. 所以,每月销售y (条)与售价x (元)的函数关系式:y 101200x =-+(x≥50). (2)由题意得:()()=10120050w x x -+-化简得:2=10170060000w x x -+-由函数解析式可知对称轴是x=85时,x≤85时,w 随x 的增加而增大.因为,围巾的每条利润不允许高于进货价的30%,那么 x≤50×(1+30%),即x≤65. 所以,当x=65时,w 取到最大值:2=106517006560000=8250w -⨯+⨯-. 所以,售价定为65元可获得最大利润,最大利润8250元.【点睛】本题考查了一次函数与二次函数在销售问题中的应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.23.(1)y=﹣x2﹣2x+3;(2)3【分析】(1)利用待定系数法确定函数关系式;(2)根据抛物线解析式求得点B、C的坐标,过点B作BE⊥x轴于点E,交直线AC于F,由直线AC的解析式和一次函数图象上点的坐标特征求得点F的坐标,然后根据三角形面积公式求解.【详解】解:(1)∵抛物线y=﹣x2+bx+c与x轴相交于A(﹣3,0),D(1,0)两点,∴930 1+=0b cb c--+=⎧⎨-+⎩,解得:2 =3bc=-⎧⎨⎩.故该抛物线解析式为y=﹣x2﹣2x+3;(2)由抛物线解析式y=﹣x2﹣2x+3,可得B(﹣1,4),C(0,3).如图,过点B作BE⊥x轴于点E,交直线AC于F,则点F的横坐标是﹣1.∵直线AC经过点A(﹣3,0),C(0,3),∴直线AC的解析式是y=x+3.把x=﹣1代入y=x+3,得y=2.则F(﹣1,2).∴BF=2.∵AO=3∴S△ABC=S△ABF +S△BCF =12BF•(AE+OE)=12BF•AO=1232⨯⨯=3.【点睛】本题考查了待定系数法求二次函数的解析式和求坐标系中三角形的面积问题,难度不大,属于基础题型,熟练掌握待定系数法求二次函数的解析式是关键.24.(12;(221【分析】(1)证明△ABE是等腰直角三角形得2BE=,再证明∠EBD EDB=∠得BE=DE,从而可得结论;(2)设AB AE m ==,则2BE DE m ==,再求出AD 的长,最后求出tan ABD ∠的值即可.【详解】 解:(1)∵四边形ABCD 是矩形∴∠90,//ABC BAD AD BC =∠=︒∵BE 平分∠ABC , ∴∠45ABE =︒∴△ABE 是等腰直角三角形,∴2BE AE =∵BD 平分∠EBC∴∠EBD CBD =∠∵//AD BC∴∠EDB CBD =∠∴∠EBD EDB =∠∴BE DE =∴2DE BE AE AE== (2)由(1)知,AB AE =设AB AE m ==,则2BE DE m ==∴(21)AD AE DE m =+=+在Rt ABD ∆中, tan 21AD ABD AB∠==+. 【点睛】 此题主要考查了矩形的性质,等三角形的判定以及垗角的正切值,证明2BE AE =是解答此题的关键.25.货船在航行途中无触礁的危险【分析】过点A 作AD ⊥BC ,垂足为D ,解直角三角形即可得到结论.【详解】解:过点A 作AD BC ⊥,垂足为DABC 30∠=︒,ACD 45∠=︒CD AD x ∴==,tan 30x BD ==︒20BC BD CD x ∴=--=解得10x =即:AD=10 ∵10>25所以货船在航行途中无触礁的危险.【点睛】本题考查了解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.26.(1)见解析;(2)1【分析】(1)由90ACB FCE ∠=∠=︒可证ACE BCF ∠=∠,由CE 是ABC ∆中线得AE=CE ,所以ACE CAE ∠=∠,从而可得BCF CAE ∠=∠,结合BFC CFA ∠=∠可证CBF ACF △△;(2)证明A BCD ∠=∠,根据1tan 2BCD ∠=利用相似三角形的性质求得11,2,4222CF BF CF ===,从而可求出BF 的值. 【详解】解:(1)证明:90ACB ∠=︒,90BCE ACE ∴∠+∠=︒,又CE CF ⊥,90BCE BCF ∴∠+∠=︒, ACE BCF ∴∠=∠又CE 是ABC ∆中线,AE CE ∴=,ACE CAE ∴∠=∠ BCF CAE ∴∠=∠又BFC CFA ∠=∠CBFACF ∴∆∆ (2)解:由(1)知CBF ACF ∆∆BF CF CB CF AF AC ∴== 又CD 是Rt ABC ∆的高,90ACB ∠=︒,90CDB ∴∠=︒90,90BCD CBD A CBD ∴∠+∠=︒∠+∠=︒,A BCD ∴∠=∠ 又1tan 2BCD ∠=, 1tan tan 2A BCD ∴∠=∠= 12CB BD AC CD ∴==, 12BF CF CB CF AF AC ∴=== 又4AF =,11,2,4222CF BF CF ∴=== 1BF ∴=.【点睛】此题主要考查了相似三角形的判定与性质以及解直角三角形,熟练掌握相关性质是解答此题的关键.。
初三数学下期中一模试卷附答案
初三数学下期中一模试卷附答案一、选择题1.如果反比例函数y=kx(k≠0)的图象经过点(﹣3,2),则它一定还经过()A.(﹣12,8)B.(﹣3,﹣2)C.(12,12)D.(1,﹣6)2.P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?()A.1条B.2条C.3条D.4条3.如图,已知直线a∥b∥c,直线m、n与直线a、b、c分别交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,则BF=()A.7B.7.5C.8D.8.54.如图,在△ABC中,DE∥BC ,12ADDB=,DE=4,则BC的长是()A.8 B.10 C.11 D.125.如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③AE DEAB BC=,④AD AEAC AB=,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有()A.①②④B.②④⑤C.①②③④D.①②③⑤6.已知两个相似三角形的面积比为 4:9,则周长的比为 ( )A.2:3B.4:9 C.3:2D.2:37.反比例函数kyx=与1(0)y kx k=-+≠在同一坐标系的图象可能为()A.B.C.D.8.在同一直角坐标系中,函数kyx=和y=kx﹣3的图象大致是()A.B.C.D.9.若△ABC∽△A′B′C′且34ABA B='',△ABC的周长为15cm,则△A′B′C′的周长为()cm.A.18B.20 C.154D.80310.如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF 的面积之比为 ( )A.1:2B.1:4C.1:5D.1:611.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的12,得到△COD,则CD的长度是()A .2B .1C .4D .25 12.若270x y -=. 则下列式子正确的是( )A .72x y =B .27x y =C .27x y =D .27x y = 二、填空题13.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”意思就是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆(如图所示),它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为_____.14.如图,在平面直角坐标系内有一点()5,12P ,那么OP 与x 轴正半轴的夹角α的余弦值为______.15.△ABC 与△A′B′C′是位似图形,且△ABC 与△A′B′C′的位似比是1:2,已知△ABC 的面积是3,则△A′B′C′的面积是_____.16.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的P 点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米.17.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面23米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).18.如图所示,在Rt △ABC 中,∠C=90°,BC=1,AC=4,把边长分别为1x ,2x ,3x ,…,n x 的n ()1n ≥个正方形依次放入△ABC 中,则第n 个正方形的边长n x =_______________(用含n 的式子表示).19.若关于x 的分式方程33122x m x x +-=--有增根,则m 的值为_____. 20.已知CD 是Rt △ABC 斜边上的高线,且AB=10,若BC=8,则cos ∠ACD= ______ .三、解答题21.已知:如图,点C ,D 在线段AB 上,△PCD 是等边三角形,且AC=1,CD=2,DB=4.求证:△ACP ∽△PDB .22.如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).(1)以原点O 为位似中心,位似比为1∶2,在y 轴的左侧,画出△ABC 放大后的图形△A 1B 1C 1,并直接写出C 1点的坐标;(2)如果点D(a ,b)在线段AB 上,请直接写出经过(1)的变化后点D 的对应点D 1的坐标.23.如图,已知反比例函数11k y x=(k 1>0)与一次函数2221(0)y k x k =+≠相交于A 、B 两点,AC ⊥x 轴于点C . 若△OAC 的面积为1,且tan ∠AOC =2 .(1)求出反比例函数与一次函数的解析式;(2)请直接写出B 点的坐标,并指出当x 为何值时,反比例函数y 1的值大于一次函数y 2的值.24.自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡200AB =米,坡度为1:3;将斜坡AB 的高度AE 降低20AC =米后,斜坡AB 改造为斜坡CD ,其坡度为1:4.求斜坡CD 的长.(结果保留根号)25.如图,AB 与CD 相交于点O ,△OBD ∽△OAC ,OD OC =35,OB =6,S △AOC =50, 求:(1)AO 的长;(2)求S△BOD【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】分别计算各点的横纵坐标之积,然后根据反比例函数图象上点的坐标特征进行判断.【详解】∵反比例函数y=kx(k≠0)的图象经过点(−3,2),∴k=−3×2=−6,∵−12×8=−4≠−6,−3×(−2)=6≠−6,12×12=6≠−6,1×(−6)=−6,则它一定还经过(1,−6).故答案选D.【点睛】本题考查了反比例函数图象上点的坐标特征,解题的关键是熟练的掌握反比例函数图象上点的坐标特征.2.C解析:C【解析】试题分析:根据相似线的定义,可知截得的三角形与△ABC有一个公共角.①公共角为∠A 时,根据相似三角形的判定:当过点P的角等于∠C时,即图中PD∥BC时,△APD∽△ACB;当过点P的角等于∠B时,即图中当PF⊥AB时,△APF∽△ABC;②公共角为∠C时,根据相似三角形的判定:当过点P的角等于∠A时,即图中P E∥AB时,△CPE∽△CAB;当过点P的角等于∠B时,根据∠CPB<60°,可知此时不成立;③公共角为∠B,不成立.解:①公共角为∠A时:当过点P的角等于∠C时,即图中PD∥BC时,△APD∽△ACB;当过点P的角等于∠B时,即图中当PF⊥AB时,△APF∽△ABC;②公共角为∠C时:当过点P的角等于∠A时,即图中P E∥AB时,△CPE∽△CAB;当过点P的角等于∠B时,∵∠CPB=∠A+∠ABP,∴PB>PC,PC=PA,∴PB>PA,∴∠PBA<∠A,∴∠CPB<60°,可知此时不成立;③公共角为∠B,不成立.综上最多有3条.故选C.3.B解析:B【解析】【分析】由直线a∥b∥c,根据平行线分线段成比例定理,即可得AC BDCE DF=,又由AC=4,CE=6,BD=3,即可求得DF的长,则可求得答案.【详解】解:∵a∥b∥c,∴AC BD CE DF=,∵AC=4,CE=6,BD=3,∴436DF =,解得:DF=92,∴937.52BF BD DF=+=+=.故选B.考点:平行线分线段成比例.4.D解析:D【解析】【分析】根据AD DB =12,可得AD AB =13,再根据DE ∥BC ,可得DE BC =AD AB ; 接下来根据DE=4,结合上步分析即可求出BC 的长.【详解】 ∵AD DB =12, ∴AD AB =13, ∵在△ABC 中,DE ∥BC , ∴DE BC =AD AB =13. ∵DE=4,∴BC=3DE=12.故答案选D.【点睛】 本题考查了平行线分线段成比例的知识,解题的关键是熟练的掌握平行线分线段成比例定理.5.A解析:A【解析】①AED B ∠=∠,且DAE CAB ∠=∠,∴ADE ACB ∽,成立.②ADE C ∠=∠且DAE CAB ∠=∠,∴ADE ACB ∽,成立. ③AE DE AB BC =,但AED 比一定与B 相等,故ADE 与ACD 不一定相似. ④AD AE AC AB=且DAE CAB ∠=∠, ∴ADE ACB ∽,成立.⑤由2AC AD AE =⋅,得AC AE AD AC=无法确定出ADE , 故不能证明:ADE 与ABC 相似.故答案为A .点睛:本题考查了相似三角形的判定定理:(1)两角对应相等的两个三角形相似;(2)两边对应成比例且夹角相等的两个三角形相似;(3)三边对应成比例的两个三角形相似;(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.6.A解析:A【分析】由于相似三角形的面积比等于相似比的平方,已知了两个相似三角形的面积比,即可求出它们的相似比;再根据相似三角形的周长比等于相似比即可得解.【详解】∵两个相似三角形的面积之比为4:9,∴两个相似三角形的相似比为2:3,∴这两个相似三角形的周长之比为2:3.故选:A【点睛】本题考查的是相似三角形的性质:相似三角形的周长比等于相似比,面积比等于相似比的平方.7.B解析:B【解析】【分析】根据反比例函数和一次函数的性质逐个对选项进行分析即可.【详解】A 根据反比例函数的图象可知,k>0,因此可得一次函数的图象应该递减,但是图象是递增的,所以A错误;B根据反比例函数的图象可知,k>0,,因此一次函数的图象应该递减,和图象吻合,所以B正确;C根据反比例函数的图象可知,k<0,因此一次函数的图象应该递增,并且过(0,1)点,但是根据图象,不过(0,1),所以C错误;D根据反比例函数的图象可知,k<0,因此一次函数的图象应该递增,但是根据图象一次函数的图象递减,所以D错误.故选B【点睛】本题主要考查反比例函数和一次函数的性质,关键点在于系数的正负判断,根据系数识别图象.8.A解析:A【解析】【分析】根据一次函数和反比例函数的特点,k≠0,所以分k>0和k<0两种情况讨论.当两函数系数k取相同符号值,两函数图象共存于同一坐标系内的即为正确答案.【详解】分两种情况讨论:①当k>0时,y=kx﹣3与y轴的交点在负半轴,过一、三、四象限,反比例函数的图象在第一、三象限,没有图像符合要求;②当k<0时,y=kx﹣3与y轴的交点在负半轴,过二、三、四象限,反比例函数的图象在第二、四象限,A符合要求.【点睛】本题考查了反比例函数的图象性质和一次函数的图象性质,关键是由k的取值确定函数所在的象限.9.B解析:B【解析】∵△ABC∽△A′B′C′,∴34 ABC ABA B C A B''=''='的周长的周长,∵△ABC的周长为15cm,∴△A′B′C′的周长为20cm.故选B.10.B解析:B【解析】试题分析:利用位似图形的性质首先得出位似比,进而得出面积比.∵以点O为位似中心,将△ABC放大得到△DEF,AD=OA,∴OA:OD=1:2,∴△ABC与△DEF的面积之比为:1:4.故选B.考点:位似变换.11.A解析:A【解析】【分析】直接利用位似图形的性质结合A点坐标可直接得出点C的坐标,即可得出答案.【详解】∵点A(2,4),过点A作AB⊥x轴于点B,将△AOB以坐标原点O为位似中心缩小为原图形的12,得到△COD,∴C(1,2),则CD的长度是2,故选A.【点睛】本题主要考查了位似变换以及坐标与图形的性质,正确把握位似图形的性质是解题关键.12.A解析:A【解析】【分析】直接利用比例的性质分别判断即可得出答案.【详解】∵2x-7y=0,∴2x=7y.A.72xy=,则2x=7y,故此选项正确;B .27x y =,则xy =14,故此选项错误; C .27x y =,则2y =7x ,故此选项错误; D .27x y =,则7x =2y ,故此选项错误. 故选A .【点睛】本题考查了比例的性质,正确将比例式变形是解题的关键.二、填空题13.四丈五尺【解析】【分析】根据同一时刻物高与影长成正比可得出结论【详解】解:设竹竿的长度为x 尺∵竹竿的影长=一丈五尺=15尺标杆长=一尺五寸=15尺影长五寸=05尺∴=解得x=45(尺)故答案为:四丈解析:四丈五尺【解析】【分析】根据同一时刻物高与影长成正比可得出结论.【详解】解:设竹竿的长度为x 尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺, ∴x 15=1.50.5, 解得x=45(尺).故答案为:四丈五尺.【点睛】本题考查的是相似三角形的应用,熟知同一时刻物髙与影长成正比是解答此题的关键.14.【解析】【详解】如图过点P 作PA⊥x 轴于点A∵P(512)∴OA=5PA=12由勾股定理得OP=∴故填:【点睛】此题考查锐角三角函数的定义先构建直角三角形确定边长即可得到所求的三角函数值 解析:513【解析】【详解】如图,过点P 作PA ⊥x 轴于点A ,∵P(5,12),∴OA=5,PA=12,由勾股定理得OP=222251213OA PA+=+=,∴5 cos13OAOPα==,故填:5 13.【点睛】此题考查锐角三角函数的定义,先构建直角三角形,确定边长即可得到所求的三角函数值. 15.12【解析】【分析】根据位似是相似的特殊形式位似比等于相似比其对应的面积比等于相似比的平方进行解答即可【详解】解:∵△ABC与△A′B′C′是位似图形位似比是1:2∴△ABC∽△A′B′C′相似比是解析:12【解析】【分析】根据位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方进行解答即可.【详解】解:∵△ABC与△A′B′C′是位似图形,位似比是1:2,∴△ABC∽△A′B′C′,相似比是1:2,∴△ABC与△A′B′C′的面积比是1:4,又△ABC的面积是3,∴△A′B′C′的面积是12,故答案为12.【点睛】本题考查的是位似变换的概念和性质,掌握位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方是解题的关键.16.5【解析】根据题意画出图形构造出△PCD∽△PAB利用相似三角形的性质解题解:过P作PF⊥AB交CD于E交AB于F如图所示设河宽为x米∵AB∥CD∴∠PDC=∠PBF∠PCD=∠PAB∴△PDC∽△解析:5【解析】根据题意画出图形,构造出△PCD∽△PAB,利用相似三角形的性质解题.解:过P作PF⊥AB,交CD于E,交AB于F,如图所示设河宽为x米.∵AB∥CD,∴∠PDC=∠PBF,∠PCD=∠PAB,∴△PDC∽△PBA,∴AB PF CD PE=,∴AB15x CD15+=,依题意CD=20米,AB=50米,∴15205015x=+,解得:x=22.5(米).答:河的宽度为22.5米.17.【解析】【分析】本题需要分段求出巷子被分成的两部分再加起来即可先在直角三角形ABC中用正切和正弦分别求出BC和AC(即梯子的长度)然后再在直角三角形DCE中用∠DCE的余弦求出DC然后把BC和DC加解析:222+【解析】【分析】本题需要分段求出巷子被分成的两部分,再加起来即可.先在直角三角形ABC中,用正切和正弦,分别求出BC和AC(即梯子的长度),然后再在直角三角形DCE中,用∠DCE 的余弦求出DC,然后把BC和DC加起来即为巷子的宽度.【详解】解:如图所示:3米,∠ACB=60°,∠DCE=45°,AC=CE.则在直角三角形ABC中,ABBC=tan∠ACB=tan60°=3,ABAC=sin∠ACB=sin60°=3,∴BC=3=233=2,AC=3=233=4,∴直角三角形DCE中,CE=AC=4,∴CDCE=cos45°=2,∴CD=CE×2=4×2=22,∴BD=2+22,故答案为:2+22.【点睛】本题需要综合应用正切、正弦.余弦来求解,注意梯子长度不变,属于中档题.18.【解析】【分析】根据正方形的对边平行证明△BDF∽△BCA然后利用相似三角形对应边成比例列出比例式即可求出第1个正方形的边长同理利用前两个小正方形上方的三角形相似根据相似三角形对应边成比例列出比例式解析:4()5n【解析】【分析】根据正方形的对边平行证明△BDF∽△BCA,然后利用相似三角形对应边成比例列出比例式即可求出第1个正方形的边长,同理利用前两个小正方形上方的三角形相似,根据相似三角形对应边成比例列出比例式即可求出前两个小正方形的边长的关系,以此类推,找出规律便可求出第n个正方形的边长.【详解】解:如下图所示,∵四边形DCEF是正方形,∴DF∥CE,∴△BDF∽△BCA,∴DF:AC=BD:BC,即x 1:4=(1-x 1):1解得x 1= 45, 同理,前两个小正方形上方的三角形相似,112121-=-x x x x x 解得x 2=x 12 同理可得,113231,-=-x x x x x 解得:33121==x x x x以此类推,第n 个正方形的边长1n 45=⎛⎫= ⎪⎝⎭nn x x . 故答案为:4()5n 【点睛】本题考查了正方形的性质,相似三角形的判定与性质,解题的关键是根据相似三角形对应边成比例找出后面正方形的边长与第一个正方形的边长的关系. 19.3【解析】【分析】把分式方程化为整式方程进而把可能的增根代入可得m 的值【详解】去分母得3x-(x-2)=m+3当增根为x=2时6=m+3∴m=3故答案为3【点睛】考查分式方程的增根问题;增根问题可按解析:3【解析】【分析】把分式方程化为整式方程,进而把可能的增根代入,可得m 的值.【详解】去分母得3x-(x-2)=m+3,当增根为x=2时,6=m+3∴m=3.故答案为3.【点睛】考查分式方程的增根问题;增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.20.【解析】试题分析:根据同角的余角相等得:∠ACD=∠B 利用同角的余弦得结论解:∵CD 是Rt△ABC 斜边上的高线∴CD⊥AB∴∠A+∠ACD=90°∵∠ACB=90°∴∠B+∠A=90°∴∠ACD=∠ 解析:45【解析】试题分析:根据同角的余角相等得:∠ACD=∠B,利用同角的余弦得结论.解:∵CD是Rt△ABC斜边上的高线,∴CD⊥AB,∴∠A+∠ACD=90°,∵∠ACB=90°,∴∠B+∠A=90°,∴∠ACD=∠B,∴cos∠ACD=cos∠B=BCAB=810=45,故答案为:4 5 .三、解答题21.见解析【解析】【分析】先证明∠ACP=∠PDB=120°,然后由△PCD为等边三角形可证明,从而可证明△ACP∽△PD B.【详解】证明:∵△PCD为等边三角形,∴∠PCD=∠PDC=60°,PC=PD=CD=2∴∠ACP=∠PDB=120°∴.∴△ACP∽△PD B.【点睛】本题考查的知识点是相似三角形的判定和等边三角形的性质,解题关键是熟记等边三角形的性质.22.(1)图见解析,C1(-6,4);(2)D1(2a,2b).【解析】【分析】(1)连接OB并延长,使BB1=OB,连接OA并延长,使AA1=OA,连接OC并延长,使CC1=OC,确定出△A1B1C1,并求出C1点坐标即可;(2)根据A与A1坐标,B与B1坐标,以及C与C1坐标的关系,确定出变化后点D的对应点D1坐标即可.【详解】(1)根据题意画出图形,如图所示:则点C 1的坐标为(-6,4);(2)变化后D 的对应点D 1的坐标为:(2a ,2b ).【点睛】运用了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.23.(1)12y x =;21y x =+;(2)B 点的坐标为(-2,-1);当0<x <1和x <-2时,y 1>y 2.【解析】【分析】(1)根据tan ∠AOC =AC OC=2,△OAC 的面积为1,确定点A 的坐标,把点A 的坐标分别代入两个解析式即可求解;(2)根据两个解析式求得交点B 的坐标,观察图象,得到当x 为何值时,反比例函数y 1的值大于一次函数y 2的值.【详解】解:(1)在Rt △OAC 中,设OC =m .∵tan ∠AOC =AC OC =2,∴AC =2×OC =2m . ∵S △OAC =12×OC×AC =12×m×2m =1,∴m 2=1.∴m =1(负值舍去). ∴A 点的坐标为(1,2).把A 点的坐标代入11k y x=中,得k 1=2. ∴反比例函数的表达式为12y x =. 把A 点的坐标代入221y k x =+中,得k 2+1=2,∴k 2=1.∴一次函数的表达式21y x =+.(2)B 点的坐标为(-2,-1).当0<x <1和x <-2时,y 1>y 2.【点睛】本题考查反比例及一次函数的的应用;待定系数法求解析式;图象的交点等,掌握反比例及一次函数的性质是本题的解题关键.24.斜坡CD的长是【解析】【分析】根据题意和锐角三角函数可以求得AE 的长,进而得到CE 的长,再根据锐角三角函数可以得到ED 的长,最后用勾股定理即可求得CD 的长.【详解】∵90AEB =︒∠,200AB =,坡度为∴tan ABE ∠==, ∴30ABE ∠=︒, ∴11002AE AB ==, ∵20AC =,∴80CE =,∵90CED ∠=︒,斜坡CD 的坡度为1:4, ∴14CE DE =, 即8014ED =, 解得,320ED =,∴CD =米,答:斜坡CD的长是【点睛】本题考查解直角三角形的应用﹣坡度坡角问题,解答本题的关键是明确题意,利用锐角三角函数和数形结合的思想解答.25.(1)10;(2)18.【解析】【分析】(1)根据相似三角形对应边之比相等可得BO AO =DO CO =35,再代入BO =6可得AO 长; (2)根据相似三角形的面积的比等于相似比的平方可得BOD AOC S S=925,进而可得S △BOD . 【详解】解:(1)∵△OBD ∽△OAC , ∴BO AO =DO CO =35∵BO =6,∴AO =10; (2)∵△OBD ∽△OAC ,DO CO =35 ∴BOD AOC S S =925∵S △AOC =50,∴S △BOD =18.【点睛】此题主要考查相似三角形的性质,解题的关键是熟知相似三角形的面积之比等于相似比的平方.。
最新九年级数学下期中第一次模拟试卷含答案

一、选择题1.如图是二次函数()20y ax bx c a =++≠图象的一部分,对称轴是直线12x =,且经过点()20,,下列说法∶①0abc >;②240b ac -<;③1x =-是关于x 的方程20ax bx c ++=的一个根;④0a b +=.其中正确的个数为( )A .1B .2C .3D .42.已知二次函数2(2)1y mx m x =+--(m 为常数,且0m ≠),( )A .若0m >,则1x <,y 随x 的增大而增大B .若0m >,则1x >,y 随x 的增大而减小C .若0m <,则1x <,y 随x 的增大而增大D .若0m <,则1x >,y 随x 的增大而减小 3.如图为二次函数y =ax 2+bx+c 的图象,其对称轴为x =1,在下列结论中:①abc >0;②若方程ax 2+bx+c =0的根是x 1、x 2,则x 1+x 2<0;③4a+2b+c <0;④当x >1时,y 随x 的增大而增大.正确的有( )A .1B .2C .3D .44.汽车刹车后行驶的距离s (单位:m )关于行驶的时间t (单位:s )的函数解析式是2156s t t =-.汽车刹车后到停下来前进了多远?( )A .10.35mB .8.375mC .8.725mD .9.375m 5.已知函数223y x x =+-及一次函数y x m =-+的图象如图所示,当直线y x m =-+与函数223y x x =+-的图象有2个交点时,m 的取值范围是( )A .3m <-B .31m -<<C .134m >或3m <-D .31m -<<或134m > 6.在平面直角坐标系中,下列二次函数的图象开口向上的是( ) A .22y x =B .221y x x =-++C .22y x x =-+D .20.5y x x =-+ 7.如图,在△ABC 中,AD 是BC 上的高,tan ∠B =cos ∠DAC ,若sin C =1213,BC =12,求AD 的长( )A .13B .12C .8D .无法判断 8.如图,在Rt ABC ∆中,90,3,2C BC AB ∠=︒==,则B 等于( )A .15︒B .20︒C .30D .60︒9.如图,ABC ∆是等边三角形,点,D E 分别在边,BC AC 上,且,BD CE AD =与BE 相交于点F .若7,1AF DF ==,则ABC ∆的边长等于( )A .572-B .582-C .582+D .572+10.在Rt △ABC 中,∠C =90°,AB =3BC ,则sin B 的值为( )A .12B .22C .32D .223 11.cos45°的值为( ) A .1 B .12 C .22 D .3212.如图,在Rt △ABC 中,∠ACB=90°,若5AC =,BC=2,则sin ∠A 的值为( )A .5B .53C .23D .25 二、填空题13.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则关于x 的一元二次方程2ax bx c ++0(0)a =≠的根为___________.14.在平面直角坐标系xOy 中,将抛物线2yx 沿着y 轴平移2个单位长度,所得抛物线的解析式为________.15.如图,点P 是双曲线()4:0C y x x=>上的一点,过点P 作x 轴的垂线交直线1:22AB y x =-于点Q ,连结,OP OQ 当点P 在曲线C 上运动,且点P 在Q 的上方时,POQ △面积的最大值是________.16.若方程20ax bx c ++=的两个根是3-和1,那么二次函数2y ax bx c =++的图象的对称轴是直线x = _____________________17.如图,从A 地到B 地需经过C 地,现城市规划需修建一条从A 到B 的笔直道路,已知180AC 米,30CAB ∠=︒,45CBA ∠=︒,则道路改直后比原来缩短了___________米.(结果精确到1米,可能用到的数据:2 1.4≈,3 1.7≈)18.在AOB 中,90AOB ∠=︒,30ABO ∠=︒,将AOB 绕顶点O 顺时针旋转,旋转角为()0180θθ︒<<︒,得到11AOB .(1)如图1,连接1AA 、1BB ,设1AOA 和1BOB 的面积分别为1S 、2S .则12:S S =__________.(2)如图2,设OB 中点为Q ,11A B 中点为P ,连接QP ,若1AO =,当θ=_______︒时,线段QP 长度最小,最小值为_____________.19.如图,在平面直角坐标系中,点O 为坐标原点,点B 的坐标为(4,0),AB ⊥x 轴,连接AO ,tan ∠AOB =54,动点C 在x 轴上,连接AC ,将△ABC 沿AC 所在直线翻折得到△ACB ',当点B '恰好落在y 轴上时,则点C 的坐标为_____.20.已知在Rt ABC 中,90C ∠=︒,1cot 3B =,2BC =,那么AC =_____________. 三、解答题21.如图,抛物线223y x x =--与x 轴交于A 、B 两点.(1)抛物线与x 轴的交点坐标为______;(2)求抛物线与坐标轴围成的ABC 的面积;(3)设(1)中的抛物线上有一个动点P ,当点P 在该抛物线上滑动到什么位置时,满足6PAB S =△,并求出此时P 点的坐标.22.如图1,在矩形ABCD 中,8AB =,6AD =,沿对角线AC 剪开,再把ACD △沿AB 方向平移得到图2,其中A D '交AC 于E ,A C ''交BC 于F .(1)在图2中,除ABC 与C DA ''△外,指出图中全等三角形(不能添加辅助线和字母)并选择一对加以证明;(2)设AA x '=.①当x 为何值时,四边形A ECF '是菱形?②设四边形A ECF '的面积为y ,求y 与x 的关系式,并求出y 最大值.23.如图,在平面直角坐标系xOy 中,已知抛物线2y ax bx c =++与x 轴交于()30A -,,()10B ,两点,与y 轴交于点()0,3C ,连接AC ,点P 为第二象限抛物线上的动点.(1)求a 、b 、c 的值;(2)连接PA 、PC 、AC ,求PAC △面积的最大值;(3)过P 作PQ AC ⊥,垂足为Q ,是否存在这样的点P 、Q ,使得CPQ CBO △△,若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.24.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45︒改为30︒.已知原传送带AB 长为42m.(1)求新传送带AC 的长度;(2)如果需要在货物着地点C 的左侧留出5m 的通道,试判断距离B 点43m 的货物MNQP 是否需要挪走,并说明理由.25.(1)()3016tan 301220212π-⎛⎫︒+-- ⎪⎝⎭ (2)解不等式组:5131131132x x x x -<+⎧⎪++⎨≥+⎪⎩ (3)解方程:22311x x x++=-- 26.如图1,直线y =34x 和直线y =﹣12x+5相交于点A ,直线y =﹣12x+5与x 轴交于点C ,点P 在线段AC 上,PD ⊥x 轴于点D ,交直线y =34x 于点Q . (1)点A 的坐标为 ;(2)当QP =OA 时,求Q 点的坐标及△APQ 的面积;(3)如图2,在(2)的条件下,∠OQP 平分线交x 轴于点M .①直接写出点M 的坐标 ; ②点N 在直线y =34x 的上方,当OQN 和OQM 全等时直接写出N 点坐标 .【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】①根据抛物线开口方向、对称轴位置、抛物线与y 轴交点位置求得a 、b 、c 的符号即可判断;②根据抛物线与x 轴的交点即可判断;③根据二次函数的对称性即可判断;④由对称轴求出=-b a 即可判断.【详解】解:①∵二次函数的图象开口向下,∴0a <,∵二次函数的图象交y 轴的正半轴于一点,∴0c >,∵对称轴是直线12x =, ∴122b a -=, ∴0b a =->,∴0abc <. 故①错误;②∵抛物线与x 轴有两个交点,∴240b ac ->,故②错误;③∵对称轴为直线12x =,且经过点()2,0, ∴抛物线与x 轴的另一个交点为()1,0-,∴1x =-是关于x 的方程20ax bx c ++=的一个根,故③正确;④∵由①中知=-b a ,∴0a b +=,故④正确;综上所述,正确的结论是③④共2个.故选:B .【点睛】本题考查了二次函数的图象和系数的关系的应用,注意:当0a >时,二次函数的图象开口向上,当0a <时,二次函数的图象开口向下.2.D解析:D【分析】先求出二次函数图象的对称轴,然后根据m 的符号分类讨论,结合图象的特征即可得出结论.【详解】 该二次函数图象的对称轴为直线21122m x m m -=-=-+, 若0m >,对于22m x m -=-无法判断其符号,故A 、B 选项不一定正确; 若0m <,则202m x m -=-<,即22m m--<1,且抛物线的开口向下, ∴当1x >时,y 随x 的增大而减小,故选:D .【点睛】此题考查的是二次函数的图象及性质,解决此题的关键是分类讨论确定对称轴的位置,再结合开口方向进行综合分析.3.C解析:C【分析】根据开口方向、对称轴、抛物线与y 轴的交点,确定a 、b 、c 的符号,根据抛物线对称轴确定x 1+x 2的符号,根据当x=2时,判断4a+2b+c 的符号,根据二次函数的增减性对④进行判断.【详解】解:①∵开口向上,∴a >0,∵对称轴在y 轴的右侧,b <0,抛物线与y 轴交于负半轴,c <0,∴abc >0,∴①正确;②从图象可知,抛物线对称轴为直线x=122x x +=1,则x 1+x 2=2>0,∴②错误; ③抛物线对称轴是x=1,根据抛物线得对称性可知当x=2和x=0时函数值相等, ∴y=4a+2b+c <0,∴③正确;④抛物线开口向上,对称轴是x=1,当x >1时,y 随x 的增大而增大,∴④正确; 故选:C【点睛】本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.4.D解析:D【分析】求出函数的最大值即可得求解.【详解】∵22575156648s t t t ⎛⎫--- ⎪⎝⎭==+, ∴当54t =时,s 取得最大值759.3758=,即汽车刹车后到停下来前进的距离是9.375m 故选D .【点睛】 本题主要考查二次函数的应用,根据题意理解其最大值的实际意义是解题的关键. 5.D解析:D【分析】作出函数223y x x =+-及一次函数y x m =-+的图象,根据图象性质讨论即可求出. 【详解】解:如图:函数223y x x =+-,当0y =时,1x =或3-,()()3010A B ∴-,,,,当31x -<<时,223y x x =--+,当直线过点A 时,1个交点,此时()03m =--+,即3m =-,当3m >-时,有2个交点,当直线过点B 时,有3个交点,此时01m =-+,即1m =, ∴1m <时有2个交点,31m ∴-<<,当直线与抛物线相切时,有3个交点,223y x x y x m⎧=--+∴⎨=-+⎩, 由()1430m =--+=, 解得:134m =, 134m ∴>时有2个交点, 综上所述,31m -<<或134m >. 【点睛】 本题考查了一次函数与二次函数的交点问题,熟练掌握二次函数的性质是解题的关键. 6.A解析:A【分析】二次函数y =ax 2+bx +c (a ≠0),①当a >0时,抛物线y =ax 2+bx +c (a ≠0)的开口向上;②当a <0时,抛物线y =ax 2+bx +c (a ≠0)的开口向下,据此判断即可.【详解】解:A 、∵a >0, ∴2y =的图象开口向上,故本选项符合题意;B 、∵a =﹣1<0,∴y =﹣x 2+2x +1的图象开口向下,故本选项不符合题意;C 、∵a =﹣2<0,∴y =﹣2x 2+x 的图象开口向下,故本选项不符合题意;D 、∵a =﹣0.5<0,∴y =﹣0.5x 2+x 的图象开口向下,故本选项不符合题意;故选:A .【点睛】本题考查二次函数的图象和性质,解答本题的关键是明确题意,利用二次函数的性质解答.7.C解析:C【分析】 根据12sin 13AD C AC ==,可设AD =12x ,由勾股定理可求出DC ,利用tan ∠B =cos ∠DAC 可求出BD =13x ,利用BC =12,求出x ,进而求解.【详解】 在Rt △ADC 中,12sin 13AD C AC ==, 设AD =12x ,则AC =13x , ∴5DC x ==,∵cos ∠DAC =sin C =1213, ∴tan B =1213, 在Rt △ABD 中,∵tan B 1213AD BD ==,∴BD =13x , ∴13x +5x =12,解得23x =, ∴AD =12x =8.故选C .【点睛】 本题考查解直角三角形,熟练掌握正切,正弦和余弦的定义是解题的关键.8.C解析:C【分析】由锐角三角函数余弦的定义即可得出∠B=30°.【详解】解:∵∠C=90°,,AB=2,∴cos 2BC B AB ==, ∴∠B=30°,故选:C .【点睛】此题考查了解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.9.C解析:C先证明△ABD ≅△BCE ,推出∠BDA=∠FDB ,BE= DA=8,再证明△BDA ~△FDB ,利用相似三角形的性质求得BD=CE=22,作EG ⊥BC于G ,根据解直角三角形的知识即可求解【详解】∵ABC ∆是等边三角形,,∴AB=BC ,∠ABD=∠C=60︒,在△ABD 和△BCE 中,60AB BC ABD C BD CE =⎧⎪∠=∠=︒⎨⎪=⎩,∴△ABD ≅△BCE ,∴∠BAD=∠CBE ,BE= DA=1+7=8,∵∠BDA=∠FDB ,∴△BDA ~△FDB ,∴BD DA FD BD =,即171BD BD+=, ∴BD=22,则CE=BD=22,作EG ⊥BC 于G ,∵∠C=60︒,∴CG=CE ⋅1cos602222︒==EG=CE ⋅3sin 60226︒== 在Rt △BEG 中,()22228658BE EG -=-=∴582故选:C【点睛】 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,特殊角的三角函数值,等边三角形各边长相等、各内角为60°的性质.关键是利用了等边三角形的性质和相似三角形的判定和性质求解,有一定的综合性.10.D【分析】设BC=a ,则AB=3a ,根据勾股定理求出AC ,再根据正弦的定义求sin B .【详解】解:设BC=a ,则AB=3a ,AC ==,sin B =33AC AB a ==, 故选:D .【点睛】本题考查了三角函数,勾股定理,解题关键是明确三角函数的意义,通过设参数,求出需要的边长.11.C解析:C【分析】直接根据特殊角的三角函数值即可得出结论;【详解】∵cos 45=°, 故选:C .【点睛】本题考查了特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键. 12.C解析:C【分析】先利用勾股定理求出AB 的长,然后再求sin ∠A 的大小.【详解】解:∵在Rt △ABC 中,AC =BC=2 ∴3=∴sin ∠A=23BC AB = 故选:C .【点睛】 本题考查锐角三角形的三角函数和勾股定理,需要注意求三角函数时,一定要是在直角三角形当中.第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题13.x1=-1x2=3【分析】关于x的一元二次方程ax2+bx+c=0(a≠0)的根即为二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点的横坐标【详解】解:根据图象知抛物线y=ax2+bx+c(解析:x1=-1,x2=3【分析】关于x的一元二次方程ax2+bx+c=0(a≠0)的根即为二次函数y=ax2+bx+c(a≠0)的图象与x 轴的交点的横坐标.【详解】解:根据图象知,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点是(-1,0),对称轴是x=1.设该抛物线与x轴的另一个交点是(x,0),则12x=1,解得,x=3,即该抛物线与x轴的另一个交点是(3,0),所以关于x的一元二次方程ax2+bx+c=0(a≠0)的根为x1=-1,x2=3.故答案是:x1=-1,x2=3.【点睛】本题考查了抛物线与x轴的交点,解题时,注意抛物线y=ax2+bx+c(a≠0)与关于x的一元二次方程ax2+bx+c=0(a≠0)间的转换.14.y=x2+2或y=x2-2【分析】根据图象的平移规律可得答案【详解】解:将抛物线y=x2沿着y轴正方向平移2个单位长度所得抛物线的解析式为y=x2+2;将抛物线y=x2沿着y轴负方向平移2个单位长度解析:y=x2+2或y=x2-2.【分析】根据图象的平移规律,可得答案.【详解】解:将抛物线y=x2沿着y轴正方向平移2个单位长度,所得抛物线的解析式为y=x2+2;将抛物线y=x2沿着y轴负方向平移2个单位长度,所得抛物线的解析式为y=x2-2;故答案是:y=x2+2或y=x2-2.【点睛】本题主要考查了二次函数与几何变换问题,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.15.3【分析】设P(x)则Q(xx−2)得到PQ=−x+2根据三角形面积公式得到S△POQ=−(x−2)2+3根据二次函数的性质即可求得最大值【详解】解:∵PQ⊥x轴∴设P(x)则Q(xx−2)∴PQ=解析:3【分析】设P (x ,4x ),则Q (x ,12x−2),得到PQ =4x −12x +2,根据三角形面积公式得到S △POQ =−14(x−2)2+3,根据二次函数的性质即可求得最大值. 【详解】解:∵PQ ⊥x 轴, ∴设P (x ,4x ),则Q (x ,12x−2), ∴PQ =4x −12x +2, ∴S △POQ =12(4x −12x +2)•x =−14(x−2)2+3, ∵−14<0, ∴△POQ 面积有最大值,最大值是3,故答案为:3.【点睛】本题考查了一次函数图象上点的坐标特征,二次函数的性质,反比例函数y =k x (k≠0)系数k 的几何意义:从反比例函数y =k x(k≠0)图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为|k|. 16.【分析】先根据题意得出抛物线与x 轴的交点坐标再由两点坐标关于抛物线的对称轴对称即可得出结论【详解】解:∵方程ax2+bx+c=0的两个根是-3和1∴二次函数y=ax2+bx+c 的图象与x 轴的交点分别解析:1-【分析】先根据题意得出抛物线与x 轴的交点坐标,再由两点坐标关于抛物线的对称轴对称即可得出结论.【详解】解:∵方程ax 2+bx+c=0的两个根是-3和1,∴二次函数y=ax 2+bx+c 的图象与x 轴的交点分别为(-3,0),(1,0).∵此两点关于对称轴对称,∴对称轴是直线x=312-+=-1. 故答案为:-1.【点睛】本题考查的是抛物线与x 轴的交点,熟知抛物线与x 轴的交点与一元二次方程根的关系是解答此题的关键.17.【分析】过点C 作CD ⊥AB 垂足为D 计算BCAB 的长度比较AC+BC 与AB 的大小即可【详解】如图过点C 作CD ⊥AB 垂足为D ∵米∴DC=BD=90AD=90BC=90∴AC+BC=180+90≈306A解析:【分析】过点C 作CD ⊥AB ,垂足为D ,计算BC ,AB 的长度,比较AC+BC 与AB 的大小即可.【详解】如图,过点C 作CD ⊥AB ,垂足为D ,∵180AC 米,30CAB ∠=︒,45CBA ∠=︒,∴DC=BD=90,AD=903,BC=902,∴AC+BC=180+902≈306,AB=AD+BD=903+90≈243,∴缩短了:306-243=63(米),故答案为:63米.【点睛】本题考查了解斜三角形,学会作高化,把斜三角形化为直角三角形,并熟练运用特殊角的三角函数值是解题的关键.18.1∶330【分析】(1)由旋转的性质解得继而证明结合30°的正切值再根据相似三角形的面积比等于相似比的平方解题即可;(2)连接根据三角形三边关系得到当在同一直线上时线段长度最小由直角三角形斜边中线的解析:1∶3 30 31. 【分析】(1)由旋转的性质,解得1111,,OA OA OB OB AOA BOB θ==∠=∠=,继而证明11()AOA BOB SAS ,结合30°的正切值,再根据相似三角形的面积比等于相似比的平方解题即可;(2)连接OP ,根据三角形三边关系得到当O Q P 、、在同一直线上时,线段QP 长度最小,由直角三角形斜边中线的性质结合含30°角的直角三角形性质,可证1OA P 是等边三角形,继而解得OP 、OQ 的长,最后由=PQ OP OQ -解题即可.【详解】解:(1)旋转1111,,OA OA OB OB AOA BOB θ∴==∠=∠=11AOA BOB ∴、均是等腰三角形11tan 30OA OA OB OB ==︒=11AOABOB ∴相似比3k = 22133k ∴== 12:13S S ∴=:故答案为:1∶3;(2)连接OP ,在OQP 中,OQ QP OP +>当O Q P 、、在同一直线上时,OP 有最小值,即=PQ OP OQ -有最小值, 当O Q P 、、在同一直线上时, P 是11A B 的中点,1111=2=O B P P A A ∴ 1130A B O ABO ∠=∠=︒ 1112OA A B ∴=11==P OP A OA ∴1OA P ∴是等边三角形,160OP A ∴∠=︒1906030AOA ∴∠=︒-︒=︒ 30θ∴=︒1OA =∴1OP =,tan 30OA OB ==︒Q为OB 中点, 122OQ OB ∴==312PQ ∴=-.【点睛】本题考查旋转的性质、直角三角形斜边的中线、含30°角的直角三角形、正切、三角形三边关系、等边三角形的判定与性质等知识,在重要考点,难度一般,掌握相关知识是解题关键.19.【分析】根据题意先求出AB =5由折叠的性质得出AB =AB =5BC =BC 过点A 作AD ⊥y 轴于点D 由勾股定理求出OB =2得出x2+22=(4﹣x )2解得x =则可得出答案【详解】解:∵tan ∠AOB =B (解析:3,02⎛⎫ ⎪⎝⎭【分析】根据题意先求出AB =5,由折叠的性质得出AB =AB'=5,BC =B'C ,过点A 作AD ⊥y 轴于点D ,由勾股定理求出OB'=2,得出x 2+22=(4﹣x )2,解得x =32,则可得出答案. 【详解】解:∵tan ∠AOB =54,B (4,0), ∴54AB OB =, ∴AB =5, ∵将△ABC 沿AC 所在直线翻折得到△ACB′,∴AB =AB'=5,BC =B'C ,过点A 作AD ⊥y 轴于点D ,∴B'D ,22AB AD -2254-3,∴OB'=2,设OC =x ,则BC =B'C =4﹣x ,Rt △OB'C 中,∵OC 2+OB'2=B'C 2,∴x 2+22=(4﹣x )2,解得x =32, ∴C (32,0). 故答案为:(32,0). 【点睛】本题考查勾股定理以及翻折问题,熟练掌握勾股定理以及折叠的性质是解题的关键. 20.6【分析】根据三角函数的定义即可求解【详解】∵cotB=∴AC==3BC=6故答案是:6【点睛】此题考查锐角三角函数的定义及运用解题关键在于掌握在直角三角形中锐角的正弦为对边比斜边余弦为邻边比斜边正解析:6【分析】根据三角函数的定义即可求解.【详解】∵cotB=BC AC, ∴AC=13BC BC cotB= =3BC=6. 故答案是:6.【点睛】此题考查锐角三角函数的定义及运用,解题关键在于掌握在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,余切为邻边比对边.三、解答题21.(1)()1,0-或()3,0;(2)6;(3)点P 的坐标为()17,3+、()17,3-、()0,3-、()2,3-.【分析】(1)令y=0,转化为一元二次方程,方程的根就是与x 轴交点的横坐标; (2)求出AB 的长度,OC 的长度,按公式计算即可;(3)利用面积公式,抛物线的解析式转化成一元二次方程求解即可.【详解】解:(1)当0y =时,2230x x --=, 解得 11x =-,23x =,∴抛物线与x 轴的交点坐标为()1,0-或()3,0,故答案为:()1,0-或()3,0.(2)由(1)点()1,0A -,()3,0B ,()0,3C-, ∴()314AB =--=,3OC =,∴14362ABC S =⨯⨯=△. (3)∵点()1,0A -,点()3,0B ,()222314y x x x =--=--, ∴此抛物线有最小值,此时4y =-,()314AB =--=,∵6PAB S =△,抛物线上有一个动点P ,∴点P 的纵坐标的绝对值为6234⨯=, ∴2233x x --=或2233x x --=-,解得,117x =,217x =,30x =,42x =,∴点P 的坐标为()17,3、()17,3-、()0,3-、()2,3-.【点睛】本题考查了二次函数与坐标轴的交点,抛物线上的内接三角形的面积,动点问题,熟练掌握性质,并能灵活运用是解题的关键.22.(1)AA E C CF ''△≌△,A BF CDE '△≌△;证明见解析 (2)①5 ②23(4)124y x =--+;12 【分析】 (1)根据矩形的性质、全等三角形的判定定理证明;(2)①设A′E=a ,A′F=b ,根据相似三角形的性质用x 表示出a 、b ,根据菱形的判定定理列出方程,解方程即可;②根据三角形的面积公式求出y 关于x 的二次函数解析式,根据二次函数的性质计算即可.【详解】解:(1)△AA′E ≌△C′CF ,△A′BF ≌△CDE ,由题意得,四边形A′DCB 是矩形,∴A′B=DC ,∴AA′=CC′,∵AB ∥CD ,∴∠BA′F=∠C′,由题意得,∠BA′F=∠A ,∴∠A=∠C′,在△AA′E 和△C′CF 中,A C AA C CAA E C CF ∠∠'⎧⎪''⎨⎪∠'∠'⎩===, ∴△AA′E ≌△C′CF (ASA );由题意得,四边形A′DCB 是矩形,∴A′B=DC ,∠B=∠D=90゜,DA′=CB ,DA′//CB ,由△AA′E ≌△C′CF ,得,A′E=FC∵四边形A′DCF 是平行四边形,∴A′F=EC ,∴Rt △A′BF ≌△CDE ;(2)①设A′E=a ,A′F=b ,在Rt △ABC 中,8AB =,6AD =,∠B=90゜∴10AC ===∵A′F ∥AC , ∴A F BA AC BA ''=,即8108b x -=,解得,4054x b -=, 同理68a x =, 解得,34a x =, 当A′E=A′F 时,四边形A′ECF 是菱形, ∴4054x -=34x , 解得,x=5, ∴当x=5时,四边形A′ECF 是菱形; ②3(8)4y A E A B x x ''=⨯=-,即364y x x =-+. 23(4)124y x =--+,y 的最大值为12. 【点睛】本题考查的是四边形的综合题,矩形的性质、相似三角形的判定和性质、全等三角形的判定和性质、二次函数的解析式的确定以及二次函数的最值的求法,掌握相关的判定定理和性质定理是解题的关键.23.(1)1a =-,2b =-,3c =;(2)278;(3)存在,57,24P ⎛⎫- ⎪⎝⎭. 【分析】(1)设抛物线的解析式为()()13y a x x =-+.将()0,3C 代入得:33a -=,抛物线的解析式化为223y x x =--+,可得1a =-,2b =-,3c =;(2)过点P 作PE x ⊥轴,交AC 于点P ,设点P 的横坐标为m ,由点P 在抛物线223y x x =--+上,设()2,23P m m m --+,可求直线AC 解析式为:3y x ,(),3E m m +,可得()()222333PE m m m m m =--+-+=--,可求()213322PAC PAE PCE S S S PE OA m m =+=⋅=--△△△配方即可; (3)假设存在,过点Q 作x 轴的平行线l ,过点P 、C 作l 的垂线,垂足为M N ,,由CPQ CBO △△, 可得13PQ OB CQ OC ==,可证PMQ QNC △△;可得13PM MQ PQ QN CN CQ ===,设(),3Q n n +,可求22PM m m n =---,MQ n m =-,QN n =-,CN n =-,可得()232n m m n -=---,()3n n m -=-,解方程即可. 【详解】解:(1)设抛物线的解析式为()()13y a x x =-+.∵将()0,3C 代入得:33a -=,解得1a =-,∴抛物线的解析式为()()13y x x =--+,即223y x x =--+,∴1a =-,2b =-,3c =;(2)过点P 作PE x ⊥轴,交AC 于点P ,设点P 的横坐标为m ,∵点P 在抛物线223y x x =--+上,∴()2,23P m m m --+, ∵直线AC 过点()30A -,、点()0,3C , ∴直线AC 解析式可求得为:3y x , ∴(),3E m m +,∴()()222333PE m m m m m =--+-+=--, ∴()213322PAC PAE PCE S S S PE OA m m =+=⋅=--△△△, ∴()223332732228PAC S m m m ⎛⎫=-+=-++ ⎪⎝⎭△, ∴当点P 的横坐标为32-时,PAC △面积的最大值为278; (3)假设存在,过点Q 作x 轴的平行线l ,过点P 、C 作l 的垂线,垂足为M N ,, ∵CPQ CBO △△, ∴PQ CQ OB OC =, ∴13PQ OB CQ OC ==, ∵∠PMQ=∠QNC=∠PQC=90°,∴∠MQP+∠CQN=90°,∠CQN+∠QCN=90°,∴∠MQP=∠NCQ ,∴PMQ QNC △△; ∴13PM MQ PQ QN CN CQ ===, 设()2,23P m m m --+,(),3Q n n +, ∴22PM m m n =---,MQ n m =-,QN n =-,CN n =-,∴()232n m m n -=---,()3n n m -=-, ∴52m =-, ∴,存在,57,24P ⎛⎫- ⎪⎝⎭.【点睛】本题考查抛物线解析式,三角形面积最值,三角形相似判定与性质,解方程组,掌握抛物线解析式,三角形面积最值,三角形相似判定与性质,解方程组,解题关键是利用相似三角形的性质构造方程组.24.(1)新传送带AC 的长度为8m ;(2)货物MNQP 需要挪走,理由见解析.【分析】(1)先根据等腰直角三角形的性质求出AD 的长,然后再根据直角三角形的性质求出AC 即可;(2)先根据余弦的定义求出CD ,然后再根据题意求出PC 的长,最后根据题意判断即可.【详解】解:(1)在Rt ABD ∆中,45ABD ︒∠=,sin 454AD AB ︒∴=⋅=在Rt ACD ∆中,30ACD ︒∠=,28AC AD ∴==,答:新传送带AC 的长度为8m ;(2)在Rt ACD ∆中,30ACD ︒∠=,cos 43CD AC ACD ∴=⋅∠=在Rt ABD ∆中,45ABD ︒∠=,4BD AD ∴==434BC CD BD ∴=-=,()4343445PC BP BC ∴=-==<,∴货物MNQP 需要挪走.【点睛】本题主要考查了解直角三角形的应用一坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的相关知识是解本题的关键.25.(1)-7;(2)x≤-1;(3)x=34-. 【分析】(1)根据特殊角的三角函数值、负指数幂、二次根式的性质及零指数幂计算即可; (2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可;(3)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】(1)原式; (2)解:5131131132x x x x -<+⎧⎪⎨++≥+⎪⎩①② 由①得:x<1,由②得:x≤-1,则不等式组的解集为x≤-1.(3)去分母得:2-x-2=3x-3,移项:-x-3x=-3,合并同类项:-4x=3,解得:x=34-, 经检验x=34-是分式方程的解; 【点睛】本题考查了解分式方程,实数的运算,以及解一元一次不等式组,解分式方程利用了转化的思想,注意要检验.26.(1)()4,3;(2)()8,6Q ;10;(3)()3,6,()1.4,4.8【分析】(1)把两个函数解析式联立方程组计算即可;(2)设P 的横坐标n ,根据勾股定理求出P ,Q 的坐标,计算即可;(3)①作MH OQ ⊥,根据勾股定理和三角函数值求出M 的坐标计算即可;②当四边形NOMQ 为平行四边形和当△NOQ 与△MOQ 关于OQ 对称时分别计算即可得到结果;【详解】(1)由题意可得: 34152y x y x ⎧=⎪⎪⎨⎪=-+⎪⎩, 化简得:31542x x =-+, 解得:4x =, 把4x =代入y =34x 中,得3y =,∴()4,3A ;故答案是()4,3;(2)如图,把0y =代入152y x =-+中,得到10x =, ∴()10,0C ,设P 的横坐标n ,把xn =代入152y x =-+得()154102y n n =-+≤≤, ∴1,52P n n ⎛⎫-+ ⎪⎝⎭, 把xn =代入34y x =得34y n =, ∴3,4Q n n ⎛⎫ ⎪⎝⎭, ∵()4,3A ,∴22435OA =+=,31555424PQ n n n ⎛⎫=--+=- ⎪⎝⎭, ∵QP OA =, ∴5554n -=, ∴8n =,∴()8,6Q ,作AG x ⊥轴,则()△115841022APQ S PQ GD ==⨯⨯-=; (3)①作MH OQ ⊥,∵MQ 平分OQP ∠,∴HM DM =,设(),0M m (m >0),则OM m =,8DM m =-, ∴8HM m =-, ∵sin HM QOD OM∠=,sin QD QOD OQ ∠=, ∴HM DQ OM OQ=, ∵()8,6Q ,∴10OQ =,6DQ =, ∴8610m m-=, ∴5m =,∴()5,0M ;②如图,当四边形NOMQ 为平行四边形时,△△NQO MOQ ≅,则NQ 由OM 平移得到,()5,0M 平移到点()8,6Q ,则853-=,则横坐标加上3,606-=,则纵坐标加上6,∵()0,0O ,∴()13,6N ;当△NOQ 与△MOQ 关于OQ 对称时,△△NOQ MOQ ≅,设()2,N a b , ∵6sin 0.610QD QOD QO ∠===, ∴0.6HM OM=,∴0.65HM =, ∴3HM =,∴226N M HM ==,作2N F x ⊥轴,则2FN M QOD ∠=∠, ∴228cos 6 4.810FN MN QOD =∠=⨯=, 26sin 6 3.610PM N M QOD =∠=⨯=, 5 3.6 1.4OF MO FM =-=-=, ∴()2 1.4,4.8N ;综上所述,符合条件的N 点的坐标为()3,6,()1.4,4.8.【点睛】本题主要考查了一次函数综合应用,结合三角函数定义、勾股定理、三角形全等计算是解题的关键.。
最新九年级数学下期中第一次模拟试卷附答案
一、选择题1.二次函数2y ax bx c =++的图象如图所示,则函数值y 0>时,x 的取值范围是( )A .x 2<-B .x 5>C .2x 5-<<D .x 2<-或x 5>2.如图,已知二次函数()20y ax bx c a =++≠的图象与x 轴交于点()1,0A -,对称轴为直线1x =,下列结论:①0abc <;②930a b c ++=;③20a b +=;④2am bm a b +<+(m 是任意实数),其中正确的是( )A .①②B .②③C .①②③D .②③④ 3.已知抛物线()()()12121y x x x x x x =--+<,抛物线与x 轴交于(,0)m ,(,0)n 两点()m n <,则m ,n ,1x ,2x 的大小关系是( )A .12x m n x <<<B .12m x x n <<<C .12m x n x <<<D .12x m x n <<< 4.如图1,在矩形ABCD 中,动点E 从点A 出发,沿A B C →→的路线运动,当点E 到达点C 时停止运动.若FE AE ⊥,交CD 于点F 设点E 运动的路程为x ,FC y =,已知y 关于x 的图象如图2所示,则m 的值为( )A 2B .2C .1D .235.函数k y x =与()20y kx k k =-≠在同一直角坐标系中的图象大致是下图中的( ) A . B . C . D . 6.已知二次函数()()20y a x m a =->的图象经过点()1,A p -,()3,B q ,且p q <,则m 的值不可能...是( ) A .2- B .2- C .0 D .527.在Rt ABC △中,如果各边长度都扩大为原来的2倍,那么锐角A 的余弦值( ) A .扩大2倍 B .缩小2倍 C .扩大4倍 D .没有变化 8.如图在Rt △ABC 中,∠ACB =90°,如果AC =3,sin B =35,那么BC 等于( )A .3B .4C .5D .69.北碚区政府计划在缙云山半山腰建立一个基站AB ,其设计图如图所示,BF ,ED 与地面平行,CD 的坡度为1:0.75i =,EF 的坡角为45︒,小王想利用所学知识测量基站顶部A 到地面的距离,若BF ED =,15CD =米,32EF =米,小王在山脚C 点处测得基站底部B 的仰角为37︒,在F 点处测得基站顶部A 的仰角为60︒,则基站顶部A 到地面的距离为( )(精确到0.1米,参考数据:3 1.73≈,sin370.60︒≈,cos370.80︒≈,tan370.75︒≈)A .21.5米B .21.9米C .22.0米D .23.9米 10.如图,将△ABC 放在每个小正方形的边长为1的网格中,点A ,B ,C 均在格点上,则tanA 的值是( )A.55B.105C.2 D.81911.如图,在菱形ABCD中,DE⊥AB,3cos5A=,BE=2,则tan∠DBE的值是()A.12B.2 C.5D.512.如图,菱形ABCD的对角线交于点O,过点A作AE⊥BC于点E,连接EO.若AC=6,BD=8,则cos∠AEO=()A.25B.35C.34D.45二、填空题13.函数y=ax2+bx+c(a≠0)图像如图所示,过点(﹣1,0),对称轴为x=2,下列结论正确的是_____.①4a+b=0;②24a+2b+3c<0;③若A(﹣3,y1),B(﹣0.5,y2),C(3.5,y3)三点都在抛物线上,y1<y2<y3;④当y1>﹣1时,y随x增大而增大.14.已知二次函数y=ax 2﹣4ax+4,当x 分别取x 1、x 2两个不同的值时,函数值相等,则当x 取x 1+x 2时,y 的值为________________________15.抛物线y =a (x ﹣2)(x ﹣2a )(a 是不等于0的整数)顶点的纵坐标是一个正整数,则a 等于_____.16.在平面直角坐标系中,把抛物线22y x =+先绕其顶点旋转180︒后,再向右平移2个单位,向下平移3个单位后的抛物线解析式为__________.17.如图是一个海绵施把,图1、图2是它的示意图,现用线段BC 表示拉手柄,线段DE 表示海绵头,其工作原理是:当拉动BC 时线段OA 能绕点O 旋转(设定转角AOQ ∠大于等于0°且小于等于180°),同时带动连杆AQ 拉着DE 向上移动.图1表示拖把的初始位置(点O 、A 、Q 三点共线,P 、Q 重合),此时45cm OQ =,图2表示拉动过程中的一种状态图,若DE 可提升的最大距离10cm PQ =.(1)请计算:OA =______cm ;AQ =_____cm .(2)当1sin 10OQA ∠=时,则PQ =______cm . 18.如图,平面直角坐标系中,矩形OABC 绕原点O 逆时针旋转30°后得到矩形ODEF ,若A (3,0),C (03E 的坐标为_________19.ABC ∆中,67.5A ,8BC =,BE AC ⊥交AC 于E ,CF AB ⊥交AB 于F ,点D 是BC 的中点.以点F 为原点,FD 所在的直线为x 轴构造平面直角坐标系,则点E 的横坐标为________.20.如图,在菱形ABCD 中,4AB =,45ABC ∠=︒,菱形ABCD 的对角线交于点O ,则ABO 的面积为__________.三、解答题21.已知函数()()1210,()y x m x m y ax m a =+--=+≠在同一平面直角坐标系中.(1)若1y 经过点()12-,,求1y 的函数表达式; (2)若2y 经过点()1,1m +,判断1y 与2y 图象交点的个数,说明理由;(3)若1y 经过点1,02⎛⎫ ⎪⎝⎭,且对任意x ,都有12y y >,请利用图象求a 的取值范围. 22.如图,在矩形ABCD 中,2AB =,4BC =,点P 是对角线BD 上的一个动点,过点P 作PF BD ⊥,交边BC 于点F (点F 与点B ,C 都不重合),点E 是射线FC 上一动点,连结PE ,ED ,并一直保持EPF FBP ∠=∠.(1)求证:EPF EBP △△∽.(2)设BP 的长为x ,DEP 的面积为y ,求y 关于x 的函数表达式,并写出自变量x 的取值范围.(3)当DEP 与BCD △相似时,求DEP 的面积.23.如图,已知某二次函数的顶点坐标是(1,4)-,且经过点(4,5)A(1)求该二次函数的表达式;(2)点(,)P m n 是该二次函数图象上一点,若点P 到y 轴的距离不大于4,请根据图象直接写出n 的取值范围.24.计算:()02202012330tan -++︒ 25.手机软件Smart Measure (智能测量)是一款非常有创意且实用性很高的数码测距工具.它可以利用手机上的摄像头和距离传感器来测量目标的距离、高度、宽度、角度和面积.测量过程非常简单;如图1、图2,打开软件后先将手机摄像头对准物体的底部按测量键,保持相同姿势,再把手机相机镜头对准测量物体的顶端按测量键,最后按下“大树键”即可测量出物体的高度智能软件的运行离不开数学原理.如图3,测量者AB 使用Smart Measure 测量一棵大树CD 的高,软件显示8m AC =,10m AD =,53CAD ∠=︒,请你根据数学知识求出大树CD 的高.(结果可保留根号)(为了计算方便,约定434sin53,cos53,tan53555︒=︒=︒=).26.(12)-1﹣2cos30°﹣【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据函数图象求出与x 轴的交点坐标,再由图象得出答案.【详解】解:有函数图象观察可知,当25x -<<时,函数值0y >.故选:C .【点睛】本题考查二次函数与不等式.掌握数形结合思想是解题关键.2.B解析:B【分析】①抛物线开口向上,对称轴为直线x =1,即可得出a >0、b <0、c <0,进而可得出abc >0,结论①错误;②由抛物线的对称轴以及与x 轴的一个交点坐标,可得出另一交点坐标为(3,0),进而可得出9a +3b +c =0,结论②正确;③由对称轴直线x=1,可得结论③正确;④2()()0am bm a b +-+≥,可得结论④错误.综上即可得出结论.【详解】解:①∵抛物线开口向上,对称轴为直线x =1,∴a >0,12b a-=,c <0, ∴b =−2a <0,∴abc >0,结论①错误; ②∵二次函数y =ax 2+bx +c (a≠0)的图象与x 轴交于点A (−1,0),对称轴为直线x =1,∴二次函数y =ax 2+bx +c (a≠0)的图象与x 轴的另一个交点为(3,0),∴9a +3b +c =0,结论②正确;③∵对称轴为直线x =1,∴12b a-=,即:b =−2a , ∴20a b +=,结论③正确;④∵222()()(2)(2)2am bm a b am am a a am am a +-+=---=-+22(21)(1)a m m a m =-+=-≥0,∴2am bm a b +≥+,结论④错误.综上所述,正确的结论有:②③.故选:B .【点睛】本题考查了抛物线与x 轴的交点、二次函数图象与系数的关系、二次函数的性质以及二次函数图象上点的坐标特征,逐一分析四条结论的正误是解题的关键.3.A解析:A【分析】根据题意画出草图,结合图象解答即可.【详解】解:当x=x 1时,y=1;当x=x 2时,y=1;又∵m<n ,()()()12121y x x x x x x =--+<的二次项系数大于0,∴函数图象大致如图所示,∴12x m n x <<<,故选A .【点睛】本题考查了二次函数的图象与性质,根据题意画出函数的大致图象是解答本题的关键. 4.D解析:D【分析】分别求出点E 在AB 、BC 段运动时函数的表达式,即可求解.【详解】解:由图2可知,AB=6,BC=10-6=4,①当点E 在AB 上运动时,y=FC=BE=AB-AE=6-x ,即y=6-x (0≤x≤6),图象为一次函数;②当点E 在BC 上运动时,如下图,则BE=x-AB=x-6,EC=BC-BE=4-(x-6)=10-x , FC=y ,AB=6,∵∠FEC+∠AEB=90°,∠AEB+∠EAB=90°,∴∠FEC=∠EAB ,∴∠CFE=∠AEB ,∴△ABE ∽△ECF , ∴BE AB CF CE=,即6610x y x -=-, 整理得:()2181061063y x x x =-+-<≤,图象为二次函数, ∵106-<, 故()2218121086363y x x x =-+-=--+有最大值,最大值为23, 即23m =, 故选:D .【点睛】本题考查的是动点图象问题,涉及到二次函数、一次函数、相似三角形等知识,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.5.B解析:B【分析】根据k>0,k<0,结合反比例函数及二次函数图象及其性质分类讨论.【详解】解:分两种情况讨论:①当k>0时,反比例函数k y x=在一、三象限,而二次函数()20y kx k k =-≠开口向上,与y 轴交点在原点下方,故C 选项错误,B 选项正确;②当k<0时,反比例函数kyx=在二、四象限,而二次函数()20y kx k k=-≠开口向下,与y轴交点在原点上方,故A选项与D选项错误.故选B.【点睛】本题考查了反比例函数图象性质和二次函数图象性质.关键是根据k>0,k<0,结合反比例函数及二次函数图象及其性质分类讨论.6.D解析:D【分析】根据二次函数图象上点的坐标特征得到m+1<3﹣m或m≤﹣1,解得即可.【详解】解:∵二次函数y=a(x﹣m)2(a>0),∴抛物线的开口向上,对称轴为直线x=m,∵图象经过点A(﹣1,p),B(3,q),且p<q,∴m+1<3﹣m或m≤﹣1解得m<1,故选:D.【点睛】本题考查了二次函数图象上点的坐标特征,熟练掌握二次函数的性质是解题的关键.7.D解析:D【分析】根据三角函数的定义和分数的基本性质联手解答即可.【详解】如图,cosA=BC AB,根据分数的基本性质,得BC AB =22BCAB,∴余弦值不变,故选D.【点睛】本题考查了锐角三角函数的定义及其分数的基本性质,熟练掌握函数的定义,灵活运用分数的基本性质是解题的关键.8.B解析:B【分析】直接利用锐角三角函数关系得出AB 的长度,然后由勾股定理求得BC 的长度.【详解】解:如图,在Rt △ABC 中,∠ACB =90°, AC =3,sin B =35, ∴sin B =AC AB , 335AB =, ∴AB =5.∴由勾股定理,得BC =2222534AB AC -=-=.故选:B .【点睛】本题考查了勾股定理,锐角三角函数的定义,熟练识记锐角三角函数的定义是解题关键,正弦:我们把锐角A 的对边a 与斜边c 的比叫做∠A 的正弦,记作sin A . 9.B解析:B【分析】根据直角三角形的边角关系及坡度、坡角的定义求解.【详解】解:如图,分别过D 、B 作DM 、BO 垂直于地面于M 、O 两点,过F 作FN 垂直于直线ED 于点F ,设DM=x ,则有:143,0.7534DM MC x MC ==∴=由勾股定理可得: 22222291516DM CM DC x x +=∴+=,, 解之得:x=12,∴DM=12,MC=9,∵32EF=,EF的坡角为45°,∴FN=NE=3,∴BO=FN+DM=3+12=15,OC=BO÷tan37°≈15÷0.75=20,∵BF=ED ,∴BF=(OC-MC-NE)÷2=4,∴AB=BF×tan60°≈4×1.73=6.92,∴AO=AB+BO=6.92+15=21.92≈21.9(米),故选B.【点睛】本题考查解直角三角形,熟练掌握直角三角形的边角关系、锐角三角函数的应用及坡度、坡角的定义是解题关键.10.D解析:D【分析】过点B作BD AC⊥,利用面积法求出BD的长,再由勾股定理求出AD的长,即可求出tanA的值.【详解】解:如图,过点B作BD AC⊥,2BC=,17AB5AC=,根据面积法,24855 BD⨯==,根据勾股定理,226419 17255AD AB BD=-=-=,∴885tan19195BDAAD===.故选:D.【点睛】本题考查锐角三角函数,解题的关键是掌握构造直角三角形求锐角三角函数的方法.11.B解析:B【分析】在直角三角形ADE 中,3AE AB BE cos 5AD AD A -===,求得AD ,AE .再求得DE ,即可得到tan ∠DBE .【详解】设菱形ABCD 边长为t .∵BE =2,∴AE =t−2. ∴3AE AB BE cos 5AD AD A -===, ∴3t 25t-=, ∴t =5.∴AE =5−2=3.∴DE4.∴tan ∠DBE =DE 4=BE 2=2. 故选:B .【点睛】本题考查了解直角三角形中三角函数的应用,要熟练掌握边角之间的关系. 12.D解析:D【分析】根据菱形的性质结合勾股定理求得BC=5,根据直角三角形斜边中线的性质证得OE=OA=OC ,证得∠AEO=∠EAO ,再利用同角的余角相等证得∠OBC=∠EAC ,利用锐角三角函数的定义即可求解.【详解】∵四边形ABCD 是菱形,且AC=6,BD=8,∴AC ⊥BD ,OB=OD=4,OA=OC=3,∴==5,∵AE ⊥BC ,OA=OC ,∴OE=OA=OC ,∴∠AEO=∠EAO ,∵AE ⊥BC ,AC ⊥BD ,∴∠OBC+∠BCO =∠EAC+∠BCO ,∴∠OBC=∠EAC ,即∠AEO=∠OBC ,∴cos ∠AEO= cos ∠OBC =45OB BC =. 故选:D .【点睛】 本题考查了锐角三角函数,菱形的性质,勾股定理,直角三角形斜边上的中线性质;熟练掌握菱形的性质是解题的关键.二、填空题13.①②③【分析】由抛物线的对称轴可判断①;由①可得出过点(﹣10)代入可得出c =﹣5a 代入化简即可判断②;根据二次函数的增减性知抛物线上点离对称轴水平距离越小函数值越大据此可判断③;由抛物线的图像的增 解析:①②③【分析】由抛物线的对称轴可判断①;由①可得出=4b a -,过点(﹣1,0),代入可得出c =﹣5a ,代入化简即可判断②;根据二次函数的增减性知抛物线上点离对称轴水平距离越小,函数值越大,据此可判断③;由抛物线的图像的增减性直接判断④.【详解】函数y =ax 2+bx +c (a ≠0)的对称轴2b x a =-, ∵ 对称轴2x =, ∴=22b a-, ∴=4b a -,∴ 4+=0a b ,故①正确;有图可知,a <0,∴=4b a -,∴ 2=8b a -,过点(﹣1,0),∴ a-b+c =0,∴ b=a+c ,即a+c=﹣4a ,∴ c =﹣5a ,∴24a +2b +3c =24a -8a -15a =a <0,故②正确;当x =0时,y =c ,∵A (﹣3,y 1),B (﹣0.5,y 2),C (3.5,y 3)三点都在抛物线上,点A 与2x =的水平距离为5,点B 与2x =的水平距离为2.5,点C 与2x =的水平距离为1.5,∵5>2.5>1.5,∴ 123y y y <<,故③正确;有图可知,当11y >-,y 随x 增大先增大后减小,故④不正确;综上,正确的有:①②③.故答案为:①②③.【点睛】本题考查的是二次函数图象与系数的关系,要求学生熟悉函数的基本性质,能熟练求解函数与坐标轴的交点及顶点的坐标等.14.4【分析】根据二次函数的性质和二次函数图象具有对称性可以求得的值从而可以求得相应的y 的值【详解】解:∵y=当x 分别取两个不同的值时函数值相等∴∴当x 取时y=故答案为4【点睛】本题考查二次函数图象上的 解析:4【分析】根据二次函数的性质和二次函数图象具有对称性,可以求得12x x +的值,从而可以求得相应的y 的值.【详解】解:∵y=()2244244ax ax a x a -+=--+,当x 分别取 12,x x 两个不同的值时,函数值相等,∴124x x +=,∴当x 取12x x +时,y=()242444a a --+=,故答案为4.【点睛】本题考查二次函数图象上的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答. 15.-1【分析】令y=0时则有则有进而可得对称轴为直线然后可求抛物线顶点纵坐标为由此可得当a 不为±1时纵坐标不为整数进而可求解a 的值【详解】解:由题意得:令y=0时则有解得:∴抛物线与x 轴交点的坐标为由 解析:-1【分析】令y=0时,则有()220a x x a ⎛⎫--= ⎪⎝⎭,则有122,2x x a ==,进而可得对称轴为直线11x a =+,然后可求抛物线顶点纵坐标为12a a--+,由此可得当a 不为±1时,纵坐标不为整数,进而可求解a 的值.【详解】解:由题意得:令y=0时,则有()220a x x a ⎛⎫--= ⎪⎝⎭, 解得:122,2x x a==, ∴抛物线与x 轴交点的坐标为()2,0,2,0a ⎛⎫ ⎪⎝⎭, 由抛物线的对称性可得对称轴为直线11x a =+, ∴把11x a =+代入抛物线解析式得顶点纵坐标为12y a a=--+, ∵顶点的纵坐标是一个正整数且a 是不等于0的整数,∴1a =±,当1a =时,y=0(不符合题意,舍去);当1a =-时,y=4,(符合题意)∴1a =-;故答案为-1.【点睛】本题主要考查二次函数的性质,熟练掌握二次函数的性质是解题的关键.16.【分析】先求出抛物线绕其顶点旋转后解析式再根据平移规律即可求解【详解】解:抛物线先绕其顶点旋转后解析式为将抛物线向右平移个单位向下平移个单位后的抛物线解析式为故答案为:【点睛】本题考查了抛物线图象与 解析:2(2)1=---y x【分析】先求出抛物线22y x =+绕其顶点旋转180︒后解析式,再根据平移规律即可求解.【详解】解:抛物线22y x =+先绕其顶点旋转180︒后解析式为22y x =-+,将抛物线22y x =-+向右平移2个单位,向下平移3个单位后的抛物线解析式为()212y x =---.故答案为:2(2)1=---y x【点睛】本题考查了抛物线图象与几何变换,熟知二次函数图象旋转与平移规律是解题关键. 17.40或【分析】(1)由题意可知:OA 定义DE 使得最大值的一半AQ =OQ-OA 即可解决问题(2)分两种情形分别画出图形解直角三角形即可解决问题【详解】解:(1)由题意故答案为540(2)当是钝角时如图解析:40 421211-或481211-【分析】(1)由题意可知:OA 定义DE 使得最大值的一半,AQ =OQ -OA 即可解决问题. (2)分两种情形分别画出图形,解直角三角形即可解决问题.【详解】解:(1)由题意11052OA cm =⨯=,45540AQ cm =-=, 故答案为5,40.(2)当OAQ ∠是钝角时,如图1中,作AH PQ ⊥于H .在Rt AHQ ∆中,1sin 10AH AQH AQ ∠==,40AQ =, 4AH ∴=,22224041211QH AQ AH ∴--在Rt QOH ∆中,223OHOA AH ,31211OQ ∴=+45(311)(4211)PQ cm ∴=-+=-, 当OAQ ∠是锐角时,如图2中,作AH OP ⊥交PO 的延长线于H .同法可得:12113OQ =,45(12113)(481211)PQ cm ∴=-=-.故答案为:421211-或481211-.【点睛】本题考查解直角三角形的应用,解题的关键是理解题意,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.18.【分析】过E 作EG ⊥AO 连接EO 先利用旋转的性质得出ED 和OD 根据三角函数可得∠EOD=30°在△OEG 中解直角三角形即可求得OG 和GE 从而得出E 点坐标【详解】解:∵A (30)C (0)∴OA=3∵四解析:(3,3)【分析】过E 作EG ⊥AO ,连接EO ,先利用旋转的性质得出ED 和OD ,根据三角函数可得∠EOD=30°,在△OEG 中解直角三角形即可求得OG 和GE ,从而得出E 点坐标.【详解】解:∵A (3,0),C (0,3),∴OA=3, 3OC =, ∵四边形OABC 为矩形,∴3AB OC ==,∠BAO=90°, 如下图,过E 作EG ⊥AO ,连接EO ,∵矩形OABC 绕原点O 逆时针旋转30°后得到矩形ODEF ,∴OD=OA=3, 3DE AB ==∠EDO=90°, ∴3tan EOD ∠=∴∠EOD=30°,∴∠EOG=∠EOD+∠DOA=60°,又∵23sin 30ED EO ==︒, ∴cos 603,sin 603,OG EO EG EO =︒==︒=∴(3,3)E .故答案为:(3,3).【点睛】本题考查解直角三角形,矩形的性质,坐标与图形变化——旋转.能正确作出辅助线,构造直角三角形是解题关键.19.【分析】连接DE 过E 作EH ⊥OD 于H 求得∠EDO =45°即可得到Rt △DEH 中求得DH 进而得出OH 即可求解【详解】如图所示连接过作于于于是的中点中点的横坐标是【点睛】本题主要考查了直角三角形斜边上中解析:422-【分析】连接DE ,过E 作EH ⊥OD 于H ,求得∠EDO =45°,即可得到Rt △DEH 中,求得DH ,进而得出OH ,即可求解.【详解】如图所示,连接DE ,过E 作EH OD ⊥于H ,BE CA ⊥于E ,CF AB ⊥于F ,D 是BC 的中点,142DE DC BC DO DB ∴=====, DCE DEC ∴∠=∠,DBO DOB ∠=∠,67.5A ∴∠=︒, 112.5ACB ABC ∴∠+∠=︒,18021802()()CDE BDO DCE DBO ∴∠+∠=︒-∠+︒-∠3602()DCE DBO =︒-∠+∠3602112.5=︒-⨯︒135=︒,45EDO ∴∠=︒,Rt DEH ∴∆中,cos 4522DH DE =︒⨯=422OH OD DH ∴=-=-,点E 的横坐标是422-.【点睛】本题主要考查了直角三角形斜边上中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.解决问题的关键是作辅助线构造等腰直角三角形.20.【分析】过A 作AE ⊥BC 于点E 则由题意可得AE 的值进一步可求得△ABO 的面积【详解】解:如图过A 作AE ⊥BC 于点E ∵AB=4∠ABC=45°∴AE=AB=∴故答案为【点睛】本题考查菱形性质和解直角三解析:22【分析】过A 作AE ⊥BC 于点E ,则由题意可得AE 的值,进一步可求得△ABO 的面积.【详解】解:如图,过A 作AE ⊥BC 于点E ,∵AB=4,∠ABC=45°,∴AE=AB sin 45︒=242= ∴1111·422222224ABO ABC S S BC AE ==⨯=⨯⨯=故答案为2 .【点睛】本题考查菱形性质和解直角三角形的综合应用,熟练掌握菱形的性质是解题关键.三、解答题21.(1)212y x x =--;(2)当1m =-时,图像1y 与2y 有一个交点;当1m ≠-时,图像1y 与2y 有两个交点,理由:见详解;(3)031a <<或310a <<【分析】(1)将()1,2-代入1y ,解关于m 的方程即可求解; (2)将点()1,1m +代入2y 求出a ,由解析式1y 和2y 联立方程组消去y 得到关于x 的一元二次方程,根据一元二次方程根的情况判断1y 与2y 交点的个数即可;(3)将1,02⎛⎫ ⎪⎝⎭代入1y 求出m 的值,把m 的值代入1y 与2y ,结合图像,根据对任意x ,都有12y y >即可求解.【详解】解:(1)将()1,2-代入1y ,得()()2111m m -=+--,解得,122,1m m =-= ,()()121y x x ∴=-+,即 212y x x =--;(2)当1m =-时,图像1y 与2y 有一个交点;当1m ≠-时,图像1y 与2y 有两个交点. 理由如下:2y 经过点()1,1m +,1m a m ∴+=+,1a ,()()121,y x m x m y x m =+--=+∴联立方程组()()1y x m x m y x m ⎧=+--⎨=+⎩,消去y ,得()2202x x m m -+=- ()()222242484410m m m m m =++=++=+≥△∴方程()2202x x m m -+=-有实数根据,当1m =-时,0=, 方程()2202x x m m -+=-有两个相等的实数根,1y 与2y 有一个交点;当1m ≠-时,0>,方程()2202x x m m -+=-有两个不相等的实数根,1y 与2y 有两个交点;综上所术,当1m =-时,图像1y 与2y 有一个交点;当1m ≠-时,图像1y 与2y 有两个交点;(3)1y 经过点1,02⎛⎫ ⎪⎝⎭, ∴ 110122m m =+--⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭, 解得,12m =-, 2121,122y x y ax ⎛⎫ ⎪⎝⎭∴=-=- 联立方程组2121212y x y ax ⎧⎛⎫=-⎪ ⎪⎪⎝⎭⎨⎪=-⎪⎩,消去y 得,()23014x a x ++=-,若方程有两个相等的实数根,图像1y 与2y 有一个交点,则()231404a =+-⨯=△, 解,得31a =±-,如图所示,对任意x ,都有12y y >,031a ∴<<或310a <<,【点睛】本题是二次函数与一次函数的综合题,考查了待定系数法求函数的解析式,二次函数与一次函数图像的交点与一元二次方程根的判别式的关系及利用图像求不等式的解集,关键在于正确理解二次函数与一次函数图像的交点与一元二次方程的关系以及数形结合的思想. 22.(1)见解析;(2)8055x <<3)54=DEP S △ 【分析】(1)直接利用相似三角形的判定定理解答即可(2)过点E 作EH BF ⊥于H ,利用相似三角形的性质,三角函数解直角三角形可得12PE PF EF BE PB PE ===,34BF BE =,再利用BHE BPF △△∽求出EH ,即可得到y 与x 的关系式,利用F 点与C 点重合的时求出x 的最大值,即可求得x 的范围(3)若DEP 与BCD △相似,分两种情况求解:当90PED ∠=︒时;当90EDP ∠=︒时,利用相似三角形的性质,等腰三角形的性质,勾股定理等知识,求解即可【详解】(1)证明:∵EPF FBP ∠=∠,PEF FEP ∠=∠.∴EPF EBP △△∽.(2)解:∵2AB CD ==,4BC AD ==,∴在Rt ABC 中22222425BD AB AD =+=+=∴21tan 42AB ADB AD ∠===.PF BD∴在Rt BPF 中,tan PF PBF BP ∠= //AD BC ADB PBF ∴∠=∠12PF AB BP AD ∴== BP x =12PF x ∴= 25DP x ∴=-∵EPF EBP △△∽. ∴12PE PF EF BE BP PE === ∴14EF BE =. ∴34BF BE =. 过点E 作EH BF ⊥于H ,EH BF ⊥,PF BD ⊥∴//EH PF ,∴BHE BPF △△∽, ∴34PF BF HE BE ==. 12PF x = ∴412323HE x x =⨯=. ∴()2112125252233y HE PD x x x x =⨯⨯=⨯⨯=-+ 当点F 与点重合时,则有1122S BD FP BC CD ⋅=⋅△BDC = 4525BC CD FP BD ⋅∴===12FP BP = 855BP ∴= x 的最大值为855∴自变量x 的取值范围:8055x <<. (3)解:若DEP 与BCD △相似,∴90PED ∠=︒或90EDP ∠=︒时,DEP 与BCD △相似.当90PED ∠=︒时,如图:∴90DPE PDE ∠+∠=︒.∵90DPE EPF ∠+∠=︒,∴PDE EPF ∠=∠.EPF EBP △△∽∴EPF FBP ∠=∠,∴DBE BDE ∠=∠,∴BE DE =.设BE a =,DE a =,4EC a =-.在Rt CDE △中,222DE EC CD ,()22242a a =-+,52a =. ∴52BE ED ==,54PE =,115525224216DEP S EP ED =⨯⨯=⨯⨯=. 当90EDP ∠=︒时,如图∵90BDC DBC ∠+∠=︒,90DBC DEB ∠+∠=︒∴BDC DEB ∠=∠又∵90DPE EPF ∠+∠=︒∵DBC EPF ∠=∠,∴BDC DPE ∠=∠∴BDC DPE DEB ∠=∠=∠在Rt DPE △中,tan tan tan 2DPE BDC DEC ∠=∠=∠=∵2CD =,∴1CE =, ∴DE∴PD , 115224DEP S DE DP =⨯⨯=△. 【点睛】本题考查了相似三角形的判定和性质,勾股定理,等腰三角形的判定和性质,三角函数解直角三角形等知识,熟练掌握相似三角形的判定和性质,以及对所学知识的综合运用是解题关键.23.(1)223y x x =--;(2)421n -.【分析】(1)设二次函数的解析式是y=a (x-h )2+k ,先代入顶点A 的坐标,再把B 的坐标代入,即可求出a ,即可得出解析式;(2)由点P 到y 轴的距离不大于4,得出 ,结合二次函数的图象可知,请根据图象直接写出n 的取值范围.【详解】解:(1)某二次函数的顶点坐标是(1,4)-,且经过点(4,5)A ,设二次函数的解析式为2(1)4y a x =--,把(4,5)A 代入得:25(41)4a =--解得:1a =,所以函数表达式为:223y x x =--.(2)点P 到y 轴的距离为||m ,∴||m ≤4,∴44m -,∵2223(1)4y x x x =--=--,在44m -时,当m=1时,有最小值n=-4;当m=-4时,有最大值n=21,∴421n -.【点睛】本题考查了待定系数法求二次函数的表达式,二次函数求最值,二次函数图象和性质的应用,求二次函数的取值范围,掌握二次函数的图象和性质的应用是解题的关键.24.133+ 【分析】 根据算术平方根,任何非零数的零次幂等于1以及特殊角的三角函数值计算即可.【详解】 解:()022********tan -++︒ =31233++⨯=1233++=133+【点睛】此题主要考查了实数运算,正确化简各数是解题关键.25.217m【分析】 过点D 作DH AC ⊥于H ,首先利用三角函数求出AH ,DH 的长度,进而求出CH 的长度,最后利用勾股定理求解即可.【详解】解:如图,过点D 作DH AC ⊥于H .在Rt ADH 中,在Rt ADH 中,cos AH CAD AD∠=, sin DH CAD AD∠=, ∴3cos53106(m)5AH AD =⋅︒≈⨯=, 4sin53108(m)5DH AD =⋅︒≈⨯=. ∵8m AC =, ∴2(m)CH AC AH =-=.∴222282217(m)CD DH CH =+=+=.【点睛】本题主要考查解直角三角形的应用,构造出直角三角形是解题的关键.26.2【分析】分别根据特殊角的三角函数值、负整数指数幂及算术平方根的性质计算出各数,再根据实数混合运算的法则.【详解】+(12)-1﹣2cos30°﹣=23--==2.【点睛】本题考查的是实数的运算,熟记负整数指数幂、算术的性质及特殊角的三角函数值是解答此题的关键.。
【典型题】初三数学下期中第一次模拟试题(附答案)

【典型题】初三数学下期中第一次模拟试题(附答案) 一、选择题1.若点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数1yx=-的图象上,并且x1<0<x2<x3,则下列各式中正确的是()A .y1<y2<y 3B.y2<y3<y1C.y1<y3<y2D.y3<y1<y2 2.如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的()A.23DEBC=B.25DEBC=C.23AEAC=D.25AEEC=3.如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=kx(x>0)的图象经过顶点B,则反比例函数的表达式为()A.y=12xB.y=24xC.y=32xD.y=40x4.如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是()A.32OBCD=B.32αβ=C.1232SS=D.1232CC=5.已知2x=3y,则下列比例式成立的是()A.B.C.D.6.如图,在矩形ABCD 中,DE AC ⊥于E ,设ADE α∠=,且3cos 5α=,5AB =,则AD 的长为( )A .3B .163C .203D .1657.图(1)所示矩形ABCD 中,BC x =,CD y =,y 与x 满足的反比例函数关系如图(2)所示,等腰直角三角形AEF 的斜边EF 过点C ,M 为EF 的中点,则下列结论正确的是( )A .当3x =时,EC EM <B .当9y =时,EC EM <C .当x 增大时,EC CF ⋅的值增大D .当x 增大时,BE DF ⋅的值不变8.如图,将一个Rt △ABC 形状的楔子从木桩的底端点P 处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8cm (如箭头所示),则木桩上升了( )A .8tan20°B .C .8sin20°D .8cos20°9.如图所示,在平面直角坐标系中,已知点A (2,4),过点A 作AB ⊥x 轴于点B .将△AOB 以坐标原点O 为位似中心缩小为原图形的12,得到△COD ,则CD 的长度是( )A .2B .1C .4D .25 10.如图,A 、B 、C 三点在正方形网格线的交点处,若将△ABC 绕着点A 逆时针旋转得到△AC′B′,则ta nB′的值为( )A .12B .24C .14D .1311.下列四个几何体中,主视图与左视图相同的几何体有( )A .1个B .2个C .3个D .4个12.给出下列函数:①y=﹣3x +2;②y=3x;③y=2x 2;④y=3x ,上述函数中符合条作“当x >1时,函数值y 随自变量x 增大而增大“的是( )A .①③B .③④C .②④D .②③ 二、填空题13.如图,在一段坡度为1∶2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为____米.14.如图,在△ABC 中,CD 、BE 分别是△ABC 的边AB 、AC 上的中线,则DF EF BF CF++=________。
初三数学下期中第一次模拟试卷附答案

一、选择题1.把二次函数243y x x =-+化成2()y a x h k =++的形式是( )A .2(2)1y x =++B .2(2)7y x =++C .2(2)1y x =--D .2(2)7y x =-- 2.一次函数y =ax +b 与二次函数y =ax 2+bx +c 在同一坐标系中的图象可能是( ) A . B .C .D .3.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列结论:①240b ac ->;②0abc >;③420a b c -+>;④30a c +<.其中,正确结论的个数是( )A .1B .2C .3D .44.已知二次函数2(2)1y mx m x =+--(m 为常数,且0m ≠),( )A .若0m >,则1x <,y 随x 的增大而增大B .若0m >,则1x >,y 随x 的增大而减小C .若0m <,则1x <,y 随x 的增大而增大D .若0m <,则1x >,y 随x 的增大而减小 5.已知二次函数y =x 2﹣4x +m 2+1(m 是常数),若当x =a 时,对应的函数值y <0,则下列结论中正确的是( )A .a ﹣4<0B .a ﹣4=0C .a ﹣4>0D .a 与4的大小关系不能确定6.当函数21(1)23a y a x x +=-++ 是二次函数时,a 的取值为( )A .1a =B .1a =±C .1a ≠D .1a =- 7.近日,重庆观音桥步行街惊现震撼的裸眼3D 未来城市,超清LED 巨幕,成功吸引了广大市民络绎不绝的前来打卡,一时间刷爆朋友圈.萱萱想了解该LED 屏GH 的高度,进行了实地测量,她从大楼底部E 点沿水平直线步行30米到达自动扶梯底端D 点,在D 点用仪器测得屏幕下端点H 的仰角为36°.然后她再沿着i=4:3长度为40米的自动扶梯到达扶梯顶端C 点,又沿水平直线行走了40米到达B 点,在B 点测得屏幕上端点G 的仰角为50°(A ,B ,C ,D ,E ,H ,G 在同一个平面内,且B ,C 和A ,D ,E 分别在同一水平线上),则该LED 屏GH 的高度约为( )(结果精确到 0.1,参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin50°≈0 .77,tan50°≈1.19)A .122.0 米B .122.9米C .111.0米D .111.9米 8.如图,在Rt ABC 中,90,4,3ACB AC BC ∠=︒==,将ABC 绕直角边AC 的中点O 旋转,得到DEF ,连接AD ,若DE 恰好经过点C ,且DE 交AB 于点G ,则tan DAG ∠的值为( )A .524B .513C .512D .7249.如图,在Rt ABC ∆中,90,3,2C BC AB ∠=︒==,则B 等于( )A .15︒B .20︒C .30D .60︒10.如图,在ABC ∆中,AC BC ⊥,30ABC ︒∠=,点D 是CB 延长线上的一点,且AB BD =,则tan DAC ∠的值为( )A .33B .23C .23+D .23- 11.在ΔABC 中,∠C =90º,AB =5,BC =3,则cos A 的值是( )A .34B .43C .35D .4512.如图,△ABC 、△FED 区域为驾驶员的盲区,驾驶员视线PB 与地面BE 的央角∠PBE =43°,视线PE 与地面BE 的夹角∠PEB =20°,点A ,F 为视线与车窗底端的交点,AF //BE ,AC ⊥BE ,FD ⊥BE .若A 点到B 点的距离AB =1.6m ,则盲区中DE 的长度是( )(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)A .2.6mB .2.8mC .3.4mD .4.5m二、填空题13.如图,二次函数2y x mx =-+的图象与x 轴交于坐标原点和()4,0,若关于x 的方程20x mx t -+=(t 为实数)在14x <<的范围内有解,则t 的取值范围是_______.14.已知二次函数2221y x mx m =-++(m 为常数),当自变量x 的值满足31x -≤≤-时,与其对应的函数值y 的最小值为5,则m 的值为__________.15.将抛物线2y x =-先向左平移1个单位长度,再向上平移2个单位长度后,得到的抛物线的解析式是______.16.道路的隔离栏通常会涂上醒目的颜色,呈抛物线形状(如图1),图2是一个长为2米,宽为1米的矩形隔离栏,中间被4根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点E ,点P )以及点A ,点B 落在同一条抛物线上,若第1根栏杆涂色部分(EF )与第2根栏杆未涂色部分(PQ )长度相等,则EF 的长度是___________.17.如图,∠DBC =30°,AB =DB ,利用此图求tan75°= _____ .18.如图,ABC ∆的顶点都是正方形网格中的格点,则cos CAB ∠=__________.19.如图所示,在四边形ABCD 中,23AD AB =,30A ∠=︒,将线段CD 绕点C 逆时针旋转90°,并延长至其3倍(即3CE CD =),过点E 作EF AB ⊥于点F ,当63AD =,3BF =,74EF =时,边BC 的长是______.20.在平面直角坐标系中,等边ABO 如图放置,其中()2,0B ,则过点A 的反比例函数的表达式为________.三、解答题21.如图,抛物线y =﹣x 2+bx +c 与x 轴相交于A (﹣3,0),D (1,0)两点,其中顶点为B .(1)求该抛物线的解析式;(2)若该抛物线与y 轴的交点为C ,求△ABC 的面积.22.某箫笛厂设计了一款成本为10元/根的箫笛,并投放市场进行试销.经过调查,发现每天的销售量y (件)与销售单价x (元)存在一次函数关系10700y x =-+. (1)销售单价定为多少时,该厂每天获取的利润最大?最大利润为多少?(2)若物价部门规定,该产品的最高销售价不得超过38元/根,那么销售单价如何定位才能获取最大利润?23.新年前夕,信业超市在销售中发现:某服装平均每天可售出20套,每件盈利40元.为了迎接新年,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.(1)要想平均每天在销售服装上盈利1200元,那么每套应降价多少元?(2)商场要想每天获取最大利润,每套应降价多少元?24.(1)计算:()2422cos 45sin 604︒︒-+(2)解方程:()2239x x -+=25.(3.14﹣π)0﹣3tan30°+|3﹣2|﹣11()2-.26.在ABC 中,90ACB ∠=︒,2CA CB ==,点P 是边AB 的中点,连接CP .(1)如图①,B 的大小=______(度),AB 的长=______;CP 的长=______; (2)延长BC 至点O ,使2OC BC =,将ABC 绕点O 逆时针旋转()0180αα︒<︒<︒得到A B C ''',点A ,B ,C ,P 的对应点分别为A ',B ',C ',P '.①如图②,当30α=︒时,求点C '到直线OB 的距离及点C '到直线AB 的距离; ②当C P ''与ABC 的一条边平行时,求点P '到直线AC 的距离(直接写出结果即可).【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式.【详解】解:()()22243443421y x x x x x =-+=-++-=--. 故选:C .【点睛】此题考查了二次函数的顶点式,掌握利用配方法将二次函数一般式转化为顶点式是解题的关键.2.B解析:B【分析】先由一次函数y ax b =+的图象得到a 、b 的正负,再与二次函数2y ax bx c =++的图象的开口方向、对称轴位置相比较即可做出判断.【详解】解:A 、由抛物线可知,a <0,x =﹣2b a <0,得b <0,由直线可知,a >0,b >0,故本选项错误;B 、由抛物线可知,a <0,x =﹣2b a <0,得b <0,由直线可知,a <0,b <0,故本选项正确;C 、由抛物线可知,a >0,x =﹣2b a >0,得b <0,由直线可知,a >0,b >0,故本选项错误;D 、由抛物线可知,a <0,x =﹣2b a<0,得b <0,由直线可知,a <0,b >0,故本选项错误.故选:B .【点睛】本题主要考查一次函数的图象、二次函数2y ax bx c =++的图象与性质,熟练掌握两函数图象与解析式的系数的关系是解答的关键.3.D解析:D【分析】根据二次函数图象的开口方向、对称轴位置、与x 轴的交点坐标等知识,逐个判断即可.【详解】解:抛物线与x 轴有两个不同的交点,因此b 2-4ac >0,故①正确;抛物线开口向上,因此a >0,对称轴为x=1>0,a 、b 异号,因此b <0,抛物线与y 轴交在负半轴,因此c <0,所以abc >0,故②正确;由图象可知,当x=-2时,y=4a-2b+c >0,故③正确;∵对称轴x=-2b a=1 ∴-b=2a当x=-1时,y=a-b+c <0,∴a+2a+c <0,即30a c +<,故④正确;综上所述,正确结论有:①②③④故选:D .【点睛】考查二次函数的图象和性质,掌握a 、b 、c 的值决定抛物线的位置以及二次函数的图象与性质,是正确判断的前提. 4.D解析:D【分析】先求出二次函数图象的对称轴,然后根据m 的符号分类讨论,结合图象的特征即可得出结论.【详解】 该二次函数图象的对称轴为直线21122m x m m -=-=-+, 若0m >,对于22m x m -=-无法判断其符号,故A 、B 选项不一定正确; 若0m <,则202m x m -=-<,即22m m--<1,且抛物线的开口向下, ∴当1x >时,y 随x 的增大而减小,故选:D .【点睛】此题考查的是二次函数的图象及性质,解决此题的关键是分类讨论确定对称轴的位置,再结合开口方向进行综合分析.5.A【分析】画出函数图象,利用图象法解决问题即可;【详解】解:∵抛物线的对称轴为422x -=-=, 抛物线与x 轴交于点A 、B .如图,设点A 、B 的横坐标分别为12x x 、,124x x +=,2121x x m =+,∴()()()22212121241641x x x x x x m -=+-=-+, ∵210m +>,∴()212x x -的最小值为16, ∴AB <4,∵当自变量x 取a 时,其相应的函数值y <0,∴可知a 表示的点在A 、B 之间,∴40a -<,故选:A .【点睛】本题考查了二次函数的性质,根据题意画出图形,利用数形结合求解是解答此题的关键. 6.D解析:D【分析】根据二次函数的定义去列式求解计算即可.【详解】∵函数21(1)23a y a x x +=-++ 是二次函数,∴a-1≠0,2a 1+=2,∴a≠1,21a =,∴1a =-,【点睛】本题考查了二次函数的定义,熟记二次函数的定义并灵活列式计算是解题的关键. 7.A解析:A【分析】作CM ⊥AE 于M ,设射线BC 交GE 于N ,则CN=ME=DM+DE ,CM=NE=NH+EH ,由三角函数定义求出EH=21.9米,由坡度求出DM=24米,NE=CM=32米,得出CN=54米,BN=94米,再由三角函数定义求出GN≈111.86米,得出GE=143.86米,即可得出答案.【详解】解:作CM ⊥AE 于M ,设射线BC 交GE 于N ,如图所示:则CN=ME=DM+DE ,CM=NE=NH+EH ,由题意得:∠GBN=50°,BC=DC=40米,DE=30米,∠EDH=36°,∵tan ∠EDH EH DE=, ∴EH=DE×tan ∠E DH≈30×0.73=21.9(米), ∵DC 的坡度为4:3CM DM =, ∴4325NE CM DC ===米,3245MD DC ==米, ∴CN=ME=DM+DE=24+30=54(米),∴BN=BC+CN=40+54=94(米),∵tan ∠GBN GN BN=, ∴GN=BN×tan ∠GBN≈94×1.19≈111.86(米),∴GE=GN+NE=111.86+32=143.86(米),∴GH=GE-EH=143.86-21.9≈121.96≈122.0 (米);故选:A .【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,能借助仰角构造直角三角形,利用三角函数解直角三角形是解题的关键.8.D解析:D【分析】连接OG,由勾股定理求出AB=5,由直角三角形的性质求出CG,CD,AD的长,由锐角三角函数的定义可得出答案.【详解】解:连接OG,在Rt△ABC中,∠C=90°,AC=4,BC=3,∴222243AC BC+=+,∵点O是AC边的中点,∴OC=OA=OD=12AC=2,∴∠GCO=∠ODC=∠BAC,∠ADC=90°,∴AG=CG,∴OG⊥AC,在Rt△ABC中,sin∠BAC=35BCAB=,cos∠BAC=45ACAB=,∴sin∠OCG=35,cos∠OCG=45,在Rt△OCG中,CG=5 cos2OCOCG=∠,在Rt△ACD中,CD=AC•cos∠OCG=165,AD=AC•sin∠OCG=125,∴DG=CD-CG=165-52=710,∴tan∠DAG=771012245DGAD==.故选:D.本题考查了旋转的性质,锐角三角函数的定义,勾股定理,直角三角形的性质,正确的作出辅助线构造直角三角形是解题的关键.9.C解析:C【分析】由锐角三角函数余弦的定义即可得出∠B=30°.【详解】解:∵∠C=90°,,AB=2,∴cos 2BC B AB ==, ∴∠B=30°,故选:C .【点睛】此题考查了解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.10.C解析:C【分析】设AC=x ,根据三角函数可得,,AB=2x ,求出DC 即可.【详解】解:设AC=x ,∵AC BC ⊥,30ABC ︒∠=,tan ∠ABC=AC BC,AC BC =,sin ∠ABC=AC AB, 12AC AB =, AB=2x ,BD=2x ,=(2x +,tan ∠DAC=2DC AC ==, 故选:C .本题考查了特殊角的三角函数和求三角函数值,解题关键是根据三角函数的定义,利用特殊角,表示出相关线段长.11.D解析:D【分析】利用勾股定理可求出AC的长,根据余弦函数的定义即可得答案.【详解】∵∠C=90°,AB=5,BC=3,∴=4,∴cosA=ACAB =45.故选:D.【点睛】考查勾股定理及锐角三角函数的定义,在直角三角形中,锐角的余弦是角的邻边与斜边的比;熟练掌握各三角函数的定义是解题的关键.12.B解析:B【分析】首先证明四边形ACDF是矩形,利用∠PBE的正弦值可求出AC的长,即可得DF的长,利用∠PEB的正切值即可得答案.【详解】∵FD⊥AB,AC⊥EB,∴DF∥AC,∵AF∥EB,∴四边形ACDF是平行四边形,∵∠ACD=90°,∴四边形ACDF是矩形,∴DF=AC,在Rt△ACB中,∵∠ACB=90°,∠ABE=43°,∴AC=AB•sin43°≈1.6×0.7=1.12(m),∴DF=AC=1.12(m),在Rt△DEF中,∵∠FDE=90°,∠PEB=20°,∴tan∠PEB=DFDE≈0.4,∴DE≈1.120.4=2.8(m),故选:B.【点睛】本题考查解直角三角形的应用及矩形的判定与性质,熟练掌握各三角函数的定义是解题关键.二、填空题13.【分析】求出函数解析式求出函数值取值范围把t 的取值范围转化为函数值的取值范围【详解】先由已知可得二次函数y=−x2+mx 的图象与x 轴交于坐标原点和(40)所以对称轴x==所以m=4代入方程y=−x2解析:04t <≤【分析】求出函数解析式,求出函数值取值范围,把t 的取值范围转化为函数值的取值范围.【详解】先由已知可得,二次函数 y=−x 2+mx 的图象与 x 轴交于坐标原点和 (4,0)所以对称轴 x=2b a -=()221m -=⨯-, 所以m=4,代入 方程y=−x 2+mx 得,y=-x 2+4x ,当x=2时,y=4即顶点坐标是(2,4)当x=1时,y=3,当x=4时,y=0由x 2−mx+t=0得 t=-x 2+4x=y因为当 1<x<4 时, 0<y≤4,所以在 1<x<4 范围内有实数解,则 t 的取值范围是0<t≤4,故答案为:0<t≤4 .【点睛】本题考查了二次函数和一元二次方程数形结合分析问题,注意函数的最低点和最高点. 14.-5或1【分析】利用配方法可得出:当x=m 时y 的最小值为1分m <-3-3≤m≤-1和m >-1三种情况考虑:当m <-3时由y 的最小值为5可得出关于m 的一元二次方程解之取其较小值;当-3≤m≤-1时y 的解析:-5或1【分析】利用配方法可得出:当x=m 时,y 的最小值为1.分m <-3,-3≤m≤-1和m >-1三种情况考虑:当m <-3时,由y 的最小值为5可得出关于m 的一元二次方程,解之取其较小值;当-3≤m≤-1时,y 的最小值为1,舍去;当m >-1时,由y 的最小值为5可得出关于m 的一元二次方程,解之取其较大值.综上,此题得解.【详解】解:∵y=x 2-2mx+m 2+1=(x-m )2+1,∴当x=m 时,y 的最小值为1.当m <-3时,在-3≤x≤-1中,y 随x 的增大而增大,∴9+6m+m 2+1=5,解得:m 1=-5,m 2=-1(舍去);当-3≤m≤-1时,y 的最小值为1,舍去;当m >-1时,在-3≤x≤-1中,y 随x 的增大而减小,∴1+2m+m 2+1=5,解得:m 1=-3(舍去),m 2=1.∴m 的值为-5或1.故答案为:-5或1.【点睛】本题考查了二次函数的最值以及二次函数图象上点的坐标特征,分m <-3,-3≤m≤-1和m >-1三种情况求出m 的值是解题的关键.15.【分析】根据左加右减上加下减的原则进行解答即可【详解】解:将抛物线向左平移1个单位所得直线解析式为:;再向上平移2个单位为:故答案为:【点睛】此题主要考查了二次函数图象与几何变换要求熟练掌握平移的规 解析:()212y x =-++【分析】根据“左加右减、上加下减”的原则进行解答即可.【详解】解:将抛物线2y x =-向左平移1个单位所得直线解析式为:()2+1y x =-; 再向上平移2个单位为:()2+21+y x =-.故答案为:()212y x =-++.【点睛】此题主要考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减. 16.4【分析】根据抛物线形状建立二次函数模型以AB 中点为原点建立坐标系xOy 通过已知线段长度求出A(10)B(-1O)由二次函数的性质确定y =ax2-a 利用PQ =EF 建立等式求出二次函数中的参数a 即可得解析:4【分析】根据抛物线形状建立二次函数模型,以AB 中点为原点,建立坐标系xOy ,通过已知线段长度求出A(1,0),B(-1,O),由二次函数的性质确定y =ax 2-a ,利用PQ =EF 建立等式,求出二次函数中的参数a ,即可得出EF 的值.【详解】解:如图,令P 下方的点为H ,以AB 中点为原点,建立坐标系xOy ,则A(1,0),B(-1,O),设抛物线的方程为y=ax 2+bx+c∴抛物线的对称轴为x=0,则2b a-=0,即b =0. ∴y =ax 2 +c .将A(1,0)代入得a+c =0,则c =-a .∴y =ax 2-a . ∵OH =2×15×12=0.2,则点H 的坐标为(-0.2,0) 同理可得:点F 的坐标为(-0.6,0).∴PH =a×(-0.2)2-a =-0.96aEF =a×(-0.6)2-a =-0.64a .又∵PQ =EF =1-(-0.96a )=-0.64a∴1+0.96a =-0.64a .解得a =58-. ∴y =58-x 2+58. ∴EF =(58-)×(-0.6)2+58=25. 故答案为:0.4.【点睛】 本题考查了二次函数的应用,解题的关键是能在几何图形中建立适当的坐标系并结合图形的特点建立等式求出二次函数表达式.17.【分析】由推出根据三角形的外角等于与它不相邻的两内角和知设表示出进一步表示根据求解【详解】解:设故答案是:【点睛】本题考查了解直角三角形的知识熟悉相关性质是解题的关键 解析:23+【分析】由AB BD =推出∠=∠A ADB ,根据三角形的外角等于与它不相邻的两内角和知15A ∠=︒,75ADC ∠=︒.设CD x =,表示出AB 、BD 、BC ,进一步表示AC .根据tan tan 75AC ADC CD 求解. 【详解】 解:ABBD =,A ADB ∴∠=∠.302DBC A , 15A ∴∠=︒,75ADC ∠=︒.设CD x =, 21sin 2CDx AB BD x DBC ,222223BC BD CD x x x , (23)AC AB BC x ,tan tan75ADCAC CD= 23=+.故答案是:23+.【点睛】本题考查了解直角三角形的知识,熟悉相关性质是解题的关键.18.【分析】根据题意和图形可以得到ACBC 和AB 的长然后根据等面积法可以求得CD 的长再利用勾股定理求得AD 的长从而可以得到cos ∠CAB 的值【详解】解:作CD ⊥AB 交AB 于点D 由图可得∵解得∴∴故答案为解析:25 【分析】根据题意和图形,可以得到AC 、BC 和AB 的长,然后根据等面积法可以求得CD 的长,再利用勾股定理求得AD 的长,从而可以得到cos ∠CAB 的值.【详解】解:作CD ⊥AB ,交AB 于点D ,由图可得,22221310,2,3332AC BC AB =+===+=∵322ABC AB CD BC S ∆⋅⨯==, 解得,2CD =, ∴2222(10)(2)22AD AC CD =-=-=, ∴2225cos 510CAB A A C D ∠===, 故答案为:25. 【点睛】 本题考查解直角三角形,解答本题的关键是明确题意,利用数形结合的思想解答. 19.【分析】由锐角三角函数可求∠DEC=30°通过证明△ADE ∽△BDC 可得由勾股定理可求AE 的长即可求解【详解】解:如图连接BDAEDE ∵将线段CD 绕点C 逆时针旋转90°并延长至其倍∴∠DCE=90°解析:258【分析】 由锐角三角函数可求∠DEC=30°,通过证明△ADE ∽△BDC ,可得12BC DC AE DE ==,由勾股定理可求AE 的长,即可求解.【详解】解:如图,连接BD ,AE ,DE ,∵将线段CD 绕点C 逆时针旋转90°3∴∠DCE=90°,CE 3CD ,∴3.tan 3DC DEC EC ∠==, ∴∠DEC=30°,∴3cos EC DEC DE ∠==1sin 2DC DEC DE ∠==, ∵233AD AB =,∴AB AD = ∴EC AB DE AD=, 又∵∠DEC=∠DAB=30°,∴△DEC ∽△DAB ,∴∠ADB=∠EDC ,DC DE DB AD =, ∴∠ADE=∠BDC ,∴△ADE ∽△BDC , ∴12BC DC AE DE ==,∵AD AB =, ∴AB=9,又∵BF=3,∴AF=6,∴254AE ===, ∴12528BC AE ==, 故答案为:258. 【点睛】 本题考查了旋转的性质,勾股定理,锐角三角函数等知识,证明△DEC ∽△DAB 是本题的关键.20.y =【分析】过点A 作AC ⊥OB 于C 设过点A 的反比例函数的表达式为y =根据等边三角形的性质得到OA =OB=2∠AOC =60°利用三角函数求出OCAC 得到点A 的坐标代入函数解析式即可【详解】解:过点A 作解析:y 【分析】过点A 作AC ⊥OB 于C ,设过点A 的反比例函数的表达式为y =k x,根据等边三角形的性质得到OA =OB=2,∠AOC =60°,利用三角函数求出OC 、AC ,得到点A 的坐标,代入函数解析式即可.【详解】解:过点A 作AC ⊥OB 于C ,设过点A 的反比例函数的表达式为y =k x , ∵△OAB 是等边三角形,()2,0B ,∴OA =OB=2,∠AOC =60°,∴OC =OA ×cos ∠AOC =2×12=1,AC =OA ×sin ∠AOC =2×32=3, ∴点A 的坐标为(1,3),∴3=1k, 解得,k =3,∴过点A 的反比例函数的表达式为y =3, 故答案为:y =3.【点睛】此题考查等边三角形的性质、反比例函数图象上点的坐标特征、锐角三角函数、待定系数法求反比例函数解析式,解题的关键是利用锐角三角函数求出OC 、AC 的长.三、解答题21.(1)y =﹣x 2﹣2x +3;(2)3【分析】(1)利用待定系数法确定函数关系式;(2)根据抛物线解析式求得点B 、C 的坐标,过点B 作BE ⊥x 轴于点E ,交直线AC 于F ,由直线AC 的解析式和一次函数图象上点的坐标特征求得点F 的坐标,然后根据三角形面积公式求解.【详解】解:(1)∵抛物线y =﹣x 2+bx +c 与x 轴相交于A (﹣3,0),D (1,0)两点, ∴9301+=0b c b c --+=⎧⎨-+⎩, 解得:2=3b c =-⎧⎨⎩.故该抛物线解析式为y =﹣x 2﹣2x +3;(2)由抛物线解析式y =﹣x 2﹣2x +3,可得B (﹣1,4),C (0,3).如图,过点B 作BE ⊥x 轴于点E ,交直线AC 于F ,则点F 的横坐标是﹣1.∵直线AC 经过点A (﹣3,0),C (0,3),∴直线AC 的解析式是y =x +3.把x =﹣1代入y =x +3,得y =2.则F (﹣1,2).∴BF =2.∵AO =3∴S △ABC =S △ABF +S △BCF =12BF •(AE+OE )=12BF •AO =1232⨯⨯=3.【点睛】本题考查了待定系数法求二次函数的解析式和求坐标系中三角形的面积问题,难度不大,属于基础题型,熟练掌握待定系数法求二次函数的解析式是关键.22.(1)40,9000元;(2)每件售价为38元,才能获取最大利润【分析】(1)首先根据题意得每件产品的利润:()10x -元,再根据二次函数的性质计算,即可得到答案;(2)结合题意,根据二次函数图像的性质计算,即可得到答案.【详解】(1)∵107000y x =-+≥∴70x ≤根据题意得,每件产品的利润:()10x -元∴该厂每天获取的利润为:()()21011070008007000x x x x -=-+--+ 当80040210x =-=⨯时,该厂每天获取的最大利润为:210408004070009000-⨯+⨯-=元;(2)根据(1)的结论,该厂每天获取的利润为:()()21011070008007000x x x x -=-+--+当40x <时,利润随x 的增大而增大;当40x >时,利润随x 的增大而减小; ∴当38x =时,即每件售价为38元,才能获取最大利润.【点睛】本题考查了二次函数、一元一次不等式的知识;解题的关键是熟练掌握二次函数的性质,从而完成求解.23.(1)应降价20元;(2)每套应降价15元【分析】(1)设每件衬衫应降价x 元,利用每件利润×总销量=总利润,列方程求解即可; (2)利用每件利润×总销量=总利润,进而求出二次函数最值即可.【详解】(1)解:设每件衬衫应降价x 元,根据题意,得()()402021200x x -+=,整理,得22604000x x -+=,解得110x =,220x =.∵尽快减少库存,∴20x答:应降价20元.(2)解:设每件衬衫应降价x 元,总利润为W 元,根据题意,得.()()40202W x x =-+2260800x x =-++, 当152b x a=-=时,利润最大, ()()4015202151250W =-+⨯=最大利润.【点睛】此题主要考查了一元二次方程以及二次函数的应用,正确利用每件利润×总销量=总利润得出关系式是解题关键.24.(1)2;(2)10x =,23x =.【分析】(1)把45°、60°的三角函数值代入计算,即可得出结果;(2)将原方程整理为一般形式,再利用提公因式法分解因式即可求得方程的根.【详解】解:(1)2cos 45sin 604︒︒-+222=⨯-+222=-+ 2=; (2)()2239x x -+=原方程可整理得:2260x x分解因式,得()230x x -=则20x =或30x -=,解得10x =,23x =.【点睛】本题考查了锐角三角函数的混合运算及解一元二次方程,掌握特殊角的三角函数值与一元二次方程的解法是解答此题的关键.25.【分析】先计算0指数、三角函数值、负指数和绝对值,再加减.【详解】解:(3.14﹣π)0﹣3tan30°2|﹣11()2-.,【点睛】本题考查了包含三角函数、0指数和负指数的实数计算,解题关键是熟记特殊角三角函数值,明确0指数、负指数的意义.26.(1)45°,;(2)①∴点C '到直线OB 的距离为2;点C '到直线AB 的距离为②4-4+5【分析】(1)根据三角形内角和定理以及勾股定理,直角三角形斜边中线的性质求解即可(2)①过点C '作C D OB '⊥,垂足为点D ,过点C '作C E AB '⊥,交BA 的延长线于点E ,连接AC ',解直角三角形求出C D '、C E '即可;②分三种情况:当//P C AC ''时,延长P C ''交OB 于H ;当//P C AB ''时,过点P '作P H OB '⊥交BO 的延长线于点H ,交A C ''于T ;当//P C AC ''时,延长P C ''交OB 于H 分别画出图形求解即可【详解】解:(1)在ABC 中,90ACB ∠=︒,2CA CB ==45B A ∴∠=∠=︒sin 2CA B AB == 点P 是AB 的中点12CP AB ∴==故答案为:45°,.(2)①过点C '作C D OB '⊥,垂足为点D ,过点C '作C E AB '⊥,交BA 的延长线于点E ,连接AC ',将ABC 绕点O 逆时针旋转α得到A B C ''',2224OC OC BC '∴===⨯=.在Rt OC D '△中,30O ∠=︒,114222C D OC ''∴==⨯=. ∴点C '到直线OB 的距离为2.2222421223OD OC C D ''=-=-==C D OB '⊥,90ACB ∠=︒,90C DB ACB '∴∠=∠=︒.//AC C D '∴.2C D '=,2AC =,C D AC '∴=.∴四边形C DCA '是平行四边形.423C A DC OC OD '∴==-=-,//C A DC ',45EAC B '∴∠=∠=︒.90904545EC A EAC ''∴∠=︒-∠=︒-︒=︒.EAC EC A ''∴∠=∠.C E AE '∴=.在Rt AC E '△中,222C E AE C A ''+=,222C A C E ''∴=.()2242322622C E C A ''==-=-. ∴点C '到直线AB 的距离为226-.②如图:当//P C AC ''时,延长P C ''交OB 于H//AC P H '90OHC AOC '∴∠=∠=︒45OC H B C P ''''=∠=︒cos 4522OH OC '∴=⋅︒=422CH OC OH ∴=-=-∴点P '到直线AC 的距离为422-如图,当//P C AB ''时,过点P '作P H OB '⊥交BO 的延长线于点H ,交A C ''于T ,由题意可得四边形OHTC '是矩形,1OH C T '==145CH OC OH ∴=+=+=∴点P '到直线AC 的距离为5如图,当//P C BC ''时,延长B A ''交BO 于点H ,可得cos 4532OH OB '=⋅︒=324CH ∴=∴点P '到直线AC 的距离为432+综上所述,点P '到直线AC 的距离为422-432+5.【点睛】本题考查了作图—旋转变换,解直角三角形,直角三角形斜边中线的性质,解题关键是理解题意,学会用分类讨论的思想思考问题.。
最新九年级数学下期中第一次模拟试卷及答案
一、选择题1.已知y 是x 的二次函数,y 与x 的部分对应值如表所示,若该二次函数图象向左平移后通过原点,则应平移( )x… 1- 0 1 2 … y … 0 3 4 3 …A .1个单位B .2个单位C .3个单位D .4个单位 2.一次函数y =ax +b 与二次函数y =ax 2+bx +c 在同一坐标系中的图象可能是( ) A . B . C . D .3.二次函数223y x =-+在14x -≤≤内的最小值是( )A .3B .2C .-29D .-304.某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为( )A .35元B .36元C .37元D .36或37元 5.飞机着陆后滑行的距离s (单位:m )与滑行的时间t (单位:s )的函数解析式是260 1.5s t t =-,那么飞机着陆后滑行多长时间才能停下来.( )A .10sB .20sC .30sD .40s6.如图,二次函数2y ax bx c =++的图象与x 轴交于,A B 两点,与y 轴负半轴交于点C ,它的对称轴为直线12x =,则下列选项中正确的是( )A .0abc <B .0a b -=C .40a c ->D .当2(1x n n =+为实数)时,y c ≤ 7.在Rt ABC ∆中,90C ∠=︒,若5sin 13A =,则cos A 的值为( ) A .512 B .813 C .1312 D .12138.如图,在Rt ABC △中,90ABC ∠=︒,4AB =,8BC =,D ,E 分别为边AB ,BC 上一点,且满足:1:3AD DB =.连接DE ,将ADBE 沿DE 翻折,点B 的对应点F 恰好落在边AC 上,则CF 的长度为( )A .1952055B .275C .52055D .3159.如图,在下列网格中,小正方形的边长均为1,点A 、B 、O 都在格点上,则AOB ∠的正弦值是( )A .31010B .22C .1010D .11010.已知ABC 的三个顶点均在正方形网格的格点上,则tan A 的值为( )A .12B .2105C .105D .25511.如图,在边长相同的小正方形组成的网格中,点A B C D 、、、都在这些小正方形的顶点上,AB CD 、相交于点P ,则tan APD ∠=( ).A .5B .3C .10D .212.如右图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC 的顶点都在格点上,则sin BAC ∠的值为( )A .45B .35C .34D .23二、填空题13.如图,在平面直角坐标中,对抛物线222y x x =-+在x 轴上方的部分进行循环反复的轴对称或中心对称变换,若点A 是该抛物线的顶点,则经过第2020次变换后所得的A点的坐标是_________.14.二次函数()22336y x x x =--≤≤的最小值是_________. 15.现从四个数1,2,1-,3-中任意选出两个不同的数,分别作为二次函数2y ax bx =+中a ,b 的值,则所得二次函数满足开口方向向下且对称轴在y 轴右侧的概率是__________.16.已知点()4,A m -,()2,B m ,()6,C n 均在抛物线2y x bx c =++上,则m ,n 的大小关系是m __________n .17.如图,∠DBC =30°,AB =DB ,利用此图求tan75°= _____ .18.在边长为4的菱形ABCD 中,∠A =60°,M 是AD 边的中点,若线段MA 绕点M 旋转得到线段MA ′,连接A ′C ,则A ′C 长度的最小值是________.19.如图,在平面直角坐标系中,点O 为坐标原点,点B 的坐标为(4,0),AB ⊥x 轴,连接AO ,tan ∠AOB =54,动点C 在x 轴上,连接AC ,将△ABC 沿AC 所在直线翻折得到△ACB ',当点B '恰好落在y 轴上时,则点C 的坐标为_____.20.如图,在山坡上种树时,要求株距(相邻两树间的水平距离)为6m .测得斜坡的斜面坡度为i =1:3(斜面坡度指坡面的铅直高度与水平宽度的比),则斜坡相邻两树间的坡面距离为_____.三、解答题21.如图,已知抛物线y =﹣x 2+bx +c 与坐标轴交于A ,B ,C 三点,其中A (﹣2,0),B (4,0).(1)求该抛物线的表达式;(2)根据图象,直接写出y >0时,x 的取值范围;(3)若要使抛物线与x 轴只有一个交点,则需将抛物线向下平移几个单位?22.如图,已知抛物线212y x bx c =++与x 轴交于A 、B 两点,与y 轴交于点C 且AB =6,抛物线的对称轴为直线x =1(1)抛物线的解析式;(2)x 轴上A 点的左侧有一点E ,满足S △ECO =4S △ACO ,求直线EC 的解析式.23.新年前夕,信业超市在销售中发现:某服装平均每天可售出20套,每件盈利40元.为了迎接新年,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.(1)要想平均每天在销售服装上盈利1200元,那么每套应降价多少元?(2)商场要想每天获取最大利润,每套应降价多少元?24.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45︒改为30︒.已知原传送带AB 长为42m .(1)求新传送带AC 的长度;(2)如果需要在货物着地点C 的左侧留出5m 的通道,试判断距离B 点43m 的货物MNQP 是否需要挪走,并说明理由.25.按要求完成下列各小题:(1)解方程:()2549x +=(2)计算:2sin 30cos 603tan 30+-26.某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB 上方150米的点C 处悬停,此时测得桥两端,A B 两点的俯角分别为65°和45°,求桥AB 的长度.(参考数据:sin650.91︒≈,cos650.42︒≈,tan65 2.14︒≈;结果精确到0.1米)【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】由表格可得点()0,3与点()2,3是关于二次函数对称轴对称的,则有二次函数的对称轴为直线0212x +==,进而可得点()1,4是二次函数的顶点,故设二次函数解析式为()214y a x =-+,然后代入点()1,0-可得二次函数解析式,最后问题可求解. 【详解】解:由表格可得点()0,3与点()2,3是关于二次函数对称轴对称的,则有二次函数的对称轴为直线0212x +==, ∴点()1,4是二次函数的顶点,设二次函数解析式为()214y a x =-+,代入点()1,0-可得:1a =-, ∴二次函数解析式为()214y x =--+, ∵该二次函数图象向左平移后通过原点,∴设平移后的解析式为()214y x b =--++, 代入原点可得:()2014b =--++,解得:123,1b b ==-(舍去),∴该二次函数的图象向左平移3个单位长度;故选C .【点睛】本题主要考查二次函数的图象与性质及平移,熟练掌握二次函数的图象与性质及平移是解题的关键. 2.B解析:B【分析】先由一次函数y ax b =+的图象得到a 、b 的正负,再与二次函数2y ax bx c =++的图象的开口方向、对称轴位置相比较即可做出判断.【详解】解:A 、由抛物线可知,a <0,x =﹣2b a <0,得b <0,由直线可知,a >0,b >0,故本选项错误;B 、由抛物线可知,a <0,x =﹣2b a <0,得b <0,由直线可知,a <0,b <0,故本选项正确;C 、由抛物线可知,a >0,x =﹣2b a >0,得b <0,由直线可知,a >0,b >0,故本选项错误;D 、由抛物线可知,a <0,x =﹣2b a<0,得b <0,由直线可知,a <0,b >0,故本选项错误.故选:B .【点睛】本题主要考查一次函数的图象、二次函数2y ax bx c =++的图象与性质,熟练掌握两函数图象与解析式的系数的关系是解答的关键.3.C解析:C【分析】根据图象,直接代入计算即可解答【详解】解:由图可知,当x=4时,函数取得最小值y 最小值=-2×16+3=-29.故选:C .【点睛】本题考查二次函数最小(大)值的求法.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.4.C解析:C【分析】根据利润=数量×每件的利润就可以求出关系式,根据(1)的解析式,将其转化为顶点式,根据二次函数的顶点式的性质就可以求出结论.【详解】解:依题意得:y=(30-20+x )(240-10x )y=-10x 2+140x+2400.∵每件首饰售价不能高于40元.∴0≤x≤10.∴求y 与x 的函数关系式为:y=-10x 2+140x+2400,x 的取值范围为0≤x≤10;∴y=-10(x-7)2+2890.∴a=-10<0.∴当x=7时,y 最大=2890.∴每件首饰的售价定为:30+7=37元.∴每件首饰的售价定为37元时,可使月销售利润最大,最大的月利润是2890元. 故选C .【点睛】本题考查了二次函数的解析式的运用,根据解析式的函数值求自变量的值的运用,二次函数的顶点式的性质的运用,解答时求出二次函数的解析式是关键.5.B解析:B【分析】当s 取最大值时,飞机停下来,求函数最大值时的自变量即可.【详解】∵当s 取最大值时,飞机停下来,∴t= 6022( 1.5)b a -=-⨯-=20, 故选:B .【点睛】本题考查了二次函数应用-飞机着陆问题,熟练把问题转化为二次函数的最值问题是解题的关键.6.D解析:D【分析】根据二次函数的图像和性质,分别对每个选项进行判断,即可得到答案.【详解】解:由图象开口向上,可知a<0,与y 轴的交点在x 轴的下方,可知c<0, 又对称轴方程为12x =,所以122b a -=>0,所以b >0, ∴abc >0,故A 错误; ∵122b a -= ∴=-a b , ∴0a b +=,故B 错误; 当12x =时,则11042y a b c =++>, ∵=-a b , ∴11042a a c -+>, ∴104a c -+>, ∴40a c -<,故C 错误;当21x n =+时,222(1)(1)y a n b n c =++++4222an an a an a c =++--+42an an c =++22(1)an n c =++;∵n 为实数,∴20an ≤,211n +≥,∴22(1)an n c c ++≤,即y c ≤,故D 正确;故选:D .【点睛】本题主要考查二次函数的图象和性质.熟练掌握图象与系数的关系以及二次函数与方程的关系是解题的关键.第II 卷(非选择题)请点击修改第II 卷的文字说明7.D解析:D【分析】 由三角函数的定义可知sin BC A AB=,可设BC=5k ,AB=13k 由勾股定理可求得12AC k =,再利用余弦的定义代入计算即可.【详解】解:如图:在Rt ABC 中,sin BC A AB =,可设BC=5k ,AB=13k . 由勾股定理可求得()()222213512AC AB BC k k k =-=-=. 所以,1212cos =1313AC k A AB k ==. 故选:D .【点睛】 本题主要考查三角函数的定义,掌握正弦、余弦函数的定义是解题的关键.8.A解析:A【分析】如图,过D 作DM AC ⊥于,M 根据已知条件先求解:,,,AD BD AC 再利用A ∠的三角函数求解,,AM DM 由对折得到:,DF 再利用勾股定理求解MF ,从而由CF AC AM MF =--可得答案.【详解】解:如图,过D 作DM AC ⊥于,M4:1:3,AB AD DB ==,13AD DB ∴==,,90ABC ∠=︒,4AB =,8BC =,22224845,AC AB BC ∴=+=+=1,AD DM AC =⊥,sin ,45DM BC A AD AC ∴=== 25DM ∴=, 同理:5cos ,45AM AB A AD AC ==== 5AM ∴=, 由对折可得:3,DF DB == 222225205355MF DF DM ⎛⎫∴=-=-= ⎪ ⎪⎝⎭,520519520545555CF AC AM MF ∴=--=-= 故选:.A【点睛】 本题考查的是轴对称的性质,勾股定理的应用,锐角三角函数的应用,掌握以上知识是解题的关键.9.C解析:C利用勾股定理求出AB 、AO 、BO 的长,再由S △ABO =12AB•h=12AO•BO•sin ∠AOB 可得答案. 【详解】解:由题意可知,AB=2,AO=224225+=,BO=222222+=,∵S △ABO =12AB•h=12AO•BO•sin ∠AOB , ∴12×2×2=12×25×22×sin ∠AOB , ∴sin ∠AOB=10, 故选:C .【点睛】 本题考查了解直角三角形,掌握三角形的面积公式是解题的关键.10.A解析:A【分析】作BD ⊥AC 于D ,根据勾股定理,可得BD 、AD 的长,根据正切为对边比邻边,可得答案.【详解】解:如图:作BD ⊥AC 于D ,,2,AD=22tanA=21222BD AD ==, 故选:A .【点睛】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.11.B解析:B【分析】设小正方形的边长为1,根据勾股定理可得AD 、AC 的值,进而可得△ADC 是等腰直角三角形,进而可得AD ⊥CD ,根据相似三角形的判定和性质可得PC =2DP ,根据等量代换和线段和差可得AD =CD =3DP ,继而即可求解.解析 设小正方形的边长为1, 由图形可知,2,2AD DC AC ===, ADC ∴是等腰直角三角形, AD DC ∴⊥.//AC BD ,2AC CP BD DP∴==, 2PC DP ∴=,3AD DC DP ∴==,tan 3AD APD DP∴∠==. 故选B .【点睛】本题考查了正方形的性质、等腰直角三角形的判定、勾股定理、相似三角形的判定及其性质以及锐角三角函数.此题难度适中,注意转化思想与数形结合思想的应用. 12.A解析:A【分析】过C 作CD AB ⊥于D ,首先根据勾股定理求出AC ,然后在Rt ACD ∆中即可求出sin BAC ∠的值.【详解】如图,过C 作CD AB ⊥于D ,则=90ADC ∠︒,222234++AC AD CD 5.4sin 5CD BAC AC ∠==. 故选:A .【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线构造直角三角形是解题的关键. 二、填空题13.【分析】观察图形可知每三次对称为一个循环组依次循环用2020除以3然后根据商和余数的情况确定出变换后的点A 所在的象限然后解答即可【详解】解:∵∴抛物线的顶点坐标为点A 第一次关于x 轴对称后在第四象限第 解析:11,22⎛⎫- ⎪⎝⎭【分析】观察图形可知每三次对称为一个循环组依次循环,用2020除以3,然后根据商和余数的情况确定出变换后的点A 所在的象限,然后解答即可.【详解】解:∵2221122=2()2()22y x x x x x =-+--=--+∴抛物线222y x x =-+的顶点坐标为11,22⎛⎫ ⎪⎝⎭点A 第一次关于x 轴对称后在第四象限,第二次关于原点对称后在第二象限,第三次关于y 轴对称后在第一象限,回到原始位置,所以每3次对称为一个循环组,∵20203=6731÷∴经过第2020次变换后所得的A 点位置第一次变换后的位置相同,在第四象限,坐标为11,22⎛⎫- ⎪⎝⎭故答案为:11,22⎛⎫- ⎪⎝⎭【点睛】本题考查了轴对称的性质,点的坐标变换规律,读懂题目信息,观察出每三次对称为一个循环组依次循环是解题的关键,也是本题的难点.14.【分析】先求出二次函数的对称轴为直线x=1a >0然后知x <1时y 随x 的增大而减小x >1时y 随x 的增大而增大再依据二次函数的增减性解答即可【详解】解:∵抛物线的对称轴为a=1>0∴x <1时y 随x 的增大解析:0【分析】先求出二次函数的对称轴为直线x=1,a >0,然后知x <1时,y 随x 的增大而减小,x >1时,y 随x 的增大而增大,再依据二次函数的增减性解答即可.【详解】解:∵抛物线的对称轴为=12b x a=-,a=1>0, ∴x <1时,y 随x 的增大而减小,x >1时,y 随x 的增大而增大.∴在36x ≤≤内,x=3时,y 有最小值,此时23233=0y =-⨯-.故答案为:0.【点睛】本题考查了二次函数的最值问题,二次函数的增减性,根据函数解析式求出对称轴是解题的关键.15.【分析】把ab 所有可能的取值及满足题目的条件通过表格列出来再根据概率的定义列式求解即可【详解】解:∵二次函数满足开口方向向下即要a<0对称轴在y 轴右侧即要求∴可以列出如下表格:其中第三和第四行数字0 解析:13【分析】把a 、b 所有可能的取值及满足题目的条件通过表格列出来,再根据概率的定义列式求解即可.【详解】解:∵二次函数满足开口方向向下即要a<0,对称轴在y 轴右侧即要求02b a->, ∴可以列出如下表格:其中第三和第四行数字0表示不满足题中某个条件 , 数字1表示满足题中某个条件, ∴由题意,只有第三和第四行两个数字都为1时才满足题目所有条件,此时a 和b 的值分别为-1和1、-1和2、-3和1、-3和2共4种情况,∴所求概率为41123=, 故答案为13. 【点睛】本题考查二次函数的性质,用列表法计算概率的方法,熟练掌握列表法的步骤及题目条件的符号表示是解题关键.16.【分析】由点AB 的坐标利用二次函数的对称性可求出b 的值利用二次函数图象上点的坐标特征可找出m 和n 的大小关系【详解】解:∵二次函数y=x2+bx+c 的图象经过点A (-4m )B (2m )∴∴b=2∵点A(解析:m n <【分析】由点A 、B 的坐标利用二次函数的对称性可求出b 的值,利用二次函数图象上点的坐标特征可找出m 和n 的大小关系.【详解】解:∵二次函数y=x 2+bx+c 的图象经过点A (-4,m )、B (2,m ), ∴42122b -+-==-, ∴b=2, ∵点A(-4,m),C (6,n )在二次函数y=x 2+bx+c 的图象上,∴m=16-8+c=8+c ;n=36+12+c=48+c ,∴m <n ,故答案为:<.【点睛】本题考查了二次函数图象上点的坐标特征以及二次函数的性质,利用二次函数图象上点的坐标特征得到m ,n 的大小是解题的关键.17.【分析】由推出根据三角形的外角等于与它不相邻的两内角和知设表示出进一步表示根据求解【详解】解:设故答案是:【点睛】本题考查了解直角三角形的知识熟悉相关性质是解题的关键解析:2+【分析】由AB BD =推出∠=∠A ADB ,根据三角形的外角等于与它不相邻的两内角和知15A ∠=︒,75ADC ∠=︒.设CD x =,表示出AB 、BD 、BC ,进一步表示AC .根据tan tan 75AC ADCCD 求解. 【详解】解:AB BD =,A ADB ∴∠=∠.302DBC A ,15A ∴∠=︒,75ADC ∠=︒.设CD x =, 21sin 2CDx AB BD x DBC , 222223BC BD CD x x x , (23)AC AB BC x ,tan tan75ADCAC CD=2=故答案是:2+【点睛】本题考查了解直角三角形的知识,熟悉相关性质是解题的关键.18.【分析】根据题意在MA的运动过程中A在以M为圆心AD为直径的圆上的弧AD上运动当AC取最小值时由两点之间线段最短知此时MAC三点共线得出A的位置进而利用锐角三角函数关系求出AC的长即可【详解】如图作解析:272-【分析】根据题意,在MA'的运动过程中,A'在以M为圆心、AD为直径的圆上的弧AD上运动,当A'C取最小值时,由两点之间线段最短知此时M、A'、C三点共线,得出A'的位置,进而利用锐角三角函数关系求出A'C的长即可.【详解】如图,作ME⊥CD于点E.∵M是AD边的中点,∴MA=2∵线段M A绕点M旋转得线段MA'.∴MA'=2∵菱形ABCD中,∠A=60°∴∠EDM =60°,在直角△MDE中,DE= MD · cos ∠EDM=121 2⨯=ME =MD · sin ∠33则EC =CD+ED=4+1=5在直角△CEM中()22225327CE ME+=+=当A'在MC上时,A'C最小,则A'C长度的最小值是7-2故答案为:7【点睛】此题主要考查了菱形的性质以及锐角三角函数关系等知识,得出A'点位置是解题关键. 19.【分析】根据题意先求出AB=5由折叠的性质得出AB=AB=5BC=BC过点A作AD⊥y轴于点D由勾股定理求出OB=2得出x2+22=(4﹣x)2解得x=则可得出答案【详解】解:∵tan ∠AOB =B ( 解析:3,02⎛⎫ ⎪⎝⎭【分析】根据题意先求出AB =5,由折叠的性质得出AB =AB'=5,BC =B'C ,过点A 作AD ⊥y 轴于点D ,由勾股定理求出OB'=2,得出x 2+22=(4﹣x )2,解得x =32,则可得出答案. 【详解】解:∵tan ∠AOB =54,B (4,0), ∴54AB OB =, ∴AB =5, ∵将△ABC 沿AC 所在直线翻折得到△ACB′, ∴AB =AB'=5,BC =B'C ,过点A 作AD ⊥y 轴于点D ,∴B'D ,22AB AD -2254-3,∴OB'=2,设OC =x ,则BC =B'C =4﹣x ,Rt △OB'C 中,∵OC 2+OB'2=B'C 2,∴x 2+22=(4﹣x )2,解得x =32, ∴C (32,0). 故答案为:(32,0). 【点睛】本题考查勾股定理以及翻折问题,熟练掌握勾股定理以及折叠的性质是解题的关键. 20.4米【分析】首先根据斜面坡度为i =1:求出株距(相邻两树间的水平距离)为6m 时的铅直高度再利用勾股定理计算出斜坡相邻两树间的坡面距离【详解】由题意水平距离为6米铅垂高度2米∴斜坡上相邻两树间的坡面距解析:【分析】首先根据斜面坡度为i =16m 时的铅直高度,再利用勾股定理计算出斜坡相邻两树间的坡面距离.【详解】由题意水平距离为6米,铅垂高度∴(m ),故答案为:【点睛】此题考查解直角三角形的应用,解题关键是掌握计算法则. 三、解答题21.(1)y =﹣x 2+2x +8;(2)当﹣2<x <4时,y >0;(3)把抛物线y =﹣x 2+2x +8向下平移9个单位,抛物线与x 轴只有一个交点.【分析】(1)把A 点和B 点坐标分别代入y=-x 2+bx+c 得到关于b 、c 的方程组,然后解方程组即可;(2)根据函数图象直接得到答案;(3)先利用配方法得到抛物线的顶点坐标,然后把抛物线的平移问题转化为点的平移问题;【详解】解:(1)把A(﹣2,0),B(4,0)代入y =﹣x 2+bx+c ,得4201640b c b c --+=⎧⎨-++=⎩, 解得28b c =⎧⎨=⎩, 抛物线解析式为y =﹣x 2+2x+8;(2)∵A(﹣2,0),B(4,0)∴由图象知,当﹣2<x <4时,y >0;(3)∵y =﹣x 2+2x+8=﹣(x ﹣1)2+9,∴抛物线的顶点坐标为(1,9),∴把抛物线y =﹣x 2+2x+8向下平移9个单位,抛物线与x 轴只有一个交点.【点睛】本题主要考查了抛物线与x 轴的交点,二次函数图象与几何变换,待定系数法确定函数关系式等知识点,注意“数形结合”数学思想的应用;22.(1)2142y x x =-++;(2)142y x =+. 【分析】(1)已知了抛物线的对称轴以及AB 的长,即可得到A 、B 的坐标,代入抛物线的解析式中求得待定系数的值,即可得出抛物线的解析式;(2)由于△ECO 和△ACO 的高都为OC ,根据等高三角形的面积比等于底边比可知:OE :OA =4:1,据此可求出E 点坐标,然后根据E 、C 坐标可用待定系数法求出直线EC 的解析式.【详解】解:(1)∵抛物线的对称轴为直线x =1,12a =-, ∴12b a-=, ∴1b =,∵AB =6, ∴A (−2,0),B (4,0),将B (4,0),1b =代入解析式212y x bx c =-++得4c =, ∴抛物线的解析式为:2142y x x =-++; (2)S △ECO =12EO•OC ,S △ACO =12AO•OC , ∵S △ECO =4S △ACO ,且OA=2,∴EO =4AO =8,∵点E 在A 点的左侧,∴E (−8,0),由抛物线的解析式得:C (0,4),设直线EC 的解析式为:y =kx +b ,将E (−8,0),C (0,4),代入得:804k b b -+=⎧⎨=⎩, 解得124k b ⎧=⎪⎨⎪=⎩,∴直线EC 的解析式为142y x =+. 【点睛】本题综合考查了二次函数的图象与性质、待定系数法求函数解析式等知识,熟练掌握二次函数的图象与性质并能准确利用待定系数法求函数解析式是解题的关键.23.(1)应降价20元;(2)每套应降价15元【分析】(1)设每件衬衫应降价x 元,利用每件利润×总销量=总利润,列方程求解即可; (2)利用每件利润×总销量=总利润,进而求出二次函数最值即可.【详解】(1)解:设每件衬衫应降价x 元,根据题意,得 ()()402021200x x -+=,整理,得22604000x x -+=,解得110x =,220x =.∵尽快减少库存,∴20x答:应降价20元.(2)解:设每件衬衫应降价x 元,总利润为W 元,根据题意,得.()()40202W x x =-+2260800x x =-++, 当152b x a=-=时,利润最大, ()()4015202151250W =-+⨯=最大利润.【点睛】此题主要考查了一元二次方程以及二次函数的应用,正确利用每件利润×总销量=总利润得出关系式是解题关键.24.(1)新传送带AC 的长度为8m ;(2)货物MNQP 需要挪走,理由见解析.【分析】(1)先根据等腰直角三角形的性质求出AD 的长,然后再根据直角三角形的性质求出AC 即可;(2)先根据余弦的定义求出CD ,然后再根据题意求出PC 的长,最后根据题意判断即可.【详解】解:(1)在Rt ABD ∆中,45ABD ︒∠=,sin 454AD AB ︒∴=⋅=在Rt ACD ∆中,30ACD ︒∠=,28AC AD ∴==,答:新传送带AC 的长度为8m ;(2)在Rt ACD ∆中,30ACD ︒∠=,cos CD AC ACD ∴=⋅∠=在Rt ABD ∆中,45ABD ︒∠=,4BD AD ∴==4BC CD BD ∴=-=,()445PC BP BC ∴=-==<,∴货物MNQP 需要挪走.【点睛】本题主要考查了解直角三角形的应用一坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的相关知识是解本题的关键.25.(1)12122x x =-=,;(2)14-【分析】(1)原方程移项后根据平方差公式分解因式,即可得到方程的解;(2)求出式中特殊角的三角函数值即可得到解答.【详解】(1)原方程可化为22x 570+-=(), ()x 1220x +-=()得:120x +=,或20x -=1212,2x x ∴=-=解:(2)原式=21122+-() 11124=+- 14=- 【点睛】本题考查一元二次方程与特殊角三角函数的应用,熟练掌握一元二次方程的解法及特殊角三角函数的值是解题关键.26.1米【分析】过点C 作CD ⊥AB ,垂足为D ,根据在C 处测得桥两端A ,B 两点的俯角分别为60°和45°,可得∠CAD=∠MCA=65°,∠CBD=∠NCB=45°,利用角的三角函数求解即可.【详解】解:如图,过点C 作CD AB ⊥,垂足为D ,由题意得65MCA A ∠=∠=︒,45NCB B ∠=∠=︒,150CD =(米),在Rt ACD ∆中,015070.1tan 65 2.14CD AD ==≈(米), 在Rt BCD ∆中,45CBD ∠=︒,∴150BD CD ==(米) ∴70.1150220.1AB AD BD =+=+=(米)答:桥AB 的长度约为220.1米.【点睛】本题考查了三角函数的运算,构造直角三角形,利用解直角三角形求边是解题的关键.。
【人教版】九年级数学下期中第一次模拟试卷带答案

一、选择题1.如图,已知点D ,E 是AB 的三等分点,DF ,EG 将ABC 分成三部分,且////DF EG BC ,图中三部分的面积分别为1S ,2S ,3S ,则123::S S S 的值为( )A .1:2:3B .1:2:4C .1:3:5D .2:3:42.在ABC 中,D ,E 分别为,BC AC 上的点,且2AC EC =,连结,AD BE ,交于点F ,设:,:x CD BD y AF FD ==,则( ) A .1y x =+B .1x y x+=C .413y x =+ D .21xy x-=- 3.如图,在△ABC 中,DE ∥BC ,∠ADE =∠EFC ,AD:BD=5:3,CF =6,则DE 的长为( )A .6B .8C .10D .124.如图,在ABC 中,中线BE ,CD 相交于点O ,连接DE ,下列结论:①12DE BC =;②12S S =△DOE △COB ;③AD OE AB OB=;④16ODE ADC S S =△△.其中结论正确的是( ).A .①②B .①③C .①②③D .①③④5.如图△BCD 中,BE ⊥CD ,AE =CE=3,BE =DE=4.BC=5,DA 的延长线交BC 于F ,则AF=( )A .1B .0.6C .1.2D .0.8 6.已知P ,Q 是线段AB 的两个黄金分割点,且AB=10,则PQ 长为( ) A .5(5-1)B .5(5+1)C .10(5-2) -D .5(3-5)7.下列函数中,y 总随x 的增大而减小的是( ) A .4y x =- B .4y x =-C .4y x=D .4y x=-8.在反比例函数13my x-=图象上有两点()11,A x y ,()22,B x y ,120x x <<,12y y <,则m 的取值范围是( )A .13m >B .13m <C .13m ≥D .13m ≤9.已知点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)是函数y =﹣2x图象上的点,且x 1<0<x 2<x 3,则y 1,y 2,y 3的大小关系是( ) A .y 1>y 2>y 3 B .y 1<y 2<y 3C .y 1>y 3>y 2D .无法确定10.如图,函数ky x=与2(0)y kx k =-+≠在同一平面直角坐标系中的图像大致( ) A . B .C .D .11.如图,矩形ABCD 的顶点A ,B 在x 轴的正半轴上,反比例函数ky x=在第一象限内的图象经过点D ,交BC 于点E .若4AB =,2CE BE =,34AD OA =,则线段BC 的长度为( )A .1B .32C .2D .2312.如图,正方形ABCD 的顶点A ,B 分别在x 轴和y 轴上与双曲线18y x=恰好交于BC 的中点E ,若2OB OA =,则ABO S △的值为( )A .6B .8C .12D .16第II 卷(非选择题)请点击修改第II 卷的文字说明参考答案二、填空题13.如图,在平行四边形ABCD 中,E 在AD 上,21AE ED =,CE 交BD 于F ,则:BCF DCF S S =△△__________.14.如图,点P 是ABC 的重心,过P 作BC 的平行线,分别交AC ,AB 于点D ,E ,作//DF EB ,交CB 于点F ,若ABC 的面积为227cm ,则DFC △的面积为______2cm .15.在ABC 中,点D 、E 分别在边AB 、AC 上,AB=12,AC=16,AE=4,若ABC 与ADE 相似,则AD=__________.16.如果23a cb d ==,其中20b d +≠,那么22a cb d +=+________. 17.已知()12,y -,()21,y -,()33,y 是反比例函数6y x=-的图象上的三个点,则1y ,2y ,3y 的大小关系是______.18.已知点(,7)M a 在反比例函数21y x=的图象上,则a=______. 19.如图,一次函数1y kx b =+的图象与反比例函数24y x=的图象交于A (1,m ),B (4,n )两点.则不等式40kx b x+-≥的解集为______.20.已知,点P (a ,b )为直线3y x =-与双曲线2y x=-的交点,则11b a -的值等于__.三、解答题21.求证:相似三角形对应边上的角平分线之比等于相似比.要求:①根据给出的ABC 及线段A B '',A '∠(A A ∠'=∠),以线段A B ''为一边,在给出的图形上用尺规作出A B C ''',使得A B C ABC ''''∽△△,不写作法,保留作图痕迹.②在已有的图形上画出一组对应角平分线,并据此写出已知、求证和证明过程.22.如果一条线段可以将一个三角形分成两个三角形,其中一个是等腰三角形,另一个三角形与原三角形相似,我们把这样的三角形叫做完美三角形,这条线段叫做这个完美三角形的完美分割线.(1)根据完美三角形的定义,老陆、栋栋、勇士分别提出如下命题: ①等腰直角三角形是完美三角形; ②含30°的直角三角形是完美三角形; ③等边三角形不是完美三角形.在上述三个命题中,是真命题的为______.(填序号)(2)如图1,在ABC 中,CD 为角平分线,40A ∠=︒,60B ∠=︒. 求证:CD 为ABC 的完美分割线.(3)如图2,在ABC 中,5AB =,6BC =,4AC =. 求证:ABC 是完美三角形.23.如图,在平面直角坐标系中,一次函数1y kx =+的图象交y 轴于点D ,与反比例函数16y x=的图象在第一象限相交于点A .过点A 分别作x 轴、y 轴的垂线,垂足为点B 、C . (1)点D 的坐标为__________; (2)当四边形OBAC 是正方形时,求k 值.24.已知A (n ,-2),B (1,4)是一次函数y =kx +b 的图象和反比例函数y=mx的图象的两个交点,直线AB 与y 轴交于点C .(1)求反比例函数和一次函数的关系式; (2)求△AOC 的面积; (3)求不等式kx +b <mx的解集(直接写出答案).25.已知一次函数y 1 = yy − (2y + 1)的图象与 x 轴和 y 轴分别交于 A 、B 两点,A (3,0),一次函数与反比例函数21ky x+=-的图象分别交于 C 、D 两点.(1)求一次函数与反比例函数解析; (2)求△OCD 的面积;(3)直接写出 y 1> y 2时,y 的取值范围.26.如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于E ,交BA 的延长线于点F .(1)求证:PA =PC ; (2)求证:PC 2=PE •PF .【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据题意易得ADFAEGABC ,则有13AD AB =,23AE AB =.进而可求得119ABC S S =,213ABC S S =,359ABCS S =,最后即可求出结果.【详解】 ∵DF ∥EG ∥BC , ∴ADF AEG ABC ,∵D 、E 是AB 的三等分点, ∴13AD AB =,23AE AB =, ∴119ABC S S =,49AEGABCSS =.∵21411993AEG ABCABCABCS S S S S S =-=-=,34599ABC AEGABCABC ABCS S SSS S =-=-=.∴123115::::1:3:5939ABCABCABCS S S S S S ==.故选C . 【点睛】本题主要考查相似三角形的判定与性质,掌握面积比等于相似比的平方是解题的关键.2.A【分析】过D 作DG ∥AC 交BE 于G ,可得△BDG ∽△BCE ,△DGF ∽△AEF ,根据相似三角形的性质可得x 与y 的数量关系. 【详解】解:如图,过D 作DG ∥AC 交BE 于G , ∴△BDG ∽△BCE ,△DGF ∽△AEF , ∴BD DG BC CE=,DG DFAE AF =,∵AC =2EC , ∴AE =CE , 则BD DFBC AF = ∴BD DFBD CD AF =+,∴BD CD AFBD DF+=, ∵x =CD :BD ,y =AF :FD , ∴1+x =y , ∴y =x +1, 故选:A ..【点睛】本题考查相似三角形的性质和应用,恰当作辅助线构建相似三角形是解题的关键.3.C解析:C 【分析】 由DE //BC 可得出53AD AE BD EC ==,∠AED =∠C ,结合∠ADE =∠EFC 可得出△ADE ∽△EFC ,根据相似三角形的性质可得出53AE DE EC FC ==,再根据CF =6,即可求出DE 的长度.解:∵DE //BC ,∴53AD AE BD EC ==,∠AED =∠C . 又∵∠ADE =∠EFC , ∴△ADE ∽△EFC ,∴53AE DE EC FC ==, ∵CF =6,∴563DE =, ∴DE =10. 故选C 【点睛】本题考查了相似三角形的判定与性质、平行线分线段成比例定理,根据平行线分线段成比例定理和相似三角形的性质列出比例式是解题的关键.4.D解析:D 【分析】先判断DE 为ABC 的中位线,则根据三角形中位线性质得到//DE BC ,12DE BC =,于是可对①进行判断;证明DOE △∽COB △,利用相似比得到12OE DE OD OB BC OC ===,14DOE COB S S =△△,则可对②进行判断;加上12AD AB =,则可对③进行判断;利用三角形面积公式得到13ODE DCE S S =△△,12DCE ADC S S =△△,则可对④进行判断. 【详解】解:∵BE 、CD 为ABC 的中线, ∴DE 为ABC 的中位线, ∴//DE BC ,12DE BC =,所以①正确; ∵//DE BC , ∴DOE △∽COB △,∴12OE DE OD OB BC OC ===,214DOE COB S DE S CB ⎛⎫== ⎪⎝⎭△△,所以②错误; ∵12AD AB =,∴AD OEAB OB=,所以③正确; ∵:1:2OD OC =,∴13ODE DCE S S =△△, ∵AE CE =,∴12DCE ADC S S =△△, ∴16ODE ADC S S =△△,所以④正确. 故选D . 【点睛】本题考查相似三角形的性质和判定,解题的关键是熟练运用相似三角形的性质和判定定理.5.B解析:B 【分析】根据条件和判断Rt △CEB ≌Rt △AED ,然后得到角相等,证明△BEC ∽△BFA ,利用比例关系计算. 【详解】 解:∵AE=3,BE=4 ∴BA=BE-AE=1 ∴在Rt △CEB 与Rt △AED 中AE CEAD CB =⎧⎨=⎩∴Rt △CEB ≌Rt △AED ∴∠EBC=∠BAF∵∠ADE+∠EAD=90°,∠BAF=∠EAD ∴∠EBC+∠BAF=90° ∵∠BEC=∠BFA=90° ∴△BEC ∽△BFA∴AF BA CE BC =即135AF = ∴AF=0.6 故选:B 【点睛】本题考查相似和全等的结合,通过全等得到角关系,然后证相似得到比例关系计算边长即可..6.C解析:C【分析】画出图像,根据黄金分割的概念写出对应线段的比值,求出AQ 、PB 的长度,再根据PQ =AQ +PB -AB 即可求出PQ 的长度.【详解】解:如图,根据黄金分割点的概念,可知512PB AQ AB AB ==, ∴AQ =PB ,AB =10,∴AQ =PB 5110555-=, ∴PQ =AQ +PB -AB =555555101052010(52)+-==.故选:C .【点睛】本题主要考查黄金分割的概念,熟记黄金分割的概念并根据黄金分割的比值列式是解题关键.7.A解析:A【分析】根据正比例函数的性质,可判断A ;根据一次函数的性质,可判断B ;根据反比例函数的性质,可判断C 、D .【详解】A 选项:y 随x 的增大而减小,符合题意,故A 正确;B 选项:y 随x 的增大而增大,不符合题意,故B 错误;C 选项:在每个象限内y 随x 的增大而减小,不符合题意,故C 错误;D 选项:在每个象限内y 随x 的增大而增大,不符合题意,故D 错误.故选:A .【点睛】本题主要考查了反比例函数的增减性,关键是要注意反比例函数在叙述增减性时必须强调在每个象限内.8.A解析:A【分析】根据反比例函数的图象与性质,可得该反比例函数图象的两个分支分别位于第二、四象限,从而可确定1-3m 的取值,进而求出m 的取值范围.【详解】解:∵120x x <<时,12y y <,∴反比例函数图象位于第二、四象限,∴1-3m <0, 解得:13m >, 故选:A .【点睛】此题主要考查了反比例函数的图象与性质,熟练掌握相关性质是解答此题的关键. 9.C解析:C【分析】根据反比例函数图象上点的坐标特征得到y 1=12x -,y 2=22x -,y 3=32x -,然后根据x 1<0<x 2<x 3比较y 1,y 2,y 3的大小.【详解】点(x 1,y 1),(x 2,y 2),(x 3,y 3)都是2y x =-的图象上的点, ∴y 1=12x -,y 2=22x -,y 3=32x -, 而x 1<0<x 2<x 3,∴y 1>y 3>y 2.故选:C .【点睛】本题考查了反比例函数图象上点的坐标特征:熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.10.B解析:B【分析】先根据反比例函数的图像,判断k 的符号,然后再判断一次函数的图像.【详解】A 中,反比例函数经过一、三象限,故k >0,则一次函数应经过一、二、四象限,错误;B 中,反比例函数经过一、三象限,故k >0,则一次函数应经过一、二、四象限,正确;C 中,反比例函数经过二、四象限,故k <0,则一次函数应经过一、二、三象限,错误;D 中,反比例函数经过二、四象限,故k <0,则一次函数应经过一、二、三象限,错误; 故选:B .【点睛】本题考查一次函数与反比例函数图像的性质,解题关键是通过函数的系数符号,判断函数图象经过的象限.11.B解析:B【分析】设OA 为4a ,则根据题干中的比例关系,可得AD=3a ,CE=2a ,BE=a ,从而得出点D 和点E 的坐标(用a 表示),代入反比例函数可求得a 的值,进而得出BC 长.【详解】设OA=4a 根据2CE BE =,34AD OA =得:AD=3a ,CE=2a ,BE=a ∴D(4a ,3a),E(4a+4,a)将这两点代入解析得; 3444k a a k a a ⎧=⎪⎪⎨⎪=⎪+⎩解得:a=12∴BC=AD=32 故选:B【点睛】本题考查反比例函数和矩形的性质,解题关键是用含有字母的式子表示出点D 、E 的坐标,然后代入解析式求解.12.C解析:C【分析】过点B 作x 轴的平行线,过点A ,C 分别作y 轴的平行线,两线相交于M ,N ,证明△ABM ≌△BCN ,可得BN=AM=2a ,CN=BM=a ,所以点C 坐标为(2a ,a ),BC 的中点E 的坐标为(a ,1.5a ),把点E 代入双曲线18y x=可得a 的值,进而得出S △ABO 的值. 【详解】如图,过点B 作x 轴的平行线,过点A ,C 分别作y 轴的平行线,两线相交于M ,N ,∵四边形ABCD 为正方形,∴∠ABC=90°,AB=BC ,∴∠ABM=90°-∠CBN=∠BCN ,∵∠M=∠N=90°,∴△ABM ≌△BCN (AAS ),∵OB=2OA ,∴设OA=a ,OB=2a ,则BN=AM=2a ,CN=BM=a ,∴点C 坐标为(2a ,a ),∵E 为BC 的中点,B (0,2a ),∴E (a ,1.5a ),把点E 代入双曲线18y x=得1.5a 2=18,a 2=12, ∴S △ABO =12a•2a=12, 故选:C .【点睛】 此题考查反比例函数k 的几何意义,三角形全等的判定和性质,解题的关键是构造全等三角形表示出点E 的坐标.二、填空题13.3【分析】证明可得结合三角形面积公式即可求得结果【详解】在平行四边形ABCD 中∵∴∵∴故答案为:3【点睛】本题考查了三角形相似的性质与判定解答本题的关键是熟练运用相似三角形的性质与判定解析:3【分析】证明DEF BCF ,可得31BF CB DF ED ==,结合三角形面积公式即可求得结果. 【详解】在平行四边形ABCD 中,AD BC =,//AD BC , ∵21AE ED =,AE ED AD +=,∴13ED AD = ∵//AD BC ,13DF ED ED BF BC AD ∴===. ∴3BCF DGF SBF S DF==. 故答案为:3.【点睛】本题考查了三角形相似的性质与判定,解答本题的关键是熟练运用相似三角形的性质与判14.3【分析】连接AP并延长交BC于G由重心的性质得AP:PG=2:1由DE//BC根据平行线分线段成比例定理可得AD:DC=AP:PG=2:1于是CD:AC=1:3再由DF//AB得出△DFC∽△AB解析:3【分析】连接AP并延长交BC于G.由重心的性质得,AP:PG=2:1.由DE//BC,根据平行线分线段成比例定理可得AD:DC=AP:PG=2:1,于是CD:AC=1:3.再由DF//AB,得出△DFC∽△ABC,根据相似三角形的性质得出S△DFC:S△ABC=1:9.【详解】解:连接AP并延长交BC于G.由重心的性质得,AP:PG=2:1.∵DE//BC,∴AD:DC=AP:PG=2:1,∴CD:AC=1:3.∵DF//AB,∴△DFC∽△ABC,∴S△DFC:S△ABC=1:9,∴S△DFC=19×S△ABC=3cm2.故答案为:3.【点睛】本题考查了三角形重心的性质,平行线分线段成比例定理,相似三角形的判定与性质,难度适中.准确作出辅助线是解题的关键.15.或【分析】分类讨论:当△ADE∽△ABC和当△AED∽△ABC根据相似的性质得出两种比例式进而解答即可【详解】如图∵∠DAE=∠BAC∴当△ADE∽△ABC∴即解得:AD=3∴当△AED∽△ABC∴解析:163或3【分析】分类讨论:当△ADE∽△ABC和当△AED∽△ABC,根据相似的性质得出两种比例式进而解答即可.【详解】∵∠DAE=∠BAC,∴当△ADE∽△ABC,∴AB ADAC AE=,即12164AD=,解得:AD=3,∴当△AED∽△ABC,∴AB AE AC AD=,即12416AD=,解得:AD=163,故答案为:163或3【点睛】本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等.16.【分析】根据已知条件得出再根据b+2d≠0即可得出答案【详解】解:∵∴∵b+2d≠0∴;故答案为:【点睛】本题考查了比例的性质熟练掌握比例的性质是解题的关键解析:2 3【分析】根据已知条件得出2223a cb d==,再根据b+2d≠0,即可得出答案.解:∵23a c b d ==, ∴2223a cb d ==, ∵b+2d≠0, ∴2223a cb d +=+; 故答案为:23. 【点睛】本题考查了比例的性质,熟练掌握比例的性质是解题的关键.17.【分析】根据反比例函数图象的性质可得其图象位于二四象限且在每个象限内y 随x 的增大而增大即可求解【详解】解:反比例函数的图象位于二四象限且在每个象限内y 随x 的增大而增大∴故答案为:【点睛】本题考查反比 解析:312y y y <<【分析】根据反比例函数图象的性质可得其图象位于二、四象限,且在每个象限内,y 随x 的增大而增大,即可求解.【详解】 解:反比例函数6y x=-的图象位于二、四象限,且在每个象限内,y 随x 的增大而增大, ∴312y y y <<,故答案为:312y y y <<.【点睛】本题考查反比例函数图象的性质,掌握反比例函数图象的性质是解题的关键. 18.3【分析】把点代入反比例函数解析式求解即可【详解】解:∵点在反比例函数的图象上∴解得故答案为:3【点睛】本题考查反比例函数上点的坐标特征掌握反比例函数上点的坐标特征是解题的关键解析:3【分析】把点(,7)M a 代入反比例函数解析式,求解即可.【详解】解:∵点(,7)M a 在反比例函数21y x=的图象上, ∴217a=,解得3a =, 故答案为:3.本题考查反比例函数上点的坐标特征,掌握反比例函数上点的坐标特征是解题的关键. 19.【分析】将不等式变形为根据AB 两点的横坐标和图象直观得出一次函数值大于或等于反比例函数值时自变量的取值范围即为不等式的解集【详解】解:由则实际上就是一次函数的值大于或等于反比例函数值时自变量x 的取值 解析:0x <,14x ≤≤【分析】 将不等式变形为4kx b x+≥,根据A 、B 两点的横坐标和图象,直观得出一次函数值大于或等于反比例函数值时自变量的取值范围,即为不等式的解集.【详解】 解:由40kx b x+-≥,则4kx b x +≥ 实际上就是一次函数的值大于或等于反比例函数值时自变量x 的取值范围,根据图象可得,其解集有两部分,即:0x <,14x ≤≤.故答案为:0x <,14x ≤≤.【点睛】本题考查反比例函数、一次函数的图象和性质,利用数形结合思想,通过图象直接得出一次函数的值大于或等于反比例函数值时自变量x 的取值范围是解题关键.20.-【分析】将点P 分别代入两函数解析式得到:b =a ﹣3b =﹣进而得到a ﹣b =3ab =﹣2将其代入求值即可【详解】∵点P (ab )为直线y =x ﹣3与双曲线y =﹣的交点∴b =a ﹣3b =﹣∴a ﹣b =3ab =﹣解析:-32【分析】 将点P 分别代入两函数解析式得到:b =a ﹣3,b =﹣2a ,进而得到a ﹣b =3,ab =﹣2.将其代入求值即可.【详解】∵点P (a ,b )为直线y =x ﹣3与双曲线y =﹣2x的交点, ∴b =a ﹣3,b =﹣2a, ∴a ﹣b =3,ab =﹣2. ∴1b ﹣1a =a b ab -=32-=﹣32. 故答案是:﹣32. 【点睛】考查了反比例函数与一次函数的交点,解题关键是是得到a ﹣b =3,ab =﹣2.三、解答题21.(1)见解析;(2)见解析【分析】(1)根据相似三角形的判定,只需作出∠Bˊ=∠B 即可得到A B C ''';(2)先根据题意写出已知、求证,再根据相似三角形的性质和角平分线定义可证得ACD A C D '''∠=∠,进而可证得ACD A C D '''∽△△,则有CD AC C D A C =''''=k . 【详解】解:(1)如图所示,A B C '''即为所求.(2)已知:如图,ABC A B C '''∽△△,相似比为k ,CD 、C D ''分别平分ACB ∠,A C B '''∠,求证:CD AC k C D A C ==''''. 证明:∵ABC A B C '''∆∆∽, ∴A A '∠=∠,ACB A C B '''∠=∠,AC k A C ='' ∵CD 、C D ''分别平分ACB ∠,A C B '''∠,∴12ACD ACB ∠=∠,12A B C C D A '∠∠'='''', ∴ACD A C D '''∠=∠,∵A A '∠=∠,∴ACD A C D '''∽△△,∴CD AC k C D A C ==''''. 【点睛】 本题考查了基本尺规作图-作与已知角相等的角、相似三角形的判定与性质,解答的关键是熟练掌握相似三角形的判定与性质,注意文字叙述性命题的证明格式.22.(1)①②③(2)证明见解析.(3)证明见解析.【分析】(1)根据等腰直角三角形的性质和完美三角形判定即可求证①;根据含30°的直角三角形的性质、角平分线的性质、完美三角形判定即可求证②;根据等边三角形的性质和完美三角形判定即可求证③;(2)由40A ∠=︒,60B ∠=︒.可得∠ACB =80°,继而判定△ABC 不是等腰三角形,△ACD 是等腰三角形,再由△BCD ∽△BAC 即可证明结论;(3)作CAD B ∠=∠,易知△CAD ∽△CBA ,继而根据相似三角形的性质可得CD 、AD 的长,继而判定△ABD 是等腰三角形,继而求证△ABC 是完美三角形.【详解】解:(1)①等腰直角三角形底边的中线将原三角形,分成两个等腰直角三角形,CD ∴为等腰直角ACB △的完美分割线,等腰直角ACB △是完美三角形,故①正确;②在Rt ACB △中,90ACB ∠=︒,30B ∠=︒,60CAB ∠=︒,当AD 平分CAB ∠时,30CAD DAB B ∠=∠=∠=︒,ACD BCA ∴∽,ADB △是等腰三角形,AD ∴是直角ACB △的完美分割线,∴含30°角的直角三角形是完美三角形,故②正确;③一条线段不可能将等边三角形分成一个等边三角形和一个等腰三角形,故等边三角形不可能是完美三角形,故③正确,∴真命题有①②③.(2)40A ∠=︒,60B ∠=︒,80ACB ∴∠=︒∴△ABC 不是等腰三角形,∵CD 平分∠ACB ,1402ACD BCD ACB ∴∠=∠=∠=︒, 40ACD A ∴∠=∠=︒, ∴△ACD 为等腰三角形,40DCB A ∠=∠=︒,CBD ABC ∠=∠,∴△BCD ∽△BAC ,CD ∴是△ABC 的完美分割线. (3)作CAD B ∠=∠,CAD B ∠=∠,C C ∠=∠,CAD CBA ∴∽△△, CA CD AD CB CA AB∴==, 4CA =,6CB =,5AB =4645CD AD ==,83CD ∴=,103AD =, 810633BD BC CD =-=-=, BD AD ∴=,ABD ∴是等腰三角形,AD ∴是ABC 的完美分割线,ABC ∴是完美三角形.【点睛】本题考查新定义的理解,各类三角形的判断及性质,相似三角形的判定及其性质的应用,解题的关键是熟练运用所学知识点.23.(1)()01,;(2)34k = 【分析】(1)根据一次函数解析式确定出D 坐标即可;(2)正方形OBAC 中,OB=AB ,OB=AB=a ,则点A (a ,a ),代入反比例解析式求出a 的值,确定出A 坐标,代入一次函数解析式求出k 的值即可.【详解】解:(1)由于点D 是一次函数y=kx+1的图象与y 轴的交点,当x=0时,y=kx+1=1,所以点D 的坐标为(0,1);故答案为:(0,1);(2)正方形OBAC中,OB=AB,设OB=AB=a,则点A(a,a),代入反比例函数解析式得a=16a,∴a2=16,∴x=4或x=-4(不合题意,含去),∴A的坐标为A(4,4),代入一次函数y=kx+1中,得4=4k+1,解得k=34.【点睛】此题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式,正方形的性质,坐标与图形性质,熟练掌握待定系数法是解本题的关键.24.(1)反比例函数关系式:4y=x;一次函数关系式:y=2x+2;(2)2;(3)x<-2或0<x<1.【分析】(1)由B点在反比例函数y=mx图象上,可求出m,再由A,B点在一次函数图象上,由待定系数法求出函数解析式;(2)由(1)可得A,C两点的坐标,从而求出△AOC的面积;(3)由图象观察函数y=mx的图象在一次函数y=kx+b图象的上方,即可求出对应的x的范围.【详解】(1)∵B(1,4)在反比例函数y=mx的图象上,∴m=4,又∵A(n,−2)在反比例函数y=mx的图象上,∴n=−2,又∵A(−2,−2),B(1,4)是一次函数y=kx+b图象上的点,∴可得224k bk b-+=-⎧⎨+=⎩,解得k=2,b=2,∴反比例函数关系式为4yx=;一次函数关系式:y=2x+2;(2)如图,过点A作AE⊥CE,由(1)可得A(−2,−2),C(0,2),∴AE=2,CO=2, ∴1122222AOC S CO AE =⨯=⨯⨯=. (3)由图象知:当0<x<1和x<−2时函数 y=m x 的图象在一次函数y=kx+b 图象的上方, ∴不等式kx+b<m x的解集为:0<x<1或x<−2. 【点睛】 本题考查一次函数与反比例函数的综合运用,灵活运用一次函数和反比例函数的图象、性质及解析式是解题关键.25.(1)13y x =-,22y x =-;(2)32;(3)1x <或2x > 【分析】(1)将点A (3,0)代入y 1 = yy − (2y + 1)即可求一次函数解析式,将k 代入21k y x +=-即可求反比例函数解析式;(2)如图所示作出辅助线,通过一次函数和反比例函数的解析式求出C 、D 的坐标,再由COD COE FOD CHD S S S S S =---矩形OEFH 计算即可;(3)结合图象以及C 、D 的坐标即可得出.【详解】解:(1)将点A (3,0)代入y 1 = yy − (2y + 1)得:3(21)0k k -+=,解得k=1,∴13y x =-,22y x=- (2)如图,连接OC ,OD ,作CE ⊥y 轴于点E ,作DF ⊥x 轴于点F ,CE,DF 交于点H , ∴212COE FOD S S ===,四边形OEFH 为矩形,由23xx-=-,解得:121,2x x==,∴(1,2),(2,1)C D--,∴CE=1,OE=2,OF=2,DF=1,CH=DH=1,∴COD COE FOD CHDS S S S S=---矩形OEFH=1322111122⨯-⨯⨯--=∴△OCD 的面积为32;(3)由(2)可知(1,2),(2,1)C D--,通过图象可知:若y1> y2,则1x<或2x>.【点睛】本题考查了反比例函数与一次函数综合问题,以及反比例函数与几何问题,解题的关键是熟练掌握反比例函数的图象和性质.26.(1)见解析;(2)见解析.【分析】(1)根据菱形的对角线平分一组对角可得∠CDB=∠ADB,然后利用“边角边”证明△APD 和△CPD全等,然后根据全等三角形对应角相等证明即可(2)利用两组角对应相等则两三角形相似,证明△APE与△FPA相似;根据相似三角形的对应边成比例及全等三角形的对应边相等即可得到结论.【详解】(1)∵四边形ABCD为菱形,∴DA=DC,∠CDB=∠ADB,在△ADP和△CDP中,AD CDBDC CBDDP DP=⎧⎪∠=∠⎨⎪=⎩,∴△ADP≌△CDP(SAS),∴PA=PC;(2)∵△ADP≌△CDP,∴∠PAD=∠PCD,∵四边形ABCD为菱形,∴DC∥AB,∴∠PCD=∠PFA,∴∠PAE=∠PFA,而∠APE=∠FPA,∴△PAE∽△PFA,∴PA:PF=PE:PA,∴PA2=PE•PF,∵PA=PC,∴PC2=PE•PF.【点睛】本题考查了相似三角形的判定,全等三角形的判定,菱形的性质等知识点,本题中依据三角形的全等或相似得出线段的相等或比例关系是解题的关键.。
【人教版】初三数学下期中第一次模拟试题含答案

一、选择题1.如图,在平行四边形ABCD 中,:2:1AE BE =,F 是AD 的中点,射线EF 与AC 交于点G ,与CD 的延长线交于点P ,则AGGC的值为( ).A .5:8B .3:8C .3:5D .2:52.如图,矩形ABCD 中,AD m =,AB n =,要使BC 边上至少存在一点P ,使ABP △、APD △、CDP 两两相似,则m 、n 间的关系式一定满足( )A .12m n ≥B .m n ≥C .32m ≥D .2m n ≥3.若点C 为线段AB 的黄金分割点,且AC BC >,则下列各式中不正确的是( ). A .::AB AC AC BC = B .35BC AB -=C .51AC AB +=D .0.618AC AB ≈4.如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚AD 和BC 交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使3OA OD =,3OB OC =),然后张开两脚,使A 、B 两个尖端分别在线段I 的两个端点上.若12AB cm =,则CD 的长是( )A .3cmB .4cmC .6cmD .8cm5.有下列四种说法:其中说法正确的有( )①两个菱形相似;②两个矩形相似;③两个平行四边形相似;④两个正方形相似. A .4个B .3个C .2个D .1个6.△ABC 与△DBC 如图放置,已知,∠ABC =∠BDC =90°,∠A =60°,BD =CD =22,将△ABC 沿BC 方向平移至△A'B'C'位置,使得A'C 边恰好经过点D ,则平移的距离是( )A .1B .22﹣2C .23﹣2D .26﹣47.如图,正方形ABCD 的顶点A 的坐标为()1,0-,点D 在反比例函数my x=的图象上,B 点在反比例函数3y x=的图像上,AB 的中点E 在y 轴上,则m 的值为( )A .-2B .-3C .-6D .-88.如图,在平面直角坐标系中,菱形OBCD 的边OB 在x 轴上,反比例函数()0ky x x=>的图象经过菱形对角线的交点,A 且与边BC 交于点F ,点C 的坐标为()8,4,则OBF ∆的面积为( )A .104 B .83C .103D .1149.下列函数是y 关于x 的反比例函数的是( )A .y =11x + B .y =21x C .y =﹣12xD .y =﹣2x 10.已知11(,)x y ,22(,)x y , 33(,)x y 是反比例函数2y x=-的图象上的三个点,且120x x <<,30x >,则123,,y y y 的大小关系是( )A .213y y y <<B .312y y y <<C .123y y y <<D .321y y y <<11.如图,矩形OABC 的顶点A 、C 分别在x 轴、y 轴上,顶点B 在第一象限,AB=1.将线段OA 绕点O 按逆时针方向旋转600得到线段OP ,连接AP ,反比例函数y=kx过P 、B 两点,则k 的值为( )A .23B .233C .43D .43312.已知点11(,)x y ,22(,)x y 均在双曲线1y x=-上,下列说法中错误的是( ) A .若12x x =,则12y y = B .若12x x =-,则12y y =- C .若120x x <<,则12y y <D .若120x x <<,则12y y >二、填空题13.如图,一次函数y =﹣34x +6的图象与x 轴交于点B ,与y 轴交于点A ,过线段AB 的中点P (4,3)作一条直线与△AOB 交于点Q ,使得所截新三角形与△AOB 相似,则点Q 坐标是_____.14.如图,已知菱形ABCD 的边长为4,点E 、F 分别是AB 、AD 上的点,若BE =AF =1,∠BAD =120°,GFEG=_____.15.已知b c c a a bk a b c+++===,0a ≠,0b ≠,0c ≠;则k =________. 16.己知034x zy ==≠,则345x y z x y z -+=++________. 17.如果反比例函数2y x=的图象经过点11(,)A x y ,22(,)B x y ,33(,)C x y 且1230x x x <<<,请比较1y 、2y 、3y 的大小为__________.18.反比例函数2(0)m y x x+=<的图象如图所示,则m 的取值范围为__________.19.已知反比例函数3y x=-,当1x >时,y 的取值范围是____ 20.已知点(,)P a b 为直线2y x =-与双曲线1y x=-的交点,则11b a -的值等于__________.三、解答题21.在如图所示的12个小正方形组成的网格中,ABC 的三个顶点都在小正方形的顶点上.仅用无刻度的直尺按要求完成下列作图.(1)在图1网格中找格点D ,作直线BD ,使直线BD 与AC 的交点P 是AC 的中点. (2)在图2网格中找格点E ,作直线BE 交AC 于点Q ,使得CQ CB =.22.作图题:如图所示,图中的小方格都是边长为1的正方形,△ABC 与△A 'B 'C '是以点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O ;(2)△A 'B 'C '与△ABC 的位似比是 ;(3)以位似中心O 为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A 'B 'C '关于点O 中心对称的△A "B "C ",并直接写出△A "B "C "各顶点的坐标. 23.如图,已知O 的半径长为1,AB 、AC 是O 的两条弦,且=AB AC ,BO 的延长线交AC 于点D ,联结OA 、OC .(1)求证:OAD ABD ∽△△.(2)当OCD 是直角三角形时,求B 、C 两点的距离.(3)记AOB 、AOD △、COD △的面积分别为1S 、2S 、3S ,如果2S 是1S 和3S 的比例中项,求OD 的长.24.如图,在矩形OABC 中,OA=3,OC=2,F 是AB 上的一个动点(F 不与A ,B 重合),过点F 的反比例函数ky x=(k >0)的图象与BC 边交于点E . (1)写出B 的坐标;(2)当F 为AB 的中点时,求反比例函数的解析式; (3)求当k 为何值时,△EFA 的面积最大,最大面积是多少?25.如图,在平面直角坐标系xOy中,直线y=2x+2与函数y=kx(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).(1)求k,m的值;(2)直接写出关于x的不等式2x+2>kx的解集;(3)若Q在x轴上,△ABQ的面积是6,求Q点坐标.26.如图,已知一次函数133 2y x=-与反比例函数2kyx=的图象相交于点A(4,n)和M(m,﹣6),与x轴相交于点B.(1)求m,n的值;(2)观察图象,当y2≥﹣6且y2≠0时,自变量x的取值范围为,若y1﹣y2<0时自变量x 的取值范围为;(3)若P点为x轴上一点, Q点为平面直角坐标系中的一点,以点A、B、P、Q为顶点的四边形为菱形,求Q点的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.D 解析:D 【分析】证明AFE △≌△()DFP AAS ,推出=AE DP ,由:2:1AE BE =,设BE k =,2AE k =,推出3AB CD k ==,5PC k =,由//AE BC ,可得AG AEGC CP=的值. 【详解】∵四边形ABCD 是平行四边形, ∴//AB PC ,AB CD =, ∴AEF P ∠=∠,∵AFE DFP ∠=∠,AF DF =, ∴AFE △≌△()DFP AAS , ∴=AE DP ,∵:2:1AE BE =,设BE k =,2AE k =, ∴3AB CD k ==,5PC k =, ∵//AE BC ,∴2255AG AE k GC CP k ===, 故选:D . 【点睛】本题考查了平行四边形的性质,全等三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是学会利用已知条件证明三角形全等、利用参数解决问题,属于中考常考题型.2.D解析:D 【分析】由于△MNP 和△DCP 相似,可得出关于MN 、PC 、NP 、CD 的比例关系式.设PC=x ,那么NP=m-x ,根据比例关系式可得出关于x 的一元二次方程,由于NC 边上至少有一点符合条件的P 点,因此方程的△≥0,由此可求出m 、n 的大小关系. 【详解】解:若设PC=x ,则NP=m-x , ∵△ABP ∽△PCD ,AB BP PC CD ∴=即,n m xx n-= 即x 2-mx+n 2=0方程有解的条件是: m 2-4n 2≥0,∴(m+2n )(m-2n )≥0,则m-2n≥0, ∴m≥2n .故选:D . 【点睛】本题是存在性问题,可以转化为方程问题,利用判断方程的解的问题来解决.3.C解析:C 【分析】根据黄金分割点的定义逐项排除即可. 【详解】解:∵点C 为线段AB 的黄金分割点,且AC BC >, ∴2AC BC AB =⋅,∴::AB AC AC BC =,则选项A 正确; ∵点C 为线段AB 的黄金分割点,且AC BC >,∴0.618AC AB =≈,则选项C 错误;选项D 正确;BC AB AC AB AB AB =-=-=,则选项B 正确. 故选:C . 【点睛】本题考查了成比例线段,熟练掌握黄金分割的定义成为解答本题关键.4.B解析:B 【分析】首先根据题意利用两组对边的比相等且夹角相等的三角形是相似三角形判定相似,然后利用相似三角形的性质求解. 【详解】∵OA =3OD ,OB =3OC , ∴3OA OBOD OC==, ∵AD 与BC 相交于点O , ∴∠AOB =∠DOC , ∴△AOB ∽△DOC , ∴3AB OADC OD==, ∵12AB cm =∴CD=12433AB ==cm, 故选B. 【点睛】本题考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定方法,学会利用相似三角形的性质解决问题,属于中考常考题型.5.D解析:D 【分析】直接利用相似图形的判定方法分别判断得出答案. 【详解】解:①两个菱形不一定相似,因为对应角不一定相等; ②两个矩形不一定相似,因为对应边不一定成比例; ③两个平行四边形不一定相似,因为形状不一定相同; ④两个正方形相似,正确. 故选:D . 【点睛】本题考查了相似多边形的判定,正确掌握判定方法是解题的关键.6.C解析:C 【分析】过点D 作DJ ⊥BC 于J ,根据勾股定理求出BC ,利用等腰直角三角形的性质求出DJ 、BJ 、JC ,利用平行线分线段成比例定理求出JC′即可解决问题. 【详解】解:过点D 作DJ ⊥BC 于J .∵DB =DC =2,∠BDC =90°, ∴BC ()()222222+4,DJ =BJ =JC =2,∵∠ABC =90°,∠A =60°, ∴∠ACB =30°, ∴AC=2AB , ∵AB 2+42=(2AB)2, ∴A′B′=AB 43, ∵DJ//A′B′,∴DJ A B ''=C J C B''', ∴434C J ',∴C′J=23,∴JB′=4﹣23,∴BB′=2﹣(4﹣23)=23﹣2.故选:C.【点睛】本题考查了平移的性质,直角三角形的性质,等腰三角形的性质,勾股定理,以及平行线分线段成比例定理.7.D解析:D【分析】作DM⊥x轴于M,BN⊥x轴于N,如图,先根据题意求得AN=2,然后证明△ADM≌△BAN得到DM=AN=2,AM=BN=3,则D(-4,2),根据待定系数法即可求得m 的值.【详解】解:作DM⊥x轴于M,BN⊥x轴于N,如图,∵点A的坐标为(-1,0),∴OA=1,∵AE=BE,BN∥y轴,∴OA=ON=1,∴AN=2,B的横坐标为1,把x=1代入3yx,得y=3,∴B(1,3),∴BN=3,∵四边形ABCD为正方形,∴AD=AB,∠DAB=90°,∴∠MAD+∠BAN=90°,而∠MAD+∠ADM=90°,∴∠BAN=∠ADM,在△ADM和△BAN中90AND ANB ADM BAN AD AB ∠∠︒⎧⎪∠∠⎨⎪⎩==== ∴△ADM ≌△BAN (AAS ),∴DM=AN=2,AM=BN=3,∴134OM OA AM =+=+= ,∴D 42-(,), ∵点D 在反比例函数m y x=,的图象上, ∴428m =-⨯=- ,故选:D .【点睛】本题考查了反比例函数图象上点的坐标特征,正方形的性质,三角形全等的判定和性质等知识,求得D 的坐标是解题的关键. 8.C解析:C【分析】根据菱形的性质可求出点A 坐标,将点A 的坐标代入到反比例函数解析式可求得k 值,即可确定函数的解析式,过点A 作AM ⊥x 轴于点M ,过点C 作CN ⊥x 轴于点N ,如图,首先在Rt △CNB 中,根据勾股定理建立方程求出OB 的长,进而可求得点B 的坐标,然后利用待定系数法可求得直线BC 的解析式,再联立直线和双曲线的解析式求出交点F 坐标,然后根据三角形的面积公式求解可.【详解】解:∵四边形OBCD 是菱形,∴OA =AC ,∵C (8,4),∴A (4,2),把点A (4,2)代入反比例函数()0k y x x =>,得到k =8, ∴反比例函数的解析式为y =8x; 过点A 作AM ⊥x 轴于点M ,过点C 作CN ⊥x 轴于点N ,如图,设OB =x ,则BC =x ,BN =8﹣x ,在Rt △CNB 中,x 2﹣(8﹣x )2=42,解得:x =5,∴点B 的坐标为(5,0),设直线BC 的函数表达式为y =ax +b ,把点B (5,0),C (8,4)代入得:∴5084a b a b +=⎧⎨+=⎩,解得:43203a b ⎧=⎪⎪⎨⎪=-⎪⎩,∴直线BC 的解析式为42033y x =-,解方程组420338y x y x⎧=-⎪⎪⎨⎪=⎪⎩,得:18x y =-⎧⎨=-⎩或643x y =⎧⎪⎨=⎪⎩, ∴点F 的坐标为F (6,43), 作FH ⊥x 轴于H ,连接OF ,∴S △OBF =12OB •FH =14105233⨯⨯=, 故选:C .【点睛】本题考查了菱形的性质、利用待定系数法求函数的解析式、两个函数的交点问题以及勾股定理等知识,属于常考题型,熟练掌握上述知识是解题的关键.9.C解析:C【分析】直接利用反比例函数的定义分别判断得出答案.【详解】解:A 、y =11x +是y 与x+1成反比例,故此选项不合题意; B 、y =21x,是y 与x 2成反比例,不符合反比例函数的定义,故此选项不合题意; C 、y =﹣12x ,符合反比例函数的定义,故此选项符合题意; D 、y =﹣2x 是正比例函数,故此选项不合题意. 故选:C .【点睛】本题考查了反比例函数的定义,正确把握定义是解题的关键.10.B解析:B【分析】先根据反比例函数2y x=-的系数20-<判断出函数图象在二、四象限,在每个象限内,y 随x 的增大而增大,再根据120x x <<,30x >,判断出1y 、2y 、3y 的大小.【详解】 解:反比例函数2y x=-中,20k =-<, ∴此函数的图象在二、四象限,在每一象限内y 随x 的增大而增大,∵120x x <<,30x >30y ,210y y >>,∴312y y y <<,故选:B .【点睛】本题考查了二次函数图象上点的坐标特征.用到的知识点为:k 0<时,反比例函数k y x=图象的分支在二、四象限,在第四象限的函数值总小于在第二象限的函数值;在同一象限内,y 随x 的增大而增大. 11.D解析:D【分析】本题先设A 点坐标(x ,0),则点B (x ,1),由等边三角性质可知P (12x)代入函数表达式即可求出结果.【详解】由题意设A 点坐标(x ,0),则点B (x ,1),将点B 代入函数式得k=x ,又由题意将线段OA 绕点O 按逆时针方向旋转60°得到线段OP ,∴OP=OA ,则△AOP 为等边三角形,∴由等边三角形性质设点P (12k),把点P=12kk , ∴k=2 k 12⨯212k ⨯, ∵k 0≠,∴,即选D . 【点睛】此题考查反比例函数,等边三角形性质,解题关键是找出点P 坐标,即运用等边三角形性质解题.12.D解析:D【分析】先把点A (x 1,y 1)、B (x 2,y 2)代入双曲线1y x =-,用y 1、y 2表示出x 1,x 2,据此进行判断.【详解】∵点(x 1,y 1),(x 2,y 2)均在双曲线1y x =-上, ∴111y x =-,221y x =-. A 、当x 1=x 2时,-11x =-21x ,即y 1=y 2,故本选项说法正确; B 、当x 1=-x 2时,-11x =21x ,即y 1=-y 2,故本选项说法正确; C 、因为双曲线1y x=-位于第二、四象限,且在每一象限内,y 随x 的增大而增大,所以当0<x 1<x 2时,y 1<y 2,故本选项说法正确; D 、因为双曲线1y x=-位于第二、四象限,且在每一象限内,y 随x 的增大而增大,所以当x 1<x 2<0时,y 1>y 2,故本选项说法错误;故选:D .【点睛】 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.二、填空题13.(03)或(0)或(40)【分析】首先确定AB 两点坐标分两种情形:①当PQ ∥OB 时②当PQ′⊥AB 时分别求解即可【详解】∵一次函数y =﹣x+6的图象与x 轴交于点B 与y 轴交于点A ∴A (06)B (80)解析:(0,3)或(74,0)或(4,0) 【分析】首先确定A ,B 两点坐标,分两种情形:①当PQ ∥OB 时,②当PQ′⊥AB 时,分别求解即可.【详解】∵一次函数y =﹣34x+6的图象与x 轴交于点B ,与y 轴交于点A ,∴A(0,6),B(8,0),∴OA=6,OB=8,AB=22OA OB+=2268+=10,如图有两种情形:①当PQ∥OB时,满足条件.∵AP=PB,∴AQ=OQ,∴Q(0,3).②当PQ′⊥AB时,满足条件.连接AQ′.∵PA=PB,PQ′⊥AB,∴Q′A=Q′B,设Q′A=Q′B=m,在Rt△AOQ′中,则有m2=62+(8﹣m)2,解得m=254,∴OQ′=8﹣254=74,∴Q′(74,0).③当PQ∥y轴时,同法可得P(4,0).综上所述,满足条件的点Q的坐标为(0,3)或(74,0)或(4,0).【点睛】本题考查一次函数的应用,相似三角形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.14.【分析】过点E作EM∥BC交AC下点M点根据菱形的性质可得△AEM是等边三角形则EM=AE=3由AF∥EM对应线段成比例即可得结论【详解】解:过点E作EM∥BC交AC于点M∵四边形ABCD是菱形∴A解析:1 3【分析】过点E作EM∥BC交AC下点M点,根据菱形的性质可得△AEM是等边三角形,则EM=AE=3,由AF∥EM,对应线段成比例即可得结论.【详解】解:过点E作EM∥BC交AC于点M,∵四边形ABCD 是菱形,∴AB =4,AD ∥BC ,∴∠AEM =∠B =60°,∠AME =∠ACB =60°,∴△AEM 是等边三角形,则EM =AE =3,∵AF ∥EM , ∴13GF AF GE EM ==, 故答案为:13. 【点睛】 本题考查了平行线分线段成比例,菱形的性质,熟练运用菱形的性质、等边三角形性质是解题的关键.15.或【分析】根据题意可分情况考虑:当时根据比例的等比性质即可求得答案;当时即代入消元即可得解【详解】解:∵∴或①当时∵∴∴∴∴②当时有∴∴综上所述或故答案是:或【点睛】本题考查了比例的等比性质分式的化 解析:2或1-【分析】根据题意可分情况考虑:当0a b c ++≠时根据比例的等比性质即可求得答案;当0a b c ++=时,即a b c +=-,代入消元即可得解.【详解】解:∵0a ≠,0b ≠,0c ≠∴0a b c ++≠或0a b c ++=①当0a b c ++≠时, ∵b c c a a b k a b c+++=== ∴b c ak +=,c a bk +=,a b ck +=∴()()()b c c a a b ak bk ck +++++=++∴()()2a b c k a b c ++=++∴()22a b c k a b c++==++ ②当0a b c ++=时,有a b c +=- ∴1a b c k c c +-===-∴综上所述,2k =或1k =-.故答案是:2或1-【点睛】本题考查了比例的等比性质、分式的化简求值等,注意需要分类讨论.16.【分析】可设则x=3ky=kz=4k 代入所求式子中求解即可【详解】解:设则x=3ky=kz=4k 则===故答案为:【点睛】本题考查比例的性质分式的求值熟练掌握比例的性质巧妙设参数是解答的关键 解析:43【分析】 可设=34x z y k ==,则x=3k ,y=k ,z=4k ,代入所求式子中求解即可. 【详解】 解:设=34x z y k ==,则x=3k ,y=k ,z=4k , 则345x y z x y z -+++ =3344354k k k k k k-+⨯++ =1612k k=43, 故答案为:43. 【点睛】本题考查比例的性质、分式的求值,熟练掌握比例的性质,巧妙设参数是解答的关键. 17.【分析】根据题意和反比例函数的性质可以得到y1y2y3的大小关系从而可以解答本题【详解】解:∵反比例函数∴在每个象限内y 随x 的增大而减小当x <0时y <0当x >0时y >0∵反比例函数的图象经过点A (x解析:213y y y <<【分析】根据题意和反比例函数的性质,可以得到y 1,y 2,y 3的大小关系,从而可以解答本题.【详解】解:∵反比例函数2y x= ∴在每个象限内,y 随x 的增大而减小,当x <0时,y <0,当x >0时,y >0,∵反比例函数2y x=的图象经过点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),且1230x x x <<<,∴213y y y <<,故答案为:213y y y <<.【点睛】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.18.【分析】直接利用反比函数图象的分布得出m+2<0进而得出答案;【详解】解:∵反比例函数图象分布在第二象限∴m+2<0解得:m <-2;故答案为:m <-2【点睛】本题考查了反比例函数图象上的性质正确掌握解析:2m <-【分析】直接利用反比函数图象的分布得出m+2<0,进而得出答案;【详解】解:∵反比例函数图象分布在第二象限,∴m+2<0,解得:m <-2;故答案为:m <-2.【点睛】本题考查了反比例函数图象上的性质,正确掌握反比例函数的增减性是解题的关键. 19.-3<y<0【分析】根据反比例函数的增减性求解【详解】在反比例函数∴函数图象在第二四象限且在每个象限内y 随x 的增大而增大当x >1时函数图象在第四象限且当x=1时y=-3∴当x >1时-3<y<0;故答解析:-3<y<0【分析】根据反比例函数的增减性求解.【详解】 在反比例函数3y x=-,30k =-<, ∴函数图象在第二、四象限,且在每个象限内y 随x 的增大而增大,当x >1时,函数图象在第四象限且当x=1时,y=-3,∴当x >1时-3<y<0;故答案为:-3<y<0.【点睛】考查反比例函数的增减性,掌握反比例函数的增减性是解题的关键,即在y=k x(k≠0)中,当k >0时,在每个象限内y 随x 的增大而减小,当k <0时,在每个象限内y 随x 的增大而增大.20.-2【分析】将点P 分别代入两函数解析式得到:b=a-2b=-进而得到a-b=2ab=-1将其代入求值即可【详解】∵点P (ab )为直线y=x-2与双曲线的交点∴b=a-2b=-∴a-b=2ab=-1∴解析:-2【分析】将点P 分别代入两函数解析式得到:b=a-2,b=-1a ,进而得到a-b=2,ab=-1.将其代入求值即可.【详解】∵点P (a ,b )为直线y=x-2与双曲线1y x=-的交点, ∴b=a-2,b=-1a , ∴a-b=2,ab=-1. ∴11b a-=2-1a b ab -==-2. 故答案是:-2.【点睛】 此题考查反比例函数与一次函数的交点,解题关键是得到a-b=2,ab=-1.三、解答题21.(1)画图见解析;(2)画图见解析.【分析】(1)根据题意画图即可;(2)由平行线性质得到MAQ NCQ ∠=∠,继而可证明AMQ CNQ ∽△△,再根据相似三角形的性质解得35CQ AC =,最后根据勾股定理解题即可. 【详解】(1)如图1所示,取格点D ,连接AD ,CD ,则四边形ABCD 为矩形,连接BD 交AC 于点P , 由于矩形对垂线互相平分,则点P 为AC 中点, 故图1中直线BD ,格点D 即为所求.(2)如图2所示,找格点M ,N ,使得2AM =,3CN =,连接MN 与AC 交于点Q , 连接BQ 并延长交格点于点E ,则格点E 即为所求.∵//AM CN ,MAQ NCQ ∴∠=∠,又AQM CQN ∠=∠(对顶角相等)AMQ CNQ ∴∽△△,23AM AQ CN CQ ∴==, 即35CQ AC =, 由勾股定理得:222AC AB BC =+,又4AB =,3BC =,22435AC ∴=+=335355CQ AC CB ∴==⨯==,故CQ CB=,∴格点E即为所求.【点睛】本题考查网格作图,涉及相似三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.22.(1)画图见解析;(2)1:2;(3)画图见解析;A"(6,0),B"(3,-2),C"(4,-4)【分析】(1)连接CC′并延长,连接BB′并延长,两延长线交于点O;(2)由OB=2OB′,即可得出△A′B′C′与△ABC的位似比为1:2;(3),连接B′O并延长,使OB″=OB′,延长A′O并延长,使OA″=OA′,C′O并延长,使OC″=OC′,连接A″B″,A″C″,B″C″,则△A″B″C″为所求,从网格中即可得出△A″B″C″各顶点的坐标.【详解】解:(1)图中点O为所求;(2)△A′B′C′与△ABC的位似比等于1:2;故答案为:1:2;(3)△A″B″C″为所求;A″(6,0);B″(3,-2);C″(4,-4).【点睛】此题考查了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.23.(1)见解析;(2)3BC=2;(3)512OD=.【分析】(1)由△AOB≌△AOC,推出∠C=∠B,由OA=OC,推出∠OAC=∠C=∠B,由∠ADO=∠ADB,即可证明△OAD∽△ABD;(2)如图2中,当△OCD是直角三角形时,需要分类讨论解决问题;(3)如图3中,作OH⊥AC于H,设OD=x.想办法用x表示AD、AB、CD,再证明AD 2=AC•CD ,列出方程即可解决问题;【详解】解:(1)在AOB 和AOC △中,OA OA AB AC OB OC =⎧⎪=⎨⎪=⎩,∴AOB AOC △≌△,C B ∴∠=∠,又∵OA OC =,OAC C B ∴∠=∠=∠,而ADO ADB ∠=∠,OAD ABD ∴∽△△.(2)如图:①当90ODC ∠=︒时,BD AC ⊥,OA OC =,AD DC ∴=,BA BC AC ∴==,ABC ∴是等边三角形,在Rt OAD 中,1OA =,30OAD ∠=︒,1122OD OA ∴==, 2232AD OA OD ∴=-=, 23BC AC AD ∴===.②90COD ∠=︒,90BOC ∠=°,22112BC =+=.③OCD ∠显然90≠︒,不需要讨论.综上所述,3BC =2.(3)如图:作OH AC ⊥于H ,设OD x =,DAO DBA ∽△△,AD OD OA DB AD AB∴==. 11AD x x AD AB∴==+. (1)AD x x ∴=+,(1)x x AB +=. 又2S 是1S 和3S 的比例中项,2213S S S ∴=⋅, 而212S AD OH =⋅,112OAC S S AC OH ==⋅△,312S CD OH =⋅⨯, 2111222AD OH AC OH CD OH ⎛⎫⎛⎫∴⋅=⋅⋅⋅ ⎪ ⎪⎝⎭⎝⎭, 即2AD AC CD =⋅,又AC AB =,(1)(1)x x CD AC AD x x +=-=+, 代入上式可得:210x x +-=, 求得512x =,或512-, 经检验,51x -=512OD ∴=. 【点睛】 本题属于圆的综合题、全等三角形的判定和性质、相似三角形的判定和性质、比例中项等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题.24.(1)B 的坐标为(3,2);(2)函数的解析式为3y x =;(3)当3k =时,S 有最大值,最大值为34.【分析】(1)根据矩形的性质即可写出B 的坐标;(2)当F 为AB 的中点时,点F 的坐标为(3,1),代入求得函数解析式即可;(3)根据图中的点的坐标表示出三角形的面积,得到关于k 的二次函数,利用二次函数求出最值即可.【详解】(1)∵在矩形OABC 中,OA=3,OC=2,∴B (3,2);(2)∵F 为AB 的中点,∴F (3,1),∵点F 在反比例函数k y x=的图象上, ∴k=3,∴该函数的解析式为3y x =; (3)由题意知E ,F 两点坐标分别为E(2k ,2),F(3,3k ), ∴EFA 12S =AF•BE 13232k k ⎛⎫=⨯- ⎪⎝⎭ 211212k k =- ()2169912k k =--+- 213(3)124k =--+, 当3k =时,S 有最大值,34S =最大值. 【点睛】 本题属于反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定反比例解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.25.(1)m =4,k =4;(2)﹣2<x <0或x >1;(3)(﹣3,0)或(1,0).【分析】(1)将点A 坐标代入直线解析式可求m 的值,再将点A 坐标代入反比例函数解析式可求k 的值;(2)解析式联立成方程组,解方程组求得B 的坐标,然后根据函数的图象即可求得不等式2x +2>k x的解集. (3)由直线解析式求得直线与x 轴的交点坐标,然后设出Q 的坐标,根据三角形面积公式得到12•|a+1|•(2+4)=6,解得a的值,即可求得点Q的坐标.【详解】解:(1)∵点A(1,m)在直线y=2x+2上,∴m=2×1+2=4,∴点A的坐标为(1,4),代入函数y=kx(k≠0)中,得4=1k,∴k=4.(2)解224y xyx=+⎧⎪⎨=⎪⎩得14xy=⎧⎨=⎩或22xy=-⎧⎨=-⎩,∴B(﹣2,﹣2),∴关于x的不等式2x+2>kx的解集是﹣2<x<0或x>1.(3)在y=2x+2中令y=0,解得x=﹣1,则直线与x轴的交点是(﹣1,0).设点Q的坐标是(a,0).∵△ABQ的面积是6,∴12•|a+1|•(2+4)=6,则|a+1|=2,解得a=1或﹣3.则点Q的坐标是(﹣3,0)或(1,0).【点睛】本题考查了一次函数与反比例函数的交点问题、坐标与图形性质、待定系数法求解析式、三角形的面积公式、解方程(组),解答的关键是熟练运用相关知识,利用数形结合方法求不等式的解集,以及利用Q点坐标表示△ABQ的面积.26.(1)m =-2,n=3;(2)x≤﹣2或x>0;0<x<4或x<﹣2;(3)点Q的坐标为(4,3)或(43)或(34,3)或(4,﹣3)【分析】(1)把点A、B的坐标代入直线的解析式求解即可;(2)满足条件y2≥﹣6且y2≠0时的x的取值范围即为反比例函数2kyx=在直线y=﹣6与x 轴之间的图象与第一象限内的图象对应的x的范围,满足y1﹣y2<0时自变量x的取值范围即为反比例函数比直线高的图象部分对应的x的取值范围,据此解答即可;(3)先求出点B的坐标,再分三种情况:①AB、BP为菱形的边,如图1;②AB为菱形的对角线,如图2;③AB为边、BP为对角线,如图3;分别利用菱形的性质和勾股定理求解即可.【详解】解:(1)把点A (4,n )和M (m , ﹣6)代入一次函数1332y x =-, 得:34332n =⨯-=,3632m -=-, ∴2m =-,3n =; (2)对2k y x=,当y 2≥﹣6且y 2≠0时,自变量x 的取值范围为x ≤﹣2或x >0; 若y 1﹣y 2<0即y 1<y 2时自变量x 的取值范围为0<x <4或x <﹣2; (3)对1332y x =-,可得点B 的坐标为(2,0), ①若AB 、BP 为菱形的边,则()()22423013AB =-+-=,若点P 在点B 右侧,如图1,则BP=AQ=AB=13,所以点Q 的坐标为(413+,3);若点P 在点B 左侧,同理可得点Q 的坐标为(413-,3);②若AB 为菱形的对角线,如图2,设点Q 坐标为(n ,3),则BQ=AQ=4-n , 过点Q 作QF ⊥x 轴于点F ,则BF=2-n ,QF=3,在Rt △BQF 中,根据勾股定理,得()()222324n n +-=-,解得34n =, ∴点Q 的坐标为(34,3);③若AB 为边、BP 为对角线,如图3,由菱形的性质知:点Q 、A 关于x 轴对称, ∴点Q 的坐标为(4,﹣3);综上,点Q 的坐标为(413,3)或(413+,3)或(34,3)或(4,﹣3). 【点睛】 本题主要考查了一次函数与反比例函数的图象与性质、菱形的性质以及勾股定理等知识,属于常考题型,熟练掌握相关知识、灵活应用数形结合的思想是解题的关键.。
【好题】初三数学下期中第一次模拟试卷含答案

【好题】初三数学下期中第一次模拟试卷含答案一、选择题1.如图所示,在△ABC中, cos B=22,sin C=35,BC=7,则△ABC的面积是()A.212B.12C.14D.212.如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=3x(x>0)、y=kx(x<0)的图象于B、C两点,若△ABC的面积为2,则k值为()A.﹣1B.1C.12-D.123.如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=kx(x>0)的图象经过顶点B,则反比例函数的表达式为()A.y=12xB.y=24xC.y=32xD.y=40x4.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是()A.AB2=AC•BC B.BC2=AC•BC C.AC 51-BC D.BC51-AC5.如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段AC 的长为()A .43B .42C .6D .4 6.如图,BC 是半圆O 的直径,D ,E 是»BC上两点,连接BD ,CE 并延长交于点A ,连接OD ,OE ,如果70A ∠︒=,那么DOE ∠的度数为( )A .35︒B .38︒C .40︒D .42︒7.若反比例函数2y x=-的图象上有两个不同的点关于y 轴的对称点都在一次函数y =-x +m 的图象上,则m 的取值范围是( ) A .22m >B .-22m <C .22-22m m >或<D .-2222m <<8.在△ABC 中,若|sinA-32|+(1-tanB)2=0,则∠C 的度数是( ) A .45° B .60°C .75°D .105° 9.如图所示,在△ABC 中,AB =6,AC =4,P 是AC 的中点,过 P 点的直线交AB 于点Q ,若以 A 、P 、Q 为顶点的三角形和以A 、B 、C 为顶点的三角形相似,则AQ 的长为 ( )A .3B .3或43C .3或34D .4310.在平面直角坐标系中,点E (﹣4,2),点F (﹣1,﹣1),以点O 为位似中心,按比例1:2把△EFO 缩小,则点E 的对应点E 的坐标为( )A .(2,﹣1)或(﹣2,1)B .(8,﹣4)或(﹣8,4)C .(2,﹣1) D .(8,﹣4) 11.如图,在△ABC 中,M 是AC 的中点,P ,Q 为BC 边上的点,且BP=PQ=CQ ,BM 与AP ,AQ 分别交于D ,E 点,则BD ∶DE ∶EM 等于A .3∶2∶1B .4∶2∶1C .5∶3∶2D .5∶2∶112.如图,在△ABC 中,AC =8,∠ABC =60°,∠C =45°,AD ⊥BC ,垂足为D ,∠ABC 的平分线交AD 于点E ,则AE 的长为A .42B .22C .823D .32二、填空题13.如图,在一段坡度为1∶2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为____米.14.在△ABC 中,∠ABC=90°,已知AB=3,BC=4,点Q 是线段AC 上的一个动点,过点Q 作AC 的垂线交直线AB 于点P ,当△PQB 为等腰三角形时,线段AP 的长为_____.15.若反比例函数y =﹣的图象经过点A(m ,3),则m 的值是_____.16.如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC ,则线段 AC 的长为________.17.如图,等腰直角三角形ABC 中, AB=4 cm.点是BC 边上的动点,以AD 为直角边作等腰直角三角形ADE.在点D 从点B 移动至点C 的过程中,点E 移动的路线长为________cm.18.如图,Rt ABC V 中,90ACB ∠=︒,直线EF BD P ,交AB 于点E ,交AC 于点G ,交AD 于点F ,若13AEG EBCG S S V 四边形,=则CF AD= .19.在 ABC V 中, 6AB = , 5AC = ,点D 在边AB 上,且 2AD = ,点E 在边AC 上,当 AE = ________时,以A 、D 、E 为顶点的三角形与 ABC V 相似.20.已知一个反比例函数的图象经过点(2,3)--,则这个反比例函数的表达式为________.三、解答题21.如图1,为放置在水平桌面l 上的台灯,底座的高AB 为5cm .长度均为20cm 的连杆BC ,CD 与AB 始终在同一水平面上.(1)旋转连杆BC ,CD ,使BCD ∠成平角,150ABC ∠=︒,如图2,求连杆端点D 离桌面l 的高度DE .(2)将(1)中的连杆CD 绕点C 逆时针旋转,使165BCD ∠=︒,如图3,问此时连杆端点D 离桌面l 的高度是增加了还是减少?增加或减少了多少?(精确到0.1cm ,参考数2 1.41≈3 1.73≈)22.计算:(1)203)330π︒-+(2)21445|5|2-︒⎛⎫+- ⎪⎝⎭(3)已知α为锐角,()2sin 152α︒-=,计算2cos 3tan 12αα-+ 23.如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于点E ,交BA 的延长线于点F .(1)求证:2PC PE PF =g ;(2)若菱形边长为8,2PE =,6EF =,求FB 的长.24.如图,已知O 是原点,,B C 两点的坐标分别为()3,1-,()2,1.(1)以点O 为位似中心,在y 轴的左侧将OBC V 扩大为原来的两倍(即新图与原图的相似比为2),画出图形,并写出点,B C 的对应点的坐标;(2)如果OBC V 内部一点M 的坐标为(),x y ,写出点M 的对应点M '的坐标.25.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC 的顶点均在格点上,点B 的坐标为(1,0).(1)在图1中画出△ABC 关于x 轴对称的△A 1B 1C 1,直接写出点C 的对应点C 1的坐标. (2)在图2中,以点O 为位似中心,将△ABC 放大,使放大后的△A 2B 2C 2与△ABC 的对应边的比为2:1(画出一种即可).直接写出点C 的对应点C 2的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A 【解析】【分析】【详解】试题分析:过点A作AD⊥BC,∵△ABC中,cosB=22,sinC=35,AC=5,∴cosB=22=BDAB,∴∠B=45°,∵sinC=35=ADAC=5AD,∴AD=3,∴CD=4,∴BD=3,则△ABC的面积是:12×AD×BC=12×3×(3+4)=212.故选A.考点:1.解直角三角形;2.压轴题.2.A解析:A【解析】【分析】连接OC、OB,如图,由于BC∥x轴,根据三角形面积公式得到S△ACB=S△OCB,再利用反比例函数系数k的几何意义得到12×|3|+12•|k|=2,然后解关于k的绝对值方程可得到满足条件的k的值.【详解】连接OC、OB,如图,∵BC∥x轴,∴S△ACB=S△OCB,而S△OCB=12×|3|+12•|k|,∴12×|3|+12•|k|=2,而k<0,∴k=﹣1,故选A.【点睛】本题考查了反比例函数系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是12|k|,且保持不变.3.C解析:C【解析】【分析】过A作AM⊥x轴于M,过B作BN⊥x轴于N,根据菱形性质得出OA=BC=AB=OC,AB ∥OC,OA∥BC,求出∠AOM=∠BCN,OM=3,AM=4,OC=OA=AB=BC=5,证△AOM ≌△BCN,求出BN=AM=4,CN=OM=3,ON=8,求出B点的坐标,把B的坐标代入y=kx求出k即可.【详解】过A作AM⊥x轴于M,过B作BN⊥x轴于N,则∠AMO=∠BNC=90°,∵四边形AOCB是菱形,∴OA=BC=AB=OC,AB∥OC,OA∥BC,∴∠AOM=∠BCN,∵A(3,4),∴OM=3,AM=4,由勾股定理得:OA=5,即OC=OA=AB=BC=5,在△AOM和△BCN中AMO BNC AOM BCN OA BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AOM ≌△BCN(AAS),∴BN=AM=4,CN=OM=3,∴ON=5+3=8,即B 点的坐标是(8,4),把B 的坐标代入y=kx 得:k=32,即y=32x, 故答案选C.【点睛】 本题考查了菱形的性质,解题的关键是熟练的掌握菱形的性质.4.D解析:D【解析】【分析】根据黄金分割的定义得出BC AC AC AB ==,从而判断各选项. 【详解】∵点C 是线段AB 的黄金分割点且AC >BC ,∴BC AC AC AB ==,即AC 2=BC•AB,故A 、B 错误;∴AC=12AB ,故C 错误;AC ,故D 正确; 故选D .【点睛】本题考查了黄金分割,掌握黄金分割的定义和性质是解题的关键.5.B解析:B【解析】【分析】由已知条件可得ABC DAC ~V V ,可得出AC BC DC AC=,可求出AC 的长. 【详解】解:由题意得:∠B =∠DAC ,∠ACB =∠ACD,所以ABC DAC ~V V ,根据“相似三角形对应边成比例”,得AC BCDC AC=,又AD 是中线,BC=8,得DC=4,代入可得AC=42,故选B.【点睛】本题主要考查相似三角形的判定与性质.灵活运用相似的性质可得出解答.6.C解析:C【解析】【分析】连接CD,由圆周角定理得出∠BDC=90°,求出∠ACD=90°-∠A=20°,再由圆周角定理得出∠DOE=2∠ACD=40°即可,【详解】连接CD,如图所示:∵BC是半圆O的直径,∴∠BDC=90°,∴∠ADC=90°,∴∠ACD=90°-∠A=20°,∴∠DOE=2∠ACD=40°,故选C.【点睛】本题考查了圆周角定理、直角三角形的性质;熟练掌握圆周角定理是解题的关键.7.C解析:C【解析】【分析】根据题意可知反比例函数2yx=-的图象上的点关于y轴的对称的点在函数2yx=上,由此可知反比例函数2yx=的图象与一次函数y=-x+m的图象有两个不同的交点,继而可得关于x的一元二次方程,再根据根的判别式即可求得答案.【详解】∵反比例函数2yx=-上有两个不同的点关于y轴对称的点在一次函数y=-x+m图象上,∴反比例函数2y x=与一次函数y =-x +m 有两个不同的交点, 联立得2y x y x m ⎧=⎪⎨⎪=-+⎩,消去y 得:2x m x =-+, 整理得:220x mx -+=,∵有两个不同的交点∴220x mx -+=有两个不相等的实数根,∴△=m 2-8>0,∴m >m <故选C.【点睛】本题考查了反比例函数图象上点的坐标特征,关于x 轴、y 轴对称的点的坐标,熟练掌握相关内容、正确理解题意是解题的关键.8.C解析:C【解析】【分析】先根据非负数的性质求出sinA 及tanB 的值,再根据特殊角的三角函数值求出∠A 及∠B 的值,由三角形内角和定理即可得出结论.【详解】∵|sin A−2|+(1−tan B )2=0, ∴tanB=1, ∴∠A=60°,∠B=45°,∴∠C=180°-∠A-∠B=180°-60°-45°=75°.故选C .【点睛】(1)非负数的性质:几个非负数的和等0,这几个非负数都为0;(2)三角形内角和等于180°.9.B解析:B【解析】AP AQ AB AC =,264AQ =,AQ=43,AP AQ AC AB =,246AQ =,AQ =3.故选B.点睛:相似常见图形(1)称为“平行线型”的相似三角形(如图,有“A 型”与“X 型”图)(2)如图:其中∠1=∠2,则△ADE ∽△ABC 称为“斜交型”的相似三角形,有“反A 共角型”、“反A 共角共边型”、 “蝶型”,如下图:10.A解析:A【解析】【分析】利用位似比为1:2,可求得点E 的对应点E′的坐标为(2,-1)或(-2,1),注意分两种情况计算.【详解】∵E (-4,2),位似比为1:2,∴点E 的对应点E′的坐标为(2,-1)或(-2,1).故选A .【点睛】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比.注意位似的两种位置关系.11.C解析:C【解析】【分析】过A 作AF ∥BC 交BM 延长线于F ,设BC=3a ,则BP=PQ=QC=a ;根据平行线间的线段对应成比例的性质分别求出BD 、BE 、BM 的长度,再来求BD ,DE ,EM 三条线段的长度,即可求得答案.【详解】过A 作AF ∥BC 交BM 延长线于F ,设3BC a =,则BP PQ QC a ===;∵AM CM =,AF ∥BC , ∴1AF AM BC CM==, ∴3AF BC a ==,∵AF ∥BP , ∴133BD BP a DF AF a ===, ∴34DF BF BD ==, ∵AF ∥BQ , ∴2233BE BQ a EF AF a ===, ∴23EF BE =,即25BF BE =, ∵AF ∥BC , ∴313BM BC a MF AF a===,∴BM MF =,即2BF BM =, ∴235420BF BF BF DE BE BD =-=-=,22510BF BF BF EM BM BE =-=-=, ∴3::::?53242010BF BF BF BD DE EM ==::. 故选:C .【点睛】 本题考查了平行线分线段成比例定理以及比例的性质,正确作出辅助线是关键.12.C解析:C【解析】【分析】由已知可知△ADC 是等腰直角三角形,根据斜边AC=8可得,在Rt △ABD 中,由∠B=60°,可得BD=tan 60AD ︒=3,再由BE 平分∠ABC ,可得∠EBD=30°,从而可求得DE 长,再根据AE=AD-DE 即可【详解】∵AD ⊥BC ,∴△ADC 是直角三角形,∵∠C=45°,∴∠DAC=45°,∴AD=DC ,∵AC=8,∴,在Rt △ABD 中,∠B=60°,∴BD=tan 60AD ︒=3, ∵BE 平分∠ABC ,∴∠EBD=30°,∴DE=BD•tan30°=33=3,∴AE=AD-DE== 故选C.【点睛】本题考查了解直角三角形的应用,熟练掌握直角三角形中边角之间的关系是解题的关键.二、填空题13.3米【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比把相应的数值代入即可【详解】解:∵坡度为1:2且株距为6米∴株距:坡面距离=2:∴坡面距离=株距×(米)【点睛】本题是将实际问题转化为解析:【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比,把相应的数值代入即可.【详解】解:∵坡度为1:2=6米,∴株距:坡面距离=2∴坡面距离=株距= 【点睛】本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.要注意坡度是坡角的正切函数. 14.或6【解析】【分析】当△PQB 为等腰三角形时有两种情况需要分类讨论:①当点P 在线段AB 上时如图1所示由三角形相似(△AQP∽△ABC)关系计算AP 的长;②当点P 在线段AB 的延长线上时如图2所示利用角 解析:53或6. 【解析】【分析】 当△PQB 为等腰三角形时,有两种情况,需要分类讨论:①当点P 在线段AB 上时,如图1所示.由三角形相似(△AQP ∽△ABC )关系计算AP 的长;②当点P 在线段AB 的延长线上时,如图2所示.利用角之间的关系,证明点B 为线段AP 的中点,从而可以求出AP .【详解】解:在Rt △ABC 中,AB =3,BC =4,由勾股定理得:AC =5.∵∠QPB 为钝角,∴当△PQB 为等腰三角形时,当点P 在线段AB 上时,如题图1所示:∵∠QPB 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =PQ ,由(1)可知,△AQP ∽△ABC , ∴,PA PQ AC BC = 即3,54PB PB -= 解得:43PB =, ∴45333AP AB PB =-=-=; 当点P 在线段AB 的延长线上时,如题图2所示:∵∠QBP 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =BQ .∵BP =BQ ,∴∠BQP =∠P ,∵90,90BQP AQB A P o o ,∠+∠=∠+∠= ∴∠AQB =∠A ,∴BQ =AB ,∴AB =BP ,点B 为线段AP 中点,∴AP =2AB =2×3=6. 综上所述,当△PQB 为等腰三角形时,AP 的长为53或6. 故答案为53或6.【点睛】本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.15.﹣2【解析】∵反比例函数y=-6x 的图象过点A (m3)∴3=-6m 解得=-2 解析:﹣2 【解析】 ∵反比例函数的图象过点A (m ,3), ∴,解得.16.【解析】已知BC=8AD 是中线可得CD=4在△CBA 和△CAD 中由∠B=∠DAC ∠C=∠C 可判定△CBA ∽△CAD 根据相似三角形的性质可得即可得AC2=CD•BC=4×8=32解得AC=4解析:2【解析】已知BC=8, AD 是中线,可得CD=4, 在△CBA 和△CAD 中, 由∠B=∠DAC ,∠C=∠C , 可判定△CBA ∽△CAD ,根据相似三角形的性质可得 AC CD BC AC= , 即可得AC 2=CD•BC=4×8=32,解得AC=42.17.【解析】试题解析:连接CE 如图:∵△ABC 和△ADE 为等腰直角三角形∴AC =ABAE=AD ∠BAC=45°∠DAE=45°即∠1+∠2=45°∠2+∠3=45°∴∠1=∠3∵∴△ACE ∽△ABD ∴∠解析:42【解析】试题解析:连接CE ,如图:∵△ABC 和△ADE 为等腰直角三角形,∴2AB ,2AD ,∠BAC=45°,∠DAE=45°,即∠1+∠2=45°,∠2+∠3=45°, ∴∠1=∠3, ∵2AC AE AB AD== ∴△ACE ∽△ABD , ∴∠ACE=∠ABC=90°,∴点D 从点B 移动至点C 的过程中,总有CE ⊥AC ,即点E 运动的轨迹为过点C 与AC 垂直的线段,22,当点D 运动到点C 时,2,∴点E 移动的路线长为2cm .18.【解析】【分析】先证△AEG ∽△ABC △AGF ∽△ACD 再利用相似三角形的对应边成比例求解【详解】解:∵EF ∥BD ∴∠AEG=∠ABC ∠AGE=∠ACB ∴△AEG ∽△ABC 且S △AEG=S 四边形EB解析:12【解析】【分析】先证△AEG ∽△ABC ,△AGF ∽△ACD 再利用相似三角形的对应边成比例求解.【详解】解:∵EF ∥BD∴∠AEG=∠ABC ,∠AGE=∠ACB ,∴△AEG ∽△ABC ,且S △AEG=13S 四边形EBCG∴S△AEG:S△ABC=1:4,∴AG:AC=1:2,又EF∥BD∴∠AGF=∠ACD,∠AFG=∠ADC,∴△AGF∽△ACD,且相似比为1:2,∴S△AFG:S△ACD=1:4,∴S△AFG1=3S四边形FDCGS△AFG1=4S△ADC∵AF:AD=GF:CD=AG:AC=1:2∵∠ACD=90°∴AF=CF=DF∴CF:AD=1:2.19.【解析】当时∵∠A=∠A∴△AED∽△ABC此时AE=;当时∵∠A=∠A∴△ADE∽△ABC此时AE=;故答案是:解析:512 35或【解析】当AE ABAD AC=时,∵∠A=∠A,∴△AED∽△ABC,此时AE=·621255 AB ADAC⨯==;当AD ABAE AC=时,∵∠A=∠A,∴△ADE∽△ABC,此时AE=·52563 AC ADAB⨯==;故答案是:125 53或.20.【解析】【分析】把已知点的坐标代入可求出k值即得到反比例函数的解析式【详解】设这个反比例函数的表达式为了则所以这个反比例函数的表达式为故答案是:【点睛】考查的是用待定系数法求反比例函数的解析式解题关解析:6 yx =【解析】【分析】把已知点的坐标代入可求出k 值,即得到反比例函数的解析式.【详解】 设这个反比例函数的表达式为了(0)k y k x=≠,则 (2)(3)6k =-⨯-=, 所以这个反比例函数的表达式为6y x =. 故答案是:6y x=. 【点睛】考查的是用待定系数法求反比例函数的解析式,解题关键是设关系式、再将已知点坐标代入,从而求解即可. 三、解答题21.(1)39.6DE cm ≈;(2)下降了,约3.2cm .【解析】【分析】(1)如图2中,作BO ⊥DE 于O .解直角三角形求出OD 即可解决问题.(2)作DF ⊥l 于F ,CP ⊥DF 于P ,BG ⊥DF 于G ,CH ⊥BG 于H .则四边形PCHG 是矩形,求出DF ,再求出DF-DE 即可解决问题.【详解】(1)过点B 作BO DE ⊥,垂足为O ,如图2,则四边形ABOE 是矩形,1509060OBD =-=o o o ∠,∴sin 6040sin 60203DO BO =⋅=⨯=o o∴203539.6DE DO OE DO AB cm =+=+=≈.(2)下降了.如图3,过点D 作DF l ⊥于点F ,过点C 作CP DF ⊥于点P ,过点B 作BG DF ⊥于点G ,过点C 作CH BG ⊥于点H ,则四边形PCHG 为矩形,∵60CBH ︒∠=,∴30BCH ︒∠=,又∵165BCD ︒∠=,∴45DCP ︒∠=, ∴sin 60103CH BC ︒==*sin 45102DP CD ==,∴DF DP PG GF DP CH AB =++=++1021035=. ∴下降高度:20351021035DE DF -=-103102=3.2cm ≈.【点睛】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.22.(1)72.(2)7;(3)﹣3 【解析】【分析】(1)先计算乘方和三角函数值,再计算加减法即可;(2先计算乘方和三角函数值、绝对值,再计算加减法即可;(3)先由特殊角的三角函数值计算出α,再代入求值即可.【详解】解:(1)原式=3﹣332 =2+32 =72. (2)原式=4﹣2×1+5 =4﹣2+5=7.(3)∵α为锐角,()2sin 152α︒-=,∴α﹣15°=45°.∴α=60°.∴2cos 3tan αα-+=﹣2×12﹣=﹣﹣=﹣.【点睛】本题考查了含特殊角的三角函数值的四则运算,掌握特殊角的三角函数值是解题的关键.23.(1)见解析;(2) 16=FB .【解析】【分析】(1)可由相似三角形AEP FAP ∆∆∽对应边成比例进行求解,也可由平行线分线段成比例定理进行求解,两者均可;(2)由题中已知线段的长度,结合(1)中的结论,再由平行线分线段成比例,即可得出结论.【详解】(1)证明:Q 四边形ABCD 是菱形, DC DA ∴=,ADP CDP ∠=∠,//DC AB ,又DP Q 是公共边,DAP DCP ∴∆≅∆,PA PC ∴=,DAP DCP ∠=∠,由//DC FA 得,F DCP ∠=∠,F DAP ∴∠=∠,又EPA APF ∠=∠QAEP FAP ∴∆∆∽,∴PA:PF=PE :PA ,2PA PE PF ∴=g2PC PE PF ∴=g .(2)2PE =Q ,6EF =,8PF ∴=,2PC PE PF =Q g ,216PC ∴=,4PC ∴=//DC FB Q ∴FB PF DC PC=, 又8DC =,∴884FB = 16FB ∴=.【点睛】本题主要考查了全等三角形的判定及性质以及菱形的性质和相似三角形的判定及性质问题,能够熟练掌握.24.(1)如图,OB C ''△即为所求,见解析;点B 的对应点的坐标为()6,2-,点C 的对应点的坐标为()4,2--;(2)点(),M x y 的对应点M '的坐标为()2,2x y --.【解析】【分析】(1)延长BO ,CO 到B′、C′,使OB′、OC′的长度是OB 、OC 的2倍.顺次连接三点即可;(2)从这两个相似三角形坐标位置关系来看,对应点的坐标正好是原坐标乘以-2的坐标,所以M 的坐标为(x ,y ),写出M 的对应点M′的坐标为(-2x ,-2y ).【详解】(1)如图,OB C ''△即为所求,点B 的对应点的坐标为()6,2-,点C 的对应点的坐标为()4,2--.(2)从这两个相似三角形坐标位置关系来看,对应点的坐标正好是原坐标乘以-2的坐标,所以M 的坐标为(x ,y ),写出M 的对应点M′的坐标为(-2x ,-2y ).【点睛】考查了直角坐标系和相似三角形的有关知识,注意做这类题时,性质是关键,看图也是关键.很多信息是需要从图上看出来的.25.(1)作图见解析;(2)作图见解析;点C 2(-6,-2)或(6,2).【解析】【分析】(1)分别作出点A 、B 、C 关于x 轴对称的点,然后顺次连接即可;(2)延长OB 到B 2,使OB 2=2OB ,按同样的方法得到点A 2、C 2,然后顺次连接,写出C 2的坐标即可.(也可以反向延长).【详解】(1)如图所示,C 1(3,-1);(2)如图所示,C2的坐标是(-6,-2)或(6,2).。
【人教版】初三数学下期中第一次模拟试卷及答案

一、选择题1.如图,在正方形ABCD中,点E是边BC的中点,连接AE,EF AE⊥交CD边于点F,已知4AB=,则CF的长为()A.1 B.5 5C.3 D.22.如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=2CE,AB=12,则AD的长为()A.4 B.6 C.5 D.83.如图,在四边形ABCD中,对角线BD平分∠ABC,∠DBC=30°,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F,若CD=2,则BF的长为()A.23B.23C.63D.434.下列相似图形不是位似图形的是()A.B.C .D .5.已知P ,Q 是线段AB 的两个黄金分割点,且AB=10,则PQ 长为( ) A .5(5-1)B .5(5+1)C .10(5-2) -D .5(3-5)6.如图,已知点E 是正方形ABCD 的边AB 边上的黄金分割点,且,AE EB >若1S 表示AE 为边长的正方形面积,2S 表示以BC 为长,BE 为宽的矩形面积,3S 表示正方形ABCD 除去1S 和2S 剩余的面积,则32:S S 的值为( )A .512- B .512+ C .352D .35+ 7.已知点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)是函数y =﹣2x图象上的点,且x 1<0<x 2<x 3,则y 1,y 2,y 3的大小关系是( ) A .y 1>y 2>y 3 B .y 1<y 2<y 3C .y 1>y 3>y 2D .无法确定8.如图,函数ky x=与2(0)y kx k =-+≠在同一平面直角坐标系中的图像大致( ) A . B .C .D .9.一次函数y =kx ﹣k 与反比例函数y =kx在同一直角坐标系内的图象大致是( )A .B .C .D .10.函数ky x=与y kx k =-(0k ≠)在同一平面直角坐标系中的大致图象是( ) A . B . C . D .11.已知点()1,3M -在双曲线ky x=上,则下列各点一定在该双曲线上的是( ) A .()3,1-B .()1,3--C .()1,3D .()3,112.给出下列函数:①y =﹣3x +2:②y =3x ;③y =﹣5x:④y =3x ,上述函数中符合条件“当x >1时,函数值y 随自变量x 增大而增大”的是( ) A .①③ B .③④ C .②④ D .②③二、填空题13.如图,D E 、分别是ABC 的边AB BC 、上的点,且//,DE AC AE CD 、相交于点O ,若:1:25DOE COA S S =△△,则BECE的值是________.14.在梯形ABCD 中,//AD BC ,两条对角线AC 、BD 相交于点O ,:1:9AODCOBSS=,那么BOC DOC S S =△△:__________.15.如图,EF 是ABC 纸片的中位线,将AEF 沿EF 所在的直线折叠,点A 落在BC 边上的点D 处,已知AEF 的面积为7,则图中阴影部分的面积为______.16.如图,在平面直角坐标系xOy 中,点D 在x 轴上,(2,0)D ,点D 的上方为点(2,1)C ,以原点O 为位似中心,相似比为1:3,在第一象限内把线段CD 扩大后得到线段AB ,则点A 的坐标为___________.17.如果反比例函数2y x=的图象经过点11(,)A x y ,22(,)B x y ,33(,)C x y 且1230x x x <<<,请比较1y 、2y 、3y 的大小为__________.18.在平面直角坐标系中,若直线2y x =-+与反比例函数ky x=的图象有2个公共点,则k 的取值范围是_________. 19.函数25(1)ny n x -=+是反比例函数,且图象位于第二、四象限内,则n =____.20.如图,在平面直角坐标系中,函数y kx =与2y x=-的图像交于A 、B 两点,过点A 作y 轴的垂线,交函数1y x=的图像于点C ,连接BC ,则ABC ∆的面积为 _________.三、解答题21.如图,已知O 的半径长为1,AB 、AC 是O 的两条弦,且=AB AC ,BO 的延长线交AC 于点D ,联结OA 、OC .(1)求证:OAD ABD ∽△△.(2)当OCD 是直角三角形时,求B 、C 两点的距离.(3)记AOB 、AOD △、COD △的面积分别为1S 、2S 、3S ,如果2S 是1S 和3S 的比例中项,求OD 的长.22.如图,ABC 内接于⊙O ,AB AC =,过点C 作AB 的垂线CD ,垂足为点E ,交O 于点F ,连接AD ,并使AD BC ∥.(1)求证:AD 为O 的切线;(2)若5AC =,2BE =,求AD 的长.23.如图,△ABC 是⊙O 的内接三角形,AD 是△ABC 的高,AE 是⊙O 的直径.求证:△ABE ~△ADC .24.已知反比例函数ky x=的图象与正比例函数2y x =的图象交于点()2,m ,求这个反比例函数的表达式,并在同一平面直角坐标系内,画出这两个函数的图象.25.已知:如图,一次函数的图象与反比例函数ky x=的图象交于A 、B 两点,且点B 的坐标为.(1)求反比例函数ky x=的表达式; (2)点在反比例函数ky x=的图象上,求△AOC 的面积; (3)在(2)的条件下,在坐标轴上找出一点P ,使△APC 为等腰三角形,请直接写出所有符合条件的点P 的坐标.26.码头工人往一艘轮船上装载货物,装完货物所需时间y (分)与装载速度x (吨 /分)之间的函数关系如图所示. (1) 这批货物的质量是多少?(2) 直接写出y 与x 之间的函数表达式;(3) 现有一批货物,要在2h 内装载完成,码头工人每分钟至少要装载多少吨货物?【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】根据相似三角形的性质与判定即可求出答案. 【详解】解:由题意可知:2BE CE ==, ∵90AEF B C ∠=∠=∠=︒,∴BAE AEB AEB CEF ∠+∠=∠+∠, ∴BAE CEF ∠=∠, ∴AEB EFC ∆∆∽, ∴AB BECE CF=, ∴422CF =, ∴1CF =, 故选:A . 【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于基础题型.2.D解析:D 【分析】先根据平行线分线段成比例定理得出比例式,代入后得出AD=23AB ,代入求出即可. 【详解】 解:∵DE ∥BC ,∴AD AEAB AC =, ∵AE=2CE ,∴2223AE CE AC EC EC ==+ 又AB=12,∴AD=23AB=8, 故选:D . 【点睛】本题考查了平行线分线段成比例定理,能根据定理得出正确的比例式是解此题的关键.3.C解析:C 【分析】连接DE ,根据直角三角形的性质求出BC ,根据勾股定理求出BD ,再求出AB ,根据DE ∥AB ,得到BDE AB DFF =,把已知数据代入计算,得到答案. 【详解】 解:连接DE ,∵∠BDC =90°,∠CBD =30°,CD =2, ∴BC =2CD =4,由勾股定理得,BD 22BC CD -2242-23 ∵E 是BC 的中点, ∴DE =12BC =BE =2, ∴∠BDE =∠CBD =30°, ∵对角线BD 平分∠ABC , ∴∠ABD =∠CBD =∠BDE , ∴DE ∥AB , ∴BDE AB DFF =, 在Rt △ABD 中,∠ABD =30°, ∴AD =12BD 3 ∴AB 22BD AD -3, ∴23DF FB =, 即2332BF BF =, 解得,BF =35故选:C . 【点睛】本题考查的是勾股定理、角平分线的性质、直角三角形30度角的性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题.4.D解析:D 【分析】根据位似变换的概念判断即可. 【详解】解:D 中两个图形,对应边不互相平行,不是位似图形, A 、B 、C 中的图形符合位似变换的定义,是位似图形,故选:D . 【点睛】本题考查的是位似变换,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形.5.C解析:C 【分析】画出图像,根据黄金分割的概念写出对应线段的比值,求出AQ 、PB 的长度,再根据PQ =AQ +PB -AB 即可求出PQ 的长度. 【详解】 解:如图,根据黄金分割点的概念,可知51PB AQ AB AB -==∴AQ =PB ,AB =10,∴AQ =PB =51105552⨯=,∴PQ =AQ +PB -AB =555555101052010(52)+-==.故选:C . 【点睛】本题主要考查黄金分割的概念,熟记黄金分割的概念并根据黄金分割的比值列式是解题关键.6.A解析:A 【分析】设正方形ABCD 的边长为a ,关键黄金分割点的性质得到51AE AB 和51BEAE -=,用a 表示出1S 、2S 和3S 的面积,再求比例. 【详解】解:设正方形ABCD 的边长为a , ∵点E 是AB 上的黄金分割点, ∴51AEAB ,则512AE a =,∴512BE AE =,则25135BE a --==⎝⎭,∵2221S AE ⎫===⎪⎪⎝⎭,2232S BE BC a =⋅=,∴)2222333222S a a a a -=--=,∴)2232:2S S a a ==. 故选:A . 【点睛】本题考查黄金分割点,解题的关键是掌握黄金分割点的性质.7.C解析:C 【分析】根据反比例函数图象上点的坐标特征得到y 1=12x -,y 2=22x -,y 3=32x -,然后根据x 1<0<x 2<x 3比较y 1,y 2,y 3的大小. 【详解】点(x 1,y 1),(x 2,y 2),(x 3,y 3)都是2y x=-的图象上的点, ∴y 1=12x -,y 2=22x -,y 3=32x -, 而x 1<0<x 2<x 3, ∴y 1>y 3>y 2. 故选:C . 【点睛】本题考查了反比例函数图象上点的坐标特征:熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.8.B解析:B 【分析】先根据反比例函数的图像,判断k 的符号,然后再判断一次函数的图像. 【详解】A 中,反比例函数经过一、三象限,故k >0,则一次函数应经过一、二、四象限,错误;B 中,反比例函数经过一、三象限,故k >0,则一次函数应经过一、二、四象限,正确;C 中,反比例函数经过二、四象限,故k <0,则一次函数应经过一、二、三象限,错误;D 中,反比例函数经过二、四象限,故k <0,则一次函数应经过一、二、三象限,错误; 故选:B .本题考查一次函数与反比例函数图像的性质,解题关键是通过函数的系数符号,判断函数图象经过的象限.9.C解析:C【分析】分别根据反比例函数及一次函数图象的特点对四个选项进行逐一分析即可.【详解】解:A.∵由反比例函数的图象在一、三象限可知,k>0k-<∴0=-的图象经过一、三、四象限.∴一次函数y kx k故本选项错误;<B.∵由反比例函数的图象在二、四象限可知,k0k->∴0=-的图象经过一、二、四象限.∴一次函数y kx k故本选项错误;<C.∵由反比例函数的图象在二、四象限可知,k0k->∴0=-的图象经过一、二、四象限.∴一次函数y kx k故本选项正确;<D.∵由反比例函数的图象在二、四象限可知,k0k->∴0=-的图象经过一、二、四象限.∴一次函数y kx k故本选项错误.故选:C【点睛】本题考查的是反比例函数、一次函数图象,解答此题的关键是先根据反比例函数所在的象限判断出k的符号,再根据一次函数的性质进行解答.10.C解析:C【分析】分k>0和k<0两种情况确定正确的选项即可.【详解】当k:>0时,反比例函数的图象位于第一、三象限,一次函数的图象交 y轴于负半轴,y 随着x的增大而增大,A选项错误,C选项符合;当k<0时,反比例函数的图象位于第二、四象限,一次函数的图象交y轴于正半轴,y 随着x的增大而增减小,B. D均错误,故选:C.此题考查反比例函数的图象,一次函数的图象,熟记函数的性质是解题的关键. 11.A解析:A【分析】先求出k=-3,再依次判断各点的横纵坐标乘积,等于-3即是在该双曲线上,否则不在.【详解】∵点()1,3M -在双曲线k y x=上, ∴133k =-⨯=-,∵3(1)3⨯-=-,∴点(3,-1)在该双曲线上,∵(1)(3)13313-⨯-=⨯=⨯=,∴点()1,3--、()1,3、()3,1均不在该双曲线上,故选:A.【点睛】此题考查反比例函数解析式,正确计算k 值是解题的关键. 12.B解析:B【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案.【详解】解:①y =﹣3x +2,当x >1时,函数值y 随自变量x 增大而减小,故此选项不符合题意; ②y =3x,当x >1时,函数值y 随自变量x 增大而减小,故此选项不符合题意; ③y =﹣5x,当x >1时,函数值y 随自变量x 增大而增大,故此选项符合题意; ④y =3x ,当x >1时,函数值y 随自变量x 增大而增大,故此选项符合题意;故选:B .【点睛】此题考查一次函数、正比例函数、反比例函数,正确把握相关性质是解题关键. 二、填空题13.【分析】先证明然后根据相似三角形的面积比等于相似比的平方求出的值继而可求的值最后可求的值【详解】解:又故答案是:【点睛】本题考查了相似三角形的判定和性质掌握相似三角形的面积比等于相似比的平方是解题关键 解析:14先证明DOE COA ∽,然后根据相似三角形的面积比等于相似比的平方求出DE AC 的值,继而可求BE BC 的值,最后可求BE EC的值. 【详解】 解://DE AC ,DOE COA ∴∽, 又:1:25DOE COA S S =△△,15DE AC ∴=, //DE AC ,BDE BAC ∴∽△△,15BE DE BC AC ∴==, 14BE EC ∴=. 故答案是:14. 【点睛】本题考查了相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题关键.14.3:1【分析】根据在梯形ABCD 中AD ∥BC 易得△AOD ∽△COB 且S △COB :S △AOD=9:1可求=3:1则S △BOC :S △DOC=3:1【详解】解:根据题意AD ∥BC ∴△AOD ∽△COB ∵S △解析:3:1【分析】根据在梯形ABCD 中,AD ∥BC ,易得△AOD ∽△COB ,且S △COB :S △AOD =9:1,可求BO OD=3:1,则S △BOC :S △DOC =3:1. 【详解】解:根据题意,AD ∥BC ,∴△AOD ∽△COB ,∵S △AOD :S △COB =1:9, ∴BO OD=3:1, 则S △BOC :S △DOC =3:1,故答案为:3:1.【点睛】本题考查了相似三角形的性质与判定,掌握相似三角形面积的比等于相似比的平方是解题的关键.15.14【分析】根据三角形的中位线定理结合相似三角形的性质可以求得△ABC 的面积再根据折叠的性质得到△DEF 的面积从而求解【详解】∵EF 是△ABC 的中位线∴EF ∥BCEF=BC ∴△AEF ∽△ACB ∴∵△解析:14【分析】根据三角形的中位线定理,结合相似三角形的性质可以求得△ABC 的面积,再根据折叠的性质得到△DEF 的面积,从而求解.【详解】∵EF 是△ABC 的中位线,∴EF ∥BC ,EF=12BC , ∴△AEF ∽△ACB , ∴22AEF ACB 1124S EF S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, ∵△AEF 的面积为7,∴△ABC 的面积=28,由折叠的性质得△DEF 的面积为7,∴图中阴影部分的面积为28-7-7=14.故答案为:14.【点睛】本题综合考查了折叠问题,三角形的中位线定理和相似三角形的判定和性质.关键是掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.16.(63)【分析】根据位似变换的性质可知△ODC ∽△OBA 相似比是根据已知数据可以求出点A 的坐标【详解】解:由题意得△ODC ∽△OBA 相似比是∴又∵∴OD=2CD=1∴OB=6AB=3∴点A 的坐标为:解析:(6,3)【分析】根据位似变换的性质可知,△ODC ∽△OBA ,相似比是1:3,根据已知数据可以求出点A 的坐标.【详解】解:由题意得,△ODC ∽△OBA ,相似比是1:3,∴13OD DC OB AB ==, 又∵(2,0)D ,(2,1)C ∴OD=2,CD=1,∴OB=6,AB=3,∴点A 的坐标为:(6,3),故答案为:(6,3).【点睛】本题考查的是位似变换,掌握位似变换与相似的关系是解题的关键,注意位似比与相似比的关系的应用.17.【分析】根据题意和反比例函数的性质可以得到y1y2y3的大小关系从而可以解答本题【详解】解:∵反比例函数∴在每个象限内y 随x 的增大而减小当x <0时y <0当x >0时y >0∵反比例函数的图象经过点A (x解析:213y y y <<【分析】根据题意和反比例函数的性质,可以得到y 1,y 2,y 3的大小关系,从而可以解答本题.【详解】解:∵反比例函数2y x= ∴在每个象限内,y 随x 的增大而减小,当x <0时,y <0,当x >0时,y >0, ∵反比例函数2y x=的图象经过点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),且1230x x x <<<,∴213y y y <<,故答案为:213y y y <<.【点睛】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.18.且【分析】联立两函数解析式消去y 得到关于x 的一元二次方程由两函数在同一直角坐标系中的图象有两个公共点得到根的判别式大于0列出关于k 的不等式求出不等式的解集即可得到k 的范围【详解】联立两解析式得:消去 解析:1k <且0k ≠【分析】联立两函数解析式,消去y 得到关于x 的一元二次方程,由两函数在同一直角坐标系中的图象有两个公共点得到根的判别式大于0,列出关于k 的不等式,求出不等式的解集即可得到k 的范围.【详解】 联立两解析式得:2y x k y x =-+⎧⎪⎨=⎪⎩, 消去y 得:220x x k -+=,∵两个函数在同一直角坐标系中的图象有两个公共点,∴24440b ac k =-=->,即1k <,则当k 满足1k <且0k ≠时,这两个函数在同一直角坐标系中的图象有两个公共点. 故答案为:1k <且0k ≠.【点睛】本题考查了一次函数与反比例函数的交点问题,把两函数图象的交点问题转化成一元二次方程根的问题是解题的关键.19.-2【分析】根据反比例函数的定义与性质解答即可【详解】根据反比函数的解析式y=(k≠0)故可知n+1≠0即n≠-1且n2-5=-1解得n=±2然后根据函数的图像在第二四三象限可知n+1<0解得n<-解析:-2.【分析】根据反比例函数的定义与性质解答即可.【详解】根据反比函数的解析式y=k x(k≠0),故可知n+1≠0,即n≠-1, 且n 2-5=-1,解得n =±2,然后根据函数的图像在第二、四三象限,可知n+1<0,解得n<-1,所以可求得n=-2.故答案为:-2【点睛】本题考查反比例函数的定义与性质,熟记定义与性质是解题的关键. 20.3【分析】连接OC 设AC 交y 轴于E 根据反比例函数k 的几何意义求出△AOC 的面积再利用反比例函数关于原点对称的性质推出OA=OB 即可解决问题【详解】解:如图连接OC 设AC 交y 轴于E ∵AC ⊥y 轴于E ∴S解析:3【分析】连接OC ,设AC 交y 轴于E .根据反比例函数k 的几何意义求出△AOC 的面积,再利用反比例函数关于原点对称的性质,推出OA=OB 即可解决问题.【详解】解:如图,连接OC 设AC 交y 轴于E .∵AC ⊥y 轴于E ,∴S △AOE =12×2=1,S △OEC =12×1=12, ∴S △AOC =32, ∵A ,B 关于原点对称,∴OA=OB ,∴S △ABC =2S △AOC =3,故答案为:3.【点睛】本题考查反比例函数与一次函数的性质,解题的关键是熟练掌握反比例函数系数k 的几何意义.三、解答题21.(1)见解析;(2)3BC =2;(3)512OD =. 【分析】(1)由△AOB ≌△AOC ,推出∠C=∠B ,由OA=OC ,推出∠OAC=∠C=∠B ,由∠ADO=∠ADB ,即可证明△OAD ∽△ABD ;(2)如图2中,当△OCD 是直角三角形时,需要分类讨论解决问题;(3)如图3中,作OH ⊥AC 于H ,设OD=x .想办法用x 表示AD 、AB 、CD ,再证明AD 2=AC•CD ,列出方程即可解决问题;【详解】解:(1)在AOB 和AOC △中, OA OA AB AC OB OC =⎧⎪=⎨⎪=⎩,∴AOB AOC △≌△,C B ∴∠=∠,又∵OA OC =,OAC C B ∴∠=∠=∠,而ADO ADB ∠=∠,OAD ABD ∴∽△△.(2)如图:①当90ODC ∠=︒时,BD AC ⊥,OA OC =,AD DC ∴=,BA BC AC ∴==,ABC ∴是等边三角形,在Rt OAD 中,1OA =,30OAD ∠=︒,1122OD OA ∴==, 2232AD OA OD ∴=-=, 23BC AC AD ∴===.②90COD ∠=︒,90BOC ∠=°,22112BC =+=.③OCD ∠显然90≠︒,不需要讨论.综上所述,3BC =或2.(3)如图:作OH AC ⊥于H ,设OD x =,DAO DBA ∽△△,AD OD OA DB AD AB ∴==. 11AD x x AD AB∴==+.AD ∴=,AB =. 又2S 是1S 和3S 的比例中项,2213S S S ∴=⋅, 而212S AD OH =⋅,112OAC S S AC OH ==⋅△,312S CD OH =⋅⨯, 2111222AD OH AC OH CD OH ⎛⎫⎛⎫∴⋅=⋅⋅⋅ ⎪ ⎪⎝⎭⎝⎭, 即2AD AC CD =⋅,又AC AB =,CD AC AD =-=, 代入上式可得:210x x +-=,求得x =,经检验,x =OD ∴=. 【点睛】 本题属于圆的综合题、全等三角形的判定和性质、相似三角形的判定和性质、比例中项等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题.22.(1)证明见解析;(2)【分析】(1)连接AO 后交DC 于点H ,交BC 于点G ,由垂径定理可知AG ⊥BC ,然后根据互余关系得到∠HAE=∠HCG ,然后利用平行关系得到∠ADE=∠HCG=∠HAE ,等量代换后可得∠HAE +∠EAD=90°;(2)根据AC 和BE 可算出AE ,然后在Rt △AEC 中算出EC ,然后证明△AED ∽△BEC ,然后利用比例关系算出DE ,在Rt △AED 中计算AD 即可.【详解】解:(1)如图,连接AO 交DC 于点H ,交BC 于点G ,则AG ⊥BC∵AG⊥BC,AB⊥DC,∠AHE=∠CHG∴∠HAE=∠HCG∵AB⊥DC∴∠ADE+∠EAD=90°∵AD∥BC∴∠ADE=∠HCG=∠HAE∴∠HAE +∠EAD=90°∴AD为O的切线(2)∵AC=AB,AC=5,BE=2∴AE=3在Rt△AEC由勾股定理可得:22-=EC AC AE=4∵AD∥BC∴△AED∽△BEC∴BE EC=AE DE∴DE=6在Rt△AED由勾股定理可得:22+=DE AEAD=35【点睛】本题主要考查圆的相关定理,掌握切线的证明方法,灵活转化角关系是证明切线的关键,在圆中计算线段长度,找准相似三角形,结合勾股定理,是解题的关键.23.见解析.【分析】根据∠AEB=∠ACB(同弧所对的圆周角相等)和AD是△ABC的高,AE是⊙O的直径,利用一个三角形的两个角与另一个三角形的两个角对应相等,即可证明.【详解】证明:∵AB=AB∴∠AEB=∠ACB(同弧所对的圆周角相等),∵AE为直径,∴∠ABE=90°(直径所对的圆周角是直角),又∵AD⊥BC,即∠ADC=90°,∴∠ABE=∠ADC,∴△ABE ∽△ADC .【点睛】此题主要考查学生对相似三角形的判定和圆周角定理的理解和掌握,解题的关键是利用同弧上的圆周角相等,先求证∠AEB =∠ACB ,然后即可得出结论.24.8y x =,见解析 【分析】 把()2,m 代入2y x =求出m 的值,利用待定系数法即可求解.【详解】解:由题意,反比例函数k y x =的图象与正比例函数2y x =的图象交于点()2,m , 则()2,m 在2y x =上,∴224m =⨯=,又∵()2,m 在k y x =上, ∴28k m ==,∴反比例函数的表达式:8y x=, 函数图象如图: .【点睛】本题考查反比例函数与一次函数的交点,掌握待定系数法求解析式是解题的关键.25.(1);(2)32;(3)(-1,0)、(0,0)、(0,1).【详解】(1)一次函数的图象过点B ,∴∴点B坐标为∵反比例函数kyx=的图象经过点B反比例函数表达式为(2)设过点A、C的直线表达式为,且其图象与轴交于点D ∵点在反比例函数的图象上∴∴点C坐标为∵点B坐标为∴点A坐标为解得:过点A、C的直线表达式为∴点D坐标为∴(3)①当点P在x轴上时,设P(m,0)∵2,22(1)2m++22(2)1m++∴22(1)2m++22(2)1m++22(2)1m++2,解得:m=0或-1②当点P在y轴上时,设P(0,n),∵2,221(2)n+-222(1)n+-∴221(2)n+-222(1)n+-221(2)n+-2解得:n=0或1综上所述:点P 的坐标可能为、、 26.(1)600t ;(2)600y x=;(3)5 【分析】 (1)根据函数图象中的数据可以求得这批货的质量;(2)设y 与x 的函数关系式是k y x=,代入函数图象中的数据即可得出结果; (3)利用函数关系式,当y=120时,得到x=5即可.【详解】解:(1)由题意可得,这批货物的质量是:1.5×400=600(t ),答:这批货物的质量是600t ; (2)设y 与x 的函数关系式是k y x =, 把(1.5,400)代入得:400 1.5k =, 解得:k=600,即y 与x 的函数关系式是600y x =; (3)2h=120min ,当y=120时,x=6005120=, 答:码头工人每分钟至少要装载5吨货物.【点睛】本题考查反比例函数的应用,解答本题的关键是求出相应的函数解析式.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学下期中第一次模拟试题及答案一、选择题1.下列说法正确的是( )A.小红小学毕业时的照片和初中毕业时的照片相似B.商店新买来的一副三角板是相似的C.所有的课本都是相似的D.国旗的五角星都是相似的2.已知一次函数y1=x-1和反比例函数y2=2x的图象在平面直角坐标系中交于A、B两点,当y1>y2时,x的取值范围是( )A.x>2B.-1<x<0C.x>2,-1<x<0D.x<2,x>03.在反比例函数y=1kx的每一条曲线上,y都随着x的增大而减小,则k的值可以是()A.-1B.1C.2D.34.如图所示,在△ABC中, cos B=22,sin C=35,BC=7,则△ABC的面积是()A.212B.12C.14D.215.如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=4:9,则AE:EC为()A.2:1 B.2:3 C.4:9 D.5:46.如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为()A.4B.3C.2D.17.如果两个相似三角形对应边之比是1:3,那么它们的对应中线之比是()A.1:3B.1:4C.1:6D.1:98.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比1:3,则AC的长是( )A.10米B.53米C.15米D.103米9.在平面直角坐标系中,将点(2,l)向右平移3个单位长度,则所得的点的坐标是()A.(0,5)B.(5,1)C.(2,4)D.(4,2)10.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的12,得到△COD,则CD的长度是()A.2 B.1 C.4 D.2511.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为()A.1.5m B.1.6m C.1.86m D.2.16m12.在反比例函数4yx的图象中,阴影部分的面积不等于4的是()A.B. C.D.二、填空题13.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FE ⊥AD ,EG =15里,HG 经过A 点,则FH =__里.14.如图,已知点A ,C 在反比例函数(0)a y a x=>的图象上,点B ,D 在反比例函(0)b y b x=<的图象上,AB ∥CD ∥x 轴,AB ,CD 在x 轴的两侧,AB=5,CD=4,AB 与CD 的距离为6,则a −b 的值是_______.15.如图,四边形ABCD 与四边形EFGH 位似,其位似中心为点O ,且43OE EA =,则FG BC=______.16.如图,在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆2AB m =,它的影子 1.6BC m =,木杆PQ 的影子有一部分落在了墙上, 1.2PM m =,0.8MN m =,则木杆PQ 的长度为______m .17.如图,已知△ABC 中,D 为边AC 上一点,P 为边AB 上一点,AB=12,AC=8,AD=6,当AP 的长度为__时,△ADP 和△ABC 相似.18.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园,以美化环境,预计花园每平方米造价为30元,学校建这个花园至少需要投资________元.19.在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数y=kx(k>0)在第一象限内过点A,且与BC交于点F.当F为BC的中点,且S△AOF=123时,OA的长为__________.20.如图,点A在双曲线y=6x(x>0)上,过点A作AB⊥x轴于点B,点C在线段AB上且BC:CA=1:2,双曲线y=kx(x>0)经过点C,则k=_____.三、解答题21.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).(1)以原点O为位似中心,位似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点的坐标;(2)如果点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.22.已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.(1)如图1,求证:AD=CD;(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.23.自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡AC=米后,斜坡AB改造为AB=米,坡度为1:3;将斜坡AB的高度AE降低20200斜坡CD,其坡度为1:4.求斜坡CD的长.(结果保留根号)24.如图,在四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,点E为AB的中点.(1)求证:△ADC∽△ACB.(2)若AD=2,AB=3,求的值.25.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P6≈2.449,结果保留整数)【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】观察图形,看它们的形状是否相同,形状相同的两个图形是相似图形.【详解】A.小明上幼儿园时的照片和初中毕业时的照片,形状不相同,不相似;B.商店新买来的一副三角板,形状不相同,不相似;C.所有的课本都是相似的,形状不相同,不相似;D.国旗的五角星都是相似的,形状相同,相似.故选D.【点睛】本题考查了相似图形,相似图形是指形状相同的图形,仔细观察看每组图形是否相同,如果相同就相似,否则就不相似.2.C解析:C【解析】【分析】因为一次函数和反比例函数交于A、B两点,可知x-1=2x,解得x=-1或x=2,进而可得A、B两点的坐标,据此,再结合函数解析式画图,据图可知当x>2时,以及当-1<x<0时,y1>y2.【详解】解方程x −1=2x,得 x =−1或x =2,那么A 点坐标是(−1,−2),B 点坐标是(2,1),如右图,当x >2时, 12y y >,以及当−1<x <0时, 12y y >.故选C.【点睛】本题考查了反比例函数与一次函数交点问题,解题的关键是能根据解析式画出函数的图象,并能根据图象解決问题3.A解析:A【解析】【分析】利用反比例函数的增减性,y 随x 的增大而减小,则求解不等式1-k>0即可.【详解】∵反比例函数y=1−kx 图象的每一条曲线上,y 随x 的增大而减小,∴1−k>0,解得k<1.故选A.【点睛】此题考查反比例函数的性质,解题关键在于根据其性质求出k 的值.4.A解析:A【解析】【分析】【详解】试题分析:过点A 作AD ⊥BC ,∵△ABC 中,2,sinC=35,AC=5,∴2BD AB ,∴∠B=45°,∵sinC=35=AD AC =5AD ,∴AD=3,∴CD=4,∴BD=3,则△ABC 的面积是:12×AD×BC=12×3×(3+4)=212.故选A .考点:1.解直角三角形;2.压轴题.5.A解析:A【解析】试题解析:∵ED ∥BC ,.DOE COB AED ACB ∴V V V V ∽,∽:4:9DOE BOC DOE COB S S V V Q V V ∽,,=:2:3.ED BC ∴=AED ACB QV V ∽,::.ED BC AE AC ∴=:2:3,?::ED BC ED BC AE AC Q ,==:2:3AE AC ∴=,:2:1.AE EC ∴=故选A.点睛:相似三角形的性质:相似三角形的面积比等于相似比的平方.6.A解析:A【解析】【分析】根据互余角性质得∠PAM =∠PBC ,进而得△PAM ∽△PBC ,可以判断①;由相似三角形得∠APM =∠BPC ,进而得∠CPM =∠APB ,从而判断②;根据对角互补,进而判断③;由△APB ∽△NAB 得AP AN BP AB=,再结合△PAM ∽△PBC 便可判断④. 【详解】解:∵AP ⊥BN ,∴∠PAM+∠PBA =90°,∵∠PBA+∠PBC =90°,∴∠PAM =∠PBC ,∵∠PMA =∠PCB ,∴△PAM ∽△PBC ,故①正确;∵△PAM ∽△PBC ,∴∠APM=∠BPC,∴∠CPM=∠APB=90°,即PM⊥PC,故②正确;∵∠MPC+∠MBC=90°+90°=180°,∴B、C、P、M四点共圆,∴∠MPB=∠MCB,故③正确;∵AP⊥BN,∴∠APN=∠APB=90°,∴∠PAN+∠ANB=90°,∵∠ANB+∠ABN=90°,∴∠PAN=∠ABN,∵∠APN=∠BPA=90°,∴△PAN∽△PBA,∴AN PA BA PB=,∵△PAM∽△PBC,∴Al AP BC BP=,∴AN AM AB BC=,∵AB=BC,∴AM=AN,故④正确;故选:A.【点睛】本题考查了相似三角形的判定和性质,正方形的性质、四点共圆,同角的余角相等,判断出PM⊥PC是解题的关键.7.A解析:A【解析】∵两个相似三角形对应边之比是1:3,∴它们的对应中线之比为1:3.故选A.点睛: 本题考查相似三角形的性质,相似三角形的对应边、对应周长,对应高、中线、角平分线的比,都等于相似比,掌握相似三角形的性质及灵活运用它是解题的关键.8.B解析:B【解析】【分析】Rt△ABC中,已知了坡比是坡面的铅直高度BC与水平宽度AC之比,通过解直角三角形即可求出水平宽度AC的长.【详解】Rt△ABC中,BC=5米,tanA=1;∴AC=BC÷故选:B.【点睛】此题主要考查学生对坡度坡角的掌握及三角函数的运用能力.9.B解析:B【解析】【分析】在平面直角坐标系中,将点(2,l)向右平移时,横坐标增加,纵坐标不变.【详解】将点(2,l)向右平移3个单位长度,则所得的点的坐标是(5,1).故选:B.【点睛】本题运用了点平移的坐标变化规律,关键是把握好规律.10.A解析:A【解析】【分析】直接利用位似图形的性质结合A点坐标可直接得出点C的坐标,即可得出答案.【详解】∵点A(2,4),过点A作AB⊥x轴于点B,将△AOB以坐标原点O为位似中心缩小为原图形的12,得到△COD,∴C(1,2),则CD的长度是2,故选A.【点睛】本题主要考查了位似变换以及坐标与图形的性质,正确把握位似图形的性质是解题关键.11.A解析:A【解析】∵BE∥AD,∴△BCE∽△ACD,∴CB CEAC CD=,即CB CEAB BC DE EC=++,∵BC=1,DE=1.8,EC=1.2∴1 1.21 1.8 1.2 AB=++∴1.2AB=1.8,∴AB=1.5m.故选A.12.B解析:B【解析】【分析】根据反比例函数kyx=中k的几何意义,过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|解答即可.【详解】解:A、图形面积为|k|=4;B、阴影是梯形,面积为6;C、D面积均为两个三角形面积之和,为2×(12|k|)=4.故选B.【点睛】主要考查了反比例函数kyx=中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=12|k|.二、填空题13.05【解析】∵EG⊥ABFH⊥ADHG经过A点∴FA∥EGEA∥FH∴∠HFA=∠AEG=90°∠FHA=∠EAG∴△GEA∽△AFH∴∵AB=9里DA=7里EG=15里∴FA=35里EA=45里∴解析:05【解析】∵EG⊥AB,FH⊥AD,HG经过A点,∴FA∥EG,EA∥FH,∴∠HFA =∠AEG =90°,∠FHA =∠EAG ,∴△GEA ∽△AFH ,∴EG EA AF FH =. ∵AB =9里,DA =7里,EG =15里,∴FA =3.5里,EA =4.5里,∴15 4.53.5FH=, 解得FH =1.05里.故答案为1.05. 14.【解析】【分析】利用反比例函数k 的几何意义得出a-b=4•OEa -b=5•OF 求出=6即可求出答案【详解】如图∵由题意知:a-b=4•OEa -b=5•OF ∴OE=OF=又∵OE+OF=6∴=6∴a-解析:403【解析】【分析】利用反比例函数k 的几何意义得出a-b=4•OE ,a-b=5•OF ,求出45a b a b --+=6,即可求出答案.【详解】如图,∵由题意知:a-b=4•OE ,a-b=5•OF ,∴OE=4a b -,OF=5a b -, 又∵OE+OF=6,∴45a b a b --+=6, ∴a-b=403, 故答案为:403. 【点睛】 本题考查了反比例函数图象上点的坐标特征,能求出方程45a b a b --+=6是解此题的关键.15.【解析】【分析】利用位似图形的性质结合位似比等于相似比得出答案【详解】四边形ABCD 与四边形EFGH 位似其位似中心为点O 且则故答案为:【点睛】本题考查了位似的性质熟练掌握位似的性质是解题的关键 解析:47 【解析】 【分析】 利用位似图形的性质结合位似比等于相似比得出答案.【详解】 Q 四边形ABCD 与四边形EFGH 位似,其位似中心为点O ,且OE 4EA 3=, OE 4OA 7∴=, 则FG OE 4BC OA 7==, 故答案为:47. 【点睛】本题考查了位似的性质,熟练掌握位似的性质是解题的关键.16.3【解析】【分析】先根据同一时刻物高与影长成正比求出QD 的影长再根据此影长列出比例式即可【详解】解:过N 点作ND ⊥PQ 于D 又∵AB=2BC=16PM=12NM=08∴PQ=QD+DP=QD+NM=1解析:3【解析】【分析】先根据同一时刻物高与影长成正比求出QD 的影长,再根据此影长列出比例式即可.【详解】解:过N 点作ND ⊥PQ 于D ,BC DN AB QD∴= 又∵AB=2,BC=1.6,PM=1.2,NM=0.8, 1.5AB DN QD BC ⋅∴==∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(m).故答案为:2.3.【点睛】在运用相似三角形的知识解决实际问题时,要能够从实际问题中抽象出简单的数学模型,然后列出相关数据的比例关系式,从而求出结论.17.4或9【解析】当△ADP∽△ACB时需有∴解得AP=9当△ADP∽△ABC时需有∴解得AP=4∴当AP的长为4或9时△ADP和△ABC相似解析:4或9.【解析】当△ADP∽△ACB时,需有AP ADAB AC=,∴6128AP=,解得AP=9.当△ADP∽△ABC时,需有AP ADAC AB=,∴6812AP=,解得AP=4.∴当AP的长为4或9时,△ADP和△ABC相似.18.【解析】【分析】如图所示作BD⊥CA于D则在直角△ABD中可以求出BD 然后求出△ABC面积;根据单价可以求出总造价【详解】如图所示AB=10AC=30∠BAC=120°作BD⊥CA于D则在直角△AB解析:6750【解析】【分析】如图所示,作BD⊥CA于D,则在直角△ABD中可以求出BD,然后求出△ABC面积;根据单价可以求出总造价.【详解】如图所示,AB=103,AC=30,∠BAC=120°,作BD⊥CA于D,则在直角△ABD中,∠BAD=60°,∴BD=ABsin60°=15,∴△ABC面积=12×AC×BD=225.又因为每平方米造价为30元,∴总造价为30×225=6750(元).【点睛】此题主要考查了运用三角函数定义解直角三角形,关键是通过作辅助线把实际问题转化为数学问题,抽象到解直角三角形中解题.19.8【解析】分析:过点A 作AH⊥OB 于点H 过点F 作FM⊥OB 于点M 设OA=x 在由已知易得:AH=OH=由此可得S△AOH=由点F 是平行四边形AOBC 的BC 边上的中点可得BF=BM=FM=由此可得S△B解析:8【解析】分析:过点A 作AH ⊥OB 于点H ,过点F 作FM ⊥OB 于点M ,设OA=x ,在由已知易得:,OH=12x ,由此可得S △AOH 2x 由点F 是平行四边形AOBC 的BC 边上的中点,可得BF=12x ,BM=14x ,FM=x ,由此可得S △BMF 2x ,由S △OAF =可得S △OBF =S △OMF =232x +,由点A 、F 都在反比例函数k y x =的图象上可得S △AOH =S △BMF ,由此即可列出关于x 的方程,解方程即可求得OA 的值. 详解:如下图,点A 作AH ⊥OB 于点H ,过点F 作FM ⊥OB 于点M ,设OA=x ,∵四边形AOBC 是平行四边形,∠AOB=60°,点F 是BC 的中点,S △OAF =∴,OH=12x ,BF=12x ,∠FBM=60°,S △OBF =∴S △AOH =28x ,BM=14x ,x ,∴S △BMF 2x ,∴S △OMF =2x , ∵由点A 、F 都在反比例函数k y x =的图象上, ∴S △AOH =S △BMF ,2=2x , 化简得:23192x =,解得:1288x x ==-,(不合题意,舍去),∴OA=8.故答案为:8.点睛:本题是一道考查“反比例函数的图象和性质及平行四边形的性质”的综合题,熟记“反比例函数的图象和性质及平行四边形的性质”是解答本题的关键.20.2【解析】【分析】根据反比例函数系数k的几何意义即可得到结论【详解】解:连接OC∵点A在双曲线y=(x>0)上过点A作AB⊥x轴于点B∴S△OAB=×6=3∵BC:CA=1:2∴S△OBC=3×=1解析:2【解析】【分析】根据反比例函数系数k的几何意义即可得到结论.【详解】解:连接OC,∵点A在双曲线y=6x(x>0)上,过点A作AB⊥x轴于点B,∴S△OAB=12×6=3,∵BC:CA=1:2,∴S△OBC=3×13=1,∵双曲线y=kx(x>0)经过点C,∴S△OBC=12|k|=1,∴|k|=2,∵双曲线y=kx(x>0)在第一象限,∴k=2,故答案为2.【点睛】本题考查了反比例函数的图象与性质,反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,熟练掌握反比例函数系数k的几何意义是解题的关键.三、解答题21.(1)图见解析,C1(-6,4);(2)D1(2a,2b).【解析】【分析】(1)连接OB并延长,使BB1=OB,连接OA并延长,使AA1=OA,连接OC并延长,使CC1=OC,确定出△A1B1C1,并求出C1点坐标即可;(2)根据A与A1坐标,B与B1坐标,以及C与C1坐标的关系,确定出变化后点D的对应点D1坐标即可.【详解】(1)根据题意画出图形,如图所示:则点C1的坐标为(-6,4);(2)变化后D的对应点D1的坐标为:(2a,2b).【点睛】运用了作图-位似变换,画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.22.(1)证明见解析;(2)△ACD、△ABE、△BCE、△BHG.【解析】分析:(1)由AC⊥BD、BF⊥CD知∠ADE+∠DAE=∠CGF+∠GCF,根据∠BGE=∠ADE=∠CGF得出∠DAE=∠GCF即可得;(2)设DE=a,先得出AE=2DE=2a、EG=DE=a、AH=HE=a、CE=AE=2a,据此知S△ADC=2a2=2S△ADE,证△ADE≌△BGE得BE=AE=2a,再分别求出S△ABE、S△ACE、S△BHG,从而得出答案.详解:(1)∵∠BGE=∠ADE,∠BGE=∠CGF,∴∠ADE=∠CGF,∵AC⊥BD、BF⊥CD,∴∠ADE+∠DAE=∠CGF+∠GCF,∴∠DAE=∠GCF,∴AD=CD;(2)设DE=a,则AE=2DE=2a,EG=DE=a,∴S△ADE=12AE×DE=12×2a×a=a2,∵BH是△ABE的中线,∴AH=HE=a,∵AD=CD、AC⊥BD,∴CE=AE=2a,则S△ADC=12AC•DE=12•(2a+2a)•a=2a2=2S△ADE;在△ADE和△BGE中,∵AED BEG DE GEADE BGE ∠∠⎧⎪⎨⎪∠∠⎩===,∴△ADE≌△BGE(ASA),∴BE=AE=2a,∴S△ABE=12AE•BE=12•(2a)•2a=2a2,S△ACE=12CE•BE=12•(2a)•2a=2a2,S△BHG=12HG•BE=12•(a+a)•2a=2a2,综上,面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.点睛:本题主要考查全等三角形的判定与性质,解题的关键是掌握等腰三角形的判定与性质及全等三角形的判定与性质.23.斜坡CD的长是【解析】【分析】根据题意和锐角三角函数可以求得AE的长,进而得到CE的长,再根据锐角三角函数可以得到ED的长,最后用勾股定理即可求得CD的长.【详解】∵90AEB =︒∠,200AB =,坡度为1:3, ∴3tan 3ABE ∠==, ∴30ABE ∠=︒, ∴11002AE AB ==, ∵20AC =,∴80CE =,∵90CED ∠=︒,斜坡CD 的坡度为1:4,∴14CE DE =, 即8014ED =, 解得,320ED =,∴22803208017CD =+=米,答:斜坡CD 的长是8017米.【点睛】本题考查解直角三角形的应用﹣坡度坡角问题,解答本题的关键是明确题意,利用锐角三角函数和数形结合的思想解答.24.(1)证明见解析;(2).【解析】【分析】(1)根据角平分线的定义得到∠DAC=∠CAB ,根据相似三角形的判定定理证明; (2)根据相似三角形的性质得到∠ACB=∠ADC=90°,根据直角三角形的性质得 到 CE=AE ,根据等腰三角形的性质、平行线的判定定理证明=,由相似三角形的性质列出比例式,计算即可.【详解】(1)证明:∵AC 平分∠DAB ,∴∠DAC=∠CAB ,∵AC 2=AB•AD ,∴= , ∴△ADC ∽△ACB ;(2)∵△ADC ∽△ACB ,∴∠ACB=∠ADC=90°,∵点 E 为 AB 的中点,∴CE=AE= AB= ,∴∠EAC=∠ECA,∴∠DAC=∠EAC,∴∠DAC=∠ECA,∴CE∥AD;∴==,∴=.【点睛】本题考查的是直角三角形的性质、平行线的判定、相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.25.此时轮船所在的B处与灯塔P的距离是98海里.【解析】【分析】过点P作PC⊥AB,则在Rt△APC中易得PC的长,再在直角△BPC中求出PB的长即可.【详解】作PC⊥AB于C点,∴∠APC=30°,∠BPC=45°,AP=80(海里),在Rt△APC中,cos∠APC=PC PA,∴PC=PA•cos∠3(海里),在Rt△PCB中,cos∠BPC=PC PB,∴PB=403cosPCBPC=∠6≈98(海里),答:此时轮船所在的B处与灯塔P的距离是98海里.【点睛】本题考查了解直角三角形的应用举例,正确添加辅助线构建直角三角形是解题的关键.。
